Prerpints.org logo
Preprint
Article

Cervical Cancer Prediction based on Imbalanced Data using Machine Learning Algorithms

Altmetrics

Downloads

89

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 September 2024

Posted:

14 September 2024

You are already at the latest version

Alerts
Abstract
Cervical Cancer affects a large part of female population that makes the prediction of this disease based on Machine Learning (ML) by outmost importance. ML algorithms can be integrated in complex intelligent agent-based systems that can offer decision support to the resident medical doctors or even to experienced medical doctors. For instance can be mentioned the situation when an experienced medical doctor diagnose a case but he/she needs expertise support that is related to another medical specialty. Data imbalance is frequent in healthcare data and has a negative influencing effect in making predictions using ML algorithms. Cancer data generally and cervical cancer data particularly are frequently imbalanced. Based on this fact the study of data imbalance impact on diverse state-of-the-art ML prediction algorithms is important. This research subject is also motivated by the fact that in many research are presented experimental evaluations of algorithms without characterization of the data on that they have been applied. Such characterizations could give clear indication to other researchers regarding the applicability of the algorithms on their specific data. Specifically, if the data have the respective characteristics than are expectable the same performance evaluation results like those in the reported research. For the study we chosed a messy real-life Cervical Cancer dataset available in a recognized data repository included a large amount of missing and noisy values. To identify the best imbalanced technique for this medical dataset, it is compared the performance of eleven important resampling methods combined with the following state-of-the-art ML models: K-Nearest Neighbours (with k values of 2 and 3), binary Logistic Regression, and Random Forest, that are frequently applied in prediction types of researches in healthcare. The studied resampling methods includes seven undersampling methods namely Condensed Nearest Neighbour, Tomek Links, Edited Nearest Neighbours, Repeated Edited Nearest Neighbours, All K-Nearest Neighbours, NearMiss, Neighbourhood Cleaning Rule, and Instance Hardness Threshold, and four oversampling methods namely Synthetic Minority Oversampling Technique (SMOTE), Adaptive Synthetic Sampling Approach for Imbalanced Learning SMOTE, Support Vector Machine SMOTE and Borderline SMOTE. In the case of the dataset for the confidence interval with 95% confidence level was between 9.23 and 16.22, while the imbalance ratio is 12.73. The obtained results show that resampling methods help the learning models to improve the classification ability of cervical cancer. The applied oversampling techniques generally showed better results than undersampling methods. In the case of Logistic Regression classifier had the highest impact on balanced techniques, while Random Forest had promising performance, even before balancing techniques and KNN2 was generally better than KNN3.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Cervical Cancer is the fourth most commonly diagnosed cancer in females around the world [1]. According to the study [2] the most important risk factors and potential predictors of Cervical Cancer are smoking, infection with sexually transmitted diseases (HIV, Sypvhilis, etc.) and hormonal contraceptives. These risk factors underlines the importance of using demographic and medical information as indicators for Cervical Cancer risk prediction. Analyzing these factors can help to understand how lifestyle choices and medical conditions correlate with the development of Cervical Cancer.
Prediction, classification particularly, decisions making generally based on imbalanced datasets can lead to diverse difficulties in data mining [3,4]. The studies in [5,6,7] present recent state-of-the-art methods for healthcare data-balancing issues with promising result. These studies also highlight that the relationship between the minority and majority class is also important because if capturing each region in the unbalanced dataset while taking in consideration the sensitivity of the ML generally, Neural Networks (NNs) particularly are more effectively able to learn the minority class with the focus near the borderline.
In this work, the main focus is on balancing issues for Cervical Cancer prediction based on messy imbalanced data. One of the scopes of this work was to study and compare a broad number of actual frequently applied data balancing methods combining with ML classification methods and evaluating this way the performance, before and after balancing on Cervical Cancer dataset. In the selection of ML classification method, several key factors were taken into consideration: K-Nearest Neighbour (KNN) makes local decisions, while not using global patterns [8], computationally efficient Logistic Regression (LR) frewuently used in medical research [9] while Random Forest (RF) is able to handle non-linear relationships well with ensemble learning [10]. These algorithm are widely used in healthcare researches when dealing with unbalanced data. However, if the scientist do not treat these problems appropriately, it can lead even to wrong interpretation of the experimental results.
The study included the following eighth undersampling methods: Condensed Nearest Neighbour (CNN), Tomek Links (TL), Edited Nearest Neighbours (ENN), Repeated Edited Nearest Neighbours (RENN), All K-Nearest Neighbours (All-KNN), NearMiss (NM), Neighbourhood Cleaning Rule (NCR), and Instance Hardness Threshold (IHT). There were also studied four oversmapling methods: Synthetic Minority Oversampling Technique (SMOTE) and Adaptive Synthetic Sampling Approach for Imbalanced Learning (ADASYN); methods based on the decision boundary: Support Vector Machine (SVM), and Borderline while the studied ML algorithms were the followings: KNN, LR and RF. By comparing these methods we provide knowledge in improving classification accuracy, while offering experimental results and also statistical characterization of the data.
Figure 1 presents the research methodology and visually summarizes a ML workflow that includes data preprocessing, sampling, feature engineering, ML training and model analysis. The study outlined the performance of the KNN, LR, and RF combined with diverse undersampling and oversampling methods on a Cervical Cancer dataset that has an Imbalance Ratio (IR) by 12.73 (the ratio of the instance number in the majority class to the instance number in the minority class). Having 7% proportion with cancer, the 95% Confidence Interval (CI) that has cancer is between 9.23% to 16.22%. The dataset has over 2500 missing values.
The research is presented under six main sections: Section 2 presents the state-of-the-art bibliographic study on balancing techniques with state-of-the-art classification algorithms in healthcare prediction, Section 3 outlines the steps of the data pre-processing and the approached model classification methodology. Based on this, Section 4 presents the results achieved when applying the various studied 11 sampling methods with the three studied ML methods, and Section 5 highlights the results comparing with similar works. Finally, the Section 6 summarizes the main ideas and proposes future work in the medical field.

2. State-of-the-art Algorithms for Prediction in Healthcare

This section analyzes the actual state-of-the-art ML models in healthcare prediction (including cancer prediction) that frequently are mentioned among the best. Sampling methods that include oversampling and undersampling can be applied combined with these methods to improve accuracy and model performance. The main difference between over- and undersampling is that oversampling increases the size of the minority class with synthetic samples, while undersampling reduces the size of the majority class leading to data loss. While prediction includes the act of predicting both numerical and categorical values, the goal of classification is specifically to predict a category, such as determining if a patient has cancer or not.

2.1. Classification Algorithms

ML models are widely used in healthcare to predict diseases, to make health record analyses with the purpose to improve medical diagnoses. In this work the following ML methods are studied: KNN, LR and RF. These ML methods are widely used in medicine for disease prediction, disease classification and risk assessment [11].

KNN algorithm

KNN is independent of data distribution [8] since it makes the prediction based on the local neighbours (where k is an integer, such as 2,3,4.. and in case of KNN2 and KNN3 consider 2 and 3 neighbors respectively) of the data points without making assumptions about the sample size and the characteristics of the data. Algorithm 1 presents the process of KNN, including parameter initialization, computation of the distance and the majority vote classification. KNN might have problems with distance calculation when works with unbalanced data because it could capture more samples from the majority class [12].
Algorithm 1 K-Nearest Neighbors Algorithm [13]
  1:
Input:
  2:
D train : Training dataset
  3:
D test : Test dataset
  4:
k: Nr of neighbors
  5:
d i s t _ m e t r i c : Distance metric function
  6:
Output:
  7:
D predicted : Predicted labels for the test dataset
  8:
Program Body
  9:
for each x test in D test  do
10:
   let d i s t a n c e s be an empty list
11:
   for each x train in D train  do
12:
     let d i s t a n c e be d i s t _ m e t r i c ( x test , x train )
13:
     let l a b e l be the label of x train
14:
     append ( d i s t a n c e , l a b e l ) to d i s t a n c e s
15:
   end for
16:
   sort d i s t a n c e s by d i s t a n c e in ascending order
17:
   let k _ n e a r e s t be the first k elements from d i s t a n c e s
18:
   let l a b e l _ c o u n t s be an empty dictionary
19:
   for each ( d i s t a n c e , l a b e l ) in k _ n e a r e s t  do
20:
     if label is not in l a b e l _ c o u n t s  then
21:
        let l a b e l _ c o u n t s [ l a b e l ] be 0
22:
     end if
23:
     increment l a b e l _ c o u n t s [ l a b e l ]
24:
   end for
25:
   let p r e d i c t e d _ l a b e l be the label with the highest count in l a b e l _ c o u n t s
26:
   assign p r e d i c t e d _ l a b e l to x test in D predicted
27:
end for
28:
Return  D predicted
Wang and Han [14] proposed a novel ensemble algorithm for unbalanced Parkinson’s disease dataset, where the KNN is used as based classifier to calculate the ensemble weights, which overcomes in different severity levels on the imbalanced distribution of the data [15]. Fuzzy KNN combined with Bonferroni means classifier makes multiple comparisons between the input data resulting easier evaluation for high-dimensional datasets (microarray and COVID-19) with minimal feature numbers [16]. In Fuzzy KNN membership degree is calculated with fuzzy membership functions. Bonferroni means classifier is an aggregation operator.

LR algorithm

LR is used to determine the outcomes of a particular data point. In binary classification, LR predicts two possible outcomes, while in multiclass classification the model can predict multiple classes. Binary (binomial) LR (bLR) is a specific form of LR [17], where the dependent variables has only two categories The applicability of LR depends on the size of the dataset meaning that having small, unbalanced datasets are used, LR can have biases towards the majority class leading incorrect prediction performance for the minority class).
Algorithm 2 presents the fundamental method of LR. The advantages of the simple bLR algorithm is that there is only simple hyperparameter-tuning as the learning rate and the numbers for epochs. bLR might struggle with hardly unbalanced data, because it results with high accuracy and low recall or precision for the minority class. More advanced LR include regularizations with penalty terms in order to keep the model’s weights small to prevent overfitting, but this lead to the decrease of the accuracy [18].
To address this issue, Firth’s penalized LR introduced a penalty term into the traditional LR model to create parameter estimates and standard errors for the LR model resulting in an improved model fitting in small health-survey related datasets [9]. [19] presented a bLR classifier with 70% PCA (dimensionality reduction of the dataset with 70% of the variance) which had the highest precision and sensitivity values compared to Elastic Net, SVM (with linear kernel), SVM (with Radial Basis Function kernel), RF and XGBoost while the researchers concluded that bLR performs well with quantitative imaging (CT and MRI scans to measure and analyze quantitative data) features as predictors. Beside predicting binary outcomes, LR can also be corporated with Least Absolute Shrinkage and Selection Operator (Lasso) regularization. Lasso LR adds a rule that discourages the model from giving importance to less relevant features [20].
Algorithm 2 Logistic Regression Algorithm [13]
  1:
Input:
  2:
D train : Training dataset
  3:
D test : Test dataset
  4:
α : Learning rate
  5:
n _ e p o c h s : Nr of training epochs
  6:
Output:
  7:
D predicted : Predicted probabilities for the test dataset
  8:
Global Data Description
  9:
θ : Parameter vector (weights), initially set to zero or random values
10:
Program Body
11:
Initialize θ to zero or random values
12:
for epoch = 1 to n _ e p o c h s  do
13:
   let g r a d i e n t s be a vector of zeros
14:
   for each ( x , y ) in D train  do
15:
     let z be the dot product of θ and x
16:
     let y ^ be the sigmoid function of z, y ^ = 1 1 + e − z
17:
     let e r r o r be y ^ − y
18:
     update g r a d i e n t s by adding ( e r r o r · x )
19:
   end for
20:
   update θ by subtracting α · g r a d i e n t s
21:
end for
22:
Prediction for D test
23:
for each x test in D test  do
24:
   let z be the dot product of θ and x test
25:
   let y ^ be the sigmoid function of z, y ^ = 1 1 + e − z
26:
   assign y ^ to x test in D predicted as the predicted probability
27:
end for
28:
Return  D predicted

RF algorithm

RF is an ensemble learning method used in classification that creates multiple decision trees during the process of training. Algorithm 3 presents the creation of bootstrap (random replacement subsets) samples for each decision tree for the forest. While creating a decision tree for each bootstrap the algorithm selects a random subset of features and votes the best split while grows till the maximal depth. This random selection of features works better with unbalanced data because it reduce the overfitting of the majority class [21].
Algorithm 3 Random Forest Algorithm [13]
  1:
Input:
  2:
D train : Training dataset
  3:
D test : Test dataset
  4:
n _ t r e e s : Number of trees in the forest (hyperparameter)
  5:
m a x _ d e p t h : Maximum depth of each tree (hyperparameter)
  6:
m i n _ s m p _ s p l i t : Minimum nr of samples to split an internal node (hyperparameter)
  7:
m i n _ s m p _ l e a f : Minimum nr of samples for leaf node (hyperparameter)
  8:
Output: D predicted : Predicted labels for the test dataset
  9:
Global Data Description: f o r e s t : List of decision trees
10:
Program Body
11:
Initialize an empty list f o r e s t
12:
for tree = 1 to n _ t r e e s  do
13:
   let b o o t s t r a p _ s a m p l e be a random subset of D train (sampling with replacement)
14:
   let t r e e be a DT initialized with m a x _ d e p t h , m i n _ s m p _ s p l i t , and m i n _ s m p _ l e a f
15:
   train t r e e on b o o t s t r a p _ s a m p l e
16:
   append t r e e to f o r e s t
17:
end for
18:
Prediction for D test
19:
for each x test in D test  do
20:
   let v o t e s be an empty dictionary
21:
   for each t r e e in f o r e s t  do
22:
     let p r e d i c t i o n be the result of t r e e on x test
23:
     increment v o t e s [ p r e d i c t i o n ] by 1
24:
   end for
25:
   let p r e d i c t e d _ l a b e l be the label with the highest count in v o t e s
26:
   assign p r e d i c t e d _ l a b e l to x test in D predicted
27:
end for
28:
Return  D predicted
Yang and Fridgeirsson [10] used Lasso LR, RF, XGBoost classifiers with random under- and oversampling methods and varied the target imbalance ratio. The study used four large health databases: three U.S. claims databases and one German EHR database, all mapped to the OMOP Common Data Model to investigate outcomes in patients with treated depression, where the initial sample was 100000. After applying 58 prediction tasks on electronic health data, the results presented that only the models for random oversampling with RF showed more variation in Receiver Operating Characteristic - Area Under the Curve (ROC-AUC) difference (compares the performance of two classification models by quantifying how much better a model is able to separate positive and negative classes compared to other model) and its general decrease compared to the original data.
Other works collected data through surveys, demonstrated by Xin and Rashid [22], where the main goal was to predict depression among women who can have anxiety due their life roles and physiological differences in Malaysia’s environment where woman can have issues with money, family, health and work. In this research the authors used SMOTE oversampling method with RF and concluded that the imbalance ratio affected the sensitivity of the RF model, which predicted the disease accurately. RF can be applied in identifying longitudinal predictors of health, while being able to discriminate poor from good self-perceived health outcomes in a 30-year cohort study [23].

2.2. Sampling Methods

2.2.1. Undersampling

To handle class imbalance, the following nearest neighbour-based methods were considered appropriate and were chosed: CNN, TL, ENN, RENN, All-KNN, NM, NCR; iterative method: IHT. For an accurate analysis, undersampling reduces the number of abundant samples to create two equally sized classes [14].
CNN undersampling technique reduces the size of the majority class by keeping the most informative instances to maintain the decision boundary. The work in [24] uses the one-pass variation of CNN called Instance-Based Learning 2 (IB2) and proposes a novel variation based algorithm on it. The researchers tested on nine datasets including variables with different types of data, from that some were related to the medical field (like: Yeast, Congenital Heart Disease, Water quality) achieving decreased computational cost for the multilabel classification process.
TL identifies pairs of samples from different classes that are the nearest neighbour to each other’s but combining with SMOTE method can balance the training dataset and is able to eliminate components that are on the wrong side of the decision. This hybrid TL approach with balanced RF in Lung cancer dataset resulted with the highest mean AUC compared to other hybrid methods Baseline and SMOTE-Edited Nearest Neighbours (SMOTE-ENN) [25].
All-KNN to make classes more separable removes samples from the majority class that have at least 1 nearest neighbour in the minority class. In the case-study of Parkinson’s Disease Tremor Severity Classification (a clinical dataset, collected from a wearable sensor from laboratory and home environments, was used) All-KNN with Artificial NN based on multi-layer perceptron (ANN-MLP)) metrics like accuracy, precision and sensitivity improved but Index of balanced accuracy (IBA) and Geometric mean stayed low [26].
RENN removes misclassified samples from the majority class until a desired class-balance is earned. The study in [11] used four imbalanced health datasets such as Diabetics, Anaemia, Lung Cancer, and Obesity which feature high-dimensional data with non-linear relationships. The researchers underlined that RENN with LR is more effective in handling lack of symmetry in datasets distribution.
ENN is a cleaning technique but eliminates misclassified samples in one step without any iterative approach. A possible application of ENN undersampling technique stands in Medicare Fraud Detection. Where in paper [27] ENN was combined with SMOTE methods on the Medicare Part B dataset. The results showed that this hybrid approach effectively balanced synthetic samples while eliminated noisy data and Decision Tree (DT) outperformed the following ML classifiers: Extreme Gradient Boosting (XGBoost), Adaptive Boosting (Adaboost), Light Gradient Boosting Machine (LGBM), LR, and RF.
NCR technique removes misclassified majority samples and improves decision boundaries. In [28] a novel clustering approach is presented that improved the quality of classification, where using K-Means algorithms the authors clustered data, then clusters object of only the majority class in a specified distance from the center are removed. For the Yeast5 protein-protein interaction network dataset, the NCR method provided the best results in Matthews Correlation Coefficient (MCC) and Cohen’s Kappa statistic (Kappa) metrics.
NM technique selectively removes majority class instances based on the distances to minority class instances (NM-1 removes the closest element and NM-2 the farthest element to the minority class). Combining NM with Principal Component Analysis (PCA) Tumuluru and Daniel [29] presented a novel approach to address the class imbalance problem in healthcare data. Using real-world dataset, the proposed model outperformed baseline classifiers in metrics like precision, recall, F1 score, AUC highlighting the possible applications in disease diagnosis, patient risk stratification, and treatment prediction. The work in [30] studied the problem of establishing the optimal number of factors in an Exploratory Factor Analysis (EFA) generally and PCA particularly, highlighting that this is a complex issue.
IHT technique removes instances from majority class and focuses on instances that are easier to classify, while removing harder identified samples. The work of Lopo and Hartomo [6] presents an evaluation of sampling techniques in healthcare insurance related fraud detection, where the IHT method (with 90% class distribution) outperformed the XGBoost, SMOTE, Random oversampling methods’ overall scores highlighting the ability to generalize well to new and unseen data in the minority and majority classes.

2.2.2. Oversampling

Datasets with less information in particular classes to be balanced, artificial samples must be generated to increase the number of rare instances [31]. To create equal class distribution by resizing the classes in this study, the following types of oversampling methods are used: methods based on the minority class: SMOTE and ADASYN; methods based on the decision boundary: SVM and Borderline.
SMOTE technique generates new instances of the minority class, resulting improved performance on the minority class prediction. There are many varieties of SMOTE preprocessing techniques namely: traditional SMOTE, Borderline-SMOTE1, Borderline-SMOTE2, SMOTE-NC, and SVM-SMOTE, which were used in a hospital mortality prediction on 126 patients with traumatic injuries. The data were extracted from the patients’ medical records. The researchers focused on the trauma patients’ status (alive/dead) as an outcome and six risk factors (age, sex, type of trauma, location of injuries, Glasgow coma scale and white blood cells). The results showed that among all SMOTE-based ML methods, RF and ANN with SMOTE and XGBoost with SMOTE-NC achieve the highest value for all evaluations metrics [31]. In [32] proposed a novel Data Augmented SMOTE Multi-Class Classifier (DASMcC) to predict Cardiovascular Diseases (CVD). To ensure that the classifier’s performance is not biased SMOTE was combined with 10-fold cross-validation technique, while XGBoost performed the best in overall performance.
SVM is ML algorithm for binary classification, where the input vector performs a non-linear mapping process to create linearly separable data in a higher-dimensional feature space. Removing correlated features and simplifying the model training process with PCA whitening results data with unit variance along in each dimension in the pretraining process of an unbalanced dataset [14]. [33] presented a novel ensemble model, which is based on the SVMs hyperplane to calculate the optional boundaries between the signed distances integrating with bLR, resulting better accuracy compared to the SVM kernel selection using datasets related to ionosphere, High Time Resolution Universe Survey (HTRU2) pulsar candidate, diabetes, and liver disorder.
Borderline oversampling is an advanced variation of SMOTE, which generates samples near the decision boundary of classes. Jo and Kim [5] proposed a novel method called minority oversampling near the borderline with a Generative Adversarial Network (OBGAN) that uses Borderline with generative adversarial network to focus on the avoiding of the mode collapse problem on small datasets. With 21 relatively small unbalanced datasets. Some of the dataset examples has the following majority/minority outcomes: Liver Cancer (have/not) with 10 features, Breast Cancer (benign/malignant) with 9 features, Prima Indians diabetes (diabetes/not) with 10 features, Blood Transfusion (not/donate) with 4 features from UCI ML Repository, Kaggle, and DataHub) and 6 benchmark methods (SMOTE, Borderline-SMOTE, ADASYN, k-means SMOTE (kmSMOTE), conditional GAN, and Generative Adversarial Minority Oversampling (GAMO) the experiments shows that OBGAN is competitive with the SMOTE-based methods and has stable performance for multiclass problems with various majority–minority ratios. ADASYN technique adapts the generation process based on the density of the distribution of minority class instances. Paper [34] proposed a DAD-net system to detect Alzheimer’s disease from images where ADASYN was able to generate new samples to balance the number of instances for every category.
This section underlines that popular health problems like Cancer, Parkinson’s disease, and Depression with their datasets, are widely used in medical field for predictive purposes. However, some datasets are affected with common data issues such as missing values, outliers, and unbalanced data. To address this challenge it is necessary to apply data manipulation techniques such as undersampling, and oversampling. Some of the available and innovative approaches incorporate algorithm modification that have promising results on healthcare prediction. For instance, SMOTE-ENN can eliminate noisy data in medical fraud detection, NCR with clusterization can eliminate class objects in protein-protein dataset, or SMOTE-data augmentation is performing well for multi class classifier in CVD disease.

3. Materials and methods

3.1. Dataset description

This study utilizes the Cervical Cancer risk factor dataset available at the UCI ML platform [35]. The data was collected from "Hospital Universitario de Caracas" in Caracas, Venezuela. There are 858 records and 36 attributes (variables). The data reveals patients’ demographic information, habits and medical history. The dataset contains 4 target variable: Hinselmann (screening test for abnormalities in the cervix), Schiller (identifies areas of concerns with iodine test), Cytology (cell abnormalities examination under microscope) and Biopsy (presence of cancer on removed tissue or cell sample). In this study we selected the biopsy as the only target variable. Because there was not data for cervical condylomatosis and AIDS, these two attributes were removed, leaving 30 variables as input.

3.2. Data Pre-processing

Clinical data in generally is affected by factors such as missing values, inconsistent data and exceptions, hence the need for pre-processing. Pre-processing is a very important step it includes both data preparation and data transformation. [29] recommended in different situations through processing to change the distribution of the data to direct the algorithms used.
Table 1 presents the attributes of the dataset, and also it is visible that the data types are Integer or Boolean. To make sure that every attribute contributes equally to the model training of the selected algorithms, the values were normalized in the [0,1] interval. Therefore the mean (1) calculation is the following:
mean = 1 N ∑ i = 1 N x i
where N is the number of samples and x i represents each sample. Standard deviation (2) calculates how much the numbers in the dataset are spread out from the mean.
stddev = 1 N ∑ i = 1 N ( x i − mean ) 2
where mean is the mean calculated previously. After the Z-score (3) the normalization is:
x normalized = x − mean stddev
where x is an individual data point, and the mean and stddev are the previously calculated values.
Missing information in the dataset can affect the statistical analysis. In the case of used dataset several patients refused to provide certain information, therefore there are many missing values, especially in the case of very intime questions like: Hormonal Contraceptives, Intrauterine Device use and sexually Transmitted Diseases (STDs).
After analyzing the data, it was visible that the patients who did not provide the intime information are exactly the same, so 105 records were eliminated, remaining 753 dates from the original dataset. The remaining null values were replaced by the median of the Integer data and the most frequently occurring value for the Boolean data.
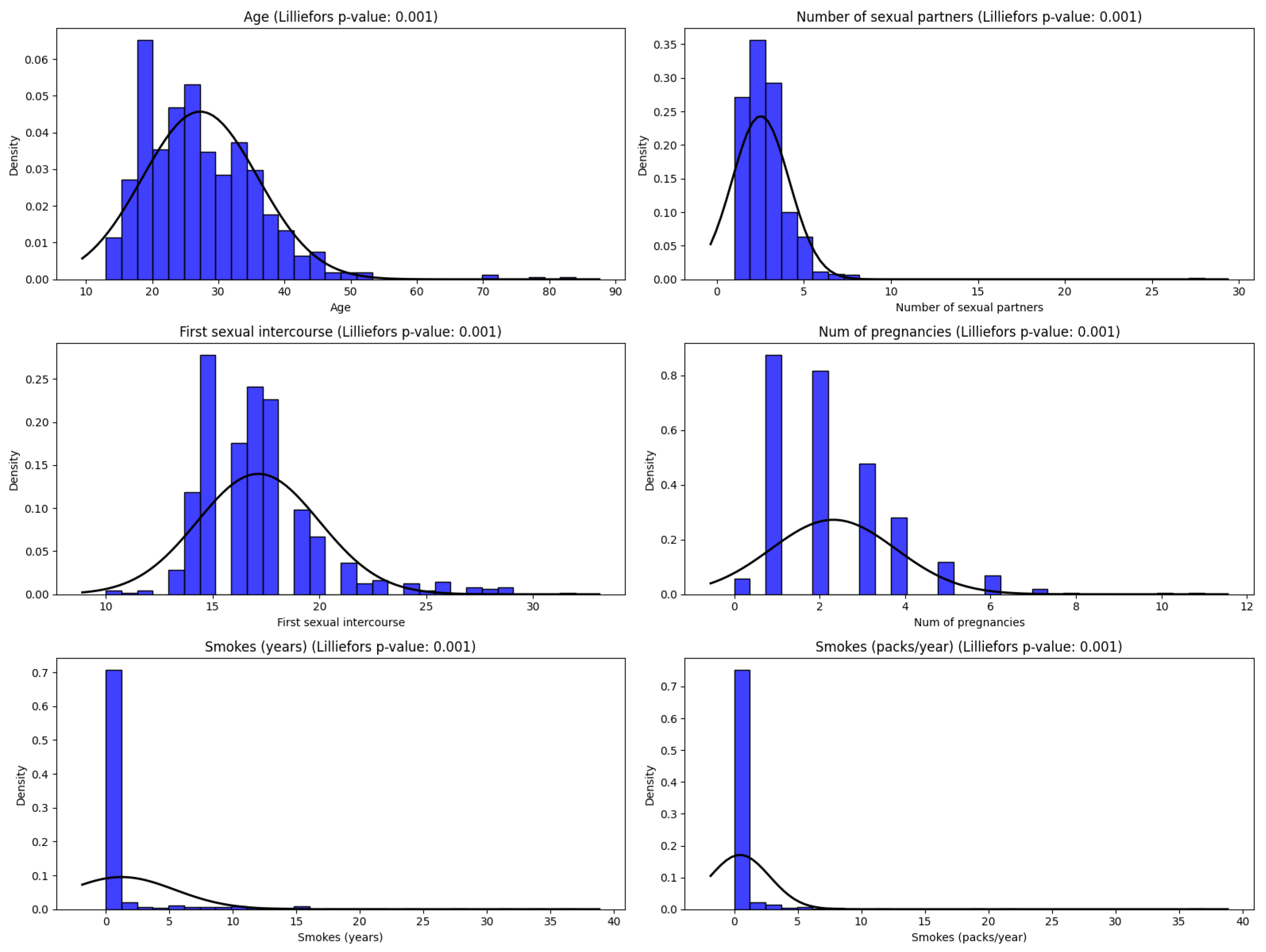
Figure 2 shows the graphical representation of the frequency distributions of some important attributes (being better predictors) form the dataset. The figure also presents the result of Lilliefors [36,37] numerical statistical test results and estimation of the distribution in case of the most important variables. It is visible the asymmetry to the right with a sudden decrease in the Number of pregnancies for a patient, being more women with 0, 1 or 2 births. In the case of the number of years in which the patient used Hormonal Contraceptives, there is also an asymmetry to the right, a fact caused by the generally young age of the women in the study. On the other hand, although the Ages of the patients are relatively young, their distribution is symmetrical.
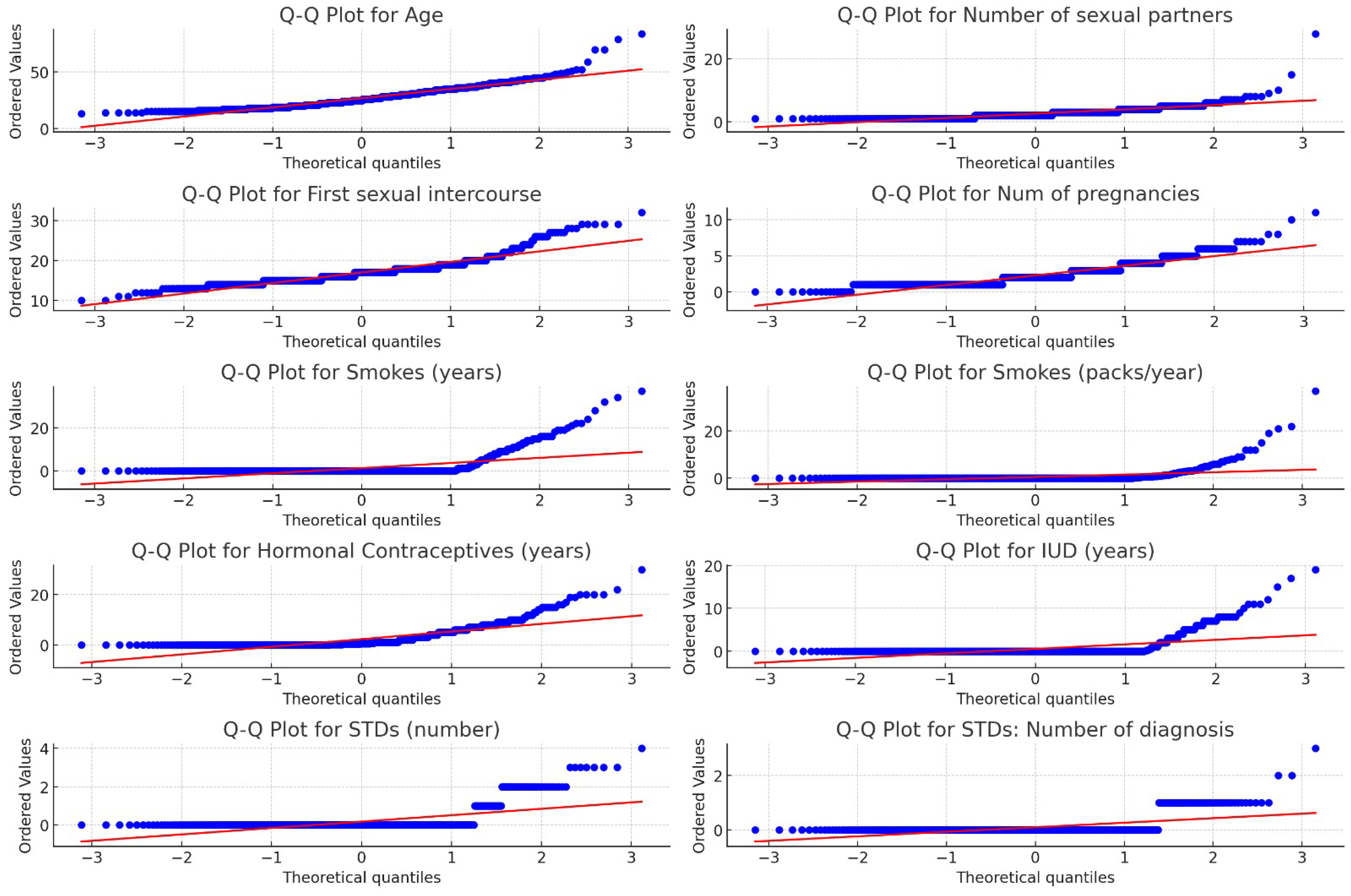
The Lilliefors test shows experimentally that the data follows a non-normal distribution and because of this median was preferred over the mean [16]. The median is also sensitive to extreme values (outliers), but it was no case for outliers in our dataset. The visual validation of the non-normal distribution is presented in Figure 3 using Q-Q plot [38] graphical representation.
Another important aspect that can be identified immediately after data preprocessing is the number of instances in each class. The data distribution was 92% of healthy patients versus 7% patients with positive biopsy.
After the data preprocessing we can calculate the imbalance ratio (IR) to measure the imbalance in a dataset. It is given by I R = n negative n positive , where n negative is the number of negative samples and n positive is the number of positive samples which is equal to 12.73.
After this the variance of the imbalance ratio can be approximated using the formula Var ( I R ) = I R 2 × 1 n positive + 1 n negative .
The Standard Error (SE) of the IR is given by S E ( I R ) = I R × 1 n positive + 1 n negative .
With 95% confidence interval (CI) for the IR is calculated as C I = I R ± Z × S E ( I R ) , where Z is the Z-score corresponding to the desired confidence level (for 95%, Z = 1.96 ) and S E ( I R ) is the SE of the IR.
Finally, the lower and upper bounds of the CI are given by Lower Bound = I R − Z × S E ( I R ) and Upper Bound = I R + Z × S E ( I R ) resulting 9.23 and 16.22 separately.

3.3. Model training and evaluation

These predictive models were implemented in Python programming language using ML libraries. The pandas library (version 1.5.3) was used for data manipulation and analysis, numpy (version 1.23.5) was employed for numerical calculations. For data visualization matplotlib (version 3.7.1) and seaborn (version 0.12.2) were utilized. The interactive visualizations were created with plotly (version 5.15.0) with the plotly.express module and plotly.io interface.
After processing the dataset, it was used to train NNs with four ML models, (KNN with k values of 2 (KNN2) and 3 (KNN3), LR and RF) using Scikit-learn and Keras. The usual values for K in KNN are 2 or 3, but there is not a well-established strategy to deciding the best K value [39]. We made experiments with with higher number of integers for K but only 2 and 3 values showed notable results.
In case of undersampling methods the most relevant parameters were the sampling_strategy (how many instances to sample used for all methods, random_state (seed for random number generation like in CNN), n_neighbours (number of neighbours to consider), max_iter (limits the number of iterations), threshold_cleaning (decides which instance to keep). Oversampling methods had the following important parameters like k_neighbors (number of nearest neighbours to use for synthetic sample generation for SVM and Borderline), m_neighbours (define the number of neighbours to consider for SVM), n_jobs (number of processors to use for parallel processing like in ADASYN). The values of the algorithms were selected based on the size of the data and class imbalance. Using estabilished guidelines from literature [19] and empirical testing also improved model performence.
In order to measure the model performance we used a common ML approach where the data was splitted into 75% training set and 25% testing set. When evaluating models for diagnosing a contagious diseases, the selected metrics must align with the goals of the diagnosis. In this case identifying all the infected individuals (even at the risk of some false positives) is more critical than missing an infected person. In order to measure this unbalanced data learning the following five evaluation metrics are selected as the performance evaluation criteria: Accuracy (%) (4), Precision (%) (5), Recall (%) (6), F1-score (%) (7), Balanced Accuracy (%) (Ba Accuracy) (8) ROC_AUC score (%) [40], class distribution: Majority (MajClass) and Minority Class (MinClass) instance number [41]. In case of a contagious disease is more important to identify infected persons (even you make mistake) than to miss an infected person (identify contagious a person even is healthy)
Table 2 Confusion Matrix presents the results obtained from classification. Correctly classified instances are True Positive (TP) and True Negative (TN), and incorrectly classified instances are False Positive (FP) and False Negative (FN) [42].
Accuracy is the most common metric in model evaluation and refers to the number of correctly labeled data points divided by the total number of examples. In other words, it’s the rate of all predictions for both classes [42]. Accuracy for binary classification:
Accuracy = T P + T N T P + T N + F P + F N
In the case of imbalanced data, accuracy is not a suitable metric when used in this form. If we have 1% of examples belonging to the minority class, we can achieve an exaggerated accuracy of 99% by predicting the majority class [42]:
Precision or Positive Predictive Value for the binary case can be interpreted as it being true in n% of cases:
Precision = T P T P + F P
and the reverse is called Recall or True Positive Rate, meaning out of the positive examples, how many were predicted as positive, or out of all sick patients, how many were correctly identified as having the disease [42]:
Recall = T P T P + F N
F1-Score is the weighted harmonic mean of Precision and Recall [42].
F 1 - Score = 2 × R e c a l l × P r e c i s i o n R e c a l l + P r e c i s i o n
Ba Accuracy is easily obtained from the rows of the confusion matrix and is the average recall from each class [42]. R e c a l l 0 = T P T P + F N and R e c a l l 1 = T P T P + F N
Ba Accuracy = ( R e c a l l 0 + R e c a l l 1 ) 2
The ROC curve and the corresponding AUC presents how well the model is capable of distinguishing between classes. The higher the AUC value, the more likely the model is to distinguish class 1 as 1 and class 0 as 0. To calculate it, a classifier and the probabilities obtained from predictions is needed. With multiple thresholds, and based on each threshold, it can categorize the predicted probabilities as false or true and calculate the True Positive Rate and False Positive Rate values.
If the AUC is closer to 1, it means it has measure of separability and also indicates which threshold is most suitable for a classifier while ROC curve is a probability curve. On the X-axis, we have the False Positive Rate, and on the Y-axis, the True Positive Rate. Each point on the curve represents a probability threshold used to determine whether an example belongs to a category.
For the metrics like accuracy, F1-score and recall, both weighted and macro forms were also calculated and presented to make the impact of imbalance visible. Macro metrics presents the unbalanced classes as equals, highlighting the minority class performance. Weighted metrics present the proportion of every class in the dataset, making a performance based on class frequency [43].
MacroPrecision (9), MacroRecall (10), and MacroF1score (11) presents the average precision, recall and F1-scores across all classes:
MacroPrecision = 1 N ∑ i = 1 N T P i T P i + F P i
MacroRecall = 1 N ∑ i = 1 N T P i T P i + F N i
MacroF 1 Score = 1 N ∑ i = 1 N 2 × T P i T P i + F P i × T P i T P i + F N i T P i T P i + F P i + T P i T P i + F N i
where N is the number of classes.
WeightedPrecision (12), MacroRecall (13), and WeightedF1score (14) presents the precision, recall and F1-scores of each class weighted by the instance number of that class:
WeightedPrecision = 1 ∑ i = 1 N | C i | ∑ i = 1 N T P i T P i + F P i × | C i |
WeightedRecall = 1 ∑ i = 1 N | C i | ∑ i = 1 N T P i T P i + F N i × | C i |
WeightedF 1 Score = 1 ∑ i = 1 N | C i | ∑ i = 1 N 2 × T P i T P i + F P i × T P i T P i + F N i T P i T P i + F P i + T P i T P i + F N i × | C i |
where | C i | is the number of instances in class i.

4. Results

The first experiment involved applying ML models using the original unbalanced dataset. For the other experiments the balanced data was used with under- and oversampling techniques. The calculated weighted average (gives more importance to values appearing more often in the data) used the number of data in the majority and minority class as weights. On the other hand the results of the macro average shows the arithmetic mean of the metric values for each class, while treating each class equally, regardless of the class size. Both averages are presented in the upcoming Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11.
In Table 3 it is centered the metrics values obtained for all algorithms with the data in their state after the initial preprocessing. We are interested in highest values (numerical values represent percentage (%)). Obtained results show that the best results were achieved by RF. The other classifiers in general have the limitation to predict the minority class.
The performance results of the ML models were obtained before applying sampling techniques
Table 4 and Table 5, for the KNN algorithm with 2 neighbors, shows the results obtained after the under- and oversampling techniques. The highest sampling values for KNN was Borderline SMOTE technique, but all methods generated much higher values than the models applied to the original dataset. ADASYN shows the least effectiveness overall, particularly in accuracy and ROC_AUC score. These insights also suggest that SVM SMOTE is an effective oversampling technique for enhancing the performance of the KNN2 model. Among the undersampling techniques, NM1 and IHT made a prediction of 78.57% and 85.71%, respectively. NCR stands out with a statistically significant ROC_AUC score of 0.80, which is notably higher than the rest. When excluding NCR, the remaining values do not show notable differences. The rest of the metrics were not better compared to the original ones.
In Table 6 and Table 7 are presents the results for KNN with 3 neighbors. For KNN3 every oversampling method worked well. In the case of undersampling NM1 and IHT produce the highest results, notable in the case of minority class prediction. NM1 also excels in class separation having 0.79 for ROC_AUC score.
Table 8 and Table 9 presents the results for the bLR. Must be noticed the good results for the AUC curve from all SMOTE methods, each excelling for some of the metrics. The Under-sampling techniques were not spectacular. CNN, TL, All-KNN, RENN, ENN, and NCR maintained a high accuracy but at the cost of ignoring the minority class, resulting poor balanced accuracy and macro metrics. NM1 and IHT handled better the minority class but this came at the expense of the overall accuracy.
Table 10 and Table 11 presents the results obtained for RF. Although this algorithm proved effective and suitable for the initial data as well, after applying both types of Sampling it obtained better results. CNN and RENN offer a better balance, achieving high accuracy while maintained reasonable performance for minority classes. It is also notable that ADASYN and NM1 technique, had values of 85.71%, respectively 100% in the detection of minority classes and a ROC_AUC score with more than 99 % in all sampling methods.
In the right side of Figure 4 it is visible a smaller area under the ROC curve and left side shows the increase of the area under the ROC curve after applying the oversampling technique.

5. Discussions

5.1. Benefits of prediction in healthcare

Using methods based on ML for solving diverse types of prediction problems can help the healthcare to be more efficient and effective. In sophisticated data analytics the ML based autonomous and intelligent systems are improved with intelligent communication technologies [44]. ML algorithms for prediction can help to make preventive strategies in decision-making ensuring that the development of the algorithm is interpretable, transparent, and takes in consideration ethical concerns [45].
Accuracy and real-time predictive analysis of disease prediction may lead to saving patients’ lives, but incorrect prediction could endanger patients’ lives. [46]. By integrating efficeint biomedical and health data the researchers can make accurate diagnosis based on ML methods to improve patient-centric treatments [47].

5.2. Scientific literature advances

The work in [48] presents similar ML algorithms for Cervical Cancer prediction. The same dataset as used in this research was analyzed with PCA, balanced with SMOTE, and distributed with 10-fold cross-validation to prevent the overfitting problem. This approach raised the accuracy, sensitivity, and ROC_AUC score of the proposed model compared to the state-of-the-art predictive models. Other Cervical Cancer work [1] used the dataset processed in this research, presents a hybrid strategy based on the combination of an oversampling method (SMOTE) and two undersampling methods (CNN and ENN) to balance the dataset. Genetic Algorithms was applied for feature selection and RF classifier provided the highest performance in G-mean (geometric mean of the recall), sensitivity, and specificity.
In the case of a larger volume of data (more than 100000 samples) or high number of missing data (more than 10% of the data), there are diverse sophisticated methods and analyses for replacing missing values. For example, Entropy-based (EB) algorithms, imputing missing values, Independent Component Analysis (ICA), Linear Discriminant Analysis (LDA) [50], removing outliers with covariance based Mahalanobis distance or treating them as special values. A combination of these techniques is described in the article [49], research concluded that ensemble model performed well under the proposed pre-processing and EB feature engineering on heart disease related dataset including 14 features.

5.3. Results of this research

We chose to use the traditional forms of KNN, LR, and RF because they are classic algorithms in ML. The bibliographic study presented that these algorithms have many improved versions, but they can also be complex or can have potential disadvantages. Focusing on these algorithms, a clear comparison served as a basis for understanding the applicability of these algorithms.
The data analyzed in the experimental evaluation of this study was highly unbalanced, with 93% of the attributes belonging to the majority class and only 7% belonging to the minority class (positive biopsy cases). The CI with 95% confidence level is between 9.23 and 16.22, while the IB is 12.73. ML algorithms applied to the unbalanced data had difficulties detecting the minority class. One of the effect of this imbalanced learning is presented by [25] highlighting those oversampling methods has higher stability than other sampling methods (undersampling and hybrid sampling), while undersampling has the worst stability.
The evaluation of the imbalanced learning techniques applied to the dataset reveal that oversampling techniques increased the performance of the models and proved to be inspired choices. KNN2 and KNN3 undersampling initially predicted 7% of the minority class, after application of sampling techniques it reached 86 %. LR reached from 0% to 93% with SMOTE technique. Even for RF, which works well even before applying the techniques, some metrics peaked. Decreasing the dimensionality of the data set did not produce major changes, but some metrics increased.

6. Conclusions

According to the bibliographic study in the medical field LR is mostly used in smaller datasets, KNN and the ensemble RF algorithms are applied in complex datasets with multiple attributes. The difference between them lies in their methodological approaches. The simple form of bLR’s parameters can be tuned easily, which works well with lower numbers of features, while KNN and RF are non-parametric methods and are able to capture interactions among features where patient data in medical research have different types of information.
To deal with missing values in non-normally distributed data, the meadian was used over the mean. This non-normality was validated by applying Lilliefors test statistical test and confirmed visually using Q-Q plot. In case of binary variables this approach is not suitable. Based on the performed research we conclude that datasets in a class with significantly less instances, leads to overfitted classifiers which are favoring to majority classes. Because of this, the samples in the minority class are hardly recognizable or incorrectly identified. This issue is present in the medical field, because in many cases the number of healthy patient records (majority class) are much higher than the records for patients diagnosed with a specified disease (minority class). This leads to ignore significant information in a minority class about a real-word medical problem that need careful examination for prediction.
In our case, none of the studied oversampling methods (SMOTE, SVM SMOTE, Borderline SMOTE, ADASYN) combined with ML methods (KNN, LR, RF) provided the best results in the case of all evaluation metrics approached. In the case of KNN it was obtained higher metric values with the Borderline SMOTE method and for RF with the ADASYN method. It is also notable that the experimental selection of KNN2 performed better than KNN3. With RF each oversampling method showed high results, even before applying sampling techniques. This fact could lead in the future to the idea of using compound classifiers while it is also important to pay attention to relevant attributes and eliminate irrelevant ones, also with the help of RF [23].
This paper presents a comprehensive review of a large number of sampling methods used for data balancing, with both over- and undersampling methods and discussed different modified versions. This study also serves as a practical guide, because having data with these characteristics, similar results can be expected by applying these algorithms with these balancing methods.
For future work, a set of hybrid classifiers (combing different classifiers, using ensemble methods or feature-level hybridization with similar feature selection methods to PCA), but also hybrid techniques of under- and oversampling could be approached on these data.

Author Contributions

“Conceptualization, Simó, Z., Muraru, M.M. and Iantovics, L.B.; methodology, Simó, Z. and Muraru, M.M.; software, Muraru, M.M. and Simó, Z.; validation, Muraru, M.M. and Simó, Z.; formal analysis, Iantovics, L.B. and Muraru, M.M.; investigation, Simó, Z. and Muraru, M.M.; resources, Muraru, M.M.; data curation, Muraru, M.M.; writing—original draft preparation, Simó, Z.; writing—review and editing, Simó, Z., Muraru, M.M. and Iantovics, L.B.; visualization, Muraru, M.M. and Simó, Z.; supervision, Iantovics, L.B.; project administration, Iantovics, L.B.; funding acquisition, Simó, Z. and Iantovics, L.B.. All authors have read and agreed to the published version of the manuscript.”

Funding

The article processing charge (APC) was funded by the Institution Organizing University Doctoral Studies (I.O.S.U.D.), the Doctoral School of Letters, Humanities and Applied Sciences, George Emil Palade University of Medicine, Pharmacy, Science, and Technology of Târgu Mureş, 540139 Târgu Mureş, Romania.

Institutional Review Board Statement

“Not applicable”

Informed Consent Statement

“Not applicable”

Data Availability Statement

The datasets used in this article are publicly available for download at: https://archive.ics.uci.edu/dataset/383/cervical+cancer+risk+factors (last accessed on 16 August 2024).

Acknowledgments

We would like to thank the Research Center on Artificial Intelligence, Data Science, and Smart Engineering (ARTEMIS) and COST Action CA22137 - Randomised Optimisation Algorithms Research Network (ROAR-NET) for the support.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ADASYN Adaptive Synthetic Sampling Approach for Imbalanced Learning
All-KNN All K-Nearest Neighbours
AUC Area Under the Curve
bLR Binary Logistic Regression
CI Confidence Interval
CNN Condensed Nearest Neighbour
EB Entropy-Based
ENN Edited Nearest Neighbours
IB2 Instance-Based Learning 2
ICA Independent Component Analysis
IHT Instance Hardness Threshold
IR Imbalance Ratio
KNN K-Nearest Neighbours
LASSO Least Absolute Shrinkage and Selection Operator
LDA Linear Discriminant Analysis
LR Logistic Regression
ML Machine Learning
NCR Neighbourhood Cleaning Rule
NNs Neural Networks
NM NearMiss
RF Random Forest
RENN Repeated Edited Nearest Neighbours
ROC Receiver Operating Characteristic
SMOTE Synthetic Minority Oversampling Technique
SVM Support Vector Machine
TL Tomek Links

References

  1. Newaz, A.; Muhtadi, S.; Haq, F.S. An intelligent decision support system for the accurate diagnosis of cervical cancer. Knowledge-Based Systems 2022, 245, 108634. [Google Scholar] [CrossRef]
  2. Bowden, S.J.; Doulgeraki, T.; Bouras, E.; et al. Risk factors for human papillomavirus infection, cervical intraepithelial neoplasia and cervical cancer: an umbrella review and follow-up Mendelian randomisation studies. BMC Medicine 2023, 21, 274. [Google Scholar] [CrossRef] [PubMed]
  3. Machado, D.; Santos Costa, V.; Brandão, P. Using Balancing Methods to Improve Glycaemia-Based Data Mining. In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 5: HEALTHINF; SciTePress, 2023; pp. 188–198. [Google Scholar] [CrossRef]
  4. Alfakeeh, A.S.; Javed, M.A. Efficient Resource Allocation in Blockchain-Assisted Health Care Systems. Applied Sciences 2023, 13, 9625. [Google Scholar] [CrossRef]
  5. Jo, W.; Kim, D. OBGAN: Minority oversampling near borderline with generative adversarial networks. Expert Systems with Applications 2022, 197, 116694. [Google Scholar] [CrossRef]
  6. Lopo, J.A.; Hartomo, K.D. Evaluating Sampling Techniques for Healthcare Insurance Fraud Detection in Imbalanced Dataset. Jurnal Ilmiah Teknik Elektro Komputer dan Informatika (JITEKI) 2023, 9, 223–238. [Google Scholar]
  7. Wang, W.; Chakraborty, G.; Chakraborty, B. Predicting the Risk of Chronic Kidney Disease (CKD) Using Machine Learning Algorithm. Applied Sciences 2021, 11, 202. [Google Scholar] [CrossRef]
  8. Papakostas, M.; Das, K.; Abouelenien, M.; Mihalcea, R.; Burzo, M. Distracted and Drowsy Driving Modeling Using Deep Physiological Representations and Multitask Learning. Applied Sciences 2021, 11, 88. [Google Scholar] [CrossRef]
  9. Suhas, S.; Manjunatha, N.; Kumar, C.N.; Benegal, V.; Rao, G.N.; Varghese, M.; Gururaj, G. Firth’s penalized logistic regression: A superior approach for analysis of data from India’s National Mental Health Survey, 2016. Indian Journal of Psychiatry 2023, 65, 1208–1213. [Google Scholar] [CrossRef]
  10. Yang, C.; Fridgeirsson, E.A.; Kors, J.A.; et al. Impact of random oversampling and random undersampling on the performance of prediction models developed using observational health data. J Big Data 2024, 11. [Google Scholar] [CrossRef]
  11. Awe, O.O.; Ojumu, J.B.; Ayanwoye, G.A.; Ojumoola, J.S.; Dias, R. Machine Learning Approaches for Handling Imbalances in Health Data Classification. In Sustainable Statistical and Data Science Methods and Practices; Awe, O.O., Vance, E.A., Eds.; Springer: Cham, 2023; pp. 19–33. [Google Scholar] [CrossRef]
  12. Sajana, T.; Rao, K.V.S.N. Machine Learning Algorithms for Health Care Data Analytics Handling Imbalanced Datasets. In Handbook of Artificial Intelligence; 2023; p. 75. [Google Scholar]
  13. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, 2009; Part of the Springer Series in Statistics (SSS). [Google Scholar]
  14. Wang, L.; Han, M.; Li, X.; Zhang, N.; Cheng, H. Review of Classification Methods on Unbalanced Data Sets. IEEE Access 2021, 9, 64606–64628. [Google Scholar] [CrossRef]
  15. Zhao, H.; Wang, R.; Lei, Y.; Liao, W.-H.; Cao, H.; Cao, J. Severity level diagnosis of Parkinson’s disease by ensemble K-nearest neighbor under imbalanced data. Expert Systems with Applications 2022, 189, 116113. [Google Scholar] [CrossRef]
  16. Vommi, A.M.; Battula, T.K. A hybrid filter-wrapper feature selection using Fuzzy KNN based on Bonferroni mean for medical datasets classification: A COVID-19 case study. Expert Systems with Applications 2023, 218, 119612. [Google Scholar] [CrossRef]
  17. Iantovics, L.B.; Enăchescu, C. Method for Data Quality Assessment of Synthetic Industrial Data. Sensors 2022, 22, 1608. [Google Scholar] [CrossRef] [PubMed]
  18. Lynam, A.L.; Dennis, J.M.; Owen, K.R.; et al. Logistic regression has similar performance to optimised machine learning algorithms in a clinical setting: application to the discrimination between type 1 and type 2 diabetes in young adults. Diagn Progn Res 2020, 4, 6. [Google Scholar] [CrossRef] [PubMed]
  19. Morgado, J.; Pereira, T.; Silva, F.; Freitas, C.; Negrão, E.; de Lima, B.F.; da Silva, M.C.; Madureira, A.J.; Ramos, I.; Hespanhol, V.; et al. Machine Learning and Feature Selection Methods for EGFR Mutation Status Prediction in Lung Cancer. Applied Sciences 2021, 11, 3273. [Google Scholar] [CrossRef]
  20. Saharan, S.S.; Nagar, P.; Creasy, K.T.; Stock, E.O.; James, F.; Malloy, M.J.; Kane, J.P. Logistic Regression and Statistical Regularization Techniques for Risk Classification of Coronary Artery Disease Using Cytokines Transported by High Density Lipoproteins. In Proceedings of the 2023 International Conference on Computational Science and Computational Intelligence (CSCI); IEEE, 2023; pp. 652–660. [Google Scholar] [CrossRef]
  21. Ayoub, S.; Mohammed Ali, A.G.; Narhimene, B. Enhanced Intrusion Detection System for Remote Healthcare. In Advances in Computing Systems and Applications; Senouci, M.R., Boulahia, S.Y., Benatia, M.A., Eds.; Lecture Notes in Networks and Systems; Springer: Cham, 2022; Volume 513, pp. 1–11. [Google Scholar] [CrossRef]
  22. Xin, L.K.; Rashid, N.b.A. Prediction of Depression among Women Using Random Oversampling and Random Forest. In Proceedings of the 2021 International Conference of Women in Data Science at Taif University (WiDSTaif); 2021; pp. 1–5. [Google Scholar] [CrossRef]
  23. Loef, B.; Wong, A.; Janssen, N.A.H.; et al. Using random forest to identify longitudinal predictors of health in a 30-year cohort study. Sci Rep 2022, 12, 10372. [Google Scholar] [CrossRef]
  24. Filippakis, P.; Ougiaroglou, S.; Evangelidis, G. Prototype Selection for Multilabel Instance-Based Learning. Information 2023, 14, 572. [Google Scholar] [CrossRef]
  25. Khushi, M.; et al. A Comparative Performance Analysis of Data Resampling Methods on Imbalance Medical Data. IEEE Access 2021, 9, 109960–109975. [Google Scholar] [CrossRef]
  26. AlMahadin, G.; Lotfi, A.; Carthy, M.M.; et al. Enhanced Parkinson’s Disease Tremor Severity Classification by Combining Signal Processing with Resampling Techniques. SN COMPUT. SCI. 2022, 3. [Google Scholar] [CrossRef]
  27. Bounab, R.; Zarour, K.; Guelib, B.; Khlifa, N. Enhancing Medicare Fraud Detection Through Machine Learning: Addressing Class Imbalance With SMOTE-ENN. IEEE Access 2024, 12, 54382–54396. [Google Scholar] [CrossRef]
  28. Bach, M.; Trofimiak, P.; Kostrzewa, D.; Werner, A. CLEANSE – Cluster-based Undersampling Method. Procedia Computer Science 2023, 225, 4541–4550. [Google Scholar] [CrossRef]
  29. Tumuluru, P.; Daniel, R.; Mahesh, G.; Lakshmi, K.D.; Mahidhar, P.; Kumar, M.V. Class Imbalance of Bio-Medical Data by Using PCA-Near Miss for Classification. In Proceedings of the 2023 5th International Conference on Inventive Research in Computing Applications (ICIRCA); Coimbatore, India; 2023; pp. 1832–1839. [Google Scholar] [CrossRef]
  30. Iantovics, L.B.; Rotar, C.; Morar, F. Survey on establishing the optimal number of factors in exploratory factor analysis applied to data mining. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2019, 9, e1294. [Google Scholar] [CrossRef]
  31. Hassanzadeh, R.; Farhadian, M.; Rafieemehr, H. Hospital mortality prediction in traumatic injuries patients: comparing different SMOTE-based machine learning algorithms. BMC Med Res Methodol 2023, 23, 101. [Google Scholar] [CrossRef] [PubMed]
  32. Sinha, N.; Kumar, M.A.G.; Joshi, A.M.; Cenkeramaddi, L.R. DASMcC: Data Augmented SMOTE Multi-Class Classifier for Prediction of Cardiovascular Diseases Using Time Series Features. IEEE Access 2023, 11, 117643–117655. [Google Scholar] [CrossRef]
  33. Bektaş, J. EKSL: An effective novel dynamic ensemble model for unbalanced datasets based on LR and SVM hyperplane-distances. Information Sciences 2022, 597, 182–192. [Google Scholar] [CrossRef]
  34. Ahmed, G.; et al. DAD-Net: Classification of Alzheimer’s Disease Using ADASYN Oversampling Technique and Optimized Neural Network. Molecules 2022, 27, 7085. [Google Scholar] [CrossRef]
  35. Cervical cancer (Risk Factors) Data Set. Available online: https://archive.ics.uci.edu/ml/datasets/Cervical+cancer (accessed on April 2024).
  36. Pinheiro, V.C.; do Carmo, J.C.; de O. Nascimento, F.A.; Miosso, C.J. System for the analysis of human balance based on accelerometers and support vector machines. Computer Methods and Programs in Biomedicine Update 2023, 4, 100123. [Google Scholar] [CrossRef]
  37. Iantovics, L. B.; Dehmer, M.; Emmert-Streib, F. MetrIntSimil—An Accurate and Robust Metric for Comparison of Similarity in Intelligence of Any Number of Cooperative Multiagent Systems. Symmetry 2018, 10, 48. [Google Scholar] [CrossRef]
  38. Darville, J.; Yavuz, A.; Runsewe, T.; Celik, N. Effective sampling for drift mitigation in machine learning using scenario selection: A microgrid case study. Applied Energy 2023, 341, 121048. [Google Scholar] [CrossRef]
  39. Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alexandria Engineering Journal 2022, 61, 279–303. [Google Scholar] [CrossRef]
  40. Naidu, G.; Zuva, T.; Sibanda, E.M. A Review of Evaluation Metrics in Machine Learning Algorithms. In Artificial Intelligence Application in Networks and Systems; CSOC 2023. Lecture Notes in Networks and Systems; Silhavy, R., Silhavy, P., Eds.; Springer: Cham, 2023; Volume 724. [Google Scholar] [CrossRef]
  41. Chen, R.J.; Wang, J.J.; Williamson, D.F.K.; et al. Algorithmic fairness in artificial intelligence for medicine and healthcare. Nature Biomedical Engineering 2023, 7, 719–742. [Google Scholar] [CrossRef] [PubMed]
  42. Ng, A.P.; Koumchatzky, N. Machine Learning Engineering with Python - Second Edition; Packt Publishing: Birmingham, UK, 2023; EAN 9781837631964; 462 pages, Paperback. [Google Scholar]
  43. Edward, J.; Rosli, M.M.; Seman, A. A New Multi-Class Rebalancing Framework for Imbalance Medical Data. IEEE Access 2023, 11, 92857–92874. [Google Scholar] [CrossRef]
  44. Manchadi, O.; Ben-Bouazza, F.-E.; Jioudi, B. Predictive Maintenance in Healthcare System: A Survey. IEEE Access 2023, 11, 61313–61330. [Google Scholar] [CrossRef]
  45. Rubinger, L.; Gazendam, A.; Ekhtiari, S.; Bhandari, M. Machine learning and artificial intelligence in research and healthcare. Injury 2023, 54 (Suppl. S3), S69–S73. [Google Scholar] [CrossRef] [PubMed]
  46. Badawy, M.; Ramadan, N.; Hefny, H.A. Healthcare predictive analytics using machine learning and deep learning techniques: a survey. Journal of Electrical Systems and Information Technology 2023, 10, 40. [Google Scholar] [CrossRef]
  47. Subrahmanya, S.V.G.; Shetty, D.K.; Patil, V.; et al. The role of data science in healthcare advancements: applications, benefits, and future prospects. Irish Journal of Medical Science 2022, 191, 1473–1483. [Google Scholar] [CrossRef]
  48. Alsmariy, R.; Healy, G.; Abdelhafez, H. Predicting Cervical Cancer using Machine Learning Methods. International Journal of Advanced Computer Science and Applications (IJACSA) 2020, 11, 7. [Google Scholar] [CrossRef]
  49. Rajendran, R.; Karthi, A. Heart Disease Prediction using Entropy Based Feature Engineering and Ensembling of Machine Learning Classifiers. Expert Systems with Applications 2022, 207, 117882. [Google Scholar] [CrossRef]
  50. Toğaçar, M.; Ergen, B.; Cömert, Z.; Özyurt, F. A Deep Feature Learning Model for Pneumonia Detection Applying a Combination of mRMR Feature Selection and Machine Learning Models. IRBM 2020, 41, 212–222. [Google Scholar] [CrossRef]
Preprints 118147 g001
Figure 1. Graphical abstract.
Figure 1. Graphical abstract.
Preprints 118147 g001
Preprints 118147 g002
Figure 2. Lilliefors normality test results.
Figure 2. Lilliefors normality test results.
Preprints 118147 g002
Preprints 118147 g003
Figure 3. A visual approach of using Q-Q Plots for distribution validation.
Figure 3. A visual approach of using Q-Q Plots for distribution validation.
Preprints 118147 g003
Preprints 118147 g004
Figure 4. ROC-AUC curve with LR before (right) and after (left) Oversampling.
Figure 4. ROC-AUC curve with LR before (right) and after (left) Oversampling.
Preprints 118147 g004
Table 1. Attributes of the dataset and their data types.
Table 1. Attributes of the dataset and their data types.
Attribute Type Attribute Type
Age int STDs:pelvic inflammatory disease bool
Number of sexual partners int STDs:genital herpes bool
First sexual intercourse (age) int STDs:molluscum contagiosum bool
Number of pregnancies int STDs:AIDS bool
Smokes bool STDs:HIV bool
Smokes (years) int STDs:Hepatitis B bool
Smokes (packs/year) int STDs:HPV bool
Hormonal Contraceptives bool STDs: Number of diagnosis int
Hormonal Contraceptives (years) int STDs: Time since first diagnosis int
IUD bool STDs: Time since last diagnosis int
IUD (years) int Dx:Cancer bool
STDs bool Dx:CIN bool
STDs (number) int Dx:HPV bool
STDs:condylomatosis bool Dx bool
STDs:cervical condylomatosis bool Hinselmann: target variable bool
STDs:vaginal condylomatosis bool Schiller: target variable bool
STDs:vulvo-perineal condylomatosis bool Cytology: target variable bool
STDs:syphilis bool Biopsy: target variable bool
Table 2. Confusion Matrix for Binary Classification.
Table 2. Confusion Matrix for Binary Classification.
Prediction
Actual Positive Negative
Positive TP FN
Negative FP TN
Table 3. Performance results of ML models (Before Sampling Techniques).
Table 3. Performance results of ML models (Before Sampling Techniques).
Metric/Sampling KNN2 KNN3 bLR RF
Accuracy 93.12 91.53 92.59 95.76
Ba Accuracy 53.57 52.71 50.00 71.42
Precision 96.54;93.59 58.98;87.93 46.29;85.73 97.81;95.95
Recall 53.57;93.12 52.71;91.53 50.00;92.59 71.42;95.76
MajClass 100 98.28 100 100
MinClass 7.14 7.14 0 42.85
F1-Score 54.87;90.26 53.33;89.30 48.07;89.03 78.88;94.96
ROC_AUC 0.61 0.63 0.71 0.99
Table 4. Performance Results of KNN2 (After Oversampling Techniques).
Table 4. Performance Results of KNN2 (After Oversampling Techniques).
Metric/Sampling SMOTE SVM SMOTE Borderline SMOTE ADASYN
Accuracy 88.35 91.01 90.47 87.83
Ba Accuracy 60.85 65.57 68.57 60.57
Precision (Mac;Wght) 59.60;89.09 66.67;90.70 66.43;91.08 58.85;87.83
Recall (Mac;Wght) 60.85;88.35 65.57;91.00 68.57;90.47 60.57;87.83
MajClass 93.14 95.43 94.29 92.57
MinClass 28.57 35.71 42.86 28.57
F1-Score (Mac;Wght) 60.17;88.71 66.09;90.85 67.41;90.76 59.58;88.36
ROC_AUC 0.72 0.74 0.74 0.72
Table 5. Performance Results of KNN2 (After Undersampling Techniques).
Table 5. Performance Results of KNN2 (After Undersampling Techniques).
Metric/Sampling CNN TL All-KNN RENN ENN NCR NM1 IHT
Accuracy 93.65 92.59 87.30 87.30 87.30 90.47 75.66 45.50
Ba Accuracy 60.42 53.28 50.42 50.42 50.42 55.42 77.00 64.00
Precision (Mac;Wght) 84.52;92.64 71.52;89.85 50.49;86.40 50.49;86.40 50.49;86.40 59.18;88.30 59.07;92.04 53.99;90.94
Recall (Mac;Wght) 60.42;93.65 53.28;92.59 50.42;87.30 50.42;87.30 50.42;87.30 55.42;90.47 77.00;75.66 64.00;45.50
MajClass 99.43 99.43 93.71 93.71 93.71 96.57 75.43 42.29
MinClass 21.43 7.14 7.14 7.14 7.14 14.29 78.57 85.71
F1-Score (Mac;Wght) 65.00;91.97 54.31;89.93 50.43;86.84 50.43;86.84 50.43;86.84 56.56;89.25 58.75;81.24 38.93;55.99
ROC_AUC 0.70 0.61 0.61 0.62 0.62 0.63 0.80 0.65
Table 6. Performance Results of KNN3 (After Oversampling Techniques).
Table 6. Performance Results of KNN3 (After Oversampling Techniques).
Metric/Sampling SMOTE SVM SMOTE Borderline SMOTE ADASYN
Accuracy 86.24 89.94 88.35 87.30
Ba Accuracy 72.85 74.85 74.00 73.42
Precision (Mac;Wght) 62.42;91.25 67.26;92.10 64.48;91.69 63.54;91.46
Recall (Mac;Wght) 72.85;86.24 74.85;89.94 74.00;88.35 73.42;87.30
MajClass 88.57 92.57 90.86 89.71
MinClass 57.14 57.14 57.14 51.47
F1-Score (Mac;Wght) 65.17;88.24 70.08;90.84 67.81;89.72 66.44;88.98
ROC_AUC 0.71 0.73 0.73 0.72
Table 7. Performance Results of KNN3 (After Undersampling Techniques).
Table 7. Performance Results of KNN3 (After Undersampling Techniques).
Metric/Sampling CNN TL All-KNN RENN ENN NCR NM1 IHT
Accuracy 90.47 91.53 86.24 86.24 87.30 88.35 69.84 43.91
Ba Accuracy 68.57 52.71 49.85 49.85 50.42 54.28 77.14 63.14
Precision (Mac;Wght) 66.43;91.08 58.98;87.93 49.85;86.24 49.85;86.24 50.49;86.40 54.94;87.54 58.13;92.40 53.80;90.82
Recall (Mac;Wght) 68.57;90.47 52.71;91.53 49.85;86.24 49.85;86.24 50.42;87.30 54.28;88.35 77.14;69.84 63.14;43.91
MajClass 94.29 98.29 92.57 92.57 93.71 94.29 68.57 40.57
MinClass 42.86 7.14 7.14 7.14 7.14 14.29 85.71 85.71
F1-Score (Mac;Wght) 67.41;90.76 53.33;89.30 49.85;86.24 49.85;86.24 50.43;86.84 54.56;87.94 55.21;77.01 37.85;54.38
ROC_AUC 0.67 0.63 0.60 0.60 0.61 0.62 0.79 0.64
Table 8. Performance Results of bLR (After Oversampling Techniques).
Table 8. Performance Results of bLR (After Oversampling Techniques).
Metric/Sampling SMOTE SVM SMOTE Borderline SMOTE ADASYN
Accuracy 86.77 88.35 86.77 85.18
Ba Accuracy 89.57 51.00 86.28 85.42
Precision (Mac;Wght) 67.72;94.66 50.89;86.50 66.49;93.92 65.12;93.70
Recall (Mac;Wght) 89.57;86.77 51.00;88.35 86.28;86.77 85.42;85.18
MajClass 86.86 94.29 86.86 85.14
MinClass 92.86 7.14 85.71 85.71
F1-Score (Mac;Wght) 72.34;89.66 50.74;87.15 70.69;89.19 68.78;88.05
ROC_AUC 0.92 0.87 0.89 0.91
Table 9. Performance Results of LR (After Undersampling Techniques).
Table 9. Performance Results of LR (After Undersampling Techniques).
Metric/Sampling CNN TL All-KNN RENN ENN NCR NM1 IHT
Accuracy 92.59 92.59 92.59 92.59 92.59 92.59 58.20 41.79
Ba Accuracy 50.00 50.00 50.00 50.00 50.00 50.00 57.71 58.71
Precision (Mac;Wght) 46.29;85.73 46.29;85.73 46.29;85.73 46.29;85.73 46.29;85.73 46.29;85.73 52.16;88.18 52.54;89.37
Recall (Mac;Wght) 50.00;92.59 50.00;92.59 50.00;92.59 50.00;92.59 50.00;92.59 50.00;92.59 57.71;58.20 58.71;41.79
MajClass 100 100 100 100 100 100 58.29 38.86
MinClass 0 0 0 0 0 0 57.14 78.57
F1-Score (Mac;Wght) 48.07;89.03 48.07;89.03 48.07;89.03 48.07;89.03 48.07;89.03 48.07;89.03 44.46;67.99 35.97;67.99
ROC_AUC 0.61 0.73 0.71 0.71 0.72 0.72 0.66 0.59
Table 10. Performance Results of RF (After Oversampling Techniques).
Table 10. Performance Results of RF (After Oversampling Techniques).
Metric/Sampling SMOTE SVM SMOTE Borderline SMOTE ADASYN
Accuracy 98.41 98.41 98.41 98.41
Ba Accuracy 92.57 92.57 92.57 98.41
Precision (Mac;Wght) 95.58;98.37 95.58;98.37 95.58;98.37 95.58;98.37
Recall (Mac;Wght) 92.57;98.41 92.57;98.41 92.57;98.41 92.57;98.41
MajClass 99.43 99.43 99.43 99.43
MinClass 85.71 85.71 85.71 85.71
F1-Score (Mac;Wght) 94.01;98.38 94.01;98.38 94.01;98.38 94.01;98.38
ROC_AUC 0.99 0.99 0.99 0.99
Table 11. Performance Results of RF (After Undersampling Techniques).
Table 11. Performance Results of RF (After Undersampling Techniques).
Metric/Sampling CNN TL All-KNN RENN ENN NCR NM1 IHT
Accuracy 98.94 95.76 95.23 97.35 96.29 96.29 95.76 76.19
Ba Accuracy 96.14 71.42 67.85 82.14 75.00 75.00 97.71 83.85
Precision (Mac;Wght) 96.14;98.94 97.81;95.95 96.14;98.94 98.07;96.43 98.07;96.43 98.07;96.43 81.81;97.30 61.02;93.58
Recall (Mac;Wght) 96.14;98.94 71.42;95.76 67.85;95.23 82.14;97.35 75.00;96.29 75.00;96.29 97.71;96.43 83.85;76.19
MajClass 99.43 100 100 100 100 100 95.43 74.86
MinClass 92.86 42.86 64.29 64.29 50 50 100 92.86
F1-Score (Mac;Wght) 96.14;98.94 78.88;94.96 75.06;94.17 82.35;95.71 82.35;95.71 82.35;95.71 87.71;96.18 60.98;81.73
ROC_AUC 0.99 0.99 1.0 1.0 0.99 0.99 0.99 0.95
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated