Prerpints.org logo
Preprint
Article

Gravitational Lensing Effects from Models of Loop Quantum Gravity with Rigorous Quantum Parameters

Altmetrics

Downloads

81

Views

78

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 September 2024

Posted:

15 September 2024

You are already at the latest version

Alerts
Abstract
Many previous works have studied gravitational lensing effects from Loop Quantum Gravity. So far, Gravitational lensing effects from Loop Quantum Gravity have only been studied by choosing large quantum parameters much larger than the Planck scale. However, by construction, the quantum parameters of the effective models of Loop Quantum Gravity are usually related to the Planck length and, thus, are extremely small. In this work, by strictly imposing the quantum parameters as initially constructed, we study the true quantum corrections of gravitational lensing effects by five effective black hole models of Loop Quantum Gravity. Our study reveals several interesting results, including the different scales of quantum corrections displayed by each model and the connection between the quantum correction of deflection angles and the quantum correction of the metric. Observables related to the gravitational lensing effect are also obtained for all models in the case of SgrA* and M87*.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Loop Quantum Gravity (LQG) is a background-independent candidate theory of quantum gravity [1,2,3]. While the full theory of LQG is very complicated, the extraction of physically observable phenomena from full LQG is extremely difficult, there have been many works obtaining the physical effects of LQG from its symmetry-reduced models with great success. One such example is Loop Quantum Cosmology (LQC) [4], from which many exciting results have been obtained. The most important result is the resolution of big bang singularity by big bounce [5,6,7]. A similar approach to simplify the theory has also been applied to many models of spherically symmetric black holes (BH) [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], also leading to the resolution of BH singulary. The latest works on LQG black holes have also produced BH models [30,31] keeping general covariance [32,33].
One of the most critical questions for a candidate theory of quantum gravity is how to test such a theory with experimental tools available now or soon to be available. So far, many works have focused on the phenomenology of LQG, studying how the theory can impact classically observable phenomena. For example, The quasinormal modes of the non-rotating LQG black holes were computed [34,35,36]. Meanwhile, [37] investigated the shadow cast by a rotating polymerized black hole constructed using the revised Newman-Janis method. The Hawking radiation spectra and evaporation of spherically symmetric LQG black holes were also studied in [38,39,40,41,42,43].
Some recent works have also investigated LQG gravitational lensing effects [44,45,46,47,48,49,50]. Gravitational lensing effects [51,52,53] describe a phenomenon where photon emitted from a distant source is deflected by a massive celestial object between the source and the observer, such as galaxies or supermassive black holes generating a strong gravitation field, leading to the bending of light trajectories and deflections of the image of the source as being received by the observer. There are two main approaches to studying the gravitational lensing effect: the weak field limits, where the light bending occurs far away from the center of the lens, inducing light deflections around or less than a few arcseconds, and the strong field limits [54,55,56,57,58,59,60], which studies the strong gravitational lensing effect happening near the photon ring the lens BH. For LQG, the focus is mainly on the strong lensing effects since the quantum correction of the theory in classical regime is most likely to be small.
There are three main goals for this work. First and foremost, most previous works studying LQG gravitational effects treat the quantum parameter as a running parameter valued in the magnitude of 1. Indeed, many interesting results can be extracted from such treatments, and one can argue that, due to the quantization ambiguity of LQG, the possibility exists to modify the regulator and quantum parameters in the theory at a fundamental level. However, it should be noted that the quantum parameters defined in the effective models of LQG are usually related to the Planck length, which is an astonishingly small number. It is doubtful that the quantum parameter can be a quantity valued at the magnitude of 1. Therefore, the most essential purpose of this work is to treat these quantum parameters seriously and to look at the quantum corrections to the gravitational lensing effect coming from these rigorously chosen quantum operators and whether there is any remote hope of detecting such quantum effects via currently available experiments.
Second, many effective BH models of LQG, such as the Ashtekar-Olmedo-Sing (AOS) and Gambini-Olmedo-Pullin (GOP) model, have yet to be tested using the gravitational lensing effects. We would also like to explore these models in our investigation of the true quantum impact of LQG on the gravitational lensing effects using rigorously imposed quantum parameters.
Third, so far, most of the works discussing the gravitational lensing effects of LQG study LQG models individually. In this paper, however, we will investigate the gravitational lensing effect of a total of five LQG effective BH models, including the AOS model, the GOP model, two newly proposed models satisfying general covariance (MC1) and (MC2), and the quantum Oppenheimer-Schneider (qOS). We hope that by making comparisons of different models of LQG, we can have a better understanding of the various scales of quantum corrections in terms of gravitational lensing effects from different effective models of LQG, their source of origin, their impacting factors in the theory, and what could make direct observations possible. We also hope that the same methodology can be applied to study other observational effects of LQG in the near future, enabling a more extensive understanding of the observational effects of the theory in regions where actual experiments are plausible.
The structure of this work is as follows: In Section 2, we briefly introduce the definitions of all five models studied, including the exact definitions and values of the quantum parameters present in each model. In the meantime, we will also provide a quick overview of how to compute the gravitational lensing effect using the strong field limit. Since this topic has been covered thoroughly by many previous works such as [45,59], we will include only the most essential steps in obtaining the deflection angle and lens observables. In section 3, we will first compute the quantum corrections of the deflection angle in all five models, then calculate the lens observables, providing comparison and analysis. In the final section of this paper, we will summarize the main results obtained in this work and provide additional insights in to how to interpret these results.

2. Technical Background

2.1. Several BH Models from Effective LQG

In this paper, we focus on the static spherically symmetric spacetimes obtained from the effective models of LQG, which in general can be described by line element:
d s 2 = − A ( r ) d t 2 + B ( r ) d r 2 + C ( r ) d Ω 2 .
Specifically, we consider the region outside of the BH horizon of the following five candidate LQG black hole (BH) models:
  • Ashtekar-Olmedo-Singh (AOS) model [61,62]:
    A A O S ( r ) = r r S 2 ϵ 1 − r S r 1 + ϵ 2 + ϵ + ϵ r S r 1 + ϵ 2 ( 2 + ϵ ) 2 − ϵ 2 r S r 1 + ϵ 16 1 + δ c 2 L 0 2 γ 2 r S 2 16 r 4 ( 1 + ϵ ) 4 , B A O S ( r ) = 1 + δ c 2 L 0 2 γ 2 r S 2 16 r 4 ϵ + r r S 1 + ϵ ( 2 + ϵ ) 2 r r S 1 + ϵ − 1 r r S 1 + ϵ ( 2 + ϵ ) 2 − ϵ 2 , C A O S ( r ) = r 2 1 + γ 2 L 0 2 δ c 2 r S 2 16 r 4 ,
    for r ∈ [ r S , ∞ ) , r S = 2 G m is the Schwarzschild radius ivn the radial coordinate r, and:
    L o δ c = 1 2 γ Δ 2 4 π 2 m 1 / 3 , ϵ + 1 = 1 + γ 2 Δ 2 π γ 2 m 2 / 3 ,
    are quantum parameters depending on both the Imirzi parameter γ and the area gap Δ = 21 . 17 l p 2 (when setting γ = 1 ), namely the minimum nonzero eigenvalue of the area operator in LQG. l p is Planck length.
  • Gambini-Olmedo-Pullin (GOP) model [18,63]:
    A G O P α ( r ) = 1 − r S r + r 0 + α Δ 4 π r S 4 r + r 0 6 1 + r S r + r 0 2 , B G O P α ( r ) = 1 + δ x 2 r + r 0 2 1 − r S r + r 0 + α Δ 4 π r S 4 r + r 0 6 1 + r S r + r 0 2 , C G O P ( r ) = r + r 0 2 ,
    where:
    r 0 = 2 G m Δ 4 π 1 / 3 ,
    α is a parameter with choices 0 and 1. The difference between these two choices is verified to be negligible concerning gravitational lensing effects.
  • Two newly proposed model satifying the minimal conditions for maintaining general covariance (MC1 and MC2) [30]:
    A M C 1 ( r ) = 1 − 2 M r + ζ M C 2 M 2 r 2 1 − 2 M r 2 , A M C 2 ( r ) = 1 − 2 M r , B M C 1 ( r ) = B M C 2 ( r ) = A M C 1 ( r ) − 1 , C M C 1 = C M C 2 = r 2 ,
    where ζ M C = 4 3 π γ 3 l p 2 M is the quantum parameter for both models. Gravitational lensing effect of this model has been studied recently in [50] by treating ζ M C as an arbitrary parameter in the order ζ M C ∼ 1 . In our paper, we stick strictly to the original theory where ζ M C = 4 3 π γ 3 l p 2 M .
  • Quantum Oppenheimer-Schneider (qOS) model [26]:
    A q O S ( r ) = 1 − 2 M r + ζ q O S M 2 r 4 , B q O S ( r ) = A q O S ( r ) − 1 , C q O S ( r ) = r 2 ,
    where ζ q O S = 16 3 γ 3 l p 2 . The gravitational lensing effect of this model has also been studied previously in [48] considering ζ q O S ∼ 1 . In this work we also keep the quantum parameter as ζ q O S = 16 3 γ 3 l p 2 .

2.2. Gravitational Lensing from Strong Field Limit and Lens Observables

Since the quantum parameters of the above mentioned BH models are value at the order of minuscule constants such as the Planck length l p or Planck area l p 2 , the quantum correction to the gravitational lensing effect is inevitably small. As a consequence, the photon trajectories whose closest distance to the lens during the trip near the photon ring have the largest impact from quantum corrections. Let the closest distance to the lens of a photon trajectories be r 0 , the minimum such distance is the BH photon sphere r m satisfying:
C ′ ( r m ) C ( r m ) = A ′ ( r m ) A ( r m ) .
For arbitrary theories with the line element (1), given impact parameter b, the deflection angle α between the source and the image can be computed as [59]:
α r 0 = I r 0 − π I r 0 = 2 ∫ r 0 ∞ 1 C A B 1 / u 2 − A / C d r
For r 0 → r m , the gravitational lensing effect can be approximated by the strong field limit. A general approach to obtain the strong field limit for BH whose line elements takes the form (1) is described in [59]. As an alternative to the original proposal, we consider the variable z = 1 − r 0 r used in [45,50], allowing for the direct conversion between z and r. The integral can then be rewritten as:
I r 0 = ∫ 0 1 R z , r 0 f z , r 0 d z ,
where we have:
R z , r 0 = 2 r 2 A ( r ) B ( r ) C 0 r 0 C ( r ) f z , r 0 = 1 A 0 − A ( r ) C 0 C ( r ) ,
where A 0 : = A ( r 0 ) and C 0 : = C ( r 0 ) . R ( z , r 0 ) is regular for r ≥ r 0 ≥ r m , while f ( z , r 0 ) is divergent in z as z → 0 , i.e., r → r 0 . We expand the divergent term f ( z , r 0 ) up to second order of z as:
f z , r 0 ∼ f 0 z , r 0 = 1 c 1 r 0 z + c 2 r 0 z 2 ,
where:
c 1 r 0 = − r 0 A 0 ′ + r 0 A 0 C 0 ′ C 0 c 2 r 0 = r 0 − 2 r 0 A 0 C 0 ′ 2 − C 0 2 2 A 0 ′ + r 0 A 0 ′ ′ + C 0 2 r 0 A 0 ′ C 0 ′ + A 0 2 C 0 ′ + r 0 2 C 0 ′ ′ 2 C 0 2
which captures the dominant contribution of the divergence as z → 0 .
Using this expansion, the integral I ( r 0 ) can be split into regular part I R ( r 0 ) and divergent part I D ( r 0 ) as:
I r 0 = I D r 0 + I R r 0 I D r 0 = ∫ 0 1 R 0 , r m f 0 z , r 0 d z I R r 0 = ∫ 0 1 R z , r 0 f z , r 0 − R 0 , r m f 0 z , r 0 d z .
As a result, the deflection angle can be computed in terms of the impact parameter b as:
α ( b ) = − a ln b b m − 1 + u + O b − b m ln b − b m ,
where:
a ≡ R 0 , r m 2 c 2 r m , u ≡ a ln δ + I R r 0 − π , δ ≡ r m 2 C ′ ′ r m C r m − A ′ ′ r m A r m .
Despite the dependence of the impact factor b in α ( b ) , using the factors a and u, several b-independent lens observables can also be extracted [45,50,59]:
  • Angle θ ∞ of the innermost image. The angle θ is defined as the observed angle between the lens BH and the image of the source as being observed after deflection via the lens. Since the photon trajectory can go around the lens multiple times before finally reaching the observer, there can be a total of n images of the source. n is not bounded since the deflection angle is unbounded for b → b m . Therefore, a limit θ ∞ ≈ b m D O L can be obtained by taking n → ∞ .
  • the angular separation s between the outermost image and the innermost image (the lower bound of the series of images as n → , since these images are unlikely to be distinguishable):
    s : = θ 1 − θ ∞ ∼ = θ ∞ e u − 2 π a .
  • the quotient μ of the flux of the outermost relativistic image to that of all other relativistic images:
    μ ∼ e 4 π a − 1 e 2 π a + e u a e 4 π a + e 2 π a + e u a
These b-independent lens observables are only dependent on the quantum parameter of the theory, thus serving as an ideal testing ground for studying the quantum correction of the gravitational lensing effect from LQG.

2.3. Exact Values of the Quantum Parameters

In this paper, we use the values of the quantum parameter in all BH models of LQG as they were originally constructed to capture the precise impact of the quantum effects. For all of the results we obtained, we set c = 1 , G = 1 , also we rescale the radial direction such that M = 1 , and the Schwarschild radius of the center BH is always r s = 2 M = 2 . This rescaling also impacts the quantum parameters due to their dependence on l p or Δ , based on the actual mass of the center black hole which varies for different cases. In this work, we choose SgrA* and M87* to study the quantum effects. For the case of SgrA*, by choosing its mass to be m SgrA ∗ = 4 . 3 × 10 6 M ⊙ and its distance to the observer to be D O L = 8 . 35 k p c , the value of the Planck length after the rescaling equals l p , SgrA ∗ = 2 r s × 1 . 61623 ∗ 10 − 35 = 2 . 54456 × 10 − 45 and Δ SgrA ∗ = 1 . 37072 × 10 − 88 . For the case of M87*, by choosing its mass to be m M 87 ∗ = 6 . 5 × 10 9 M ⊙ and its distance to the observer to be D O L = 16 . 8 M p c , the Planck length after the rescaling equals l p , M 87 ∗ = 1 . 68333 × 10 − 48 and Δ M 87 ∗ = 5 . 99871 × 10 − 95 .
Here we provide a collection of the exact values of quantum parameters we use in for all five models mentioned above:
  • AOS model: Δ = 1 . 37072 × 10 − 88 for SgrA* and Δ = 5 . 99871 × 10 − 95 for M87*.
  • GOP model: Δ = 1 . 37072 × 10 − 88 for SgrA* and Δ = 5 . 99871 × 10 − 95 for M87*.
  • MC1 and MC2 models: ζ M C = 1 . 18713 × 10 − 44 for SgrA* and ζ M C = 7 . 85333 × 10 − 48 for M87*.
  • qOS model: ζ q O S = 1 . 79435 × 10 − 88 for SgrA* and ζ q O S = 7 . 85268 × 10 − 95 for M87*.

3. Main Results

3.1. Deflecting Angle α

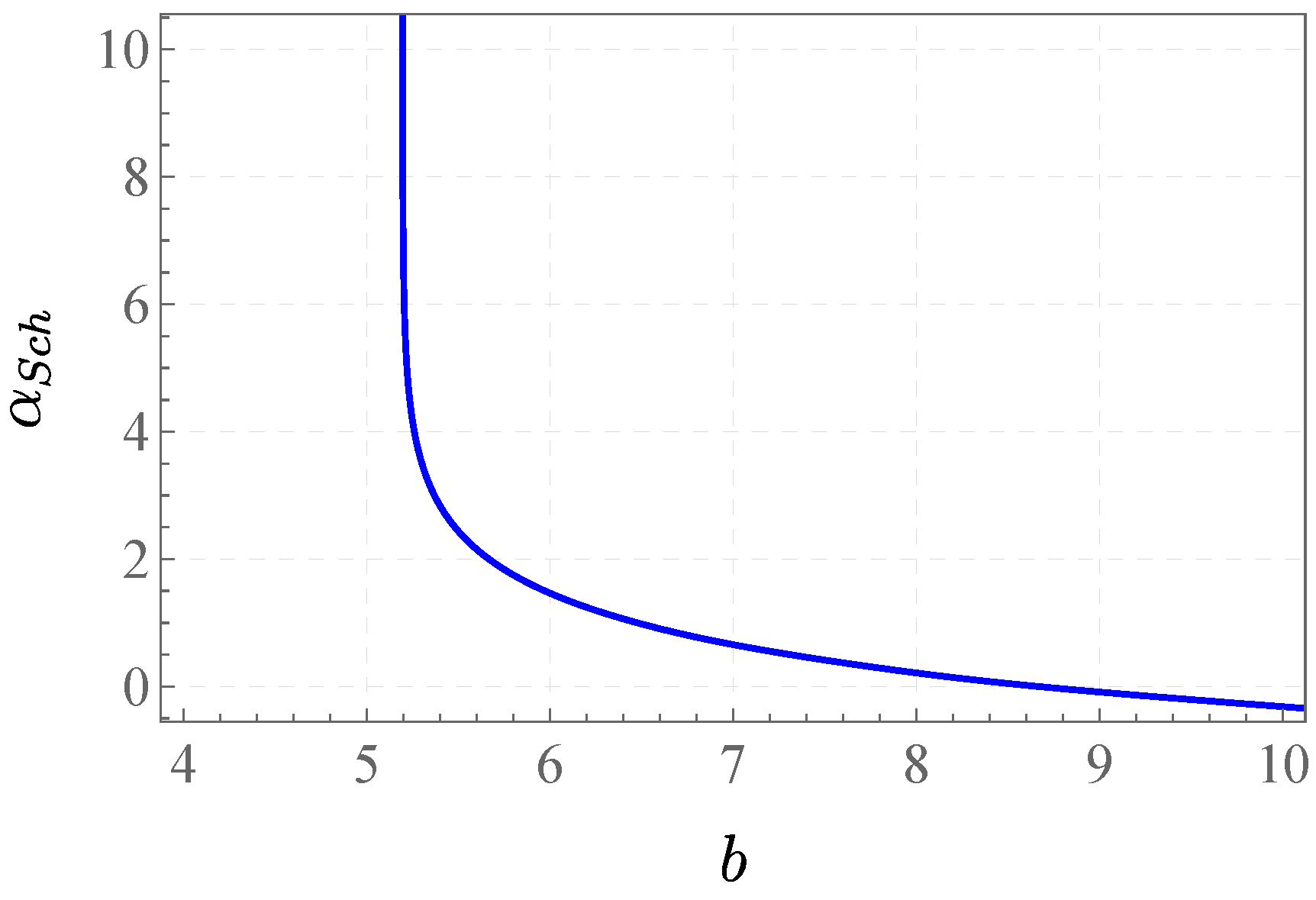
In this subsection, we show the quantum corrections of BH models of LQG on the gravitational lensing effect by computing the deflection angle versus the impact parameter b. Using eqn. (9), the deflection angle can be computed for
Figure 1 shows the results for the deflection angle with respect to the impact factor b. Since the quantum parameters we use for all models are extremely small (as shown in Table ), all of the results for the deflection angles are very close to the Schwarzschild case:
α S c h ≈ − L o g [ 0 . 19245 b − 1 ] − 0 . 40023 ,
for M = 1 . The difference can not be shown on Figure 1 as the curve for each model overlaps. To characterize the quantum effects of different models, we consider both the exact difference D α and relative difference R α between the deflection angle α L Q G of each LQG BH model and α S c h of the Schwarzschild BH:
D α ( b ) : = α L Q G ( b ) − α S c h ( b ) , R α ( b ) : = α L Q G ( b ) − α S c h ( b ) α S c h ( b ) .
Moreover, for the case of deflecting angle, we consider the case where the impact factor is very near to the innermost possible impact factor b m = 5 . 19615 for Schwarzschild BH. A log-log graph (Figure) can be produced in this region by defining the relative difference R b of the impact factor b to b m :
R b : = b − b m b m .
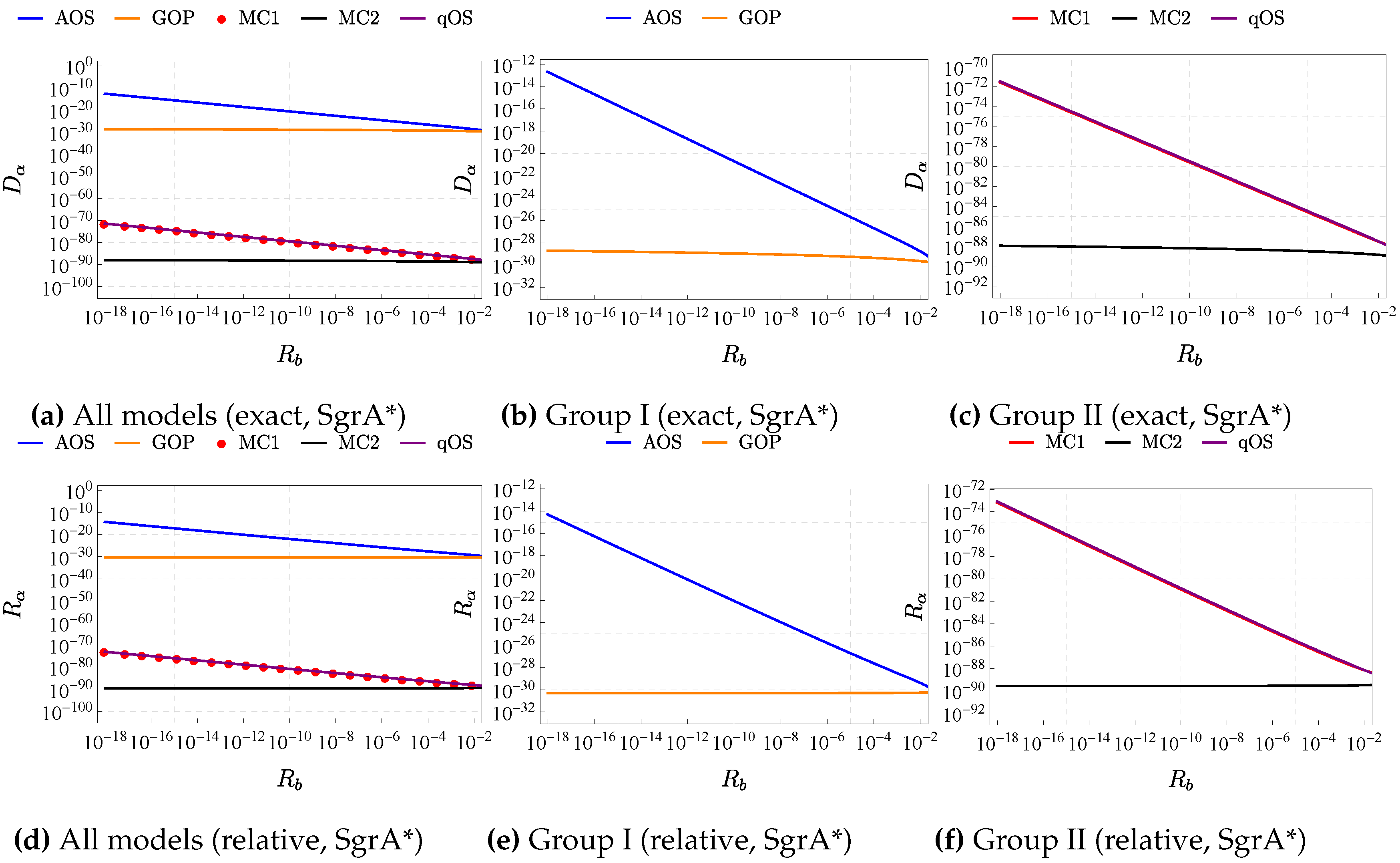
Figure 2 shows the Log 10 - Log 10 graph of the exact difference D α and relative difference R α of the deflection angle α between LQG BH models and Schwarzschild BH versus the relative distance R b to Schwarzschild b m . All results are obtained using input data from SgrA ∗ . (a) and (d) shows the results for all five models, where red dots instead of curves depict results corresponding to the MC1 model because of the overlap with the qOS model. In (b)(c)(e)(f), the five models are further divided into two groups based on the values of their results.
Several facts can be read from this figure: First, despite the overall minor quantum corrections obtained, the five models can be split into two distinct groups using their values of R α and D α : Both AOS and GOP models are put into group I due to their relatively large quantum corrections to α , while the other three models, namely MC1, MC2 and qOS models, all have minor quantum corrections to α . Second, the results for q O S and M C 1 models are very similar, making them almost indistinguishable in Figure 2. This shows that both models are closely related, at least in the region outside the photon ring.
Interestingly, the quantum correction of deflection angles of models AOS, MC1, and qOS increase much faster than models GOP and MC2 as R b → 0 . A careful look into the theories indicates that the quantum correction of A ( r ) of all former three models is significantly larger as b → b m . At the same time, A M C 2 ( r ) = A S c h ( r ) and A G O P ( r ) has only minimal quantum corrections compares to B G O P ( r ) . Recall from (8) that the location of the photon sphere is impacted by both A ( r ) and C ( r ) , which suggests that the patterns of these results might be related to the specific way in which the metric tensor is quantum corrected. In particular, large changes in A ( r ) might lead to the minimal impacting factor of the model deviating from the Schwarzschild BH. As a result, since R b is defined by computing the relative difference of b over the Scharzschild minimal impacting factor b m , S c h , b → b m does not apply to both the Schwarzschild BH and the LQG model at the same time. This can further boost the difference in deflecting angle α .
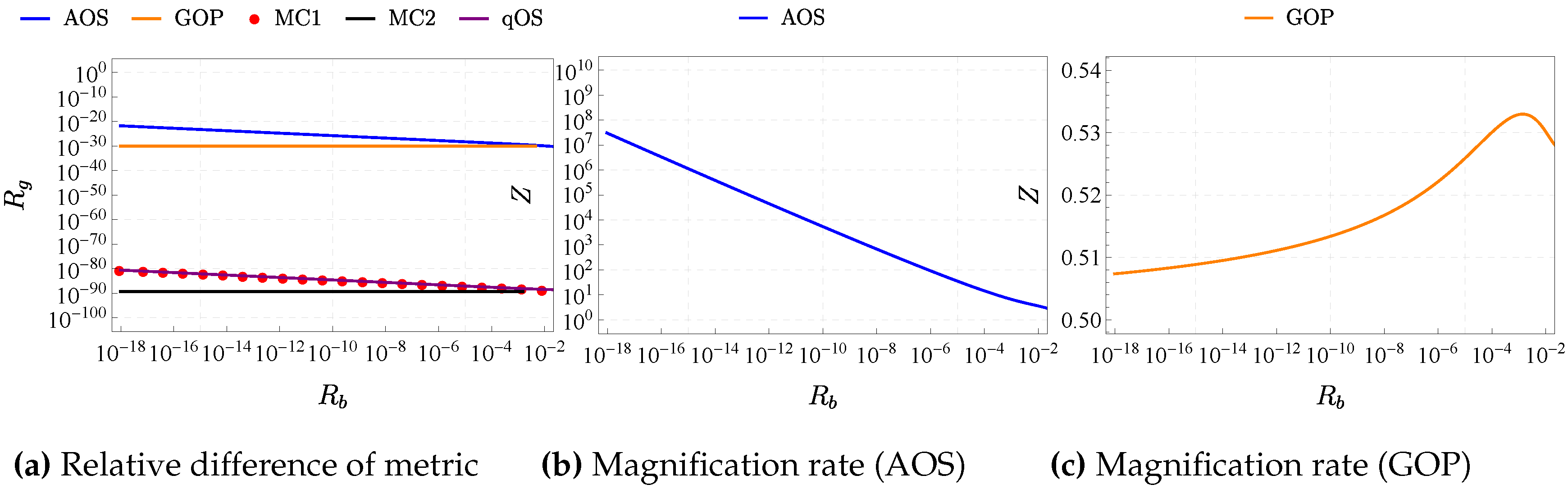
To further investigate this finding, we plot the relative difference of A A O S ( r ) , A M C 1 ( r ) and A q O S ( r ) versus R b , as well as the relative difference of B G O P and B M C 2 versus R b in Figure 3. Since the relative difference of the deflection angle and the relative difference of metric components both reflect on the level of quantum correction, we further define the following magnification rate Z:
Z : = R α / R g ,
where:
R g : = A ( r ) − A S c h ( r ) A S c h ( r ) For AOS , MC 1 , qOS , B ( r ) − B S c h ( r ) B S c h ( r ) For GOP , MC 2.
Figure 3 shows the relation between the quantum corrections of metric and the quantum corrections of deflection angle α . Figure 3 (a) shows the relative difference of metric for all five models. When comparing the results in Figure 3 (a) with Figure 2 (d), it is straightforward to see that the relative quantum corrections of the metric is significantly smaller than the quantum corrections of the relative deflection angle α for the models: AOS, MC1, and qOS. For GOS and MC2 models, however, the difference is not apparent.
The same conclusion is further supported by Figure 3 (b) and Figure 3 (c). Figure 3 (b) shows the magnification rate Z versus R b in the AOS model. As R b goes to 0, i.e., when b → b m , S c h , Z becomes increasingly larger, reaching 10 7 . This suggests that in this region, the relative quantum correction on the deflection angle is much higher than the relative quantum correction of the metric, significantly boosting the detectability of the theory in this region. Figure 3 (c) shows the magnification rate Z versus R b in the GOP model. Being different from Figure 3 (b), as R b goes to 0, Z becomes stable at around Z = 0 . 5 . This suggests that in the GOP model, the relative quantum correction on the deflection angle is not boosted when compared to the relative quantum correction of the metric.

3.2. Lense Observables

Despite all the quantum corrections we have obtained, linking any real physical observations to these quantum effects is still challenging. This is because the deflection angle α is not invariant to the change in b, which can vary drastically for actual individual sources. Moreover, since the impact of quantum effects occurs only when b → b m , S c h , it is unlikely that any effects in this region will be straightforwardly observable.
Therefore, to detect quantum gravitational corrections from gravitational lensing effects, we turn to computing the quantum effects of lens observables. These observables are directly detectable by observations and only depend on the quantum parameter of each specific model. Therefore, these observables could offer us a direct link between the quantum effects and direct observations.
Table 1 and Table 2 shows the Observables of SgrA ∗ and M 87 ∗ . Each table contains three data sections, corresponding to θ ∞ , s, and μ m , respectively. Within each section, both the exact value of observables and their relative difference to their Schwarzschild counterparts are included. "Sch" stands for Schwarschild BH, for which all the relative differences read 0.
By comparing the data computed, it appears that the lens observables obtained from SgrA ∗ have larger quantum corrections than from M 87 ∗ . For the most significant relative quantum corrections, the value from SgrA ∗ is typically around 100 times larger than from M 87 ∗ . This indicates that the quantum effects generated by the BH models of LQG can be very sensitive to the characteristics of the center BH.
Also, as can be seen from both Table 1 and Table 2, AOS model has the largest quantum corrections of θ ∞ and s, while GOP model has the largest quantum correction of μ m . The quantum corrections generated by models MC1, MC2, and qOS are significantly smaller, making them even harder to detect. The relative difference of θ ∞ is 0 for the MC2 model due to the fact that it shares the exact same A ( r ) and C ( r ) as Schwarzschild BH. Its only quantum effect comes from B ( r ) .

4. Discussion

In this work, we have studied the quantum corrections to the gravitational lensing effect induced by five different LQG black hole models, where the quantum parameter is obtained authentic to the original theories for all cases. Using the strong field limit method, we successfully computed the deflection angles, as well as lens observables from these models. We have made the following key discoveries:
First, we discovered that although the quantum effects are very small for all five models, their actual value can vary enormously: the impacts of quantum corrections of the AOS and GOP models are much higher than the impact generated by MC1, MC2, and qOS, forming two different groups of theories based the scale of quantum effects generated by each model. This might indicate the underlying connections and differences among different effective LQG models.
Second, the quantum corrections of the deflection angles are roughly in the same order as the quantum corrections of the metric tensor. Meanwhile, the ratio between the quantum corrections of the deflection angle and the quantum corrections of the metric is shown to increase drastically for AOS, MC1, and qOS models, with the impacting parameter b being very close to the minimal impacting factor b m for Schwarzschild BH. It remains to be discovered whether such drastic increase can have real observable effects, which can help with the detection of quantum effects from these models.
Third, lens observables obtained from SgrA ∗ have larger quantum corrections than from M 87 ∗ . For the most significant relative quantum corrections, the value from SgrA ∗ is typically around 100 times larger than that from M 87 ∗ , indicating that the center BH with different properties can have very different quantum corrections to the gravitational lensing effects.
As expected, the quantum impacts we obtained in this work are minimal due to the quantum parameters valued at the Planck scale. Nonetheless, noting that the largest quantum corrections we obtained are at the order of ∼ 10 − 30 , we argue that there are still at least four directions to improve the detection of the quantum effects of LQG:
  • Based on our study in this work, we discovered that the characteristics of the lens object play an essential role in the gravitational lensing effect. Comparing the results obtained for SgrA* and M87*, the relative differences of the lens observables to the observables for Scharzschild BH are at least 100 times larger for SgrA* than M87*. This result suggests that by discovering new lens objects, it is possible to make the quantum effect larger on the observables, possibly even larger by orders of magnitudes, making them much easier to detect.
  • The remaining quantization ambiguities might also make the actual quantum effects larger. For example, during the discretization phase of LQG quantization, the minimum spacing of lattices is usually associated with the area gap, which is chosen to be the minimum nonzero eigenvalue of the area operator in loop quantum gravity. This treatment gives the smallest such area gaps in the theory. However, it is not necessarily the only choice of the lattice spacing, which could contribute to larger quantum parameters of the model and thus render its quantum effects larger.
  • New models from LQG. So far, the works on studying the gravitational lens effects of LQG models have only explored some effective models of the symmetry-reduced theory of LQG. In this work, we have shown that the quantum effects of different BH models of LQG can be extremely different. Thus it is possible that some future models, such as the effective models of full canonical LQG and spin foam models which both contain additional quantum corrections, can produce different results than the effective models we studied.
  • Future advances in observing and measuring gravitational lensing effects may further increase the experimental precision of such observations. This may further narrow the gap between the actual detection range and LQG quantum corrections.
By combining all four above-mentioned approaches, it is still possible to narrow down the gap between the actual detection range and the scale of the quantum corrections by several orders of magnitudes, or even tens of orders of magnitudes, making the verification of the effects of quantum gravity much more tangible.

References

  1. T. Thiemann, Modern Canonical Quantum General Relativity. Cambridge Monographs on Mathematical Physics. Cambridge University Press, 2007.
  2. C. Rovelli and F. Vidotto, Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory. Cambridge Monographs on Mathematical Physics. Cambridge University Press, 11, 2014.
  3. A. Ashtekar and J. Pullin, eds., Loop Quantum Gravity: The First 30 Years, vol. 4 of 100 Years of General Relativity. World Scientific, 2017.
  4. A. Ashtekar and P. Singh, Loop Quantum Cosmology: A Status Report, Class. Quant. Grav. 28 (2011) 213001. [arXiv:1108.0893]. [CrossRef]
  5. A. Ashtekar, T. Pawlowski, and P. Singh, Quantum nature of the big bang, Phys. Rev. Lett. 96 (2006) 141301, [gr-qc/0602086]. [CrossRef]
  6. A. Ashtekar, T. Pawlowski, and P. Singh, Quantum Nature of the Big Bang: An Analytical and Numerical Investigation. I., Phys. Rev. D 73 (2006) 124038, [gr-qc/0604013]. [CrossRef]
  7. A. Ashtekar, T. Pawlowski, and P. Singh, Quantum Nature of the Big Bang: Improved dynamics, Phys. Rev. D 74 (2006) 084003, [gr-qc/0607039]. [CrossRef]
  8. L. Modesto, Loop quantum black hole, Class. Quant. Grav. 23 (2006) 5587–5602, [gr-qc/0509078]. [CrossRef]
  9. M. Campiglia, R. Gambini, and J. Pullin, Loop quantization of spherically symmetric midi-superspaces, Class. Quant. Grav. 24 (2007) 3649–3672, [gr-qc/0703135]. [CrossRef]
  10. F. Caravelli and L. Modesto, Spinning Loop Black Holes, Class. Quant. Grav. 27 (2010) 245022, [arXiv:1006.0232]. [CrossRef]
  11. J. F. Barbero G. and A. Perez, Quantum Geometry and Black Holes, pp. 241–279. WSP, 2017. arXiv:1501.02963. [CrossRef]
  12. A. Perez, Black Holes in Loop Quantum Gravity, Rept. Prog. Phys. 80 (2017), no. 12 126901, [arXiv:1703.09149]. [CrossRef]
  13. A. Corichi and P. Singh, Loop quantization of the Schwarzschild interior revisited, Class. Quant. Grav. 33 (2016), no. 5 055006, [arXiv:1506.08015]. [CrossRef]
  14. J. Olmedo, S. Saini, and P. Singh, From black holes to white holes: a quantum gravitational, symmetric bounce, Class. Quant. Grav. 34 (2017), no. 22 225011, [arXiv:1707.07333]. [CrossRef]
  15. A. Ashtekar, J. Olmedo, and P. Singh, Quantum Transfiguration of Kruskal Black Holes, Phys. Rev. Lett. 121 (2018), no. 24 241301, [arXiv:1806.00648]. [CrossRef]
  16. N. Bodendorfer, F. M. Mele, and J. Münch, Effective Quantum Extended Spacetime of Polymer Schwarzschild Black Hole, Class. Quant. Grav. 36 (2019), no. 19 195015, [arXiv:1902.04542]. [CrossRef]
  17. C. Liu, T. Zhu, Q. Wu, K. Jusufi, M. Jamil, M. Azreg-Aïnou, and A. Wang, Shadow and quasinormal modes of a rotating loop quantum black hole, Phys. Rev. D 101 (2020), no. 8 084001, [arXiv:2003.00477]. [Erratum: Phys.Rev.D 103, 089902 (2021)]. [CrossRef]
  18. R. Gambini, J. Olmedo, and J. Pullin, Spherically symmetric loop quantum gravity: analysis of improved dynamics, Class. Quant. Grav. 37 (2020), no. 20 205012, [arXiv:2006.01513]. [CrossRef]
  19. J. G. Kelly, R. Santacruz, and E. Wilson-Ewing, Effective loop quantum gravity framework for vacuum spherically symmetric spacetimes, Phys. Rev. D 102 (2020), no. 10 106024, [arXiv:2006.09302]. [CrossRef]
  20. J. Lin and X. Zhang, Effective four-dimensional loop quantum black hole with a cosmological constant, Phys. Rev. D 110 (2024), no. 2 026002, [arXiv:2402.13638]. [CrossRef]
  21. N. Bodendorfer, F. M. Mele, and J. Münch, (b,v)-type variables for black to white hole transitions in effective loop quantum gravity, Phys. Lett. B 819 (2021) 136390, [arXiv:1911.12646]. [CrossRef]
  22. N. Bodendorfer, F. M. Mele, and J. Münch, Mass and Horizon Dirac Observables in Effective Models of Quantum Black-to-White Hole Transition, Class. Quant. Grav. 38 (2021), no. 9 095002, [arXiv:1912.00774]. [CrossRef]
  23. Y.-L. Liu, Z.-Q. Feng, and X.-D. Zhang, Solar system constraints of a polymer black hole in loop quantum gravity, Phys. Rev. D 105 (2022) 084068, [arXiv:2201.10202]. [CrossRef]
  24. F. Sartini and M. Geiller, Quantum dynamics of the black hole interior in loop quantum cosmology, Phys. Rev. D 103 (2021), no. 6 066014, [arXiv:2010.07056]. [CrossRef]
  25. M. Han and H. Liu, Improved effective dynamics of loop-quantum-gravity black hole and Nariai limit, Class. Quant. Grav. 39 (2022), no. 3 035011, [arXiv:2012.05729]. [CrossRef]
  26. J. Lewandowski, Y. Ma, J. Yang, and C. Zhang, Quantum Oppenheimer-Snyder and Swiss Cheese Models, Phys. Rev. Lett. 130 (2023), no. 10 101501, [arXiv:2210.02253]. [CrossRef]
  27. X. Zhang, Loop Quantum Black Hole, Universe 9 (2023), no. 7 313, [arXiv:2308.10184]. [CrossRef]
  28. K. Giesel, H. Liu, E. Rullit, P. Singh, and S. A. Weigl, Embedding generalized LTB models in polymerized spherically symmetric spacetimes, arXiv:2308.10949. [CrossRef]
  29. K. Giesel, H. Liu, P. Singh, and S. A. Weigl, Regular black holes and their relationship to polymerized models and mimetic gravity, arXiv:2405.03554. [CrossRef]
  30. C. Zhang, J. Lewandowski, Y. Ma, and J. Yang, Black Holes and Covariance in Effective Quantum Gravity, arXiv:2407.10168. [CrossRef]
  31. I. H. Belfaqih, M. Bojowald, S. Brahma, and E. I. Duque, Black holes in effective loop quantum gravity: Covariant holonomy modifications, arXiv:2407.12087. [CrossRef]
  32. M. Bojowald and G. M. Paily, Deformed General Relativity and Effective Actions from Loop Quantum Gravity, Phys. Rev. D 86 (2012) 104018, [arXiv:1112.1899]. [CrossRef]
  33. M. Bojowald, S. Brahma, and J. D. Reyes, Covariance in models of loop quantum gravity: Spherical symmetry, Phys. Rev. D 92 (2015), no. 4 045043, [arXiv:1507.00329]. [CrossRef]
  34. F. Moulin, K. Martineau, J. Grain, and A. Barrau, Quantum fields in the background spacetime of a polymeric loop black hole, Class. Quant. Grav. 36 (2019), no. 12 125003, [arXiv:1808.00207]. [CrossRef]
  35. F. Moulin, A. Barrau, and K. Martineau, An overview of quasinormal modes in modified and extended gravity, Universe 5 (2019), no. 9 202, [arXiv:1908.06311]. [CrossRef]
  36. D. del Corral and J. Olmedo, Breaking of isospectrality of quasinormal modes in nonrotating loop quantum gravity black holes, Phys. Rev. D 105 (2022), no. 6 064053, [arXiv:2201.09584]. [CrossRef]
  37. S. Brahma, C.-Y. Chen, and D.-h. Yeom, Testing Loop Quantum Gravity from Observational Consequences of Nonsingular Rotating Black Holes, Phys. Rev. Lett. 126 (2021), no. 18 181301, [arXiv:2012.08785]. [CrossRef]
  38. A. Barrau, T. Cailleteau, X. Cao, J. Diaz-Polo, and J. Grain, Probing Loop Quantum Gravity with Evaporating Black Holes, Phys. Rev. Lett. 107 (2011) 251301, [arXiv:1109.4239]. [CrossRef]
  39. R. Gambini and J. Pullin, Hawking radiation from a spherical loop quantum gravity black hole, Class. Quant. Grav. 31 (2014) 115003, [arXiv:1312.3595]. [CrossRef]
  40. A. Barrau, X. Cao, K. Noui, and A. Perez, Black hole spectroscopy from Loop Quantum Gravity models, Phys. Rev. D 92 (2015), no. 12 124046, [arXiv:1504.05352]. [CrossRef]
  41. A. Ashtekar, Black Hole evaporation: A Perspective from Loop Quantum Gravity, Universe 6 (2020), no. 2 21, [arXiv:2001.08833]. [CrossRef]
  42. A. Arbey, J. Auffinger, M. Geiller, E. R. Livine, and F. Sartini, Hawking radiation by spherically-symmetric static black holes for all spins: Teukolsky equations and potentials, Phys. Rev. D 103 (2021), no. 10 104010, [arXiv:2101.02951]. [CrossRef]
  43. A. Arbey, J. Auffinger, M. Geiller, E. R. Livine, and F. Sartini, Hawking radiation by spherically-symmetric static black holes for all spins. II. Numerical emission rates, analytical limits, and new constraints, Phys. Rev. D 104 (2021), no. 8 084016, [arXiv:2107.03293]. [CrossRef]
  44. S. Sahu, K. Lochan, and D. Narasimha, Gravitational lensing by self-dual black holes in loop quantum gravity, Phys. Rev. D 91 (2015) 063001, [arXiv:1502.05619]. [CrossRef]
  45. Q.-M. Fu and X. Zhang, Gravitational lensing by a black hole in effective loop quantum gravity, Phys. Rev. D 105 (2022), no. 6 064020, [arXiv:2111.07223]. [CrossRef]
  46. J. Kumar, S. U. Islam, and S. G. Ghosh, Strong gravitational lensing by loop quantum gravity motivated rotating black holes and EHT observations, Eur. Phys. J. C 83 (2023), no. 11 1014, [arXiv:2305.04336]. [CrossRef]
  47. E. L. B. Junior, F. S. N. Lobo, M. E. Rodrigues, and H. A. Vieira, Gravitational lens effect of a holonomy corrected Schwarzschild black hole, Phys. Rev. D 109 (2024), no. 2 024004, [arXiv:2309.02658]. [CrossRef]
  48. L. Zhao, M. Tang, and Z. Xu, The Lensing Effect of Quantum-Corrected Black Hole and Parameter Constraints from EHT Observations, arXiv:2403.18606. [CrossRef]
  49. Y. Dong, The gravitational lensing by rotating black holes in loop quantum gravity, Nucl. Phys. B 1005 (2024) 116612. [CrossRef]
  50. H. Liu, M.-Y. Lai, X.-Y. Pan, H. Huang, and D.-C. Zou, Gravitational lensing effect of black holes in effective quantum gravity, arXiv:2408.11603. [CrossRef]
  51. F. W. Dyson, A. S. Eddington, and C. Davidson, Ix. a determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of may 29, 1919, Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 220 (1920), no. 571-581 291–333. [CrossRef]
  52. S. Liebes, Gravitational Lenses, Phys. Rev. 133 (1964) B835–B844. [CrossRef]
  53. R. A. Society, [Monthly notices of the Royal Astronomical Society/Letters]; Monthly notices of the Royal Astronomical Society. Letters [Elektronische Ressource], vol. 29. Oxford University Press, 1870.
  54. C. G. Darwin, The gravity field of a particle, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 249 (1959), no. 1257 180–194. [CrossRef]
  55. H. C. Ohanian, The black hole as a gravitational “lens”, American Journal of Physics 55 (1987), no. 5 428–432. [CrossRef]
  56. S. Frittelli, T. P. Kling, and E. T. Newman, Space-time perspective of Schwarzschild lensing, Phys. Rev. D 61 (2000) 064021, [gr-qc/0001037]. [CrossRef]
  57. K. S. Virbhadra and G. F. R. Ellis, Schwarzschild black hole lensing, Phys. Rev. D 62 (2000) 084003, [astro-ph/9904193]. [CrossRef]
  58. V. Bozza, S. Capozziello, G. Iovane, and G. Scarpetta, Strong field limit of black hole gravitational lensing, Gen. Rel. Grav. 33 (2001) 1535–1548, [gr-qc/0102068]. [CrossRef]
  59. V. Bozza, Gravitational lensing in the strong field limit, Phys. Rev. D 66 (2002) 103001, [gr-qc/0208075]. [CrossRef]
  60. K. S. Virbhadra, Relativistic images of Schwarzschild black hole lensing, Phys. Rev. D 79 (2009) 083004, [arXiv:0810.2109]. [CrossRef]
  61. A. Ashtekar, J. Olmedo, and P. Singh, Quantum extension of the Kruskal spacetime, Phys. Rev. D 98 (2018), no. 12 126003, [arXiv:1806.02406]. [CrossRef]
  62. A. Ashtekar and J. Olmedo, Properties of a recent quantum extension of the Kruskal geometry, Int. J. Mod. Phys. D 29 (2020), no. 10 2050076, [arXiv:2005.02309]. [CrossRef]
  63. R. Gambini, J. Olmedo, and J. Pullin, Loop Quantum Black Hole Extensions Within the Improved Dynamics, Front. Astron. Space Sci. 8 (2021) 74, [arXiv:2012.14212]. [CrossRef]
Preprints 118218 g001
Figure 1. Deflection angle α with respect to impact factor b. All of the models investigated in this paper share the same curve with Schwarzschild BH.
Figure 1. Deflection angle α with respect to impact factor b. All of the models investigated in this paper share the same curve with Schwarzschild BH.
Preprints 118218 g001
Preprints 118218 g002
Figure 2. Log 10 - Log 10 graph of the exact difference D α and relative difference R α of the deflection angle α between LQG BH models and Schwarzschild BH versus the relative distance R b to Schwarzschild b m . All results are obtained using input data from SgrA ∗ . (a) and (d) shows the results for all five models, where red dots instead of curves depict results corresponding to the MC1 model because of the overlap with the qOS model. In (b)(c)(e)(f), the five models are further divided into two groups based on the values of their results.
Figure 2. Log 10 - Log 10 graph of the exact difference D α and relative difference R α of the deflection angle α between LQG BH models and Schwarzschild BH versus the relative distance R b to Schwarzschild b m . All results are obtained using input data from SgrA ∗ . (a) and (d) shows the results for all five models, where red dots instead of curves depict results corresponding to the MC1 model because of the overlap with the qOS model. In (b)(c)(e)(f), the five models are further divided into two groups based on the values of their results.
Preprints 118218 g002
Preprints 118218 g003
Figure 3. The relation between the quantum corrections of metric and the quantum corrections of deflection angle α . (a): Relative difference of metric for all five models. (b) The Magnification rate Z for the AOS model, indicating the quantum effect is magnified significantly by the deflection angle compared to the metric’s quantum correction. (c) The Magnification rate Z for the GOP model. No magnification is observed.
Figure 3. The relation between the quantum corrections of metric and the quantum corrections of deflection angle α . (a): Relative difference of metric for all five models. (b) The Magnification rate Z for the AOS model, indicating the quantum effect is magnified significantly by the deflection angle compared to the metric’s quantum correction. (c) The Magnification rate Z for the GOP model. No magnification is observed.
Preprints 118218 g003
Table 1. Observables of SgrA ∗
Table 1. Observables of SgrA ∗
type Sch AOS GOP MC1 MC2 qOS
θ ∞ 26.42 26.42 26.42 26.42 26.42 26.42
θ ∞ − θ ∞ , Sch θ ∞ , Sch 0 − 2.0155 × 10 − 31 − 1.29278 × 10 − 91 − 2.60978 × 10 − 90 0 − 3.32287 × 10 − 90
s 0.03306 0.03306 0.03306 0.03306 0.03306 0.03306
s − s , Sch s , Sch 0 4.12221 × 10 − 30 3.20814 × 10 − 30 − 4.08044 × 10 − 89 − 1.88176 × 10 − 89 5.31267 × 10 − 89
μ m 6.82121 6.82121 6.82121 6.82121 6.82121 6.82121
μ m − μ m , Sch μ m , Sch 0 − 3.10219 × 10 − 31 − 4.6598 × 10 − 31 5.22227 × 10 − 90 2.61119 × 10 − 90 − 9.97707 × 10 − 90
Table 2. Observables of M 87 ∗
Table 2. Observables of M 87 ∗
type Sch AOS GOP MC1 MC2 qOS
θ ∞ 19.8509 19.8509 19.8509 19.8509 19.8509 19.8509
θ ∞ − θ ∞ , Sch θ ∞ , Sch 0 − 1.53022 × 10 − 33 − 5.65763 × 10 − 98 − 1.14213 × 10 − 96 0 − 1.4542 × 10 − 96
s 0.02484 0.02484 0.02484 0.02484 0.02484 0.02484
s − s , Sch s , Sch 0 3.12968 × 10 − 32 2.4357 × 10 − 32 − 1.78574 × 10 − 95 − 8.23521 × 10 − 96 2.325 × 10 − 95
μ m 6.82121 6.82121 6.82121 6.82121 6.82121 6.82121
μ m − μ m , Sch μ m , Sch 0 − 2.35526 × 10 − 33 − 3.53783 × 10 − 33 2.28544 × 10 − 96 1.14274 × 10 − 96 − 4.3663 × 10 − 96
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated