A Soft Exoskeleton System Based-On Segmented Composite Proprioceptive Bending Actuators for Hand Rehabilitation ADL Tasks

Preprint

Article

A Soft Exoskeleton System Based-On Segmented Composite Proprioceptive Bending Actuators for Hand Rehabilitation ADL Tasks

Altmetrics

Downloads

125

Views

Comments

A peer-reviewed article of this preprint also exists.

Kai Li

Daohui Zhang^*,

Yaqi Chu^*,Xingang Zhao,Shuheng Ren,Xudong Hou

Kai Li

Daohui Zhang^*,

Yaqi Chu^*,Xingang Zhao,Shuheng Ren,Xudong Hou

This version is not peer-reviewed

Submitted:

16 September 2024

Posted:

16 September 2024

You are already at the latest version

Alerts

Abstract

Soft pneumatic actuators/robotics have received significant interest in the medical and health fields, due to their intrinsic elasticity and simple control strategies enabling desired interaction. However, current soft hand pneumatic exoskeletons often exhibit uniform deformation, mismatch the profile of the interacted objects, and seldom quantify the assistive effects during activities of daily life (ADL), such as extension angle and joint stiffness predicted. The lack of quantification poses challenges to the effective and sustainable advancement of rehabilitation technology. This paper introduces the design, modeling, and testing of pneumatic bioinspired Segmented Composite Proprioceptive Bending Actuators (SCPBAs) for hand rehabilitation in ADL tasks. The actuator’s soft-joint/rigid-bone segmented structure, inspired by the human finger anatomy, provides a superior fit compared to traditional continuous structures. A quasi-static model is established to predict the bending angles based on geometrical parameters. The SCPBAs also include a quantitative evaluation of joint stiffness and extension angle utilizing proprioceptive bending information. Additionally, a soft under-actuated hand exoskeleton equipped with SCPBAs demonstrates its potential in ADL rehabilitation scenarios.

Keywords:

Subject: Engineering - Bioengineering

1. Introduction

Stroke is a leading cause of disability worldwide, with over 13.7 million new patients annually. Stroke survivors of suffer from motor dysfunction and require external assistance for basic activities of daily life (ADL), which is crucial for maintaining quality of life [1]. The absence of independence in ADL diminishes their quality of life and reduces life satisfaction. Unfortunately, approximately 65% of stroke survivors face hand impairments that significantly impede their ability to perform ADL tasks [2]. Thus, various mechanical exoskeletons have been developed to aid in hand rehabilitation and restore independence in their life [3,4].

Traditional hand rehabilitation systems typically rely on rigid links and electric motors [5], which have the distinctive characteristics of cumbersome support, easily causing secondary damage with wearers, and blocking normal motion in performing ADL. Thus, a wearable hand rehabilitation exoskeleton made of soft/elastic material came into being, possessing the advantages of lightweight, high power-to-weight ratio, low material cost and comfort with its counterpart [6]. Polygerinos .et al developed an elastomer-based robotic glove to augment hand rehabilitation for individuals with function grasp pathologies at home, which could carry out gross and precise grasping [7]. Yap et al. presented a fully fabric-based bidirectional soft glove design to assist hand-impaired patients, which can realize active finger flexion and extension for training [8]. Correia et al. performed a textile-based soft robotic glove controlled by the user with a button and then conducted it in thirteen tetraplegic patients using the Jebsen Taylor Hand Function Test et., which showed the effectiveness of this system [9]. Li et al. proposed a variable stiffness pneumatic actuator coupled with a multi-stage articulated steel layer and verified the extension effect of the actuator over a clenched artificial hand with damper force associated with hyperfunction [10].

Various soft gloves have been conducted in typical hand rehabilitation scenarios to validate their performance [9,11,12,13,14], but few exoskeleton systems can directly quantitatively characterize the assistant effect after wearing in ADL tasks, such as extension angle and joint stiffness predicted. The existing hand function scale of the Modified Ashworth Scale (MAS) is subjective and affected by the doctor’s experience, which is not conducive to evaluation [15,16]. Shi et al. replicated the standalone desktop device to measure the passive joint moment and angle for the MCP joint in the index finger [17]. However, the bulky size of the bench limits the potential to characterize the other joints and use portability. Heung et al. introduced a soft-composited rehabilitation actuator that objectively reflects the condition of post-stroke, which is validated by simulations and experiments [18,19]. Matsunaga et al. combined information from a joint modular soft actuator and a marker-less hand joint position acquisition device to finger joint stiffness estimation in a telerehabilitation environment [20]. However, it has limited potential for wide applications because the standing condition requires an external camera to supervise the bending process. Matsunaga et al. proposed ANN-based models to simultaneously estimate the stiffness of the DIP, PIP, and MCP joint for index fingers [21]. Still, it is challenging to prove the validity of the stiffness estimation methods and requires training data from dummy fingers using machine learning. Moreover, the primary function of these systems is almost used to characterize performance, which cannot simultaneously be employed in rehabilitation ADL tasks.

For different bioinspired soft robotic systems designed for hand rehabilitation/assistance, as listed in Table A3., rehabilitation training modes are various explored for the ‘human-soft exoskeleton’ integrated system in ADL. Sui et al. engineered a soft-packaged rehabilitation glove with tight integration of sensing, actuation, human-machine interference, and closed-loop algorithm to regain fine motor skills in hand rehabilitation [12]. Zhou et al. applied a state machine controller based on signals from the integrated sensors to detect users’ intuition in hand-object interactions, driving the corresponding actuator at maximum operation pressure [22]. Chen et al. provided a tendon-driven soft hand exoskeleton with a hybrid configuration based on a graphical user interface (GUI) open-loop control strategy, in which the training paradigm parameters are directly predefined by the kinematic model [23]. Chen et al. also accomplished dexterous hand/forearm manipulation with the assistance of a foot-controlled interface by utilizing the unaffected foot movements as command signals, which is an open-loop limb mapping control scheme [24]. Tang et al. proposed a model-based online learning adaptive control algorithm for a wearable soft robotic glove by predefined trajectory, taking its interaction with the human fingers into account [25]. Lai et al. focused on a soft pneumatic glove with HPAs for assisting ADL tasks and developed two customized finger force products for quantifying finger function enhanced in patients [26].

In this study, we proposed a soft hand exoskeleton system made by segmented composite proprioceptive bending actuators (SCPBAs), which incorporate the fiber-elastic body and stiffness compensation layer integrated bending perception, to realize the finger joint stiffness predicted, reversely stretching motion and rehabilitation training in ADL tasks simultaneously. First, the bio-design principle and fabrication for the SCPBAs are presented. The soft-joint/rigid-bone segmented configuration inspired by the anatomy of the human finger is put forward in the proposed SCPBAs, which perfectly matches the traced profile and displays the conformable segmented bending deformation when interacting with the human finger in rehabilitation. Next, the improved analytical mode of the SCPBAs for both the free space and constrained space are presented. The stiffness compensation layer integrated proprioceptive sensors attached to the bottom of the SCPBAs, can monitor the bending deformation and reversely extend for hand dysfunction, such as clamp-shape hand. A reorganized analytical model established the relationship between the inflated pressure, bending angle, and joint stiffness, is also applied to evaluate finger joint stiffness index in finger-actuator integrated condition. Then, performance characterizations using the dummy/mannequin finger and task-oriented training strategies are conducted. The soft hand exoskeleton realized the bending deformation feedback as well as rehabilitation training in ADL tasks, such as tripod pinch and tip pinch.

2. Design and Fabrication of the SCPBAs

In this section, based on our previous work [27], the proposed SCPBAs inspired by the anatomy of the human finger are formulated first. Then, the improved modular molding design method is used to prototype the actuator, which is also called secondary post-processing.

2.1. The Bio-Inspiration and Implementation of the SCPBAs

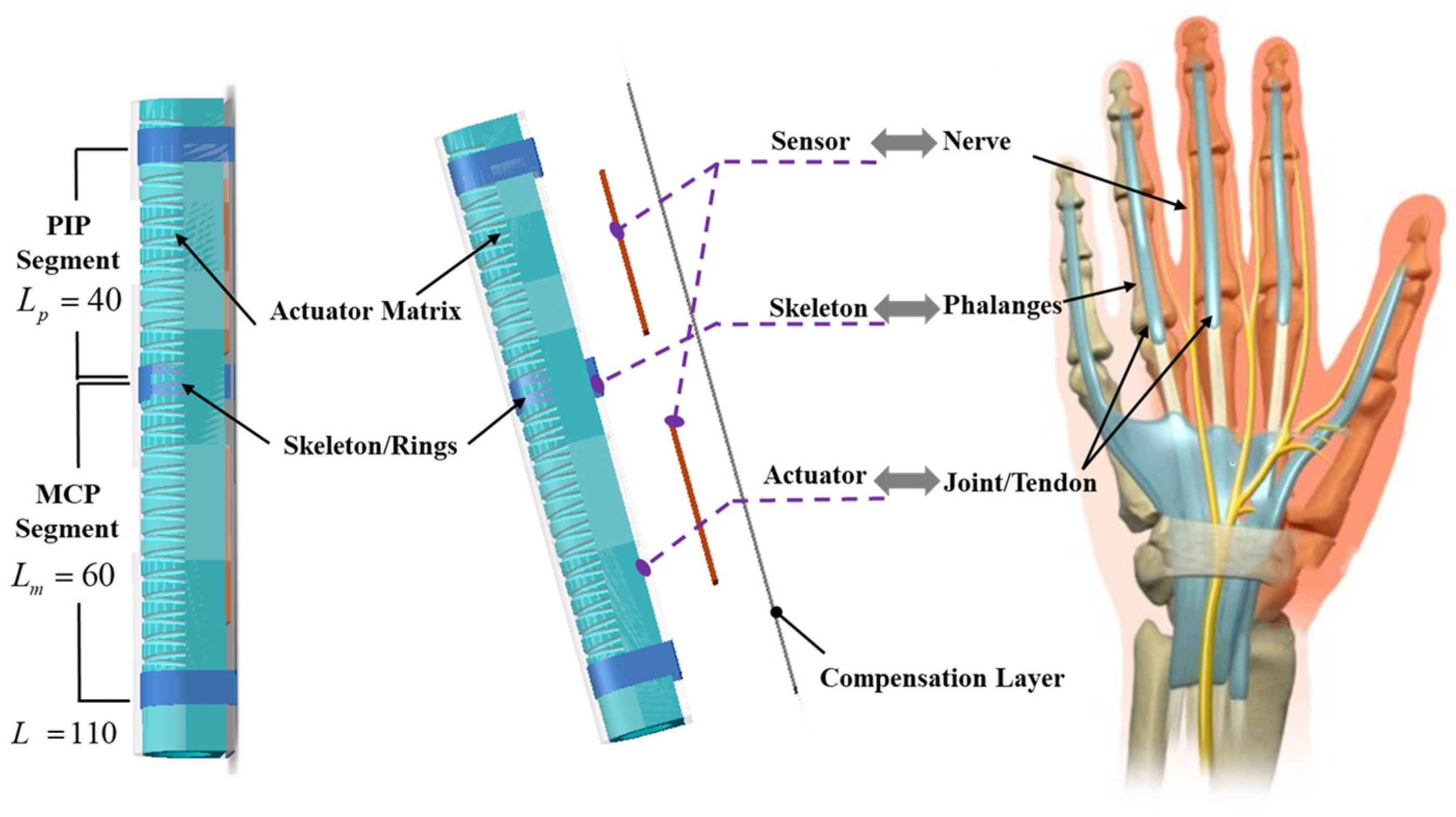
From the anatomical diagram of the hand/finger in Figure 1 [27,28], the organizational structure of the finger consists of linkage skeleton/phalanges, and muscle tendons/ligaments. First, from the perspective of hand motor function, the skeleton/phalanges have been linked with three joints, including the metacarpophalangeal joint (MCP), the proximal interphalangeal joint (PIP), and the distal interphalangeal joint (DIP). The tendon transforms the actuation force from muscle to the corresponding finger joint. From the ontology sensing function, the skin acts as a soft cushion and also as the proprioceptor, which can guarantee non-destructive interaction and also provide information on perception.

Considering the two aforementioned aspects of the finger/digit, the proposed bionic segmented composite proprioceptive bending actuators (SCPBAs) can greatly conform to the profiles of the finger, and also provide feedback motion information in real-time, as follows:

1). From the perspective of structural bionics firstly, distinguishing from traditional FRAs, the SCPBAs assembly incorporated rigid rings not only mimic simply the soft-joint/rigid-bone anatomy of the fingers, but it provides multi-joint/segmented bending morphing, which can enhance the conformability interaction of the finger joint. In other words, the proposed SCPBAs can promote segmented bending on the flexible joint section and keep the matrix from deforming in the rigid phalangeal sections where bending is not desired under the whole actuated process. This secondary post-processing method called mechanical programming relies on utilizing the materials’ mechanical properties.

2). Next, to realize the sensing function of the fingers abovementioned, the stiffness-compensating layer with the sensing function element was attached to the bottom surface of the SCPBAs, which can simultaneously enhance body stiffness and monitor bending deformation.

As shown in Figure 1, functional elements, such as silicone body enwound with fiber-reinforced layer, and stiffness compensating layer with bending sensors, are correspondingly imitated different modules of the human finger, which are integrated into the bioinspired SCPBAs design. However, the DIP joint contributes only 15% to the function grip. Thus, the proposed SCPBAs for wearable exoskeleton are double-segmented and lack covering the DIP joint.

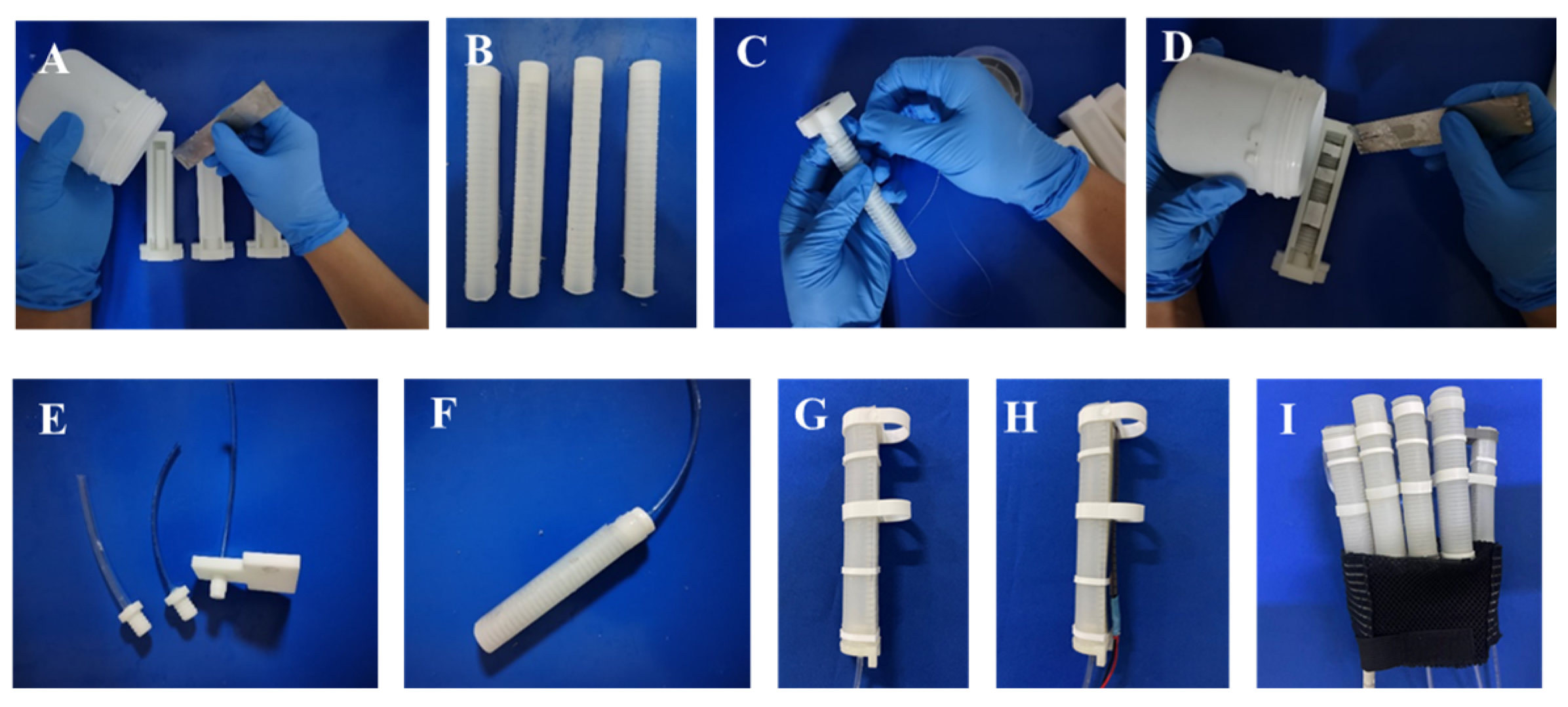
2.2. Actuator Fabrication

The proposed SCPBAs have the advantages of scalable fabrication, personalized customization, and low cost. Also, according to the personalized finger parameters, such as the length, the spacing between the rigid and flexible segments can be configured arbitrarily to fulfill requirements. The silicone matrix of the SCPBAs appears like semi-obround shape, with curved soft joints and non-curved rigid segments spaced apart that allow multi-joint under-actuated bending entirely. The main fabrication processes consist of multi-steps as follows. (1) molding the inner soft body; (2) affixing the bottom strain limiting layer and winding the double helix fiber wires, (3) encapsulating the entire body with mixed silicone rubber secondly to prevent shifting, (4) fixing the restraint retaining rings with mounting holes as non-curved rigid segment, (5) installing the tailored stiffness compensating layer attached bending sensors to the grooves in rings, and (6) sealing the open end with hub, as shown in Figure 2.

The steps (1)-(3) and (6) of fabrication and assembly of the bioinspired actuator are detailed in our previous study [27]. The steps (4) and (5) integrated multi-function fusion processes are concisely described here.

Step (4): The restraint retaining rings have the same structural parameters (width: 8 mm) with the installed holes, which are made of resin by the 3d printer and act as the phalanges of the finger, as shown in Figure 2G.

Step (5): The stiffness compensating layer (SUS 304 stainless steel sheet with different thicknesses) with flexible bending sensors (Flex Sensor) in Figure 2H, which correspond to the bending joint, are placed in the positioning slot by the interference fit.

3. Mathematical Modeling of the SCPBAs

In this section, we explicitly formulate the relationship between input pressure, bending angle, and joint stiffness to pursued the behavior of the SCPBAs [18,19]. Firstly, the bending model with input pressure was developed in free space, describing the motion characteristics of the actuation under different thicknesses of the stiffness compensation layer. Next, it has been taken into consideration the wearer’s hand status, such as finger spasticity or hypertonia, which is prevalent in stroke survivors. Besides, three quantitative indexes have been proposed to describe the SCPBAs specifically.

Evaluation Index 1: Bending Resistance $B R$
Evaluation Index 2: Extension Angle (degree) $θ_{0} - θ$
Evaluation Index 3: Stiffness Evaluation (Nm/rad) $K_{J}$

3.1. Bending Model in Free Space

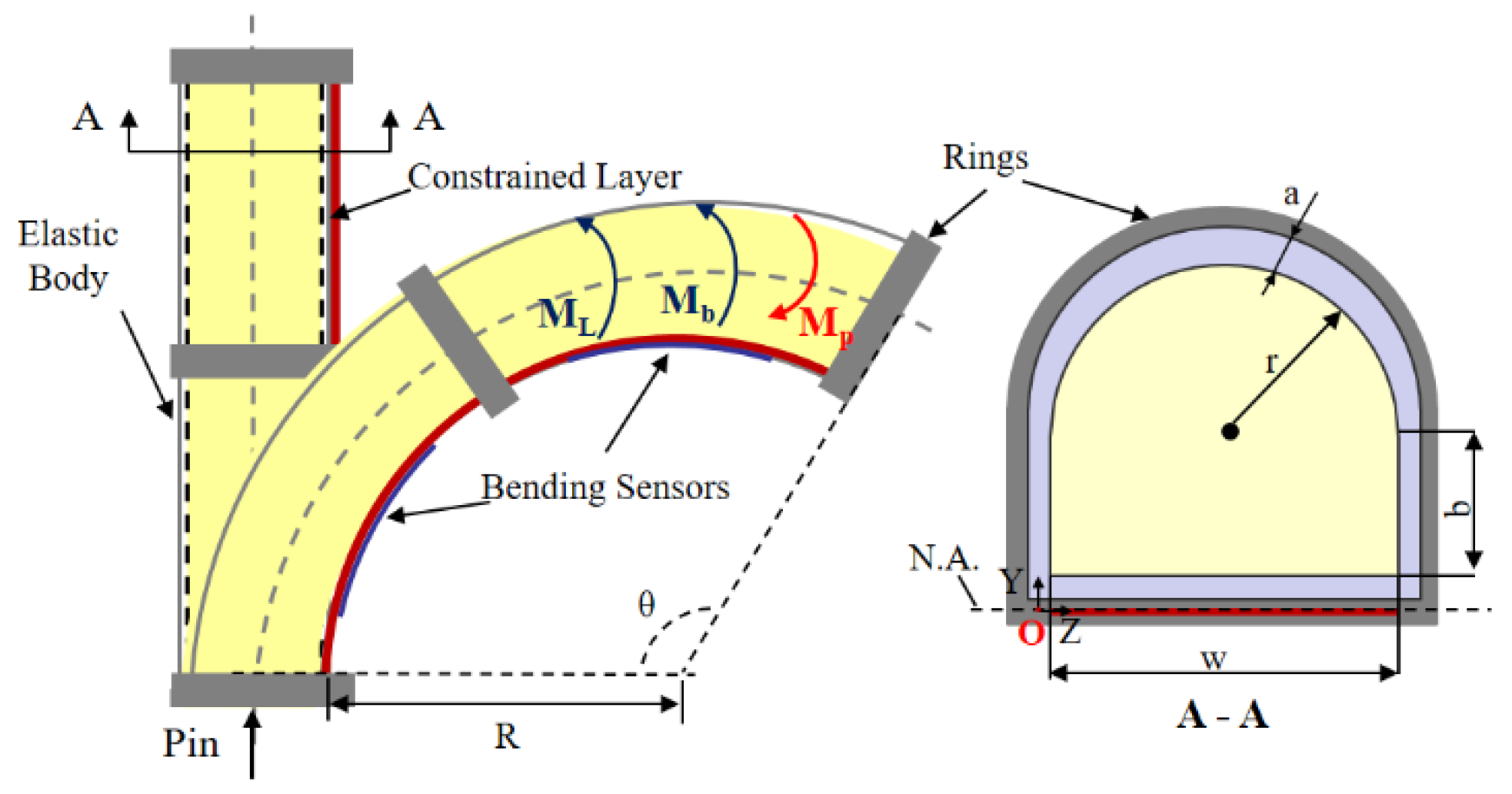
In the free space as shown in Figure 3, the bending torque equilibrium equation is composed of the inflation pressure, the elastic-based body, and the bottom stiffness compensation layer, thus

M_{P} = M_{b} + M_{L}

(1)

M_{P}

is the bending moment induced by the input pressure P_in, comprising the hemi-circular shape

M_{H C}

and rectangle shape

M_{R}

. The sum moment of the actuator can be described as follows:

\begin{array}{l} M_{P} = M_{R} + M_{H C} \\ = \int_{0}^{b} w P_{i n} (y + a + \frac{t}{2}) d y + \int_{0}^{r} 2 \sqrt{r^{2} - y^{2}} P_{i n} (y + a + b + \frac{t}{2}) d y \\ = [w (a b + \frac{b t}{2} + \frac{b^{2}}{2}) + \frac{π r^{2}}{2} (a + b + \frac{t}{2}) + \frac{2 r^{3}}{3}] P_{i n} \end{array}

(2)

M_{b}

is the bending moment composed of the elastic bending torque in the bottom part

M_{b o t t o m}

, side part

M_{s i d e}

and top part

M_{t o p}

, i.e.

M_{b} = M_{t o p} + M_{s i d e} + M_{b o t t o m}

. The proposed actuator body is fabricated from silicone rubber (Dragonskin 30, Smooth on Inc.), which can be molded as an Ogden first-order hyper-elastic model. Its strain energy is given by the following:

W (λ_{1}, λ_{2}, λ_{3}) = \frac{μ_{1}}{α_{1}} ({λ_{1}}^{α_{1}} + {λ_{2}}^{α_{1}} + {λ_{3}}^{α_{1}} - 3)

(3)

where the material coefficient

α_{1}

is the strain-hardening exponent,

μ

is the initial shear modulus of the material, and

μ_{1} = \frac{2 μ}{α_{1}}

. The estimated values of the coefficient

μ_{1} = 75449 k P a

and

α_{1} = 5.836

can be acquired from a uniaxial compression test. The principal nominal stresses

s_{i}

can be obtain

s_{i} = μ_{1} ({λ_{i}}^{α_{1}} - {λ_{i}}^{- α_{1}})

, for

i = 1, 2, 3

. Coefficient

λ_{1}, λ_{2}

, and

λ_{3}

denote the elongation in the directions of axial, circumferential, and radial, respectively. The circumferential direction wrapped around the non-stretchable fibers and induced

λ_{2} = 1

Approximation For the sake of convenience, we use the Maclaurin series for stress

s

to acquire the numerical representation between the input pressure and bending angle output, i.e.,

s = μ_{1} (λ^{α_{1}} - λ^{- α_{1}}) \approx \frac{2 μ_{1} α_{1} θ}{L} y

. Then, the corresponding partial bending torques are depicted as:

\begin{array}{l} M_{t o p} = 2 \int_{0}^{a} (\int_{0}^{\frac{π}{2}} s_{t o p} ((r + τ) ((r + τ) \sin ϕ + (a + b + \frac{t}{2}))) d ϕ) d τ \\ \approx θ \frac{μ_{1} α_{1}}{L} [π {(a + b + \frac{t}{2})}^{2} (a^{2} + 2 a r) + \frac{4 π}{3} (a + b + \frac{t}{2}) [{(a + r)}^{3} - r^{3}] + \frac{π}{4} [{(a + r)}^{4} - r^{4}]] \end{array}

(4)

M_{s i d e} = 2 \int_{\frac{t}{2}}^{\frac{t}{2} + a + b} a y s_{s i d e} d y \approx 2 \int_{\frac{t}{2}}^{\frac{t}{2} + a + b} a \frac{2 μ_{1} α_{1} θ}{L} y^{2} d y = θ \frac{4 μ_{1} α_{1} a}{3 L} [{(\frac{t}{2} + a + b)}^{3} - {(\frac{t}{2})}^{3}]

(5)

M_{b o t t o m} = \int_{\frac{t}{2}}^{\frac{t}{2} + a} w y s_{b o t t o m} d y \approx \int_{\frac{t}{2}}^{\frac{t}{2} + a} w \frac{2 μ_{1} α_{1} θ}{L} y^{2} d y = θ \frac{2 μ_{1} α_{1} w}{3 L} [{(\frac{t}{2} + a)}^{3} - {(\frac{t}{2})}^{3}]

(6)

M_{L}

is the bending moment by the bottom stiffness compensation layer. We used the SUS304 stainless steel plate for the stiffness compensation layer in this study. The bending moment

M_{L}

is defined by:

M_{L} = θ \frac{E_{L} (w + 2 a) t^{3}}{12 (1 - ν^{3}) L}

(7)

where the Young’s modulus

E_{L} = 194020 M P a

and the Poisson’s ratio

v = 0.3

To sum up, the explicit linear form of the relationship between input pressure and the bending angle output can be represented by the following:

θ = \frac{A}{B + C + D + E} P_{i n}

(8)

Such that

\begin{array}{l} A = w (a b + \frac{b t}{2} + \frac{b^{2}}{2}) + \frac{π r^{2}}{2} (a + b + \frac{t}{2}) + \frac{2 r^{3}}{3} \\ B = \frac{μ_{1} α_{1}}{L} [π {(a + b + \frac{t}{2})}^{2} (a^{2} + 2 a r) + \frac{4 π}{3} (a + b + \frac{t}{2}) [{(a + r)}^{3} - r^{3}] + \frac{π}{4} [{(a + r)}^{4} - r^{4}]] \\ C = \frac{4 μ_{1} α_{1} a}{3 L} [{(\frac{t}{2} + a + b)}^{3} - {(\frac{t}{2})}^{3}], D = \frac{2 μ_{1} α_{1} w}{3 L} [{(\frac{t}{2} + a)}^{3} - {(\frac{t}{2})}^{3}], E = \frac{E (w + 2 a) t^{3}}{12 (1 - ν^{3}) L} \end{array}

Evaluation Index 1: Bending Resistance $B R$

Previous studies demonstrated that different parameters of the traditional FRAs (e.g. wall width, inner chamber height and width, and actuator length) alter the bending behaviors. In this section, the bending resistance

(B R)

is presented to evaluate the difficulty of bending deformation, defined by the ratio of the elastic matrix and the compensation layer stored over the supplied bending torque:

B R = \frac{M_{b} + M_{L}}{M_{P}}

(9)

Besides, the lower bending resistance (BR) indicates that the actuator is easier to bend with less pressure.

3.2. Bending Model in Constrained Space

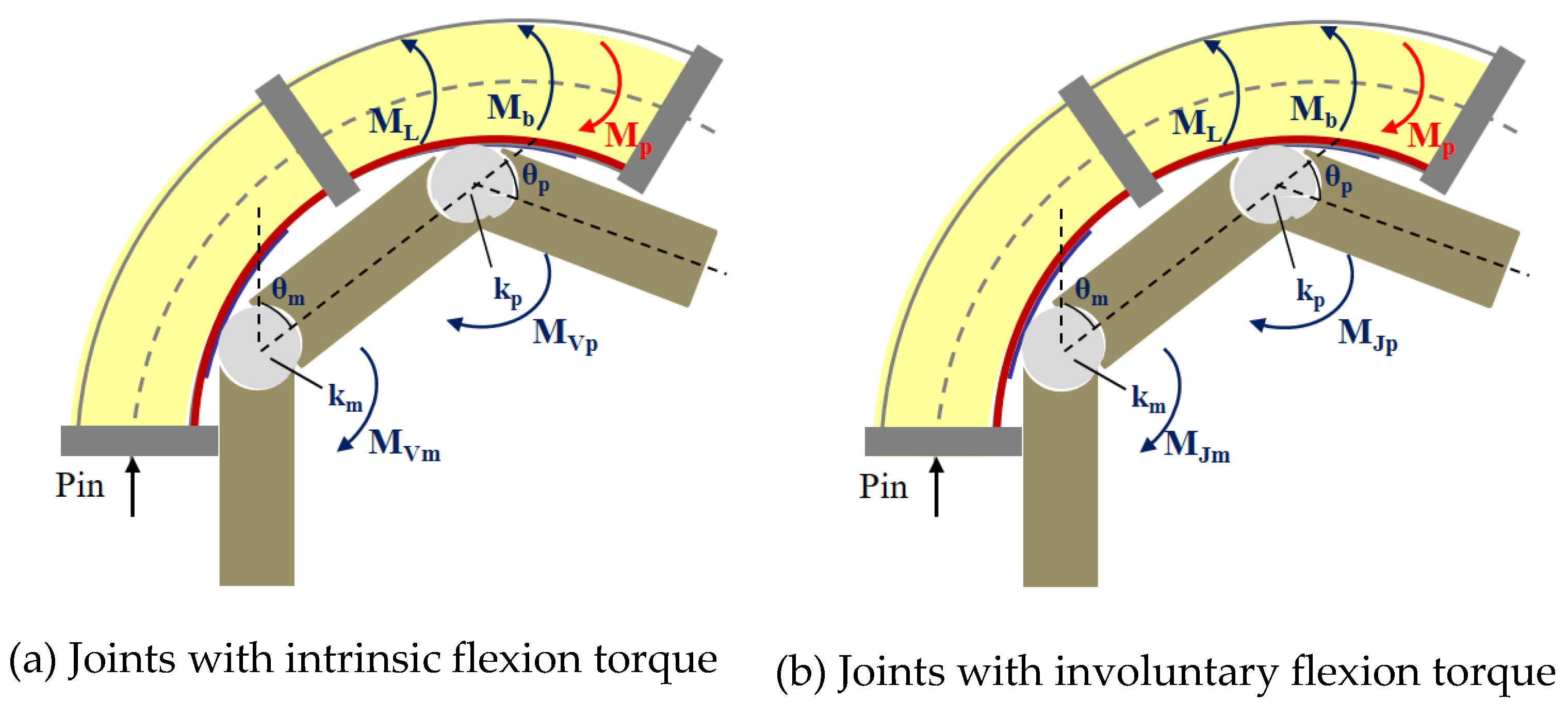
Most ADL tasks depend on finger flexibility, which not only includes finger flexion, but stretching motion are equally important, especially for the digit joint hypertonia of the subjects. Hence, joint stiffness and extension angle are utilized to describe quantitatively scenarios above mentioned. In this section, the human-machine coupling interaction factor (e.g. joint stiffness) is researched. As shown in Figure 4, it is obvious that the wear’s finger muscular tone/joint stiffness impacts the bending motion, when the SCPBAs are coupled with a mannequin finger. Then, two different scenarios are investigated as follows:

3.2.1. Constrained Space with Intrinsic/Voluntary Flexion Torque

For able-bodied subjects, their fingers tend to curl inward naturally and show an initial position (

θ_{0}

) due to the muscular tone display in finger flexors (e.g., flexor digitorum profunda) being larger than in finger extensors (e.g., extensor digitorum profunda), when there is no exerted involuntary flexion torque. Passive extension resistance at the joints, indicated as intrinsic joint stiffness

(K_{V})

, would be created to resist opposing movement when the flexor muscles stretch from the fixed position

(θ_{0})

Assumed that the finger joint angle is consistent with the actuator-finger coupled segmented bending angle

(θ)

, the relationship between input pressure and coupled segmented angle can be redefined by the intrinsic flexion torque

M_{V}

. Figure 4a describes the improved moment equilibrium around the finger joints.

Case I:

0 \leq θ \leq θ_{0}

(intrinsic flexion torque

M_{V}

exists in extension movement,

M_{P}

may be zero)

M_{P} + M_{V} = M_{b} + M_{L}, M_{V} = K_{V} (θ - θ_{0}), M_{V} = M_{V m} + M_{V p}

(10)

θ = \frac{A P_{i n} - K_{v} θ_{0}}{B + C + D + E - K_{v}}

(11)

Case II:

θ > θ_{0}

(intrinsic flexion torque

{M^{'}}_{V}

exists in flexion movement,

M_{P}

is not zero)

M_{P} = M_{b} + M_{L} + {M^{'}}_{V}, {M^{'}}_{V} = {K^{'}}_{V} (θ - θ_{0}), {M^{'}}_{V} = {M^{'}}_{V m} + {M^{'}}_{V p}

(12)

θ = \frac{A P_{i n} + {K^{'}}_{v} θ_{0}}{B + C + D + E + {K^{'}}_{v}}

(13)

3.2.2. Constrained Space with Involuntary Flexion Torque

For subjects with hand dysfunction (e.g. stroke survivors), strong extension resistance indicated as intrinsic joint stiffness (K_J) would be also induced due to the excess tone in finger flexors, called hypertonia. The involuntary flexion torque (M_J) generated by extension resistance (K_J) causes the finger to bend, or even a hooked shape. The following analysis quantify the resistance due to hypertonia in terms of the joint stiffness.

Case I:

0 \leq θ \leq θ_{0}

(intrinsic flexion torque M_J exists in extension movement, M_P may be zero)

M_{P} + M_{J} = M_{b} + M_{L}, M_{J} = K_{J} (θ - θ_{0}), M_{J} = M_{J m} + M_{J p}

(14)

θ = \frac{A P_{i n} - K_{J} θ_{0}}{B + C + D + E - K_{J}}

(15)

Case II:

θ > θ_{0}

(intrinsic flexion torque

M_{J}

is absent in flexion movement)

M_{P} = M_{b} + M_{L} + {M^{'}}_{J}, {M^{'}}_{J} = {K^{'}}_{J} (θ - θ_{0}), {M^{'}}_{J} = {M^{'}}_{J m} + {M^{'}}_{J p}

(16)

θ = \frac{A P_{i n} + {K^{'}}_{J} θ_{0}}{B + C + D + E + {K^{'}}_{J}}

(17)

To sum up, the intrinsic joint stiffness

K_{V}

and the involuntary stiffness

K_{J}

are presented in two different constrained scenarios, respectively. Since the major design consideration is for stroke survivors, only the joint stiffness upon extending the fingers is of interest (especially for the maximum extending angles

θ_{0} - θ, θ = θ_{s \max}, M_{p} = 0

), and then the corresponding elastic coefficient (

K_{J}

) are the desired results. Further flexion of the fingers after the initial angle

θ_{0}

would not be researched into stiffness estimation. In the bending state of the SCPBAs, the cutoff pressure P is defined as soon as the measured MCP angle exceeds its upper limit (

θ_{0}

), and therefore the SCPBAs is no further enabled.

Evaluation Index 2: Extension Angle $θ_{0} - θ$

The extension angle refers to the reverse extension of the hand caused by the stretching of the bottom rigid compensation layer when the finger is wearing the actuator. The difference between this angle and the initial angle is the angle being sought.

Evaluation Index 3: Stiffness Evaluation $K_{J}$

Case I:

0 \leq θ \leq θ_{0}

(intrinsic flexion torque

M_{J}

exists in extension movement,

M_{P}

may be zero)

K_{J} = \frac{(B + C + D + E) θ - A P_{i n}}{θ - θ_{0}}

(18)

Case II:

θ > θ_{0}

(intrinsic flexion torque

M_{J}

is absent in flexion movement)

{K^{'}}_{J} = \frac{A P_{i n} - (B + C + D + E) θ}{θ - θ_{0}}

(19)

extension angle reaches its maximum (i.e.

θ_{0} - θ, θ = θ_{s \max}, M_{p} = 0

4. Performance Characterization of the SCPBAs

4.1. Experiment Setup

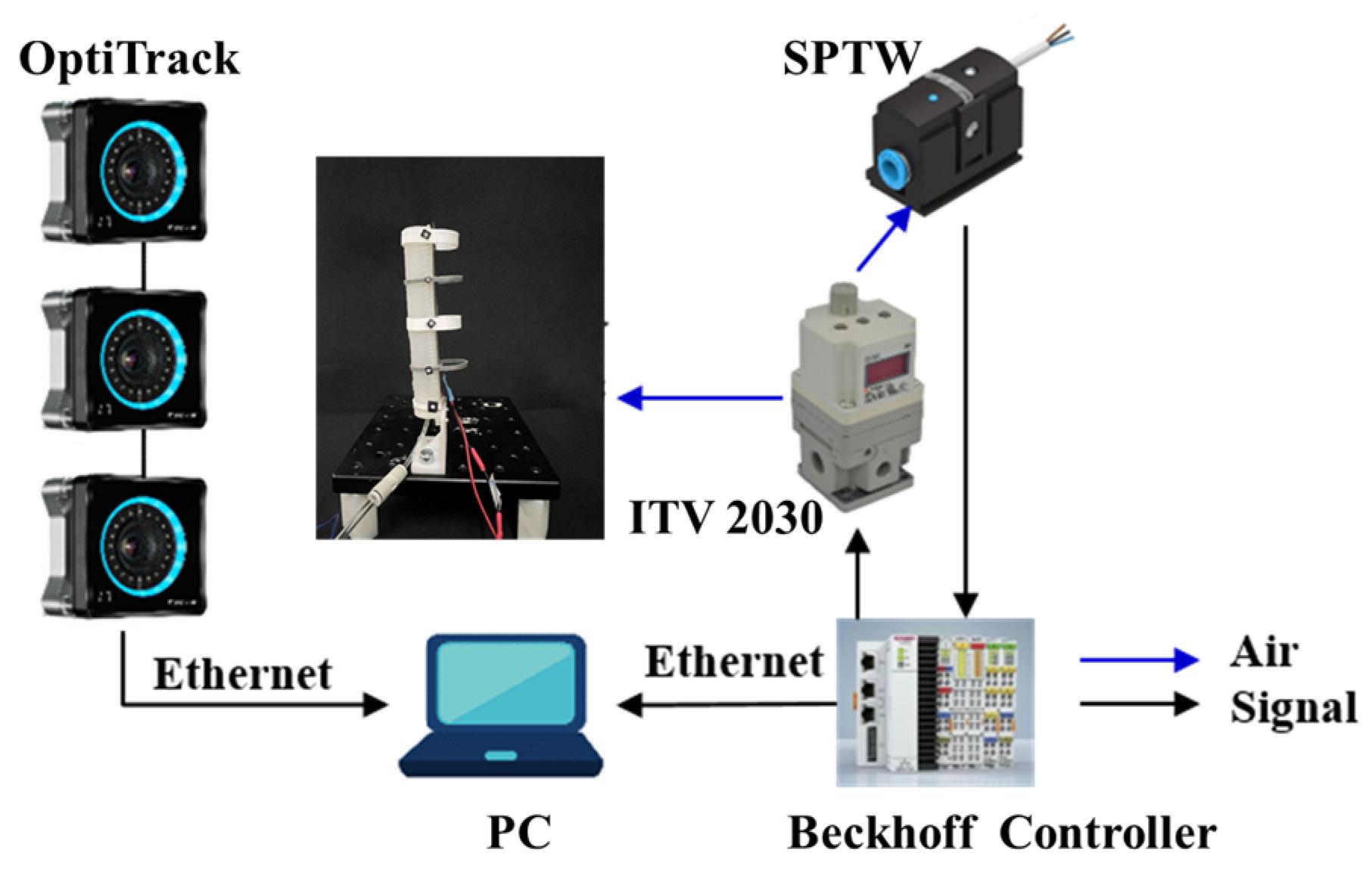
To evaluate the bending performance and verify the analytical model, the proposed SCPBAs were clamped vertically upward to inflate repeatedly, reducing the influence of gravity. As shown in Figure 5, a filter regulator (MS4-LFR-1/4, Festo Inc., Germany) is used to filter and limit the maximum value of input pressure by manual operation in the inlet. The pressurized air regulated from the proportional solenoid valves (ITV2030, SMC, Japan) is continuously adjusted and then flows into the SCPBAs and a pressure sensor (SPTW-P6R-G14-VD-M12, Festo, Germany) monitoring the channels’ air pressure real-time. Besides, the SCPBAs’ bending angles can be monitored by the commercial bending sensors attached to the bottom of the actuator, which can calibrated by three optical cameras (Optitrack, NaturalPoint, Germany) based on the relative position of the reflective markers. Data from the cameras were streamed to a PC by Motive, and to be synchronized with the pressure signal and voltages in Beckhoff. The inflated pressure is applied in steps of 40 kPa until it reaches 180 kPa and doesn’t occur failure.

4.1.1. Characterization of the Embedding Flexible Bending Sensor

In this section, the coupled flexible bending sensors are calibrated to facilitate the ontology bending perception of the SCPBAs, which are conducted on the relationship between the electric signals (i.e. the voltage value) and the bending angles. The bending angles are indicated by the relative position of pasted reflective markers, which are captured using the OptiTrack system with 30Hz. For the sake of accuracy, the SCPBAs are actuated within a short interval of 20 kPa to retain data.

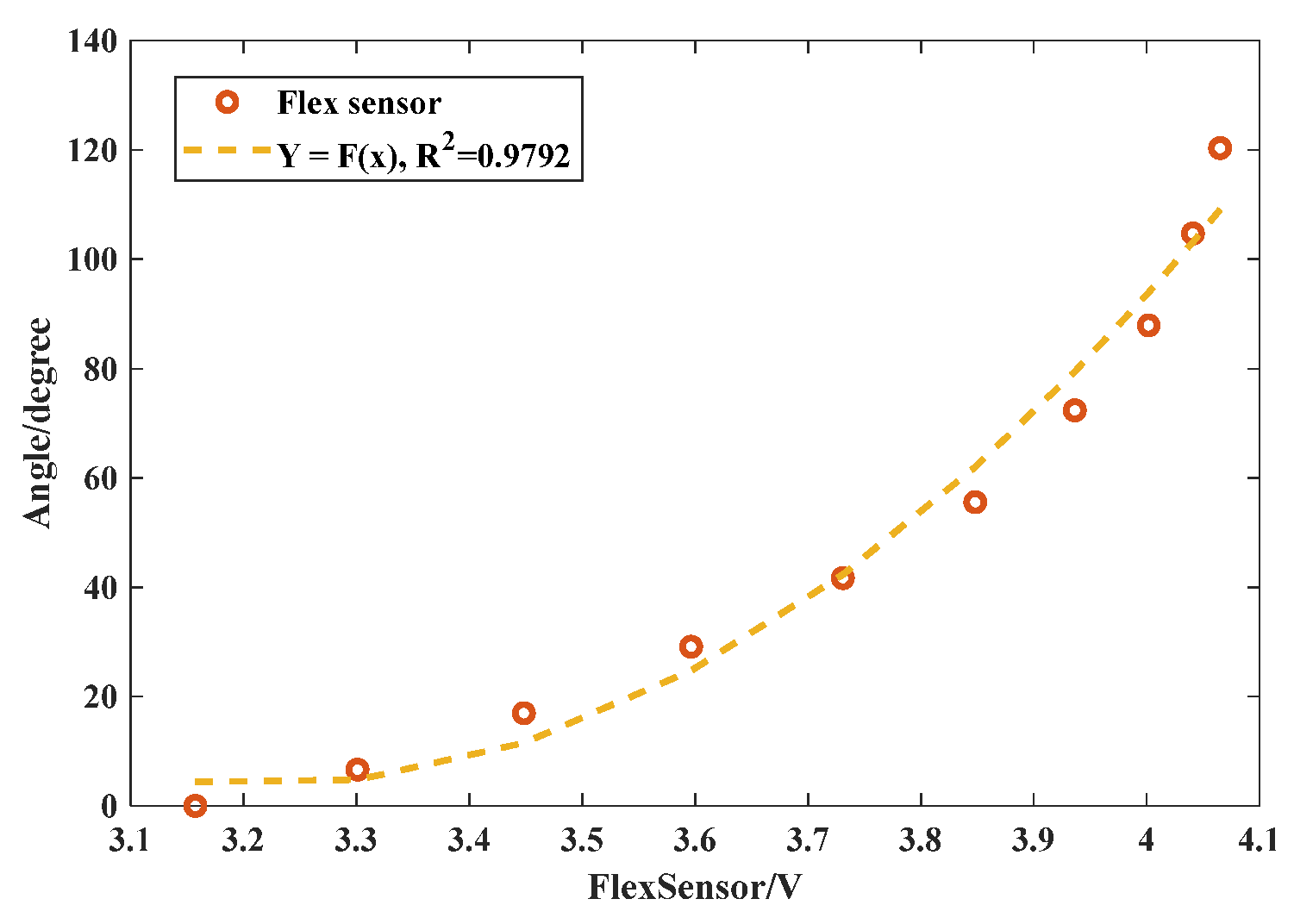
The bending angles of the sensor were captured by three cameras and calculated in Matlab, and then plotted in Figure 6 (as the scatters shows) with the corresponded voltage. The dotted line indicates the fitted curves derive from experimental results. The inset table shows the quadratic function model

Y = 147.1068 x^{2} - 947.1210 x + 1528 . 2692

, and the determination coefficient

R^{2} = 0.9792

of the sensor. The coefficient

R^{2}

is closed to 100%, which indicated the fitted model

Y = f (x)

matches the real scenarios, and then the bending kinematics are constructed in a real-time manner.

4.2. Bending Angle Measurement in Free Space

4.2.1. Changing the Stiffness-Compensating Layer Thickness

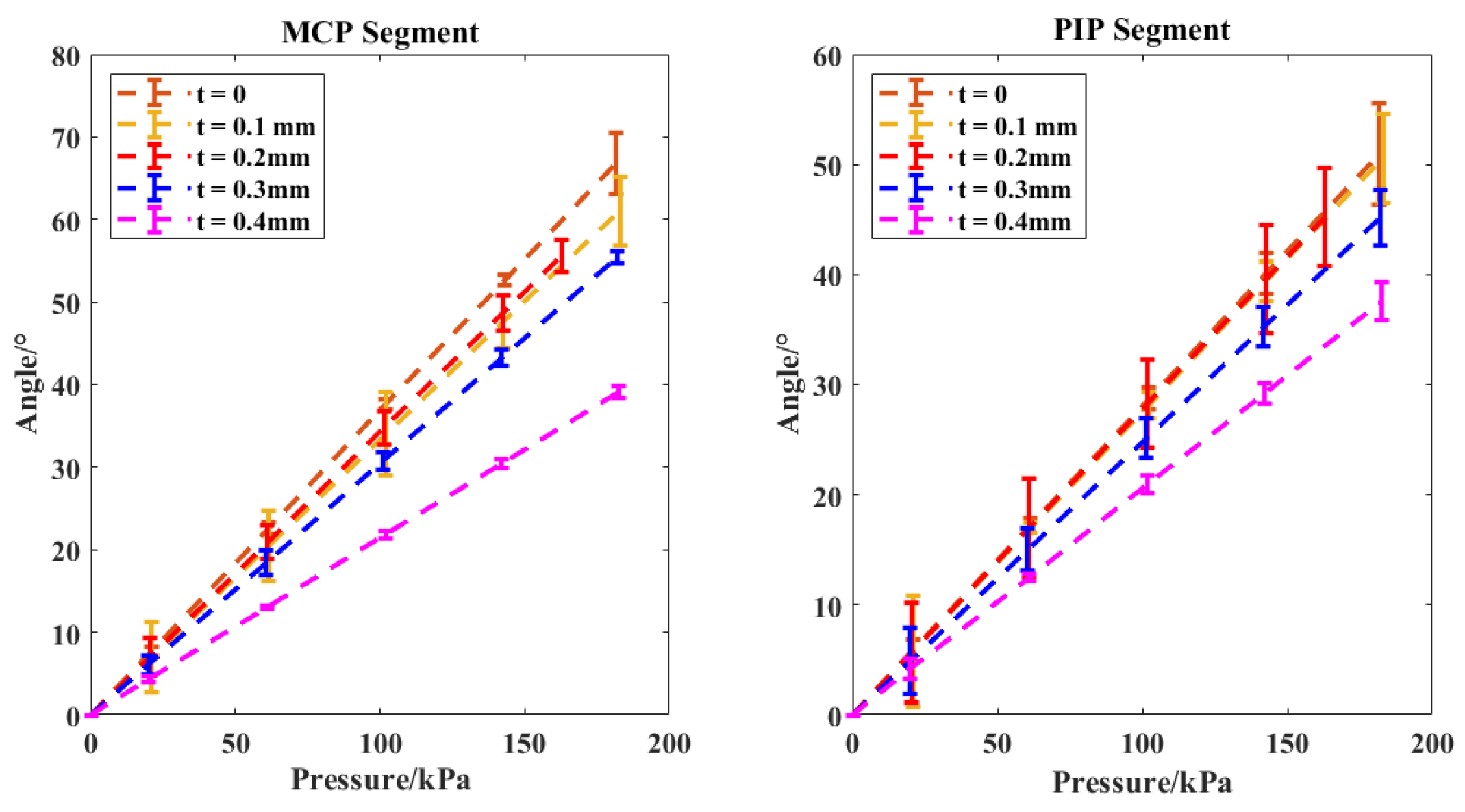
This section first investigated the proposed SCPBAs composed of hollow elastic hemi-obround with rigid rings in free space. The major parameters for the hybrid actuator are

(a, b, r, w, L) = (3.3, 7.5, 7.5, 15, 110)

. Four pieces of stiffness-compensating layers that are 0.1, 0.2, 0.3, and 0.4 mm thickness, have 15 mm width and 60 mm (MCP segment) or 40 mm (PIP segment) length, and where they are compared in terms of their bending angle

θ_{m}

and

θ_{p}

, respectively.

As shown in Figure 7, all the soft joint angles keep the linear relationships with input pressure. Compared with the traditional fiber-reinforced actuators without a stiffness-compensating layer (FRAs, t = 0 mm), the total bending angles versus the inflated pressure of the proposed SCPBAs decreased clearly. At 180 kPa, an increase in the thickness of the stiffness-compensating layer from 0.1 mm (50% of standard size, i.e., 0.2 mm) to 0.2mm to 0.3 mm (150% of standard size) to 0.4 mm (200% of standard size) at both the MCP and PIP segments decreased the magnitude of

θ_{m}

from 61°, 59° to 55°and 39°, whereas the FRAs reached 67°. In addition, the magnitude of

θ_{p}

decreased from 50°, 49°to 45° and 37°, and the FRAs reached 51°. Hence, with the increase of the thickness of the stiffness-compensating layer, the corresponding actuator allocates more energy to prompt stiffness-compensating layer bending and then results in the reduction in total angle as depicted by the bending resistance.

Evaluation Index: Bending Resistance $B R$

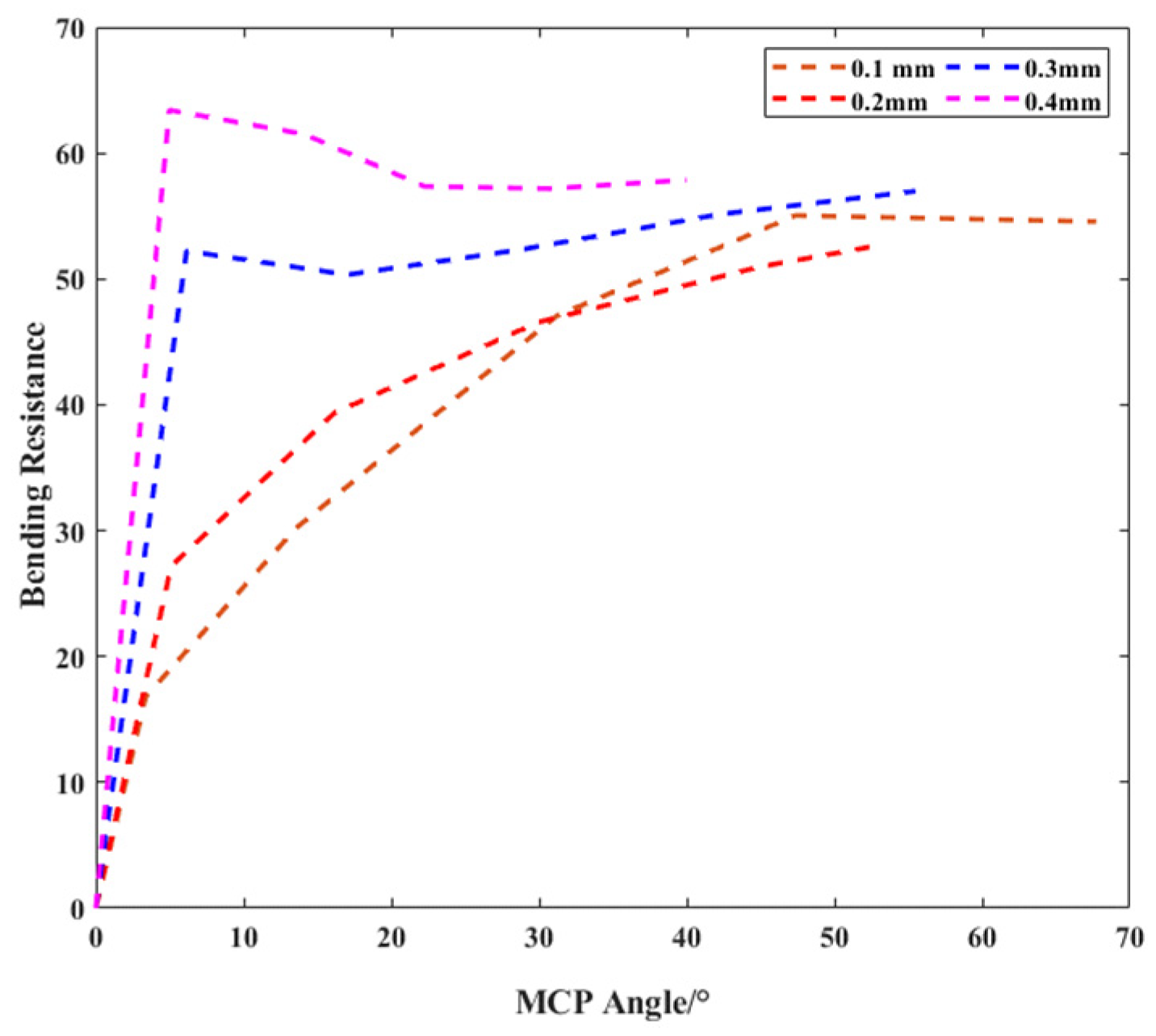
Previous studies demonstrated that different parameters of the soft actuators could alter the bending behaviors (e.g. wall width, inner chamber height and width, and actuator length). In this section, the bending resistance is reported to measure the difficulty of bending deformation when the stiffness compensation layers are integrated, defined by the ratio of the elastic matrix moment over the supplied bending torque:

B R = \frac{M_{b} + M_{L}}{M_{P}}

(20)

In Figure 8, the lower bending resistance (BR) indicates that the actuator is easier to bend with less pressure. Also, the thicker the stiffness compensation layer is, the greater the corresponding bending resistance value is. The maximum bending resistance value could reach to 63, when the 0.4mm layer is integrated.

4.3. Bending Angle Measurement with Involuntary Flexion Torque

For subjects with hand dysfunction (e.g. stroke survivors), the modified Ashworth scale (MAS) is an assessment used in rehabilitation fields, which relies on the extensive experience of the rehabilitation physician to obtain the muscle tone level of the hand. Moreover, the corresponding relationship between the MAS scores and the joint stiffness magnitudes has been researched [15,17,18,20], as summarized in Table 1. It’s obvious that the healthy subjects have lower joint stiffness with no voluntary flexion torque, so this scenario could be classified as a special case of involuntary flexion torque (with hand dysfunction) to explore.

4.3.1. Extension Angle and Joint Stiffness Evaluation on the Dummy Finger

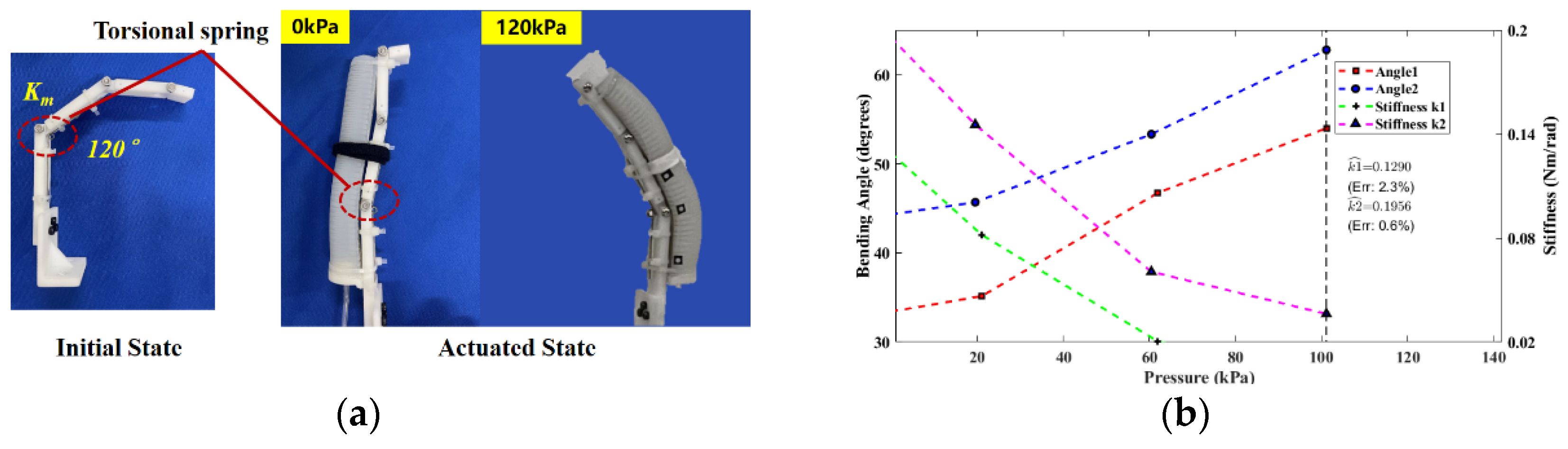
Considering the thickness (t=0.2mm) and the deformation recovery property of the bottom stiffness compensation layer, two 3D printed index fingers with torsional springs (k₁ = 0.1321 Nm/rad and k₂ = 0.1968 Nm/rad) are installed with only at the MCP joint positions fingers, which are designed to mimic the affected fingers (Figure 9). The SCBAs with t= 0.2mm are only tested on the MCP segment in this section, as parameters indicated in Table A1. The theoretical stiffness of the used torsional spring k_T (Nm/rad) can be calculated on the following formula:

k_{T} = \frac{E I}{180 D n}, I = \frac{π d^{4}}{64}

(21)

where

k_{T}

is the stiffness coefficient of the torsion spring,

E = 197000 M P a

is the elastic modulus of spring material. The

D, n, d

indicate the mean diameter, number of windings, and the diameter of the spring wire for the torsional spring as shown in Table A2, respectively.

For both stiffness dummy fingers, the trend of the analysis results is consistent. As shown in Figure 9, the cutoff pressure (P = 102kPa) is chosen for the upper limits of measured MCP joint angles and predicted stiffness. The end of the actuation of the SCPBAs is disabled when the pressure is out of range. Since the experimental sample adopted the left-turning torsional spring, its elastic coefficient decreases with the flexion direction in the extension phase. Hence, when the passive extension angle reaches the maximum and the SCPBAs are not actuated (

θ = θ_{s \max}, M_{p} = 0

), then the corresponding elastic coefficient (

K_{J}

) are the desired results. The estimated errors of the predicted stiffness are all less than 2.5%, which is far less than 8% in Reference [18], and the minimum predicted error is 0.6% (Table 2). Besides, a maximum extending bending angle of 22.3° is observed on the lower stiffness finger at 0kPa. Although satisfactory results are demonstrated in slight spasticity with middle stiffness (0.04-0.5 Nm/rad), it is obvious that the estimated error is higher in the small stiffness. It may be because the elastic potential energy stored in the actuator is greater than the torsion spring when P_in =0, and the energy is mainly distributed on the PIP joint, so resulting in a larger error for MCP joint evaluation.

5. Soft Robotic Glove with the SCPBAs for Task-Oriented Rehabilitation Training

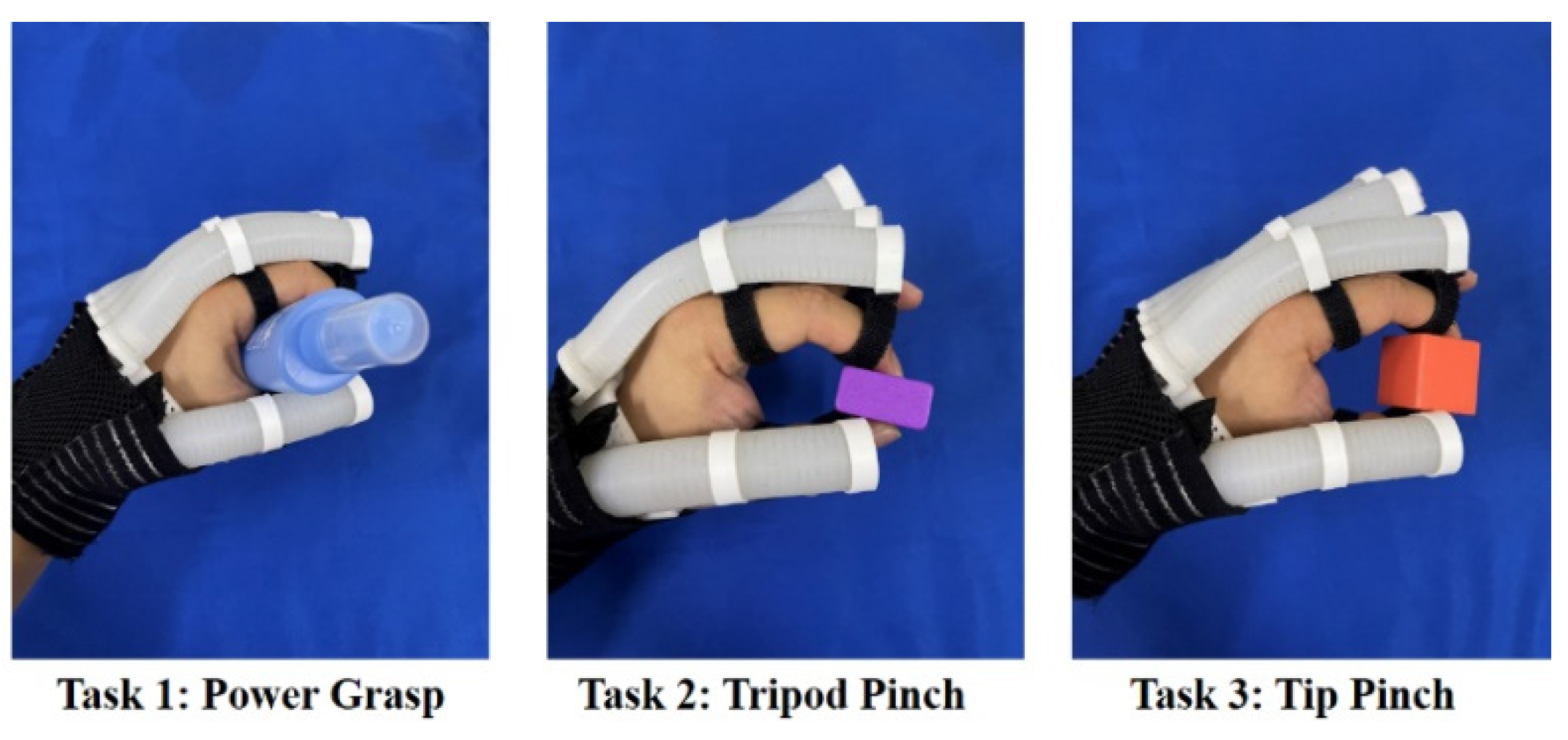
The following experiments were conducted to verify the rehabilitation assistance of a soft hand exoskeleton with the proposed SCPBAs in ADL tasks. First, based on the resin support and tailored Velcro loop, a customized soft hand exoskeleton with the SCPBAs is displayed in Figure 10, which can achieve compatible motion and interaction with the hand safely and steadily. The lengths for the SCPBAs in the hand-wearable scenario are anthropomorphic, which agrees with the anatomical results. Then, three grasping scenarios in ADL tasks were demonstrated. Under an inflating pressure of 200kPa, the soft exoskeleton can pick up objects with different postures, such as tip pinch.

5.1. Pre-Defined ADL Tasks

Several meaningful ADL tasks have been designed to help improve hand function, and also conducted to verify the validity of the proposed training. Moreover, these three-hand grasping types, such as power grasp (all five fingers), tripod pinch (thumb, index, and middle fingers), and tip pinch (thumb and index fingers), are frequently used during ADL tasks. Thus, in this study, three ADL tasks are selected a s power grasping an elliptical bottle (task 1), tripod pinching a medium-sized cuboid woodblock (task 2), and tip pinching a small-sized cubic woodblock (task 3), as shown in Figure 11. These selected objects are common in standard hand function tests such as the Box and Blocks Test (BBT). These three hand gestures are widely appeared in a variety of tasks, helping subjects with abnormal function to complete daily assistance and improve the quality of life.

5.2. Task-Oriented Rehabilitation Strategy

From the perspective of a physiatrist conducting professional rehabilitation, the task-oriented rehabilitation framework is established. These three tasks are executed consecutively from task 1 to task 3. For a total rehabilitation trial, each task is required to perform thrice lasting 20-22 s (5 s grasping object + 10 s holding object + 5 -7s releasing object). Thus, it takes 60 seconds to repeat the task three times alone and one trial takes around 3 minutes (i.e., 3 tasks × 60 seconds per task). Besides, if participants aim to achieve a rehabilitation session with one hour, each session consisting of 20 repetitions (3 minutes × 20 = 1 hour) is recommended, which could also have a rest of 2 minutes between two consecutive trials to avoid muscle fatigue.

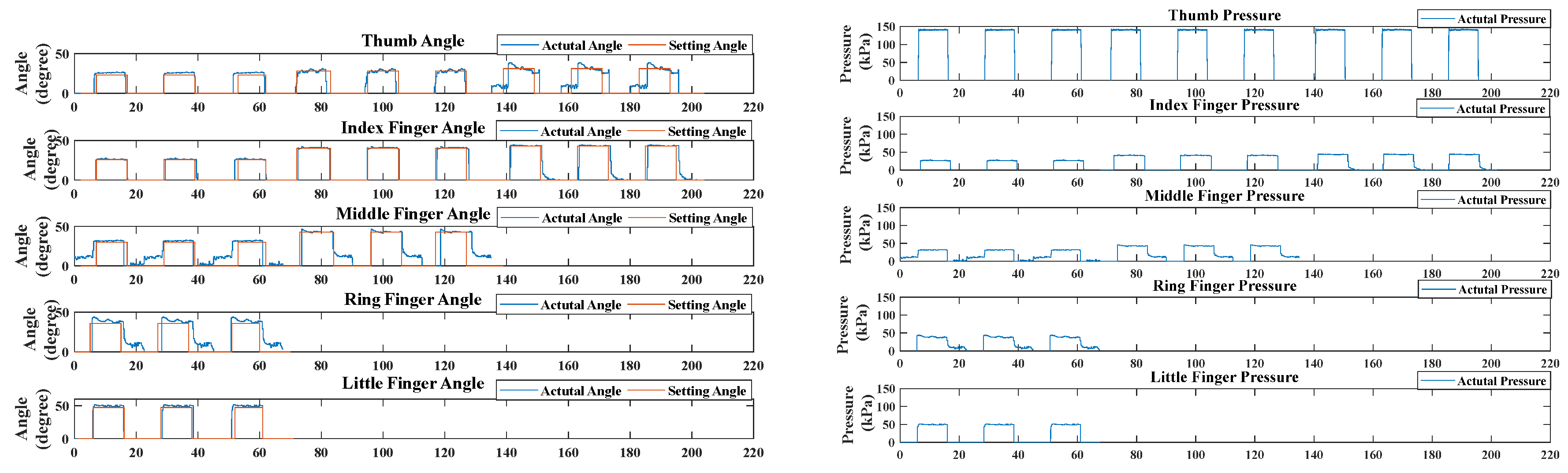
Enabled by the bending sensors, joint angles can be detected at a sampling rate of 10 Hz. Hence, the difference between the desired and actual bending angle can be calculated in real-time. Before starting the rehabilitation training, we first build the mapping relationship between the SCPBAs bending angles and different tasks. And then taking the average of experimental results as a desired aim. Table 3 demonstrates the realized bending angles of the five fingers for three different tasks. The connective symbol (-) denotes that the changes in finger bending angles for this task are ignored or the related fingers are free motion during training.

Figure 11 shows the bending angle and internal pressure as a function of time t in the rehabilitation training trial process, which also represents the switch-mode rehabilitation from power grasp (task 1) to tripod pinch (task 2) to tip pinch (task 3). The red solid curve represents the actual bending angle of the involved fingers and the blue curves show the corresponding setting bending angles.

AB subject followed the experimental procedure and performed the task-oriented training modality. As depicted in Figure 12, the training commenced with a hand relaxation phase, transitioning to a hand closure phase. During the hand closure phase, which lasted for 5 seconds, the target angle increase was triggered by a task-specific timer. The soft pneumatic glove then assisted in reaching the target angles during the hand holding phase. For instance, the thumb achieved its target angle with a rapid response (within less than 2 seconds) and minimal overshoot (less than 5% of the target angle). Stability was maintained within 5 seconds, with the angle varying no more than 2% from the target. After 10 seconds, the target angle reduction commenced, and the hand closure and hand holding phases alternated. By adjusting the bending rate for each finger, the participant was able to achieve the required hand movements. The trial concluded with the sequential and repeated execution of three tasks. Moreover, Table 4 shows that the monitoring error of the embedded bending sensor is as low as 6%, with an angle error of approximately 2°.

6. Conclusions

In conclusion, this paper presented the design, modeling, and testing of the pneumatic bioinspired segmented composite proprioceptive bending actuators (SCPBAs) for rehabilitation hand ADL tasks training. Contributions of this research mainly include the following: 1) The SCPBAs take inspiration from the anatomy of human fingers, which makes the actuator match the finger profile and attain compatible motion coupled with a finger. 2) The proposed SCPBAs have significant advantages in the accuracy of joint stiffness evaluation and extension angle. 3) The soft hand exoskeleton based on the SCPBAs integrated the proprioceptive stiffness compensation layer, could monitor the bending deformation and safety pressure in ADL tasks. Under the input pressure of 180kPa, the proposed SCPBAs drive fingers to 113° with the maximum extension angle of 22.3°.

In future work, utilizing multi-material three-dimensional technologies could realize multi-gradient hardness customized design for stroke patients in hand rehabilitation training. Moreover, a feedback control system with flexible electronics sensing for wearable devices will be researched to enable more precision motion, accurately assess the motor function, monitor the whole rehabilitation training process, and achieve active training by users’ intention.

Author Contributions

Conceptualization, X.Z., K.L and D.Z.; methodology, K.L. and Y.C.; software, K.L., S.R. and Y.C.; validation, K.L., S.R. and X.H.; formal analysis, K.L., and Y.C.; investigation, resources, data curation, X.Z., K.L, Y.C. and D.Z.; writing—original draft preparation, K.L.; writing—review and editing, X.Z., K.L, Y.C. and D.Z.; visualization, K.L., S.R., X.H. and Y.C.; supervision, project administration, funding acquisition, X.Z. and D.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded in part by the National Natural Science Foundation of China (92048302, 62273336, 61903360, 62203430, U20A20197), the National Key Research and Development Program of China (2022YFF1202500 and 2022YFF1202502), the Liaoning Revitalization Talents Program (XLYC1908030), China Postdoctoral Science Foundation funded project (2019M661155, 2022M723312), and Natural Science Foundation of Liaoning Province (2022-BS-025).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Parameters for the SCPBAs.

Values(mm)	Interpretations
$a = 3.3$	Wall thickness
$r = 7.5$	Internal circular radius
$b = 7.5$	Internal rectangular height
$w = 15$	Internal chamber width
$t = 0.2$	Thickness of bottom constrained layer
$L = 110, L_{m} = 60, L_{p} = 40$	Length of internal chamber, MCP segment, PIP segment, respectively
$θ_{m}, θ_{p}$	Bending angle of MCP segment and PIP segment, respectively

Table A2. Structural parameters of torsion springs.

Torsional spring	TS1	TS2
d (mm)	0.8	0.8
D (mm)	4	3
n	3	3
$θ_{0}$ (degrees)	120	120
$k_{T}$ (Nm/rad)	0.1321	0.1968

Table A3. Comparison between existing representative works and our proposed composite hand exoskeleton.

Hand Exoskeletons	Actuator structure	Joint number of each actuator	Bending Sensor	Applications on assistance	Applications on assessment
Polygerinos et al., 2015 [7,29]	Fiber reinforced elastomers	3	No	Yes	No
Yap et al., 2017 [30]	Fabric-reinforced elastomers with pleated structure	1	No	Yes	No
Heung et al., 2019 [19]	Fiber-reinforced elastomers with composite layer	2	No	Yes	No
Heung. et al., 2020 [18]	Fiber-reinforced elastomers with composite layer	2	No	Yes	Yes
Ma et al., 2022 [31]	Fiber-reinforced elastomers with three-air-chamber structure	1	No	Yes	No
Li et al, 2023 [10]	Fiber-reinforced elastomers with multi-stage articulated layer	3	No	Yes	No
Heung et al., 2023 [32]	Bellow-based elastomers	2	Resistive bending sensors	Yes	No
This work	Segmented composite bending actuators	2	Resistive bending sensors	Yes	Yes

References

Johnson, C.O.; Feigin, V.L. Global, regional, and national burden of stroke, 1990-2016: a systematic analysis for the Global Burden of Disease Study 2016. Lancet Neurol 2019, 18, 439–458. [Google Scholar] [CrossRef] [PubMed]
Dobkin Bruce, H. Rehabilitation after Stroke. New England Journal of Medicine 2005, 352, 1677–1684. [Google Scholar] [CrossRef] [PubMed]
Gassert, R.; Dietz, V. Rehabilitation robots for the treatment of sensorimotor deficits: a neurophysiological perspective. Journal of neuroengineering and rehabilitation 2018, 15, 1–15. [Google Scholar] [CrossRef] [PubMed]
Tong, Y.; Liu, J. Review of Research and Development of Supernumerary Robotic Limbs. IEEE/CAA Journal of Automatica Sinica 2021, 8, 929–952. [Google Scholar] [CrossRef]
Gull, M.A.; Bai, S.; Bak, T. A review on design of upper limb exoskeletons. Robotics 2020, 9, 16. [Google Scholar] [CrossRef]
Liu, Q.; Zuo, J.; Zhu, C.; Xie, S.Q. Design and control of soft rehabilitation robots actuated by pneumatic muscles: State of the art. Future Generation Computer Systems 2020, 113, 620–634. [Google Scholar] [CrossRef]
Polygerinos, P.; Galloway, K.C.; Savage, E.; Herman, M.; O’Donnell, K.; Walsh, C.J. Soft robotic glove for hand rehabilitation and task specific training. In Proceedings of the 2015 IEEE international conference on robotics and automation (ICRA); 2015; pp. 2913–2919. [Google Scholar]
Yap, H.K.; Khin, P.M.; Koh, T.H.; Sun, Y.; Liang, X.; Lim, J.H.; Yeow, C.-H. A fully fabric-based bidirectional soft robotic glove for assistance and rehabilitation of hand impaired patients. IEEE Robotics and Automation Letters 2017, 2, 1383–1390. [Google Scholar] [CrossRef]
Correia, C.; Nuckols, K.; Wagner, D.; Zhou, Y.M.; Clarke, M.; Orzel, D.; Solinsky, R.; Paganoni, S.; Walsh, C.J. Improving Grasp Function After Spinal Cord Injury With a Soft Robotic Glove. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2020, 28, 1407–1415. [Google Scholar] [CrossRef]
Li, X.; Hao, Y.; Zhang, J.; Wang, C.; Li, D.; Zhang, J. Design, Modeling and Experiments of a Variable Stiffness Soft Robotic Glove for Stroke Patients With Clenched Fist Deformity. IEEE Robotics and Automation Letters 2023, 8, 4044–4051. [Google Scholar] [CrossRef]
Nuckols, K.; Hohimer, C.J.; Glover, C.; de Lucena, D.S.; Moyo, W.; Wagner, D.; Cloutier, A.; Lin, D.J.; Walsh, C.J. Effects of a Soft Robotic Glove using a High Repetition Protocol in Chronic Stroke: A Pilot Study. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob); 2020; pp. 428–433. [Google Scholar]
Sui, M.; Ouyang, Y.; Jin, H.; Chai, Z.; Wei, C.; Li, J.; Xu, M.; Li, W.; Wang, L.; Zhang, S. A soft-packaged and portable rehabilitation glove capable of closed-loop fine motor skills. Nature Machine Intelligence 2023, 5, 1149–1160. [Google Scholar] [CrossRef]
Connolly, F.; Wagner, D.A.; Walsh, C.J.; Bertoldi, K. Sew-free anisotropic textile composites for rapid design and manufacturing of soft wearable robots. Extreme Mechanics Letters 2019, 27, 52–58. [Google Scholar] [CrossRef]
Ge, L.; Chen, F.; Wang, D.; Zhang, Y.; Han, D.; Wang, T.; Gu, G. Design, modeling, and evaluation of fabric-based pneumatic actuators for soft wearable assistive gloves. Soft robotics 2020, 7, 583–596. [Google Scholar] [CrossRef] [PubMed]
Kamper, D.G.; Rymer, W.Z. Quantitative features of the stretch response of extrinsic finger muscles in hemiparetic stroke. Muscle & Nerve 2000, 23, 954–961. [Google Scholar]
Dionysian, E.; Kabo, J.M.; Dorey, F.J.; Meals, R.A. Proximal Interphalangeal Joint Stiffness: Measurement and Analysis. The Journal of Hand Surgery 2005, 30, 573–579. [Google Scholar] [CrossRef]
Shi, X.Q.; Heung, H.L.; Tang, Z.Q.; Tong, K.Y.; Li, Z. Verification of Finger Joint Stiffness Estimation Method With Soft Robotic Actuator. Frontiers in Bioengineering and Biotechnology 2020, 8. [Google Scholar] [CrossRef]
Heung, H.L.; Tang, Z.Q.; Shi, X.Q.; Tong, K.Y.; Li, Z. Soft rehabilitation actuator with integrated post-stroke finger spasticity evaluation. Frontiers in bioengineering and biotechnology 2020, 8, 111. [Google Scholar] [CrossRef]
Heung, K.H.L.; Tong, R.K.Y.; Lau, A.T.H.; Li, Z. Robotic Glove with Soft-Elastic Composite Actuators for Assisting Activities of Daily Living. Soft Robot 2019, 6, 289–304. [Google Scholar] [CrossRef]
Matsunaga, F.; Kokubu, S.; Tortos Vinocour, P.E.; Ke, M.-T.; Hsueh, Y.-H.; Huang, S.Y.; Gomez-Tames, J.; Yu, W. Finger Joint Stiffness Estimation with Joint Modular Soft Actuators for Hand Telerehabilitation. Robotics 2023, 12. [Google Scholar] [CrossRef]
Matsunaga, F.; Oba, E.; Ke, M.T.; Hsueh, Y.H.; Huang, S.Y.; Gomez-Tames, J.; Yu, W. Machine-Learning-Based Accurate Finger Joint Stiffness Estimation With Joint Modular Soft Actuators. IEEE Robotics and Automation Letters 2024, 9, 7047–7054. [Google Scholar] [CrossRef]
Zhou, Y.M.; Wagner, D.; Nuckols, K.; Heimgartner, R.; Correia, C.; Clarke, M.; Orzel, D.; O’Neill, C.; Solinsky, R.; Paganoni, S. Soft robotic glove with integrated sensing for intuitive grasping assistance post spinal cord injury. In Proceedings of the 2019 International conference on robotics and automation (ICRA); 2019; pp. 9059–9065. [Google Scholar]
Chen, W.; Li, G.; Li, N.; Wang, W.; Yu, P.; Wang, R.; Xue, X.; Zhao, X.; Liu, L. Soft Exoskeleton With Fully Actuated Thumb Movements for Grasping Assistance. IEEE Transactions on Robotics 2022. [Google Scholar] [CrossRef]
Chen, W.; Li, G.; Li, N.; Wang, W.; Yu, P.; Wang, R.; Xue, X.; Zhao, X.; Liu, L. Restoring Voluntary Bimanual Activities of Patients With Chronic Hemiparesis Through a Foot-Controlled Hand/Forearm Exoskeleton. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2023, 31, 769–778. [Google Scholar] [CrossRef] [PubMed]
Tang, Z.Q.; Heung, H.L.; Shi, X.Q.; Tong, K.Y.; Li, Z. Probabilistic Model-Based Learning Control of a Soft Pneumatic Glove for Hand Rehabilitation. IEEE Transactions on Biomedical Engineering 2022, 69, 1016–1028. [Google Scholar] [CrossRef] [PubMed]
Lai, J.; Song, A.; Wang, J.; Lu, Y.; Wu, T.; Li, H.; Xu, B.; Wei, X. A Novel Soft Glove Utilizing Honeycomb Pneumatic Actuators (HPAs) for Assisting Activities of Daily Living. IEEE Transactions on Neural Systems and Rehabilitation Engineering 2023, 31, 3223–3233. [Google Scholar] [CrossRef] [PubMed]
Li, K.; Zhang, D.; Chu, Y.; Zhao, X. Bioinspired Segmented Hybrid Bending Pneumatic Actuators for Rehabilitation/Assisting Training. In Proceedings of the 2023 29th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), 21-24 Nov. 2023; pp. 1–6. [Google Scholar]
Bazira, P.J. Surgical anatomy of the hand. Surgery (Oxford) 2022, 40, 155–162. [Google Scholar] [CrossRef]
Yap, H.K.; Lim, J.H.; Nasrallah, F.; Goh, J.C.; Yeow, R.C. A soft exoskeleton for hand assistive and rehabilitation application using pneumatic actuators with variable stiffness. In Proceedings of the 2015 IEEE international conference on robotics and automation (ICRA); 2015; pp. 4967–4972. [Google Scholar]
Yap, H.K.; Lim, J.H.; Nasrallah, F.; Yeow, C.-H. Design and preliminary feasibility study of a soft robotic glove for hand function assistance in stroke survivors. Frontiers in neuroscience 2017, 11, 547. [Google Scholar] [CrossRef]
Ma, K.; Jiang, Z.; Gao, S.; Cao, X.; Xu, F. Design and Analysis of Fiber-Reinforced Soft Actuators for Wearable Hand Rehabilitation Device. IEEE Robotics and Automation Letters 2022, 7, 6115–6122. [Google Scholar] [CrossRef]
Heung, K.H.L.; Li, H.; Wong, T.W.L.; Ng, S.S.M. Assistive robotic hand with bi-directional soft actuator for hand impaired patients. Frontiers in Bioengineering and Biotechnology 2023, 11. [Google Scholar] [CrossRef]

Figure 1. Biomimetic design and concept of the proposed SCPBAs.

Figure 2. Fabrication and assembly of the SCPBAs.

Figure 3. Illustration of the proposed SCPBAs bending deformation in free space.

Figure 4. The diagram of bending deformation in constrained space considering finger joint stiffness.

Figure 5. The experimental setup of the SCPBAs.

Figure 6. The voltage magnitude and corresponding angle of the soft Flex sensor on the SCPBAs.

Figure 7. The relationship between the input pressure and output angle with various thicknesses of the stiffness-compensation in free space for MCP and PIP segment, respectively. The experimental data are represented by all trials’ mean and standard deviation. The dashed lines represent the modeling analytical results.

Figure 8. Bending resistance (BR)/Efficiency comparison of the different thicknesses of the stiffness-compensating layer.

Figure 9. Stiffness estimation of the index finger MCP joint: (a) the dummy finger coupled with torsional spring, (b) the measured MCP joint angles and estimated stiffness.

Figure 10. The predefined three ADL tasks.

Figure 11. Experimental results of an able-bodied subject. (a) The task-oriented training strategy during the three tasks. (b) Pressure values for achieving setting angles.

Table 1. The corresponding relationships between the MAS scores and the reference MCP joint stiffness [15,17,18,20].

Subject Condition	Stiffness Level	MAS Score	MCP Reference Stiffness $(N m / r a d$ )
Healthy	Low Stiffness	0	$\leq 0.04$
Slight spasticity	Middle Stiffness	1+	$(0.04, 0.5)$
Moderate-to-serve spasticity	Large Stiffness	$\geq 2$	$\geq 0.5$

Table 2. The two evaluation indexes of the proposed SCPBAs for middle stiffness.

Stiffness Condition	Extension Angle(degree)		Stiffness Estimated (Nm/rad)
Stiffness Condition	Ref. [10]	This work	Reference Stiffness	Estimated Value	Error (%)
1+, Middle Stiffness $(0.04, 0.5)$ ,Slight spasticity	[8.2°, 19.8°]	22.3	0.1321	0.1290	2.3
	[8.2°, 19.8°]	16.8	0.1968	0.1956	0.6

Table 3. Experimental targeted angles for three ADL tasks.

Tasks	Thumb	Index Finger	Middle Finger	Ring Finger	Little Finger
Task 1	23°	26°	30°	36°	47°
Task 2	28°	40°	43°	-	-
Task 3	31°	43°	-	-	-

Table 4. Monitoring errors in rehabilitation training process.

Tasks	Thumb	Index Finger	Middle Finger	Ring Finger	Little Finger
Task 1	12.63%	6.04%	6.07%	9.47%	15.90%
Task 2	9.35%	8.27%	5.93%	-	-
Task 3	8.79%	10.26%	-	-	-

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Soft Exoskeleton System Based-On Segmented Composite Proprioceptive Bending Actuators for Hand Rehabilitation ADL Tasks

Abstract

1. Introduction

2. Design and Fabrication of the SCPBAs

2.1. The Bio-Inspiration and Implementation of the SCPBAs

2.2. Actuator Fabrication

3. Mathematical Modeling of the SCPBAs

3.1. Bending Model in Free Space

3.2. Bending Model in Constrained Space

3.2.1. Constrained Space with Intrinsic/Voluntary Flexion Torque

3.2.2. Constrained Space with Involuntary Flexion Torque

4. Performance Characterization of the SCPBAs

4.1. Experiment Setup

4.1.1. Characterization of the Embedding Flexible Bending Sensor

4.2. Bending Angle Measurement in Free Space

4.2.1. Changing the Stiffness-Compensating Layer Thickness

4.3. Bending Angle Measurement with Involuntary Flexion Torque

4.3.1. Extension Angle and Joint Stiffness Evaluation on the Dummy Finger

5. Soft Robotic Glove with the SCPBAs for Task-Oriented Rehabilitation Training

5.1. Pre-Defined ADL Tasks

5.2. Task-Oriented Rehabilitation Strategy

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe