Submitted:
14 September 2024
Posted:
16 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Electric Fish Optimization Algorithm and Its Problems
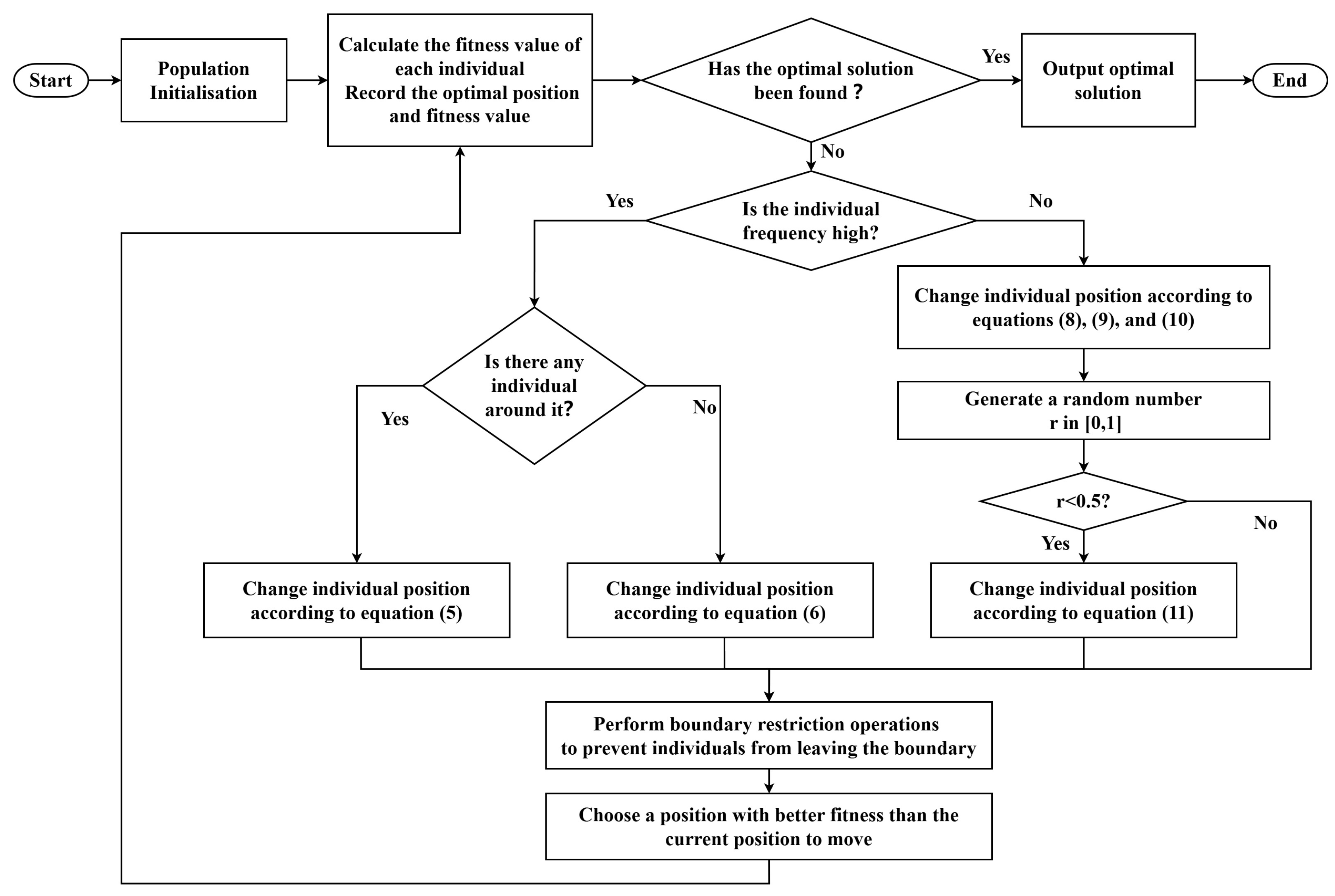
2.1. Electric Fish Optimization Algorithm
2.2. Problems Encountered by EFO
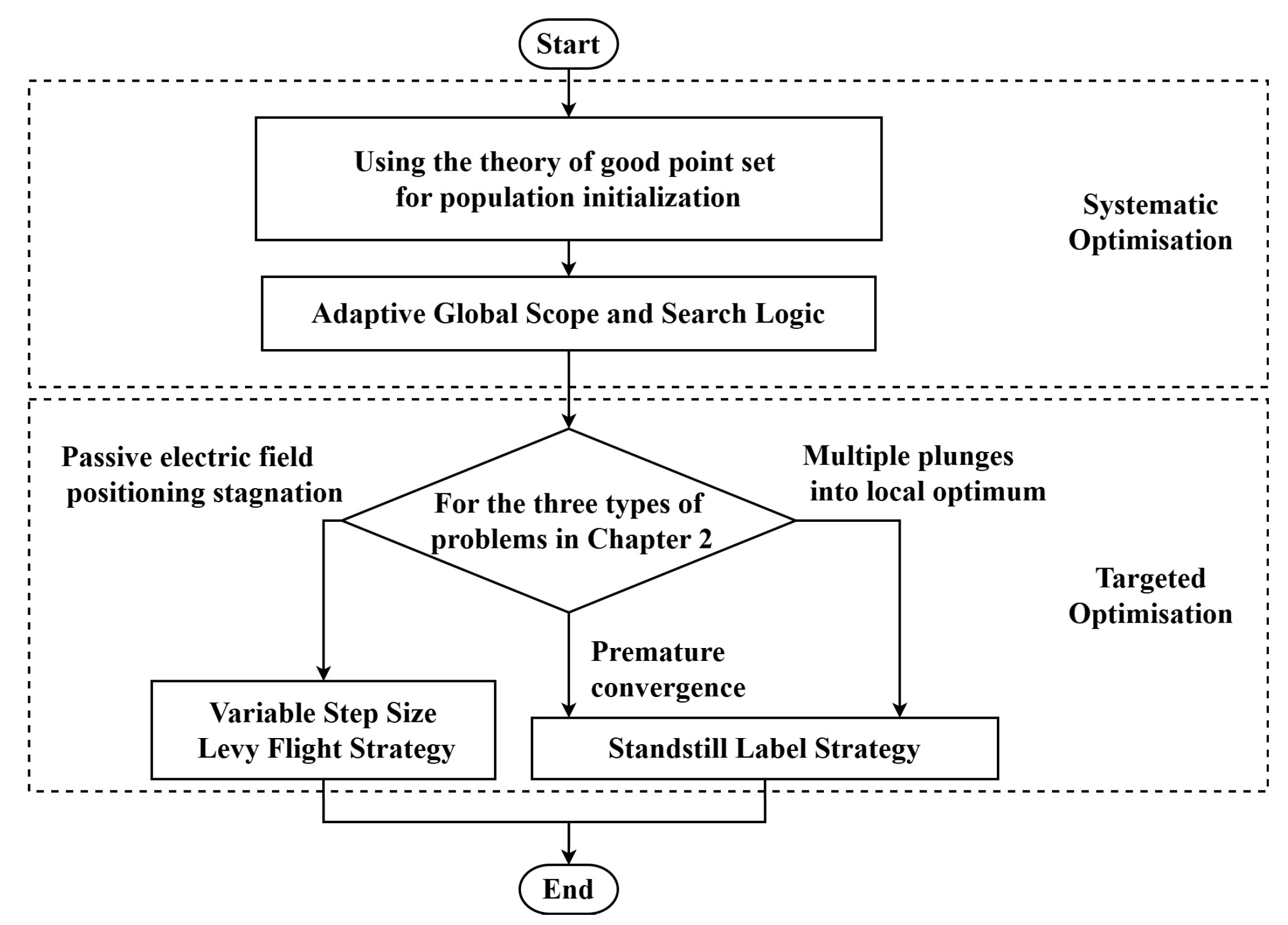
3. The SLLF-EFO Algorithm Proposed in This Article
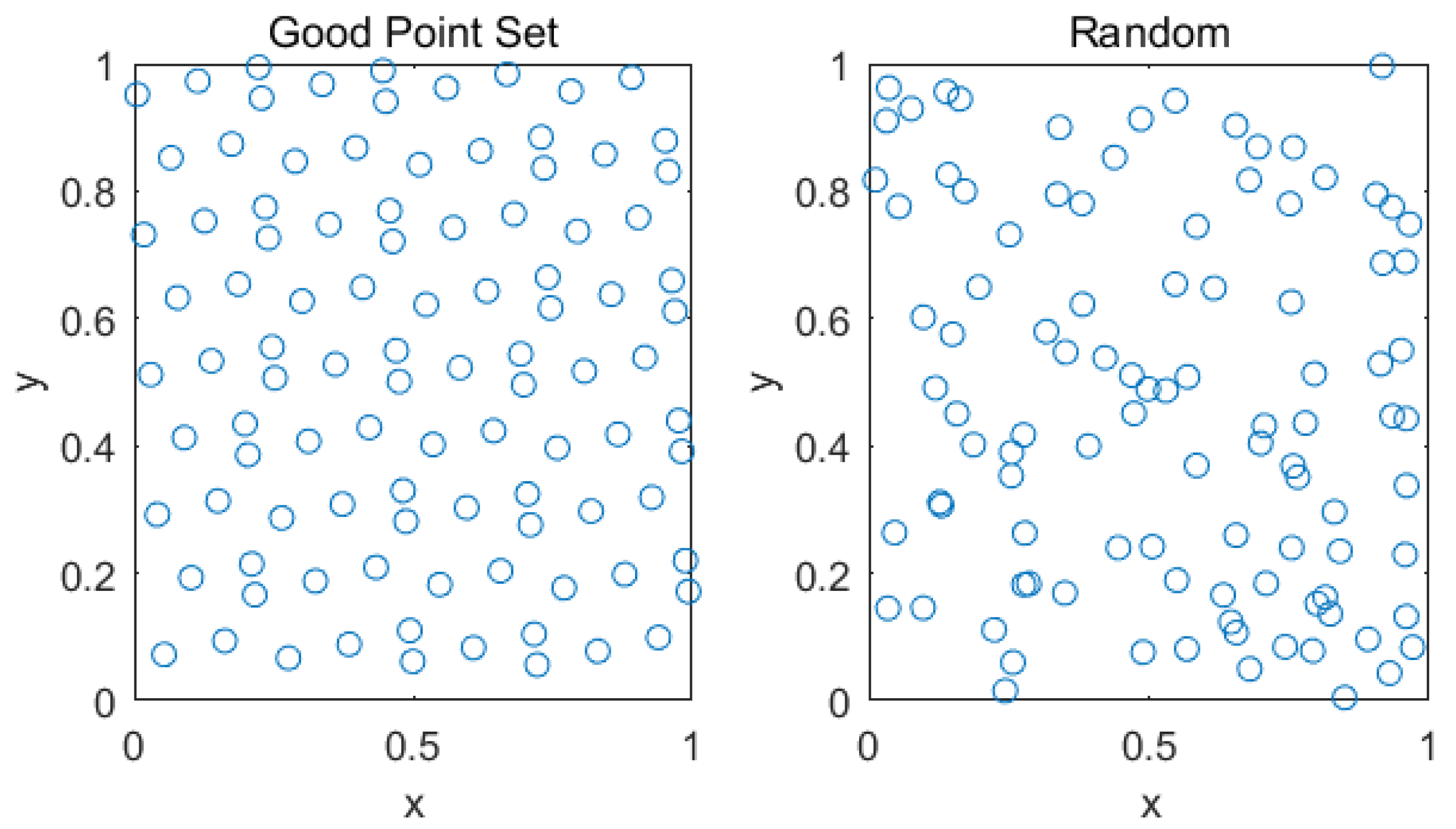
3.1. Population Initialisation
3.2. Adaptive Global Scope and Search Logic
3.2.1. Adaptive Global Scope
3.2.2. Optimization of Individual Selection Strategy for Active Electric Field Localization
3.2.3. Introduction of Golden Sine Operator
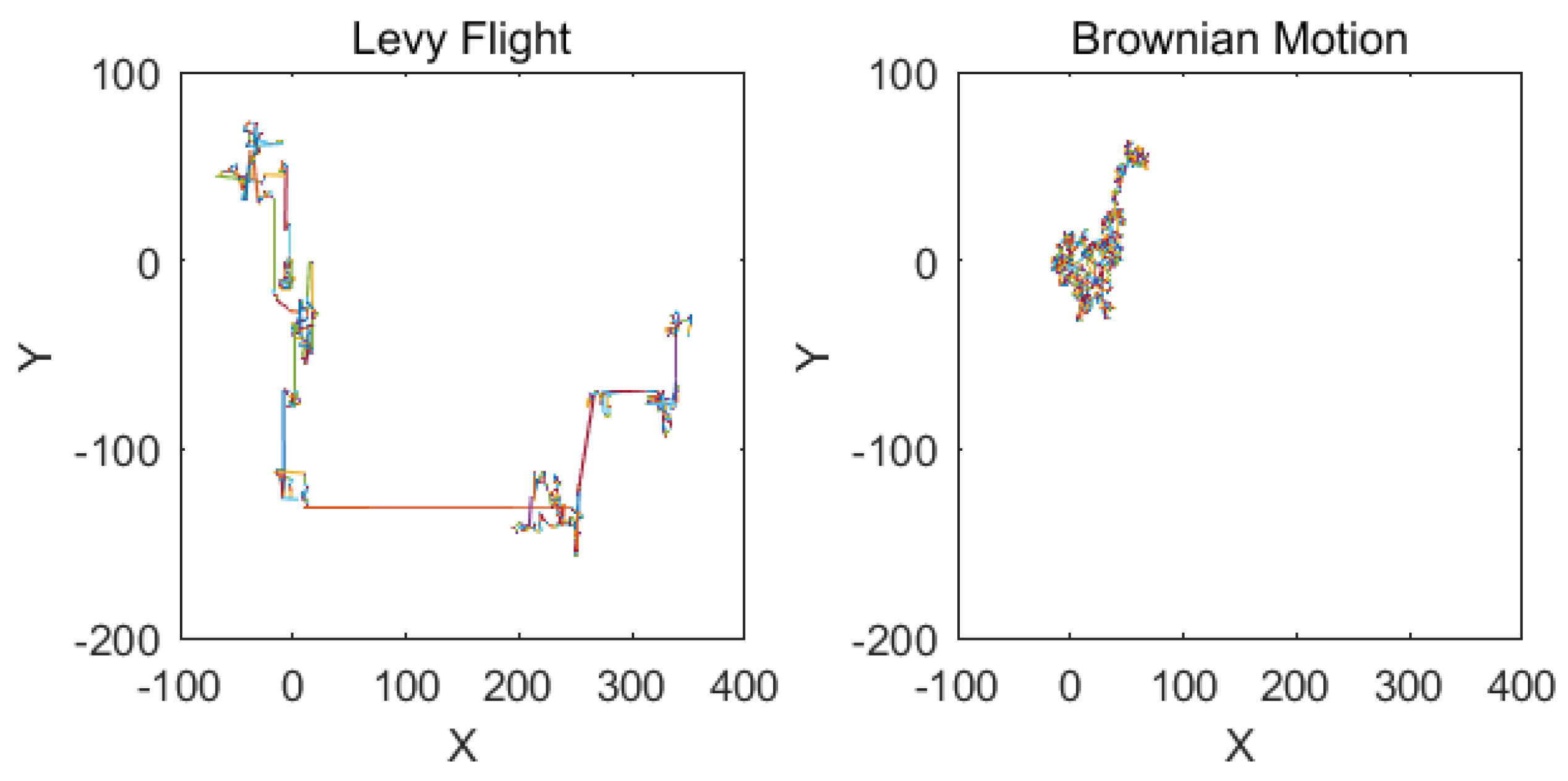
3.3. Variable Step Size Levy Flight Strategy
3.3.1. Levy Flight Strategy
3.3.2. Variable Step Movement Logic
3.4. Standstill Label Strategy
4. Experiments Based on Benchmark Functions
4.1. Test Functions and Comparison Algorithms
4.2. Speed Comparison with Other Algorithms
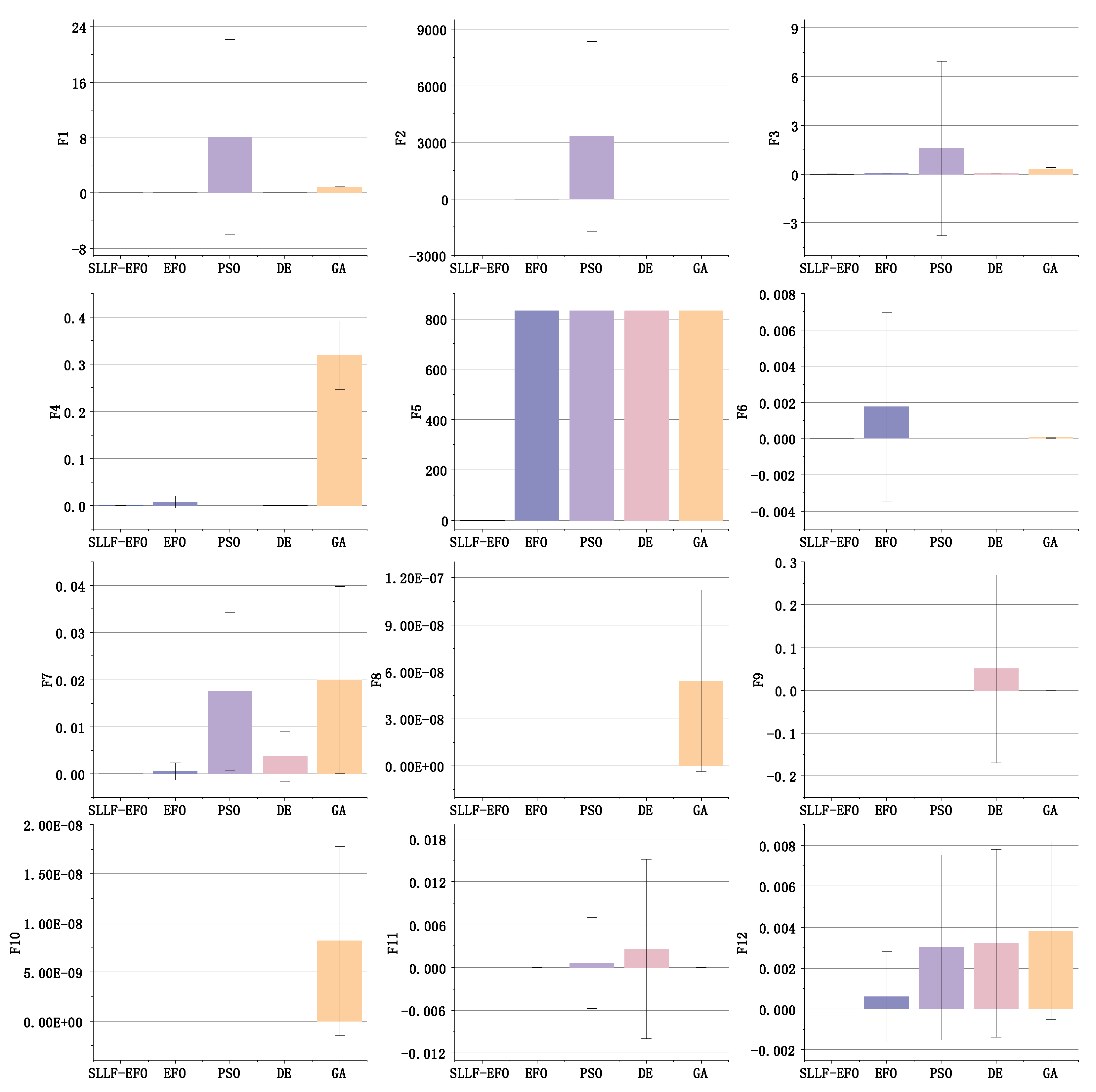
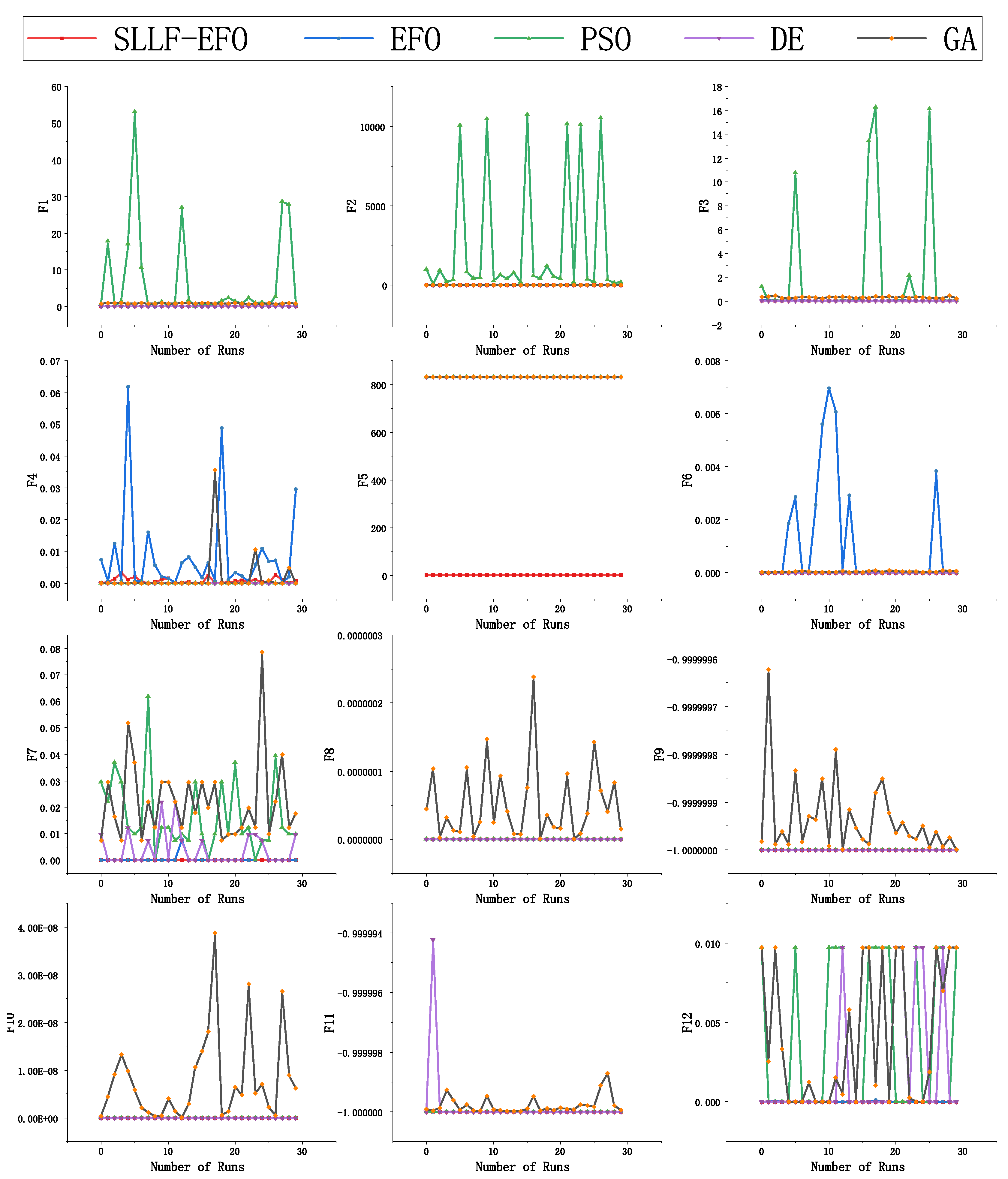
4.3. Accuracy Comparison with Other Algorithms
5. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Darvishpoor, S.; Darvishpour, A.; Escarcega, M.; Hassanalian, M. Nature-inspired algorithms from oceans to space: A comprehensive review of heuristic and meta-heuristic optimization algorithms and their potential applications in drones. Drones 2023, 7, 427. [Google Scholar] [CrossRef]
- Yilmaz, S.; Sen, S. Electric fish optimization: A new heuristic algorithm inspired by electrolocation. Neural Computing and Applications 2020, 32, 11543–11578. [Google Scholar] [CrossRef]
- Deepa, J.; Madhavan, P. ABT-GAMNet: A novel adaptive Boundary-aware transformer with Gated attention mechanism for automated skin lesion segmentation. Biomedical Signal Processing and Control 2023, 84, 104971. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Abualigah, L.; Ewees, A.A.; Al-Qaness, M.A.; Yousri, D.; Alshathri, S.; Abd Elaziz, M. An electric fish-based arithmetic optimization algorithm for feature selection. Entropy 2021, 23, 1189. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.S.; Karri, G.R. Eeoa: Cost and energy efficient task scheduling in a cloud-fog framework. Sensors 2023, 23, 2445. [Google Scholar] [CrossRef] [PubMed]
- Rao, Y.S.; Madhu, R. Hybrid dragonfly with electric fish optimization-based multi user massive MIMO system: Optimization model for computation and communication power. Wireless Personal Communications 2021, 120, 2519–2543. [Google Scholar] [CrossRef]
- Anirudh Reddy, R.; Venkatram, N. Intelligent energy efficient routing in wireless body area network with mobile sink nodes using horse electric fish optimization. Peer-to-Peer Networking and Applications, 2024; 1–25. [Google Scholar]
- Viswanadham, Y.V.R.S.; Jayavel, K. Design & Development of Hybrid Electric Fish-Harris Hawks Optimization-Based Privacy Preservation of Data in Supply Chain Network with Block Chain Technology. International Journal of Information Technology & Decision Making, 2023; 1–32. [Google Scholar]
- Yılmaz, S.; Sen, S. Classification with the electric fish optimization algorithm. 2020 28th Signal Processing and Communications Applications Conference (SIU). IEEE, 2020, pp. 1–4.
- Yıldız, Y.A.; Akkaş, Ö.P.; Saka, M.; Çoban, M.; Eke, İ. Electric fish optimization for economic load dispatch problem. Niğde Ömer Halisdemir Üniversitesi Mühendislik Bilimleri Dergisi, 13, 1–1.
- Vaishnavi, T.; Sheeba Joice, C. A novel self adaptive-electric fish optimization-based multi-lane changing and merging control strategy on connected and autonomous vehicle. Wireless Networks 2022, 28, 3077–3099. [Google Scholar] [CrossRef]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. A comparative review of approaches to prevent premature convergence in GA. Applied Soft Computing 2014, 24, 1047–1077. [Google Scholar] [CrossRef]
- Nakisa, B.; Ahmad Nazri, M.Z.; Rastgoo, M.N.; Abdullah, S. A survey: Particle swarm optimization based algorithms to solve premature convergence problem. Journal of Computer Science 2014, 10, 1758–1765. [Google Scholar] [CrossRef]
- Li, Y.; Lin, X.; Liu, J. An improved gray wolf optimization algorithm to solve engineering problems. Sustainability 2021, 13, 3208. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Particle swarm optimization: Global best or local best? 2013 BRICS congress on computational intelligence and 11th Brazilian congress on computational intelligence. IEEE, 2013; 124–135. [Google Scholar]
- Islam, S.M.; Das, S.; Ghosh, S.; Roy, S.; Suganthan, P.N. An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2011, 42, 482–500. [Google Scholar] [CrossRef] [PubMed]
- Hua, L. The application of number theory in approximate analysis. Science Press, 1978; 1–99. [Google Scholar]
- ZHANG L, Z.B. Good Point Set Based Genetic Algorithm. CHINESE JOURNAL OF COMPUTERS-CHINESE EDITION- 2001, 24, 917–922. [Google Scholar]
- Chen, Y.X.; Liang, X.M.; Huang, Y. Improved quantum particle swarm optimization based on good-point set. Journal of Central South University (Science and Technology) 2013, 4, 1409–1414. [Google Scholar]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Advances in Electrical & Computer Engineering 2017, 17. [Google Scholar]
- Zhang, J.; Wang, J.S. Improved whale optimization algorithm based on nonlinear adaptive weight and golden sine operator. IEEE Access 2020, 8, 77013–77048. [Google Scholar] [CrossRef]
- Xie, W.; Wang, J.S.; Tao, Y. Improved black hole algorithm based on golden sine operator and levy flight operator. IEEE Access 2019, 7, 161459–161486. [Google Scholar] [CrossRef]
- Drysdale, P.; Robinson, P. Lévy random walks in finite systems. Physical Review E 1998, 58, 5382. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, B. A novel ant colony optimization algorithm with Levy flight. Ieee Access 2020, 8, 67205–67213. [Google Scholar] [CrossRef]
- Heidari, A.A.; Pahlavani, P. An efficient modified grey wolf optimizer with Lévy flight for optimization tasks. Applied Soft Computing 2017, 60, 115–134. [Google Scholar] [CrossRef]
- Gong Ran, Shi Wenjuan, Z.Z. Optimization Algorithm for Slime Mould Based on Chaotic Mapping and Levy Flight. Computer & Digital Engineering 2023, 51, 361–367. [Google Scholar]
- Mantegna, R.N. Fast, accurate algorithm for numerical simulation of Levy stable stochastic processes. Physical Review E 1994, 49, 4677. [Google Scholar] [CrossRef] [PubMed]
- Bacaër, N. Verhulst and the logistic Equation (1838). A short history of mathematical population dynamics, 2011; 35–39. [Google Scholar]
- Kyurkchiev, N. A family of recurrence generated sigmoidal functions based on the Verhulst logistic function. Some approximation and modelling aspects. Biomath Communications 2016, 3. [Google Scholar] [CrossRef]
- Ma, Y.N.; Gong, Y.J.; Xiao, C.F.; Gao, Y.; Zhang, J. Path planning for autonomous underwater vehicles: An ant colony algorithm incorporating alarm pheromone. IEEE Transactions on Vehicular Technology 2018, 68, 141–154. [Google Scholar] [CrossRef]
- Castillo-Villar, K.K. Metaheuristic algorithms applied to bioenergy supply chain problems: theory, review, challenges, and future. Energies 2014, 7, 7640–7672. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. Computational intelligence for multimedia big data on the cloud with engineering applications, 2018; 185–231. [Google Scholar]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Systems with Applications 2021, 166, 113917. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.H.; Tang, F.; Huang, D.X. Improved particle swarm optimization combined with chaos. Chaos, Solitons & Fractals 2005, 25, 1261–1271. [Google Scholar]
- Guo, W.; Liu, T.; Dai, F.; Xu, P. An improved whale optimization algorithm for forecasting water resources demand. Applied Soft Computing 2020, 86, 105925. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95-international conference on neural networks. ieee, 1995; Vol. 4, 1942–1948. [Google Scholar]
- Price, K.V. Differential evolution. Handbook of optimization: From classical to modern approach, 2013; 187–214. [Google Scholar]
- Holland, J.H. Adaptation in natural and artificial systems: An introductory analysis with applications to biology, control, and artificial intelligence, 1992.
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. International Journal of Mathematical Modelling and Numerical Optimisation 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Li, F.; Guo, W.; Deng, X.; Wang, J.; Ge, L.; Guan, X. A hybrid shuffled frog leaping algorithm and its performance assessment in Multi-Dimensional symmetric function. Symmetry 2022, 14, 131. [Google Scholar] [CrossRef]
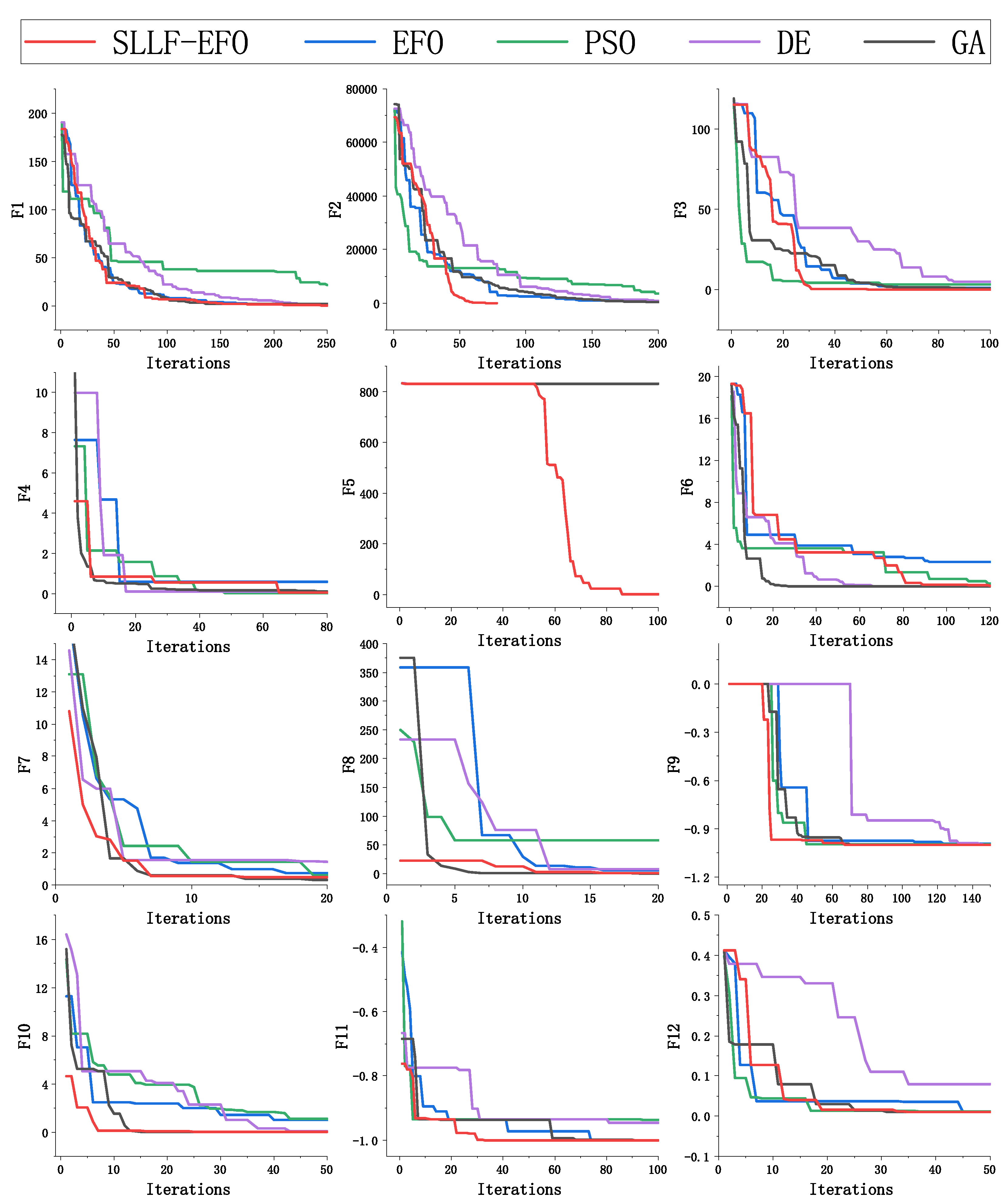
| Serial Number | Functin | Search Scope | Dimension | Optimum Value |
|---|---|---|---|---|
| F1 | Sphere | [-5.12,5.12] | 30 | 0 |
| F2 | Step | [-100,100] | 30 | 0 |
| F3 | Quartic | [-1.28,1.28] | 30 | 0 |
| F4 | Rosenbrock | [-5,10] | 30 | 0 |
| F5 | Schwefel | [-500,500] | 30 | 0 |
| F6 | Ackley | [-32,32] | 30 | 0 |
| F7 | Griewank | [-600,600] | 30 | 0 |
| F8 | Bohachevsky | [-100,100] | 2 | 0 |
| F9 | Easom | [-100,100] | 2 | -1 |
| F10 | Rastrigin | [-5.12,5.12] | 2 | 0 |
| F11 | Drop-Wave | [-5.12,5.12] | 2 | -1 |
| F12 | Schaffer N6 | [-10,10] | 2 | 0 |
| Function | Index | SLLF-EFO | EFO | PSO | DE | GA | SIF |
|---|---|---|---|---|---|---|---|
| F1 | — | Exceed | Exceed | Exceed | Exceed | Exceed | — |
| F2 | Min-Iter | 62 | 1005 | 2000 | 481 | 361 | 13.64 |
| Max-Iter | 441 | 2000 | 2000 | 572 | 827 | ||
| Mean-Iter | 112.17 | 1530.15 | 2000 | 540.34 | 502.61 | ||
| Over-Num | 0 | 4 | 100 | 0 | 0 | ||
| F3 | — | Exceed | Exceed | Exceed | Exceed | Exceed | — |
| F4 | Min-Iter | 2000 | 2000 | 831 | 2000 | 2000 | — |
| Max-Iter | 2000 | 2000 | 1291 | 2000 | 2000 | ||
| Mean-Iter | 2000 | 2000 | 1009.67 | 2000 | 2000 | ||
| Over-Num | 100 | 100 | 0 | 100 | 100 | ||
| F5 | — | Exceed | Exceed | Exceed | Exceed | Exceed | — |
| F6 | Min-Iter | 730 | 938 | 797 | 379 | 2000 | 1.57 |
| Max-Iter | 2000 | 2000 | 1158 | 464 | 2000 | ||
| Mean-Iter | 994.52 | 1563.65 | 1005.98 | 422.67 | 2000 | ||
| Over-Num | 6 | 31 | 0 | 0 | 100 | ||
| F7 | Min-Iter | 327 | 781 | 804 | 410 | 2000 | 1.32 |
| Max-Iter | 2000 | 2000 | 2000 | 2000 | 2000 | ||
| Mean-Iter | 1350.48 | 1789.35 | 1875.16 | 1093.83 | 2000 | ||
| Over-Num | 13 | 68 | 88 | 40 | 100 | ||
| F8 | Min-Iter | 109 | 157 | 514 | 207 | 2000 | 1.90 |
| Max-Iter | 139 | 801 | 1074 | 283 | 2000 | ||
| Mean-Iter | 122.51 | 223.23 | 798.59 | 250.04 | 2000 | ||
| Over-Num | 0 | 0 | 0 | 0 | 100 | ||
| F9 | Min-Iter | 375 | 803 | 529 | 259 | 2000 | 2.33 |
| Max-Iter | 1483 | 1970 | 1007 | 2000 | 2000 | ||
| Mean-Iter | 596.18 | 1388.08 | 773.71 | 431.93 | 2000 | ||
| Over-Num | 0 | 0 | 0 | 5 | 100 | ||
| F10 | Min-Iter | 105 | 187 | 517 | 181 | 2000 | 2.00 |
| Max-Iter | 229 | 756 | 1054 | 260 | 2000 | ||
| Mean-Iter | 140.89 | 281.13 | 761.67 | 226.42 | 2000 | ||
| Over-Num | 0 | 0 | 0 | 0 | 100 | ||
| F11 | Min-Iter | 162 | 403 | 506 | 371 | 2000 | 3.30 |
| Max-Iter | 582 | 2000 | 2000 | 2000 | 2000 | ||
| Mean-Iter | 263.02 | 868.33 | 771.86 | 550.53 | 2000 | ||
| Over-Num | 0 | 10 | 1 | 4 | 100 | ||
| F12 | Min-Iter | 302 | 931 | 585 | 510 | 2000 | 2.38 |
| Max-Iter | 2000 | 2000 | 2000 | 2000 | 2000 | ||
| Mean-Iter | 796.27 | 1894.89 | 1218.83 | 1263.89 | 2000 | ||
| Over-Num | 4 | 72 | 31 | 33 | 100 |
| Functions | Index | SLLF-EFO | EFO | PSO | DE | GA | Ratio |
|---|---|---|---|---|---|---|---|
| F1 | Mean | 8.078069590 | 0.801900988 | 105.37 | |||
| Std | 14.08101851 | 0.116547399 | 31.29 | ||||
| F2 | Mean | 0 | 0.04 | 3306.32 | 0 | 0 | Extremely High |
| Std | 0 | 0.196946386 | 5036.425121 | 0 | 0 | Extremely High | |
| F3 | Mean | 0.003147740 | 0.038953813 | 1.582964707 | 0.026996480 | 0.326350667 | 12.38 |
| Std | 0.001781311 | 0.012436167 | 5.361322043 | 0.006638658 | 0.067290692 | 6.98 | |
| F4 | Mean | 0.000854922 | 0.007367849 | 0 | 0.319380700 | 8.62 | |
| Std | 0.000884378 | 0.012963790 | 0 | 0.073208760 | 14.66 | ||
| F5 | Mean | 831.8099376 | 831.8099376 | 831.8099376 | 831.8099376 | ||
| Std | 0 | 0 | 0 | 0 | — | ||
| F6 | Mean | 0.001767313 | 0 | 0 | |||
| Std | 0.005219645 | 0 | 0 | ||||
| F7 | Mean | 0.000504985 | 0.017456368 | 0.003697774 | 0.019963270 | ||
| Std | 0.001886713 | 0.016805818 | 0.005273292 | 0.019810354 | |||
| F8 | Mean | 0 | 0 | 0 | 0 | — | |
| Std | 0 | 0 | 0 | 0 | — | ||
| F9 | Mean | -1 | -1 | -1 | -0.95 | -0.999999957 | — |
| Std | 0 | 0 | 0 | 0.219042914 | — | ||
| F10 | Mean | 0 | 0 | 0 | 0 | — | |
| Std | 0 | 0 | 0 | 0 | — | ||
| F11 | Mean | -1 | -0.999999843 | -0.999362453 | -0.997449813 | -0.999999729 | Extremely High |
| Std | 0 | 0.006375467 | 0.012556252 | Extremely High | |||
| F12 | Mean | 0.000614620 | 0.003011932 | 0.003206250 | 0.003819688 | ||
| Std | 0.002198893 | 0.004516180 | 0.004591560 | 0.004323915 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




