Preprint
Article
Power Signal Histograms: A Method of Power Grid Data Compression on the Edge for Real-time Incipient Fault Forensics
Altmetrics
Downloads
45
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
13 September 2024
Posted:
16 September 2024
You are already at the latest version
Alerts
Abstract
Across the power grid infrastructure, deployed power transmission systems are susceptible to incipient faults that interrupt standard operations. These incipient faults can range from being benign in impact to causing massive hardware damage and even loss of life. The power grid is continuously monitored, and incipient faults are recorded by Digital Fault Recorders (DFRs) to mitigate such outcomes. DFR recorded data allows power quality forensics and event analysis, but this capability comes at the cost of high data storage and data transmission requirements. It is common for data older than two weeks to be overwritten due to storage limitations and without being analyzed. This inhibits the creation of long-term data libraries that would enable incipient fault forensics and the characterization of behavior that precedes them, which limits the development and implementation of preventive measures; thus, there is a critical need to reduce DFR recorded data storage requirements. This work addresses this critical need by leveraging the cyclic and residual histograms and introducing the frequency, and Root Means Squared (RMS) histograms, which alleviate current high data storage requirements and provides effective Incipient Fault Prediction (IFP). The residual, frequency, and RMS histograms are an extension of the cyclic histogram, reduce the date storage requirement by up to 99.58%, can be generated on the DFR without interrupting its normal operations, and are capable of predicting voltage arcing six hours before it is strong enough to trigger a DFR recorded event.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Power utilities have and continue to employ “smart” devices within their generation, transmission, and distribution infrastructure, leading to an ever-growing amount of data recording and storage. Historically, power utility personnel have processed, analyzed, and learned from this data using by-hand approaches; however, these approaches (i) rely heavily upon the knowledge, experience, and expertise of the person or persons conducting the analysis, (ii) are often conducted days or weeks after the data was recorded if at all thus limiting the value of the analysis, and (iii) are hindered by the fact that power utilities often lack sufficient personnel and other resources (e.g., funds, time, computation, storage) to conduct dedicated and continuous processing and analysis of smart device recorded data.
A Digital Fault Recorder (DFR) is a smart device employed by power utilities to comply with some North American Electric Corporation (NERC) standards and monitor key substations and transmission lines. The Electric Power Research Institute (EPRI) defines a DFR as a device capable of digitizing and recording oscillography (OSG) data (e.g., three-phase sinusoidal voltage), sequence of events, and faults [1]. DFRs can monitor analog voltages, current lines, buses, and numerous digital inputs. Figure 1 provides examples of a Capacitive Voltage Transformer (CVT) event, Figure 1a, and a loose connection induced arcing event, Figure 1b, recorded using a DFR sampling at 960 Hz and occuring on a 161 kV line. This work focuses on the DFR’s continuous digitization and recording of the nominal (a.k.a., non-faulted) sinusoidal three-phase voltage and current waveforms. Due to limited personnel, funds, time, and storage capacity, it is common for power utilities to not analyze or look at these waveforms and to overwrite the recordings every two to three weeks, thus hindering and even prohibiting the generation of actionable intelligence, incipient fault detection, and fault prediction by power utility personnel. Overwriting of the recorded data not only results in the potential loss of actionable information, but also prevents creation of long-term data libraries essential to incipient fault forensics and characterization of the behavior that precedes them; thus, prohibiting development and implementation of preventive or corrective measures. The work in [2] and [3] are the first, and up to this point the only, compression algorithms proposed for power signals. The cyclic and residual histograms provide reduced, two-dimensional representations of OSG data and capture the likelihood a power signal’s magnitude achieves a specific value at a given sample point within a cycle and over time.
Incipient Fault Detection (IFD) uses waveform analytics to identify faults occurring within a recorded fault. There has been demonstrated success with identifying various event types that occur during grid operations [3,4,5,6,7,8,9]. While these methods are useful in identifying and validating the occurrence of events, Incipient Fault Prediction (IFP) targets predicting these events before they occur, allowing event prevention through preemptive measures. This (i) maintains nominal grid operations, (ii) prevents hardware from being damaged, and (iii) reduces risk to maintenance crews. The work in [10] demonstrates the ability to use an increased frequency of previous events to forecast the likelihood of a more critical failure but does not use the recorded waveform data, only the log of prior events. The work in [11] presents a correlation-based approach that accurately predicts an event ten milliseconds before the event occurs. Current research has shown that the earliest detection possible is only forty seconds before an event occurrence on a deployed grid [12]. The authors of [13] predict a series of line interruptions, voltage dips, and ground faults with 89% true-positive accuracy one hour preceding the fault. The authors used Root-Means Squared (RMS) data sampled at 1Hz and a random forest classifier to predict fault likelihood. The work in [2] introduces IFD using cyclic and residual histograms as data-efficient storage techniques. While the data is reduced, these histograms are designed for IFD. This work assesses the viability of using these histograms for IFP. Deployed DFRs are designed for performing only standard grid monitoring operations. Thus, the computational capability of the DFR is limited. These computational limitations include reduced processor, memory, and storage. Because of these limitations, any new functionality must be implemented in a computationally efficient way to ensure way that does not interfere with standard operations. The contributions of this work are summarized as follows.
- The proposed method of power histogram compression reduces data storage requirements by % compared to the original waveform.
- The power histograms are validated with IFP experiments using DFR power grid event data recorded using OSG files. The IFP enabling code is available v.i.a. GitHub [14].
- The ability of the histograms to store actionable data is assessed using three use cases: Capacitive Voltage Transformer (CVT) failure, arcing due to a loose connection, and DFR sampling error. All use case data is recorded by DFRs deployed within an operational power transmission system.
- The power histogram compression enables IFP that is statistical; thus, it does not require Machine Learning/Deep Learning (ML/DL).
- The IFP approach based on the power histograms is less computationally complex, transparent, and explainable versus ML/DL-based approaches, making it tractable to ease operational use and integration.
- The power histograms enabled an IFP approach that predicts an event seven hours before the DFR is triggered, facilitating remedial action.
- The power histograms allow DFR to observe once, generate the corresponding histograms, and store them for future IPF detection.
Our IFP approach predicts CVT failure and arcing one hour and six hours before the DFR triggering threshold is satisfied, facilitating preventive maintenance or repair.
2. Background
2.1. Power Transmission Recording
DFRs are designed to monitor and store power line transmissions continuously. DFRs read voltage and current waveforms at an event sampling rate, , typically greater than the continuous storage sampling rate, . DFRs store an event’s -sampled waveform for subsequent analysis. The three-phase voltage and current waveforms are downsampled to the storage sampling rate and recorded in an OSG file regardless of whether an event has been detected within the twenty-four-hour monitored period. These OSG files typically require 20 Gb to 50 Gb of memory based on the number of monitored lines. Other datasets, such as Oak Ridge National Laboratory’s Grid Event Signature Library, provide various fault types [15]. To our knowledge, no publicly available databases provide recordings that include the twenty-four hours preceding the detected fault. The authors hope other power-quality researchers can use our open-source software to create long-term 24/7 public datasets for further power-quality research [14]. It is estimated that a year’s worth of histograms, generated at one-hour intervals from two hundred deployed DFRs with an average of six lines (i.e., three voltage and three current), would require 12 Gb of storage space; thus, providing a tractable means for creating a histogram-based library. Such a library would allow new, timely preventative or corrective action methods that enhance power grid operations by predicting various event types.
2.2. Power Line Histograms
This section details Cyclic, Residual, Frequency, and RMS histogram generation.
2.2.1. Time Synchronization
The cyclic histogram is the average per-cycle behavior over the sampling period. It is processed relative to a sine function (i.e., sample is zero, sample is negative, and sample is positive). Due to DFR clock drift and source voltage frequency drift, each cycle must be detected and time-synchronized before creating the histograms. This synchronization begins by detecting a recorded cycle. A recorded cycle’s start is determined to be two consecutive samples: the first is negative, and the second is positive (i.e., a negative-to-positive zero crossing). The cyclic histogram-generating process then skips forward three-quarters of the number of Samples per Cycle (SPC). For example, if the SPC is 16, the function skips forward 12 samples. The end of the cycle is determined to be the next negative-to-positive zero crossing. The actual sampled value is never zero, so the function estimates the time at which the sampled cycle is zero by calculating the slope between the negative and positive samples around the zero crossing,
where x is the sampled waveform, n is the negative sample index before the positive sample index , and is the time between sample points. The initial zero point is,
The second time offset is calculated using the estimated end of the cycle. Next, is created with and as its starting and ending points with steps of . The detected cycle is interpolated into the time-synchronized cycle using and stored for cyclic histogram creation. The end of cycle i is the start of cycle . This process is repeated until the cyclic histogram-generating process reaches the waveform’s end.
2.2.2. Cyclic Histogram
The cyclic histogram is a per-sample Probability Mass Function (PMF). The number of histograms calculated equals the number of SPC plus one. Because each point in the cycle has different minimums and maximums, the histogram limits are set globally based on the minimum and maximum values observed within the cycles. Figure 2a provides a representative illustration of a cyclic histogram. The cyclic histogram allows utility personnel to confirm successful time-synchronization visually by ensuring that the cyclic histogram resembles a sine function with a magnitude associated with bus rating. Our code [14] generates a metadata file that states the number of cycles captured by the time synchronization algorithm. This information can detect abnormal recording behavior, such as complete line outages.
2.2.3. Residual Histogram
Residual histogram generation begins by subtracting an ideal cycle from every time-synchronized cycle. The residual histogram highlights imperfections imposed by (i) nominal line behavior, (ii) power disturbance events, and (iii) behavior that may occur before an event or fault. The residual histogram is calculated over a smaller voltage range than the cyclic histogram, which presents abnormalities with greater clarity. The ideal cycle is one cycle of the sine function oscillating at the power system’s fundamental frequency, which in the United States is 60 Hz. The ideal cycle’s magnitude is the same as the operational voltage and is determined using the bus RMS voltage by,
where is the voltage RMS value. For example, a 161kV bus will have a operational voltage of kV. After subtracting the ideal cycle, the per-sample PMFs are generated. The number of histogram bins and voltage range are conditionally set to normalize the voltage steps across different residual histograms. If the observed voltage range is kV, the global voltage range is set to kV, and the number of histogram bins is set to . If the global voltage range is less than kV but greater than kV, the global voltage range is set to kV and the number of histogram bins is set to . Otherwise, the global voltage range is set to kV with histogram bins. This ensures all residual histograms have the same voltage step size. The per-sample PMFs are generated using the selected global voltage range and number of histogram bins to create the residual histogram. A representative illustration of a residual histogram is shown in Figure 2b.
2.3. Frequency and RMS Histograms
2.3.1. Frequency Histogram Calculation
The frequency histogram is the waveform’s dominant frequency PMFs over time. The dominant frequency is calculated by generating the Power Spectral Density (PSD) across a user-defined bandwidth, which is a small window (i.e., smaller than ) around the fundamental transmission frequency (e.g., 60 Hz). This enables the calculation of an Alternate Discrete Fourier Transform (A-DFT) instead of the Fast Fourier Transform (FFT). The FFT calculates the frequency response from , which leads to the processing of additional frequencies not used for histogram generation and wastes computational resources. The A-DFT processes frequencies within the desired and much smaller user-defined bandwidth, resulting in a more efficient implementation. The A-DFT-based PSD is,
where are the waveform samples in window w, is the window length used to calculate the PSD, f is the dominant frequency in the user-defined bandwidth at which is maximum, t is the user-defined bandwidth-determined time vector. The function is the same value for all calculations of , thus it is calculated once and the resulting array stored for later use. This is advantageous because the exponential function is computationally expensive, so precalculation of significantly reduces the time needed to compute Equation (4). This process repeats until the dominant frequency is calculated for each window. The frequency histogram is the PMF of all dominant frequencies within the histogram’s bin limits, equal to the user-defined bandwidth. A representative frequency histogram is shown in Figure 2c.
2.3.2. RMS Histogram
The RMS histogram is generated using the frequency histogram window and step sizes. First, the average energy over each window is calculated by,
Once all windows’ average energy is calculated, the RMS histogram is the PMF of all average energy values. A representative illustration of an RMS histogram is shown in Figure 2d.
2.4. Operational Power System Use Cases
IFP capability is assessed on three use cases: (i) CVT Failure, (ii) Loose Connection, and (iii) DFR Sampling Error. All results are based on utility-provided .OSG files generated from deployed DFRs monitoring a real-world power transmission system. For each of the three cases, line recordings are provided for a total of twenty-four hours preceding the last reported event at a sampling rate of 960 Hz and a precision of 16-bits (a.k.a. half-precision) For all three cases, only voltage lines are uses for analysis.
2.4.1. Use Case #1: Capacitive Voltage Transformer Failure
CVTs supply voltage to protective relays. Our IFP approach applies to relays incapable of CVT detection and predicts CVT failure using the waveforms recorded using the storage sampling rate, . CVT failure occurs when enough capacitive elements fail and cause an explosion, which poses a severe risk to equipment and utility personnel that may be nearby when the failure occurs. CVT failures can be characterized by a single phase reaching a peak-to-peak voltage 10% higher than that phase’s average peak-to-peak value for at least three cycles. A representative illustration of a CVT failure event is shown in Figure 1a. This characterization effectively identifies CVT failures during the event [3]; however, these methods are often implemented after the event (i.e., the event-triggered DFR recording) or during the event at the earliest. Thus, new approaches are needed to predict CVT failure (a.k.a. before the DFR recording is triggered) to facilitate the implementation of event prevention measures.
2.4.2. Use Case #2: Loose Connection
A loose bus connection can cause arcing, Figure 1b. This can be a loose screw or poor contact between the lines and the bus. The loose connection increases the dielectric constant within the connection and increases power draw, wasting energy. Additionally, arcing can lead to a fire if timely corrective actions are not taken. Figure 1b shows an arcing event around ms. After the event, each line phase is rotated , which is evident by the post-event phase of Phase A being equal to the pre-event phase of Phase C.
2.4.3. Use Case #3: DFR Sampling Error
Automated fault detection and identification algorithms, such as those in [3,4,5,6,7,8,9], assume the DFR is correctly sampling the continuous waveforms. However, methods for ensuring accurate measurement and correct sampling are needed. This use case focuses on the latter and is facilitated by the frequency histogram. Like the clock drift mentioned in Section 2.2.2, the DFR may impose other unintentional anomalies onto the recorded, sampled waveform that interfere with fault detection and prediction. Clock skew can manifest in frequency, where the frequency behavior drifts outside the nominal operating frequency tolerance. This frequency tolerance is Hz for the data used herein.
3. Methodology
This section describes generating actionable information using either array- or vector-based metrics. The array-based metric generates actionable information from the cyclic or residual histogram, while the frequency or RMS histograms are used for vector-based actionable information generation. Both metrics allow for measuring a line’s statistics over time, which serves as the actionable information for IFP.
3.1. Array-Based Metric
The array-based metric is the per-sample cross-correlation computed between a reference histogram and the histograms generated from the storage sampled waveform. The reference histogram is generated from the storage sampled waveform before a DFR triggering event. For example, suppose a DFR-triggering CVT failure event occurs at 15:03, and histograms are generated every 5 minutes. In that case, our IFP approach uses the histogram generated from the waveform samples within the 14:55 to 15:00 time window as the reference histogram. The per-sample cross-correlation is calculated by,
where is the reference histogram, H is the histogram generated using one of the four approaches in Section 2, b is the given bin, is the number of bins, and n is the sample within the span of the cycle. This produces a vector where zero is low similarity, and one is an exact match.
3.2. Vector-Based Metric
The vector-based metric is the variance of the frequency or RMS histogram. The PMF’s variance is calculated as,
where y is an array representing the histogram’s support, h is the bin’s probability, is the number of histogram bins, is the step size between bins, and is the mean,
4. Results
Results are generated using real-world, known occurrences of CVT failure, arcing, and DFR sampling error events within an operational power transmission system. All three events are voltage-related, only the voltage waveforms are used. However, the presented IFP approach can be used for current waveform manifesting events. The voltage waveforms are sampled at =960 Hz or 16 SPC. The residual, RMS, and frequency histograms are used for CVT failure, arcing, and DFR sampling error event IFP, respectively. The other histograms are neglected because their corresponding metrics did not provide sufficient actionable information to enable IFP. Table 1 lists each use case, the histogram used for IFP, and the IFP time before the DFR triggering event occurs.
The histograms are generated using data collected over a twenty-four-hour period. Three CVT failure and arcing events are present in the DFR recorded data, and their presence is confirmed by power utility personnel. The DFR triggering events are marked using vertical red lines in Figure 3 and Figure 4. To enable comparative assessment and determine the minimum amount of time over which histograms must be generated to facilitate IFP, histograms are generated every five, ten, thirty, and sixty minutes. When comparing the memory required to store the unprocessed, raw waveforms to our histogram-based approach, the amount of memory needed to store the histograms is %, %, %, and % lower when generating them every five, ten, thirty, or sixty minutes, respectively. The presented results show that while the data size is significantly reduced, actionable information is retained.
4.1. Use Case #1: CVT Failure Events Prediction Results
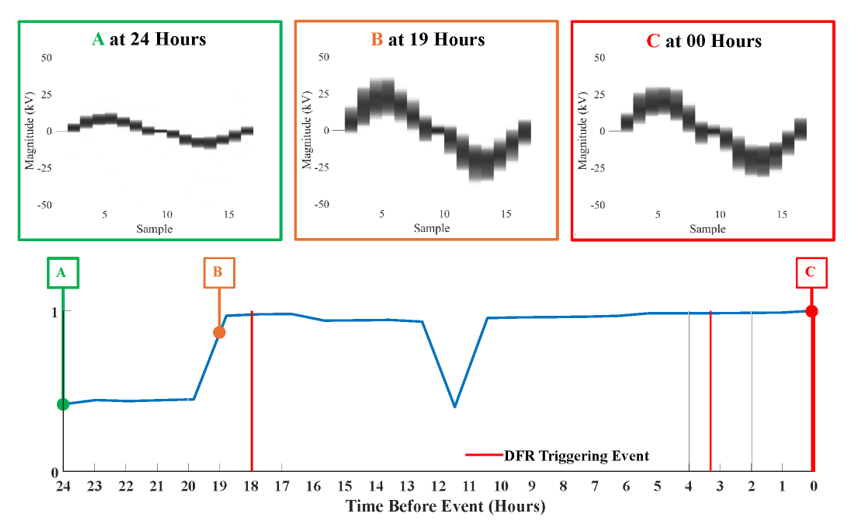
Residual histograms are calculated per Section 2.2.3 with bins per sample. Figure 3 shows array-based metric values using residual histograms–generated every five, ten, thirty, and sixty minutes–cross-correlated with the corresponding interval’s reference residual histogram. The array-based metric measures the similarity between the reference histogram and those generated from the storage sampled waveform(s). Figure 3 presents the average of each array-based metric for residual histograms generated every five, Figure 3a, ten, Figure 3b, thirty, Figure 3c, and sixty, Figure 3d, minutes.
The array-based metric for the residual histograms generated every five minutes, Figure 3a provides inconsistent (i.e., the value varies from to ) actionable information (a.k.a., prediction of CVT failure) 1 hour before the first DFR triggering CVT failure. The array-based metric becomes more consistent, approaching the first CVT event at 18 hours and remaining consistent throughout the processing period. There is one drop in the array-based metric value approximately 12 hours before the last DFR triggering CVT failure event. However, the noisy nature of the metric using the five-minute interval residual histograms may make it difficult to set a threshold or other measure that consistently predicts CVT failure before the DFR is triggered.
Figure 3b shows the array-based metric for residual histograms generated every ten minutes. As in Figure 3a, CVT failure prediction is inconsistent 1 hour before the first DFR triggering CVT failure event but becomes and remains relatively consistent afterward. Here, the metric is noisy and suffers a drop around 16 hours before the last DFR triggering CVT failure event. This drop and relatively long recovery may also make it difficult to set a threshold or measure that consistently predicts CVT failure before the DFR is triggered.
The array-based metric for thirty-minute generated residual histograms is shown in Figure 3c. The behavior is inverted when compared to the five, ten, and sixty-minute interval results shown in Figure 3a, Figure 3b, and Figure 3d, respectively. Again, the array-based metric is inconsistent for the first four hours (i.e., 24 to 20 hours before the first recorded CVT failure event), thus limiting its IFP value. The array-based metric value does become more consistent after the first four hours but does not predict any of the CVT failure events before the DFR is triggered, thus negating its IFP potential.
Figure 3d shows the array-based metric for the residual histograms generated every sixty minutes. The metric is consistently low before the first DFR triggering CVT failure event that occurs 18 hours before the third and final event. The array-based metric’s value reaches (a.k.a., high similarity) one hour before the first CVT failure event triggers the DFR, and the value is higher than for the remaining processing period except for the low value a little under 12 hours before the final event. It is important to note that the array-based metric is high (i.e., above ) at least one hour before all three CVT failure events trigger the DFR, thus providing IFP actionable information. Additionally, residual histograms generated every sixty minutes have the lowest memory requirements compared to the other three time intervals and unprocessed waveforms.
The cross-correlation values presented in Figure 3 are calculated using the reference residual histogram generated using the OSG data corresponding to the DFR’s last (a.k.a., most recent) triggering CVT failure event and designated “zero hour” in Figure 3. The CVT failure events occurring eighteen and three hours before the last DFR triggering CVT failure event are considered “blind tests” of the presented IFP approach. The high CVT failure likelihood value (i.e., a cross-correlation value above 0.9) one hour before the DFR triggering CVT failure event occurs at hour eighteen shows the viability of the presented cross-correlation-based IFP approach. It also indicates that a DCR can generate a histogram from a single event’s OSG data and then use it as a reference for IFP before the event grows strong enough to trigger a DFR event recording.
4.2. Use Case #2: Voltage Arcing Event Prediction Results
The RMS histograms are calculated using a window size of 60 cycles, 960 samples, a step size of 30 cycles or a total of 480 samples, and 256 bins per histogram. The results presented in Figure 4 show the absolute difference in RMS variance between Phase A and Phase B histograms in five, Figure 4a, ten, Figure 4b, thirty, Figure 4c, and sixty, Figure 4d minute intervals over a twenty-four-hour period. The arcing events occurred between these two phases, but a similar approach can be applied to arcing between any combination of two or more phases. DFR-triggering arcing events occur six and four hours before the third event at . IFP necessitates the detection of the significant voltage variations that can occur during an arcing event. These voltage variations are due to increasing or changing resistance for a loose connection.
The vector-based metric for five-minute generated RMS histograms is shown in Figure 4a. It shows that the RMS variance difference is largest 24, 22, , and 7 hours before the first arcing event; however, the difference is erratic, making IFP difficult because there is no clear point at which arcing is definitively predicted due to multiple high variance points.
Figure 4b shows the vector-based metric for RMS histograms generated every ten minutes. The absolute difference is smoother than the five-minute interval case, Figure 4a, but remains sufficiently erratic to minimize its IFP value.
The absolute difference of RMS variance calculated using RMS histograms generated every thirty minutes is shown in Figure 4c. The RMS variance’s absolute difference is smoother than in the previous two cases, offering a lower initial value 24 hours before the third arcing event. The absolute difference is less than 10V hours before the last event and remains less than 10V until 15 hours before peaking hours before the final event and hours before the first arcing event. Despite its IFP potential, the thirty-minute-based results are still not a good predictor of arcing because the highest absolute difference in RMS variance occurs 18 hours and 24 hours before the first and last arcing events.
The vector-based metric for sixty-minute generated RMS histograms is shown in Figure 4d. The absolute difference does not exceed 20V until 13 hours before the final event and 7 hours before the first event. The single maximum occurs 7 hours before the first event provides an IFP potential that utility personnel can act on. As noted at the end of Section 4.1, the sixty-minute-based histograms are advantageous because they require the least memory.
4.3. Use Case #3: Sampling Error Detection Results
Figure 5 shows the frequency histogram of a voltage waveform recorded by a DFR with faulty Digital Signal Processor (DSP) firmware. Only the sixty-minute interval histogram is displayed because the other four exhibit the same behavior. Figure 5 shows the PMF residing at the edges of the histogram limits and outside the Hz operating tolerance. It is unknown when utility personnel detected this particular DFR sampling error; however, this specific DFR-imposed measurement error can be detected whenever most of a PMF’s total area resided outside the Hz tolerance.
4.4. Process Times
Table 2 presents the runtime in milliseconds to perform the cycle synchronization, residual calculation, and frequency and energy processes individually. Due to the frequency and energy calculations being based on the same windowing approach, they are calculated within the same defined function. They are, therefore, included together when presenting the runtime. The code in [14] includes an option to include the runtime in the generated metadata file for further profiling by power quality researchers. The results are generated using a laboratory DFR connected to a Dell Laptop with an Intel© i5 4210H 2C/2T mobile Central Processing Unit (CPU) and 8Gb of Double Data Rate 3 (DDR3) Random Access Memory (RAM). The CPU is limited to running at a Ghz core clock. Histogram processing is performed Python with each function is written as separate definition. Each definition is decorated with a Just In Time (JIT) compilation that utilizes the NUMBA library for function acceleration. Each function is run initially to be compiled and cached. Function runtimes are based on using the cached, accelerated version of each function. When generating the histograms using sixty-minute intervals, the runtime does not exceed one second; thus, the runtime is less than % of the overall operational time.
5. Conclusion
A histogram-based IFP approach is presented and validated using three use cases with data collected in an operational power transmission system. Actionable information–generated using sixty-minute interval residual histograms–predicts a CVT failure event one hour before triggering the DFR. Additionally, the RMS histogram–via the absolute difference in the RMS variance between transmission lines–predicts arcing seven hours before the arcing is sufficient to trigger the DFR. Lastly, the frequency histogram permits the detection of improper DFR sampling. One of the benefits of generating the cyclic, residual, frequency, and RMS histograms is that they allow for creating long-term power grid behavior libraries. This is because the histograms, generated every sixty minutes over twenty-four hours, require only % (a.k.a., a % reduction) of the memory needed to store the same period’s DFR-recorded OSG files. These histogram libraries could be used to develop more analytical methods to predict more event types with sufficient lead time to enable preventative or corrective actions that ultimately improve power grid operations. In this work, histogram-based IFP is assessed using three use cases, so additional research is needed to identify the full set of events for which the presented approach is viable.
Author Contributions
Conceptualization, J.T. and T.C.; methodology, J.T.; software, J.T.; validation, A.M., T.C.; formal analysis, J.T.; investigation, J.T.; resources, A.M., D.R.; data curation, A.M.; writing—original draft preparation, J.T., D.R.; writing—review and editing, J.T., D.R.; visualization, J.T.; supervision, D.R, A.M.; project administration, A.M., D.R.; funding acquisition, D.R., A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Tennessee Valley Authority (TVA) funding.
Data Availability Statement
While the data used in this dataset is not public, the code used to generate all histograms is available at https://github.com/utc-simcenter/learning-from-power-signals-public.
Acknowledgments
The authors would like to thank Jonathan Boyd and Nathan Hooker of the Tennessee Valley Authority, whose input and assistance made this work possible.
Conflicts of Interest
The authors declare no conflict of interest
Abbreviations
The following abbreviations are used in this manuscript:
| A-DFT | Alternative Discrete Fourier Transform |
| CVT | Capactive Voltage Transformer |
| DFR | Digital Fault Recorder |
| DL | Deep Learning |
| EPRI | Electrical Power Research Institute |
| FFT | Fast Fourier Transform |
| IFD | Incipient Fault Detection |
| IFP | Incipient Fault Prediction |
| JIT | Just In Time |
| ML | Machine Learning |
| NERC | North American Electric Corporation |
| OSG | OScilloGraphy |
| PMF | Probability Mass Function |
| RMS | Root Means Squared |
| SPC | Samples Per Cycle |
References
- Demcko, J.; Selin, D. Digital Fault Recorders in Power Plant Applications. Technical Report 102 0233. Electric Power Research Institute (EPRI), Palo Alto, California, 2010. [Google Scholar]
- Cooke, T. Condensing pq data and visualization analytics. IEEE Power & Energy Society General Meeting, 2015.
- Boyd, J.; Tyler, J.; Murphy, A.; Reising, D. Learning from Power Signals: An Automated Approach to Electrical Disturbance Identification within a Power Transmission System. Sensors 2024, 24. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, A.; Aguado, J.; Martín, F.; López, J.; Muñoz, F.; Ruiz, J. Rule-based classification of power quality disturbances using S-transform. Electric Power Systems Research 2012, 86. [Google Scholar] [CrossRef]
- Kapoor, R.; Gupta, R.; Son, L.H.; Jha, S.; Kumar, R. Boosting performance of power quality event identification with KL Divergence measure and standard deviation. Measurements 2018, 126. [Google Scholar] [CrossRef]
- De, S.; Debnath, S. Real-time cross-correlation-based technique for detection and classification of power quality disturbances. IET Generation, Transmission & Distribution 2018, 12, https. [Google Scholar] [CrossRef]
- Pilario, K.; Cao, Y.; Shafiee, M. Incipient fault detection, diagnosis, and prognosis using canonical variate dissimilarity analysis. In Computer Aided Chemical Engineering; Elsevier, 2019; Vol. 46.
- Wilson, A.; Reising, D.; Hay, R.; Johnson, R.; Karrar, A.; Loveless, T. Automated identification of electrical disturbance waveforms within an operational smart power grid. IEEE Transactions on Smart Grid 2020, 11. [Google Scholar] [CrossRef]
- Mannon, T.; Suggs, J.; Reising, D.; Hay, R. Automated Identification of Re-Closing Events in an Operational Smart Power Grid. IEEE SoutheastCon, 2020.
- Moghe, R.; Mousavi, M.J. Trend analysis techniques for incipient fault prediction. IEEE Power & Energy Society General Meeting, 2009. [CrossRef]
- Samet, H.; Khaleghian, S.; Tajdinian, M.; Ghanbari, T.; Terzija, V. A similarity-based framework for incipient fault detection in underground power cables. International Journal of Electrical Power & Energy Systems 2021, 133. [Google Scholar] [CrossRef]
- Hoffman, V.; Michalowska, K.; Andersen, C.; TorsÆter, B. Incipient Fualt Prediction in Power Quality Monitoring. CIRED 2019. [Google Scholar]
- Tyvold, T.; Nybakk, T.; Andresen, C.; Hoffmann, V. Impact of the Temporal Distribution of Faults on Prediction of Voltage Anomalies in the Power Grid. International Conference on Smart Energy Systems and Technologies (SEST), 2020. [CrossRef]
- Tyler, J.; Reising, D. Learning from Power Signals. https://github.com/utc-simcenter/learning-from-power-signals-public, 2023.
- Oak Ridge National Laboratory and Lawrence Livermore National Laboratory. Grid Event Signature Library (GESL) 2024.
Figure 1.
Representative illustrations of two operational power grid event use cases. Both Capacitive Voltage Transformer (CVT) and arching events are recorded to an OSG file generated by a DFR sampling the voltage waveforms at 960 Hz.
Figure 1.
Representative illustrations of two operational power grid event use cases. Both Capacitive Voltage Transformer (CVT) and arching events are recorded to an OSG file generated by a DFR sampling the voltage waveforms at 960 Hz.
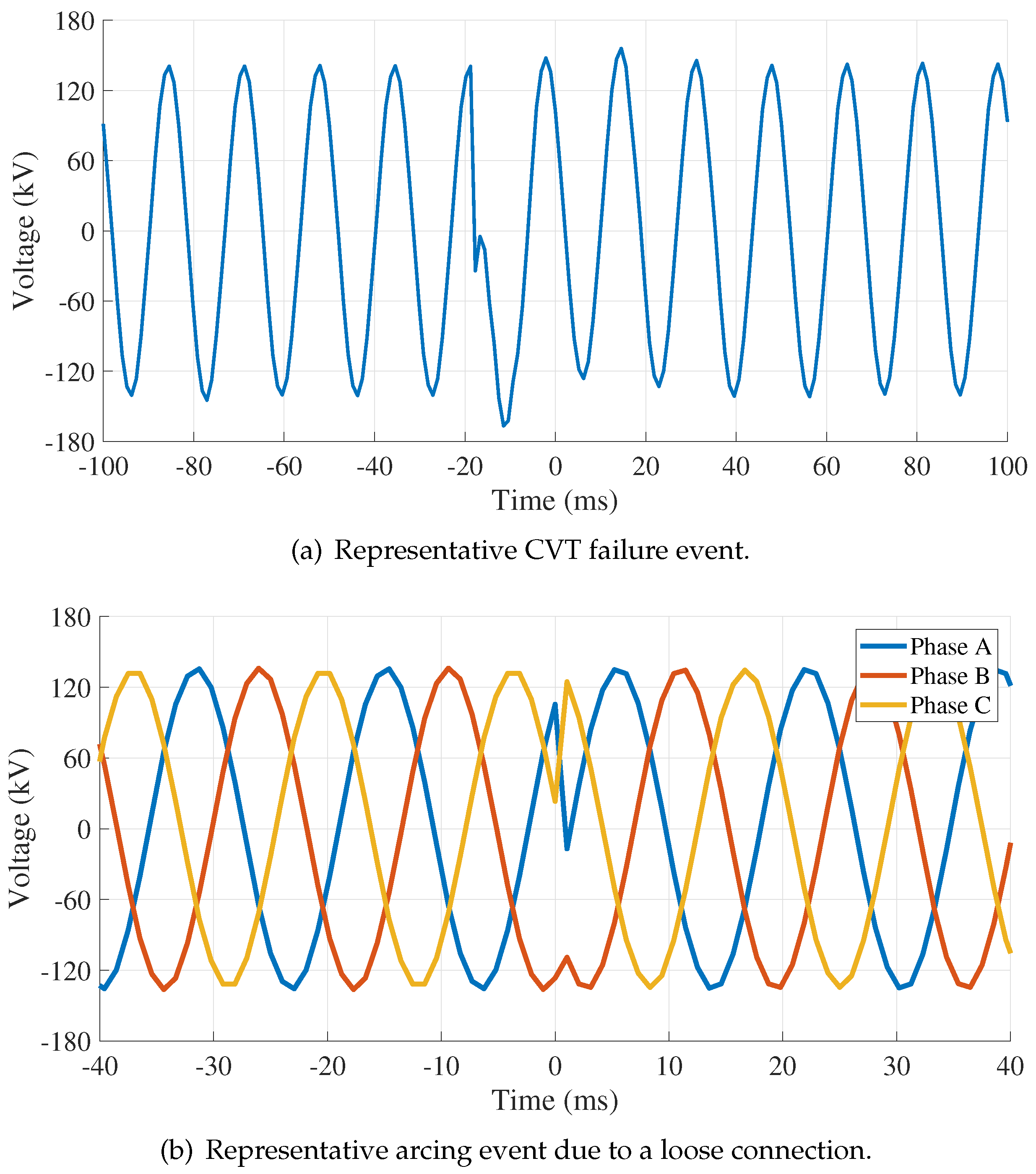
Figure 2.
Representative cyclic, residual, frequency, and RMS histograms generated using one hour of a 161 kV bus line with a transmission frequency of 60 Hz.
Figure 2.
Representative cyclic, residual, frequency, and RMS histograms generated using one hour of a 161 kV bus line with a transmission frequency of 60 Hz.
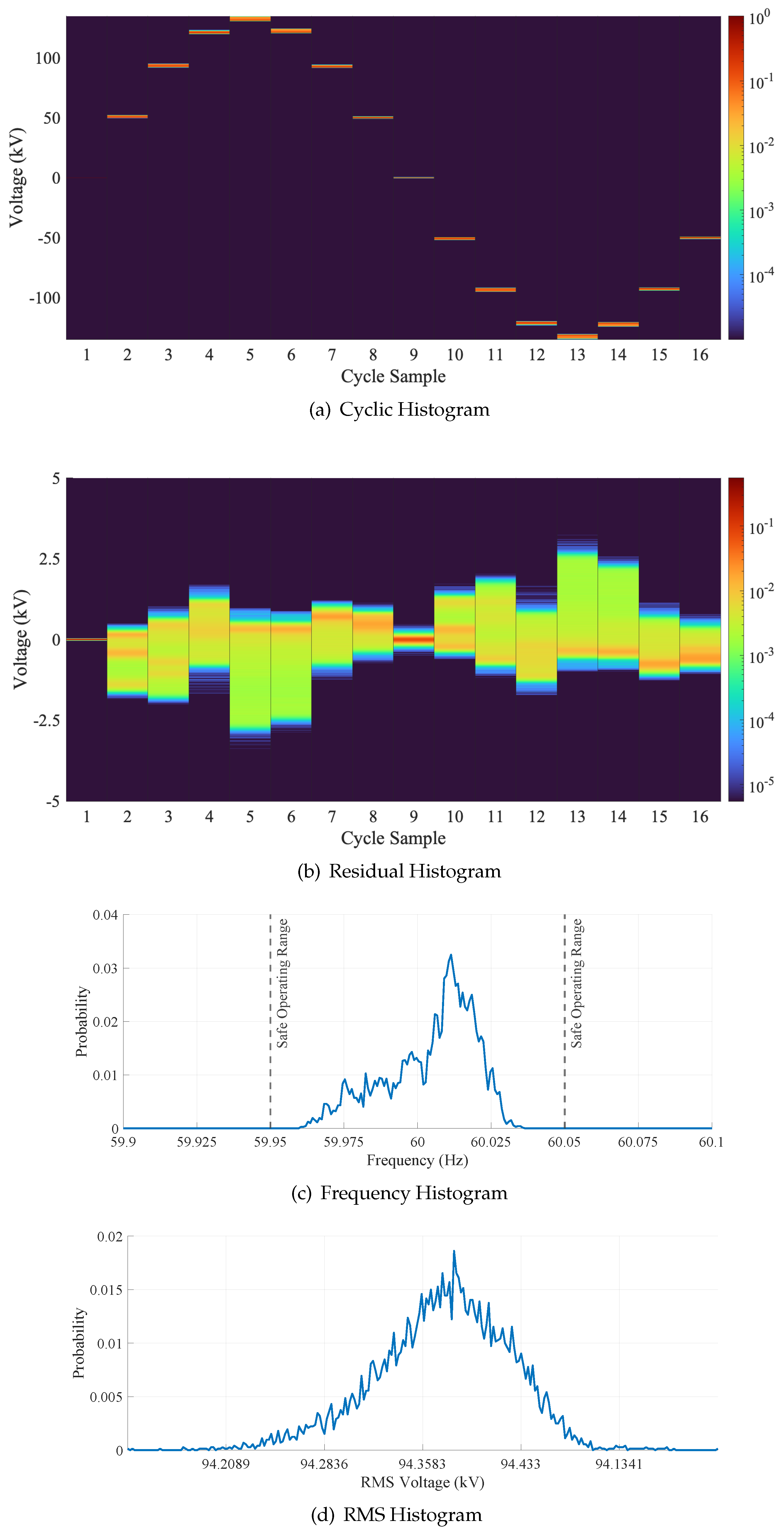
Figure 3.
Use Case #1: CVT Failure Event IFP: The average per-sample cross-correlation calculated between the reference residual histogram and the residual histograms generated for a twenty-four-hour period. Histograms are generated every five, ten, thirty, and sixty minutes.
Figure 3.
Use Case #1: CVT Failure Event IFP: The average per-sample cross-correlation calculated between the reference residual histogram and the residual histograms generated for a twenty-four-hour period. Histograms are generated every five, ten, thirty, and sixty minutes.
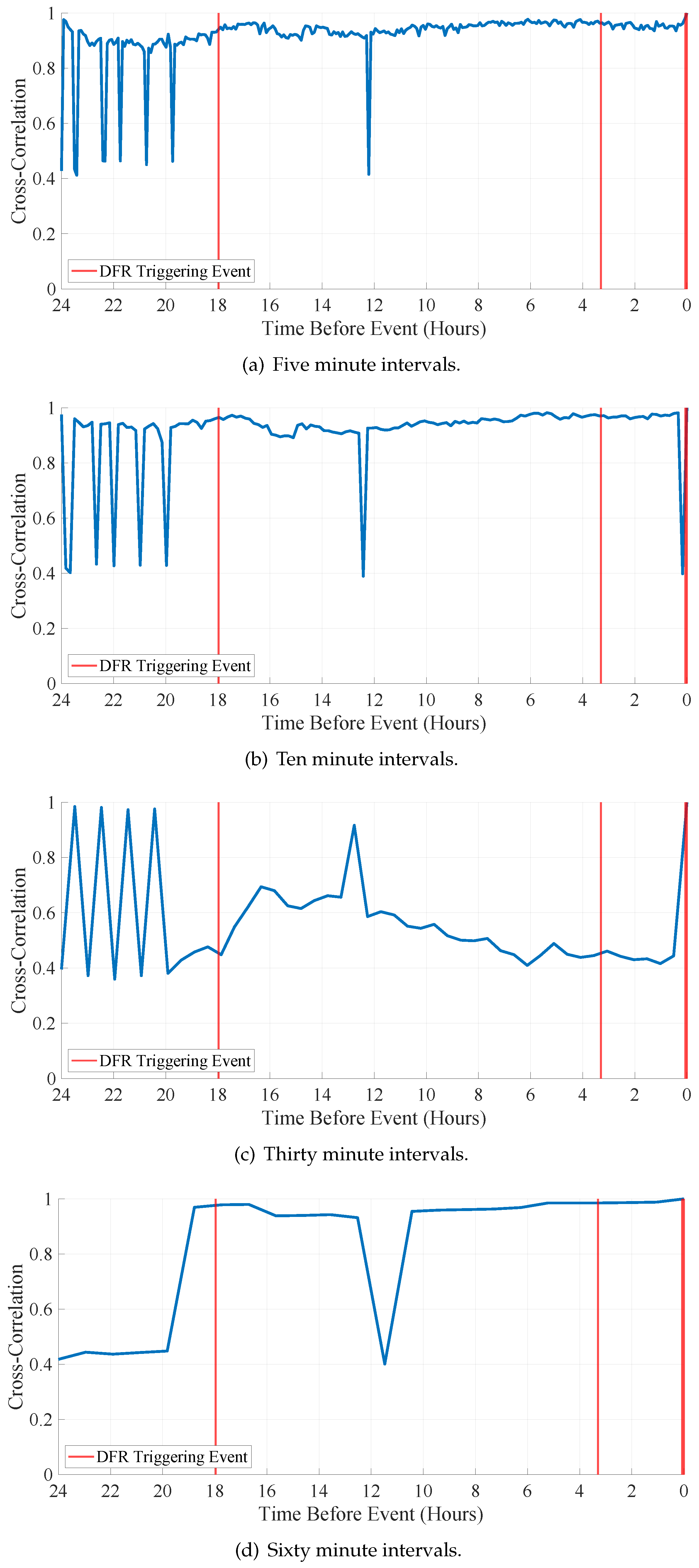
Figure 4.
Use Case #2: Arcing Event IFP: The absolute difference in RMS histogram variance between two 161 kV transmission lines for twenty-four hours. Histograms are generated every five, ten, thirty, and sixty minutes.
Figure 4.
Use Case #2: Arcing Event IFP: The absolute difference in RMS histogram variance between two 161 kV transmission lines for twenty-four hours. Histograms are generated every five, ten, thirty, and sixty minutes.
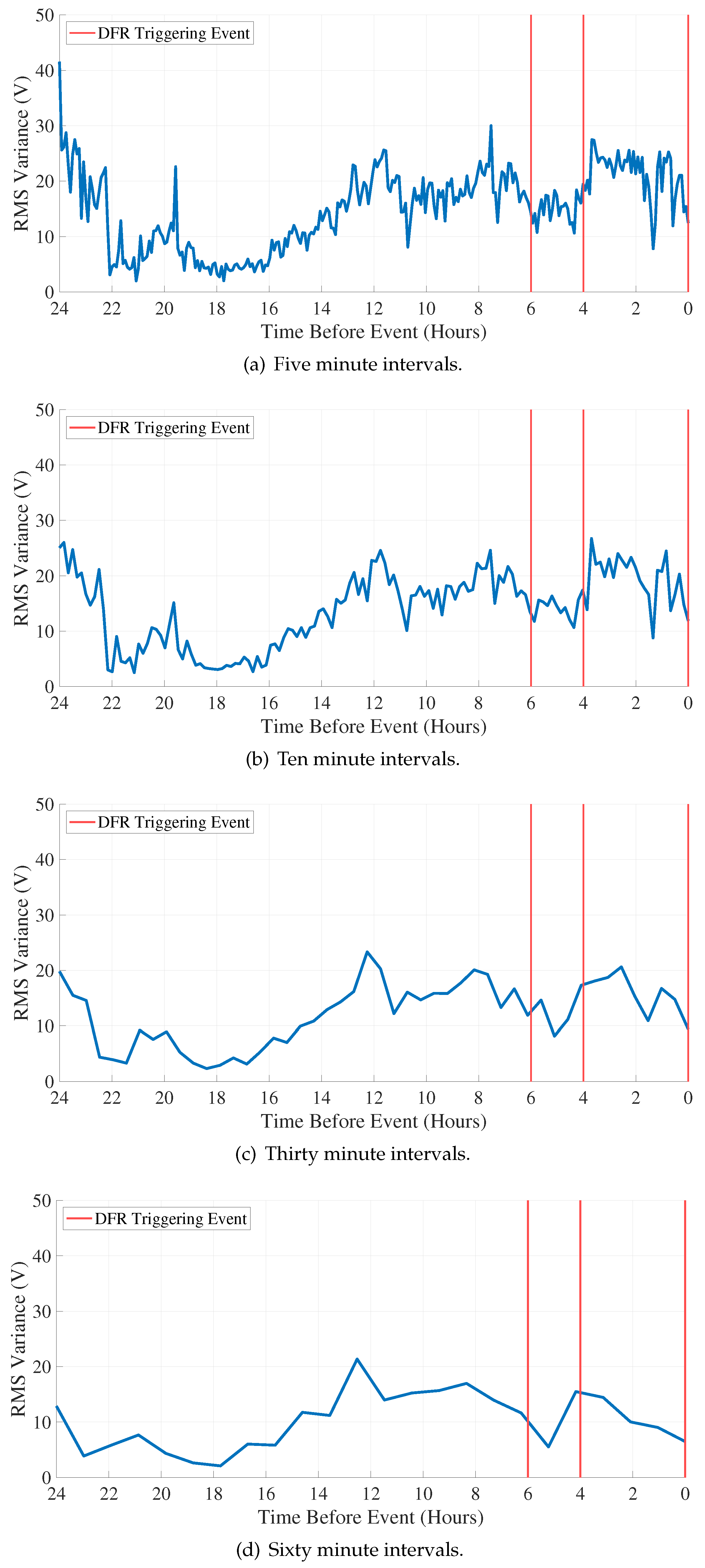
Figure 5.
Use Case #3: DFR Sampling Error: Frequency histograms generated from data recorded by a DFR with a fault DSP chip firmware.
Figure 5.
Use Case #3: DFR Sampling Error: Frequency histograms generated from data recorded by a DFR with a fault DSP chip firmware.
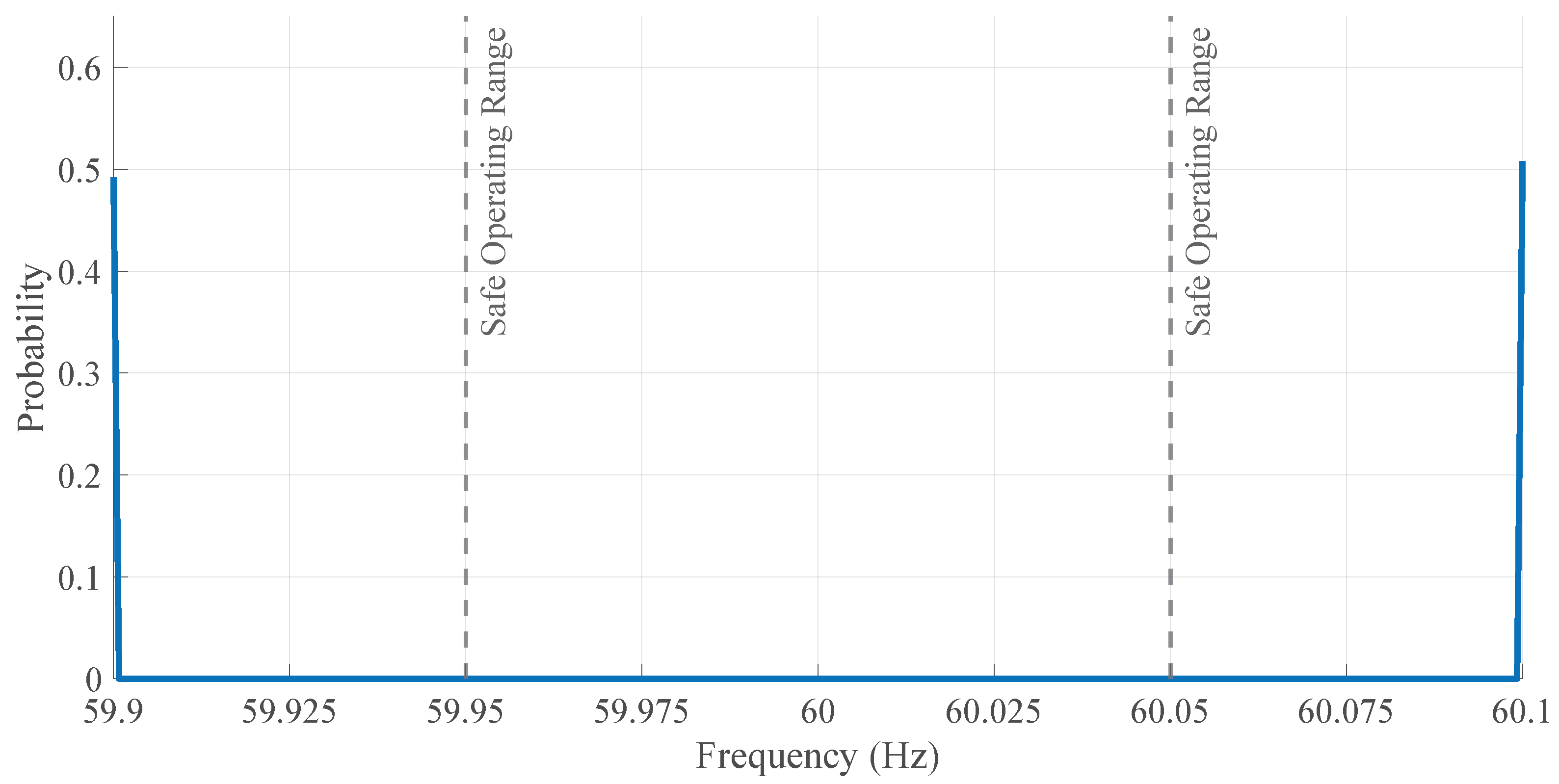
Table 1.
Table listing each use case, the corresponding histogram used for IFP of the selected use case, and the IFP approach’s predicted time before DFR triggering event occurrence.
Table 1.
Table listing each use case, the corresponding histogram used for IFP of the selected use case, and the IFP approach’s predicted time before DFR triggering event occurrence.
 |
Table 2.
Task runtime in milliseconds when calculating the cyclic, residual, frequency, and energy histograms at sixty-, thirty-, ten-, and five-minute intervals.
Table 2.
Task runtime in milliseconds when calculating the cyclic, residual, frequency, and energy histograms at sixty-, thirty-, ten-, and five-minute intervals.
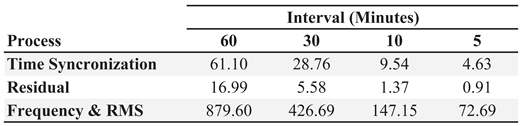 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







