Prerpints.org logo
Preprint
Article

Preparation and Refinement Mechanism of a New Master Alloy Al-5Ti-1B-1RE Refiner

Altmetrics

Downloads

54

Views

27

Comments

0

Submitted:

16 September 2024

Posted:

17 September 2024

You are already at the latest version

Alerts
Abstract
To obtain high quality grain refiner, a new Al-5Ti-1B-1RE master alloy grain refiner was synthesised by melt-matching method. Thermodynamic calculations and kinetic analyses, which were seriously missing from the study of key issues during the preparation process, were investigated. The microstructure and properties, comparison of the refining effect of different grain refiners on industrial pure aluminium and its refining mechanism were analysed with the help of X-ray diffraction (XRD), optical microscopy (OM), scanning electron microscopy (SEM) and energy spectroscopy, transmission electron microscopy (TEM) and an electronic universal testing machine (CSS-44100). The experimental results show that the second-phase particles in the Al-5Ti-1B-1RE master alloy matrix synthesised by the melt-matching method are mainly TiB2、 A13Ti、Ti2A120RE, etc. The magnitude of the free energy ΔG of the synthesis reaction is calculated to be ΔGTiB2<ΔGAl3Ti<ΔGTi2A120RE. When the temperature is low (undercooling ΔT is large), the nucleation rate N mainly depends on the kinetic atomic diffusion activation energy Q, while the thermodynamic nucleation work becomes a secondary factor, and vice versa. The industrial pure aluminum refined by the new grain refiner has almost transformed from coarse columnar crystals to fine equiaxed crystals, with an average grain size of 70.2 μm, which was 36.18% and 20.66% smaller than that refined by domestic and imported Al-Ti-B wire master alloy grain refiner, and its mechanical properties of tensile strength σb was increased by 11.94%, 8.29%, and elongation at break δ was improved by 31.79%, 17.41%, respectively. The main mechanism for refining pure aluminum in Al-5Ti-1B-1RE master alloy is the formation of TiA13 on TiB2 particles, the release of RE atoms from Ti2A120RE phase surrounding TiAl3, and the partial transformation into TiA13 phase, which promotes the dual nucleation refinement mechanism and the pinning effect of rare earth elements on grain boundaries.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

Aluminium and aluminium alloys have a wide range of applications in aerospace, manufacturing, transportation and mobile communications in automotive and other fields due to their excellent thermal conductivity, low density, high specific strength, and good process properties [1,2,3,4]. The grain refinement treatment of aluminium and aluminium alloys has always been a research hot spot. Since the introduction of Al-Ti-B master alloy grain refiner, it has rapidly become the most efficient and widely used grain refiner in aluminium and aluminium alloys with high efficiency grain refining effect, which is a major breakthrough in the grain refining treatment technology [5,6]. It is currently used by approximately 75% of users worldwide and is recognised as one of the most effective grain refiners for aluminium and aluminium alloys [7,8]. With the increasing application of Al-Ti-B master alloy grain refiners in modern aluminum industry, it has been found that their performance defects limit their use in the rolling of high-grade foil materials. The refining effect of high-strength aluminum alloys containing elements such as Zr and Cr is weakened or even lost, resulting in uneven grain structure, known as “grain refiner poisoning” phenomenon, making it difficult to obtain high-quality aluminum products [9,10,11]. And with the increasing use of aluminium and aluminium alloys, the demand for high quality grain refiners is also increasing. Due to the late start of research on grain refiners in China and the blockade of related core technologies by foreign countries, the second particles TiAl3 and TiB2 in the prepared Al-Ti-B grain refiners have larger sizes, fewer quantities, and more severe agglomeration. The refinement effect and product purity are significantly inferior to similar foreign products, and high-quality Al-Ti-B grain refiners need to be imported in large quantities [12]. Therefore, the development of efficient, clean and stable grain refiner is imminent to solve the shortage of Al-Ti-B grain refiner, which is of great practical significance and economic benefits to the development of China's aluminium processing industry.
Therefore, domestic and foreign materials science and technology workers have been exploring a new generation of grain refiner will reduce or eliminate the “grain refiner poisoning”, as a key topic of current research. In recent years, it has been found that the role of rare earth refinement, purification and other functions and the refinement of Al-5Ti-1B master alloy can be effectively combined to develop a new type of Al-5Ti-1B-1RE mater alloy grain refiner, which can significantly improve the refining performance of the grain refiner and can reduce or eliminate the phenomenon of“grain refiner poisoning” [13,14,15]. The synthesis and preparation methods of Al-5Ti-1B-1RE master alloy are constantly evolving and improving, with various advantages and disadvantages for each synthesis method [16,17,18,19,20]. However, the melt-matching method has the advantages of fast reaction, low synthesis temperature, low energy consumption, and low pollution, and stands out among many synthesis methods [21,22,23]. A new Al-5Ti-1B-1RE master alloy grain refiner was synthesized by introducing rare earth elements during the synthesis of Al-Ti-B master alloy. Materials science and technology workers to improve the domestic Al-5Ti-1B-1RE grain refiner grain refining performance, carried out a lot of research work and achieved certain results, but still failed to have a breakthrough. The reasons for this are related to the lack of systematic and detailed thermodynamics calculations and kinetic analysis of the preparation process of Al-5Ti-1B-1RE grain refiner, the lack of in-depth research on the refining mechanism and the control of the second phase, and the lack of key technologies. This is the bottleneck in the development of obtaining high-quality Al-5Ti-1B-1RE grain refiner. At present, the research on the grain refinement mechanism of aluminum and aluminum alloys mainly focuses on two aspects [24,25]: first, the theoretical research on the modeling method of the grain refinement mechanism of aluminum and aluminum alloys. Second, based on the theoretical study, the refinement methods of aluminum and aluminum alloys are formulated and optimized, which mainly include physical methods such as controlling the cooling rate, vibration, stirring, and ultrasonic treatment of the melt, and chemical methods such as the addition of grain refiners. At present, there are various nucleation theories in the study of the refinement mechanism of Al-5Ti-1B-1RE grain refiner, but no consensus has been reached [26,27,28]. The fine dispersed second phase in grain refiner is the key to improving their refining performance and has been recognized. In this paper, thermodynamic calculations, kinetic analysis, and the refinement mechanism of Al-5Ti-1B-1RE grain refiner synthesis and preparation were carried out in order to provide a useful reference for the research and development of high-quality grain refiners. It also provides a solid theoretical foundation and practical reference value for fully tapping into the potential of materials, expanding the application of aluminum and aluminum alloys in China's new energy vehicles and meeting the demand for lightweight manufacturing.

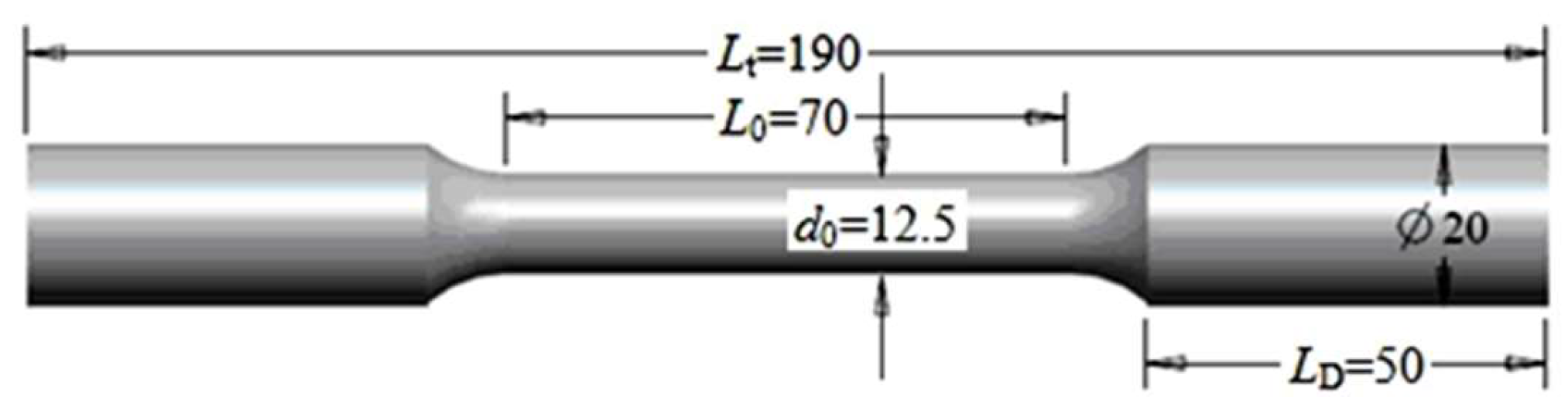
2. Test Materials and Methods

2.1. Test Materials

The main materials used are: pure aluminum, aluminum powder, potassium fluoroborate (w (KBF4)≥98.00%), titanium powder (w (Ti)%≥99.00%), cerium lanthanum rich rare earth, hexachloroethane (C2Cl6), covering agent, grain refiner, degassing agent, coating, graphite stirring rod, JJ-1 precision booster electric mixer and other auxiliary materials and tools. When calculating the alloy element composition, the upper limit value of the burning loss is taken for the alloy elements with high burning loss.

2.2. Methods

2.2.1. Al-5Ti-1B-1RE Master Alloy Synthesized by Melt-Matching Method

After the titanium powder, aluminum powder, potassium fluoborate (KBF4) and hexachloroethane (C2Cl6), which were removed from the water, were proportioned according to the appropriate stoichiometric ratios, they were fully ball-milled on a high-speed ball mill, then taken out, and pressed into blocks under a certain amount of stress on a universal test tensile machine. Then the graphite crucible with a certain mass of pure aluminum was placed in the SG2-7.5-12 well type resistance furnace to heat up to 730℃. A certain thickness of special covering agent was added on the surface of Al melt, and it was stirred and stripped of slag after the pure aluminum was completely melted. The furnace temperature was raised to 830℃, the treated briquettes and mixed rare earth RE were wrapped with aluminum foil and then pressed into the middle and lower part of the melt in batches with graphite bellows, the aluminum melt was stirred with graphite rods and JJ-1 precision power increasing electric stirrer and the reaction was fully carried out by holding the temperature for 20 min and stirring once every 5 min to fully react. The temperature was lowered to 780 ℃, refined, degassed, and stood for 5 minutes until the slag floated up. The slag was thoroughly removed, and the alloy liquid in the crucible was poured into the mold to synthesize the Al-5Ti-1B-1RE master alloy grain refiner.

2.2.2. Refinement Test Process

The graphite crucible containing equal mass of pure aluminium was placed in four well resistance furnaces of KSL-12-JY type with the same conditions to be heated, and the temperature was raised to 730 ℃. After the aluminum melt was completely melted, perform slag removal, degassing, refining, slag removal, and pour the 0th group of pure aluminum samples. And the pure aluminium specimen of group 0 was poured. Subsequently to the first, second, third group of molten pure industrial aluminium were added to the intermediate alloy grain refiner in the actual production of the amount of addition as a standard: are 0.20% of the molten aluminium, i.e., Ti (wt%) = 0.01% of the domestic, imported Al-5Ti-1B wire master alloy grain refiner, and self-made Al-5Ti-1B-1RE master alloy grain refiners were added. The mixture was thoroughly stirred and held for 5 minutes. After slag removal, degassing, refining, and slag removal, these three sets of samples were poured in sequence. After cooling, the poured specimen was prepared into a metallographic sample for observation and processed into a tensile specimen according to the standard GB/T16865-2013. The tensile performance test was carried out on a WDW-10 microcomputer controlled electronic universal testing machine. The total length of the tensile specimen was 190 mm, of which the length of the two clamped ends of the specimen was 50 mm, the diameter of the original cross-section of the parallel length of the specimen was 12.5 mm, and the specimen marking distance before the application of force at room temperature was 70 mm, as shown in Figure 1. The tensile speed was 0.5 mm/min at room temperature. After pulling off the two parts of the specimen closely butted together, the axis of the two parts were located in the same straight line, measuring the specimen after pulling off the standard distance. The tensile strength σb is the stress corresponding to the maximum test force Nb of the specimen during pull-off, and its value is the maximum test force divided by the original cross-sectional area A0 of the specimen [29]:
σ b = N b A 0
The elongation after fractureδ is the percentage of the elongation of the gauge length of the specimen after fracture to the original gauge length
δ = L 1 − L 0 L 0 × 100 %
where: L0—the original gauge length of the specimen; L1—the gauge length of the sample after being pulled apart. To ensure the accuracy of the tensile test data, 5 specimens were stretched in each group and the average value is taken.

3. Results and Analysis

3.1. Phase Analysis of Grain Refiner for Al-5Ti-1B-1RE Master Alloy

The Al-5Ti-1B-1RE intermediate alloy prepared by melt-matching synthesis was analysed for physical phase by XRD diffraction technique. The phase analysis of Al-5Ti-1B-1RE master alloy synthesized by melt-matching method was carried out using XRD diffraction technology. The chemical composition analysis was carried out using German Spike SPECTRO MAXx mm06 direct reading spectrometer. The microstructure of the second phase was analyzed using scanning electron microscopy (SEM), energy dispersive spectrometer, and transmission electron microscopy (TEM). The refinement effect of industrial pure aluminum was observed and analyzed using optical microscope (OM). In the process of synthesis and preparation, when hexachloroethane was pre-pressed into a block and pressed into the aluminum liquid, the absorption rate of the reactants can be greatly increased. The main reason for this was that hexachloroethane produced a large amount of gas at high temperatures, which can play a role in rapid stirring, so that the aluminum powder, titanium powder and potassium fluoborate were fully dispersed and in contact with the melt. C2Cl6 is a white crystal with a density of 2.091 g/cm3 and a sublimation temperature of 185.5℃. It produces the following reaction when pressed into an aluminum liquid [30]:
C2Cl6 → C2Cl4 + Cl2
2Al + 3Cl2 → AlCl3
3C2Cl6 + 2Al → 3C2Cl4 + 2AlCl3
The boiling point of the reaction product C2Cl4 is 121℃, and participates in refining together with AlCl3, so that the titanium powder and potassium fluoroborate absorption will be greatly improved. The Al-5Ti-1B-1RE master alloy grain refiner synthesized at a reaction temperature of 830 ℃ was subjected to X-ray diffraction phase analysis, as shown in Figure 2.
From Figure 2, it can be seen that during the reaction process, in addition to the diffraction peaks of Al phase, there are also diffraction peaks of TiA13, TiB2 and Ti2A120RE phases. This indicated that Ti, which was supersaturated in the Al melt, should have been synthesized with Al to form the TiA13 phase. However, due to the introduction of RE elements, its activity in the Al melt was very high and the surface energy was also very high, in order to reduce the surface energy and its solid solubility in the aluminum melt was very low, there was a free state of the RE elements involved in the reaction of A1 and Ti to generate the Ti2A120RE phase, i.e., Ti2A120Ce and Ti2A120La phase. Due to the fact that KBF4 and Ti powder were added to the aluminum melt in the form of pressed blocks, the atomic density and reactivity were significantly lower than those of RE added in bulk. Therefore, they preferentially interacted with the Al melt. It mainly underwent the following reactions (6) - (9) [31]:
2KBF4(l)+3Al(l)=AlB2+KAlF4(l)
Ti(s) +3Al (l) =TiAl3(s)
AlB2(s) +TiAl3(s) =TiB2+4Al (l)
14Al+2TiA13+RE=Ti2A120RE
As the synthesis reaction proceeded the Ti2A120RE phase was increasing and the amount of TiA13 phase was decreasing. However, the reaction (7) proceeded sufficiently due to the excess of added Ti elements, so there was still residual TiA13 phase present in the Al melt after TiA13 was fully involved in the reaction (9). The TiB2 phase was very stable, and it did not react with RE, and no titanium-boron rare-earth compounds were detected at the end of the reaction. So the second phase in the synthesized and prepared refiner was mainly TiA13, TiB2, Ti2A120RE phases, as shown in Figure 2. The chemical composition of the synthesized and prepared Al-5Ti-1B-1RE master alloy refiner was examined as shown in Table 1, and from the data, it can be indicated that the synthesized chemical composition achieved the chemical composition of the design goal.
The morphological characteristics and distribution of the second phase in the synthesized and prepared Al-5Ti-1B-1RE master alloy were analyzed by scanning electron microscopy (SEM) and energy spectroscopy (EDS). Synthesis reaction temperature of 830 ℃, as shown in Figure 3, in which the size of the larger gray blocky, with obvious angular phase, as pointed out A in Figure 3. After further analysis by energy spectroscopy, as shown in Figure 3b, it mainly contained two elements of aluminum and titanium, with an atomic percentage content ratio of Ti:Al ≈ 1:3, which can be determined as TiA13. The appearance shape was similar to TiA13, with a larger size and a whitish surface, as indicated by B in Figure 3. According to the energy spectrum analysis, as shown in Figure 3 (c), it mainly contained titanium, aluminum, and rare earth elements, with an atomic percentage ratio of Ti: Al: RE ≈ 2:20:1. Based on Figure 2, it can be determined that the Ti2A120RE phase was composed of Al, A13Ti, and RE, and had a complex face-centered cubic structure. The small-sized black gray particles distributed in the matrix, as indicated by C in Figure 3, were analyzed by energy spectrum. As shown in Figure 3d, they mainly contain two elements, titanium and boron, and were distributed in the aluminum matrix. Their atomic percentage ratio was Ti: B ≈ 1:2. Combined with Figure 2, it can be determined that they were TiB2 phase, which had good chemical stability and did not react with RE. RE mainly acted as a surfactant, dispersant, and catalyst in aluminum melt, adsorbing and forming a liquid film at the solid-liquid interface, hindering the contact between particles, reducing the surface tension of the interface, reducing the contact and repulsive force between second phase particles, reducing agglomeration, and making TiB2 particles more evenly distributed. It was extremely beneficial for improving the surface wettability and grain refinement of TiA13 and TiB2 in aluminum melt.
From the TEM image of TiB2 in the Al-5Ti-1B-1RE master alloy at a synthesis temperature of 830 ℃ in Figure 4, it can be clearly observed that TiB2 had a relatively regular hexagonal shape with a tendency to aggregate, as indicated by the red arrow in Figure 4. TiB2 particles aggregated together, with a cluster size of approximately 1.2μm, while the size of the individual TiB2 particles is about 0.6 μm, as indicated by the arrows in Figure. 4. When evaluating TiB2 contained in aluminum master alloy refiners, the standard specifies [32]: the size of loose TiB2 agglomerates ≤ 25μm, the presence of no dense TiB2 agglomerates and TiB2 particles with a size ≤ 2μm should account for more than 90% with a roughly uniform and dispersed distribution. The TiB2 agglomerate size in the Al-5Ti-1B-1RE master alloy prepared at synthesis temperature was approximately 1.0 μm ≤ 25μm, with more than 90% of TiB2 particles having sizes ≤ 2 μm and no dense TiB2 agglomerates present. This indicated that the TiB2 particle size in the grain refiner prepared by this process had reached the standard specification.

3.2. Calculation and Analysis of Thermodynamics

Computational analysis of thermodynamics, which was seriously missing from the study of key issues in the preparation process, was carried out during the synthesis of Al-5Ti-1B-1RE master alloys prepared by the melt-matching method due to the approximate Ti/B mass ratio of 5:1 exceeding the mass ratio of Ti and B in TiB2 (2.2׃1). Therefore, the main reaction products of KBF4 and Ti in the aluminium alloy melt at atmospheric pressure 1103.15K (temperature 830 °C) are AlB2, TiAl3 and TiB2, whose thermodynamic calculations were in accordance with the conditions of the standard reaction heat effect method calculations, which were carried out by the Kirchhoff equations for the first approximation of the standard reaction heat effect [33]:
Δ G T θ = ( Δ H 298 θ ± Σ Δ H p h a s e ) − T ( Δ S 298 θ ± Σ Δ H p h a s e T p h a s e )
Where: Δ H p h a s e and Δ H p h a s e T p h a s e are the heat and entropy of phase transition of a substance. If the substance undergoing phase transition is a product in the reaction, it is marked with a positive sign, and if it is a reactant, it is marked with a negative sign.
During the synthesis of the prepared Al-5Ti-1B-1RE master alloys by the melt-matching method, the main reactions occurring were as follows:
2KBF4(l)+3Al(l) =AlB2+2KAlF4(l)
Δ G 1 θ ( AlB 2 ) = - 48072 + 36 . 363 T
=-48072+36.363×1103.15=-7928.15655
Ti(s) +3Al (l) =TiAl3(s)
Δ G 2 θ ( TiAl 3 ) = - 18227 + 15 . 712   T
=-18227+15.712×1103.15=-894.3072
AlB2(s) +TiAl3(s) =TiB2(s) +4Al (l)
Δ G 3 θ ( TiB 2 ) = - 73381 + 38 . 996 T
=-73381+38.996×1103.15=-30362.5626
According to the thermodynamic data for the standard reaction Gibbs free energy change ∆G ≤ 0, the reaction proceeds spontaneously to the right. When the synthesis temperature was 1103.15 K (830 °C), it was calculated that (1) Δ G 1 θ ( AlB 2 ) = -48072 + 36.363 × 1103.15= -7928.15655 kJ•mol-1< 0, AlB2 can be produced in the aluminium melt. When Δ G 1 θ ( AlB 2 ) ≥ 0 , the temperature T1 ≥ 1322.00 K (1048.85 ℃), the reaction (11) proceed to the left and AlB2 cannot stabilise, since the refiner synthesis temperature was at atmospheric pressure 830 ℃ < 1048.85 ℃, AlB2 can stabilise at 830 ℃. When Δ G 2 θ ( TiAl 3 ) = -18227+15.712 × 1103.15=-894.3072kJ• mol-1<0, reaction (12) proceeded to the right to generate TiAl3. When Δ G 2 θ ( TiAl 3 ) ≥ 0 , the temperature T2 ≥ 1160.07K (886.92 ℃), reaction (12) proceeded to the left, and TiAl3 could not exist stably. TiAl3 decomposed and dissolved. Since the synthesis temperature of the grain refiner was at atmospheric pressure 830 ℃ ＜ 886.92 ℃, TiAl3 could exist stably at 830 ℃.When Δ G 3 θ ( TiB 2 ) = -73381+38.996T3=-73381+38.996 × 1103.15
=-30362.5626 kJ • mol-1<0, reaction (13) proceeded to the right, producing TiB2, which had a much lower free energy ∆ G than AlB2. When Δ G 3 0 ( TiB 2 ) ≥ 0 , T3 ≥ 1881.76 K (1608.61℃), the reaction (13) proceedsed to the left and TiB2 cannot be stabilised. TiB2 can be stabilised in the synthesis process at atmospheric pressure of 830°C. After adding Al-5Ti-1B-RE refiner to the melt, Al3Ti was dissolved and excess Ti was released into the melt. Due to the more negative Gibbs free energy of TiB2 compared to AlB2 and Al3Ti, from a thermodynamic perspective, AlB2 was extremely unstable in high-temperature A1-Ti-B-RE melts. As the reaction time prolonged, the transformation of AlB2 to TiB2 occurred, i.e., chemical reaction Equation (8): AlB2(s) +TiAl3(s) =TiB2+4Al (l). At the same time, the melting point of AlB2 (950 ℃) was much lower than that of TiB2 phase (2980 ℃), so Ti in the melt tends to combine with B to form TiB2. According to the principle of minimum energy in the system, the system always needs to adjust itself to reach the lowest energy and be in a stable equilibrium state. Therefore, reaction Equation (8) was sufficient to fully occur, ensuring the stable existence of TiB2 particles in the aluminum melt. Under the influence of gravity, the second phases TiB2 and TiAl3 generated by the reaction enter the aluminium melt, where TiAl3 interacted with it due to the presence of rare earths in the melt:
14 Al + 2 TiA 1 3 + RE = Ti 2 A 1 20 RE  
Δ G 4 θ ( Ti 2 A 1 20 RE ) = - 227024 + 74 . 837 T 4  
=-227024+74.837×1103.15=-144467.56345 kJ·mol-1< 0
When the synthesis temperature was 1103.15 K (830 °C), by calculating (1) Δ G 1 θ ( Ti 2 A 1 20 RE ) = -227024 + 74.837 × 1103.15 = -144467.56345 kJ·mol-1< 0, the result was the production of Ti2A120RE. When T4 ≥ 3033.58 K (2760.43 ℃), Δ G 4 θ ( Ti 2 A 1 20 RE ) ≥ 0 , the reaction (14) proceeds to the left, Ti2A120RE can not be stabilised, and Ti2A120RE decomposed and dissolved, and since the refinement agent synthesis temperature was at atmospheric pressure 830℃ < 2760.43℃, Ti2A120RE can be stabilised at 830 ℃. According to the free energies, it can be determined that the synthesis temperature of the grain refiner was 830 ℃, and each reaction (11) - (14) can proceed to the right.
The Gibbs free energy was the lowest in the chemical reaction for synthesizing Ti2A120RE, indicating its best stability. According to the Gibbs free energy function of Equation (14), it can be calculated that at a temperature of T=1103.15 K, ΔG=-144467.56345 kJ • mol-1. The lowest value indicated a very good trend of spontaneous chemical reaction, which was also the fundamental reason why the melt matching reaction method can significantly reduce production costs. Therefore, the synthesis temperature not only affected the thermodynamic process of the reaction, but also caused changes in the composition and structural state of the melt by affecting the stability of the compound, and inherited this change into the solid structure. Therefore, when the synthesis temperature was higher than a certain value, the decomposition of certain phases (e.g. TiAl3, etc.) occurred, which changed the structure of the melt composition, thus affecting the kinetic process of crystallisation.

3.3. Crystallization Kinetics Analysis

The total free energy of the system decreases as the crystal size grows with the growth of the nucleus during the crystallisation process. The reaction continues in a direction that is conducive to the growth of the crystal nucleus. The growth of crystal nuclei is considered to be a process in which atoms in the liquid phase migrate to the surface of the crystal nucleus, i.e., the liquid-solid interface advances towards the liquid phase. During the solidification process, there are two types of atomic migration occurring simultaneously at the liquid-solid interface, namely, the migration of atoms from the liquid phase to the solid phase and the migration of atoms from the solid phase to the liquid phase. If N represented the number of atoms that migrate per unit area in time t, then [34]:
R F   =   ( d N dt ) F = A F G F N L ν L exp ( - O F κ T )
R m   =   ( d N dt ) m = A m G m N s ν s exp ( - O m κ T )
Where: RF - the solidification rate, Rm - melting rate, AF - the probabilities of liquid phase atoms reaching the solid phase, Am solid phase atoms reaching the liquid phase and being able to settle (without being bounced back due to collisions), GF - the probabilities of liquid phase atoms transitioning to solid phase, Gm -the probabilities of solid phase atoms transitioning to liquid phase, NL - the atomic migration numbers per unit area of liquid at the interface, Ns the atomic migration numbers per unit area of solid phases at the interface, νL - the vibrational frequencies of the atoms in the liquid, νs - the vibrational frequencies of the atoms in the solid phases, QF - the activation energies of the atoms for the leaps from the liquid phase to the solid phase, Qm - the activation energies of the atoms for the leaps from the solid phase to the liquid phase.
If Ti (interface temperature) = Tm (melting point temperature), then RF = Rm, Solidification and melting were in dynamic equilibrium, i.e., the number of atoms that migrated from the liquid phase to the solid phase nucleus was equal to the number of atoms that migrated from the nucleus to the liquid phase, so the nucleus cannot grow. To promote the growth of crystal nuclei, that was, to push the solid-liquid interface into the liquid phase, RF >Rm was required. The interface temperature Ti that satisfied this condition must be lower than the melting point temperature Tm, that was, there must be a certain dynamic (kinetic) undercooling degree ΔTk (ΔTk = Tm – Ti) at the interface . The dynamic undercooling ΔTk was necessary for achieving net atomic transport from liquid to solid at the interface. And in the supercooled liquid, a large number of phase undulations of varying sizes sprang up every instant. At a certain temperature, the probability of phase fluctuations of different sizes occurring varied. The probability of phase fluctuations occurring in both large and small sizes was small, and there was a limit value rmax for the largest phase fluctuations occurring at each temperature. The size of rmax was related to temperature. The higher the temperature, the smaller the rmax size, and the lower the temperature, the larger the rmax size. The larger phase fluctuations that appeared in supercooled liquids were likely to transform into crystal nuclei during crystallization, and these phase fluctuations were the germ of the crystal nucleus, namely the crystal embryo. The effect of crystal embryo on the crystallisation kinetic process, the nucleation rate (I) of the solid phase precipitated from the liquid phase [35]:
I = k N V P exp [ - 16 π σ α L 3 f ( θ ) 3 K b Δ S 2 Δ T 2 ]
Where: I - nucleation rate; k - coefficient of Boltzmann's constant with respect to atomic diffusion; N V P - number of nuclei in the melt; ΔS - entropy of nucleation; ΔT - supercooling of nucleation.
According to Equation (17), the nucleation rate I was directly proportional to the number of embryos N V P in the melt, and increased exponentially with the increase of nucleation undercooling ΔT. Therefore, when preparing Al-5Ti-1B-1RE master alloy by melt matching method, the solid-liquid interface advanced towards the liquid phase when the solidification rate RF >Rm melting rate. If the undercooling degree ΔT of nucleation was larger and the critical number of embryos N V P was greater, the nucleation rate I was higher, vice versa. The higher the melt temperature, the smaller the nucleation supercooling ΔT, the stronger the diffusion of atoms, the smaller phases may merge and grow preferentially and the smaller the number of critical embryos, the lower the nucleation rate I was.
From the above, it can be seen that when the Al-5Ti-1B-1RE master alloy was prepared by the melt-matching method, the nucleation rate I of the undercooled liquid mainly depended on the thermodynamic nucleation work at higher temperatures (with lower undercooling ΔT), and the activation energy Q of dynamic atomic diffusion became a secondary factor. When the temperature was low (with a large degree of undercooling ΔT), the nucleation rate N mainly depended on the kinetic atomic diffusion activation energy Q, while the thermodynamic nucleation work became a secondary factor. When the temperature was appropriate, there was a certain degree of undercooling ΔT, and the thermodynamic nucleation rate I1 and the dynamic nucleation rate I2 had an optimal combination. At this point, the nucleation rate I reached its maximum value and a “peak” appeared on the nucleation rate curve, which was inherited into the solid structure.
Preprints 118364 g005
Figure 5. Relationship curve between nucleation rate I and undercooling ΔT.
Figure 5. Relationship curve between nucleation rate I and undercooling ΔT.
Preprints 118364 g005

3.4. Refinement Analysis of Different Grain Refiners

3.4.1. Analysis of Refining Effects of Different Grain Refiners

The self-made Al-5Ti-1B-1RE master alloy grain refiner was used to refine industrial grade aluminium in comparison with the home-made Al-Ti-B wire and the Al-Ti-B wire master alloy grain refiner manufactured by the British company LSM under the same refining test conditions. The unrefined pure aluminium microstructure was coarse columnar crystals with hardly a single intact grain placed in the field of view, as shown in Figure 6a. The grain size of industrial pure aluminium was significantly reduced by the master alloy grain refiner. When adding domestic Al-Ti-B wire master alloy grain refiner, most of them were equiaxed crystals, but there were still a considerable number of coarse grains, with an average grain diameter of 95.6 μm. And some of the grains had sharp corners, which was detrimental to the mechanical properties of refined pure aluminium, and played a weakening effect. In the green circles in Figure 6b, the grains indicated by the red arrows had obvious sharp corners. When the imported Al-Ti-B wire mastrer alloy was added, its grain size was smaller than that of the domestic Al-Ti-B wire master alloy refiner added in equal amount, but the grain size was still somewhat uneven, with an average grain diameter of 84.7 μm, and there were few grains with sharp corners in the grains. This indicates that the effect of imported Al-Ti-B wire master alloy was better than that of domestic Al-Ti-B wire master alloy, and its refinement effect was shown in Figure 6c. When the self-made Al-5Ti-1B-1RE master alloy grain refiner was added, the grain size was significantly refined, and most of them had been transformed into fine equiaxed crystals. The grain size was smaller than that of domestic and imported Al-Ti-B wire master alloy grain refiner, and the average grain diameter was 70.2 μm. There was an obvious advantage in the refining effect and grain uniformity, as shown in Figure 6d. The industrial pure aluminium refined by the self-made Al-5Ti-1B-1RE master alloy grain refiner had rounded grains, close to the equiaxed grain shape, with little cutting effect on the matrix, and its high level of refinement was assessed to have reached the fine grain level in terms of average grain diameter [36].

3.4.2. Analysis of Refining Properties of Different Grain Refiners

The mechanical tensile properties of industrial pure aluminium refined by different grain refiners were tested and the results are shown in Figure 7. Unrefined industrial pure aluminum, domestically produced Al-Ti-B wire master alloy grain refiner, Al-Ti-B wire master alloy grain refiner produced by LSM company in the UK and self-made Al-5Ti-1B-1RE master alloy grain refiner refined industrial pure aluminum were marked as Group 0, Group 1, Group 2, and Group 3 specimens respectively, and the tensile strength σb and elongation at break δ of each group of tensile specimens were measured. From the test results of tensile properties of the specimens, it can be seen that the tensile strength σb and elongation at break δ of the specimens of group 0, group 1, group 2 and group 3 increased in order. And their tensile strength σb was 53.00 MPa, 67.00 MPa (26.42% higher than pure aluminium σb), 69.26 MPa (30.68% higher than pure aluminium σb), 75.00 MPa (41.51% higher than pure aluminium σb), respectively. The tensile strength σb of group 3 was increased by 11.94% and 8.29% compared to group 1 and group 2 specimens, respectively.The elongation rates at break δ were 23.38%, 39.20% (increased by 67.59% compared to pure aluminum δ), 44.00% (increased by 88.54% compared to pure aluminum δ) and 51.66% (increased by 120.96% compared to pure aluminum δ), respectively. The elongation δ of group 3 increased by 31.79% and 17.41% compared to group 1 and 2 specimens, respectively. The tensile strength σb and elongation at break δ of Group 1, Group 2 and Group 3 specimens were increased compared to Group 0 specimens tensile, especially Group 3 specimens were significantly increased, which also corresponded to the effect of different types of master alloy refiners refining in Figure 6.
The grain size directly determined the mechanical properties of aluminum and aluminum alloys. The level of mechanical properties also directly reflected the degree of grain refinement, as expressed by the Hall Petch formula [37]:
σ = σ0 + Kd-1/2
Where:σ0 - constant represents the resistance to deformation within the crystal, which is approximately 2-3 times the critical shear stress in the slip direction of a single crystal on the slip plane. K-constant characterizes the influence of grain boundaries on deformation, which depends on the structure. According to Equation (18), the tensile strength σ of polycrystalline materials is linearly related to the reciprocal of the square root of their grain diameter d, and the smaller the grain size, the higher the strength. This indicates that with the addition of grain refiners to industrial pure aluminium, the number of non-spontaneous nucleation of its second phase particles increases significantly, effectively promoting nucleation and grain refinement. The smaller the grain size, the more grain boundaries there are, and the greater the deformation resistance, the higher the macroscopic tensile strength. On the other hand, under the same external force, the smaller the grain size, the more uniform the deformation of each grain, and the lower the probability of stress concentration. Cracks are less likely to initiate and propagate, and can withstand a larger amount of deformation before fracture, resulting in higher macroscopic plasticity. When using self-made Al-5Ti-1B-1RE master alloy to refine pure aluminum, a large number of effective second phase nucleation particles were released in a short period of time, generating new nucleation particles before the growth of the melt, hindering the growth of columnar crystals, and changing the crystal growth morphology towards fine equiaxed crystals, promoting grain refinement and improving the toughness of the materials. The mechanical properties of pure aluminum refined by adding self-made Al-5Ti-1B-1RE master alloy were significantly better than those of industrial pure aluminum refined by adding an equal amount of Al-5Ti-1B wire mater alloy, as shown in Figure 7. In addition, the presence of inclusions, impurities or gases in the industrial pure aluminium melt can lead to the presence of various defects in the crystals, such as porosity, porosity, etc., which significantly reduced the overall performance of industrial pure aluminium [38]. However, the RE element itself has the function of purifying aluminum melt, significantly reducing impurities and defects such as pores in pure aluminum, and improving mechanical properties. Therefore, group 3 specimens have the smallest grain size and the highest tensile strength σb and elongation at break δ.

3.4.3. Analysis of Refinement Mechanism of Al-5Ti-1B-1RE Mater Alloy

As the second phase of Al-5Ti-1B-1RE master alloy is mainly TiA13, TiB2 and Ti2A120RE, when added to the industrial pure aluminium melt, TiA13 melting point was 440 ℃ quickly dissolved. TiB2 had a high melting point of 2980 ℃ and still existed in solid form in the melt. TiB2 and TiA13 in the melt had good wettability due to their small wetting angle. The planes formed by the strong covalent bond network of B-B in the TiB2 crystal structure provided the possibility for TiA13 to nucleate on its surface. Therefore, Ti preferentially formed a Ti rich layer around TiB2 particles, with TiB2 particles as the center and TiAl3 forming around TiB2, as shown in Figure 8a,b, in the areas indicated by red arrows A and B. The energy spectrum region scanning analysis was carried out, which mainly containing Al, Ti, B and a small amount of RE, as shown in Figure 8c. Combined with the X-ray diffraction results in Figure 2 and the morphological characteristics of the second phase particles in the Al-5Ti-1B-1RE master alloy, it can be determined that the central black particle material was TiB2, and the phases surrounding TiB2 were mainly TiAl3 and rare earth phases. Ti formed a TiA13 coating layer, namely Ti+3A1⇋TiA13. During the solidification process, a large amount of TiB2 wrapped in a thin layer of TiA13 served as an effective nucleation substrate for α-Al, promoting nucleation and refining the α-Al grains [39].
Simultaneously conducting regional scanning analysis on points C and D in Figure 8a, it was found that regions A and B have the same analysis results. On the other hand, the RE element released by the dissolution of the second phase particle Ti2A120RE phase forms a protective thin layer on the surface of TiA13, i.e., Ti2A120RE⇋14Al+2TiA13+RE, and the energy spectrum analysis of the E and F regions in Figure 8b was shown in Figure 8d, in which the E grey region mainly contained the two elements of aluminium and titanium, and its atomic percentage content ratio was Ti:Al≈1:3, it can be determined that the substance was TiA13. The white region of phase F, which surrounds the bulk TiA13 phase E, was then analysed by energy spectroscopy to contain Ti, Al, and RE with an atomic percentage ratio of Ti: Al: RE ≈ 2:20:1, as shown in Figure 8e. Combined with the results of X-ray diffraction in Figure 1, it can be judged to be the Ti2A120RE phase with a complex face-centred cubic structure. At the same time, due to the release of RE atoms from the Ti2A120RE phase surrounding TiAl3, which was partially converted into TiA13 phase to promote the formation of TiA13 on the surface of TiB2. The TiA13 phase can exist in the aluminium melt for a longer period of time and the refining effect lasted for a longer period of time, which protected the formation of TiA13 on TiB2 grains, i.e., it further promoted nucleation and α-Al grain refinement, as shown in the schematic diagram of the dual nucleation theory in Figure 9, which was consistent with the dual nucleation refinement theory proposed by P.S. Mohanty et al [40].
In addition, the rare earth elements themselves played a positive role in refining pure aluminium, with a portion of the rare earth elements being pushed up to the grain boundaries during solidification process. Due to the RE atomic radius of 0.174-0.204 nm, which was larger than the aluminium atomic radius of 0.143 nm, and the solid solubility in aluminium was extremely low, the precipitation of rare earth elements to cause α-Al lattice distortion, with a strong pinning of grain boundaries and subgranular boundaries, which played a role in refining the grain.
The other part of rare earth elements mainly played a role in promoting the protection of the dual nucleation TiA13 and TiB2 phase during the refinement process. To obtain good refining effect, in the synthesis and preparation of Al-5Ti-1B-1RE master alloy to ensured that TiB2 in the mass ratio of Ti B > 47.867 2 × 10.811 = 2.21 , that was, in addition to the generation of TiB2, the Ti mass to had a surplus, the generation of TiA13, which was a prerequisite for obtaining effective nucleation of TiA13 phase and TiB2 phase. The self-made Al-5Ti-1B-1RE master alloy with Ti B = 5 1 > 2.21 can obtain effective nucleation and better refinement effect.

4. Conclusions

(1)
When synthesizing a new Al-5Ti-1B-1RE master alloy grain refiner by melt matching method, the reaction generated by the second phase TiB2 and TiAl3 into the aluminium melt, Interaction with TiAl3 due to the presence of rare earths in the melt: 14Al+2TiAl3+ RE=Ti2Al20RE.
(2)
When the new Al-5Ti-1B-1RE master alloy grain refiner was synthesised by the melt-mixing method at synthesis temperature of 1103.15 K (830 °C), it was calculated that the magnitude of Gibbs free energy ΔG was ΔGTi2Al20RE<ΔGTiB2<ΔGAl3Ti.
(3)
When the temperature was appropriate, there was a certain degree of subcooling ΔT, the thermodynamic nucleation rate I1 and the kinetic nucleation rate I2 had an optimal fit, at which time the nucleation rate I reached the maximum value, and a “peak”appeared on the nucleation rate curve.
(4)
The mechanical properties of pure aluminum refined by Al-5Ti-1B-1RE master alloy were significantly better than those of pure aluminum added with equal amounts of domestic and imported Al-5Ti-1B wire master alloy. The tensile strength σb and elongation δ were increased by 11.94%, 8.29%, and 31.79%, 17.41%, respectively.
(5)
The refining mechanism of Al-5Ti-1B-1RE master alloy for industrial pure aluminum was a dual nucleation refining mechanism. Due to the addition of RE elements, the refining effect lasts longer.

Author Contributions

Conceptualization, Z.W. and S.W.; methodology, Z.W.; validation, S.W. and X.L.; formal analysis, Q.Y.; investigation, Q.Y. and L.L.; resources, S.W.; data curation, C.D.; writing—original draft preparation, Z.W. and S.M.; writing—review and editing, Z.W. and S.W.; supervision, X.L. and L.L.; funding acquisition, Z.W., Q.Y. and C.D.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China, No.52104375, Major Project of Basic Science (Natural Science) Research of Institution of Higher Education of Jiangsu Province, China, No.22KJA460010, Huai'an Science and Technology Bureau Project, Jiangsu Province, China, No. HABL202206.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhao, H.; Chakraborty, P.; Ponge, D.; Hickel, T.; Sun, B.; Wu, H.; Gault, T.; Raabel, D. Hydrogen trapping and embrittlement in high-strength Al alloys. Nature. 2022, 602, 437–441. [Google Scholar] [CrossRef]
  2. Wang, Z.; Liu, X.; Dong, C.; Chen, J.; Liu., L. Thermal Fatigue Crack Propagation Process and Mechanism of Multicomponent Al-7Si-0.3Mg Alloy. Crystals 2023, 13, 1068. [Google Scholar] [CrossRef]
  3. Njuguna, B.; Li, J.; Tan, Y.; Sun, Q.; Li, P. Grain refinement of primary silicon in hypereutectic Al-Si alloys by different P-containing compounds. China Foundry. 2021, 18, 37–44. [Google Scholar] [CrossRef]
  4. Dong, X.; Feng, L.; Wang, S.; Ji, G.; Addad, A.; Yang, H.; Nyberg, E.; Ji, S. On the exceptional creep resistance in a die-cast Gd-containing Mg alloy with Al addition. Acta Mater. 2022, 232, 117957. [Google Scholar] [CrossRef]
  5. Gao, P.; Zhou, T.; Xu, X.; Gao, Z.; Chen, Li. Refinement Mechanism Research of Al3Ni Phase in Ni-7050 Alloy. Rare Met. Mater. Eng., 2013, 42, 0006–0013. [Google Scholar]
  6. Sotlz, U.; Sommer, F.; Sutttart, B. Phase Equilibrium of Aluminum-Rich AlTiB Alloys-Solubility of TiB2 in Aluminum Melts. Alum. 1995, 350–355. [Google Scholar]
  7. Birol, Y. Performance of Al–5Ti–1B and Al–3B grain refiners in investment casting of AlSi7Mg0.3 alloy with preheated ceramic moulds. Int J Cast Metal Res. 2013, 26, 283．. [Google Scholar] [CrossRef]
  8. Wang, Z.; Si, N. Synthesis and Refinement Performance of the New Al-Ti-B-RE Master Alloy Grain Refiner. Rare Met. Mater. Eng. 2015, 44, 2970–2975. [Google Scholar]
  9. Zhao, Hong-Liang.; Yue, J.; Gao, Y.; Weng, K. Grain and dendrite refinement of A356 alloy with Al-Ti-C-RE master alloy. Rare Met. 2013, 32, 12–17. [CrossRef]
  10. Chen, Y.; Xu, Q.; Huang, T. Microstructure of Al-Ti-B-RE Master Alloy and Its Mechanism of Refining Pure Aluminum. J. Chin.Rare Earth Soc. 2007, 25, 597–602. [Google Scholar]
  11. Yu, L.; Liu, X. Ti transition zone on the interface between TiC and aluminum melt and its influence on melt viscosity. J. Mater Pro Tech. 2007, 182, 519–524. [Google Scholar] [CrossRef]
  12. Li, H.; Chai, L.; Ma, T.; Chen, Z. Synthesis of Al-5Ti-1B Refiner by Melt Recation Method. J. Mater Eng. 2017, 45, 39–45. [Google Scholar]
  13. Wang, Z.; Zhang, Q.; Zhang, M.; Liu, J.; Lv, J. Effect of Refinement and Modification on Microstructure, Properties and Eutectic Silicon Growth Mechanism of Cast A356 Aluminum Alloy. Rare Met. Mater. Eng. 2020, 49, 2665–2673. [Google Scholar]
  14. Chen, Y.; Xu, Q.; Huang, T. Refining performance and long time efficiency of Al-Ti-B-RE master alloy. The Chin. J.Nonferrous Met. 2007, 17, 1232–1239. [Google Scholar]
  15. Han, H.; Lü, C.; Miao, H. Fabrication of a New Mg-50%Al4C3-6%Ce Master Alloy and Its Refinement Mechanism on AZ91D Alloy. Rare Met. Mater. Eng. 2013, 42, 0028–0031. [Google Scholar]
  16. Fan, G.; Wang, M.; Liu, Z.; Liu, Z.; Weng, Y.; Song, T. Grain refinement effects of titanium added to commercial pure aluminum by electrolysis and by master alloys. Chin. J.Nonferrous Met. 2004, 14, 250–254. [Google Scholar]
  17. Nikitin, V.; Wan, Q.; Kandalova1, E.; Makarenko, A.; Yong, L. Preparation of Al-Ti-B grain refiner by SHS technology. Scripta Materialia, 2000, 42, 561–566. [Google Scholar] [CrossRef]
  18. Wang, S.; Wang, M.; Liu, Z.; Liu, Z.; Song, T.; Weng, Y.; Zuo, X. Grain Refining of Aluminum Alloy with Titanium Added by Electrolysis and Structure and Properties of A-l Si Alloy Prepared with It. Light Alloy Fabrication Technology, 2005, 33, 21–24. [Google Scholar]
  19. Murty, B.; Kori, S. Venkateswarlu; Bhat, R.; Chakraborty, M. Manufacture of Al-Ti-B master alloys by the reaction of complex halide salts with molten aluminum. J. Mater Pro Tech. 1999, 89-90, 152–158. [Google Scholar] [CrossRef]
  20. Yu, Y.; Qiu, Z.; Zhang, M.; Xia, A. Development of Aluminum Boron and Aluminum Titanium Boron Master Alloys. Light Met. 1988, 31–33. [Google Scholar]
  21. Yang, S.; Yang, G. Electrolytic production of aluminum alloy. Beijing: Metallurgical Industry Press. 2010.
  22. Lan, Y.; Zhu, Z. Master Alloys for Aluminum Alloys and Their Current Status. Light Met. 2004, 49–51. [Google Scholar]
  23. Yang, S.; Yang, G.; Gu, S. Electrolytic production of aluminum based alloys. Special casting & nonferrous alloys. 2001, 102–104. [Google Scholar]
  24. Yan, J.; Li, P.; Zuo, X.; Zhou, Y.; Luo, X. Research Progress of Al-Ti-B Grain Refiner: Mechanism Analysis and Second Phases Controlling. Mater Rev B: Rev Papers. 2020, 34, 09152–09163. [Google Scholar]
  25. Huang, J.; Sun, M.; Zhang, Y.; Weng, Q.; Chen, Z.; Ma, Q.; Cai, D. Research progress of grain refinement behavior of Al-Ti-B in Al-Si alloys. Nonferrous Met. Mater. Eng. 2022, 43, 47–60. [Google Scholar]
  26. Wang., K.; Cui, C.; Wang, Q.; Liu, S.; Gu, C. The microstructure and formation mechanism of core-shell-like TiAl3/Ti2Al20Ce in melt-spun Al-Ti-B-Re grain refiner. Mater. Lett. 2012, 153–156. [Google Scholar] [CrossRef]
  27. Wang, K.; Cui, C.; Wang, Q.; Zhao, L.; Hu, Y. Microstructure of Al-5Ti-1B-1RE nanoribbon and its refining efficiency on as-cast A356 alloys. J. Rare Earths. 2013, 31, 313–317. [Google Scholar] [CrossRef]
  28. Yang, L.; Zhang, L.; Jiang, H.; He, J.; Zhao, J. Mechanism of grain refinement in Al-Cu alloy by adding trace La and Al-5Ti-1B. Acta Phys. Sin. 2023, 72, 086401–086408. [Google Scholar] [CrossRef]
  29. Cui, Z.; Tan, Y. Metallography and heat treatment. Beijing: China Machine Press.2007.
  30. Huang, Z. Composition optimization, microstructure and properties research of cast AlSi7Cu2Mg alloy. Taiyuan: Master's thesis from North China University. 2009.
  31. Wang, Z.; Si, N. The Effect of the Morphology and Distribution of the Second Phases of Al-Ti-B-RE Master Alloys on Refining Commercially Pure Aluminum. Rare Met. Mater. Eng. 2015, 44, 1494–1498. [Google Scholar]
  32. Liu, X.; Bian, X. Master alloy for microstructure refinement of aluminum alloy. Changsha: Central South University Press. 2012.
  33. Ye, D.; Hu, J. Practical Handbook of the Thermodynamic Data for Inorganic Substances. Beijing: Metallurgical Industry Press, 2002.
  34. Wang, Z. Fundamentals of Materials Science. Beijing: China Machine Press. 2023.
  35. Cai, Xun. Fundamentals of Materials Science and Engineering. Shanghai: Shanghai Jiao Tong University Press. 2017.
  36. Chen, X.; Geng, H.; Li, Y. Quantitative metallographic analysis of modification level of hypoeutectic Al-Si alloys. Acta Metall Sin. 2005, 41, 891–896. [Google Scholar]
  37. Wang, Y.; Yuan, L.; Yang, L.; Peng, L.; Ding, W. Strengthening-Toughening of High-Strength Al-Zn Cast Aluminum Alloys: Research Progress and Prospects. Rare Met. Mater. Eng. 2023, 52, 3954–3970. [Google Scholar]
  38. Shi, B.; Pan, F.; Chen, X.; Tang, A.; Peng, J. Research and Development of Purification Technologies of Aluminum Alloy Melt. Mater Rev. 2009, 23, 45–48. [Google Scholar]
  39. Wang, M.; Huang, D.; Jiang, H. Research progress of aluminum alloys for automobiles. Heat Treat Met. 2006, 31, 34–38. [Google Scholar]
  40. Lan, Y.; Guo, P.; Zhang, J. The Effect of Rare-earth on the Refining Property of the Al-Ti-B-RE Master Alloys. Foundry Tech. 2005, 26, 774–775. [Google Scholar]
Preprints 118364 g001
Figure 1. Dimensions of tensile specimen at room temperature (mm).
Figure 1. Dimensions of tensile specimen at room temperature (mm).
Preprints 118364 g001
Preprints 118364 g002
Figure 2. X-ray diffraction pattern of Al-5Ti-1B-1RE master alloy refiner.
Figure 2. X-ray diffraction pattern of Al-5Ti-1B-1RE master alloy refiner.
Preprints 118364 g002
Preprints 118364 g003
Figure 3. The microstructures of the second phase particles: (a) and EDAX of the secondary phases of. Al-5Ti-1B-1RE master alloy: (b) A phase; (c) B phase; (d) C phase.
Figure 3. The microstructures of the second phase particles: (a) and EDAX of the secondary phases of. Al-5Ti-1B-1RE master alloy: (b) A phase; (c) B phase; (d) C phase.
Preprints 118364 g003
Preprints 118364 g004
Figure 4. TEM of TiB2 of Al-5Ti-1B-1RE master alloy at synthetic temperature 830℃.
Figure 4. TEM of TiB2 of Al-5Ti-1B-1RE master alloy at synthetic temperature 830℃.
Preprints 118364 g004
Preprints 118364 g006
Figure 6. Comparison about refining effect of different kinds of refiners: (a) Al-5Ti-1B master alloy made in our country; (b) Al-5Ti-1B master alloy imported; (c) Al-5Ti-1B-1RE master alloy refiners.
Figure 6. Comparison about refining effect of different kinds of refiners: (a) Al-5Ti-1B master alloy made in our country; (b) Al-5Ti-1B master alloy imported; (c) Al-5Ti-1B-1RE master alloy refiners.
Preprints 118364 g006
Preprints 118364 g007
Figure 7. The mechanical properties of pure aluminum before and after adding different grain refiners: (a) the 0th group-the pure Al unrefined; (b) the first group-adding Al-Ti-B made in our country; (c) the second group-adding Al-Ti-B imported; (d) the third group-adding self-made Al-5Ti-1B-1RE refiners.
Figure 7. The mechanical properties of pure aluminum before and after adding different grain refiners: (a) the 0th group-the pure Al unrefined; (b) the first group-adding Al-Ti-B made in our country; (c) the second group-adding Al-Ti-B imported; (d) the third group-adding self-made Al-5Ti-1B-1RE refiners.
Preprints 118364 g007
Preprints 118364 g008
Figure 8. SEM micrographs of nucleus and EDS analysis results: (a) SEM of the secondary phase of Al-5Ti-1B-1RE; (b) EDAX of A, B; (c) SEM of the secondary phase of Al-5Ti-1B-1RE; (d) EDAX of E; (e) EDAX of F
Figure 8. SEM micrographs of nucleus and EDS analysis results: (a) SEM of the secondary phase of Al-5Ti-1B-1RE; (b) EDAX of A, B; (c) SEM of the secondary phase of Al-5Ti-1B-1RE; (d) EDAX of E; (e) EDAX of F
Preprints 118364 g008
Preprints 118364 g009
Figure 9. Schematic diagram of the duplex nucleation theory.
Figure 9. Schematic diagram of the duplex nucleation theory.
Preprints 118364 g009
Table 1. The chemical compositions of Al-5Ti-1B-1RE master alloy (wt. %).
Table 1. The chemical compositions of Al-5Ti-1B-1RE master alloy (wt. %).
Alloying Element Ti B RE Fe Si Cu Ni Al
Nominal composition 5.00 1.00 1.00 ≤0.20 ≤0.20 ≤0.10 ≤0.10 Bal
Actual measurement value 5.06 0.93 0.95 0.14 0.12 0.04 0.05 Bal
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated