Preprint
Article
Regressive Machine Learning for Real-Time Monitoring of Bed-Based Patients
Altmetrics
Downloads
133
Views
103
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
16 September 2024
Posted:
17 September 2024
Read the latest preprint version here
Alerts
Abstract
This research presents an ensemble model developed to enhance the safety of bedridden patients in healthcare settings. The model utilizes a unique dataset capturing six typical movements performed by patients laying in bed, such as rolling over, falling off the bed, etc. The aim is to automate the classification of these movements, thereby enabling real-time monitoring of patients without the constant presence of hospital personnel in the room, a common practice in current healthcare settings. The dataset is preprocessed and balanced using the Synthetic Minority Over-sampling Technique, and then split into training and test sets for model training and evaluation. Three different models are explored: a Decision Tree Regressor, a Gradient Boosting Regressor, and a Bagging Regressor. The Bagging Regressor is an ensemble model that utilizes the Decision Tree Regressor as its base regressor. Each model’s performance is evaluated using accuracy, R2 score, and Mean Squared Error on both the training and test sets. The ensemble model demonstrates promising results, indicating the potential of machine learning to improve patient safety in healthcare settings. The study also employs K-Fold cross-validation and learning curves to validate the robustness of the ensemble model. This research contributes to the growing body of knowledge on the application of machine learning in healthcare and opens up new avenues for improving patient safety through real-time monitoring and classification of patient movements.
Keywords:
Subject: Medicine and Pharmacology - Clinical Medicine
1. Introduction
Falls among bed-bound patients, particularly older adults, remain a persistent issue. The incidence of falls is high, with about one-third of adults aged 65 and older experiencing falls annually, leading to injuries and increased healthcare needs [1]. About 10% of fatal falls in the elderly occur in the hospital. Falls can be costly as well, leading to increased treatment and extended hospital stays, usually resulting in 60% higher medical expenses. This issue is especially relevant in both hospital and home care settings, where achieving effective fall prevention strategies is difficult due to lack of resources and staff education [2].
Preventing falls in bed-bound patients requires systematic approaches, such as identifying individual risk factors and providing tailored interventions. These may include strength and balance training for patients who can perform limited movements, proper use of bed alarms, and positioning techniques to reduce fall risk. Employee involvement and scenario-based training, such as workshops, are also key in successful fall prevention measures [3].
Falls are the leading cause of injury among adults aged ≧65 years (i.e., older adults) in the United States [4]. Falls are preventable, and health-care providers can help their older patients reduce their risk for falls. Screening older patients for fall risk, assessing modifiable risk factors (e.g., use of psychoactive medications or poor gait and balance), and recommending interventions to reduce this risk (e.g., medication management or referral to physical therapy) can prevent older adult falls [4]. Falls can lead to serious consequences such as fractures, head injuries, reduced mobility, premature long-term care admissions, and even death, especially considering that 30% of fallers will fall again [5].
Gait and balance disorders are multifactorial, common causes of falls, especially in older adults with other comorbidities and underlying medical conditions [6]. Cognitive impairment also is associated with an increased risk of falls [6], including impaired visuospatial function, psychomotor speed, executive function, and attention [7]. This can be attributed to neurologic diseases such as Parkinson disease or neurocognitive disorders such as dementia [8]. Current literature does not document sufficient evidence for effective fall prevention intervention in this population [9]. Frailty and deconditioning, due to a mix of factors such as unintentional weight loss, muscle weakness, and low physical activity are associated with falls [8]. Polypharmacy and the use of certain medications, such as opioids, vasodilators, antihistamines, antidepressants, and B-blockers, are associated with increased fall risk [6]. With older populations, medication reconciliation becomes increasingly important as managing multiple comorbidities and medical problems leads to conflicting side effect profiles.
These factors are often exacerbated by each other - the effect of psychotropic medications on gait and balance is known, along with wandering behavior and poor situational awareness associated with impaired cognition, impulsivity, and poor balance control [7]. Nonmedical reasons, such as unsafe home environments and poor footwear, can also contribute [4,5]. Adherence to fall prevention recommendations and referrals is a factor that should be explored further [10].
Today, inpatient and long-term care use multiple observation modalities to prevent falls. These methods include the use of human resources, technological resources, or even both. The most traditional and well-known method is one-to-one observation, wherein hospital staff are assigned to a patient to stay nearby and monitor them at all times [11]. Although a well-used modality, the efficacy of one-to-one depends on the abilities of the staff to both keep a constant watch on the patient and to make clinical predictions regarding what actions or movements may lead to falls. Additionally, one-to-one as a monitoring method is costly and resource consuming [12]. By assigning a member of the hospital staff to constantly monitor a single patient, there are fewer staff on the floor available to do other tasks for other patients. Reducing the number of staff that can serve other patients increases the workload on other staff members and decreases the care said staff can deliver to each individual patient. As the cost of one-to-one is that which pays the hospital staff, it is a costly modality.
As technology has advanced, inpatient settings have been able to implement cameras into patient monitoring [11]. The accessibility of the camera has offered an efficient and less costly method of patient monitoring [13]. With it, a single hospital staff is no longer required to dedicate their entire day to a single patient. As such, there are more staff available to work on the floors and the work can be distributed more effectively. Additionally, a single - or just a few - staff member(s) can be utilized to monitor multiple patients at once. Although they may need to be trained to utilize the technology as best as possible, staff can integrate their own creative and clinical decision-making skills to optimize monitoring. The largest issue with camera monitoring, however, is the inability to take rapid action, making it overall a more passive modality [14]. As staff are monitoring a patient online, if a patient does experience a fall, the monitoring staff is unable to take action themselves and must instead inform other staff on the respective floor to help the patient. Additional costs for camera monitoring are attributed mostly to the initial investment as well as maintenance of camera equipment.
Bed alarms are another prominent modality used to reduce fall risk [11]. Functioning by alerting staff of when a patient is off the bed yet requiring fewer costs and less personnel allocation, the bed alarm is an intuitive tool in fall risk management [15]. By directly alerting staff of an adverse event, it expedites the spread of information and the time to action. However, bed alarms are only effective after an event has already occurred, making alarms another passive modality [16]. Although effective in making patients feel more secure and hastening a call to action, bed alarms are ineffective in actively reducing falls.
Using machine learning to monitor bed bound patients can mitigate the current issues associated with monitoring bed-bound patients. Current literature on machine learning for fall detection and prevention indicate that many studies use wearable inertial measurement units (IMU), which generate data that will be analyzed by a machine learning algorithm. Some of the machine learning algorithms include, Support Vector Machine (SVM), Artificial Neural Network (ANN), Random Forest (RF), k-Nearest Neighbors (kNN), k-means, Linear Discriminant Analysis (LDA) [10]. Each algorithm has its own benefits and shortcomings depending on the specific data that is fed. Overall, the accuracy, sensitivity and specificity of fall detection and prevention was comparable among the different machine learning algorithms, with SVM having an accuracy of 98%, kNN having an accuracy of 99%, ANN having an accuracy of 95.25% when using an IMU sensor at the waist [10]. Sensor location is another important aspect as different studies place the sensor in different locations in the body to maximize the data that can be captured. Most studies seem to place the sensors at the waist.
2. Materials and Methods
This section begins with the `Data Collection’ subsection, which explains the use of a mannequin model and sensors to capture and transmit data related to patient movements. This is followed by the `Machine Learning’ subsection, where the preparation of the dataset for machine learning is discussed, including the normalization of features and the handling of class imbalance. The `Models’ subsection introduces the three machine learning models used in the study, while the `Evaluation’ subsection describes the evaluation of these models using the R-squared score and mean squared error. The `Cross-Validation’ subsection further elaborates on the use of KFold Cross-Validation in the machine learning pipeline. Finally, the ’Calculating Confusion Matrix’ subsection details the use of a confusion matrix to evaluate the performance of the models, including a strategy to categorize the continuous output of regression models into discrete classes.
2.1. Data Collection
In this study, we utilized a high-fidelity mannequin, a tool commonly used in medical education and simulation centers, to simulate the various movements typically experienced by inpatient individuals in a bed setting. This mannequin, often employed by medical students for practicing diverse patient scenarios, was adapted to replicate the common movements and positions of bedridden patients.
To accurately capture these movements, we equipped the mannequin with Movella DOT sensors. These are wearable sensor development platforms known for their signal processing and sensor fusion framework, making them particularly optimized for applications involving human movement. The Movella DOT sensors, which include an accelerometer, a gyroscope, and a magnetometer, were strategically placed on the mannequin, as shown in Figure 1. These sensors recorded velocities, accelerations, and Euler angles at specific time intervals, providing a comprehensive dataset of the mannequin’s movements. The data was transmitted wirelessly via Bluetooth to eliminate any potential interference from cables.
The accelerometer measured the acceleration of the mannequin’s movements, the gyroscope captured the rotational speed, and the magnetometer recorded the magnetic field. The data from these individual components were then combined using sensor fusion algorithms to accurately calculate the mannequin’s orientation.
This approach of using a high-fidelity mannequin and sensors like Movella DOT has enabled us to gather precise and reliable data on the movements typically experienced by inpatients. The movements were then categorized into six distinct labels: “Roll right” (0), “Roll left” (1), “Drop right” (2), “Drop left” (3), “Breathing” (4), and “Seizure” (5). These labels represent the most common movements and positions experienced by inpatients, providing a comprehensive understanding of patient behavior in a bed setting.
2.2. Machine Learning
The methodology involves the application of ensemble machine learning models on a given dataset. The dataset is first loaded into the Python environment using the pandas library. The dataset is divided into features (X) and the target variable (y). The features are all columns except the first one, and the target is the first column. The features are then normalized to be between 0 and 1 using the MinMaxScaler from the sklearn.preprocessing module. This is done to ensure that all features have the same scale and that the model is not biased towards features with larger scales.
In our dataset, we observe an imbalance in the distribution of classes within the target variable. This imbalance can potentially lead to a model bias, where the model might overfit to the majority class and underperform when predicting the minority class. To mitigate this issue, we employ the Synthetic Minority Over-sampling Technique (SMOTE), which is a technique that generates synthetic data for the minority class, thereby balancing the class distribution. The process of synthetic data generation involves calculating the k nearest neighbors for each instance in the minority class, randomly choosing one of these neighbors, and creating a synthetic instance at a random point on the line segment connecting the two instances. This can be represented by the following formula:
where is the synthetic instance, is the instance from the minority class, is the randomly chosen neighbor, and is a random number between 0 and 1.
The sampling strategy, to mitigate the imbalance in the dataset, is set such that each class in the target variable has 200 instances. The random state is set to 42 for reproducibility. This is a common practice in machine learning where a specific seed is set for the random number generator. This allows the results to be reproduced exactly, as the same “random” numbers will be generated each time the code is run.
The data is then split into training and test sets, with 80% of the data used for training and 20% used for testing. The random state is again set to 42 for reproducibility. Several models are then fitted to the training data, including the Decision Tree Regressor, Gradient Boosting Regressor, and Bagging Regressor.
2.3. Models
Following a review of various models, taking into account their performance, complexity, and susceptibility to overfitting, the decision was made to employ the Decision Tree Regressor, the Gradient Boosting Regressor, and the Bagging Regressor. The Bagging Regressor is an ensemble model that primarily uses the Decision Tree Regressor as its base regressor. Detailed descriptions of all three models are provided below.
The Decision Tree Regressor (DTR) is a simple model that splits the features at certain thresholds to make predictions. The formula for a decision tree can be represented as:
where Y is the output, X is the input, are the regions of the feature space that result from the splits, are the constants (mean of the target variable in the region ), and I is the indicator function.
The Gradient Boosting Regressor (GBR) is a more complex model that fits new predictors to the residual errors of the previous predictor. The formula for gradient boosting can be represented as:
where is the boosted model at step is the boosted model at the previous step, are the regions of the feature space that result from the splits, are are the optimal coefficients, and I is the indicator function.
The Bagging Regressor (BR) is an ensemble model that fits base regressors each on random subsets of the original dataset and then aggregate their individual predictions to form a final prediction. The formula for bagging can be represented as:
where is the final prediction, B is the number of base regressors, and are the base regressors. In the context of a Bagging Regressor, base regressors are the individual models that are trained on different subsets of the original dataset. The final prediction of the Bagging Regressor is typically an average of the predictions made by each of these base regressors. In this study, the number of base regressors (B) is 50. It means that the Bagging Regressor is training 50 separate instances of its base regressor on different subsets of the data. These 50 models collectively make up the Bagging Regressor. In Python, BR is implemented using the DTR as the base regressor. BR enhances the performance of DTR by reducing overfitting and improving prediction accuracy.
2.4. Evaluation
The models are evaluated using the R-squared (R2) score, and mean squared error (MSE) on both the training and test sets. In a regression problem, the goal is to predict a continuous outcome variable from one or more predictor variables. The performance of regression models is typically assessed using error metrics that quantify the difference between the predicted and actual values. Two of the most common metrics are MSE and R2. MSE is the average of the squared differences between the predicted and actual values. It is a measure of the model’s prediction error. A lower MSE indicates a better fit of the model to the data, as it means the model’s predictions are closer to the actual values. In contrast, accuracy and Area Under the Curve (AUC) are metrics typically used for classification problems, where the goal is to predict a categorical outcome. Accuracy measures the proportion of correct predictions, while AUC measures the ability of the model to distinguish between classes. These metrics are not suitable for regression problems because regression predictions are not categorical, but continuous. Hence, MSE and R2 are used in regression problems because they provide meaningful measures of the model’s ability to predict continuous outcomes.
MSE is the average of the squared differences between the predicted and actual values. It is a measure of the model’s prediction error. A lower MSE indicates a better fit of the model to the data, as it means the model’s predictions are closer to the actual values.
where are the actual values, are the predicted values, and n is the number of observations.
R2, also known as the coefficient of determination, measures the proportion of the variance in the dependent variable that is predictable from the independent variables. It ranges from 0 to 1, with 1 indicating that the model perfectly predicts the actual values and 0 indicating that the model does not explain any of the variability of the response data around its mean. A higher R2 indicates a better fit of the model to the data. The formula for R2 is:
where is the sum of squares of residuals and is is the total sum of squares.
In the context of this research, it remains beneficial to compute accuracy, particularly because the continuous predictions are classified into bins corresponding to a target categorical variable expressed numerically. In this case, a continuous variable representing different movements of bedridden patients is binned, and the predictions are subsequently categorized into labels such as “Roll right” (0), “Roll left” (1), “Drop right” (2), “Drop left” (3), “Breathing” (4), and “Seizure” (5).
2.5. Cross-Validation
The machine learning pipeline utilized uses cross-validation to evaluate the performance of the resulting model. A technique called KFold Cross-Validation is utilized. This method involves breaking down the training data into several sections, specifically 10 in this case. These sections are often referred to as “folds”. To make sure the results can be replicated, a specific “random state” is set. Think of it as setting a seed for a random number generator. In this context, the seed is 42. Moreover, the data is “shuffled” before it’s divided into folds. This is to ensure that the sequence of the data doesn’t influence the outcomes of the model training.
Once the data is divided into folds, the ensemble model undergoes training and evaluation several times. In each cycle, a different fold of the data is set aside for evaluation while the model is trained on the remaining data. The model’s performance in each cycle is assessed and a score is given. This process is repeated for each fold of the data, resulting in a collection of scores. In mathematical terms, if we consider n as the total number of data points and k as the number of folds, the model will be trained k times. Each time, it will be trained on data points and evaluated on data points. The final outcome is an array of k scores, one for each cycle.
2.6. Calculating Confusion Matrix
The confusion matrix is a table that is used to describe the performance of a classification model (or “classifier”) on a set of test data for which the true values are known. It allows visualization of the performance of an algorithm. The model makes a prediction for each sample in the test set. A confusion matrix is traditionally used for evaluating classification models; however, by employing a binning strategy to categorize the continuous output of regression models into discrete classes, it becomes possible to calculate a confusion matrix for regression models as well.
Since the Bagging Regressor’s output is continuous, to make these predictions meaningful in the context of categorical labels, they need to be categorized into bins. Binning is used as a method to convert continuous predictions from a Bagging Regressor into categorical labels. It is used to segment and sort data values into bins. Bin edges [-0.5, 0.5, 1.5, 2.5, 3.5, 4.5, 5.5] are used to categorize the continuous predictions from the Bagging Regressor into one of the six categories represented by the labels “Roll right” (0), “Roll left” (1), “Drop right” (2), “Drop left” (3), “Breathing” (4), and “Seizure” (5). Each bin edge represents the boundary between two categories. For example, a prediction value of 0.3 would fall into the bin between -0.5 and 0.5, and would be labeled as ’Roll right’. A prediction value of 1.7 would fall into the bin between 1.5 and 2.5, and would be labeled as ’Roll left’, and so on.
Finally, the confusion matrix is calculated using the true test labels and the predicted test labels, which have been transformed into numerical form. The resulting confusion matrix provides an additional evaluation of the Bagging Regressor model’s performance. To reiterate, this approach allows us to effectively evaluate a model that produces continuous output by using a binning strategy.
3. Results
In the pursuit of identifying the most appropriate machine learning regressors for the given dataset, an initial analysis was conducted on a selection of commonly used regressors. The findings of this analysis are presented in the Table 1, with the algorithms arranged in descending order of performance.
The GBR emerged as the superior performer. This machine learning model is adept at detecting intricate patterns within the data. However, it is susceptible to overfitting, as it constructs trees in a sequential manner, with each new tree designed to rectify errors made by its predecessors. As the model incorporates more trees, it becomes increasingly expressive, which, if not properly managed, can lead to overfitting.
The Random Forest, the second-best performer, shares GBR’s ability to discern complex patterns in the data. However, it too is prone to overfitting, particularly when dealing with noisy data. This is attributed to the Random Forest’s methodology of constructing numerous deep trees, each trained on a different data subset. While this can result in a model that fits the training data exceptionally well, it may perform poorly on unseen data.
In contrast, the DTR is less likely to overfit due to its simplicity. Decision trees are generally more interpretable and can handle both numerical and categorical data. Despite this, they can still overfit if allowed to grow excessively deep, although this is typically easier to control than in more complex models.
Given the circumstances, we opted for the BR, an ensemble model that incorporates the DTR as its base regressor. This method takes advantage of DTR’s inherent ability to counteract overfitting. While the GBR or Random Forest may offer marginally better MSE and R2 values, their use heightens the overfitting problem with our dataset. The slight improvement in these metrics does not justify their use if they contribute to overfitting issues.
The Table 3 presents a comparative evaluation of three distinct models: DTR, GBR, and BR. The performance of these models is assessed using metrics such as Accuracy, R2 (for both training and testing datasets), and MSE (for both training and testing datasets).
The DTR model demonstrates an accuracy of 0.892, an R2 score of 1.000 for the training data, and an R2 score of 0.939 for the test data. The MSE for the training data is 0.000, suggesting no error, while the MSE for the test data is 0.167. The GBR model exhibits a slightly higher accuracy of 0.908, an R2 score of 0.990 for the training data, and an R2 score of 0.943 for the test data. The MSE for the training data is 0.031, and for the test data, it’s 0.156.
The ensemble model, i.e., BR, outperforms both individual models with an accuracy of 0.950, an R2 score of 0.996 for the training data, and an R2 score of 0.959 for the test data. The MSE for the training data is 0.012, and for the test data, it is 0.112.
3.1. Cross-Validation
The Table 4 compares the performance of a model with and without the SMOT. The metrics used for comparison are the mean and standard deviation. The mean represents the average performance of the model, while the standard deviation measures the variability of the model’s performance.
It can be observed that the model performs better when SMOT is used, as indicated by the higher mean score. The standard deviation is also lower with SMOT, suggesting that the model’s performance is more consistent when this technique is used.
3.2. Learning Curves
Learning curves are a diagnostic tool in machine learning that provide insights into how well a model is learning from the training data and generalizing to unseen data. They plot the model’s performance on both the training and cross-validation datasets over a series of training iterations. The training score reflects how well the model fits the training data. The cross-validation score, on the other hand, indicates how well the model generalizes to unseen data. If the training score is significantly higher than the validation score, it suggests that the model might be overfitting, meaning it is too complex and is fitting the noise in the training data rather than the underlying pattern (as seen in Figure 2a). The point where the training score and cross-validation score converge is considered a good indication of the optimal model complexity (as seen in Figure 2b).
Note, that the maximum training sizes (in Figure 2) are different with and without SMOT because SMOT creates synthetic examples of the minority class, effectively increasing the size of the training data. This allows the model to be trained with more data when SMOT is used.
The learning curves in Figure 2a start with a significant gap of 60 score points between the training and cross-validation scores. This large gap indicates that the model is initially overfitting the training data, meaning it performs well on the training data but poorly on the unseen cross-validation data. As the model is trained with more data, the cross-validation score rises, suggesting that the model is learning and generalizing better. However, by the maximum training size, the curves are still far apart, indicating that the model is still overfitting. This suggests that the model has learned the training data too well and is not generalizing well to unseen data.
The learning curves in Figure 2b start with a smaller gap of 15 score points between the training and cross-validation scores. This smaller gap suggests that the model is not overfitting as much as in the case without SMOTE. As the model is trained with more data, the cross-validation score rises and converges with the training score by approximately halfway between the smallest and largest training size. Once converged, the two scores remain close for the rest of the training size, from the middle to the maximum. This sustained convergence indicates that the model is generalizing well to unseen data and is not overfitting or underfitting. The use of SMOT, which creates synthetic examples of the minority class, seems to help the model learn better and generalize better to unseen data.
3.3. Confusion Matrix
The confusion matrix, shown in Figure 3, represents a 6-class classification problem. The classes are: Roll right (0), Roll left (1), Drop right (2), Drop left (3), Breathing (4), and Seizure (5). The rows of the matrix represent the actual classes, while the columns represent the predicted classes by the machine learning model. The diagonal elements represent the number of points for which the predicted label is equal to the true label, while off-diagonal elements are those that are mislabeled by the classifier. The higher the diagonal values of the confusion matrix the better, indicating many correct predictions.
The model correctly predicted all 39 instances of Roll right (0), as there are no off-diagonal elements in the first row. Similarly, the model correctly predicted all 38 instances of Roll left (1), as there are no off-diagonal elements in the second row. For Drop right (2), the model correctly predicted 39 instances, but misclassified 1 instance as Roll left (1) and 1 instance as Drop left (3). For Drop left (3), the model correctly predicted 47 instances, but misclassified 2 instances as Roll right (0) and 1 instance as Roll left (1). For Breathing (4), the model correctly predicted 34 instances, but misclassified 2 instances as Seizure (5). For Seizure (5), the model correctly predicted 31 instances, but misclassified 5 instances as Breathing (4).
Overall, the model seems to be doing well in predicting the classes, as the majority of the predictions fall on the diagonal (correct predictions). However, there are some misclassifications, particularly between Breathing (4) and Seizure (5), and to a lesser extent between Drop right (2) and Drop left (3), and Drop left (3) and Roll right (0) and Roll left (1).
4. Discussion
The main utility of utilizing sensor-based surveillance is the effectiveness in continuously monitoring patients while avoiding privacy concerns of other technologies, such as AI-based video surveillance. In one study, the authors utilized a security framework which had successfully maintained both privacy and security in the healthcare setting. The recording system was activated only as a response to health or security concerns. Additionally, only medical professionals (nurses, doctors) may access the encrypted video data. The ability to balance privacy and security in video-based patient monitoring systems. The regression model in the current study did not rely on video surveillance which ensures absolute privacy by utilizing the Movella DOT sensors [17]. In another study which used Internet of Things (IOT) Sensors and artificial intelligence to monitor patient activities and alerts healthcare professionals to recent changes. It was found that with the use of the CNN-UUGRU deep learning model, which outperforms existing models in terms of accuracy (97.7%) and precision (96.8%) in identifying human activities based on sensor data [18]. Additionally, this sensor-based system can predict possible falls based on behavioral and physiological data, as discussed in fall prevention research by El-Bendary et al [19]. These systems not only detect immediate threats but also help predict falls before they occur, utilizing patient history and sensor fusion technology.
Integration of AI systems with electronic record systems has also been briefly investigated by a systematic review published in 2021. Incorporating EHR data not only enhances the predictive power of these models but also allows for the creation of personalized care plans based on a combination of sensor-based movement data and detailed patient histories. For example, patients with a history of mobility issues or chronic diseases that impact their movement (such as arthritis or Parkinson’s disease) could have higher-risk scores calculated by the model, which can trigger early intervention measures. In line with this, Lee et al.’s systematic review (2020) emphasizes that integrating predictive models into EHR systems significantly improves clinical outcomes, particularly in critical care settings like sepsis management and thrombotic disorder prevention [20].
Usmani et al. conducted a systematic review of fall detection and prevention using machine learning, emphasizing the growing use of wearable sensors, such as inertial measurement units (IMUs), to capture patient movements. Their review highlights the effectiveness of machine learning models like Support Vector Machines (SVM), Random Forests (RF), and Artificial Neural Networks (ANN), all achieving high accuracy rates (up to 99%) in fall detection. By including EMR data, such as mobility restrictions, history of falls, and cognitive impairments, alongside sensor data, the predictive accuracy of the regression models could be optimized. This integration would allow the system to generate alerts that are personalized to the patient’s specific condition and treatment regimen, creating a more dynamic and proactive fall prevention system [16].
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets analyzed in this study, as well as the software used for their analysis, are available online. The corresponding references to these datasets and software are included in the article. Any additional information or data not provided in the article can be obtained upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Linnerud, S.; Kvael, L.A.H.; Graverholt, B.; Idland, G.; Taraldsen, K.; Brovold, T. Stakeholder development of an implementation strategy for fall prevention in Norwegian home care – a qualitative co-creation approach. BMC Health Services Research 2023, 23. [Google Scholar] [CrossRef] [PubMed]
- Karen, B. Pearson, MLIS, M.; Andrew F. Coburn, P. Evidence-based Falls Prevention in Critical Access Hospitals, 2011.
- Jennifer Van Pelt, M. Fall Prevention: Fall Prevention in Hospitals. Today’s Geriatric Medicine 2023, 16, 28. [Google Scholar]
- Morello, R.T.; Soh, S.E.; Behm, K.; Egan, A.; Ayton, D.; Hill, K.; Flicker, L.; Etherton-Beer, C.D.; Arendts, G.; Waldron, N.; Redfern, J.; Haines, T.; Lowthian, J.; Nyman, S.R.; Cameron, P.; Fairhall, N.; Barker, A.L. Multifactorial falls prevention programmes for older adults presenting to the emergency department with a fall: systematic review and meta-analysis. Injury Prevention 2019, 25, 557–564. [Google Scholar] [CrossRef] [PubMed]
- Ang, G.; Low, S.; How, C. Approach to falls among the elderly in the community. Singapore Medical Journal 2020, 61, 116–121. [Google Scholar] [CrossRef] [PubMed]
- Cuevas-Trisan, R. Balance Problems and Fall Risks in the Elderly. Physical Medicine and Rehabilitation Clinics of North America 2017, 28, 727–737. [Google Scholar] [CrossRef] [PubMed]
- Whitney, J.; Close, J.C.; Jackson, S.H.; Lord, S.R. Understanding Risk of Falls in People With Cognitive Impairment Living in Residential Care. Journal of the American Medical Directors Association 2012, 13, 535–540. [Google Scholar] [CrossRef] [PubMed]
- Colón-Emeric, C.S.; McDermott, C.L.; Lee, D.S.; Berry, S.D. Risk Assessment and Prevention of Falls in Older Community-Dwelling Adults: A Review. JAMA 2024, 331, 1397. [Google Scholar] [CrossRef] [PubMed]
- NICE. Clinical Guideline 161. Falls: assessment and prevention of falls in older people. https://www.nice.org.uk/guidance/cg161, 2014. Accessed , 2014. 19 December.
- LeLaurin, J.H.; Shorr, R.I. Preventing Falls in Hospitalized Patients. Clinics in Geriatric Medicine 2019, 35, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Rausch, D.L.; Bjorklund, P. Decreasing the costs of constant observation. The Journal of nursing administration 2010, 40, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Cournan, M.; Fusco-Gessick, B.; Wright, L. Improving Patient Safety Through Video Monitoring. Rehabilitation nursing : the official journal of the Association of Rehabilitation Nurses 2018, 43, 111–115. [Google Scholar] [CrossRef] [PubMed]
- Woltsche, R.; Mullan, L.; Wynter, K.; Rasmussen, B. Preventing Patient Falls Overnight Using Video Monitoring: A Clinical Evaluation. International journal of environmental research and public health 2022, 19, 13735. [Google Scholar] [CrossRef] [PubMed]
- Seow, J.P.; Chua, T.L.; Aloweni, F.; Lim, S.H.; Ang, S.Y. Effectiveness of an integrated three-mode bed exit alarm system in reducing inpatient falls within an acute care setting. Japan Journal of Nursing Science 2021, 19. [Google Scholar] [CrossRef] [PubMed]
- Mileski, M.; Brooks, M.; Topinka, J.B.; Hamilton, G.; Land, C.; Mitchell, T.; Mosley, B.; McClay, R. Alarming and/or Alerting Device Effectiveness in Reducing Falls in Long-Term Care (LTC) Facilities? A Systematic Review. Healthcare 2019, 7, 51. [Google Scholar] [CrossRef] [PubMed]
- Usmani, S.; Saboor, A.; Haris, M.; Khan, M.A.; Park, H. Latest Research Trends in Fall Detection and Prevention Using Machine Learning: A Systematic Review. Sensors 2021, 21, 5134. [Google Scholar] [CrossRef] [PubMed]
- Braeken, A.; Porambage, P.; Gurtov, A.; Ylianttila, M. Secure and Efficient Reactive Video Surveillance for Patient Monitoring. Sensors 2016, 16, 32. [Google Scholar] [CrossRef] [PubMed]
- Palanisamy, P.; Padmanabhan, A.; Ramasamy, A.; Subramaniam, S. Remote Patient Activity Monitoring System by Integrating IoT Sensors and Artificial Intelligence Techniques. Sensors 2023, 23, 5869. [Google Scholar] [CrossRef] [PubMed]
- El-Bendary, N.; Tan, Q.; Pivot, F.C.; Lam, A. Fall Detection and Prevention for the Elderly: A Review of Trends and Challenges. International Journal on Smart Sensing and Intelligent Systems 2013, 6, 1230–1266. [Google Scholar] [CrossRef]
- Lee, T.C.; Shah, N.U.; Haack, A.; Baxter, S.L. Clinical Implementation of Predictive Models Embedded within Electronic Health Record Systems: A Systematic Review. Informatics 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Illustration of pitch, roll, and yaw relative to a patient in both supine and sitting positions.
Figure 1.
Illustration of pitch, roll, and yaw relative to a patient in both supine and sitting positions.
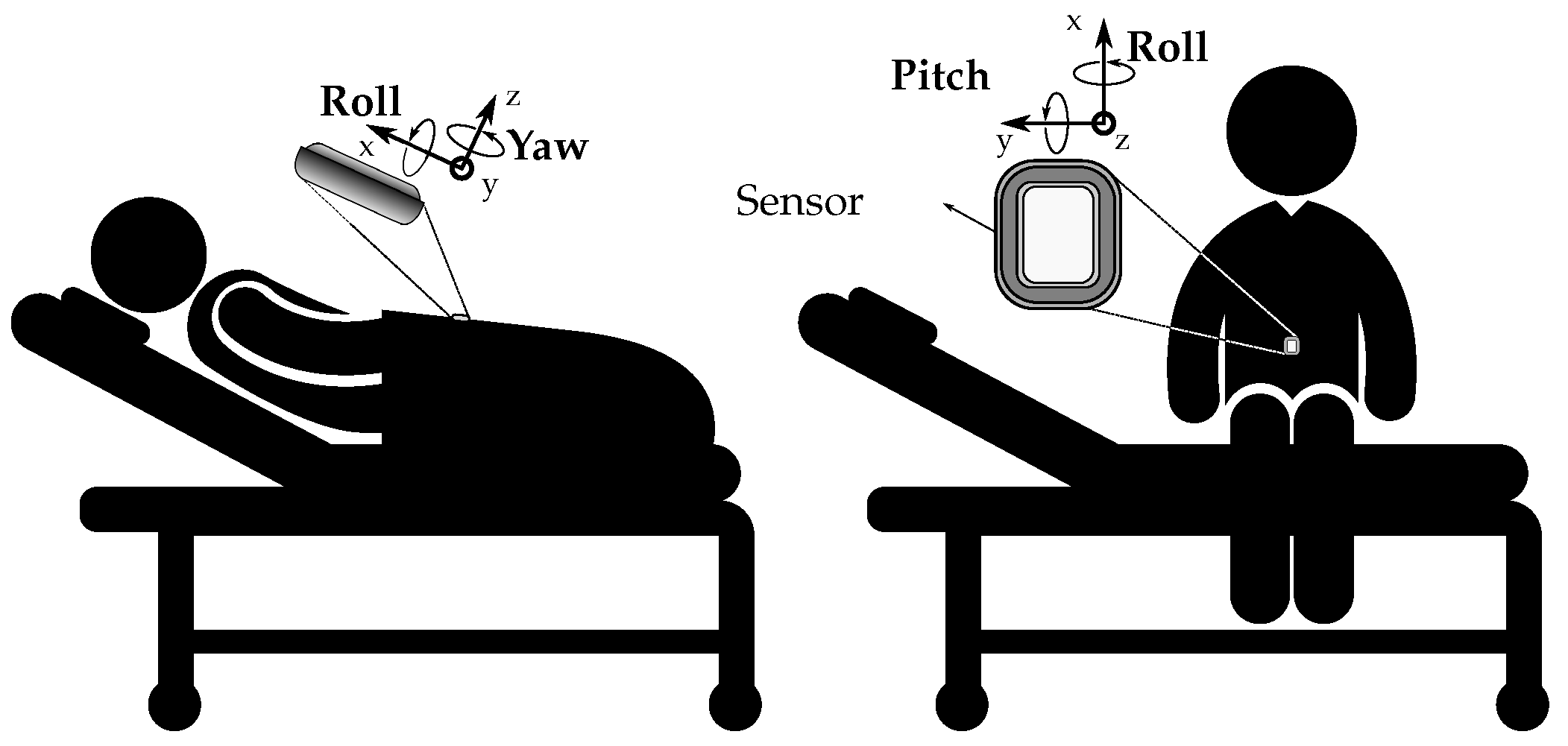
Figure 2.
The performance of the ensemble model on the training and validation sets over a series of training iterations. Part (a) shows the learning curve without the application of SMOT, while part (b) demonstrates the learning curve with SMOT. The use of SMOT appears to enhance the model’s ability to handle imbalanced datasets, as evidenced by the improved performance in part (b).
Figure 2.
The performance of the ensemble model on the training and validation sets over a series of training iterations. Part (a) shows the learning curve without the application of SMOT, while part (b) demonstrates the learning curve with SMOT. The use of SMOT appears to enhance the model’s ability to handle imbalanced datasets, as evidenced by the improved performance in part (b).
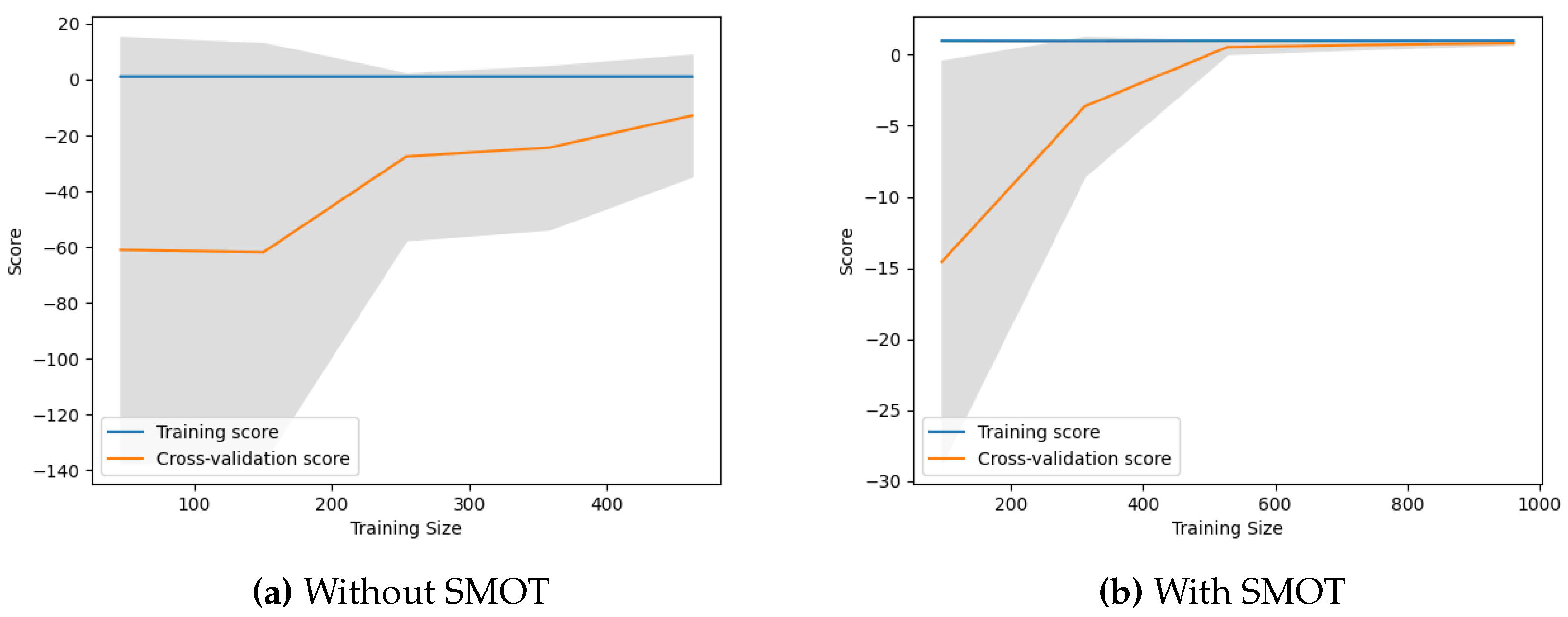
Figure 3.
Confusion matrix heatmap for the model. The x-axis represents the predicted labels and the y-axis represents the actual labels. The color intensity in each cell corresponds to the number of instances, with darker colors indicating higher numbers. The actual numbers are also included in each cell of the heatmap.
Figure 3.
Confusion matrix heatmap for the model. The x-axis represents the predicted labels and the y-axis represents the actual labels. The color intensity in each cell corresponds to the number of instances, with darker colors indicating higher numbers. The actual numbers are also included in each cell of the heatmap.
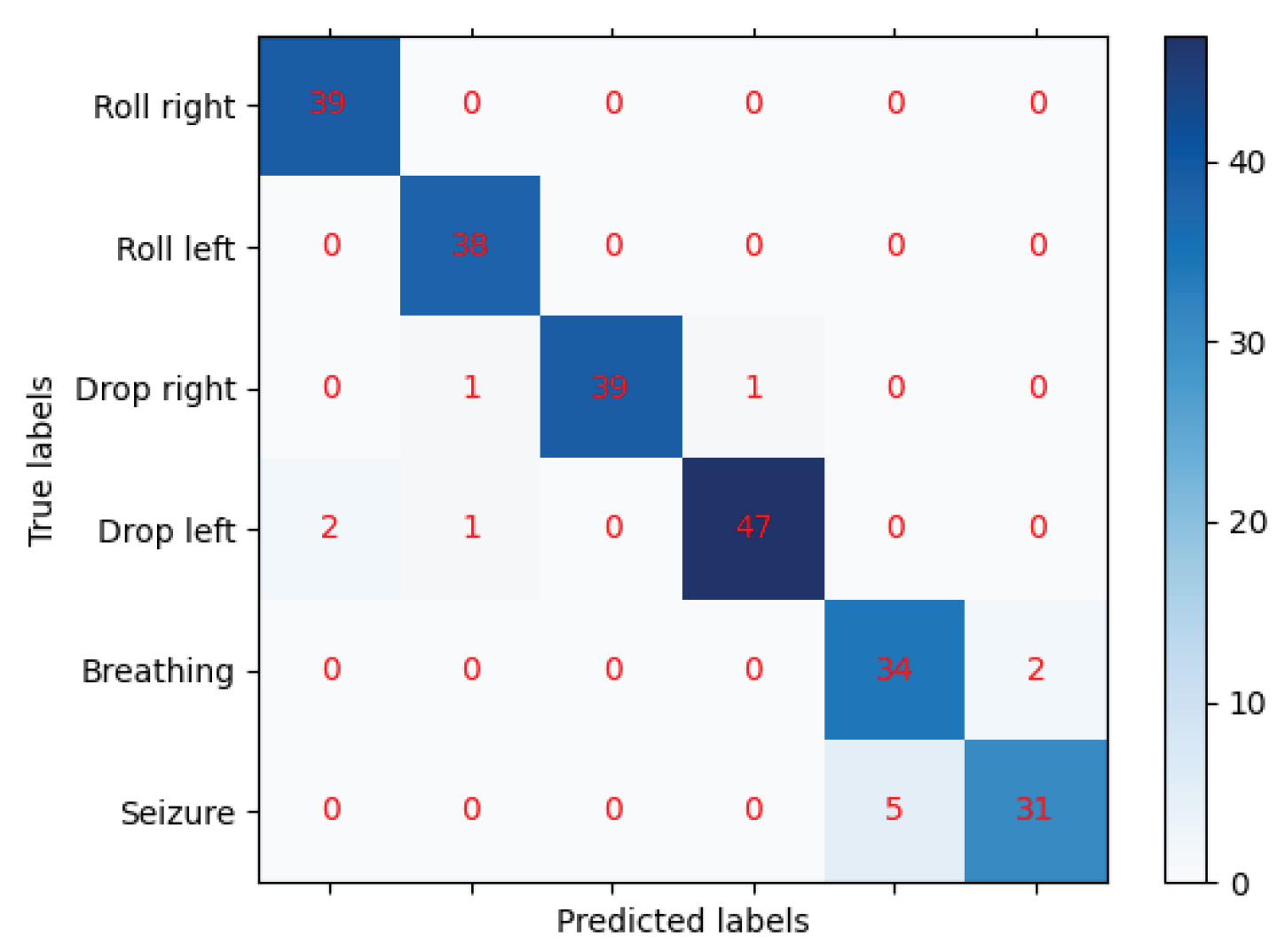
Table 1.
Performance Comparison of Different Regressors.
| Regressor: | MSE: | R2: |
|---|---|---|
| Gradient Boosting | 0.093 | 0.970 |
| Random Forest | 0.120 | 0.962 |
| Decision Tree | 0.138 | 0.956 |
| Support Vector | 0.220 | 0.930 |
| K-Nearest Neighbors | 0.322 | 0.897 |
| Linear | 19.419 | -5.209 |
Table 2.
Performance Comparison of Decision Tree Regressor, Gradient Boosting Regressor, and their Ensemble, without SMOT.
Table 2.
Performance Comparison of Decision Tree Regressor, Gradient Boosting Regressor, and their Ensemble, without SMOT.
| Model | Accuracy | R2 (Train) | R2 (Test) | MSE (Train) | MSE (Test) |
|---|---|---|---|---|---|
| DTR | 0.8362 | 1.000 | 0.9035 | 0.000 | 0.3017 |
| GBR | 0.8621 | 0.9925 | 0.9702 | 0.0219 | 0.0932 |
| BR | 0.8621 | 0.9915 | 0.9592 | 0.0247 | 0.1276 |
Table 3.
Performance Comparison of Decision Tree Regressor, Gradient Boosting Regressor, and their Ensemble, with SMOT.
Table 3.
Performance Comparison of Decision Tree Regressor, Gradient Boosting Regressor, and their Ensemble, with SMOT.
| Model | Accuracy | R2 (Train) | R2 (Test) | MSE (Train) | MSE (Test) |
|---|---|---|---|---|---|
| DTR | 0.892 | 1.000 | 0.939 | 0.000 | 0.167 |
| GBR | 0.908 | 0.990 | 0.943 | 0.031 | 0.156 |
| BR | 0.950 | 0.996 | 0.959 | 0.012 | 0.112 |
Table 4.
Performance Comparison of Ensemble Model with and without SMOT.
| Technique: | Mean: | Standard Deviation: |
|---|---|---|
| Without SMOT | 0.9374 | 0.0258 |
| With SMOT | 0.9705 | 0.0146 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







