Prerpints.org logo
Preprint
Article

Fuzzy Logic based Energy Management Strategy for Hybrid Fuel Cell Electric Ship's Power and Propulsion System

Altmetrics

Downloads

87

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 September 2024

Posted:

17 September 2024

You are already at the latest version

Alerts
Abstract
The growing use of proton-exchange membrane fuel cells (PEMFC) in hybrid propulsion systems, aimed at replacing traditional internal combustion engines and reducing greenhouse gas emis-sions. Effective power distribution between the fuel cell and the energy storage system (ESS) is crucial, which has led to a growing emphasis on developing energy management systems (EMS) to efficiently implement this integration. To address this goal, this study examines the performance of a fuzzy logic rule-based strategy for a hybrid fuel cell propulsion system in a small hydro-gen-powered passenger vessel. The primary objective is to optimize fuel efficiency, with particular attention to reducing hydrogen consumption. The analysis is carried out under typical operating conditions encountered during a river trip. Comparisons between the proposed strategy with other approaches —control-based, optimization-based and deterministic rule-based— are con-ducted to verify the effectiveness of the proposed strategy. Simulation results indicated that EMS based on fuzzy logic mechanisms was the most successful in reducing fuel consumption. The superior performance of this method stems from its ability to adaptively manage power distri-bution between the fuel cell and energy storage systems.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

In recent times, environmental pollution has emerged as a critical concern that significantly impacts the well-being of humans and other living organisms on earth. This growing issue has driven extensive research efforts to develop renewable energy sources as a sustainable solution for the future of humanity. According to the International Renewable Energy Agency (IRENA), a total of 131 countries have committed to reaching net-zero emissions, encompassing 88% of global emissions. Hydrogen plays a vital role in decarbonizing sectors such as heavy industry and transport. It is expected to contribute 10% to emission reductions [1].
The proton exchange membrane fuel cell (PEMFC) is considered the most suitable and efficient hydrogen-based system, making it a promising candidate for integration with traditional energy devices like batteries or/and supercapacitors (SC) in hybrid systems [2]. Its lower operating temperatures and superior energy conversion rates distinguish the PEMFC from other fuel cell types [3]. However, its slow dynamic response and inability to recover excess energy present significant challenges for its widespread use as a standalone energy source. These issues can lead to problems such as fuel starvation, membrane drying, ultimately causing degradation of its lifetime [4]. Therefore, it is essential to integrate the PEMFC with other interconnected electrical storage devices [5]. In such configuration, the energy storage systems manage the sudden variations in load demands, allowing the fuel cell to run consistently at peak efficiency. By preventing the fuel cell from being overloaded during times of high power demand, this configuration lowers fuel consumption and improves overall efficiency [6].
The integration of ESS with fuel cells has been considered in many transport applications. For example, ref. [7,8] compares various energy management schemes for a fuel-cell-based emergency power system in an electric aircraft, including lithium-ion batteries, supercapacitors and converters. The same configuration was examined in [9], to supply power and allow energy recovery during regenerative braking in a hybrid tramway. Similarly, study [10] evaluates energy management strategies but in this case for hybrid fuel cell-battery autonomous underwater vehicles.
These examples highlight the versatility and adaptability of ESS and fuel cell integration across various transport platforms. While much of the existing research on EMS has been heavily focused on automotive applications, recent studies have begun exploring EMS in marine settings, particularly for their potential to reduce emissions and improve fuel efficiency [11]. Ships, ranging from passenger vessels [12] to large commercial ships [13], are increasingly being equipped with hybrid systems that combine a source of fuel and storage systems.
The optimal distribution of required power between the fuel cell and the energy storage system is a challenging task for hybrid fuel cell propulsion systems, requiring the development of an energy management strategy [14]. Following the historical literature for hybrid propulsion systems, creating a successful EMS is an important field of study [15,16,17,18]. Reducing greenhouse gas emissions [19], lowering operating expenses [20], lightening the weight of the power system [21], and reducing stress on power system components [22] to prolong their lifespan are some objectives of an energy management plan. Other objectives include optimizing navigation endurance by maintaining the battery state of charge (SOC) [23] or frequency [24] and bus voltage at a desired level [25].
One notable study [26] delves into the design and optimization of a hybrid energy storage system (HESS) for marine vessels, aiming to boost power system performance and extend fuel cell lifespan. The proposed EMS leverages support vector machines and frequency control, alongside a multi-objective optimization approach, resulting in an HESS that meets power demands efficiently while enhancing power quality and device longevity. Another study [27] introduces a fuzzy logic-based EMS for hybrid fuel cell ships, integrating a PEMFC, battery, and ultra-capacitor. Simulations reveal this strategy’s effectiveness in optimizing power distribution, reducing dynamic stress on the fuel cell, and maintaining optimal charge levels in the battery and ultra-capacitor, ultimately improving system efficiency and fuel economy. Additionally, for smaller vessels [28], an EMS has been developed that requires the fuel cell to meet average power demands, utilizing the energy storage system to handle fluctuations, thereby ensuring consistent power supply and efficient energy usage.
Given the complexity and importance of developing an effective energy management strategy for hybrid propulsion systems, various methods have been explored to address the associated challenges. Traditional approaches such as real-time optimization [29,30], metaheuristic optimization techniques [31,32], and model predictive control [33,34] have been widely utilized in EMS development. However, one area that remains underexplored in this specific field is the application of fuzzy logic control, which could offer significant advantages in handling the inherent uncertainties and non-linearities of hybrid systems.
This paper focuses on implementing energy management techniques for hybrid fuel cell systems in small ships. It compares various energy management strategies and aims to reduce energy consumption. The chapter also explores an advanced control method: fuzzy logic to handle complexities in hybrid propulsion systems. The goal is to contribute to sustainable marine technologies, leading to reduced fuel consumption, lower emissions, and more efficient marine operations. The key contributions of the following study can be summarized as follows:
  • Address the growing interest in hybrid fuel cell propulsion systems by examining a small fuel cell-powered vessel during a river trip;
  • Conduct a comparative study of five distinct energy management strategies—control-based, optimization-based, deterministic rule-based, and fuzzy logic rule-based—highlighting their effectiveness in managing power allocation in hybrid transport fuel cell systems;
  • Evaluation of these strategies based on total hydrogen consumption during a 300-second real data driving cycle that included docking, acceleration, and cruising phases. This analysis include assessments of total energy consumption, battery state of charge, and the performance of fuel cells, batteries, and supercapacitors;
  • Analyze how initial SOC levels affect hydrogen consumption for each strategy across various initial battery state of charge levels, specifically at 55%, 65%, 75%, and 85%;
  • Provide valuable insights into how different EMS impact overall efficiency and system longevity, contributing to improved power management practices in hybrid fuel cell propulsion systems.
The study is structured as follows: Section 2 introduces the hybrid fuel cell electric ship under study, detailing the hybrid system’s components and their roles within the system architecture. Section 3 discusses the energy management strategies used to dynamically allocate power among the fuel cell, energy storage devices, and loads. Section 4 presents simulation results, comparing the effectiveness of various approaches in terms of energy consumption and system efficiency. Finally, Section 5 summarizes the findings, offering conclusions and suggestions for future research to enhance hybrid fuel cell transportation systems.

2. Description of the Fuel Cell Vessel

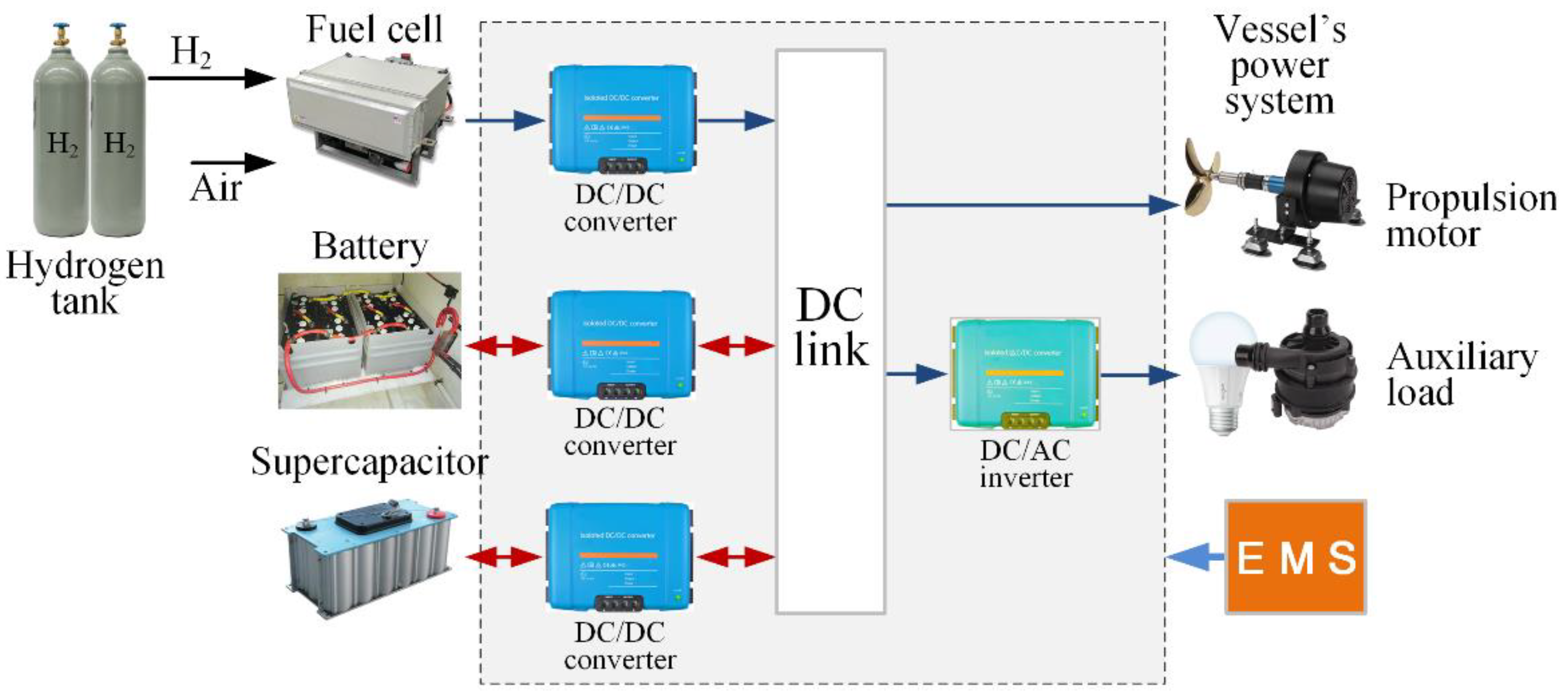
This paper presents a hybrid power system for a hydrogen passenger vessel, which uses a PEMFC as the primary DC power source and a lithium-ion battery bank and supercapacitor for additional energy storage, as seen in Figure 1. The fuel cell can handle load demands ranging from 0 to 12 kW, while the battery bank and SC provide additional power. The hybrid system ensures a balanced power supply by utilizing the rapid response capabilities of the batteries and supercapacitors to handle sudden power spikes. The vessel (with specifications detailed in Table 1) is designed for river trips and has two 15 hp electric propulsion motors for navigation and maneuvering. It also has a main fuel tank pressurized at 350 bar, allowing 24 hours of continuous operation without refueling. The vessel also has three auxiliary bottle tanks, providing flexibility and extended operational capability.
The integration of the fuel cell with the battery and SC storage systems is pivotal for maintaining the vessel’s performance during dynamic load conditions. The energy storage components are designed to enhance load handling by supporting the fuel cell in managing rapid load changes and peak demands, ensuring smooth operation without overburdening the fuel cell. By distributing the load efficiently among the fuel cell, batteries and supercapacitors, the hybrid system minimizes total energy consumption and enhances the vessel’s energy efficiency. The main fuel tank and auxiliary bottle tanks provide sufficient hydrogen storage to support extended operational periods, making the vessel suitable for long-duration trips without frequent refueling.
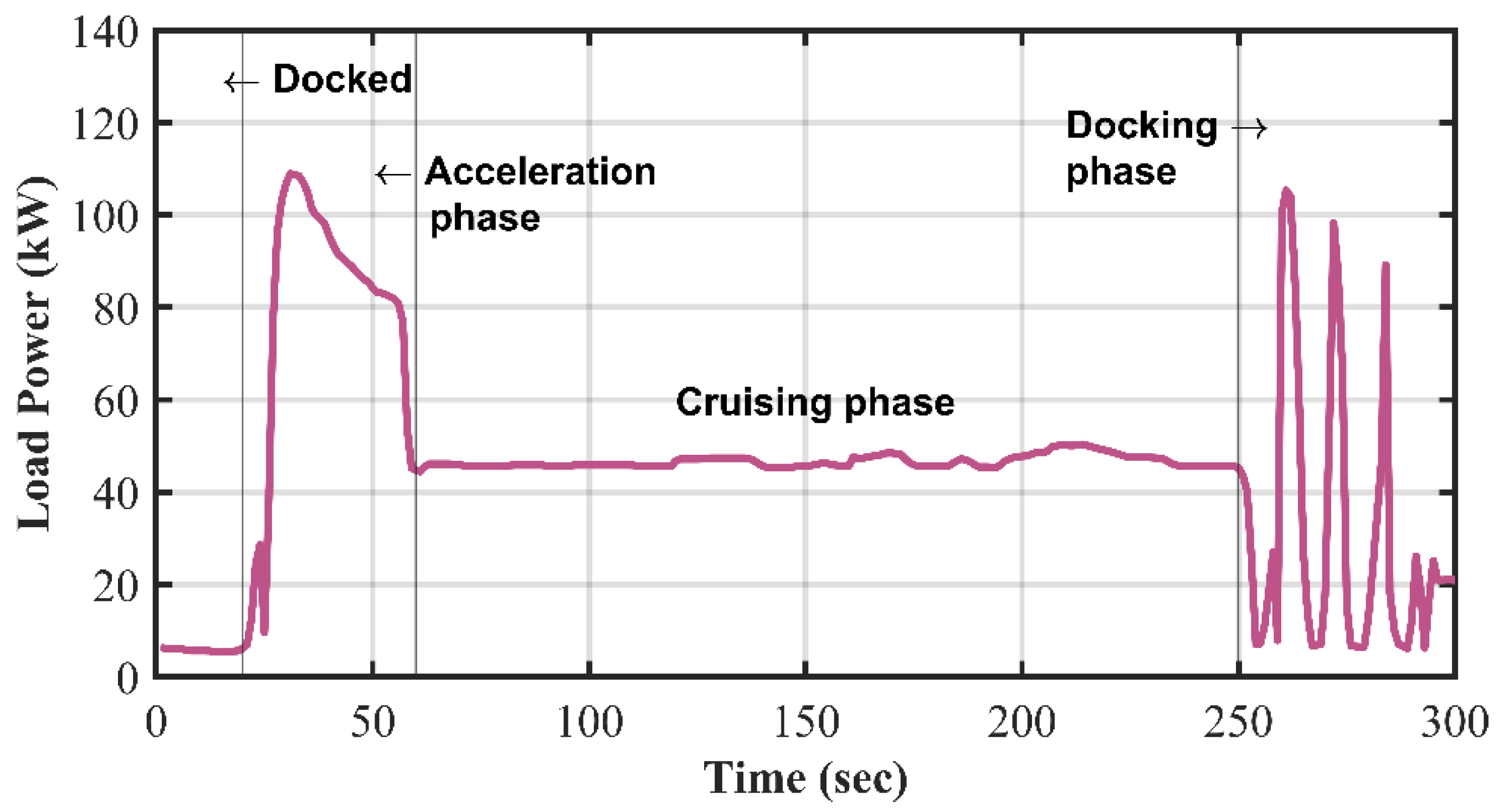
A measurement of the power requirements for a typical driving cycle of the vessel is depicted in Figure 2. This measurement encompasses both propulsion and auxiliary power needs. According to the data, the vessel remains docked for the initial 20 seconds before commencing its journey. This is followed by a 40-second acceleration period during which the vessel reaches its cruising speed. Once at cruising speed, the vessel maintains this speed for approximately 190 seconds. Finally, the vessel enters a 50-second docking phase, bringing the total time for the entire maneuver to 300 seconds [12].
Understanding these power requirements is essential for optimizing the energy management strategy of the hybrid fuel cell/battery/supercapacitor system. By analyzing the power needs during each phase of the driving cycle, the EMS can be fine-tuned to allocate power efficiently, reduce fuel consumption, and maintain optimal performance of the vessel’s hybrid power system. A detailed description of the components of the hybrid fuel system is provided below.

2.1. PEMFC Model

A generic PEMFC model is used in this study, which consists of an anode, cathode, and electrolyte [6]. The fuel cell uses a platinum catalyst to separate hydrogen into two opposite charges. The positive protons move to the cathode, while the negatively charged electrons pass through an external load, creating a voltage difference across the terminals. Within the fuel cell, concentration, activation, and ohmic losses occur, resulting in potential differences. These losses, can be expressed as follows,
V fc = E th − V al − V ol − V cl
where Vcl refers to the concentration voltage loss, Val represents the activation voltage loss and Vol is the ohmic voltage loss. Eth is the thermodynamic potential, which can be calculated by the following equation,
E th = 1.229 − 0.85 ⋅ 10 − 3 ( T − 298.15 ) + 4.3085 ⋅ 10 − 5 T ln P H 2 P o 2
where PH2 and PO2 denote the partial pressures of hydrogen and oxygen, respectively, and T is the cell temperature in Kelvin. In turn, the voltage loss during activation can be expressed as follows,
V al = − η 1 + η 2 T + η 3 T ln C O 2 + η 4 T ln ( 1 )
where CO2 is the oxygen concentration and η1, η2, η3, η4 are the parametric factors of the FC model. The equivalent resistance of the FC is what causes the ohmic voltage loss and is evaluated as,
V ol = I R m + R c
where the equivalent resistance of the membrane to proton conduction is denoted by Rm, while RC is the equivalent resistance of the contact to electron conduction. The concentration voltage drop can be explained as,
V cl = − β ln 1 − I / A I max
The variation in reactant concentration at the electrode surface causes the concentration voltage drop. Imax is the highest current density and β is the concentration loss constant [35].
V st = n V fc = n E th − V al − V ol − V cl

2.2. Battery Model

This study uses Li-ion batteries due to their superior energy density compared to other batteries like NiMH, lead-acid, or NiCd. The state of charge is considered for optimal performance, and polarization resistance is calculated using filtered battery current for simulation stability [3]. The battery voltage for the Li-ion battery model is expressed as,
V b = E 0 − K Q Q − q ⋅ q − R bat ⋅ i + A bat e − B ⋅ q − K Q Q − q i *
where E0 represents the battery’s constant voltage. The actual battery charge is represented by q, while Q denotes the total battery capacity, both measured in Ah. The filtered battery current is denoted by i*. The symbols Abat and Β are the exponential zone amplitude (V) and time constant inverse (Ah)-1, respectively. Rbat refers to the internal resistance of the battery [36]. The term K(Q/(Q-q)) of Eq. (7) is referred to as the polarization resistance and the term K(Q/(Q-q))q is known as the polarization voltage.

2.3. Supercapacitor Model

Supercapacitors are similar to electrostatic or electrolytic capacitors but have higher energy storage and release due to their high capacitance. They consist of two porous carbon electrodes submerged in an electrolyte, with negative and positive charges moving towards each other. This results in two layers at each electrode, known as a double-layer capacitor. The Stern model, which integrates Helmholtz and Gouy-Chapman models, is used in this study [26]. The capacitance of an SC can be described as,
C = 1 C h + 1 C gc − 1
The Helmholtz and Gouy-Chapman capacitance are given by,
C h = N e ε ε 0 A i l C gc = D Q cc 2 N e R T sinh Q cc N e 2 A i 8 R T ε ε 0 m c
where the parameter Ne represents the number of electrode layers. Also, the permittivities of the electrolyte material and free space are denoted by ε and ε0, respectively, both measured in (F/m). The Helmholtz layer length, or molecular radius, is indicated by l (m). Ai is the interfacial area between the electrodes and the electrolyte (m2), while mc is the molar concentration (mol/m3). The symbol Qcc denotes the electric charge of the cell (C) [8].

2.4. Power Converters

The fuel cell and the energy storage systems are connected to the dc bus via DC/DC converters, which enable voltage conversion (step-up and step-down) and provide precise control over the current and DC bus voltage. DC/DC converters can be modeled using either switching models or average-value models. Switching models are used for design and analyzing pulse-width-modulated (PWM) schemes but require short sampling times, making simulations time-consuming. Average-value models (used in this study), which replace switches with controlled voltage/current sources, reduce simulation time by omitting switching harmonics while still preserving converter dynamics, allowing for longer sampling times and more efficient simulations [6].

3. Energy Management Strategies

Energy management strategies are essential for optimizing the performance and efficiency of hybrid propulsion systems. These strategies involve the careful coordination and control of different energy sources, such as diesel engines, fuel cells, electric motors, batteries, and renewable energy systems like solar or wind. By effectively managing the energy flow between these sources, these strategies ensure that the vessel operates with maximum efficiency. In hybrid propulsion systems, energy management is particularly important as it allows the vessel to seamlessly switch between power sources depending on the operational demands, such as cruising, docking, or maneuvering [37]. This not only enhances the system’s overall energy efficiency but also extends the lifespan of the propulsion components and contributes to more sustainable maritime operations by minimizing the environmental impact.
This paper explored three distinct categories of energy management strategies: optimization-based, control-based, and rule-based strategies. Optimization-based strategies mainly use algorithms to continuously adjust the energy distribution for optimal efficiency, often relying on real-time data and predictive models. Control-based strategies, on the other hand, focus on maintaining the desired performance levels by dynamically controlling the energy flow according to predefined control laws, often employing feedback loops to adjust for deviations in performance. Rule-based strategies are more straightforward, using predefined rules to govern the energy management decisions. These can be further categorized into deterministic and fuzzy logic rule-based approaches. Deterministic rule-based strategies apply specific, fixed rules that dictate energy management actions based on clear, binary conditions, making them simple but less adaptable to varying conditions. In contrast, fuzzy logic rule-based strategies introduce a level of flexibility by handling uncertainties and imprecise inputs, allowing for smoother transitions between different operating modes and better performance in complex, real-world scenarios. Table 2 presents a comparison of the advantages and drawbacks of each technique.
Each of these state-of-the-art energy management approaches is designed to address specific challenges in fuel cell propulsion systems, ensuring that the vessel reduces hydrogen consumption to a minimum, extends the lifespan of batteries and supercapacitors, and maintains their SOC within a narrow and optimal range.
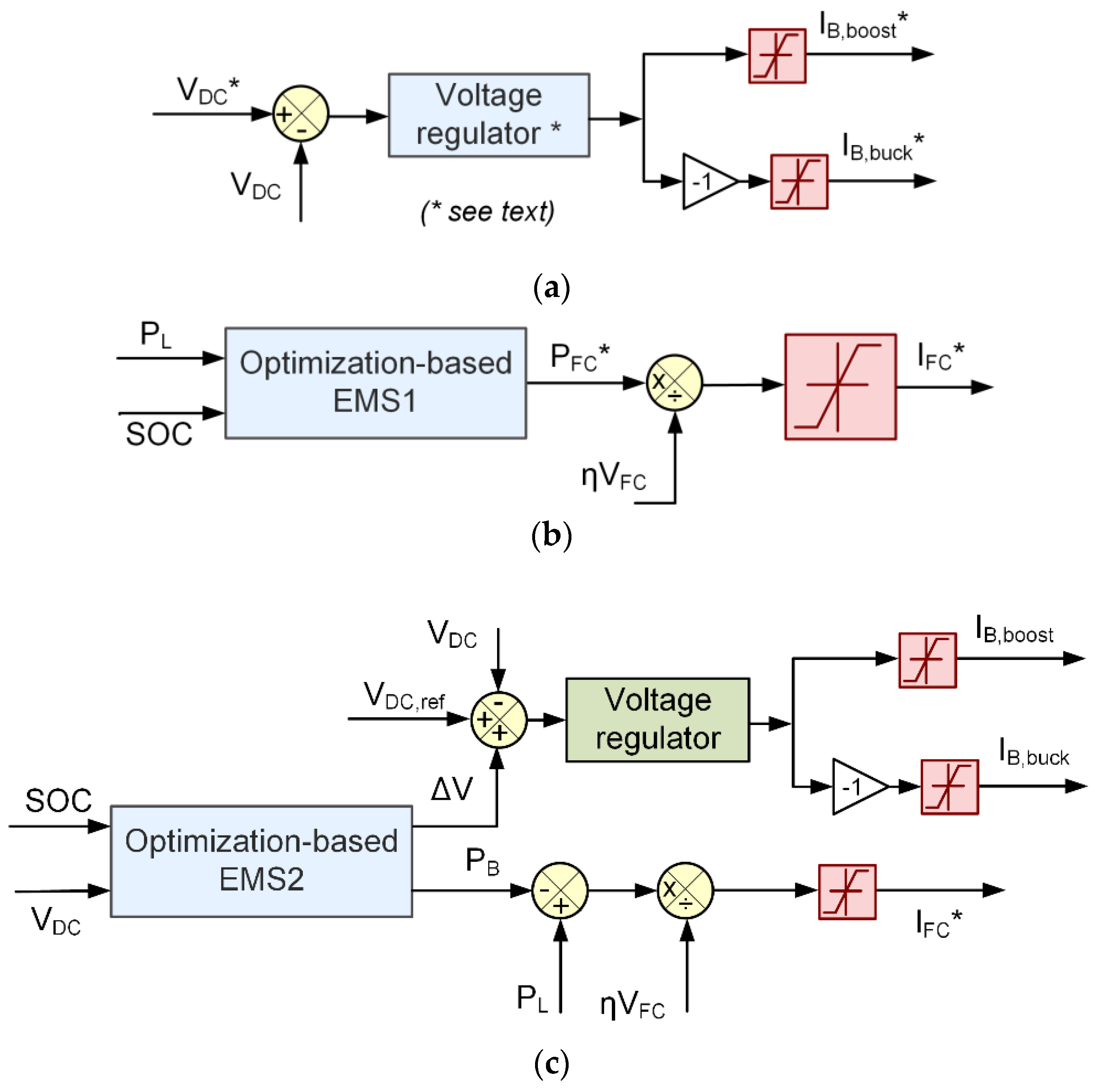
In order to guarantee an equitable and thorough comparison of the various energy management systems, each scheme is created in compliance with the same specifications. The battery power maintained between a maximum of 4 kW and a minimum of -1.2 kW, while the battery SOC remained within the range of 50% to 90%. The fuel cell power was required to operate between a maximum of 12 kW and a minimum of 0 kW. Additionally, the DC bus voltage kept within the limits of 280 V as the maximum and 250 V as the minimum. Controlling the DC bus voltage, via battery converters is a crucial part of the EMS implementation. A simple proportional-integral (PI) controller is used to create this control mechanism, which is shown in Figure 3a. This voltage control is used in each of the five EMS presented below.
The primary differentiation among the various EMS lies in the approach used to determine the reference power for the fuel cell. Each EMS employs a distinct strategy for setting the fuel cell’s reference power. The subsequent sections of this chapter will provide a detailed explanation of each energy management scheme considered. These explanations will cover the methodologies used for determining the fuel cell reference power, the rationale behind each approach, and how these strategies affect the management of energy flows within the system.

3.1. Optimization-Based EMS (OB-EMS)

Optimization-based energy management strategies are designed to ensure that a system operates at its optimal level by minimizing a defined cost function while adhering to specific constraints [38]. The core of such an EMS is the cost function, which serves as a metric to assess and guide the system’s performance. This function typically incorporates various weights to assign penalties to different operational aspects. For example, if the battery’s state of charge nears its lower limit, the cost function is designed to impose a significant penalty on battery usage to prevent over-discharge. Similarly, if the fuel cell or supercapacitor is not operating efficiently, the cost function will adjust to reflect these inefficiencies. The optimization process continuously assesses and adjusts the power distribution among the fuel cell, battery, and SC systems based on these penalties, aiming to minimize overall costs while ensuring that all operational constraints are respected. This method not only optimizes efficiency but also safeguards critical components from harmful operating conditions, thereby improving the durability and reliability of the energy systems.

3.1.1. Fuel Cell Hydrogen Consumption Minimization (OB-EMS1)

The primary objective of the first optimization-based energy management strategy (OB-EMS1) is to reduce fuel consumption by strategically limiting the hydrogen used by the fuel cell. This is accomplished by optimizing the distribution of power among the available energy sources, ensuring that the fuel cell operates at peak efficiency [39]. OB-EMS1 utilizes a cost function that focuses on minimizing fuel usage while still satisfying the system’s energy requirements. This cost function is designed to penalize excessive fuel consumption, thereby steering the system to use the fuel cell only when absolutely necessary and at optimal power levels. The block diagram of the technique is shown in Figure 3b, and the following formulation of the optimization problem can be used:
minimize     J = ( P FC + γ P B ) ⋅ Δ Τ
The objective function is constrained by the following equalities and inequalities
P L = P FC + P B
γ = 1 − 2 m S O C B − 0.5 S O C B , max + S O C B , min S O C B , max + S O C B , min
0 ≤ γ ≤ 2 P B , min ≤ P B ≤ P B , max P FC , min ≤ P FC ≤ P FC , max
where the fuel cell power, battery power, and load demand are denoted, respectively, by PFC, PB, and PL. The sample time, ΔT, and the penalty coefficient, γ, are indicated. The battery’s minimal and maximum states of charge are shown by SOCB,min and SOCB,max, respectively. The minimum and maximum fuel cell power are denoted by PFC,min and PFC,max, respectively. The minimum and maximum battery power are denoted by PB,min and PB,max, respectively.

3.1.2. Battery and SC Maximization Usage (OB-EMS2)

The primary aim of the second optimization-based energy management strategy (OB-EMS2) is to decrease hydrogen consumption by deliberately increasing the power demand on the supercapacitor and battery, while staying within their operational limits [40]. This strategy is outlined in Figure 3c, which shows the EMS configuration. The voltage of the DC bus, along with the states of charge of the battery and supercapacitor, are key inputs for the EMS method. These inputs are used to generate outputs such as the reference power for the battery and the charge or discharge voltage (ΔV) for the SC [26].
To establish the reference power required for the fuel cell, OB-EMS2 compares the battery’s power output with the load’s power demand. This comparison determines the fuel cell current (IFC*). Additionally, the EMS evaluates the supercapacitor’s status by comparing the actual DC bus voltage with the sum of the capacitor’s voltage and the reference DC bus voltage (Vdc_ref). This comparison indicates whether the SC needs to be charged or discharged, thereby optimizing its role in meeting load demands and minimizing reliance on the fuel cell. The optimization formula is detailed in the EMS block and is expressed mathematically as follows:
max     F = P B Δ T + 1 2 C Δ V 2
The following inequalities limit the objective function, which aims to maximize the energy provided by the battery and supercapacitor over a predetermined period of time:
P B Δ Τ ≤ ( S O C B − S O C B , min ) V B Q P B , min ≤ P B ≤ P B , max V DC , min ≤ V DC ≤ V DC , max
where VDC,min and VDC,max are the minimum and maximum limits of the DC bus voltage, respectively, and C is the supercapacitor’s rated capacitance. VB is the battery’s rated capacity, and Q is its nominal voltage.

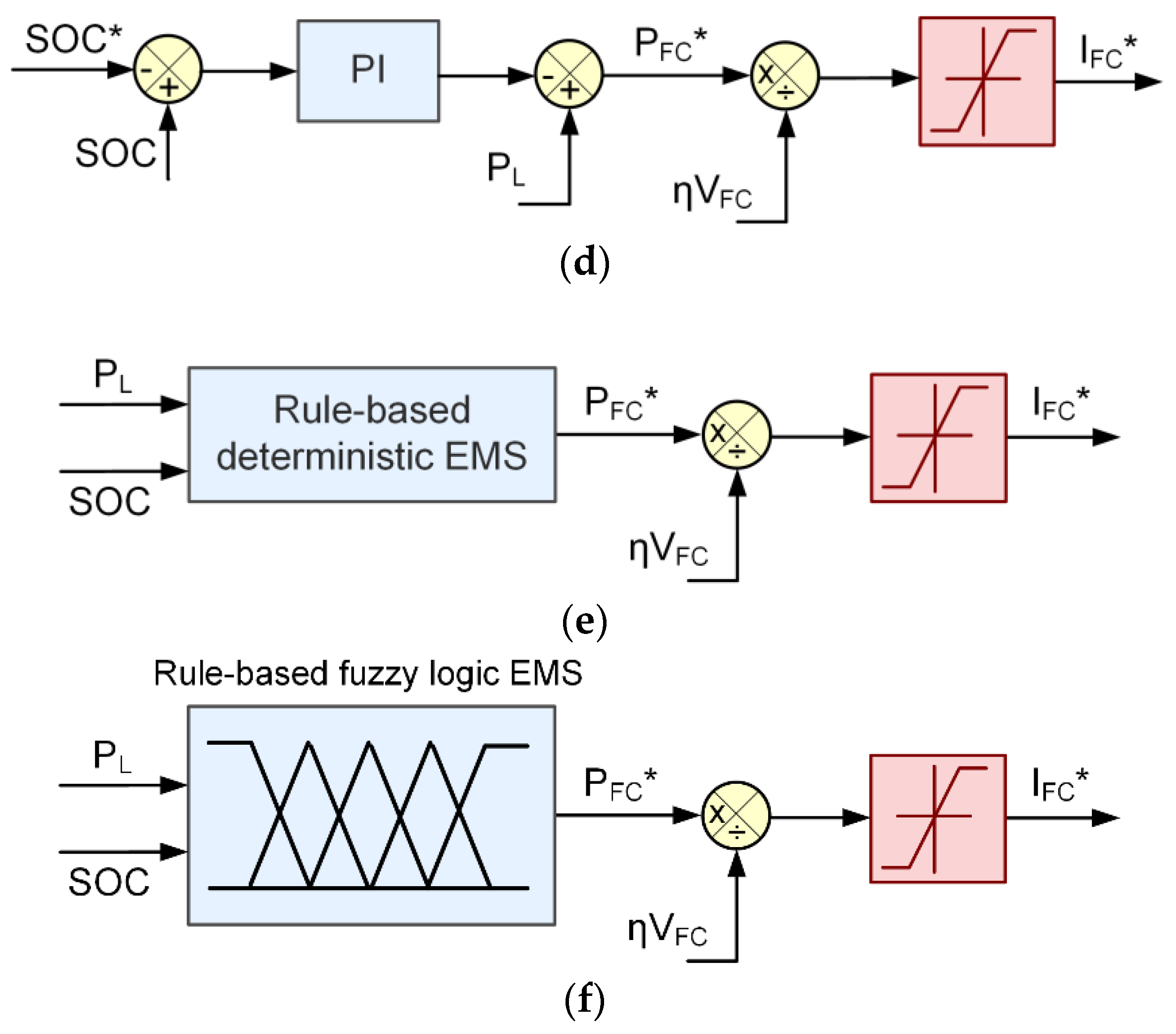
3.2. Control-Based EMS (CB-EMS)

Fuel cell power is calculated by subtracting the battery’s power from the load power, which is the sum of all resource powers. The battery’s power is managed using a Proportional-Integral (PI) controller, which operates based on both current and past input signal values. The PI controller minimizes deviations from the desired power output and adjusts the battery’s power output to ensure optimal power level. When the battery’s SOC is above the average value and FC power is low, the PI controller allows maximum power supply, while when the SOC falls below; the controller ensures full power supply. The PI controller’s transfer function ensures efficient power management across the system. The block diagram of this control-based EMS is illustrated in Figure 3d. Τhe PI controller’s transfer function is designed to execute this control task efficiently, ensuring smooth power management across the system as follows:
P Β = S O C B * − S O C B K p + K i s
The fuel cell’s output current IFC is then calculated based on the PFC obtained from the controller and the fuel cell output voltage VFC.

3.3. Rule-Based Deterministic EMS (RBD-EMS)

The rule-based deterministic EMS (Figure 3e) operates as a finite-state machine, making it the simplest among the EMS options used. The power setpoint for the fuel cell is established based on the battery’s state of charge, and the corresponding battery power can be calculated using Equation (11). The strategy is incorporated into a look-up table of eight states, as shown in Table 3.

3.4. Rule-Based Fuzzy Logic EMS (RBFL-EMS)

The rule-based fuzzy logic EMS, which utilizes a Mamdani fuzzy inference system [30], is designed in a manner similar to the RBD-EMS. The key benefit of using fuzzy logic is its ability to prevent abrupt changes between states, leading to smoother transitions due to its continuous-valued logic. Similar to the deterministic EMS, the fuzzy logic controller also uses the battery state of charge and the power load as inputs and the output is the power of fuel cell, as depicted in Figure 3f.
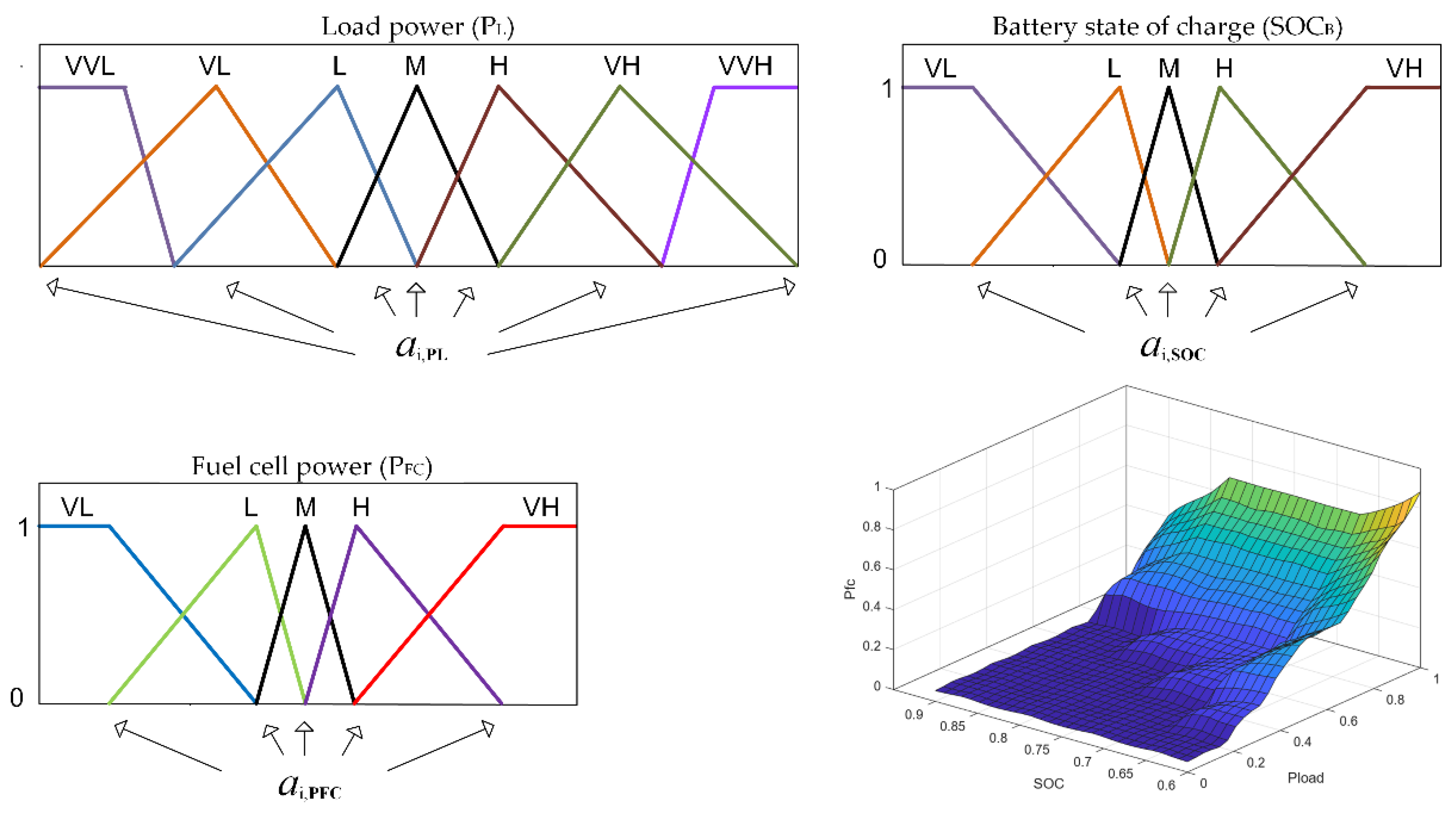
In brief, fuzzy logic control consists of three sequential stages or phases, namely: fuzzification, the inference system and the defuzzification process. The fuzzification step is responsible for converting the input’s value from its normal state to a mapped fuzzy value [2]. Each variable, whether input or output, is mapped through fuzzy membership functions (MF), which describe the degree of belonging of each variable to the MF within the range [0, 1]. A value of 1 denotes full belonging to the MF, while 0 implies that the variable’s value does not belong to the MF at all. The inference system uses a rule base that contains a set of “if-then” rules to process the fuzzy input values. Each rule describes a relationship between fuzzy inputs and fuzzy outputs. The inference engine combines the rules to derive fuzzy output values based on the fuzzy input values. Finally, the defuzzification step involves selecting a single, precise value from the fuzzy output set, which can be used as the final control action.
In this study, the fuzzy logic controller uses two input variables: the state of charge of the battery (SOCB) and the required power load (PL), with one output variable being the required power of the fuel cell (PFC). The controller employs a set of IF-THEN rules to connect the inputs to the output. The IF part of each rule, known as the antecedent, defines the condition under which the rule applies, while the THEN part, or consequent, specifies the values of the output variable [27]. The membership degree of the antecedent in each rule is assessed, and the consequent values are averaged and weighted based on these degrees. Triangular and trapezoidal membership functions are used for the fuzzy inputs and output, as illustrated in Figure 4.
There are five linguistic terms for SOCB input and PFC output, including VL (very low), L (low), M (medium), H (high) and VH (very high), with the fuzzy field scope [0, 1]. The PL input is characterized by seven linguistic terms, VVL (very very low), VL (very low), L (low), M (medium), H (high), VH (very high) and VHH (very very high) within the range [0, 1].
When the vessel is accelerating and the load power demand is high, the fuel cell system, the battery and the SC should supply power to the ship simultaneously. The fuel cell system adjusts its power output based on the state of charge of the battery. If the SOCB is very low or low, the fuel cell generates a high output to compensate for the low battery charge, providing the necessary power to meet the demand. As the SOCB increases to medium, the fuel cell output decreases to medium level, balancing the need for both battery charging and power delivery. Similarly, when SOCB is high or very high, the fuel cell maintains a medium output, ensuring efficient power management without overloading the system or excessively charging the battery. When the ship is cruising at a constant speed and the required power is stable, the distribution of power among the power sources is complex, and depends on the battery SOC. If the SOCB is very low, the fuel cell responds with a very low output, reflecting minimal power generation due to the low battery charge. When SOCB reaches medium or high, the fuel cell maintains a medium output, efficiently balancing power delivery to meet the demand while preserving battery health. When the ship is decelerating and the load power demand is very low, if the SOCB is less than the desired value, the fuel cell system delivers power in order to increase the SOC of the battery. If the SOCB is higher than the desired level (high), the battery will supply power. If SOC value is near the desired value, fuel cell supplies all the demand power.
The membership function parameters ai,SOC (i=1...5), ai,PL (i=1...7) and ai,PFC (i=1...5) on the horizontal axis of Figure 4 represent the points that define the boundaries of the membership functions. These are critical points where the transition occurs between different levels of membership in each fuzzy set. Selecting the parameters for the membership functions typically involves a trial-and-error process and requires a lengthy experimental procedure to determine the optimal parameters. To address this issue, a recent optimization algorithm is employed in this study to identify the optimal set of parameters that minimizes a specific criterion which is the hydrogen consumption. The algorithm iteratively adjusted the positions of the parameters within the defined range, searching for the optimal configuration that yields the best control performance. This approach ensures that the fuzzy sets are optimally distributed, providing accurate and adaptive system responses.
The fuel cellʹs operational mode is established by its associated membership function and the corresponding rule table (Table 4). The fuzzy reasoning process is carried out using the Mamdani inference method, which governs the decision-making rules. During the operation, the fuzzy strategy efficiently allocates the necessary power to each energy source, ensuring not only that the workload demand is fully met but also that the SOC is maintained. These parameters must be accurately set to prevent overcharging or deep discharging.

4. Simulation Results and Discussion

To thoroughly assess the performance of the EMS, they are tested against the load profile provided in Section 2, using the simulation model described therein. The power distributions vary depending on the chosen EMS, clearly illustrating the distinct operational characteristics of each strategy. For a fair comparison, identical PEMFC and ESS models with consistent initial conditions are employed in four scenarios, according to the initial battery SOC. Thus, in the present study was considered the case for initial SOC 55%, 65%, 75% and 85%. Indicatively, the plots for initial SOC 65% and 85% are shown; the other two cases show similar results. 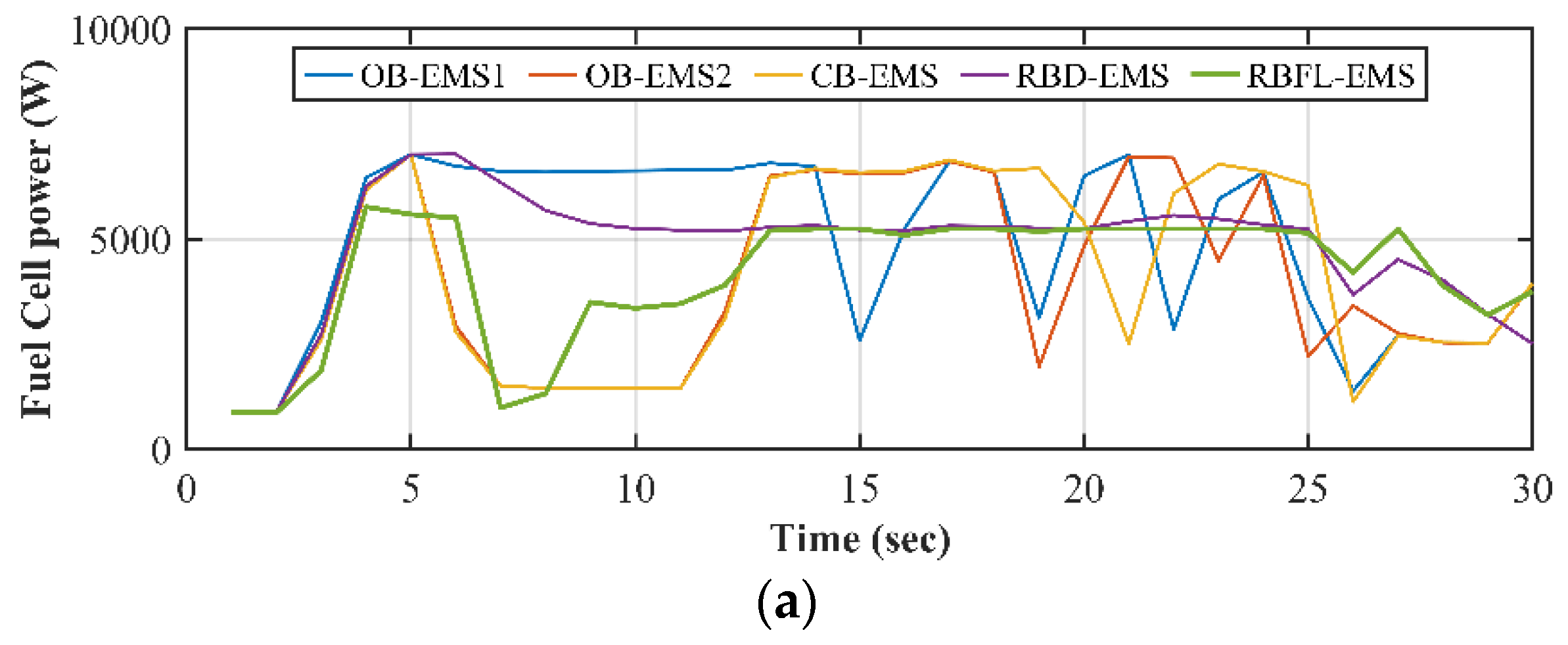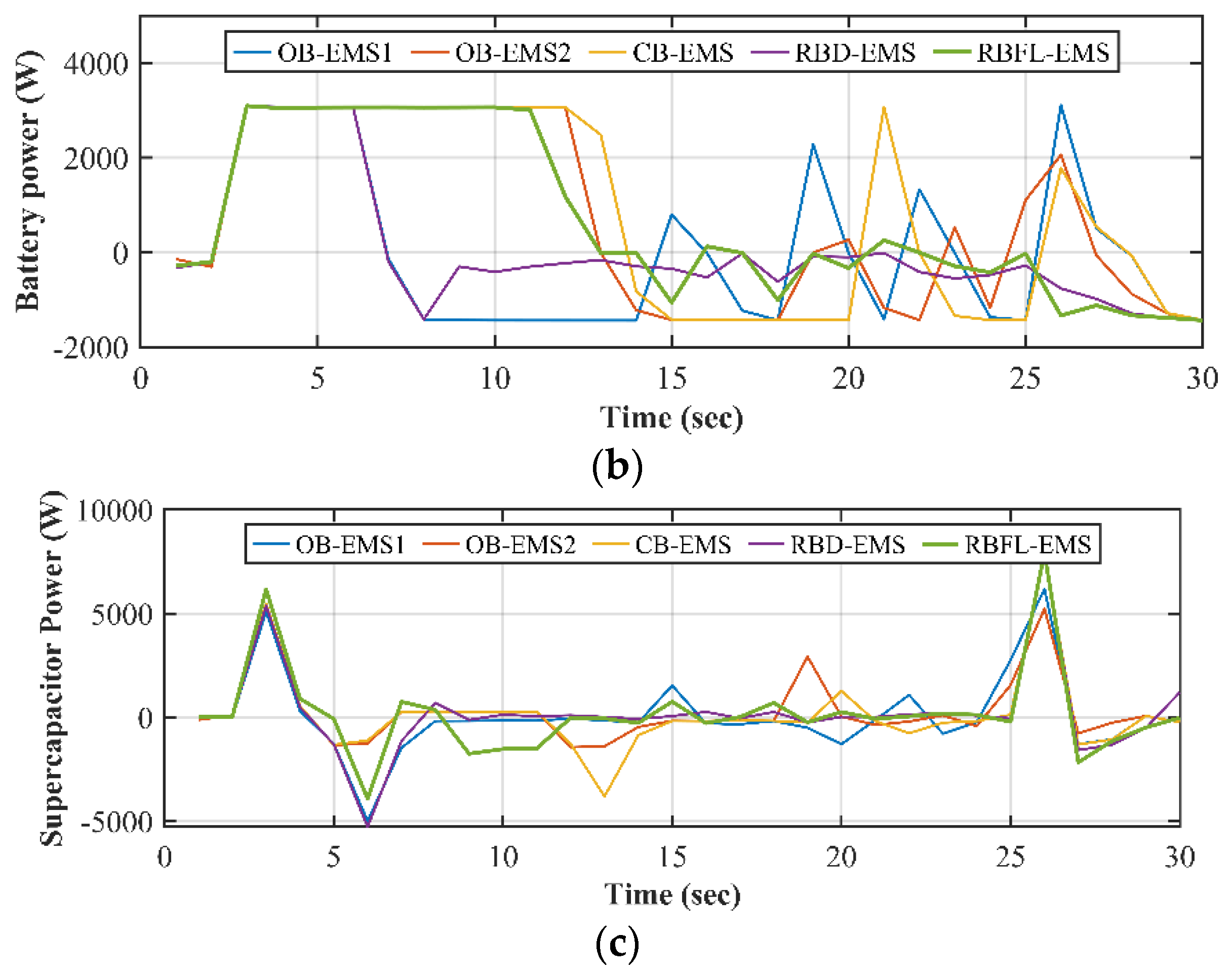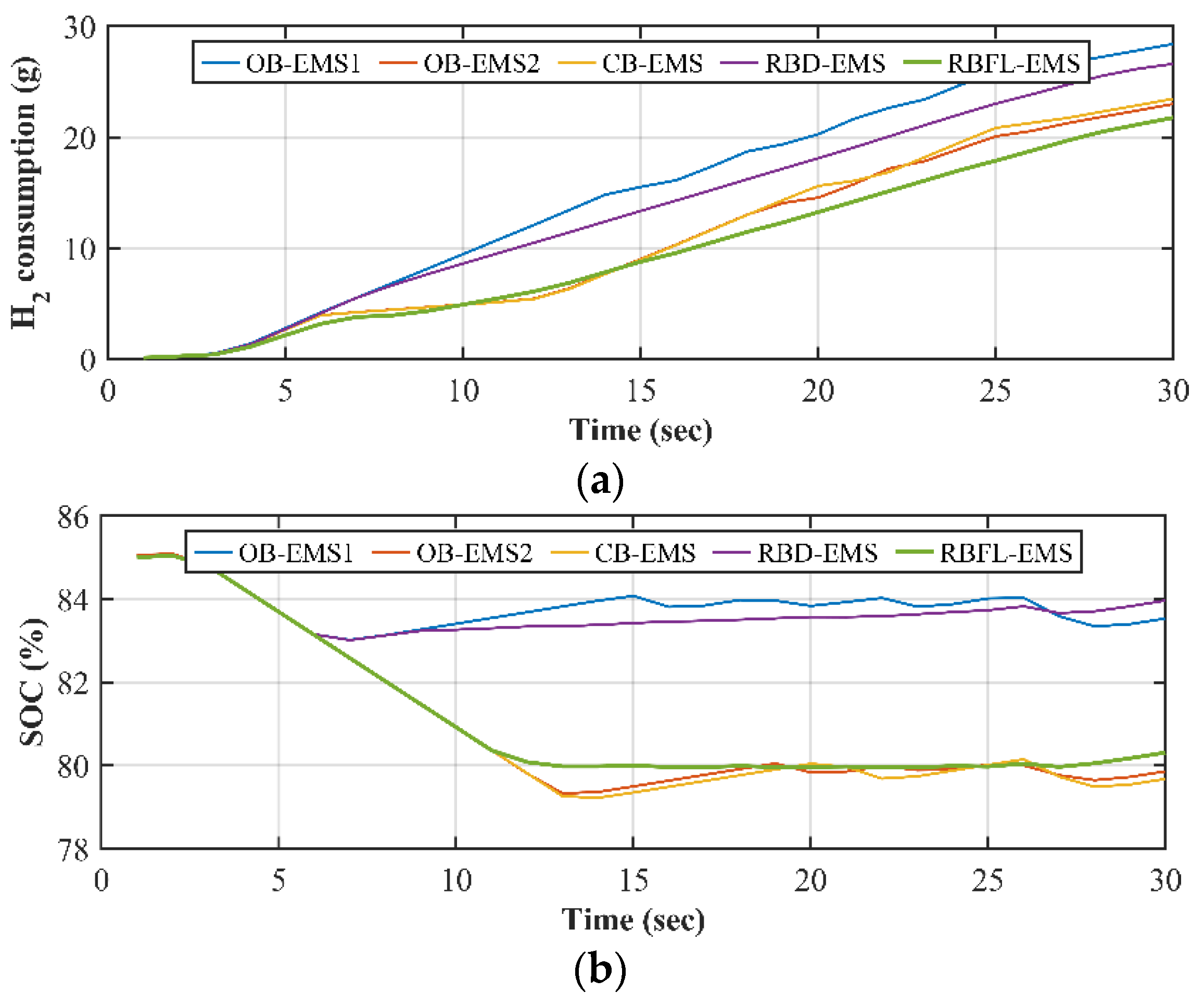Figure 5, Figure 6, Figure 7 and Figure 8 present the resulting power distributions, alongside the transient behaviors of the battery SOC and hydrogen consumption for both cases. These figures effectively demonstrate the influence of different initial SOC levels on the overall system performance.
These figures also illustrate the behavior of the EMS over the predefined 300 seconds period. Additionally, key metrics such as hydrogen consumption, average power of the fuel cell and ESS are summarized in Table 5. Key operational points (Figure 5 and Figure 7) are as follows:
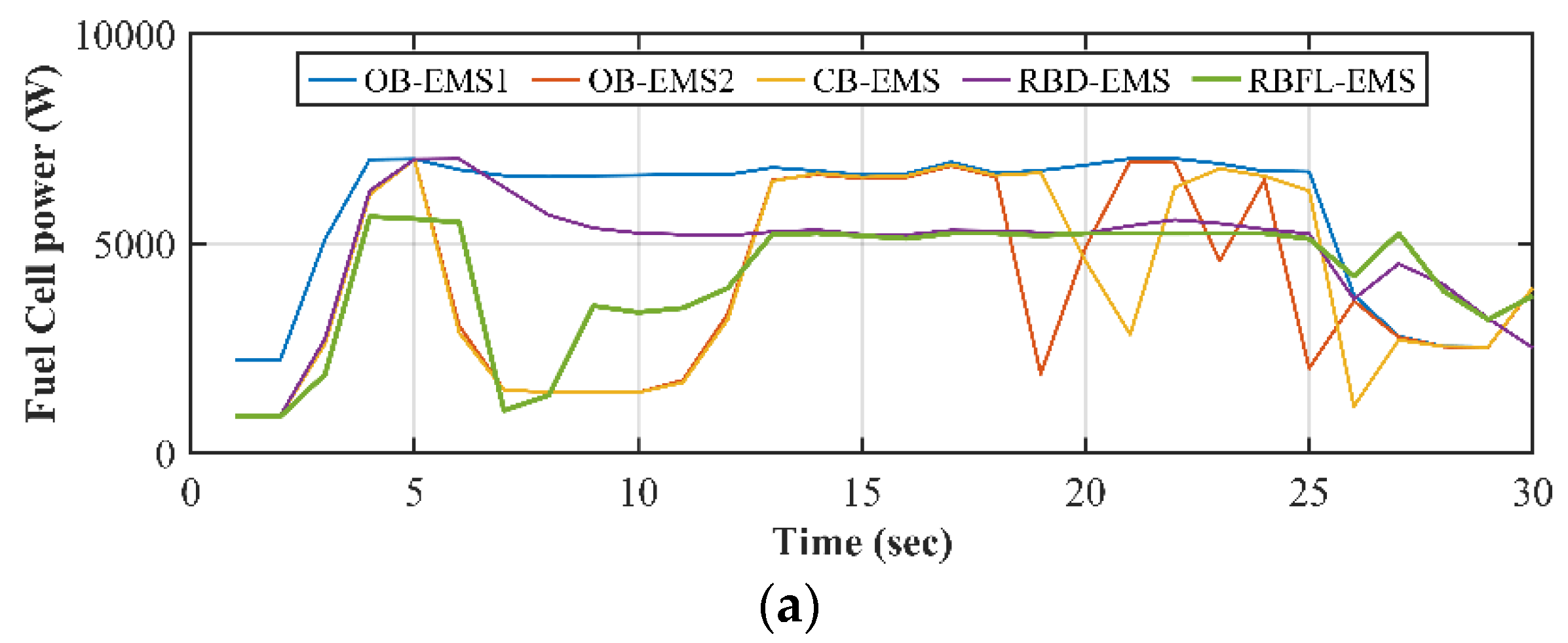
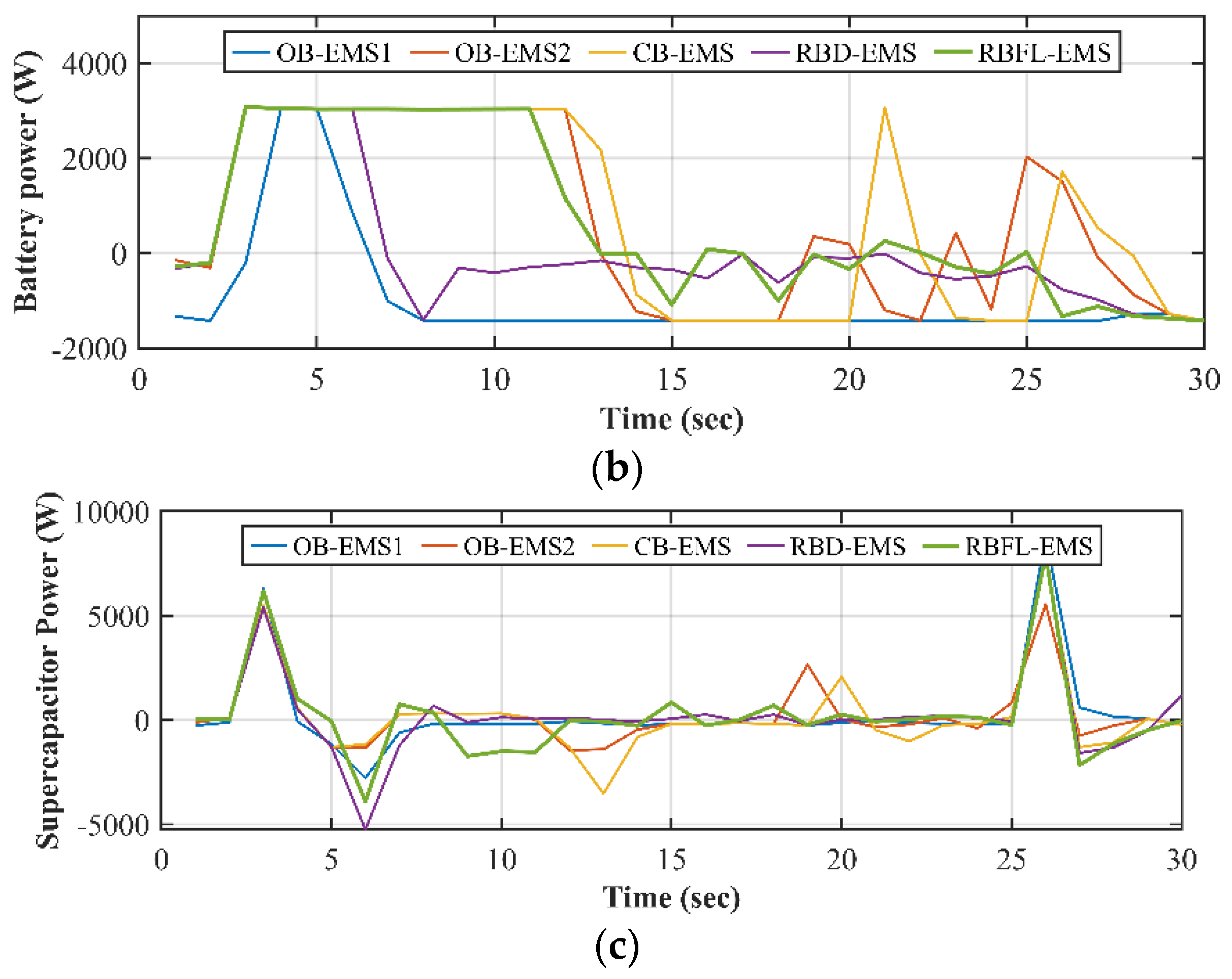
  • Initial/Acceleration Phase (t=0-60 sec.): All strategies start with a rapid increase in fuel cell power output at the beginning of the cycle, indicating the system’s response to an initial high-power demand phase. OB-EMS1, OB-EMS2, CB-EMS and RBD-EMS show a sharp surge, with power levels exceeding 7500 W, while RBFL-EMS peaks at much lower power level around 6000 W. All the strategies provide a sharp positive battery output, maintaining close to 3000 W initially. The SC power spikes up, with OB-EMS1 and RBFL-EMS, reaching as high as 7000 W. This indicates a large amount of power discharge, to assist in meeting an initial high load demand, such as during acceleration. Conversely, all the others EMS exhibit a more moderate power surge, peaking around 5500 W. This suggests these strategies are less reliant on supercapacitor power during the initial phase.
  • Cruising Phase (t=60-250 sec.): OB-EMS1 maintains a relatively high and steady fuel cell power output (around 6500 W) for a significant portion of the time. The RBD-EMS shows a decrease but stabilizes at a lower power level (~5000 W). OB-EMS2, CB-EMS and RBFL-EMS show variations, with the RBFL-EMS method fluctuating at lower power values. As for the battery, it appears that the above three strategies use the battery energy, while OB-EMS1 draws energy to charge the battery during cruising. The RBD-EMS shows consistent low negative power in the early phase, indicating continuous regeneration, and then fluctuates between small positive and negative values. The SC power for all strategies remains relatively low, but the behaviors diverge. OB-EMS2, CB-EMS and RBFL-EMS demonstrate mild oscillations in both the positive and negative directions, indicating periods of alternating discharge and recharge. RBD-EMS and OB-EMS1 show more stable power outputs, with smaller fluctuations. Their power remains close to zero for most of this period, suggesting a more conservative approach to SC usage, possibly to preserve its charge for later stages.
  • Docking Phase (t=250-300 sec.): Towards the end of the cycle, all strategies show a decline in fuel cell power output. This indicates a period where the system’s load is reduced, due to lower energy demand as part of a shutdown process. Notably, OB-EMS2, and CB-EMS experience more pronounced drops, with multiple sharp decreases in power, while OB-EMS1, RBD-EMS and RBFL-EMS taper off more gradually and consistently. Figure 5b and Figure 7b shows increased power fluctuations across all strategies. CB-EMS and OB-EMS2 experiences large, frequent oscillations in battery power, both positive and negative, indicating dynamic energy management that balances between charging and discharging. OB-EMS1 still exhibit fairly stable power though shows some minor variations in power output. RBD-EMS and RBFL-EMS remain relatively stable with small oscillations, further emphasizing their conservative power management approach. In the final phase, all strategies exhibit sharp fluctuations in SC power. Both positive and negative spikes are observed, with values reaching up to 8000 W and as low as -5000 W, especially for CB-EMS, OB-EMS2, and RBFL-EMS. These frequent power changes suggest that the supercapacitor is being heavily utilized to balance the system’s energy demands. The SC is rapidly discharging to provide power and then recharging quickly, reflecting a highly dynamic load environment. RBD-EMS and OB-EMS1 show smaller fluctuations compared to other strategies, implying that they are utilizing the SC more conservatively, resulting in lower energy bursts and more controlled power management.
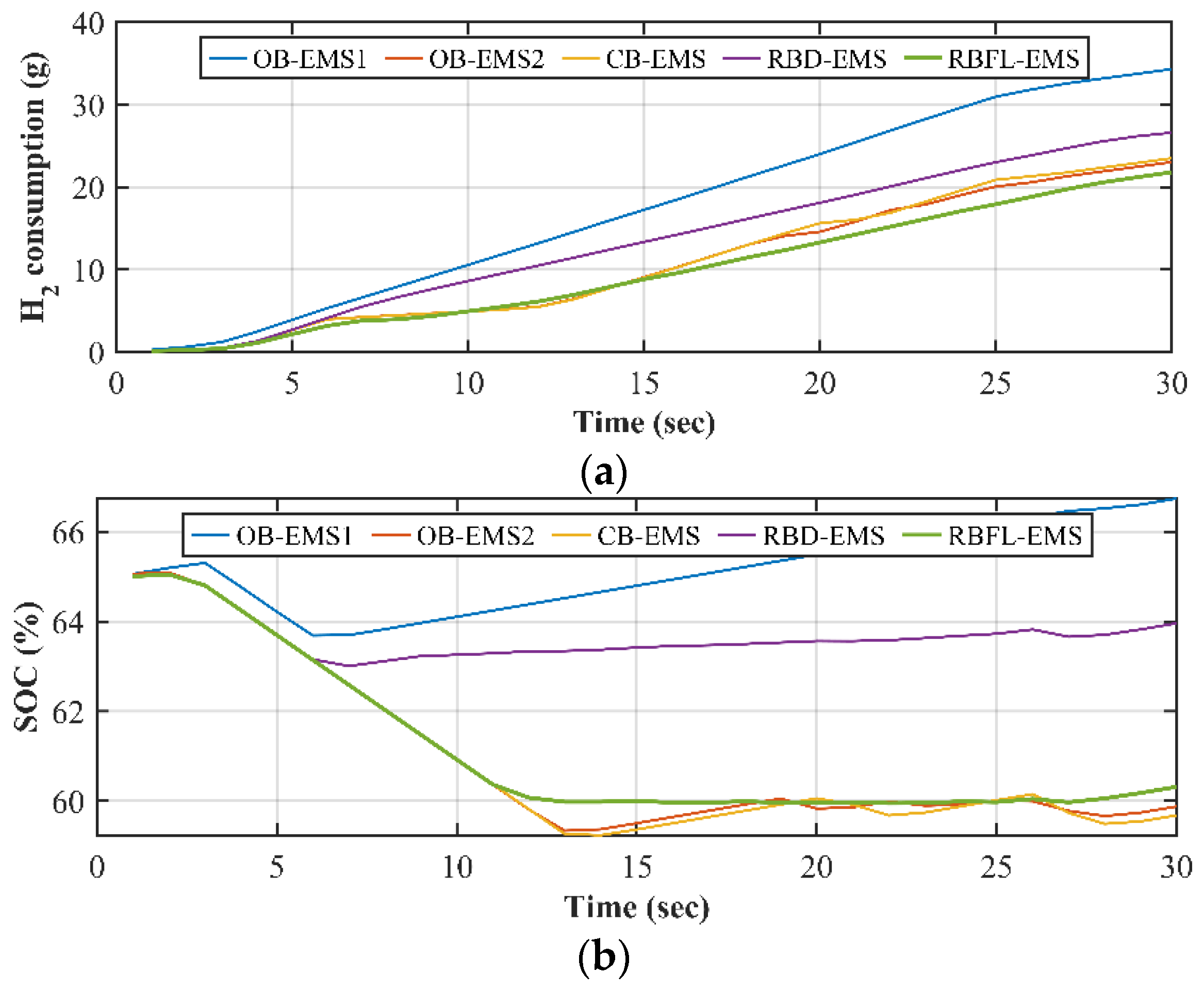
Figure 6a and Figure 8a displays the hydrogen consumption (in grams) over time for the five different energy management strategies. In the early phase (from 0 to 60 seconds), all strategies exhibit an increase in hydrogen consumption, though the rates vary slightly. RBFL-EMS shows the steepest descent in H₂ consumption from the beginning, indicating that this strategy consumes less hydrogen early on compared to the others. During acceleration phase, the consumption of hydrogen continues in a linear fashion for all strategies. This suggests a steady demand for hydrogen as the system operates at cruising speed.
Figure 6b, shows the state of charge of the battery. At the start (~0 to 60 seconds), all strategies begin with nearly identical SOC values around 65%. However, there is a noticeable divergence in SOC depletion patterns among the different EMS strategies shortly after the initial period. The OB-EMS1 strategy shows an increase in SOC over time, indicating an improvement in battery charge. In contrast, OB-EMS2 experiences an initial drop before stabilizing around 60%, reflecting some discharge followed by a maintained SOC. Similarly, CB-EMS also drops initially but then stabilizes at around 60%. RBD-EMS shows a gradual downward trend, with the SOC reducing to approximately 62%. Meanwhile, RBFL-EMS experiences an initial drop, followed by slight fluctuations, eventually stabilizing just above 60%.
Table 5 indicates that the RBD-EMS and the OB-EMS1 primarily depend on the fuel cell for power, leading to the highest hydrogen consumption. In contrast, the OB-EMS2, CB-EMS and RBFL-EMS utilize both the fuel cell and the ESS to meet load demands. RBFL-EMS is more efficient in terms of hydrogen consumption and seem to prioritize battery power for energy use, leading to lower average hydrogen consumption 63.67% compared to RBD-EMS and 66.78% compared to OB-EMS1.
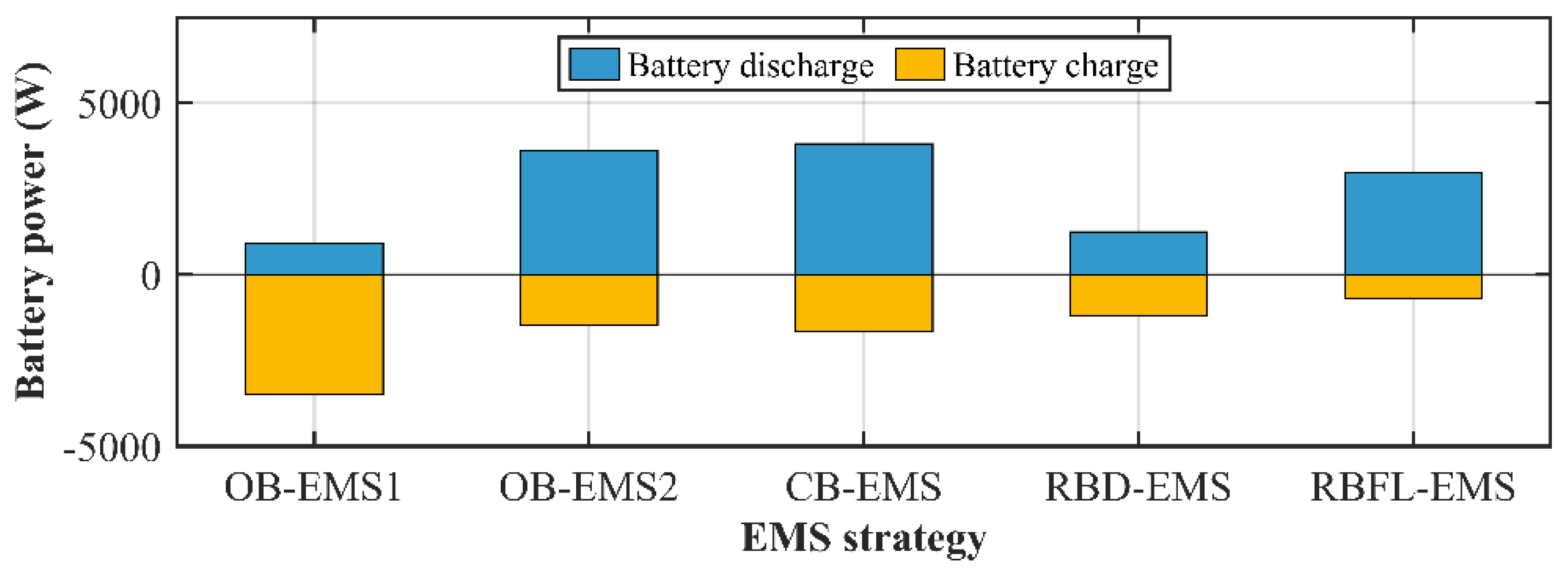
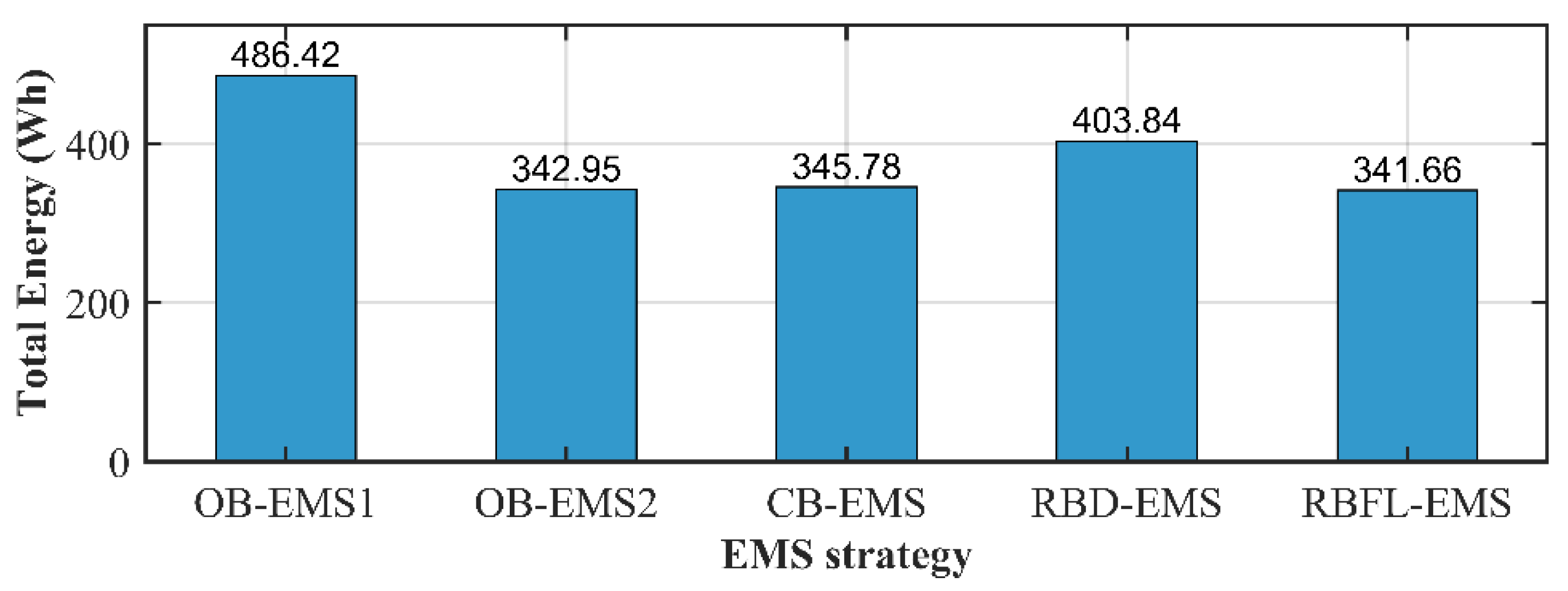
Figure 9 illustrates a comparison of total battery energy for various EMS strategies, starting with an initial SOC of 65%, where the blue bars represent battery discharge and the yellow bars indicate battery charge. OB-EMS1 has a discharge battery energy around 4000W, with 900 W dedicated to battery discharging. OB-EMS2 and CB-EMS show total discharge energy around 5000 W, with 3800 W from discharging, demonstrating a more balanced distribution between charge and discharge compared to OB-EMS1. RBD-EMS shows 1200 W of charging and 1200 W of discharging, making it one of the least battery-using strategies overall. Lastly, RBFL-EMS exhibits the lowest charge energy at 700 W, with 3000 W from battery discharging, making it the least energy-consuming strategy.
As presented in Figure 10, the RBFL-EMS exhibits lower energy consumption compared to the four other EMS approaches across different initial battery SOC levels. Indicatively for the initial SOC 65%, the highest energy savings, 29.76%, are achieved in comparison to the OB-EMS1, while the lowest energy savings, 0.37%, are observed when compared to the OB-EMS2.
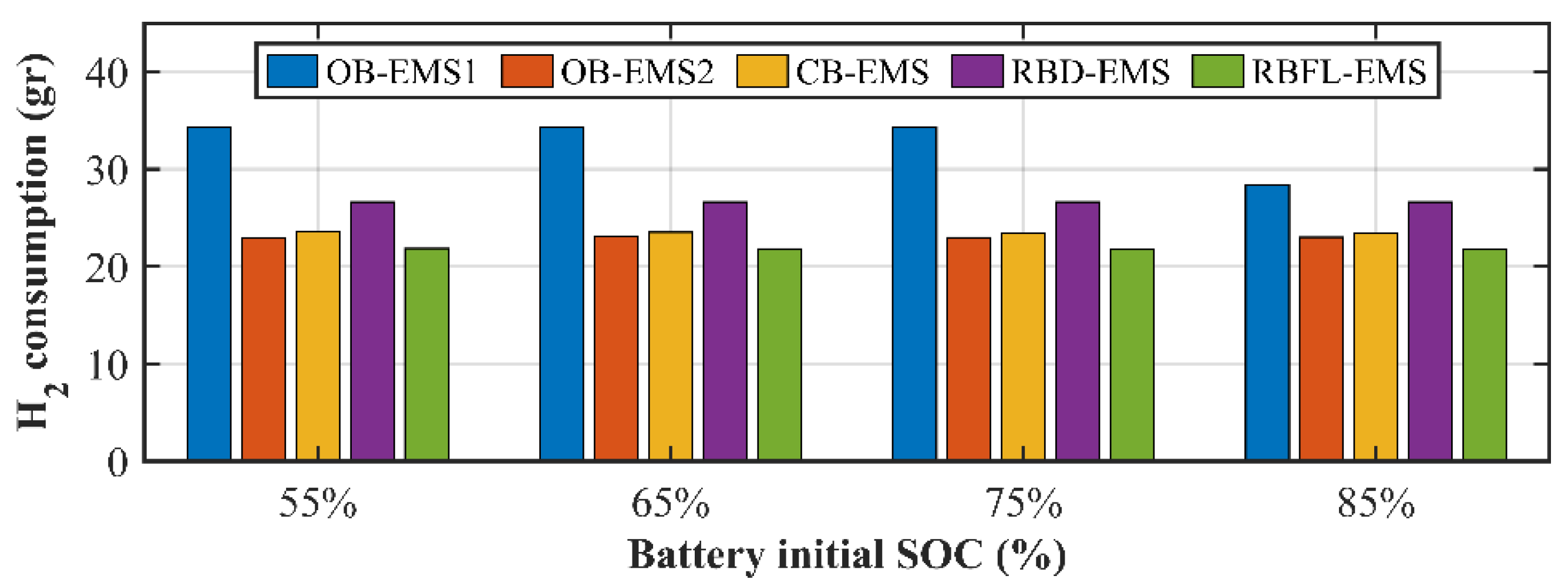
Finally, Figure 11 illustrates the impact of different initial battery SOC levels (55%, 65%, 75%, and 85%) on hydrogen consumption for the different EMS strategies. The RBFL-EMS exhibits the lowest hydrogen consumption across different initial battery SOC levels, as it prioritizes supplying the load power from the battery system whenever feasible. In particularly, the RBFL-EMS reduces hydrogen consumption by 36.35% and 17.92% compared to the OB-EMS1 and RBD-EMS, respectively, while showing approximately the same hydrogen consumption as the OB-EMS2 and CB-EMS with a reduction of 4.7% and 7.2% respectively.

5. Conclusions

The growing interest in hybrid fuel cell propulsion systems for transportation is driven by their exceptional efficiency, low noise levels, and low emissions. These features make them a compelling alternative to conventional internal combustion engines, particularly as the focus on reducing environmental impact and enhancing sustainability intensifies. The performance of hybrid fuel cell systems is closely linked to how power is allocated among the various components within the system. Proper power management is essential for maximizing overall efficiency, sustaining performance levels, and prolonging the lifespan of the system. Numerous EMS have been explored, each designed with specific objectives in mind, addressing unique operational demands and constraints.
This study provides a comparative analysis of five distinct energy management strategies -control-based, optimization-based, deterministic rule-based and fuzzy logic rule-based-, focusing on total hydrogen consumption for a small hydrogen-powered passenger vessel operating in a river trip scenario. During a 300-second driving cycle, which included docking, acceleration, and cruising phases, the strategies were evaluated based on total energy consumption, battery state of charge, and the performance of the fuel cell, battery, and supercapacitor. The simulation results indicated that the fuzzy logic rule-based energy management strategy excelled in minimizing fuel consumption.
It shows a steeper decline in hydrogen use from the early phase, and prioritizes energy supply from the battery system, resulting in the lowest overall hydrogen consumption across various initial SOC levels. The RBFL-EMS demonstrates significant hydrogen savings of 63.67% compared to the RBD-EMS and 66.78% compared to OB-EMS1. Moreover, the RBFL-EMS achieves the highest energy savings of 29.76% when compared to OB-EMS1 and the lowest savings of 0.37% compared to OB-EMS2. Overall, RBFL-EMS proves to be the most energy-efficient strategy, optimizing both hydrogen and battery energy usage while ensuring lower consumption rates, making it a highly effective choice for fuel cell and energy storage system management.
Future work should focus on real-time implementation and validation of the RBFL-EMS strategy in real-world environments to address practical challenges. Incorporating machine learning and AI could enhance predictive capabilities and optimize energy management. Integrating renewable energy sources, such as solar or wind, into hybrid systems would further reduce hydrogen consumption and boost sustainability. Multi-objective optimization, balancing hydrogen use, costs, emissions, and system longevity, should also be explored. Additionally, scalability of the RBFL-EMS to larger transportation systems and the integration of advanced energy storage technologies could unlock further efficiency gains across various applications.

Author Contributions

Conceptualization, E.N. and Y.L.K.; methodology, E.N.; software, Y.L.K.; validation, E.N.; formal analysis, E.N. and J.-F.C.; investigation, E.N.; resources, E.N.; data curation, E.N.; writing—original draft preparation, E.N.; writing—review and editing, Y.L.K. and J.-F.C.; visualization, Y.L.K.; supervision, Y.L.K. and J.-F.C.; project administration, Y.L.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data are available upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. IRENA. International Renewable Energy Agency. Available online: https://www.irena.org/Energy-Transition/Technolo- gy/Hydrogen (accessed on September 2024).
  2. Trinh, H.-A.; Truong, H.-V.-A.; Ahn, K.K. Development of Fuzzy-Adaptive Control Based Energy Management Strategy for PEM Fuel Cell Hybrid Tramway System. Appl. Sci. 2022, 12, 3880. [Google Scholar] [CrossRef]
  3. Kunde, C.; Hanke-Rauschenbach, R.; Mangold, M.; Kienle, A.; Sundmacher, K.; Wagner, S.; Hahn, R. Temperature and Humidity Control of a Micro PEM Fuel Cell Stack. Fuel Cells. 2010, 10, 949–959. [Google Scholar] [CrossRef]
  4. Arce, A.; Real, A.J.d.; Bordons, C.; Ramirez, D.R. Real-Time Implementation of a Constrained MPC for Efficient Airflow Control in a PEMFuel Cell. IEEE Trans. Ind. Electron. 2010, 57, 1892–1905. [Google Scholar] [CrossRef]
  5. Nivolianiti, E.; Karnavas, Y.L.; Charpentier, J.-F. Energy management of shipboard microgrids integrating energy storage systems: A review. Renew. Sustain. Energy Rev. 2024, 189, 114012. [Google Scholar] [CrossRef]
  6. Njoya Motapon, S.; Dessaint, L.-A.; Al-Haddad, K. A Comparative Study of Energy Management Schemes for a Fuel-Cell Hybrid Emergency Power System of More-Electric Aircraft. IEEE Trans. Ind. Electron. 2014, 61(3), 1320–1334. [Google Scholar] [CrossRef]
  7. Li, L.; Bai, J.; Xu, J.; Chang, M.; Qiao, L. A Conceptual Sizing Method and Energy Management Strategy for Hybrid-Electric Aircraft. 2023 Asia-Pacific International Symposium on Aerospace Technology (APISAT 2023) Proceedings. APISAT 2023. Singapore, Oct. 2023, Lecture Notes in Electrical Engineering.
  8. Çınar, H.; Kandemir, I. Active Energy Management Based on Meta-Heuristic Algorithms of Fuel Cell/Battery/Supercapacitor Energy Storage System for Aircraft. Aerospace. 2021, 8, 85. [Google Scholar] [CrossRef]
  9. Torreglosa, J. P.; García, P. Predictive Control for the Energy Management of a Fuel-Cell–Battery–Supercapacitor Tramway. IEEE Trans. Ind. Inf. 2014, 10, 276–285. [Google Scholar] [CrossRef]
  10. Deutsch, C.; Chiche, A.; Bhat, S.; Lagergren, C.; Lindbergh, G.; Kuttenkeuler, J. Evaluation of energy management strategies for fuel cell/battery-powered underwater vehicles against field trial data. Energy Convers. Manag. 2022, 14, 100193. [Google Scholar] [CrossRef]
  11. Inal, O.B.; Charpentier, J.-F.; Deniz, C. Hybrid power and propulsion systems for ships: Current status and future challenges. Renew. Sustain. Energy Rev. 2022, 156, 111965. [Google Scholar] [CrossRef]
  12. Han, J.; Charpentier, J.-F.; Tang, T. An Energy Management System of a Fuel Cell/Battery Hybrid Boat. Energies. 2014, 7, 2799–2820. [Google Scholar] [CrossRef]
  13. Karkosiński, D.; Rosiński, W.A.; Deinrych, P.; Potrykus, S. Onboard Energy Storage and Power Management Systems for All-Electric Cargo Vessel Concept. Energies. 2021, 14, 1048. [Google Scholar] [CrossRef]
  14. Bassam, A. M.; Phillips, A. B.; Turnock, S. R.; Wilson, P. A. An improved energy management strategy for a hybrid fuel cell/battery passenger vessel. Int. J. Hydrogen Energy. 2016, 41, 22453–22464. [Google Scholar] [CrossRef]
  15. ie, P.; Guerrero, J. M.; Tan, S.; Bazmohammadi, N.; Vasquez, J. C.; Mehrzadi, M.; Al-Turki, Y. Optimization-Based Power and Energy Management System in Shipboard Microgrid: A Review. IEEE Syst. J. 2021, 1–13. [Google Scholar] [CrossRef]
  16. Jaramillo Jimenez, V.; Kim, H.; Munim, Z.H. A review of ship energy efficiency research and directions towards emission reduction in the maritime industry. J. Clean. Prod. 2022, 366, 132888. [Google Scholar] [CrossRef]
  17. Nuchturee, C.; Li, T.; Xia, H. Energy efficiency of integrated electric propulsion for ships – A review. Renewable and Sustainable Energy Rev. 2020, 134, 110145. [Google Scholar] [CrossRef]
  18. Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. Optimising design and power management in energy-efficient marine vessel power systems: a literature review. J. Mar. Eng. Technol. 2018, 1–10. [Google Scholar] [CrossRef]
  19. Fang, S.; Xu, Y. Multi-objective robust energy management for all-electric shipboard microgrid under uncertain wind and wave. Int. J. Electr. Power Energy Syst. 2020, 117, 105600. [Google Scholar] [CrossRef]
  20. Papari, B.; Cox, R.; Edrington, C. S.; Ozkan, G.; Hoang, P. H.; Deb, N. Enhancement of Energy Management in the Shipboard Power Systems Based on Recursive Distributed Load Shedding Model. 2019 IEEE Electric Ship Technologies Symposium (ESTS). Washington, DC, USA, Aug. 2019. [CrossRef]
  21. Tao, Y.; Qiu, J.; Lai, S.; Sun, X.; Zhao, J. Flexible Voyage Scheduling and Coordinated Energy Management Strategy of All-Electric Ships and Seaport Microgrid. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3211–3222. [Google Scholar] [CrossRef]
  22. Chu, K.; Qi, Z.; Tong, X.; Zhou, X.; Bai, L. A State Machine EMS Based on Equivalent Consumption Minimization for Hybrid Power System in UAVs. Proceedings of 3rd 2023 International Conference on Autonomous Unmanned Systems (3rd ICAUS 2023). ICAUS 2023. Lecture Notes in Electrical Engineering, 1176. Springer, Singapore.
  23. Oo, T. Z.; Kong, A. W. -K. Real-Time Energy Management for Marine Applications Using Markov Approximation. IEEE Trans. Power Syst. 2023, 38, 4341–4354. [CrossRef]
  24. Karnavas, Y.L.; Nivolianiti, E. Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm. Appl. Sci. 2023, 13, 6128. [Google Scholar] [CrossRef]
  25. Edrington, C. S.; Ozkan, G.; Papari, B.; Gonsoulin, D. E.; Perkins, D.; Vu, T. V.; Vahedi, H. Distributed energy management for ship power systems with distributed energy storage. J. Mar. Eng. Technol. 2019, 1–14. [Google Scholar] [CrossRef]
  26. Chen, H.; Zhang, Z.; Guan, C.; Gao, H. Optimization of sizing and frequency control in battery/supercapacitor hybrid energy storage system for fuel cell ship. Energy. 2020, 197, 117285. [Google Scholar] [CrossRef]
  27. Zhu, L.; Han, J.; Peng, D.; Wang, T.; Tang, T.; Charpentier, J.-F. Fuzzy logic based energy management strategy for a fuel cell/battery/ultra-capacitor hybrid ship. 2014 First International Conference on Green Energy ICGE 2014. Sfax, Tunisia, March. 2014. [CrossRef]
  28. Shih, N.-C.; Weng, B.-J.; Lee, J.-Y.; Hsiao, Y.-C. Development of a 20 kW generic hybrid fuel cell power system for small ships and underwater vehicles. Int. J. Hydrogen Energy. 2014, 39, 13894–13901. [Google Scholar] [CrossRef]
  29. Chua, L. W. Y.; Tjahjowidodo, T.; Seet, G. G. L.; Chan, R. Implementation of Optimization-Based Power Management for All-Electric Hybrid Vessels. IEEE Access. 2018, 6, 74339–74354. [Google Scholar] [CrossRef]
  30. Kalikatzarakis, M.; Geertsma, R. D.; Boonen, E. J.; Visser, K.; Negenborn, R. R. Ship energy management for hybrid propulsion and power supply with shore charging. Control Eng. Pract. 2018, 76, 133–154. [Google Scholar] [CrossRef]
  31. Wen, S.; Zhao, T.; Tang, Y.; Xu, Y.; Fang, S.; Zhu, M.; Ding, Z. Joint Energy Management and Voyage Scheduling for All-Electric Ships Using Dynamic Real-Time Electricity Price of Onshore Power. 2020 IEEE/IAS 56th Industrial and Commercial Power Systems Technical Conference (I&CPS). Las Vegas, Nevada, USA, Jul. 2020. [CrossRef]
  32. Huang, Y.; Lan, H.; Hong, Y.-Y.; Wen, S.; Fang, S. Joint Voyage Scheduling and Economic Dispatch for All-Electric Ships with Virtual Energy Storage Systems. Energy. 2019, 116268. [Google Scholar] [CrossRef]
  33. Edrington, C. S.; Ozkan, G.; Papari, B.; Gonsoulin, D. E.; Perkins, D.; Vu, T. V.; Vahedi, H. Distributed energy management for ship power systems with distributed energy storage. J. Mar. Eng. Technol. 2019, 1–14. [Google Scholar] [CrossRef]
  34. Hou, J.; Sun, J.; Hofmann, H. Control development and performance evaluation for battery/flywheel hybrid energy storage solutions to mitigate load fluctuations in all-electric ship propulsion systems. Appl. Energy. 2018, 212, 919–930. [Google Scholar] [CrossRef]
  35. Njoya Motapon, S.; Dessaint, L.-A.; Al-Haddad, K. A Comparative Study of Energy Management Schemes for a Fuel-Cell Hybrid Emergency Power System of More-Electric Aircraft. IEEE Trans. Ind. Electron. 2014, 61, 1320–1334. [Google Scholar] [CrossRef]
  36. García, P.; Torreglosa, J. P.; Fernández, L. M.; Jurado, F. Viability study of a FC-battery-SC tramway controlled by equivalent consumption minimization strategy. Int. J. Hydrogen Energy. 2012, 37, 9368–9382. [Google Scholar] [CrossRef]
  37. Nuchturee, C.; Li, T.; Xia, H. Energy Efficiency of Integrated Electric Propulsion for Ships—A Review. Renew. Sustain. Energy Rev. 2020, 134, 110145. [Google Scholar] [CrossRef]
  38. Xie, P.; Guerrero, J.M.; Tan, S.; Bazmohammadi, N.; Vasquez, J.C.; Mehrzadi, M.; Al-Turki, Y. Optimization-Based Power and Energy Management System in Shipboard Microgrid: A Review. IEEE Syst. J. 2021, 16, 578–590. [Google Scholar] [CrossRef]
  39. Zhang, H.B.; Li, Q.; Wang, H.Q.; Li, Q.Y.; Qin, G.F.; Wu, Q. A review of energy management optimization based on the equivalent consumption minimization strategy for fuel cell hybrid power systems. Fuel Cells 2022, 22, 116–130. [Google Scholar] [CrossRef]
  40. Rezk, H.; Nassef, A.M.; Abdelkareem, M.A.; Alami, A.H.; Fathy, A. Comparison among various energy management strategies for reducing hydrogen consumption in a hybrid fuel cell/supercapacitor/battery system. Int. J. Hydrogen Energy 2019. [Google Scholar] [CrossRef]
Preprints 118269 g001
Figure 1. The configuration of the passenger vessel under study.
Figure 1. The configuration of the passenger vessel under study.
Preprints 118269 g001
Preprints 118269 g002
Figure 2. Typical load characteristics for a typical power driving cycle.
Figure 2. Typical load characteristics for a typical power driving cycle.
Preprints 118269 g002
Preprints 118269 g003aPreprints 118269 g003b
Figure 3. Energy management schemes: (a) DC bus voltage control common to all EMS, (b) Optimization-based EMS-1 (OB-EMS1), (c) Optimization-based EMS-2 (OB-EMS2), (d) Control-based EMS (CB-EMS), (e) Rule-based deterministic EMS (RBD-EMS), (f) Rule-based fuzzy logic EMS (RBFL-EMS).
Figure 3. Energy management schemes: (a) DC bus voltage control common to all EMS, (b) Optimization-based EMS-1 (OB-EMS1), (c) Optimization-based EMS-2 (OB-EMS2), (d) Control-based EMS (CB-EMS), (e) Rule-based deterministic EMS (RBD-EMS), (f) Rule-based fuzzy logic EMS (RBFL-EMS).
Preprints 118269 g003aPreprints 118269 g003b
Preprints 118269 g004
Figure 4. Membership functions of the RBFL-EMS input and output variables and the corresponding designed inference system control surface.
Figure 4. Membership functions of the RBFL-EMS input and output variables and the corresponding designed inference system control surface.
Preprints 118269 g004
Preprints 118269 g005aPreprints 118269 g005b
Figure 5. Comparison of power distribution from energy sources for battery initial SOC 65% (a) fuel cell; (b) battery; (c) supercapacitor.
Figure 5. Comparison of power distribution from energy sources for battery initial SOC 65% (a) fuel cell; (b) battery; (c) supercapacitor.
Preprints 118269 g005aPreprints 118269 g005b
Preprints 118269 g006
Figure 6. Time responses for battery initial SOC 65% for the five different strategies, (a) H2 consumption and (b) battery SOC.
Figure 6. Time responses for battery initial SOC 65% for the five different strategies, (a) H2 consumption and (b) battery SOC.
Preprints 118269 g006
Preprints 118269 g007aPreprints 118269 g007b
Figure 7. Comparison of power distribution from energy sources for battery initial SOC 85% (a) fuel cell; (b) battery; (c) supercapacitor.
Figure 7. Comparison of power distribution from energy sources for battery initial SOC 85% (a) fuel cell; (b) battery; (c) supercapacitor.
Preprints 118269 g007aPreprints 118269 g007b
Preprints 118269 g008
Figure 8. Time responses for battery initial SOC 65% for the five different strategies, (a) H2 consumption and (b) battery SOC.
Figure 8. Time responses for battery initial SOC 65% for the five different strategies, (a) H2 consumption and (b) battery SOC.
Preprints 118269 g008
Preprints 118269 g009
Figure 9. Total battery energy comparison for battery initial SOC equal to 65%.
Figure 9. Total battery energy comparison for battery initial SOC equal to 65%.
Preprints 118269 g009
Preprints 118269 g010
Figure 10. Total consumed energy comparison for battery initial SOC equal to 65%.
Figure 10. Total consumed energy comparison for battery initial SOC equal to 65%.
Preprints 118269 g010
Preprints 118269 g011
Figure 11. Impact of different initial battery SOC on hydrogen consumption.
Figure 11. Impact of different initial battery SOC on hydrogen consumption.
Preprints 118269 g011
Table 1. Specifications of the hydrogen passenger vessel.
Table 1. Specifications of the hydrogen passenger vessel.
Specification Data
Powering 1x PEMFC 12 kW,
1x 40 Ah/ 48V Lithium-Ion battery
1x SC stack 15.6 F
Engine 2x DC permanent magnet motors (2x15 hp)
Capacity 12 passengers
Length 12 m
Beam 3.96 m
Draft 0.76 m
Airdraft 2.16 m
Displacement 3000 kg
Max speed 7 knots
Table 2. Advantages and disadvantages of energy management strategies.
Table 2. Advantages and disadvantages of energy management strategies.
Method Advantages Disadvantages
Optimization-based ✓ adaptable to varying operational conditions ✕ Complexity in implementation
use recent information ✕ High computational demand
Control-based ✓ effective in managing specific operational objectives ✕ Limits to predefined control laws
✓ simple to implement ✕ not adapt well to unpredicted changes
Rule-based:
deterministic		 ✓ simple and reliable ✕ requires prior knowledge
✓ high real-time performance ✕ lacks flexibility in complex scenarios
Rule-based:
Fuzzy logic		 ✓ adaptability and ease of adjustment ✕ based on experience
✓ handles uncertainties ✕ difficulty operating complex systems
Table 3. Deterministic rule-based states.
Table 3. Deterministic rule-based states.
State Condition Decision/Statement
PL SOCB
1 PL < PFC,min SOCB > SOCB,max PFC* = PFC,min
2 PFC,min ≤ PL ≤ PFC_max SOCB > SOCB,max PFC* =PL
3 PL ≥ PFC,max SOCB > SOCB,max PFC* =PFC,max
4 PL < PFC,opt SOCB,min ≤ SOCB ≤ SOCB,max PFC* =PFC,opt
5 PFC,opt ≤ PL ≤ PFC_max SOCB,min ≤ SOCB ≤ SOCB,max PFC* =PL
6 PL ≥ PFC,max SOCB,min ≤ SOCB ≤ SOCB,max PFC* = PFC,max
7 PL < PFC,max SOCB < SOCB,min PFC* = PL - PB,min
8 PL ≥ PFC,max SOCB < SOCB,min PFC* = PFC,max
Table 4. The fuzzy association matrix (FAM) developed here.
Table 4. The fuzzy association matrix (FAM) developed here.
SOCB
VL L M H VH
PL VVL VL VL VL VL VL
VL VL VL VL VL VL
L L VL VL VL VL
M M L VL VL VL
H M L L VL VL
VH H M M M L
VVH VH H H H M
Table 5. Key metrics from the simulation results of the different EMS.
Table 5. Key metrics from the simulation results of the different EMS.
EMS H2
consumption
(gr)		 Battery
SOC
(average)
(%)		 Fuel cell
Power
(average)
(W)		 Battery
power
(average)
(W)
SOC 55% OB-EMS1 34.33 55.12 5837.72 -856.11
OB-EMS2 22.92 51.04 4109.45 746.44
CB-EMS 23.56 51.01 4157.85 710.54
RBD-EMS 26.62 53.68 4845.95 17.99
RBFL-EMS 21.85 51.19 4072.45 753.07
SOC 65% OB-EMS1 34.33 65.13 5837.02 -858.65
OB-EMS2 23.05 61.06 4103.12 721.14
CB-EMS 23.51 61.01 4149.35 721.47
RBD-EMS 26.62 63.68 4846.08 18.06
RBFL-EMS 21.82 61.20 4099.91 759.49
SOC 75% OB-EMS1 34.32 75.13 5836.25 -861.12
OB-EMS2 22.98 71.06 4098.86 729.84
CB-EMS 23.47 71.01 4142.25 728.56
RBD-EMS 26.62 73.86 4846.17 17.86
RBFL-EMS 21.80 71.20 4090.91 764.46
SOC 85% OB-EMS1 28.41 83.85 4945.35 -30.38
OB-EMS2 23.00 81.06 4095.12 730.91
CB-EMS 23.47 81.01 4142.36 728.91
RBD-EMS 26.62 83.69 4846.25 17.75
RBFL-EMS 21.77 81.20 4090.32 767.78
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated