Prerpints.org logo
Preprint
Concept Paper

Automating Portfolio Replication with Stock Market Algorithms

Altmetrics

Downloads

48

Views

24

Comments

0

This version is not peer-reviewed

Predictive Analytics and Fault Diagnosis of Machines with Machine Learning Techniques

Submitted:

17 September 2024

Posted:

20 September 2024

You are already at the latest version

Alerts
Abstract
This study aims to explore methods for automating the replication of correlated portfolios across shares using various algorithms. The goal is to select one algorithm for implementation in a visualization tool that will facilitate portfolio building. The dynamics of the stock market provide a comprehensive view of the global economy, acting as a catalyst for stakeholders to participate and benefit various sectors financially, primarily through investments in companies that yield returns and contribute to the economy. The evaluation and comparison of these algorithms are crucial for making well-informed decisions regarding the core objectives of the study. Ultimately, a determination will be made as to whether the program can effectively analyse data from Yahoo finance to provide a quick overview of the financial market state of companies in the S&P 500 US stock prices.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In the financial services industry, the process of constructing a portfolio requires a viable amount of time and effort. Visualizing portfolio data is crucial as it demonstrates the significance of optimizing portfolio weights and maximizing diversification for accurate predictions [1,2]. Furthermore, we will illustrate how machine learning can enhance portfolio construction by learning hierarchical relationships from the close value matrix. To measure portfolio performance, we will utilize instruments that offer insight into their performance relative to our objectives [3]. These metrics are typically compared to a benchmark that represents an overview of the investment universe rather than traditional investment opportunities like the S&P 500 index for U.S. equities or the risk-free interest rate for fixed-income assets. Therefore, this study aims to assess specific performance measurements and employ various approaches to optimize portfolio performance in interaction with the market and calculate relevant performance statistics [4,5,6,7,8,9].
Portfolio management is a critical concept that involves balancing risk-return trade-offs to minimize operational costs and maximize profits. In this study, we introduce k-means clustering as a method for computing and visualizing key features and comparing performance against other algorithms. Subsequently, we will train, test, and tune linear models for regression and classification using cross-validation to achieve robust out-of-sample performance. These models will then be integrated into the framework for defining and back-testing algorithmic trading strategies. Incorporating a wider range of information into machine learning models will lead to more accurate predictions, capturing more complex patterns than other methods. As a result, various approaches have been developed to optimize portfolios, including the application of machine learning to learn hierarchical assets and to treat assets as either complements or substitutes within the portfolio risk profile.
The study is as follows; similar papers are shown in the following section. The empirical investigation is described in Section III. The result analysis is covered in Section IV, and in Section V, we wrap up the investigation with some conclusions and plans for future research.

2. Related Works

In our comprehensive literature review, we delved into the realm of machine learning [10] and explored various methods for analyzing the financial market such as [11] to assist investors in making well-informed trading decisions. The primary objective of this review was to assess existing approaches, classify their relevance to the specific issue of stock market dynamics, and determine the most suitable pre-trade and backend logic for the study. The reinforcement learning approaches such as [12] for trading emerged as the most fitting, given its capacity to yield-distributed the training data and its management with the model of a return-maximizing agent operating in an uncertain, dynamic environment, akin to an investor or trading strategy interacting with financial markets. Additionally, the application of narrow AI for trade based on machine learning entails the use of substantial datasets and sophisticated algorithms to augment the accuracy of future predictions [13]. Furthermore, when dealing with raw data, machine learning is required to identify similarities without prior instruction through unsupervised learning such as [14]. Notably, the trial-and-error approach of reinforcement learning can be implemented to address the challenge of discovering and applying dynamic trading strategies, enabling machine learning algorithms to proactively select or even create their training data [15,16,17,18,19].

3. Empirical Study

As a result of time and complexity constraints, the study specification has undergone several changes. Notably, the integration of machine learning has remained a crucial requirement for conducting time series clustering. However, due to the lack of available research material pertinent to our study’s objectives, a cautious approach was adopted. While the study yielded excellent results, it is important to note that this concept has not been replicated by other academics. Subsequently, the objectives was redesigned using a different set of features following extensive research efforts. As a consequence, the study specification will no longer include strategies such as the differentiation of company names or sector separation. Instead, our tool will utilize a classifier to assess the relevance of the selected dataset. During the model training phase, a systematic approach will be adopted to ascertain the optimal cluster number, enabling the model to identify prevailing trends. The updated study specifications that reflect the minor adjustments made, categorized into functional and non-functional requirements are as follows [20,21,22,23,24,25]:
  • Functional Requirements: Import CSV historical dataset from Yahoo finance, recognize trends/patterns, separate different industries/sectors, distinguish notable differences and utilize real data, processing time not to exceed 10 seconds, portfolio visualization for strategic planning, and minimize UI complexity and ensure user-friendliness for all types of investors.
  • Non-Functional Requirements: The visual application will feature machine learning and intuitive design to facilitate the handling of large datasets, the system will be compatible with a MacOS desktop with an M1 chip, as this is the designated operating system, the model is required to provide distinct scores for each cluster for grouping purposes, without displaying these scores to the user, and error handling for entering an invalid dataset is a required feature.

3.1. Pre-Implementation

The study design can be broadly divided into three main parts. Firstly, the design of the web craneage; secondly, the classified; and thirdly, the web application. Each of these components’ designs has evolved over the course of the year, and any modifications from the original design will be thoroughly initiated in the subsequent sections. The successful development of vision-based recognition systems capable of autonomously navigating complex historical datasets relies on the creation of an association model. This model must effectively learn the relationships between different stocks and their corresponding weights should be trained to extract features from relevant trends, illustrate their topology and influence, and accurately associate them with the appropriate outputs. The three primary functions of the model can be categorized as follows:
  • Data Collection and Preparation: Upon collection, the data undergoes how be-trade into selected machine learning algorithms. Tools such as the elbow method play a crucial role in identifying the desired information. Additionally, the sampling of inputs in time series can be enhanced by utilizing more complex algorithms like the Self-Organizing Map (SOM). However, due to time complexity with the SOM algorithm has been excluded.
  • K-Means Clustering: Repeated trends by the optimal number of clusters, each respective centroid within our time series dataset.
  • T-Distributed Stochastic Neighbour Embedding (t-SNE): It is a non-linear algorithm that can capture complex data structures beyond hyperplanes. Although it requires assumptions to reach a solution, t-SNE is a powerful tool for visualizing high-dimensional data. In the context of stock market analysis, an unsupervised learning approach is employed to enable the clustering of similar stocks. This is achieved by presenting the algorithm with data captured from companies within the S&P 500, spanning multiple industries such as real estate, healthcare, energy, and more. By navigating this financial data, the algorithm can learn to recognize and imitate patterns, ultimately facilitating the clustering of stocks with similar characteristics. This application of t-SNE enables the visualization and analysis of complex stock market dynamics, providing valuable insights into the relationships between different stocks and industries.

3.2. Post-Implementation

The development phase encompasses the implementation of the design and associated technologies at each level. Similar to the design phase, the development phase involved three stages: data extraction, k-means clustering development, and t-distributed stochastic neighbour embedding development. Any deviations from the original plan are thoroughly elaborated upon within their respective sections, as there have been some adjustments since the initial development plan was formulated. Python was chosen as the development language due to its extensive standard library and user-friendly nature. Additionally, Python provides a comprehensive set of tools that can be seamlessly integrated into the study, supported by an active online community. In addition, data distribution and visualization play a pivotal role in the field of data science. Broadly, there are two categories of visualizations in data science: metric plots and data distribution plots. While metric plots form a routine component of a data scientist’s daily workflow, data visualization algorithms are comparatively less prevalent. Metric-based visualizations include Kullback-Leibler (KL) divergence scores between datasets and time series plots reflecting metric values, among others. Essentially, data visualization enables a more profound understanding of the data and facilitates the development of improved methods, such as t-SNE, albeit the metrics alone are generally sufficient in most scenarios.

3.2.1. Collecting and preparing the data

The foundation of an Algorithmic Trading (AT) system lies in establishing an infrastructure capable of processing real-time data and maintaining a repository of historical data to compute fundamental, technical, and quantitative metrics essential for scalable pretrade analysis. The historical data utilized in this study is sourced from the Yahoo finance database for the period 2020-21, encompassing all companies in the S&P 500 index. Effective management of this data necessitates the implementation of a time series decomposition approach, which serves as a crucial abstraction for pattern recognition methods. In time series analysis, systematic components are typically classified into consistent or linear components that can be described and modelled and non-systematic components that cannot be directly modelled. Systematic components in time series analysis are delineated as follows:
  • Level or Cycle: This component reflects a time series’ tendency to rise and fall at varying rates and is often employed in the analysis of business cycles.
  • Trend: The trend component describes the overall direction of the series, indicating increasing or decreasing values. It can also exhibit a positive or negative trend, or may not exhibit a trend at all.
  • Seasonality: Unlike the cycle component, seasonality pertains to data that rises and falls at consistent rates during a recurring short-term cycle.
Additionally, a non-systematic component known as noise or remainder is present within the time series analysis. The residual component is the random fluctuation in the data that remains after removing the trend, cycle, and seasonal components from the time series data. When working with historical data, it is advisable to utilize a seasonally adjusted time series. This type of time series excludes the seasonal component, allowing for a focused analysis of the overall trend in the data. Additionally, decomposing the time series enables adjustments such as translation, rotation, and rescaling of the original features to capture significant variations within the seasonal component. This facilitates the investigation of the factors contributing to the observed data fluctuations. The nature of a time series can often be discerned based on its variation, with the choice between an additive and multiplicative model informed by the series’ characteristics. In this case, a multiplicative seasonal decomposition was chosen due to the varying magnitude of the seasonal component over time; alternatively, an additive or linear series could have been utilized. Despite the data being aggregated monthly, the analysis focuses on a yearly period, necessitating a 12-month setting.

3.2.2. K-Means Clustering

This section delves into an unsupervised machine-learning technique that can effectively extract meaningful patterns from data without the need for predetermined outcome labels. This method involves grouping data points based on their similarities, independent of their labels. The measure of similarity typically relies on a distance metric, often the Euclidean distance. However, the complex nature of the data points adds a layer of intricacy, particularly in the context of time series clustering. This process often involves transforming time series data into tables, grouping columns based on time indices or aggregations, and then forming clusters by minimizing the total sum of squares for each group. The k-means algorithm, commonly used for this purpose, classifies data into a specified number of clusters, regardless of whether that number is optimal. As a result, users are advised to critically assess the appropriateness of the chosen number of clusters. One validation technique we employed the elbow method to determine the optimal number of clusters. Subsequently, we utilized the open-source SciPy library to conduct k-means clustering on Numpy arrays. The Vg module facilitates k-means clustering by providing a vector quantization tool, which aids in minimizing distortion and enhancing accuracy. The distortion is typically calculated using the Euclidean distance between centroids and vectors. We handle convergence through parameters that determine centroid initialization, treatment of empty clusters, and the presence of finite numbers in the input matrix. This method returns centroids and their respective clusters based on the input vector. While this approach offers simplicity, flexibility, and compatibility with large datasets, it does have drawbacks. These include the need to manually define the number of centroids, susceptibility to errors, and reliance on the initial to the centroids.

3.2.3. T-Distributed Stochastic Neighbour Embedding (T-SNE)

The t-SNE algorithm is designed to capture and preserve both local and global structures of high-dimensional data, including clusters. By preserving the neighbourhood structure of the data, t-SNE aims to mitigate some of the issues associated with SNE. The algorithm accomplishes this by defining a Gaussian probability distribution over the potential neighbours of each point and minimizing the difference between probability distributions in higher and lower dimensions. Tod of machine learning, t-SNE has gained popularity for its ability to create two-dimensional maps from high-dimensional data. Its versatility has made it an increasingly popular dimensionality reduction technique, although its flexibility can make it challenging to interpret. While the algorithm can adjust visualizations in a way that obscures the underlying data, studying t-SNE behaviour in simple cases can provide insights into its workings. Creating an asymmetric probability matrix using perplexity, a measure from information theory that assesses how well a probability distribution predicts a sample, is a crucial step in the t-SNE process. The choice of perplexity significantly impacts the embedding between local and global aspects of the dataset. Selecting an appropriate perplexity value is vital, as a high perplexity can cause clusters to merge into a single large cluster, while a low value can produce numerous insignificant close clusters. In our case, a perplexity of 75 provided a meaningful representation of the global geometry.

3.3. Evaluation Criteria

A combination of unit testing, integration testing, and user testing will be employed to evaluate the functional and non-functional requirements of the study. The study’s success will be contingent on the software meeting all specified criteria and machine learning acting as an efficient alternative to standard stock screeners accordingly:
  • Diversification: It is a crucial evaluation metric for charts. To ensure diversification among stocks, the software will encompass various industry sectors such as consumer discretionary, consumer staples, energy, financials, healthcare, industrials, utilities, and real estate. Assuming a one-year company timeline cycle, the minimum interval will be 12 months. Users will have the option to most-distribute dues.
  • Cost Efficiency: Once the software identifies a suitable time series, it should incur reasonable computational costs and be straightforward for users to manage. This will also involve assessing empty clusters to ensure that the provided data lacks recognizable patterns.
  • Trading Benefits: The program will enhance users’ trading activities by facilitating the identification of similarities among selected stocks and categorizing time series data sourced from the Yahoo finance platform for their study and analysis.
  • Back testing: The practice of back testing involves simulating an algorithm using historical data in order to generate performance metrics that can be applied to new market scenarios. In addition to the inherent uncertainty in predicting market trends, the manner in which the algorithm is implemented can also impact the results, leading to an increased risk of misinterpreting patterns that were observed within the historical data as applicable to future data.
  • Pipeline API: The Pipeline API streamlines the process of computing factors for a wide range of securities by leveraging historical data. It enhances efficiency by adhering to an event-driven architecture and employs vectorized factor computation when feasible. However, we did not delve deeply into the testing phase.
  • Elbow Method: The elbow method is a technique used to determine the optimal value of k in k-means clustering. The ideal value of k is identified by analyzing the sum of squared distances between data points and their clusters. The goal is to identify an inflexion point where the sum of squared distances flattens out, resembling an “elbow” on the graph. This method involves running k-means clustering for a range of k values and calculating the sum of squared distances for each value. By plotting the sum of squared distances values on a line chart, we can visually identify the “elbow”, which represents the optimal k value. It’s important to select a small k value with a low sum of squared distances, as increasing k can lead to diminishing returns. However, the elbow method may not always be successful, particularly when the data is not well-clustered. In such cases, alternative methods for determining the optimal k, such as computing silhouette scores, should be considered.
  • Silhouette Coefficient: The silhouette coefficient is a measure that assesses how similar a data point is within a cluster (cohesion) relative to other clusters (separation). To begin, a range of k values (e.g., 1 to 10) is chosen for each value, and the silhouette scores are then plotted. The primary difference between the elbow method and the silhouette coefficient is that the elbow method only computes the Euclidean distance, whereas the silhouette coefficient takes into account variables such as skewness, variance, high-low differences, and so on. Due to its computational simplicity, the elbow method is more suitable than the silhouette score for datasets with a smaller size or time complexity. Silhouette analysis scores have an advantage over the elbow method because they enable the evaluation of clusters based on multiple criteria, making it very likely that the most optimal number of clusters in k-means can be determined.

4. Result Analysis

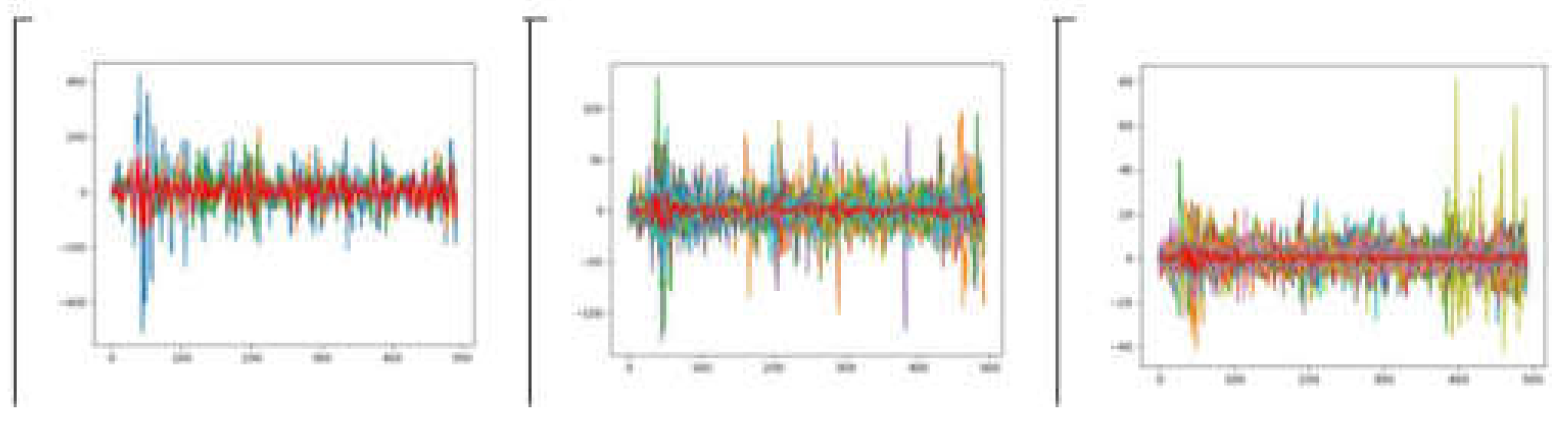
This study is cantered around the development of a unique stock screener, setting it apart from others. Its aim is to provide an innovative approach for visualizing the dynamics of capital markets in order to effectively construct portfolios. Due to time and complexity constraints, one of the proposed techniques, the SOM algorithm, was excluded from the study. Additionally, we opted not to integrate platforms such as TensorFlow or Keras as they were not deemed essential for the core functionality of the study. The study has achieved partial success in meeting its objectives. Our analysis indicates that optimal results in k-means clustering are obtained when k=3. As a result, three distinct clusters were identified as illustrated in Figure 1 demonstrating discernible trends shared by similar companies, with the red centroid representing the centre of each cluster essentially the average of the cluster.
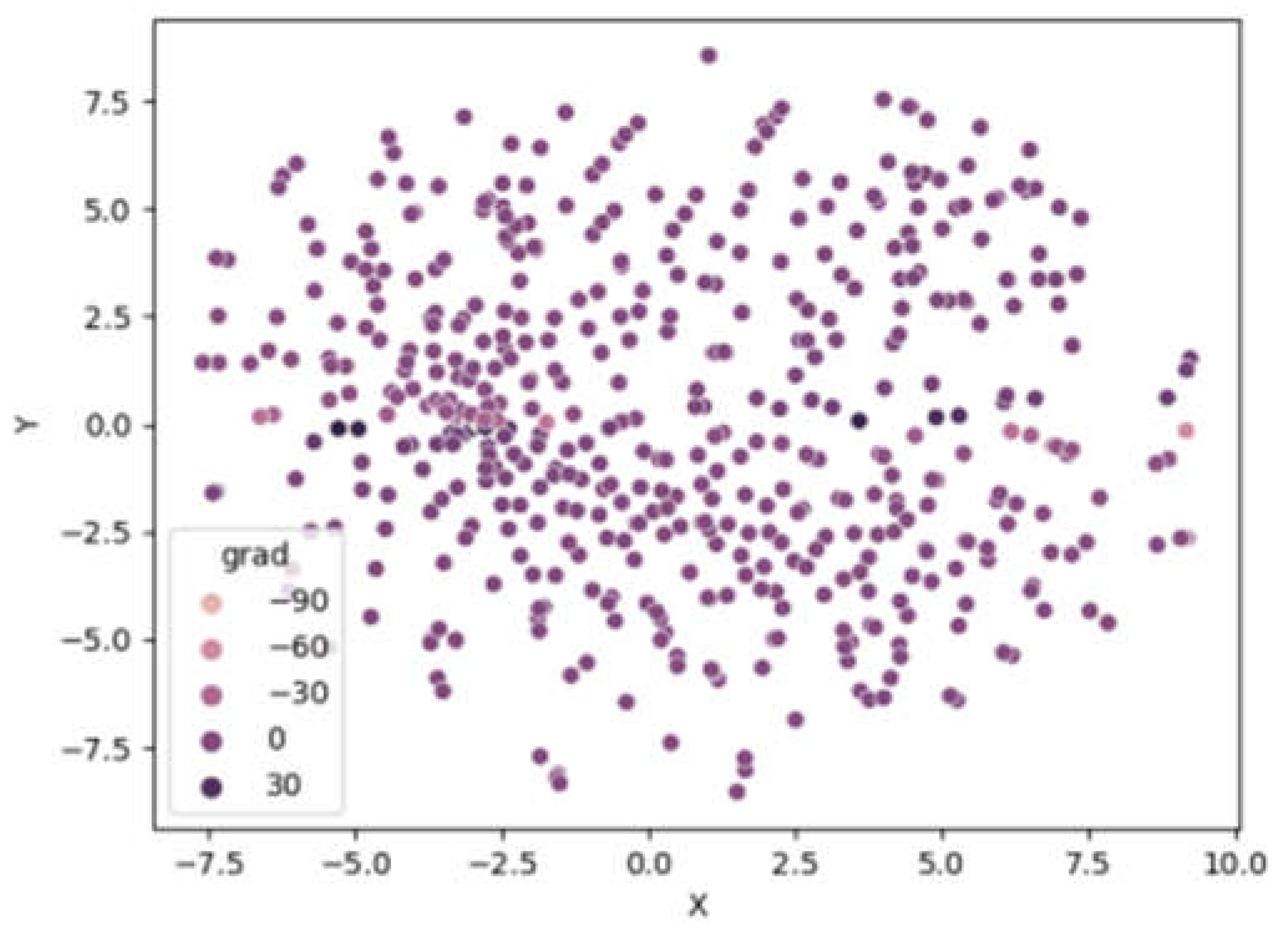
Figure 2 serves a similar function as k-means clustering. Clusters are not readily distinguishable from one another. However, the legend indicates five distinct clusters. We found that a perplexity value of 75 yielded the best global geometry compared to other values tested, and verbose 1 allowed for observation of the program’s computational performance. The concept of cross-validation involves using a training sample to make predictions and a validation sample to verify the accuracy of those predictions. This technique is commonly employed to evaluate the predictive performance of an algorithm. In this particular study, the use of a specific dataset may have introduced bias and it could be beneficial to consider alternative time periods or eliminate certain data points in order to draw more precise conclusions. When discussing the t-SNE algorithm, it is important to highlight the Kullback-Leibler divergence (KL divergence), which is rooted in mathematical probability theory and information theory and is widely utilized in the data mining literature. KL divergence compares two probabilistic distributions over the same variable or measure, indicating the “distance” between the two distributions. It is crucial to note that KL divergence is not a metric measure and does not provide a distance measure, but rather a measure of dissimilarity between the distributions.
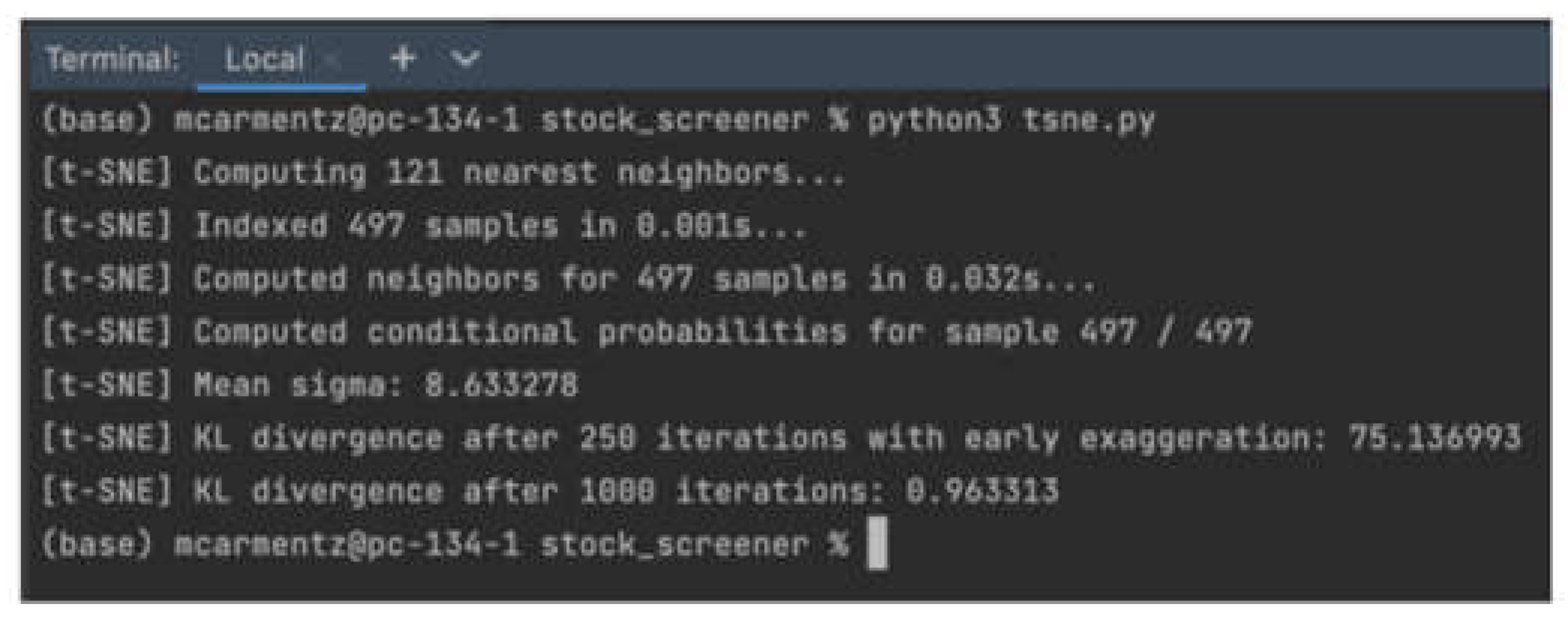
An assessment of performance functional requirements demonstrates that the clusters in the t_sne.py successfully converge in less than 1 second for 497 out of 497 conditional probability samples. Figure 3 presents the computational output for the t-sne function. In this study, the primary focus is on analyzing historical capital time series. It should be noted that the methods employed may not be suitable for linear datasets. However, adjustments can be made to accommodate various types of assets with historical prices at different intervals such as minute, hour, daily, weekly, monthly, or yearly. It’s important to acknowledge that unpredictable factors such as inflation rates, financial crises, wars, or events like COVID-19 may have had an influence that is not fully captured by conventional trends and have been accounted for as normal patterns. It’s worth mentioning that the k-means clustering method has limitations, such as the need for manual definition of the number of centroids, which can be prone to errors, and reliance on the initial values of each centroid. Similarly, the t-SNE algorithm does not guarantee convergence to a global optimum of its cost function.

5. Conclusions

This study has explored the intersection of machine learning and investment trading, leveraging the explosive growth of digital data and the emergence of global business and technology trends. Despite some limitations and areas for improvement, the study has achieved its primary objectives and has provided valuable experience in software development and a useful tool for investment decisions. The study has also highlighted the potential for future developments in the application of machine learning to trading, including automation, synthetic training data, and quantum computing. The study has also demonstrated the effectiveness of k-means clustering and the elbow method in optimizing cluster selection. Future work will explore additional algorithms, such as Self-Organising Maps (SOM), and incorporate sentiment analysis, technical indicators, and news data to enhance the tool’s capabilities. Overall, this study has been a modest success and has provided a solid foundation for future research and development in this field.

Funding

No funds, grants, or other support was received.

Data Availability

Data will be made on reasonable request.

Conflict of Interest

The authors declare that they have no known competing for financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Code Availability

Code will be made on reasonable request.

References

  1. Kumar, A.; Dodda, S.; Kamuni, N.; Arora, R.K. Unveiling the Impact of Macroeconomic Policies: A Double Machine Learning Approach to Analyzing Interest Rate Effects on Financial Markets. 2024. Available online: https://arxiv.org/abs/2404.07225v1 (accessed on 5 May 2024).
  2. Arora, R.; Gera, S.; Saxena, M. Mitigating security risks on privacy of sensitive data used in cloud-based ERP applications. In Proceedings of the Proceedings of the 2021 8th International Conference on Computing for Sustainable Global Development, INDIACom 2021; 2021; pp. 458–463. [Google Scholar] [CrossRef]
  3. Soni, A. Advancing Household Robotics: Deep Interactive Reinforcement Learning for Efficient Training and Enhanced Performance. J. Electr. Syst. 2024, 20, 1349–1355. [Google Scholar] [CrossRef]
  4. Kashyap, G.S.; Siddiqui, A.; Siddiqui, R.; Malik, K.; Wazir, S.; Brownlee, A.E.I. Prediction of Suicidal Risk Using Machine Learning Models, 25 December 2021. Available online: https://papers.ssrn.com/abstract=4709789 (accessed on 4 February 2024).
  5. Kaur, P.; Kashyap, G.S.; Kumar, A.; Nafis, M.T.; Kumar, S.; Shokeen, V. From Text to Transformation: A Comprehensive Review of Large Language Models’ Versatility. 2024. Available online: https://arxiv.org/abs/2402.16142v1 (accessed on 21 March 2024).
  6. Kashyap, G.S.; Sohlot, J.; Siddiqui, A.; Siddiqui, R.; Malik, K.; Wazir, S.; Brownlee, A.E.I. Detection of a facemask in real-time using deep learning methods: Prevention of Covid 19. 2024. Available online: https://arxiv.org/abs/2401.15675v1 (accessed on 4 February 2024).
  7. Kashyap, G.S.; Wazir, S.; Hamdard, J.; Delhi, N.; Malik, I.K.; Sehgal, V.K.; Dhakar, R. Revolutionizing Agriculture: A Comprehensive Review of Artificial Intelligence Techniques in Farming. 2024. [CrossRef]
  8. Kanojia, M.; Kamani, P.; Kashyap, G.S.; Naz, S.; Wazir, S.; Chauhan, A. Alternative Agriculture Land-Use Transformation Pathways by Partial-Equilibrium Agricultural Sector Model: A Mathematical Approach. 2023. Available online: https://arxiv.org/abs/2308.11632v1 (accessed on 16 September 2023).
  9. Habib, H.; Kashyap, G.S.; Tabassum, N.; Nafis, T. Stock Price Prediction Using Artificial Intelligence Based on LSTM– Deep Learning Model. In Artificial Intelligence & Blockchain in Cyber Physical Systems: Technologies & Applications; CRC Press, 2023; pp. 93–99. ISBN 9781000981957. [CrossRef]
  10. Roy, S.S.; Chopra, R.; Lee, K.C.; Spampinato, C.; Mohammadi-Ivatlood, B. Random forest, gradient boosted machines and deep neural network for stock price forecasting: A comparative analysis on South Korean companies. Int. J. Ad Hoc Ubiquitous Comput. 2020, 33, 62–71. [Google Scholar] [CrossRef]
  11. Saifan, R.; Sharif, K.; Abu-Ghazaleh, M.; Abdel-Majeed, M. Investigating algorithmic stock market trading using ensemble machine learning methods. Inform. 2020, 44, 311–325. [Google Scholar] [CrossRef]
  12. Ang, A.; Piazzesi, M. A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables. J. Monet. Econ. 2003, 50, 745–787. [Google Scholar] [CrossRef]
  13. Chopra, V.K.; Ziemba, W.T. The effect of errors in means, variances, and covariances on optimal portfolio choice. In The Kelly Capital Growth Investment Criterion: Theory And Practice; 2011; pp. 249–257 ISBN 9789814293501. [CrossRef]
  14. Swamy, D.V. Impact of Macroeconomic and Endogenous Factors on Non Performing Bank Assets. SSRN Electron. J. 2012. [Google Scholar] [CrossRef]
  15. Kanaparthi, V.K. Navigating Uncertainty: Enhancing Markowitz Asset Allocation Strategies through Out-of-Sample Analysis. 2023. [CrossRef]
  16. Kanaparthi, V. Robustness Evaluation of LSTM-based Deep Learning Models for Bitcoin Price Prediction in the Presence of Random Disturbances. 2024. [CrossRef]
  17. Kanaparthi, V. Evaluating Financial Risk in the Transition from EONIA to ESTER: A TimeGAN Approach with Enhanced VaR Estimations. 2024. [CrossRef]
  18. Kanaparthi, V. Transformational application of Artificial Intelligence and Machine learning in Financial Technologies and Financial services: A bibliometric review. 2024. [CrossRef]
  19. Kanaparthi, V. AI-based Personalization and Trust in Digital Finance. 2024. Available online: https://arxiv.org/abs/2401.15700v1 (accessed on 4 February 2024).
  20. Wazir, S.; Kashyap, G.S.; Saxena, P. MLOps: A Review. 2023. Available online: https://arxiv.org/abs/2308.10908v1 (accessed on 16 September 2023).
  21. Marwah, N.; Singh, V.K.; Kashyap, G.S.; Wazir, S. An analysis of the robustness of UAV agriculture field coverage using multi-agent reinforcement learning. Int. J. Inf. Technol. 2023, 15, 2317–2327. [Google Scholar] [CrossRef]
  22. Wazir, S.; Kashyap, G.S.; Malik, K.; Brownlee, A.E.I. Predicting the Infection Level of COVID-19 Virus Using Normal Distribution-Based Approximation Model and PSO. In; Springer, Cham, 2023; pp. 75–91. [CrossRef]
  23. Kashyap, G.S.; Malik, K.; Wazir, S.; Khan, R. Using Machine Learning to Quantify the Multimedia Risk Due to Fuzzing. Multimed. Tools Appl. 2022, 81, 36685–36698. [Google Scholar] [CrossRef]
  24. Naz, S.; Kashyap, G.S. Enhancing the predictive capability of a mathematical model for pseudomonas aeruginosa through artificial neural networks. Int. J. Inf. Technol. 2024, 2024, 1–10. [Google Scholar] [CrossRef]
  25. Alharbi, F.; Kashyap, G.S. Empowering Network Security through Advanced Analysis of Malware Samples: Leveraging System Metrics and Network Log Data for Informed Decision-Making. Int. J. Networked Distrib. Comput. 2024, 1–15. [Google Scholar] [CrossRef]
Preprints 118405 g001
Figure 1. Using the k-means clustering method to group time series.
Figure 1. Using the k-means clustering method to group time series.
Preprints 118405 g001
Preprints 118405 g002
Figure 2. Clusters using t-SNE.
Figure 2. Clusters using t-SNE.
Preprints 118405 g002
Preprints 118405 g003
Figure 3. tsne.py output logging.
Figure 3. tsne.py output logging.
Preprints 118405 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated