Prerpints.org logo
Preprint
Article

Search for True Ternary Fission in the Reaction 40Ar+208 Pb

Altmetrics

Downloads

71

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 September 2024

Posted:

18 September 2024

You are already at the latest version

Alerts
Abstract
The true ternary fission, the fission of a nucleus into three fragments of nearly equal mass, is an elusive and poorly known process influenced by shell effects. It has been envisaged an increase of the probability of this process with respect to the binary fission, very low in spontaneous and neutron-induced fission, by adopting heavy-ion induced reactions due to the possibility to increase the fissility parameter and the excitation energy of the compound nuclei. Nuclei with mass number around A=250, accessible in heavy-ion induced reactions, are favorable and should be investigated. It is still debated if the process takes place in a single step, direct ternary fission, or in two steps, sequential ternary fission. The purpose of this work is to define experimental conditions and observables that allow the disentangling of the products from the direct and sequential ternary fission as well as from the usual most probable binary fission. This step is essential to gain insight on the ternary fission dynamics and on the binary to ternary fission competition. The method proposed here is to simulate the kinematics of the ternary and binary fission processes to compute the energy distributions and angular correlations of direct and sequential ternary fission products, as well as those of binary fission. The reaction taken as benchmark is 40Ar+208Pb at 230 MeV supposed to form the 248Fm* compound nucleus. The simulation results have been filtered by considering the response function of a multi-coincidence detection system virtually constructed using the Geant4 simulation toolkit. The simulations support the possibility to separate the products of different multimodal fission decays with the proposed setup that consequently represents an effective tool to get insight on ternary fission from the observables selected.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

The process of induced nuclear fission, namely the division of a nucleus into two lighter nuclei, the so called binary fission (BF), was first proposed by Meitner and Frisch [1] as an attempt to interpret the data from O. Hahn and F. Strassmann [2,3] obtained bombarding Uranium with neutrons. The qualitative explanation of the induced fission process was provided within the framework of the Liquid Drop Model (LDM) that was introduced a few years earlier by Bohr [4]. In 1939 Bohr and Wheeler formalized Meitner’s and Frisch’s intuition in their seminal paper [5].
Fission can take place also spontaneously as later discovered by G.N. Flerov and K.A. Petrzhak in 1941. In the case of nuclear reactions induced by heavy ions, projectile and target may fuse first to form a compound nucleus (CN), that later on may split into lighter nuclei, the so-called fission fragments, if energetically allowed.
Shortly after the discovery of binary fission, the breakup of heavy nuclei into three fragments, the ternary fission (TF), was theoretically predicted still on the base of the LDM [6,7]. LDM calculations, involving only the initial and final states, indicate that by increasing the CN charge TF becomes indeed energetically possible. In particular, the energy release is higher than that from BF if the number of fission fragments of fairly equal mass is bigger than 2 [8,9]. Experimental evidence of TF, consisting in the evidence of long range alpha particles emitted in connection with spontaneous fission, was first presented by Alvarez and collaborators [10]. In the same years also ternary and quaternary fission, consisting in the emission of much heavier light fragments with mass up to 32 atomic mass units, was identified by San-Tsiang, Zah-Wei, Chastel, and Vigneron [11,12].
Many experimental works have been devoted to the study of spontaneous and neutron-induced fission, i.e. in nuclei at low excitation energy. In these studies it has emerged that mostly alpha particles are emitted as a ternary particle (TP) in a plane perpendicular to the fragment separation axis, with some degree of distortion toward the light fragment direction due to the Coulomb focusing of the heavier fragment [13,14]. Furthermore, the average alpha particle energy is nearly constant, around 16 MeV [15], but disagreement has been reported for the TF/BF ratios, e.g., in the spontaneous fission of 252Cf ≈ 0.1 % [16] and 0.24 ± 0.02 % [17] were obtained in different measurements.
Still further efforts are necessary to consolidate the present knowledge about ternary fission. By using heavy-ion induced reactions heavier nuclei with higher fissility parameters and excitation energies become accessible. This change of the entrance channel conditions largely affect not only the TF, but also other competing processes accompanied by alpha-particle emission, as for instance quasifission and pre-theramalization stages of the formation of the compound nucleus [18,19,20]. The analysis of double-differential α spectra, measured in coincidence with two fission fragments from very heavy composite systems, evidenced alpha multiplicities much larger than those expected from extrapolation of the TF data [18]. These observations support the view that the alpha particles appear from nuclear matter fluctuations occurring in the neck of the fissioning system or from the CN before the scission and cannot be used to probe the potential energy surface (PES) at the scission configuration [21,22].
The breakup of a nucleus into three fragments of nearly equal mass ( A 1 ≃ A 2 ≃ A 3 ) is known as true ternary fission (TTF). This process may occur following two different paths, to be distinguished experimentally: (i) in one step, known as direct ternary fission (DTF) [23], or (ii) in two subsequent binary breakups, known as sequential ternary fission (STF) [24]. In both cases three fragments emerge, but the kinematics is expected to be different. In STF, the first step is an asymmetrical binary fission (AsymBF). It produces one light and one heavy fragment. If the heavy fragment excitation energy is sufficient to overcome the its fission barrier, in turn, it splits in two fragments within a time scale of 10 − 20 s [23]. The mixing of STF and DTF events is one of the major issues in the experimental observation of TTF.
Experimental evidence of the TTF has been claimed since the 60’s [25]. A review of early experimental results can be found in ref. [23]. The production of ternary fragments, such as F, Ne, Na, Mg, Al, and Si isotopes, up to A=35 has been identified by Gönnenwein et al. [26] in neutron-induced fission on 242 Am target. However TTF probability turned out to be very low. Typical values are those observed in thermal neutrons induced fission of 235U where a TTF event occurs every 6.7 ( ± 3.0 ) 10 6 BF ones [27]. The low excitation energy seems to be a hindering factor of the TTF probability that in addition decreases exponentially with the increase of ternary fragment mass [28,29]. Because of this, TTF is still a poorly known process and its occurrence in superheavy nuclei (SHN) is not experimentally confirmed [21,30,31,32]. Yet, it is worth to mention that the search of TF was mainly performed in spontaneous and neutron-induced fission which gives access to fissioning nuclei with a neutron to proton ratios nearly constant and with atomic numbers in the narrow region Z = 90 - 98 [33,34,35,36,37,38,39,40].
The conditions favoring the breakup in more than two fragments were suggested by Swiatecki [8]. Within the framework of the liquid drop model the probability of true ternary fission increases rapidly as Z 2 / A increases [8]. Many models have been proposed which include shell effects in the calculation of the PES. According to Diehl et al. [9] TTF is hindered by a double saddle path, where the second saddle is higher in energy. With the increase of the charge of the nucleus, the second saddle tend to vanish and eventually disappears making TTF becomes accessible. Theoretical studies on 252Cf [41,42] and on the giant nuclear system 238 U + 238 U [29] also indicate similar shell effects for TTF. Minima for tripartitions composed by magic nuclei appear in the PES proposed in ref. [43,44]. These indications are supported by recent observation of TTF in the spontaneous fission of 252Cf and in neutron induced fission of 235U [43,45,46,47,48]. In both cases, the observation of TTF producing nuclei with masses close to the magic 132Sn, 70 Ni , and 48 Ca isotopes was claimed [45,46].
Further experimental results can be found in [25,49,50]. Particularly interesting are the systematics on 40Ar induced reactions [49,51] where one could expect a TTF/BF ratio up to 3% [51] and a cross sections of about 0.5 mb for TTF having a ternary fragment with A > 23 .
By using heavy-ion induced reactions it would be possible to test the above conditions that are supposed to ignite TTF by changing the neutron to proton ratio of the fissioning nucleus and its excitation energy. However, any experiment devoted to the detection of the TTF has to deal with the overlap of DTF and STF fragments. Therefore an analysis of the possible detector configurations has to be planned carefully.
This article aims at establishing the guidelines to disentangle the products of DTF and STF mechanisms by analyzing the angular correlations and energies expected for TTF fragments to be identified in mass and charge. The reaction 40 Ar + 208 Pb at the beam energy of 230 MeV, producing 248 Fm ∗ ( Z 2 / A = 40.3), is chosen as a case study to search for TTF. The beam energy is chosen so to keep the excitation energy low enough to be able to be sensitive to shell effects. The same reaction was exploited by Price et al. [52] by using mica and glass as a solid material to detect heavy ions tracks and rebuild the kinematics. They claim a value of 4 × 10 − 3 for the ratio TTF/BF. The present availability of modern devices well suited for measuring the kinetic energies and performing the (A,Z) identification of heavy fragments over a wide mass range [53,54,55,56,57] motivates this study.
The article is organized as it follows. In Section 2.1 and Section 2.2, we briefly highlight, for both DTF and STF processes, the kinematics equations and the resulting angular and energy distributions built on conservation laws. In Section 2.3, the asymBF and symmetric BF (symBF) events are discussed. A possible apparatus and computed observables for STF, DTF, and BF decays, by considering the events collected in 1 week of beam time, are described in Section 2.4 and Section 3, respectively. Finally, remarks and conclusions are given in Section 4.

2. Materials and Methods

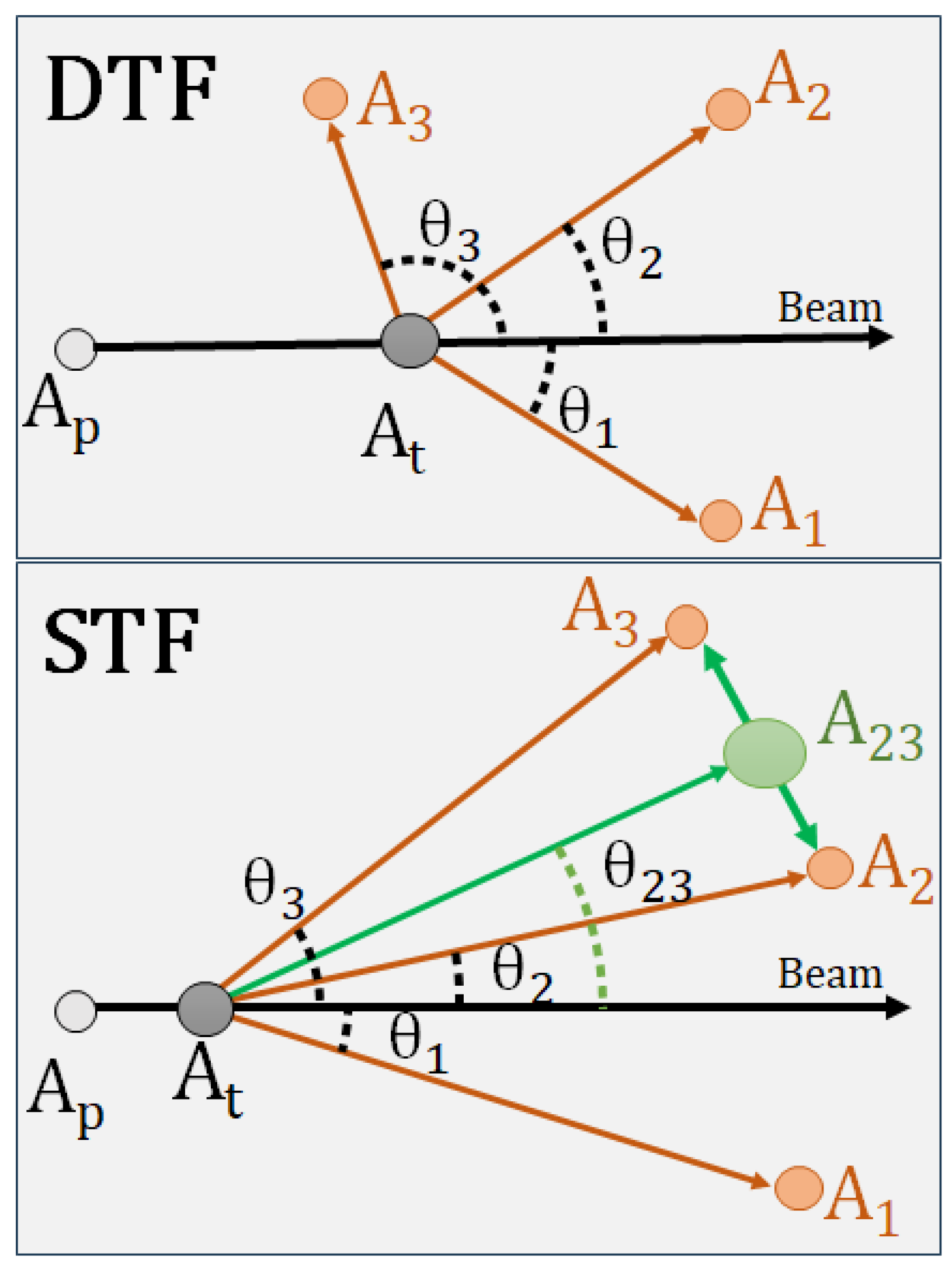
2.1. Kinematics of DTF and STF Decay Mechanisms

Ternary fission fragments originated during DTF and STF decays are characterized by different kinematics given the single or dual step nature. Among all the possibilities trajectories, only those belonging to the same plane have been taken into account. A schematic view of both processes is shown in Figure 1.
Hence, the velocity vector of each fragment is described by 2 variables: the absolute value of velocity and the polar angle ( θ ). Known a priori are the projectile ( A p , Z p ) nucleus, the target ( A t , Z t ) nucleus, and the energy of the projectile that impinges on a fixed target ( E p ). For a detailed description of the evolution of the reaction, the mass and the atomic numbers of the fragment have to be fixed by assigning mass values M ( A i , Z i ) . From now on, we consider known the masses of the fragments, which we will indicate in synthetic form, not making explicit reference to the dependence on the atomic number and on the mass number, namely M ( A i , Z i ) = M i with i = 1 , 2 , 3 . A 23 is the mass number of the intermediate fragment in STF. The actual mass values are taken from [58] and the Q values of the process involved in DTF and STF can be computed.
By taking into account the energy and momentum conservation laws, we deduced the equations describing the DTF and STF events for fixed tripartitions. In all calculations, we assume that the fragments are cold, namely, the excitation energy of the system is fully converted into kinetic energy of the fragments. We made this assumption at each separation stage by neglecting the amount of energy dissipated by particle evaporation and/or transformed in deformation of the fragments.
Assuming that all fragment velocity vectors belong to the same reaction plane, nine variables (mass, energy and angle of each fragment) describe the kinematics of the exit channel. By fixing the mass tripartition ( M 1 , M 2 , M 3 ), the kinetic energy and the emission angle of the fragment 1 ( E 1 and θ 1 ) and the emission angle of fragment 2 ( θ 2 ), and by considering the energy and momentum conservation laws, the remaining three quantities, namely the kinetic energy of fragment 2 ( E 2 ) and the kinetic energy and the emission angle of the fragment 3 ( E 3 and θ 3 ), are calculated. The angles are given with respect to the beam direction and are positive in the anticlockwise direction.

2.1.1. One-step decay: Direct Ternary Fission

The kinematic plot for DTF is shown in the top panel of Figure 1. The tripartition occurs suddenly. Energy conservation for three body decay allows having a velocity of the third fragment in the following way:
v 3 = 2 ( E p + Q ) − M 1 v 1 2 − M 2 v 2 2 M 3 1 / 2 .
The Q-value in the above equation is defined as
Q = M p + M t − ∑ i = 1 3 M i ,
where M p , M t and M i are the masses of the projectile, target and of the i-th product nucleus, respectively.
By considering momentum conservation law, the angle of the third fragment and the velocity of the second fragment can be expressed, respectively, as:
θ 3 = c o s − 1 M p v p − M 1 v 1 c o s ( θ 1 ) − M 2 v 2 c o s ( θ 2 ) M 3 { 2 ( E p + Q ) − M 1 v 1 2 − M 2 v 2 2 }
v 2 = − M 1 v 1 s i n ( θ 1 ) + M 3 v 3 s i n ( θ 3 ) M 2 s i n ( θ 2 )
So, replacing the values of v 3 and θ 3 , the solutions of v 2 are:
v 2 = − β ± β 2 − 4 α γ 2 α ,
where,
α = M 2 ( M 2 + M 3 ) β = 2 M 2 { M 1 v 1 cos ( θ 1 − θ 2 ) − 2 E p M p cos ( θ 2 ) } γ = M 1 v 1 ( M 1 v 1 + M 3 ( v 1 − 2 ( E p + Q ) ) − 8 E p M p cos ( θ 1 ) ) + 2 M p E p
Now, if we substitute the value of v 2 found in term of known parameters in the v 3 and θ 3 expressions we obtain the three equations for E 2 , E 3 and θ 3 as function of the three input parameters ( E 1 , θ 1 and θ 2 ) for each ternary fragmentation.

2.1.2. Two-steps decay: Sequential Ternary Fission

At the first step the compound nucleus of mass number A C N breaks into two fragments: ( A 23 and A 1 ). The Total Kinetic Energy (TKE, the sum of the kinetic energy of the two fragments ( A 23 and A 1 ) is calculated considering no excitation of the fragments. The velocity plot for STF is shown in the bottom panel of Figure 1. At each decay step, the fragments are emitted on the opposite sides in the center of mass of the fissioning nucleus. The velocities of the fragments in the lab frame are obtained by summing up the cm velocities with the proper velocity of the source in the cm frame, namely v → c m in the first step and v → 23 , c m in the second one.
We now analyze the kinematics of this two-step TF. Before the collision, the center-of-mass velocity is given by:
v c m = M p v p M p + M t = 2 E p M p M p + M t .
By using the momentum conservation law along the axis identified by the beam vector and the orthogonal one we have:
M 1 v 1 cos ( θ 1 ) + M 23 v 23 cos ( θ 23 ) = ( M 1 + M 23 ) v c m M 1 v 1 sin ( θ 1 ) + M 23 v 23 sin ( θ 23 ) = 0
From which we obtain:
θ 23 = cot − 1 cot ( θ 1 ) − ( M 1 + M 23 ) v c m M 1 v 1 sin ( θ 1 ) v 23 = − M 1 v 1 sin ( θ 1 ) M 23 sin ( θ 23 )
Recursively by knowing the initial condition of the second fissioning nucleus ( A 23 → A 2 + A 3 ) and by using both the energy and momentum conservation laws we obtain:
M 2 v 2 cos ( θ 2 ) + M 3 v 3 cos ( θ 3 ) = M 23 v 23 cos ( θ 23 ) M 2 v 2 sin ( θ 2 ) + M 3 v 3 sin ( θ 3 ) = M 23 v 23 sin ( θ 23 ) 1 2 M 2 v 2 2 + 1 2 M 3 v 3 2 = 1 2 M 23 v 23 2 + Q 2
Thus, the angle and the velocity of the third fragment and the velocity of the second fragment are:
cos θ 3 = 1 M 3 V 3 M 23 v 23 cos ( θ 23 ) − M 2 v 2 cos ( θ 2 )
v 3 = M 23 v 23 2 + 2 Q 2 − M 2 v 2 2 M 3 1 2
v 2 = − β ± β 2 − 4 α γ 2 α
where,
α = M 2 ( M 2 + M 3 ) β = − 2 M 2 M 23 v 23 cos ( θ 2 − θ 23 ) γ = M 23 2 v 23 2 − M 3 M 23 v 23 2 − 2 M 3 Q 2 .
Then, by substituting the value of v 2 in the expression of v 3 and θ 3 , the three equations for E 2 , E 3 and θ 3 as function of the three input parameters ( E 1 , θ 1 and θ 2 ) for each ternary-fragmentation are obtained.

2.2. DTF and STF Differences in Energy and Angular Distributions

The identification of the experimental signatures of the TTF mechanisms requires the selection of experimental conditions allowing to distinguish between DTF and STF on an event-by-event basis. We have simulated mass, charge, kinetic energy, and angular distributions of the fragments originating from these two mechanisms and searched for the experimental conditions for collecting valuable data. We consider the experimental feasibility of a measurement where the velocities of the three fragments are co-planar because angular momentum conservation arguments imposes this constraint (see discussions in [59,60,61]).
The 40 Ar + 208 Pb at E lab = 230 MeV reaction has been selected as it is addressed as a favorable pathway for TTF in theoretical works [52]. Furthermore, most of the features of the binary fission of this reaction were already well established in previous studies [62,63,64,65,66]. For instance, recently, ejectile production has been studied in mass, charge and energy distributions, and cross sections of the different transfer channels leading to the production of neutron-rich heavy isotopes [62,63]. Moreover, the spontaneous fission of fermium isotopes has been studied in prompt neutron emission in 246Fm [66] and in α accompanied cold ternary fission in 257Fm [67].
First and foremost, we explored the possibility of TTF according to the Three Cluster Model (TCM) that pictures ternary fission of heavy nuclei as a clustering effect [41,42]. The Ternary Fission Potential (TFP) is computed from the values of the binding energies of the fragments, Coulomb interaction, and Yukawa plus exponential nuclear attractive potential among the three fragments. Out of a large number of possible three body tripartitions, by applying the condition A 1 ≥ A 2 ≥ A 3 the possible fragment combinations are reduced to a subset of 299774 combinations. In the model, the geometrical arrangement of the three fragments, at the contact stage, are limited to be collinear or equatorial [42,68]. For both scission configurations, the TFP’s satisfying the condition A 1 ≥ A 2 ≥ A 3 have been calculated as a function of the three fragments atomic numbers ( Z 1 , Z 2 , and Z 3 ) and are presented in Figure 2 as a Dalitz plot.
In collinear configurations, the region of absolute minima corresponds to the emission of a heavy fragment with Z 1 ≈ 76 , Z 2 ≈ 22 and Z 3 ≈ 2 . In the equatorial configurations the region of minima, in addition to the very asymmetric masses common to the collinear configurations, includes also more symmetric configurations up to ( Z 1 = Z 2 = 50 ). However, the TFP shows in both configurations also local minima for Z 1 , Z 2 , and Z 3 values of 50, 30, and 20 ,respectively, indicated by arrows in Figure 2. These atomic numbers correspond to Sn, Zn, and Ca nuclei that are the magic nuclei candidates for TTF in our investigation. In particular we focused on 8 TTF combinations. These combinations are characterized by having two out of three fragments as double magic nuclei to follow the indication of the calculations presented in [29,32,69]. The TFP of these combinations for collinear and equatorial configurations are presented in Figure 3. The deepest minimum corresponds to combinations with 48Ca. Among the combinations including 48Ca, the 132 Sn + 68 Zn + 48 Ca tripartition has been considered in more detail in sec. 2.2.3 to present how the DTF and STF products can be experimentally separated.

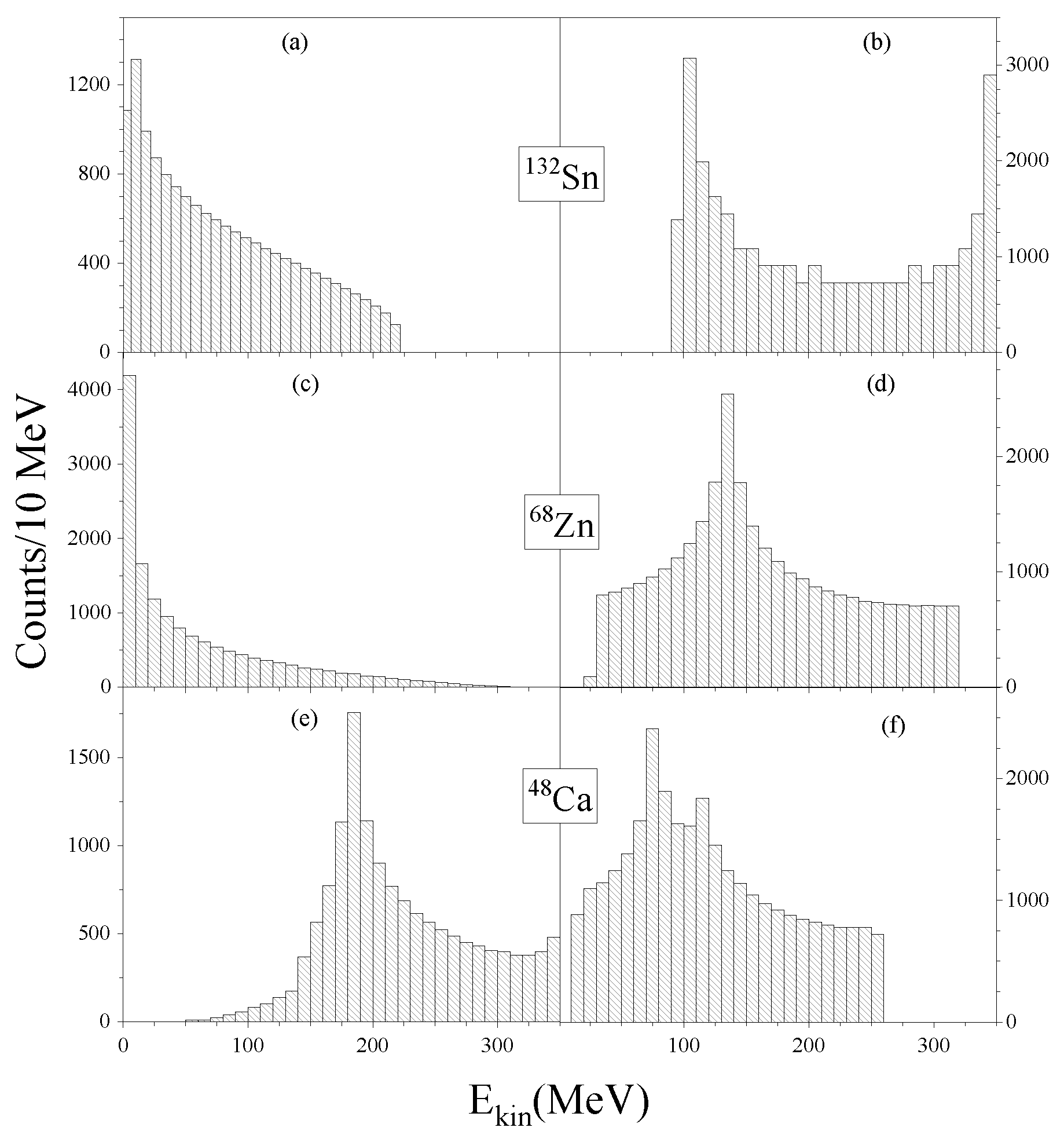
2.2.1. Energy Distributions

The ternary fragment kinetic energies and emission angles in DTF and STF mechanisms are reported in Figure 4 and Figure 5. They are calculated according to the equations described in Section 2.1. As input parameters we considered: (i) all mass and atomic numbers of the above-discussed three-fragment combinations to calculate nuclear masses and reaction Q-values; (ii) kinetic energies ranging from 1 to 350 MeV with 1 MeV step and emission angles ranging from 0 to − 180 ∘ with 5 ∘ step for the heavy fragment A 1 ; (iii) emission angles ranging from 0 to 180 ∘ with 5 ∘ step for the medium fragment A 2 . Only configurations with fragments A 1 and A 2 emitted on opposite sides with respect to the beam direction have been selected. This constraint is chosen to simulate the detector geometry of a typical setup (see later in Section 2.4).
As shown in Figure 4, kinetic energies larger than 270 MeV appear only in DTF mechanisms. Since the kinetic energy is mainly of Coulomb origin, this effect is related to the strength of the repulsion at the specific stage at which the repulsion occurs and on the atomic number of the fragments. Clearly, for DTF the highest energy of the third fragment is consistent with the repulsion of the medium and heavy fragments with lowest kinetic energies.
For the STF, Coulomb repulsion acts during two steps. In the first step, Coulomb repulsion is responsible of the velocity of the fragments A 1 and A 23 . The second step produces a repulsion of nearly equal strength. The configuration that guarantees very low energy of A 2 and A 3 is therefore not possible. The overlapped kinematics imposes further constraints. Consequently, the heavier fragment can reach energies up to 350 MeV, and the configurations with low E 1 and E 2 are not possible.

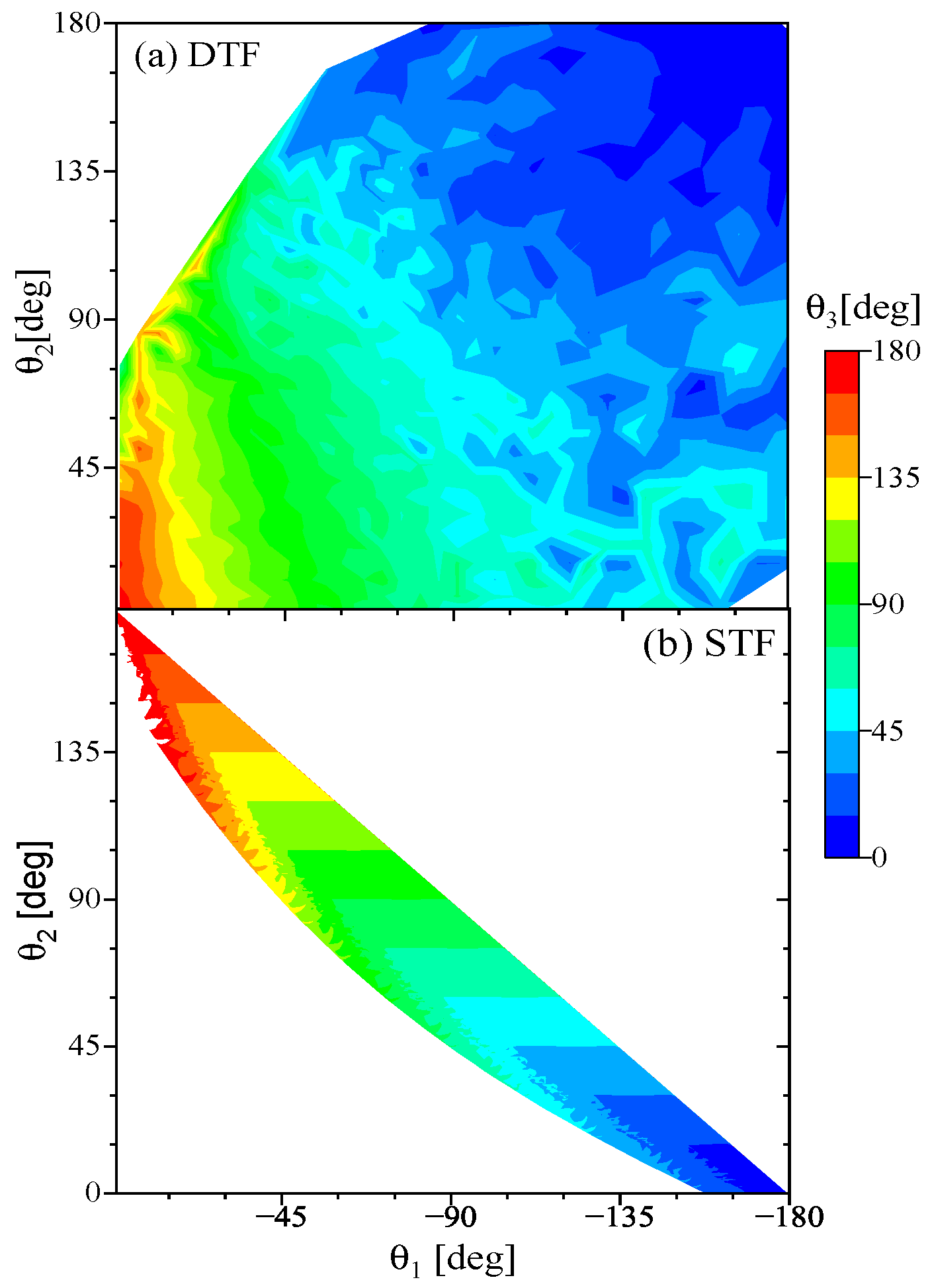
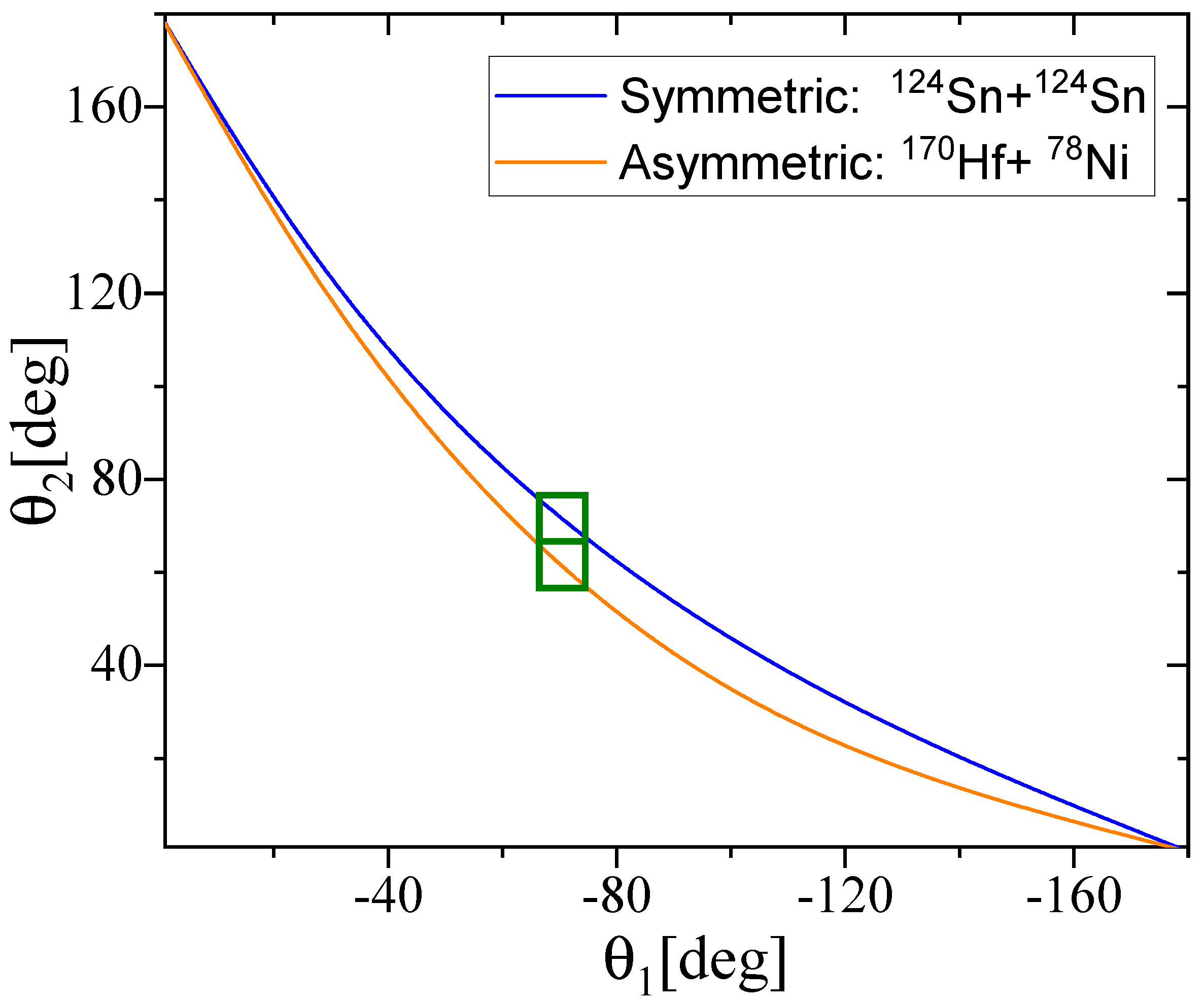
2.2.2. Angular Distributions

The decay mechanisms largely affect also the angular correlations of the reaction products. By considering only the ternary decay occurring in-plane the resulting emission angles in the laboratory system are presented in Figure 5. The fragment angle ( θ 3 ), as function of the heavier fragment angles, θ 1 and θ 2 , is computed when the fragments are emitted on opposite sides with respect to the beam direction. In DTF calculations, once the light fragment direction ( θ 3 ) is fixed (i.e., a detector is mounted at some fixed angle), there exists an interval of θ 1 and θ 2 corresponding to it. By analyzing the DTF distribution in detail we observe that the fragment A 3 is emitted at the backward angles ( θ 3 > 90 ∘ ), when the two heavier fragments move at small angles in the forward ( θ 1 = − 50 ∘ − 0 ∘ and θ 2 = 0 ∘ − 50 ∘ ). This behavior depend not only on the decay mechanism, but also on the fact that the beam energy is not very high compared to the Coulomb repulsion energies involved in the process.
Completely different is the behavior of TTF events produced by the STF mechanism. Indeed, for a fixed θ 1 value, the θ 2 and θ 3 values are very similar and their ranges of variability are narrower than those observed in DTF calculations. Furthermore, the two heaviest fragments are never emitted at the same angle, i.e. if θ 1 = − 40 ∘ , θ 2 and θ 3 would be more than 100 ∘ and vice versa. Obviously, this is a consequence of the two step process and its kinematics where the A 1 and A 23 fragments move apart in opposite directions in the center of the mass frame. The only exception occurs for the cases of θ 1 = − θ 2 at around 70 ∘ . Therefore, to collect STF events very stringent constraints should be considered for positioning the detectors.

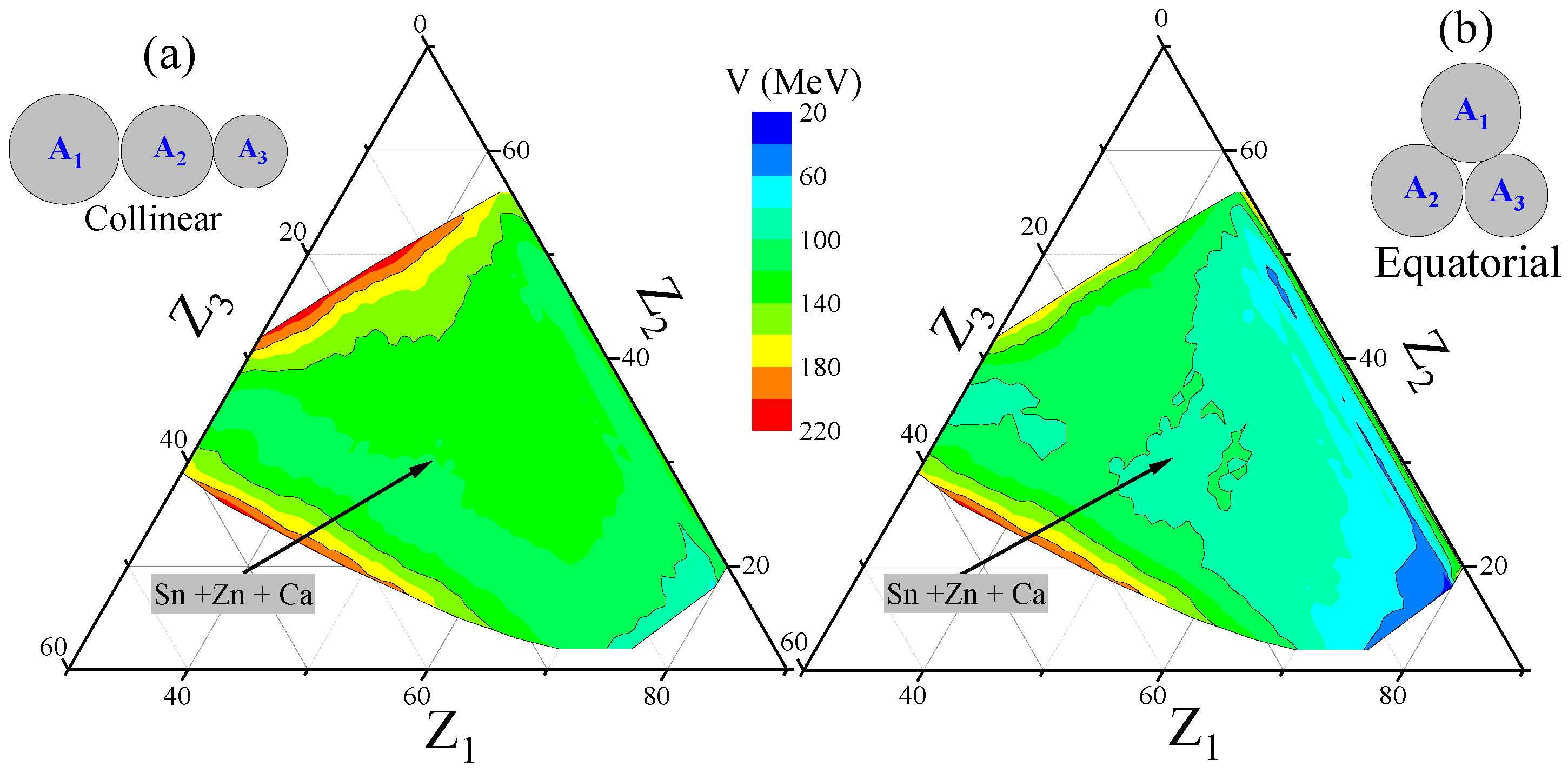
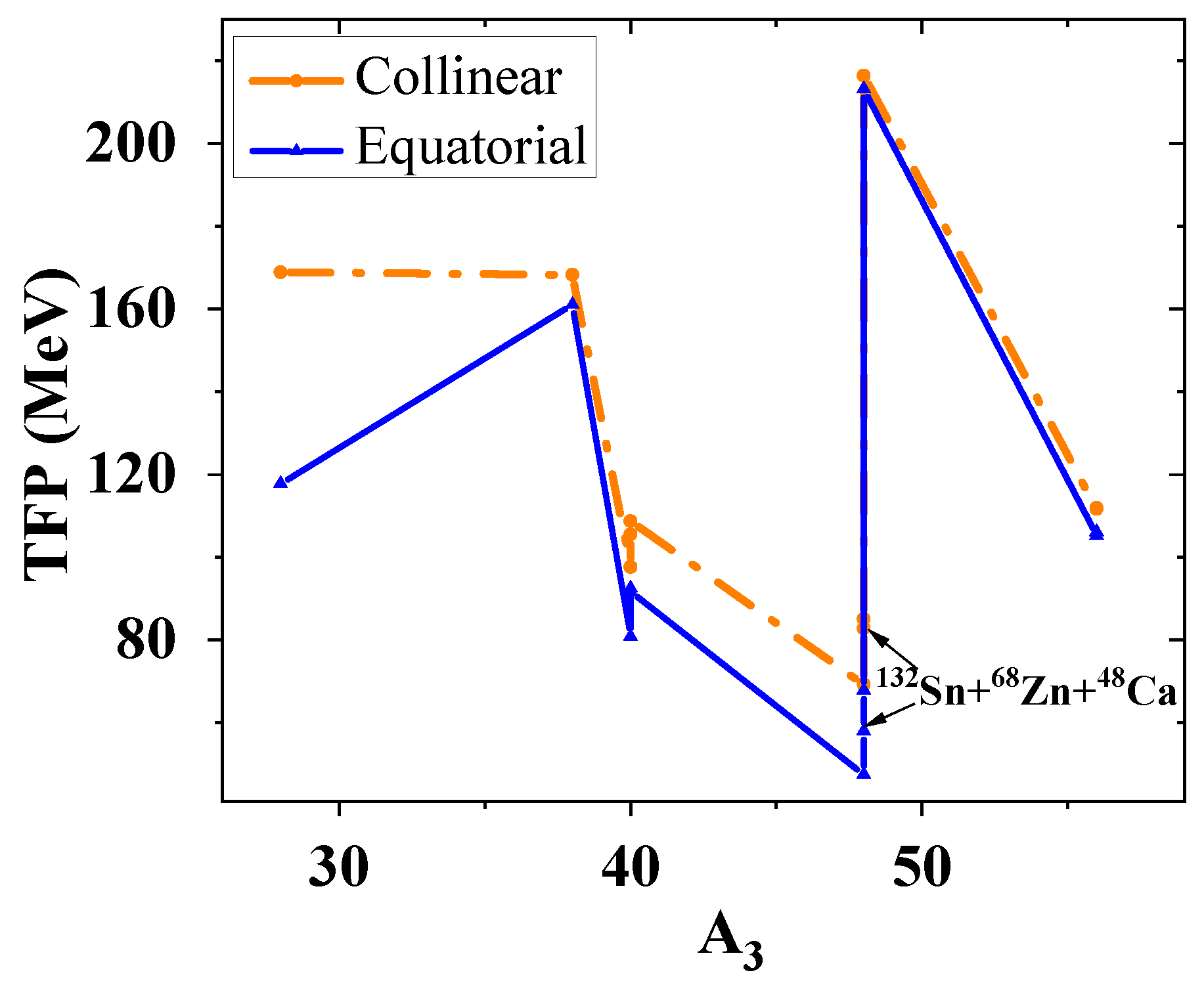
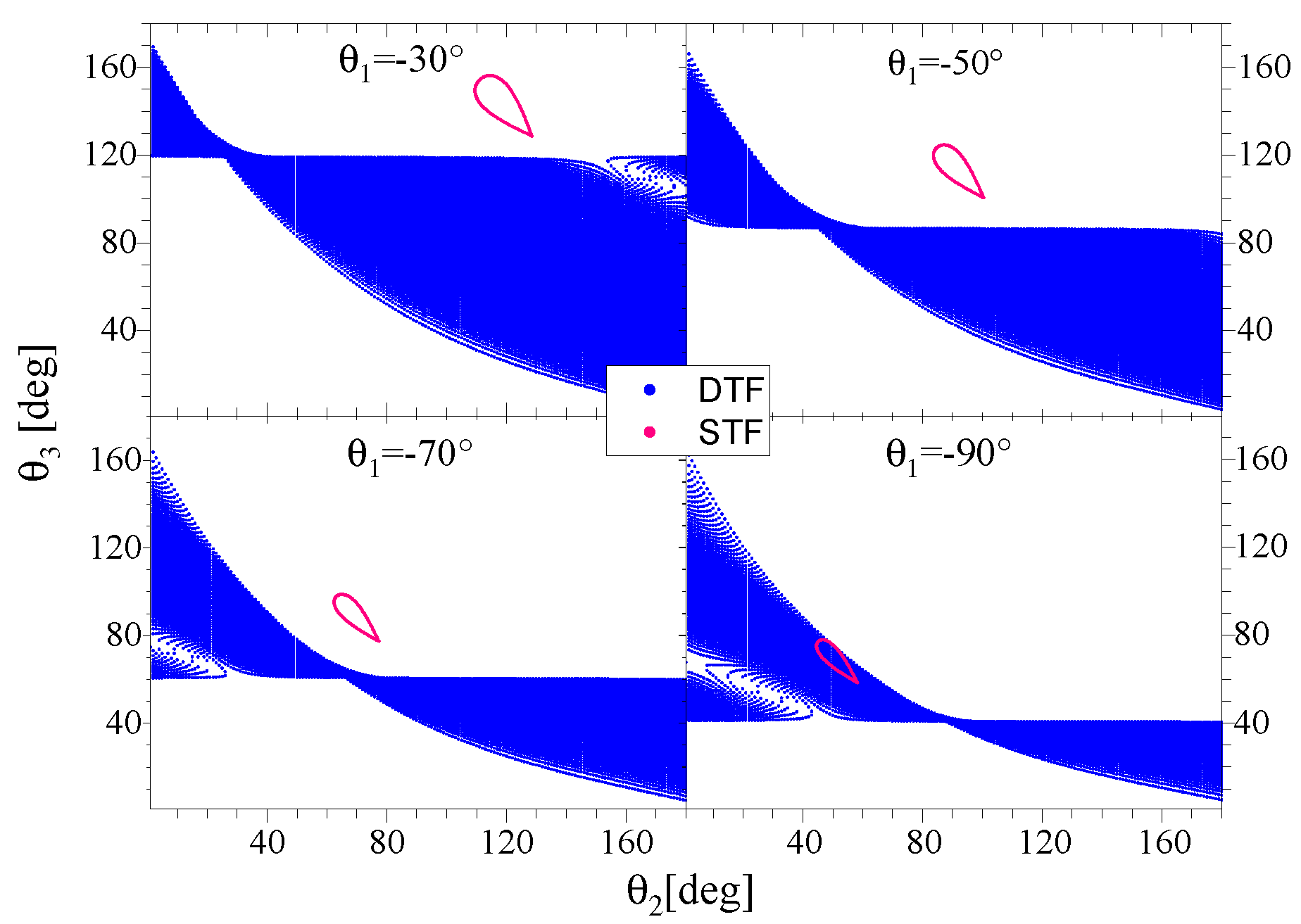
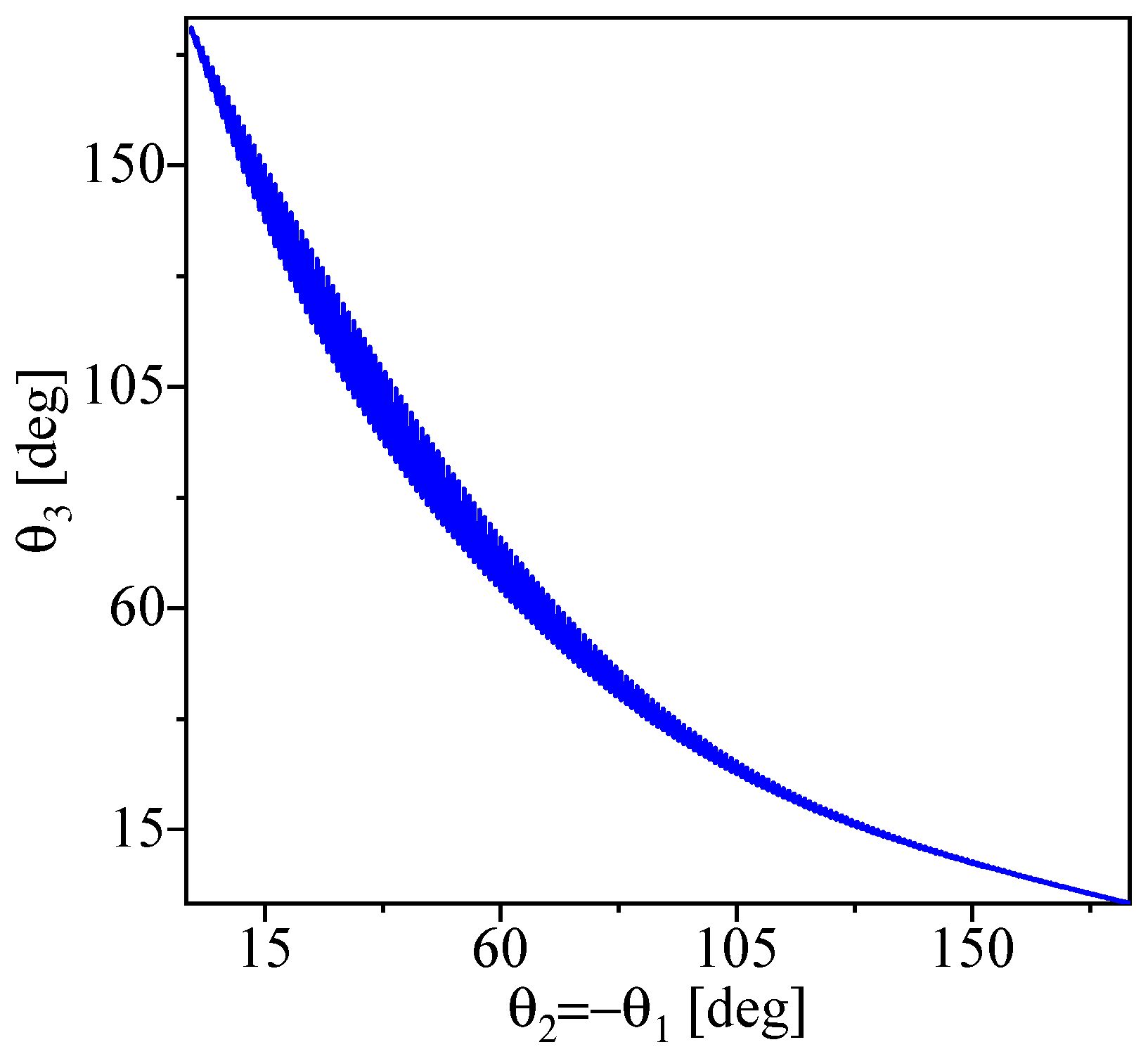
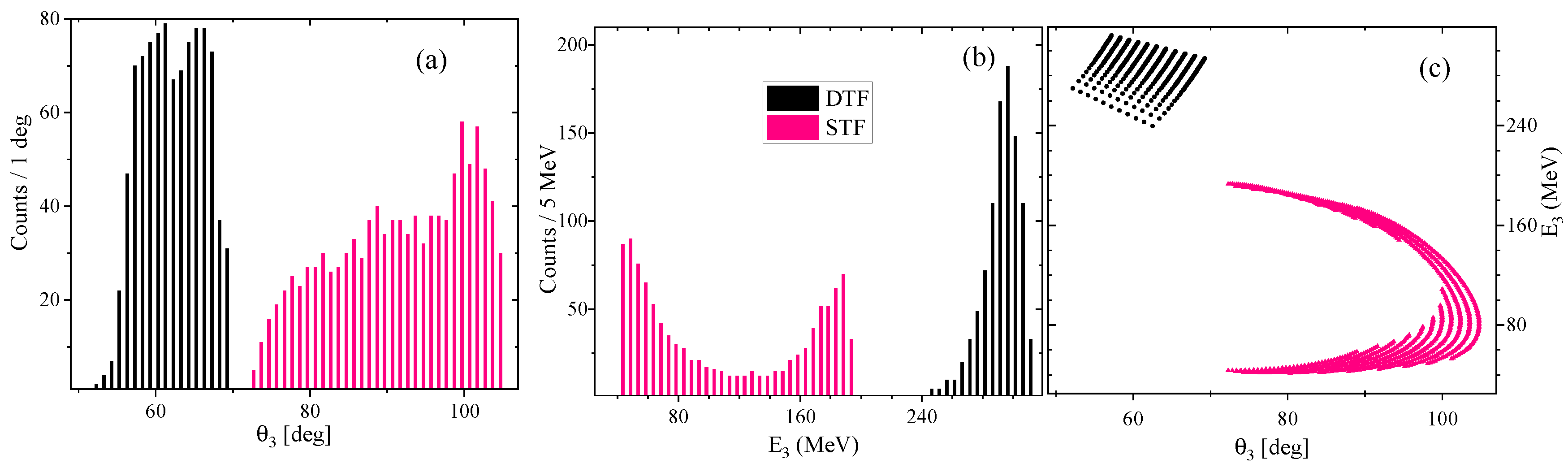
2.2.3. Disentangling of DTF and STF in the 132 Sn + 68 Zn + 48 Ca Tripartition

To gain insight on how to optimize the experimental conditions to collect fragments from TTF, the energy and angular distributions of the tripartition 132 Sn + 68 Zn + 48 Ca has been taken as a reference.
The computed energy distributions of these three fragments are shown in the left and right panel of Figure 6 for DTF and STF, respectively. We observe that the kinetic energies of the middle (68Zn) and heavy (132Sn) fragments in most of DTF cases can reach much lower kinetic energies (down to 1 - 50 MeV) with respect to those in STF, where the fragments are emitted with the maximum amplitudes at 120 MeV and 140 MeV, respectively. We underline that the peaks in the distributions are due to the facts the same energy can be obtained from different combinations of energies and angles of the other two fragments. Thus, being the total available energy the same for both processes, the energies of light fragments (48Ca) result much larger in DTF. The kinetic energy of 48Ca fragments in DTF can go up to 350 MeV and the maximum probability is at around 180 MeV, whereas in STF the 48Ca kinetic energy does not exceed 260 MeV and the maximum probability is reached at below 100 MeV.
Although these distributions show marked differences, they imply the simultaneous measurement of energy, mass, and atomic numbers over a large angular range if the aim is the disentanglement of the origin of the production mechanism. Thus, for planning an experimental investigation the limited angular coverage of the used detectors has to be taken into account.
In Figure 7, the angular correlations between 48Ca and 68Zn fragments are shown. The angular correlations are presented for DTF and STF for fixed values of the 132Sn emission angle. We note that for a 132Sn emitted at the forward direction ( θ 1 ≥ − 90 ∘ ), the same tern of angles does not correspond to both the DTF and STF events, i.e. they are separable simply by collecting coincidence events from detector placed at different angles. However, to define the mechanism responsible for the TF it is convenient to perform measurements in which we can collect products of both mechanisms simultaneously and exploit other observables to disentangle each contribution.
The results shown in Figure 7, for a specific tripartition, reflect what has been previously shown in Figure 5, i.e. wider distributions correspond to DTF whereas, in STF, only very narrow regions are found for the 68Zn and 48Ca angles.
This is a general trend except for the configurations in which the θ 1 = − θ 2 . In this case also the θ 3 distribution of DTF is narrower as shown in Figure 8. Thus, with detectors covering only a small section of the solid angle, it would be possible to measure the θ 3 distribution. Particularly interesting are the events collected in the two-coincidence mode from detectors in θ 1 = − θ 2 = − 70 ∘ configuration because they include middle and heavy fragments produced by both the DTF and STF mechanisms.
The dynamics of the DTF and STF processes affect also the energy of the fragments. At the separation stages, indeed, the different Coulomb repulsion drives the trajectories and determines the observed kinetic energy distributions. In Figure 9, we present the energies 68Zn and 48Ca for fixed 132Sn angles (same values considered in Figure 7).
Being the angular distribution of DTF fragments broader a similar trend is expected for the kinetic energy intervals. Thus, we observe 68Zn and 48Ca kinetic energies distributed over a wide interval ranging from few MeV up to about 300 MeV and form 50 MeV up to 350 MeV (blue lines), respectively, whereas the narrower angular distributions of STF produce strong correlations between the Zn and Ca kinetic energies as indicated by the red lines. In Figure 9 we observe that the phase space of 68Zn and 48Ca energies for the STF and DTF are not overlapping except for few points corresponding to the 132Sn emitted at θ 1 = − 90 ∘ , where also an overlap in the angular distributions is observed. Consequently, the kinetic energies of fragments are observables sensitive to the tripartition mechanism. The indications of the competition among the two ternary mechanisms, obtained by performing measurements of angular distributions, can be confirmed by measuring the energy spectra of a single fragment in coincidence with 132Sn measured at a fixed angle.
The correlations presented so far allow to identify guidelines to select observables and detector locations if exclusive measurements have to be planned to disentangle fragments from DTF or STF mechanisms.
In Figure 10 the 48Ca angular and energy distributions, under the condition of angular symmetric emission of the medium and heavy fragment, i.e. θ 1 = − θ 2 = − 70 ∘ , are presented. The 48Ca fragments are emitted at 60 ∘ ± 10 ∘ and 90 ∘ ± 15 ∘ for DTF and STF, respectively. Furthermore, these events correspond also to well separated kinetic energy ranges 40-190 MeV and 240-310 MeV for STF and DTF, respectively, as shown in Figure 10b. Therefore, by including two detectors covering these angles a solid event-by-event identification of DTF and SFT products is possible.

2.3. Collection of Binary Fission Events

TTF is considered as a rare process compared to BF. Although the total energy released in ternary events is larger than that of BF, ternary probability is hindered by larger barriers. Sophisticated three-center shell model calculations [70] indicate a significant reduction of the ternary fission barrier with the increase of the nuclear mass. Furthermore, it is expected that this barrier becomes rather low (or vanishes completely) in the case of SHN. Therefore, by considering that the ternary fission decay can be rather probable in very heavy nuclei [29], it is interesting not only to determine what is the possible decay mechanisms taking place but also its occurrence with respect to binary fission. The simultaneous measurement of ternary and binary events would allow us to reach this goal.
In this contest the 40 Ar + 208 Pb at 230 MeV reaction is convenient because the folding angles goes from 140 ∘ , for the symmetric fission, to 130 ∘ , for the asymmetric fission involving the 78Ni fragment as shown in Figure 11.
The events of other possible asymmetric channels have not been plotted because they will overlap with BF, elastic and QE events, whose fragment masses are very close to 132Sn and 208Pb doubly magic nuclei.
BF events can be collected with two detectors symmetrical placed at 70 ∘ on the opposite side of the beam direction. By covering the angle at about 60 ∘ in coincidence with the detector at − 70 ∘ also the very asymmetric fission events would be collected.

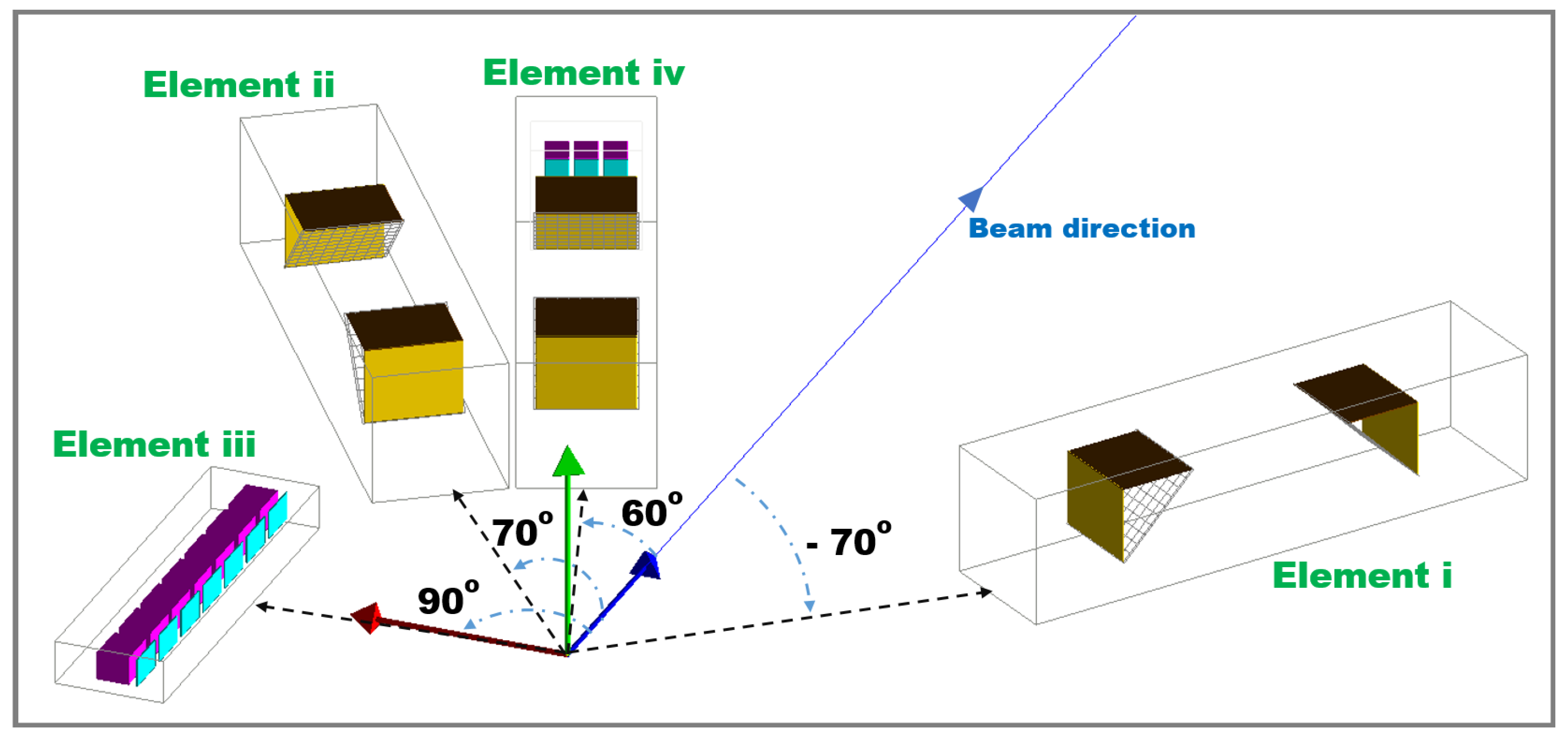
2.4. Detection Apparatus

We present here an example for an arrangement of existing detectors, inspired by the correlations discussed above, to perform measurements aimed at highlighting the occurrence of DTF and STF.
The apparatus is shown in Figure 12, It consist of 4 detection elements mounted in the horizontal plane (our reaction plane) and centered around the target. The polar angles with respect to the beam direction (the z axis) are positive in anticlockwise. The four elements are named as follows:
  • (i) a TOF arm at − 70 ∘ ± 5 ∘ ;
  • (ii) a TOF arm at 70 ∘ ± 5 ∘ ;
  • (iii) a string of 7 telescope detector covering 50 ∘ and centered at 90 ∘ ;
  • (iv) a system of a TOF arm combined with a squared array of telescope detectors at 60 ∘ ± 5 ∘ .
Each TOF arm consists of a start and a stop detector, position sensitive, that allow the ion to pass through with a relatively small energy loss. The telescope detector consists of two-stages and is made by a thin (20 μ m ) and a thick ( 300 μ m ) Si detectors. A string of 7 telescopes, mounted in a single raw, would be used for the construction of the detection element (iii). The same telescopes are mounted in a squared array downstream the stop detector of arm (iv) which will be able to collect therefore TOF and residual energy of the particles passing through.
Each telescope can be used to identify the charge of the lighter ion by exploiting the Δ E − E technique. The use of several telescopes in a raw (element (iii)) allows accessing the angular distributions over a wide angular range centered at 90 ∘ . Example of expected angular and energy distributions for the light fragment in STF events are shown in Figure 10. At the forward angles the narrower angular distribution calculated for the DTF events, instead, can be measured by exploiting the high spatial resolution of TOF detector mounted upstream in the element (iv).
The TOF detectors, featuring the (i), (ii) and (iv) detection elements, can be realized by using two TOSCA units [71] coaxially mounted downstream and acting as start and stop detectors, respectively. The TOSCA units represent the core detection elements. These detectors, developed for a wide variety of experiments as those described in [72,73], have been successfully adopted for the study of binary fission and quasifission in 2023, and of multinucleon transfer reactions in 2024 at JYFL and GSI, respectively. Each unit measures the time and the (x, y) position of charged particles passing through a thin layer mounted orthogonal to the reaction plane. The TOSCA units, represented with triangular prisms in Figure 12, offer a state-of-the-art spatial and time resolutions. By performing coincidence measurements between the two TOSCA units of each TOF detector the velocity vectors of particles can be determined. By crossing thin layers (few μ m ) of a plastic material the variations of trajectories and energies of particles are minimal, so further independent measurements can be performed. Thus, by mounting the telescope array downstream the stop detector in element (iv) we can also measure the mass, charge, and energy of light fragments with a single detection element.
For collecting valuable data an effective trigger scheme able to collect events produced by different decay processes should be arranged. A single event occurs when each sensitive part of a detection element produces a valid signal, i.e. the detectors of each element should be arranged in AND mode. Then, by considering the different number of products and distributions featuring them, the OR mode between the following event conditions can be adopted:
  • (a) coincidences between (i) and (ii) elements;
  • (b) coincidences between (i) and (iii) elements;
  • (d) coincidences between (i), (ii) and (iii) elements;
  • (e) single event form (iv) and (iii) elements.
The trigger conditions a and b will provide the data for separating BF and TF decays discussed in sec. 2.3, while the trigger conditions c and d will be used to investigate the observables featuring the DTF and STF mechanisms, respectively, as the energy and angular correlations of the fission fragments. The condition e will be used to characterize fragments from the different processes and will be useful for the experimental measurements of the detection efficiency.

2.5. Rates Estimates

In order to evidence the differences among competing processes following the collisions a sufficient statistics have to be collected. The TTF involving lighter fragment mass A > 23 , for the 40 Ar + 208 Pb reaction at 230 MeV, has been evaluated to be around 5 mb. This value is determined by considering: a TTF to BF cross-sections ratio of about 0.7%, according to the 40 Ar induced reactions systematics with a beam energy of 230 MeV on 208Pb target [49,51], and a fusion-fission cross section of 700 mb, calculated with the Bass model. Furthermore, we considered the sharing among the possible tripartitions energetically allowed. Although this is a very large number, by considering the increase of the probability to emit two doubly-magic nuclei per fission decay and the A 3 > 23 , we can expect a branching of 1% for the 132 Sn + 68 Zn + 48 Ca tripartition. This tripartition, indeed, coincides with one of the deepest minima of TFP built by considering both DTF and STF mechanisms, as discussed in Section 2.2. So we can estimate a cross section of 50 μ b for this specific tripartition. This gross estimate is corroborated by the 9.4 μ b of 28Mg in coincidence with two fission fragments measured in the 4 He + 238 U reaction at E ∗ =118 MeV [74]. This value, according the systematics [23], is, indeed, expected to be lower than our, because it involves tripartitions with only one doubly-magic nucleus, and it is performed at lower beam energy and in a composite system with lower fissility parameter ( Z 2 / A ), 36.6 instead of 40.3 for the 40 Ar + 208 Pb reaction.
Along with the production yield, also the detection efficiency have to be considered. The proposed setup is intended for the collection of both double and triple coincidence events. The double events are necessary for the BF yield and can be used to provide a description of the TTF by estimating the properties of missing fragments as done in several previous experiment. However, a definitive identification of TTF requires the direct and simultaneous measurement of three fragments. By considering the experimental efficiency of 4% for double coincidence events, typical of the two-arm TOF spectrometer with similar size and intrinsic efficiency of those considered here, we can assume 0.8% as minimum detection efficiency for triple coincidence events. The deduced efficiency is in line with the value obtained in a very recent experiment performed with the TOF spectrometer CORSET arranged for measuring ternary reaction products [54].
In conclusion, by considering the estimated cross section and detection efficiency, and assuming to use a beam intensity of 20 pnA ( 1.2 · 10 11 pps) on a 208Pb target 0.2 μ g / c m 2 thick, about 200 events of 132 Sn + 68 Zn + 48 Ca tripartition can be collected per day. Therefore, in the plots (Figure 13 , Figure 14 and Figure 16), extracted by considering double and triple coincidence modes, 2000 events can be collected in 10 days of beam time provided by existing accelerator facilities such as LNL (Italy) or JYFL (Finland). The cross-sections for BF, order of magnitude larger, as well as the larger detection efficiency makes the collection of thousands of BF events achievable in few hours with the experimental conditions described above.
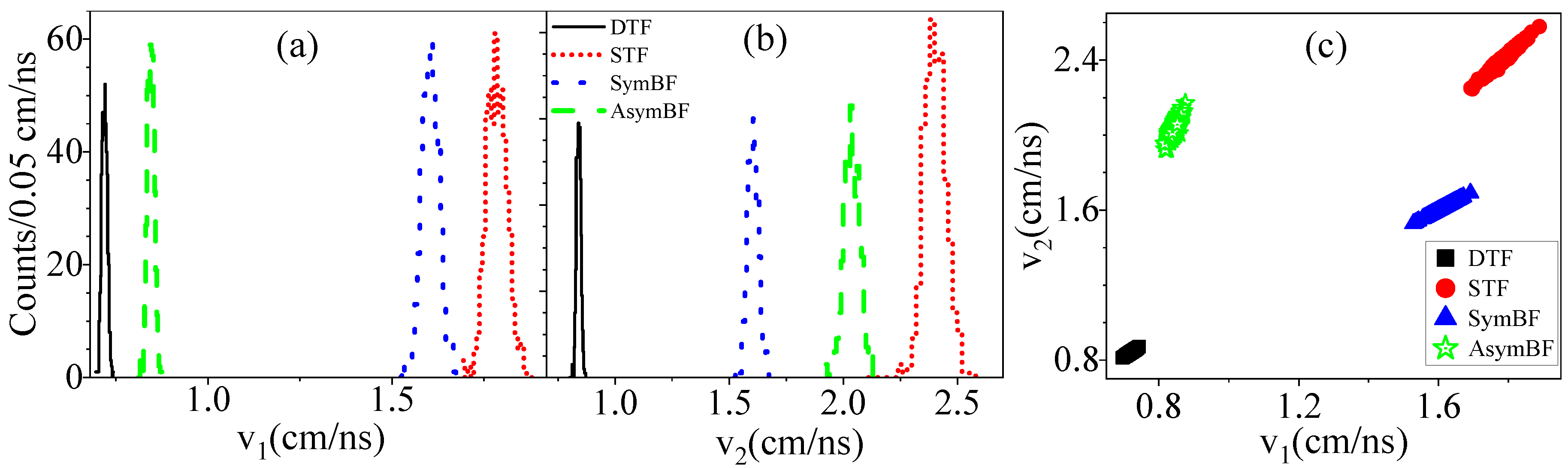
Preprints 118445 g013
Figure 13. Velocity distributions of coincident events ( θ 2 = − θ 1 = 70 ∘ ). The spectra at θ 1 (a) and θ 2 (b) correspond to the heavier and middle mass fragments in the case of TF, respectively. In asymmetric BF the heavier fragment is measured at θ 1 . The location of the coincident events in the two-dimensional matrix v 1 vs v 2 are shown in panel (c).
Figure 13. Velocity distributions of coincident events ( θ 2 = − θ 1 = 70 ∘ ). The spectra at θ 1 (a) and θ 2 (b) correspond to the heavier and middle mass fragments in the case of TF, respectively. In asymmetric BF the heavier fragment is measured at θ 1 . The location of the coincident events in the two-dimensional matrix v 1 vs v 2 are shown in panel (c).
Preprints 118445 g013
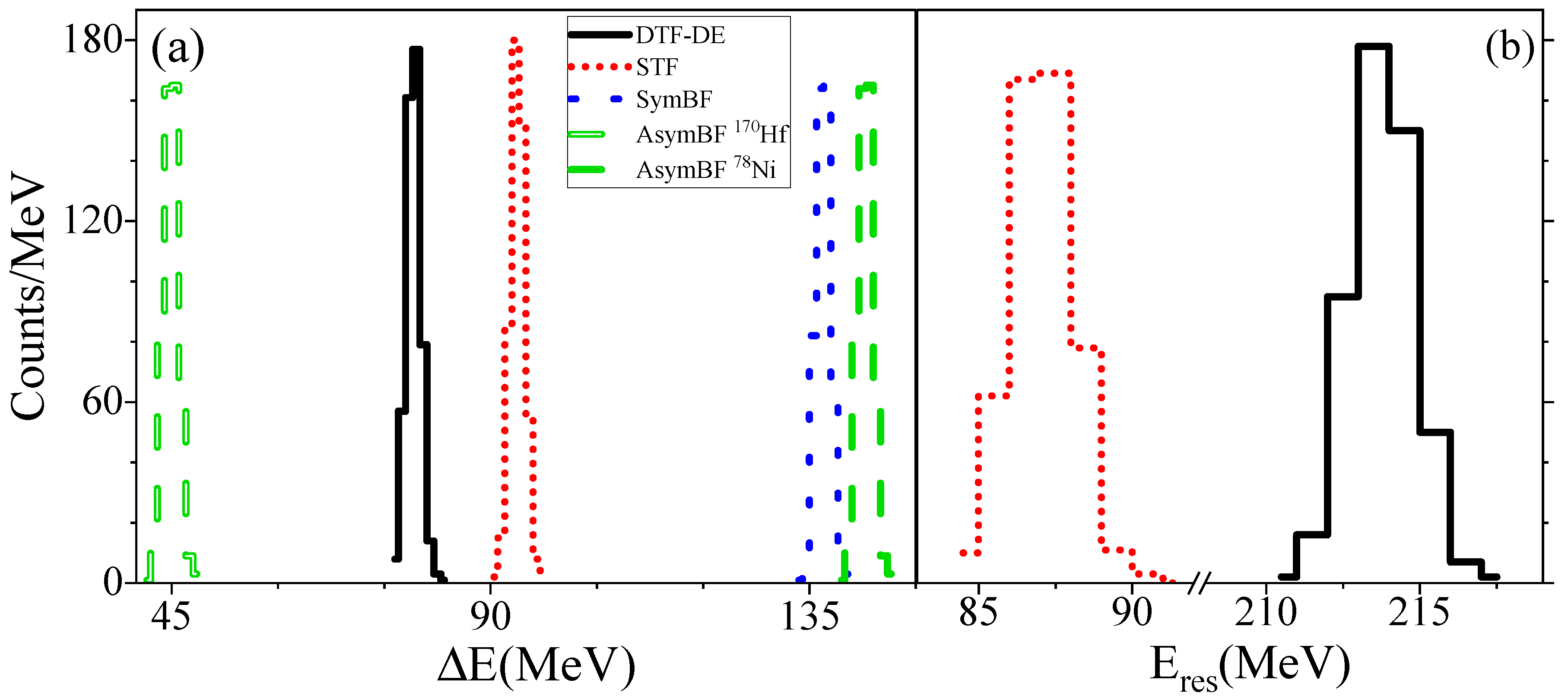
Preprints 118445 g014
Figure 14. Energy spectra measured with the two stages telescope detector at θ 1 = 90 ∘ ± 15 ∘ . The spectra are simulated for the thin Δ E (a) and thick E r e s (b) detectors in the case of the 4 processes taken into account.
Figure 14. Energy spectra measured with the two stages telescope detector at θ 1 = 90 ∘ ± 15 ∘ . The spectra are simulated for the thin Δ E (a) and thick E r e s (b) detectors in the case of the 4 processes taken into account.
Preprints 118445 g014
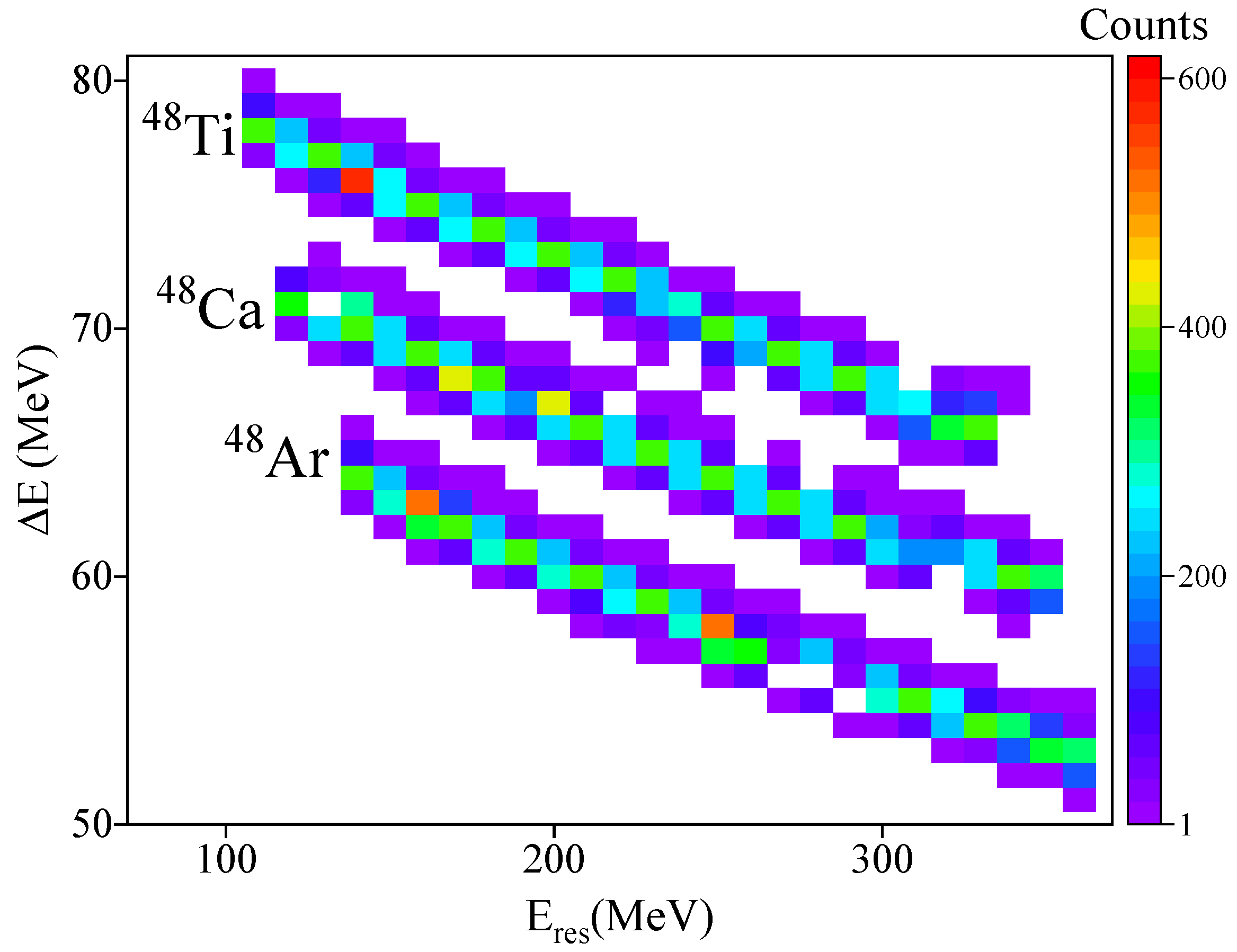
Preprints 118445 g015
Figure 15. Δ E − E matrix of nuclei with A=48 and different atomic numbers. The width of the distribution in Δ E depends mainly on the energy resolution of the detectors. Here we assume for both detectors an energy resolution (FWHM) of 900 keV.
Figure 15. Δ E − E matrix of nuclei with A=48 and different atomic numbers. The width of the distribution in Δ E depends mainly on the energy resolution of the detectors. Here we assume for both detectors an energy resolution (FWHM) of 900 keV.
Preprints 118445 g015

3. Geant4 – Simulation Results

The geometry of the detection apparatus includes both active and passive elements. Both of these, along with the detector geometry, have been included in a simulation based on the Geant4 [75,76]. Geant4 is a versatile toolkit used to simulate the passage of particles through matter. It was developed for high energy physics to construct virtual experimental setups with detectors and now it is used by a wider community. In this work, Geant4 was used to model a setup for detection ternary decays of composite systems. The simulation tracked the ions’ time of interaction, position, and energy loss in the detector, providing essential insights into their interaction with the detector materials. The G4EmLivermorePhysics class was employed which is ideal for modeling electromagnetic interactions of ions with energies in the tens of MeV range. This class includes precise energy loss data for the ions and detection materials. The decay processes were managed using G4DecayPhysics class, which handled potential radioactive decay of unstable ions. These combined models ensured accurate simulation of the ions’ interaction with the detector, including the tracking of their decay when applicable.
The aim is to filter the simulated events with a realistic example of a detection setup and evaluate the feasibility of an experiment. The complete simulated setup includes the 4 detection elements described in sec. 2.4.
By including the resolution and efficiency of existing devices we determined the capability to separate events produced by the different processes taking place as well as the geometrical constraints in shaping such a detection apparatus.

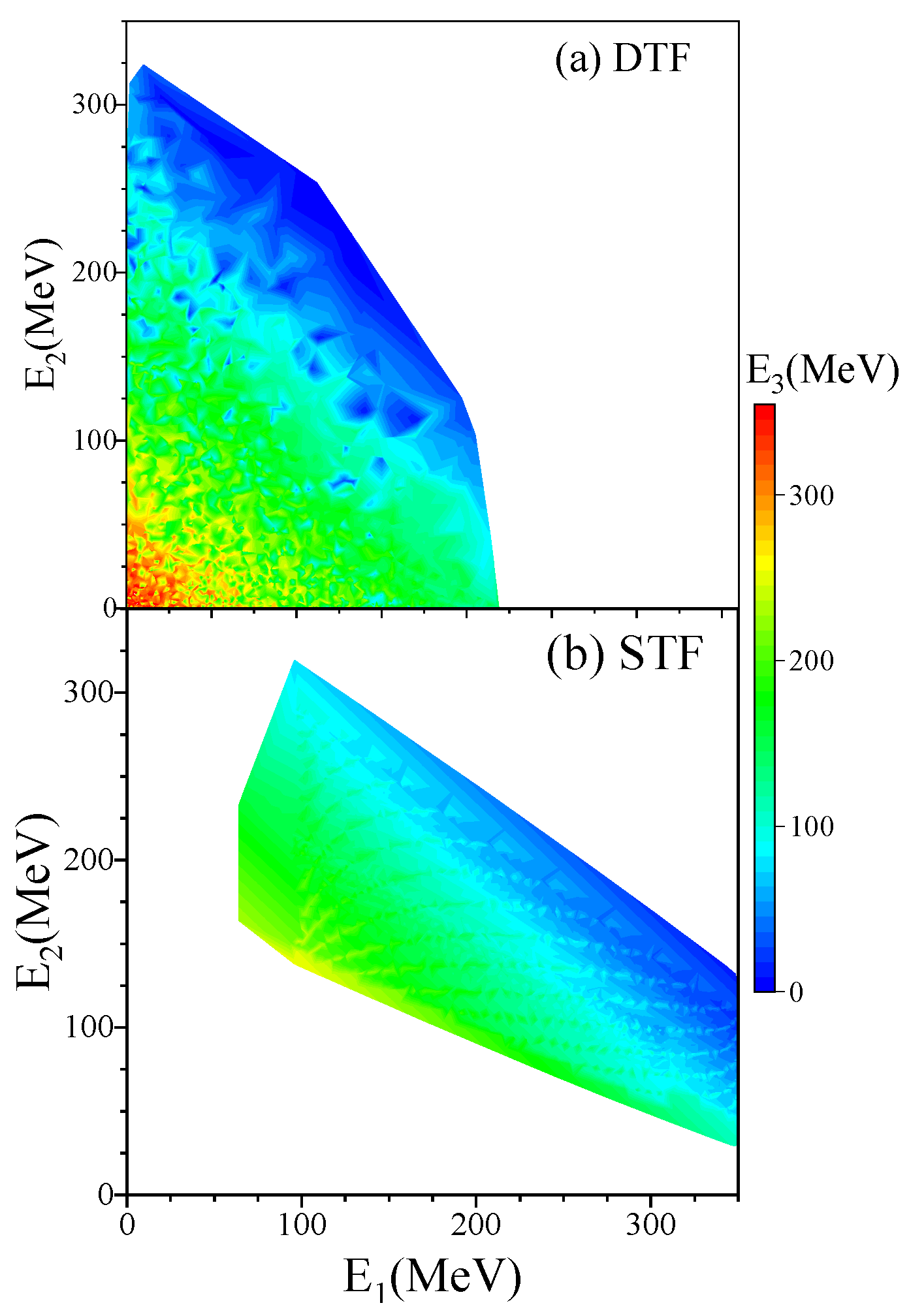
3.1. Correlated velocities in forward detectors

According to the above discussion two TOF detectors placed at − 70 ∘ ± 5 ∘ and 70 ∘ ± 5 ∘ will measure the time and position of the particle passing through a thin ( 190 μ g / c m 2 ) Mylar layer.
The time and flight path experimentally measured in a similar devices with lower performances show Gaussian distributions featured by 150 ps and 2 mm full width at half-maximum (FWHM), see [53]. Therefore, the time and flight path values resulting from the simulations were smeared with Gaussian distributions whose widths correspond to the aforementioned FWHM values. The resulting velocity distributions ( v 1 and v 2 ) with the typical Gaussian distributions are shown in Figs. 13a,b. In the velocity spectra the peaks corresponding to the products of different mechanisms result as well separated. The separation and tagging of events results in being much more effective by simultaneously considering the two-velocity correlation plot, as indicated by the well separated loci shown in Figure 13c.

3.2. Identification of Light Ions at Backward Direction for STF Characterization

A string of two-stages telescopes centered at around 90 ∘ and covering a wide polar angle represents the element (iii). This detection element is mainly included for the characterization of STF events by measuring the angular and energy distributions of light fragments shown in Figure 10. The granularity of the array will provide the angular distribution, while the use of two-stages telescopes is motivated by the interest in both measuring the energies and identifying the Z of lighter fragments. Then, we have considered for the first stage a 20 μ m thick Si detector, which produces the ( Δ E ) signal and only partially slowes down the light ions, and for the second stage a 300 μ m thick Si detector that is sufficiently thick for collecting the residual energies ( E r e s ) of the ions expected. The dependence of energy resolution of Si detector on atomic mass (A) and energy (E) of heavy ions can be taken into account by considering the empirical formula proposed in [77]:
Δ E E = 5 × 10 − 3 1 + 0.01 A E A .
Accordingly, we considered an upper limit for our measurements of 900 keV, corresponding to ions with mass A=50 at E=300 MeV. The energy resolutions of detectors have been introduced in our simulations with the same approach described for the time and position resolutions of the TOF detector. The energy spectra at 90 ∘ ± 15 ∘ for ions with masses ranging from A=48 to A=176 are shown in Figure 14a and b for the thin ( Δ E ) and thick ( E r e s ) detectors, respectively. The two peaks in the E r e s spectrum correspond to the light fragments of 48Ca with energies larger than 100 MeV as those produced by DTF and STF decay. Indeed, only low Z ions can pass through the 20 μ m Si layer of Δ E detector. The heavier fragments from SymBF and AsymBF reactions, due the larger energy loss, will be stopped and their kinetic energies will be collected in the Δ E detector only.
The energy peaks of the fragments from different processes are well separated in the ( Δ E ) spectra, see Figure 14a. Although the use of a single thin detector would be sufficient to disentangle them, the use of a second detector stage is important for two reasons: (i) by measuring the total kinetic energies of all products it is possible to achieve a comprehensive description of the reaction mechanism without making any further assumption on the reaction channel and kinematics; (ii) by using the Δ E − E technique for the identification of the Z of the lightest fragments, it is possible to separate fragments having the same energy and mass but different Z. For instance, in Figure 15, we present a Δ E − E plot for several fragments of mass number A=48 and energy ranging from 125 to 350 MeV.

3.3. Identification of Light Ions at forward Direction for DTF Characterization

The detection element (iv) placed at most forward direction consists of a TOF arm combined with a square array of two-stages telescopes. This detection element is required to collect the light fragments of DTF events when the heavier and middle mass are emitted at − 70 ∘ and 70 ∘ , respectively. Therefore, to cover the maximum emission angle of lightest fragments, as shown in Figure 10a, detection element (iv) is centered at 60 ∘ ± 5 ∘ . With this element, we intend to measure simultaneously and independently the velocity vectors and energies of the ions. The method adopted for simulating these quantities is the same used in the other detection elements, see 3.1 and 3.2. As before, we consider also the same values of time, position, and energy resolution for the active parts. By performing a measurement with this detection element a clear identification of all ions is achievable. Also in this case the energy measurement obtained with the thin detectors would be sufficient to disentangle the products of different processes. This confirms that the trajectories after passing through the thin layers of TOF detectors are practically undisturbed. However, in order to get complete information on the angular distribution of these light ions emitted with a narrower distribution the use of a TOF detector sensitive to the position would provide very valuable data. Furthermore, an even better clear separation can be easily reached by combining the information collected by using all sensitive elements. An idea of the separation reachable can be provided by looking at the Δ E − v matrix shown in Figure 16.
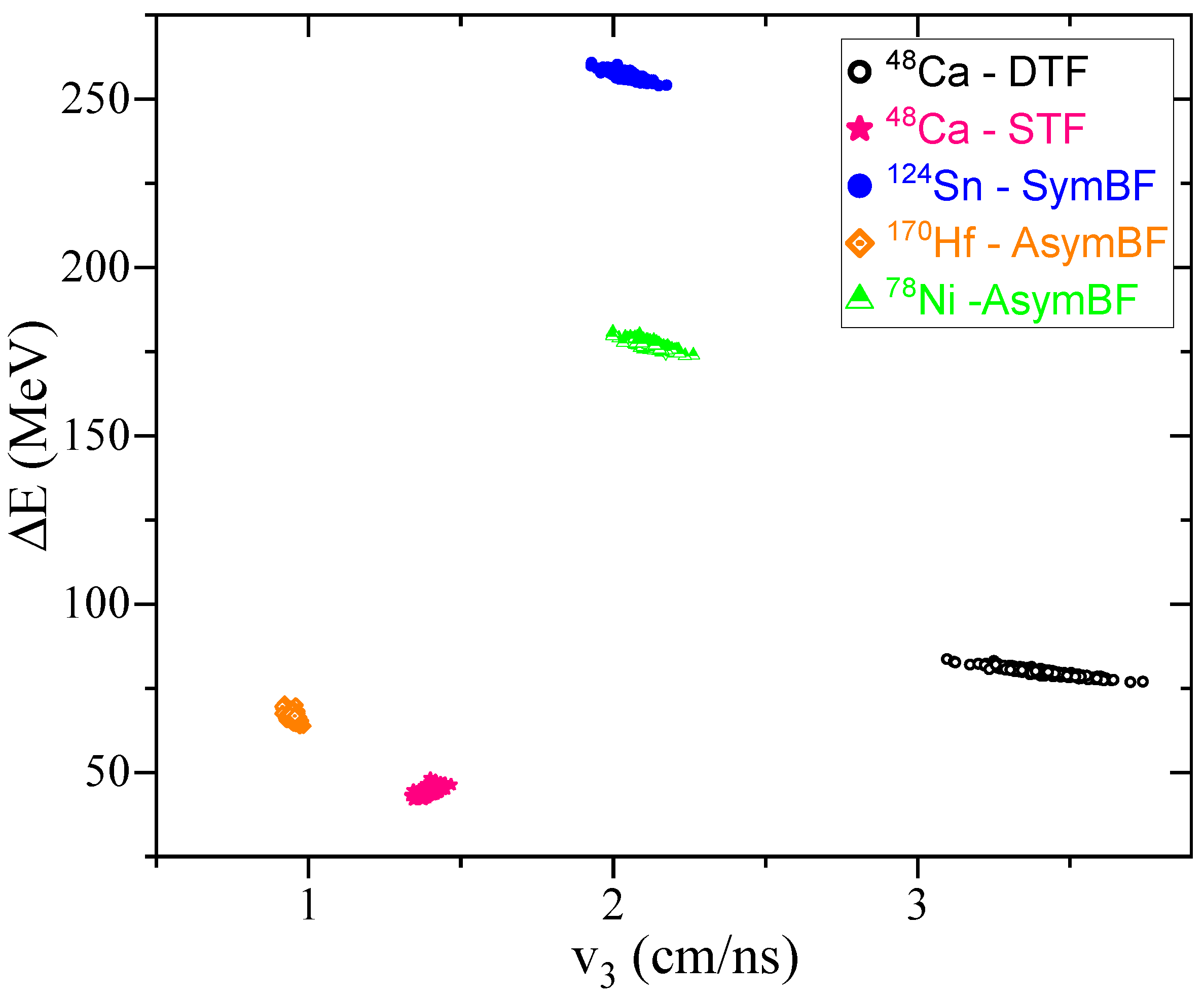
Preprints 118445 g016
Figure 16. Energy-velocity matrix of fragments emitted at 60 ∘ ± 5 ∘ .
Figure 16. Energy-velocity matrix of fragments emitted at 60 ∘ ± 5 ∘ .
Preprints 118445 g016
By considering the capability to perform a direct mass identification given by this element, i.e. obtained by the independent measurement of the velocity and energy of the ions, further indication can be achieved. For instance it will be possible to determine the masses most abundantly produced by all involved processes.

4. Discussion and Conclusions

The existing information on ternary fission has been mainly collected by studying the spontaneous and neutron induced fission when the influence of shell effects are not damped by excitation energies. By studying nuclei in the region of masses around A=250 large changes in mass and TKE distributions of binary decay products have been evidenced. These changes are related to the dynamical evolution of the processes. Also, the dynamical evolution of the ternary fission is still debated. The peculiarities of this region of nuclei, accessible in heavy-ion induced reactions, due to the reduction of fission barriers could be favorable also for investigating the ternary fission.
In this work, we have studied the kinematics of the possible decay processes of 248Fm∗ compound nuclei produced in the 40 Ar + 208 Pb reaction at 230 MeV with the aim to define the observables to distinguish DTF, STF, and BF events.
The fragments’ energy and angular distributions have been calculated for the most probable ternary fragmentations chosen by the corresponding minima in TFP surfaces. It is found that by fixing the emission angles of the two heavier fragments the resulting energy and angular correlations are very different in DTF and STF processes. To define specific experimental conditions, the ternary fragmentation 132 Sn + 68 Zn + 48 Ca , corresponding to a minimum value in the TFP surface due to the two doubly magic products, has been considered. The comparative analysis of the products’ angular and energy distributions has been considered for distinguishing the events originating from the different TF processes and symmetric and asymmetric binary fission events expected to be the main decay channels of the reaction. Thus, a multi-coincidence apparatus involving state-of-art detection elements, such as the TOSCA units and two-stages Si detector telescope array, has been proposed for collecting valuable data.
The calculations filtered by implementing a realistic apparatus response function within the Geant4 simulation toolkit framework have been used to simulate the experimental observables. The simulation results indicate that binary and ternary fission events can be simultaneously measured and clearly separated by exploiting the differences in the energy, velocity, and angular distributions of the fragments.
Estimated yields of TF, by considering the systematics on 40Ar induced fission reactions, the efficiency of proposed setup and the available beam intensity, indicate the possibility to collect valuable data. Then, in conclusion, the proposed experimental investigation seems to be well suited to evidence the TF in heavy-ion induced reactions, determine the ratio between TF and BF occurrences, and progress in the knowledge of TF fission dynamics.
It is not excluded that during ternary fission neutrons can be produced. It would be useful to measure their multiplicities because the ternary neutrons can feed the cycles of reactions used for nuclear energy production and neutron transport as summarized in [78,79].

Acknowledgments

This work was supported in part by the Italian Ministry of Foreign Affairs and International Cooperation (MAECI) under contract PGR12399.

Abbreviations

Binary Fission BF
Liquid Drop Model LDM
Compound Nucleus CN
Ternary Fission TF
Ternary Particle TP
Ternary Fission Potential TFP
Potential Energy Surface PES
True Ternary Fission TTF
Direct Ternary Fission DTF
Sequential Ternary Fission STF
Asymmetrical Binary Fission AsymBF
Total Kinetic Energy TKE
Symmetrical Binary Fission SymBF
Time Of Flight TOF

References

  1. Meitner, L.; Frisch, O.R. Disintegration of uranium by neutrons: a new type of nuclear reaction. Nature 1939, 143, 239. [Google Scholar] [CrossRef]
  2. Hahn, O.; Strassmann, F. Uber den nachweis und das verhalten der bei der bestrahlung des urans mittels neutronen entstehenden erdalkalimetalle. Naturwissenschaften 1939, 27, 11–15. [Google Scholar] [CrossRef]
  3. Hahn, O.; Strassmann, F. Nachweis der entstehung aktiver bariumisotope aus uran und thorium durch neutronenbestrahlung; nachweis weiterer aktiver bruchst¨ucke bei der uranspaltung; nachweis weiterer aktiver bruchst¨ucke bei der uranspaltung. Naturwissenschaften 1939, 27, 89–95. [Google Scholar] [CrossRef]
  4. Bohr, N. Nature 1936, 137, 344–348. [CrossRef]
  5. Bohr, N.; Wheeler, J.A. Phys. Rev. 1939, 56, 426–450. [CrossRef]
  6. Present, R.; Wheeler, J. The Mechanism of nuclear fission. Phys. Rev. 1939, 56, 426. [Google Scholar] [CrossRef]
  7. Present, R. Possibility of ternary fission. Phys. Rev. 1941, 59, 466. [Google Scholar]
  8. Grad, H.; Rubin, H. Peaceful uses of atomic energy. Proc. 2nd Int. Conf.(Geneva, 1958), 1958, Vol. 31, p. 100.
  9. Diehl, H.; Greiner, W. Theory of ternary fission in the liquid drop model. Nuclear Physics A 1974, 229, 29–46. [Google Scholar] [CrossRef]
  10. Alvarez, L.; Farwell, G.; Segre, E.; Wiegand, C. Phys. Rev. 1947, 71, 327. [CrossRef]
  11. San-Tsiang; Zah-Wei; Chastel; Vigneron, L. On the New Fission Processes of Uranium Nuclei. Phys. Rev. 1947, 71, 382. [Google Scholar] [CrossRef]
  12. San-Tsiang, T.; Zah-Wei, H.; Vigneron, L.; Chastel, R. Ternary and Quaternary Fission of Uranium Nuclei. Nature 1947, 159, 773. [Google Scholar] [CrossRef]
  13. Gönnenwein, F. Nucl. Phys. A 2004, 734, 213–216. [CrossRef]
  14. Gönnenwein, F.; Mutterer, M.; Kopatch, Y. Europhys. News 2005, 36, 11. [CrossRef]
  15. Wagemans, C.; Deruytter, A. The emission of Long-Range α-particles in the thermal neurtron induced fission of 233U, 235U, and 239Pu. Zeitschrift für Physik A Atoms and Nuclei 1975, 275, 149–156. [Google Scholar] [CrossRef]
  16. Papka, P.; Beck, C. Cluster in Nuclei: Experimental Perspectives. Cluster in Nuclei 212, 2, 299. [CrossRef]
  17. Muga, M.L.; Bowman, H.R.; Thompson, S.G. Tripartition in the Spontaneous-Fission Decay of Cf252. Phys. Rev. 1961, 121, 270. [Google Scholar] [CrossRef]
  18. Rubchenya, V.; Alexandrov, A.; Khlebnikov, S.; Lyapin, V.; Maslov, V.; Penionzhkevich, Y.E.; Prete, G.; Sobolev, Y.G.; Tyurin, G.; Trzaska, W.; others. Light particle accompanied quasifission in superheavy composite systems. Physics of Atomic Nuclei 2006, 69, 1388–1398. [Google Scholar] [CrossRef]
  19. Duek, E.; Ajitanand, N.; Alexander, J.M.; Logan, D.; Kildir, M.; Kowalski, L.; Vaz, L.C.; Guerreau, D.; Zisman, M.; Kaplan, M.; others. Mechanisms for emission of 4 He in the reactions of 334 MeV 40 Ar with 238 U. Zeitschrift für Physik A Atoms and Nuclei 1984, 317, 83–100. [Google Scholar] [CrossRef]
  20. Vardaci, E.; Kaplan, M.; Parker, W.E.; Moses, D.J.; Boger, J.; Gilfoyle, G.; McMahan, M.; Montoya, M. Search for ternary fragmentation in the reaction 856 MeV 98Mo+ 51V: kinematic probing of intermediate-mass-fragment emissions. Physics Letters B 2000, 480, 239–244. [Google Scholar] [CrossRef]
  21. Wagemans, C. Ternary Fission in The Nuclear Fission Process. CRC Press, Boca Raton, FL 1991.
  22. Gönnenwein, F. World Scientific, Singapore 1999, p. 59.
  23. Brandt, R. Angew. Chem. internat. 1971, 10, 890. [CrossRef] [PubMed]
  24. Vijayaraghavan, K.; von Oertzen, W.; Balasubramaniam, M. Kinetic energies of cluster fragments in ternary fission of 252Cf. Eur. Phys. J. A 2012, 48, 27. [Google Scholar] [CrossRef]
  25. Iyer, R.; Cobble, J. Evidence of ternary fission at lower energies. Physical Review Letters 1966, 17, 541. [Google Scholar] [CrossRef]
  26. Gönnenwein, F.; Möller, A.; Crön, M.; Hesse, M.; Wöstheinrich, M.; Faust, H.; Fioni, G.; Oberstedt, S. Nuovo Cimento A 1997, 110, 1089. [CrossRef]
  27. L. Rosen, A.H. Symmetrical tripartition of U235, by thermal neutrons. Phys. Rev. 1950, 78, 533. [Google Scholar] [CrossRef]
  28. Schall, P.; Heeg, P.; Mutterer, M.; Theobald, J. On symmetric tripartition in the spontaneous fission of 252Cf. Phys. Lett. B 1987, 191, 339. [Google Scholar] [CrossRef]
  29. Zagrebaev, V.; Karpov, A.; Greiner, W. True ternary fission of superheavy nuclei. Phys. Rev. C 2010, 81, 044608. [Google Scholar] [CrossRef]
  30. Vijayaraghavan, K.; Balasubramaniam, M.; von Oertzen, W. True ternary fission. Phys. Rev. C 2015, 91, 044616. [Google Scholar] [CrossRef]
  31. von Oertzen, W.; Nasirov, A. True ternary fission, the collinear decay into fragments of similar size in the 252Cf(sf) and 235U(nth,f) reactions. Phys. Lett. B 2014, 734, 234–238. [Google Scholar] [CrossRef]
  32. Poenaru, D.; Gherghescu, R.; Greiner, W.; Nagame, Y.; Hamilton, J.; Ramayya, A. True ternary fission. Romanian Reports in Physics 2003, 55, 549–554. [Google Scholar]
  33. Hamilton, J.H.; Ramayya, A.V.; Kormicki, J.; Ma, W.C.; Lu, Q.; Shi1, D.; Deng, J.K.; Zhu, S.J.; Sandulescu, A.; Greiner, W.; Akopian, G.M.T.; Oganessian, Y.T.; Popeko, G.S.; Daniel, A.V.; Kliman, J.; Polhorsky, V.; Morhac, M.; Cole, J.D.; Aryaeinejad, R.; Lee, I.Y.; Johnson, N.R.; McGowan, F.K. Zero neutron emission in spontaneous fission of 252Cf: a form of cluster radioactivity. J. Phys. G: Nucl. Part. Phys. 1994, 20, L85. [Google Scholar] [CrossRef]
  34. Ter-Akopian, G.M.; Hamilton, J.H.; Oganessian, Y.T.; Kormicki, J.; Popeko, G.S.; Daniel, A.V.; Ramayya, A.V.; Lu, Q.; Butler-Moore, K.; Ma, W.C.; Deng, J.K.; Shi, D.; Kliman, J.; Polhorsky, V.; Morhac, M.; Greiner, W.; Sandelescu, A.; Cole, J.D.; Aryaeinejad, R.; Johnson, N.R.; Lee, I.Y.; McGowan, F.K. Phys. Rev. Lett. 1994, 73, 1477. [CrossRef]
  35. Hamilton, J.H.; Ramayya, A.V.; Hwang, J.K.; Kormicki, J.; Babu, B.R.S.; Sandulescu, A.; Florescu, A.; Greiner, W.; Ter-Akopian, G.M.; Oganessian, Y.T.; Daniel, A.V.; Zhu, S.J.; Wang, M.G.; Ginter, T.; Deng, J.K.; Ma, W.C.; Popeko, G.S.; Lu, Q.H.; Jones, E.; Dodder, R.; Gore, P.; Nazarewicz, W.; Rasmussen, J.O.; Asztalos, S.; Lee, I.Y.; Chu, S.Y.; Gregorich, K.E.; Macchiavelli, A.O.; Mohar, M.F.; Prussin, S.; Stoyer, M.A.; Lougheed, R.W.; Moody, K.J.; Wild, J.F.; Bernstein, L.A.; Becker, J.A.; Cole, J.D.; Aryaeinejad, R.; Dardenne, Y.X.; Drigert, M.W.; Butler-Moore, K.; Donangelo, R.; Griffin, H.C. New cold and ultra hot binary and cold ternary spontaneous fission modes for 252Cf and new band structures with gammasphere. Prog. Part. Nucl. Phys. 1997, 38, 273–287. [Google Scholar] [CrossRef]
  36. Ramayya, A.V.; Hamilton, J.H.; Hwang, J.K.; Peker, L.K.; Kormicki, J.; Babu, B.R.S.; Ginter, T.N.; Sandulescu, A.; Florescu, A.; Carstoiu, F.; Greiner, W.; Ter-Akopian, G.M.; Oganessian, Y.T.; Daniel, A.V.; Ma, W.C.; Varmette, P.G.; Rasmussen, J.O.; Asztalos, S.J.; Chu, S.Y.; Gregorich, K.E.; Macchiavelli, A.O.; Macleod, R.W.; Cole, J.D.; Aryaeinejad, R.; Butler-Moore, K.; Drigert, M.W.; Stoyer, M.A.; Bernstein, L.A.; Lougheed, R.W.; Moody, K.J.; Prussin, S.G.; Zhu, S.J.; Griffin, H.C.; Donangelo, R. Cold (neutronless) α ternary fission of 252Cf. Phys. Rev. C 1998, 57, 2370. [Google Scholar] [CrossRef]
  37. Ramayya, A.V.; Hwang, J.K.; Hamilton, J.H.; Sandulescu, A.; Florescu, A.; Ter-Akopian, G.M.; Daniel, A.V.; Oganessian, Y.T.; Popeko, G.S.; Greiner, W.; Cole, J.D. Observation of 10Be Emission in the Cold Ternary Spontaneous Fission of 252Cf. Phys. Rev. Lett. 1998, 81, 947. [Google Scholar] [CrossRef]
  38. Kopatch, Y.N.; Mutterer, M.; Schwalm, D.; Thirolf, P.; Gönnenwein, F. 5He, 7He, and 8Li(E* = 2.26MeV) intermediate ternary. Phys. Rev. C 2002, 65, 044614. [Google Scholar] [CrossRef]
  39. Daniel, A.V.; Ter-Akopian, G.M.; Hamilton, J.H.; Ramayya, A.V.; Kormicki, J.; Popeko, G.S.; Fomichev, A.S.; Rodin, A.M.; Oganessian, Y.T.; Cole, J.D.; Hwang, J.K.; Luo, Y.X.; Fong, D.; Gore, P.; Jandel, M.; Kliman, J.; Krupa, L.; Rasmussen, J.O.; Wu, S.C.; Lee, I.Y.; Stoyer, M.A.; Donangelo, R.; Greiner, W. Phys. Rev. C 2004, 69, 041305. [CrossRef]
  40. Ter-Akopian, G.; Daniel, A.V.; Fomichev, A.S.; Popeko, G.S.; Rodin, A.M.; Oganessian, Y.T.; Hamilton, J.H.; Ramayya, A.V.; Kormicki, J.; Hwang, J.K.; Fong, D.; Gore, P.; Cole, J.D.; Jandel, M.; Kliman, J.; Krupa, L.; Rasmussen, J.O.; Lee, I.Y.; Macchiavelli, A.O.; Fallon, P.; Stoyer, M.A.; Donangelo, R.; Wu, S.C.; Greiner, W. Phys. At. Nuclei 2004, 67, 1860. [CrossRef]
  41. Manimaran, K.; Balasubramaniam, M. Ternary fission fragmentation of 252Cf for all possible third fragments. Eur. Phys. J. A 2010, 45, 293. [Google Scholar] [CrossRef]
  42. Manimaran, K.; Balasubramaniam, M. All possible ternary fragmentations of 252Cf in collinear configuration. Phys. Rev. C 2011, 83, 034609. [Google Scholar] [CrossRef]
  43. Pyatkov, Y.; Kamanin, D.; Kopach, Y.; Alexandrov, A.; Alexandrova, I.; Borzakov, S.; Voronov, Y.; Zhuchko, V.; Kuznetsova, E.; Panteleev, T.; Tyukavkin, A. Collinear cluster tri-partition channel in reaction 235U(nth,f). Phys. Atom. Nucl. 2010, 73, 1309–1316. [Google Scholar] [CrossRef]
  44. Poenaru, D.; W. Greiner, J.H.; Ramayya, A.; Hourany, E.; Gherghescu, R. Multicluster accompanied fission. Phys. Rev. C 1999, 59, 3457. [Google Scholar] [CrossRef]
  45. Pyatkov, Y.; Trzaska, W.; Khlebnikov, S. Island of the high yields of 252Cf(sf) collinear tripartition in the fragment mass space. Rom. Rep. Phys. 2007, 59, 569. [Google Scholar]
  46. Pyatkov, Y.; Kamanin, D.; von Oertzen, W.; Alexandrov, A.; Alexandrova, I.; Falomkina, O.; Kondratjev, N.; Kopatch, Y.; Kuznetsova, E.; Lavrova, Y.; Tyukavkin, A.; Trzaska, W.; Zhuhcko, V. Collinear cluster tri-partition of 252Cf(sf) and in the 235U(nth,f) reaction. Eur. Phys. J. A 2010, 45, 29. [Google Scholar] [CrossRef]
  47. Pyatkov, Y.; Kamanin, D.; Alexandrov, A.; Alexandrova, I.; Kondratuev, N.; Kuznetsova, E.; Jacobs, N.; Malaza, V.; Minh, D.P.; Zhuchko, V. Presumable scenario of one of the collinear cluster tripartition modes. Int. J. Mod. Phys. E 2010, 20, 1008. [Google Scholar] [CrossRef]
  48. Pyatkov, Y.; Kamanin, D.; von Oertzen, W.; Alexandrov, A.; Alexandrova, I.; Falomkina, O.; Jacobs, N.; Kondratjev, N.; Kuznetsova, E.; Lavrova, Y.; Malaza, V.; Ryabov, Y.; Strekalovsky, O.; Tyukavkin, A.; Zhuchko, V. Collinear cluster tri-partition (CCT) of 252Cf(sf): New aspects from neutron gated data. Eur. Phys. J. A 2012, 48, 94. [Google Scholar] [CrossRef]
  49. Karamyan, S. Sov. J. Nucl. Phys. 1967, 5, 559.
  50. Vandenbosch, R.; Huizenga, J.R. Nuclear Fission; Academic Press, 1973.
  51. Perelygin, V.; Shadieva, N.; Tretiakova, S.; Boos, A.; Brandt, R. Ternary fission produced in Au, Bi, Th and U with Ar ions. Nuclear Physics, Section A 1969, 127, 577–585. [Google Scholar] [CrossRef]
  52. Price, P.; Fleischer, R.; Walker, R.; Hubbard, E. Ternary Fission of Heavy Compound Nucleis. Proceedings of the Third Conference on Reactions Between Complex Nuclei: Held at Asilomar (Pacific Grove, California), edited by Albert Ghiorso, R. M. Diamond and H. E. Conzett, Berkeley: University of California Press 1963, pp. 332–337. [CrossRef]
  53. Badala, A.; Cognata, M.L.; Nania, R.; Osipenko, M.; Piantelli, S.; Turrisi, R.; Barion, L.; Capra, S.; Carbone, D.; Carnesecchi, F.; Casula, E.; Chatterjee, C.; Ciani, G.; Depalo, R.; Nitto, A.D.; Fantini, A.; Goasduff, A.; Guardo, G.; Kraan, A.C.; Manna, A.; Marsicano, L.; Martorana, N.; Morales-Gallegos, L.; Naselli, E.; Scordo, A.; Valdre, S.; Volpe, G. Riv. Nuovo Cim. 2022, 45, 189–276. [CrossRef]
  54. Kozulin, E.; Knyazheva, G.; Karpov, A.; Saiko, V.; Bogachev, A.; Itkis, I.; Novikov, K.; Vorobiev, I.; Pchelintsev, I.; Savelieva, E.; others. Detailed study of multinucleon transfer features in the Xe 136+ U 238 reaction. Physical Review C 2024, 109, 034616. [Google Scholar] [CrossRef]
  55. Kozulin, E.; Knyazheva, G.; Itkis, I.; Kozulina, N.; Loktev, T.; Novikov, K.; Harca, I. Shell effects in fission, quasifission and multinucleon transfer reaction. Journal of Physics: Conference Series 2014, 515, 012010. [Google Scholar] [CrossRef]
  56. Di Nitto, A.; Vardaci, E.; La Rana, G.; Nadtochy, P.N.; Prete, G. Evaporation channel as a tool to study fission dynamics. Nucl. Phys. A 2018, 971, 21–34. [Google Scholar] [CrossRef]
  57. Ramos, D.; Caamano, M.; Farget, F.; Rodriguez-Tajes, C.; Lemasson, A.; Schmitt, C.; Audouin, L.; Benlliure, J.; Casarejos, E.; Clement, E.; others. NSR Query Results. Phys. Rev. C 2023, 107, L021601. [Google Scholar] [CrossRef]
  58. Wang, M.; Huang, W.; Kondev6, F.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references. Chinese Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
  59. Di Nitto, A.; Vardaci, E.; Brondi, A.; La Rana, G.; Cinausero, M.; Gelli, N.; Moro, R.; Nadtochy, P.N.; Prete, G.; Vanzanella, A. Clustering effects in 48Cr composite nuclei produced via the 24Mg +24Mg reaction. Phys. Rev. C 2016, 93, 044602. [Google Scholar] [CrossRef]
  60. Di Nitto, A.; Vardaci, E.; Davide, F.; La Rana, G.; Ashaduzzaman, M.; Mercogliano, D.; Setaro, P.A.; Banerjee, T.; Vanzanella, A.; Bianco, D.; Cinausero, M.; Gelli, N.; Loffredo, F.; Quarto, M. Clustering effects in 36Ar nuclei produced via the 24Mg+12C reaction. Phys. Rev. C 2023, 107, 024615. [Google Scholar] [CrossRef]
  61. Moro, R.; Brondi, A.; Gelli, N.; Barbui, M.; Boiano, A.; Cinausero, M.; Di Nitto, A.; Fabris, D.; Fioretto, E.; La Rana, G.; Lucarelli, F.; Lunardon, M.; Montagnoli, G.; Ordine, A.; Prete, G.; Rizzi, V.; Trotta, M.; Vardaci, E. Compound nucleus evaporative decay as a probe for the isospin dependence of the level density. Eur. Phys. J. A 2012, 48, 159. [Google Scholar] [CrossRef]
  62. Mijatovic, T.; Szilner, S.; Corradi, L.; Montanari, D.; Courtin, S.; Fioretto, E.; Gadea, A.; Goasduff, A.; Haas, F.; Malenica, D.J.; Montagnoli, G.; Pollarolo, G.; Prepolec, L.; Scarlassara, F.; Soic, N.; Stefanini, A.; Tokic, V.; Ur, C.; Dobon, J.V. The pairing correlation study in the 40Ar +208Pb reaction. AIP Conference Proceedings 2015, 1681, 060012. [Google Scholar] [CrossRef]
  63. Mijatovic, T.; Szilner, S.; Corradi, L.; Montanari, D.; Pollarolo, G.; Fioretto, E.; Gadea, A.; Goasduff, A.; Malenica, D.J.; Marginean, N.; Milin, M.; Montagnoli, G.; Scarlassara, F.; Soic, N.; Stefanini, A.M.; Ur, C.; Valiente-Dobon, J. Multinucleon transfer reactions in the 40Ar +208Pb system. Phys. Rev. C 2016, 94, 064616. [Google Scholar] [CrossRef]
  64. Strobele, H.; Brockmann, R.; Harris, J.; Riess, F.; Sandoval, A.; Stock, R.; Wolf, K.; Pugh, H.; Schroeder, L.; Renfordt, R.; Tittel, K.; Maie, M. Charged-particle exclusive analysis of central Ar + KCl and Ar + Pb reactions at 1.8 and 0.8 GeV/nucleon. Phys. Rev. C 1983, 27, 1349. [Google Scholar] [CrossRef]
  65. Grabe, B. Phys. Rev. C 1992, 45, R5–R8. [CrossRef]
  66. Isaev, A.; Mukhin, R.; Andreev, A.; Bychkov, M.; Chelnokov, M.; Chepigin, V.; Devaraja, H.; Dorvaux, O.; Forge, M.; Gall, B.; Hauschild, K.; Izosimov, I.; Kessaci, K.; Kuznetsova, A.; Lopez-Martens, A.; Malyshev, O.; Popeko, A.; Popov, Y.; Rahmatinejad, A.; Sailaubekov, B.; Shneidman, T.; Sokol, E.; Svirikhin, A.; Testov, D.; Tezekbayeva, M.; Yeremin, A.; Zamyatin, N.; Zhumadilov, K. Prompt neutron emission in the spontaneous fission of 246Fm. Eur. Phys. J. A 2022, 58, 108. [Google Scholar] [CrossRef]
  67. Manjunatha, H.; Sowmya, N.; Sridhar, K.; Seenappa, L. A study of probable alpha-ternary fission fragments of 257Fm. J. Radioanal. Nucl. Chem. 2017, 314, 991–999. [Google Scholar] [CrossRef]
  68. Vijayaraghavan, K.; Lakshmi, V.G.; Prema, P.; Balasubramaniam, M. Equatorial, collinear trajectories in the ternary fission of Cf252 for various third fragments. J. Phys. G: Nucl. Part. Phys. 2019, 46, 025103. [Google Scholar] [CrossRef]
  69. Poenaru, D.; Gherghescu, R.; Greiner, W. Complex fission phenomena. Nucl. Phys. A 2005, 747, 182. [Google Scholar] [CrossRef]
  70. Degheidy, A.; Maruhn, J. Z. Phys. A 1979, 290, 205–2012. [CrossRef]
  71. Vardaci, E.; et al.. TOSCA:A Time-of-Flight sub-nanosecond Spectrometer for Charged radiation Applications. in preparation.
  72. Vardaci, E.; Pulcini, A.; Kozulin, E.M.; Matea, I.; Verney, D.; Maj, A.; Schmitt, C.; Itkis, I.M.; Knyazheva, G.N.; Novikov, K.; Kozulina, N.; Harca, I.M.; Kolesov, I.V.; Saveleva, K.; Kirakosyan, V.V.; Dorvaux, O.; Ciemala, M.; Brambilla, S.; Ashaduzzaman, M.; De Canditiis, B.; Di Nitto, A.; Quero, D.; Parascandolo, C.; Pierroutsakou, D.; Rath, P.K.; Sposito, G.; La Rana, G.; Bracco, A.; Camera, F.; Stezowski, O.; Borcea, C.; Calinescu, S.; Petrone, C.; Wilson, J. Using γ rays to disentangle fusion-fission and quasifission near the Coulomb barrier: A test of principle in the fusion-fission and quasielastic channels. Phys. Rev. C 2020, 101, 064612. [Google Scholar] [CrossRef]
  73. Agodi, C.; Cappuzzello, F.; Cardella, G.; Cirrone, G.A.P.; De Filippo, E.; Di Pietro, A.; Gargano, A.; La Cognata, M.; Mascali, D.; Milluzzo, G.; Nania, R.; Petringa, G.; Pidatella, A.; Pirrone, S.; Pizzone, R.G.; Rapisarda, G.G.; Sergi, M.L.; Tudisco, S.; Valiente-Dobón, J.J.; Vardaci, E.; Abramczyk, H.; Acosta, L.; Adsley, P.; Amaducci, S.; Banerjee, T.; Batani, D.; Bellone, J.; Bertulani, C.; Biri, S.; Bogachev, A.; Bonanno, A.; Bonasera, A.; Borcea, C.; Borghesi, M.; Bortolussi, S.; Boscolo, D.; Brischetto, G.A.; Burrello, S.; Busso, M.; Calabrese, S.; Calinescu, S.; Calvo, D.; Capirossi, V.; Carbone, D.; Cardinali, A.; Casini, G.; Catalano, R.; Cavallaro, M.; Ceccuzzi, S.; Celona, L.; Cherubini, S.; Chieffi, A.; Ciraldo, I.; Ciullo, G.; Colonna, M.; Cosentino, L.; Cuttone, G.; D’Agata, G.; De Gregorio, G.; Degl’Innocenti, S.; Delaunay, F.; Di Donato, L.; Di Nitto, A.; Dickel, T.; Doria, D.; Ducret, J.E.; Durante, M.; Esposito, J.; Farrokhi, F.; Fernandez Garcia, J.P.; Figuera, P.; Fisichella, M.; Fulop, Z.; Galatá, A.; Galaviz Redondo, D.; Gambacurta, D.; Gammino, S.; Geraci, E.; Gizzi, L.; Gnoffo, B.; Groppi, F.; Guardo, G.L.; Guarrera, M.; Hayakawa, S.; Horst, F.; Hou, S.Q.; Jarota, A.; José, J.; Kar, S.; Karpov, A.; Kierzkowska-Pawlak, H.; Kiss, G.G.; Knyazheva, G.; Koivisto, H.; Koop, B.; Kozulin, E.; Kumar, D.; Kurmanova, A.; La Rana, G.; Labate, L.; Lamia, L.; Lanza, E.G.; Lay, J.A.; Lattuada, D.; Lenske, H.; Limongi, M.; Lipoglavsek, M.; Lombardo, I.; Mairani, A.; Manetti, S.; Marafini, M.; Marcucci, L.; Margarone, D.; Martorana, N.S.; Maunoury, L.; Mauro, G.S.; Mazzaglia, M.; Mein, S.; Mengoni, A.; Milin, M.; Mishra, B.; Mou, L.; Mrazek, J.; Nadtochy, P.; Naselli, E.; Nicolai, P.; Novikov, K.; Oliva, A.A.; Pagano, A.; Pagano, E.V.; Palmerini, S.; Papa, M.; Parodi, K.; Patera, V.; Pellumaj, J.; Petrone, C.; Piantelli, S.; Pierroutsakou, D.; Pinna, F.; Politi, G.; Postuma, I.; Prajapati, P. Prada Moroni, P.G.; Pupillo, G.v Raffestin, D.; Racz, R.; Reidel, C.A.; Rifuggiato, D.; Risitano, F.; Rizzo, F.; Roca Maza, X.; Romano, S.; Roso, L.; Rotaru, F.; Russo, A.D.; Russotto, P.; Saiko, V.; Santonocito, D.; Santopinto, E.; Sarri, G.; Sartirana, D.; Schuy, C.; Sgouros, O.; Simonucci, S.; Sorbello, G.; Soukeras, V.; Spartá, R.; Spatafora, A.; Stanoiu, M.; Taioli, S.; Tessonnier, T.; Thirolf, P.; Tognelli, E.; Torresi, D.; Torrisi, G.; Trache, L.; Traini, G.; Trimarchi, M.; Tsikata, S.; Tumino, A.; Tyczkowski, J.; Yamaguchi, H.; Vercesi, V.; Vidana, I.; Volpe, L.; Weber, U. Nuclear physics midterm plan at LNS. The European Physical Journal Plus 2023, 138, 1038. [Google Scholar] [CrossRef]
  74. Iyer, R.; Cobble, J. Ternary Fission of U 238 Induced by Intermediate-Energy Helium Ions. Physical Review 1968, 172, 1186. [Google Scholar] [CrossRef]
  75. Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; Behner, F.; Bellagamba, L.; Boudreau, J.; Broglia, L.; Brunengo, A.; Burkhardt, H.; Chauvie, S.; Chuma, J.; Chytracek, R.; Cooperman, G.; Cosmo, G.; Degtyarenko, P.; Dell’Acqua, A.; Depaola, G.; Dietrich, D.; Enami, R.; Feliciello, A.; Ferguson, C.; Fesefeldt, H.; Folger, G.; Foppiano, F.; Forti, A.; Garelli, S.; Giani, S.; Giannitrapani, R.; Gibin, D.; Gómez Cadenas, J.; González, I.; Gracia Abril, G.; Greeniaus, G.; Greiner, W.; Grichine, V.; Grossheim, A.; Guatelli, S.; Gumplinger, P.; Hamatsu, R.; Hashimoto, K.; Hasui, H.; Heikkinen, A.; Howard, A.; Ivanchenko, V.; Johnson, A.; Jones, F.; Kallenbach, J.; Kanaya, N.; Kawabata, M.; Kawabata, Y.; Kawaguti, M.; Kelner, S.; Kent, P.; Kimura, A.; Kodama, T.; Kokoulin, R.; Kossov, M.; Kurashige, H.; Lamanna, E.; Lampén, T.; Lara, V.; Lefebure, V.; Lei, F.; Liendl, M.; Lockman, W.; Longo, F.; Magni, S.; Maire, M.; Medernach, E.; Minamimoto, K.; Mora de Freitas, P.; Morita, Y.; Murakami, K.; Nagamatu, M.; Nartallo, R.; Nieminen, P.; Nishimura, T.; Ohtsubo, K.; Okamura, M.; O’Neale, S.; Oohata, Y.; Paech, K.; Perl, J.; Pfeiffer, A.; Pia, M.; Ranjard, F.; Rybin, A.; Sadilov, S.; Di Salvo, E.; Santin, G.; Sasaki, T.; Savvas, N.; Sawada, Y.; Scherer, S.; Sei, S.; Sirotenko, V.; Smith, D.; Starkov, N.; Stoecker, H.; Sulkimo, J.; Takahata, M.; Tanaka, S.; Tcherniaev, E.; Safai Tehrani, E.; Tropeano, M.; Truscott, P.; Uno, H.; Urban, L.; Urban, P.; Verderi, M.; Walkden, A.; Wander, W.; Weber, H.; Wellisch, J.; Wenaus, T.; Williams, D.; Wright, D.; Yamada, T.; Yoshida, H.; Zschiesche, D. Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2003, 506, 250–303. [Google Scholar] [CrossRef]
  76. Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; Beck, B.; Bogdanov, A.; Brandt, D.; Brown, J.; Burkhardt, H.; Canal, P.; Cano-Ott, D.; Chauvie, S.; Cho, K.; Cirrone, G.; Cooperman, G.; Cortés-Giraldo, M.; Cosmo, G.; Cuttone, G.; Depaola, G.; Desorgher, L.; Dong, X.; Dotti, A.; Elvira, V.; Folger, G.; Francis, Z.; Galoyan, A.; Garnier, L.; Gayer, M.; Genser, K.; Grichine, V.; Guatelli, S.; Guèye, P.; Gumplinger, P.; Howard, A.; Hřivnáčová, I.; Hwang, S.; Incerti, S.; Ivanchenko, A.; Ivanchenko, V.; Jones, F.; Jun, S.; Kaitaniemi, P.; Karakatsanis, N.; Karamitros, M.; Kelsey, M.; Kimura, A.; Koi, T.; Kurashige, H.; Lechner, A.; Lee, S.; Longo, F.; Maire, M.; Mancusi, D.; Mantero, A.; Mendoza, E.; Morgan, B.; Murakami, K.; Nikitina, T.; Pandola, L.; Paprocki, P.; Perl, J.; Petrović, I.; Pia, M.; Pokorski, W.; Quesada, J.; Raine, M.; Reis, M.; Ribon, A.; Ristić Fira, A.; Romano, F.; Russo, G.; Santin, G.; Sasaki, T.; Sawkey, D.; Shin, J.; Strakovsky, I.; Taborda, A.; Tanaka, S.; Tomé, B.; Toshito, T.; Tran, H.; Truscott, P.; Urban, L.; Uzhinsky, V.; Verbeke, J.; Verderi, M.; Wendt, B.; Wenzel, H.; Wright, D.; Wright, D.; Yamashita, T.; Yarba, J.; Yoshida, H. Recent developments in Geant4. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2016, 835, 186–225. [Google Scholar] [CrossRef]
  77. Bass, R.; Czarnecki, J.; Zitzmann, R. Nuclear Instruments and Methods, 1975; 130, 125–133. [CrossRef]
  78. Cetnar, J.; Stanisz, P.; Oettingen, M. Linear Chain Method for Numerical Modelling of Burnup Systems. Energies 2021, 14, 1520. [Google Scholar] [CrossRef]
  79. Stanisz, P.; Oettingen, M.; Cetnar, J. Development of a Trajectory Period Folding Method for Burnup Calculations. Energies 2022, 15, 2245. [Google Scholar] [CrossRef]
Preprints 118445 g001
Figure 1. In-plane kinematic plots of direct ternary fission (DTF-top) and sequential ternary fission(STF - bottom). In the DTF a simultaneous formation of the A 1 , A 2 and A 3 fragments occurs. In STF the first binary scission produces the A 1 and A 23 fragments, the subsequent binary scission of the A 23 fragment produces the final products A 2 and A 3 .
Figure 1. In-plane kinematic plots of direct ternary fission (DTF-top) and sequential ternary fission(STF - bottom). In the DTF a simultaneous formation of the A 1 , A 2 and A 3 fragments occurs. In STF the first binary scission produces the A 1 and A 23 fragments, the subsequent binary scission of the A 23 fragment produces the final products A 2 and A 3 .
Preprints 118445 g001
Preprints 118445 g002
Figure 2. Dalitz plot of the potential energies for collinear (a) and equatorial (b) ternary fragmentations of 248Fm (Z=100). The potential energies are calculated as a function of the charge numbers with the constraint for the fragment masses A 1 ≥ A 2 ≥ A 3 .
Figure 2. Dalitz plot of the potential energies for collinear (a) and equatorial (b) ternary fragmentations of 248Fm (Z=100). The potential energies are calculated as a function of the charge numbers with the constraint for the fragment masses A 1 ≥ A 2 ≥ A 3 .
Preprints 118445 g002
Preprints 118445 g003
Figure 3. Potential Energy of a ternary fragmentation involving two out of three double magic nuclei in collinear and equatorial configurations.
Figure 3. Potential Energy of a ternary fragmentation involving two out of three double magic nuclei in collinear and equatorial configurations.
Preprints 118445 g003
Preprints 118445 g004
Figure 4. Kinetic energies of light fragments E 3 presented as a function of E 1 and E 2 by assuming DTF (a) and STF (b) mechanisms. The calculations have been performed with the conditions: A 1 ≥ A 2 ≥ A 3 , emission of A 1 and A 2 on the opposite side with respect to the beam direction and wide range for the A 1 energies. See the text for more details.
Figure 4. Kinetic energies of light fragments E 3 presented as a function of E 1 and E 2 by assuming DTF (a) and STF (b) mechanisms. The calculations have been performed with the conditions: A 1 ≥ A 2 ≥ A 3 , emission of A 1 and A 2 on the opposite side with respect to the beam direction and wide range for the A 1 energies. See the text for more details.
Preprints 118445 g004
Preprints 118445 g005
Figure 5. Emission angles of light fragment θ 3 as a function of the heavy ( θ 1 ) and medium ( θ 2 ) mass angles in the laboratory system calculated considering the DTF (a) and STF (b) mechanisms. In the calculations A 1 ≥ A 2 ≥ A 3 and two of the three fragments are doubly magic nuclei. See the text for more details.
Figure 5. Emission angles of light fragment θ 3 as a function of the heavy ( θ 1 ) and medium ( θ 2 ) mass angles in the laboratory system calculated considering the DTF (a) and STF (b) mechanisms. In the calculations A 1 ≥ A 2 ≥ A 3 and two of the three fragments are doubly magic nuclei. See the text for more details.
Preprints 118445 g005
Preprints 118445 g006
Figure 6. Kinetic energies of the product of 132 Sn + 68 Zn + 48 Ca tripartition. The products of the DTF and STF mechanisms are shown in the left and right panels, respectively.
Figure 6. Kinetic energies of the product of 132 Sn + 68 Zn + 48 Ca tripartition. The products of the DTF and STF mechanisms are shown in the left and right panels, respectively.
Preprints 118445 g006
Preprints 118445 g007
Figure 7. Angular correlations of the 132 Sn + 68 Zn + 48 Ca tripartition. The DTF (blue) and STF (pink) angular correlations θ 2 vs θ 3 are presented for the a fixed heavy fragment angle θ 1 reported in the top of each panel.
Figure 7. Angular correlations of the 132 Sn + 68 Zn + 48 Ca tripartition. The DTF (blue) and STF (pink) angular correlations θ 2 vs θ 3 are presented for the a fixed heavy fragment angle θ 1 reported in the top of each panel.
Preprints 118445 g007
Preprints 118445 g008
Figure 8. DTF angular correlations of the 132 Sn + 68 Zn + 48 Ca tripartition for θ 2 =- θ 1 .
Figure 8. DTF angular correlations of the 132 Sn + 68 Zn + 48 Ca tripartition for θ 2 =- θ 1 .
Preprints 118445 g008
Preprints 118445 g009
Figure 9. Energies of 68Zn and 48Ca. Different emission angles ( θ 1 ) of 132Sn in DTF (blue) and STF (red) for the 132 Sn + 68 Zn + 48 Ca fragmentation have been considered.
Figure 9. Energies of 68Zn and 48Ca. Different emission angles ( θ 1 ) of 132Sn in DTF (blue) and STF (red) for the 132 Sn + 68 Zn + 48 Ca fragmentation have been considered.
Preprints 118445 g009
Preprints 118445 g010
Figure 10. Energies and angles of the light fragments from the 132 Sn + 68 Zn + 48 Ca tripartition. Under the condition of angle symmetric emission of the medium and heavy fragment at θ 1 = − θ 2 = − 70 ∘ , in panels (a) and (b) are shown the angular and energy distributions of the 48Ca fragments, while in panel (c) it is shown the angle vs. energy correlations assuming both DTF (black) and STF (pink) processes. For details on energy, angular intervals and steps considered in calculations see the text.
Figure 10. Energies and angles of the light fragments from the 132 Sn + 68 Zn + 48 Ca tripartition. Under the condition of angle symmetric emission of the medium and heavy fragment at θ 1 = − θ 2 = − 70 ∘ , in panels (a) and (b) are shown the angular and energy distributions of the 48Ca fragments, while in panel (c) it is shown the angle vs. energy correlations assuming both DTF (black) and STF (pink) processes. For details on energy, angular intervals and steps considered in calculations see the text.
Preprints 118445 g010
Preprints 118445 g011
Figure 11. Angular correlations of BF events. The distributions of fragment 2 ( θ 2 ) vs fragment 1 ( θ 1 ) for symmetric (blue line) and asymmetric fission (orange line). The green boxes represent the two angular ranges covered by the detection setup proposed in Sec. 2.4.
Figure 11. Angular correlations of BF events. The distributions of fragment 2 ( θ 2 ) vs fragment 1 ( θ 1 ) for symmetric (blue line) and asymmetric fission (orange line). The green boxes represent the two angular ranges covered by the detection setup proposed in Sec. 2.4.
Preprints 118445 g011
Preprints 118445 g012
Figure 12. Schematic draw of the detection apparatus consisting of three different detector types. The blue line superimposed to the z axis (blue arrow) identifies the beam direction. See the text for more details.
Figure 12. Schematic draw of the detection apparatus consisting of three different detector types. The blue line superimposed to the z axis (blue arrow) identifies the beam direction. See the text for more details.
Preprints 118445 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated