Prerpints.org logo
Preprint
Article

Enhancement of the Elastocaloric Performance of Natural Rubber by Forced Air Convection

Altmetrics

Downloads

106

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts
Abstract
We study the enhancement of the elastocaloric effect in natural rubber by using forced air convection in order to favour heat extraction during the elongation stage of an stretching-unstretching cycle. Elastocaloric performance is quantified by means of the adiabatic undercooling that occurs after a fast removal of the stress, measured by infrared thermography. To ensure accurate measurements, spatial averages on thermal maps of the sample surface are performed since undercooled samples display heterogeneities caused by various factors. The influence of the stretching velocity and the air velocity is analysed. The results show that, given the fact that the stretching velocities should be high enough to improve the cooling power, there is an optimal air velocity that provides maximum adiabatic undercooling. Our experiments have also allowed us to characterise the dependence of the Newton heat transfer coefficient on the air convection velocity. We have shown that this coefficient may show an enhancement up to 600% for air velocities around 4 m/s.
Keywords: 
Subject: Physical Sciences  -   Thermodynamics

1. Introduction

Many current efforts to develop environmentally friendly refrigeration are based on the elastocaloric effect in solids [1]. Very recently, there have been promising developments in prototypes using shape memory alloys and a regenerative technique, which feature very large cooling powers and outstanding temperature spans above 50°C [2,3,4]. While these cooling performances largely overcome those reported for any other solid-state caloric technique [3], they require the application of large stresses which are challenging to achieve. By contrast, natural rubber (NR) has been found to exhibit giant elastocaloric effects at very low applied stress by virtue of its strain-induced crystallisation transition [5,6,7,8,9], which makes this material an excellent candidate for high-efficiency elastocaloric devices. When the polymeric chains are stretched, they show a collective behaviour that favours their arrangement into small regions of crystallites with entropy significantly lower than that of their disordered and unstretched state. When stress is suddenly (adiabatically) released from the crystallised state, the increase in entropy associated with the reverse transition (amorphisation) results in a large sample undercooling.
Adiabatic temperature changes below − 10 K have been reported when stress is released on a previously stretched sample under uniaxial forces at room temperature. Moreover, when the samples are stressed by both uniaxial forces and twisting, maximum undercooling ranging from − 12 K to − 68 K has been claimed [10,11].
The development of NR-based elastocaloric refrigerators [12,13,14] faces various challenges. The main ones are due to the low thermal conductivity of NR to the hot and cold reservoirs, which constrains the high-frequency operation of a cooling cycle. In a simple cyclic refrigerator, the environment (air or water at room temperature) functions as a hot reservoir, and heat is extracted from the NR refrigerant to the environment after adiabatically or isothermally stretching. Ideally, the low-entropy crystallised state is maximised when elongated at room temperature. When the process is reversed, stress is released adiabatically, and the cold reservoir below room temperature draws heat from the NR sample. This allows the refrigerant to return to its original amorphous state at room temperature and start the cycle again. Recently, a comparison between samples of different thicknesses evidenced that the slow heat transfer between rubber and air during natural convection delays the kinetics of strain-induced crystallisation [15], which might have a big impact on the elastocaloric performance of future refrigeration devices.
Heat transfer from NR to air was studied 25 years ago [16,17] using unstressed hot cylindrical samples. Assuming a Newtonian behaviour, the authors considered a linear relation
d Q d t = − h A Δ T
where Δ T is the temperature difference between air and rubber, d Q / d t is the rate of heat loss, A is the sample surface and h is the heat transfer coefficient. The transient evolution of the temperature in the centre of the sample during cooling to air was compared to finite element simulations. The most accurate comparison yielded h ≃   17.4 W m−2 K−1. To our knowledge, there is no available data on heat transport coefficients for samples that have been heated or cooled by internal elastocaloric effects and/or forced air convection.
In this work, we examine the heat extraction from NR during the stretching stage of the cycle when in contact with air at room temperature. We conduct a comparative analysis of natural and forced convection and also delve into the impact of stretching velocity. Our end goal is to enhance the elastocaloric effect, measured as the adiabatic undercooling that occurs following a fast stress release from the elongated crystallised phase.
The paper is organised as follows: in Section 2, we describe the experimental details. In Section 3, we report the effect of the stretching velocity and the air convection velocity on the elastocaloric undercooling as well as the values determined for the Newtonian heat transfer coefficients under different convection conditions. We summarise and conclude in Section 4.

2. Materials and Methods

2.1. Sample

The natural rubber of this study is an SMR (Standard Malaysian Rubber) CV60 (Mooney Viscosity ML 1 + 4, 100 °C: 55–60), supplied by the company Akrochem (USA), with 0.15% of hydroxylamine added to the latex stage to prevent the raw rubber stiffening while storing. The NR was masticated inside the chamber of an internal mixer (Brabender Plastic-Corder W50EHT, Brabender GmbH & Co., Germany) at a temperature of 80 °C for 5 min and a rotation speed of 40 rpm. After 10 minutes, the vulcanising agent dicumyl peroxide (DCP) was added (1.5 wt% of the NR) and mixed for 5 min. The masterbatch containing NR and DCP was vulcanised according to the estimated optimal time at 170 °C [18] under 4 MPa. In order to perform the elastocaloric test, flat dogbone-shaped specimens were extracted from hot-moulded sheets by die-cutting with a specimen preparation punching machine (CEAST). The dimensions of the parallelepipedic sample neck, where crystallisation concentrates, are: a = 15   mm , length; b = 4   mm , width; and c = 1   mm thickness.

2.2. Experimental Setup

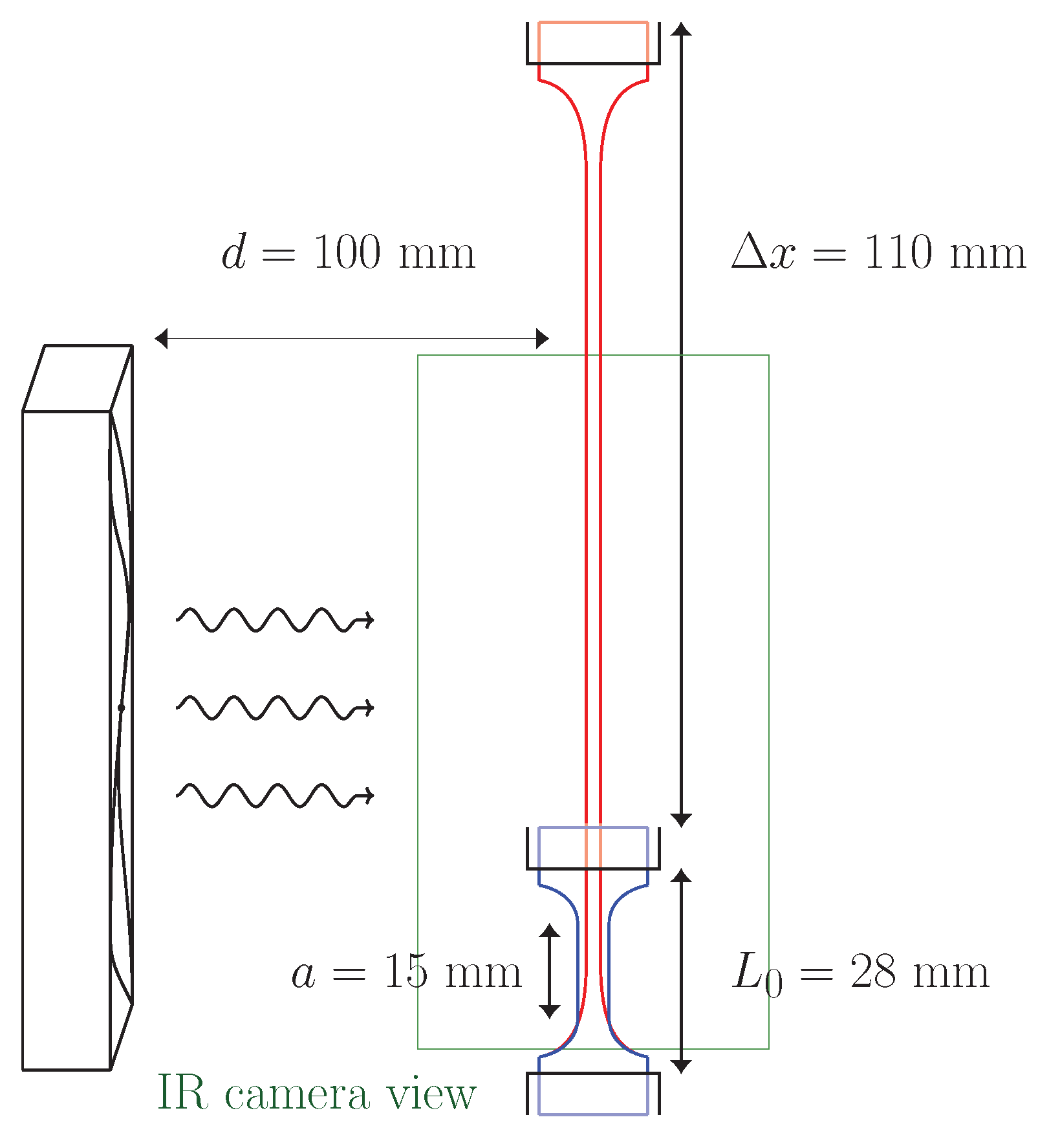
Stretching-unstretching experiments were carried out using a Zwick/Roell Z005 materials testing machine equipped with a 500 N load cell and an optical extensometer. Stretching protocols were performed with displacement control, and data was recorded at 10 samples/s. Figure 1 shows a schematic representation of the setup.
To capture thermal maps of the central and bottom parts of the sample surface, an Infratec 8800 infrared camera framing at a rate of 25Hz was used. For the 250x512 pixel maps, the framing frequency was restricted to 5Hz. The force and displacement data from the materials testing machine was transferred to the IR camera software (IRBIS 3 Professional) for synchronisation. The camera lens was placed at 650 mm from the sample surface. The spatial resolution of the maps was 5.12 pixels/mm. The entire experiment was surrounded by a polystyrene cage to prevent external infrared radiation reflections. Ambient temperature was approximately constant at T 0 = 22 ± 1 °C.
For forced convection experiments, a 24 V brushless DC fan (Orion, OD9238-24HBVXC) was placed at a distance of 100 mm from the sample axis. Forced airflow was parallel to the 4 mm× 15 mm flat faces of the sample. The fan diameter was 90 mm, and its centre was at 45 mm from the sample base.
The fan was calibrated in a separate blank experiment by changing the applied voltage in the range 5 V − 20 V and measuring the air speed v air at the position of the centre of the sample using an anemometer. For this range of voltages, airspeed was in the range 0 − 5 m /s.
The sample was attached to the testing machine using steel grips. Prior to any experiment, the sample was always subjected to 5 conditioning cycles that imposed a grip-to-grip elongation of Δ x = 110   mm . After the conditioning protocol, the initial position of the grips for subsequent experiments was modified to have a zero force reading ( | F | ≲ 0.01   N ), resulting in an initial grip-to-grip length of L 0 ≃ 28   mm .

2.3. Elastocaloric Cycling Protocol

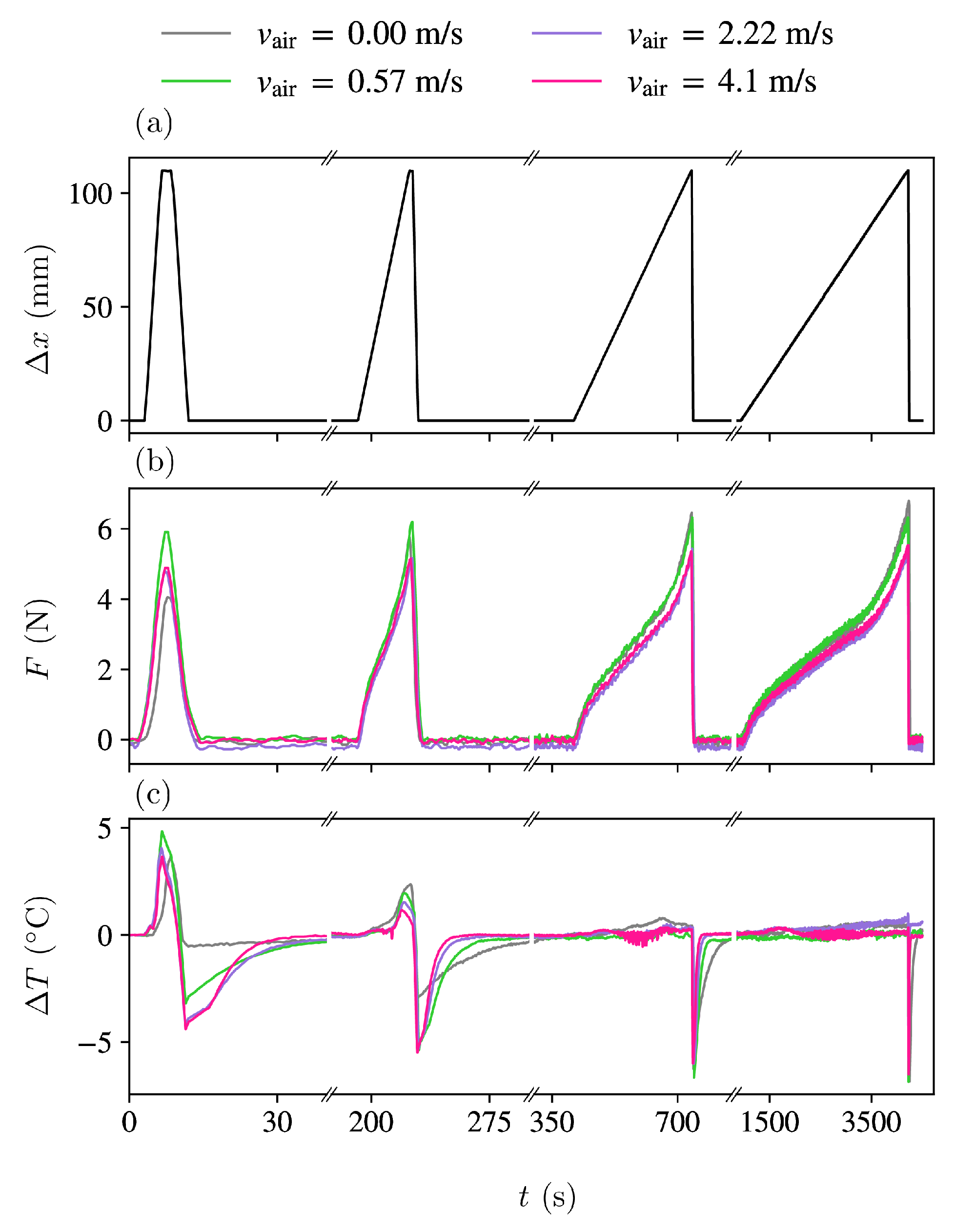
Figure 2 (a) illustrates the stretching protocols, wherein a lengthening of Δ x = 110   mm is imposed at varying velocities. The experiment involved four rounds of stretching-unstretching cycles, each one with a brief 2-second pause. A long thermalisation pause of 1800 seconds was implemented between each cycle. The elongation ramps were carried out at stretching velocities of v = 2000 , 200, 20 and 2 mm/min, respectively, and the unstretching ramps were always at high speed (2000 mm/min). During forced convection measurements, the fan was operated solely during the stretching process and was turned off at the beginning of the brief two-second pause prior to rapid unstretching. The goal was to minimise heat exchange during the unstretching process, resulting in maximum undercooling from enhanced adiabatic conditions.
The stretching ratio in the centre of the dogbone samples was λ = 5.2 for elongations of Δ x = 110   mm , as determined independently in a separate experiment by tracking paint marks (separated 13 mm) with the optical extensometer. It should be noted that this value differs from the commonly used total stretching ratio λ total = a + Δ x a = 8.33 , which is computed assuming that only the neck of the dogbone sample is elongating. The difference in these two values evidences that the heads of the sample contribute significantly to the total elongation. In the following, we will use λ = 5.2 .
In Figure 2(b), the measured force is plotted against time for various scenarios at selected loading velocities v and air velocities v a i r . It is evident that the force required to reach the elongated state varies as a function of both parameters v and v a i r .

2.4. Sample Temperature Determination

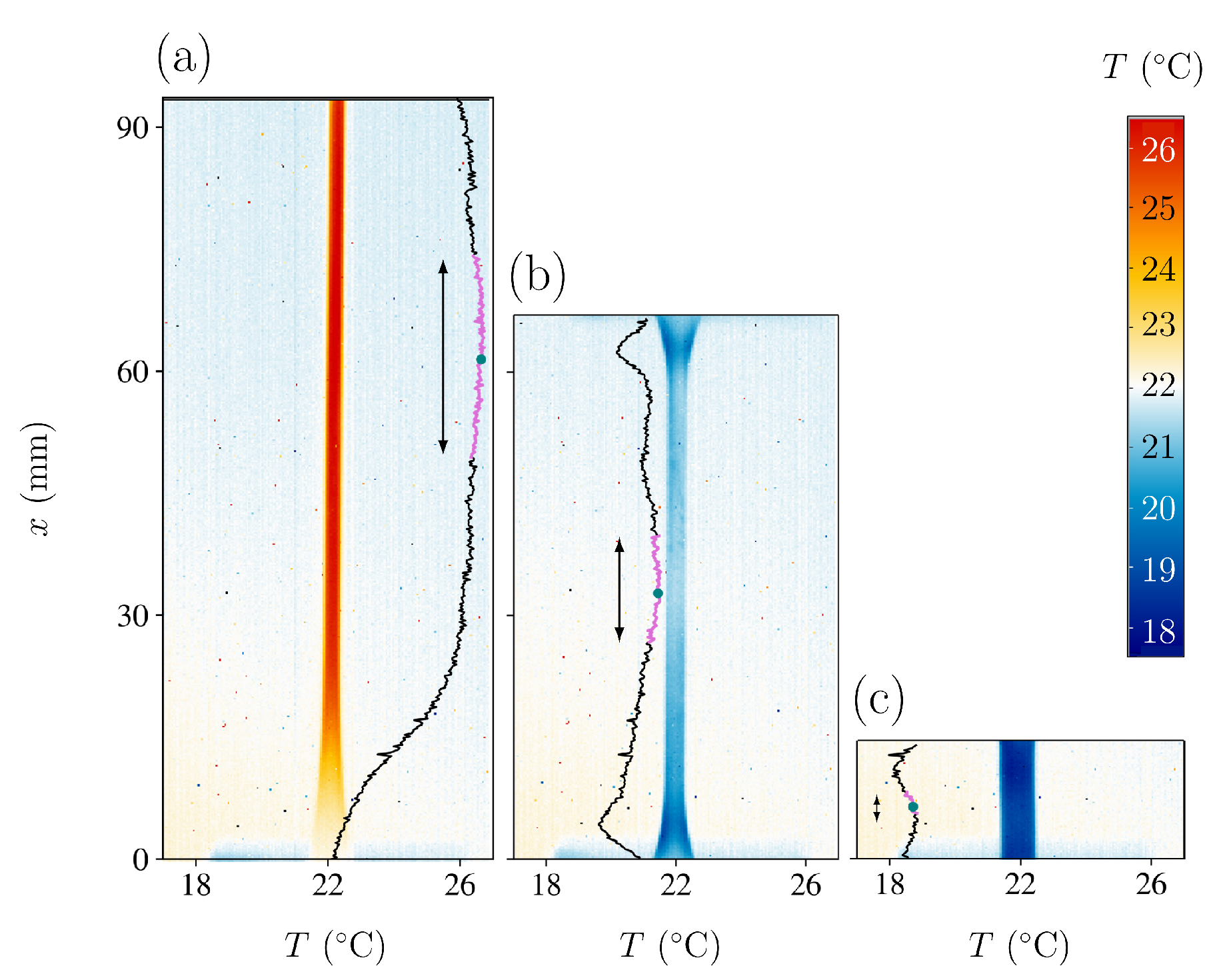
Figure 3 shows three examples of temperature maps of the sample at v a i r = 0.57 m / s and v = 2000   mm / min . Panel 3(a) displays the sample at an instant right after the stretching stage. The sample temperature is above room temperature due to the latent heat release during crystallisation. Panel 3(b) corresponds to an intermediate frame during the fast unstretching stage, and panel 3(c) corresponds to the final frame after total stress removal. In the latter case, the sample is several degrees below room temperature due to the heat absorption in the amorphisation transition. Notice that in Figure 3(a) the sample cannot be imaged at full length due to the limited field of view of the camera. However, the central region is always within the frame.
The black vertical curves indicate the temperature along the central vertical axis of the sample. The values can be read on the horizontal bottom axis. As can be seen, the sample temperature is heterogeneous, with regions that display undercooling variations of more than 2°C and temperature gradients larger than 0.5°C/mm.
These temperature heterogeneities observed immediately after the unstretching stage may result from stress heterogeneities within the stretched sample that affect locally the crystallisation degree. These in turn might be caused by differences in sample width, heterogeneities in sample composition, heat conduction towards the grips, heterogeneities in the air convection, etc. Even in the case that convection is natural (without a fan), the displacement of the sample points in the upper part of the sample is faster than the displacement of the sample points in the lower part. Furthermore, when the experiment is performed with forced convection (fan switched on), the airflow can also be inhomogeneous, depending on the fan speed.
For these reasons, to ensure an accurate measurement of the elastocaloric effect, we have characterised the sample temperature T by considering an average of the central part of the neck with a length of 20% of its total length. For every snapshot in Figure 3, we have indicated the central point (green dot) and the averaged segment in magenta. This protocol might give lower undercooling values than other estimations reported in the literature that might have characterised the elastocaloric effect by measuring undercooling at the point with the lowest temperature. In particular, it can be noted that close to the ends of the sample, there are regions displaying larger undercooling than the averaged central region.
A second possible source of errors in determining the sample temperature could be due to the change in the roughness of the NR surface when comparing the stretched and unstretched samples. The influence of roughness in emissivity is a well-studied effect in the literature [19,20]. To estimate the temperature variations of this effect, we measured the sample temperature in the two states (stretched and unstretched) after long waiting times at room temperatures. The temperature readings were consistent within a margin of ± 0.3 K, which is comparable to the estimated room temperature fluctuations.
Figure 2(c) shows the difference between the average sample temperature and the room temperature corresponding to each study case. Note that for low values of v and high values of v a i r , the sample temperature remains nearly constant throughout the whole loading step, thus approaching an isothermal stretching protocol. On the contrary, for high stretching velocity v and v a i r = 0 (natural convection), the process is close to adiabaticity, and the sample shows high overheating during the loading step. In all cases, the high velocity of the unstretching step in the absence of forced air convection yields large undercooling.

3. Results and Discussion

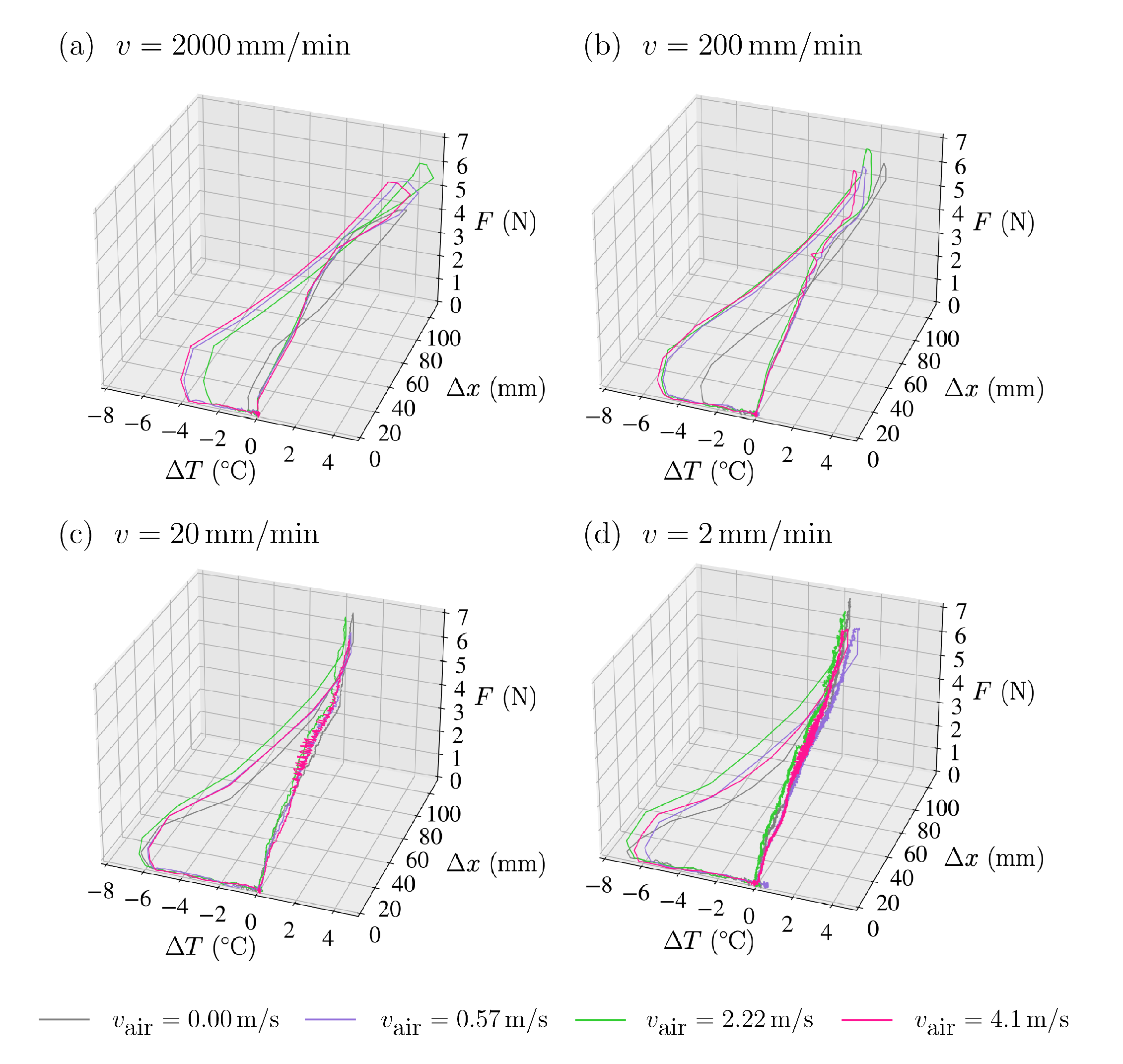
Given the out-of-equilibrium behaviour of rubber, the elastocaloric effect is better described by a three-dimensional trajectory in the F − Δ x − Δ T diagram. The various analysed scenarios are depicted in Figure 4. Each plot corresponds to a different stretching velocity: (a) v = 2000   mm / min , (b) v = 200   mm / min , (c) v = 20   mm / min and (d) v = 2   mm / min .
The cycles start at Δ T = T − T 0 = 0 and show an increasing F vs Δ x trajectory. Trajectories display a clear shift to high temperatures when stretched rapidly (a and b), which diminishes as v a i r increases. The overheating occurs approximately in the second half of the trajectory, which signals the region of large deformations where crystallisation occurs. In contrast, the trajectory remains rather isothermal regardless of the air velocity for the slow stretching cases (c and d).
Regarding the undercooling steps, which occur at a fast rate in the absence of forced convection, a significant undercooling is noticed by the trajectories moving towards the left side of the graphs. Higher levels of undercooling, reaching almost Δ T u n s t r = − 8 ∘ C, are attained when the sample is subjected to slow stretching and prolonged exposure to large deformations, which favours crystallisation.
It is worth noting that for the fastest stretching experiments in which the sample remained in a deformed state for shorter periods (panel (a) in Figure 4), increasing v a i r values rendered a deeper undercooling. In this regard, magenta and violet lines show undercooling of Δ T u n s t r ∼ -6°C, clearly more negative than the green and black lines. This is indicative that increasing heat extraction during fast stretching favours crystallisation.

3.1. Elastocaloric Adiabatic Undercooling

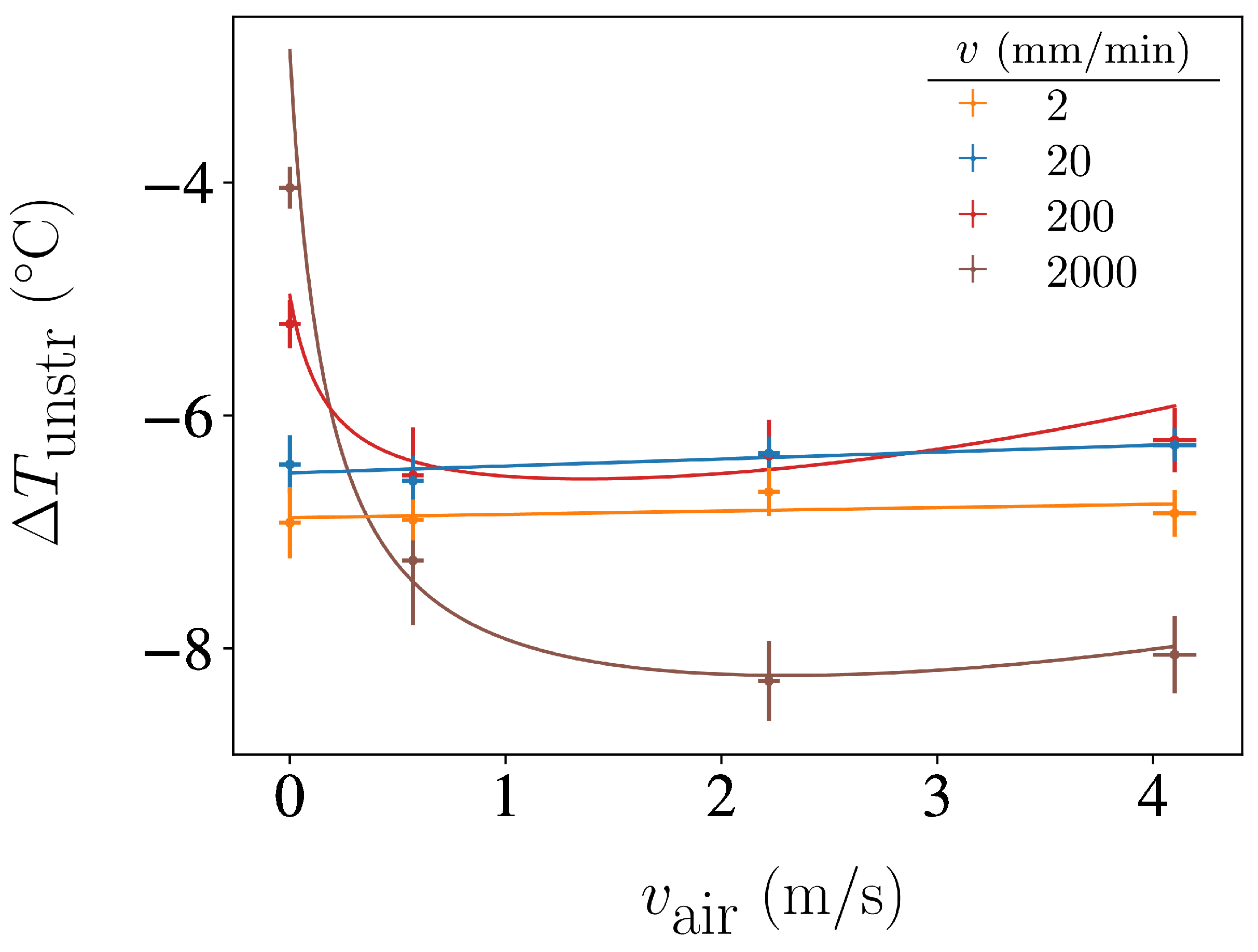
To better understand the effect of forced convection during the stretching stage, in Figure 5 we have compiled the values of the maximum undercooling values Δ T u n s t r as a function of the air velocity v a i r for each stretching velocity v. As can be observed, forced convection enhances undercooling in the case of fast stretching experiments, while it has nearly negligible influence in the case of slow stretching experiments. This suggests that when rubber is stretched fast, there is competition between heat release and crystallisation growth. In the presence of this competition, forced convection can promote crystallisation. However, if the stretching process is sufficiently slow, heat extraction no longer limits crystallisation.
The reason why the curves for high stretching velocities display a minimum is unclear. One possible explanation for why the highest v a i r values result in decreased undercooling is that turbulent airflow can negatively impact forced convection heat extraction efficiency.
The observed Δ T u n s t r undercooling values range from -8°C to -6°C, which are slightly lower compared to those found in the literature for similar stretching ratios in natural rubber (such as -9°C in Ref. [7]). This might be due to the fact that we report a surface average rather than the temperature of the coolest region of the sample.

3.2. Newton Heat Transfer Coefficient

To quantitatively model the effect of air convection on the dissipation of internally generated heat at the crystallisation transition, we conducted experiments maintaining constant air velocity for a prolonged period after stretching or unstretching. Temperature evolution during these periods was analysed to derive the Newton heat transfer coefficient in each case.
Assuming that losses to air are the main source of thermal changes during such pauses at constant elongation, one can integrate Eq. 1 to obtain an exponential time evolution for the temperature
T ( t ) = T 0 − ( T 0 − T i ) · e − t / τ ,
where T 0 is the ambient temperature, T i is the initial temperature immediately following either stretching or unstretching, and t is the time elapsed since the pause has begun. The time constant τ that can be fitted from the experimental data, is given by
τ = ρ N R C N R l c h ,
where ρ N R is the density of NR, C N R is the specific heat capacity of NR and l c = V / A is a characteristic length that measures the sample volume V to area A ratio.
Note that since volume changes of NR under stretching are very small l c = λ − 1 / 2 · V 0 / A 0 , where V 0 / A 0 = b c 2 ( b + c ) is the volume to area ratio of the unstretched sample. Hence, stretching favours the effect of convection since it decreases l c . This is an advantage of using convection as a heat exchange mechanism in the stretched sample after crystallisation.
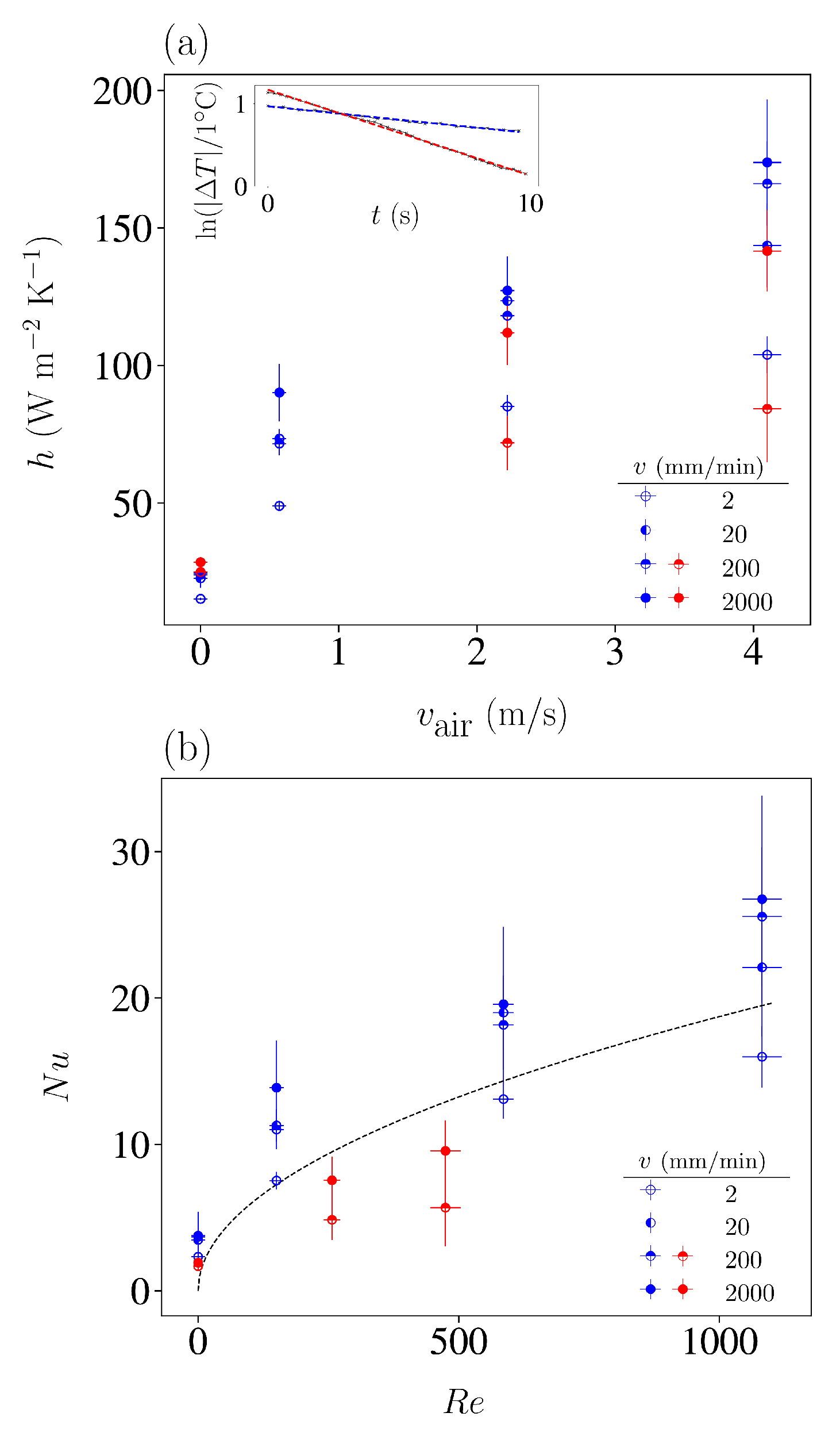
The main panel of Figure 6(a) compiles the obtained values of h as a function of air velocity. Values indicated with red symbols correspond to long pauses with constant air velocity after stretching at velocity v. Blue symbols correspond to experiments in which the sample was stretched at selected stretching velocities and subsequently unstretched to different undercooled states. To calculate the value of h based on the fitted values of τ we have used C N R = 1880 J / ( k g K ) [21], ρ N R = 950 k g / m 3 (as determined in our lab), and l c = λ − 1 V 0 / A 0 = 1.75 × 10 − 4 m for the stretched sample and l c = V 0 / A 0 = 4 × 10 − 4 m for the unstretched samples.
Examples of the experimental fits of the exponential decay in Eq. 2 are shown in the inset of Figure 6. They correspond to the thermal equilibration during long pauses without air convection ( v a i r = 0 ) in two cases: the red curve corresponds to an experiment in which the sample heats up after loading at v = 2000 mm/min, and the blue curve to an experiment in which the sample first heats up loading at v = 2000 mm/min and is subsequently unstretched at an undercooled state. Although the uncertainties in the fit of these exponential decays are small, we have considered also the uncertainites in the determination of T 0 in order to estimate the error bars in h. Note that the different cases correspond to fits in which the initial states have different temperatures T i as a consequence of the internal elastocaloric heating or cooling.
An increase in air velocity consistently results in a significant rise in the coefficient h. For v a i r > 4 m/s, the gain in h is typically larger than 100% in comparison to the scenarios without forced air convection, and for v a i r = 4 m/s they top values of 600%.
Figure 6(b) displays the same data using the standard definitions of the adimensional Nusselt number and Reynolds number
N u = h w κ a i r , R e = v a i r w μ a i r ,
where κ a i r = 2.7 × 10 − 2 W m−1 K−1 is the air thermal conductivity, μ a i r = 1.516 × 10 − 5 m2/s is the air kinematic viscosity, and w is a characteristic length of the forced convection problem which corresponds to the width of the sample along the air direction. For the unstretched sample (blue symbols), it corresponds to the sample width w = b = 4 mm, and for the stretched sample (red symbols), it corresponds to w = b / λ = 1.75 mm.
The obtained Reynolds numbers are clearly below the critical value R e ≃ 3500 , which indicates that we are not in a turbulent regime. Although our experimental situation does not strictly correspond to a stationary state, but rather to a relaxation towards equilibrium, we can satisfactorily compare the observed trend of N u vs. R e with the dependence
N u = 0.664 R e 1 / 2 P r 1 / 3 ,
where P r = 0.71 is the Prandtl number for air, as proposed for forced convection problems [22].

4. Conclusions

We have conducted a series of experiments aimed at exploring the enhancement of the efficiency and the cooling power of an elastocaloric refrigeration cycle based on natural rubber. Our focus has been on using forced air convection for the heat dissipation between the refrigerant and the hot reservoir. The cycles included a stretching stage carried out at different velocities, followed by a unstretching stage always performed at maximum velocity to reach adiabatic conditions.
To enhance the maximum undercooling Δ T u n s t r , it is convenient to ensure isothermal conditions during the stretching stage that are achievable by driving the sample at a very low stretching velocity. However, this strategy is detrimental to the frequency of the refrigeration cycle of an operating device. Based on the limitation that the cycle frequency is generally to be maximised, it has been demonstrated that an alternative approach is to implement forced air convection while in the stretching stage. At a set stretching velocity, there is an optimal v a i r value that provides the highest level of undercooling. Besides, the experiments have allowed determining the Newton heat transfer coefficient h for samples that were overheated or undercooled by an internal elastocaloric effect, for different air velocities. Depending on the initial thermal conditions, the enhancement of the heat transfer coefficient can be as large as 600% for air velocities of v a i r = 4 m/s.
These findings open promising perspectives for the design of future elastocaloric cooling prototypes based on natural rubber using air convective heat exchange to the hot source.

Author Contributions

E.Valdés: Data acquisition and curation, Formal analysis, Investigation, Visualisation. E.Stern-Taulats: Writing – review & editing, Methodology, Conceptualisation, Funding acquisition. N.Candau: Sample provider, Methodology, Conceptualisation. L.Mañosa: Methodology, Conceptualisation, Writing – review & editing. E.Vives: Methodology, Conceptualisation, Writing – review & editing, Funding acquisition, Project administration, Resources, Supervision.

Funding

We acknowledge financial support from Spanish Ministry of Science and Innovation (MCIN/AEI/ 10.13039/501100011033) and European Union (NextGenerationEU/PRTR) under grants PID2020-113549RB-I00/AEI and TED2021-129952B-C32/AEI. We also acknowledge support from Generalitat de Catalunya (AGAUR) under grants 2021SGR00328 and 2021LLAV00080. E Stern-Taulats acknowledges financial support from Spanish Ministry of Science and Innovation under Grant IJC2020-043957-I. N. Candau acknowledges the Spanish Ministry of Science and Innovation (Project TED2021-129952A-C33), and the research group eb-POLICOM of the Generalitat de Catalunya (Grant 2021SGR01042).

Data Availability Statement

Data will be made available upon reasonable request.

Acknowledgments

We acknowledge Antoni Vives, Quim Badosa and Jonathan Gebbia for technical support. We also acknowledge Antoni Planes for useful suggestions.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Nomenclature

A sample neck surface
A 0 initial sample neck surface
a sample neck length
b sample neck width
c sample neck thickness
d fan sample distance
C N R specific heat capacity of natural rubber
Δ T Difference between sample average surface temperature and room temperature
Δ T u n s t r Minimum diference between sample average surface temperature and room temperature
after fast unstretching
F force
h heat transfer coefficient
L 0 initial grip-to-grip length
l c characteristic length measuring the neck volume-to-surface ratio
λ local stretching ratio in the neck center
λ t o t a l total stretching ratio
N u Nusselt number
P r Prandtl number
Q heat
R e Reynolds number
ρ N R density
T average surface temperature of the sample
T 0 room temperature
T i initial temperature
t time
τ characteristic time constant for thermal relaxation
V sample neck volume
V 0 initial sample neck volume
v stretching velocity
v a i r average air velocity
w forced convection characteristic length
Δ x sample elongation

References

  1. Mañosa, L.; Planes, A. Materials with Giant Mechanocaloric Effects: Cooling by Strength. Advanced Materials 2017, 29, 1–25. [Google Scholar] [CrossRef] [PubMed]
  2. Ahcin, Z.; Dall’Olio, S.; Zerovnik, A.; Baskovic, U.Z.; Porenta, L.; Kabirifar, P.; Cerar, J.; Zupan, S.; Brojan, M.; Klemenc, J.; Tusek, J. High-performance cooling and heat pumping based on fatigue-resistant elastocaloric effect in compression. Joule 2023, 6, 2338–2357. [Google Scholar] [CrossRef] [PubMed]
  3. Qian, S.; Catalini, D.; Muehlbauer, J.; Liu, B.; Mevada, H.; Hou, H.; Hwang, Y.; Radermacher, R.; Takeuchi, I. High-performance multimode elastocaloric cooling system. Science 2023, 380, 722–727. [Google Scholar] [CrossRef] [PubMed]
  4. G.Zhou.; Y.Zhu.; S.Yao.; Q.Sun. Giant temperature span and cooling power in elastocaloric regenerator. Joule 2023, pending, 1–18. [CrossRef]
  5. Guyomar, D.; Li, Y.; Sebald, G.; Cottinet, P.J.; Ducharne, B.; Capsal, J.F. Elastocaloric modeling of natural rubber. Appl. Thermal Eng. 2013, 57, 33–38. [Google Scholar] [CrossRef]
  6. Xie, Z.; Sebald, G.; Guyomar, D. Comparison of direct and indirect measurement of the elastocaloric efect in natural rubber. Appl. Phys. Lett. 2016, 108, 041901. [Google Scholar] [CrossRef]
  7. Candau, N.; Vives, E.; Fernández-Renna, A.I.; Maspoch, M. Elastocaloric effect in vulcanized natural rubber and natural/wastes rubber blends. Polymer 2021, 236. [Google Scholar] [CrossRef]
  8. James, H.M.; Guth, E. Theory of Elastic Properties of Rubber. The Journal of Chemical Physics 1943, 11, 455. [Google Scholar] [CrossRef]
  9. Gu, Q.; Zaïri, F.; Guo, X. Thermodynamics and mechanics of stretch-induced crystallization in rubbers. Physical Review E 2018, 97, 1–13. [Google Scholar] [CrossRef]
  10. Mei, G.; Li, J.; Feng, D.; Qian, D.; Liu, Z. Twistocaloric modeling of elastomer fibers and experimental validation. Macromolecular Rapid Communications 2023. [Google Scholar] [CrossRef]
  11. Liu, B.; yumei wang.; Zhu, S.; Theodorakis, P.; Song, F.; Rachid, B.; Chen, K. A Lower Temperature Difference of The Elastocaloric Effect by Natural Rubber. Research Square 2023. [CrossRef]
  12. Sebald, G.; Komiya, A.; Jay, J.; Coativy, G.; Lebrun, L. Regenerative cooling using elastocaloric rubber: Analytical model and experiments: analytical model and experiments. Journal of Applied Physics 2020, 127. [Google Scholar] [CrossRef]
  13. S.Zhang.; Q.Yang.; C.Li.; et al. Solid-state cooling by elastocaloric polymer with uniform chain-lengths. Nature Communications 2022, 13. [CrossRef]
  14. Sebald, G.; Lombardi, G.; Coativy, G.; Jay, J.; Lebrun, L. High performance polymer-based regenerative elastocaloric cooler. Applied Thermal Engineering 2023, 223, 1–28. [Google Scholar] [CrossRef]
  15. Haissoune, H.; Chenal, J.M.; Chazeau, L.; Sebald, G.; Morfin, I.; Lebrun, L.; Dalmas, F.; Coativy, G. Elastocaloric effect: Impact of heat transfer on strain-induced crystallization kinetics of natural rubber. Polymer 2022, 263. [Google Scholar] [CrossRef]
  16. P.Sae-oui.; Freakley, P.; P.S.Oubridge. Determination of heat transfer coefficient of rubber to air. Plastic Rubber and Composites 1999, 28, 65–68. [CrossRef]
  17. P.Sae-oui. Effect of specimen geometry on heat transfer coefficient of rubber to air. Songklanakarin Journal of Science and Technology 2000, 22.
  18. J.Kruželák.; Sýkora, R.; I.Hudec. Peroxide vulcanization of natural rubber. Part I: effect of temperature and peroxide concentration. Journal of Polymer Engineering 2014, 34, 617–624. [CrossRef]
  19. B.Rousseau.; M.Chabin.; P.Echegut.; A.Sin.; F.Weiss.; P.Odier. High emissivity of a rough Pr2 Ni O4 coating. Applied Physics Letters 2001, 79, 3633–3635. [CrossRef]
  20. Wen, C.D.; Mudawar, I. Modelling the effects of surface roughness on the emissivity of aluminium alloys. Internationl Journal of Heat and Mass Transfer 2006, 49, 4279–4289. [Google Scholar] [CrossRef]
  21. N.Bekkedahl.; H.Matheson. Heat capacity, entropy and free nergy of rubber hydrocarbon. Journal of research of teh National Bureau of Standards 1935, 15, 503–515. [CrossRef]
  22. F.P.Incropera.; D.P.DeWitt.; T.L.Bergman.; A.S.Lavine., Fundamentals of Heat and Mass Transfer. John Wiley & Sons: Hoboken, NJ, USA, 2006; chapter 7; p. 410.
Preprints 118521 g001
Figure 1. Schematic representation of the sample in both stretched and unstretched positions, as well as the location and size of the fan. The green rectangle indicates the area captured by the IR camera.
Figure 1. Schematic representation of the sample in both stretched and unstretched positions, as well as the location and size of the fan. The green rectangle indicates the area captured by the IR camera.
Preprints 118521 g001
Preprints 118521 g002
Figure 2. (a) Mechanical protocol consisting in four stretching steps (from left to right) at v = 2000, 200, 20 and 2 mm/min followed by fast unstretching at 2000 mm/min, with a 2-second pause in-between. Long pauses of 180 s separate the cycles. (b) Corresponding behaviour of the applied force for each of the four air velocities v a i r as indicated by the line colour. (c) The behaviour of the temperature in the centre of the sample at each v a i r . Note that the horizontal scale of these graphs is discontinuous and that each segment is plotted on a different time scale.
Figure 2. (a) Mechanical protocol consisting in four stretching steps (from left to right) at v = 2000, 200, 20 and 2 mm/min followed by fast unstretching at 2000 mm/min, with a 2-second pause in-between. Long pauses of 180 s separate the cycles. (b) Corresponding behaviour of the applied force for each of the four air velocities v a i r as indicated by the line colour. (c) The behaviour of the temperature in the centre of the sample at each v a i r . Note that the horizontal scale of these graphs is discontinuous and that each segment is plotted on a different time scale.
Preprints 118521 g002
Preprints 118521 g003
Figure 3. (a) IR camera view and central temperature profile of the sample at its maximum elongation. (b) IR camera view and central temperature profile in an intermediate position during the unstretching stage. (c) IR camera view and central temperature profile of the sample after returning to its initial position. On each temperaure profile we have indicated with violet color the region that has been used in order to determine the sample temperature T ( t ) . The vertical length of this region corresponds to 20% of the total length L ( t ) of the sample.
Figure 3. (a) IR camera view and central temperature profile of the sample at its maximum elongation. (b) IR camera view and central temperature profile in an intermediate position during the unstretching stage. (c) IR camera view and central temperature profile of the sample after returning to its initial position. On each temperaure profile we have indicated with violet color the region that has been used in order to determine the sample temperature T ( t ) . The vertical length of this region corresponds to 20% of the total length L ( t ) of the sample.
Preprints 118521 g003
Preprints 118521 g004
Figure 4. Applied force F (in N) vs. elongation Δ x (in mm) vs. change of the average surface temperature Δ T of NR (in °C) for all loading-unloading cycles. The stretching velocities are (a) 2000 mm/min, (b) 200 mm/min, (c) 20 mm/min and (d) 2 mm/min. In all cases, unloading is at 2000 mm/min. The colour of each curve indicates the convective air velocity v a i r , as shown in the legend below.
Figure 4. Applied force F (in N) vs. elongation Δ x (in mm) vs. change of the average surface temperature Δ T of NR (in °C) for all loading-unloading cycles. The stretching velocities are (a) 2000 mm/min, (b) 200 mm/min, (c) 20 mm/min and (d) 2 mm/min. In all cases, unloading is at 2000 mm/min. The colour of each curve indicates the convective air velocity v a i r , as shown in the legend below.
Preprints 118521 g004
Preprints 118521 g005
Figure 5. Maximum undercooling at the centre of the rubber sample achieved from rapid unstretching after stretching at different velocities v, as a function of the velocity of air convection v a i r during the stretching stage.
Figure 5. Maximum undercooling at the centre of the rubber sample achieved from rapid unstretching after stretching at different velocities v, as a function of the velocity of air convection v a i r during the stretching stage.
Preprints 118521 g005
Preprints 118521 g006
Figure 6. (a) Estimated Newton convection coefficient for NR stretched at various loading velocities and subjected to different air velocities, acting as a sink (blue) and as a source of heat (red). Vertical error bars have been estimated by considering the propagation of the uncertainties in the room temperature determination that propagate when fitting of Eq.2. Inset shows examples of the fitted curves for the temperature change Δ T ≡ T ( t ) − T 0 corresponding to long thermal relaxations after a loading stage with v = 200 mm / min and no air convection. (b) The same data is represented as the Nusselt number N u as a function of Reynolds number R e , as explained in the text. The dashed line shows the standard relation between these adimensional numbers proposed for forced convection.
Figure 6. (a) Estimated Newton convection coefficient for NR stretched at various loading velocities and subjected to different air velocities, acting as a sink (blue) and as a source of heat (red). Vertical error bars have been estimated by considering the propagation of the uncertainties in the room temperature determination that propagate when fitting of Eq.2. Inset shows examples of the fitted curves for the temperature change Δ T ≡ T ( t ) − T 0 corresponding to long thermal relaxations after a loading stage with v = 200 mm / min and no air convection. (b) The same data is represented as the Nusselt number N u as a function of Reynolds number R e , as explained in the text. The dashed line shows the standard relation between these adimensional numbers proposed for forced convection.
Preprints 118521 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated