Prerpints.org logo
Preprint
Review

Sustainability in Long-term Surface Mine Planning: A Systematic Review of Operations Research Applications

This version is not peer-reviewed.

Submitted:

18 September 2024

Posted:

19 September 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
The mining industry, critical for global resource supply, has historically been linked to significant environmental degradation and social challenges including habitat disruption, water and soil contamination as well as fatalities. But recently the industry has been undergoing a transformative change to meet evolving environmental and societal expectations. Operations Research (OR) provides essential tools and techniques to optimize decision-making processes in this context. This paper presents a comprehensive review of different OR methods and their applications in balancing economic, social and environmental objectives in surface mine planning. By evaluating the strengths and limitations of these techniques, this review offers valuable insights for researchers and practitioners aiming to improve production efficiency and sustainability through advanced planning strategies.
Keywords: 
Subject: 
Engineering  -   Mining and Mineral Processing

1. Introduction

1.1. Sustainability

In the literature sustainable development (SD) has several definitions. The definition that remains the most frequently cited today, was introduced by the United Nations' World Commission on Environment and Development in 1987 as: “Sustainable development is development that meets the needs of the present without compromising the ability of future generations to meet their own needs” [1].
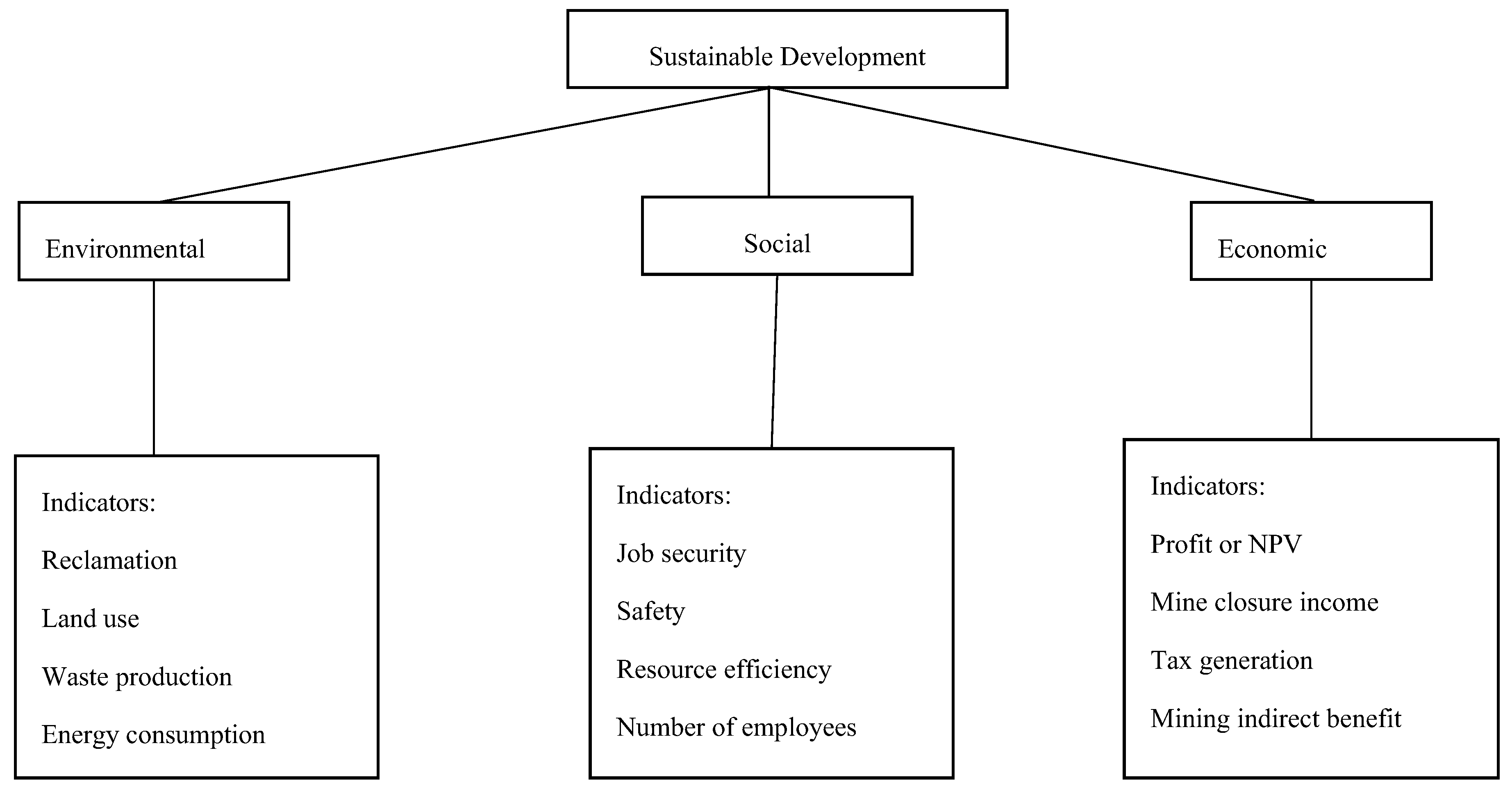
Since that time, various researchers have introduced different definitions of SD. However, the primary characteristic of SD is its holistic nature, encompassing diverse aspects of human needs. Environment, society, and economy are three pivotal aspects of sustainability that should be considered concurrently in any decision-making process. In mining engineering, these three principles can be connected to various indicators, some of which are illustrated in Figure 1. These indicators are utilized to ensure that industries are acting responsibly [2]. Environmental considerations focus on minimizing ecological damage and ensuring that mining activities do not leave a lasting negative impact on the environment. Social indicators emphasize the importance of mining operations in providing employment, ensuring safety, and maintaining social welfare. Economic indicators ensure that mining activities are financially sustainable and contribute positively to the local and national economy.
Following the acceptance of SD concept, numerous companies and governments began incorporating SD aspects into their activities and scholars started to discuss some of its dimensions in various sectors like Energy [3], Construction [4], urban planning [5,6] and community and agriculture [7].
Villas-Boas et al. (2005) distinguished between two terms, sustainability and SD, despite their often interchangeable use. They noted that sustainability pertains to the resilience of social and environmental systems, enabling them to endure external shocks and recover to normal operations. According to this view, sustainability does not apply to non-renewable minerals. In contrast, SD involves combining environmental policies with development strategies to meet present and future human needs, improve life quality, and safeguard the environment essential for life. Considering this framework, minerals are explicitly included within the scope of SD [8].
In the mining industry, where operations often have significant environmental and social impacts, it is essential to establish a framework for assessing and improving the sustainability of projects while balancing the three pillars of sustainable development. OR optimization methods are among the most widely utilized by specialists to achieve this goal. In this research, our focus is specifically on the application of these methods in surface mine planning.

1.2. Surface Mine Planning

Mine planning refers to the process of determining how an ore deposit will be exploited over the lifespan of a mining operation. The primary goal is to create an efficient system for extracting and supplying minerals to the market, ensuring minimal costs while adhering to the regulations. Decisions made at this stage are critical, as they have the most significant and lasting impact on the mine's future. It relies on all factors that planning engineers deem crucial for the proposed mine’s eventual success. This process is both strategic and tactical, initially focusing on long-term objectives derived from strategic factors, then shifting to more intricate short-term planning stages, which are influenced by tactical factors. The latter stages are a direct outcome of the former [9].
Surface mining (such as open pit mining) is recognized as an appropriate approach for extracting mineral resources or ore deposits situated at shallow depths and it is the most practiced and more efficient method compared to underground mining. However, when ore deposits are located at significant depths, the volume of waste material that must be removed can become prohibitively large, making surface mining economically impractical. This highlights the importance of economic feasibility in selecting a mining method. If surface mining is determined to be the best approach, efforts focus on developing reserves and infrastructure suitable to the specific mineral commodity being extracted [10]. Efficient and timely use of resource is also a crucial for maintaining profitability and competitiveness in surface mining operations [11].
In open pit mining, As the surface of the land is excavated, a progressively deeper pit is created until the mining operation concludes. Before extraction of ore can commence, the overburden must be removed. Haul roads typically wind through the mine from the bottom of the pit to the surface. By dividing the deposit into blocks, determining the value of each block, and creating a geometric model of the deposit, we can address the pit design problem. This approach helps establish the ultimate pit limit, determine the cutoff grade, and plan long-term production.
The dynamic nature of surface mining environments presents unique challenges that require sophisticated algorithms and methods to effectively manage the complexities of mine planning tasks, and this make it an active area of research, encouraging the development of innovative approaches. Nowadays optimization methods are essential in addressing mine planning challenges, focusing on cost reduction and profit maximization using advanced algorithms [12].

1.3. Sustainable Mine Planning

One of the key industries influencing economic, social, and environmental benefits is the mining sector. SD was likely first introduced to the mining industry in the early 1990s, at events such as the Rio Summit in 1992 [13]. However, in recent years integration of SD into this industry is gaining more attention as the demand for raw materials and their products, along with the environmental impacts resulting from extraction, continues to increase [14]. It was demonstrated that all aspects of SD can be negatively impacted by the mining industry despite its benefits. Amirshenava and Osanloo (2019) evaluated the impact of mining activities on three SD elements and calculated the relative severity score for each of the suggested indicators. However, the principles of SD, which are essential for reducing the negative impacts of mining activities during the design phase, are often overlooked [15]. To date, standard practices for resource evaluation, planning, and mine design have not sufficiently incorporated SD concepts. The most widely used methods for economic and engineering assessments in the mining industry's feasibility and design projects have failed to fully embrace sustainability principles [16]. Key reasons for this include:
  • Sustainability considerations are often addressed late in the project, after major decisions affecting social and environmental factors have been made.
  • Sustainability efforts focus on mitigating effects and implementing control measures, rather than being incorporated into the initial mine design and operational planning stages [17].
Asr et al. noted that all the SD studies in mine planning have concentrated on three main topics: determining the optimum cut-off grade (COG), the ultimate pit limit (UPL), and production planning [16]. Some of these studies addressed all three aspects of SD, while others focused on only two or even a single aspect, primarily economic. While each aspect is significant, even focusing on just one can provide valuable insights.
There are several review papers on mine planning, each offering various perspectives on the topic. However, none of these papers examine mine planning from the standpoint of OR methods. This gap highlights the need for a comprehensive review focusing on the application of OR techniques in mine planning to provide insights into their pros and cons for optimizing mining operations.
In this study, we will highlight OR methods developed and applied to optimize sustainable long term mine planning in surface mining operations. Additionally, by conducting a comparative analysis of these methodologies, we aim to highlight their effectiveness, limitations, and potential to improve the efficiency and profitability of surface mining operations. This understanding can enable mining companies to optimize their processes and adapt to the changing demands of the industry.
The rest of this research is structured as follows: The next section gives information about the research methodology, followed by an overview of exact and metaheuristic methods that appear in the literature. In the fourth stage we discussed the strengths and weaknesses of the methods presented in the previous section. The final section presents future opportunities and provides a conclusion of the objectives.

2. Research Methodology

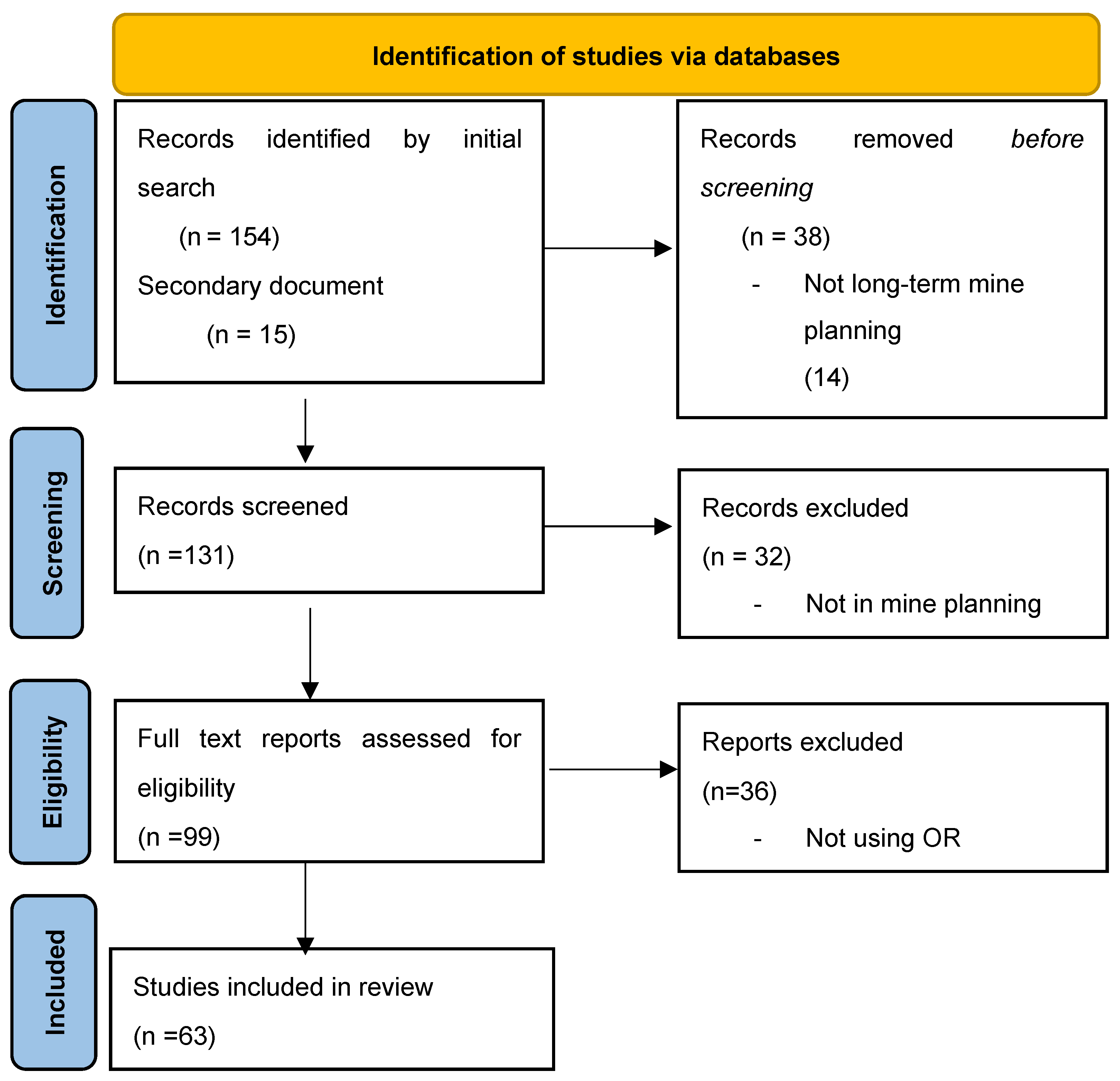
The aim of this literature review is to examine research that has employed OR methods for sustainable long-term mine planning. A systematic review was performed, starting with extracting English papers published in prominent journals. To compile the literature for this review, we conducted a comprehensive search using Scopus, which resulted in identifying 154 relevant papers published between 1980 and 2024. The search was performed using the following keywords within the title, abstract, and keywords:
"(sustainability OR sustainable OR sustainable mining OR NPV OR environment OR social) AND (production planning OR mine planning OR production scheduling OR open pit)"
In addition to these, we included 15 more papers that, although not part of the initial search results, were referenced as secondary documents in Scopus. These secondary documents were deemed significant for providing a broader perspective on the subject matter.
We did not include "operations research" or "OR" in the keywords because, based on experience, many papers utilize OR methods to optimize processes without explicitly mentioning the term "OR" within the text. To further narrow down the scope, 106 articles were excluded at different stages of the review process for various reasons, such as:
  • The article did not apply an OR method.
  • The article did not focus on long-term mine planning.
  • The article was not related to the topic for any other reason.
Preprints 118640 g002
Preprints 118640 g002
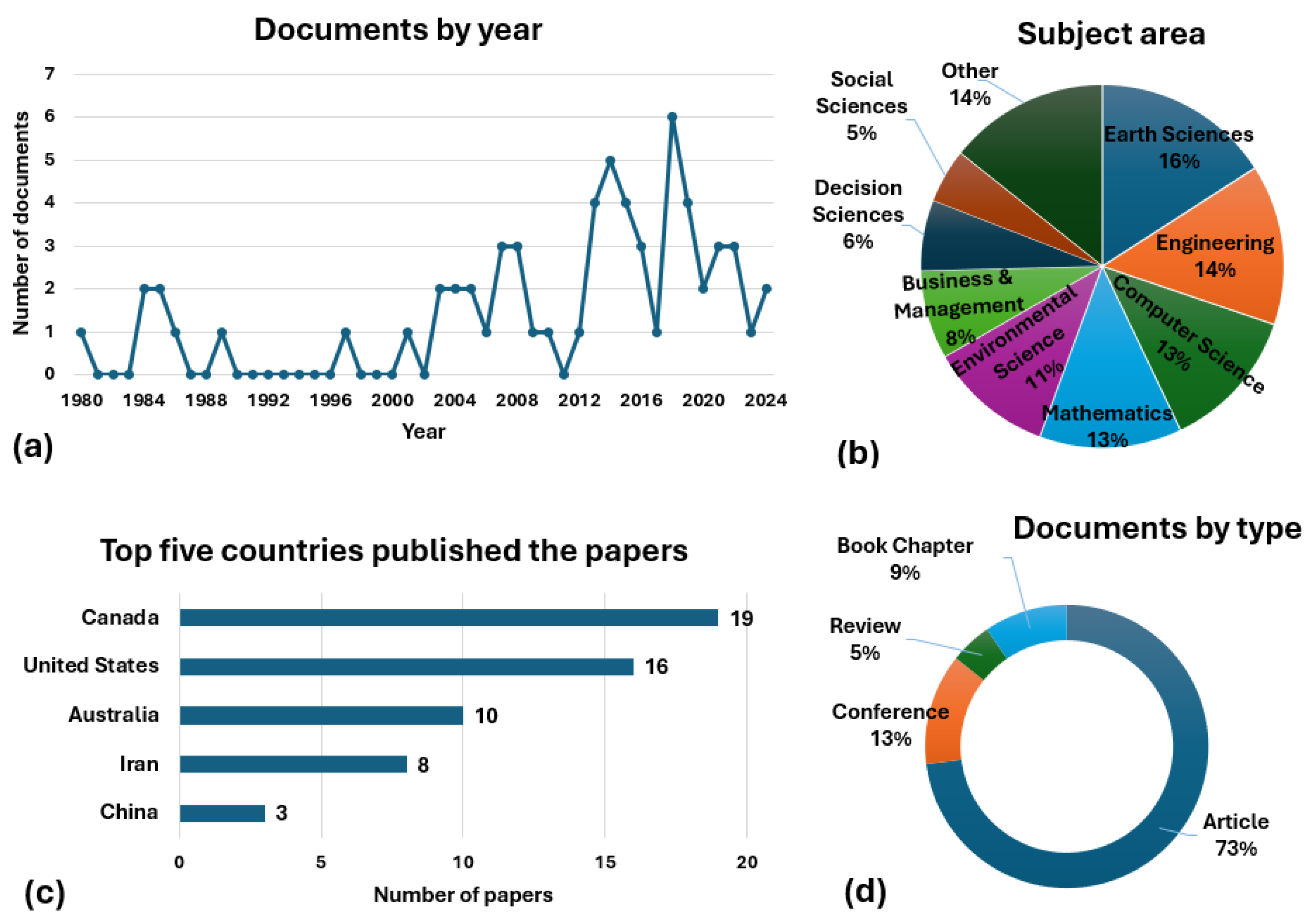
Following these guidelines, 63 papers were selected. First, these papers were analyzed based on year, subject area, document type, and country, as shown in Figure 3a, 3b, 3c, and 3d. The graphs show that the majority of the documents are journal papers from the last 20 years, predominantly from Canada, the United States, and Australia. Figure 2d illustrates that the subject areas defined by the database based on journal scope, article content, and keywords, primarily include Earth Sciences, Engineering, and Computer Science.
This review encompasses a significant portion of recent papers in the field of sustainable mine planning from the perspective of OR methods used. At the end, the opportunities for future research were identified.

3. OR Methodologies

OR and computer technology were introduced into mining engineering in the late 1950, to enhance the economic efficiency of mining development, consider a broader spectrum of factors, and optimize design and development processes [18]. In this section, we will explore the OR optimization methods and algorithms and their application in different stages of long-term surface mine planning in the context of SD.

a. Exact Methods

Exact methods guarantee finding the best possible solution for an optimization problem. These methods are usually applicable to smaller or well-defined problems due to their computational intensity.

3.1.1. Linear Programming (LP)

Linear optimization or Linear Programming is a technique used to achieve the best possible solution when the relationships between variables are linear, with both objectives and constraints expressed as linear equations. This method is among the most utilized approaches in mine production scheduling. A basic formulation of the problem with fundamental constraints can be illustrated as follows:
Max ∑ i = 1 I ∑ t = 1 T c i t x i t
s. t. ∑ t = 1 T x i t ≤ 1           ∀   i = 1,2 … I (Reserve constraints)
       x i t ≤ ∑ k = 1 t x i ′ k ∀ i = 1,2 … I ;       ∀ t = 1,2 … T ;     ∀ i ′ ∈ B i , (Slope constraints)
       ∑ i = 1 I w i ∗ x i t ≤ M ¯ t      ∀   t = 1,2 … T             (Mining capacity constraints)
∑ i = 1 I o i ∗ w i ∗ x i t ≤ O ¯ t ∀ t = 1,2 … T       (Processing capacity constraints)
Where:
c i t = discounted economic value of block i if mined in period t;
x i t = {1, if block i is mined in period t; 0, otherwise};
I= total number of blocks;
T=total number of periods;
B i = Set of blocks that must be excavated before block i;
i = blocks index, i=1,2⋅⋅⋅I;
t = time period index, t=1,2⋅⋅⋅T;
i ′ = index of blocks that must be excavated before block i;
M ¯ t = maximum mining capacity available during period t;
wi = tonnage of the block;
O ¯ t = maximum processing capacity available during period t;
o i = {1, if block i is ore; 0, otherwise};
Burgher and Erickson (1984) explored the integration of reclamation cost with production scheduling using a linear optimization approach. They analyzed how optimal production schedules for a small coal mine are affected by reclamation requirements and a fluctuating discount rate. Their findings show that a higher discount rate encourages production to be moved forward, while reclamation requirements tend to delay production. This delay occurs because reclamation adds extra costs, which mine managers prefer to postpone, as these costs are reduced when discounted over time [19].
Some studies leverage the integration of linear programming (LP) with other methods, such as integer programming. Mixed Integer Linear Programming (MILP) can be especially beneficial when certain variables must be integers. Caccetta and Kelsey (2001) applied MILP to optimize the extraction of waste blocks [20], whereas Badiozamani and Askari-Nasab (2014) used it to incorporate reclamation and tailings cost into the Net Present Value (NPV) objective function. These researchers emphasized the importance of integrating mining operations with environmental benchmarks, where comprehensive schedule meets the tailing capacity constraint and adheres to the production of the necessary reclamation material [21]. Recently, a new framework (LCA-MILP) was introduced to integrate environmental data from life cycle assessment (LCA) with MILP. This approach focused on dust emissions and greenhouse gases (GHGs) in open pit mine planning, achieving an 11.05% reduction in GHG emissions while maintaining over 93% of the basic NPV [22].
In another study, researchers developed a simultaneous mixed integer programming (SimMIP) model to optimize ore production as well as waste dump scheduling in mining complex. Unlike traditional two-step methods that separate ore and waste scheduling, SimMIP creates both schedules concurrently. It dynamically evaluates the economic value of possible routes for a mining block from source to destination, balancing NPV optimization with waste management strategies considering factors such as acid mine drainage (AMD) and greenhouse gas (GHG) emissions. When applied to a gold mining complex, the SimMIP model demonstrated superior performance in maximizing NPV, encapsulating potentially acid-forming (PAF) waste, and reducing GHG emissions [23]. MILP has also been employed by other researchers to address waste rock handling while optimizing mine scheduling [24,25,26,27,28].
Despite its frequent use in literature, addressing large-scale problems with MILP remains challenging due to computational complexity. This issue can be mitigated by techniques such as block clustering or using heuristic or meta-heuristic methods. In this regard, Lamghari et al. (2015) introduced a two-phase hybrid solution method. In the first phase, a series of LP problems is solved to generate an initial solution, followed by the second phase, where a variable neighborhood descent (VND) procedure refines this solution. This method was tested on instances derived from real mineral deposits and benchmark instances from literature. The efficiency of SH-VND was evaluated using upper bounds provided by CPLEX, and its performance was compared to recent methods from the literature and an alternate method in commercial mine planning software. Results indicate that SH-VND outperforms existing approaches, enabling mine planners to obtain high-quality solutions in shorter computational times. It can solve large problem instances quickly and manage more complex variations of the open-pit mine production scheduling problem [29].

3.1.2. Multi Criteria Decision Making (MCDM)

MCDM also known as Multi-criteria analysis (MCA), encompasses a range of methods used to assist in decision-making when options are assessed based on multiple criteria, especially when these criteria are measured in different units that cannot easily be converted. Although there are various MCA methods, they all rely on data normalization and the assignment of weights to the criteria to produce a combined score for each option. MCA methods are primarily categorized into two types: Multi-Objective Decision Making (MODM) and Multi-Attribute Decision Making (MADM). We will discuss these categories separately in the following sections.

3.1.2.1. Multi Objective Decision Making (MODM)

This method aims to find the optimal solution when there are multiple desired goals, often with conflicting optimization directions. Goal programming (GP), a subset of multi-objective optimization, is used to manage these conflicting objectives by assigning each a specific target value. Deviations from these targets, whether above or below, are quantified, and the aim is to minimize these undesired deviations through an achievement function. GP provides flexibility in formulating and prioritizing various goals, as well as allowing a certain level of interaction between the decision maker and the optimization process [30,31].
Ben-Awuah et al. (2012) applied Mixed Integer Linear Goal Programming (MILGP) in Production Scheduling and Waste Disposal Planning for Oil Sands mining. Their goal was to maximize NPV by determining the best schedule and destination for ore, dyke material, and waste extraction using mining-cuts derived from block clustering techniques. The schedule is designed to meet key factors for oil sands profitability and sustainability, such as maximizing NPV and creating timely tailings storage areas. Additionally, decision makers have the right to determine goal deviation variables, penalty costs, and priorities to achieve a balanced schedule and enhanced NPV. Trade-offs can also be made between achieving specific goals and maximizing NPV or minimizing dyke construction costs [32].
In a similar study, Ben-Awuah et al. (2018) developed an expanded model utilizing MILGP with the primary aim of optimizing NPV and minimizing waste dump construction costs. The methodology encompasses preprocessing the block economic model to reduce the number of variables by defining an UPL and grouping mining blocks into mining cuts at various levels or benches within the UPL. Then, a method is utilized to solve the GP formulation for the revised problem. Comparative analysis showed that this approach outperforms schedules and waste dump plans produced by the commercial mine scheduling software, Whittle. The MILGP model allocated more ore for extraction in the early years, resulting in an increased NPV [33].
Later, Maremi et al. (2021) applied MILGP to long-term production planning (LTPP) with an innovative strategy for waste management that involves dyke construction and backfilling activities. This approach, implemented for oil sands production and tailings disposal planning, simultaneously schedules production, reclamation, and dyke material while optimizing the size, shape, and location of in-pit tailings cells. It also generates optimal annual targets for mining and processing within an integrated mine planning and waste management framework. The direct combination of this practical mine planning and waste management approach offers several benefits, including reduced environmental footprint of external tailing facilities, advancement of progressive closure, and support for sustainable waste disposal planning [34].

3.1.2.2. Multi Attribute Decision Making (MADM)

MADM is a specific type of MCA that deals with decisions involving multiple attributes for the alternatives that are usually conflicting. The aim of MCDM/A is to offer a process for selecting, ranking, describing, classifying, and sorting alternatives according to a set of decision criteria [35]. It is a widely used approach for weighting and ranking problems with diverse options [36], and several studies have utilized it to evaluate various situations considering SD indicators in mining engineering areas [37,38]. However, it is not limited to mining; MADM has been used to assist decision-making processes in SD contexts for numerous other areas, such as energy, tourism, and transport [39,40,41]. Odell (2004) used MADM for UPL design and integrated the social and environmental criteria in assessing different scenarios of UPL based on mine life [42]. Another attempt was made by Adibi et al. (2015) to select UPL based on three indexes of SD. They converted UPL problem to a MADM problem and then used TOPSIS methodology to choose the best solution. This method proposes a UPL with higher social and economic scores. However, it also results in a larger pit and more waste being mined [43].

3.1.3. Data Envelop Analysis (DEA)

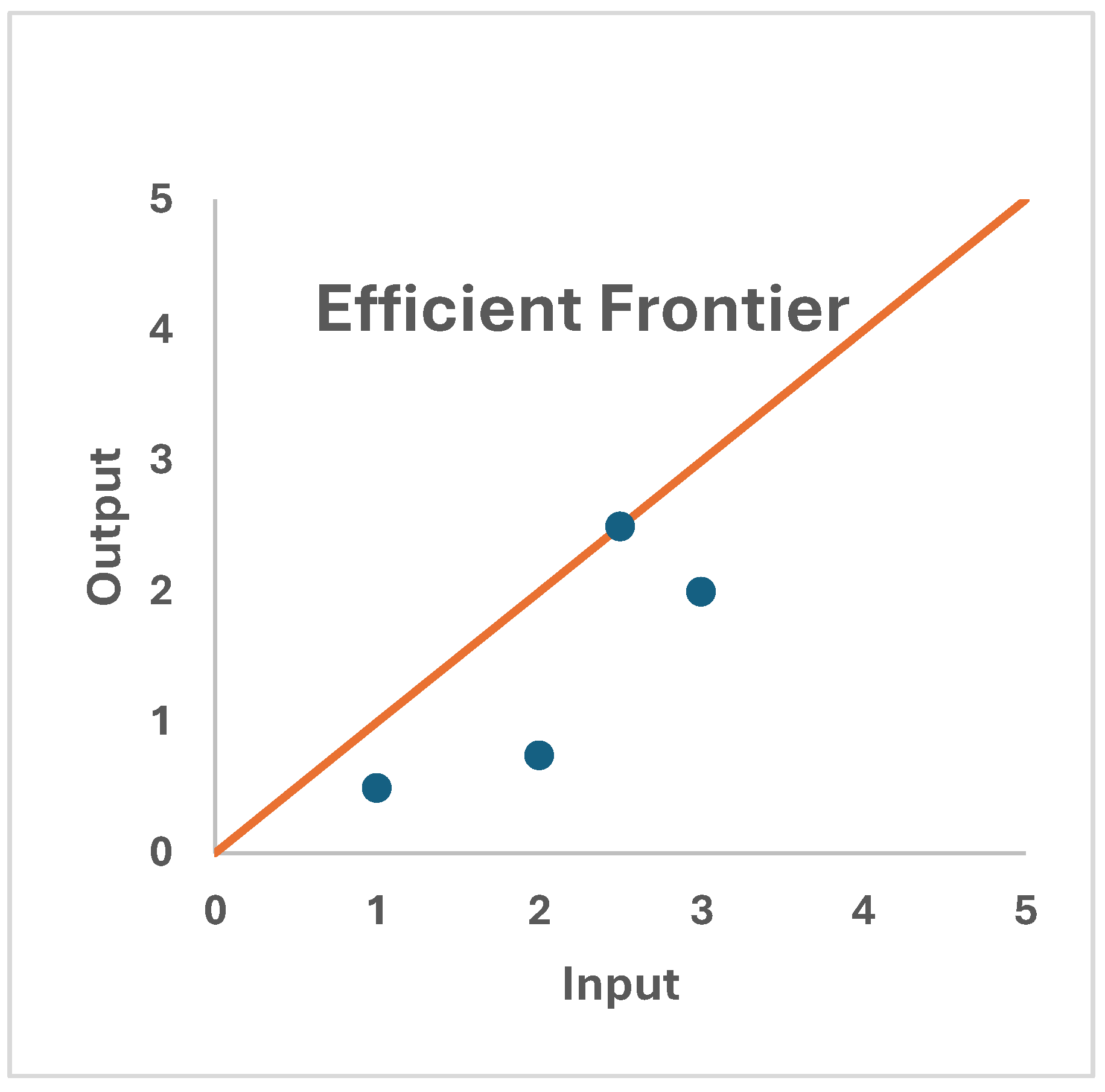
DEA is a non-parametric approach to measure productive efficiency of decision-making units (DMUs) by creating an objective function and evaluating each alternative. It is especially valuable for comparing relative performance when multiple inputs and outputs make direct comparison challenging.
Efficiency is generally the ratio of output to input, represented by:
Efficiency = output / input = (u₁y₁ + ... + uₛyₛ) / (v₁x₁ + ... + vₘxₘ),
where x and y represent the input and output variables, respectively, and u and v are their associated weights.
The most efficient Decision-Making Unit (DMU) scores a value of 1, while the remaining DMUs are compared against it, receiving scores between 0 and 1 (Figure 4). DEA is a useful tool because it integrates diverse data types into a single efficiency score.
Moradi and Osanloo (2015) quantified the criteria for SD and allocated their shares as 26% for environmental factors, 38% for economic factors, and 36% for social factors when designing UPL using DEA [44]. While this method could be beneficial in mine planning for its focus on economic efficiency and input-output relationships, it is primarily an economic model and may not adequately incorporate environmental and social considerations. Additionally, it requires a significant amount of accurate data to be effective.

3.1.4. Lane Algorithm

Lane’s algorithm is a practice to determine COG considering three main constraints of mining, milling/treatment, and refining along with their related costs and capacities. The Lane’s model is able to make proper use of the capacities of mining operations to increase the NPV (with consideration of discount rate) and total profit value of the whole project (not discounted) under fixed economic conditions. Applying this method, Ramirez-Rodriguezm and Rozgonyi (2004) considered the cost of reconstruction in COG optimization and proved that integrating the environmental requirement of SD can have an essential impact on COG and mine profitability [45]. In a similar research paper, rehabilitation cost was inserted into COG optimization problem, and this resulted in decreasing the COG and increasing the achievable NPV of the process [46].
Lane’s (1964, 1988) [47,48] method has been extensively utilized, but it has notable limitations highlighted by several researchers. There are some flaws in the derivation for maximizing profit and determining the optimal COG, where a key aspect was overlooked. Moreover, during differentiation, COG was inconsistently treated—first as a constant and later as a variable [49]. Because of these limitations, the method may not be suitable for identifying the optimum COG in all scenarios and for all deposit types [50].

3.1.5. Dynamic Programing (DP)

In mathematical optimization, DP usually simplifies a decision by breaking it down into a series of sequential decision steps over time. A sequence of value functions determines the value of the system at each state and time [51]. In their recent study, De Lara and colleagues developed a dynamic optimization technique to tackle the open-pit block scheduling problem, a major challenge in mining due to its complexity. They introduced heuristics based on index strategies, which provide a suboptimal solution, and set upper and lower bounds for NPV. The findings were promising, as index strategies demonstrated speed and scalability for large mining cases. This supports their use, especially in scenarios requiring rapid planning simulations and NPV calculations [52]. Additionally, this methodology was used in research in which ecological costs like carbon emission and damaged land costs, were incorporated into open pit production scheduling. Geologically optimal pushbacks that maximize metal extraction are initially created within the ultimate pit. These pushbacks are subsequently prioritized through DP to derive the most favorable production schedule, integrating ecological costs into the economic evaluation criteria. It was shown that incorporating ecological costs into the schedule results in a different sequence with lower production rates and an extended mine life. This approach reduces the total present value of ecological costs by 2.8% and increases the overall net present value by 2.5% compared to schedules without ecological costs. However, it slightly decreases the purely economic gain (NPV calculated without ecological costs) [53].

3.1.6. Lagrangian Relaxation (LR)

In mathematical optimization, LR is a method used to simplify complex constrained optimization problems. By relaxing the constraints, it converts a difficult problem into a more manageable one. The solution to this relaxed problem provides an approximation of the original problem, offering valuable insights. This technique handles inequality constraints by introducing a Lagrange multiplier, which penalizes constraint violations. Instead of enforcing strict inequality constraints, these penalties are incorporated into the optimization process. As a result, solving the relaxed problem is often more practical than addressing the original problem directly [54]. Various adaptations of LR have been developed for large-scale optimization problems [55]. However, the effectiveness of this method in converging to optimal solution hinges upon the values assigned to the lagrangian parameters initially and during adjustments [56].
The considerable size of mine scheduling problems makes it challenging to solve them using simple integer programming formulations alone. Consequently, various decomposition and aggregation methods have been commonly used in previous research [57]. Dagdelen improved this approach by employing LR and dividing the constraints into two types: constraints forming a network, such as sequencing constraints, and side constraints, which pertain to production and processing capacities [58]. Kawahata (2006) incorporated LR techniques into the large-scale MILP problem to reduce its size and accelerate the solution process, while still focusing on optimizing production and processing capacities [59].
When developing an LR model for a specific instance of the open pit block sequencing (OPBS) problems, it is challenging to decide which resource constraints to dualize and which to keep explicit. Lambert and Newman (2014) introduced the Maximum Value Feasible Pit method and a tailored LR approach to dualize several resource constraints. These formulations considerably shorten solution times compared to directly solving the original problem or using an Initial Integer Feasible Solution (IIFS). They also presented an algorithm for generating an IIFS, which they applied to the OPBS problem (Lambert & Newman, 2014).
Rahimi and Ghasemzadeh (2015) employed this method to optimize leaching and concentration cut-off grades as well as annual cashflows by analyzing the bio-heap leaching method. Environmental and social costs were integrated into the problem to make it a sustainable process. Bio-heap leaching of low-grade copper ore has been found to enhance the NPV of copper mines while minimizing environmental harm [60]. In a different study, an enhanced version of LR known as Temporally Decomposed Greedy Lagrangian Relaxation (TDGLR) was utilized to optimize scheduling problems by simultaneously addressing NPV and carbon emissions. By reducing the problem space, this method was demonstrated to be more efficient and faster than MIP using several datasets, particularly for larger instances where MIP struggles to generate feasible solutions [61].

3.1.7. Stochastic Programming

Stochastic programming is a framework used to address problems involving uncertainty. In stochastic programs, some or all of the problem parameters are uncertain but follow known probability distributions. Unlike deterministic optimization, which assumes precise knowledge of all parameters, stochastic programming seeks to find a solution that not only optimizes a specific criterion but also effectively manages the uncertainty in the parameters. Given that many real-world decisions in mining engineering involve uncertainty, stochastic programming has been widely utilized in this field for over twenty years. Traditionally, open pit mine design and planning relied on a single deterministic block model despite various sources of uncertainty due to sparse drill hole data. To address this, Menabde et al. (2018) developed a novel mathematical algorithm for mine optimization with orebody uncertainty. Their approach simultaneously focuses on optimization of the extraction sequence and COG. Using the MIP technique and employing a set of equally probable orebody realizations, the algorithm can significantly improve the expected NPV. The use of variable COG optimized under uncertainty evaluated through conditionally simulated orebodies also enhances accuracy and performance. Applying this method on a simple and rescaled problem and using the variable COG on the mean grade block model showed a 20% increase in NPV over the base case, while further optimization using all orebody realizations produced an additional 4.1% increase [62]. This method, known as Stochastic Integer Programming (SIP), has been employed in various research studies focused on mine scheduling optimization with the aim of maximizing NPV while utilizing several simulated scenarios for the orebody [63,64].
Remele et al. (2018) introduced a two-stage SIP approach to optimize NPV while ensuring that waste and tailings are disposed of within the mined-out sections of a pit. The objective function was split into two parts: first, optimizing the average discounted cash flows for various scenarios, and second, penalizing deviations from the minimum production goals. Their innovative method determines the extraction sequence of mining blocks as well as the allocation of strips for waste storage (destination policy). The approach accounts for geological uncertainties, such as metal grades, type of material, and chemical compositions. Applied to an iron ore deposit, the model demonstrated that utilizing in-pit storage significantly reduces re-handling costs during the rehabilitation stage, minimizes environmental impact, and addresses the challenge of limited external material storage space [65].
In a different study, researchers employed simultaneous stochastic optimization to tackle the issues of material uncertainty and waste variability in a gold mining complex. Considering the impact of uncertainty, the model aims to concurrently optimize cut-off grade, waste management, stockpiling, and processing decisions, while establishing the production schedule as the target outcome. The implementation focused on maximizing the value of the products sold. The results show significant improvements over the base case, particularly in meeting environmental, permitting, and processing targets. By reducing the total waste produced by treating it as a mining product, the new schedule requires a lower mining rate. Even though less material is mined and lower grades are sent to the processing facility, the total metal production remains unchanged over the life of the mine. This decrease in mining rate reduces costs and equipment expenditures, which results in a 6% increase in NPV [66].
Several studies have considered different types of uncertainty in mine planning and scheduling. Dimitrakopoulos (2018) reviewed various techniques used in Mine Design and Production Scheduling, categorizing them into two groups:
  • Algorithms based on simulated annealing [64,67,68].
  • Algorithms based on stochastic integer programming [62,63,69,70,71].
The same study introduced a new framework to enhance common approaches by integrating both stochastic modeling of orebodies and stochastic optimization in a complementary way. Using a copper deposit as an example, the author compared the results to the industry's ‘best practice’ which involves a conventional schedule based on a single estimated orebody model and Whittle’s approach [72]. The study demonstrated that the stochastic framework increases production schedule value by approximately 25%, regardless of which of the two methods is applied. Additionally, stochastic optimal pit limits were approximately 15% larger in total tonnage compared to traditional (deterministic) optimal pit limits. This difference extends the mine's lifespan and increases the NPV by about 10% compared to conventional pit limits using stochastic production scheduling. [73].

3.2. Metaheuristic Algorithms

In mathematical optimization, a metaheuristic is an advanced procedure intended to discover, generate, or select a heuristic (partial search algorithm) that can offer a sufficiently good solution to an optimization problem. In mine production scheduling, various metaheuristic methods have been used to tackle the complexities of optimization. In this section, we will explore some of the commonly applied approaches.

3.2.1. Genetic Algorithm (GA)

GA is an optimization technique that simulates the process of natural selection from biological evolution.
As mentioned in the previous section, the LR algorithm does not always guarantee convergence to the optimal solution. To address this limitation, Moosavi and colleagues (2014) developed a hybrid algorithm that combines LR with GA to solve the scheduling problem with a grade blending constraint, which is essential for maintaining the desired average grade in materials delivered to various processing facilities. By using LR, this approach tackles the computational challenges of the original problem, particularly related to mining and processing capacity, as well as the grade blending constraints. The method integrates these constraints into the objective function and uses penalties as lagrangian multipliers to avoid violations. GA provides the initial population and updates the lagrangian parameters through mutation and crossover. By numerical results they showed that LA-GA method performs better in terms of convergence speed and attaining highly near-optimal solution [74].
A Multi-Objective Genetic Algorithm (MOGA) is a tailored form of genetic algorithms specifically designed to handle multi-objective optimization problems by using a search mechanism that simultaneously finds optimal solutions across multiple objectives. Azhar et al. (2023) used MOGA to integrate carbon costs into mine production scheduling. Their method was proven effective in generating Pareto fronts, allowing for the simultaneous consideration of both NPV and carbon costs [75].

3.2.2. Particle Swarm Optimization (PSO)

PSO is inspired by the collective behavior seen in bird flocking. It manages a group of particles that explore the solution space by taking into account their own experiences as well as those of neighboring particles, allowing it to solve large-scale complex problems. In this algorithm, each particle in the swarm represents a potential solution. Initially, every particle is given a starting position and velocity. As the algorithm iterates, it continuously updates the position and velocity of each particle based on how desirable their current solutions are. This process continues until the algorithm converges on an optimal or near-optimal solution for the given problem. Using this algorithm, Khan and Niemann (2014) developed a new method for optimizing long-term production scheduling. Their research centered on applying this computationally efficient metaheuristic technique to tackle the complexities of mine production scheduling. They proposed a procedure to assess various PSO algorithm variants, and compared their performance, seeking the most effective solution for this difficult optimization problem. To minimize constraint violations, they incorporated a penalty into the objective function [76]. Several researchers have employed the PSO algorithm to address uncertainty in mining scheduling such as Geological factors [77] and grade uncertainty [78,79].

3.2.3. Simulated Annealing (SA)

SA is an optimization method inspired by the metallurgical annealing process, where materials are heated and then gradually cooled. Developed by Kirkpatrick et al. in 1983, SA is particularly well-suited for combinatorial optimization problems with large search spaces and non-linear or discontinuous objective functions. The process begins with an initial solution and systematically explores the solution space through iterations, accepting new solutions based on a probability distribution. At the beginning, the algorithm allows the acceptance of worse solutions with a higher probability, similar to the high-temperature phase in the annealing. As the algorithm advances, the temperature parameter decreases, gradually lowering the likelihood of accepting worse solutions, mimicking the cooling process [80].
Goodfellow and Dimitrakopoulos (2013) applied the Simulated Annealing (SA) algorithm in a modified scheduling model to address the pushback design challenge in mining operations with grade uncertainty. Their method improved the conventional phase design by introducing two distinct formulations aimed at minimizing deviations from phase production targets across different simulated grade scenarios. Applying these formulations at a copper mining operation led to a significantly improved solution, marked by reduced variability in achieving production goals [81]. Subsequently, Goodfellow and Dimitrakopoulos (2016) developed a framework for globally optimizing scheduling problems by integrating non-linear relationships that are typically overlooked due to the complexities of non-linear optimization. Three solvers, utilizing a mix of SA, PSO, and differential evolution, were devised, and evaluated. Experimental results from a copper and gold mining complex showed that the algorithm could generate solutions that reduce the risk of failing to meet production targets, resulting in a 6.6% increase in NPV compared to deterministic design and a 22.6% higher NPV than commercial software [82].
Similarly, Kumral (2013) proposed a solution approach, combining GP and SA, to address a modified scheduling model dealing with both scheduling and COG problems under grade uncertainty. The method initially aims to minimize capacity constraint violations (mining and processing) while creating a schedule that meets a specified NPV, along with reserve and block precedence constraints. Subsequently, SA iteratively refines the initial solution over multiple iterations, making adjustments to the mining period and COG for randomly selected blocks. When applied to a gold mining operation, this hybrid approach proved effective, with SA significantly improving the initial solution generated by GP [83].
After reviewing the selected papers, they were summarized based on several factors: area of mine planning, primary objective, sustainability dimensions considered (economic, environmental, or social), and modeling method used in Table 1.

4. Discussion

Exact methods strive to find the globally optimal solution but can be impractical for large-scale problems. LP offers a mathematically rigorous framework for formulating and solving optimization problems, making it well-suited for representing mining objectives, various constraints, and decision variables. LP can effectively model large-scale problems, and a variety of software and solvers have been developed to handle such challenges [12].
In mine production planning, mathematical programming models such as LP, MIP, MILP, and GP can handle multiple material types, destinations and elements, and they yield solutions within known bounds of optimality. As solutions approach optimality, they often produce production schedules with higher NPVs compared to those achieved from heuristic optimization techniques. Consequently, there has been extensive research into applying mathematical programming models to the LTPP problem, primarily using LP, MIP, and MILP. However, as it is mentioned before, these applications typically result in large-scale optimization problems with lengthy solution times [57,84].
While LP is a useful tool in this field, it's important to recognize that the relationships between decision variables and constraints are not always linear. Many real-world mining constraints, such as ore grades, processing capacities, and equipment availability, often demonstrate non-linear behavior. Representing these constraints with linear programs can result in inaccurate outcomes and suboptimal decisions. Additionally, LP solutions are typically continuous, which may not translate into feasible operational decisions (decision variables like the number of mining blocks to extract) in a mining context. Although MILP can handle discrete decision variables, the inclusion of integer constraints can greatly increase solution times and pose significant computational challenges in large-scale mine scheduling problems [29]. Sensitivity is another concern with LP, as even minor changes in input parameters like resource grade can lead to significant shifts in the optimal solution, making LP solutions less robust in dynamic mining environments. This limitation can be mitigated by multi objective optimization, as its solutions tend to be more robust and resilient to changes in input parameters within the dynamic mining context [85].
The primary advantage of dynamic programming is that it ensures the discovery of the optimal solution for problems with an optimal substructure. This means the best overall solution can be constructed from the optimal solutions of smaller subproblems. This characteristic guarantees that dynamic programming solutions are globally optimal. However, this approach requires more memory and involves higher computational complexity [86].
Lagrangian relaxation provides a powerful and flexible method for solving constrained optimization problems, enhancing computational efficiency by converting a complex constrained problem into a series of simpler, unconstrained problems. However, it may face convergence issues, particularly in non-linear cases, and does not guarantee finding the globally optimal solution to the original problem. This limitation is also present in metaheuristic algorithms, potentially affecting confidence in the solutions obtained. Despite this, the capability of metaheuristic algorithms to address complex, nonlinear, large-scale, and non-convex optimization problems, which are common in mine scheduling, remains significant.
Based on Table 1, LP, DP, LR, stochastic programming, and metaheuristics are among the most commonly used methods in surface mine planning that considered SD aspects. Table 2 provides a summary of the advantages and drawbacks of these methods.
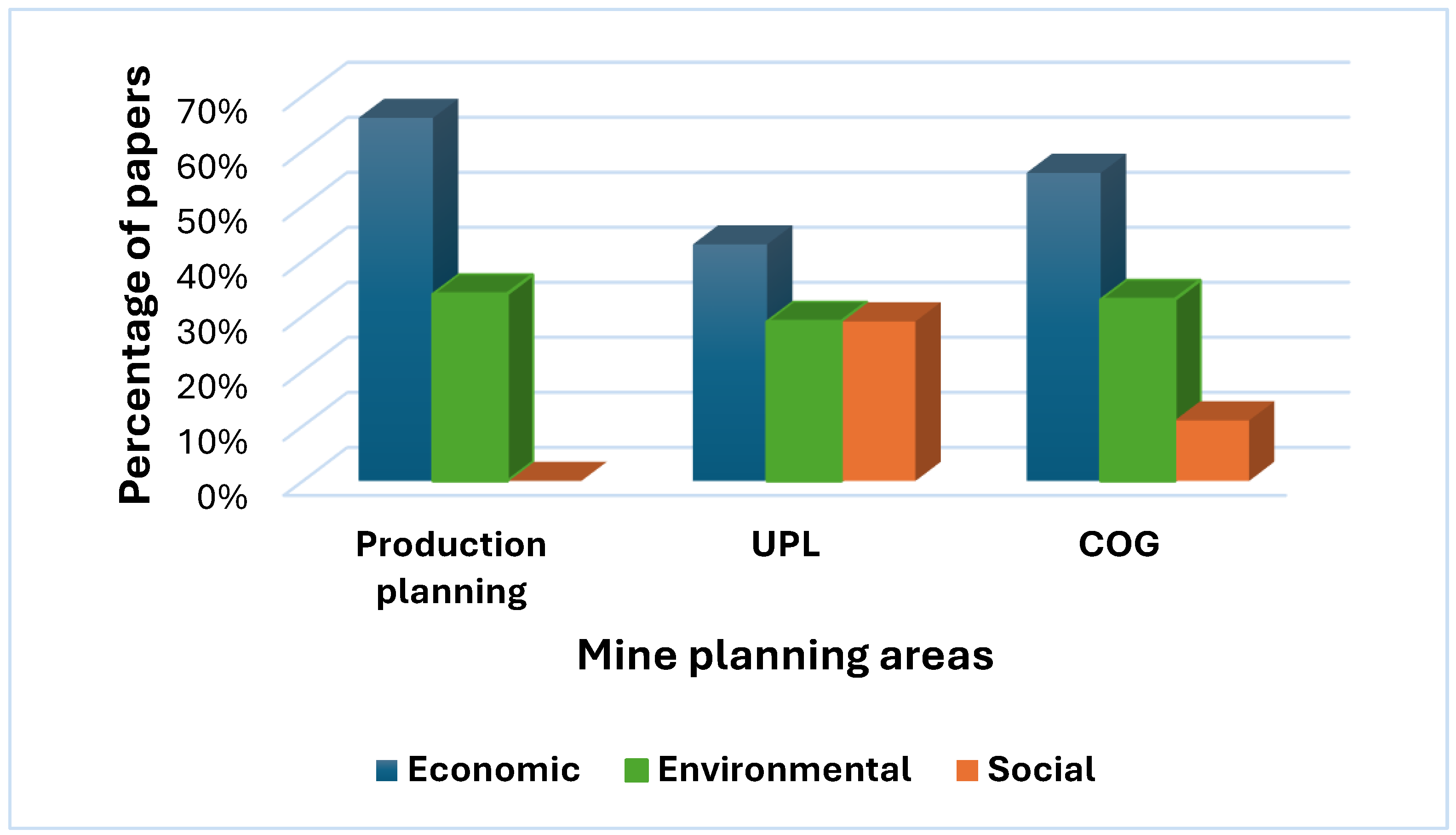
Through the review of related articles in this paper, several gaps in the field of sustainable mine production planning have been identified. Notably, the aspect of social sustainability has been largely overlooked. As shown in Figure 5, no published research has yet examined the integration of social factors with production scheduling optimization in surface mining operations. Future studies should explore the impact of indicators such as safety standards, community health, and the social effects of mining activities, including vibration, on local populations. Addressing these gaps will contribute to a more holistic approach to sustainable mining operations, ensuring that economic, environmental, and social factors are balanced in the planning process.
Additionally, from the OR perspective, our review reveals that certain advanced methodologies have yet to be applied to sustainable mine planning. Approaches such as multi-level optimization and fuzzy logic, which have shown considerable potential in other fields, remain underutilized in this domain. These methods could offer significant benefits, allowing for more robust and adaptable decision-making when dealing with uncertainty and complexity.
Multi- level optimization is particularly relevant when dealing with conflicting objectives, as it allows for a hierarchical decision-making process where one objective is prioritized at one level, and the other is considered at a subsequent level.
In the context of sustainable mine planning, economic objectives often conflict with social and environmental goals. Two-level optimization allows the decision-making process to be structured in a hierarchical manner. For instance, at the first level, the optimization could focus on maximizing NPV, ensuring that the economic viability of the mining operation is secured. At the second level, within the constraints set by the first level, the optimization could focus on minimizing negative social and environmental impacts. This structure mirrors the real-world scenario where economic viability is a prerequisite, but sustainability considerations are also crucial.
It also offers flexibility in model design. Different formulations can be used depending on the specific needs of the mine planning problem. For instance, if minimizing environmental impact is more critical in a particular context, the optimization levels can be reversed or adjusted accordingly. This adaptability makes it a suitable approach for a wide range of mining operations with varying priorities and constraints.
Fuzzy logic is another approach that should receive more attention in sustainable mining. In this field, factors such as environmental impact and social implications are often uncertain or difficult to quantify precisely, alongside operational factors like ore grade and market prices. Fuzzy logic is specifically designed to manage such uncertainty and ambiguity by incorporating imprecise data into the decision-making process. This makes it particularly suitable for sustainable mine production planning, where the exact trade-offs between economic, social, and environmental objectives may not always be clear. Additionally, it can be integrated with other optimization methods, such as multi-level optimization, to enhance their ability to handle uncertainty and complex trade-offs. However, the specific applicability and effectiveness of these approaches would depend on the precise formulation of the problem and the nature of the mining operation in question. Further research and model testing would be necessary to validate their utility in this context.

5. Conclusion

Mining companies face a complex and critical challenge when developing long-term plans that must balance economic returns with the environmental and social impacts on the communities. OR methods have proven to be effective tools for addressing these intricate sustainable decision-making problems, particularly in the mining sector, where multiple conflicting criteria, subjective evaluations, uncertainties, and the involvement of diverse stakeholders are common challenges.
This paper presented a comprehensive review of the literature on OR methods applied to assess sustainability in long term surface mining. We analyzed 59 articles, categorizing them based on the focus areas of surface mine planning (UPL, COG, and production planning), the methods employed to model and solve the problem, and the sustainability dimensions considered. Our review emphasizes the need for advanced planning and scheduling optimization techniques that integrate a mix of primary methods to address these complex problems more efficiently, both in terms of time and solution quality, ultimately supporting practitioners in enhancing production while achieving sustainability goals.
Future research should place greater emphasis on incorporating the social dimension, particularly in mine production planning, and addressing project uncertainties to develop more realistic models and practical solutions that align more closely with the evolving needs of the mining industry.

Author Contributions

Conceptualization, M.A. and A.A.; methodology, M.A. and S.O.A.; formal analysis, M.A.; investigation, M.A.; resources, A.A.; data curation, M.A. and S.A; writing—original draft preparation, M.A. and S.A.; writing—review and editing, M.A. and A.A. and S.O.A.; visualization, A.A. and S.O.A.; supervision, A.A.; project administration, A.A.; funding acquisition, A.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. WORLD COMMISSION ON ENVIRONMENT AND DEVELOPMENT. 1987.
  2. Hale, J.; Legun, K.; Campbell, H.; Carolan, M. Social Sustainability Indicators as Performance. Elsevier 2019. [Google Scholar] [CrossRef]
  3. Afshari, H.; Agnihotri, S.; Searcy, C.; Jaber, M.Y. Social Sustainability Indicators: A Comprehensive Review with Application in the Energy Sector. Elsevier 2022. [Google Scholar] [CrossRef]
  4. Rostamnezhad, M.; Thaheem, M. Social Sustainability in Construction Projects—a Systematic Review of Assessment Indicators and Taxonomy. Sustainability 2022. [Google Scholar] [CrossRef]
  5. NEAMŢU, B. Measuring the Social Sustainability of Urban Communities: The Role of Local Authorities. Transylvanian Review of Administrative Sciences 2012. [Google Scholar]
  6. Sharifi, A. Urban Sustainability Assessment: An Overview and Bibliometric Analysis. Ecol Indic 2021. [Google Scholar] [CrossRef]
  7. Bathaei, A.; Štreimikienė, D. A Systematic Review of Agricultural Sustainability Indicators. Agriculture 2023. [Google Scholar] [CrossRef]
  8. Villas Boas, R.C.; Solar, S.; Shields, D.; Anciaux, P. A Review on Indicators of Sustainability: For the Mineral Extraction Industries; CETEM/MCT/CNPq/CYTED/IMPC: Rio de Janeiro, 2005. [Google Scholar]
  9. Holloway, E.; Cowie, S. Mine Planning and the Crucial Role of Geology. SEG Discovery 2019, 16–27. [Google Scholar] [CrossRef]
  10. Darling, P. SME Mining Engineering Handbook, Third Edition - Google Books. Available online: https://books.google.com/books?hl=en&lr=&id=5uq-kdfHLWUC&oi=fnd&pg=PP1&dq=Darling,+2011&ots=wrpgukx13H&sig=Bn9sIoZEDfdk5T6elvx4AQJnt_k#v=onepage&q=Darling%2C%202011&f=false (accessed on 15 July 2024).
  11. Githiria, J. Review of Mathematical Models Applied in Open-Pit Mining. Springer Series in Geomechanics and Geoengineering 2020, 92–102. [Google Scholar] [CrossRef]
  12. Newman, A.M.; Rubio, E.; Caro, R.; Weintraub, A.; Eurek, K. A Review of Operations Research in Mine Planning. Interfaces (Providence) 2010, 40, 222–245. [Google Scholar] [CrossRef]
  13. Laurence, D. Establishing a Sustainable Mining Operation: An Overview. J Clean Prod 2011. [Google Scholar] [CrossRef]
  14. Gorman, M.; Dzombak, D. A Review of Sustainable Mining and Resource Management: Transitioning from the Life Cycle of the Mine to the Life Cycle of the Mineral. Conservation and Recycling 2018. [Google Scholar] [CrossRef]
  15. Amirshenava, S.; Osanloo, M. A Hybrid Semi-Quantitative Approach for Impact Assessment of Mining Activities on Sustainable Development Indexes. J Clean Prod 2019, 218, 823–834. [Google Scholar] [CrossRef]
  16. Asr, E.T.; Kakaie, R.; Ataei, M.; Tavakoli Mohammadi, M.R. A Review of Studies on Sustainable Development in Mining Life Cycle. J Clean Prod 2019, 229, 213–231. [Google Scholar] [CrossRef]
  17. Muñoz, J.I.; Guzmán, R.R.; Botín, J.A. Development of a Methodology That Integrates Environmental and Social Attributes in the Ore Resource Evaluation and Mine Planning. Int J Min Miner Eng 2014, 5, 38–58. [Google Scholar] [CrossRef]
  18. Wang, J.; Liu, Y.; Li, Y.; Wang, L. 60 Years Development and Prospect of Mining Systems Engineering. Journal of the China Coal Society 2024, 49, 261–279. [Google Scholar] [CrossRef]
  19. Burgher, K.; Erickson, E. The Optimization of Coal Mine Production Schedules Using Linear Programming: An Example That Determines the Effects of Reclamation Costs and Interest Rates. Elsevier 1984. [Google Scholar] [CrossRef]
  20. Caccetta, L.; Kelsey, P.J. Models for Mine Site Rehabilitation. In Proceedings of the CaccetInProc. MODSIM 2001 International Congress on Modelling and Simulation; 2001; pp. 2155–2160.
  21. Badiozamani, M.; Askari-Nasab, H. Integration of Reclamation and Tailings Management in Oil Sands Surface Mine Planning. Environmental modelling & software 2014. [Google Scholar]
  22. Mirzehi, M.; Moradi Afrapoli, A. Sustainable Long-Term Production Planning of Open Pit Mines: An Integrated Framework for Concurrent Economical and Environmental Optimization. Resources Policy 2024, 94, 105131. [Google Scholar] [CrossRef]
  23. Lin, J.; Asad, M.W.A.; Topal, E.; Chang, P.; Huang, J.; Lin, W. A Novel Model for Sustainable Production Scheduling of an Open-Pit Mining Complex Considering Waste Encapsulation. Resources Policy 2024, 91, 104949. [Google Scholar] [CrossRef]
  24. Williams, D.; Topal, E.; Zhang, N. Development of a Rock Dump Scheduling Model Using Linear Programming. In Proceedings of the Proceedings of the First International Seminar on the Management of Rock Dumps, Stockpiles and Heap Leach Pads, March 5 2008. [Google Scholar]
  25. Li, Y.; Topal, E.; Ramazan, S. Optimising the Long-Term Mine Waste Management and Truck Schedule in a Largescale Open Pit Mine. Transactions of the Institutions of Mining and Metallurgy, Section A: Mining Technology 2016, 125, 35–46. [Google Scholar] [CrossRef]
  26. Li, Y.; Topal, E.; Williams, D. Waste Rock Dumping Optimisation Using Mixed Integer Programming (MIP). Int J Min Reclam Environ 2013, 27, 425–436. [Google Scholar] [CrossRef]
  27. Fu, Z.; Asad, M.W.A.; Topal, E. A New Model for Open-Pit Production and Waste-Dump Scheduling. Engineering Optimization 2019, 51, 718–732. [Google Scholar] [CrossRef]
  28. Das, R.; Topal, E.; Mardaneh, E. Improved Optimised Scheduling in Stratified Deposits in Open Pit Mines–Using in-Pit Dumping. Int J Min Reclam Environ 2022, 36, 287–304. [Google Scholar] [CrossRef]
  29. Lamghari, A.; Dimitrakopoulos, R.; Ferland, J.A. A Hybrid Method Based on Linear Programming and Variable Neighborhood Descent for Scheduling Production in Open-Pit Mines. Journal of Global Optimization 2015, 63, 555–582. [Google Scholar] [CrossRef]
  30. Zeleny, M. Multiple Objectives in Mathematical Programming: Letting the Man In. Comput Oper Res 1980, 7, 1–4. [Google Scholar] [CrossRef]
  31. Hannan, E.L. An Assessment of Some Criticisms of Goal Programming. Comput Oper Res 1985, 12, 525–541. [Google Scholar] [CrossRef]
  32. Ben-Awuah, E.; Askari-Nasab, H.; Awuah-Offei, K. Production Scheduling and Waste Disposal Planning for Oil Sands Mining Using Goal Programming. Journal of Environmental Informatics 2012, 20, 20–33. [Google Scholar] [CrossRef]
  33. Ben-Awuah, E.; Askari-Nasab, H.; Maremi, A.; Navid, &; Hosseini, S. ; Hosseini, N.S. Implementation of a Goal Programming Framework for Production and Dyke Material Planning. Int J Min Reclam Environ 2018, 32, 536–563. [Google Scholar] [CrossRef]
  34. Maremi, A.; Ben-Awuah, E.; Askari-Nasab, H. Multi-Objective Mathematical Programming Framework for Integrated Oil Sands Mine Planning and Tailings Disposal Optimization. 2021. [Google Scholar]
  35. Kandakoglu, A.; Frini, A.; Ben Amor, S. Multicriteria Decision Making for Sustainable Development: A Systematic Review. Journal of Multi-Criteria Decision Analysis 2019, 26, 202–251. [Google Scholar] [CrossRef]
  36. Sitorus, F.; Cilliers, J.J.; Brito-Parada, P.R. Multi-Criteria Decision Making for the Choice Problem in Mining and Mineral Processing: Applications and Trends. Expert Syst Appl 2019, 121, 393–417. [Google Scholar] [CrossRef]
  37. Si, H.; Bi, H.; Li, X.; Yang, C. Environmental Evaluation for Sustainable Development of Coal Mining in Qijiang, Western China. Int J Coal Geol 2010, 81, 163–168. [Google Scholar] [CrossRef]
  38. Agarski, B.; Hadzistevic, M.; Budak, I.; Moraca, S.; Vukelic, D. Comparison of Approaches to Weighting of Multiple Criteria for Selecting Equipment to Optimize Performance and Safety. International Journal of Occupational Safety and Ergonomics 2019, 25, 228–240. [Google Scholar] [CrossRef] [PubMed]
  39. Mardani, A.; Jusoh, A.; Zavadskas, E.; Cavallaro, F. Sustainable and Renewable Energy: An Overview of the Application of Multiple Criteria Decision Making Techniques and Approaches. Sustainability 2015, 7, 13947–13984. [Google Scholar] [CrossRef]
  40. Garabinović, D.; Papić, M.; Kostić, M. Multi-Criteria Decision Making Trends in Ecotourism and Sustainable Tourism. cyberleninka.ru 2021, 68, 321–340. [Google Scholar] [CrossRef]
  41. Broniewicz, E.; Ogrodnik, K. A Comparative Evaluation of Multi-Criteria Analysis Methods for Sustainable Transport. Energies (Basel) 2021, 14. [Google Scholar] [CrossRef]
  42. Jane Odell, C.B. Integration of Sustainability into the Mine Design Process. 2004.
  43. Adibi, N.; Ataee-Pour, M.; Rahmanpour, M. Integration of Sustainable Development Concepts in Open Pit Mine Design. J Clean Prod 2015, 108, 1037–1049. [Google Scholar] [CrossRef]
  44. Moradi, G.; Osanloo, M. Prioritizing Sustainable Development Criteria Affecting Open Pit Mine Design: A Mathematical Model. Procedia Earth and Planetary Science 2015, 15, 813–820. [Google Scholar] [CrossRef]
  45. Ramirez-Rodriguezm, G.D.; Rozgonyi, T.G. Evaluating the Impact of Environmental Considerations in Open Pit Mine Design and Planning. In Proceedings of the Proceedings of the Eighth International Symposium on Environmental Issues and Waste Management in Energy and Mineral Production; 2004; pp. 125–131. [Google Scholar]
  46. Gholamnejad, J. Determination of the Optimum Cutoff Grade Considering Environmental Cost. J. Int. Environmental Application & Science 2008, 3, 186–194. [Google Scholar]
  47. Lane, K. The Economic Definition of Ore: Cut-off Grades in Theory and Practice; Mining Journal Books, 1988.
  48. Lane, K. CHOOSING THE OPTIMUM CUT-OFF GRADE 1964, 59, 811–829.
  49. Dagdelen, K.; Kawahata, K. Cut-off Grade Optimization for Large Scale Multi-Mine, Multi-Process Mining Operations.; PROCEEDINGS OF INTERNATIONAL SYMPOSIUM ON ENVIRONMENTAL ISSUES AND WASTE MANAGEMENT IN ENERGY AND MINERAL PRODUCTION (SWEMP), January 1 2007; pp. 226–233.
  50. Asad, M.W.A. Cutoff Grade Optimization Algorithm with Stockpiling Option for Open Pit Mining Operations of Two Economic Minerals. International Journal of Surface Mining, Reclamation and Environment 2005, 19, 176–187. [Google Scholar] [CrossRef]
  51. De Lara, M.; Doyen, L. Sustainable Management of Natural Resources: Mathematical Models and Methods; 2008. ISBN 9783540790730.
  52. De Lara, M.; Morales, N.; Beeker, N. Adaptive Strategies for The Open-Pit Mine Optimal Scheduling Problem. J. Int. Environmental Application & Science 2021, 3, 186–194. [Google Scholar]
  53. Xu, X.; Gu, X.; Wang, Q.; Gao, X.; Liu, J.; Wang, Z. Production Scheduling Optimization Considering Ecological Costs for Open Pit Metal Mines. J Clean Prod 2018, 210–221. [Google Scholar] [CrossRef]
  54. Ahuja, R.; Magnanti, T.; Orlin, J. Network Flows, 1988.
  55. Fisher, M.L. The Lagrangian Relaxation Method for Solving Integer Programming Problems. Manage Sci 2004, 50, 1861–1871. [Google Scholar] [CrossRef]
  56. Poore, A.B.; Robertson, A.J. A New Lagrangian Relaxation Based Algorithm for a Class of Multidimensional Assignment Problems. Comput Optim Appl 1997, 8, 129–150. [Google Scholar] [CrossRef]
  57. Dagdelen, K. Optimum Multi Period Open Pit Mine Production Scheduling. PhD, Colorado School of Mine, 1985.
  58. Dagdelen, K. Optimum Open Pit Mine Production Scheduling by Lagrangian Parameterization. In Proceedings of the 19th APCOM; 1986; pp. 127–142. [Google Scholar]
  59. Kawahata, K. New Algorithm to Solve Large Scale Mine Production Scheduling Problems by Using the Lagrangian Relaxation Method, A. PhD, Colorado School of Mine, 2006.
  60. Rahimi, E.; Ghasemzadeh, H. A New Algorithm to Determine Optimum Cut-off Grades Considering Technical, Economical, Environmental and Social Aspects. Resources Policy 2015, 46, 51–63. [Google Scholar] [CrossRef]
  61. Azhar, N.A.B.; Gunawan, A.; Cheng, S.-F.; Leonardi, E. A Carbon-Aware Planning Framework for Production Scheduling in Mining Logistics. In Proceedings of the International Conference on Computational Logistics. Cham: Springer International Publishing; Cham, 2022; Vol. 13557. [Google Scholar]
  62. Menabde, M.; Froyland, G.; Stone, P.; Yeates, G.A. Mining Schedule Optimisation for Conditionally Simulated Orebodies. Advances in Applied Strategic Mine Planning 2018, 91–100. [Google Scholar]
  63. Leite, A.; Dimitrakopoulos, R. Stochastic Optimization of Mine Production Scheduling with Uncertain Ore/Metal/Waste Supply. Int J Min Sci Technol 2014, 24, 755–762. [Google Scholar] [CrossRef]
  64. Albor Consuegra, F.; Dimitrakopoulos, R. Stochastic Mine Design Optimisation Based on Simulated Annealing: Pit Limits, Production Schedules, Multiple Orebody Scenarios and Sensitivity Analysis. Mining Technology 2009, 118, 79–90. [Google Scholar] [CrossRef]
  65. Adrien Rimélé, M.; Dimitrakopoulos, R.; Gamache, M. A Stochastic Optimization Method with In-Pit Waste and Tailings Disposal for Open Pit Life-of-Mine Production Planning. Resources Policy 2018, 57, 112–121. [Google Scholar] [CrossRef]
  66. Levinson, Z.; Dimitrakopoulos, R. Simultaneous Stochastic Optimisation of an Open-Pit Gold Mining Complex with Waste Management. Int J Min Reclam Environ 2020, 34, 415–429. [Google Scholar] [CrossRef]
  67. Godoy, M.; Dimitrakopoulos, R. Managing Risk and Waste Mining in Long-Term Production Scheduling of Open-Pit Mines. SME transactions 2004, 316. [Google Scholar]
  68. Leite, A.; Dimitrakopoulos, R. Stochastic Optimisation Model for Open Pit Mine Planning: Application and Risk Analysis at Copper Deposit. Mining Technology 2007, 116, 109–118. [Google Scholar] [CrossRef]
  69. Ramazan, S.; Dimitrakopoulos, R. Production Scheduling with Uncertain Supply: A New Solution to the Open Pit Mining Problem. Optimization and Engineering 2013, 14, 361–380. [Google Scholar] [CrossRef]
  70. Montiel, L.; Dimitrakopoulos, Roussos. ; Kawahata, K. Globally Optimising Open-Pit and Underground Mining Operations under Geological Uncertainty. Mining Technology 2016, 125, 2–14. [Google Scholar] [CrossRef]
  71. Goodfellow, R.; Dimitrakopoulos, R. Simultaneous Stochastic Optimization of Mining Complexes and Mineral Value Chains. Math Geosci 2017, 49, 341–360. [Google Scholar] [CrossRef]
  72. Whittle, J. A Decade of Open Pit Mine Planning and Optimization-the Craft of Turning Algorithms into Packages. 1999.
  73. Dimitrakopoulos, R. Stochastic Mine Planning—Methods, Examples and Value in an Uncertain World; Advances in Applied Strategic Mine Planning, 2018; ISBN 9783319693200. [Google Scholar]
  74. Moosavi, E.; Gholamnejad, J.; Ataee-Pour, M.; Khorram, E. Improvement of Lagrangian Relaxation Performance for Open Pit Mines Constrained Long-Term Production Scheduling Problem. J Cent South Univ 2014, 21, 2848–2856. [Google Scholar] [CrossRef]
  75. Azhar, N.A.B.; Gunawan, A.; Cheng, S.-F.; Leonardi, E. Carbon-Aware Mine Planning with a Novel Multi-Objective Framework. In Proceedings of the In Proceedings of the Fourteenth International Conference on Computational Logistics, Berlin, Germany; 2023; pp. 6–8. [Google Scholar]
  76. Khan, A.; C Niemann-Delius, C. Production Scheduling of Open Pit Mines Using Particle Swarm Optimization Algorithm. Advances in Operations Research 2014, 2014. [Google Scholar] [CrossRef]
  77. Gilani, S.; Sattarvand, J.; Hajihassani, M.; Abdullah, S. A Stochastic Particle Swarm Based Model for Long Term Production Planning of Open Pit Mines Considering the Geological Uncertainty. Resources Policy 2020, 68. [Google Scholar] [CrossRef]
  78. Tolouei, K.; Moosavi, E.; Hossein, A.; Tabrizi, B.; Afzal, P.; Abbas, &; Bazzazi, A. ; Bazzazi, A.A. An Optimisation Approach for Uncertainty-Based Long-Term Production Scheduling in Open-Pit Mines Using Meta-Heuristic Algorithms. Int J Min Reclam Environ 2021, 35, 115–140. [Google Scholar] [CrossRef]
  79. Khan, A. Long-Term Production Scheduling of Open Pit Mines Using Particle Swarm and Bat Algorithms under Grade Uncertainty. J South Afr Inst Min Metall 2018, 118, 361–368. [Google Scholar] [CrossRef]
  80. Kirkpatrick, S. Optimization by Simulated Annealing: Quantitative Studies. J Stat Phys 1984, 34, 975–986. [Google Scholar] [CrossRef]
  81. Goodfellow, R.; Dimitrakopoulos, R. Algorithmic Integration of Geological Uncertainty in Pushback Designs for Complex Multiprocess Open Pit Mines. Mining Technology 2013, 122, 67–77. [Google Scholar] [CrossRef]
  82. Goodfellow, R.; Dimitrakopoulos, R. Global Optimization of Open Pit Mining Complexes with Uncertainty. Appl Soft Comput 2016, 40, 292–304. [Google Scholar] [CrossRef]
  83. Kumral, M. Optimizing Ore–Waste Discrimination and Block Sequencing through Simulated Annealing. Appl Soft Comput 2013, 13, 3737–3744. [Google Scholar] [CrossRef]
  84. Caccetta, L.; Hill, S.P. An Application of Branch and Cut to Open Pit Mine Scheduling. Journal of Global Optimization 2003, 27, 349–365. [Google Scholar] [CrossRef]
  85. Coello, C.A.C. Evolutionary Algorithms for Solving Multi-Objective Problems. Springer 2007. [Google Scholar]
  86. Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2022.
Preprints 118640 g001
Figure 1. Sustainable development principles and indicators.
Figure 1. Sustainable development principles and indicators.
Preprints 118640 g001
Preprints 118640 g002
Figure 2. Different phases of systematic review.
Figure 2. Different phases of systematic review.
Preprints 118640 g002
Preprints 118640 g003
Figure 3. Distribution of the papers based on different factors.
Figure 3. Distribution of the papers based on different factors.
Preprints 118640 g003
Preprints 118640 g004
Figure 4. DEA method.
Figure 4. DEA method.
Preprints 118640 g004
Preprints 118640 g005
Figure 5. Papers distribution based on SD factors.
Figure 5. Papers distribution based on SD factors.
Preprints 118640 g005
Table 1. Summary of reviewed papers.
Table 1. Summary of reviewed papers.
Reference Area Primary objective SD aspect OR method
Burgher and Erickson, 1984 Production planning Considered reclamation cost into the optimization of production schedule Economic
Environmental		 LP
Caccetta and Kelsey, 2001 Production planning Presented a system for waste block removal Economic
Environmental		 MILP
Badiozamani and Askari-Nasab, 2014 Production planning Integrated reclamation and tailings cost into NPV optimization Economic
Environmental
Mirzehi & Moradi Afrapoli, 2024 Production planning Considered dust emissions and greenhouse gases into the optimization of production schedule Economic
Environmental
Lin et al., 2024 Production planning Optimized production and waste dump scheduling simultaneously (Maximize NPV and Minimize GHG and AMD) Economic
Environmental		 MIP
Lamghari et al., 2015 Production planning Introduced a hybrid method using LP and variable neighborhood descent (VND) procedure
 Economics LP & VND
Ben-Awuah et al., 2012 Production planning Maximize NPV by determining the best schedule and destination for ore, dyke material, and waste extraction using mining-cuts Economic
Environmental		 MODM
Ben-Awuah et al., 2018 Production planning Proposed an expanded model to
maximize the NPV and minimize waste dump construction costs 		Economic
Environmental
Maremi et al., 2021 Production planning Presented a framework for optimizing mine scheduling as well as shape, size and location of tailing-cells Economic
Environmental
Odell, 2004 UPL Integrated the social and environmental criteria in evaluating various scenarios of UPL based on mine life Environmental Social MADM
Adibi et al., 2015 UPL Presented a method to select UPL base on SD Economic
Environmental
Social
Moradi and Osanloo, 2015 UPL Quantified SD criteria. The share of environmental, economic and social is 26, 38 and 36%, respectively Economic
Environmental
Social		 DEA
Ramirez-Rodriguezm and Rozgonyi, 2004 COG Applied the cost of reconstruction in cut-off grade optimization
 Economic Environmental
 Lane Algorithm
Gholamnejad, 2008 COG Inserted the cost of rehabilitation in cut-off grade optimization Economic Environmental
De Lara et al., 2020 Production planning Provided upper and lower bound for NPV in the deterministic case using index strategies, and a theoretical framework for cases under uncertainty Economic DP
Xu et al., 2018 Production planning Ecological costs like carbon emission and damaged land costs, were incorporated into production scheduling. Economic
Environmental
Dagdelen, 1986 Production planning Decomposed large scale linear program resulted in an improved discounted cash flow Economic LR
Kawahata, 2006 Production planning Presented two subproblems to tighten the feasible region for MILP, resulting in reduction in size of the model and improvement in solution time Economic
Lambert and Newman, 2014 Production planning Presented Maximum Value Feasible Pit to determine which constraints should be dualize in LR, and obtained a near-optimum solution more quickly Economic
Rahimi and Ghasemzadeh, 2015 COG Determined leaching and concentration optimum COG and annual cashflows by analyzing the bio heap leaching method. Economic
Environmental
Social
Azhar et al., 2022 Production planning An enhanced version of LR was utilized to address NPV and carbon emissions. Economic
Environmental
Menabde and Dimitrakopoulos, 2018 Production planning & COG Optimizing NPV using MIP technique and employing a set of equally probable orebody realizations Economic
 Stochastic integer programming
Remele et al. (2018) Production planning Optimizing NPV and waste and tailing disposal considering geological uncertainties Economic
Environmental
Levinson, 2022 Production planning & COG Employed simultaneous stochastic optimization to optimize COG, waste management, stockpiling, and processing decisions under material uncertainty and waste variability Economic
Environmental
Dimitrakopoulos, 2018 Production planning & UPL Combined stochastic modeling of orebodies with stochastic optimization in a complementary way Economics
Moosavi et al., 2014 Production planning Employed Genetic algorithm to provide the initial population as well as updated lagrangian parameters Economic GA
Azhar et al., 2023 Production planning Incorporated the carbon cost in mine planning using multi objective optimization Economic Environmental
 MOGA
Khan & C Niemann-Delius, 2014 Production planning Developed a procedure to assess different PSO algorithm variants and compared their function Economic PSO
Goodfellow & Dimitrakopoulos, 2013 Production planning Created a method to reduce deviations from phase production goals across different simulated grade scenarios Economic SA
Goodfellow & Dimitrakopoulos, 2016 Production planning Introduced a framework for globally optimizing scheduling problems by integrating non-linear relationships Economic
Kumral, 2013 Production planning & COG proposed a solution approach for combining GP and SA, to minimize violations of capacity constraints Economic SA & GP
Table 2. Summary of optimization methods for surface mine planning.
Table 2. Summary of optimization methods for surface mine planning.
Method Advantages Disadvantages
LP
  • Capable of modeling large scale problems
  • Supported by different software and solvers
  • Incapable of addressing non-linear behavior in real-world mining constraints, such as ore grades, processing capacities, and equipment availability.
  • LP solutions are usually continuous and may not always align with practical operational decisions.
  • Less robust and highly sensitive to variations
DP
  • Guarantee obtaining the optimal solution when there is an optimal substructure
  • Demand more memory and involves computational complexity
LR
  • Effective and adaptable for addressing constrained optimization problems.
  • Enhance computational efficiency by breaking down a complex constrained problem into a series of simpler, unconstrained problems.
  • May face convergence problems, especially in non-linear scenarios.
  • Do not ensure discovering the globally optimal solution
Stochastic programming
  • Incorporate uncertainty, leading to more robust and reliable decision making
  • Enhance risk management
  • High complexity
  • Computationally intensive, resulting in longer solution time
  • Data-intensive, requiring detailed probabilistic information
Metaheuristic
  • Address complex, nonlinear, large-scale, and non-convex optimization problems
  • Do not guarantee the discovery of globally optimal solution
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated