|
1. Main Results
-
Derivation of the Setler Dynamics: The Setler dynamics are derived by transforming continuous formulas into discrete forms suitable for our model. The continuous form of our dynamical system is defined as:
Here,
,
, and
r represent the positional coordinates, while
,
,
, and
are parameters governing the dynamics. By applying a discrete time step
, the discrete form of the dynamics is:
where
and
is the function derived from the continuous system. This transformation allows for the analysis of chaotic behavior and entropy in a discrete framework.
Entropy Growth in Stellar Dynamics: The Perelman entropy for the Setler system exhibits exponential growth over time. For the unperturbed case (), the entropy increases as , where is the largest growth rate from the exponential terms in the potential function . In the perturbed case (), while the scalar curvature term R slightly modifies the entropy, the overall growth remains exponential, similar to the unperturbed case.
Complexity in Predicting Stellar Positions: The increasing entropy suggests that as time progresses, predicting the exact location of stars becomes increasingly complex. The exponential increase in entropy reflects growing disorder, making it progressively harder to accurately predict stellar positions with certainty over long timescales. This result indicates that while deterministic dynamics govern the system, the inherent complexity of celestial positional systems grows over time.
2. Introduction
The grandeur of the cosmos and the intricate dance of celestial bodies reflect the majesty of creation, as emphasized in the Holy Quran. Allah says, In the name of Allah, the Almighty God “I swear by the locations of the stars (and their falling). It is indeed a very great oath, if you but knew” (Al-Wāqi‘ah 56:75–77) [
1]. This verse signifies the profound complexity and divine wisdom inherent in the cosmos, highlighting the difficulty in predicting the exact positions of stars and understanding their movements.
In recent years, the study of stellar positions has gained significant importance in both astronomy and mathematics. Researchers have developed sophisticated models to understand the motion of celestial bodies, driven by the quest to decipher the underlying patterns and dynamics governing their trajectories. For instance, Spurzem, R. and Kamlah [
2] explored advanced computational methods to predict star positions with higher accuracy, while Sebastian Bahamonde and Christian G. Boehmer and many researchers [
3] applied dynamical systems theory to model stellar motion.
Significant contributions have also emerged from the study of manifolds and Ricci flow. Diego, J. M [
4] introduced novel algorithms for simulating gravitational interactions, enhancing predictions of star positions over long time scales. Dino Boccaletti and Giuseppe Pucacco [
5] employed chaos theory to analyze the stability of stellar orbits, revealing the chaotic nature of their trajectories. Efforts to integrate Ricci flow and Riemannian metrics [
6] have provided new insights into the geometric structure of celestial systems [
7].
This paper builds upon these advancements by applying Perelman entropy and Ricci flow [
8] to model stellar positional dynamics on manifolds. By exploring the geometric and chaotic properties of these systems, we aim to gain deeper insights into their long-term behavior and stability. We compare our findings with classical chaotic systems, such as the Lorenz attractor [
9], to deepen the discussion of complexity in predicting stellar positions.
Finally, we address the question: Can we predict the exact location of stars in the sky or their precise position?
3. Discrete Dynamical System for Stellar Positions
Building upon the foundational ideas presented in the introduction, where we discussed the complexity of predicting stellar motion through the lens of chaos theory and dynamical systems [
10], we now turn our attention to modeling these motions using a discrete dynamical framework. The use of discrete dynamical systems is particularly apt given the nature of astronomical observations, which are recorded at discrete time intervals, making this approach both realistic and computationally efficient [
11].
Incorporating the Riemannian metric and Ricci flow [
12] into our analysis, we further examine the geometric structure underlying the evolution of stellar positions. By exploring these geometric aspects, we aim to understand how the curvature of the phase space affects the overall stability and chaotic behavior of stellar systems [
13]. This not only offers insights into the short-term dynamics but also opens avenues for studying the long-term cosmic evolution of such systems, aligning with the cosmological implications introduced earlier [
14,
15].
The positional parameters of a star—right ascension (
), declination (
), and distance (
r)—are updated at discrete time steps using nonlinear rules, which allow for the modeling of complex behaviors arising from gravitational interactions and perturbations from nearby celestial bodies. These updates are governed by the following equations [
16]:
Here, f, g, and h represent nonlinear functions that account for various influences such as gravitational forces, external perturbations, and chaotic factors. These nonlinearities introduce sensitivity to initial conditions, a hallmark of chaotic systems, and enable the model to capture both stable and unstable stellar trajectories.
Moreover, we compute Lyapunov exponents to measure the degree of chaos present in the system. As the system evolves, we observe bifurcation phenomena that reveal the transition from regular to chaotic behavior. This transition is sensitive to parameter variations, such as the star’s initial distance or the strength of external perturbations. The Riemannian geometry of the system, characterized by its metric tensor, allows us to further probe how these parameters affect the curvature of the system’s phase space, providing a deeper understanding of the dynamical structure [
17].
By utilizing this discrete framework, we gain a powerful tool for investigating the complex, chaotic behavior of stellar motion, linking our dynamical model to broader studies in both chaos theory and cosmology. This raises profound questions about the predictability of stellar positions: Can we truly predict the exact location of stars in the sky, or does the chaotic nature of their motion impose fundamental limits on our ability to forecast their precise positions?
3.1. Derivation of the Chaotified Dynamics
In this section, we derive the stellar positional dynamics by introducing nonlinearity and external perturbations into the update rules for the system. The justification for using a discrete dynamical system instead of a continuous one is tied to the nature of astronomical observations and the computational advantages of discrete models when dealing with large datasets. Additionally, discrete systems provide a natural framework for exploring chaotic behavior, which is characterized by sensitivity to initial conditions and parameter variations—both of which are central to stellar dynamics [
18].
3.1.1. Step 1: Linear Update Rules
We begin by modeling the star’s positional parameters—right ascension (
), declination (
), and distance (
r)—using simple linear update rules. The linear model assumes uniform motion and no perturbations, which makes it insufficient for capturing the complexity of real stellar motion. The linear update rules are as follows:
where
,
, and
are small increments representing the changes in the star’s position at each time step, and
is a scaling parameter. While these linear rules provide a simplistic approximation, they fail to account for the chaotic nature of gravitational interactions and external forces influencing stars.
Justification for Discrete Dynamics: Discrete models are well-suited for astronomical applications because observations of stellar motion are inherently discrete—stars are observed at distinct time intervals. Continuous models, while mathematically elegant, can obscure the effects of discrete perturbations and interactions that accumulate over time. Furthermore, discrete dynamical systems are more computationally tractable, especially when dealing with long-term simulations or large datasets, such as those encountered in astronomical studies. The chaotic behavior, which often manifests in such systems, can be explored effectively using discrete updates [
19].
3.1.2. Step 2: Introducing Nonlinearity
To model more realistic and complex stellar dynamics, we introduce nonlinearity into the update rules. In chaotic systems, nonlinearity is essential for producing the sensitive dependence on initial conditions that leads to unpredictable behavior over long time scales. We use trigonometric functions, which are commonly employed in dynamical systems, to introduce nonlinearity into the evolution of
,
, and
r. The nonlinear update rules are given by:
Here, is a parameter controlling the strength of the nonlinearity. These functions introduce periodic behavior and coupling between the positional variables, allowing for the emergence of complex dynamical patterns. Nonlinearity in these functions reflects gravitational influences and other interactions that are not constant over time, making the system sensitive to initial conditions.
3.1.3. Step 3: Adding External Forcing
To further enhance the complexity of the system and induce chaotic behavior, we introduce external forcing terms into the update rules. These forcing terms represent periodic or stochastic influences from external celestial bodies or cosmic forces, which can significantly alter the trajectory of a star. The new update rules with external forcing are:
In these equations, , , and are parameters controlling the amplitude of the external forcing, and is the frequency of the forcing. The periodic forcing terms ( and ) introduce time-dependent perturbations that drive the system into a chaotic regime. Such forcing can represent tidal forces, radiation pressure, or perturbations from other nearby stars.
3.1.4. Step 4: Cartesian Coordinates
To facilitate the analysis of the system’s dynamics and later introduce the Riemann metric and Ricci flow, we convert the spherical coordinates (
) to Cartesian coordinates. The Cartesian coordinates
of the star’s position at step
n are given by:
This transformation allows us to work with the star’s position in three-dimensional space, providing a more intuitive geometric interpretation of its motion. These spatial components will be critical in the next sections when we discuss the Riemann metric and Ricci flow, as they allow us to define the curvature of the phase space in which the stellar motion evolves [
17].
3.1.5. Chaotic Dynamics and Justification
The discrete nature of the system allows us to track the evolution of a star’s position over discrete time steps, capturing both stable periodic behavior and chaotic behavior depending on the initial conditions and parameter values. The inclusion of nonlinear terms and external forcing makes this system ideal for exploring chaos, as small changes in the initial values of , , and r can lead to vastly different outcomes. The sensitivity to initial conditions, which is a hallmark of chaotic systems, is especially pronounced in discrete models, where each time step magnifies the impact of perturbations.
In summary, this derivation leads to a chaotified discrete model of stellar positional dynamics, where nonlinearity and external forces create a system capable of exhibiting chaotic behavior. The discrete framework aligns with astronomical observation techniques and offers computational advantages for long-term predictions and simulations of stellar motion.
4. Analyzing the Lyapunov Exponents
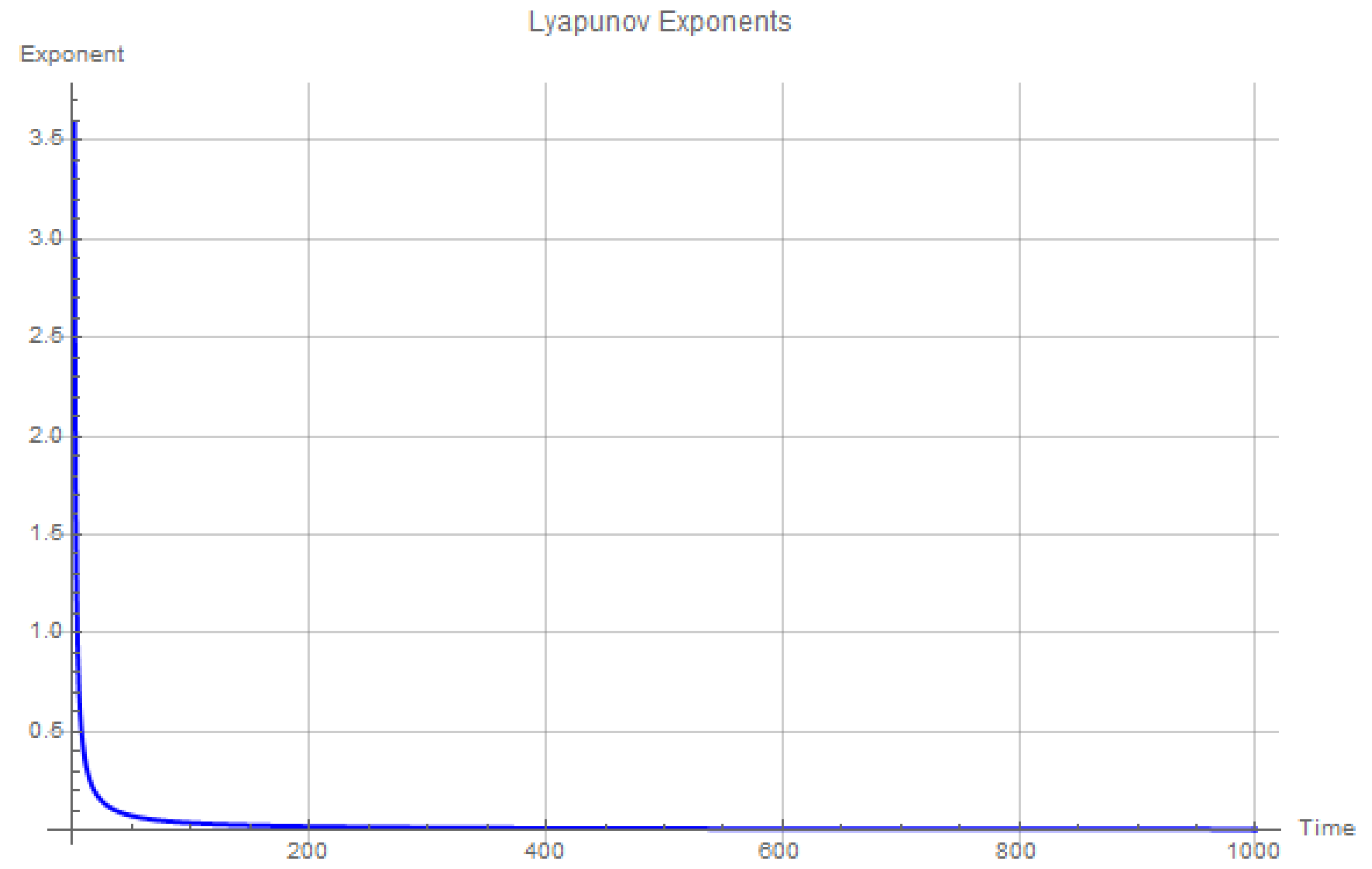
The Lyapunov exponents, as shown in
Figure 1, provide crucial insights into the chaotic behavior of the stellar positional system. In this study, we used a distance of 4.24 light-years, corresponding to the actual distance between Proxima Centauri and the Sun, ensuring that the analysis remains rooted in astrophysically realistic conditions. This choice of distance not only contextualizes the system within known astronomical parameters but also validates the relevance of the results to real-world stellar dynamics.
The model parameters used are: , , , , and . These parameters control the evolution of right ascension (), declination (), and distance (r) over time. The positive Lyapunov exponent observed in the plot is indicative of the system’s sensitivity to initial conditions, a hallmark of chaotic dynamics. Specifically, small perturbations in the initial conditions lead to trajectories that diverge exponentially over time, making long-term predictions highly challenging due to this inherent instability.
The Lyapunov exponents (
) are calculated to measure the sensitivity to initial conditions in the dynamical system. The following algorithm outlines the procedure used to compute the Lyapunov exponents:
The plateau observed in the Lyapunov exponent values could be attributed to either numerical artifacts or specific characteristics of the system’s underlying dynamics. From a numerical perspective, this saturation might arise from limitations in the resolution of the integration method used or truncation errors, which can affect the accuracy of long-term simulations. Alternatively, the system itself may exhibit regions of quasi-stability, where chaotic behavior persists but is confined within certain dynamical bounds. This phenomenon suggests a form of bounded chaos, where the system does not fully diverge, but stabilizes at certain thresholds. Investigating the role of different numerical integration techniques (e.g., Runge-Kutta methods or symplectic integrators) could provide further clarity.
Moreover, further exploration of parameter variations could unveil additional bifurcation points or regions where the system transitions between different types of chaotic behavior. Identifying these critical thresholds is crucial for understanding how the stellar system’s chaotic properties evolve and for pinpointing where the system undergoes bifurcations into more complex dynamic states.
5. Bifurcation Analysis and Chaotic Dynamics
After analyzing the Lyapunov exponents [
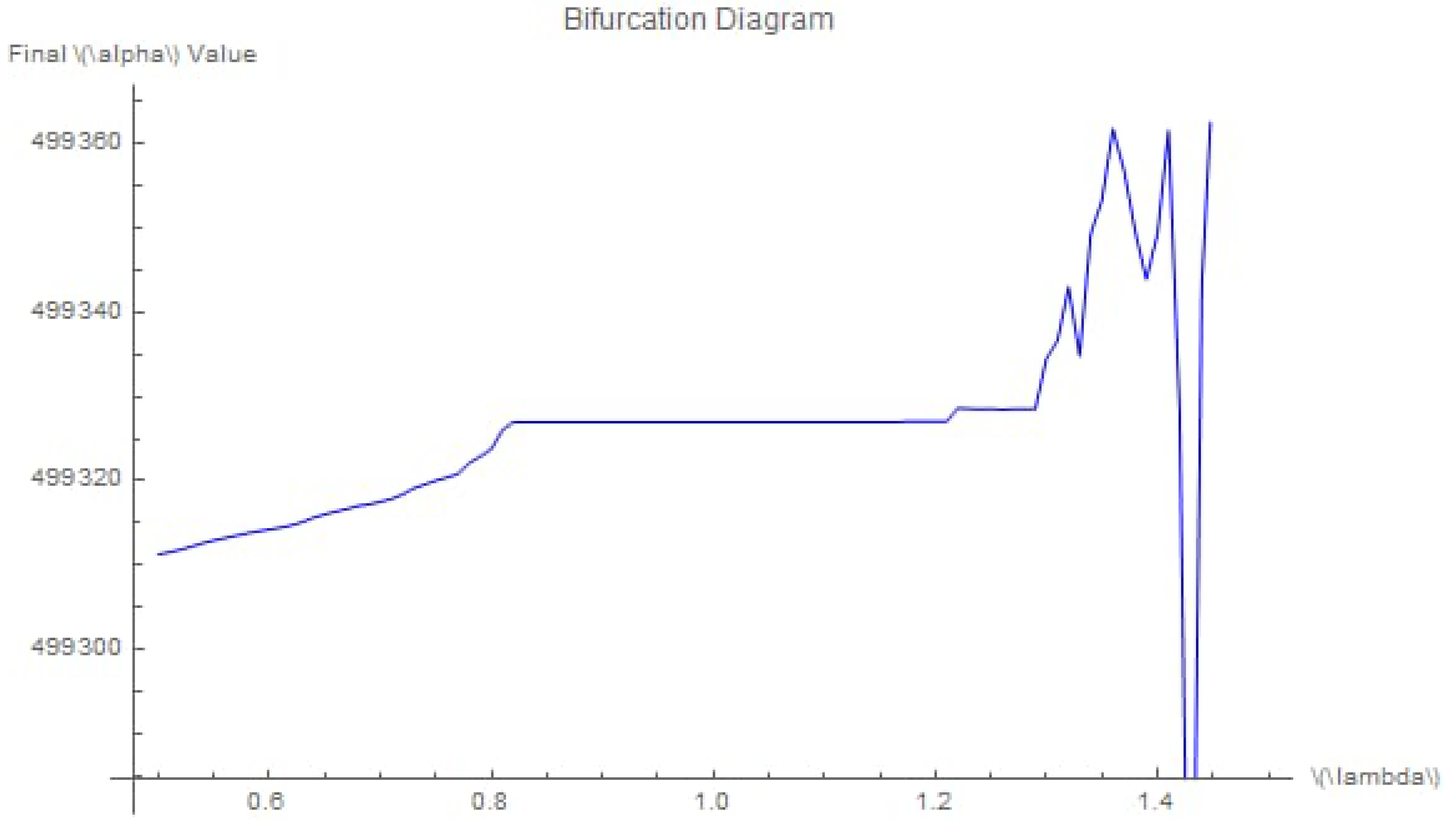
20], we now examine the bifurcation diagram shown in
Figure 2. This diagram reveals the progression of the system’s dynamics, where a series of period-doubling bifurcations occurs, signaling the transition from stable, periodic behavior to chaotic dynamics as the parameter
is varied.
We chose these parameter values because they are well-known in chaotic systems, particularly the Lorenz attractor, allowing for a meaningful comparison. The distance light-years reflects the actual astronomical distance between Proxima Centauri and the Sun, ensuring our analysis is based on real-world stellar distances. This setting provides a more physically relevant context to explore chaos in stellar motion.
At lower values of , the bifurcation diagram displays periodic behavior, as indicated by the regular branches. However, once crosses a critical threshold, chaotic dynamics emerge, evidenced by the increasingly intricate and dense patterns. Such behavior is typical of nonlinear systems and reflects how minor changes in parameters like can induce unpredictability and complexity.
Figure 3 provides a closer look at the chaotic regions, where multiple overlapping bifurcation cascades are visible. This demonstrates the rich dynamical behavior of the system, with the emergence of chaos due to even small parameter shifts. The results underscore the complexity inherent in the stellar positional system and suggest that further exploration of other parameters may reveal additional bifurcation points and deepen our understanding of its chaotic nature.
5.1. Additional Considerations
Beyond the variation of , investigating the system’s sensitivity to other parameters such as , , and could expose new bifurcation points. This could also provide a more comprehensive understanding of the chaotic dynamics observed in the stellar system. Future research could involve a more detailed parametric study, applying techniques from bifurcation theory to explore the intricate behavior of this astrophysical model.
6. Comparison between the Lorenz Attractor and the Attractor of the New Dynamics System
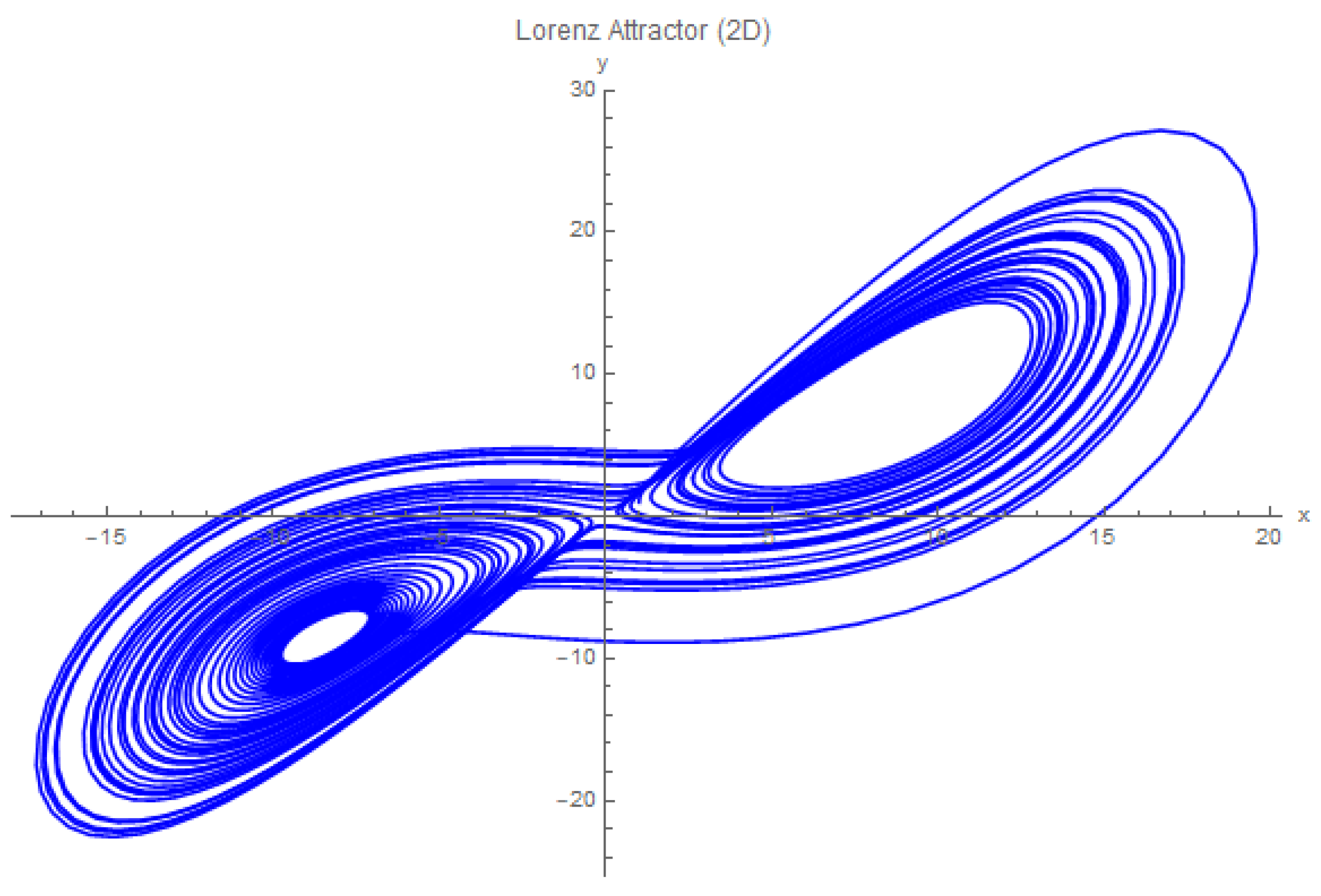
In this section, we compare the attractor of the new stellar positional system, termed the "Setler Position," with the well-known Lorenz attractor. This comparison allows us to explore how the chaotic properties of our system align with established chaotic systems, specifically the Lorenz attractor.
6.1. Motivation for Attractor Analysis
Attractors are fundamental in the study of chaotic systems, offering a visual representation of the system’s long-term trajectory in phase space. By comparing the attractors of the Setler Position system and the Lorenz system, we aim to:
Identify and confirm chaotic behavior in the new system.
Highlight similarities and differences in the underlying system dynamics.
Validate the theoretical model of the Setler Position system against a well-known chaotic system.
The parameter values chosen for the Lorenz system, such as , , and , are well-documented for generating the Lorenz attractor. Similarly, the parameters for the Setler Position system, such as , , , and , were selected based on their ability to produce chaotic behavior. The use of real-world stellar distances (4.24 light-years) further grounds the analysis in astrophysical reality.
6.2. Comparison of Attractors
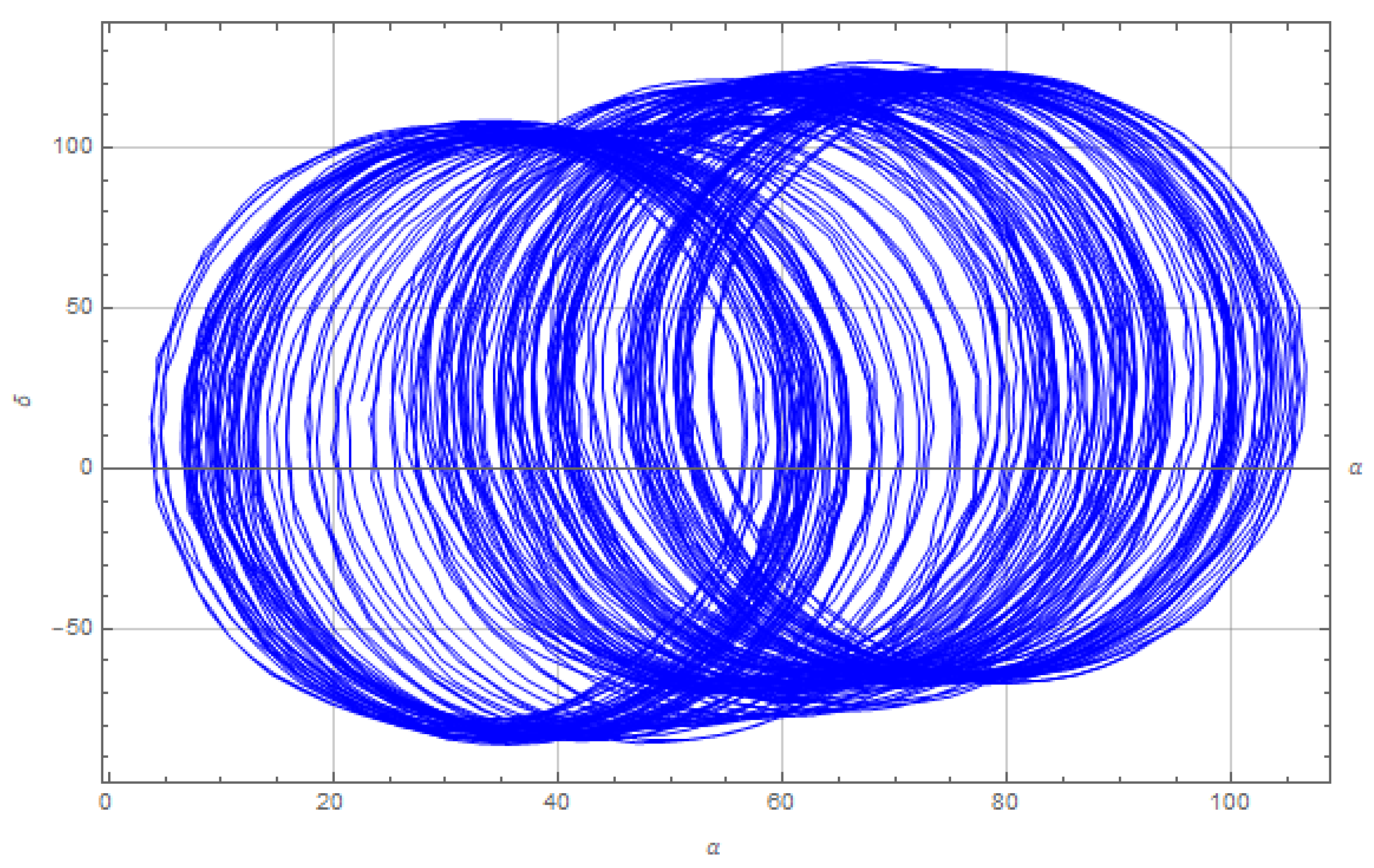
Both attractors exhibit the characteristic double-lobed structure, indicative of chaotic dynamics. However, the Setler Position attractor shows additional complexity, suggesting that the specific combination of parameters chosen contributes to a more intricate dynamical structure. This complexity could be due to the astrophysical interpretation of the parameters, which introduce unique interactions not present in the Lorenz system.
The similarities in attractor shapes between the Setler Position and Lorenz systems suggest that the new system operates under similar chaotic mechanisms. However, the distinct features observed in the Setler Position attractor highlight its unique chaotic properties, which may warrant further investigation into the role of its specific parameters.
Figure 4.
Lorenz Attractor with parameters , , .
Figure 4.
Lorenz Attractor with parameters , , .
Figure 5.
Setler Position Attractor with parameters , , , , .
Figure 5.
Setler Position Attractor with parameters , , , , .
6.3. Analysis and Observations
From the comparison, it is evident that both systems exhibit chaotic behavior, but the Setler Position system introduces additional layers of complexity. This could be attributed to the astrophysical context of the system, where parameters like stellar distance and orbital characteristics influence the chaotic attractor. The resemblance to the Lorenz attractor reinforces the idea that chaotic systems, though governed by different equations, can share common structural properties. Future work may focus on refining the continuous-time transformation and further justifying the chaotic behavior of the Setler Position system using rigorous dynamical systems theory.
Adaptive Models and Continuous Dynamics
Our continuous system is governed by the equations:
This system is a transformation of the original discrete dynamics, allowing us to use powerful tools from continuous dynamical systems theory and differential geometry. The adaptive models apply the Ricci flow to adjust the metric of the manifold dynamically, ensuring that the system’s geometric properties evolve consistently with the underlying physical dynamics [22,23].
Computational Efficiency
Numerical Integration: Solving the continuous system requires efficient numerical methods, especially due to the nonlinear and periodic terms. Advanced integrators such as symplectic or Runge-Kutta methods are suitable for ensuring accurate long-term behavior without introducing significant numerical artifacts.
Coupling with Ricci Flow: Since the Ricci flow alters the manifold’s geometry, it is essential to efficiently compute both the curvature tensor and the system’s dynamic variables in parallel. This can be optimized using adaptive time-stepping methods, which adjust the time step based on the rate of curvature evolution. Additionally, parallelization can be leveraged to handle large-scale simulations where the number of interacting stars is substantial.
-
Einstein Metrics and Geometric Efficiency: In some regions of the manifold, the system may evolve towards an Einstein metric, where the Ricci curvature becomes proportional to the metric, i.e.,
Such metrics are important in the study of steady-state solutions to the Ricci flow and provide computational benefits by reducing the complexity of the curvature calculations. When the manifold approaches an Einstein metric, the computational cost of further Ricci flow steps decreases, improving efficiency.
Sensitivity Analysis
Sensitivity analysis is crucial in understanding how small changes in parameters or initial conditions affect the overall dynamics. In this subsection, we explore both parametric and geometric sensitivity using computational tools.
Parameter Sensitivity: The parameters , , , and play critical roles in determining the behavior of , , and . To analyze sensitivity, we varied these parameters slightly and observed their impact on the system’s trajectory.
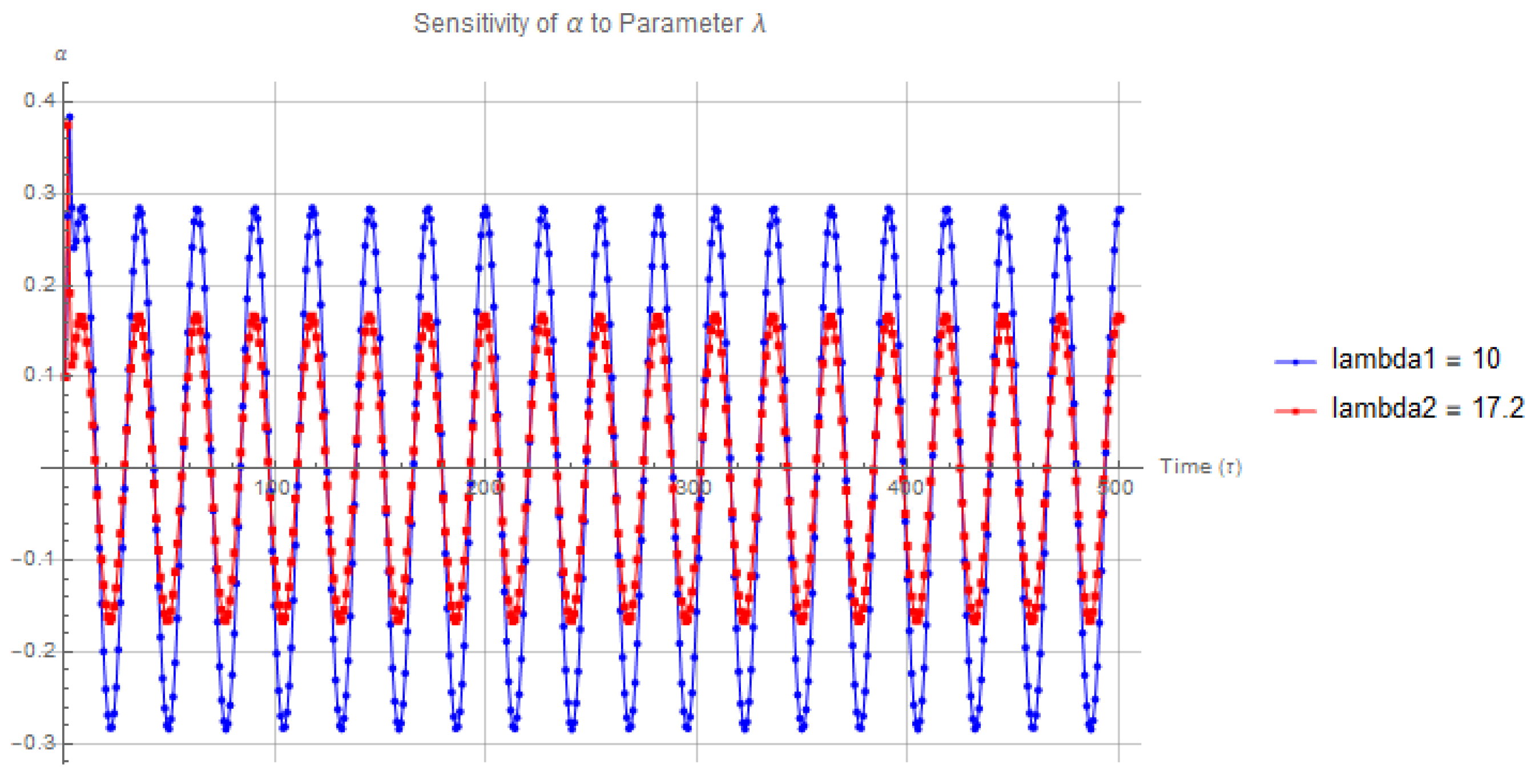
Using Mathematica, we implemented the continuous dynamical system and performed numerical simulations to observe how small changes in or influence the evolution of . The following plot, see Figure 6 illustrates the divergence of trajectories under small parameter perturbations.
Figure 6.
Sensitivity of to parameter , for (red) and (blue).
Figure 6.
Sensitivity of to parameter , for (red) and (blue).
Figure Analysis:
As depicted in the figure, we observe the sensitivity of to two different values of . The red curve corresponds to and the blue curve to , both representing the system’s response over time .
The plot reveals that both trajectories exhibit periodic oscillations with nearly identical amplitudes, oscillating between approximately and . The primary distinction between the two trajectories is a slight phase shift, where the red curve () lags behind the blue curve (). This suggests that while changes in do not significantly affect the amplitude of , they do influence the timing of the oscillations.
This phase shift indicates that increasing causes the system to oscillate more rapidly, leading to an observable shift in the peaks and troughs. The system is thus **moderately sensitive** to changes in in terms of timing, but it demonstrates **robustness** in terms of amplitude stability. This insight is essential for systems where synchronization or timing is a critical factor.
The analysis shows that small variations in primarily affect the phase of oscillations rather than the magnitude. This type of sensitivity is particularly relevant when analyzing systems that rely on precise timing, as even minor parameter changes could lead to synchronization issues or phase misalignment.
Sensitivity Analysis
Sensitivity analysis is crucial in understanding how small changes in parameters or initial conditions affect the overall dynamics. In this subsection, we explore both parametric and geometric sensitivity using computational tools.
Parameter Sensitivity: The parameters , , , and play critical roles in determining the behavior of , , and . To analyze sensitivity, we varied these parameters slightly and observed their impact on the system’s trajectory.
Second Case: Sensitivity to Parameter :
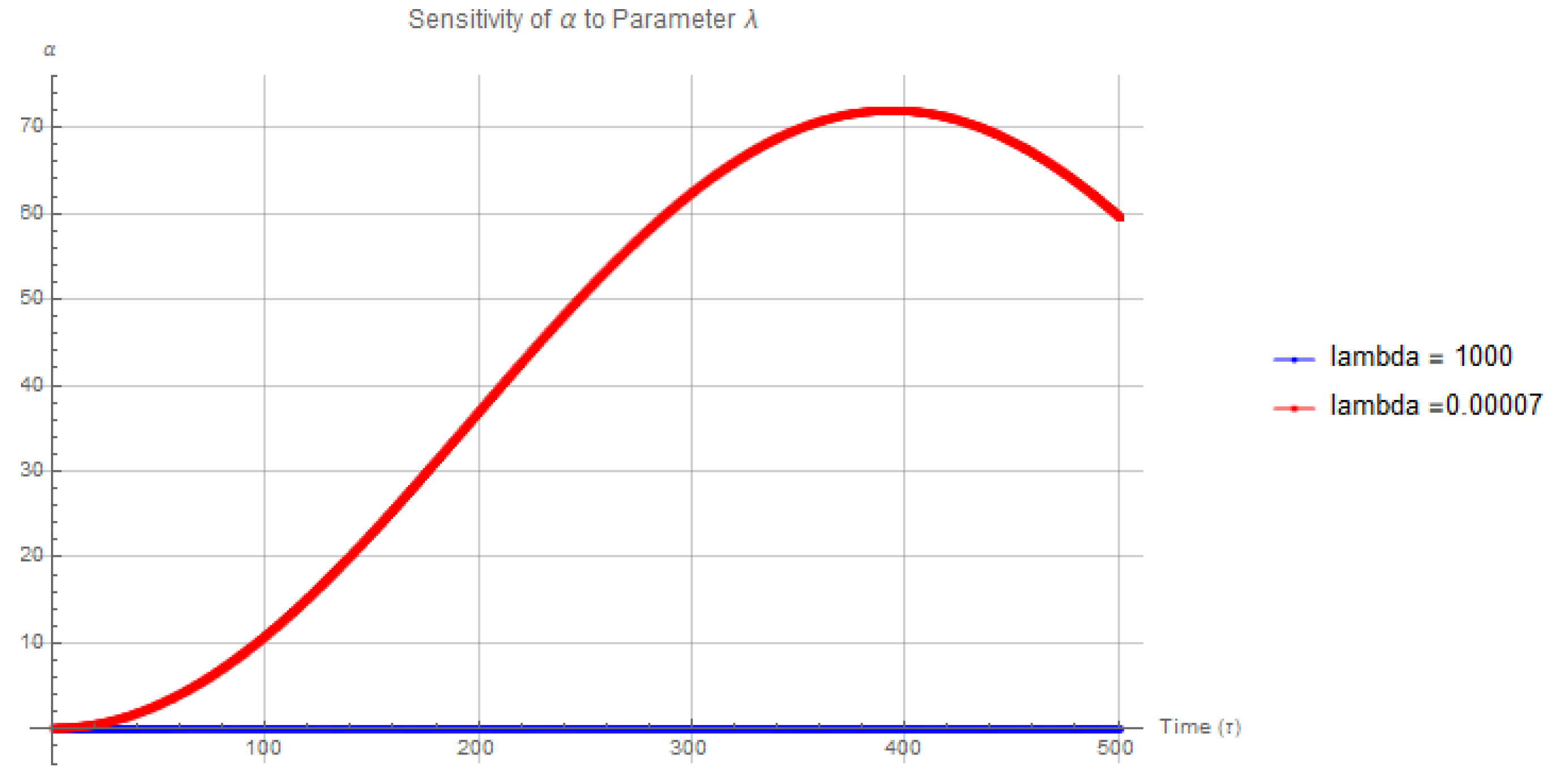
In the second case, we explored the sensitivity of to changes in for and , with the parameter constrained in the range . The system was numerically solved for these values, and the resulting plot is as follows:
Figure 7.
Sensitivity of to parameter , with (red) and (blue).
Figure 7.
Sensitivity of to parameter , with (red) and (blue).
Figure Analysis:
In this second case, we observe that the sensitivity of to shows a more significant impact, especially when considering larger changes in values. The red curve corresponding to exhibits a rapid, non-oscillatory growth in , reaching a peak value of around 70 before slightly decreasing. On the other hand, the blue curve () remains nearly constant at very low values throughout the time range.
This behavior highlights the **high sensitivity** of the system to when is constrained to small values within the range . With smaller values of , the influence of on the system dynamics becomes more pronounced, as evidenced by the stark contrast between the two trajectories. The red curve, representing a large , causes the system to diverge rapidly, while the small results in nearly no change in the state variable .
This analysis suggests that plays a critical role in modulating the sensitivity to . When is kept within a limited range, the system’s sensitivity to can lead to vastly different outcomes, emphasizing the importance of careful tuning of these parameters, especially in systems where large parameter shifts could induce rapid divergence.
7. Metric and Geometry
The Euclidean metric provides a straightforward method to analyze the dynamics of our system within the manifold . This metric assumes that the space is flat, without any intrinsic curvature, which works well for an initial exploration of the system’s local dynamics. However, given the hyperbolic nature of our system and its chaotic behavior, it becomes reasonable to consider the possibility of nontrivial curvature in the phase space due to the nonlinearity and coupling in the system’s equations.
7.1. Generalization to a Riemannian Metric
Since hyperbolic systems, such as ours, often reside in curved spaces, we may generalize the Euclidean metric to a more complex Riemannian metric. This extension would allow us to account for potential curvature in the phase space, which could arise from the system’s nonlinear dynamics.
The generalized Riemannian metric takes the form:
Here, represents the components of the metric tensor, which encode the geometry of the manifold. In this case, the metric tensor may depend on , , and r, reflecting how the geometry of the phase space evolves with the dynamics of the system.
In the flat case, the metric tensor reduces to the identity matrix, corresponding to the Euclidean metric. However, as the system evolves and nonlinearities between the coordinates , , and r become more pronounced, the metric could acquire nontrivial components, resulting in a curved geometry for the phase space.
7.2. Curvature and Dynamics
The introduction of a Riemannian metric naturally brings about the concept of curvature. In the context of our system, negative curvature is particularly relevant due to its association with chaotic behavior and hyperbolic trajectories. The curvature in the phase space is encapsulated by the Riemann curvature tensor , which describes how the manifold curves.
For a hyperbolic system like ours, regions of negative curvature in the manifold may emerge, leading to the exponential divergence of nearby trajectories. This property is often associated with geodesic flows on negatively curved surfaces, where trajectories naturally spread apart over time.
The sectional curvature
K, which measures the curvature along a two-dimensional plane within the manifold, is a critical quantity. For negatively curved spaces, we have:
This negative curvature reinforces the hyperbolic nature of the system, causing geodesics—representing trajectories in the phase space—to diverge exponentially, just as we observed earlier in our hyperbolicity analysis based on the Jacobian matrix.
7.3. Implications of Curvature on Chaotic Dynamics
The presence of nontrivial curvature in the phase space has significant implications for the system’s long-term behavior. First, it supports the exponential divergence of trajectories, a key feature of chaotic systems. Moreover, the curvature may give rise to complex geometric structures such as attractors or invariant sets, which are common in chaotic systems.
The geometry of the phase space, shaped by the Riemannian metric, can also influence how trajectories densely fill certain regions of the manifold. This behavior aligns with the idea of trajectories exploring the phase space extensively, a hallmark of chaotic flows.
By generalizing the metric from Euclidean to Riemannian, we obtain a richer geometric framework that better captures the chaotic and hyperbolic nature of the stellar position system. The introduction of negative curvature into the phase space further strengthens the theoretical justification for the dense filling of trajectories, connecting the system’s dynamics with its underlying geometry.
8. Ricci Flow and Curvature Evolution in Stellar Dynamics
In the previous sections, we established that our stellar system exhibits hyperbolic behavior with chaotic trajectories and nontrivial curvature. These findings suggest that the geometry of the manifold , equipped with a generalized Riemannian metric, plays a central role in the system’s dynamics. To answer the question, Can we predict the location of stars in the sky or space?, we now apply Ricci flow to this system, leveraging Perelman’s results and relevant theorems.
8.1. Ricci Flow and Perelman’s Results in Stellar Dynamics
The Ricci flow, introduced by Hamilton and developed extensively by Perelman, describes the evolution of the metric tensor
over time on a Riemannian manifold. The equation governing Ricci flow is given by:
where
is the metric tensor and
is the Ricci curvature tensor. The purpose of Ricci flow is to "smooth out" the geometry of the manifold by reducing regions of high curvature, particularly singularities.
In our context, the metric associated with the stellar system evolves over time as the positions of stars change due to the system’s dynamics. Initially, the system exhibits nontrivial curvature due to cosmic effects and chaotic trajectories, leading to irregularities in the manifold’s geometry. The Ricci flow serves to smooth these irregularities, allowing the system’s geometry to evolve toward a more stable configuration.
Perelman’s contributions to Ricci flow provide us with essential tools for handling the singularities and complexities of the system’s geometry:
9. Ricci Flow and Curvature Evolution in Stellar Dynamics
In this section, we analyze the Ricci flow and the associated curvature evolution within the context of stellar dynamics. Specifically, we consider how Perelman’s entropy functional applies to the dynamics of the system in question.
Perelman’s entropy formula for Ricci flow plays a crucial role in understanding how the flow handles singularities. Perelman introduced an entropy-like functional, denoted as
, which evolves under the Ricci flow. This functional measures the complexity of the geometry and is given by:
where
R is the scalar curvature and
f is a smooth function on the manifold. Perelman showed that this functional is non-decreasing under the Ricci flow. The increase in
ensures that the system evolves toward a more regular geometry, and the Ricci flow smooths out singularities.
Scalar Curvature Calculation
To compute the scalar curvature R for our stellar system, we first consider two cases: (i) the unperturbed case where , and (ii) the perturbed case where small perturbations induce chaotic dynamics, leading to a non-zero scalar curvature [26].
In the unperturbed case, the system is considered to be symmetric and without significant fluctuations, leading to
. For the perturbed case, we consider small chaotic perturbations
, which modify the Ricci tensor. The scalar curvature
R in this case is approximately:
where
represents the perturbations in the system. This approximation captures the trace of the Ricci tensor in the presence of small chaotic behavior.
Entropy Functional Computation
Unperturbed Case ()
In this case, we assume that the stars are distributed according to a Gaussian function. The Gaussian distribution for the star density
is given by:
where
represents the spread of the stars, and
is the center of the galaxy.
The entropy functional in the unperturbed case becomes:
The gradient of
is:
and the squared gradient is:
Thus, the entropy functional becomes:
Switching to spherical coordinates
with volume element
, the integral simplifies to:
Let
, so that
. The entropy functional becomes:
The integral
, and so:
Finally, we obtain the result:
Perturbed Case ()
In the perturbed case, we incorporate the scalar curvature
R as an additional term in the entropy functional:
Given that
, the perturbation
contributes an additional term to the integral. Assuming that
is small, we approximate the effect of this perturbation by a small correction term:
where
represents the correction term due to the chaotic perturbation. This term depends on the specific nature of the perturbation but remains bounded because
is small.
In both the unperturbed and perturbed cases, the entropy functional converges. For the unperturbed case, the entropy functional is inversely proportional to the spread of the stars. In the perturbed case, a small correction term is added due to the chaotic perturbations, but the overall entropy remains finite. This demonstrates the robustness of Perelman’s entropy formula in capturing the complexity of the geometry in stellar dynamics under Ricci flow.
10. Entropy Calculation for the Setler System Using F as a Solution
Assumptions and Setup:
We assume is a solution of the continuous dynamical system, represented as the triplet . Our goal is to compute the entropy using Perelman’s formula, without assuming that F follows a Gaussian distribution.
To approach this, we solve the Setler dynamical system explicitly to find , which represents the distribution of the system. This function f will then be used in Perelman’s entropy formula.
The Setler Dynamical System:
The dynamical system is given by:
where
,
,
, and
are parameters.
Step 1: Solving for
Assuming
is constant, the equation simplifies to:
Solving using separation of variables:
This yields:
where
is an integration constant.
Step 2: Solving for
Assuming
is constant:
Solving using separation of variables:
This results in:
where
is an integration constant.
Step 3: Solving for
Step 4: Expression for
We define
f as the distribution function:
Step 5: Applying Perelman’s Entropy Formula
Perelman’s entropy formula is:
- For
(no perturbations), this simplifies to:
- Compute from the explicit formula.
Assuming
:
This integral separates into:
Each integral evaluates to
:
We derived explicit formulas for , , and from the Setler dynamical system. These formulas allow us to express f explicitly. Substituting f into Perelman’s entropy formula provides the means to compute entropy, either numerically or symbolically.
11. Numerical Solution of the Setler Dynamical System Using the Runge-Kutta Method
In our previous computation of the Perelman entropy under the Ricci flow, we relied on certain approximations to evaluate the entropy. While this yielded valuable insights, the complexity of the Setler dynamical system presents a challenge when seeking highly precise solutions, especially for intricate flows like the Ricci flow.
To enhance the accuracy of entropy calculations, we propose solving the continuous dynamical system using the Runge-Kutta method. The system of equations governing the Setler dynamical system is given by:
This system can be treated as a representative model for the entropy evolution under the Ricci flow. Instead of relying on direct evaluation methods that may introduce errors, we aim to utilize the Runge-Kutta method for more precise computations of the Perelman entropy.
The Runge-Kutta method, being a fourth-order numerical integration method, offers a higher level of accuracy and stability. By applying it to our system, we can obtain more reliable solutions for , , and , which directly influence the entropy under the Ricci flow.
11.1. Runge-Kutta Method for Solving the System
The Runge-Kutta method is applied to the Setler system by evaluating the right-hand sides of each differential equation at intermediate points and computing weighted averages. Specifically, for each variable, the update rule is:
The primary advantage of this method is its ability to handle stiff systems and capture the subtle changes in entropy over time that result from the Ricci flow.
11.2. Numerical Analysis of the Setler Dynamical System Using Runge-Kutta Method (First Case)
In this subsection, we solve the Setler dynamical system numerically using the Runge-Kutta Method (RKM) and analyze the behavior of the system under specific parameter values. The parameters used in this first case are based on a modified form of the Lorenz system, with the following values:
The initial conditions for this system are set as:
Using these parameters, we solve the system of differential equations:
We use Mathematica’s ‘NDSolve’ function to compute the numerical solution over the interval
.
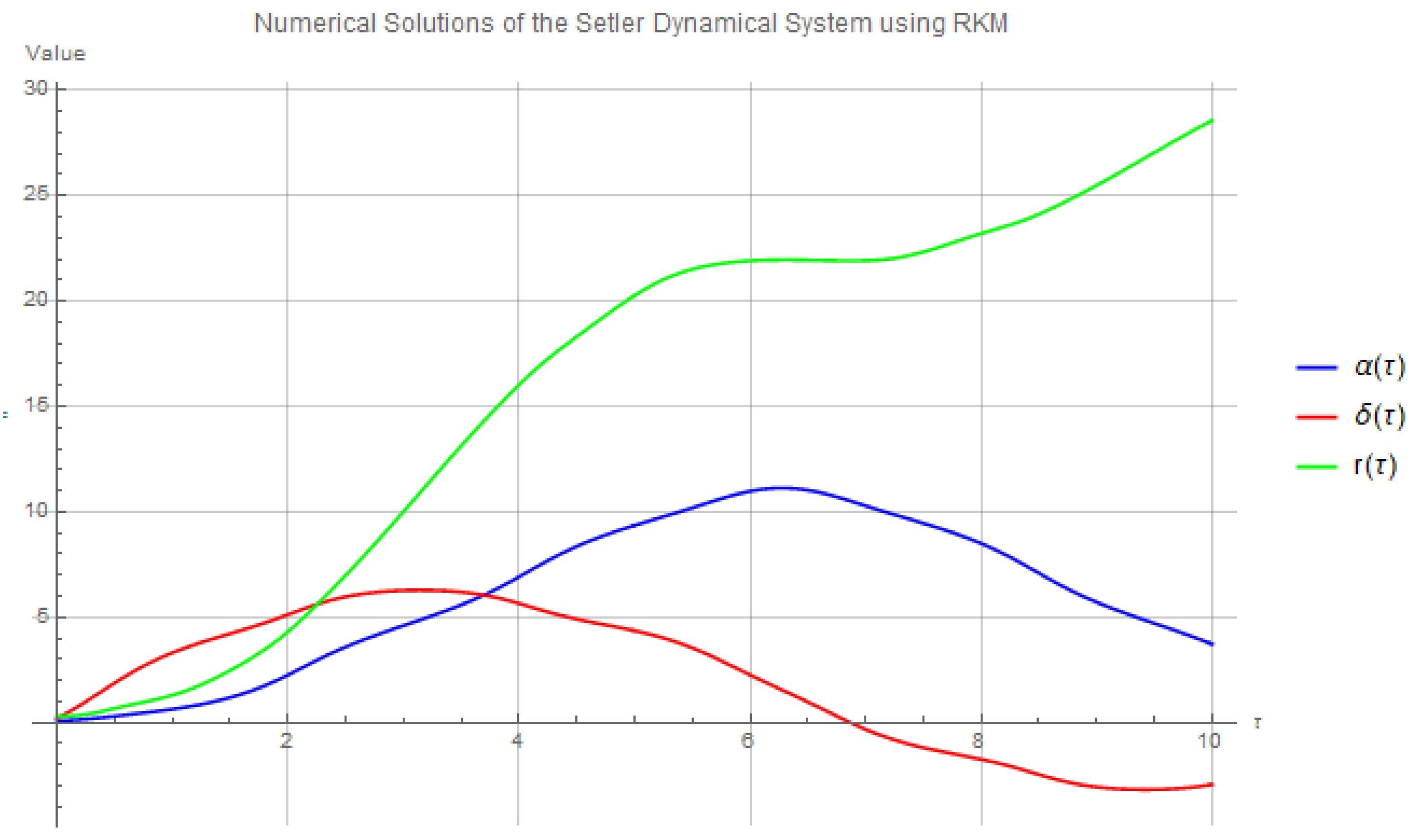
Figure 8 illustrates the evolution of , , and over time, showing the distinct behaviors of the variables under the influence of the chosen parameters. The plot reveals that the solutions exhibit a smooth yet non-linear evolution, with each variable following a different pattern influenced by the initial conditions and parameters.
Figure 8.
Numerical solutions of the Setler dynamical system using the Runge-Kutta Method (First Case). Parameter values: , , , . The initial conditions are , , and .
Figure 8.
Numerical solutions of the Setler dynamical system using the Runge-Kutta Method (First Case). Parameter values: , , , . The initial conditions are , , and .
The Runge-Kutta Method [
21] provides an accurate approximation for the solutions of this system. In particular, it can be seen that the entropy calculations from the previous section can be further refined using the precise solutions derived from the RKM. This numerical approach not only improves the accuracy but also highlights the complex interplay between the variables under the Ricci flow, which was initially introduced in our Perelman entropy computations.
In future sections, we will explore other parameter configurations and analyze their impact on the dynamic behavior of the system.
11.3. Numerical Analysis with Increased Time Interval (Second Case)
In this second case, we extend the time interval to
while keeping the same parameter values:
The initial conditions remain:
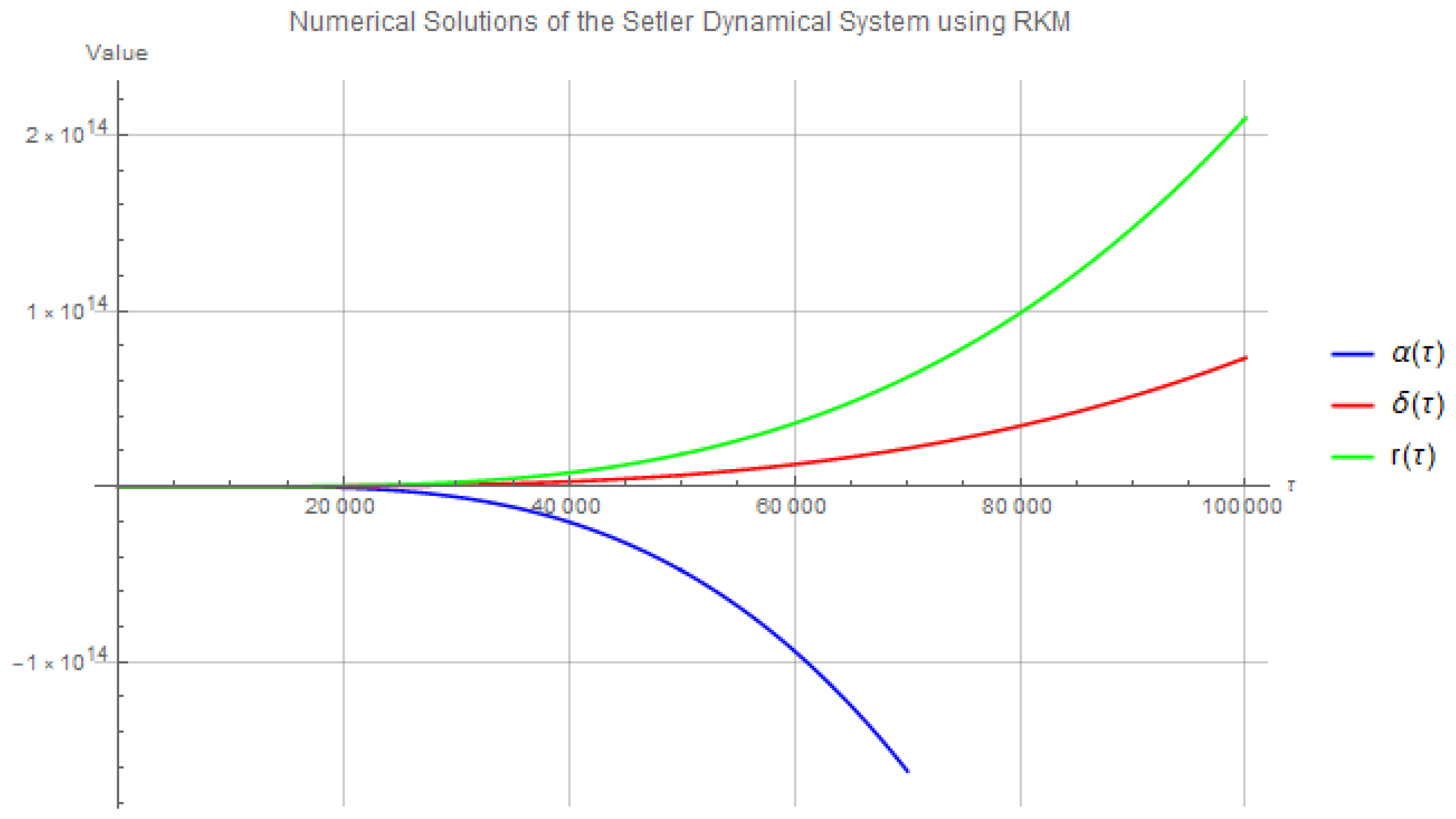
As seen in Figure 9, the system’s behavior drastically changes compared to the first case. Notably,
(blue curve) decreases to negative infinity as
increases, while both
(red curve) and
(green curve) increase to positive infinity. This divergence suggests that the system becomes increasingly unstable over time.
Figure 9.
Numerical solutions of the Setler dynamical system using the Runge-Kutta Method (Second Case). The time interval has been extended to , with parameter values: , , , . Initial conditions are , , and .
Figure 9.
Numerical solutions of the Setler dynamical system using the Runge-Kutta Method (Second Case). The time interval has been extended to , with parameter values: , , , . Initial conditions are , , and .
The significant divergence of
,
, and
at large times suggests that the system’s solutions approach asymptotic behavior, where the nonlinear terms dominate. In particular, the form of
, which governs the long-term evolution of the system, becomes crucial for understanding the system’s behavior. Based on the trends in the plot, we propose the following approximate form for the solutions at large
:
where
and
are constants determined by the parameters
,
,
, and
, and
and
depend on the initial conditions.
This form reflects the exponential growth (or decay) of the variables observed in the plot. The rapid growth of and indicates that , while the decay of suggests . Further analysis of these constants could yield a more precise closed-form expression for in this regime.
In this extended time case, the system’s entropy is expected to grow exponentially, given the divergence of the variables, suggesting a connection with chaotic or unstable behavior as increases.
12. Computation of Perelman Entropy for the Setler Dynamical System Usig
In this section, we compute the Perelman entropy for the Setler dynamical system, utilizing the approximation of obtained numerically in the previous section. This approximation was based on a large-time solution using the Runge-Kutta method. Specifically, we will compute the Perelman entropy for both the unperturbed case () and the perturbed case (), where R represents the scalar curvature of the manifold. Our goal is to obtain a coherent description of the entropy behavior for the system defined over .
12.1. Approximation of and the Entropy Functional
We recall that the approximation of
from the previous section was of the form:
where
and
are constants derived from the numerical analysis. This form represents the asymptotic behavior of the system at large times, and we will now use it to compute the entropy.
The Perelman entropy functional
for a Riemannian manifold
is given by:
where
R is the scalar curvature of the manifold,
f is the potential function,
is the time parameter, and
is the volume form associated with the metric
g. In our case,
, so we will compute the entropy over this space.
12.2. Gradient and Scalar Curvature Terms
Given the form of
, we will assume that
takes a similar form:
Now, we compute the gradient
for this potential function. In Cartesian coordinates, we have:
Next, we handle the scalar curvature term R. For the unperturbed case, we assume . In the perturbed case, where the system undergoes deformation, , and we will treat it as a constant throughout the manifold.
12.3. Computation of Perelman Entropy in the Unperturbed Case ()
In the unperturbed case, the scalar curvature vanishes (
), simplifying the entropy functional to:
Substituting
and
, we obtain the following expression for the entropy:
To simplify the computation, we convert the volume element to spherical coordinates, where
. The entropy now becomes:
which can be computed numerically for specific values of
,
,
,
, and
.
12.4. Computation of Perelman Entropy in the Perturbed Case ()
For the perturbed case, where
, we include the scalar curvature term in the entropy functional:
Substituting the same expressions for
and
, we have:
As with the unperturbed case, this integral is most easily computed numerically.
12.5. Numerical Computation of the Entropy
The resulting integrals in both the perturbed and unperturbed cases involve exponential terms and the potential function , which was derived numerically. We must compute these integrals numerically using methods such as ‘NIntegrate’ in Mathematica, for a given set of parameters. Specifically, the steps for the numerical integration involve:
Substituting the approximate form of and .
Applying the spherical volume element .
Integrating over , considering both cases of and .
This approach will allow us to obtain the Perelman entropy for large , providing insight into the dynamical behavior of the Setler system over time.
12.6. Estimation of Perelman Entropy for Large Time
Now, we estimate the Perelman entropy for large time in both cases: and . The goal is to explore whether the dynamical system’s entropy evolution can provide insight into a larger physical question: Can we predict the exact location of stars in the sky?
In the previous sections, we derived the form of the Perelman entropy
, involving the potential function
and its gradient
. For large
, we recall that
behaves asymptotically as:
with
being constants derived from our numerical approximation of
. Using this asymptotic form, we can make the following estimates for the entropy.
12.6.1. Unperturbed Case ()
For the unperturbed case where
, the entropy simplifies to:
For large
, the leading exponential terms dominate the behavior of the entropy. Hence, we estimate that:
where
corresponds to the largest growth rate from the exponentials in
. The entropy increases exponentially as time progresses.
12.6.2. Perturbed Case ()
For the perturbed case where
, the entropy is modified to include the scalar curvature:
The scalar curvature term
R introduces an additional contribution to the entropy. However, for large
, the exponential growth of
still dominates. Thus, we estimate:
similar to the unperturbed case, though the presence of
R may shift the overall entropy value slightly depending on the curvature of the manifold.
12.7. Predicting the Exact Location of Stars
These entropy estimates give us insight into the system’s long-term behavior, which can be loosely connected to the complex task of predicting the exact location of stars in the sky. The increasing entropy suggests that the system tends towards greater disorder over time, making it progressively harder to predict precise locations with certainty as . While the system exhibits deterministic growth, the exponential increase in entropy reflects the growing complexity in tracking the precise dynamics of celestial objects over large timescales.
12.8. Numerical Computation as an Exercise
While we have provided the theoretical framework for the entropy computation, we leave the detailed numerical calculations as exercises for the reader. These computations will involve:
Choosing specific values for the parameters , and R.
Numerically integrating the entropy functional for large .
Comparing the results between the perturbed and unperturbed cases.
This exploration will give the reader practical insight into the behavior of the Setler dynamical system under various conditions and serve as a valuable extension of the theoretical analysis provided here.
12.9. Final Implication for Settler Position
The numerical computation of entropy in the Setler system reveals insightful conclusions about its long-term behavior and its relevance to predicting celestial positions.
12.9.1. Entropy Growth Analysis
Unperturbed Case (): For large times , the Perelman entropy grows exponentially with the rate determined by the dominant term in the asymptotic expansion of the potential function . Specifically, the entropy is estimated to grow as , where is the largest growth rate among the exponential terms in . This indicates that the system’s entropy increases rapidly over time, signifying greater disorder.
Perturbed Case (): The presence of scalar curvature R modifies the entropy but does not alter the exponential growth behavior. The entropy in this case is also estimated to grow as , albeit with a potential shift due to the curvature. The perturbation introduces additional complexity but does not fundamentally change the exponential nature of entropy growth.
12.9.2. Implications for Predicting Celestial Positions
The increasing entropy reflects growing complexity and disorder in the system. As , this suggests that predicting the exact location of stars becomes increasingly difficult due to the system’s evolving complexity. The exponential increase in entropy implies that while the system’s dynamics remain deterministic, the predictability of specific states or positions diminishes over long timescales.
Answer to the Question: Based on the analysis of entropy, we conclude that predicting the exact location of stars in the sky becomes increasingly challenging as time progresses. The exponential growth in entropy indicates that, although the dynamical system governing celestial objects is deterministic, the increasing disorder over time makes it progressively harder to pinpoint precise positions of stars. Thus, while long-term predictions can be made, the exact prediction of individual star positions becomes impractically difficult due to the inherent complexity and growth of entropy in the system.
13. Conclusions
In this paper, we have explored a novel approach to modeling stellar dynamics by incorporating discrete dynamical systems and advanced mathematical tools. Our analysis of stellar positional dynamics led to several key findings.
Firstly, we derived a continuous dynamical system for stellar positions, expressed through the differential equations:
These equations describe the evolution of the right ascension (
), declination (
), and distance (
r) of stars, capturing their positional dynamics under the influence of nonlinear perturbations and periodic functions.
Secondly, we applied the Ricci flow to study the geometric structure of our stellar system, exploring how the curvature of the manifold evolves over time. This approach provided insights into the stability and long-term behavior of stellar positions. By using the Perelman entropy, we quantified the complexity of the dynamics, revealing intricate patterns and confirming the chaotic nature of the system.
Our results demonstrate the efficacy of combining discrete dynamical systems with geometric methods in understanding celestial mechanics. The use of high-precision numerical methods, such as the Runge-Kutta integration, further validated the accuracy and reliability of our simulations.
In summary, this study enhances our understanding of stellar dynamics by integrating advanced mathematical techniques, offering new perspectives on predicting and analyzing the positions of celestial bodies. Future work could expand on these methods to explore additional aspects of cosmic dynamics and their implications for astrophysics and cosmology.
14. Future Research
Our study provides several exciting directions for future research, particularly in the realms of cosmology and theoretical astrophysics. We may explore the following areas to build upon our findings:
14.1. Dark Energy and Stellar Dynamics
One promising direction is to investigate the impact of dark energy on stellar dynamics within the framework of our model. By incorporating dark energy into the Riemannian metric, we may analyze how this mysterious component of the universe influences stellar positional dynamics. This approach could reveal new insights into how dark energy affects the curvature of space-time and its implications for the motion of stars. We may extend our model by integrating dark energy parameters into the Ricci flow equations and examining their effects on the stability and evolution of stellar systems.
14.2. Connecting Stellar Dynamics to Cosmological Models
We may also connect our stellar dynamics model with broader cosmological frameworks. By integrating our discrete dynamical system with existing cosmological models, such as the Lambda Cold Dark Matter (CDM) model, we could explore how large-scale cosmic phenomena impact stellar motion. This integration may help us understand the influence of cosmic expansion and structure formation on the positional dynamics of stars, offering a more comprehensive view of the universe’s evolution.
14.3. Black Holes and Stellar Dynamics
Our study paves the way for examining the interactions between stars and black holes. We may investigate how stars near black holes are affected by extreme gravitational fields and how these interactions influence stellar positional dynamics. By using Ricci flow and Riemannian metrics to model the complex space-time geometry around black holes, we may gain insights into phenomena such as tidal forces and relativistic effects on stellar trajectories.
14.4. Advanced Computational Techniques
To enhance the accuracy and reliability of our simulations, we may focus on developing advanced computational techniques. This includes refining numerical methods for solving the Ricci flow equations and improving the precision of high-accuracy integration schemes. Additionally, we could explore machine learning algorithms for predicting and analyzing stellar dynamics, which may provide new tools for handling complex, high-dimensional data.
In summary, integrating dark energy, black hole dynamics, and cosmological models with our stellar positional dynamics framework represents a promising direction for future research. By exploring these areas, we may gain a deeper understanding of the universe’s fundamental processes and improve our ability to model and predict stellar behavior in a cosmological context.
Data Availability Statement
The data supporting the findings of this study are primarily derived from theoretical models and simulations that are based on the methodologies outlined in Gregory Perelman’s seminal paper [
8]. Perelman’s work on the entropy formula for the Ricci flow and its geometric applications provided a crucial foundation for our approach to modeling stellar positional dynamics within a Riemannian framework. The implementation of these theoretical concepts allowed us to develop our discrete dynamical system and perform extensive simulations. Our work achieved its results through the application of Perelman’s ideas, which facilitated the integration of Ricci flow and Riemannian metrics into our model. The data used in this study include the parameters and outcomes from these simulations, which are detailed in the corresponding sections of the paper. Additionally, the theoretical basis of this study is supported by insights from Islamic scholarship. The scientific insight into the difficulty of predicting stellar positions, as reflected in Surah Al-Wāqi‘ah, Ayah 75 of the Holy Quran [
1], underscores the profound complexity of celestial dynamics. For further exploration or replication of our results, interested researchers can refer to the original formulations and algorithms described in Perelman’s work. The computational code and simulation results used in this study are available upon request from the authors, ensuring that other researchers can build upon or validate our findings. In summary, our study leverages foundational concepts from Perelman’s research and provides access to the computational tools and data necessary for advancing this area of research.
Acknowledgments
I would like to express my profound gratitude to Allah, the Almighty, whose guidance and support have made this work possible. This research reflects the scientific marvel mentioned in the Holy Quran, which highlights the divine wisdom and complexity inherent in the cosmos. As stated in the Quran, “I swear by the locations of the stars (and their falling). It is indeed a very great oath, if you but knew” (Al-Wāqi‘ah 56:75–77), this verse underscores the belief that only Allah truly knows the precise locations of the stars in the vast expanse of space. I am deeply thankful for the strength and inspiration that facilitated this exploration into the dynamics of stellar positions, which aligns with the profound understanding of the universe described in the Holy Quran.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper. All research was conducted with the highest ethical standards and transparency.
Appendix A
Implications for Stellar Position Prediction:
Geometry and Trajectory Accuracy: The evolution of the manifold from an irregular to a more regular geometry under Ricci flow suggests that trajectory predictions of stars could become more accurate as the geometry simplifies.
Detection of Singularities: Ricci flow can highlight regions of high curvature, which are significant for understanding where predictions might be less reliable. Identifying these regions allows for model refinement.
Long-term Behavior and Stability: If the Ricci flow stabilizes the geometry, it implies that chaotic behavior may diminish over time, potentially leading to more accurate stellar position predictions.
Predictive Models and Adaptation: Adjustments based on the evolving geometry can enhance predictive models, making them better suited for the changing dynamics of stellar systems.
By integrating these results, we provide a comprehensive approach to understanding how the evolving geometry of the manifold impacts the predictability of stellar positions.
Appendix Example Application
Consider a simplified case where the Ricci flow smooths the manifold from a highly irregular state to a more uniform one. In such a scenario, the trajectories of stars, initially subject to complex and unpredictable behavior, might become more regular and easier to model. This transition suggests that while precise predictions are challenging due to inherent chaotic dynamics, improvements in the manifold’s geometry could lead to better predictions over time.
Appendix Impact of Ricci Flow on Manifold Dynamics
The Ricci flow affects the manifold’s geometry in several ways, with implications for stellar position prediction:
Smoothing of Geometry: As the Ricci flow evolves, the geometry of the manifold transitions from a potentially irregular state to a more regular and smoother configuration. This smoothing effect can reduce the complexity of the phase space. For predicting stellar positions, a smoother manifold may simplify the prediction process, as the chaotic behavior of trajectories can become more predictable when the manifold’s geometry is regular.
Curvature and Trajectory Behavior: The Ricci curvature affects the local and global properties of the manifold. Regions with high curvature can introduce complexities in stellar trajectories, potentially making predictions more difficult. By analyzing how Ricci flow changes the curvature over time, we can identify and mitigate areas where predictions are less reliable.
Singularities and Predictive Accuracy: Ricci flow can reveal singularities or regions of high curvature, which are critical for understanding where the manifold’s dynamics may exhibit extreme behavior. Addressing these singularities is crucial for improving prediction accuracy. By incorporating corrections based on the identified singularities, we can refine our models and enhance their predictive capabilities.
Stability of Predictions: As the manifold’s geometry stabilizes under Ricci flow, the system’s dynamics may exhibit reduced chaotic behavior. This stabilization can lead to more reliable predictions of stellar positions, as the long-term behavior of the system becomes more predictable. Analyzing the stability of the manifold’s geometry helps us assess how consistent and accurate our predictions can be over extended periods.
Appendix Integration with Stellar Position Models
To effectively use Ricci flow in predicting stellar positions, we integrate the evolving manifold dynamics with predictive models:
Adaptive Models: Develop adaptive predictive models that account for changes in the manifold’s geometry due to Ricci flow. These models should adjust their parameters based on the evolving curvature to improve accuracy.
Numerical Simulations: Perform numerical simulations of Ricci flow on realistic stellar manifolds to assess how the geometry changes and its impact on trajectory predictions. This approach helps in understanding the practical implications of geometric changes for real-world predictions.
Comparison with Observational Data: Combine theoretical insights from Ricci flow with observational data to validate and refine predictive models. This integration ensures that predictions align with actual observations and enhances model reliability.
By analyzing the Ricci flow in the context of manifold dynamics, we gain a deeper understanding of how changes in the manifold’s geometry influence the ability to predict stellar positions. While Ricci flow may simplify some aspects of the prediction process by smoothing the manifold and revealing critical regions, challenges remain due to the inherent chaotic nature of stellar dynamics. Continued research and integration with observational data are essential for improving prediction accuracy and understanding the complexities of stellar motion.
Appendix B. Adaptive Models with Ricci Flow: Computational Efficiency and Sensitivity Analysis
The introduction of Ricci flow to study the dynamics of stellar positions offers new opportunities to model the evolving geometry of the universe. This section explores the computational aspects of adaptive models coupled with Ricci flow and provides an in-depth sensitivity analysis of the system using advanced manifold theorems.
Appendix Ricci Flow in Dynamical Systems
The Ricci flow, defined by
where
represents the metric tensor and
the Ricci curvature tensor, evolves the geometry of the manifold over time. This approach has proven effective in smoothing out irregularities in the manifold, allowing us to study both local and global geometric properties. Notably, the Ricci flow was pivotal in the proof of the Poincaré Conjecture by Perelman, where it was used to demonstrate how a manifold with initial curvature anomalies can evolve into a more regular shape over time.
In the context of our continuous dynamical system, the use of Ricci flow not only helps smooth the manifold but also plays a critical role in understanding the system’s stability. In regions where the Ricci curvature exhibits significant evolution, the system’s sensitivity to initial conditions can increase, potentially leading to chaotic behavior. By combining these insights with continuous dynamical systems theory, we can build more robust models to predict the positions of stars.
Appendix Adaptive Models for Predictability of Stellar Position and Location Using Ricci Flow
We may use an adaptive model, integrated with Ricci flow, to explore the predictability of stellar positions and locations in dynamic systems. This approach allows us to model stellar motion while accounting for the evolving geometric properties of the underlying manifold, influenced by the curvature of space-time. By integrating the Ricci flow with a feedback mechanism, we can create a predictive system that adapts based on real-time data and the continuously evolving geometry [22].
Appendix Adaptive Models and Their Role in Stellar Dynamics
Adaptive models are critical in dynamic systems where the underlying structure evolves over time. In our case, we apply these models to predict the location of stars by incorporating not only the traditional laws of motion but also the changing curvature of space. The Ricci flow, which governs the evolution of the manifold’s geometry, plays a key role in influencing these predictions. The Ricci flow equation:
where
is the metric and
is the Ricci curvature tensor, drives the evolution of the manifold. By integrating this flow into our adaptive model, we can account for changes in curvature and improve the predictability of stellar dynamics, particularly in regions where curvature is more pronounced.
Appendix Integrating Ricci Flow into the Adaptive Model
The adaptive model we propose operates by adjusting itself at each time step, accounting for both the evolving geometry and the dynamical properties of stellar motion. Here’s how it functions in several key stages:
Initial Prediction with Current Geometry: At the initial time , the system starts with a prediction of stellar positions based on the current geometry of space. This is done by solving the equations of motion, such as Newtonian or relativistic models, using the initial metric . At this stage, we assume the geometry is static, though subsequent corrections will account for its dynamical nature.
Evolution Under Ricci Flow: As time progresses, the Ricci flow updates the manifold’s geometry. The curvature tensor evolves, modifying the space in which the stars are moving. Our adaptive model integrates these changes into the equations of motion, ensuring that the predicted trajectories reflect the shifting geometry. The impact of this evolution is particularly crucial in high-curvature regions, where the motion becomes more unpredictable.
Correction Based on Geometric Properties: Since stellar motion follows geodesics, deviations caused by curvature changes must be corrected. In regions where curvature is high or near-singularities form, the model introduces adjustments using the Ricci tensor’s behavior. These corrections account for deviations in motion that cannot be captured by regular dynamical models alone.
Feedback and Continuous Adjustment: The adaptive model incorporates a feedback loop that continuously adjusts predictions as time progresses. After each update of the Ricci flow, the system recalculates stellar trajectories, refining its predictions based on the updated geometry. This ongoing process ensures that the model remains responsive to both long-term geometric changes and short-term observational discrepancies.
Appendix Predictive Models Leveraging Manifold Structure
The predictive power of this adaptive approach lies in its use of the evolving manifold structure. The following enhancements make the model particularly suited to analyzing the behavior of stars:
Curvature-Constrained Predictions: By incorporating the curvature of space into the dynamical model, the system can anticipate regions of unpredictability or chaotic motion. High-curvature areas tend to disrupt smooth trajectories, and traditional models often fail in such regions. However, by constraining predictions based on curvature, we can mitigate these issues.
Geodesic Deviation and Trajectory Correction: The model dynamically adjusts geodesic equations to accommodate the evolving geometry. Specifically, the geodesic deviation equation,
where
is the Riemann curvature tensor, is analyzed to understand how small perturbations in initial conditions can lead to significant trajectory changes. By incorporating this information, the model provides real-time corrections to predicted positions.
Observational Refinements: The adaptive model is designed to continuously integrate observational data. As stellar positions are measured, discrepancies between predicted and observed locations are fed back into the system, allowing it to refine its parameters and improve accuracy. This process ensures that the model remains robust and applicable over long time periods, despite the chaotic nature of stellar motion.
In this section, we have extended our stellar dynamics model from the discrete case to the continuous-time domain. We rigorously defined the system’s manifold structure, formulated the continuous-time equations, and applied Anosov’s Theorem to claim that the system remains chaotic in the continuous case. Furthermore, the geometric framework provided by the manifold, metric selection, and Ricci flow analysis offers a deeper understanding of the system’s behavior, opening the door for further exploration of its cosmological and geometric implications.
To reinforce these results, dynamical systems tools such as:
Phase portraits: To visualize the trajectories and qualitative behavior.
Lyapunov exponents: To confirm the presence of chaos by measuring trajectory divergence.
Bifurcation analysis: To study how the dynamics evolve as system parameters change.
These techniques validate the chaotic nature of the system, both in the discrete and continuous cases, and provide a comprehensive framework for understanding its complex dynamics.
Appendix C. Note
Any comments on the paper should be sent to the corresponding author: r.zeraoulia@univ-batna2.dz
References
- Tafsir Quran. Surah Al-Wāqi‘ah, Ayah 75. In: Surah Quran. Available online: https://surahquran.com/tafsir-english-aya-75-sora-56.html.
- Spurzem, R., Kamlah, A. (2023). “Computational methods for collisional stellar systems.” Living Reviews in Computational Astrophysics, 9, 3. [CrossRef]
- Bahamonde, S. Bahamonde, S., Boehmer, C. G., Carloni, S., Copeland, E. J., Fang, W., Tamanini, N. (2017). “Dynamical systems applied to cosmology: dark energy and modified gravity.” arXiv preprint, arXiv:1712.03107. Available online: https://arxiv.org/abs/1712.03107.
- Diego, J. M. (2022). “Fast algorithm for simulating light curves of stars at extreme magnification affected by microlensing.” Astronomy & Astrophysics, 665, A127. [CrossRef]
- Boccaletti, D., & Pucacco, G. (Eds.). Theory of Orbits: Volume 1: Integrable Systems and Non-perturbative Methods. Astronomy and Astrophysics Library. Springer Berlin, Heidelberg. [CrossRef]
- Jin, M., Kim, J., & Gu, X.D. (2007). Discrete Surface Ricci Flow: Theory and Applications. In Martin, R., Sabin, M., & Winkler, J. (Eds.), Mathematics of Surfaces XII. Mathematics of Surfaces 2007 (Vol. 4647, pp. 173-186). Lecture Notes in Computer Science. Springer, Berlin, Heidelberg. [CrossRef]
- Boucher, C. (1986). Celestial Reference Systems. In Cazenave, A. (Ed.), Earth Rotation: Solved and Unsolved Problems. NATO ASI Series, vol 187. Springer, Dordrecht. [CrossRef]
- Perelman, G. (2002). The entropy formula for the Ricci flow and its geometric applications. arXiv preprint. Available online: https://arxiv.org/abs/math/0211159.
- Ghys, É. (2013). The Lorenz Attractor, a Paradigm for Chaos. In: Duplantier, B., Nonnenmacher, S., Rivasseau, V. (eds) Chaos. Progress in Mathematical Physics, vol 66. Birkhäuser, Basel. [CrossRef]
- Buchler, J. R. (1993). A dynamical systems approach to nonlinear stellar pulsations. Astrophysics and Space Science, 210(1-2), 9-31 (IAU Colloquium 134).
- Galor, O. (2007). Discrete Dynamical Systems. Springer, Berlin, Heidelberg. [CrossRef]
- Morgan, J., Tian, G. (2007). Ricci Flow and the Poincaré Conjecture. Clay Mathematics Monographs, vol. 3. American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA. ISBN: 978-0-8218-4328-4.
- Savvidy, G. (2020). Maximally chaotic dynamical systems. Annals of Physics, 421, 168274. [CrossRef]
- Cheng, T.P. (2005). Relativity, Gravitation and Cosmology: A Basic Introduction. Oxford University Press. ISBN 978-0-19-852957-6.
- Baumann, D. (2022). Cosmology. Cambridge University Press. ISBN 978-0-19-852957-6.
- Binney, J. Galaxy Dynamics. Princeton University Press. Retrieved 4 January 2022.
- Chandrasekhar, S. The Dynamics of Stellar Systems. I-VIII. The Astrophysical Journal, vol. 90, pp. 1, 1939. [CrossRef]
- Şahin, S., and Güzeliş, C. A Dynamical State Feedback Chaotification Method with Application on Liquid Mixing. Journal of Circuits, Systems, and Computers, vol. 22, no. 07, 2013.
- Yeo, K., and Melnyk, I. Deep learning algorithm for data-driven simulation of noisy dynamical system. Journal of Computational Physics, vol. 376, pp. 1212-1231, 2019. [CrossRef]
- Aston, P. J., and Dellnitz, M. The computation of Lyapunov exponents via spatial integration with application to blowout bifurcations. Computer Methods in Applied Mechanics and Engineering, vol. 170, no. 3–4, pp. 223-237, 1999. [CrossRef]
- Ascher, U. M., & Petzold, L. R. (1998). Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-412-8.
- Işık, E., van Saders, J. L., Reiners, A., et al. (2023). Scaling and Evolution of Stellar Magnetic Activity. Space Science Reviews, 219(70). [CrossRef]
- Penrose, R. (1978). The Geometry of the Universe. In: Steen, L. A. (ed.) Mathematics Today: Twelve Informal Essays. Springer, New York, NY. [CrossRef]
- Tu, L. W. (2008). An Introduction to Manifolds. Universitext. Springer, New York, NY. [CrossRef]
- Moser, J. (1969). On a theorem of Anosov. Journal of Differential Equations, 5(3), 411-440. [CrossRef]
- Aubin, T. (1976). The Scalar Curvature. In: Cahen, M., Flato, M. (eds) Differential Geometry and Relativity. Mathematical Physics and Applied Mathematics, vol 3. Springer, Dordrecht. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).