Prerpints.org logo
Preprint
Article

Insider Threat Detection Form Irregular Login Patterns with Metaheuristic Optimized AdaBoost

Altmetrics

Downloads

64

Views

19

Comments

0

Submitted:

18 September 2024

Posted:

20 September 2024

You are already at the latest version

Alerts
Abstract
This paper addresses a critical concern in intrusion detection within the broader realm of cyber security, particularly focusing on login activity involving the majority of normal users. Utilizing the AdaBoost classifier, the study employs various optimizers to enhance performance by selecting optimal control parameters. A specially tailored version of Crayfish Optimization Algorithm (COA) is introduced to cater to the unique requirements of this investigation. Through a comparative analysis of a simulated publicly available dataset, models optimized by the modified algorithm demonstrate superior outcomes, achieving an accuracy of 94.6128% and displaying an adaptive convergence rate capable of navigating local minima to identify optimal solutions. The best-performing model undergoes SHapley Additive exPlanations (SHAP) analysis to identify key contributing features. Limitations arise from the computational intensity of the optimization process, necessitating consideration of limited populations and smaller numbers of estimators during simulations. Future endeavors will extend the methodology to incorporate additional user actions in classification, with a focus on addressing computational constraints as hardware advancements occur. Proposed, modified algorithm could be applied to deal with various optimization tasks, beyond the scope of this study.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In modern, complex information systems, cyber security intrusion detection plays an ever-increasingly important role [1]. Ransomware attacks and data breaches, often initialized by insiders [2], cost organizations millions with many institutions being forced to shut down due to loss of trust or finance. Due to the ever-evolving topology of cybersecurity, administrators and security specialists often struggle to keep up with new developments [3].
One promising approach, capable of adapting to the changing landscape of security in the digital realm is the application of artificial intelligence (AI). Algorithms from this class have ability to discern patterns and effectively learn from observations of data. This allows the application and adaptation of AI with minimal programming required. Additionally, algorithms learn from new data and are therefore capable of adapting to new developments as well [4].
There are several challenges to the proper application of AI in cyber security. The first one is data availability. Companies are often hesitant to make data concerning attacks publicly available and therefore real-world data is scarce. The second challenge is associated with parameter selections. Namely, algorithms are often designed with good general performance in mind, however, to be well suited to a specific task, parameter tuning is required in order to adjust the algorithm to the available data. This process can often be NP-hard due to the large search spaces when considering options for parameters.
A class of algorithms often selected by researchers to tackle hyperparameter tuning are metaheuristic algorithms [5]. These algorithms take a randomness-driven approach and often borrow inspiration from search strategies observed in nature to handle and guide optimizations toward an optimal solution. These algorithms have even been shown to tackle NP-hard problems with acceptable results and within realistic time constraints, however, a true optimal solution is not guaranteed.
This work seeks to explore the potential of the AdaBoost classifier in order to handle detection of insider threats within an organization. A publicly available simulated cyber security dataset is used, and user login patterns are analyzed in order to detect malicious actors. Additionally, a modified version of the recently introduced crayfish optimization algorithm (COA) [6] is introduced specifically for the needs of this study.
The main contributions of this work can be outlined as the following:
  • This is proposal for new insider threat detection framework based on the AdaBoost algorithm to boost institution cyber security,
  • We present a novel, modified version of the COA designed to overcome some of the observed shortcomings of the original,
  • We have conducted evaluation of several contemporary optimizers in order to determine their advantages and disadvantages when optimizing AdaBoost for cyber security.
Proper management of cyberspace refers to the application of the following principles: responsibility, transparency, rule of law, participation of the entire audience in cyberspace, institutional responsiveness, effectiveness of institutional and individual roles, as well as efficiency in operations. The basic problem in ensuring cyber security is the definition of legal norms and institutions that would monitor the flow of data and actions in cyberspace, as well as ensure the privacy rights of users. U.S. Congress still struggles to establish a system that provides essential privacy protection while retaining investigative capabilities [7]. Cybersecurity and privacy protection are subjects of intensive research [8], as well as governments’ considerations around the world. In 2023 Australia has established its 2023-2030 Australian Cyber Security Strategy [9].
The interconnected nature of cyberspace, "without borders", poses a real problem for the traditional framework of territorial application of laws [10]. Data and cyber activities are generated on servers that may fall under the jurisdiction of one state, while users or cyber victims may fall under the jurisdiction of another state or legal system [11].
It is often considered that laws applicable to offline activities should also apply to online activities, but clear characterization of such actions in practice is difficult to achieve. Cybersecurity raises complex legal questions primarily related to the right to privacy and freedom of expression. This complexity is further compounded by public-private collaboration and the related legal issues concerning responsibility and control. The issue of monitoring activities and data flows is complicated due to the diverse nature of actors involved in cyberspace. According to the broadest understanding, national oversight institutions oversee the work of various agencies or functional lines of administration. Consequently, state-level parliamentary committees may oversee the work of intelligence services, armed forces, or judicial bodies. On the other hand, public-private collaboration in the field of cybersecurity goes beyond the boundaries of individual agencies, leading to a collision of expert understandings of cyber activities and surveillance mandates. The consequence of this collision is the existence of a large number of cases where surveillance is either inadequate or nonexistent. Regarding the overlap of responsibilities and control, the procedures of each government agency are linked in a chain of accountability from the first to the last.
In cyberspace, chains of command can be disrupted by the involvement of private actors and the establishment of public-private collaboration mechanisms. In practice, there may be IT companies that engage with government agencies and work exclusively for the state, but this relationship is often much more complex and obscured by numerous information asymmetries that reduce transparency and hinder the smooth and successful functioning of surveillance and control mechanisms [12].
The oversight boards in each government should control the government agencies for which they are directly responsible. In this way, there may be an omission of private partners of these agencies from the oversight space, even in cases when they are directly funded or closely collaborate with these agencies. The technical specificity of characterizing cyberspace further complicates the traditional problems faced by national parliamentarians tasked with overseeing the security sector, leading to reduced effective accountability. Difficulties in reliably identifying perpetrators of cybercrimes can lead to hindered or even nonexistent accountability of the security sector to civilian authorities, contributing to a culture of impunity for these criminal acts. Thus, the judicial sector may grant special powers to law enforcement and intelligence agencies through issuing search warrants. This fact is particularly important in the context of communication interception. In practice, judicial oversight is often circumvented or restricted for reasons of national security preservation under emergency conditions.
As a model of good legislation, we can mention the National Cyber Security Strategy of Sweden from 2016, which regulates issues from the legal regulation of ICT to the protection of critical infrastructure. However, it seems that there is not just one committee or subcommittee dealing solely with cybersecurity. Unlike most national cybersecurity strategies, the Swedish strategy includes strategic principles and an action plan that helps parliament hold both public and private actors accountable in the process of controlling cyber security. The principle of the rule of law is interpreted by international courts, such as the European Court of Human Rights (ECHR). This court has developed a rule-of-law test stating that "all restrictions on fundamental rights must be based on clear, precise, accessible, and predictable legal provisions and must pursue legitimate aims in a manner that is necessary and proportionate to the aim in question, and there must be an effective, preferably judicial, remedy". Consequently, authorities in states demand that private companies who own social media platforms ensure that their services do not harbor violent extremists and terrorists. To meet these demands, governments [13], and private companies holding social media, have developed specific terms and codes of conduct to control the content posted on these platforms, and generally, apply legal rules in the digital world. In this way, they have de facto established rules and norms on the Internet. However, these terms and rules are not the same on all platforms, creating ambiguity and legal uncertainties regarding the type of content prohibited on each platform.
Hackers and various agencies routinely engage in eavesdropping on private conversations and intercept them at the "back door". In other words, when it comes to state security, there is no truly established need for the application of the rule of law, although we have at least basic principles that could form the basis of such an important part of the universal fortress of human rights. With the increasing partnership between law enforcement agencies and intelligence and security services, this weakening of the rule of law threatens to spread and be transferred to the police and prosecutors. The lack of clear legal frameworks in this area, both domestically and internationally, poses an additional threat to the rule of law on the Internet and in the global digital environment [14].
Numerous existing approaches attempt to address cyber security, with traditional techniques like firewalls [15] and block lists proving useful over time [16]. However, rapid developments and the emergence of zero-day [17] vulnerabilities make it challenging for administrators to keep up with attackers. To adapt to the fast-paced information age, new techniques are imperative.
IoT networks are frequent targets for DDoS and DoS attacks [18], where relatively simple devices can disrupt operations on a massive scale and compromise information about their environment and users. Additionally, insider actors seeking revenge for perceived unfair treatment pose a significant threat vector [19].
A noticeable research gap exists in insider threat detection, creating a void in the field. This investigation aims to explore the potential of AI for preventing insiders from causing harm to organizations by focusing on user behavior classification. By addressing this gap, the research contributes to advancing methods that can better safeguard against evolving cyber security challenges, particularly in the context of insider threats.
AdaBoost [20] utilized an iterative approach in order to cast an approximation of the Bayes classifier. This is done by combining several weaker classifiers. From a starting point of an unweighted sample used to train the model, this approach builds a group of classifiers. If a miss classification occurs, the weights of each classifier are reduced and if a correct classification is made weights are incremented. The error of a weak classifier εt can be determined as given by Equation (1):
ε t = ∑ i = 1 N ω i , t I h t x i ≠ y i ∑ i = 1 N ω i , t ,
where εt denotes the weighted error of the weak learner in the t-th iteration. The variable N represents the number of training instances. The term ωi,t corresponds to the weight of the i-th instance in the t-th iteration. The expression ht(xi) signifies the prediction made by the weak learner for the i-th instance in the t-th iteration. The variable yi represents the true label of the i-th instance. Additionally, the function I(·) is an indicator function that equals 1 if the condition within the parentheses is true and 0 otherwise.
Further classifiers are built based on the attained weights and the weight adjustment process is repeated. Large groups of classifiers are usually assembled in order to create accurate classification. A score is given to each of these sub-models, and a linear model is constructed by their combination. The classifier weight in the ensemble can be determined according to Equation (2):
α t = 1 2 ln 1 − ε t ε t
where weight αt, assigned to each weak learner in the final ensemble, is calculated based on its performance. It depends on the weighted error εt and is used to determine the contribution of the weak learner to the final combined model. To update weights Equation (3) is used:
ω i , t + 1 = ω i , t exp − α t y i h t x i ,
where ωi,t represents the weight of the i-th instance in the t-th iteration, αt denotes the weight of the weak learner in the t-th iteration, yi stands for the true label of the i-th instance, and ht(xi) signifies the prediction of the weak learner for the i-th instance in the t-th iteration.
AdaBoost algorithm is well suited to binary classification problems. However, it does struggle with multi-class classification problems. As the challenge in this work is a binary classification problem, this algorithm is selected for optimization.
Hyperparameter selection can often be difficult in practice. There is currently no unified approach for selection. Researchers often resort to computationally expensive complete search techniques or a trial-and-error process. When dealing with a mixed set of parameters this challenge can quickly form a mixed NP-hard problem. Therefore, techniques capable of addressing this category of challenge are required.
Taking a heuristic approach is often preferable. Metaheuristic optimizers have demonstrated ability to handle NP-hard problems, often drawing inspiration from natural phenomena. Some notable examples include the genetic algorithm (GA) [21], particle swarm optimization (PSO) [22], firefly algorithm (FA) [23], sine cosine algorithm (SCA) [24], whale optimization algorithm (WOA) [25], reptile search algorithm (RSA) [26] and COLSHADE [27]. The driving reason for so many algorithms comes from the no free-lunch theorem of optimization (NFL) [28] that states that no single approach is perfectly suited to all challenges and across all metrics. Therefore, constant experimentation is needed to determine the most suitable optimizer for a given task.
Hybridization of existing algorithms is a popular approach for researchers to overcome some of the observed drawbacks of optimizers. Metaheuristics is successfully applied in several fields of optimization, including finance [29], medicine [30,31], computer security [32], renewable power generation [33] and may others [34].

2. Materials and Methods

This section describes the base methods and algorithms that served as inspiration for our work. Following that, the potential for improvements is described alongside the modifications aimed at improving performance. Finally, the algorithm pseudocode is presented.

2.1. Original Crayfish Optimization Algorithm

The Crayfish optimization algorithm (COA) is a recently created metaheuristic algorithm depicting the behavior of crayfish, also known as crayfish, a form of crustacean, in a natural setting [6]. These animals belong to the infraorder Astacidea family and make freshwater such as lakes and rivers their home. They are omnivores, foraging the floor of the body of water for nutritious meals.
Algorithm emulates crayfish summer resort behavior which entails the crayfish searching for cool caves when the temperatures are high. This behavior acts as the algorithm’s exploration stage. Next, these animals compete for the best shelter. Foraging, which happens when the temperatures allow, is also modeled. Competing and foraging are used as exploitation stages in COA.
As is the norm with swarm intelligence, the population of crayfish P is initialized in the beginning stage of the algorithm. To manage the stages of exploration and exploitation, temperature is represented by a random constant defined by the Equation (4):
t e m p = r a n d × 15 + 20
The summer retreat behavior happens when the temperature is higher than 30°C, in which case the crayfish look for a cool shelter from the heat, such as caves. Temperatures between 15°C and 30°C are suitable for crayfish feeding, with 25°C being ideal. Since most reliable foraging behavior happens in the range of 20°C to 30°C, the model’s temperature ranges from 20°C to 35°C. The mathematical representation of the feeding behavior of crayfish may be seen in Equation (5):
p = C 1 1 2 π σ exp − t e m p − μ 2 2 σ 2 .
In this expression, µ marks the thriving weather for crayfish, while C1 and σ serve the purpose of controlling the food intake of crayfish at varying temperatures.
When temp>30, the stage of exploring starts. The shelter crayfish take from the heat is modeled by Equation (6):
X s h a d e = X G + X L 2
where, XL marks the current colony optimal positioning, while XG marks the best possible place gained, in regards to the number of iterations.
Whether the crayfish competes for the shelter is randomly dictated by the variable value rand. In case this value is lesser than 0.5, no competition between crayfish for the shelter occurs. Since there is no obstacle, the crayfish will enter the cave without issue, per the Equation (7) and Equation (8):
X t + 1 i , j = X t i , j + C 2 × r a n d X s h a d e − X t i , j
C 2 = 2 − t T
C2 denotes a decreasing curve, T marks the topmost number of repetitions, and t marks live iteration, while t+1 depicts the repetition number for the next generation.
During the high temperatures, the crayfish seek shelter. This shelter or cave is a symbol of the best possible solution. In the summer resort stage, the crayfish head towards the cave thus nearing the optimal solution. The closer to the cave they are, the better COA‘s potential for exploitation becomes, and the faster the algorithm converges.
When rand≥0.5, there is competition between crayfish for the shelter. This competition has played the role of the start of the exploitation stage. The conflict is represented by the Equation (9) and Equation (10):
X t + 1 i , j = X t i , j − X t Z j + X s h a d e
z = r o u n d r a n d N − 1 + 1
where z marks the crayfish’s random individual.
In the competition phase, crayfish fight with each other. Crayfish Xi adapt their position in relation to another crayfish’s position Xz. This adaptation of positions expands the search range of COA, thereby boosting the algorithm’s exploration capacity.
The crayfish feed in temperatures below or equal to 30°C. When such conditions are met, the crayfish moves towards the food. Location of the food Xfood and its size Q are decided as defined by Equation (11) and Equation (12):
X f o o d = X G
Q = C 3 × r a n d f i t n e s s i f i t n e s s f o o d
In this context, C3 stands for the food factor representing the biggest food source, with a constant value of 3. The fitness variable denotes the fitness value of the i-th crayfish, whereas fitnessfood indicates the fitness value linked to the food’s location.
In the case when the food is too big, and Q>(C3+1)/2, the process of tearing up the food is depicted in Equation (13):
X f o o d = exp − Q X f o o d
When the food is small enough, Q<(C3+1)/2, the crayfish will simply eat the food, as given by Equation (14):
X t + 1 i , j = X t i , j − X f o o d p + p × r a n d X t i , j
During the foraging phase, crayfish employ various feeding tactics depending on the size of their food denoted by Q, where the food location Xfood signifies the ideal solution. They will move closer to the food of readily edible size. Conversely, when Q is excessively large, meaning a substantial disparity between the crayfish and the optimal solution, Xfood will be decreased, thereby drawing it nearer to the meal.

2.2. Hybrid COA

Despite the admirable performance demonstrated by the COA, as a recently introduced algorithm, there is still plenty of room to explore potential improvements. To that end, this work introduced two new mechanisms into the original COA.
The initial modification incorporates quasi-reflective learning (QRL) [35] in the first T iterations. Following each iteration, the worst solutions are replaced by new solutions generated based on Equation (15):
A z q r = r a d l b z + u b z 2 ,   a
where lb and ub denote lower and upper bounds of the search space and rad denotes a random value within the given interval. The newly generated solution is not subjected to objective function evaluation thus the computational complexity of the modified algorithm is kept consistent with the original.
When examining optimization metaheuristics, it becomes crucial to find an equilibrium between exploration and exploitation. In order to enhance exploitation, a supplementary adjustment is incorporated, drawing inspiration from the widely recognized firefly algorithm (FA) [23]. The FA simulates the courtship behaviors of bioluminescent beetles through mathematical modeling, where individuals emitting brighter light attract those in their vicinity. The brightness of each agent is computed according to a problem-dependent objective function, outlined in Equation (16):
F i = f X i
Several environmental factors are also simulated to replicate real-world conditions such as light fading depending on the distance between agents, as well as the characteristics of the medium of propagation. The basic search mechanism of the FA is shown by Equation (17):
X i t + 1 = X i t + β e − γ   r i , j 2 X j t − X i t + α ε i t
Equation (17) is commonly swapped for Equation (18) to improve computational performance, where β0 represents the attractiveness at r=0:
β r = β 0 1 + γ × r 2
In these formulas, Xi(t) represents the current position of agent i at a specific iteration t, and rij denotes the current position of agent j during the corresponding iteration t. The parameter β signifies the separation between agents indexed as i and j serving as a metric for their mutual attraction. β is termed the agent attraction coefficient, γ denotes the light absorption coefficient, α controls the degree of randomness, and εi(t) represents a stochastic vector.
Although the introduced search mechanism of the FA does enhance convergence, it is crucial to strike a balance throughout the optimization process. The firefly search mechanism becomes active only in the latter half of the optimization interactions. After each of these iterations, a pseudo-random value is generated within the range [0, 1] and compared to a threshold value ψ. If the generated value surpasses ψ, the firefly search is initiated; otherwise, a normal COA search is employed. The value of ψ is determined empirically to yield optimal results for the given problem, typically set at 0.6.
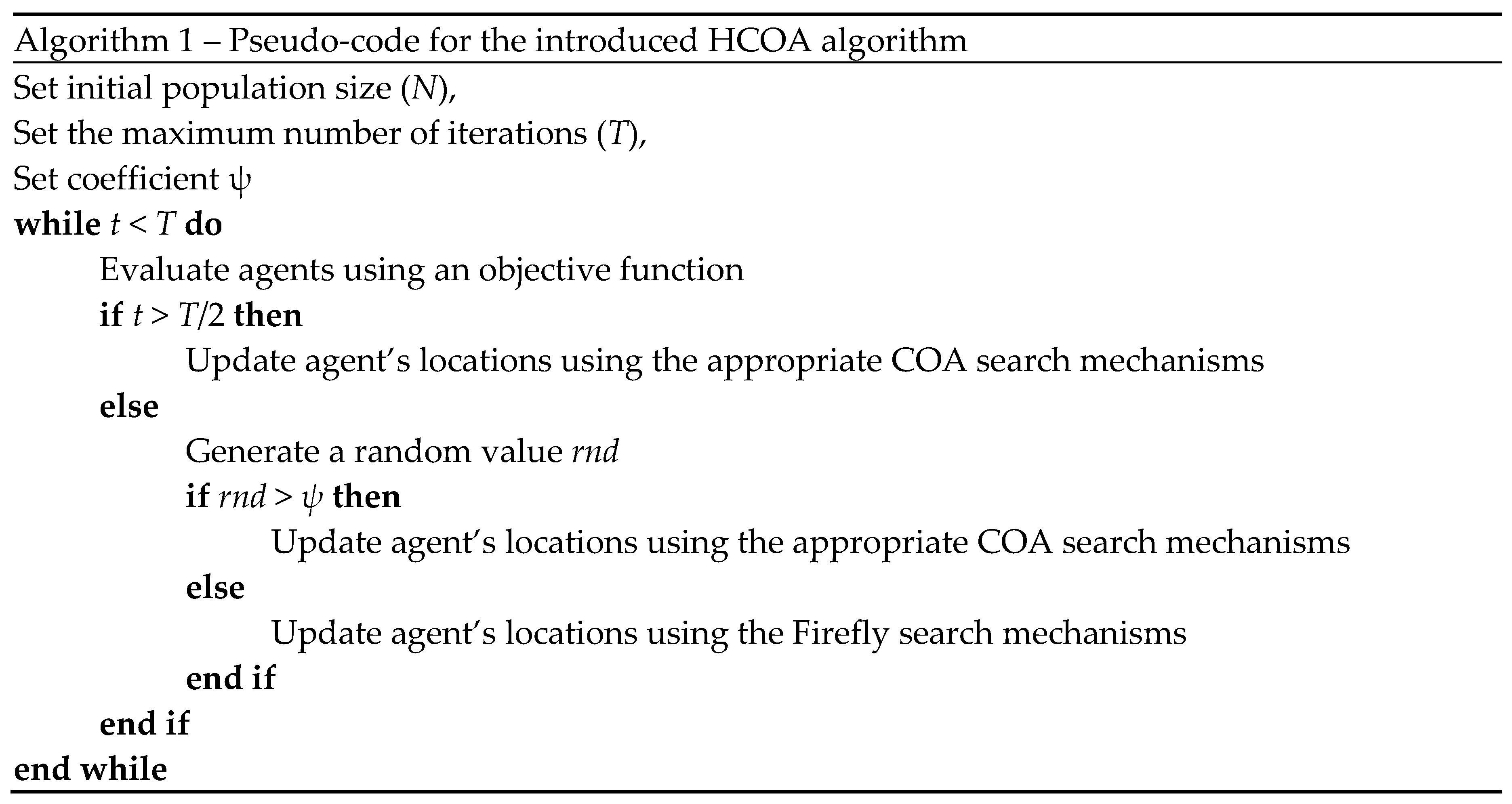
The described algorithm is dubbed the hybrid COA(HCOA). The pseudocode for the described algorithm is provided in the following Algorithm 1 pseudocode:
Preprints 118612 i001

3. Experimental Results

To facilitate experimentation a publicly accessible simulated dataset is utilized provided by the Carnegie Mellon University CERT Division Software Engineering Institute [36]. The dataset was accessed on January 25, 2023. and is publicly available [37]. While this dataset contains information on several malicious insider threat users and their activities our work focuses on logon activities and their relative period.
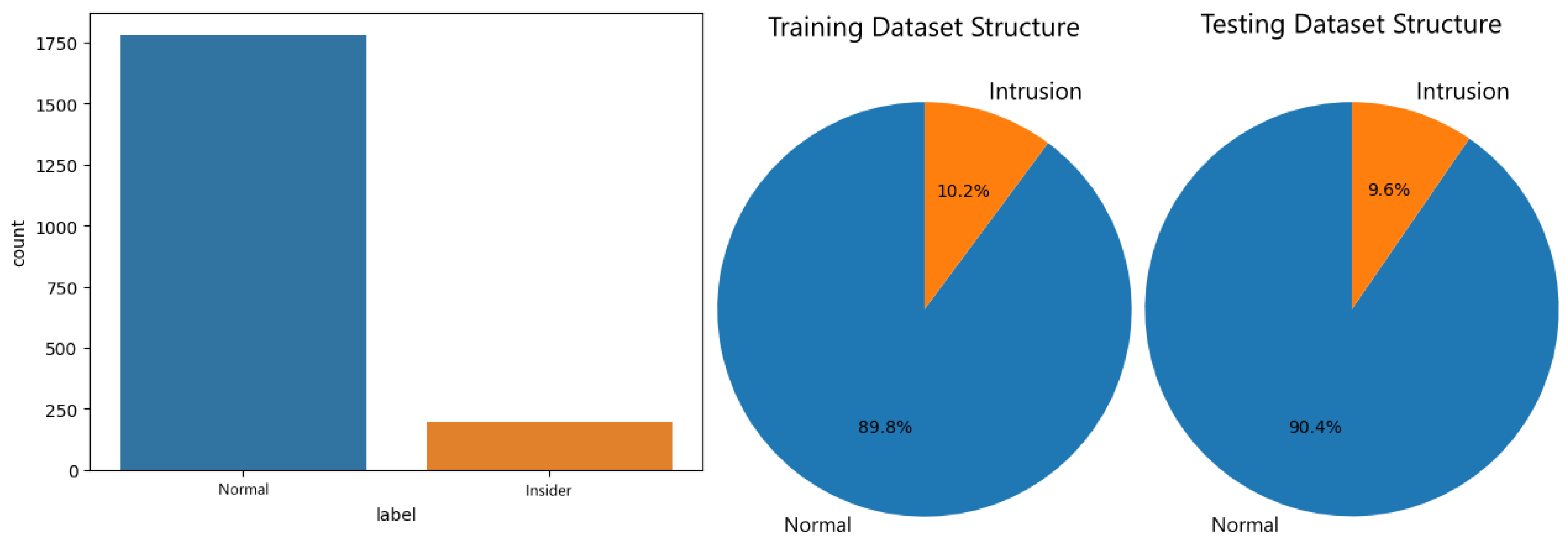
To reflect real-world scenarios dataset is heavily imbalanced with malicious actor activities being a minority. A total of 854661 samples represent normal users with only 198 samples being malicious actors. To facilitate model training, the majority class is down-sampled to a 9:1 ratio of normal to malicious activities. During testing 1782 samples represent normal user activity and 198 malicious. The datasets are further split into training and testing with 70% allocated to train respective models and 30% withheld for evaluations. The dataset structure, as well as the structure of the training and testing portions, are shown in Figure 1.
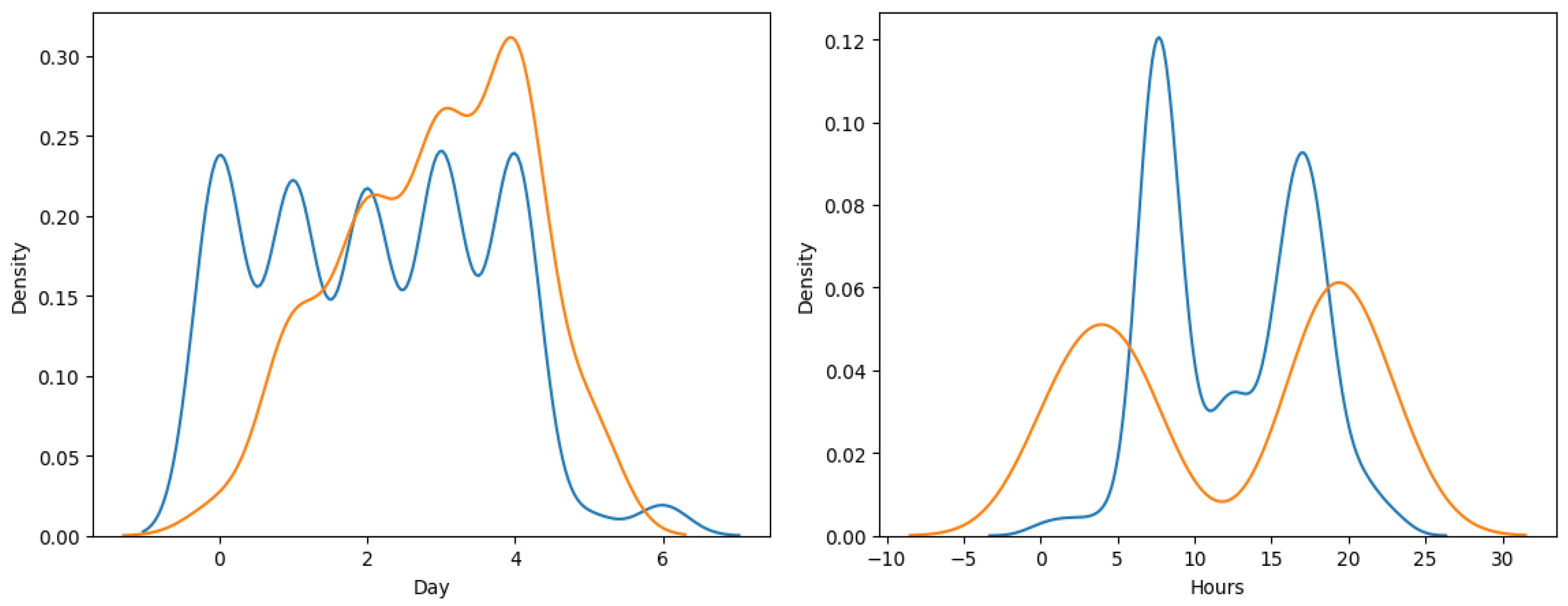
Time of access features are considered in this experiment. Specifically, the day of access and time of day. Interesting patterns can be observed in the behavior of user access with insider threats often accessing machines outside of regular work hours. Additionally, insiders prefer accessing machines later in the week. The distribution of normal and malicious user access can be seen in Figure 2.
Several contemporary optimizers were included in a comparative analysis with the introduced optimizer: COA [6], GA [21], PSO [22], FA [23], SCA [24], WOA [25], RSA [26] and COLSHADE [27]. Algorithms were independently implemented in Python using standard machine-learning libraries provided by Sklearn. Additional supporting libraries utilized include Pandas and Numpy. Optimizers are implemented with parameters set to the values suggested in the original works.
Optimizes are tasked with selecting optimal control parameter values for the AdaBoost algorithms. These parameters and their respective ranges are the number of estimators [10, 50], depth [1, 10] and learning rate [0.1, 2]. A relatively modest number of estimators is used due to the heavy computational demands of the optimization. Each optimizer was allocated a population size of ten and allowed 15 iterations to improve attained solutions. Finally, the experimentation is repeated 30 times in independent executions to account for the randomness inherent in the application of metaheuristics.
To guide the optimization Cohen’s kappa metric is utilized due to this metric’s ability to evaluate classifications of imbalanced data well. The Cohen’s kappa score is determined by Equation (19):
k = c 0 − c e 1 − c e
Further metrics are tracked to ensure thorough comparisons. These include a set of standard classification metrics used to get a comprehensive overview of algorithm performances including accuracy shown in Equation (20), precision Equation (21), recall Equation (22) and f1-score in Equation (23):
Accuracy = Number   of   Correct   Pr edictions Total   Number   of   Pr edictions
Pr ecision = True   Positives True   Positives + False   Positives
Re call = True   Positives True   Positives + False   Negatives
f 1 − score = 2 × Pr ecision × Re call Pr ecision + Re call
Additionally, error rates are recorded for each algorithm determined by Equation (24):
Error   rate = 1 − Accuracy
Error rate is the complement of accuracy and represents the proportion of incorrectly classified instances. It is the ratio of the number of misclassifications to the total number of instances. This is a convenient way to represent the error rate in terms of more intuitive accuracy metric.

3.1. Simulation Outcomes

Simulation results in terms of objective and indicator function are provided in Table 1 and Table 2 respectively. As evident, introduced optimizer attained the best outcomes with the best scoring of 0.711939, mean scoring of 0.673919, and median executions scoring of 0.672113 in terms of objective function results. The best outcomes in terms of the worst-case performance are demonstrated by the FA attaining an objective function score of 0.630255.
These results are somewhat similar to the results in terms of an indicator function, with the introduced optimizer matching the best performance of 0.053872, sharing first place with the WOA, and attaining the best outcomes in mean and median executions scoring 0.057239 and 0.056397 respectively. The PSO attained the best outcomes in the worst-case execution scoring 0.062290.
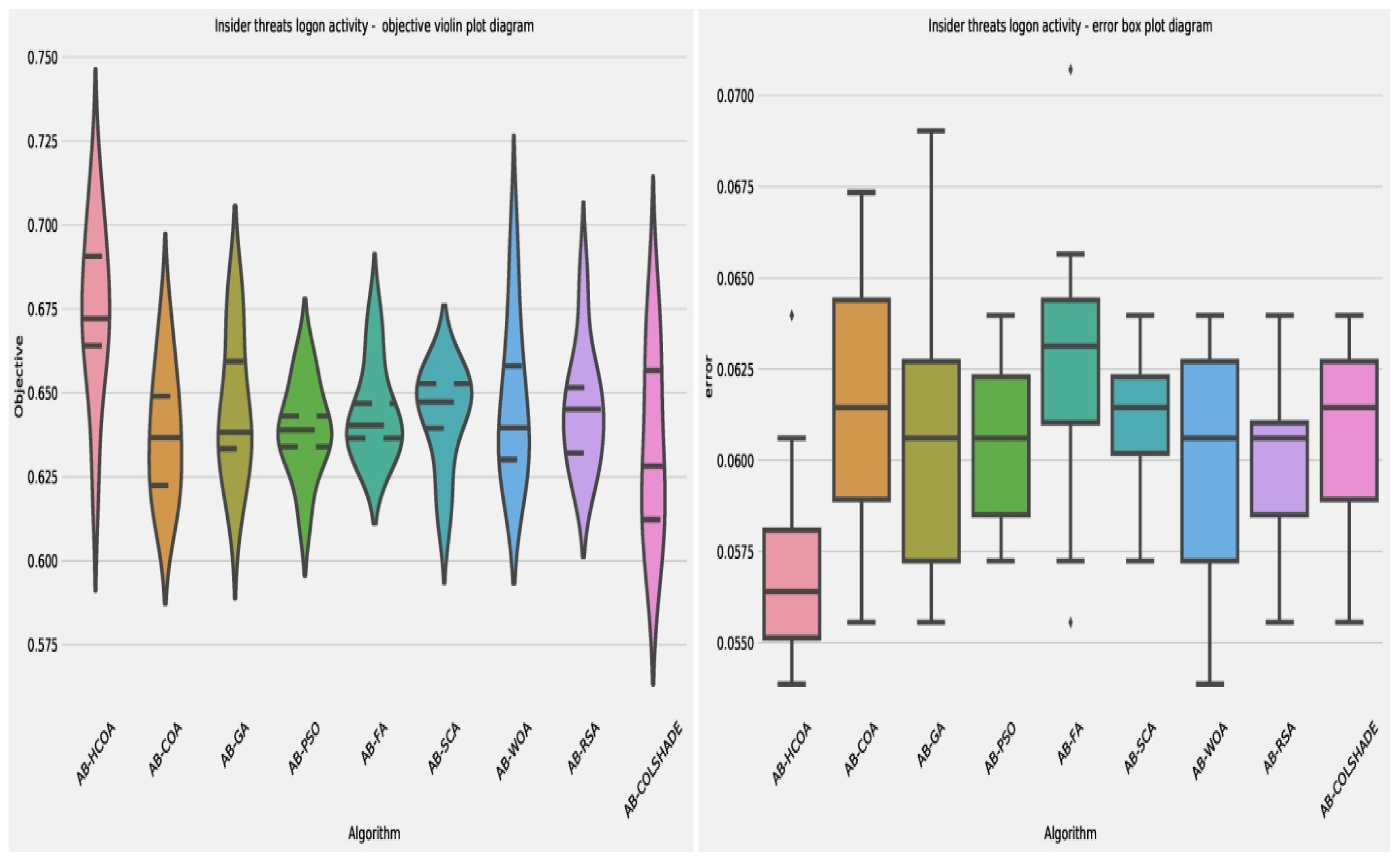
Comparisons in terms of algorithm stability can be viewed in Table 1 and Table 2 in terms of objective and indicator functions as well. In terms of stability, the PSO and SCA attained the highest rate of stability in comparison to other tested optimizes. However, they did not demonstrate the best performance. Visual comparisons are provided in Figure 3. While the introduced optimizer showcases a relatively low stability in terms of objective function it nonetheless demonstrates the best outcomes. Additionally, in terms of indicator function, the introduced optimizers show the highest outcomes, outperforming all other algorithms.
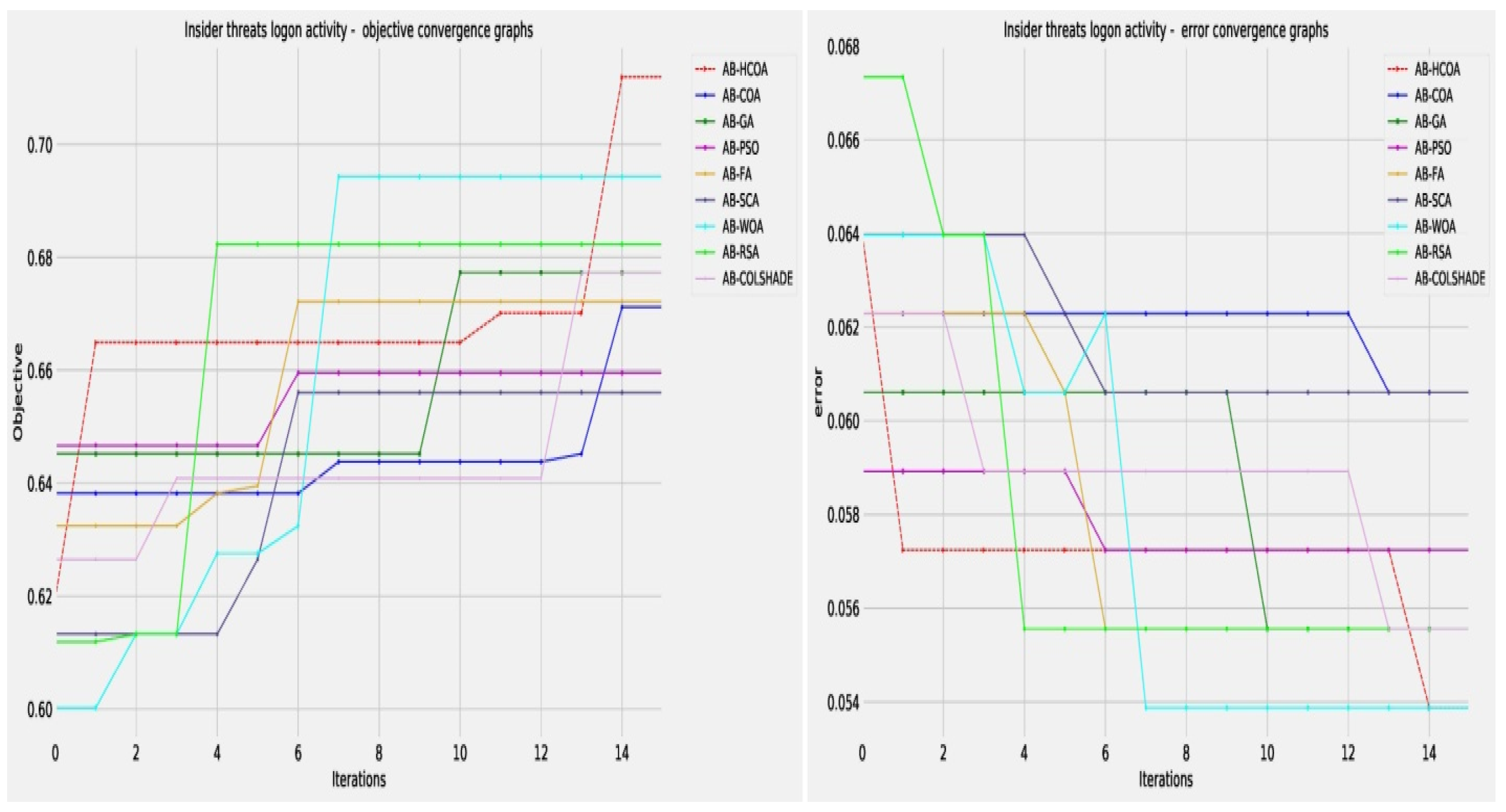
Comparisons in terms of convergence rate are provided in terms of objective as well as indicator function in Table 2. A clear influence of the introduced modifications is evident in the modified version of the algorithm over the baseline.
While many algorithms converge towards a local minimum, the modified version locates the best solution towards the final executions suggesting that the introduced alterations have introduced an improvement.
Figure 4 shows the objective and indicator functions’ outcome convergence plots.
Detail metric comparisons between the best-constructed models are provided in Table 3. A clear dominance in terms of best outcomes is showcased by the introduced algorithm, with only the FA outperforming the algorithm in terms of precision for insider threat detection. However, this is to be somewhat expected as in accordance with the NFL [28] no single optimizer is equally suited to all challenges across all metrics.
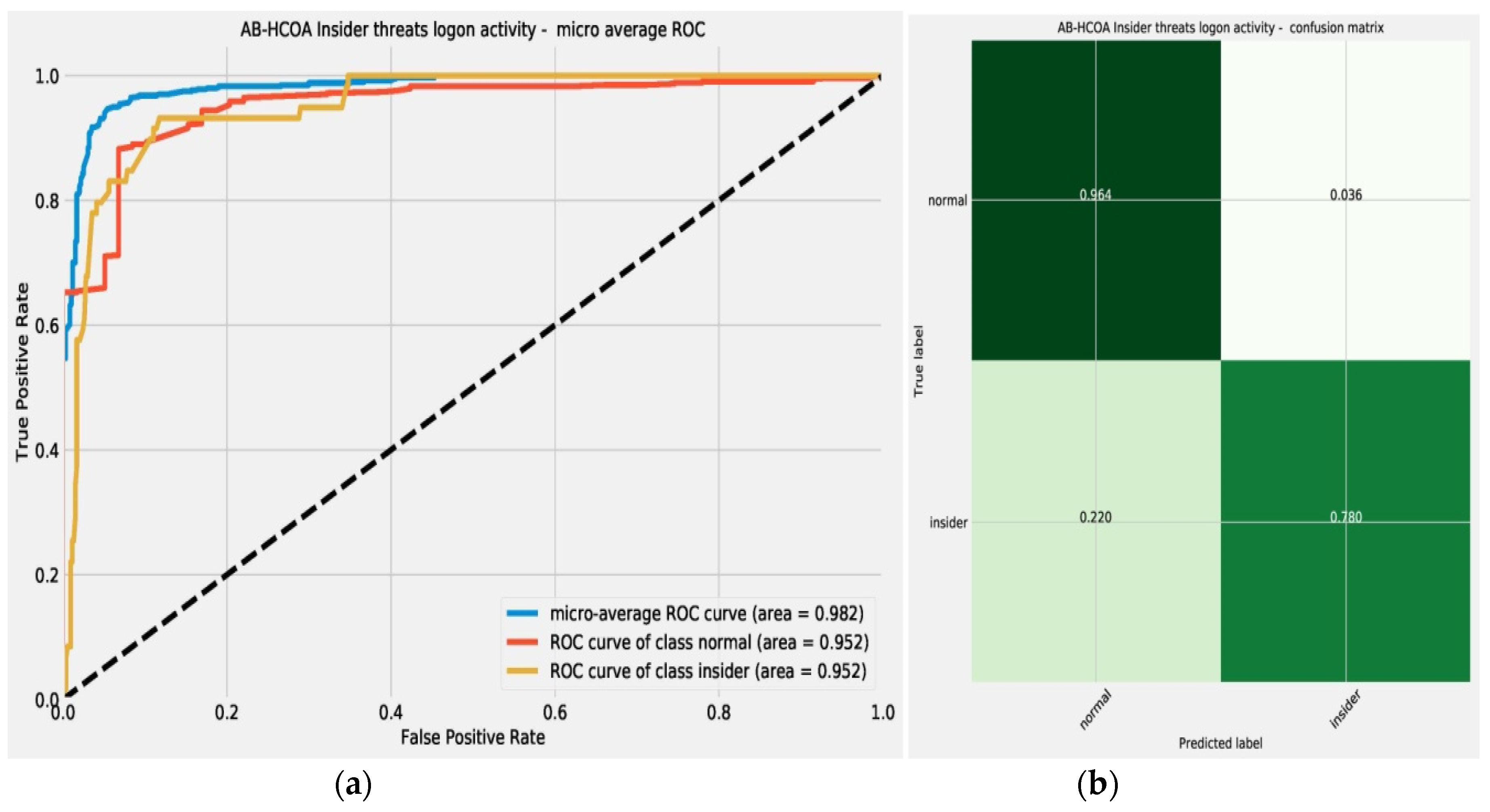
Graphical presentation of the outcomes for the best model in terms of confusion matrix and ROC are provided in Figure 5.
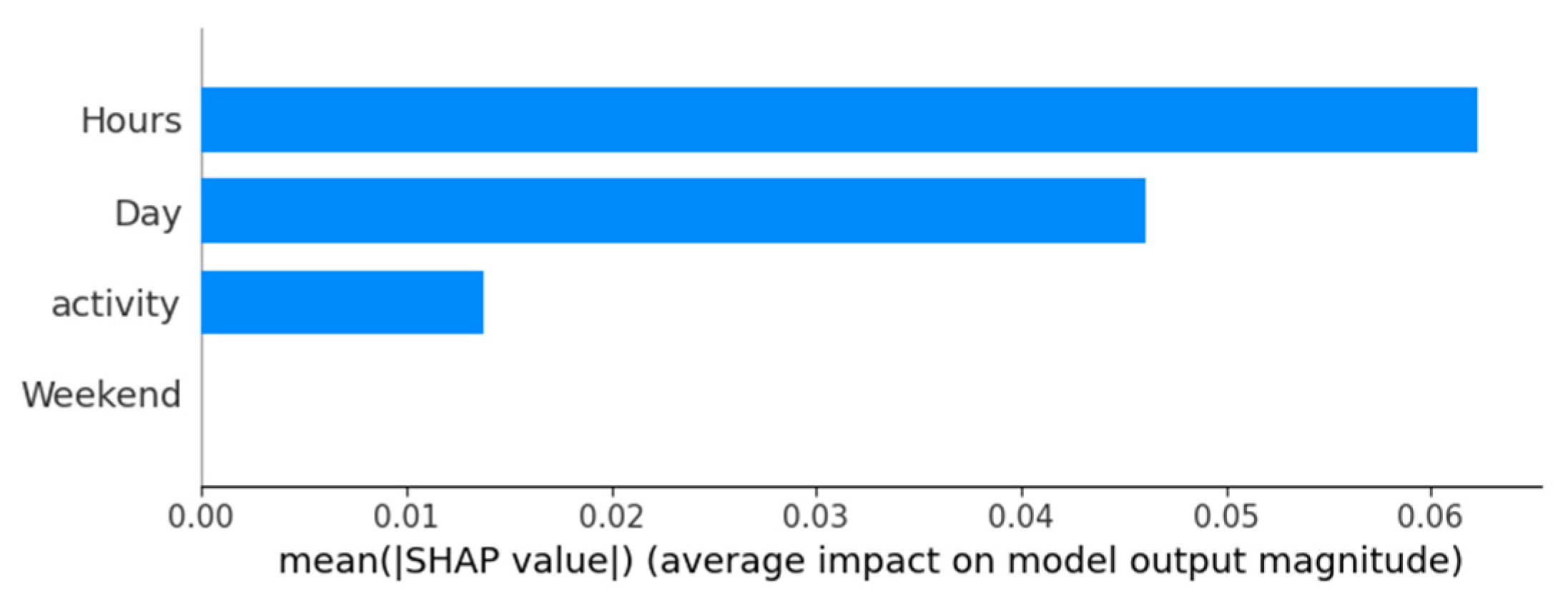
Additional sample additive explanations (SHAP) analysis [38] is conducted to determine the feature importance for the best models’ decision-making process. The outcomes are presented in Figure 6. SHAP interpretation suggests that the time of the day, and the day of the week play an important role in user activity being classified correctly. Additionally, the type of activity (logon or logoff) is considered. However, if an activity occurs on a weekend that is not considered important for the classification, likely due to this information being redundant with the day of the week being available.
Finally, the parameter selections made by each optimizer for the respective best-constructed model are provided in Table 4.

5. Conclusions

This work attempts to solve the problem of intrusion detection, based on login activity, within a greater context of cyber security, for a majority of normal users. AdaBoost classifier is applied to improve performance. Several optimizers are tasked with selecting optimal control parameters. Additionally, a modified version of COA algorithm is introduced specifically for this investigation. A comparative analysis is conducted, with several contemporary optimizers on a simulated, publicly available, dataset. The models optimized by the introduced modified algorithm attained the best outcomes demonstrating an accuracy of 94.6128% and an adaptive convergence rate that was capable of overcoming local minima and locating the best solution. Additionally, the best-constructed model was subjected to SHAP analysis in order to determine the key contributing features.
Some limitations associated with this research are due to the heavy computational constraints of the optimization process. Namely, the training and evaluation process requires training of many models, therefore limited populations and smaller numbers of estimators are considered during the simulations.
Future works will focus on further expanding the methodology, by incorporating other user actions in the classification. The computational constraint-associated limitations hope to be addressed as more powerful hardware becomes available. Finally, other optimization tasks will be improved by the introduced novel, modified algorithms.

Author Contributions

Conceptualization, L.J. and N.B.; methodology, N.B.; software, N.B. and L.J.; validation, M.S. and F.M.; formal analysis, Ž.S.; investigation, Ž.S. and F.M.; resources, Ž.S.; data curation, M.S.; writing—original draft preparation, L.J.; writing—review and editing, M.S. and F.M.; visualization, L.J.; supervision, N.B.; project administration, M.S.; funding acquisition, Ž.S. All authors have read and agreed to the published version of the manuscript

Informed Consent Statement

Not applicable.

Data Availability Statement

The dataset was accessed on January 25, 2023. and is publicly available from https://kilthub.cmu.edu/articles/dataset/Insider_Threat_Test_Dataset/%2012841247.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gupta, B.; Gupta, B.; Srinivasagopalan, S. Handbook of research on intrusion detection systems (Intrusion detection systems); IGI Global: Hershey, Pennsylvania, 2020. [Google Scholar]
  2. Insider threats and Insider Intrusion Detection. International journal of recent technology and engineering 2019, 8, 158–166. [CrossRef]
  3. N. T N and D. Pramod, "Insider Intrusion Detection Techniques: A State-of-the-Art Review," The Journal of computer information systems, vol. ahead-of-print, no. ahead-of-print, pp. 1–18, 2024. [CrossRef]
  4. Ferrag, M.A.; Maglaras, L.; Moschoyiannis, S.; Janicke, H. Deep learning for cyber security intrusion detection: Approaches, datasets, and comparative study. Journal of information security and applications 2020, 50, 102419. [Google Scholar] [CrossRef]
  5. Hassan, I.H.; Mohammed, A.; Masama, M.A. Chapter 6 - Metaheuristic algorithms in network intrusion detection. In Comprehensive Metaheuristics; Mirjalili, S., Gandomi, A.H., Eds.; Academic Press, 2023; pp. 95–129. [Google Scholar]
  6. Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish optimization algorithm. The Artificial intelligence review 2023, 56, 1919–1979. [Google Scholar] [CrossRef]
  7. Kosseff, J. Defining Cybersecurity Law. Iowa law review 2018, 103, 985–1031. [Google Scholar]
  8. Moallem, A. HCI for Cybersecurity, Privacy and Trust : 6th International Conference, HCI-CPT 2024, Held as Part of the 26th HCI International Conference, HCII 2024, Washington, DC, USA, June 29 – July 4, 2024, Proceedings, Part I, Lecture Notes in Computer Science, 14728, 1st ed.; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
  9. 2023-2030 Australian Cyber Security Strategy. 2023. Available online: https://www.homeaffairs.gov.au/about-us/our-portfolios/cyber-security/strategy/2023-2030-australian-cyber-security-strategy.
  10. Svantesson, D. J. B.; Kloza, D. Trans-Atlantic data privacy relations as a challenge for democracy; European integration and democracy series; Intersentia: Cambridge, UK, 2017; Volume 4. [Google Scholar]
  11. Papakonstantinou, V. Cybersecurity as praxis and as a state: The EU law path towards acknowledgement of a new right to cybersecurity? The computer law and security report 2022, 44, 105653. [Google Scholar] [CrossRef]
  12. Lukings, M.; Habibi Lashkari, A. Understanding Cybersecurity Law and Digital Privacy : A Common Law Perspective, Future of Business and Finance, 1st ed.; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
  13. Savin, A. I.; Trzaskowski, J. Research handbook on EU internet law; Research handbooks in European law series; Edward Elgar Publishing: Northampton, 2023. [Google Scholar]
  14. Pohl, J. H. International Data Transfers and Cybersecurity: Three Regulatory Approaches and Their Implications; Cambridge University Press: Cambridge, UK, 2023; pp. 134–160. [Google Scholar]
  15. Ullrich, J.; Cropper, J.; Frühwirt, P.; Weippl, E. The role and security of firewalls in cyber-physical cloud computing. EURASIP Journal on Information Security 2016, 2016, 1. [Google Scholar] [CrossRef]
  16. S. Thapa and A. M. Dissanayaka, "The Role of Intrusion Detection/Prevention Systems in Modern Computer Networks: A Review," 2020.
  17. Bilge, L.; Dumitraş, T. Before we knew it: an empirical study of zero-day attacks in the real world. In Proceedings of the 2012 ACM conference on Computer and communications security, Raleigh, North Carolina, USA; 2012. [Google Scholar] [CrossRef]
  18. Džaferović, E.; Sokol, A.; Almisreb, A.A.; Mohd Norzeli, S. DoS and DDoS vulnerability of IoT: A review. Sustainable Engineering and Innovation 2019, 1, 43–48. [Google Scholar] [CrossRef]
  19. Kandias, M.; Mylonas, A.; Virvilis, N.; Theoharidou, M.; Gritzalis, D. An Insider Threat Prediction Model; Springer: Berlin/Heidelberg, Germany; pp. 26–37. [CrossRef]
  20. Hastie, T.J.; Rosset, S.; Zhu, J.; Zou, H. Multi-class AdaBoost ∗. Statistics and Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
  21. Holland, J.H. Genetic Algorithms. Scientific American 1992, 267, 66–73. [Google Scholar] [CrossRef]
  22. J. Kennedy and R. Eberhart, "Particle swarm optimization," 1995, vol. 4: IEEE, pp. 1942–1948 vol.4. [CrossRef]
  23. Xin-She, Y.; He, X. Firefly Algorithm: Recent Advances and Applications. arXiv 2013, arXiv:1308.3898. [Google Scholar]
  24. Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowledge-based systems 2016, 96, 120–133. [Google Scholar] [CrossRef]
  25. Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Advances in engineering software (1992) 2016, 95, 51–67. [Google Scholar] [CrossRef]
  26. Abualigah, L.; Elaziz, M.A.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Systems with Applications 2022, 191, 116158. [Google Scholar] [CrossRef]
  27. J. Gurrola-Ramos, A. Hernàndez-Aguirre, and O. Dalmau-Cedeño, "COLSHADE for Real-World Single-Objective Constrained optimization Problems," in 2020 IEEE Congress on Evolutionary Computation (CEC), 19-24 July 2020 2020, pp. 1–8. [CrossRef]
  28. Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation 1997, 1, 67–82. [Google Scholar] [CrossRef]
  29. N. Bacanin, M. Zivkovic, L. Jovanovic, M. Ivanovic, and T. A. Rashid, "Training a Multilayer Perception for Modeling Stock Price Index Predictions Using Modified Whale Optimization Algorithm," in Computational Vision and Bio-Inspired Computing, Singapore, S. Smys, J. M. R. S. Tavares, and V. E. Balas, Eds., 2022// 2022: Springer Singapore, pp. 415–430.
  30. Minic, A.; Jovanovic, L.; Bacanin, N.; Stoean, C.; Zivkovic, M.; Spalevic, P.; Petrovic, A.; Dobrojevic, M.; Stoean, R. Applying Recurrent Neural Networks for Anomaly Detection in Electrocardiogram Sensor Data. Sensors 2023, 23, 9878. [Google Scholar] [CrossRef] [PubMed]
  31. M. Zivkovic, L. Jovanovic, M. Ivanovic, A. Krdzic, N. Bacanin, and I. Strumberger, "Feature Selection Using Modified Sine Cosine Algorithm with COVID-19 Dataset," in Evolutionary Computing and Mobile Sustainable Networks, Singapore, V. Suma, X. Fernando, K.-L. Du, and H. Wang, Eds., 2022// 2022: Springer Singapore, pp. 15–31.
  32. N. AlHosni et al., "The XGBoost Model for Network Intrusion Detection Boosted by Enhanced Sine Cosine Algorithm," in Third International Conference on Image Processing and Capsule Networks, Cham, J. I.-Z. Chen, J. M. R. S. Tavares, and F. Shi, Eds., 2022// 2022: Springer International Publishing, pp. 213–228.
  33. Damaševičius, R.; Jovanovic, L.; Petrovic, A.; Zivkovic, M.; Bacanin, N.; Jovanovic, D.; Antonijevic, M. Decomposition aided attention-based recurrent neural networks for multistep ahead time-series forecasting of renewable power generation. PeerJ Comput Sci 2024, 10, e1795. [Google Scholar] [CrossRef] [PubMed]
  34. Mirjalili, S. A.; Gandomi, A. H. Comprehensive metaheuristics : algorithms and applications; Academic Press: London, UK, 2023. [Google Scholar]
  35. Luo, W.; Yu, X. Quasi-reflection based multi-strategy cuckoo search for parameter estimation of photovoltaic solar modules. Solar Energy 2022, 243, 264–278. [Google Scholar] [CrossRef]
  36. J. Glasser and B. Lindauer, "Bridging the Gap: A Pragmatic Approach to Generating Insider Threat Data," in 2013 IEEE Security and Privacy Workshops, 23-24 May 2013 2013, pp. 98–104. [CrossRef]
  37. B. Lindauer, "Insider Threat Test Dataset," ed: Carnegie Mellon University, 2020.
  38. Lundberg S M, L.S.I. A unified approach to interpreting model predictions. Advances in Neural Information Processing Systems 2017, 30, 4765–4774. [Google Scholar] [CrossRef]
Preprints 118612 g001
Figure 1. Dataset training and testing structure.
Figure 1. Dataset training and testing structure.
Preprints 118612 g001
Preprints 118612 g002
Figure 2. Normal, shown in blue, and insider thread user distributions shown in orange color.
Figure 2. Normal, shown in blue, and insider thread user distributions shown in orange color.
Preprints 118612 g002
Preprints 118612 g003
Figure 3. Objective and indicator function outcome distributions over 30 independent runs.
Figure 3. Objective and indicator function outcome distributions over 30 independent runs.
Preprints 118612 g003
Preprints 118612 g004
Figure 4. Objective and indicator function outcome convergence plots.
Figure 4. Objective and indicator function outcome convergence plots.
Preprints 118612 g004
Preprints 118612 g005
Figure 5. (a) Best performing model ROC; (b) Confusion matrix.
Figure 5. (a) Best performing model ROC; (b) Confusion matrix.
Preprints 118612 g005
Preprints 118612 g006
Figure 6. SHAP analysis outcomes for the best model.
Figure 6. SHAP analysis outcomes for the best model.
Preprints 118612 g006
Table 1. Objective function outcomes for the best worst mean and median runs.
Table 1. Objective function outcomes for the best worst mean and median runs.
Method Best Worst Mean Median Std Var
AB-HCOA 0.711939 0.625510 0.673919 0.672113 0.024330 0.000592
AB-COA 0.671187 0.613295 0.637825 0.636679 0.018445 0.000340
AB-GA 0.677333 0.617112 0.645781 0.638252 0.019972 0.000399
AB-PSO 0.659553 0.614028 0.638885 0.638874 0.012979 0.000168
AB-FA 0.672196 0.630255 0.644348 0.640337 0.013494 0.000182
AB-SCA 0.656084 0.613295 0.642558 0.647218 0.014036 0.000197
AB-WOA 0.694297 0.625510 0.647621 0.639584 0.022794 0.000520
AB-RSA 0.682312 0.625510 0.645486 0.645056 0.017144 0.000294
AB-COLSHADE 0.055556 0.063973 0.060816 0.061448 0.002719 7.40E-06
Table 2. Indicator function outcomes for the best worst mean and median runs.
Table 2. Indicator function outcomes for the best worst mean and median runs.
Method Best Worst Mean Median Std Var
AB-HCOA 0.053872 0.063973 0.057239 0.056397 0.003260 1.06E-05
AB-COA 0.060606 0.063973 0.061658 0.061448 0.003663 1.34E-05
AB-GA 0.055556 0.069024 0.060816 0.060606 0.004075 1.66E-05
AB-PSO 0.057239 0.062290 0.060396 0.060606 0.002296 5.27E-06
AB-FA 0.055556 0.065657 0.062710 0.063131 0.004434 1.97E-05
AB-SCA 0.060606 0.063973 0.061027 0.061448 0.002018 4.07E-06
AB-WOA 0.053872 0.063973 0.059975 0.060606 0.003464 1.20E-05
AB-RSA 0.055556 0.063973 0.059975 0.060606 0.002516 6.33E-06
AB-COLSHADE 0.055556 0.063973 0.060816 0.061448 0.002719 7.40E-06
Table 3. Metrics comparisons between the best performing models constructed by each optimizer.
Table 3. Metrics comparisons between the best performing models constructed by each optimizer.
Method metric normal insider accuracy macro avg weighted avg
AB-HCOA precision
recall
f1-score		 0.975425
0.964486
0.969925 		0.707692
0.779661
0.741935 		0.946128
0.946128
0.946128		 0.841559
0.872073
0.855930 		0.948832
0.946128
0.947279
AB-COA precision
recall
f1-score		 0.969868
0.962617
0.966229		 0.682540
0.728814
0.704918		 0.939394
0.939394
0.939394		 0.826204
0.845715
0.835573		 0.9413297
0.939394
0.940274
AB-GA precision
recall
f1-score		 0.964815
0.973832
0.969302		 0.740741
0.677966
0.707965		 0.944444
0.944444
0.944444		 0.852778
0.825899
0.838633		 0.942558
0.944444
0.943345
AB-PSO precision
recall
f1-score		 0.961326
0.975701
0.968460		 0.745098
0.644068
0.690909		 0.942761
0.942761
0.942761		 0.853212
0.809884
0.829685		 0.939849
0.942761
0.940892
AB-FA precision
recall
f1-score		 0.963100
0.975701
0.969359		 0.750000
0.661017
0.702703		 0.944444
0.944444
0.944444		 0.856550
0.818359
0.836031		 0.941933
0.944444
0.942873
AB-SCA precision
recall
f1-score		 0.964618
0.968224
0.966418		 0.701754
0.677966
0.689655		 0.939394
0.939394
0.939394		 0.833186
0.823095
0.828037		 0.938509
0.939394
0.938928
AB-WOA precision
recall
f1-score		 0.968343
0.971963
0.970149		 0.736842
0.711864
0.724138		 0.946128
0.946128
0.946128		 0.852592
0.841914
0.847144		 0.945348
0.946128
0.945714
AB-RSA precision
recall
f1-score		 0.966543
0.971963
0.969245		 0.732143
0.694915
0.713043		 0.944444
0.944444
0.944444		 0.849343
0.833439
0.841144		 0.943261
0.944444
0.943797
AB-COLSHADE precision
recall
f1-score		 0.964815
0.973832
0.969302		 0.740741
0.677966
0.707965		 0.944444
0.944444
0.944444		 0.852778
0.825899
0.838633		 0.942558
0.944444
0.943345
support 535 59
Table 4. Parameter selections for the respective best-performing model made by each optimizer.
Table 4. Parameter selections for the respective best-performing model made by each optimizer.
Method p1 p2 p3
AB-HCOA 34 4 1.941851
AB-COA 50 3 1.958571
AB-GA 42 2 1.557575
AB-PSO 30 2 1.522928
AB-FA 41 2 1.470723
AB-SCA 20 2 1.685248
AB-WOA 50 2 1.815289
AB-RSA 50 2 1.839656
AB-COLSHADE 43 2 1.469586
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated