On a New Innovative Steam-Based Method for Teaching Cycloidal Curves in Engineering Higher Education

Robotics offers innovative possibilities at all levels of education, which should be considered when planning the teaching process for certain topics of engineering mathematics in higher education. In this paper, we present a new teaching-learning technique using STEAM-based methods to explore the properties of cycloidal curves for Computer Science Engineering BSc students. Frontal teaching, which is part of the tradition of higher education, has been complemented with teaching methods that meet the generational needs of students: problem-based learning, integration of STEAM-based methods and project-based learning. We have developed a new methodological model that combines the advantages of the traditional teaching method with new forms of teaching that have proven to be effective in teaching Generation Z. The four-stage methodological model uses a variety of didactical approaches because each stage applies a different type of learning technique to make the learning process interesting, motivating and effective. One of the main pillars of the model is the use of Desmos dynamic geometry software to create animations, and the other is the use of educational robotics to support visualisation. The implementation of educational robotics and its potential for teaching cycloidal curves is discussed in detail. The effectiveness of the method was investigated with first-year undergraduate students in computer science engineering. Quantitative studies were carried out to test the effectiveness of the new teaching technique. The experimental results strongly indicate the value of using the four-stage methodological model to implement active learning in the field of cycloidal curves.

Keywords:

Subject: Computer Science and Mathematics - Other

1. Introduction

Understanding scientific and mathematical knowledge and practices, as well as technological and engineering practices, has become a priority for national education programs across the world [1]. STEAM (Science, Technology, Engineering, Art, Mathematics) has recently become a standard part of higher education internationally, with many universities adapting their curriculum to integrate it [2]. STEAM is the evolution of STEM (Science, Technology, Engineering, Mathematics), which was first introduced by the US National Science Foundation (NSF) in the 1990’s [3]. STEM was initially developed to address the ongoing low performance of students from the Western world in mathematics and science in international assessments and to encourage students to pursue careers in these fields [3]. In 2010, Bybee called for quality science education that includes technology and engineering: "A true STEM education should increase students’ understanding of how things work and improve their use of technologies. ...Engineering is directly involved in problem solving and innovation, two themes with high priorities on every nation’s agenda ...the creation of high-quality, integrated instruction and materials, as well as the placement of problems associated with grand challenges of society at the centre of study". The extension of STEM to STEAM was first proposed in 2013 [5]. As the name STEAM suggests, there is a crucial focus on encouraging students to think in a broader perspective than that of each individual subject [6]. STEAM has been shown to improve conceptual and deep understanding of the subjects covered. Kang in 2019 conducted a literature review of six studies, which included analysing 256 papers from schools that provide STEAM education, and the results demonstrated that there is a positive and immediate effect on the student’s conceptual understanding. The methods of STEAM education are now widely used and applied at all levels of education, including higher education.

1.1. What Is Engineering Mathematics?

Engineering mathematics has two distinct but interconnected facets. On one hand, it serves as the foundation for engineering programs, typically taught by mathematicians. On the other hand, mathematics is an integral component of engineering science, providing the tools and framework for understanding and solving complex problems [8]. Over the past decade, advancements in technology have significantly impacted the field. New algorithms and methods have emerged to help engineers analyse large databases, build predictive models, and solve optimisation problems [9]. The increasing power of computers has enabled the application of complex numerical methods and simulation techniques, supporting engineers in modelling and understanding intricate physical phenomena such as fluid dynamics, structural analysis, and electromagnetic design [10,11,12]. While still in its early stages, quantum computing offers immense potential to further revolutionise engineering mathematics [13,14]. We can expect breakthroughs in complex optimisation problems and simulations, potentially influencing engineering design and research [15]. These innovations and methods empower engineers to work more efficiently on technical challenges and open new opportunities for developing and applying technology.

Engineering students’ training in mathematics is a top priority. The field relies heavily on mathematical principles, with foundational subjects like calculus, differential equations, linear algebra, and statistics being crucial for understanding and solving engineering problems. A robust mathematical background equips engineers with critical thinking and problem-solving skills, enabling them to design systems, troubleshoot issues, and optimise processes [15,16]. As modern engineering increasingly leverages sophisticated technology, a deep understanding of advanced mathematical algorithms becomes essential [17]. Fields like Artificial Intelligence (AI) and Machine Learning (ML) require extensive knowledge of linear algebra, calculus, and probability [18]. Engineering innovation and research continually push the boundaries of mathematical knowledge, necessitating that engineers working on cutting-edge technologies, such as quantum computing or advanced materials, possess a comprehensive understanding of both applied and theoretical mathematics [19,20]. Ultimately, mathematics is the foundation upon which engineering principles are built, equipping students with the skills to solve complex problems, innovate, and excel in a technologically advanced and interdisciplinary world. Teaching mathematics to engineers in higher education requires a thoughtful and well-structured approach to meet the needs of the profession and prepare students for the future challenges they will face [8,21].

Engineering mathematics education should provide a strong foundation in core subjects, demonstrating theoretical concepts through practical examples that showcase their real-world applications in engineering problem-solving. Rogovchenko and Rogovchenko argue that mathematical modelling projects can effectively develop students’ mathematical competency, enhance their understanding of engineering concepts, and improve their communication and collaboration skills. They provide a specific project example in their work, concluding that such projects are crucial for developing the necessary skills for engineering success. Education should embrace modern software and technologies [23], using computer simulations to reinforce theoretical knowledge and provide students with practical experience. Integrating project-based learning (PjBL) is essential, as it allows students to engage in significant projects and real-life case studies, enhancing their problem-solving and analytical skills. Interactive classrooms, where students are actively encouraged to participate in solving problems and understanding concepts [24], foster a more dynamic and engaging learning environment. The curriculum must adapt to technological advancements, equipping students with the knowledge and skills to effectively utilize new educational technologies to maximize their learning and prepare them for continuous professional development [25].

1.2. STEAM-Based Education and Educational Robotics

Technology and innovation play an increasingly important role in modern life, and education must evolve based on innovation and technological progress to keep pace with a changing world. Digital technologies have made a paradigm shift in the entire education system [25]. STEAM-based education is gaining increasing prominence at universities [26], which is particularly important for engineering higher education. Today’s university students increasingly demand educational methods that they find engaging, relevant, and interactive. STEAM education offers a dynamic and attractive learning experience [27]. Many contemporary challenges are complex and multidisciplinary in nature. The STEAM approach allows university students to combine knowledge from various scientific and artistic fields to understand and address these challenges. The spread of problem-based learning is a consequence of the realisation that learners are left with minimal knowledge after learning through traditional, frontal teaching methods and find it difficult to apply the knowledge they acquire in other contexts. Problem-based learning provides a learning environment where learners can use and reinforce prior knowledge, learn in real-life contexts and develop their knowledge in individual or small group work [28]. Developments over the past decade have led to the availability of a wide range of robotic learning tools, all with the common goal of innovation and motivating learners in the learning process.

Robotics and computational thinking are valuable tools for developing STEAM pedagogy and promoting the inclusion and integration of diverse groups of students. There are many robotic teaching tools at our disposal intended to encourage innovation and motivation of students during the learning process. As robots are increasingly common in our world, it is essential to integrate them into education [29,30]. Robots have clearly opened up new possibilities in teaching and learning. Educational robotics (ER), which involves the use of robotic techniques in education, is seen as a groundbreaking learning tool that enhances the learning environment, transforms teaching and learning methods and fosters a new educational ecosystem [31]. Of course, most of the educational applications of ER focus on robotics-related subjects such as robot programming, robot building and artificial intelligence [32,33,34].

LEGO Education focused on STEM-based learning from the beginning, even before this acronym was standard [35,36]. The collaboration with MIT has played a crucial role in developing LEGO’s robotics products. LOGO is a programming language developed in the 1960s at MIT, designed to make coding accessible for children. Its most famous feature is the turtle, a simple robot or on-screen graphic that can be controlled with commands, teaching basic programming concepts like sequencing and loops [37]. In the mid-1980s, the LOGO research group began collaborating with the LEGO group because LEGO Group recognised the potential of teaching and learning with robots [35]. The partnership between LOGO and LEGO brought programming to life, starting with LEGO/LOGO, which combined LEGO building with LOGO code. The history of LEGO robots dates back to the end of the 20th century when the LEGO Group started developing robotic kits. The first significant step was introducing the LEGO Technic series in the late 1970s, which allowed users to build more complex mechanical models. The programmable brick revolutionised the process by allowing LEGO creations to be independent and mobile, paving the way for LEGO Mindstorms [38]. Various generations of LEGO robotics kits have been released in the last twenty years: Mindstorms NXT in 2006, NXT 2.0 in 2009, and Mindstorms EV3 in 2013. Souza et al. conducted a systematic review of the literature analysing the use of LEGO robotics technology as an instrument for teaching, considering the robotics kits and their programming environments as a combination of teaching methodologies and practices. In 2018, it was reported that the most commonly used environment and programming languages are LabVIEW and LEGO’s block-based programming language. Additionally, Souza et al. found that LEGO Robotics is utilised for teaching programming, interdisciplinary subjects, participating in tournaments, robotics, and computational thinking. Furthermore, LEGO® Robotics has been successfully used by students across various levels, including K-12, undergraduate, and graduate programs. The most recent product in the evolution of LEGO robots, SPIKE Prime, was released in 2020 and is already very popular [39]. One reason for this is probably that the robot can be programmed in several ways, and one option is the Scratch programming language [35]. Ersozlu et al. used a scientometrics analysis to map data from the scientific literature based on different kinds of published research and found that computational thinking (CT) in mathematics education was mostly about teaching computational skills and computer programming through practical and algorithmic thinking in engineering and STEM education, especially at the higher education level. In addition, Scratch has been the dominant tool used to teach programming skills at all levels of schooling, including higher education.

Educational robotics has been successfully used for many years as a tool to make learning more experiential and effective [41]. Combining educational robotics with problem-based learning is not a new idea, and educational software developed for LEGO Education robot kits (WeDo 2.0, EV3, SPIKE Prime, SPIKE Essential) includes learning projects that essentially implement problem-based learning as an integral part of the design of the educational software [35]. However, these projects focus on basic physical, biological and social science knowledge and on learning robot programming concepts [42]. In order to target STEAM-based methodology in higher education, it is necessary to develop new robot constructs and build student projects around them.

Despite the potential of integrating robotics into teaching and learning, this integration has not yet been fully explored in university practice, especially in higher mathematics education.

1.3. Importance and Teaching of Cycloidal Curves

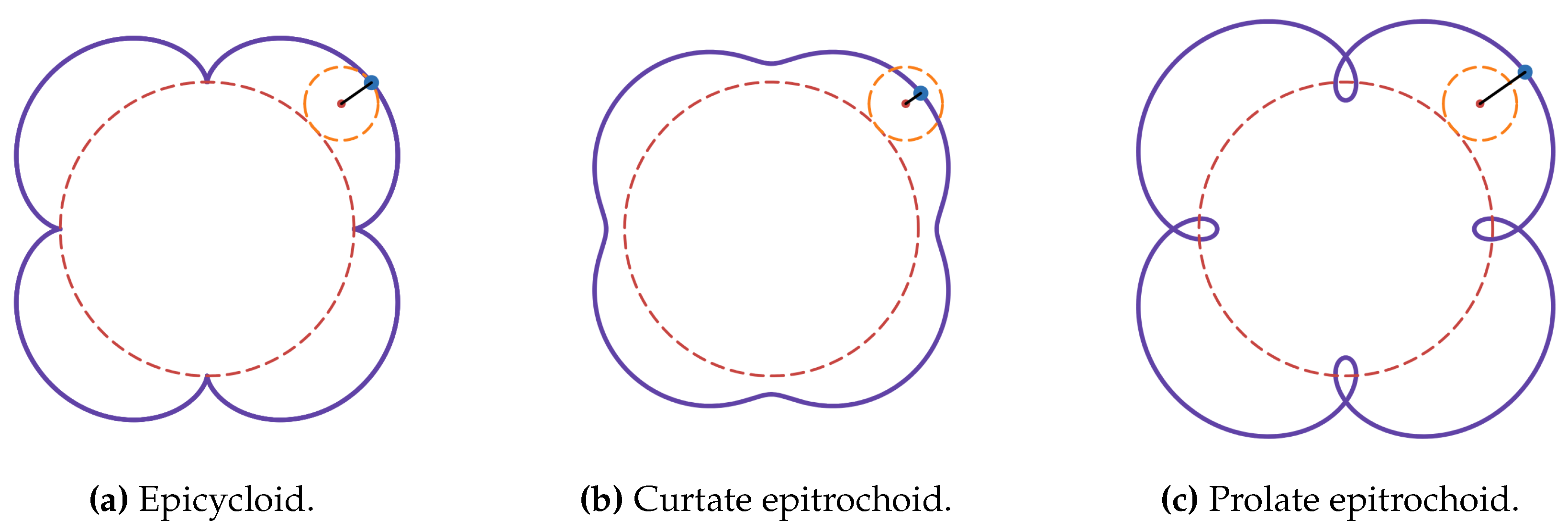
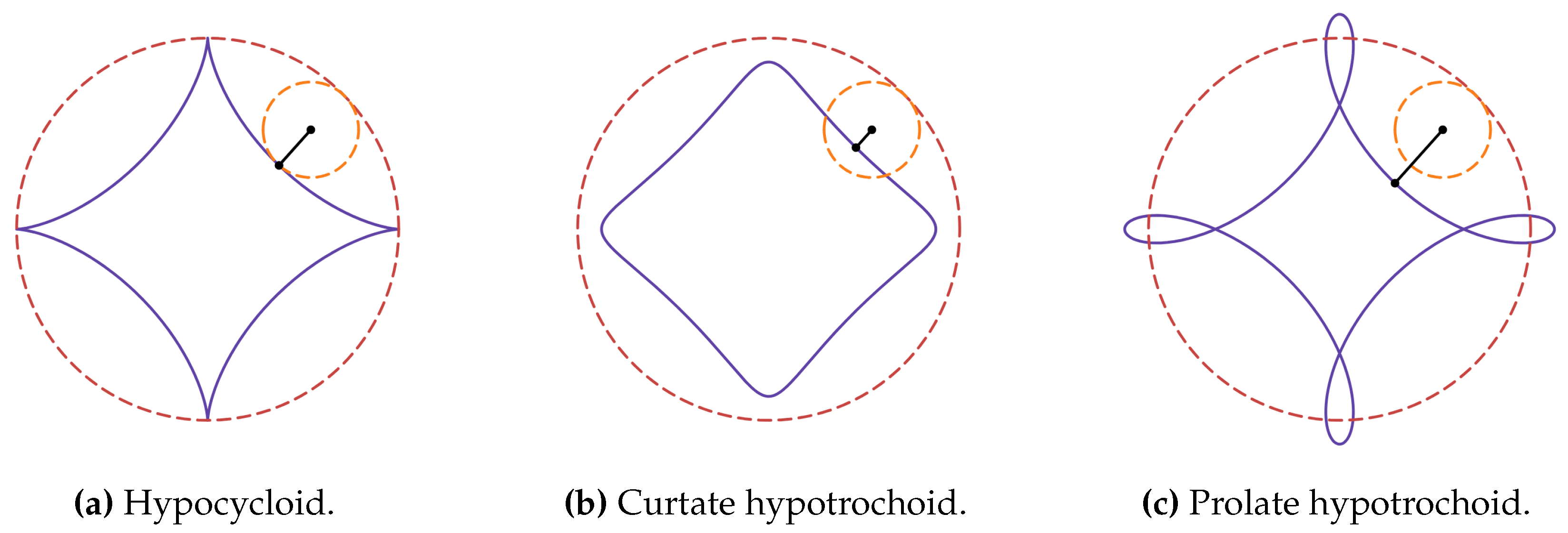
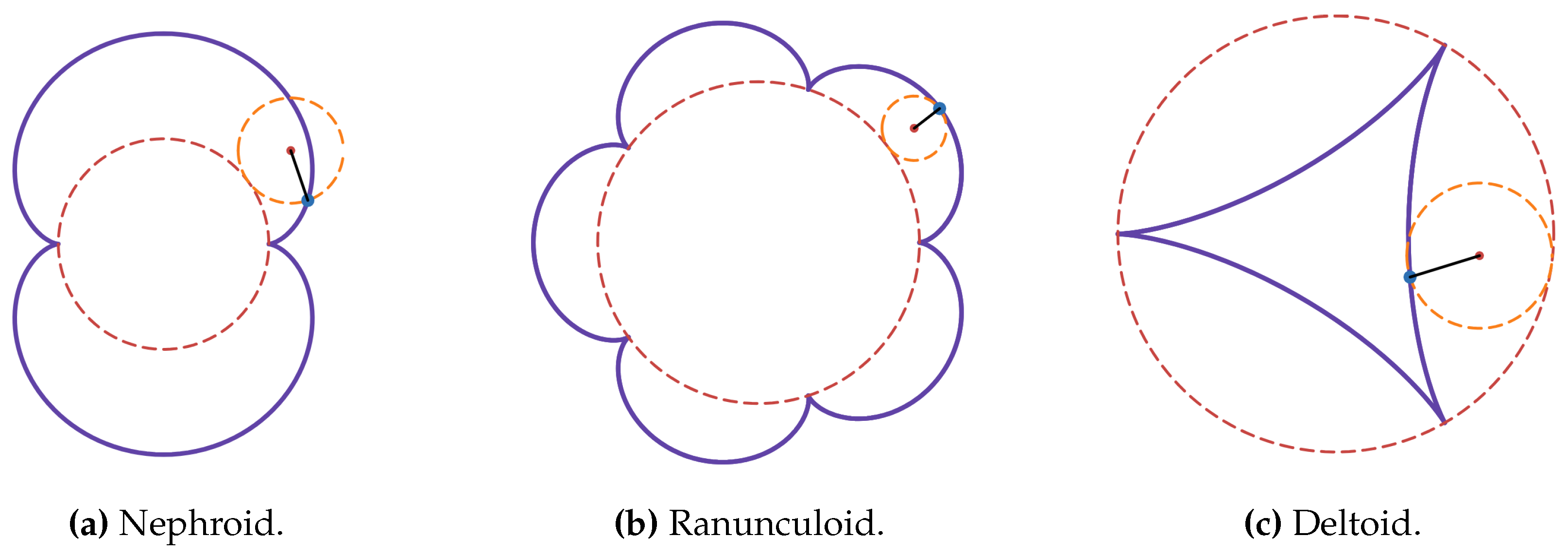
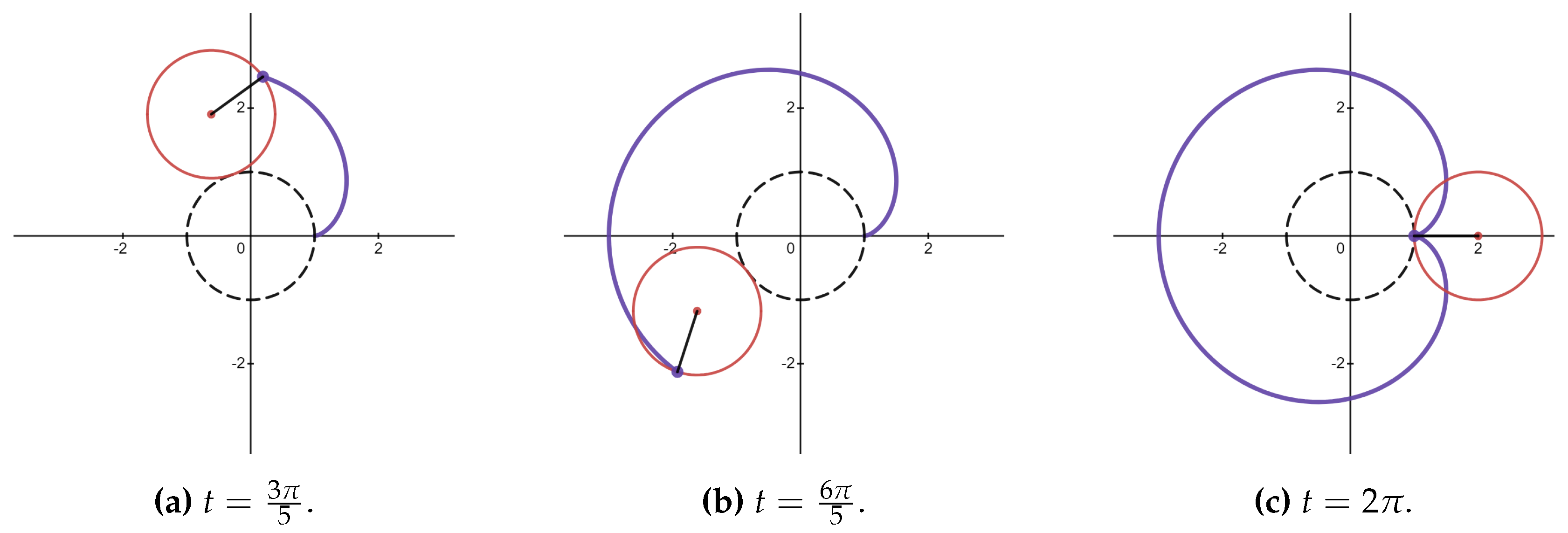
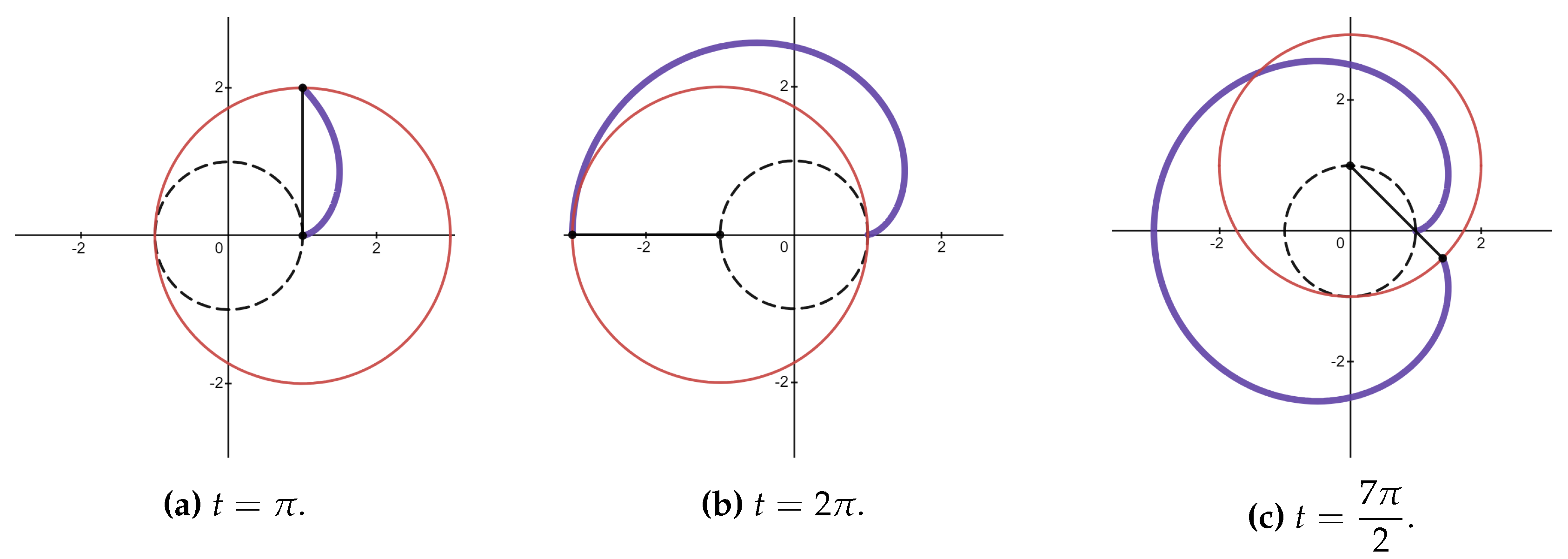
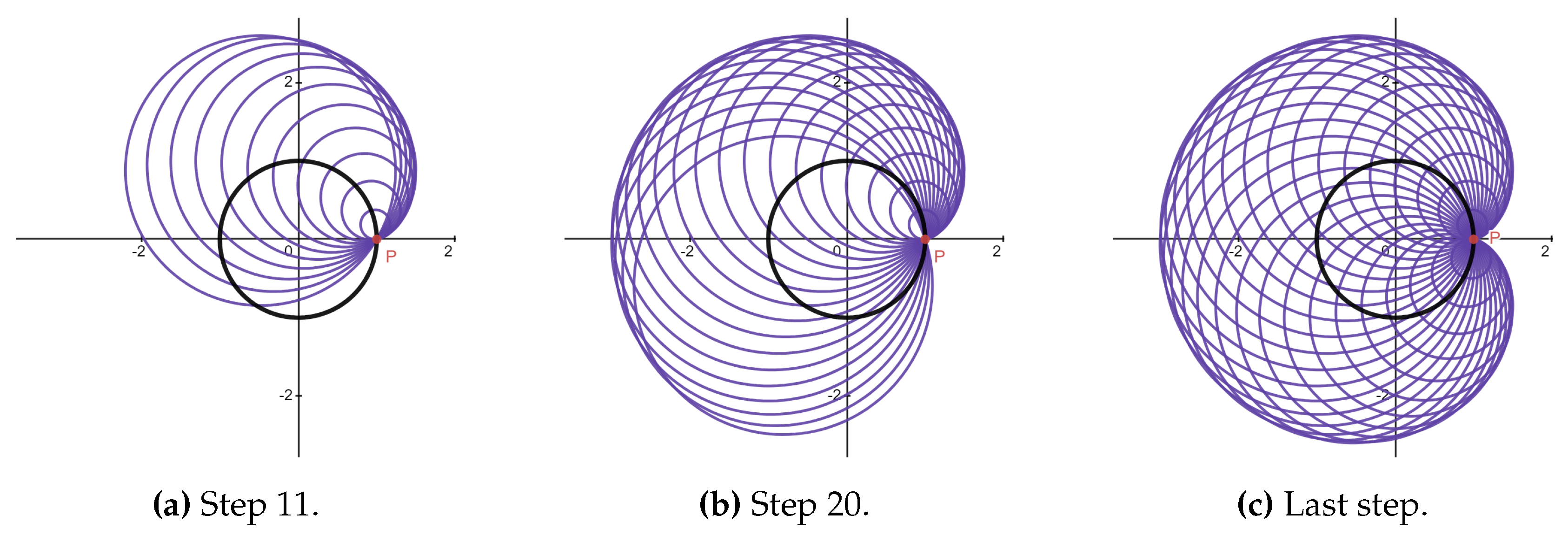
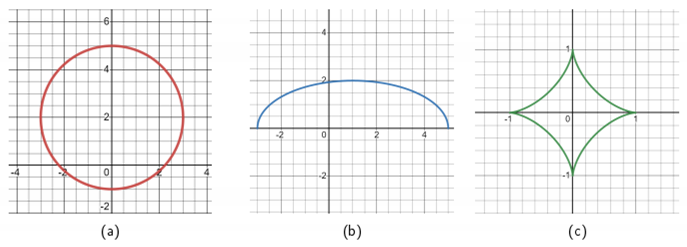
Roulette is a path traced by the point fixed on a curve that is rolling on another fixed curve [43]. Cycloidal curves are a family of roulettes generated by the motion of a point attached to a circle as the circle rolls along a fixed straight line or another circle. These curves include trochoids, epitrochoids and hypotrochoids, as shown in Table 1.

The parametric equations and graphs of the cycloidal curves are given in Appendix 6. We note that the term central trochoid encompasses both epitrochoids and hypotrochoids [44]. The centre of a central trochoid curve is defined as the centre of the fixed circle.

In engineering mathematics, theory and application go hand in hand. Cycloidal curves are very useful in practical life. In 1694, Philip de la Hire published a complete mathematical analysis of epicycloids and recommended an involute curve for designing gear teeth. However, in practice, it was not used for another 150 years. In 1733, Charles Camus expanded la Hire’s work and developed theories of mechanisms. Twenty years later, in 1754, Leonard Euler worked out design principles for involute gearing. Felix Wankel developed the Wankel Rotary Engine in the 1920s. Initially developed as an air compressor, the engine is now used in automobiles. The rotor is an equilateral triangle with curved sides, and the bore is an epitrochoid curve. Nowadays, epitrochoids can be found in important mechanical parts such as gears with epitrochoidal tooth profiles, cams and epitrochoidal-shaped housings for rotary internal combustion engines and rotary piston pumps. For the last case, the epitrochoid curve notes the path that the rotor tip of the eccentric shaft traces out upon revolving [45]. Hypocycloid curves also have many important applications in engineering. One of these is the use of the astroid shape in the process of moving bus doors [46]. In addition, central epi- and hypotrochoids can be used, for example, in surveillance or spatial coverage applications, as periodic motion primitives for human dancers or for performing complex choreographic patterns in small autonomous vehicles [47], as well as in the context of autonomous robot navigation with collision-free and decoupled multi-robot path planning [48]. Cycloidal curves are used in roller coaster design, architecture (Kimbell Art Museum, Hopkins Center for the Arts), and the creation of geometric patterns for stained glass windows, mosaics, and textiles [49].

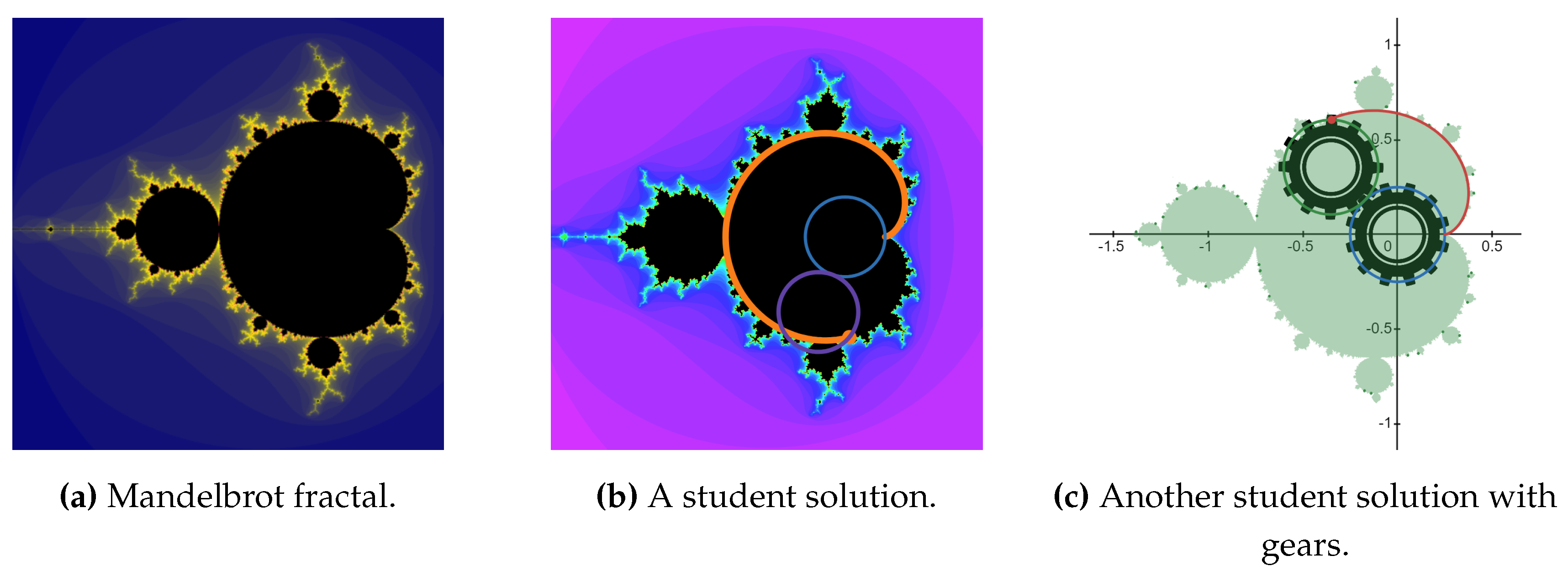
The wide range of applications above shows that cycloidal curves represent fundamental mathematical and geometric concepts indispensable in various engineering fields. In his 1913 article, Epsteen summarized the minimum content to be taught in engineering mathematics, emphasizing the importance of higher plane curves in the curriculum, including cycloids, hypocycloids and epicycloids. These curves are extremely important for mathematical foundations because the knowledge associated with them becomes relevant in the context of kinematic analysis and mechanical design. Cycloidal curves help engineering students better understand motion and force transfer principles, especially in mechanical systems [51]. By studying such curves, students learn the precise design and efficient calculations that are essential for a variety of engineering applications. In addition, the presentation of cycloidal curves is also important in modelling the behaviour of physical motions, such as the behaviour of a pendulum [52]. In modern computer-aided design programs, the accurate representation of cycloidal curves allows the efficient design of complex mechanical components. Cycloidal curves are not only mathematical curiosities but also fundamental tools for solving engineering problems.

In university engineering mathematics education, cycloidal curves were taught in the 18th and 19th centuries using geometric and analytical methods. Students usually learned from hand-drawn diagrams and understood mathematical equations involved in on-the-spot demonstrations and geometric proofs [53,54]. Kinematic models and mechanical devices were used for illustration because the derivation of the equations of cycloidal curves and the representation requires visualisation [55]. Several of these constructions are included in Schilling’s famous collection of kinematic models [56]. Kinematics, the study of motion, played an important role in understanding cycloidal curves, especially in analysing mechanical systems and motions. The emphasis was on geometric insights and classical physical examples. Traditional teaching methods for students at universities are outdated and not effective enough [52]. In today’s education, modern technologies and computer simulations are now used to help understand the knowledge of cycloidal curves. Several didactical articles deal with visualising cycloidal curves using dynamic geometric software or simulation embedded in a remote experiment [52,57,58]. These methods have many advantages in terms of visualisation, but they do not provide direct experimental experience. The recent research of Tessema et al. highlights the importance of a realistic, hands-on approach to learning in mathematics education, particularly in the study of geometry. Traditionally, drawing cycloidal curves is a lengthy process that requires engineering drawing knowledge. A simpler and faster way to produce curves is to have a robot draw the curve during an ER activity. By building and then testing the drawing robots, students gain first-hand experiences [60,61,62,63,64].

1.4. 4C Learning Approach

LEGO’s philosophy is that effective learning can only be achieved through a holistic approach because learning has creative, cognitive, social and emotional aspects. The LEGO 4C principle is a pedagogical model developed by LEGO Education, focusing on four fundamental key competencies in learning [65]. The LEGO 4C learning approach is characterised by its hands-on, inquiry-based, and collaborative nature, which aligns with constructivist and experiential learning theories. It engages students in active learning experiences where they actively construct knowledge, explore concepts, and solve problems.

By integrating the four Cs into educational activities, the LEGO 4C learning approach aims to foster creativity, critical thinking, collaboration, and communication skills in students, preparing them for success in the 21st century [66]. These key competencies are as follows:

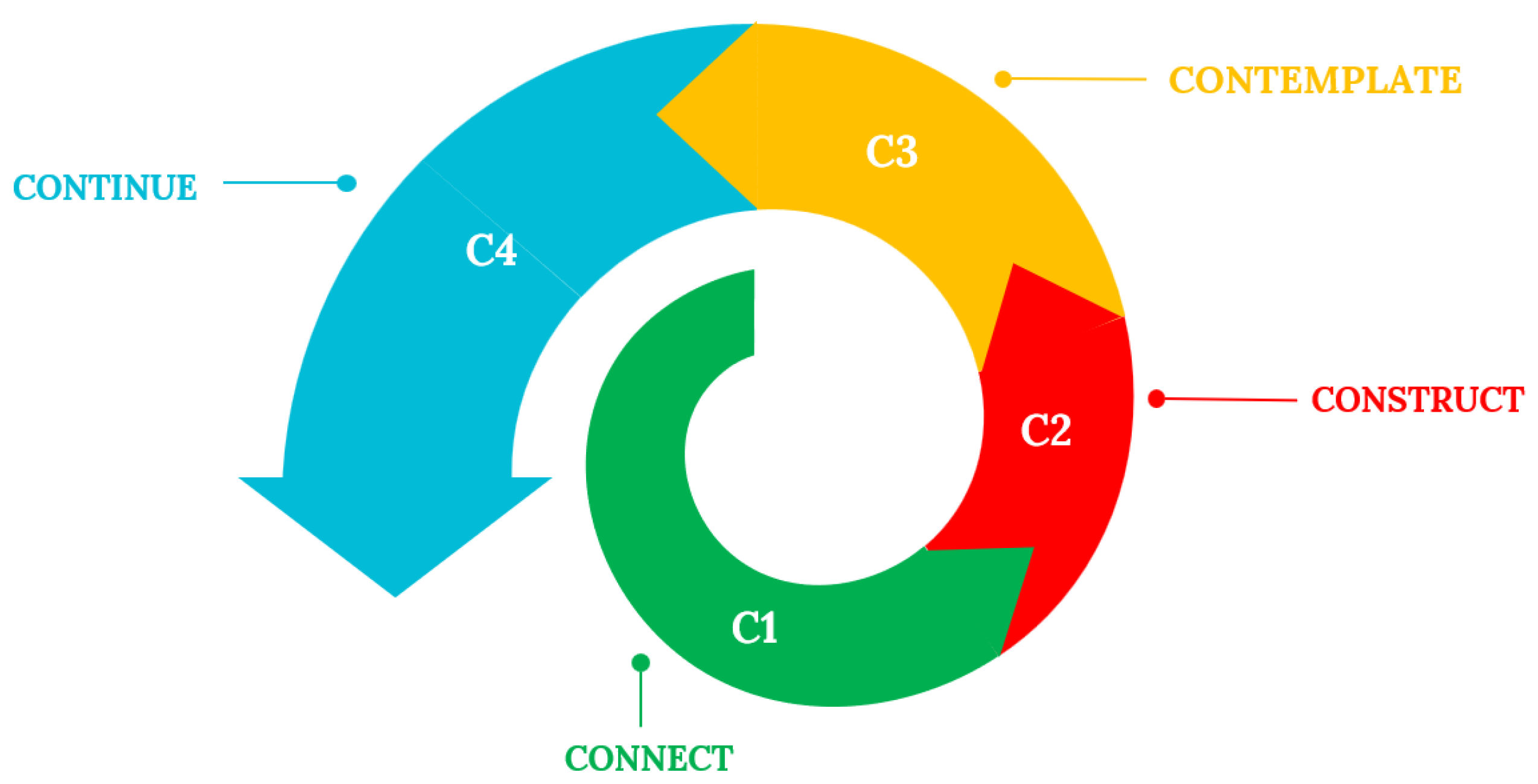
Connect: This first C stands for connection, meaning establishing a connection. Students should be given the opportunity to connect with the subject matter and recognize its relevant and interesting context. This allows learning to more closely align with students’ everyday lives and experiences.
Construct: The second C is construction, which means allowing students to create or build something. This could be a physical model, a project work, or a digital creation. The act of constructing enables students to deepen and apply their learning.
Contemplate: The third C is contemplate, which encourages students to reflect on the things they have created and what they have learned. This includes reflection and self-reflection, as well as critical evaluation of the application of what they have learned.
Continue: The final C is continue, which means giving students the opportunity to further develop, apply, and share what they have learned and created with others. This process can help sustain learning and apply what has been learned in practical ways.

These four phases are steps in an iterative process that should often be seen as a learning spiral (Figure 1); the four links are not a single linear structure but a process of interlocking and dynamic circulation [66]. The LEGO 4C principle is a framework applied to learning and teaching that helps students establish a closer connection with the subject matter and apply experiential and hands-on learning methods. This allows for a deeper understanding of learning and enriches the learning experience.

The LEGO 4C methodology has mainly gained ground in primary and secondary education [65]. The 4C principle can also be applied in higher education because of the generational shift. We propose a methodological model based on the 4C principle to process the curriculum on cycloidal curves. Engineering students naturally show a keen interest in robotics and ICT tools, which aligns with their chosen specialisation. To help them discover the secrets of cycloidal curves, we have developed a methodology combining frontal teaching with problem-based learning, educational robotics, and dynamic geometric software in project-based learning.

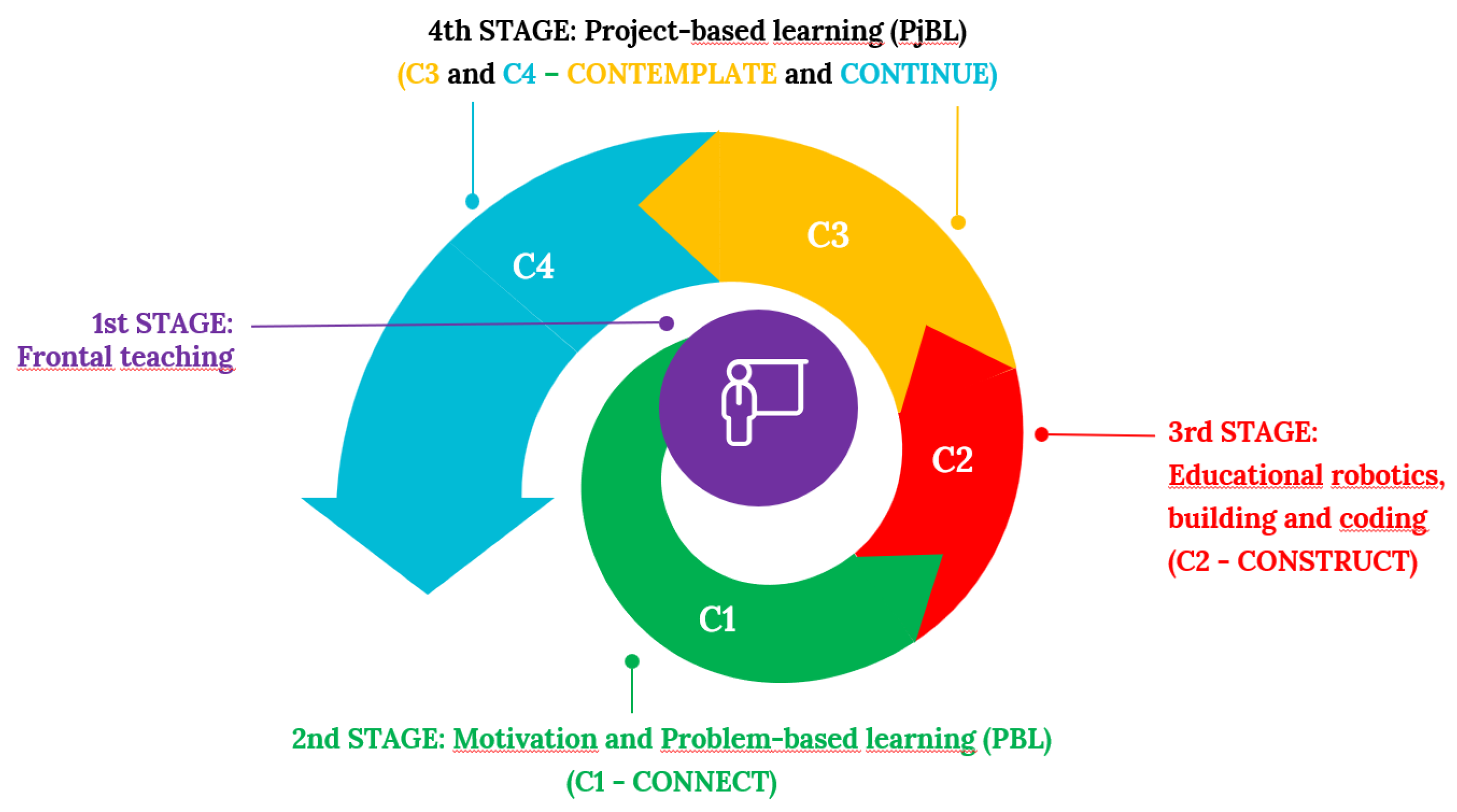
1.5. The Four-Stage Methodological Model for Learning Cycloidal Curves

The first element of the four-stage model for learning cycloidal curves is frontal teaching (lecture and practice), where the theoretical material is presented, covering cycloidal curves (Figure 2). In fact, many studies have been carried out over the last two decades on the disadvantages of frontal teaching. However, it is still the dominant teaching method in higher education [67]. Ganyaupfu investigated that the teacher-student interactive method was the most effective teaching method over the teacher-centred approach because direct teaching is efficient in transferring knowledge but is not sufficient for deeper understanding, problem-solving and creativity. Innovative teaching incorporates technology into the teaching-learning process to create a rich and helpful learning experience for students and a rewarding teaching experience for teachers [69,70]. It should not necessarily be abandoned for large courses and frontal teaching, but it should be complemented by techniques where students are not passive participants. There is evidence that lectures can effectively and structurally communicate information, model reasoning, and motivate students, particularly when adequately supported by other activities [71].

After the theoretical grounding, the topic of plane curves can be continued in specialised seminars. The second stage is to start working according to the 4C principle. The problem statement explores the possibility of producing a curve experimentally. We note that seminars are extracurricular activities. In the second phase, the focus is on attracting attention and motivation. Where possible, we choose demonstration experiments that students can carry out in small groups, documenting them and giving them the opportunity to gain direct experience. Problem-based learning (PBL) is achieved through the formulation of real-life tasks. Given that Connect aims to revive knowledge related to what has been learned previously, students are actively involved in solving the problems formulated. It is worthwhile to revive the most important theoretical knowledge; for this purpose, visualisation solutions and animations can be used in the case of cycloidal plane curves.

The third stage uses STEAM-based methods: building and programming drawing robots, and understanding how robots work. The educational robot kits give students the opportunity to explore a curve under investigation in small group activities. Working with robots requires providing building instructions for appropriate drawing robot designs and sharing conditions for working with robots. For four years, the authors have been designing drawing robots whose operating mechanisms can be mathematically deduced with precision. Using the LEGO Education SPIKE Prime robot set, educational robots have been designed to produce a wide range of representatives of the cycloidal curve family.

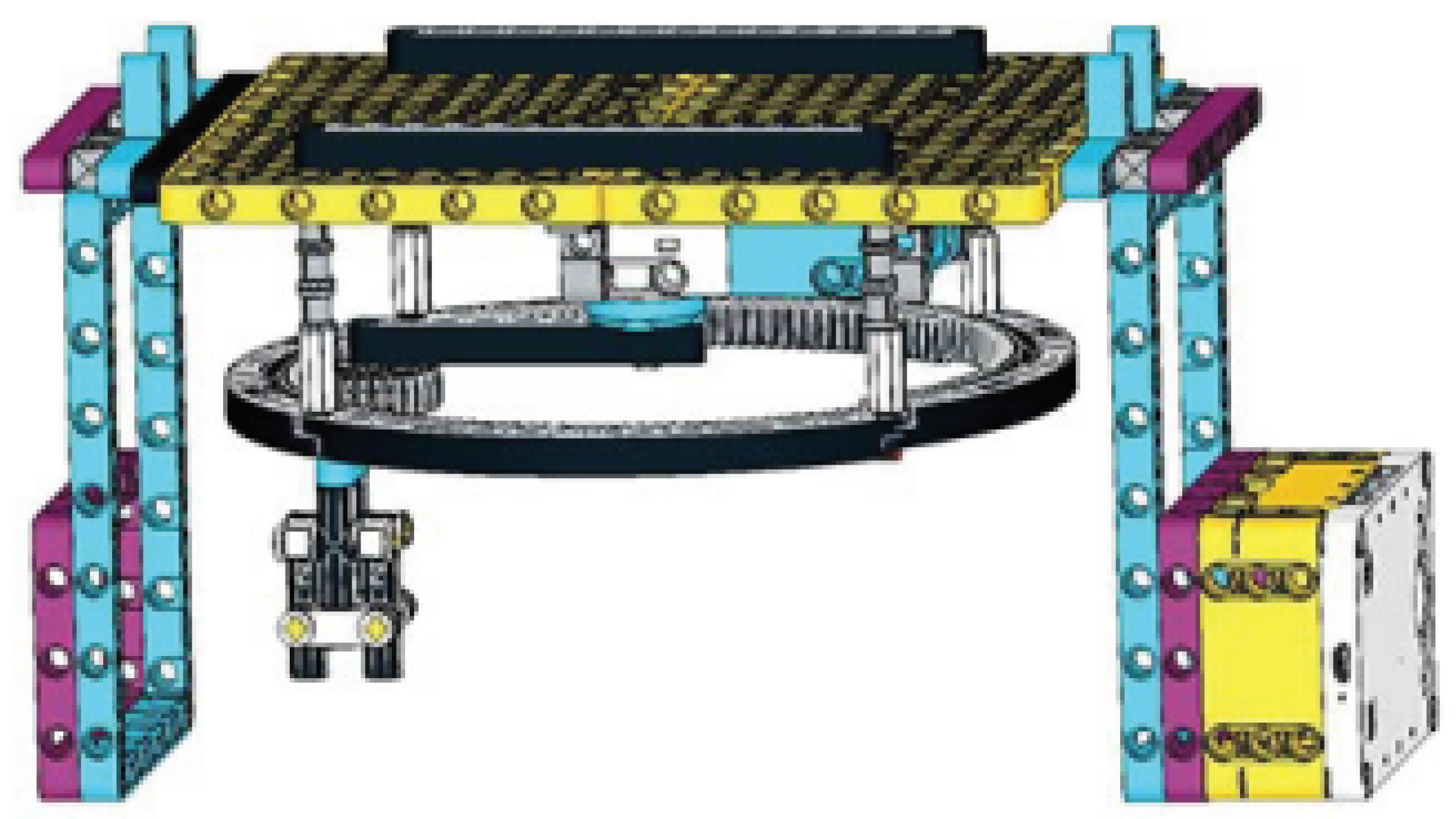
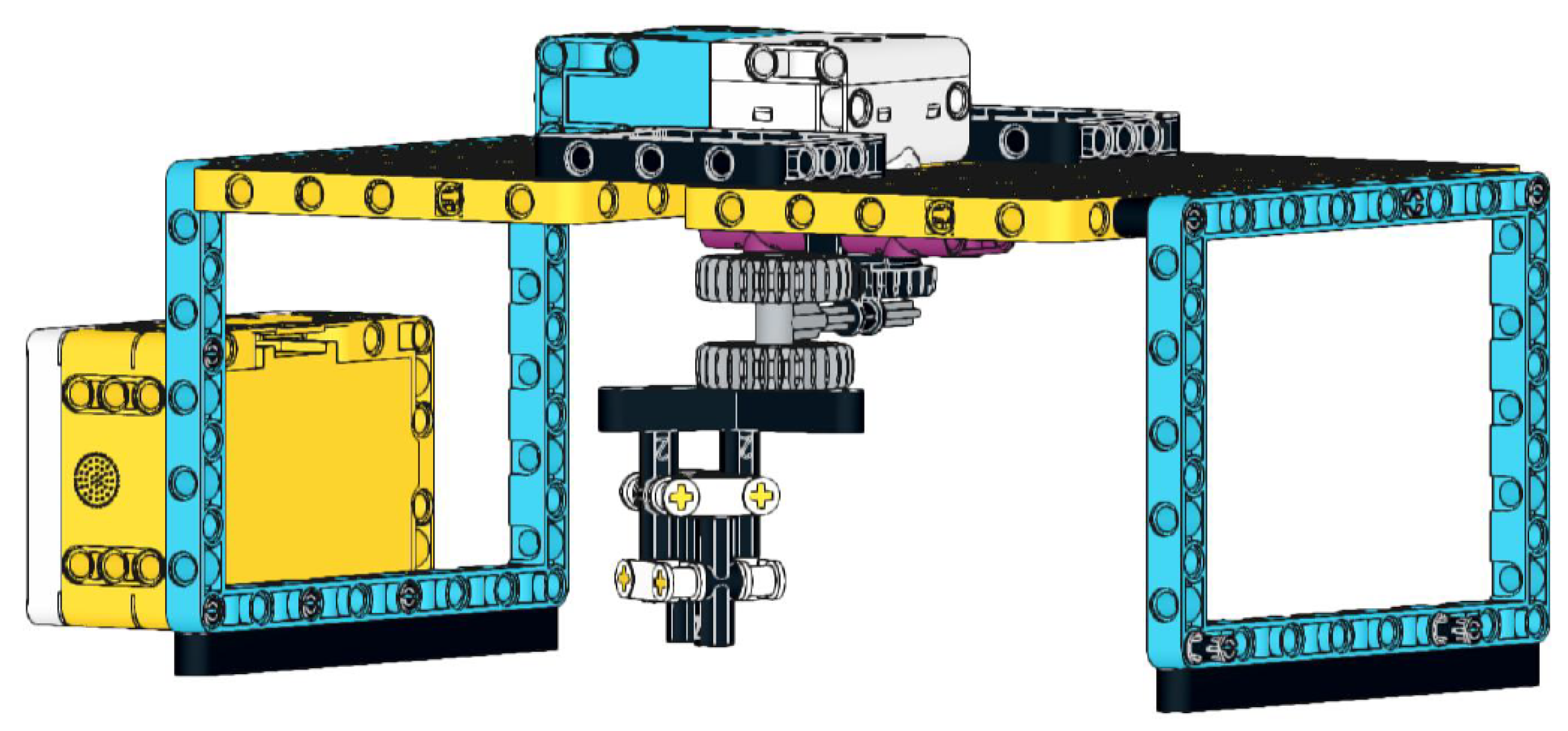
In spirograph-like robot models, gears are used to model the circles that generate the cycloidal curves. The aim of [60] was to introduce the hypotrochoid family of curves and to give ideas and tools for teaching the topic. The general parametric equations of hypotrochoids were given, and several special curves that can be derived from these equations were shown. In addition, a drawing robot called Spikograph 1.0 (see Figure 3), modelled on a Spirograph toy, was presented, which can draw different hypotrochoids, giving students a physical experience. This robot uses LEGO gears to model the slip-free rolling of the circles, and knowing the gears’ sizes, the parametric equations of the drawn curves can be easily written.

Spikograph 1.0 gave the idea to design Spikograph 2.0 (Figure 4) for drawing epitrochoid curves; this drawing robot was presented in [61]. The factor that most determines which epitrochoids can be drawn with the robot is the size of the suitable gears in the LEGO Education SPIKE Prime set. The diameters of the circles that define the epitrochoid correspond to the rolling diameters of the gears that model them. The rolling diameter of a gear is the diameter of an idealised disc that allows it to roll on the equivalent idealised disc of another gear that is usually meshing with it. This dimension is easy to determine since the rolling diameter of any LEGO gear, expressed in mm, is equal to the number of teeth on it.

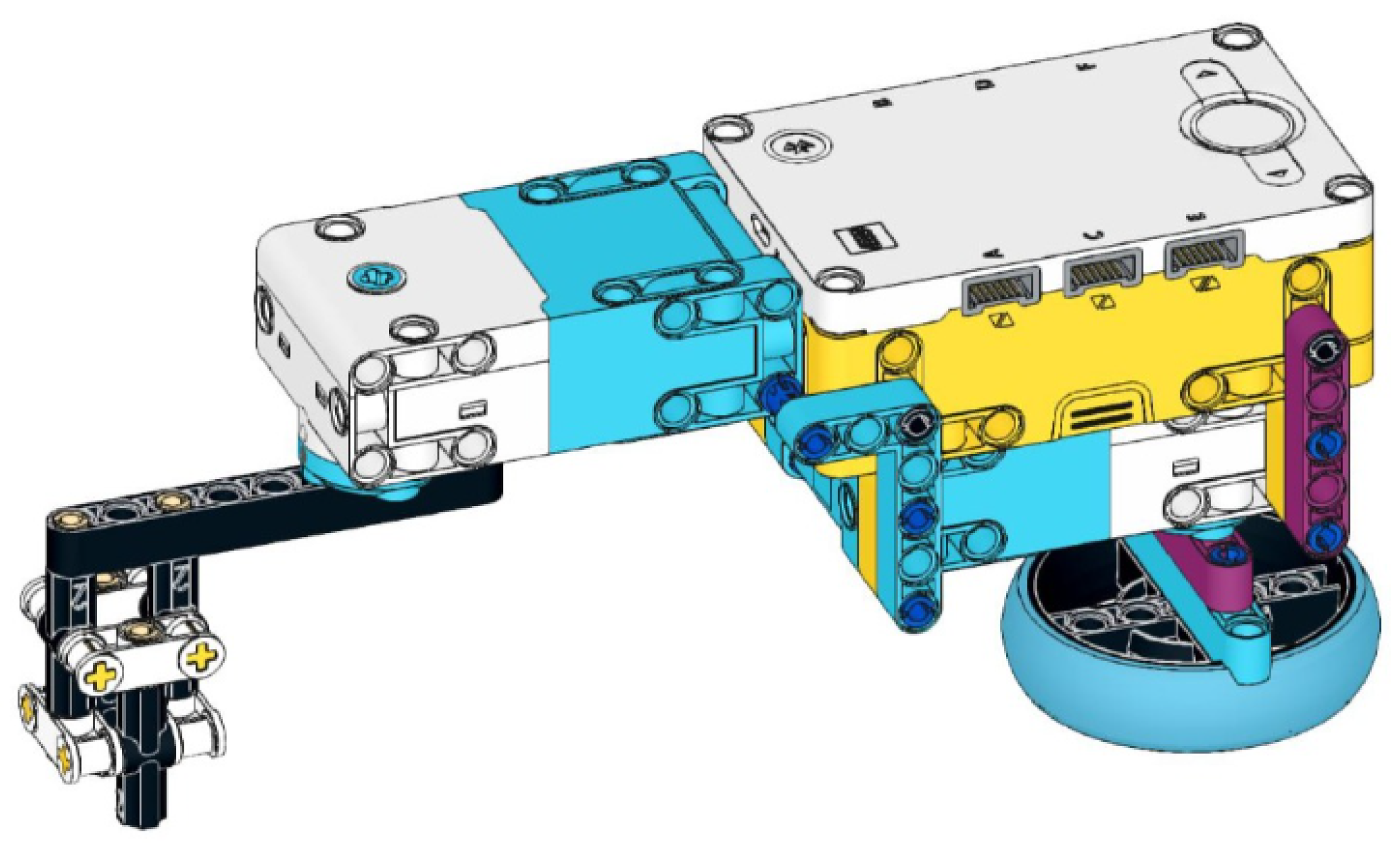
Students can work not only with these two gearing robots in the seminars. Although Spirograph-like robots are an excellent way to illustrate the production of many notable plane curves, the principle of operation of robots in the industry follows a different path. It is important that students can work through real-life tasks on various projects; therefore, the use of a SCARA-style robot design is also possible in the seminar series (see Figure 5). The SCARA robot is one of the common types of industrial robots [72]. The SCARA name stands for Selective Compliance Articulated Robot Arm. The main feature of the SCARA robot is that it has a jointed 2-link arm driven by two independent motors [73]. It is well-known that the plots generated by a Spirograph toy can also be drawn using a 2-link planar or SCARA robot after computing the inverse kinematics to get the joint angles needed to perform the correct movements. It is also a known fact that the Spirograph toy is not able to draw all types of trochoidal curves; only the curtate types can be created. However, Spirograph-like and SCARA-style robots can draw all three types of central trochoids [63,64].

Thanks to their construction, robots can draw an infinite number of cycloidal curves. However, the number of curves that can be drawn in the Spirograph toy is finite. Table 2 summarises the central trochoids that can be drawn with the Spirograph, only LEGO gears and racks [74], and the various educational LEGO drawing robots. The SCARA-style robot can be used to draw all types of central trochoids, but its principle of operation does not follow the usual definition of curve generation. A big advantage of the robot versions using gears is that the generation of curves is based on the definition. Exploring the potential of drawing robots and how to integrate them into the educational process is an ongoing process of active research.

The construction phase of the 4C principle is where the robot is built and programmed. Writing the program is also considered design because the robot can only operate with the right program. In the case of Spirograph-like robots, this refers to the operation of a single motor, whereas in the case of a SCARA-style robot, it refers to the coordinated operation of two motors.

The LEGO SPIKE Prime robot hub can be programmed in three ways, one of which includes the Scratch programming language. Developed by Mitchel Resnick at the MIT Media Lab, Scratch is an evolution of the LOGO language. This visual, block-based coding language features a drag-and-drop interface, making programming accessible and enjoyable for users [35]. Programs for drawing robots are created in Scratch using the original software designed for the LEGO SPIKE Prime robot.

In the contemplate phase, the synthesis is given through the solution of a project task, where the task is to create an animation modelling the robot’s working principle. Students can work on the project independently or in groups, allowing for exchange and knowledge sharing. Project-based learning (PjBL) can be a very effective way to learn mathematics. PjBL involves students working on complex, real-life problems that require them to apply mathematical knowledge and skills. This approach helps students link theoretical knowledge with practical applications and develops their problem-solving and collaboration skills [75]. In project-based learning, it is important that the projects are genuinely interesting and relevant to the students and that they solve real problems [76]. The teacher has a key role to play in guiding and supporting students through the projects and helping them to understand the relationships and mathematical principles. Projects can also help students to see how mathematics relates to their everyday lives and to solve real-world problems. Relevant literature suggests that the link between PjBL and dynamic geometric software (DGS) is extremely useful in mathematics education [77,78]. DGS refers to computer software that allows the visualization and manipulation of functions, curves, and geometric shapes. These software can help students understand and visualize mathematical concepts that they can apply in PjBL projects. With DGS, students can see geometric constructions and shapes in real-time, resulting in a visual understanding that supports students in handling abstract mathematical concepts better. The DGS provides an interactive platform through which students can experiment and modify geometric constructions on their own, significantly contributing to the development of active learning and an experimental approach. The link between theoretical and practical aspects is greatly facilitated by using DGS, as students can immediately see how functions, geometric shapes and relationships change when they change parameters or manipulate constructs. Experiences have shown that the combined use of PjBL and DGS helps make mathematics teaching more interactive and understandable [78,79,80]. Students will be able to apply the mathematical knowledge they have acquired through DGS in real projects and will be able to combine theoretical and practical aspects more easily.

In the fourth stage of 4C, additional project tasks are connected to the studied curve. It is recommended that homework be solved using DGS. There are different types and versions of DGS. One of the most commonly used DGS is GeoGebra [79]. The application can be used for geometric and algebraic analysis. It offers several tools for visualising functions, drawing and manipulating geometric shapes and understanding mathematical concepts [80]. Desmos was originally a graphing calculator application but has since been extended to include DGS functionality. Desmos is a compelling application for visualising functions and curves and helping to understand mathematical expressions [81], so it is worth using this DGS for engineering mathematics courses. Another advantage is that Desmos is also an excellent tool for project-based learning. Real-time graphs, data visualisation, and interactive shape generation help students present their projects clearly and interestingly and provide opportunities for collaboration and interaction between students. For example, several students can collaborate on a project and see each other’s work in real time. In Desmos, students are able to animate graphs, which can help them better understand mathematical relationships and changes [82].

A well-designed methodology helps to structure and manage the learning process. It sets out the expected goals and outcomes for learners and the steps to be followed to achieve them. Based on the 4C principle, the four-stage methodological model for learning cycloidal curves considers learners’ individual needs, interests and abilities. It provides a flexible structure for differentiated learning experiences to ensure all students succeed. This method creates a motivating and engaging learning environment. Students enjoy learning through exciting and challenging tasks, contributing to long-term engagement and success.

Using the four-stage model for learning cycloidal curves, ellipses, cycloids, cardioids, astroids, and roses were discussed. The application of the four-stage model for learning cycloidal curves is illustrated in Appendix 7 with the example of teaching cardioid.

2. Materials and Methods

2.1. General Background

Many good practices are related to teaching 2-dimensional plane curves, including cycloidal curves, where the teaching model supports knowledge development through different visualisation techniques. However, no methodological model was found on cycloidal curves, where STEAM-based education is integrated consistently into university practice. The need for this development and research was motivated by the fact that central trochoids are the most crucial two-dimensional plane geometric patterns widely used in real-life practice (see SubSection 1.3); however, alternative methods for teaching them in higher education were not available to provide students with first-hand experiences.

A new learning structure was created after a thorough study of the literature in the framework of Lithuanian-Hungarian cooperation. The new methodological model, the four-stage methodology for learning cycloidal curves (see SubSection 1.5), considers generational needs while making optimal use of the University of Miskolc’s available infrastructure because the training centre of the University of Miskolc has 24 LEGO Education SPIKE Prime educational robotics kits. The development started in May 2023. Researchers from the Šiauliai State Institute of Higher Education and the University of Miskolc jointly worked. Based on the previous experience [62], the researcher team compiled the additional teaching material needed to apply the new methodological model according to the 4C principle (SubSection 1.4). We have rethought the drawing robots’ construction and created building guides with the seminar material. We have sorted the problems related to cycloidal curves and selected them thematically for the seminars. The complete development of the four-stage methodological model for teaching cycloidal curves took half a year.

A methodology model is well-designed if it is based on scientific research and pedagogical principles. The four-stage methodology model for learning cycloidal curves is based on the 4C principle, which is the result of research conducted by LEGO Education and is, therefore, scientifically sound. In order to make the same claim about the overall structure, measurements have been carried out in the spring semester of the academic year 2023/24 to provide empirical evidence of the effectiveness of the four-stage model for learning cycloidal curves. The experiment was carried out in Miskolc, Northern Hungary. The research presented in this article continues the Lithuanian-Hungarian research conducted between June 2021 and June 2023 with 27 students at the University of Miskolc. The previous research focused only on a new, innovative approach to teaching the cardioid curve [62].

2.2. Research Design

The study used exploratory research, a quasi-experimental research design, and quantitative observation to assess the impact of the four-stage model for learning cycloidal curves. The quasi-experimental approach was necessary because it was impossible to randomly assign computer science engineering students to the experimental and control groups. The experiment was carried out in connection with the Calculus II course.

In the first part of the study, we used a post-test-only design. In the spring semester, the cycloidal curve topic is the first part of the Calculus II syllabus. All students who took the Calculus II course were absolved of the Calculus I course in the autumn semester, so all participants had a basic knowledge of the topic of engineering mathematics. A control group study was conducted, in which the experimental group learned using the four-stage model for learning cycloidal curves, while the control group was taught in a traditional format. The control group participated solely in traditional frontal lectures and practical lessons, whereas the experimental group benefited moreover from additional activities based on the four-stage model for learning cycloidal curves. The post-test-only design allows for a clear comparison between the intervention and control groups, helping to isolate the effect of the treatment. Table 3 summarises activities during the Calculus II course.

In the second part of the study, a between-groups design was used. This framework allows the effectiveness of the intervention to be assessed across different groups of participants. Based on their prior knowledge, the experimental group was divided into three sub-groups (below-average, average, and above-average performers). The average score of the question papers in Calculus I was used to form the groups. The post-test results were examined group-by-group to explore whether the method could be used effectively regardless of prior knowledge.

2.3. Sample and Ethics

The effectiveness of the four-stage methodology model for learning cycloidal curves was tested with Hungarian Computer Science Engineering BSc students at the University of Miskolc.

The experimental group comprised 36 students (86.11% male, 13.89% female). The control group comprised 62 students (93.55% male, 6.45% female). The total sample compared 98 students, consisting of 89 men (90.82%) and 9 women (9.18%), as shown in Figure 6. All participants are full-time BSc students and aged between 19 and 22. The experimental group and the control group were of different sizes, but the statistical method chosen to analyse the data is not sensitive to differences in group size.

At the beginning of the semester, students were informed that up to 40 students could participate in six extra Robotic-STEAM (R-STEAM) seminars during the semester. Students could register voluntarily. Participants agreed to attend all six seminar sessions and to prepare solutions for the homework assignments. Four of the applicants failed to meet this condition, resulting in an experimental group of 36. The groups in the practical sessions were mixed, i.e., the control and experimental groups were not separated during the frontal teaching. Cycloidal curves are usually covered in the first 4 weeks of the semester. The lectures and practical sessions were held as usual during the experiment in the first four weeks. However, six extra seminars were held so that the experiment took place in the first six weeks of the semester. Only members of the experimental group attended the R-STEAM seminars. Due to the limited number of robots and the training centre’s limited capacity, the seminars were divided into groups of 20 students.

At the beginning of the semester, students were informed of the research’s aims, and all agreed to participate. The study followed the ethical standards set out in the University of Miskolc’s Code of Ethics.

2.4. Intervention and Instruments

The Calculus II course lasted 13 weeks and consisted of three 45-minute lectures and two 45-minute practical problem sessions weekly. Students learned the same material and solved the same exercises during practice sessions. The participants attended the same lectures, while their practice sessions were taught in groups of 20 students on average. There were five practice groups. The teachers of the practice groups consulted each week on the main issues related to the course in order to avoid teacher influence, so the structure of the practice sessions was similar in each group.

The learning processes of the experimental and control groups were synchronised during frontal teaching. Both groups heard the same theoretical material in the lectures, and in the exercises, they took the same types of tasks, working from the same exercise book. The first stage in the four-stage methodological model for learning cycloidal curves is frontal teaching, which was implemented under the same conditions for both the experimental and control groups. The control group did not receive any other intervention.

The experimental group members (36 students) participated in six extra R-STEAM seminars, one weekly for six weeks, where STEAM-based supplementary training was implemented to support the frontal teaching of the theoretical material. A full description of one of the six seminars can be found in Appendix 7. The second and third stages of the teaching-learning process were implemented in the seminars according to the 4C principle. The last stage involved extracurricular activities in the form of project work. In these out-class activities, the experimental group students solved homework projects using DGS, as shown in the last column in Table 3.

The post-test, the question paper of Calculus II, was written in the seventh week of the semester. The scores obtained on the question paper were used for the statistical analysis. The task set used for the question paper was the same for the experimental and control groups. Experienced teachers marked the question papers. The question paper exercises were marked using a detailed scoring guide prepared by the lecturer, which included the sub-scores and scoring information. All post-test tasks, along with their corresponding score values, can be found in Appendix 8.

2.5. Research Questions

When introducing a new educational model, it is crucial to address several key research questions to ensure its effectiveness, impact, and sustainability. This research aimed to demonstrate the positive effects of the four-stage methodological model for learning cycloidal curves, so the research questions were the following:

RQ1: Can a positive effect of the four-step model on the learning of cycloidal curves be demonstrated after its introduction in an undergraduate engineering mathematics course?
RQ2: Which group of students use the new learning model most effectively regarding academic performance?

The participants’ question paper results were analysed using statistical methods to answer the two research questions regarding effectiveness and learning outcomes.

3. Data Analysis and Results

In the experiment, the control group was larger (62 participants) than the experimental group (36 participants). The DATAtab statistical calculator was used to analyse the data. Table 4 shows the two groups’ statistical key figures. The maximum possible score on the question paper was 50. The experimental group has a higher mean score (42.17) compared to the control group (27.15). Similarly, the median score for the experimental group (45) is higher than that of the control group (27). The standard deviations and variances are similar, indicating a comparable level of spread or variability in scores within both groups. However, the experimental group has a slightly higher standard deviation (8.56) compared to the control group (8.18). The range for the control group (7 to 46) is wider compared to the experimental group (24 to 50). The 95% confidence interval for the mean score of the control group (

25.07 - 29.22

) does not overlap with that of the experimental group (

39.27 - 45.07

), reinforcing the conclusion that the experimental group scores significantly higher. The data show that the experimental group shows significantly higher performance in scores compared to the control group, with higher mean, median, and mode. The confidence intervals for the means do not overlap, suggesting a statistically significant difference between the groups. The variability within each group is similar, but the experimental group has a slightly higher spread around the median.

The violin plot of the sample combined with the box plot includes all the essential data: a marker for the median, a box indicating the interquartile range, and all points of the sample, so it shows the entire distribution of the data (see Figure 7).

The violin plot is a powerful visual tool that vividly illustrates the distribution of scores for the control and experimental groups. The distribution in the control group is centred around a score of 27, which aligns with the group’s median and mean scores. The distribution in the experimental group is centred around a score of 45, corresponding to the group’s median and mean scores. The plot clearly shows that the experimental group achieved higher scores than the control group. Additionally, the width of the violin plot at any given score indicates the density of scores at that level, highlighting the distribution’s shape and spread. The kernel density estimation (KDE) method generates the violin plot to smooth the distribution. This method estimates the density of the data, and during the smoothing process, the estimated density may overlap the actual minimum and maximum of the data at some points. Therefore, we can see the "stretches" of the violin plot beyond the actual boundaries of the data.

3.1. Response to Research Question RQ1

The statistical results showed that the experimental group had a higher average score than the control group. However, a statistical hypothesis test is needed to conclude that the experimental group did indeed score better than the control group. The following hypotheses were formulated to answer research question RQ1:

Null hypothesis: There is no difference between the experimental and control groups concerning the dependent variable.
Alternative hypothesis: There is a difference regarding the dependent variable between the experimental group and the control group.

Table 5 shows the results of three different statistical tests used to assess whether the data follow a normal distribution.

A high p-value (greater than 0.05) suggests that the data do not significantly deviate from normality. In our case, the results of the different tests are contradictory; the results are mixed. The Kolmogorov-Smirnov test shows no significant difference between the two samples, while other tests (Shapiro-Wilk and Anderson-Darling) do. The Shapiro-Wilk and Anderson-Darling tests suggest the data do not follow a normal distribution. To compare the two samples, we used a non-parametric test, the Mann-Whitney U test, which does not assume a normal data distribution. This test helped to determine whether the medians of the two samples were significantly different. Table 6 shows the results of a Mann-Whitney U-test, which is used to analyse whether there is a difference between the two groups.

The Mann-Whitney U Statistic value (U) is 247. The U value represents the number of times a score from one group precedes a score from the other group in the ranked list of all scores. A smaller U value indicates that the ranks of one group are generally lower than the ranks of the other group, suggesting a difference in the distributions of the two groups. The value of 247 is indeed low compared to the maximum possible value, which means that the scores of the experimental group are generally higher than those of the control group. The maximum value of the U statistic is the product of two sample sizes:

U_{m a x} = 36 \cdot 62 = 2232 .

The z-value (standardised test statistic) is -6.42. This is the standardised deviation from the mean value in a normal distribution, which is used to determine the significance of the U-statistic. The negative z value indicates that the experimental group scores significantly higher. The asymptotic p-value is <0.001. This value represents the probability of observing a test statistic as extreme as, or more extreme than, the observed value under the null hypothesis (which posits no difference between the groups). A p-value of <0.001 is below the common significance threshold of 0.05, suggesting that the result is significant at the 5% level. Another way of calculating the p-value is the exact p-value, which is often used for small sample sizes. It’s slightly smaller than the asymptotic p-value and also indicates a significant result at the 5% significance level. The r value is 0.65. This is a measure of effect size and indicates the magnitude of the difference between groups. The r-value, a measure of effect size, is calculated for the Mann-Whitney U test as follows:

r = \frac{| z |}{\sqrt{N_{t o t a l}}},

where z is the standardised z-value from the test, and N is the total sample size, i.e., the sum of the sizes of the two groups. The interpretation of effect size values was established by the statistician Jacob Cohen in 1988 [83]. A value of 0.65 indicates a high effect size, which shows that the difference is not only statistically significant but also of practical significance.

In summary, the Mann-Whitney U-test showed that the difference between the control group and the experimental group with respect to the dependent variable was statistically significant. The results of the Mann-Whitney U test indicate that the experimental group achieved significantly better results than the control group. The low U-value (247) indicates that the experimental group ranks higher, and this conclusion is reinforced by the very low p-values and the significant effect size. This suggests that the experimental intervention was more effective than the control. Thus, the null hypothesis was rejected, which answers research question RQ1.

3.2. Response to Research Question RQ2

In the experimental group, we tested whether we could find a correlation between the results of the question paper on cycloidal curves and past performance. Given the differences in prior knowledge, we wanted to see what relationship could be identified in the sample. For this study, we used participants’ Calculus I average scores. The Calculus II course is in the spring semester; of course, it can only be taken if the Calculus I course was absolved in the previous semester. Similar to Calculus II requirements, Calculus I requires students to write two 50-point question papers during the semester. Three subgroups were formed based on the average of the scores on these two papers. Subgroups of below-average (G1), average (G2), and above-average performers (G3) were created using the usual technique in psychological experiments. The sample mean and standard deviation were used to calculate the lower and upper bounds of the middle interval. Students who performed in the mean

\pm 0.5 \times

standard deviation range were assigned to group G2. The intervals for the selection are the following:

G 1 = [25, 28.445), G 2 = [28.445, 33.755], G 3 = (33.755, 44] .

With this selection method

| G 1 | = 13

| G 2 | = 12

és

| G 3 | = 11

, as can be seen in Figure 8.

Once the three subgroups were formed, the results of the question papers on cycloidal curves were examined group by group. Table 7 shows the data of descriptive statistics. The mean and median values are similar across the three groups, indicating that the means of the data are not significantly different (see Figure 9). However, the median for G1 is slightly lower (43) compared to the median for G2 (46.5) and G3 (47). The standard deviation and variance are similar in magnitude across all three groups. Still, the variance and standard deviation for the G1 group are slightly higher, suggesting greater variability among the G1 data. The minimum and maximum values are in a similar range.

The following two hypotheses were formulated and tested to answer research question RQ2:

Null hypothesis: There is no difference between the three categories of the experimental group in terms of the dependent variable (scores of the question paper on cycloidal curves).
Alternative hypothesis: There is a difference between the three categories of the experimental group in terms of the dependent variable (scores of the question paper on cycloidal curves).

The Kruskal-Wallis non-parametric test was used to determine whether there was a significant difference between the groups because the normality condition was not met in the sample. Table 8 shows the results.

χ^{2}

is the test statistic for the Kruskal-Wallis test. A value of 0.99 suggests there is not much difference between the groups. The larger the

χ^{2}

value, the more evidence there is for differences between the groups. A lower

χ^{2}

value usually suggests that the differences between the groups are not as pronounced. The degrees of freedom in this case are 2. The degrees of freedom for the Kruskal-Wallis test is one less than the number of groups being compared. We have three subgroups, so the degrees of freedom are 2. The resulting p-value was 0.611, meaning that there was no statistically significant difference between the medians of the three groups. This is consistent with the statistical characteristics where means and medians were similar. Typically, a p-value less than 0.05 is considered statistically significant.

Based on the data and the Kruskal-Wallis test results, there is no statistically significant difference among the three subgroups (G1, G2, and G3). The means and medians of the subgroups are very similar, and the variability is also comparable across the subgroups. The p-value of 0.611 indicates that any observed differences are likely due to random chance rather than a true effect. In summary, based on the results of the Kruskal-Wallis test, a p-value of 0.611 indicates that there is no statistically significant difference between the subgroups tested. We retain the null hypothesis, which means that the four-stage model for learning cycloidal curves helped students achieve better academic results regardless of their individual mathematical competencies. Thus, we can answer the RQ2 research question: the four-stage methodology for learning cycloidal curves supports learning achievement regardless of individual differences in prior knowledge; it is not only effective for a certain group of students.

4. Discussion and Conclusions

This research delved into the potential of a novel four-stage methodology for teaching cycloidal curves in university engineering mathematics education, aiming to determine its effectiveness and suitability for diverse student populations. The new learning model implements STEAM-based education in engineering mathematics using ER and DGS.

In the experiment, we conducted a control group study involving 98 first-year Computer Engineering BSc students. In the first part of the study, we employed a post-test-only design, which means we collected data only after the intervention without administering a pre-test beforehand. By skipping the pre-test, we reduced the risk of biases arising from participants being aware of the study’s purpose or goals, which might otherwise affect how they respond or behave during the post-test. As a result, this design helped provide a more precise and more accurate evaluation of the intervention’s impact based solely on the post-test results. In the second part of the study, we used a between-groups design. This approach enabled us to compare the effects of the intervention among different subgroups of participants.

Two research questions were formulated and answered by analysing the scores of the question paper written in a classroom setting. Both the descriptive statistics data and the result of the hypothesis test support the answers to research questions RQ1 and RQ2, so the treatment used is an effective tool for learning cycloidal curves.

In hypothesis testing to answer research question RQ1, we employed a non-parametric test, specifically the Mann-Whitney U test, due to the non-normal distribution of the data. The Mann-Whitney U test demonstrated a statistically significant difference concerning the dependent variable between the control and experimental groups. Expressly, the results indicated that the experimental group achieved significantly better outcomes than the control group. The low U-value (247) suggested higher rankings for the experimental group, which was further supported by very low p-values and a significant effect size. These findings imply that the experimental intervention was more effective than the control. We compared the results with the study conducted by Coufal , which utilised the LEGO Mindstorms EV3 kit. Both experiments demonstrated similarly strong results. In the research by Coufal , a comparable main research design was employed, featuring a pedagogical experiment that included both experimental and control groups, alongside skill and knowledge assessment through testing. A significant contribution of their study was its verification of the positive impact of educational robotics and project-based learning on developing student competencies, a finding that our experiment corroborates. Additionally, a content analysis technique used in one of the other experiments with the LEGO Mindstorms EV3 robot indicated that project-based learning, when combined with robotics activities within a STEM curriculum framework, significantly benefits students [85]. We also concur with the findings of Goh and Ali , who reported positive outcomes in their educational experiment with the LEGO NXT robot. They emphasised the necessity for improved teaching methods to inspire courses, provide more comprehensive support for students facing mathematical challenges, and foster a community atmosphere among STEM learners.

In the experimental group, three subgroups were formed based on students’ previous results in Calculus I to answer research question RQ2. The Kruskal-Wallis test yielded a p-value of 0.611, indicating no statistically significant difference between the subgroups. This suggests that the four-stage model for learning cycloidal curves contributed to improved academic outcomes regardless of students’ individual mathematical competencies, demonstrating its effectiveness across diverse student groups. In our research, we found that the four-stage methodological model for learning cycloidal curves is an effective approach to the learning process. Our results show that the method can be applied positively to students with below-average, average, and above-average mathematical knowledge.

The experiment indirectly validated Pritchard ’s claim that the frontal teaching method can effectively teach mathematics, and thus engineering mathematics, if it is complemented with activities that motivate students. Our research also supports Hassidov ’s findings that the teaching method employed in mathematics classrooms is a key and highly influential factor in students’ mathematical development. Additionally, it emphasizes the importance of integrating frontal teaching with computer-based mathematical activities. Recent technological innovations have accelerated the integration of digital technologies into mathematics education [88]. The systematic analysis of Cevikbas et al. showed that the most popular technologies in the category of digital resources for mathematical modelling were DGSs. While the four-stage model for learning about cycloidal curves relies heavily on DGS, it also introduces students to an alternative modelling technique by integrating ER, providing them with tangible physical experiences. Additionally, the experiment suggested that, aligning with the findings of Tessema et al. , realistic hands-on experiences are essential to the mathematics learning process. This approach ensures that students are actively engaged in learning, fostering a deeper understanding of the subject matter.

4.1. Limitations

Introducing educational robotics into higher education presents several challenges that must be addressed while planning and implementing robotic activities. Adequate laboratories and technical infrastructure are essential for robotics programs. Robotic tools and software often have technical problems and bugs that require time and expertise, hindering the smooth running of classes and reducing the overall learning experience.

The narrowest cross-section is LEGO robot kits. There are good examples of LEGO robots being used in higher education; for example, Avanzato and Udvardy and Beszédes show educational applications of the LEGO Mindstorms EV3 system. However, the LEGO EV3 robotics kit was released in 2013, and since then, many newer technologies and robotic tools have entered the market. Newer kits like the LEGO Education SPIKE Prime feature more advanced sensors, motors, and programming capabilities. Technology evolves rapidly, the EV3’s programming environment is nowadays less user-friendly and modern compared to newer systems that are more intuitive and support multiple programming languages, such as Scratch and Python; moreover, the LEGO education SPIKE Prime are more modular and flexible, better suited to the needs of various educational levels and projects. These kits are more accessible to assemble and modify, which is particularly important in education.

The research was conducted at one university and only involved students in computer science engineering. Further research is needed to test the methodology in different universities and with various groups of students. The lack of demographic diversity may be a limitation of our methodological experiment, as the results of experiments in homogeneous groups are difficult to generalise. If the participants are not representative of the different demographic characteristics of the society, the results may be biased and may not reflect the real situation or the different reactions of different groups. The lack of demographic diversity in the experiment meant that important factors such as cultural differences, the impact of social background or the different experiences of different age groups could not be taken into account when interpreting the results. The study’s small sample size (98 participants) is a major limitation. This small sample size may limit the generalizability of the findings to the larger population. A larger sample would provide more robust and reliable results.

Nowadays, the gender distribution in engineering higher education remains unequal. The proportion of females is much lower than males in engineering and computer science [91,92]. The sample in this article was predominantly male (90.82%). This may have affected the study’s results. Future research may wish to use a more gender-balanced sample. However, it may also be interesting to repeat the experiment in a course with a higher proportion of female to explore whether the results remain consistent across diverse populations. Unfortunately, we could not conduct such experiments either at the University of Miskolc or at the Šiauliai State Higher Education Institution because the sex ratios of the students did not allow it.

One of the main limitations of the quasi-experimental research design used in the experiment is that it does not allow randomly allocating participants into groups. This means that the experimental and control group members may not be equally representative of the whole population. Because of the lack of random grouping, it is impossible to determine whether the substantial differences observed are due to the experimental intervention or the result of pre-existing differences. Quasi-experimental research design is often used in educational experiments [93], as random assignment is usually not feasible for ethical or practical reasons; it was the case in our experiment too.

The research focused on only one subject: teaching cycloid curves. Further development and research are needed to test the four-step methodological model in other subjects, as the ER activity requires the creation of appropriate robot constructs and projects.

5. Considerations for Future Research

It is crucial to recognise that while the research design and sample size may raise some questions regarding the overall robustness of the research findings, they do not inherently undermine the validity of the results. Nonetheless, these limitations must be carefully considered when interpreting the study’s outcomes. To enhance the reliability of future inquiries, it is essential to evaluate the effectiveness of the four-stage methodology for learning cycloidal curves using a larger and more diverse sample size. Specifically, ensuring a more balanced gender representation and incorporating a wider demographic of subjects will provide a more comprehensive understanding of the methodology’s impact.

The findings from this experiment suggest that the four-stage approach for learning cycloidal curves holds promise in facilitating the learning process of cycloidal curves. This potential of the four-stage approach for learning cycloidal curves to significantly enhance the learning process is a reason for hope. However, to establish more definitive conclusions, it is imperative to conduct additional studies in this area. Exploring the application of this methodology across various educational institutions and among different student demographics would provide valuable insights and strengthen the generalizability of the results.

In the current study, we relied solely on quantitative measures to assess the outcomes, which limited the understanding of the participants’ experiences and attitudes. For future iterations of this experiment, it will be vital to integrate qualitative tools, including soliciting student feedback through questionnaires. By gathering participants’ perspectives on the four-stage methodology for learning cycloidal curves, we will not only enrich the data but also better understand the subjective experiences of students, thus providing a more holistic view of the methodology’s effectiveness and areas for improvement.

Author Contributions

The authors contributed equally to this paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study followed the ethical standards laid down in the Ethics Code of the University of Miskolc.

Informed Consent Statement

Informed consent was obtained from all participants involved in the study.

Data Availability Statement

The data presented in this study are available on request from the corresponding author due to ethical reasons.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

ER	Educational Robotics
PBL	Problem-based Learning
PjBL	Project-based Learning
DGS	Dynamic Geometry Software

6. Equations and Graphs of Cycloidal Curves

The curve is a cycloid when the curve is generated by a point on the circumference of a circle that rolls along a straight line. The name of the curve, cycloid, originates from Galileo Galilei, who studied the curve in detail [94]. If the fixed curve is a circle and the generating point lies on the circumference of the rolling circle, then the cycloidal curve is called an epicycloid or a hypocycloid, depending on whether the rolling circle is situated outside or inside the fixed circle [95]. All main types of cycloidal curve families are summarised in Table 1. We note that epi- and hypotrochoid curves were first described by Albrecht Dürer in his work “Instruction in measurement with compasses and straight edge” in 1525. Dürer called these curves spider lines because the lines he used to construct the curves looked like a spider [45]. Cycloidal curves were named by Ole Rømer in 1674 while studying the best form for gear teeth. The claim that Ole Rømer was the first to propose using cycloidal curves for gear tooth profiles can be found in the works of Gottfried Wilhelm von Leibniz and Christian Huygens. Unfortunately, this cannot be directly proven because Rømer’s published work was destroyed in the great fire of 1728 in Copenhagen [96].

The parametric equations of a plane curve are usually given by two different functions depending on the same variable, in the form

(x (t), y (t))

for some real parameter t, where x and y are continuous functions of t. If a circle of radius r rolls around the outside of a fixed circle of radius R, and the generating point (pole) P is attached to the moving circle a distance d from its centre, the parametric equations of the epitrochoid traced by P are

\begin{matrix} x (t) & = (R + r) cos t - d cos (\frac{R + r}{r} t), \\ y (t) & = (R + r) sin t - d sin (\frac{R + r}{r} t), \end{matrix}

(1)

where the independent variable

t \in R

denotes the angle between a line through the centre of both circles and the x-axis [97]. In the sequel, the quantities

R, r

and d in (1) will be referred to as parametric constants, and d will be called the pole distance. Considering the geometric interpretation of cycloidal curves, we assume that the parametric constants R and r are positive real numbers and d is a non-negative real number. Three cases can be distinguished depending on the relation between d and r. In the case, if

d = r

, then the curve is an epicycloid (Figure 10), if

d < r

then it is a curtate epitrochoid (Figure 10), and in case of

d > r

, the curve is a prolate epitrochoid (Figure 10). An epicycloid always touches the fixed circle

(d = r)

; a curtate epitrochoid does not touch the fixed circle

(d < r)

, while a prolate epitrochoid crosses it

(d > r)

Figure 10. Epitrochoids

(R = 4 r)

. (Figures were created using Desmos.)

Figure 10. Epitrochoids

(R = 4 r)

. (Figures were created using Desmos.)

If a circle of radius r rolls around the inside of a fixed circle of radius R, and the pole P is attached to the moving circle a distance d from its centre, so the parametric equations of the hypotrochoid traced by P are

\begin{matrix} x (t) & = (R - r) cos t + d cos (\frac{R - r}{r} t), \\ y (t) & = (R - r) sin t - d sin (\frac{R - r}{r} t), \end{matrix}

(2)

where

t \in R

[97]. Three cases can be distinguished based on the relative values of d and r. If the distance from the fixed point on the moving circle to the centre is equal to the radius of the moving circle

(d = r)

, then the curve is a hypocycloid. If the point is within the radius of the inner circle

(d < r)

, the curve is a curtate hypotrochoid. In the case of

d > r

, it is a prolate hypotrochoid. A hypocycloid touches the fixed circle

(d = r)

; a curtate hypotrochoid does never touch the fixed circle

(d < r)

, and a prolate hypotrochoid crosses it

(d > r)

Figure 11. Hypotrochoids (

R = 4 r

). (Figures were created using Desmos.)

Figure 11. Hypotrochoids (

R = 4 r

). (Figures were created using Desmos.)

In addition to this grouping, further important curves can be obtained by a particular choice of parametric constants. For example, if

d = 0

, it can be easily seen from equations (1) and (2) that the curves are circles with radius

R + r

and

R - r

(

r < R

). A hypotrochoid with

R = 2 r

r \neq d

is an ellipse. The cardioid is an epicycloid with parametric constants

d = r = R

, and the hypocycloid with

d = r = \frac{R}{4}

is an astroid (Figure 11a). For hypocycloids and epicycloids consider the fraction

r / R = p / q

, where p and q are relatively prime natural numbers. Then, the denominator q of the reduced fraction has an important meaning since q gives the number of cusps, where a cusp is defined as a point in which the curve meets the fixed circle. For example, the cardioid is a 1-cusped epicycloid, the nephroid is a 2-cusped epicycloid (Figure 12a), and an epicycloid with five cusps is called a ranunculoid (Figure 12b). A 2-cusped hypocycloid (Tusi couple) is a line segment, a 3-cusped hypocycloid is a deltoid (Figure 12c), and the astroid is a 4-cusped hypocycloid (Figure 11a). A trochoid can have infinitely many cusps if the

r / R

ratio is not rational; in this case, the generating circle will never return to its initial position, and the curve will keep having new cusps as the circle keeps rolling around the base circle [43,54,97].

Figure 12. Multi-cusped epi- and hypocycloids. (Figures were created using Desmos.)

7. Teaching Cardioid Using the Four-Stage Model for Learning Cycloidal Curves

One of the most interesting shapes in the varied world of two-dimensional curves is the cardioid, which belongs to the family of epicycloids. Its practical applications have kept it in the spotlight today. The methodology developed to teach the cardioid curve is presented below, starting from the second stage, using the elements of the 4C principle.

7.1. Connect

In the seminar that follows the theoretical presentation, it is worthwhile to make the connection from at least three different angles. First, a brief overview of the history of cardioid is given, and the use of the cardioid in practical life is discussed. Then, the cardioid is represented as a caustic curve, followed by a revival and demonstration of the fact of the double generation property. The animations produced by the Desmos graphing calculator support well the visual representation of the two types of cardioid curve generation.

7.1.1. History and Practical Applications of Cardioids

There is no certainty about who discovered the cardioid. There is written evidence that in 1637, the amateur mathematician Étienne Pascal - father of Blaise Pascal - investigated the more general case of the cardioid, the limaçon, but not the cardioid specifically. In 1674, the Danish astronomer Ole Rømer considered the cardioid when he was searching for the optimal gear tooth shape, and several sources credit him with the discovery [95,98]. The cardioid as an epicycloid was investigated in 1691 by Jacob Ozaniaill, and afterwards, it appeared in the works of several prominent mathematicians. Bernoulli, L’ Hospital, Maclaurin, Cramer and many others also worked with the cardioid [99]. In 1708, Philippe de la Hire was the first to calculate the arc length of the cardioid [98]. Its name comes from the Greek word for heart. Interestingly, it was not until 1741 when Johann Castillon gave the curve its name in a paper in the Royal Society’s Philosophical Transactions.

The cardioid curve has intrigued mathematicians for centuries because of its properties, its graph’s beauty and practical applications [97,98]. The cardioid appears in many seemingly diverse areas of mathematics, playing an essential role in fractal geometry; for example, the central figure of the famous Mandelbrot set is a cardioid curve [98]. Cardioid shapes appear on rolls and bobbins to ensure the uniform layering of yarn in the textile industry and in the signal strength pattern of a type of radio antenna [100]. The cardioid antenna takes its name from the shape of the radiating beam. Typically a single-band antenna, it is most commonly used in terrestrial communications. The use of cardioid-shaped fractals in antennas allows coverage of all commercial frequency bands in the 1.8-30 GHz frequency range while maintaining the small size of the antenna due to the space-filling capability of the fractals; therefore, fractal antennas can be used in energy harvesting systems as well as IoT, WLAN, mobile MIMO and satellite communication systems and radars [101]. In parallel, the cardioid also plays a significant role in audio engineering because a cardioid directional pattern in a microphone provides a relatively wide pick-up zone [102]. When audio engineers need an unidirectional microphone - one highly sensitive to sounds generated directly in front of the microphone and less sensitive to those generated next to or behind it - they use a microphone with cardioid directionality [103]. Cardioid finds various applications in complex analysis, plant physiology, and engineering [102]. From a didactical point of view, the wide and illustrative practical use of cardioid antennas and microphones offers an excellent opportunity to motivate engineering students and raise their awareness of the interesting properties of cardioid.

7.1.2. A Popular Experiment: Cardioid in a Cup

In the literature on teaching cardioid, the cupping experiment to demonstrate the caustic property is almost invariably mentioned because it requires minimal equipment and is easy to perform [102,104]. It can be performed not only with an empty cup but also with a liquid, for example, coffee or tea, on which the heart curve can be displayed. Using the flashlight function of mobile phones, it is easy to form the cardioid by illuminating it from the rim of the cup, and the photo can be taken with another phone so that in a few minutes we can have a good quality photo of the cardioid curve (Figure 13a). With this experiment, we prove that the caustic curve for the circle is a cardioid if the light rays are emitted from a fixed point on the circle and reflected back from the circle according to the laws of physics (Figure 13b).

Figure 13. Cardioid, as a caustic curve of the circle. The Flower string art with six cardioids made by .

The cardioid is then obtained as an envelope of lines, but only the caustic curve is visible in the cup, not the lines (the light rays). In string art, the principle of producing a caustic curve is often used, where the straight lines are modelled with a thread [106,107], so that not only the envelope curve is visible, but also the straight lines (segments), as can be seen in Figure 13c. Because of its simplicity, the cup experiment is a good choice to stimulate interest, but the exploration and solution of the related phenomenon should be placed at the end of the seminar, which will establish the framework and thus provide a sense of completeness for the participants.

7.1.3. Double Generation Theorem

The cardioid can be derived in a surprisingly wide variety of ways. It is most often defined as an epicycloid: a cardioid is a plane curve followed by a fixed point on the circumference of a circle of radius r as the circle rolls without sliding along a fixed circle of radius r [43]. The parametric equations for the cardioid curve are:

\begin{matrix} \begin{matrix} x (t) & = r (2 cos t - cos 2 t) \\ y (t) & = r (2 sin t - sin 2 t), \end{matrix} \end{matrix}

(3)

where

t \in [0, 2 π] .

The derivation of (3) can be found in [95]. Figure 14 shows three steps from the production by animation for the cardioid in equation (3) when

r = 1

. The period is equal to the circumference of the moving circle, so it is

2 π

in this case.

Figure 14. Generating the cardioid as epicycloid for

r = 1

. (Figures were created using Desmos.)Animation of the generation: https://www.desmos.com/calculator/dlz1jubuzy

Figure 14. Generating the cardioid as epicycloid for

r = 1

. (Figures were created using Desmos.)Animation of the generation: https://www.desmos.com/calculator/dlz1jubuzy

Usually, the cardioid is approached only from the epicycloid point of view in the lecture and does not discuss other possibilities. However, due to the dual generating property, the cardioid can also be specified as a hypocycloid (see Figure 15). The cardioid is the trace of a point on the circumference of a circle of radius

R = 2 r

, where the circle rolls "inside" a fixed circle of radius r without sliding [95]. Double generation is easily illustrated by making spectacular Desmos animations.

Figure 15. Generating the cardioid as hypocycloid for

r = 1

and

R = 2 r = 2

. (Figures were created using Desmos.) Animation of the generation: https://www.desmos.com/calculator/vgts1kwl1k

Figure 15. Generating the cardioid as hypocycloid for

r = 1

and

R = 2 r = 2

. (Figures were created using Desmos.) Animation of the generation: https://www.desmos.com/calculator/vgts1kwl1k

7.2. Construct

Based on the cup experiment, the question naturally arises: how can we plot the cardioid curve with high accuracy? Another way to gain direct experience is to take advantage of STEAM-based education by using educational robotics to draw the cardioid curve. The Spikograph 2.0 robot (see Figure 4) is operated by a simple program: a single turn of the motor produces the cardioid curve. We created a detailed construction manual for the robot using Studio 2.0 software. The robot can be quickly built in a short time. Small groups of up to 3-4 students are recommended for building and testing. To build the basic robot, we used double gears (46372) with 28 mm diameter and teeth on both sides to model the moving circles and a turntable (LEGO Turntable, 4652236) of the same size to model the fixed circle (Figure 16a). The rolling gears are rotated by the motor, and a continuously adjustable shaft has been used for the linkage to allow easy gear changes during the rebuild. The felt-tip pen is fixed to a circumferential point on the moving gear. The rolling gears were doubled to solve the problem of precise positioning and stable mounting of the drawing head. With this construction version, the pen holder head can be fixed at several points using a LEGO Technic lever. Cardioids of different sizes can be drawn by rebuilding the robot after replacing the gears. In Figure 16b, LEGO Technic gears with 40 teeth (364902) were used for the construction. In this case, the positioning of the axis for rotation is different from that when using the turntable. The application of the 40th gear is advantageous because the length of the strings passing through the cusp from the perimeter points of the drawn curve is 8 cm, so the area and the length of the arc can be easily calculated using integral calculus. Building and drawing takes about 20 minutes, including rebuilding, if properly prepared. In the article [63], we discussed in detail the process of drawing cardioid curves by LEGO robots, together with the theoretical background. In addition, we have presented guided projects based on the use of cardioid drawing robots.

Figure 16. Cardioid drawing Spikograph 2.0 robot. (The first subfigure was made with Studio 2.0 software, the second two are self-made photos.)

7.3. Contemplate

The word fractal was coined in 1975 by mathematician Benoit Mandelbrot to describe a set of shapes whose infinitely complex self-similar forms reveal repetition. The dazzling computer-generated images of fractals capture the attention and motivate the interest of students in mathematics more than any other mathematical discovery in the last century [98]. The Mandelbrot set is defined as the set of complex numbers

c \in C

such that the sequence

{z_{n}}

defined by the recursion

z_{n} = z_{n - 1}^{2} + c

with initial value

z_{0} = 0

remains bounded for all

n \geq 0

[108]. The Mandelbrot set features a fundamental cardioid shape adorned with numerous bulbs directly attached to it [109]. The main cardioid is the big heart-shaped region of the Mandelbrot fractal.

The project task in the contemplate phase was connected to the main cardioid in the Mandelbrot fractal. The aim was to animate the generation of the cardioid in the fractal, where the rolling of the circles over each other results in the points of the cardioid curve. Two solutions were proposed to visualise the Mandelbrot set. In the first, the Mandelbrot set can be loaded into Desmos as an image, in which case the image can be positioned arbitrarily. In the second one, the fractal is generated in Desmos, and the path to the iteration is provided to the students. The project’s aim was to generate a central cardioid shape using circles. Considering that the groups working on the project started with their own ideas, the initial cardioids had different sizes and orientations, resulting in different solutions.

The earlier stage of the methodology provided significant support for the task because, essentially, the robot’s operation had to be modelled with animation; all the knowledge was provided, and the students were also shown the animation of cardioid production as both epi- and hypocycloid when the double generation theorem was presented. The effectiveness of the work with robots was indicated by the fact that among the solutions, there were animations where the gears appeared, as seen in Figure 17.

Figure 17. Mandlbrot fractal and student solutions for the project. (The first subfigure was generated using the free Mandelbrot Set Explorer generator, the last two figures were created using Desmos.)

7.4. Continue

The last stage of the methodology was implemented by setting interesting project tasks that could be solved with the Desmos dynamic geometry software, focusing mainly on cardioid visualisation. The cardioid can be constructed as an envelope of curves in several different ways. When generating a cardioid, several animation options are possible, the most common one being to display the members of the curve family one after the other. A common feature of all animations is the use of lists. In creating attractive solutions, students are also introduced to properties of the cardioid that go beyond the basic knowledge required by the curriculum.

7.4.1. Cardioid as the Envelope of a Pencil of Circles

Consider a given circle (the generator circle) and a distinguished point P on the generator circle. The set of all circles that pass through P and have their centres on the generator circle form a pencil of circles. The envelope of this pencil is a cardioid [43].

Figure 18. Cardioid as the envelope of a pencil of circles. (Figures were created using Desmos.) Animation of the generation: https://www.desmos.com/calculator/nvkxenx7ek

The diameter of the resulting cardioid is twice the diameter of the fixed circle, and its cusp is at point P. The cardioid was generated in 34-step iterations using the Desmos graphing calculator to create Figure18.

7.4.2. Evolute and Involute

Several simple student projects can be formulated to investigate the tangent lines. A spectacular figure can be drawn by plotting the cardioid tangents (Figure 19a). The meaning of evolute is the locus of the centre of curvature or the envelope of the normals of a curve. Like for all cycloidal curves, the evolute of the cardioid is a mirror-image cardioid, but not of the same size (Figure 19b). The parametric equations of the evolute:

\begin{matrix} \begin{matrix} x (t) & = \frac{1}{3} r (2 cos t + cos 2 t) \\ y (t) & = \frac{1}{3} r (2 sin t + sin 2 t), \end{matrix} \end{matrix}

(4)

where

t \in [0, 2 π]

, when we have the cardioid defined by (3) .

If the plane curves

g_{1}

and

g_{2}

are given, and the curve

g_{2}

is the evolute of

g_{1}

, then

g_{1}

is the involute of

g_{2}

. We can make the previous problem more complex by sketching the involute of the given cardioid (3). The involute of the cardioid is a mirror-image cardioid in a bigger size. The parametric equations of the involute:

\begin{matrix} \begin{matrix} x (t) & = 3 r (2 cos t + cos 2 t) \\ y (t) & = 3 r (2 sin t + sin 2 t), \end{matrix} \end{matrix}

(5)

t \in [0, 2 π]

. The number of iterations is 61 for the first two subfigures and 51 for the third in Figure 19. To solve these exercises, one needs to know the parametric equations of the cardioid in vector form, the derivative of the parametrically defined curve, and the equations of tangent and normal of a curve.

Figure 19. Cardioids drawn with tangent and normal lines. (Figures were created using Desmos.) Animation of the generation of the evolute: https://www.desmos.com/calculator/vsdi02x51i

8. The Post-Test

How is a cardioid curve generated? (5 points)
How many points of intersection do the following two parametric curves have? (3 points)

$\{\begin{matrix} x (t) = 3 cos t \\ y (t) = 3 sin t \end{matrix}, 0 \leq t \leq π \{\begin{matrix} x (t) = 4 cos t \\ y (t) = 2 sin t \end{matrix}, 0 \leq t \leq 2 π$
Identify the curves shown in the following figures and write down the parametric equations for all three curves. (9 points)
Find $\frac{d y}{d x}$ and find an equation of the tangent line to the given curve at $t_{0} = \frac{π}{4}$ . Sketch the curve and the tangent line in the Cartesian coordinate system. (9 points)

$\{\begin{matrix} x (t) = {cos}^{3} t \\ y (t) = {sin}^{3} t, & t \in [0, 2 π] \end{matrix}$
Calculate the area and circumference of the sector bounded by the curve $r (φ) = 6 sin φ$ , $φ \in [0, π]$ using integral calculus. Make a sketch! Give the Cartesian coordinate equation of the curve. (10 points)
Sketch the curve below and determine its arc length. (5 points)

$\{\begin{matrix} x (t) = t - sin t \\ y (t) = 1 - cos t, & t \in [0, 2 π] \end{matrix}$
Find the area inside the cardioid $r (θ) = 1 + cos θ$ and outside the circle $r = 1$ . (9 points)

References

Kelley, T.R.; Knowles, J.G. A conceptual framework for integrated STEM education. International Journal of STEM Education 2016, 3, 1–11. [Google Scholar] [CrossRef]
de la Garza, A. , Internationalisation in Higher Education as a Catalyst to STEAM. In The STEAM Revolution: Transdisciplinary Approaches to Science, Technology, Engineering, Arts, Humanities and Mathematics; de la Garza, A.; Travis, C., Eds.; Springer International Publishing, 2019; pp. 143–154. [CrossRef]
Herranen, J.; Fooladi, E.C.; Milner-Bolotin, M. Promoting STEAM in Education. LUMAT Special Issue 2021, 9, 1–8. [Google Scholar] [CrossRef]
Bybee, R.W. What is STEAM Education? Science 2010, 329, 995. [Google Scholar] [CrossRef] [PubMed]
Catterall, L.G. A Brief History of STEM and STEAM from an Inadvertent Insider. The STEAM Journal 2017, 3, 1–15. [Google Scholar] [CrossRef]
Graham, M.A. Deconstructing the Bright Future of STEAM and Design Thinking. Art Education 2020, 73, 6–12. [Google Scholar] [CrossRef]
Kang, N.H. A review of the effect of integrated STEM or STEAM (science, technology, engineering, arts, and mathematics) education in South Korea. Asia-Pacific Science Education 2019, 5, 1–22. [Google Scholar] [CrossRef]
Pepin, B.; Biehler, R.; Gueudet, G. Mathematics in Engineering Education: a Review of the Recent Literature with a View towards Innovative Practices. Int. J. Res. Undergrad. Math. Ed. 2021, 7, 163–188. [Google Scholar] [CrossRef]
Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: taxonomy, applications, and open challenges. Artificial Intelligence Review 2023, 56, 13187–13257. [Google Scholar] [CrossRef]
Vinuesa, R.; Brunton, S.; McKeon, B. The transformative potential of machine learning for experiments in fluid mechanics. Nature Reviews Physics 2023, 5, 536–545. [Google Scholar] [CrossRef]
Lorenzis, L.D.; Düster, A. (Eds.) Modeling in Engineering Using Innovative Numerical Methods for Solids and Fluids; Springer Cham, 2020. [CrossRef]
Duffy, A.; Zhang, G. Electromagnetic Design and Analysis in Electrical Power Conversion and Usage. Energies 2023, 16. [Google Scholar] [CrossRef]
Sepúlveda, S.; Cravero, A.; Fonseca, G.; Antonelli, L. Systematic Review on Requirements Engineering in Quantum Computing: Insights and Future Directions. Electronics 2024, 13. [Google Scholar] [CrossRef]
Wang, Y.; Kim, J.E.; Suresh, K. Opportunities and Challenges of Quantum Computing for Engineering Optimization. Journal of Computing and Information Science in Engineering 2023, 23, 060817. [Google Scholar] [CrossRef]
Martins, J.R.R.A.; Ning, A. Engineering Design Optimization; Cambridge University Press, 2021.
Insorio, A.O.; Librada, A.R.P. Enhancing Mathematical Critical Thinking and Problem-Solving Skills through Emergenetics® as a Grouping Mechanism. Contemporary Mathematics and Science Education 2021, 2, ep21002. [Google Scholar] [CrossRef] [PubMed]
Mitin, V.V.; Romanov, D.A.; Polis, M.P. Modern Advanced Mathematics for Engineers; Wiley-Interscience, 2001.
Singh, K. The Role of Mathematics in Artificial Intelligence and Machine Learning. International Journal for Research Publication and Seminar 2023, 14, 186–197. [Google Scholar] [CrossRef]
Beretta, E.; Gandolfi, A.; Sastri, C. Mathematics and Innovation in Engineering. Key Engineering Materials 2008, 380, 3–14. [Google Scholar] [CrossRef]
Muhammed-Amin, D. Emerging Trends in Applied Mathematics. Cihan University-Erbil Scientific Journal 2024, 8, 36–40. [Google Scholar] [CrossRef]
Diane Harris, Laura Black, P. H.M.B.P.J.W.a. Mathematics and its value for engineering students: what are the implications for teaching? International Journal of Mathematical Education in Science and Technology 2015, 46, 321–336. [Google Scholar] [CrossRef]
Rogovchenko, Y.; Rogovchenko, S. Promoting engineering students’ learning with mathematical modelling projects. SEFI 50th Annual conference of The European Society for Engineering Education. "Towards a new future in engineering education, new scenarios that European alliances of tech universities open up", 2022, pp. 643–652. [CrossRef]
Gjonbalaj, Q.D.; Gjoka, L. Engineering Mathematics and Modern Technology. International Journal of Educational Technology and Learning 2018, 2, 8–13. [Google Scholar] [CrossRef]
Ivanov, V.; Pavlenko, I.; Evtuhov, A.; Trojanowska, J. Major Challenges in Engineering Education. Augmented Reality for Engineering Graphics; Springer Nature Switzerland: Cham, 2024; pp. 1–11. [Google Scholar] [CrossRef]
Haleem, A.; Javaid, M.; Qadri, M.A.; Suman, R. Understanding the role of digital technologies in education: A review. Sustainable Operations and Computers 2022, 3, 275–285. [Google Scholar] [CrossRef]
Carter, C.E.; Barnett, H.; Burns, K.; Cohen, N.; Durall, E.; Lordick, D.; Nack, F.; Newman, A.; Ussher, S. Defining STEAM Approaches for Higher Education. European Journal of STEM Education 2021, 6, 13. [Google Scholar] [CrossRef]
Boiko, A.; A, N. ; I., K.; GrasVelazquez, A. The attractiveness of Science, Technology, Engineering and Mathematics subjects. Results from five countries; European Schoolnet, Brussels., 2019.
Graaff, E.; Kolmos, A. Characteristics of Problem-Based Learning. International Journal of Engineering Education 2003, 19, 657–662. [Google Scholar]
Merino, P.P.; Castro, M.; Merino, J.; Restivo, M.; Peixoto, A.; González, C.; Menacho, A.; Loro, F.; Sancristobal, E.; Blázquez, M.; Díaz, P.; Plaza, I.; Fondón, I.; Sarmiento, A.; Civantos, I.; Fernandez, C.; Lord, S.; Rover, D.; Chan, R.; Strachan, R. Educational Robotics for All: Gender, Diversity, and Inclusion in STEAM. 2020 IEEE Learning With MOOCS (LWMOOCS). IEEE, 2020, pp. 19–24. [CrossRef]
Mubin, O.; Stevens, C.J.; Shahid, S.; Mahmud, A.A.; Dong, J.J. A review of the applicability of robots in education. Technology for Education and Learning 2013, 1, 1–7. [Google Scholar] [CrossRef]
Nilüfer Atman Uslu; Yavuz, G. Ö.; Usluel, Y.K. A systematic review study on educational robotics and robots. Interactive Learning Environments 2023, 31, 5874–5898. [Google Scholar] [CrossRef]
Mitnik, R.; Recabarren, M.; Nussbaum, M.; Soto, A. Collaborative robotic instruction: A graph teaching experience. Computers & Education 2009, 53, 330–342. [Google Scholar] [CrossRef]
Souza, I.M.L.; Andrade, W.L.; Sampaio, L.M.R.; Araujo, A.L.S.O. A Systematic Review on the use of LEGO® Robotics in Education. 2018 IEEE Frontiers in Education Conference (FIE), 2018, pp. 1–9. [CrossRef]
Čelarević, A.; Mrakić, I. Application of educational robots in teaching. Nauka i tehnologija 2023, 11, 8–16. [Google Scholar] [CrossRef]
Körei, A.; Szilágyi, S. From Scratch to Python - Lego Robots as Motivational Tools for Coding. Multidiszciplináris Tudományok 2022, 12, 247–255. [Google Scholar] [CrossRef]
Ruiz, F.; Zapatera, A.; Montés, N.; Rosillo-Guerrero, N. From STEM to STEAM using LEGO MINDSTORMS in Learning Projects Obtained from LOMCE. INTED2019 Proceedings. IATED, 2019, 13th International Technology, Education and Development Conference, pp. 5592–5598. [CrossRef]
Martin, F.; Mikhak, B.; Resnick, M.; Silverman, B.; Berg, R. , To Mindstorms and Beyond: Evolution of a Construction Kit for Magical Machines. In Robots for Kids: Exploring New Technologies for Learning Experiences; Druin, A.; Hendler, J., Eds.; Morgan Kaufman Academic Press, San Francisco, 2000.
Üçgül, M. History and Educational Potential of LEGO Mindstorms NXT. Mersin Üniversitesi Eğitim Fakültesi Dergisi 2013, 9, 127–137. [Google Scholar]
Petrovič, P. Spike Up Prime Interest in Physics. Robotics in Education; Lepuschitz, W., Merdan, M., Koppensteiner, G., Balogh, R., Obdržálek, D., Eds.; Springer International Publishing: Springer Cham, 2021; pp. 146–160. [Google Scholar] [CrossRef]
Ersozlu, Z.; Swartz, M.; Skourdoumbis, A. Developing Computational Thinking through Mathematics: An Evaluative Scientific Mapping. Education Sciences 2023, 13. [Google Scholar] [CrossRef]
Darmawansah, D.; Hwang, G.J.; Chen, M.R.A.; Liang, J.C. Trends and research foci of robotics-based STEM education: a systematic review from diverse angles based on the technology-based learning model. International Journal of STEM Education 2023, 10. [Google Scholar] [CrossRef]
Barak, M.; Zadok, Y. Robotics projects and learning concepts in science, technology and problem solving. International Journal of Technology and Design Education 2009, 19, 289–307. [Google Scholar] [CrossRef]
Lockwood, H. A Book of Curves; Cambridge U.P., 1967.
Hotton, S. A geometric invariant for the study of planar curves and its application to spiral tip meander, 2016. arXiv:1602.07758. [CrossRef]
Omirou, S.L.; Nearchou, A.C. An epitrochoidal pocket—A new canned cycle for CNC milling machines. Robotics and Computer-Integrated Manufacturing 2009, 25, 73–80. [Google Scholar] [CrossRef]
Wang, B.; Geng, Y.; Chu, J. Generation and application of hypocycloid and astroid. Journal of Physics: Conference Series 2019, 1345, 032085. [Google Scholar] [CrossRef]
Tsiotras, P.; Castro, L. , The Artistic Geometry of Consensus Protocols. In Controls and Art, Inquiries at the Intersection of the Subjective and the Objective; Springer Nature Switzerland, 2014; pp. 129–153.
Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. SHP: Smooth Hypocycloidal Paths with Collision-Free and Decoupled Multi-Robot Path Planning. International Journal of Advanced Robotic Systems 2016, 13, 133. [Google Scholar] [CrossRef]
Raicu, L.; Rugescu, A.M.M. Cycling curves and their applications. Journal of Industrial Design and Engineering Graphics 2015, 10, 55–58. [Google Scholar]
Epsteen, S. Minimum Courses in Engineering Mathematics. The American Mathematical Monthly 1913, 20, 47–52. [Google Scholar] [CrossRef]
More, M. Mathematics and engineering in real life through mathematical competitions. International Journal of Mathematical Education in Science and Technology 2018, 49, 305–321. [Google Scholar] [CrossRef]
Palka, L. .; Schauer, F..; Dostal, P.. Modelling of the simple pendulum Experiment. MATEC Web of Conferences 2016, 76, 04037. [Google Scholar] [CrossRef]
Miller, J.S. Cycloid generator. American Journal of Physics 1959, 27, 62. [Google Scholar] [CrossRef]
Tosun, M.; Ersoy, S. Rolling Circles of Motions: Yesterday and Today. Models and Theories in Social Systems; Flaut, C., Hošková-Mayerová, Š., Flaut, D., Eds.; Springer International Publishing: Cham, 2019; pp. 211–222. [Google Scholar] [CrossRef]
Roussel, R.; Cani, M.P.; Léon, J.C.; Mitra, N.J. Exploratory design of mechanical devices with motion constraints. Computers & Graphics 2018, 74, 244–256. [Google Scholar] [CrossRef]
Shell-Gellasch, A. Hands on History: A Resource for Teaching Mathematics; The Mathematical Association of America, 2008.
Kabaca, T. A model teaching for the cycloid curves by the use of dynamic software with multiple representations approach. African Journal of Mathematics and Computer Science Research 2013, 6, 40–50. [Google Scholar] [CrossRef]
Phan-Yamada, T.; Gwin, E. Hypocycloids and Hypotrochoids. MathAMATYC Educator 2014, 6, 1–3. [Google Scholar]
Tessema, G.; Michael, K.; Areaya, S. Realist hands-on learning approach and its contributions to learners’ conceptual understanding and problem-solving skills on solid geometry. Pedagogical Research 2024, 9, em0186. [Google Scholar] [CrossRef]
Körei, A.; Szilágyi, S. Displaying parametric curves with virtual and physical tools. The Teaching of Mathematics 2022, XXV, 61–73. [Google Scholar] [CrossRef]
Körei, A.; Szilágyi, S. Discovering epitrochoid curves with STEAM-based learning methods. Annales Mathematicae et Informaticae, p. Accepted manuscript. 2024. [Google Scholar] [CrossRef]
Körei, A.; Szilágyi, S.; Vaičiulyte, I. Task design for teaching cardioid curve with dynamic geometry software and educational robotics in university practice. Problems of Education in the 21st Century 2023, 81, 840–860. [Google Scholar] [CrossRef]
Körei, A.; Szilágyi, S. How to Draw Cardioids with LEGO Robots: A Technical-Mathematical Project in Higher Education. Robotics in Education; Balogh, R., Obdržálek, D., Christoforou, E., Eds.; Springer Nature Switzerland: Cham, 2023; pp. 37–48. [Google Scholar] [CrossRef]
Körei, A.; Szilágyi, S. Using Educational Robotics to Explore and Teach Trochoidal Curves. Advanced Research in Technologies, Information, Innovation and Sustainability; Guarda, T., Portela, F., Diaz-Nafria, J.M., Eds.; Springer Nature Switzerland: Cham, 2024; pp. 87–101. [Google Scholar] [CrossRef]
He, T.; Hu, X. Practical Research on Robotics Teaching in Elementary School Based on 4C Teaching Method: The Example of LEGO Educational Robotics. Curriculum and Teaching Methodology 2022, 5, 13–18. [Google Scholar] [CrossRef]
Yang, Y.; Yang, W.Y.Y. STEAM Activity Design Based on 4C Education Concept - Take tie-dye of traditional culture as an example. Frontiers in Educational Research 2020, 3, 7–14. [Google Scholar] [CrossRef]
Deng, Z. A quantitative overview of the approaches influencing traditional and new teaching methods on technical college students. Soft Computing 2023. [Google Scholar] [CrossRef]
Ganyaupfu, E. Teaching Methods and Students’ Academic Performance. International Journal of Humanities and Social Science Invention 2013, 2, 29–35. [Google Scholar]
Khairnar, C.M. Advance Pedagogy: Innovative Methods of Teaching and Learning. International Journal of Information and Education Technology 2015, 5, 869–872. [Google Scholar] [CrossRef]
Fiksl, M.; Flogie, A.; Aberšek, B. Innovative teaching/learning methods to improve science, technology and engineering classroom climate and interest. Journal of Baltic Science Education 2017, 16, 1009–1019. [Google Scholar] [CrossRef]
Pritchard, D. Where learning starts? A framework for thinking about lectures in university mathematics. International Journal of Mathematical Education in Science and Technology 2010, 41, 609–623. [Google Scholar] [CrossRef]
Singh, G.; Banga, V. Robots and its types for industrial applications. Materials Today: Proceedings 2022, 60, 1779–1786. [Google Scholar] [CrossRef]
Chen, D.; Zeng, Z.; Guan, Y.; Zhu, H.; Zhang, T. SCARA Robots Developed with Modular Method. 2020 IEEE International Conference on Mechatronics and Automation (ICMA), 2020, pp. 454–459. [CrossRef]
Körei, A.; Szilágyi, S. Parametric Graph Project - Using LEGO Gears for Drawing Curves. Advanced Research in Technologies, Information, Innovation and Sustainability; Guarda, T., Portela, F., Augusto, M.F., Eds.; Springer Nature Switzerland: Cham, 2022; pp. 101–114. [Google Scholar] [CrossRef]
Fisher, D.; Kusumah, Y.S.; Dahlan, J.A. Project-based learning in mathematics: A literature review. Journal of Physics: Conference Series 2020, 1657, 012032. [Google Scholar] [CrossRef]
Zhou, C. The Impact of the Project-Based Learning Method on Students. BCP Education & Psychology 2023, 9, 20–25. [Google Scholar] [CrossRef]
Ng, W.L.; Teo, B.C.; Yeo, J.B.W.; Ho, W.K.; Teo, K.M. , T.L.; Kaur, B.; Tay, E.G., Eds.; Springer Singapore: Singapore, 2019; pp. 313–348. doi:10.1007/978-981-13-3573-0_14.Education. In Mathematics Education in Singapore; Toh, T.L., Kaur, B., Tay, E.G., Eds.; Springer Singapore: Singapore, 2019; pp. 313–348. [Google Scholar] [CrossRef]
Juandi, D.; Kusumah, Y.S.; Tamur, M.; Perbowo, K.S.; Siagian, M.D.; Sulastri, R.; Negara, H.R.P. The Effectiveness of Dynamic Geometry Software Applications in Learning Mathematics: A Meta-Analysis Study. International Journal of Interactive Mobile Technologies 2021, 15, 18–37. [Google Scholar] [CrossRef]
İbili, E. The Use of Dynamic Geometry Software from a Pedagogical Perspective: Current Status and Future Prospects. Journal of Computer and Education Research 2019, 7, 337–355. [Google Scholar] [CrossRef]
Juandi, D.; Priatna, N. Discovery learning model with GeoGebra assisted for improvement mathematical visual thinking ability. Journal of Physics: Conference Series 2018, 1013, 012209. [Google Scholar] [CrossRef]
Garfinkel, K.; Albrecht, M. The Art of Curve Stitching: A Creative Mathematics Project for Students. The Mathematics Teacher 2018, 112, 60–66. [Google Scholar] [CrossRef]
Chorney, S. Classroom practice and craft knowledge in teaching mathematics using Desmos: challenges and strategies. International Journal of Mathematical Education in Science and Technology 2022, 53, 3203–3227. [Google Scholar] [CrossRef]
Cohen, P. Statistical Power Analysis for the Behavioral Sciences; Routledge, 1988. [CrossRef]
Coufal, P. Project-Based STEM Learning Using Educational Robotics as the Development of Student Problem-Solving Competence. Mathematics 2022, 10. [Google Scholar] [CrossRef]
Hsu, R.C.; Tsai, T.H. Assessing the Impact of a Project-Based Learning Robotics Course with Integrating of STEM Education Using Content Analysis Method. European Journal of STEM Education 2022, 7, 09. [Google Scholar] [CrossRef] [PubMed]
Goh, H.; Ali, M.B.B. Robotics as a tool to STEM learning. International Journal for Innovation Education and Research 2014, 2, 66–78. [Google Scholar] [CrossRef]
Hassidov, D. How Teaching Method (Alternative/Frontal) Affects Achievement in Mathematics for Boys and Girls in Grades Four to Six Who Are Learning in a Computer-Assisted Environment. Creative Education 2019, 10, 1425–1443. [Google Scholar] [CrossRef]
Cevikbas, M.; Greefrath, G.; Siller, H.S. Advantages and challenges of using digital technologies in mathematical modelling education – a descriptive systematic literature review. Frontiers in Education 2023, 8, 1142556. [Google Scholar] [CrossRef]
Avanzato, R. Mobile robotics for freshman design, research, and high school outreach. Proceedings of 2000 IEEE International Conference on Systems, Man & Cyberbetics - Cyberbetics Evolving to Systems, Humans, Organizations, and their Complex Interactions, 2000, Vol. 1, pp. 736–738. [CrossRef]
Udvardy, P.; Beszédes, B. Educational application of LEGO Mindstorms EV3 system by using different simulation environments. 15th International Symposium on Applied Informatics and Related Areas organized in the frame of Hungarian Science Festival, Óbuda University, Székesfehérvár 2020, 2020, pp. 133–136. [Google Scholar]
Charlesworth, T.E.; Banaji, M.R. Gender in Science, Technology, Engineering, and Mathematics: Issues, Causes, Solutions. Journal of Neuroscience 2019, 39, 7228–7243. [Google Scholar] [CrossRef] [PubMed]
Jaccheri, L.; Pereira, C.; Fast, S. Gender Issues in Computer Science: Lessons Learnt and Reflections for the Future. 2020 22nd International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), 2020, pp. 9–16. [CrossRef]
Gopalan, M.; Rosinger, K.; Ahn, J.B. Use of Quasi-Experimental Research Designs in Education Research: Growth, Promise, and Challenges. Review of Research in Education 2020, 44, 218–243. [Google Scholar] [CrossRef]
Whitman, E.A. Some Historical Notes on the Cycloid. The American Mathematical Monthly 1943, 50, 309–315. [Google Scholar] [CrossRef]
Yates, R.C. Curves and Their Properties, Classics in Mathematics Education. Vol. 4; National Council of Teachers of Mathematics, 1974.
Figliolini, G.; Stachel, H.; Angeles, J. On Martin Disteli’s spatial cycloidal gearing. Mechanism and Machine Theory 2013, 60, 73–89. [Google Scholar] [CrossRef]
Lawrence, J.D. A Catalog of Special Plane Curves; Dover Publications, 1972.
Pickover, C.A. The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics; Sterling Publishing Co. Inc., 2012.
Archibald, R.C. The Cardioid and Tricuspid: Quartics with Three Cusps. Annals of Mathematics 1903, 4, 95–104. [Google Scholar] [CrossRef]
Thomas, G.B.; Weir, M.D.; Giordano, F.R. Thomas’ Calculus (11th ed.); Pearson Education Inc., Addison-Wesely, 2005.
Lazović, L.; Jokanovic, B.; Rubez̆ić, V.; Radovanovic, M.; Jovanović, A. Fractal Cardioid Slot Antenna for Super Wideband Applications. Electronics 2022, 11, 1043. [Google Scholar] [CrossRef]
Karjanto, N.; Yermukanova, B. Integral of radical trigonometric functions revisited. The Mathematics Enthusiast 2016, 13, 243–254. [Google Scholar] [CrossRef]
Rohani, B.; Kamiyama, K.; Arai, H. Cardioid type pattern optimization using characteristic mode analysis. 12th European Conference on Antennas and Propagation (EuCAP 2018), 2018, pp. 1–3. [CrossRef]
Shukla, A. On teaching mathematics to gifted students: some enrichment ideas and educational activities. 2022; arXiv:math.HO/1911.10726]. [Google Scholar] [CrossRef]
Kaydeekat. Flower String Art. https://www.instructables.com/Flower-String-Art/.
Richeson, D. Residue designs, string art, and number theory. Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture; Torrence, J.H.E.; Fong, C.; Seaton, K., Eds. Tessellations Publishing, 2023, p. 365–368.
von Renesse, C.; Ecke, V. Discovering The Art of Mathematics: Using String Art to Investigate Calculus. PRIMUS 2016, 26, 283–296. [Google Scholar] [CrossRef]
Bittner, D.; Cheong, L.; Gates, D.; Nguyen, H. New approximations for the area of the Mandelbrot set. Involve, a Journal of Mathematics 2017, 10, 555–572. [Google Scholar] [CrossRef]
Devaney, R.L. The Mandelbrot Set, the Farey Tree, and the Fibonacci Sequence. The American Mathematical Monthly 1999, 106, 289–302. [Google Scholar] [CrossRef]

Figure 1. The LEGO 4C methodological spiral. (Figure was created using Microsoft PowerPoint.)

Figure 2. Scheme of the four-stage methodological model for learning cycloidal curves. (Figure was created using Microsoft PowerPoint.)

Figure 3. Spikograph 1.0 drawing robot. (Figure was created using Studio 2.0 software.)

Figure 4. Spikograph 2.0 drawing robot. (Figure was created using Studio 2.0 software.)

Figure 5. SCARA-style LEGO robot. (Figure was created using Studio 2.0 software.)

Figure 6. Sankey diagram of the full sample to visualise gender and groups. (Figure was created using DATAtab.)

Figure 7. Violin plot combined with box plot. (Figure was created using DATAtab.)

Figure 8. Multi-vari chart of the experimental group according to average scores related to the Calculus I course. (Figure was created using DATAtab.)

Figure 9. Bar chart of the subgroups of the experimental group showing mean scores and standard deviations. (Figure was created using DATAtab.)

Table 1. Classification of cycloidal curves.

	Cycloidal curves
	(a circle rolling on another circle or a line)
	Epitrochoids	Trochoids	Hypotrochoids
	(a circle rolling outside another circle)	(a circle rolling on a line)	(a circle rolling inside another circle)
The tracing point is on the circumference of the moving circle	Epicycloid	Cycloid	Hypocycloid
The tracing point is inside the moving circle	Curtate epitrochoid	Curtate cycloid	Curtate hypotrochoid
The tracing point is outside the moving circle	Prolate epitrochoid	Prolate cycloid	Prolate hypotrochoid

Table 2. Drawing central trochoids with didactic tools.

	Central trochoid curves
	(a circle rolling on another circle)
	Epitrochoids			Hypotrochoids
	Curtate	Epicycloid	Prolate	Curtate	Hypocycloid	Prolate
Spirograph toy	Yes	No	No	Yes	No	No
LEGO gears, racks	Yes	No	No	Yes	No	No
Spikograph 1.0 robot	No	No	No	Yes	Yes	Yes
Spikograph 2.0 robot	Yes	Yes	Yes	No	No	No
SCARA-style robot	Yes	Yes	Yes	Yes	Yes	Yes

Table 3. Activities during Calculus II course.

	Cycloidal curves
	Frontal teaching		Other activities
	(Stage 1)		(Stage 2 and Stage 3)		(Stage 4)
Topic	Lectures	Practical sessions	R-STEAM seminars	In-class DGS tasks	Homework projects
	(academic hours)			(exercises)
Circles, ellipses	3	2	2	2	4
Trochoids	3	2	2	2	3
Epitrochoids	2	1	2	3	2
Cardioid	1	1	2	2	2
Hypotrochoids	2	1	2	3	2
Astroid	1	1	2	2	2

Table 4. Descriptive Statistics for Both Groups.

	Experimental Group	Control Group
N	36	62
Mean	42.17	27.15
Median	45	27
Mode	50	25
Std. Deviation	8.56	8.18
Variance	73.34	66.88
Minimum	24	7
Maximum	50	46

Table 5. Different statistical tests to check the normality.

	Experimental Group		Control Group
	Statistics	p	Statistics	p
Kolmogorov-Smirnov	0.21	0.075	0.12	0.287
Shapiro-Wilk	0.84	<0.01	0.97	0.172
Anderson-Darling	2.17	<0.01	0.78	0.042

Table 6. Mann-Whitney U-test values.

	U	z	asymptotic p	exact p	r
Mann-Whitney U-test	247	-6.42	<0.001	<0.001	0.65

Table 7. Descriptive Statistics for Groups G1, G2 and G3.

	G1	G2	G3
N	13	12	11
Mean	40.31	43.25	43.18
Median	43	46.5	47
Mode	50	50	50
Std. Deviation	9.13	8.09	8.81
Variance	83.4	65.48	77.56
Minimum	24	29	25
Maximum	50	50	50

Table 8. Kruskal-Wallis test values

	$χ^{2}$	df	p
Kruskal-Wallis test	0.99	2	0.611

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On a New Innovative Steam-Based Method for Teaching Cycloidal Curves in Engineering Higher Education

Abstract

1. Introduction

1.1. What Is Engineering Mathematics?

1.2. STEAM-Based Education and Educational Robotics

1.3. Importance and Teaching of Cycloidal Curves

1.4. 4C Learning Approach

1.5. The Four-Stage Methodological Model for Learning Cycloidal Curves

2. Materials and Methods

2.1. General Background

2.2. Research Design

2.3. Sample and Ethics

2.4. Intervention and Instruments

2.5. Research Questions

3. Data Analysis and Results

3.1. Response to Research Question RQ1

3.2. Response to Research Question RQ2

4. Discussion and Conclusions

4.1. Limitations

5. Considerations for Future Research

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

6. Equations and Graphs of Cycloidal Curves

7. Teaching Cardioid Using the Four-Stage Model for Learning Cycloidal Curves

7.1. Connect

7.1.1. History and Practical Applications of Cardioids

7.1.2. A Popular Experiment: Cardioid in a Cup

7.1.3. Double Generation Theorem

7.2. Construct

7.3. Contemplate

7.4. Continue

7.4.1. Cardioid as the Envelope of a Pencil of Circles

7.4.2. Evolute and Involute

8. The Post-Test

References

MDPI Initiatives

Important Links

Subscribe