One-X Property Conjecture, Stochastic Orders and Implied Volatility Surface Construction

Preprint

Article

One-X Property Conjecture, Stochastic Orders and Implied Volatility Surface Construction

Altmetrics

Downloads

Views

Comments

Zeyu Cao^*,Siqiao Zhao,Shaosai Huang

This version is not peer-reviewed

Submitted:

16 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts

Abstract

In this work, we explore Conjecture 1 proposed in the newly released pioneering paper “Volatility transformers: an optimal transport-inspired approach to arbitrage-free shaping of implied volatility surfaces” by Zetocha Valer, which posits that the “One-X” property is both a necessary and sufficient condition for convex order between non-negative continuous strictly increasing distributions with the same mean. We provide a counterexample demonstrating that the conjecture, as originally stated, does not hold. By examining stochastic orders, particularly the increasing convex order, and the “One-X” property, we propose an enhanced version of the conjecture which is shown to be valid. Furthermore, we discuss the implications of these findings in the context of equity implied volatility fitting and the construction of implied volatility surfaces, highlighting the challenges posed by real-market conditions. In the end, we propose several applications in implied volatility surface construction or simulation.

Keywords:

Subject: Business, Economics and Management - Finance

1. Introduction

Ever since the birth of Black-Sholes theory ?? and local volatility ??, construction of the implied volatility (IV) surface that is free of arbitrage has been an active research area. Although it may seem to be a simple task at the first glance, as pointed out in ??, constructing arbitrage-free IV surfaces that fit specific market conditions remains a challenging task for many sell-side institutions.

In a recent work [Zet23] of Zetocha, an optimal transport-inspired approach has been introduced to understand the arbitrage-free shaping of IV surfaces. In this approach, a fundamental concept that mathematically describes the calendar no-arbitrage is the convex order “

\leq_{c x}

” : for random variables X and Y, we say

X \leq_{c x} Y

if for any convex function

φ

, it holds

\begin{matrix} E [φ (X)] \leq E [φ (Y)] . \end{matrix}

(1)

Given a set of random variables

X_{1}, \dots, X_{n}

in convex order, i.e.

X_{i} \leq_{c x} X_{i + 1}

(

i = 1, \dots, n - 1

), they become the marginals of a martingale measure (thus being arbitrage-free); see Theorem 2.6 of [BeJu16] or Theorem 8 of [Str65]. It is therefore desirable to produce sequences of random variables that obey consecutive convex orders.

Notice however, that checking (1) for each and every single convex function

φ

is usually impossible in applications. A more natural and practical ordering between two random variables X and Y with the same mean is the so-called “One-X” order: we say

X \leq_{O n e - X} Y

if there is some

c > 0

such that

\begin{matrix} \forall t < c, F_{X} (t) < F_{Y} (t) and \forall t > c, F_{X} (t) > F_{Y} (t), \end{matrix}

(2)

where

F_{X}

and

F_{Y}

are the cumulative distribution functions (CDF’s) of X and Y, respectively. In this situation, the graphs of

F_{X}

and

F_{Y}

intersects at the single point

(c, F_{X} (c))

. Usually, by inspecting the graphs of the corresponding CDF’s, one could easily check the One-X order between a pair of random variables.

Besides the convenience, a key property mentioned in Theorem 3 of [Zet23] (see also Lemma 2 of [Ohl69]) is that for random variables X and Y with the same mean,

X \leq_{O n e - X} Y

implies that

X \leq_{c x} Y

. Moreover, the One-X order is preserved under the optimal transport maps generated from continuous and strictly increasing functions defined on

R_{+}

; for more detailed discussions see Section 6.2 of [Zet23].

It is natural to guess whether these two orderings are actually equivalent: as asked by Conjecture 1 of [Zet23], when

E [X] = E [Y]

and the CDF’s are both continuous and strictly increasing, is it true that

X \leq_{c x} Y

implies

X \leq_{O n e - X} Y

To answer this question, let us examine these concepts in a broader scope: both the convex order and the One-X order have their corresponding parts in the study of actuarial science, and their relations have been studied in the seminal work of [Mül96]. In fact, unlike the convex order, the One-X order (or the dangerousness order in the language of actuarial science) is not necessarily transitive, and as shown in [Mül96], it is the transitive closure “

\leq_{D^{*}}

” of the One-X order that becomes equivalent to the convex order. We therefore expect a negative answer to the above mentioned conjecture. In the next section we will rigorously define the ordering concepts and summarize their relations. Then in Section 3 we will present a counterexample to Conjecture 1 of [Zet23].

It still leaves us wondering to what extent could we reverse the implication of the convex order by the One-X order, and we will restrict our attention to the class of distributions induced by implied density functions, whose existence would already eliminate the butterfly arbitrage. More specifically, we will focus on the class of log Gaussian mixtures, which are sufficiently generic since they are weakly dense in the space of all probability distributions. After discussing this in more details in Section 4, we will prove a theorem in Section 5 where for each pair of random variables with equal mean and in convex order, we find finitely many consecutive One-X inequalities interpolating between them.

In the last section, we will extend our discussion on several aspects of the IV surface construction and highlight a novel approach: we propose to apply the martingale interpolation techniques to the construction of the intermediate implied density functions at maturities with poor liquidity; we will also discuss a framework of synthetic IV generation that harnesses the power of machine learning.

2. Background

In this section, we will first recall the definitions and properties of some well-known stochastic orders between one-dimensional random variables, which will be used intensively in the later sections. Then we will introduce the dangerousness and the One-X property which enable us to state and understand the meaning of the conjecture in [Zet23].

2.1. Stochastic Orders and Their Properties

In this section we present rigorous mathematical definitions of the related stochastic orders, as well as some useful properties. We assume that there are two random variables X and Y with CDF’s

F_{X}

and

F_{Y}

respectively.

Definition 1.

X is smaller than Y in the increasing convex order, denoted as

X \leq_{i c x} Y

, if for any real-valued increasing convex function f,

\begin{matrix} E [f (X)] \leq E [f (Y)], \end{matrix}

(3)

provided both expectations exist.

Since any increasing convex function can be obtained as the limit of linear combinations of the functions in the form

ϕ (x) = {(x - z)}^{+}

z \in [0, \infty)

, (3) in the above definition can be replaced by

\begin{matrix} \forall z \geq 0, E [{(X - z)}^{+}] \leq E [{(Y - z)}^{+}] . \end{matrix}

(4)

Using integration by parts it is also easy to show that (4) is equivalent to the following integral inequality of their corresponding CDF’s:

\begin{matrix} \forall z \geq 0, \int_{z}^{\infty} (1 - F_{X} (x)) d x \leq \int_{z}^{\infty} (1 - F_{Y} (y)) d y . \end{matrix}

(5)

If we replace increasing convex function by convex function, then X is called smaller than Y in convex order, denoted as

X \leq_{c x} Y

; recall (1). When

E [X] = E [Y]

, one can show that these two orders are equivalent, i.e.

X \leq_{i c x} Y \Leftrightarrow X \leq_{c x} Y

; see Theorem 4.A.35 of [SS07] for more details. Under the assumption that

E [X] = E [Y]

, we can therefore use these two definitions in an exchangeable manner.

Lemma 1.

[Theorem 2.3.10 [BRM15]] Let X and Y be two random variables. Then

X \leq_{i c x} Y

if and only if

ϕ (X) \leq_{i c x} ϕ (Y)

for all real valued increasing convex function

ϕ

In particular, as multiplication by a positive constant is an increasing convex function, we have

\begin{matrix} X \leq_{i c x} Y \Leftrightarrow \forall c > 0, c X \leq_{i c x} c Y . \end{matrix}

(6)

Lemma 2.

[Theorem 2.3.13 [BRM15]] Let

X_{1}, \dots, X_{n}

and

Y_{1}, \dots, Y_{n}

be two sets of independent random variables. If

X_{i} \leq_{i c x} Y_{i}

for all

i = 1, \dots, n

, then

\begin{matrix} \sum_{i = 1}^{n} X_{i} \leq_{i c x} \sum_{i = 1}^{n} Y_{i} . \end{matrix}

We therefore have the following useful corollary for the construction of the counterexample:

Corollary 1.

Given two sets of independent random variables

X_{1}, \dots, X_{n}

and

Y_{1}, \dots, Y_{n}

such that

X_{i} \leq_{i c x} Y_{i}

for all

i = 1, \dots, n

. If

c_{1}, \dots, c_{n}

are positive numbers, then

\begin{matrix} \sum_{i = 1}^{n} c_{i} X_{i} \leq_{i c x} \sum_{i = 1}^{n} c_{i} Y_{i} . \end{matrix}

2.2. One-X Order and A Related Conjecture

To recall the One-X order defined in (2), we start with the more general definition of the dangerousness ordering which has been introduced to the study of the actuarial science by [Mül96].

Definition 2.

Given non-negative one-dimensional random variables X and Y whose CDF’s are

F_{X}

and

F_{Y}

respectively, X is called less dangerous than Y, denoted by

X \leq_{D} Y

, if there exists some

c \geq 0

such that

F_{X} \leq F_{Y}

over

[0, c)

F_{X} \geq F_{Y}

over

(c, \infty)

, and

E (X) \leq E (Y)

. When

E (X) = E (Y)

is required, this relation is called One-X in [Zet23]; in this case we will write

X \leq_{O n e - X} Y

As mentioned before, we have the following implication: Theorem 1. [Theorem 3 of [Zet23]] Given non-negative one-dimensional random variables X and Y such that

E [X] = E [Y]

, then

X \leq_{O n e - X} Y \Rightarrow X \leq_{c x} Y

. The inverse to this theorem is conjectured by Zetocha: Conjecture 1. [Conjecture 1 of [Zet23]] Given non-negative one-dimensional random variables X and Y whose CDF’s are

F_{X}

and

F_{Y}

respectively. Suppose

F_{X}

and

F_{Y}

are continuous and strictly increasing functions on

R_{+}

, and

E [X] = E [Y]

, then

X \leq_{c x} Y \Rightarrow X \leq_{O n e - X} Y

By providing a counterexample to this conjecture in the next section, will show that a single One-X inequality is not enough for a pair of random variables satisfying the convex ordering.

2.3. Inter-disciplinary Concept Comparison

Till now, we have seen several orderings such as the convex order, the One-X order, and the dangerousness order. Some of these concepts occur in financial mathematics, and some of them originates from actuarial science. In this subsection we will try to make a more systematic summary of these concepts and some results, aiming to build a dictionary between some of the important concepts from the two fields.

For the sake of simplicity, we will work under the assumption that all the distributions are non-negative, continuous and with the same mean. Given two random variables X and Y with continuous, strictly increasing CDF’s and the same mean, the following table briefly summarizes the various orderings in different contexts:

Financial Mathematics Concepts	Actuarial Science Concepts
One-X Order: $X \leq_{O n e - X} Y$	Less Dangerous: $X \leq_{D} Y$
Increasing Convex Order: $X \leq_{i c x} Y$	Stop-loss Order: $X \leq_{s l} Y$
Convex Order: $X \leq_{c x} Y$	Transitive closure of $\leq_{D}$ : $X \leq_{D^{*}} Y$ .

In each of the first two rows, the concepts are mathematically defined in identical manners. The two concepts in the third row are shown to be equivalent by Corollary 4.4 [Mül96]. Moreover, the lack of transitivity of $\leq_{O n e - X}$ or $\leq_{D}$ makes them inequivalent to $\leq_{c x}$ , and their transitive closure $\leq_{D^{*}}$ is defined as following: $X \leq_{D^{*}} Y$ if there is a sequence of random variables ${X_{n}}_{n = 1}^{\infty}$ such that $X = X_{1}$ , $X_{n} \leq_{D} X_{n + 1}$ and that $X_{n} \to Y$ weakly. Notice that under the assumption $E [X] = E [Y]$ , it consequently holds that $E [X] = E [X_{n}]$ for all $n = 1, 2, 3, \dots$ .

3. A Counterexample to Conjecture 1

In this section, we begin with reviewing some conditions on the existence of (increasing) convex-order between two distributions belonging to some specific exponential families. We will then construct two random variables with the same finite mean that are in convex order; moreover, they have continuous and strictly increasing CDF’s, but their CDF’s cross more than once: this violates the corresponding One-X inequality and becomes a counterexample to Conjecture 1.

3.1. (Increasing) Convex Order Between Exponential Family Distributions

We will consider the Gamma and the Weibull distributions. Conditions on the existence of increasing convex order between two given Gamma or Weibull distributions are given following their definitions. We follow [BRM15] for the notations and the main results in this part.

Definition 3.

(Gamma Distribution) A non-negative continuous one-dimensional random variable X follows the Gamma distribution, denoted by

X \sim G (α, β)

, if its probability density function (PDF) is given by

\begin{matrix} f (x) = \frac{x^{α - 1} e^{(- \frac{x}{β})}}{β^{α} Γ (α)}, x \in (0, \infty), \end{matrix}

where

α > 0

is called shape parameter,

β > 0

is called scale parameter.

X \sim G (α, β)

, then

E [X] = α β

Definition 4.

[Weibull Distribution] A non-negative continuous one-dimensional random variable X follows the Weibull distribution, denoted by

X \sim W (α, β)

, if its CDF is given by

\begin{matrix} F (x) = 1 - e^{- {(\frac{x}{α})}^{β}}, x \in (0, \infty), \end{matrix}

where

α > 0

is called scale parameter,

β > 0

is called shape parameter. If

X \sim W (α, β)

, then

E [X] = α Γ (1 + \frac{1}{β})

Given two random variables which follow either the Gamma or the Weibull distributions, let’s state some sufficient conditions to guarantee the existence of increasing convex order relation between them. These sufficient conditions are adopted from Section 2.9.1 of [BRM15]:

Lemma 3.

Given two random variables

X_{i} \sim G (α_{i}, β_{i}), i = 1, 2

, if

α_{1} > α_{2}

and

α_{1} β_{1} \leq α_{2} β_{2}

, then

X_{1} \leq_{i c x} X_{2}

. If

α_{1} β_{1} = α_{2} β_{2}

, then

X_{1} \leq_{c x} X_{2}

Given

X_{i} \sim W (α_{i}, β_{i}), i = 1, 2

, if

β_{1} > β_{2}

and

α_{1} Γ (1 + 1 / β_{1}) \leq α_{2} Γ (1 + 1 / β_{2})

, then

X_{1} \leq_{i c x} X_{2}

. If

α_{1} Γ (1 + 1 / β_{1}) = α_{2} Γ (1 + 1 / β_{2})

, then

X_{1} \leq_{c x} X_{2}

. Here we rely on the fact that if two non-negative random variables with the same mean follow increasing convex order, then they are in convex order; see Theorem 4.A.35 of [SS07].

3.2. The Counterexample

We consider the following random variables with the same mean:

\begin{matrix} X_{i} = 0.5 Y_{i 1} + 0.2 Y_{i 2} + 0.3 Y_{i 3} (i = 1, 2), \end{matrix}

where the six independent random variables are

$Y_{11} \sim G (3, 1 / 3)$ , $Y_{12} \sim G (10, 3)$ , $Y_{13} \sim W (0.5, 1)$ ;
$Y_{21} \sim G (1 / 3, 3)$ , $Y_{22} \sim G (3, 10)$ , $Y_{23} \sim W (1 / 12, 1 / 3)$ .

By Lemma 3, it is clear that

Y_{11} \leq_{c x} Y_{21}

Y_{12} \leq_{c x} Y_{22}

for the two pairs of Gamma distributions, and each pair share the same mean. For the pair of Weibull distributions

Y_{13}

and

Y_{23}

, notice that

β_{13} = 1 > 1 / 3 = β_{23}

; moreover, since

Γ (1 + 1 / β_{13}) = Γ (2) = 1

and

Γ (1 + 1 / β_{23}) = Γ (4) = 6

, it follows

\begin{matrix} \frac{Γ (1 + 1 / β_{13})}{Γ (1 + 1 / β_{23})} = \frac{1}{6} = \frac{α_{23}}{α_{13}} . \end{matrix}

Therefore

Y_{13} \leq_{i c x} Y_{23}

by Lemma 3. Since

X_{i}

(

i = 1, 2

) are positive linear combinations of

Y_{i j}

’s, we have

X_{1} \leq_{c x} X_{2}

by Corollary 1.

We can also plot the CDF’s of each pair of

Y_{1 j}

and

Y_{2 j}

(

j = 1, 2, 3

), and their CDF’s satisfy the One-X inequality for each j. According to Theorem 3 of [Zet23], we can therefore conclude that

Y_{1 j} \leq_{c x} Y_{2 j}

for each

j = 1, 2, 3

; this is consistent with our analysis above. The plots of each pair of CDF’s can be seen in Figure 1.

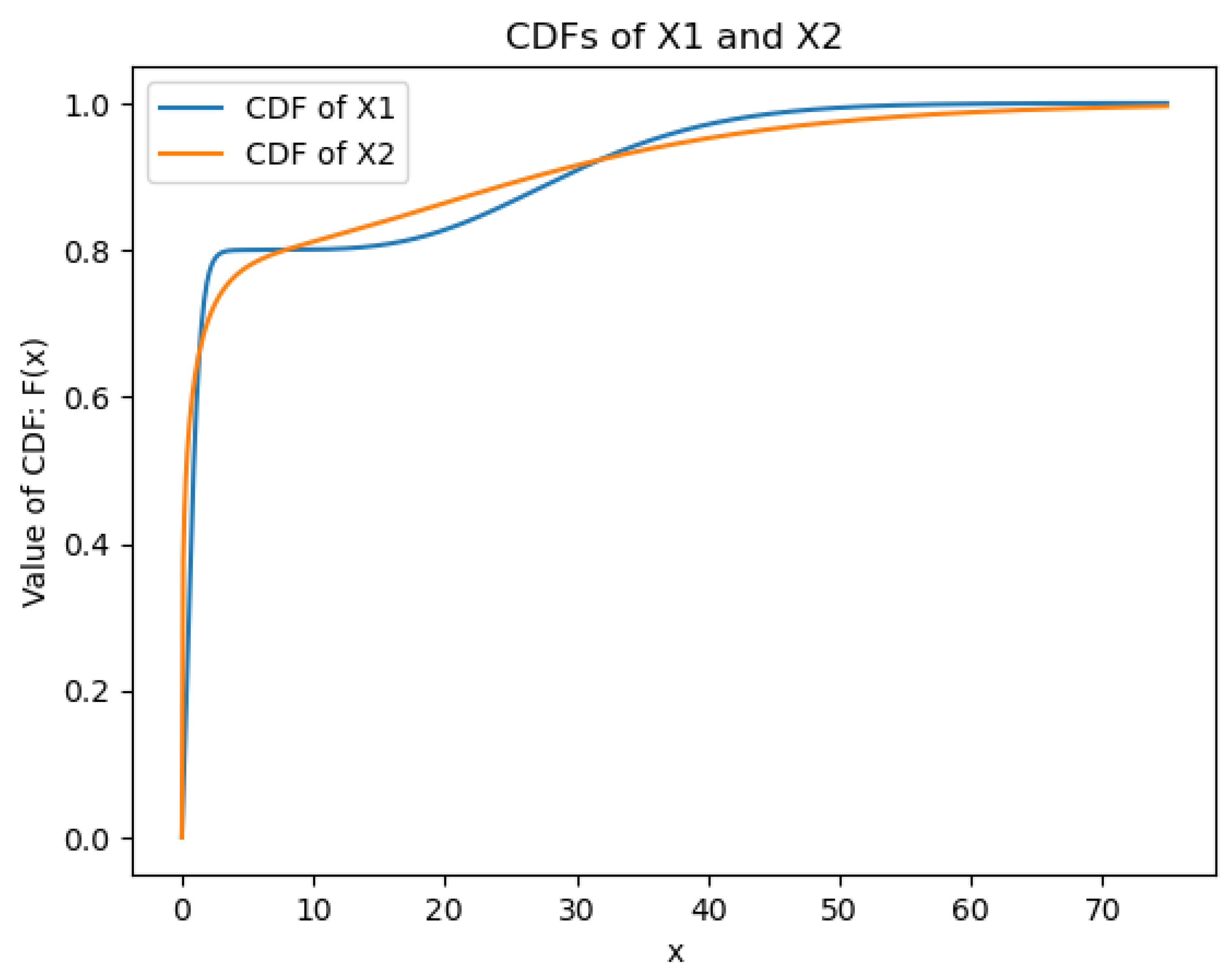
To conclude our argument on this counterexample, let us plot the CDF’s of probability distributions

X_{1}

and

X_{2}

in Figure 2, where we can easily see that they intersect more than once, as we can numerically check that

\begin{matrix} F_{X_{1}} (0.5) = 0.28521275 & < 0.54714305 = F_{X_{2}} (0.5), \\ F_{X_{1}} (3) = 0.7961403 & > 0.74182055 = F_{X_{2}} (3), \end{matrix}

but on the other hand

\begin{matrix} F_{X_{1}} (20) = 0.82747431 & < 0.86400305 = F_{X_{2}} (20), \\ F_{X_{1}} (40) = 0.97101896 & > 0.95225997 = F_{X_{2}} (40) . \end{matrix}

Therefore

X_{1} {\leq ̸}_{O n e - X} X_{2}

, but we have already shown that

X_{1} \leq_{c x} X_{2}

. This completes the counterexample.

4. Underlying Density and log Gaussian Mixtures

Although Conjecture 1 fails in the most general scenario, we may focus on smaller classes of distributions and obtain a partial inverse to the implication “

\leq_{O n e - X} \Rightarrow \leq_{c x}

”. To determine which classes of distributions are viable in practice, let us recall the context that motivates the conjecture: equity implied volatility fitting and gap filling.

There are several very popular IV surface construction methods, besides the well-known parametric method such as stochastic volatility inspired IV surface [Gat04], another major approach is through the construction of implied density per time-slice. One benefit of this method is that the existence of implied density function implies no butterfly arbitrage. Consequently, the main challenge remains to deal with the calendar arbitrage, for which the existence of One-X orders will play a key role.

When the underlying is of equity class, the existence of dividends brings challenges into the construction of IV and local volatility surface. One way to bypass this is the pure stock process [Bue10]: assume that the equity price is

S_{t}

, the pure stock

X_{t}

is defined as

S_{t} = A_{t} + B_{t} X_{t}

where

A_{t} + B_{t} = F_{t}

and

F_{t}

is the stock’s forward price. As shown in [Bue10],

X_{t}

is a positive martingale with

E [X_{t}] = 1

, and all the pricing theories can be transformed from

S_{t}

X_{t}

. In particular, the construction of IV surface or the implied density will be associated with the

X_{t}

process.

Notice that the implied density in [Zet23] obeys log normal distribution. This assumption helps to explain the theoretical foundations explicitly and facilitates the implementation of the proposed IV surface construction method. However, as pointed out in [GP23], a single log normal distribution alone suffers the difficulty of fitting the IV smile in the real market, especially before the companies’ earning dates when the implied volatility smile may become W-shape. Therefore, we propose to use mixtures of log normal distributions (aka log Gaussian mixtures) to fit the implied density functions. The rational of this proposal is based on the well-known fact that Gaussian mixtures are dense in the set of probability distributions; see P65 [GBC16].

Before moving to the modification of the conjecture, let’s consider the number of intersections of two continuous probability distributions defined on

[0, \infty)

Preposition 4.1.

Given two random variables

X_{i}

(

i = 1, 2

) whose CDF’s, denoted by

F_{X_{i}}

respectively, are defined on

[0, \infty)

, if their CDF’s are real-analytic, then the number of intersections of

F_{X_{1}}

and

F_{X_{2}}

is at most countable. If we further assume that the density function of

X_{2}

dominates that of

X_{1}

, then there are finitely many intersections.

Proof.

We begin with covering

[0, \infty)

\cup_{n = 0}^{\infty} [n, n + 1]

. Define

h : = F_{X_{2}} - F_{X_{1}}

, h is also analytical whose zero points correspond to the intersection numbers of

F_{X_{1}}

and

F_{X_{2}}

. Let’s show that over each sub-interval

[n, n + 1]

, h has finitely many zeros, thus, it has at most countably many zeros.

[n, n + 1]

is a compact set in

R^{1}

. If h has infinitely many zeros, then by Bolzano-Weierstrass Theorem, the set of zeros has a convergent sub-sequence in

[n, n + 1]

. Therefore, by identity theorem, h must be zero on all of

[n, n + 1]

which implied h is identically zero. This is a contradiction to the assumption that

X_{1}

and

X_{2}

are different.

Let’s denote the density functions by

f_{i}

i = 1, 2

. If

X_{2}

dominates

X_{1}

, then

{lim}_{x \to \infty} \frac{f_{2} (x)}{f_{1} (x)} = \infty

. Thus, there exists a positive number A such that

F_{X_{1}}

and

F_{X_{2}}

intersects at most once over

[A, \infty)

. Following the same argument as above, we can show that

F_{X_{1}}

and

F_{X_{2}}

only intersect finite many times over

[0, A]

. Thus, if

X_{2}

dominates

X_{1}

, their CDF’s have only finitely many intersection points.

Remark 4.2.

Many common density functions have the properties described in Proposition 4.1., with the log Gaussian mixtures being the primary examples. Such a distribution is usually our first choice to model the implied density distribution of the underlying. Therefore, from a piratical point of view, given two listed maturities

T_{1}

T_{2}

with corresponding implied distribution

M_{1}

M_{2}

, it is reasonable to assume that their CDF’s intersect at finitely many points.

5. One-X Interpolation Between Convex Ordered Pairs

As mentioned in Section 2.3, the One-X order (or the dangerousness order) is not transitive, and its transitive closure requires inserting extra terms in between two random variables satisfying the convex order. Theoretically there might be infinitely many intermediate terms appearing, but for practical purpose there are often only finitely many such terms. We have the following

Theorem 2.

Given two non-negative one-dimensional random variables X and Y which share the same mean, and their CDF’s,

F_{X}

and

F_{Y}

, cross finitely many times (say, n times), then

X \leq_{c x} Y

if and only if there exists a sequence of random variables

Z_{1}, Z_{2}, \dots, Z_{n}

such that

X = Z_{1}

Y = Z_{n}

, and

Z_{i} \leq_{O n e - X} Z_{i + 1}

for

i = 1, 2, . . ., n - 1

Proof.

The if part is relatively straight forward. By Theorem 3 of [Zet23], the One-X order implies the convex order. Thus, for any

i < n

Z_{i} \leq_{O n e - X} Z_{i + 1}

implies that

E [Z_{i}] = E [Z_{i + 1}]

and

Z_{i} \leq_{c x} Z_{i + 1}

. These two properties are both transitive, and thus

X = Z_{1} \leq_{c x} Z_{n} = Y

. (Notice that if one fixes n as 2, then this is the original conjecture).

Now, let us prove the only if part. By Theorem III.1.3 of [KGvH94] or Theorem 1.1, Chapter IV of [Hür08],

X \leq_{c v} Y

and n intersections of the CDF’s implies that there exists a sequence of random variables

{Z_{i}}_{i = 1}^{n}

such that

X = Z_{1}

Y = Z_{n}

Z_{i} \leq_{D} Z_{i + 1}

, for

i = 1, 2, . . ., n - 1

. By Definition 1, this implies

E [Z_{i}] \leq E [Z_{i + 1}]

; however, notice that

E [Z_{1}] = E [X] = E [Y] = E [Z_{n}]

, and thus, all the random variables in this sequence share the same mean which shows that

Z_{i} \leq_{o n e - X} Z_{i + 1}

, for

i = 1, 2, \dots, n - 1

Remark 5.1.

When

F_{X}

and

F_{Y}

cross possibly infinitely many times, one needs to replace the finite sequence

{Z_{i}}_{i = 0}^{n}

in Theorem 2 by a possibly infinite sequence which convergences to Y in both distribution and mean (which is called “stop-loss convergence"). A proof of this generalization can be found in Section 4 of [Mül96]; compare also the transitive closure

\leq_{D^{*}}

of the dangerousness order mentioned in Section 2.3.

As discussed in Section 4, the log Gaussian mixtures are the most natural class of distributions to work with. For such distributions we have the following

Corollary 2.

Given two random variables X and Y whose distributions are log Gaussian mixtures; suppose

E [X] = E [Y]

, then

X \leq_{c x} Y

if and only if there exists a sequence of random variables

Z_{1}, Z_{2}, \dots, Z_{n}

such that

X = Z_{1}

Y = Z_{n}

, and

Z_{i} \leq_{O n e - X} Z_{i + 1}

for

i = 1, 2, . . ., n - 1

. This is an obvious consequence of Theorem 2, Proposition 4.1. and Remark 4.2..

6. IV Surface Construction and Future Work

From the discussions of previous sections, we can see that the proposed models in [Zet22] and [Zet23] may have difficulties in dealing with more complicated implied volatility construction problems such as the W-shape before earning dates. We need more sophisticated models to fit the IV smiles better, and as discussed in Section 4, a good candidate is the log Gaussian mixtures introduced in [GP23].

Since our focus is on fitting the implied density function instead of the IV curve per listed maturity, it is well-known that there is no concern about the butterfly arbitrage, which is ruled out by the very existence of the implied density function. We only need to eliminate the calendar arbitrage, which is related to the convex order of the implied densities at different maturities; see Theorem 2.6 of [BeJu16] or Theorem 8 of [Str65].

6.1. Criteria for log Gaussian Mixtures to Obey Convex Order

In this subsection, without loss of generality, we will be working with the pure stock process

X_{t}

as mentioned in Section 4. Assume that there are two listed maturities

T_{1} < T_{2}

, each having an implied density function

f_{i}

(

i = 1, 2

) which is the marginal density function of the process

X_{t}

T_{i}

. Assuming

f_{i}

(

i = 1, 2

) have log Gaussian mixture distributions, we would like to guarantee that there is no calendar arbitrage between them, which means

f_{1} = X_{T_{1}} \leq_{c x} X_{T_{2}} = f_{2}

under our assumptions.

There are relatively easy criteria when the implied density functions are from some common probability families such as normal, exponential, etc. [BRM15]. However, to the best knowledge of the authors, when the density functions are complicated functions such as the log Gaussian mixture distributions, there is no good theoretical criteria to compare their convex order. Here we discuss some feasible ways to compare the convex order between two mixture of lognormal from a computational point of view.

By Lemma 1, we can further assume that the density functions are mixtures of normal distributions instead of lognormal distributions.

\begin{matrix} f_{i} (x) = \sum_{j = 1}^{n_{i}} p_{i j} φ_{i j} (x) \end{matrix}

where

p_{i j} \geq 0

and

\sum_{j = 1}^{n_{i}} p_{i j} = 1

;

φ_{i j}

is the PDF of a normal random variable whose mean is

μ_{i j}

and whose standard deviation is

σ_{i j}

Then we have

\begin{matrix} X_{T_{1}} \leq_{c x} X_{T_{2}} \\ \Leftrightarrow & \forall z, E [{(X_{T_{1}} - z)}^{+}] \leq E [{(X_{T_{2}} - z)}^{+}] \\ \Leftrightarrow & \forall z, \sum_{j = 1}^{n_{1}} p_{1 j} \int_{z}^{\infty} (1 - Φ_{1 j} (x)) d x \leq \sum_{k = 1}^{n_{2}} p_{2 k} \int_{z}^{\infty} (1 - Φ_{2 k} (x)) d x \\ \Leftrightarrow & min_{z \in R} L (z) \geq 0, \end{matrix}

where

Φ_{i j}

is the CDF of normal random variable whose mean is

μ_{i j}

and whose standard deviation is

σ_{i j}

, and we define the function

\begin{matrix} L (z) : = \int_{z}^{\infty} (\sum_{j = 1}^{n_{1}} p_{1 j} Φ_{1 j} (x) - \sum_{k = 1}^{n_{2}} p_{2 k} Φ_{2 k} (x)) d x . \end{matrix}

As discussed in Remark 4.2., it is reasonable to assume that the CDF’s of

X_{T_{1}}

and

X_{T_{2}}

has finitely many intersections. Notice that the CDF of

X_{T_{i}}

\sum_{l = 1}^{n_{1}} p_{i l} Φ_{i l} (x)

, and we see that

L^{'} (x) = 0

has only finitely many solutions:

x_{1}, x_{2}, \dots, x_{d}

, and

\begin{matrix} min_{z \in R_{+}} L (z) = min {L (x_{1}), \dots, L (x_{d})} . \end{matrix}

With the help of the following theorem, one can reduce the complexity of calculating

L (x_{m})

Theorem 3.

[Theorem 1.3, Chapter IV [Hür08]] Let

X, Y

be two random variables whose means are

μ_{X}

μ_{Y}

, whose CDF’s are

F_{X} (x)

F_{Y} (x)

, and whose stop-loss transforms are respectively

\begin{matrix} π_{X} (x) : = \int_{x}^{\infty} (1 - F_{X} (x)) d x and π_{Y} (x) : = \int_{x}^{\infty} (1 - F_{Y} (x)) d x . \end{matrix}

Suppose that their CDF’s cross

d \geq 1

times at points

x_{1}, \dots, x_{d}

, then one has

X \leq_{i c x} Y

if and only if one of the following is fulfilled:

1.: the first sign change of the difference $F_{Y} (x) - F_{X} (x)$ occurs from − to +, there is an even number of crossing points $d = 2 m$ , and the following inequalities hold:

$\begin{matrix} π_{X} (x_{2 j - 1}) \leq π_{Y} (x_{2 j - 1}), j = 1, 2, \dots, m; \end{matrix}$
2.: the first sign change of the difference $F_{Y} (x) - F_{X} (x)$ occurs from + to −, there is an odd number of crossing points $d = 2 m + 1$ , and the following inequalities hold:

$\begin{matrix} μ_{X} \leq μ_{Y}, and π_{X} (x_{2 j}) \leq π_{Y} (x_{2 j}), j = 1, 2, \dots, m . \end{matrix}$

Notice that

L (x) = π_{X_{T_{1}}} (x) - π_{X_{T_{2}}} (x)

, and thus Theorem 3 can help reduce almost half of the calculations of

L (x_{i})

(

i = 1, 2, \dots, d

6.2. Remarks on IV Surface Construction

Along with the fast developing and growth of machine learning, many researchers have applied machine learning/deep learning techniques into the financial filed. One of the first areas where machine/deep learning achieves exciting success is the prediction on various assets’s prices. Deep learning, particularly models like Long Short-Term Memory (LSTM) networks, has significantly advanced the field of finance by enhancing stock prediction. In stock prediction, LSTM networks excel at analyzing vast amounts of historical and real-time data to identify complex temporal patterns and trends, thereby improving the accuracy of forecasting models compared to traditional statistical methods, see for instance [FTZ24]. Another very active research topic in recent years is Generative Adversarial Networks (GANs) and its variants. They are employed to create synthetic financial data, which is invaluable for augmenting datasets, testing trading strategies, and enhancing the robustness of predictive models. Recently, these deep learning methodologies have been extended to the modeling of implied volatility surfaces, allowing for more precise pricing of derivatives and better risk management by capturing the intricate dynamics of option markets [VC23]. These applications underscore the versatility and power of deep learning in transforming financial analysis and decision-making.

In this part, inspired by the applications of deep learning mentioned above, we will discuss some common practical issues encountered in IV surface fitting, and propose several feasible methods to tackle them. Following the same spirit of the series of papers [Zet22,Zet23], we first discuss implied density interpolation, and then consider synthetic IV generation.

IV Interpolation

It is not an uncommon case that for three listed maturities $T_{1} < T_{2} < T_{3}$ , there are high quality quotes on $T_{1}$ and $T_{3}$ while at $T_{2}$ there are few reasonable bid/ask quote pairs for periods of time. In this case, we can fit implied density functions at $T_{1}$ and $T_{3}$ , and we can assume that there is no calendar arbitrage between them. To get an implied density function at $T_{2}$ , one can do martingale interpolation that guarantees no-arbitrage among the three implied density functions.

Ever since the introduction of martingale optimal transport (MOT) [HL17], martingale interpolation has become an attractive research area. In [HL17], a straightforward generalization of the McCann’s interpolations from optimal transport (OT) is introduced, and can be viewed as martingale version of McCann’s interpolations (Definition 2.9, [HL17]). Later, [BBHK17], from a probabilistic point of view, proposes a Benamou–Brenier-type formulation of the martingale transport problem for given distributions $μ$ , $ν$ in convex order. The unique solution $M_{t}$ to their problem is a Markov martingale with several remarkable properties: in a specific way, it replicates the movement of a Brownian particle as closely as possible, subject to the conditions $M_{0} \sim μ$ and $M_{1} \sim ν$ . Similar to McCann’s displacement interpolation, $M_{t}$ offers a time-consistent interpolation between $μ$ , $ν$ as two margins. Recently, [KM23] suggests a new framework. The authors introduce randomized arcade processes (RAP) which can match any finite sequence of target random variables (in convex order) at fixed times across the entire probability space. This makes RAP a powerful tool for strong stochastic interpolation between target random variables. Then they introduce filtered arcade martingales (FAM) which are martingales constructed using the filtrations generated by RAP. They provide an almost-sure solution to the martingale interpolation problem and reveal an underlying stochastic filtering structure. The paper shows that FAM can be informed by Bayesian updating when the underlying RAP is conditionally-Markov, which adds an additional layer of sophistication to the interpolation process.

These martingale interpolation methods are all good candidates for our implied density interpolation purpose. Particularly, the last one which is inspired by the information-based approach [BHM21] helps provide more reasonablely interpolated results. We believe that such frameworks or methods are suitable for implied density function, and thus IV interpolation, especially for the pure stock process in equity or swaption in fixed income. In other words, as long as the underlying asset can be modelled as a martingale process, then the above discussed martingale interpolation methods can be applied for implied density/IV interpolation.

The purpose of this interpolated implied density function at $T_{2}$ is two-folds. On the one hand, it can provide an educated guess when there are few quotes; on the other hand, when there are a few good bid/ask quotes but not enough for a good fitting, one can use the interpolated implied density function as a reference when applying one’s own IV fitting method. For example, one can fit one’s own implied density model and minimize the Kullback–Leibler divergence between the fitted result and the interpolated one to avoid unexpected behaviours when searching for the local minimum of the IV fitting loss function. One can also use the interpolated implied density function to generate enough artificial mid quotes and fit a set of parameters for one’s own model. This set of parameters can be used as a good initial guess to better fit one’s own model with respect to the available (but not enough) market data.

Though several financial applications have been proposed, it seems that the current paper is one of the first work considering to apply martingale interpolation to implied density interpolation for maturities with poor liquidity and discussing the proper situation to apply this technique.
Synthetic IV generation

Along with the rapid growth of generative AI such as generative adversarial nets (GAN) ??, variational autoencoder (VAE) ??, diffusion model ?? etc, synthetic data generation and its application in financial industry has become an active research area; see, for instance, the pioneer work ??. The properly generated synthetic financial data gives an extra edge in back-testing and risk management on trading/hedging strategies. Since one of the most important components in equity option market is the IV surface, we consider synthetic IV curve generation on a given listed maturity.

Instead of pure non-parametric methods which focus on the direct generation of the IV curve, we propose to apply a more parametric method. For instance, when dealing with pure stock price, for a given listed maturity T, we can assume that the implied density function is of the form

$f_{T} (x) : = \sum_{i = 1}^{n} p_{i} g_{i} (x),$

(7)

where n is a fixed large enough integer to generate the required IV smile, $p_{i} \geq 0$ represents the probability $f_{T} = g_{i}$ such that $\sum_{i = 1}^{n} p_{i} = 1$ , and $g_{i}$ is the PDF of a log Gaussian distribution whose mean is $μ_{i}$ and whose standard deviation is $σ_{i}$ . Then instead of learning the distribution of the IV curve itself, one can try to learn the distribution of the set of parameters $(n, p_{1}, . . ., p_{n}, μ_{1}, . . ., μ_{n}, . . ., σ_{1}, . . ., σ_{n})$ , using the various generative AI algorithms mentioned above. This approach has the following benefits:

–

the problem is reduced to a finite dimensional learning problem which is more feasible;

–

with the help of (7), the generated IV curve has no butterfly arbitrage naturally; moreover, due to its parametric form, the resulted IV curve is smoother and stabler;

–

due to its parametric form, it is easier to estimate useful quantities such as skewness and kurtosis of the underlying distribution, and compare them with the shape of the IV curve.

Also, notice the fact that mixtures of Gaussian distributions are dense in the set of probability distributions with respect to the weak topology, with a properly chosen n, our assumption will lose minimal information. Moreover, we can apply the above arguments to both bid and ask quotes instead of the sole mid quotes.

Above we discuss and propose several ideas in IV interpolation and synthetic IV generation for back-testing. In a forthcoming paper, we will implement these ideas and study their effects through simulated and real-world data 1.

References

BHL+20. Hans Buehler, Blanka Horvath, Terry Lyons, Imanol Perez Arribas, and Ben Wood. A data-driven market simulator for small data environments. Preprint arXiv:2006.14498, 2020. [CrossRef]
BRM15. F. Belzunce, C. M. Riquelme and J. Mulero. An Introduction to Stochastic Orders. Elsevier Science, 2015.
BBHK17. Julio Backhoff-Veraguas, Mathias Beiglböck, Martin Huesmann, Sigrid Källblad. Martingale Benamou–Brenier: a probabilistic perspective. Preprint arXiv:1708.04869, 2017. [CrossRef]
BeJu16. M. Beiglböck and N. Juilet. On a problem of optimal transport under marginal martingale constructions. Ann. Probab. 441: 42-106, 2016.
BS73. Fischer Black and Myron Scholes. The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81(3): 637-654, 1973.
BHM21. D. Brody, L. P. Hughston and A. Macrina. Financial Informatics: An Information-based Approach to Asset Pricing. G - Reference, Information and Interdisciplinary Subjects Series. World Scientific, 2021.
Bue10. Hans Buehler. Volatility and dividends-volatility modelling with cash dividends and simple credit risk. Available at SSRN, 2010.
DK94. Emanuel Derman and Iraj Kani. Riding on a smile. Risk, 7(2): 32–39, 1994.
D+94. Bruno Dupire et al. Pricing with a smile. Risk, 7(1) 18–20, 1994.
FTZ24. Xiaojing Fan, Chunliang Tao, and Jianyu Zhao. Advanced stock price prediction with xlstm-based models: Improving long-term forecasting. Preprints, August 2024. [CrossRef]
Gat04. Jim Gatheral. A parsimonious arbitrage-free implied volatility parameterization with application to the valuation of volatility derivatives. Presentation at Global Derivatives & Risk Management, Madrid, page 0, 2004.
GP23. Paul Glasserman and Dab Pirjol. W-shaped implied volatility curves and the Gaussian mixture model. Quantitative Finance, 23(4): 557-577, 2023. [CrossRef]
GBC16. Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning, MIT press, 2016.
GPAM+14. Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville and Yoshua Bengio. Generative adversarial nets. Advances in neural information processing systems, 27, 2014.
HL17. P. Henry-Labordère. Model-free Hedging: A Martingale Optimal Transport Viewpoint. Chapman & Hall/CRC financial mathematics series. CRC Press, 2017.
HJA20. Jonathan Ho, Ajay Jain and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in neural information processing systems, 33: 6840-6851, 2020.
Hür08. Werner Hürlimann. Extremal moment methods and stochastic orders. Boletin de la Associacion Matematica Venezolana, 15(2): 153-301, 2008.
KGvH94. R. Kaas, M. J. Goovaerts, and A. E. van Heerwaarden, A.E. Ordering of Actuarial Risks. Caire education series. CAIRE, 1994.
KM23. Georges Kassis and Andera Macrina. Arcade Processes for Informed Martingale Interpolation and Transport. Preprint arXiv:2301.05936, 2023. [CrossRef]
KW13. Diederik P. Kingma and Max Welling. Auto-encoding variational bayes. Preprint arXiv:1312.6114, 2013. [CrossRef]
Mül96. Alfred Müller. Orderings of risks: A comparative study via stop-loss transforms. Insurance: Mathematics and Economics, 17(3): 215-222, 1996. [CrossRef]
Ohl69. J. B. Ohlin. On a class of measures of dispersion with application to optimal reinsurance. ASTIN Bullentin, 5: 249-266, 1969. [CrossRef]
SS07. M. Shaked and J. G. Shanthikumar. Stochastic Orders. Springer Series in Statistics. Springer New York, 2007.
Str65. V. Strassen. The existence of probability measures with given marginals. Ann. Math. Statist. 36: 423-439, 1965. [CrossRef]
VC23. Milena Vuletic and Rama Cont. Volgan: a generative model for arbitrage-free implied volatility surfaces. Available at SSRN, 2023.
Zet22. Valer Zetocha. The Longitude: managing implied volatility of illiquid assets. Available at SSRN, 2022.
Zet23. Valer Zetocha. Volatility Transformers: an optimal transport-inspired approach to arbitrage-free shaping of implied volatility surfaces. Available at SSRN, 2023.
zha23. Siqiao Zhao. PolyModel: Portfolio Construction and Financial Network Analysis. PhD thesis, Stony Brook University, 2023.

1	Most of this work is based on or inspired by the last part of the second author’s PhD thesis[zha23], and all the contents are for pure academic research only.

Figure 1. Comparing the CDF’s of the individual components

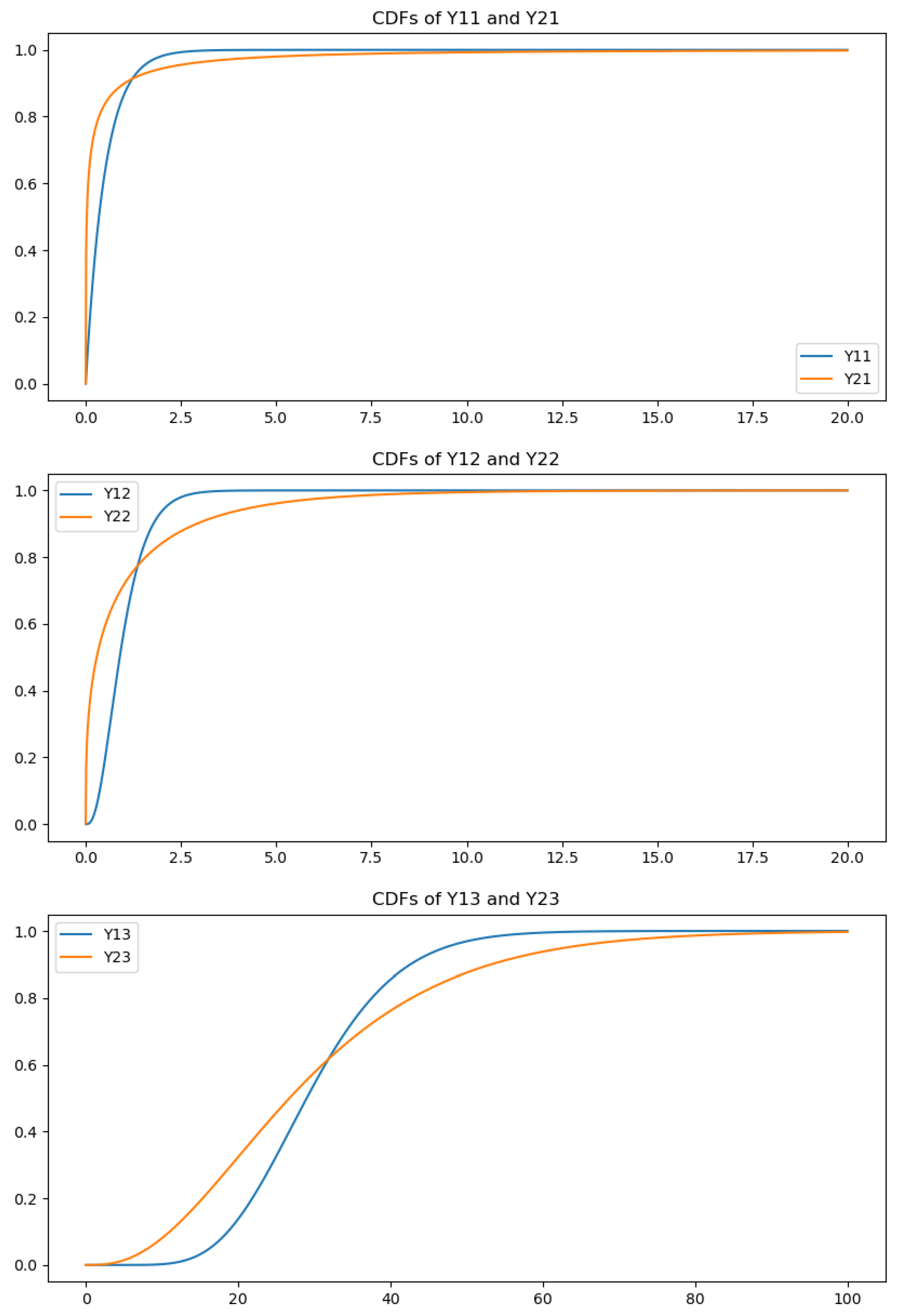
Figure 2. Comparing the CDF’s of

X_{1}

and

X_{2}

Figure 2. Comparing the CDF’s of

X_{1}

and

X_{2}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

One-X Property Conjecture, Stochastic Orders and Implied Volatility Surface Construction

Abstract

1. Introduction

2. Background

2.1. Stochastic Orders and Their Properties

2.2. One-X Order and A Related Conjecture

2.3. Inter-disciplinary Concept Comparison

3. A Counterexample to Conjecture 1

3.1. (Increasing) Convex Order Between Exponential Family Distributions

3.2. The Counterexample

4. Underlying Density and log Gaussian Mixtures

5. One-X Interpolation Between Convex Ordered Pairs

6. IV Surface Construction and Future Work

6.1. Criteria for log Gaussian Mixtures to Obey Convex Order

6.2. Remarks on IV Surface Construction

References

MDPI Initiatives

Important Links

Subscribe