Prerpints.org logo
Preprint
Article

PerFuSIT: Personalized Fuzzy Logic Strategies for Intelligent Tutoring of Programming

Altmetrics

Downloads

62

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 September 2024

Posted:

20 September 2024

You are already at the latest version

Alerts
Abstract
Recent advancements in Intelligent Tutoring Systems (ITS), driven by Artificial Intelligence (AI), have attracted substantial research interest, particularly in the domain of computer programming education. Given the diversity in learners' backgrounds, cognitive abilities, and learning paces, the development of personalized tutoring strategies to support effective attainment of learning objectives has become a critical challenge. This paper introduces PerFuSIT (Personalized Fuzzy Logic Strategies for Intelligent Tutoring of Programming), an innovative fuzzy logic-based module designed to select the most appropriate tutoring strategy from five available options, based on individual learner characteristics. The available strategies include revisiting previous content, progressing to the next topic, providing supplementary materials, assigning additional exercises, or advising the learner to take a break. PerFuSIT's decision-making process incorporates a range of learner-specific parameters, such as performance metrics, error types, indicators of carelessness, frequency of help requests, and the time required to complete tasks. Embedded within the traditional ITS framework, PerFuSIT introduces a sophisticated reasoning mechanism for dynamically determining the optimal instructional approach. Experimental evaluations demonstrate that PerFuSIT significantly enhances learner performance and improves the overall efficacy of interactions with the ITS. The findings highlight the potential of fuzzy logic to optimize adaptive tutoring strategies by customizing instruction to individual learners' strengths and weaknesses, thereby providing more effective and personalized educational support in programming instruction.
Keywords: 
Subject: Computer Science and Mathematics  -   Other

1. Introduction

In recent years, the fields of digital learning and educational technology have experienced significant advancements. Intelligent Tutoring Systems (ITS) and the integration of Artificial Intelligence (AI) have important contribution to these advancements. ITS offer adaptive and personalized learning experiences that address the unique educational needs and preferences of individual learners [1,2,3,4]. They incorporate AI techniques that model effectively the learner’s characteristics and needs and make the system able to respond to them emulating the way of thinking and the reactions of a human tutor [5,6,7,8,9]. This has as a result, the enhancement of the learner’s performance, engagement and overall educational outcomes.
Considering the importance and necessity of computer programming skills across various disciplines, substantial research has been conducted on advanced tutoring systems for teaching these skills [10,11,12]. Computer programming education benefits significantly from these advancements. This is due to the fact that learners of computer programming have, usually, diverse backgrounds, characteristics, needs and learning pace [13,14]. Also, computer programming is a rapidly evolving field, which requires frequent updates and personalized instruction. Numerous researchers have developed ITSs for computer programming education [15,16,17,18,19,20,21,22]. Despite these efforts, educational outcomes in programming courses need further enhancement [23,24,25,26,27].
There are various challenges of an ITS for computer programming education. Particularly, they include modeling of complex and vague data, like students’ knowledge and skill levels [28,29,30], a flexible error diagnosis mechanism that can identify a variety of error types (i.e syntax errors, logic errors) [31,32], sophisticated decision making processes and real-time data processing that allow the provision of targeted personalized feedback [33,34] and dynamic adjustments of the tutoring strategies and processes. An AI technique that is able to address these chalenges is fuzzy logic, a reasoning approach that effectively manages uncertainty by calculating with words and imitating the human way of thinking [35,36]. More specifically, fuzzy logic enables a more effective representation of students knowledge level using linguistic terms [37,38,39], can detect and interpret errors in a more flexible way [40,41], and can emulate a human tutor cognitive processes and reactions through fuzzy rules, providing nuanced feedback [42,43].
In the view of the above, this paper introduces PerFuSIT (Personalized Fuzzy Logic Strategies for Intelligent Tutoring of Programming), an innovative fuzzy logic-based module that is responsible for selecting the most appropriate tutoring strategy based on characteristics of learners within an intelligent system for teaching computer programming. PerFuSIT leverages fuzzy logic to model the inherent uncertainty and variability in learner performance and educational needs and adapt dynamically the tytoring strategies. More specifically, PerFuSIT is a Fuzzy Inference System that takes into account for each learner, her/his performance, types of errors, carelessness, frequency of help requests, and required time to solve exercises, and selects the most optimal tutoring strategy for her/him, consulting the tutoring model and applying a set of fuzzy rules. PerFuSIT is a module of a comprehensive web-based ITS that teaches computer programming (Figure 1). The presented system has been used by undergraduate students of the department of Informatics of the University of Piraeus in Greece. The evaluation results show that PerFuSIT enhances learners’ performance and the efficacy of their interactions with the system. The findings indicate that PerFuSIT is a significant advancement in the development of intelligent tutoring systems for computer programming, with the potential to impact the broader landscape of personalized education. It showcases how fuzzy logic can be leveraged to develop more intelligent, adaptive, and effective learning systems.

2. Literature Review

In literature review there are works that concern the development of ITS for computer programming, which leverage fuzzy logic to provide personalized and adaptive learning experiences, but they are limited. Particularly, in [44], the authors used a fuzzy logic-based mechanism to determine the students’ skill level in a tutoring system for the programming language C. However, no personalized feedback and instructional processes are derived from each individual student. Also, Photoboard [45] is another ITS that uses fuzzy logic to identify the knowledge level of novice learners in computer programming. Furthermore, in [46], the authors developed NanoDoc, an adaptive serious game for teaching the programming concepts of sequence and iteration to elementary school students. NanoDoc incorporates fuzzy logic to describe student knowledge level and provides the appropriate working examples according to it until s/he obtain the required knowldege level. Another serious game that incorporated fuzzy logic for offering adaptivity is FuzzEG [47]. FuzzEG describes the learner’s knwoledge level through fuzzy sets and decides about the level of difficulty of the quizzes and the extension of the game scenario so as the learner can interact with more educational content using a set of fuzzy rules. Both serious games fuzzy logic-based adaptation aimed to modeling the students knowledge level and determining the difficulty of exercises. Also, in [48], the authors present a computer programming serious game, which uses a fuzzy logic-based mechanism that models the student’ skills and decides about the difficulty of the game’s mission. Thus, the game adapt its challenges to each individual learner skills to support her/him on learning computer programming, but it does not provide any other instructional adjustemnet. In [49], the authors developed COALA system that uses fuzzy logic to assess the program (code) that a student writes in a tutoring systems for computer programming. COALA uses fuzzy logic to represent a variety of parametes concerning the student program, like lines of code and complexity, and through fuzzy rules generates feedback including ways of correcting and improving the program quality. Similarly, to the aforementioned works, neither COALA provides a comprehensive adaptive instructional strategy. In addition, in [50], the authors present FuzKSD, a fuzzy logic-based mechanism, which is incorporated in a web-based ITS that teaches the programming language C. The operation of FuzKSD is based on fuzzy sets and fuzzy rules. Its aim is to identify dynamically the student’s knowledge level and its changes and model the learning or forgetting process. In this way, the system decides for each learner if s/he needs to repeat the current domain chapter, if s/he has to be transitted to the next one, or s/he has to return to a previous one to revise it. The presented system provide adaptive instruction, however it is restricted to which chapter of the learning material each indiividual student has to read.
Regarding the above, we conclude that although fuzzy logic has been used for providing adaptive learning features in tutoring systems for computer programming, its use is limited. More specifically, fuzzy logic is ussually used for modeling the student konwledge or skill level and determining the difficulty of the provided educational content and her/his transition or not to the next chapter of the knowledge domain. Despite these advancements, the application of fuzzy logic for providing more nuanced adaptive instructional actions, like giving access to supplemental educational material or asking to solve more exercises or advising to have a rest, to each individual learner needs further investigation. The presented mechanism aims to dynamically adapt instructional strategies based on continuous assessment of learner performance and learning profile leveraging through a fuzzy logic-based mechanism.

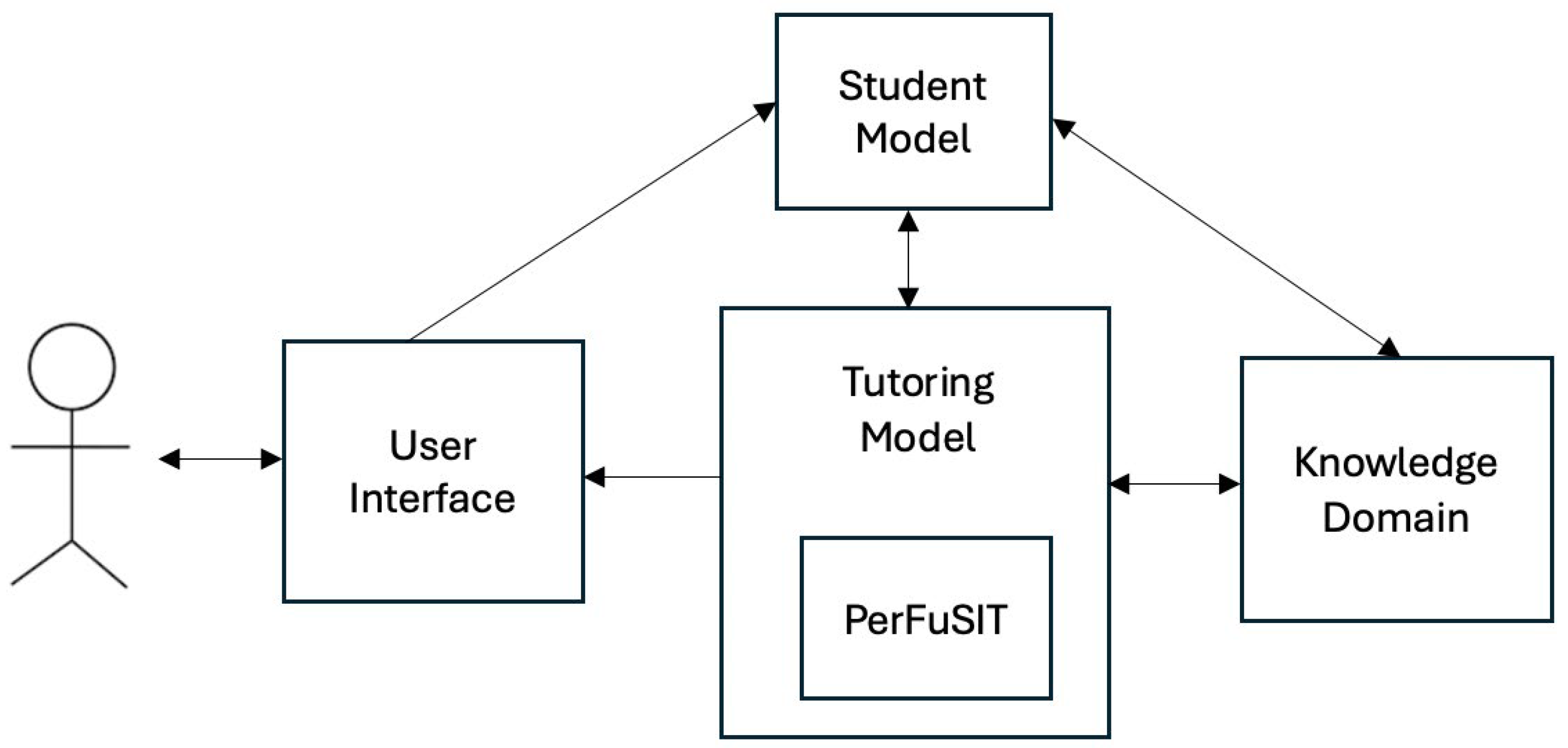
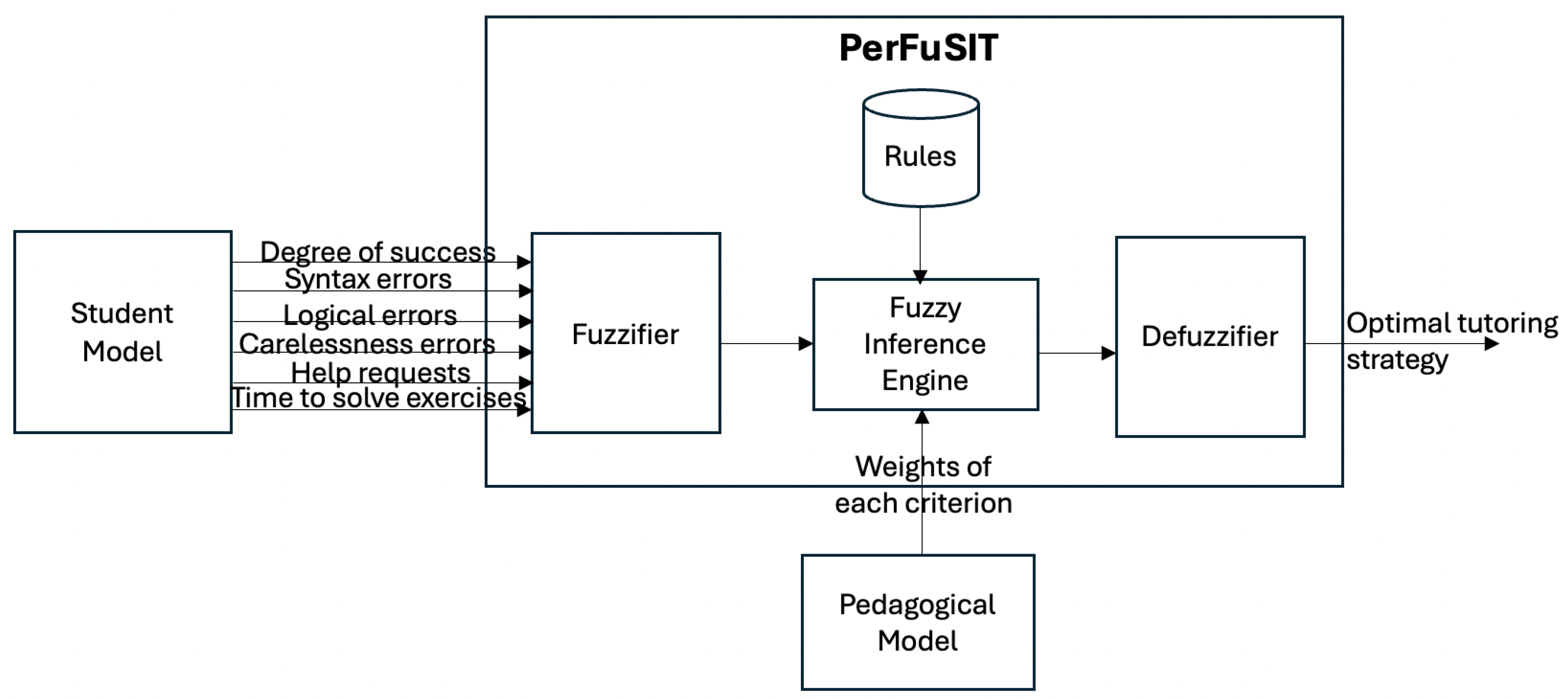
3. PerFuSIT

PerFuSIT is an innovative fuzzy-based mechanism for providing personalized tutoring strategies in an intelligent tutoring system that teaches computer programming (Figure 2). In more details, PerFuSIT takes as input the student’s degree of success in the knowledge domain, the percentage of syntax and logical errors s/he does, the frequency of mistakes that happen due to carelessness, the frequency of help requests and the time s/he needs to solve exercises. These data are provided by the student model. Also, PerFuSIT takes as input the weights of each criterion. The weights are stored in the pedagogical model and are defined by tutors and experts in computer programming. The input data are fuzzified and PerFuSIT applies weights and a set of fuzzy rules over them to decide about the most appropriate tutoring strategy among five available, ranging from reviewing a chapter or moving to a next one, to providing supplemental content and additional exercises.

3.1. Available Tytoring Strategies

The available tutoring strategies among of which PerFuSIT has to select the most appropriate for each individual learner are the following:
  • A1: Review the chapter
  • A2: Move to the next chapter
  • A3: Access supplemental resources
  • A4: Practice additional exercises
  • A5: Take a break
The aim of PerFuSIT is to define how significant and educational effective is each one of the available tutoring strategies for each individual learner. This significance and effectiveness are described though the following five fuzzy sets (Table 1): ‘Very Low’ (VL), ‘Low’ (L), ‘Average’ (A), ‘Much’ (M), ‘Very Much’ (VM). These fuzzy sets and their intervals were determined based on the knowledge and experience of 8 computer programming teachers and 3 intelligent tutoring system developers. All participant teachers had 7 years at least experience in teaching computer programming and 3 of them had, also, involved in related to computer programming curriculum development. Furthermore, the 3 developers had 5 years at least experience in developing ITS.

3.2. Input Data and Weights

The input data concern learner performance and individualized learning parameters of the learner’s profile. Particularly, the input data are:
a)
the learner’s degree of success (it is calculated with a maximum value of 100),
b)
the learner’s syntax errors (it is calculated as percentage of the overall errors),
c)
the learner’s logical errors (it is calculated as percentage of the overall errors),
d)
the learner’s errors due to carelessness (it is calculated as percentage of the overall errors),
e)
the frequency of help requests (it is calculated as percentage of the total available aids),
f)
the mean time the learner needs to solve exercises (it is calculated as percentage of the total available time for solving an exercise).
The crisp values of the above data are fuzzified to the following five fuzzy sets (Table 2): ‘Very Low’ (VL), ‘Low’ (L), ‘Medium’ (M), ‘High’ (H), ‘Very High’ (VH).
Weights are defined for each parameter and declare how much each parameter (i.e syntax errors) contributes to apply a tutoring action (i.e., provide supplemental content). A weight can take one of the following four values:
  • Very low (VL): 0.1
  • Low (L): 0.3
  • Average (A): 0.5
  • Μuch (Μ): 0.8
  • Very Much (VM): 1
For example, a very low degree of success indicates that the learner has to review the current chapter very much, or a very high percentage of carelessness errors implies very much that the learner needs to take a break. Similarly, a medium percentage of syntax errors indicate an average possibility of providing additional exercises, while a high frequency of help requests implies that the learner needs supplemental resources. In Table 3, Table 4, Table 5, Table 6, Table 7, and Table 8 the defined weights of each parameter for each tutoring strategy are presented. Both the fuzzy sets for the input data, as well as the weights of them for each input parameter were defined by the 11 experts (8 computer programming teachers and 3 intelligent tutoring system developers), that were referred to the Subsection 3.1.

3.3. The Fuzzy Rules

Below, the PerFuSIT’s fuzzy rules are presented. For each input data there are 25 fuzzy sets (5 rules for each action). There are 150 fuzzy rules in total. They are of the following format: “If ‘input_parameter’ is X then Ai is Y”, where input_parameter ∈ {degree of success, syntax errors, logical errors, carelessness errors, help requests, time to solve exercises}, X ∈ {VL, L, M, H, VH}, i∈[1,5] and Y ∈ {VL, L, A, M, VM}. Some examples of the set of fuzzy rules follow:
  • If ‘degree of success’ is ‘M’ then A1 is ‘A’.
  • If ‘degree of success’ is ‘H’ then A3 is ‘VL’.
  • If ‘syntax errors’ is ‘L’ then A2 is ‘M’.
  • If ‘logical errors’ is ‘VH’ then A5 is ‘M’.
  • If ‘carelessness errors’ is ‘VH’ then A5 is ‘VM’.
  • If ‘help requests’ is ‘M’ then A1 is ‘L’.
  • If ‘time to solve exercises’ is ‘M’ then A3 is ‘A’.
All the rules are presented in Table 9, Table 10, Table 11, Table 12, Table 13, and Table 14. Also, these rules, were defined based on the experience and knowledge of the 11 experts (8 computer programming teachers and 3 intelligent tutoring system developers), that were referred to the Subsection 3.1.

3.4. The Procedure of PerFuSIT Operation

Below the steps of the PerFuSIT’s operation are presented.
  • Step 1: Definitions of the criteria weights for each tutoring strategy
  • Step 2: Get the values of the criteria from the log files of the system
  • Step 3: Input data fuzzification
  • Step 4: Application of the fuzzy rules
  • Step 5: Output calculation for each rule
  • Step 6: Weights application to the outputs
  • Step 7: Results aggregation
  • Step 8: Defuzzification of the aggregated result
  • Step 9: Rank the results
  • Step 10: Selection of the appropriate tutoring strategy

4. Use Case Scenarios

In this section example of use clearly illustrate the operation of PerFuSIT. Let’s have five learners, whose performance and individuallized parameters of their learning profiles are presented in Table 15. The fuzzified input values for these five learners are presented in Table 16 and Table 17.
Then, the fuzzy rules are applied. For example, for Maria the following fuzzy rules are triggered:
1)
If ‘degree of success’ is ‘M’ then A1 is ‘A’.
2)
If ‘degree of success’ is ‘M’ then A2 is ‘L’.
3)
If ‘degree of success’ is ‘M’ then A3 is ‘A’.
4)
If ‘degree of success’ is ‘M’ then A4 is ‘A’.
5)
If ‘degree of success’ is ‘M’ then A5 is ‘A’.
6)
If ‘degree of success’ is ‘H’ then A1 is ‘L’.
7)
If ‘degree of success’ is ‘H’ then A2 is ‘M’.
8)
If ‘degree of success’ is ‘H’ then A3 is ‘VL’.
9)
If ‘degree of success’ is ‘H’ then A4 is ‘VL’.
10)
If ‘degree of success’ is ‘H’ then A5 is ‘VL’.
11)
If ‘syntax errors’ is ‘VL’ then A1 is ‘VL’.
12)
If ‘syntax errors’ is ‘VL’ then A2 is ‘VM’.
13)
If ‘syntax errors’ is ‘VL’ then A3 is ‘VL’.
14)
If ‘syntax errors’ is ‘VL’ then A4 is ‘VL’.
15)
If ‘syntax errors’ is ‘VL’ then A5 is ‘VL’.
16)
If ‘syntax errors’ is ‘L’ then A1 is ‘VL’.
17)
If ‘syntax errors’ is ‘L’ then A2 is ‘M’.
18)
If ‘syntax errors’ is ‘L’ then A3 is ‘VL’.
19)
If ‘syntax errors’ is ‘L’ then A4 is ‘VL’.
20)
If ‘syntax errors’ is ‘L’ then A5 is ‘VL’.
21)
If ‘logical errors’ is ‘M’ then A1 is ‘A’.
22)
If ‘logical errors’ is ‘M’ then A2 is ‘A’.
23)
If ‘logical errors’ is ‘M’ then A3 is ‘A’.
24)
If ‘logical errors’ is ‘M’ then A4 is ‘M’.
25)
If ‘logical errors’ is ‘M’ then A5 is ‘A’.
26)
If ‘logical errors’ is ‘H’ then A1 is ‘M’.
27)
If ‘logical errors’ is ‘H’ then A2 is ‘VL’.
28)
If ‘logical errors’ is ‘H’ then A3 is ‘M’.
29)
If ‘logical errors’ is ‘H’ then A4 is ‘VM’.
30)
If ‘logical errors’ is ‘H’ then A5 is ‘M’.
31)
If ‘carelessness errors’ is ‘VL’ then A1 is ‘VL’.
32)
If ‘carelessness errors’ is ‘VL’ then A2 is ‘VL’.
33)
If ‘carelessness errors’ is ‘VL’ then A3 is ‘VL’.
34)
If ‘carelessness errors’ is ‘VL’ then A4 is ‘VL’.
35)
If ‘carelessness errors’ is ‘VL’ then A5 is ‘VL’.
36)
If ‘help requests’ is ‘L’ then A1 is ‘VL’.
37)
If ‘help requests’ is ‘L’ then A2 is ‘M’.
38)
If ‘help requests’ is ‘L’ then A3 is ‘L’.
39)
If ‘help requests’ is ‘L’ then A4 is ‘L’.
40)
If ‘help requests’ is ‘L’ then A5 is ‘VL’.
41)
If ‘help requests’ is ‘M’ then A1 is ‘L’.
42)
If ‘help requests’ is ‘M’ then A2 is ‘A’.
43)
If ‘help requests’ is ‘M’ then A3 is ‘A’.
44)
If ‘help requests’ is ‘M’ then A4 is ‘A’.
45)
If ‘help requests’ is ‘M’ then A5 is ‘A’.
46)
If ‘time to solve exercises’ is ‘M’ then A1 is ‘L’.
47)
If ‘time to solve exercises’ is ‘M’ then A2 is ‘A’.
48)
If ‘time to solve exercises’ is ‘M’ then A3 is ‘A’.
49)
If ‘time to solve exercises’ is ‘M’ then A4 is ‘A’.
50)
If ‘time to solve exercises’ is ‘M’ then A5 is ‘L’.
51)
If ‘time to solve exercises’ is ‘H’ then A1 is ‘A’.
52)
If ‘time to solve exercises’ is ‘H’ then A2 is ‘L’.
53)
If ‘time to solve exercises’ is ‘H’ then A3 is ‘M’.
54)
If ‘time to solve exercises’ is ‘H’ then A4 is ‘M’.
55)
If ‘time to solve exercises’ is ‘H’ then A5 is ‘A’.
Then, the outputs of the rules are adjusted according to the weights. For example, the weight of ‘degree of success’ for A1 is very high and for A3 is high. So, the membership value of the outputs of the rules 1 and 6 are multiplied by 1 and the membership value of the outputs of the rules 3 and 8 are multiplied by 0.8. On the other hand, the weight of ‘logical errors’ for A5 is average. So, the membership value of the outputs of the corresponding rules (25 and 30) are multiplied by 0.5. Furthermore, the weight of ‘carelessness errors’ for A1 is very low and for A4 is low. So, the membership value of the output of the rule 31 is multiplied by 0.1 and the membership value of the output of the rule 34 is multiplied by 0.3. The results of applying the fuzzy rules and the weights for the five learners are depicted in Table 18, Table 19, Table 20, Table 21, and Table 22. In Table 23, the final weighted outputs of the rules for all the learners are presented.
The aggregation of the rules’ outputs is done using the centroid method. The crisp aggregated results are depicted in Table 24. According to them, Maria will be provided more practice exercises, John and Alex will be transited to the next chapter of the educational content, Kate will be provided with supplemental educational resources to read, and Jason will be advised to take a break.

5. Evaluation

5.1. The Method

To evaluate the PerFuSIT’s ability and effectiveness in helping learners to acquire knowledge and accomplish the learning goal, an experiment was conducted. Particularly, a group of undegraduate students of Informatics utilized the ITS, which incorporates PerFuSIT, for a duration of 5 weeks. Following this period, they took a test to assess the computer programming knowledge they had acquired. The test had a maximum possible score of 10, signifying an excellent level of knowledge. Furthremore, the mean number of learners’ interactions with the ITS during the period of 5 weeks was calculated gathering the appropriate data from the log files. One interaction is calculated each time a learner reads the content of a chapter and answers the corresponding test. Therefore, if a student reads 3 times a chapter and answers to the corresponding test until s/he passed it and be moved to the next chapter, the system will consider that s/he performed 3 interactions. Then, both the average performance of the learners of the above group as their mean number of interactions with the ITS were compared with the corresponding values of learners from the same undergraduate program in Informatics of another group, who used, during the same period, another version of the ITS, with the same educational content and structure, but without the PerFuSIT. It has to be emphasized that the version of the ITS, from which PerFuSIT is absent, adapts the educational content to each individual learner based only to her/his performance, as is the case with most intelligent and adaptive tutoring systems. For example, if a student’s performance is 42%, then the system recommends her/him to revise the current chapter of the educational material. However, if her/his degree of success is 80%, the system transits the learner to the next chapter. T-tests [51] were used to ensure the accuracy and the statistical significance of the difference of the mean values of the aforementioned metrics.

5.2. The Test-Bed

In the evaluation process, 114 undergraduate students of the department of Informatics of the University of Piraeus in Greece, participated. They were divided into two equal number groups: PerFuSIT_group and No_PerFuSIT_group. The students of the first group utilized the ITS, which incorporates PerFuSIT, while the No_PerFuSIT_group utilized another version of the ITS, with the same educational content and structure, but without the PerFuSIT. The learners of both groups utilized the systems for a period of 5 weeks. During this period, they were attending lectures on computer programming. Before, the students used the ITSs, they attended a detailed demonstration of them. Additionally, comprehensive user manuals were provided. Furthermore, online help and support were available throughout the usage period. There was an equal distribution between the two groups, regarding the characteristics of the learners (Table 25).

5.3. The Results

The evaluation results show that the integration of PerFuSIT, enhances learners’ performance and the efficacy of their interactions with the system. Particularly, the mean performance score was 8.51 for PerFuSIT_group and 7.02 for No_ PerFuSIT_group (Table 26). Therefore, there is an increase of 14.9% in student performance. This increase is statistically significance, since the ‘P(T<=t) two-tail’ value of the t-test is less than 0.05.
In addition, the average number of interactions with ITS was reduced by 15.3% with the PerFuSIT integration. In more details, the mean number of interactions was 45.83 for PerFuSIT_group and 54.11 for No_PerFuSIT_group (Table 27). The difference in the mean number of interactions between the two groups is significant, as indicated by the value of ‘P(T<=t) two-tail’, which is lower than 0.05. Consequently, PerFuSIT allows the learner to complete a knowledge domain chapter and reach the learning goal with fewer interactions. As a result, PerFuSIT allows learners to achieve better performance while requiring fewer interactions with the system.

6. Discussion

The development and implementation of PerFuSIT is a significant advancement in the field of adaptive learning technologies, particularly for tutoring systems for computer programming. The ability of PerFuSIT to adjust dynamically the tutoring strategies based on a variety of data of the learning profile of a student indicates the contribution to the development of more intelligent, adaptive, and effective learning systems. Unlike other intelligent tutoring systems that use fuzzy logic primarily to model student knowledge or skill levels and determine the difficulty of educational content or whether a learner should progress to the next chapter, PerFuSIT’s fuzzy inference mechanism enables real-time adjustments to more nuanced tutoring strategies, such as providing access to additional educational materials, assigning more exercises, or suggesting a break. This approach offers more targeted and responsive feedback to better support the instruction process and help learners to reach the learning objectives.
The experimental results, which indicate improvements in both learner performance and interaction efficacy, provide strong evidence of the benefits of PerFuSIT. Particularly, PerFuSIT contributes to the performance improvement and, also, allows the learner to complete a knowledge domain chapter and reach the learning goal with fewer interactions. Therefore, it allows learners to perform better while interacting lower times with the system. These findings underscore the significant contribution of PerFuSIT to the effective learning in the computer programming education. Furthrmore, they highlight the potential of fuzzy logic to improve adaptive learning technologies, offering more supportive and effective personalized tutoring strategies in computer programming instruction.

7. Conclusion

In this paper, an innovative fuzzy-based mechanism, called PerFuSIT, for providing personalized tutoring strategies within an intelligent tutoring system for computer programming is presented. PerFuSIT takes into account several data of the students’ learning profiles and by leveraging fuzzy logic adapts dynamically adapt the tutoring strategy that are appropriate for each individual student. In such a way, it provides a more nuanced and responsive feedback to the diverse needs of learners, supporting the instructional process of computer programming.
The experimental results confirm that PerFuSIT contributes to improved learner performance and more efficient interactions within the tutoring system. These findings highlight the value of incorporating fuzzy logic into adaptive learning technologies, particularly in environments where learners have diverse needs and learning paces. They indicate that PerFuSIT constitute a major advancement in the development of intelligent tutoring systems for computer programming. This can, also, influence the wider field of personalized education. Furthermore, the presented mechanism can be leveraged to develop more intelligent, adaptive, and effective learning systems.
In the future, emotional and motivational indicators have to be taken into consideration in the learners’ needs to provide a more advanced personalized tutoring process. Furthermore, we intend to incorporate PerFuSIT into ITS of other domain knowledge that computer programming.

Author Contributions

Conceptualization, K.C. and M.V.; methodology, K.C.; software, K.C.; validation, K.C. and M.V.; writing—original draft preparation, K.C.; visualization, K.C.; supervision, M.V.; project administration, K.C. and M.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Goenaga, S.; Navarro, L.; Quintero M, C.G.; Pardo, M. Imitating human emotions with a nao robot as interviewer playing the role of vocational tutor. Electronics 2020, 9(6), 971. [Google Scholar] [CrossRef]
  2. Minn, S. AI-assisted knowledge assessment techniques for adaptive learning environments. Computers and Education: Artificial Intelligence 2022, 3, 100050. [Google Scholar]
  3. Alrakhawi, H.A.; Jamiat, N.U.R.U.L.L.I.Z.A.M.; Abu-Naser, S.S. Intelligent tutoring systems in education: A systematic review of usage, tools, effects and evaluation. Journal of Theoretical and Applied Information Technology 2023, 101(4), 1205–1226. [Google Scholar]
  4. Alrakhawi, H.A.; Jamiat, N.; Umar, I.N.; Abu-Naser, S.S. Improvement of Students Achievement by Using Intelligent Tutoring Systems-A Bibliometric Analysis and Reviews. Journal of Theoretical and Applied Information Technology 2023, 101(11). [Google Scholar]
  5. Roessingh, J.J.; Poppinga, G.; van Oijen, J.; Toubman, A. Application of artificial intelligence to adaptive instruction-combining the concepts. In Adaptive Instructional Systems: First International Conference, AIS 2019, Held as Part of the 21st HCI International Conference, HCII 2019, Orlando, FL, USA, 26–31 July 2019, Proceedings 21; Springer International Publishing: Cham, Switzerland, 2019; pp. 542–556. [Google Scholar]
  6. Sottilare, R. Agent-based methods in support of adaptive instructional decisions. In Proceedings of the International Conference on Human-Computer Interaction, Copenhagen, Denmark, 19–21 July 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 164–175. [Google Scholar]
  7. AlShaikh, F.; Hewahi, N. AI and machine learning techniques in the development of Intelligent Tutoring System: A review. In Proceedings of the IEEE 2021 International Conference on innovation and Intelligence for informatics, computing, and technologies (3ICT), Zallaq, Bahrain, 29–30 September 2021; pp. 403–410. [Google Scholar]
  8. Shan Wang, Fang Wang, Zhen Zhu, Jingxuan Wang, Tam Tran, Zhao Du, Artificial intelligence in education: A systematic literature review. Expert Systems with Applications 2024, 252 Pt A, 124167, ISSN 0957-4174. [CrossRef]
  9. Vuković, I.; Kuk, K.; Čisar, P.; Banđur, M.; Banđur, Đ.; Milić, N.; Popović, B. Multi-agent system observer: Intelligent support for engaged e-learning. Electronics 2021, 10(12), 1370. [Google Scholar] [CrossRef]
  10. Hooshyar, D.; Binti Ahmad, R.; Wang, M.; Yousefi, M.; Fathi, M.; Lim, H. Development and evaluation of a game-based bayesian intelligent tutoring system for teaching programming. Journal of Educational Computing Research 2018, 56(6), 775–801. [Google Scholar] [CrossRef]
  11. Figueiredo, J.; García-Peñalvo, F.J. Intelligent tutoring systems approach to introductory programming courses. In Proceedings of the Eighth International Conference on Technological Ecosystems for Enhancing Multiculturality, Salamanca, Spain, 21–23 October 2020; pp. 34–39. [Google Scholar]
  12. Chrysafiadi, K.; Virvou, M.; Tsihrintzis, G.A. A fuzzy-based evaluation of E-learning acceptance and effectiveness by computer science students in Greece in the period of COVID-19. Electronics 2023, 12(2), 428. [Google Scholar] [CrossRef]
  13. Navarro-Cota, C.; Molina, A.I.; Redondo, M.A.; Lacave, C. Individual differences in computer programming: A systematic review. Behaviour & Information Technology 2024, 1–19. [Google Scholar]
  14. Lacave, C.; Molina, A.I. The Impact of COVID-19 in Collaborative Programming. Understanding the Needs of Undergraduate Computer Science Students. Electronics 2021, 10, 1728. [Google Scholar] [CrossRef]
  15. Castro-Schez, J.J.; Glez-Morcillo, C.; Albusac, J.; Vallejo, D. An intelligent tutoring system for supporting active learning: A case study on predictive parsing learning. Information Sciences 2021, 544, 446–468. [Google Scholar] [CrossRef] [PubMed]
  16. Vesin, B.; Mangaroska, K.; Akhuseyinoglu, K.; Giannakos, M. Adaptive assessment and content recommendation in online programming courses: On the use of elo-rating. ACM Transactions on Computing Education (TOCE) 2022, 22(3), 1–27. [Google Scholar] [CrossRef]
  17. Van Petegem, C.; Dawyndt, P.; Mesuere, B. Dodona: Learn to code with a virtual co-teacher that supports active learning. In Proceedings of the 2023 Conference on Innovation and Technology in Computer Science Education V. 2, Turku, Finland, 7–12 June 2023; p. 633. [Google Scholar]
  18. Day, M.; Penumala, M.R.; Gonzalez-Sanchez, J. Annete: An intelligent tutoring companion embedded into the eclipse IDE. In Proceedings of the 2019 IEEE First International Conference on Cognitive Machine Intelligence (CogMI), Los Angeles, CA, USA, 12–14 December 2019; pp. 71–80. [Google Scholar]
  19. Huang, Y.; Brusilovsky, P.; Guerra, J.; Koedinger, K.; Schunn, C. Supporting skill integration in an intelligent tutoring system for code tracing. Journal of Computer Assisted Learning 2023, 39(2), 477–500. [Google Scholar] [CrossRef]
  20. Elkot, M.A. Embedding adaptation levels within intelligent tutoring systems for developing programming skills and improving learning efficiency. International Journal of Advanced Computer Science and Applications 2019, 10(12). [Google Scholar] [CrossRef]
  21. Francisco, R.E.; de Oliveira Silva, F. Intelligent Tutoring System for Computer Science Education and the Use of Artificial Intelligence: A Literature Review. CSEDU 2022, 1, 338–345. [Google Scholar]
  22. Crow, T.; Luxton-Reilly, A.; Wuensche, B. Intelligent tutoring systems for programming education: A systematic review. In Proceedings of the 20th Australasian Computing Education Conference, Brisbane, Australia, 30 January 2018–2 February 2018; pp. 53–62. [Google Scholar]
  23. Medeiros, R.P.; Ramalho, G.L.; Falcão, T.P. A systematic literature review on teaching and learning introductory programming in higher education. IEEE Transactions on Education 2019, 62(2), 77–90. [Google Scholar] [CrossRef]
  24. Lacave, C.; Molina, A.I.; Cruz-Lemus, J.A. Learning Analytics to identify dropout factors of Computer Science studies through Bayesian networks. Behaviour & Information Technology 2018, 37(10–11), 993–1007. [Google Scholar]
  25. Dirzyte, A.; Perminas, A.; Kaminskis, L.; Žebrauskas, G.; Sederevičiūtė–Pačiauskienė, Ž.; Šliogerienė, J.;... & Gajdosikiene, I. Factors contributing to dropping out of adults’ programming e-learning. Heliyon 2023, 9(12).
  26. Yulianto, B.; Prabowo, H.; Kosala, R. Comparing the effectiveness of digital contents for improving learning outcomes in computer programming for autodidact students. Journal of e-Learning and Knowledge Society 2016, 12(1). [Google Scholar]
  27. Zinovieva, I.S.; Artemchuk, V.O.; Iatsyshyn, A.V.; Popov, O.O.; Kovach, V.O.; Iatsyshyn, A.V.;... & Radchenko, O.V. The use of online coding platforms as additional distance tools in programming education. Journal of physics: Conference Series 2021, 1840(1), 012029.
  28. Desmarais, M.C.; Baker, R.S.D. A review of recent advances in learner and skill modeling in intelligent learning environments. User Modeling and User-Adapted Interaction 2012, 22, 9–38. [Google Scholar] [CrossRef]
  29. Binh, H.T.; Trung, N.Q.; Duy, B.T. Responsive student model in an intelligent tutoring system and its evaluation. Education and information technologies 2021, 26(4), 4969–4991. [Google Scholar] [CrossRef]
  30. Ramírez-Noriega, A.; Juárez-Ramírez, R.; Jiménez, S.; Martínez-Ramírez, Y. Knowledge representation in intelligent tutoring system. In Proceedings of the International Conference on Advanced Intelligent Systems and Informatics 2016; Springer International Publishing: Cham, Switzerland, 2017; pp. 12–21. [Google Scholar]
  31. Le, N.T.; Pinkwart, N. Adding weights to constraints in intelligent tutoring systems: Does it improve the error diagnosis? In Towards Ubiquitous Learning: 6th European Conference of Technology Enhanced Learning, EC-TEL 2011, Palermo, Italy, 20–23 September 2011; Proceedings 6; Springer: Berlin/Heidelberg, Germany, 2011; pp. 233–247. [Google Scholar]
  32. McCall, D. Novice Programmer Errors-Analysis and Diagnostics; University of Kent: Kent, UK, 2016. [Google Scholar]
  33. Jamaludin, N.H.; Romli, R. Analysis of the Effectiveness of Feedback Provision in Intelligent Tutoring Systems. In International Conference on Computing and Informatics; Springer Nature: Singapore, 2023; pp. 168–179. [Google Scholar]
  34. Keuning, H.; Jeuring, J.; Heeren, B. A systematic literature review of automated feedback generation for programming exercises. ACM Transactions on Computing Education (TOCE) 2018, 19(1), 1–43. [Google Scholar] [CrossRef]
  35. Zadeh, L.A. Fuzzy Sets. Information and Control 1965, 8(3), 338–353. [Google Scholar] [CrossRef]
  36. Chrysafiadi, K. The Role of Fuzzy Logic in Artificial Intelligence and Smart Applications. In Fuzzy Logic-Based Software Systems; Springer International Publishing: Cham, Switzerland, 2023; pp. 25–29. [Google Scholar]
  37. K. Chrysafiadi, S. K. Chrysafiadi, S. Papadimitriou, M. Virvou, Cognitive-based adaptive scenarios in educational games using fuzzy reasoning. Knowl.-Based Syst. 2022, 109111. [Google Scholar] [CrossRef]
  38. Yu, Y.X.; Gong, H.P.; Liu, H.C.; Mou, X. Knowledge representation and reasoning using fuzzy Petri nets: A literature review and bibliometric analysis. Artificial Intelligence Review 2023, 56(7), 6241–6265. [Google Scholar] [CrossRef]
  39. Karaci, A. Intelligent tutoring system model based on fuzzy logic and constraint-based student model. Neural Computing and Applications 2019, 31(8), 3619–3628. [Google Scholar] [CrossRef]
  40. Chrysafiadi, K.; Virvou, M. Evaluating the learning outcomes of a fuzzy-based Intelligent Tutoring System. In Proceedings of the 2021 IEEE 33rd International Conference on Tools with Artificial Intelligence (ICTAI), Washington, DC, USA, 1–3 November 2021; pp. 1392–1397. [Google Scholar]
  41. Hsieh, T.-C.; Lee, M.-C.; Su, C.-Y. Designing and implementing a personalized remedial learning system for enhancing the programming learning. Journal of Educational Technology & Society 2013, 16(4), 32–46. [Google Scholar]
  42. Hostetter, J.W.; Abdelshiheed, M.; Barnes, T.; Chi, M. Leveraging fuzzy logic towards more explainable reinforcement learning-induced pedagogical policies on intelligent tutoring systems. In Proceedings of the 2023 IEEE International Conference on Fuzzy Systems (FUZZ), Incheon, Republic of Korea, 13–17 August 2023; pp. 1–7. [Google Scholar]
  43. Lasfeto, D.B.; Ulfa, S. Modeling of online learning strategies based on fuzzy expert systems and self-directed learning readiness: The effect on learning outcomes. Journal of Educational Computing Research 2023, 60(8), 2081–2104. [Google Scholar] [CrossRef]
  44. Yazid, M.A.A.F.M.; Sahabudin, N.A.; Raffei, A.F.M.; Remli, M.A. C Programming Skill Levels Determination Using Fuzzy Logic. In Proceedings of the IEEE 2021 International Conference on Software Engineering & Computer Systems and 4th International Conference on Computational Science and Information Management (ICSECS-ICOCSIM), Pekan, Malaysia, 24–26 August 2021; pp. 399–404. [Google Scholar]
  45. Hurtado, C.; Licea, G.; García-Valdez, M.; Quezada, A.; Castañón-Puga, M. Teaching Computer Programming as Well-Defined Domain for Beginners with Protoboard. In Trends and Innovations in Information Systems and Technologies: Volume 2 8; Springer International Publishing: Cham, Switzerland, 2020; pp. 262–271. [Google Scholar]
  46. Toukiloglou, P.; Xinogalos, S. NanoDoc: Designing an adaptive serious game for programming with working examples support. In European Conference on Games Based Learning, September 2022; Volume 16, No. 1, pp. 628–636.
  47. Toukiloglou, P.; Xinogalos, S. NanoDoc: Designing an adaptive serious game for programming with working examples support. In Proceedings of the European Conference on Games Based Learning, Lisbon, Portugal, 6–7 October 2022; No. 1; Volume 16, pp. 628–636. [Google Scholar]
  48. Vahldick, A.; Mendes, A.J.; Marcelino, M.J. Dynamic difficulty adjustment through a learning analytics model in a casual serious game for computer programming learning. EAI Endorsed Transactions on Serious Games 2017, 4(13). [Google Scholar] [CrossRef]
  49. Jurado, F.; Redondo, M.A.; Ortega, M. Using fuzzy logic applied to software metrics and test cases to assess programming assignments and give advice. Journal of Network and Computer Applications 2012, 35(2), 695–712. [Google Scholar] [CrossRef]
  50. Chrysafiadi, K.; Virvou, M. Fuzzy logic for adaptive instruction in an e-learning environment for computer programming. IEEE transactions on Fuzzy Systems 2014, 23(1), 164–177. [Google Scholar] [CrossRef]
  51. Pallant, J. SPSS survival manual: A step by step guide to data analysis using IBM SPSS; Routledge: London, UK, 2020. [Google Scholar]
Preprints 118697 g001
Figure 1. ITS that incororates PerFuSIT.
Figure 1. ITS that incororates PerFuSIT.
Preprints 118697 g001
Preprints 118697 g002
Figure 2. The architecture of PerFuSIT.
Figure 2. The architecture of PerFuSIT.
Preprints 118697 g002
Table 1. Fuzzy sets for tutoring strategies significance.
Table 1. Fuzzy sets for tutoring strategies significance.
Fuzzy set partition Membership function
Very Low (VL) (0, 0, 20) μ V L x = 0 ,     x ≥ 20 20 − x 20 ,   0 ≤ x ≤ 20
Low (L) (10, 30, 50) μ L x = x − 10 20 ,   10 ≤ x ≤ 30   0 ,   x ≤ 10   o r   x ≥ 50 50 − x 20 ,   30 ≤ x ≤ 50
Average (A) (30, 50, 80) μ A x = x − 30 20 ,   30 ≤ x ≤ 50   0 ,   x ≤ 30   o r   x ≥ 80 80 − x 30 ,   50 ≤ x ≤ 80
Much (M) (50, 80, 90) μ M x = x − 50 30 ,   50 ≤ x ≤ 80   0 ,   x ≤ 50   o r   x ≥ 90 90 − x 10 ,   80 ≤ x ≤ 90
Very Much (VM) (80, 100, 100) μ V M x = 0 ,     x ≤ 80 x − 80 20 ,   80 ≤ x ≤ 100  
Table 2. Fuzzy sets for input variables.
Table 2. Fuzzy sets for input variables.
Fuzzy set partition Membership function
Very Low (VL) (0, 0, 20) μ V L x = 0 ,     x ≥ 20 20 − x 20 ,   0 ≤ x ≤ 20
Low (L) (10, 30, 50) μ L x = x − 10 20 ,   10 ≤ x ≤ 30   0 ,   x ≤ 10   o r   x ≥ 50 50 − x 20 ,   30 ≤ x ≤ 50
Medium (M) (30, 50, 80) μ M x = x − 30 20 ,   30 ≤ x ≤ 50   0 ,   x ≤ 30   o r   x ≥ 80 80 − x 30 ,   50 ≤ x ≤ 80
High (H) (50, 80, 90) μ H x = x − 50 30 ,   50 ≤ x ≤ 80   0 ,   x ≤ 50   o r   x ≥ 90 90 − x 10 ,   80 ≤ x ≤ 90
Very High (VH) (80, 100, 100) μ V H x = 0 ,     x ≤ 80 x − 80 20 ,   80 ≤ x ≤ 100  
Table 3. The weights of degree of success for each tutoring strategy.
Table 3. The weights of degree of success for each tutoring strategy.
degree Very Low Low Medium High Very High
A1 VM M A L VL
A2 VL VL L M VM
A3 M M A VL VL
A4 L L A VL VL
A5 M M A VL VL
Table 4. The weights of syntax errors for each tutoring strategy.
Table 4. The weights of syntax errors for each tutoring strategy.
syntax Very Low Low Medium High Very High
A1 VL VL A M VM
A2 VM M A VL VL
A3 VL VL L A A
A4 VL VL A M M
A5 VL VL A M M
Table 5. The weights of logical errors for each tutoring strategy.
Table 5. The weights of logical errors for each tutoring strategy.
logical Very Low Low Medium High Very High
A1 VL VL A M VM
A2 VM M A VL VL
A3 VL L A M VM
A4 VL L M VM VM
A5 VL VL A M M
Table 6. The weights of carelessness errors for each tutoring strategy.
Table 6. The weights of carelessness errors for each tutoring strategy.
carelessness Very Low Low Medium High Very High
A1 VL VL VL L L
A2 VL VL VL VL VL
A3 VL VL VL VL VL
A4 VL VL M M M
A5 VL VL M VM VM
Table 7. The weights of help requests for each tutoring strategy.
Table 7. The weights of help requests for each tutoring strategy.
Help requests Very Low Low Medium High Very High
A1 VL VL L A A
A2 M M A L VL
A3 VL L A M VM
A4 VL L A M VM
A5 VL VL L M M
Table 8. The weights of required time to solve exercises for each tutoring strategy.
Table 8. The weights of required time to solve exercises for each tutoring strategy.
Time Very Low Low Medium High Very High
A1 VL VL L A A
A2 M A A L L
A3 VL VL A M VM
A4 VL VL A M VM
A5 VL VL L A M
Table 9. Fuzzy rules concerning the degree of success.
Table 9. Fuzzy rules concerning the degree of success.
degree of success Very Low Low Medium High Very High
A1 VM M A L VL
A2 VL VL L M VM
A3 M M A VL VL
A4 L L A VL VL
A5 M M A VL VL
Table 10. Fuzzy rules concerning syntax errors.
Table 10. Fuzzy rules concerning syntax errors.
Syntax errors Very Low Low Medium High Very High
A1 VL VL A M VM
A2 VM M A VL VL
A3 VL VL L A A
A4 VL VL A M M
A5 VL VL A M M
Table 11. Fuzzy rules concerning logical errors.
Table 11. Fuzzy rules concerning logical errors.
Logical errors Very Low Low Medium High Very High
A1 VL VL A M VM
A2 VM M A VL VL
A3 VL L A M VM
A4 VL L M VM VM
A5 VL VL A M M
Table 12. Fuzzy rules concerning carelessness errors.
Table 12. Fuzzy rules concerning carelessness errors.
Carelessness errors Very Low Low Medium High Very High
A1 VL VL VL L L
A2 VL VL VL VL VL
A3 VL VL VL VL VL
A4 VL VL M M M
A5 VL VL M VM VM
Table 13. Fuzzy rules concerning help requests.
Table 13. Fuzzy rules concerning help requests.
Help requests Very Low Low Medium High Very High
A1 VL VL L A A
A2 M M A L VL
A3 VL L A M VM
A4 VL L A M VM
A5 VL VL L M M
Table 14. Fuzzy rules concerning required time to solve exercises.
Table 14. Fuzzy rules concerning required time to solve exercises.
Time to solve exercises Very Low Low Medium High Very High
A1 VL VL L A A
A2 M A A L L
A3 VL VL A M VM
A4 VL VL A M VM
A5 VL VL L A M
Table 15. Learning profiles of the students.
Table 15. Learning profiles of the students.
degree syntax logical carelessness Help requests time
Maria 62% 18% 60% 5% 32% 58%
John 75% 32% 15% 12% 60% 76%
Alex 86% 45% 23% 35% 12% 65%
Kate 58% 40% 20% 7% 80% 10%
Jason 65% 25% 62% 48% 35% 85%
Table 16. Fuzzified values of the learners’ profiles data.
Table 16. Fuzzified values of the learners’ profiles data.
degree syntax logical carelessness Help requests time
Maria (0, 0, 0.6, 0.4, 0) (0.1, 0.4, 0, 0, 0) (0, 0, 0.67, 0.33, 0) (0.75, 0, 0, 0, 0) (0, 0.9, 0.1, 0, 0) (0, 0, 0.73, 0.27, 0)
John (0, 0, 0.167, 0.83,0) (0, 0.9, 0.1, 0, 0) (0.25, 0.25, 0, 0, 0) (0.4, 0.1, 0, 0, 0) (0, 0, 0.67, 0.33, 0) (0, 0, 0.13, 0.87, 0)
Alex (0, 0, 0, 0.4, 0.3) (0, 0.25, 0.75, 0, 0) (0, 0.65, 0, 0, 0) (0, 0.75, 0.25, 0, 0) (0.4, 0.1, 0, 0, 0) (0, 0, 0.5, 0.5, 0)
Kate (0, 0, 0.73, 0.267, 0) (0, 0.5, 0.5, 0, 0) (0, 0.5, 0, 0, 0) (0.65, 0, 0, 0, 0) (0, 0, 0, 1, 0) (0.5, 0, 0, 0, 0)
Jason (0, 0, 0.5, 0.5, 0) (0, 0.75, 0, 0, 0) (0, 0, 0.6, 0.4, 0) (0, 0.1, 0.9, 0, 0) (0, 0.75, 0.25, 0, 0) (0, 0, 0, 0.5, 0.25)
Table 17. Input variables’ fuzzy sets and their membership values for each learner.
Table 17. Input variables’ fuzzy sets and their membership values for each learner.
degree syntax logical carelessness Help requests time
Maria ‘M’ with μM(x)=0.6
&
‘H’ with μH(x)=0.4		 ‘VL’ with μVL(x)=0.1
&
‘L’ with μL(x)=0.4		 ‘M’ with μM(x)=0.67
&
‘H’ with μH(x)=0.33		 ‘VL’ with μVL(x)=0.75 ‘L’ with μL(x)=0.9
&
‘M’ with μM(x)=0.1		 ‘M’ with μM(x)=0.73
&
‘H’ with μH(x)=0.27
John ‘M’ with μM(x)=0.167
&
‘H’ with μH(x)=0.83		 ‘L’ with μL(x)=0.9
&
‘M’ with μM(x)=0.1		 ‘VL’ with μVL(x)=0.25
&
‘L’ with μL(x)=0.25		 ‘VL’ with μVL(x)=0.4
&
‘L’ with μL(x)=0.1		 ‘M’ with μM(x)=0.67
&
‘H’ with μH(x)=0.33		 ‘M’ with μM(x)=0.13
&
‘H’ with μH(x)=0.87
Alex ‘H’ with μH(x)=0.4
&
‘VH’ with μVH(x)=0.3		 ‘L’ with μL(x)=0.25
&
‘M’ with μM(x)=0.75		 ‘L’ with μL(x)=0.65 ‘L’ with μL(x)=0.75
&
‘M’ with μM(x)=0.25		 ‘VL’ with μVL(x)=0.4
&
‘L’ with μL(x)=0.1		 ‘M’ with μM(x)=0.5
&
‘H’ with μH(x)=0.5
Kate ‘M’ with μM(x)=0.73
&
‘H’ with μH(x)=0.267		 ‘L’ with μL(x)=0.5
&
‘M’ with μM(x)=0.5		 ‘L’ with μL(x)=0.5 ‘VL’ with μM(x)=0.65 ‘H’ with μH(x)=1 ‘VL’ with μVL(x)=0.5
Jason ‘M’ with μM(x)=0.4
&
‘H’ with μH(x)=0.5		 ‘L’ with μL(x)=0.75 ‘M’ with μM(x)=0.6
&
‘H’ with μH(x)=0.4		 ‘L’ with μL(x)=0.1
&
‘M’ with μM(x)=0.9		 ‘L’ with μL(x)=0.75
&
‘M’ with μM(x)=0.25		 ‘H’ with μH(x)=0.5
&
‘VH’ with μVH(x)=0.25
Table 18. Fuzzy rules output for Maria.
Table 18. Fuzzy rules output for Maria.
Degree syntax logical carelessness Help requests time
A1 A with μA=0.6 VL with μVL=0.08 A with μA=0.536 VL with μVL=0.075 VL with μVL=0.9 L with μL=0.219
L with μL=0.4 VL with μL=0.32 M with μM=0.264 L with μL=0.1 A with μA=0.081
A2 L with μL=0.6 VM with μVM=0.08 A with μA=0.536 VL with μVL=0.075 M with μM=0.9 A with μA=0.219
M with μM=0.4 M with μM=0.32 VL with μVL=0.264 A with μA=0.1 L with μL=0.081
A3 A with μA=0.48 VL with μVL=0.03 A with μA=0.67 VL with μVL=0.075 L with μL=0.9 A with μA=0.219
VL with μVL=0.32 VL with μVL=0.12 M with μM=0.33 A with μA=0.1 M with μM=0.081
A4 A with μA=0.48 VL with μVL=0.03 M with μM=0.67 VL with μVL=0.225 L with μL=0.45 A with μA=0.584
VL with μVL=0.32 VL with μVL=0.12 VM with μVM=0.33 A with μA=0.05 M with μM=0.216
A5 A with μA=0.3 VL with μVL=0.05 A with μA=0.335 VL with μVL=0.75 VL with μVL=0.45 L with μL=0.584
VL with μVL=0.2 VL with μVL=0.2 M with μM=0.165 L with μL=0.05 A with μA=0.216
Table 19. Fuzzy rules output for John.
Table 19. Fuzzy rules output for John.
Degree syntax logical carelessness Help requests time
A1 A with μA=0.167 VL with μVL=0.72 VL with μVL=0.2 VL with μVL=0.04 L with μL=0.67 L with μL=0.039
L with μL=0.83 A with μA=0.08 VL with μVL=0.2 VL with μVL=0.01 A with μA=0.33 A with μA=0.261
A2 L with μL=0.167 M with μM=0.72 VM with μVM=0.2 VL with μVL=0.04 A with μA=0.67 A with μA=0.039
M with μM=0.83 A with μA=0.08 M with μM=0.2 VL with μVL=0.01 L with μL=0.33 L with μL=0.261
A3 A with μA=0.134 VL with μVL=0.27 VL with μVL=0.25 VL with μVL=0.04 A with μA=0.67 A with μA=0.039
VL with μVL=0.664 L with μL=0.03 L with μL=0.25 VL with μVL=0.01 M with μM=0.33 M with μM=0.261
A4 A with μA=0.134 VL with μVL=0.27 VL with μVL=0.25 VL with μVL=0.12 A with μA=0.335 A with μA=0.104
VL with μVL=0.664 A with μA=0.03 L with μL=0.25 VL with μVL=0.03 M with μM=0.165 M with μM=0.7
A5 A with μA=0.084 VL with μVL=0.45 VL with μVL=0.125 VL with μVL=0.4 L with μL=0.335 L with μL=0.104
VL with μVL=0.415 A with μA=0.05 L with μL=0.125 VL with μVL=0.1 M with μM=0.165 A with μA=0.7
Table 20. Fuzzy rules output for Alex.
Table 20. Fuzzy rules output for Alex.
Degree syntax logical carelessness Help requests time
A1 L with μL=0.4 VL with μVL=0.2 VL with μVL=0.52 VL with μVL=0.075 VL with μVL=0.4 L with μL=0.15
VL with μVL=0.3 A with μA=0.6 VL with μVL=0.025 VL with μVL=0.1 A with μA=0.15
A2 M with μM=0.4 M with μM=0.2 M with μML=0.52 VL with μVL=0.075 M with μM=0.4 A with μA=0.15
VM with μVM=0.3 A with μA=0.06 VL with μVL=0.025 M with μM=0.1 L with μL=0.15
A3 VL with μVL=0.32 VL with μVL=0.075 L with μL=0.65 VL with μVL=0.075 VL with μVL=0.4 A with μA=0.15
VL with μVL=0.24 L with μL=0.225 VL with μVL=0.025 L with μL=0.1 M with μM=0.15
A4 VL with μVL=0.32 VL with μVL=0.075 L with μL=0.65 VL with μVL=0.225 VL with μVL=0.2 A with μA=0.4
VL with μVL=0.24 A with μA=0.225 M with μM=0.075 L with μL=0.05 M with μM=0.4
A5 VL with μVL=0.2 VL with μVL=0.125 VL with μVL=0.325 VL with μVL=0.75 VL with μVL=0.2 L with μL=0.4
VL with μVL=0.15 A with μA=0.375 M with μM=0.25 VL with μVL=0.05 A with μA=0.4
Table 21. Fuzzy rules output for Kate.
Table 21. Fuzzy rules output for Kate.
Degree syntax logical carelessness Help requests time
A1 A with μA=0.73 VL with μVL=0.4 VL with μVL=0.4 VL with μVL=0.065 A with μA=0.8 VL with μVL=0.15
L with μL=0.267 A with μA=0.4
A2 L with μL=0.73 M with μM=0.4 M with μM=0.4 VL with μVL=0.065 L with μL=0.8 M with μM=0.15
M with μM=0.267 A with μA=0.4
A3 A with μA=0.584 VL with μVL=0.15 L with μL=0.5 VL with μVL=0.065 M with μM=0.8 VL with μVL=0.15
VL with μVL=0.214 L with μL=0.15
A4 A with μA=0.584 VL with μVL=0.15 L with μL=0.5 VL with μVL=0.195 M with μM=0.5 VL with μVL=0.4
VL with μVL=0.214 A with μA=0.15
A5 A with μA=0.365 VL with μVL=0.25 VL with μVL=0.25 VL with μVL=0.65 M with μM=0.5 VL with μVL=0.4
VL with μVL=0.133 A with μA=0.25
Table 22. Fuzzy rules output for Jason.
Table 22. Fuzzy rules output for Jason.
Degree syntax logical carelessness Help requests time
A1 A with μA=0.4 VL with μVL=0.6 A with μA=0.48 VL with μVL=0.01 VL with μVL=0.6 A with μA=0.15
L with μL=0.5 M with μM=0.32 VL with μVL=0.09 L with μL=0.2 A with μA=0.075
A2 L with μL=0.4 M with μM=0.6 A with μA=0.48 VL with μVL=0.01 M with μM=0.6 L with μL=0.15
M with μM=0.5 VL with μVL=0.32 VL with μVL=0.09 A with μA=0.2 L with μL=0.075
A3 A with μA=0.32 VL with μVL=0.225 A with μA=0.6 VL with μVL=0.01 L with μL=0.6 M with μM=0.15
VL with μVL=0.4 M with μM=0.4 VL with μVL=0.09 A with μA=0.2 VM with μVM=0.075
A4 A with μA=0.32 VL with μVL=0.225 M with μM=0.6 VL with μVL=0.03 L with μL=0.375 M with μM=0.4
VL with μVL=0.4 VM with μVM=0.4 M with μM=0.27 A with μA=0.125 VM with μVM=0.2
A5 A with μA=0.2 VL with μVL=0.375 A with μA=0.3 VL with μVL=0.1 VL with μVL=0.375 A with μA=0.4
VL with μVL=0.25 M with μM=0.2 M with μM=0.9 L with μL=0.125 M with μM=0.2
Table 23. The weighted outputs.
Table 23. The weighted outputs.
A1 A2 A3 A4 A5
Maria
  • VL with μVL=0.9
  • L with μL=0.4
  • A with μA=0.8
  • M with μM=0.264
  • VL with μVL=0.264
  • L with μL=0.6
  • A with μA=0.536
  • M with μM=0.9
  • VM with μVM=0.08
  • VL with μVL=0.32
  • L with μL=0.9
  • A with μA=0.67
  • M with μM=0.33
  • VL with μVL=0.32
  • L with μL=0.45
  • A with μA=0.584
  • M with μM=0.7
  • VM with μVM=0.33
  • VL with μVL=0.75
  • L with μL=0.584
  • A with μA=0.335
  • M with μM=0.165
John
  • VL with μVL=0.72
  • L with μL=0.83
  • A with μA=0.33
  • VL with μVL=0.04
  • L with μL=0.33
  • A with μA=0.67
  • M with μM=0.83
  • VM with μVM=0.2
  • VL with μVL=0.664
  • L with μL=0.25
  • A with μA=0.67
  • M with μM=0.33
  • VL with μVL=0.664
  • L with μL=0.25
  • A with μA=0.335
  • M with μM=0.7
  • VL with μVL=0.45
  • L with μL=0.335
  • A with μA=0.7
  • M with μM=0.165
Alex
  • VL with μVL=0.52
  • L with μL=0.4
  • A with μA=0.6
  • VL with μVL=0.3
  • L with μL=0.15
  • A with μA=0.15
  • M with μM=0.52
  • VM with μVM=0.3
  • VL with μVL=0.4
  • L with μL=0.65
  • A with μA=0.15
  • M with μM=0.15
  • VL with μVL=0.32
  • L with μL=0.65
  • A with μA=0.4
  • M with μM=0.4
  • VL with μVL=0.2
  • L with μL=0.4
  • A with μA=0.375
  • M with μM=0.25
Kate
  • VL with μVL=0.4
  • L with μL=0.267
  • A with μA=0.8
  • VL with μVL=0.065
  • L with μL=0.8
  • A with μA=0.4
  • M with μM=0.4
  • VL with μVL=0.214
  • L with μL=0.5
  • A with μA=0.584
  • M with μM=0.8
  • VL with μVL=0.4
  • L with μL=0.5
  • A with μA=0.584
  • M with μM=0.5
  • VL with μVL=0.65
  • A with μA=0.365
  • M with μM=0.5
Jason
  • VL with μVL=0.6
  • L with μL=0.5
  • A with μA=0.48
  • M with μM=0.32
  • VL with μVL=0.32
  • L with μL=0.4
  • A with μA=0.48
  • M with μM=0.6
  • VL with μVL=0.4
  • L with μL=0.6
  • A with μA=0.6
  • M with μM=0.4
  • VM with μVM=0.075
  • VL with μVL=0.4
  • L with μL=0.375
  • A with μA=0.32
  • M with μM=0.6
  • VM with μVM=0.4
  • VL with μVL=0.375
  • L with μL=0.125
  • A with μA=0.4
  • M with μM=0.9
Table 24. The final crisp aggregated outputs.
Table 24. The final crisp aggregated outputs.
A1 A2 A3 A4 A5
Maria 40.06 51.81 43.26 52.94 35.95
John 32.64 59.38 43.51 47.42 42.37
Alex 38.38 57.29 34.05 43.62 44.79
Kate 41.67 46.45 50.99 45.94 47.36
Jason 40.94 48.77 44.91 52.96 53.44
Table 25. Participants’ characteristics and their distribution.
Table 25. Participants’ characteristics and their distribution.
Gender
Male Female
PerFuSIT_group 32 25
No_PerFuSIT_group 35 22
Age
18-20 21-23 23+
PerFuSIT_group 37 13 7
No_PerFuSIT_group 39 13 5
Background on computer programming
none low medium high
PerFuSIT_group 24 28 5 0
No_PerFuSIT_group 26 25 4 2
Experience in using computers
none low medium high
PerFuSIT_group 0 0 4 53
No_PerFuSIT_group 0 0 7 50
Experience in interacting with tutoring systems
none low medium high
PerFuSIT_group 17 10 23 7
No_PerFuSIT_group 14 16 18 9
Table 26. T-test results concerning the mean performance.
Table 26. T-test results concerning the mean performance.
No_PerFuSIT_group PerFuSIT_group
Mean 7.01754386 8.50877193
Variance 1.946115288 1.468671679
Observations 57 57
Pooled Variance 1.707393484
Hypothesized Mean Difference 0
df 112
t Stat -6.092558252
P(T<=t) one-tail 8.03134E-09
t Critical one-tail 1.658572629
P(T<=t) two-tail 1.60627E-08
t Critical two-tail 1.981371815
Table 27. T-test results concerning the mean number of interactions.
Table 27. T-test results concerning the mean number of interactions.
No_PerFuSIT_group PerFuSIT_group
Mean 54.1052632 45.8245614
Variance 253.845865 184.9686717
Observations 57 57
Pooled Variance 219.407268
Hypothesized Mean Difference 0
df 112
t Stat 2.98444835
P(T<=t) one-tail 0.00174425
t Critical one-tail 1.65857263
P(T<=t) two-tail 0.00348849
t Critical two-tail 1.98137181
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated