On the Salient Limits of Strings of Assembly Theory

Preprint

Article

On the Salient Limits of Strings of Assembly Theory

Altmetrics

Downloads

331

Views

397

Comments

Wawrzyniec Bieniawski

,Piotr Masierak,

Szymon Łukaszyk^*

Andrzej Tomski

Wawrzyniec Bieniawski

,Piotr Masierak,

Szymon Łukaszyk^*

Andrzej Tomski

This version is not peer-reviewed

Submitted:

30 September 2024

Posted:

03 October 2024

Read the latest preprint version here

Alerts

Abstract

We consider the formation of strings of any natural radix b within the framework of assembly theory. In particular, we show that the upper bound of the assembly index depends on the radix b both quantitatively and qualitatively, and the longest length N of a string that has the assembly index of N-k is given by N_(N-k)=b²+b+3k-2 for k={1,2,3}. We also provide two particular forms of such strings. For k=1 such odd length strings are nearly balanced and there are four such different strings if b=2 and seventy-two if b=3. Since these results are valid also for b=1, assembly theory subsumes information theory.

Keywords:

Subject: Physical Sciences - Mathematical Physics

1. Introduction

Assembly theory (AT), formulated in 2017, introduced the concept of an initial pool [1].

Definition 1.

We call a set

P_{0} (b) {0, 1, \dots, b - 1}

that contains

b \in N

different basic symbols c, the initial assembly pool.

The reader will find numerous results on AT in refs. [1,2,3,4,5,6,7,8,9,10], for example. Here, we extend the results of our previous study [9] concerning bitstrings to strings of any natural radix b. We consider the formation of strings

C_{k}^{(N, b)}

of length N containing symbols from the initial assembly pool

P_{0} (b)

within the AT framework in consecutive assembly steps from basic symbols c and strings assembled in previous steps.

In fact, any embodiment of AT, with basic symbols representing LEGO® blocks, chemical bonds, graphs, monomers, etc. assembled in any n-dimensional space (

n \in C

) [11] corresponds to the string AT version. This is because in AT an assembly step always consists in joining two parts only, which can be thought of as the left and right fragments of the newly formed string. Put simply, AT explains and quantifies selection and evolution [7] but it is through the word (aka string or message), in particular a nucleotide sequence in the case of

b = 4

, all AT things come into existence [12].

Definition 2.

We call a set

P_{s} (b)

that contains basic symbols and strings assembled in previous steps

{1, 2, \dots, s - 1}

the working assembly pool.

An assembly step s may consist of

C_{k}^{(2, b)} = c_{1} \circ c_{2}, C_{k}^{(N_{l} + 1, b)} = C_{l}^{(N_{l}, b)} \circ c_{2}, C_{k}^{(1 + N_{m}, b)} = c_{1} \circ C_{m}^{(N_{m}, b)}, C_{k}^{(N_{l} + N_{m}, b)} = C_{l}^{(N_{l}, b)} \circ C_{m}^{(N_{m}, b)},

(1)

where

c_{1}, c_{2} \in P_{0} (b)

C_{l}^{(N_{l}, b)}, C_{m}^{(N_{m}, b)} \in P_{s - 1} (b)

, and

C_{k} \in P_{s} (b)

. We note that the joining operator "∘", in general, does not commute. Using Definitions 1 and 2, the assembly index (ASI) of a string is the minimal achievable value of a difference between the cardinalities of the working and initial assembly pools leading to this string, since at each assembly step the cardinality of the working assembly pool increases by one. Therefore, the working assembly pool 2 cannot be identified with the initial assembly pool 1; the initial assembly pool 1 must not contain strings of basic symbols (see Appendix G).

2. Results

Theorems 1 and 2 were already stated in our previous study [9] for

b = 2

. We restate them here

\forall b

for clarity.

Theorem 1.

A quadruplet is the shortest string that allows for more than one ASI for all b.

Proof.

N = 2

provides

b^{2}

available doublets with unit ASI.

N = 3

provides

b^{3}

available triplets with ASI equal to two. Only

N = 4

provides

b^{4}

quadruplets that include b quadruplets

C_{k, \min}^{(4, b)} = [* * * *]

and

b (b - 1)

quadruplets

C_{l, \min}^{(4, b)} = [* ★ * ★]

with ASI equal to two, while the ASI of the remaining quadruplets is three. For example, to assemble the quadruplet

C_{k, \min}^{(4, 4)} = [0202]

, we need to assemble the doublet

[02]

and reuse it from the first step pol

P_{1}

, while there is nothing available to reuse, in the case of the quadruplet

C_{l}^{(4, 4)} = [0123]

. □

Where the symbol value can be arbitrary, we write * assuming that it is the same within the string. If we allow for the 2^nd possibility different from *, we write ★. Furthermore, we consider the degenerate case of

b = 1

Theorem 2.

The smallest ASI

a^{(N)} (C_{\min})

as a function of N corresponds to the shortest addition chain for N (OEIS A003313) for all b.

Proof.

Strings

C_{\min}

for which

a^{(N)} (C_{\min}) = min_{k} ({a^{(N, b)} (C_{k})})

\forall k \in {1, 2, \dots, b^{N}}

can be formed in subsequent steps s by joining the longest string assembled so far with itself until

N = 2^{s}

is reached. Therefore, if

N = 2^{s}

, then

min_{k} ({a^{(2^{s})} (C_{k})}) = s = {log}_{2} (N)

. Only

b^{2}

strings have such ASI if

N = 2^{s}

, including respectively b and

b (b - 1)

strings

C_{k}^{(2^{s}, b)} = [* * \dots], C_{l}^{(2^{s}, b)} = [* ★ * ★ \dots],

(2)

and the assembly pathway of each of the strings (2) is unique. At each assembly step, its length doubles.

An addition chain for

N \in N

having the shortest length

s \in N

(commonly denoted as

l (N)

) is defined as a sequence

1 = a_{0} < a_{1} < \dots < a_{s} = N

of integers such that

\forall j \geq 1

a_{j} = a_{k} + a_{l}

for

l \leq k < j

. The first step in creating an addition chain for N is always

a_{1} = 1 + 1 = 2

and this corresponds to assembling a doublet

[* *]

[* ★]

from the initial assembly pool

P_{0} (b)

. Thus, the lower bound for s of the addition chain for N,

s \geq {log}_{2} (N)

is achieved for

N = 2^{s}

b^{2}

strings (2).

The second step in creating an addition chain can be

a_{2} = 1 + 1 = 2

a_{2} = 1 + 2 = 3

. Thus, finding the shortest addition chain for N corresponds to finding the ASI of a string containing basic symbols and/or doublets and/or triplets containing these doublets for

N \neq 2^{s}

since due to Theorem 1 only they provide the same assembly indices

{0, 1, 2}

. □

At least some of the following six simple theorems are useful for further consideration.

Theorem 3.

The strings

C_{\min}^{(2^{s}, b)}

can contain at most two symbols if

b > 1

. Other minimal ASI strings of length

N \neq 2^{s}

can contain at most three symbols if

b > 2

Proof.

Minimal ASI strings of length

N = 2^{s}

are formed by joining the newly assembled string to itself, where a clear or mixed doublet is created in the first step. Minimal ASI strings of other lengths admit a doublet and a triplet containing this doublet and an additional basic symbol.

To formally prove the first part, we can also use mathematical induction on the asembly step s. If

s = 1

, then the minimal strings

C_{\min}^{(2, b)}

are doublets of the form

[c_{1} c_{2}]

, where

c_{1}, c_{2} \in P_{0} (b)

. If

c_{1} = c_{2}

, the string contains one distinct symbol, and if

c_{1} \neq c_{2}

, the string contains two distinct symbols. In both cases, the number of distinct symbols does not exceed two. Now assume that for some

k \in N

, all minimal strings

C_{\min}^{(2^{k}, b)}

contain at most two distinct symbols. We must show that

C_{\min}^{(2^{k + 1}, b)}

also contains at most two distinct symbols. Consider constructing

C_{\min}^{(2^{k + 1}, b)}

by joining two identical minimal strings

C_{\min}^{(2^{k}, b)}

C_{\min}^{(2^{k + 1}, b)} = C_{\min}^{(2^{k}, b)} \circ C_{\min}^{(2^{k}, b)},

(3)

with each other. By the inductive hypothesis, each

C_{\min}^{(2^{k}, b)}

contains at most two distinct symbols. Therefore, their concatenation also contains at most two distinct symbols. By induction, for all

s \in N

, the minimal string

C_{\min}^{(2^{s}, b)}

contains at most two distinct symbols.

We will now show that other minimal ASI strings of length

N \neq 2^{s}

can contain at most three distinct symbols if

b > 2

. We provide the construction of minimal ASI strings with three symbols. In the first step

s = 1

, we create a doublet

[c_{1} c_{2}]

where

c_{1}, c_{2} \in P_{0} (b)

and

c_{1} \neq c_{2}

. Next, we combine the existing doublet

[c_{1} c_{2}]

with a new symbol

c_{3} \in P_{0} (b)

where

c_{3} \notin {c_{1}, c_{2}}

. This forms a triplet

[c_{1} c_{2} c_{3}]

, introducing a third distinct symbol and further increasing the ASI by 1. We continue assembling by joining the longest string formed so far with itself or with previously formed strings, maintaining the minimal increase in ASI.

Assume a contrario that there exists a minimal ASI string

C_{\min}^{(N, b)}

of length

N \neq 2^{s}

that contains four or more distinct symbols. To incorporate a fourth symbol, at least one additional assembly step is required beyond what is needed for the three symbols. This additional step implies an increase in ASI, which contradicts the minimality of

C_{\min}^{(N, b)}

. Thus, Theorem 3 is proven. □

Theorem 4.

A string containing the same three doublets has the same ASI as a string containing two pairs of the same doublets, provided that both strings have the same distributions of other repetitions and have the same lengths.

Proof.

Without loss of generality (w.l.o.g.), consider the following two strings of the same length

N + 8

with

* ★ \neq 01

and the same distributions of other repetitions (if there are any other repetitions)

C_{k} = [\dots 01 \dots 01 \dots 01 \dots * ★ \dots], C_{l} = [\dots 01 \dots 01 \dots 22 \dots 22 \dots],

(4)

where

* ★ \neq 01

. Creating a doublet takes one assembly step. Each appending of a doublet to an assembled string counts as another assembly step. Hence, in a general case (i.e., for strings

C_{k}

C_{l}

containing also other symbols), the string

C_{k}

requires six additional assembly steps, the same as the string

C_{l}

, which completes the proof. □

Theorem 5.

A string containing the same three doublets has the same ASI as a string containing the same two triplets, provided that both strings have the same distributions of other repetitions.

Proof.

W.l.o.g. consider the following two strings of the same length

N + 6

with the same distributions of other repetitions

C_{k} = [\dots 01 \dots 01 \dots 01 \dots], C_{l} = [\dots 010 \dots 010 \dots] .

(5)

Creating a triplet takes two assembly steps. Hence, in the general case, the string

C_{k}

requires four additional assembly steps, the same as the string

C_{l}

, which completes the proof. □

Theorem 6.

A string containing the same two quadruplets of the minimum ASI has the same ASI as a string containing the same three triplets, provided that both strings have the same distributions of other repetitions and have the same lengths.

Proof.

W.l.o.g. consider the following two strings of the same length

N + 9

with the same distributions of other repetitions

C_{k} = [\dots 0101 \dots 0101 \dots ★ \dots], C_{l} = [\dots 010 \dots 010 \dots 010 \dots] .

(6)

Creating such a quadruplet takes two assembly steps. Hence, in a general case, the string

C_{k}

requires five additional assembly steps, the same as the string

C_{l}

, which completes the proof. □

Theorem 7.

A string containing the same two quadruplets of the maximum ASI has the same ASI as a string containing a doublet and the same two triplets based on this doublet, provided that both strings have the same distributions of other repetitions.

Proof.

W.l.o.g. consider the following two strings of the same length

N + 8

with the same distributions of other repetitions

C_{k} = [\dots 0001 \dots 0001 \dots], C_{l} = [\dots 110 \dots 10 \dots 110 \dots] .

(7)

Creating such a quadruplet takes three assembly steps. Hence, in a general case, the string

C_{k}

requires five additional assembly steps, the same as the string

C_{l}

, which completes the proof. □

Theorem 8.

A string containing the same two doublets and the same two triplets not based on this doublet has the same ASI as a string containing a doublet and the same two triplets based on this doublet, provided that both strings have the same distributions of other repetitions and have the same lengths.

Proof.

W.l.o.g. consider the following two strings of the same length

N + 8

with the same distributions of other repetitions

C_{k} = [\dots 110 \dots 00 \dots 110 \dots 00 \dots], C_{l} = [\dots 110 \dots 10 \dots 110 \dots * ★ \dots],

(8)

where

* ★ \notin {11, 10}

. In a general case, the string

C_{k}

requires seven additional assembly steps, the same as the string

C_{l}

, which completes the proof. □

The seven-bit string is the longest string that can have the maximum ASI

a_{\max}^{(7, 2)} = 7 - 1 = 6

. There are four such bitstrings containing two clear triplets and the starting bit at the end or the ending bit at the start, that is

[* * * ★ ★ ★ *] and [★ * * * ★ ★ ★],

(9)

and their lengths cannot be increased without a repetition of a doublet, which keeps the ASI at the same level

a_{\max}^{(8, 2)} = 8 - 2 = 6

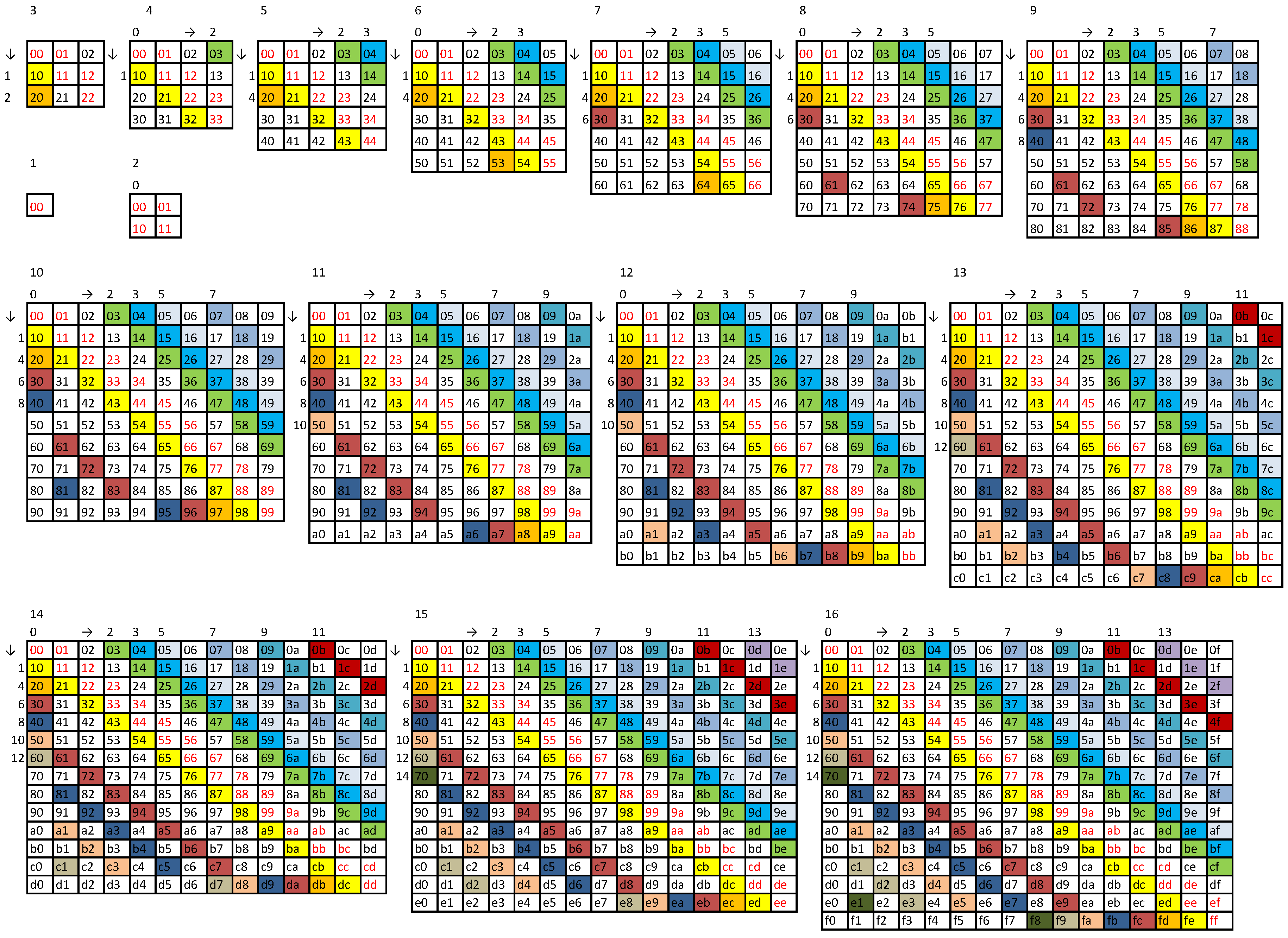
This observation and Theorem 2 motivated us to develop a general method to construct the longest possible string having the ASI

a_{\max}^{(N, b)} (C_{(N - 1)}) = N - 1

, as a function of the radix b. We denote the length of this string by

N_{(N - 1)}

N_{(N - 1)} (b)

, and we call this string a

C_{(N - 1)}

string.

After a few groping try-outs, we eventually reached two stable methods (cf. Appendices, Method A and Method B). In both methods, we start with an initial balanced string of length

3 b

containing b clear triplets ordered as

[0001112 \dots (b - 2) (b - 1) (b - 1) (b - 1)] .

(10)

The doublets that can be inserted into the initial string (10) can be arranged in a

b \times b

matrix

(11)

where the crossed out entries on a diagonal cannot be reused, as they would create repetitions in this string. If we assume that we shall not insert doublets between the clear triplets of the string (10), we can also cross out the entries in the first superdiagonal of the matrix (11). The strings of odd lengths generated by these general methods are not only the longest but also the most balanced. This can be stated in the following theorem.

Theorem 9

(

C_{(N - 1)}

string). The longest length of a string that has the ASI of

N - 1

is given by

N_{(N - 1)} = 3 b + {(b - 1)}^{2} = b^{2} + b + 1

(12)

(OEIS A353887) and this string is nearly balanced, that is

N_{(N - 1)} = b N_{c} + 1,

(13)

where

N_{c} = b + 1

is the number of occurrences of all but one symbol within the string, and its Shannon entropy is

\begin{matrix} H (C_{(N - 1)}) = - \sum_{c = 0}^{b - 1} p_{c} {log}_{2} (p_{c}) & = - (b - 1) \frac{N_{(N - 1)} - 1}{b N_{(N - 1)}} {log}_{2} (\frac{N_{(N - 1)} - 1}{b N_{(N - 1)}}) - \frac{N_{(N - 1)} - 1 + b}{b N_{(N - 1)}} {log}_{2} (\frac{N_{(N - 1)} - 1 + b}{b N_{(N - 1)}}) = \\ = \frac{1 - b^{2}}{b^{2} + b + 1} {log}_{2} (\frac{b + 1}{b^{2} + b + 1}) - \frac{b + 2}{b^{2} + b + 1} {log}_{2} (\frac{b + 2}{b^{2} + b + 1}) ≲ l o g_{2} (b) . \end{matrix}

(14)

The proof of the Theorem 9 is given in Appendix C. Although the case for

b = 1

is degenerate, as no information can be conveyed using only one symbol (

H (C_{(N - 1)}) = 0

in this case), the formula (12) yields the correct result; the string

[000]

is the longest string with

a_{\max}^{(N, 1)} = N - 1

by Theorem 1, as for

b = 1

the upper and the lower bound on the ASI are the same,

a_{\max}^{(N, 1)} = a_{\min}^{(N)}

(OEIS A003313). Thus, AT subsumes information theory.

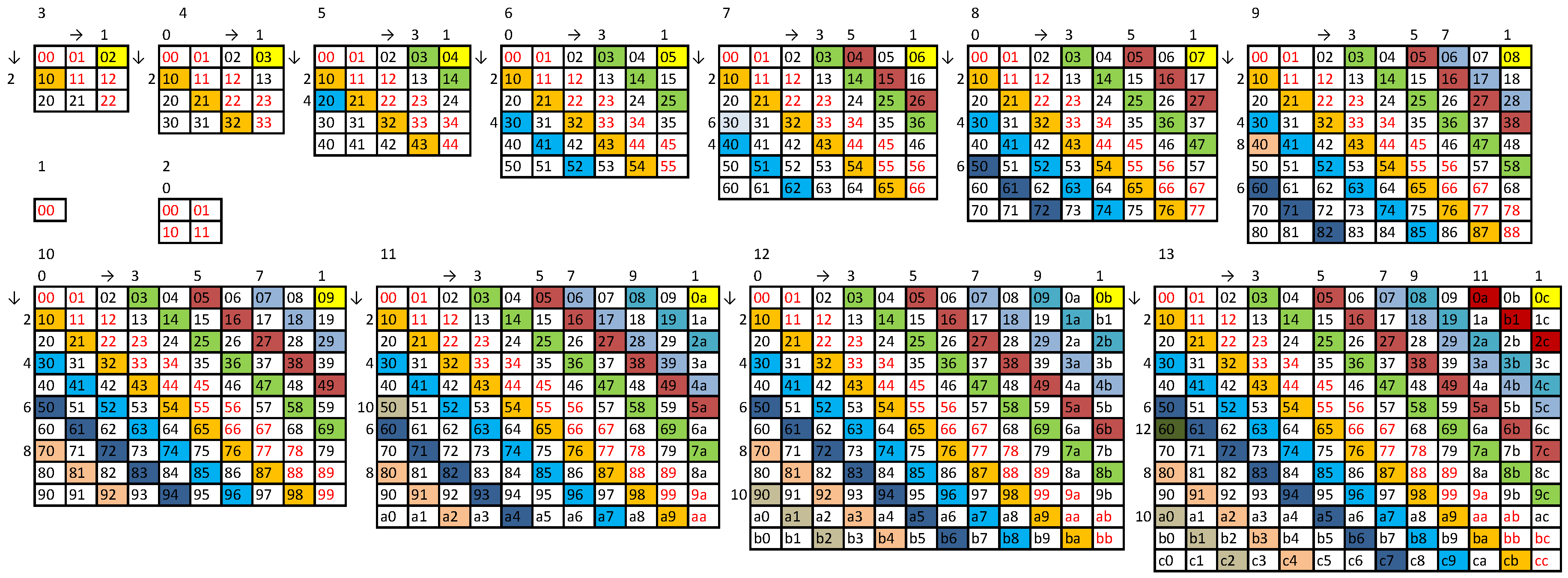
Subsequently, we considered other

C_{(N - k)}

strings for

k > 1

with the maximum ASI

a_{\max} (C_{(N - k)}) = N - k

Theorem 10

(

C_{(N - 2)}

string). For all

b > 1

the longest length of a string that has the ASI of

N - 2

is given by

N_{(N - 2)} = N_{(N - 1)} + 3

or equivalently by

N_{(N - 2)} = b^{2} + b + 4,

(15)

and

N_{(N - 2)} = (b - 2) N_{c} + (N_{c} + 1) + (N_{c} + 3) = b N_{c} + 4,

(16)

where

N_{c} = b + 1

is the number of occurrences of all but two symbols within the string, and its Shannon entropy is

\begin{matrix} H (C_{(N - 2)}) & = - \frac{b^{2} - b - 2}{b^{2} + b + 4} {log}_{2} (\frac{b + 1}{b^{2} + b + 4}) - \frac{b + 2}{b^{2} + b + 4} {log}_{2} (\frac{b + 2}{b^{2} + b + 4}) - \frac{b + 4}{b^{2} + b + 4} {log}_{2} (\frac{b + 4}{b^{2} + b + 4}) . \end{matrix}

(17)

The entropy

H (C_{(N - 2)}) ≲ {log}_{2} (b)

for

b ⪆ 1.6398

The proof of the Theorem 10 is given in Appendix E. In general,

C_{(N - 2)}

string must contain a clear quadruplet (

b b b b

) and a pattern binding the symbols adjoining this quadruplet, such as

[\dots a b b b b c \dots a b c \dots]

[\dots a b b b b a b a \dots]

, etc., so that any

C_{(N - 2)}

string contains only one pair of repeated doublets

a b

b b

, or

{b c, b a}

. For example, for

N = 10

, sixteen bitstrings

\begin{matrix} [0100011110], [0111100010], [0111101000], [\underset{̲}{0100001110}], \\ [0001011110], [0001111010], [0101111000], [0111000010] \end{matrix}

(18)

(an additional eight are given by swapping 0 with 1) have the ASI

a = N - 2 = 8

, where the underlined string (18) is the one that is created for

b = 2

in Appendix E.

Theorem 11

(

C_{(N - 3)}

string). For all

b > 2

the longest length of a string that has the ASI of

N - 3

is given by

N_{(N - 3)} = N_{(N - 1)} + 6

. or equivalently by

N_{(N - 3)} = b^{2} + b + 7,

(19)

and

N_{(N - 3)} = (b - 3) N_{c} + (N_{c} + 1) + (N_{c} + 2) + (N_{c} + 4) = b N_{c} + 7,

(20)

where

N_{c} = b + 1

is the number of occurrences of all but three symbols within the string, and its Shannon entropy is

\begin{matrix} H (C_{(N - 3)}) & = - \frac{b^{2} - 2 b - 3}{b^{2} + b + 7} {log}_{2} (\frac{b + 1}{b^{2} + b + 7}) - \frac{b + 2}{b^{2} + b + 7} {log}_{2} (\frac{b + 2}{b^{2} + b + 7}) \\ - \frac{b + 3}{b^{2} + b + 7} {log}_{2} (\frac{b + 3}{b^{2} + b + 7}) - \frac{b + 5}{b^{2} + b + 7} {log}_{2} (\frac{b + 5}{b^{2} + b + 7}) . \end{matrix}

(21)

The entropy

H (C_{(N - 3)}) ≲ {log}_{2} (b)

for

b ⪆ 2.4033

The proof of the Theorem 11 is given in Appendix F.

3. Conclusions

We have shown that the shape of the upper bound of the assembly index depends on the size b of the initial assembly pool

P_{0}

. The behavior of the upper ASI bound for larger b requires further research. There is one string of length

N_{(N - 1)} (1) = 3

, four strings of length

N_{(N - 1)} (2) = 7

, seventy-two strings of length

N_{(N - 1)} (3) = 13

(cf. Appendix D). Determining

N_{(N - 1)} (b)

for

b \geq 4

requires further research.

Author Contributions

WB: First concept of a general method for constructing the string of length

N_{(N - 1)}

leading to Theorem 9; outline of the general Method A; proposition of Theorem 8 numerous clarity corrections and improvements; PM: outline of the general Method B; numerous clarity corrections and improvements; AT: formal proof of Theorem 3; proof that the Shannon entropy (14) can be approximated by

{log}_{2} (b)

for large b; numerous clarity corrections and improvements; SŁ: The remaining part of the study.

Funding

This research received no external funding.

Institutional Review Board Statement

In this section, you should add the Institutional Review Board Statement and approval number, if relevant to your study. You might choose to exclude this statement if the study did not require ethical approval. Please note that the Editorial Office might ask you for further information. Please add “The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of NAME OF INSTITUTE (protocol code XXX and date of approval).” for studies involving humans. OR “The animal study protocol was approved by the Institutional Review Board (or Ethics Committee) of NAME OF INSTITUTE (protocol code XXX and date of approval).” for studies involving animals. OR “Ethical review and approval were waived for this study due to REASON (please provide a detailed justification).” OR “Not applicable” for studies not involving humans or animals.

Data Availability Statement

The public repository for the code written in the MATLAB computational environment and C++ is given under the link https://github.com/szluk/Evolution_of_Information (accessed on 19 September 2024).

Acknowledgments

The authors thank Mariola Bala for motivation. SŁ thanks his wife, Magdalena Bartocha, for her everlasting support, and his partner and friend, Renata Sobajda, for her prayers.

Conflicts of Interest

Authors Wawrzyniec Bieniawski and Piotr Masierak were employed by the company Łukaszyk Patent Attorneys. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix A. Method A

We start with a string of clear triplets (10). In the 1^st step, we create a string containing doublets on the first subdiagonal of the matrix (11) starting with 10

[102132 \dots (b - 2) (b - 3) (b - 1) (b - 2)],

(A1)

and we append it to the string (10). With this step, we also eliminate the doublets on the second superdiagonal starting with the doublet 02, as well as the doublet

(b - 1) 1

. In the 2^nd step, we create a string containing doublets on the third superdiagonal beginning with the doublet 03

[0314 \dots (b - 5) (b - 2) (b - 4) (b - 1)],

(A2)

and append it to the string created so far. With this step, we also remove the doublet

(b - 2) 0

and the middle part of the second subdiagonal containing

{31, 42, \dots, (b - 2) (b - 4)}

. And so on. Finally, we append 0 if b is even. This process is illustrated in Figure A1 and for

3 \leq b \leq 13

generates the following

C_{(N - 1)}

strings

\begin{matrix} [000111222 | 10 | 20], \\ [000111222333 | 102132 | 03 | 0], \\ [000111222333444 | 10213243 | 0314 | 20 | 40], \\ [000111222333444555 | 1021324354 | 031425 | 0415 | 2053 | 0], \\ [000111222333444555666 | 102132435465 | 03142536 | 041526 | 2064 | 0516 | 30], \\ [000111222333444555666777 | 10213243546576 | 0314253647 | 04152637 | 2075 | 051627 | 306174 | 0], \\ [\dots | 1021324354657687 | 031425364758 | 0415263748 | 2086 | 05162738 | 30617285 | 0718 | 40], \\ [\dots | 102132435465768798 | 03142536475869 | 041526374859 | 2097 | 0516273849 | \\ 3061728396 | 071829 | 408195 | 0], \\ [\dots | 102132435465768798 a 9 | 031425364758697 a | 0415263748596 a | 20 a 8 | \\ 05162738495 a | 3061728394 a 7 | 0718293 a | 408192 a 6 | 091 a | 50], \\ [\dots | 102132435465768798 a 9 b a | 031425364758697 a 8 b | 0415263748596 a 7 b | 20 b 9 | \\ 05162738495 a 6 b | 3061728394 a 5 b 8 | 0718293 a 4 b | 408192 a 3 b 7 | 091 a 2 b | 50 a 1 b 6 | 0], \\ [\dots | 102132435465768798 a 9 b a c b | 031425364758697 a 8 b 9 c | 0415263748596 a 7 b 8 c | 20 c a | \\ 05162738495 a 6 b 7 c | 3061728394 a 5 b 6 c 9 | 0718293 a 4 b 5 c | 408192 a 3 b 4 c 8 | 091 a 2 b 3 c | 50 a 1 b 2 c 7 | 0 b 1 c | 60] . \end{matrix}

(A3)

Figure A1. Doublet matrices for

1 \leq b \leq 16

showing the creation of

N_{(N - 1)}

strings according to Method Appendix A. Colored doublets are appended to the initial string of clear triplets in the order indicated by arrows starting from the 1^st column or row. Finally, 0 is appended at the end, if b is even.

Figure A1. Doublet matrices for

1 \leq b \leq 16

showing the creation of

N_{(N - 1)}

Appendix B. Method B

This method is similar to the Method Appendix A. We also start with a string of clear triplets (10) and the matrix of doublets (11) with a crossed diagonal and the first superdiagonal. In the first step, we append the doublet

0 (b - 1)

(top right doublet of the matrix of doublets (11)) at the end of the string (10). Next, we generally perform the following pairs of iterations:

we check subsequent subdiagonals until we find one that does not contain a doublet present in the string created so far, we append it at the end of this string, and proceed to step 2;
we check subsequent superdiagonals until we find one that does not contain a doublet present in the string created so far, we append it at the end of this string, and proceed to step 1.

Finally, we append 0 if b is even. The method is illustrated in Figure A2 and for

3 \leq b \leq 13

generates the

C_{(N - 1)}

strings in the form

\begin{matrix} [000111222 | 0210], \\ [000111222333 | 03 | 102132 | 0], \\ [000111222333444 | 04 | 10213243 | 0314 | 20], \\ [000111222333444555 | 05 | 1021324354 | 031425 | 304152 | 0], \\ [000111222333444555666 | 06 | 102132435465 | 03142536 | 405162 | 041526 | 30], \\ [000111222333444555666777 | 07 | 10213243546576 | 0314253647 | 3041526374 | 051627 | 506172 | 0], \\ [\dots | 08 | 1021324354657687 | 031425364758 | 304152637485 | 05162738 | 607182 | 061728 | 40], \\ [\dots | 09 | 102132435465768798 | 03142536475869 | 30415263748596 | 0516273849 | 5061728394 | 071829 | 708192 | 0], \\ [\dots | 0 a | 102132435465768798 a 9 | 031425364758697 a | 30415263748596 a 7 | 05162738495 a | \\ 60718293 a 4 | 061728394 a | 8091 a 2 | 08192 a | 50], \\ [\dots | 0 b | 102132435465768798 a 9 b a | 031425364758697 a 8 b | 30415263748596 a 7 b 8 | 05162738495 a 6 b | \\ 5061728394 a 5 b 6 | 0718293 a 4 b | 708192 a 3 b 4 | 091 a 2 b | 90 a 1 b 2 | 0], \\ [\dots | 0 c | 102132435465768798 a 9 b a c b | 031425364758697 a 8 b 9 c | 30415263748596 a 7 b 8 c 9 | 05162738495 a 6 b 7 c | \\ 5061728394 a 5 b 6 c 7 | 0718293 a 4 b 5 c | 8091 a 2 b 3 c 4 | 08192 a 3 b 4 c | a 0 b 1 c 2 | 0 a 1 b 2 c | 60] . \end{matrix}

(A4)

Figure A2. Doublet matrices for

1 \leq b \leq 13

showing the creation of

N_{(N - 1)}

strings according to Method Appendix B. Colored doublets are appended to the initial string of clear triplets in the order indicated by arrows starting from the 1^st column or row. Finally, 0 is appended at the end, if b is even.

Figure A2. Doublet matrices for

1 \leq b \leq 13

showing the creation of

N_{(N - 1)}

Appendix C. Proof of C_(N−1) String Theorem

The

N_{(N - 1)}

given by the formula (12) is an odd number for all b. The first element

3 b

is the length of the initial string (10) containing b clear triplets and

b^{2} - b - (b - 1)

is the number of doublets available in the matrix (11) after crossing out b doublets on its diagonal and

b - 1

doublets on its superdiagonal that are present in the starting string (10). By definition, a

C_{(N - 1)}

string cannot have any repetitions. To be the longest, it must contain all doublets in the matrix (11) and all clear triplets. Furthermore, to be the most patternless, this string must maximize Shannon entropy; must be the most balanced. For the string of the form (13) the fractions in the Shannon entropy are

p_{0} = \frac{N_{c} + 1}{N_{(N - 1)}}, p_{1, 2, \dots, b - 1} = \frac{N_{c}}{N_{(N - 1)}},

(A5)

where w.l.o.g. we assume that the symbol occurring

N_{c} (b) + 1

times within the string is

c = 0

. To see that the Shannon entropy (14) of a

C_{(N - 1)}

string can be approximated by

{log}_{2} (b)

for large b, first notice that

1 - b^{2} < 0

and

b^{2} + b + 1 > 0, \forall b > 1

. Furthermore,

\forall b > 0

b + 1 ≪ b^{2} + b + 1

, which implies that the first term

{log}_{2} (\frac{b + 1}{b^{2} + b + 1}) < 0 .

(A6)

Similarly the second term,

{log}_{2} (\frac{b + 2}{b^{2} + b + 1}) < 0 .

(A7)

Hence, the entropy (14) can be approximated by the dominant contribution from the first term, which is

{log}_{2} (b) .

The strings given by (12) are not the shortest possible ones. Strings satisfying the equation (13) and satisfying

min (b N_{c} (b) + 1) > N_{(N - 1)} (b - 1)

are given by

b^{2} + 1

(OEIS A002522). They can be constructed to contain all possible doublets but without any triplets, starting with an initial balanced string of length

2 b

containing b clear doublets ordered from the main diagonal of the doublet matrix (11). Furthermore, their entropies are smaller than the entropies of the strings given by the equation (12). Namely

\forall b > 1

\frac{1 - b^{2}}{b^{2} + b + 1} {log}_{2} (\frac{b + 1}{b^{2} + b + 1}) - \frac{b + 2}{b^{2} + b + 1} {log}_{2} (\frac{b + 2}{b^{2} + b + 1}) > \frac{b (1 - b)}{b^{2} + 1} {log}_{2} (\frac{b}{b^{2} + 1}) - \frac{b + 1}{b^{2} + 1} {log}_{2} (\frac{b + 1}{b^{2} + 1}) .

(A8)

Now, assume a contrario that a string

C_{(N - 1)}^{'}

longer than

N_{(N - 1)}

can be constructed, say of length

N_{(N - 1)}^{'} = N_{(N - 1)} + 1

. But in this case, the corresponding

H (C_{(N - 1)}^{'}) < H (C_{(N - 1)})

. The string of the length given by the formula (12) maximizes the Shannon entropy if it must additionally satisfy the relation (13). Thus, Theorem 9 is proven.

Appendix D. Number of $C_{(N - 1)}^{(13, 3)}$ Strings

For

b = 3

, only two doublets can be introduced without repetitions into the initial string (10), leading to twelve unique strings of length

N_{(N - 1)} = 13

\begin{matrix} [000111222 | 0210], [000111222 | 1020], [20 | 21 | 000111222], [21 | 02 | 000111222], [0001112 | 02 | 22 | 10], [0001112 | 10 | 22 | 20], \\ [21 | 000 | 20 | 111222], [000 | 20 | 111222 | 10], [02 | 000111222 | 10], [20 | 00 | 21 | 0111222], [21 | 0001112 | 02 | 22], [21 | 000111222 | 02] . \end{matrix}

(A9)

Finally, we have to multiply the cardinality of this set by

3! = 6

to account for permutations. For example, the first string

[0001112220210]

, is equivalent to five strings

[0002221110120]

[1110002221201]

[1112220001021]

[2220001112102]

, and

[2221110002012]

. Hence, there are seventy-two different strings of length

N_{(N - 1)} (3) = 13

Appendix E. Proof of C_(N−1) String Theorem

For

b = 1

N_{(N - 2)} (1) = N_{(N - 1)} (1) + 2 = 5

, as the ASI of

[00000]

is the same as the ASI of

[000000]

C_{(N - 1)}

string contains all doublets. Hence, inserting any basic symbol into any position inevitably leads to a repetition of a doublet. W.l.o.g. we append it at the start of the

C_{(N - 1)}

string, obtaining a string

C_{k} = [* 000111222 \dots], a_{\max}^{(N_{(N - 1)} + 1, b)} (C_{k}) = N - 2 .

(A10)

Another symbol can be introduced to this string without an additional doublet repetition provided that it adjoins the previously introduced symbol, which gives a string

C_{l} = [★ * 000111222 \dots], a_{\max}^{(N_{(N - 1)} + 2, b)} (C_{l}) = N - 2,

(A11)

leading to the repetition of the doublet

★ *

* 0

but not both of them (here we allow

★ = *

). Hence, both length and the ASI of this string increase by one. Finally, 0 can be appended at the start of this string without an additional doublet repetition provided that

★ = 1

and

* = 0

and the string becomes

C_{(N - 2)} = [010000111222 \dots], a_{\max}^{(N_{(N - 1)} + 3, b)} (C_{(N - 2)}) = N - 2,

(A12)

leading to the mutually exclusive repetition of the doublet 01, 10 or 00, so that also both length and the ASI of this string increase by one. An insertion of another symbol into the string (A12) at any position will maintain or even decrease the ASI of this newly formed string. For example, appending 0 at the start of the

C_{(N - 2)}

string (A12)

[0010000111222 \dots] .

(A13)

creates a 001 triplet based on 00 doublet leading to a decrease of the ASI of this longer string to

a = N - 4

as compared to

a = N - 2

of the string (A12). Thus, Theorem 10 is proven.

For the string of the form (16) the fractions in the Shannon entropy are

p_{0} = \frac{N_{c} + 3}{N_{(N - 2)}}, p_{1} = \frac{N_{c} + 1}{N_{(N - 2)}}, p_{2, \dots, b - 1} = \frac{N_{c}}{N_{(N - 2)}},

(A14)

where w.l.o.g. we assume that the symbol occurring

N_{c} (b) + 1

times within the string is

c = 0

, which leads to Shannon entropy (17).

Appendix F. Proof of C (N-3) String Theorem

N_{(N - 3)} (1) = N_{(N - 1)} (1) + 4 = 7

, as the ASIs of strings of seven and eight same symbols is three. The appending 0 at the start of the

C_{(N - 2)}

string (A12) decreases of the ASI of this longer string to

a = N - 4

(cf. Appendix E. Thus, w.l.o.g. we append

* \neq 0

at the start of the

C_{(N - 2)}

string (15)

C_{k} = [* 010000111222 \dots], a_{\max}^{(N_{(N - 1)} + 4, b)} (C_{k}) = N - 3 .

(A15)

* = 1

, we have the same three doublets 10. Otherwise, we have two pairs of the same doublets

* 0

and 10. Both cases are equivalent by Theorem 4. An insertion of another symbol to this string may maintain or even decrease the ASI of this newly formed string. To maximize its ASI, another symbol must adjoin *. Hence, we append ★ at the start, where

\forall ★

and

\forall * \neq 0

, a string

C_{l} = [★ * 010000111222 \dots], a_{\max}^{(N_{(N - 1)} + 5, b)} (C_{l}) = N - 3,

(A16)

has an increased length and ASI. If

b = 2

we have

C_{l}^{(12, 2)} = [★ * 0100001110],

(A17)

and

\begin{matrix} C_{1}^{(12, 2)} & = [000100001110], a (C_{1}^{(12, 2)}) = 12 - 4 = 8, \\ C_{2}^{(12, 2)} & = [110100001110], a (C_{2}^{(12, 2)}) = 8, \\ C_{3}^{(12, 2)} & = [100100001110], a (C_{3}^{(12, 2)}) = 8, \end{matrix}

(A18)

Hence, we must take

★ * = 01

in the string (A17) to obtain the string

C_{(N - 3)}^{(12, 2)} = [010100001110], a_{\max}^{(N_{(N - 1)} + 5, 2)} (C_{(N - 3)}^{(12, 2)}) = 12 - 3 = 9,

(A19)

that cannot be further extended along with the ASI. Therefore,

N_{(N - 3)} (2) = N_{(N - 1)} (2) + 5 = 12

for

b = 2

For

b > 2

, w.l.o.g. we assume

★ = 1

* = 2

and append 0 at the start of the string (A17) to obtain

C_{(N - 3)} = [012010000111222 \dots], a_{\max}^{(N_{(N - 1)} + 6, b)} (C_{(N - 3)}) = N - 3,

(A20)

and the ASI of this newly formed string increases again. However, the insertion of another symbol into this string will maintain or even decrease the ASI of this newly formed string. Thus, Theorem 11 is proven.

Appendix G. Misunderstanding Assembly Pools

Consider the following mapping [13] between a working assembly pool

P_{3} (5)

containing five basic symbols and three strings made of these symbols and the initial assembly pool of radix

b = 8

\begin{matrix} P_{3} (5) & \leftrightarrow P_{0} (8) \\ 0 & \leftrightarrow 0 \\ 1 & \leftrightarrow 1 \\ 2 & \leftrightarrow 2 \\ 3 & \leftrightarrow 3 \\ 4 & \leftrightarrow 4 \\ 20 & \leftrightarrow 5 \\ 201 & \leftrightarrow 6 \\ 2012 & \leftrightarrow 7 \end{matrix}

(A21)

Now consider the string

C_{k}^{(11, 5)} = [20123242012]

(A22)

assembled beginning with the initial assembly pool

P_{0} (5)

and having the ASI

a^{(11, 5)} (C_{k}) = 7

only two steps above

a_{\min}^{(11)} = 5

. We can assemble the string

C_{l}^{(8, 8)} = [20123247]

(A23)

of length

N = 8

in 7 steps with the initial assembly pool

P_{0} (8)

and then, using the mapping (A21), it will correspond to the string (A22). However, as we have shown in Section 2,

N_{(N - 1)} (8) = 73 \neq 7

. In fact the latter string (A23) should be assembled as

C_{m}^{(5, 8)} = [73247]

(A24)

with the ASI

a^{(5, 8)} (C_{m}) = 5 - 1 = 4

and with the initial assembly pool

P_{0} (8)

, as

2012 \leftrightarrow 7

according to the mapping (A21). Hence, considering a set

P_{3} (5)

as the initial assembly pool is a gross misunderstanding; there is only one initial assembly pool for a given b and many different working assembly pools for

b > 1

and

s > 1

(

P_{1} (1) = {0, 00}

References

Marshall, S.M.; Murray, A.R.G.; Cronin, L. A probabilistic framework for identifying biosignatures using Pathway Complexity. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2017, 375, 20160342. [Google Scholar] [CrossRef] [PubMed]
Imari Walker, S.; Cronin, L.; Drew, A.; Domagal-Goldman, S.; Fisher, T.; Line, M. Probabilistic Biosignature Frameworks. In Planetary Astrobiology; Meadows, V.; Arney, G.; Schmidt, B.; Des Marais, D.J., Eds.; University of Arizona Press, 2019; pp. 1–1. [CrossRef]
Planetary astrobiology; Meadows, V.S.; Arney, G.N.; Schmidt, B.E.; Des Marais, D.J.; University of Arizona space science series, The University of Arizona Press (Eds.) Houston: Lunar and Planetary Institute: Tucson, 2020. [Google Scholar]
Liu, Y.; Mathis, C.; Bajczyk, M.D.; Marshall, S.M.; Wilbraham, L.; Cronin, L. Exploring and mapping chemical space with molecular assembly trees. Science Advances 2021, 7, eabj2465. [Google Scholar] [CrossRef] [PubMed]
Marshall, S.M.; Mathis, C.; Carrick, E.; Keenan, G.; Cooper, G.J.T.; Graham, H.; Craven, M.; Gromski, P.S.; Moore, D.G.; Walker, S.I.; Cronin, L. Identifying molecules as biosignatures with assembly theory and mass spectrometry. Nature Communications 2021, 12, 3033. [Google Scholar] [CrossRef] [PubMed]
Marshall, S.M.; Moore, D.G.; Murray, A.R.G.; Walker, S.I.; Cronin, L. Formalising the Pathways to Life Using Assembly Spaces. Entropy 2022, 24, 884. [Google Scholar] [CrossRef] [PubMed]
Sharma, A.; Czégel, D.; Lachmann, M.; Kempes, C.P.; Walker, S.I.; Cronin, L. Assembly theory explains and quantifies selection and evolution. Nature 2023, 622, 321–328. [Google Scholar] [CrossRef] [PubMed]
Jirasek, M.; Sharma, A.; Bame, J.R.; Mehr, S.H.M.; Bell, N.; Marshall, S.M.; Mathis, C.; MacLeod, A.; Cooper, G.J.T.; Swart, M.; Mollfulleda, R.; Cronin, L. Investigating and Quantifying Molecular Complexity Using Assembly Theory and Spectroscopy. ACS Central Science 2024, 10, 1054–1064. [Google Scholar] [CrossRef] [PubMed]
Łukaszyk, S.; Bieniawski, W. Assembly Theory of Binary Messages. Mathematics 2024, 12, 1600. [Google Scholar] [CrossRef]
Raubitzek, S.; Schatten, A.; König, P.; Marica, E.; Eresheim, S.; Mallinger, K. Autocatalytic Sets and Assembly Theory: A Toy Model Perspective. Entropy 2024, 26, 808. [Google Scholar] [CrossRef] [PubMed]
Łukaszyk, S.; Tomski, A. Omnidimensional Convex Polytopes. Symmetry 2023, 15. [Google Scholar] [CrossRef]
Book of John [1.3], c90.
Ozelim, L.; Uthamacumaran, A.; Abrahão, F.S.; Hernández-Orozco, S.; Kiani, N.A.; Tegnér, J.; Zenil, H. Assembly Theory Reduced to Shannon Entropy and Rendered Redundant by Naive Statistical Algorithms, 2024. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Salient Limits of Strings of Assembly Theory

Abstract

1. Introduction

2. Results

3. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Method A

Appendix B. Method B

Appendix C. Proof of C(N−1) String Theorem

Appendix D. Number of C ( N − 1 ) ( 13 , 3 ) Strings

Appendix E. Proof of C(N−1) String Theorem

Appendix F. Proof of C (N-3) String Theorem

Appendix G. Misunderstanding Assembly Pools

References

MDPI Initiatives

Important Links

Subscribe

Appendix C. Proof of C_(N−1) String Theorem

Appendix D. Number of $C_{(N - 1)}^{(13, 3)}$ Strings

Appendix E. Proof of C_(N−1) String Theorem