Preprint

Hypothesis

Quantum Relativity

Altmetrics

Downloads

Views

128

Comments

Ahmed Mohamed Ismail^*,

Samira Ezzat Mohamed

Ahmed Mohamed Ismail^*,

Samira Ezzat Mohamed

This version is not peer-reviewed

Abstract

This research answers the knowledge gap regarding the explanation of the quantum jump of the electron. This scientific paper aims to complete Einstein's research regarding general relativity and attempt to link general relativity to quantum laws.

Keywords:

Submitted:

19 September 2024

Posted:

22 September 2024

Read the latest preprint version here

Alerts

Abstract

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

This research was created for the purpose of answering questions about physics phenomena that have not been answered. Such as explaining the phenomenon of the quantum jump of the electron and the phenomenon of cumulative entanglement. What happens in the phenomenon of the quantum jump of the electron is that when we give the electron energy, this energy causes the electron to move from the energy level that it occupies to the higher energy level without crossing the distance between the two orbits, which leads to the occurrence of the phenomenon of the quantum jump of the electron [1] (Svidzinsky et al., 2014).

The role of this scientific paper is to provide a scientific explanation of how the quantum leap occurs without crossing the distance between the orbits. The theory of quantum entanglement is a connection between two quantum entangled particles. If one particle is observed, the other particle is affected by it at the same moment. This is what Einstein objected to; because when the electron traveled this distance in the same period of time, this would lead to the existence of a speed faster than the speed of light. Einstein proved it in special relativity. The maximum speed in the universe is the speed of light. Therefore, the phenomenon of quantum entanglement does not agree with Einstein’s laws. After the validity of quantum laws was proven. There has become a conflict between the laws of relativity that apply to the universe and the quantum laws that apply to atoms. This scientific paper aims to resolve this conflict between the laws of relativity and quantum laws. By establishing a law derived from the laws of relativity to apply to quantum laws. (Equation (1)).

This law in Equation (1) is known as quantum relativity because it links the laws of relativity and quantum theory. This law is derived from general relativity. The law works to explain the phenomenon of the quantum leap and the phenomenon of quantum entanglement, as it explains that when energy is given to the atom, the atom does not gain energy, but rather space-time gains that energy. We will discuss the interpretation of this theory in detail later.

The goal of this scientific research is to answer the explanation of the phenomenon of quantum leap and quantum entanglement and to add some modifications in the Bohr model.

2. Equations

These laws want to explain the results of the final derivation process of this research and what this research wants to prove.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(h_{p} \times C)}^{4}} T_{μ ν}

(1)

where G_µν represents the Einstein tensor, e is the electron charge, G is the universal gravitational constant, T_µν is the energy-momentum tensor, me is the electron mass, h_p is the Planck constant, ε₀ is the vacuum permittivity, r_n is the Bohr radius, Z is the atomic number, n is the energy level, C is the speed of light. This is a law that links the four constants (gravity, electron charge, Planck constant, and speed) into one law.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n \times λ)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(E_{n})}^{4}} T_{μ ν}

(2)

where E_n represents the photon energy, λ is the wavelength. This law explains the final result of the derivation. This law proves the creation of a relationship that links the photon energy and curvature of space-time.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(λ)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(E_{t})}^{4}} T_{μ ν}

(3)

where E_t represents the energy of the total photon.

E_{(p)}^{2} = \frac{{(2 π \times n)}^{4} \times {(2 \times ε_{0})}^{2}}{{(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(ℏ \times C)}^{5}}{{(e)}^{4} \times G}

(4)

where E_p represents the Planck energy. This law links Planck energy with other cosmological constants.

E = \frac{n^{2} \times h_{(a)}^{2} \times 2 K E}{{(Z)}^{2}} + n \times P \times \frac{ω}{k \times α \times Z}

(5)

E = m \times C^{2} + P \times C

where E represents the energy, h_(a) is the atomic constant, KE is the kinetic energy, P is the momentum,

ω

is the angular velocity, k is the wave vector, and

α

is the fine-structure constant. This law explains the final result of the derivation. This law proves the creation of a relationship that links energy and kinetic energy. That the lost kinetic energy comes out in the form of radiant energy.

E = ℏ \times C \times n \times k

(6)

E = n \times h_{(p)} \times ν

where

ℏ

represents the reduced Planck constant,

ν

is the frequency. This law explains the final result of the derivation. This law proves the creation of a relationship that links the energy of the total photon and wave vector.

H = \frac{e^{4} \times {({(k_{e})}_{{(m)}_{1}})}^{2} \times G}{{(ℏ \times C)}^{3}}

(7)

{({(k_{e})}_{{(m)}_{1}})}^{2} = {(m_{e})}^{2} \times k_{e}^{2} = \frac{{(m_{e})}^{2}}{{(4 π \times ε_{0})}^{2}}

where H represents the Cosmic Constant (David cosmological constant),

{(k_{e})}_{{(m)}_{1}}

is the Agglomerated mass permittivity constant,

k_{e}

is the Coulomb constant. This law works to link the four constants (gravity, electron charge, Planck constant, and speed) into one law.

X = \frac{e^{2} \times {(k_{e})}_{m} \times G}{{(ℏ \times C)}^{2}}

(8)

{(k_{e})}_{m} = {(m_{e})}^{2} \times k_{e} = \frac{{(m_{e})}^{2}}{(4 π \times ε_{0})}

X = α \times R = \frac{α \times {(m_{e})}^{2}}{{(m_{p})}^{2}} = \frac{α \times {(m_{e})}^{2} \times G}{ℏ \times C} = \frac{e^{2} \times {(m_{e})}^{2} \times G}{(4 π \times ε_{0}) \times {(ℏ \times C)}^{2}} = \frac{e^{2} \times {(k_{e})}_{m} \times G}{{(ℏ \times C)}^{2}}

where X represents the unknown force X (David constant),

{(k_{e})}_{m}

is the mass permittivity constant. This is a law that links the four constants (gravity, electron charge, Planck constant, and speed) into one law.

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times \bar{ℏ} \times e^{2} \times {(Z)}^{2}}{n^{2} \times E^{2}} T_{μ ν}

(9)

where

\bar{ℏ}

represents the multiverse constant. This law wants to prove is the creation of a relationship that links the curvature of space-time and the energy of the total photon.

n^{2} \times ℏ^{2} = {(k_{e})}_{{(m)}_{1}} \times r \times e^{2}

(10)

{(k_{e})}_{{(m)}_{1}} = (m_{e}) \times k_{e} = \frac{(m_{e})}{(4 π \times ε_{0})}

This law affects the Planck constant and the charge of the electron.

2. Notes between the Laws

Equation (6), this scientific formula explains the relationship between the energy of the total photon and the wave vector. In other words, the wave vector and the energy are the same.

h_{(a)} = \frac{1}{α} = \frac{R}{X}

(11)

where R represents the Cosmic mass constant. The atomic constant is the reciprocal of the fine-structure constant.

α = \frac{n \times v}{C} α = \frac{n^{2} \times λ_{(e)}}{2 π \times α_{0}}

(12)

where

λ_{(e)}

represents the Compton wavelength,

v

is the speed. This law explains the relationship between the fine-structure constant and the speed.

R = \frac{{(m^{e})}^{2}}{{(m_{p})}^{2}}

(13)

where

m_{p}

represents the Planck mass.

\bar{ℏ} = k_{e} \times X = \frac{e^{2} \times {(m_{e})}^{2}}{{(4 π \times ε_{0})}^{2} \times ℏ \times C \times {(m_{p})}^{2}} = \frac{H \times ℏ \times C}{e^{2}} = \frac{H \times k_{e}}{α}

(14)

\bar{ℏ} = \frac{e^{2} \times {({(k_{e})}_{{(m)}_{1}})}^{2} \times G}{{(ℏ \times C)}^{2}}

This law works to link the four constants (gravity, electron charge, Planck constant, and speed of light) into one law.

E = \frac{n^{2} \times h_{(a)}^{2} \times 2 K E}{{(Z)}^{2}}

(15)

This law proves that lost kinetic energy comes out in the form of radiant energy.

Derivation of Equations

K E = \frac{1}{2} \times m \times v^{2}

(16)

Kinetic Energy Equation

a = \frac{v^{2}}{r}

(17)

We associate acceleration with kinetic energy equation.

K E = \frac{1}{2} \times m \times v^{2} \frac{r}{r}

K E = \frac{1}{2} \times a \times m \times r

(18)

v = \frac{d}{t} = \frac{2 π \times r}{T}

(19)

Then we link Equation (16) to periodic time.

2 K E = {(\frac{2 π \times r}{T})}^{2} \times m

(20)

{(T)}^{2} = \frac{{(2 π \times r)}^{2} \times m}{2 K E}

T = 2 π r \sqrt{\frac{m}{2 K E}}

(21)

T = \frac{n^{2}}{ν \times α}

(22)

There is a relationship between frequency and the fine structure constant and its relationship to periodic time. Then we link Equations (21) and (22).

ν = \frac{n^{2} \times \sqrt{2 K E}}{2 π r \times α \times \sqrt{m}}

(23)

ν = \frac{C}{λ}

(24)

Then we work on introducing the wavelength into the Equation (23).

λ = \frac{2 π r \times α \times C \times \sqrt{m}}{n^{2} \times \sqrt{2 K E}}

(25)

λ^{2} = \frac{{(2 π r)}^{2} α^{2} \times C^{2} \times m}{n^{4} \times 2 K E}

E = m \times C^{2}

Then we work on introducing the energy into the Equation (25).

E = \frac{n^{4} \times 2 K E \times λ^{2}}{{(2 π r)}^{2} \times α^{2}}

(26)

k = \frac{2 π}{λ}

(27)

Then we work on introducing the wave vector into the Equation (26).

E = \frac{n^{4} \times 2 K E}{α^{2} \times k^{2} \times {(r_{n} \times Z)}^{2}}

(28)

What this law aims to prove is the creation of a relationship that links energy and kinetic energy. That the lost kinetic energy comes out in the form of radiant energy.

k = \frac{P}{ℏ}

(29)

Then we work on introducing the wave vector into the Equation (28).

E = \frac{n^{4} \times ℏ^{2} \times 2 K E}{P^{2} \times {(r_{n})}^{2} \times α^{2} \times {(Z)}^{2}}

(30)

L = n \times ℏ = P \times r_{n}

(31)

Then we work on introducing the angular momentum into the Equation (30).

E = \frac{n^{2} \times L^{2} \times 2 K E}{L^{2} \times α^{2} \times {(Z)}^{2}}

E = \frac{n^{2} \times 2 K E}{α^{2} \times {(Z)}^{2}}

(32)

E = \frac{n^{2} \times 2 K E}{α^{2} \times {(Z)}^{2}}

We will commence the following derivation, starting from (32).

h_{(a)} = \frac{1}{α} = \frac{C \times (Z)}{n \times v}

(33)

Then we work on introducing the atomic constant into the Equation (32). Which relates to me, the reciprocal of the fine-structure constant and the electron velocity.

E = \frac{n^{2} \times h_{(a)}^{2} \times 2 K E}{{(Z)}^{2}}

E = m \times C^{2}

m \times C^{2} = \frac{n^{2} \times h_{(a)}^{2} \times 2 K E}{{(Z)}^{2}}

2 K E = m \times v^{2}

m \times C^{2} = \frac{n^{2} \times h_{(a)}^{2} \times m \times v^{2}}{{(Z)}^{2}}

The mass is removed from the ends.

h_{(a)}^{2} = \frac{C^{2} \times {(Z)}^{2}}{n^{2} \times v^{2}}

The atomic constant establishes the relationship between speed and n is the energy level, C is the speed of light.

E = \frac{n^{2} \times 2 K E}{α^{2} \times {(Z)}^{2}}

We will commence the following derivation, starting from (32).

2 K E = a \times m \times r_{n}

Then we link Equations (18) and (32).

E = \frac{n^{2} \times a \times m \times r_{n}}{α^{2} \times {(Z)}^{2}}

(34)

a = \frac{G \times m \times α}{R^{2} \times {(r_{n})}^{2}}

After, that, we linked the acceleration to the Equation (34).

E = \frac{G \times m^{2} \times n^{2}}{R^{2} \times α \times r_{n} \times {(Z)}^{2}} \frac{C^{4}}{C^{4}}

E = m \times C^{2}

E = \frac{n^{2} \times G \times E^{2}}{R^{2} \times α \times r_{n} \times C^{4} \times {(Z)}^{2}} \frac{8 π}{8 π}

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times G}{C^{4}} T_{μ ν}

(35)

After, that, we linked the general relativity to the equation.

r = \frac{G_{μ ν} + Λ g_{μ ν} \times E \times n^{2}}{R^{2} \times α \times 8 π \times T_{μ ν} \times {(Z)}^{2}}

(36)

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times R^{2} \times α \times r_{n} \times {(Z)}^{2}}{n^{2} \times E} T_{μ ν}

This equation is considered the most important equation because it links energy and general relativity.

h_{(a)} = \frac{1}{α} = \frac{R^{2}}{X}

R^{2} = \frac{{(m_{e})}^{2}}{{(m_{p})}^{2}}

X = α \times R^{2} = \frac{α \times {(m_{e})}^{2}}{{(m_{p})}^{2}} = \frac{α \times {(m_{e})}^{2} \times G}{ℏ \times C} = \frac{e^{2} \times {(m_{e})}^{2} \times G}{(4 π \times ε_{0}) \times {(ℏ \times C)}^{2}} = \frac{e^{2} \times {(k_{e})}_{m} \times G}{{(ℏ \times C)}^{2}}

These equations are used to calculate the value of X and the value of R in order, to obtain the value of the atomic constant that is used in the kinetic quantum relativity equation.

{(k_{e})}_{m} = {(m_{p})}^{2} \times k_{e} = \frac{{(m_{p})}^{2}}{(4 π \times ε_{0})}

m_{(p)}^{2} = \frac{F_{p} \times ℏ}{C^{3}} = \frac{ℏ \times C}{G}

Planck’s mass can be used to connect it, to me, the vacuum permittivity.

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times R^{2} \times α \times r_{n} \times {(Z)}^{2}}{n^{2} \times E} T_{μ ν}

We will commence the following derivation, starting from (36).

X = α \times R^{2} = \frac{α \times {(m_{e})}^{2}}{{(m_{p})}^{2}}

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times X \times r_{n} \times {(Z)}^{2}}{n^{2} \times E} T_{μ ν} \frac{α}{α}

α = k_{e} \times \frac{e^{2}}{ℏ \times C}

(37)

After, that, we linked the fine-structure constant to the Equation (36).

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times X \times r_{n} \times {(Z)}^{2} \times k_{e} \times e^{2}}{n^{2} \times E \times ℏ \times C \times α} T_{μ ν}

E_{t} = E \times α

\bar{ℏ} = k_{e} \times X = \frac{e^{2} \times {(m_{e})}^{2}}{{(4 π \times ε_{0})}^{2} \times ℏ \times C \times {(m_{p})}^{2}} = \frac{H \times ℏ \times C}{e^{2}} = \frac{H \times k_{e}}{α}

(38)

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times e^{2} \times \bar{ℏ} \times r_{n} \times {(Z)}^{2}}{n^{2} \times ℏ \times C \times E_{t}} T_{μ ν}

(39)

This law proves the creation of a relationship that links the curvature of space-time and the energy of the total photon.

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times H \times r_{n} \times {(Z)}^{2}}{n^{2} \times E} T_{μ ν}

(40)

After, that, we linked the Equations (38) and (39).

E = ℏ \times C \times n \times k

k = \frac{n}{r}

(41)

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times H \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times ℏ \times C} T_{μ ν}

(42)

After, that, we linked the Equations (6), (40) and (41).

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times H \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times ℏ \times C} T_{μ ν}

We will commence the following derivation, starting from (42).

H = α \times X

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times α \times X \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times ℏ \times C} T_{μ ν}

X = α \times R

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times α^{2} \times R \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times ℏ \times C} T_{μ ν}

(43)

α = \frac{1}{4 π \times ε_{0}} \times \frac{e^{2}}{ℏ \times C}

α = k_{e} \times \frac{e^{2}}{ℏ \times C} \frac{1}{(ℏ \times C)}

\frac{α}{ℏ \times C} = k_{e} \times \frac{e^{2}}{{(ℏ \times C)}^{2}}

(44)

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times α \times k_{e} \times e^{2} \times R \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times {(ℏ \times C)}^{2}} T_{μ ν}

(45)

After, that, we linked the Equations (43) and (44).

S = k_{e} \times R

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times α \times S \times e^{2} \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times {(ℏ \times C)}^{2}} T_{μ ν}

\bar{ℏ} = α \times S

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times \bar{ℏ} \times e^{2} \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times {(ℏ \times C)}^{2}} T_{μ ν}

E = ℏ \times C \times n \times k

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times \bar{ℏ} \times k^{2} \times e^{2} \times r_{n}^{2} \times {(Z)}^{2}}{n^{2} \times E^{2}} T_{μ ν}

k = \frac{n}{r}

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times \bar{ℏ} \times e^{2} \times {(Z)}^{2}}{n^{2} \times E^{2}} T_{μ ν}

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times H \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times ℏ \times C} T_{μ ν}

We will commence the following derivation, starting from (9).

H = \frac{e^{4} \times {({k_{e}}_{{(m)}_{1}})}^{2} \times G}{{(ℏ \times C)}^{3}}

Then we link Equations (7) and (9).

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times e^{4} \times {({k_{e}}_{{(m)}_{1}})}^{2} \times G \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times {(ℏ \times C)}^{4}} T_{μ ν}

{({k_{e}}_{{(m)}_{1}})}^{2} = {(m_{e})}^{2} \times k_{e}^{2} = \frac{{(m_{e})}^{2}}{{(4 π \times ε_{0})}^{2}}

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times e^{4} \times {(m_{e})}^{2} \times G \times r_{n}^{2} \times {(Z)}^{2}}{n^{4} \times {(4 π \times ε_{0})}^{2} \times {(ℏ \times C)}^{4}} T_{μ ν}

(46)

2 π \times r = n \times λ

2 π = \frac{n \times λ}{r}

(47)

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times e^{4} \times {(m_{e} \times Z)}^{2} \times G \times {(r_{n})}^{4}}{n^{6} \times {(ℏ \times C)}^{4} \times {(2 ε_{0})}^{2} \times {(λ)}^{2}} T_{μ ν}

(48)

After, that, we linked the Equations (46) and (47).

G_{μ ν} + Λ g_{μ ν} = \frac{2 π \times e^{4} \times {(m_{e} \times Z)}^{2} \times G \times {(r_{n})}^{4}}{n^{6} \times {(ℏ \times C)}^{4} \times {(ε_{0})}^{2} \times {(λ)}^{2}} T_{μ ν}

(49)

After dividing 2 by

8 π

G_{μ ν} + Λ g_{μ ν} = \frac{((2 π) \times {(r_{n})}^{4}) \times {(m_{e} \times Z)}^{2}}{({(n)}^{6} \times {(λ)}^{2}) \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(ℏ \times C)}^{4}} T_{μ ν}

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{5} \times {(r_{n})}^{4}) \times {(m_{e} \times Z)}^{2}}{({(n)}^{6} \times {(λ)}^{2}) \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(h_{p} \times C)}^{4}} T_{μ ν}

(50)

Reduced Planck constant is Planck’s constant divided by

2 π .

k = \frac{2 π}{λ}

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{4}) \times k^{2} \times {(m_{e} \times Z)}^{2}}{{(n)}^{6} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(h_{p} \times C)}^{4}} T_{μ ν}

(51)

k = \frac{n}{r_{n}}

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(h_{p} \times C)}^{4}} T_{μ ν}

After, we linked the wave vector to the Equation (51).

E = \frac{n^{2} \times 2 K E}{{(α \times Z)}^{2}}

We will commence the following derivation, starting from (32).

α^{2} = \frac{H}{R}

E = \frac{n^{2} \times R \times 2 K E}{H \times {(Z)}^{2}}

(52)

After, we linked the fine-structure constant to the Equation (32).

R = \frac{{(m_{e})}^{2}}{{(m_{p})}^{2}}

E = \frac{n^{2} \times {(m_{e})}^{2} \times 2 K E}{H \times {(m_{p} \times Z)}^{2}}

After, that, we linked the Equations (13) and (52).

C^{2} = \frac{E}{m}

C^{2} = \frac{n^{2} \times (m_{e}) \times 2 K E}{H \times {(m_{p} \times Z)}^{2}} \frac{{(2 π \times C)}^{2}}{{(2 π \times C)}^{2}}

E_{(p)} = 2 π \times m_{p} \times {(C)}^{2}

E_{(p)}^{2} = \frac{{(2 π)}^{2} \times n^{2} \times m_{e} \times {(C)}^{2} \times 2 K E}{H \times {(Z)}^{2}}

(53)

p^{2} = m_{e} \times 2 K E

E_{(p)}^{2} = \frac{{(2 π)}^{2} \times n^{2} \times p^{2} \times C^{2}}{H \times {(Z)}^{2}} \frac{{(r)}^{2}}{{(r)}^{2}}

After, that, we linked the momentum to the Equation (53).

n \times ℏ = p \times r

E_{(p)}^{2} = \frac{{(2 π)}^{2} \times n^{4} \times ℏ^{2} \times C^{2}}{H \times r^{2} \times {(Z)}^{2}}

(54)

H = \frac{e^{4} \times {(m_{e} \times r)}^{2} \times G}{{(2 \times ε_{0} \times n \times λ)}^{2} \times {(ℏ \times C)}^{3}}

(55)

E_{(p)}^{2} = \frac{{(2 π)}^{2} \times n^{6} \times {(ℏ \times C)}^{5} \times {(2 \times ε_{0})}^{2} \times {(λ)}^{2}}{e^{4} \times G \times r^{4} \times {(Z e \times m_{e})}^{2}}

After, that, we linked the(David cosmological constant) to the Equation (54).

E_{(p)}^{2} = \frac{{(2 π)}^{2} \times ({(n)}^{6} \times {(λ)}^{2}) \times {(2 \times ε_{0})}^{2}}{{(r_{n})}^{4} \times {(m_{e} \times Z)}^{2}} \frac{{(ℏ \times C)}^{5}}{{(e)}^{4} \times G}

2 π \times r = n \times λ

E_{(p)}^{2} = \frac{{(2 π)}^{4} \times ({(n)}^{4}) \times {(2 \times ε_{0})}^{2}}{{(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(ℏ \times C)}^{5}}{{(e)}^{4} \times G}

(56)

H = \frac{e^{4} \times {(m_{e})}^{2} \times G}{{(4 π \times ε_{0})}^{2} \times {(ℏ \times C)}^{3}}

We will commence the following derivation, starting from (7).

2 π \times r = n \times λ

H = \frac{e^{4} \times {(m_{e} \times r)}^{2} \times G}{{(2 \times ε_{0} \times n \times λ)}^{2} \times {(ℏ \times C)}^{3}}

(57)

H = α^{2} \times R = \frac{α^{2} \times {(m_{e})}^{2}}{{(m_{p})}^{2}} = \frac{α^{2} \times {(m_{e})}^{2} \times G}{ℏ \times C} = \frac{e^{4} \times {(m_{e})}^{2} \times G}{{(4 π \times ε_{0})}^{2} \times {(ℏ \times C)}^{3}}

(58)

H = \frac{α^{2} \times h^{2} \times G}{λ_{(e)}^{2} \times ℏ \times c^{3}} = α^{2} \times t_{(p)}^{2} \times ω_{(c)}^{2} = \frac{e^{4} \times {({(k_{e})}_{{(m)}_{1}})}^{2} \times G}{{(ℏ \times C)}^{3}}

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(h_{p} \times C)}^{4}} T_{μ ν}

We will commence the following derivation, starting from (51).

{(\frac{h_{p}}{e^{2}})}^{2} = {(\frac{μ_{0} \times C}{2 α})}^{2}

where

μ_{0}

Vacuum permeability.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n)}^{4} \times {(μ_{0} \times ε_{0})}^{2}} \frac{{(2 α)}^{2} \times G}{{(h_{p})}^{2} \times {(C)}^{6}} T_{μ ν}

(59)

{(ε_{0} \times h_{p} \times C)}^{2} = {(\frac{e^{2}}{2 α})}^{2}

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n)}^{4} \times {(μ_{0})}^{2}} \frac{{(2 α)}^{4} \times G}{{(e \times C)}^{4}} T_{μ ν}

(60)

E_{(p)}^{2} = \frac{{(2 π)}^{4} \times ({(n)}^{4}) \times {(2 \times ε_{0})}^{2}}{{(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(ℏ \times C)}^{5}}{{(e)}^{4} \times G}

We will commence the following derivation, starting from (56).

E_{(p)}^{2} = \frac{{(2 π)}^{4} \times ({(n)}^{4}) \times {(2 \times ε_{0})}^{2}}{{(2 π)}^{5} \times {(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(h_{p} \times C)}^{5}}{{(e)}^{4} \times G}

E_{(p)}^{2} = \frac{{(n)}^{4} \times {(2 \times ε_{0})}^{2}}{(2 π) \times {(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(h_{p} \times C)}^{5}}{{(e)}^{4} \times G}

h_{p} = \frac{μ_{0} \times C \times e^{2}}{2 α}

E_{(p)}^{2} = \frac{{(n)}^{4} \times μ_{0} \times {(2 \times ε_{0})}^{2}}{(2 π) \times {(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(h_{p})}^{4} \times {(C)}^{6}}{{(e)}^{2} \times G \times 2 α}

(61)

{(ε_{0} \times h_{p} \times C)}^{2} = {(\frac{e^{2}}{2 α})}^{2}

E_{(p)}^{2} = \frac{{(n)}^{4} \times μ_{0} \times {(2)}^{2} \times {(e)}^{2}}{(2 π) \times {(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(h_{p})}^{2} \times {(C)}^{4}}{G \times {(2 α)}^{3}} \frac{{(C)}^{2}}{{(C)}^{2}}

(62)

{(\frac{h_{p}}{C})}^{2} = {(\frac{μ_{0} \times e^{2}}{2 α})}^{2}

E_{(p)}^{2} = \frac{{(n)}^{4} \times {(μ_{0})}^{3} \times {(2)}^{2}}{(2 π) \times {(r_{n})}^{2} \times {(m_{e} \times Z)}^{2}} \frac{{(e \times C)}^{6}}{G \times {(2 α)}^{5}}

(63)

5. The Hypothesis on Which the Equation Is Based

Here we will review the most important hypotheses that led to arriving at this equation, the details of the equation, the answers that explain this equation, and the defects that faced the Bohr model and the method of solving it.

The problems with Bohr model began when it could not explain the following:

How does the electron remain stable in its orbit, since it is assumed that bodies accelerating around the nucleus, such as the electron, emit energy, and this emitted energy carries all wavelengths?

This is something that Bohr could not answer [2] (Udema, 2017).

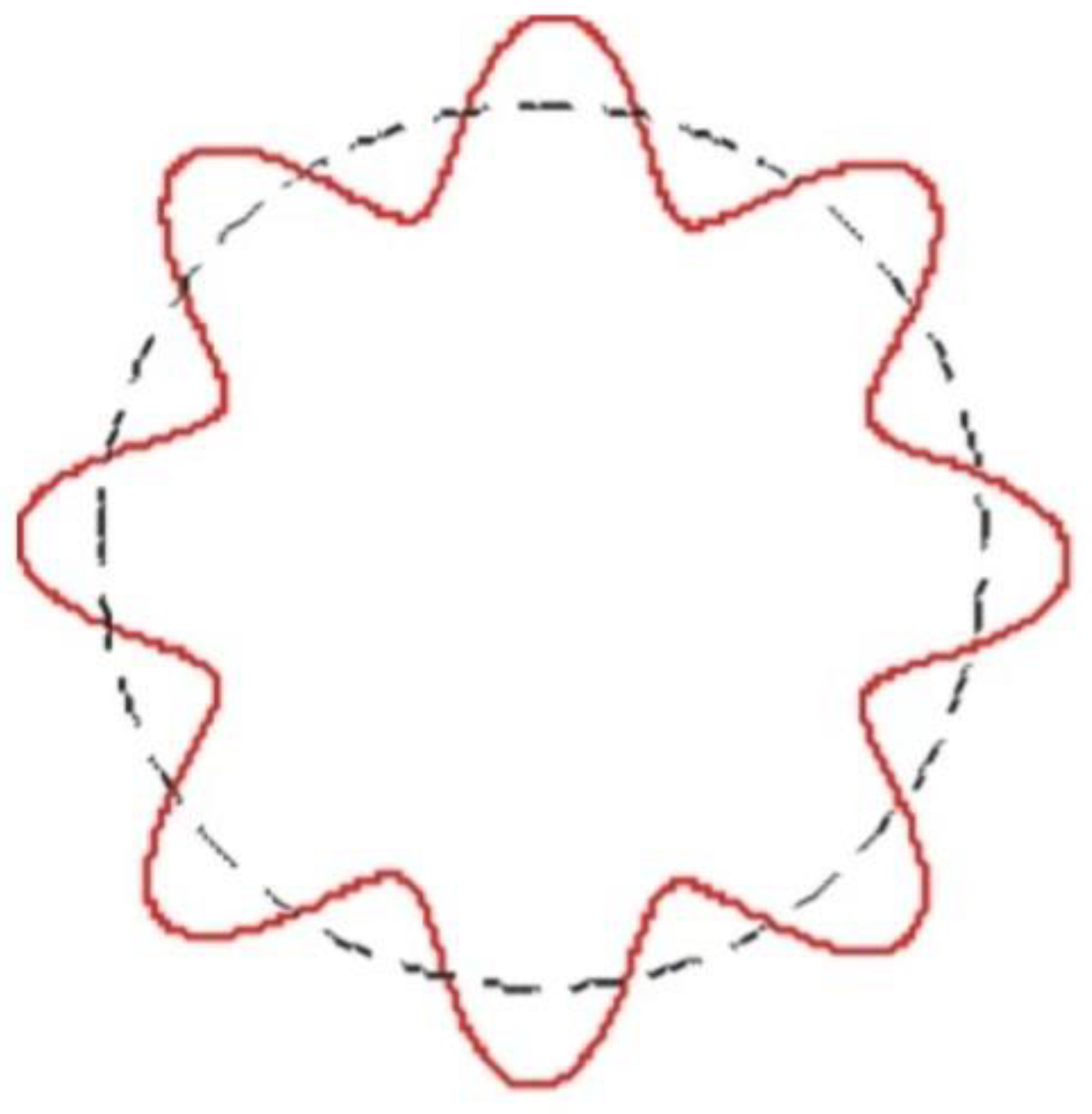
Well, this scientific paper will answer that and will also explain quantum entanglement. As a result of the movement of electrons on the fabric of space-time in a straight line. Because the straight line passes around the nucleus. Then the electron passes, forming a great circle around the nucleus. Therefore, the electron moves in a straight line and the electron does not need to expend energy. This makes the electron not, emit energy and be in a stable state.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n \times λ)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(E_{n})}^{4}} T_{μ ν}

Explanation of the hypothesis of electron quantum jump.

How the quantum jump of occurs?

The electron rotates in the orbit specified for it in the atom at a certain speed proportional to the orbit, so that it is fixed in its orbit and the atom is stable, but the matter is different when energy is added to the atom. What has been measured is that when the atom gains energy, the electrons gain this energy, work to make a quantum jump without crossing the distance between the two orbits. But my equations interpreted this in a way that linked relativity and the quantum world. The interpretation of the law is as follows: When you give energy to the atom, the electron does not gain energy, but rather the fabric of space-time acquires this energy. Then it works on contraction the level with the highest energy until an overlap occurs between the level with the highest energy and the orbit occupied by the electron. So the quantum leap occurs, meaning that the issue is relative between the electron and the electron observer. From, the point of view of the electron, it is moving in position. When interference occurs between the two orbits, the electron does not notice it, but from the point of view of the electron observer, what happens? The electron disappears from the level that it occupies and appears in the upper orbit, that is a quantum jump occurs. This wave interference is achieved through this law.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n \times λ)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(E_{n})}^{4}} T_{μ ν}

Because the equation connects more than one equation into a single equation. As

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times G}{C^{4}} T_{μ ν}

Δ E_{n} = \frac{h_{p} \times C}{λ}

n \times λ = 2 π \times r_{n}

How quantum entanglement occurs?

What happens is that the electron connects to the other electron through space-time, as space-time acts like a quantum tunnel that connects the two electrons. In this way, the electron does not penetrate the speed of light, But in relation to large objects, you see that it has crossed the speed of light.

This hypothesis was based on scientific foundations, the most important of which is:

1) the connection between relativity and quantum mechanics occurs via quantum entanglement and loop gravitational entanglement.

2) quantum entanglement occurs by the contraction of space-time.

3) space-time contraction occurs by space-time absorbing energy.

4) the quantum jump of the electron occurs as a result of the contraction of space-time.

4. Method

My name is Ahmed. I have made a theoretical derivation of the equation of general relativity as explained in this research for the purpose of obtaining an equation that can be applied within the quantum world so that it describes the movement of the electron during the quantum jump in the Bohr model. After that, the researcher Samira reviewed the research and verified it, and then she worked on applying this theory to the movement of the electron during the occurrence of the quantum leap, using previous research and matching it with the results of this equation to determine its validity.

This part of the research will explain the spectrum of the hydrogen atom in a new way, as the results presented in these tables from previous research match the results extracted from the equation, and this is consistent with the validity of this equation. Because the new equation is consistent with the photon energy equation. We will discuss that part of the research in the results and discussion.

Table 1 this table shows the measurement results of one of the previous researches related to the spectrum of the hydrogen atom in the Balmer series [3] (Nanni, 2015).

Table 1 the theoretical results are obtained through the wavelength equation located above the tables

Tables 2 and 3 shows the results of measuring the hydrogen atom [3] (Nanni, 2015).

These tables show the measurement results of one of the previous researches related to the spectrum of the hydrogen atom.

Table 4 shows the results of the Humphreys series measurement.[3] (Nanni, 2015)

Table 4 this table shows the measurement results of one of the previous researches related to the spectrum of the hydrogen atom in the Humphreys series

Table 5 shows the measurement results tested [3] (Nanni, 2015).

Table 5 it represents the theoretical and experimental value of the hydrogen atom. Using the photon energy law mentioned above, this table.

Figure 1. Bohr hydrogen atomic model incorporating de Broglie’s [4] (Jordan, 2024).

This drawing, taken from previous research, shows how the quantum leap occurs through interference, as my equation showed. When interference occurs between the orbit occupied by the electron and the energy level higher than the electron’s orbit, it occurs in the form of wave interference of this type as a result of a contraction in the fabric of space-time. The black circle represents the orbit occupied by the electron, while the red color represents how interference occurs from the orbit higher than the orbit occupied by the electron in the form of wave interference.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n \times λ)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(E_{n})}^{4}} T_{μ ν}

Because the equation connects more than one equation into a single equation. As

G_{μ ν} + Λ g_{μ ν} = \frac{8 π \times G}{C^{4}} T_{μ ν}

Δ E_{n} = \frac{h_{p} \times C}{λ}

n \times λ = 2 π \times r_{n}

Figure 2. The observed emission line spectrum of atomic hydrogen in chapter 2 atoms.[5] (Manini, 2020).

Table (6) shows the measurement results of one of the previous researches related to the spectrum of the hydrogen atom in chapter 2 atoms [5] (Manini, 2020).

This shape is a result of the fact that the electron, after a quantum leap occurred as a result of an interference between the orbital that it occupies and the energy level above it, was in an unstable state. Therefore, when the highest level of energy returns to its position, it releases energy in the form of spectral lines. These lines are determined according to the amount of energy, as shown in the picture.

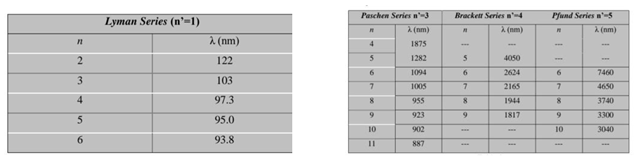
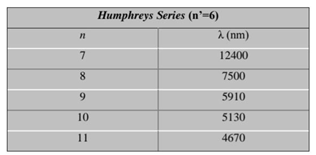
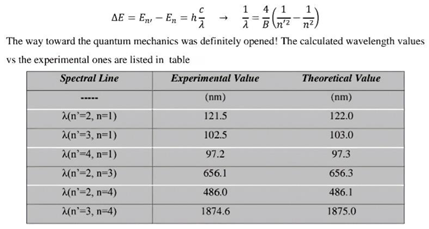
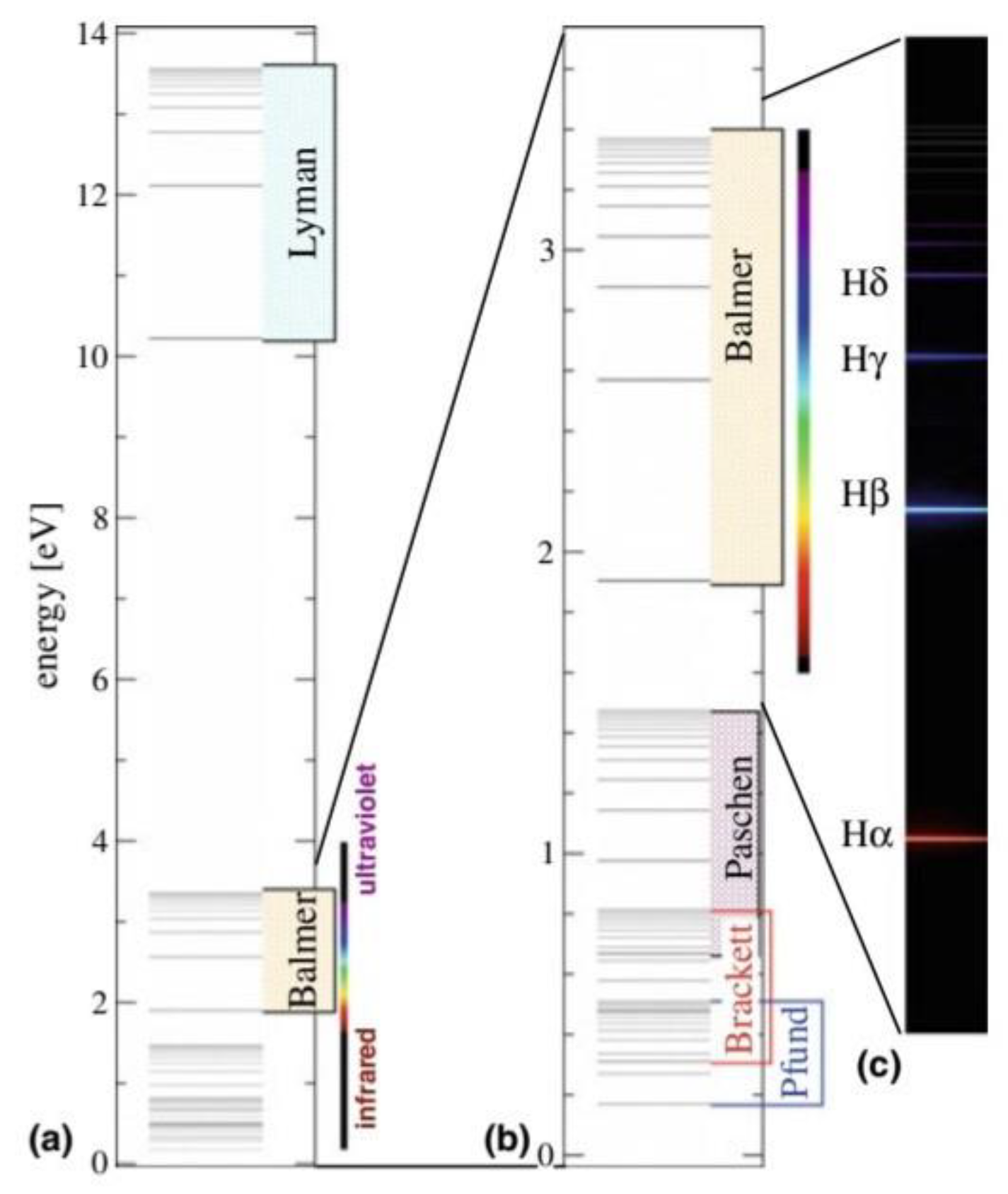
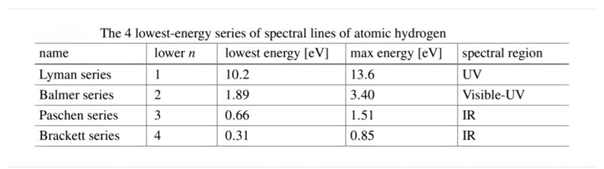
7. Results and Discussion

This scientific research aims to prove a theory by comparing the practical results of this theory with the original results and making the comparison in a table. We will discuss that here .

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(h_{p} \times C)}^{4}} T_{μ ν}

\frac{G_{μ ν} + Λ g_{μ ν}}{T_{μ ν}} = \frac{8 π \times G}{C^{4}} = 2.0766474428 \times 10^{- 43}

(64)

r_{n}^{2} = \frac{2.800285118 \times 10^{- 21} \times {(n)}^{4}}{{(Z)}^{2}}

After substituting the constants into equation number 1. This derivation proves that the equation can be applied to the Bohr radius.

G_{μ ν} + Λ g_{μ ν} = \frac{({(2 π)}^{3} \times {(r_{n})}^{2}) \times {(m_{e} \times Z)}^{2}}{{(n \times λ)}^{4} \times {(ε_{0})}^{2}} \frac{{(e)}^{4} \times G}{{(E_{n})}^{4}} T_{μ ν}

\frac{G_{μ ν} + Λ g_{μ ν}}{T_{μ ν}} = \frac{8 π \times G}{C^{4}} = 2.0766474428 \times 10^{- 43}

Δ E_{n} = 0.17043774059 e V \times \frac{{(r_{n} \times Z)}^{\frac{2}{4}}}{n \times λ}

(65)

After, that, we linked the equation number (2, 64). The unit of measurement for photon energy is electron volt (eV), the wavelength is (nm), and Bohr radius is a (nm).

Δ E_{n} = \frac{h_{p} \times C}{λ} = \frac{1239.8419637 e V n m}{λ}

(65)

Photon energy equation.

Table 7. Comparing my theoretical results through my equation with previous results.

Theoretical value (My work) Experimental value
Spectral Line	Energy		λ		λ
λ(n’=2, n=1)	10.204269824	eV	121.50227162	nm	121.5 nm
λ(n’=3, n=1)	12.093949421	eV	102.51754168	nm	102.5 nm
λ(n’=4, n=1)	12.75533728	eV	97.201817292	nm	97.20 nm
λ(n’=3, n=2)	1.8896795971	eV	656.1122667	nm	656.1 nm
λ(n’=4, n=2)	2.5510674561	eV	486.00908641	nm	486.0 nm
λ(n’=4, n=3)	0.66138785898 eV		1874.6064763	nm	1874.6 nm

The results of the experimental value were obtained by using the results of previous research on the hydrogen atom. I prove in Table 7 that the results of the equations are identical to their original results in Table 5, which indicates the validity of this law.

Δ E_{n} = E_{2} - E_{1}

Δ E_{n} = \frac{- 13.605693099 e V}{1} \times (\frac{{(Z)}^{2}}{{(n_{2})}^{2}} - \frac{{(Z)}^{2}}{{(n_{1})}^{2}})

Δ E_{n} = 0.17043774059 e V \times \frac{{((0.052917720265 n m \times {(n)}^{2}) \times Z)}^{\frac{2}{4}}}{n \times λ}

These are the results of a relationship between energy and wavelength. The observed results show that whenever the energy increases, the wavelength decreases, as shown by this equation in the hydrogen atom.

5. Conclusions

After the idea of research has been clarified using theoretical and practical scientific evidence to explain the phenomenon of the quantum leap and quantum entanglement from a new perspective, these equations would be used in the following:

1) serving humanity in the advancement of scientific research.

2) using these equations to explore space and quantum world.

3) using these equations in developing communications machines.

References

Svidzinsky, A. Scully, M. Bohr’s molecular model, a century later. Physics T. 2014, 67, 33-39. [CrossRef]
Udema, I. I. Renaissance of Bohr’s model via derived alternative equation. American J. Mod. Phys 2017, 6, 23-31. [CrossRef]
Nanni, L. The hydrogen atom: A review on the birth of modern quantum mechanics. Physics 2015. [CrossRef]
Jordan, R. B. Principles of Inorganic Chemistry. Springer N., 2024; pp. 1--18. [CrossRef]
Manini, N. Introduction to the physics of matter: basic atomic, molecular, and solid-state physics. Springer N., 2020; pp. 11--16. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Quantum Relativity

Abstract

Abstract

1. Introduction

2. Equations

2. Notes between the Laws

Derivation of Equations

Kinetic Energy Equation

5. The Hypothesis on Which the Equation Is Based

4. Method

7. Results and Discussion

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe