Prerpints.org logo
Preprint
Article

Large Eddy Simulation of the Flow past a Circular Cylinder at Re=130,000: Effects of Numerical Platforms and Single- and Double-Precision Arithmetic

Altmetrics

Downloads

78

Views

110

Comments

0

This version is not peer-reviewed

Submitted:

17 September 2024

Posted:

23 September 2024

You are already at the latest version

Alerts
Abstract
Numerical simulations of the sub-critical flow past a circular cylinder at the Reynolds number, Re=130,000 are performed using two numerical platforms, commercial, Ansys Fluent and open source, OpenFoam (finite volume method and large eddy simulation based on a differential equation for the sub-grid kinetic energy). An overview of the available experimental data and similar large eddy simulation studies is presented. A detailed analysis of all accumulated data demonstrates satisfactory agreement between them with a dispersion of the order of 10% (for the main integral flow parameters). A detailed comparison of the results obtained by single- and double-precision numerical methods using Ansys Fluent did not reveal any noticeable discrepancies for the integral and local flow parameters, as well as spectral characteristics. It is shown that the behavior of the dynamic system of the fluid dynamic equations computed with single precision is stable by Lyapunov and does not lead to any loss of accuracy. The reconstructed attractors of the dynamic systems in the phase space are limited by an ellipsoid.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

The results of large-eddy simulation of the flow over a circular cylinder for the Reynolds number Re = 130,000 are presented. This work is a logical continuation of previous studies, where the large-eddy simulation was verified on external aerodynamic problems of various bluff bodies for the Reynolds numbers, Re = 3,900 [18,21,26], Re = 20,000 [19], Re = 40,000 − 50,000 [22,23,24]. The present results can be used as a basis for further development of active flow control and boundary layer separation technology using trapped vortex cells [25].
The goals and objectives are as follows:
  • verification and validation of the large eddy simulation (LES) to study turbulent separated flows and external aerodynamic problems for Reynolds numbers of practical interest. Review of available experimental data and similar results obtained using LES. Comparison of results computed using two platforms, Ansys Fluent [3] and OpenFOAM [43].
  • Evaluation of the accuracy of LES using coarse and medium-size computational grids with the number of cells in the range of 10 − 25 million, which is of practical interest in industry.
  • Analysis of results obtained using single-precision arithmetic. As a rule, the use of numerical methods and algorithms with single precision allows achieving a significant increase in computational efficiency due to a decrease in the RAM memory consumption and low-level optimization in programming both classical processors (CPU) and graphics accelerators (GPU).
  • Further application of stability theory and Lyapunov metrics to analyze the turbulent flows as dynamic systems.
The flow over a circular cylinder at different Reynolds and Mach numbers is a generally recognized benchmark in both computational and experimental aerodynamics. For the specific Reynolds number, Re = 130,000 , the pioneering LES work can be considered Breuer’s [5], which investigated numerical schemes, computational grids, and subgrid scale models. Cao and Tamura [7] focus on the study of three-dimensional vortex structures in the wake of a cylinder by analyzing the periodicity (modulation) of time series of aerodynamic coefficients. Lloyd and James [16] test LES on fairly coarse computational grids for the Reynolds numbers, Re = 63,000 − 500,000 . Yeon et al. [45] present detailed results of numerical simulation for the several flow regimes: sub-critical ( Re = 126,000 ), critical ( Re = 250,000 ) and post-critical ( Re = 757,000 ). Much attention is paid to estimating the required linear size of the computational domain in the spanwise direction. For Re = 126,000 , a fairly satisfactory agreement between predictions and experimental data was obtained. Plata et al. [34] utilize an adapted LES based on the Galerkin method for the Reynolds numbers, Re = 3,900 , Re = 20,000 , and Re = 140,000 .
The work of Cantwell and Coles [8] can be considered as a fundamental experimental study, where in addition to the integral flow parameters (such as forces, vortex shedding frequency and pressure coefficient) local distributions of the velocity field in the streamwise and vertical directions are given, which is an important aspect for validation and verification of the LES technique. In addition to the work of Cantwell and Coles [8], a number of experimental studies are available in the literature, where alternative data can be found, but mainly limited to integral characteristics [2,15,29,37].
Available data on the effect of floating-point arithmetic on the accuracy of computational fluid dynamics (CFD) problems are limited to the work of Brogi et al. [6], where the effect of single-, double- and mixed-precision (SP, DP and SPDP hereinafter, respectively) arithmetic was presented using the OpenFOAM toolbox. They showed, on the one hand, that the use of SP and DP for a number of laminar flows does not affect the accuracy of the solution. On the other hand, for a number of the turbulent flows, the opposite results were obtained. For the turbulent flows, round-off errors in nonlinear terms of the Navier-Stokes equations lead to an increase of high-frequency disturbances (or noise), and, in some cases, can lead to solution’s divergence for systems of linear algebraic equations. Thus, Brogi et al. [6] failed to obtain a converged solution for the isotropic decaying turbulence test case using the `rhoPimpleFoam’ application and single-precision arithmetic. Here, they recommend using the concept of mixed-precision arithmetic, SPDP, implemented in OpenFOAM (starting from v1906), where matrix operations are computed within DP and all other underlying code is compiled and executed within SP. They also show the importance of the turbulence model and the grid cell sizes, i.e., implicit numerical diffusion can compensate the high-frequency perturbations caused by rounding errors in the case where the linear scales of the smallest eddy structures are comparable or smaller than the size of the grid cell.
The article is presented in five parts. The first two sections are devoted to the problem statement and aspects of numerical and mathematical modeling. Then the main results are presented and compared with the already available experimental and numerical data. The fourth part provides a brief discussion and critical review. At the end, the main conclusions are presented.

2. Problem Statement, Computational Grid And Brief Aspects Of Mathematical Modeling And Numerical Methods

A brief problem statement, description of the computational domain and finite-volume grids, as well as some aspects of mathematical modeling and numerical methods are presented.
The turbulent flow is characterized by the following Reynolds and Mach numbers: Re = ρ ∞ U ∞ D / μ ∞ = 130,000 , M = U ∞ / a ∞ = 0.05 , respectively. Here ρ is the density, U is the velocity, a is the speed of sound, μ is the dynamic molecular viscosity, D is the diameter of cylinder. The subscript ∞ indicates the flow parameters at the inlet boundary.

2.1. Computational Grids

Numerical simulations are performed on two types of meshes:
  • unstructured, hexahedral with different levels of adaptation (Figure 1b-d; here and below the abbreviation HM is used). The computational domain is defined as a rectangular parallelepiped with dimensions 30 D × 20 D × 10 D in the x, y and z directions, respectively. As a starting point, the computational block is divided into 60 × 40 × 20 nodes. Next, the grid was successively adapted in three iterations with a coefficient of 2 × 2 × 2 in the regions from y / D = − 4 to y / D = 4 , y / D = − 2.25 to y / D = 2.25 and y / D = − 1.9 to y / D = 1.9 . The cylindrical region with a radius of 1.75 , located in the center of the Cartesian coordinates, was adapted at the next level with the same coefficient. The last iteration was applied to a rectangular region with dimensions x / D = − 1 to x / D = 2 and from y / D = − 1 to y / D = 1 . Grid adaptation at all levels completely covered the computational region in the spanwise direction. Thus, the circumferential grid resolution of the cylinder is N θ = 184 , and along the span, N z = 640 ( L z / D = 0.0156 ). For adequate resolution of the boundary layer on the surface of the cylinder, a viscous sub-grid was added with a minimum dimensionless cell height, y + = h 1 s t / D = 4 × 10 − 4 , an expansion factor of 1.04 , and a total number of layers of 40, respectively. The total grid size is 2.43 × 10 7 cells.
  • curvilinear, orthogonal O-type (Figure 1, e-g; here and below the abbreviation OM is used) with a dimension of 444 × 444 × 64 ( 1.36 × 10 7 cells) in the x, y and z directions, respectively. The length of the computational domain in the streamwise direction is 25 × D , and in the spanwise direction, L z = π × D . The grid nodes are radially relaxed from the cylinder towards the outflow boundary with a dimensionless height of the first cell y + = r / D = 1.25 × 10 − 4 and an expansion coefficient in the radial direction of 1.06 .

3. Brief Aspects Of Numerical Simulations

Large eddy simulation is performed using CFD platforms Ansys Fluent 2021R1 [3] and OpenFOAM v2212[43] (hereinafter, the abbreviations AF and OF are used, respectively). To close the filtered, Favre-averaged Navier-Stokes equations, the differential subgrid scale model for the turbulence kinetic energy (k-model) and its dynamic modification [11,41,46] are used. Both numerical platforms are based on the finite volume method (FVM) implemented as a pressure-based solver [13] using a limited central differencing scheme of the second-order (bounded CDS-2) for the velocity, a second-order upwind scheme (SOU) for the remaining nonlinear convective terms and an implicit Euler method (bounded BDF-2) for time integration [10]. The time integration step is chosen to ensure that the local Courant number is less than one, C F L < 1 . The system of linear algebraic equations is solved using the algebraic multigrid method (AMG) accompanied by the additive correction strategy [12] and the classical iterative Gauss-Seidel procedure in AF and the symmetric iterative Gauss-Seidel method for all dependent variables except pressure, which is calculated using the geometric multigrid method (GAMG) [44] in OF.
For spectral analysis of time series, the classical methods of the fast Fourier transform (FFT), Welch periodograms [42] and continuous wavelet transform (CWT) are used, which detailed description can be found in [18]. The Lyapunov metric, described in detail in our previous work [26], is used to study the phase properties of dynamic systems.
The formulation of boundary and initial conditions is similar to that presented earlier [18] with the exception of setting the velocity field at the inlet boundary, and corresponds to the free-stream values of the Reynolds and Mach numbers, Re = 130,000 and M = 0.05 . The perfect gas model is used to account for compressibility. Molecular viscosity and thermal conductivity are assumed to be constant. The Prandtl number was taken to be 0.75 , and the ratio of specific heat capacities was 1.4 .
The characteristic convective time is defined as the ratio of the streamwise length of the computational domain to the free-stream velocity, τ c o n v = L x / U ∞ . The solution is considered statistically converged after τ c o n v > 4 . To obtain statistically independent data, time averaging is performed over an interval equal to N v s = 25 (here N v s is the vortex shedding cycle or the period of oscillatory motion). The averaging operator is denoted as 〈〉.

4. Results

The runs matrix is given in Table 1. It should be noted that LES using OF were performed on an unstructured hexahedral grid, while the O-type grid was used to study the effects of single- and double-precision arithmetic using AF. The following subgrid scale models were tested: the differential model for the kinetic energy (or the k-model, with coefficients C k = 0.07 and C ϵ = 1.042 , hereinafter TKE) and its dynamic modification (hereinafter dTKE). The results are compared with experimental data of Achenbach [2], Cantwell and Coles [8], Schewe [37], Norberg [29], Lim and Li [15], and LES data presented by Breuer [5], Cao and Tamura [7], Lloyd and James [16], Yeon et al. [45] and Plata et al. [34]. A critical remark should be done here: in physical experiments of external aerodynamics, an important factor is the turbulence intensity and the uniformity of the incoming flow, which in turn is determined by the quality of a wind tunnel. Sometimes there is a possibility that the laminar-turbulent transition will occur directly in the boundary layer before its separation from the bluff body surface. In this case, a number of integral parameters, such as the separation angle, pulsations of the lift coefficient, and the length of the recirculation zone can be significantly overestimated/underestimated. In addition, a flow bifurcation is possible, as in the case of the flow over a circular cylinder at Re = 3,900 [26].

4.1. Unsteady Flow Field

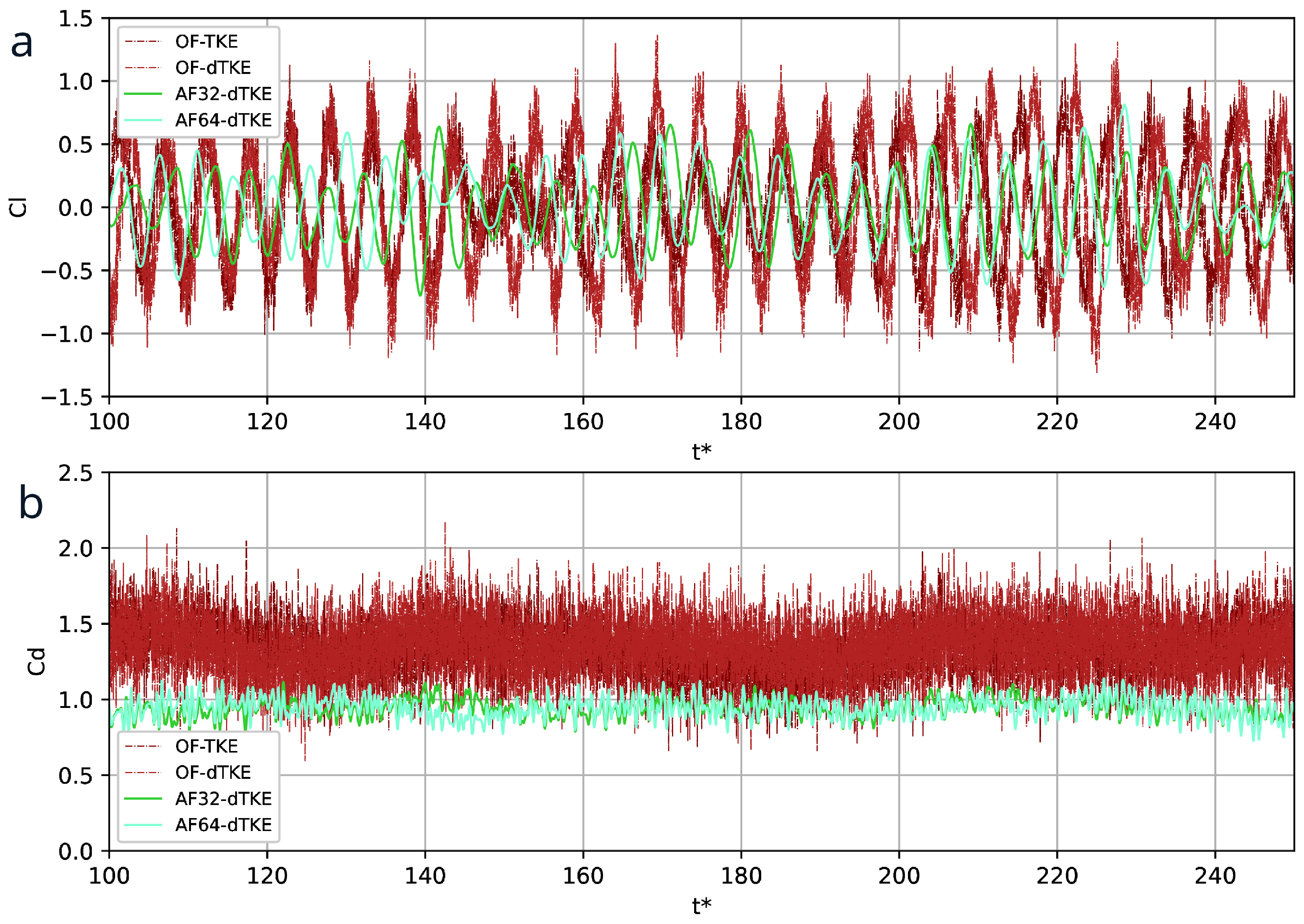
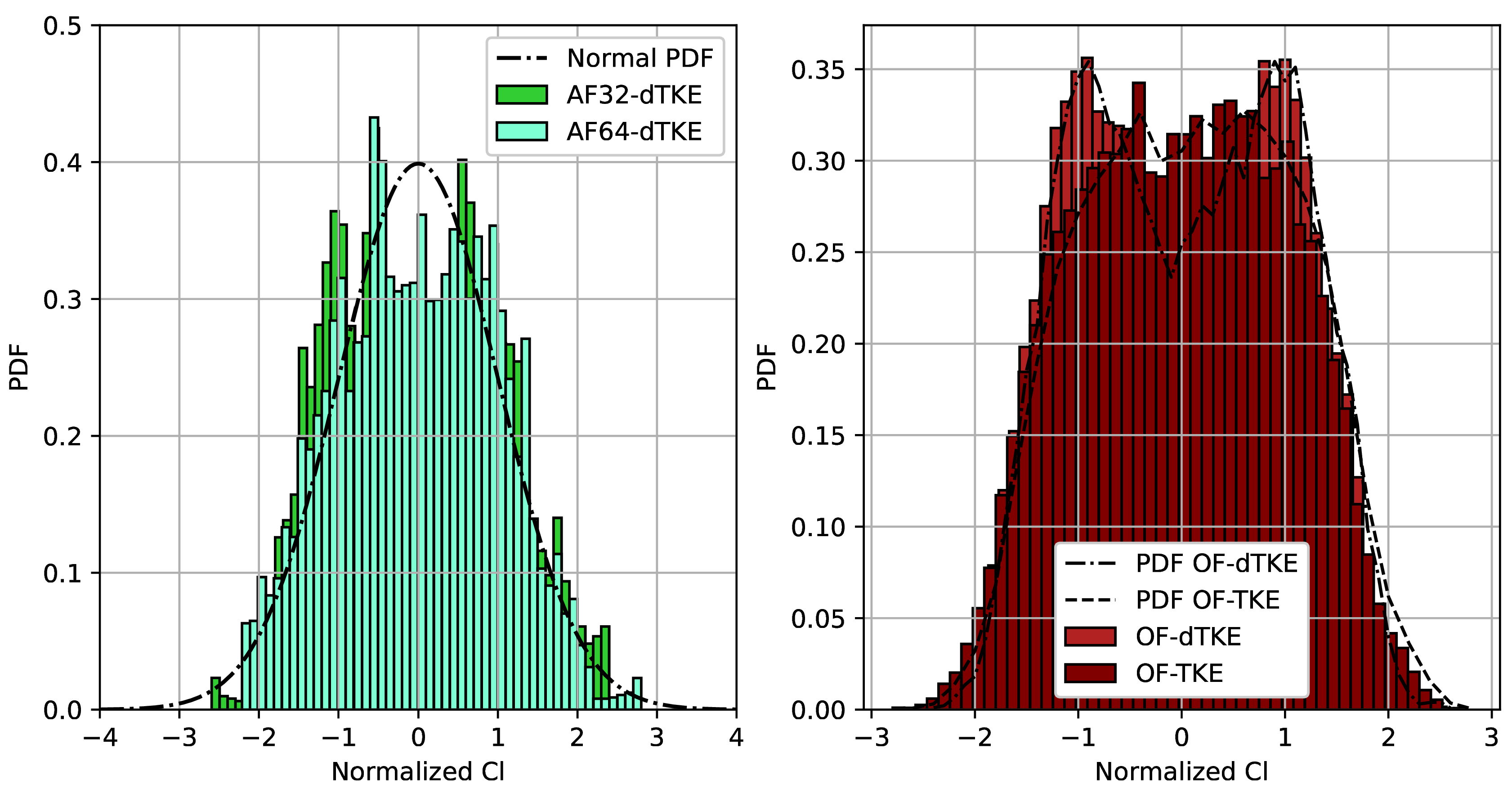
The dynamics of the lift and drag coefficients over time is shown in Figure 2. Figure 3 illustrates the formation of a vortex street and coherent energy structures using the Q-criterion, Q = S 2 − Ω 2 = 10 4 (where S is the strain rate tensor and Ω is the vorticity). Figure 4 shows the probability density function of the normalized lift coefficient C l . Two different forms of probability distribution obtained for the AF32-dTKE, AF64-TKE and OF-TKE, OF-dTKE runs, respectively, are clearly visible. OF-TKE and OF-dTKE have a distribution close to bi-modal, having two widely spaced and symmetrical peaks. For AF32-dTKE and AF64-dTKE, the histograms reproduce the shape of the Gaussian curve (or normal distribution) quite well. In practice, for the sub-critical flow over a cylinder, the normal distribution of C l obtained by Schewe [37], as well as in numerical results by Cao and Tamura [7], is confirmed. The physical interpretation of this phenomenon is that random modulations of amplitude and frequency during the formation and shedding of vortices and their subsequent convection downstream the wake contribute to the formation of a distribution close to normal [7]. The difference in distribution density between AF32-dTKE, AF64-TKE and OF-TKE, OF-dTKE, may explain the observed difference in aerodynamic coefficients observed in Figure 2.

4.2. Integral Parameters

Table 2 presents the main integral flow parameters, such as the lift ( C l ), drag ( C d ) and pressure base suction ( C p b ) coefficients, the Strouhal number ( St p ), the separation zone length ( L r ) and the primary boundary layer separation angle θ s .
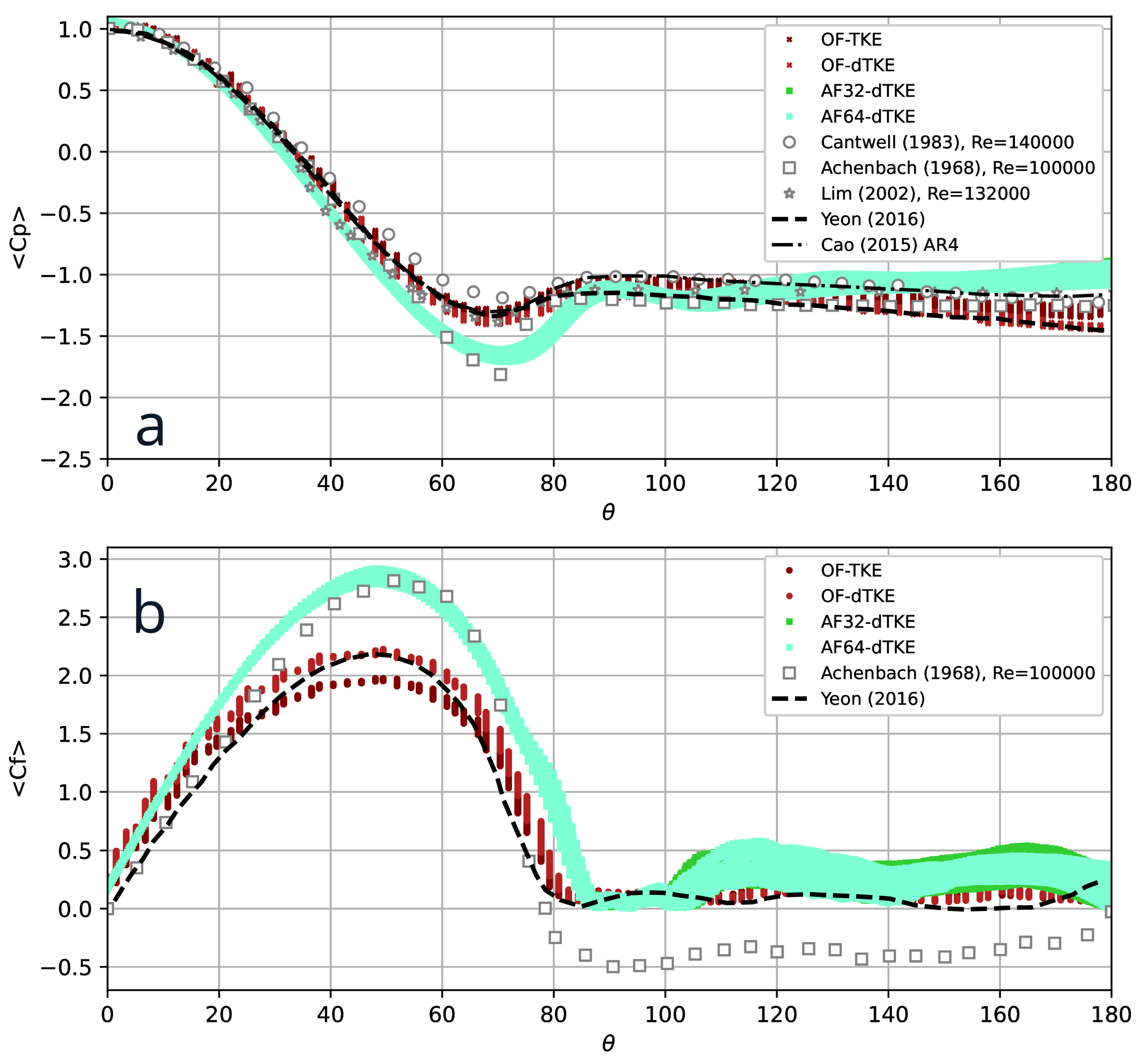
The distribution of the pressure coefficient 〈 C p 〉 = 2 ( 〈 p 〉 − p ∞ ) / ( ρ ∞ U ∞ 2 ) (here p ∞ is the free-stream pressure) over a circular cylinder is shown in Figure 5,a. The numerical results obtained by OF-TKE, OF-dTKE are in satisfactory agreement with experiments of Cantwell and Cowles [8] and Lim and Li [15], as well as with numerical data of Cao and Tamura [7] and Yeon et al. [45], while the 〈 C p 〉 distributions by AF32-dTKE and AF64-dTKE better approximate experimental data of Achenbach [2].
In Figure 5,b the friction coefficient along the cylinder surface 〈 C τ 〉 = 2 ( 〈 τ 〉 − p ∞ ) / ( ρ ∞ U ∞ 2 ) (here τ is the friction) obtained in the present LES is compared with experiment by Achenbach [2]. The OF-TKE, OF-dTKE runs are in satisfactory agreement with numerical data by Yeon et al. [45], and qualitatively reproduce the distribution of 〈 C τ 〉 by Achenbach [2]. It should be noted that the experimental measurements of Achenbach [2] for Re = 100,000 are used. The AF32-dTKE and AF64-dTKE runs show qualitative agreement with data by Achenbach [2] starting from the stagnation point ( θ s = 0 ∘ ) to the separation point θ ≈ 80 ∘ . The separation angle θ s is determined from the condition of zero shear stress on the cylinder surface. From experiments of Achenbach [2] and Cantwell and Cowles [8] the boundary layer separation occurs at θ s = 77 − 78 ∘ . The computed values of θ s are slightly overestimated θ s = 83 − 85 ∘ but consistent with data by Yeon et al. [45] ( θ s = 81 ∘ ). In the results by Breuer [5] the separation point is shifted even further downstream θ s = 91 − 94 ∘ . The nature of the curves 〈 C τ 〉 obtained in the simulations on the back side of the cylinder indicates the presence of secondary vortex structures, however, due to the lack of experimental data, their quantitative assessment is not given here.
The mean base suction coefficient 〈 C p , b 〉 is defined as the pressure coefficient on the cylinder surface at the point θ = 180 ∘ . Its computed values by OF-TKE, OF-dTKE, AF32-dTKE and AF64-dTKE were 〈 − C p , b 〉 = 1.36 and 〈 − C p , b 〉 = 1.01 , respectively. At the same time, experimental results yield values in the range 〈 − C p , b 〉 = 1.15 − 1.25 [2,8,15]. A wide range of values of 〈 C p , b 〉 is also observed in available LES works: from 〈 − C p , b 〉 = 0.86 − 1.01 [16] to 〈 − C p , b 〉 = 1.51 − 1.64 [5,34,45].
The base suction pressure coefficient is related to the drag ( C d ) and lift ( C l ) coefficients, which are calculated by integrating the pressure over the cylinder surface: C d = 2 F x / ( ρ ∞ U ∞ 2 A ) and C l = 2 F y / ( ρ ∞ U ∞ 2 A ) . Here F x and F y are the forces acting on the cylinder in the streamwise and vertical directions, respectively. A = L z × D is the surface area of the cylinder projected along the span. The mean drag coefficient was 〈 C d 〉 = 1.34 for OF-TKE, OF-dTKE and 〈 C d 〉 = 0.94 for AF32-dTKE and AF64-dTKE, respectively. While the experimental value of the drag coefficient converges to 〈 C d 〉 = 1.2 [2,8,15,37], the numerical values obtained from different LES studies show a large scatter 〈 C d 〉 = 0.89 − 1.43 [5,7,16,34,45]. It is interesting to note that the mean value predicted by LES including the present results converges to 〈 C d 〉 = 1.19 ± 0.2 % with a dispersion of about 20 % . The lift coefficient pulsations obtained in the present work ( 〈 C l ′ 〉 = 0.27 − 0.41 ) are consistent with available experimental ( 〈 C l ′ 〉 = 0.25 − 0.52 [8,29,37]) and numerical data ( 〈 C l ′ 〉 = 0.3 − 0.63 [7,16,45]).
An important parameter is the length of the recirculation zone L r . It is well-known that the measurement of L r in experiments often strongly depends on the early laminar-turbulent transition in separated shear layers, usually caused by the incoming turbulence intensity, when the early transition corresponds to a shorter length of the separated zone [14,26]. From the LES point of view, important parameters are the statistical convergence [33], the free-stream turbulence intensity [26], the spanwise length of the computational domain [7] and, in general, the numerical dissipation of the computational methodology (grids, convective schemes, algorithms, etc.) [5,16,34,45]. The experimental values of the recirculation zone length are limited by data of Cantwell and Cowles [8], L r = 0.4 − 0.5 . These values correlate quite satisfactorily with numerical data by [5,34,45], L r = 0.42 − 0.63 and the present results by OF-TKE and OF-dTKE, L r = 0.55 − 0.58 . At the same time, AF32-dTKE and AF64-dTKE show L r = 0.68 , when the length of the separation zone significantly exceeds the experimental measurements [8].

4.3. First And Second Order Statistics

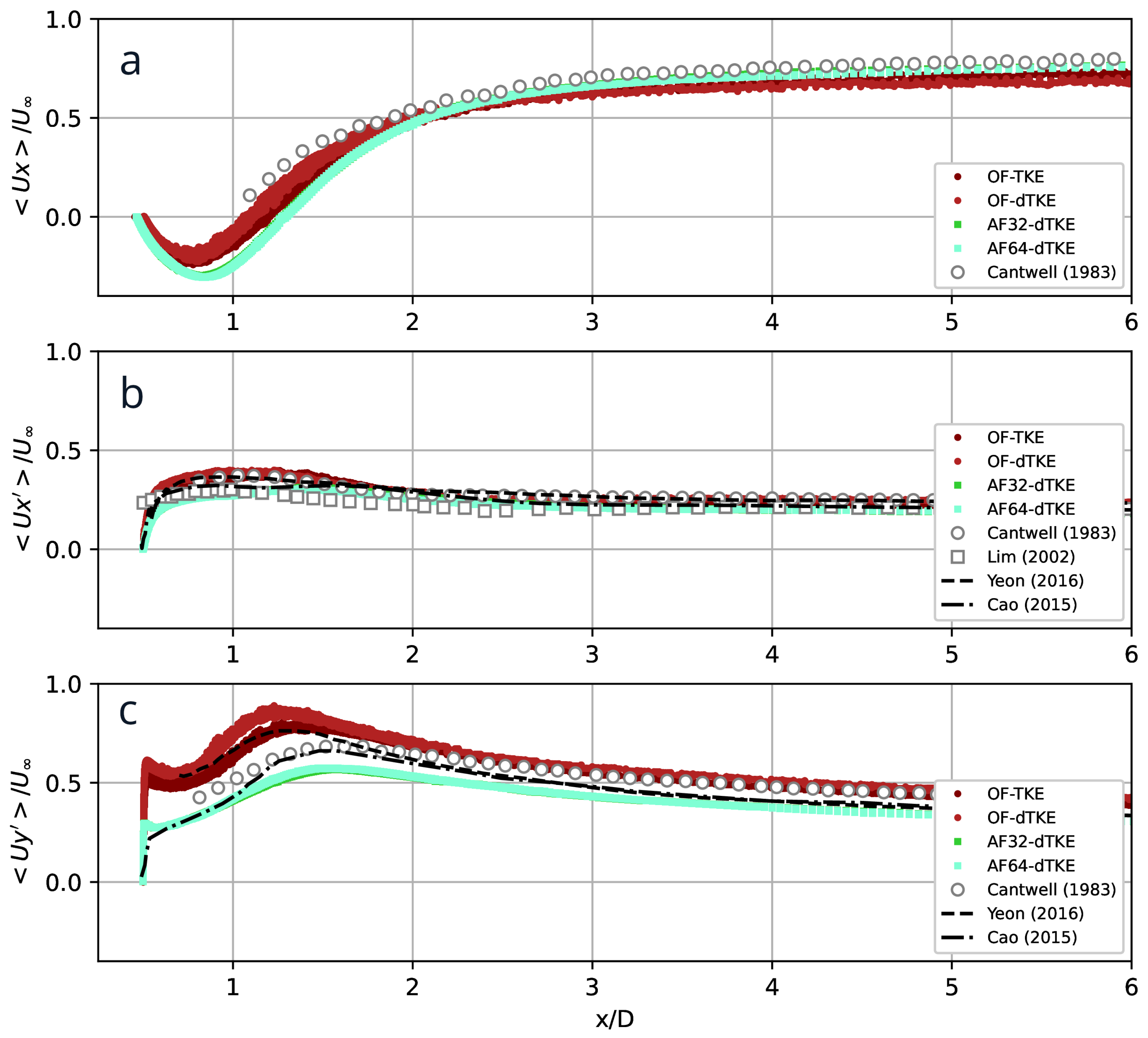
The distribution of the streamwise velocity U x along the central axis is shown in Figure 6,a. It is clearly seen that the present LES are in satisfactory agreement with experiment by Cantwell and Coles [8] in the far wake ( x / D > 2 ), while in the vicinity of the cylinder the results generally overestimate the length of the recirculation zone. It is interesting to note that the flow intensity (minimum values of the streamwise velocity) in the core of the separation zone obtained by AF32-dTKE and AF64-dTKE differs by approximately 1.5 times from the values obtained by OF-TKE and OF-dTKE. The pulsations of the streamwise velocity U x ′ along the central axis (Figure 6,b) obtained by OF-TKE and OF-dTKE are in satisfactory agreement with measurements by Cantwell and Coles [8] and with LES data by Cao and Tamura [7] and Yeon et al. [45]. The results by AF32-dTKE and AF64-dTKE are closer to experiment by Lim and Lee [15].
The predicted pulsations of the vertical velocity U y ′ along the central axis and experiment data by Cantwell and Coles [8] are compared in Figure 6,c. The results by AF32-dTKE and AF64-dTKE match numerical data by Cao and Tamura [7] and are underestimated by about 15 % compared to experiment of Cantwell and Coles [8]. The results by OF-TKE and OF-dTKE diverge by about 30 % from the physical measurements in the near wake ( x / D < 2 ), after which they begin to converge smoothly. The same trend is observed for LES results by Yeon et al. [45].
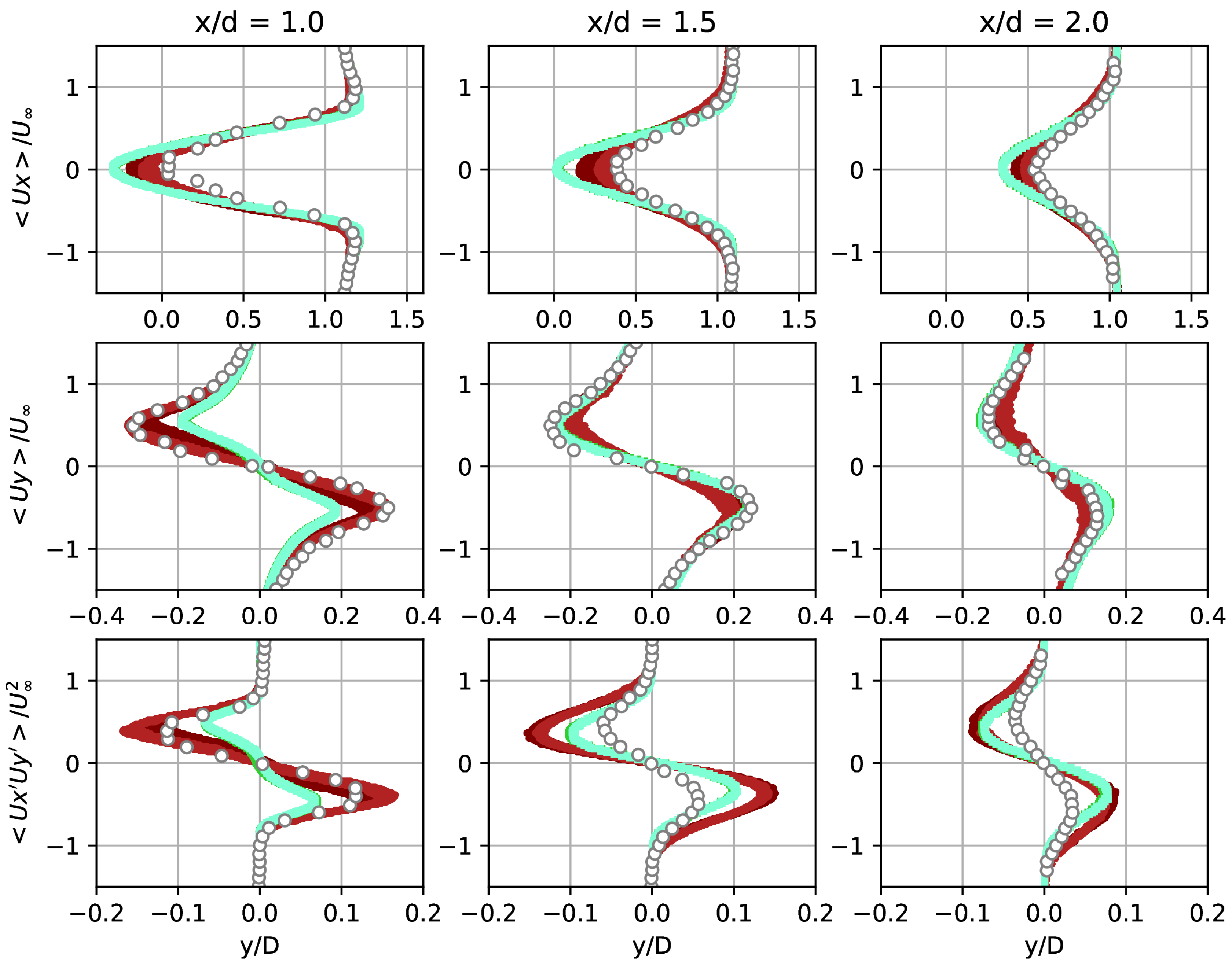
In Figure 7 the predicted and experimental profiles of the mean streamwise and vertical velocities in the radial cross-section of the computational domain are compared at x / D = 1 , 1.5 , and 2. The deficit observed in the present LES in all three cross-sections for the streamwise velocity with respect to the experimental data is explained by the general overestimated value of the separation zone length. For the vertical velocity, satisfactory agreement was obtained between the present LES and experiment by Cantwell and Coles [8], with the exception of x / D = 1 , where a small disagreement is also observed for AF32-dTKE and AF64-dTKE. Figure 7 shows the radial profiles of the root-mean-square values of the normal Reynolds stresses, 〈 U x ′ U y ′ 〉 , where, in general, qualitative agreement between the present and experimental data is observed. The discrepancies for the peak values are approximately 20 % .

4.4. One-Dimensional Energy Spectra

The flow over a circular cylinder at Re = 130,000 belongs to the sub-critical regime, when the boundary layers remain laminar ( 1000 < Re < 200,000 ). In this range of Reynolds numbers, both absolute and convective instability are present: asymmetric vortex shedding (Benard/von Kármán instability) and Kelvin-Helmholtz (KH) instability in the shear layer [35]. The vortex instability is periodic and has a characteristic frequency f v s = St U ∞ / D , where St is the Strouhal number. Using FFT for the vertical velocity in the near wake of the cylinder ( x / D = 1.5 , y / D = 0 ) the computed Strouhal numbers were, St = 0.19 for AF32-dTKE and AF64-dTKE, and St = 0.21 for OF-TKE and OF-dTKE, respectively. It should be noted that if FFT applied for the lift coefficient, the Strouhal numbers are slightly different: St = 0.19 and St = 0.18 for AF32-dTKE,AF64-dTKE and OF-TKE, OF-dTKE, respectively. The experimental value of the Strouhal number for Re = 130000 varies within St = 0.18 − 0.20 [8,15,29,37]. The LES data from Table 2 also show a small dispersion, St = 0.177 − 0.22 .
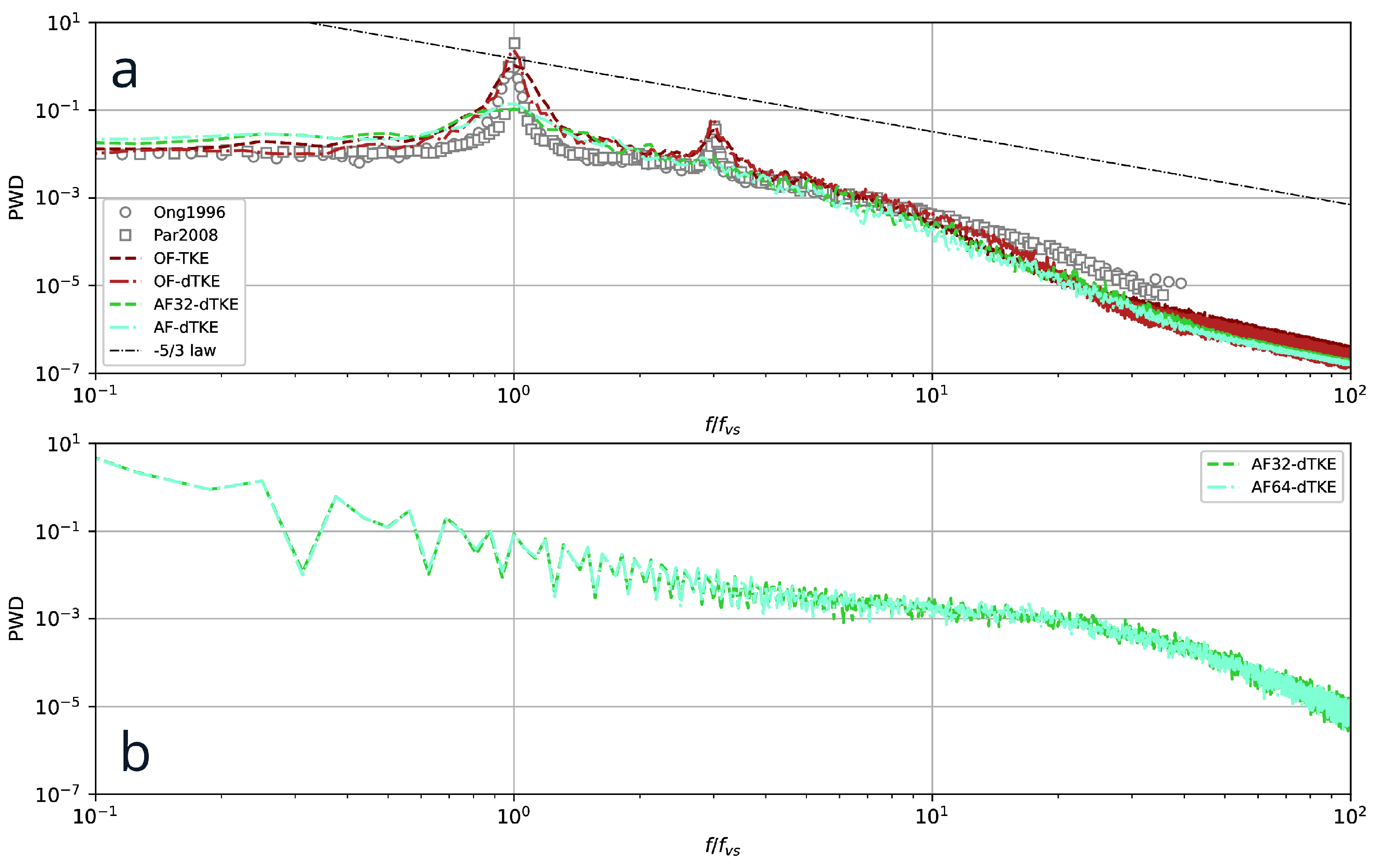
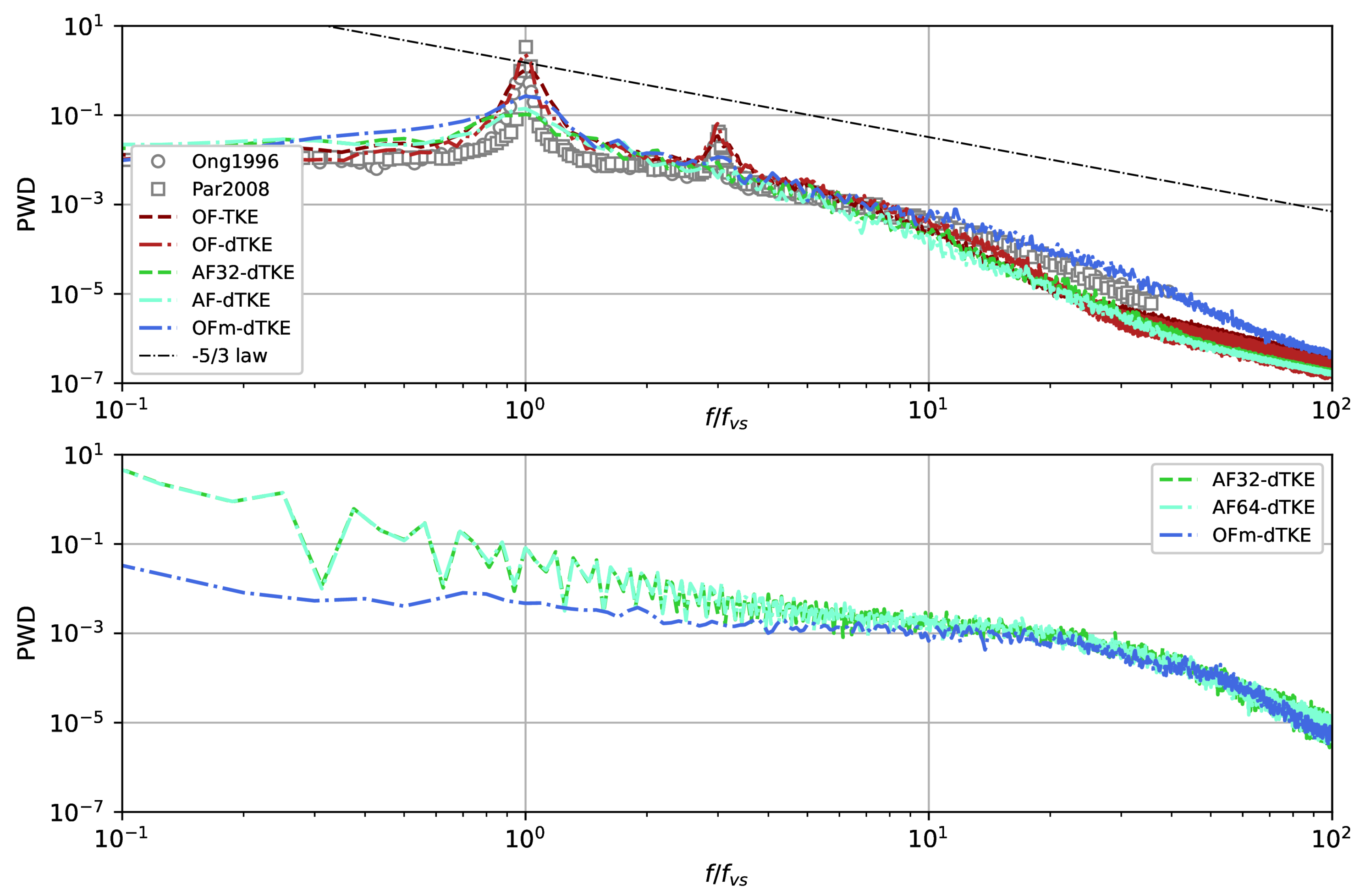
In Figure 8,a the one-dimensional energy spectra, normalized by the characteristic Strouhal frequency ( f v s ), are compared with the experimental measurements of Ong and Wallace [31], Parnaudeau et al. [33] and the − 5 / 3 power law. The Welch’s periodogram technique [42] is used to smooth the spectral curves. Also, to increase the statistical significance [14] the spectra are averaged in the spanwise direction. It is well known that the effect of excessive dissipation of the numerical method usually leads to rapid attenuation of the spectrum and unsatisfactory reproduction of the inertial interval [14,18,27]. In the present work the inertial interval is clearly reproduced over a wide range of wave numbers, which agrees well with experiments by Ong and Wallace [31] and Parnaudeau et al. [33]. The presence of small-scale, coherent energy structures that remain active far from the cylinder, shown in Figure 3. All predicted curves in Figure 8,a collapse satisfactorily, up to f / f v s ≈ 1 , after which they begin to decay slowly.
The dynamics of boundary layer separation is similar to the mixing layer, when the length of the recirculation zone is large enough. The Kelvin–Helmholtz (KH) mechanism underlying the shear layer instability has a characteristic frequency f k h ) for Re > 1200 , with which the mixing layer collapses into highly concentrated vortices [39]. At present, a sufficiently large amount of experimental data has accumulated to analyze the dependence of the characteristic frequency of the mixing layer on the Reynolds number for various simple geometric figures. 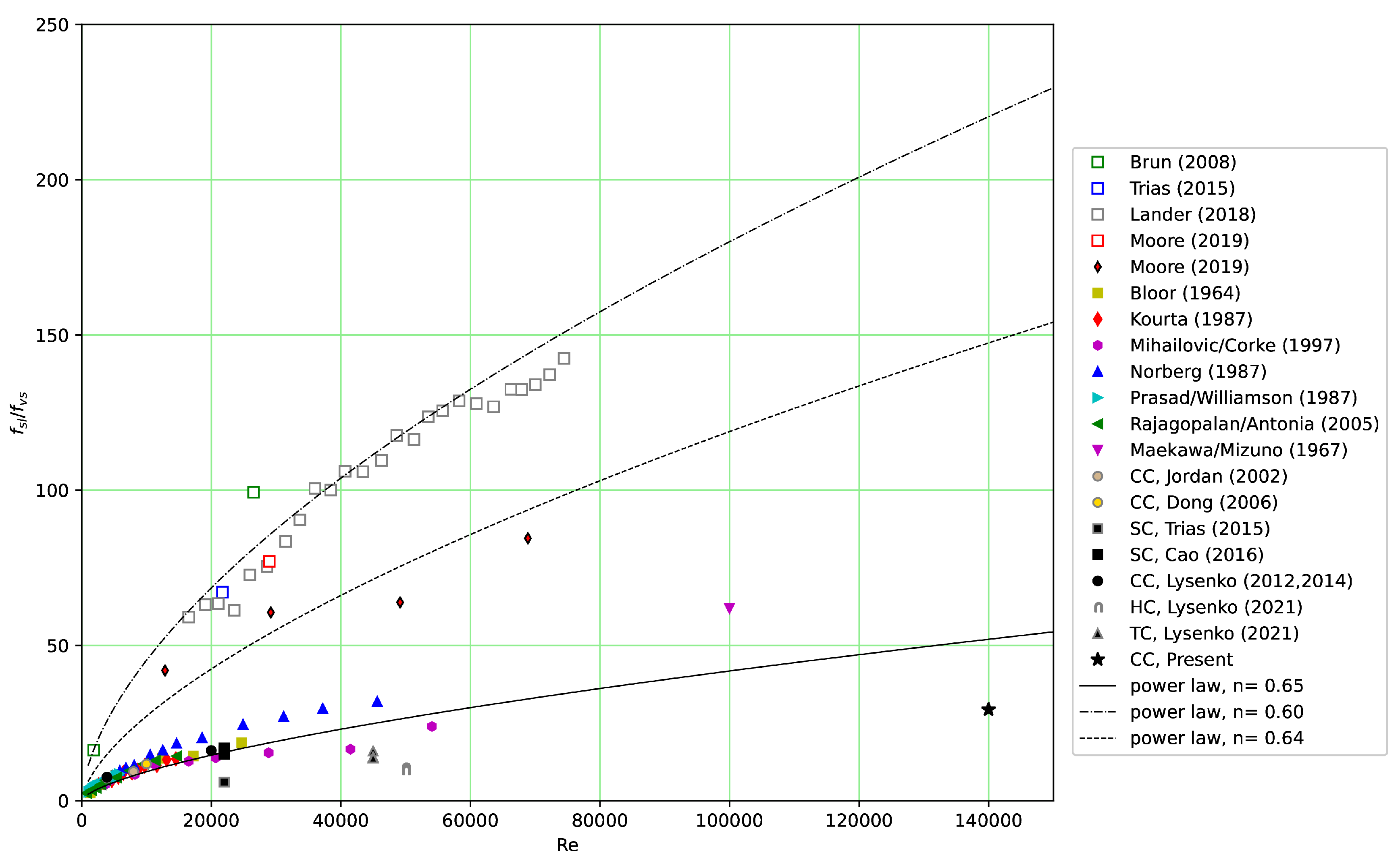Some data are presented in Figure 9, and the reader can find a further analysis of them in [23,24].
In the LES framework of the flow over a circular cylinder at Re = 3,900 [18] and Re = 20,000 [19] the values f k h / f v s = 7 − 8 and f k h / f v s = 16.2 were computed, respectively. These results are in good agreement with the available experimental and numerical results [9]. In the work of Cao and Tamura [7] for Re = 130,000 the numerical values of the characteristic peak frequencies f k h / f v s = 15 − 17 are presented. The present LES for Re = 130,000 (AF32-dTKE and AF64-dTKE) are in the range of f k h / f v s ≈ 28.9 . Based on these numbers, it is possible to show a quadratic dependence of the characteristic instability frequency on the Reynolds number of the form Re taking into account the thickness and separation velocity of the laminar boundary layer, which is in good agreement with Bloor [4], who established the exponent, n = 0.67 : f k h / f v s = A × Re 0.67 . The present results are well approximated by the adjusted value n = 0.65 (Figure 9).
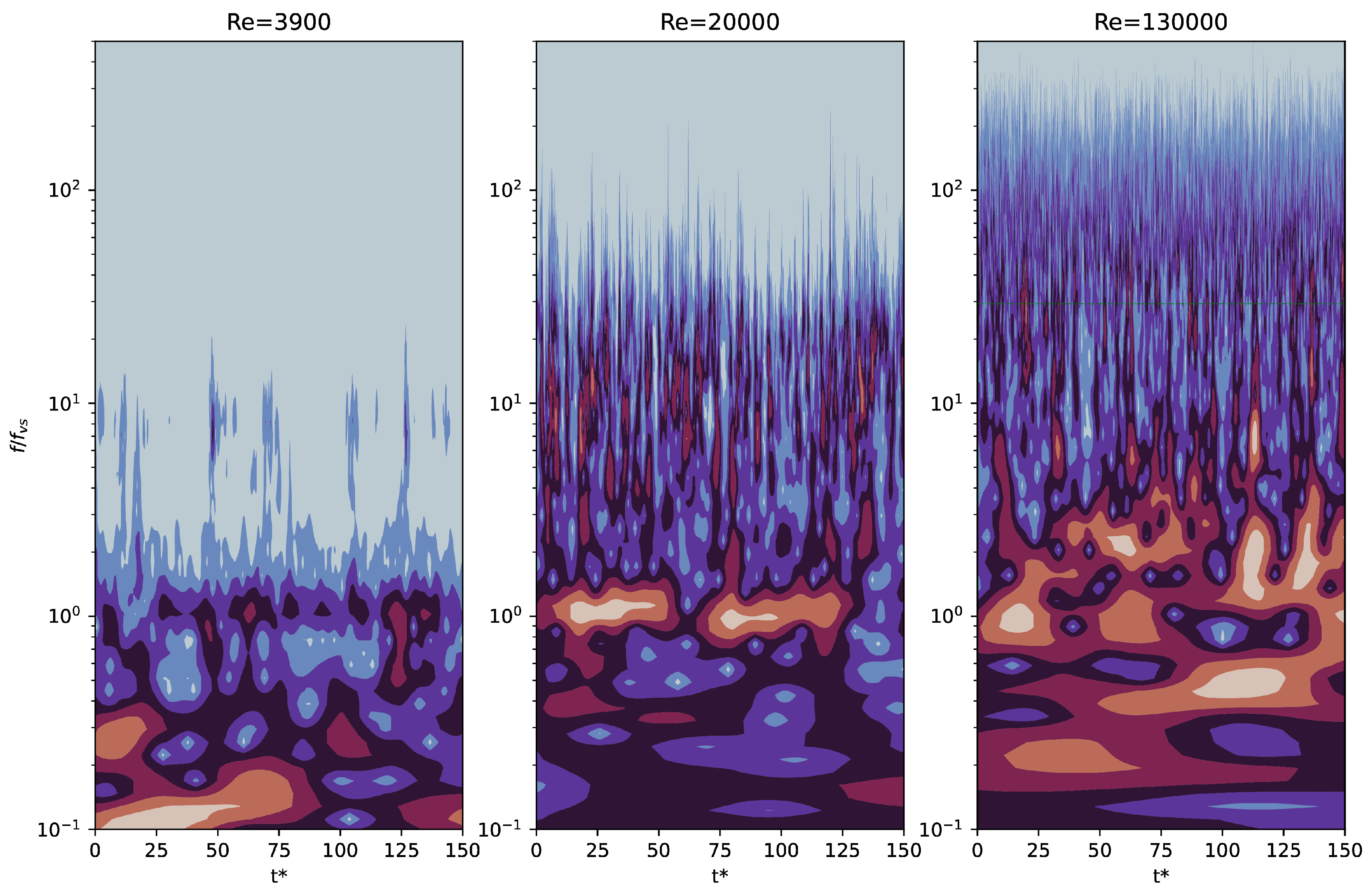
Figure 8,b shows the curves of the energy spectra, where a relatively broadband frequency range of f k h / f v s is visible. To quantitatively estimate the average frequency of the KH instability, the one-dimensional wavelet transform is used. Figure 10 presents the CWT results for the vertical velocity measured in the shear layer near the vicinity of the circular cylinder for the different Reynolds numbers. It is clearly seen that both the BK and KH instabilities occur only periodically and have an intermittent character. The KH peaks do not always appear at the same frequency, but are localized in a certain frequency range and also depend on time. A tendency for the energy density to increase with increasing Reynolds number is clearly visible.

4.5. Lyapunov Metric

In this section, an attempt is made to quantitatively and qualitatively estimate the difference between the two dynamic systems AF32 and AF64 using the Lyapunov metric. The modified procedure, proposed by Nastak et al. [28] and later adapted by Lysenko [26], is used for LES of the flow over a circular cylinder.
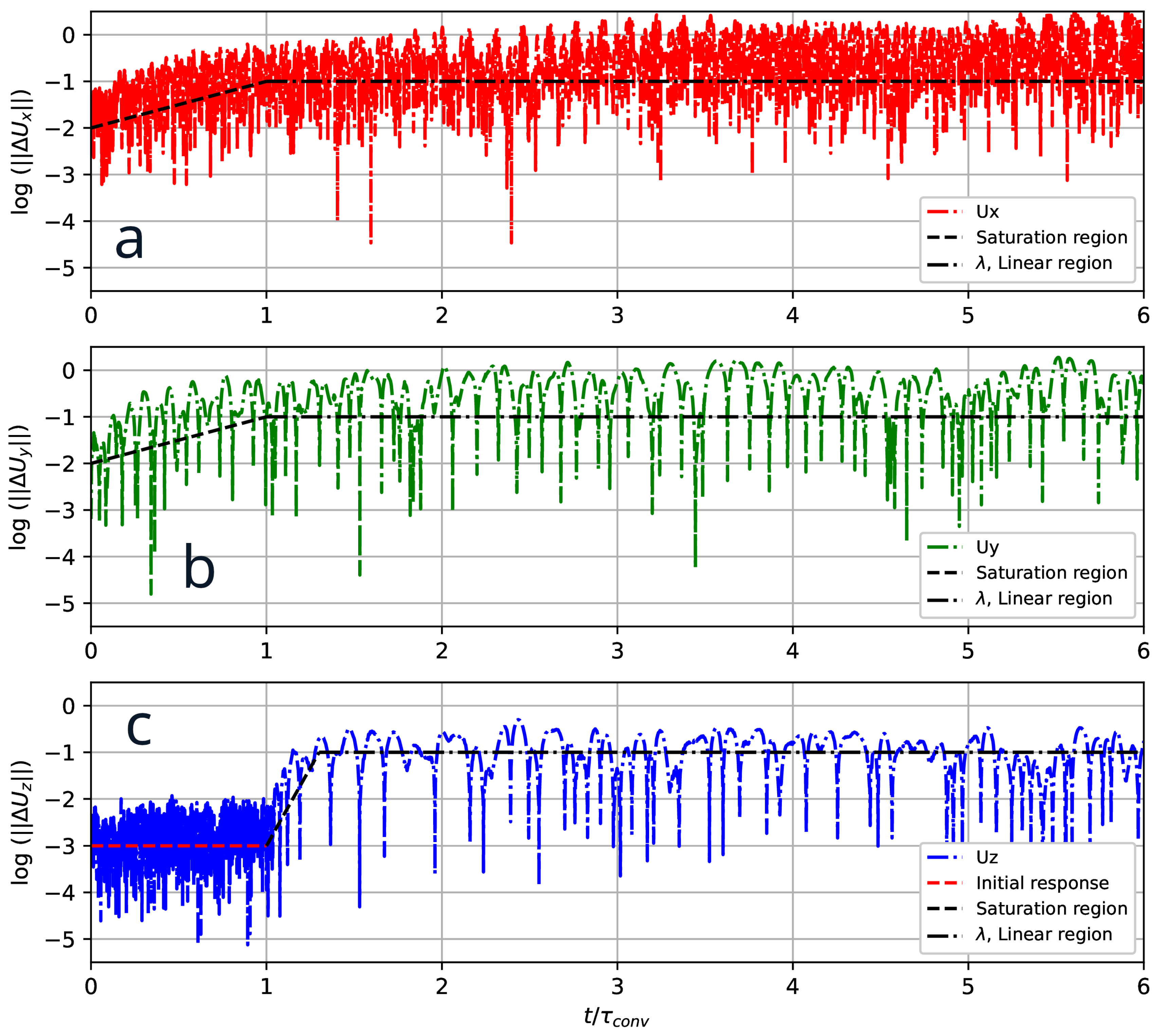
To solve the problem, the same numerical methodology and computational grid (similar to AF32 and AF64) are utilized. Two scenarios are investigated. In the first case, single-precision arithmetic is used, in the second – double-precision. Simulations start at the same time t 0 . Both solutions are initialized with statistically converged data after reaching the convective time τ c o n v = 4 . Figure 11 compares the difference in phase trajectories obtained for two solutions, AF32 and AF64. To calculate the divergence, the L 2 -norm is used and it is assumed that the process is ergodic (the Lyapunov exponent does not depend on the initial conditions, when the level of initial perturbations is sufficiently small ϵ ≪ 1 [32]). In this case, the initial perturbations are the loss of accuracy due to round-off errors when going from DP to SP, i.e., for the C and C++ programming languages (in which both numerical platforms are implemented), ϵ ≈ ∥ 2 − 52 − 2 − 23 ∥ . The presented time evolution of the separation is similar to the work of Nastak et al. [28] and contains two separate regions: the linear region and the saturation region. It can be noted that the divergence increases with time, when the velocity fields first diverge from small structures to larger homogeneous isotropic structures over time [26,28]. Also, in Figure 11,c there is a well-defined region of the so-called initial pulse (the initial response region) [28], which is absent in the phase trajectories for the streamwise and vertical velocities.
The Lyapunov exponent is estimated from the slope of the separation curve in the logarithmic region and is shown as dashed lines in Figure 11. The slope of the Lyapunov exponent is related to the predictability time [28], which corresponds to t p ∼ 1.5 τ c o n v . In practice, the predictability time shows how quickly a dynamic system will transit from one state to another [26]. According to [28], the predictability time and the Lyapunov exponent can be used as quantitative information about the time horizon over which the phase transition can be modeled. The Lyapunov metric can also be used to study the stability of dynamic systems. So an important conclusion and a direct consequence of Figure 11 is that the dynamic system AF32 is stable by Lyapunov [17]. From Figure 11 it is clearly seen that after reaching the predictability time, saturation occurs, since the divergence of phase trajectories reaches an asymptotic: a statistically stationary state of both systems is reached.
Under some considerations it can be assumed that the concepts of turbulence and chaos are closely related [1,26,36]. Thus, the concept of an attractor for nonlinear dynamic systems from the chaos theory can be applied to the analysis the turbulent flows described by the Navier–Stokes equations. To reconstruct attractors, i.e., states of the phase space or the evolution of the system from the initial conditions, one can use a three-dimensional time signal of the computed norm of the dimension p, ∥ L p ∥ ≡ 1 / V ∫ V ( · ) p d V 1 / p (where V is the volume of the computational domain) using the Takens embedding method [38] in the same spirit as Alberti et al. [1] and Lysenko [26]. In practice, the second-order norm can be used to examine the behavior of the attractor in the phase space: Θ ( t ) = d ∥ U x ∥ d t , d ∥ U y ∥ d t , d ∥ U z ∥ d t (here the symbol t denotes time). 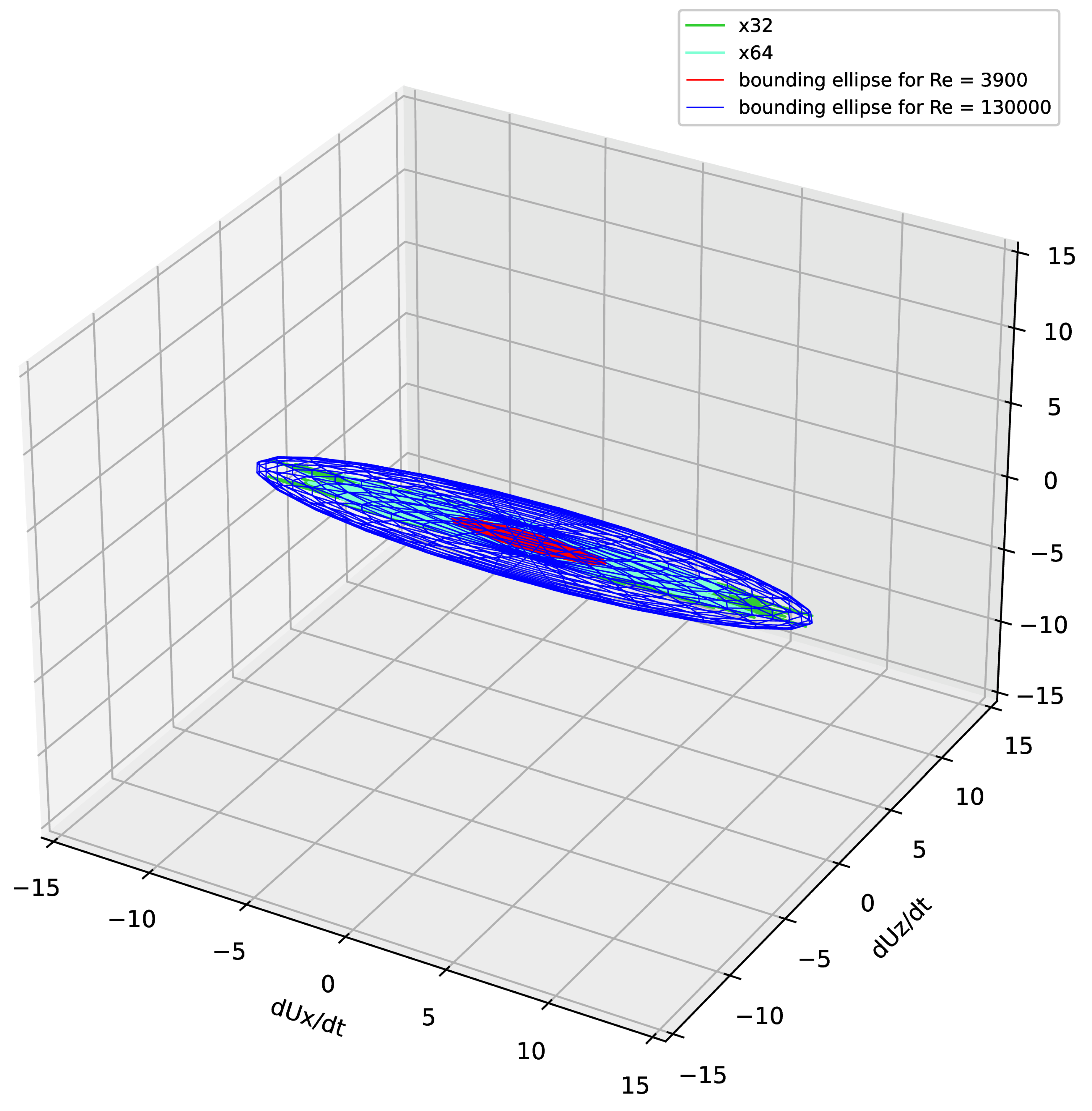Figure 12 shows the evolution of the AF32 and AF64 attractors in the three-dimensional space, as well as the results by Lysenko [26] for Re = 3,900 . It is evident that the results for Re = 3,900 and Re = 130,000 are quite consistent, and the dimension of the attractors for Re = 130,000 significantly exceeds the case for Re = 3,900 . Similar to Lysenko [26], all systems are limited to simple geometric figures, ellipsoids.

5. Discussion

Large eddy simulations of the flow over a circular cylinder at Re = 130,000 were carried out in order to assess the following goals and objectives:
  • further validation and verification of LES for external aerodynamics and turbulent separated flows. Previously, the turbulent flows over a circular ( Re = 3,900 [18,21,26] and Re = 20,000 [19]), semi-circular ( Re = 50,000 [24]) and triangular ( Re = 45,000 [22,23]) cylinders were studied in detail. The differential subgrid scale k-model (with constants C k = 0.07 and C ϵ = 1.048 ) and its dynamic modification are tested. In the present work, the Reynolds number was increased by almost an order of magnitude to Re = 130,000 . Also, in addition to OF, numerical simulations was extended to use the commercial CFD code AF.
  • investigation of LES and related numerical methods using single-precision arithmetic, which is also due to several factors. The most important is the possibility of more efficient use of computational resources: on the one hand, numerical methods using SP arithmetic use less RAM memory, and, as a rule, provide a small performance gain ( ≈ 10 − 20 % ) when using classical CPUs. On the other hand, they allow achieving significant acceleration on graphics accelerators, which are usually optimized for single-precision calculations, as well as on hybrid CPU-GPU systems.
    As mentioned above, OF provides the ability to perform simulations using mixed-precision arithmetic, SPDP. To test it, another special run (OFm-dTKE) was performed using the O-type grid. In this case, the problem was setup as closely as possible to match the AF32-dTKE and AF64-dTKE runs. On the one hand, the predicted integral flow characteristics (Table 2) converge with a small variation to data by AF32-dTKE and AF64-dTKE, which indicates reasonable consistency of the two numerical platforms. On the other hand, the numerical method implemented in OF, even for the SPDP case, has a smaller numerical diffusion, which is clearly seen in Figure 13, where the one-dimensional energy spectra are compared. Numerical dissipation is clearly visible for AF32-dTKE and AF64-dTKE runs. It should be noted that it was not possible to obtain a final physical solution using OF with single-precision arithmetic (similar to Brogi et al. [6]). Most likely, this is due to the fact that the linear algebra algorithms implemented in OF are more sensitive to high-frequency perturbations due to round-off errors. It is also worth emphasizing that in the present work, the dynamic differential subgrid scale model for the kinetic energy was used, which is strictly dissipative under the condition when turbulent viscosity is positive [10], i.e., it makes a certain contribution to the suppression of high-frequency oscillations, which together with the algebraic multigrid method implemented in AF allows to effectively simulate the turbulent flows with single precision.
  • qualitative and quantitative testing of LES implemented in two numerical platforms AF and OF, using coarse and medium-sized computational grids (10-25M cells) for the Reynolds number of practical interest ( Re = 130,000 ). Curved, orthogonal O-type (OM) and unstructured, hexahedral (HM) meshes, with several levels of adaptation computational are used.
In general, the present LES reproduced the physics of the flow over a cylinder, consisting of several important mechanisms. First of all, the occurrence of the Kelvin-Heimholtz instability in the separated shear layers, further growth and development of disturbances on the discontinuity interface and the subsequent laminar-turbulent transition, the development of vortex cores and their convection downstream (asymmetric vortex formation or Benard/von Kármán instability). The vortex dynamics in the wake, characterized by the Strouhal number, are in satisfactory agreement with the available data. Since it was not possible to find any values for the Kelvin-Heimholtz instability for the Reynolds number Re = 130,000 , the values obtained in this work are difficult to quantify. Qualitatively, they are well approximated by the value n = 0.65 for the power-law dependence proposed by Bloor [4]. The root-mean-square values of lift pulsations are in good agreement with the available LES and experimental data. The predicted drag coefficients are within the values presented in the literature. While the results of physical modeling suggest that the drag coefficient has converged to a certain value, LES shows a fairly large dispersion of ≈ 20 % . Another important parameter is the length of the separation zone. The present work shows a quite large discrepancies between simulations and measurements. Other authors also show significant scatter. It should be noted that for a given Reynolds number, there is only one experiment [8]. The variety of factors that influence quality of LES is wide (computational grids and its dimensions, boundary conditions, convective schemes, subgrid scale models, numerical methods, etc.), and it is difficult to single out several fundamental ones that influence the prediction of C d and L r .
Despite the fact that, in general, satisfactory agreement has been achieved for a number of integral and local parameters, the found deviations for C d and L r indicate that this test case for Re = 130000 is still a ’challenge’ problem for the large eddy simulations. This is primarily due to limited computational resources, which are usually bounded by the following factors:
  • the overall performance of the computing system, which is usually limited by the execution time (the time per step per grid node, which is now effectively fixed, since the processor clock rate does not increase), the number of effective MPI nodes, which depends on the problem size and the network communication rate. Parallel efficiency is also usually limited to about 70 % of the theoretical one, in the case when pressure-based algorithms are used and the stability condition C F L < 1 imposed by the computational grid and the boundary layer resolution ( y + );
  • the final period of time integration (the total number of time integration steps), consisting of the interval required to obtain a statistically converged flow field (reaching the self-oscillatory regime, of the order of several τ c o n v ) and the time segment required to get time-averaged data (usually several tens of N v s ).
It is important to note that in the Breuer’s pioneering work [5] (published about twenty-five years ago) high-performance computing (HPC) systems like NEC SX-4 and VP300/VP700 ( included in the TOP500 list at that time1) were used for LES. The results of Lysenko et al. [18] for Re = 3,900 (published about twelve years ago) were performed on the Stallo (HPC) using 256 cores, when a typical simulation took about two weeks. For the runs performed by Lysenko et al. [22,23,24] for Re = 45,000 − 50,000 , the Vilje 2 HPC was used with 128-256 cores in parallel and the typical simulation time was also about two weeks. Thus, the forecast about LES applications for the Reynolds numbers of practical interest made by Breuer [5] about two and a half decades ago is confirmed yet. In the present study, the simulations were performed on work stations with Intel Gold 6142 (32 cores) and I9-13900 (32 cores) CPUs with the typical time about two weeks as well.
A detailed analysis and comparison of the results calculated using SP and DP revealed minimal discrepancies for both integral and local characteristics, as well as for one-dimensional spectra between AF32-dTKE and AF64-dTKE runs, respectively. It is also important that the AF32-dTKE calculation is stable by Lyapunov, and properties of its attractor in the phase space are the same as for AF64-dTKE. Of course, these are strictly preliminary, but quite important results for machine learning problems in aerodynamics [40]. In the future, it will be necessary to conduct studies for other Reynolds and Mach numbers, as well as other classes of the turbulent separated flows.

6. Conclusions

In this paper we continued testing the large eddy simulation implemented in two numerical platforms AF and OF for the flow over a circular cylinder at Re = 130,000 . The priority was given to studying the possibility of LES to reproduce a complex physical phenomena of the flow for a given Reynolds number using computational grids of medium size (10-25M cells), which is of interested for practical engineering applications. In general, satisfactory results were obtained, despite the existing some discrepancies between the present results and relevant data from the literature. The discrepancies can be explained both by the specifics of numerical simulations (various computational grids, convective schemes, subgrid scale models, algorithms and methods for solving the Navier-Stokes equations) and by the methods for collecting and acquisition of physical measurements (as noted earlier, the location of the laminar-turbulent transition, which is very sensitive to the turbulence intensity of the incoming flow, is critically important).
The second important aspect is validation of LES using single-precision arithmetic. In practice, the use of SP allows to reduce the RAM costs and obtain a small performance gain (in this paper ≈ 20 % ) for classical CPUs and, in theory, a significant performance gain for GPUs. The important practical conclusion for engineering applications, as well as for the development of machine learning algorithms, is that the differences between the two runs with SP and DP using AF are negligible for all integral, local and spectral characteristics of the flow. In addition, it is shown that the numerical methodology using SP arithmetic is stable by Lyapunov. The special run using the concept of mixed precision arithmetic implemented in OF showed satisfactory convergence with the results predicted by AF, which indicates a significant degree of consistency of these numerical platforms. It worth to notice, that an attempt to use OF with SP to predict this flow was failed. In this case it seems that the linear algebra solvers implemented in OF are more sensitive to round-off errors and the related high-frequency noise.
The next important step to continue this work is seen as further testing of the numerical methods for the critical and post-critical flows over a circular cylinder, as well as increasing the Mach number to study the compressibility effect.

Funding

This research received no external funding

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Dataset available on request from the authors

Conflicts of Interest

The authors declare no conflicts of interest

Abbreviations

The following abbreviations are used in this manuscript:
AF Ansys Fluent
AMG Algebraic Multigrid Method
BDF Backward Differencing Formula
CDS Central Differencing Scheme
CFD Computational Fluid Dynamics
CPU Central Processing Unit
CWT Continuous Wavelet Transform
DP Double-precision
FFT Fast Fourier transform
FVM Finite Volume Method
GAMG Geometric Multigrid Method
GPU Graphics Processing Unit
HPC High Performance computing
LES Large Eddy Simulation
KH Kelvin–Helmholtz Instability
OF OpenFOAM
PDF Probability Density Distribution
RAM Random-Access Memory
SOU Second-order Upwind Scheme
SP Single-precision
SPDP mixed-precision
TKE Turbulence kinetic energy

References

  1. Alberti, T.; Daviaud, F.; Donner, R.V.; Dubrulle, B.; Faranda, D.; Lucarini, V. Chameleon attractors in a turbulent flow. Chaos Solitons Fractals 2023, 168, 113195. [Google Scholar] [CrossRef]
  2. Achenbach, E. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re = 5×106. J Fluid Mech 1968, 34, 625–639. [Google Scholar] [CrossRef]
  3. ANSYS FLUENT 2021SRb. Theory guide. Tech. rep., Ansys Inc. (2021).
  4. Bloor, M. The transition to turbulence in the wake of a circular cylinder. J Fluid Mech 1964, 19, 290–304. [Google Scholar] [CrossRef]
  5. Breuer, M. A challenging test case for large eddy simulation: High Reynolds number circular cylinder flow. Int J Heat Fluid Flow 2000, 21, 648–654. [Google Scholar] [CrossRef]
  6. Brogi, F.; Bnà, S.; Boga, G.; Amati, G.; Esposti Ongaro, T.; Cerminara, M. On floating point precision in computational fluid dynamics using OpenFOAM. Future Generation Computer Systems 2024, 152, 1–16. [Google Scholar] [CrossRef]
  7. Cao, Y.; Tamura, T. Numerical investigations into effects of three-dimensional wake patterns on unsteady aerodynamic characteristics of a circular cylinder at Re=1.3×105. J Fluids Struct 2015, 59, 351–369. [Google Scholar] [CrossRef]
  8. Cantwell, B.; Coles, D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J Fluid Mech 1983, 136, 321–374. [Google Scholar] [CrossRef]
  9. Dong, S.; Karniadakis, G.E.; Ekmekci, A.; Rockwell, D. A combined direct numerical simulation particle image velocimetry study of the turbulent air wake. J Fluid Mech 2006, 569, 185–207. [Google Scholar] [CrossRef]
  10. Geurts, B. Elements of direct and large-eddy simulation, R.T.Edwards, Philadelphia (2004).
  11. Horiuti, K. Large eddy simulation of turbulent channel flow by one-equation modeling. J Phys Soc Jpn 1985, 54, 2855–2865. [Google Scholar] [CrossRef]
  12. Hutchinson, B.; Raithby, G. A multigrid method based on the additive correction strategy. J Numer Heat Transfer 1986, 9, 511–37. [Google Scholar] [CrossRef]
  13. Issa, R. Solution of the implicitly discretized fluid flow equations by operator splitting. J Comput Phys 1986, 62, 40–65. [Google Scholar] [CrossRef]
  14. Kravchenko, A.; Moin, P. Numerical studies of flow over a circular cylinder at Re = 3900. Phys Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
  15. Hee-Chang Lim, H.-C.; Lee, S-J. Flow control of circular cylinders with longitudinal grooved surfaces. AIAA J 2002, 40, 2027–2036. [Google Scholar] [CrossRef]
  16. Lloyd, T.P.; James, M. Large eddy simulations of a circular cylinder at Reynolds numbers surrounding the drag crisis. Applied Ocean Research 2016, 59, 676–686. [Google Scholar] [CrossRef]
  17. Lyapunov, A.M. The general problem of the stability of motion. Int J Control 1992, 55, 521–790. [Google Scholar] [CrossRef]
  18. Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFOAM toolbox. Flow Turbul Combust 2012, 89, 491–518. [Google Scholar] [CrossRef]
  19. Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 2×104. Flow Turbul Combust 2014, 92, 673–698. [Google Scholar] [CrossRef]
  20. Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Numerical simulations of the Sandia flame D using the Eddy Dissipation Concept. Flow Turbul Combust 2014, 93, 665–687. [Google Scholar] [CrossRef]
  21. Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Towards simulation of far-field aerodynamic sound from a circular cylinder using OpenFOAM. I J Aeroacoustics 2014, 13, 141–168. [Google Scholar] [CrossRef]
  22. Lysenko, D.A.; Ertesvåg, I.S. Reynolds-Averaged, Scale-Adaptive and Large-Eddy Simulations of Premixed Bluff-Body Combustion Using the Eddy Dissipation Concept. Flow Turbulence Combust 2018, 100, 721–768. [Google Scholar] [CrossRef]
  23. Lysenko, D.A.; Ertesvåg, I.S. Assessment of algebraic subgrid scale models for the flow over a triangular cylinder at Re = 45000. Ocean Eng 2021, 222, 108559. [Google Scholar] [CrossRef]
  24. Lysenko, D.A.; Donskov, M.; Ertesvåg, I.S. Large-eddy simulations of the flow over a semi-circular cylinder at Re = 50000. Comput Fluids 2021, 228, 10505. [Google Scholar] [CrossRef]
  25. Lysenko, D.A.; Donskov, M.; Ertesvåg, I.S. Large-eddy simulations of the flow past a bluff-body with active flow control based on trapped vortex cells at Re = 50000. Ocean Eng 2023, 280, 114496. [Google Scholar] [CrossRef]
  26. Lysenko, D.A. Free stream turbulence intensity effects on the flow over a circular cylinder at Re = 3900: bifurcation,attractors and Lyapunov metric. Ocean Eng 2023, 287, 115787. [Google Scholar] [CrossRef]
  27. Ma, X.; Karamanos, G.-S.; Karniadakis, G.E. Dynamics and low-dimensionality of a turbulent near wake. J Fluid Mech 2000, 410, 29–65. [Google Scholar] [CrossRef]
  28. Nastac, G.; Labahn, J.W.; Magri, L.; Ihme, M. Lyapunov exponent as a metric for assessing the dynamic content and predictability of large-eddy simulations. Phys Rev Fluids 2017, 2, 094606. [Google Scholar] [CrossRef]
  29. Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J Wind Eng Ind Aerodyn 1993, 49, 187–196. [Google Scholar] [CrossRef]
  30. Norberg, C. Experimental investigation of the flow around a circular cylinder: Influence of aspect ratio. J Fluid Mech 1994, 258, 287–316. [Google Scholar] [CrossRef]
  31. Ong, L.; Wallace, J. The velocity field of the turbulent very near wake of a circular cylinder. Exp Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
  32. Oseledets, V.I. Multiplicative ergodic theorem. Characteristic Lyapunov exponents of dynamical systems. Tr. Mosk. Mat. Obs. 1968, 19, 179–210. [Google Scholar]
  33. Parnaudeau, P.; Carlier, J.; Heitz, D.; Lamballais, E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900. Phys Fluids 2008, 20, 085101. [Google Scholar] [CrossRef]
  34. Plata, M.; Lamballais, E.; Naddei, F. On the performance of a high-order multiscale DG approach to LES at increasing Reynolds number. Comput. Fluids 2019, 194, 104306. [Google Scholar] [CrossRef]
  35. Prasad, A.; Williamson, C.H.K. The instability of the shear layer separating from a bluff body. J Fluid Mech 1997, 333, 375–402. [Google Scholar] [CrossRef]
  36. Ruelle, D.; Takens, F. On the nature of turbulence. Communications Math Phys. 1971, 23, 343–344. [Google Scholar] [CrossRef]
  37. Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
  38. Takens, F. Detecting strange attractors in turbulence. 1981, 898, 366–381. [Google Scholar] [CrossRef]
  39. Shanbhogue, S.J.; Husain, S.; Lieuwen, T. Lean blowoff of bluff body stabilized flames: Scaling and dynamics. Prog Energy Combust Sci 2009, 35, 98–120. [Google Scholar] [CrossRef]
  40. Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies 2023, 16, 2343. [Google Scholar] [CrossRef]
  41. Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J Comput Phys 1975, 18, 376–404. [Google Scholar] [CrossRef]
  42. Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust 1967, 15, 70–73. [Google Scholar] [CrossRef]
  43. Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. J Comput Phys 1998, 12, 620–631. [Google Scholar] [CrossRef]
  44. Wesseling, P.; Oosterlee, C.W. Geometric multigrid with applications to computational fluid dynamics. Comput. Appl. Math. 2001, 128, 311–334. [Google Scholar] [CrossRef]
  45. Yeon, S.M.; Yang, J.; Stern, F. Large-eddy simulation of the flow past a circular cylinder at sub- to super-critical Reynolds numbers. Applied Ocean Research 2016, 59, 663–675. [Google Scholar] [CrossRef]
  46. Yoshizawa, A. Statistical theory for compressible shear flows, with the application to subgrid modelling. Phys Fluids 1986, 29, 1416–1429. [Google Scholar] [CrossRef]
1
https://www.top500.org/
2
https://www.sigma2.no/content/vilje
Preprints 118472 g001
Figure 1. General view of the curvilinear, orthogonal and unstructured, hexahedral meshes and computational domain (b,d,e,g), their frontal view and zoom in the vicinity of the cylinder (c,f). x, y and z are Cartesian coordinates in the longitudinal, vertical and spanwise directions, θ and r are circumferential and radial coordinates
Figure 1. General view of the curvilinear, orthogonal and unstructured, hexahedral meshes and computational domain (b,d,e,g), their frontal view and zoom in the vicinity of the cylinder (c,f). x, y and z are Cartesian coordinates in the longitudinal, vertical and spanwise directions, θ and r are circumferential and radial coordinates
Preprints 118472 g001
Preprints 118472 g002
Figure 2. Time evolution of the lift C l (a) and drag C d (b) coefficients over ≈ 30 oscillation periods for the flow over a circular cylinder at Re = 130 , 000
Figure 2. Time evolution of the lift C l (a) and drag C d (b) coefficients over ≈ 30 oscillation periods for the flow over a circular cylinder at Re = 130 , 000
Preprints 118472 g002
Preprints 118472 g003
Figure 3. Visualization of a vortex shedding downstream of a circular cylinder at Re = 130 , 000 using the Q-criterion, Q = 10 4 : OF-dTKE(a) and AF64-dTKE(b)
Figure 3. Visualization of a vortex shedding downstream of a circular cylinder at Re = 130 , 000 using the Q-criterion, Q = 10 4 : OF-dTKE(a) and AF64-dTKE(b)
Preprints 118472 g003
Preprints 118472 g004
Figure 4. Probability density distribution (PDF) of the lift coefficient normalized by its root mean square value
Figure 4. Probability density distribution (PDF) of the lift coefficient normalized by its root mean square value
Preprints 118472 g004
Preprints 118472 g005
Figure 5. Comparison of the pressure (a) and friction (b) coefficient over the cylinder surface ( θ s = 0 – stagnation point) for the flow over a circular cylinder at Re = 130 , 000 . Note that the present results are not averaged in the spanwise direction in order to show their variation over L z
Figure 5. Comparison of the pressure (a) and friction (b) coefficient over the cylinder surface ( θ s = 0 – stagnation point) for the flow over a circular cylinder at Re = 130 , 000 . Note that the present results are not averaged in the spanwise direction in order to show their variation over L z
Preprints 118472 g005
Preprints 118472 g006
Figure 6. Distribution of the mean streamwise velocity (a), as well as the RMS values of the streamwise (b) and vertical (c) velocity along the central axis for the flow over a circular cylinder at Re = 130 , 000
Figure 6. Distribution of the mean streamwise velocity (a), as well as the RMS values of the streamwise (b) and vertical (c) velocity along the central axis for the flow over a circular cylinder at Re = 130 , 000
Preprints 118472 g006
Preprints 118472 g007
Figure 7. Radial profiles of the meas streamwise and vertical velocities, as well as the Reynolds stress U x ′ U y ′ in the near wake ( x / D = 1.0 , 1.5 , 2.0 ) for the flow over a circular cylinder at Re = 130 , 000
Figure 7. Radial profiles of the meas streamwise and vertical velocities, as well as the Reynolds stress U x ′ U y ′ in the near wake ( x / D = 1.0 , 1.5 , 2.0 ) for the flow over a circular cylinder at Re = 130 , 000
Preprints 118472 g007
Preprints 118472 g008
Figure 8. One-dimensional energy spectra of the vertical velocity in the near wake of a circular cylinder (a) and shear layer instability (b) at Re = 130 , 000 . Signals measured at points x / D = 1.5 , y / D = 0 (a) and x / D = 0.15 , y / D = 0.5 with multiple distributions along the span
Figure 8. One-dimensional energy spectra of the vertical velocity in the near wake of a circular cylinder (a) and shear layer instability (b) at Re = 130 , 000 . Signals measured at points x / D = 1.5 , y / D = 0 (a) and x / D = 0.15 , y / D = 0.5 with multiple distributions along the span
Preprints 118472 g008
Preprints 118472 g009
Figure 9. Dependence of the characteristic frequency of the separated shear layers on the Reynolds number: results of numerical and physical modeling
Figure 9. Dependence of the characteristic frequency of the separated shear layers on the Reynolds number: results of numerical and physical modeling
Preprints 118472 g009
Preprints 118472 g010
Figure 10. Energy scalogram of wavelet coefficients for the vertical velocity in the wake of circular cylinder in a separated shear layer, calculated using CWT for Re = 3 , 900 ([18]), 20 , 000 ([18]) and 130 , 000 (AF64-dTKE runs). Here t * = t U ∞ / D is the dimensionless time. The dashed line shows the average frequency of the broadband interval f k h / f v s = 28.9 for Re = 130 , 000
Figure 10. Energy scalogram of wavelet coefficients for the vertical velocity in the wake of circular cylinder in a separated shear layer, calculated using CWT for Re = 3 , 900 ([18]), 20 , 000 ([18]) and 130 , 000 (AF64-dTKE runs). Here t * = t U ∞ / D is the dimensionless time. The dashed line shows the average frequency of the broadband interval f k h / f v s = 28.9 for Re = 130 , 000
Preprints 118472 g010
Preprints 118472 g011
Figure 11. Divergence in streamwise (a), vertical (b), and spanwise (c) velocities between two solutions obtained using single-precision (AF32) and double-precision (AF64) arithmetic for the flow over a circular cylinder at Re = 130 , 000 . The time scale is normalized using the convective time, τ c o n v . The dashed lines represent the linear region, and the dash-dotted lines represent the saturation region
Figure 11. Divergence in streamwise (a), vertical (b), and spanwise (c) velocities between two solutions obtained using single-precision (AF32) and double-precision (AF64) arithmetic for the flow over a circular cylinder at Re = 130 , 000 . The time scale is normalized using the convective time, τ c o n v . The dashed lines represent the linear region, and the dash-dotted lines represent the saturation region
Preprints 118472 g011
Preprints 118472 g012
Figure 12. Attractors of nonlinear systems AF32-dTKE and AF64-dTKE for the flow over a circular cylinder at Re = 130 , 000 , as well as their bounding ellipsoids, in the three-dimensional space. For the sake of completeness, similar results for Re = 3 , 900 [26] are presented
Figure 12. Attractors of nonlinear systems AF32-dTKE and AF64-dTKE for the flow over a circular cylinder at Re = 130 , 000 , as well as their bounding ellipsoids, in the three-dimensional space. For the sake of completeness, similar results for Re = 3 , 900 [26] are presented
Preprints 118472 g012
Preprints 118472 g013
Figure 13. One-dimensional energy spectra of the vertical velocity in the near wake of a circular cylinder (a) and shear layer instability (b) for the flow over a circular cylinder at Re = 130 , 000 . Signals measured at points x / D = 1.5 , y / D = 0 (a) and x / D = 0.15 , y / D = 0.5
Figure 13. One-dimensional energy spectra of the vertical velocity in the near wake of a circular cylinder (a) and shear layer instability (b) for the flow over a circular cylinder at Re = 130 , 000 . Signals measured at points x / D = 1.5 , y / D = 0 (a) and x / D = 0.15 , y / D = 0.5
Preprints 118472 g013
Table 1. Runs matrix: numerical platform, floating-point arithmetic, computational grid, and subgrid scale model
Table 1. Runs matrix: numerical platform, floating-point arithmetic, computational grid, and subgrid scale model
Run CFD code Precision Mesh TM
OF-TKE OF DP HM TKE
OF-dTKE OF DP HM dTKE
OFm-dTKE OF SPDP OM dTKE
AF32-dTKE AF SP OM dTKE
AF64-dTKE AF DP OM dTKE
Table 2. Review of experimental and LES studies for the turbulent flow over a circular cylinder at Re = 130 , 000 : parameters and integral characteristics
Table 2. Review of experimental and LES studies for the turbulent flow over a circular cylinder at Re = 130 , 000 : parameters and integral characteristics
Source Method 〈 C d 〉 〈 C l ′ 〉 St − 〈 C p , b 〉 〈 L r / D 〉 θ s
Achenbach [2] HWA 1.19 1.25 78
Cantwell & Coles [8] HWA 1.24 0.52 0.179 1.21 0.4-0.5 77
Schewe [37] HWA 1.17 0.25 0.20
Norberg [29] 0.49 0.185
Lim & Lee [15] HWA 1.2 0.185 1.15
Breuer (DC) [5] LES 1.28 0.22 1.51 0.46 94
Breuer (D3) [5] LES 1.37 0.21 1.6 0.42 91
Cao & Tamura [7] LES 1.16 0.3 0.2
Lloyd & James (4C) [16] LES 1.00 0.63 0.177 1.01
Lloyd & James (4F) [16] LES 0.89 0.5 0.203 0.86
Yeon et al. [45] LES 1.37 0.62 0.2 1.64 0.63 81
Plata et al. [34] LES 1.43 0.19 1.59 0.5
Present work
OF − TKE LES 1.33 0.41 0.19 1.36 0.55 83o
OF − dTKE LES 1.34 0.53 0.19 1.37 0.58 83o
OFm − dTKE LES 0.98 0.55 0.18 1.03 0.62 89o
AF 32 − dTKE LES 0.94 0.28 0.21 1.01 0.68 85o
AF 64 − dTKE LES 0.94 0.27 0.21 1.01 0.68 85o
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated