Prerpints.org logo
Preprint
Article

Enhancing Precision of Forest Growing Stock Volume in the Estonian National Forest Inventory with Different Predictive Techniques and Remote Sensing Data

Altmetrics

Downloads

71

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 September 2024

Posted:

23 September 2024

You are already at the latest version

Alerts
Abstract
Estimating Forest growing stock volume (GSV) is crucial for forest growth and resource management, as it reflects forest productivity. National measurements are laborious and costly, however integrating satellite data such as optical, Synthetic Aperture Radar (SAR), and Airborne Laser Scanning (ALS) with National Forest Inventory (NFI) data and machine learning (ML) methods has transformed forest management. In this study, Random Forest (RF), Support Vector Regression (SVR), and Extreme Gradient Boosting (XGBoost) were used to predict GSV using Estonian NFI data, Sentinel-2 imagery, and ALS point cloud data. Four variable combinations were tested: CO1 (vegetation indices and LiDAR), CO2 (vegetation indices and individual band reflectance), CO3 (LiDAR and individual band reflectance), and CO4 (a combination of vegetation indices, individual band reflectance, and LiDAR). Across Estonia's geographical regions, RF consistently delivered the best performance. In the northwest (NW), RF achieved an R² of 0.63 and an RMSE of 125.39 m³/plot. In the southwest (SW), it achieved an R² of 0.73 and an RMSE of 128.86 m³/plot. In the northeast (NE), RF achieved an R² of 0.64 and an RMSE of 133.77 m³/plot, and an R² of 0.70 and an RMSE of 120.72 m³/plot was achieved in the southeast (SE). These results underscore RF's precision in predicting GSV across diverse environments, though refining variable selection and improving tree species data could further enhance accuracy.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Forest and its ecosystems play a vital role in the overall health and sustainability of the planet earth, providing indispensable services such as carbon sequestration, biodiversity conservation, and water regulation [1,2]. These ecosystems support a vast array of life forming processes for both plant and animal species, contributing to ecological functionality, stability, and resilience [3,4]. In addition, they offer economic benefits through the provision of resources such as timber and non-timber forest products (NTFPs), highlighting their multifaceted importance [5]. Forest growing stock volume (GSV) is a critical metric in forestry resources assessments (FRA), representing the total volume of all living trees within a given area [6,7], serving as an indicator for measuring the forest management capability, forest quality, and carbon sequestration potential [8]. The accurate estimation of this essential variable is pivotal for sustainable forest management, conservation practices, quantification of ecosystem services, and aid in providing detailed information to support decision making mechanism [9,10]. Advances in remote sensing data capturing technology and machine learning (ML) algorithms have significantly enhanced the precision and efficiency of GSV assessments, casing a fundamental change in estimation thereby providing valuable insights for resource management [11,12].
Traditional and Remote Sensing (RS) based estimation methods in assessing GSV offer distinct advantages and present challenges, shaping their complementary roles in forest inventory and management. Traditional methods, such as field sampling and harvesting data, provide accurate measurements at localized scales by directly observing tree dimensions and timber volume [6]. However, the fieldwork for acquiring data for forest growing stock volume at a larger scale is challenging [13] and holistically, these approaches are labour-intensive, costly, and may lack continuous coverage over large, forested area [14]. Conversely, the RS method offers significant advancements by providing spatially explicit and continuous assessments of forest related variables. With a long history of remote sensing data availability, different data sources have been utilized to estimate forest variables out of which optical satellite imagery such as Landsat has been widely used [15]. The synoptic coverage, moderate ground cover resolution, high repetitive coverage, and free access policy makes some optical RS the most widely used [15,16,17] meanwhile, While RS methods enhance efficiency and coverage, it is expedient to note that they cannot emphatically replace field sampling methods. They require careful calibration and validation with ground-truth data from traditional methods to ensure accuracy and precision [18]. Integration of both approaches through hybrid methodologies facilitates comprehensive GSV assessments [19], leveraging the strengths of RS for broad-scale monitoring and the precision of traditional methods for validation and localized accuracy.
Optical sensors usually provide detailed information on the horizontal structure of forest vegetation based on the configuration, meanwhile, information about the vertical structure is not presented. On the contrary, LiDAR remote sensing can provide both horizontal and vertical information, depending on the configuration of the LiDAR system used and therefore, it is well suited for describing forest structure [20,21]. The use of optical imagery with high resolution for estimating GSV has proven to be effective for example, Mura et al. [22] explored the capabilities of the sentinel-2 for predicting growing stock volume in Italy. Zhou & Feng [8] compared the precision of sentinel-2 and Landsat 8 OLI in estimating forest stock volume and concluded that sentinel-2 based model achieved higher accuracy. Hence the choice of integrating LiDAR metric and Sentinel-2 data in our current study. Research efforts geared towards the usage of Airborne laser scanning (ALS) in the estimation of GSV has proven its resourcefulness as a valuable data source [13,23,24,25,26]. Lindgren et al [27] emphasized that in addition to ALS, there are many other sources of remote sensing data that could be used for automated prediction of forest variables like GSV However, lack of good prediction accuracy has reduced their use in operational forest management.
In providing more accurate, non-destructive frequent updates, remotely sensed data can improve the quality of forest inventory database, thus, the synergy between traditional and RS methods in GSV estimation not only enhances forest management practices but also supports sustainable resource utilization and conservation efforts on a global scale thereby improving the resources management activities [19,28,29,30,31]. Integrating LiDAR and optical remote sensing data for estimating forest biophysical parameters presents some associated challenges necessitating careful attention, robust methodologies, and many a time a hybrid method that leverages the strengths of both LiDAR and optical sensors while mitigating their limitations. Researchers have addressed these challenges through various innovative approaches for example, Hudak et al. [32] proved that the integration of LiDAR and optical remote sensing data significantly improves forest inventory accuracy, most especially in predicting forest structure attributes when LiDAR is combined with multispectral imagery. Asner et al. [33] stressed the importance of ground-based calibration and validation to achieve accurate carbon stock estimates with airborne LiDAR. Fernández-Landa et al. [34] analyzed the effectiveness of combining national wide LiDAR information and optical imagery to estimate forest variables and concluded that this integration may lead to an increase in estimation accuracy most especially when the species are homogenized.
Several modelling techniques either as parametric (e.g., multiple linear regression, logistic regression, geographically weighted regression) and non-parametric (e.g., k-nearest neighbors (k-NN), random forests, artificial neural networks, gradient nearest neighbor (GNN), support vector machines, and decision trees) have been used to establish the relationship between the response variables (forest variables) and predictor variables (remote sensing derived variables) [8,23,35,36,37,38,39]. Machine learning algorithms such as Random Forests, Support Vector Machines, Extreme Gradient Boosting, and Artificial Neural Networks (ANN) are some of the commonest ML algorithms used for forest variables estimation and they have demonstrated superiority and proven efficient in estimating GSV, outperforming traditional methods, highlighting their robustness across diverse datasets and varying forest ecological conditions [8,11,36,37,40,41].
The aim of our research was to assess the predictability of forest growing stock volume across various Cartesian planes in Estonia, corresponding to the flight schedules of ALS based on forestry purpose, by utilizing three ML algorithms to analyse NFI plot data alongside multimodal remote sensing data. We integrated ALS height percentile with multispectral data, to create a comprehensive dataset for the analysis and incorporates ground-truth data from NFI plots to enhance the accuracy of remote sensing data interpretations and model training. We applied and compared the performance of three distinct machine learning algorithms such as RF, SVR, and XGBoost to predict forest growing stock volume, focusing on their accuracy and reliability at the plot level to ensure localized accuracy in forest growing stock volume. By achieving these objectives, the research aimed to advance the understanding of forest growing stock volume estimation using multimodal remote sensing data and machine learning techniques, ultimately contributing to more effective and sustainable forest management in Estonia.

2. Materials and Methods

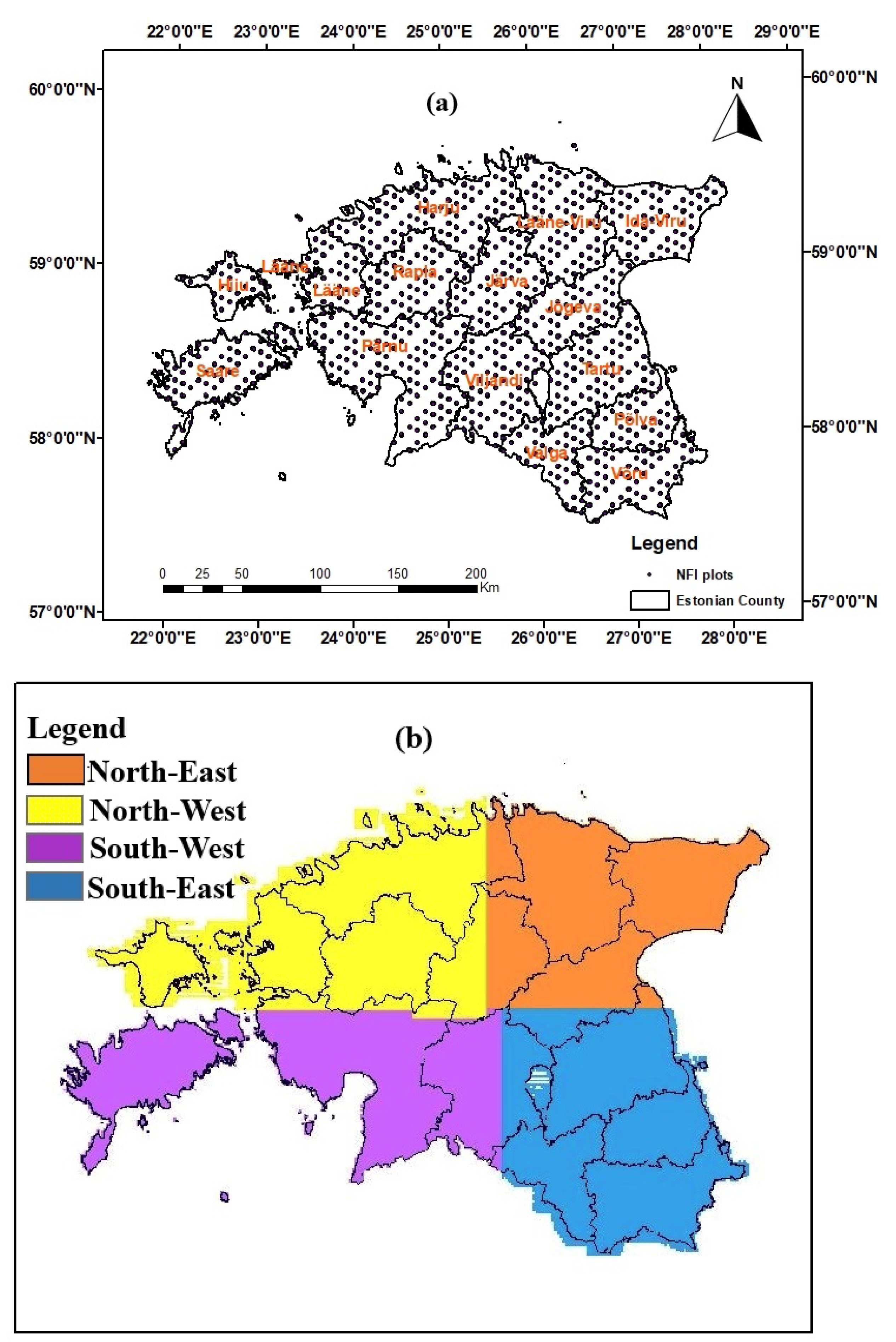
2.1. Study Area

The study area (Estonia) covers an approximately landmass of 45,339 km2 and located in Northern Europe on the shore of the Baltic Sea. It borders the Baltic Sea and the Gulf of Finland. Forest in Estonia account for about 53.6% approximately 23,308 km2 of its landmass [42]. It is situated between latitudes 57°30'34" N to 59°49'12" N and longitudes 21°45'49" E to 28°12'44" E. as shown in Figure 1a. [43]. Forests in Estonia are as defined by its Forest Act [44] and it covers 2.2 million ha of its total landmass which account for approximately half of the county’s land area [45]. The main common tree species composition that contributes majorly in the growing stock volume quantification are Scots pine (Pinus sylvestris L.) which account for about 34% coverage of the forest area, downy birch (Betula Pubescens Ehrh) and silver birch (B. Pendula Roth) dominating about 31% of the forested land, Norway spruce (Picea abies (L.) Karst) with a share of 16% and species like European aspen (Populus tremela L.), grey alder (Alnus incana (L.) Moench), black alder (A. glutinosa (L.) Gaertn, and common ash (Fraxinus excelsior L) [45]. Their coverage in space is either linear or cluster resulting into heterogenous or homogenous stand with an average stand size of 1.25 ha [23,46]. The mean annual temperature is 4.7°C; in February, it is -6.6°C, and in July, it is 16.3°C, while the mean annual precipitation is 500 to 700 mm [43]. Thirteen (13) toil taxa were identified and categorized into Automorphic soils (Leptosols, Cambisols, Luvisols, Planosols, Podzoluvisols, Podzols, Arenosols), different Gleysols, and Histosols (mires and bogs). Fluvisols (alluvial and saline littoral soils) and Technogenic formation on reclaimed land [47].

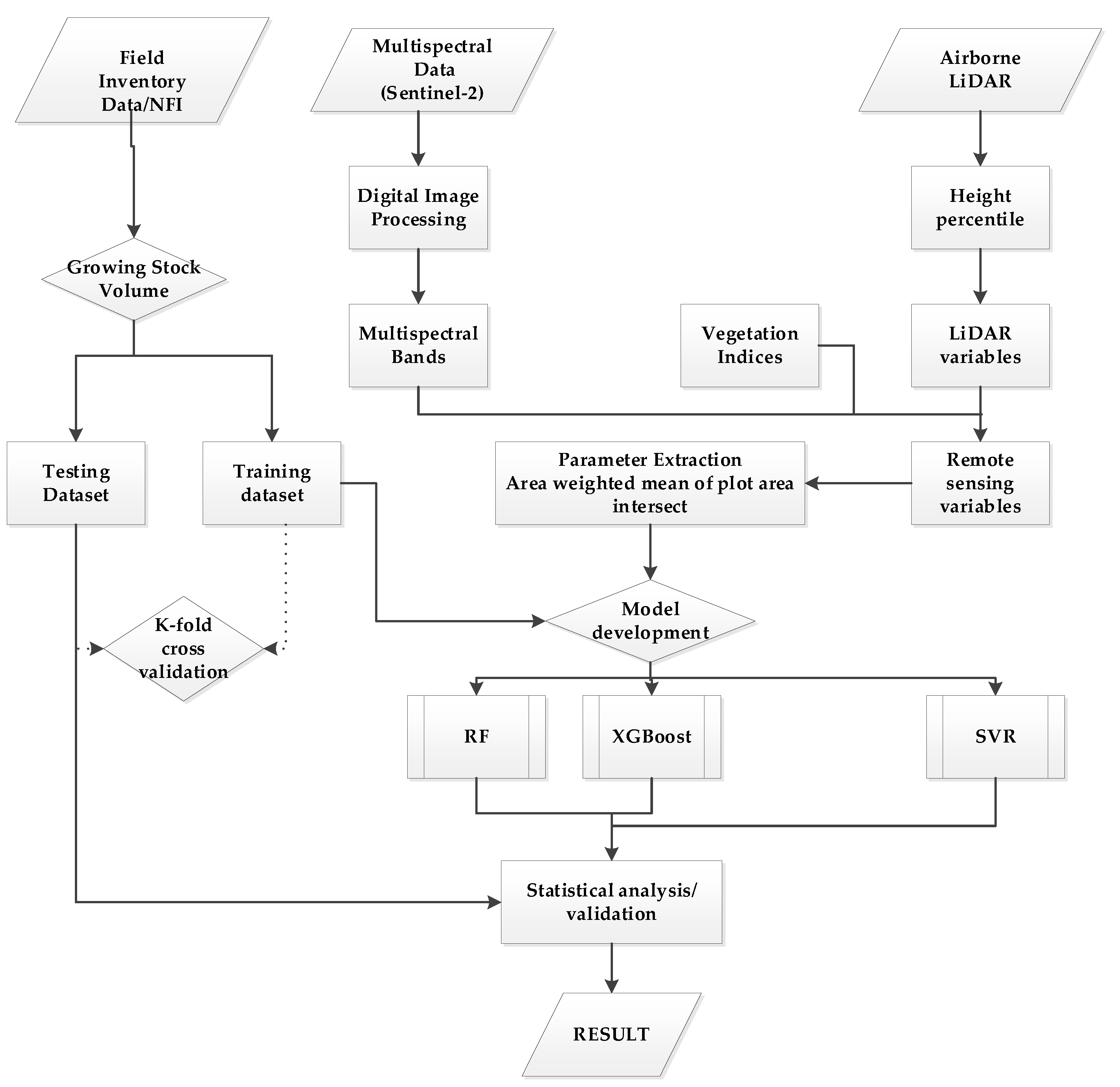
2.2. General Overview of Methods

This study estimates the forest Growing Stock Volume (GSV) by combining multi-sensor remote sensing and National Forest Inventory data using RF, Extreme Gradient Boosting (XGBoost), and Support Vector Regression (SVR) regression algorithms. The methodology flow-chart is shown in Figure 2.

2.3. Estonian National Forest Inventory

As part of the intensive forest management scheme, National Forest inventory (NFI) are conducted in Estonian with a five-year repeat cycle. The first NFI covering the whole country is dated back to 1999 [48] and was designed to give a description of Estonia’s forests. Currently, the NFI gives more robust information about the distribution of land by land-use classes, the afforestation and growing stock of non-forest land etc. It is designed as an annual research effort, which, using optimal methods, enhances the continuous updating of its architectural database. A network of sample plots, covering the entire country with the same sampling intensity, has been designed for five years with 20% yearly coverage and a potential of increasing frequencies. This is designed in a way that allow one-fifth of the total sample plots to be inventory yearly and further enhance a revisit measurement of the permanent sample plots after each complete cycle (five years). The network of sample plots in Estonian NFI is spatially distributed on a national grid of 5 km x 5 km quadrangle as determined by the L-EST coordinates system with the same sampling intensity. Three types of circular sample plots with fixed-radius are used in the NFI but for the purpose of this study, volume-based sample plots are used. Sample plots are organized into permanent clusters and temporary clusters that form 800 x 800-meter squares. Detailed methodology for the NFI is described in the Estonia global forest resources assessment [49]. For the purpose of this study, sample plots in the 2018-2022 cycle were used

2.4. Field Inventory Measurement

As an element of the thorough data acquisition strategies, a systematic sampling technique without pre-stratification was adopted in the Estonia NFI. Within each circular sample plots, trees diameter at breast height (dbh) of trees with dbh ≥ 5 cm was recorded at 1.3 m height above the ground. Height was recorded for some trees according to the criteria that allow for dbh to height estimation with minimal prediction error in accordance to NFI criteria using (Equation (1)), information such as species, age, sample plot center coordinates etc. were also recorded within the 10 m and 7 m radii sample plot using handheld GPS. Trees dbh was measured using a caliper with ±1.0 mm accuracy while height measurement was done using Vertex. The sample plots were further stratified into NE, SE, SW, and NW category in other to align with the aerial laser scanning based partitioning of Estonia (Figure 1b). Region specific growing stock volume equation (Equation (2)) was used to estimate the volume of trees in each plot. The volume of sample plots was then calculated by summing the volume of all the trees in the sample plot.
Nc = B A n
GSV = a 1 + a 2 ∗ h + a 3 ∗ f ∗ ( t / ( t + 5.0 ) ) c 1 + c 2 ∗ h
where Nc is the total number of tree count for height measurement, BA is the plot basal area in m2/ha and n is the maximum number of trees in the plot, G S V is the growing stock volume of each tress, a 1 , a 2 , a 3 , c 1 , c 2 are species-based constants, h is the tree height, t is the age, f is dummy variable with value of 1 if sample plot is on any island in Estonia.
Outliers was detected and removed through the use of PauTa Criterion where the outlier is statistically calculated and removed rather than a manual specification of outliers’ threshold. A threshold is determined according to a certain probability and any error exceeding this is taken to be a gross error rather than a random error. A numerical distribution interval of (µ − 3σ, µ + 3σ) was used as this explained the largest proportion of any given data [50]. Data point with values less than μ-3σ or greater than μ + 3σ were deleted before the regression analysis to ensure that the data assumed a normal distribution. Table 1 shows the geographical characterization of the GSV

2.5. Remote Sensing Data

To establish the relationship between Growing stock volume and remote sensing data, this study utilized both optical satellite data (Sentinel -2) and ALS height percentile data. The sentinel-2 images that covers each cartesian plane were downloaded from Copernicus Open Access Hub (https://dataspace.copernicus.eu.) images contained rich spectral information and were downloaded based on selection criteria such as maximum cloud cover <2% and sensor uniformity in cases where multiple sensors were available. A full representation of each plane contains a mosaic of maximum of 4 or 3 scenes. The selected bands ranges from band 2 through 8, 8A, 11 and 12 (Table 2). Each product was corrected from top-of-atmosphere (TOA) reflectance and processed into orthoimage bottom-of-atmosphere (BOA) surface reflectance using sen2cor version 2.11 of the sentinel application platform (SNAP) and then resampled into 10 m resolution. Cloud and cloud shadow were determined and masked using ESA SNAP and overlapping points on the pixel that were not properly classified were manually removed using R studio. Points were converted into shapefile (20 m x 20 m vector box) using the bounding box technique and was used to extract the corresponding band reflectance values using a weighted mean approach which extract the average value of pixels that interest with the shapefile.

2.6. LiDAR Data

In Estonia, airborne laser observation is carried out by the Estonian Land board on a yearly basis during the spring and summer period. The country is divided into four and a quarter is covered in the spring and a quarter in summer (Figure 1b) The summer flight program is designed to allow for forestry application. In this study a total of eleven (11) height percentile (Table 2) were used and these correspond to data collected during the summer of 2018, 2019, 2020, and 2021 using the Reigl VQ – 1560i airborne laser scanning system. The system was configured to operate at an altitude of 1200 m (mapping of densely populated areas), 2000 m (mapping with imaging priority) and 2600 m during the spring and 3100 m in the summer time for forestry mapping.

2.7. Independent Variable Screening

A total of thirty-six (36) variables were pooled from the Sentinel -2 and LidAR data (Table 2). In other to avoid multicollinearity among independent variables, Boruta feature selection method and Variance inflation factors (VIFs) were employed. First, we used the Boruta feature selection to rank all the independent variables according to their importance as a function of their Z-score value secondly, in other to enrich the selection processes, VIFs were estimated among the remaining predictor variables and variables with VIFs lower than five (5) were considered an indicator of multicollinearity and filtered appropriately. We explored four different combinations of variables such as (i). VIs combined with Band Reflectance Values and LiDAR data. (ii). VIs combined with Band Reflectance Values. (iii). VIs combined with LiDAR data. (iv). Band Reflectance Values combined with LiDAR data. For each year, a total of eleven (15) spectra vegetation indices (VIs) (Table 2) were estimated using R studio. The height percentile and band reflectance are as described under section (LiDAR) and (sentinel-2) respectively.

2.8. Regression Analysis

Three (3) non-parametric models were constructed and compared using R statistical software. These models encompass Random Forest (RF), Support Vector Regression (SVR), and XGBoost.

2.8.1. Random Forest Regression

The Random Forest (RF) is a CART decision model [51] and one of the most commonly used non-parametric methods to establish the relationship between dependent and independent variables. It is a machine-learning process where regression is based on a decision tree characterized by a selection of a subset from training data by a random sampling method with replacement. This bootstrapping process extracts a set of n data repeatedly and randomly from the sample data as a training dataset (approximately two-thirds), and the remaining one-third which are left out of the bag (OOB) are used to estimate the error and to assign level of importance to the dependent variables. Handling redundancy in predictors when the number of predictors is very large which tends to aggravate into multi-collinearity is properly minimized and overfitting is prevented [52]. For this study, the RF was constructed using the R package RandomForest [53]. It was initially calibrated with the default value of ntree and subsequently varied with a step of 500. The number of feature variable at each split (mtry) was determine using the tuneRF function. This function facilitates the tuning of the hyperparameter mtry by searching for the optimal value that minimizes the Out-of-Bag (OOB) error estimate.

2.8.2. Support Vector Regression (SVR)

The support vector regression (SVR) is a supervised machine learning algorithms that handles the prediction of continuous numeric values. It is a derivative of support vector machine (SVM) which was developed by Vapnik et al. [54] and it uses a kernel function to linearize a non-linear regression by mapping the input data into a high-dimensional function space [55]. This method has been proven to be one of the popular algorithms used for regression analysis to estimate forest related variables using remotely sensed data [15,30,39]. It uses a set of functions to estimate the regression model and engage the Structural Risk Minimization (SRM) to minimize model error and overfitting problem [30,56] In this study, the radial basis function kernel (RBF) was used to train the model as it has a few parameters tunning and was implemented in R using the “e1071” R package.

2.8.3. Extreme Gradient Boosting

Extreme Gradient Boosting (XGBoost) is one of the most effective advanced Machine learning whose iteratives is based on gradient boosting framework. XGBoost was proposed by Chen et al. [57] to support both classification and regression models using the reg:logistics and reg:linear as a loss function for its classification and regression algorithms respectively. It applies the second-order Taylor expansion to the objective function and uses the combination of first and second order derivative to approximate the objective function more accurately to arrive at a more precise definition that facilitate optimization [58]. It introduces a regularization term into the objective function to prevent overfitting and enhance the creation of a simpler models. As an ensemble learning method, XGBoost combine multiple base learners to obtain a single prediction that is more robust towards achieving a better predictive accuracy.

2.9. Model Evaluation

The total sample plots in each quadrant (Table 1) were randomly portioned into 70% and 30% subsets, the first was used as training dataset and the latter was used as the testing data set for the built model. In other to avoid the risk associated with overfitting and to obtain a more reliable estimate of machine learning based models, a k-fold cross validation technique is always a vital step. This method partitions the original sample into k equal number of subset and iteratively choose different partition for training and validation dataset. Each partition is used as the testing set only once while the remaining k-1 subset are used as the training sample in a leave-one-out cross validation method (LOOCV). A parallel processing technique was employed to speed up the computational speed of the LOOCV using the parallel package in R. Performance metrics such as Root Mean Square Error (RMSE) and coefficient of determination (R²) were calculated based on the predictions made on the testing dataset using 10-fold cross-validation.
R M S E = ∑ i = 1 n ( y ~ i − y i ) 2 n
R M S E % = R M S E ȳ . 100 %
R 2 = 1 − ∑ i = 1 n ( y i − y ~ i ) 2 ∑ i = 1 n ( y i − y ̄ i ) 2
where n is the number of observations, y i is the actual GSV of the ith plot, y ~ i is the predicted GSV of the ith plot, and y ̄ i is the mean of the actual GSV.

3. Results

A total of 14880 sample plots were selected from the NFI data following the removal of outliers through PauTa criteria. The share of each quadrant is represented in Table 1 where the largest share (3852) is on the NE zone followed by the NW with 3712 sample plots while the SE and SW has a share of 3665 and 3651 respectively. Four (4) variables combinations as discussed in section 2 were used in training the three predictive models i.e., RF, SVR and XGBoost. A maximum of a 10-fold cross validation was considered sufficient enough to optimize the model according to minimum RMSE and a considerable coefficient of determination. The sample plots in each share were used to generate a corresponding model and each model’s performance metrics is explained as follows.

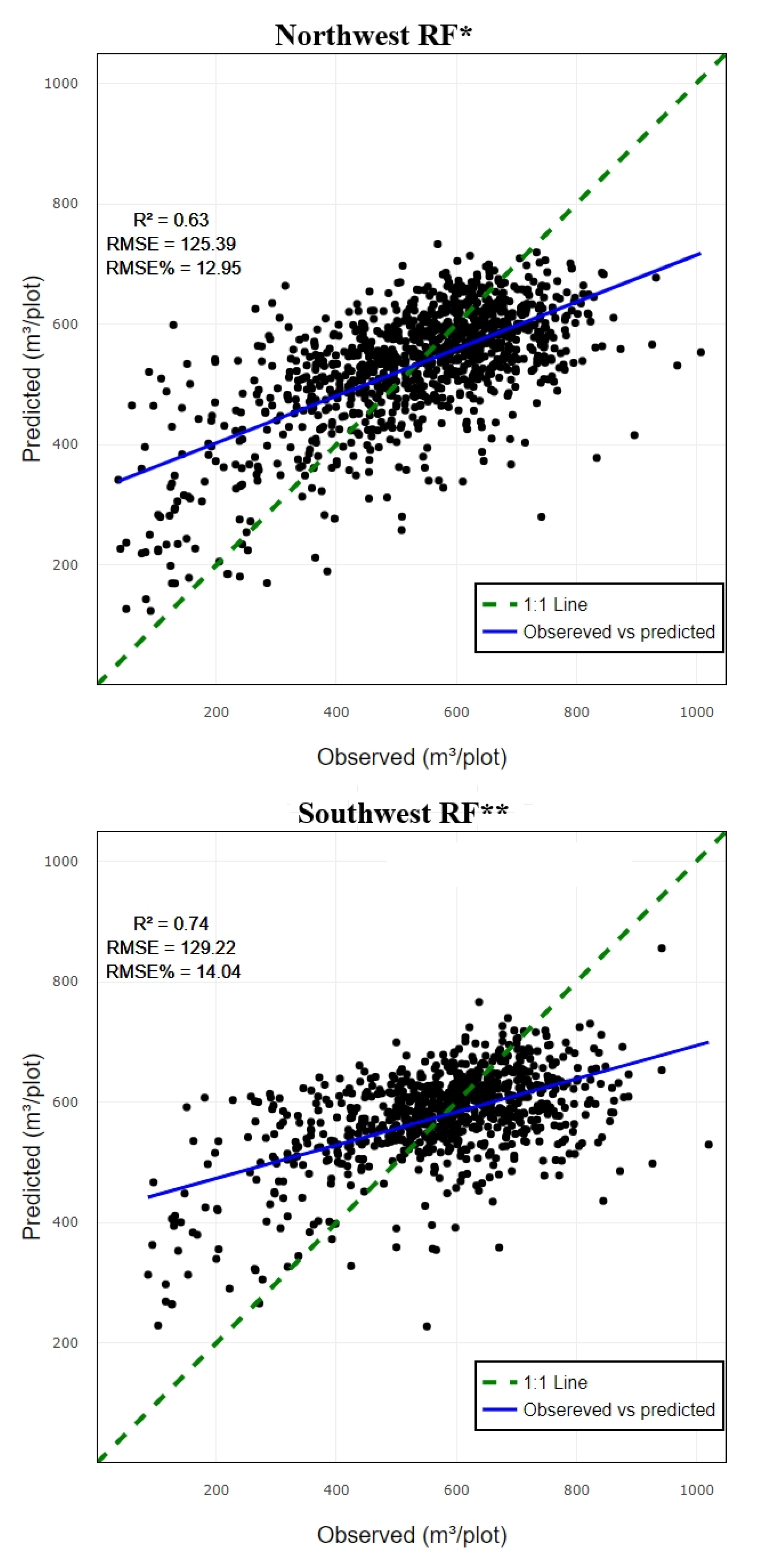
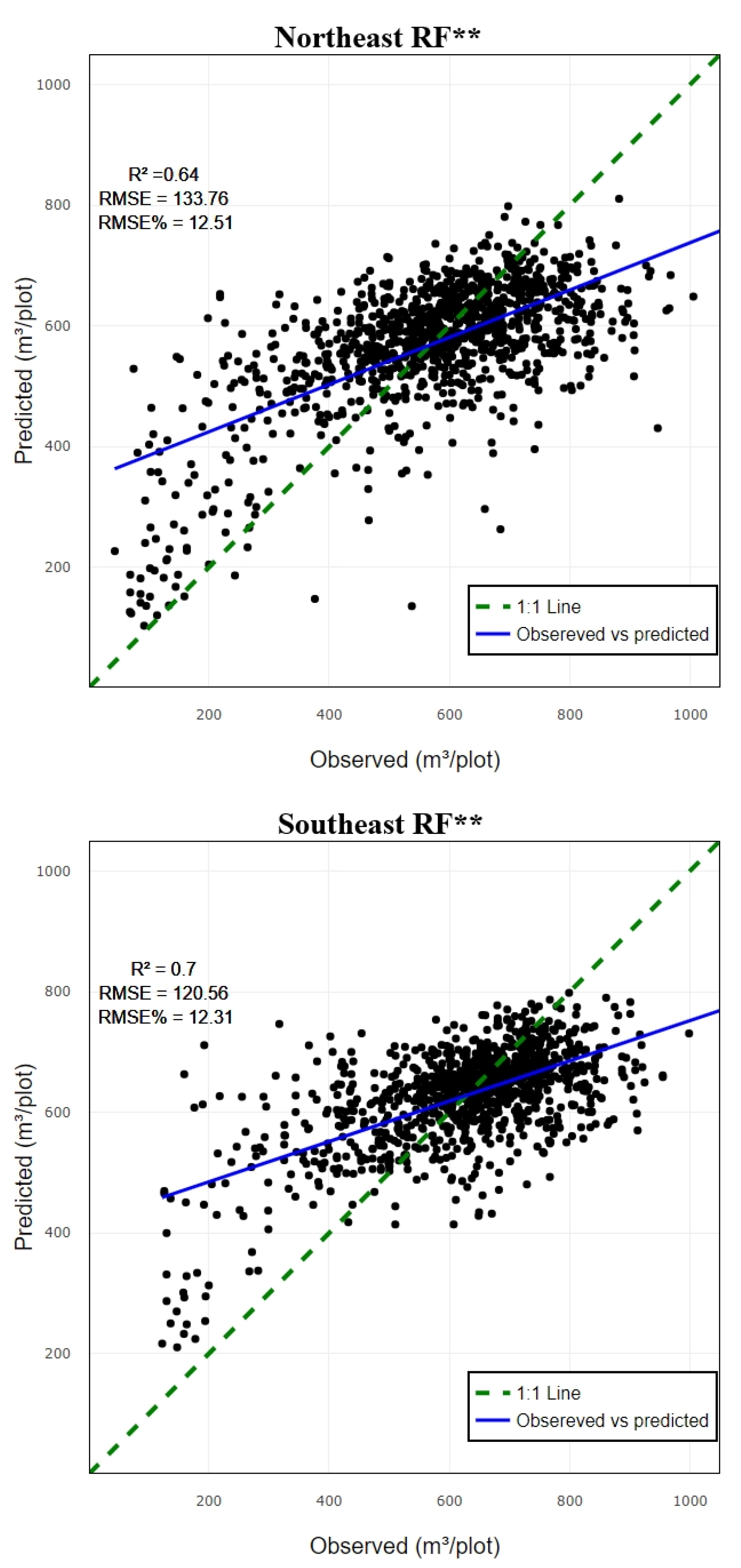
3.1. Performance Assessment Based on Random Forest Predictive Model

The performance metrics for the RF-based model for each combination of variables at the quadrant level are illustrated in Table 3. In the NW zone, RMSE values ranged from 125.39 m³/plot to 141.84 m³/plot for CO3 and CO1 categories respectively, with CO4 and CO3 showing relatively close performance R² values of 0.64 (CO4) and 0.63 (CO3). The CO4 seems to have a relatively higher RMSE (126.74 m³/plot) and a higher RMSE% (13.09) as compared to the CO3 (Table 3) with this, preference was given to the combination with the lowest RMSE and RMSE%. The highest R² (0.78) also corresponds to a larger RMSE (141.84) as with the CO1 model, this necessitates the choice of CO3 variable combination for the best performance at this zone. In the SW zone, RMSE varied from 126.85 m³/plot to 139.21 m³/plot for CO3 and CO1 respectively. In this zone, the CO4 variable combination exhibited a good fit with an RMSE of 129.22 m³/plot, R² of 0.74 and RMSE% of 14.04. Although, the CO1 and CO2 models shows a higher R² of 0.79 and 0.77 yet, their associated RMSE is larger as compare to the CO4 combination (Table 3).
For the NE zone, CO4 yielded the best results with an R² of 0.64 and an RMSE of 133.77 m³/plot, followed by CO3 model with an R² of 0.61 and an RMSE of 132.17 m³/plot. The highest R² and RMSE under this zone also correspond to the CO2 and CO1 which is accompanied by a higher RMSE. Similarly, in the SE zone, CO4 variables performed the best with an R² of 0.70 and an RMSE of 120.56 m³/plot, followed by the CO3 variables with an R² 0.68 and an RMSE of 119.35 m³/plot. Although, CO1 had the highest R² (0.81) and RMSE (135.49), the emphasis on minimizing the RMSE favored the CO4 variables as the variability explain under this combination is on an average good.

3.2. Performance Assessment Based on Support Vector Regression

Support vector regression model carried out at quadrant level using each variable combinations is as presented in Table 3. In the NW zone, the best performance in terms of the lowest RMSE and RMSE% is the CO3-generated model having an R² of 0.52, RMSE of 123.41 m³/plot and an RMSE% of 12.74%. However, this model captured less variability compared to its RF counterpart (Table 3). A notable trend of a consistent highest R² value across each quadrant is exhibited by CO1 model and also, it is characterized by the highest RMSE. In the NW zone, for instance, the CO1 variable achieves an R² of 0.81 and an RMSE of 150.01 m³/plot, indicating significant error when applied to the 3712 plots within the zone.
In the SW zone, CO1 variable produced an R² value of 0.79 and an RMSE of 141.35 m³/plot, while CO4 and CO3 both achieved an R² value of 0.64. However, the CO3 model has the lowest RMSE (124.53 m³/plot) compared to CO4 (129.57 m³/plot). Despite CO2's relatively average performance with an R² of 0.74 and an RMSE of 136.17 m³/plot, the CO3 model is deemed more suitable with an RMSE of 124.53 m³/plot. The range of coefficient of determination in the NE zone is between 0.43 – 0.65 where the CO1 and CO2 explain the same variability with an R² of 0.65. However, the RMSE in CO1 is 4.37 m³/plot higher than CO2. The CO3 model exhibits the lowest RMSE (129.83 m³/plot) and RMSE% (12.14), although its R² (0.43) is the lowest among all variable combinations. On average, CO4 performs notably better with an R² of 0.60 and an RMSE of 138.98 m³/plot. In the SE zone, CO1 demonstrates the highest R² (0.86) and RMSE (144.46 m³/plot), while CO3 exhibits the lowest R² (0.63) and corresponding lowest RMSE (116.43 m³/plot). Although the CO3 and CO4 models shows a relatively good fit, selecting CO4 (R² = 0.68, RMSE = 122.34 m³/plot) is justifiable. In comparison with the RF model, a better precision is obtained with the RF using CO4 model.
Table 4. Support Vector Regression performance metric.
Table 4. Support Vector Regression performance metric.
Variables R² RMSE RMSE%
CO1 NW 0.81 150.01 15.49
CO2 0.53 130.53 13.48
CO3 0.52 123.41 12.74
CO4 0.51 125.05 12.91
CO1 SW 0.79 141.35 15.36
CO2 0.74 136.17 14.79
CO3 0.64 124.53 13.53
CO4 0.64 129.57 14.08
CO1 NE 0.65 153.53 14.06
CO2 0.65 149.16 13.95
CO3 0.43 129.83 12.14
CO4 0.6 138.98 13
CO1 SE 0.86 144.46 14.76
CO2 0.79 132.45 13.52
CO3 0.63 116.43 11.89
CO4 0.68 122.34 12.5

3.3. Performance assessment based on Extreme gradient boosting

The XGBoost outperform the SVR in the NW zone meanwhile, a similar performance was achieved within the variable combination of RF and XGBoost models. Notably, for the CO4 variable, both models (XGBoost and RF) had the same R² value of 0.64 and closely correlated RMSE values, differing by only 0.59 m³/plot. For the CO1 model, both XGBoost and RF also achieved an R² of 0.78, though XGBoost had a higher RMSE of 1.8 m³/plot compared to the RF model. An R² of 0.61 for XGBoost was found in the CO3 model, with an RMSE of 124.63 m³/plot, highlighting the robustness of CO3 variables for growing stock volume estimation.
In the SW zone, we compared the unit differences in performance metrics and found that the CO4 model-based algorithm met our goals best, with an R² of 0.69 and the lowest RMSE of 128.29 m³/plot. This was followed by the CO3 model with an R² of 0.68 and an RMSE of 129.32 m³/plot. As with the other models, the CO1 variable yielded the highest R² of 0.77, with an RMSE of 139.39 m³/plot. At the NE zone, the RMSE are in the range of 132.58 m3/plot to 148.16 m3/plot which is similar to the range obtained with RF. The CO3 produced a more accurate estimate considering its R² and RMSE of 0.60 and 132.58 m3/plot respectively. In the NE zone, the RMSE values range from 132.63 m³/plot to 148.16 m³/plot, similar to the range obtained with RF. The CO3 model provided a more accurate estimate, with an R² of 0.60 and an RMSE of 132.63 m³/plot.
Comparing the results obtained in the SE zone based on the four variable combinations, we found the CO3 model to be the most precise, with an R² of 0.65 and an RMSE of 119.48 m³/plot. The CO4 model also achieved an R² of 0.65, but its associated RMSE is 123.36 m³/plot, which is 4.18 m³/plot higher than CO3, making CO3 the preferred model. The CO2 model shows an increased R² of 0.75 but a decreased accuracy, with an RMSE of 131.40 m³/plot. Although the CO1 model has the highest R² of 0.80, its associated RMSE of 138.01 m³/plot indicates a notable decrease in predictive power.
Table 5. XGBoost performance metric.
Table 5. XGBoost performance metric.
Variables R² RMSE RMSE%
CO1 NW 0.78 143.67 14.84
CO2 0.68 133.77 13.81
CO3 0.61 124.46 12.85
CO4 0.64 126.15 13.03
CO1 SW 0.77 139.37 15.19
CO2 0.74 136.17 14.79
CO3 0.68 129.32 14.05
CO4 0.69 128.29 13.94
CO1 NE 0.69 139.63 13.09
CO2 0.72 148.16 13.86
CO3 0.6 132.63 12.4
CO4 0.59 134.25 12.56
CO1 SE 0.8 138.01 14.1
CO2 0.75 131.4 13.4
CO3 0.65 119.48 12.17
CO4 0.65 123.36 12.6

3.4. Model Predictive Power at Each Quadrant/ Comparative Analysis of Predictive Model

In all quadrants, the RF algorithms proves to be the most effective. For instance, RF algorithm with the CO3 variable combination proves to be the best predictive model in the NW zone, with the SVR-based model achieving the lowest RMSE of 123.41 m³/plot, followed by the CO3-XGBoost model with an RMSE of 124.63 m³/plot; however, considering the differences in R² values and associated RMSEs, the RF-based model with an R² value of 0.63 and an RMSE value of 125.39 m³/plot is more preferable (Figure 3 NW_RF), and the CO3 variable combination demonstrates robust performance, consistently yielding the lowest RMSE values across all three predictive model. In the SW zone, the RF algorithm again outperforms other models in estimating GSV based on the CO4 variable combination (Figure 3 SW_RF), although the SVR model achieved the lowest RMSE, it also showed more scattering with an R² of 0.6; shifting focus to the NE zone, the RF algorithms using the CO4 variable combination yield more preferable results (Figure NE_FR), followed by the XGBoost model using the CO3 variable combination, with the least effective results found in the SVR model (Table 6); turning to the SE zone, the use of RF-based algorithms with the CO4 variable combination also shows appreciable performance (Figure 4 SE_RF), outperforming the SVR and XGBoost models (Table 6), yet as observed in other zones, the lowest RMSE does not necessarily correspond to the RF-based model; nonetheless, the minimal differences in performance metrics among these predictive models favour the RF model, and generally, the SVR yields the lowest RMSE across all quadrants and predictive models, but its CO1 and CO2-based models are characterized by relatively high RMSE values.

4. Discussion

In this study, we demonstrated the prediction of forest tree growing stock volume using three predictive algorithms such as RF, SVM and XGBoost. In other to enrich our prediction, we made use of Estonian National Forest Inventory data, Sentinel 2, and LiDAR height percentile data as the use of multi-source data has the potential of improving the prediction of growing stock volume [37,40,59]. Our study presented a pioneering model estimation of plot GSV using a complete cycle NFI over Estonia forest and at such provide an architectural framework for comparative study in the country. We used four variable combinations derived from the remotely sensed data as explained in section 2 of this article. These includes; LiDAR and Vegetation Indices (CO1), Lidar and band reflectance (CO2), Vegetation Indices and band reflectance value (CO3), band reflectance value, vegetation indices and LiDAR height percentile (CO4). In our characterization, we examined which of the machine learning algorithms performs best and also delved into variable importance and their associated sources.
Notably, in all the quadrant, the RF based algorithm outperformed other predictive algorithms (Table 6). Although the lowest RMSE does not necessarily correspond to the RF model, nonetheless, the associated unit differences between the performance metric favors the RF model. For example, in the NW, the RF achieved an R² of 0.63 and an RMSE of 125.39 m³/plot, followed by the XGBoost with an R² of 0.64 and an RMSE of 126.15 m³/plot, the lowest RMSE correspond to the SVR algorithm with an R² value of 0.52 and an RMSE value of 123.41 m³/plot. The lowest RMSE of 124.53 m³/plot in the SW also corresponds to the SVR whereas, the best predictive model was found in the RF models with an R² 0.74 and an RMSE of 129.22 m³/plot. This further establish the strength of RF algorithms in estimating forest variables.
The use of RF to estimate GSV has been demonstrated overtime, in some cases, it is used exclusively [14,37,60] and in some, it was used comparatively with other ML algorithms [36,37,40]. For example, Chirici et al. [40] used two non-parametric and two parametric prediction methods (RF, K-NN, MLR and GWR) to produce a wall – wall spatial prediction of growing stock volume using Italian NFI plot and remotely sensed data and concluded that RF forest algorithm produced the best accuracy. Although the variable used in their prediction is not the same as ours. In our study, we do not consider the environmental factors, nor distinguish the forest type and species at each quadrant level this of course we believe would have help to further homogenized our findings. For example, Estonia is characterized by both coniferous and deciduous tree species. Lang et al. [23] in their research to facilitate the construction of maps for forest height, standing wood volume and tree species composition in Estonia suggested that for a more reliable prediction, empirical data can be divided into subset that account for variability before fitting the model.
The use of optical remote sensing data for the prediction of forest variable is usually accompanied with issue relating to saturation and this is believed to have effect on the accuracy of the predicted variables. Areas within the forest with dense canopy closure are highly susceptible to saturation problem as the optical sensor only capture horizontal information about the forest. One of the ways to possibly reduce this impact is the inclusion of vegetation indices derived from red edge band [61,62] and also through the inclusion of satellite data that captures the vertical information about the forest structure. Hence, we incorporated the height percentile data from LiDAR metric and vegetation indices derived from red edge bands (table 2). As seen from the results of our findings, combination that incorporated vegetation indices, band reflectance values and height percentile data consistently yielded the best results in each quadrant except in the NW quadrant where combination of bands reflectance number and height percentile is considered to be more accurate (table 3). Although the unit difference between the performance metrics of the CO3 and CO4 variable combinations at this quadrant is not well pronounced having an RMSE of 125.39 m³/plot and an R² value of 0.63 in the CO3 and an RMSE 126.7 m³/plot and an R² value of 0.64 in the CO3 (table 3).
When band reflectance and height percentiles were used, this approach yields the lowest RMSE across all quadrants and the three predictive models (Table 3, Table 4 and Table 5). Additionally, incorporating vegetation indices further improves the coefficient of determination (R²). For example, in the SW zone, adding vegetation indices improves the R² by 4.11% and decreases the RMSE by 1.56%. Similarly, in the NE zone, there is a 4.7% improvement in R² and a 1.19% decrease in RMSE. In the SE zone, the R² increases by 2.86% and the RMSE decreases by 1.13%. The CO1 and CO2 combination consistently yields significantly higher R² values and an erroneous RMSEs (Table 3, Table 4 and Table 5).
Lahssini et al. [59] was of the opinion that the availability of multimodal remote sensing data alone does not necessarily guarantee better performance; instead, how these data are integrated is crucial. Appendix A shows how the various variable were integrated and ranked in order of their importance. Based on the prediction in the NW quadrant, LiDAR height percentile and band reflectance number shows a good fit in GSV prediction with height percentile at p95, p90 and p50 the most important height percentile variable this had been established by other studies [63,64,65] and the red edge band 7 and 5 are the most important band reflectance number this correspond to other research where the red edge bands had been established to outperformed other bands in forest variable prediction [8,66,67].
In the SW, NE and SE quadrat where the combination of height percentile, individual band reflectance value and vegetation indices proved to be the most efficient combination in GSV prediction, the height percentile at p95, p90, p80 and p50 are crucial among the height percentile variables, followed by individual band reflectance values. This correspond to [63,64,68] where these height percentiles were also reported to contribute effective to forest variables prediction. Among the individual band reflectance number, the red edge and SWIR are the most commonly reported bands that correlate with GSV. Our findings further establish this where the SWIR1, SWIR2, red edge bands were part of the most important variable that contribute significantly to the GSV prediction except in the NE quadrant where red edge band 6 was removed.
In our research, we only examine the effect of the inclusion of various band reflective value, vegetation indices and height percentile data on the overall performance and reliability of GSV prediction meanwhile the initial performance of ML algorithm can be improved with hybrid model [37,69]. For instance, in Hu et al. [37], accuracy of three machine learning including RF, SVR and an artificial neural network (ANN) were improved by building a hybrid model as an extension of these ML these later yielded an improvement by reducing the initial RMSE of RF by 11.45 %, and an increase in the associated R² by 2.17% for the SVR, the RMSE was reduced by 20.37% and the R² increased by 7% these are called ordinary kriging model hybrid.

5. Conclusions

Estimating and quantifying forest related variables such as aboveground biomass and growing stock volume are becoming increasingly important and there already exist considerable research finding on this, nonetheless, there exist a dearth of comprehensive research effort in Estonia. The primary aim of this study was to enhance the estimation of growing stock volume by integrating data from National Forest Inventory, Sentinel 2, and LiDAR, employing three predictive algorithms such as RF, SVR, and XGBoost. Our findings reveal that the combined use of height percentile, band reflectance value, and vegetation indices significantly improves the accuracy of GSV predictions. The combination of band reflectance value and height percentile also exhibited a promising trend. Among the predictive algorithms tested, RF demonstrated the best performance, yielding the most considerable accuracy at each quadrant. The most occurring height percentile variable are P95, p90 and p50 while the occurrence of the red edge and SWIR bands are significant notable. Despite the promising outcomes of our study, certain research gap exists that need addressing. For example, the variability of forest types and conditions across different geographical regions suggests that further testing and refinement of these methods are necessary. Efforts should attempt to homogenized the tree species in each quadrant into individual strata before modelling and additionally, integrating other data sources, such ecological, climatological, and experimenting with emerging machine learning techniques could further enhance prediction accuracy. In conclusion, the enriched estimation of growing stock volume using NFI, Sentinel 2, and LiDAR data, combined with advanced predictive algorithms, offers a robust tool for forest management. This approach promises significant benefits for sustainable forestry practices and ecosystem monitoring, paving the way for more informed and effective climate smart decision-making in forest conservation and management.

Author Contributions

Conceptualization, T.O. and A.S.; methodology, T.O., A.S.; formal analysis, T.O. and A.S.; writing—original draft preparation, T.O.; writing—review and editing, T.O and A.S.; supervision, A.S.; funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Estonian Research Council, grant number PRG2214.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

We extend our sincere thanks to the Estonian Land Board for supplying the LiDAR data. Additionally, we appreciate the efforts of all authors whose contributions were vital to the development and completion of this paper

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Preprints 118888 i001Preprints 118888 i002

References

  1. Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
  2. Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
  3. Mori, A.S.; Furukawa, T.; Sasaki, T. Response Diversity Determines the Resilience of Ecosystems to Environmental Change. Biological Reviews 2013, 88, 349–364. [Google Scholar] [CrossRef] [PubMed]
  4. Sing, L.; Metzger, M.J.; Paterson, J.S.; Ray, D. A Review of the Effects of Forest Management Intensity on Ecosystem Services for Northern European Temperate Forests with a Focus on the UK. Forestry: An International Journal of Forest Research 2018, 91, 151–164. [Google Scholar] [CrossRef]
  5. Belcher, B.; Ruíz-Pérez, M.; Achdiawan, R. Global Patterns and Trends in the Use and Management of Commercial NTFPs: Implications for Livelihoods and Conservation. World Development 2005, 33, 1435–1452. [Google Scholar] [CrossRef]
  6. Brown, S. Measuring Carbon in Forests: Current Status and Future Challenges. Environmental Pollution 2002, 116, 363–372. [Google Scholar] [CrossRef]
  7. Chirici, G.; McRoberts, R.E.; Winter, S.; Bertini, R.; Brändli, U.-B.; Asensio, I.A.; Bastrup-Birk, A.; Rondeux, J.; Barsoum, N.; Marchetti, M. National Forest Inventory Contributions to Forest Biodiversity Monitoring. Forest Science 2012, 58, 257–268. [Google Scholar] [CrossRef]
  8. Zhou, Y.; Feng, Z. Estimation of Forest Stock Volume Using Sentinel-2 MSI, Landsat 8 OLI Imagery and Forest Inventory Data. Forests 2023, 14, 1345. [Google Scholar] [CrossRef]
  9. FAO Global Forest Resources Assessment Report, Estonia Global Forest Resources Assessment. (accessed on 15 November 2022).
  10. Næsset, E. Practical Large-Scale Forest Stand Inventory Using a Small-Footprint Airborne Scanning Laser. Scandinavian Journal of Forest Research 2004, 19, 164–179. [Google Scholar] [CrossRef]
  11. Breidenbach, J.; Anton-Fernandez, C.; Petersson, H.; Mcroberts, R.E.; Astrup, R. Quantifying the Model-Related Variability of Biomass Stock and Change Estimates in the Norwegian National Forest Inventory. Forest Science 2014, 60, 25–33. [Google Scholar] [CrossRef]
  12. Wulder, M.A.; White, J.C.; Fournier, R.A.; Luther, J.E.; Magnussen, S. Spatially Explicit Large Area Biomass Estimation: Three Approaches Using Forest Inventory and Remotely Sensed Imagery in a GIS. Sensors 2008, 8, 529–560. [Google Scholar] [CrossRef] [PubMed]
  13. Kangas, A.; Astrup, R.; Breidenbach, J.; Fridman, J.; Gobakken, T.; Korhonen, K.T.; Maltamo, M.; Nilsson, M.; Nord-Larsen, T.; Næsset, E.; et al. Remote Sensing and Forest Inventories in Nordic Countries – Roadmap for the Future. Scandinavian Journal of Forest Research 2018, 33, 397–412. [Google Scholar] [CrossRef]
  14. Wang, X.; Zhang, C.; Qiang, Z.; Xu, W.; Fan, J. A New Forest Growing Stock Volume Estimation Model Based on AdaBoost and Random Forest Model. Forests 2024, 15, 260. [Google Scholar] [CrossRef]
  15. Du, C.; Fan, W.; Ma, Y.; Jin, H.I.; Zhen, Z. The Effect of Synergistic Approaches of Features and Ensemble Learning Algorith on Aboveground Biomass Estimation of Natural Secondary Forests Based on Als and Landsat 8. Sensors 2021, 21. [Google Scholar] [CrossRef]
  16. Asner, G.P.; Knapp, D.E.; Martin, R.E.; Tupayachi, R.; Anderson, C.B.; Mascaro, J.; Sinca, F.; Chadwick, K.D.; Higgins, M.; Farfan, W.; et al. Targeted Carbon Conservation at National Scales with High-Resolution Monitoring. Proceedings of the National Academy of Sciences 2014, 111. [Google Scholar] [CrossRef]
  17. Loveland, T.R.; Irons, J.R. Landsat 8: The Plans, the Reality, and the Legacy. Remote Sensing of Environment 2016, 185, 1–6. [Google Scholar] [CrossRef]
  18. Gobakken, T.; Næsset, E. Assessing Effects of Laser Point Density, Ground Sampling Intensity, and Field Sample Plot Size on Biophysical Stand Properties Derived from Airborne Laser Scanner Data. Canadian Journal of Forest Research 2008, 38, 1095–1109. [Google Scholar] [CrossRef]
  19. Rosema, A.; Verhoef, W.; Noorbergen, H.; Borgesius, J.J. A New Forest Light Interaction Model in Support of Forest Monitoring. Remote Sensing of Environment 1992, 42, 23–41. [Google Scholar] [CrossRef]
  20. Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR Remote Sensing of Forest Structure. Progress in Physical Geography: Earth and Environment 2003, 27, 88–106. [Google Scholar] [CrossRef]
  21. White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Canadian Journal of Remote Sensing 2016, 42, 619–641. [Google Scholar] [CrossRef]
  22. Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the Capabilities of the Sentinel-2 Multi Spectral Instrument for Predicting Growing Stock Volume in Forest Ecosystems. International Journal of Applied Earth Observation and Geoinformation 2018, 66, 126–134. [Google Scholar] [CrossRef]
  23. Lang, M.; Sims, A.; Pärna, K.; Kangro, R.; Möls, M.; Mõistus, M.; Kiviste, A.; Tee, M.; Vajakas, T.; Rennel, M. Remote-Sensing Support for the Estonian National Forest Inventory, Facilitating the Construction of Maps for Forest Height, Standing-Wood Volume, and Tree Species Composition Kaugseirel Põhinev Lahendus Eesti Statistilise Metsainventuuri Jaoks Puistute Kõrguse, Tüvemahu Ja Liigilise Koosseisu Kaartide Koostamiseks. Forestry Studies 2020, 73, 77–97. [Google Scholar] [CrossRef]
  24. McRoberts, R.E.; Tomppo, E.O.; Næsset, E. Advances and Emerging Issues in National Forest Inventories. Scandinavian Journal of Forest Research 2010, 25, 368–381. [Google Scholar] [CrossRef]
  25. Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sensing of Environment 2002, 80, 88–99. [Google Scholar] [CrossRef]
  26. Nilsson, M.; Nordkvist, K.; Jonzén, J.; Lindgren, N.; Axensten, P.; Wallerman, J.; Egberth, M.; Larsson, S.; Nilsson, L.; Eriksson, J.; et al. A Nationwide Forest Attribute Map of Sweden Predicted Using Airborne Laser Scanning Data and Field Data from the National Forest Inventory. Remote Sensing of Environment 2017, 194, 447–454. [Google Scholar] [CrossRef]
  27. Lindgren, N.; Olsson, H.; Nyström, K.; Nyström, M.; Ståhl, G. Data Assimilation of Growing Stock Volume Using a Sequence of Remote Sensing Data from Different Sensors. Canadian Journal of Remote Sensing 2022, 48, 127–143. [Google Scholar] [CrossRef]
  28. Allan Sims Principles of National Forest Inventory Methods. In Definition and Uncertainty of Forests. Managing Forest Ecosystems; Springer, 2022; Vol. 43.
  29. Chowdhury, T.A.; Thiel, C.; Schmullius, C. Growing Stock Volume Estimation from L-Band ALOS PALSAR Polarimetric Coherence in Siberian Forest. Remote Sensing of Environment 2014, 155, 129–144. [Google Scholar] [CrossRef]
  30. Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. International Journal of Digital Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
  31. Zharko, V.O.; Bartalev, S.A.; Sidorenkov, V.M. Forest Growing Stock Volume Estimation Using Optical Remote Sensing over Snow-Covered Ground: A Case Study for Sentinel-2 Data and the Russian Southern Taiga Region. Remote Sensing Letters 2020, 11, 677–686. [Google Scholar] [CrossRef]
  32. Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of Lidar and Landsat ETM+ Data for Estimating and Mapping Forest Canopy Height. Remote Sensing of Environment 2002, 82, 397–416. [Google Scholar] [CrossRef]
  33. Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; van Breugel, M. A Universal Airborne LiDAR Approach for Tropical Forest Carbon Mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
  34. Fernández-Landa, A.; Fernández-Moya, J.; Tomé, J.L.; Algeet-Abarquero, N.; Guillén-Climent, M.L.; Vallejo, R.; Sandoval, V.; Marchamalo, M. High Resolution Forest Inventory of Pure and Mixed Stands at Regional Level Combining National Forest Inventory Field Plots, Landsat, and Low Density Lidar. International Journal of Remote Sensing 2018, 39, 4830–4844. [Google Scholar] [CrossRef]
  35. Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A Meta-Analysis and Review of the Literature on the k-Nearest Neighbors Technique for Forestry Applications That Use Remotely Sensed Data. Remote Sensing of Environment 2016, 176, 282–294. [Google Scholar] [CrossRef]
  36. Hawryło, P.; Francini, S.; Chirici, G.; Giannetti, F.; Parkitna, K.; Krok, G.; Mitelsztedt, K.; Lisańczuk, M.; Stereńczak, K.; Ciesielski, M.; et al. The Use of Remotely Sensed Data and Polish NFI Plots for Prediction of Growing Stock Volume Using Different Predictive Methods. Remote Sensing 2020, 12, 3331. [Google Scholar] [CrossRef]
  37. Hu, T.; Sun, Y.; Jia, W.; Li, D.; Zou, M.; Zhang, M. Study on the Estimation of Forest Volume Based on Multi-Source Data. Sensors 2021, 21, 7796. [Google Scholar] [CrossRef] [PubMed]
  38. Myroniuk, V.; Bell, D.M.; Gregory, M.J.; Vasylyshyn, R.; Bilous, A. Uncovering Forest Dynamics Using Historical Forest Inventory Data and Landsat Time Series. Forest Ecology and Management 2022, 513, 120184. [Google Scholar] [CrossRef]
  39. Singh, C.; Karan, S.K.; Sardar, P.; Samadder, S.R. Remote Sensing-Based Biomass Estimation of Dry Deciduous Tropical Forest Using Machine Learning and Ensemble Analysis. Journal of Environmental Management 2022, 308. [Google Scholar] [CrossRef]
  40. Chirici, G.; Giannetti, F.; McRoberts, R.E.; Travaglini, D.; Pecchi, M.; Maselli, F.; Chiesi, M.; Corona, P. Wall-to-Wall Spatial Prediction of Growing Stock Volume Based on Italian National Forest Inventory Plots and Remotely Sensed Data. International Journal of Applied Earth Observation and Geoinformation 2020, 84, 101959. [Google Scholar] [CrossRef]
  41. Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest Neighbor Imputation of Species-Level, Plot-Scale Forest Structure Attributes from LiDAR Data. Remote Sensing of Environment 2008, 112, 2232–2245. [Google Scholar] [CrossRef]
  42. Forest. 2020 Yearbook Forest 2018.(Aastaraamat Mets 2018).; Raudsaar, M., Siimon, K.L.,. Valgepea, M. (eds.)., Ed.; Tallinn, Keskkonnaagentuur.
  43. Raukas, A. Briefly about Estonia. Dynamiques environnementales 2018, 284–291. [Google Scholar] [CrossRef]
  44. RT Forest Act. Riigiteataja I 2006, 30, 232.
  45. Raudsaar M; Merenäkk M; Valgepea M Yearbook Forest 2013 2014.
  46. Adermann V Eesti Metsad 2010 [Estonian Forests 2010 Available at Http://Www.Digar.Ee/Id/Nlib-Digar:258209; 2012.
  47. Reintam L . . Soil Objectives. In: Raukas, A. (Ed.). Estonian Environment: Past, Present and Future. Ministry of the Environment of Estonia, Environment Information Centre 1996, 106–108.
  48. Kohava, P. Forests in Estonia 1999 (Eesti Metsad 1999). 2000, 44.
  49. FRA Estonia GLOBAL FOREST RESOURCES ASSESSMENT 2015 COUNTRY REPORT; 2015.
  50. Zhang, C.; Gao, Z.; Null, S.Y.; Li, P. Edge Detectors Based on Pauta Criterion with Application to Hybrid Compact-WENO Finite Difference Scheme. AAMM 2023, 15, 1379–1406. [Google Scholar] [CrossRef]
  51. Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  52. Breiman, L. Bagging Predictors; Kluwer Academic Publishers, 1996; Vol. 24, pp. 123–140;
  53. Liaw, A.; Wiener, M. Classification and Regression by randomForest; 2002; Vol. 2;
  54. Vapnik, V.S.; Golowich, A. Smola Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing. Advances in Neural Information Processing Systems 1997, 9, 281–287. [Google Scholar]
  55. Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and Evaluation of Three Methods for Estimating Forest above Ground Biomass Using TM and GLAS Data. Remote Sensing 2017, 9. [Google Scholar] [CrossRef]
  56. Dibike, Y.B.; Velickov, S.; Solomatine, D.; Abbott, M.B. Model Induction with Support Vector Machines: Introduction and Applications. Journal of Computing in Civil Engineering 2001, 15, 208–216. [Google Scholar] [CrossRef]
  57. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery, August 13 2016; Vol. 13–17-August-2016, pp. 785–794.
  58. Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10. [Google Scholar] [CrossRef]
  59. Lahssini, K.; Teste, F.; Dayal, K.R.; Durrieu, S.; Ienco, D.; Monnet, J.-M. Combining LiDAR Metrics and Sentinel-2 Imagery to Estimate Basal Area and Wood Volume in Complex Forest Environment via Neural Networks. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 4337–4348. [Google Scholar] [CrossRef]
  60. Ma, T.; Hu, Y.; Wang, J.; Beckline, M.; Pang, D.; Chen, L.; Ni, X.; Li, X. A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China. Remote Sensing 2023, 15, 1853. [Google Scholar] [CrossRef]
  61. Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the Capabilities of Sentinel-2 for Quantitative Estimation of Biophysical Variables in Vegetation. ISPRS Journal of Photogrammetry and Remote Sensing 2013, 82, 83–92. [Google Scholar] [CrossRef]
  62. Yu, T.; Pang, Y.; Liang, X.; Jia, W.; Bai, Y.; Fan, Y.; Chen, D.; Liu, X.; Deng, G.; Li, C.; et al. China’s Larch Stock Volume Estimation Using Sentinel-2 and LiDAR Data. Geo-spatial Information Science 2023, 26, 392–405. [Google Scholar] [CrossRef]
  63. Leite, R.V.; Amaral, C.H. do; Pires, R. de P.; Silva, C.A.; Soares, C.P.B.; Macedo, R.P.; Silva, A.A.L. da; Broadbent, E.N.; Mohan, M.; Leite, H.G. Estimating Stem Volume in Eucalyptus Plantations Using Airborne LiDAR: A Comparison of Area- and Individual Tree-Based Approaches. Remote Sensing 2020, 12, 1513. [Google Scholar] [CrossRef]
  64. Lin, W.; Lu, Y.; Li, G.; Jiang, X.; Lu, D. A Comparative Analysis of Modeling Approaches and Canopy Height-Based Data Sources for Mapping Forest Growing Stock Volume in a Northern Subtropical Ecosystem of China. GIScience & Remote Sensing 2022, 59, 568–589. [Google Scholar] [CrossRef]
  65. Saarela, S.; Grafström, A.; Ståhl, G.; Kangas, A.; Holopainen, M.; Tuominen, S.; Nordkvist, K.; Hyyppä, J. Model-Assisted Estimation of Growing Stock Volume Using Different Combinations of LiDAR and Landsat Data as Auxiliary Information. Remote Sensing of Environment 2015, 158, 431–440. [Google Scholar] [CrossRef]
  66. Fang, G.; He, X.; Weng, Y.; Fang, L. Texture Features Derived from Sentinel-2 Vegetation Indices for Estimating and Mapping Forest Growing Stock Volume. Remote Sensing 2023, 15, 2821. [Google Scholar] [CrossRef]
  67. Korhonen, L.; Hadi; Packalen, P. ; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the Estimation of Boreal Forest Canopy Cover and Leaf Area Index. Remote Sensing of Environment 2017, 195, 259–274. [Google Scholar] [CrossRef]
  68. Saarela, S.; Wästlund, A.; Holmström, E.; Mensah, A.A.; Holm, S.; Nilsson, M.; Fridman, J.; Ståhl, G. Mapping Aboveground Biomass and Its Prediction Uncertainty Using LiDAR and Field Data, Accounting for Tree-Level Allometric and LiDAR Model Errors. Forest Ecosystems 2020, 7. [Google Scholar] [CrossRef]
  69. Chen, L.; Ren, C.; Zhang, B.; Wang, Z. Multi-Sensor Prediction of Stand Volume by a Hybrid Model of Support Vector Machine for Regression Kriging. Forests 2020, 11, 296. [Google Scholar] [CrossRef]
Preprints 118888 g001
Figure 1. Cluster network (a) of the Estonia NFI permanent and temporary plot (2018-2022), Cartogram of the elevation model of the land cover (b).
Figure 1. Cluster network (a) of the Estonia NFI permanent and temporary plot (2018-2022), Cartogram of the elevation model of the land cover (b).
Preprints 118888 g001
Preprints 118888 g002
Figure 2. Methodology flowchart for the study.
Figure 2. Methodology flowchart for the study.
Preprints 118888 g002
Preprints 118888 g003aPreprints 118888 g003b
Figure 3. Scatter plot of observed vs. predicted GSV values for the validation plots using the best predictive model. The symbols * and ** represent the CO3 and CO4 combinations, respectively. Northwest RF, Southwest RF, Northeast RF, and Southeast RF denote the Random Forest-based models for the northwest, southwest, northeast, and southeast regions, respectively.
Figure 3. Scatter plot of observed vs. predicted GSV values for the validation plots using the best predictive model. The symbols * and ** represent the CO3 and CO4 combinations, respectively. Northwest RF, Southwest RF, Northeast RF, and Southeast RF denote the Random Forest-based models for the northwest, southwest, northeast, and southeast regions, respectively.
Preprints 118888 g003aPreprints 118888 g003b
Table 1. Descriptive characteristics for GSV (m³/plot).
Table 1. Descriptive characteristics for GSV (m³/plot).
Zone No. of plot Min Max Mean SD
N/W 3712 36.89 1007.01 531.42 162.36
S/W 3651 80.8 1038.24 573.22 153.58
N/E 3852 31.76 1101.03 569.59 175.65
S/E 3665 122.08 1101.03 625.40 147.57
All 14880 31.76 1101.03 575.13 163.78
Table 2. Source and description of variables.
Table 2. Source and description of variables.
Variable Description
Sentinel 2 Blue B2
single band Green B3
Red B4
Red edge 1 B5
Red edge 2 B6
Red edge 3 B7
NIR B8
NIR narrow B8A
SWIR B11
SWIR B12
Veg. indices NDVI (B08-B04)/(B08+B04)
ARI1 (1 / B03) - (1 / B05)
MARI (1 / B03) - (1 / B05) * B07
ARVI (B8A - B04 - y * (B04 - B02)) / (B8A + B04 - y * (B04 - B02))
NDVIre705 (B08-B05)/(B08+B05)
NDVIre740 (B08-B06)/(B08+B06)
NDVIre783 (B08-B07)/(B08+B07)
EVI 2.5*(B08-B04)/(BO8+2.4*B04+1)
SAVI (B08-B04) *(1+L)/ (BO8+B04+L)
MCARI ((B05 - B04) - 0.2 * (B05 - B03)) * (B05 / B04)
Clgreen (B07)/(B03-1)
ND11 (B07-B05)/(B07+B05)
chlre (B07)/(B05-1)
GNDVI B08-BO3) / (B08+B03
MSAVI 0.5*(2 * B08 + 1 - sqrt ((2 * B08 + 1)^2 - 8 * (B08 - B04)))
Airborne Lidar p25 Height percentile of 25%
p50 Height percentile of 50%
p60 Height percentile of 60%
p70 Height percentile of 70%
p75 Height percentile of 75%
p80 Height percentile of 80%
p90 Height percentile of 90%
p95 Height percentile of 95%
first_returns_above number of first return laser pulses
percentage_all percentage of all laser pulses
total_first_return total number of first return laser pulses
Table 3. Random Forest performance metric.
Table 3. Random Forest performance metric.
Variables R² RMSE RMSE%
CO1 NW 0.78 141.84 14.65
CO2 0.69 133.1 13.74
CO3 0.63 125.39 12.95
CO4 0.64 126.74 13.09
CO1 SW 0.79 139.21 15.12
CO2 0.77 138.57 15.05
CO3 0.7 126.85 13.78
CO4 0.74 129.22 14.04
CO1 NE 0.73 141.51 13.23
CO2 0.74 147.2 13.77
CO3 0.61 132.17 12.36
CO4 0.64 133.77 12.51
CO1 SE 0.81 135.49 13.84
CO2 0.74 128.41 13.12
CO3 0.68 119.35 12.19
CO4 0.7 120.56 12.32
Table 6. comparative metrics.
Table 6. comparative metrics.
Quadrant RF SVR XGBoost
R² RMSE R² RMSE R² RMSE
NW 0.64* 125.39 0.52* 123.41 0.64** 126.15
SW 0.74** 129.22 0.64* 124.53 0.69** 128.29
NE 0.64** 133.77 0.60** 138.98 0.60* 132.63
SE 0.70** 120.56 0.68** 122.34 0.65* 123.66
Where * and ** are the CO3 and CO4 combination respectively.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated