Prerpints.org logo
Preprint
Article

A New Approach to Fermat’s Last Theorem with Several Examples

Altmetrics

Downloads

81

Views

81

Comments

0

Submitted:

23 September 2024

Posted:

23 September 2024

You are already at the latest version

Alerts
Abstract
These counterexamples have shown the relationships between the power of a Pythagorean equation and Pythagorean’s triples. There are three positive integers that satisfy Fermat’s equation when the power n is equal to 2 in the case of the Pythagorean theorem and it’s applicable relationships in right triangles. On the other hand, as the power varies from positive to negative integers or any integers other than 2, such as in the case of Fermat’s last theorem, the hypotenuse z of a right triangle tends to be equal to one of the sides x or y of the triangle and the other side tends to be equal to zero. And the application of this idea describes the behavior of a mass object in motion. Since the total energy of the object is the sum of its energy in motion and its rest energy, at a particular power n, the total energy of the object tends to be equal to either the rest energy or the photon energy.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

Ancient Mesopotamian is one of the most significant early development of mathematics, begins about 3rd millennium BCE to the fall of Babylon in 539BCE, mathematics are been used for measuring and for keeping tracks of quantities. Mathematics is written in Cuneiform script, in form of clay inscribed. Mesopotamian worked on many mathematical topics which includes Babylonian numerals, Algebra and arithmetic, Geometry and Pythagoreans theorem, before the development of other sophisticated topics.
Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It was named after a Greek philosopher Pythagoras, who was born around 570BC. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule has been in use during 20th to 16th centuries BC, over a thousand years before Pythagoras was born.
Between 2000BC and 1786BC, Egyptian Middle Kingdom Berlin Papyrus 6619 includes a problem whose solution is related to the Pythagorean triple 6:8:10, but the problem does not mention any triangle. The Mesopotamian tablet Plimpton 322, written between 1790 and 1750 BC contains many entries that are closely related to Pythagorean triples.
Between 8th and 5th century BC, Baudhayana Shulba Sutra, contains a statement of the Pythagorean Theorem and the Pythagorean triples both as a special case of isosceles right triangle and in the general case as Apastamba Shulba Sutra around 6th century BC.
During the 5th century AD, Byzantine Neoplatonic philosopher and mathematician Proclus wrote two arithmetic rules for generating special Pythagorean triples. The one attributed to Pythagoras starts from an odd number (c. 570 – c. 495 BC).
The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven give a reasoning for the Pythagorean Theorem for the 3:4:5 triangle, in China it is called “Gougu theorem”
Carl Boyer states that the Pythagorean Theorem in the Śulba-sũtram may have been influenced by ancient Mesopotamian mathematics, but there is no conclusive evidence in favor or opposition of this possibility.
Pythagorean Theorem is used in construction and geometry in the ancient times till date. The theorem states that the square of the hypotenuse z is equal to the sum of the squares of the other two sides x, y of a right triangle. The theorem has been proven countless time with different methods which include geometric and algebraic methods. It can be written as an equation relating the lengths of the sides x, y, and hypotenuse z, generally known as the Pythagorean equation.
If z denotes the length of the hypotenuse and x and y denote the other two lengths of the legs of a right triangle perpendicular to each other, then the Pythagorean theorem can be expressed in Pythagorean equation: {\displaystyle b={\sqrt {c^{2}-a^{2}}}.}
x 2 +   y 2 =   z 2
For example, it can be deduced using simple mathematics, that if only the lengths of the legs of the right triangle are known and the hypotenuse is unknown, then the length of the hypotenuse can be calculated with the following equations
z =   x 2 +   y 2  
Colloquially, if the length of the hypotenuse and one length of the leg is known, then the length of the other legs can be calculated as
x =   z 2 −   y 2
Or
y =   z 2 −   x 2  
Any triple integers x, y, and z that satisfy the equation above is called Pythagorean’s triples, and there are infinitely numerous triples and methods of generating them which have been studied by different cultures such as the Babylonians, Ancient Greek, Chinese, and Indian mathematicians. Thus far, the knowledge of the Pythagorean Theorem based on the history can be classified into four parts: the knowledge of Pythagorean triples, the knowledge of the relationship among the sides of a right triangle as shown in equation 2, 3 & 4, the knowledge of the relationships among adjacent angles, and the knowledge of the proofs of the theorem within some deductive system. Another knowledge of Pythagorean equation that should be considered on this topic is the knowledge of the relationship between the Pythagorean’s triples and the power of the equation.
However, the simplest equation likely to explain the relationships between the power of the equation and the triples is called Fermat’s Last Theorem. It is an example of a Diophantine’s equation.
Diophantus of Alexandra was an Alexandra mathematician and an author of series of books called Arithmetica. His texts deal with solving algebraic equations which includes Diophantine equations, Diophantine geometry, and Diophantine approximations which are all based on Number theory. Diophantus wrote on polygonal numbers, a topic of great interest to Pythagoras. One of the editions of Diophantus’s book was translated to Latin and published by Claude Bachet in 1621.
Many years after, while Pierre de Fermat was studying Diophantine’s equation; he came across a problem and he wrote in the margin of his copy of the Arithmetica close to Diophantus’s sum of squares problem that “it is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher that the second, into two like powers. I have discovered a truly marvelous proof of this, which this margin is too narrow to contain”. That is there is no positive integer solution for the equation 5 below if n > 2 . This is the equation that relates the power and the Pythagorean’s triples.
x n + y n = z n
In 1670, five years after the death of Pierre de Fermat, a new edition of his book augmented with his comments was published by his son Clément-Samuel Fermat. The augment was that, there is no three positive integers x, y and z, that can fit into the equation 5 above if the power n is any integer but not 2. It was not clear whether Fermat actually have a valid proof for the general proof of the equation. Rather a specific proofs by him survived, the case where n=4, no general proof was found. The methods of Fermat marvelous proof he claimed to have had for the general solution are unknown, perhaps it would have been an elementary method by comparison based on the level of the mathematical knowledge at his time.
Fermat used infinite descent method in his special case where n = 4 to show that the area of a right triangle with integer sides can never be equal the square of an integer. Quite a number of alternative proofs of this case were developed after. In 1676, Frénicle de Bess, Leonhard Euler in 1738, Kausler in 1802, Peter Barlow in 1811, Adrien-Marie Legendre in 1830, Schopis in 1825, Olry Terquem in 1846, Joseph Bertrand in 1851, Victor Lebesgue in 1853 - 1862, Théophile Pépin in 1883, Tafelmacher in 1893, David Hilbert in 1897, Bendz in 1901, Gambioli in 1901, Leopold Kronecker in 1901, Bang in 1905, Sommer in 1907, Bottari in 1908, Karel Rychlík in 1910, Nutzhorn in 1912, Robert Carmichael in 1913, Hancock in 1931, Gheorghe Vrănceanu in 1966, Grant and Perella in 1999, Barbara in 2007, and Dolan in 2011.
Other proofs for special case were focused on the odd prime exponents such as 3, 5, and 7. And the first person to work on the special case n =3 is Abu-Mahmud Khojandi in the 10th century but his approach toward the proof was incorrect. Leonhard Euler in 1770 used Fermat approach infinite descent but it was discovered to contained major gap. Afterward, many independent proofs were published by Kausler in 1802, Legendre in 1823-1830, Calzolari in 1855, Gabriel Lamé in 1865, Peter Guthrie Tait in 1872, Günther in 1878, Gambioli in 1901, Krey in 1909, Rychlík in 1910, Stockhaus in 1910, Carmichael in 1915, Johannes van der Corput in 1915, Axel Thue in 1917, and Duarte in 1944.
Around 1825 the special case n=5 was independently proved by Legendre and Peter Gustav Lejeune Dirichlet, followed by alternative proofs developed by Carl Friedrich Gauss in 1875, Lebesgue in 1843, Lamé in 1847, Gambioli in 1901, Werebrusow in 1905, Rychlík in 1910, Van der Corput in 1915, and Guy Terjanian in 1987. And the complicated special case n = 7 was introduced by Lamé in 1839. And later simplified in 1840 by Lebesgue, and the more simplified proofs were published in 1864, 1874 and 1876 by Angelo Genocchi. In 1876 alternative proofs were developed by Théophile Pépin and Edmond Maillet in 1897. Other proofs for n = 6 were published by Kausler, Thue, Tafelmacher, Lind, Kapferer, Swift, and Breusch. While Kapferer and Breusch each published a proof for the case n = 10. Likewise, Dirichlet in 1832 and Terjanian each published a proof for the case n = 14. A significant proof for the general solution was first worked on by a French mathematician Sophie Germain; she approached the theorem using mathematical induction and several other new methods to prove Fermat's Last Theorem for all exponents. Using mathematical induction; she was able to show that, if no integers raised to the prime exponent p{\displaystyle p^{\mathrm {th} }} were adjacent modulo{\displaystyle \theta } θ   θ , then θ {\displaystyle \theta } must divide the product x y z , as she defined a set of auxiliary prime number θ {\displaystyle \theta } constructed from a prime exponent {\displaystyle p} p through the equation {\displaystyle \theta =2hp+1} θ = 2 h p + 1 , where h is defined as any integer that cannot be divided by 3 . This proof would have established Fermat's Last Theorem, since the product x y z {\displaystyle xyz} can have at most a finite number of prime factors. With all her efforts and trials she did not succeeded in proving the first case of Fermat's Last Theorem for all even exponents, specifically for{\displaystyle n=2p}, n = 2 p that was later proved by Guy Terjanian in 1977. The first prove that show that Fermat’s last theorem holds for infinitely many odd primes was published by Leonard dleman, Roger Heath-Brown and Étienne Fouvry in 1985.
Around the year 1955, two Japanese mathematicians Goro Shimura and Yutaka Taniyama observed a possible link between two distinct branches of mathematics; elliptic curves and modular forms. The modularity theorem states that every elliptic curve is modular, meaning that all elliptic curves can be associated with a unique modular form. It was known as the Taniyama–Shimura conjecture and was considered as a mere statement with less attention, but was taken more seriously when André Weil found supporting evidence. Though, it was extraordinarily difficult and perhaps inaccessible to proof. In 1984, a German mathematician Gerhard Frey proposed a link between Fermat's equation and the modularity theorem. He stated that if Fermat's equation had any solution (a, b, c) for exponent p > 2, then it could be shown that the semi-stable elliptic curve equation 6 below
y 2 = x x − a p x + b p
would have unusual properties that it was unlikely to be modular. Following this strategy, a proof of Fermat's Last Theorem required two steps. First, it was necessary to prove the modularity theorem which seemed to be difficult. Second, it was necessary to show that Frey's intuition was correct: that if an elliptic curve were constructed in this way, the resulting elliptic curve could not be modular using a set of numbers that were a solution of Fermat's equation. Frey showed that this was plausible but did not go as far as giving a full proof. The missing piece "epsilon conjecture" also known as Ribet's theorem was identified by French mathematician Jean-Pierre Serre who gave an almost-complete proof.
An English mathematician Andrew Wiles committed his life to solve the second half: proving a special case of the modularity theorem for semi-stable elliptic curves. Initially, Wiles approached the problem using induction based on Galois Theory, while the method seems difficult, he extended horizontal Iwasawa theory for inductive argument. The theory was not feasible to the problem, later he discovered an Euler system developed by Victor Kolyvagin and Matthias Flach.
In June 1993, Wiles was fully ready to present his result, however an error was detected during the peer review that part of the results was incorrect. He spent closed to a year trying to fix the error with the help of his former student Richard Taylor without success. And he was about given up when he discovered that Iwasawa theory and the Kolyvagin–Flach approaches were each inadequate on their own, but together they could be made powerful enough to fix the error. In 2015, Wiles was awarded the prestigious Nobel Prize for his work solving one of the most difficult mathematical problems –Fermat’s Last Theorem.
The methods used by Wiles and other mathematician including Fermat himself are based on the infinite descent, either in its original form or the form of descent on elliptic curves or abelian varieties. The original equation as simple as it is, it can be understood using simple arithmetic principles. It is widely known that there are many positive three integers that satisfy the equation where the power n = 2 , and those three integers are called Pythagoreans triples, while the equation where n = 2 is called Pythagorean’s equation. On the other hand, Fermat’s last theorem states that there is no positive integer that satisfies the equation x n + y n = z n if the power n   ≠ 2 . In counter example to the statement made by Pierre de Fermat, and also to explain the relationship between the power of the equation and the Pythagorean’s triples, this article show that using simple arithmetic principles “the hypotenuse of a right triangle tends to be equal to the one side of the triangle and the other side tends to be equal to zero or serves as zero as a result of power variation; i.e. the value of the hypotenuse z tends to be equal to the value of y, while x tends to be equal to zero as the power n increases (x → 0, z → y), and at the other hand as the power n decreases the value of the hypotenuse z tends to be equal to the value of x, while y tends to be equal to zero (y → 0, z → x)”. Therefore, there exist three positive integers x, y and z that satisfy Fermat’s last theorem at a particular positive and negative power n, though one of the integer has to be equal to zero in the process, while the other two integers are equal. It application describes why mass psrticles cannot attain the speed of light, in other word; the energy of a matter (mass particle) in motion is assumed to possess the sum of the energy of the particle in motion and the rest energy of the particle, using mass-momentum energy relation. Many literatures on why mass particles cannot attain the speed of light attested that as the particle approaches the speed of light, the mass of the particle increases, so does the energy required to move it. And experimentally, it is extremely difficult to achieve that huge amount of energy for an increasing mass of a particle to attain the speed of light. Rather, nth root theorem show that as the particle approaches the speed of light, the total energy of the particle in motion also known as the relativistic energy tends to be equal to a photon energy while the rest energy of the particle tends to be equal to the zero. This supported the fact that only the particles with zero rest mass (photon) would be able to attain the speed of light.

2. Methods

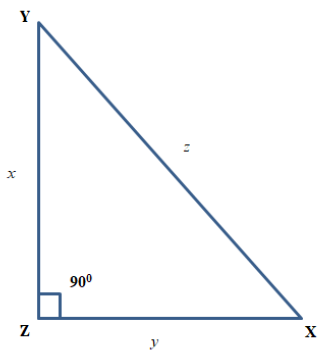
Example 1: By Converse of Pythagorean Theorem. Suppose that x, y and z be three positive integers with ( x 2 + y 2 = z 2 ), then there exist a right triangle XYZ with length x, y, and z. In this case Z = 90 0
Preprints 119001 g001
Figure 1. Right angle triangle XYZ. Without loss of generality we assume that ( x 2 + y 2 = z 2 ).
Figure 1. Right angle triangle XYZ. Without loss of generality we assume that ( x 2 + y 2 = z 2 ).
Preprints 119001 g001
Example 2:  x n + y n = z n has a positive integer solution as the power n varies, where the hypotenuses z of the right triangle tends to be equal to one of the term x or y (the base or perpendicular of the triangle) on the other side of the equality sign, while the other term tends to be equal to zero, and the triangle collapsed to a straight line.
Proof: by homogeneity of the exponents and the rules of logical reasoning (i.e. the algebraic principle of Pythagorean and general reasoning). We assume that x, y and z are positive integers and primitively prime while the exponent n are whole numbers.
Case 1: Pythagoras equation in the case where n = 2 such as the equation 1 above. Where we have x 2 + y 2 = z 2
And x= base, y= perpendicular, z= hypotenuse, also x < y < z
Lemma (a); suppose we know the values of base x and the perpendicular y of a right triangle, then we can find the hypotenuse z, by making z the subject of the formula. Make z the subject of the formula from eqn. 1
z = x 2 + y 2
Therefore, the value of z is the square root of the sum of the squares of the two other terms (x and y).
Lemma (b); suppose we know the values for the hypotenuse z and the base x of a right angle triangle, then we can find the perpendicular y, by making y the subject of the formula. Make y the subject of the formula from eqn. 1
y = z 2 − x 2  
Therefore, the value of y is the square root of the difference of the square of the other two terms (z and x).
Lemma (c); suppose we know the values for the hypotenuse z and the perpendicular y of a right angle triangle, then we can find the base x, by making x the subject of the formula. Make x the subject of the formula from eqn. 1
x = z 2 − y 2  
Therefore, the value of x is the square root of the difference of the square of the two other terms (z and y).
Case 2: Pythagorean equation in the case where power n > 2 ; Fermat last theorem –there is no positive integer solution for the equation x n + y n = z n if n > 2 . Rather as the power n increases far beyond 2, the value of z tends to be equal to y, while x tends to be equal to zero, and at a particular power n, the both sides of the equality sign are equal
And x= base, y= perpendicular, z= hypotenuse, also x < y < z
x n + y n = z n
Then at n > > > > > 2
X ↓ 0 n + Y ↓ y n = Z ↓ y n  
Lemma (a); suppose we have a right triangle with base x, perpendicular y, and hypotenuse z to be positive integers and primitively prime numbers; they are Pythagorean’s triples. Then, we assumed that the eqn. 7. is equal at power n > > > > > 2 . then, we make the hypotenuse z the subject of the formula as the power n increases, while the value of the base x and the perpendicular y remain constant. Make z the subject of the formula from eqn. 7.
z n = x n + y n  
Then
z = x n + y n n
Assuming the value of x and y is known and remain constant, while the value of z is unknown and to be determined as the power n increases, at n > > > > > 2 . the equation will change to the form as follows at a certain power n
x n + y n n = y
Therefore,
x n + y n   ≈   y n
Since the eqn. 10 above is approximated, then taking the nth root at both sides of the equation
x n + y n n = y n n
y = y
where z   → y and x → 0
Lemma (b); suppose we know the values for the base x and the hypotenuse z of a right triangle is known and they remain constant, while the value for the perpendicular y is determined as the power n increases. Then, we make y the subject of the formula. Make y the subject of the formula from eqn. 7
y = z n − x n n
Assuming the value of y is been determined as the power n increases while the value of z and x remain constant, at n > > > > > 2 . Then, the equation changes to the form as follows
z n − x n ≈   z n
And taking the nth root of both sides of the eqn. 14
z n − x n n = z n n
z = z
where y → z and x → 0
Lemma (c); suppose we have the value of z and y and we have to determine the value of x as the power n increases. Then we make x the subject of the formula. Make x the subject of the formula from eqn. ii. Then,
x = z n − y n n
Assuming the value of x is been determined as the power n increases while the value of z and y remain constant, n > > > > > 2 .
z n − y n n   ≈   z
So, x neither equal to z nor y. rather x   ≈ z while y   ≠   z   n o r   0  
Case 3: equation similar to Fermat’s last theorem, where the exponent n < 2 has no positive integer solution. Rather as the power n decreases, the value of the hypotenuse z tends to be equal to x while the value of y tends to be equal to zero, and at a particular negative power n, the both sides of the equality sign are equal
And x= base, y= perpendicular, z= hypotenuse, also x < y < z
x − n + y − n = z − n
Then at n ≪ ≪ ≪ ≪ 2
X ↓ x − n + Y ↓ 0 − n = Z ↓ x − n  
Lemma (a); suppose we have x, y, and z to be positive integers and primitively prime numbers. We assumed that the eqn. 7. is equal at a power n   ≪ ≪ ≪ ≪ 2 . then, we make z the subject of the formula as the power n decreases, while the value of x and y remain constant. Make z the subject of the formula from eqn. 19.
z − n = x − n + y − n
Then
z = x − n + y − n − n
And if the value of z is been determined as the power n decreases while the value for x and y remain constant, n   ≪ ≪ ≪ ≪ 2 .
x − n + y − n − n = x
Therefore,
x − n + y − n   ≅   x − n
And taking the -nth root at both sides of the equation
x − n + y − n − n = x − n − n
x = x
where z   → x and y → 0
Lemma (b); suppose we have to determine the value for y as the power n decreases while the value of z and x remain constant. Then, we make y the subject of the formula. Make y the subject of the formula from eqn. 19.
y = z − n − x − n − n
Assuming the value of y is to be determined as the power -n decreases while the value of z and x remain constant, n   ≪ ≪ ≪ ≪ 2 .
z − n − x − n − n = a − b i
The value of y becomes a complex expression, where a ≅ x
Lemma (c); suppose we have the value of z and y, and we have to determine the value of x as the power decreases. Then we make x the subject of the formula. Make x the subject of the formula from eqn. 19. Then,
x = z − n − y − n − n
Assuming the value of x is been determined as the power -n decreases while the value of z and y remain constant, n   ≪ ≪ ≪ ≪ 2 .
z − n − y − n − n = c − d i
The value of x becomes a complex expression, where c ≅ y

3. Results/Applicataion

In special theory of relativity, where the observer observes different motions due to the observer’s frame of reference. There are two similar equations that describe objects or particles.
I.
E = m 0 c 2
Where E = energy of an an object or particle at rest, m 0 = rest mass of the particle, c = speed of light. This equation is correct only when an object or particle is not moving.
II.
E = γ m 0 c 2
Where E = energy of an object or partcle in motion, gamma γ = 1 1 − v 2 c 2 , v = object velocity relative to the observer, c = speed of light, m 0 = rest mass of an object or particle.
This equation is related to object or particle in motion, travellig with a velocity v. In motion, as the velocity of a particle increases towards the speed of light, gamma ( γ ) increases, while the energy of the particle increases. The two equations above does not apply for massless particles such as the particle of light –photons; they only applied for particles with rest mass and speeds below the speed of light, particle at rest. Although, there is an equation that applies universally for both particles with mass and without mass, and even particles in motion and at rest; which is known as the mass-momentum energy. For the purpose of this article, we focus on mass particles in motion and at rest. Thus we examine what gamma stands for in this equation. Generally, it is a quantity that expresses how much the measurements of time, length, and other physical properties changes for a particle in motion, it is also called the Lorentz factor.
In a physical sense, gamma is the ratio of the energy of a particle in motion to its energy at rest, as expressed matthematically in the equation bellow,
γ = 1 1 − v 2 c 2 = E m o t i o n E r e s t
Where E m o t i o n = is the energy of a paticle in motion, E r e s t = energy of a particle at rest γ = gamma hold for mass particles with velocity v ( 0 < v < c ), c = speed of light. Square both sides of the equation, we have the following
1 1 − v 2 c 2 2 = E m o t i o n 2 E r e s t 2
1 1 − v 2 c 2 = E m o t i o n 2 E r e s t 2
E r e s t 2 = E m o t i o n 2 1 − v 2 c 2
And we have,
E r e s t 2 = E m o t i o n 2 − E m o t i o n 2   v 2 c 2
From the equation above, the rest energy of a mass particle in motion is the difference between its energy in motion and the velocity quotient energy ( β ).
Velocity quotient is the product of the energy of a particle in motion and the ratio of the velocity of a particle and the constant speed of light ( β = v 2 c 2 ). Rearraging the equation, we have that the total energy of a particle in motion is equivalent to the sum of the rest energy of the particle and the velocity quotient energy of that particle, as expressed below
E m o t i o n 2 = E r e s t 2 + E m o t i o n 2   v 2 c 2
In more details we have
E T E M 2 = m c 2 2 + γ m c 2 .   v c 2
where E T E M = total energy of a particle in motion, and other teams as defined above.
This Pythagoreans form of the equation of a particle in motion shows that the total energy a particle experience in motion is the sum of its rest energy and its velocity quotient energy, where the velocity ranges ( 0 < v < c ), and the power of the equation is equal to 2 (i.e. n = 2).
Using the principle of nth root theorem, where the power n of the equation varies from negative power to the very large positive integer,
E T E M n = m c 2 n + γ m c 2 .   v c n
As the energy level (power n) increases, the rest energy of a particle tends to be equal to zero while its total energy tends to be equal to the velocity quotient energy, making the velocity quotient β = 1, that is the velocity of the particle is equivalent to the constant speed of light, and the particle can only be describe as a massless particle -photon.
E T E M n = γ m c 2 .   v c n
where, E r e s t n   → 0 , velocty quotient ( β ) = v c = 1
Likewise, as the energy level (power n) decreases, the total energy of the particle tends to be equal to the rest energy and the velocity quotient energy is equal to zero, that is the particle is totally at rest, since the value for its velocity quotient is equal to zero.
E T E M − n = m c 2 − n
where γ m c 2 . v c − n → 0 , velocity quotient ( β ) = v c = 0

4. Discusion/Conclusion

In counter examples to Fermat equation, and to explaining the relationship between the Pythagorean’s triples and the power of the equation as they varies. The article shows that using simple arithmetic approach, “the hypotenuse of a right triangle tends to be equal to the one side of the right triangle and the other side tends to be equal to zero or serves as zero at the same time as a result of power variation; i.e. the value of the hypotenuse z tends to be equal to the value of y, while x is tends to be equal to zero as the power n increases, and at the other hand as the power n decreases the value of the hypotenuse z tends to be equal to the value of x, while y tends to be equal to zero”. Making it more profound that there is a relationship between the Pythagoreans’ triples and the power of the equation, just as there were other studies of Pythagoreans equation, such as the knowledge of the Pythagrean’s equation. The application of this principle is used to explain the motion of a mass particles as they experience both the rest energy and the velocity qoutient energy at a power n=2. While the variatio of the power explain the behaviour of a massless particle at a very high level of power n of the equation, and the mass particle at rest at a very lower level of power n. The principle shows that massless particles exist at a high positive power n, while the rest energy exist at the a low negative power n. In conclusion, at a negative power n, the velocity quotient of a particle is equal to zero, which describes a particle with a rest mass. While the velocity quotient of a particle is equal to 1, at a very high positive power n, describing the photon particles.

References

  1. B. Christophe, C. Brian, D. Fred, R. Taylor, (2001). "On the modularity of elliptic curves over {\displaystyle \mathbf {Q} }: Wild 3-adic exercises". Journal of the American Mathematical Society. 14 (4): 843–939. [CrossRef]
  2. G. Ayodele. “nth root theorem: a contradictory theory to Fermat’s last theorem” 2022. ttps://www.researchgate.net/publication/358397176_nth_root_theorem_a_contradictory_theory_to_Fermat's_last_theorem.
  3. C. Davide, (2016). "Fermat's last theorem earns Andrew Wiles the Abel Prize". Nature. 531 (7594): 287. Bibcode:2016Natur.531..287C. [CrossRef] [PubMed]
  4. W. Eric, Weisstein, (2021). "Fermat's Last Theorem". MathWorld – A Wolfram Web Resource. Retrieved 7 May 2021.
  5. Wiles, (1995). "Modular elliptic curves and Fermat's Last Theorem" (PDF). Annals of Mathematics. 141 (3): 448. JSTOR 2118559. OCLC 37032255. Frey's suggestion, in the notation of the following theorem, was to show that the (hypothetical) elliptic curve y2 = x(x + up)(x – vp) could not be modular. [CrossRef]
  6. R. Ken, (1990). "On modular representations of Gal(Q/Q) arising from modular forms" (PDF). Inventiones Mathematicae. 100 (2): 432. Bibcode:1990InMat.100..431R. hdl:10338.dmlcz/147454. MR 1047143. S2CID 120614740. [CrossRef]
  7. J. Stillwell. "Elements of Number Theory". New York: Springer-Verlag. 2003. pp. 110–112. ISBN 0-387-95587-9. Retrieved 17 March 2016.
  8. T. Heath. “Diophantus of Alexandria”. Second Edition, Cambridge University Press, 1910, reprinted by Dover, NY, 1964, pp. 144–145.
  9. F. J. Duarte. "Sobre la ecuación x3 + y3 + z3 = 0". Boletín de la Academia de Ciencias Físicas, Matemáticas y Naturales (Caracas). 1944, 8: 971–979.
  10. L. Freeman. "Fermat's Last Theorem: Proof for n = 5". 2005. Retrieved 23 May 2009.
  11. A. S. Werebrusow. "On the equation x5 + y5 = Az5 (in Russian)". Moskov. Math. Samml. 1905, 25: 466–473.
  12. K. Rychlik. "On Fermat's last theorem for n = 5 (in Bohemian)". Časopis Pěst. Mat. 1910, 39: 185–195, 305–317.
  13. L. Freeman. "Fermat's Last Theorem: Proof for n = 7". 2006. Retrieved 23 May 2009.
  14. P. Ribenboim. “13 Lectures on Fermat's Last Theorem”. New York: Springer Verlag. 1979; p. 202. ISBN 978-0-387-90432-0.
  15. S. Wagstaff Jr. "The irregular primes to 125000". Mathematics of Computation. American Mathematical Society. 1978, 32 (142): 583–591. JSTOR 2006167. (PDF) Archived 24 October 2012 at the Wayback Machine. [CrossRef]
  16. H. J. David. "Examples of eventual counterexamples, answer by J.D. Hamkins". mathoverflow.net. 2010. Retrieved 15 June 2017.
  17. S. Singh. "Fermat's Last Theorem". 1997; ISBN 1-85702-521-0.
  18. G. Frey. "Links between stable elliptic curves and certain diophantine equations". Annales Universitatis Saraviensis. Series Mathematicae. 1986, 1: 1–40.
  19. R. Ken. "On modular representations of Gal(Q/Q) arising from modular forms" (PDF). Inventiones Mathematicae. 1990, 100 (2): 431–476. Bibcode:1990InMat.100..431R. [CrossRef]
  20. S. Singh. 199743–551. JSTOR 2118559. OCLC 37032255. Archived from the original (PDF) on 28 June 2003. [CrossRef]
  21. R. Taylor, A. Wiles. "Ring theoretic properties of certain Hecke algebras". Annals of Mathematics. 1995, 141 (3): 553–572. JSTOR 2118560. OCLC 37032255. Archived from the original on 27 November 2001. [CrossRef]
  22. B. June, L. Imre, G. Timothy. “The Princeton Companion to Mathematics”. Princeton University Press. 2008; pp. 361–362. ISBN 9781400830398.
  23. D. Noam, Elkies. "The ABC's of Number Theory" (PDF). The Harvard College Mathematics Review. 2007, 1 (1).
  24. M. Waldschmidt. "Open Diophantine Problems". Moscow Mathematical Journal. 2004, 4: 245–305. arXiv:math/0312440. S2CID 11845578. [CrossRef]
  25. C. Richard, P. Carl. “Prime Numbers: A Computational Perspective”. Springer. 2000; p. 417. ISBN 978-0387-25282-7.
  26. C. Tianxin, C. Deyi, Z. Yong. "A new generalization of Fermat's Last Theorem". Journal of Number Theory. 2015, 149: 33–45. arXiv:1310.0897. S2CID 119732583. [CrossRef]
  27. M. Preda. "A Cyclotomic Investigation of the Catalan–Fermat Conjecture". Mathematica Gottingensis, 2007.
  28. H.W. Lenstra Jr. "On the inverse Fermat equation". Discrete Mathematics. 1992, 106–107: 329–331. [CrossRef]
  29. M. Newman. "A radical diophantine equation". Journal of Number Theory. 1981, 13 (4): 495–498. [CrossRef]
  30. B. D. Curtis, A. M. W. Glass, S. J. Gábor. "Fermat's last theorem for rational exponents". American Mathematical Monthly. 2004, 111 (4): 322–329. JSTOR 4145241. MR 2057186. [CrossRef]
  31. D. Noam, Elkies. "ABC implies Mordell". International Mathematics Research Notices. 1991 (7): 99–109. Our proof generalizes the known implication "effective ABC [right arrow] eventual Fermat" which was the original motivation for the ABC conjecture. [CrossRef]
  32. C. Breuil, B. Conrad, F. Diamond, and R. Taylor. “On the modularity of elliptic curves over Q: wild 3-adic exercises.” Journal of the American Mathematical Society 2001, 14, (2001) 843–939.
  33. G. Cornell, J.H. Silverman, G. Stevens. “Modular forms and Fermat’s Last Theorem.” Springer, 1998.
  34. G. Faltings. “The proof of Fermat’s last theorem by R. Taylor and A. Wiles, Notices of the American Mathematical Society” 1995, 42 (1995), 743–746. 18.783 Spring 2017, Lecture #26, Page 8.
  35. G. Frey, (1986). “Links between stable elliptic curves and certain diophantine equations.”, Annales Universitatis Saraviensis. Series Mathematicae 1 (1986), 1–40.
  36. C. Khare, J. P. Wintenberger. “Serre’s modularity conjecture (I).” Inventiones Mathematicae 178 (2009), 485–586.
  37. B. Mazur. “Rational isogenies of prime degree”, Invent. Math. 1978, 44, 129–162.
  38. J. S. Milne. “Elliptic curves, BookSurge Publishers”. 2006.
  39. K. Ribet. “On modular representations of Gal(Q=Q) arising from modular forms, Inventiones” Mathematicae 1990, 100 (1990), 431–476.
  40. K. Ribet. “Galois representations and modular forms”, Bulletin of the AMS 32 (1995), 375–402.
  41. J. H. Silverman. “Advanced topics in the arithmetic of elliptic curves”, Springer, 1994.
  42. R. Taylor, A. Wiles. Ring-theoretic properties of certain Hecke algebras, Annals of Mathematics 141 (1995), 553–572.
  43. A. Wiles. Modular elliptic curves and Fermat’s last theorem, Annals of Mathematics 141 (1995), 443-551.
  44. J. Buhler, R. Crandell, R. Ernvall, T. Metsänkylä. "Irregular primes and cyclotomic invariants to four million". Mathematics of Computation. American Mathematical Society. 1993, 61 (203): 151–153. Bibcode:1993MaCom..61..151B. JSTOR 2152942. [CrossRef]
  45. D. Fred. "On Deformation Rings and Hecke Rings". The Annals of Mathematics. 1996, 144 (1): 137–166. JSTOR 2118586. [CrossRef]
  46. C. Brian, D. Fred, R. Taylor. "Modularity of certain potentially Barsotti-Tate Galois representations". Journal of the American Mathematical Society. 1999, 12 (2): 521–567. . ISSN 0894-0347. [CrossRef]
  47. J.R. Forshaw; A.G. Smith. Dynamics and Relativity. Wiley. 2009; pp. 258–259. ISBN 978-0-470-01460-8.
  48. J.A. Wheeler; C. Misner; K.S. Thorne (). Gravitation. W.H. Freeman & Co. 1973; pp. 201, 649, 1188. ISBN 0-7167-0344-0.
  49. G. Feinberg (1967). "Possibility of faster-than-light particles". Physical Review. 159 (5): 1089–1105. Bibcode:1967PhRv..159.1089F. [CrossRef]
  50. Z.Y.Wang (2016). "Modern Theory for Electromagnetic Metamaterials". Plasmonics. 11 (2): 503–508. [CrossRef]
  51. Okun, Lev B. "The Concept of Mass". Physics Today. 1989, 42 (6): 31–36. Bibcode:1989PhT....42f..31O. ISSN 0031-9228. [CrossRef]
  52. J, Max. Concepts of mass in contemporary physics and philosophy. Princeton, N.J.: Princeton University Press. 2000; p. 51. ISBN 978-1-4008-1219-6. OCLC 614715841.
  53. E, Erik; V, Kjell. "The classical and relativistic concepts of mass". Foundations of Physics. 1976, 6 (1): 115– 124. Bibcode:1976FoPh....6..115E. ISSN 0015-9018. S2CID 120139174. [CrossRef]
  54. Ives, Herbert E. "Derivation of the Mass-Energy Relation". Journal of the Optical Society of America. 1952, 42 (8): 540. ISSN 0030-3941. [CrossRef]
  55. S, John; T, Roberto. "Einstein's first derivation of mass–energy equivalence". American Journal of Physics. 1982, 50 (8): 760–763. Bibcode:1982AmJPh..50..760S. ISSN 0002-9505. Archived from the original on 2019-05-28. Retrieved 2020-10-14. [CrossRef]
  56. Ohanian, Hans C. "Did Einstein prove E=mc2?". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 2009, 40 (2): 167–173. Bibcode:2009SHPMP..40..167O. Retrieved 2020-10-14. [CrossRef]
  57. V, Roger. "Integer solutions of a−2 + b−2 = d−2". Mathematical Gazette. 1999, 83 (497): 269–271. JSTOR 3619056. S2CID 123267065. [CrossRef]
  58. R, Jennifer. "The upside-down Pythagorean Theorem". Mathematical Gazette. 2008, 92: 313–317. S2CID 125989951. [CrossRef]
  59. L, Serge, (2002). Algebra. Graduate Texts in Mathematics. Vol. 211. Springer-Verlag New York. p. 196.
  60. K, Daniel; RJ. Kolenkow (2010) [1973]. “An Introduction to Mechanics”. Cambridge University Press. pp. 499–500. ISBN 978-0-521-19821-9.
  61. J.R. Forshaw; A.G. Smith (2009). ‘Dynamics and Relativity”. Wiley. pp. 149, 249. ISBN 978-0-470-01460-8.
  62. D. McMahon (2006). “Relativity”. DeMystified. Mc Graw Hill (USA). p. 20. ISBN 0-07-145545-0.
  63. D. McMahon. Quantum Field Theory. DeMystified. Mc Graw Hill (USA). 2008; pp. 11, 88. ISBN 978-0-07-154382-8.
  64. G, Walter. "The Compton effect according to Schrödinger's theory". Z. Phys. 1926, 40: 117–133. S2CID 122254400. [CrossRef]
  65. D, Paul. "The Quantum Theory of the Electron". Proc. Roy. Soc. London Ser. A. 1928, 117 (778): 610–624. Bibcode:1928RSPSA.117..610D. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated