Prerpints.org logo
Preprint
Article

Interpretable Regression Models for Predicting and Optimizing Hydrogen Production in Co-Gasification Process

Altmetrics

Downloads

48

Views

34

Comments

0

This version is not peer-reviewed

Submitted:

20 September 2024

Posted:

23 September 2024

You are already at the latest version

Alerts
Abstract
Renewable energy is essential to environmental sustainability and ranks high among the United Nations strategic goals. In this context, as opposed to conventional biomass gasification, co-gasification emerges as a promising technological pathway to effectively combine the distinct benefits of various gasification feedstocks in order to generate hydrogen-rich syngas. The goal of achieving net-zero emissions has further raised the demand for biomass co-gasification. However, the complicated reactions involved in co-gasification process pose challenge in optimizing the process parameters for increased productivity and performance. To the author’s knowledge, there is no consensus regarding the most suitable machine learning (ML) based regression models for optimizing biomass-plastics co-gasification process, as no prior research has examined the effectiveness of different regression models for this process. Further, the practical application of ML models is adversely affected by their black box nature and lack of interpretability. To address these gaps, the objective of the currect research is two-fold: Firstly, to model the co-gasification process using seven different ML algorithms. Secondly, to develop an evaluation framework and assess model interpretability to select an ideal model for co-gasification interpretation and optimization. The support vector regression(SVR) model demonstrated the most reliable predictive performance. The study employed learning curve analysis and cross validation analysis to substantiate the model predictive performance and exhibit its potential to generalize. Beyond performance analysis, Shapely additive explanation, (SHAP) is first explored in the realm of cogasification to interpret the prediction of the studied models from global and local perspective. The research findings are expected to provide valuable insights to better understand and optimize biomass-plastics cogasification process for H2-rich syngas production.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Rapid industrialization and population growth have resulted in a significant hike in energy demand. Approximately 80% of worldwide energy comes from fossil fuels, which may potentially raise the greenhouse gas (GHG) emissions, particularly carbon dioxide C O 2 [1]. The far-reaching consequences of this trend with detrimental effects on the ecosystem has alarmed the world leaders and policymakers, to move towards an environmentally benign energy source. Parallel to this, worldwide plastic production has increased steadily in order to satisfy the demands of the international market. Plastics, being composed of petroleum-based materials, have contributed to the depletion of non-renewable fossil fuels as a consequence of this phenomenon. Beyond that, the accumulation of plastic waste without a proper disposal system endangers the health of humans and animals by contaminating groundwater [2]. This has necessitated urgent research for a sustainable treatment of plastic waste. Numerous approaches have been utilized to alleviate this issue but recycling plastic waste into fuels rich in energy has been recognized as the most favorable strategy to address challenges faced globally, and move towards a more sustainable future [3]. Considering the rapid growth in energy consumption and the pressing environmental issues, the pursuit of clean energy production is vitally important research endeavor. Hydrogen is widely acknowledged as a potential clean energy carrier due to its applicability and versatility. Moreover, in the field of transportation, hydrogen has the potential to serve as a carbon-free green substitute for traditional fossil fuel-powered internal combustion engines. The rapid development of hydrogen technology and growing energy demand has driven many countries to prioritize hydrogen development in their national strategies and implement measures to meet their sustainability development goals [4]. Hydrogen being globally recognized as an important energy carrier in international decarbonization strategies, there is rising attentiveness to establish the sustainability of hydrogen production. The plastic wastes containing hydrocarbons are considered as an excellent feed for hydrogen production with minimal GHG emissions [5]. The majority of nations are therefore eager to promote innovations in clean hydrogen production from plastic wastes and boost their economy [6].
Thermochemical methods have recently received increased attention from scientific community, governments and industry as a promising versatile platform for producing hydrogen-rich gases from plastic wastes due to its high conversion efficiency and high process yield [7]. Amongst all diverse thermochemical methods, gasification has stood out as a key technology to provide a significant framework for large-scale conversion of plastic wastes with reduced GHG emissions. As evidenced from recent literature [8], co-gasification of plastic wastes with biomass have attracted a great deal of attention because of its synergistic effects to enhance the energy conversion efficiency and reduce significant secondary pollution that are often associated with plastic gasification. However, the paucity of literature on biomass-plastics co-gasification clearly indicates its infancy stage with substantial needs for further research and improvements. Besides its promising features, the biomass-plastics co-gasification is not yet deployed at industrial scale owing to its ill-defined phenomena influenced by various internal and external process parameters. Therefore, modeling such a complex process using computational fluid dynamics is challenging [9]. Accordingly, many experiments are required to gain a deep understanding of design, optimize, control, and scale up of co-gasification process. However, due to limitations in time and resources, researchers often find it challenging to explore high dimensional parameter space with experimental trials. Thus, it is of the utmost importance to understand and maximize the impact of process parameters on hydrogen production especially during co-gasification process with the available limited experimental data.
With the beginning of the 4th industrial revolution and technological breakthroughs, ML technology [10], a branch of artificial intelligence, has been reported as an effective tool for addressing the above-mentioned bottlenecks. This powerful technique has proven effective in uncovering trends and patterns within co-gasification datasets without requiring deep understanding of the underlying physicochemical mechanics. In addition, ML not only enables to circumvent experimental measurements but also utilizes sophisticated computational methods to understand complex chemical reactions that are challenging to model mathematically and establish models with high accuracy [11]. With its unique characteristics, ML has been widely applied in various research publications to simulate gasification [12]. However, identifying the most suitable and reliable ML algorithm is a crucial step to realize the full potential of ML algorithm, it is worth noting that no studies have investigated the significant performance of different ML algorithms for estimating hydrogen production, especially from biomass-plastics co-gasification process. Also, it is surprising that there is indeed a glaring lack of attempt to understand the performance of the ML algorithms with limited experimental data. Therefore, there is a need for a consensus on best ML algorithm to determine the optimal process parameters for maximizing hydrogen production from biomass-plastics co-gasification with the available limited experimental data. It is essential to address these gaps in order to successfully commercialize this technology and widely implement it as a solution to decrease GHG emissions, while also addressing the increasing need for liquid fuel.
To fill this gap of knowledge, this is the first study that delves to investigate a wide range of ML regression models for estimating hydrogen production accuracy from biomass-plastics co-gasification process. The ML models selected for comparison includes linear regression (LR), decision tree regression (DTR), random forest regression (RFR), gradient boosting regression (GBR), support vector regression (SVR), and multilayer perceptron (MLP). The rationale for selecting these ML models was based on their strong performance reported in the relevant literature [13]. Furthermore, they are widely utilized in the field of biomass conversion. These models are assessed using the currently available, limited amount of experimental data. All models are configured using a standardized model configuration to maintain consistent model complexity and enable a meaningful comparison. The comprehensive assessment results illustrate the respective benefits and generalization ability of developed regression models in precisely capturing the intricate connection between the process parameters and hydrogen production with regard to biomass-plastics co-gasification process.
The outcome of this research is expected to hold considerable importance in terms of enhancing and optimizing co-gasification systems involving biomass and plastics. Such advancements could result in increased efficiency and efficacy in the utilization of these invaluable resources. This knowledge has significant promise for promoting the advancement of economically efficient and environmentally friendly co-gasification systems for biomass-plastics.These findings can help researchers and business executives to maximize the advantages of biomass-plastics co-gasification while reducing its negative effects on the environment. In conclusion, this work makes a valuable contribution to the progress of sustainable energy technology and the shift towards a more environmentally friendly and sustainable future.

2. Machine Learning Models

2.1. k-Nearest Neighbor (KNN) Regression

KNN regression is a non-parametric ML technique that is widely recognized for its simplicity and ease of implementation [14]. This approach is mostly used when there is a lack of prior knowledge regarding the distribution of data. The implementation of KNN utilizes instance-based learning, which operates on the fundamental principle that the nearest neighbors have the greatest potential to impact the prediction. Against this background, the approach uses the output of its neighbors to predict the outcome of the test sample rather than learning the mapping from training set. Hence, choosing a method to calculate the distance between test and training data is the first step in developing this algorithm. Euclidean distance is commonly observed in this context.
KNN is regarded as a lazy learner as it saves the training data and starts learning process when test data is presented for prediction. For instance, To determine which training dataset samples are the k-nearest to a given X, KNN calculates the distance d i between X and each sample x i in the training dataset D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) . It then picks the k samples with the shortest distance. Finally, it provides the k-nearest neighbor’s weighted average as follows [14].
Y ^ = ∑ i = 1 k y i ( X )
Two key aspects impact prediction results: k value and distance measuring method. Small k values make outcomes vulnerable to adjacent noise. If k is significant, irrelevant points can be considered. The optimal k value is usually computed via cross-validation.

2.2. Decision Tree Regression (DTR)

Recently, DTR has grown popular due to its ease of implementation, interpretability, and low computing cost. In contrast to LR models that utilize a single regression function, whether parametric or non-parametric, across the entire dataset and incorporates all independent variables as predictors, the DTR model employs stratified regression analysis and applies different regression models to stratified samples of the independent variables with varying relationships to the dependent variable. More crucially, they can handle non-linear interactions between features, which many other ML algorithms cannot, and finds the most essential features that influence decision-making.
The fundamental principle underlying the use of DTR is to divide complicated decision into simpler ones and create easier-to-interpret prediction. To this end, DTR employ a recursive partitioning of training samples D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) into homogeneous subsets at each node based on the partitioning criteria such as Information gain and Gini impurity [15]. This partitioning is carried out by dividing the predicator space into distinct regions R j (where j = 1 to J) that represents the terminal nodes. Each region j is assigned with a constant γ j and the tree ϕ T P is mathematically modelled as follows [15],
Y ^ = ϕ T P ( X , θ ) = ∑ j = 1 J γ j I ( X ∈ R j ) w h e r e
I ( X ∈ R j ) = 1 , if X ∈ R j 0 , otherwise
The efficacy of the DTR model relies on the process of identifying the optimal hyperparameter θ through the minimization of the prediction error, which is mathematically represented as:
θ ^ = a r g m i n θ ∑ i = 1 N L ( y i , y ^ i )
where y i is the outcome of the input sample x i and L ( . ) is loss function. For regression problem, the loss function is mean square error. θ ^ represents the optimized hyperparameter. Against this background, the DTR may overfit if the depth of the tree is extremely high by learning too fine training data details. This phenomenon has the potential to result in generalization on unseen data. conversely, an extreme low tree depth may lead to under-fitting. Therefore, the tuning of tree depth is of utmost importance. Although decision trees have some limitations, they may successfully address the issue of missing data by employing techniques such as weighted impurity and attribute splitting.

2.3. Support Vector Regression (SVR)

support vector machine (SVM) is among the most popular ML algorithms for classification problems on the basis of statistical learning theory. SVR is a modified version of SVM that has been specifically developed to address high dimensionality, nonlinearity, and limited sample sizes in regression problems. In contrast to previous regression models, SVR focuses on minimizing the generalization error instead of minimizing the sum of squared errors between predicted and actual outcomes [15]. In addition, it utilizes the advantages of kernel function to effectively capture and represent non-linear correlation between the input and output data in a higher-dimensional space. SVR eventually achieves generalized regression efficiency by adequately minimizing both the observed distribution error and training error.
In a broad context, SVR endeavors to identify a function that adequately captures the correlation between x i and y i within the provided training dataset D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) , as seen below ([15]).
Y ^ = ∑ i = 1 N α i ⁢ K ( x i , x j ) + b w h e r e
K ( x i , x j ) = exp ∥ x i − x j ∥ 2 2 σ 2
In this case, α i and b are the support vectors and bias term respectively, determined during training. The kernel function, denoted as K, aims to map the feature space onto a higher dimension. As a result, features that are not linearly separable in lower dimensions can achieve linear separability in higher dimensions. The selection of kernel function is a crucial task in SVR and the primary kernel functions used within SVR framework includes, namely linear, polynomial, sigmoid, and radial basis function (RBF). This study uses RBF kernel defined in Eqn-(5).
Following the selection of a kernel, the empirical risk minimization strategy can be leveraged using a robust insensitive loss function given in Eqn-(7) to train SVR and achieve an optimal solution. Thus, the support vectors and bias determined by minimizing Eqn-(6), can subsequently be utilized to make predictions using Eqn-(4).
J = ∑ i = 1 m L ϵ ( y i ^ , y i )
L ϵ = 0 , if y i − y i ^ ≤ ϵ y i − y i ^ − ϵ , otherwise

2.4. Gradient Boosting Regression(GBR)

GBR is another ensemble variant of DTR proposed by Friedman. It incorporates boosting learning approach and gradient descent method to effectively identify the limits of weak learners and enhance their prediction accuracy. MART, an acronym for Multiple Additive Regression Trees, is a specialized version of gradient boosting that has been tailored exclusively for regression purposes [16]. In general, boosting methods consist three fundamental components: an ensemble model, weak learners, and a loss function. In this context, weak learners refer to models that exhibit a strong bias with the training dataset and produces outputs that are not noteworthy. Unlike RFR, GBR redefines boosting as a numerical optimization problem and iteratively adds a weak learner to the ensemble model using gradient descent to minimize the loss function. Mathematically, GBR model over M trees can be described as [16]:
Y ^ = G m ( X ) = G m − 1 ( X ) + α ϕ T P ( X , θ )
Here T ( x , θ m ) is the weak classifier generated in m t h iteration, θ m is determined minimizing the loss function which can be described as:
θ ^ m = a r g m i n θ ∑ i = 1 N L ( y i , y ^ i )
where G m − 1 ( X ) is the previous tree residue and GBR minimizes the θ ^ m to establish the parameters of the resulting ensemble. Training process seeks to lower the loss function as much as possible to find the local or global optimal solution. Thus, GBR can help reduce bias and variation in prediction results particularly when applied to small datasets. Therefore, this study utilized GBR to predict hydrogen production in a small-dataset environment.

2.5. Random Forest Regression (RFR)

RFR is a variation of DTR model that was introduced by Breiman with an aim to improve the performance of decision tree models leveraging bagging ensemble learning method [17]. Within this learning framework, RFR improves DTR generalization by incorporating randomness at two levels. First, the tree construction process begins utilizing bootstrap sampling with replacement to randomly select the training datasets T b (where b = 1 to B) from the complete training dataset T. Second, during the tree partitioning process, RFR endeavors to identify the most favorable partition by either examining the whole predicator space or by utilizing the maximum number of predicator variables m. Mathematically, the final random forest with B trees T b (where b = 1 to B) is represented as follows [17],
Y ^ = Φ T B , P ( X ) = ∑ b = 1 B ϕ T b , m ( X )
Thus, RFR gains potential to eliminate DTR overfitting by leveraging the benefits of ensemble learning and random sampling. Furthermore,the RFR inherent cross validation ability with bootstrapped samples estimates realistic prediction error during training, making it appropriate for real-time application. Nevertheless in real practice, RF structure must be managed with an adequate amount of trees to balance accuracy and computational burden.

2.6. Multilayer Percepttron (MLP)

MLP is a specific category of artificial neural network. It emulates the neural structure of human brain to address a problem, and can be employed for regression or classification tasks. The success of MLP-based neural networks in a wide range of applications depends on their ability to accurately approximate any function to any desired level of accuracy [18]. The MLP model consists of three sorts of layers: an input layer, one or more hidden layers, and an output layer. The nodes within each layer are interconnected by weighted connections to minimize the discrepancy between the output of the network and the desired output. The output signals of a Multilayer Perceptron (MLP) are determined by the summation of the inputs from the previous layer, which is then adjusted by a basic nonlinear activation function as given below [18],
Y ^ = A c t _ f u n ( ∑ N = 1 f W N . l X N )
In this context, the variables f and l represent the input process parameters and the number of nodes, respectively. Additionally, wide variety of activation functions that can be used, includes linear, sigmoid, softmax, tanh, and rectified linear unit (RELU). In general, backpropagation strategy is used to optimize the model parameters during the training process. This is done by modifying the bias and weights at each epoch, gradually reducing the output error as described in Eqn-(11). Thus, the strategy facilitates MLP achieve enhanced precision.

3. Model Design and Implementation

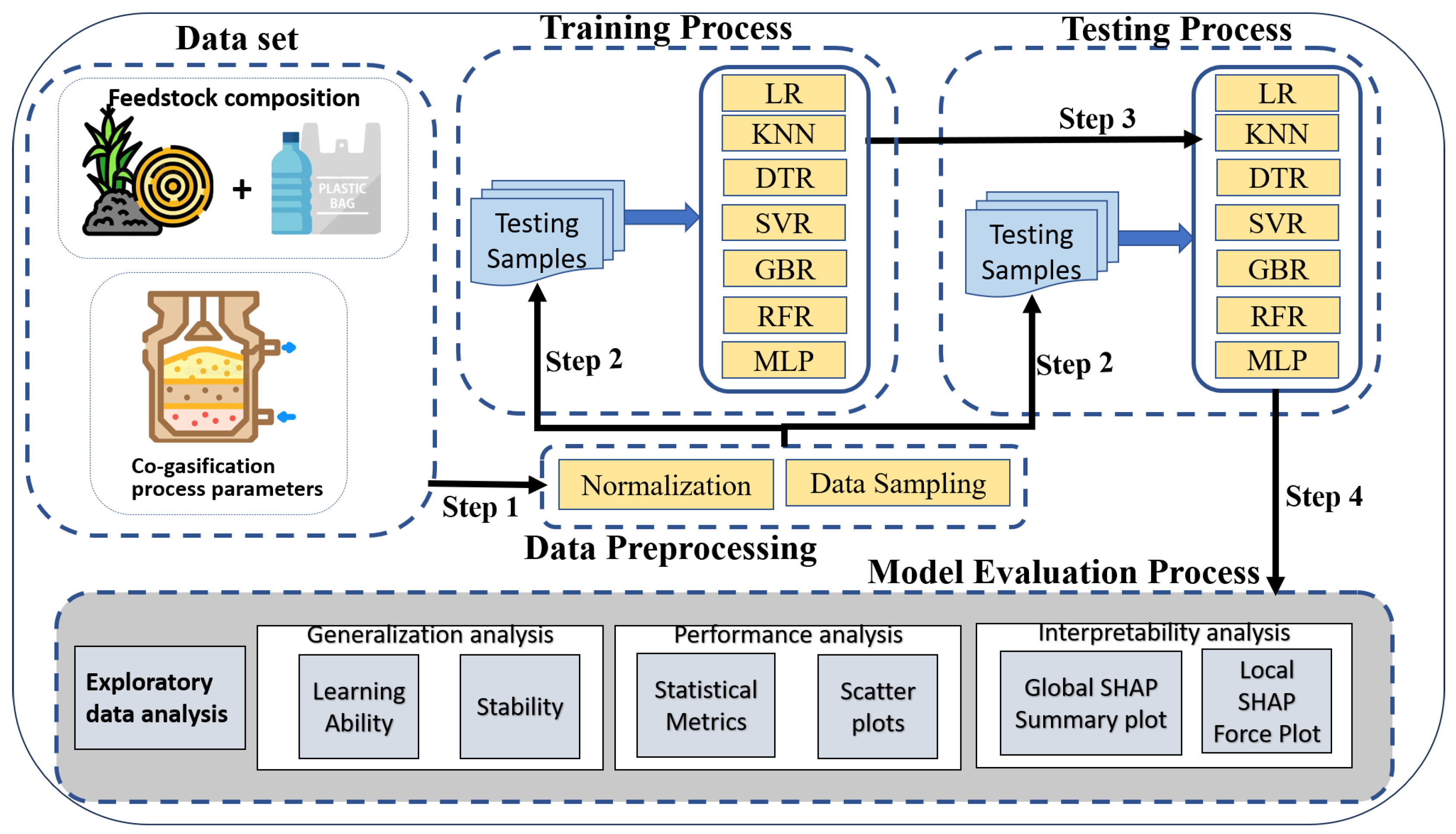
The evaluation process framework is depicted in Figure 1. The figure depicts the relationship between techniques and practices discussed under the section-Section 2. The step-wise exploration of the methodology adopted for comprehensive analysis of selected predictive models for hydrogen production is as follows,

3.1. Data Description

The research data utilized in this study was sourced from prior literature on the co-gasification of waste plastic and rubber, as documented by [19,20]. The dataset comprises 30 independent experiments carried out in a central composite design, wherein the independent variables include HDPE particle, Rubber seed shell (RSS) biomass particle size, plastic quantity in the mixture and gasification temperature. The quantity of hydrogen generated during the co-gasification of plastic and rubber waste was measured as the dependent variable. The experiment was conducted using a thermogravimetric analyzer that was connected to a mass spectrometer. Table 1 displays the descriptive statistics of the data. The HDPE particle size, biomass RSS particle size, plastic composition in the mixture and gasification temperature were measured in the range of 0.13 to 0.63mm, 0.13 to 0.63 mm, 0% to 40% and 500 ∘ to 900 ∘ respectively. 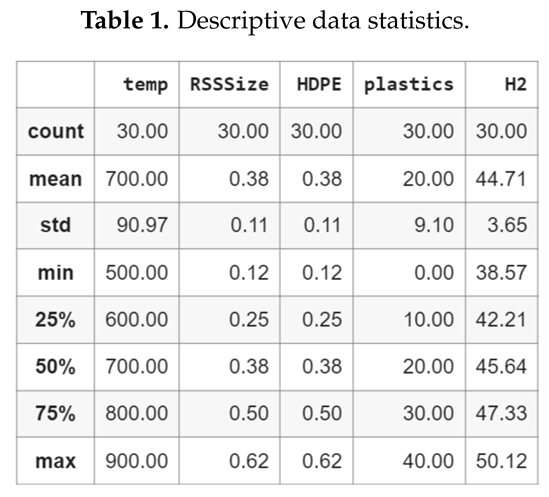Preprints 118852 i001
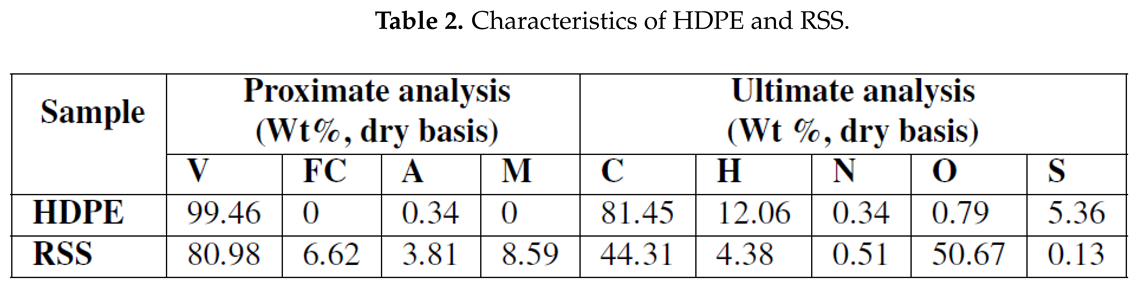
Table 2 presents the characteristics of the primary raw materials used in this investigation. Here, The elemental analyzer and thermogravimetry analyzer, respectively, were used to perform the ultimate and proximate analyses of these feedstocks. As illustrated in Table-Table 2, the proximate analysis reports the elemental composition of volatile matters(V), fixed carbon(FC), ash (A) and moisture content (M) in the raw materials. While ultimate analysis determines the elemental composition of carbon, hydrogen, nitrogen and oxygen content in the raw materials.Additional information regarding the dataset can be found elsewhere [20]. Preprints 118852 i002

3.2. Data Preparation

Data preparation is a crucial step that must be undertaken prior to model training. This process guarantees optimal performance and promotes competence in the generated models.Data format must be consistent for ML algorithms. To achieve this, feature scaling, the process of ensuring that all features are normalized to a consistent range is essential in data preprocessing to reduce model complexity and accelerating the learning process. It also enables every feature to contribute evenly and prevents model bias. As discussed in the subsection-Section 3.1, the features collected from cogasification process have different scales, different distributions and sometimes outliers. This study uses min-max normalization to normalize all features as defined below [21],
x ¯ = x − m i n ( x ) m a x ( x ) − m i n ( x )

3.3. Model Implementation

ML models chosen for investigation in this study are developed using the sklearn library in python. Apart from that, in specific, python libraries such as statsmodel, seaborn and matplotlib were utilized for conducting exploratory data analysis with purpose to gain insights into the relationship between predictors and the target variable. Furthermore, the study made use of the Jupyter notebook interface provided by the Google Colaboratory platform [22]. This interface offers a highly interactive programming environment for Python, eliminating the need for local system setup. All tests in this study were conducted using this platform. As stated in the literature, the efficacy of a machine learning algorithm is dependent upon the quality of the training and testing data employed during the model development process. The diversified training and testing datasets are essential for accurately assessing the true performance of a model, since they mitigate the potential biases that may arise from over-fitting or under-fitting the model to the training data. Taking into account this fact, stratified sampling was adopted to split the study dataset using the most common split ratio 80:20. This indicates that 80% of the data are used for training and remaining 20% for testing set [23].
Following the process of data splitting, the initial step involves the implementation of selected ML models with baseline hyperparameter configurations. These models are then trained using a 10-fold cross validation (10-CV) technique, which aims to provide more reliable and stable estimates. The aforementioned models are labeled as unoptimized machine learning models. For the second task, we reimplemented all models specifying the hyperparameter space for each ML model. Subsequently, a 10-CV was utilized to determine the optimal hyperparameters for all models. The ML models developed using the optimal hyperparameters have been designated as tuned models.

3.4. Model hyperparameter tuning

Hyperparameters refer to the parameters that are used to define the architecture of a model. The process of selecting appropriate hyperparameter values for a given ML algorithm and dataset is crucial [24]. Hyperparameters play a significant role in controlling the model learning process and can greatly affect the effectiveness of ML models. The objective of hyperparameter tuning is to enhance the generalization performance of the model by identifying the optimal values for the hyperparameters that yield the most favorable out-of-sample performance.
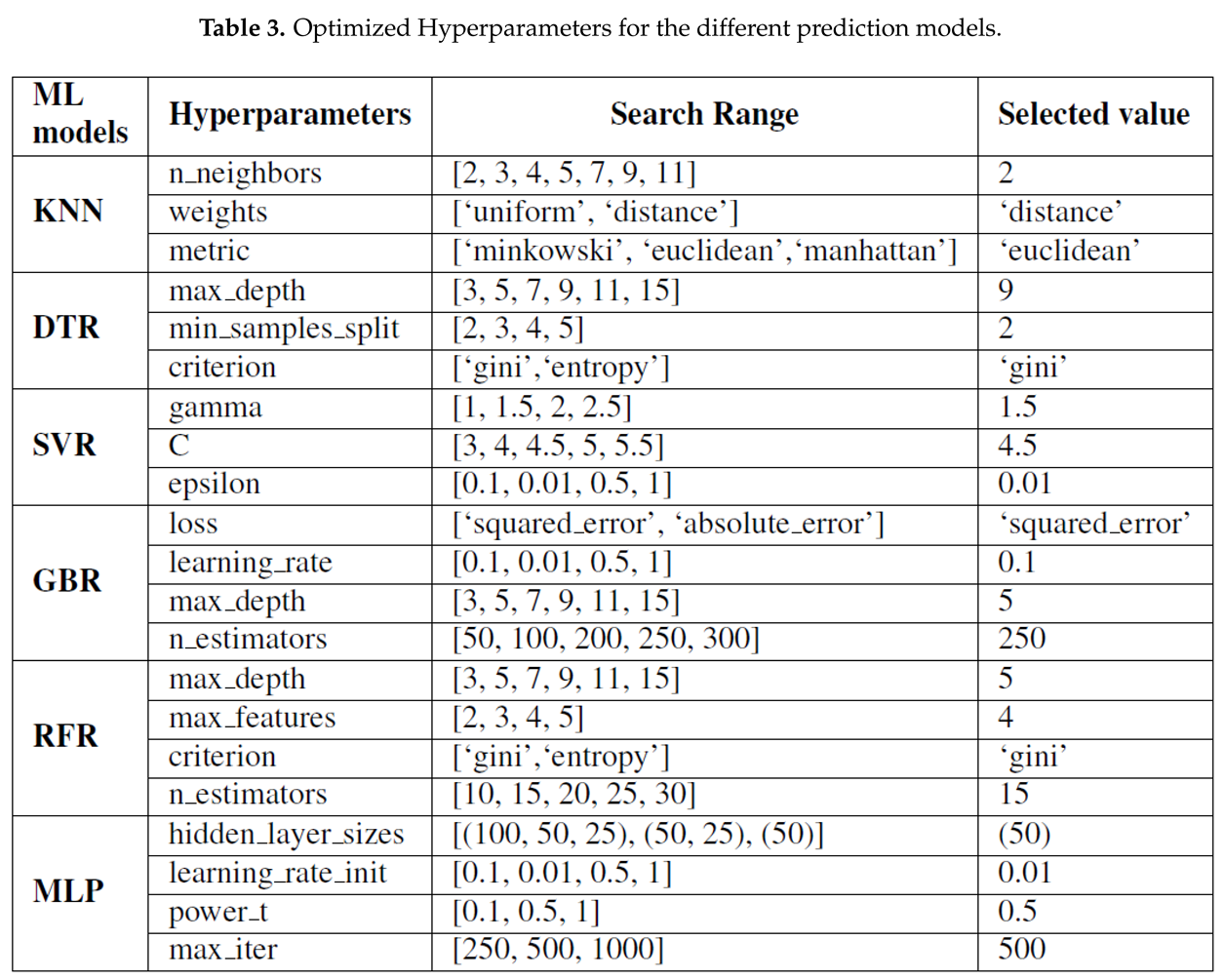
The cross-validated grid search function (GridSearchCV) in python is employed with negated MAE as scoring parameter to analyze every possible combination of hyperparameters and determine the optimal set that maximizes generalization performance. Finally, to evaluate how well the best found combination generalises, we measure its score on the hold-out test set. Table 3 provides insight into the hyperparameter space for all machine learning models. Preprints 118852 i003

4. Results and Discussion

The assessment of the developed ML models is utmost importance in order to select the ideal model for accurate prediction of hydrogen production in a co-gasification process. Within this framework, experiments are designed to evaluate the developed models across three dimensions, such as its generalization ability, prediction error, and interpretability. This section presents the result analysis to compare the effectiveness of the seven regression models for prediction of hydrogen production. Finally, the section concludes by presenting the most important contribution made by the models chosen in this study.

4.1. Exploratory data analysis (EDA)

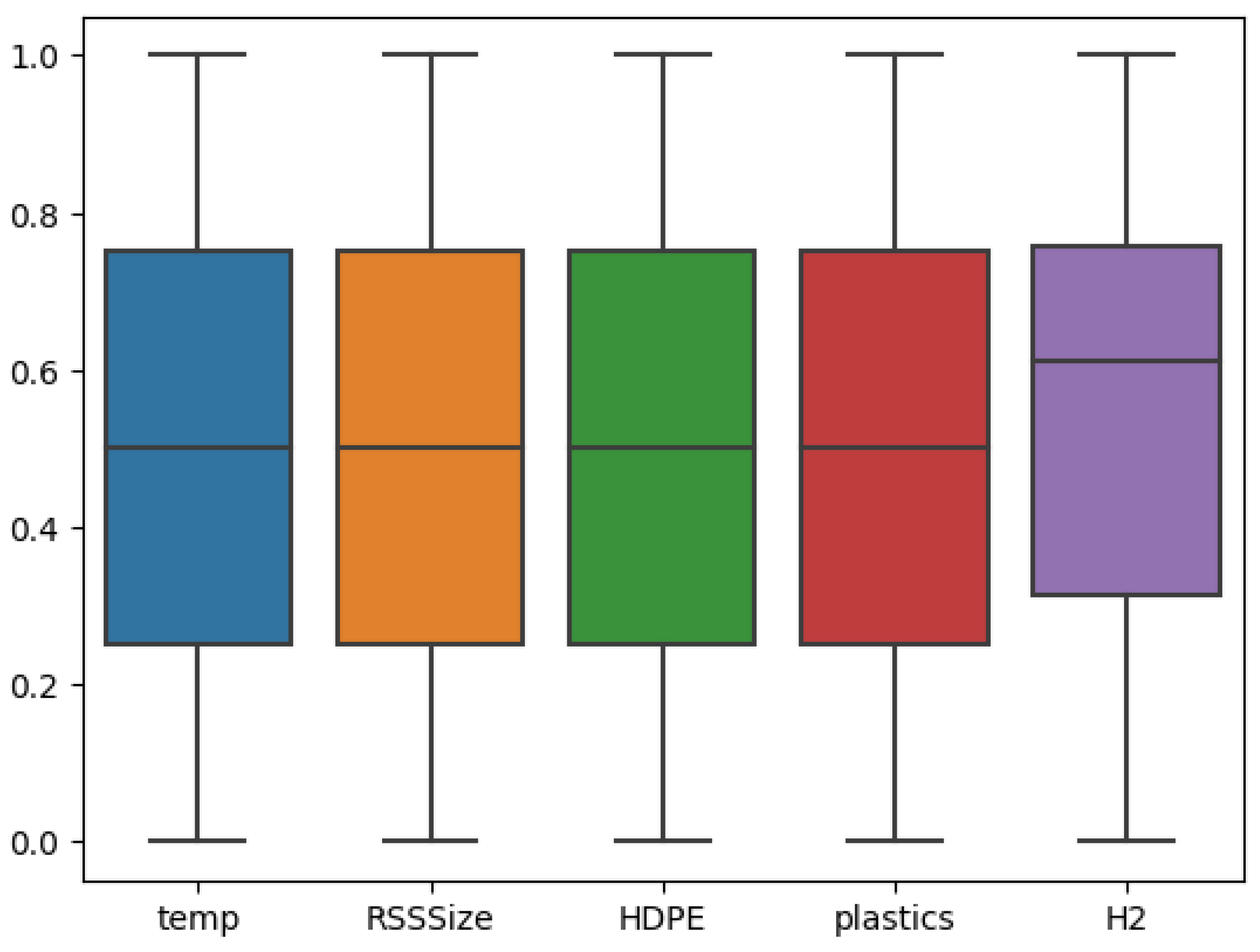
As a first step, the research data presented in Data description section is preprocessed based on the procedure outlined in the section-Section 3. Subsequently, the preprocessed data was subjected to analysis using a statistical technique known as EDA. Briefly, EDA is a most important step in ML that need to be conducted before model development to understand and prepare the study data [25]. In EDA, the first task is to examine the presence of outliers in the modeling data set and to investigate the data homogeneity. For this purpose, Python’s boxplot is shown in Figure 2. Observing these results, it is obvious that the dataset has no outliers and distribution of all input features of interest are in reasonable range, making them suitable for developing the predictive models.
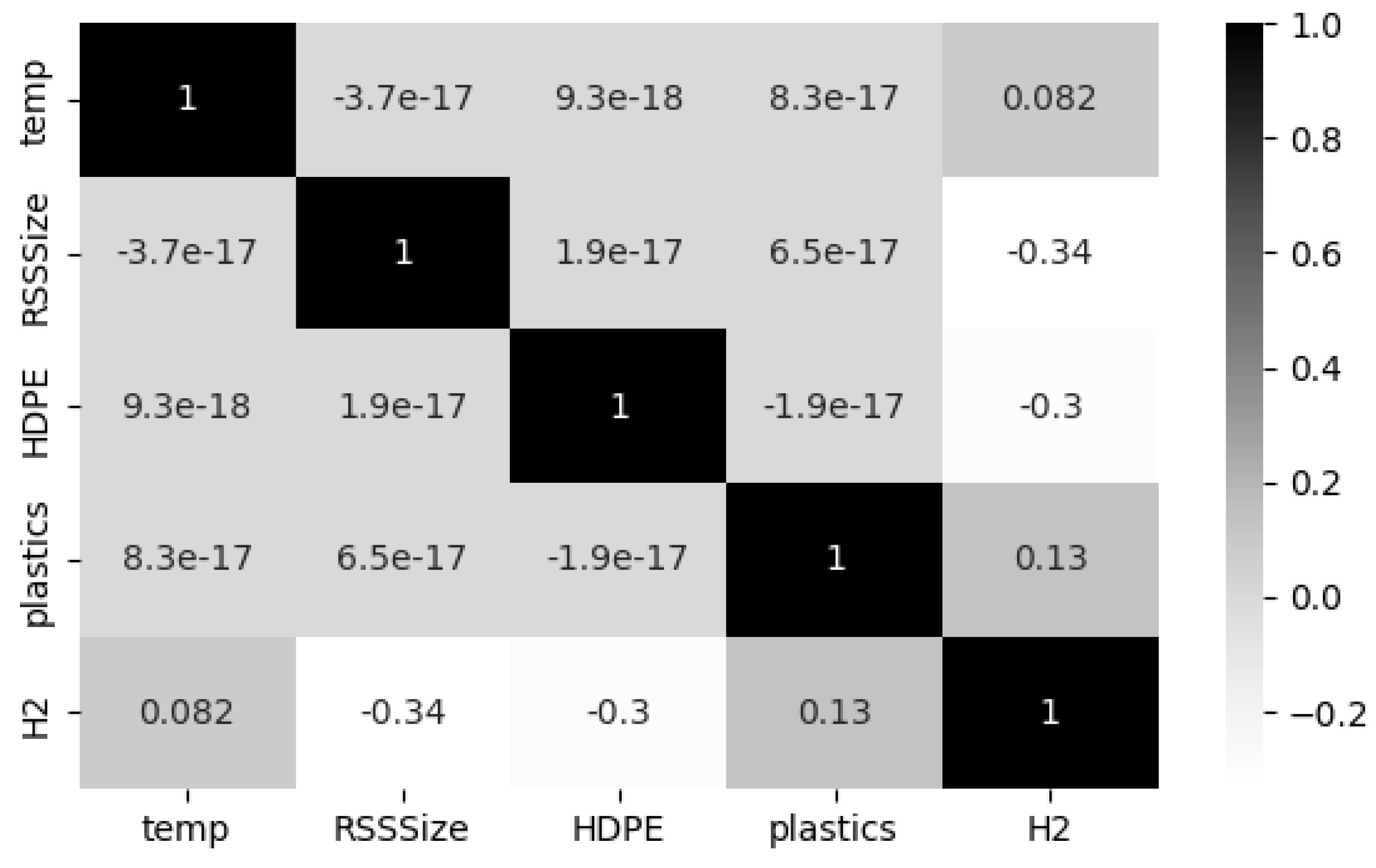
Furthermore, Pearson Correlation Coefficient (PCC) analysis was conducted to unveil the relationships among all parameters in the co-gasification process. This process enables to identify the co-linearity between input features and eradicate the overlapping effect of input features. Ideally, | P C C | = 1 represents strong data correlation, whereas | P C C | = 0 signifies the absence of correlation. Further, it is a standard practice to consider only one variable for model development, when | P C C | between two variables is greater than 0.6 [26]. The Seaborn heatmap illustrated in Figure 3. demonstrates the degree of dependency between the input process parameters and the target variable hydrogen production. From careful observation of the figure, it is evident that the correlation coefficients between the four process parameters is < 0.01 , declaring they are not correlated to each other. Also, it is worthy to observe that the operating temperature and quantity of plastics shows positive correlation on hydrogen production, with the correction co-efficient of 0.082 and 0.13 respectively. Whereas the other two process parameters such as RSS size and HDPE size shows negative correlation on hydrogen production with a co-efficient of -0.34 and -0.3 respectively. These observations imply that all these four process parameters have varying influences on the hydrogen production and are required to be considered for model development.

4.2. Model Generalization Analysis

After ensuring the quality of the study data and acquiring a thorough understanding of its characteristics from EDA analysis, the chosen seven different ML models are developed and trained following the procedures outlined in the section-Section 3. The primary objective of the first set of experimental analyses is to investigate the potential of the developed ML models for their generalization ability on the available research data. This investigation is conducted from two distinct perspectives, which will be delineated in the following sections.

4.2.1. Model Learning Ability

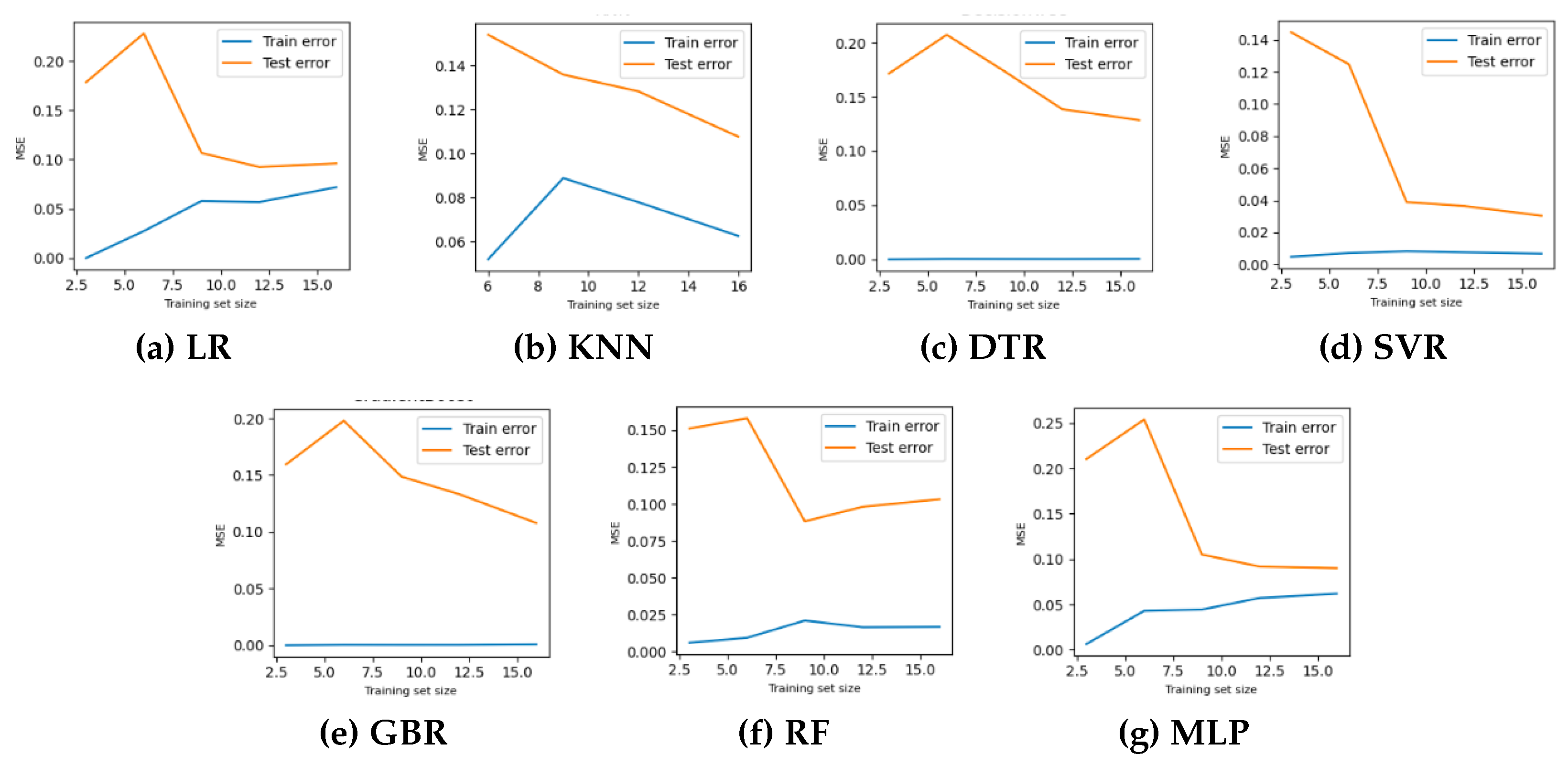
Learning curves are widely recognized as a valuable tool in ML for visually representing the training progress over time. The scholarly literature suggests utilizing learning curves to analyze ML models as they can assist in identifying over-fitting or under-fitting and can contribute to improving the performance of the models [27]. Acknowledging the benefits of the learning curves, it is employed in this study to investigate the performance of the ML models for hydrogen predication in co-gasification process. 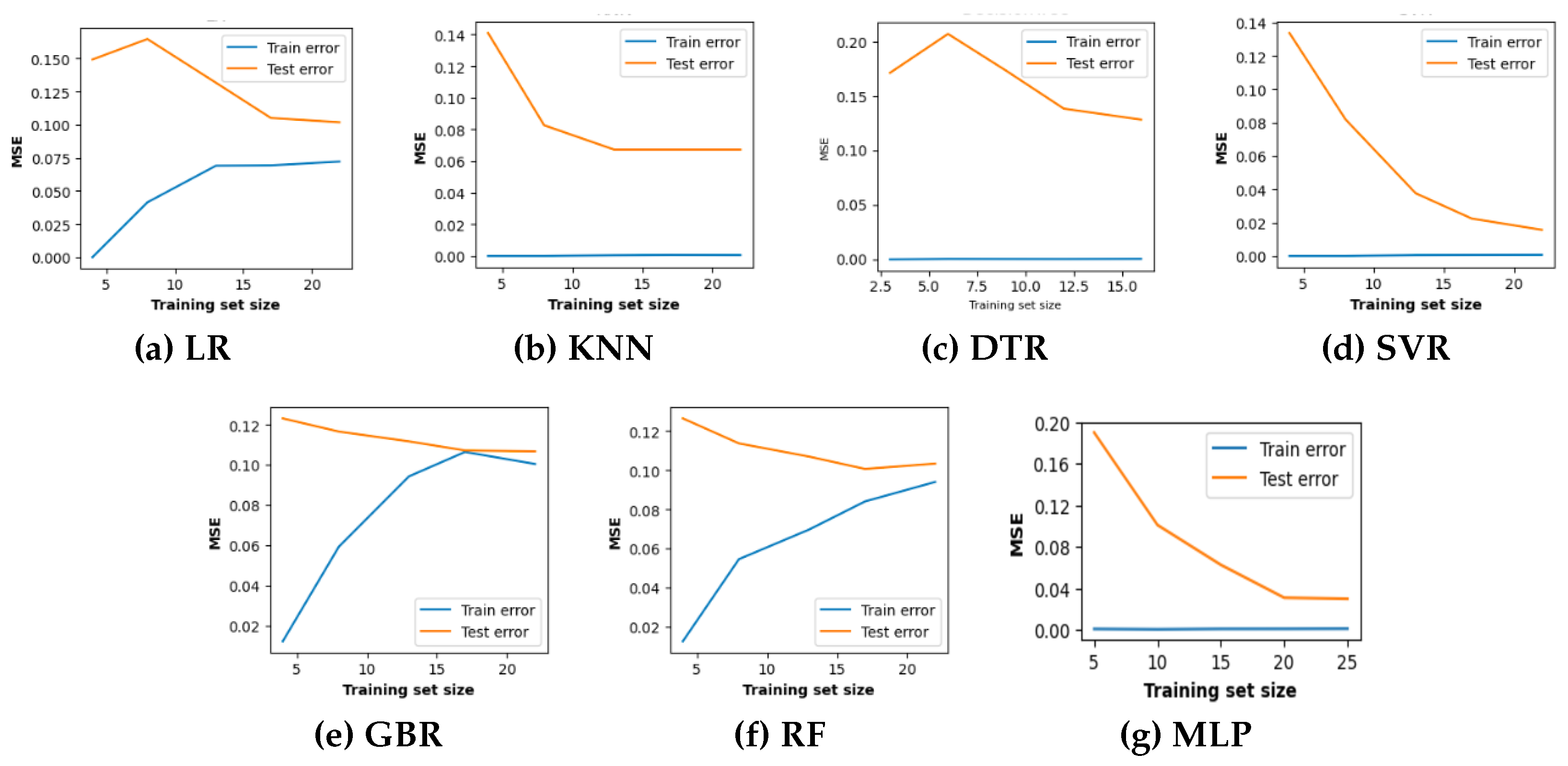The corresponding results for the four machine learning models with hyperparameter optimization are depicted in Figure 5, while their respective baselines are shown in Figure 4. The learning curve is shown by two solid lines: orange for the training data and green for the testing data. In this context, the MSE is utilized to evaluate the predictive performance of the models as they advance in their learning process. In general, the errors observed on the testing dataset serve as indicator of model generalization, whereas errors observed on the training dataset provide insights into the goodness-of-fit. Consequently, researchers recommend generalization as a `gold standard’ for model selection as it reflects the model’s ability to adapt to a new data and make accurate prediction.
Keeping this in mind and observing the MSE value in Figure 4 and Figure 5, it is evident that the learning curves of all the competing models except for KNN and MLP, exhibit only minor differences on hyperparameter optimization. This finding confirms that the hyperparameter optimization do not have substantial influence on predictive performance for the dataset under examination. Now the carefully observing the learning curves of all optimized models, it can be seen that for all the models except LR, the MSE value for training set (blue line) is minimized irrespective of the number of training samples. The goodness-of-fit with all the competing models except LR affirms the non-linear relationship between the process parameters for hydrogen prediction in co-gasification process. Nevertheless, the observation of predictive performance on testing set reveals two points, First, to our surprise, the tree-based models overfit on the training set. Second, the KNN, SVR and MLP models demonstrate better effectiveness with low MSE scores approx 0.05 for testing dataset, particularly as the size of the training dataset increases. As a result, these three models present an improved ability to generalize and show lower variance when tested with unseen test data. More specifically, SVR and MLP models reaches the minimum MSE score of 0.025 and, as a consequence, would not get any advantages from further training with additional data.

4.2.2. Model Stability

Model stability that assesses how consistently a ML model makes accurate predictions across training data is utmost importance to draw an informed decision regarding model selection. Currently, cross-validation is widely accepted in the field of ML and data analysis, and considered as a universal tool to assess the stability of a model to generalize beyond its training set [28]. More importantly, the variance of CV serves as a stable error measurement to assess how accurately the model prediction generalizes over a set of independent data. If the variance is low, then the model can be deemed stable and considered the most suitable model for accurate prediction.
The primary attraction for CV encompasses three distinct aspects, first its simplicity to use. Second attraction, its sensitivity to the functional form dimension of model complexity, in contrast to other generalization criteria such as Akaike and Bayesian Information Criterion. Third attraction, it offers a confidence measure for estimating generalization error especially when the training set used to develop a ML model is small. Therefore, it is indeed imperative to utilize CV within a co-gasification framework, considering the challenges and costs of acquiring large datasets in this framework.
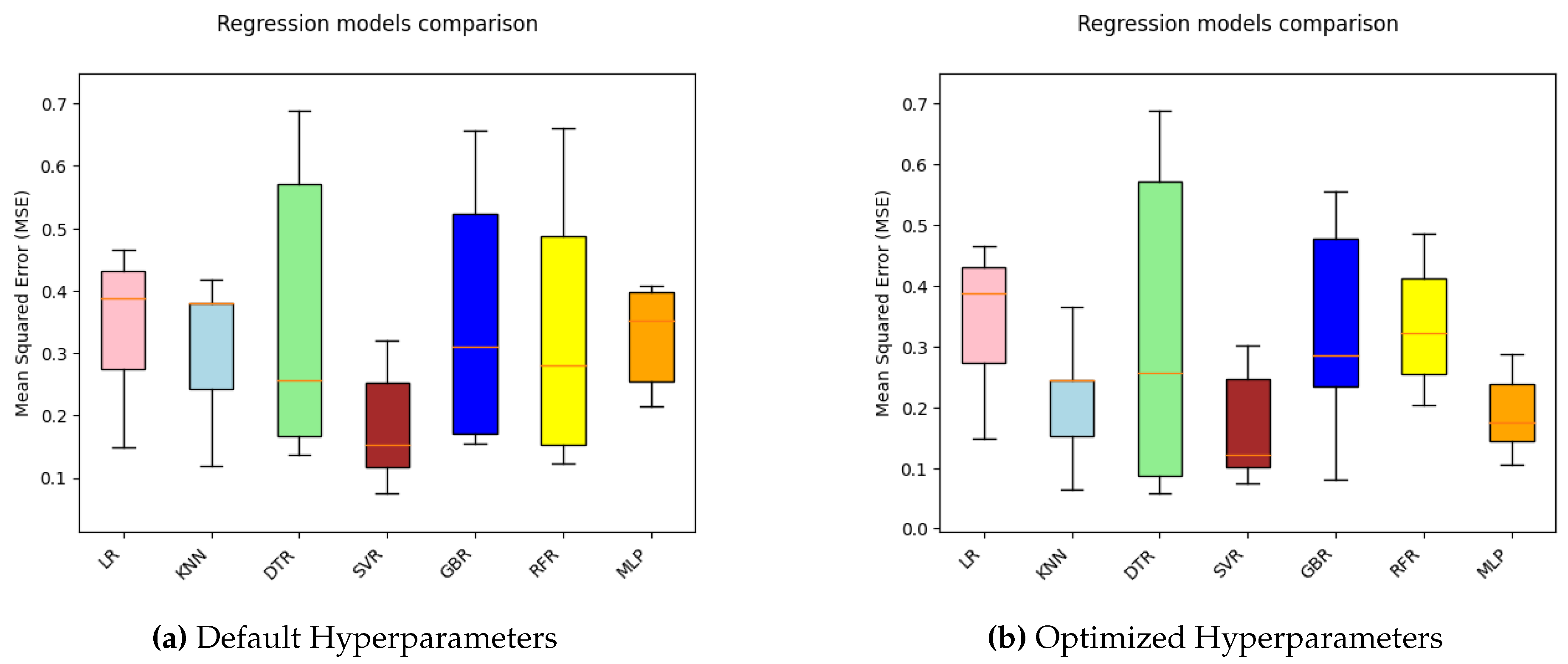
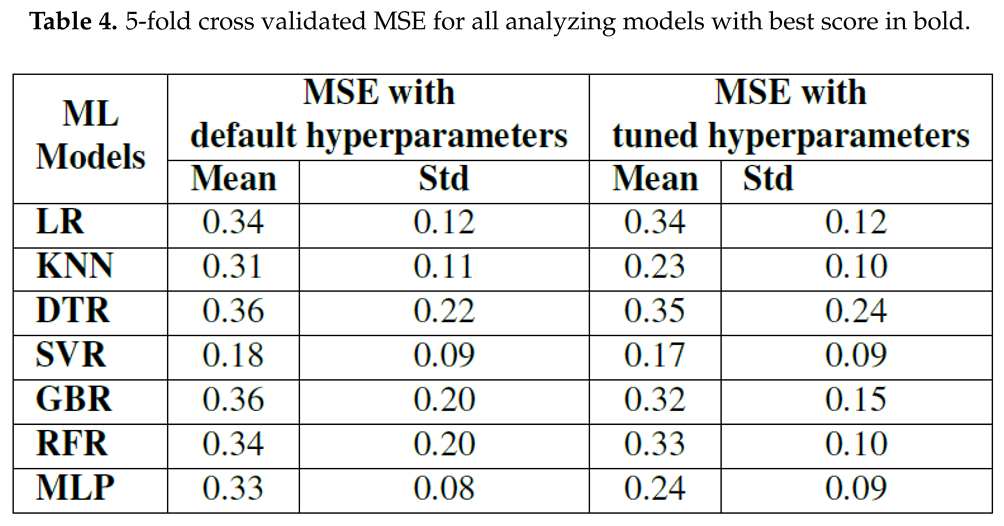
Realizing its benefits, this research work employs CV with MSE as its objective function to compare the stability of the developed ML models. Next, the mean and standard deviation (std) over the 5-fold CV results of all the ML models developed with default and optimal hyperparameters are presented in Table 4. In order to enhance the comprehensibility of the findings, a visual representation of the CV results is illustrated using box plot in Figure 6.
Observing the mean and std of CV results, it is evident that only SVR model displays the lowest CV score with mean and std of 0.18 and 0.09 respectively. Conversely, all other ML models yield relatively larger CV scores. While comparing the CV results of all ML models trained with default and optimized hyperparameters, it is apparent that except LR and DTR, all other ML models demonstrate enhanced prediction performance with hyperparameter optimization.
Visual inspection of the box plot clearly indicates that SVR presents a comparatively lower median value than other competing ML models. Also, it can be seen that KNN and MLP models with tuned hyperparameters display smaller box compared to other models and conforms their stable performance with minor variations in results across the folds. This finding is consistent with the learning curve behavior illustrated in Figure 5. Preprints 118852 i004

4.3. Prediction Performance Analysis

The second set of experimental analyses aims to evaluate and compare the efficacy of the developed ML models for predicting hydrogen production in co-gasification process. In this direction, experiments were devised to train the developed ML models using the training set that comprises 80% of the research dataset. The trained ML models were subsequently assessed using the testing set created with the remaining 20% of the research data. The prediction performance measured on testing set are presented and compared both quantitatively and qualitatively as follows,

4.3.1. Quantitative Statistical Metrics

The best performing model cannot be determined by merely comparing the models using a single assessment metric. 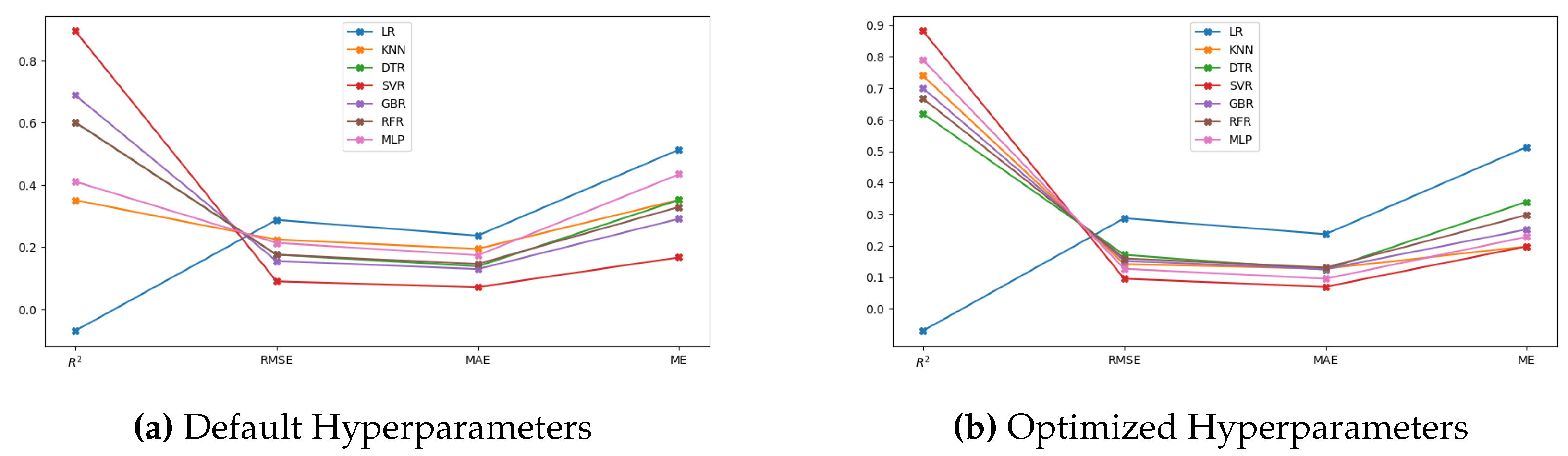Consequently, at this phase of analysis, the prediction performance of the developed ML models is compared employing four different statistical measures namely, coefficient of determination ( R 2 ) , root mean squared error (RMSE), mean absolute error (MAE) and max error (ME) to examine the correlation between the predicted test results and the measured H2 yield [29]. Table 5 presents these statistical measures as a standard indicator to compare and analyze the performance of all the analyzing ML models with default and optimized hyperparameters for hydrogen yield prediction in co-gasification. Figure Table 5 displays a line graph of the same data for easier interpretation. 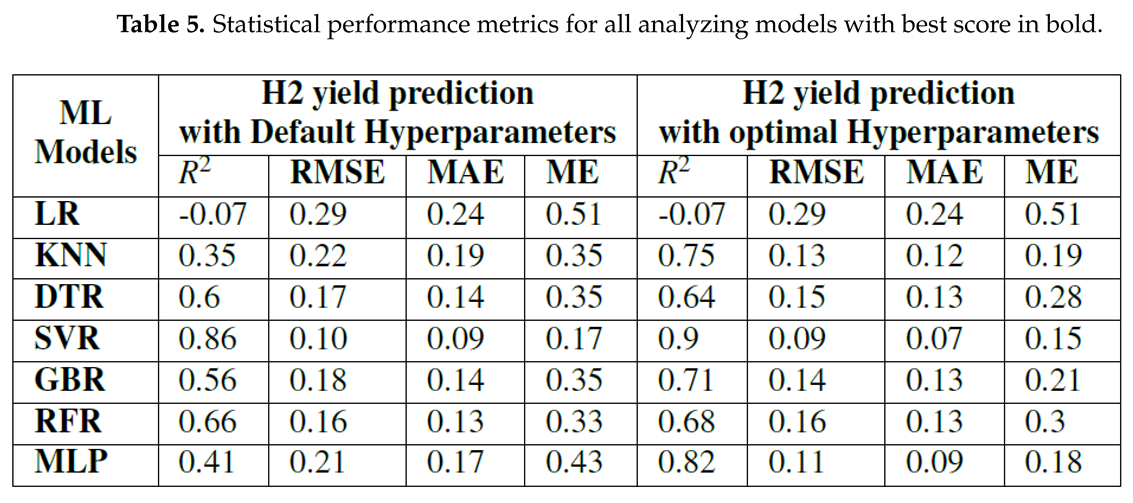Preprints 118852 i005
In this context, ( R 2 ) value closer to unity along with reduced values of RMSE, MAE and ME are recognized as key performance indicators for an idle model with improved prediction performance. In this viewpoint, comparing the results between default and optimized hyperparameters reveal that the optimization process enhances the key performance indicators across all prediction models, except LR. This finding supports two claims: First, the importance of hyperparameter optimization while developing a prediction model for co-gasification process. Second, the accuracy of the hyperparameter optimization procedure is validated by the good-fitting exhibited by all non-linear ML models for co-gasification process. The marginal performance of LR might be attributed to its limited capacity to effectively capture the intricate relationships present within the study data.
From the vertical comparison of the results through different prediction models with optimized hyperparameters, the lowered statistical error measures validates that the predictive models have successfully captured the impact of all input parameters to accurately predict the hydrogen yield in the co-gasification process. In particular, SVR appears to be the most potential prediction model with the lowest error values (RMSE, MAE and ME) and highest R 2 value of 0.9. MLP follows the same trend and achieves the second-best prediction performance with a R 2 greater than 0.8 compared to other competing ML models. Although GBR and KNN failed to exhibit good generalization ability when cross validated with the whole research data, their prediction performance on 20% testing set is deemed satisfactory with R 2 > 0.7 . This finding suggests that by strengthening the training dataset, the predictive performance of these non-linear models can be enhanced.

4.3.2. Qualitative Scatter Plot

The scatter plot, together with a regression line, is widely acknowledged as a versatile and very valuable method for visually and statistically evaluating the correlation between model predictions and the observed values [30]. It is commonly employed as a primary approach to examine the accuracy of model predictions within data driven research. In light of this foundation, the present study employs scatter plot-based regression analysis to provide more empirical evidence for the findings obtained in the previous sections.
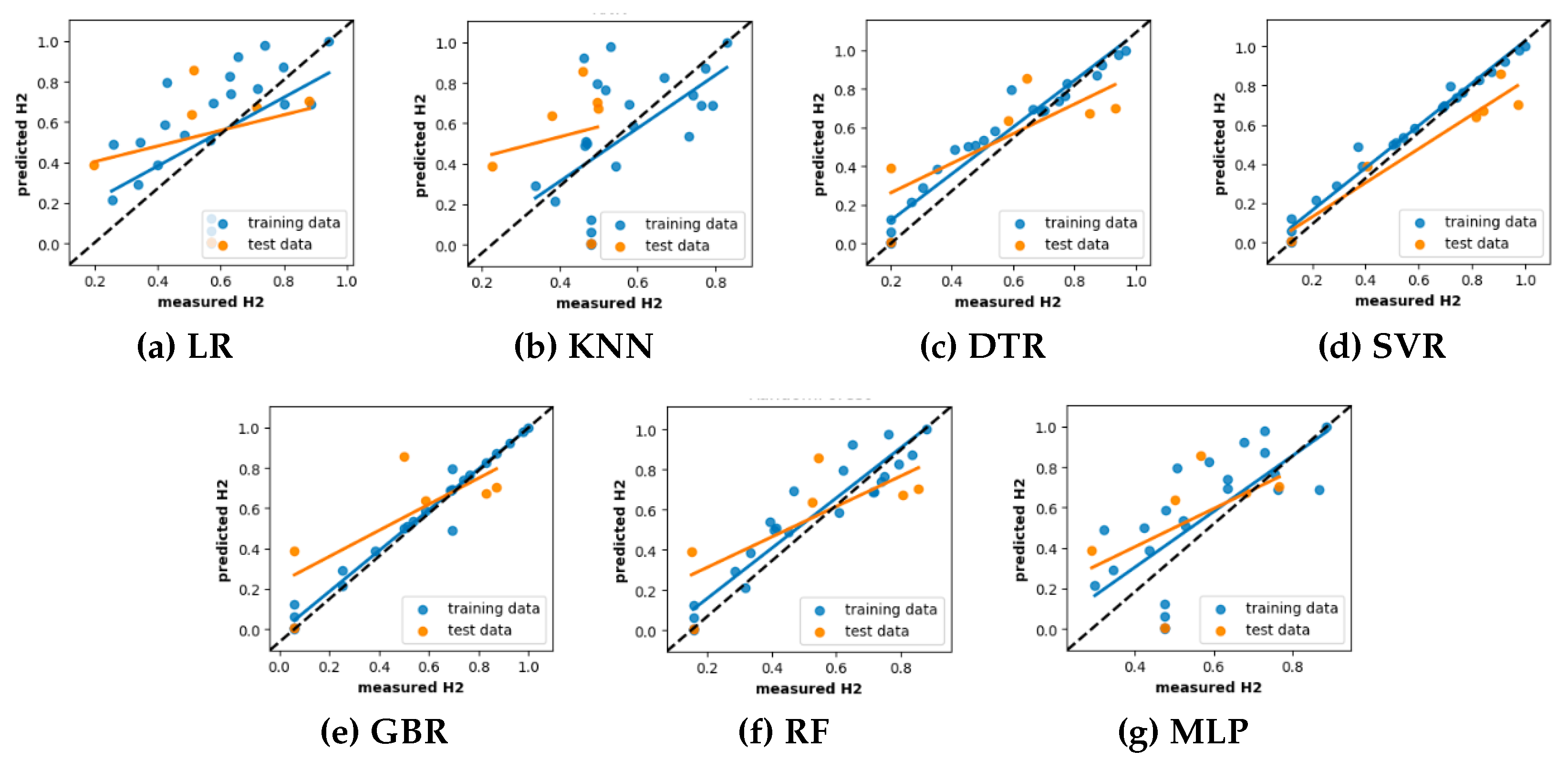
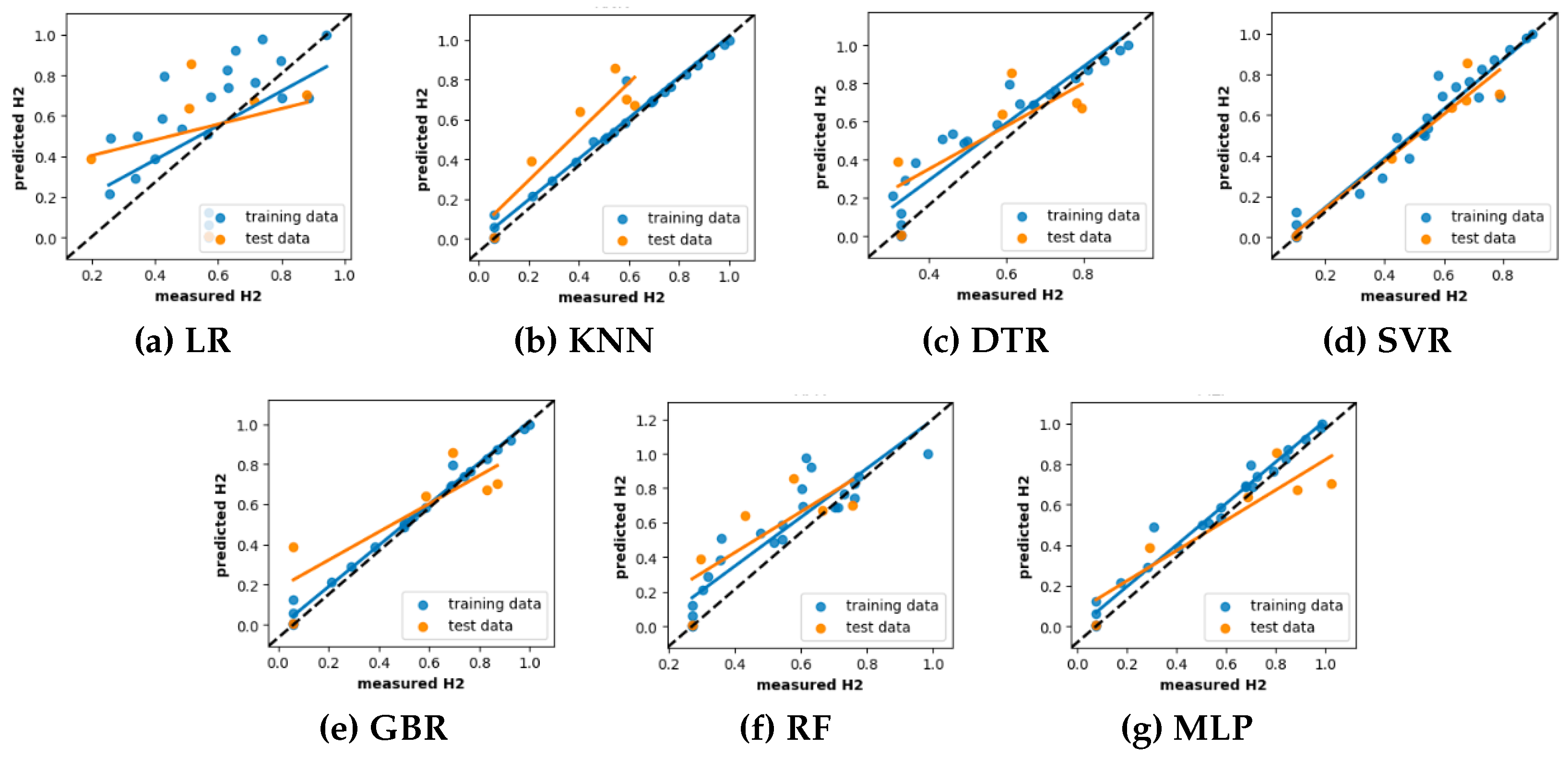
Here, the vertical distance from the regression line to a specific point indicates the prediction error for that sample. As a result, a prediction model is deemed effective exhibits minimal errors, and their predictions tend to cluster around the regression line. For an ideal regression model, their prediction align perfectly with the actual measurements, resulting in all data points falling precisely along the diagonal line known as the [1:1] regression line. The scatter plots illustrating the experimentally observed and predicted hydrogen yield for the ML models developed with default and tuned hyperparameters are shown in Figure 8 and Figure 9, respectively. Here, The [1:1] regression line is shown by the black dashed line at a 45 degree angle and the data distribution represented by the blue and orange color corresponds to the training and testing predictions, respectively.
Analyzing the figures in Figure 8 and Figure 9, it is evident that LR exhibits more scattered prediction with the testing and training set. The observed inferior performance of LR in comparison to other ML models further substantiates the non-linear behavior of hydrogen production with the process parameters. One unexpected observation is that DTR and RFR which showed overfit on training set in learning curve, have shown scattered predictions even with training set. This condition may be attributed to the hard rule-based learning approach employed by the DTR and RFR. Anotehr notable observation is that, with the exception of DTR and RFR, all other ML models exhibit a close clustering of predictions around the regression line. This finding adds more support for their ability to effectively describe the non-linear correlation between hydrogen production and the process parameters.

4.4. Model Interpretation

In practice, if a researcher finds a ML model with an acceptable level of accuracy, the subsequent step involves gaining insight into the prediction process and making informed decision in light of expert domain knowledge. Unfortunately, the black-box mechanism of ML models presents challenges in understanding the impact and influence of input parameters on target within the modeling process. This experimental analysis takes a step further to address the problem at hand by analyzing the interpretability of the developed ML models and rationalize their predictions, irrespective of their complexity [31]. The post-hoc interpretability analysis integrates the Shapley approach with the developed ML models to provide substantial insights into the final prediction of the model from both local and global perspectives [32]. The subsections that follow will explore these findings in further detail.

4.4.1. Global Explanation with Summary Plot

The Global explanation, also known as the dataset-level explanation, has proven crucial in understanding the underlying association between the features and the final predictions based on the complete model [33]. This section explores the global explanation of the Shapley method for all the developed ML models using the summary plot [34]. One benefit of utilizing the Shapley summary plot for global analysis is that it not only effectively depicts the significance of features but also highlights the positive and negative associations that these features have with the target.
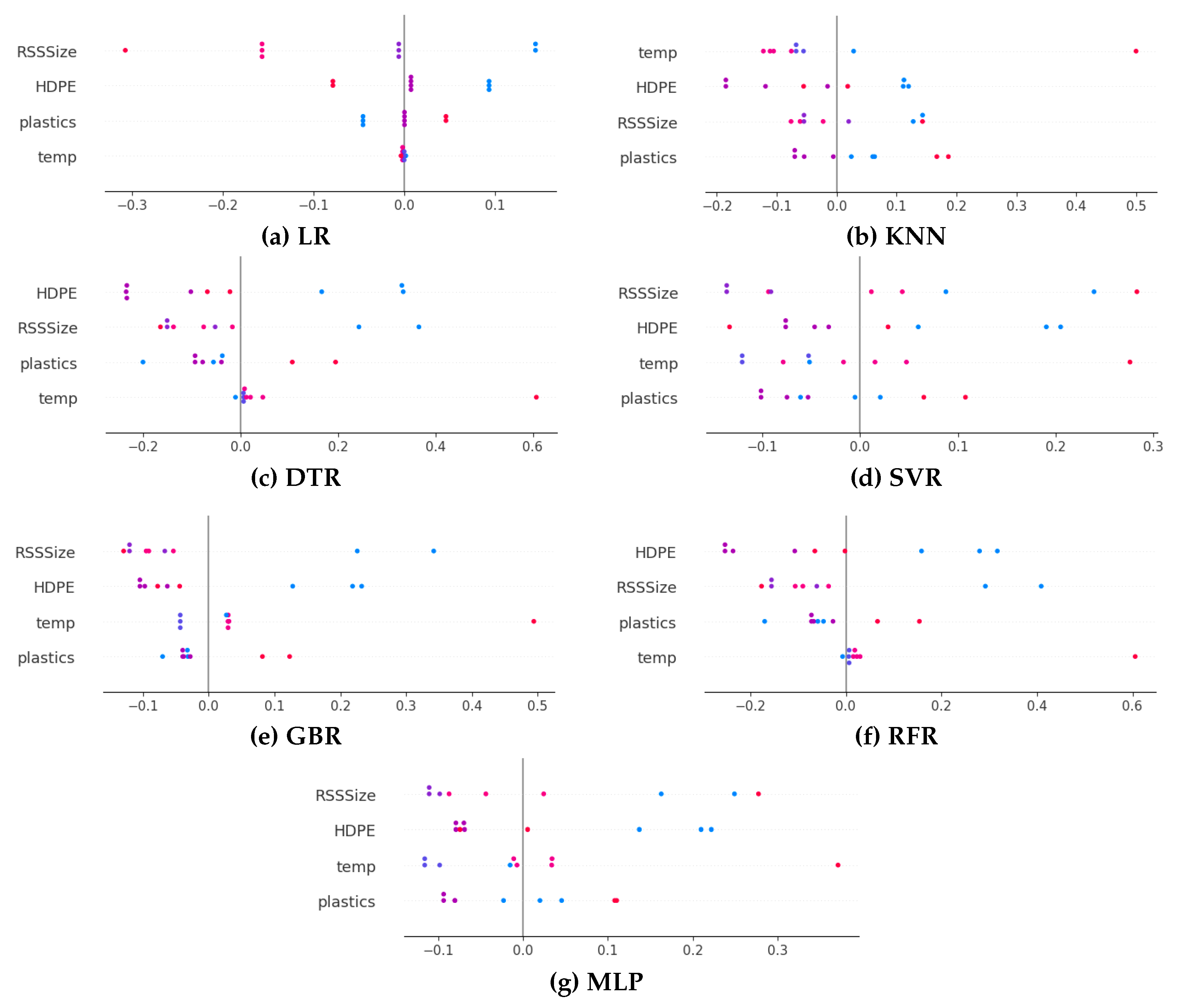
Figure 10 displays the SHAP summary plots for all the developed ML models on the testing dataset. These plots depict the shapley values associated with each process parameter utilized in predicting hydrogen generation throughout the biomass-plastics cogasification process. On the X axis, the positive shapley value signifies an increase in hydrogen production during co-gasification, whereas a negative value signifies a decrease in production. The relative importance of each process parameter is depicted along the Y axis, with the most crucial one at the top and the least crucial one toward the bottom. Each dot within the summary plot corresponds to a sample in the dataset, visually representing the impact of that sample on the model output.
The analysis of the summary plot in Figure 10 reveals that on average all the process parameters are most important influential factors for hydrogen production during biomass-plastics co-gasification. The dots spread across the summary plots of all ML models for these process parameters provide credence to this finding. Interestingly, we can see that only KNN, SVM, GBR and MLP recognize HDPE, RSSize and temp as the most dominant process parameters compared to plastics. This explanation regarding the effects of process parameters is consistent with the majority of the co-gasification process literature and prior knowledge in the field.
More specifically, the careful analysis of data distribution on X axis indicates that KNN, MLP, and SVM were effective in holding a mixed effect of HDPE and RSSize on hydrogen generation while GBR exhibiting a negative impact contradicts the experimental observation that supports the mixed impact for HDPE and RSSize parameters. Likewise, as opposed to exhibiting a mixed correlation with temperature, MLP considers a positive effect with regard to temperature and do not comply with empirical observations. Surprisingly, the global explanation provided by the KNN and SVM models are in agreement with the previously published literature and experimental observations on cogasification.

4.4.2. Local Explanation with Force Plot

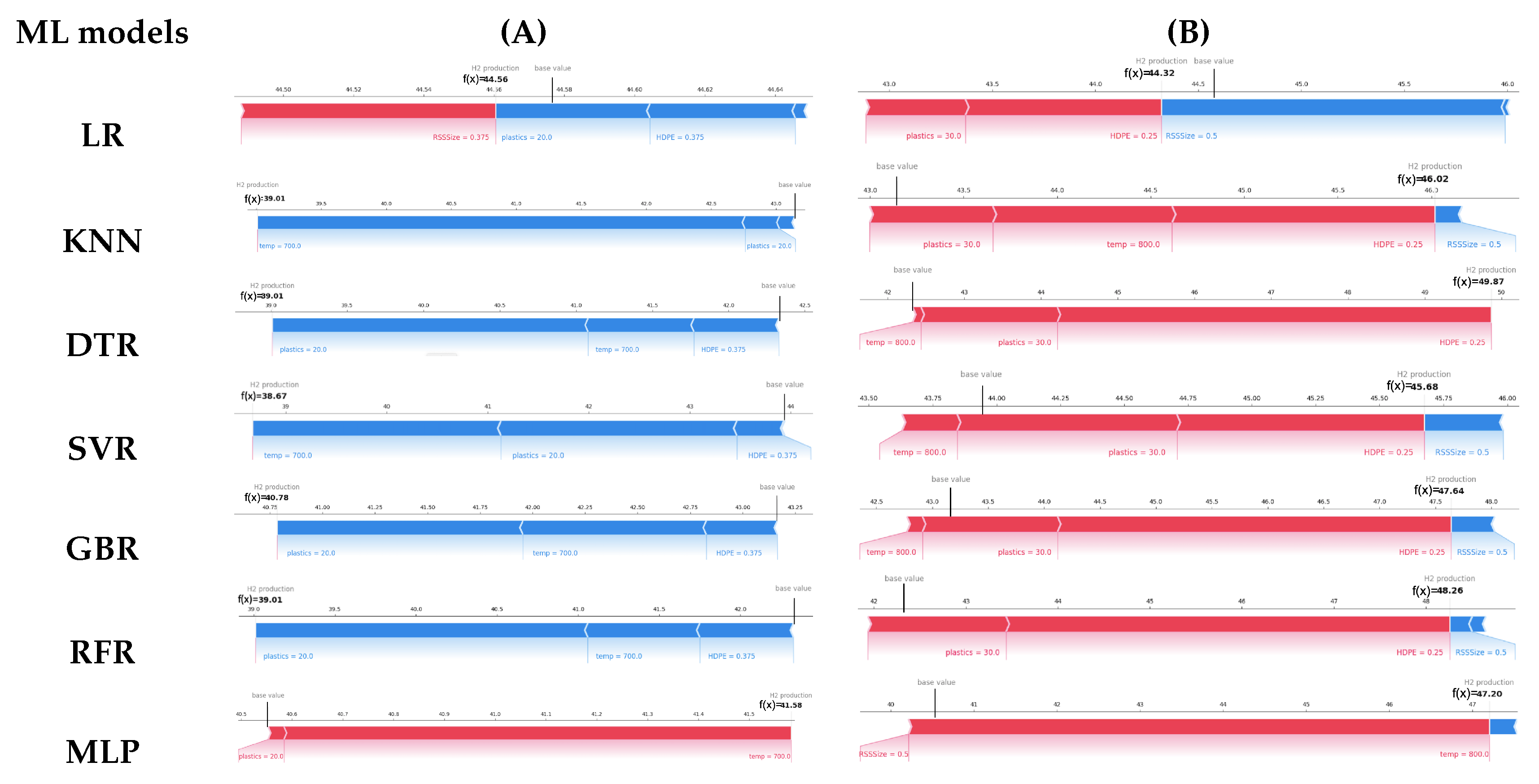
As discussed above, the global explanation describes the model as a whole, illuminating the relative importance of process parameters and their influence on hydrogen production. Conversely, local explanation, also known as individual prediction explanation, is essential to elucidate the impact of process parameters on a specific model prediction. Further, the importance of local explanation becomes evident in achieving optimum values for process parameters when a global explanation fails to capture the local behavior of complex models. This phenomenon is mainly observed in the co-gasification process, wherein the model demonstrates varying behavior across different combinations of process parameters. Given the importance of local explanation, this section examines the local interpretability of all the developed ML models using the Shapley force plot, which has garnered considerable attention in recent times due to its appealing features.
Figure 11 (A) and Figure 11(B) shows the SHAP force plots for two separate instances selected from the testing dataset with process parameters for low and high hydrogen production prediction respectively. Each of these plots display two values: the base value, which is the average model output, and the model prediction for that instance. These plots clearly illustrate how the process parameters drives the model prediction from the baseline value for the instance under consideration. The process parameters that drive prediction value lower are visually represented in the color blue, while those drive prediction value higher are visually represented in the color red.
In the specific case depicted in Fig.Figure 11(A), the hydrogen production recorded during the co-gasification experiment amounts to 38.625. Upon detailed examination of Fig.Figure 11(A), it becomes evident that, with the only exception of MLP, the prediction result is less than the base value for all ML models. The majority of machine learning models concur that the primary cause for the decrease in hydrogen generation is attributed to low values of process parameters such as temperature, plastic percentage, and HDPE size. Additionally, it is noteworthy to observe, that among all the developed ML models, only SVR model exhibits a more precise outcome of 38.67.
Conversely, the hydrogen production recorded during co-gasification experiment for the case shown in Figure 11(B) is 48.212. A careful examination of these figures reveal that with the exception of LR, all other ML models provide prediction result that are higher than their baseline value. In this case, the RFR model surprisingly exhibited the most accurate estimate of hydrogen production. However, it is evident from its force plot that it ignored the fact that a higher temperature enhances hydrogen production. In the similar vein, both DTR and MLP models disregarded the adverse impact of RSSize on hydrogen production. Thus, only KNN, SVR, and GBR models were more successful in explaining the positive influence of temperature, plastic percentage, and HDPE size as well as the negative impact of RSSize on hydrogen generation, despite their prediction result was not significantly better in this case.

5. Conclusion

This study investigated the performance of seven different ML models including LR, KNN, DTR, SVR, GBR, RFR and MLP for predicting and optimizing the hydrogen production based on the process parameters for biomass-plastics co-gasification process. To this end, exploratory data analysis was conducted as a preliminary step to assess the quality of the study dataset before utilizing it to train the selected ML models. Eventually, after optimizing the hyperparameters of all the trained ML models, a comprehensive set of experiments was devised to evaluate the performance of these models across three dimensions including generalization ability, prediction capabilities and interpretability. Based on the results, it could be concluded that:
  • The generalization ability analysis based on qualitative and quantitative grounds using learning curve and CV, revealed that SVR and MLP models had a greater potential for generalization compared to other competing models with a minimum MSE score of approximately 0.025.
  • The prediction performance analysis using quantitative statistical metrics and qualitatively scatter plots further substantiated the potential of SVR demonstrating its efficacy in capturing the complex nonlinear relationship between hydrogen production and process parameters with an excellent prediction accuracy of approximately 0.25.
  • The interpretability analysis of the developed ML models at global and local level using Shap summary plot and force plot respectively revealed that KNN, SVR and GBR model were more successful in reliably elucidating the influence of the process parameters on hydrogen production and concurred with both the experimental observations and previously published literature.

Acknowledgments

The author extend her appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/01/29695).

References

  1. Yoro, K.O.; Daramola, M.O. CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in carbon capture; Elsevier, 2020; pp. 3–28.
  2. Mangal, M.; Rao, C.V.; Banerjee, T. Bioplastic: an eco-friendly alternative to non-biodegradable plastic. Polymer International 2023, 72, 984–996. [Google Scholar] [CrossRef]
  3. Thew, C.X.E.; Lee, Z.S.; Srinophakun, P.; Ooi, C.W. Recent advances and challenges in sustainable management of plastic waste using biodegradation approach. Bioresource Technology 2023, 374, 128772. [Google Scholar] [CrossRef] [PubMed]
  4. Züttel, A.; Remhof, A.; Borgschulte, A.; Friedrichs, O. Hydrogen: the future energy carrier. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2010, 368, 3329–3342. [Google Scholar] [CrossRef] [PubMed]
  5. Ismail, M.M.; Dincer, I. A new renewable energy based integrated gasification system for hydrogen production from plastic wastes. Energy 2023, 270, 126869. [Google Scholar] [CrossRef]
  6. Sikiru, S.; Oladosu, T.L.; Amosa, T.I.; Olutoki, J.O.; Ansari, M.; Abioye, K.J.; Rehman, Z.U.; Soleimani, H. Hydrogen-powered horizons: Transformative technologies in clean energy generation, distribution, and storage for sustainable innovation. International Journal of Hydrogen Energy 2024, 56, 1152–1182. [Google Scholar] [CrossRef]
  7. Wang, Y.; Wu, J.J. Thermochemical conversion of biomass: Potential future prospects. Renewable and Sustainable Energy Reviews 2023, 187, 113754. [Google Scholar] [CrossRef]
  8. Yek, P.N.Y.; Chan, Y.H.; Foong, S.Y.; Mahari, W.A.W.; Chen, X.; Liew, R.K.; Ma, N.L.; Tsang, Y.F.; Sonne, C.; Cheng, Y.W.; others. Co-processing plastics waste and biomass by pyrolysis–gasification: a review. Environmental Chemistry Letters 2024, 22, 171–188. [Google Scholar] [CrossRef]
  9. Ramos, A.; Monteiro, E.; Silva, V.; Rouboa, A. Co-gasification and recent developments on waste-to-energy conversion: A review. Renewable and Sustainable Energy Reviews 2018, 81, 380–398. [Google Scholar] [CrossRef]
  10. Naqvi, S.R.; Ullah, Z.; Taqvi, S.A.A.; Khan, M.N.A.; Farooq, W.; Mehran, M.T.; Juchelková, D.; Štěpanec, L.; others. Applications of machine learning in thermochemical conversion of biomass-A review. Fuel 2023, 332, 126055. [Google Scholar]
  11. Dodo, U.A.; Ashigwuike, E.C.; Abba, S.I. Machine learning models for biomass energy content prediction: a correlation-based optimal feature selection approach. Bioresource Technology Reports 2022, 19, 101167. [Google Scholar] [CrossRef]
  12. Devasahayam, S. Deep learning models in Python for predicting hydrogen production: A comparative study. Energy 2023, 280, 128088. [Google Scholar] [CrossRef]
  13. Ascher, S.; Wang, X.; Watson, I.; Sloan, W.; You, S. Interpretable machine learning to model biomass and waste gasification. Bioresource Technology 2022, 364, 128062. [Google Scholar] [CrossRef] [PubMed]
  14. Wang, Z.; Peng, X.; Xia, A.; Shah, A.A.; Yan, H.; Huang, Y.; Zhu, X.; Zhu, X.; Liao, Q. Comparison of machine learning methods for predicting the methane production from anaerobic digestion of lignocellulosic biomass. Energy 2023, 263, 125883. [Google Scholar] [CrossRef]
  15. Ozbas, E.E.; Aksu, D.; Ongen, A.; Aydin, M.A.; Ozcan, H.K. Hydrogen production via biomass gasification, and modeling by supervised machine learning algorithms. International Journal of Hydrogen Energy 2019, 44, 17260–17268. [Google Scholar] [CrossRef]
  16. Wen, H.T.; Lu, J.H.; Phuc, M.X. Applying artificial intelligence to predict the composition of syngas using rice husks: A comparison of artificial neural networks and gradient boosting regression. Energies 2021, 14, 2932. [Google Scholar] [CrossRef]
  17. Xue, L.; Liu, Y.; Xiong, Y.; Liu, Y.; Cui, X.; Lei, G. A data-driven shale gas production forecasting method based on the multi-objective random forest regression. Journal of Petroleum Science and Engineering 2021, 196, 107801. [Google Scholar] [CrossRef]
  18. Bienvenido-Huertas, D.; Rubio-Bellido, C.; Solís-Guzmán, J.; Oliveira, M.J. Experimental characterisation of the periodic thermal properties of walls using artificial intelligence. Energy 2020, 203, 117871. [Google Scholar] [CrossRef]
  19. Chin, B.L.F.; Yusup, S.; Al Shoaibi, A.; Kannan, P.; Srinivasakannan, C.; Sulaiman, S.A. Optimization study of catalytic co-gasification of rubber seed shell and high density polyethylene waste for hydrogen production using response surface methodology. Advances in bioprocess technology 2015, 209–223. [Google Scholar]
  20. Ayodele, B.V.; Mustapa, S.I.; Kanthasamy, R.; Zwawi, M.; Cheng, C.K. Modeling the prediction of hydrogen production by co-gasification of plastic and rubber wastes using machine learning algorithms. International Journal of Energy Research 2021, 45, 9580–9594. [Google Scholar] [CrossRef]
  21. Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv preprint 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
  22. Bisong, E.; Bisong, E. Google colaboratory. Building machine learning and deep learning models on google cloud platform: a comprehensive guide for beginners 2019, 59–64. [Google Scholar]
  23. Xu, Y.; Goodacre, R. On splitting training and validation set: a comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. Journal of analysis and testing 2018, 2, 249–262. [Google Scholar] [CrossRef]
  24. Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L.; others. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2023, 13, e1484. [Google Scholar] [CrossRef]
  25. Data, M.C.; Komorowski, M.; Marshall, D.C.; Salciccioli, J.D.; Crutain, Y. Exploratory data analysis. Secondary analysis of electronic health records 2016, 185–203. [Google Scholar]
  26. McDonald, J.H.; Dunn, K.W. Statistical tests for measures of colocalization in biological microscopy. Journal of microscopy 2013, 252, 295–302. [Google Scholar] [CrossRef]
  27. Perlich, C. ; others. Learning Curves in Machine Learning., 2010.
  28. Wong, T.T.; Yeh, P.Y. Reliable accuracy estimates from k-fold cross validation. IEEE Transactions on Knowledge and Data Engineering 2019, 32, 1586–1594. [Google Scholar] [CrossRef]
  29. Vaiyapuri, T.; Binbusayyis, A. Application of deep autoencoder as an one-class classifier for unsupervised network intrusion detection: a comparative evaluation. PeerJ Computer Science 2020, 6, e327. [Google Scholar] [CrossRef]
  30. Nguyen, Q.V.; Miller, N.; Arness, D.; Huang, W.; Huang, M.L.; Simoff, S. Evaluation on interactive visualization data with scatterplots. Visual Informatics 2020, 4, 1–10. [Google Scholar] [CrossRef]
  31. Das, D.; Ito, J.; Kadowaki, T.; Tsuda, K. An interpretable machine learning model for diagnosis of Alzheimer’s disease. PeerJ 2019, 7, e6543. [Google Scholar] [CrossRef]
  32. Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nature machine intelligence 2020, 2, 56–67. [Google Scholar] [CrossRef]
  33. Nguyen, V.G.; Sharma, P.; Ağbulut, Ü.; Le, H.S.; Cao, D.N.; Dzida, M.; Osman, S.M.; Le, H.C.; Tran, V.D. Improving the prediction of biochar production from various biomass sources through the implementation of eXplainable machine learning approaches. International Journal of Green Energy 2024, 1–28. [Google Scholar] [CrossRef]
  34. Giudici, P.; Raffinetti, E. Shapley-Lorenz eXplainable artificial intelligence. Expert systems with applications 2021, 167, 114104. [Google Scholar] [CrossRef]
Preprints 118852 g001
Figure 1. Evaluation framework of Explainable ML models for hydrogen production prediction.
Figure 1. Evaluation framework of Explainable ML models for hydrogen production prediction.
Preprints 118852 g001
Preprints 118852 g002
Figure 2. Heat map for Correlation analysis.
Figure 2. Heat map for Correlation analysis.
Preprints 118852 g002
Preprints 118852 g003
Figure 3. Heat map for Correlation analysis.
Figure 3. Heat map for Correlation analysis.
Preprints 118852 g003
Preprints 118852 g004
Figure 4. Learning curve analysis of different ML models with default hyperparameters.
Figure 4. Learning curve analysis of different ML models with default hyperparameters.
Preprints 118852 g004
Preprints 118852 g005
Figure 5. Learning curve analysis of different ML models with optimized hyperparameters.
Figure 5. Learning curve analysis of different ML models with optimized hyperparameters.
Preprints 118852 g005
Preprints 118852 g006
Figure 6. Box plot analysis of 5-fold cross validation for all analysing models.
Figure 6. Box plot analysis of 5-fold cross validation for all analysing models.
Preprints 118852 g006
Preprints 118852 g007
Figure 7. Line graph illustrating the statistical Performance metrics for all analysing models.
Figure 7. Line graph illustrating the statistical Performance metrics for all analysing models.
Preprints 118852 g007
Preprints 118852 g008
Figure 8. Prediction performance analysis of different ML models with default hyperparameters.
Figure 8. Prediction performance analysis of different ML models with default hyperparameters.
Preprints 118852 g008
Preprints 118852 g009
Figure 9. Prediction performance analysis of different ML models with optimized hyperparameters.
Figure 9. Prediction performance analysis of different ML models with optimized hyperparameters.
Preprints 118852 g009
Preprints 118852 g010
Figure 10. SHAP summart plot of the developed ML models on the testing dataset.
Figure 10. SHAP summart plot of the developed ML models on the testing dataset.
Preprints 118852 g010
Preprints 118852 g011
Figure 11. SHAP force plot of the developed ML models for two different instance that yield low and high hydrogen.
Figure 11. SHAP force plot of the developed ML models for two different instance that yield low and high hydrogen.
Preprints 118852 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated