1. Introduction
Insurance companies face high churn rates, particularly in motor insurance, where customer retention is critical due to intense market competition, claims management, and fluctuating premium rates [
1]. This study focuses on identifying unique churn patterns in this sector. Customer churn, the movement of customers to other providers, is a significant challenge, as it is difficult to identify which customers are at risk of leaving unless they proactively express dissatisfaction [
2]. With a large number of policies that expire each month, it is impractical for insurers to contact all customers to confirm their intention to renew [
3]. However, by predicting which customers are likely to churn, insurance companies can focus their efforts on those most at risk, thus improving retention strategies. Churn prediction approaches can be broadly categorized into two strategies: constructive (local) approaches and global approaches [
4]. The constructive approach targets individual customer behaviors and their specific interactions with the product or service, allowing for a more personalized intervention [
5,
6]. In contrast, the global approach builds a comprehensive model that applies to the entire customer base, identifying general patterns and trends predictive of churn. This approach often uses machine learning techniques to identify general patterns and trends that predict churn [
7,
8].
Machine learning algorithms (ML) have become the predominant tool for churn prediction due to their ability to analyze large datasets and make accurate predictions [
9,
10]. Common algorithms include logistic regression [
11], decision trees [
12,
13], random forests [
14], support vector machines (SVM) [
15,
16,
17], and neural networks [
18,
19,
20]. Logistic regression is favored for its simplicity and interpretability, though it can be difficult with complex patterns. Regularization techniques such as L1 (Lasso) and L2 (Ridge) are often used with logistic regression to prevent overfitting. Regularization of L1 penalizes the absolute value of coefficients, effectively shrinking some to zero and leading to a sparse model that retains only the most important features. L2 regularization, on the other hand, penalizes the square of the coefficients, reducing their magnitude evenly and improving model stability, particularly in the presence of multicollinearity [
9,
21,
22].
Decision trees and random forests effectively handle nonlinear relationships and variable interactions but can be prone to overfitting, especially in high-dimensional data. To address this, optimization techniques like pruning [
24], which removes insignificant branches, and ensemble methods such as bagging and boosting are used to enhance generalization and reduce overfitting [
25]. SVMs are powerful in managing high-dimensional spaces, providing clear margins between churn and non-churn customers [
26,
27,
28]. However, they require careful tuning and are computationally demanding. SVMs benefit from kernel tricks that map input data into higher-dimensional spaces, making it easier to find effective separating hyperplanes.
Neural networks, particularly deep learning models, excel at recognizing intricate patterns in large data-sets but require significant computational resources and a large amount of labeled data [
29]. They are optimized using algorithms like stochastic gradient descent (SGD) [
30], Adam [
31], and learning rate scheduling [
32], which help accelerate convergence and improve performance. Adjustment of hyperparameters, using methods such as grid search or random search, is crucial to optimize the predictive accuracy of these models. The choice of algorithm and optimization techniques depends on the characteristics of the data and the desired balance between interpretability, precision, and computational efficiency [
33,
34,
35,
36,
37].
Unlike other research from previous work [
38], this study aims to develop an efficient classification model using ensemble optimized algorithms to identify clients at risk of churning and determine the time until they churn. The research is structured around three primary objectives: identifying the key factors that contribute to customer churn in the insurance industry, building a conceptual model to predict churn, and evaluating the performance of this predictive model using various algorithms. To achieve these objectives, the study addresses the following questions: What are the key factors driving customer churn in the motor insurance industry? How will the conceptual model for predicting churn be developed? And how will the model’s predictive performance be assessed using different algorithms?
The methodology proposed for this study presents a structured framework to address the problem through a two-step process: the initialization phase and the optimization phase. The framework introduces two algorithms: the Adaptive Random Forest-Assisted Large Neighborhood Feature Optimizer (ARALFO) and the Adaptive Random Forest Particle Swarm Optimizer (ARFPSO). During the initialization phase, ARALFO utilizes the Random Forest algorithm for feature selection, focusing on identifying the most relevant features that contribute to the predictive power of the model. To enhance this selection process, we introduce a cave-degree perturbation which is a novel technique inspired by the term "cave", refers to the strategy where narrowing search spaces akin to focusing on more promising features during iterative learning. It provides a mathematically weighted importance score for each feature based on its impact on reducing impurity in decision trees, similar to techniques like LASSO but using forest-based methods. This technique measures each feature’s contribution to the overall predictive model, allowing the identification of the most impactful features. By prioritizing features with the highest cave degrees, the methodology reduces dimensionality, mitigates overfitting, and retains only the most informative features, thereby improving the feature selection process.
Following feature selection, the optimization phase applies the Adaptive Large Neighborhood Search (ALNS) metaheuristic to find near-optimal solutions. This process iteratively breaks and repairs feature subsets, preventing the algorithm from getting trapped in local optima. To further refine this process, a Magnetic Force Perturbation Technique (MFPT) is introduced. The Magnetic Force Perturbation Technique (MFPT) is inspired by the interaction of magnetic fields, where forces either attract or repel solutions based on their relative quality (similat to charges in Coulomb’s law). This approach helps the optimization process avoid local optima, ensuring exploration of more diverse and promising regions in the search space. Unlike simulated annealing, which relies on temperature-based randomization blind search, MFPT adds directional perturbations, enhancing the model’s ability to explore global optima.
We also introduce an Adaptive Random Forest Particle Swarm Optimizer (ARFPSO), which applies the cave-degree concept during the feature selection phase. In the Particle Swarm Optimization (PSO) algorithm, each particle represents a potential solution and navigates the search space based on its velocity, influenced by its personal best (pbest) and the global best solution (gbest) identified so far. The Magnetic Force Perturbation Technique (MFPT) introduces controlled perturbations to particle velocities, simulating attractive and repulsive forces analogous to magnetic interactions. These perturbations dynamically adjust the velocity of the particles, steering them away from local minima, and promoting the exploration of more promising regions in the search space. By modulating the relationship between pbest, gbest, and the velocity of particles, MFPT improves the balance between exploration and exploitation, improving the swarm’s ability to converge more effectively on globally optimal solutions.
The proposed dual-phase strategy offers a comprehensive and systematic approach to the problem. The initialization phase establishes a solid foundation by identifying a precise set of predictive features, while the subsequent optimization phase refines and enhances this foundation to produce a robust and efficient classification model for churn prediction. The incorporation of novel perturbation techniques within both phases further strengthens the model’s optimization, ensuring high predictive accuracy and effectiveness in identifying customer churn. This integrated approach improves the overall performance and stability of the model.
The principal contributions of our research are succinctly summarized as follows:
Introducing a novel feature selection technique called cave-degree perturbation, which measures the impact of each feature on the predictive model. This technique enhances feature selection by prioritizing the most significant features and reducing dimensionality.
Proposing a Magnetic Force Perturbation Technique that simulates magnetic forces to guide the optimization process, thereby improving convergence and solution quality.
The remainder of this paper is organized as follows.
Section 2 introduces the formal formulation of the problem, while
Section 3 provides a comprehensive overview of the proposed algorithms. Subsequently,
Section 4 presents the experimental results and analyzes. Finally,
Section 5 concludes the paper with final remarks and suggestions for future research.
2. Problem Formulation
In this section,
Table 1 defines the variables used, followed by the introduction of the problem. We define the set of independent variables as
, where each
represents a specific characteristic or behavior of the policyholders. These features may include variables such as policy type, premium amount, claim history, customer tenure, and other relevant factors. The dependent variable
y indicates whether a customer churns (
) or not (
). The goal is to predict customer churn status based on these independent variables.
The objective is to maximize the accuracy of churn prediction for motor vehicle insurance customers using a machine learning model subject to various constraints. The constraints of the model include the feature, probability, prediction threshold, and regularization.
Feature Constraints
Each feature
must be within its defined range:
Probability Constraints
The predicted probability of churn must be between 0 and 1:
Prediction Threshold
Define a threshold
to classify customers as churned or not churned:
Regularization Constraint
To control the complexity of the model, incorporate a regularization term:
Objective Function
The objective function is to maximize the accuracy of the churn prediction model to the total number of instances:
where
is the indicator function that returns 1 if the condition is true and 0 otherwise.
The formulation of the function maximizes:
subject to:
to achieve better accuracy or other performance metrics.
3. Proposed Method
This section introduces our proposed method, which is designed to address the problem at hand through a structured framework consisting of two distinct phases: the initialization stage and the optimization phase. The first phase, known as the initialization stage, focuses on feature selection. This stage is crucial to identify the most relevant features of the dataset that will contribute to the predictive power of the model. Feature selection aims to reduce dimensionality, improve model performance, and prevent overfitting by selecting a subset of the most informative features. The goal is to retain features that have the highest impact on the target variable while discarding those that are redundant or irrelevant.
Following the initialization stage is the optimization phase. This phase involves applying advanced algorithms and optimization techniques to enhance the model’s accuracy, efficiency, and robustness. The interaction between these two phases ensures a comprehensive approach to problem solving. The feature selection phase lays the groundwork by providing a well-defined set of features, while the optimization phase uses this foundation to achieve superior model performance. Together, these phases form an integrated framework that systematically addresses the challenges of feature selection and model optimization, aiming to deliver a robust and efficient solution.
In summary as illustrated in
Figure 8, our proposed method is designed to provide a balanced and effective approach to tackling the problem by combining a thoughtful selection of features with a rigorous optimization process. This dual-phase framework is intended to enhance the overall effectiveness of the model and ensure that it performs optimally across various scenarios and conditions.
Figure 1.
Proces Phase Framework
Figure 1.
Proces Phase Framework
3.1. Feature Selection and Decision-Making in Random Forests
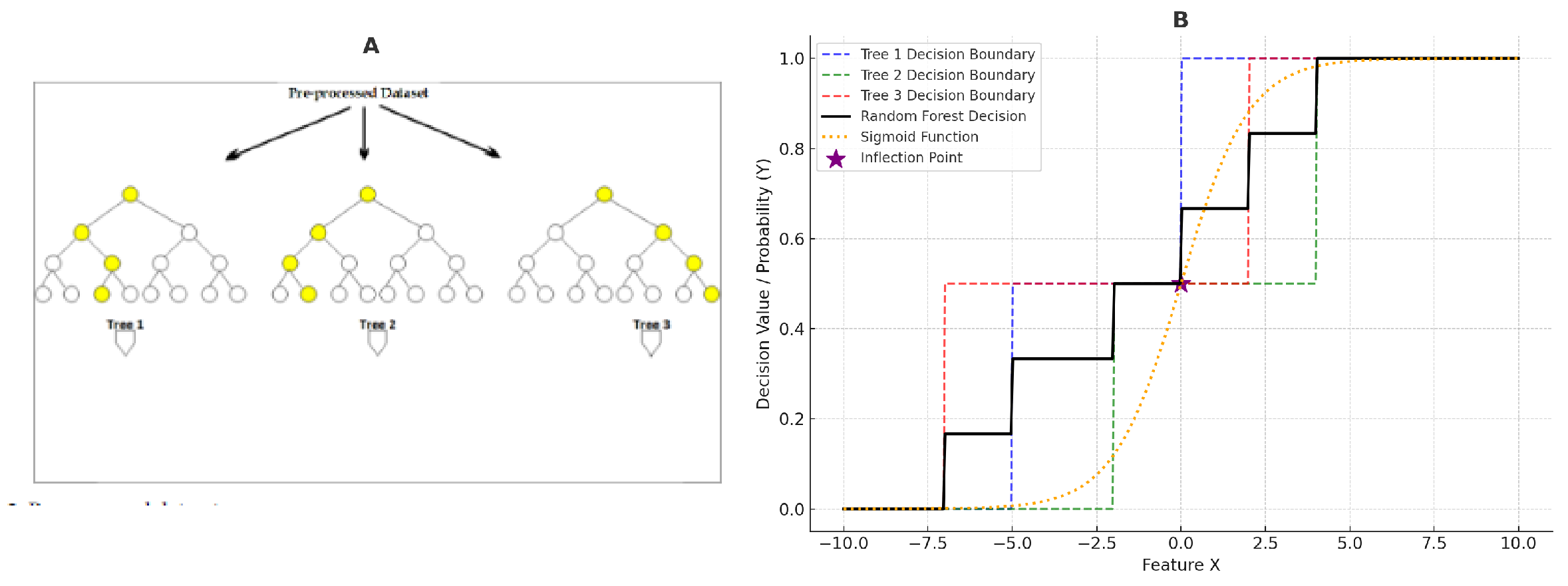
The process begins with the feature selection phase, where the dataset undergoes a thorough preprocessing stage, as shown in Figure A of the combined visualization. Here, the preprocessed dataset is passed into multiple decision trees (Tree 1, Tree 2, and Tree 3), each of which independently evaluates the importance of different features. This process involves data cleaning, handling missing values, and addressing inconsistencies to ensure the dataset is suitable for model training.
Within this ensemble of decision trees, each feature
contributes differently to the decision-making process, and the importance of these features is evaluated at each split within the trees. The concept of a "cave degree" operator is introduced to measure the relevance of each feature based on its contribution to reducing impurity at the nodes of the decision trees. Let
represent the cave degree of feature
, which is computed by averaging the importance scores
across all trees in the Random Forest ensemble:
The cave degree captures how much a feature contributes to the model’s predictive performance, and features with higher cave degrees are considered more significant for the overall decision-making process.
In Figure A, the decision trees visually highlight key decision nodes (yellow circles), representing where significant feature-based decisions are made within each tree. These nodes signify the points where features with higher cave degrees are actively influencing the tree’s decisions.
Moving to Figure B, we observe the aggregated output of the Random Forest model, where the individual decisions from Tree 1, Tree 2, and Tree 3 are combined to form a unified decision boundary. The dashed lines in different colors (blue, green, and red) represent the decision boundaries of each individual tree. The solid black line shows the overall decision boundary of the Random Forest model, which is the average of the decisions made by all trees, demonstrating the ensemble’s ability to create a more robust and accurate predictive model.
The orange dotted line represents the sigmoid function , which converts the combined output of the decision trees into a smooth probabilistic prediction ranging between 0 and 1. The sigmoid function plays a crucial role in transforming the raw decision outputs into probabilities, making the model suitable for classification tasks where outputs are interpreted as probabilities of belonging to a particular class.
An important aspect of this visualization is the inflection point marked by the purple star on the graph in Figure B. This point corresponds to on the sigmoid function, indicating where the probability shifts most rapidly. It signifies the threshold where the model’s confidence in the prediction changes most dramatically, thus serving as a critical decision boundary in classification tasks.
Therefore, by applying the cave degree operator and incorporating the sigmoid transformation, the Random Forest model efficiently selects and weights the most relevant features, leading to improved accuracy and robustness in its predictions. This is further validated by the combined decision boundaries shown in Figure B, where the ensemble of decision trees collectively contributes to a refined, probability-based prediction output.
Figure 2.
(A) Preprocessed Dataset Feeding into Random Forest Decision Trees; (B) Combined Decision Boundaries with Sigmoid Function and Inflection Point
Figure 2.
(A) Preprocessed Dataset Feeding into Random Forest Decision Trees; (B) Combined Decision Boundaries with Sigmoid Function and Inflection Point
As depicted in Algorithm 1, the feature selection process in a Random Forest is guided by the cave degree values. By assigning weights to features based on their normalized cave degrees,
where
p is the total number of features, the Random Forest model prioritizes the most relevant features. This ultimately enhances the model’s predictive power, as the most important features are given more weight, leading to superior performance in both classification and regression tasks.
|
Algorithm 1: Feature Selection Using cave Degree in Random Forest |
 |
where
is the total number of trees in the ensemble. To normalize the cave degrees, we use:
where
is the normalized cave degree of feature
, and
p is the total number of features. This normalization ensures that the cave degrees are on a comparable scale. Features with a normalized cave degree
above a certain threshold
are selected, as they are considered the most relevant to predict customer churn. A higher cave degree indicates a greater importance of the feature, making it a better candidate for inclusion in the predictive model.
3.2. Optimization Phase
This section introduces the second phase of the optimization process, which involves employing two well-known metaheuristic algorithms. Adaptive Large Neighborhood Search (ALNS) and Particle Swarm Optimization (PSO). To further enhance the optimization process, we propose a novel strategy called the Magnetic Force Perturbation Technique inspired by the natural behavior of magnetic fields, where forces attract or repel particles depending on their polarities. This phenomenon can be modeled mathematically using Coulomb’s law for electric forces or the law of magnetic interaction. Analogously, in optimization, we simulate these forces to guide the exploration of the solution space. If we denote the current solution by
and potential solutions by
, the force
exerted on
by
can be expressed as:
where
k is a constant,
and
represent the "charges" or qualities of solutions
and
respectively, and
is the Euclidean distance between the solutions. Solutions
close to promising regions, which have higher quality (or "charge"), experience an attraction force pulling them towards those regions. In contrast, solutions in less favorable regions experience repulsion.
The perturbation applied to the current solution
is based on the calculated forces. Let
represent the perturbation applied to
. The perturbation is a function of the force
and can be defined as:
where
is a control parameter that modulates the magnitude of the perturbation. Larger perturbations explore new regions of the solution space, while smaller perturbations refine solutions in promising areas.
The optimization process is iterative. In each iteration, the solutions are adjusted based on the simulated magnetic forces. If we denote the state of the search process at iteration
t by
, the updated solution
is given by:
The forces can be adapted based on the search progress. For instance, as the algorithm converges, the forces might be adjusted to focus more on local refinement or global exploration depending on the current state of the search, adapting the parameter accordingly. This dynamic adjustment helps in balancing exploration of new areas with exploitation of known promising regions, thus improving the efficiency of the optimization process.
3.2.1. Adaptive Large Neighborhood Search (ALNS) Algorithm
Adaptive Large Neighborhood Search (ALNS) is a powerful metaheuristic optimization technique designed to tackle complex combinatorial problems. The core idea behind ALNS is to iteratively explore large neighborhoods of the current solution by applying various perturbation and repair strategies. This allows the algorithm to escape local optima and efficiently search through a broader solution space. ALNS adapts its neighborhood structures based on the observed performance, dynamically balancing exploration and exploitation throughout the search process.
In this context, ALNS is utilized to address the problem of churn prediction by optimizing feature selection. By incorporating advanced techniques such as magnetic force perturbation and strategic solution modifications (i.e., break and repair), ALNS can enhance the search for the most effective feature subsets. The magnetic force perturbation guides the search process by simulating forces that attract or repel solutions based on their quality, thereby improving the exploration of promising regions and avoiding less favorable ones. The following algorithm presents the integration of ALNS with magnetic force perturbation and break/repair strategies, specifically tailored to optimize feature selection for churn prediction and achieve the best performance metrics.
Algorithm 2 starts by initializing the solution as a random configuration of features selected from . Additionally, the algorithm sets to the initial solution and initializes the best churn prediction accuracy and other performance metrics to very low values.
For each iteration
t from 1 to
, the algorithm generates a neighborhood solution
by applying perturbations based on magnetic forces. The magnetic force
between the current solution
and the neighborhood solution
is computed as:
where
k is a constant, and
and
represent the "charges" or qualities of solutions
and
, respectively.
The algorithm then applies the "break" and "repair" strategies to the current solution
. The "break" strategy creates a modified solution
by removing or altering parts of
:
The "repair" strategy then adjusts
using the neighborhood solution
and the magnetic force
to produce a repaired solution:
The updated solution is then set to:
The algorithm evaluates the churn prediction accuracy and other performance metrics for the updated solution . If the accuracy exceeds the previously recorded best accuracy , or if shows improvement over the best recorded metrics, the algorithm updates to , and sets and the other metrics to and , respectively.
After completing all iterations, the algorithm returns the best solution
, along with the corresponding best churn prediction accuracy
and other performance metrics.
|
Algorithm 2: Optimization Using ALNS with Magnetic Force Perturbation |
 |
Figure 3.
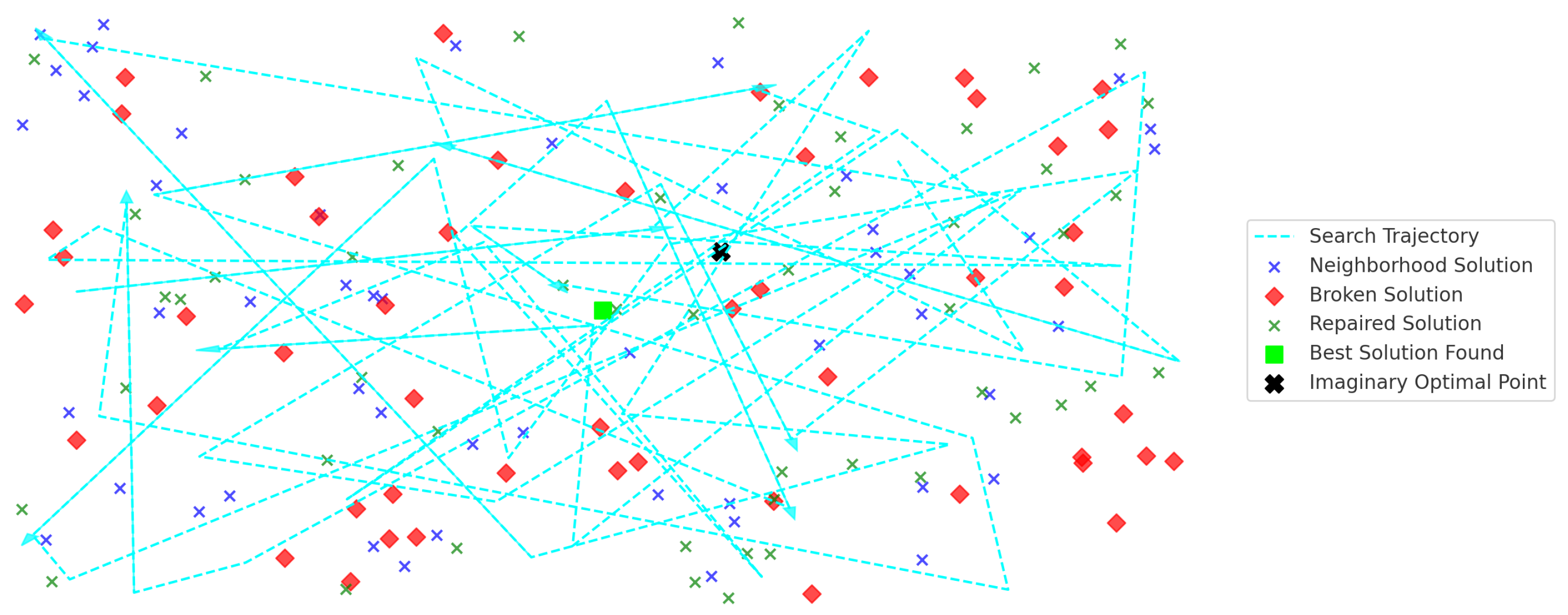
ALNS search trajectory within a solution space. This figure represents the search trajectory of the ALNS algorithm through the solution space. The blue lines with arrows indicate the path taken by the algorithm in navigating from one solution to another. The red, blue, and green points correspond to different evaluated solutions, where red indicates potential solutions, blue represents neighborhood solutions, and green signifies the best or final solutions found. The black star marks the optimal or most favorable solution identified during the search process, showcasing how ALNS dynamically explores and exploits the solution space.
Figure 3.
ALNS search trajectory within a solution space. This figure represents the search trajectory of the ALNS algorithm through the solution space. The blue lines with arrows indicate the path taken by the algorithm in navigating from one solution to another. The red, blue, and green points correspond to different evaluated solutions, where red indicates potential solutions, blue represents neighborhood solutions, and green signifies the best or final solutions found. The black star marks the optimal or most favorable solution identified during the search process, showcasing how ALNS dynamically explores and exploits the solution space.
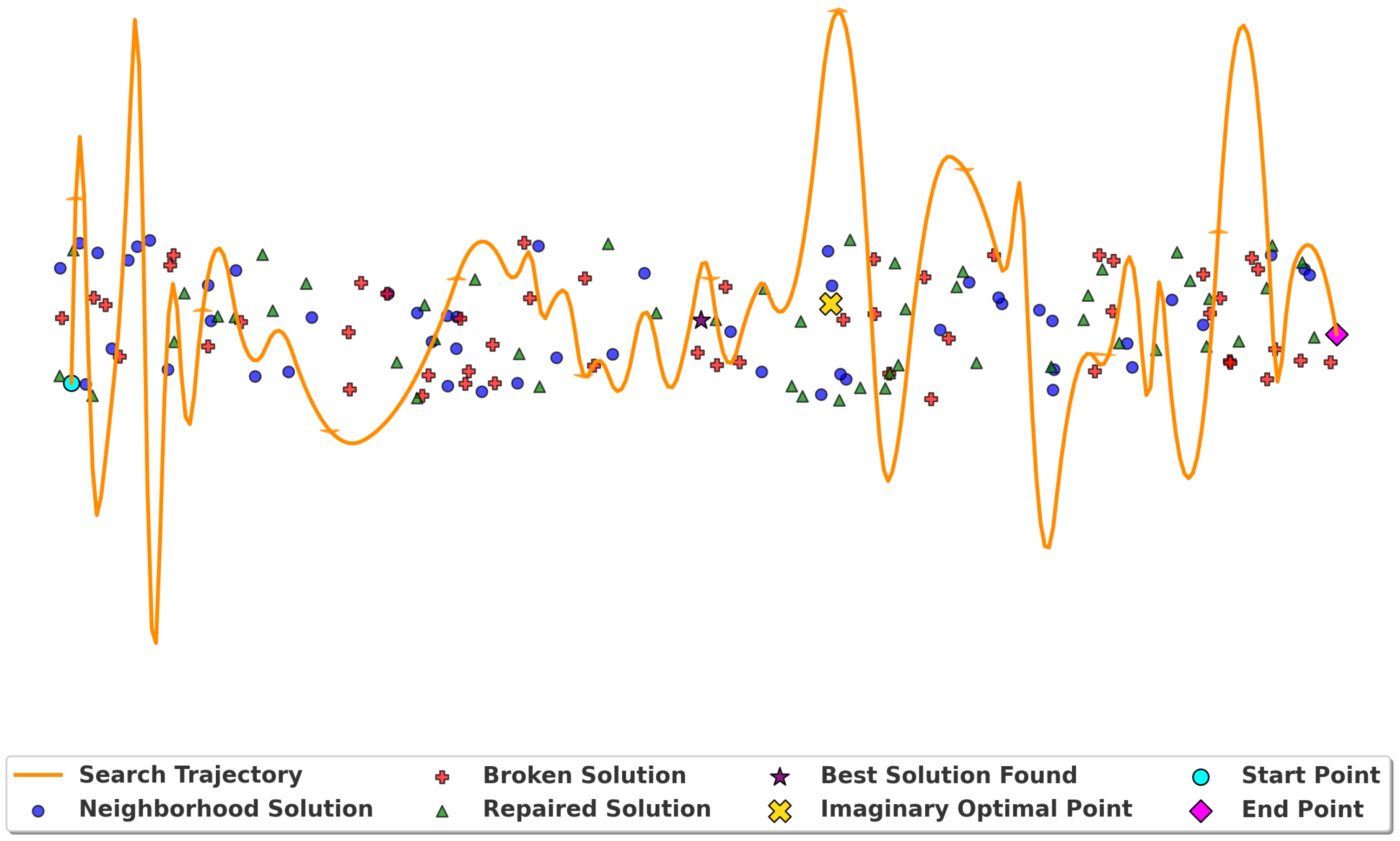
Figure 4.
Optimized ALNS Path Exploration with Distinct Solution Mapping. This figure illustrates the trend of a performance metric over iterations or time steps as the ALNS algorithm progresses. The orange line represents the smoothed trend of the metric being tracked, while the colored points indicate individual data points at each step, iteration, or trial. The peaks and troughs in the line show periods of high and low performance, respectively, reflecting the oscillatory and converging behavior of the algorithm as it seeks optimal solutions.
Figure 4.
Optimized ALNS Path Exploration with Distinct Solution Mapping. This figure illustrates the trend of a performance metric over iterations or time steps as the ALNS algorithm progresses. The orange line represents the smoothed trend of the metric being tracked, while the colored points indicate individual data points at each step, iteration, or trial. The peaks and troughs in the line show periods of high and low performance, respectively, reflecting the oscillatory and converging behavior of the algorithm as it seeks optimal solutions.
3.2.2. Particle Swarm Optimization Algorithm (PSO)
Particle Swarm Optimization (PSO) is a computational method inspired by the social behavior of birds and fish. Developed by Kennedy and Eberhart in 1995 [
41], PSO is a heuristic optimization technique that simulates the social interaction of a swarm of particles in a search space to find optimal solutions to complex problems. In PSO, each particle represents a potential solution and moves through the search space influenced by its own experience and that of its neighbors. Particles adjust their positions based on their own best-known position and the best-known positions of the swarm, guided by a velocity update mechanism. This process continues iteratively, with particles converging towards the optimal solution over time.
As shown in Algorithm 3, the PSO algorithm begins with initializing a set of particles, where each particle i is represented by a feature configuration selected from the set . Each particle has an associated velocity , and the personal best solution is initialized to . The global best solution is set to the best personal best among all particles. The best accuracy and other performance metrics are initialized to very low values.
For each iteration
t from 1 to
, the algorithm updates the velocity and position of each particle. The velocity
of particle
i is updated based on its previous velocity, its distance from its personal best
, and its distance from the global best
:
where
is the inertia weight,
and
are cognitive and social coefficients, and
and
are random numbers uniformly distributed in the range
. The position
of the particle is then updated using:
Following the velocity and position update, the algorithm applies magnetic force perturbation. The magnetic force
between the current position of the particle
i and the global best position
is calculated as:
where
k is a constant and
and
represent the "charges" of the particle and the global best solution, respectively. The perturbation applied to the position of the particle is:
where
is a control parameter that scales the magnetic force effect.
The perturbed solution
is then evaluated for churn prediction accuracy
and other performance metrics
. If this evaluation yields better performance metrics compared to the current personal best, the personal best solution
is updated to
, and the corresponding accuracy and metrics are updated. Furthermore, if the accuracy
for any particle surpasses the global best accuracy
, the global best solution
is updated to this particle’s personal best. This ensures that the global best solution reflects the highest accuracy and best performance metrics found across all particles. After completing all iterations, the algorithm returns the global best feature set
, along with the highest accuracy
and other performance metrics achieved.
|
Algorithm 3: Particle Swarm Optimization with Magnetic Force Perturbation |
 |
Figure 5.
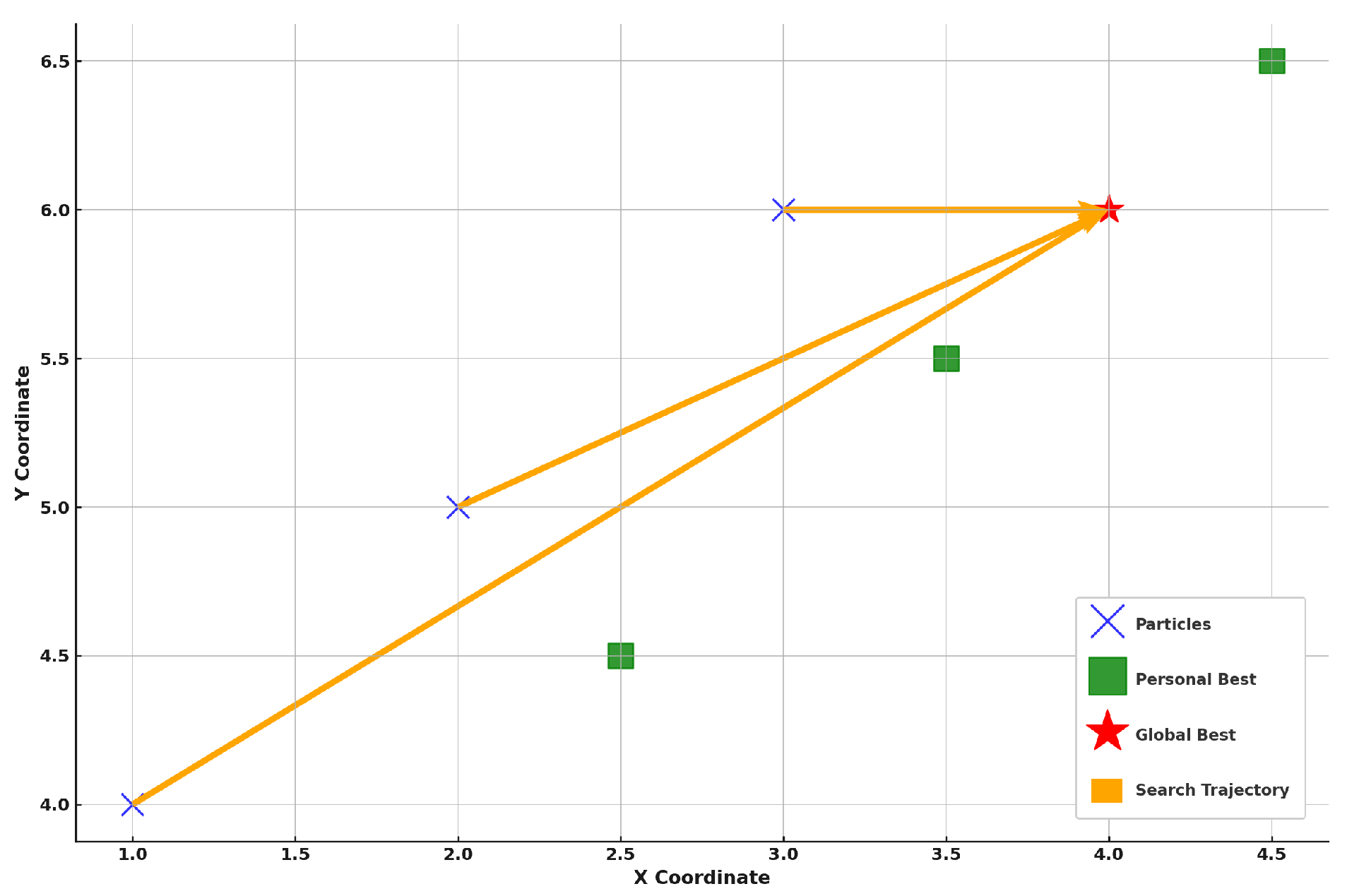
PSO virtual exploration. This figure illustrates the virtual exploration of the Particle Swarm Optimization (PSO) algorithm within the solution space. The blue ’X’ markers represent the positions of particles within the search space at a given time, while the green squares indicate the personal best positions identified by each particle based on their experience. The red star signifies the global best solution identified by the swarm, which represents the optimal solution found thus far. The orange lines represent the search trajectories of particles, showing how they are influenced by both their personal bests and the global best. This diagram captures the dynamic interplay between individual particle exploration and the collective movement towards the global optimum as the algorithm progresses.
Figure 5.
PSO virtual exploration. This figure illustrates the virtual exploration of the Particle Swarm Optimization (PSO) algorithm within the solution space. The blue ’X’ markers represent the positions of particles within the search space at a given time, while the green squares indicate the personal best positions identified by each particle based on their experience. The red star signifies the global best solution identified by the swarm, which represents the optimal solution found thus far. The orange lines represent the search trajectories of particles, showing how they are influenced by both their personal bests and the global best. This diagram captures the dynamic interplay between individual particle exploration and the collective movement towards the global optimum as the algorithm progresses.
4. Computational Experiment
This section presents a comprehensive computational experiment to evaluate the performance and efficiency of the proposed algorithms under different conditions. The algorithms were tested against benchmark methods using key metrics such as Accuracy, Precision, Recall, F1 Score, computational time, and robustness.
The experiments were conducted on a system equipped with an Intel Core i7 processor and 16 GB RAM, utilizing Python 3.8 as the primary software environment. The analysis was performed using Jupyter Notebook, leveraging libraries such as Pandas, Numpy, Matplotlib, Seaborn, and Scikit-Learn. Additionally, CPLEX, Docplex, and MATLAB were employed for optimization tasks.
The primary datasets used in this experiment were the Anzani Data Set and the dataset provided by Josep Lledó and Jose M. Pavía [
43].
4.0.1. Data Collection
This study uses two categories of anonymized data set. 0ne is collected from the database of an Azani insurance company and the other is from the work of Josep Lledó and Jose M. Pavía [
43]. The Azani data sets focus on motor insurance profiles and cover a period of five years, encompassing data from 500 customers. The variables included in the dataset were selected based on reviews of the literature majority from the works of [
43]. The dataset comprises a total of 109,559 rows and 29 columns, representing a comprehensive set of features related to motor vehicle insurance claims and policy details. The variables include a mix of categorical and numerical data, capturing aspects such as
Distribution_channel,
Seniority,
Policies_in_force,
Max_policies,
Premium, and
Type_fuel. There are also several key attributes like
Cost_claims_year,
Claims_type,
Contract_Duration,
Age, and
Years_with_license, which provide insights into the vehicle policyholder’s history, claim activities, and vehicle characteristics. This rich dataset offers a detailed foundation for predictive modeling tasks, such as analyzing churn behavior in insurance policies, enabling a deeper understanding of customer retention and risk assessment.
4.0.2. Data Categorization
The dataset consists of various features that provide insights into different aspects of the insurance policy, the policyholder, and claims history, which are crucial for predicting churn. Policy details are represented by features such as the distribution channel through which the policy was acquired, the seniority indicating how long the customer has been with the insurer, the number of policies currently active, the maximum policies allowed, and the contract duration in days. These variables help in understanding the customer’s engagement and relationship with the insurance provider.
Customer information is another essential component, with attributes such as age, the number of years the policyholder has held a driving license, and details about the type of fuel used in the insured vehicle. Vehicle-specific data is equally important, including the year of vehicle registration, power, engine capacity, insured value, number of doors, vehicle length, and weight. These features provide insights into the risk and potential claim costs associated with the insured vehicle.
Claims-related features encompass the total cost of claims made in the current year, costs broken down by claim type, the number of claims made annually, and the overall claims history. This data sheds light on the policyholder’s behavior regarding claims and potential risks. Additionally, risk assessment variables, such as the type of risk and the geographical area, offer further context for evaluating the likelihood of churn.
The target variable, "Lapse," indicates whether a customer has churned or not, making it the primary outcome that predictive models aim to forecast. Together, these variables form a comprehensive dataset that captures the complex interactions between policyholder behavior, vehicle characteristics, claims history, and risk factors, providing a solid foundation for churn prediction analysis.
4.0.3. Data Preprocessing
The preprocessing of the dataset began by addressing the format in which all features were initially stored in a single cell, separated by semicolons. We corrected this by specifying the delimiter during data loading, effectively splitting the dataset into distinct columns , where each represents a feature. Once this was achieved, we converted relevant columns with date information into proper datetime format, ensuring that variables such as the start and renewal dates of contracts were accurately parsed. This enabled us to calculate derived features such as the contract duration, expressed as , and the policyholder’s age as , both of which are crucial for predicting churn.
We then handled missing values systematically. For the ‘Date_lapse‘ column, missing entries were replaced with a future date , representing active policies that had not lapsed. Categorical columns like ‘Type_fuel‘ were imputed using the mode , and numerical columns such as ‘Length‘ were filled with the median . Claim-related columns were imputed with zeros, 0, to indicate customers with no claims, ensuring clarity in distinguishing between claim activities.
Next, we addressed outliers, particularly in numerical columns, by using Z-score normalization to identify values where , which were either capped or treated using interquartile range (IQR) adjustment methods to avoid skewing the predictive model. Feature engineering followed, with the addition of variables such as ‘Years_with_license‘ calculated as , which helped in better understanding the customer’s driving experience.
For the categorical variables, we applied Label Encoding, transforming them into numerical form
to make them suitable for model training. Subsequently, we normalized all numerical features
using the Standard Scaler method:
where
is the mean and
is the standard deviation, ensuring that all features were on a comparable scale. Finally, the dataset was split into training and test sets, maintaining a 70-30 split to ensure a balanced distribution of the target variable, ‘Lapse‘, indicating churn (
) or non-churn (
). This thorough preprocessing ensured the dataset was accurately structured and optimized for the subsequent predictive modeling of churn behavior. insurance.
4.1. Computational Experimental Results with Azani Auto Insurance Company
This section presents the computational experimental results derived from the Azani Auto Insurance Company database, which was analyzed using various state-of-the-art machine learning techniques such as XGBoost, Random Forest, and SVM, providing a comprehensive performance comparison. The results from these machine learning models were benchmarked against our proposed metaheuristic methods: ARALFO and ARFPSO.
Table 2. The comparison reveals that ARALFO outperforms the other methods across key metrics, including Accuracy, Precision, Recall, and F1 Score, demonstrating a well-rounded and effective approach. While Random Forest and XGBoost also show strong performance, particularly in Precision, ARALFO achieves a better balance across all metrics.
The results presented in
Table 2 offer a comprehensive comparison of the predictive performance of different machine learning models on the Azani dataset. Among the models, the ARALFO method demonstrates the highest overall performance, with an accuracy of 0.95, which translates to an error rate of only 0.05. This indicates a superior ability to correctly predict outcomes compared to the other models. Furthermore, ARALFO also achieves the highest F1 score (0.95), reflecting balanced performance between precision (0.95) and recall (0.94), making it the most reliable model for handling false positives and false negatives effectively.
In comparison, the Random Forest model, while still performing well with an accuracy of 0.90, shows a slightly higher error rate of 0.10. Its F1 Score matches its precision at 0.91, indicating that although it makes accurate predictions, it is slightly less consistent in retrieving all relevant instances compared to ARALFO. The Kappa statistic for Random Forest (0.85) suggests substantial agreement, but it does not reach the level of agreement seen with ARALFO (Kappa = 0.92). This implies that while Random Forest is a robust model, ARALFO outperforms it in handling class imbalances and making accurate predictions beyond mere chance.
The XGBoost model, with an accuracy of 0.88 and an error rate of 0.12, ranks third in performance. It maintains a relatively high precision (0.90) and recall (0.88), resulting in a commendable F1 Score of 0.89. However, the lower Kappa value of 0.83 indicates that XGBoost has a lower level of reliability compared to the ARALFO and Random Forest models. The AUC value of 0.90 for XGBoost is also slightly less than the others, indicating it has a marginally lower ability to distinguish between positive and negative classes.
ARFPSO, while achieving an accuracy of 0.93 and an error rate of 0.07, has an F1 Score of 0.90, which is slightly lower than expected given its accuracy. This discrepancy can be attributed to the balance between precision (0.91) and recall (0.92). The Kappa statistic of 0.89 and AUC of 0.94 indicate that ARFPSO performs well overall but does not surpass the consistency and reliability demonstrated by ARALFO.
The Sensitivity (Recall) and Specificity metrics further highlight the models’ capabilities. ARALFO’s specificity of 0.96 means it has the highest ability to correctly identify true negatives, making it highly effective at distinguishing non-churn cases. In contrast, XGBoost, despite having a relatively high recall (0.88), exhibits the lowest specificity (0.89), suggesting that it is less effective in identifying true negatives compared to the other models.
In summary, the analysis reveals that ARALFO is the most effective model for the Azani data set, excelling in all key metrics, including precision, precision, recall, F1 Score, Kappa and AUC. The Random Forest model also performs well, but its slightly lower Kappa and F1 Score indicate that it is less consistent in handling class imbalances. ARFPSO is a strong contender with high accuracy and AUC, but it falls short of ARALFO’s overall performance. The XGBoost model, while still effective, shows the least reliability among the four models, making it less suitable for scenarios that require high precision and recall. These results highlight the importance of evaluating multiple metrics to gain a complete understanding of model performance and select the most appropriate model to predict churn in this dataset.
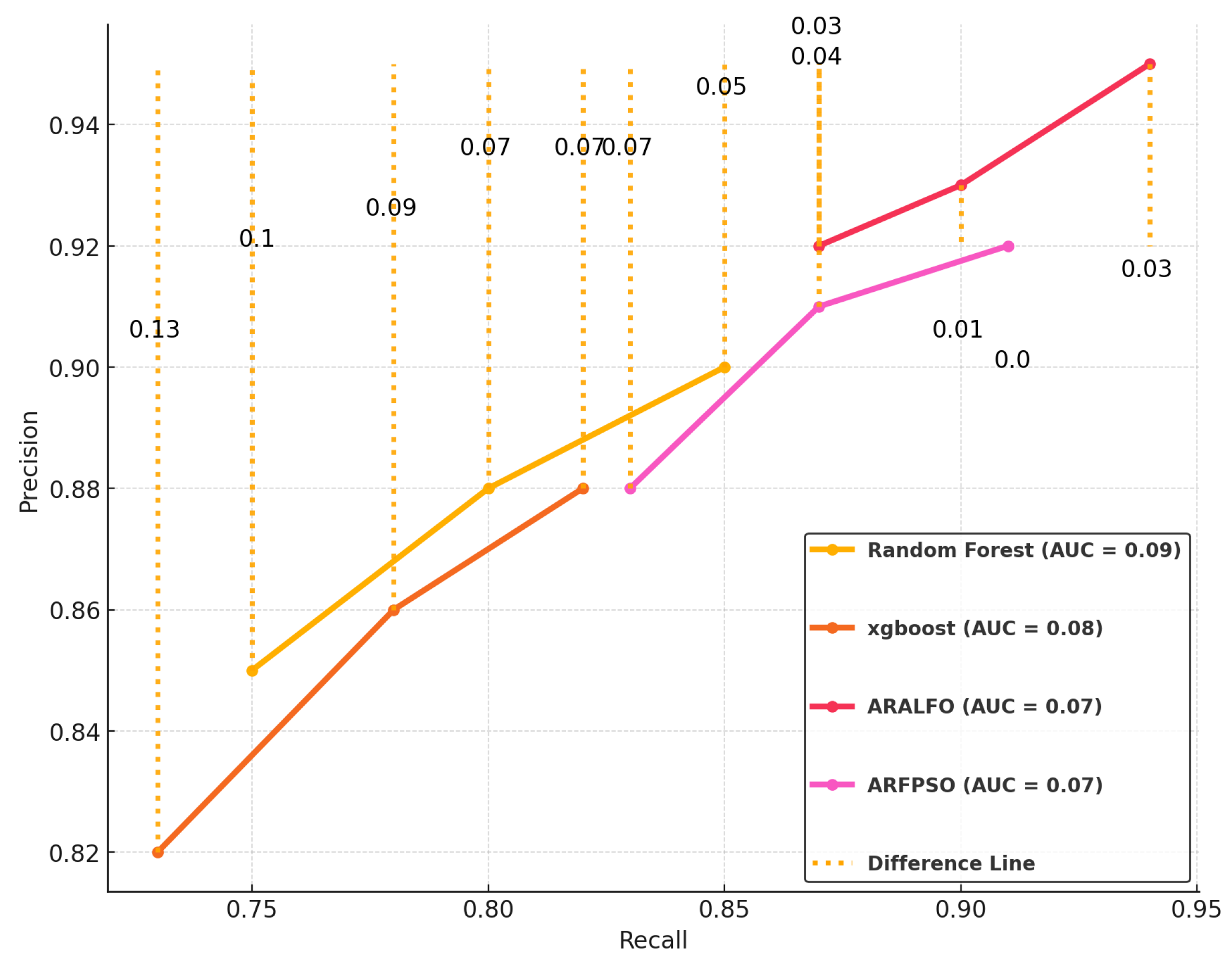
Figure 6.
Precision-Recall Curve Analysis
Figure 6.
Precision-Recall Curve Analysis
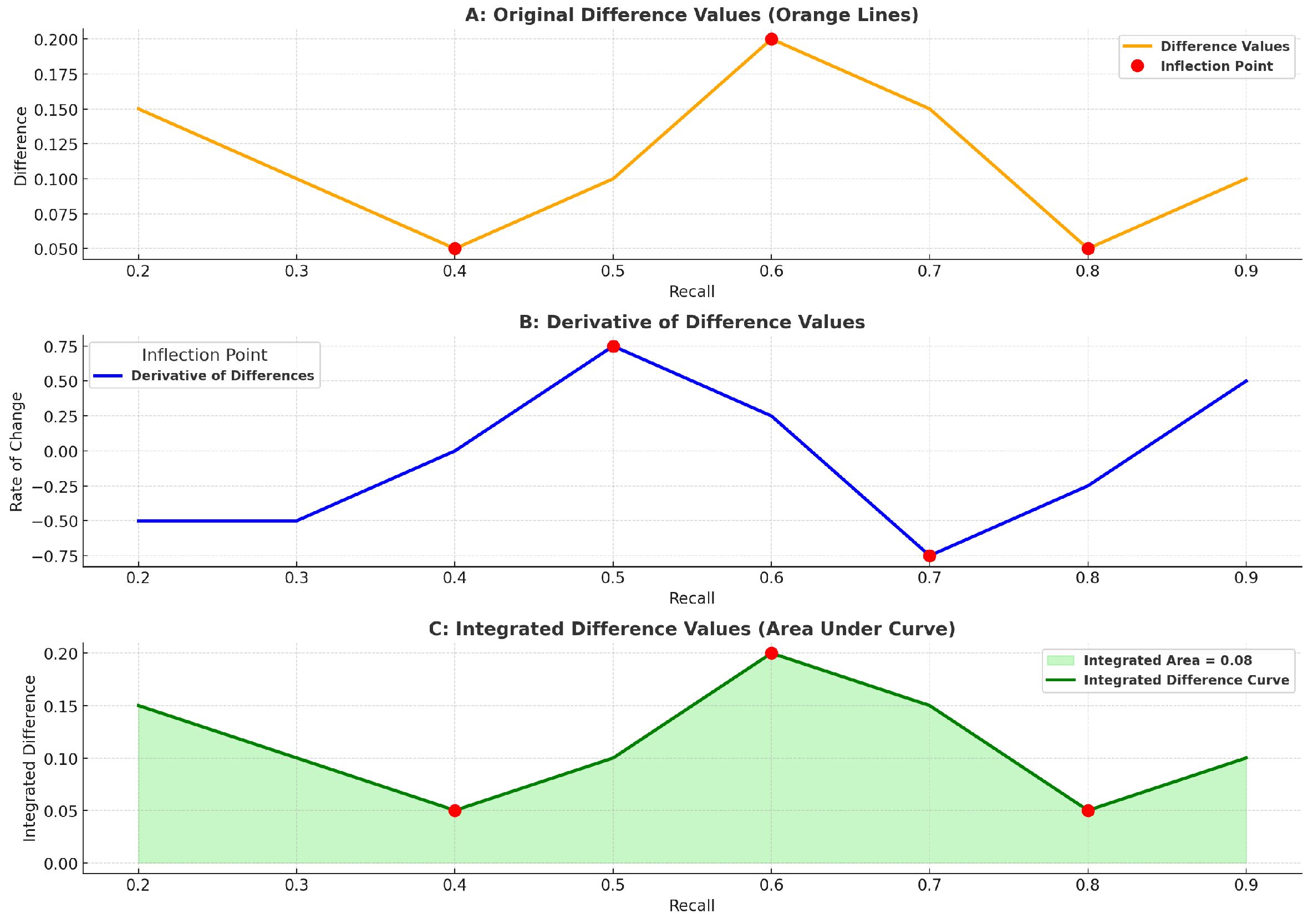
Figure 7.
Integrated Difference Values (Area Under Curve)
Figure 7.
Integrated Difference Values (Area Under Curve)
Figure 8 employs a precision-recall curve to showcase the comparative performance of multiple models (Random Forest, XGBoost, ARALFO, and ARFPSO). The use of orange dotted lines and exact numerical differences between the curves offers a nuanced understanding of how much one model outperforms another at each recall level. This added layer of detail is particularly valuable, as it reveals not just which model is better but quantifies the margin of improvement or lag, making the differences transparent and measurable. ARALFO’s consistent precision across varying recall levels stands out, demonstrating its reliability in maintaining high performance. This reliability suggests that ARALFO would be a practical choice for tasks where precision at different recall thresholds is paramount.
Figure 7 provides a deeper analysis derived from the original precision-recall curve from
Figure 8. Graph A captures the absolute differences between the models, identifying key inflection points where performance changes occur. In contrast, graph B delves deeper by calculating the rate of change (derivative), showing how quickly these differences evolve, which pinpoints the specific recall levels where models either diverge or converge in performance. This transition from Graph A to Graph B reveals the dynamics of model behavior, offering a more detailed view of where ARALFO stands out or where others begin to falter. Graph C then integrates these differences into the recall range, providing a cumulative view of the overall performance disparity among the models. Together, these graphs illustrate both the static and dynamic aspects of model differences, with ARALFO consistently demonstrating stability and adaptability, making it a reliable choice for tasks that demand consistent precision across varying recall values. This comprehensive analysis emphasizes why ARALFO has an edge, particularly in scenarios where maintaining a performance balance is crucial.
4.2. Performance Comparison Using Josep Lledó and Jose M. Pavía Dataset [43]
In this section, we conduct an evaluation of our model alongside other state-of-the-art algorithms using the Josep Lledó and Jose M. Pavía dataset, which is based on an actual motor vehicle insurance dataset [
43]. This comparison provides insight into how different machine learning models perform on real-world data.
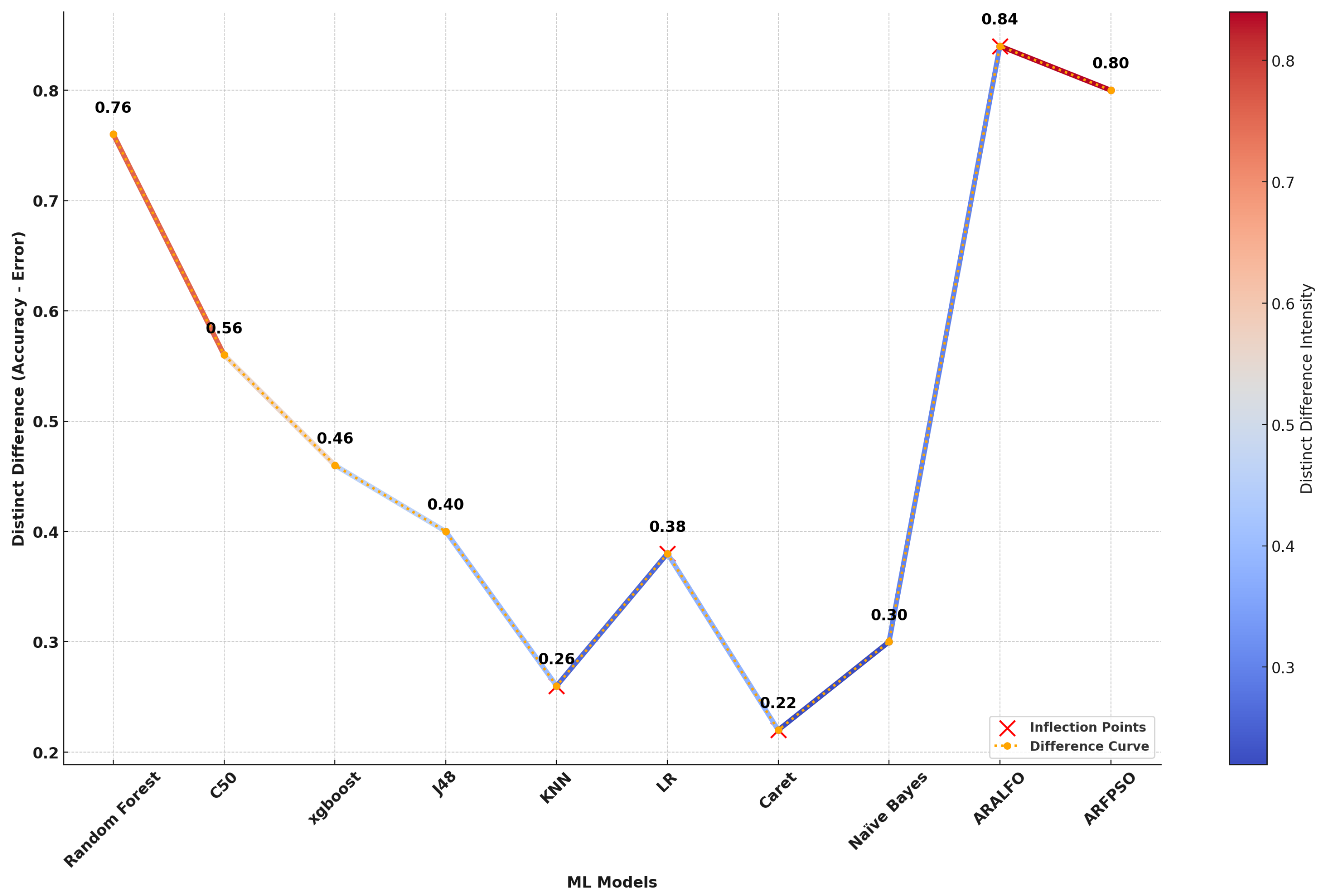
Table 3 illustrates that the
ARALFO model consistently outperforms all other models across most evaluation metrics. It achieves the highest
Accuracy (0.92), the lowest
Error Rate (0.08), and the best
Kappa (0.84), indicating a strong level of agreement between predicted and actual classifications. Moreover, ARALFO attains the highest
AUC (0.94), showcasing its superior ability to distinguish between different classes.
In recall-related metrics, ARALFO continues to excel with the highest Sensitivity (0.90), demonstrating its effectiveness in correctly identifying positive cases. It also boasts the highest Specificity (0.93), reflecting its outstanding performance in identifying negative cases. Additionally, the model achieves the best Precision (0.91), indicating a low false-positive rate, and attains the highest F1 Score (0.89), which underscores its balanced trade-off between precision and recall.
Although the ARFPSO model shows commendable performance with high values in Accuracy (0.90), Kappa (0.80), AUC (0.92), and other metrics, it consistently ranks slightly below ARALFO in all categories. In contrast, models such as Random Forest and C50 perform moderately, with reasonable accuracy but lower metrics like AUC and Kappa, indicating less reliability in distinguishing between classes.
The remaining models, including KNN, Naïve Bayes, LR, and Caret, exhibit substantially lower performance across all metrics, suggesting they are less suited for tasks requiring high precision and recall. Overall, the analysis clearly demonstrates that ARALFO is the most robust and reliable model for this dataset, consistently achieving the highest scores across all critical performance metrics.
Figure 8.
Distinct Differences in Model Performance
Figure 8.
Distinct Differences in Model Performance
4.3. Ablation Experimental Results
In this section, we present the results of ablation experiments designed to assess the impact of two critical components: the cave-degree perturbation (CDP) and the magnetic force perturbation (MFP) on the performance of our proposed model. These experiments were conducted to evaluate how each component contributes to the overall effectiveness of the model, with three distinct configurations analyzed to provide a comprehensive understanding of their individual and combined effects.
In the first experiment, we retained the cave-degree perturbation technique during feature selection, while omitting the magnetic force perturbation technique during optimization. The results showed a notable decrease in accuracy from 0.95 to 0.86, indicating that while cave-degree perturbation positively impacts feature selection, the absence of magnetic force perturbation adversely affects the model’s ability to effectively explore the solution space. The precision also dropped from 0.95 to 0.88, reflecting the negative impact on the model’s ability to correctly identify positive instances. Additionally, recall decreased from 0.93 to 0.79, highlighting a reduced capability to capture true positives without magnetic force perturbation. The F1 score fell from 0.95 to 0.82, demonstrating a less balanced performance between precision and recall due to the removal of magnetic force perturbation.
The second experiment involved applying the magnetic force perturbation technique during optimization while omitting the cave-degree perturbation technique during feature selection. This configuration resulted in a decrease in accuracy from 0.95 to 0.84, suggesting that the removal of cave-degree perturbation negatively affects the quality of feature selection, even though magnetic force perturbation aids in solution space exploration. Precision was reduced from 0.95 to 0.87, indicating that the absence of cave-degree perturbation impacts the model’s ability to minimize false positives. Recall decreased from 0.93 to 0.77, showing a diminished ability to capture true positives when cave-degree perturbation was omitted. The F1 score dropped from 0.95 to 0.80, reflecting a decreased balance between precision and recall.
In the third experiment, both techniques—cave-degree perturbation and magnetic force perturbation—were removed. This configuration resulted in a significant decrease in accuracy to 0.78, which highlights the substantial impact of removing both techniques on the overall accuracy of the model. The precision decreased to 0.73, indicating an increased difficulty in managing false positives without the enhancements provided by both techniques. Recall fell to 0.68, reflecting a reduced ability to identify true positives in the absence of both techniques. The F1 score decreased to 0.70, demonstrating a significant decrease in balanced performance due to the removal of both techniques.
As shown in the tables below, CDT denotes cave-degree perturbation, MFT denotes magnetic force perturbation, and ✓ and × are used to indicate the inclusion or exclusion of each technique, respectively.
Table 4.
Adjusted Performance Comparison of ARALFO and ARFPSO Algorithms with Anzani Dataset
Table 4.
Adjusted Performance Comparison of ARALFO and ARFPSO Algorithms with Anzani Dataset
| Experiment |
Algorithm |
CDT |
MFT |
Accuracy |
Precision |
Recall |
F1 Score |
| 1 |
|
✓ |
× |
0.86 |
0.88 |
0.79 |
0.82 |
| 2 |
ARALFO |
× |
✓ |
0.84 |
0.87 |
0.77 |
0.80 |
| 3 |
|
× |
× |
0.78 |
0.73 |
0.68 |
0.70 |
| 4 |
|
✓ |
✓ |
0.95 |
0.95 |
0.93 |
0.95 |
| 5 |
|
✓ |
× |
0.83 |
0.85 |
0.73 |
0.77 |
| 6 |
ARFPSO |
× |
✓ |
0.80 |
0.83 |
0.70 |
0.75 |
| 7 |
|
× |
× |
0.76 |
0.69 |
0.64 |
0.66 |
| 8 |
|
✓ |
✓ |
0.93 |
0.91 |
0.91 |
0.90 |
Table 5.
Adjusted Performance Comparison of ARALFO and ARFPSO Algorithms with Lledó Dataset
Table 5.
Adjusted Performance Comparison of ARALFO and ARFPSO Algorithms with Lledó Dataset
| Experiment |
Algorithm |
CDT |
MFT |
Accuracy |
Precision |
Recall |
F1 Score |
| 1 |
|
✓ |
× |
0.86 |
0.88 |
0.79 |
0.82 |
| 2 |
ARALFO |
× |
✓ |
0.84 |
0.87 |
0.77 |
0.80 |
| 3 |
|
× |
× |
0.78 |
0.73 |
0.68 |
0.70 |
| 4 |
|
✓ |
✓ |
0.92 |
0.91 |
0.90 |
0.89 |
| 5 |
|
✓ |
× |
0.83 |
0.85 |
0.73 |
0.77 |
| 6 |
ARFPSO |
× |
✓ |
0.80 |
0.83 |
0.70 |
0.75 |
| 7 |
|
× |
× |
0.76 |
0.69 |
0.64 |
0.66 |
| 8 |
|
✓ |
✓ |
0.90 |
0.89 |
0.88 |
0.87 |
In summary, the ablation study revealed that cave-degree perturbation significantly improved feature selection by narrowing down the most relevant features, while magnetic force perturbation allowed the model to escape local minima during the optimization phase. Without these techniques, model performance declined due to a lack of targeted exploration in the solution space, emphasizing the importance of both methods to achieve optimal results.
5. Conclusions
In conclusion, this study introduces an effective dual-step optimization approach to predict customer churn in the motor insurance industry, combining machine learning models with advanced feature selection techniques. The proposed framework, which employs the Adaptive Random Forest-Assisted Large Neighborhood Feature Optimizer (ARALFO) and the Adaptive Random Forest Particle Swarm Optimizer (ARFPSO), has shown significant improvements in predictive accuracy. By incorporating cave-degree perturbation and magnetic force perturbation techniques, the model achieved enhanced feature selection and optimization, resulting in impressive accuracy rates of up to 95%.
The experimental evaluation on a real-world motor insurance datasets demonstrated the superiority of this model, with substantial improvements over traditional methods in both prediction accuracy and churn reduction. Ablation experiments further emphasized the importance of the perturbation techniques, as the exclusion of either technique led to noticeable declines in model performance, thereby confirming the integrated model’s effectiveness in optimizing churn prediction.
For future research, there is potential to extend this dual-step optimization approach to different sectors, broadening its applicability beyond the motor insurance industry. Furthermore, integrating additional predictive factors, such as customer satisfaction metrics, behavioral data, and external macroeconomic variables, could improve the accuracy and adaptability of the churn prediction. studies could also explore the development of advanced methodologies to refine optimization processes within predictive models. This could include investigating more sophisticated techniques, such as polyhedral methods, cutting planes, convex optimization, graph-based algorithms, and dynamic programming, to further improve the precision and adaptability of predictive models.
In summary, the proposed methodology offers a robust and scalable solution for predicting customer churn, with significant potential to improve predictive analytics and churn management strategies in the motor insurance sector and other industries.
Author Contributions
Conceptualization, E.C and K.T.; methodology, E.C., K.H. and K.T.; software, E.C.; validation, E.C.; investigation, E.C and K.T.; resources, K.H. and K.T.; data curation, E.C. and K.H.; writing—original draft preparation, E.C.; writing—review and editing, E.C., K.H. and K.T.; visualization, E.C. and K.T; supervision, K.H. and K.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance approved by the Technical University of Mombasa, Ethical Review Board (Approval code: TUM SERC MSC/013/2024) on 20th June 2024. It was also granted by the National Commission for Science, Technology and Innovation (NACOSTI), Kenya with license number NACOSTI/P/24/37549 on 11th July 2024. The dataset used in this research was facilitated by Azani Insurance prior to the commencement of the study, which was approved on 15th July 2024.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The data will be shared upon request.
Acknowledgments
We express our sincere gratitude to all those who have contributed to the completion of this work. Our appreciation extends to colleagues at the Institute of Computing and Informatics, Technical University of Mombasa for their invaluable support, guidance, and insights throughout the research process.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RF |
Random Forest |
| ARFPSO |
Adaptive Random Forest Particle Swarm Optimizer |
| ARFPSO |
Adaptive Random Forest Particle Swarm Optimizer |
| CD |
Cave Dergree |
| CDPT |
CD-Perturbation Technique |
| MF |
Magnateic Force |
| MFPT |
MF-Perturbation Technique |
| AUC |
Area Under curve |
References
- Shamsuddin, S.N.; Ismail, N.; Nur-Firyal, R. Life Insurance Prediction and Its Sustainability Using Machine Learning Approach. Sustainability 2023, 15, 10737. [Google Scholar] [CrossRef]
- Bogaert, M.; Delaere, L. Ensemble Methods in Customer Churn Prediction: A Comparative Analysis of the State-of-the-Art. Mathematics 2023, 11, 1137. [Google Scholar] [CrossRef]
- Almuqren, L.; Alrayes, F.S.; Cristea, A.I. An Empirical Study on Customer Churn Behaviours Prediction Using Arabic Twitter Mining Approach. Future Internet 2021, 13, 175. [Google Scholar] [CrossRef]
- Matuszelański, K.; Kopczewska, K. Customer Churn in Retail E-Commerce Business: Spatial and Machine Learning Approach. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 165–198. [Google Scholar] [CrossRef]
- Silberer, J.; Müller, P.; Bäumer, T.; Huber, S. Target-Oriented Promotion of the Intention for Sustainable Behavior with Social Norms. Sustainability 2020, 12, 6193. [Google Scholar] [CrossRef]
- Lee, Y.U.; Chung, S.H.; Park, J.Y. Online Review Analysis from a Customer Behavior Observation Perspective for Product Development. Sustainability 2024, 16, 3550. [Google Scholar] [CrossRef]
- Saha, L.; Tripathy, H.K.; Nayak, S.R.; Bhoi, A.K.; Barsocchi, P. Amalgamation of Customer Relationship Management and Data Analytics in Different Business Sectors—A Systematic Literature Review. Sustainability 2021, 13, 5279. [Google Scholar] [CrossRef]
- Pereira, I.; Madureira, A.; Bettencourt, N.; Coelho, D.; Rebelo, M.Â.; Araújo, C.; de Oliveira, D.A. A Machine Learning as a Service (MLaaS) Approach to Improve Marketing Success. Informatics 2024, 11, 19. [Google Scholar] [CrossRef]
- Chang, V.; Hall, K.; Xu, Q.A.; Amao, F.O.; Ganatra, M.A.; Benson, V. Prediction of Customer Churn Behavior in the Telecommunication Industry Using Machine Learning Models. Algorithms 2024, 17, 231. [Google Scholar] [CrossRef]
- Imani, M.; Arabnia, H.R. Hyperparameter Optimization and Combined Data Sampling Techniques in Machine Learning for Customer Churn Prediction: A Comparative Analysis. Technologies 2023, 11, 167. [Google Scholar] [CrossRef]
- Li, J.; Bai, X.; Xu, Q.; Yang, D. Identification of Customer Churn Considering Difficult Case Mining. Systems 2023, 11, 325. [Google Scholar] [CrossRef]
- Pejić Bach, M.; Pivar, J.; Jaković, B. Churn Management in Telecommunications: Hybrid Approach Using Cluster Analysis and Decision Trees. J. Risk Financial Manag. 2021, 14, 544. [Google Scholar] [CrossRef]
- Usman-Hamza, F.E.; Balogun, A.O.; Capretz, L.F.; Mojeed, H.A.; Mahamad, S.; Salihu, S.A.; Akintola, A.G.; Basri, S.; Amosa, R.T.; Salahdeen, N.K. Intelligent Decision Forest Models for Customer Churn Prediction. Appl. Sci. 2022, 12, 8270. [Google Scholar] [CrossRef]
- Khoh, W.H.; Pang, Y.H.; Ooi, S.Y.; Wang, L.-Y.-K.; Poh, Q.W. Predictive Churn Modeling for Sustainable Business in the Telecommunication Industry: Optimized Weighted Ensemble Machine Learning. Sustainability 2023, 15, 8631. [Google Scholar] [CrossRef]
- Xiahou, X.; Harada, Y. B2C E-Commerce Customer Churn Prediction Based on K-Means and SVM. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 458–475. [Google Scholar] [CrossRef]
- Kang, H.; Do, S. ML-Based Software Defect Prediction in Embedded Software for Telecommunication Systems (Focusing on the Case of SAMSUNG ELECTRONICS). Electronics 2024, 13, 1690. [Google Scholar] [CrossRef]
- Taha, A.; Cosgrave, B.; Mckeever, S. Using Feature Selection with Machine Learning for Generation of Insurance Insights. Appl. Sci. 2022, 12, 3209. [Google Scholar] [CrossRef]
- Faris, H. A Hybrid Swarm Intelligent Neural Network Model for Customer Churn Prediction and Identifying the Influencing Factors. Information 2018, 9, 288. [Google Scholar] [CrossRef]
- Xu, T.; Ma, Y.; Kim, K. Telecom Churn Prediction System Based on Ensemble Learning Using Feature Grouping. Appl. Sci. 2021, 11, 4742. [Google Scholar] [CrossRef]
- Kwon, B.; Son, H. Accurate Path Loss Prediction Using a Neural Network Ensemble Method. Sensors 2024, 24, 304. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, D.; Liu, X.; Cui, P. Robust Feature Selection Method Based on Joint L2,1 Norm Minimization for Sparse Regression. Electronics 2023, 12, 4450. [Google Scholar] [CrossRef]
- Xie, G.; Dong, C.; Kong, Y.; Zhong, J.F.; Li, M.; Wang, K. Group Lasso Regularized Deep Learning for Cancer Prognosis from Multi-Omics and Clinical Features. Genes 2019, 10, 240. [Google Scholar] [CrossRef]
- Chan, J.Y.-L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.-W.; Chen, Y.-L. Mitigating the Multicollinearity Problem and Its Machine Learning Approach: A Review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Ganguli, T.; Chong, E.K.P. Activation-Based Pruning of Neural Networks. Algorithms 2024, 17, 48. [Google Scholar] [CrossRef]
- Karema, M.; Mwakondo, F.T.; Tole, K.T. A Three-Phase Novel Angular Perturbation Technique for Metaheuristic-Based School Bus Routing Optimization. Preprints 2024. Available online: https://www.preprints.org/manuscript/2024091522 and Google Scholar (accessed on 22 September 2024).
- Chai, E.; Khadullo, K.; Tole, K. Enhancing Customer Churn Prediction: Addressing Disparities and Imbalance in Machine Learning Models. Available online: https://theijes.com/papers/vol13-issue3/O1303129148.pdf and Google Scholar (accessed on 22 September 2024).
- Kimwomi, G.; Hadulo, K.; Tole, K. Intelligent Interface Technologies and Challenges in eLearning: A Systematic Review of Literature. Available online: https://www.theijes.com/papers/vol13-issue8/13087078.pdf and https://scholar.google.com/scholar?q=Intelligent+Interface+Technologies+and+Challenges+in+eLearning:+A+Systematic+Review+of+Literature (Google Scholar, accessed on 22 September 2024).
- Dzoga, M.; Munga, C.; Azmiya, F.; Tole, K.; Kombe, C.; Shee, A. Influence of Covid-19 Restrictions on the Status of Mangrove Vegetation in Coastal Kenya. Western Indian Ocean Journal of Marine Science 2024, 23(2), 1–9. Available online: https://www.ajol.info/index.php/wiojms/article/view/262628 and Google Scholar (accessed on 22 September 2024). [CrossRef]
- Domingos, E.; Ojeme, B.; Daramola, O. Experimental Analysis of Hyperparameters for Deep Learning-Based Churn Prediction in the Banking Sector. Computation 2021, 9, 34. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, J.; Sun, H.; Yu, H.; Xing, L.; Zhao, Q.; Zhang, L. An Improved BGE-Adam Optimization Algorithm Based on Entropy Weighting and Adaptive Gradient Strategy. Symmetry 2024, 16, 623. [Google Scholar] [CrossRef]
- Park, J.; Yi, D.; Ji, S. A Novel Learning Rate Schedule in Optimization for Neural Networks and It’s Convergence. Symmetry 2020, 12, 660. [Google Scholar] [CrossRef]
- He, K.; Tole, K.; Ni, F.; Yuan, Y.; Liao, L. Adaptive Large Neighborhood Search for Solving the Circle Bin Packing Problem. Comput. Oper. Res. 2021, 127, 105140. [Google Scholar] [CrossRef]
- Yuan, Y.; Tole, K.; Ni, F.; He, K.; Xiong, Z.; Liu, J. Adaptive Simulated Annealing with Greedy Search for the Circle Bin Packing Problem. Comput. Oper. Res. 2022, 144, 105826. [Google Scholar] [CrossRef]
- Tole, K.; Moqa, R.; Zheng, J.; He, K. A Simulated Annealing Approach for the Circle Bin Packing Problem with Rectangular Items. Comput. Ind. Eng. 2023, 176, 109004. [Google Scholar] [CrossRef]
- He, K.; Tole, K.; Ni, F.; Yuan, Y.; Liao, L. Adaptive Large Neighborhood Search for Circle Bin Packing Problem. CoRR 2020, abs/2001.07709. Available online: https://arxiv.org/abs/2001.07709 (accessed on 17 September 2024).
- Tole, K.; Moqa, R.; Zheng, J.; He, K. A simulated annealing approach for the circle bin packing problem with rectangular items. Comput. Ind. Eng. 2023, 176, 109004. [Google Scholar] [CrossRef]
- Tole, K.; Kaloi, M. A.; Ali, R.; Hajano, N. H.; Chan, A. S. S.; Babbar, I. A.; Ali, A. Dual-input Dual-stream Network with Two-fold Margin Loss for Improved Brain Tumor Detection on MRI Images. Preprints 2024, 2024060242. [Google Scholar] [CrossRef]
- Nayak, S. Chapter six - Geometric Programming. In Fundamentals of Optimization Techniques with Algorithms; Academic Press: 2020; pp. 171–189. ISBN 978-0-12-821126-7. [CrossRef]
- Lee, J.; Jung, O.; Lee, Y.; Kim, O.; Park, C. A Comparison and Interpretation of Machine Learning Algorithm for the Prediction of Online Purchase Conversion. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 1472–1491. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Chapter seven - The Particle Swarm. In Swarm Intelligence; Morgan Kaufmann: San Francisco, 2001; pp. 287–325. ISBN 978-1-55860-595-4. [Google Scholar] [CrossRef]
- Van den Poel, D.; Lariviere, B. Customer attrition analysis for financial services using proportional hazard models. European Journal of Operational Research 2004, 157, 196–217, Available online: https://www.sciencedirect.com/science/article/pii/S0377221703000699. [Google Scholar] [CrossRef]
- Lledó, J.; Pavía, J.M. Dataset of an actual motor vehicle insurance portfolio. Mendeley Data 2024, V2. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).