Preprint
Article
From Single Shot to Structure: End-to-End Network based Deflectometry for Specular Free-Form Surface Reconstruction
Altmetrics
Downloads
90
Views
104
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
23 September 2024
Posted:
25 September 2024
You are already at the latest version
Alerts
Abstract
Deflectometry is a key component in the precise measurement of specular (mirrored) surfaces, however traditional methods often lack an end-to-end approach that performs 3D reconstruction in a single shot with high accuracy and generalizes across different free-form surfaces. This paper introduces a novel deep neural network (DNN)-based approach for end-to-end 3D reconstruction of free-form specular surfaces using single-shot deflectometry. Our proposed network, VUDNet, innovatively combines discriminative and generative components to accurately interpret orthogonal fringe patterns and generate high-fidelity 3D surface reconstructions. By leveraging a hybrid architecture integrating a Variational Autoencoder (VAE) and a modified U-Net, VUDNet excels in both depth estimation and detail refinement, achieving superior performance in challenging environments. Extensive data simulation using Blender, leading to a dataset which we are making available, ensures robust training and enables the network to generalize across diverse scenarios. Experimental results demonstrate the strong performance of VUDNet, setting a new standard for 3D surface reconstruction. The implementation of VUDNet is available on GitHub at https://github.com/hadious/VUDNet.
Keywords:
Subject: Computer Science and Mathematics - Computer Vision and Graphics
1. Introduction
In recent years, rapid advancements in optical-based industries have significantly influenced sectors such as microelectronics [1,2,3] and automotive design [4,5,6], leading to a strong demand for highly accurate methods for measuring specular surfaces [7,8]. Deflectometry [9,10,11] is an optical measurement technique which relies upon the reflection of structured light patterns from an unknown surface to infer its shape. Deflectometry is highly effective for measuring specular surfaces due to its accuracy, speed, and non-contact approach, making it particularly suitable for capturing detailed surface variations [12]. Additionally, free-form surface reconstruction [13,14] is crucial for modeling complex, irregular shapes found in advanced optical systems [15]. Together, these methods enhance precision and innovation in optical manufacturing.
The more specific context of single-shot deflectometry [16,17,18], performing deflectometry based on only a single image, is crucial for several reasons, particularly for high-speed imaging of fast dynamically changing surfaces. This includes applications such as fast-moving or morphing specular surfaces like liquids (water, metals), where capturing multiple images is impractical due to the rapidly changing nature of the surface. Additionally, in industrial scanning, single-shot deflectometry enhances efficiency by eliminating the need for multiple images, important for quality control of reflective objects [9]. For example, in General Fusion’s Magnetised Target Fusion technology scheme, measurement of the 3D shape of an imploding specular liquid metal vortex to compress plasma to generate nuclear fusion with microsecond precision is required [19]. Traditional methods [10] require multiple captures and complex setups to obtain surface-gradient information in perpendicular directions, which can be time-consuming and problematically inefficient for dynamic applications.
To further enhance the efficiency and accuracy of single-shot deflectometry, recent research has explored the use of composite fringe patterns in deep learning-based 3D surface measurement techniques [17,20]. These composite patterns are particularly effective in addressing the challenges associated with single-shot deflectometry, such as encoding complex surface details in a single capture. Historically, in the use of fringe patterns for surface measurement, vertical and horizontal patterns are often combined into a single composite pattern. The separation of these orthogonal fringe patterns into their individual components is crucial for accurate analysis and has traditionally been achieved through methods like the 2D Fourier algorithm [21], which despite its utility, often results in phase errors and spectrum aliasing [22].
In contrast, in this paper we propose a novel deep neural network (DNN)-based approach designed for the end-to-end 3D reconstruction of free-form surfaces. Our network, VUDNet, processes 2D images captured from a surface onto which an orthogonal fringe pattern is projected (See Figure 1). This discriminative-generative hybrid network excels in depth estimation. To the best of our knowledge, VUDNet represents the first DNN-based approach in deflectometry, pioneering the use of generative methods for depth estimation.
The integration of both generative and discriminative components in our network is pivotal for achieving high-fidelity 3D surface reconstruction. The discriminative part of the network is essential for accurately identifying and interpreting the orthogonal fringe patterns projected onto the specular surface. This involves extracting meaningful features from an image, which are crucial for determining the gradient information necessary for depth estimation. The discriminative model’s ability to parse complex visual patterns with precision directly impacts the accuracy of the subsequent 3D reconstruction.
On the other hand, the generative component plays a crucial role in translating the extracted gradient information into a coherent 3D representation. The generative model excels in learning and representing the underlying data distribution through embedding representations [23,24]. These embeddings capture the intricate details and variations of the surface, allowing the reconstruction of a highly detailed and accurate 3D shape. The learned embeddings are vital because they encapsulate the spatial relationships and depth cues that are not readily apparent in the raw 2D images [24]. This deep representation allows the generative model to fill in gaps and correct any inconsistencies in the depth information, resulting in a precise 3D reconstruction. This synergy between the two models not only enhances the overall performance of the network but also ensures that the 3D reconstructions are both geometrically precise and visually coherent.
Paper Contributions:
- Novel DNN-Based Approach for Deflectometry: We introduce VUDNet, the first deep neural network (DNN) designed specifically for end-to-end 3D reconstruction of free-form specular surfaces using single-shot deflectometry. VUDNet leverages a hybrid architecture that combines the strengths of both generative and discriminative models, ensuring high accuracy and generalization.
- Dataset Simulation: To train and evaluate our model, we have simulated an extensive dataset. This dataset, which includes a variety of deformed specular surfaces and their corresponding depth maps, will be made publicly available to support future research in this field.
- Robust Performance in Challenging Environments: Experimental results demonstrate that VUDNet significantly outperforms existing methods in reconstructing 3D surfaces from single-shot 2D images, particularly in challenging environments. Our network demonstrates the ability to generalize across diverse scenarios.
2. Background
Deflectometry has high accuracy, speed, and is non-contact, making it suitable for a variety of industrial applications [9]. However, traditional deflectometry methods, such as phase-shifting techniques, require multiple images to be captured in order to obtain surface gradients in two perpendicular directions [9,17]. This process can be time-consuming and inefficient, particularly for dynamic or real-time applications.
Single-shot deflectometry has been developed to overcome these limitations [9,17,18,25,26]. Seo et al. developed a single-shot freeform surface profiler based on spatially phase-shifted lateral shearing interferometry [17]. This approach, while simplifying the measurement process, still struggles with complex surface geometries. Phase measuring profilometry has also seen advancements, with deep learning methods enhancing measurement capabilities [27,28]. Working from a single image significantly reduces the time required for surface measurement, however there are resulting challenges in interpreting the complex patterns reflected by specular surfaces, especially those with low reflectivity or intricate geometries.
The application of deep learning in optical metrology, including deflectometry, has shown significant promise [12,17,26,29]. Deep learning models can learn complex patterns and provide robust phase retrieval from noisy or low-quality data. DYNet++ [17] utilizes deep learning for single-shot deflectometry, capable of retrieving phase information from composite patterns even in challenging conditions with both closed- and open-loop fringe patterns.
Wang et al. proposed a deep-learning-based deflectometric method for freeform surface measurement [26]. Their approach involves devising a deep neural network specifically for freeform surface reconstruction. This method offers a solution for the general measurement of freeform surfaces while minimizing measurement errors caused by noise and system geometry calibration.
3. Method
The architecture of our proposed network represents a sophisticated blend of specialized components designed to tackle the unique challenges of reconstructing 3D specular surfaces from single-shot 2D images. Central to this architecture are two main components: the discriminative and generative branches which form a novel hybrid depth estimator network. Our proposed model is an ensemble of a Variational Auto Encoder (VAE) [30,31,32] and a modified U-Net [33] architecture, adapted here to enhance depth map refinement. This section details each component’s role and functionality within our network, elucidating how they collectively contribute to 3D surface reconstruction. Figure 2 illustrates the comprehensive architecture of our network.
3.1. Problem Formulation
In this work, we address the challenge of reconstructing a 3D surface from a single-shot 2D image of an orthogonal sinusoidal fringe pattern reflected on a specular surface. To formulate the problem, we introduce the following notations and definitions:
- : The 2D reflected image of a pattern reflected by surface .
- : The ground truth depth map corresponding to surface .
- : The estimated depth map produced by our network.
- : The MLP function that combines the outputs of the VAE and U-Net to produce .
- : camera parameters.
- : The projection to render a 2D image I from surface .
- : The function mapping a 3D point to depth.
- The objective is to develop a hybrid depth estimator network, VUDNet, that integrates both generative and discriminative modeling approaches. To train and evaluate our model we simulate a comprehensive dataset that includes 2D images I and corresponding ground truth depth maps . The generated dataset captures the complex interactions of light with specular surfaces, providing a robust foundation for training our hybrid depth estimator network. This approach ensures that our model can generalize well to real-world scenarios involving specular reflections.
3.2. Architecture Overview
The VUDNet architecture integrates a Variational Auto Encoder (VAE) and a modified U-Net, both of which are provided with an input 2D image I, the reflection of pattern on some unknown surface . The VAE is a generative model that aims to learn the underlying distribution of the data, providing a coarse estimation of the depth map. In contrast, the U-Net is a discriminative model designed to refine this estimation, yielding a finer and more precise depth map. The hybrid nature of our architecture leverages the strengths of both generative and discriminative approaches, creating a comprehensive depth estimation model.
The VAE component of our architecture consists of an encoder function that compresses the input image into a latent space representation , followed by a decoder function that reconstructs the depth map from this latent representation, producing depth estimate . This process allows the VAE to capture and model the complex variations in specular surfaces. On the other hand, the modified U-Net architecture, tailored for depth estimation, employs a series of downsampling and upsampling layers specifically structured to refine the depth map, producing estimate . Unlike the traditional U-Net, our modified version diminishes the effect of skip connections to prevent the direct transfer of the texture information present in the patterning of input image I, thereby ensuring that the output is a detailed depth map rather than a combination of depth and texture features.
The output depth maps from both the VAE and the modified U-Net are then fed into a fully connected Multi-Layer Perceptron (MLP) that serves as an ensemble method. Let denote the MLP function that combines the depth maps from the two networks:
Such an ensemble approach is beneficial for several reasons:
- Reduced Overfitting: Ensemble methods inherently reduce the risk of overfitting [34]. They are known for their ability to improve generalization by leveraging the strengths of multiple models and mitigating individual model biases [34]. In our work, this is especially true as we combine one discriminative model and one generative model. Each model captures different aspects of the data distribution, and their combination leads to a more generalizable solution.
- Complementary Strengths: The VAE’s ability to model complex data distributions complements the U-Net’s strength in preserving spatial details, making the ensemble approach particularly effective for depth estimation tasks.
- Improved Performance: Hybrid models that incorporate both generative and discriminative components have been shown to outperform single-method models in various tasks [35,36,37]. This combination harnesses the power of both methodologies, leading to improved performance in reconstructing 3D surfaces from 2D images.
3.3. Loss Function
The loss function used in our network is a composite of reconstruction loss and regularization terms. This combination is designed to ensure that the network not only accurately reconstructs the desired output but also maintains generalization capabilities and prevents overfitting [38]. The reconstruction loss directly measures the difference between the predicted and true values, ensuring precise output generation. Meanwhile, the regularization terms add constraints that promote smoother and more robust model predictions, enhancing the overall performance and stability of the network [39]. The VAE component of the loss,
consists of a Mean Squared Error (MSE) reconstruction loss (left) and a Kullback-Leibler (KL) divergence for regularization (right). Here is a weighting factor, is the posterior distribution, and is the prior distribution.
For the modified U-Net component,
there is again an MSE term (left), but additionally a Total Variation (TV) regularization [40] term (right), controlled by weighting factor , which encourages spatial smoothness in the predicted depth map by penalizing large gradients [41] and reducing noise [42], leading to improved generalization and robustness [43].
The final output from the MLP ensemble is optimized using a combined loss function from both VAE and U-Net losses:
Statistically, the integration of these loss terms ensures that the model benefits from both global structural understanding (via VAE) and local detail refinement (via U-Net). The MLP ensemble leverages this dual optimization, effectively balancing bias and variance trade-offs [44]. This approach mitigates the risk of overfitting through regularization while maintaining high reconstruction accuracy, resulting in a model that performs well across varied and unseen data distributions [45].
3.4. VUDNet Discussion
Ensemble methods combine multiple models to improve overall performance by leveraging the strengths of each model [46]. In the context of this work, our results showcase a compelling strategy by ensembling a discriminative model (U-Net) with a generative model (VAE) through an MLP, harnessing the complementary advantages of both types of models. Drawing on the theoretical foundations provided by Bishop and Lasserre’s work [47], we can explore the benefits of such an ensemble.
Ensembling helps to mitigate overfitting by combining models that have different error patterns [48]. Let and be the errors of the U-Net and VAE, respectively. The combined error can be expressed as:
where is a weight learned by the MLP. By appropriately weighting the errors of the U-Net and VAE, the ensemble can reduce the overall error variance. If the errors of U-Net and VAE are uncorrelated, the covariance term drops out, leading to a reduced overall variance. In our work, this is the case because the VAE and U-Net approach the problem from different angles: the VAE focuses on capturing the global structure and underlying distribution of the data, while the U-Net emphasizes local details and spatial relationships. Consequently, the sources of their errors are fundamentally different and likely unrelated. Since and are not strictly independent, we assume:
If approaches zero, the covariance term becomes negligible, and the ensemble error approaches the minimum possible value based on the variances of the individual models. The optimal weight balances the contributions of the VAE and U-Net, leveraging their complementary strengths to reduce the overall error. Even with a non-zero , the error of the ensemble model still has the potential to be lower than the individual errors:
Given an adequate learning process to learn the optimal weights, the ensemble model combines the strengths of both VAE and U-Net, reducing the overall error through weighted averaging.
4. Dataset Development
To the best of our knowledge, there is no public dataset available for specular free-form surface reconstruction, therefore we have generated our own synthetic dataset, which is introduced in this section.
By creating a virtual environment that approximates key optical aspects of real-world conditions for a reflective textured surface according to physical laws of reflection embedded in the Blender Cycles ray-tracing engine, we can systematically explore the nuances of specular surface reconstruction. This section details the precise setup and execution of our simulation environment, ensuring that every aspect, from lighting and camera positioning to surface properties, is meticulously configured to generate reliable and varied datasets necessary for robust training.
4.1. Setting Up the Simulation Environment
The simulation environment was created using Blender, the Cycles ray-tracing engine, for its ability to produce realistic, physically accurate simulations. This level of realism ensures that the synthetic data closely mimic real-world conditions, thereby improving model robustness and reliability. Simple reflection models often fail to account for optical phenomena such as diffraction, scattering, and the intricate interplay of light with micro-surface textures. In contrast, Blender’s comprehensive simulation environment allows for the accurate replication of these effects, providing a more robust and realistic dataset.
The Cycles engine has been validated in numerous scientific studies [49,50,51] for its ability to simulate complex optical phenomena. Additionally, the open-source nature of Blender, its extensive online support, and the convenience of programming through Python make it an ideal choice for automated dataset generation. Despite some limitations with caustics and computational cost, Cycles provides a balanced trade-off between usability and precision, making it suitable for our purposes. By leveraging the advanced features of Blender’s Cycles engine, we ensure that our synthetic data is both realistic and scientifically valid.
A fixed camera, fixed pattern and surface settings were configured to replicate a realistic scenario for deflectometry, including the use of an orthogonal sinusoidal fringe pattern. This pattern is projected onto a specular object, and the reflected fringes are recorded by a camera. A substantial number of images were captured under these settings, providing a robust foundation for training based on fringe patterns. Figure 3 illustrates this environment for visual clarity.
4.2. Dataset Generation
To generate the dataset, 2D images were rendered from the simulated environment using Blender’s Cycles ray-tracing engine. For each image sample, the surface was uniquely deformed by a specified mechanism (detailed in Section 4.4), to ensure variability in the dataset, with an associated depth map . Each 2D image was rendered based on the specific surface reflectance characteristics, camera settings, and the surface topology. The optical ray tracing setup in Cycles was configured with a maximum sample count of 4096, ensuring high-quality image generation. Total bounces were set to 12, diffuse bounces to 4, glossy bounces to 4, transmission bounces to 12, and transparent bounces to 8.
4.3. Pattern
We utilize a fixed orthogonal sinusoidal fringe pattern, , which remains constant throughout the measurement process. A fixed pattern design is particularly advantageous for industrial applications where the pattern needs to be forged, printed, or otherwise permanently established. Unlike dynamic systems, such as in [22], where an LCD changes the pattern with every shot, our fixed pattern ensures consistency and reliability in scenarios where altering the pattern is impractical or impossible.
The fixed orthogonal sinusoidal fringe pattern is represented as:
for mean intensity , modulation amplitude , periods , and phase shifts .
This pattern is projected onto the surface, and the reflected image is captured. The orthogonal nature of the pattern ensures that gradient information is obtained in both the x and y directions, which is crucial for 3D reconstruction. By maintaining a fixed pattern, we ensure that our system can be reliably deployed in industrial applications without the need for complex pattern generation mechanisms, providing a stable and efficient solution for 3D surface measurement.
4.4. Shape Deformations
To have a diverse array of geometric features, we systematically introduced deformations to a plane surface :
Here represents the set of parameters that conditions the projection. These deformations were designed to simulate realistic scenarios, to increase the likelihood of network generalizability from training data to real-world applications.
Surface Generation:
The surface generation process involved modifying a base planar surface by integrating various shapes, such as hemispheres, to resemble convex structures and by applying parametric deformations to create concave forms. Each surface was assigned a specular material to mimic realistic lighting interactions, crucial for representing real-world scenarios.
- Shape Integration: To generate convex-like surfaces, multiple convex shapes, primarily hemispheres, were superimposed onto a base planar surface at randomized positions and scales.
- Parametric Deformations: To generate concave surfaces, the planar surface was deformed using a set of parametric functions , such as parabolic and sinusoidal transformations. These functions control the depth and curvature of the deformation, sculpting the surface into various forms.
- Randomization: To enhance diversity, the parameters involved in both convex-like shape integration (size , position , and the number of hemispheres ) and concave deformations were randomized, resulting in a wide range of surface topologies , featuring variations from subtle indentations to pronounced curvatures.
- Specular Material Assignment: All generated surfaces were assigned a specular material to ensure that the generated data accurately represented real-world scenarios, where surface reflectivity significantly impacts depth perception.
Data Capture:
Following the creation of these surfaces, we rendered 2D images and captured corresponding depth maps. This process involved
- Rendering 2D Images: Each deformed surface was rendered under controlled lighting conditions to capture the specular reflections characteristic of real-world environments.
- Depth Map Acquisition: Depth maps were generated for each configuration, providing the precise geometric ground-truth information essential for training.
This methodical approach to generating a diverse and realistic dataset enables our deep learning model to learn robust features applicable across a wide range of real-world surfaces.
4.5. Depth Map Standardization
Depth maps generated from simulations often require standardization to ensure consistency and accuracy in subsequent processing steps. Algorithm 1 illustrates the process we employ for this standardization. The algorithm begins with the calculation of the centroid of the depth map, providing a central reference point for further transformations. Principal Component Analysis (PCA) is then used to determine the primary axes of variance in the data, identifying the principal components that describe the orientation of the surface in the 3D space. The PCA eigenvectors lead to a rotation matrix, ensuring that the surface data are oriented with the XY plane, with the Z-axis representing height. The transformation aligns the centroid of the depth map to the origin, standardizing the position and orientation. Finally, the depth values are normalized to a predefined range of .
| Algorithm 1 Normalize and Align Depth Map |
|
4.6. Data Preparation
The dataset used in our study consists of a diverse set of depth maps generated from simulated environments, totaling 400 images. We included 250 concave surface samples and 150 convex-like ones, as our research indicated that concave surfaces present more complexity, and so were emphasized in our simulations. Each image is pixels in size and is rendered in greyscale. The dataset is divided into training, validation, and test sets, with used for training, for validation, and for testing. This division ensures a robust evaluation of the model’s performance across different data splits and helps in assessing generalization.
5. Results and Discussion
Figure 4 qualitatively demonstrates the success of our model. The predicted depth map exhibits a high degree of smoothness, indicating effective regularization and the absence of noise or artifacts. The image shows no visible outliers, suggesting consistent accuracy across the surface. Most significantly, there is no discernible presence of the orthogonal fringe pattern that would have been strikingly present in the input image, highlighting VUNet’s ability to reconstruct the underlying surface geometry without retaining or passing through the pattern information.
Figure 5 presents a comparison between the ground truth and predicted depth maps for a randomly selected sample. The left images display the ground truth depth map, while the right images show the depth map predicted by our VUDNet model. The predicted depth map is smoother than the original, due to the regularization term. Nevertheless, the estimates still retains a high degree of fine detail. The visual comparison suggests that the model has effectively captured the essential features of the surface, aligning well with the expected characteristics observed in the ground truth data. This smoothing effect helps to manage the noise and artifacts typically associated with specular surfaces.
The visualization of the VAE representation, as illustrated in Figure 6, demonstrates a remarkable separation of the representation space. This clustering effect indicates that the VAE has successfully formed a coherent representation space where intrinsic features of different surfaces are well captured and recognizable. In this context, a cluster in the VAE’s representation space refers to a grouping of data points in the latent space that share similar underlying features. Ideally, the separation of these clusters is crucial for feature learning, as it allows the VAE to distinguish between various surface characteristics effectively. In Figure 6, the points represent the data points in the latent space rather than the original data points themselves, emphasizing the VAE’s ability to encode distinct features. Regarding the comment about the partitioning of images, it should be noted that this separation results from applying the t-SNE method [52] to visualize the latent space, showcasing the ideal separability achieved in the learned representation.
The intrinsic features extracted by the VAE enable the network to distinguish between different types of surfaces, which is crucial for accurate depth estimation. The well-defined clusters suggest that the VAE can identify and learn the underlying patterns in the data, leading to potent feature extraction. This capability is essential for generalizing the network’s performance across diverse and complex surface geometries.
Figure 7 further supports the effectiveness of the VAE representation. The scattering of the samples based on their features shows that similar data points are located near each other in the representation space. This proximity indicates that the VAE can effectively group similar surfaces, enhancing the network’s ability to perform accurate depth estimation. The close grouping of similar samples demonstrates the VAE’s proficiency in feature extraction, ensuring that surfaces with similar characteristics are represented similarly in the latent space.
The VAE’s ability to maintain these clusters and scatter plots signifies its strength in capturing and representing the essential features of the input data. This representation plays a critical role in the subsequent stages of depth estimation, where accurate and reliable feature extraction is paramount.
Although our method employs an ensemble of a VAE and U-Net, we focus on visualizing the latent representation of the VAE. As highlighted in prior research [32], VAEs are designed to learn compact, informative latent spaces [53,54,55] that capture the underlying structure of the data. In contrast, U-Net primarily performs pixel-level refinement, working directly in the image space without explicitly learning a latent representation [33]. Therefore, the U-Net’s contribution is more appropriately assessed through its impact on the final depth maps, rather than through latent space visualization.
Table 1 demonstrates the remarkable performance of VUDNet.
The quantitative metrics presented in Table 1 demonstrate the network’s capability to achieve high accuracy and consistency in depth estimation. Specifically, the VUDNet model shows significantly lower Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and LogError compared to the comparator DYNet++ [17] and D-UNet [29] models. The lower errors across all metrics highlight the superior performance of the VUDNet’s hybrid architecture in providing precise and reliable 3D surface reconstructions.
The effective combination of VAE and U-Net components, along with the MLP ensemble, allows VUDNet to capture intricate surface details while maintaining overall structural coherence. The distinct separation in the VAE representation space indicates successful feature extraction, validating the model’s ability to generalize across diverse and complex surface geometries.
6. Conclusions
In this paper, we introduced VUDNet, an innovative deep neural network designed for the end-to-end 3D reconstruction of specular free-form surfaces using single-shot deflectometry. Our approach uniquely combines the strengths of both generative and discriminative models by integrating a Variational Autoencoder (VAE) and a modified U-Net. This hybrid architecture excels in depth estimation and detail refinement, providing high-fidelity reconstructions that surpass the performance of existing methods. Our dataset, which allows for network training on a diverse range of scenarios, is being made publicly available to support future work in this domain.
Experimental results demonstrate that VUDNet achieves incredible reconstruction accuracy from single-shot 2D images, with an RMSE error one fourth as large (or better) in comparison to competing state-of-the-art methods). The integration of both MSE and TV regularization terms in the loss function promotes spatial smoothness and reduces noise, leading to visually coherent depth maps. The findings of this study set a new standard for single-shot deflectometry, showcasing the potential of deep learning in advancing optical metrology for specular surfaces.
In future work, we plan to explore the application of VUDNet to other forms of surface measurement and extend our approach to dynamic and real-time scenarios. Additionally, we aim to investigate the integration of more advanced generative models to further improve the robustness of depth estimation in diverse and complex environments.
Author Contributions
Conceptualization, M.Hadi Sepanj, Saed Moradi and Paul Fieguth; Formal analysis, M.Hadi Sepanj; Funding acquisition, Claire Preston, Anthony Lee and Paul Fieguth; Methodology, M.Hadi Sepanj, Saed Moradi and Amir Nazemi; Project administration, Paul Fieguth; Resources, Claire Preston and Anthony Lee; Software, M.Hadi Sepanj; Supervision, Paul Fieguth; Validation, M.Hadi Sepanj; Visualization, M.Hadi Sepanj; Writing – original draft, M.Hadi Sepanj; Writing – review & editing, Saed Moradi, Amir Nazemi, Claire Preston, Anthony Lee and Paul Fieguth.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kwak, H.; Kim, J. Semiconductor multilayer nanometrology with machine learning. Nanomanufacturing and Metrology 2023, 6, 15. [Google Scholar] [CrossRef]
- Li, T.; Wang, S.; Luo, Y.; Wan, J.; Luo, Z.; Chen, M. 3D Vision and Intelligent On-line Inspection in SMT Microelectronic Packaging: A Review. IEEE Journal of Emerging and Selected Topics in Industrial Electronics 2024. [Google Scholar] [CrossRef]
- Jangra, P.; Duhan, M. Comparative analysis of devices working on optical and spintronic based principle. Journal of Optics 2024, 53, 1629–1649. [Google Scholar] [CrossRef]
- Flores-Fuentes, W.; Arellano-Vega, E.; Sergiyenko, O.; Alba-Corpus, I.Y.; Rodríguez-Quiñonez, J.C.; Castro-Toscano, M.J.; González-Navarro, F.F.; Vasavi, S.; Miranda-Vega, J.E.; Hernández-Balbuena, D.; et al. Surface color estimation in 3D spatial coordinate remote sensing by a technical vision system. Optical and Quantum Electronics 2024, 56, 406. [Google Scholar] [CrossRef]
- Li, T.; Polette, A.; Lou, R.; Jubert, M.; Nozais, D.; Pernot, J.P. Machine Learning-Based 3D Scan Coverage Prediction for Smart-Control Applications. Computer-Aided Design 2024, 103775. [Google Scholar] [CrossRef]
- Prauzek, M.; Hercik, R.; Konecny, J.; Mikolajek, M.; Stankus, M.; Koziorek, J.; Martinek, R. An optical-based sensor for automotive exhaust gas temperature measurement. IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Rak, G.; Hočevar, M.; Kolbl Repinc, S.; Novak, L.; Bizjan, B. A review on methods for measurement of free water surface. Sensors 2023, 23, 1842. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, R.; Zhao, J.; Wu, J.; Fu, S.; Chen, Y.; Sun, Y. Low coherence measurement methods for industrial parts with large surface reflectance variations. IEEE Transactions on Instrumentation and Measurement 2023. [Google Scholar] [CrossRef]
- Burke, J.; Pak, A.; Höfer, S.; Ziebarth, M.; Roschani, M.; Beyerer, J. Deflectometry for specular surfaces: an overview. Advanced Optical Technologies 2023, 12, 1237687. [Google Scholar] [CrossRef]
- Huang, L.; Idir, M.; Zuo, C.; Asundi, A. Review of phase measuring deflectometry. Optics and Lasers in Engineering 2018, 107, 247–257. [Google Scholar] [CrossRef]
- Häusler, G.; Faber, C.; Olesch, E.; Ettl, S. Deflectometry vs. interferometry. Optical measurement systems for industrial inspection VIII; SPIE, 2013; Volume 8788, pp. 367–377. [Google Scholar]
- Guan, J.; Li, J.; Yang, X.; Chen, X.; Xi, J. Defect detection method for specular surfaces based on deflectometry and deep learning. Optical Engineering 2022, 61, 061407–061407. [Google Scholar] [CrossRef]
- Wójcik, A.; Niemczewska-Wójcik, M.; Sładek, J. Assessment of free-form surfaces’ reconstruction accuracy. Metrology and Measurement Systems 2017, 24, 303–312. [Google Scholar] [CrossRef]
- Orumi, M.A.B.; Sepanj, M.H.; Famouri, M.; Azimifar, Z.; Wong, A. Unsupervised Deep Shape from Template. In Image Analysis and Recognition: 16th International Conference, ICIAR 2019, Waterloo, ON, Canada, August 27–29, 2019; Proceedings, Part I 16; Springer, 2019; pp. 440–451. [Google Scholar]
- Jiang, X.J.; Scott, P.J. Advanced metrology: freeform surfaces; Academic Press, 2020. [Google Scholar]
- Qiao, G.; Huang, Y.; Song, Y.; Yue, H.; Liu, Y. A single-shot phase retrieval method for phase measuring deflectometry based on deep learning. Optics Communications 2020, 476, 126303. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Ghim, Y.S.; Rhee, H.G. DYnet++: A deep learning based single-shot phase-measuring deflectometry for the 3D measurement of complex free-form surfaces. IEEE Transactions on Industrial Electronics 2023. [Google Scholar] [CrossRef]
- Liang, H.; Sauer, T.; Faber, C. Using wavelet transform to evaluate single-shot phase measuring deflectometry data. In Applications of Digital Image Processing XLIII; SPIE, 2020; Volume 11510, pp. 404–410. [Google Scholar]
- Mangione, N.S.; Wu, H.; Preston, C.; Lee, A.M.; Entezami, S.; Ségas, R.; Forysinski, P.W.; Suponitsky, V. Shape manipulation of a rotating liquid liner imploded by arrays of pneumatic pistons: Experimental and numerical study. Fusion Engineering and Design 2024, 198, 114087. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Li, Y.; Tao, T.; Han, J.; Chen, Q.; Zuo, C. Single-shot absolute 3D shape measurement with deep-learning-based color fringe projection profilometry. Optics Letters 2020, 45, 1842–1845. [Google Scholar] [CrossRef]
- Chang, H.T.; Lin, T.Y.; Chuang, C.H.; Chen, C.Y.; Ho, C.C.; Chang, C.Y. Separation of two-dimensional mixed circular fringe patterns based on spectral projection property in fractional Fourier transform domain. Applied Sciences 2021, 11, 859. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, J.; Jiang, X.; Fan, L.; Wei, C.; Yue, H.; Liu, Y. High-precision dynamic three-dimensional shape measurement of specular surfaces based on deep learning. Optics Express 2023, 31, 17437–17449. [Google Scholar] [CrossRef]
- Dupont, E.; Whye Teh, Y.; Doucet, A. Generative Models as Distributions of Functions. In Proceedings of The 25th International Conference on Artificial Intelligence and Statistic; Camps-Valls, G., Ruiz, F.J.R., Valera, I., Eds.; PMLR, 2022; Volume 151, Proceedings of Machine Learning Research; pp. 2989–3015. [Google Scholar]
- Lavrač, N.; Podpečan, V.; Robnik-Šikonja, M. Representation Learning: Propositionalization and Embeddings; Springer, 2021. [Google Scholar]
- Nguyen, M.T.; Ghim, Y.S.; Rhee, H.G. One-shot deflectometry for high-speed inline inspection of specular quasi-plane surfaces. Optics and Lasers in Engineering 2021, 147, 106728. [Google Scholar] [CrossRef]
- Wang, J.; Wang, T.; Xu, B.; Willomitzer, O.C.; et al. Accurate Eye Tracking from Dense 3D Surface Reconstructions using Single-Shot Deflectometry. arXiv 2023, arXiv:2308.07298. [Google Scholar]
- Li, W.; Liu, T.; Tai, M.; Zhong, Y. Three-dimensional measurement for specular reflection surface based on deep learning and phase measuring profilometry. Optik 2022, 271, 169983. [Google Scholar] [CrossRef]
- Suresh, V.; Zheng, Y.; Li, B. PMENet: phase map enhancement for Fourier transform profilometry using deep learning. Measurement Science and Technology 2021, 32, 105001. [Google Scholar] [CrossRef]
- Dou, J.; Wang, D.; Yu, Q.; Kong, M.; Liu, L.; Xu, X.; Liang, R. Deep-learning-based deflectometry for freeform surface measurement. Optics Letters 2022, 47, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Lopez, R.; Regier, J.; Jordan, M.I.; Yosef, N. Information constraints on auto-encoding variational bayes. Advances in neural information processing systems 2018, 31. [Google Scholar]
- Pu, Y.; Gan, Z.; Henao, R.; Yuan, X.; Li, C.; Stevens, A.; Carin, L. Variational autoencoder for deep learning of images, labels and captions. Advances in neural information processing systems 2016, 29. [Google Scholar]
- Pinheiro Cinelli, L.; Araújo Marins, M.; Barros da Silva, E.A.; Lima Netto, S. Variational autoencoder. In Variational Methods for Machine Learning with Applications to Deep Networks; Springer, 2021; pp. 111–149. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015; proceedings, part III 18; Springer 2015; pp. 234–241. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In International workshop on multiple classifier systems; Springer, 2000; pp. 1–15. [Google Scholar]
- Ye, Y.; Ji, S. A Hybrid Generative and Discriminative PointNet on Unordered Point Sets. arXiv 2024, arXiv:2404.12925. [Google Scholar]
- Garcia Satorras, V.; Akata, Z.; Welling, M. Combining generative and discriminative models for hybrid inference. Advances in Neural Information Processing Systems 2019, 32. [Google Scholar]
- Kou, G.; Chen, H.; Hefni, M.A. Improved hybrid resampling and ensemble model for imbalance learning and credit evaluation. Journal of Management Science and Engineering 2022, 7, 511–529. [Google Scholar] [CrossRef]
- Roelofs, R. Measuring Generalization and overfitting in Machine learning. University of California: Berkeley, 2019. [Google Scholar]
- Ying, X. An overview of overfitting and its solutions. Journal of physics: Conference series 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Kobler, E.; Effland, A.; Kunisch, K.; Pock, T. Total deep variation: A stable regularization method for inverse problems. IEEE transactions on pattern analysis and machine intelligence 2021, 44, 9163–9180. [Google Scholar] [CrossRef] [PubMed]
- Baiju, P.; Antony, S.L.; George, S.N. An intelligent framework for transmission map estimation in image dehazing using total variation regularized low-rank approximation. The Visual Computer 2022, 38, 2357–2372. [Google Scholar] [CrossRef]
- Ibrahim, M.M.; Liu, Q.; Khan, R.; Yang, J.; Adeli, E.; Yang, Y. Depth map artefacts reduction: A review. IET Image Processing 2020, 14, 2630–2644. [Google Scholar] [CrossRef]
- Aotani, T.; Kobayashi, T.; Sugimoto, K. Meta-optimization of bias-variance trade-off in stochastic model learning. IEEE Access 2021, 9, 148783–148799. [Google Scholar] [CrossRef]
- Pourtaheri, Z.K.; Zahiri, S.H. Ensemble classifiers with improved overfitting. In Proceedings of the 2016 1st conference on swarm intelligence and evolutionary computation (CSIEC); IEEE, 2016; pp. 93–97. [Google Scholar]
- Abimannan, S.; El-Alfy, E.S.M.; Chang, Y.S.; Hussain, S.; Shukla, S.; Satheesh, D. Ensemble multifeatured deep learning models and applications: A survey. IEEE Access 2023. [Google Scholar] [CrossRef]
- Bernardo, J.; Bayarri, M.; Berger, J.; Dawid, A.; Heckerman, D.; Smith, A.; West, M. Generative or discriminative? getting the best of both worlds. Bayesian statistics 2007, 8, 3–24. [Google Scholar]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Engineering Applications of Artificial Intelligence 2022, 115, 105151. [Google Scholar] [CrossRef]
- Koch, M.; Rosselló, J.M.; Lechner, C.; Lauterborn, W.; Eisener, J.; Mettin, R. Theory-assisted optical ray tracing to extract cavitation-bubble shapes from experiment. Experiments in Fluids 2021, 62, 1–19. [Google Scholar] [CrossRef]
- Kiuchi, S.; Koizumi, N. Simulating the appearance of mid-air imaging with micro-mirror array plates. Computers & Graphics 2021, 96, 14–23. [Google Scholar]
- Villa, J.; Mcmahon, J.; Nesnas, I. Image Rendering and Terrain Generation of Planetary Surfaces Using Source-Available Tools. In Proceedings of the 46th Annual AAS Guidance, Navigation & Control Conference, Breckenridge, CO, USA; 2023; pp. 1–24. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. Journal of machine learning research 2008, 9. [Google Scholar]
- Yee-King, M. Latent spaces: A creative approach. In The Language of Creative AI: Practices, Aesthetics and Structures; Springer, 2022; pp. 137–154. [Google Scholar]
- Gelada, C.; Kumar, S.; Buckman, J.; Nachum, O.; Bellemare, M.G. Deepmdp: Learning continuous latent space models for representation learning. In International conference on machine learning; PMLR, 2019; pp. 2170–2179. [Google Scholar]
- Fries, W.D.; He, X.; Choi, Y. Lasdi: Parametric latent space dynamics identification. Computer Methods in Applied Mechanics and Engineering 2022, 399, 115436. [Google Scholar] [CrossRef]
Figure 1.
Overview of the context faced by this paper: A known fringe pattern (left) is reflected by some shape of interest, and the resulting reflection is captured by a camera. Our proposed method, VUDNet, reconstructs the estimated shape based on the observed image, trained on a dataset of simulated reflections.
Figure 1.
Overview of the context faced by this paper: A known fringe pattern (left) is reflected by some shape of interest, and the resulting reflection is captured by a camera. Our proposed method, VUDNet, reconstructs the estimated shape based on the observed image, trained on a dataset of simulated reflections.
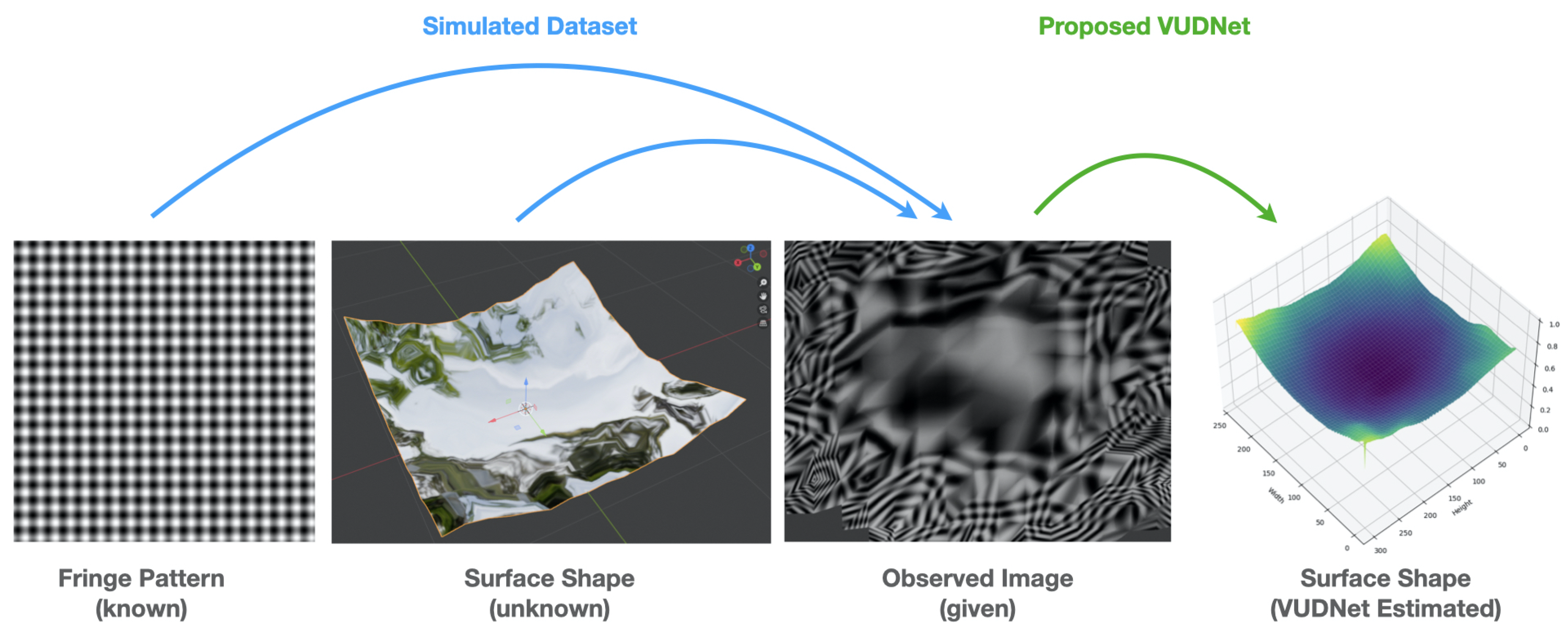
Figure 2.
General architecture of the proposed VUDNet for end-to-end 3D reconstruction of specular free-form surfaces. The network integrates a Variational Autoencoder (VAE, bottom) for coarse depth estimation and a modified U-Net (top) for detail refinement. The ensemble approach leverages both generative and discriminative components, combining their outputs (right) to produce accurate depth maps from single-shot 2D images.
Figure 2.
General architecture of the proposed VUDNet for end-to-end 3D reconstruction of specular free-form surfaces. The network integrates a Variational Autoencoder (VAE, bottom) for coarse depth estimation and a modified U-Net (top) for detail refinement. The ensemble approach leverages both generative and discriminative components, combining their outputs (right) to produce accurate depth maps from single-shot 2D images.
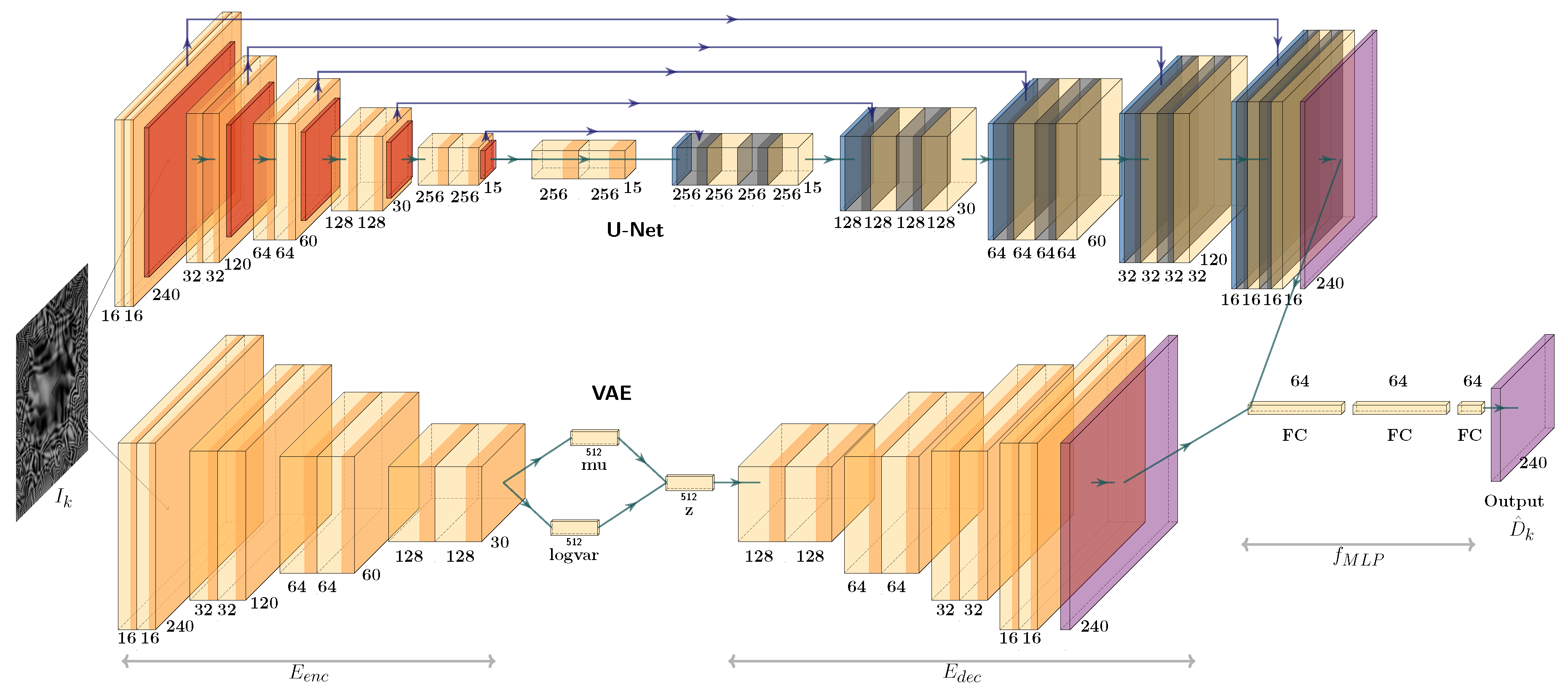
Figure 3.
Simulation environment setup for generating the dataset. The environment includes a fixed camera, a fixed pattern, and various surface settings to replicate realistic deflectometry scenarios. An orthogonal sinusoidal fringe pattern is projected onto specular objects, and the reflected fringes are captured by the camera. This setup ensures the generation of a robust and varied dataset, essential for training the VUDNet to accurately reconstruct 3D surfaces from single-shot 2D images. Since this image is a direct screenshot from the Blender environment, the surface is reflecting the simulated world background. The reflection of the pattern plane on the surface is visible to the camera.
Figure 3.
Simulation environment setup for generating the dataset. The environment includes a fixed camera, a fixed pattern, and various surface settings to replicate realistic deflectometry scenarios. An orthogonal sinusoidal fringe pattern is projected onto specular objects, and the reflected fringes are captured by the camera. This setup ensures the generation of a robust and varied dataset, essential for training the VUDNet to accurately reconstruct 3D surfaces from single-shot 2D images. Since this image is a direct screenshot from the Blender environment, the surface is reflecting the simulated world background. The reflection of the pattern plane on the surface is visible to the camera.
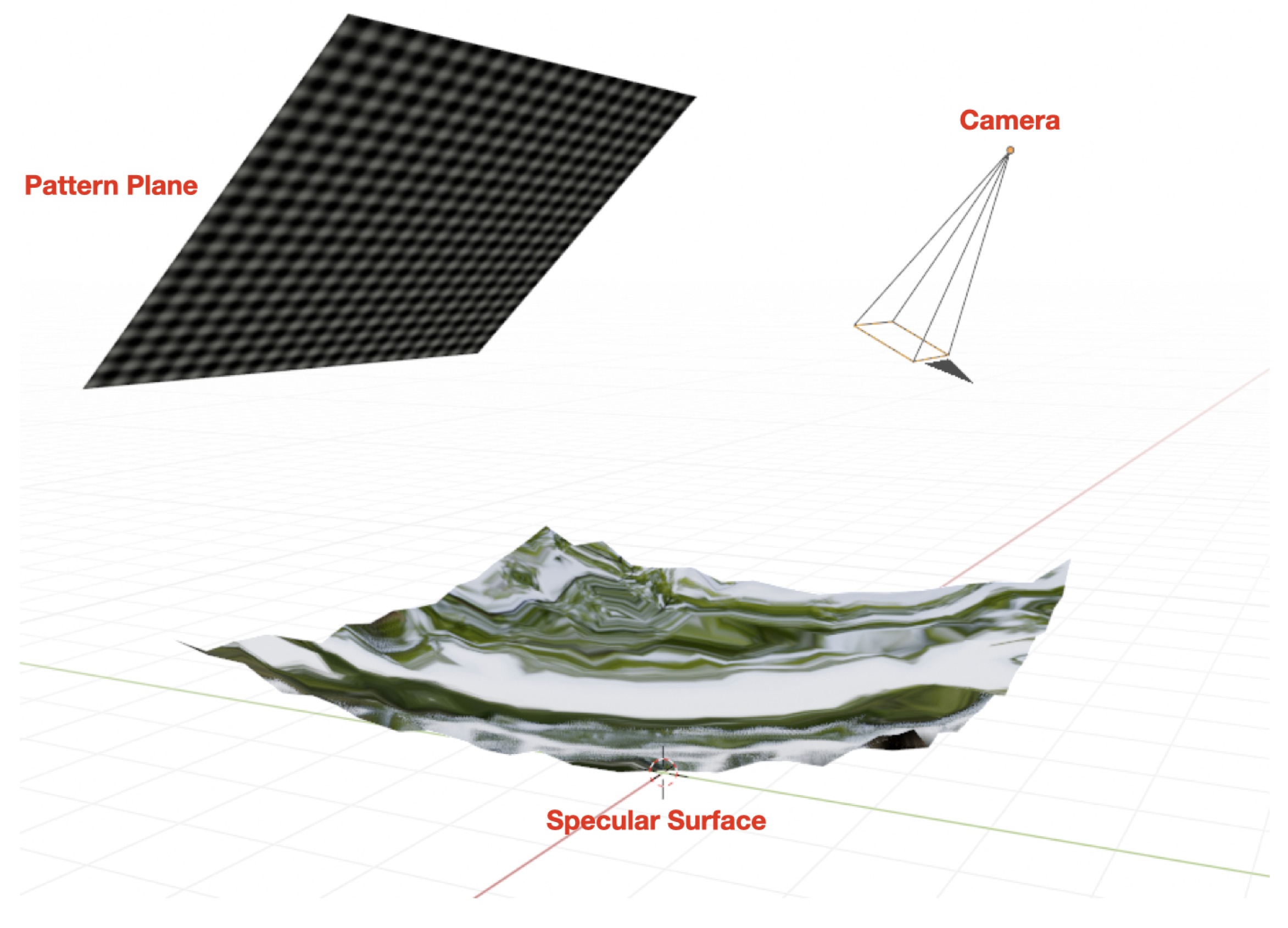
Figure 4.
Mean Squared Error (MSE) difference between the ground truth depth map and the predicted depth map from our VUDNet model for a selected sample, showing smoothness, effective regularization, absence of outliers, and no visible orthogonal fringe patterns, demonstrating the model’s accuracy.
Figure 4.
Mean Squared Error (MSE) difference between the ground truth depth map and the predicted depth map from our VUDNet model for a selected sample, showing smoothness, effective regularization, absence of outliers, and no visible orthogonal fringe patterns, demonstrating the model’s accuracy.
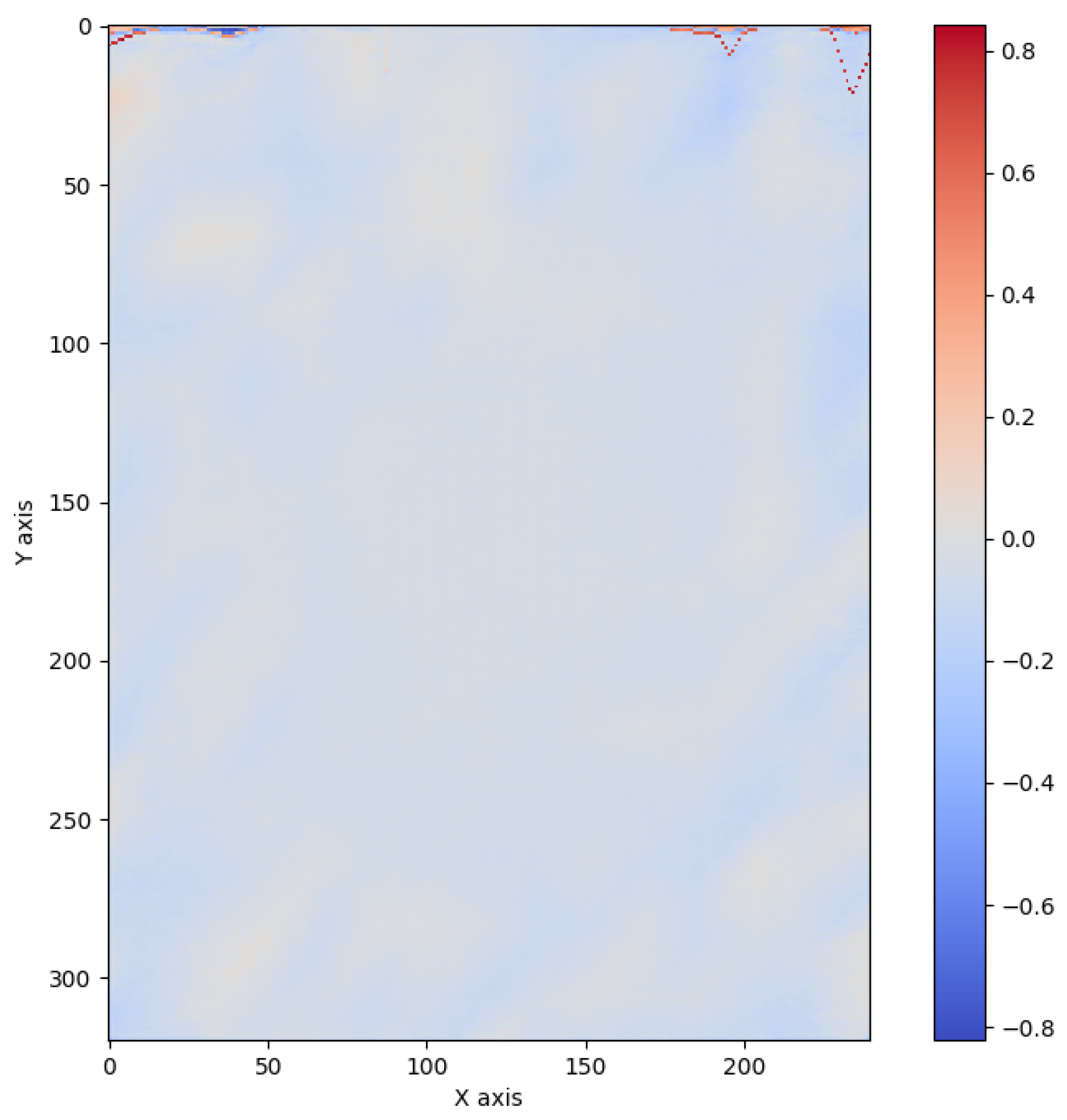
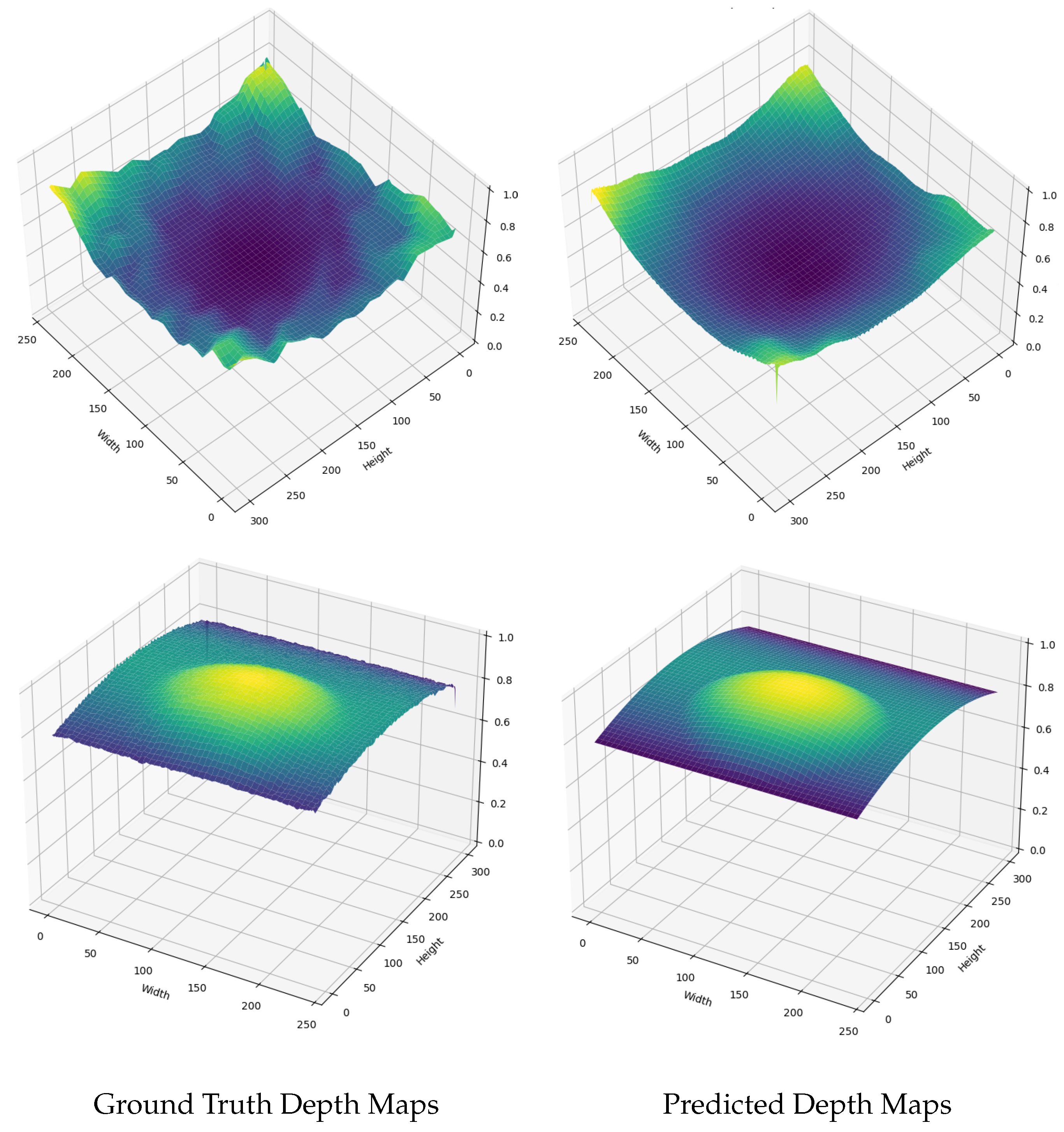
Figure 5.
Comparison of ground truth (left) and VUDNet-estimated depth maps (right), showing effective noise reduction and fine detail retention. The top images showcase a result for a concave sample, while the bottom images represent an example of the convex-like case.
Figure 5.
Comparison of ground truth (left) and VUDNet-estimated depth maps (right), showing effective noise reduction and fine detail retention. The top images showcase a result for a concave sample, while the bottom images represent an example of the convex-like case.
| Ground Truth Depth Maps | Predicted Depth Maps |
Figure 6.
VAE representation (trained on the complete dataset) showcasing distinct separation of clusters in the latent space, indicating effective differentiation of surface characteristics and potent feature extraction, crucial for accurate depth estimation and generalization across diverse surface geometries. The four images on the right correspond to the selected points in the latent space (left image). It is evident that images from different clusters belong to the same category, highlighting the network’s ability to identify underlying similarities despite variations in surface characteristics.
Figure 6.
VAE representation (trained on the complete dataset) showcasing distinct separation of clusters in the latent space, indicating effective differentiation of surface characteristics and potent feature extraction, crucial for accurate depth estimation and generalization across diverse surface geometries. The four images on the right correspond to the selected points in the latent space (left image). It is evident that images from different clusters belong to the same category, highlighting the network’s ability to identify underlying similarities despite variations in surface characteristics.
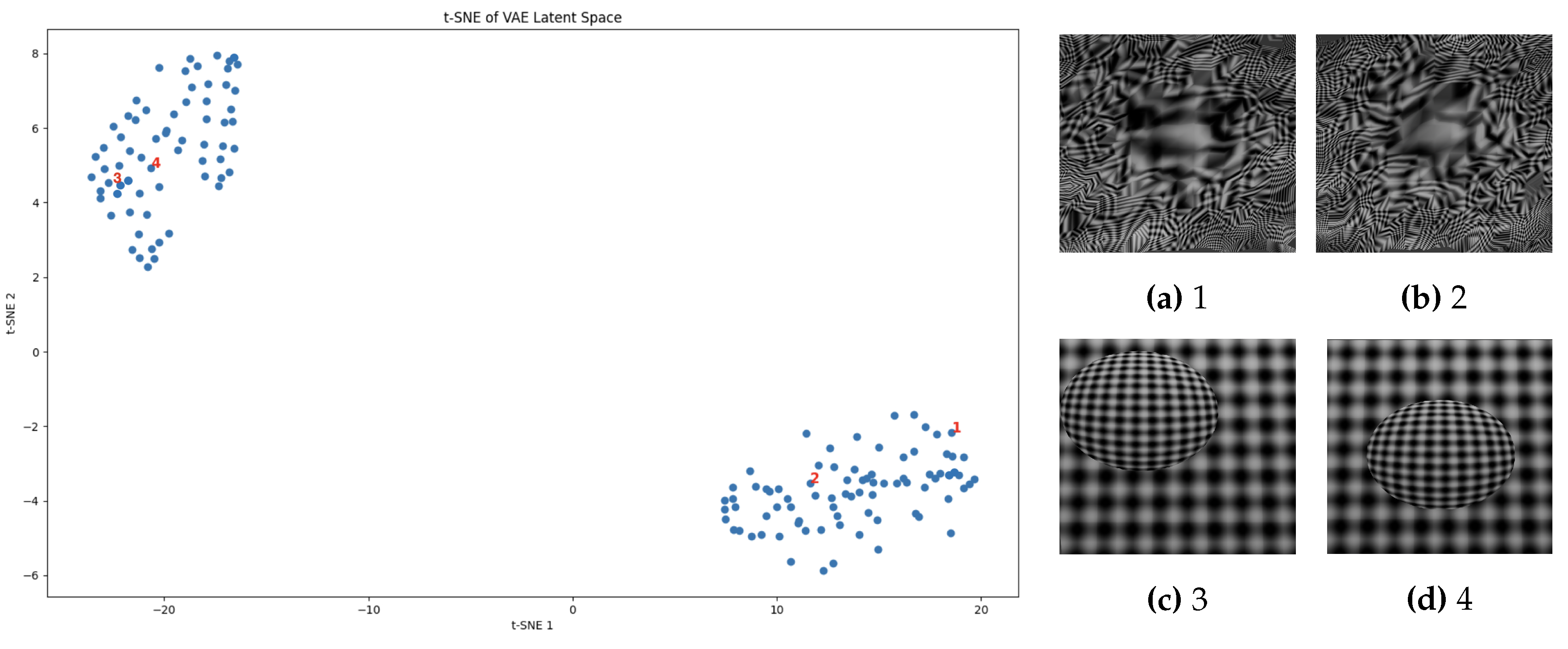
Figure 7.
VAE representation (trained exclusively on concave data) demonstrating effective distribution of data points (each point in the figure illustrate the data equivalent in the latent space), indicating proficient feature extraction and grouping of surfaces with similar characteristics in the latent space, which is crucial for accurate depth estimation. The images on the right correspond to the selected points in the latent space (left image). It is clear that images positioned closer together share more similarities in reflection shape, while those farther apart are less similar, even though they belong to the same category. This emphasizes the network’s capability to capture underlying similarities despite variations in surface characteristics within the same category.
Figure 7.
VAE representation (trained exclusively on concave data) demonstrating effective distribution of data points (each point in the figure illustrate the data equivalent in the latent space), indicating proficient feature extraction and grouping of surfaces with similar characteristics in the latent space, which is crucial for accurate depth estimation. The images on the right correspond to the selected points in the latent space (left image). It is clear that images positioned closer together share more similarities in reflection shape, while those farther apart are less similar, even though they belong to the same category. This emphasizes the network’s capability to capture underlying similarities despite variations in surface characteristics within the same category.
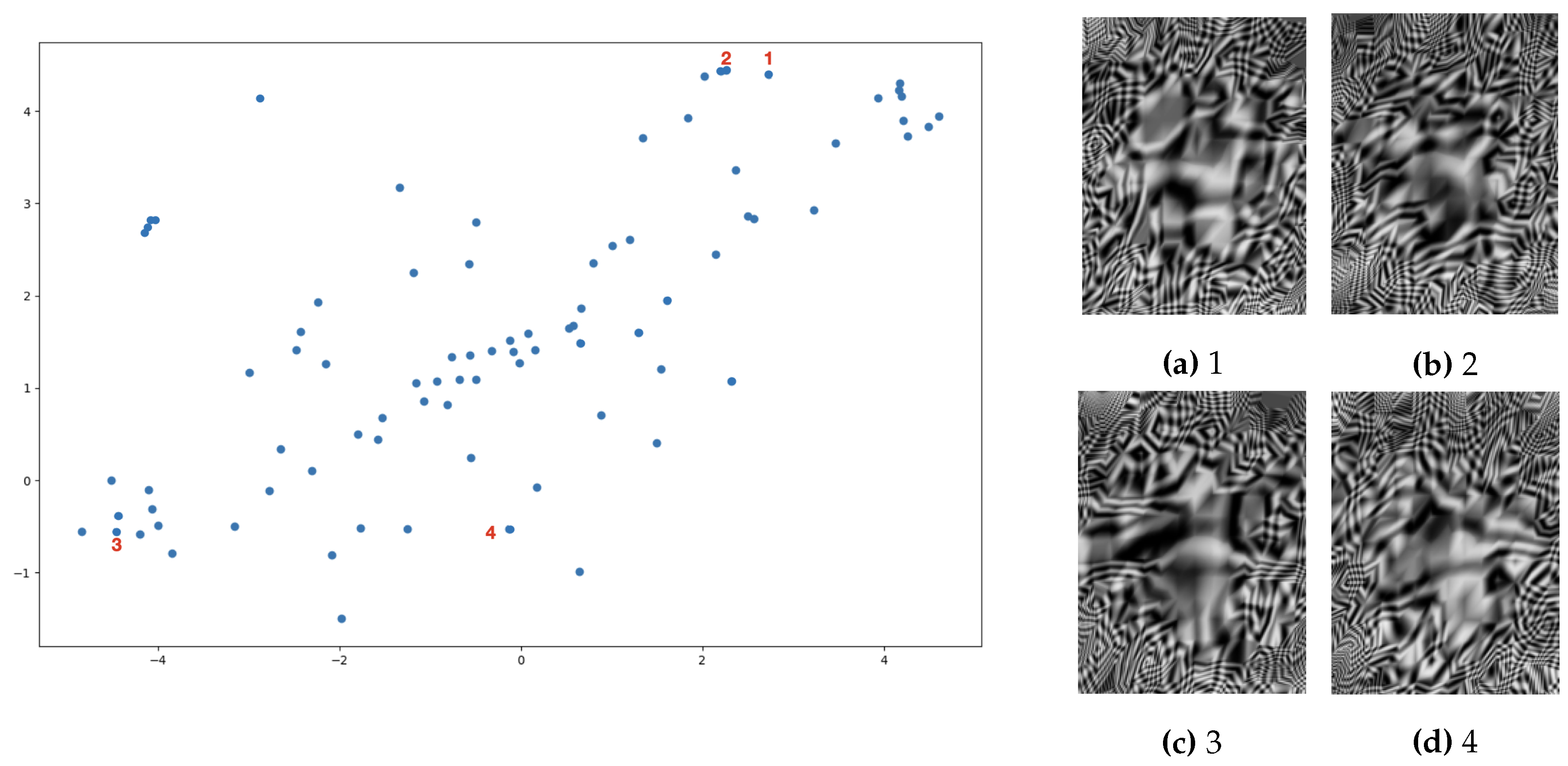
Table 1.
Performance comparison of different models on our generated dataset. VUDNet has reconstruction errors approximately one fourth that of competing methods, under all three criteria of Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Log Error.
Table 1.
Performance comparison of different models on our generated dataset. VUDNet has reconstruction errors approximately one fourth that of competing methods, under all three criteria of Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Log Error.
| Model | MAE | RMSE | LogError |
|---|---|---|---|
| VUDNet (On Concave) | 0.0443 | 0.0600 | 0.0122 |
| VUDNet (On Convex) | 0.0168 | 0.0218 | 0.0038 |
| VUDNet (General) | 0.0355 | 0.0470 | 0.0090 |
| 0.1607 | 0.1987 | 0.0790 | |
| (General) | 0.2052 | 0.2245 | 0.0451 |
* DYNet++ plus reconstructing the surface by zonal integration for reconstructing the surfaces as mentioned in [17]. Since there is no publicly available on the DYNET++ dataset, we were unable to test on their dataset, so we implemented their method on our dataset. ** For D-UNet [29], as there are no publicly available data or code, we implemented it based on [29] and tested it on our proposed dataset.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







