Investigation of Tunable Work Function, Electrostatic Force Microscopy and Band Structure of TiO2 Nanoparticles using Kelvin Probe Force Microscopy

The tunable work function of titanium dioxide (TiO₂) nanoparticles of various sizes was measured using the Kelvin Probe Force Microscopy (KPFM) technique. The analysis of the contact potential difference (CPD) across TiO₂ nanoparticles of different sizes revealed a clear relationship between nanoparticle size, surface roughness, and work function. The study observed work function values ranging from 4.49 eV to 4.57 eV for particle sizes between 3 nm and 85 nm, which were higher than those of bulk TiO₂, likely due to quantum confinement effects. Additionally, electrostatic force microscopy (EFM) measurements showed significant charge-trapping behavior within TiO₂ nanoparticles under different applied bias voltages. The optical analysis also revealed a quantum confinement-induced band gap of 3.35 eV, larger than that of bulk TiO₂, and distinct photoluminescence peaks at 383 nm and 403 nm, corresponding to near-band-edge excitonic emissions and defect-related states. By analyzing the conduction band (CB) and valence band (VB) of TiO₂ nanoparticles using KPFM, the CB and VB positions were calculated based on work function data and bandgap. The results indicated that as particle size increases, both CB and VB energies shift slightly towards lower values, where smaller nanoparticles exhibit larger band gaps and higher work functions.

Keywords:

Subject: Physical Sciences - Condensed Matter Physics

1. Introduction

Nanotechnology has completely transformed material science by allowing for the manipulation of materials at the atomic and molecular levels. This has led to the creation of nanomaterials with unique properties. Titanium dioxide (TiO₂) nanoparticles are especially intriguing because they can be used in a variety of applications such as photocatalysis, UV filtration, optoelectronics, and energy conversion[1,2]. These properties at the nanoscale level make TiO₂ ideal for a wide range of technological uses. At the nanoscale, materials are affected by quantum effects, surface phenomena, and structural morphology. Key factors that heavily influence the electronic properties of TiO₂ nanoparticles are particle size, surface roughness, and defects[3]. It has traditionally been challenging to understand the changes in work function based on nanoparticle size, morphology, and defects due to the limitations of conventional measurement techniques[4,5]. However, Kelvin probe force microscopy (KPFM) is an effective scanning probe microscopy (SPM) technique for characterizing the work function and local electrostatic potential of conductive or semiconductor materials at the nanoscale. Kelvin probe force microscopy (KPFM) is a technique that combines atomic force microscopy (AFM) and surface potential mapping using the principle of KPFM[6,7,8]. In KPFM, the electrostatic interaction between the tip and the surface controls the cantilever’s oscillation, unlike conventional AFM image acquisition. This uses a dual-signal detection scheme, with a DC signal to generate a force proportional to the difference in work function between the tip and surface, and an AC voltage to lead to the oscillation of the cantilever. When the frequency of the AC voltage matches the cantilever resonance frequency, a KPFM signal is generated. This allows for surface potential mapping[9,10,11]. Determining conduction band (CB) and valance band (VB) positions of semiconductor NPs is crucial for understanding their properties and applications. We used KPFM to investigate the band positions of semiconductor NPs and establish a correlation between their work function and band structure. This approach allows for precise determination of band edge positions of materials[12,13,14,15].

This research utilized Kelvin Probe Force Microscopy (KPFM) and Electrostatic Force Microscopy (EFM) to explore the electronic characteristics of TiO₂ nanoparticles at the nanoscale. KPFM accurately measures the work function by detecting the contact potential difference (CPD), while EFM investigates the behavior of charge trapping of TiO2 nanoparticles. Additionally, photoluminescence and absorption spectroscopy were employed to examine the optical properties of the TiO2 nanoparticles. The combination of KPFM and EFM with optical analysis provides a comprehensive understanding of the electronic and optical properties of TiO₂ nanoparticles based on their size, emphasizing the importance of adjusting nanoparticle size and surface morphology to achieve specific characteristics. This article offers a detailed analysis of the work function, electronic structure, and optical properties of TiO₂ nanoparticles, focusing on the effects of nanoparticle size and surface morphology. The results of this study not only enhance our understanding of TiO₂ nanomaterials but also provide practical recommendations for tailoring their properties to enhance performance in various technological applications.

2. Materials and Methods

Nanoparticles of TiO2 measuring less than 100nm in size were purchased from Sigma-Aldrich.The TiO2 was applied to a variety of surfaces, such as mica sheets, glass, and P-type silicon substrates, for different types of analysis. The scanning probe microscopy (SPM-9700HT, Shimadzu, Tokyo, Japan) was utilized to assess the morphology, KPFM, and EFM characteristics of the TiO2. AFM and KPFM were employed to investigate the electrical properties and work function, allowing for a precise determination of the morphology and surface potential. The substrates were carefully positioned on a piezoelectric stage for examination, and a conductive probe made of PtSi was affixed to the end of the cantilever to generate its topography. KPFM enhanced the analysis by producing images of the surface potential and topographic map at each scan point. The interaction between the probe and the sample surface comprised an electrostatic force component, providing valuable data on the surface potential. Proper sample preparation was essential for accurate mapping, with each sample attached to carbon tape and securely fastened to a steel disc for stability during scanning. The scanning was conducted at a speed of 0.5 Hz and a resolution of 256 × 256 pixels, yielding high-definition images with a spatial resolution of 0.2 nm. To obtain the measurements, Nanoworld provided a conductive tip Pt/Ir –coating with resonance frequency 75 k Hz and force constant 2.8 N/m. The acquisition of UV-visible absorption spectra was conducted utilizing a UV-2600i spectrophotometer produced by Shimadzu in Tokyo, Japan. Concurrently, photoluminescence spectra were recorded employing an RF-6000 spectrofluorometer, also manufactured by Shimadzu in Tokyo, Japan.

3. Results and Discussion

3.1. AFM and Surface Roughness of TiO₂ Nanoparticles

The results shown in Figure 1, displaying the Atomic Force Microscopy (AFM) analysis of TiO₂ nanoparticles, reveals significant insights into their surface topography and roughness. In panel (a), the topographic image showed how the nanoparticles were spread out on the surface, reaching heights of around 99.52 nm. The distribution of nanoparticle sizes was presented in the histogram in panel (b), a particle size distribution histogram based on data extracted from approximately 1800 nanoparticles in the image in Figure (1). Analysis using particle measurement software is revealing an average size of approximately 21 nm, with most particles falling between 10 to 30 nm. Panel (c) identified specific areas (A-B, C-D, and E-F) for a detailed examination of surface roughness and height, while panel d line profiles offered precise measurements of the surface roughness. Area A-B had the highest roughness (Ra) at 9.66 nm, with a particle height of 33 nm. In the C-D area, the Ra was slightly lower at 8.06 nm, with a height of 25.6 nm. In contrast, the E-F area had the smoothest surface, with an Ra of 0.95 nm and a height of 7 nm. These differences in roughness across different sections indicated an uneven distribution of nanoparticle sizes and surface textures. It is also important to note that as the nanoparticle size decreases, the surface roughness also decreases, which can be attributed to several key factors. As the nanoparticle size diminishes, the surface area to volume ratio increases significantly, resulting in a more uniform distribution of surface atoms and a smoother overall surface. Additionally, smaller nanoparticles tend to have fewer crystal defects and imperfections, leading to a smoother surface with fewer irregularities.

Figure 1. a) Atomic force microscopy (AFM) topography images of TiO2 nanoparticles on a mica substrate, Scan sizes of 8 µm × 8 µm (A). (b) Particle size distribution histogram , (c) high resolution topography images of TiO2 nanoparticles on a mica substrate Scan sizes of 3.3 µm × 3.3 µm ( (d) roughness analysis for TiO2 nanoparticles identified in the image (c).

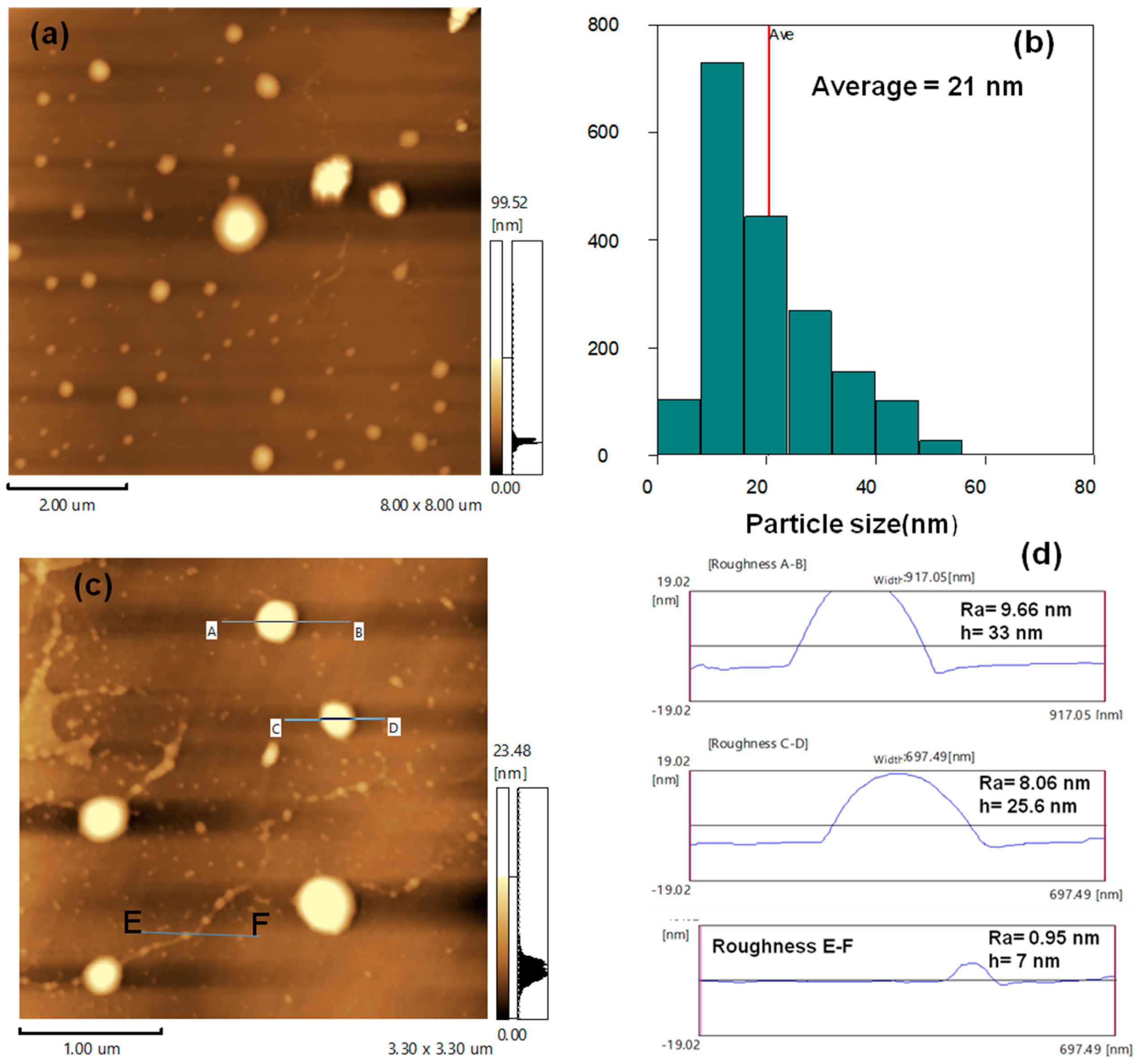
3.2. Kelvin Probe Force Microscopy of TiO₂NPs

Kelvin probe Force Microscopy is being utilized to analyze the properties of variable sizes for TiO2 nanoparticles and how their work function can be altered. A conductive probe allows for a thorough examination of the sample’s surface and its electrical characteristics. Through precise scanning and manipulation of the probe’s interaction with a constant force oscillation, we are able to gather data on the surface’s physical attributes, elevations, and electrical voltage distribution. This approach provides insight into the contact potential difference (CPD) and the electrical relationship between the probe and the sample. Figure 2 depicts images captured with the Atomic Force Microscopy (AFM) and Kelvin Probe Force Microscopy (KPFM) of titanium dioxide (TiO2) nanoparticles of different sizes. The scan size is 3.30×3.30 μm and shows a varied distribution of surface potentials indicated by the color contrast.

The potential scale on Figure 2 (c) and Figure (g) ranges from 6.14 Volt to 6.26 Volt, and from 6.12 Volt to 6.34 Volt, with brighter regions representing higher surface potentials. These differences in surface potential are due to variations in nanoparticle size. Line profiles taken from Figuer (d) and Figuer (h) offer detailed data about the surface potential along specific cross-sections of the TiO2 nanoparticles. The average Contact Potential Difference (CPD) for various sizes (3 nm, 8 nm, 25 nm, 33 nm, 73 nm, and 85 nm) of TiO2 nanoparticles, as shown in Figure 2(d) and Figuer (h), are 10 mV, 12 mV, 40 mV, 50 mV, 60 mV, and 90 mV, respectively[16]. The KPFM scan reveals a non-uniform surface potential distribution across the TiO2 nanoparticles, which is likely connected to the electronic structure of the nanoparticles. It is noted that larger particles have higher surface potentials due to their lower curvature and associated lower surface energy. This information is important for understanding the behavior and properties of TiO2 nanoparticles. In Figure 3, you can see the surface potential of a reference sample of Highly Ordered Pyrolytic Graphite (HOPG), grade ZYA, using KPFM. The sample has a mosaic spread of 0.4 ± 0.1◦ and measures 10 mm x 10 mm with a thickness of 1 mm.

It was provided by (MikroMasch,Wetzlar, Germany). Figure 3(b) displays the (CPD) of graphite substrate, which is approximatly 30 mV. This value offers important information about the surface properties and behavior of HOPG.

KPFM is a technique utilized to evaluate the work function of TiO₂ nanoparticles by analyzing the contact potential difference between the tip and the sample. This difference is connected to the variance in work function between the tip and sample, which allows for precise measurements at a nanoscale level, making it possible to analyze the work function of each TiO₂ nanoparticle.

The equation (1) can be employed to calculate the difference in work function associated with the CPD between the tip and the sample.

ϕ_{s a m p l e} = ϕ_{t i p} - e V_{C P D} 1

Where ‘e’ represents the charge of a single electron, and

V_{C P D}

refers to the Contact Potential Difference, which is the potential difference between the probe tip and the sample’s surface. To accurately determine the work function of TiO2 nanoparticles, it is essential to first establish the work function of the cantilever in the instrument. Calibration is essential for reliable measurements with a known reference for standardization. This research uses graphite sample with a work function of 4.5 to 5 eV, for precise calibration. By applying the identical equation (1) in the analysis of TiO2 nanoparticles in conjunction with HOPG substrates, it becomes possible to develop unique equations that are tailored to the characteristics of each substrate typ. The work function of the TiO2 nanoparticle substrate is denoted as

ϕ_{T i O 2}

and the specific Contact Potential Difference for the TiO2 nanoparticle substrate as V_{(CPD, TiO2)}. Similarly, when we specify the work function for the HOPG substrate as

ϕ_{H O P G}

and its unique Contact Potential Difference as V _{(CPD, HOPG)}, we arrive at an equations for the TiO2 and HOPG substrate as follows:

ϕ_{T i O 2} = ϕ_{t i p} - e V_{(C P D, T i O 2)} 2

Φ_{H O P G} = ϕ_{t i p} - e V_{(C P D, H O P G)} 3

By taking the difference between equation 2 and equation 3, a novel equation is derived that outlines the correlation between the work functions of TiO2 nanoparticles and the reference sample of Graphite, as demonstrated below:

ϕ_{T i O 2} = ϕ_{H O P G} + e (V_{(C P D, H O P G)} - V_{(C P D, T i O 2)}) 4

Utilizing equation (4) and examining the CPD values derived from Figure 2 and Figure 3, along with the documented work function values for highly oriented pyrolytic graphite (HOPG)[17], the work function of TiO2 nanoparticles of different sizes has been accurately calculated. The specific values obtained are outlined in Table 1, ranging from 4.49 eV to 4.57 eV. It is interesting to note that these values are higher than the work function of bulk TiO2, which is approximately 4.2 eV[18,19]. Several key factors influence the variation in work function values between TiO2 nanoparticles and bulk TiO2. A primary factor is quantum confinement due to the small size of nanoparticles, which limits electron mobility and raises energy levels. Consequently, more energy is needed to free an electron, resulting in a higher work function in nanoparticles compared to bulk TiO2. Additionally, nanoparticles have a greater surface area-to-volume ratio, altering the behavior of surface atoms and enhancing surface energy, thereby modifying the electronic structure and increasing work function. The unique morphology and surface features of nanoparticles significantly contribute to these changes. Moreover, their crystalline structure and defect presence also affect the work function, as variations in crystallinity and defects influence electronic properties. Figure 4 shows the correlation between work function and TiO2 nanoparticle size, indicating that larger particles lead to a decreased work function. This phenomenon is due to the isotropic surface curvature of symmetrical spheres. Moreover, smaller particles exhibit a higher work function, linked to the beneficial effects of curvature noted in research [20,21,22]. Equation (5) illustrates that smaller nanoparticles rely more on their surface characteristics.

ϕ_{E}^{s} = ϕ_{E}^{0} + \frac{1}{2 π ϵ} (\frac{e^{2}}{r_{a}}) 5

This highlights the link between quantum mechanics and electrostatics in a nanoscale regime, where properties vary by size and differ from bulk materials [23].

The relationship between the roughness of a surface and the work function of nanoparticles has a significant impact on their electronic properties and can be comprehensively studied using Kelvin Probe Force Microscopy (KPFM). Surface roughness refers to the small and large variations in the topography of nanoparticle surfaces, which affect the local electronic environment and, ultimately, the work function – the minimum energy required to extract an electron from the surface to the vacuum level. As surface roughness increases, the irregularities on the surface create local variations in electron density and electrostatic potential. These surface characteristics can result in increased electric fields at sharp protrusions or edges, making electron emission easier and lowering the work function. In a study of TiO2 nanoparticles, it was found that as surface roughness increased from 0.58 nm to 30 nm with the growth of nanoparticle size (from 3 nm to 85 nm in diameter), the work function decreased from 4.57 eV to 4.49 eV (refer to Table 1). This trend shows that larger particles with rougher surfaces had a lower energy barrier for electron emission compared to smaller, smoother particles. The slight decrease in work function with increasing roughness can be attributed to more pronounced local electric fields on rougher surfaces, reducing the energy needed for electron removal. These findings are consistent with similar studies in nanomaterials, indicating that increased surface roughness typically leads to a decrease in work function due to electrostatic and quantum effects at the nanoscale.

3.3. Electrostatic Force Microscopy of TiO₂NPs

The phenomenon of charge trapping in TiO₂ semiconductor nanoparticles significantly impacts their electronic and optoelectronic properties. Electrostatic Force Microscopy (EFM) is a powerful technique used to study this behavior at the nanoscale. Titanium dioxide (TiO₂) nanoparticles are widely studied for various applications, and charge trapping plays a critical role due to their large surface area and electronic properties. In semiconductor nanoparticles like TiO₂, charge trapping occurs when electrons or holes become localized in defect sites within the material, which can be intrinsic (such as oxygen vacancies) or extrinsic (such as impurities or surface states)[24,25]. EFM, a scanning probe technique, measures electrostatic forces between a charged tip and the sample surface and can detect charge trapping in nanoparticles by observing shifts in the phase or amplitude of the oscillating probe. By scanning the tip over the surface, EFM can map the distribution of trapped charges across the TiO₂ nanoparticles, providing insights into defect locations and the dynamics of charge trapping and de-trapping processes[26,27]. Figure 5 displays EFM features a range of images and cross sections related to TiO₂ nanoparticles, including topography images, EFM images at different bias voltages, and three-dimensional projections. Cross sections showing the height and EFM signal at both +6V and -6V biases are also provided for further analysis. Utilizing electrostatic force microscopy (EFM) to examine TiO₂ nanoparticles reveals significant differences in the nanoparticles’ electrostatic behavior when subjected to positive and negative bias voltages. For instance, under a +6V bias, the EFM image illustrates areas of increased electrostatic interaction, indicating a stronger attraction between the tip and the positively charged surface. However, under a -6V bias, the EFM image displays a contrast reversal, with darker regions signifying stronger repulsion or different charge accumulation on the nanoparticle surfaces. The increase in voltage at the nanoparticle peak under negative bias suggests charge accumulation, potentially due to defects or localized charge trapping. These images showcase the changes in the electrostatic environment under applied bias and highlight EFM’s sensitivity to local charges and potential differences. The cross-sectional profiles further validate this behavior, demonstrating a 19 mV variation in voltage under both positive and negative biases with opposite signs, indicating that the charge distribution changes direction depending on the applied field’s polarity. The potential distribution also differs between the positive and negative bias EFM images, with the positive bias resulting in lower potential regions within the nanoparticles, indicating charge depletion or differing interactions with the electric field[28].

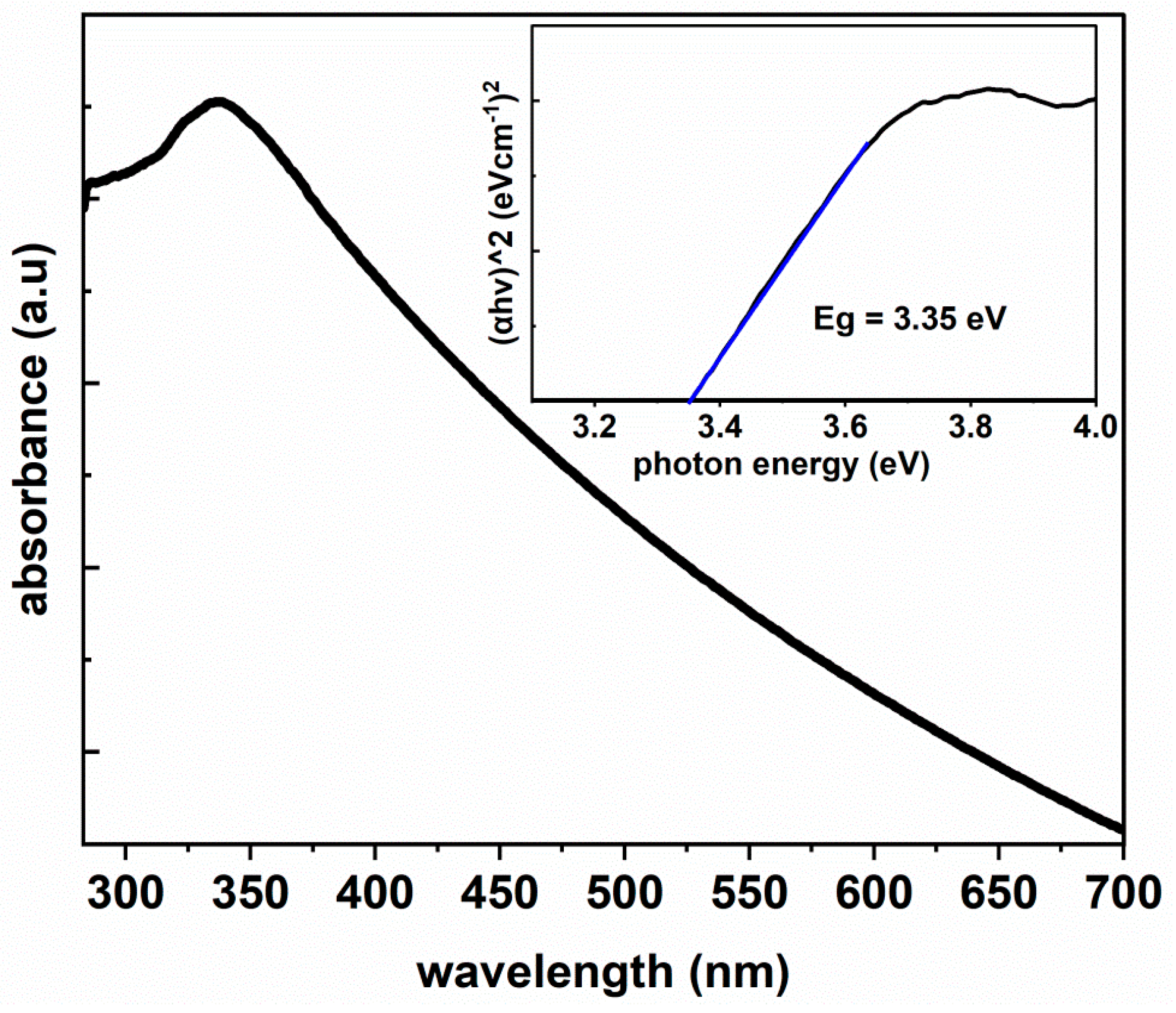
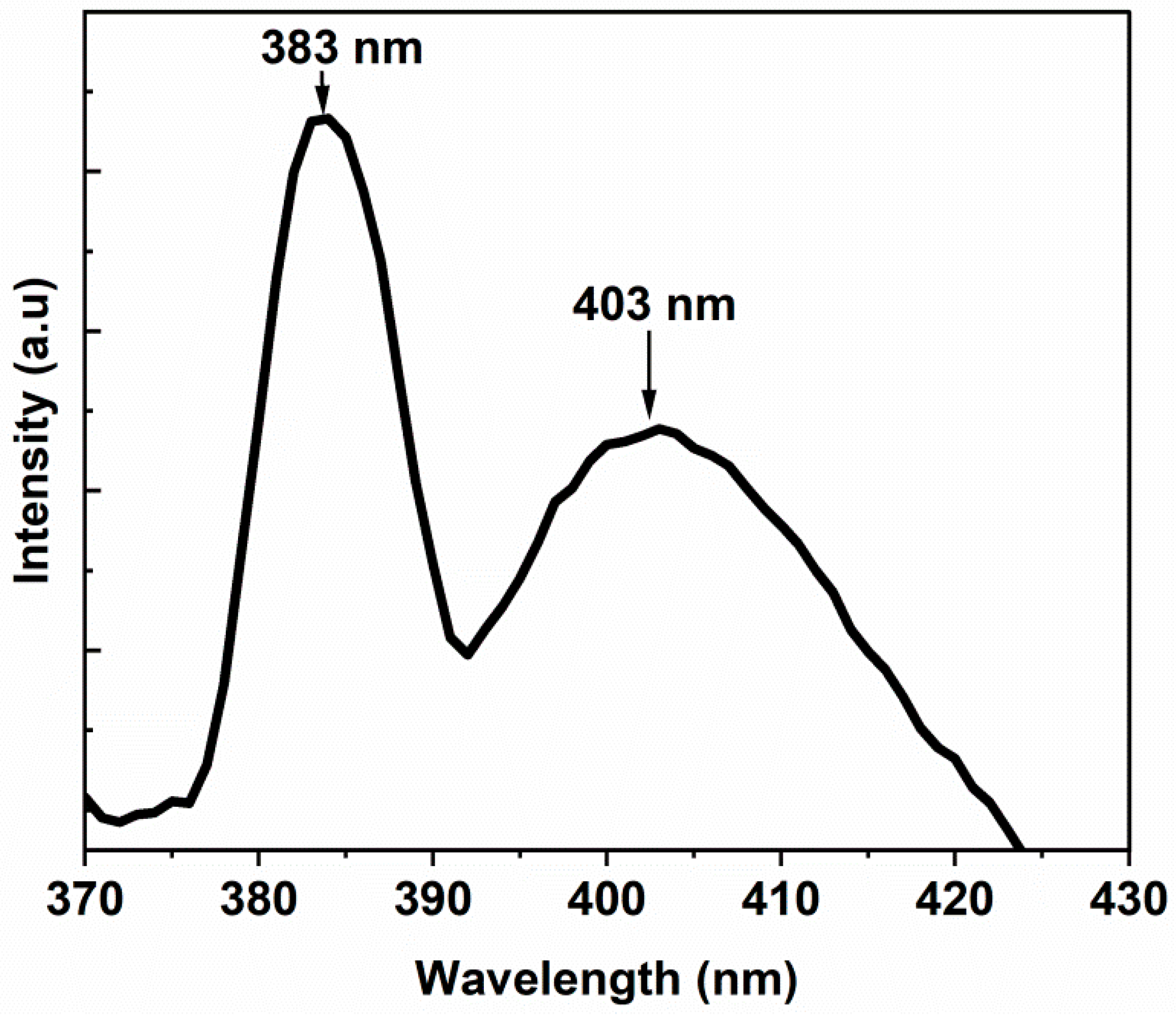
3.4. Optical Properties

The absorption spectrum of TiO₂ nanoparticles is shown in Figure 6, illustrating a significant absorption in the UV region followed by a gradual decline as the wavelength increases from approximately 300 nm to 700 nm. This spectrum is typical of semiconductor nanoparticles, where photon absorption causes electronic transitions from the valence band to the conduction band. The Tauc plot, included as an inset, provides a method for calculating the optical band gap of the nanoparticles By graphing (αhν)² as a function of photon energy (hν). The linear portion of the plot is used to determine the band gap energy, revealing a value of 3.35 eV for the TiO₂ nanoparticles[29,30,31]. It is observed that TiO2 nanoparticles have a significantly higher band gap energy than bulk TiO2, typically around 3.2 eV for the anatase phase. This increase in band gap is due to the quantum confinement effect as the nanoparticles approach the exciton Bohr radius, causing the continuous energy bands of bulk material to be divided into discrete energy levels. This results in a widening of the band gap as the particle size decreases. The band gap increase to 3.35 eV in TiO2 nanoparticles indicates that these particles are small enough to experience significant quantum confinement[32,33]. This wider band gap means that TiO2 nanoparticles absorb light at shorter wavelengths, making them more effective at absorbing ultraviolet (UV) light. This makes them suitable for applications in UV filtration, photocatalysis, and solar energy harvesting. The shift in absorbance towards higher energies can enhance the efficiency of TiO2 nanoparticles in these applications, especially under UV irradiation, where they can generate more energetic charge carriers compared to bulk counterparts.

Figure 6. Absorbance spectrum of TiO2 nanoparticles, inset – Tauc plot for energy band gap calculation.

Figure 7 depicts the photoluminescence (PL) spectrum of TiO2 nanoparticles, displaying two distinct emission peaks at 383 nm and 403 nm. The 383 nm peak is attributed to higher energy transitions, likely stemming from near-band-edge emissions resulting from the recombination of free or shallowly trapped excitons within the TiO2 structure. In contrast, the 403 nm emission suggests the existence of defect states or oxygen vacancies, creating localized energy states within the bandgap and allowing for radiative recombination at lower energies compared to the band-edge transitions. The presence of multiple emission peaks indicates the existence of various recombination centers within the nanoparticles. The sharp 383 nm peak represents a relatively pure transition near the band edge, while the broader 403 nm peak indicates emissions related to defects[34,35]. The significance of these emission peaks lies in their implications for the optical properties and potential applications of TiO2 nanoparticles. Understanding the origins and characteristics of these peaks can provide valuable insights into the electronic structure and defect chemistry of TiO2. The near-band-edge emissions at 383 nm are particularly important as they indicate the presence of free or shallowly trapped excitons, which play a crucial role in the photocatalytic and photoelectrochemical processes of TiO2. By studying and manipulating these excitonic transitions, researchers can develop strategies to enhance the efficiency and performance of TiO2-based devices, such as solar cells, sensors, and photocatalysts. On the other hand, the 403 nm emission peak linked to defect states or oxygen vacancies presents interesting possibilities for customizing and controlling the photoluminescence properties of TiO2 nanoparticles[36]. Understanding the nature and distribution of these defect states is crucial for optimizing the luminescent properties of TiO2, as well as for designing novel materials with tailored optical responses.

Figure 7. Photoluminescence (PL) spectrum of TiO2 nanoparticles.

3.5. Determination of $E_{c}$ and $E_{v}$ Using KPFM

Studying CB and VB with KPFM is essential for understanding electronic characteristics at the nanoscale. To determine the conduction band (CB) and valence band (VB) of TiO2 using Kelvin Probe Force Microscopy (KPFM), the first step involves carefully preparing the TiO2 nanoparticles for analysis. Once the nanoparticles are prepared, the KPFM technique measures their work function. KPFM works by bringing a conductive tip close to the surface of the TiO2 nanoparticles and applying an electrical bias to the tip, creating a force between the tip and the nanoparticles. Manipulating this force allows for the determination of the work function of the TiO2 nanoparticles. The work function represents the energy required to remove an electron from the material to the vacuum level and is crucial in understanding the electronic properties of TiO2. The Fermi level position provides essential information about the energy band structure of the material, while UV-Vis spectroscopy is utilized to estimate the bandgap of TiO2. Based on UV-Vis spectroscopy, the bandgap of TiO2 is determined to be approximately 3.35 eV. Knowledge of the Fermi level position and the bandgap makes it possible to compute the CB and VB positions. For n-type TiO2, the Fermi level is assumed to be near the minimum conduction band. Based on this assumption, the CB position can be directly derived from the work function obtained from the KPFM measurement. To determine the VB position, the bandgap is subtracted from the CB position. From a mathematical perspective, the CB position can be calculated as the negative value of the work function in electron volts (eV), and the VB position can be determined as the negative value of the combined sum of the work function and the bandgap in electron volts (eV) according to the following equations.

E_{c} (e V) = - w o r k f u n c t i o n (- \emptyset) 6

E_{v} (e V) = - w o r k f u n c t i o n (e V) - B a n d g a b (e V) 7

By utilizing KPFM and UV-Vis spectroscopy, along with precise computations based on the measured parameters, the conduction band and valence band of TiO2 nanoparticles can be identified. The results of the calculation for the conduction band and valence band for variable sizes of TiO2 nanoparticles are presented in Table 1. It can be observed from Table 1 that there is a slight change in the conduction band (CB) and valence band (VB) energies as the particle size increases, which is also reflected in the work function. For particles of 3 nm, the conduction band is at -4.57 eV, and the valence band is at -7.92 eV. These values shift slightly to -4.49 eV (CB) and -7.84 eV (VB) for 85 nm particles. The decrease in the work function is linked to slight shifts in the conduction and valence band energies, suggesting that as the particles grow larger, their energy bands move towards lower energies. The link between the decrease in the work function and the shift in the conduction and valence band energies with increasing particle size in TiO₂ nanoparticles can be explained by quantum confinement effects and surface phenomena. Quantum confinement effects dominate when nanoparticles are very small (typically less than 10 nm), resulting in quantized energy levels and larger band gaps, which increases the work function because of the need for more energy to move an electron. As the nanoparticle size increases, the quantum confinement effect weakens, causing the energy levels to become closer to those in the bulk material and the band gap to narrow. This results in the reduction of the work function as less energy is needed to remove an electron from the particle’s surface. Surface States and Roughness also play a role, with larger particles having increased surface roughness and more surface states, which can lower the energy barrier for electron emission, reducing the effective work function.

5. Conclusions

This study provides a thorough analysis of the work function, band structure, and electrostatic properties of TiO₂ nanoparticles (NPs) based on their size, using Kelvin Probe Force Microscopy (KPFM) and Electrostatic Force Microscopy (EFM). The research reveals a strong link between nanoparticle size, surface roughness, and the work function of TiO₂ NPs, which ranges from 4.49 eV to 4.57 eV for particles between 3 nm and 85 nm. The higher work function of the nanoparticles compared to bulk TiO₂ (typically 4.2 eV) is mainly due to quantum confinement effects. As nanoparticle size increases, surface roughness also increases, leading to a decrease in the work function due to reduced surface curvature and associated decrease in surface energy. Additionally, the study highlights the role of charge trapping in TiO₂ NPs, as revealed by EFM under different bias voltages. Furthermore, optical analysis demonstrates the impact of quantum confinement on TiO₂ NPs, with a measured band gap of 3.35 eV, higher than the typical bulk value of 3.2 eV for anatase TiO₂. Photoluminescence analysis shows emission peaks at 383 nm and 403 nm, indicating near-band-edge excitonic transitions and defect-related states, respectively. Moreover, KPFM and UV-Vis spectroscopy show that the conduction band (CB) and valence band (VB) energies of TiO₂ nanoparticles slightly shift with increasing particle size, accompanied by a decrease in the work function. This study provides valuable insights into the versatile electronic and optical properties of TiO₂ nanoparticles, influenced by size, surface roughness, and defects. The findings are crucial for advancing the design and improvement of TiO₂-based materials for various applications, including photocatalysis, UV filtration, and optoelectronic devices.

Author Contributions

Conceptualization, I.M.; methodology, I.M.; validation, I.M., N.Q.;J.G and S.T.M.; data curation, I.M., N.Q.;J.G and S.T.M.; writing—original draft preparation, I.M.; writing—review and editing, I.M., N.Q.; J.G; and S.T.M. All authors have read and agreed to the published version of the manuscript

Funding

This research received no external funding

Data Availability Statement

Data will be made available on request.

Acknowledgments

The authors are grateful to Palestine Technical University-Kadoorie (PTUK) and United Arab Emirate University for the facilities and support .

Conflicts of Interest

The authors declare no conflicts of interest.

References

Parrino, F.; Palmisano, L. Titanium Dioxide (TiO2) and Its Applications; Elsevier Science, 2020; ISBN 978-0-12-820434-4.
Akakuru, O.U.; Iqbal, Z.M.; Wu, A. TiO Nanoparticles. In TiO2 Nanoparticles; John Wiley & Sons, Ltd., 2020; pp. 1–66 ISBN 978-3-527-82543-1.
Abdullah, E.A. Band Edge Positions as a Key Parameter to a Systematic Design of Heterogeneous Photocatalyst. Eur. J. Chem. 2019, 10, 82–94. [Google Scholar] [CrossRef]
Li, D.; Song, H.; Meng, X.; Shen, T.; Sun, J.; Han, W.; Wang, X. Effects of Particle Size on the Structure and Photocatalytic Performance by Alkali-Treated TiO2. Nanomaterials 2020, 10, 546. [Google Scholar] [CrossRef] [PubMed]
Tesfaye Jule, L.; Ramaswamy, K.; Bekele, B.; Saka, A.; Nagaprasad, N. Experimental Investigation on the Impacts of Annealing Temperatures on Titanium Dioxide Nanoparticles Structure, Size and Optical Properties Synthesized through Sol-Gel Methods. Materials Today: Proceedings 2021, 45, 5752–5758. [Google Scholar] [CrossRef]
Glatzel, T.; Gysin, U.; Meyer, E. Kelvin Probe Force Microscopy for Material Characterization. Microscopy 2022, 71, i165–i173. [Google Scholar] [CrossRef]
Kim, Y.-M.; Lee, J.; Jeon, D.-J.; Oh, S.-E.; Yeo, J.-S. Advanced Atomic Force Microscopy-Based Techniques for Nanoscale Characterization of Switching Devices for Emerging Neuromorphic Applications. Applied Microscopy 2021, 51, 7. [Google Scholar] [CrossRef] [PubMed]
Wang, J.; Zhang, H.; Cao, G.; Xie, L.; Huang, W. Injection and Retention Characterization of Trapped Charges in Electret Films by Electrostatic Force Microscopy and Kelvin Probe Force Microscopy. physica status solidi (a) 2020, 217, 2000190. [Google Scholar] [CrossRef]
Checa, M.; Neumayer, S.M.; Tsai, W.-Y.; Collins, L. Advanced Modes of Electrostatic and Kelvin Probe Force Microscopy for Energy Applications. In Atomic Force Microscopy for Energy Research; CRC Press, 2022 ISBN 978-1-00-317404-2.
Zhang, H.; Gao, H.; Geng, J.; Meng, X.; Xie, H. Torsional Harmonic Kelvin Probe Force Microscopy for High-Sensitivity Mapping of Surface Potential. IEEE Transactions on Industrial Electronics 2022, 69, 1654–1662. [Google Scholar] [CrossRef]
Chen, S.; Dong, H.; Yang, J. Surface Potential/Charge Sensing Techniques and Applications. Sensors 2020, 20, 1690. [Google Scholar] [CrossRef]
Zhang, W.; Chen, Y. Experimental Determination of Conduction and Valence Bands of Semiconductor Nanoparticles Using Kelvin Probe Force Microscopy. J Nanopart Res 2013, 15, 1334. [Google Scholar] [CrossRef]
Henning, A.; Günzburger, G.; Jöhr, R.; Rosenwaks, Y.; Bozic-Weber, B.; Housecroft, C.E.; Constable, E.C.; Meyer, E.; Glatzel, T. Kelvin Probe Force Microscopy of Nanocrystalline TiO2 Photoelectrodes. Beilstein J Nanotechnol 2013, 4, 418–428. [Google Scholar] [CrossRef]
Melitz, W.; Shen, J.; Lee, S.; Lee, J.S.; Kummel, A.C.; Droopad, R.; Yu, E.T. Scanning Tunneling Spectroscopy and Kelvin Probe Force Microscopy Investigation of Fermi Energy Level Pinning Mechanism on InAs and InGaAs Clean Surfaces. Journal of Applied Physics 2010, 108, 023711. [Google Scholar] [CrossRef]
Lanzoni, E.M.; Gallet, T.; Spindler, C.; Ramírez, O.; Boumenou, C.K.; Siebentritt, S.; Redinger, A. The Impact of Kelvin Probe Force Microscopy Operation Modes and Environment on Grain Boundary Band Bending in Perovskite and Cu(In,Ga)Se2<math><msub Is=“true”><mrow Is=“true”></Mrow><mrow Is=“true”><mn Is=“true”>2</Mn></Mrow></Msub></Math> Solar Cells. Nano Energy 2021, 88, 106270. [Google Scholar] [CrossRef]
Miyazaki, M.; Wen, H.F.; Zhang, Q.; Adachi, Y.; Brndiar, J.; Štich, I.; Li, Y.J.; Sugawara, Y. Imaging the Surface Potential at the Steps on the Rutile TiO ₂ (110) Surface by Kelvin Probe Force Microscopy. Beilstein J. Nanotechnol. 2019, 10, 1228–1236. [Google Scholar] [CrossRef] [PubMed]
Musa, I.; Faqi, R. Structural, Electrostatic Force Microscopy, Work Function, and Optical Characterization of Pure and Al-Doped ZnO Nanoparticles. Results in Materials 2024, 22, 100570. [Google Scholar] [CrossRef]
Fakhouri, H.; Arefi-Khonsari, F.; Jaiswal, A.K.; Pulpytel, J. Enhanced Visible Light Photoactivity and Charge Separation in TiO2/TiN Bilayer Thin Films. Applied Catalysis A: General 2015, 492, 83–92. [Google Scholar] [CrossRef]
Mansfeldova, V.; Zlamalova, M.; Tarabkova, H.; Janda, P.; Vorokhta, M.; Piliai, L.; Kavan, L. Work Function of TiO ₂ (Anatase, Rutile, and Brookite) Single Crystals: Effects of the Environment. J. Phys. Chem. C 2021, 125, 1902–1912. [Google Scholar] [CrossRef]
Kaur, J.; Kant, R. Curvature-Induced Anomalous Enhancement in the Work Function of Nanostructures. J. Phys. Chem. Lett. 2015, 6, 2870–2874. [Google Scholar] [CrossRef]
Taylor, K.J.; Pettiette-Hall, C.L.; Cheshnovsky, O.; Smalley, R.E. Ultraviolet Photoelectron Spectra of Coinage Metal Clusters. The Journal of Chemical Physics 1992, 96, 3319–3329. [Google Scholar] [CrossRef]
Musa, I.; Ghabboun, J. Work Function, Electrostatic Force Microscopy, Tunable Photoluminescence of Gold Nanoparticles, and Plasmonic Interaction of Gold Nanoparticles/Rhodamine 6G Nanocomposite. Plasmonics 2024. [Google Scholar] [CrossRef]
Vollath, D.; Fischer, F.D.; Holec, D. Surface Energy of Nanoparticles – Influence of Particle Size and Structure. Beilstein J. Nanotechnol. 2018, 9, 2265–2276. [Google Scholar] [CrossRef]
Khoury, D.E. Towards the Use of Electrostatic Force Microscopy to Study Interphases in Nanodielectric Materials. phdthesis, Université Montpellier, 2017.
Marchi, F.; Dianoux, R.; Smilde, H.J.H.; Mur, P.; Comin, F.; Chevrier, J. Characterisation of Trapped Electric Charge Carriers Behaviour at Nanometer Scale by Electrostatic Force Microscopy. Journal of Electrostatics 2008, 66, 538–547. [Google Scholar] [CrossRef]
Kaja, K.; Mariolle, D.; Chevalier, N.; Naja, A.; Jouiad, M. Sub-10 Nm Spatial Resolution for Electrical Properties Measurements Using Bimodal Excitation in Electric Force Microscopy. Review of Scientific Instruments 2021, 92, 023703. [Google Scholar] [CrossRef] [PubMed]
Chen, G.; Xu, Z. Charge Trapping and Detrapping in Polymeric Materials. Journal of Applied Physics 2009, 106, 123707. [Google Scholar] [CrossRef]
Silva-Pinto, E.; Neves, B.R.A. Charge Injection on Insulators via Scanning Probe Microscopy Techniques: Towards Data Storage Devices. Journal of Nanoscience and Nanotechnology 2010, 10, 4204–4212. [Google Scholar] [CrossRef]
Fidalgo, A.; Letichevsky, S.; Santos, B.F. Assessment of TiO2 Band Gap from Structural Parameters Using Artificial Neural Networks. Journal of Photochemistry and Photobiology A: Chemistry 2021, 405, 112870. [Google Scholar] [CrossRef]
Safiay, N.M.; Rani, R.A.; Azhar, N.E.A.; Khusaimi, Z.; Hamzah, F.; Rusop, M. Influence of Different Annealing Temperatures on the Structural and Optical Properties of TiO 2 Nanoparticles Synthesized via Sol-Gel Method: Potential Application as UV Sensor. Indonesian Journal of Chemistry 2021, 21, 279–285. [Google Scholar] [CrossRef]
Mithun, M.H.; Sayed, A.; Rahaman, I. The Effect of Band-Gap on TiO2 Thin Film Considering Various Parameters. Proceedings of Engineering and Technology Innovation 2021, 19, 45–52. [Google Scholar] [CrossRef]
Sharma, S.; Venkata Dhanunjaya Reddy, A.; Jayarambabu, N.; Vikram Manoj Kumar, N.; Saineetha, A.; Venkateswara Rao, K.; Kailasa, S. Synthesis and Characterization of Titanium Dioxide Nanopowder for Various Energy and Environmental Applications. Materials Today: Proceedings 2020, 26, 158–161. [Google Scholar] [CrossRef]
D’Elia, D.; Beauger, C.; Hochepied, J.-F.; Rigacci, A.; Berger, M.-H.; Keller, N.; Keller-Spitzer, V.; Suzuki, Y.; Valmalette, J.-C.; Benabdesselam, M.; et al. Impact of Three Different TiO2 Morphologies on Hydrogen Evolution by Methanol Assisted Water Splitting: Nanoparticles, Nanotubes and Aerogels. International Journal of Hydrogen Energy 2011, 36, 14360–14373. [Google Scholar] [CrossRef]
Sampaio, M.J.; Yu, Z.; Lopes, J.C.; Tavares, P.B.; Silva, C.G.; Liu, L.; Faria, J.L. Light-Driven Oxygen Evolution from Water Oxidation with Immobilised TiO2 Engineered for High Performance. Sci Rep 2021, 11, 21306. [Google Scholar] [CrossRef]
Abdullah, S.A.; Sahdan, M.Z.; Nafarizal, N.; Saim, H.; Bakri, A.S.; Cik Rohaida, C.H.; Adriyanto, F.; Sari, Y. Photoluminescence Study of Trap-State Defect on TiO ₂ Thin Films at Different Substrate Temperature via RF Magnetron Sputtering. J. Phys.: Conf. Ser. 2018, 995, 012067. [Google Scholar] [CrossRef]
Mahesh, A.; Jawahar, I.N.; V, B. Photoluminescence, Photocurrent Response and Photocatalytic Activity of Hydrothermally Derived Nanocrystalline Zno with Native Point Defects 2023.

Figure 2. KPFM of variable sizes of TiO2 nanoparticles deposited on Si substate (a) and (e) Topography (b) Topography profiles along lines A-B(1),C-D(2),E-F(3),and G-H(4) extract from image (a),(f) Topography profiles of particles 5 and 6 from image (e). (c) and (g) Surface potential. (d) and (h) surface potential profiles of variable sizes TiO2 nanoparticles along lines (1-6) in image (c) and (g).

Figure 3. (a) KPFM image of reference substrate (HOPG), (b) (CPD) of HOPG extract from image (a).

Figure 4. Work function and contact potential difference (CPD) of variable sizes of TiO2 nanoparticles.

Figure 5. (a) AFM image of TiO2 nanostructure, (b) EFM of the TiO2 nanostructure bias voltage at positive 6 V, (c) EFM of the TiO2 nanostructure bias voltage at negative 6 Volt, (d,e,f) Three-dimensional images of AFM and EFM of TiO2 nanostructures, (g) profile height of TiO2 nanostructures, (h) EFM profile of TiO2 nanostructures at positive 6 Volt, (i) EFM profile of TiO2 nanoparticles at negative 6 Volt.

Table 1. Contact potential difference, work function and band structure of TiO2 nanoparticles properties.

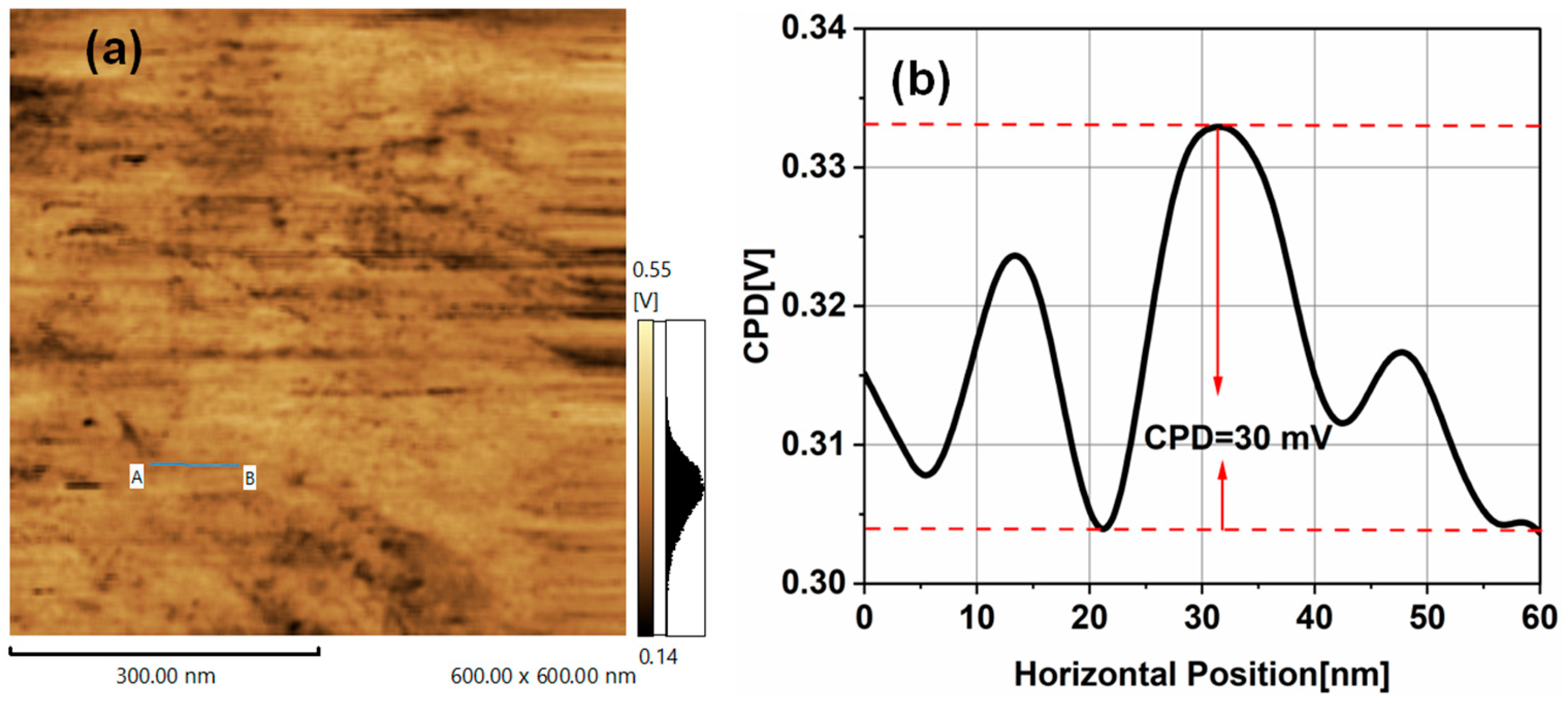
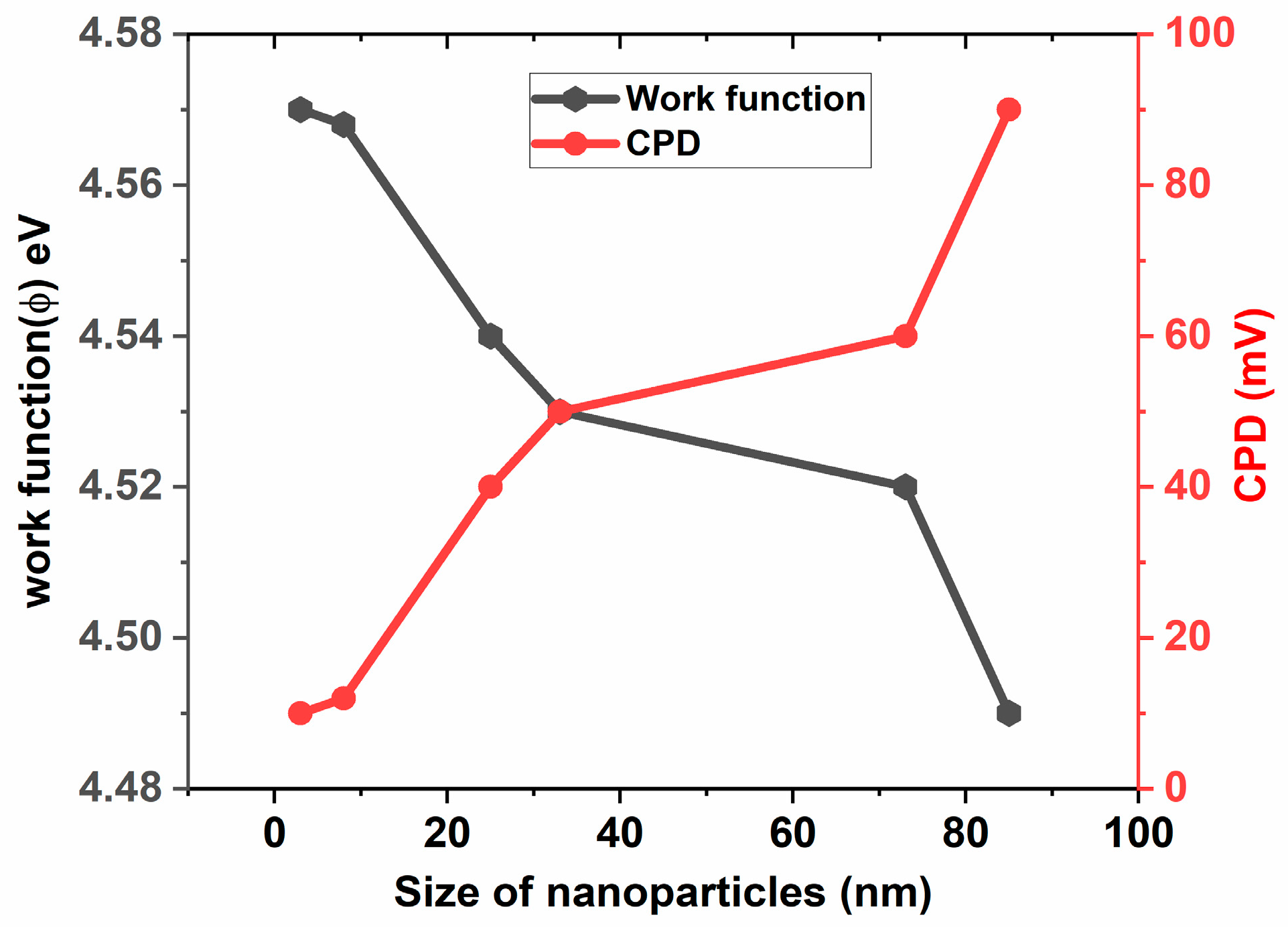
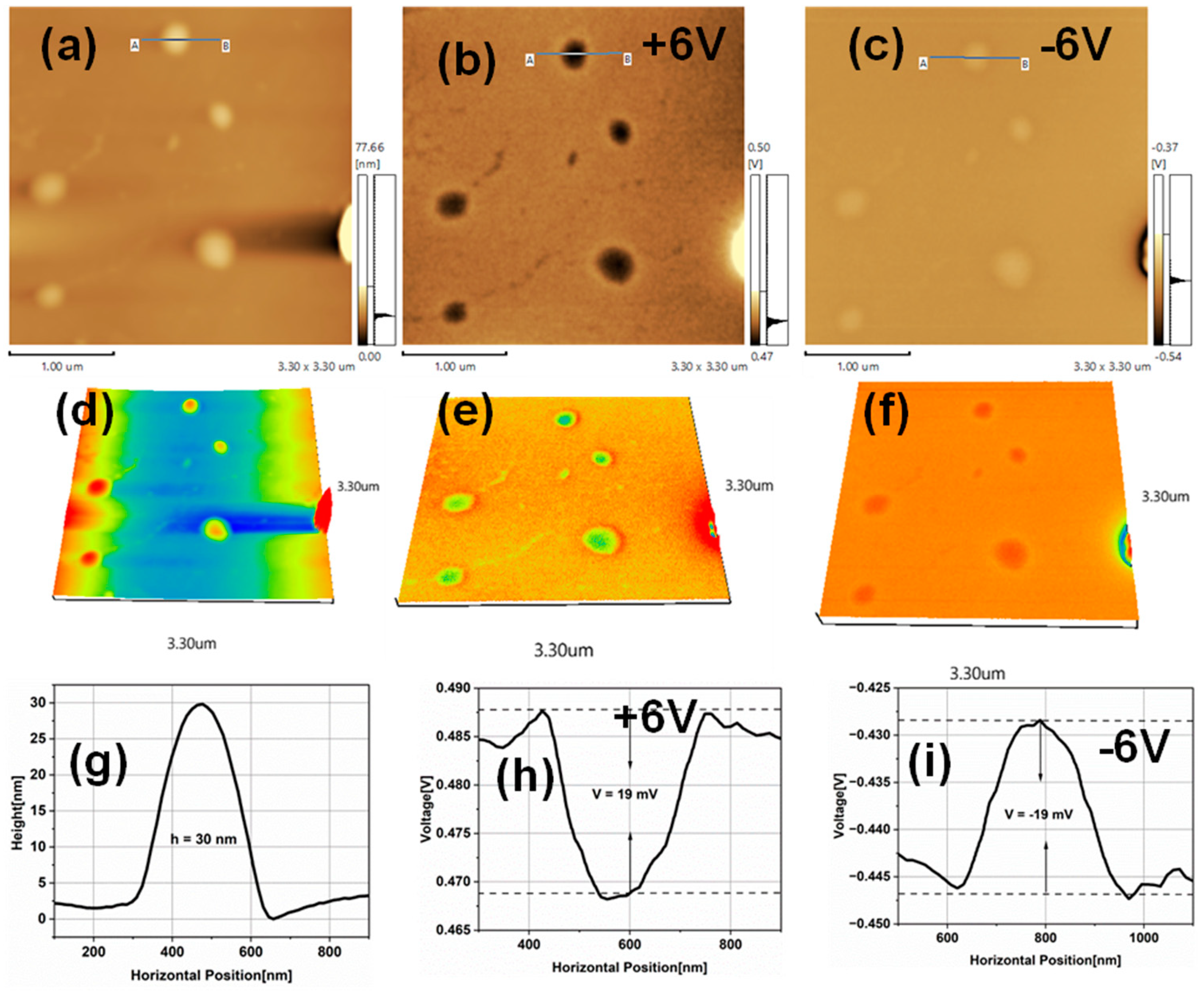
Particle Size (nm)	surface roughness (nm)	CPD (mV)	Work function(Φ) (eV)	Conduction band (eV)	Valance band (eV)
3	0.58	10	4.57	-4.57	-7.92
8	0.95	12	4.568	-4.568	-7.918
25	8.06	40	4.54	-4.54	-7.89
33	9.66	50	4.53	-4.53	-7.88
73	23.92	60	4.52	-4.52	-7.87
85	30.57	90	4.49	-4.49	-7.84

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer