Preprint
Article
Fragility Analysis of Buried Operating Steel Pipeline Under Longitudinal Permanent Ground Deformation
Altmetrics
Downloads
60
Views
107
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 September 2024
Posted:
25 September 2024
You are already at the latest version
Alerts
Abstract
Structural integrity of buried pipelines is threatened by the effects of Permanent Ground Deformation (PGD), resulting from seismic-induced landslides and lateral spreading due to liquefaction parallel to the pipeline axis, requiring accurate analysis of the system performance. Analytical fragility functions allow to estimate the likelihood of seismic damage along the pipeline, supporting design engineers and network operators in prioritizing resource allocation for mitigative or remedial measures in spatially distributed lifeline systems.
To efficiently and accurately evaluate the seismic fragility of buried operating steel pipeline under longitudinal PGD, this study develops an analytical model considering the asymmetric pipeline material behavior in tension and compression under varying operational loads. The validated model is further implemented within a fragility function calculation framework based on Monte Carlo Simulation (MCS), allowing to assess the probability of exceedance of the pipeline performance limit states conditioned to the intensity of PGD.
The evaluated fragility surfaces showed that the pipeline probability of exceeding the performance criteria increases for larger soil displacement and lengths, as well as cover depths, because of the greater mobilized soil reaction counteracting pipeline deformation. Additionally, the performed Global Sensitivity Analysis (GSA) highlighted the influence of the PGD and soil-pipeline interaction parameters, as well as the effect of the service loads on structural performance, requiring proper consideration in pipeline system modeling and design.
Finally, the proposed analytical fragility function calculation framework provides a useful methodology for effectively assessing the performance of operating pipelines under longitudinal PGD, quantifying the effect of the uncertain parameters impacting structural response.
Keywords:
Subject: Engineering - Civil Engineering
1. Introduction
Buried continuous pipelines are vulnerable to the effects of Permanent Ground Deformation (PGD) resulting from seismic-induced landslides, faulting, and lateral spreading due to liquefaction. The pipeline response depends on its orientation with respect to the direction of the ground movement, that is generally a combination of transverse and longitudinal ground movement, occurring perpendicular and parallel to the pipeline axis, respectively. Transverse PGD induce predominant shear and bending stresses at the margins of the PGD zone, similar to the fault crossing problem investigated by many researchers during the last 50 years (Kennedy et al. 1977, Karamitros et al. 2011, Trifonov and Cherniy 2011, Sarvanis and Karamanos, 2017, Banushi and Squeglia, 2018). Conversely, longitudinal PGD results in axial compression and tension in the pipeline that may ultimately lead to local buckling and tensile rupture, respectively. According to previous investigations (O’Rourke and Nordberg, 1991, 1992a; O’Rourke and Liu, 2012; Suzuki and Hagio, 1990), buried continuous pipelines are significantly more vulnerable to PGD in longitudinal direction, requiring detailed analysis of the system performance under this hazard.
The response of buried continuous pipelines subjected to longitudinal PGD depends on the pipe deformation capacity in operating conditions, soil-structure interaction, as well as the amount of ground movement δ, its spatial extent Lb, and pattern of ground deformation (Figure 1).
The rigid block pattern, defined by a downslope movement δ within the soil block length Lb, induces localized relative soil-pipeline displacement at the margins, resulting in largest pipe strains, compared to other distributive geometries considered by O’Rourke and Nordberg (1992a). Consequently, this pattern has been extensively employed within simple analytical or more complex numerical methods to assess the pipeline performance under longitudinal PGD (O’Rourke and Nordberg 1992a; 1992b; O’Rourke et al., 1995; ALA 2005; IITK-07, 2007; Toprak et al., 2010; Wijewickreme et al., 2005; Wham and Davis 2019; Banushi and Wham, 2021; Bain et al., 2024).
The analytical structural models are more computationally efficient, compared to the complex numerical analysis approach, which requires further expertise of the engineer to analyse the models for use in routine engineering applications (C-CORE et al. 2009).
The existing analytical models for assessing the deformation of buried continuous pipelines subjected to longitudinal PGD consider the pipe material either as linear elastic (O’Rourke and Nordberg 1992a; 1992b) or inelastic, following a Ramberg-Osgood stress-strain relationship equal in tension and compression (O’Rourke et al., 1995; Bain et al., 2024).
Two conditions are established for which the pipeline deformation demand is assessed, depending on whether the soil block length Lb is short (case I) or long (case II) enough to fully mobilize soil reaction along the pipeline under the imposed ground displacement. The pipeline design force is computed as the minimum between the ultimate soil reaction transferable to the pipe over a length of Lb/2 (case I) and the force computed assuming the pipeline fully compliant with the soil (case II), as recommended by the 2005 ALA guideline. This model predicts that half the total applied soil load is resisted in tension and half in compression, because of the assumed symmetric configuration of the soil-pipeline system, including the material constitutive relationships in tension and compression.
This is not representative for pipelines of materials with different stress-strain relationship in tension and compression under uniaxial or biaxial stress state conditions, resulting in asymmetric pipeline loading and strain demand in the tensile and compressive ground deformation zone.
Therefore, to accurately assess the pipeline performance under longitudinal PGD, it is necessary to adopt analytical methods considering an asymmetric nonlinear material behavior of the operating pipeline in tension and compression as well as the elastoplastic axial soil-pipeline interaction (e.g. Banushi and Squeglia 2018; Schaumann et al. 2005).
The analytical models can be efficiently implemented within a seismic fragility analysis framework to evaluate the structural performance considering the uncertainties of the system parameters.
Pipeline fragility assessment requires proper consideration of the variability of the physical characteristics of the soil-pipe system, including the material strength properties, the soil cover depth, and pipe operational loads such as temperature difference and internal pressure (Honneger et al., 2014; Banushi et al. 2017, 2018; Tsatsis et al., 2022).
These uncertainties are considered within a probabilistic framework like the Monte Carlo Simulation (MCS), employing a large number of soil-pipeline system samples, generated by random sampling of the input system parameters, based on their probability distribution.
The generated seismic demand samples are compared with the structural capacity values associated with a certain performance limit state, allowing to estimate the associated probability of exceedance as a function of the level of seismic intensity measure, IM (Zhou, 2012; Toprak and Cirmiktili, 2021). The latter is defined by a group of representative seismic ground motion parameters, e.g. the peak ground displacement δ, and the length of the PGD zone Lb. Conversely, the structural limit states are defined on the basis of an adequate Engineering Demand Parameter (EDP), e.g. the peak longitudinal strain, describing the system performance (Elnashai and Di Sarno 2015; Di Sarno and Elnashai, 2019)
The analytical fragility relationships represent a useful design tool, allowing to identify precise locations of pipeline damage, that is fundamental in evaluating pipeline seismic performance and prioritizing resource allocation for mitigative or remedial measures in spatially distributed lifeline systems.
To efficiently evaluate the seismic fragility of buried operating steel pipelines under longitudinal PGD, this study develops an analytical model considering the nonlinear properties of system, and the effect of the service loads, that is validated through accurate finite element analysis. The analytical model is further implemented within a fragility function calculation framework based on Monte Carlo Simulation (MCS), allowing to evaluate the probability of exceedance of the pipeline performance limit states conditioned to the ground displacement hazard. Furthermore, to quantify the influence of the uncertain input parameters on the predicted pipeline performance, this study conducts Global Sensitivity Analysis (GSA), based on the Sobol’s variance decomposition method, using MCS to calculate the Sobol’s sensitivity indices.
First, this paper presents the methodology adopted to evaluate seismic fragility of buried pipelines subjected to longitudinal PGD, using an accurate analytical model considering the asymmetric pipeline material behavior in tension and compression under varying service loads.
Then, the obtained fragility analysis results are carefully discussed and compared with data reported in other research publications, highlighting the main factors influencing the seismic performance of buried operating pipelines, considering the system uncertainties. Finally, the conclusion section highlights the contributions of the present paper to the state-of-the-art practice and research of pipeline seismic design, suggesting further important perspectives related to the addressed issues.
2. Methodology
This section presents the adopted methodology to assess the seismic fragility of buried operating pipelines subjected to longitudinal PGD. First, the developed analytical model is described, allowing to evaluate the buried operating pipeline performance under longitudinal PGD, as a function of the system nonlinearities and operation loads. Second, it defines the pipeline performance limit states evaluated through the structural analysis. Then, the analytical model results are compared to the finite element analysis results, demonstrating the validity of the proposed analytical procedure. Finally, it presents a probabilistic framework, based on Monte Carlo Simulation (MCS), to evaluate the fragility functions and quantify the effect of system uncertainties.
2.1. Analytical Model for Assessment of the Continuous Pipeline Response under Longitudinal PGD
This paragraph describes the developed analytical model for assessing the performance of buried continuous pipelines under longitudinal PGD, considering the nonlinear material constitutive relationships, force equilibrium, and displacement compatibility along the pipe-soil system. This algorithm allows implementation of the asymmetric nonlinear stress-strain relationship for the pipe material in tension and compression, as well as the elastoplastic axial soil-pipeline interaction, accurately assessing the response of the system subjected to this geohazard.
The ground deformation is idealized as rigid-block movement, defined by a downslope movement δ over a block length Lb, resulting in a tension crack of width δ at the upslope end and a compression ridge over a distance δ on the downslope end (Figure 2a). The soil displacement assumes a constant value δ within the PGD zone, while being zero on either side of it.
The moving soil block tends to pull the pipe along with it, resulting in localized relative soil-pipeline displacement at the margins of the PGD zone, and associated resistance forces on either side of the sliding block head and toe. This results in a maximum pipeline axial force at the head and maximum axial compression force at the toe, decreasing linearly thereupon due to the sliding soil friction (fs). Beyond this zone, the relative soil-pipeline displacement is negligible, and the pipeline displacement matches that of the ground (case II). As the soil displacement increases reaching a critical value δ = δcr, the relative soil-pipeline displacement and associated friction reaction are mobilized over the entire soil block length, and the pipeline deformation remains constant thereafter (case I).
Evidently, the region of the soil-pipeline system beyond the soil block behaves like a pull-out test in tension (region I and region II) and compression (region II and region IV), with the end displacement applied the pipe points underlying the tension crack and compression bulge, respectively (Figure 2a). The total pipeline elongation at each side the soil block head i.e., in region 1 (Up1) and region 2 (Up2), is equal to the magnitude of the overall pipeline contraction at each side of the toe of the sliding block, i.e., in region 3 (Up3) and region 4 (Up4).
The strain demand is calculated using the analytical model developed by Banushi (2017) evaluating the structural response of a continuous buried pipeline, subjected to a pullout force one end (x = 0). The resulting pipeline displacement is obtained by integrating the axial strains associated with the axial force distribution along the pipeline, considering the beam on elastic foundation theory for the static friction length, and the force equilibrium for the frictional sliding length (Figure 2b and 2c). The model employs the theory of plasticity for modeling the pipe material based on normality plastic flow rule, the von Mises yield criterion, and isotropic strain hardening, accounting for the initial axial thermal strains and biaxial stress state in the pipe due to internal pressure.
The pipe material is assumed to have a piecewise stress-strain curve, defined by the engineering strain-stress values (εi, σi), either in tension (ε > 0) or in compression (ε < 0), where
Ei = (σi-σi-1)/(εi-εi-1) is the slope of the i-th segment constituting the pipe multi-linear stress-strain relationship (Figure 3a). The pipe-soil interaction is modeled using an elastic-perfectly plastic force-displacement relationship, the maximum soil friction force per unit length of the pipeline fs, and the relative soil-pipeline displacement at onset of friction sliding u0, where k=fs/u0 is the rigidity of friction interaction (Figure 3b).
The analytical formulation for evaluating the buried pipeline displacement ΔL subjected to a pull-out force F is reported in Table 1, considering an unanchored length (La) sufficiently long so that the pipeline response is unaffected by far-end boundary conditions. This analytical solution allows to evaluate the The analytical formulation for evaluating the buried pipeline displacement ΔL subjected to a pull-out force F is reported in Table 1, considering an unanchored length (La) sufficiently long so that the pipeline response is unaffected by far-end boundary conditions. This analytical solution allows to evaluate the elongation of the pipeline ΔL under the pull-out force F, as an explicit function of the associated axial strain ε.
Considering that for the case II (δ ≤ δcr), the magnitude of the total pipeline displacement in tension (Up1+Up2), and compression (Up3+Up4) are equal to the ground displacement δ, the latter can be expressed as a function of the maximum pipeline strain in tension and compression, at the soil block head and toe, respectively:
where α=√(k/E1A), being A the cross-section area of the pipe, E1 the elastic stiffness of the pipe material (Figure 3a), k the elastic rigidity of the soil-pipe friction interaction (Figure 3b), Le the length of the static friction zone in tension (region 2) and compression (region 3). Moreover, δcr is the soil displacement corresponding to the transition from case II to case I, when the friction reaction is mobilized over the entire soil block length, and the pipeline displacement remains constant, with maximum magnitude equal to δcr − u0.
The critical soil displacement value δcr can be easily determined considering that, the axial force difference in the pipe between the head and toe of the soil block is equal to overall friction force mobilized in-between (ΔFmax = fsLb), while the amount of pipeline elongation in region I is equal to the magnitude of pipeline contraction in region IV, considering the functional relationships indicated in Table 2. Most importantly, Equation (1) allows to determine the amount of critical ground displacement (δcr,i) corresponding to the achievement of the level of pipe axial strain associated with a certain performance limit state, either in tension or compression.
2.2. Deformation Capacity and Performance Limit States for the Steel Pipeline
In this study, the pipeline response is assessed in terms of the critical ground displacement corresponding to the achievement of maximum allowable longitudinal compression and tension strains, associated with normal operability and pressure integrity performance goal.
2.2.1. Normal Operability Limit (NOL) State
It is expected that the pipeline maintains its functionality after a seismic event, and the induced longitudinal strains are limited to avoid excessive distortion of the pipe cross-section impairing the passage of internal pigs for cleaning and inspection of material leakage. According to the 2001 ALA Guideline, the longitudinal compression strain limit, associated with the onset of local buckling, is given by:
with,
where p is the difference between the pipe internal and external pressure, E is the elastic modulus of the pipe material, t is the pipeline thickness, D is the pipeline diameter, and Dmin is minimum pipe diameter because of ovalization.
To maintain normal operability, the 2001 ALA Guideline recommends limiting the magnitude of longitudinal tensile strain to εt1 = 2%.
2.2.2. The Pressure Integrity Limit (PIL) State
It accepts significant pipe ovalization and wrinkle formation without loss of containment, that may subsequently result in pipe wall folding and associated excessive tensile strains, leading to crack initiation and ultimate rupture. To guarantee the pressure integrity performance requirement, the longitudinal compressive strain limit is evaluated as εc2 = 1.76 t/D. The allowable longitudinal tensile strain limit is assumed to be εt2 = 4% (ALA 2001, Honegger and Nyman, 2004).
Evidently, the pipeline performance is controlled by its behavior in compression, being the magnitude of the strain limit associated with the normal operability (NOL) (Equation 2) lower than that in tension (2%), for typical ranges of the diameter to thickness D/t ratio in onshore pipeline applications.
2.3. Validation of the Analytical Model
The proposed analytical model is validated against numerical simulation evaluating the response of buried operating pipeline under longitudinal PGD, using the finite element software ABAQUS/Standard (ABAQUS, 2022). First, the system performance is analyzed numerically within the beam on Winkler foundation theory. Then, the numerical results are compared with those obtained using the state-of-the-art analytical procedure (O’Rourke et al. 1995; IITK-07, 2007; O’Rourke and Liu, 2012) and the proposed analytical model, demonstrating the capacity of the latter to accurately evaluate the pipeline response.
The calculation example considers the X42 steel grade pipeline with diameter of 20 inch and thickness of 7.1 mm, buried in dense sand with a cover depth Hc = 1.5 m, measured from the soil surface to the pipe crown. The analyzed soil-pipeline parameters are summarized in Table 2.
The pipeline performance is evaluated considering the presence and absence of service loads, including internal pressure P, and temperature variation ΔT, demonstrating the accuracy of the proposed analytical method to assess system response in operating conditions.
The unpressurized pipeline (P = 0 MPa) has no temperature variation with respect to its installation temperature (ΔT = 0°C). Conversely, the pressurized pipeline is assumed to operate at an average temperature of ΔT = 50°C, compared to the pipe installation temperature, and internal pressure P = 4.4 MPa, which is 75% of the maximum allowed pressure, Pmax, according to ASME B31.4 (2002):
2.3.1. Finite Element Analysis of the Soil-Pipeline System
Within the numerical approach, the pipeline is modeled using the PIPE22H beam element type implemented in Abaqus/Standard (ABAQUS, 2022), particularly suitable to model long, slender pipelines with a thin-walled circular cross section, allowing the possibility to specify external or internal pressure. Instead, the longitudinal soil-pipeline interaction is modeled with uniaxial spring elements SPRING2 connected at each node of the pipeline on one end, while being assigned the far-field ground motion at the other end through the boundary conditions. The adopted mesh size for the beam pipe elements is 0.10 m, based on the mesh sensitivity study performed herein, assuring efficiency and accuracy of the numerical solution.
The X42 steel grade pipe material model is defined within the von Mises plasticity theory with nonlinear hardening, considering an uniaxial engineering stress-strain curve based on the Ramberg-Osgood relationship with material parameters n = 15 and r = 32, Young modulus E = 210 GPa, and yield stress σy = 290 MPa. The elasto-plastic force displacement relationship of the soil springs is defined by the sliding soil friction force per unit length of the pipeline, fs = 26.8 kN/m, and the relative soil-pipe displacement at the onset of friction sliding, u0 = 3 mm, calculated according to the ALA guidelines (ALA 2001), assuming compacted dense sand with friction angle ϕ = 40° (Table 2).
The lengths of steel pipeline–soil system is equal 1000 m, so that the system response to the imposed ground displacement is representative of an infinitely long segmented pipeline, unaffected by far-end boundary conditions. The assumed soil block length is Lb = 300 m (case II), located at the center of the soil–pipeline system so that its midpoint lies on the pipeline bisector.
The numerical analysis is conducted in two consecutive steps. First, the internal pressure and temperature variation are applied in the pipeline, while the pipeline ends and the free ends of the soil springs are restrained in the longitudinal direction. Second, the soil block movement δ = 4 m is applied statically with a maximum step increment equal to Δδ = 1 mm, at the free nodes of the soil springs within the soil block length, while outside of the moving block the soil nodes remain fixed. On each step increment, the nonlinear equilibrium equations are solved iteratively by the Newton–Raphson method, allowing the assessment of system performance at any level of applied ground displacement, until material failure.
2.3.2. Comparison between Numerical and Analytical Solutions
Figure 4 shows a comparison between the numerical and analytical model results assessing the performance of the pressurized and unpressurized pipeline in terms of the maximum axial strains in tension and compression, as a function of the ground displacement δ. Overall, the peak pipe strain magnitudes in the tensile and compressive PGD zone increase monotonically with the ground movement, progressively reaching the performance limit states of NO and PI at critical values of ground displacement δcr, based on the operating conditions (Table 3).
The conventional model results agree well with the numerical analysis only for the case of unpressurized pipeline under tension, while diverging significantly for the pressurized pipeline, with a percent difference exceeding 5% (Table 3). Conversely, comparison between the proposed analytical model and the numerical simulation results showed excellent agreement for both cases of pipeline operating conditions. Specifically, the percent difference between the pipeline performance results for these two methods does not exceed 0.9% (Table 3), demonstrating the greater accuracy of this analytical procedure to assess system response, compared with the conventional method.
Finally, the proposed analytical model, evaluating the response of the buried operating pipeline, subjected to longitudinal PGD, can be implemented in most programming languages (e.g., Python, Matlab) for further parametric analysis.
2.4. Critical Soil Displacement (δcr) and Length (Lcr) for the Performance Limit States of the Operating Pipeline
As the soil displacement δ increases (case II), the maximum magnitude of the pipeline axial force and associated strain at both margins of the PGD zone increases monotonically (Equation (1)), until the soil reaction mobilizes fully over the entire soil block length Lb (case I). Herein, the total soil load (fsLb) over the PGD zone is resisted by the developed pipe axial force that is maximum at the head (Ft,max) and and toe (Fc,max) of the sliding soil block. Therefore, the critical soil length Lcr, associated with full mobilization of the soil reaction (case I) for a given value of soil displacement, δ, is directly proportional to the overall pipe load at the edges of the PGD zone (Lcr = (Ft,max−Fc,max)/fs). Consequently, the pipeline deformation demand will reach a certain limit state only if the soil displacement δ and block length Lb are equal or greater than the critical soil displacement δcr and length Lcr corresponding to that performance criteria, respectively.
Figure 5 shows the variation of the critical soil block length Lcr as a function of the ground displacement δ, indicating the critical values associated with the achievement of the performance limit states in the pressurized (Pi/Pmax=0.75, ΔT=50°C) and unpressurized pipeline (Pi/Pmax=0, ΔT=0°C). Furthermore, the distribution of the of axial strain, stress, force, displacement, and soil friction reaction along the pressurized and unpressurized pipeline for increasing values of the applied ground movement d is presented in Appendix I, illustrating the different system response for case I and case II.
Clearly, the pipeline response depends on the operating loads, with the performance limit states in compression being reached for lower levels of critical soil displacement and length in the pressurized pipeline, compared to the unpressurized one.
Interestingly, the pressurized and unpressurized pipeline satisfy all performance criteria for soil block lengths Lb shorter than 145 m and 254 m, respectively, for any value of the applied ground displacement, δ. Conversely, the pipeline will fail to satisfy any limit state for values of the soil block length Lb and ground displacement δ exceeding 0.79 m and 280 m, respectively (Figure 5).
Figure 6 and Figure 7 show the maximum pipe strain magnitude as a function of the ground deformation demand (δ, Lb), for the pressurized and unpressurized pipeline respectively, highlighting the critical PGD values (δcr,i, Lcr,i) corresponding to the achievement of the performance limit states.
Clearly, the curve of the critical soil block length Lcr as a function of the ground displacement δ separates the PGD demand characterizing case I of short soil block (Lb < Lcr) from that of case II of long soil block (Lb > Lcr). Hence, the strain isolines are defined by two horizontal half-lines parallel to the δ and Lb axis, intersecting on the critical curve, as shown in Figure 6 and Figure 7.
2.5. Uncertainty Analysis
The deterministic analysis procedure adopted in the previous section assumes precise knowledge of the system parameters. However, all problem variables are characterized by a certain degree of uncertainty, including the material strength, and the seismic loading. To quantify the effect of these uncertainties on the pipeline performance, this study develops a robust fragility analysis framework based on Monte Carlo Simulation (MCS). The latter considers a large number of soil-pipeline system samples, generated by random sampling of the input system parameters, based on their probability distribution. The generated seismic demand samples are compared with the structural capacity values associated with each performance limit state, allowing to estimate the associated probability of exceedance conditioned to the level of ground motion intensity measure, IM, represented by the vector (δ, Lb).
To investigate the effect of the soil cover depth Hc, three different values between 1.0 m and 2.0 m are considered, representative of typical onshore pipeline installations. The soil strength parameters, i.e. the longitudinal soil reaction per unit length of pipeline fs, and relative soil-pipe displacement at friction sliding, u0 are assumed to follow a normal distribution, with the mean values derived according to ALA 2001, and a coefficient of variation COV = 30% (Propescu et al., 2005; Zhou 2012; Ni et al., 2018). The uncertainty of the X42 steel grade pipe material is modeled considering that the yield strength follows a normal distribution, with mean value σy = 290 MPa and a small COV = 3.5%, representing the low variability of the steel properties.
Table 4.
Probabilistic characteristics of the input parameters.
| Parameters | Units | Distribution | Mean or range | COV | |
|---|---|---|---|---|---|
| Pipe | Pressure, P | KPa | Uniform | [0, 5846.4] | |
| Temperature, T | °C | Uniform | [0, 50] | ||
| Yield strength, σy | MPa | Normal | 290 | 0.035 | |
| Cover depth, Hc | m | - | [1, 1.5, 2] | ||
| Soil | Soil friction reaction per unit pipe length, fs | KN/m | Normal | [19.2, 26.8, 34.4] | 0.3 |
| Relative soil-pipe displacement at friction sliding, u0 | mm | Normal | 3 | 0.3 |
The limit state functions for normal operability (NOL) and pressure integrity (PIL) in tension and compression are expressed in terms of the system demand (δ, Lb) and capacity (δcr,i, Lcr,i) corresponding to each performance criteria:
The probability of exceeding the normal operability (NOL), and the pressure integrity limit (PIL) state conditioned to the PGD intensity measure level (δ, Lb) is given by the joint union of the associated damage states in tension and compression:
P[NOL|(δ, Lb)] = P [(max(gt1) ≤ 0 ∪ max(gc1) ≤ 0|(δ, Lb)]
P[PIL|(δ, Lb)] = P [(max(gt2) ≤ 0 ∪ max(gc2) ≤ 0|(δ, Lb)]
These probabilities can be effectively calculated using the Monte Carlo Simulation (MCS) method, as summarized in the following key steps:
- definition of the uncertain input parameters and their probability distributions,
- generation of a sample set of the system random variables, considering their probability distributions,
- evaluation of the pipeline displacement capacities, δt1, δt2, δc1, δc2, equal to the ground displacement level associated with the achievement of the pipeline performance limit states, using Equation (1), and the corresponding values of the critical soil length Lcr = (Ft,max−Fc,max)/fs.
- evaluation of the limit state functions, as the difference between the calculated system capacity (δcr,i, Lcr,i) and demand (δ, Lb) using Equations (5-8),
- evaluation of the indicator functions, I1i(δ, Lb) = (max(gt1) ≤ 0 ∪ max(gc1) ≤ 0), and I2i(δ, Lb) = (max(gt2) ≤ 0 ∪ max(gc2) ≤ 0), that are equal to the unity provided unsatisfactory performance for the normal operability and pressure integrity limit state, respectively, and zero otherwise.
- repetition of the steps (1) to (5) N times, to obtain N sample values of I1i(δ, Lb), I2i(δ, Lb), counting the unsatisfactory performance for the normal operability (NOL), and the pressure integrity limit (PIL) state, respectively,
- evaluation of the probability of exceedance of the normal operability (NOL), and the pressure integrity limit (PIL) state, for a given PGD intensity (δ, Lb), as the ratio between the total sum of I1i(δ, Lb) and I2i(δ, Lb) to the sample size N:
The described algorithm can be easily implemented within most programming languages, like Python (Van Rossum 2015), to evaluate the fragility surfaces representing the conditional probability of the system reaching a performance limit state, as a function of the seismic demand.
3. Fragility Surfaces
This section presents the fragility analysis results of the buried operating steel pipeline subjected to longitudinal PGD, obtained using the methodology described in paragraph 2.5.
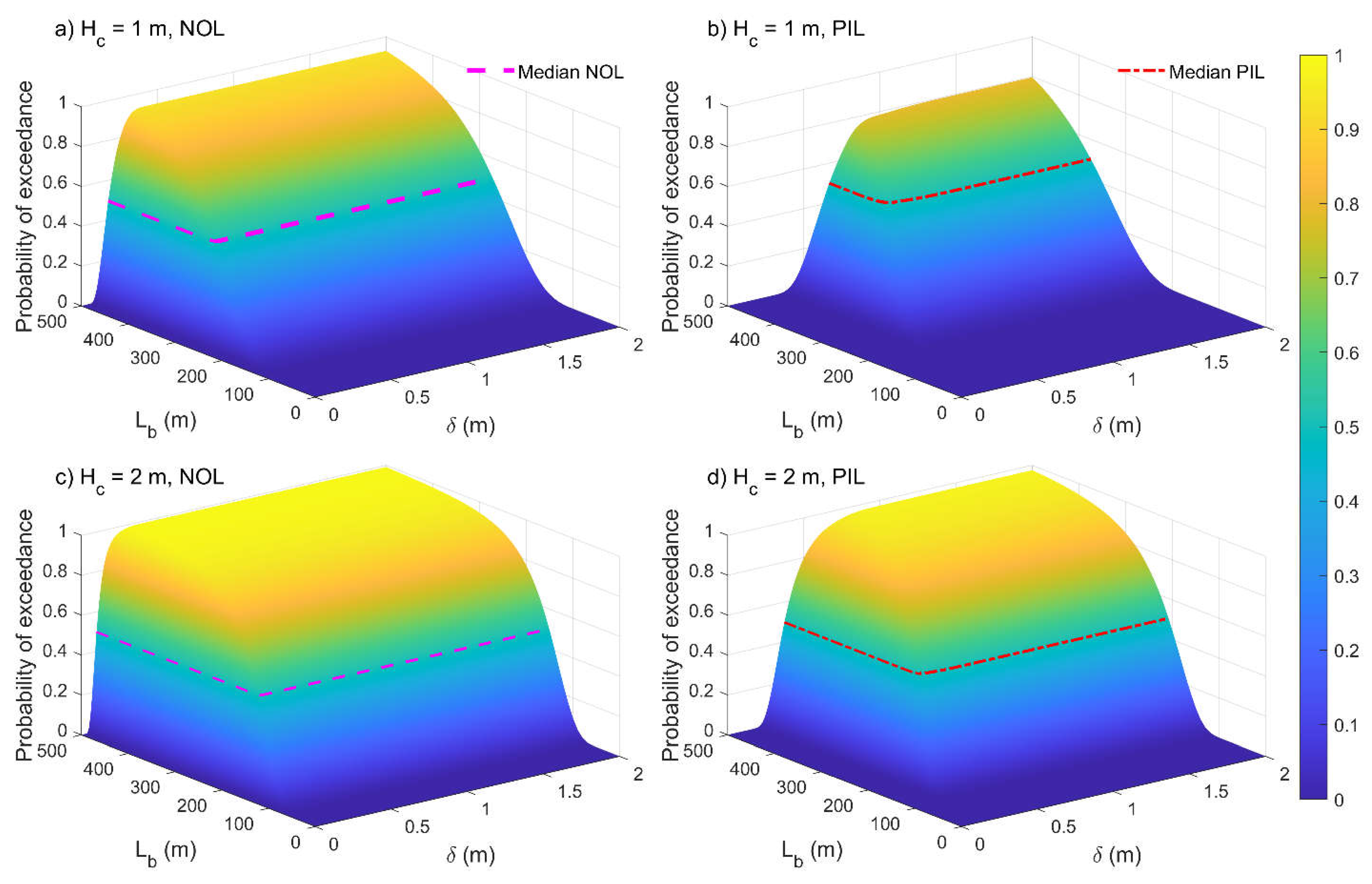
The evaluated fragility surfaces represent the probability of exceedance of the pipeline performance limit states conditioned to the ground displacement hazard (δ, Lb), as shown in Figure 8.
Clearly, the pipeline probability of reaching the performance criteria increases for larger soil displacement δ and lengths Lb, being greater for the NOL compared to the PIL limit state. This is consistent with pipeline deformation response observed previously for the deterministic analysis (Figure 6 and Figure 7), with the iso-probability lines defined by two horizontal half-lines parallel to the δ and Lb axis, as shown in Figure 8.
Specifically, the median values of soil displacement (δ, Lb), corresponding to 50% probability of reaching the NOL and PIL criteria are (0.128m, 194.2m) and (0.480m, 267.4m), as indicated in Figure 8.
These critical values exceed the ones evaluated deterministically (Figure 5) by about 30% and 10%, for the NOL and PIL limit state, respectively, highlighting the need to adopt appropriate safety factors within the deterministic design approach.
To investigate the effect of the cover depth Hc on the pipeline performance, the fragility functions are evaluated considering a minimum cover depth value Hc = 1 m and a maximum Hc = 2 m. This induces a directly proportional variation in the soil friction reaction per unit pipe length fs, according to ALA 2001.
Clearly, the pipeline probability of exceedance of the performance limit states for a given PGD level (δ, Lb) increases with greater burial depths and consequent soil friction reaction. Specifically, the median values of ground displacement intensity (δ, Lb), corresponding to 50% probability of reaching the NOL criteria are (0.18m, 266.35m) and (0.10m, 147.85m) for the shallower (Hc = 1m) and deeper (Hc = 2m) soil cover depth, respectively. Likewise, a critical PGD intensity of (δ, Lb) of (0.67m, 366.79m) and (0.37m, 203.61m) is needed to achieve a 50% probability of reaching the PIL criteria for the former (Hc = 1m) and latter (Hc = 2m) pipe burial condition.
This is consistent with current pipeline design guidelines prescriptions, recommending to use shallow burial depths, light weight backfill and pipe coating with low friction coefficient to minimize the intensity of soil-pipeline interaction, optimizing system performance (PRCI 2004; CEN 2006).
The obtained fragility surfaces permit to assess the probability of exceedance of the pipeline performance limit states for any given PGD intensity (δ, Lb), considering the uncertainties of the system geometric and mechanical characteristics, including the varying operational loads.
Figure 9.
Fragility surface of the buried pipeline for different cover depths and performance limit states: a) Hc = 1.0 m, NOL; b) Hc = 1.0 m, PIL and c) Hc = 2.0 m, NOL; d) Hc = 2.0 m, PIL.
Figure 9.
Fragility surface of the buried pipeline for different cover depths and performance limit states: a) Hc = 1.0 m, NOL; b) Hc = 1.0 m, PIL and c) Hc = 2.0 m, NOL; d) Hc = 2.0 m, PIL.
4. Global Sensitivity Analysis
This section presents the results of the global sensitivity analysis (GSA) conducted to quantify the uncertainty (variance) of the model prediction y = g(x1, x2, …, xm), attributed to each input random variable xi. This method has the advantage of considering the sensitivity over the entire input space, including the nonlinear interaction effects between the system variables, allowing to identify those parameters that have the greatest influence on the model output.
The adopted GSA procedure is based on the Sobol’s variance decomposition method, in which the total variance of model output V = Var(y) is decomposed into component variances resulting from individual parameters Vi and their interactions Vijk (Sobol, 1990).
Specifically, the first-order Sobol index Si of an input variable xi represents the fraction of the output variance attributed to xi (Si = Vi /V), while the higher order Sobol indexes Sijk indicate the impact of input parameter interaction on the output results (Sijk = Vijk /V). Finally, the total-order index STi quantifies the overall effects of one input parameter xi including its interaction with all other variables on the model output, and is defined as the sum of all sensitivity indices involving xi (STi = Si + Σi≠jSij + Σi≠j≠kSijk + …).
To accurately estimate the first order and total Sobol indices this study performs a double-loop Monte Carlo integration procedure (Saltelli, 2002).
The estimated influence of the input random variables on the achievement of the pipeline performance limit states, based on Sobol’s sensitivity indexes, is shown in Figure 10.
The soil block length Lb is the most influential parameter, with a first-order sensitivity index Si of 51.2% and 38.1% for the NOL and PIL limit states, respectively, and a total sensitivity indexes STi greater than 72% for both performance limit states. This is evident, since the length of the PGD zone Lb controls the pipeline deformation demand, where each limit state is achieved provided that the soil block length value exceeds the correspondent critical threshold (Lb≥Lcr,i).
The second most significant variable is the soil friction reaction per unit pipe length fs, with a first-order sensitivity index Si of 7.8% and 8.7% for the NOL and PIL limit states, respectively, and a total sensitivity indexes STi greater than 32% for both damage levels. The third most influential parameter for the PIL limit state is the soil displacement δ, with an associated first order sensitivity index Si of 12.8% and a total sensitivity index STi of 33.2 %.
Interestingly, the pipeline operating temperature is the third most influential parameter for the NOL limit state, with a first order sensitivity index Si and a total sensitivity index STi of 1.6% and 15.2 %, respectively. This is consistent with the results of the sensitivity analysis conducted in Tsatsis et al. (2022), quantifying the effect of uncertainties of the pipeline system subjected to longitudinal PGD, including the significant impact of operational loads.
While the first-order sensitivity indexes for the internal pressure Pi, are negligible (Si < 1%), the total sensitivity indexes STi reach 10.7% and 5.5% for the NOL and PIL limit state respectively, highlighting the considerable interaction effects of Pi with the other input variables.
The least influential input random variables are the pipe yield strength σy and relative soil-pipe displacement at friction sliding u0, with associated total sensitivity indexes STi less than 4.5% and 0.3%, respectively.
This is consistent with the simplified assumptions adopted in existing analytical models of buried pipelines under longitudinal PGD, that conservatively neglect the relative soil-pipeline displacement at friction sliding u0 (O’Rourke et al., 1995).
The use of both sensitivity indexes allows a comprehensive understanding of the influence of the input variables on the performance limit state function, highlighting the importance of interaction effects between the soil-pipeline system parameters.
5. Conclusions
This study develops an analytical model that accurately and efficiently evaluates the performance of buried operating pipelines under longitudinal PGD, considering the asymmetric pipeline material behavior in tension and compression under varying operational loads. Further comparison of the proposed analytical model with detailed finite element analysis results showed excellent agreement, demonstrating its capacity to accurately assess the pipeline response as a function of the system parameters. The analytical model was efficiently implemented within a fragility function calculation framework based on MCS, allowing to assess the probability of exceedance of the pipeline performance limit states conditioned to the PGD intensity (δ, Lb), considering the system uncertainties.
The evaluated fragility surfaces showed that the pipeline probability of reaching the performance criteria increases for larger soil displacement δ and lengths Lb, as well as cover depths Hc, because of the greater mobilized soil reaction counteracting pipeline deformation. This requires implementation of proper engineering design solutions that minimize the risk of pipeline damage, for example, by adopting shallow soil cover depths, light weight backfill, and low-friction pipe coating.
The performed GSA allowed to quantify the uncertainty of the pipeline performance assessment attributed to each random system parameter, considering the sensitivity over the entire input space, including the nonlinear interaction effects between variables. The PGD length (Lb) resulted the most influential parameter on the exceedance of the NOL and PIL performance limit states, followed by the soil friction per unit pipe length (fs) and ground displacement (δ), based on the fist-order and total order Sobol indices. This is consistent with the expected system performance, since the intensity of PGD and soil-pipeline interaction directly controls the pipeline deformation demand.
The significant total sensitivity indexes of the temperature variation (ΔT) and internal pressure (Pi) for the NOL limit state demonstrated the importance of their interaction effects with the other input variables, requiring proper consideration in pipeline system modeling and design.
Finally, the proposed analytical fragility function calculation framework, provides a useful methodology for effectively assessing the performance of operating pipelines under longitudinal PGD, quantifying the effect of the uncertain parameters impacting system response.
Appendix A
This appendix presents the seismic performance of the pressurized and unpressurized pipeline analyzed in Section 2.3 in terms of axial strain, stress, force, displacement, and soil friction reaction along its axis for increasing values of ground movement d, for case I and case II.
The moving soil block induces localized relative soil-pipeline displacement at the margins of the PGD zone, and associated resistance forces. This results in a maximum pipeline axial force at the sliding block head and maximum axial compression force at the toe, decreasing linearly thereupon due to the sliding soil friction (fs). Beyond this zone, the relative soil-pipeline displacement is negligible, and the pipeline displacement matches that of the ground until the soil reaction mobilizes fully along the entire soil block length Lb (Case I), remaining constant thereafter.
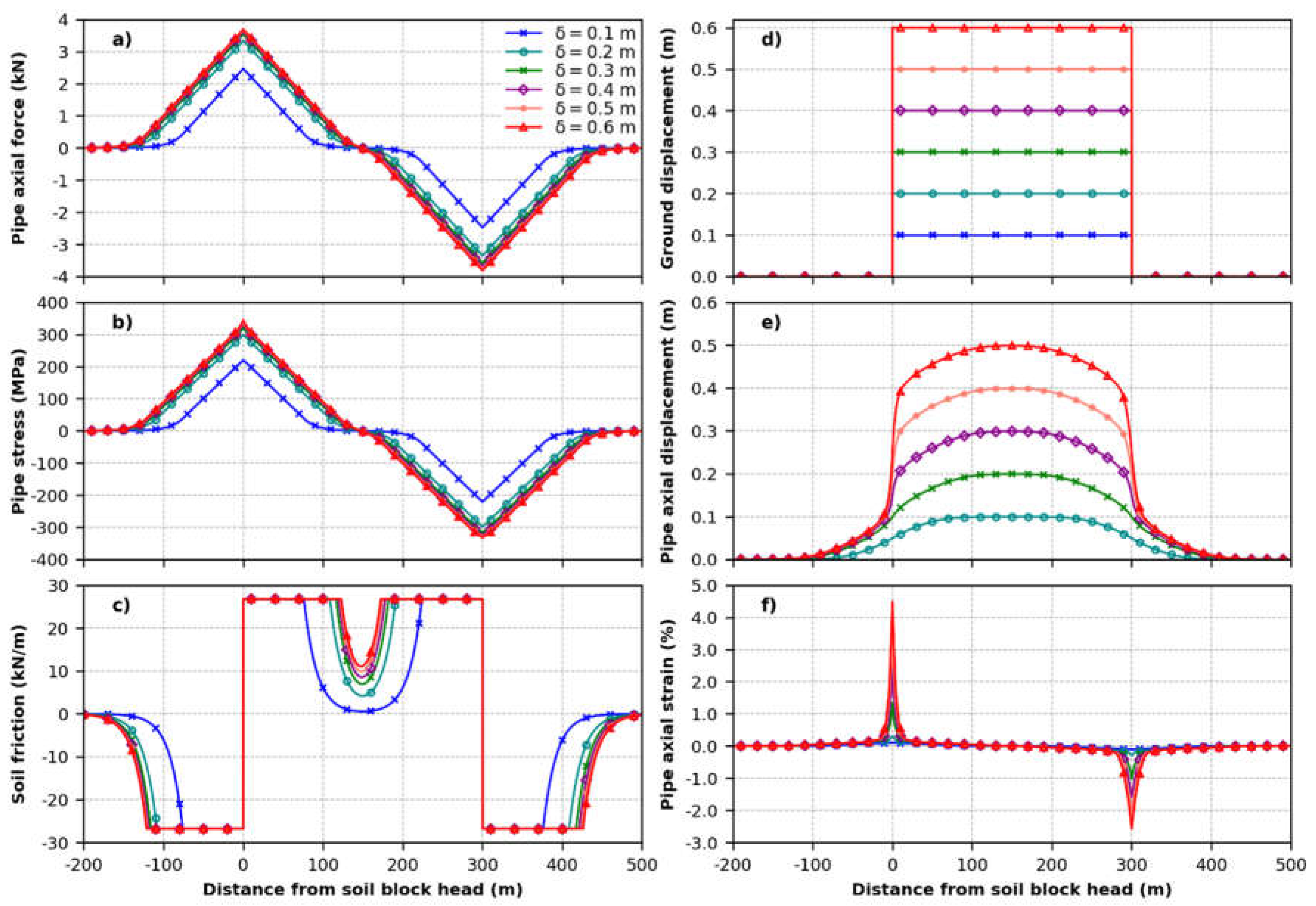
The length of the PGD Lb is a critical geotechnical parameter, determining whether the pipeline performance criteria are exceeded for increasing ground displacements d, as shown in Figure A1 and Figure A2, indicating the pressurized and unpressurized pipe response, respectively, for Lb=200m (case I). Conversely, the response of the pressurized and unpressurized pipeline subjected to long soil block movement (Lb = 300 m) is shown in Figure A3 and Figure A4 respectively.
The operating pipeline exhibits an asymmetric response along its axis is in tension and compression, compared to the non-operating pipeline, as evident from the resulting axial force, stress, strain, displacement, and soil friction reaction indicated in Figure A1, Figure A2, Figure A3 and Figure A4.
The maximum pipeline displacement corresponding to full mobilization of the soil reaction for the pressurized and unpressurized pipeline under short soil block (Lb=200m) movement is equal to 0.12m (Figure A1) and 0.23m (Figure A2), respectively. This is consistent the critical ground displacement and associated soil block length values (d, Lb) shown in Figure 5. The pressurized pipeline reaches the compressive strain limit for the NOL criteria (0.62%) for a soil displacement of 0.1m (Figure A1-d), whereas the unpressurized pipeline remains elastic, with a maximum axial strain of 0.11% (Figure A2-d). This further highlights the influence of the operating loads of pipeline performance, as discussed throughout the paper.
For case II (Lb = 300 m), the pressurized and unpressurized pipeline exceed the PIL limit state for a ground displacement d of 0.42 m (Figure A3) and 0.57 m (Figure A4), respectively, confirming the detrimental effect of the operating loads on the pipeline performance, as observed in Section 2.4.
Figure A1.
Response of the pressurized pipeline (Pi/Pmax=0.75, ΔT=50°C) to longitudinal PGD with block length Lb = 200 m (case I): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
Figure A1.
Response of the pressurized pipeline (Pi/Pmax=0.75, ΔT=50°C) to longitudinal PGD with block length Lb = 200 m (case I): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.

Figure A2.
Response of the unpressurized pipeline (Pi/Pmax=0, ΔT=0°C) to longitudinal PGD with block length Lb = 200 m (case I): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
Figure A2.
Response of the unpressurized pipeline (Pi/Pmax=0, ΔT=0°C) to longitudinal PGD with block length Lb = 200 m (case I): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
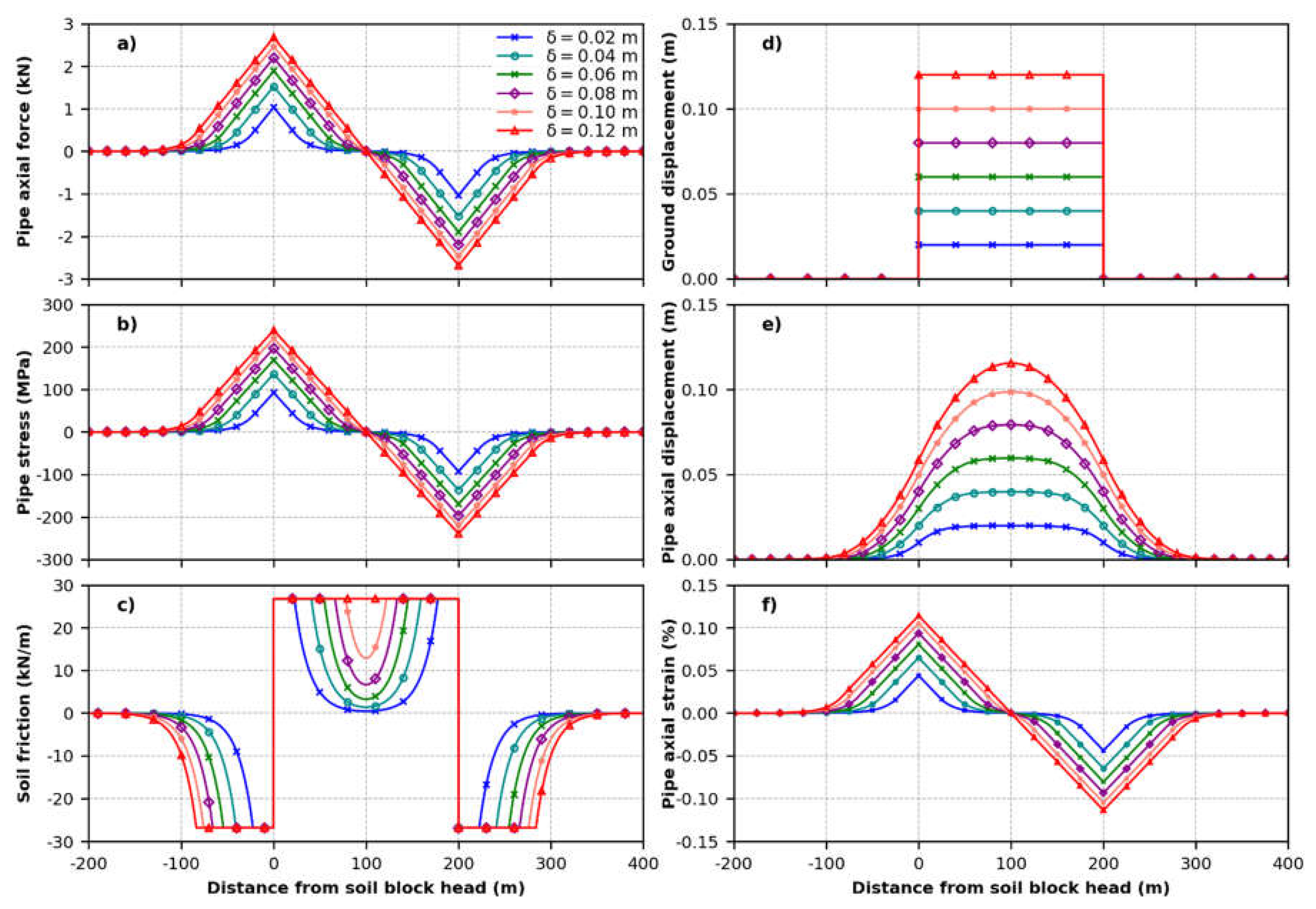
Figure A3.
Response of the pressurized pipeline (Pi/Pmax=0.75, ΔT=50°C) to longitudinal PGD with block length Lb = 300 m (case II): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
Figure A3.
Response of the pressurized pipeline (Pi/Pmax=0.75, ΔT=50°C) to longitudinal PGD with block length Lb = 300 m (case II): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
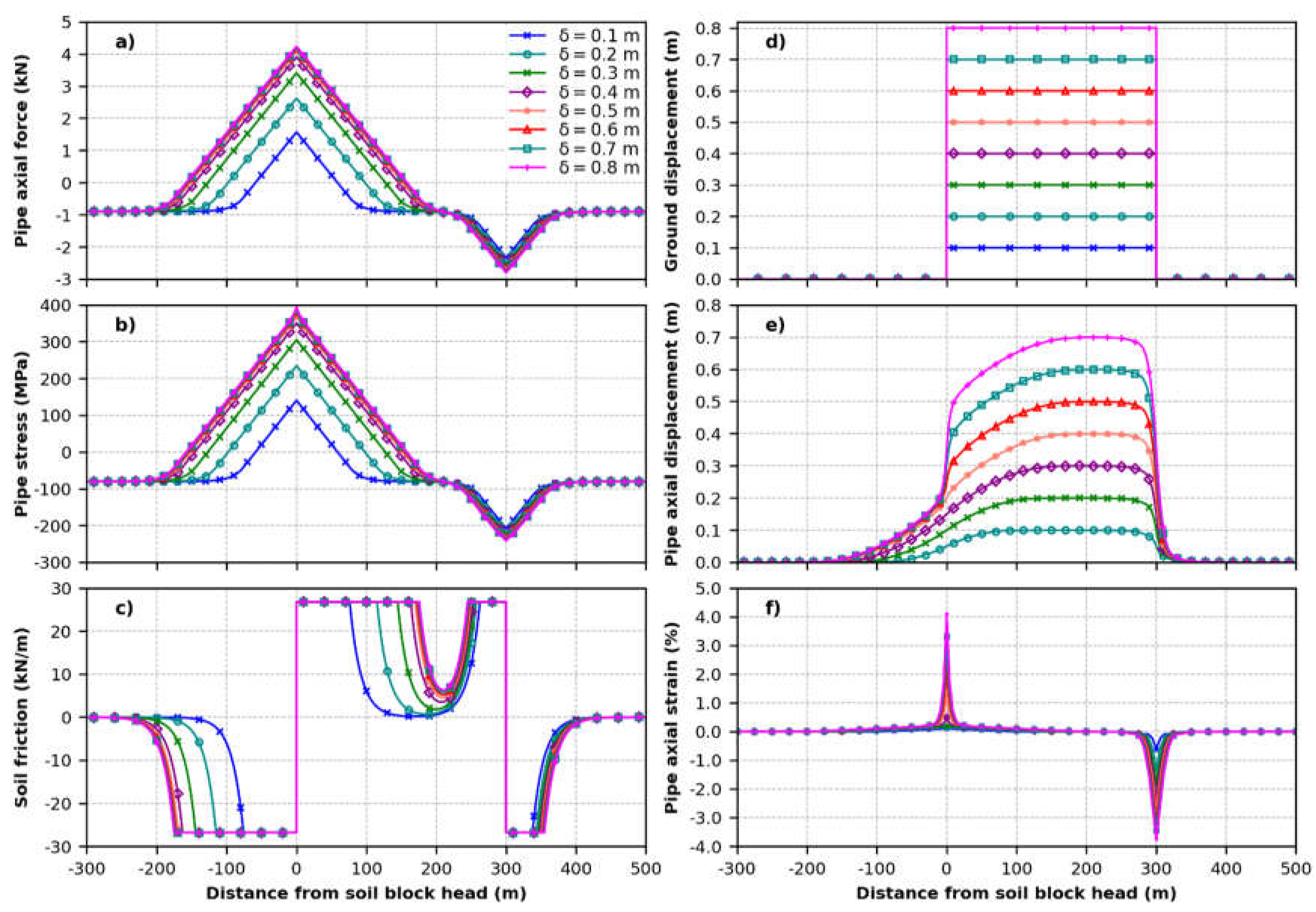
Figure A4.
Response of the pressurized pipeline (Pi/Pmax=0, ΔT=0°C) to longitudinal PGD with block length Lb = 300 m (case II): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
Figure A4.
Response of the pressurized pipeline (Pi/Pmax=0, ΔT=0°C) to longitudinal PGD with block length Lb = 300 m (case II): (a) pipe axial force; (b) pipe axial stress; (c) soil friction; (d) ground displacement; (e) pipe axial displacement; (f) pipe axial strain vs. distance from tension crack.
References
- ABAQUS. 2022. User’s guide, Simulia, Providence, RI, USA.
- ALA 2001. Guidelines for the design of buried steel pipe. American Lifeline Alliance (ALA), Washington, DC.
- ALA. 2005. Seismic guidelines for water pipelines. American Lifelines Alliance (ALA), Washington, D.C.
- ASME. 2002. Pipeline transportation systems for liquid hydrocarbons and other liquids. ASME B31.4. New York.
- Bain C. A., O’Rourke T. D., Bray J. D. 2024. Pipeline Response to Seismic Displacement at Balboa Boulevard during the 1994 Northridge Earthquake. Journal of Geotechnical and Geoenvironmental Engineering, 150(2), 04023139.
- Banushi, G. Seismic design of buried steel pipelines [Doctoral dissertation]. 2017. [CrossRef]
- Banushi G., Squeglia N., Thiele K., Salvatore W. 2017. Finite element analysis of operating buried pipelines subjected to strike-slip fault movement. In proceedings, 12th Pipeline Technology Conference. EITEP Institute, Hannover, Germany.
- Banushi G., Squeglia N. 2018. Seismic analysis of a buried operating steel pipeline with emphasis on the equivalent-boundary conditions. Journal of Pipeline Systems Engineering and Practice, ASCE; 9(3): 04018005. [CrossRef]
- Banushi G., Squeglia N., Thiele K. 2018. Innovative analysis of a buried operating pipeline subjected to strike-slip fault movement. Soil Dynamics and Earthquake Engineering; 107: 234–249. [CrossRef]
- Banushi G., Wham B. P. 2021. Deformation capacity of buried hybrid-segmented pipelines under longitudinal permanent ground deformation. Canadian Geotechnical Journal, 58(8): 1095-1117. [CrossRef]
- Bartlett S.F., Youd T.L. 1992. Empirical analysis of horizontal ground displacement generated by liquefaction-induced lateral spreads. Technical Report NCEER-92-0021. National Center for Earthquake Engineering Research, Buffalo, NY.
- CEN (European Committee for Standardization). 2006. Design of structures for earthquake resistance. 4: Silos, tanks and pipelines. Eurocode 8 EN 1998-4, Brussels, Belgium.
- C-CORE; DG Honegger Consulting, and SSD Inc. 2009. Guidelines for constructing natural gas and liquid hydrocarbon pipelines through areas prone to landslide and subsidence hazards, Design, Materials, and Construction Committee of Pipeline Research Council International, Inc., Chantilly, VA.
- Di Sarno L., Karagiannakis G. 2020. On the seismic fragility of pipe rack-piping systems considering soil–structure interaction. Bulletin of earthquake engineering; 18(6):2723–57. [CrossRef]
- Di-Sarno, L., Elnashai, A. S. 2021. Seismic Fragility Relationships for Structures. In Advances in Assessment and Modeling of Earthquake Loss (pp. 189-222). Springer International Publishing.
- Elnashai A.S., Di Sarno L. 2015. Fundamentals of earthquake engineering. From source to fragility. Wiley and Sons, UK.
- Hamada M., O’Rourke, T.D. 1992, Large Ground Deformations and Their Effects on Lifelines, Japanese Case Studies of Liquefaction and Lifeline Performance During Past Earthquakes, Technical Report NCEER-92-0001, Multidisciplinary Center for Earthquake Engineering Research, Buffalo, New York.
- Honegger D.G., Nyman D. 2004. PRCI Guidelines for the Seismic Design and Assessment of Natural Gas and Liquid Hydrocarbon Pipelines. Pipeline Research Council International. Technical Toolboxes, Houston, Texas.
- Honegger D. G., Wijewickreme D., Youd T. L. 2014. Regional pipeline vulnerability assessment based upon probabilistic lateral spread hazard characterization. In Proceedings, 10th national conference on earthquake engineering; EERI, Oakland.
- Karamitros D. K., Bouckovalas G. D., Kouretzis G. P., Gkesouli V. 2011. An analytical method for strength verification of buried steel pipelines at normal fault crossings. Soil Dynamics and Earthquake Engineering; 31(11), 1452-1464. [CrossRef]
- Kennedy R. P., Williamson R. A., Chow A. M. 1977. Fault movement effects on buried oil pipeline. Transportation Engineering Journal of ASCE; 103(5), 617-633.
- Ni P., Mangalathu S., Yi Y. 2018. Fragility analysis of continuous pipelines subjected to transverse permanent ground deformation. Soils and Foundations, 58(6), 1400-1413. [CrossRef]
- O'Rourke M., Nordberg G. 1991. Analysis procedures for buried pipelines subject to longitudinal and transverse permanent ground deformation. In Proceedings, 3rd Japan–US Workshop on Earthquake Resistant Design of Lifeline Facilities and Countermeasures for Soil Liquefaction, San Francisco, Calif. Multidisciplinary Center for Earthquake Engineering Research, Buffalo, NY Technical Report NCEER-91-0001; 439-453.
- O’Rourke M.J., Nordberg C. 1992a. Behavior of buried pipelines subject to permanent ground deformation. In Proceedings of 10th World Conference on Earthquake Engineering; Madrid, Spain, 19–24 July, 1992. International Association for Earthquake Engineering. 5411–5416.
- O’Rourke M.J., Nordberg C. 1992b. Longitudinal permanent ground deformation effects on buried continuous pipelines. Technical report NCEER-92-0014. National Center for Earthquake Engineering Research, Buffalo, NY.
- O’Rourke M.J., Liu X.J., Flores-Berrones R. 1995, Steel pipe wrinkling due to longitudinal permanent ground deformation, Journal of Transportation Engineering; 121(5), 443-451. [CrossRef]
- Popescu R., Deodatis G., Nobahar A. 2005. Effects of random heterogeneity of soil properties on bearing capacity. Probabilistic Engineering Mechanics; 20(4): 324–341. [CrossRef]
- Saltelli A. 2002. Making best use of model evaluations to compute sensitivity indices. Computer physics communications, 145(2), 280-297. [CrossRef]
- Sarvanis G. C., Karamanos S. A. 2017. Analytical model for the strain analysis of continuous buried pipelines in geohazard areas. Engineering structures; 152: 57-69. [CrossRef]
- Schaumann P., Keindorf C., Brüggemann, H. 2005. Elasto-plastic bearing behavior of steel pipes exposed to internal pressure and bending. International Ocean and Polar Engineering Conference. ISOPE.
- Sobol’ I. M. 1990. Sensitivity estimates for nonlinear mathematical models. Matematicheskoe Modelirovanie 2, 112–118.
- Suzuki N., Hagio A. 1990. Safety assessment of welded pipelines undergoing large ground deformation. In ASCE Pipeline Design and Installation. 108-119.
- Toprak S., Cetin O. A., Nacaroglu E., Koc A. C. 2010. Pipeline performance under longitudinal permanent ground deformation. In 14th European Conference on Earthquake Engineering.
- Toprak, S., Cirmiktili, O. Y. 2021. Reliability-Based Analyses and Design of Pipelines' Underground Movements during Earthquakes. In Reliability-Based Analysis and Design of Structures and Infrastructure (pp. 365-380). CRC Press.
- Trifonov O. V., Cherniy V. P. 2012. Elastoplastic stress–strain analysis of buried steel pipelines subjected to fault displacements with account for service loads. Soil Dynamics and Earthquake Engineering; 33(1): 54-62. [CrossRef]
- Tsatsis A., Alvertos A., Gerolymos N. 2022. Fragility analysis of a pipeline under slope failure-induced displacements occurring parallel to its axis. Engineering Structures; 262: 114331. [CrossRef]
- Van Rossum, G. 2015. Python 2.7.10 language reference. Samurai Media Limited, Hong Kong.
- Wham B. P., Davis C. A. 2019. Buried continuous and segmented pipelines subjected to longitudinal permanent ground deformation. Journal of Pipeline Systems Engineering and Practice; 10(4): 04019036. [CrossRef]
- Wijewickreme D., Honegger D., Mitchell A., Fitzell, T. 2005. Seismic vulnerability assessment and retrofit of a major natural gas pipeline system: a case history. Earthquake spectra; 21(2): 539-567. [CrossRef]
- Zhou, W. 2012. Reliability of pressurized pipelines subjected to longitudinal ground movement. Structure and Infrastructure Engineering; 8(12): 1123-1135.
Figure 1.
Pipeline subjected to longitudinal PGD: a) 3D view, b) 2D schematic representation.
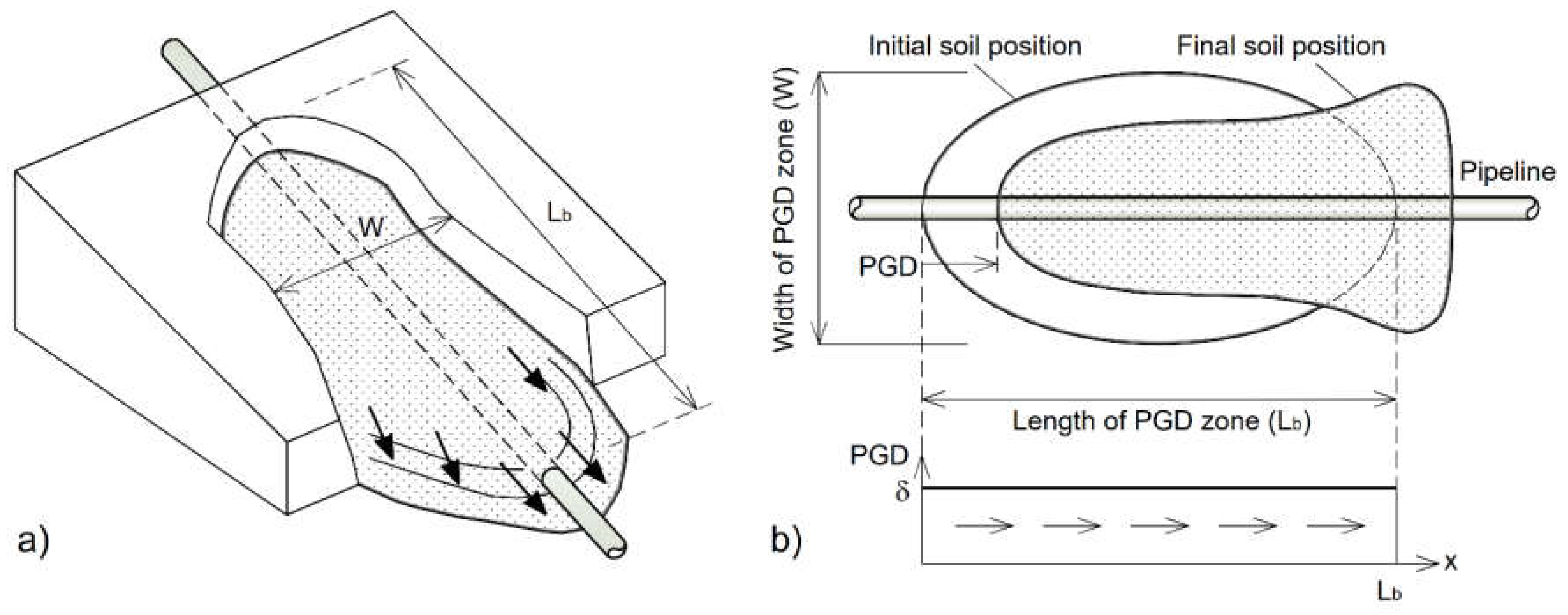
Figure 2.
a) Schematic representation of the buried pipeline displacement subjected to longitudinal soil block movement (case II), including b) soil-pipeline system behaving like a pull-out test in tension (region I) c) force equilibrium in the axial direction of the pipe element of infinitesimal length dx.
Figure 2.
a) Schematic representation of the buried pipeline displacement subjected to longitudinal soil block movement (case II), including b) soil-pipeline system behaving like a pull-out test in tension (region I) c) force equilibrium in the axial direction of the pipe element of infinitesimal length dx.
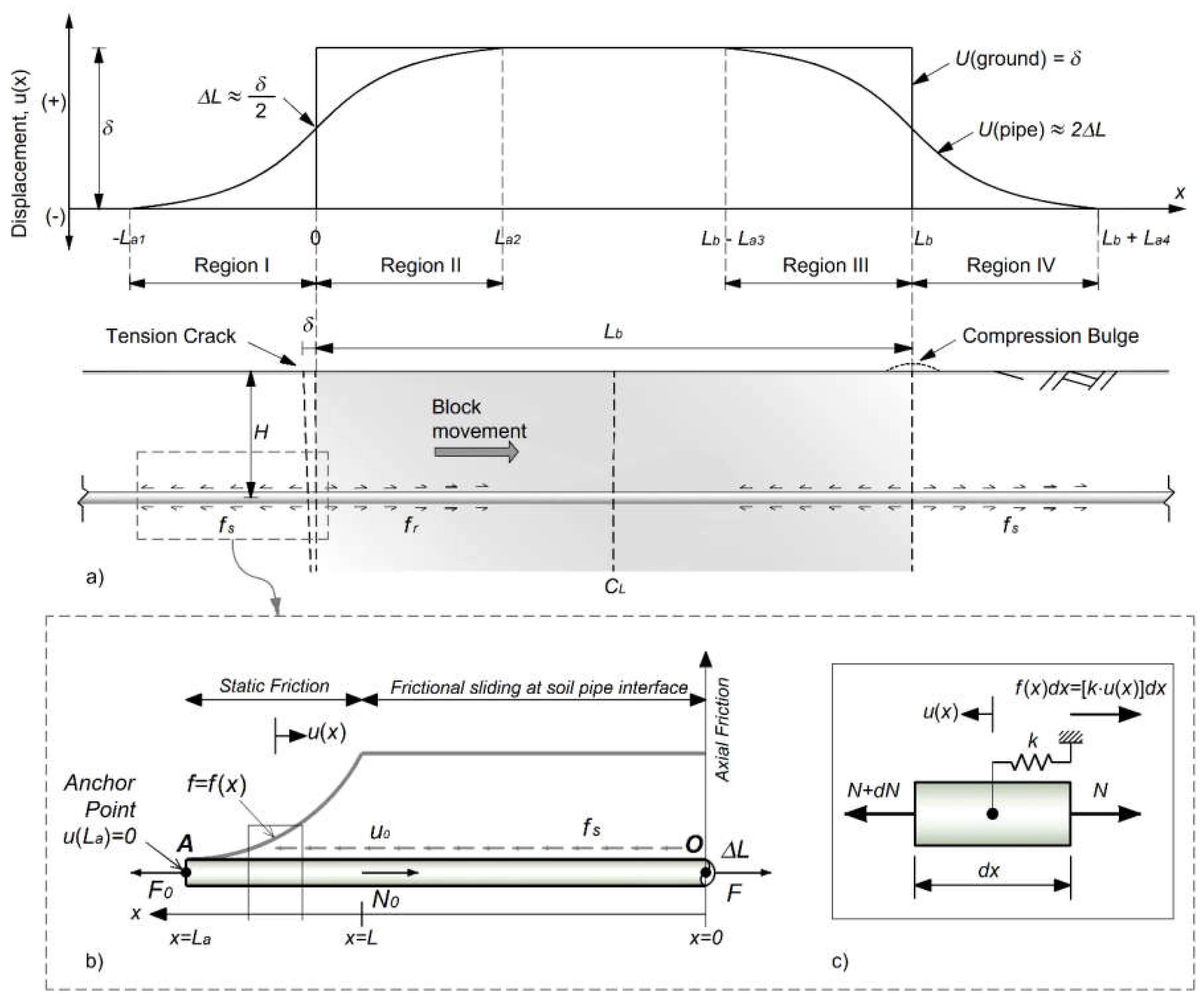
Figure 3.
Schematic representation of the axial constitutive behavior of the (a) pipeline material; (b) pipe-soil interaction.
Figure 3.
Schematic representation of the axial constitutive behavior of the (a) pipeline material; (b) pipe-soil interaction.
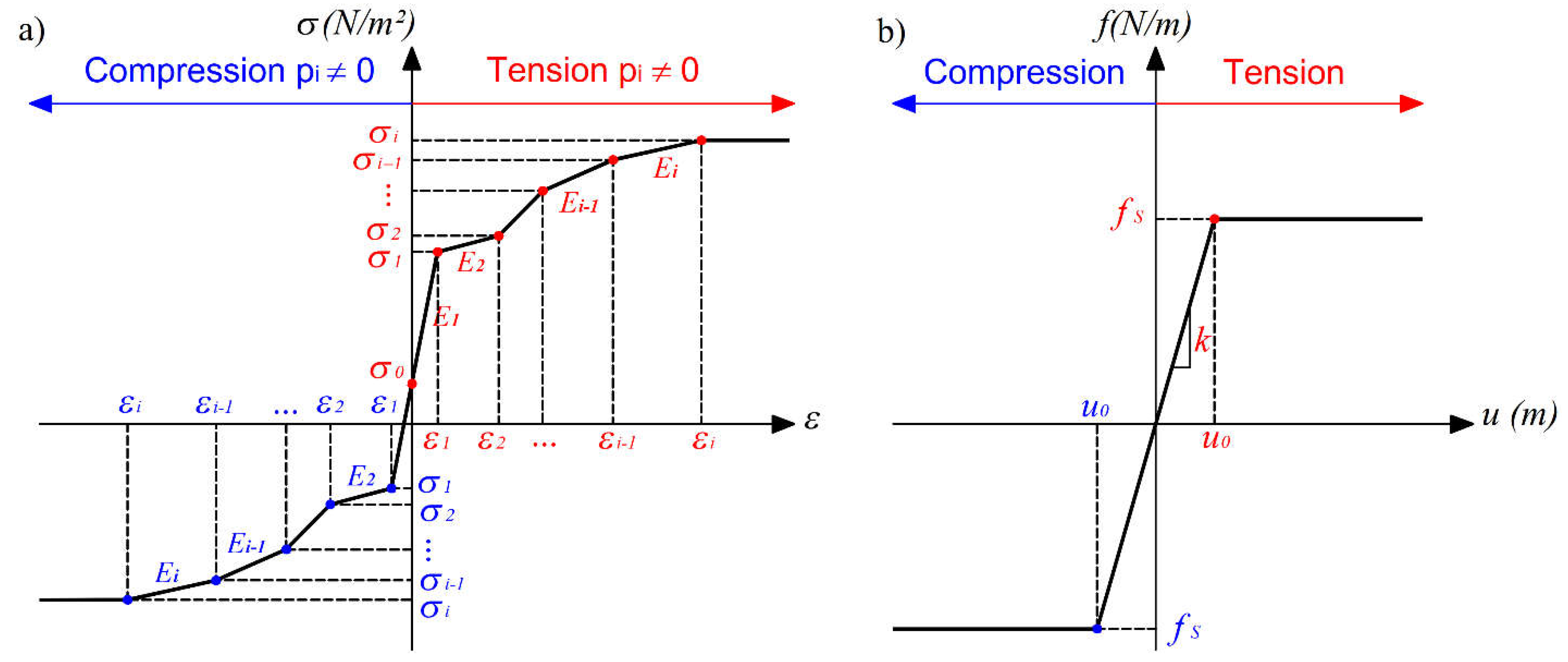
Figure 4.
Comparison between the numerical and analytical models evaluating the pipeline performance under longitudinal PGD (Lb = 300m) in terms of maximum tensile and compressive pipe strain as a function of the ground displacement δ.
Figure 4.
Comparison between the numerical and analytical models evaluating the pipeline performance under longitudinal PGD (Lb = 300m) in terms of maximum tensile and compressive pipe strain as a function of the ground displacement δ.
Figure 5.
Variation of the critical soil block length, Lcr = (Ft,max−Fc,max)/fs, as a function of the ground displacement δ, with indication of the critical values associated with the achievement of the pipeline performance limit states.
Figure 5.
Variation of the critical soil block length, Lcr = (Ft,max−Fc,max)/fs, as a function of the ground displacement δ, with indication of the critical values associated with the achievement of the pipeline performance limit states.
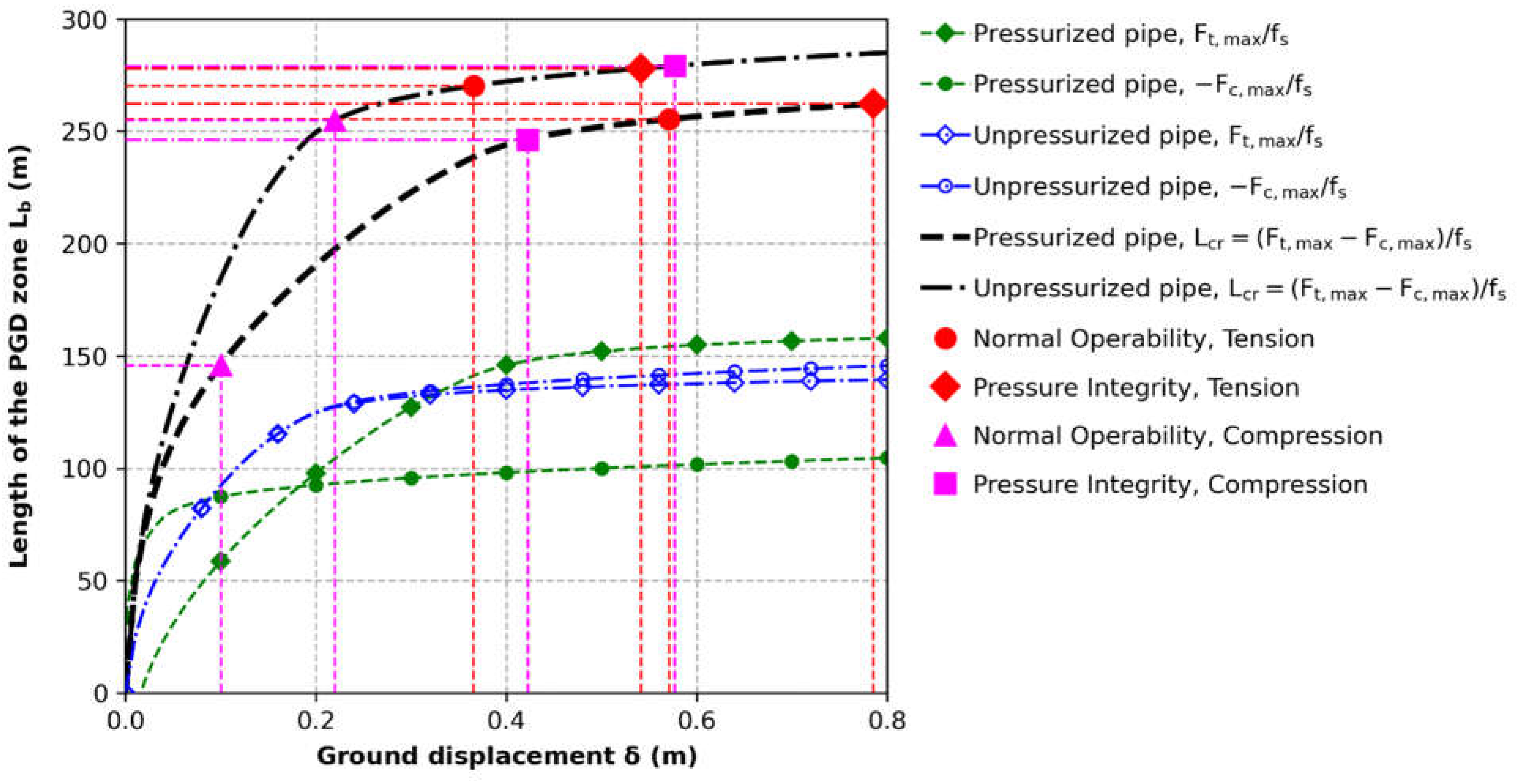
Figure 6.
Peak axial strain magnitude in the pressurized pipeline (Pi/Pmax=0.75, ΔT=50°C) as a function of the PGD length Lb and displacement δ in a) tension and b) compression. The dashed horizontal curves represent the strain isolines corresponding to the NOL and PIL performance limit states.
Figure 6.
Peak axial strain magnitude in the pressurized pipeline (Pi/Pmax=0.75, ΔT=50°C) as a function of the PGD length Lb and displacement δ in a) tension and b) compression. The dashed horizontal curves represent the strain isolines corresponding to the NOL and PIL performance limit states.
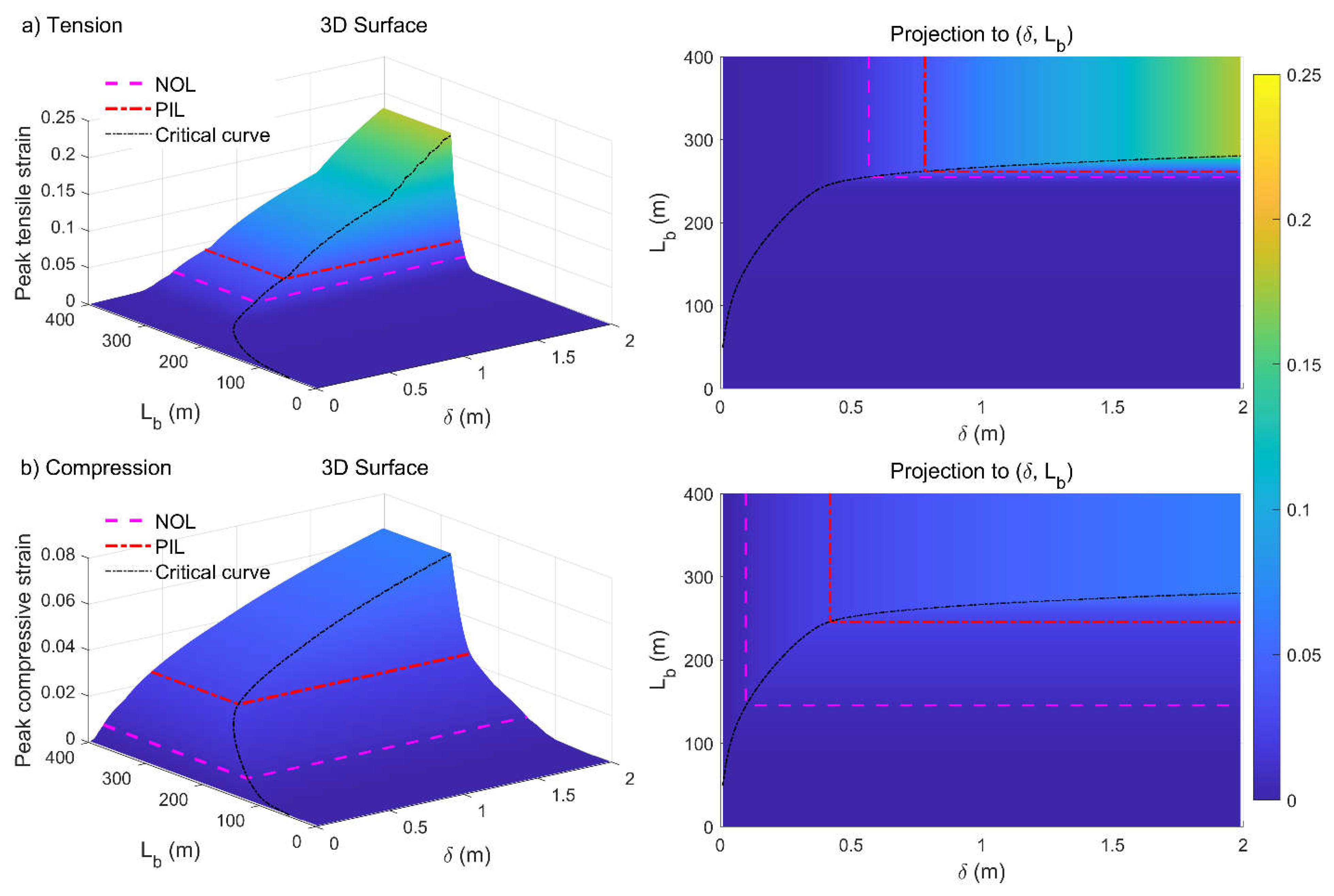
Figure 7.
Peak axial strain magnitude in the unpressurized pipeline (Pi/Pmax=0, ΔT=0°C) as a function of the PGD length Lb and displacement δ in a) tension and b) compression; The dashed horizontal curves represent the strain isolines corresponding to the NOL and PIL performance limit states.
Figure 7.
Peak axial strain magnitude in the unpressurized pipeline (Pi/Pmax=0, ΔT=0°C) as a function of the PGD length Lb and displacement δ in a) tension and b) compression; The dashed horizontal curves represent the strain isolines corresponding to the NOL and PIL performance limit states.
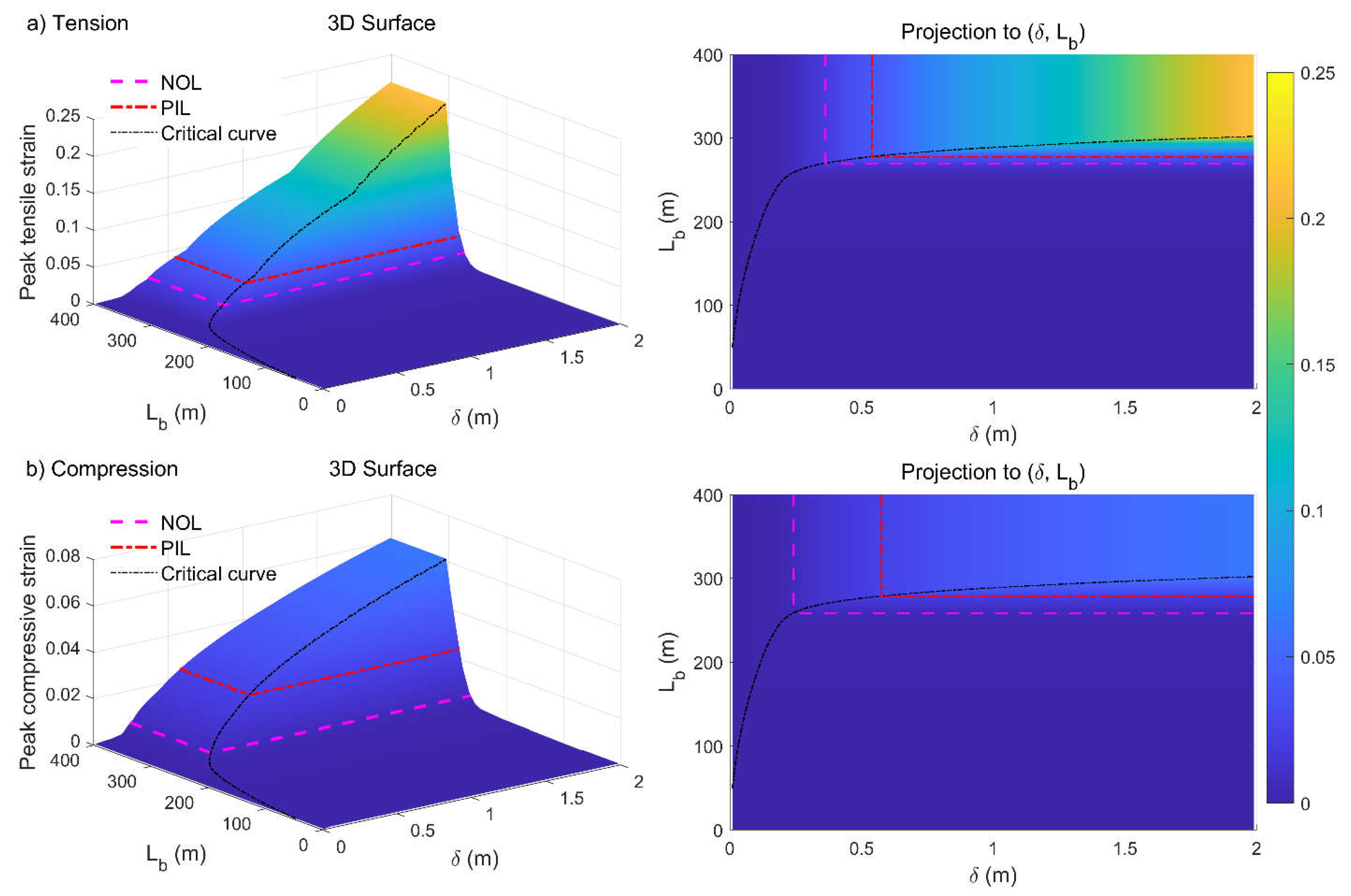
Figure 8.
Fragility surface of the buried pipeline (Hc = 1.5m) for: a) Normal Operability Limit (NOL) and b) Pressure Integrity Limit (PIL).
Figure 8.
Fragility surface of the buried pipeline (Hc = 1.5m) for: a) Normal Operability Limit (NOL) and b) Pressure Integrity Limit (PIL).
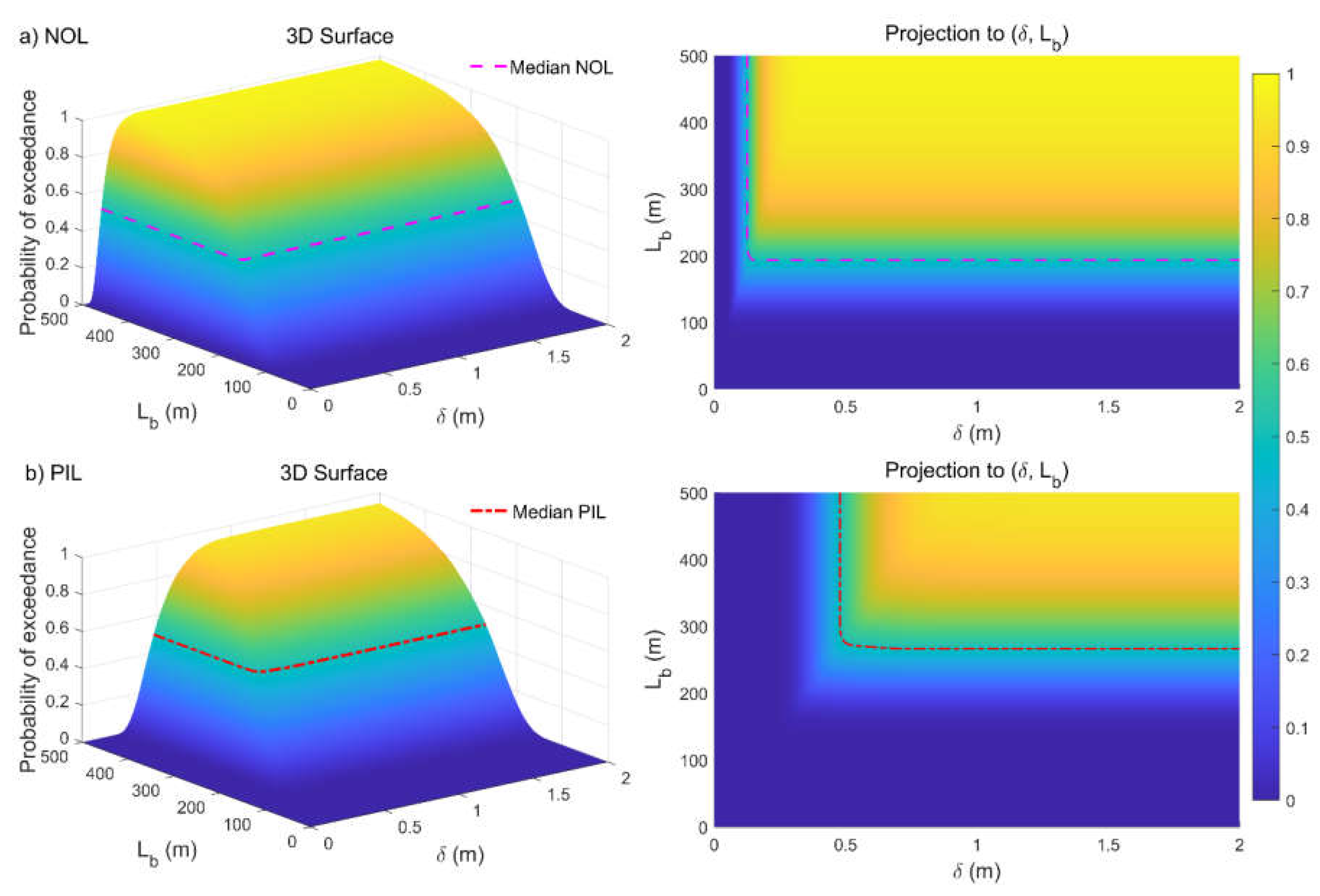
Figure 10.
Comparison of the first order and total order sensitivity indexes of the system input parameters for the a) NOL and b) PIL performance limit state.
Figure 10.
Comparison of the first order and total order sensitivity indexes of the system input parameters for the a) NOL and b) PIL performance limit state.
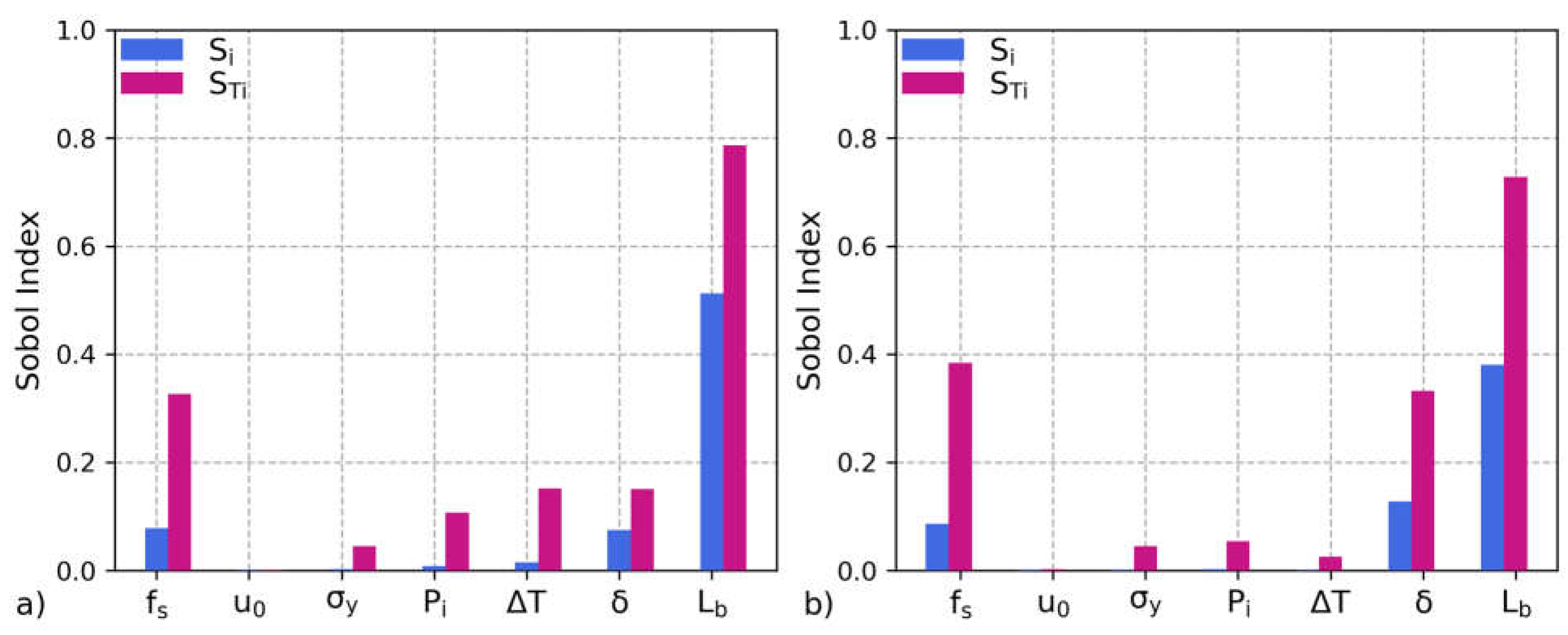
Table 1.
Analytical formulation for evaluating response of the buried pipeline displacement ΔL subjected to a pull-out force F (Banushi, 2017).
Table 1.
Analytical formulation for evaluating response of the buried pipeline displacement ΔL subjected to a pull-out force F (Banushi, 2017).
| i | F-interval | ΔL | Pipe axial force F |
|---|---|---|---|
| 1 | |||
| >1 |
Table 2.
Pipe-soil system parameters.
| Parameters | Units | |
|---|---|---|
| Pipe diameter, D | 0.508 | m |
| Pipe wall thickness, t | 7.1 | mm |
| Pipe elastic modulus, E | 210 | GPa |
| Poisson's ratio, ν | 0.3 | |
| Pipe yield stress, σy | 290 | MPa |
| Pipe cover depth, Hc | 1.5 | m |
| Soil density, γ | 18.0 | kN/m3 |
| Soil friction angle, ϕ | 40 | ° |
| Pipe-soil interface friction angle, δi | 28 | ° |
| Soil pressure at rest, K0 | 1 | |
| Soil friction reaction per unit pipe length, fs | 26.8 | kN/m |
| Relative soil-pipe displacement at friction sliding, u0 | 3 | mm |
Table 3.
Critical ground displacement δcr,i corresponding to the achievement of the normal operability (NOL) and pressure integrity (PI) limit states, in tension and compression, according to the numerical and analytical methods.
Table 3.
Critical ground displacement δcr,i corresponding to the achievement of the normal operability (NOL) and pressure integrity (PI) limit states, in tension and compression, according to the numerical and analytical methods.
| Analysis method | Normal Operability Limit | Pressure Integrity Limit | |||
|---|---|---|---|---|---|
| Tension | Compression | Tension | Compression | ||
| δt1 (m) | δc1 (m) | δt2 (m) | δc2 (m) | ||
| Pressurized pipeline | numerical | 0.5706 | 0.0996 | 0.7835 | 0.4192 |
| analytical | 0.5710 | 0.1001 | 0.7854 | 0.4226 | |
| % difference | 0.06% | 0.51% | 0.24% | 0.81% | |
| conventional | 0.3440 | 0.2327 | 0.5179 | 0.3988 | |
| % difference | 65.90% | -57.18% | 51.30% | 5.09% | |
| Unpressurized pipeline | numerical | 0.3656 | 0.2200 | 0.5420 | 0.5738 |
| analytical | 0.3655 | 0.2199 | 0.5415 | 0.5773 | |
| % difference | -0.02% | -0.06% | -0.08% | 0.61% | |
| conventional | 0.3511 | 0.2069 | 0.5249 | 0.3917 | |
| % difference | 4.12% | 6.35% | 3.24% | 46.48% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






