Submitted:
24 September 2024
Posted:
25 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Human Lower Extremity Anatomy
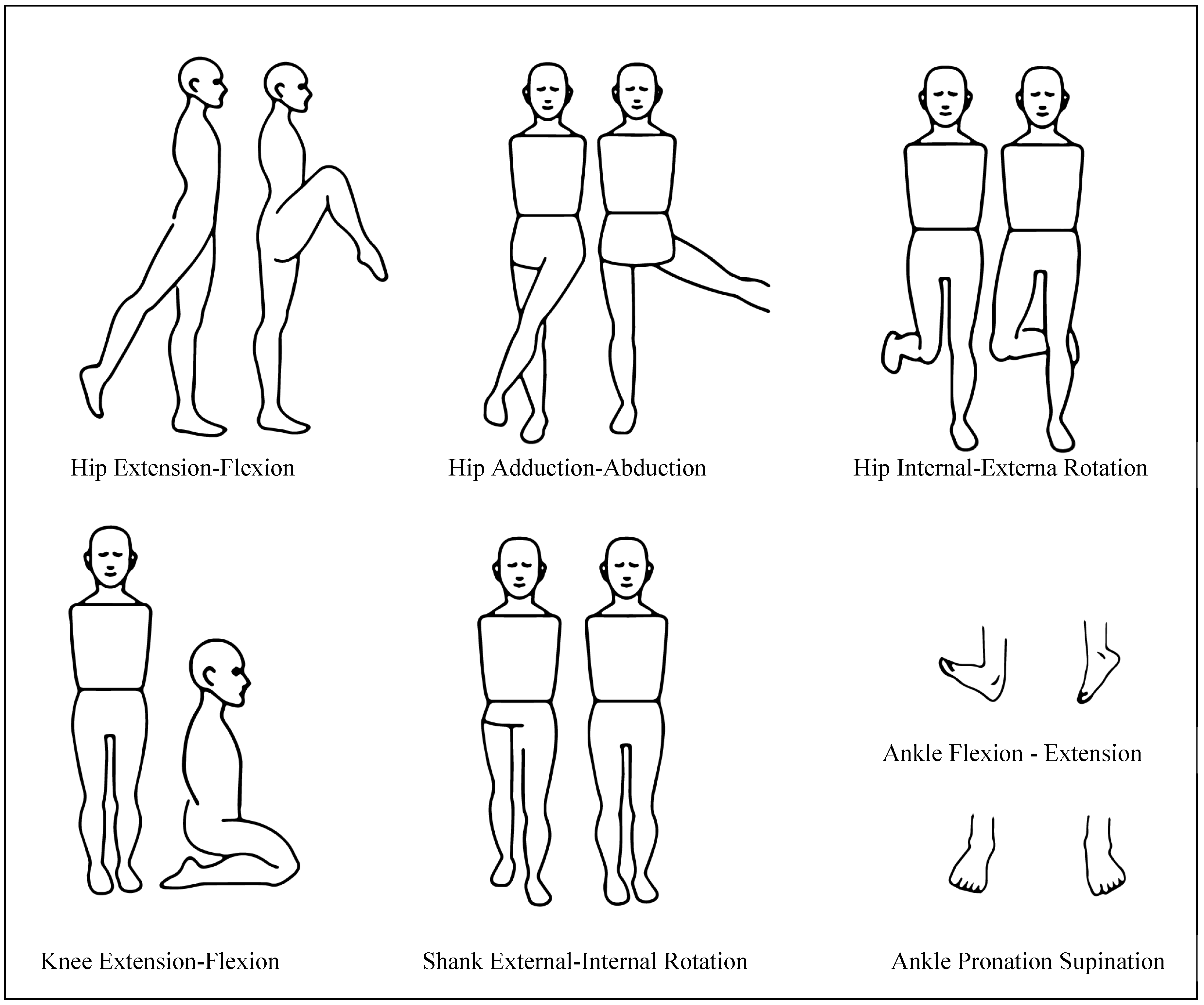
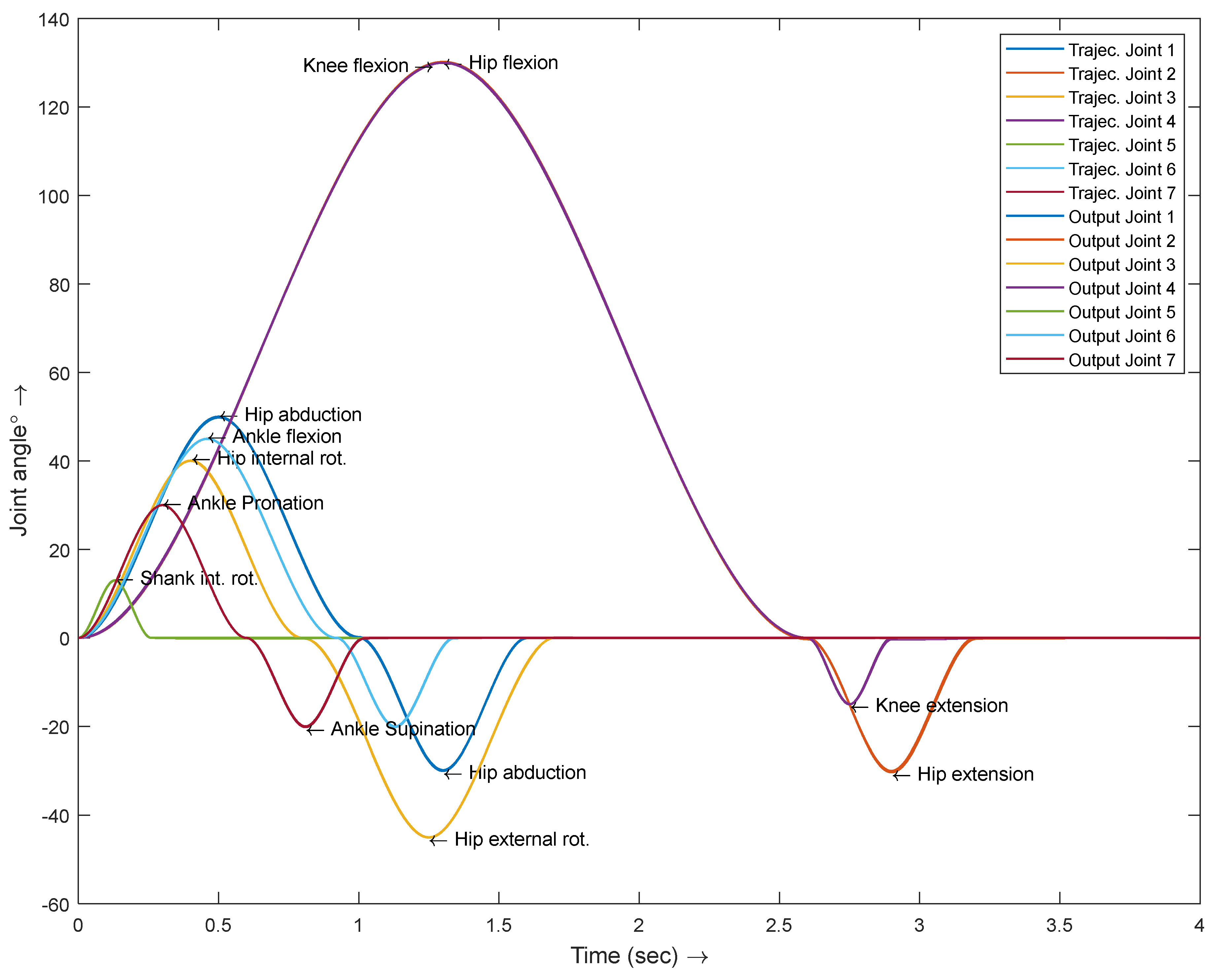
2.1. Human Lower Extremity Ranges of Motion
2.2. Human Lower Extremity Anthropometric Parameters
3. Human Lower Extremity Kinematic and Dynamic Modeling

3.1. Kinematic and Dynamic Modeling
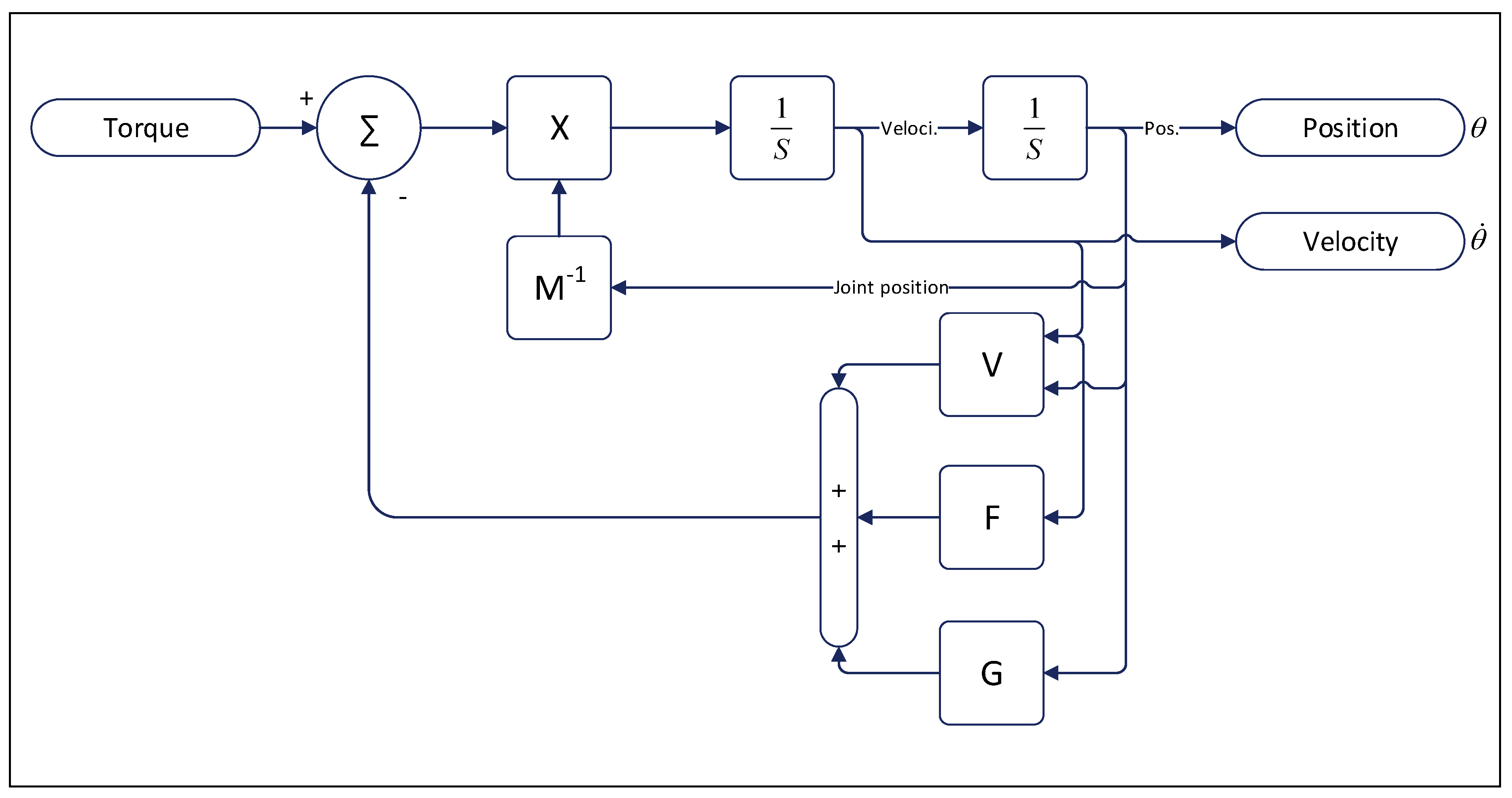
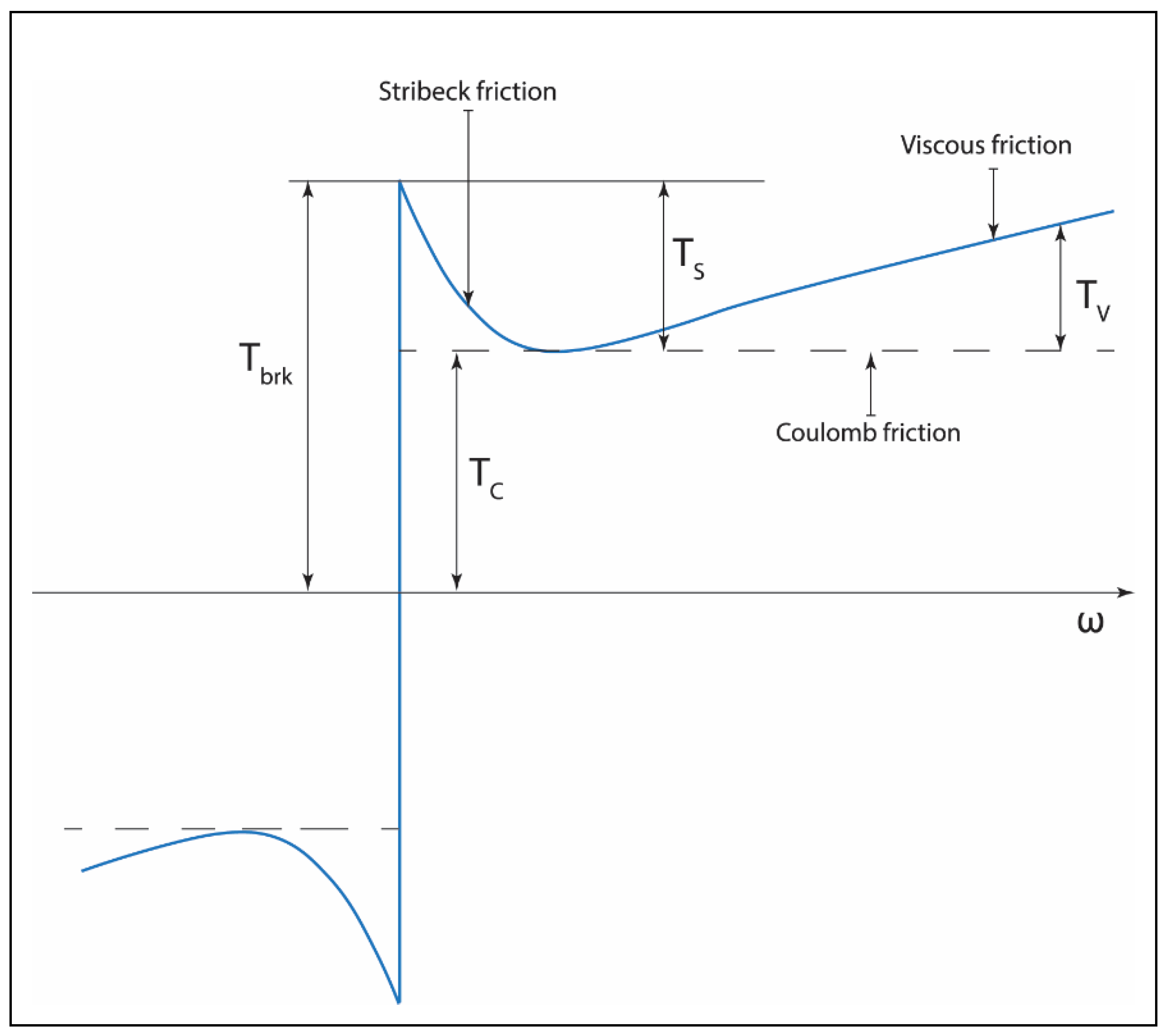
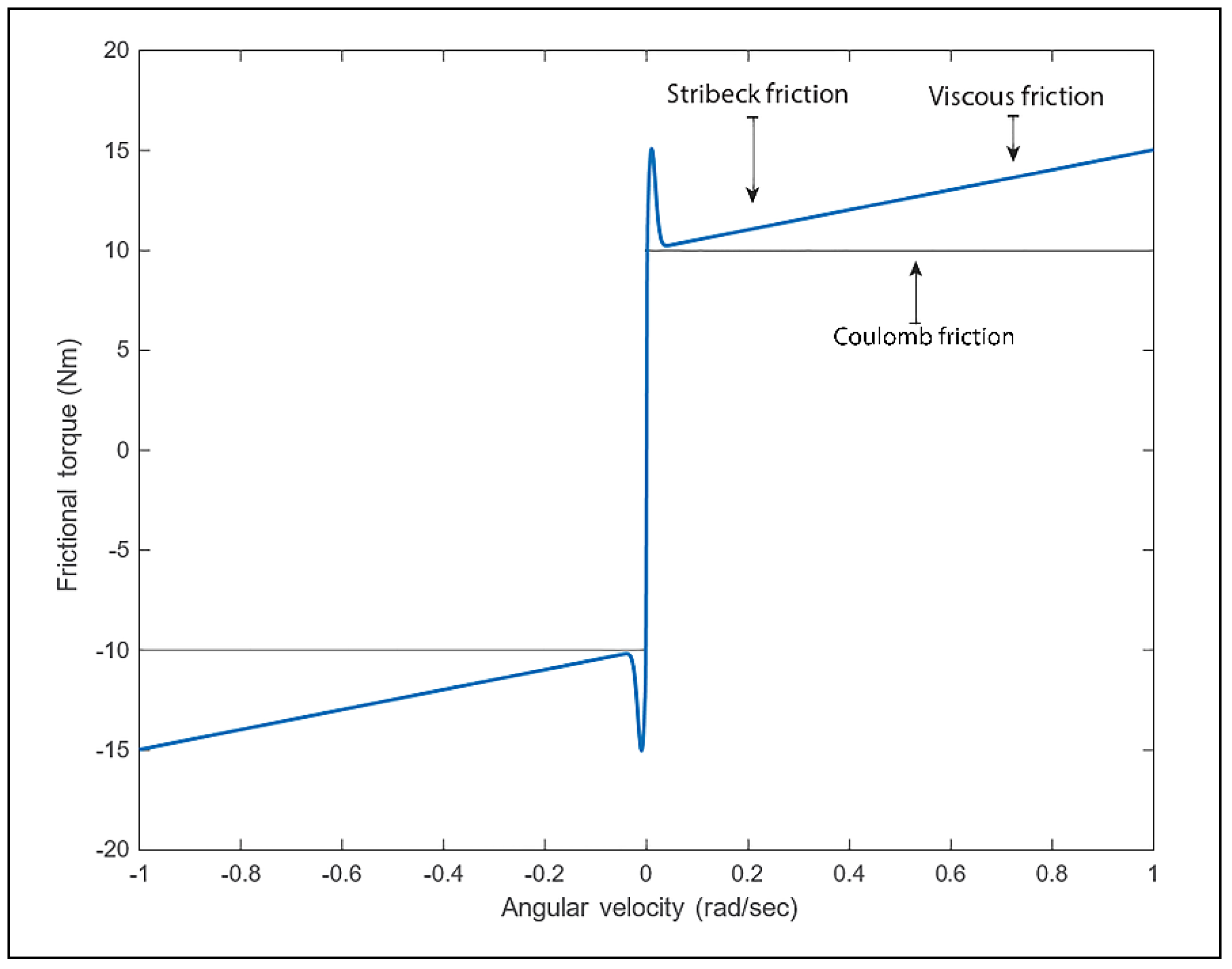
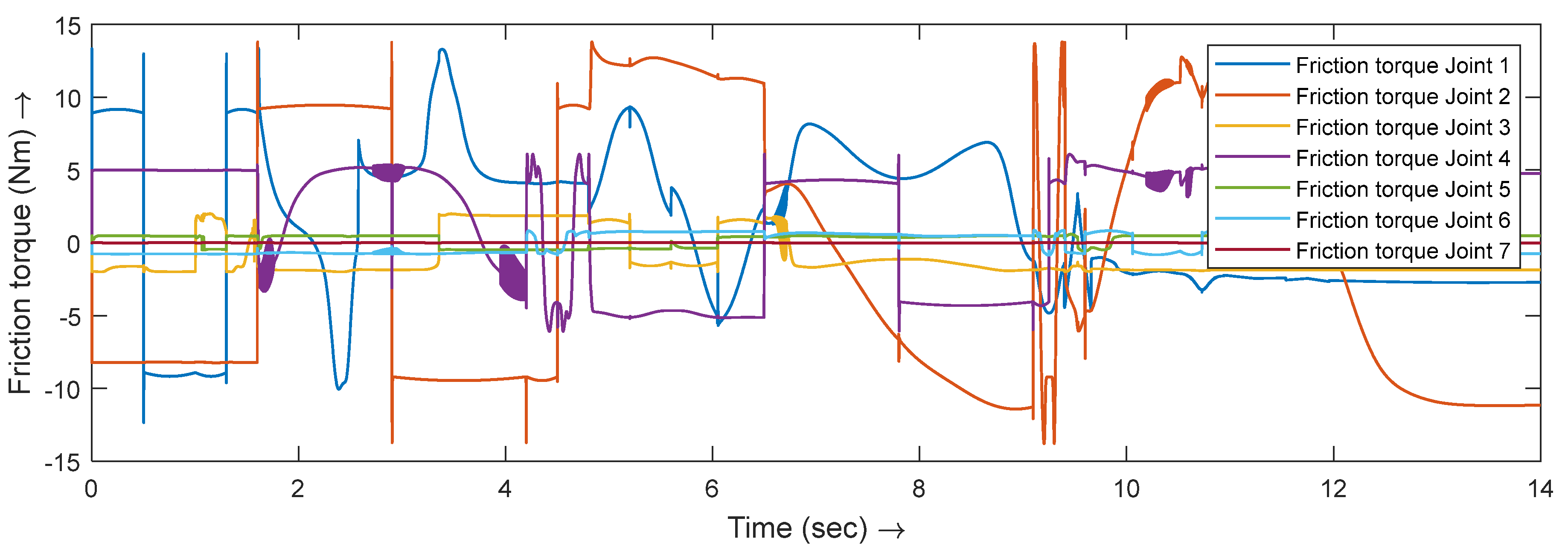
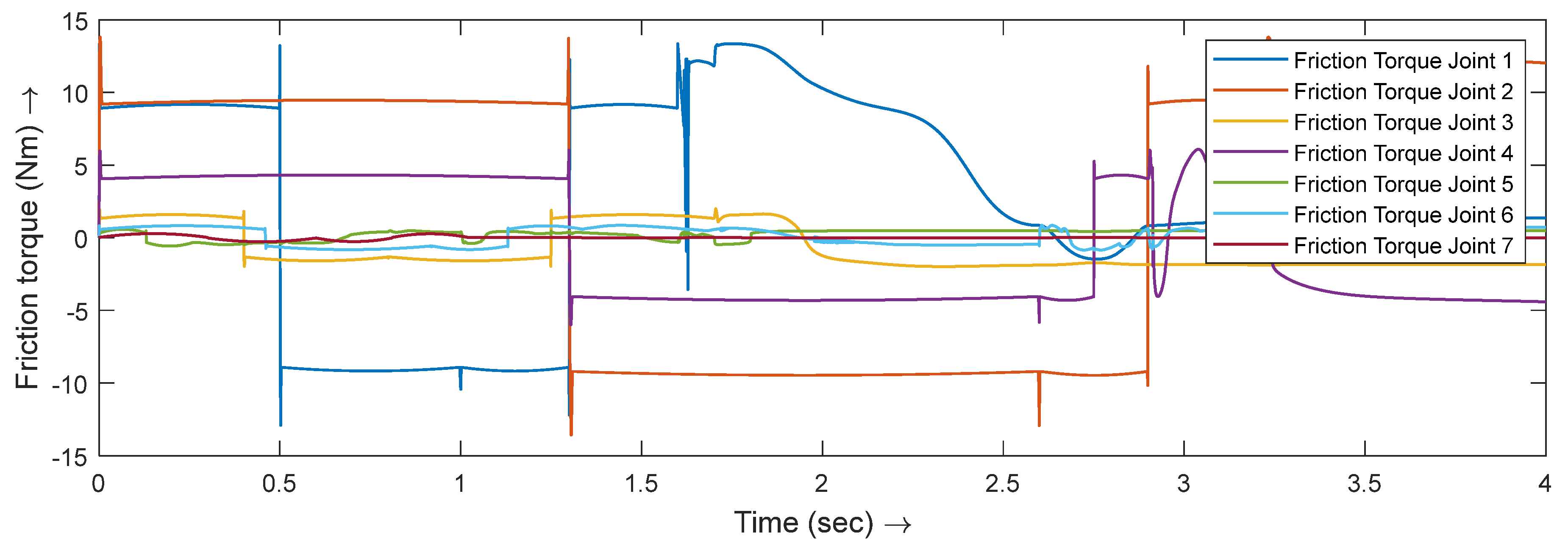
3.2. Friction Modeling
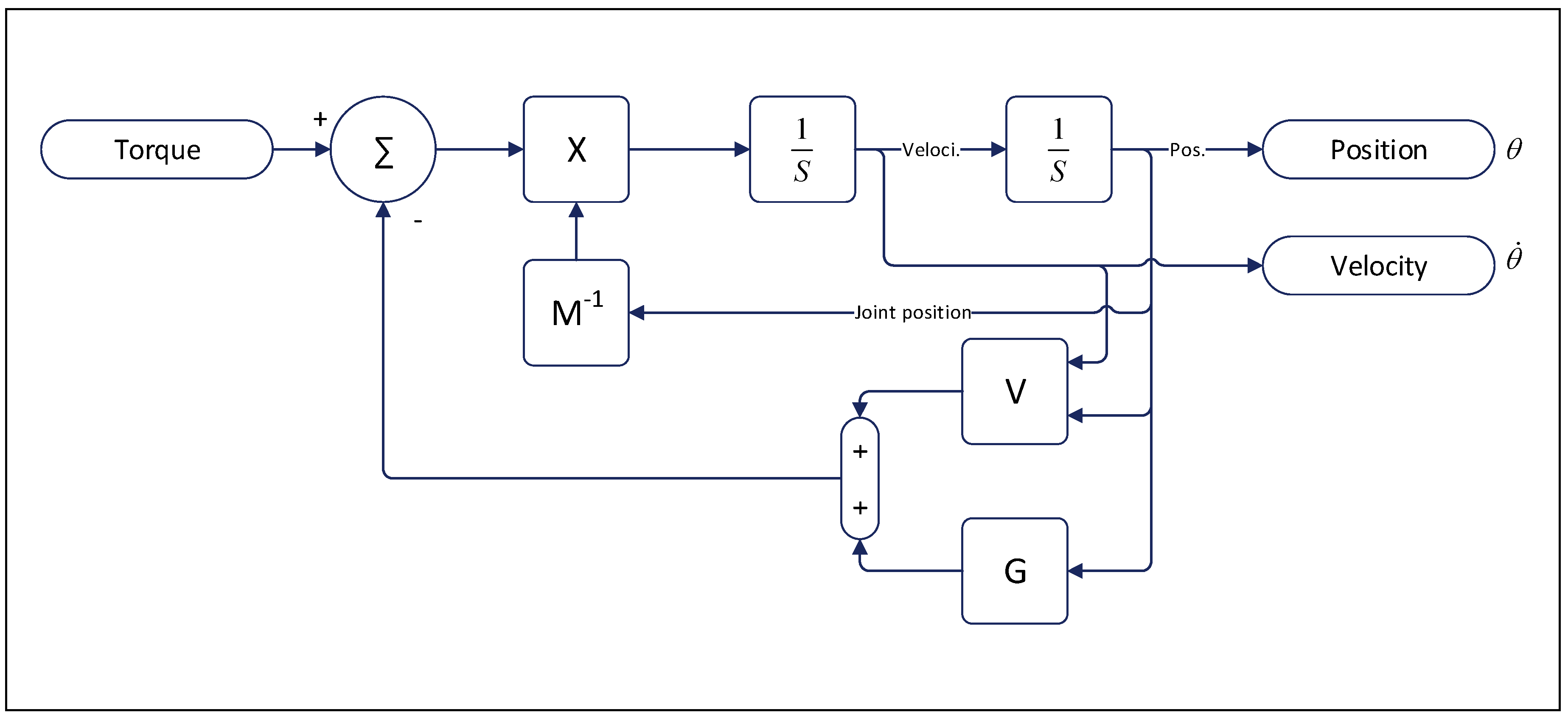
4. Realistic Model Reference Computed Torque Control
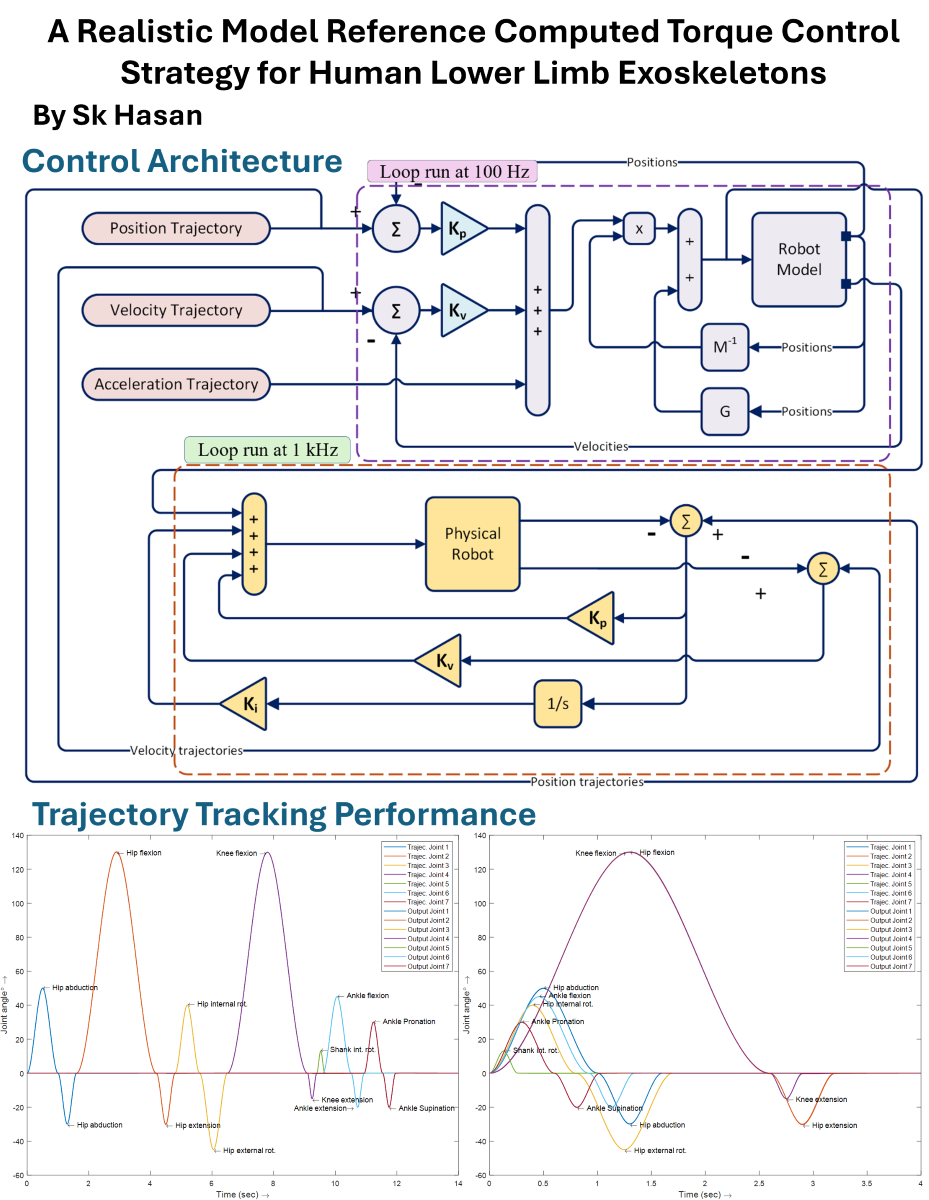
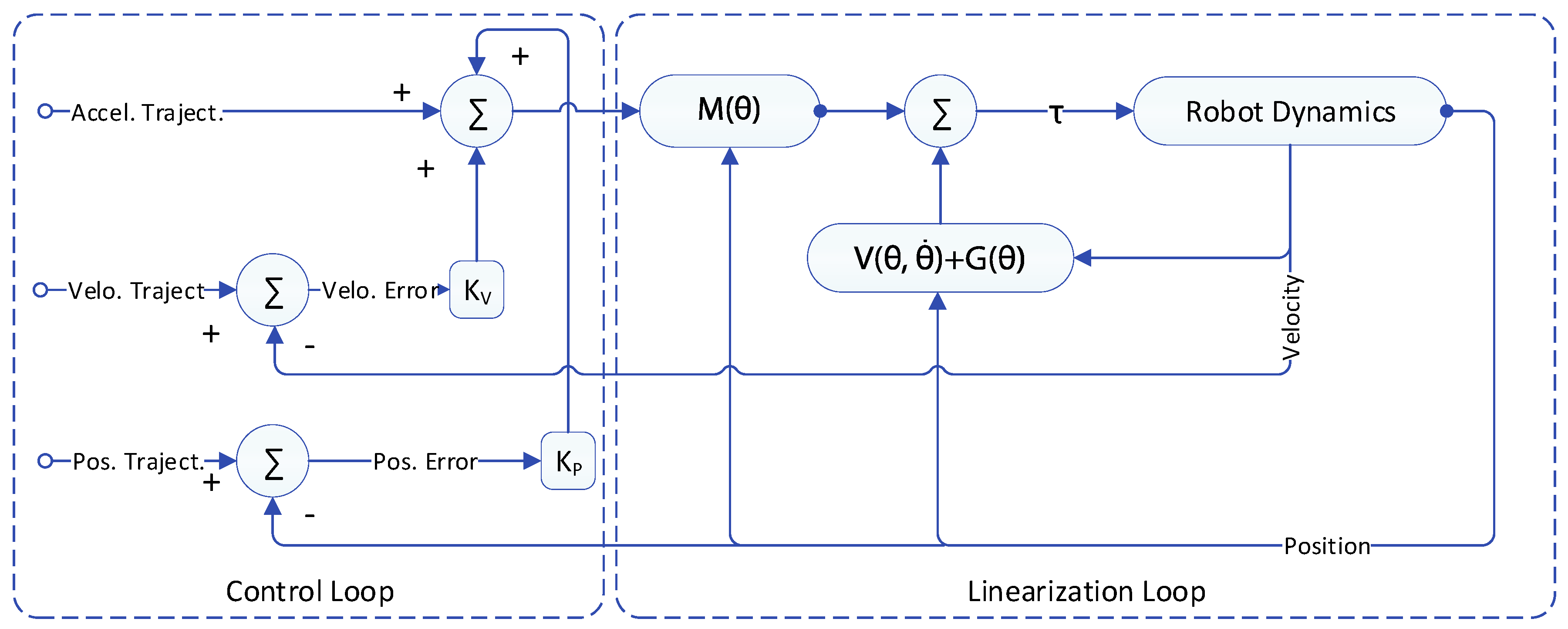
4.1. Computed Torque Controller:
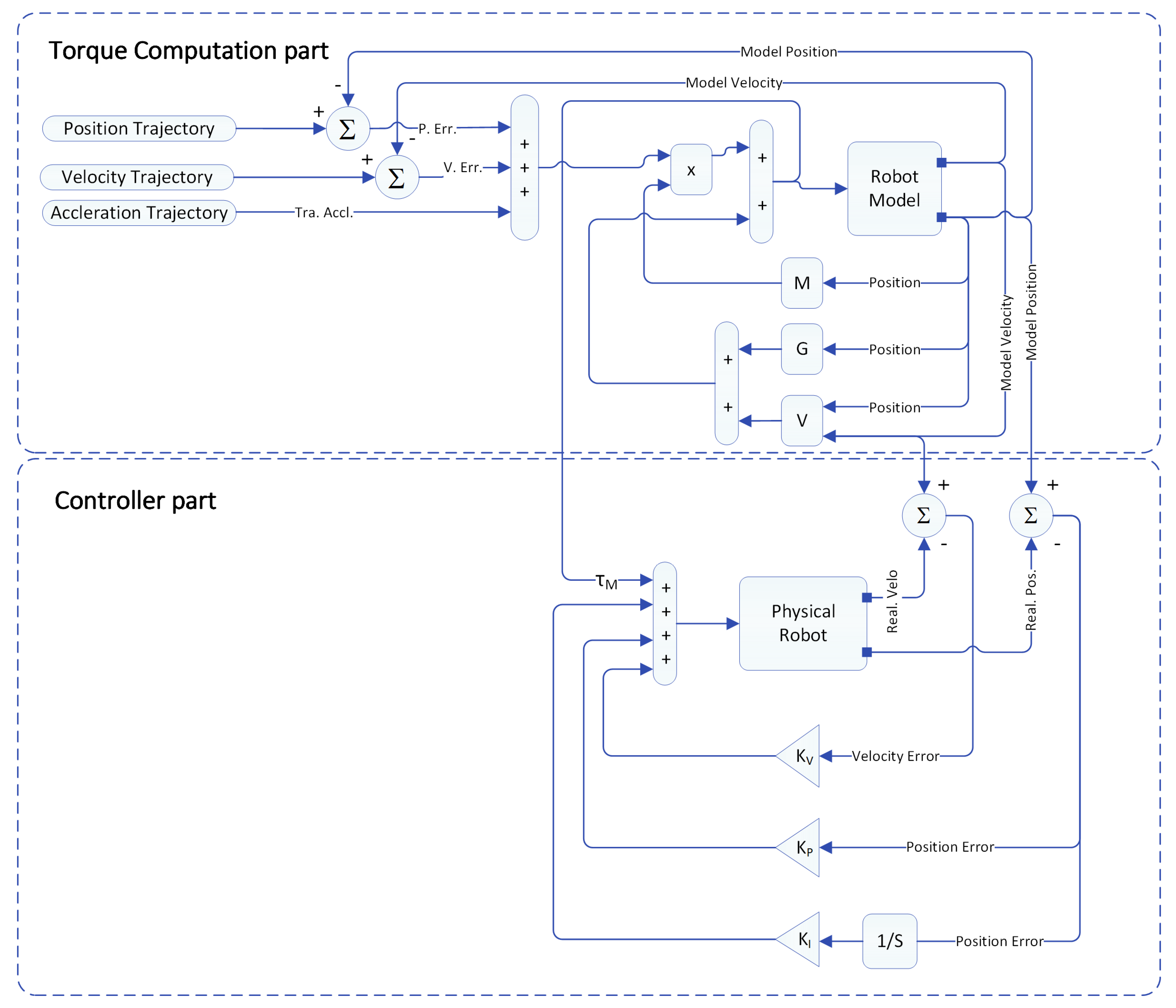
4.2. Model Reference Computed Torque Controller
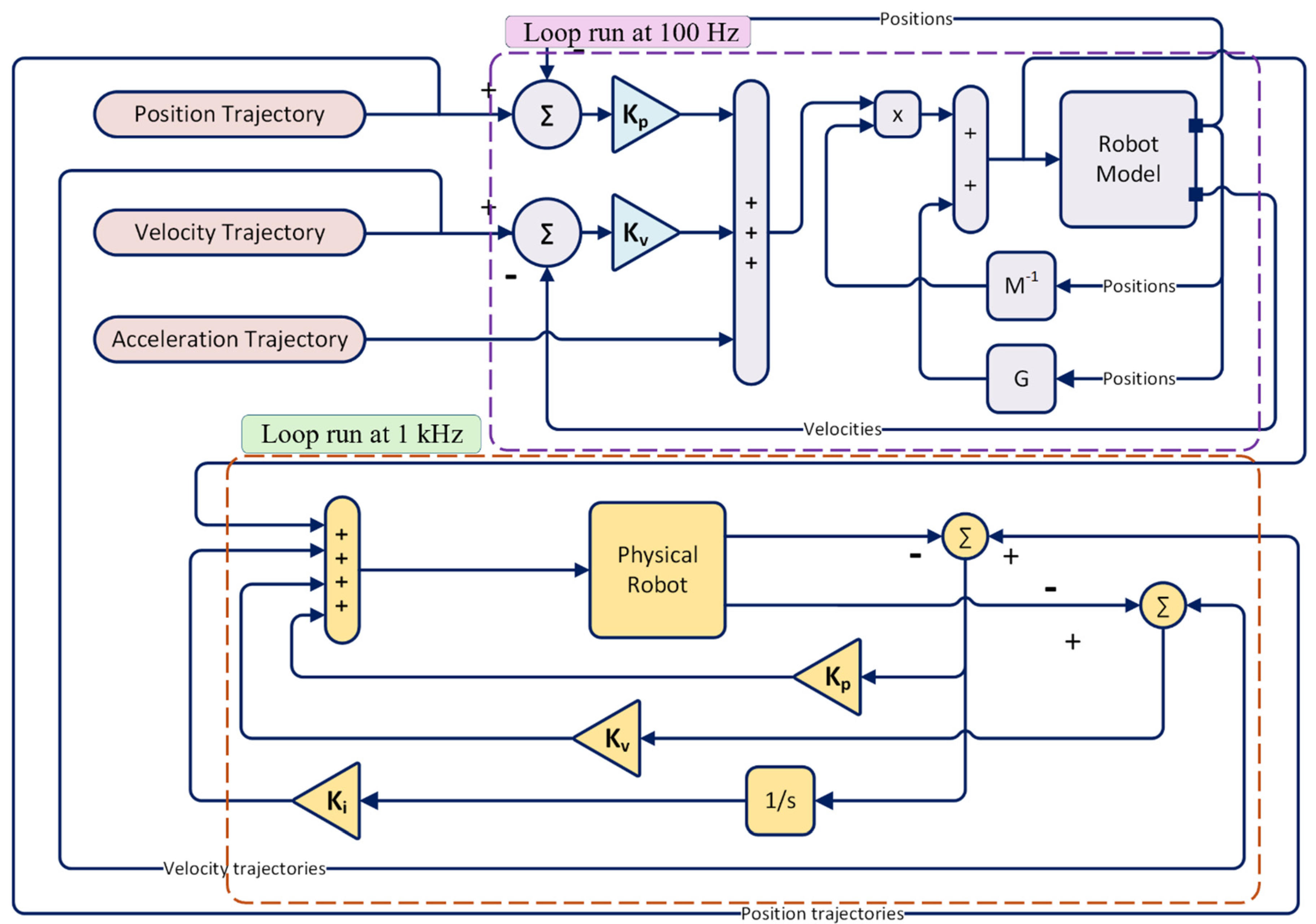
4.3. Realistic Model Reference Computed Torque Controller
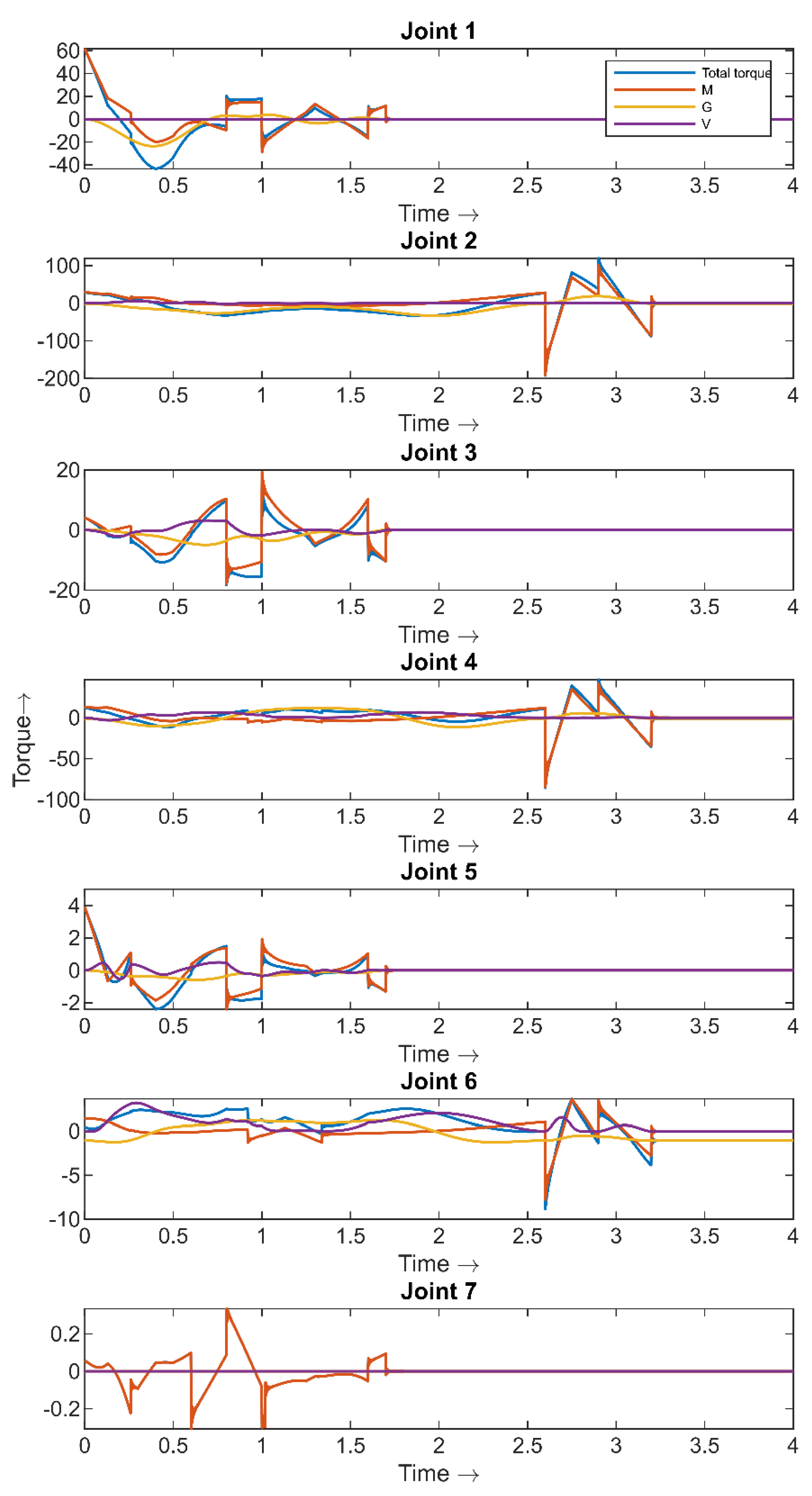
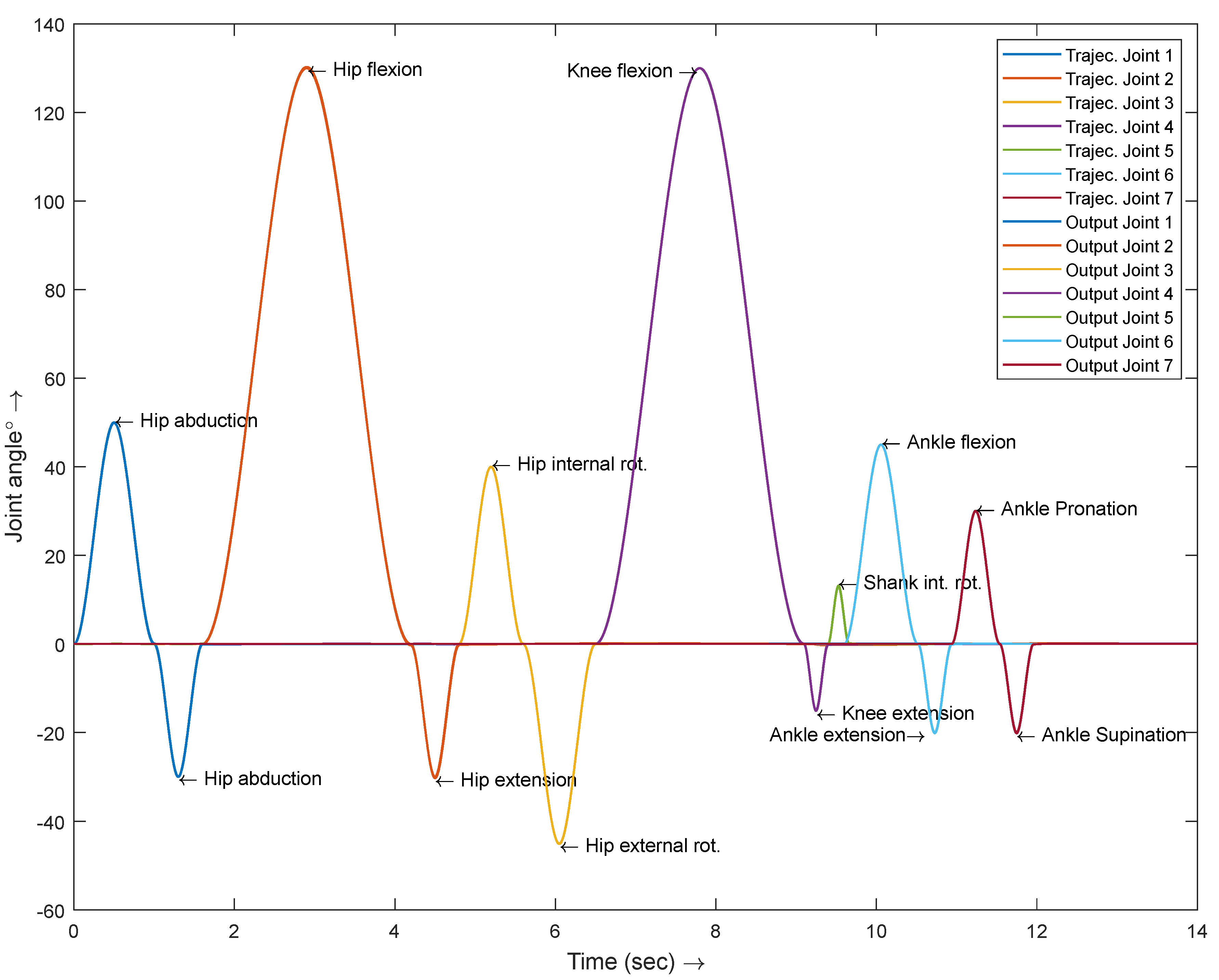
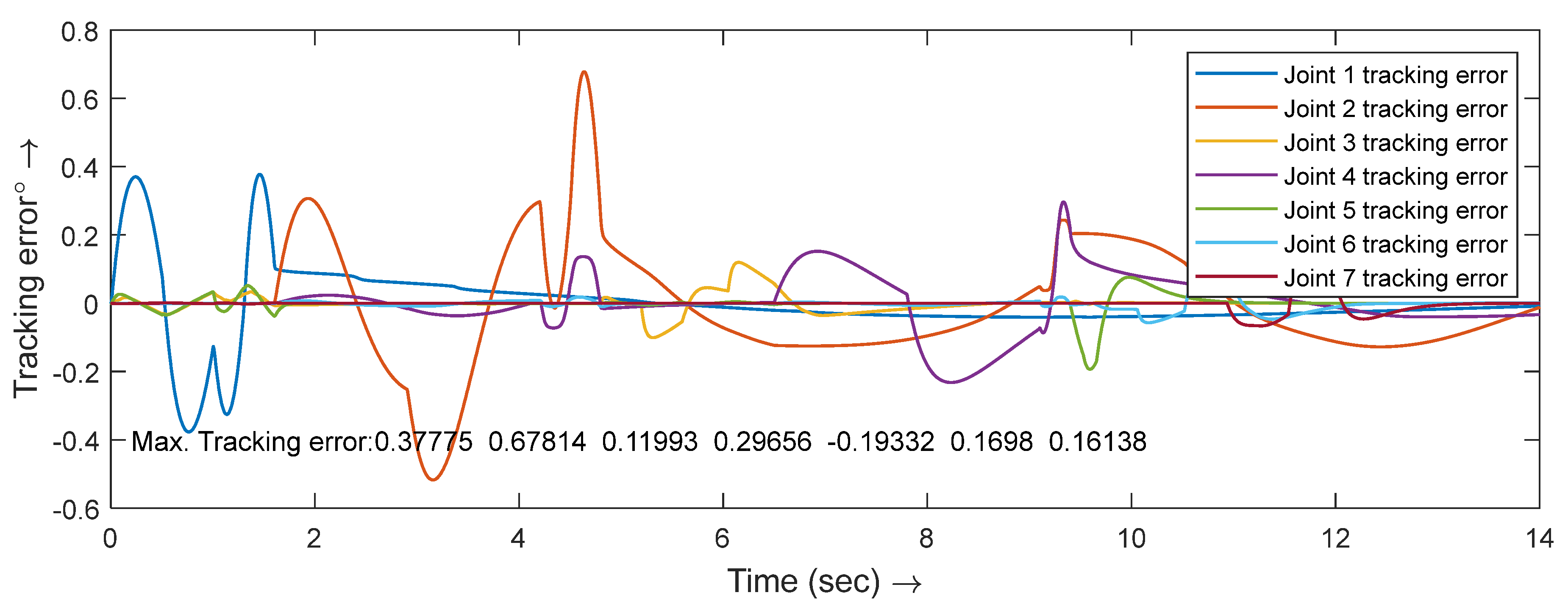
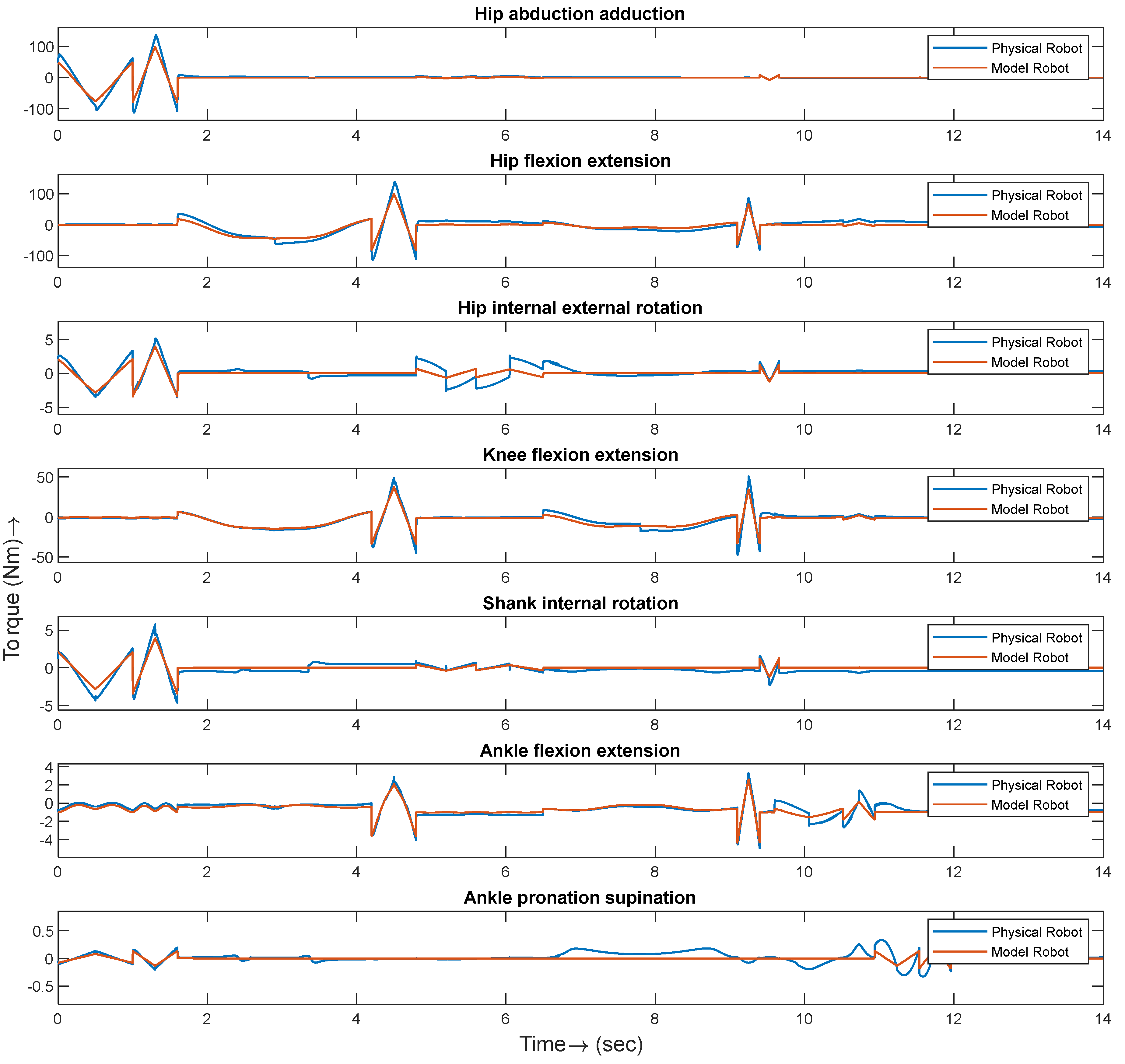
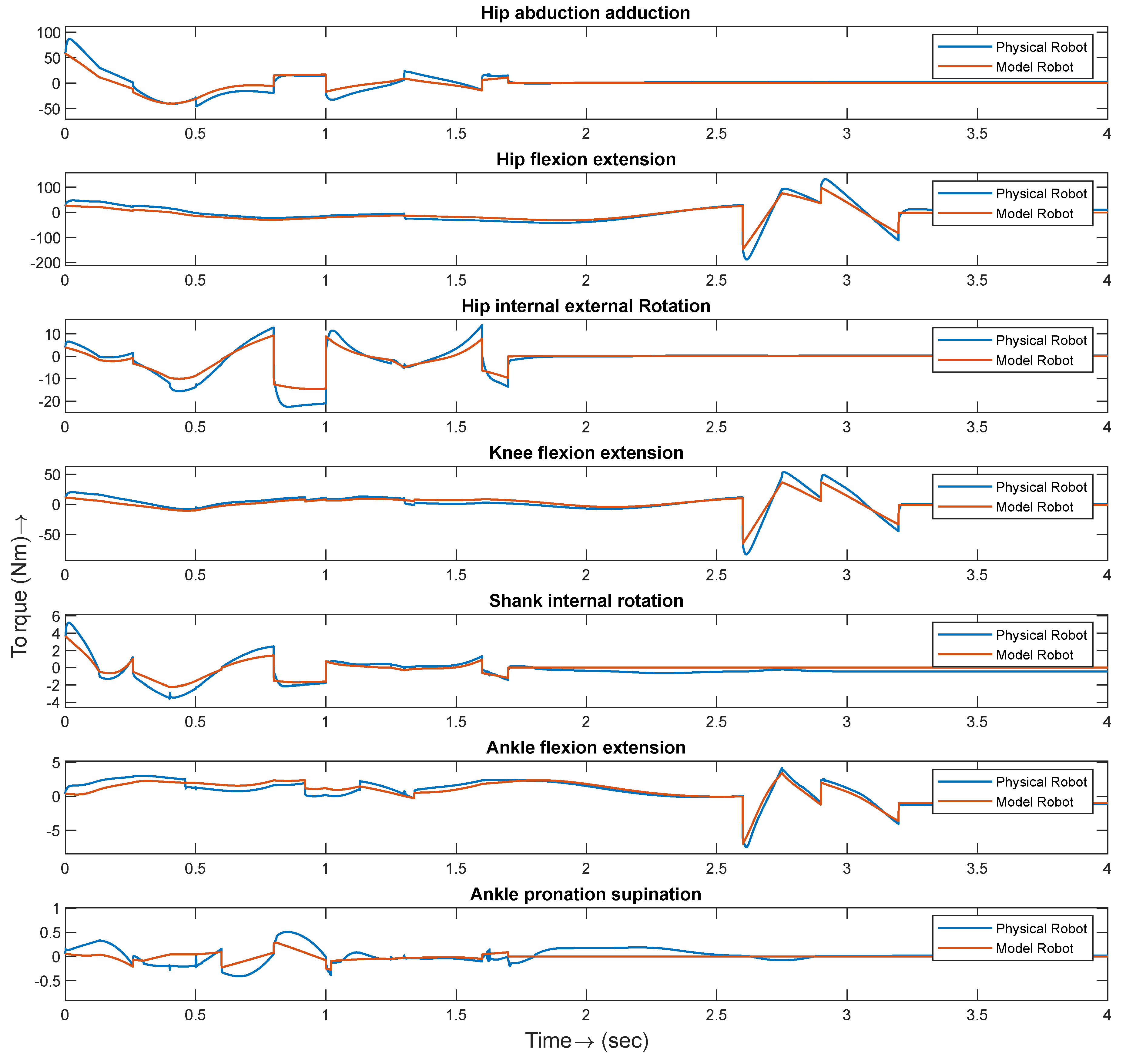
5. Simulation Results and Discussion
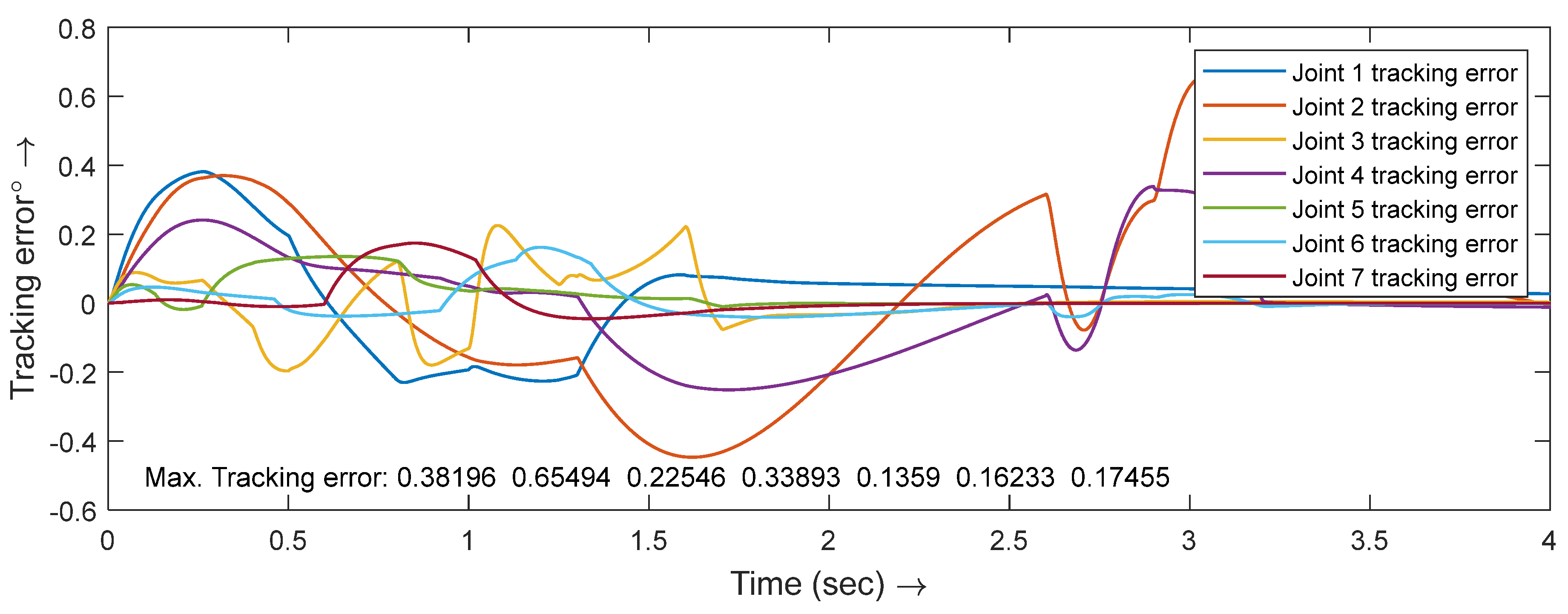
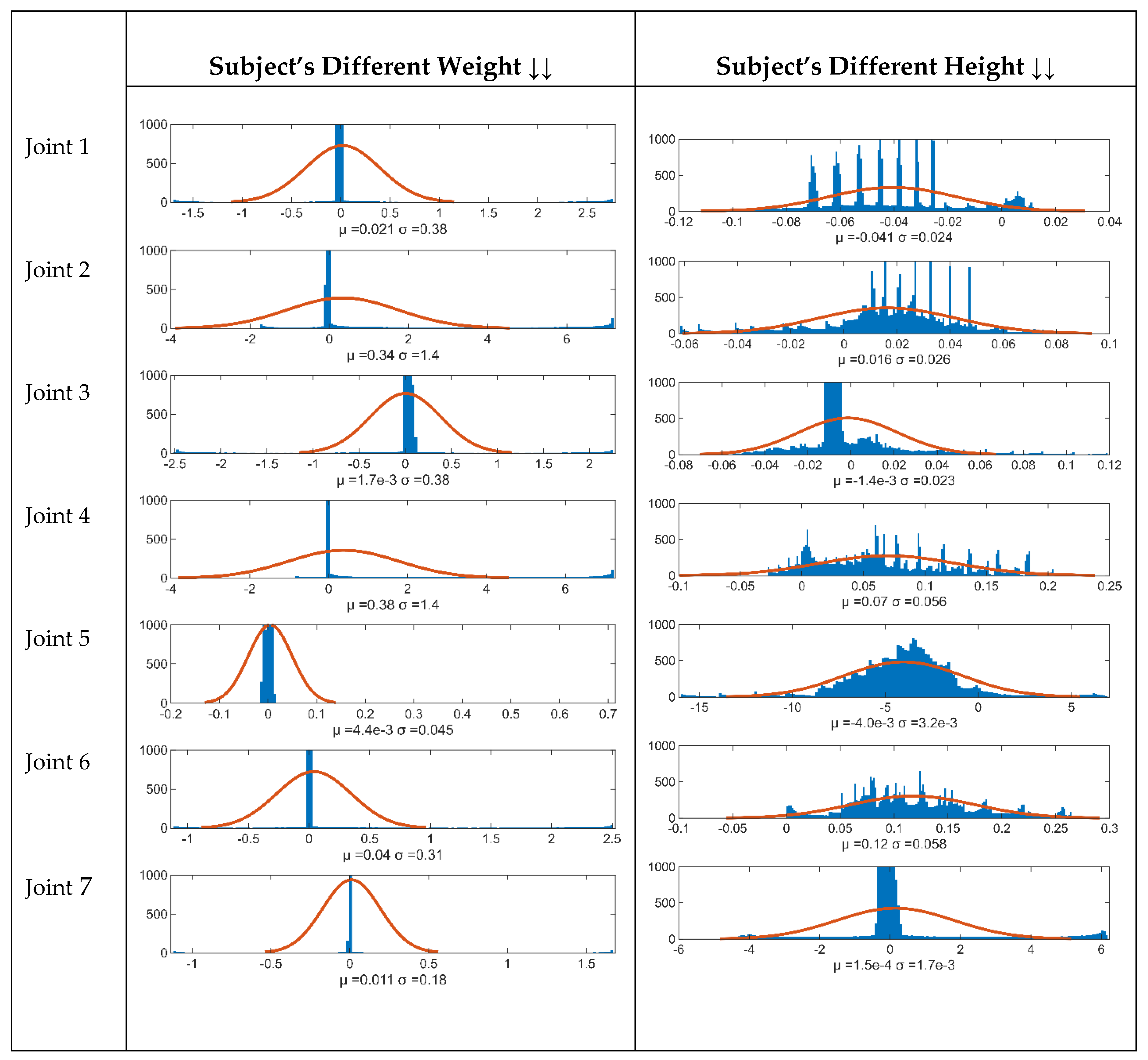
6. Controller Performance Verification
Conclusions
References
- K. Kyoungchul and J. Doyoung, “Design and control of an exoskeleton for the elderly and patients,” IEEE/ASME Transactions on Mechatronics, vol. 11, pp. 428-432, 2006.
- K. Kong, H. Moon, B. Hwang, D. Jeon, and M. Tomizuka, “Impedance Compensation of SUBAR for Back-Drivable Force-Mode Actuation,” IEEE Transactions on Robotics, vol. 25, pp. 512-521, 2009. [CrossRef]
- Colombo, Gery, Joerg, Matthias, Schreier, Reinhard, et al., “Treadmill training of paraplegic patients using a robotic orthosis.,” Journal of Rehabilitation Research & Development vol. 37, pp. 693-700, 2000.
- M. Bernhardt, M. Frey, G. Colombo, and R. Riener, “Hybrid force-position control yields cooperative behaviour of the rehabilitation robot LOKOMAT,” in 9th International Conference on Rehabilitation Robotics, 2005. ICORR 2005., 2005, pp. 536-539.
- J. F. Veneman, R. Kruidhof, E. E. G. Hekman, R. Ekkelenkamp, E. H. F. V. Asseldonk, and H. v. d. Kooij, “Design and Evaluation of the LOPES Exoskeleton Robot for Interactive Gait Rehabilitation,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 15, pp. 379-386, 2007. [CrossRef]
- J. F. Veneman, R. Ekkelenkamp, R. Kruidhof, F. C. T. v. d. Helm, and H. v. d. Kooij, “Design of a series elastic- and Bowden cable-based actuation system for use as torque-actuator in exoskeleton-type training,” in 9th International Conference on Rehabilitation Robotics, 2005. ICORR 2005., 2005, pp. 496-499.
- S. K. Banala, S. K. Agrawal, and J. P. Scholz, “Active Leg Exoskeleton (ALEX) for Gait Rehabilitation of Motor-Impaired Patients,” in 2007 IEEE 10th International Conference on Rehabilitation Robotics, 2007, pp. 401-407.
- S. K. Agrawal, S. K. Banala, A. Fattah, V. Sangwan, V. Krishnamoorthy, J. P. Scholz, et al., “Assessment of Motion of a Swing Leg and Gait Rehabilitation With a Gravity Balancing Exoskeleton,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 15, pp. 410-420, 2007. [CrossRef]
- S. H. Kim, S. K. Banala, E. A. Brackbill, S. K. Agrawal, V. Krishnamoorthy, and J. P. Scholz, “Robot-assisted modifications of gait in healthy individuals,” Experimental Brain Research, vol. 202, pp. 809-824, 2010/05/01 2010.
- P. Stegall, K. N. Winfree, and S. K. Agrawal, “Degrees-of-freedom of a robotic exoskeleton and human adaptation to new gait templates,” in 2012 IEEE International Conference on Robotics and Automation, 2012, pp. 4986-4991.
- H. Kawamoto and Y. Sankai, “Power assist method based on phase sequence driven by interaction between human and robot suit,” in RO-MAN 2004. 13th IEEE International Workshop on Robot and Human Interactive Communication (IEEE Catalog No.04TH8759), 2004, pp. 491-496.
- G. M. Kenta Suzuki, H. Kawamoto, Y. Hasegawa, and Y. Sankai, “Intention-Based Walking Support for Paraplegia Patients with Robot Suit HAL.pdf,” 2005. [CrossRef]
- H. Kawamoto, T. Hayashi, T. Sakurai, K. Eguchi, and Y. Sankai, “Development of single leg version of HAL for hemiplegia,” in 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2009, pp. 5038-5043.
- G. Zeilig, H. Weingarden, M. Zwecker, I. Dudkiewicz, A. Bloch, and A. Esquenazi, “Safety and tolerance of the ReWalk exoskeleton suit for ambulation by people with complete spinal cord injury: a pilot study,” J Spinal Cord Med, vol. 35, pp. 96-101, Mar 2012.
- A. Esquenazi, M. Talaty, A. Packel, and M. Saulino, “The ReWalk Powered Exoskeleton to Restore Ambulatory Function to Individuals with Thoracic-Level Motor-Complete Spinal Cord Injury,” American Journal of Physical Medicine & Rehabilitation, vol. 91, 2012. [CrossRef]
- D. Shi, W. Zhang, W. Zhang, and X. Ding, “A Review on Lower Limb Rehabilitation Exoskeleton Robots,” Chinese Journal of Mechanical Engineering, vol. 32, p. 74, 2019/08/30 2019.
- E. Strickland. (2011). Good-bye, Wheelchair, Hello Exoskeleton. Available: http://spectrum.ieee.org/biomedical/bionics/goodbye-wheelchair-hello-exoskeleton.
- R. J. Farris, H. A. Quintero, S. A. Murray, K. H. Ha, C. Hartigan, and M. Goldfarb, “A Preliminary Assessment of Legged Mobility Provided by a Lower Limb Exoskeleton for Persons With Paraplegia,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 22, pp. 482-490, 2014. [CrossRef]
- D. Sanz-Merodio, M. Cestari, J. C. Arevalo, and E. Garcia, “Control Motion Approach of a Lower Limb Orthosis to Reduce Energy Consumption,” International Journal of Advanced Robotic Systems, vol. 9, p. 232, 2012/12/06 2012. [CrossRef]
- P. D. Neuhaus, J. H. Noorden, T. J. Craig, T. Torres, J. Kirschbaum, and J. E. Pratt, “Design and evaluation of Mina: A robotic orthosis for paraplegics,” in 2011 IEEE International Conference on Rehabilitation Robotics, 2011, pp. 1-8.
- L. Wang, S. Wang, E. H. F. v. Asseldonk, and H. v. d. Kooij, “Actively controlled lateral gait assistance in a lower limb exoskeleton,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2013, pp. 965-970.
- J.-H. Kim, J. W. Han, D. Y. Kim, and Y. S. Baek, “Design of a Walking Assistance Lower Limb Exoskeleton for Paraplegic Patients and Hardware Validation Using CoP,” International Journal of Advanced Robotic Systems, vol. 10, p. 113, 2013/02/01 2013. [CrossRef]
- K. Hian Kai, J. H. Noorden, M. Missel, T. Craig, J. E. Pratt, and P. D. Neuhaus, “Development of the IHMC Mobility Assist Exoskeleton,” in 2009 IEEE International Conference on Robotics and Automation, 2009, pp. 2556-2562.
- N. L. Tagliamonte, F. Sergi, G. Carpino, D. Accoto, and E. Guglielmelli, “Human-robot interaction tests on a novel robot for gait assistance,” in 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), 2013, pp. 1-6.
- Y. Mori, J. Okada, and K. Takayama, “Development of a standing style transfer system “ABLE” for disabled lower limbs,” IEEE/ASME Transactions on Mechatronics, vol. 11, pp. 372-380, 2006. [CrossRef]
- T. Yoshimitsu and K. Yamamoto, “Development of a power assist suit for nursing work,” in SICE 2004 Annual Conference, 2004, pp. 577-580 vol. 1.
- K. Yamamoto, M. Ishii, H. Noborisaka, and K. Hyodo, “Stand alone wearable power assisting suit - sensing and control systems,” in RO-MAN 2004. 13th IEEE International Workshop on Robot and Human Interactive Communication (IEEE Catalog No.04TH8759), 2004, pp. 661-666.
- A. B. Zoss, H. Kazerooni, and A. Chu, “Biomechanical design of the Berkeley lower extremity exoskeleton (BLEEX),” IEEE/ASME Transactions on Mechatronics, vol. 11, pp. 128-138, 2006. [CrossRef]
- H. Kazerooni, R. Steger, and L. Huang, “Hybrid Control of the Berkeley Lower Extremity Exoskeleton (BLEEX),” The International Journal of Robotics Research, vol. 25, pp. 561-573, 2006.
- B. Chen, C.-H. Zhong, X. Zhao, H. Ma, X. Guan, X. Li, et al., “A wearable exoskeleton suit for motion assistance to paralysed patients,” Journal of Orthopaedic Translation, vol. 11, pp. 7-18, 2017/10/01/ 2017. [CrossRef]
- B. Chen, C. Zhong, X. Zhao, H. Ma, L. Qin, and W. Liao, “Reference Joint Trajectories Generation of CUHK-EXO Exoskeleton for System Balance in Walking Assistance,” IEEE Access, vol. 7, pp. 33809-33821, 2019. [CrossRef]
- S. Hyon, J. Morimoto, T. Matsubara, T. Noda, and M. Kawato, “XoR: Hybrid drive exoskeleton robot that can balance,” in 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2011, pp. 3975-3981.
- D. Nguyen-Tuong and J. Peters, Learning Robot Dynamics for Computed Torque Control Using Local Gaussian Processes Regression, 2008.
- T. Kurz. (2015). Normal Ranges of Joint Motion. Available: http://web.mit.edu/tkd/stretch/stretching_8.html.
- A. A. o. O. Surgeons., Joint Motion: Methods of Measuring and Recording: Chicago : American Academy of Orthopaedic Surgeons, 1965.
- F. P. Kendall, E. K. McCreary, P. G. Provance, M. M. Rodgers, and W. A. Romani, Muscles: Testing and Function, with Posture and Pain, 5th ed.: LWW, 2005.
- G. Nikolova and Y. Toshev, “Comparison of two approaches for calculation of the geometric and inertial characteristics of the human body of the Bulgarian population,” Acta of Bioengineering and Biomechanics, vol. 10, pp. 3-8, 2008.
- J. J. Craig, Introduction to robotics : mechanics and control: Pearson/Prentice Hall, Upper Saddle River, N.J., 2005.
- S. Liu and G. S. Chen, “Dynamics and Control of Robotic Manipulators with Contact and Friction,” 2018.
- E. Pennestrì, V. Rossi, P. Salvini, and P. P. Valentini, “Review and comparison of dry friction force models,” Nonlinear Dynamics, vol. 83, pp. 1785-1801, 2016/03/01 2016. [CrossRef]
- J.-L. Ha, R.-F. Fung, C.-F. Han, and J.-R. Chang, “Effects of Frictional Models on the Dynamic Response of the Impact Drive Mechanism,” Journal of Vibration and Acoustics, vol. 128, pp. 88-96, 2005. [CrossRef]
- S. K. Hasan and A. K. Dhingra, “Development of a model reference computed torque controller for a human lower extremity exoskeleton robot,” Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, vol. 235, pp. 1615-1637, 2021/10/01 2021. [CrossRef]
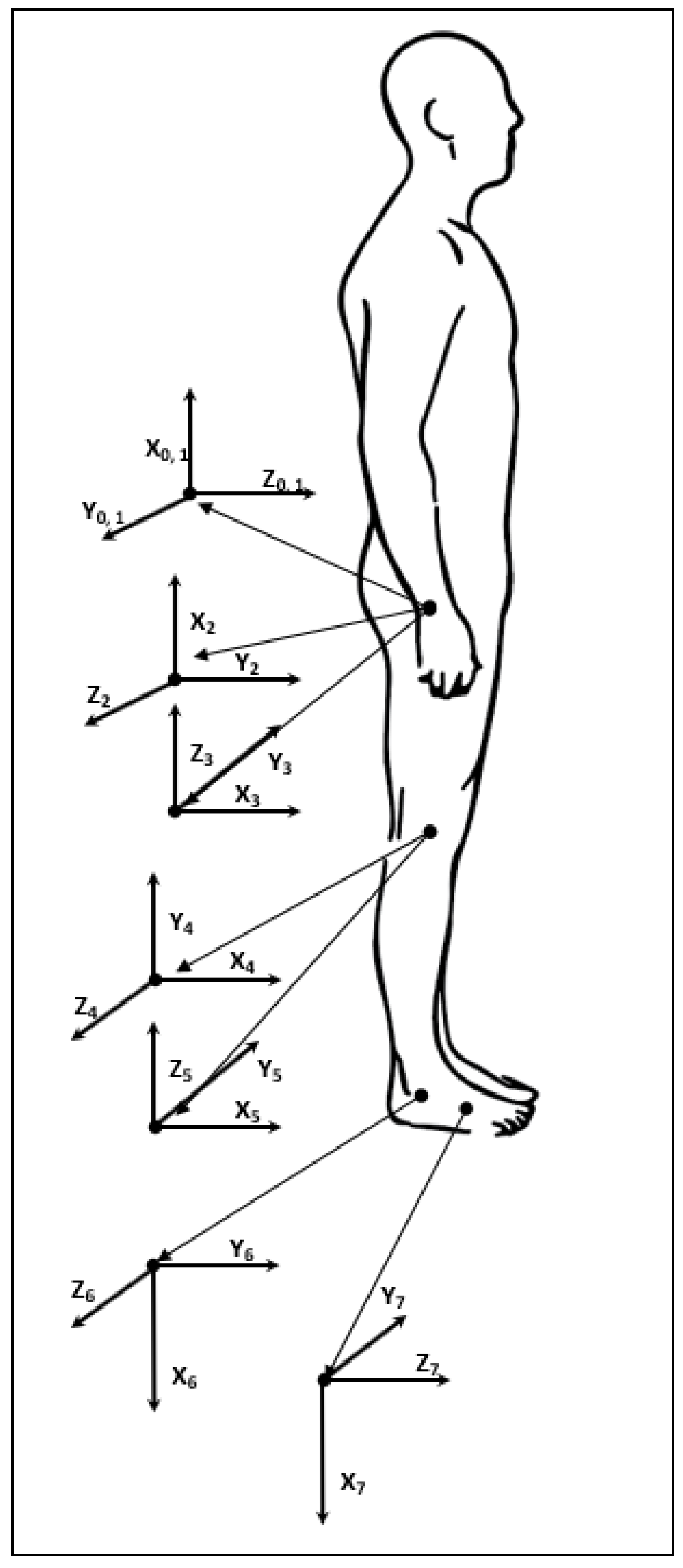
| # | Device name | Actuated joints | Control algorithm | Remarks | Ref. |
| 1. | EXPO and SUBAR |
Hip: F-E (A) Knee: F-E (A) Ankle: (U) Double legs |
EXPO utilizes a Fuzzy logic controller, while SUBAR is developed with an Impedance controller | The use of the impedance controller in SUBAR offers greater user comfort compared to EXPO | [1,2] |
| 2. | Lokomoat | Pelvis: V.M. (U) Hip: F-E (A) Knee: F-E (A) Ankle: F-E (U) Double legs |
Patient-Driven Motion Reinforcement (PDMR) techniques were used to implement the Hybrid Force Position Control System | The PDMR method enables patients to walk at their preferred speed and gait pattern | [3,4] |
| 3. | Lopes | Pelvis: L-R, F-B Hip: F-E(A) A-A (A) Knee: F-E (A) Double legs |
An impedance control scheme was implemented | The impedance controller enabled the creation of a virtual therapist action | [5,6] |
| 4. | ALEX | Trunk: 3 DOF Hip: F-E (A), A-A(U) Knee: F-E (A) Ankle: F-E(U) Single leg |
A force field controller was implemented, allowing the system to apply appropriate force to follow the desired trajectory | The force field controller enabled the development of the assist-as-needed control technique, which is crucial for active and active-assist types of physical therapy | [7,8,9,10] |
| 5. | HAL | Hip: F-E (A) Knee: F-E (A) Ankle: F-E (U) Single leg |
HAL single-leg version operates using a hybrid controller that combines Cybernetic Voluntary Control (CVC) and Cybernetic Autonomous Control (CAC). CVC offers physical support based on the user’s voluntary muscle activity, while CAC functions using pre-recorded trajectories | CVC is effective when the user has strong voluntary muscle signals, while CAC is more suitable when those signals are weak. This allows the system to accommodate all types of patients | [11,12,13] |
| 6. | REWALK | Hip: F-E(A) Knee: F-E(A) Foot: F-E(U) Double legs |
It operates using pre-recorded trajectories, with a tilt sensor determining the trunk angle to select the most appropriate trajectory for the user’s condition | The literature lacks a detailed description of the low-level controller | [14,15] |
| 7. | ELEGS | Hip: A-A (U) F-E (A) Knee: F-E (A) Ankle: F-E (U) |
A finite state machine is used to maneuver a series of states. |
Different controllers were developed for different states. | [16,17] |
| 8. | Vanderbilt Exoskeleton | Hip: F-E (A) Knee: F-E (A) Double legs |
Runs based on preprogrammed trajectories. It has settings for different modes like sitting to stand, walk, stair ascent/descent | The literature lacks a detailed description of the low-level controller | [18] |
| 9. | ATLAS | Hip: F-E (A) Knee: F-E (A) Ankle: F-E(U) |
It was developed by integrating a finite state machine with a PD controller, with specific proportional and derivative gains, along with defined entry and exit conditions for each state | The finite state machine, combined with varying gains, functions similarly to a gain scheduling mechanism | [19] |
| 10. | MINA | Hip: F-E (A) Knee: F-E (A) Ankle: F-E(U) Double legs |
MINA operates using a PD controller and functions in two phases: the recording phase, where trajectories are collected from healthy subjects, and the running phase, during which the robot follows the pre-recorded trajectories | The use of a PD controller for a type I system is well justified, as it ensures both stability and accuracy | [20] |
| 11. | Mind walker | Hip: A-A (A) F-E(A) Knee: F-E(A) Ankle: F-E (U) Double legs |
A joint impedance controller is integrated with a Finite State Machine, where state transitions are triggered by shifts in the center of mass. | This approach is highly effective for controlling walking assistance in lower limb exoskeleton robots. The inclusion of an impedance controller allows the robot to easily match its impedance with the user. | [21] |
| 12. | Walking assistance lower limb exoskeleton | Hip: F-E (A) A-A (U) Knee: F-E (A) Ankle: U Double Legs |
The walking assistance robot operates using a finite state machine, with state transitions triggered by the location of the Center of Pressure, determined through data from the inclinometer | The inclinometer mounted on the backbone measures the torso angle. | [22] |
| 13. | IHMC mobility assist exoskeleton | Hip: F-E (A), A-A (A), R-R (U) Knee: F-E (A) Ankle: F-E (U) Double Legs |
System operates based on torque and position control, with a PD controller used in both cases. | The PD controller is employed for both position and torque control, with greater emphasis placed on system robustness than on tracking accuracy | [23] |
| 14. | Lower-limb power assist exoskeleton |
Hip: F-E(A) Knee: F-E(A) Ankle: U |
A PI velocity control loop is placed within a PI torque control loop. | More emphasis was placed on accuracy rather than the robustness of the control system. | [24] |
| 15. | ABLE | Hip: F-E Knee: F-E Ankle: F-E |
Powered by a PD controller, the mobile platform, lower limb orthosis, and telescopic crutch operate in synchrony | More focus was given on the stability and disturbance rejection rather than tracking accuracy. | [25] |
| 16. | Nurse robot suit | Supports shoulder, waist, legs | PID control technique | PID control algorithms were employed to achieve a balance between stability and accuracy | [26,27] |
| 17. | BLEEX | Hip: F-E (A), A-A (A), R (U) Knee: F-E (A) Ankle: A-A(U), F-E(A) R |
The BLEEX robot operates with a hybrid controller, consisting of two separate controllers: one for the swing phase and another for the stance phase. The swing phase demands high velocity with low torque, while the stance phase requires low velocity with high torque | The combination of the position controller and the positive feedback-based sensitivity controller performed efficiently, resulting in minimal tracking error | [28,29] |
| 18. | CUHK-Exo | Hip: F-E (A), R Knee: F-E (A) Ankle: F-E(P) |
At the lower level, a PD controller is utilized, while the upper level employs the Offline Design and Online Modification (ODOM) control technique | Accurately calculating the center of pressure is impractical, but the use of the ODOM adaptation method enhances its functionality | [30,31] |
| 19. | Xor | Hip: F-E (A), R(U) Knee: F-E (A) Ankle: F-E(P), A-A(U) |
The system operates on a hybrid driving concept, with pneumatic artificial muscles serving as gravity balancers and an electric motor acting as a compensator | A comparison with the PD controller demonstrates the effectiveness of the proposed controller. | [32] |
| Gesture name | Joint variable | Link offset | Link length | Link twist |
| Hip Abduction/Adduction | ||||
| Hip Flexion/Extension | ||||
| Hip Internal/External rotation | ||||
| Knee Flexion/Extension | ||||
| Knee Internal rotation | ||||
| Ankle Dorsiflexion/Plantarflexion | ||||
| Ankle Pronation/Supination | 0 |
| Subject mass | 163 lb (73.95 kg) |
Distance between proximal joint and | Thigh | 6.69 in (170 cm) | ||
| Shank | 7.48 in (18.92 cm) | |||||
| Foot | 4.5 in (11.5 cm) | |||||
| Subject height | 67 in (170.18 cm) |
Thigh inertia () |
(0.0151) |
0 | 0 | |
| Thigh Mass | 12.45 lb (5.65 kg) |
0 | (0.070) | 0 | ||
| 0 | 0 |
(0.070) |
||||
| Shank mass | 7.67 lb (3.48 kg) |
Shank inertia |
(0.06480) |
0 | 0 | |
| Foot Mass | 2.05 lb (0.93 kg) |
0 |
(0.0107) |
0 | ||
| 0 | 0 |
(0.0620) |
||||
| Thigh-length | 16.14 in (41 cm) |
Foot inertia |
(0.001) |
0 | 0 | |
| Shank length | 18.89 in (48.79 cm) |
0 |
(0.0037) |
0 | ||
| 0 | 0 |
(0.0041) |
||||
| Foot length | 10.23 in (25.88 cm) |
PD controller gains Loop 1 | PID controller gains Loop 2 | |||
| [500, 500, 500, 500, 500, 500, 500] | [104, 104, 104, 104, 104, 104, 104] | |||||
|
|
[7500, 7500, 7500, 7500, 7500, 7500, 7500] |
[250, 250, 250, 250, 250, 250, 250] | ||||
|
|
[55x103, 50x103, 55 x102, 3x102, 55x102, 55x102, 55x102] | |||||
| Subject’s Weight | Subject’s Height |
| 150 lbs. | 50 inch |
| 160 lbs. | 55 inch |
| 170 lbs. | 60 inch |
| 180 lbs. | 65 inch |
| 190 lbs. | 70inch |
| 200 lbs. | 75 inch |
| Trajectory tracking Error | Weight | Max Error(99.70% coverage) | Height | Max Error(99.70% coverage) | ||
| Median | STD | Median | STD | |||
| Joint 1 | 0.021 | 0.38 | 1.16 | -0.041 | 0.024 | 0.113 |
| Joint 2 | 0.34 | 1.4 | 4.54 | 0.016 | 0.026 | 0.094 |
| Joint 3 | 1.7x10-3 | 0.38 | 1.14 | -1.4x10-3 | 0.023 | 0.070 |
| Joint 4 | 0.38 | 1.4 | 4.58 | 0.07 | 0.056 | 0.238 |
| Joint 5 | 4.4x10-3 | 0.045 | 0.13 | -4x10-3 | 0.023 | 0.073 |
| Joint 6 | 0.04 | 0.31 | 0.97 | 0.07 | 0.056 | 0.238 |
| Joint 7 | 0.011 | 0.18 | 0.55 | -4.0x10-3 | 3.2x10-3 | 0.0136 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




