Preprint
Review
Introduction to General Theory of Relativity and Interpretation of Geometrical Quantities
Altmetrics
Downloads
51
Views
50
Comments
0
This version is not peer-reviewed
Covariance, Objectivity and Evolution Equations in Either Classical or Quantum Gravity and Quantum Mechanics
Submitted:
25 September 2024
Posted:
25 September 2024
You are already at the latest version
Alerts
Abstract
In this paper, we will describe the general theory of relativity. The special theory of relativity is based on the ideal inertial frames. These ideal inertial frames are assumed to exist in every event in space-time. In contrast, in the general theory of relativity, we do not have to make that assumption. Additionally, the space-time is considered to be part of the solution to the motion. Moreover, interpretation of geometrical quantities is introduced.
Keywords:
Subject: Physical Sciences - Theoretical Physics
I. Postulates of the General Theory of Relativity
Einstein postulated two principles of the general theory of relativity:
- 1)
- The laws of physics have the same form for every observer in an accelerated or not reference frame.
- 2)
- The principle of the equivalence, which states that in the neighbourhood of every point in space, the gravitational field is equivalent to the existence of an accelerated reference frame relative to which there are no gravitational effects.
In the special theory of relativity, the inertial frames were used to describe the laws of physics. However, according to E. Mach’s principle [27], inertial properties depend on the presence of other bodies in the universe. For example, to determine an inertial frame in the laboratory frame on Earth, we have to take into account that Earth is a body that rotates around itself and the Sun.
According to the principle of equivalence, the gravitational mass for each object can be considered to be chosen equal to its inertial mass. Based on the Newtonian mechanics, mass has two distinguished properties. First is the gravitational property as an attraction for other masses through the gravitation’s Newton law:
where is the Newton’s gravitation constant (), is the mass of any object above the surface of the Earth (with mass M) at a distance r (close to the surface) from the centre of the Earth. (Note that , where R is the distance from the surface point to the centre of Earth and h is the height of the mass from the surface of Earth. Here, it is assumed that such that ). In Eq. (1), g is the gravitation acceleration:
where R is the distance from the centre of Earth to its surface. Eq. (1) indicates that bigger the mass stronger the attractive force ; however, Eq. (2) indicates that the acceleration of that mass does not influence its acceleration g.
The second property is the inertial property of the mass, expressed through the second law of Newton in the form:
where is the inertial mass of the same object moving under the resultant force with acceleration a. As that the property, the inertial mass indicates the resistance of the object to acceleration. In the Newtonian mechanics, is chosen such that
That is, and are considered numerically equal. However, experimentally, it is found that and are proportional to each other, and experimentally that proportionality constant is found within an accuracy of . Theoretically, the answer to that concerns is given by Einstein in 1916 with his general theory of relativity, who postulated that and are proportional to each other as a basic connection between the two unique concepts. Suppose a person in an elevator at rest. Then, that person is in a uniform gravitational field , and if that person drops an object, then the acceleration of the object relative to the floor of the elevator is g.
Now, suppose that the elevator is accelerated upwards by an external field with an acceleration . The person (and hence the object in his hands) is in a region where gravity does not exist. If that person drops the same object, then again that object undergoes the same acceleration relative to the floor of the elevator.
That “thought experiment” suggests that we can not distinguish between the two cases, and is an evidence of the two postulated principles by Einstein. That is, the physics is the same for observers in an inertial frame and an accelerated frame. Furthermore, it indicates that the gravitational mass and the inertial mass are equivalent.
Besides, consider an experiment in an elevator with laser light by an observer. If the observer sends a light pulse towards the wall of the elevator, when the elevator is accelerated upwards by an external force, then as the elevator moves up, the pulse strikes a spot which is not the same as it would have been when the elevator is at rest. That is, the trajectory of the light pulse bends downwards as the elevator accelerates upward. Based on the first postulate of the Einstein, we can not distinguish this phenomenon with the light pulse in a reference frame of the elevator accelerating with another non-accelerating reference frame in the gravitational field; therefore, the light beam bends downward by a gravitational field. Note that the experiments have already shown that a small bending exists.
Moreover, the time scales are changed in the presence of gravity. In particular, a clock runs slower under the influence of gravity than a clock located in the places where the gravity is negligible. For example, it has been detected that the frequencies of the radiation by the atoms in the presence of the strong gravity field are red-shifted to lower frequencies compared with the same frequencies in the absence or weak gravitational field. That is observed in the spectra of the atoms in massive stars and Earth by measuring the frequencies of the gamma rays emitted from nuclei that were separated vertically by a certain distance, so the gravitation field strength was varying.
It is a consequence of the general theory of the relativity that if we consider two identical clocks, one in the first floor of a high building and the other on the upper floors, for instance on the 10th floor, the one that is on the first floor run slower than the clock on the 10th floor because the gravity is more influential on the first floor compared to the 10th floor.
Another evidence of the general theory of relativity is the application of the so-called Global Positioning System (GPS) unit, which employs the relativistic correction of the time calculations when it analyses the signals received from the orbiting satellites. Note the clocks on the surface of the Earth run slower than the identical clocks in the Earth-orbiting satellites because they experience a stronger gravitation field of the Earth’s surface [27].
A consequence of the second postulate of Einstein is that the gravitation field may be made negligible at any point by an appropriate choice of the reference frame, such as a freely falling object as a reference frame. Also, Einstein introduced a concept that is known as curvature of space-time in which the gravitational strength can be specified in every point [1]. In fact, according to Einstein, the Newtonian concept of gravitation force does not exist, but rather every mass causes a curvature of space-time in its neighbourhood, which is followed by all freely moving objects in that space-time. Therefore, the two masses, which are at a distance r from each other, cause the curving of the space-time in between, and hence the two masses move towards each other.
As an evidence of the curved space-time of the general theory of relativity would be the deflection of the light ray passing near the Sun due to the curvature of the space-time caused by the Sun’s mass. Indeed, this is confirmed by the detection of the starlight bending near the Sun during one of the total solar eclipse.
Another consequence of the curvature of the space-time, in extreme cases, is the creation of the so-called black holes. That occurs when the mass concentration becomes very large, for example, when a massive star collapses to a small volume. Within a certain distance from the centre of the black hole, the curvature of the space-time is so extreme that it will not allow any matter, information, or even the light to escape. Note that recently there are reports that the creation of the black holes have been observed [28].
Also, the general theory of relativity predicts the existence of the so-called gravitational waves from the moving masses. More importantly, very recently, these waves are directly experimentally observed.
II. Gravitational Field in General Theory of Relativity
The general theory of relativity is mathematically described under the framework of non-Euclidean geometry. A common term used is the geodesic, giving the paths of the shortest distance. In general theory, the objects move along the geodesics of space-time. Assume that a set of geodesics starts parallel to each other. If the gravitational effects in the region extended by the geodesics are uniform, then the geodesics will remain parallel. However, if these gravitational effects are nonuniform within that region, the geodesics will deviate and start either approaching or receding each other. According to the general theory, the geodesic deviation is used as a measure of the gravitational field.
Note the analogy with the first law of Newton, which states that if there are no external forces, then the object continues moving along a straight line without acceleration.
As an example, we consider two objects separated by a distance of along the horizontal direction. Assume that the objects drop simultaneously from the same height above the surface of the Earth. Based on the principle of equivalence, locally, very close to each object and neglecting the gravitational mass of the objects, we can treat the region as an inertial frame. That is, in a local region of either object, the gravity can be made to vanish by the choice of the inertial reference frame. That system corresponds to a local to either object free fall frame, which will be used as an observer inertial system. As the objects fall toward the surface of Earth, their separation decreases. The change in their separation is a local measure of the gravitational effect of Earth since the choice of the frame can not neglect it. Fall itself of each object is not considered a gravitational effect because the selection of the frame can eliminate it, such as a frame that is accelerated by external forces with acceleration upward.
In Figure 1, we show two geodesics, where two 4-vector fields are defined at each point, namely the 4-velocity field of motion along the geodesic, and the separation field vector between two geodesics along the horizontal direction.
Let be a time when in each geodesic, there were observed test particles at the head and tail of the vector . The proper time will be used at the tail of the deviation vector, and the head is at the point where the other test particle is at the same time. Note that as the motion of test particles progress along the geodesics, the proper times of the two test particles are not the same. In the Newtonian approximation, the equation of motion for the separation between the test particles is given by [22]
where is the length along the geodesic.
In Eq. (5), R is a constant that depends on the distance to the centre of Earth. Eq. (5) indicates that the acceleration of the distance between the two geodesics is proportional to their separation, . Solution of Eq. (5) is given as (assuming an initial phase equal to zero):
For the case of a two-dimensional example of the geodesics on the surface of a sphere, we assume that initially the two geodesics are parallel. Then, they meet after they have traveled th of the circumference of the sphere, that is:
where a is the radius of the sphere. Therefore,
Solving it for R, we obtain
Thus, R represents the gaussian curvature of the surface of the sphere, a two-dimensional space, which is product of two gaussian curvatures, namely and along the two separate one-dimensional directions on the sphere’s surface.
III. Some Aspects of Fundamental Tensor
The invariant expression of the square of a linear element is written as
where . In Eq. (10), is a covariant second rank tensor, which is symmetric: . That tensor is also called by Einstein as fundamental tensor because of its role in physics basis of understanding the gravitation. Based on Einstein, the contravariant second rank tensor, , is defined such that
where
and in Eq. (11), based on Einstein’s rule, the repeating indices up-down indicate summation.
Therefore, based on Einstein, the contravariant tensor is defined by calculating the determinant of covariant tensor , then for each element of we can consider the co-factor and divide it by g to determine . That is, in terms of matrix notations, is the inverse of . Therefore,
or in matrix form , where is a diagonal matrix with all diagonal elements equal to 1. Eq. (10) can also be written as
we can write
Combining Eq. (14) and Eq. (15), we write that
Eq. (16) indicates that is the contravariant form of the same second rank tensor .
The tensor , which is a covariant second rank tensor obeys the Lorentz transformation (a physical quantity can be defined in terms of a contravariant vector in four-dimensional space or , respectively, in the inertial frame S and , if between them there exists a relation as follows:
That is, is given as
); that is:
Taking the determinant of both sides in Eq. (19), and using the properties of the multiplication of determinants, we can write:
where is the matrix given by:
which the so-called Lorentz transformation tensor. It can be seen that is a symmetric matrix.
Denoting by and , we can write
We can now apply the rule of transformation of the volume in the four-dimensional space for an element of volume
Using Jacobi’s theorem, in the new coordinates
Combining Eq. (22) and Eq. (24), we obtain that
We can denote by the absolute value of g to have a positive number, then Eq. (25) reduces to
Eq. (26) implies the invariance of , characterises the hyperbolic nature of the space-time continuum, as stated by Einstein. Moreover, gives the magnitude of the four-dimensional element of the volume in a local reference frame in the same sense as in the spacial theory of relativity of a rod-clock measurement. Therefore, based on the time form and the space-like volume form, the scaled space-time volume form is
where g is the determinant of the covariant form . Furthermore, is dependent on the point in the four-dimensional space-time space, , according to the general theory of relativity. That is in contrast to special theory of relativity, where there exists a finite region in four-dimensional space such that are assumed to be constant.
In the general theory of relativity, the elements physically describe the gravitational field concerning the chosen reference frame, and they are no longer constant but functions of the four-dimensional space point ; that is, they depend on both space and time. Furthermore, if we describe the motion of a free particle, then its movement in the new coordinates will be a curved nonuniform motion. The law of this motion will be independent of the nature of the moving particle, and, based on Einstein, it can be interpreted as a motion under the influence of the gravitation field, which occurs because of the dependence of on .
In contrast, based on the special theory of relativity that may apply to a particular four-dimensional region with some properly chosen coordinate reference frame, then has components constant, the free particle moves relative to this frame with uniform motion in a straight line.
Therefore, if we are no longer able to chose a coordinate system, where the special theory of relativity applies to a finite region of the space-time, then we should consider that elements describe the gravitation field. They are a function of the four-dimensional space point .
IV. Motion of a Particle in Gravitation Field
We now describe the motion of a point-like particle in the presence of the gravitation field. In particular, we will derive the equation of the geodesic line. For that, we will use the formalism for describing the motion of a free particle from the special theory of relativity viewpoint.
We call again the principle of the least action. The action integral I is defined as a time integral of Lagrangian function L along a possible path of the particle. The path that we would like to know the equation. The action integral is written as:
where the integral is evaluated in the proper time interval between and measured in the local coordinate system of particle. In Eq. (28), s represents a parameter in the sense that it is monotonically increasing function of , that is, . Furthermore, represents the magnitude of the element length along the geodesic line given by Eq. (10), which is Lorentz invariant.
First, we write Eq. (28) in the following form:
where
is some 4-vector velocity related to the particle, which is a function of . We can define an effective Lagrangian as:
which is a function of particle position in four-dimensional space and its 4-vector velocity . Eq. (29) reduces to
We can now use the principle of least action to determine the equation of geodesic line, which corresponds to the shortest path. However, in contrast to special theory of relativity case, is also a function of .
We can obtain the solution in the following covariance form, known as Lagrangian equations:
where is given by Eq. (31). We can evaluate the second term, and obtained:
and for the first term, we got
We can write Eq. (36) in a more convenient form as follows:
Now, we can assume that the element length is along the geodesic line, that is, ; furthermore, we take it such that . Then, Eq. (35) and Eq. (37), reduce to
and
We can take the derivative of the expression in Eq. (39) with respect to s, and we obtain
Combining Eq. (38) and Eq. (40) in Eq. (34), we obtain
for . For convenience the rescaled space-time metric can be defined [29]:
In addition, we can replace , and obtain Eq. (41) as follows for :
or,
where the following Christoffel’s tensor is introduced
Combining Eq. (44) and Eq. (45), we write
We can multiply both sides of Eq. (46) by the contravariant metric tensor and use , to get
where
Eq. (47) and Eq. (48) represent the geodesic line equation of a particle in gravitational field.
It is important to emphasise that Eq. (50) is general; that is, it is valid to describe the geodesic line equation independently of the coordinate reference frame. If we consider two reference frames, the coordinate reference system in which the particle is free and not subject to any external forces and the coordinate reference system in which there exists a gravitation field described by the dependence of metric tensor on the positions of the four-dimensional point . Then, in particle moves, according to the special theory of relativity, in a straight geodesic line uniformly. Eq. (50) applies for the motion of the free particle by taking constant, and hence . On the other hand, if we consider the motion of a particle in the coordinate system in which are not constant, then the particle moves in a gravitation field, and hence . Therefore, Eq. (50) describes the motion in any arbitrary coordinate reference frame, either or . The term on the right-hand side can also be interpreted as the 4-gradient of a gravitational potential. That is, it is a contravariant field vector.
V. Absolute and Covariant Derivatives of Vectors and Tensors with Covariant Representation
Consider a vector undergoing a parallel translation between infinitesimal nearby points and . The changes on the covariant components of are that are linearly dependent on the values of the covariant components . To describe that, we can consider that the scalar product is invariant under the parallel translation, that is
where the summation is assumed over the repeating indices. Thus, the dot product between two vectors represents a physical quantity that has a magnitude but no direction, and hence, it does not change from point to point. Therefore,
or
We can assume a linear dependence between and via Christoffel’s symbols:
Furthermore, using Eq. (53), we write
If we change the summation index on the left of Eq. (55), we obtain
After rearranging, it gives
Since is an arbitrary chosen contravariant vector, then Eq. (57) implies that
which indicates a linear dependence between the covariant components and the change in the covariant components of vector undergoing a parallel translation between infinitesimally close points and .
The difference between the evaluated vector and , and the change of vector upon the parallel translation from points and is defined as the absolute covariant differential in terms of the covariant components :
Combining Eq. (58) and Eq. (59) yields
or,
Note that the repeated indices represent summation.
It is important to note that if the surface is flat, then in a Cartesian coordinate system, also called Galilean, the volume is rectangular and . Therefore, for a flat surface
indicating that both contravariant and covariant absolute differential components reduce to the respective ordinary differential components, and they are identical.
In contrast, Eq. (61) represents the covariant absolute differential of the component in a curvilinear coordinate system for curved surfaces.
Similarly, we can calculate the absolute differential of a contravariant vector :
Using the linearity , and substituting it in Eq. (63), it gives
Furthermore, the covariant derivative can be introduced as the following:
Consider now the case when the vectors are expressed in terms of the contravariant components. The contravariant tensor is expressed as a product of their contravariant components:
For a parallel translation, the differential of is given as
Using the linearity expressions for both and in terms of Christoffel’s symbols, we obtain
Eq. (68) suggests that
The absolute differential of the contravariant tensor is
Using Eq. (69) and Eq. (70), it can be found that
Thus, the covariant derivative of the contravariant tensor is as the following:
VI. Relativistic Tidal Forces
The tidal forces have also been described in the framework of Newtonian mechanics. These represent forces that exist because of the gravitational waves. It is interesting to describe these forces in the context of the general theory of relativity. It has been shown that Riemann tensor is used to express the second derivatives of the gravitational potential in the equation of motion for the separation of two nearby particles moving in the gravitation field, where each can be described by Eq. (50).
For that, we consider two nearby geodesic lines, each described by Eq. (50), that represent the motion of two freely falling objects. Let represents the four-dimensional position of the first object, and that of the second falling object. The trajectories of two falling objects are described by the following equations:
for . The same proper time is used to describe the motion along each geodesic. It is important to note that the geodesic lines are very close to each other and are parallel to each other at . We would like to describe the time evolution of the difference: .
First, a Taylor expansion of Christoffel’s symbol about the position of the first object, , is obtained:
Then, the equation of the second object (see Eq. (73)) becomes (for )
or, we obtain the approximate equation by ignoring the terms second order on :
Using the geodesic line equation for the first object from Eq. (73), we obtain:
Employing Eq. (64), we obtain absolute derivative as
Taking the second absolute derivative, we get
where is the 4-velocity of the first object. We can use the following identity:
where summation over repeated indices is considered. Then, Eq. (80) becomes
Combining Eq. (79) and Eq. (82), we get
Using Eq. (73), we can write
Substituting Eq. (84) into Eq. (83), we obtain
We can relabel some of the indices in Eq. (85) and obtain
where
is the famous Riemann tensor. Eq. (86) is written in more convenient form:
Eq. (88) is first order in small 4-vector difference ; that is, it ignores higher order terms . Eq. (88) describes the relative acceleration of the two objects initially and being their initial motions that describe the flow along the geodesic. On the other hand, (where is some parameter) describes the motion from one geodesic to the other. Another interpretation of Riemann tensor, as description of the curvature of the surface, is given in Figure 2. The two vectors and describe the flow along each geodesic form a parallelogram. Then, a vector can be translated parallel along that parallelogram. The deviation of the vector would be proportional to Riemann tensor:
where the minus sign indicates that the vector can either increase or decrease its length. Note that Eq. (88) can be generalised to a family of the geodesics parameterised as , where s is a parameter describing the family of geodesics and is the proper time describing the geodesic flow. Let be the 4-vector characterising the motion from one geodesic to another nearby geodesic within the same family, and representing the flow along a geodesic. Then, we would find that if the 4-vector is transported parallel along the geodesic flow, its second covariant derivative is related to Riemann tensor as in Eq. (88).
Time solution of Eq. (88) is determined by the curvature of space-time, which is represented by Riemann tensor. It has been applied to strong gravity to test the limits of the general theory of relativity. Contraction of the Riemann tensor produces the so-called Ricci tensor with components defined as
By definition, the curvature scalar R is defined as
Note that those equations become Newtonian gravitational field theory equations for weak gravitational fields and when speed is much lower than that of the light. Besides, they converge to special theory results, if there is no gravitational field. It is important to mention that these equations predict the existence of the gravitational waves from moving masses, as predicted by Einstein [30], which are very recently detected experimentally [31].
VII. Gravitation Field Equations
First, we will discuss the gravitation field equations in the absence of matter. According to Einstein, with matter should be understood everything that is not gravitation field; that is, including the electromagnetic field; however, in some future work, we will discuss the possibility of joining the gravitation and electromagnetic fields in a unified field. The main idea is to generate gravitation field equations that are Lorentz invariant. From Eq. (50), if there is no gravitation field, then . Therefore, are the components of the gravitation field. In addition, from Eq. (87), if , then Riemann tensor components vanish, . However, Riemann tensor elements are not the components of the gravitation field. That is, if , then Riemann tensor elements are necessary zero. Based on the formalism of the general theory of relativity, the gravitation field causes curvature of the four-dimensional space, that is the space-time. However, the gravitational field is described by the metric tensor , and precisely on the dependence of on the 4-vector positions , and hence based on its definition contains the components of the gravitation field. On the other hand, Riemann tensor is a mathematical object to describe the curvature of the space-time (in general, of any multi-dimensional space), and therefore, it is necessary for it to vanish if . Mathematically, it is also sufficient, but based on the general theory of relativity the components of the gravitation field are described by . Based on this introduction, we expect that gravitation field equations in the absence of matter to be expressed in terms of the components of .
The least action principle can be used with a Lagrangian given by:
and , where g is the determinant of . Then, the action integral is
where is a proper time indicating the flow along the geodesic. Using the principle of the least action, we have
where
where in the third line the indices and are swapped and the symmetric property of metric tensor are use.
We can use the following identity:
to obtain
Using Eq. (45) and Eq. (48), we can write:
Therefore,
Therefore, Eq. (97) can be written as
We can now write Lagrangian equation by considering it (as also indicated from Eq. (100)) as a function of and its derivative (so-called velocity)
as follows:
where the second equation is a constraint. Eq. (102) give Lagrangian equations of gravitation in a Lorentz invariant form.
Using Eq. (100), we have
Substituting Eq. (103) into Eq. (102), we obtain
Eq. (104) are know as Einstein’s equations of gravitation field in the absence of matter.
To write Eq. (104) in terms of physical quantities, such as energy and momentum, Einstein introduced some other important quantities. For that, first we multiply both sides of the first expression in Eq. (102) by :
Using the following identity, we have
Combining Eq. (107) and Eq. (108) yields
Introducing the tensor
where
Then,
The symmetric tensor is called energy-momentum density tensor. The expressions in Eq. (111) imply the conservation law of energy-momentum. Furthermore, describes the energy component. is related to the universal gravitation constant as defined by Newton’s mechanics. To Eq. (111), we have also to add the constraint .
Moreover, the energy-momentum density tensor can be related to the geometry of the space-time. In particular, using the gravitation field equations, Eq. (104), it is found in covariant form that [32]
Furthermore, the components of Einstein’s second rank tensor are introduced as
Therefore, Einstein’s tensor becomes proportional to the energy-momentum density tensor, , given as
To obtain the gravitation field equations of Einstein in the presence of matter again the principle of least action is used [3]:
where is the action of the gravitational field and is the action of the matter. Here,
and
where is the energy-momentum density tensor of the matter (macroscopic masses, current charge densities, including the electromagnetic field), and is Newton’s gravitation constant:
In Eq. (117) and Eq. (119), the integration is over all space. Substituting Eq. (117) and Eq. (119) into Eq. (116), we obtain
In Eq. (120), since are arbitrary, then Eq. (120) implies that
Eq. (121) is rearranged as follows:
where
Note that the SI units of are
The SI units of (the energy-momentum density tensor of the matter) are
and hence, the SI units of are
(Note that is a dimensionless tensor.)
Eq. (122) indicates that the energy-momentum density tensor of the matter (including the macroscopic masses, current charge densities, and the electromagnetic field) influences on the components of the tensor , which determine the curvature of space-time. That can be considered as a mechanism of conservation for the transformation of energy-momentum to the energy-momentum needed to cause a change in curvature of space-time. To demonstrate that, we can consider the divergence of each of those tensors. For instance, in general, we expect that the divergence of is such that . On the other hand, , as shown by Eq. (111). Therefore, to compensate for that is added the term , which related to the scalar curvature R and the metric of the space-time, which represents the presence of gravitation field. As an interpretation regarding Ricci’s tensor , Eq. (90), it represents the average curvature that we would find if we investigate all planes involving the 4-vector .
Eq. (122) was later modified by Einstein to the following expression to allow the solution to be consistent with the observation of a static universe.
The cosmological constant is a constant parameter, which depends on the metric [7,26]. Furthermore, is proportional to the total energy density concerning the metric under consideration. Therefore, there will be different cosmological constants for different metrics. For instance, is positive concerning Friedmann-Lemaître-Robertson-Walker metric (de Sitter space), see also Ref. [18]; however, is negative for the metric of the celestial body (anti-de Sitter space). Thus, the cosmological constant is connected to the cosmology in the universe under the Friedmann-Lemaître-Robertson-Walker metric. In the case of Friedmann-Lemaître-Robertson-Walker metric, the cosmological constant has a value of . In contrast, is a universal constant, and hence it is the same constant in every reference frame.
VIII. On Interpretation of Geometrical Quantities
In the following, the physical and geometrical interpretation of the Ricci tensor, Riemann tensor, and scalar curvature is discussed. Besides, a physical interpretation of Einstein’s tensor is described. Note that the derivations presented here are also shown elsewhere [33]; however, we will describe all the derivations in details for the sake of clarity, and we will also give graphical illustrations when possible. For further reading material, concerning this section, we can suggest [2,8,17].
A. Gauss’s Curvature Measure
First, consider a curve in a two-dimensional space, as shown in Figure 3. At any given point, the effective radius of the circle turning at the same rate as the curvature of the curve at the same point can be determined. Then, by definition, the Gauss’ curvature is given as
Now, consider a two-dimensional surface immersed in a three-dimensional space. In that case, two different curvatures can be identified, as illustrated in Figure 4:
Thus, the intrinsic Gauss’s curvature is defined as product of two curvatures
Imagine a point in a three-dimensional space and suppose one moves along the geodesics in all directions a distance e. That is going to form a circle, as shown in Figure 5. If the space is flat, then the circumference of that circle is
On the other hand, if the space is curved, then the circle will be either smaller or greater in size, depending on the curvature of the space. For example, for a sphere with radius (see also Figure 5), the circumference can be shown to be
It can be seen that the deviation includes a term of the second order concerning the ratio from the flat space. The Gauss’s intrinsic curvature is defined as
which is product of two extrinsic curvatures of a spherical surface.
Therefore, can be interpreted as a measure of the degree of deviation of the circumference of the circle in a curved space compare with circumference of that circle in a flat space. Besides, that deviation is quadratic (see Eq. (132)), as would also be interpreted by the Riemann tensor, which depends on the second derivative of the metric tensor .
B. Interpretation of Riemann Tensor, Ricci Tensor, and Scalar Curvature
Let us consider two non-parallel vectors and at a point in a curved space. These two vectors determine a two-dimensional subspace. Furthermore, the curvature of that subspace, the Riemann tensor , times the area of the parallelogram formed by the vectors squared, determines the curvature of that subspace; that is,
Therefore, the Riemann tensor can be seen as a set of Gaussian curvatures. On the interpretation of the Ricci tensor, note that Ricci tensor is , and hence the Ricci tensor is the average of the Gaussian curvatures of the subspaces defined by the vectors . For instance, suppose we are calculating the average curvature of all planes including the vector ; for that, we can take a collection of orthonormal vectors and perform the average
Note that Eq. (135) represents an area weighted curvature.
In a three-dimensional space, scalar curvature indicates deviation of the surface area of a generalised sphere in a curved space from its surface area in a flat surface. For that, consider a sphere of radius r with centre at the point , which is constructed as a set of all points that have a geodesic distance r from the centre , as illustrated in Figure 6. In the curved space the surface area of that sphere is smaller compare with the same sphere in a flat space.
Now, consider a space-time point , and let be the point a distance away from in an arbitrary direction. The set of orthonormal vectors at the point is also chosen, which represent the Riemann normal coordinates at the point in the space-time. Any unit vector at the point is considered a linear superposition of the basis vectors . The coordinates of a point at a short distance along the geodesic from in the direction is determined by solving the geodesic equation
The solution of Eq. (136) can be approximated as
Note that in Riemann normal coordinates the tensor is 0 to 0th order in . Using the symmetry of in all three lower indices:
Then, Eq. (137) can be written as
Note that represent coordinates of the points on the sphere starting at and moving a geodesic distance in the direction . The surface element area is given as
where the change in the coordinate with the change in the direction:
where is a set of variables representing the change in the direction. Furthermore,
The Taylor expansion of the metric gives
Thus,
where
Moreover,
where is Ricci tensor. Substituting Eq. (146) into Eq. (144), we obtain that
In Eq. (140), the determinant is
We can now introduce the Riemann polar coordinates ; therefore, the new metric in the polar coordinates relates to the metric in the Riemann normal coordinates as the following:
The explicit forms of the covariant components are
where
The contravariant components are calculated as
From Eq. (149), the inverse relationship is
Substituting Eq. (152) into Eq. (153), we have
which is an expression used to determine the curvature of the space-time.
In Eq. (156), the first term is related to the flat space. Therefore, defining the flat space surface area element as
Comparing Eq. (155) with Eq. (157), we conclude that the second term in Eq. (155) represents the deviation of the surface area element in the curved space from the flat space. Thus,
where the term cancels because of the anti-symmetry of the Riemann tensor in the first two or last two indices, and multiplication by causes contraction. Therefore, the surface area of the sphere embedded in a curved space is given as
where the integration is over all possible angles, gives the surface area of the sphere in the flat Euclidean space, and hence
Thus,
where it is used that
From Eq. (161), it can be found that the scalar curvature is
Eq. (163) indicates that the scalar curvature has the same meaning as the Gaussian curvature.
C. Interpretation of Einstein’s Tensor
The Einstein’s tensor definition is
Now, suppose that Riemann tensor is known at some point in four-dimensional space-time. Also, suppose that one is interested on calculating the scalar curvature of the three-dimensional space (corresponding to the spatial dimensions of space-time). Moreover, the three-dimensional subspace is orthogonal to a vector , which represents the direction of time in the space-time and it is normalised to one. Consider the projection of metric tensor onto the three-dimensional space given as . The curvature of the three-dimensional space is then given as
Eq. (165) indicates that the curvature of the three-dimensional subspace orthogonal to the unit vector , , equals minus two times the Einstein’s tensor contracted with the vector . In other words, if one choses a direction for the time (represented by the direction of unit vector ), Einstein’s tensor characterises the spatial dimensional scalar curvature, as in Eq. (165). Note that the minus sign in Eq. (165) is because the space-time has a negative metric.
On the other hand, we know that (from Eq. (122)), where is the energy-momentum density of the matter. Furthermore, the contraction of the tensor with the time-like unit vector yields the energy density w in the reference frame can be defined by :
Thus, combining Eq. (165) and Eq. (166), we get
which indicates that scalar curvature of the spatial dimensions of space-time equals the energy density in an arbitrary reference frame up to a factor ; that is, the energy density represents the curvature of the spatial dimensions and it is independent of the chosen reference frame.
Note that the minus sign in Eq. (167) is due to the fact that the spatial dimensions of space-time have a negative metric; that is, the curvature of a sphere in the spatial dimensions is negative for that metric.
D. Newton Gravity
Consider the space-time and a volume element spanned by a set of four vectors , which are linearly independent. Suppose a parameter , representing the time, and the direction of the time flow. Furthermore, we would like to describe the time evolution of the three-dimensional space volume, characterising the spatial dimension of space-time, which is along the vector ; that is, it is a volume transverse to a vector that describes the motion from one geodesic to another. Thus, all the points inside the volume are moving along the geodesics. In a flat space, that volume corresponds to the volume of a constant solid angle and constant radial width moving along the geodesics. Although the space is flat, the volume element is increasing quadratically in time, and hence the second time derivative is different from zero.
Moreover, we would like to describe time evolution of the deviation on the volume element between the curved and flat space:
That can be described by Eq. (88) as (where ):
Integration over all spatial dimensions, we obtain
From Eq. (122):
Contracting both sides with , we can get
where T is the trace of the energy-momentum density tensor.
Combining Eq. (171) and Eq. (172), we write
By contraction with time-like unit vector , Eq. (173) becomes the motion of the matter equation as
If the vector is described by a slow motion, then it describes the same motion as the rest frame, and hence . Then, Eq. (175) can also be written as
Substituting Eq. (175) into Eq. (170), we obtain
where is the enclosed mass in the volume V and . For objects that are moving slowly, the covariant derivatives equal the standard time derivatives, and thus Eq. (176) becomes
where standard volume of a sphere is used; that is, higher order terms are omitted.
IX. Conclusions
We described an introduction to general theory of relativity. Furthermore, an interpretation of geometrical quantities was introduced.
References
- Edited by M. J. Klein, A. J. Kox, and R. Schulman. The Collected Papers of Albert Einstein: The Berlin Years: Writings, 1914-1917, Vol 6. Princeton University Press, (2016).
- R. M. Wald. General Relativity. The University of Chicago Press, (1984).
- L. D. Landau and E. M. Lifshitz. The Classical Theory of Fields. Pergamon Press, (1971).
- S. B. Rüster. The fundamental conservation law in the theory of general relativity: an unconventional approach is feasible and correct. Parana Journal of Science and Education, 6(9), 1-11, (2020).
- S. B. Rüster. Why in general relativity the energy density of the gravitational field must be localizable?. Parana Journal of Science and Education, 7(1), 1-9, (2021).
- S. B. Rüster. Energy is Conserved in General Relativity. Parana Journal of Science and Education, 8(6), 13-22, (2022).
- S. B. Rüster. Energy Conservation in General Relativity and Flat Rotation Curves of Spiral Galaxies. Parana Journal of Science and Education, 9(6), 20-27, (2023).
- R. P. Feynman. Feynman Lectures on Gravity. Addison Wesley, (1995).
- G. Hooft. Introduction to general relativity. Utrecht University, Utrecht, 2010.
- D. Giulini. The Rich Structure of Minkowski Space. Part of the Fundamental Theories of Physics. FTPH, Vol. 165, (2009).
- S. Barak. Electric Charge and its Field as Deformed Space. Applied Physics Research, 11(4), 29-40, (2019). [CrossRef]
- F. Cabral and F. S. N. Lobo. Electrodynamics and Space-time Geometry: Foundations. Foundations of Physics, 47, 208-228, (2017). [CrossRef]
- M. Born and L. Infeld. Foundations of the New Field Theory. In: Proc. Royal Soc. A 144, 852, (1934). [CrossRef]
- E. Bergshoeff et al. The Born-Infeld Action from Conformal Invariance of the Open Superstring. In: Phys. Lett. B 188, 1, (1987). [CrossRef]
- A. A. Chernitskii. On unification of gravitation and electromagnetism in the framework of a general-relativistic approach. Gravitation and Cosmology. 15, 151-153, (2009). [CrossRef]
- G. Boillat. Nonlinear Electrodynamics: Lagrangians and Equations of Motion. In: J. Math. Phys. 11, 941, (1970). [CrossRef]
- M. Nakahara. Geometry, Topology, and Physics. Institute of Physics Publishing, (1996). [CrossRef]
- B. P. Schmidt and N. B. Suntzeff and M. M. Phillips and R. A. Schommer and A. Clocchiatti and R. P. Kirshner and P. Garnavich and P. Challis and B. Leibundgut and J. Spyromilio and A. G. Riess and A. V. Filippenko and M. Hamuy and R. C. Smith and C. Hogan and C. Stubbs and A. Diercks and D. Reiss and R. Gilliland and J. Tonry and J. Maza and A. Dressler and J. Walsh and R. Ciardullo. The High-Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type Ia Supernovae The Astrophysical Journal, 507(1), 46, (1998). [CrossRef]
- H. Sykja. Bazat e Elektrodinamikës. SHBUT, (2006).
- D. J. Griffiths. Introduction to Electrodynamics. Prentice Hall, 3rd Edition, (1999).
- H. Kamberaj. Electromagnetism. With Solved Problems. Springer Nature, (2022).
- J. D. Jackson. Classical Electrodynamics. John Wiley & Sons, 3rd Edition, (1999).
- H. Goldstein, C. Poole, and J. Safko. Classical Mechanics. Third Edition. Addison Wesley, (2002).
- U. J. Nöckel. Maxwell’s equations as mechanical law. Eur. J. Phys., 43(4), 045202, (2022). [CrossRef]
- M. A. Jaswon. Mechanical Interpretation of Maxwell’s Equations. Nature, 224, 1303-1304, (1969). [CrossRef]
- S. B. Rüster. The Importance of the Cosmological Constant for Understanding Dark Matter and Dark Energy. Parana Journal of Science and Education, 6(5), 1-8, (2020). http://doi.org/10.6084/m9.figshare.12645395.
- D. Holliday, R. Resnick, and J. Walker. Fundamentals of Physics. John Wiley & Sons, (2011).
- D. Clery. Event Horizon Telescope Images Second Black Hole’s Jets. Science, 373, 6553, (2021). [CrossRef]
- M. Modugno and D. Saller and J. Tolksdorf. Classification of infinitesimal symmetries in covariant classical mechanics. J. Math. Phys., (2006). [CrossRef]
- A. Einstein. Die Feldgleichungen der Gravitation. Preuss. Akad. Wiss. Berlin Sitzungsber, 47, 844-847, (1915).
- B. P. Abbott et al. LIGO Scientific Collaboration and Virgo Collaboration, Observation of Gravitation Waves from a Binary Black Hole Merger. Phys. Rev. Lett., 116, 061102, 2016; B. P. Abbott et al., LIGO Scientific Collaboration and Virgo Collaboration, GW170817: Observation of Gravitation Waves from a Binary Neutron Star Inspiral, Phys. Rev. Lett., 119, 161101, (2017). [CrossRef]
- A. Einstein. The Collected Papers of Albert Einstein: The Berlin Years: Writings, 1914-1917, Vol 6, Edited by M. J. Klein, A. J. Kox, and R. Schulman.
- L. C. Loveridge. Physical and Geometrical Interpretations of the Riemann Tensor, Ricci Tensor, and Scalar Curvature. 2016, http://arxiv.org/abs/gr-qc/0401099v1. [CrossRef]
Figure 1.
The 4-velocity and the separation vector along two geodesics.
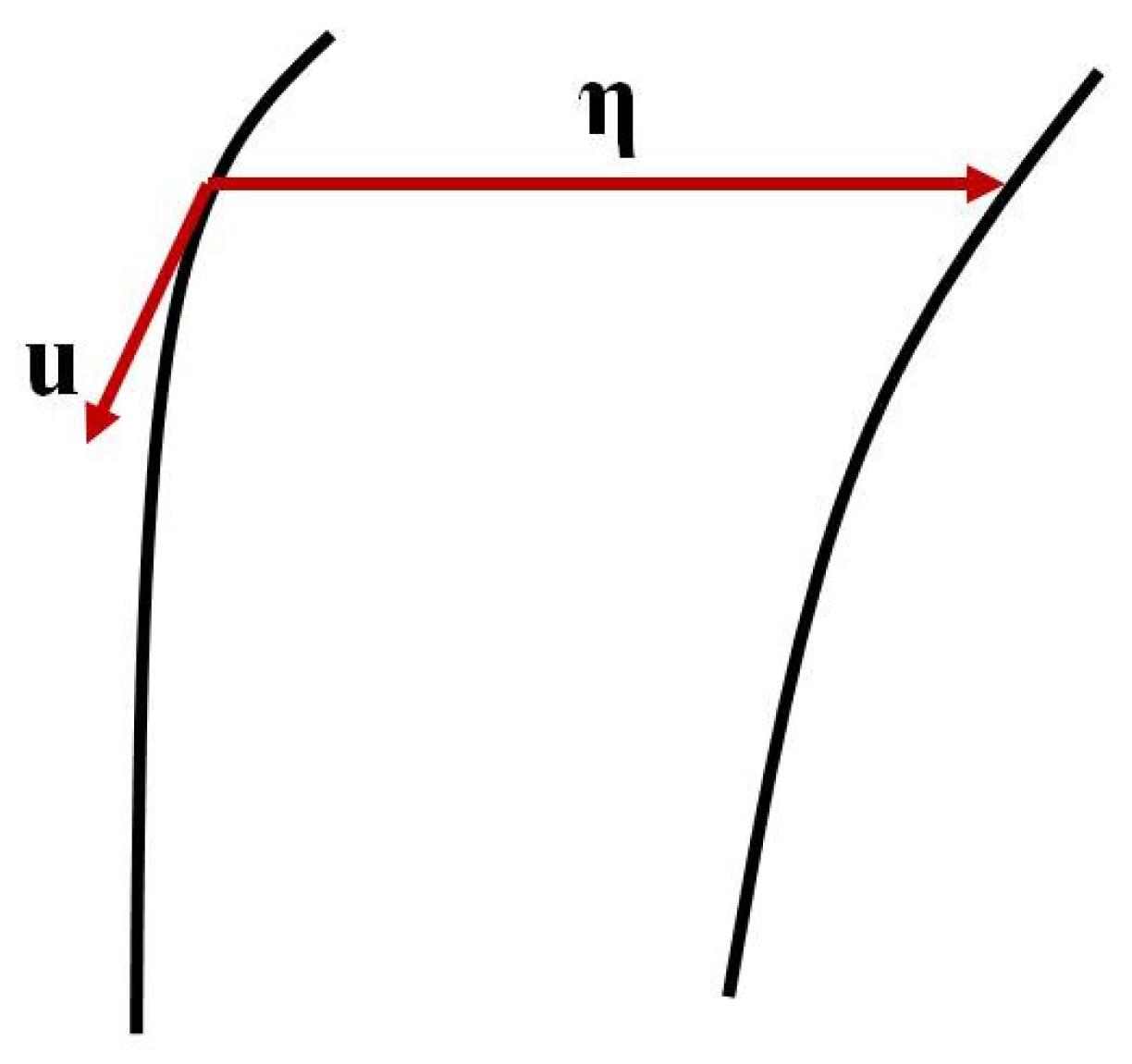
Figure 2.
The 4-velocity and along two geodesic lines indicating the flow along each geodesic and the 4-vector transported parallel.
Figure 2.
The 4-velocity and along two geodesic lines indicating the flow along each geodesic and the 4-vector transported parallel.
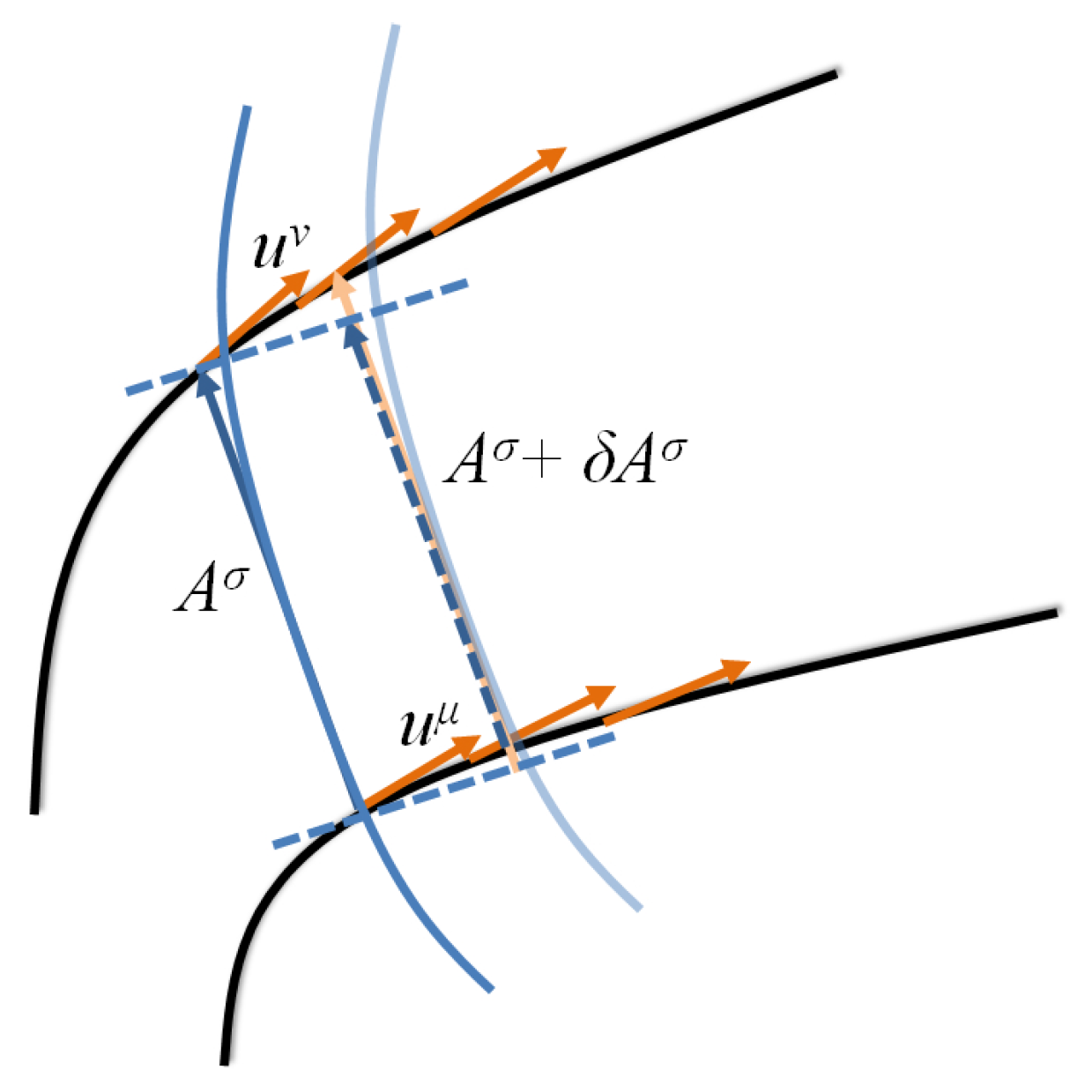
Figure 3.
The curvature in the two-dimensional space.
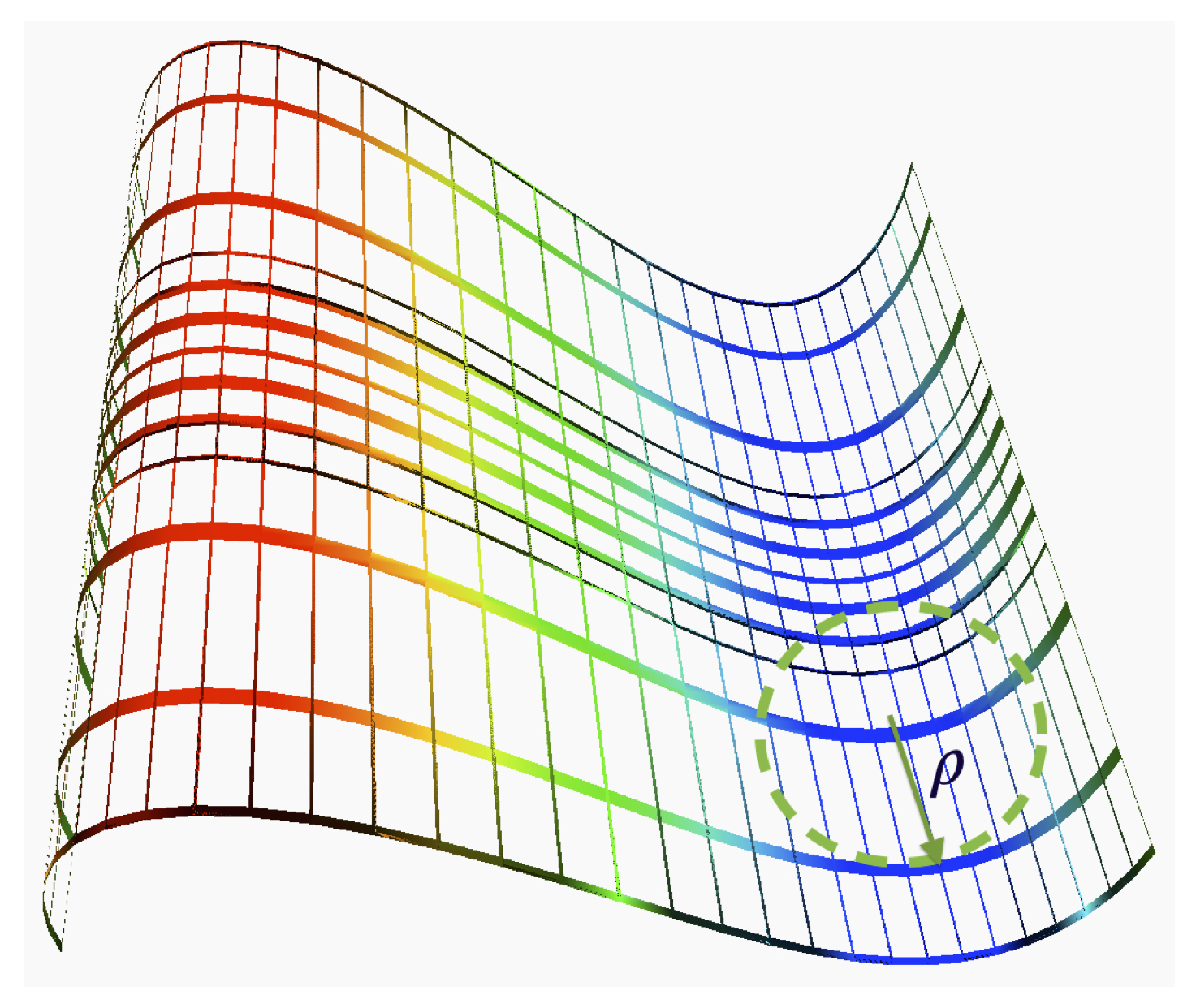
Figure 4.
The curvatures in the three-dimensional space.

Figure 5.
The map of a circle with radius e on a flat surface and on the surface of a sphere with radius .
Figure 5.
The map of a circle with radius e on a flat surface and on the surface of a sphere with radius .
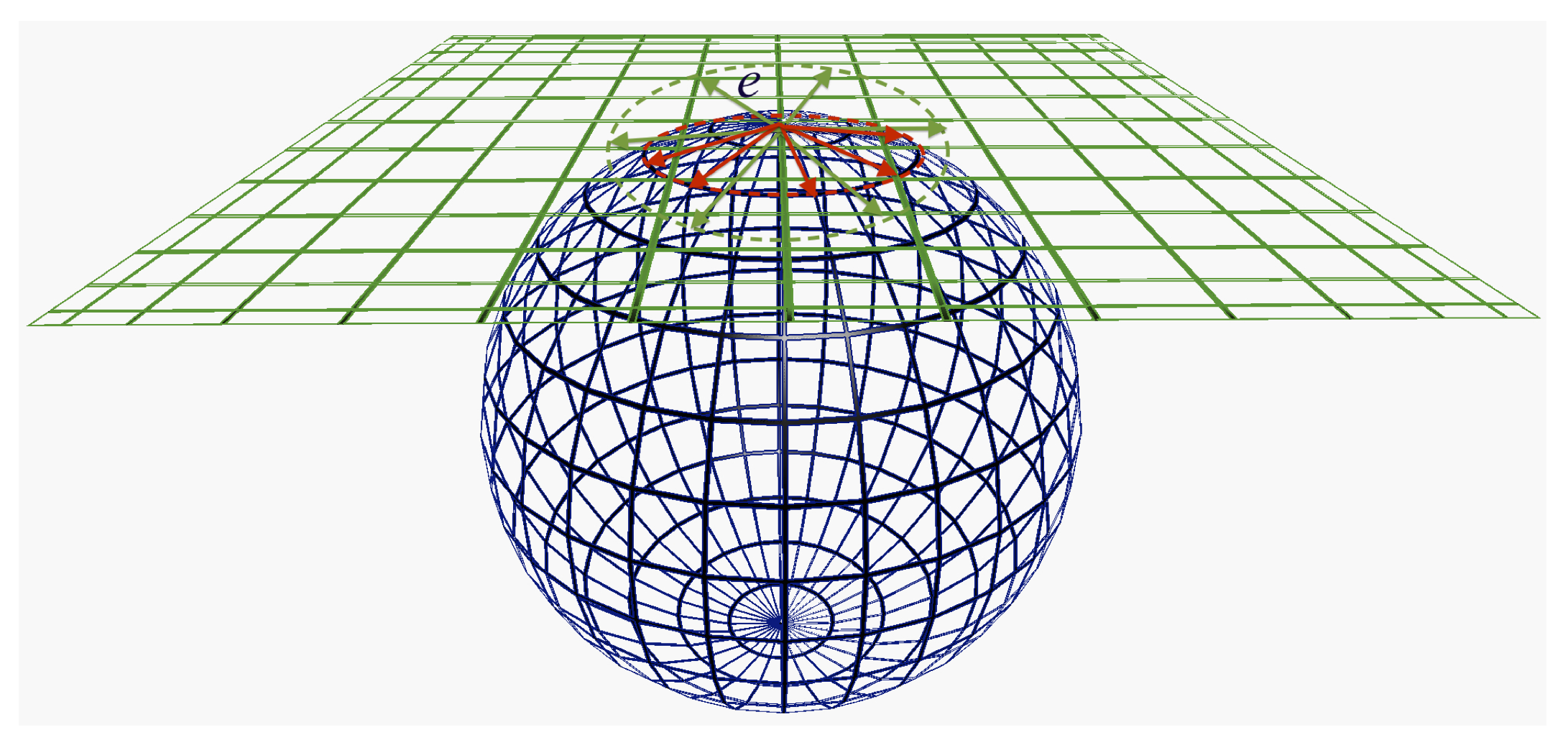
Figure 6.
(Left) Construction of a sphere with radius r by moving from the point (centre of sphere) along the geodesic with a distance r in a flat space. (Right) Construction of a sphere with radius by moving from the point (centre of sphere) along the geodesic with a distance r in a curved space.
Figure 6.
(Left) Construction of a sphere with radius r by moving from the point (centre of sphere) along the geodesic with a distance r in a flat space. (Right) Construction of a sphere with radius by moving from the point (centre of sphere) along the geodesic with a distance r in a curved space.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





