Are Markets Naturally Random? Machine Learning Approach to Quantifying Randomness

Preprint

Article

Are Markets Naturally Random? Machine Learning Approach to Quantifying Randomness

Altmetrics

Downloads

Views

Comments

Philipp Bogdan^*

This version is not peer-reviewed

Submitted:

23 September 2024

Posted:

25 September 2024

You are already at the latest version

Alerts

Abstract

From some perspective, every natural phenomenon is just a combination of many elementary random events clustering and forming a pattern. Nonetheless, the nature of random events differs from one field of study to another. This research is an attempt to determine whether volatile stock price movement, considered random, accords to the randomness of real world phenomena. To accomplish the task, a deep learning model was built, trained on preprocessed data and evaluated to calculate it's accuracy. The acquired results were then compared, and it turned out that stock prices are very similar in randomness to natural phenomena as the model trained on large amounts of stock data was increasing the accuracy of predictions of all real world parameters.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Since the beginning of human era, nature has been available for humans to observe. It provided people with all they needed: food, entertainment, freedom. Nature was the backbone of human living, so describing it, interpreting its rules and predicting natural events was essential for survival. At first, people themselves have developed certain skills to predict physical events, e.g. the trajectory of a projectile or the time required to boil some water. Then, sciences like statistics and physics were created, which allowed to make very accurate predictions. Nevertheless, there still were many phenomena which were hard to predict without vast computational capacities. As computer technology advanced at the dawn of the 21st century, powerful tools for predicting and understanding nature became available. Despite their broad potential applications, these newly developed computational forecasting methods have primarily been used to analyze and predict a narrow range of events, such as stock markets and weather. Whilst we have been increasingly successful in working with these particular phenomena, predicting many other naturally occurring events has been left out.

It may be totally unreasonable to even try predicting some seemingly random things, like air quality or solar activity, but doing so might yield some tangible results. This paper explores the limitations of basic forecasting from available data.

In the Machine Learning(ML) field it is often said that quality of data plays a more significant role than the model used, that is why here more attention is paid to preprocessing data and feature engineering than to designing the model architecture.

Predicting events has proven to be very useful for identifying anomalies in advance to be able to prepare for them and mitigate possible destructive outcomes. One important notion is that some events are more predictable than others, which should be caused by fundamental reasons like the number of random variables influencing the result. Here, only the similarity in randomness of stock prices and various natural phenomena is studied. It is based on the assumption, that if a model works better in forecasting certain concepts(achieves better accuracy results), it suggests that these concepts can be compared in predictability. Nonetheless, it suggests that the topic can be extended further, allowing for new metrics measuring randomness to be inferred.

2. Background

More than three decades ago [1] presented an excursion on the computational power of a single perceptron and extended the topic with Multi-Layer Perceptron (MLP), the base of Artificial Neural Network (ANN), which is the foundation of modern models. Despite the technology being available, the techniques were rarely used, because there wasn’t enough computational power available to solve difficult tasks more efficiently than with traditional methods. Nevertheless, those models weren’t useless - Dewdney provides an example of Rietman-Frye small ANN model called POLARNET, consisting of just 30 neurons in a single hidden layer. It achieved a remarkable accuracy of 95% in transforming polar coordinates into Cartesian form.

Time series data analysis and forecasting is a subject which has also been studied intensely for the last couple of decades. The most popular solutions so far are traditional and Machine Learning techniques such as: Regression, ARIMA-like models, SVMs, discussed by [2,3,4], and Neural Networks1 which were used in this research.

[5] studied different models for predicting stock prices in Iran for different categories like metals and diversified financials. It was suggested that among the most well-known tree-based and neural network models, Long Short-Term Memory (LSTM) works the best for predicting markets, but it is the most computationally demanding.

LSTM networks, in particular, have proved to be very effective in solving a range of different tasks. They had been the state-of-the-art deep learning method before transformers came around after the famous landmark paper “Attention is all you need" by [6]2. Using LSTM networks OpenAI built a model which defeated Team Liquid, the strongest competitive human team of the time in Dota 2 computer game3, voice assistant Alexa received a huge advancement, responding more comprehensively, and big financial companies could predict stock prices much better. [7] delved deep into the topic of LSTM networks. They have explored the application of different LSTM models, like BLSTM or CNN-LSTM, and found which of them work the best for a selection of classic ML tasks(time-series forecasting, computer vision, etc.).

Another highly effective type of model which could be used in this research is Convolutional Neural Network (CNN). Those networks perform so-called convolutions on data. For more details on how CNNs work, see: [8]. Their main advantage comes from their in-built compatibility with 2- and 3-dimensional data. They employ certain techniques called kernels which can very efficiently detect patterns in the data. The revolutionary AlexNet model, proposed by [9], established CNNs to be the best in solving visual tasks like image classification or object detection. For example, a CNN model was used by [10] to detect breast cancer from scans, allowing to prevent it at early stages. After the AlexNet success, many more non-visual applications were found as extensive research in the topic was conducted. Moreover, according to [11], novel applications are still being found, even though the most of the modern machine learning research is conducted on transformer technology which is flooding the scientific field over the recent years. Convolutional models are known for their effectiveness in time-series analysis, but they were not used here, because they require a different approach for preprocessing the data.

3. Models

3.1. Neural Networks

For forecasting, LSTM and ANN models were used. The latter is a well-known tool for analysing data and solving tasks like classification, regression and anomaly detection. ANN is used here as a benchmark model. It is made of neurons ordered in 3 main layers. These are: input layer, hidden layer and output layer. All neurons are fully connected to all neurons from the next layer, except for output layer, and such layers are called dense. These connections(previously known as synapses, in parallel to human brain neural structure) are assigned different weights which is the main network’s capacity to think.

Figure 1. General ANN structure. The circles are neurons and each connection is assigned a weight to it.

The neural networks themselves are no more than complex structures operating basic operations like multiplication and addition on many numbers. To be trained, a network requires a dataset which is a list of input-output pairs of values. The learning process consists of 2 main stages: feedforward4 and backpropagation.

3.2. Feedforward

During feedforward the model loads the input values in its first layer. These are then multiplied by the weights and passed to the first hidden layer. Weights and biases of each layer of the model can be represented neatly as the following matrices

w^{l}

and

b^{l}

, respectively. The activation values matrix

a^{l}

is also mentioned below.

w^{l} = (\begin{matrix} w_{11}^{l} & w_{12}^{l} & \dots & w_{1 k}^{l} \\ w_{21}^{l} & w_{22}^{l} & \dots & w_{2 k}^{l} \\ ⋱ \\ w_{j 1}^{l} & w_{j 2}^{l} & \dots & w_{j k}^{l} \end{matrix}) b^{l} = (\begin{matrix} b_{1}^{l} \\ b_{2}^{l} \\ ⋮ \\ b_{j}^{l} \end{matrix}) a^{l} = (\begin{matrix} a_{1}^{l} \\ a_{2}^{l} \\ ⋮ \\ a_{j}^{l} \end{matrix})

Here, l is the number of a layer to which the weights and biases are attached. Each weight

w_{j k}^{l}

goes from k-th neuron in

(l - 1)

-th layer to j-th neuron in l-th layer. Note, that each row in the weight matrix represents all the weights attached to j-th neuron in the l-th layer, going from the

(l - 1)

-th layer. Similarly, bias

b_{j}^{l}

is assigned to j-th neuron in l-th layer.

For each neuron at each hidden layer weighted sum of activations from the previous layer is added to the bias at the neuron to get the z value, and then a sigmoid function

σ (x)

is applied to the result to get the activation. For each j-th neuron at l-th layer its activation

a_{j}^{l}

is obtained through the following equations (1.1) and (2.1) as described before.

z_{j}^{l} = \sum_{k} w_{j k}^{l} a_{k}^{l - 1} + b_{j}^{l}

(1.1)

a_{j}^{l} = σ (z_{j}^{l})

(2.1)

The same can be written way more neatly in the matrix form.

z^{l} = w^{l} a^{l - 1} + b^{l}

(1.2)

a^{l} = σ (z^{l})

(2.2)

These results continue to be passed forward to then, finally, terminate at the output layer neurons. The output of the network is then compared to the dataset output values and a loss function is calculated. The goal which the network aims to achieve is to find a set of weights and biases which minimise the mean loss over the whole dataset.

3.3. Backpropagation

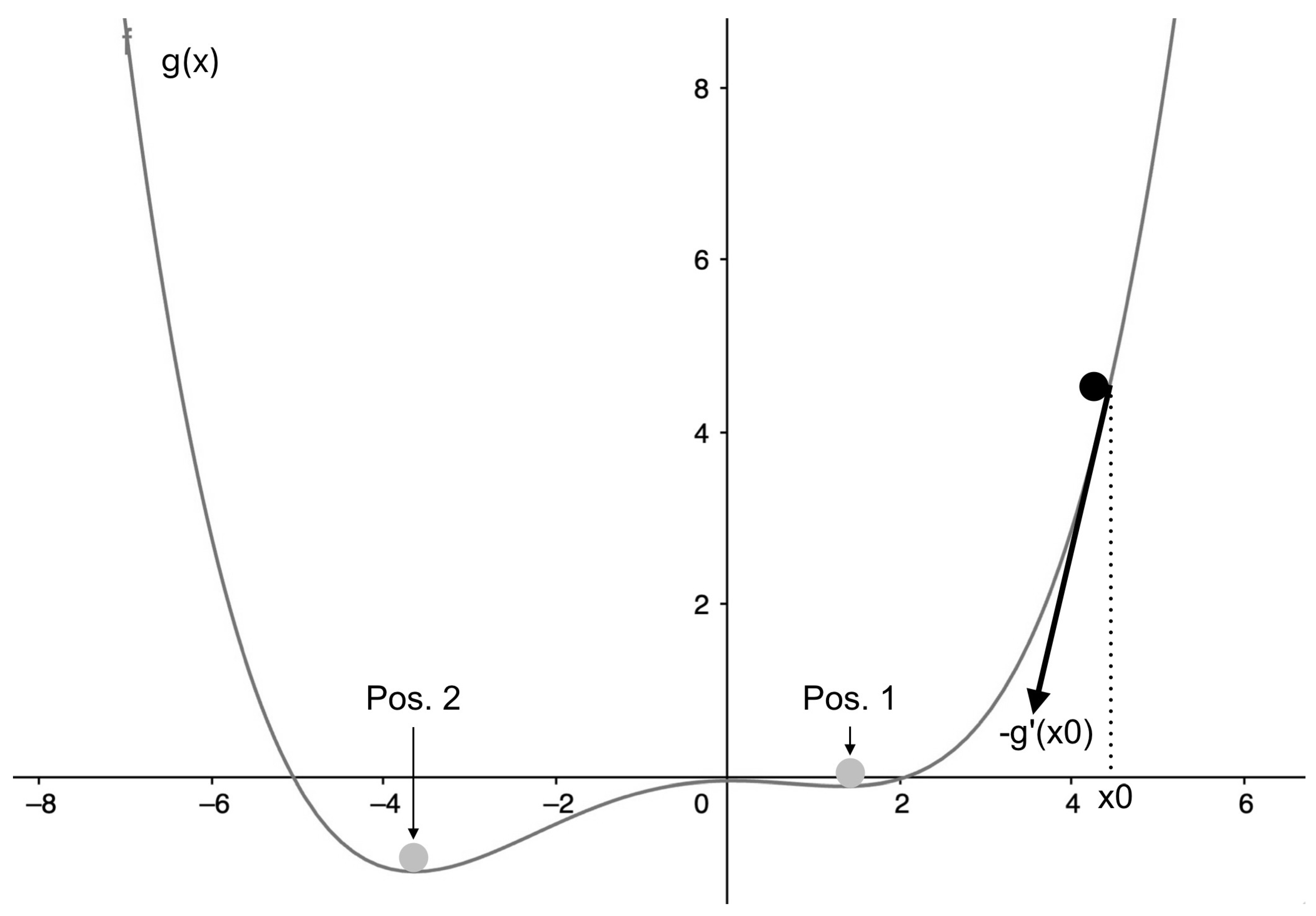
To learn the network needs to have an algorithm to change the weights in a way which results in reduction of loss. This process is based on backpropagation and it is called gradient descent. Probably the best way to think about it is to imagine a single-variable arbitrary loss function g(x). Here, the only variable we can change is x. Starting at a randomly initialised position

x_{0}

, the gradient of the function in respect to x is calculated at this point using

g^{'} (x)

like in Figure 2. To get to the minimum of the function it is convenient to imagine a ball which tries to roll down the into the valley. To get there, it needs to go against the initial gradient at each point. So, the adjustment to the x is some coefficient5

η

times the negative gradient in respect to x.

Δ x = - η g^{'} (x_{0})

(3.1)

x = x_{0} + Δ x

(4.1)

Equation (4.1) makes the adjustment to the variable x. Next, the process is repeated until the ball terminates at position 1.

It is clear that this position is not the true minimum of the function, but rather a local minimum. This is a problem, as the true minimum of the function at position 2 is what needs to be achieved. For solving that, the initial position can be initialised again, so that the ball might appear at a more favourable place, e.g. on the left of the graph, where it will eventually terminate at the true minimum. In general, many models can be created with different random initialisations, the performance of which will then be compared and the best will be chosen to be used further. Another common way of getting around this problem is to create an ensemble of these models and estimate an answer to the problem by summarising the answers of each individual model.

The problem discussed before used just 1 variable, but in reality there can be any number of variables6. To take account for these many variables, multivariable calculus should be introduced. Let’s call v the vector containing all n variables, and call

\nabla g

the gradient vector of the function g.

v = {(\begin{matrix} v_{1} & v_{2} & \dots & v_{n} \end{matrix})}^{T} \nabla g = {(\begin{matrix} \frac{\partial g}{\partial v_{1}} & \frac{\partial g}{\partial v_{2}} & \dots & \frac{\partial g}{\partial v_{n}} \end{matrix})}^{T}

Δ v = - η \nabla g

(3.2)

v = v + Δ v

(4.2)

Equations (3.2) and (4.2) are versions of (3.1) and (4.1), extended to work with multiple variables. Equation (4.2) is an algorithmic one, rather than mathematical, updating vector v to account for changes (

Δ v

The key problem here is to calculate all of those partial derivatives to build

\nabla g

. Here is where the backpropagation algorithm is applied. It calculates the values of partial derivatives from the error between the acquired output of the model and the required output in the dataset. This algorithm won’t be described in detail here, as it is lengthy and complicated.

For a detailed and comprehensive dive into the basics of neural networks, gradient descent, backpropagation and more, Nielsen (2018) e-book [12] can be consulted.

3.4. LSTM

LSTM network is a bit different from ANN. It is a type of Recurrent Neural Network (RNN), because it passes the values from the previous feedforward onto the next, allowing for remembering some temporary patterns in the data. It has weights and biases and the difference from ANN models is in the hidden layer neurons. Instead of neurons it has long short-term memory units. Each unit has 4 main sections: memory cell, input gate, output gate and forget gate. The cell stores the data and it is like a vessel which is operated by the three gates. Each gate has two states: it is either open or closed. Gate functionality is described below:

Input gate receives important data and stores it into the cell when it is opened, and doesn’t receive any data considered less valuable when it is closed.
Output gate outputs any relevant information from the cell when it is opened, and doesn’t output anything when it is closed.
Forget gate discards any irrelevant data from the cell when it is opened, and is inactive when it is closed.

During the learning process the gates are trained to determine which information is important or relevant, therefore changing their state to either closed or opened.

3.5. Layer Architecture

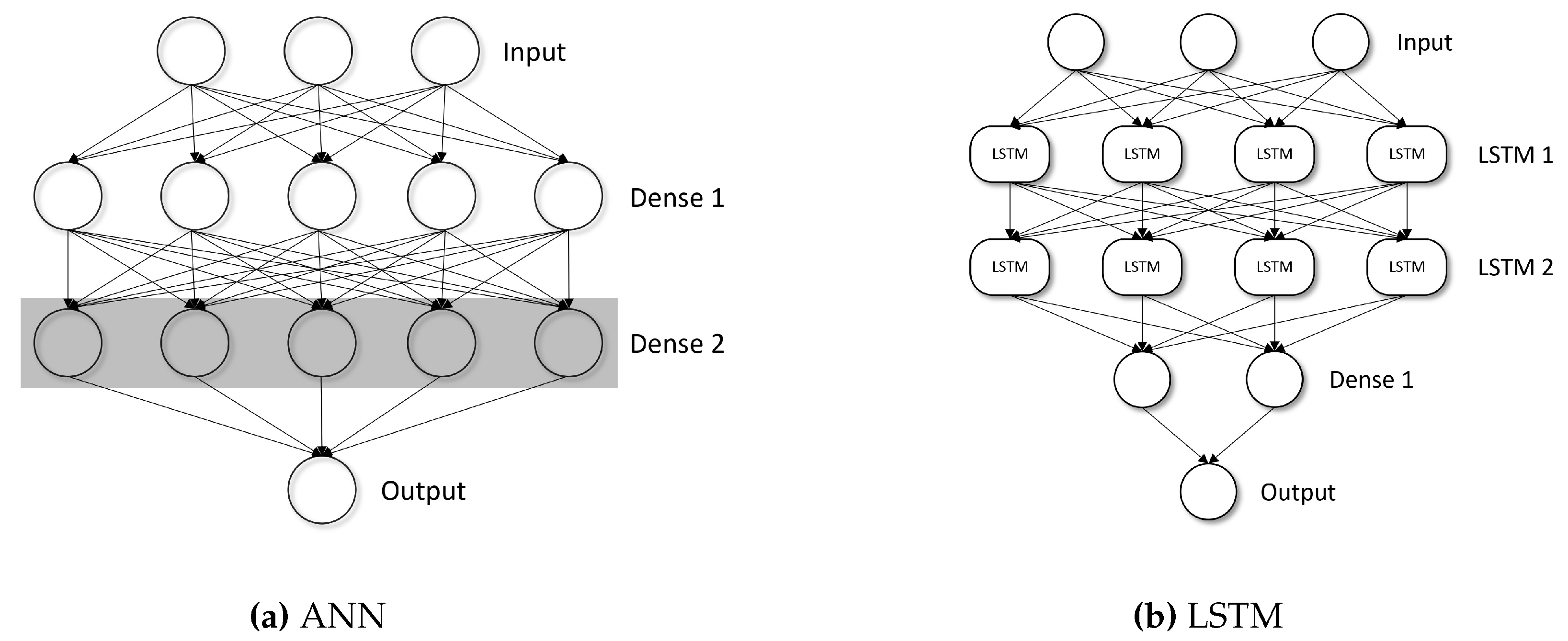
As mentioned previously, 2 models were built: ANN- and LSTM-based. They were implemented in Python7 programming language using keras high-level API, built on top of tensorflow library. Figure 3 displays the models used in the research. They are both considered deep neural networks, as they have more than one hidden layer each.

The ANN model is very much like the general ANN described before, except that a special technique called dropout was used at the transition from Dense 1 to Dense 2. It has one main parameter

α

, called rate. The dropout technique is active only at training stage. During forward pass, when it gets to the dropout layer,

α

random neurons are removed8. One heuristic is used during this process: the weights, connected to the neurons of the layer are scaled by a factor of

\frac{1}{1 - α}

to keep the overall sum of the inputs the same as before. This is required, because the load on each individual neuron is increased during the training due to the removal of some neurons. The idea behind using dropout is to decrease the internal dependencies of neurons upon each other for better generalisation.

Five layers make up the LSTM model. It has the same input and output layers as the ANN model, and the difference is in the hidden layers. The first too hidden layers are composed of LSTM units. This allows the network to remember and absorb certain temporary and long-term patterns, which is crucial for analysing time-series data. In addition to those, there is a dense layer, extracting the main features.

In terms of numbers: the ANN model has 128 units in both hidden layers and it has around 16k parameters, whereas the LSTM model has 64 units in the first two LSTM layers and 32 units in the dense layer, and uses about 52k parameters.

4. Data

4.1. Sources

The data for stocks was taken for the top 100 NASDAQ-listed companies by capitalisation. Two APIs were used for fetching the data: Yahoo Finance for OHLCV9 values and AlphaVantage for indicator10 data. In addition to those, TradingView API was tried for indicator data, but it only gives recommendations on whether to buy/hold/sell a stock, based on indicator analysis, not the indicator values required.

4.2. Selecting Data

Initially, one might think that the more data is fed into a model, the more reliable the prediction output. It sounds reasonable, but in reality it turns out to be more complicated than that. If different data features are not independent from each other, they are considered overlapping, which creates noise. For example, there are four different values for price feature, and, in essence, they all represent the same property. Introducing all of them into the model simultaneously results in a much worse performance than if, say, only one of those values was taken or if they were summarised into a lower number of values which would retain the main properties of all of them. This is a powerful machine learning technique called dimensionality reduction11 and it is crucial for training an effective model. For example, initially there were 13 different numbers representing some information for each day in the dataset, and the model trained on all of them was very random and chaotic. The model wouldn’t provide with any good results until the dimensionality of the input was reduced to just 3 values. There is a further discussion on this, later in the paper.

As all the four price values basically represent the same thing, only the close values were left in the dataset, because the target price is also a close value. In addition to price, there was volume and a single indicator values for each trading day. The same issue was encountered with indicators. At first, there were 8 different indicators used, but for the same reason as with price, it had to be reduced. In essence, indicators are derived from price which has already been included, nevertheless one indicator was decided to be left in the dataset. There was the following selection of different indicators: AD, OBV, ADX, AROON, RSI, STOCK, CCI, MACD12. Each of them were used in the dataset and evaluated by the ANN model to determine the most effective one.

One important preprocessing technique used during the comparison is standardisation. It is crucial when using neural networks, as neurons learn the most effectively when the input is in the range

[- 1, 1]

. It stems from the sigmoid function having the most sensitivity around the

[- 1, 1]

range, and not being able to distinguish large numbers. For example, if the classic sigmoid function

σ (x) = \frac{1}{1 + e^{- x}}

is applied to 1000 and 1000000, the results are 1 and 1, respectively, which doesn’t help at all. Thus, the data should be standardised, which means its values should be scaled to a range close to

[- 1, 1]

. There exist different approaches, and 3 of these were used in this research: no standardisation, custom standardisation and StandardScaler from scikit-learn python library. The StandardScaler inputs an array of some data, calculates its mean, standard deviation and outputs statistical z values13 with those normal distribution parameters:

z = \frac{x - μ}{σ}

where x - input value,

μ

- mean,

σ

- standard deviation.

Table 1 shows prediction results for the 8 indicators and 3 standardisation techniques mentioned before. The model was set to train for 50 epochs14 with an early stopping of 5-epoch patience15. If the model reaches 50-th epoch it means there is still some capacity to learn left in the training dataset, and the model generalises well with the parameters chosen. Clearly, with raw data(no standardisation) the results are terrible and even negative error is present. In contrast to that, the results are far more accurate and similar when custom and standard(scikit learn StandardScaler) methods are used. Analysing this table, AD indicator with custom standardisation was chosen as the input data in the main dataset.

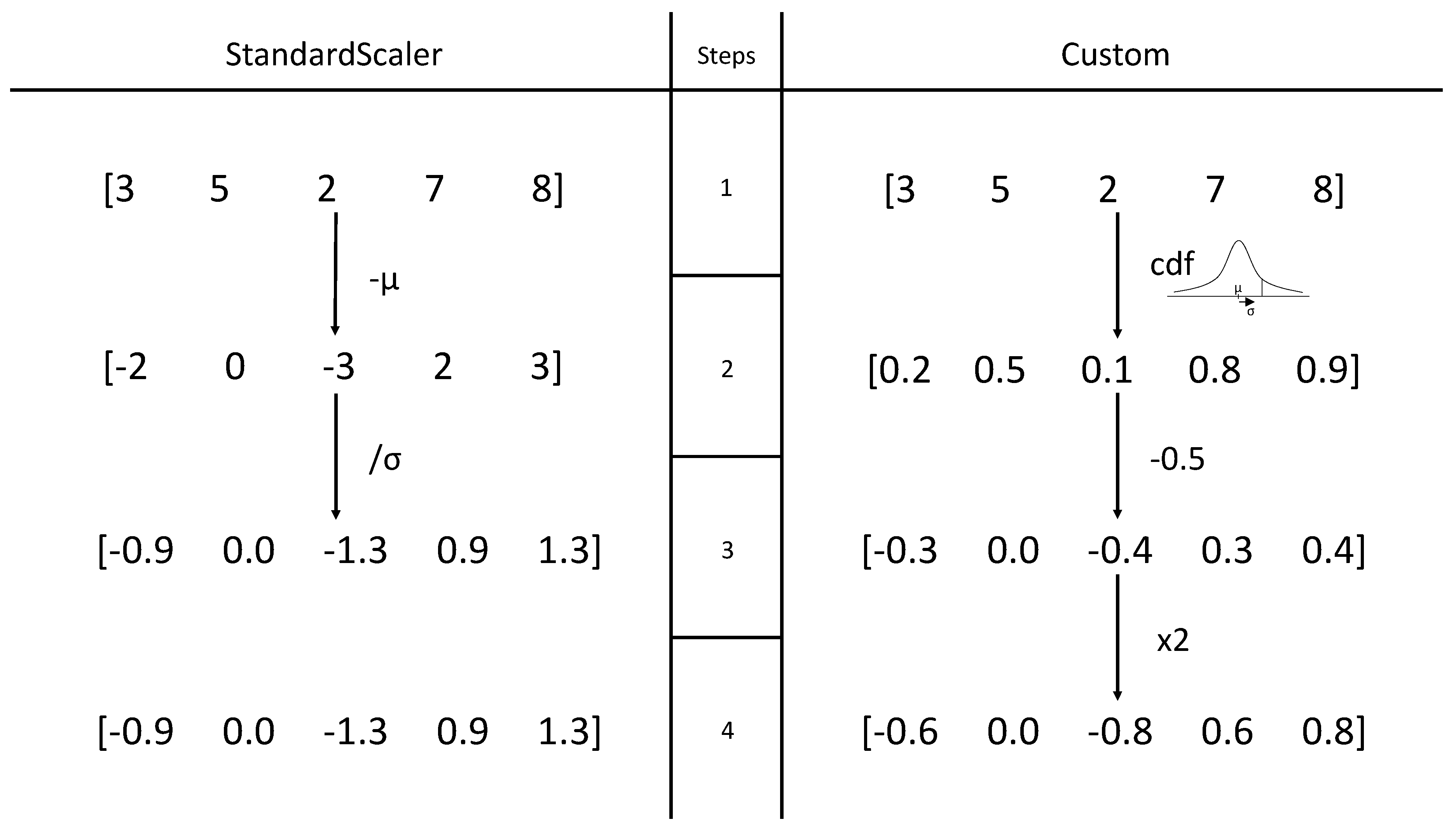
4.3. Custom Standardisation

The basis of the custom method is normal distribution, the same as in StandardScaler, but the approach is different. Figure 4 shows the difference between the two approaches. The function takes an array as an input and one more parameter, called n. Let’s go through the algorithm of custom standardisation with an array

[3, 5, 2, 7, 8]

as an example input. Iterating through each entry in the array the method first calculates the mean and standard deviation of n entries before in the array, including the current one. If there were less entries before than n, the algorithm uses all the entries before the current one. Then it calculates the cumulative distribution function with the current entry as an input using normal distribution with the previously calculated mean and standard deviation values. It results in a number in the range

[0, 1]

. To scale it to the range

[- 1, 1]

, 2 additional steps are required: first

0.5

is substracted from the number and then it is multiplied by 2.

The advantages of that method over StandardScaler is that, first, all the numbers in the inputted array are scaled to

[- 1, 1]

range, which is very beneficial for neural networks to work in a stable fashion. The second advantage is that the method standardises each entry not by the whole array, but rather by the last n entries. This approach is deeply intertwined with the nature of stock prices and time-series data, because when given an array of all entries, each entry represents some value at a certain time period, and each such entry had only the information about the entries before itself.

Another benefit of the latter technique is that the n parameter allows to have additional control over the data. It introduces relevancy to the data, which is very suitable for time-series analysis16. As the standardisation is not uniformly applied for each entry as in the former method, but rather each entry is standardised with an account for only the preceding data. Combined, these properties allow the custom standardisation to absorb the complexities of the time-series data features better than scikit-learn StandardScaler.

4.4. Parsing Data

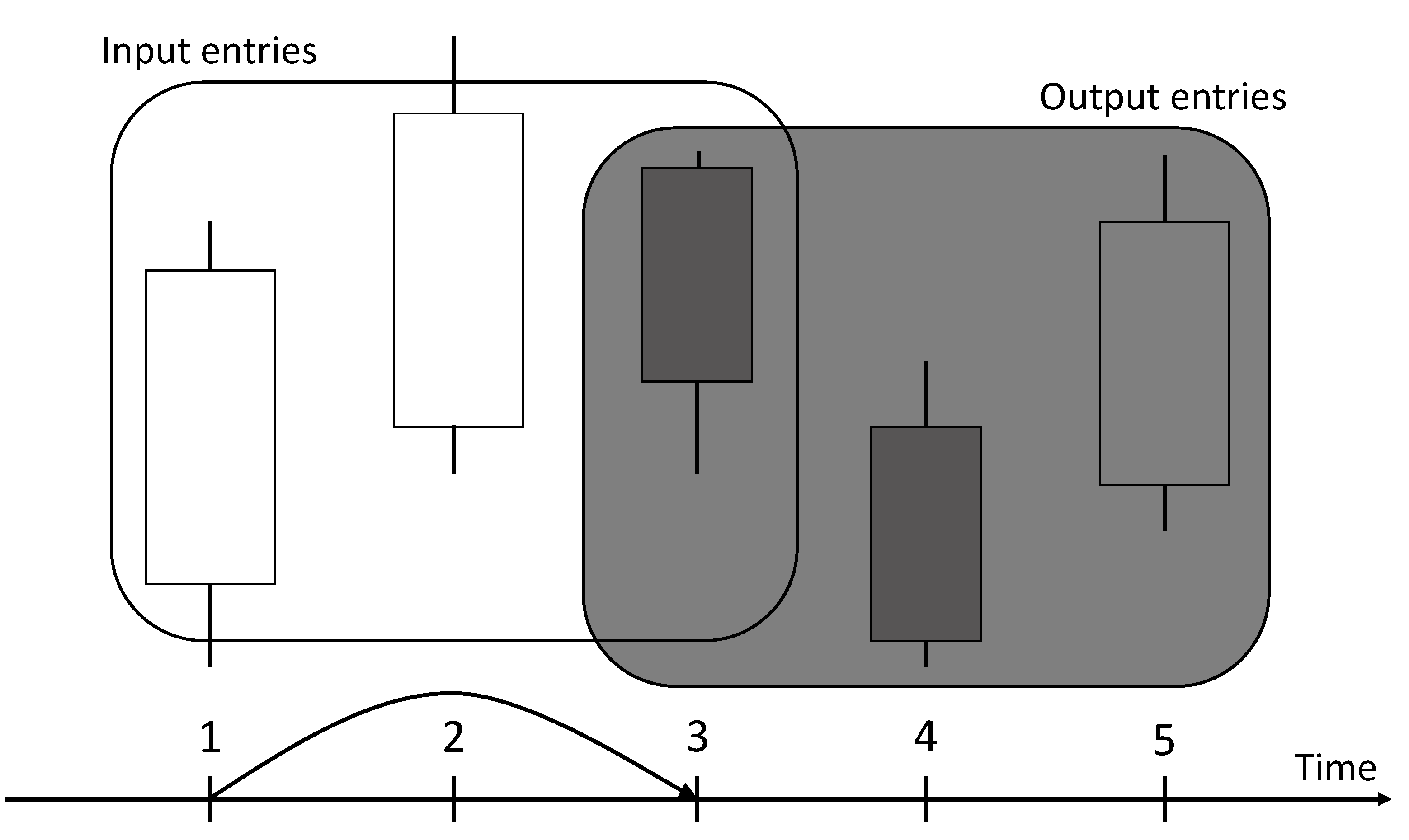
For the network to train effectively, it requires a proper dataset. As mentioned previously, the training process needs two arrays for inputs and outputs. To predict the future based on the past, the input values should be of some data before the output values. If each trading day is imagined as a candlestick17, then for each t candles as an input, the output would be t candles s days ahead (t and s are named after

t i m e s t e p

and

s t r i d e

variable names used in the code, respectively). Figure 5 illustrates this approach.

An experiment showed that with different values of t and s, the accuracy changed. While tuning these parameters, it turned out that the best performance is achieved when

t = 3

and

s = 1

. This configuration was chosen, i.e. sets of 3 adjacent candles with the time difference between inputs and outputs of 1 day made up the dataset used.

4.5. Dimensions

After applying the preprocessing described previously, the dataset consisted of entries of 3 values each. Each entry would conform to the following vector format: [ClosePrice, VolumeValue, IndicatorValue]. Here, VolumeValue and IndicatorValue are standardised and ClosePrice is raw. Even though the number of values in each entry was reduced from 13 to 3, the price value still was the main feature which could be left on its own. So, several tests were conducted to determine which configuration is better: the one with 3 values [ClosePrice, VolumeValue, IndicatorValue] or the one with just 1 value [ClosePrice].

Sometimes in data science a technique called Principal Component Analysis(PCA) is used to reduce the ambiguity of data spread. It is due to most commonly data being more distinctly split on some other coordinate axes than the original one. This method creates a new coordinate system on the same data and then translates the data onto the newly created axes. Nevertheless, PCA technique wasn’t used here, for the sake of simplicity and demonstration convenience.

Throughout the research the Mean Absolute Percentage Error (MAPE) loss function was mainly used. It calculates the mean deviation from the target value across the whole dataset, and it is given in %.

The results are displayed in Table 2. Here, only the top 10 NASDAQ companies are taken for demonstration. It is clear, that 1 value entries outperform 3 value entries by around 2 times. It might have happened due to many reasons: the model available is too small to analyse high-dimensional data or some other preprocessing technique should have been used on the data. It seems like in this research, the more simplistic the approach, the better the performance. As an outcome, 1 value entries are used in the Results section.

5. Results

The main idea was to build a base stock-trained model, fine-tune it on the real-world data and then compare to a model just trained on real-world data. For that there needs to be a well-performing reliable base model. The architecture for the latter was the LSTM model, and 2 training datasets were taken: the top 100 and top 20 NASDAQ companies by capitalisation.

Table 3 illustrates the accuracy18 of 3 models. Base 20 and base 100 differ by their dataset and standard model is the ANN model that had been trained just on the company stock price data which it is evaluated on. To summarise, it is evident that the base 100 model works better in terms of generalisation and overall performance than the base 20 model, and the standard model is the best to spot some specifics of data. For example, Nvidia has experienced a period of a very rapid stock price growth due to the boom of AI(as of 2024), which is unusual for the most companies in the dataset, resulting in standard model vastly outperforming both base models. However, with stable companies like Google the base models work better than the standard model19.

For fetching real-world phenomena data, datasets from kaggle.com and data.world websites were used. These are arbitrary and not bound to any theme or topic. The data acquired was preprocessed in a similar way to the stock data and parsed into training datasets, compatible with the models used.

Table 4 shows how well the models, developed here, predict real-world data. The solar wind density dataset has time difference of 5 minutes between values, whereas the simpler dataset has the previous values averaged, so that each entry contains data for 1 day, reducing the dataset size significantly.

The models were trained and evaluated on each dataset for 30 times and the mean error is displayed in the table. In addition to that, for each dataset, standard deviation of evaluation result was taken and hypothesis testing was conducted to determine whether the fine-tuned model does, in fact, outperform the standard model and it is not a coincidence:

H_{0} : μ_{1} \leq μ_{2}

H_{1} : μ_{1} > μ_{2}

, where

μ_{1}

is for fine-tuned mean and

μ_{2}

is for standard model mean performance. T-distribution was then used to to reject

H_{0}

with 1% significance level. On each dataset the fine-tuned model predicts better than the standard model with more than 99% confidence.

It is clear, that, on average, the error obtained here is greater than with stock prices. Also, fine-tuned model which is the base 100 model additionally trained on the real-world data, performs the best out of the three models tested.

6. Conclusion

A lot of different datasets were fetched to achieve the best performance. Four different values for stock prices, one value for volume and 8 more different indicator values were available. Despite this huge initial dimensionality of the data available for each entry, after some tests it was found that when filtering all the data to just a single price value the performance was the best. In theory, the additional data should have helped the predictions, but one reason why it hasn’t might be that the model was too small, or the architecture wasn’t very effective. A further research would explore the topic using larger models, with non-sequential architecture and some additional layers to help the prediction. In addition to that, a CNN model with a completely different parsing process should be devised as it is capable to outperform the models used.

The models built have achieved a good performance on the stock prices, but did worse when evaluated on real-world phenomena. Nevertheless, when comparing the error, it turned out that the fine-tuned model was increasing the performance of the simple standard model. It means that the randomness incorporated into the base model when trained on stock prices is similar to the randomness of the phenomena studied, namely global temperature, air quality, solar winds density, covid deaths and soybean vegetation index. The more fine-tuning increased standard model’s accuracy on a dataset, the more those natural events are alike with the markets, in terms of randomness.

The results are quite convincing, nevertheless they might not be true, because several assumptions and heuristics made could be wrong. For that reason there needs to be a further study on them with rigorous proof and statistical background.

To conclude, this research has showed that markets are, indeed, naturally random and their randomness aligns with that of the natural phenomena chosen, meaning that the individual actions of people trading stocks can be looked at from a completely different perspective and analysed as the natural phenomena do. The latter notion might inspire philosophical discussions on whether humans are purely individual or they are a part of some bigger system, which explains us better than we do ourselves now.

Notes

1	These are very common, nevertheless there are many more methods not mentioned. Comparison of those models and a discussion on why ML techniques might be more powerful is available here: link.
2	This paper has devised and popularised the transformer technique based on attention mechanism. Today, transformer is the state-of-the-art method in ML, and it forms the foundation of the Large Language Models like ChatGPT, Claude and others.
3	A concise article on that is available on OpenAI website: link.
4	Feedforward is sometimes called forward pass.
5	This coefficient is called learning rate. The more the coefficient, the quicker the descent, but if it’s too great, the ball might go past the minimum and result in unstable movement.
6	For example, modern Large Language Models (LLMs) use billions or even trillions of variables (also known as parameters): Meta’s Llama-3 has 8 billion parameters and OpenAI’s ChatGPT-4 has 1.76 trillion parameters. Read link for more details about the sizes of the modern LLM models and the computational power required to train them.
7	The whole code used in the research is available on GitHub: link.
8	To be specific, they are not removed, but rather their values are set to zero which doesn’t change the logic overall, and just simplifies the abstraction.
9	OHLC - Open, High, Low, Close, Volume. For each trading day these four price values and volume amount(i.e. how much stocks were traded) are available.
10	Indicators are some functions which take the price values as an input and output a single number, which carries some technical information and may help a trader to decide whether to buy the stock.
11	This is a process of reducing the dimensions of inputs, to remove noise from the data and assist the predictive model. A more detailed discussion is available here: link.
12	The indicators selected are described in the following article: link.
13	These z values are different from those previously discussed in the Neural Networks section. They represent the value if it was rescaled to a normal distribution $X \sim N (0, 1)$ .
14	A single epoch represents the model using the full dataset once. If there is more than 1 epoch, it means the model continues learning on the dataset already used previously, using the same data. Here, training for 50 epochs means that the model uses each input-output pair for 50 times if the training hasn’t been stopped before the last epoch.
15	Patience is the main parameter in early stopping which is the number of epochs with no improvement of results required for the network to stop training on the data and mitigate overfitting. Overfitting is a common problem in machine learning and it occurs when a model stops learning from the data to generalise, but rather achieves the best accuracy on the training dataset at the cost of becoming worse overall.
16	For example, with this technique the values 10 and 100 days ago are distinguished, and the more recent value is given a bigger impact on standardising the current value.
17	A diagram explaining candlesticks is available on this website: link.
18	In some sense error, which is actually shown in the table, is a metric of accuracy, and in comparative context, those two words are used interchangeably here. Note, that the more the accuracy, the less the error.
19	By comparing the performance of standard and base models on some company, its volatility can be inferred. If base model outperforms the standard model, then the company stocks are stable and low-volatile. Otherwise, the opposite is true.

References

Dewdney, A. The New Turing Omnibus; W. H. Freeman & Co.: USA, 1993. [Google Scholar]
Sarstedt, M.; Mooi, E. , Regression Analysis; Springer, 2014; pp. 193–233. [CrossRef]
Fattah, J.; Ezzine, L.; Aman, Z.; Moussami, H.; Lachhab, A. Forecasting of demand using ARIMA model. International Journal of Engineering Business Management 2018, 10, 184797901880867. [Google Scholar] [CrossRef]
Hearst, M.; Dumais, S.; Osman, E.; Platt, J.; Scholkopf, B. Support vector machines. Intelligent Systems and their Applications, IEEE 1998, 13, 18–28. [Google Scholar] [CrossRef]
Nabipour, M.; Nayyeri, P.; Jabani, H.; Mosavi, A.; Salwana, E.; S. , S. Deep Learning for Stock Market Prediction. Entropy 2020, 22. [Google Scholar] [CrossRef] [PubMed]
Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N. ; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Advances in neural information processing systems, 2017, pp. 5998–6008.
Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artificial Intelligence Review 2020, 53. [Google Scholar] [CrossRef]
Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. 2017 International Conference on Engineering and Technology (ICET), 2017, pp. 1–6. [CrossRef]
Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems; Pereira, F.; Burges, C.; Bottou, L.; Weinberger, K., Eds. Curran Associates, Inc., 2012, Vol. 25.
Khalid, A.; Mehmood, A.; Alabrah, A.; Alkhamees, B.F.; Amin, F.; AlSalman, H.; Choi, G.S. Breast Cancer Detection and Prevention Using Machine Learning. Diagnostics (Basel) 2023, 13. [Google Scholar] [CrossRef] [PubMed]
Ersavas, T.; Smith, M.A.; Mattick, J.S. Novel applications of Convolutional Neural Networks in the age of Transformers. Scientific Reports 2024, 14, 10000. [Google Scholar] [CrossRef] [PubMed]
Nielsen, M.A. Neural Networks and Deep Learning, 2018.

Figure 2. Gradient descent can be imagined as a ball rolling down a hill.

Figure 3. Architectures of the models used. The circles here are neurons(perceptrons) and rounded rectangles are LSTM units described previously. The shaded Dense 2 region represents dropout technique used at the previous Dense 1 layer. These are not to scale in number of neurons with the actual models used.

Figure 4. Comparison between the standardisation methods.

Figure 5. A representation of data parsing. In this example

t = 3

and

s = 2

. This means that each input consists of 3 candles, and the output also consists of 3 candles 2 days ahead. Therefore, the leading candle in the input is candle 1 and the leading candle in the output is candle 3.

Figure 5. A representation of data parsing. In this example

t = 3

and

s = 2

Table 1. A comparison of 8 indicators with 3 different standardisation techniques used. The highlighted entries are the ones outperforming the others.

Method	Indicator	Best Loss	Stopped, epoch	Error
Raw	OBV	3653	31	9.84%
	AD	2116	24	-24.41%
	ADX	8377	9	-74.57%
	AROON	15553	13	-87.87%
	RSI	6204	17	-61.24%
	STOCH	8870	27	-70.06%
	CCI	10870	12	-101.95%
	MACD	8424	11	-71.36%
Custom	OBV	6.38	25	0.51%
	AD	6.29	30	0.34%
	ADX	6.59	50	0.33%
	AROON	6.56	30	0.35%
	RSI	7.64	23	0.38%
	STOCH	6.40	21	0.39%
	CCI	6.79	50	0.31%
	MACD	6.81	25	0.33%
Standard	OBV	6.89	50	0.37%
	AD	6.31	44	0.38%
	ADX	6.63	30	0.37%
	AROON	6.05	40	0.24%
	RSI	6.30	50	0.36%
	STOCH	6.27	49	0.33%
	CCI	6.69	30	0.38%
	MACD	6.67	28	0.38%

Table 2. Performance comparison for different input dimensions.

Name	Symbol	Error, %
Name	Symbol	3 values	1 value
Microsoft	MSFT	2.48	1.29
Apple	AAPL	3.63	1.67
Nvidia	NVDA	6.72	2.50
Broadcom	AVGO	3.09	1.59
Amazon	AMZN	4.00	1.98
Meta	META	3.32	1.64
Tesla	TSLA	5.15	2.47
GoogleA	GOOGL	3.06	1.34
GoogleC	GOOG	2.57	1.42
Costco	COST	2.30	1.16

Table 3. Accuracy data for different models. Note, that standard model here can be interpreted as Base 1, as it was trained on a single company.

Name	Symbol	Error, %
Name	Symbol	Standard	Base 20	Base 100
Microsoft	MSFT	1.49	1.01	1.04
Apple	AAPL	2.61	150.32	8.77
Nvidia	NVDA	3.68	710.39	56.65
Broadcom	AVGO	4.77	4.55	5.83
Amazon	AMZN	1.77	54.16	2.14
Meta	META	2.19	1.23	1.24
Tesla	TSLA	2.31	19.73	1.73
GoogleA	GOOGL	1.26	1.27	1.00
GoogleC	GOOG	1.42	0.87	1.02
Costco	COST	2.12	1.34	1.97

Table 4. Performance of different models on real-world datasets. The best performing model on each dataset is highlighted.

Dataset	Error, %
Dataset	Standard	Base 100	Fine-tuned
Global Temperature	5.73	3.55	3.54
Air quality, PM10 (ug/m3)	12.66	8.42	8.03
Solar winds density simpler	30.17	22.53	19.53
Covid deaths	46.13	53.84	35.60
Soybeans South America	46.08	63.69	31.99

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Are Markets Naturally Random? Machine Learning Approach to Quantifying Randomness

Abstract

1. Introduction

2. Background

3. Models

3.1. Neural Networks

3.2. Feedforward

3.3. Backpropagation

3.4. LSTM

3.5. Layer Architecture

4. Data

4.1. Sources

4.2. Selecting Data

4.3. Custom Standardisation

4.4. Parsing Data

4.5. Dimensions

5. Results

6. Conclusion

Notes

References

MDPI Initiatives

Important Links

Subscribe