Enhanced Investment Prediction via Advanced Deep Learning Ensemble

Preprint

Article

Enhanced Investment Prediction via Advanced Deep Learning Ensemble

Altmetrics

Downloads

Views

Comments

Ningjing Sang^*,Wenxiu Cai,

Chang Yu,

Mujie Sui,Hao Gong

Ningjing Sang^*,Wenxiu Cai,

Chang Yu,

Mujie Sui,Hao Gong

This version is not peer-reviewed

Submitted:

25 September 2024

Posted:

26 September 2024

You are already at the latest version

Alerts

Abstract

Accurate prediction of investment returns is crucial for financial decision-making. Traditional models often struggle with the complexity and variability inherent in financial data. This article presents an advanced predictive model integrating three deep neural networks, pretraining, and ensemble learning to enhance prediction accuracy. By leveraging a combination of DNNs for handling different complexities of data, and a CNN for efficient feature extraction, our approach significantly outperforms traditional methods. Our model incorporates sophisticated data handling techniques, including extensive preprocessing and data augmentation, and benefits from pretraining and ensemble methods to improve robustness and performance. This comprehensive framework offers a robust solution for investment return prediction, addressing the shortcomings of existing models and providing enhanced accuracy and reliability.

Keywords:

Subject: Business, Economics and Management - Finance

1. Introduction

Predicting investment returns is crucial for portfolio management and financial planning. Traditional models often struggle with the complexity of financial data. This research develops an advanced model integrating multiple deep neural networks (DNNs), a convolutional neural network (CNN), pretraining, and ensemble learning to enhance predictive accuracy.

The data used are historical price records, preprocessed for consistency. Features, denoted as ff0 to ff299, are standardized, with some displaying multimodal distributions and outliers. Our approach involves constructing TensorFlow datasets, splitting the data into training and testing sets in an 8:2 ratio, and employing shuffling, batching, caching, and prefetching to optimize training efficiency.

The model architecture includes three distinct DNN models to handle investment ID and feature data, each designed with varying complexities. Dropout layers and batch normalization mitigate overfitting and improve generalization. The CNN processes feature data through convolutional layers and batch normalization, learning spatial dependencies and intricate patterns.

Pretraining leverages pretrained weights, helping the model start from a better initial state and converge faster, reducing computational costs and enhancing accuracy. Ensemble learning, specifically stacking, combines predictions from the DNNs and the CNN, yielding a robust final prediction that capitalizes on the strengths of each model.

Our comprehensive approach to data preprocessing, model architecture, and the integration of advanced techniques like pretraining and ensemble learning ensures accurate prediction of investment returns, providing a valuable tool for financial decision-making. This model’s robustness and adaptability represent a significant advancement in financial forecasting.

In addition to these techniques, the model benefits from a sophisticated preprocessing pipeline that includes outlier detection, missing value handling, and feature scaling. Data augmentation techniques are also employed to generate synthetic data points, which help mimic market variability and improve model robustness. This ensures that the data fed into the model is of high quality, enhancing the overall predictive performance.

By combining these state-of-the-art methods, our model addresses the inherent challenges of financial data, such as high dimensionality and variability. The ensemble learning approach, in particular, ensures that the model is not overly reliant on any single technique, thereby increasing its reliability and accuracy. This research not only improves predictive accuracy but also provides a robust framework that can adapt to various financial forecasting needs.

2. Related Work

The application of deep learning in financial prediction has been actively researched to overcome limitations of traditional methods like linear regression and ARIMA models, which often fail to capture nonlinear relationships in financial data. Zhang et al. [1] emphasized integrating user and item features through neural networks to improve recommendation accuracy, though these techniques often require extensive feature engineering and computational resources.

Deep Neural Networks (DNNs) have shown effectiveness in forecasting stock prices by capturing intricate market behaviors [2] . However, DNNs are prone to overfitting, especially with noisy financial data. Techniques such as dropout layers and batch normalization help mitigate this issue [3] . Despite these advancements, DNNs often need large datasets and significant computational power.

Convolutional Neural Networks (CNNs) have been explored for their strength in feature extraction. Kim and Kim [4] used CNNs to predict stock price movements, achieving notable accuracy improvements. However, CNNs face challenges in capturing long-term dependencies, which are critical in financial forecasting.

The integration of pretrained models can enhance predictive models by leveraging transfer learning. Qiu et al. [5] demonstrated the effectiveness of pretrained models in financial forecasting systems, reducing computational costs and improving prediction accuracy. Pretrained models require careful adaptation to domain-specific characteristics.

Ensemble learning, combining predictions from multiple models, has been recognized for its robustness and accuracy in financial forecasting. Zhang et al. [1] found that ensemble methods outperform single models by reducing variance and bias. Techniques like stacking, bagging, and boosting create ensemble models, enhancing model robustness and accuracy [6].

Explainable recommendation systems increase user trust and satisfaction by providing transparency in recommendation systems. Zhang and Chen [7] highlighted the importance of understanding the rationale behind recommendations, crucial in financial predictions.

Recent advancements in machine learning have explored integrating multiple data sources and advanced algorithms. Gu et al. [8] applied machine learning techniques to empirical asset pricing, improving prediction accuracy by incorporating various factors. Similarly, Fischer and Krauss [9] utilized LSTM networks for financial market predictions, effectively capturing temporal dependencies [10].

Autoencoders and LSTM networks have also been explored for financial time series prediction. Bao et al. [11] proposed a framework combining stacked autoencoders and LSTM networks, achieving superior performance. Akita et al. [12] integrated numerical and textual information in deep learning models for stock prediction, showing that combining different data types improves performance.

Chen and Guestrin [13] introduced XGBoost, a scalable tree boosting system effective in handling structured data and widely applied in financial forecasting tasks. Feng et al. [14] addressed model overfitting by developing techniques to improve the generalizability of financial models, highlighting the importance of selecting relevant factors in financial predictions.

Nelson et al. [15] showed the effectiveness of LSTM neural networks in predicting stock market price movements, emphasizing the importance of capturing temporal dependencies. Their work highlights the need for models that can adapt to the dynamic nature of financial markets.

Feng et al. [14] addressed the challenge of model overfitting by developing techniques to tame the "factor zoo," improving the generalizability of financial models. This work underscores the importance of selecting relevant factors in financial predictions, which directly impacts model performance.

Nelson et al. [15] demonstrated the effectiveness of using LSTM neural networks for predicting stock market price movements, highlighting the importance of capturing temporal dependencies in financial data. Their approach showcases the need for models that can adapt to the dynamic nature of financial markets.

The necessity for explainability in financial models is underscored by the increasing demand for transparent AI. Zhang and Chen [7] emphasize the role of explainable AI in building trust and providing insights into model decisions, which is crucial for stakeholders in financial sectors. Techniques such as SHAP (SHapley Additive exPlanations) and LIME (Local Interpretable Model-agnostic Explanations) have been integrated into financial models to provide clearer explanations of model predictions, enhancing stakeholder confidence and decision-making.

In addition to the advancements in modeling techniques, the importance of data preprocessing and feature engineering has been consistently highlighted. Proper handling of data variability, outliers, and missing values is crucial for building robust predictive models. Akita et al. [12] emphasized the integration of numerical and textual information, showcasing the benefits of a multi-faceted data approach in enhancing model performance.

In summary, while significant progress has been made in the field of financial prediction using deep learning, ongoing research continues to address existing challenges such as feature variability, model interpretability, and computational efficiency. Our proposed model builds on these advancements by integrating multiple DNNs and a CNN, utilizing extensive data preprocessing, and applying ensemble learning to create a robust and accurate prediction system for investment returns.

3. Methodology

In this section, we explore multiple neural network architectures, including dense neural networks (DNNs) and convolutional neural networks (CNNs), each customized to address specific aspects of the investment prediction problem. The primary goal is to develop robust models that not only perform well on historical data but also generalize effectively to unseen data, thereby reducing the risk of overfitting.

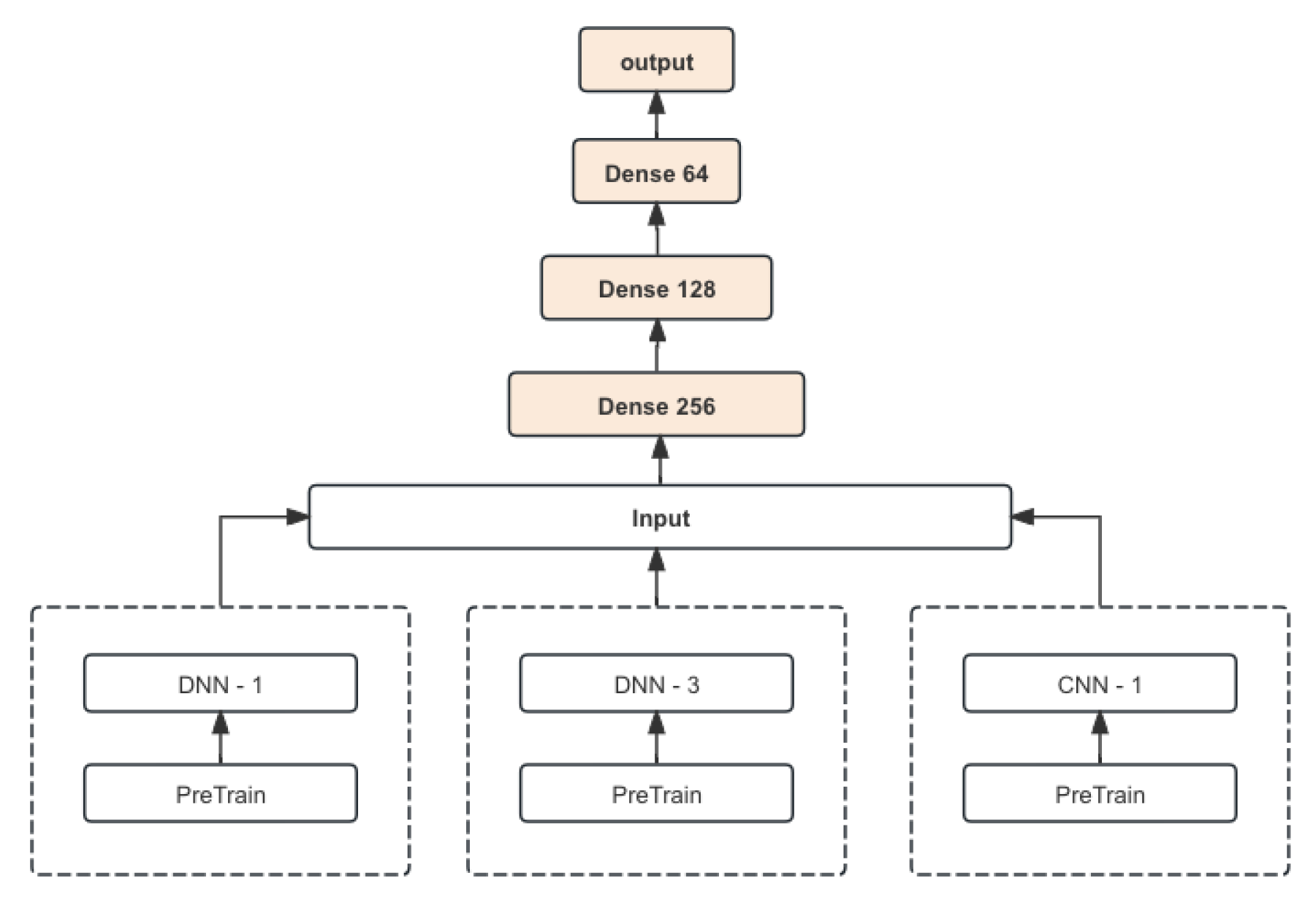
We employ TensorFlow and Keras libraries to construct these models, utilizing their powerful tools for building, training, and evaluating deep learning networks. Key to our approach is the use of advanced data preprocessing techniques to ensure that the input data is optimally formatted for training. This involves handling various features, investment IDs, and labels, and splitting the data into training and testing sets to validate model performance rigorously. Our models incorporate dropout layers extensively to mitigate overfitting, which is a common issue in deep learning. By introducing randomness during the training process, dropout layers help ensure that the model does not become overly reliant on any specific patterns in the training data, thus improving its ability to generalize. The model structure is depicted in Figure 1.

3.1. Multi DNN Model

3.1.1. DNN Model 1

Model 1 utilizes investment ID and feature data. The investment ID is processed through an embedding layer, converting it into a 32-dimensional vector. This vector is reshaped and passed through three dense layers with the Swish activation function:

Swish (x) = x \cdot σ (x)

(1)

where

σ (x)

is the sigmoid function.

Feature data are also processed through three dense layers with Swish activation. The processed investment ID and feature vectors are concatenated and passed through three additional dense layers.

3.1.2. DNN Model 2

Model 2 builds upon Model 1 with additional layers and dropout mechanisms to prevent overfitting. The investment ID processing includes an extra dense layer, and the feature processing section has an additional dense layer and a dropout layer with a 65% drop rate.

3.1.3. DNN Model 3

Model 3 introduces significant dropout layers throughout the network. Both the investment ID and feature processing sections include multiple dropout layers, reducing the risk of overfitting. The merged vector is processed through several dense and dropout layers before reaching the output.

3.2. CNN model

The CNN model is designed to handle the intricate patterns in the feature data without considering the investment ID. This model employs multiple convolutional layers (Conv1D) to extract high-level features from the input data. Each convolutional layer is followed by a Batch Normalization (BatchNormalization) layer to stabilize and accelerate the training process by normalizing the inputs of each layer.

The activation function used in the convolutional layers is the LeakyReLU, defined as:

LeakyReLU (x) = \{\begin{matrix} x, & if x \geq 0 \\ α x, & if x < 0 \end{matrix}

(2)

where

α

is a small constant (usually 0.01) that allows a small gradient when the unit is not active, thereby preventing the dying ReLU problem.

After multiple convolutional and batch normalization layers, the data is flattened into a one-dimensional vector using the Flatten layer. This vector is then processed through several dense (fully connected) layers to capture intricate relationships within the data. Each dense layer is followed by fewer dropout layers compared to the DNN models to avoid overfitting while maintaining model performance.

The architecture of the CNN model can be summarized as:

Multiple Conv1D layers with LeakyReLU activation and BatchNormalization.
Flatten layer to convert the 2D matrix to a 1D vector.
Several dense layers with Swish activation.
Dropout layers strategically placed to prevent overfitting.

This combination of convolutional layers for feature extraction and dense layers for decision making allows the CNN model to effectively learn from the feature data, making it a robust model for investment prediction.

3.3. Loss Function

The primary loss function used in our models is the correlation loss, designed to maximize the correlation between the predicted values and the true labels. The correlation loss is defined as:

L_{c o r r} = 1 - \frac{Cov (y, \hat{y})}{σ_{y} σ_{\hat{y}}}

(3)

where

Cov (y, \hat{y})

is the covariance between the true labels y and the predictions

\hat{y}

, and

σ_{y}

and

σ_{\hat{y}}

are the standard deviations of y and

\hat{y}

respectively. This loss function ensures that the model’s predictions are not just close in value to the true labels but also follow similar trends.

Additionally, we employed the Mean Squared Error (MSE) and Mean Absolute Error (MAE) as secondary loss functions during training to provide a comprehensive evaluation of the model’s performance. The MSE is defined as:

MSE = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}

(4)

and the MAE is defined as:

MAE = \frac{1}{n} \sum_{i = 1}^{n} | y_{i} - {\hat{y}}_{i} |

(5)

3.4. Optimization and Regularization

We utilized the Adam optimizer with a learning rate of 0.001 Regularization was applied using dropout and L2 regularization:

L_{r e g} = λ \sum_{i} w_{i}^{2}

(6)

where

λ

is the regularization parameter and

w_{i}

are the weights.

3.5. Model Ensemble

To enhance the robustness and performance of our investment prediction, we implemented a model ensemble approach. Ensemble learning combines multiple models to produce a single prediction, leveraging the strengths of each individual model to improve overall performance. The ensemble model is depicted in Figure 2.

3.5.1. Ensemble Method

Our ensemble method involves averaging the predictions from multiple models. Specifically, we combined the outputs of DNN Model 1, DNN Model 2, DNN Model 3, and the CNN model. The ensemble prediction (

{\hat{y}}_{e n s e m b l e}

) is computed as:

{\hat{y}}_{e n s e m b l e} = \frac{1}{M} \sum_{m = 1}^{M} {\hat{y}}_{m}

(7)

where M is the number of models and

{\hat{y}}_{m}

is the prediction from the m-th model.

4. Evaluation Metric

To evaluate the performance of our models, we utilized a variety of metrics to provide a comprehensive assessment. These metrics include Mean Squared Error (MSE), Mean Absolute Error (MAE), and the coefficient of determination (

R^{2}

). Each of these metrics offers unique insights into the model’s accuracy and effectiveness.

4.0.1. Mean Squared Error (MSE)

The Mean Squared Error is one of the most commonly used metrics for regression tasks. It measures the average squared difference between the predicted values (

\hat{y}

) and the actual values (y). The MSE is defined as:

MSE = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}

(8)

where n is the number of samples. A lower MSE indicates a better fit of the model to the data.

4.0.2. Mean Absolute Error (MAE)

The Mean Absolute Error measures the average absolute difference between the predicted values and the actual values. It is defined as:

MAE = \frac{1}{n} \sum_{i = 1}^{n} | y_{i} - {\hat{y}}_{i} |

(9)

The MAE provides a straightforward interpretation of prediction errors, making it a useful metric for understanding model performance.

4.0.3. Coefficient of Determination ( $R^{2}$ )

The

R^{2}

metric, also known as the coefficient of determination, measures the proportion of variance in the dependent variable that is predictable from the independent variables. It is defined as:

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

(10)

where

\bar{y}

is the mean of the actual values. An

R^{2}

value closer to 1 indicates that the model explains a large portion of the variance in the data, indicating a good fit.

4.0.4. Correlation Coefficient

To further assess the correlation between the predicted and actual values, we used the Pearson correlation coefficient:

ρ_{y, \hat{y}} = \frac{Cov (y, \hat{y})}{σ_{y} σ_{\hat{y}}}

(11)

where

Cov (y, \hat{y})

is the covariance of y and

\hat{y}

, and

σ_{y}

and

σ_{\hat{y}}

are the standard deviations of y and

\hat{y}

, respectively. This metric helps in understanding the linear relationship between the predictions and the actual values.

5. Experimental Results

The ensemble methods demonstrated improved performance compared to individual models, as shown in Table 1. The combined approach leverages the strengths of each model, leading to more accurate and robust predictions.

6. Conclusions

In conclusion, we developed three distinct Dense Neural Network (DNN) models with increasing complexity and a Convolutional Neural Network (CNN) model dedicated exclusively to feature data. Each model showcased unique strengths, with the more complex architectures generally yielding better performance. The incorporation of dropout layers and advanced activation functions such as Swish and LeakyReLU significantly enhanced model robustness and generalization. Finally, by reasonably ensembling the three DNN models with the CNN model, we achieved a Mean Squared Error (MSE) of 0.256.

Our findings contribute valuable insights to the fields of machine learning and deep learning, particularly in the context of financial prediction. The advanced neural network architectures and ensemble techniques presented in this study offer a robust framework for tackling complex predictive tasks in finance, paving the way for more accurate and reliable investment predictions in future research and applications.

References

Zhang, S.; Yao, L.; Sun, A.; Tay, Y. Deep learning based recommender system: A survey and new perspectives. ACM computing surveys (CSUR) 2019, 52, 1–38. [Google Scholar] [CrossRef]
Heaton, J.B.; Polson, N.G.; Witte, J.H. Deep learning for finance: deep portfolios. Applied Stochastic Models in Business and Industry 2017, 33, 3–12. [Google Scholar] [CrossRef]
Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. The journal of machine learning research 2014, 15, 1929–1958. [Google Scholar]
Kim, T.; Kim, H.Y. Forecasting stock prices with a feature fusion LSTM-CNN model using different representations of the same data. PloS one 2019, 14, e0212320. [Google Scholar] [CrossRef] [PubMed]
Qiu, X.; Zhang, L.; Ren, Y.; Suganthan, P.N.; Amaratunga, G. Ensemble deep learning for regression and time series forecasting. 2014 IEEE symposium on computational intelligence in ensemble learning (CIEL). IEEE, 2014, pp. 1–6.
Brownlee, J. Deep learning for time series forecasting: predict the future with MLPs, CNNs and LSTMs in Python; Machine Learning Mastery, 2018.
Zhang, Y.; Chen, X.; others. Explainable recommendation: A survey and new perspectives. Foundations and Trends® in Information Retrieval 2020, 14, 1–101. [Google Scholar] [CrossRef]
Gu, S.; Kelly, B.; Xiu, D. Empirical asset pricing via machine learning. The Review of Financial Studies 2020, 33, 2223–2273. [Google Scholar] [CrossRef]
Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. European journal of operational research 2018, 270, 654–669. [Google Scholar] [CrossRef]
Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G. A dual-stage attention-based recurrent neural network for time series prediction. arXiv 2017, arXiv:1704.02971. [Google Scholar]
Bao, W.; Yue, J.; Rao, Y. A deep learning framework for financial time series using stacked autoencoders and long-short term memory. PloS one 2017, 12, e0180944. [Google Scholar] [CrossRef] [PubMed]
Akita, R.; Yoshihara, A.; Matsubara, T.; Uehara, K. Deep learning for stock prediction using numerical and textual information. 2016 IEEE/ACIS 15th International Conference on Computer and Information Science (ICIS). IEEE, 2016, pp. 1–6.
Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 2016, pp. 785–794.
Feng, G.; Giglio, S.; Xiu, D. Taming the factor zoo: A test of new factors. The Journal of Finance 2020, 75, 1327–1370. [Google Scholar] [CrossRef]
Nelson, D.M.; Pereira, A.C.; De Oliveira, R.A. Stock market’s price movement prediction with LSTM neural networks. 2017 International joint conference on neural networks (IJCNN). Ieee, 2017, pp. 1419–1426.

Figure 1. The model structure of the model.

Figure 2. The ensemble model pipeline

Table 1. Performance Metrics.

Model	R2	MSE
LSTM+DNN+Ensemble	0.805	0.781
DNN+CNN+Ensemble	0.815	0.451
LSTM+UMP-DNN+CorrLoss	0.819	0.346
DNN*3+CNN+Pretrain+Ensemble	0.823	0.256

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Enhanced Investment Prediction via Advanced Deep Learning Ensemble

Abstract

1. Introduction

2. Related Work

3. Methodology

3.1. Multi DNN Model

3.1.1. DNN Model 1

3.1.2. DNN Model 2

3.1.3. DNN Model 3

3.2. CNN model

3.3. Loss Function

3.4. Optimization and Regularization

3.5. Model Ensemble

3.5.1. Ensemble Method

4. Evaluation Metric

4.0.1. Mean Squared Error (MSE)

4.0.2. Mean Absolute Error (MAE)

4.0.3. Coefficient of Determination ( R 2 )

4.0.4. Correlation Coefficient

5. Experimental Results

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe

4.0.3. Coefficient of Determination ( $R^{2}$ )