Preprint
Article
On Deadlock Analysis and Characterization of Labeled Petri Nets with Undistinguishable and Unobservable Transitions
Altmetrics
Downloads
80
Views
32
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 September 2024
Posted:
25 September 2024
You are already at the latest version
Alerts
Abstract
This work addresses the analysis and characterization of deadlocks in discrete-event systems modeled by labeled Petri nets (LPNs) with undistinguishable and unobservable transitions. To provide a solution for the notorious problem, it is essential to present an effective characterization such that deadlock control and synthesis are technically and methodologically possible. To this end, we introduce the notion of dangerous implicit vectors (DIVs) which implicitly threaten the system deadlock-freedom. The set of dead markings is divided into two subsets: dead basis markings (DBMs) and dangerous implicit markings (DIMs). An algorithm is designed to compute the sets of DIVs and DIMs at a given basis state of a system. Moreover, by virtue of linear algebraic equations, we formulate sufficient conditions to identify the existence of blocking markings in an LPN. Finally, an algorithm is developed to construct an observed graph that is a compact representation of the reachability graph of a Petri net with respect to the existence of dead reaches. At the end of this paper, experiment results that illustrate the correctness and effectiveness of the reported solution are presented.
Keywords:
Subject: Computer Science and Mathematics - Computer Science
1. Introduction
Nowadays, the use of artificial dynamical systems is remarkably increasing in view of the enormous evolution of computer technology. The most important characteristic of these systems is determined by the occurrence of asynchronous events such that they are naturally and soundly labeled as discrete-event systems (DESs). In fact, many contemporary cyber-physical systems can be investigated from the view of discrete-event systems, where the procedure of system analysis and synthesis greatly depends on system mathematical models [1]. Without such a mathematical model, it would be impossible to analyze and control the behavior of a system. Different models are used to achieve this goal such as Petri nets, automata, Markov chains, etc. However, Petri nets have been recognized as one of the most powerful tools for modeling dynamic discrete-event systems. The increasing interest in Petri nets is stimulated by their modeling power and a mathematical arsenal supporting the analysis of the modeled systems through the usage of linear algebra and engineering optimization techniques. Nevertheless, several fundamental problems remain open. Among them, we in this research center around the deadlock problem, which is an important issue in designing automated systems [2] and has received much attention from the community of computer science and systems control engineering [3,4,5].
Researchers and practitioners have developed an array of deadlock resolution methods such as the early work by Zhang and Holloway [6], where a controlled Petri net model is used for a forbidden state avoidance issue under partial event observation and the initial marking of the net model is assume to be known. In [7,8] Li and Wonham seminally explore the use of state-feedback control of discrete-event systems under partial state observation, where a plant is modeled with a finite state automaton in which an event can be controllable (observable) or uncontrollable (unobservable). Their goal is to find necessary and sufficient conditions for the existence of “optimal” state feedback control laws given a control specification represented by a finite state automaton. Proposed in [13] is a deadlock characterization and a control procedure based on an observer of a plant, which is actually what an external agent can observe, representing the system output from the lens of outside observation. By virtue of the characterization, a systematic procedure is presented for deadlock recovery, i.e., a deadlock state can be guided/recovered to a predefined normal state. The main contribution is that the observer, the controller, and the deadlock recovery algorithm are all based on the same linear algebraic techniques. Later, Giua and Seatzu [10], based on the previously mentioned characterization, use generalized mutual exclusion constraints (GMECs) to ensure the control objective, where a plant is modeled with a Petri net and a GMEC serves as the control specification. They explore a recovery procedure and present a deadlock recovery algorithm using linear algebraic techniques. In these studies, contrary to the supervisory control theory in the Ramadge-Wonham framework [45], all transitions are in general assumed to be controllable and observable, and ordinary Petri nets are usually used to model systems. Partially to this end, but not limited to, the methodologies of deadlock analysis and control derived from Petri nets are not as general as those from the Ramadge-Wonham paradigm.
In the literature, people have followed three main lines to deal with the problem of deadlocks in DESs modeled with Petri nets. First, we mention the deadlock prevention principle [19,21,22,23,24,25] which is an offline computation procedure that imposes restrictions on system evolution to prevent the reachability of dead markings. The prevention is ensured by forbidding all first-met bad markings (FBMs) that represent the first entry from the live zone (LZ) to the dead zone (DZ) that are the partition of the reachability graph of a plant, where the initial state that is assumed to be legal belongs to the live zone.
Contrary to deadlock prevention principle, deadlock avoidance [26,27,28,29,30,31] is an on-line mechanism used to handle the blocking problem in Petri nets. As the mechanism proceeds online, at each state, a proper decision is made and issued to the actuators among all possible evolutions, aiming to avoid deadlocks and keep the system never trapped in a deadlock state. However, similar to the previously mentioned method, deadlock avoidance uses the notions of LZ and DZ to achieve this purpose. Although it generally leads to higher resource utilization and throughput, overly aggressive policies are still not able to totally eliminate all deadlocks in some cases. From here comes the necessity to use deadlock recovery strategies. Note that a recovery scheme is usually used in the scenario where deadlocks do not cause serious consequences. To summarize, conservative methods eliminate all unsafe states and deadlocks, and often some good states, thereby degrading the system performance. On the other hand, they are intended to be easy to implement. Finally, we briefly explain deadlock detection and recovery techniques [32,33,34,35]. The difference between this mechanism and the aforementioned two methodologies is that a deadlock detection and recovery approach permits the occurrence of a deadlock. Once it occurs, it is detected and then a recovery policy is initialized to guide and navigate the system to a predefined deadlock-free state, by simply reallocating the resources held by the system processes. The efficiency and efficacy of this approach depend upon the response time of the implemented algorithms for deadlock detection and recovery. In general, these algorithms require a large amount of data and may become complex when several types of shared resources are considered [36].
To summarize, the deadlock problem has often been discussed in the literature and several original theoretical approaches have been proposed [9,10,11,12,13] to solve it. While the previous works usually use ordinary Petri nets to model a system where all transitions are observable (the occurrence of any transition can be detected) and distinguishable (different transitions carry different labels), we deal, in this paper, with the issue of deadlock analysis and control in labeled Petri nets where transitions can be unobservable and undistinguishable since labeled Petri nets are an important framework of discrete-event systems and their liveness is usually a prerequisite for many problems such as fault diagnosis, opacity verification and enforcement, and state estimation [14]. We are motivated by the importance of defining deadlock and controlling a discrete-event system to ensure the correct and safe functioning of large complex systems. More preciously, the importance of defining the deadlock problem optimally will lead consequently to finding an optimal solution to guarantee the deadlock-freeness of the studied system. Moreover, given the lack of work treating this problem in labeled Petri nets, our contributions clearly appear.
This paper will be divided into seven main sections. Section 2 provides a background on Petri nets and gives the necessary notations. Section 3 introduces a study of basis reachability graphs. In Section 4, we give reachability and basis reachability graph analysis for the deadlock problem. An algorithm is developed to define an observed graph as a compact representation of the reachability graph of a Petri net with respect to the existence of dead reaches in Section 5. Experiment results are utilized to illustrate the proposed method in Section 6. Finally, Section 7 concludes the paper, along with future topics in the direction.
2. Preliminaries
2.1. Automata
A non-deterministic finite-state automaton (NFA) is a quadruple , where X is the finite set of states, is the alphabet (usually finite), is the transition relation with , where is the empty string describing unobservable events, and is the initial state. The transition relation specifies the dynamics of the NFA: if , then from state x the occurrence of event yields the state . In particular, given any state , we have . The transition relation can be extended to , where if there exists a sequence of events and states such that generates the word , for , and , for .
An event e is said to be defined at state if there exists a state such that . An NFA is simply denoted as in the case where the initial state could be any state in X or the initial state is of no interest. The generated language of an automaton from a state is defined as
Given a set of states , we define the language generated from the states in set Y as:
2.2. Petri Nets
In this section, we review basic definitions of Petri nets. For more details we refer readers to [15] and [17].
Definition 1.
(Petri net). A Petri net is a quadruple , where P is a finite and non-empty set of places; T is a finite and non-empty set of transitions; and are respectively the pre- and post- incidence functions that specify the arcs directed from places to transitions, and vice versa 1. We use to represent the incidence matrix of a Petri net. The cardinality of the set of places is denoted as and that of the set of transitions is .
The input and output sets of a node are defined by • and , respectively, with is the set of all directed arcs from transitions to places or from places to transitions, specified by the pre- and post incidence functions. This notation can be extended to a set of nodes as follows: given , one has • and . A marking of a net is a mapping that assigns to each place a non-negative integer number of tokens. We denote by the marking of a place p at the marking M. For computational convenience, a marking can be represented by a vector of size m. A Petri net system is a net N with initial marking . Graphically, places are represented by circles and transitions by bars while black dots are used to represent tokens that flow among the places via transition firing. As to be seen, using the enabling and firing rules, the dynamics of a Petri net is defined. In fact, their role is to determine the flow of tokens between places, thus specifying how the initial marking can evolve.
Definition 2.
(Firing Rule). Given a Petri net system , a transition is enabled at a marking M if . An enabled transition can fire, yielding a new marking such that . We write to denote that the sequence of transitions is enabled at and to denote that the firing of σ yields . Given a sequence , the function associates with a transition sequence σ in the Parikh vector , i.e., if transition t appears k times in σ.
Definition 3.
(Reachable Marking). A marking M is reachable in if there exists a sequence σ such that . The set of all markings reachable from defines the reachability set of , denoted by , i.e., .
A Petri net system is bounded if there exists a non-negative integer such that for any place and for any reachable marking , holds. A marking M is said to be a deadlock or dead marking if no transition is enabled at M. A Petri net is said to be deadlock-free if at least one transition is enabled at every reachable marking. A transition t is said to be live at if for any , there exists a feasible sequence of transitions at M such that and t is enabled at . A Petri net is said to be live at a marking if all transitions are live at the marking.
Definition 4.
(Induced Subnet). Given a net and a subset of its transitions, the –induced subnet of N is a net , where (resp., ) is the restriction of (resp., ) to .
The net can be thought of as a net obtained from N by removing all transitions in , which is also written as . An essential notion in Petri net structural analysis is siphon [18]. A nonempty set is a siphon if •. A siphon is said to be minimal if there is no siphon contained in it as a proper subset. Siphons are a major structural technique for deadlock control in a Petri net system.
3. Labeled Petri Nets
For more details about labeled Petri nets, we refer the readers to [16]. A labeled Petri net (LPN) is a quadruple , where
- -
- E is the alphabet, i.e., the set of labels;
- -
- is a Petri net system;
- -
- is the labeling function that assigns to a transition either a symbol from E or the empty string .
As usual, is used to denote the set of silent (unobservable) transitions, i.e., the set of transitions labeled with the empty string . Hence, founded on this type of events, the set of transitions can be partitioned into two disjoint sets , where is the set of observable transitions and is called the set of unobservable transitions. By extending the labeling function to firing sequences , we define and
An example of an LPN is shown in Figure 1, where is the set of places and is the set of transitions with , , , , and . Note that we will refer to this example in Section 4.
Given an LPN and a marking , the language generated by G from M is defined as
Furthermore, given a set of markings of G, we define the language generated from the markings in Y as
A string belonging to is called an observation. Let be an observation of an LPN . We define
as the set of markings consistent with . We also define the set of markings generating as
By definition, once the word (string) is observed, the sets and are non-empty sets. Given an observation , is a prefix of , if and only if there exists a string such that . We write to denote the prefix set of with and . For a set of observations , we define the prefix-closure of L as . In plain words, consists of all the prefixes of all the strings in L. It is trivial that and for any string , if L is not empty.
4. Minimal Explanation and Basis Reachability Graph
The concept of basis reachability graph is proposed in [39,40], which serves as a compact way to represent the reachability set of an LPN to solve fault diagnosis and many other problems in the context of discrete-event systems. It has been used to address the issues related to observability, e.g., diagnosability and opacity verification and enforcement problems [39,40,41]. A generalization of the basis reachability graph is proposed by Ma and his colleagues in [38], where a more fundamental structure that only contains basis markings independently from the system’s partition is defined. In this section, we will provide some basic definitions that will be used in the following.
4.1. Minimal Explanation and Minimal E-Vector
Definition 5.
(Basis Partition [38]). Given a Petri net , a pair is called a basis partition of T if it satisfies:
In a basis partition , the sets and are called the explicit transition set and the implicit transition set, respectively. That is, a basis partition is a partition of T into and such that the –induced subnet is acyclic. We denote and .
Given a Petri net , a basis partition , a marking M, and a transition , we define the set of explanations of transition t at marking M as
In plain words, the firing of any implicit sequence leads the system to a new marking at which the explicit transition t is enabled. Moreover, the set of e-vectors (explanation vectors), which represents the set of firing vectors associated with the firing sequences in is defined as
We also define the set of minimal explanations of transition t at marking M as
The corresponding set of minimal explanation vectors is
4.2. Basis Reachability Graph
Definition 6.
(Basis Marking). Given a Petri net with an initial marking and a basis partition , its basis marking set is defined as follows:
- ;
- If , then the predicate holds:
where is the incidence matrix of N restricted to the transition set . A marking M in is called a basis marking of with respect to .
Definition 7.
(Basis Reachability Graph). Given a bounded net with an initial marking and a basis partition , its basis reachability graph (BRG) is a non-deterministic finite state automaton, represented by a quadruple such that
- the state set is the set of basis markings;
- the event set is the set of pairs ;
- the transition relation Δ is:
- the initial state is the initial marking .
Algorithm 1 iteratively computes basis markings and constructs a BRG. We use to denote the BRG of a net with basis partition . If no confusion arises, it is simply written as .

By instructions (4–13), this algorithm computes the set of all minimal explanations of each selected marking M and associates each explanation with a new marking defined by the state equation of a basis marking . Each new marking is defined as an unchecked marking and this procedure runs iteratively until there are no unchecked markings. For a bounded Petri net, based on , Algorithm 1 terminates in a finite time.
5. Deadlock Analysis
In this section, we will give a brief overview of reachability graph-based methodologies dealing with the deadlock problem in a DES modeled with Petri nets. In fact, when treating the problem, we can distinguish between structure and reachability graph analysis. In this paper, we are interested in the latter, providing effective solutions for the deadlock problem for an LPN.
5.1. Analysis of Reachability Graph
In [43], Uzam and Zhou propose to split a reachability graph of a net model into two parts: a deadlock zone (DZ) and a live zone (LZ). The former may contain deadlock states (markings), partial deadlock states, and states that inevitably lead a system to deadlocks or livelocks. A live zone constitutes the remaining good states of the reachability graph representing the optimal system behavior. We show in Figure 2 the partition of the reachability graph of some LPN. By a slight abuse of notation, we use and to denote the sets of markings in the deadlock zone and live zone, respectively.
The set of legal markings is defined as . An MTSI (marking/transition separation instance) is a pair of a marking M and a transition t, denoted as , whose set is defined as , where M is called a dangerous marking. The set of good markings is defined as , where defines the set of dangerous markings, i.e., the set of deadlock states (markings) and the states which inevitably lead to deadlocks. Hence, by removing all dangerous markings from , we obtain the set of good markings. In the following, we recall some definitions originally from [20].
The transitions in a Petri net model are classified into two parts: critical and good ones, whose sets are denoted as and , respectively, where and . From a reachability graph, we can see that the liveness can be guaranteed by implementing all MTSIs.
For a transition t, a legal marking M is called a t-good marking if t is not enabled at M, or with being a legal marking; M is called a t-dangerous marking if with is an illegal marking. The sets of t-good and t-dangerous markings are denoted as and , respectively. Let t be a transition and M a t-good marking. M is called a t-enabled good marking if ; otherwise, M is called a t-disabled good marking. The sets of t-enabled (resp., t-disabled) good markings is denoted by (resp., ). Thus, and can be defined as and . Let t be a critical transition and M a t-dangerous marking. is called a t-critical MTSI. defines the set of t-critical MTSIs [37].
5.2. Analysis of Basis Reachability Graph
Under the assumption that the -induced subnet is acyclic, the study in [39,40] proposes the original BRG to solve the fault diagnosis problem. A generalization of BRG has been introduced later in [38]. The proposed graph well preserves the information on the reachability set, as well as on the evolution behavior of the Petri net, while its structure is usually much more compact than the conventional reachability graph and the state explosion problem is to some extent mitigated. In this subsection, we focus on analyzing deadlocks based on BRGs and studying their effectiveness in characterizing deadlocks in systems modeled by LPN.
Definition 8.
[38] Given a net , a basis partition , and a basis marking , the implicit reach of , denoted by , is defined as
By definition, the implicit reach of a basis marking is the set of markings reachable from by firing only implicit transitions.
Corollary 1.
[38] Given a Petri net and its BRG , it holds
As Corollary 1 shows, we can easily observe that the union of the implicit reaches of all basis markings equals the set of reachable markings. The main contribution of a BRG is that of preventing the exhaustive exploration of all reachable states. In fact, to construct a BRG, one only needs to explore the minimal e-vectors for each basis marking and observable transition. However, this may ignore useful information about deadlock markings. Let us now introduce the following definitions that are essential and critical to formalize and develop the main results in this paper.
Definition 9.
Given a marking M and an explicit transition , the set of entire explanations at M is defined as
We also define the set of entire explanation vectors as
Similarly, we introduce the set of entire minimal explanations at M as
and its corresponding set of entire minimal e-vectors as
In other words, represents the set of all implicit sequences whose firing at the marking M enables an explicit transition , while is the set of all minimal implicit sequences feasible at , at which any explicit transition is enabled. The number of arcs in a BRG, where is the input vertices, is equal to the cardinality of .
Lemma 1.
Given an LPN , a basis partition , and an implicit transition , a basis marking is reachable from another basis marking if it satisfies
with , and .
Proof.
This result stems from the state equation of a basis marking. Since and , we have one and only one for some i. In other words, we have at least one basis marking such that
Based on the state equation of a basis marking, if , then for all and for all , we have
Thus, we conclude that is a reachable basis marking. □
As indicated by the lemma, a marking M is a reachable basis marking if there exists, at least, another reachable basis marking from which M can be reachable by firing a minimal explanation followed by its corresponding explicit transition .
Definition 10.
Given an LPN , a basis partition , and an implicit transition , a marking M is a dead basis marking (DBM) if it satisfies the following linear system:
In words, a marking M is said to be a DBM if there exists a basis marking , from which it is reachable, by firing with a minimal explanation of , and there does not exist any implicit sequence feasible at that can enable an explicit transition. Note that, despite the set of entire explanations at is empty, the set of implicit reaches could not be. From Definition 10, we derive the following sufficient condition for deadlock existence in an LPN.
Theorem 1.
(Sufficient Condition) Given an LPN , a basis partition , a DBM , and a marking , the following predicate holds:
Proof.
The fact that is a DBM implies . We have and for all such that , it holds , leading to the truth of . □
Proposition 1.
Given an LPN , a basis partition , and a marking M. If M is a BDM, then holds.
Proof.
The proof of Proposition 1 derives from Theorem 1. Suppose that M is a dead basis marking. Theorem 1 has shown . We conclude that from M only the markings in are reachable. Hence, holds. □
Theorem 1 gives a sufficient condition to make decision about the safeness of a basis marking’s reaches. In fact, once the set of entire explanations feasible at is empty, we can easily conclude that only implicit transitions can be feasible at . This means that the reachability set of the basis marking is equal to its implicit reach. Note that a BRG is founded under the assumption of acyclicity of the -induced subnet. Therefore, there does not exist any implicit sequence feasible at that can return the system to its optimal behavior. In this case, any marking reachable from ( with ) should be necessarily a dead state, a partial deadlock state, or an inevitable state that leads to deadlocks.
Example 1.
Let us consider the LPN in Figure 3, whose transition partition is with and . The initial marking is . As shown in Figure 4, the reachability graph contains seven markings, from which we can easily extract the deadlock zone . The BRG of this example is visualized in Figure 5. The basis marking is a DBM since it is reachable from by firing , where and . Consider the implicit reach of , holds. By Proposition 1, we have .
Although DMBs are covered by a BRG, it is not able to fully characterize the deadlock problem in an LPN. In fact, the basis reachability graph covers only deadlock states reachable by firing minimal explanations, neglecting thus other feasible implicit events that may threaten the system and lead to deadlocks. To clearly explain this point, let us introduce Example 2 which illustrates the weakness of a BRG in deadlock recognization.
Example 2.
Consider the Petri net in Figure 1 with an initial marking , where , , and for other places. The set of transitions T is divided into and .
The reachability graph of the net model, shown in Figure 6, has five reachable markings. The firing of from the marking leads the system to a dead marking . While considering a basis partition with and , Figure 7 defines its BRG. As shown in the figure, this graph is composed of three basis markings. Regarding deadlocks, it gives . However, since this dead state is not reachable by firing a minimal explanation, the BRG of this example does not contain any DBM and the sequence of transitions leading the system to the deadlock zone is not taken into account by the BRG. Thus, the weakness of a BRG facing this type of deadlock clearly appears.
In this section, we have shown that using the original BRG we cannot fully address the deadlock problem. Thus, in the next section, we will introduce new concepts that are able to deal with deadlock characterization and analysis in an LPN.
6. Dangerous Implicit Reaches
In this section, we propose new concepts that enable us to identify the existence of deadlocks in systems modeled by an LPN. A system under consideration in this research is supposed to be arbitrarily labeled, i.e., no condition or restriction is imposed on the labeling function . Hence, the system may contain undistinguishable transitions, i.e., at a marking M, two (or more) enabled transitions may share the same label (e.g., a). We denote the set of undistinguishable transitions with respect to a label as . Moreover, the set of distinguishable transitions in an LPN is denoted by . By definition, holds, where is the set of undistinguishable transitions. Hence, the set of transitions can be partitioned as follows , where is the set of undistinguishable transitions but observable, i.e., , where .
Consider a system modeled with an LPN and consistent with the aforementioned description. With respect to the concept of basis reachability graph, we can classify the set of implicit reachable states from each basis marking to three main subsets: minimal explanations, non minimal explanations, and non explanation sequences. As we have proven in the previous section, if a deadlock state is reachable by firing an explicit transition preceded by one of its minimal explanations, the BRG can identify such a deadlock state. However, the BRG is still unable to identify deadlocks reachable by firing non minimal explanations or implicit sequences that can never belong to the set of entire explanations.
6.1. Dangerous Implicit Markings (DIMs) and Dangerous Implicit Vectors (DIVs)
At the beginning of this subsection, let us introduce some results that will be used in the following to minimize the related computations.
Theorem 2.
Suppose that is firable starting from a marking with in an PLN. It holds:
Proof.
Let and . This implies that . Suppose that is firable from with . Then, we have . Hence we get the following system
which indicates . Accordingly, we conclude that from we necessarily have and the reachable marking is . □
Corollary 2.
Given two sequences , where , , and , suppose that there is a marking from which are firable sequentially with . If is firable from with , then holds.
Proof.
The proof of this corollary derives from Theorem 2. In fact, suppose that from a marking we have . This implies that (1) with and . If , then (2) and . By (1) and (2) we conclude and . □
As a matter of fact, Corollary 2 is a generalization of Theorem 2. In what follows, we touch upon a primary notion called dangerous implicit marking which is pivotal to the development of this research.
Definition 11.
Given an LPN , a basis marking , and a vector , let with and such that . Then is said to be a dangerous implicit vector (DIV) while is called a dangerous implicit marking (DIM).
Thus, we define the set of Dangerous Implicit Vectors (DIVs) at by
Moreover, we define the set of Dangerous Implicit Markings (DIMs) reachable from as
In words, consider a basis marking and a vector feasible at . The vector is dangerous because it can never be an explanation vector of any explicit transition at , i.e., for any feasible implicit sequence of transition at , where is the marking reachable by firing from , the sequence can never belong to the set of entire explanations at . In this case, the marking reachable by firing an implicit sequence from , with , is called a dangerous implicit marking.
Theorem 3.
Given an LPN , a basis marking , and a sequence of implicit transitions satisfying:
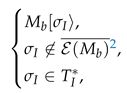 let be a set of markings, where denotes the prefix set of .3 Then, for any , .
let be a set of markings, where denotes the prefix set of .3 Then, for any , .
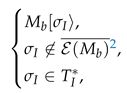
Proof.
Let be a basis marking and be two implicit sequences with . Suppose that and verify Theorem 3. Since and , we have . Let us consider now . We aim to prove that for all , .
- (a)
- By , . Moreover, there does not exist such that due to .
- (b)
- As known, the -induced subnet is acyclic, implying that the predicate holds: : . That is to say, from the marking , we cannot co-reach by firing only implicit transitions.
By (a) and (b), we conclude that for all , holds. □
In simple words, consider an LPN , an arbitrary basis partition , and a basis marking . Under the assumption that the -induced subnet is acyclic, we have proven by Theorem 3 that any marking reached by firing an implicit sequence that does not belong to , the prefix-closure of the set of entire explanations , is either a dead marking or a marking that inevitably leads the system to a blocking state. Thus, belongs necessarily to the dead Zone (DZ).
Proposition 2.
Given an LPN , a basis marking , and a dangerous implicit vector with , is a DIM and for all such that , holds.
Proof.
Given a basis marking and a sequence of implicit transitions firable from with , suppose that is a DIV, i.e., there does not exist such that . This implies that for all , there does not exist such that . We have for all such that , is true and thus by Theorem 3, holds. □
By virtue of DIV and DIM notions, Proposition 2 represents a generalization of Theorem 3. In fact, when checking the safeness of each non dead-basis marking, if an implicit vector is feasible at a basis marking () and there does not exist any explanation vector feasible at such that , we do not need to check the maximal cardinality that the implicit vector can reach, since it is certain by Proposition 2 that we will never find a vector included in the set of entire e-vectors.
In the following, Algorithm 2 is introduced to check the safeness of each non-dead basis marking. Given a basis marking and its set of entire e-vectors , the role of the proposed algorithm is to check if there exists any DIV, i.e., any implicit vector feasible at and does not belong to the set of entire explanations , that can threaten the system deadlock-freedom, thereby providing more information about deadlocks that can be reached from the basis marking .

Algorithm 2 works in a breadth-first manner. Considering the set of entire explanation vectors, this algorithm checks whether there exist any undesirable implicit vectors that can fire and lead to deadlocks. A first test is done by step 6 to verify the existence of the sufficient condition given by Theorem 3 and Proposition 2. Specifically, the matrix defines the set of entire e-vectors. If there does not exist any row in C such that , the conditions given by Theorem 3 and Proposition 2 are satisfied. Hence, the reached marking will be added to the set of dangerous implicit markings without adding it to the set . A second condition is introduced by step 9 of Algorithm 2. Indeed, this test aims to minimize the computation by checking whether the conditions in Theorem 2 and Corollary 2 are satisfied. Once becomes empty, a set of dangerous implicit vectors DIVs and its corresponding set of implicit dangerous markings DIMs are obtained by .
Proposition 3.
The complexity of Algorithm 2 is .
Proof.
In the worst case, the first step of the algorithm, i.e., the while loop, takes time of , where represents the number of implicit transitions of the studied Petri net. In the second step, browsing through the matrix takes the time of . The third step considers the checking of the existence of the new implicit vector in the two matrices B and of size and respectively, with being the cardinality of the set of entire e-vectors of . Therefore, the total cost for “the else if statement” is . Finally, the asymptotic total cost of Algorithm 2 is . □
Although, in the worst case, the number of iterations of Algorithm 2 may grow exponentially with the diameter (i.e., length of the maximal path) of the implicit subnet, in most practical cases, this number is quite reasonable, and Algorithm 2 has good performance since each iteration mainly consists of simple additions or comparisons of vectors.
Example 3.
Let us consider the Petri net system shown in Figure 8, which consists of 9 places and 8 transitions . The transition set partition is defined by with and . Consider the initial marking . The reachability graph, shown in Figure 9, contains 16 reachable markings, 12 of which are legal markings and 4 of which are deadlock markings. In Figure 10, we present its BRG composed of 6 markings.
Let us focus on the basis marking which is the marking in the reachability graph. As shown in the BRG, is not a DBM. However, from the reachability graph one observes that is a dead marking reachable implicitly from and neglected by the BRG. By applying Algorithm 2, we can easily obtain with and . In fact, the set of entire e-vectors at contains only one element which belongs to . However, the vector is feasible from . Since there does not exist any vector such that , is a dangerous implicit vector at and is its corresponding DIM. As Theorem 3 and Proposition 3 indicate, this DIM belongs to the dead zone DZ.
6.2. Non Minimal Explanations
As we have previously mentioned, the concept of dangerous implicit markings is able to deal with the deadlock states reachable by an implicit sequence that can never be an explanation of any explicit transition at a given basis marking. However, in this subsection, we touch upon the last type of dead markings reachable from a basis marking which is a non minimal explanation. In plain words, the principle of the basis reachability graph is to find the minimal implicit path to activate each explicit transition. By this principle, non minimal explanations will not be considered.
Proposition 4.
Given an LPN , a basis partition , a marking M, and a sequence such that , if , is not a dead marking.
Proof.
Let be a marking and be a sequence of implicit transitions firable from M. signifies that there exists a transition such that . We can then conclude that does not lead to a dead marking. □
By definition, an explanation is a sequence of implicit transitions feasible at a given basis marking to enable an explicit transition. Thus, we conclude that a marking reachable from a basis one by firing an explanation of any explicit transition is not a dead marking.
Theorem 4.
Given an LPN , a basis marking , an explicit transition , and that is a non minimal explanation vector of at , let be a marking reachable by firing preceded by , an explanation consistent with . If M is a dead marking, then there exists a basis marking reachable from by firing , where is a minimal explanation of at in comparison with , from which a dangerous implicit marking M is reachable, i.e., , and .
Proof.
Consider a basis marking , an implicit transition , and a non minimal explanation vector , i.e., . Suppose that is a dead marking. The fact that is a non minimal e-vector implies that there exists an e-vector verifying . That is to say that there exists a vector such that . Thus we have
We conclude that M can be reached from the basis marking by firing an implicit sequence of transitions such that . However, M is a dead marking. Hence, there does not exist any e-vector such that . Finally, we obtain . □
By Theorem 4, we have proved that if a dead state is reachable by firing a non minimal explanation, we can certainly reach it by firing only implicit transitions from a basis marking. Thus, the concept of dangerous implicit reach can cover this type of dead reachable states and identify dangerous sequences leading to such markings.
Example 4.
Consider again the LPN in Figure 8 whose unobservable subnet is acyclic. Let us focus our attention on the basis marking . The set of explanations of at is . Therefore, we have and . In the BRG, only the minimal explanation is considered. Although this minimal explanation leads the system to a legal state, we can observe that according to the reachability graph, the non minimal explanations and conduct the system inevitably to the dead state . Since with is the minimal explanation in comparison with the aforementioned two explanations, one sees .
7. Observed Graph: A Deadlock Characterization for Labeled Petri Nets
In this section, we propose a new graph that is able to fully characterize deadlocks in systems modeled by labeled Petri nets.
Definition 12.
(Observed Graph) Given a bounded Petri net with an initial marking and a basis partition , the observed graph of the Petri net is a non-deterministic finite state automaton that is a quadruple , where
-
the state set is the set of observed markings with:
- -
- the state set being the set of observed basis markings;
- -
- the state set being the set of observed dead markings;
- the event set is the set of pairs ;
-
the transition relation is with:
- -
- -
- the initial state is the initial marking .
Algorithm 3 presents a method to calculate the observed graph . By steps (3–16), we first compute the original BRG. By step 7, the set of entire explanation is computed. Steps (17–21) check the existence of the sufficient condition given by Theorem 1. If the tested marking M is a DBM, then we add it to the set of dead markings , assign a tag to M, and return to step 2 to check another marking without tag from if there exists. If the first sufficient condition of Theorem 1 is not satisfied, by steps (18–21) we check the safeness of the implicit reaches of the marking M. If (the set of dangerous implicit vectors and its corresponding markings computed by Algorithm 2) is not empty, for all we add the reachable implicit marking to and to . This procedure runs iteratively until there is no unchecked marking in . For a bounded Petri net, based on , Algorithm 3 terminates in a finite time.

We first consider the complexity of the observed graph , i.e., the number of observed markings in it. In the worst case, when each transition in the net system has a self-loop, the partition is and , the observed graph has the same complexity as the basis reachability graph and the reachability graph, i.e., . Despite in the aforementioned case has the same complexity as a reachability graph and BRG, we note that in practice we can usually find a basis partition in which , under which is much more compact than the reachability graph, i.e., and more precisely , where represents the number of dead markings.
Theorem 5.
Given an LPN and its observed graph , if there is no dead marking in , G is a deadlock-free net.
Proof.
This is trivial. Suppose that the observed graph of G does not contain any dead observed markings. There is no marking in G that can be a deadlock state at which no transition is enabled, which completes the proof. □
Example 5.
Consider again the Petri net system given by Figure 8 . The set of deadlock markings is . In Figure 10, we present the BRG composed of 6 markings. However, only one dead marking exists in the BRG.
Using Algorithm 3, we construct the observed graph of the Petri net system. The resulting graph is shown in Figure 11, which contains 8 markings. From , the set of DIVS and DIMs are . By steps (20–21), we add to and to . However, is defined as a dead basis marking (DBM). Since , we tag as an old node and execute step 2 to check the existence of marking without a tag in . Considering Theorem 1, there is no need to check the safeness of the implicit reaches of . Similarly to , at we have and its value is . Thus a new node and a new relation will be added to and , respectively.
8. Experimental Results
In this section, we will introduce the experimental results of this work. A flexible manufacturing system is used to illustrate the proposed deadlock characterization policy for labeled Petri nets. The Petri net model of the system shown in Figure 12 is a pure and bounded Petri net taken from [44]. In the net, there are 13 places and 10 transitions . Given the system partition with and and the initial marking , Figure 13 shows that the net has 32 reachable markings, 28 of which are legal markings depicted in solid lines and 4 of which are deadlock ones depicted in dashed lines. The set of deadlock markings is .
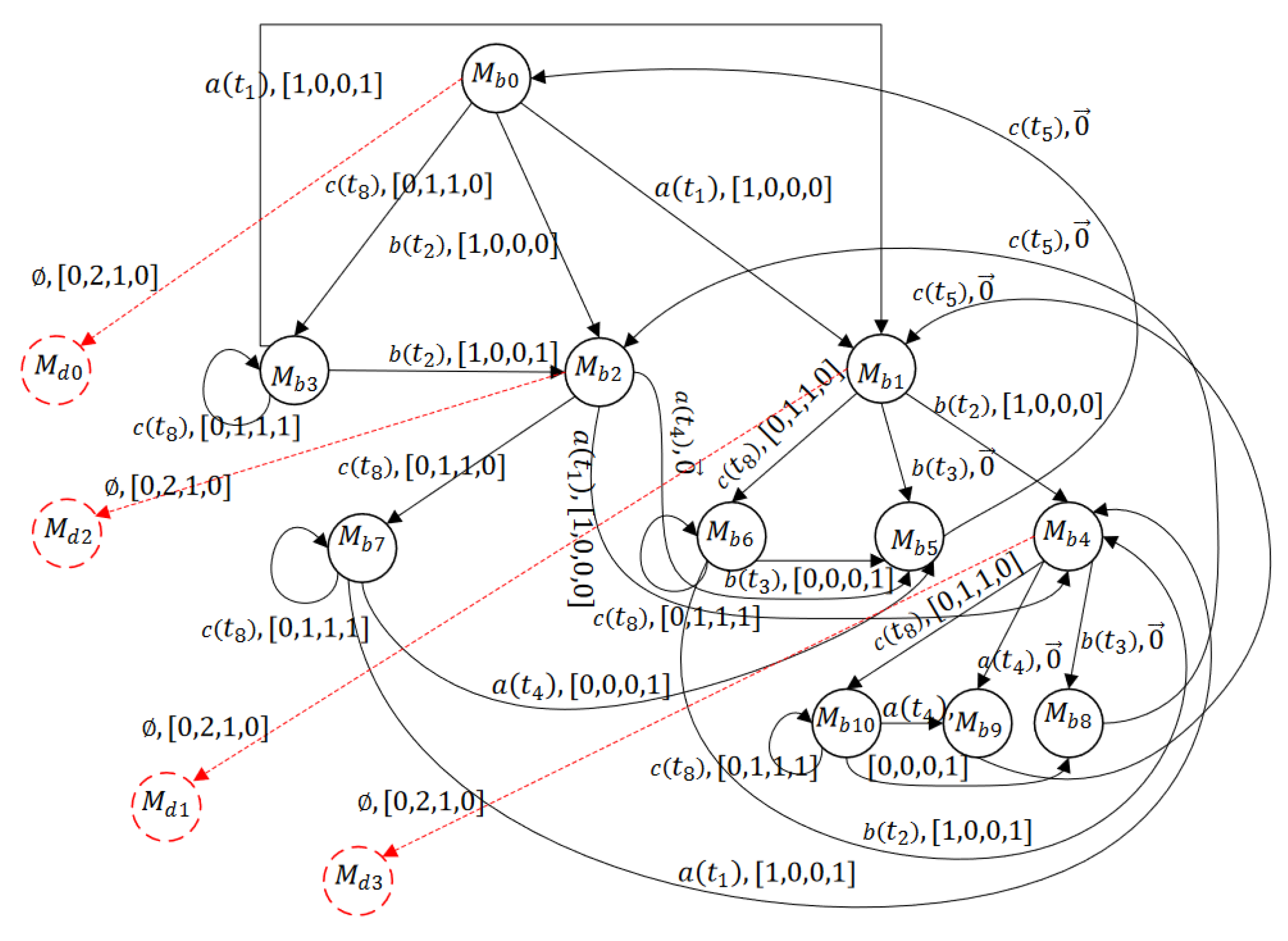
In Figure 14, we present the basis reachability graph of the net system. As the BRG shows, the number of basis markings is . However, none of the dead markings appears in the BRG, i.e., for all , . We construct the observed graph with Algorithm 3. The number of markings is . We observe that and . From the marking we have Thus the dead markings is added to the observed graph since it represents a dangerous implicit reachable marking. As the same as , the computation of the set of DIVs and DIMs results in and a new dead node is added. From the marking we also have a dangerous implicit reach given by since Finally, from the marking we have and a dead observed marking is added to the observed graph.
9. Conclusion and Future Work
This paper addresses the deadlock characterization and analysis in labeled Petri nets whose transitions can be unobservable and undistinguishable. In the first part of the paper, we show that the notion of BRG cannot define and characterize correctly and accurately the deadlock problem in an LPN. We propose a first algorithm to compute the max-cardinality of the implicit vector that can fire from a given state of the system. After that, we introduce two sufficient conditions described by linear algebraic equations that will be useful to construct the observed graph. Then, we provide an algorithm to computing the observed graph. Finally, experimental results implemented using the C # tool expose the correctness and effectiveness of the proposed solution. To move forward, future research in this framework will focus on using observed graphs to ensure the deadlock-freeness and to study the liveness enforcement of systems modeled by labeled Petri nets.
Author Contributions
Conceptualization, L.Z. and Z.A.; methodology, Z.A.; software, Z.A.; formal analysis, L.Z.; writing—original draft preparation, Z.A.; writing—review and editing, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DES | Discrete-event system |
| LPN | Labeled Petri net |
| BRG | Basis reachability graph |
| DIM | Dangerous implicit marking |
| DIV | Dangerous implicit vector |
References
- Liang, Y.; Liu, G.Y.; El-Sherbeeny, A. M. Polynomial-time verification of decentralized fault pattern diagnosability for discrete-event systems. Mathematics 2023, 11, 3398. [Google Scholar] [CrossRef]
- Li, Y.Y.; Chen, Y.F.; Zhou, R. A set covering approach to design maximally permissive supervisors for flexible manufacturing systems. Mathematics 2024, 12, 1687. [Google Scholar] [CrossRef]
- Dou, H.; You, D.; Wang, S. G.; Zhou, M.C. Designing liveness-enforcing supervisors for manufacturing systems by using maximally good step graphs of Petri nets. IEEE Transactions on Automation Science and Engineering 2024. [Google Scholar] [CrossRef]
- Zhang, R.P.; Feng, Y.X.; Yang, Y.K.; Li, X.L.; Li, H.N. Polynomial-complexity deadlock avoidance policy for tasks offloading in satellite edge computing with data-dependent constraints and limited buffers. IEEE Transactions on Aerospace and Electronic Systems 2024. [Google Scholar] [CrossRef]
- Qi, H.D.; Wang, J.L.; Yan, C.G.; Jiang, C.J. The probabilistic liveness decision method of unbounded Petri nets based on machine learning. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2024, 54, 1070–1081. [Google Scholar] [CrossRef]
- Zhang, L.; Holloway, L.E. Forbidden state avoidance in controlled Petri nets under partial observation. In Proceedings of the 33rd Allerton Conference on Communication, Control, and Computing, Monticello, Illinois, USA, 27-29 September 1995; pp. 146–155. [Google Scholar]
- Li, Y.; Wonham, W.M. Controllability and observability in the state-feedback control of discrete-event systems. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, Texas, USA, December 1989; pp. 203–208. [Google Scholar]
- Zhou, Y.; Hu, H. S.; Deng, G. L.; Cheng, K.; Lin, S. W.; Liu, Y.; Ding, Z. H. Distributed motion control for multiple mobile robots using discrete-event systems and model predictive control. IEEE Trans. Syst., Man, Cybern.: Syst. 2024, 54, 997–1010. [Google Scholar] [CrossRef]
- Giua, A.; Seatzu, C.; Basile, F. Observer-based state-feedback control of timed Petri nets with deadlock recovery. IEEE Trans. Autom. Control 2004, 49, 17–29. [Google Scholar] [CrossRef]
- Giua, A.; Seatzu, C. Deadlock characterization for Petri nets controlled using GMECs and observers. In Proceedings of the 2003 American Control Conference, Denver, Colorado, USA; 2003; pp. 320–325. [Google Scholar]
- Chen, F.; Barkaoui, K. Maximally permissive Petri net supervisors for flexible manufacturing systems with uncontrollable and unobservable transitions. Asian J. Control 2014, 16, 1646–1658. [Google Scholar] [CrossRef]
- Corona, D.; Giua, A.; Seatzu, C. Marking estimation of Petri nets with silent transitions. In Proceedings of the 43rd IEEE Conference on Decision and Control, Paradise Island, Bahamas; 2004; pp. 966–971. [Google Scholar]
- Basile, F.; Chiacchio, P.; Giua, A.; Seatzu, C. Deadlock recovery of Petri net models controlled using observers. In Proceedings of the 8th IEEE Conference on Emerging Technologies and Factory Automation, Antibes, France; 2001; pp. 441–449. [Google Scholar]
- Ren, K.X.; Zhang, Z.P.; Xia, C.Y. Event-based fault diagnosis of networked discrete event systems. IEEE Transactions on Circuits and Systems II: Express Briefs 2022, 69, 1787–1791. [Google Scholar] [CrossRef]
- Murata, T. Petri nets: Properties, analysis, and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Peterson, J.L. Petri Net Theory and the Modelling of Systems; Prentice-Hall: New Jersey, USA, 1981. [Google Scholar]
- Cassandras, C.G.; Lafortune, S. Introduction to Discrete Event Systems, 2nd ed.; Springer: New York, USA, 2008. [Google Scholar]
- Li, Z.; Zhao, M. On controllability of dependent siphons for deadlock prevention in generalized Petri nets. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2008, 38, 369–384. [Google Scholar]
- Chen, Y.F.; Li, Z.W. On structural minimality of optimal supervisors for flexible manufacturing systems. Automatica 2012, 48, 2647–2656. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, Z.W.; Al-Ahmari, A. Nonpure Petri net supervisors for optimal deadlock control of flexible manufacturing systems. IEEE Trans. Syst., Man, Cybern., Syst. 2013, 43, 252–265. [Google Scholar] [CrossRef]
- Ezpeleta, J.; Colom, J.M.; Martinez, J.A. A Petri net based deadlock prevention policy for flexible manufacturing systems. IEEE Trans. Robot. Autom. 1995, 11, 173–142. [Google Scholar] [CrossRef]
- Fanti, M.P.; Zhou, M.C. Deadlock control methods in automated manufacturing systems. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2004, 34, 5–22. [Google Scholar] [CrossRef]
- Lautenbach, K.; Ridder, H. The linear algebra of deadlock avoidance–A Petri net approach. Institute of Software Technology, University of Koblenz-Landau, Koblenz, Germany, Tech. Rep. No. 25–96, 1996.
- Wang, S.G.; You, D.; Wang, C.Y. Optimal supervisor synthesis for Petri nets with uncontrollable transitions: A bottom-Up algorithm. J. Inf. Sci. 2016, 363, 261–273. [Google Scholar] [CrossRef]
- Xing, K.Y.; Zhou, M.C.; Wang, F.; Liu, H.X.; Tian, F. Resource-transition circuits and siphons for deadlock control of automated manufacturing systems. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2011, 41, 74–84. [Google Scholar] [CrossRef]
- Ezpeleta, J.; Rcalde, L. A deadlock avoidance approach for non-sequential resource allocation systems. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2004, 34, 93–101. [Google Scholar] [CrossRef]
- Hsieh, F.S. Fault-tolerant deadlock avoidance algorithm for assembly processes. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2004, 34, 65–79. [Google Scholar] [CrossRef]
- Wu, N.Q.; Zhou, M.; Li, Z.W. Resource oriented Petri net for deadlock avoidance in flexible assembly systems. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2008, 38, 56–69. [Google Scholar]
- Wu, N.Q.; Zhou, M.C. Modeling, analysis and control of dual-arm cluster tools with residency rime constraint and activity time variation based on Petri nets. IEEE Trans. Autom. Sci. Eng. 2012, 9, 446–454. [Google Scholar]
- Wu, N.Q.; Zhou, M.C. Schedulability analysis and optimal scheduling of dual-arm cluster tools with residency time constraint and activity time Variation. IEEE Trans. Autom. Sci. Eng. 2012, 9, 203–209. [Google Scholar]
- Xing, K.Y.; Zhou, M.C.; Liu, H.X.; Tian, F. Optimal Petri-net-based polynomial-complexity deadlock-avoidance policies for automated manufacturing systems. IEEE Trans. Syst., Man, Cybern. A, Syst., Humans 2009, 39, 188–199. [Google Scholar] [CrossRef]
- Dotoli, M.; Fanti, M.P. Deadlock detection and avoidance strategies for automated storage and retrieval systems. IEEE Trans. Syst., Man, Cybern. C, Appl., Rev. 2007, 37, 541–552. [Google Scholar] [CrossRef]
- Huang, Y.S.; Pan, Y.L.; Su, P.J. Transition-based deadlock detection and recovery policy for FMSs using graph technique. ACM Trans. Embed. Comput. Syst. 2013, 12, 11:1–11:13. [Google Scholar] [CrossRef]
- Kumaran, T.K.; Chang, W.; Cho, H.; Wysk, R.A. A structured approach to deadlock detection, avoidance and resolution in flexible manufacturing systems. Int. J. Prod. Res. 1994, 32, 2361–2379. [Google Scholar] [CrossRef]
- Wysk, R.A.; Yang, N.S.; Joshi, S. Resolution of deadlocks in flexible manufacturing systems: Avoidance and recovery approaches. J. Manuf. Syst. 1994, 13, 128–138. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.W.; Al-Ahmari, A.; Wu, N.Q.; Qu, T. Deadlock recovery for flexible manufacturing systems modeled with Petri nets. J. Inf. Sci. 2017, 381, 290–303. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.W.; Barkaoui, K. Maximally permissive Petri net supervisors with a novel structure. In Proceedings of the 12th IFAC/IEEE International Workshop on Discrete Event Systems, Cachan, France; 2014; pp. 80–85. [Google Scholar]
- Ma, Z.Y.; Tong, Y.; Li, Z.W.; Giua, A. Basis marking representation of Petri net reachability spaces and its application to the reachability problem. IEEE Trans. Autom. Control 2017, 62, 1078–1093. [Google Scholar] [CrossRef]
- Cabasino, M.; Giua, A.; Seatzu, C. Fault detection for discrete event systems using Petri nets with unobservable transitions. Automatica 2010, 46, 1531–1539. [Google Scholar] [CrossRef]
- Cabasino, M.; Giua, A.; Pocci, M.; Seatzu, C. Discrete event diagnosis using labeled Petri nets: An application to manufacturing systems. Control Eng. Pract. 2011, 19, 989–1001. [Google Scholar] [CrossRef]
- Tong, Y.; Li, Z.W.; Seatzu, C.; Giua, A. Verification of state-Based opacity using Petri nets. IEEE Trans. Autom. Control 2017, 62, 2823–2837. [Google Scholar] [CrossRef]
- Giua, A.; Seatzu, C. Fault detection for discrete event systems using Petri nets with unobservable transitions. In Proceedings of the 44th IEEE International Conference on Decision and Control, Seville, Spain; 2005; pp. 6323–6328. [Google Scholar]
- Uzam, M.; Zhou, M.C. An improved iterative synthesis method for liveness enforcing supervisors of flexible manufacturing systems. Int. J. Prod. Res. 2006, 44, 1987–2030. [Google Scholar] [CrossRef]
- Zhang, X.; Uzam, M. Transition-based deadlock control policy using reachability graph for flexible manufacturing systems. Advances Mech. Eng. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Wonham, W.; Cai, K. Supervisory Control of Discrete-Event Systems; Springer: Cham, 2018. [Google Scholar]
| 1 | In this work, we use to denote the set of non-negative integers. |
| 2 |
denotes the prefix-closure of . |
| 3 |
denotes the prefix set of . |
Figure 1.
A labeled Petri net.
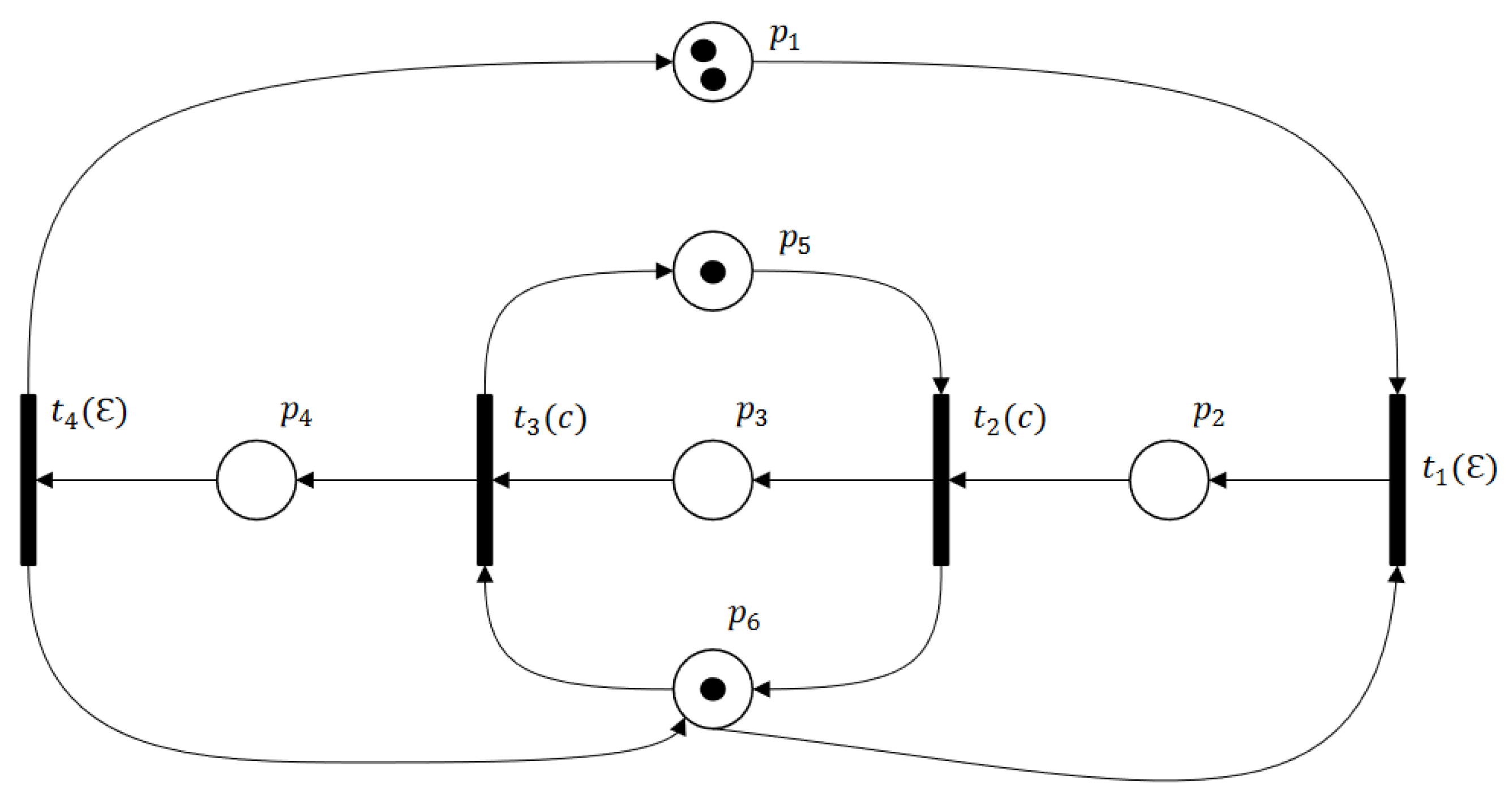
Figure 2.
Partitioned reachability graph of an LPN.
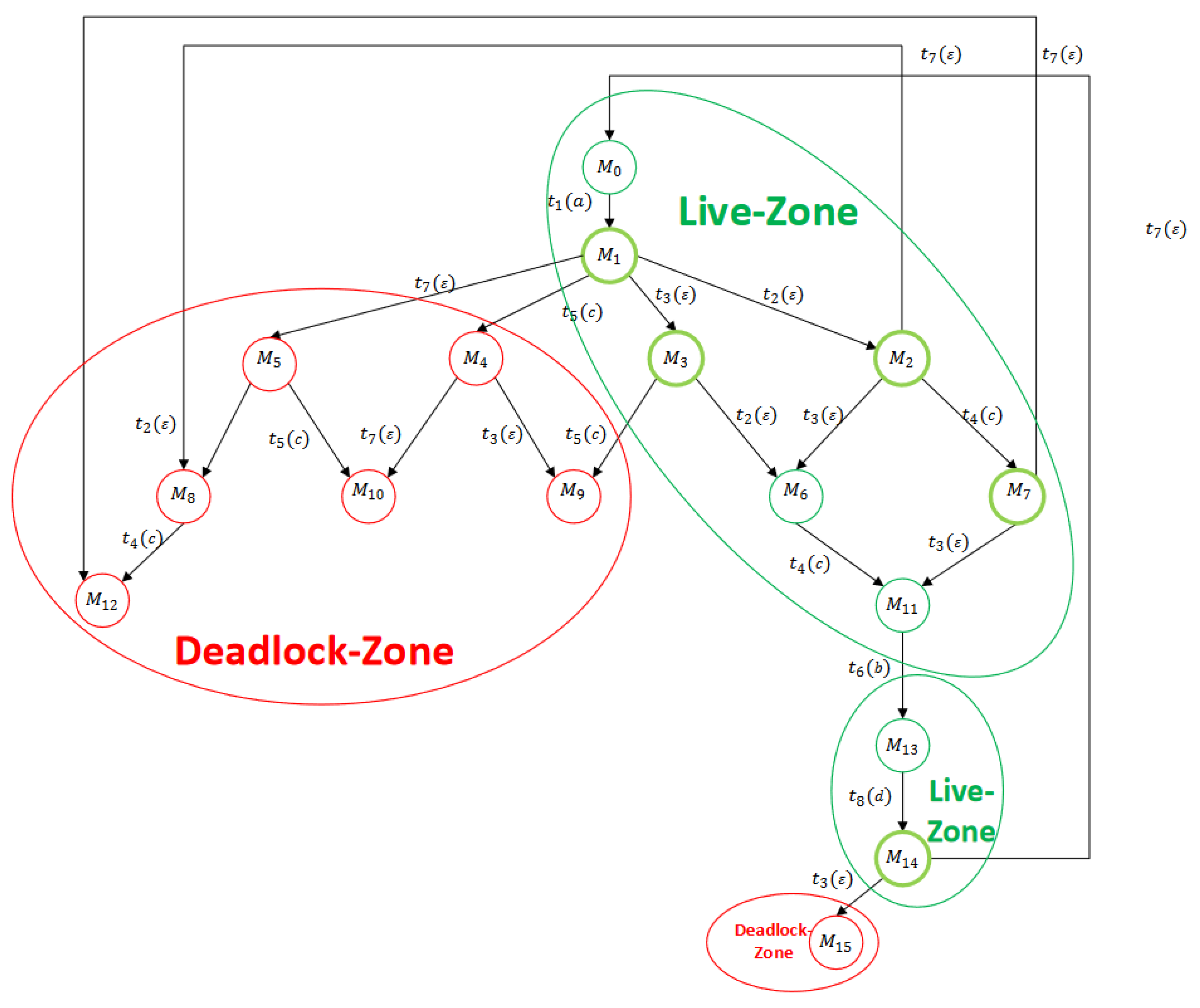
Figure 3.
A labeled Petri net.
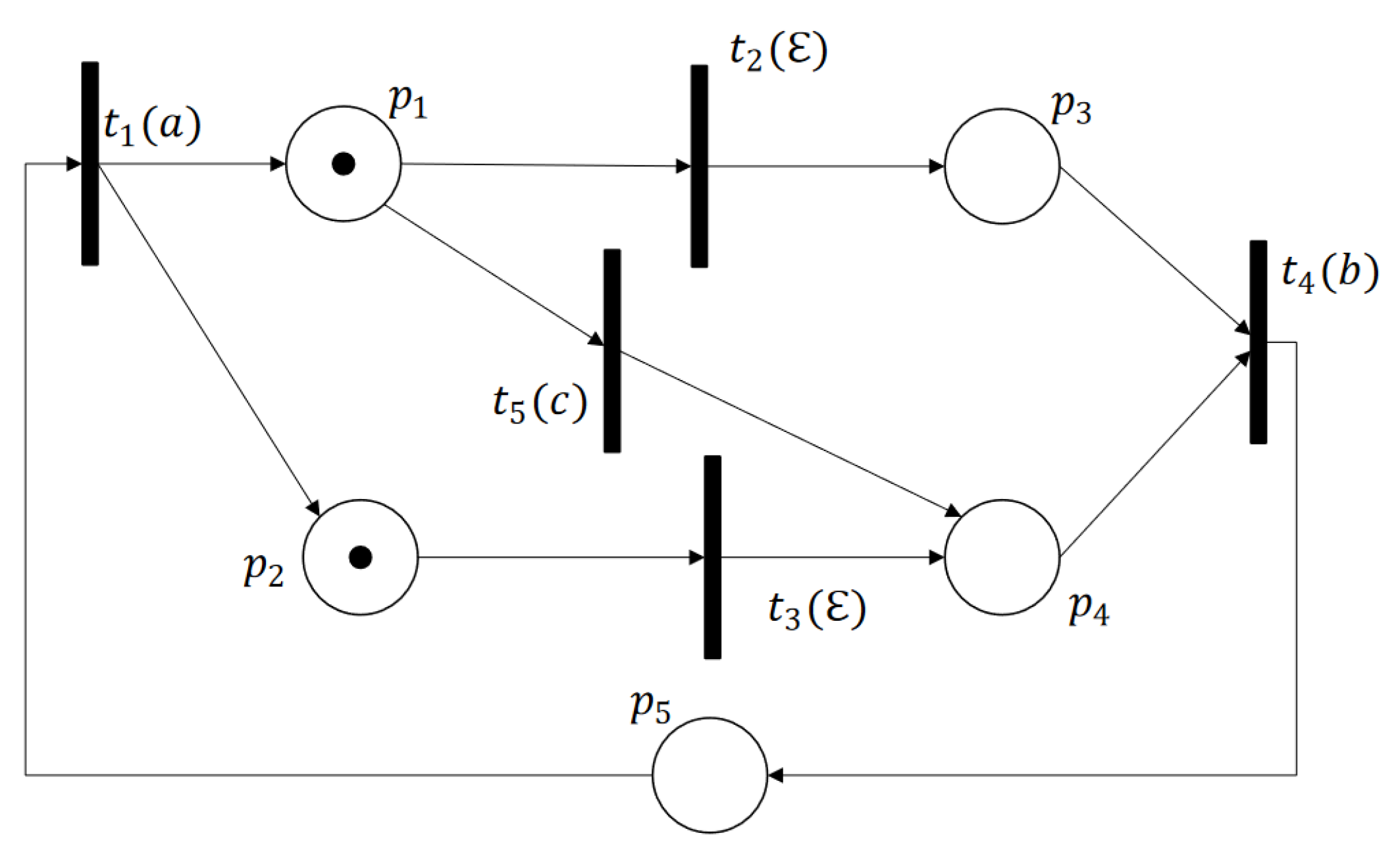
Figure 4.
Reachability graph of the LPN in Figure 3.
Figure 4.
Reachability graph of the LPN in Figure 3.
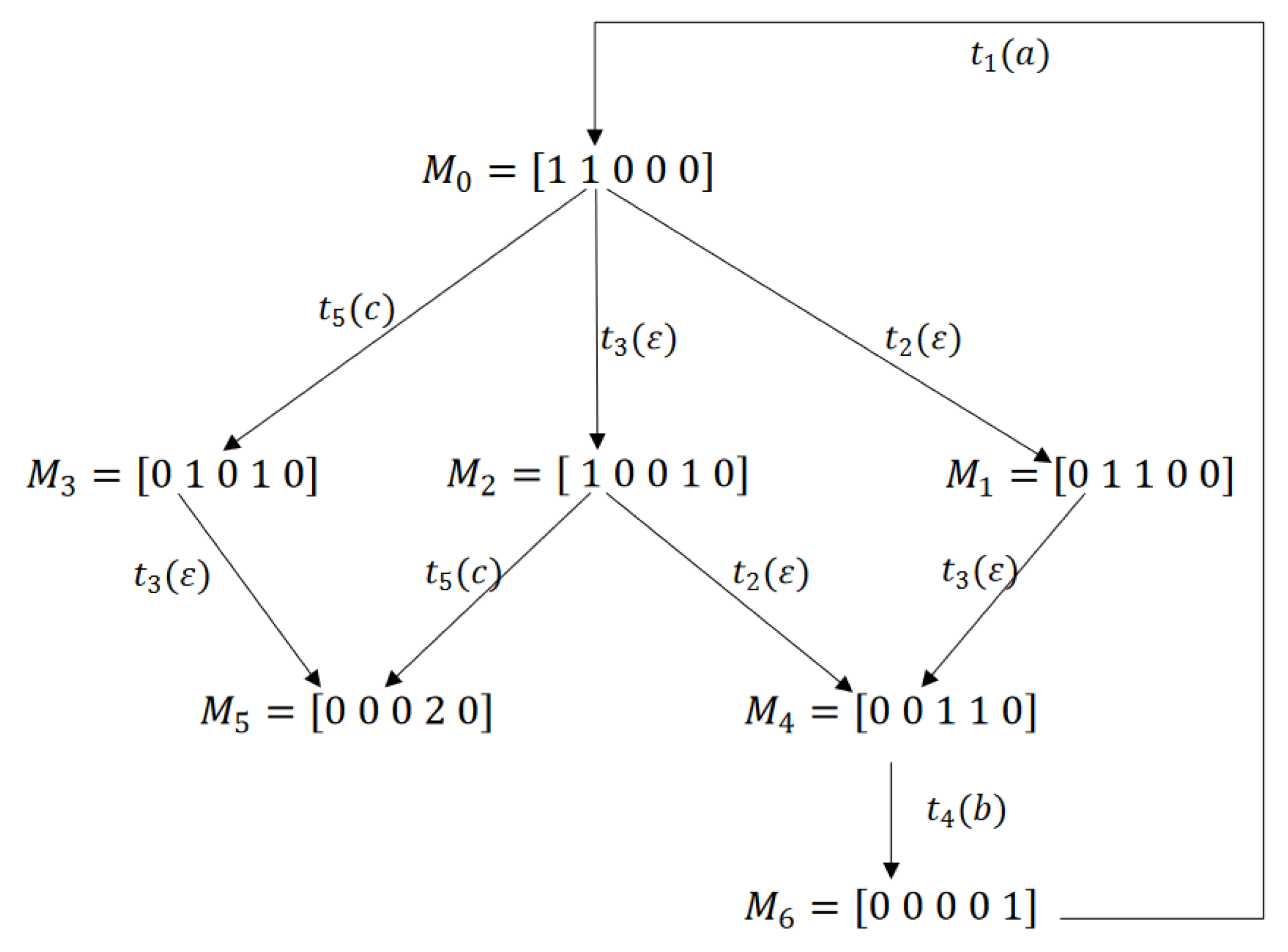
Figure 5.
The BRG of the LPN in Figure 3.
Figure 5.
The BRG of the LPN in Figure 3.
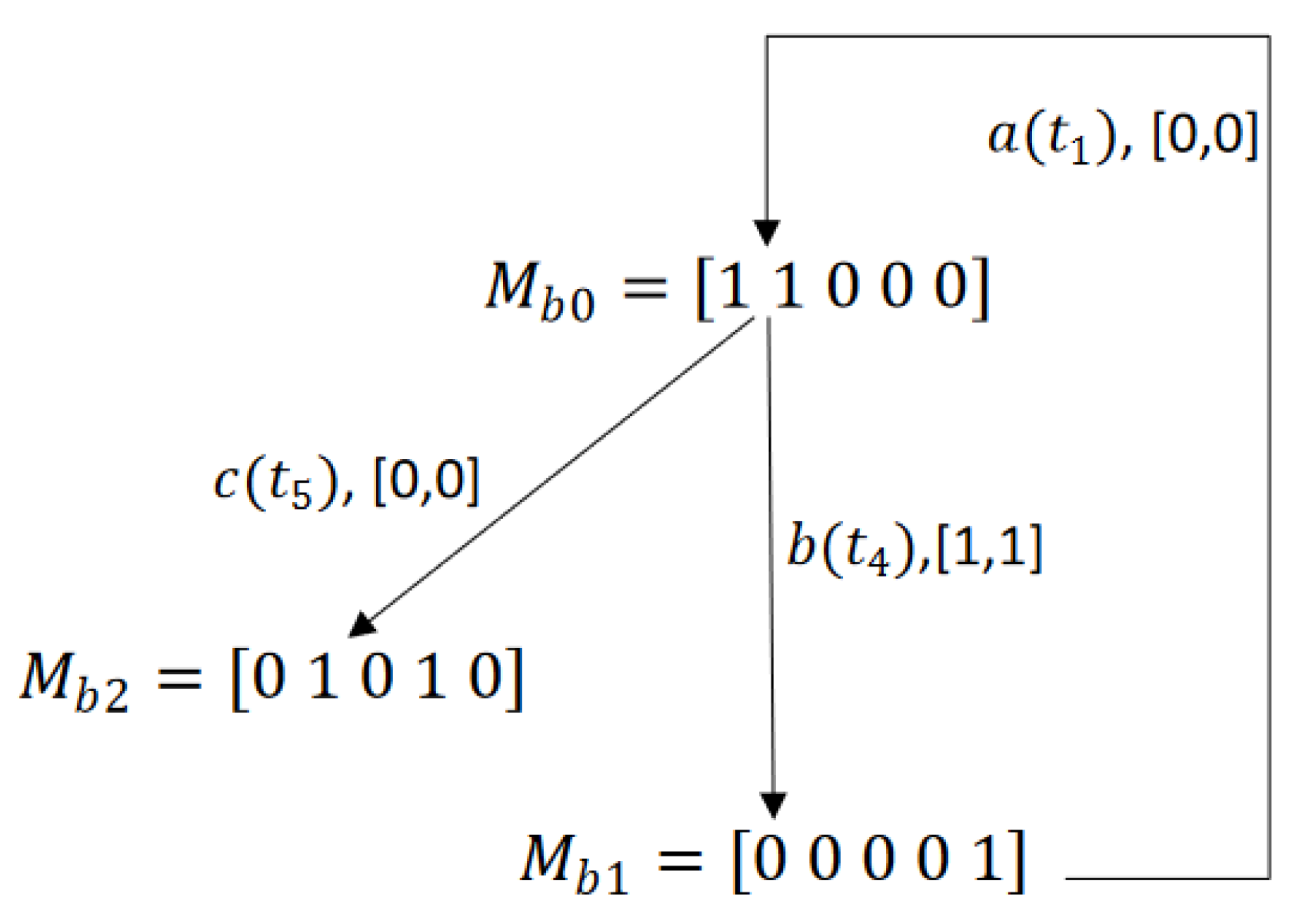
Figure 6.
RG of the LPN in Figure 1.
Figure 6.
RG of the LPN in Figure 1.
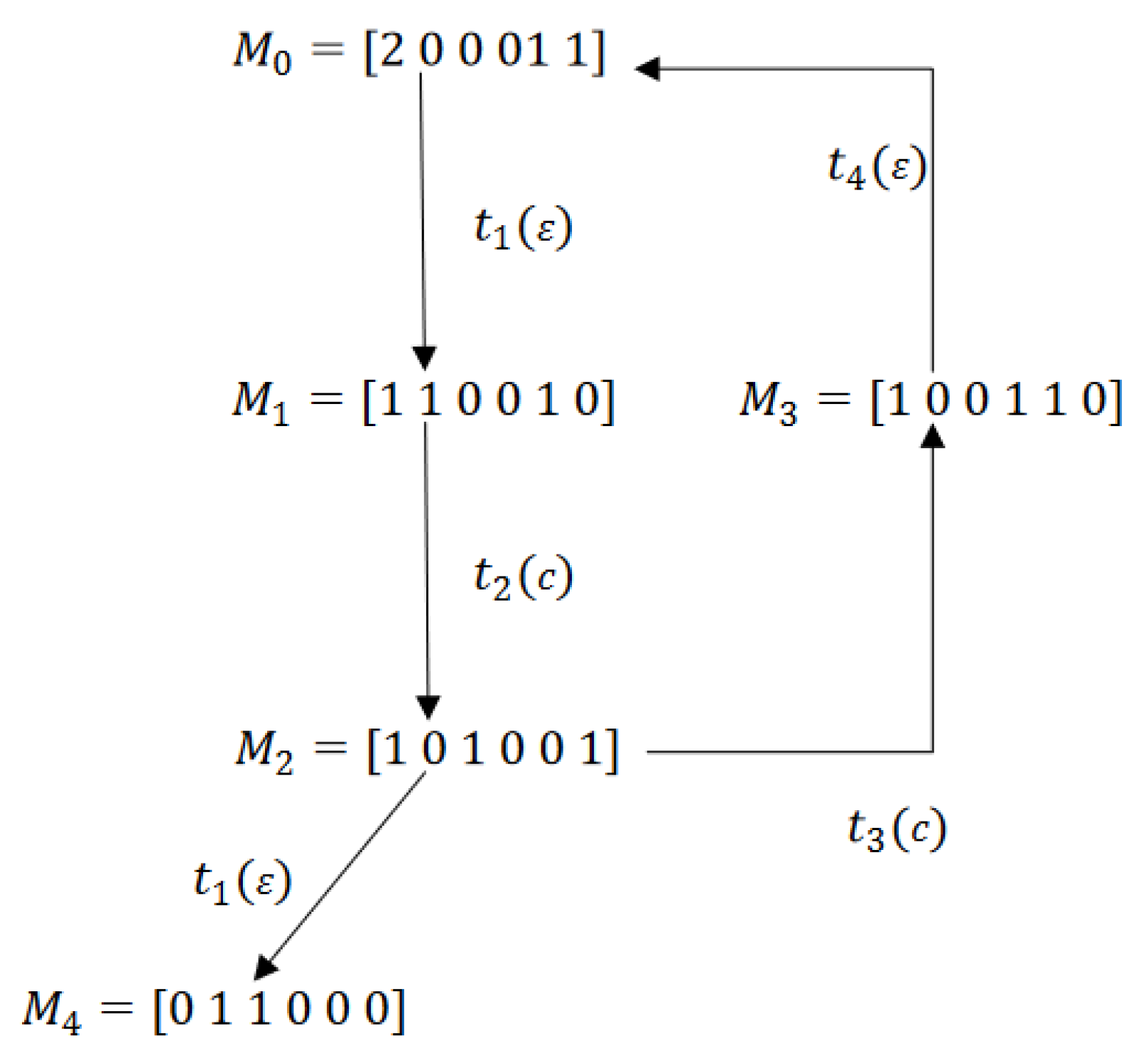
Figure 7.
BRG of the LPN in Figure 1.
Figure 7.
BRG of the LPN in Figure 1.
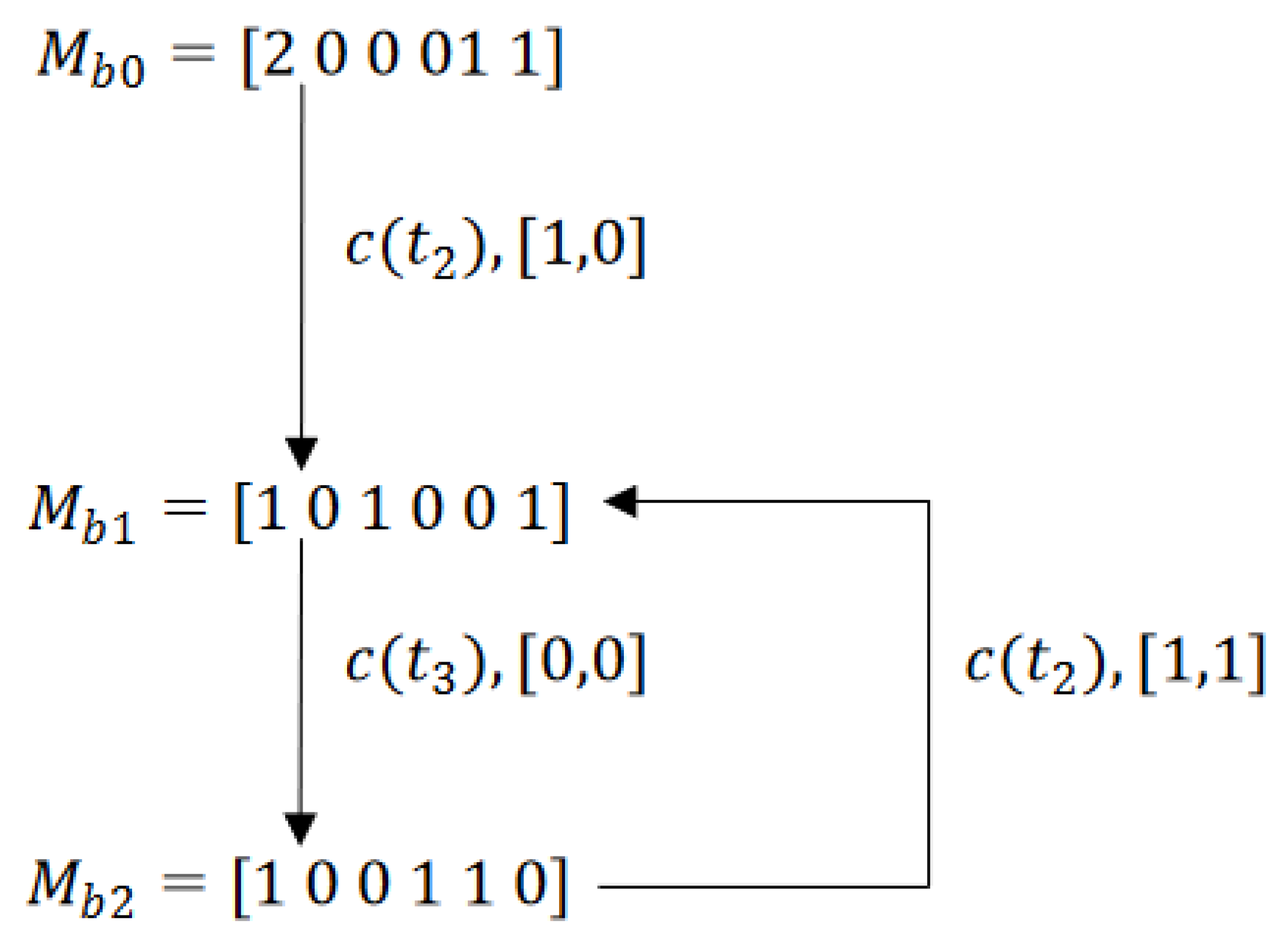
Figure 8.
A labeled Petri net.

Figure 9.
Reachability graph of an LPN.
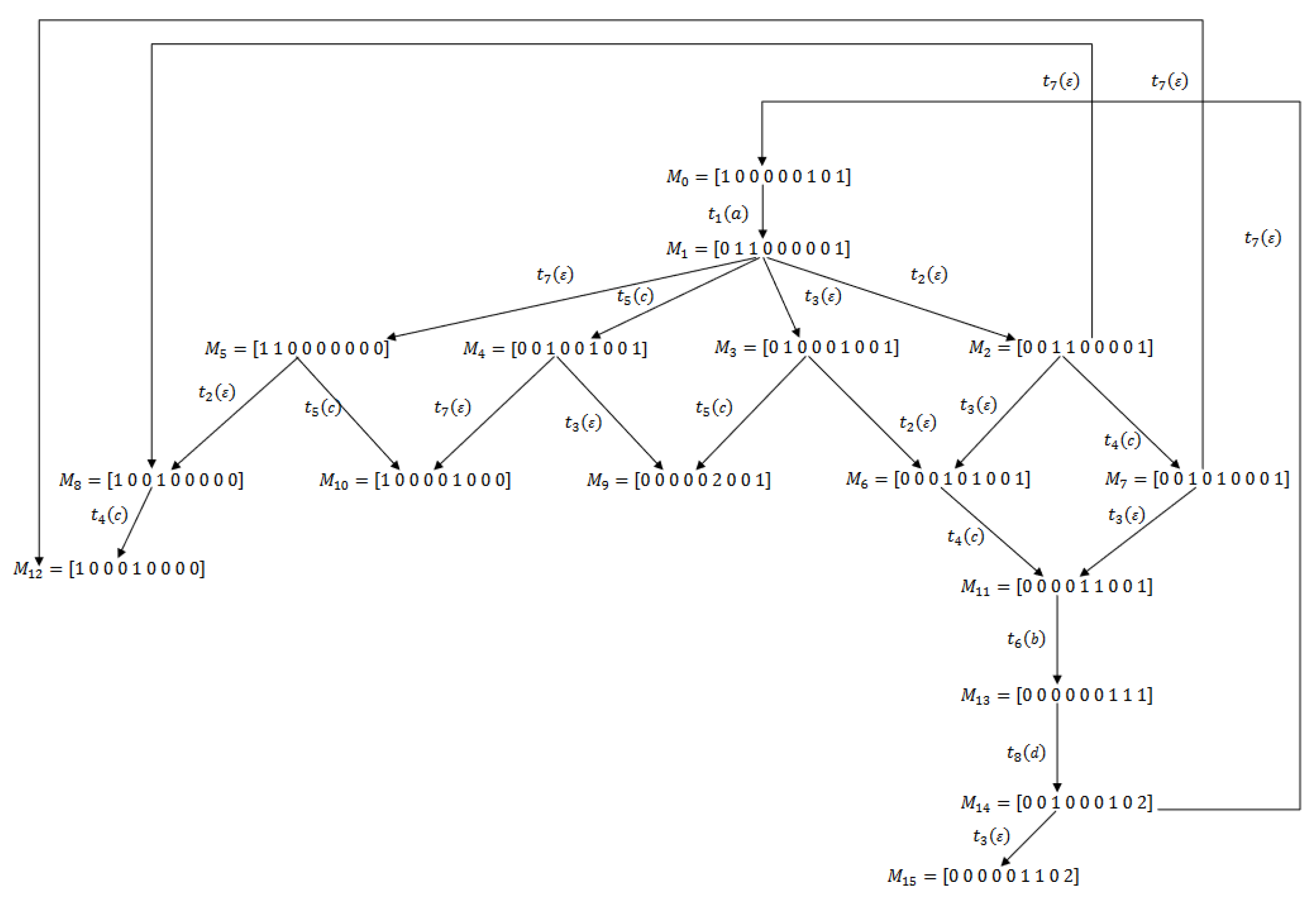
Figure 10.
BRG of the LPN in Example 2.
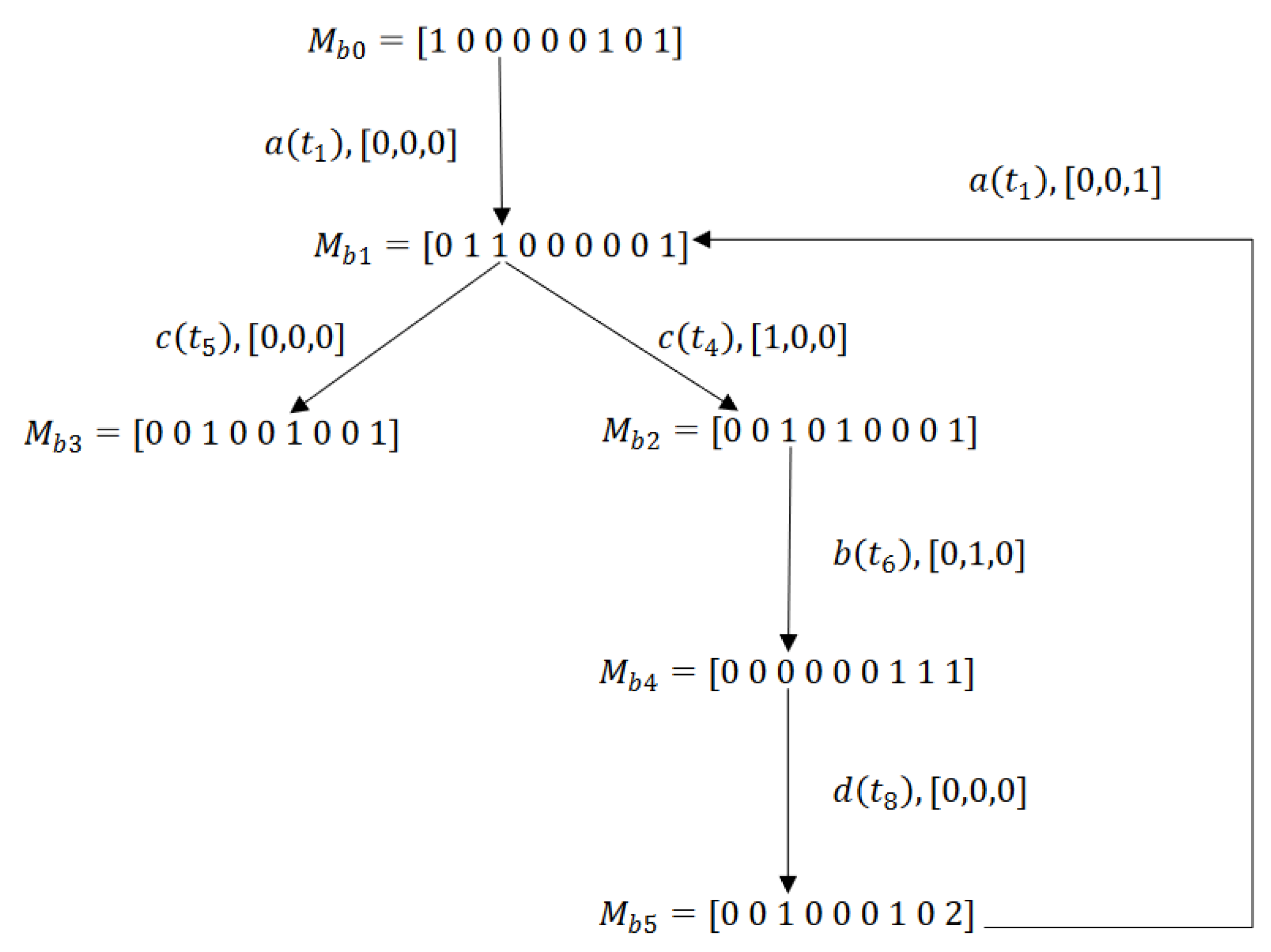
Figure 11.
Observed graph of the LPN in Example 2.
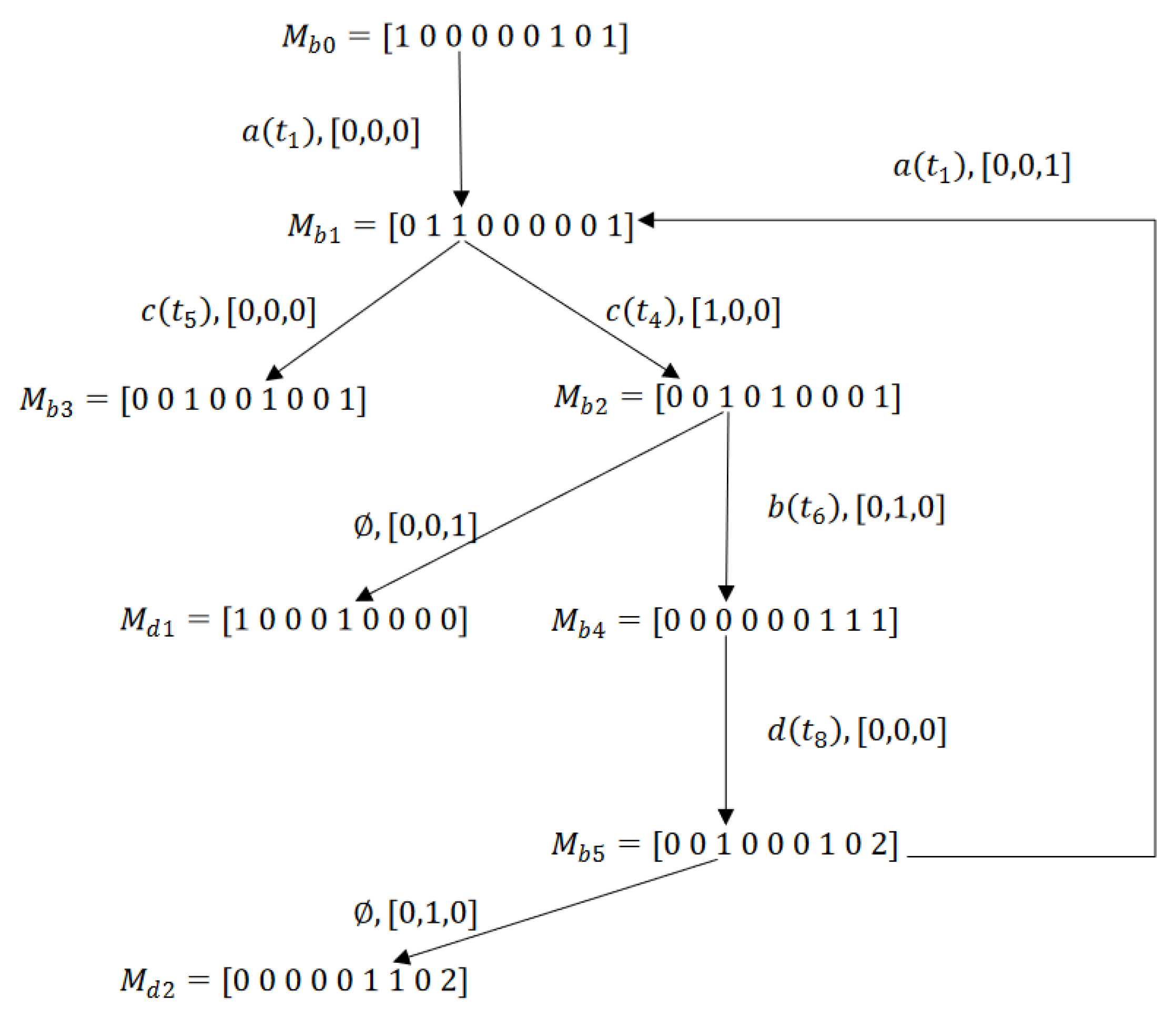
Figure 12.
Labeled Petri net of Example 3.
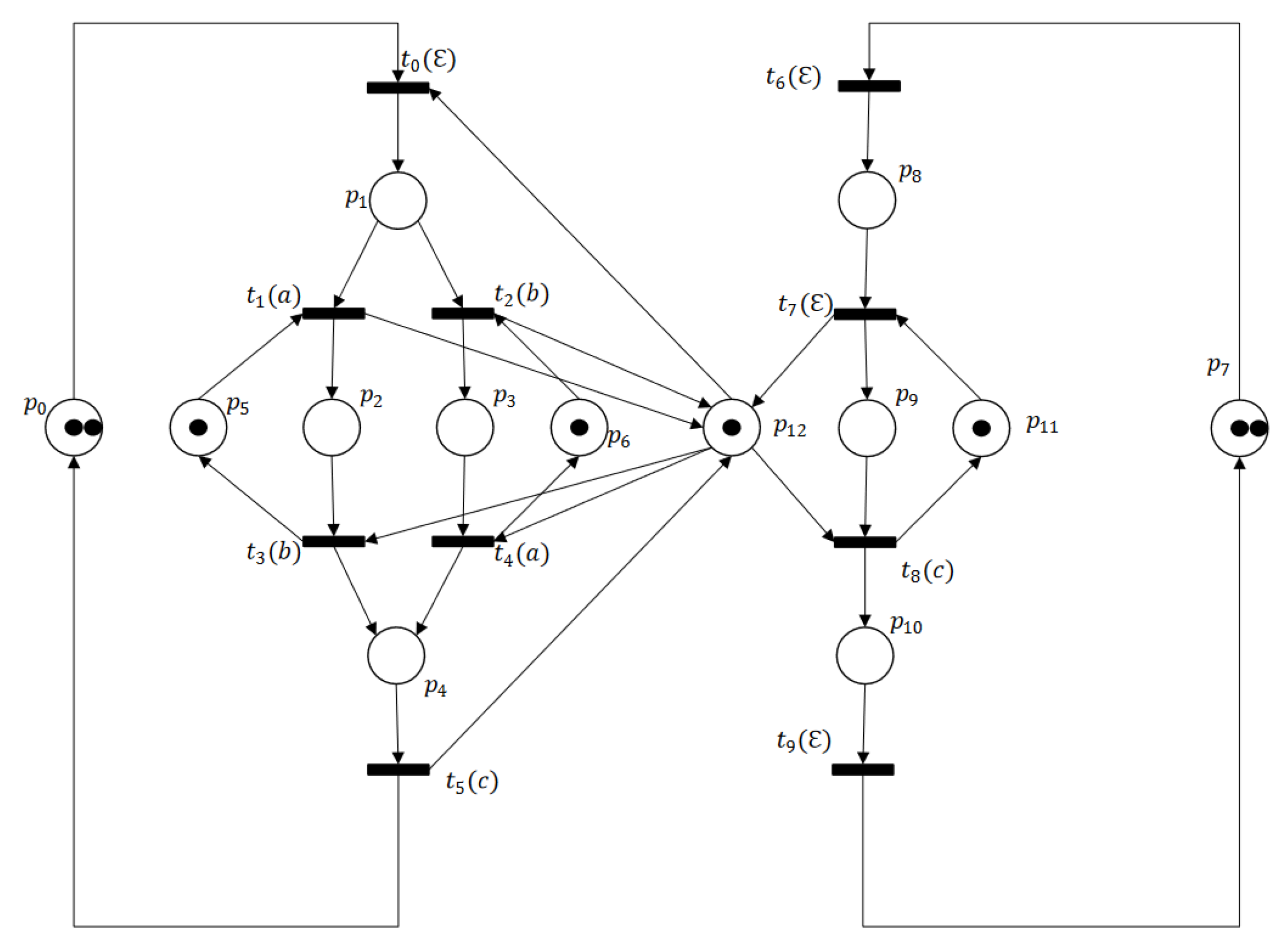
Figure 13.
Reachability graph of the LPN in Example 3.
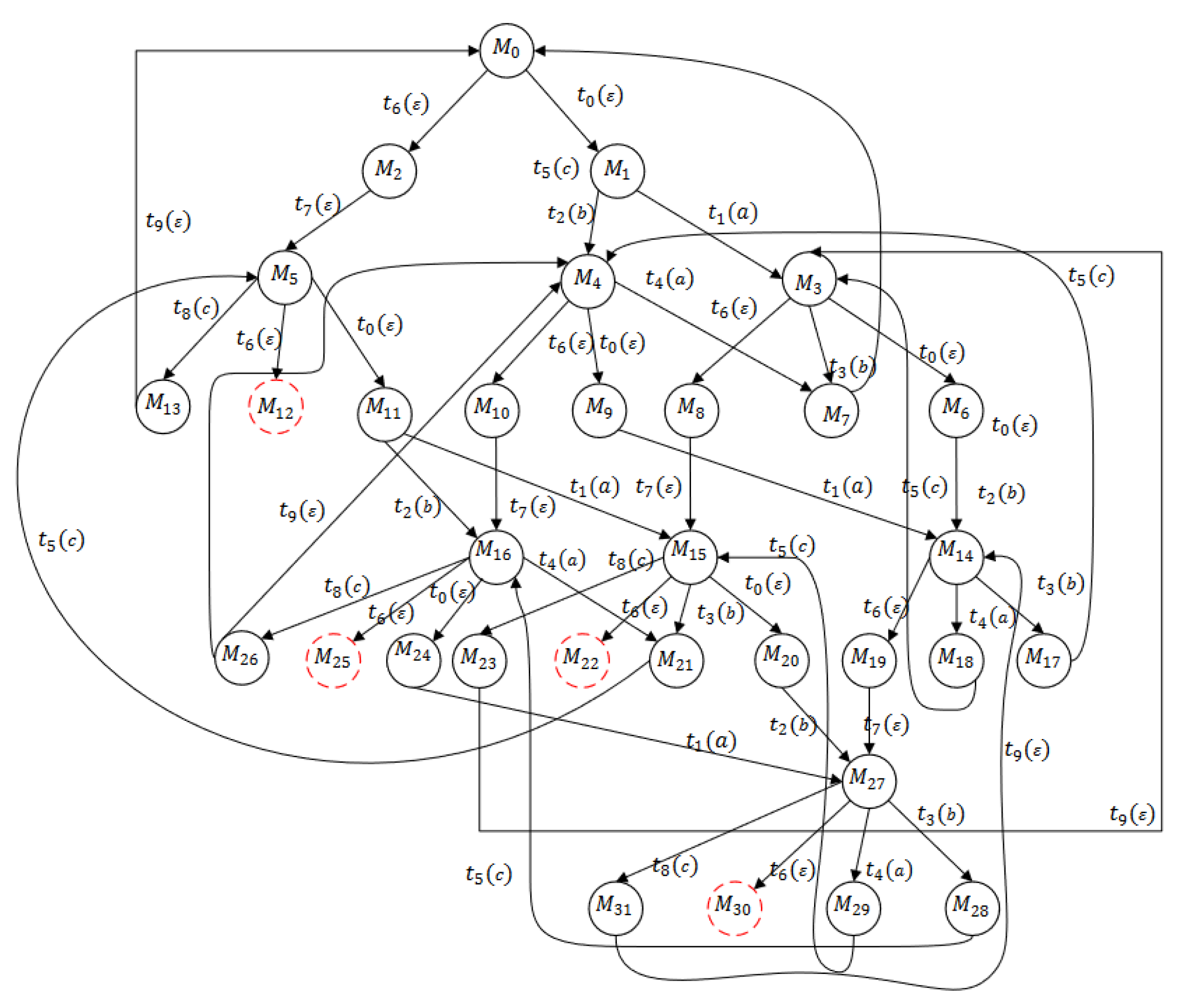
Figure 14.
BRG of the LPN in Example 3.
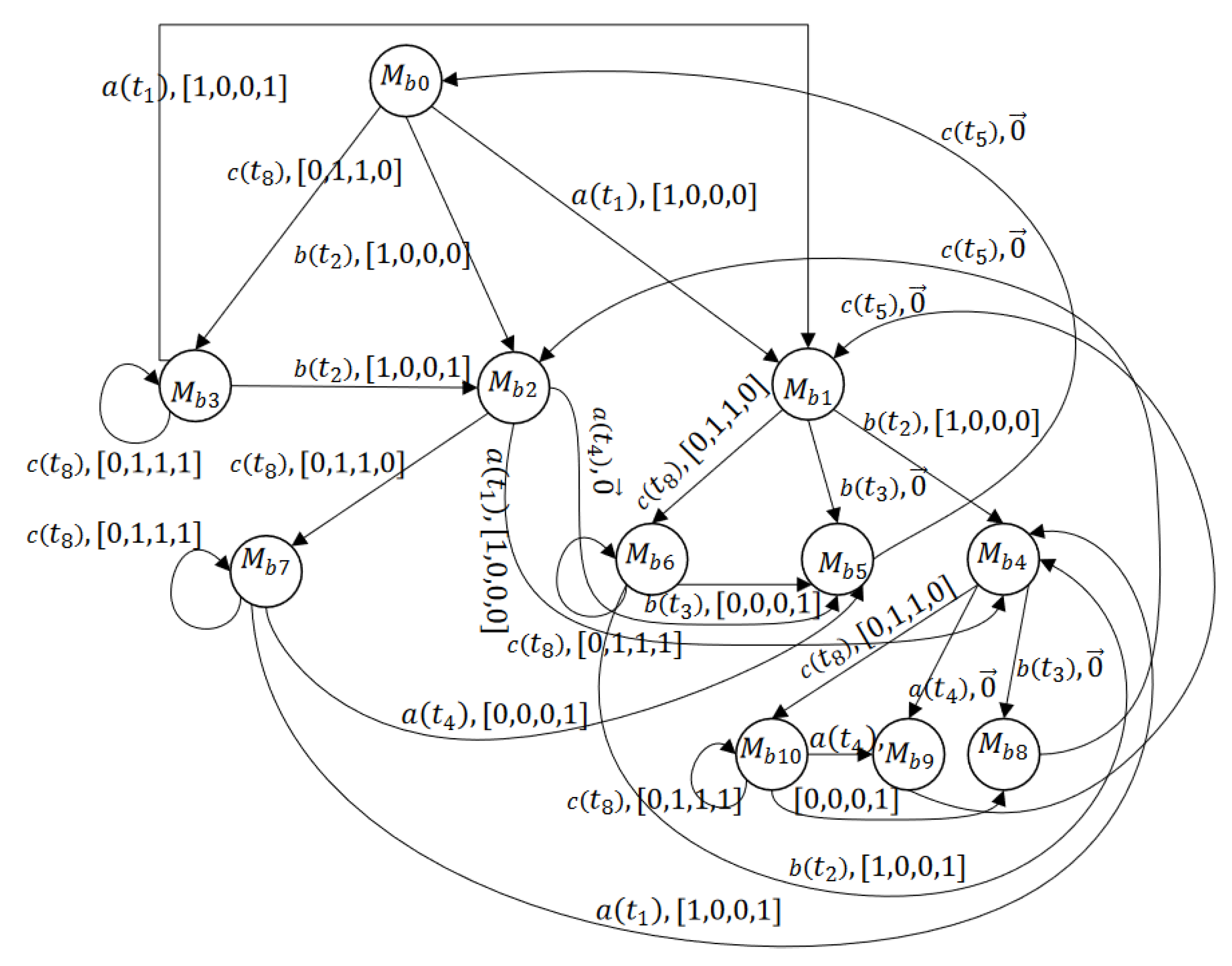
Figure 15.
Observed graph of the LPN in Example 3.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




