Prerpints.org logo
Preprint
Article

EEG Signal Correlation Study Towards Possible Epileptic Foci Localization

Altmetrics

Downloads

80

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 September 2024

Posted:

26 September 2024

You are already at the latest version

Alerts
Abstract
The precise localisation of epileptic foci with the help of EEG or ECoG signals is still a clinical challenge that is rarely successful, except in the case of foci that are very close to the surface and allow a clear assignment to a single electrode. On the research side, dipole reconstruction of instantaneous excitation fields via the lead-field matrix or the evaluation of time-dependent phase shifts in the measurements seem to be still possible and are under development. For the latter, we have investigated the necessary correlation of signals in the time range up to a few hundred milliseconds in an EEG of a healthy subject (self-experiment). We find periods of up to 190 msec in length in which a correlation over short latencies succeeds very well, alternating with periods in which long-range correlations occur while the short latencies come to a standstill. An automatic propagation time focus localisation to be developed therefore appears possible if an underlying state monitoring system independently recognises the suitable time periods and then successfully performs the comparatively shortest-range triangulation calculations over these.
Keywords: 
Subject: Biology and Life Sciences  -   Neuroscience and Neurology

1. Introduction

The localisation of one signal source (Electric Source Imaging [1,2], ESI) in the midst of a concert of multiple sources is one of the main challenges of brain research [3]. We cur-rently have to rely on EEG, ECoG, PET, MEG or fMRI data to detect single sources [4,5], and in the future dipole field measurements which are subject of research [6] will be added to this list.
In addition to fundamental knowledge-guided research, it is the demand in clinical use that drives such considerations, especially in the area of localisation of seizure foci (i.e. in cases of focal epilepsy [3]) in patients who are difficult to treat with medication [7] and who can be made seizure-free by resection of the epileptogenic brain tissue [3,8]. Since the extent of the failures also increases with the size of the resected tissue [9], attempts are made to keep the resected tissue small. To do this, it is essential to localise the focus precisely, usually by placing subdural ECoG electrodes, which have a typical distance of 1 cm, preoperatively. This achieves, roughly estimated, a spatial resolution of about 1 cm [10], although in other places people talk about millimetre-accurate spatial localization [11]. Recent studies, with high-density electrode arrays with only 1 mm electrode spacing, which had exactly this increases precision in resolution as their goal [12], showed other local phenomena such as mini-ictus but no clear increase in localisation. Alternatively, it is common nowadays to implant several intracranial SEEG electrodes [13,14,15] but prior indication for placement must already be obtained from non-invasive studies. The typical interelectrode distance is on the order of 1 cm [16], however multiple designs are in the works with a goal to constantly improve the resolution and bring it to the level of animal studies of tens of micrometers [17]. The imaging techniques PET and fMRI, which are often cited, also achieve localisation at the centimetre level.
In general, however, the mathematical analysis of EEG or, better still, ECoG data is associated with the immediately plausible idea of localisation from the comparison of many measurement points. Two mayor methods are conceivable:
The first method is based on the known location analysis of earthquake waves, which pheno-typically comes close to ictal events. Here we have primary and secondary (near-surface) waves that propagate at 2–8 km/sec and approx. 3 km/sec, respectively. With the known data on the structure of the earth's crust, the epicenters can be determined with an accuracy of a few 10 km, given the earth's radius of 6400 km. If this procedure were applied to ictal events [18], then with neuronal signal conduction velocities of 30 to 70 m/s and an actual maximum time resolution of EEG and ECoG data of 1 ms, spatial resolutions of only 3 to 7 cm would be achieved.
In the second approach, the limits described above lead to the assumption of an instantaneous propagation of the electrical fields [19]. Here, from the EEG and ECoG data recorded at a multitude of electrodes [20,21], dipoles in the brain volume are reconstructed, which contribute to the overall picture of the electrode recording.
Other approaches that of course need mentioning are the development of wavelet entropy apps and sliding window [22] techniques as well as Kalman filtering [1]. More over we can learn by clinical applications of localized applied electric fields for artificial ictus generation [23] or, which is even more promising, epilepsy suppression [24].
Both models have, beneath a general challenge of inverse modeling, their limitations [25] in the possible causes of the seizure. These may lie at the level of singular neurons, where the self-inhibition mechanisms of the ion channels may be suspended. Another level might be at groups of pyramidal or subpyramidal-pyramidal clusters [26,27]. These may be electrical synapses or in the course of the neuronal-plastic development [28] of an epileptic predisposition of structures which also build recurrent signaling pathways [29] that exhibit an inherent tendency to giant postsynaptic potentials or overshoots [30]. The latter two approaches have anatomical-structural prerequisites that would favor direct neuronal latency analysis. However, the overall picture would in any case be a superimposition of delayed neuronal signal transmissions with instantaneous field propagation, which are attenuated in magnitude, for example, by glial tissue.
The aim of the present study is to examine the extent to which neurally delayed signals could be used for focus localisation. Firstly, such localisations require time domains of high latency-related correlations, which would have a stimulus transmission or delay modelling as their basis. Secondly, in the presence of correlation, it is necessary to examine the extent to which, these not only exhibit characteristics of synchronicity, but also a directionality as an expression of upstream and downstream processing levels.

2. Design Considerations

The mathematical-physical model of delay-based epileptic excitation requires feedback loops with characteristic loop propagation times τL. These can range from short-range temporal lobe epilepsy, in which localisation is often successful with conventional electrode systems and centimetre-accurate resolution or τL ≈ 0.15 ms [12]. On the other hand, in extreme cases, long-range excitation loops are conceivable that run over a commissure with paths of 2 x 14 cm and path durations of around 8 ms and additional delays per synapse between 0.5 and 2 ms [31] and possible synaptic summation periods [32,33] of the same dimension. In total, loop durations of 10 msec and more are conceivable here. In terms of magnitude, this fits perfectly into the picture of the usual ictal frequencies of up to 200 Hz.
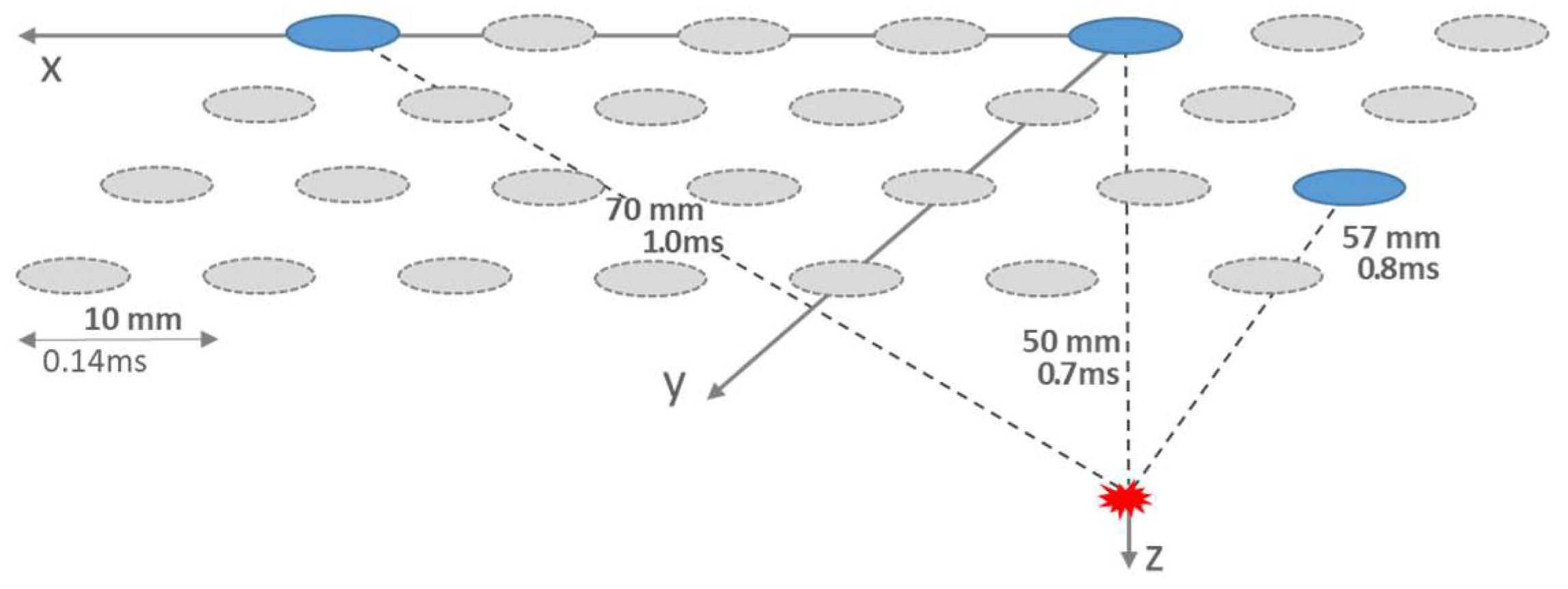
The necessary decoding of travel time differences into the spatial localisation of sources is achieved by calculating the intersection points of three spherical surfaces under the electrode points with radii that can be determined from the travel time differences and the propagation speed [34]. The triangulation is illustrated in Figure 1 for a source depth of z = 50 mm under an electrode at the origin of a Cartesian x,y,z coordinate system and two further electrodes, which were assumed to be 5 positions further in the x-direction and two diagonal positions. The calculated transit time differences were 0.1 ms and 0.3 ms [29]. Consequently, the temporal resolution limit should be at least 0.1 ms [30], which relates to a resolution in the frequency range of 10 kHz or, for sampling according to the Nyquist condition 20 kHz. This would be at the technical limit of today's electrophysiology devices.
For a later clinical realisation of a focus localisation system, the attempt with a simple linear model would undoubtedly fall short. Rather, a model would have to be designed that dynamically and adaptively tracks the permanent reorganisation of active signalling pathways in the CNS. Based on the current state of science and technology, this appears possible with continuously running self-learning algorithms [31,32] in augmentation of work done 50 years before [33]. Whilst some insights in the necessity to stable phases of neuronal representation that provide a currently valid ‘linear image’ of current latencies have been gained in the early 2000 decade [34], a remaining question is still whether periods or EEG or ECoG epochs exist in which self-learning algorithms can provide and optimise themselves. Mathematically, this is equivalent to the search for time periods in which the correlation between the individual EEG signals is sufficiently high.
Such cross-correlations of EEG data have already been used in related applications [35]. They have also been used to train support vector machines [36] to derive motor signals for BCIs [37] or to detect brain-heart disorders in focal epilepsies [38].
However, the idea that the signal transmission via neurons could be visible in EEG data is controversial and instead a transmission only via white matter is proposed [39].

3. Experimental and Results

For a fundamental analysis of correlation periods, there is no need to use measurement data from epilepsy patients. Instead, data from healthy subjects can be evaluated. This was done in the form of a study by one of the co-authors in a self-experiment. At the time of the data collection, the person was in generally good health, of sound mind, had no known (neurological) preexisting conditions and had a generally good level of fitness in terms of sports physiology. The data collection was carried out while the person was awake and with his eyes open.
A 64-channel high-density EEG from BRAIN PRODUCTS was used. Using BRAINVISION pro-fessional ANALYZER2.1® software, the impedance of the electrodes on the coupled EEG cap was checked to see if it was below the usual standard of 15 kOhm @ 1kHz. The data collection took place in a lit anechoic room with playback of acoustic stimuli, some of which were responded to by pressing a button. In total, data from four runs of seven minutes each were recorded. The following data analysis only uses non-event-related sections. The data were recorded at 1kHz and downsampled to 100Hz which was sufficient for further latency analysis.
The determination of the correlation r of two channels p and q, shifted by a temporal latency Δ, is carried out according to a modified Bravais-Pearson equation (1)
r p , q ∆ = 1 n   ∑ i = 1 n p i − p ¯ q i + ∆ − q ¯ 1 n ∑ i = 1 n p i − p ¯ 2 · 1 n ∑ i = 1 n q i + ∆ − q ¯ 2
by direct comparison of the respective value pairs of EEG amplitudes shifted by the latency. The calculated correlation coefficients can assume values between +1 (highest linear dependency) and -1 (antiphase course); values around zero indicate incoherence. A total of 530 sec recording time was examined per channel pairing for preset latencies of 10, 20, 30, 50, 70, 100, 200, 250, 300, 400 and 500 ms.
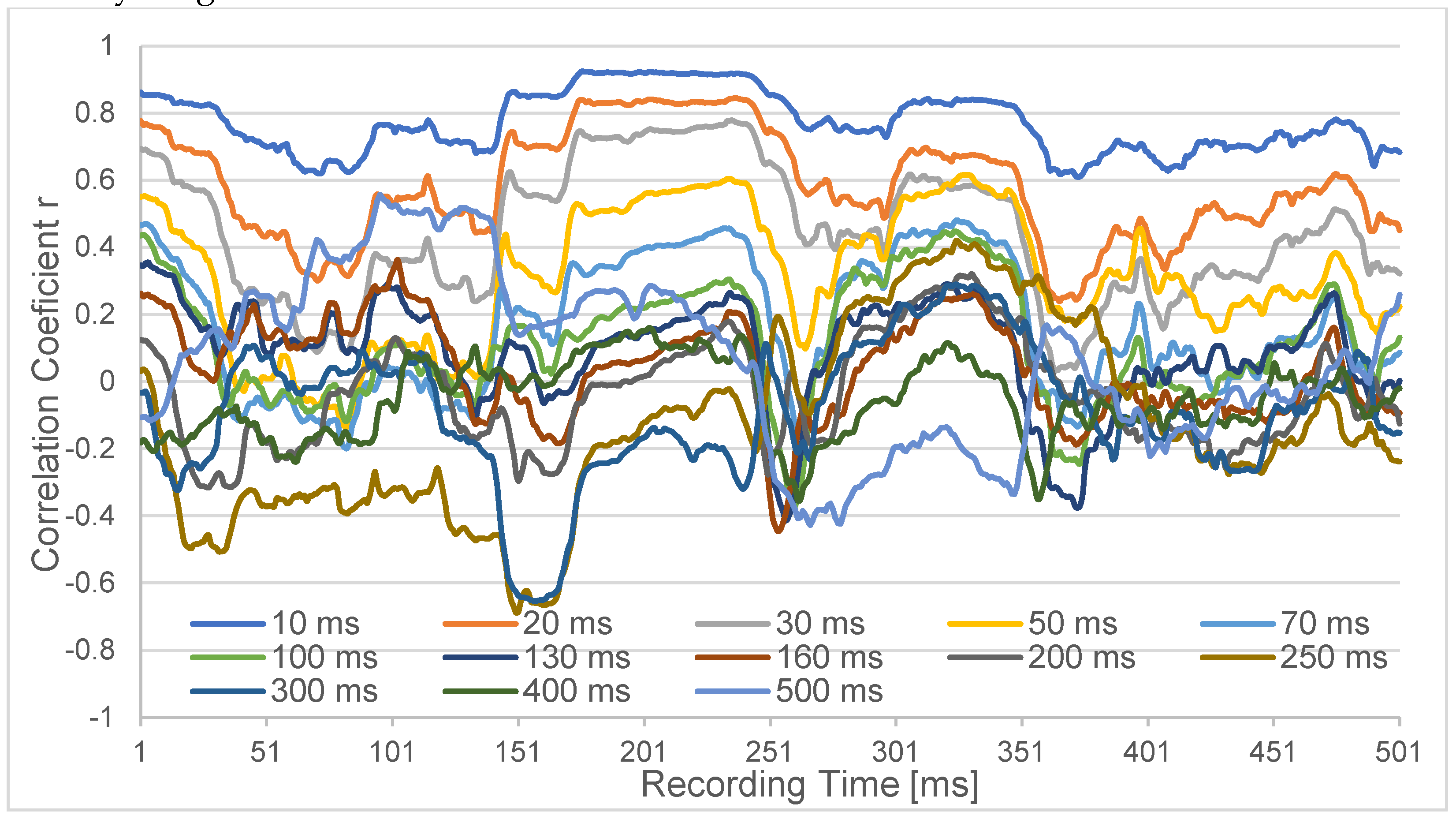
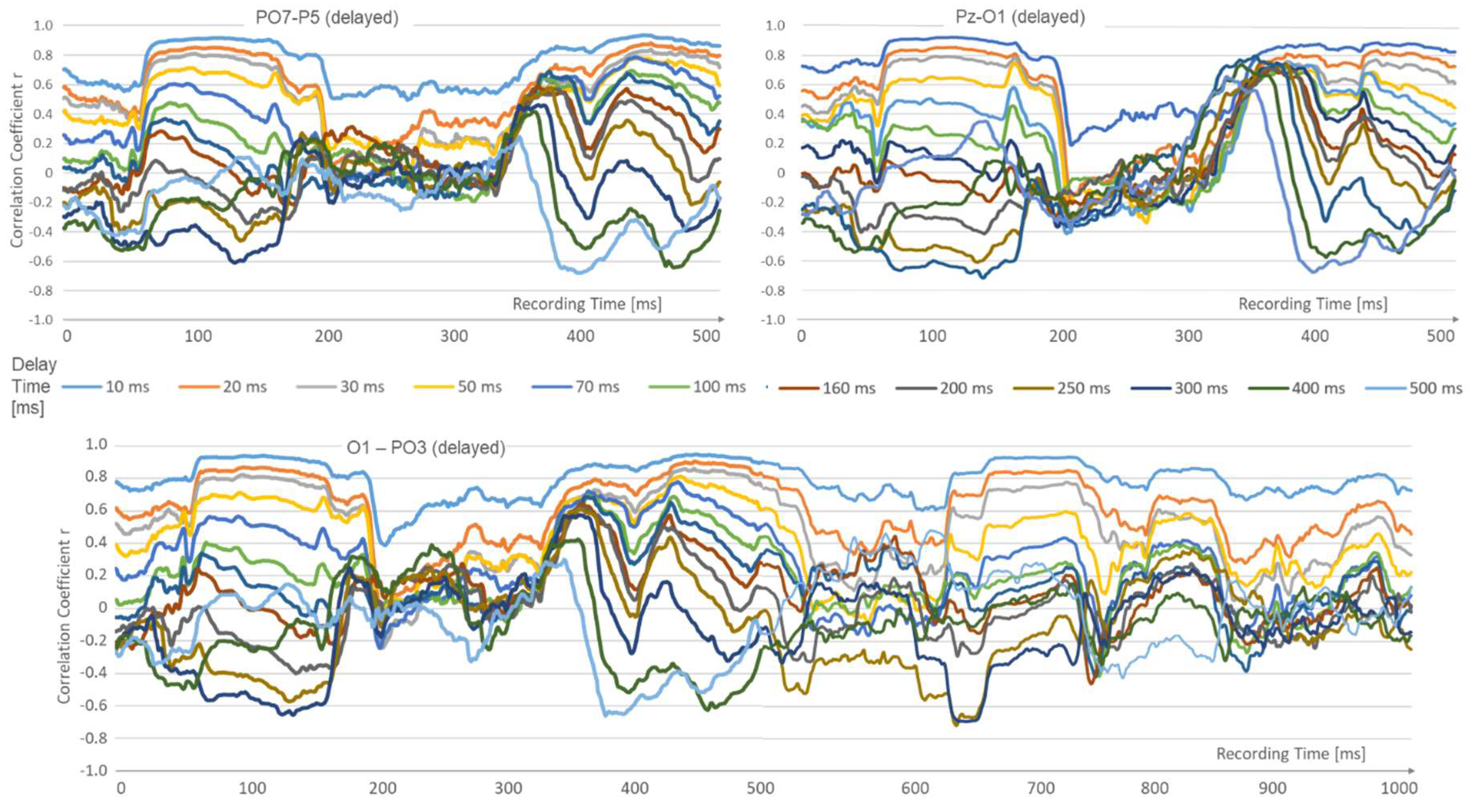
The results were time-resolved progressions of 500 ms (p-) duration each, as shown in Figure 2 for both monopolar channels Oz and PO3 for the different latencies. While the short latencies up to 30 ms are consistently positively correlated, the longer latencies up to 300 ms fluctuate around zero, and the very long latencies tend to be anticorrelated.
For a first overview 34 EE-recording channels above one visual and auditory hemisphere underwent the correlation test over one full recording span of 530 sec. With one exception all initial correlation coefficients reach almost 50%. 18 out of 34 reached average r-values exceeding 0,7 corresponding to a coefficient of determination r2 of 49% (Table 1). Amongst the latter it is found that the latencies with respect to this limit tend to be shorter over the visual cortex than over the auditory areas.
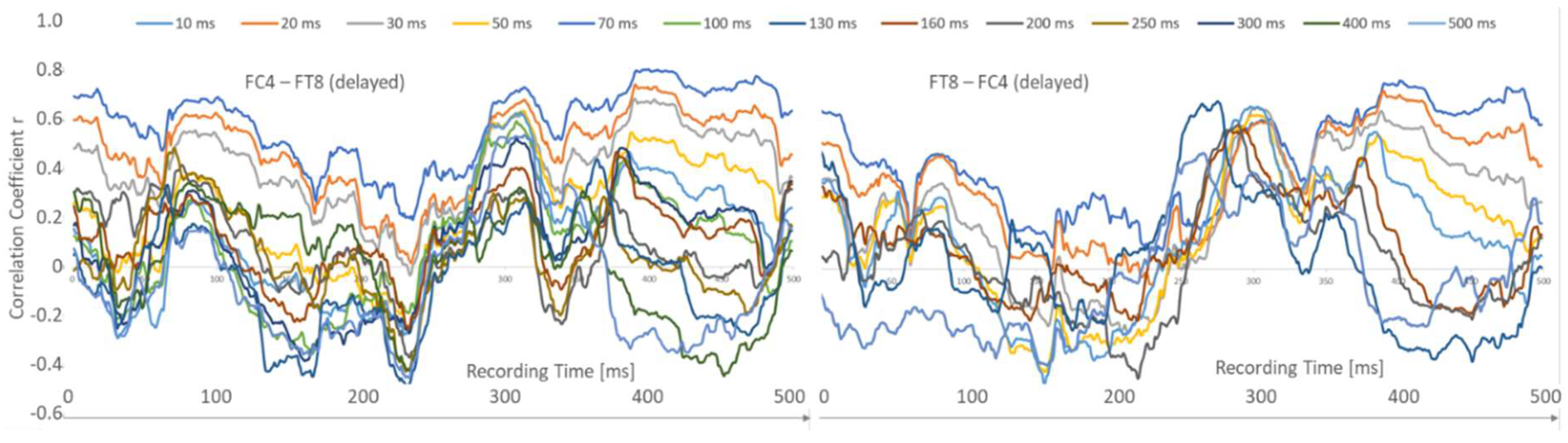
Next, the criterion of directionality was examined. For example, the pairing FC4 – FT8 (neighbours afternext) shows very similar 10 ms and 20 ms curves but different mean r-values. On the other hand, the correlation curves for the 70 ms to 200 ms latencies were clearly different from each other (Figure 3).
Furthermore, a measure of directionality was sought. It proved to be advantageous to calculate the relative deviation of the correlations r of EEG data p and q as follows and to find the maximum of this. For the present data, this results in values in the percentage range
Directionality = M a x ( ∆ ) A B S   r p , q + ∆ − r ( q ,   p + ∆ ) r p , q + ∆ + r ( q ,   p + ∆ ) · 2
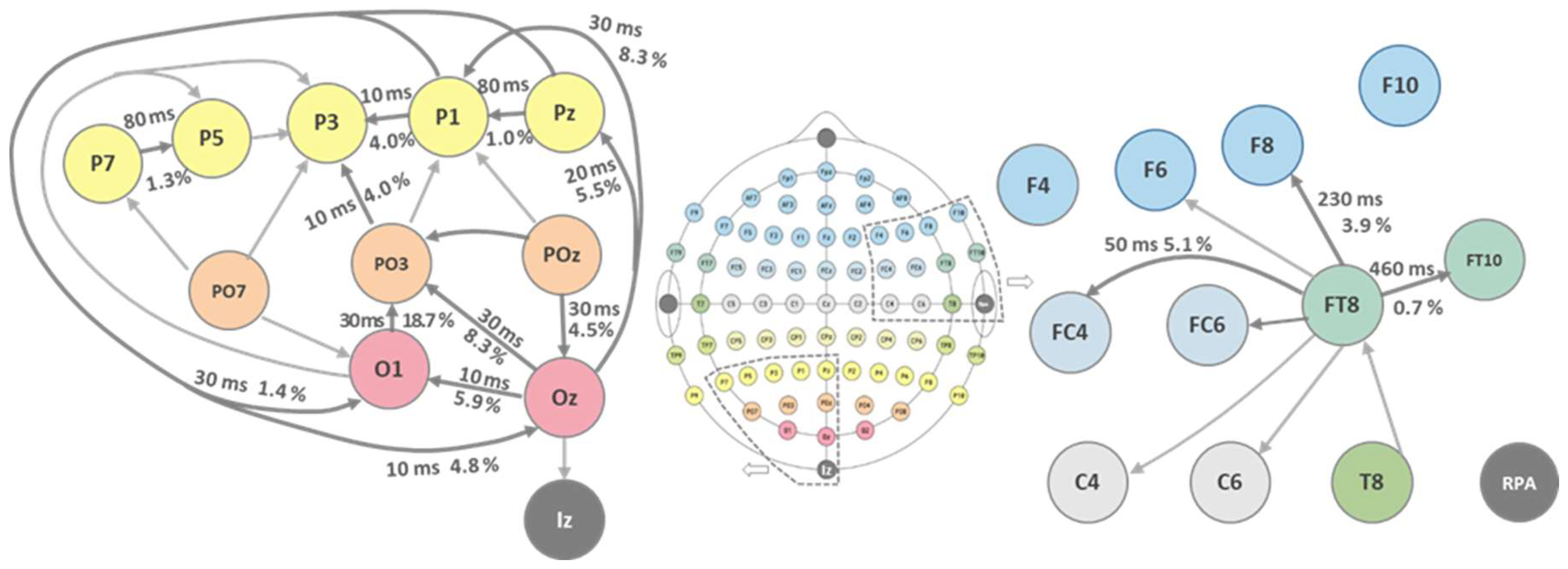
Likewise, the dominant source can be identified by comparing the signs at the maxima. The results of these calculations are listed in Table 2. The directionality values lie in the range of few % to 23 %. However, from both the latency data and source identification, a sound picture arises as can be seen from Figure 4 for the occipital visual and temporal auditory lobe EEG data.
Another frequently occurring observation in these analyses is a change of epochs: those with high correlation, decreasing from short latencies to longer ones, are contrasted with others that show a quasi-reversal of latency. Here, the correlation collapses at short latencies, while the longer latencies up to 500 ms become increasingly positive. This epoch change occurs in periods of approximately 190 - 220 ms.

4. Discussion

Without supra-individual generalisation, which a case study does not allow, we have as a result that EEG data can be successfully correlated, which on the one hand is in line with the results of Tang [22] and Bruns [40]. On the other hand, we now have numerical latency values and a practical confidence measure that can substantiate the modelling. The different latency data obtained for the correlation over the visual pathway compared to the auditory system, with shorter or significantly longer latencies at the confidence threshold, are equally reflected in daily clinical experience with evoked potentials [1,46] and underline the validity of the approach taken. In particular, this is achieved quasi online, since there was no stimulus-synchronous synchronisation.
The correlation of the EEG electrode data of the nearest and second neighbours shows a transmitter-receiver structure in the range of 10%, which is consistent with the SoA knowledge about primary, secondary and associative fields. We see this as proof that neuronal functional structures are involved in the formation of EEG signals and that transmission does not only occur through the white matter [38].
The fact that it is possible to identify epochs of stable states on the basis of EEG latency correlation data appears to be new. The correlation dominance of short latency (10–70 ms) transitions into states with positive correlations of long latencies (200–500 ms), with short latencies hardly correlated at all. The periods of these epoches are in the range of 190–220 ms, which is reminiscent of alpha wave periods and generalised brain states, as examined, for example, by Kringelbach and Deco [3,47]. However, this is asking for a further comparison with existing connectivity methods, like Granger causality or the multitude of DTFs [48,49,50].
In general, the results point to various closed-loop circuits. We estimate and identify the delays in these control loops during our correlation methodology. This should eventually provide clues for future modelling [12]. Overall, the proposed model is consistent with the ongoing development of classifiers for ictus detection, as reviewed by Dümpelmann [8] and Mégevand [1], as well as with stimulus localisation.

5. Conclusions

Having the previous findings well discussed, we suppose that an EEG- od ECoG-based source localization algorithm could be favorable that adds, for instance to dipole localization, propagational terms. They could use
(a)
linearly simplified neural signaling (weighted signal speed and transition delays) for small area, underlying source localizations,
(b)
a set of “brain state models” according to a) that merge into another, and
(c)
an adaptive, machine-learning mechanism that develops those brain states (within recurring 200 ms sequences) and recognizes those states.
If such an algorithm can be developed, an epileptic focus localization could be realized, trained during presurgical EEG- or ECoG-recordings and could be useful in all cases where the brain states according to a)-c) are not actually switched in the event of ictusses. Algorithm development and introduction of methods of artificial intelligence in clinical diagnosis would be next steps to validate the proposed procedure based on our pilot data. Simple underlying methods would also help to proceed towards 'explainable AI' approaches for situations in which effects of diagnostic decisions would end in surgical resection of brain areas eventually removing seizure onset zones.

Author Contributions

Conceptualization, T.D. and T.S.; methodology, T.D. data acquisitions and measurements A.H.; validation, T.S. and D.W.; data curation, writing and original draft preparation, T.D.; review and editing, T.D. and D.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially co-funded by “EEG/ECoG based Neuroimaging” by German DFG, project 511765241 as well as National Science Centre, Poland, grant number 2022/04/Y/NZ4/00063. The main funding came from EU Horizon 2020 project “MDOT” grant number 814654.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data will be posted during publication approval.

Acknowledgments

We gratefully acknowledge the contribution of Dr. Brilliant who performed the EEG recordings a Hannover Medical School.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Mégevand P, Hamid L, Dümpelmann M, Heers M, New horizons in clinical electric source imaging, Z. Epileptol. 2019 32:187–193. [CrossRef]
  2. Kaiboriboon K, Lüders H O, Hamaneh M, Turnbull J, Lhatoo S D, EEG source imaging in epilepsy—practicalities and pitfalls, Nature Reviews Neurology 8, 498-507 (2012).
  3. Vorwerk J, Wolters CH, Baumgarten D. Global sensitivity of EEG source analysis to tissue conductivity uncertainties. Front Hum Neurosci. 2024 Mar 12;18:1335212. [CrossRef]
  4. Schmitt F. C.; Stefan H; Holtkamp M (Eds.): Epileptische Anfälle und Epilepsien im Erwachsenenalter : Diagnostik und Therapie. Berlin, Heidelberg : Springer Berlin / Heidelberg, 2021, p21–28.
  5. Tamilia E; Madsen J. R., Grant P E; Pearl P L; Papadelis C, Current and Emerging Potential of Magnetoencephalography in the Detection and Localization of High-Frequency Oscillations in Epilepsy. In: Frontiers in neurology 8 (2017), p14.
  6. Liu Y, Su H, Li C. Effect of Inverse Solutions, Connectivity Measures, and Node Sizes on EEG Source Network: A Simultaneous EEG Study. IEEE Trans Neural Syst Rehabil Eng. 2024;32:2644-2653. [CrossRef]
  7. Kwan P, Brodie M J, Early identification of refractory epilepsy. In: The New England journal of medicine 342 (2000), 5, p314–319.
  8. Dümpelmann M, Early seizure detection for closed loop direct neurostimulation devices in epilepsy. In: Journal of neural engineering 16 (2019), 4, p41001.
  9. Bauer S, Rosenow F, Anfälle, in. Diener H-C, Steinmetz H, Kastrup O (eds.) Referenz Neurologie. Stuttgart, New York : Georg Thieme Verlag, 2019 pp158-172.
  10. Todaro C, Marzetti L, Valdés Sosa PA, Valdés-Hernandez PA, Pizzella V. Mapping Brain Activity with Electrocorticography: Resolution Properties and Robustness of Inverse Solutions. Brain Topogr. 2019 Jul;32(4):583-598. [CrossRef]
  11. Medina-Pizarro M, Spencer D D, Damisah E C, Recent advances in epilepsy surgery. In: Current Opinion in Neurology. 36, 2, (2023), p95. [CrossRef]
  12. Sun J, Barth K, Qiao S, Chiang C-H, Wang C, Rahimpour S, Trumpis M, Duraivel S, Dubey A, Wingel K E, Rachinskiy I, Voinas A E, Ferrentiono B, Southwell D G, Haglund M M, Friedmann A H, Lad S P, Doyle W K, Solzbacher F, Cogans G, Sinha S R, Devore S, Devinskiy O, Friedman D, Pesaran B, Viventi J, Intraoperative microseizure detection using a high-density micro-electrocorticography electrode array. In: Brain communications 4 (2022), Nr. 3, fcac122.
  13. Jobst B C, Bartolomei F, Diehl B, et al. Intracranial EEG in the 21st Century. Epilepsy Currents. 2020;20(4):180-188.
  14. Parvizi, J., Kastner, S. Promises and limitations of human intracranial electroencephalography. Nat Neurosci 21, 474–483 (2018). [CrossRef]
  15. Mercier M R, Dubarry A-S, Tadel François, Avanzini Pietro, Axmacher N, Cellier D, Del Vecchio M, Hamilton L S, Dora Hermes D, Kahana M J, Knight R T, Llorens A, Megevand P, Melloni L, Miller K J, Piai V, Puce A, Ramsey N F, Schwiedrzik C M, Smith S E, Stolk A, Swann N C, Vansteensel M J, Voytek B, Wang L, Lachaux J-P, Oostenveld R, Advances in human intracranial electroencephalography research, guidelines and good practices, NeuroImage, Volume 260, 2022, 119438. [CrossRef]
  16. Lhatoo S D, Kahane P, Lüders H O (eds.), Invasive studies of the human epileptic brain : principles and practice, Oxford University Press, 2019.
  17. Lee K, Paulk A C, Ro Y G et al., Flexible, scalable, high channel count stereo-electrode for recording in the human brain. Nat Commun 15, 218 (2024). [CrossRef]
  18. Rampp S, Scherg M, Grundlagen der Quellenlokalisation. In: Zeitschrift für Epileptologie 31 (2018), 3, pp170–178.
  19. Moller C, Behandlung von Potentialsingularitaten bei der EEG/MEG-basierten Rekonstruktion dipolarer Stromquellen in Finite-Elemente-Volumenleitermodellen des menschlichen Kopfes. Dissertation Erlangen University (2005).
  20. Łęski S, Wójcik D K, Tereszczuk J, Świejkowski D, Kublik E, Wróbel A, Inverse Current-Source Density in three dimensions, Neuroinformatics 5 (2007) 207.
  21. Chintaluri C, Bejtka M, Średniawa W, Czerwiński M, Dzik J M, Jędrzejewska-Szmek J, Kondrakiewicz K, Kublik E, Wójcik D K,, What we can and what we cannot see with extracellular multielectrodes, (2021), PLoS Comput Biol 17(5): e1008615. [CrossRef]
  22. Tang X, Zhang X, Cai D, Du J, Liu W, An epileptic focus location method based on ECoG. In: Biomedical materials and engineering 26 Suppl 1 (2015), p1053-1058.
  23. Kang W, Ju C, Joo J, Lee J, Shon Y-M, Park S-M, Closed-Loop Direct Control of Seizure Focus in a Rodent Model of Temporal Lobe Epilepsy via Localized Electric Fields Applied Sequentially Nat Commun. 2022;13(1):7805. [CrossRef]
  24. Takeuchi Y, Harangozo M, Pedraza L, Foldi T, Kozak G,Li Q, Berenyi A, Closed-loop stimulation of the medial septum terminates epileptic seizures doi:10.1093/brain/awaa450 BRAIN 2021: 144; 885–908 | 885.
  25. Scharfman H E, The neurobiology of epilepsy. Curr Neurol Neurosci Rep. 2007 Jul;7(4):348-54. [CrossRef]
  26. Matsumoto R, Ajmone-Marsan C. Cortical cellular phenomena in experimental epilepsy: ictal manifestations. Exp Neurol 1964;80:305–326. [PubMed: 14142796].
  27. Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P, et al. Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature 1996;378:75–78. [PubMed: 7477292.
  28. Traub R D, Michelson-Law H, Bibbig A E, et al. Gap junctions, fast oscillations and the initiation of seizures. Adv Exp Med Biol 2004;548:110–122. [PubMed: 15250590].
  29. Sutula T P, Dudek F E, Unmasking recurrent excitation generated by mossy fiber sprouting in the epileptic dentate gyrus: an emergent property of a complex system. In: Scharfman H E (ed), The Dentate Gyrus: A Comprehensive Guide to Structure, Function, and Clinical Implications. Amsterdam: Elsevier; 2007.
  30. Brown T H, Johnston D, The synaptic nature of the paroxysmal depolarization shift in hippocampal neurons. Ann Neurol 1984;16:S65–S71. [PubMed: 6095744].
  31. Sabatini B L, Regher W G, (1999). Timing of synaptic transmission, Annu. Rev. Physiol. 61, 521–542.
  32. Bröhl T, Rings T, Lehnertz K, Von Interaktionen zu Interaktionsnetzwerken: Zeitabhängige funktionelle Netzwerke am Beispiel der Epilepsie. In: Klinische Neurophysiologie 51 (2020), 03, pp132–143.
  33. Boudkkazi S, Carlier E, Ankri N, Caillard O, Giraud P, Fronzaroli-Molinieres L, Debanne D, Release-Dependent Variations in Synaptic Latency: A Putative Code for Short- and Long-Term Synaptic Dynamics, Neuron 56, pp (2007). [CrossRef]
  34. Seek M, Gschwind M, High-Density-Elektroenzephalografie, in Schmitt F. C.; Stefan H; Holtkamp M (Eds.): Epileptische Anfälle und Epilepsien im Erwachsenenalter : Diagnostik und Therapie. Berlin, Heidelberg : Springer Berlin / Heidelberg, 2021, p21–28.
  35. Marcoleta J P, Nogueira W, Doll T, Distributed mixed signal demultiplexer for electrocorticography electrodes. In: Biomedical physics & engineering express 6 (2020), 5, p55006.
  36. Ha S; Akinin A, Park J, Kim C, WANG H, Maier C, Mercier P P, Cauwenberghs G, Silicon-Integrated High-Density Electrocortical Interfaces. In: Proceedings of the IEEE 105 (2017), 1, pp11–33.
  37. Kiral-Kornek I, et al 2017 Epileptic seizure prediction using big data and deep learning: toward a mobile system EBioMedicine 27 103–11.
  38. Acharya R U, Oh S L, Hagiwara Y, Tan J H and Adeli H 2017 Deep convolutional neural network for the automated detection and diagnosis of seizure using EEG signals Comput. Biol. Med. 415–6 190–8.
  39. Deppisch J, Die Zeitstruktur neuronaler Repräsentation : Modellierung und Identifikation neuronaler Assemblies als kollektive Erregungszustände des visuellen Systems, Dissertation Frankfurt am Main University (Physics) 1994.
  40. Bruns A, Amplitudenkopplung zwischen Kortexsignalen: Ein bislang ungenutzter Indikator für kooperative Hirnprozesse im Menschen, Dissertation Marburg university, 2003.
  41. Knyazev GG, Savostyanov AN, Bocharov AV, Aftanas LI. EEG cross-frequency correlations as a marker of predisposition to affective disorders. Heliyon. 2019 Nov 29;5(11):e02942. [CrossRef]
  42. Chandaka S, Chatterjee A, Munshi S, Cross-correlation aided support vector machine classifier for classification of EEG signals, Expert Systems with Applications, 36, 2, (part 1) 2009, pp1329-1336. [CrossRef]
  43. Al-dabag, M.L., Ozkurt, N. EEG motor movement classification based on cross-correlation with effective channel. SIViP 13, 567–573 (2019). [CrossRef]
  44. Frassineti L, Catrambone V, Lanatà A, Valenza G, Impaired brain-heart axis in focal epilepsy: Alterations in information flow and implications for seizure dynamics. Network Neuroscience 2024; 8 (2): 541–556. [CrossRef]
  45. Bhavsar R, Sun Y, Helian N, Davey N, Mayor D, Steffert T, The Correlation between EEG Signals as Measured in Different Positions on Scalp Varying with Distance, Procedia Computer Science, 123, 2018, pp92-97. [CrossRef]
  46. Pernet C, Garrido M I, Gramfort A, Maurits N, Michel C M, Pang E, Samelin R, Schoffelen J M; Valdes-sosa P A, Puce A, Issues and recommendations from the OHBM COBIDAS MEEG committee for reproducible EEG and MEG research. In: Nature neuroscience 23 (2020), Nr. 12, S. 1473–1483.
  47. Kringelbach M L, Deco G, Brain States and Transitions: Insights from Computational Neuroscience, Cell Reports, Volume 32, Issue 10, 2020, 108128. [CrossRef]
  48. Korzeniewska A, Mańczak M, Kamiński M, Blinowska K J, Kasicki S, Determination of information flow direction among brain structures by a modified directed transfer function (dDTF) method, Journal of Neuroscience Methods, Volume 125, Issues 1–2, 2003, pp195-207, ISSN 0165-0270. [CrossRef]
  49. Kamiński M, Ding M, Truccolo W, et al., Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol Cybern 85, pp145–157 (2001). [CrossRef]
  50. Wilke C, Van Drongelen W, Kohrman M, He B. (2010), Neocortical seizure foci localization by means of a directed transfer function method. Epilepsia, 51: pp564-572. [CrossRef]
Preprints 119298 g001
Figure 1. Triangulation scheme of an ictal source in the depth of about 50 mm with electrodes of 10 mm spacing. Neural propagation leads to different transit times of 0.7 ms, 0.8 ms and 1.0 ms respectively.
Figure 1. Triangulation scheme of an ictal source in the depth of about 50 mm with electrodes of 10 mm spacing. Neural propagation leads to different transit times of 0.7 ms, 0.8 ms and 1.0 ms respectively.
Preprints 119298 g001
Preprints 119298 g002
Figure 2. Correlation coefficient r of cannels Oz and PO3 within a 500 msec correlation interval. The x-axis denotes Oz time over 500 ms against which PO3 was delayed by 10 ms up to 500 ms. For the shorter delays always positive correlation is found, which tends to zero around 100 ms and turns into partial anticorrelation for delays < 250 ms.
Figure 2. Correlation coefficient r of cannels Oz and PO3 within a 500 msec correlation interval. The x-axis denotes Oz time over 500 ms against which PO3 was delayed by 10 ms up to 500 ms. For the shorter delays always positive correlation is found, which tends to zero around 100 ms and turns into partial anticorrelation for delays < 250 ms.
Preprints 119298 g002
Preprints 119298 g003
Figure 3. Correlation difference of the pairing FC4-FT8 versus FT8-FC4.
Figure 3. Correlation difference of the pairing FC4-FT8 versus FT8-FC4.
Preprints 119298 g003
Preprints 119298 g004
Figure 4. Directionalities of the EEG-correlations depicted for the visual and auditory cortices. The informational flux is yield in a correct way. So do the latencies which are short for the more primary areas and get prolonged for the more associative spots.
Figure 4. Directionalities of the EEG-correlations depicted for the visual and auditory cortices. The informational flux is yield in a correct way. So do the latencies which are short for the more primary areas and get prolonged for the more associative spots.
Preprints 119298 g004
Preprints 119298 g005
Figure 5. The correlation analysis over several spots and longer times reveals phases of strong short correlations which alternate with periods where the longer delays gain strength.
Figure 5. The correlation analysis over several spots and longer times reveals phases of strong short correlations which alternate with periods where the longer delays gain strength.
Preprints 119298 g005
Table 1. Correlation overview on 34 EEG-channels from the visual and auditory cortex. Almost all correlations start from r > 0,5. From the 34 parings 18 reached the r = 0,7 threshold with latencies of 10 ms and longer.
Table 1. Correlation overview on 34 EEG-channels from the visual and auditory cortex. Almost all correlations start from r > 0,5. From the 34 parings 18 reached the r = 0,7 threshold with latencies of 10 ms and longer.
Locked Channel Iz Oz Oz Oz O1 PO3 POz POz PO3 PO3 O1 PO7 PO7 PO3 PO7 P7 P5
Delayed Channel Oz O1 POz PO3 PO3 POz Pz P1 P1 P3 PO7 P7 P5 PO7 P3 P5 P3
Corr. Coeff. @ 10 ms 0.58 0.7 0.75 0.76 0.75 0.76 0.77 0.66 0.63 0.71 0.49 0.7 0.83 0.59 0.59 0.81 0.67
Latency [ms] @r = 0.7 0 10 30 30 30 30 30 0 0 10 00 80 0 0 80 0
Locked Channel P3 P1 P7 P5 P3 P1 Pz Pz P1 FT10 FT8 FT8 FT8 C6 FT8 FC4 FT8
Delayed Channel P1 Pz O1 O1 O1 O1 O1 Oz Oz FT8 F8 FC6 F6 FT8 T8 FT8 C4
Corr. Coeff. @ 10 ms 0.71 0.83 0.78 0.64 0.57. 0.75 0.71 0.73 0.76 0.89 0.8 0.69 0.29 0.69 0.5 0.74 0.64
Latency [ms] @r = 0.7 10 80 60 0 0 30 10 20 30 460 230 0 0 0 0 50 0
Table 2. Directionality and source identification calculated from EEG correlation data.
Table 2. Directionality and source identification calculated from EEG correlation data.
Locked Channel Iz Oz Oz Oz O1 PO3 POz POz PO3 PO3 O1 PO7 PO7 PO3 PO7 P7 P5
Delayed Channel Oz O1 POz PO3 PO3 POz Pz P1 P1 P3 PO7 P7 P5 PO7 P3 P5 P3
Directionality [%] 6.8 5.9 4.5 8.3 19.7 4.3 5.9 8.9 4.4 4.0 7.6 6.9 2.6 2.7 8.0 1.3 10.6
Source Oz Oz POz Oz O1 POz POz POz PO3 PO3 PO7 PO7 PO7 PO3 PO7 P7 P5
Locked Channel P3 P1 P7 P5 P3 P1 Pz Pz P1 FT10 FT8 FT8 FT8 C6 FT8 FC4 FT8
Delayed Channel P1 Pz O1 O1 O1 O1 O1 Oz Oz FT8 F8 FC6 F6 FT8 T8 FT8 C4
Directionality [%] 4.0 1.0 2.3 1.5 10.4 1.4 2.7 5.5 8.3 0.7 3.9 3.4 23.5 3.8 1.9 5.1 12.6
Source P1 Pz O1 O1 O1 P1 Pz Oz Oz FT9 FT8 FT8 FT8 FT8 T8 FT8 FT8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated