Submitted:
25 September 2024
Posted:
26 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Analysis
3. Results and Discussions
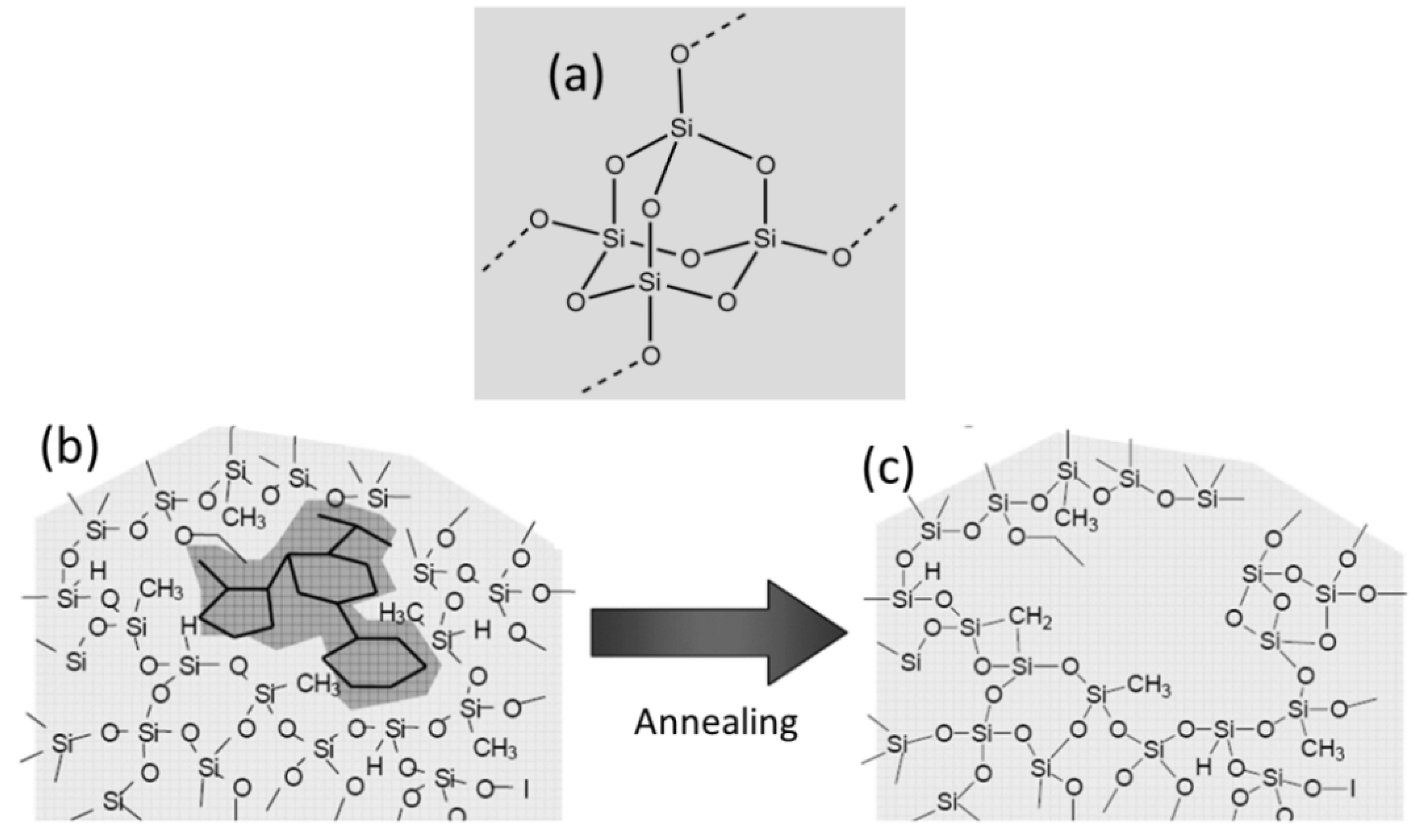
3.1. Chemical Composition
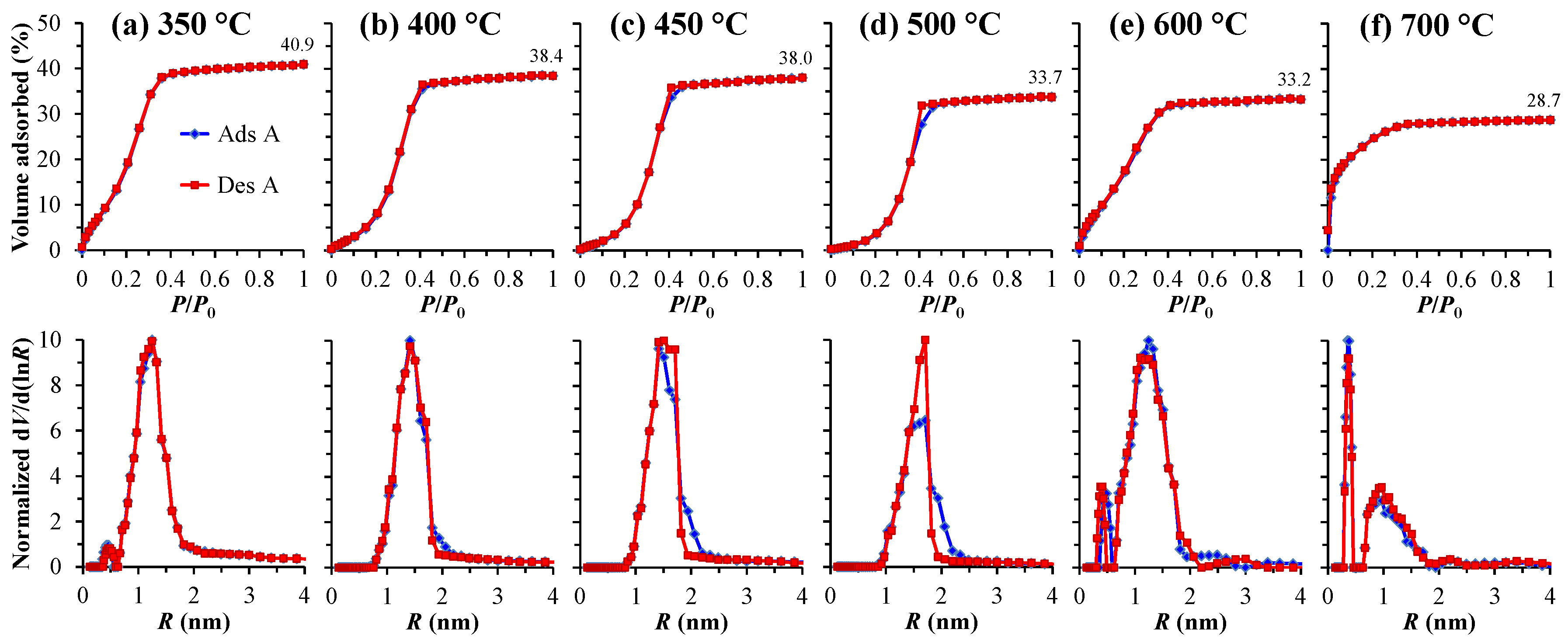
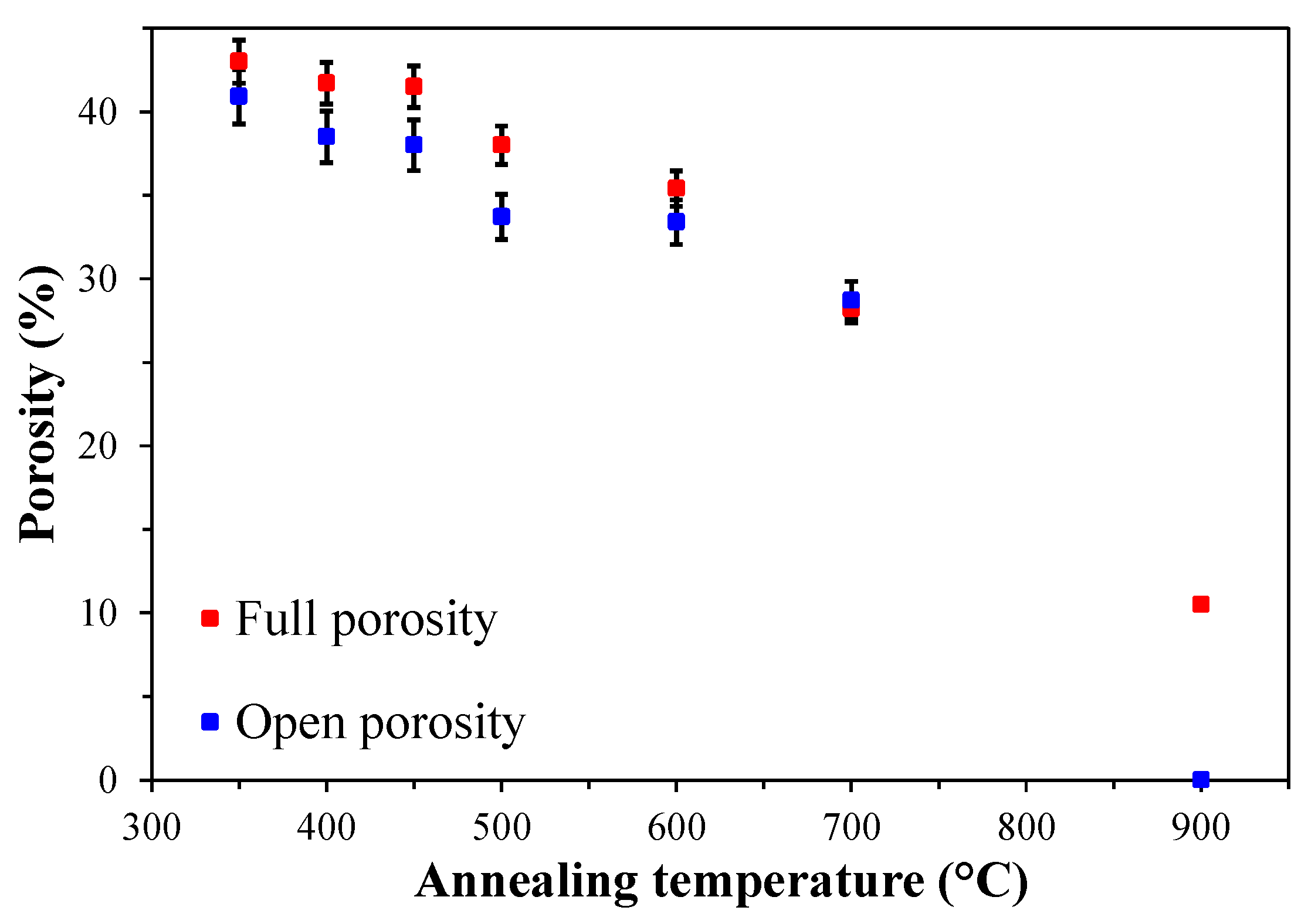
3.2. Spectroscopic Ellipsometry (SE) and Ellipsometric Porometry (EP) Data
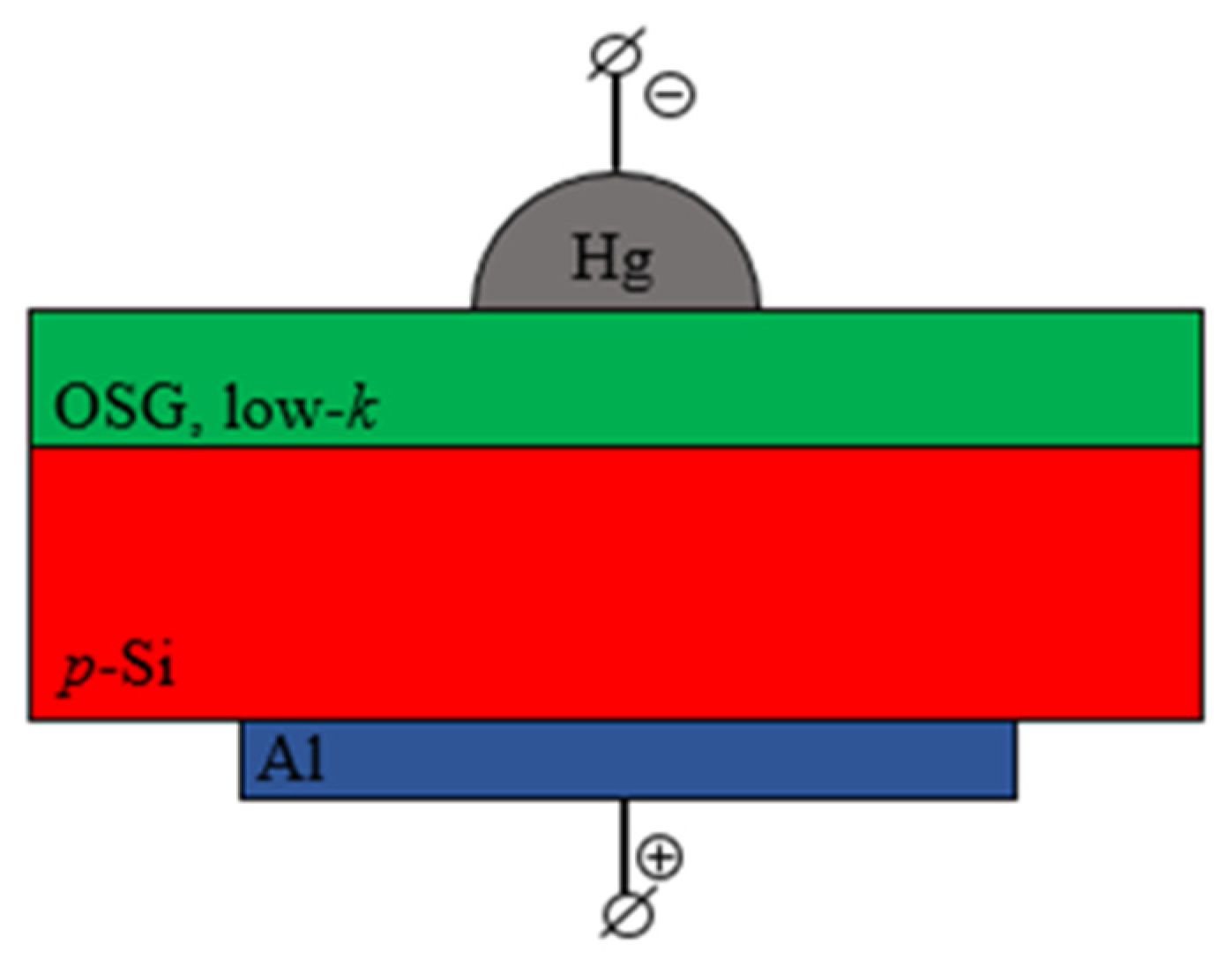
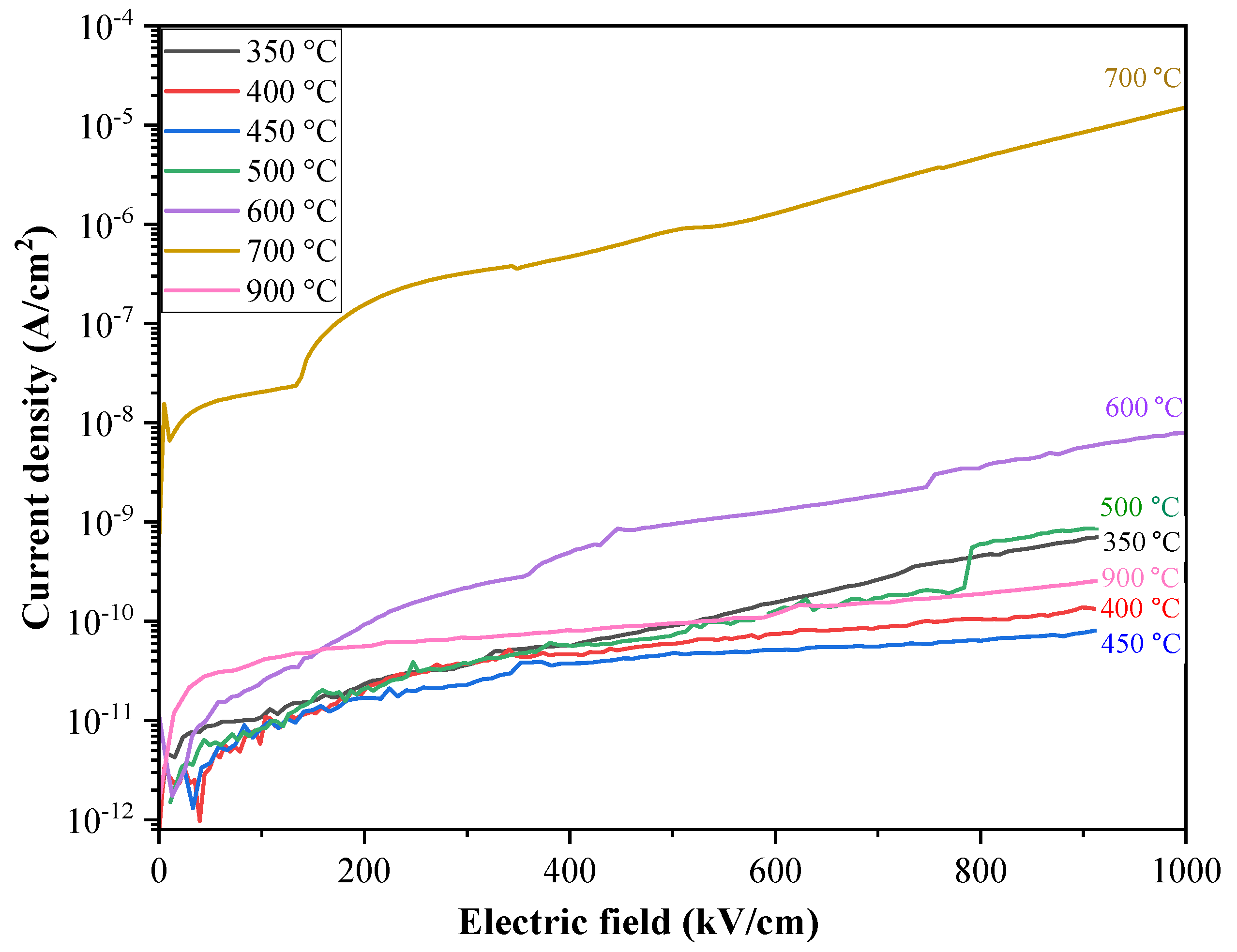
3.3. Electrical Properties
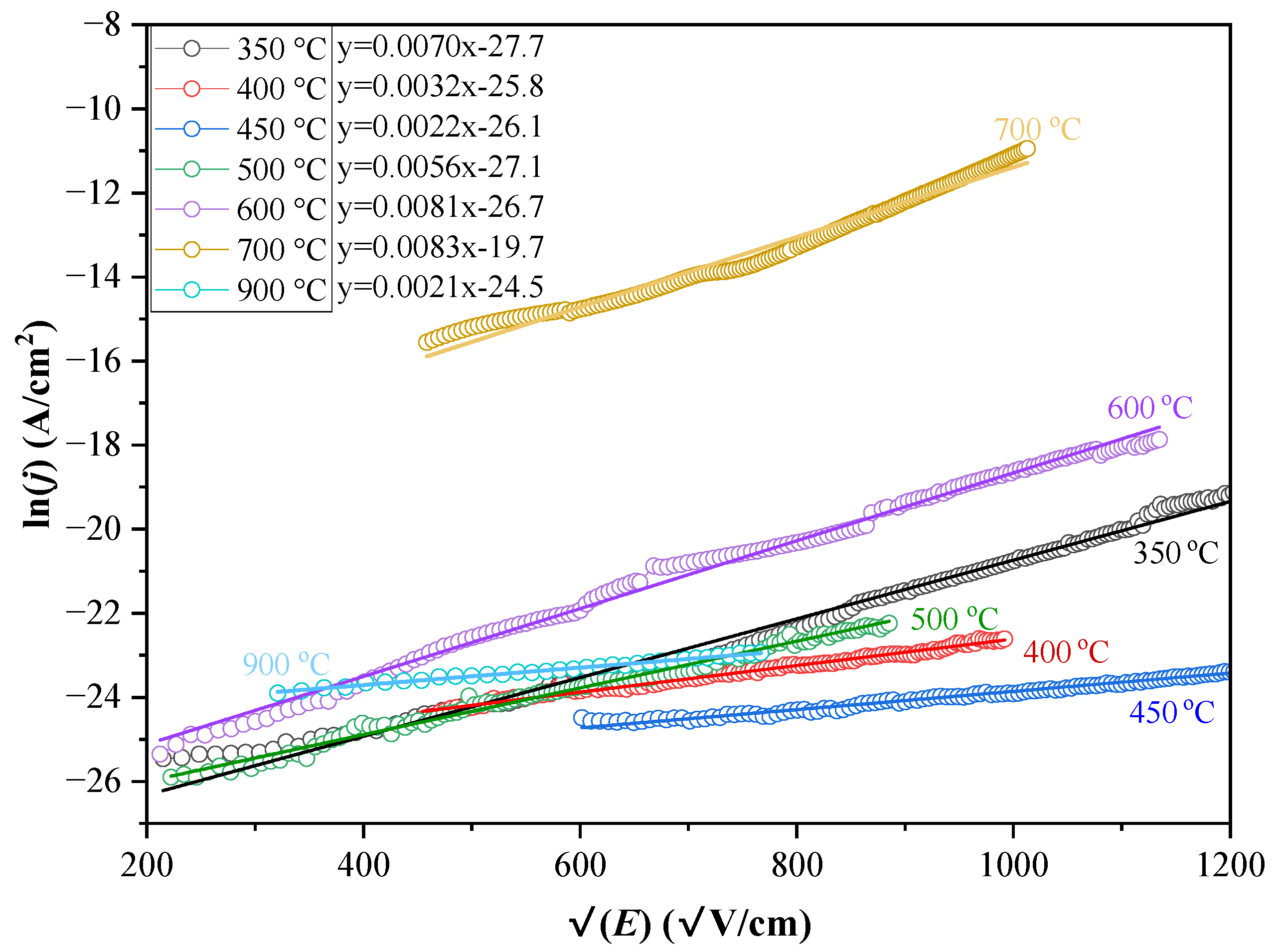
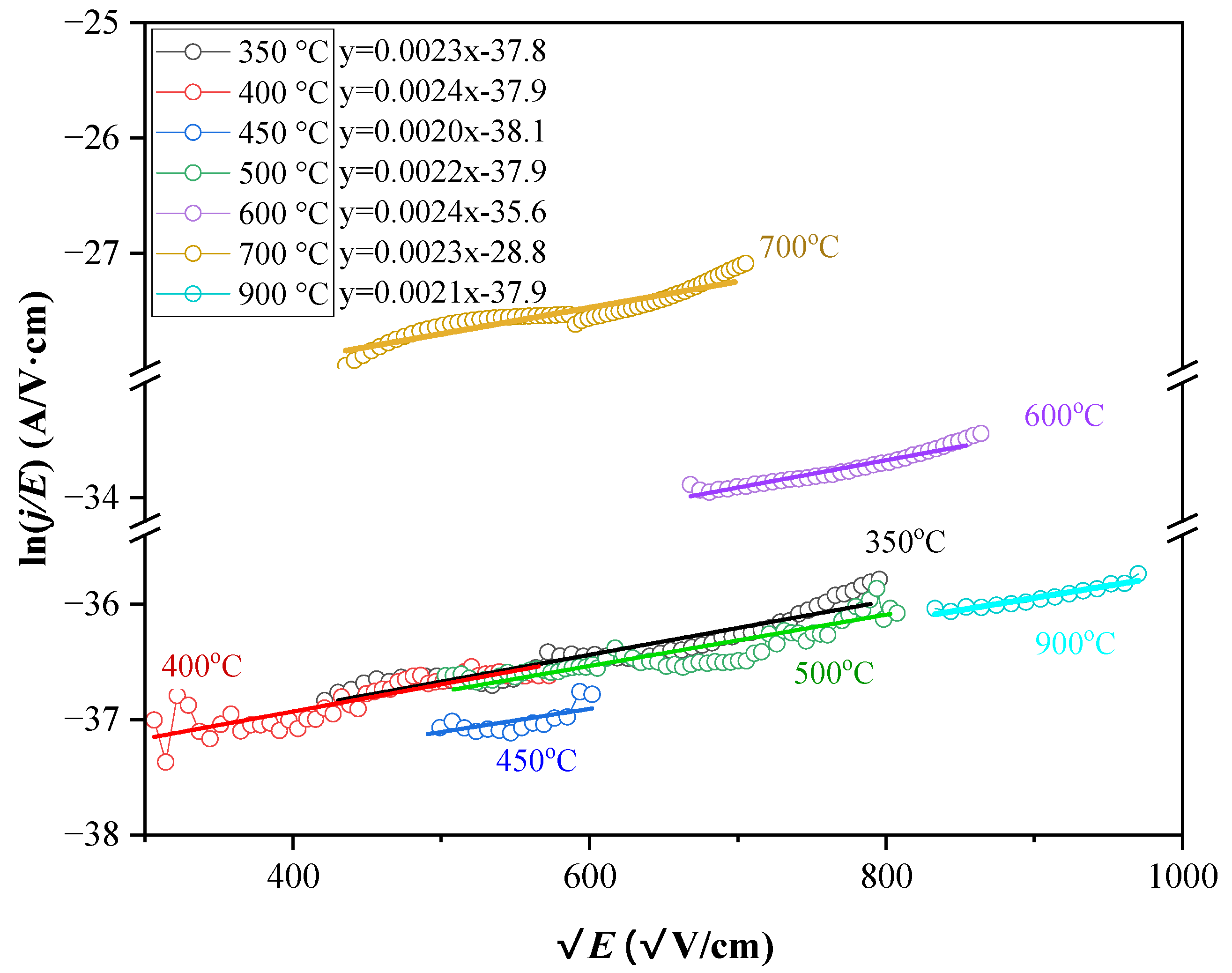
3.4. Discussion of the Leakage Mechanism
3.4.1. Verification of NG Model
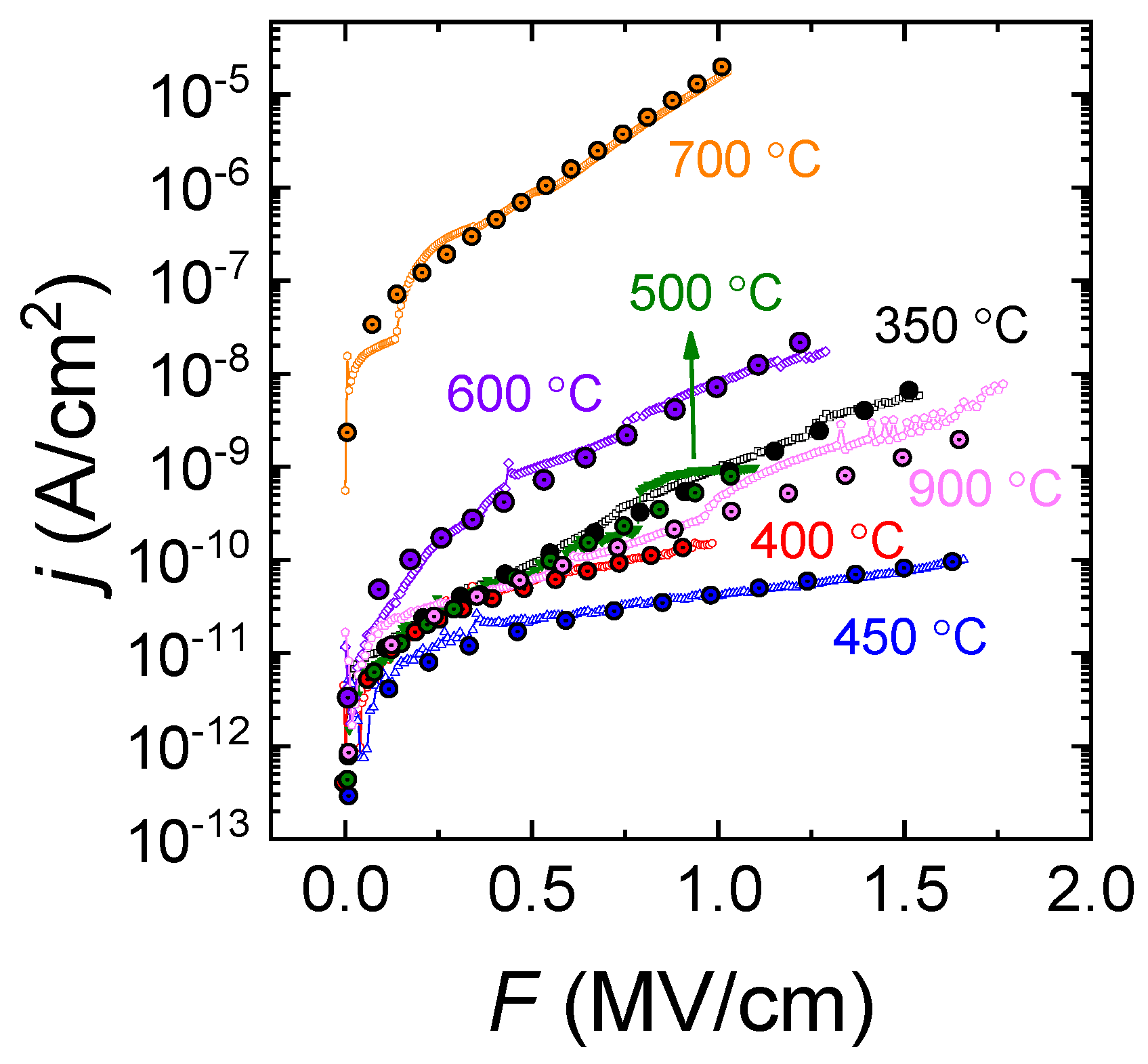
3.4.2. Verification of SE and PF Models
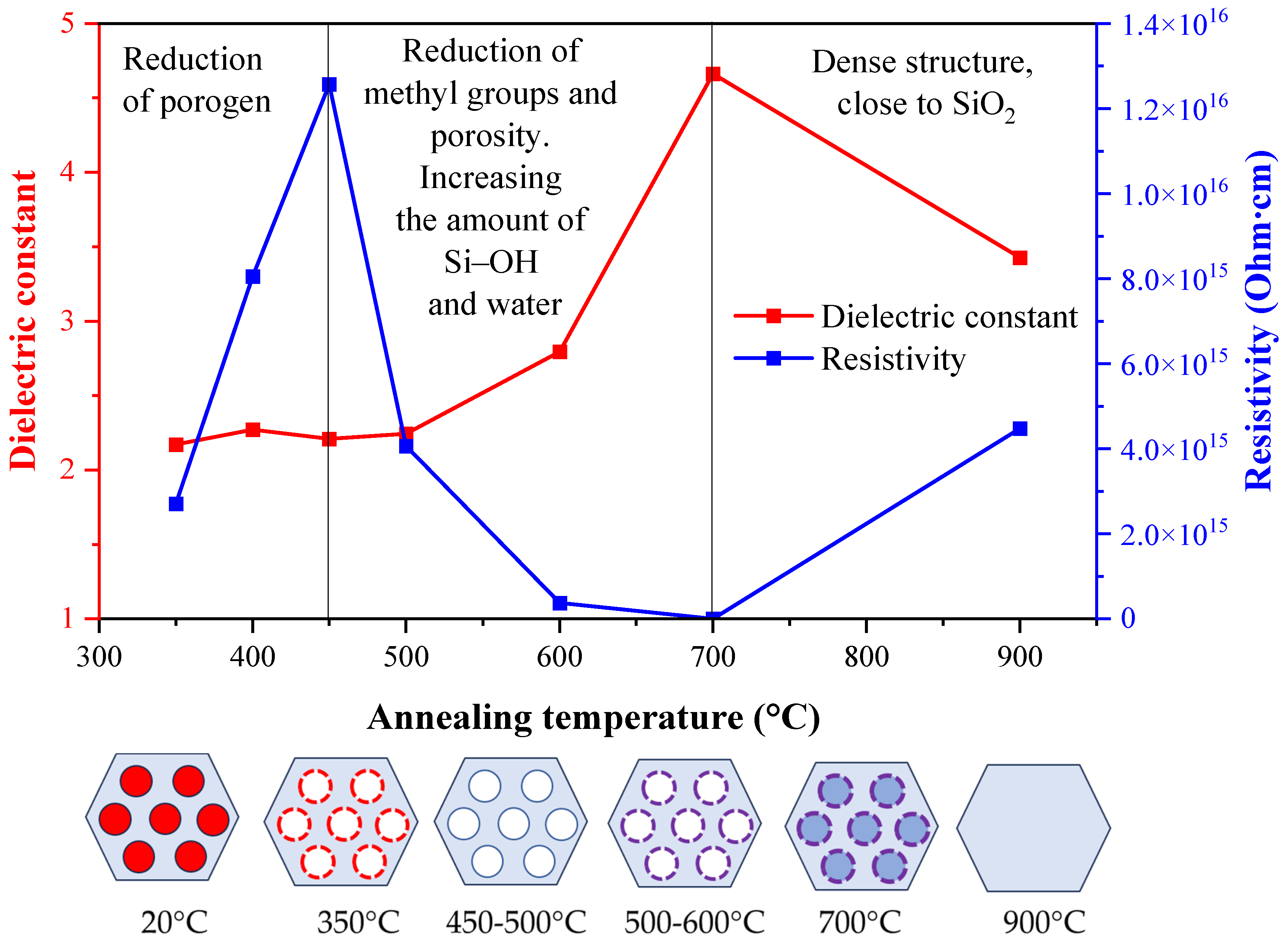
4. Conclusion
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Bohr, M.T. Interconnect scaling—the real limiter to high performance ULSI. Solid State Technol. 1996, 39, 105–111. [Google Scholar] [CrossRef]
- Havemann, R.H.; Hutchby, J.A. High-performance interconnects: An integration overview. Proc. IEEE 2001, 89, 586–601. [Google Scholar] [CrossRef]
- Moon, J.H.; Jeong, E.; Kim, S.; Kim, T.; Oh, E.; Lee, K.; Han, H.; Kim, Y.K. Materials quest for advanced interconnect metallization in integrated circuits. Adv. Sci. 2023, 10, 2207321. [Google Scholar] [CrossRef]
- Volksen, W.; Miller, R.D.; Dubois, G. Low dielectric constant materials. Chem. Rev. 2010, 110, 56–110. [Google Scholar] [CrossRef] [PubMed]
- Grill, A.; Gates, S.M.; Ryan, T.E.; Nguyen, S.V.; Priyadarshini, D. Progress in the development and understanding of advanced low k and ultralow k dielectrics for very large-scale integrated interconnects—State of the art. Appl. Phys. Rev. 2014, 1, 011306. [Google Scholar] [CrossRef]
- Michalak, D.J.; Blackwell, J.M.; Torres, J.M.; Sengupta, A.; Kreno, L.E.; Clarke, J.S.; Pantuso, D. Porosity scaling strategies for low-k films. J. Mater. Res. 2015, 30, 3363–3385. [Google Scholar] [CrossRef]
- Baklanov, M.R.; Gismatulin, A.A.; Naumov, S.; Perevalov, T.V.; Gritsenko, V.A.; Vishnevskiy, A.S.; Rakhimova, T.V.; Vorotilov, K.A. Comprehensive Review on the Impact of Chemical Composition, Plasma Treatment, and Vacuum Ultraviolet (VUV) Irradiation on the Electrical Properties of Organosilicate Films. Polymers 2024, 16, 2230. [Google Scholar] [CrossRef]
- Baklanov, M.R.; Jousseaume, V.; Rakhimova, T.V.; Lopaev, D.V.; Mankelevich, Y.A.; Afanas’ev, V.V.; Shohet, J.L.; King, S.W.; Ryan, E.T. Impact of VUV photons on SiO2 and organosilicate low-k dielectrics: General behavior, practical applications, and atomic models. Appl. Phys. Rev. 2019, 6, 011301. [Google Scholar] [CrossRef]
- Grill, A.; Neumayer, D.A. Structure of low dielectric constant to extreme low dielectric constant SiCOH films: Fourier transform infrared spectroscopy characterization. J. Appl. Phys. 2003, 94, 6697–6707. [Google Scholar] [CrossRef]
- Afanas’ev, V.V.; Keunen, K.; Stesmans, A.; Jivanescu, M.; Tőkei, Z.; Baklanov, M.R.; Beyer, G.P. Electron spin resonance study of defects in low-κ oxide insulators (κ = 2.5–2.0). Microelectron. Eng. 2011, 88, 1503–1506. [Google Scholar] [CrossRef]
- Pomorski, T.A.; Bittel, B.C.; Lenahan, P.M.; Mays, E.; Ege, C.; Bielefeld, J.; Michalak, D.; King, S.W. Defect structure and electronic properties of SiOC: H films used for back end of line dielectrics. J. Appl. Phys. 2014, 115, 234508. [Google Scholar] [CrossRef]
- King, S.W.; French, B.; Mays, E. Detection of defect states in low-k dielectrics using reflection electron energy loss spectroscopy. J. Appl. Phys. 2013, 113, 044109. [Google Scholar] [CrossRef]
- Lauer, J.L.; Sinha, H.; Nichols, M.T.; Antonelli, G.A.; Nishi, Y.; Shohet, J.L. Charge trapping within UV and vacuum UV irradiated low-k porous organosilicate dielectrics. JES 2010, 157, G177. [Google Scholar] [CrossRef]
- Liniger, E.G.; Shaw, T.M.; Cohen, S.A.; Leung, P.K.; Gates, S.M.; Bonilla, G.; Canaperi, D.F.; Rao, S.P. Processing and moisture effects on TDDB for Cu/ULK BEOL structures. Microelectron. Eng. 2012, 92, 130–133. [Google Scholar] [CrossRef]
- Lloyd, J.R.; Shaw, T.M.; Liniger, E.G. Effect of moisture on the time dependent dielectric breakdown (TDDB) behavior in an ultra-low-k (ULK) dielectric. In 2005 IEEE International Integrated Reliability Workshop, South Lake Tahoe, CA, USA, 17–20 October 2005. [Google Scholar] [CrossRef]
- Michelon, J.; Hoofman, R.J. Moisture influence on porous low-k reliability. IEEE Trans. Device Mater. Reliab. 2006, 6, 169–174. [Google Scholar] [CrossRef]
- Li, Y.; Ciofi, I.; Carbonell, L.; Heylen, N.; Van Aelst, J.; Baklanov, M.R.; Groeseneken, G.; Maex, K.; Tőkei, Z. Influence of absorbed water components on SiOCH low-k reliability. J. Appl. Phys. 2008, 104, 034113. [Google Scholar] [CrossRef]
- Cheng, Y.L.; Leon, K.W.; Huang, J.F.; Chang, W.Y.; Chang, Y.M.; Leu, J. Effect of moisture on electrical properties and reliability of low dielectric constant materials. Microelectron. Eng. 2014, 114, 12–16. [Google Scholar] [CrossRef]
- Krishtab, M.; Afanas’ev, V.; Stesmans, A.; De Gendt, S. Leakage current induced by surfactant residues in self-assembly based ultralow-k dielectric materials. Appl. Phys. Lett. 2017, 111, 032908. [Google Scholar] [CrossRef]
- Sze, S.M.; Li, Y.; Ng, K.K. Physics of Semiconductor Devices, 2nd ed.; Wiley: New York, 1981; pp. 44–60. [Google Scholar]
- Wu, C.; Li, Y.; Baklanov, M.R.; Croes, K. Electrical reliability challenges of advanced low-k dielectrics. ECS J. Solid State Sci. Technol. 2014, 4, N3065–N3070. [Google Scholar] [CrossRef]
- Nasyrov, K.A.; Gritsenko, V.A. Charge transport in dielectrics via tunneling between traps. J. Appl. Phys. 2011, 109, 097705. [Google Scholar] [CrossRef]
- Vishnevskiy, A.S.; Naumov, S.; Seregin, D.S.; Wu, Y.H.; Chuang, W.T.; Rasadujjaman, M.; Zhang, J.; Leu, J.; Vorotilov, K.A.; Baklanov, M.R. Effects of Methyl Terminal and Carbon Bridging Groups Ratio on Critical Properties of Porous Organosilicate Glass Films. Materials 2020, 13, 4484. [Google Scholar] [CrossRef] [PubMed]
- Baklanov, B.M.; Mogilnikov, K.P.; Polovinkin, V.G.; Dultsev, F.N. Determination of pore size distribution in thin films by ellipsometric porosimetry. J. Vac. Sci. Technol. 2000, 18, 1385–1391. [Google Scholar] [CrossRef]
- Iacopi, F.; Travaly, Y.; Eyckens, B.; Waldfried, C.; Abell, T.; Guyer, E.P.; Gage, D.M.; Dauskardt, R.H.; Sajavaara, T.; Houthoofd, K.; et al. Short-ranged structural rearrangement and enhancement of mechanical properties of organosilicate glasses induced by ultraviolet radiation. J. Appl. Phys. 2006, 99, 053511. [Google Scholar] [CrossRef]
- Woignier, T.; Prassas, M.; Duffours, L. Sintering of aerogels for glass synthesis, J. Sol. Gel Sci. Technol 2019, 90, 76–86. [Google Scholar] [CrossRef]
- Sawamura, K.I.; Furuhata, T.; Sekine, Y.; Kikuchi, E.; Subramanian, B.; Matsukata, M. Zeolite Membrane for Dehydration of Isopropylalcohol−Water Mixture by Vapor Permeation. ACS Appl. Mater. Interfaces 2015, 7, 13728–13730. [Google Scholar] [CrossRef] [PubMed]
- Marsik, P.; Verdonck, P.; De Roest, D.; Baklanov, M.R. Porogen residues detection in optical properties of low-k dielectrics cured by ultraviolet radiation. Thin Solid Films 2010, 518, 4266–4272. [Google Scholar] [CrossRef]
- Baklanov, M.R.; Zhao, L.; Van Besien, E.; Pantouvaki, M. Effect of porogen residue on electrical characteristics of ultra low-k materials. Microelectron. Eng. 2011, 88, 990–993. [Google Scholar] [CrossRef]
- Van Besien, E.; Pantouvaki, M.; Zhao, L.; De Roest, D.; Baklanov, M.R.; Tőkei, Z.; Beyer, G. Influence of porosity on electrical properties of low-k dielectrics. Microelectron. Eng. 2012, 92, 59–61. [Google Scholar] [CrossRef]
- Proost, J.; Baklanov, M.; Maex, K.; Delaey, L. Compensation effect during water desorption from siloxane-based spin-on dielectric thin films. J. Vac. Sci. Technol. 2000, 18, 303–306. [Google Scholar] [CrossRef]
- Lloyd, J.R.; Liniger, E.; Shaw, T.M. Simple model for time-dependent dielectric breakdown in inter-and intralevel low-k dielectrics. J. Appl. Phys. 2005, 98, 084109. [Google Scholar] [CrossRef]
- Wu, C.; Li, Y.; Barbarin, Y.; Ciofi, I.; Tang, B.; Kauerauf, T.; Croes, K.; Bommels, J.; De Wolf, I.; Tőkei, Z. Towards the understanding of intrinsic degradation and breakdown mechanisms of a SiOCH low-k dielectric. 2014 IEEE International Reliability Physics Symposium, Waikoloa, HI, USA, 01–05 June 2014; pp. 3A.2.1–3A.2.6. [Google Scholar] [CrossRef]
- Gischia, G.; Croes, K.; Groeseneken, G.; Tőkei, Zs.; Afanas’ev, V.; Zhao, L. Study of leakage mechanism and trap density in porous low-k materials. IEEE International Reliability Physics Symposium (IRPS), Anaheim, CA, USA, 02–06 May 2010; pp. 549–555. [Google Scholar] [CrossRef]
- Wu, C.; Li, Y.; Barbarin, Y.; Ciofi, I.; Croes, K.; Bömmels, J.; De Wolf, I.; Tőkei, Z. Correlation between field dependent electrical conduction and dielectric breakdown in a SiCOH based low-k (k = 2.0). Appl. Phys. Lett. 2013, 103, 032904. [Google Scholar] [CrossRef]
- Skuja, L. Optically active oxygen-deficiency-related centers in amorphous silicon dioxide. J. Non-Cryst. Solids 1998, 239, 16–48. [Google Scholar] [CrossRef]
- Salh, R. Defect Related Luminescence in Silicon Dioxide Network: A Review. In Crystalline Silicon - Properties and Uses; InTech, 2011; pp. 135–172. [Google Scholar] [CrossRef]
- Trukhin, A.; Smits, K.; Chikvaidze, G.; Dyuzheva, T.; Lityagina, L. Luminescence of silicon Dioxide—silica glass, α-quartz and stishovite. Open Phys. 2011, 9, 1106–1113. [Google Scholar] [CrossRef]
- Trukhin, A.N.; Goldberg, M.; Jansons, J.; Fitting, H.J.; Tale, I.A. Silicon dioxide thin film luminescence in comparison with bulk silica. J. Non-Cryst. Solids 1998, 223, 114–122. [Google Scholar] [CrossRef]
- Pustovarov, V.A.; Zatsepin, A.F.; Biryukov, D.Y.; Aliev, V.S.; Iskhakzay, R.K.; Gritsenko, V.A. Synchrotron-Excited Luminescence and Converting of Defects and Quantum Dots in Modified Silica Films. J. Non-Cryst. Solids 2023, 602, 122077. [Google Scholar] [CrossRef]
- Rasadujjaman, M.; Zhang, J.; Spassky, D.A.; Naumov, S.; Vishnevskiy, A.S.; Vorotilov, K.A.; Yan, J.; Zhang, J.; Baklanov, M.R. UV-Excited Luminescence in Porous Organosilica Films with Various Organic Components. Nanomaterials 2023, 13, 1419. [Google Scholar] [CrossRef]
- Sze, S.M. Current Transport and Maximum Dielectric Strength of Silicon Nitride Films. J. Appl. Phys 1965, 38, 2951–2956. [Google Scholar] [CrossRef]
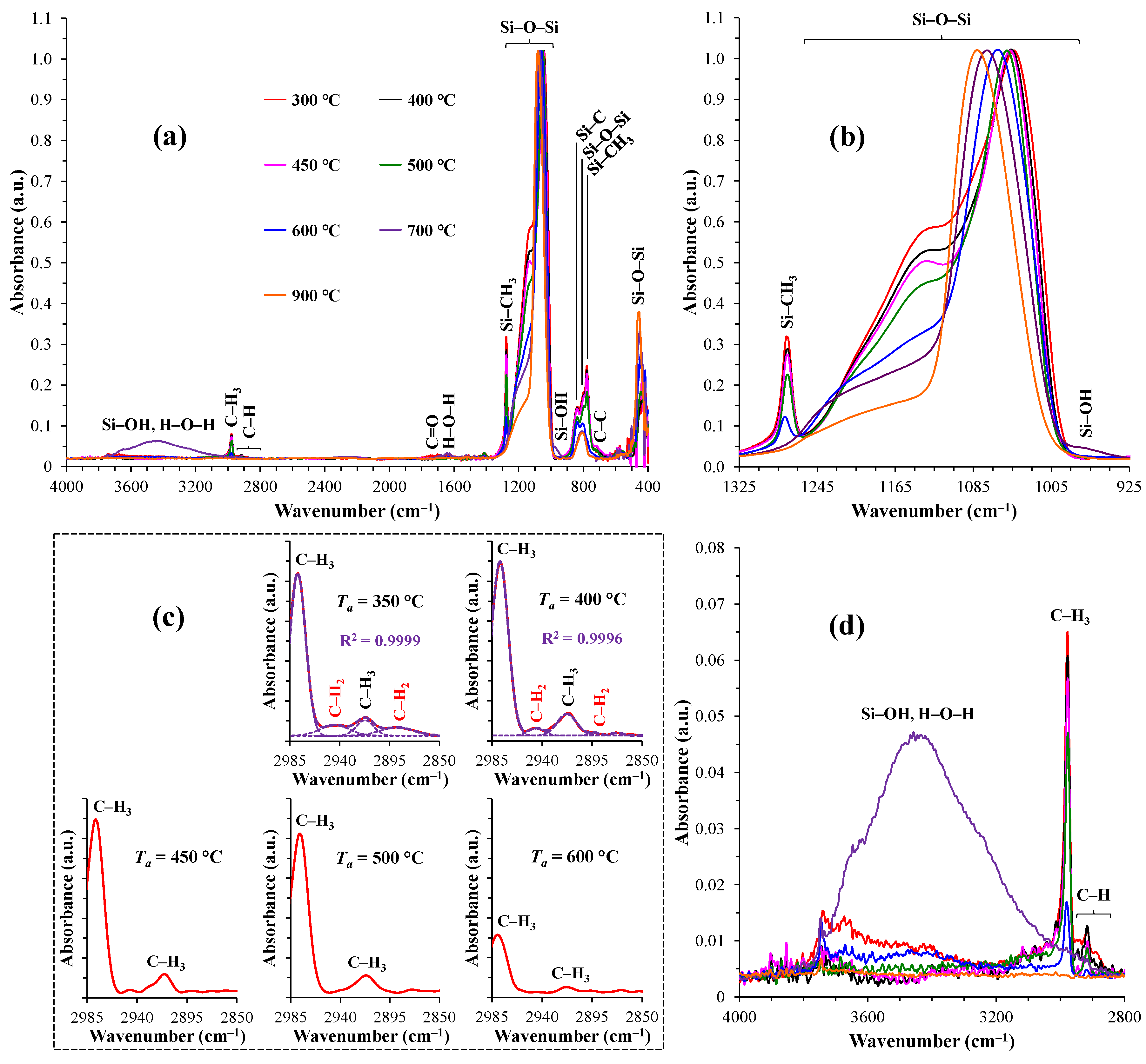
| Annealing temperature Та (°С) |
Inetwork/Icage | Relative areas of characteristic peaks/bands Si–O–Si (×1000) | ||||
|---|---|---|---|---|---|---|
| Si–OH, H–O–H |
C–H | C–H3 | Si–CH3 | Si–OH | ||
| 350 | 1.76 | 31.0 | 14.3 | 7.0 | 26.2 | 0.4 |
| 400 | 1.96 | 4.3 | 15.7 | 7.2 | 23.8 | 0.1 |
| 450 | 2.10 | 6.8 | 12.8 | 7.1 | 23.6 | – |
| 500 | 2.29 | 15.9 | 8.5 | 7.1 | 18.4 | – |
| 600 | 4.61 | 19.2 | 2.6 | 1.9 | 5.9 | – |
| 700 | 5.16 | 180.2 | – | – | – | – |
| 900 | 7.22 | 1.5 | – | – | – | – |
| Annealing temperature Ta (°С) |
Thickness d (nm) |
Shrinkage ∆d (%) |
Refractive index n |
Average radius pores 〈R〉 (nm) |
Open porosity Vopen (%) |
Relative (full) porosity VLL (%) |
Young’s modulus (GPa) |
|---|---|---|---|---|---|---|---|
| 350 | 324 | 0 | 1.248 | 1.15 | 40.9 | 43.0 | 1.9 |
| 400 | 305 | 5.9 | 1.253 | 1.37 | 38.5 | 41.7 | 2.4 |
| 450 | 301 | 7.1 | 1.257 | 1.44 | 38.0 | 41.5 | 2.6 |
| 500 | 273 | 15.7 | 1.272 | 1.51 | 33.7 | 38.0 | 3.7 |
| 600 | 233 | 28.1 | 1.280 | 1.09 | 33.4 | 35.4 | 4.6 |
| 700 | 195 | 39.8 | 1.310 | 0.40 | 28.7 | 28.2 | 11.6 |
| 900 | 170 | 47.6 | 1.392 | – | ~0 | 10.5 | – |
| Annealing temperature Ta (°С) |
Thermal energy of ionization, WT (eV) |
Optical energy of ionization, Wopt (eV) |
The traps concentration N (cm–3) |
|---|---|---|---|
| 350 | 1.6 | 3.2 | 1.0×1020 |
| 400 | 1.6 | 3.2 | 8.0×1021 |
| 450 | 1.6 | 3.2 | 5.0×1022 |
| 500 | 1.6 | 3.2 | 9.0×1019 |
| 600 | 1.2 | 2.4 | 6.0×1019 |
| 700 | 1.2 | 2.4 | 3.0×1019 |
| 900 | 1.6 | 3.2 | 3.0×1020 |
| Annealing temperature Ta (°С) |
εi | n2 | |
|---|---|---|---|
| Poole–Frenkel | Schottky | ||
| 350 | 1.5841 | 0.2556 | 1.557 |
| 400 | 1.5441 | 0.2153 | 1.571 |
| 450 | 1.4096 | 1.6837 | 1.581 |
| 500 | 1.7293 | 0.0711 | 1.617 |
| 600 | 1.5311 | 0.0973 | 1.639 |
| 700 | 1.6689 | 0.1745 | 1.717 |
| 900 | 1.9316 | 0.5017 | 1.937 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





