Newton's Law of Gravity Is Valid Only When Gravitational Lensing Has a Negligible Impact

1. Introduction

The long-standing puzzle of galaxy rotation has intrigued astronomers and physicists for decades[1,2]. Specifically, the observed rotational velocities of galaxies do not align with predictions based on Newtonian dynamics[3]. In spiral galaxies, particularly at greater distances from their centers, the observed rotation speeds are significantly higher than those predicted by classical mechanics. According to Newton’s law of gravitation, these rotational speeds should decrease with increasing distance from the galactic center. However, observations show that these velocities remain relatively constant or even increase. This discrepancy has led to extensive research, with two main explanations emerging.

The first explanation suggests that Newtonian mechanics holds but that an unseen form of matter, known as dark matter[4,5], exists within galaxies. Dark matter does not emit light or energy, rendering it undetectable by conventional methods, but its mass is hypothesized to provide the additional gravitational pull required to explain the higher rotation speeds. The existence of dark matter would thus reconcile the observed velocities with predictions based on gravitational theory.

The second explanation proposes that the laws of gravity themselves may differ on large, cosmic scales. This theory, known as Modified Newtonian Dynamics (MOND)[6,7], suggests that Newton’s law of gravitation is valid only under certain conditions and that gravity weakens less rapidly with distance than Newton’s inverse-square law predicts. MOND offers an alternative framework that negates the need for dark matter, though this remains a contentious topic within the scientific community.

Adding further complexity, recent observations have shown that certain galaxies exhibit rotational behavior consistent with Newtonian predictions[8]. This finding deepens the debate between dark matter advocates and proponents of modified gravity. The fact that some galaxies conform to Newtonian dynamics while others do not suggests that additional factors, possibly linked to the scale or structure of galaxies, may influence gravitational behavior on a cosmic scale.

Our study begins by revisiting the fundamental nature of gravitational forces when gravitational lensing[9,10] is negligible. Consider two spherically symmetric objects, denoted as a and b, with uniformly distributed mass in space. According to Newton’s law of gravitation, the gravitational attraction between these two objects arises from the interaction of their respective gravitational fields. In this context, gravitons—the hypothetical energy particles that mediate gravitational forces—act as the carriers of gravitational energy.

In the absence of other objects, the gravitons surrounding object a are uniformly directed toward its center, maintaining the equilibrium of its gravitational field. In this state, no net force acts on object a, as the forces exerted by its field cancel out. However, when both objects a and b are present in the same region of space, each begins to absorb gravitons from the other’s gravitational field. When object a absorbs gravitons from object b, it experiences a force $F_{ab}$, directed toward object b. Similarly, object b absorbs gravitons from the field of object a, resulting in a corresponding force $F_{ba}$, also directed toward object b.

Gravitons, as carriers of energy, are influenced by gravitational forces. According to Einstein’s general theory of relativity[11], the path of photons is deflected by gravitational lensing. In a similar manner, gravitons are also subject to gravitational lensing, particularly in the presence of massive objects. However, in Newton’s analysis of gravitational forces within the solar system—such as in experiments[12] measuring gravitational attraction between smaller objects—the effect of gravitational lensing was negligible due to the relatively low mass of the objects involved. In these cases, the influence of gravitational lensing on gravitons can be ignored, and Newton’s law of gravitation holds.

When analyzing galactic rotation, however, the gravitational lensing effect caused by massive black holes[13] at the centers of galaxies becomes significant due to the enormous mass of these black holes and the cosmic scale of the galaxies. Gravitons, which carry gravitational energy, experience notable deflection over such large distances. Consider a system consisting of a small-mass object a and a massive black hole b. As object a absorbs gravitons from the gravitational field of black hole b, it experiences a force $F_{ab}$ , directed toward b.

Moreover, due to gravitational lensing, object a loses gravitons from its own gravitational field, both through direct absorption by black hole b and through deflection caused by b’s gravitational lensing effect. Some of these deflected gravitons are not directed back toward object a, further disrupting the equilibrium of its gravitational field. This imbalance—where the force on object a becomes larger than that on b—is amplified by the gravitational lensing effect, even though the forces remain opposite in direction.

From this analysis, we conclude that Newton’s law of gravitation is an approximation that holds only when gravitational lensing is negligible. In cases where gravitational lensing has a significant effect, the actual gravitational force on an object exceeds the value predicted by Newton’s law. Specifically, the lensing effect caused by massive objects, such as Massive black holes at the centre of galaxies, leads to a stronger gravitational force than Newtonian mechanics would suggest. This phenomenon helps explain the discrepancy between the predicted and observed rotational velocities of galaxies, where Newtonian models underestimate these velocities.

In conclusion, our analysis of the gravitational effects of lensing offers a fresh theoretical approach to understanding galactic rotation. This framework provides a more detailed explanation of the influence of gravitational lensing from the central black hole on surrounding objects, highlighting the discrepancy between the actual gravitational force and the predictions made by Newton’s gravitational law. Our findings lay a solid foundation for future research into the role of gravitational lensing in large-scale cosmic systems. Given the prevalence of supermassive black holes at the centers of galaxies and the vast number of stars within them, a deeper comprehension of how lensing affects galactic dynamics is essential to addressing the ongoing challenge of galaxy rotation.

2. Method

Based on Einstein’s mass-energy equation, $E=m{c}^2$, all matter in the universe can be understood as forms of energy. This includes both the energy of particles traveling at the speed of light, such as photons, and the energy within objects that possess rest mass, like elementary particles that constitute matter. According to the law of gravity, any object with mass generates a gravitational field. To quantify the strength of this gravitational field for objects of different masses, we define the total energy $E_g$ of gravitons absorbed per unit time by the gravitational field of an object with mass m. This energy is given by the following expression, where $\lambda \left(m\right)$ is a function dependent on m:

$$E_g=\lambda \left(m\right)m{c}^2$$

(1)

Building on this, the strength of the gravitational field $E_g^r$ at a distance r from the gravitational source is given by the following equation:

$$E_g^r={\displaystyle \frac{\lambda \left(m\right)m{c}^2}{4\pi r^2}}$$

(2)

We begin by examining the generation of gravitational force in the scenario where the effect of gravitational lensing can be neglected. In this case, we focus on two spherically symmetric masses, object a and object b, that are uniformly distributed in space. According to the law of gravitation, the gravitational force between these two objects arises from the presence of their respective gravitational fields. These fields are composed of energy carriers known as gravitons.

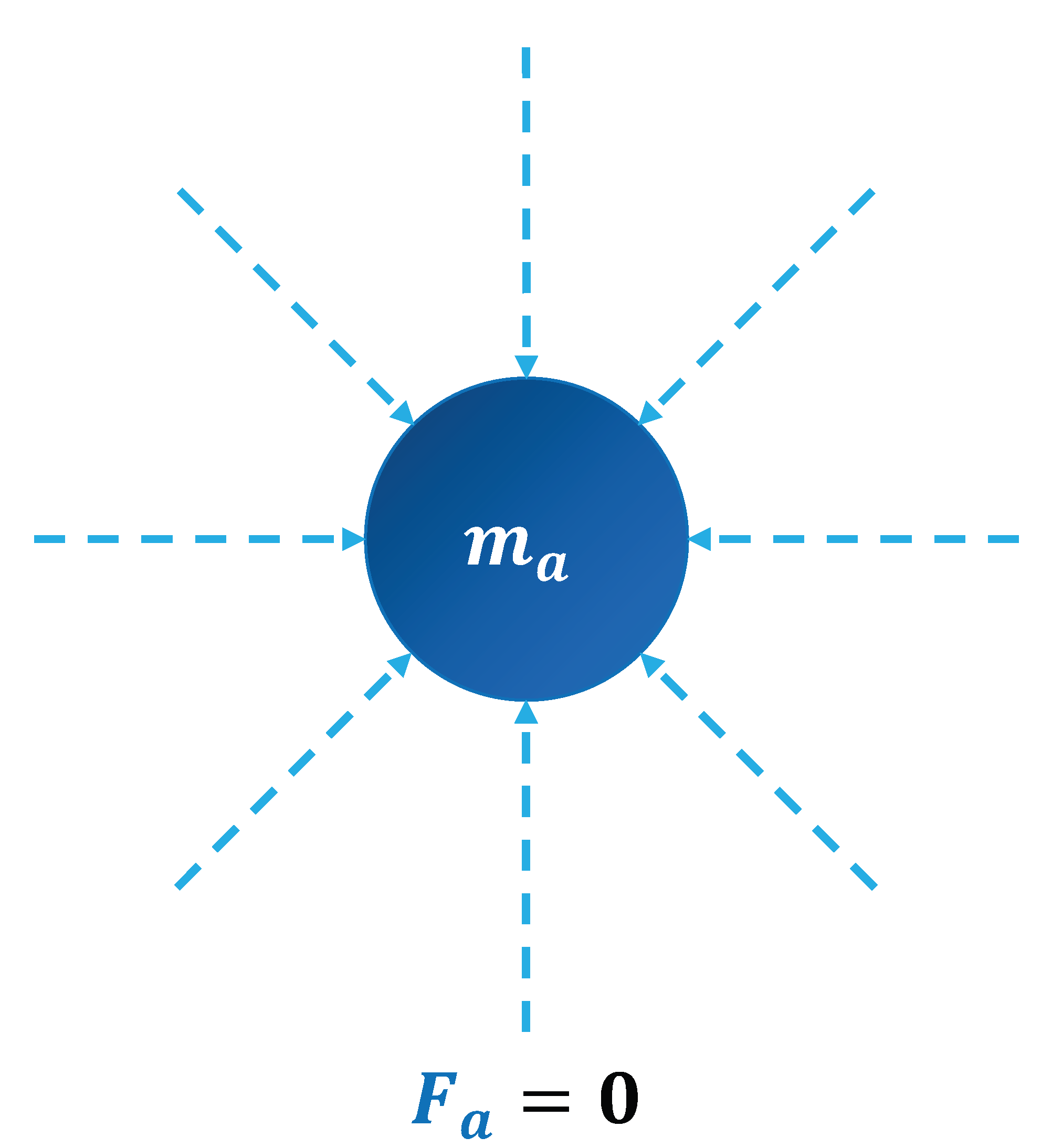
To simplify the analysis, we first consider a single object a in isolation, as shown in Figure 1. Since there are no other objects to interact with, all gravitons in the gravitational field of object a are directed toward the center of the field. In this state, object a remains in equilibrium, experiencing no net force from its own gravitational field.

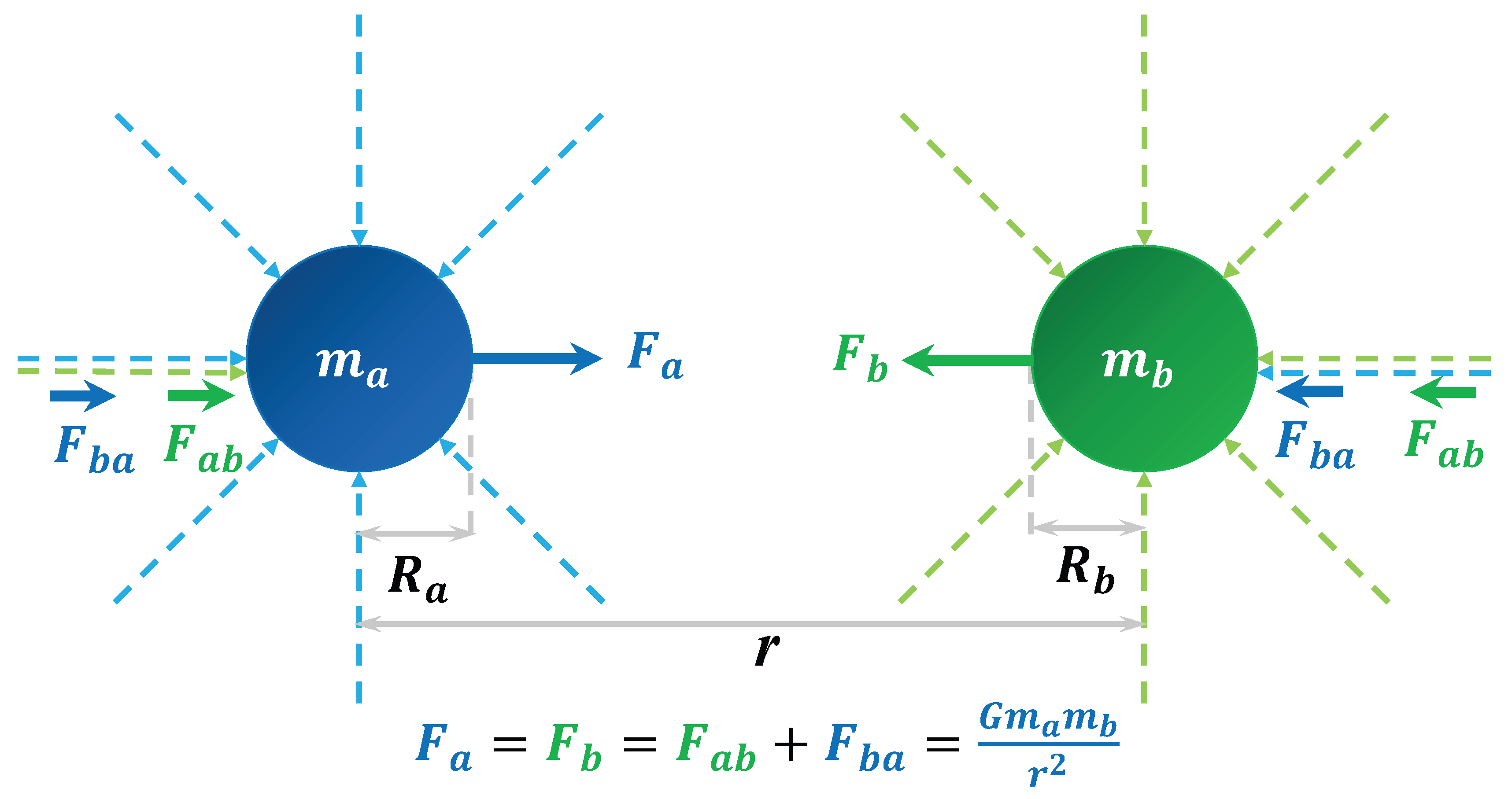
Now, consider the case where both object a and object b exist in the same space, as shown in Figure 2. Due to their interaction, object a absorbs gravitons from the gravitational field of object b, resulting in a force $F_{ab}$ directed towards object b. Simultaneously, object b absorbs gravitons from the gravitational field of object a, causing object a’s original equilibrium to be disturbed. This leads to a second force, $F_{ba}$, acting on object a, which is also directed towards object b. It is important to note that, in the absence of spacetime curvature effects, the force $F_{ba}$ arises only after the gravitons absorbed by object b take a time interval of $r/c$ to act on object a, where r is the distance between the two objects and c is the speed of light. In summary, the gravitational interaction between two objects is the result of the superposition of two forces: $F_{ab}$ and $F_{ba}$, which are equal in magnitude and opposite in direction.

We define the total energy of the gravitons absorbed by object a from the gravitational field of object b as $E_{ab}$, and similarly, the energy absorbed by object b from the field of object a as $E_{ba}$. Assuming that $r\gg R_a$ and $R_b$, where $R_a$ and $R_b$ are the radii of the two objects, we can approximate that the absorbed gravitons pass through the objects in parallel. Under this condition, the forces $F_{ab}$ and $F_{ba}$ satisfy the following expression:

$$F_{ab}={\displaystyle \frac{E_{ab}}{c}}$$

(3)

$$F_{ba}={\displaystyle \frac{E_{ba}}{c}}$$

(4)

Gravitons possess a certain degree of penetrating power. For example, even when a satellite orbiting Earth is blocked by the planet, the satellite’s timing is still influenced by the Sun’s gravitational force. To quantify this penetrating power, we introduce a variable, $\gamma$, which measures the penetrating force of gravitons. The unit of $\gamma$ is ${\mathrm{m}}^2{\mathrm{kg}}^{-1}$. For each object, there is a parameter $\beta$, which depends on the object’s radius R, density $\rho$, and mass m. The value of $\beta$ satisfies the following equation:

$$\beta =2R\rho \gamma$$

(5)

For any object a, ${\beta }_a>0$. When ${\beta }_a\le 1$, the graviton can penetrate the maximum thickness of object a. However, the penetrating power of gravitons has an upper limit. When ${\beta }_a>1$, the graviton cannot penetrate the maximum thickness of object a, and only a portion of object a can absorb gravitons from the gravitational field. It is well understood that photons cannot penetrate black holes, meaning that any photon entering the Schwarzschild radius of a black hole is completely absorbed. Since gravitons also carry energy, they are assumed to behave similarly and cannot penetrate a black hole.

To analyze the gravitational force on object a, we first consider the partial force $F_{ab}$ directed towards object b, which results from object a absorbing gravitons from the gravitational field of object b. The total energy of gravitons, $E_{ab}$, absorbed by object a depends on whether ${\beta }_a$ is greater than 1 or not. We consider two cases:

Case 1: When ${\beta }_a\le 1$

In this case, the graviton can penetrate the maximum thickness of object a. Consequently, the mass at all positions within object a will absorb gravitons from object b’s gravitational field, which are parallel to the gravitons incident on object a. The total absorbed energy $E_{ab}$ satisfies the following equation:

$$E_{ab}={\displaystyle \frac{\lambda \left(m_b\right)m_b{c}^2\gamma m_a}{4\pi r^2}}$$

(6)

Case 2: When ${\beta }_a>1$ and object a is not a black hole

Here, the graviton cannot penetrate the maximum thickness of object a. Only a portion of object a can absorb gravitons from object b’s gravitational field, which are parallel to the gravitons incident on object a. The energy $E_{ab}$ absorbed in this scenario satisfies the following equation:

$$E_{ab}={\displaystyle \frac{\lambda \left(m_b\right)m_b{c}^2}{4\pi r^2}}\left[\pi R_a^2\left(1-{\displaystyle \frac{1}{{\beta }_a^2}}\right)+{\displaystyle \frac{\gamma m_a}{{\beta }_a^3}}\right]$$

(7)

Case 3: When object a is a Schwarzschild black hole

In this case, gravitons cannot penetrate any part of the Schwarzschild black hole. All gravitons from the gravitational field of object b, which are parallel and incident within the Schwarzschild radius $R_a^s$ of the black hole a, are fully absorbed by object a. The energy $E_{ab}$ absorbed in this case satisfies the following equation:

$$E_{ab}={\displaystyle \frac{\lambda \left(m_b\right)m_b{c}^2\pi {R_a^s}^2}{4\pi r^2}}$$

(8)

In analyzing the loss of gravitons in the gravitational field of object a due to the influence of object b, we observe a disruption in the equilibrium of object a’s gravitational field. This disruption introduces an additional force component on object a directed toward object b, denoted as $F_a^{loss}$. We must consider whether to account for the gravitational lensing effect caused by object b and its impact on the graviton loss in object a’s field. The total energy of gravitons lost from object a’s gravitational field is defined as $E_a^{\mathrm{loss}}$.

2.1. When Gravitational Lensing Effects can be Neglected

In cases where the gravitational lensing effect of object b is negligible, the total energy loss of gravitons in the gravitational field of object a, denoted $E_a^{loss}$, is equal to the total energy of gravitons absorbed by object b from the gravitational field of object a, denoted $E_{ba}$. The energy $E_{ba}$ follows the same law as the previously described $E_{ab}$.

$$E_a^{loss}=E_{ba}$$

(9)

For ${\beta }_b\le 1$, gravitons can penetrate object b at its maximum thickness. Thus, all mass within object b absorbs gravitons from the gravitational field of object a, parallel to the incident gravitons. In this case, $E_{ba}$ satisfies the following relation:

$$E_{ba}={\displaystyle \frac{\lambda \left(m_a\right)m_a{c}^2\gamma m_b}{4\pi r^2}}$$

(10)

For ${\beta }_b>1$, in a non-black hole scenario, gravitons cannot penetrate the maximum thickness of object b. Consequently, only part of object b can absorb the gravitons from object a’s gravitational field. In this case, $E_{ba}$ follows this expression:

$$E_{ba}={\displaystyle \frac{\lambda \left(m_a\right)m_a{c}^2}{4\pi r^2}}\left\{\pi R_a^2\left(1-{\displaystyle \frac{1}{{\beta }_a^2}}\right)+{\displaystyle \frac{\gamma m_a}{{\beta }_a^3}}\right\}$$

(11)

Given that r is significantly larger than both $R_a$ and $R_b$, we can assume that the graviton is absorbed by the object while maintaining alignment with the direction of the line connecting the two objects. Under these conditions, the gravitational force $F_a$ acting on object a is described by the following expression:

$$F_a={\displaystyle \frac{E_{ab}+E_{ba}}{c}}$$

(12)

In cases where both ${\beta }_a$ and ${\beta }_b$ are less than 1, the force $F_a$ conforms to the following relationship:

$$F_a={\displaystyle \frac{(\lambda \left(m_a\right)+\lambda \left(m_b\right))\gamma m_a{m}_{b}c}{4\pi r^2}}={\displaystyle \frac{G{m}_a{m}_b}{r^2}}$$

(13)

From the equation above, it can be observed that the gravitational force acting on object a follows Newton’s law of universal gravitation,when ignoring the additional graviton loss due to object b’s gravitational lensing effect.

Furthermore, given that the gravitational forces between objects of different masses m within the solar system consistently align with Newton’s law, we can assume that $\lambda \left(m\right)$ is a constant independent of the mass of the objects involved. Thus, $\lambda \left(m\right)=\lambda$. Under these conditions, Newton’s law of universal gravitation is expressed by the following equation:

$$F_{Newton}={\displaystyle \frac{G{m}_a{m}_b}{r^2}}={\displaystyle \frac{\lambda \gamma m_a{m}_{b}c}{2\pi r^2}}$$

(14)

2.2. When Gravitational Lensing Effects cannot be Neglected

When the gravitational lensing effect from object b, which is considered a massive Swashian black hole at the center of the galaxy, causes significant additional graviton loss in the gravitational field of object a (denoted as $E_b^{lens}$), the total energy of gravitons lost in object a’s gravitational field, $E_a^{loss}$, becomes greater than the total energy absorbed by object b, $E_{ba}$. Thus, the energy loss $E_a^{loss}$ in the gravitational field of object a exceeds the gravitons absorbed by object b. This graviton loss is described by the following expression:

$$E_a^{loss}=E_b^{lens}+E_{ba}>E_{ba}$$

(15)

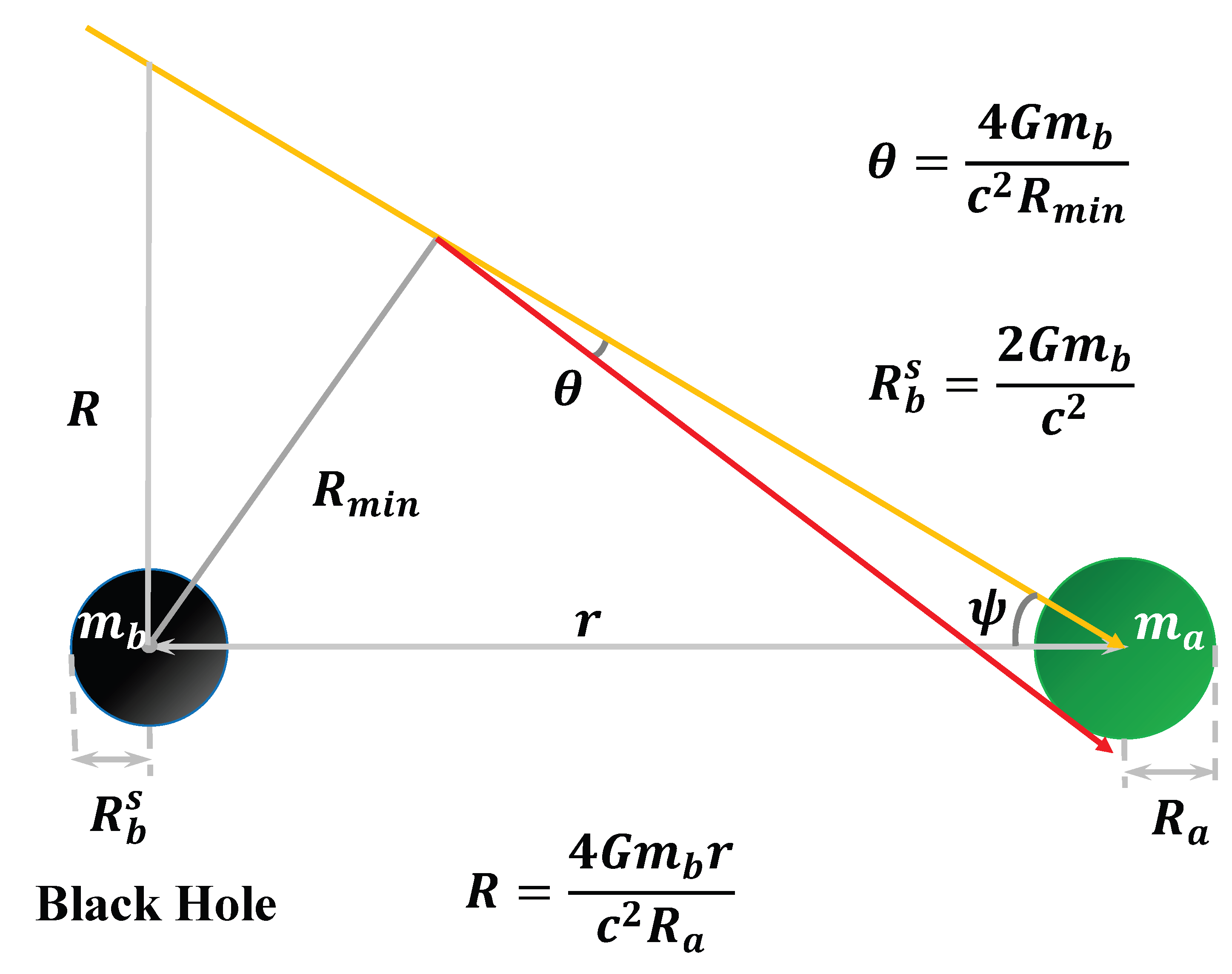
Under the influence of object b’s gravitational lens, as shown in Figure 3,the graviton propagation direction is deflected at a galactic scale. The deflection angle $\theta$ is given by:

$$\theta ={\displaystyle \frac{4G{m}_b}{c^2{R}_{min}}}$$

(16)

Where $R_{min}$ represents the shortest distance to the center of object b during the propagation of gravitons, influenced by the gravitational lensing effect of object b. In this analysis, the distance r refers to the galactic scale, meaning that the distance between object a and the black hole b is very large, with r being significantly greater than both $R_a$ and $R_b^s$. Since gravitons propagate at the speed of light, the angle $\theta$ becomes very small, allowing the approximation $sin\left(\theta \right)\approx \theta$. Under this approximation, the path of the graviton can be considered a hyperbolic curve with high curvature. Therefore, we can assume that $R_{min}$ is approximately equal to the distance from object b to the yellow line. It is important to note that the conclusions drawn from this analysis are not directly applicable when object a is relatively close to the black hole. $R_{min}$ satisfies the following relation:

$$R_a={\displaystyle \frac{r\theta R_{min}}{R}}$$

(17)

Then R and $\psi$ satisfies the following expression:

$$R={\displaystyle \frac{4G{m}_{b}r}{c^2{R}_a}}={\displaystyle \frac{2R_b^{s}r}{R_a}}$$

(18)

$$cos\left(\psi \right)={\displaystyle \frac{r}{\sqrt{R^2+r^2}}}={\displaystyle \frac{1}{\sqrt{{\left(\frac{2R_b^s}{R_a}\right)}^2+1}}}$$

(19)

The total energy $E_a^{\mathrm{loss}}$, accounting for gravitons lost at an angle $\psi$, satisfies the following relationship:

$$E_a^{loss}={\int }_0^{\psi }{\displaystyle \frac{\lambda m_a{c}^2}{4\pi R_a^2}}2\pi R_{a}sin\left(\theta \right)R_{a}d\theta ={\displaystyle \frac{\lambda m_a{c}^2}{2}}\left[1-{\displaystyle \frac{1}{\sqrt{1+{\left(\frac{2R_s}{R_a}\right)}^2}}}\right]$$

(20)

$E_a^{loss}$ includes the energy $E_{ba}$ directly absorbed by the Swahili black hole b:

$$E_{ba}={\displaystyle \frac{\lambda m_a{c}^2\pi {R_b^s}^2}{4\pi r^2}}$$

(21)

The additional energy loss due to gravitational lensing by the Swahili black hole b, denoted as $E_b^{\mathrm{lens}}$, is expressed as:

$$E_b^{lens}=E_a^{loss}-E_{ba}={\displaystyle \frac{\lambda m_a{c}^2}{2}}\left[1-{\displaystyle \frac{1}{\sqrt{1+{\left(\frac{2R_s}{R_a}\right)}^2}}}\right]-{\displaystyle \frac{\lambda m_a{c}^2\pi {R_b^s}^2}{4\pi r^2}}$$

(22)

where $E_b^{\mathrm{lens}}>0$.

Since there is an angle between the direction of the graviton lost by object a and the line connecting a and b, it can no longer be assumed that the graviton remains parallel to the connecting line. Consequently, the force $F_a^{\mathrm{loss}}$ on object a, due to the energy loss $E_a^{\mathrm{loss}}$, satisfies the following expression:

$$F_a^{loss}={\int }_0^{\psi }{\displaystyle \frac{\lambda m_{a}c}{4\pi R_a^2}}cos\left(\theta \right)2\pi R_{a}sin\left(\theta \right)R_{a}d\theta ={\displaystyle \frac{\lambda m_{a}c{\left(\frac{R_b^s}{R_a}\right)}^2}{1+{\left(\frac{2R_b^s}{R_a}\right)}^2}}>F_{ba}$$

(23)

$$F_{ba}={\displaystyle \frac{\lambda m_{a}c\pi {R_b^s}^2}{4\pi r^2}}$$

(24)

It is evident that, under the gravitational lensing effect of the Swahili black hole b, the fractional force $F_a^{loss}$ on object a becomes independent of r at galactic scales. When ${\beta }_a\le 1$, the total gravitational force $F_a$ acting on object a is expressed as:

$$F_a=F_{ab}+F_a^{loss}={\displaystyle \frac{\lambda m_b\gamma m_{a}c}{4\pi r^2}}+{\displaystyle \frac{\lambda m_{a}c{\left(\frac{R_b^s}{R_a}\right)}^2}{1+4{\left(\frac{R_b^s}{R_a}\right)}^2}}={\displaystyle \frac{F_{Newton}}{2}}+{\displaystyle \frac{\lambda m_{a}c{\left(\frac{R_b^s}{R_a}\right)}^2}{1+4{\left(\frac{R_b^s}{R_a}\right)}^2}}$$

(25)

For sufficiently large values of r (i.e., when $r\gg R_b^s$ and $R_a$), the force $F_b$ on the Swahili black hole b satisfies the following equation:

$$F_b=F_{ab}+F_{ba}={\displaystyle \frac{\left[\lambda m_b\gamma +\lambda \pi {R_b^s}^2\right]m_{a}c}{4\pi r^2}}={\displaystyle \frac{F_{Newton}}{2}}\left(1+{\displaystyle \frac{\pi {R_s^b}^2}{\gamma m_b}}\right)<F_a$$

(26)

$$F_a-F_{Newton}={\displaystyle \frac{\lambda m_{a}c{\left(\frac{R_b^s}{R_a}\right)}^2}{1+4{\left(\frac{R_b^s}{R_a}\right)}^2}}-{\displaystyle \frac{\lambda m_b\gamma m_{a}c}{4\pi r^2}}$$

(27)

Based on the analysis above, it is clear that the gravitational force on object a does not follow Newton’s formula for universal gravitation when the gravitational lensing effect from object b results in a significant loss of gravitons in the gravitational field of object a. At galactic scales, the gravitational force on object a deviates from Newton’s predictions $F_{Newton}$ , and the discrepancy increases with the distance between the two objects.

It is worth noting that our analysis begins with the assumption that there are lonly two objects in space: object a with ${\beta }_a<1$ and object b, which has a massive black hole at the center of the galaxy. There exist some gravitons in the gravitational field of object a, which are deflected by the gravitational lensing effect of black hole b, do not propagate to object a. However, these gravitons are not lost; they continue to propagate in the direction established by their deflection. When examining the rotation of a galaxy with many objects, it is crucial to account for how these deflected gravitons, which continue to travel through space, influence the gravitational force on other objects. Consequently, gravitational formulae derived for scenarios involving only two objects are insufficient for analyzing the complex gravitational interactions in a galaxy. A more comprehensive analysis is needed to address the intricate effects of many objects and the central black hole’s gravitational lensing on galactic rotation.

3. Conclusions

Our analysis highlights the critical role of gravitational lensing in explaining the discrepancies observed in galactic rotation. Newton’s law of gravitation, while effective in many cases, is shown to be an approximation that holds only when the effects of gravitational lensing are negligible. When lensing effects caused by massive objects, such as Massive black holes at the centre of galaxies, are significant, the actual gravitational force exerted on objects exceeds the predictions made by Newton’s inverse-square law. This insight provides a compelling explanation for the higher-than-expected rotational velocities of galaxies, where Newtonian dynamics underestimates these velocities. This framework not only challenges the conventional reliance on dark matter but also offers a refined understanding of gravitational forces at galactic scales. Further research into the effects of gravitational lensing will be crucial for advancing our understanding of cosmic dynamics and refining gravitational models at large scales.