Principles of Integration Science Its Content, Methods, and Significance

Preprint

Article

Principles of Integration Science Its Content, Methods, and Significance

Altmetrics

Downloads

Views

Comments

Yingrui Yang^*

This version is not peer-reviewed

Submitted:

26 September 2024

Posted:

27 September 2024

You are already at the latest version

Alerts

Abstract

Interdisciplinary research consists of many levels and pathways. One research level that has emerged since the early 21st century is called integration science. Specifically, we focus on a research pathway that structurally integrates social sciences with theoretical physics from perspectives of dynamic analysis. Building on nearly 20 years of prior work, this paper proposes a basic theory of integration science, laying the theoretical foundation for its subsequent development. The significance of integration science operates on three levels. First, identifying structural connections between different disciplines helps in our holistic understanding of natural and social phenomena. Second, generally speaking, the current level of conceptualization and modeling in natural sciences, especially physics, is ahead of social sciences. Integration science research can help elevate the level of conceptualization and modeling in social sciences. Third, the structural similarity across different disciplines reflects the shared thinking of scientists from various fields. Integration science is not simply a synthesis of knowledge from different disciplines. The standard of integration science is to enable social sciences and natural sciences to share the same mathematical structures, thereby possessing a unified mathematical language for description. The empirical basis of integration science is discussed, proposing a unified theory of interdisciplinary scientific observation. This includes concepts like the directionality of scientific observation and the orthogonal principle, the concept of observational disturbance and the diagonal law, defining low and high disturbance quadrants, and discussing why different disturbance quadrants follow their respective mathematical paths. The basic theory of integration science is proposed. The application of category theory in integration science is introduced, along with the necessary semantic supplements. The fundamental concepts of integration mathematics are proposed, defining concepts like integration points, lines, plans, and bulks, and discussing their algebraic and functional analysis methods, thereby laying the mathematical foundation for the integration science. The structural force hypothesis is proposed, along with an axiomatic system of structural forces, thereby laying the philosophical foundation for integrative science. Based on prior work, specific cases of integrative points, lines, plans, and bulks are provided.

Keywords:

Subject: Social Sciences - Cognitive Science

1. Introduction

Since the latter half of the 20th century, interdisciplinary research has been thriving. This type of research encompasses various levels and approaches. This paper aims to focus on one specific area of research that has emerged since the early 21st century, known as integrative science. Specifically, this paper addresses a research approach that structurally integrates social sciences and theoretical physics within a dynamical context. This approach is deeply rooted in the Bourbaki structuralist tradition. In this tradition, Douglas Hofstadter [1] and Roger Penrose [2] are considered the most prominent figures in the last 30 years.

Social sciences and natural sciences have traditionally been studied separately, with clear boundaries between them. So how can they be integrated? Integration does not mean, nor is it possible, to turn social sciences like economics or psychology into natural sciences like physics, nor vice versa. The meaning of integration science operates on three levels. First, finding structural connections between different disciplines helps us understand natural and social phenomena in a holistic manner. Second, generally speaking, the level of conceptualization and modeling in current natural sciences, particularly physics, is ahead of social sciences. Integrative science research can help elevate the conceptualization and modeling levels of social sciences. Third, the structural similarities between different disciplines reflect the intellectual commonalities among scientists in these fields. Therefore, integrative science is an upgraded version of cognitive science and serves as a foundational path for interdisciplinary research. Integration science is not a simple amalgamation of knowledge from different disciplines. Discovering structural connections between different fields often involves complex conceptual abstraction and structured development. The standard for integration science is to allow social sciences and natural sciences to share the same mathematical structures, thereby enabling a unified mathematical language. This goal reflects the essence and vitality of scientific life. It is not only an appreciation of the beauty of mathematics but also a bridging of scientific domains and, more importantly, a pursuit of scientific truth.

The rest of this paper is structured as follows: Section 2, titled "Principles of Scientific Observation," discusses the directionality and the orthogonality principle of scientific observations, observational disturbance levels, the diagonal rule, low and high disturbance zones, and two different mathematical paths. Section 3, titled "Mathematical Foundations of Integration Theory," covers category theory, integrative argument mathematics (defining concepts such as integrative points, lines, surfaces, and bodies / bulks), and the defense of the structural force hypothesis. Section 4, Section 5, Section 6 and Section 7 present case studies on integrative points, lines, surfaces, and bulks, respectively. This part involves three interrelated standard models: the Standard Model of particle physics, the Standard Model of economic dynamics, and the Standard Model of cognitive dynamics. Section 8 provides a general discussion. It is worth emphasizing that Section 3.2 and Section 3.3, which cover the meta-mathematical foundations of the integration theory and the structural force hypothesis, are the technical core of this paper.

The narrative design of this paper aims to be as self-contained as possible. The physics concepts mentioned mainly pertain to quantum field theory. General readers do not need to be overly concerned with these concepts. This paper briefly reviews the context of integrative science presented in several of my previous papers (see references). These papers explain the relevant physics concepts. Readers interested in a deeper understanding of these concepts can refer to the book by Zhengxing Wang [3] or a more comprehensive work by Tony Zee [4].

2. Principles of Scientific Observation

2.1. Directionality and Orthogonality Principle of Scientific Observation

Economics, psychology, and physics fundamentally belong to empirical sciences. Theories in empirical sciences are, and can only be, hypothetical, termed scientific hypotheses, because scientists can only observe samples and not the entire population. Scientific hypotheses require experimental support, making scientific observation indispensable. In this sense, the language of empirical science is statistics, and its methodology is inductive.

In physics, the observer, as the subject of observation, observes the external physical world. The term "external" suggests an inherent sense of directionality in scientific observation. Conceptually abstracting this, we can refer to it as outward observation. In psychology and cognitive science, the observer observes the internal mental world, referred to as inward observation. In economics, empirical research relies on data. Data provided in the public domain are obtained from statistical analyses of past economic phenomena. Data collected in laboratories come from post-experimental statistical analysis. In short, various data reflect the observation of history, termed backward observation. It is well-known that economists are never satisfied with just speaking about history; economics has a need and impulse to make predictions about the future. Extending the observational telescope into the future is called forward observation.

Faced with these directional observations, we can further abstract and establish the concept of the "directionality" of scientific observation. We see that observations in different empirical disciplines have different directions, yet these different kinds of scientific observations ultimately converge under the concept of directionality. But what is the significance of this convergence? The first thing we can do is "orthogonalize" these different scientific observation directions. In mathematical language, this is called trivialization. Orthogonalization can be characterized by a function: generally, two directions that are the same are assigned a value of 1, and different ones are assigned a value of 0. Clearly, mutually perpendicular directions are a special case of orthogonalization. The formula for this is:

Now, let's use a bit of imagination. First, draw a horizontal axis to represent the mental world, which corresponds to inward observation. Next, draw a vertical axis to represent the physical world, which corresponds to outward observation. Then, draw a diagonal axis from the lower left through the origin to the upper right, representing the economic world, with forward observation slanting upward and backward, see Figure 1 below.

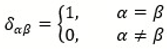
2.2. Observation Interference and the Diagonal Rule

Please focus on the orthogonal framework in Figure 1 above. As is customary, this framework is divided into four quadrants, with the upper right being the first quadrant, and the lower left being the third quadrant, following a counterclockwise order. Now, in Figure 2 below, start by marking quantum mechanics at the top of the vertical physical axis, and Newtonian mechanics at the bottom, passing through the origin. Next, mark higher-order cognition at the right end of the mental horizontal axis, and lower-order cognition at the left end. Additionally, on the economic diagonal axis passing through the origin, mark forward observation at the upper right end, and backward observation at the lower left end. In this virtual diagram, quantum mechanics, higher-order cognition, and economic forward observation are concentrated in the first quadrant, while Newtonian mechanics, lower-order cognition, and economic backward observation are concentrated in the third quadrant. The first and third quadrants are diagonally opposite, which is known as the Diagonal Rule. This rule has two meanings.

The first layer of meaning indicates that, in the first quadrant, quantum mechanics and quantum field theory lead high-level cognition and economic forward-looking observations, and the models are appropriate. In the third quadrant, classical Newtonian mechanics leads low-level cognition and economic backward-looking observations, and the models are also appropriate. In the second quadrant, if quantum mechanics leads low-level cognition and economic backward-looking observations, it is considered excessive. In the fourth quadrant, if Newtonian mechanics leads high-level cognition and economic forward-looking observations, it is considered insufficient.

The second layer of meaning is that the first quadrant can be described as a high-disturbance observation zone, while the third quadrant can be described as a low-disturbance observation zone. Here, the concept of "observation disturbance" is introduced by Dirac: the higher the degree of disturbance in observation, the smaller the world we can observe. In Newtonian mechanics, the disturbance level in our observation is low, making it suitable for observing the macroscopic world. In quantum mechanics, the disturbance level is high, making it suitable for observing the microscopic world. The field bridging these two is called "mesoscopic physics." Some argue that quantum physics is also used in observing the macroscopic world, such as in cosmology; this refers to the study of microscopic phenomena within the classical macroscopic world.

What is observation diturbance? Simply put, it is the limitation of experimental methods and observational tools. We know that every science has its boundaries. According to Popper’s philosophy of science, having boundaries allows for falsifiability (disprovablility), which is essential for science. Theories without boundaries are akin to religion, as they lack falsifiability. The boundaries of an empirical science largely depend on the limitations of its experimental methods and observational tools. Improving experimental methods and enhancing observational tools can only shift these boundaries, not remove them. It is remarkable that physicist Dirac transformed this reality into the concept of observational disturbance. Disturbance is not an inherent concept of a physical system but a meta-concept regarding a physical system. Establishing meta-concepts is one of the signs of a mature basic theory.

2.3. Low Disturbance Zone

We need to explain why quantum mechanics and high-level cognition, as well as economic forward-looking observations, coexist in high-interference zones, while Newtonian mechanics and low-level cognition, as well as economic backward-looking observations, coexist in low-interference zones.

Newtonian mechanics is characterized by its observation of phenomena with direct observability. Newton, sitting under an apple tree, could observe an apple falling from the tree and its trajectory. Although seemingly mundane, this phenomenon is a chance alignment of natural factors, including human visual capability, apple size, and falling speed. The empirical foundation of Newtonian mechanics is direct observability. The human eye can observe the falling apple because, relatively speaking, the apple is large and moving slowly. This can be termed "large/slow" physics. Regardless of advancements in observational tools, even using high-energy accelerators and radio telescopes, these tools are merely extensions of the human eye. Scientists are human beings and the observation subjects.

The term "low" in lower-order cognition should not be misunderstood as denoting a lower rank but rather low disturbance. This term can be contrasted with "low" in low-energy physics. Low-level cognition is derived from traditional psychophysics, studying perception, attention, perception, hearing, vision, and human-computer interaction, among other subfields. For example, in a computerized visual experiment, different points of varying colors, shapes, sizes, and positions are sequentially presented on a screen. Subjects make judgments and responses based on pre-understood experimental instructions by clicking different keys. This type of experimental task is called a "priming task." The response time for each click task is usually measured in microseconds. The judgments for each click task are relatively simple. In such simple and rapid mental activities, the opportunity for data noise is very low, meaning the interference in observation is low. Typically, a psychological experiment is conducted within 40 to 60 minutes to achieve optimal mental performance. It is conceivable that thousands of click tasks can be completed in a 60-minute period. With such high task density, behavioral performance can be approximated as a learning curve. This learning curve is akin to the trajectory of an apple falling. These experiments can be described as observing "simple/fast" cognitive processes.

Backward-looking observations in economics, also known as empirical research in economics, including experimental economics, fall into this category. Empirical research relies on data. Whether the data is collected in the public domain or obtained in a laboratory, data validity indicates that events have already occurred. Therefore, data reflects observations of past events, i.e., historical observations. When presenting these data, they are often made into charts and curves. These curves are similar in function to the apple's falling curve and the low-level cognition learning curve. Backward-looking observations of history are lower in interference compared to forward-looking observations of the future. While there can be various interferences in backward-looking observations of economic events, they are "process" interferences that can theoretically be ignored.

2.4. High Disturbance Zone

Quantum mechanics is in the high-disturbance zone. The elementary particles and their motion states observed in quantum mechanics experiments are often difficult to observe directly. For example, massless bosons or "confined" fermion quarks. Additionally, elementary particles move close to or at the speed of light. As a result, elementary particles are very small (sometimes just with some residual energy) and move very fast, making high interference inevitable in observation. This type of physical observation can be termed "small/fast" observations.

The Heisenberg Uncertainty Principle is the best interpretation of high-disturbance. The Uncertainty Principle, also known as the Principle of Uncertainty, states that the position and momentum of a particle cannot both be precisely measured simultaneously. The more accurately one is measured, the less accurately the other can be determined. In other words, both are uncertain quantities. Similarly, energy and time also form a pair of quantities subject to the Uncertainty Principle. Observations of two uncertain quantities are sensitive to the order of measurement; the sequence of measurement affects the results, and their difference is not zero. This is known as the "non-commutativity law." Establishing a non-commutative relationship in a field is, in this sense, the realization of quantization.

In quantum mechanics and quantum field theory, dynamic analysis involves source analysis, of whch the source is called the charge, requiring consideration of various particle states. Thus, particles possess internal space. This internal space is rotational, thus termed as the dynamic phase space; its rotational angular momentum is called "spin," which is an intrinsic property of elementary particles and has no comparable reference in Newtonian mechanics. The intrinsic properties of particles are difficult to observe directly. To establish the local symmetry of different particle states, a concept called "gauge field" is introduced to balance phase changes in phase space. Simultaneously, a differential operation called "covariant derivative" is introduced to balance the rate of phase change. These are not directly observable and are fundamental reasons for the high degree of disturbance in quantum physical observations.

In a certain sense, higher-order cognition is the language of economics. Its research scope is broad, but it has three main subdomains: reasoning, decision-making, and game theory. This is because each of these subfields has its normative theory, namely logic, decision theory, and game theory. In other words, every specific observational task used in experiments has a "standard" rational answer. Various misconceptions, illusions, hueristics, biases, and irrational answers are relative to the standard rational answer. For example, in reasoning experiments, after providing a set of premises, a conclusion, either valid or invalid, is given to the subject to make a "yes/no" judgment. This type of experimental task is called the evaluation task. In contrast to the priming tasks used in lower-order cognition experiments, higher-order cognition experiments typically use verbal tasks.

In higher cognition experiments, observation arises from several aspects. First, because subjects need to read and understand a verbal task, their response time significantly increases, measured in minutes/seconds; microseconds are negligible. During this relatively long period, process noise, such as distraction, increases significantly. Second, within a 40-60 minute experiment period, each experimental trail takes significantly longer time, reducing the number of trails significantly. In other words, the limited observational results do not form a well-approximated learning curve. Third, and most crucially, solving a verbal reasoning task should have certain mental representation and mental process predicted by theoretical models, called "task structure." Compared to lower-order cognition, the task structure of higher cognition observations is much more complex, termed as "complex/slow" cognitive tasks. The objective data we can directly observe are accuracy rates or error rates and the time taken. However, we cannot directly observe the mental processes involved in complex task structures. In other words, we can observe whether the subject got it right or wrong, but it is difficult to observe how the subject arrived at the result. This is the main source of high disturbance.

Economists have always had an impulse for forward-looking observations. Theoretically, economics textbooks tell us not to consider sunk costs, letting the past remain in the past. Economics emphasizes efficiency, which is defined by marginal utility; marginal utility refers to the benefit of investing one more unit of resource. Here, "one more unit" implies future tense or at least general present tense, rather than past tense. Observing future economic phenomena, uncertainty factors increase dramatically, which is a general source of high disturbance in forward-looking observations and is easy to understand. Specific observations in the market require more in-depth analysis.

2.5. Two Mathematical Paths

The above describes what constitutes low-interference and high-interference zones. What is the significance? The significance lies in distinguishing the different mathematical paths in the two regions. Penrose [2], in "The Road to Reality," states: "Calculus is absolutely essential for understanding theoretical physics. In a field where calculus can be applied, it is possible to apply more advanced mathematics." This is self-evident in the low-interference zone; Newton and Leibniz were indeed the inventors of calculus. In the low-interference zone, Newtonian mechanics' apple falling curve, low-level cognition learning curves, and backward-looking economic data curves can all be approximately depicted as smooth curves, meaning they can be represented as continuous functions and are almost everywhere differentiable.

However, in the high-disturbance zone, the path to calculus is "winding and lengthy." Von Neumann [17], in "Mathematical Foundations of Quantum Mechanics," points out that quantum mechanical experimental observations can all be reduced to a type of "yes/no" measurement. Penrose’s book [2] also provides a dedicated section on this (§22.6). Simplified, suppose there is a particle emitter and a particle detector called a "yes gate." When the emitter excites a particle, if the detector receives it, the particle is said to have entered the yes gate; if the detector does not receive it, it is not said that the particle was not excited but that it entered the "no gate." This description is different from Newtonian mechanics and counterintuitive but is a stroke of genius in quantum mechanics. Similarly, in higher cognition experiments, getting a task right is akin to entering the YES-gate; getting it wrong is not said to be due to inadequate effort but to entering the NO-gate. Likewise, in economic forward observations, accurate predictions enter the YES- Gate, and inaccurate ones enter the No- Gate. Regardless of which gate is entered, economists have made their efforts. Such "yes/no" type observations are mathematically represented by the Dirac δ-function, which is referred to here as the Dirac function for convenience.

This function is composed of two formulas. The first formula states that when an excited particle enters the "yes gate" (detector, correct answer, or predicted future event), the function value is infinite; when the excited particle enters the "no gate" (not detected, incorrect answer, or inaccurate prediction), the function value is zero. The second formula is the indefinite integral of the first formula and equals a constant. Here, the second formula tells us that regardless of whether the particle enters the "yes gate" or the "no gate," the particle has already been excited. In philosophical terms, the first formula of the Dirac function can be seen as its epistemological support, while the second formula represents its ontological commitment. The Dirac function almost perfectly characterizes "yes/no" type observations, yet it is not a mathematically well-defined function.

It was not until the development of mathematical distribution theory that the second formula of the original Dirac function—i.e., the integral formula—was used as a starting point for making ontological commitments. The first formula of the original function is used as the integrand, called the testing function, to provide an epistemological pathway, requiring this testing function to have at least one supporting point. This supporting point is the excited particle captured by the original quantum measurement detector, the correct answer in solving a verbal problem in higher cognition, such as a reasoning problem, or a predicted future economic event in economic forward-looking observations. By traversing this path, the high-disturbance zone can finally apply calculus legally and appropriately, laying a solid foundation for introducing more advanced mathematical tools.

There is a popular game called the "20-Questions" game, also known as the mind-reading game. One player thinks of something, such as an apple, and the other player can ask up to 20 "yes/no" questions, such as: "Is it a tool?" "Is it some food?" "Is it some meat?" "Is it some grain?" and so on, gradually approaching the correct answer. The renowned American theoretical physicist John Wheeler once wrote that quantum physical observations are akin to playing the 20-Questions game with nature. Similarly, observations in higher cognition are like playing the 20-Questions game with the mental world, and economic forward observations are like playing the same game with future economic events. Wheeler’s words capture the essence of microscopic scientific observations.

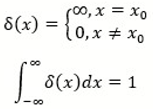
3. Mathematical Foundations of Integration Theory

3.1. Application of Category Theory

When integrating social sciences with physics, it first involves the mathematics used in physics. In logical terms, these mathematical contents are referred to as object language mathematics. Integrative theory itself also needs to be described using mathematical language as much as possible, which is known as meta-mathematics. The meta-mathematics of integrative theory is essentially mathematical category theory. For example, in "Categorical Dynamics," we used quantum electrodynamics as a functor structure to establish natural transformations between market dynamics fragments and reasoning dynamics fragments, as illustrated in Figure 3.

At the same time, a natural transformation characterization of isospin was also provided, as illustrated in Figure 4.

Recently, in "The Cognitive Gauge Structure of Philosophy Encountering Statistics " [12], a natural transformation between philosophy and statistics was established in the context of definability within gauge structures, as shown in Figure 5 below.

More generally, consider a structure, such as the aforementioned normative structure, denoted as Y. Let there be two domain fragments with normative structures, denoted as objects

X_{1}

and

X_{2}

. Suppose there are morphisms

F_{1}

Y \to X_{1}

and

F_{2}

Y \to X_{2}

. From the composition of the two morphisms, denoted ⟨

F_{1}

∣

F_{2}

⟩, one can obtain the product of the two objects, denoted as

X_{1} \times X_{2}

, as illustrated in Figure 6.

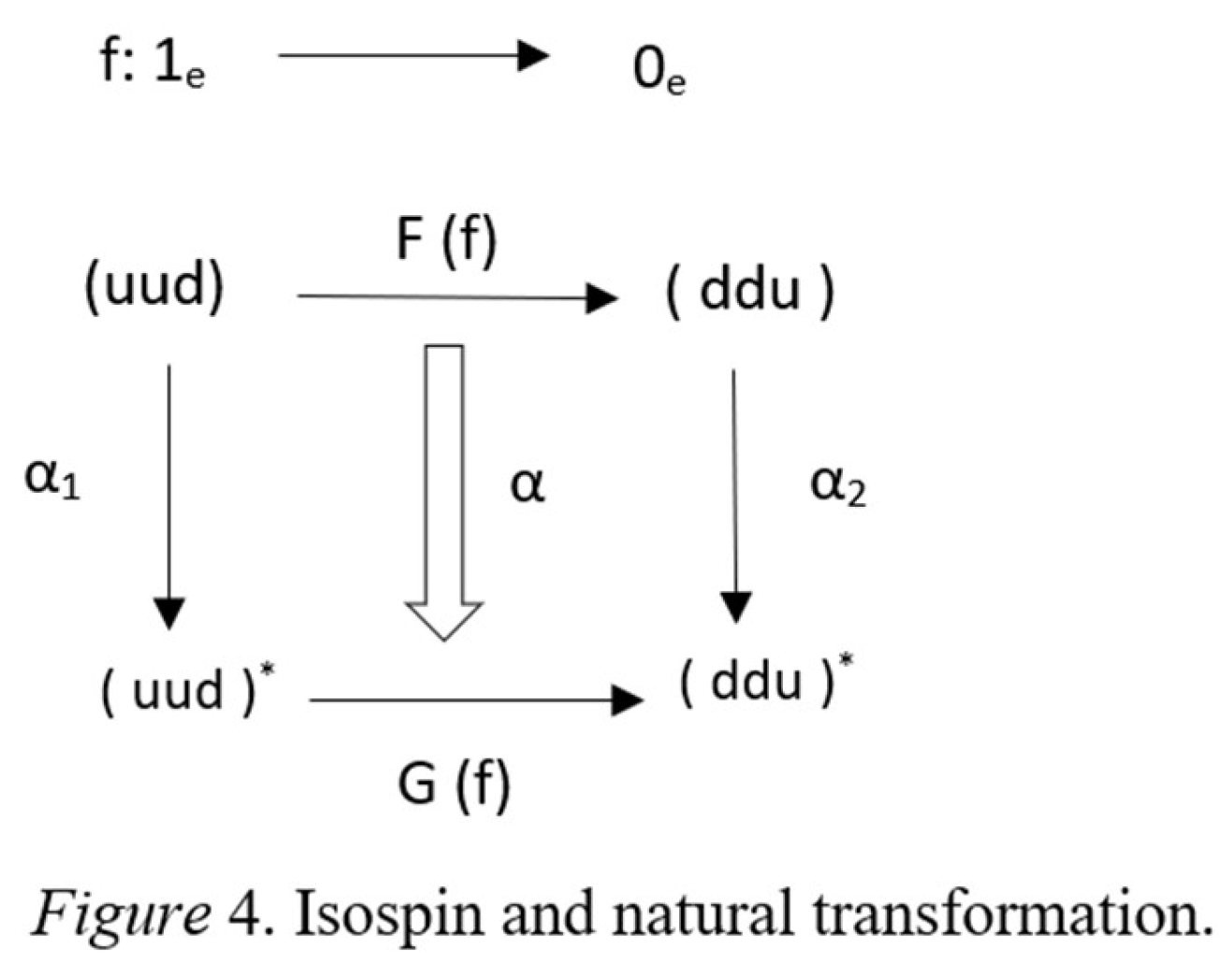
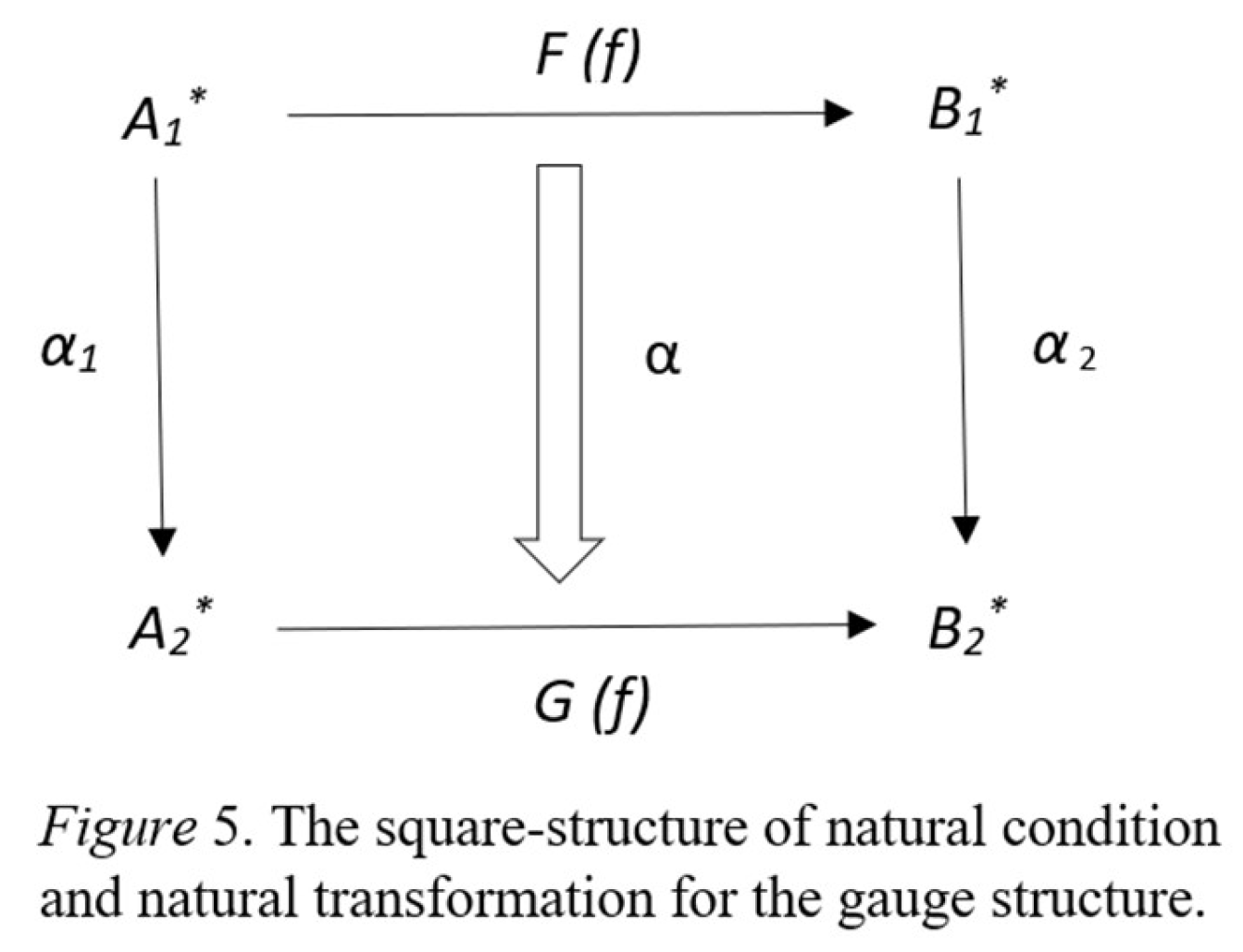
3.2. The Mathematical Foundations of Integration Theory

Category theory reflects profound structuralist ideas and has strong general characterizations. In recent years, we have seen many significant developments in this area. Category theory aligns so well with the ideas of integration science that it should be the primary language for its mathematical depiction. However, due to the general nature of category theory, applying it to characterize a specific domain can cause that domain to lose its distinctive features. Logic reminds us that between category theory and integrative theory, there needs to be a semantics known as the metamathematics of integrative theory. Below, we introduce some fundamental concepts of integrative geometry.

Definition 1: Integrative Point. If two or more domains share a structure, this structure is called an integrative point between them. This situation is known as 1st-order integration.

Definition 2: Integrative Line. If two domains share two or more integrative points, these structures form an integrative line between the two domains. This situation is known as 2nd-order integration.

Definition 3: Integration Surface (plane). If more than two domains share an integration line, they form an integration surface (plane). This situation is also called the 3rd-order integration.

Definition 4: Integration Body (bulk). If more than two domains share more than one integrative plane, they form an integrative body. This situation is also called higher-order integration.

Definition 5: Zero-order Integration. Lastly, a domain is considered to always be integrable with itself, it is counted as 0^th-order (null) integration.

It is not difficult to see that various geometric properties can be discussed based on the above-defined basic concepts of integrative geometry. For example, an integration line can be characterized as a vector, whose rotation produces a geometric phase. We can also discuss its algebraic properties. For example:

Proposition 1: An integrative point, considered as a product operation in category theory, with all 0th-order integrations as unit integrative points, forms a semigroup with all objects satisfying this integrative point.

We can also discuss its analytical properties. For example:

Proposition 2: An integrative point, considered as a function over all domains, is characterized as a Dirac delta function; where the integrative point is the support point. Domains satisfying the integrative point structure take the value of 1, while those not satisfying it take the value of 0. From the perspective of observation, this is a special type of "yes/no" observation. From a logical perspective, it is a form of binary logic.

Proposition 3: Dynamical Isospin: If an integrative point represents a structural force, then any two integrated domains form an isospin, which can be characterized by Weyl spinors. If more than two domains share an integrative point, it is termed as an isospin multiplet.

Proposition 4: A set of integration points as a basis implies that when two domains share this set of integration points, it signifies a linear transformation between the two bases.

3.3. The Hypothesis of Structural Force

We believe that structure is both the manifestation and carrier of the structural force. Structural force is not a mere analogy or metaphor but a scientific hypothesis. Structural force is the ontological commitment of integration science. Scientific hypotheses must be based on observation. Unquestionably, nothing is more universal than structural phenomena. Based on this, we propose:

Axiom 1: There exists a structural force, and various structures are both its manifestation and carrier.

Structural force cannot be reduced to the four natural forces defined in physics, nor to any social forces or mental forces. We propose:

Axiom 2: Structural force is irreducible, meaning no path exists to reduce structural force to other forces.

Thus, we can consider the hypothesis of structural force as independent of any existing axiomatic system, neither provable nor disprovable. Therefore, we have:

Axiom 3: The hypothesis of structural force is independent.

Clearly, the hypothesis of structural force is consistent with existing scientific hypotheses, poses no contradiction, and is beneficial for scientific development. Thus:

Axiom 4: Structural force is benignly defined.

In the history of philosophy, there was Bergson's intuitiionistic phenomenology. Correspondingly, there were Heyting's intuitionistic logic and mathematics. Intuitionistic mathematics only accepts constructive proofs and does not accept proofs of existence. The integration theory of structural force differs; we have:

Axiom 5: In the concept of integration theory, existence proofs are constructions and a special case of constructive proofs.

In the development of science and human knowledge, countless facts demonstrate that structure is portable from one domain to another. Especially in the study of big data, artificial intelligence, and virtual worlds, structural portability has even become a path dependency. This is essentially the core idea of the book, “Gödel, Escher, Bach: An Eternal Golden Braid”, by Hofstadter [1] . To summarize, we have:

Axiom 6: Structure has portability from one domain to other domains.

These six axioms form the axiomatic system of integration theory. The concept of structural force might seem abrupt to general readers. This is due to sensory, perceptual, and cognitive reasons, all of which need explanation. First, physics tells us there are four natural forces, with electromagnetism and gravity being commonly known. However, when strong and weak forces are mentioned, there might be surprise, not to mention structural force, which feels similar. Second, when discussing forces, one naturally thinks of Newton, Einstein, or Maxwell, which are significant. Structure is seen everywhere: a house with three rooms and a hall is a structure; a book with 16 chapters is a structure; a social system is a structure; the syntax of a language is a structure. How does structure become a force? This is the darkness under the lamp of perception. All these can be understood. For readers interested in the concept of structure, I recommend Xu Guangxian’s book, Material Structure, as a reference [16].

What truly needs explanation is the cognition of force. Force is a concept in classical physics. In modern particle physics, forces are characterized by their mediators. For example, electromagnetism is characterized by photons, and the strong force by gluons, collectively known as bosons. Particles are characterized using field theory language, where particles are depicted by their fields, such as the photon field and the gluon field. Now, conceptualizing structural force as a general structural field is more understandable. Imagine a space where each point represents an arbitrary structure, which constitutes the structural field. The mediator of structural force can be called a structural particle. In quantum mechanics, a particle is characterized by its wave function. Hence, a structural particle is at least a function, taking various structures as values. In quantum field theory, the wave function is an operator. A structural operator can represent any structure.

Once upon a time, the Bourbaki structuralist school was highly influential, covering mathematics with set theory language and profoundly impacting natural sciences, social sciences, and even humanities. Yet today, it seems intermittent. Why? Because it lacked force! It was so focused on structure but fell short of making a commitment to structural force. Today, as mathematical category theory becomes increasingly sophisticated, with significant progress, scientists still approach it with reverence but keep their distance, seldom applying it. Why? Because it lacks force! Category theory aims to study structures but has not crossed the shallow waters to make a commitment to structural force.

It is often commented that shared structures between different domains are merely analogies, somewhat dismissive. Scientists often say they listen to the voice of nature; can they not hear the call of structural force? This is not just prejudice but also shortsightedness. Not to mention that analogy itself is an important method of scientific discovery. If you can perceive that structural force pervades all scientific domains and is omnipresent, you will certainly feel awe.

Science emphasizes empirical evidence, based on experiments and observations. In physics, there is atomic structure; in biology, the DNA double helix structure; in chemistry, crystal structure. In social sciences, structures are also ubiquitous. Is the overlap of structures merely coincidence? Discovering new structures is the mission of science, and discovering shared structures between natural sciences, social sciences, and even humanities is a rightful respect for structural force.

Structural force can build bridges between disciplines, support human knowledge, serve as a channel for human cognition, and provide a path dependency for scientific development. Integrative science is the study of structural force. Structural force can guide us to many unexpected scientific discoveries and even help find mathematical and physical models for many so-called common-sense phenomena. Here are some examples:

Example 1: Guided by quantum chromodynamics, we have discovered that consciousness can be divided into eight types.

Example 2: Freud’s personality theory (discussing three types of needs: id, ego, and superego) and the Platonic tradition in epistemology (discussing three elements of cognition: truth-seeking, belief-seeking, and verification) were originally unrelated. They can both be characterized by Gell-Mann’s three-color charge, showing a unified three-dimensional internal space in mathematical and physical terms.

Example 3: The concept of fractional charge helps us understand fractional market charge and fractional logical charge.

Example 4: Guided by the weak isospin dynamics, we understand that economic externalities can cause isospin between achievement and fear impulses, as well as isospin between market charge and market residual.

Example 5: From the properties of the Higgs field, we understand the three meta-properties of ordinary rationality. Additionally, from the Higgs mechanism, we understand the mechanism of ordinary rationality.

Example 6: From the concept of the Goldstone field, we have developed a model about the effects of emotions.

Example 7: By examining the history of modern theoretical physics, we have discovered 14 characteristic phases of psychological life.

In my nearly 20 years of integrated scientific research experience, I have continuously felt the impact of structural force. As long as you keep striving to unveil the mysterious veil of mathematical physics, you will continually reap rewards in social sciences and experience the profound impact of "large pearls and small pearls falling onto a jade plate." On a quiet, contemplative night, you ponder where this structure comes from: Is structure natural or social, material or mental? The Riemann Hypothesis—has its proof yet to be discovered, or has it yet to be conceived? Gradually, your speculative thoughts seem to drift away from traditional philosophical thinking, and your vision becomes blurred. In the concept of integrated theory philosophy, there is no distinction between society and nature, or between mind and matter. In the face of structural force, society and nature are of the same root, and social sciences and natural sciences are intertwined branches.

The structurer is a valiant general, expanding the territory of science and defending all directions. Structure is the foundation of the building, relied upon by engineering and highlighting brilliance. Structure is crafted with unique skill, a template of divine tools, seamlessly natural. Structure is material, shrouded in elegant gauze, a gift of nature. Structure is the mind, meticulously sculpted, a dedication of intellect. Structure is very busy, serving many masters, calling from left to right. Structure is abundant, layered and scattered, with winding paths leading to tranquility. Structure is regulation, cosmic laws, societal order. Structure is human reason, actions and inactions, thoughts and considerations. Structure is physics, symmetry and defects, groups in mathematics. Structure is a framework, the flesh and bones of a body, stately and shaped. The article is structure, divided into sections and paragraphs, with layout and planning. Is structure the right path, a smooth road extending far into the distance? With structural force at your side, science can be done, science can achieve (Yes, science can, science can make it).

Studying structural theory is an inherent part of cognitive science. Logically speaking, the structures obtained through observation are descriptive structures. Structures derived through reasoning are necessary structures. And structures obtained through imagination are accidental structures. Both necessary and accidental structures are modal structures. Descriptive structures have primary priority, stronger than modal structures.

To emphasize, Section 3.2 and Section 3.3 are the core of this paper. Their core role is to locate the scattered work of integrated science across multiple articles within the unified framework of integrated science meta-mathematics. In other words, the meta-mathematics of integration theory is the framework of this paper and also the framework of integrated science. Next, we will introduce new developments in integration theory, discussing specific cases of integration points, integration lines, integration surfaces, and integration bodies.

4. Integration Point Cases

Here, we first introduce two cases of integration points. The first case involves two fields sharing a single integration point, while the second case involves multiple fields sharing a single integration point.

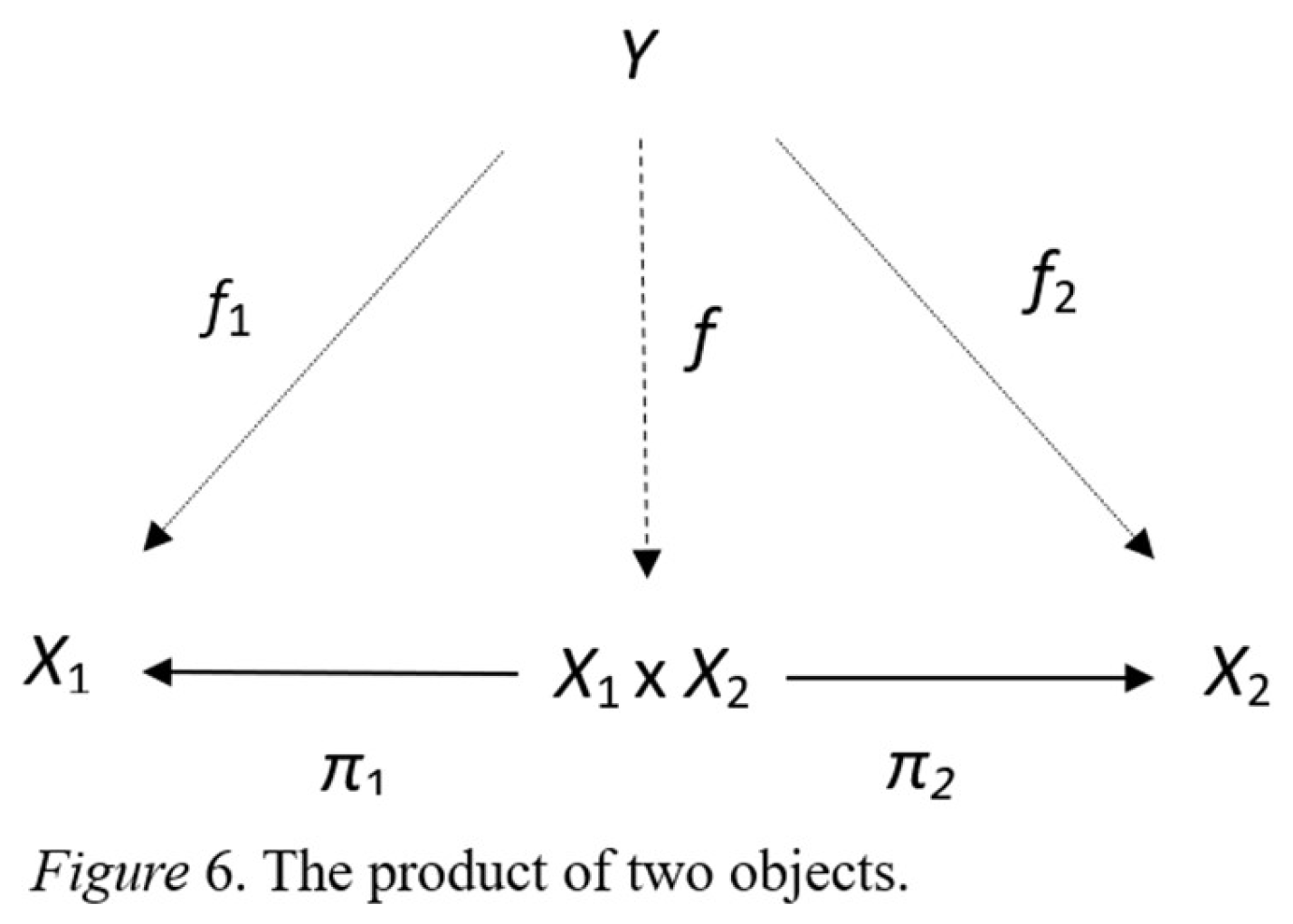
4.1. Two Fields Sharing a Single Integration Point

In "Philosophy Encountering the Cognitive Normative Structure of Statistics" [12], we first define normative structure. To construct a normative structure, one must distinguish between two levels: the global level and the local level. Each level must further distinguish between two tiers, known as normative potential and normative field strength. This forms a double-layered, double-tiered four-box structure. Clearly, categorizing this requires four components: global normative potential, global normative field strength, local normative potential, and local normative field strength. The distinction between global and local lies in that the former is independent of individual differences, while the latter must consider individual differences. The distinction between normative potential and normative field strength can be generally explained through calculus. A definite integral is considered normative potential, where the integrand is the normative field strength, and the constant in the formula is termed normative degrees of freedom. It is evident that deriving normative field strength from normative potential requires some differential operation, thereby eliminating the normative degrees of freedom. It should be noted that this methodology must be sufficiently general at the global level, without individual differences; yet at the local level, it must be covariant, encompassing individual differences. Additionally, normative structure is constrained by normative principles: if global symmetry cannot be established, then local symmetry cannot be established.

We have not only discovered normative structure in people's philosophical thinking pathways but also found similar normative structures in recent developments in statistics. Thus, as an integration point, this structural phenomenon can be used to integrate the seemingly distant fields of philosophy and statistics.

In a complex philosophical system, one can distinguish between the emergence of philosophical knowledge and the underlying cognitive fluctuations and transitions of philosophers. From a dynamic perspective, this distinction can identify potential energy and kinetic energy. For example, we define original metaphysics as global philosophical normative potential and add-on philosophies (such as philosophy of science) as global philosophical normative field strength. This is based not only on the analysis of the current expressions of philosophers' understanding but also on judgments of their cognitive intentions. This is why we refer to it as cognitive normative structure rather than simply normative structure. Philosophy is closely related to linguistics. Here, we are not referring to the philosophy of language familiar to philosophers, but rather to philosophical language. Philosophical inquiry and philosophical response involve not only philosophical thinking but also linguistic expression. Chomsky's distinction between competence and performance helps us understand philosophical language and philosophical behavior. Philosophical cognition is a form of intellectual ability, while philosophical expression is a form of intellectual performance. In cognitive normative structure, individual philosophical cognition is local normative potential, while its philosophical expression is normative field strength. We know more or less how to discuss philosophical issues in cognitive science; we also need to learn how to discuss cognitive science issues in philosophy.

In standard statistical inference statistics, the traditional method is to use the sample mean xˉ to estimate the population mean μ (e.g., t-test). Under this statistical concept, what is the cognitive intention of statisticians, what do they aim to achieve, and what cognitive channel do they choose? It can be judged that statisticians actually assume that the population mean is global normative potential, and the sample mean is global normative field strength because this selected sample serves to estimate the properties of the population. This is akin to introducing a random sampling model, where each sample is considered a point, and the mean of all sample points' data is used to estimate the overall mean of the operational results. This can still be viewed as a global estimate, where the global phase is an arbitrary statistical constant, i.e.,

θ = C

. The rule here is that as long as the mean is taken or the phase is set as a constant, it rises to the global level.

At the local level of statistics, we first introduce the observation operation set Ω={ω_i}. Ω is a countably infinite set with a measure of zero. We introduce a variable x_i to traverse all operations in Ω. Now consider the power set P(Ω), where each element is a possible random sample. This is the local normative potential. In the random sampling model, the dynamic phase is a function of the random sample variable

x^{j}

, i.e., θ = θ(

x^{j}

). Each phase comes from a sample complex, corresponding to a Born probability. Thus, the Born trace formed during random sampling is the local gauge field strength. This describes the cognitive intention of statisticians, which is to construct a locally relevant statistical path. Hence, this construction is not merely a gauge structure but a cognitive gauge structure. This represents a cognitive emergence in interdisciplinary research.

In this case, a single integration point, namely the cognitive gauge structure, has been established between philosophy and statistics (see Table 1).

4.2. Multiple Fields Sharing a Single Integration Point

We know that language ability is the most fundamental function of psychological life. In the paper "The Integrated Structure of Language and Language Behavior and Its Psychologized Path: Psychological Life and Theoretical Physics Part II" [6], we discussed a fundamental special language structure known as the "dual-leg structure," which consists of syntax and semantics. This dual-leg structure can serve as a language characterization tool across logical language, decision theory language, game theory language, set theory language, quantum mechanics language, normative field theory language, intrinsic dynamical geometrization language, and so on. In other words, using the dual-leg structure as an integration point can unify specific languages across different fields. Here, we will briefly introduce the first four fields mentioned.

The stability of natural language depends on the stability of its syntactic and grammatical structure, while its determinacy is reflected in its semantics. Thus, the stability and determinacy of natural language are based on the separation of syntactic-grammatical structure from semantics. This separation is not given freely; it is an advanced stage of the long-term evolution of language. It is often overlooked how miraculous the formation of syntactic-grammatical structures is in human language evolution. Even more amazing is that humans invented semantics, which determines the meaning of language expressions, truly a masterpiece of ingenuity. This allows humans to stand and walk using only two linguistic "legs," freeing up two mental "hands" to engage in more complex tasks. Upright walking is a milestone in human evolution and also in the evolution of human language.

The stability and determinacy brought by the syntactic-grammatical structure and its semantics, known as the dual-leg structure of language, are more clearly reflected in formal and scientific languages. To learn a subject, one must first become familiar with its language, separate its syntactic-grammatical structure from its semantics, and then understand the meta-properties combining the two. Here, we briefly mention analyses of eight such scientific language dual-leg structures: Logic, Decision Theory, Game Theory, Meta-Mathematics, Quantum Mechanics Wave Functions, Gauge Field Theory, Set Theory, and Geometric Program of Particle Physics Standard Model.

4.2.1. Standard Dual-Leg Structure of Logic and Formal Language

A logical system's dual-leg structure has two standard components: formal syntax and formal semantics (also called models). Standard logic has its own standards, requiring that its syntactic structure and its semantics are dual and equivalent. This equivalence is established through the relationship between provability and validity. If all proofs are valid, the logic system is said to be semantically coherent. If all valid formulas or inferences are provable, the logic system is said to be complete. Coherence and completeness are overall properties of the logic system, also known as meta-properties, like a bidirectional bridge connecting logical syntax and semantics, even though they are constructed independently. Propositional logic exhibits coherence and completeness.

4.2.2. Syntax Structure and Utility Semantics in Decision Theory

The classic axiomatized decision theory syntax is a three-layer structure:

Selection Set: A collection of choices or options.
Outcome Set: Each choice can produce a set of possible outcomes.
Characterization: Each outcome is characterized by two properties, desire and feasibility.

To pose a decision theory problem, it must be placed within this syntactic structure. Solving a decision theory problem requires establishing a total preference relation on the selection set, meaning any two choices must be compared, and one must be preferred over the other; a "no preference" option is not allowed. This is known as semantic inquiry.

The classic decision theory syntax structure is constructed from top to bottom, while its semantics must be defined from bottom to top. The decision theory meaning of desire is money. Regardless of the desire, under the decision theory meaning, it must be converted into a monetary value. The next concept is the feasibility of an outcome. Note that a choice can produce several or many possible outcomes, and the decision-maker's weight assigned to these outcomes varies. The weight distribution assigned to all possible outcomes of a choice is called a strategy. To convert this strategy into a probability distribution, mathematical normalization is required, meaning all probabilities in the distribution must sum to 1. This is because all possible outcomes belong to the same choice, and if this choice is considered the optimal preference, it becomes a reality, with a probability of 1. With this normalized probability distribution, probabilities can be assigned to possible outcomes. Thus, the decision theory semantics of syntactic feasibility is its probability.

An outcome is characterized by its two syntactic attributes: desire and feasibility. The decision theory semantics of desire is money, and the semantics of feasibility is probability; their product is called utility. Therefore, the decision theory semantics of a syntactic outcome is its utility. This is the origin of the name for decision theory utility semantics. This is the second layer, known as the outcome layer. Moving up one layer brings us back to the options layer. An option can produce several or many possible outcomes, each with its semantic utility; the sum of these utilities is called the mathematical expectation. Thus, the decision theory semantics of a syntactic option is its mathematical expectation. This meaning in decision theory is referred to as utility semantics.

The system meta-property of decision theory requires that the syntactic structure and utility semantics are comparable in strength, meaning that for any two options, one is preferred over the other if and only if its mathematical expectation is greater. This is known as the decision theory representation theorem.

4.2.3. Syntax Structure and Utility Semantics in Game Theory

Modern game theory has flourished under the so-called Nash framework. Nash not only rigorously defined cooperative and non-cooperative games using mathematical language but also proved their systemic meta-properties, namely Nash solutions and Nash equilibria, thereby establishing the basic framework for game theory research. Here, we use non-cooperative games as an example.

The syntax structure of non-cooperative games is not complex, but there is a conceptual challenge.

4.: Assumption: Let N be the number of players in the game.
5.: Action Sets: Each player has a set of possible actions, denoted as $A_{i}$ . This is similar to individual decision theory, with no cognitive difficulty.
6.: Situation: Consider an n-tuple of possible actions ( $a_{1}$ ,…, $a_{i}$ ,…, $a_{n}$ ), where each player selects an action from their set of possible actions. This n-tuple is called a situation. A game is the collection of all possible situations, which is the Cartesian product of all players' action sets, denoted as X1n $A_{i}$ . This is like a film reel composed of individual frames.

The essential difference from individual decision theory is that each player does not establish a preference relation on their own action set but rather on the set of all situations. The meta-property of non-cooperative games is often referred to as Nash equilibrium, which is a purely syntactic property. A Nash equilibrium is a special situation that must be considered for each player, denoted as (ai∗,a−i∗), satisfying the following condition: for each player i, ai∗≻iai for all ai∈Ai. The game-theoretic meaning of a situation is called its utility. Similar to decision theory, utility is a linear function of value and probability, so the semantics of non-cooperative games is referred to as utility semantics.

4.2.4. Dual-Leg Structure of Set Theory Language

Set theory is the universal language of contemporary mathematics. The Bourbaki structuralist school made significant contributions in this area. Recently, the author proposed a method for directly generating the dual-leg structure from sets.

Consider a set A. Its power set, denoted P(A), is the set of all subsets of A. Let a be an arbitrary element of A, denoted a∈A, meaning a belongsto A, where the symbol ∈ indicates membership. Let B be an arbitrary subset of A, denoted B⊆A, meaning A contains B or B is contained inA, where the symbol ⊆ indicates inclusion. Clearly, B∈P(A). The definition of the power set is given by P(A)={B∣B⊆A}, meaning B∈P(A) if and only if B⊆A. In logical terms, B∈P(A) is called the extension of P(A), and B⊆A is called the intension of P(A). Thus, through verbal analysis of the power set, we construct the extension syntax and intension semantics of set theoretic language, also known as "membership syntax" and "inclusion semantics," denoted as ∈ syntax and ⊆ semantics, respectively. This dual-leg structure is self-generated from the inherent structure of set theory language, hence it is general. The meta-properties of this generated dual-leg structure are evident, being both complete and coherent, as each member of the power set refers to a unique subset of the set. In category theory, the collection of all referential methods for a category is called the index set.

The above discussion illustrates that using the dual-leg structure of natural language as an integration point can unify at least four specific scientific languages (see Table 2).

5. Integration Line Case Study

In "Psychological Characteristics and Society: Psychological Life and Theoretical Physics" [5], we propose a completely new theory of psychological life, using theoretical physics as a model and method, specifically discussing five characteristic phases of psychological life. The first is the "Embracing Phase," characterized by certainty and a sense of security, as depicted by Newtonian mechanics. The second is the "Contradiction Phase," where the psychological characteristics involve the entanglement and conflict between ideals and reality, described by quantum mechanics and special relativity in their debates about remote quantum entanglement and local causality. The third is the "Reintegration Phase," where psychological characteristics involve the integration of ideals and reality, recognition of personal conditions and individual differences, and re-engagement with society. This is first depicted by the concept of proper time and momentum cone in special relativity, and later by the conceptual parts of gauge field theory. Note: Quantum field theory is an integration of special relativity and quantum mechanics. The fourth is the "Civic Phase," characterized by a psychological commitment to the structure of the external environment, as depicted by the dynamics analysis and symmetry groups of gauge field theory. During the Civic Phase, there is a global symmetry demand concerning social norms, a local symmetry desire regarding individual differences, and a normative transformation concept regarding everyday reality. The fifth is the "Sentimental Phase," where psychological characteristics reflect the equivalence principle between the geometric and algebraic descriptions of psychological gravity, as depicted by general relativity. The inequality of psychological advantages makes the psychosocial environment a curved space, and Pareto improvements in psychological welfare represent the curvature of this psychosocial space. Additionally, psychological life includes other characteristic phases that are not discussed in detail in this text.

From the above, it is clear that, with each psychological characteristic phase as an integration point, there exists a series of integration points between psychological life and theoretical physics, forming a rich integration line (see Table 3).

6. Integration Surface Case Studies

First, it should be noted that in my nearly 20 years of research in integrative science up to the present, the development of cognitive dynamics has reached a basic level of maturity. The standard model of cognitive dynamics [13] includes reasoning dynamics, sub-cognitive dynamics, and knowledge acquisition externality dynamics. This paper does not elaborate on this part. Here, we provide three integration surface case studies. The first involves market dynamics, reasoning dynamics, and quantum electrodynamics, collectively referred to as U(1) dynamics. The second involves sub-economic dynamics, sub-cognitive dynamics, and quantum chromodynamics, collectively referred to as SU(3) dynamics. The third involves economic externality dynamics, cognitive externality dynamics, and weak force dynamics (including weak isospin dynamics and the electroweak model), collectively referred to as SU(2) dynamics.

6.1. U(1) Dynamics Integration Surface

In the article "Principles of Market Dynamics: Economic Dynamics and the Standard Model (II)" [8], based on classical electrodynamics and using quantum electrodynamics as a reference model framework, we constructed a market dynamics system. This construction consistently adheres to the principles of Bourbaki structuralism. Market dynamics studies the interactions between price, demand, and supply. Quantum electrodynamics studies the interactions among photons, electrons, and positrons. Both fall under the category of U(1) dynamics and share the U(1) symmetry group. Market dynamics introduces the concept of market charge and defines demand and supply accordingly. By examining market hesitation phenomena, spin is introduced as an intrinsic property of demand and supply. Thus, demand and supply can be defined by Dirac spinors. Through the introduction of money cones and price shells, virtual prices are defined; demand and supply interact through the exchange of virtual prices. These interactions can be described by Feynman diagrams. The cognitive field has the function of polarized decision-making, described by a magnetic field.

Market dynamics considers that the socio-economic system itself is an experiment, with each market participant acting as an observer. We established the non-commutative relationships of market observations and the market version of the uncertainty principle, defining the quantum version of the "invisible hand." Based on classical electrodynamics, we discussed the relationship between the price field and the Maxwell field, and introduced the concept of gauge potentials. Higher-order cognition (including game theory, decision-making, and reasoning) causes market fluctuations (including mesoscopic and quantum fluctuations). Various intrinsic fluctuation phenomena in the market are fundamental to understanding both market participants' cognition and market phase transitions. We defined six components of the market wave function: global phase factor, global gauge potential and global gauge field strength, as well as local phase factor, local gauge potential, and local gauge field strength. Gauge transformations are a fascinating part of quantum electrodynamics and market dynamics. The gauge principle demonstrates that global symmetry is a necessary condition for local symmetry. Four operators are introduced: the Newtonian mean operator, the Einstein money cone operator, the Schrödinger evolution operator, and the Dirac field theory operator. These four operators are applied to the market wave function to present four operator states of the market wave function. Changes in operator states are referred to as phase transitions in the market wave function.

Using the same construction methods and processes as for market dynamics, reasoning dynamics is also a U(1) dynamics system. Reasoning dynamics introduces logical charge as the source for active dynamics analysis, defining syntactic reasoning through mental logic theory (characterized by negative charge; [14]) and semantic reasoning through mental model theory (characterized by positive charge) [15]. In the process of logical thinking, moving logical charges generate logical flow (characterized by electric current) and are accompanied by cognitive fields (characterized by magnetic fields). Considering a reasoning problem, whether a conclusion holds for a set of premises, the reasoner may experience hesitation during the thought process, known as the spin of logical charge. Just as the magnetic field polarizes electrons, the cognitive field polarizes hesitation to make a judgment about the conclusion. Reasoning dynamics has a clear gauge structure. Its global gauge potential is the logician, and its global gauge field strength is the specific logical system. The local gauge potential is the reasoning ability of the individual reasoner, and the local gauge field strength is the individual reasoner's performance in reasoning behavior.

It is known that quantum electrodynamics provides a series of possible positive points, forming a potential integration line. From the above discussion, we can see that quantum electrodynamics, market dynamics, and reasoning dynamics share this integration line, forming an integration surface for U(1) dynamics (see Table 4 below).

This integration surface satisfies the U(1) symmetry group and is thus also referred to as the U(1) integration surface.

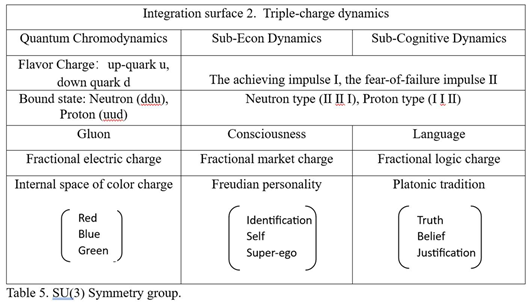
6.2. SU(3) Dynamics Integration Surface

In the paper "Principles of Sub-Economic Dynamics: Economic Dynamics and the Standard Model (III)" [9], sub-economic dynamics theory is constructed using quantum chromodynamics (QCD) as a conceptual and modeling tool. The term "sub" in sub-economic dynamics (sub-econ dynamics) derives from "subatomic." In physics, subatomic dynamics primarily studies the interactions between quarks and their bound states with gluons, which is the most fundamental level of matter structure in current scientific understanding. In economic dynamics, sub-economic dynamics primarily investigates the interactions between impulses and their bound states with consciousness, representing the deepest level of mental structure. In the theoretical physics standard model, subatomic dynamics is known as quantum chromodynamics (QCD). In the economic dynamics standard model, sub-economic dynamics uses quantum chromodynamics as its theoretical model, and both share the mathematical SU(3) symmetry group.

Sub-economic dynamics explores the relationship between people's economic impulse structures and market behavior. It discusses the deep structure of free markets. Sub-economic dynamics forms the psychological foundation of market dynamics. Sub-economic dynamics and quantum chromodynamics share an integration line, including a series of integration points. The first integration point involves economic impulses and quarks, including achievement impulse and up quarks, fear impulse and down quarks. Other integration points involve flavor charge, generational effects, neutron-like bound states, proton-like bound states, gluons and consciousness, fractional charges and fractional market charges, and gauge transformations. The most notable integration point is color charge. Quarks carry three types of color charges (red, blue, green), meaning quarks have a three-dimensional internal space. Correspondingly, applying Freud's personality theory, economic impulses also have their three-dimensional internal space. The three dimensions are the id (Identification), ego (Self), and superego (Superego), each characterized by one of the three color charges. For clarification, the id represents basic survival needs such as food, housing, and reproduction. The ego represents social needs such as education, employment, and social interaction. The superego represents spiritual or psychological needs such as faith, honor, and the afterlife.

Similarly, within the framework of quantum chromodynamics, we constructed sub-cognitive dynamics. The main difference between sub-cognitive dynamics and sub-economic dynamics is that it applies the Platonic tradition from epistemology to construct the three-dimensional internal space of the knowledge impulse. The Platonic tradition holds that to know a piece of knowledge, three conditions must be met: the pursuit of truth, belief, and verification. These three conditions are characterized by three types of color charges, forming the three-dimensional internal space of the knowledge impulse.

From the above discussion, it is evident that sub-economic dynamics and sub-cognitive dynamics share a rich integration line with quantum chromodynamics, forming an integration surface for SU(3) dynamics (see Table 5).

As a meta-integration point, the three types of dynamics here share the mathematical SU(3) symmetry group, so this integration surface is also referred to as the SU(3) integration surface.

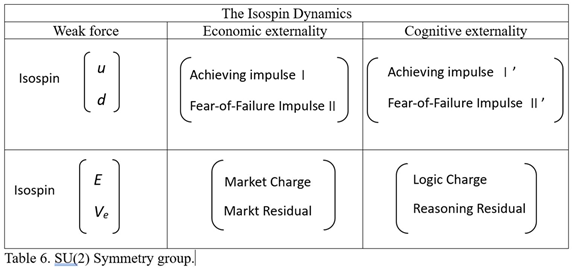
6.3. Isospin Integration Surface

Economic externalities are undoubtedly a significant aspect of economics. In the paper "Principles of Economic Externality Dynamics: Economic Dynamics and the Standard Model (III)" [9], we proposed a new economic externality dynamics model using the weak force theory from physics as a reference framework. The gauge field theory of weak force is rich in content. In this paper, we use its isospin model method to construct two economic isospin models. The first is the isospin between economic achievement impulses and economic fear impulses under the influence of economic externalities. The second is the isospin between market behavior and market residuals. Additionally, in our previous work on cognitive externality dynamics [13], we constructed two similar cognitive isospin models. The first is the isospin between cognitive achievement impulses and cognitive fear impulses under the influence of cognitive externalities. The second is the isospin between reasoning behavior and problem-solving residuals.

The weak force can alter the flavor charge of quarks. For example, protons (uud) and neutrons (ddu) are two bound states that differ by the flavor charge of just one quark; otherwise, their components and binding methods are the same, making them twins with different names. When the weak force changes a down quark (d) in a neutron to an up quark (u), the neutron decays into a proton (along with an electron and an anti-neutrino). This is called weak isospin, denoted as(uud ddu) or (d u). Similarly, economic externalities can alter the flavor charge of economic impulses, and cognitive externalities can alter the flavor charge of cognitive impulses. All three share the mathematical symmetry group SU(2) (see Table 6).

Moreover, under interactions with weak charges, electrons and anti-neutrinos also form isospins. Similarly, under interactions with economic externalities, market charges and market residuals form isospins. Likewise, under interactions with cognitive externalities, logical charges and problem-solving residuals form isospins. All three share the mathematical symmetry group SU(2) (see Table 6).

7. Standard Model Integration System

In the paper "Outline of Categorical Dynamics (I)" [11], we introduced our previous work on how to integrate the standard model of particle physics (hereinafter referred to as the Standard Model) into dynamics analysis of social sciences. The approach involves embedding the structure of the Standard Model into the dynamics analysis of social sciences to construct new dynamics systems. Generally, the Standard Model consists of four components: quantum electrodynamics, quantum chromodynamics, isospin dynamics, and the Higgs mechanism. Using this theoretical framework, we constructed two sets of social science standard models: economic dynamics and mental dynamics. Correspondingly, economic dynamics comprises market dynamics, sub-economic dynamics, economic externality dynamics, and ordinary rationality mechanisms, while cognitive dynamics comprises reasoning dynamics, sub-cognitive dynamics, cognitive externality dynamics, and ordinary rationality mechanisms. In summary, this previous work encompasses three standard models and a total of 12 types of dynamics analysis. Below is the integrative characterization of the overall work (see Table 7).

In this diagram, reading horizontally by row represents the previous description of the preliminary work. However, reading vertically by column reveals four integration surfaces. The first is the U(1) dynamics integration surface, which includes quantum electrodynamics, market dynamics, and reasoning dynamics. The second is the SU(3) dynamics integration surface, which includes quantum chromodynamics, sub-economic dynamics, and sub-cognitive dynamics. The third is the isospin dynamics integration surface, which includes flavor charge and lepton isospin, economic impulse isospin, and cognitive impulse isospin. These three dynamics integration surfaces are described using the language of gauge field theory and are characterized by different gauge symmetries, namely the U(1) symmetry group, the SU(3) symmetry group, and the SU(2) symmetry group, respectively. (Additionally, the fourth is the Higgs mechanism integration surface, which is not detailed here.) Therefore, the Standard Model is commonly expressed through the integration of these three symmetry groups. Gauge field theory is a part of quantum field theory, and the Standard Model is regarded as a unified field theory of the three fundamental forces of nature (excluding gravity), namely electromagnetism, the strong force, and the weak force. We now see that these three integration surfaces form an integrated Standard Model system spanning three domains.

8. General Discussion

Since the latter half of the 20th century, interdisciplinary research has flourished. Interdisciplinary research comprises many levels and paths. One emerging research area since the early 21st century is called integrative science. Specifically, we focus on the research path of structural integration between social sciences and theoretical physics in a dynamical sense. Building on nearly 20 years of preliminary work, this paper proposes the basic theory of integration science, laying the theoretical foundation for its subsequent development.

In the introduction, this paper discussed three levels of meaning in integration science. First, finding structural connections between different disciplines helps us achieve a holistic understanding of natural and social phenomena. Second, the conceptualization and modeling levels of natural sciences, especially physics, are generally ahead of those in social sciences. Integration science research helps elevate the conceptualization and modeling levels of social sciences. Third, the structural connectivity between different disciplines reflects the cognitive alignment of scientists across fields. Integration science is not merely a synthesis of different disciplinary knowledge. The standard of integration science is to enable social sciences and natural sciences to share the same mathematical structure, thereby having a unified mathematical language for characterization.

Section 2 of this paper discusses the empirical foundation of integration science and proposes a unified theory of interdisciplinary scientific observations. This includes the directional concept of scientific observations and orthogonality principles, the concept of observational disturbance and the diagonal rule, defining low-disturbance and high-disturbance quadrants, and discussing why different disturbance quadrants have distinct mathematical pathways.

Section 3 is the core of the paper, presenting the basic theory of integration science. It first introduces how to apply mathematical category theory in integration science and proposes necessary semantic supplements. Subsection 3.2 is crucial, presenting the fundamental concepts of integration theory mathematics, defining integration points, integration lines, integration surfaces, and integration systems, and discussing their algebraic and functional analysis methods, thus laying the mathematical foundation for integration science. Subsection 3.3 introduces the Structural Force Hypothesis and provides an axiomatic system for structural force, laying the philosophical foundation for integration science. Based on the previous work, Section 4, Section 5, Section 6 and Section 7 provide specific cases of integration points, integration lines, integration surfaces, and integration bulks.

With the preliminary ideas of integration theoretic mathematics proposed, further development of integration science will not only cover more detailed fields but also require further development of its meta-mathematical theory. The introduction of the Structural Force Hypothesis prepares the groundwork for developing structural dynamics theory, which involves introducing the concept of structural charge. This dynamics should satisfy gauge structure, having both global and local levels. At the global level, general integration structural analysis is conducted without considering individual differences. At the local level, individual differences must be considered, including people's understanding of structural concepts and their structural thinking. Finally, we also anticipate further discussion on the Structural Force Hypothesis to deepen our understanding of the philosophical foundation of integration science.

References

Hofstadter, D. (1979/1995). Gödel, Escher, Bach: An Eternal Golden Braid. Basic Basic Books Inc. New York.
Penrose, R. (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Alfred A. Knopf.
Wang, Z. (2008). Elementaty Quantum Field Theory. Peking University Press, Beijing.
Zee, T. (2003). Quantum Field Theory in a Nutshell. Princeton University Press, Princeton.
Yang, Y. Psychological Character Periods and Society: Psychological Life and Theoretical Physics I. Science, Economy, Society 2022, 40. [Google Scholar]
Yang, Y. The Integration Structure of Language and Linguistic Behavior and Its Psychologization Path: Psychological Life and Theoretical Physics II. Science, Economy, Society, 2022; 40. [Google Scholar]
Yang, Y. (2022). The Content, Methods, and Significance of Economic Dynamics: Economic Dynamics and the Standard Model I. Science, Economy, Society, Vol. 40, No. 5. China. Preprint in English. Yang, Y. Contents, Methods, and Significance of the Economic Dynamics: Economics Dynamics and Standard Model (I). Preprints 2024, 2024080810. [CrossRef]
Yang, Y. Principles of Market Dynamics: Economic Dynamics and the Standard Model II. Science, Economy, Society, 2023; 41. [Google Scholar]
Yang, Y. Principles of Sub-Economic Dynamics: Economic Dynamics and the Standard Model III. Science, Economy, Society, 2023; 41. [Google Scholar]
Preprint in English: Yang, Y. Principles of the Sub-Econ Dynamics: The Econ-Dynamics and the Standard Model (Ⅲ). Preprints 2024, 2024071843. Yang, Y. (2023). Principles of Economic Externality Dynamics: Economic Dynamics and the Standard Model V. Science, Economy, Society, Vol. 41, No. 5. China. [CrossRef]
Yang, Y. Principles of Economic Externality Dynamics Economic Dynamics and the Standard Model (V). Journal of Electrical Electronics Engineering 2024, 3, 01–13. [Google Scholar] [CrossRef]
Yang, Y. Outline of Categorical Dynamics: From Theoretical Physics to Social Sciences. Cognitive Science 2022, 6. [Google Scholar]
Yang, Y. Philosophy Encounters Statistics with the Cognitive Gauge Structure. Cognitive Science 2023, 7. [Google Scholar]
Yang, Y. (2023). The Content, Methods, and Significance of Higher-Order Cognitive Research. Academic Frontiers, 2023. [Google Scholar]
Yang, Y., Braine, M.D.S., & O'Brien, D.P. (1998). Some empirical justifications of one mental predicate-logic model. In M.D.S. Braine & D.P. O'Brien (Eds.), Mental Logic, Chapter 12, pp. 333-365. Mahwah, NJ: Lawrence Erlbaum Associates.
Yang, Y.; Johnson-Laird, P.N. Illusions in quantified reasoning: How to make impossible seem possible, and vice versa. Memory & Cognition 2000, 28, 452–465. [Google Scholar] [CrossRef]
Xu, G. (2010). Material Structure. Science Press, Beijing.
von Neuman, J. (1955/1983), The Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton, New Jersey.

Figure 1.

Figure 2.

Figure 3.

Figure 4.

Figure 5.

Figure 6.

Table 1. Integration Points - Normative Structure.

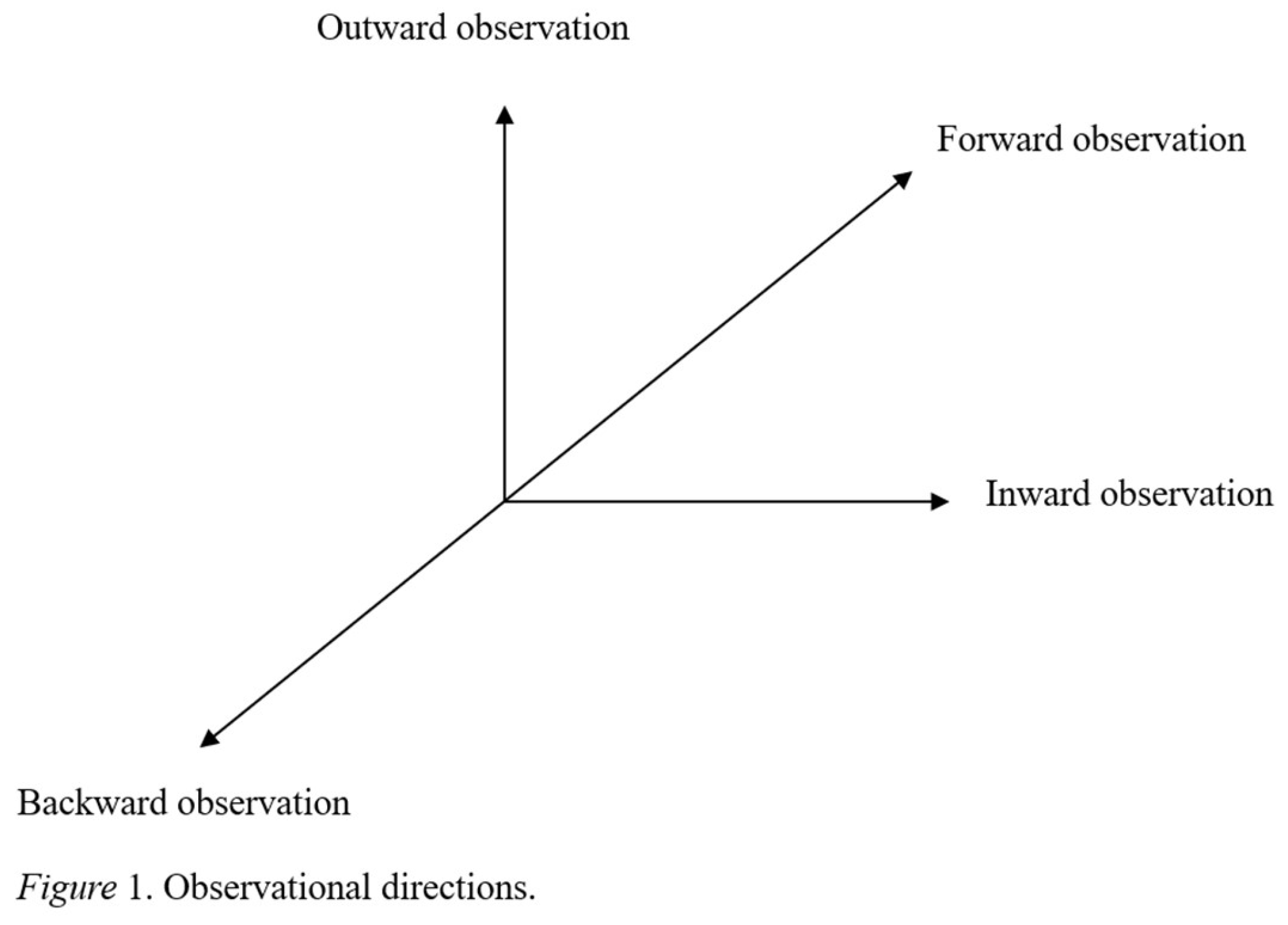
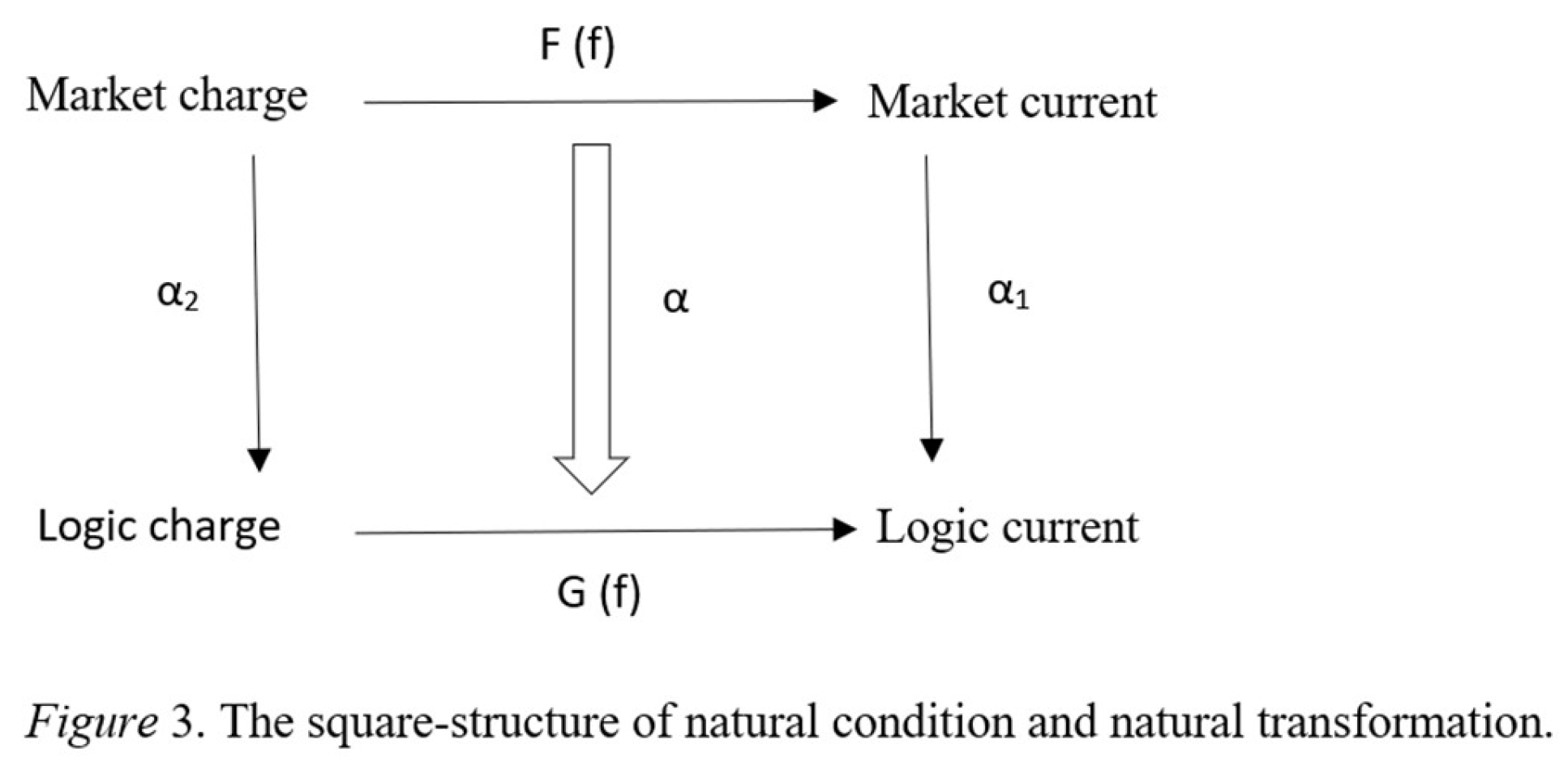
Gauge Structure
Gauge Structure	Philosophy	Statistics
Global Gauge Potential	Metaphysics	Population
Global Gauge Field Strength	Add-on Philosophy	Population Mean
Local Gauge Potential	Cognitive Philosophy, Individual Philosophical Ability	Stochastic Sampling
Local Gauge Field Strength	Cognitive Philosophy, Individual Philosophical Expression	Sample Probability

Table 2. Multiple state of leg structure.

One more integration point
Syntax/Semantics Two-leg mechanism	Logic, decision theory, game theory, set theory, etc.

Table 3. Psychological characteristic phases and their physical model.

Integration line
Psychological life characteristic phase	Theoretical physics
Embracing phase	Newtonian mechanics
Phase of conflict	Quantum mechanics and special relativity
Re-entry phase	Proper time, momentum cone Gauge field theory concept
Citizenship phase	gauge field theory model
Emotional phase	general relativity

Table 4. Integration surface 1. U(1) symmetry.

Single Charge Dynamics
Quantum Electrodynamics	Market Dynamics	Reasoning Dynamics
Electric Charge	Market Charge	Logical Charge
Spin Up Spin Down	Buying Not Buying	Valid / Yes Invalid / No
Magnetic Field	Economic Cognitive Field	Reasoning Cognitive Field
Global Gauge Potential	Economic Rationality or Rational Man	Logician or Logic
Global Gauge Field Strength	Perfect Competitive Market	A Specific Logical System or A Set of Reasoning Experiment items
Local Gauge Potential	Individual Consumer Budget	Reasoner Ability
Local Gauge Field Strength	Individual Consumer Consumption	Reasoner Performance
Light Cone	Money Cone	Language Cone

Table 5.

Table 6.

Table 7. Standard Model integration. U (1)

\otimes

SU (2)

\otimes

SU (3) is the direct product of three symmetry groups.

Table 7. Standard Model integration. U (1)

\otimes

SU (2)

\otimes

SU (3) is the direct product of three symmetry groups.

Three Standard models
Integration Surface	Integration Surface 1	Integration Surface 2	Integration Surface 3	Integration Surface 4
Standard Model	Quantum Electrodynamics	Quantum Chromodynamics	Weak Force Model	Higgs Mechanism
Economic Dynamics	Market Dynamics	Subeconomic Dynamics	Economic Externality Dynamics	Ordinary Rationality Mechanism
Epistemic Dynamics	Reasoning Dynamics	Subcognitive Dynamics	Cognitive Externality Dynamics	Ordinary Rationality Mechanism
Number Of Charges	Single Charge Dynamics	Three Charge Dynamics	Isospinal Dynamics	Complex Scalar Field
Gauge Symmetry Group	U (1) Symmetry Group	SU (3) Symmetry Group	SU (2) Symmetry Group	Spontaneous Symmetry Breaking

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Principles of Integration Science Its Content, Methods, and Significance

Abstract

1. Introduction

2. Principles of Scientific Observation

2.1. Directionality and Orthogonality Principle of Scientific Observation

2.2. Observation Interference and the Diagonal Rule

2.3. Low Disturbance Zone

2.4. High Disturbance Zone

2.5. Two Mathematical Paths

3. Mathematical Foundations of Integration Theory

3.1. Application of Category Theory

3.2. The Mathematical Foundations of Integration Theory

3.3. The Hypothesis of Structural Force

4. Integration Point Cases

4.1. Two Fields Sharing a Single Integration Point

4.2. Multiple Fields Sharing a Single Integration Point

4.2.1. Standard Dual-Leg Structure of Logic and Formal Language

4.2.2. Syntax Structure and Utility Semantics in Decision Theory

4.2.3. Syntax Structure and Utility Semantics in Game Theory

4.2.4. Dual-Leg Structure of Set Theory Language

5. Integration Line Case Study

6. Integration Surface Case Studies

6.1. U(1) Dynamics Integration Surface

6.2. SU(3) Dynamics Integration Surface

6.3. Isospin Integration Surface

7. Standard Model Integration System

8. General Discussion

References

MDPI Initiatives

Important Links

Subscribe