Prerpints.org logo
Preprint
Review

Mathematical Problems of Artificial Intelligence and Their Solution Through the Universality of the Zeta Function

Altmetrics

Downloads

67

Views

46

Comments

0

This version is not peer-reviewed

Submitted:

26 September 2024

Posted:

27 September 2024

Read the latest preprint version here

Alerts
Abstract
Artificial Intelligence (AI) faces several mathematical challenges, such as optimization, generalization, interpretability of models, and phase transitions. These problems significantly limit the application of AI in critical areas such as medicine, autonomous systems, and finance. This paper examines the main mathematical problems of AI and proposes solutions based on the use of the universality of the Riemann zeta function.
Keywords: 
Subject: Computer Science and Mathematics  -   Other

1. Introduction

Currently, we are witnessing remarkable progress in the field of AI. The advances in AI are preparing humanity for the emergence of General Intelligence (AGI). However, problems with energy consumption raise doubts about its near arrival. We believe that the only hope lies in the universality of the Riemann zeta function and its constructive application. This hope was formulated by the fathers of modern mathematics, who saw the Riemann Hypothesis as a sort of “Holy Grail” of science, the discovery of which will bring immeasurable knowledge. As the great mathematician David Hilbert once said in response to the question of what would interest him in 500 years: “Only the Riemann Hypothesis.” It is appropriate to admire all our predecessors who see the development of science and humanity over millennia.
The mathematical foundations of artificial intelligence include several key areas, such as probability theory, statistics, linear algebra, optimization, and information theory. These disciplines provide the necessary tools for solving complex tasks related to AI learning and development. However, despite significant progress in this area, AI faces an increasing number of mathematical problems that need to be solved for the further effective development of technologies.
In recent years, there has been a significant increase in energy consumption due to the development of AI. For example, statistical data show that AI’s energy consumption increased from 0.1% of global consumption in 2023 to 2 % in 2024. This growth implies the need to either slow down the development of AI due to energy resource constraints, create new energy sources, or develop more efficient computational algorithms that can significantly reduce energy consumption.
One of the most pressing issues is the problem of turbulence—a type of information flow that humanity has not yet been able to effectively process. Solving such problems with AI could influence progress in areas such as high-temperature superconductivity, phase transitions, the creation of new materials, and thermonuclear fusion. Thus, AI will play a key role in solving global scientific problems, and the mathematical methods used to address these problems will become an important aspect of its further development.
In this paper, we will examine the main mathematical disciplines playing an important role in AI development and analyze the problems limiting its efficiency, proposing our approaches based on global scientific achievements and systematizing them for AI development.

2. Mathematical Disciplines and Their Problems

Probability Theory and Statistics: Probability theory and statistics are the foundation for modeling uncertainty and AI learning. These disciplines provide tools for building predictive models, such as Bayesian methods and probabilistic graphical models.
Problems: The main issues are related to estimating uncertainty, handling incomplete and noisy data. Probabilistic models require significant computational resources to account for all factors of uncertainty.
Linear Algebra: Linear algebra is used for data analysis, working with high-dimensional spaces, and performing basic operations in neural networks. It is also important for dimensionality reduction methods such as Principal Component Analysis (PCA).
Problems: As data volumes increase, the computational complexity of operations in high-dimensional spaces grows exponentially, creating the so-called “curse of dimensionality.”
Optimization Theory: Optimization is the foundation of most machine learning algorithms. Gradient descent and its modifications are used to minimize loss functions and find the best solutions.
Problems: The main challenges include the presence of local minima, slow convergence, and complexity in multidimensional spaces, which require significant computational resources.
Differential Equations: Differential equations are used to model dynamic systems, such as recurrent neural networks and LSTMs. They are important for describing changes over time and predicting based on data.
Problems: Nonlinear differential equations are difficult to solve in real time, making their application computationally expensive.
Information Theory: Information theory plays a key role in encoding and transmitting data with minimal loss. It is also important for minimizing entropy and improving the efficiency of model learning.
Problems: Balancing entropy and the amount of data, especially in the presence of noise, is a complex task that requires large computational resources.
Computability Theory: Computability theory helps define which problems can be solved with algorithms and where the limits of AI applicability lie.
Problems: Determining problems that cannot be solved algorithmically, especially in the context of creating strong AI.
Stochastic Methods and Random Process Theory: These methods are used to handle uncertainty and noise, including algorithms like Monte Carlo methods and stochastic gradient descent.
Problems: Optimizing random processes under limited resources remains a complex task.
Neural Networks and Deep Learning: Deep neural networks consist of complex multilayer structures involving linear transformations and nonlinear activation functions. These networks are widely used for solving AI tasks such as pattern recognition and natural language processing.
Problems: The main issues include interpretability of neural network decisions, overfitting, and generalization. These problems require significant computational resources to solve.

3. Detailed Problem Descriptions

Probability Theory and Statistics: Probabilistic methods play a key role in machine learning and AI, especially in tasks like supervised and unsupervised learning. Bayesian methods, probabilistic graphical models, and maximum likelihood methods are widely applied.
Problems: The main mathematical problem involves uncertainty estimation and developing methods for working with probabilistic models in the presence of incomplete data or significant noise.
Linear Algebra: Used for data analysis and working with high-dimensional spaces, which is critical for neural networks and dimensionality reduction methods like PCA. Analyzing data and working with high-dimensional spaces are critical aspects of machine learning and AI tasks, especially for neural networks. The high dimensionality of data increases computational and modeling complexity, making effective data processing methods essential.
Dimensionality reduction methods, such as PCA (Principal Component Analysis), are used to reduce the number of features (variables) while retaining the most significant information. PCA helps to:
Reduce computational complexity; Decrease the likelihood of overfitting; Improve data visualization in 2D and 3D; Accelerate model training. This method allows identifying key components, which is especially important in tasks with thousands of features, such as image processing, text, or genetic data, where the original data have high dimensionality.
Problems: The “curse of dimensionality,” where working with large datasets becomes computationally complex.
Optimization Theory: Optimization is the foundation for most machine learning algorithms. Gradient descent and its modifications are used to minimize loss functions.
Problems: Local minima and slow convergence in multidimensional spaces remain a challenge.
Differential Equations: Used for modeling dynamic systems, such as recurrent neural networks and LSTMs.
Problems: Solving nonlinear differential equations in real-time is a significant mathematical difficulty.
Information Theory: Evaluates how to encode and transmit information with minimal losses, which is related to reducing entropy and minimizing losses during model training.
Problems: Balancing entropy and data quantity when training models with noisy data.
Computability Theory: The main task of this theory is to define which problems can be solved by algorithms and study the limits of computation. It plays an important role in understanding which tasks are computable and which are not, which is especially important for developing efficient AI algorithms.
Problems: In the context of strong AI, the most important problem is unsolvable tasks that cannot be solved algorithmically, such as the halting problem. This places fundamental limitations on the creation of strong AI capable of solving any task. Other tasks, such as computing all consequences of complex systems or working with systems with chaotic dynamics, may also turn out to be uncomputable within existing algorithmic approaches.
Stochastic Methods and Random Process Theory: These methods are used in AI algorithms to work with uncertainty and noise, such as Monte Carlo methods and stochastic gradient descent.
Problems: Efficiently handling uncertainty and optimizing random processes under limited resources remains a complex task.
Neural Networks and Deep Learning: Deep neural networks are based on multilayered structures, including linear transformations and nonlinear activation functions.
Problems: The main problem is the explainability (interpretability) of neural network decisions, as well as overfitting and generalization.

4. The Main Result and Its Consequences

In this section, we present the main mathematical results that can serve as a unified foundation for overcoming the mathematical problems of AI outlined above. We want to start the presentation of these results with a diagram depicting this function in Figure 1.
In [6], Voronin proved the following universality theorem for the Riemann Zeta function. Let D be any closed disc contained in the strip 1 / 2 < ℜ ( z ) < 1 . Let f be any non-vanishing continuous function on D which is analytic in the interior of D. Let ϵ > 0 . Then there exist real numbers t such that
sup z ∈ D ζ ( z + i t ) − f ( z ) < ϵ .
Voronin mentions in [6] that the analogue of this result for an arbitrary Dirichlet L-function is valid.
In [7], Theorem (Joint universality of Dirichlet L-function):
Let k > 1 , and let Z 1 , ⋯ , Z n be distinct Dirichlet characters modulo k. For 1 ≤ j ≤ n , let D j be a simply connected compact subset of C , and let f j be a non-vanishing continuous function on D j , which is analytic in the interior (if any) of D j . Then the set of all t ∈ R for which
sup 1 ≤ j ≤ n sup z ∈ D j L ( z + i t , Z j ) − f j ( z ) < ϵ
has positive lower density for every ϵ > 0 .
The constructive universality of the Riemann zeta function, developed in [12,13] Theorem Constructive Universality of the Zeta Function:
Let
. . . s − n , s − n . . . . s − n + 1 . . . . s − 1 , s 1 , s 2 . . . . s n . . i s z e r o s ζ f u n c t i o n
I m ( s i ) < I m ( s ) < I m ( s i + 1 )
I m ( s ) = c o n s t
Then
sup s , I m s n < I m s < I m s n + 1 | l n ( | ζ ( s ) | ) θ ( R e ( s ) − 1 / 2 − δ ) | | < C I m ( s ) δ
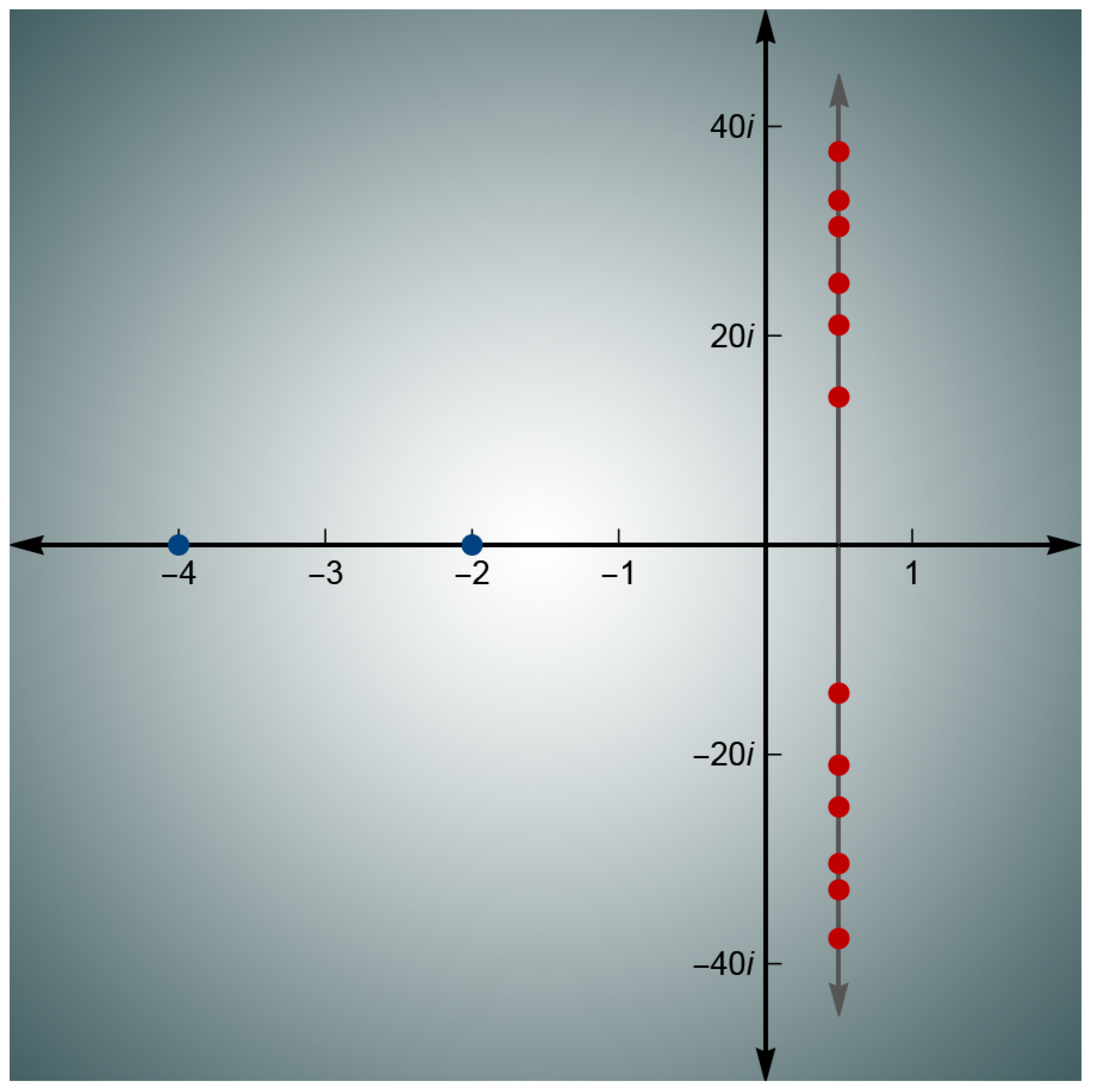
and its zeros can be used for global approximation of loss functions and avoiding local minima. The zeros of the zeta function can be viewed as key points for analyzing high-dimensional spaces of loss functions [8]. This will accelerate the optimization process and achieve better convergence. The critical line and zeros of the zeta function are shown in Figure 2

5. The Universality of the Riemann Zeta Function as a Unified Mathematical Foundation for AI Problems

Let us consider the first mathematical problem of AI—probability theory. Of course, probability theory is a vast area of mathematics, but choosing the appropriate measure to describe current processes becomes a problem, especially in turbulent conditions. We believe that the results that combine quantum statistics with the zeros of the zeta function could form the basis for solving both the turbulence problem and the task of constructing measures for AI.
Replacing random measures with quantum statistics based on the zeros of the zeta function in the context of AI and Global AI represents an interesting and deep direction of research. It offers a new way of modeling uncertainty, learning, and prediction in complex systems.
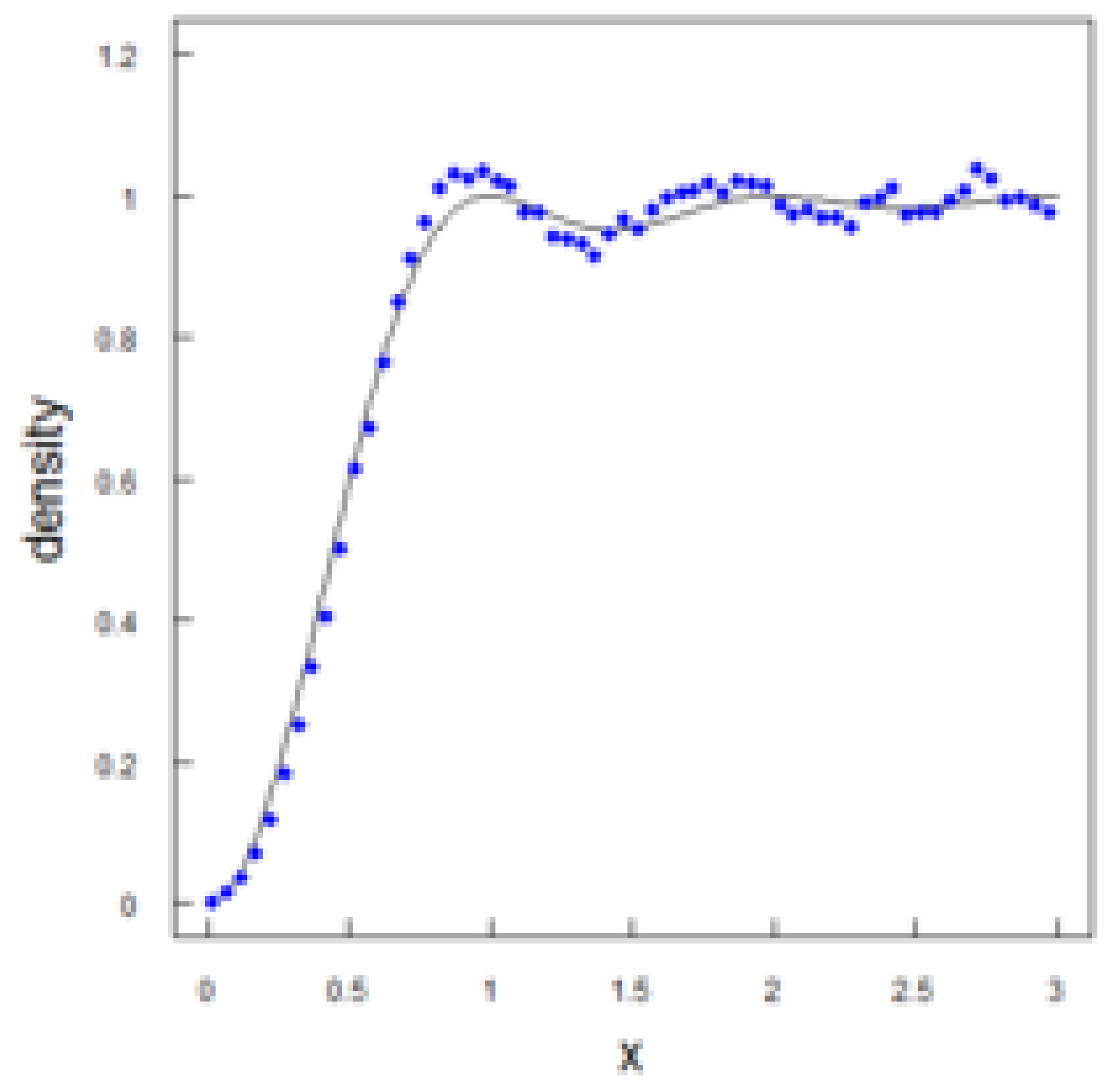
1. Quantum Statistics and Uncertainty in AI: In modern AI systems, uncertainty is often modeled through probabilistic methods such as Bayesian networks, stochastic processes, and distributions. Quantum statistics could offer more accurate methods for describing uncertainty. The zeros of the zeta function can be used as generators of a statistical measure for complex dynamic systems where uncertainty and chaotic behavior play a key role. The figure showing the connection of the zeros with quantum statistics is shown in Figure 3, which was obtained in [3].
2. Connection with Global AI: The task of building Global AI (AGI) is to create AI capable of solving a wide range of tasks at a level far superior to human intelligence. This requires powerful methods for working with incomplete information and complex dependencies. The zeros of the zeta function can improve AGI’s ability to predict chaotic and complex dynamics in real-time.
3. A Priori Measure for Bayesian AI Systems: Choosing an a priori measure in Bayesian AI systems is a serious task. Replacing the classical a priori measure with a distribution based on the zeros of the zeta function could improve the determination of initial probabilities under uncertainty, as the chaos measure is the distribution of the zeros of the zeta function, as shown in works [2,3,8]
4. Quantum AI: Combining quantum computing and AI could significantly accelerate learning and data processing. The zeros of the zeta function can form the basis for creating probabilistic models in quantum AI, where quantum superpositions and entanglements enhance computational capabilities. To move into the field of quantum AI, we propose relying on the results of Berry, Keating, Montgomery, Odlyzko, and Durmagambetov [2,3,8,12,13], which allow these results to become a serious theory.

6. Linear Algebra

The main problem in using linear algebra methods in AI is the issue of data dimensionality growth. Within the theory of constructive universality, this problem is reduced to replacing datasets with a single point representing the entire dataset. Transformations, such as the Hilbert transform or Fourier transform, can be reduced to analytic functions that are constructively encoded by a single point on the complex plane according to Voronin’s universality theorem and constructively implemented in [12].

7. Differential Equations

: Differential equations are used to model dynamic systems, such as recurrent neural networks and LSTMs. To study differential equations through the zeta function, equations of the form can be considered:
y ˙ = A y + f ( y , t )
Applying the Hilbert transform, we obtain:
z ˙ = A z + F ( z )
where z = T y , and F ( z ) = T f ( y , t ) .
Using the results of works [12,13], we can formulate:
z = ζ ( s )
s ˙ = A ζ ( s ) + F ( ζ ( s ) ) ζ ˙
s | k = k 0 = s 0
We reduce the problem’s solution to constructing the trajectory of the parameter s. Since we are between the zeros of the Riemann zeta function, the problem of determining the moment of turbulence is solved in parallel—the moment when the parameter k hits the zeros of the zeta function. This allows tracking which zero we will hit and understanding the nature of the arising instability. This approach provides an important leap in understanding the nature of things and can serve as the basis for describing phase transitions.
This method solves the phase transition problem for both AI and new material production technologies. Furthermore, in the context of financial markets, it can describe the “black swan” phenomenon. In medicine, this approach describes critical health conditions, and in thermonuclear fusion, it allows avoiding disruptions in the technology’s operating mode.

8. Information Theory

Information theory evaluates how to encode and transmit information with minimal losses, which is related to reducing entropy and minimizing losses in model training.
Problems: Balancing entropy and data quantity when training models with noise is a complex task. The universality of the zeta function represents a new approach to encoding and decoding data: signals are replaced by points on the critical line. This fundamentally changes the learning technology—instead of learning from large volumes of data, the process focuses on key points on the critical line. In areas close to the zeros of the zeta function, learning will yield opposite results with minimal data changes.

9. Computability Theory

Computability theory is important for determining which problems can be solved with algorithms and for studying the limits of AI capabilities. Now we can classify tasks for each set of input data located between two zeros of the zeta function. According to the universality theorem, all datasets are transformed into points on the critical line. We can observe cyclical processes or an approach to critical points—the zeros of the zeta function. The process may stop either by approaching zero or by nearly periodicity, according to Poincaré’s theorem.

10. Optimization Problems

Local minima and slow convergence in multidimensional spaces present significant challenges. The universality of the zeta function and its tabulated values help eliminate these problems, reducing them to simple computational tasks. Optimizing stochastic processes under limited resources remains an important task, especially in AI systems requiring large data processing or real-time operations.

11. Neural Networks and Deep Learning

Deep neural networks consist of multilayered structures involving linear transformations and nonlinear activation functions. Multilayered neural networks can be viewed as multilayered “boxes” built from the zeros of the zeta function. If all the zeros of the zeta function are considered, one can obtain an infinitely layered neural network capable of performing Global Intelligence functions. Activation functions can be viewed as phases of the zeta function’s zeros.

12. Understanding Intelligence Through the Zeta Function

Processes described through the values of the zeta function, located to the right of the line Re ( s ) = 1 / 2 in the critical strip of the Riemann zeta function, correspond to the observable world. The processes described by the values of the zeta function to the left are their reflections, symbolizing fundamental processes influencing the physical world. This symmetry emphasizes the importance of the zeta function in understanding AI. AI is engaged in prediction, and the values of the zeta function can be considered part of this prediction.
Suppose we observe a process that occurs simultaneously in both the brain and outside of it. The universality of the zeta function lies in its ability to describe both processes. For example, the registration of signals by sensors and the subsequent decoding of records can be described through the zeta function. Interpretation becomes a shift from one point to another on the critical line.

13. Interpretability and the Future of Global Intelligence

Global Intelligence will be able to analyze and predict processes, relying on both explicit and hidden aspects. The nonlinear symmetry of the zeta function provides a new metaphor for solving the problem of AI interpretability, making it more predictable and efficient, as outlined in all aspects of our research. The development of AI is directly related to understanding human intelligence, which requires a deep understanding of brain function.
We suggest that the remarkable symmetry inherent in living organisms may be associated with the symmetry of the zeta function, which represents a computational system implementing the prediction mechanism through the zeros of the zeta function. The complete decoding of the brain’s hemispheres’ work and their connection with the symmetry of the zeta function seems to us a natural step toward creating global intelligence.
One example of this process is the functioning of the visual system. Vision, by its nature, is a two-dimensional sensor system, but thanks to holographic processing in the brain, it is transformed into three-dimensional images. We suggest that retinal follicles can be interpreted as a natural realization of the zeta function’s zeros. This assumption allows us to understand how information entering the retina is processed by the brain, synchronizing with biorhythms such as the heartbeat, which acts as the brain’s “clock generator.”
Thus, the right hemisphere of the brain processes data related to the right side of the zeta function’s critical line, and the left hemisphere processes the left. This synchronous process forms the perception of temporal and spatial coordinates, creating awareness of the past and present.
Continuing this thought about the brain’s work, one can assume that similar principles operate in the Universe. For example, black holes can be associated with the zeros of the Riemann zeta function, leading to an even deeper understanding of the principles of the microcosm and macrocosm, which humanity has pondered since ancient times.

References

  1. Goodfellow, I., Bengio, Y., Courville, A. (2016). Deep Learning. MIT Press.
  2. Montgomery, H. L. (1973). The pair correlation of zeros of the zeta function. Proceedings of Symposia in Pure Mathematics.
  3. Odlyzko A. On the distribution of spacings between zeros of the zeta function (Engl.) // Mathematics of Computation[Engl.]: journal. — Providence, R.I.: American Mathematical Society, 1987. — Vol. 48, iss. 177. — P. 273—308.
  4. Ribeiro, M. T., Singh, S., & Guestrin, C. (2016). “Why Should I Trust You?” Explaining the Predictions of Any Classifier. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
  5. Gaspard, P. (2005). Chaos, Scattering and Statistical Mechanics. Cambridge Nonlinear Science Series.
  6. Voronin, S. M. (1975). Theorem on the Universality of the Riemann Zeta-Function. Mathematics of the USSR-Izvestija.
  7. Bagchi, B. (1981). Statistical behaviour and universality properties of the Riemann zeta-function and other allied Dirichlet series. PhD thesis, Indian Statistical Institute, Kolkata.
  8. Berry, M. V., & Keating, J. P. (1999). The Riemann Zeros and Eigenvalue Asymptotics. SIAM Review.
  9. Ivic, A. (2003). The Riemann Zeta-Function: Theory and Applications. Dover Publications.
  10. Haake, F. (2001). Quantum Signatures of Chaos. Springer Series in Synergetics.
  11. Sierra, G., & Townsend, P. K. (2000). The Landau model and the Riemann zeros. Physics Letters B.
  12. Durmagambetov, A. A. (2023). A new functional relation for the Riemann zeta functions. Presented at TWMS Congress-2023.
  13. Durmagambetov, A. A. (2024). Theoretical Foundations for Creating Fast Algorithms Based on Constructive Methods of Universality. Preprints 2024. [CrossRef]
Preprints 119480 g001
Figure 1.
Figure 1.
Preprints 119480 g001
Preprints 119480 g002
Figure 2.
Figure 2.
Preprints 119480 g002
Preprints 119480 g003
Figure 3.
Figure 3.
Preprints 119480 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated