Prerpints.org logo
Preprint
Article

Trajectory Planning and Performance Atlases of a New Omnidirectional Conveyor

Altmetrics

Downloads

58

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 September 2024

Posted:

27 September 2024

You are already at the latest version

Alerts
Abstract
This paper proposes an omnidirectional conveyor as a novel alternative to existing omnidirectional conveyors. With symmetric and compact layout, this new structure ensures consistent kinematics and enhanced flexibility in trajectory planning. The kinematic model of the proposed omnidirectional conveyor is developed and verified through simulation in CoppeliaSim. Four typical classes of trajectories are generated and verified in the simulation environment. Using PID control, the actual trajectories of a package on the conveyor closely match the desired trajectories. In addition, this paper outlines the workspace and corresponding wheel patterns for the conveyor, demonstrating how different supported wheel patterns emerge when packages move across various areas of the conveyor. The discussion extends to fault tolerance and obstacle avoidance, examining the workspace and wheel patterns with one or two omni wheels failed. Furthermore, this paper provides a comprehensive analysis on the feasible desired movements for the packages on the conveyor under the constrained wheel speed. This provides insights and guidance on trajectory planning and design of the conveyor.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

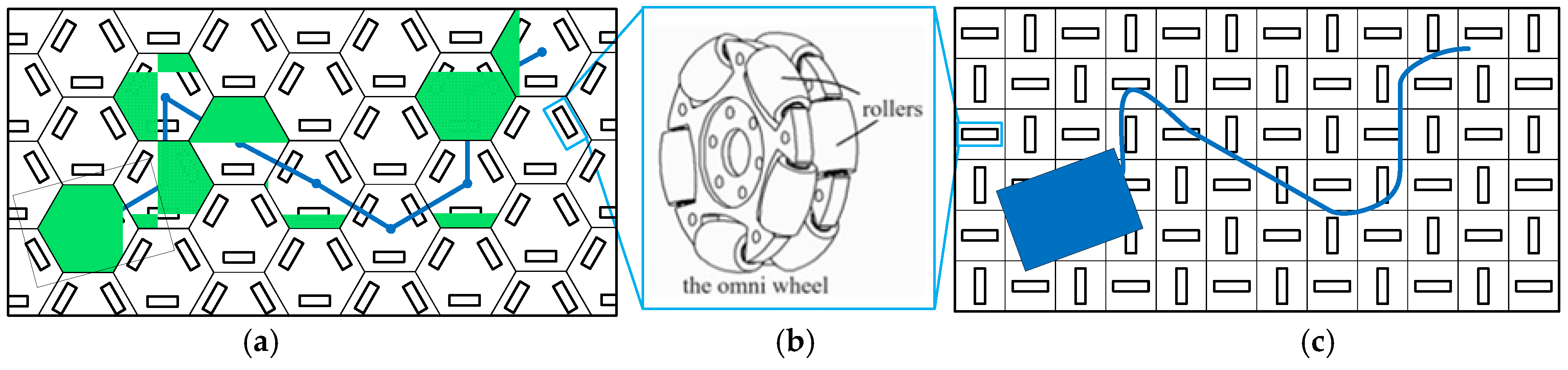
In recent decades, an omnidirectional conveyor system has been introduced as automated means of transportation of packages, goods, parts and materials in the manufacturing and logistics industries [1,2]. The omnidirectional conveyor has the ability to move packages concurrently and independently in rotation and translation in the conveyor plane thanks to an array of omni wheels [3,4]. The omni wheels consist of a base wheel with a number of rollers evenly attached around the circumference of the wheel hub, as shown in Figure 1b. The rollers are oriented with their axes perpendicular to the axis of the base wheel in order to create additional mobility. With various wheel patterns, the omni wheels are commonly aligned to generate in-plane motion with three degrees of freedom.
The advantages of the omnidirectional conveyor over conventional conveyor transfer solutions are that they are compact and flexible in transportation and deploying [5,6]. Conventional conveyor technology is characterized by rollers and powered belts, which can only fulfill simple transferring tasks, namely moving objects on a straight line [7,8]. Thus, conventional conveyor systems are not suited to develop more flexible and adaptable production lines or logistics systems in the context of smart factories. To address this issue, many types of conveyors have been developed such as the flexible conveyor [9], cognitive conveyor [10], and grid-sorter [11] etc. However, these designs have limited mobilities and make path planning be conducted in a simple manner. As a result, more advanced operations such as sorting, palletizing, and depalletizing, etc. cannot be realized.
The omnidirectional wheeled conveyors come as a whole new solution for addressing the above limitations of a conveyor. Various conveyor types with different wheel patterns have been developed [12,13,14,15]. Among the various patterns, the most popular one is the omni cellular conveyor [16,17,18,19,20], which consists of an array of regular hexagon modules with three identical omni wheels, as shown in Figure 1a. This conveyor shares kinematic similarities with the three-omni-wheeled mobile robots [21,22,23]. Extensive research efforts have been devoted to trajectory tracking [24], path planning [25], dynamics [26] and control [27] of the cellular conveyor. However, the kinematics of the wheel patterns that are in-between the adjacent regular hexagon modules have not been utilized for moving the packages. In this work, the other two triangular wheel patterns between the hexagon modules are identified and one of them is proved to be feasible. The feasible patterns between the modules are oriented rather randomly compared to the triangular pattern in the hexagon module, making controlling and analyses of the conveyor rather difficult if not impossible. As a result, the path planning usually are conducted in the module-to-module manner [28,29]. And a greater number of wheels are thus needed. In addition, the feasible minimum size of the package and density of the wheel distributions have not been investigated. The operation of the conveyor relies on experience provided the package can always cover at least one module. Further, while the cellular conveyor has fault tolerance capabilities, when a wheel fails, the entire module has to be deactivated, causing packages to be bypassed. In reality, some areas within affected module may remain functional, making the complete deactivation of the module inefficient. This approach leads to wasted potential and reduces the feasible areas for trajectory planning.
To address these problems, this paper proposes a novel omnidirectional conveyor. The proposed conveyor consists of a mixed array of horizontal and vertical omni wheels with a symmetric structure, as shown in Figure 1c. Similar to the cellular conveyor, although a four-wheeled pattern is identified to contribute the basic kinematics of the conveyor, as highlighted in Figure 1c, the package actually moves with a number of different wheel patterns depending on the location and size of the packages. It means everywhere the package moves, there is a corresponding pattern. Unlike the wheel patterns in-between the modules for the cellular conveyor, the wheels that occur everywhere on the conveyor are either horizontal and vertical, making kinematics and control of the proposed conveyor with great ease and consistency. The trajectory planning scheme can thus be conducted in a continuous manner rather than the module-to-module manner. Therefore, in this design, the basic module is the individual wheels. If one of the wheels fails, only the failed wheel is deactivated. In this work, a comprehensive study will be conducted in depicting the feasible workspace for the conveyor with different package sizes and the failure of wheels occurs. The minimum number of wheels ensuring the whole areas of the conveyor are feasible is then identified. Further, based on the minimum wheel number layout, comprehensive analyses have been conducted to determine the feasible desired velocities of the package under constrained wheel velocities. This study reveals that some theoretically feasible areas may become infeasible if the desired package velocities are unachievable due to the wheel velocity limits.
The remainder of this paper is organized as follows: the kinematic model of our proposed conveyor is established in Section 2. Section 3 develops the mathematics of the trajectory planning problem. The trajectory planning is then verified using CoppeliaSim software in Section 4. Section 5 illustrates the workspace of the conveyor based on different wheel patterns. Furthermore, workspace and the corresponding wheel patterns for the conveyor with failure of one or two omni wheels are discussed in Section 6. Last but not least, under constrained wheel speed, the feasible motions in velocity level are discussed and related feasible areas are depicted in Section 7. Finally, conclusion remarks and future research plan are given in Section 8.

2. Kinematic Modelling

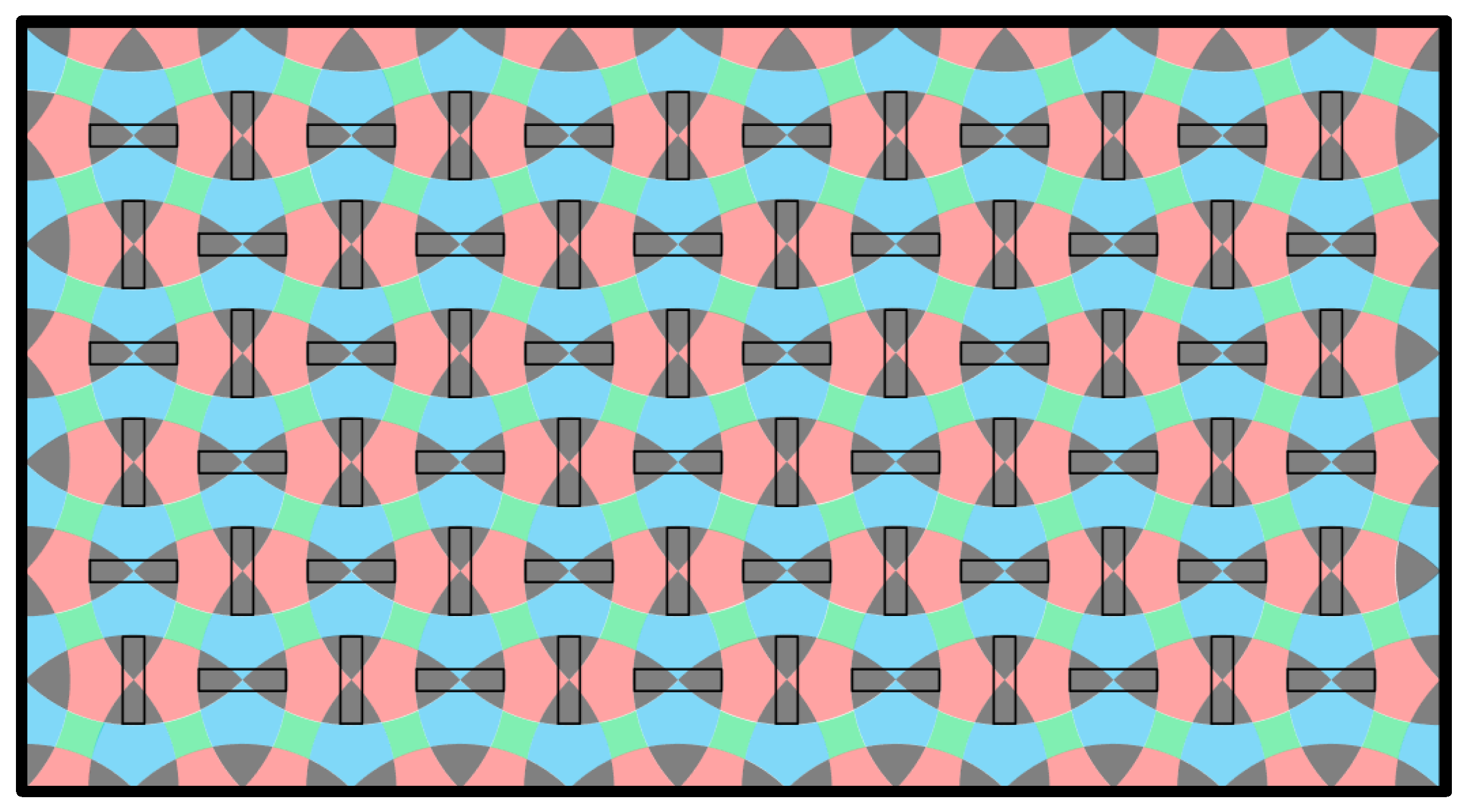
The structure of the proposed omnidirectional conveyor is depicted as shown in Figure 1, where the omni wheels are arranged in an array evenly distributed on the platform with the horizontal and vertical wheels adjacent to each other. It shares similarities with the three-omni-wheel conveyor as a repeated core pattern of four omni wheels. However, the supporting wheels are not necessarily to be the four-wheel pattern. The covered wheels actually can form various patterns depending on the size and location of the package on it, which will exert an influence on the workspace and performances of the conveyor.
In this section, a kinematic model is established to reveal the relationship between wheel rotational velocity and the package velocity. The package, goods, or other materials on the conveyor are referred as “box” hereinafter for simplicity. As shown in Figure 2, the position of the box center O ' is described by x , y relative to the world frame {W} attached to the conveyor. The base frame {b} is attached to the center of the box. The angle between the axis x of the world frame and the axis x of the base frame, i.e., θ , represents the box rotational angle. Apparently, x ˙ , y ˙ and θ ˙ denote the box translational velocities in axes x and y directions and the box rotational velocity, with respect to the world frame.
Based on rigid body kinematics, the rotational velocity of each wheel can be derived as in (1).
u 1 h n u 2 h n u 1 v n u 2 v n = 1 r 1 1 0 0 0 0 1 1 − ( n − 1 ) d − h 1 y n − 1 d + h 2 y − ( n − 1 ) d − h 1 x n − 1 d + h 2 x x ˙ y ˙ θ ˙
where h i x and h i y ( i = 1 , 2 ) denote the horizontal and vertical positions of the vertical and the horizontal wheels with respect to the box center, respectively. n refers to the serial number of rows of horizontal wheels or columns of vertical wheels counting from the center of the box. For example, n = 1 represents the nearest wheels to the box center. u i h n and u i v n ( i = 1 , 2 ) are rotational velocities of the horizontal and vertical wheels, respectively. r is the radius of the omni wheel. d is the wheel distance in both horizontal and vertical directions. Equation (1) can be rewritten as u = T q where u and q refer to the wheel and box velocity vectors, respectively. T represents the transformation matrix. Clearly, the transformation matrix is redundant and the rank is three. The redundant wheels lead to stable support of the box. In contrast, the existing cellular conveyor have basic module with three wheels, and the kinematics is not redundant.
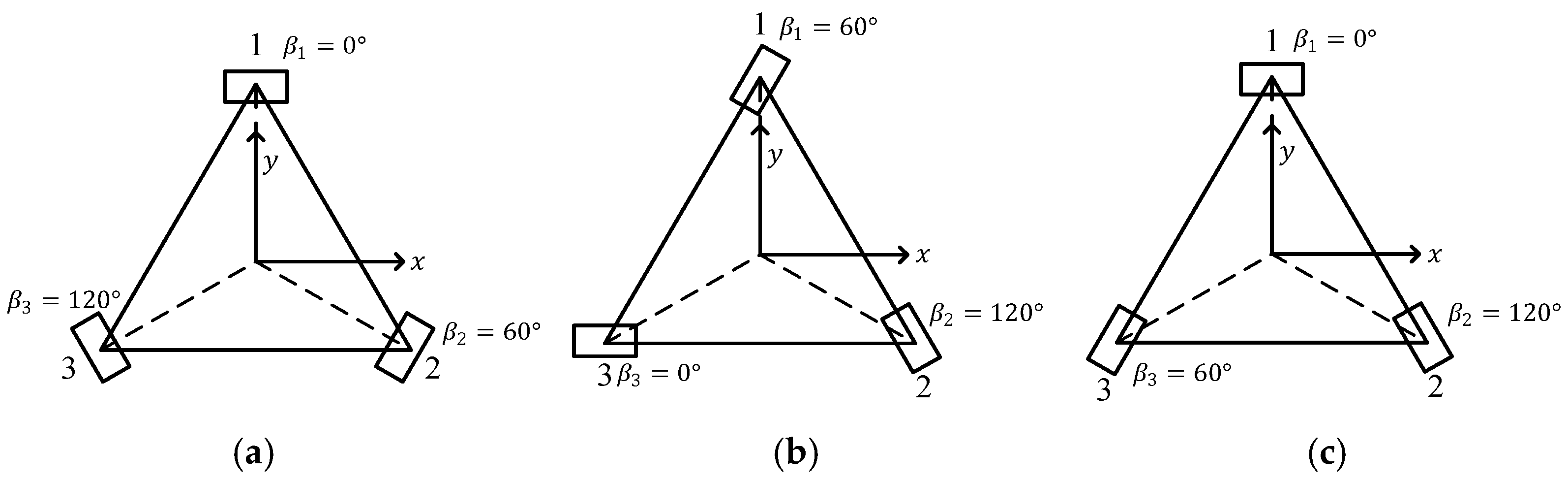
In order to compare our proposed conveyor to the cellular conveyor, the kinematics for the cellular conveyor are also discussed here. According to literatures, only the triangular wheel pattern within each module is utilized, as shown in Figure 3a. However, there exist another two triangular wheel patterns between adjacent modules, as shown in Figure 3b,c. In order to simplify the discussion, the equilateral triangle for the three-wheel patterns is assumed.
The kinematic models for the three triangular wheel patterns are developed as in (2) ~ (4), respectively.
u 1 u 2 u 3 = 1 r − R 0 1 0 R 0 1 2 3 2 − R 0 − 1 2 3 2 θ ˙ x ˙ y ˙
u 1 u 2 u 3 = 1 r − 1 2 R 0 1 2 3 2 1 2 R 0 − 1 2 3 2 1 2 R 0 1 0 θ ˙ x ˙ y ˙
u 1 u 2 u 3 = 1 r − R 0 1 0 1 2 R 0 − 1 2 3 2 − 1 2 R 0 1 2 3 2 θ ˙ x ˙ y ˙
where R 0 refers to the circumscribed circle of the triangle. It is seen that, the transformation matrix of (4) is singular and the rank is equal to two rather than three making the third type of wheel pattern infeasible for all translational movements and rotations. However, according to the cellular conveyor layout, adding one wheel to the infeasible pattern to form a diamond wheel pattern with four wheels will result in a feasible pattern. This is because any adjacent triangular pattern to the infeasible pattern in Figure 3c is one of the feasible patterns in Figure 3a,b. As a result, all of the diamond wheel patterns with four wheels are feasible. However, because the patterns in Figure 3b,c are oriented rather randomly compared to the pattern in the hexagon module as in Figure 3a, the actual control and analysis of the conveyor based on the two patterns are rather difficult if not impossible. As a result, according to the literature, the path planning was conducted only in the module-to-module manner.

3. Trajectory Planning

In this section, we will consider methods of computing a trajectory that describes the desired motion of the box on the conveyor. Usually, a trajectory is generated with given initial and final positions and orientations by human and then further specified by a couple of choices of functions that define these trajectories. The choice of functions could be linear, polynomial, circular, and sinusoidal etc., as long as it satisfied the boundary conditions. Sometimes we wish to allow path to be specified that include intermediate via points, then additional continuous conditions at the via points are required to be satisfied. In general, it is desirable for the motion of the box to be smooth. For this purpose, the trajectory function should be continuous and has a continuous first derivative.
In what follows, we will consider four types of trajectories that are typical for actual applications: a prescribed trajectory [30], trajectories defined by intermediate via points [31], trajectories defined by Bezier curves [32], and trajectories with combined straight-line and pure rotations [33]. These trajectory planning problems are formulated in this section and verified through simulation in the next section.

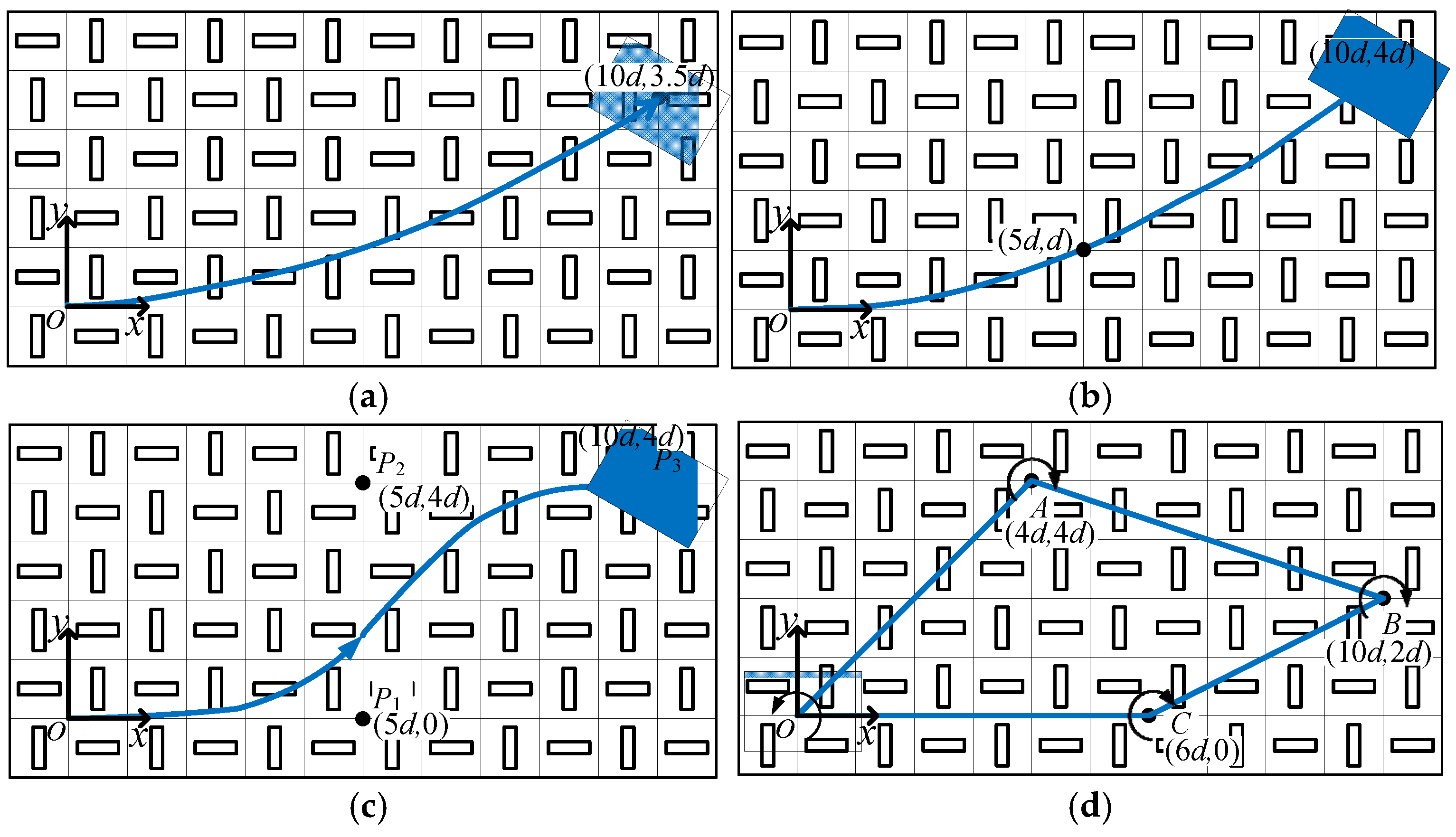
3.1. Case 1: Trajectories Specified by Particular Functions

The first type of trajectory generation problem concerns the box following a prescribed trajectory defined by functions. Here, the parabolic trajectory is taken as an example. As shown in Figure 4a, the box travels from the origin of the world frame to location ( 10 d , 3.5 d ) , in 7 seconds, following a trajectory function as in (5), rigorously, where x and y are horizontal and vertical positions relative to the world frame.
y t = 1 2 x t 2
We consider a simple linear form of x ( t ) , as in (6). To rigorously follow the trajectory, y ( t ) is calculated by substituting (6) into (5), as in (7).
x t = a t + b
y t = 1 2 a 2 t 2 + a b t + 1 2 b 2
where a and b are unknown coefficients. With (6) and (7), the velocity along this path is clearly: x ˙ t = a ; y ˙ t = a 2 t + a b . The orientation of the box is assumed to be tangent to the trajectory and directed forward. Of course, it can be defined otherwise. Thus, we have
t a n θ = y ' = x
Obviously, the orientation angle θ ( t ) is not independent; rather, it is related to the translational position of the vehicle. From (5), we can derive the orientation angle θ ( t ) and its derivative, i.e., the rotational velocity of the vehicle θ ˙ ( t ) , as in (9) and (10).
θ ( t ) = a r c t a n ⁡ ( a t + b )
θ ˙ ( t ) = a 1 + ( a t + b ) 2
Given the initial and goal locations, i.e., ( 0 , 0 ) and ( 10 d , 3.5 d ) for initial and goal locations, respectively, the unknown parameters a and b can be computed. The calculated box velocities x ˙ t , y ˙ t , and θ ˙ ( t ) , are then converted into the angular velocity of each wheel using (1). It should be noted that the initial velocity for the box is not zero in this example, to generate a smoother trajectory, the initial velocity may be zero. For this purpose, higher degree of functions may be used rather than a linear one as in (6). In this case, more constraints need to be used to specify a particular curve.
Preprints 119479 g004
Figure 4. The box following four trajectories: (a) a parabolic trajectory; (b) two segments of cubic polynomials through a via point; (c) a cubic Bezier curve; (d) trajectories of straightlines and pure rotations.
Figure 4. The box following four trajectories: (a) a parabolic trajectory; (b) two segments of cubic polynomials through a via point; (c) a cubic Bezier curve; (d) trajectories of straightlines and pure rotations.
Preprints 119479 g004

3.2. Case 2: Trajectories Include via Points

The second type of trajectory considered in this section concerns the box pass through a set of via points. Clearly, more via points included in the trajectory result in more constraints to be specified to derive the unknowns of the trajectory functions. A simple case with only one via point is examined in this section. As shown in Figure 4b, the initial, via and goal points are defined as ( 0 , 0 ) , ( 5 d , d ) and ( 10 d , 4 d ) , respectively. Unlike the first trajectory example, that is, the orientation of the box is tangent to the trajectory all the time, in this case, the orientation of the box is tangent to the trajectory only at the initial, via and goal points. The rotational speed is specified to be constant. The box is to move 3 seconds from the initial position to the via points and it takes another 4 seconds to arrive at the goal point. To make the whole trajectory smooth, the trajectory, velocity and acceleration at the via point should be continuous. In addition, velocity of the box at the initial and goal points is required to be zero. Here, we use polynomials as the trajectory function. And all these mentioned constraints uniquely specified two particular cubic polynomials, as in (11) and (12).
x i t = a i 0 + a i 1 t + a i 2 t 2 + a i 3 t 3
y i t = b i 0 + b i 1 t + b i 2 t 2 + b i 3 t 3
where the i = 1 and i = 2 refers to the trajectory segment OA and AB, respectively. x i t and y i t refer to the box locations in axis x and y, respectively. Combining above mentioned constraints yields the 16 equations in 16 unknown coefficients. Solving for the sixteen coefficients, it is easy to derive the box velocities in the two trajectory segments, i.e., x ˙ 1 t , y ˙ 1 t , x ˙ 2 t , and y ˙ 2 t . By application of the kinematics, the angular velocity of each wheel can be computed. Compared to the first trajectory of a simple parabolic curve, this trajectory is defined by an extra via point and more constraints are employed to make the trajectory smoother. Based on this example, trajectory that include more via points could be defined and obviously, it requires more constraints to solve the unknowns.

3.3. Case 3: Bezier Curves

The third type of trajectory that is commonly used in trajectory planning is the Bezier curves. Here, cubic Bezier curve is used. The cubic Bezier curve requires four given points, as shown in Figure 4c. The box travel from starting point P 0 ( 0 , 0 ) to reach the end point P 3 ( 10 d , 4 d ) . The trajectory is further shaped by the other two points P 1 ( 5 d , 0 ) and P 2 ( 5 d , 4 d ) such that the curve is tangent to line P 0 P 1 ¯ and P 2 P 3 ¯ . The detailed equation for the cubic Bezier curve is in (13).
B t = ( 1 − t ) 3 P 0 + 3 ( 1 − t ) 2 t P 1 + 3 1 − t t 2 P 2 + t 3 P 3
where t ∈ ( 0,1 )   P i = ( x i t , y i ( t ) ) T ( i = 0 , 1 , 2 , 3 ), and B t = ( x t , y ( t ) ) T . From (13) it is seen that, four points is required to uniquely specify the cubic Bezier curve, which essentially is the polynomials. The Bezier curve is also frequently applied in Computer-Aided-Design (CAD) for drawing complex smooth curves. If a trajectory is defined through human-drawings combined with the CAD software, the Bezier curve can be considerably useful.

3.4. Case 4: Trajectories through Straightline Segments and Pure Rotations

The fourth type of trajectory generation problem concerns the box passing through a set of via points that are connected through straight lines. The orientation of the box remains unchanged when moving along the straight lines until it come to rest at each via point. The orientation of the box only changes at the initial and via points to make the orientation of the box the same as the incline angle of the next straight-line segment, as shown in Figure 4d. In this case, the translational and rotational motions are separated. Constant rotational velocity of 1 rad/s at the stopping points are assumed to simplify the trajectory planning. Cubic polynomials are used for the line segments, as in (14) ~ (19).
x i t = a i 0 + a i 1 t + a i 2 t 2 + a i 3 t 3
y 1 t = x 1 t
y 2 t = − 1 3 x 2 t
y 3 t = 1 2 x 3 t
y 4 t = 0
y 5 t = 0
where i = 1 refers to segment OA, i = 2 refers to the next line segment AB, and so on. For each line segment, it is assumed that the box velocity at the start and end locations are zero. The time spent at the line segments OA, AB, BC, and CO is set to be 4, 6, 4, and 6 seconds, respectively. Solving for the sixteen unknowns, trajectories of each line segments are determined. Then, using (1), the wheel rotational velocities can be calculated.

4. Simulation Analyses

4.1. Creating a 3D Model in CoppeliaSim

In this section, the 3D model of the omnidirectional conveyor is created in CoppeliaSim software (version 4.5.1). Since the omni wheel has complex structures, it is built in professional CAD software (Solidworks, version 2022) and then imported to the CoppeliaSim. Firstly, the CAD model of an omni wheel is downloaded from GrabCAD website. Secondly, the base placer, shaft connector, and wheel base of the omni wheel are merged together to make a single stationary base part. Then, the CAD model of the omni wheel is converted to URDF (Universal Robot Description Format) format, with clearly defined hierarchy of the wheel rollers and the single stationary base and coordinate systems. The URDF format of the omni wheel is finally imported to CoppeliaSim.
The omni wheels and the platform is set as non-respondable to each other, thus simplifying the cuboid body structure design and decreasing computational cost. The schematic top view of the conveyor is presented in Figure 5, where the wheel horizontal and vertical distances are all equal to d = 0.07 m . The box is modeled as cuboid directly with the edge size equal to 0.21 m and its radius of inscribed circle is 0.105 m , slightly larger than 2 d in order to ensure everywhere on the conveyor is feasible for trajectory generation. 2 d is the minimum size of the box to ensure everywhere on the conveyor it is feasible to move and rotate. Detailed feasible areas are depicted in Section 5 and Section 6.
The wheel joints, as indicated in red color, are set to dynamic mode. The joints of the rollers are set as free control mode such that the rollers rotate passively. The conveyor is interfaced with Python child script using the regular API, provided by CoppeliaSim.

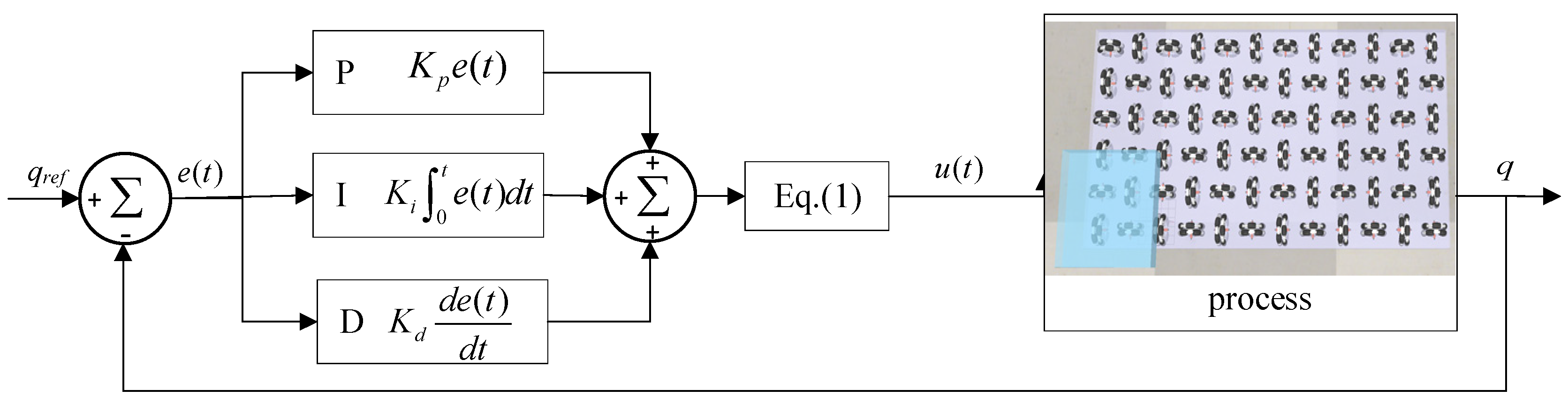
4.2. Trajectory Generation with PID Control

To reduce the tracking errors, the PID control strategy is applied. As shown in Figure 6, the tracking error of the box positions and orientations in world frame e ( t ) can be calculated readily, and fed to the PID controller to generate the control signal, i.e., the box velocity with respect to the global frame, ( θ ˙ , x ˙ , y ˙ ) . Then the box velocity is used to obtain the wheel rotational velocities by using (1).

4.3. Simulation Results

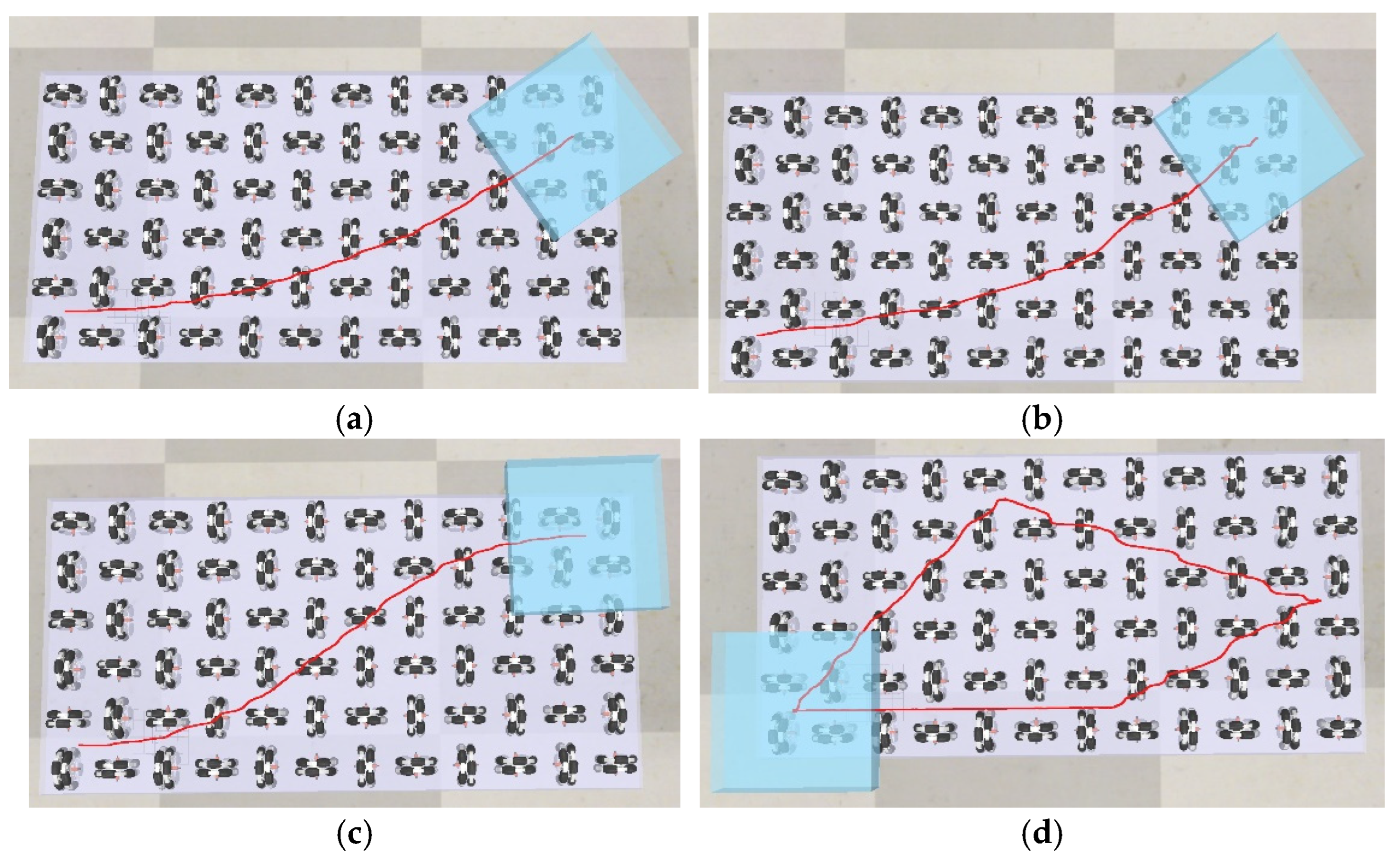
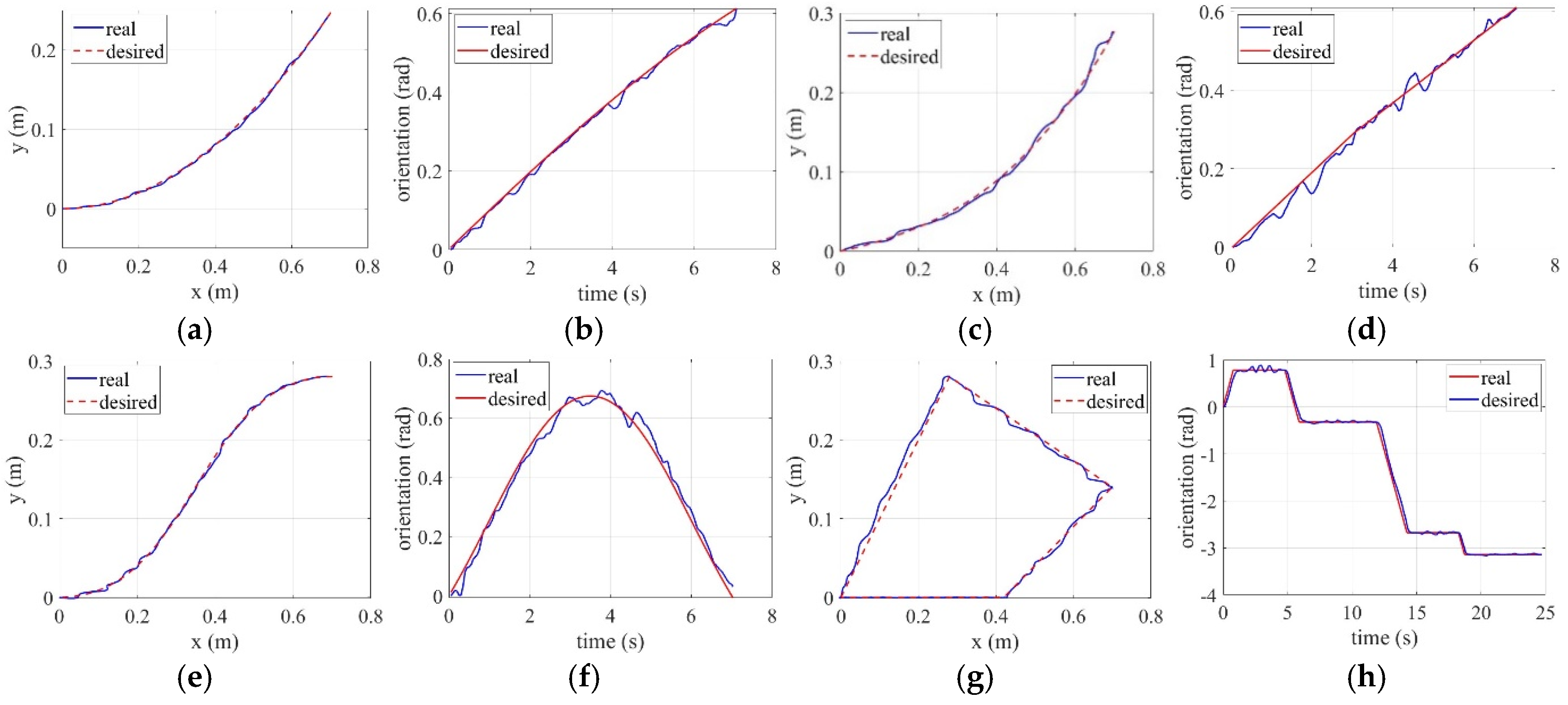
The snapshot of the final trajectory planning result is depicted in Figure 7. The actual trajectories are depicted in red color. During the simulations, only the wheels being covered by the box are rotating while other wheels remain stationary to reduce the computational and simulation time. The simulation time interval is set to 0.05 seconds for one cycle of computations. Figure 8 illustrates the trajectory following results for the four trajectory cases, in which it shows that the actual and desired trajectories and orientations agree well with each other.

5. Workspace and Wheel Patterns

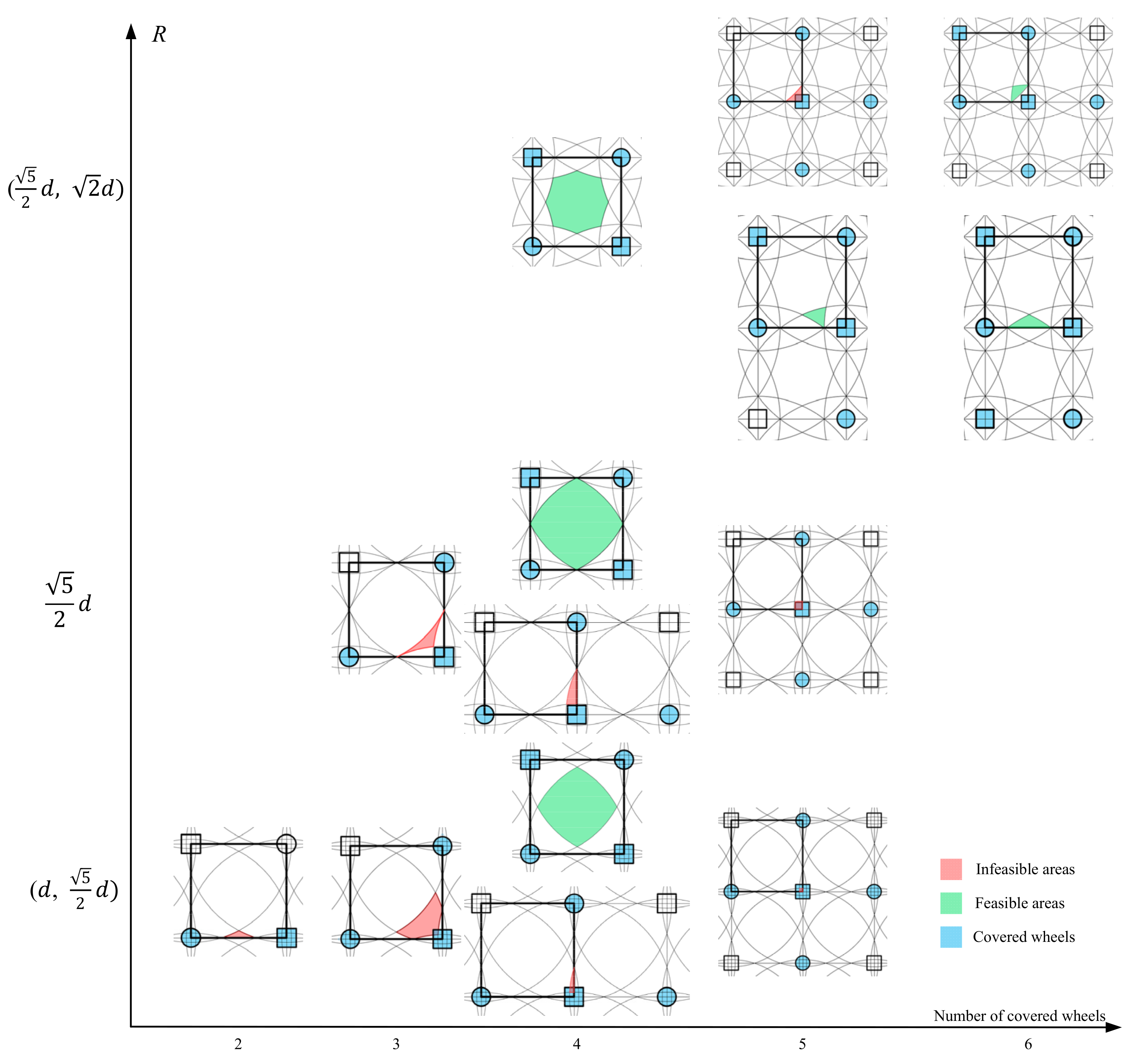
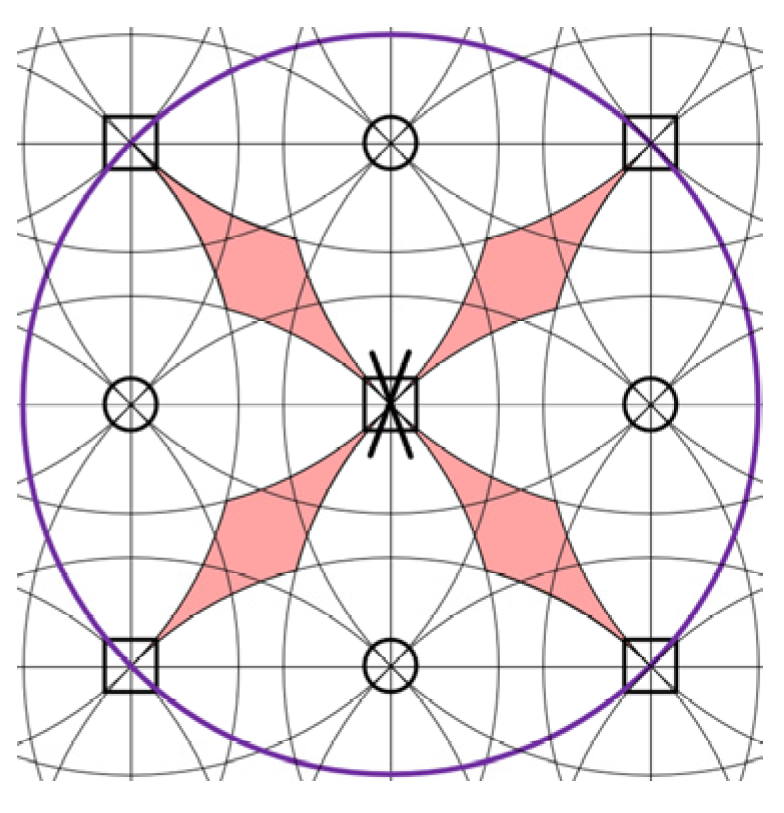
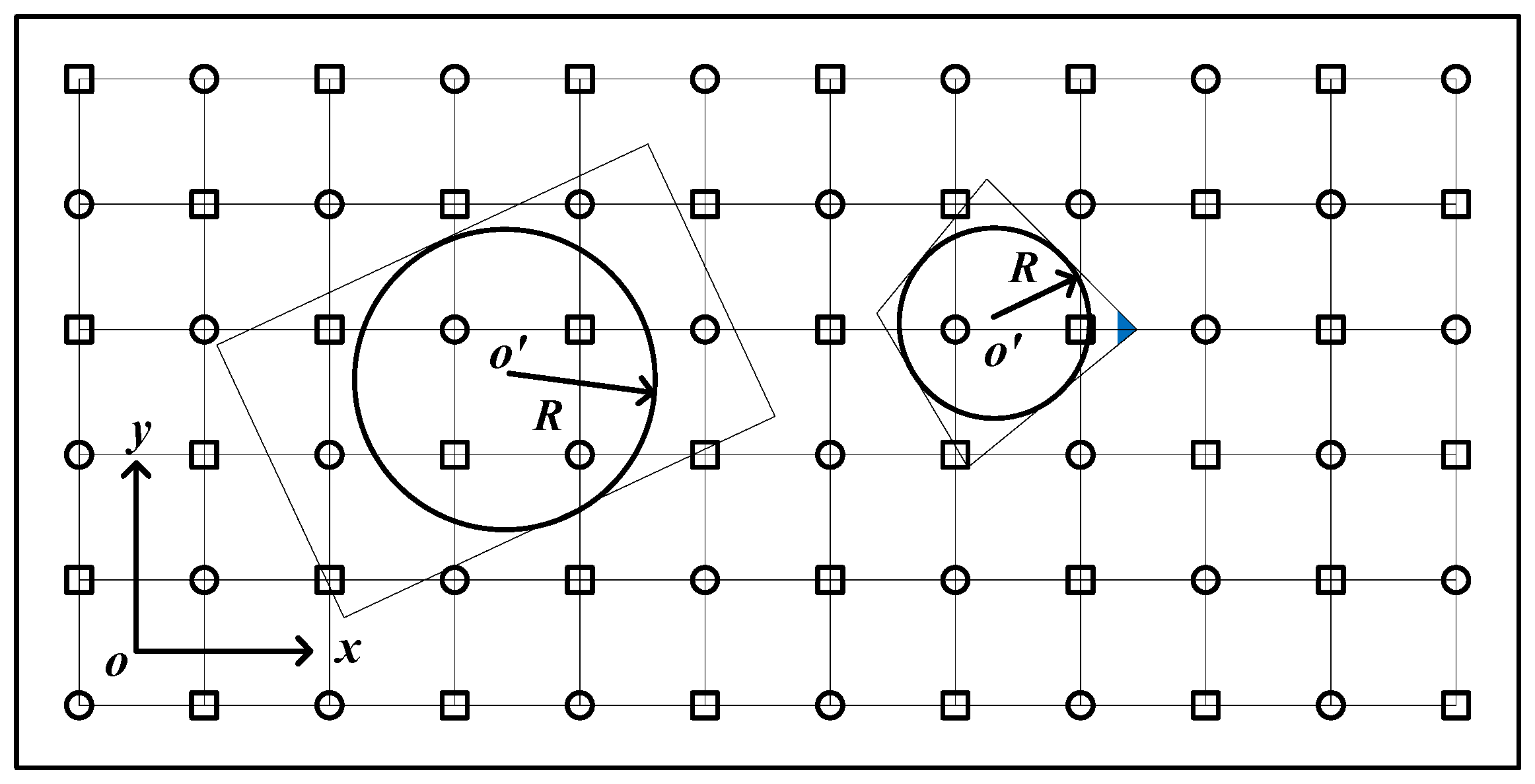
We have seen in previous sections that the proposed omnidirectional conveyor is feasible for transfer and rotation of the box on it. However, in fact, not all areas for box of different sizes, moving on different areas with different orientations are feasible. As shown in Figure 9, the number of wheels and associated wheel patterns covered by the box may vary if the box shape or size changes or if the box moved to different areas with different orientations. In practice, it should be clear that whether a particular area is feasible for a box to translate or rotate, and what is the minimum size of the box? To answer these questions, an inscribed circle located at the center of a box is used to represent the shape and size of a box, as shown in Figure 9. The inscribed circle is used as the representation circle for reasons that, if the inscribed circle can cover a wheel pattern that is feasible for moving and rotating the circle, then the original box that covers at least the same wheel pattern as the representation circle does apparently feasible. The circle ensures that the wheel pattern remain unchanged with changing of the orientation. In Figure 9 and hereinafter, we have used a small square and a circle to replace the omni wheels for simplicity such that the squares and circles represent horizontal and vertical wheels, respectively or vice versa.
Apparently, if we draw a circle on the conveyor with its center located at one of the wheel centers, i.e., the center of the small square or the small circle as shown in Figure 9, with its radius being the same as the radius of the inscribed circle of the box, then if the box (represented by the inscribed circle) is moved to inside of the circle, the corresponding wheel will be covered by the box. The wheel at which the circle locates its center will not be covered by the box if it moves outside the boundary circle. If two boundary circles corresponding to two wheels have an intersection, the related two wheels will both be covered by the inscribed circle of a box if the box is located within the intersection area. With these, we can draw all the boundary circles for every wheels. These boundary circles have divided the conveyor into many small areas. Within different small areas, the number of covered wheels and its pattern may vary.
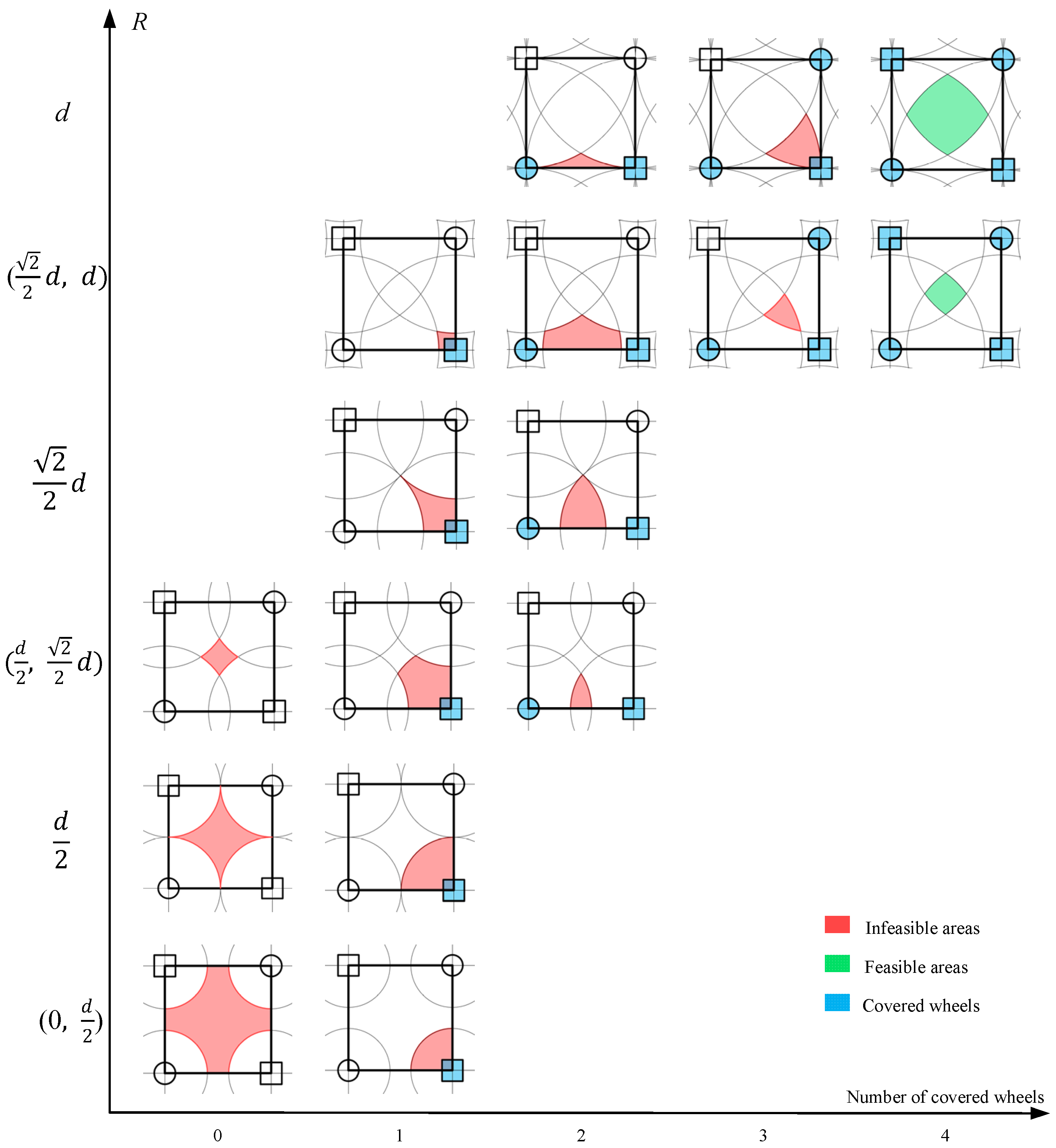
It is clearly to find that a four-wheeled pattern makes a square that repeated over the conveyor. And the small intersection areas for each four-wheel square are the same. As a result, we only have to investigate the feasible areas within a four-wheel square. For small radius of the inscribed circle, the number of covered wheels is generally lesser than the one with larger radius. We have drawn all the possible wheel patterns with the inscribed circle radius ranging from smaller than d / 2 to greater than ( 10 d ) / 2 , as shown in Figure 10, Figure 11 and Figure 12. The shaded intersection areas refer to the location of the center of the inscribed circle, and the highlighted wheels are corresponding covered wheels. Due to symmetry, only one of the identical areas are shaded for simplicity, one can deduce the other corresponding symmetric areas that shares identical wheel patterns.
It is seen from Figure 10 that when the radius of the inscribed circle is less or equal to the wheel distance d , the number of covered wheels is never above four. Obviously, wheel patterns with 0, 1, 2, and 3 wheels are incapable of driving the box to any translational and rotational velocities and hence infeasible. When the radius of the inscribed circle of the box is equal to d , only the central area is feasible as it has four wheels. However, since its feasible area is surrounded by infeasible areas, the overall conveyor is infeasible for generating an actual trajectory. As a result, when the radius of the maximum inscribed circle is no larger than d , the conveyor cannot be used. In other words, if the horizontal or vertical wheel distance d exceeds the radius of the inscribed circle R , then the conveyor is unusable. The red and green colors refer to the infeasible and feasible areas, respectively.
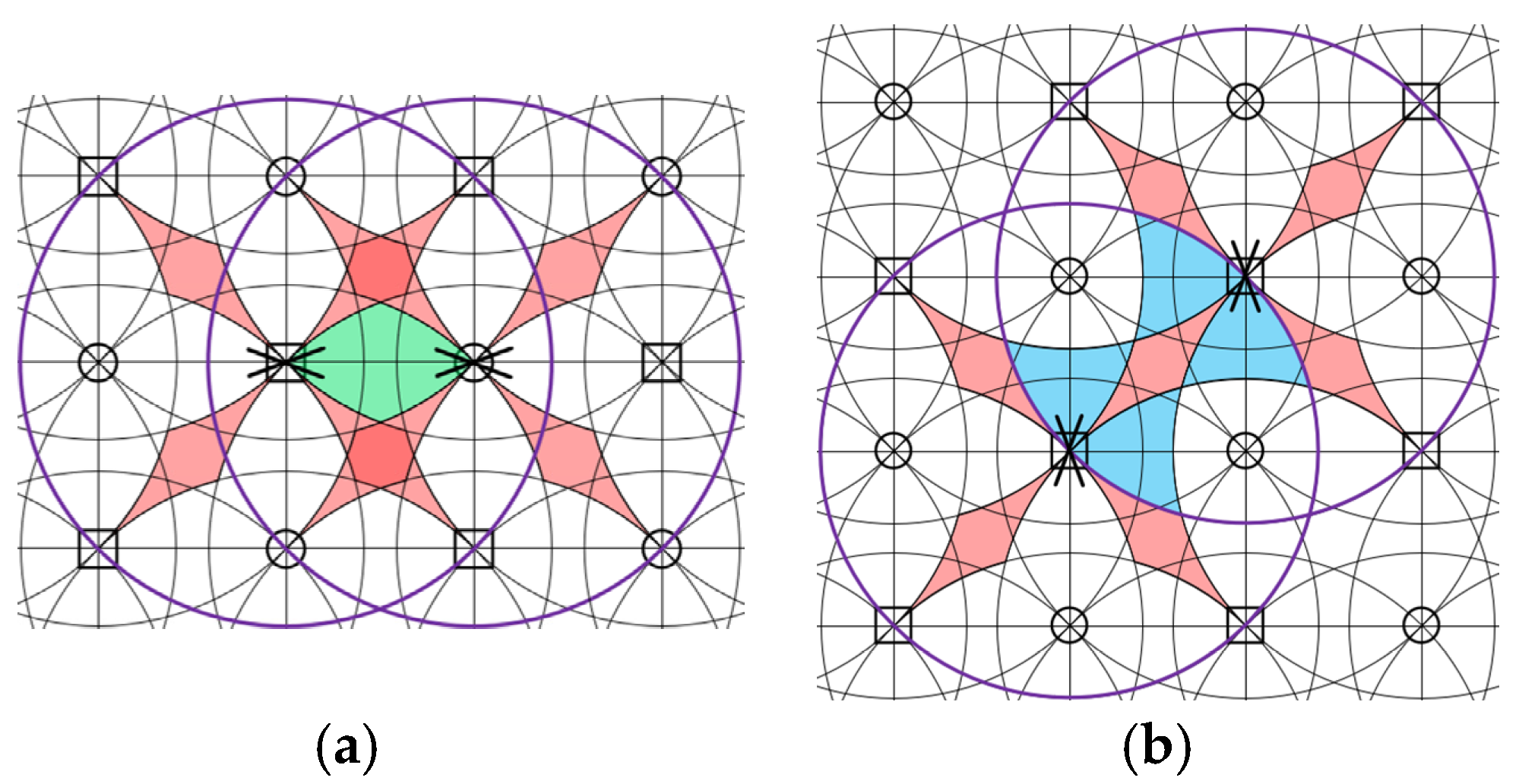
Similarly, as shown in Figure 11, when the radius of the inscribed circle is smaller than 5 d / 2 , there appears new wheel patterns with four and five wheels. However, the new emerged pattern is also infeasible for there is only one horizontal wheels with three or four vertical wheels (or only one vertical wheels with three or four horizontal wheels). Only feasible area occurs around the center of the four-wheel square, but these feasible areas are isolated by infeasible areas same as in Figure 10, making the whole conveyor infeasible. When the radius of the inscribed circle is equal to 5 d / 2 , the central feasible area connected to each other via a point. It is critical feasible for using the conveyor. When the radius of the inscribed circle increased to be in the range of 5 d / 2 , 2 d , new wheel patterns of five and six wheels emerge. The new emerged patterns turn out to be feasible and adjacent to the feasible area of the four-wheel pattern. In this case, the conveyor has a whole connected feasible area and the box can be transferred in this combined area. However, the connecting areas are narrow compared to the wide feasible area of the four-wheel pattern. The box has to move precisely in those narrow areas and a possible deviation can cause the box to move to the infeasible areas.
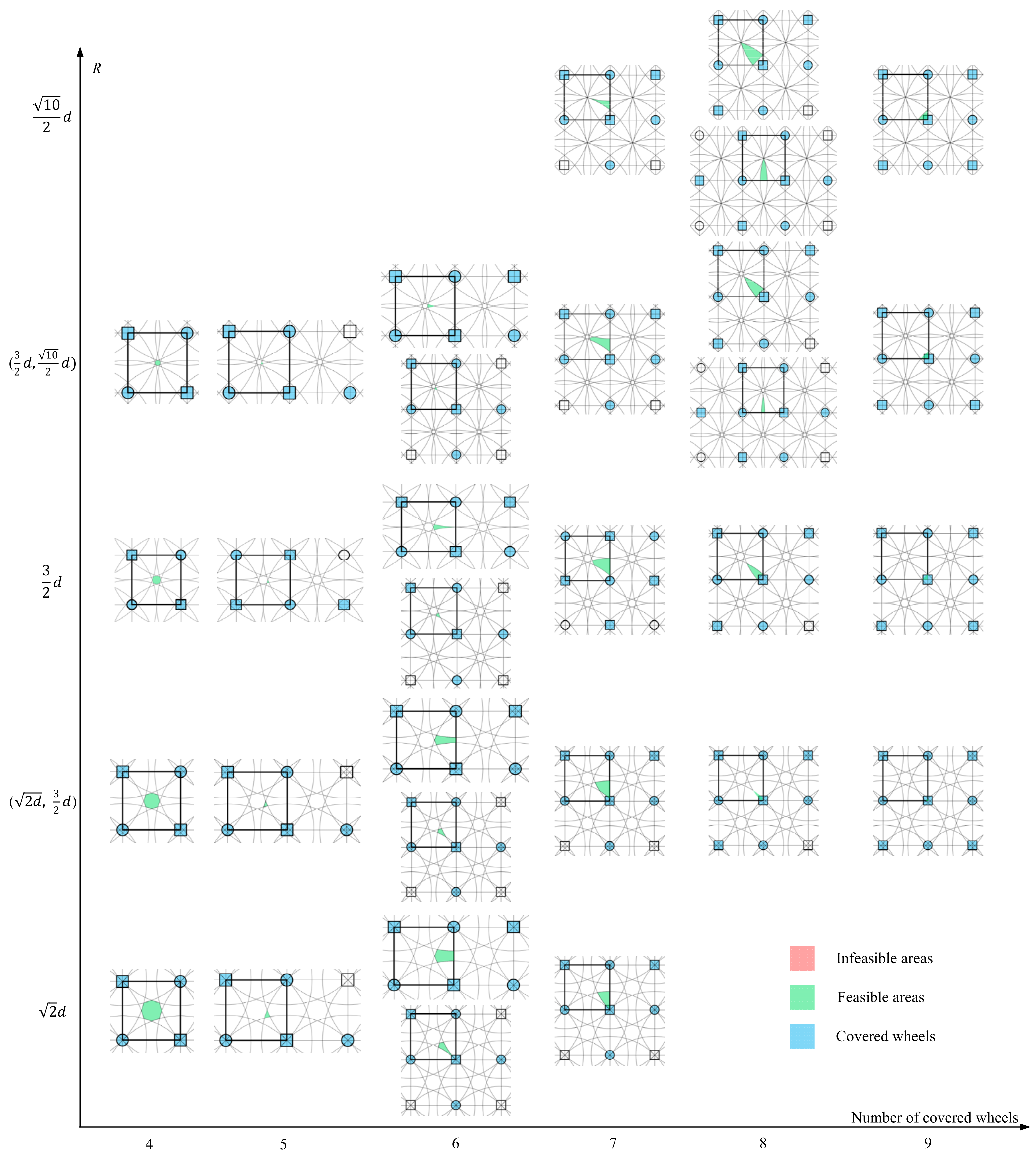
When the radius of the maximum inscribed circle is equal to or greater than 2 d , there is no infeasible areas and the whole conveyor is everywhere feasible, as illustrated in Figure 12. As the radius of the representation circle increases, new wheel patterns with more wheels emerges. When the radius increased to be equal to 10 d / 2 , at least seven wheels are covered by the box. Clearly, more covered wheels make the transfer and rotation more stable and can bare heavier box with greater wheel fault tolerance capability. In contrast, smaller number of wheels are less cost effective and the system is simpler. At this point, the radius of 2 d is optimal in minimizing the number of wheels and cost of the conveyor. In fact, the size of an actual box is greater than the inscribed circle which means potentially more wheels may be covered, leading to the transfer of a box more reliable.
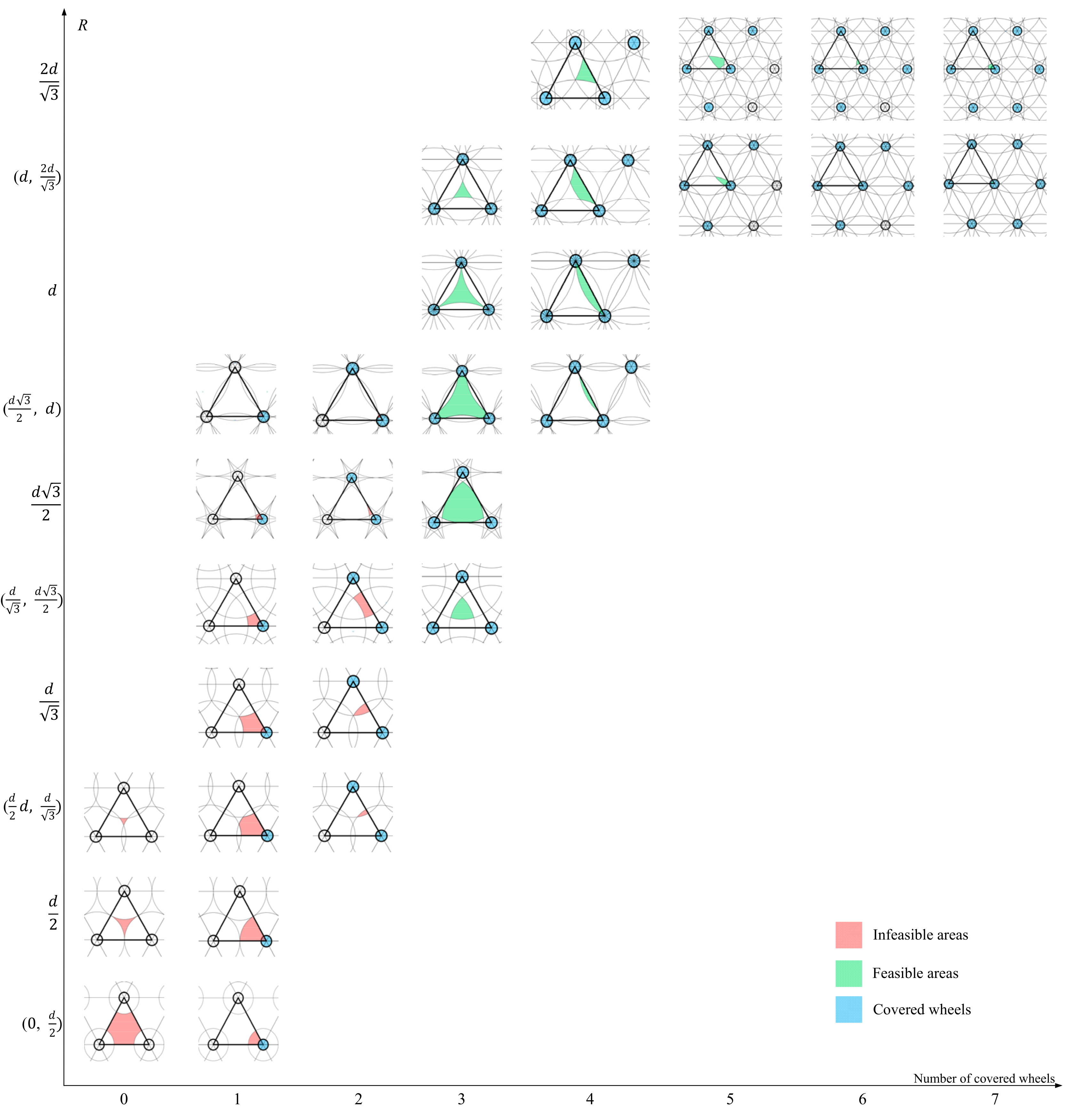
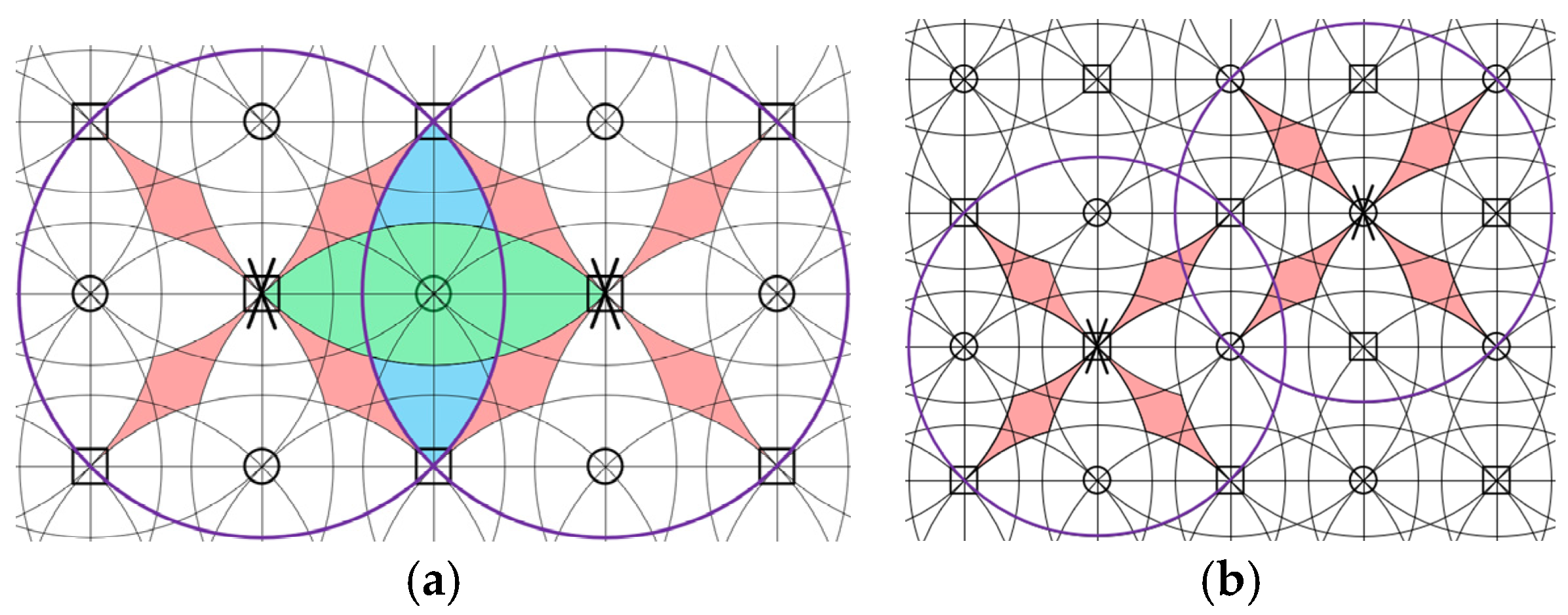
To further compare the proposed omnidirectional conveyor with the existing cellular conveyor, the feasible areas and wheel patterns for the cellular conveyor are illustrated as shown in Figure 13. It is seen that until the box size was increased to be at least equal to 2 d / 3 , the whole areas are feasible. Similar to the proposed conveyor, further increasing the box size will result in more complex wheel patterns with more covered wheels. The box size less than 2 d / 3 results in either infeasible areas with 0, 1, 2, and 3 wheels or discontinuous areas with the triangle patterns. Since any four-wheeled patterns that emerge are comprised of one feasible triangle pattern, the four-wheeled pattern is feasible. In contrast to the diamond shape of the four-wheeled pattern for the cellular conveyor, the four-wheeled pattern of our proposed conveyor is square thus allowing the isotropic supporting of the box. More critically, the diamond shape of the four-wheeled pattern is oriented rather randomly making actual controlling difficult. As a result, the actual control of the cellular conveyor is based on the hexagon modules.
It is also interesting to find that, if we draw a circumscribed circle with radius R 0 for the three-wheel pattern of the cellular conveyor and the four-wheel pattern of the proposed conveyor, the minimum radius of the inscribed circle of the box for ensuring the whole conveyor feasible are both equal to 2 R 0 (which is 2 d for the proposed conveyor and 2 d / 3 for the cellular conveyor). This makes the cellular conveyor is better than the proposed conveyor in reducing the number of wheels. However, because the difficult in using the other wheel patterns, the conveyor is utilized based on the hexagon module. And a greater number of wheels are thus needed compared to our proposed conveyor to ensure at every time there is at least one of the modules is covered.

6. Fault Tolerance

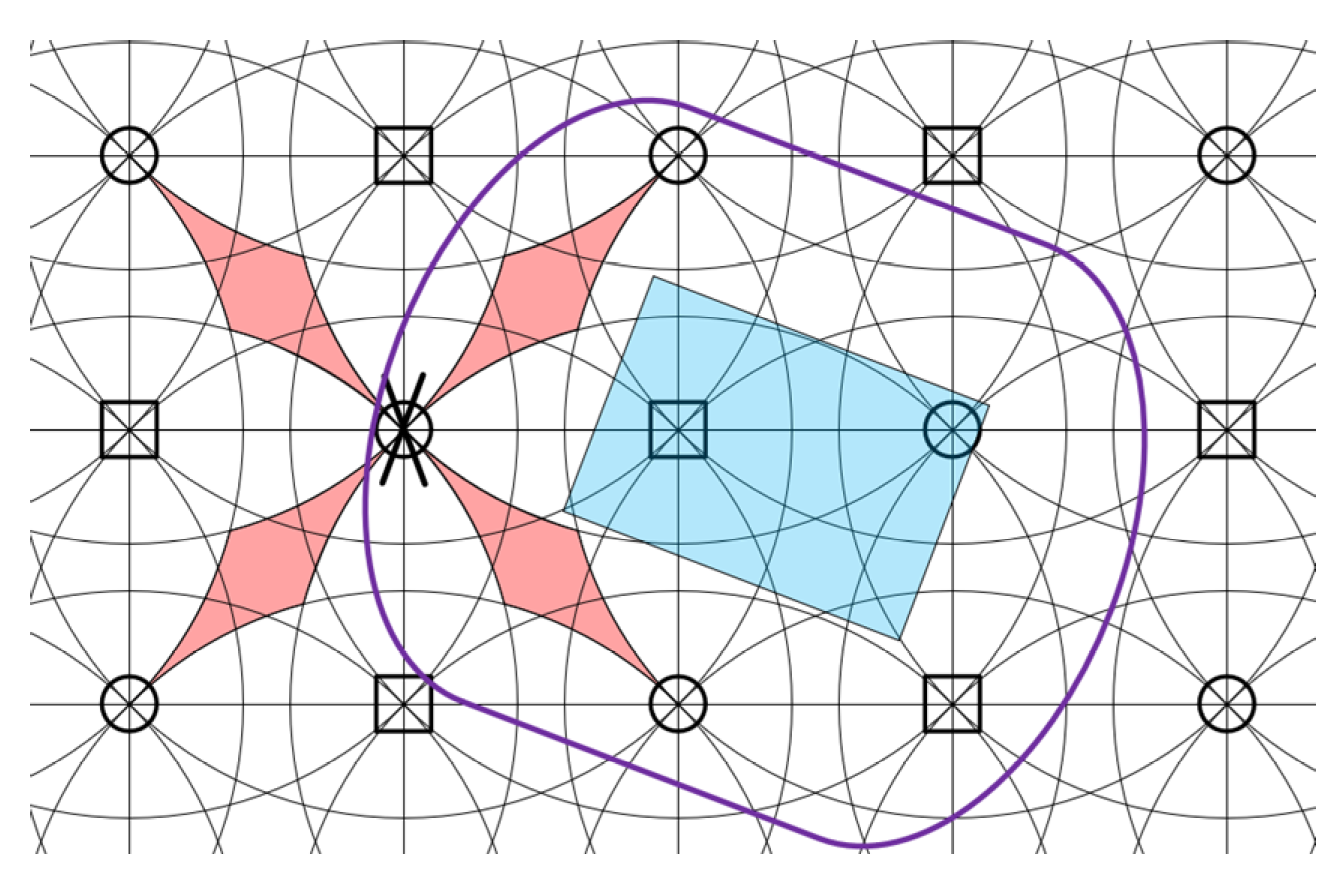
Section 5 discusses the feasible areas of the conveyor for different box sizes under the assumption that all the omni wheels are well conditioned. In practice, the conveyor should have the ability of fault tolerance of the wheels to increase the productivity of the conveyor. Obviously, failed wheels will change the wheel patterns and therefore may cause a feasible area to be infeasible. This section will study this issue and redraw the workspace to provide insights and guidance on trajectory planning.
From Section 5, it is found that 2 d is the minimum radius of the inscribed circle that is feasible everywhere on the conveyor. In other words, the maximum wheel distance d should be R / 2 to ensure that the overall conveyor is feasible for box with the radius R of its inscribed circle. In which case, the conveyor can have minimum number of wheels and the whole area is feasible. So, in this section, we discuss the fault tolerance issue with the radius of the represented circle to be equal to 2 d . Other sizes can be derived using the same logic.
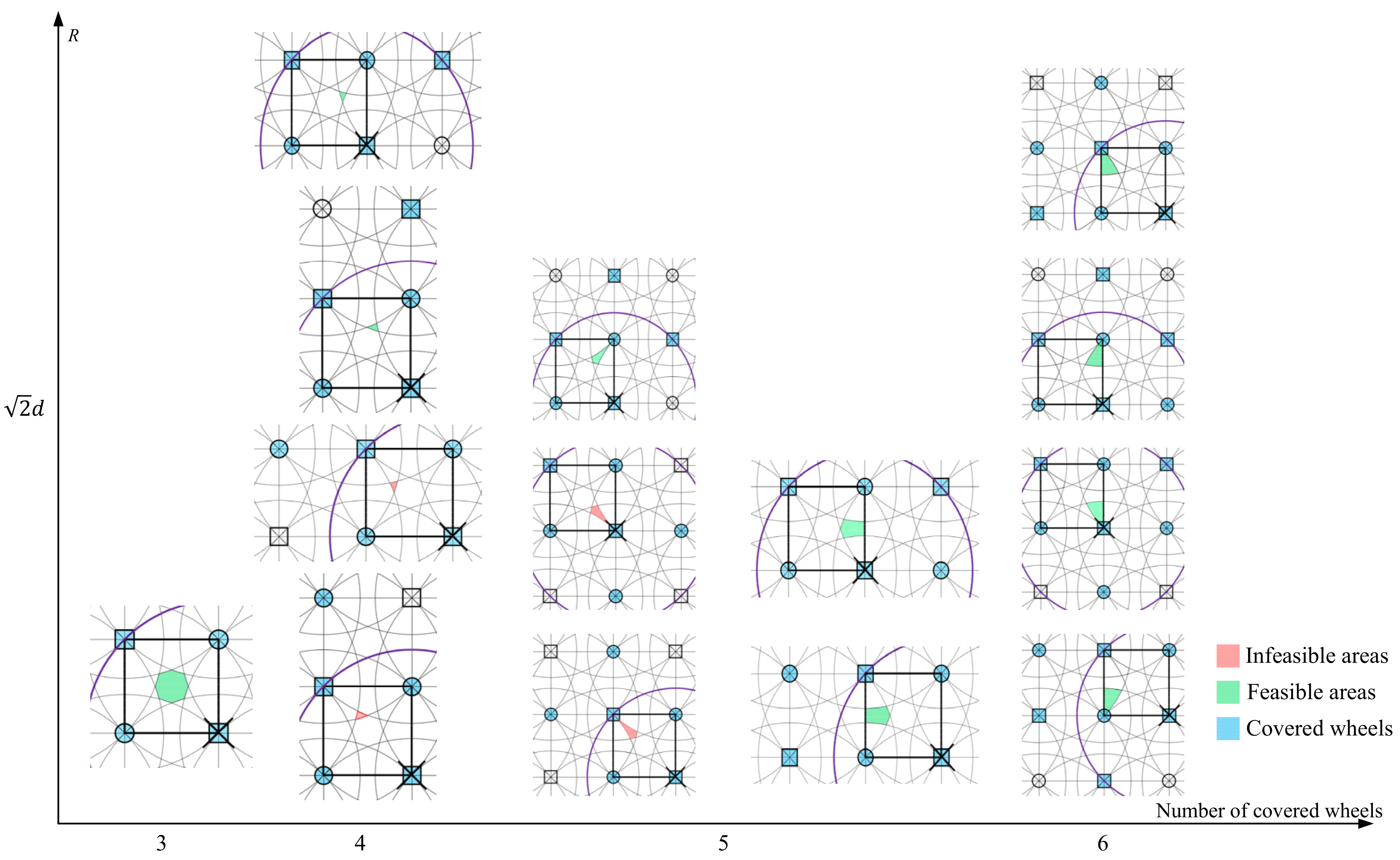
The distinct wheel patterns for different areas are depicted for only once in Figure 14. Different areas sharing the same wheel pattern can be easily deduced. As compared to Figure 12, decreasing of the number of wheels leads to pattern changes. Originally, all the areas are feasible and all the patterns are feasible patterns. Due to a loss of one of the covered wheels, the feasible pattern may become infeasible one and the corresponding area is invalid. To find the feasible area, first a boundary circle is drawn with its center located at the failed wheel such that the area outside the boundary circle is not affected by the failed wheel. The areas inside the boundary circle maybe feasible or infeasible depending on the wheel patterns.
It can be seen from Figure 14 that, there emerged new wheel patterns due to loss of the failed wheel. The feasible and infeasible areas are shaded with green and red, respectively. The areas with identical wheel patterns are not presented in Figure 14 to avoid complexity. Combined with the infeasible areas together, the whole infeasible area in red color is depicted as shown in Figure 15. Clearly, all the areas within the boundary circle are affected by the failed patterns, but not all of them turn to be infeasible. The infeasible areas consist of four independent parts with a symmetric layout.
If two omni wheels are failed at the same time, the feasible and infeasible areas are depicted as shown in Figure 16 and Figure 17, where the area identified by blue refers to the new infeasible areas caused by combined two failed wheels. The green area is theoretical feasible and because it is isolated by infeasible areas, it becomes infeasible either. If two failed wheels have two wheels in between, the boundary circles do not intersect to each other, and all the infeasible areas are caused solely by the two failed wheels independently.
Based on the above discussions, the trajectory planning must be conducted in the feasible areas. Commonly, the conveyor is used in situations where many boxes are presented. Trajectory planning must ensure no collision occurs between the boxes. Figure 18 illustrates the feasible areas for collision avoidance with one wheel fails. It is seen that the infeasible areas consist of the union areas of both the infeasible area due to wheel failures and the infeasible areas generated by the obstacles.

7. Feasible Motions under Constrained Wheel Velocity

In Section 5, it is seen that the wheel patterns depend on the size and location of the box. It has been found that when the radius of the inscribed circle of the box is greater than or at least equal to 2 d , all the areas are feasible. However, the feasibility is based on the assumption that the wheel rotational velocity is unbounded. When the wheel rotational velocity has a limit, parts of the feasible areas may become infeasible. Here, each wheel is assumed to be identical and the maximum rotational velocity cannot exceed a certain value, denoted as u m a x ( > 0 ) . The maximum translational wheel velocity is thus V m a x = u m a x r .
The translational velocity of the horizontal wheel above and below the box center can be written as in (20) and (21), respectively.
V 1 x = x ˙ − n − 1 d + h 1 y θ ˙  
V 2 x = x ˙ + n − 1 d + h 2 y θ ˙  
With constrained wheel velocity, it is obviously to have V 1 x ≤ V m a x and V 2 x ≤ V m a x , which can be rewritten as
− V m a x ≤ x ˙ − n − 1 d + h 1 y θ ˙ ≤ V m a x  
− V m a x ≤ x ˙ + n − 1 d + h 2 y θ ˙ ≤ V m a x
Same results can be derived for the vertical wheels, as in (24) and (25), respectively.
− V m a x ≤ y ˙ − n − 1 d + h 1 x θ ˙ ≤ V m a x
− V m a x ≤ y ˙ + n − 1 d + h 2 x θ ˙ ≤ V m a x  
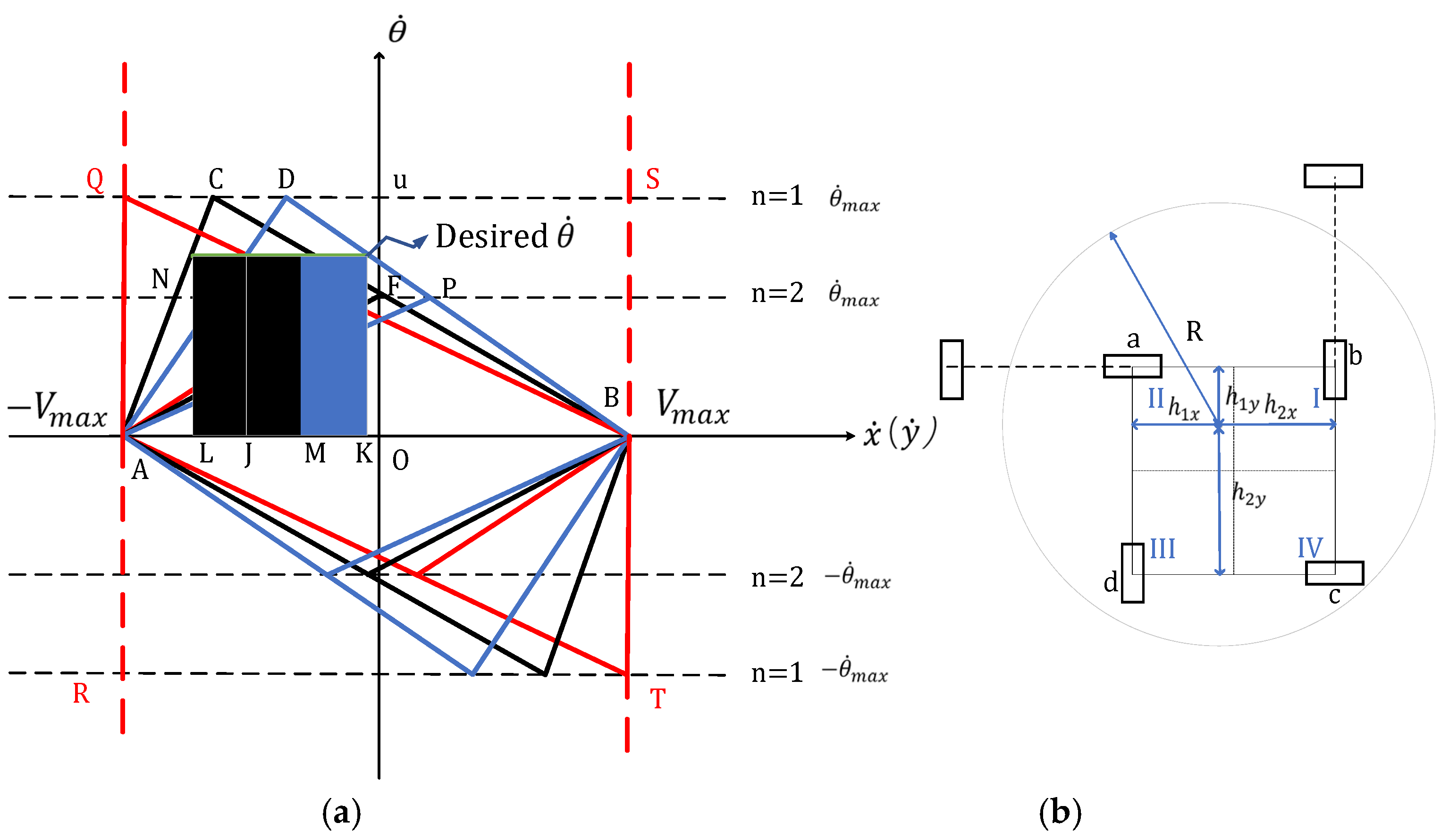
Equations (22)~(25) can be conveniently represented graphically as in Figure 19. Figure 19b shows the inscribed circle locating its center at the II quadrant of the covered four-wheel square area, and Figure 17a depicts the relevant feasible areas and boundaries, generated by (22) ~ (25). The black line indicates the feasible area for horizontal velocity of the box x ˙ and rotational velocity of the box θ ˙ . The green line represents the feasible area for vertical velocity y ˙ and rotational velocity θ ˙ of the box. Above the horizontal axis, the areas are feasible for clockwise rotation of the box, and below the horizontal axis, the areas relate to the counterclockwise rotation of the box. Due to symmetry, here, only the upper part of the horizontal axis is considered.
If the inscribed circle of a box only covers the four wheels that form a square, as shown in Figure 19b, the feasible areas for the horizontal and vertical wheels form a parallelogram, respectively. The upper parts form a triangle. For example, if the desired horizontal and rotational velocities of the box which are represented by the inscribed circle are within the triangle ABC, it is achievable with the constrained wheel velocity. The triangle ABD indicates the feasible desired vertical and rotational velocities of a box. If we draw a horizontal line indicating the desired rotational velocity of a box: θ ˙ , then the corresponding feasible horizontal and vertical velocities are within the ranges L M ¯ and J K ¯ , respectively.
It is easily to find that the area of the feasible triangle areas is irrelevant to the location of the box and calculated to be constant value: 2 V m a x 2 n − 1 d . Obviously, greater the value of n , that is, farther the wheel covered, smaller the feasible areas the desired trajectory can be achieved. Here in this work, we only consider n = 1 ,   2 . Because the area is constant, the height of the triangle is also constant. As a result, the maximum feasible desired rotational velocity for the box is θ ˙ m a x = 2 V m a x n − 1 d . The corresponding feasible translational velocity of the box is x ˙ = V m a x n − 1 d ( h 1 y − h 2 y ) and y ˙ = V m a x n − 1 d ( h 1 x − h 2 x ) . All the feasible triangle is located with its upper vertex on the horizontal line: θ ˙ m a x = 2 V m a x n − 1 d .
Based on Equations (22)~(25), it is seen that if the upper vertex of the feasible triangle is approaching left, the location of the box center is approaching up to the horizontal wheel and left to the vertical wheel. On the contrary, if the upper vertex of the feasible triangle is approaching right, the location of the box center is approaching down to the horizontal wheel and right to the vertical wheel. If the feasible triangle is right located in the middle, i.e., the upper vertex is located on the vertical axis, the box center is right located in the center of the four-wheel square. To extremes, if the box center is moved to the same location to the vertical or horizontal wheels, i.e., h i x = h i y = 0   ( i = 1,2 ) , the upper vertex of the feasible triangle is located on the point Q or S , as indicated in red in Figure 19a.
From the discussion of previous sections, the four-wheel pattern only occurs in particular areas of the overall workspace. If there is an upper horizontal wheel being covered, the feasible area for horizontal velocity x ˙ of the box ∆ A B C reduces to ∆ A B F . The added horizontal wheel has no effect on the feasible area for the vertical velocity y ˙ which still is ∆ A B D . If the box center is moving across the boundary that causes the wheel pattern to turn from the four-wheel pattern to the four-wheel with one more upper horizontal wheel pattern, the desired velocity within the area ∆ A F C will on longer be feasible.
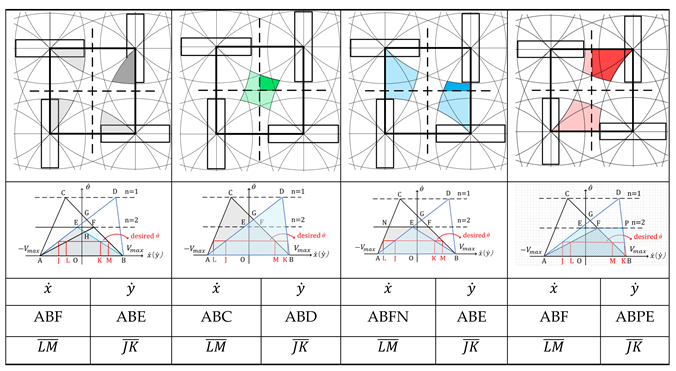
Clearly, different locations of the box center result in different wheel patterns. From the above findings, the feasible area for different patterns may become different as well. In this work, the feasible area is summarized as in Table 1. Here, we only present the case when box radius is equal to 2 d . Row two of the Table 1 refer to the feasible area for desired velocities for the corresponding area in row one in dark color and other identical areas are indicated in light color.
It is seen from Table 1 that, the feasible areas in the second row corresponds to box locations within the quadrant I, as shown in Figure 19b, such that the horizontal and vertical velocity feasible areas are located to the left and right of the vertical axis, respectively. The feasible areas of desired trajectory velocities for counterclockwise rotational motions are symmetric about the origin of the coordinate frame and thus omitted for simplicity. For the same desired rotational velocity θ ˙ , the desired horizontal and vertical velocities are within the ranges L M ¯ and J K ¯ , respectively, as illustrated in the second row of Table 1.
In summary, overall feasible areas for the desired velocities are illustrated in Figure 20, where the meanings of the colors are the same as in Table 1. It is found that if the box is moved along the blue areas, the desired horizontal velocity of the box can be larger than the desired vertical velocity. The desired vertical velocity of the box can be larger than the desired horizontal velocity if the box is moved to the red areas. The desired velocity ranges for the horizontal and vertical directions are the same when the box is moved to areas in green and grey areas. The desired velocity for the green areas can be larger than the grey areas. From Figure 20, it is seen that there exists a time-optimal path if the box moves horizontal on the blue and green areas and vertical on the red and green areas. It is noted that because the kinematics of the cellular conveyor is coupled, the feasible areas for the desired velocities are not likely to be depicted in the plane. Rather, it can only be illustrated in the space making analyses difficult. Due to the decoupled characteristics of the proposed conveyor, the kinematic analyses can be carried out concisely.

8. Conclusions

In this work, we have proposed a new omnidirectional conveyor. Kinematic model has been established and trajectory planning of four example typical trajectories has been achieved and verified via simulations. Results have been provided to show that the actual trajectories with PID control are well in line with the desired trajectories. In addition, the workspace and wheel patterns for box with different sizes have been depicted and analyzed. Furthermore, the workspace and wheel patterns for the conveyor with failed wheels have been investigated in order to provide guidance for trajectory planning. On the velocity level, the feasible areas for the trajectory planning have been comprehensively studied, showing that on the velocity level, some areas within the feasible workspace may become infeasible under the constrained wheel rotational velocity. In comparison to the existing cellular counterpart, our proposed conveyor ensures consistent and decoupled kinematics and lesser number of wheels are needed thus saving the cost.
In summary, this paper has three major contributions. Firstly, this paper proposed a new omnidirectional conveyor. Secondly, trajectory planning has been achieved and verified using PID control. Thirdly, the paper has presented workspace of the conveyor for boxes with different sizes and feasible areas in case of wheel failures. Finally, with assumption of constrained wheel velocity, this work further depicted the feasible areas for the desired box velocities thus paving the way for trajectory planning and optimal control. Based on this work, our ongoing work will be focusing on dynamic issues, obstacle avoidance, optimal control, and actual experiments of our proposed omnidirectional conveyor.

Author Contributions

Conceptualization, Z.Z.; methodology, Z.Z. and X.Z.; software, Z.Z., T.S., and Z.W.; validation, Z.Z.; formal analysis, Z.Z.; investigation, T.S.; resources, Z.Z. and T.S.; data curation, Z.Z. and Z.W.; writing—original draft preparation, Z.Z.; writing—review and editing, X.Z, Z.Z.; visualization, T.S., Z.W. and Z.Z.; supervision, X.Z.; project administration, Z.Z.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research and the APC were funded by National Natural Science Foundation of China, grant number 52005407.

Data Availability Statement

CoppeliaSim simulation model files and codes can be found via: https://github.com/BeginPy/A-new-omnidirectional-conveyor.git.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Firvida, M.B.; Thamer, H.; Uriarte, C.; Freitag, M. Decentralized Omnidirectional Route Planning and Reservation for Highly Flexible Material Flow Systems with Small-Scaled Conveyor Modules. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Turin, Italy, 4-7 September 2018; pp. 685–692. [CrossRef]
  2. Zaman, M.Q.; Wu, H.-M. Intelligent Motion Control Design for an Omnidirectional Conveyor System. IEEE Access 2023, 11, 47351–47361. [Google Scholar] [CrossRef]
  3. Shabalina, K.; Sagitov, A.; Magid, E. Comparative Analysis of Mobile Robot Wheels Design. In Proceedings of the 2018 11th International Conference on Developments in eSystems Engineering (DeSE), 2018; pp. 175–179. [CrossRef]
  4. Song, J.B.; Byun, K.S. Design and Control of a Four-Wheeled Omnidirectional Mobile Robot with Steerable Omnidirectional Wheels. Journal of Robotic Systems 2004, 21, 193–208. [Google Scholar] [CrossRef]
  5. Cofaru, N.F.; Rizescu, C.I.; Pleşea, A.I.; Rizescu, D.; Inţă, M. Modular Transport and Sorting System with Omnidirectional Wheels. MATEC Web of Conferences 2021, 343. [Google Scholar] [CrossRef]
  6. Uriarte, C.; Asphandiar, A.; Thamer, H.; Benggolo, A.; Freitag, M. Control strategies for small-scaled conveyor modules enabling highly flexible material flow systems. Procedia CIRP 2019, 79, 433–438. [Google Scholar] [CrossRef]
  7. Sint, T.H. Design and Implementation of Automatic Omnidirectional Conveyor Belt System. Thesis, National University of Singapore, Singapore, 2021. https://doi.org/10.13140/RG.2.2.15416.97283. National University of Singapore. Available online: https://www.researchgate.net/publication/381008250. [CrossRef]
  8. Fedorko, G.; Ivančo, V. Analysis of Force Ratios in Conveyor Belt of Classic Belt Conveyor. Procedia Engineering 2012, 48, 123–128. [Google Scholar] [CrossRef]
  9. Gaiardelli, S.; Carra, D.; Spellini, S.; Fummi, F. Dynamic Job and Conveyor-Based Transport Joint Scheduling in Flexible Manufacturing Systems. Applied Sciences 2024, 14. [Google Scholar] [CrossRef]
  10. Kruhn, T.; Radosavac, M.; Shchekutin, N.; Overmeyer, L. Decentralized and Dynamic Routing for a Cognitive Conveyor. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Wollongong, NSW, Australia, 9-12 July 2013; pp. 436–441. [CrossRef]
  11. Kim, K.; Hong, Y.-G. Industrial General Reinforcement Learning Control Framework System Based on Intelligent Edge. In Proceedings of the 2020 22nd International Conference on Advanced Communication Technology (ICACT), Phoenix Park, PyeongChang, South Korea, 16-19 February 2020; pp. 414–418. [CrossRef]
  12. Abu-Radeh, Y.; Shahateet, N.; Tarwa, S.; Tahbob, R.; Takrouri, W. Omni-Directional Sorting Conveyor. Palestine Polytechnic University, Hebron-Palestine, 2023. Available at: scholar.ppu.edu/handle/123456789/9025.
  13. Zhou, Z.; Zhang, H.; Liu, K.; Ma, F.; Lu, S.; Zhou, J.; Ma, L. Design of a Two-Dimensional Conveyor Platform with Cargo Pose Recognition and Adjustment Capabilities. Sensors 2023, 23. [Google Scholar] [CrossRef] [PubMed]
  14. Salazar, E.B.; Escudero, B.N.; Minango, S.N.R. Omnidirectional Transport System for Classification and Quality Control using Artificial Vision. In Proceedings of the Proceedings of the 2019 3rd International Conference on Virtual and Augmented Reality Simulations, 2019; pp. 62–66. [CrossRef]
  15. orner, M.; Benedikt, F.; Grimmel, F.; Hulin, T. SwarmRail: A Novel Overhead Robot System for Indoor Transport and Mobile Manipulation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May-31 August 2020; pp. 5905–5911. [CrossRef]
  16. Youssef, A.W.; Elhusseiny, N.M.; Shehata, O.M.; Shihata, L.A.; Azab, E. Kinematic modeling and control of omnidirectional wheeled cellular conveyor. Mechatronics 2022, 87. [CrossRef]
  17. Keek, J.S.; Loh, S.L.; Hanafi, A.N.; Cheong, T.H. Pre-slippage detection and counter-slippage for e-pattern omniwheeled cellular conveyor. Bulletin of Electrical Engineering and Informatics 2024, 13, 2298–2309. [Google Scholar] [CrossRef]
  18. Keek, J.S.; Loh, S.L.; Chong, S.H. Design and Control System Setup of an E-Pattern Omniwheeled Cellular Conveyor. Machines 2021, 9. [Google Scholar] [CrossRef]
  19. Uriarte, C.; Kunaschk, S. Omnidirectional Conveying System Module, Modular Omnidirectional Conveying System and Omnidirectional Conveying System. Patent application DE 10 2012 014 181 A1, BIBA - Bremer Institut für Produktion und Logistik GmbH, Bremen, Germany, 2014. Available online: https://register.dpma.de/Patentregister/Patenten/DE/DE102012014181A1/index.html.de.
  20. Sun, T.; Zhang, Y.; Zhang, H.; Wang, P.; Zhao, Y.; Liu, G. Three-Wheel Driven Omnidirectional Reconfigurable Conveyor Belt Design. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22-24 November 2019; pp. 101–105. [CrossRef]
  21. Ismaela, O.Y.; Hedley, J. Analysis, Design, and Implementation of an Omnidirectional Mobile Robot Platform. American Scientific Research Journal for Engineering, Technology, and Sciences (ASRJETS) 2016, 22(1), 195-209. Available online: http://asrjetsjournal.org/.
  22. Liu, Y.; Zhu, J.J.; Williams, R.L.; Wu, J. Omni-directional mobile robot controller based on trajectory linearization. Robotics and Autonomous Systems 2008, 56, 461–479. [Google Scholar] [CrossRef]
  23. Galgamuwa, G.I.R.K.; Liyanage, L.K.G.; Ekanayake, M.P.B.; Samaranayake, B.G.L.T. Simplified Controller for Three Wheeled Omni Directional Mobile Robot. In Proceedings of the 2015 IEEE 10th International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 18-20 August 2015; pp. 314–319. [CrossRef]
  24. Zhang, H.; Zhou, Z.; Lu, S.; Wang, H.; Yan, B.; Si, X. Design of reconfigurable transfer palletizing platform based on omnidirectional wheels. In Proceedings of the 2022 China Automation Congress (CAC), 2022; pp. 2455–2460. [CrossRef]
  25. Zaher, W.; Youssef, A.W.; Shihata, L.A.; Azab, E.; Mashaly, M. Omnidirectional-Wheel Conveyor Path Planning and Sorting Using Reinforcement Learning Algorithms. IEEE Access 2022, 10, 27945–27959. [Google Scholar] [CrossRef]
  26. Bi, Z.M.; Wang, L. Dynamic control model of a cobot with three omni-wheels. Robotics and Computer-Integrated Manufacturing 2010, 26, 558–563. [Google Scholar] [CrossRef]
  27. Sanghai, R.A.; Saundalkar, P.P.; Mallick, J.A.; Shah, B. Sort X Consignment Sorter using an Omnidirectional Wheel Array for the Logistics Industry. In Proceedings of the 2020 International Conference on Convergence to Digital World - Quo Vadis (ICCDW), 2020; pp. 1–5. [CrossRef]
  28. Wolfe, K.C.; Kutzer, M.D.M.; Armand, M.; Chirikjian, G.S. Trajectory Generation and Steering Optimization for Self-Assembly of a Modular Robotic System. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA 2010), Anchorage, AK, USA, 3-8 May 2010; pp. 4996–5001. [CrossRef]
  29. Feng, S.; Liu, Y.; Pressgrove, I.; Ben-Tzvi, P. Autonomous Alignment and Docking Control for a Self-Reconfigurable Modular Mobile Robotic System. Robotics 2024, 13. [CrossRef]
  30. Stampa, M.; Rohrig, C.; Kunemund, F.; Hes, D. Estimation of Energy Consumption on Arbitrary Trajectories of an Omnidirectional Automated Guided Vehicle. In Proceedings of the 2015 IEEE 8th International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Warsaw, Poland, 7-9 September 2015; pp. 873–878. [CrossRef]
  31. Cservenák, Á. Path and Trajectory Planning for an Automated Carrier Vehicle Equipped with Two Conveyor Belts Used in Manufacturing Supply. Manufacturing Technology 2021, 21, 164–183. [Google Scholar] [CrossRef]
  32. Cservenák, Á. Path and Trajectory Planning for an Automated Carrier Vehicle Equipped with two Conveyor Belts used in Manufacturing Supply. Manufacturing Technology 2021, 21, 164–183. [Google Scholar] [CrossRef]
  33. Renny Simba, K.; Uchiyama, N.; Sano, S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bézier curves. Robotics and Computer-Integrated Manufacturing 2016, 41, 31–42. [Google Scholar] [CrossRef]
Preprints 119479 g001
Figure 1. Diagram of omnidirectional conveyors. (a) the three-omni-wheeled cellular conveyor; (b) the omni wheel; (c) our proposed conveyor.
Figure 1. Diagram of omnidirectional conveyors. (a) the three-omni-wheeled cellular conveyor; (b) the omni wheel; (c) our proposed conveyor.
Preprints 119479 g001
Preprints 119479 g002
Figure 2. Kinematic representation of the omnidirectional conveyor.
Figure 2. Kinematic representation of the omnidirectional conveyor.
Preprints 119479 g002
Preprints 119479 g003
Figure 3. Three triangular wheel patterns in the cellular conveyor. (a) feasible wheel pattern in the module; (b) feasible wheel pattern in-between the modules; (c) infeasible wheel pattern in-between the modules.
Figure 3. Three triangular wheel patterns in the cellular conveyor. (a) feasible wheel pattern in the module; (b) feasible wheel pattern in-between the modules; (c) infeasible wheel pattern in-between the modules.
Preprints 119479 g003
Preprints 119479 g005
Figure 5. A top view screen shot of an omnidirectional conveyor model in CoppeliaSim.
Figure 5. A top view screen shot of an omnidirectional conveyor model in CoppeliaSim.
Preprints 119479 g005
Preprints 119479 g006
Figure 6. Block diagram of the omnidirectional conveyor under PID control.
Figure 6. Block diagram of the omnidirectional conveyor under PID control.
Preprints 119479 g006
Preprints 119479 g007
Figure 7. A top view screenshot of actual trajectories in CoppeliaSim. (a) case 1; (b) case 2; (c) case 3; (d) case 4.
Figure 7. A top view screenshot of actual trajectories in CoppeliaSim. (a) case 1; (b) case 2; (c) case 3; (d) case 4.
Preprints 119479 g007
Preprints 119479 g008
Figure 8. Simulation results. (a) trajectory of case 1; (b) orientation of case 1; (c) trajectory of case 2; (d) orientation of case 2; (e) trajectory of case 3; (f) orientation of case 3; (g) trajectory of case 4; (h) orientation of case 4.
Figure 8. Simulation results. (a) trajectory of case 1; (b) orientation of case 1; (c) trajectory of case 2; (d) orientation of case 2; (e) trajectory of case 3; (f) orientation of case 3; (g) trajectory of case 4; (h) orientation of case 4.
Preprints 119479 g008
Preprints 119479 g009
Figure 9. An inscribed circle for representation of the box.
Figure 9. An inscribed circle for representation of the box.
Preprints 119479 g009
Preprints 119479 g010
Figure 10. Workspace and wheel patterns: part 1.
Figure 10. Workspace and wheel patterns: part 1.
Preprints 119479 g010
Preprints 119479 g011
Figure 11. Workspace and wheel patterns: part 2.
Figure 11. Workspace and wheel patterns: part 2.
Preprints 119479 g011
Preprints 119479 g012
Figure 12. Workspace and wheel patterns: part 3.
Figure 12. Workspace and wheel patterns: part 3.
Preprints 119479 g012
Preprints 119479 g013
Figure 13. Workspace and wheel patterns for the cellular conveyor.
Figure 13. Workspace and wheel patterns for the cellular conveyor.
Preprints 119479 g013
Preprints 119479 g014
Figure 14. Workspace of the conveyor with one failed wheel.
Figure 14. Workspace of the conveyor with one failed wheel.
Preprints 119479 g014
Preprints 119479 g015
Figure 15. Infeasible areas with one wheel failed.
Figure 15. Infeasible areas with one wheel failed.
Preprints 119479 g015
Preprints 119479 g016
Figure 16. Infeasible areas with two adjacent wheels failed. (a) horizontal or vertical adjacent failed wheels; (b) diagonal adjacent failed wheels.
Figure 16. Infeasible areas with two adjacent wheels failed. (a) horizontal or vertical adjacent failed wheels; (b) diagonal adjacent failed wheels.
Preprints 119479 g016
Preprints 119479 g017
Figure 17. Infeasible areas with two wheels failed (with one normal wheel in-between). (a) horizontal or vertical failed wheels; (b) diagonal failed wheels.
Figure 17. Infeasible areas with two wheels failed (with one normal wheel in-between). (a) horizontal or vertical failed wheels; (b) diagonal failed wheels.
Preprints 119479 g017
Preprints 119479 g018
Figure 18. Feasible area for collision avoidance.
Figure 18. Feasible area for collision avoidance.
Preprints 119479 g018
Preprints 119479 g019
Figure 19. Feasible areas with constrained wheel velocity. (a) feasible areas for desired movements; (b) box location and wheel patterns.
Figure 19. Feasible areas with constrained wheel velocity. (a) feasible areas for desired movements; (b) box location and wheel patterns.
Preprints 119479 g019
Preprints 119479 g020
Figure 20. Vehicle trajectory and orientation.
Figure 20. Vehicle trajectory and orientation.
Preprints 119479 g020
Table 1. Feasible areas for desired velocities.
Table 1. Feasible areas for desired velocities.
Preprints 119479 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated