Probabilities on a Heyting Algebra

Preprint

Article

Probabilities on a Heyting Algebra

Altmetrics

Downloads

Views

Comments

Jean-Pascal Laedermann^*

This version is not peer-reviewed

Submitted:

24 September 2024

Posted:

30 September 2024

You are already at the latest version

Alerts

Abstract

Probability is initially defined on a Boolean algebra or a lattice of projectors. We propose here to start from a Heyting algebra.

Keywords:

Subject: Computer Science and Mathematics - Logic

1. Introduction

Probabilities are usually defined over Boolean algebras. In the finite case, it is sufficient to give the values for the atoms. We show here that it is possible to generalize them to Heyting algebras, starting from the prime filters, in other words on the spectrum of the algebra. Surprisingly, it is also possible to define them in a quantum manner, using projectors.

2. Affine Measures

We place ourselves in a finite Heyting algebra

H

. The set of its filters will be denoted

F

and the subset of its prime filters

Φ

, which is the co-spectrum of

H

1. The finiteness of the algebra implies that all filters are principal. G will be the subset of prime filter infs. A filter can be seen as a set of propositions validated at a certain time, or as the intension of a formal object.

Definition

An affine measure on

H

is an application

μ : H \to R

that verifies

(i) μ (a \lor b) + μ (a \land b) = μ (a) + μ (b)

If, in addition, we have

μ (⊥) = 0

μ (⊤) = 1

and

a ⩽ b ⟹ μ (a) ⩽ μ (b)

, it becomes a probability.

Let

t = (a, b)

. It is useful to introduce a deviation matrix translating relation (i) with Kronecker indices:

Δ_{c}^{t} = δ_{c}^{a \lor b} + δ_{c}^{a \land b} - δ_{c}^{a} - δ_{c}^{b}

We can see that the affine measures verify

Δ μ = 0

2, i.e.

μ \in K e r Δ

Let

O_{a}^{b} = (a ⩽ b) = \{\begin{matrix} 1 & i f a ⩽ b \\ 0 & o t h e r w i s e \end{matrix}

be the matrix of the order relation of

H

Proposition

\forall t . Δ_{a}^{t} O_{f}^{a} = 0 ⟺ f \in G o r f = ⊥ o r f = ⊤

Demonstration

The relation on the left is

O_{f}^{a \land b} + O_{f}^{a \lor b} - O_{f}^{a} - O_{f}^{b} = 0

, or

(a \land b ⩾ f) + (a \lor b ⩾ f) = (a ⩾ f) + (b ⩾ f)

↑ f

is prime, we have

f ⩽ a \lor b ⟺ f ⩽ a o r f ⩽ b

, and

f ⩽ a \land b ⟺ f ⩽ a a n d f ⩽ b

Apart from the trivial cases

f = ⊥ o r ⊤

, let’s look at the various possibilities:

\begin{matrix} f ⩽ a & f ⩽ b & (f ⩽ a) + (f ⩽ b) & (f ⩽ a \lor b) + (f ⩽ a \land b) \\ 0 & 0 & 0 + 0 & 0 + 0 \\ 0 & 1 & 0 + 1 & 1 + 0 \\ 1 & 0 & 1 + 0 & 1 + 0 \\ 1 & 1 & 1 + 1 & 1 + 1 \end{matrix}

And if

f \notin G

, we find

a ≱ f, b ≱ f, a \lor b ⩾ f, a \land b ≱ f

and the relation is false.

qed

Let’s denote by

{(O | G)}_{g}^{g^{'}} = O_{g}^{g^{'}}

the restriction of the order relation to G. The strict order implies that

\exists n . {(O | G - I d)}^{n} = 0

. Let

A = I d - O | G

and

S^{n} = \sum_{i \in n} A^{i}

. We see easily that

S^{n} \cdot O | G = I d

O | G

is therefore invertible. The matrix

O_{a}^{b}

is then of rank

| G |

and all affine measures are obtained by

μ^{a} = O_{g}^{a} π^{g}

(summation restricted to G). Suppose

π^{g}

is a classical probability on G. Since the elements of O and

π

are positive or zero, the growth of

μ

is guaranteed. For

a = ⊥

, the sum is empty, i.e. zero, and if

a = ⊤

the sum is total and equals 1.

The result is

Theorem

Any probability is of the form

μ^{a} = O_{g}^{a} π^{g} = \sum_{g ⩽ a} π^{g}

where

π

is a classical probability on the set G, i.e.

π^{g} ⩾ 0, \sum_{g} π^{g} = 1

3. Antichains

It is also possible to express these probabilities using the antichains of the algebra.

Proposition

μ (a) = \sum_{g \in M a x (G \cap ↓ a)} μ (g)

Demonstration

M a x (G \cap ↓ a)

is the set of maximal elements of

{g ⩽ a}

. This is an antichain, since none of these maxima is comparable to any other.

a = ⊥

, the antichain is empty, and we have

μ (⊥)

= 0. If

a \in G

, we get the definition of

μ

on prime filter infs. For other elements, the

M a x

ensures that

π^{g}

are not counted more than once.

qed

Notes

The probability

μ

is first defined on G, which is generally much smaller than

H

. It is extended to the other elements by the sum of its values on the antichains of G.

Let’s denote the antichains of G by

A C (G)

. An order relation is defined by

α, β \in A C (G) α ⩽ β ⟺ M a x (α \cup β) = β

This order makes it a distributive lattice isomorphic to

H^{o p}

, via

i (α) = ⋁ α i^{- 1} (a) = M a x (G \cap [⊥, a])

4. Projectors

Let

H

be a Hilbert space of dimension

| G |

and

JH

be the set of its orthogonal projectors. If

J, K \in JH

, let

J \lor K

be the projector on the subspace generated by the union of their images, and

J \land K

that on their intersection. We also introduce a natural order relation

J ⩽ K

given by

I m J \subseteq I m K

We know that if

[J, K] = 0

, then

J \lor K = J + K - J K

and

J \land K = J K

Let

| β_{g} 〉

be an orthonormal basis of

H

and

| β_{g} 〉 〈 β_{g} |

be the associated projectors. The latter commutate and verify exactly (i).

Hence the

Theorem

Let

J : H \to JH

be given by

J (a) = \sum_{g ⩽ a} | β_{g} 〉 〈 β_{g} |

J is a monomorphism of distributive lattices.

Any probability on

H

can be written as

μ^{a} = 〈 ψ | J (a) | ψ 〉

where

ψ

is a vector of norm 1, in other words a amplitude of probability in the quantum sense.

Notes

If we denote by

ψ^{g}

the coordinates of

ψ

in the

β_{g}

basis, we obtain

π^{g} = {| ψ^{g} |}^{2}

Generally speaking, we don’t have

J (\neg a) = I d - J (a)

. Better still, if

I d - J (a) = j (b)

, we can easily show that

a = \neg b

b = \neg a

a \lor \neg a = b \lor \neg b = ⊤

a = \neg a

and

b = \neg b

5. Conditioning vs. Quantum Reduction

The notion of conditional probability can be traced back to the classical definition:

μ (a | b) = \frac{μ (a \land b)}{μ (b)}

Theorem

Let

j_{b} : ψ \mapsto \frac{J (b) | ψ 〉}{∥ J (b) | ψ 〉 ∥}

, then

μ (a | b) = 〈 j_{b} ψ | J (a) | j_{b} ψ 〉

The demonstration is obvious, given the commutativity of the

J (a)

projectors.

j_{b}

is a quantum reduction operator. It is unitary, but not linear.

6. Integration and Differentiation

Since

π^{g}

is a classical probability on G, we can introduce random variables

X : G \to R

and calculate integrals as

\int X d μ = X_{g} π^{g}

. But

O_{g}^{g^{'}}

is invertible, and we get

\int X d μ = X_{g} {(\overset{- 1}{O | G})}_{g^{'}}^{g} μ^{g^{'}}

. This expression uses only the values of

μ

on G.

{(O | G)}^{- 1}

appears as a differentiation operator. This confirms that

μ

is in fact a cumulative probability.

7. Discussion

7.1. Commutative Windows

The set of projectors

J {(a)}_{a \in H}

with connectors

\lor, \land

is a commutative subalgebra of

JH

. It is a classical window on a quantum space in the sense of Isham-Doering [1], a context in the sense of Kochen-Specker [2]. The above theorems open a door to quantum modeling based on intuitionistic logic.

7.2. Square Roots

The introduction of the probability amplitude as a square root is closely related to the search for non-informative a priori in Bayesian statistical decision theory. For example, if the aim of a sequence of experiments is to estimate a probability

π^{g}

by realization frequencies

\frac{N^{g}}{N}

, we can define, thanks to the Fisher information, an a priori of Jeffreys which has interesting invariance properties [3]. This a priori has a density on the simplex of dimension

| G | - 1

. The vector

{(\sqrt{π^{g}})}_{g \in G}

has quadratic norm 1, and the density image by

\sqrt{}

is the uniform measure [4] on the sphere

S^{| G | - 1}

7.3. Non Commutative Extension

The

β

basis can be replaced by a partition of the identity

\sum_{g} B_{g} = I d

, where the

B_{g}

are orthogonal projectors of a Hilbert of sufficient dimension. Such a partition can be, for example, that of the eigenprojectors of a Hermitian operator whose eigenvalues are arbitrary, provided they are distinct for distinct projectors. This allows the coexistence of several operators that may only commute on certain subspaces, i.e. the coexistence of algebras for which the inter-algebra conjunction (∧) is only defined under certain conditions.

7.4. Superpositions

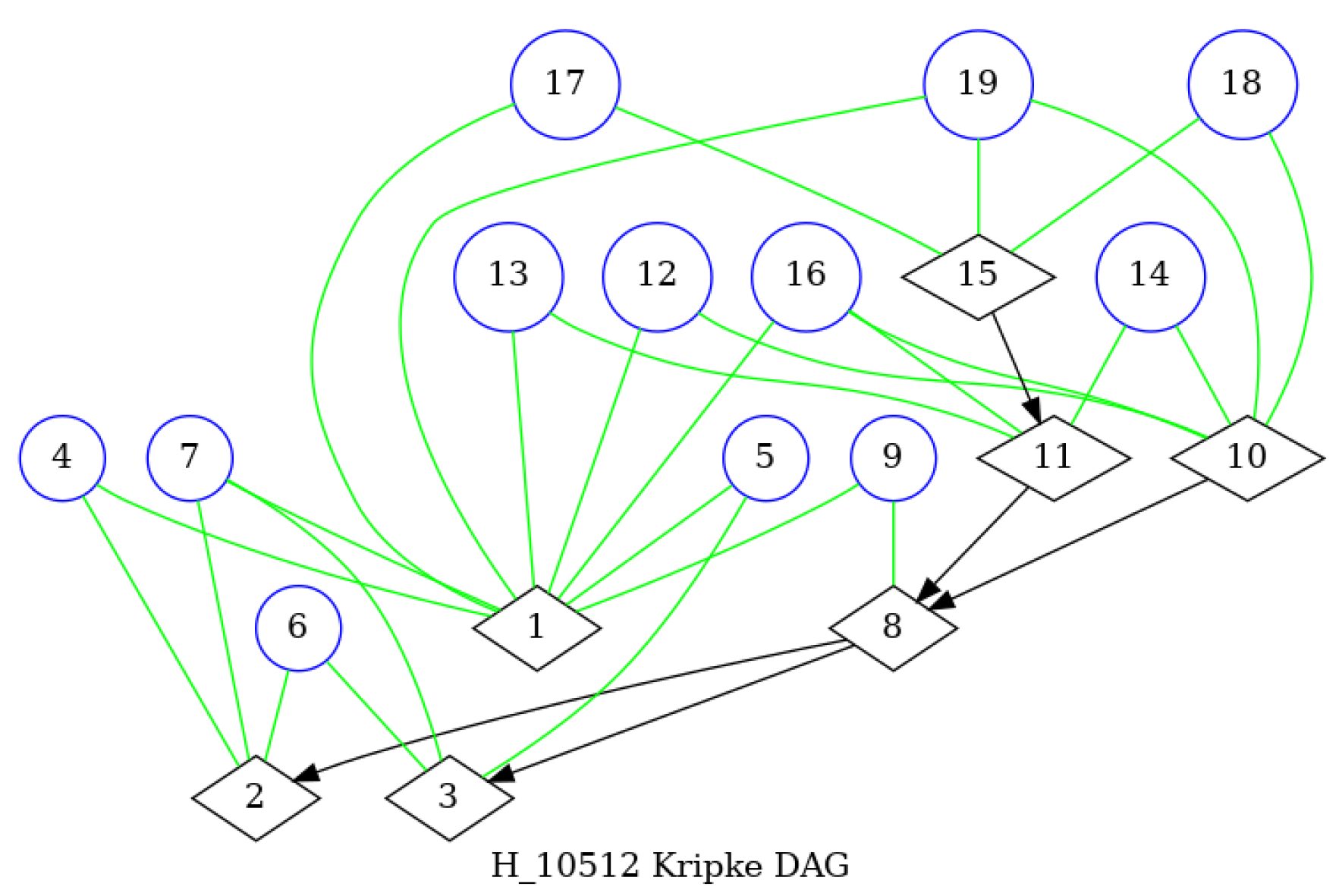
The non-prime filters f of

F

also qualify as validating systems of propositions, but they admit disjunctions that have the following property

\exists a, b . a \lor b \in f a n d a \notin f a n d b \notin f

These disjunctions, which we might call floating, are related to superpositions of quantum states. In Kripke’s semantics for intuitionistic logic, these filters are not among the admissible worlds [5].

7.5. Boole Algebras

When the algebra is Boolean, we retrieve classical probability because all prime filters are ultrafilters.

7.6. Stone Representation

The idea of replacing atoms by prime filters is obviously directly inspired by the famous Stone representation theorem.

7.7. Similarities

The linking of

Φ

prime filters,

J (a)

projectors and G antichains emerges from the following considerations:

If the intersection of two prime filters is prime, one is in the other.

If two orthogonal projectors commute, either they are orthogonal, or one is less than the other.

If the union of two maximal antichains is an antichain, one is in the other.

7.8. Code

All these results have been confirmed by computer. The code is written in C++, and the matrix calculations are performed by the eigen3 library. [6]

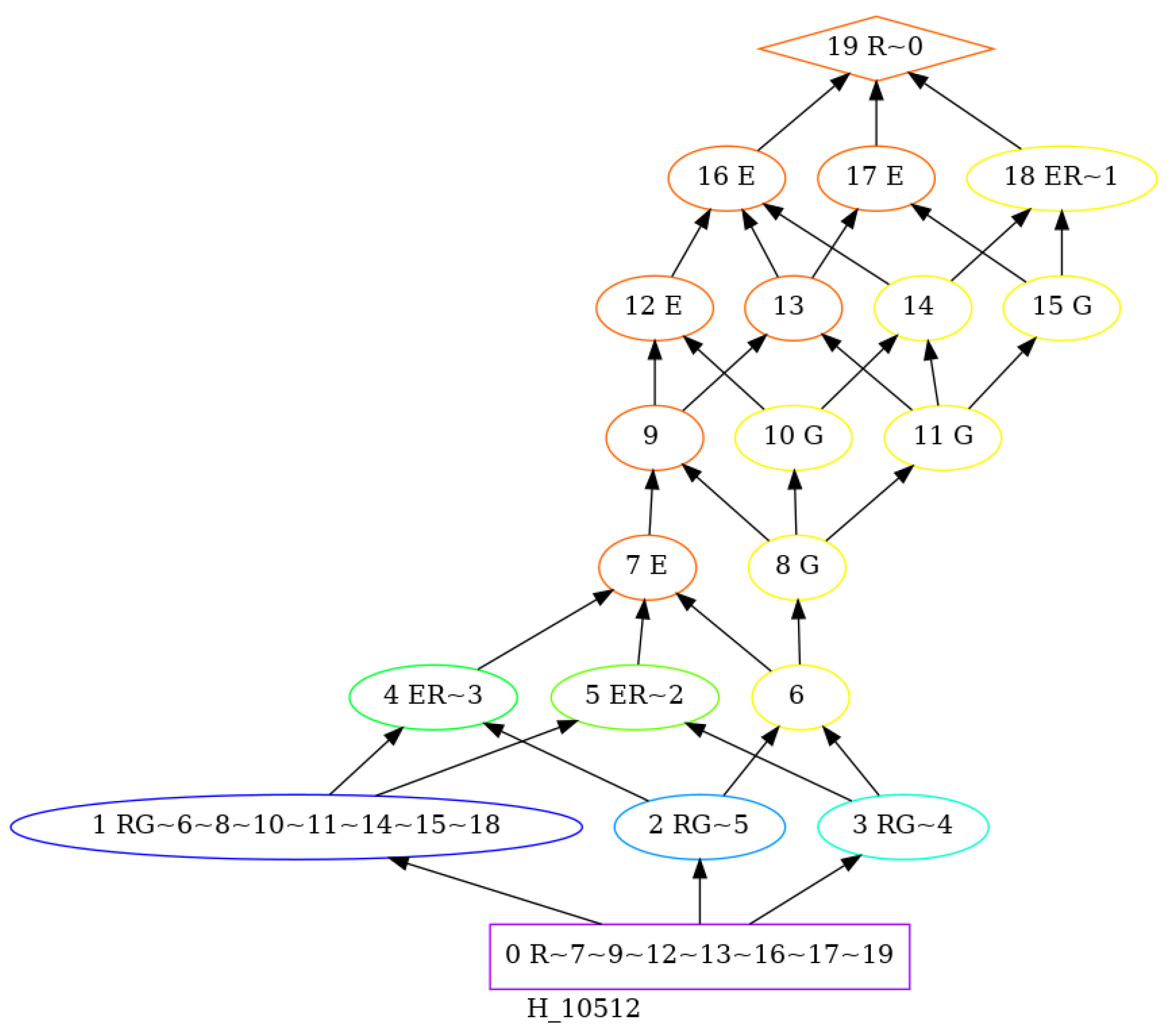
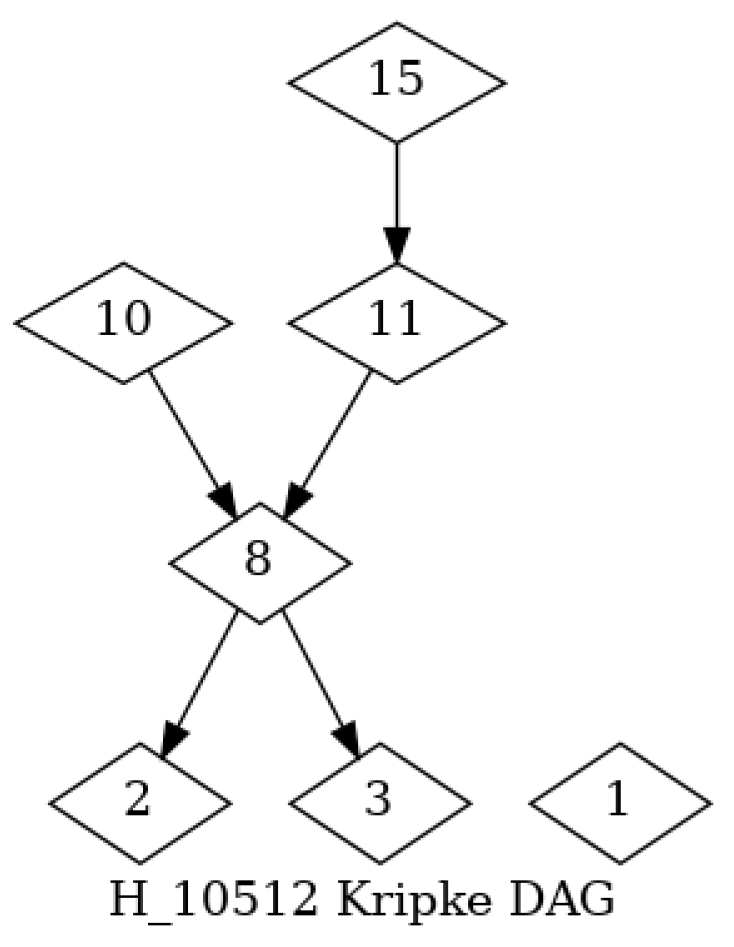
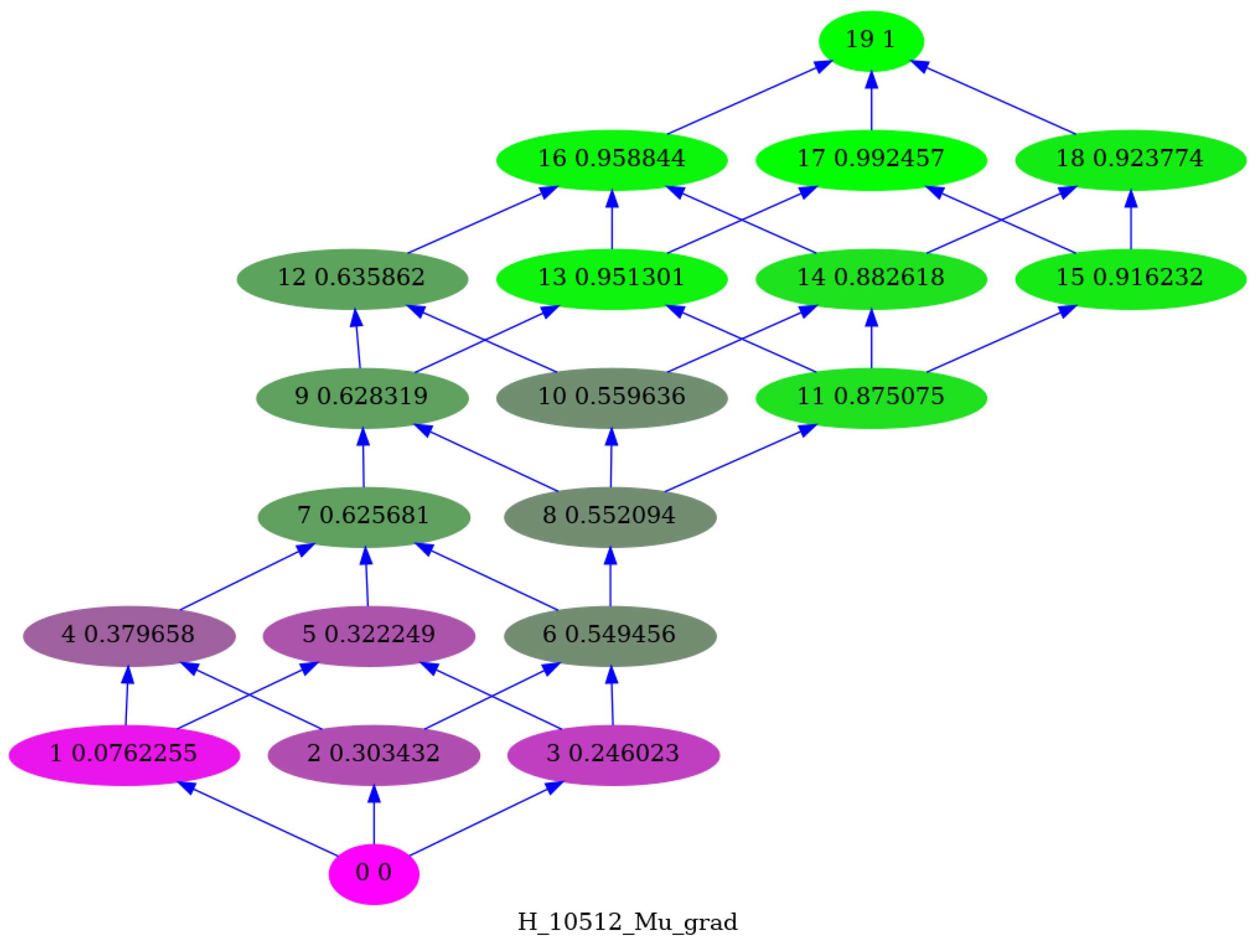
8. Example

These notions have been implemented and used to present Figure 1, Figure 2, Figure 3 and Figure 4. The Heyting algebra is obtained by the antichains of an arbitrary ordered set G, and the probability

μ

by a uniform random draw of the probability amplitude

ψ

Notes

1	The term spectrum is usually reserved for ideals.
2	We’ll also use index notation with Einstein’s summation convention. Here, we would have $\forall t . Δ_{a}^{t} μ^{a} = 0$ .

References

Doering, A., Isham, C. What is a Thing?: Topos Theory in the Foundations of Physics. Preprint at https://arxiv.org/abs/0803.0417 (2008).
Wikipedia: The Kochen-Specker Theorem. https://en.wikipedia.org/wiki/Kochen-Specker_theorem (2024).
Bernardo, J.M., Smith, A.F.M. Bayesian Theory. John Wiley and Sons LTD, Chichester (2000).
Laedermann, J.-P. Sur l’estimation des répartitions discrètes. Unpublished (2005).
Wikipedia: Semantics of intuitionistic logic. https://en.wikipedia.org/wiki/Kripke_semantics (2024).
Eigen Eigen 3. https://eigen.tuxfamily.org/index.php?title=Main_Page (2024).

Figure 1. Hasse diagram of a Heyting algebra. The G are the infs of prime filters, the E the sups of prime ideals, and the R the regular elements (

a = \neg \neg a

). The ∼ signs describe the reciprocal image of the negation operator. Colors are iso-negation classes. In particular, the inf 7 filter is the Jacobson filter, intersection of ultrafilters, whose infs are 1, 2 and 3.

Figure 1. Hasse diagram of a Heyting algebra. The G are the infs of prime filters, the E the sups of prime ideals, and the R the regular elements (

a = \neg \neg a

Figure 2. Order relationship restricted to primary filter infs. If we think of a prime filter as a world of Kripke [5] whose propositions are the elements, the arrows indicate the possible time courses, which go in the opposite direction to the order of the algebra. Indeed, the lower the inf, the greater the filter and the greater the number of propositions it validates. The existence of these arrows is guaranteed by the persistence requirement. There are two connected components, so the algebra is a product.

Figure 3. Extension of

μ^{g}

by antichains. To obtain the prob of an element outside G, we sum the probs of the ends of its outgoing arrows.

Figure 3. Extension of

μ^{g}

by antichains. To obtain the prob of an element outside G, we sum the probs of the ends of its outgoing arrows.

Figure 4. Probability. Incidentally, we can introduce a notion of information by

- log μ

. ⊤ contains no information because

log μ (⊤) = log 1 = 0

, while

- log μ (⊥) = - log 0 = \infty

suggests that infinite information would be needed to demonstrate the absurd.

Figure 4. Probability. Incidentally, we can introduce a notion of information by

- log μ

. ⊤ contains no information because

log μ (⊤) = log 1 = 0

, while

- log μ (⊥) = - log 0 = \infty

suggests that infinite information would be needed to demonstrate the absurd.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Probabilities on a Heyting Algebra

Abstract

1. Introduction

2. Affine Measures

3. Antichains

4. Projectors

5. Conditioning vs. Quantum Reduction

6. Integration and Differentiation

7. Discussion

7.1. Commutative Windows

7.2. Square Roots

7.3. Non Commutative Extension

7.4. Superpositions

7.5. Boole Algebras

7.6. Stone Representation

7.7. Similarities

7.8. Code

8. Example

Notes

References

MDPI Initiatives

Important Links

Subscribe