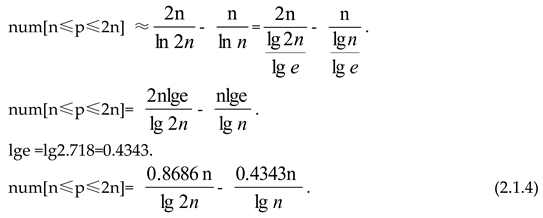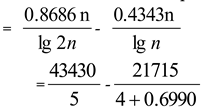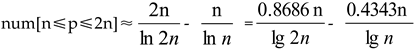Section 5,The 4 genetic codes of the conjecture,
the proof of Goldbach's conjecture
Hou Shao-Sheng1, Ma Lin-Jun2
(1 Anyang Mathematical Society, Henan Province, China; 2 Department of Mathematics, Sun Yat-sen University, Guangzhou City, Guangdong Province, China)
Hou Shao-Sheng Email: ayhss@163.com.
Abstract The mathematical formula of Hou Shaosheng's theorem is as follows:
num(2n=q+(2n-q))=num(2n=pi+pj)+ num(2n=ht+hu)
+ num(2n=ps+hr)+ num(2n=hk+pd). (3.3.0)
The 4 inferences of Hou Shaosheng's theorem are as follows:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Among them, the convention is: 3≤q≤n,q is odd.
pi, pj, ps, pd are all odd prime numbers; ht, hu, hr, hk are all odd composite numbers.
And pi≤pj, ht≤hu, ps≤hr, hk≤pd.
pi, ht, ps, hk, ∈[3,n]; pj, hu, hr, pd∈[n,2n-3].
4 inferential formulas provide a reliable theoretical basis for proving Goldbach's conjecture.
The basic task of this section is to uncover the 4 genetic codes that make Goldbach's conjecture valid, based on 4 inferential formulas. Moreover, as long as one genetic code exists, Goldbach's conjecture will continue to hold true. The paper proved that there were at least three of the four genetic codes, which proved Goldbach's conjecture once and for all.
Keyword Goldbach conjecture; Continue to be established;
genetic code.
[Document ID] A [Document number]
5.0. Theorem 6. If n Is an Odd Prime, then 2n=n+n, the Conjecture is True
Proof Since 2n=n+n, if n is an odd prime, then n+n is already the sum of two odd prime numbers, so the conjecture works.
As for Goldbach's conjecture 2n=pi+pj, some sources say that the computer has verified that 6≤2n≤1010, and Goldbach's conjecture is valid. As we have already said, if n is an odd prime, then the conjecture naturally holds. Therefore, in the following study of the conjecture, n is generally assumed to be composite number and relatively large, for example, 1000≤2n.
5.1 Let num(3≤p≤2k-3)=num(3≤p≤2n-3)+1, k=n+1,
Then at 2k,the conjecture must be true.
(After that, if not specified, always set k=n+1)
Theorem 7.If num(3≤p≤2k-3)=num(3≤p≤2n-3)+1, where k=n+1, then 2k must can be expressed as the sum of two odd prime numbers, that is, if 2k=2 (n+1), Goldbach's conjecture must be true.
Proof because
num(3≤p≤2k-3)=num(3≤p≤2n-3)+1.
And k=n+1, so we have:
num(3≤p≤2k-3)
=num(3≤p≤2n-1)
=num(3≤p≤2n-3)+1 (5.1.1)
(5.1.1) indicates that the number of odd prime p in the interval
[3,2n-1] is 1 more than that in the interval [3,2n-3].
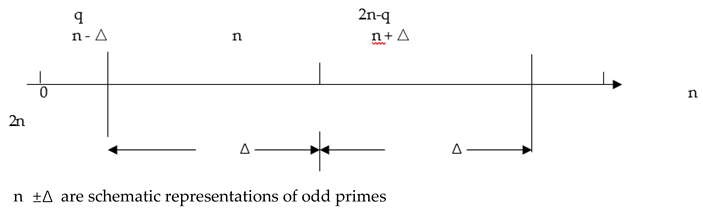
There are only two more integers in the interval [3,2n-1] than in the interval [3,2n-3] : 2n-2,2n-1. Obviously, 2n-2 is even and 2n-1 is odd number. So, one extra odd prime can only be 2n-1.
Because k=n+1, 2k-3=2n-1. So in the figure below, 2k-3 and 2n-1 are the same point.
as shown in the figure: In the interval [3,2n-1], there are only two more integers than in the interval [3,2n-3] : 2n-2,2n-1.
So there must be:
2k=2(n+1)=3+(2n-1). (5.1.2)
Since 3 and (2n-1) are both odd prime numbers, so for 2k=2(n+1), the conjecture is true.
Theorem 7 has been proved.
5.2. The Application Value of Theorem 7
The above proof reveals an important secret: let k=n+1, if (2n-1) is an odd prime number, regardless of whether n is odd or even, then 2k must can be expressed as the sum of two odd prime numbers, that is, 2k conjecture must be true.
If (2n-1) is an odd prime, then 2k=2 (n+1) must can be expressed as the sum of two odd prime numbers, that is, 2k must be true.
This theorem provides a theoretical basis for supposing (2n-1) to be an odd composite number when proving conjectures by classification.
If (2n-1) is an odd prime, then 2k=2 (n+1) must can be expressed as the sum of two odd prime numbers, So the conjecture must be true at 2k.
This situation, in practice, is not uncommon.
See 1:
When n=3, 2n-1=2×3-1= 5, 5 is an odd prime number.
So we have 2k=2 (n+1)
=2×4= (2×3-1)+3.
See 2:
When n=4, 2n-1=2×4-1= 7, 7 is an odd prime.
So we have 2k=2 (n+1)
=2×5= (2×4-1)+3.
See 3:
when n=6, 2n-1=2×6-1=11,11 is an odd prime.
So we have 2k=2(n+1)
=2×7=(2×6-1)+3.
See 4:
When n=7, 2n-1=2×7-1= 13,13 is an odd prime number.
So we have 2k=2(n+1)
=2×8=(2×7-1)+3.
Above, we give 4 examples. These 4 examples show that the situation expressed by theorem 7 exists in practice.
However, not every n applies to theorem 7. For example, n=5, 2n-1=9. 9 is not an odd prime and does not satisfy that (2n-1) is an odd prime, so it does not apply to theorem 7.
If (2n-1) is not an odd prime number, for such n, to prove that 2 (n+1), the conjecture must hold, we need to apply a series of subsequent theories, and gradually solve.
5.3 In proving the conjecture, we can assume that the conjecture holds for 2n and that k=(n+1) is composite number.
If not specified, always set k=n+1 thereafter.
If n is an odd prime, 2n=n+n, then obviously the conjecture works.
And since (2n-1) is an odd prime,2k=3+(2n-1),2k is the sum of two odd prime numbers.
That is, as long as (2n-1) is an odd prime, for such n we already have: 2(n+1)=2k=3+ (2n-1),2(n+1) is already the sum of two odd prime numbers.
So, if we assume that the conjecture is true for 2n and to prove that the conjecture must be true for 2k, we can assume that (2n-1) is odd composite. As for (2n-1) being an odd composite number, whether this condition must be used depends on the specific situation. Put this condition here in case you need it.
And we know that for 6≤2n≤106, our conjecture is true. So we can assume that 2n is true.
Let 3≤n, k=n+1, and if k is an odd prime, then the conjecture works at 2k. So we'll work on the conjecture Always set k=n+1, and k is composite number.
Therefore, in proving the conjecture later, we can assume that the conjecture holds for 2n, and that k(=n+1) is composite number. As long as you can prove that the 2k conjecture is true under these conditions, then the conjecture must be true.
k(=n+1) is a composite number, which can be divided into k(=n+1) is an odd composite number and an even composite number.
(2n-1) is composite number, and only odd composite numbers are possible.
Please read this section carefully, and do not ignore it because it has no proof of theorems and no derivation of formulas. Actually, this section is very important. Because this section is the link between the previous and the next, is the most important logical process in the proof of conjecture.
5.4 Minimum and maximum values of num(2k=pi++pj+).
Theorem 8. Suppose that the conjecture is true for 2n, that is:
num(3≤p≤n)=num(2n=pi+pj)+ num(2n=ps+hr); (4.0.1)
num(n≤p≤2n-3)=num(2n=pi+pj)+ num(2n=hk+pd); (4.0.3)
num(2n=pi+pj)≥1.
A: If one of (pi+2), (pj+2), (hr+2), (hk+2) is an odd prime, then the conjecture holds for 2k, k=n+1.
B: And (pi+2), (pj+2), (hr+2), (hk+2) are the sum of the number of odd primes, which is the maximum value of num(2k=pi++pj+). To wit:
num(2k=pi++pj+)≤num((pi+2)∈P)+num((pj+2)∈P)
+num((hr+2)∈P)+num((hk+2)∈P)
(pi+2)∈P means that pi+2 is an odd prime, num((pi+2)∈P) means that pi+2 is the number of odd prime numbers, and the same applies to the rest. (P is the set of odd prime numbers).
(pi, pj, ps, pd, pi+, pj+, are all odd prime numbers).
C: And num((pj+2)∈P)+num((hr+2)∈P), is the minimum value of
num(2k=pi++pj+). To wit:
num((pj+2)∈P)+num((hr+2)∈P) ≤ num(2k=pi++pj+).
Proof Firstly, part of the inference of Hou Shao-sheng's theorem (Theorem 4) is quoted as follows:
About the formula:
num(2n=q+(2n-q))=num(2n=pi+pj)+ num(2n=ht+hu)
+ num(2n=ps+hr)+ num(2n=hk+pd). (3.3.0)
always have:
num (3≤p≤n)= num(2n=pi+pj)+ num(2n=ps+hr); (4.0.1)
num (n≤p≤2n-3)= num(2n=pi+pj)+ num(2n=hk+pd). (4.0.3)
(1) The following proves theorem content A, as follows:
because
2k=2n+2
=(pi+2)+pj =pi+(pj+2) . (5.4.1)
So, as long as one of (pi+2) is an odd prime, or one of (pj+2) is an odd prime, 2k is already the sum of two odd prime numbers, so at 2k, the conjecture is true.
also because
2k=2n+2
=ps+hr+2=ps+(hr+2). (5.4.2)
That is to say, as long as one of (hr+2) is an odd prime, 2k is already the sum of two odd prime numbers, so at 2k, the conjecture is true.
(hr+2) is an odd prime number, which exists in all 8 examples. And the larger num (2n=ps+hr), the more odd prime numbers (hr+2) are.
also because
2k=2n+2
=hk+pd+2=(hk+2)+pd. (5.4.3)
That is to say, as long as one of (hk+2) is an odd prime, 2k is already the sum of two odd prime numbers, So at 2k, the conjecture is true.
At lest one of (hk+2) is an odd prime number, which exists in all 8 examples. And the larger num(2n=hk+pd)is, the more odd primes (hk+2) are.
Note that if num (2n=pi+pj) =m, and m is a positive integer, then there are m number of 2n=pi+pj, then there are m number of pi, then there are m of pj, and so on.
From (4.0.1), (4.0.3) we can see that if there is a pi+2=pi+1 that is an odd prime, or a pj+2=pj+1 that is an odd prime, or a hr+2=p that is an odd prime, or a hk+2=p that is an odd prime, then the conjecture must be true at 2k.
We have noticed that when (pi+2), (pj+2), (hr+2), (hk+2) are odd prime numbers,then
2k=(pi+2)+pj, 2k=pi+(pj+2), 2k=ps+(hr+2), 2k=(hk+2)+pd,
Every 2k is the sum of two odd prime numbers. As long as one of them exists, it proves that the 2k time conjecture is true.
Theorem content A proves the end.
(2) Theorem content B is proved as follows:
From the above, if (pi+2), (pj+2), (hr+2), (hk+2) are odd prime numbers, then 2k=(pi+2)+pj, 2k=pi+(pj+2), 2k=ps+(hr+2), 2k=(hk+2)+pd,
Each 2k is the sum of two odd prime numbers. As long as one of them exists,
it proves that the 2k time conjecture is true.
And (pi+2), (pj+2), (hr+2), (hk+2) are the sum of the number of odd primes, which is the maximum value of num(2k=pi++pj+). To wit:
num(2k=pi++pj+)≤num((pi+2)∈P)+num((pj+2)∈P)
+num((hr+2)∈P)+num((hk+2)∈P)
This provedtheoremcontentB.
(3) The following proof theorem content C, as follows:
Let num((pi+2) ∈P) indicate that pi+2 is the number of odd prime numbers.
Let num((pj+2)∈P)=m1, (m1 is a non-negative integer), that is, there are m1 odd primes of pj+2.
If 1 number of pj+2 is an odd prime, then 1 number of pi+(pj+2) is the sum of 2 odd prime numbers, and there is 1 of 2k=pi++pj+.
Let num((pj+2) ∈P)=m1, that is, there are m1 number of pj+2 which is odd prime numbers,then there are m1 number of pi+(pj+2) is the sum of two odd prime numbers, there are m1 number of 2k=pi++pj+.
Replacing m1 with num((pj+2)∈P) in the above sentence gives the following statement:
If num((pj+2)∈P). there are num((pj+2)∈P) of pj+2 which is odd prime, there are num((pj+2)∈P) of pi+(pj+2) which is the sum of two odd primes, there are num((pj+2)∈P) of 2k=pi++pj+ . The same goes for others.
Let num((hr+2)∈P)=m2, (m2 is a non-negative integer),that is, there are m2 number of hr+2 which is odd prime numbers,then there are m2 number of hr+2 that is odd prime numbers.
If one number of hr+2 is an odd prime, then there is one number of ps+(hr+2) is the sum of two odd prime numbers, and there is one 2k=pi++pj+ .
If m2 number of hr+2 is odd primes,then there are m2 number of ps+(hr+2) is the sum of two odd primes, and there are m2 number of 2k=pi++pj+ .
If num((hr+2)∈P), there are num((hr+2)∈P) of hr+2 which is odd prime, there are num((hr+2)∈P) of ps+(hr+2) which is the sum of two odd primes, there are num((hr+2)∈P) of 2k=pi++pj+ . The same goes for others.
We notice that since there is no repetition between pi,ps , there is no repetition between pi+(pj+2),ps+(hr+2).
So num((pj+2)∈P)+num((hr+2)∈P)is the minimum value of
num(2k=pi++pj+).
so has:
num((pj+2)∈P)+num((hr+2)∈P) ≤ num(2k=pi++pj+).
This proved theorem content C.
Theorem 8 has been proved.
5.5 Theorem 9. If num (2n=ps+hr) =0, Goldbach's conjecture must be true.
Proof Because the 2n conjecture is true, there must be:
num(3≤p≤n)= num(2n=pi+pj)+ num(2n=ps+hr). (4.0.1)
Among num(2n=pi+pj)≥1.
However, it is possible that num(2n=ps+hr)=0.
If num(2n=ps+hr)=0,
there must be: num(3≤p≤n)=num(2n=pi+pj).
This shows that pi in (2n=pi+pj) is all the odd prime numbers p in the interval [3,n].
Let the smallest odd prime in pi be p1, then p1=3, that is, p1 is the first odd prime 3 in the interval [3,n]. So at least one of pi+2 is an odd prime.
Because at least one of pi+2 is an odd prime, and because:
num(2n=pi+pj)= num(2n+2=pi+2+pj)
= num(2k=(pi+2)+pj).
We know that there are sister primes in the interval [3,n].
Let the ith odd prime be pi, and pi+2=pi+1 is the odd prime, and pi+1 is the (i+1)th odd prime.
Here, pi is the ith odd prime number, and pi+1 is the (i+1)th odd prime number. pi, pi+1 is a sister prime number.
Then:
2k=(pi+2)+pj
=pi+1+pj.
So 2k time is a good guess.
From the above proof, we can see that when num(2n=ps+hr)=0, Goldbach's conjecture must be true.
Therefore, when proving the conjecture below, it can be assumed that num (2n=ps+hr) ≥1, And just consider that k=(n+1) is composite. Since k is an odd prime, the conjecture is obviously true at 2k.
Theorem 9, complete proof.
5.6 Theorem 10. If pi+2is an odd prime, or hr+2is an odd prime, Goldbach's conjecture must be true.
Proof Since k=n+1 is composite number, there must be:
num(3≤p≤k)=num(3≤p≤n) (5.6.1)
Quote (4.0.1) as follows:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr). (4.0.1)
From (5.6.1) and (4.0.1), there must be:
num(3≤p≤k)= num(3≤p≤n)
=num(2n=pi+pj)+num(2n=ps+hr)
=num(2n+2=pi+2+pj)+num(2n+2=ps+hr+2) (5.6.2)
=num(2k=pi+2+pj)+num(2k=ps+hr+2), k=n+1. (5.6.3)
From (5.6.3) :
2k=pi+2+pj
=(pi+2)+pj
=pi+(2+pj)
If one of(pi+2)is an odd prime, then(pi+2)+pj is already the sum of 2 odd prime numbers. So 2k=(pi+2)+pj, 2k is already the sum of 2 odd prime numbers. So the 2k time conjecture works.
If one of(2+pj)is an odd prime, then pi+(2+pj)is already the sum of 2 odd prime numbers. So 2k=pi+(2+pj), 2k is already the sum of 2 odd prime numbers. So the 2k time conjecture works.
From (5.6.3) :
2k=ps+hr+2
=ps+(hr+2)
If one of(hr+2)is an odd prime, then ps +(hr+2)is already the sum of 2 odd prime numbers. So 2k=ps+(hr+2), 2k is already the sum of 2 odd prime numbers. So the 2k time conjecture works.
This proves that if there is a pi+2 that is an odd prime, or a 2+pj that is an odd prime, or a hr+2 that is an odd prime, then the conjecture must be true at 2k. That Goldbach's conjecture must be true.
Theorem 10 is proved.
Theorem 10 proves that if pi+2 is an odd prime, or hr+2 is an odd prime, Goldbach's conjecture must be true. However, this theorem is not answered: there must be pi+2 which is an odd prime numbers, or there must be hr+2 which is an odd prime numbers, to ensure that Goldbach's conjecture is true.
The task that pi+2 must be an odd prime, or that hr+2 must be an odd prime, requires theorem 17.
If someone checks every even number up to 3× one by one, Goldbach's conjecture is true. This fact tells us that Goldbach's conjecture is true for every even number in the interval [6, 3×].
Let's say 2n,2(n+1), no less than 6, no greater than 3×, why is the conjecture true for 2n, and true for 2(n+1)? It works for 2n, it works for 2(n+1), so what's the secret? The result of our research is the following 4 major theoretical questions raised by the authors.
5.7 Four major theoretical questions raised by the author; The four genetic codes of Goldbach's conjecture.
Goldbach's conjecture at 2n is expressed as 2n=pi+pj; Goldbach's conjecture for 2 (n+1), we use 2(n+1)=pi++pj+, pi+, pj+, are odd prime numbers.
In the study of 4 major theoretical problems, the term 2(n+1)=pi++pj+ is involved. To do this, we need to give it a definition.
Definition: Let qi and qj both be odd prime numbers, and 2(n+1)=qi+qj, then we say (define) 2(n+1)=qi+qj, which is the source of 2(n+1)=pi++pj+.
We're working on Goldbach's conjecture. We have to ask: what is the nature of Goldbach's conjecture? Some people would say that the essence is: as long as 3≤n, then 2n=pi+pj can be true. We say this answer is correct, but it misses the point.
So, what's the point? The key is: why is the conjecture true for 2n, and true for 2(n+1)? Or, if 2n=pi+pj is true, 2k=pi++pj+ where does come from? 2k=pi++pj+ How is composed?
This part will reveal the most mysterious and essential recurrence relation of Goldbach's conjecture. The recursion relation here means that if the conjecture is true at 2n, it must lead to the conjecture being true at 2 (n+1).
5.7.1 Question 1: Assuming 2n is true, where does 2k=pi++pj+ come from? Or, why do assumptions persist?
We have theorem 11 to answer as follows:
Theorem 11: If the 2n conjecture is true, then2k=pi++pj+ has the following 4 sources, as long as 1 source exists, the 2k conjecture is guaranteed to continue to be true.
The 4 sources of2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+.
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+.
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+.
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
Each of these 4 sources is a theorem. Because they have the same form, they're put together as a theorem.
4 sources of expression, very simple, are what if, then what. If what is the condition of the theorem, then what is the conclusion of the theorem. From the condition of the theorem, to the conclusion of the theorem, there is no other intermediate link, causality, very direct, so it is no longer proved.
At this point, the only question the reader should ask is, is it possible that none of the 4 ifs exist? This is the most central issue, and this is the issue that we are most concerned about. As a proof of the conjecture, this question must be answered.
As an answer to the core question, theorem 17 will prove:
If the Goldbach conjecture holds for 2n and k (=n+1) is composite number, then at least one of (pi+2), (hr+2) is an odd prime, which guarantees that the conjecture holds for 2k.
Theorem 11, theoretically gives 4 sources of 2k=pi++pj+.
Note that 2k=ht+2+hu, either 2k=(ht+2)+hu, or 2k=ht+(2+hu), cannot be the sum of 2 odd prime numbers. So it can't be one of 2k=pi++pj+, so 2k=pi++pj+, there are only 4 sources above.
The 4 sources of 2k=pi++pj+ essentially answer the close relationship between the 2n conjecture and the 2k conjecture.
As long as one of these 4 sources exists, 2k time conjecture must be true!
These 4 sources are the decisive factors and fundamental guarantees for the continuation of the conjecture.
These 4 sources are the 4 genetic codes of Goldbach's conjecture.
These 4 sources are the fundamental mystery of the persistence of Goldbach's conjecture.
Note that the first 2k=(pi+2)+pj of the 4 sources. when (pi+2) is an odd prime, because pi, (pi+2), are both odd primes, so pi, (pi+2), is a sister prime, and pi is the smaller of the sister primes.
The second 2k=pi+(pj+2) of the 4 sources , when (pj+2) is an odd prime, since pj, (pj+2), are both odd primes, so pj, (pj+2), is a sister prime, and pj is the smaller of the sister primes.
The third 2k=ps+(hr+2) of the 4 sources, originally hr is an odd composite number, when (hr+2) is an odd prime, ps+(hr+2) becomes the sum of 2 odd primes. The significance of this event is that it connects 2n=ps+hr with 2k=ps+(hr+2), completing the transition from the non-Goldbach conjecture (2n=ps+hr) to Goldbach's conjecture(2k=pi++pj+)!
The fourth 2k=(hk+2)+pd of the 4 sources, originally hk is an odd composite number, and when (hk+2) is an odd prime number, (hk+2)+pd becomes the sum of 2 odd primes. The significance of this event is that it connects 2n=hk+pd with 2k=(hk+2)+pd, completing the transition from the non-Goldbach conjecture (2n=hk+pd) to Goldbach's conjecture(2k=pi++pj+)!
So, two of the 4 sources of 2k=pi++pj+ are realized with the help of the smaller of the sister primes; Two are realized by means of the non-Goldbach conjecture.
Question 1.1: As n increases, the number of (2n=pi+pj) increases in a wave.
2k=2(n+1)=pi++pj+ has 4 sources, which is the fundamental reason why num(2n=pi+pj) gradually waves up as n increases.
In some materials, especially at
https://en.wikipedia.org/wiki/Goldbach’s_conjecture the odd primes slash the intersection of graphics, further enriches our perceptual knowledge. Although these data know that num (2n=pi+pj) increases with the increase of n, they do not indicate the reason for the gradual increase.
Numerous researchers of Goldbach's conjecture, through a limited number of mathematical examples, have found that as n increases, the number of (2n=pi+pj) gradually increases in a wave pattern. This discovery is a contribution and deserves recognition. However, no one knows that 2k=2(n+1)=pi++pj+ has 4 sources, so no one has mathematically explained the gradual increase in the number of (2n=pi+pj).
To explain the gradual increase in num(2n=pi+pj), we use the following 2 mathematical formulas.
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
Let's say k=n+1, and let's compare num(3≤p≤n), num(3≤p≤k).
If k is composite number, whether k is odd composite number or even composite number, there is:
num(3≤p≤n)=num(3≤p≤k).
That is to say, if k is composite number, num(3≤p≤n) does not change as n increases by l from n to k. That is, num(3≤p≤n) does not change.
When n changes to k,num(3≤p≤n)=num(3≤p≤k), it is known from (4.0.1) that the total number of num(2n=pi+pj) +num (2n=ps+hr) does not change. However,num(2n=pi+pj), num(2n=ps+hr), can be changed. This change will cause a wave change in num(2n=pi+pj), num(2n=ps+hr).
If k is an odd prime, there is always:
num(3≤p≤n)+1=num(3≤p≤k).
That is to say, if k is an odd prime, num(3≤p≤n), because n increases by 1, and as n changes from n to k, num(3≤p≤k) increases by 1 compared to num(3≤p≤n), the change occurs.
When n changes to k,num(3≤p≤k) increases by 1 compared with
num(3≤p≤n), and it can be seen from (4.0.1) that the total number of num(2n=pi+pj)+ num(2n=ps+hr)increases by 1. num (2n=pi+pj), num (2n=ps+hr), must change. It is likely to increase num (2n=pi+pj).
⑴ If the conjecture is true for 2n, it is accepted that
1≤num (2n=pi+pj). There is no doubt that the greater num (2n=pi+pj), the greater the number of (2n=pi+pj). The more 2n=pi+pj, the more pi+2, the more pj+2. Not every pi+2, not every pj+2, is an odd prime, but the more chances pi+2, pj+2, is an odd prime, the more pi+2, pj+2, is an odd prime.
If pi+2, pj+2, are odd prime numbers, each 2k=(pi+2)+pj, each 2k=pi+ (2+pj), becomes one of(2k=pi++pj+). Causes an increase in the number of (2k=pi++pj+).
⑵ Assuming that the conjecture is true for 2n, in general, 1≤
num(2n=ps+hr). The greater num (2n=ps+hr), the greater the number of (2n=ps+hr). The more we have (2n=ps+hr), the more we have (hr+2). Although not every (hr+2) is an odd prime, the more chances (hr+2) is an odd prime, the more (hr+2) is an odd prime.
If (hr+2) is an odd prime, every 2k=ps+(hr+2) becomes one of(2k=pi++pj+). Causes an increase in the number of (2k=pi++pj+).
2n=ps+hr, not one of (2n=pi+pj). If 2k=ps+(hr+2) becomes one of (2k=pi++pj+), this is a process from 2n=ps+hr to(2k=pi++pj+). This is an important factor that the num(2k=pi++pj+)of increase .
⑶ Assuming that the conjecture is true for 2n, in general, 1≤num (2n=hk+pd). There is no doubt that the greater num (2n=hk+pd), the greater the number of (2n=hk+pd). The more (2n=hk+pd) there is, the more (hk+2) there is. Although not every (hk+2) is an odd prime, the more chances (hk+2) is an odd prime, the more (hk+2) is an odd prime.
If (hk+2) is an odd prime, every 2k=(hk+2)+pd becomes one of(2k=pi++pj+). Causes an increase in the number of (2k=pi++pj+).
2n=hk+pd, not one of (2n=pi+pj). If 2k=(hk+2)+pd becomes one of (2k=pi++pj+), this is a process from 2n=hk+pd to(2k=pi++pj+). This is an important factor that the num(2k=pi++pj+)of increase .
Theorem 11 theoretically proves that 2k=2(n+1)=pi++pj+ has 4 sources. Now, let's test theorem 11 with a mathematical example.
Verification question 1: 2k=2(n+1)=pi++pj+, there are four sources.
The following example, 3, is the third of the 8 mathematical examples in 3.2: Instance 3. Now verify the 4 sources of 2k=pi++pj+ with example 3.
Example 3. 2n=2×51=102
=1+101=3+99=5+97=7+95=9+93=11+91=13+89=15+87=17+85=
=19+83=21+81=23+79=25+77=27+75=29+73=31+71=33+69=35+67
=37+65=39+63=41+61=43+59=45+57=47+55=49+53=51+51.
Note: Numbers underlined are prime numbers. If the number is not underlined, it is a composite number.
Theorem 11 proves that 2k=2(n+1)=pi++pj+ has 4 sources. These 4 sources are fully confirmed in Example 3. See below for specific verification.
Verify the first source of 2k=2(n+1)=pi++pj+as follows:
num(2×51=pi+pj)=8.
These 8 number of 2×51=pi+pj are as follows:
2×51 =5+97 =13+89 =19+83 =23+79 =29+73 =31+71 =41+61 =43+59.
2n=pi+pj, (pi +2)are odd prime numbers:
(5+2); (29+2);(41+2).
2k=2(n+1)=(pi+2)+pj. 2k is the sum of 2 odd prime numbers, such as:
2k=(5+2)+97 ;2k=(29+2)+73 ; 2k=(41+2)+61.
Verify the second source of2k=2(n+1)=pi++pj+, as follows:
2n=pi+pj,(pj+2)are odd prime numbers:
(71+2);(59+2).
2k=2(n+1)=pi+(pj+2), 2k is the sum of 2 odd prime numbers, which is:
2k=31+(71+2); 2k=43+(59+2).
Note: (29+2)+73, repeated with 31+(71+2). (41+2)+61, repeat with 43+(59+2). We're shading the duplicators.
Verify the third source of 2k=2(n+1)=pi++pj+, as follows:
num(2n=ps+hr)=6.
The 6 number of 2×51=ps+hr are: 2×51= 3+99= 7+95= 11++91= 17+85= 37+65= 47+55.
2n=ps+hr,(hr+2) are odd prime numbers: (99+2); (95+2); (65+2).
2k=2(n+1)=ps+(hr+2), 2k is the sum of 2 odd prime numbers, which is:
2k=3+(99+2); 2k=7+(95+2); 2k=37+(65+2).
Verify the fourth source of 2k=2(n+1)=pi++pj+, as follows:
num(2n=hk+pd)=2.
These 2 number of 2n=hk+pd are as follows:
2n=35+67; 2n=49+53;
2n=hk+pd, (hk+2)are odd prime numbers: (35+2).
2k=2(n+1)=(hk+2)+pd, 2k is the sum of 2 odd prime numbers, which is:
2k=(35+2)+67.
(The character shading is repeated and can be ignored.)
For example, the above facts are taken as examples:
(5+2)+97, like 7+(95+2), is the sum of the same 2 numbers, and 7+(95+2) is the repeat.
37+(65+2)and (35+2)+67 are the sum of the same 2 numbers, and (35+2)+67 is the repeat.
The above facts show that the 4 sources of 2k=2(n+1)=pi++pj+ all appear in Example 3, and the theory and practice are completely consistent.
Above we get 9 number of 2k=2(n+1)=pi++pj+, of which there are 4 repetitions. So there are no repetitions(2k=pi++pj+),only 5.
After comparison, these 5 are exactly the same as the actual situation in example 2 (2(51+1)).
Us from(2n=2×51=102=1+101=3+99=······=49+53=51+51.), got 2k=
2(51+1)=pi++pj+ is all about.
The reader should appreciate that the 4 sources would rather repeat the same data (with character shading), and never give up the opportunity to ensure that the conjecture continues to hold.
The appearance of the duplicate data explains the 4 sources and provides multiple guarantees for the establishment of Goldbach's conjecture. If only one(2k=pi++pj+)occurs once, the conjecture is guaranteed. If(2k=pi++pj+)occurs m times in total, the conjecture is guaranteed m times. This is one of the mysteries of the persistence of conjecture.
Since(2k=pi++pj+)has only 4 sources,(2k=pi++pj+)can occur at most 4 times for the same (2k=pi++pj+). Because in the same source, there can be no duplication. For example, 2k=2(n+1)=pi++pj+ the fourth source: 2n=hk+pd, when one (hk+2) is an odd prime, 2k= (hk+2) +pd, forming a 2k=pi++pj+, it is impossible to appear 2 identical 2k=(hk+2)+pd.
5.7.2 Question 2: Where does 2k=ps++hr+ come from? Will the 4 sources of 2k=2(n+1)=pi++pj+ use up 2n resources and hinder the source of 2k=ps++hr+?
We have theorem 12 answers as follows:
Theorem 12: If the conjecture is true for 2n, then 2k=ps++hr+has4sources:
If one of(pj+2)is an odd composite number, then 2k=pi+(pj+2) becomes one of 2k=ps++hr+.
If one of (hr+2) is an odd composite number, then 2k=ps+(hr+2) becomes one of 2k=ps++hr+.
If one of (ps+2) is an odd prime, then 2k=(ps+2)+hr becomes one of 2k=ps++hr+ .
If one of (ht+2) is an odd prime, then 2k=(ht+2)+hu becomes one of 2k=ps++hr+.
Each of the 4 sources of 2k=ps++hr+ above is a theorem. Because the causal relationship between the condition and the conclusion is very direct, it can no longer be proved.
2k=ps++hr+ There are only 4 sources mentioned above. Because 2k=hk+2+pd, neither 2k=(hk+2)+pd, nor 2k=hk+(2+pd), can be the sum of 1 odd prime + 1 odd composite number. So it can't be one of 2k=ps++hr+, it can't be a source of it.
2k=2(n+1)=ps++hr+ has 4 sources, which is why num(2n=ps+hr) is gradually increasing in waves.
The reason why num(2n=ps+hr) gradually increases in waves can still be explained by mathematical formulas. In this regard, we see above (Problem 1.1: As n increases, the number of (2n=pi+pj) increases in a wave.) Examples have been given, which are omitted here for the sake of shortening space.
Theorem 12, in theory, proves that 2k=2(n+1)=ps++hr+ has 4 sources. Let's test theorem 12 with a mathematical example.
Verification question 2: 2k=2(n+1)=ps++hr+ 4 sources.
Example 3 below, the third of the 8 mathematical examples in 3.2, now uses example 3 to verify the 4 sources of 2k=ps++hr+.
Example 3. 2n=2×51=102
=1+101=3+99=5+97=7+95=······=41+61=43+59=45+57=47+55=49+53=51+51.
The number is underlined. The number is an odd prime. None digits with underscores are odd composite numbers.
Theorem 12 proves that 2k=2(n+1)=ps++hr+ has 4 sources. These 4 sources are fully confirmed in Example 3. See below for specific verification.
Verify the first source of 2k=2(n+1)=ps++hr+, as follows.
num(2×51=pi+pj)=8.
These 8 number of 2×51=pi+pj as follows:
2×51=5+97=13+89=19+83=23+79=29+73=31+71=41+61=43+59.
2n=pi+pj, (pj+2)are odd composite numbers:
5+(97+2)=13+(89+2)=19+(83+2)=23+(79+2)=29+(73+2)=41+(61+2).
Verify the second source of 2k=2(n+1)=ps++hr+, as follows.
num (2n=ps+hr)=6.
These 6 number of 2n=ps+hr are as follows:
2×51=3+99=7+95=11+91=17+85=37+65=47+55.
2n=ps+hr,(hr+2) are odd composite numbers:
11+(91+2)=17+(85+2)=47+(55+2).
Verify the third source of 2k=2(n+1)=ps++hr+, as follows.
num(2n=ps+hr)=6.
These 6 number of 2n=ps+hr are as follows:
2×51=3+99=7+95=11+91=17+85=37+65=47+55.
2n=ps+hr,(ps+2) are odd prime numbers:
(3+2)+99=(11+2)+91=(17+2)+85.
(3+2)+99, repeat with 5+(97+2), (11+2)+91 repeat with 13+(89+2),
(17+2)+85 is repeated with 19+(83+2).
Verify the fourth source of 2k=2 (n+1) =ps++hr+, as follows.
num(2×51=ht+hu)=9.
These 9number of 2n=2×51=ht+huare as follows:
2n=9+93; 2n=15+87; 2n=21+81; 2n=25+77; 2n=27+75;
2n=33+69; 2n=39+63; 2n=45+57; 2n=51+51.
2n=ht+hu, (ht+2) are odd prime numbers:
(9+2)+93=(15+2)+87=(21+2)+81=(27+2)+75=(39+2)+63=(45+2)+57.
(The character shading is repeated and can be ignored.)
The above facts show that the 4 sources of 2k=2(n+1)=ps++hr+ are exactly consistent with mathematical examples.
Us from(2n=2×51=102=1+101=3+99=······=49+53=51+51.), got it
num(2(51+1)=ps++hr+)=9. The data is exactly the same as in example 2
(2(51+1)).
Above, we have completed the verification task of 2k=2 (n+1) =ps++hr+ 4 sources.
In order to facilitate later references if necessary, we make the following summary.
Summary:
Us from(2n=2×51=102=1+101=3+99=······=49+53=51+51.), got it
num(2(51+1)=ps++hr+)=9.
These 9 number of 2(51+1)=2(n+1)=ps++hr+ as follows.
From the first source of 2k=2(n+1)=ps++hr+, as follows:
2n=pi+pj, and pj+2 are odd composite numbers:
5+(97+2)=13+(89+2)=19+(83+2)=23+(79+2)=29+(73+2)=41+(61+2).
From the second sourceof2k=2(n+1)=ps++hr+, as follows:
2n=ps+hr,(hr+2) are odd composite numbers:
11+(91+2)=17+(85+2)=47+(55+2).
From the third source of 2k=2(n+1)=ps++hr+,as follows:
2n=ps+hr, (ps+2) are odd prime numbers:
(3+2)+99=(11+2)+91=(17+2)+85.
From the fourth source of 2k=2(n+1)=ps++hr+, as follows:
2n=ht+hu, (ht+2) are odd prime numbers:
(9+2)+93=(15+2)+87=(21+2)+81=(27+2)+75=(39+2)+63=(45+2)+57.
(The character shading is repeated and can be ignored.)
Us from(2n=2×51=102=1+101=3+99=······=49+53=51+51.), got it
num(2(51+1)=ps++hr+)=9.The data is exactly the same as in example 2
(2(51+1)).
From the above 4 sources, the obtained 2k=2(n+1)=ps++hr+ is summarized as follows:
5+(97+2)=13+(89+2)=19+(83+2)=23+(79+2)=29+(73+2)=41+(61+2).
11+(91+2)=17+(85+2)=47+(55+2).
(3+2)+99=(11+2)+91=(17+2)+85.
(9+2)+93=(15+2)+87=(21+2)+81=(27+2)+75=(39+2)+63=(45+2)+57.
The shadow is the duplicator.
Please pay attention to 1, the following:
5+(97+2)=13+(89+2)=19+(83+2)=23+(79+2)=29+(73+2)=41+(61+2).
2k=pi +(pj+2) is the sum of an odd prime number and an odd composite number.
Please pay attention to 2, the following:
11+(91+2)=17+(85+2)=47+(55+2).
2k=ps+(hr+2) is the sum of an odd prime number and an odd composite number.
It should also be noted that there is no repetition between 2k=pi+(pj+2)and 2k=ps+(hr+2)! And they're all part of 2k=2(n+1)=ps++hr+ . This example shows that in 2k=2(n+1)=ps++hr+ , if you want to reject 2k=pi+(pj+2), or reject 2k=ps+(hr+2), there is no reason.
5.7.3 Question 3: 2k=ht++hu+ Where does come from? We have theorem 13 answers as follows.
Theorem 13: If the conjecture holds for 2n, then2k=ht++hu+ has the following 4 sources:
If one of (ps+2) is odd composite number, then 2k=(ps+2)+hr becomes one of 2k=ht++hu+.
If one of (ht+2) is odd composite number, then 2k=(ht+2)+hu becomes one of 2k=ht++hu+.
If one of (hu+2) is odd composite number, then 2k=ht+(hu+2) becomes one of 2k=ht++hu+.
If one of (pd+2) is odd composite number, then 2k=hk+(pd+2) becomes one of 2k=ht++hu+.
Above, 2k=ht++hu+ 4 sources, each proposition is a theorem. Because the causal relationship between the condition and the conclusion is very direct, it can no longer be proved.
Above, we give 4 sources for 2k=ht++hu+. This is why num(2n=ht+hu), the wave form, increases rapidly as n increases! It is still possible to explain the reason for the rapid increase of num(2n=ht+hu) in a mathematical formula, but for the sake of compression, it is omitted here.
2k=ht++hu+, there are only 4 sources mentioned above. Because 2k=pi+2+pj, neither 2k= (pi+2) +pj, nor 2k=pi+ (2+pj), can be the sum of one odd composite number plus one odd composite number. So it can't be a source of 2k=ht++hu+.
Theorem 13 theoretically proves that 2k=2(n+1)=ht++hu+ has 4 sources. Let's test theorem 13 with a mathematical example.
Verification question 3: 2k=2(n+1)=ht++hu+ 4 sources.
Example 3, which is the third of the 8 mathematical examples in 3.2, is now used to verify 2k=2(n+1)=ht++hu+ 4 sources.
Example 3. 2n=2×51=102
=1+101=3+99=5+97=7+95=······=41+61=43+59=45+57=47+55
=49+53=51+51.
Theorem 13 proves that 2k=2(n+1)=ht++hu+ has 4 sources. These 4 sources are fully confirmed in Example 3. See below for specific verification.
Verify the first source of 2k=2(n+1)=ht++hu+, as follows.
num(2×51=ht+hu)=9.
These 9number of2n=2×51=ht+huare as follows:
2n=9+93; 2n=15+87; 2n=21+81; 2n=25+77; 2n=27+75;
2n=33+69; 2n=39+63; 2n=45+57; 2n=51+51.
2n=ht+hu, and (ht+2) are odd composite numbers:
(25+2)+77=(33+2)+69.
Verify the second source of 2k=2(n+1)=ht++hu+, as follows.
2n=ht+hu, (hu+2) are odd composite numbers:
9+(93+2)=27+(75+2)=39+(63+2).
Verify the third source of 2k=2(n+1)=ht++hu+, as follows.
num(2n=ps+hr)=6.
These 6 number of 2n=ps+hr are as follows:
2n=3+99; 2n=7+95; 2n=11+91; 2n=17+85; 2n=37+65;
2n=47+55;
2n=ps+hr, (ps+2) are odd composite numbers:
(7+2)+95=(37+2)+65=(47+2)+55.
Verify the fourth source of 2k=2(n+1)=ht++hu+, as follows.
num(2n=hk+pd)=2.
These two number of 2n=hk+pd are as follows:
2n=35+67; 2n=49+53;
2k=hk+pd, and (pd+2) are odd composite numbers:
35+(67+2)=49+(53+2).
(The character shading is repeated and can be ignored.)
The above facts show that the 4 sources of 2k=2(n+1)=ht++hu+ are exactly consistent with mathematical examples.
Us from (2n=2×51=102=1+101=3+99=······=49+53=51+51.), obtained the num(2(51+1)=ht++hu+)=5. The data is exactly the same as in example 2 (2 (51+1)).
We should note that 2k=2(n+1)=ht++hu+ 4 sources, in mathematical practice, it is preferable to repeat the data, but never give up the data that should be.
5.7.4 Question 4: Where does2k=hk++pd+ come from? We have theorem 14 answers as follows.
Theorem 14: If the conjecture is true for 2n,2k=hk++pd+ has the following 4 sources:
If one of (pi+2) is odd composite number , then 2k=(pi+2)+pj becomes one of 2k=hk++pd+;
If one of (hu+2) is odd prime, then 2k=ht+(hu+2) becomes one of 2k=hk++pd+;
If one of (hk+2) is odd composite number, then 2k=(hk+2)+pd becomes one of 2k=hk++pd+;
If one of (pd+2) is odd prime, then 2k=hk+(2+pd) becomes one of 2k=hk++pd+;
Above, there are 4 sources of 2k=hk++pd+, each of which is a theorem. Because the causal relationship between the condition and the conclusion is very direct, it can no longer be proved.
Above we give 4 sources of 2k=hk++pd+. This is why num (2n=hk+pd) waves gradually increase as n increases! The reason for the gradual increase of num (2n=hk+pd) wave can still be explained by mathematical formula, but for the sake of space, it is omitted here!
2k=hk++pd+, there are only 4 sources mentioned above. Because 2k=ps+2+hr, neither 2k=(ps+2)+hr, nor 2k=ps+ (2+hr), can be the sum of one odd composite number plus one odd prime number. So it can't be a source of 2k=hk++pd+.
Theorem 14 theoretically proves that 2k=2(n+1)=hk++pd+ has 4 sources. Let's verify theorem 14 with a mathematical example.
Verification question 4: 2k=2(n+1)=hk++pd+ 4 sources.
Example 3 below, which is the third of the 8 mathematical examples in 3.2, is now used to verify 2k=2(n+1)=hk++pd+ 4 sources.
Example 3. 2n=2×51=102
=1+101=3+99=5+97=7+95=······=41+61=43+59=45+57=47+55
=49+53=51+51.
Theorem 14 theoretically proves that 2k=2(n+1)=hk++pd+ has 4 sources. These 4 sources are fully confirmed in Example 3. See below for specific verification.
Verify the first source of 2k=2(n+1)=hk++pd+, as follows.
num(2×51=pi+pj)=8.
These 8 number of 2×51=pi+pj, as follows:
5+97=13+89=19+83=23+79=29+73=31+71=41+61=43+59.
2n=pi+pj, (pi+2) are odd composite numbers:
(13+2)+89=(19+2)+83=(23+2)+79=(31+2)+71=(43+2)+59.
Verify the second source of 2k=2(n+1)=hk++pd+, as follows.
num(2×51=ht+hu)=9.
These 9 number of 2n=2×51=ht+hu are as follows:
2n=9+93; 2n=15+87; 2n=21+81; 2n=25+77; 2n=27+75;
2n=33+69; 2n=39+63; 2n=45+57; 2n=51+51.
2n=ht+hu, (hu+2) are odd prime numbers:
15+(87+2)=21+(81+2)=25+(77+2)=33+(69+2)=45+(57+2)=51+(51+2).
Verify the third source of 2k=2(n+1)=hk++pd+, as follows.
num(2n=hk+pd)=2.
These two number of 2n=hk+pd are as follows:
2n=35+67; 2n=49+53;
2n=hk+pd, and (hk+2) are odd composite numbers: (49+2)+53.
Verify the fourth source of2k=2(n+1)=hk++pd+, as follows.
num(2n=hk+pd)=2.
These two number of 2n=hk+pd are as follows:
2n=35+67; 2n=49+53;
2n=hk+pd, (pd+2) is an odd prime number, not one in this case. However, this cannot be used to negate the existence of odd prime numbers (pd+2), much less to negate the theorem 14. It is now confirmed by example 2 that there are indeed (pd+2) odd prime numbers.
Example 2. 2×52=104
=1+103=3+101=5+99=7+97=9+95=11+93=13+91=15+89=17+87=
=19+85=21+83=23+81=25+79=27+77=29+75=31+73=33+71=35+69
=37+67=39+65=41+63=43+61=45+59=47+57=49+55=51+53.
In this case, num(2n=hk+pd)=6.
These 6 number of 2n=hk+pd are as follows:
2n=15+89, 2n=21+83, 2n=25+79, 2n=33+71, 2n=45+59, 2n=51+53.
2n=hk+pd, (pd+2) are odd prime numbers: 33+(71+2), 45+(59+2).
The above facts show that the four sources of 2k=2(n+1)=hk++pd+ are exactly consistent with mathematical examples.
Us from(2n=2×51=102=1+101=3+99=······=49+53=51+51.), obtained the num(2(n+1)=2(51+1)=hk++pd+)=6. The data is exactly the same as in example 2 (2(51+1)).
We should note that 2k=2(n+1)=hk++pd+ 4 sources, in mathematical examples, it is preferable to repeat the data, but never give up the data that should be.
Four big theoretical questions, and that concludes.
5.8 Summary of 4 major theoretical problems and 4 Genetic code problems
The 4 major theoretical problems are the core theoretical problems in the proof of Goldbach conjecture, which is a major breakthrough and great harvest in our study of Goldbach conjecture.
Goldbach's conjecture holds, essentially, because it holds for 2n, and it still holds for 2(n+1).
The proof of Goldbach's conjecture must answer: If the conjecture is true for 2n, why is it still true for 2(n+1)? What is the close relationship between the establishment of 2n and the establishment of 2k?
4 major theoretical questions are theoretically answered: the close relationship between 2n holds and 2k(k=n+1) holds.
Theorem 11 answers: If the conjecture is true at 2n, then 2k=pi++pj+ has 4 sources, and as long as one source exists, the conjecture will continue to be true at 2k. This is the most important discovery and central theory in the proof of the conjecture.
Theorem 12 answers: If the conjecture is true for 2n, then 2k=ps++hr+ has 4 sources.
Theorem 13 answers: If the conjecture is true for 2n, then 2k=ht++hu+ has 4 sources.
Theorem 14 answers: If the conjecture is true for 2n, then 2k=hk++pd+ has four sources.
The 4 major theoretical questions not only theoretically answer the close relationship between the establishment of 2n and the establishment of 2k(k=n+1), but also accept the strict test of case 3 and case 2.
Inspection instructions:
2k=pi++pj+ has 4 sources; fully unified with complex mathematical examples.
2k=ps++hr+ has 4 sources; fully unified with complex mathematical examples.
2k=ht++hu+ has 4 sources; fully unified with complex mathematical examples.
2k=hk++pd+ has 4 sources; fully unified with complex mathematical examples.
The test shows that Hou Shaosheng's theorem is correct, the inference of Hou Shaosheng's theorem is correct, and the theory of four sources is correct. Readers are welcome to test with other examples.
Above, we have made all kinds of theoretical preparations for proving Goldbach's conjecture, but only the above theoretical preparations are not enough, we must also study the classification of odd prime numbers, we must also study the relationship between all odd composite numbers and the number of odd prime numbers in the interval [3,n]. It is also necessary to study the relationship between all the odd composite numbers and the number of odd primes in the interval [n, 2n-3].
Professor Liang Yixing, who was the dean of the School of Mathematics at Xiamen University before he retired, and Professor Zhu Huilin, once asked the question. They, along with Ma Linjun, a professor at Sun Yat-sen University, and Zeng Hongbiao, who graduated from Wuhan University with a master's degree in mathematics and is a professor in the United States,
raised similar questions in the first draft of their paper, forcing Hou to dig deeper. After six years and hundreds of revisions, the present proof was finally formed.
I sincerely thank Professors Ma Linjun, Zeng Hongbiao, Liang Yixing and others for their questions and important contributions. My sincere thanks to Dr. Liu Xiaoqian and Li Canzhang, who graduated from the Chinese Academy of Mathematics, for their 6-7 years of repeated review.
Let's first define three new concepts about odd prime numbers.
5.9 Odd prime after odd composite number, odd prime after odd prime number, independent odd prime number.
Definition 1: Let h be an odd composite number, if h+2 is an odd prime p, that is, if h+2=p, this paper calls this kind of odd primes p are odd primes after odd composite numbers,or prime numbers after odd composite numbers.
Definition 2: Let pi be an odd prime, if pi+2 is an odd prime p, that is, if pi+2=p, this paper calls this kind of odd primes p are odd primes after odd primes, or prime numbers after odd primes.
Definition 3: Let p be an odd prime number, and if p-2, p+2, are both odd composite numbers, then the odd prime p is called an independent odd prime number, or independent prime number. The independent prime must be the prime after the odd composite number.
According to the above definition, all odd prime numbers greater than 3 can be divided into twokind:
The first kind, An odd prime after an odd composite number.
For example, 9+2=11,15 +2= 17,21 +2=23, 27+2=29. 11,17, 23, 29, that's the prime after the odd composite number.
The secondkind,anodd prime numbers afteranodd prime numbers.
For example, 3+2=5, 5+2= 7, 11+2= 13, 17+2=19. 5, 7, 13, 19, that's the prime after the odd prime.
In fact, if pi+2=pi+1, usually piand pi+1are called sister primes.
If pi is the ith odd prime number, pi+1 is the (i+1)th odd prime number, And pi+2=pi+1, then pi+1 is an odd prime after an odd prime.
3 is an odd prime number, but it is neither an odd prime after an odd composite number nor an odd prime after an odd prime. 3 is the first odd prime number.
5.10 3,5,7 is the only three sister prime number.
Theorem 15: 3,5,7 is the only 3 sister primes, and there can be no other 3 odd primes that are 3 sister primes.
Proof 3,5,7, is the only 3 sister primes, that is,there can be no three odd primes other than 3,5,7 that are 3 sister primes.
The proof for this conclusion is as follows:
Suppose pi, pi+2, pi+4, are three sister primes, 3 < pi .
Because pi is an odd prime number, so pi =3m+1; Or pi=3m+2.
If pi=3m+1, then pi+2=3m+3=3(m+1), which contradicts that pi+2 is an odd prime.
If pi=3m+2, then pi+4=3m+6=3(m+2), which contradicts that pi+4 is an odd prime.
Theorem 15, complete proof.
5.11 [3, n] The number of odd primes after odd composite numbers in the interval.
The number of odd primes after odd composite numbers in the interval [n, 2n-3].
Theorem 16A: (ht+2) and (hk+2), contain all the odd primes p after odd composite numbers in the interval [3, n]. After 11≤n, in the interval [3, n], there is at least one odd prime p are odd primes after odd composite numbers. After 50≤n, in the interval [3, n], 50% or more of the number of odd primes p are odd primes after odd composite numbers.
Theorem 16B: (hu+2) and (hr+2) contains all the odd primes p after odd composite numbers in the interval [n, 2n-3]. In the interval [n,2n-3], 50% or more of the number of odd primes p are odd primes after odd composite numbers.
Note: ht, hk, hu and hr here are ht, hk, hu and hr in Hou Shaosheng's theorem.
Theorem 16C: Of (ht+2) and (hk+2), at least one is an odd prime.
Of (hu+2) and (hr+2), at least one is an odd prime.
Theorem 16D: Let h be an odd composite number in the interval [n, 2n-3], and if h+2 is an odd prime and 2n-1 is an odd composite number, then there must be odd primes (h+2) in the interval [n, 2n-3].
ProofWe first quote the inference of Hou Shaosheng's theorem (theorem 4) as follows:
About the formula:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
always have:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Among them, the convention is: 3≤q≤n, q is odd. n≤2n-q≤2n-3;
pi, pj, ps, pd are all odd prime numbers; ht, hu, hr, hk are all odd composite numbers.
And: pi≤pj, ht≤hu, ps≤hr, hk≤pd.
pi, ht, ps, hk, ∈[3,n]; pj, hu, hr, pd∈[n,2n-3].
Please note that: (4.0.1), (4.0.2), (4.0.3), (4.0.4), are directly derived from Hou Shao-sheng's theorem, so the expression of these 4 equations will always be the same, regardless of whether num (2n=pi+pj) =0. It has nothing to do with whether the conjecture is true. In other words, even if the num(2n=pi+pj)=0, (4.0.1), (4.0.2), (4.0.3), (4.0.4), still is established.
According to (4.0.2),ht, hk are all the odd composite numbers h in the interval [3, n];
According to (4.0.4), hu, hr, are all the odd composite numbers h in the interval [n, 2n-3].
Since 3(2m+1) is an odd composite number, and (m is a positive integer), it follows that the odd composite number h in the interval [3,n] and [n,2n-3] is abundant. Because ht, hk is all the odd composite numbers h in the interval [3,n]; hu, hr, is all the odd composite numbers h in the interval [n,2n-3], so ht, hk, hu, hr, is rich, and it follows that (ht+2), (hk+2), (hu+2), (hr+2) is rich.
Theorem 16A is as follows.
Theorem 16A: (ht+2) and (hk+2), contain all the odd primes p after odd composite numbers in the interval [3, n]. After 11≤n, in the interval [3, n], there is at least one odd prime p are odd primes after odd composite numbers. After 50≤n, in the interval [3, n], 50% or more of the number of odd primes p are odd primes after odd composite numbers.
Theorem 16A is proved as follows:
From the concept can be known:
If h is all the odd composite numbers in the interval [3, n], then h+2 contains all the odd prime numbers p after the odd composite numbers in the interval [3, n].
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
(4.0.2) The mathematical meaning of the formula is:
The only odd composite numbers in the interval [3, n] are: ht, hk; And the number of odd composite h in the interval [3, n] is equal to the number of ht + the number of hk.
That is,ht,hk, is all the odd composite numbers h in the interval [3, n].
Therefore, (ht+2) and (hk+2) contain all the odd primes p after odd composite numbers in the interval [3, n].
This proves the statement of theorem 16A:
(ht+2) and (hk+2), contain all the odd primes p after odd composite numbers in the interval [3, n].
The following must be proved:
In the interval [3,n], 50% or more of the number of odd primes p are odd primes after odd composite numbers, 50≤n.
The proof is as follows:
The interval [3, n] is divided into two intervals [3, 50] and
[50, n].
A: There are a total of 14 odd prime numbers in the interval [3, 50]. As follows:
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Among them, odd prime number after odd composite number, there are a total of 7. As follows:
11,17,23,29,37, 41,47.
The actual inspection shows that 50% of the number of odd primes p in the interval [3, 50] are odd primes after odd composite numbers.
B: In the interval [50, n], there are no 3 sister primes. So, any odd prime number is either one of the two sister primes or an independent odd prime number.
Because, of the 2 sister odd primes (pi, pi+2), (pi+2 is an odd prime), there must be a pi, and only one pi is an odd prime after the odd composite number;
Any independent odd prime number p is an odd prime after an odd composite number.
Therefore, in the interval [50, n], 50% or more of the number of odd primes p are odd primes after odd composite numbers, 50<n.
By synthesizing the above A and B, we can see that in the interval [3, n], 50% or more of the number of odd prime numbers p is the odd prime number after the odd composite number, 50<n.
This proves that:
After 50≤n, in the interval [3, n], 50% or more of the number of odd primes p are odd primes after odd composite numbers.
Since 11 is an odd prime after an odd composite number, after 11≤n, there is at least one odd prime after an odd composite number in the interval [3, n].
At this point, the contents of theorem 16A are proved.
Theorem 16B is as follows:
(hu+2)and (hr+2), contain all the odd primes p after odd composite numbers in the interval [n, 2n-3]. In the interval [n, 2n-3], 50% or more of the number of odd primes p are odd primes after odd composite numbers, 10≤n.
Note: ht, hk, hu and hr here are ht, hk, hu and hr in Hou Shaosheng's theorem.
Theorem 16B is proved as follows:
First quote (4.0.4) as follows:
num(n≤h≤2n-3)=num (2n=ht+hu) +num (2n=ps+hr). (4.0.4)
The mathematical meaning of (4.0.4) is:
The only odd composite numbers in the interval [n, 2n-3] are: hu and hr; And the number of odd composite h in the interval [n, 2n-3] is equal to the number of hu + the number of hr.
That is, hu, hr, is all the odd composite numbers h in the interval [n, 2n-3].
Let all odd composite numbers in the interval [n, 2n-3] be h, then h+2 contains all odd primes after odd composite numbers in the interval [n, 2n-3].
Therefore, (hu+2) and (hr+2) contain all the odd primes p after the odd composite numbers in the interval [n, 2n-3].
This proves a statement in theorem 16B:
(hu+2) and (hr+2), contain all the odd primes p after odd composite numbers in the interval [n, 2n-3].
Let's prove another sentence from theorem 16B:
In the interval [n, 2n-3], 50% or more of the number of odd primes p are odd primes after odd composite numbers, 10≤n.
All odd numbers q in the interval [n, 2n-3] are either odd prime numbers p or odd composite numbers h. In 2.1.2, theorem 2 has been proved:
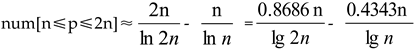
If n=10 is substituted into this formula, num[10≤p≤20] > 2 is obtained.
The actual test shows that num[10≤p≤20]=4, because 11,13,17, 19, ∈[10,20].
We have shown that num[n≤p≤2n] is an increasing function of n, n→∞. The calculation can prove that as long as 10≤n, there is
num[n≤p≤2n] > 2. This shows that after 10≤n, there are at least three odd prime numbers in the interval [n, 2n].
Since 3,5,7 is the only 3-sister odd prime number, there can be no 3-sister odd prime numbers in the interval [n, 2n], 3 < n. Therefore, when we talk about sister odd prime numbers below, we refer to 2 sister odd prime numbers unless otherwise specified.
Let 10<n, considering that n=pi,pi+2=pi+1, there are possible special cases, in the interval [n, 2n-3], as long as the number of odd primes is not less than 3, the odd prime p after the odd composite number must exist. This is because if n=pi, n+2=pi+2=pi+1, then pi, pi+1, is already a 2 sister prime, since there is no 3-sister prime, then the third odd prime pi+2, must be an odd prime after an odd composite number. That is, between pi+1 and pi+2 , there is at least one odd composite number h.
Since there are no 3-sister primes in the interval [n, 2n-3] after 10<n, there are either 2 sister primes or no 2 sister primes in the interval [n, 2n-3]. This shows that for every two prime numbers arranged from smallest to largest, at least one is an odd prime after an odd composite number.
This means that 50% or more of the number of odd primes p in the interval [n, 2n-3] are odd primes after odd composite numbers, 10≤n.
This proves another statement in theorem 16B:
In the interval [n, 2n-3], 50% or more of the number of odd primes p are odd primes after odd composite numbers, 10≤n.
At this point, the contents of theorem 16B are proved.
Let's prove theorem 16C.
Theorem 16C is as follows:
At least one of the (ht+2) and (hk+2) is an odd prime.
In both (hu+2) and (hr+2), at least one is an odd prime.
Theorem 16C is proved as follows.
Theorem 16A states that: (ht+2) and (hk+2) contain all the odd primes p after odd composite numbers in the interval [3, n].
Since 11 is an odd prime after an odd composite number, so long as 11≤n, then the odd prime p after odd composite number in the interval [3,n] must exist. These odd prime numbers p after odd composite numbers are all formed by odd composite numbers h+2.
Since (ht+2) and (hk+2) contain all the odd primes p after the odd composite numbers in the interval [3, n], at least one of (ht+2) and (hk+2) is an odd prime.
At least one of the (ht+2) and (hk+2) is an odd prime. Proof complete.
The following proof:
In both (hu+2) and (hr+2), at least one is an odd prime.
The proof is as follows.
Theorem 16B states that: (hu+2) and (hr+2) contain all the odd primes p after odd composite numbers in the interval [n, 2n-3]. In the interval [n, 2n-3], 50% or more of the number of odd primes p are odd primes after odd composite numbers.
Since (hu+2) and (hr+2) contain all the odd primes p after the odd composite numbers in the interval [n, 2n-3], at least one of (hu+2) and (hr+2) is an odd prime number.
In both (hu+2) and (hr+2), at least one is an odd prime. Proof complete.
Theorem 16C, complete proof.
Let's prove theorem 16D.
Theorem 16D, as follows.
Let h be an odd composite number in the interval [n, 2n-3], and if h+2 is an odd prime and 2n-1 is an odd composite number, then there must be an odd prime h+2 in the interval [n, 2n-3].
Theorem 16D is proved as follows:
Since h is an odd composite number in the interval [n, 2n-3], h≤2n-3, and therefore h+2≤2n-1. Since 2n-1 is assumed to be odd composite number, if h+2 is odd prime, must be h+2 < 2n-1. Since 2n-2 is even, there must be h+2≤2n-3. That is, if h+2 is an odd prime, then the odd prime h+2≤2n-3 . It's the odd prime h+2 in the interval [n, 2n-3].
Theorem 16D, complete proof.
Theorem 16 will play an important role in the proof of Goldbach's conjecture.
Finally, we emphasize that theorem 16 is a fundamental theorem. This theorem uncovers the transition from the odd composite number h to the odd prime h+2 after the odd composite number.
Theorem 16, finished proving.
5.12 Theorem 17: If the conjecture is true at 2n and k (=n+1)
is composite number, then at least one of (pi+2), (hr+2) is an
odd prime, which guarantees that the conjecture is true at 2k.
Proof:To prove theorem 17, first quote the theorem that will be used, and then prove theorem 17.
(1) Quote theorem 11 as follows:
Theorem 11: If the 2n conjecture is true, then 2k=pi++pj+ has the following 4 sources, as long as one of the sources exists, it will ensure that the conjecture continues to be true at 2k.
The 4 sources of 2k=pi++pj+are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+;
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
If the Goldbach conjecture holds for 2n, 2k=pi++pj+ has 4 sources, so long as one source exists, the conjecture will continue to hold for 2k. So, to prove the conjecture, you just need to prove the existence of a source.
Conversely, if the Goldbach conjecture is true at 2n, and if it is not true at 2k, then none of the 4 sources of 2k=pi++pj+ can exist.
As a proof by contradiction, if the conjecture is not valid when 2k is assumed, it is assumed that: 2k=pi++pj+ 4 sources, none of which exist; As long as the contradiction can be found according to rigorous mathematical reasoning, it is proved that 2k=pi++pj+ 4 sources, at least one of the existence. That proves the 2k conjecture. That's the mathematical idea behind proving Theorem 17.
(2) The inference of Hou Shaosheng's theorem is quoted as follows:
About the formula:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+ num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
There is always:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=gsh(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Among them, the convention is: 3≤q≤n, q is odd.
pi, pj, ps, pd are all odd prime numbers; ht, hu, hr, hk are all odd composite numbers.
And: pi≤pj, ht≤hu, ps≤hr, hk≤pd.
pi, ht, ps, hk, ∈[3,n]; pj, hu, hr, pd∈[n,2n-3].
Under our theoretical system, if the conjecture is true for 2n, it is accepted that the above (4.0.1), (4.0.2), (4.0.3), (4.0.4) are also true. Therefore, the simultaneous holding of (4.0.1), (4.0.2), (4.0.3), (4.0.4) is also the theoretical basis for our proof of theorem 17, in particular the admission that: 1≤num(2n=pi+pj).
(3)If the conjecture is true for 2n and k (=n+1) is composite number, then at least one of (pi+2), (hr+2) is an odd prime, which guarantees that the conjecture must be true for 2k.
The proof is as follows.
Because 2k=k+k, if k is an odd prime number, 2k is already the sum of two odd prime numbers, and the guess is natural stand.
So, as long as it can be shown that k is composite number, the 2k conjecture must be true, then Goldbach's guess If you want it, it will be true.
Therefore, in the following proof, it is not distinguished whether k is an even composite number or an odd composite number. Just assume k
It's composite number.
Specific proof is as follows:
The reference (4.0.1) is as follows.
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr) (4.0.1)
If the conjecture is true for 2n, it is accepted that (4.0.1) is true, where: 1≤num(2n=pi+pj).
(4.0.1), is the object of our study below.
Since k (=n+1) is composite number, it is obtained by (4.0.1) :
num(3≤p≤k)
=num(3≤p≤n)
=num(2n=pi+pj)+num(2n=ps+hr) (4.0.1)
=num(2n+2=pi+2+pj)+num(2n+2=ps+hr+2)
=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
that's it:
num(3≤p≤k)=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
From (4.0.1) to (5.12.1), each step of the derivation process is based on mathematical definitions, or mathematical axioms, or mathematical theorems. So (5.12.1) must be true.
We know from (5.12.1) that as long as one of (pi+2) is an odd prime, there must be at least one 2k=(pi+2)+pj, and 2k is the sum of two odd prime numbers (pi+2), pj, to ensure that the conjecture must be true at 2k.
If none (pi+2) is an odd prime, then every (pi+2) is an odd composite number.
It is also known from (5.12.1) that as long as one of (hr+2) is an odd prime, there must be at least one 2k= ps+(hr+2), and 2k is the sum of two odd prime numbers ps, (hr+2), which guarantees that the conjecture must be true at 2k.
If none (hr+2) is an odd prime, then every (hr+2) is an odd composite number.
Therefore, whether at least one of (pi+2) is an odd prime number is one of the keys to proving Goldbach's conjecture.
Similarly, whether at least one of (hr+2) is an odd prime is another key to proving Goldbach's conjecture.
A sufficient condition for at least one of (pi+2) to be an odd prime is that at least one in pi is the lesser of the sister primes.
Note: If pi is the smaller of the sister primes, there must be (pi+2) that is odd primes.
Depending on whether at least one pi in (2n=pi+pj) is the smaller of the sister primes, pi can be divided into 2 classes.
first kind: In pi, at least one pi is the smaller of the sister primes. So at least one (pi+2) is an odd prime, which guarantees that the conjecture is true at 2k.
For this category, there is no need to write a written argument.
second kind: In pi, none of the pi is the lesser of the sister primes, so none (pi+2) is an odd prime; So every(pi+2)is an odd composite number.
For the second kind of pi, we must prove that at least one of (hr+2) is an odd prime. So there is at least one 2k=ps+(hr+2), where 2k is the sum of two odd prime numbers ps, (hr+2), which guarantees that the conjecture is true at 2k.
It can be obtained from (5.12.1) :
num(3≤p≤k)-num(2k=ps+(hr+2))=num(2k=(pi+2)+pj) (5.12.2)
By (5.12.1) must be true, we can see that (5.12.2) must be true.
That is to say, both sides of the equal sign must have the same number and the same name.
However, if (pi+2) is not an odd prime, then (5.12.2) must not be true. This proof uses the mathematical implication that if (pi+2) is not an odd prime, (5.12.2) must not be true to prove theorem 17. The concrete proof is as follows.
In (5.12.2), according to our convention, ps≤(hr+2), (pi+2)≤pj, so ps, (pi+2), are within the interval [3, k].
(hr+2), pj, both in the range [k, 2k-3]. pi, pj, ps are odd prime numbers.
(pi+2),(hr+2),whether it is an odd prime number or an odd composite number, is what needs to be discussed below.
The following, through the way of debating questions and answers, proves that 2k, Goldbach conjecture must be true.
Question 1: Is at least one (hr+2) an odd prime?
If at least one (hr+2) is an odd prime, then the Goldbach conjecture holds for 2k.
This is because 2k=ps+(hr+2), with at least one 2k, is already the sum of an odd prime ps and an odd prime (hr+2). So at 2k, Goldbach's conjecture is established.
If there is not at least one (hr+2) that is an odd prime,that is, every (hr+2) is an odd composite number.
Next, we continue our argumentative question and answer under the assumption that each (hr+2) is an odd composite number.
Question 2: Under the assumption that every (hr+2) is an odd composite number, is at least one (pi+2) an odd prime number?
If at least one (pi+2) is an odd prime, then the Goldbach conjecture holds for 2k.
This is because 2k=(pi+2)+pj, with at least one 2k, is already the sum of an odd prime (pi+2) and the odd prime pj. So at 2k, Goldbach's conjecture is established.
If there is not at least one (pi+2) that is an odd prime,So every (pi+2) is an odd composite number.
From problem 1 and problem 2, we can see that the conditions for the following discussion are: every (pi+2), every (hr+2) is an odd composite number.
Next, we continue our argumentative question and answer under the assumption that each (pi+2) and each (hr+2) are odd composite numbers.
Each (pi+2) is an odd composite number, that is, the smaller of the sister primes that do not exist in pi.
Question 3: Under the assumption that every (pi+2) and every (hr+2) are odd composite numbers, does (5.12.2) still hold?
(5.12.2), is a mathematical equation, both sides of the equal sign, must have the same number, the name of the thing must be the same.
num(3≤p≤k)-num(2k=ps+(hr+2))=num(2k=(pi+2)+pj) (5.12.2)
From the derivation process of 5.12.2), we can know that (5.12.2) must be established and (5.12.2) should be established.
However, under the assumption that every (pi+2), every (hr+2), is an odd composite number, (5.12.2) cannot be held. This means the hypothesis is not valid! (pi+2), (hr+2), at least one of them is an odd prime number! So theorem 17 is true. That's the logic below.
If one (pi+2) is an odd prime, or one (hr+2) is an odd prime, then Goldbach's conjecture is established.
To prevent us from proving the conjecture, we must assume that every (pi+2) is odd composite number and every (hr+2) is odd composite number.
Next, we proceed with the inference under the assumption that each (hr+2) and each (pi+2) are odd composite numbers.We shall show that the assumptions here contradict the results obtained by further inference. This is proof by contradiction.
Now analyze (5.12.2) as follows.
On the left side of the equal sign, num(3≤p≤k) is the number of all the odd prime numbers p in the interval [3, k].
Every ps is an odd prime, so it's known. There is no doubt.
Each (hr+2), according to the above assumptions, is an odd composite number.
So every 2k=ps+(hr+2), every 2k is the sum of an odd prime ps and an odd composite number (hr+2).
Since ps is a partial odd prime in the interval [3, k], num (2k=ps+(hr+2)) is the number of partial odd prime ps in the interval [3, k]. It is also the number of odd composite numbers (hr+2) in the interval [k, 2k-3].
So, num(3≤p≤k)-num (2k=ps+(hr+2)) is the number of all odd primes p in the interval [3, k], minus the number of partial odd primes ps in the interval [3, k].
Therefore,num(3≤p≤k)-num (2k=ps+(hr+2)) is the number of partial odd prime numbers p in the interval [3, k].
(5.12.2), is a mathematical equation. On the right side of the equals sign, num(2k=(pi+2)+pj), must also be the number of partial odd prime p in the interval [3, k]. This is a necessary condition for the establishment of (5.12.2).
num(2k=(pi+2)+pj), must also be the number of partial odd prime numbers p in the interval [3, k]; It follows that every (pi+2) must be an odd prime p in the interval [3, k].However, this contradicts the previous: it must be assumed that every (pi+2) is odd composite number and every (hr+2) is odd composite number.
The proof of theorem 17 is now completely complete. However, for the reader to see more, the inferences continue.
If one of (pi+2) is not an odd prime p in the interval [3, k],
num(2k=(pi+2)+pj) cannot be the number of partial odd prime p in the interval [3, k].
num(2k=(pi+2)+pj)represents the number of(2k=(pi+2)+pj)according to the definition (1.2 Meaning of mathematical symbols in the paper).
The number of (2k=(pi+2)+pj) is the number of (pi+2) in the interval [3, k], which is also the number of pj in the interval [k, 2k-3].
Since every (pi+2) must be an odd prime p in the interval [3, k], the conjecture holds for 2k. As a proof of the conjecture, this is quite the end of it.
Above, we have proved that at 2k, Goldbach's conjecture holds.
Our main logical procedure for proving the conjecture is: In order to prevent proving Goldbach's conjecture, we must assume that every
(pi+2), every (hr+2), is an odd composite number; Under this assumption, num (2k=(pi+2)+pj) must be the number of odd composite numbers (pi+2) in the interval [3, k]. However, this contradicts the necessary condition for (5.12.2) to hold: num (2k=(pi+2)+pj) must be the number of odd primes p in the interval [3, k], so (pi+2) must be odd primes! Therefore, the assumption that every (pi+2), every (hr+2), is an odd composite number cannot be held. So at least one of (pi+2), (hr+2), is an odd prime. This is the main logical process for proving theorem 17. This proof, in fact, is proof by contradiction.
The proof of theorem 17 ends here.
(3) The role of sister primes in the proof of Goldbach's conjecture.
Some readers may ask: The key step in your proof is to assume that every (pi+2) is an odd composite number, and every (hr+2) is an odd composite number, which follows: num (2k=(pi+2)+pj) is the number of odd composite numbers (pi+2) in the interval [3, k].This contradicts the fact that num (2k=(pi+2)+pj) must be the number of odd prime numbers p in the interval [3, k].
Asking 1: If you don't assume that every pi+2 is an odd composite number, does theorem 17 still hold?
Answer: True.If we do not assume that every (pi+2) is an odd composite number, that is, at least one of (pi+2) is an odd prime, which is consistent with theorem 17, then at least one of (pi+2), (hr+2), is an odd prime number.
A sufficient condition for each (pi+2) to be odd composite number is that pi is either the largest of the (3,5,7) sister primes, or the larger of the other sister primes, or an independent odd prime. If every (pi+2) is an odd composite number, then at least one of (hr+2) is an odd prime number, as theorem 17 states.
A sufficient condition for (pi+2) to be an odd prime is that pi is the lesser of the (3,5,7) sister primes 3, or 5, or the lesser of the other sister primes.
As long as one (pi+2) is an odd prime, 2k=(pi+2)+pj, 2k is already the sum of two odd prime numbers, and Goldbach's conjecture is guaranteed.
Above is the role of sister primes in the proof of Goldbach's conjecture.
Below, we first demonstrate with example 8 that every (pi+2) is an example of an odd composite number and does exist.The main proof procedure of theorem 17 above is verified with example 8.
Since instance 8, each of which (pi+2) is a odd composite number, has certain particularity, and then use instance 3 to verify the main proof process of theorem 17 above. Example 3 is the example 3 used many times in the paper.
(4) Each of these (pi+2) is an example of an odd composite number that does exist.
Some readers wonder if there are actual examples: every one of them (pi+2) is an odd composite number.
Answer: Each of these (pi+2) is an example of an odd composite number that does exist.
Take a look at example 8 below.
Example 8. 2×19=38
=1+37=3+35=5+33=7+31=9+29=11+27=13+25=15+23=17+21=19+19.
In this example:
num(2×19=q+(2n-q))=9. num(19≤p≤2×19-3)=4.
num(19≤h≤2×19-3)=5.
num(2n=pi+pj)=2. num(2n=ht+hu)=0. num(2n=ps+hr)=5.
num(2n=hk+pd)=2. num(3≤p≤35)=10. num(3≤h≤35)=7.
num(3≤p≤19)=7. num(3≤h≤19)=2.
The above data fully satisfy the following formula:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+ num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Note that num(2n=ht+hu)=0. It indicates that 2n is small. When 2n is slightly larger, num(2n=pi+pj), num(2n=ht+hu), num(2n=ps+hr), and
num(2n=hk+pd) should all be no less than 1.
num(3≤p≤19)=7 > num(3≤h≤19)=2. That also means that 2n is small. When 2n is larger, the value should be: num(3≤p≤n)≤num(3≤h≤n).
num(3≤p≤n)≤num(3≤h≤n) indicates that the number of odd primes in the interval [3,n] is not greater than the number of odd composite numbers.
look again
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr) (4.0.1)
num(3≤p≤19)=7. The seven odd prime numbers are: 3, 5, 7, 11, 13, 17, 19.
num(2×19=pi+pj)=2. The 2 number of(2×19=pi+pj) are:
2×19=7+31, 2×19=19+19.
num(2n=ps+hr)=5. The 5 number of (2×19=ps+hr)are as follows:
2×19=3+35; 2×19=5+33; 2×19=11+27; 2×19=13+25; 2×19=17+21.
The above data are in full agreement with the formula (4.0.1). The test is as follows:
Num(2n=pi+pj)+num(2n=ps+hr)
=2+5
=7=num(3≤p≤19).
The test shows that the above data are in full agreement with the formula (4.0.1).
Of particular note: num(2×19=pi+pj)=2. These two number of
(2×19=pi+pj) are:
2×19=7+31; 2×19=19+19.
This means that the two of pi in(2×19=pi+pj)are 7 and 19.
7 is the largest prime of the sister primes (3,5,7).
19 is the larger prime of the sister primes (17,19).That is, in the pi of instance 8, there is no smaller of the sister
primes.
We notice that in the pi of example 8, there is no smaller of the sister primes because num(2×19=pi+pj)=2. In other words, it's because n=19 is relatively small.
Look again:
7+2=9. 9 is an odd composite number.
19+2=21. 21 is an odd composite number.
That is, in example 8, every (pi+2) is an odd composite number, not an odd prime number.
Example 8 tells us that there are instances where each (pi+2) is an odd composite number. This shows that it is impossible to prove Goldbach's conjecture by proving that at least one of (pi+2) is an odd prime number.
Example 8 tells us that every pi in (2n=pi+pj) is the greater of the sister primes, or the largest of (3,5,7), and therefore every (pi+2) is an odd composite number, and such practical examples exist. So the smaller of the sister primes, all in ps of (2n=ps+hr), there are practical examples of this.
In Example 8, num(2n=ps+hr)=5. The five number of (2n=ps+hr) are as follows:
2×19=3+35; 2×19=5+33; 2×19=11+27; 2×19=13+25; 2×19=17+21.
The five of ps are as follows:
3; 5; 11; 13; 17.
3,5, is the smaller of the (3, 5, 7) sister primes.
11 is the smaller of the (11, 13) sister primes.
17, is the smaller of the (17, 19) sister primes.
In the interval [3, n], which in this case is the interval [3, 19], all the odd primes are as follows:
3, 5, 7, 11, 13, 17, 19.
The smaller of the sister primes are: 3, 5, 11, 17. They're all in ps. 13 is the greater of the (11, 13) sister primes. However, this cannot be denied: the smaller of the sister primes are all in ps.
Example 8 tells you and me that it is never possible to prove Goldbach's conjecture by proving that at least one of (pi+2) is an odd prime.
Since it is impossible to prove that at least one of (pi+2) is an odd prime, we prove theorem 17 that at least one of (pi+2) and (hr+2) is an odd prime! This completes the proof of Goldbach's conjecture.
(6) Verify theorem 17 and its main proof process with example 8.
(6.1) Verify theorem 17 with example 8.
Theorem 17: If the conjecture is true at 2n and k (=n+1) is compositenumber, then at least one of (pi+2), (hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Example 8 is as follows:
Example 8. 2×19=38
=1+37=3+35=5+33=7+31=9+29=11+27=13+25=15+23=17+21=19+19.
In Example 8: num(2×19=pi+pj)=2. The two number of (2×19=pi+pj) are: 2×19=7+31;2×19=19+19.
This means that the two of pi in(2×19=pi+pj)are 7 and 19.
7 is the largest of the sister primes (3,5,7); 19 is the greater of
the sister prime numbers (17,19).
7+2=9. 9 is an odd composite number.
19+2=21, 21 is an odd composite number.
That is, in example 8, each pi in(2n=pi+pj)is either the largest of the sister primes, Or 7, the largest of the sister primes (3,5.7). Or, in pi, there is no smaller of the sister primes. So every pi+2 is an odd composite number.
Since every (pi+2) is an odd composite number, theorem 17 tells us that at least one of (hr+2) is an odd prime number, which guarantees that the conjecture holds for 2k.
Whether this is actually the case, the test is as follows:
In Example 8, num(2n=ps+hr)=5. The five number of(2n=ps+hr)are as
follows:
2×19=3+35; 2×19=5+33; 2×19=11+27; 2×19=13+25; 2×19=17+21.
The five number of ps are as follows:
3; 5; 11; 13; 17.
The five number of hr are as follows:
35; 33; 27; 25; 21.
Each hr+2 is as follows:
35+2=37; 33+2=35; 27+2=29; 25+2=27; 21+2=23.
hr+2, is an odd prime number, as follows:
35+2=37; 27+2=29; 21+2=23.
Since every (pi+2) is an odd composite number, according to theorem 17, at least one of (hr+2) is an odd prime number, which guarantees that the conjecture is true at 2k.
In example 8, three number of (hr+2) are odd prime numbers: 35+2=37; 27+2=29; 21+2=23.
The result of verifying theorem 17 with example 8 shows that the actual situation of example 8 is completely consistent with theorem 17.
(6.2) Verify the main proof process of theorem 17 with example 8.
(5.12.2), is a mathematical equation, both sides of the equal sign, should have the same quantity, the same name of things.
num(3≤p≤k)-num(2k=ps+(hr+2))=num(2k=(pi+2)+pj) (5.12.2)
Obviously,num(3≤p≤k)-num(2k=ps+(hr+2)), on the left side of the equals sign, is the number of partial odd prime p in the interval [3, k], without any doubt.
(5.12.2), is a mathematical equation where num(2k=(pi+2)+pj), on the right side of the equal sign, must also be the number of partial odd primes p in the interval [3, k]. This is a necessary condition for the establishment of (5.12.2).
Since num(2k=(pi+2)+pj)must also be the number of partial odd prime numbers p in the interval [3, k], every (pi+2) must be an odd prime number p in the interval [3, k]; Otherwise, num(2k=(pi+2)+pj) cannot be the number of partial odd prime p in the interval [3, k]. Since each (pi+2) is an odd prime p in the interval [3, k], the conjecture is established at 2k. Thus, (5.12.2), the necessary condition for the establishment is: 2k, the conjecture is established.
If one of (pi+2) is an odd prime, or one of (hr+2) is an odd prime, then Goldbach's conjecture is established.
To prevent us from proving the conjecture, we must assume that every (pi+2) is odd compositenumberand every (hr+2) is odd compositenumber.
In Example 8, num(2×19=pi+pj)=2. The two number of (2×19=pi+pj)are:
2×19=7+31;2×19=19+19.
Since num(2×19=pi+pj)=2. There are 2 number of (pi+2).
These 2 number of (pi+2) are: (7+2), (19+2).
(7+2)=9. 9 is an odd composite number.
(19+2)=21, 21 is an odd composite number.
Because instance 8 only has these 2 number of (pi+2), which are (7+2)= 9,9 is odd composite number; (19+2)=21, 21 is an odd composite number. So every (pi+2) is an odd composite number. So num(2k=(pi+2)+pj), is the number of odd composite numbers (pi+2) in the interval [3, k]; Contradicts
num(2k=(pi+2)+pj), which must be the number of odd prime p in the interval [3, k]. This contradiction illustrates: the assumption that every (pi+2) is odd composite number and every (hr+2) is odd composite number is not true. That is, (pi+2), (hr+2), at least one of them is an odd prime.
The above verification results are in complete agreement with the proof process of theorem 17.
Verify theorem 17 with example 8, and this is the end.
(7) Verify theorem 17 and its main proof process with example 3.
(7.1) Verify theorem 17 with example 3.
Since in instance 8, each (pi+2) is an odd composite number and has particularity, we will use example 3 to verify theorem 17.
Example 3. 2×51=102
=1+101=3+99=5+97=7+95=9+93=11+91=13+89=15+87=17+85=19+83=21+81
=23+79=25+77=27+75=29+73=31+71=33+69=35+67=37+65=39+63=41+61
=43+59=45+57=47+55=49+53=51+51.
Theorem 17: If the conjecture is true at 2n and k (=n+1) is compositenumber, then at least one of (pi+2), (hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
In Example 3, num(2×51=pi+pj) =8.
These 8 number of 2×51=pi+pj, as follows:
2n=5+97; 2n=13+89; 2n=19+83; 2n=23+79; 2n=29+73;
2n=31+71; 2n=41+61; 2n=43+59;
Among, 8 number of pi are as follows:
5, 13, 19, 23, 29, 31, 41, 43.
In the 8 number of pi above, pi+2, are odd prime numbers as follows:
5+2=7; 29+2=31; 41+2= 43.
So, 2k=2(n+1)=(pi+2)+pj, 2k is the sum of two odd prime numbers, as
follows:
2k=(5+2)+97; 2k=(29+2)+73; 2k=(41+2)+61.Any one of the above three 2k is sufficient to guarantee the Goldbach
conjecture for 2k=2 (n+1)!
The above fact shows that in 2n=pi+pj, as long as there is a pi+2, which is an odd prime number, then 2k=2(n+1), Goldbach's conjecture must be true.
In 2n=pi+pj, a sufficient condition for one of pi+2 to be an odd prime is that one of pi is the smaller of the sister primes.
Similarly, in 2n=pi+pj, as long as there is a pj+2, which is an odd prime number, then 2k=2(n+1), Goldbach's conjecture must be true.
In 2n=pi+pj, pi is either the smaller of the sister primes, or it is not; pi must be one of them.
pi is not the smaller of the sister primes, and there are only two possibilities: pi is the larger (or largest) of the sister primes, or it is an independent odd prime. In both cases, pi+2 is not an odd prime, it's an odd composite number.
In Example 3 :num(2n=ps+hr) =6.
These 6 number of 2n=ps+hr are as follows:
2n=3+99; 2n=7+95; 2n=11+91; 2n=17+85; 2n=37+65;
2n=47+55;
Among them, 6 number of hr, as follows:
99;95;91; 85;65;55.
In the 6 number of hr above, hr+2, are odd prime numbers as follows:
99+2=101; 95+2=97; 65+2=67.
So, 2k=2(n+1)=ps+(hr+2), 2k is the sum of two odd prime numbers, as follows:
2k=3+(99+2); 2k=7+(95+2); 2k=37+(65+2).
Any one of the above three 2k is sufficient to guarantee the Goldbach conjecture for 2k=2 (n+1)!
We see that in example 3, pi has the smaller of the sister primes; There are also the larger of the sister primes. This is completely different from example 8.
Example 3: In pi, at least oneofpiis the smaller prime of the sister primes, so at least oneof(pi+2) is an odd prime. So there is at least one 2k=(pi+2)+pj, where 2k is the sum of two odd primes (pi+2), pj, which guarantees that the conjecture holds for 2k.
The above logic tells us that in pi, as long as one piis the smaller prime of the sister primes, the 2k time conjecture is guaranteed to be true. Thus, the proof of the conjecture only needs to prove that in pi, no piis a smaller prime number, and the conjecture still holds at 2k.
In the proof of theorem 17, assuming that every (pi+2) is an odd composite number, essentially assuming that no pi is a smaller prime of sister prime, we still prove that the 2k conjecture holds. The others, of course, at least one of pi is the smaller prime of the sister primes, and the conjecture is certainly true, and no further proof is needed.
(5.12.2), is a mathematical equation, both sides of the equal sign, should have the same quantity, the same name of things.
num(3≤p≤k)-num(2k=ps+(hr+2))=num(2k=(pi+2)+pj) (5.12.2)
Obviously, num(3≤p≤k)-num(2k=ps+(hr+2)) is the number of partial odd prime p in the interval [3, k], without any doubt.
(5.12.2), is a mathematical equation where num (2k=(pi+2)+pj), on the right side of the equal sign, must also be [3, k] the number of odd primes p in the interval. Each (pi+2) in (2k=(pi+2)+pj) must be an odd prime p in the interval [3, k]. Because, if there is a (pi+2) that is not an odd prime p in the interval [3, k], num(2k=(pi+2)+pj), it cannot be the number of odd prime p in the interval [3, k].
If there is a (pi+2) that is an odd prime p in the interval [3, k], then Goldbach's conjecture is established. If any (pi+2) is not an odd prime p in the interval [3, k], then any (pi+2) is an odd composite number h in the interval [3, k]; num (2k=(pi+2)+pj) is the number of odd composite number h in the interval [3, k]. This contradicts num (2k=(pi+2)+pj), which must be the number of odd prime numbers p in the interval [3, k].
If some (pi+2) is an odd prime p in the interval [3, k]; The others (pi+2) are odd composite numbers h in the interval [3, k]; num(2k=(pi+2)+pj)
is not the number of odd primes p in the interval [3, k]. This contradicts num(2k=(pi+2)+pj), which must be the number of odd prime numbers p in the interval [3, k]. Example 3 falls into this category.
After the above verification, we know that the case of example 3 is still included in the proof of theorem 17.
(pi+2) in (2k=(pi+2)+pj), there are only three cases.
In the first case, each (pi+2) is a odd composite number h in the
interval [3, k]. Example 8 falls into this category.
In the second case, some of (pi+2) are odd prime numbers p in the interval [3, k]; Others of (pi+2), are odd composite number h in the interval [3, k]; Example 3 falls into this category.
Since some of (pi+2) are odd prime numbers p in the interval [3, k], the conjecture holds at 2k.
In the third case, each (pi+2) is an odd prime p in the interval
[3, k]. There must be 2k=2n+2=(pi+2)+pj. 2k is already the sum of two odd prime numbers. This is already included in the proof of theorem 17.
After the above test, we know that: (pi+2), the three possible cases, all included in the proof of theorem 17. Therefore, the proof process of theorem 17 is absolutely rigorous and absolutely comprehensive! Verify theorem 17 with example 3, and this is the end.
(8)Readers may raise the following questions, and answer them as follows.
(8.1) Some experts ask why you use 2k=(pi+2)+pj instead of 2k=(pi+1)+(pj+1)?
The answer is as follows: 2n+2=2k=(pi+2+pj) =(pi+1)+ (pj+1), which is numerically valid. However, since pi and pj are both odd prime numbers, pi+1 and pj+1 are both even numbers. So 2k=(pi+1)+ (pj+1), is 2k expressed as the sum of two even numbers. This has nothing to do with the 2k conjecture. In other words, 2k=(pi+1)+ (pj+1) is meaningless for the study of Goldbach's conjecture. So we're not going to consider the form 2k=(pi+1)+ (pj+1).
Above is the answer to the question (8.1).
(8.2) Some experts ask, you use 2k=(pi+2)+pj, in (2k=(pi+2)+pj), did not lose the prime number 3?
The answer is as follows: In order to answer the questions of the experts on this subject, we have previously added some findings on sister prime numbers.
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr) (4.0.1)
We know that there must be sister primes in the interval [3,n].However,it is not certain that pi must contain the smaller of the sister primes.
If the mth odd prime is pm, and pm+2=pm+1, pm+1 is the (m+1)th odd prime. We call pm the smaller of the sister prime numbers; pm+1 is the larger of the sister primes.
If at least one of the pi is the smaller of the sister primes, then it is immediately certain that at least one of (pi+2) is an odd prime.
So there is at least one 2k=(pi+2)+pj, 2k is already the sum of two odd prime numbers (pi+2), pj. So Goldbach's conjecture is established.
Example 8, in pi, none is the smaller of the sister primes; The smaller of the sister primes, all in ps.
Example 8 tells us that it is never possible to prove that at least one of pi is the smaller of the sister primes.
The existence of example 8 has brought endless difficulties and troubles to the proof of Goldbach's conjecture. The above theorem 17 and its proof successfully avoid this endless difficulty and annoyance.
Now we can answer your questions. Experts ask, if you use 2k=(pi+2)+pj, don't you lose the prime 3?
The answer is as follows: If you think that one pi is the smaller of the sister primes, then at least one (pi+2) is already an odd prime, then the conjecture is established.
If you think that no pi is the lesser of the sister primes, you think that every pi is the greater of the sister primes, so (pi+2) are all odd composite numbers.
Under the above assumption, each (pi+2) is an odd composite number.
So, where is the odd prime number 3? Under the above assumption, it
should be said with certainty that 3 is one of the odd prime numbers ps. Also, the smaller of the sister primes are in ps.
num(3≤p≤k)=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
Because 3 is one of the odd prime numbers ps, it is not thrown away. The smaller of each sister prime, including 3,5, is in ps and is not thrown away.
The above is the answer to the question (8.2).
(8.3) Some experts say that in (5.12.1), num (2k=(pi+2)+pj) represents the number of odd prime pi. Does not represent the number of pi+2. Answer as follows: Do you think num(2k=(pi+2)+pj) represents the number of odd primes pi, not (pi+2). First of all, your understanding is inconsistent with the definition of the meaning of mathematical symbols in (1.2 the meaning of mathematical symbols in the paper), so it is wrong.
Second, you're not treating pi+2 as a number. See: (3+2) =5, (5+2) =7, (7+2) =9, (9+2) =11,..., 5,7,9,11... is a number. You interpret a parenthesis (pi+2) as two numbers. This contradicts the intention of the paper. If you say so, you only look at pi in (pi+2). So, let me ask you, where did the +2 go?
In this article, we always treat the parentheses (pi+2) and similar representations as a number. Look at the text before you ask your question, in bold bold:
Question 1: Is at least oneof(hr+2) an odd prime?
Question 2: Under the assumption that every (hr+2) is an odd composite
number, is at least oneof(pi+2) an odd prime number?
Fromquestion1 andquestion2, we can see that the basis of the following discussion is: every (pi+2), every (hr+2) is an odd composite number.
Question 3: Is (5.12.1) still true under the assumption that every (pi+2), every (hr+2), is an odd composite number?
This proves that the assumption that every (pi+2), every (hr+2), is an odd composite number is not valid! It proves that at least one of (pi+2), (hr+2), is an odd prime. So at 2k, Goldbach's conjecture works.
You see, the above (hr+2), (pi+2), every time they are mentioned, are they not as a number?
The above is the answer to the question (8.3).
(8.4) The expert asks: (pi+2), (hr+2), at least one of which is an odd prime, is this consistent with the previous theorem?
The answers are as follows. Theorem 11: If the 2n conjecture is true, then 2k=pi++pj+ has the following 4 sources, as long as one of the sources exists, it will ensure that the conjecture continues to be true at 2k.
The 4 sources of 2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of(pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
Theorem 11 simply says:If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
It is not certain that at least one of (pi+2), (hr+2), is an odd prime number; There is no guarantee that at least one 2k=pi++pj+ exists; There's just no guarantee that Goldbach's conjecture is true.
So, at least one of (pi+2), (hr+2) is an odd prime, which is a step further than theorem 11. Absolutely sure, at least one 2k=pi++pj+ exists, which is a completely positive conclusion. It's exactly the same as theorem 11, but it goes one step further and makes a completely positive conclusion.
The above is the answer to the question (8.4).
(8.5) The reader asks:In each of the eight mathematical instances in the paper, is at least one of them (pi+2), (hr+2) an odd prime?
Answer as follows:We examined each of the eight mathematical examples. Every mathematical instance, in (pi+2), (hr+2), has at least one odd prime.
Earlier, we did a written test for Example 3 and Example 8, which the reader has reviewed.
Readers are welcome to write their own new mathematical examples, test theorems 17. And we hope you will publish your examples and test results. It is best to send your examples and test results to Hou Shaosheng.
Example 3 is shown as follows.
Example 3. 2n=2×51=102
=1+101=3+99=5+97=7+95=······=41+61=43+59=45+57=47+55
=49+53=51+51.
Example 3, above, is the third of the eight mathematical examples in the paper: Example 3. Now use example 3 to verify that at least one of the (pi+2), (hr+2) numbers is an odd prime.
Verify the first source of 2k=2(n+1)=pi++pj+as follows:
num(2×51=pi+pj)=8.
These 8 number of 2×51=pi+pj are:
2×51= 5+97 = 13+89 = 19+83 = 23+79
= 29+73 = 31+71 = 41+61 = 43+59.
2n=pi+pj,(pi+2) are odd prime numbers:
(5+2)+97 =(29+2)+73 =(41+2)+61.
This verifies that at least one of (pi+2) is an odd prime.
For every (pi+2) that is an odd prime, there is a 2k=(pi+2)+pj, which becomes one of 2k=pi++pj+.
For example, since 2×51=5+97, and(5+2)is an odd prime,
So 2×(51+1)=(5+2)+97.
2×(51+1) is already the sum of two odd prime numbers.
For example, since 2×51=29+73, and (29+2) is an odd prime,
So 2×(51+1)=(29+2)+73.
2×(51+1) is already the sum of two odd prime numbers.
......
This verifies that for every (pi+2) that is an odd prime, there is a 2k=(pi+2)+pj, which becomes one of 2k=pi++pj+.
Verify the third source of2k=2(n+1)=pi++pj+ as follows:
num(2n=ps+hr)=6.
The 6 number of 2×51=ps+hr are:
2×51= 3+99 = 7+95 = 11+91 = 17+85 = 37+65 = 47+55.
2n=ps+hr,(hr+2) are odd prime numbers: 3+(99+2)= 7+(95+2)
= 37+(65+2).
This verifies that (hr+2) is an odd prime number.
For each (hr+2) that is an odd prime, there is a 2k=ps+(hr+2), which becomes one of 2k=pi++pj+.
For example, since 2×51= 3+99, and (99+2)is an odd prime,
So 2×(51+1)=3+(99+2).
2×(51+1) is already the sum of two odd prime numbers.
For example, since 2×51=7+95, and (95+2)is an odd prime,
So 2×(51+1)=7+(95+2).
2×(51+1) is already the sum of two odd prime numbers.
......
This verifies that if one of (hr+2) is an odd prime, then 2k=ps+(hr+2)
becomes one of 2k=pi++pj+.
The reader should appreciate that the four sources of 2k=pi++pj+ would rather repeat the same data, (Character under shadow), and never give up the opportunity to ensure that the conjecture continues to hold.
The appearance of the duplicate data explains the four sources, which provides multiple guarantees for the establishment of Goldbach's conjecture. If only one(2k=pi++pj+)occurs once, the conjecture is guaranteed. If(2k=pi++pj+)occurs m times in total, the conjecture is guaranteed m times. This is one of the mysteries of the persistence of conjecture.
Since(2k=pi++pj+)has only four sources,(2k=pi++pj+)can occur at most four times for the same(2k=pi++pj+). Because in the same source, there can be no duplication.
Above is the answer to the question (8.5).
(9)Some notes on (5.12.1).
(5.12.1) is as follows:
num(3≤p≤k)=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
Note: num(3≤p≤k) indicates the number of odd primes p in the interval [3, k].
In (5.12.1), (pi+2), ps, are in the interval [3, k].
pj, (hr+2), are all in the interval [k, 2k-3].
pj, ps is an odd prime number.
(pi+2), (hr+2), whether it is an odd prime number or an odd composite
number, is what needs to be discussed below.
The inference of Hou Shaosheng's theorem when quoting theorem 5:2k is as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
Among them, it is agreed:
pi+, pj+, ps+, pd+, are all odd prime numbers; ht+, hu+, hr+, hk+, are all odd composite numbers.
And: pi+≤pj+, ht+≤hu+, ps+≤hr+, hk+≤pd+.
pi+, ht+, ps+, hk+, ∈[3,k]; pj+, hu+, hr+, pd+, ∈[n,2k-3].
(9.1) Note 1: If one of (pi+2) is an odd prime in the interval
[3, k], one of (hr+2) is odd composite number in the interval [k, 2k-3]. In this case,
num(3≤p≤k)=num(2k=(pi+2)+pj)+ num(2k=ps+(hr+2)) (5.12.1)
Among:
2k=(pi+2)+pj becomes one of 2k=pi++pj+.
2k=ps+(hr+2) becomes one of 2k=ps++hr+.
(9.2) Note 2: Where does all 2k=pi++pj+ in (4.3.1) come from?
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
Theorem 11: If the 2n conjecture is true, then 2k=pi++pj+ has the
following four sources, as long as one of the sources exists, it will ensure that the conjecture continues to be true at 2k.
The 4 sources of 2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
(9.3) Note 3: If one of (pi+2)is an odd prime in the interval [3, k], one of (hr+2) is odd prime number in the interval [k, 2k-3], where
num(3≤p≤k)=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
Among:
2k=(pi+2)+pj becomes one of 2k=pi++pj+.
2k=ps+(hr+2) becomes one of 2k=pi++pj+.
2k=(pi+2)+pj, 2k=ps+(hr+2), are all part of num(2k=pi++pj+).
Moreover, it is possible that (pi+2)=ps and pj=(hr+2).
If (pi+2)=ps, pj=(hr+2), then 2k=(pi+2)+pj, 2k=ps+(hr+2), are repeated.
(9.4) Note 4: Expert asked: Does 2k=ps++hr+ in (4.3.1) no longer exist?
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
In general, 2k=ps++hr+, there is: 1≤num(2k=ps++hr+).
num(2k=ps++hr+)=0. only when k is small.
For example, k=5, 2k=10=1+9=3+7=5+5.
In this example, 2×5=3+7, 2×5=5+5. Both are one of 2k=pi++pj+.In this example, num(2k=ps++hr+)=0.
Where does 2k=ps++hr+ in (4.3.1) come from?Theorem 12:
If the conjecture is true for 2n, then 2k=ps++hr+ has four
sources:
If one of (pj+2) is an odd composite number, then 2k=pi+(pj+2) becomes
one of 2k=ps++hr+;
If one of (hr+2) is an odd composite number, then 2k=ps+(hr+2) becomes
one of 2k=ps++hr+;
If one of (ps+2) is an odd prime, then 2k=(ps+2)+hr becomes one of
2k=ps++hr+;
If one of (ht+2) is an odd prime, then 2k=(ht+2)+hu becomes one of
2k=ps++hr+.
(9.5) Note 5: If one of (pi+2) is an odd composite number in the interval [3, k], one of (hr+2) is odd composite number in the interval [k, 2k-3], where
num(3≤p≤k)=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
Among:
2k=(pi+2)+pj becomes one of 2k=hk++pd+.This 2k=hk++pd+ must be transferred
from (5.12.1) to (4.3.2), (4.3.3) to become one of num (2k=hk++pd+).It is a process of returning to the source.
2k=ps+(hr+2) becomes one of 2k=ps++hr+. This 2k=ps++hr+ must be transferred
from (5.12.1) to (4.3.1), (4.3.4) to become one of num (2k=ps++hr+).It is a process of returning to the source.
Similar situations encountered should be dealt with in this way, and will not be discussed too much.
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
(9.6) Note 6: The reader asks: Where does all of 2k=hk++pd+ come from?
Theorem 14: If the conjecture is true for 2n, 2k=hk++pd+ has the following 4 sources:
If one of (pi+2) is odd composite, then 2k=(pi+2)+pj becomes one of 2k=hk++pd+;
If one of (hu+2) is odd prime, then 2k=ht+(hu+2) becomes one of 2k=hk++pd+;
If one of (hk+2) is odd composite, then 2k=(hk+2)+pd becomes one of 2k=hk++pd+;
If one of (pd+2) is an odd prime, then 2k=hk+(2+pd) becomes one of 2k=hk++pd+.
(9.7) Note 7: If one of(pi+2) is an odd composite number in the interval [3, k], one of (hr+2) is odd prime number in the interval [k, 2k-3], where
num(3≤p≤k)=num(2k=(pi+2)+pj)+num(2k=ps+(hr+2)) (5.12.1)
Among:
2k=(pi+2)+pj becomes one of 2k=hk++pd+.
2k=ps+(hr+2) becomes one of 2k=pi++pj+.
(9.8)Note 8: Where does all 2k=ht++hu+ in (4.3.2) come from?
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
Theorem 13: If the conjecture holds for 2n, then 2k=ht++hu+ has the following four sources:
If one of (ps+2) is odd composite, then 2k=(ps+2)+hr becomes one of 2k=ht++hu+.
If one of (ht+2) is odd composite, then 2k=(ht+2)+hu becomes one of 2k=ht++hu+.
If one of (hu+2) is odd composite, then 2k=ht+ (hu+2) becomes one of 2k=ht++hu+.
If one of (pd+2) is odd composite, then 2k=hk+ (pd+2) becomes one of 2k=ht++hu+.
A statement on theorem 17, over.
5.13 Theorem 18: If the conjecture is true at 2n and k (=n+1) is composite, then at least oneof(hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
To prove theorem 18, first quote the related theorem and then prove theorem 18.
Proof: (1) Quote theorem 11 as follows:
Theorem 11: If the 2n conjecture is true, then 2k=pi++pj+ has the following four sources, as long as one of the sources exists, it will ensure that the conjecture continues to be true at 2k.
The 4 sources of 2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+;
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
If the Goldbach conjecture holds for 2n, 2k=pi++pj+ has four sources, so long as one source exists, the conjecture will continue to hold for 2k. So, to prove the conjecture, you just need to prove the existence of a source.
Conversely, if the Goldbach conjecture is true at 2n, and if it is not true at 2k, then none of the 4 sources of 2k=pi++pj+ can exist.
As a proof by contradiction, if the conjecture is not valid for 2k , that is,2k=pi++pj+ 4 sources, none of which exist;As long as the contradiction can be found according to rigorous mathematical reasoning, it is proved that 2k=pi++pj+ 4 sources, at least one of the existence. That proves the 2k conjecture. That's the mathematical idea proving theorem 18.
(2) The inference of Hou Shaosheng's theorem is quoted as follows:
About the formula:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
There is always:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Among them, the convention is: 3≤q≤n, q is odd.
pi, pj, ps, pd are all odd prime numbers; ht, hu, hr, hk are all odd composite numbers.
And: pi≤pj, ht≤hu, ps≤hr, hk≤pd.
pi, ht, ps, hk, ∈[3,n]; pj, hu, hr, pd∈[n,2n-3].
Under our theoretical system, if the conjecture is true for 2n, it is accepted that the above (4.0.1), (4.0.2), (4.0.3), (4.0.4) are also true. Therefore, the simultaneous holding of (4.0.1), (4.0.2), (4.0.3), (4.0.4) is also the theoretical basis for our proof of theorem 18, in particular the admission that: 1≤num(2n=pi+pj).
(3) Quote theorem 5 (theinferenceof Hou Shaosheng's theorem at 2k) as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
Quote (4.0.4) as follows.
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
(4.0.4) indicates that hu, hr, are the all odd composite numbers in the interval [n,2n-3].
(4.0.4) Indicates that num(n≤h≤2n-3) is equal to the number of odd composite number hu + the number of odd composite number hr.
If n in (4.0.4) is replaced by k, we get:
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
(4.3.4), is k time, Hou Shaosheng theorem of inference formula.
(4.3.4) It is stated that num(k≤h≤2k-3) is equal to the number of
odd composite number hu+ + the number of odd composite number hr+.
(4)At least one of (hu+2) and (hr+2) is an odd prime number.
Quote theorem 16C as follows:
At least one of the (ht+2) and (hk+2) is an odd prime.
In both (hu+2) and (hr+2), at least one is an odd prime.
(5) Theorem 18: If the conjecture is true at 2n and k (=n+1) is composite, then at least oneof(hr+2) is an odd prime, which guarantees that the conjecture must be true at 2k.
The proof is as follows.
(5.1) Assuming that 2n-1 is an odd prime number, the conjecture must hold for 2k.
If 2n-1 is an odd prime, then it must be: 2k=2(n+1)=3+(2n-1).
So 2k is the sum of the odd prime number 3 and the odd prime number 2n-1, and the conjecture holds for 2k. So let's say that 2n-1 is an odd prime number, so we don't need to talk about it anymore.
Now let's say that 2n-1 is odd composite, and the conjecture must be true.
(5.2) Suppose that 2n-1 is the odd composite number, and the number relationship between the odd composite number h in the interval [n, 2n-3] and [k, 2k-3] is as follows.
A If n is an odd composite number, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3).
B If n is an odd prime number, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: To the right of the above equation, -1, is to subtract an odd composite number (2n-1) = (2k-3).
C If n is even, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note:To the right of the above equation, -1, is to subtract an odd composite number (2n-1)=(2k-3).
The proof is as follows.
Please refer the reader to the picture below.
[n, 2n-3] has one more integer n than [k, 2k-3], but two fewer
integers: 2n-2, 2n-1.
Note: n+1=k, where K is composite number; 2n-1=2k-3, 2n-1, which is
odd composite number.
n is an even number, an odd prime number, and an odd composite
number, which need to be studied separately.
Since we are dealing with the number of odd composite number h in the intervals [n,2n-3] and [k,2k-3], we have nothing to do with the even numbers n, 2n-2. It has nothing to do with odd prime p.
A If n is odd composite number, since 2n-1 is also odd composite number, the number of odd composite number h in the interval [n,2n-3] and [k,2k-3] is equal; Except for n and (2n-1), these two odd composite numbers, the other odd composite numbers h are the same. so has:
num(n≤h≤2n-3)=num(k≤h≤2k-3).
B If n is an odd prime, since 2n-1 is an odd composite number, then [n,2n-3] is 1 less than the number of odd composite number h in the interval [k,2k-3]; 1, refers to an odd composite number (2n-1); The other odd composite numbers are the same. So there are:
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: To the right of the above equation, -1, is to subtract an odd composite number (2n-1) = (2k-3).
C If n is even, since 2n-1 is an odd composite number, [n,2n-3] is 1 less than the number of odd composite number h in the interval [k,2k-3]; 1, refers to an odd composite number (2n-1); The other odd composite numbers are the same. so has:
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: To the right of the above equation, -1, is to subtract an odd composite number (2n-1) = (2k-3).
A,B,C, three conclusions have been proved.
The following, for A,B,C, 3 conclusions, respectively prove the conjectures are valid.
(5.3) Suppose that 2n-1 is an odd composite number;
A If n is an odd composite number, there must be
num(n
≤
h
≤
2n-3)=num(k
≤
h
≤
2k-3).
Under these conditions, the conjecture must be true.
The proof is as follows.
From num(n≤h≤2n-3)=num(k≤h≤2k-3), there must be:
num(k≤h≤2k-3)
=num(n≤h≤2n-3)
=num(2n=ht+hu)+num(2n=ps+hr) (4.0.4)
=num(2n+2=ht+2+hu)+num(2n+2=ps+2+hr)
=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)). (5.13.1)
That's it :
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
The derivation process of each step above has mathematical axioms, theorems, definitions, and bases, so (5.13.1) must be true!
Our aim is to prove that there must be (2+hr) that is odd prime numbers. Thus 2k=ps+(2+hr), and at least one 2k is the sum of the odd prime ps and the odd prime (2+hr).
The proof is as follows:
Theorem 16C states that at least one of (2+hu) and (2+hr) is an odd prime number.
The following proof by contradiction shows that at least oneof(2+hr) is an odd prime number.
Theorem 16C states that at least one of (ht+2) and (hk+2) is an odd prime number.
In both (hu+2) and (hr+2), at least one is an odd prime.
Suppose each (2+hr) is an odd composite number. According to theorem 16C, at least one of (2+hu) is an odd prime number.
Now analyze (5.13.1) as follows.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
On the left side of the equal sign, num(k≤h≤2k-3) is the number of all the odd composite number h in the interval [k, 2k-3].
(5.13.1), is a mathematical equation, on the right of the equals sign,
num(2k=ht+(2+hu))+ num(2k=ps+(2+hr)),
It must also be the number of all odd composite number h in the interval
[k, 2k-3]. This is a necessary condition for (5.13.1) to be established.
It can be seen that num(2k=ht+(2+hu)), num(2k=ps+(2+hr)), must be the number of partial odd composite numbers h in the interval [k, 2k-3]. Otherwise, it contradicts the mathematical principle that only numbers with the same name can be equal, and only numbers with the same name can be added or subtracted.
num(2k=ht+(2+hu))represents the number of (2k=ht+(2+hu))according to the definition (1.2 Meaning of mathematical symbols in the paper).
number of (2k=ht+(2+hu)) is the number of ht in the interval [3, k]; Of course is also the number of (2+hu) in the interval [k, 2k-3].
Since num(2k=ht+(2+hu))must be the number of partial odd composite numbers h in the interval [k, 2k-3], every (2+hu) must be the odd composite number h in the interval [k, 2k-3]; Otherwise, num(2k=ht+(2+hu)) cannot be the number of odd composite number h in the interval [k, 2k-3].
Each (2+hu) must be an odd composite number h in the interval [k, 2k-3]; Contradicted by the fact that at least oneof(2+hu) is an odd prime.
Therefore, the assumption that every (2+hr) is an odd composite number is not true. So at least oneof(2+hr) is an odd prime.
At least oneof(2+hr) is an odd prime, which guarantees that at 2k, the conjecture must be true.
A If n is an odd composite number, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3).
Under these conditions, the conjecture must be true. Proof is finished.
(5.3.1) Answer 9 relevant questions
The following 9 questions, experts and readers, are likely to be asked, and we offer to answer them below.
Problem 1: (2+hr) is an odd prime number, which also contradicts (2+hu), (2+hr), which must both be odd composite numbers. How do you solve it?
Answer 1: If some (2+hr) are odd prime numbers, then 2k=ps+(2+hr), 2k is already the sum of odd prime numbers ps and odd prime numbers (2+hr). 2k=ps+(2+hr), already one of the four sources of 2k=pi++pj+ .
To be more specific, 2k=ps+(2+hr) is the third of the four sources of 2k=pi++pj+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
Theorem 11: The 4 sources of 2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+;
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
At this point, 2k=ps+(2+hr) should be removed from (5.13.1). After copying, transfer to position of(2k=pi++pj+)in (4.3.1), (4.3.3). Make it part of num(2k=pi++pj+). Because 2k=pi++pj+ has four sources, 2k=ps+(2+hr), if k is relatively large, can only be part of num(2k=pi++pj+), not all of it.
2k=pi++pj+ in (4.3.1) and (4.3.3) is formed after the convergence of the four sources of 2k=pi++pj+.
To quote Theorem 5: The inference of Hou Shaosheng's theorem in 2k is as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
Note that we moved 2k=ps+(2+hr) from (5.13.1), copied it, and moved it to position of(2k=pi++pj+)in (4.3.1), (4.3.3). Make it part of
num(2k=pi++pj+). This process, after proving 2k, does not affect the proof that the conjecture is established.
Problem 2: If some (2+hr) are odd composite numbers, then 2k=ps+(2+hr), 2k is already the sum of odd prime ps and odd composite numbers (2+hr). 2k=ps+(2+hr) is already one of 2k=ps++hr+.
To be more specific, 2k=ps+(2+hr) is the second of four sources for 2k=ps++hr+.
Theorem 12: If the conjecture is true for 2n, then 2k=ps++hr+ has four sources:
If one of (pj+2) is an odd composite number, then 2k=pi+(pj+2) becomes one of 2k=ps++hr+;
If one of (hr+2) is an odd composite number, then 2k=ps+(hr+2) becomes one of 2k=ps++hr+;
If one of (ps+2) is an odd prime, then 2k=(ps+2)+hr becomes one of 2k=ps++hr+;
If one of (ht+2) is an odd prime, then 2k=(ht+2)+hu becomes one of 2k=ps++hr+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+ num(2k=ps+(2+hr)) (5.13.1)
If some (2+hr) are odd composites number, 2k=ps+(2+hr) is left in the position of 2k=ps+(2+hr) in (5.13.1) as part of 2k=ps++hr+. The four sources of 2k=ps++hr+, when brought together, replace the position of 2k=ps+(2+hr) in (5.13.1).
Problem 3: If some (ps+2) are odd prime numbers, then 2k=(ps+2)+hr, 2k is already the sum of odd prime numbers (ps+2) and odd composite numbers hr. 2k=(ps+2)+hr, already one of 2k=ps++hr+.
To be more specific, 2k=(ps+2)+hr is the third of the four sources for 2k=ps++hr+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
At this time, 2k=(ps+2)+hr is retained in the position of 2k=ps+(2+hr) in (5.13.1), becoming one of the four sources of 2k=ps++hr+.
The four sources of 2k=ps++hr+, when brought together, replace the position of 2k=ps+(2+hr) in (5.13.1).
Problem 4: If some (ps+2) are odd composite numbers, then 2k=(ps+2)+hr, 2k is already the sum of odd composite numbers (ps+2) and odd composite numbers hr. 2k=(ps+2)+hr, already one of 2k=ht++hu+.
To be more specific, 2k=(ps+2)+hr is the first of four sources for 2k=ht++hu+.
Theorem 13: If the conjecture holds for 2n, then 2k=ht++hu+ has the following four sources:
If one of (ps+2) is an odd composite number, then 2k=(ps+2)+hr becomes one of 2k=ht++hu+.
If one of (ht+2) is an odd composite number, then 2k=(ht+2)+hu becomes one of 2k=ht++hu+.
If one of (hu+2) is odd composite number, then 2k=ht+(hu+2) becomes one of 2k=ht++hu+.
If one of (pd+2) is odd composite number, then 2k=hk+(pd+2) becomes one of 2k=ht++hu+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
At this time, 2k=(ps+2)+hr is retained in the position of 2k=ht+(2+hu) in (5.13.1), becoming one of the four sources of 2k=ht++hu+.
The four sources of 2k=ht++hu+, when aggregated, replace the position of 2k=ht+(2+hu) in (5.13.1).
Problem 5: If some (2+hu) are odd prime numbers, then 2k=ht+(2+hu), 2k is already the sum of odd composite numbers ht and odd prime numbers (2+hu). 2k=ht+(2+hu) is already one of 2k=hk++pd+.
To be more specific, 2k=ht+(2+hu) is the second of the four sources of 2k=hk++pd+.
Theorem 14: If the conjecture is true for 2n, 2k=hk++pd+ has the following four sources:
If one of (pi+2) is odd composite , then 2k=(pi+2)+pj becomes one of 2k=hk++pd+;
If one of (hu+2) is an odd prime, then 2k=ht+(hu+2) becomes one of 2k=hk++pd+;
If one of (hk+2) is odd composite, then 2k=(hk+2)+pd becomes one of 2k=hk++pd+;
If one of (pd+2) is an odd prime, then 2k=hk+(2+pd) becomes one of 2k=hk++pd+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
At this time, 2k=ht+(2+hu) should be removed from (5.13.1), copied, and transferred to(2k=hk++pd+) in (4.3.2), (4.3.3). Make it part of
num(2k=hk++pd+). Because 2k=hk++pd+ has four sources, 2k=ht+(2+hu), in the case of k is relatively large, can only be a part of num(2k=hk++pd+), not all.
2k=hk++pd+ in (4.3.2) and (4.3.3) is formed after the convergence of four sources of 2k=hk++pd+.
To quote Theorem 5: The inference of Hou Shaosheng's theorem in 2k is as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
Problem 6: If some (2+hu) are odd composite numbers, then 2k=ht+(2+hu), 2k is already the sum of odd composite numbers ht and odd composite numbers (2+hu). 2k=ht+(2+hu), already one of 2k=ht++hu+.
Specifically, 2k=ht+(2+hu) is the third of the four sources for 2k=ht++hu+.
Theorem 13: If the conjecture holds for 2n, then 2k=ht++hu+ has the following four sources:
If one of (ps+2) is odd composite number, then 2k=(ps+2)+hr becomes one of 2k=ht++hu+.
If one of (ht+2) is odd composite number, then 2k=(ht+2)+hu becomes one of 2k=ht++hu+.
If one of (hu+2) is odd composite number, then 2k=ht+(hu+2) becomes one of 2k=ht++hu+.
If one of (pd+2) is odd composite number,then 2k=hk+(pd+2) becomes one of 2k=ht++hu+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+ num(2k=ps+(2+hr)) (5.13.1)
At this time, 2k=ht+(2+hu) should be retained in the position of 2k=ht+(2+hu) in (5.13.1). Also copy, move 2k=ht+(2+hu) to the position 2k=ht++hu+ in (4.3.2), (4.3.4) and become part of num(2k=ht++hu+). Because 2k=ht++hu+ has four sources, 2k=ht+(2+hu), in the case of k is relatively large, can only be a part of num(2k=ht++hu+), not all.
To quote Theorem 5: The inference of Hou Shaosheng's theorem in 2k is as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
2k=ht++hu+ in (4.3.2) and (4.3.4) is formed after the convergence of four sources of 2k=ht++hu+. When the four sources of 2k=ht++hu+ are aggregated, the position of 2k=ht+(2+hu) in (5.13.1) is replaced.
Problem 7: If some (ht+2) are odd prime numbers, then 2k=(ht+2)+hu, 2k is already the sum of odd prime numbers (ht+2) and odd composite numbers hu. 2k=(ht+2)+hu, already one of 2k=ps++hr+.
Specifically, 2k=(ht+2)+hu is the fourth of the four sources for 2k=ps++hr+.
Theorem 12: If the conjecture is true for 2n, then 2k=ps++hr+ has four sources:
If one of (pj+2) is an odd composite number, then 2k=pi+(pj+2) becomes one of 2k=ps++hr+;
If one of (hr+2) is an odd composite number, then 2k=ps+(hr+2) becomes one of 2k=ps++hr+;
If one of (ps+2) is an odd prime, then 2k=(ps+2)+hr becomes one of 2k=ps++hr+;
If one of (ht+2) is an odd prime, then 2k=(ht+2)+hu becomes one of 2k=ps++hr+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
At this time, 2k=(ht+2)+hu should be retained in the position of 2k=ps+(2+hr) in (5.13.1). Also copy, move 2k=(ht+2)+hu to 2k=ps++hr+ in (4.3.1), (4.3.4) and become part of num(2k=ps++hr+). Because 2k=ps++hr+ has four sources, 2k=(ht+2)+hu, if k is larger, can only be part of
num(2k=ps++hr+), not all of it.
To quote Theorem 5: The inference of Hou Shaosheng's theorem in 2k is as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
2k=ps++hr+ in (4.3.1) and (4.3.4) is formed after the convergence of four sources of 2k=ps++hr+. When the four sources of 2k=ps++hr+ are aggregated, the position of 2k=ps+(2+hr) in (5.13.1) is replaced.
Problem 8: If some (ht+2) are odd composite numbers, then 2k=(ht+2)+hu, 2k is already the sum of odd composite numbers (ht+2) and odd composite numbers hu. 2k=(ht+2)+hu, already one of 2k=ht++hu+.
To be more specific, 2k=(ht+2)+hu is the second of four sources for 2k=ht++hu+.
Theorem 13: Assuming the conjecture is true for 2n, 2k=ht++hu+ has the following four sources:
If one of (ps+2) is odd composite number, then 2k=(ps+2)+hr becomes one of 2k=ht++hu+.
If one of (ht+2) is odd composite number, then 2k=(ht+2)+hu becomes one of 2k=ht++hu+.
If one of (hu+2) is odd composite number, then 2k=ht+(hu+2) becomes one of 2k=ht++hu+.
If one of (pd+2) is odd composite number, then 2k=hk+(pd+2) becomes one of 2k=ht++hu+.
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+ num(2k=ps+(2+hr)) (5.13.1)
At this time, 2k=(ht+2)+hu should be retained in the position of 2k=ht+(2+hu) in (5.13.1). Also copy, move 2k=(ht+2)+hu to 2k=ht++hu+ in (4.3.2), (4.3.4) to become part of num(2k=ht++hu+). Because 2k=ht++hu+ has four sources, 2k=(ht+2)+hu, in the case of k is relatively large, can only be a part of num(2k=ht++hu+), not all.
To quote Theorem 5: The inference of Hou Shaosheng's theorem in 2k is as follows:
num(3≤p≤k)=num(2k=pi++pj+)+num(2k=ps++hr+). (4.3.1)
num(3≤h≤k)=num(2k=ht++hu+)+num(2k=hk++pd+). (4.3.2)
num(k≤p≤2k-3)=num(2k=pi++pj+)+num(2k=hk++pd+). (4.3.3)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
2k=ht++hu+ in (4.3.2) and (4.3.4) is formed after the convergence of four sources of 2k=ht++hu+. When the four sources of 2k=ht++hu+ are aggregated, the position of 2k=ht+(2+hu) in (5.13.1) is replaced.
Question 9: With 2k=ht++hu+ replace (5.13.1) 2k=ht+(2+hu),With 2k=ps++hr+ to replace (5.13.1) 2k=ps+(2+hr) after, (5.13.1) will evolve into (4.3.4).
num(k≤h≤2k-3)=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.1)
num(k≤h≤2k-3)=num(2k=ht++hu+)+num(2k=ps++hr+). (4.3.4)
The evolution process described above is extremely complex. It is a process of great differentiation, great reorganization, recombination, and reintegration. Generally speaking, from the great differentiation to the return of the team, the following eight situations are involved.
A: From 2n=pi+pj, to 2n+2=pi+2+pj, to 2k=(pi+2)+pj; It must be studied separately that (pi+2) is an odd prime number; (pi+2) is an odd composite number.
If pi+2 is an odd prime; 2k=(pi+2)+pj, will return to 2k=pi++pj+.
If pi+2 is odd composite; 2k=(pi+2)+pj, will return to 2k=hk++pd+.
B: From 2n=pi+pj, to 2n+2=pi+2+pj, to 2k=pi+(2+pj). It is necessary to study separately that (2+pj) is an odd prime number and (2+pj) is an odd composite number.
If (2+pj) is an odd prime; 2k=pi+(2+pj), will return to 2k=pi++pj+.
If (2+pj) is odd composite number; 2k=pi+(2+pj), will return to 2k=ps++hr+.
C: From 2n=ps+hr, to 2n+2=ps+2+hr, to 2k= (ps+2) +hr. It must be studied separately that (ps+2) is an odd prime number and (ps+2) is an odd composite number.
If (ps+2) is an odd prime; 2k=(ps+2)+hr, will return to 2k=ps++hr+.
If (ps+2) is odd composite number; 2k=(ps+2)+hr, will return to 2k=ht++hu+.
D: From 2n=ps+hr, to 2n+2=ps+2+hr, to 2k=ps+(2+hr). It must be studied separately that (2+hr) is an odd prime number and (2+hr) is an odd composite number.
If (2+hr) is an odd prime; 2k=ps+(2+hr), will return to 2k=pi++pj+.
If (2+hr) is odd composite number; 2k=ps+(2+hr), will return to 2k=ps++hr+.
E: From 2n=ht+hu, to 2n+2=ht+2+hu, to 2k= (ht+2) +hu. It must be studied separately that (ht+2) is an odd prime number and (ht+2) is an odd composite number.
If (ht+2) is an odd prime; 2k=(ht+2)+hu, will return to 2k=ps++hr+.
If (ht+2) is an odd composite number;2k=(ht+2)+hu,will return to 2k=ht++hu+.
F: From 2n=ht+hu, to 2n+2=ht+2+hu, to 2k=ht+(2+hu). We must study separately that (2+hu) is an odd prime number and (2+hu) is an odd composite number.
If (2+hu) is an odd prime; 2k=ht+(2+hu), will return to 2k=hk++pd+.
If (2+hu) is an odd composite number; 2k=ht+(2+hu), will return to 2k=ht++hu+.
G: From 2n=hk+pd, to 2n+2=hk+2+pd, to 2k=(hk+2)+pd. It must be studied separately that (hk+2) is an odd prime number and (hk+2) is an odd composite number.
If (hk+2) is an odd prime; 2k=(hk+2)+pd, will return to 2k=pi++pj+.
If (hk+2) is an odd composite number; 2k=(hk+2)+pd, will return to 2k=hk++pd+.
H: From 2n=hk+pd, to 2n+2=hk+2+pd, to 2k=hk+(2+pd). It must be studied separately that (2+pd) is an odd prime number and (2+pd) is an odd composite number.
If (2+pd) is an odd prime; 2k=hk+(2+pd), will return to 2k=hk++pd+.
If (2+pd) is an odd composite number; 2k=hk+(2+pd), will return to 2k=ht++hu+.
In the above 8 cases, return to 2k=pi++pj+, in 4 cases. In these four cases, there are four sources of 2k=pi++pj+, and only these four sources.
Back at 2k=ps++hr+, there are 4 scenarios. In these four cases, there are four sources of 2k=ps++hr+, and only these four sources.
Back to 2k=ht++hu+ , there are 4 scenarios. In these four cases, there are four sources of 2k=ht++hu+, and only these four sources.
Back to 2k=hk++pd+, there are 4 cases. These four cases, previously called 2k=hk++pd+ 4 sources, and only these 4 sources.
Question 10: The above answers to the nine questions have been very comprehensive. The answer to 9 questions, essentially applicable: Theorem 17, theorem 18, theorem 19 after the proof of the description. In mathematics, we often use empathy to prove, not to prove. Therefore, after the proof of theorem 17, after the proof of B and C in theorem 18, after the proof of theorem 19, the answers to the above nine questions will not be repeated.
After you have reviewed the proof of theorem 17, the proof of A,B, and C in theorem 18, and the proof of theorem 19, if you still have questions, please look at the answers to the above 9 questions.
(5.4) Suppose that 2n-1 is an odd composite number.
B If n is an odd prime number, there must be
num(n
≤
h
≤
2n-3)=num(k
≤
h
≤
2k-3)-1.
Note: On the right side of the formula, -1, is to subtract an odd composite number (2n-1) = (2k-3).
Under these conditions, the conjecture must be true.
The proof is as follows.
From num(n≤h≤2n-3)=num(k≤h≤2k-3)-1, we can get:
num(k≤h≤2k-3)-1
=num(n≤h≤2n-3)
=num(2n=ht+hu)+num(2n=ps+hr) (4.0.4)
=num(2n+2=ht+2+hu)+num(2n+2=ps+2+hr)
=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)). (5.13.2)
that's it
num(k≤h≤2k-3)-1=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.2)
The derivation process of each step above has mathematical axioms, theorems, definitions, and bases, so (5.13.2) must be true!
Our aim is to prove that there must be (2+hr) that is odd prime numbers. 2k=ps+(2+hr), 2k is the sum of the odd prime ps and the odd prime (2+hr).
The proof is as follows:
Theorem 16C states that at least one of (2+hu) and (2+hr) is an odd
prime number.
The following proof by contradiction shows that at least one (2+hr)
is an odd prime number.
Suppose each (2+hr) is an odd composite number.
Theorem 16C states that at least one of (2+hu) is an odd prime number.
Now analyze (5.13.2) as follows.
On the left side of the equal sign, num(k≤h≤2k-3) is the number of
all the odd composite number h in the interval [k, 2k-3].
Therefore, num(k≤h≤2k-3)-1 is the number of partial odd composite
number h in the interval [k, 2k-3].
(5.13.2), is a mathematical equation, on the right of the equals sign,
num(2k=ht+(2+hu))+num(2k=ps+(2+hr)),
it must also be the number of partial odd composite numbers h in the interval [k, 2k-3]. This is a necessary condition for the establishment of (5.13.2).
It can be seen that num(2k=ht+(2+hu)), num(2k=ps+(2+hr)), must be the number of partial odd composite numbers h in the interval [k, 2k-3]. Otherwise, it contradicts the mathematical principle that only numbers with the same name can be equal, and only numbers with the same name can be added or subtracted.
num(2k=ht+(2+hu)) represents the number of (2k=ht+(2+hu)) according to the definition (1.2 Meaning of mathematical symbols in the paper).
Number of (2k=ht+(2+hu)) is the number of ht in the interval [3, k]; Of course is also the number of (2+hu)in the interval [k, 2k-3].
Since num(2k=ht+(2+hu)) must be the number of partial odd composite numbers h in the interval [k, 2k-3],therefore, every (2+hu) must be the odd composite number h in the interval [k,2k-3]; Otherwise, num(2k=ht+(2+hu)) cannot be the number of odd composite number h in the interval [k, 2k-3].
Each (2+hu) must be an odd composite number h in the interval [k, 2k-3]; Contradicted by the fact that at least one of (2+hu) is an odd prime.
Therefore, the assumption that every (2+hr) is an odd composite number is not true. So at least one of (2+hr) is an odd prime.
At least one of (2+hr) is an odd prime, which guarantees that at 2k, the conjecture must be true.
This paper is accompanied by 8 mathematical examples. In every instance, at least one of (2+hr) is an odd prime p.
Some readers will ask: If a certain (2+hr) is an odd prime number, it also contradicts that every (2+hr) must be an odd composite number. What do you do?
The answer is as follows: At this point, 2k=ps+(2+hr), 2k is already the sum of the odd prime ps and the odd prime (2+hr), 2k, the conjecture is established.
At this point, 2k=ps+(2+hr) should be removed from (5.13.2). After copying, transfer to position of(2k=pi++pj+) in (4.3.1), (4.3.3). Make it part of num(2k=pi++pj+).
Regarding this issue, (4.3.1) answer 9 relevant questions with detailed answers. Please refer to.
B If n is an odd prime number, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: On the right side of the formula, -1, is to subtract an odd
composite number (2n-1) = (2k-3).
Under these conditions, the conjecture must be true.
End of proof.
(5.5) Suppose that 2n-1 is an odd composite number.
C If n is even, there must be num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: On the right side of the formula ,-1, is to subtract an odd
composite number (2n-1) = (2k-3).
Under these conditions, the conjecture must be true.
The proof is as follows.
From num(n≤h≤2n-3)=num(k≤h≤2k-3)-1, there must be:
num(k≤h≤2k-3)-1
=num(n≤h≤2n-3)
=num(2n=ht+hu)+num(2n=ps+hr) (4.0.4)
=num(2n+2=ht+2+hu)+num(2n+2=ps+2+hr)
=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)). (5.13.3)
That Is:
num(k≤h≤2k-3)-1=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.3)
The derivation process of each step above has mathematical axioms, theorems, definitions, and bases, so (5.13.3) must be true!
Our aim is to show that at least one of (2+hr) is an odd prime number.
2k=ps+(2+hr), 2k is the sum of the odd prime ps and the odd prime (2+hr).
The proof is as follows:
Theorem 16C states that at least one of (2+hu) and (2+hr) is an odd
prime number.
The following proof by contradiction shows that at least one of (2+hr)
is an odd prime number.
Suppose each (2+hr) is an odd composite number.
Theorem 16C states that at least one of (2+hu) is an odd prime number.
Now analyze (5.13.3) as follows.
On the left side of the equal sign, num(k≤h≤2k-3) is the number of all the odd composite number h in the interval [k, 2k-3].
Therefore, num(k≤h≤2k-3)-1 is the number of partial odd composite number h in the interval [k, 2k-3].
num(k≤h≤2k-3)-1=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.3)
(5.13.3), is a mathematical equation,
num(2k=ht+(2+hu)+num(2k=ps+(2+hr))
It must also be the number of partial odd composite numbers h in the interval [k, 2k-3]. This is a necessary condition for the establishment of (5.13.3).
It can be seen that num(2k=ht+(2+hu)),num(2k=ps+(2+hr)), must be the
number of partial odd composite numbers h in the interval [k, 2k-3]. Otherwise, it contradicts the mathematical principle that only
numbers with the same name can be equal, and only numbers with the same
name can be added or subtracted.
num(2k=ht+(2+hu)) represents the number of (2k=ht+(2+hu)) according to the definition (1.2 Meaning of mathematical symbols in the paper).
number of (2k=ht+(2+hu)) is the number of ht in the interval [3, k]; Of course is also the number of (2+hu) in the interval [k, 2k-3].
Since num(2k=ht+(2+hu)) must be the number of partial odd composite numbers h in the interval [k,2k-3], therefore, every (2+hu) must be the odd composite number h in the interval [k,2k-3]; Otherwise, num(2k=ht+(2+hu)) cannot be the number of odd composite number h in the interval [k, 2k-3].
Each (2+hu) must be an odd composite number h in the interval
[k, 2k-3]; Contradicted by the fact that at least one (2+hu) is an odd prime.
Therefore, the assumption that every (2+hr) is an odd composite number is not valid.
So at least one of (2+hr) is an odd prime.
At least one of (2+hr) is an odd prime, which guarantees that at 2k, the conjecture must be true.
C If n is even, there must be num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: On the right side of the formula, -1, is to subtract an odd composite number (2n-1) = (2k-3).
Under these conditions, the conjecture must be true.
Theorem 18, end of proof
This paper is accompanied by 8 mathematical examples. In every instance, at least one of (2+hr) is an odd prime p.
Experts and readers are welcome to test theorem 18 with their own examples.
(5.5.1) : Answer questions that readers may have.
Question: 2k=ps+(2+hr), (2+hr) is an odd prime number, does it not
contradict that every (2+hu), every (2+hr), must be an odd composite number in the interval [k,2k-3]?
Answer the question: Contradictory. To resolve this contradiction, when (2+hr) is an odd prime, we need to move 2k=ps+(2+hr) out of (5.13.3); Move to the (2k=pi++pj+)location of (4.3.1), (4.3.3), making it part of (2k=pi++pj+).
Regarding this issue, (5.3.1) answer 9 relevant questions with detailed answers. Please refer to.
(5.6) : Appendix: The original text of proof by contradiction in a small dictionary of mathematics, for readers' reference.
The original text of the proof by contradiction in the mathematical dictionary is as follows:
proof by contradiction Proof by contradiction is the equivalent proposition of proving a proposition - the inverse negative proposition. Thus the original proposition is proved indirectly. The general steps of proof by contradiction are: (1) Assume that the opposite of the conclusion is true; ② Draw wrong conclusions based on reason;③ To assert the opposite of the conclusion is wrong; ④ To assert the positive side of the conclusion is correct.
If there is only one case on the opposite side of the conclusion, it is sufficient to conclude that this case is not true. This proof by contradiction is called reduction;
If there is more than one case on the opposite side of the conclusion, it is necessary to refute each case one by one in order to affirm the positive truth of the conclusion. This kind of proof by contradiction is called exhaustion.
Example 1 We know that in △ABC, ∠B≠∠C. Seek confirmation: AB≠AC.
Proof (Use the reductive method) : If AB≠AC is not true, then AB=AC. Then ∠B=∠C, and the known contradiction.So AB≠AC.
(So much for quoting the original dictionary of mathematics).
Any expert or reader who cannot find a specific error in the above proof should admit that we have proved the conjecture. Please recommend this proof to a famous magazine for publication and make your contribution to the proof of Goldbach's conjecture.
(5.7) : Summary of theorem 18 proof work:
5.13 This part is to prove theorem 18: If the conjecture is true for 2n and k (=n+1) is composite, then at least one of (hr+2) is an odd prime, which guarantees that the conjecture is true for 2k.
We want to complete the proof of theorem 18 using the formula (4.0.4).
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr) (4.0.4)
num(k≤h≤2k-3)-1=num(2k=ht+(2+hu))+num(2k=ps+(2+hr)) (5.13.3)
There are two basic reasons for choosing (4.0.4). The first, (4.0.4) exists 2n=ps+hr, from which we get 2k=ps+(2+hr). The second, hu and hr, are odd composite numbers. However, theorem 16C has proved that at least one of (2+hu),(2+hr), is an odd prime. Moreover, when (2+hu) is an odd prime, it is not satisfied (5.13.3). These basic conditions provide us with the most favorable basis for proving theorem 18.
In order to prove theorem 18, the relationship between
num(n≤h≤2n-3) and num(k≤h≤2k-3) must be studied. Otherwise, there's no proof to begin with.
In (5.1), we prove that if 2n-1 is an odd prime number, the conjecture must be true for 2k.
In (5.2), we first assume that 2n-1 is odd composite number. Then we assume that n is odd composite number, n is odd prime, and n is even. The following three relationships are obtained.
A If n is an odd composite number, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3).
B If n is an odd prime number, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: On the right side of the formula, -1, is to subtract an odd composite number (2n-1) = (2k-3).
C If n is even, there must be
num(n≤h≤2n-3)=num(k≤h≤2k-3)-1.
Note: On the right side of the formula, -1, is to subtract an odd composite number (2n-1) = (2k-3).
For the above three relations, it is necessary to prove separately that (2+hr) is an odd prime number. The whole proof of 5.13 was carried out under the guidance of this mathematical thought.
For the above three relations, we have separately proved that (2+hr) exists as odd prime numbers. So there is at least one 2k=ps+(2+hr), 2k is the sum of the odd prime ps and the odd prime (2+hr), 2k, the conjecture is established.
So the proof of theorem 18 is complete.
Theorem 18, finished proving.
Theorem 18 proves that if the conjecture is true for 2n and k (=n+1) is composite number, then at least one of (hr+2) is an odd prime, which guarantees that the conjecture is true for 2k.
Theorem 18 proves that a source of 2k=pi++pj+ must exist. One source is: if one of (hr+2) is an odd prime, then 2k=ps+(2+hr) is a source of 2k=pi++pj+. Theorem 18 affirms that there must be a number (hr+2) that is an odd prime, which guarantees that the conjecture holds at 2k.
Similar to theorem 18, Theorem 19 will prove that another source of 2k=pi++pj+ must exist. Another source is: if one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+. Theorem 19 affirms that there must be a number (hk+2) that is an odd prime, which guarantees that the conjecture holds for 2k.
5.14 Theorem 19: If the conjecture is true for 2n and k (=n+1) is a composite number h, then at least one of (hk+2) is an odd prime p, which guarantees that the conjecture is true for 2k.
Proof: (1) Quote theorem 11 as follows:
Theorem 11: If the 2n conjecture is true, then 2k=pi++pj+ has the
following four sources, as long as one of the sources exists, it will ensure that the conjecture continues to be true at 2k.
The 4 sources of 2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+;
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
If the Goldbach conjecture holds for 2n, 2k=pi++pj+ has four sources, so long as one source exists, the conjecture will continue to hold for 2k. So, to prove the conjecture, you just need to prove the existence of a source.
Conversely, if the Goldbach conjecture is true at 2n, and if it is not true at 2k, then none of the four sources of 2k=pi++pj+ can exist.
As a proof by contradiction, if the conjecture is not valid when 2k is assumed, it is assumed that: 2k=pi++pj+ 4 sources, none of which exist; As long as the contradiction can be found according to rigorous mathematical reasoning, it is proved that 2k=pi++pj+ 4 sources, at least one of the existence. That proves the 2k conjecture. That's the mathematical idea behind proving theorem 19.
(2) The inference of Hou Shaosheng's theorem is as follows:
About the formula:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
There is always:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Among them, the convention is: 3≤q≤n,q is odd.
pi, pj, ps, pd, are all odd prime numbers; ht, hu, hr, hk are all odd composite numbers.
And pi≤pj, ht≤hu, ps≤hr, hk≤pd.
pi, ht, ps, hk, ∈[3,n]; pj, hu, hr, pd∈[n,2n-3].
Under our theoretical system, if the conjecture is true for 2n, it is accepted that the above (4.0.1), (4.0.2), (4.0.3), (4.0.4) are also true. Therefore, the simultaneous holding of (4.0.1), (4.0.2), (4.0.3), and (4.0.4) is also the theoretical basis for our proof of theorem 19, in particular the admission that 1≤num(2n=hk+pd).
(3)It is only necessary to prove that when k is a composite number h, Goldbach's conjecture holds for 2k.
Since 2k=k+k, if k is an odd prime p,2k is already the sum of two odd prime numbers, and the conjecture naturally holds.
Therefore, as long as it can be shown that k is a composite number h, the 2k conjecture must hold, then Goldbach's conjecture must hold.
k is a composite number h, and in general, it is necessary to distinguish between k being an odd composite number h and k being an even composite number h.
(4) At least one of (ht+2) and (hk+2) is an odd prime p.
Quote theorem 16C as follows:
In both (ht+2) and (hk+2), at least one is an odd prime p.
In both (hu+2) and (hr+2), at least one is an odd prime p.
(5)If k is a composite number h, then at least oneof(hk+2) is an odd prime p, ensuring that the conjecture holds for 2k.
In the following proof, it is necessary to distinguish between k being an even composite number h and k being an odd composite number h, given separately prove it.
(5.1) If k is aoddcomposite number h, then at least oneof(hk+2) is an odd prime p, ensuring that the conjecture holds for 2k.
Specific proof is as follows:
Quote (4.0.2) below.
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd). (4.0.2)
By assuming that the conjecture is true for 2n, we admit that (4.0.2)
is true.
(4.0.2) is the object of our next study.
Since k (=n+1) is an odd composite number, n is an even number. It can
be obtained from (4.0.2) :
num(3≤h≤k)
=num(3≤h≤n)+1
=num(2n=ht+hu)+num(2n=hk+pd)+1
=num(2n+2=ht+2+hu)+num(2n+2=hk+2+pd)+1
=num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd)+1 (5.14.1)
That is:
num(3≤h≤k)=num(2k=(ht+2)+hu)+ num(2k=(hk+2)+pd)+1 (5.14.1)
Note: To the right of the above formula ,+1, is to add an odd composite number k (=n+1), K of course in the interval [3, k].
Each of these steps is based on a mathematical definition, or a mathematical axiom, or a mathematical theorem. So (5.14.1) must be true.
Now analyze (5.14.1) as follows:
num(3≤h≤k) is the number of odd composite number h in the interval [3, k].
Because (5.14.1) is true, according to our convention, (ht+2)≤hu, (hk+2)≤pd, so in (5.14.1), (ht+2), (hk+2), are within the interval [3, k].
hu, pd, all in the range [k, 2k-3].
hu, is odd composite number; pd is an odd prime number.
ht, hk, are both odd composite numbers, both in the interval [3, n].
(ht+2), (hk+2), whether the odd prime number p or the odd composite number h, is what needs to be discussed below.
The following, through the way of debating questions and answers, proves that 2k, Goldbach conjecture must be true.
Problem 1: If there is a (hk+2 ) is an odd prime p, Goldbach's conjecture is established.
Theorem 16C states that at least one of (ht+2) and (hk+2) is an odd prime p.
If at least one of (hk+2) is an odd prime p, then the Goldbach conjecture holds for 2k.
This is because, in (2k=(hk+2)+pd), there is at least one 2k, which is already the sum of the odd prime (hk+2) and the odd prime pd. So at 2k, Goldbach's conjecture is established.
If there is not at least one of (hk+2) that is an odd prime p, then every (hk+2) is an odd composite number h.
Now, under the assumption that each (hk+2) is an odd composite number h, we will continue our argumentative question and answer.
Problem 2: Under the assumption that every (hk+2) is an odd composite number h, at least one of (ht+2) is an odd prime number p. Theorem 16C states that at least one of (ht+2) and (hk+2) is an odd prime p.
If every (hk+2) is an odd composite number h, then at least one of (ht+2) is an odd prime number p.
Next, we continue our argumentative question and answer under the assumption that every (hk+2) is an odd composite number h and at least one of (ht+2) is an odd prime number p.
Problem3: If every (hk+2) is an odd composite number h and at least oneof(ht+2) is an odd prime number p, does (5.14.1) still hold?
num(3≤h≤k)=num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd)+1 (5.14.1)
(5.14.1), is a mathematical equation, both sides of the equal sign, should have the same quantity, the same name of things.
On the left side of the equal sign, num(3≤h≤k) is the number of odd composite number h in the interval [3, k].
To the right of the equal sign, num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd)+1 must also be the number of odd composite numbers h in the interval
[3, k].
It follows that num(2k=(ht+2)+hu), num(2k=(hk+2)+pd), 1, must all be the number of odd composite numbers h in the interval [3, k].
Conversely, if num(2k=(ht+2)+hu), num(2k=(hk+2)+pd), 1, one is not
the number of odd composite number h in the interval [3, k], their sum, cannot be the number of odd composite numbers h in the interval [3, k].
Since it is assumed that every (hk+2) is an odd composite number h in the interval [3, k], according to the definition (1.2 Meaning of mathematical notation in the paper), num (2k=(hk+2)+pd) represents the number of odd composite numbers (hk+2) in the interval [3, k].
Now note: to the right of the above formula, +1, is to add an odd composite number k (=n+1), K of course in the interval [3, k].
It can be seen from the note that 1 refers to an odd composite number k (=n+1), and K is of course in the interval [3, k]. Thus, 1 is the number of odd composite number h in the interval [3, k].
Since num (2k=(ht+2)+hu) must be the number of odd composite numbers h in the interval [3, k],therefore, every (ht+2) must be the odd composite number h in the interval [3, k].
Conversely,If there is a (ht+2) that is not an odd composite number h in the interval [3, k], According to the definition (1.2 Meaning of mathematical notation in the paper), num (2k=(ht+2)+hu) is not the number of odd composite numbers h in the interval [3, k].
Note that every (ht+2) must be an odd composite number h in the interval [3, k], contradicting the assumption that at least oneof(ht+2) is an odd prime number p.
Above, we derive the contradiction under the assumption that every (hk+2) is an odd composite number h and at least oneof(ht+2) is an odd prime number p.
This proves that the assumption that every (hk+2) is an odd composite number h, and at least oneof(ht+2) is an odd prime number p, is not valid! Since at least one of (hk+2), (ht+2) is an odd prime p,thereforeat least one of (hk+2) is an odd prime p. So at 2k, Goldbach's conjecture works.
The main logical procedure for proving our conjecture is to assume that every (hk+2) is an odd composite number h, and at least oneof(ht+2) is an odd prime number p, and then derive the contradiction, so the hypothesis cannot be established. And since at least one of (hk+2), (ht+2) is an odd prime p,therefore,at least one of (hk+2) is an odd prime p. So at 2k, Goldbach's conjecture works.
Above, we have proved that Goldbach's conjecture holds when k is a odd composite number h.
It is shown below that if k is an even composite number h, Goldbach's conjecture holds.
(5.2) If k is an even composite number h, then at least oneof(hk+2) is an odd prime p, in 2k, the conjecture must hold.
Specific proof is as follows:
Quote (4.0.2) below.
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
By assuming that the conjecture is true for 2n, we admit that (4.0.2) is true.
(4.0.2) is the object of our next study.
Since k(=n+1) is an even composite number, from (4.0.2):
num(3≤h≤k)
=num(3≤h≤n)
=num(2n=ht+hu)+num(2n=hk+pd)
=num(2n+2=ht+2+hu)+num(2n+2=hk+2+pd)
=num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd) (5.14.2)
that's it
num(3≤h≤k)=num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd) (5.14.2)
Each of these steps is based on a mathematical definition, or a mathematical axiom, or a mathematical theorem. So (5.14.2) must be true.
Now analyze (5.14.2) as follows:
num(3≤h≤k) is the number of odd composite numbers h in the interval
[3, k].
Because (5.14.2) is true, and because we agree that (ht+2)≤hu; (hk+2)
≤pd; So in (5.14.2), (ht+2), (hk+2), are all in the interval [3, k].
hu, pd, all in the interval[k, 2k-3].
hu, is odd composite number; pd is an odd prime number.
ht, hk, are both odd composite numbers, both in the interval [3, n].
(ht+2), (hk+2), whether it is odd prime number or odd composite number, is what needs to be discussed below.
The following, through the way of debating questions and answers, proves that 2k, Goldbach conjecture must be true.
Problem 1: If there is oneof(hk+2)is an odd prime number, Goldbach's conjecture is established.
If at least one of(hk+2) is an odd prime, then the Goldbach conjecture holds for 2k.
This is because 2k=(hk+2)+pd, with at least one 2k, is already the sum of the odd prime number (hk+2) and the odd prime number pd. So at 2k, Goldbach's conjecture is established.
If there is not at least one of (hk+2) that is an odd prime, then every (hk+2) is an odd composite number.
Now, under the assumption that each (hk+2) is an odd composite number, we will continue our argumentative question and answer.
Problem 2: Under the assumption that every (hk+2) is an odd composite number, at least one of (ht+2) is an odd prime number.
Theorem 16C states that at least one of (ht+2) and (hk+2) is an odd prime p.
Since every (hk+2) is assumed to be an odd composite number h,therefore,at least one of (ht+2) is an odd prime number p.
Next, we continue our argumentative question and answer under the assumption that every (hk+2) is an odd composite number h and at least one of (ht+2) is an odd prime number p.
problem3: If every (hk+2) is an odd composite number h and at least oneof(ht+2) is an odd prime number p, does (5.14.2) still hold?
num(3≤h≤k)=num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd) (5.14.2)
(5.14.2), is a mathematical equation, both sides of the equal sign, should have the same quantity, the same name of things.
On the left side of the equal sign, num(3≤h≤k) is the number of odd composite numbers h in the interval [3, k].
To the right of the equal sign, num(2k=(ht+2)+hu)+num(2k=(hk+2)+pd) must also be the number of odd composite numbers h in the interval
[3, k].
It follows that num(2k=(ht+2)+hu),num(2k=(hk+2)+pd), must be the number of odd composite numbers h in the interval [3, k].
Conversely, if num(2k=(ht+2)+hu), num(2k=(hk+2)+pd), one of them is not the number of odd composite numbers h in the interval [3, k], their sum, cannot be the number of odd composite numbers h in the interval
[3, k].
Since it is assumed that every (hk+2) is an odd composite number h in the interval [3, k],therefore, num (2k=(hk+2)+pd) is the number of odd composite numbers (hk+2) in the interval [3, k], according to the definition (meaning of mathematical notation in 1.2 paper).
Since num (2k=(ht+2)+hu) must be the number of odd composite numbers h in the interval [3, k], therefore,every (ht+2) must be the odd composite number h in the interval [3, k].
Conversely, if there is a (ht+2) that is not an odd composite number h in the interval [3, k], num (2k=(ht+2)+hu) is not the number of odd composite numbers h in the interval [3, k] according to the definition (meaning of mathematical notation in 1.2 paper).
Note that every (ht+2) must be an odd composite number h in the interval [3, k], contradicting the assumption that at least oneof(ht+2) is an odd prime number p.
Above, we derive the contradiction under the assumption that every (hk+2) is an odd composite number h and at least oneof(ht+2) is an odd prime number p.
This proves that the assumption that every (hk+2) is an odd composite numbersh, and at least oneof(ht+2) is an odd prime number p, is not valid! Since at least one of (hk+2), (ht+2) is an odd prime p,therefore ,at least one of (hk+2) is an odd prime p. So at 2k, Goldbach's conjecture works.
The main logical procedure for proving our conjecture is to assume that every (hk+2) is an odd composite numbersh, and at least oneof(ht+2) is an odd prime number p, and then derive the contradiction, so the hypothesis cannot be established. And since at least one of (hk+2), (ht+2) is an odd prime p, therefore,at least one of (hk+2) is an odd prime p. So at 2k, Goldbach's conjecture works.
This proves that if k is an even composite number, Goldbach's conjecture holds.
(6) At 2k, Goldbach's conjecture is valid
In (5.1) and (5.2) above, we have respectively proved that Goldbach's conjecture is valid when k is an odd composite number h and when k is an even composite number h. This proves that as long as k is a composite number h, at 2k Goldbach's conjecture holds.
Also because Goldbach's conjecture holds when k is an odd prime p,therefore, 2k is any positive integer Goldbach's conjecture is all true.
(7) The 8 mathematical examples in the paper are completely consistent with theorem 19
In the paper, there are 8 mathematical examples. We examined each of these examples. In every example, at least one of (hk+2) is an odd prime p. Such that 2k=(hk+2)+pd, at least one of 2k is the sum of the odd prime number (hk+2) and the odd prime number pd, guaranteeing the Goldbach conjecture at 2k.
Theorem 19, end of proof.
Please note to the reader:
Theorem 17 is an independent proof of Goldbach's conjecture.
Theorem 18 is an independent proof of Goldbach's conjecture.
Theorem 19 is another independent proof of Goldbach's conjecture.
Three proofs, if only one of them is correct, Goldbach's conjecture is true.
We, the prover, are, of course, sure that all three proofs are correct. Otherwise I wouldn't ask you to review it. At the same time, you are welcome to put forward valuable comments, we will refer to your comments, modify the paper better. You are welcome to participate and contribute to the proof of Goldbach's conjecture.
5.15 Summary of proof of conjecture:
From numerous concrete mathematical examples, the abstract mathematical theory (proposition) is raised, and then the abstract mathematical theory is proved as a mathematical theorem; The mathematical theorems we have obtained must be tested by mathematical examples. This is the mathematical idea and method followed by this proof of Goldbach's conjecture.
If the Goldbach conjecture holds for 2n, and proves that it holds for 2k, from n to k(=n+1), it appears that the difference is only one integer. However, it caused great changes.
If 2n=pi+pj is true, then pi and pj are symmetric with respect to n.
If 2k=pi++pj+ is true, then pi+, pj+ is symmetric with respect to k.
It should be noted that in the interval [3, n] and [3, k], the odd primes are exactly the same if k is composite number. That is, where the number of odd primes is equal, and the same odd prime is in the interval [3, n] and [3, k].
In the interval [n, 2n-3] and [k, 2k-3], where k is composite number, the odd primes are exactly the same except for n and 2k-3.
In the figure below, k=n+1, 2k-3=2n-1.
At 2n, the inference of Hou Shaosheng's theorem has the following four formulas:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-3)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-3)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Of these 4 formulas, there are only 4 basic formulas, as follows:
2n=pi+pj, 2n=ps+hr, 2n=ht+hu, 2n=hk+pd.
and that 2n+2=pi+2+pj, 2n+2=ps+2+hr, 2n+2=ht+2+hu, 2n+2=hk+2+pd.
Further there are:
2k=pi+2+pj, 2k=ps+2+hr, 2k=ht+2+hu, 2k=hk+2+pd.
2n+2=2k, that's what every schoolboy knows.
Hou Shao-sheng's theorem is the theoretical basis for proving Goldbach's conjecture. The proof of Hou's theorem was the first hurdle. Before proving Hou Shaosheng's theorem, no one knows the content of Hou Shaosheng's theorem, which is the biggest difficulty encountered in proving it. After obtaining Hou Shao-sheng's theorem, how to obtain the inference of Hou Shao-sheng's theorem is the second difficulty.
After proving Hou's theorem and its inferences, the difficulty of proving the conjecture is how to prove that at least one of the odd prime numbers is in (pi+2), or in (2+pj), or in (2+hr), or in (hk+2).
This is what all the above proof is about.
2n=pi+pj. pi, pj are symmetric about n;
2n=ps+hr. ps, hr are symmetric about n;
2n=ht+hu. ht, hu are symmetric about n;
2n=hk+pd. hk, pd are symmetric about n.
From 2n=pi+pj, 2n=ps+hr, 2n=ht+hu, 2n=hk+pd,
to 2k=pi++pj+, 2k=ps++hr+, 2k=ht++hu+, 2k=hk++pd+,
it is a process from quantitative change to qualitative change .
We have proved with new theories and methods that:If the conjecture is true at 2n, then the conjecture must be true at 2k.
The above proof shows that the theoretical system we have established is absolutely rigorous and correct. It can prove Goldbach's conjecture under various harsh conditions.
The above proof answers the core question:Do the four sources of 2k=pi++pj+not exist,at the same time? Now you can beabsolutely certain: 4 sourcesof2k=pi++pj+, at the same time do not exist, completely impossible. If only one of these four sources exists, the 2k conjecture is guaranteed. This is the decisive factor and the fundamental guarantee of the continuity of the conjecture.
The four sources of2k=pi++pj+are the fundamental guarantee that Goldbach's conjecture must be true.
The four sources of2k=pi++pj+are the genetic code that Goldbach's conjecture must hold.
The four sources of2k=pi++pj+are the mysteries that Goldbach's conjecture must be true
5.12 Theorem 17, we proved: if the conjecture is true for 2n and k (=n+1) is composite number, then at least one of (pi+2), (hr+2) is an odd prime number, which guarantees that the conjecture must be true for 2k.
Theorem 17, proved two sources of 2k=pi++pj+: 2k=(pi+2)+pj , 2k=ps+(hr+2), at least one of them exists.
5.13 Theorem 18, we proved: if the conjecture is true for 2n and k (=n+1) is composite number, then at least one of (hr+2) is an odd prime number, which guarantees that the conjecture must be true for 2k.
Theorem 18, proved one source of 2k=pi++pj+:2k=ps+(hr+2) must exist.
5.14 Theorem 19, we proved: if the conjecture is true for 2n and k (=n+1) is composite number, then at least one of (hk+2) is an odd prime number, which guarantees that the conjecture must be true for 2k.
Theorem 19, proved one source of 2k=pi++pj+:2k=(hk+2)+pd must exist.
Theorem 17, theorem 18, and theorem 19 are theorems that exist independently of each other. Any one of them would guarantee Goldbach's conjecture. If you want to disprove our proof of Goldbach's conjecture, you must find specific mathematical errors in each of the above three proofs!
So much for the proof of Goldbach's conjecture.
5.16 A Note
The above proof of Goldbach's conjecture is a proof of conjecture under the second theoretical system.
In 1967, Hou learned about Chen Jingrun and Goldbach's conjecture. In 1977, Hou Shaosheng proved the sufficient and necessary condition theorem of conjectures. In 2000, after 23 years of preparation, he gave the first proof of Goldbach's conjecture. In 2006, in the Guangming Daily Press, published the monograph "Proof of Goldbach's conjecture·Proof of Fermat's last conjecture ". 1,000 volumes of Chinese books have been circulated so far, and no one has found fundamental mathematical errors.
The proof of Goldbach's conjecture in the book is the first proof of Goldbach's conjecture given by Hou Shaosheng, that is, the proof of Goldbach's conjecture under the first theoretical system. The proof under the first theoretical system has three core mathematical ideas.
The first core mathematical idea is that proved that theorem of the sufficient and necessary condition that the conjecture is hold,and insists that a proof satisfies the theorem of sufficient and necessary conditions is a correct proof, and a proof does not satisfy the theorems of sufficient and necessary conditions must be wrong.
The second core mathematical idea is: It is proved that the single digits is all the odd composite numbers of 1,3,7,9, and are only the function values of 10 odd composite number formulas.Thus, all positive integers can be divided into 17 classes: the single digits is all the odd composite numbers of 1,3,7,9, divided into 10 classes; The single digit is all the odd composite numbers of 5, divided into 1 class;the single digits is all even numbers of 2,4,6,8,0, divided into 5 classes; All prime numbers, as 1 class.
The third core mathematical idea is that if n is a prime number, 2n, the conjecture naturally holds, without the need for proof. For the remaining 16 classes of composite numbers, classification proof. When proving a certain class of composite numbers, the other composite numbers are excluded, the interference is eliminated to the maximum extent, and the conditions for proving are created.
In fact, Goldbach's conjecture is divided into 17 small conjectures and proved separately. It's like a piece of cake that you can't eat all at once, so we divide it into 17 pieces and then eat each piece one by one.
The core mathematical idea of the second theoretical system is to uncover the genetic code between the 2n conjecture and the 2 (n+1) conjecture.
The second theoretical system is based on Hou Shao-sheng's identity 2n=q+(2n-q). This identity has three most valuable properties: first, it is an identity;Second, this identity contains all the possibilities of factorization of 2n into the sum of two integers; The third one, q, takes an odd number, 2n is just the sum of two odd numbers.In this way, all forms of decomposition that are irrelevant to the conjecture are deleted, and all elements that may be relevant to the conjecture are retained. We obtained all the elements that to prove conjecture.
The proof of Hou Shaosheng's theorem is a great achievement under the second theoretical system, and also a major breakthrough in the history of Goldbach's conjecture. The mathematical expression of Hou Shaosheng's theorem contains all the elements needed to prove the conjecture, which provides a solid theoretical basis for proving the conjecture.
The four inferential formulas of Hou Shaosheng's theorem provide specific and highly targeted mathematical formulas for the proof of conjectures.
The four major theoretical questions put forward by the author reveal the mystery of Goldbach's conjecture that there are only four genetic codes, and as long as there is a genetic code, the conjecture is guaranteed to continue to be true!
Under the second theoretical system, Hou Shaosheng proved theorem 17, theorem 18 and theorem 19. These three theorems exist independently of each other.Any one of these theorems is sufficient to ensure that the proof of the conjecture is completely completed.
Let real mathematicians review the proofs under the second theoretical system, and spare no efforts to teach and comment. Hou Shaosheng looks forward to your guidance and cooperation, and looks forward to your joint publication in the world's most famous magazine.
On November 15, 2007, Professor Ma Linjun and Professor Li Baitian of Sun Yat-sen University, after reviewing the Chinese book for half a year, wrote in the written Proof Materials: Wang Yuan, Chen Jingrun and other famous mathematicians said that it would be difficult to find a new mathematical idea to prove Goldbach's conjecturing in 1,000 years, and now Hou Shaosheng has solved the problem. We have studied "1+1" for decades, and Hou's research results are of the highest level within the scope of our knowledge, which has the basis for holding expert meetings and deserves the help and support of the government.
After Chen Jingrun proved 1+2, mathematicians all over the world almost recognized that the theory and method of 1+2 can not provide any help for proving 1+1! To prove 1+1, one has to look for new mathematical ideas.
In 1992, Wang Yuan, Chen Jingrun, Pan Chengdong, Yang Le, four academicians of the Chinese Academy of Sciences held a press conference, openly said: in another 1,000 years will be difficult to find a new mathematical idea to prove the conjecture, let alone prove 1+1!
In 2006, Wang Yuan said on CCTV4: I am firmly against the Chinese trying to prove 1+1.Because it's impossible!
Since Chen Jingrun proved 1+2, Wang Yuan, and Pan Chengdong proved 1+4, the leading position in the world and the absolute authority in China, their remarks made the proof of Goldbach's conjecture enter a frozen period: No magazine in the world is willing to review the "proof of Goldbach's conjecture", and in China there is a major tragedy that the review did not find the problem and did not dare to publish it!
In October 2013, Beijing Today Keyuan magazine published Hou Shaosheng's "New Mathematical Thought to Prove Goldbach Conjecture" and "Defect of Eratosthenes screening method ,and Ideal final screening method". Two papers, Hou Shaosheng invited Beijing Today Keyuan magazine editor Chen Jiazhong personally sent to Wang Yuan. Wang Yuan promised to give an explanation. Until Wang Yuan died, he did not give an explanation. Wang Yuan claimed to be proficient in screening; And said that it would be difficult to find new mathematical ideas to prove the conjecture for another 1,000 years. However, in the face of two papers, he was dumb!!
I sincerely hope that some competent mathematician will cooperate with me and publish a proof of Goldbach's conjecture! Let mathematicians around the world get out of the quagmire of proving Goldbach's conjecture, and end the sad history of the Chinese nation without mathematical theorems!
For references, see the end.
Section 6,Summary of the proof process of Goldbach conjecture
6.1 Study the three historical stages of Goldbach's conjecture
In 1742, Goldbach and Euler proposed the Goldbach conjecture. For 282 years, countless mathematicians have tried to prove it.
The period from 1742 to 1920 was a period of constant testing of Goldbach's conjecture. At this stage, by expanding the scope of the test, humans are convinced that the conjecture is highly likely to be correct.This is the first historical stage in the study of conjecture. The most important thing at this stage was that Goldbach made the conjecture, and then Euler published the conjecture and hoped that future mathematicians would prove it.
From 1920 to 1977, humans used electronic computers to verify Goldbach's conjecture on a larger scale. At this stage, the 9+9 proof method was created, and the 1+2 proof method was developed by Chen Jingrun. But mathematicians, including Chen, believed that to prove the conjecture, new mathematical ideas had to be sought. According to the Academy of Mathematics of the Chinese Academy of Sciences, it will be difficult to find new mathematical ideas to prove conjectures in another 1,000 years.
From 1977 to 2020, this is the third historical phase hypothesized by human research. The outstanding feature of this stage is that in 1977, Hou Shaosheng proved the sufficient and necessary condition theorem of Goldbach's conjecture in an unpublished manuscript. And the conclusion is drawn: if the proof satisfies the theorem of sufficient and necessary conditions, the proof is correct; If the proof does not satisfy the sufficient and necessary conditions theorem, the proof must be wrong. This new mathematical idea ended the history of groping in the dark and pointed the way to proving Goldbach's conjecture.
What is more valuable is that under the guidance of the theorem of sufficient and necessary conditions, after 23 years of hard and meticulous work, a series of problems satisfying the theorem of sufficient and necessary conditions have been creatively solved. And a proof of Goldbach's conjecture is written (Method 1).In 2006, he published the Proof of Goldbach's Conjecture and the Proof of Fermar's Last Conjecture. So far no one has been able to deny any a of the proofs.
6.2 Hou Shaosheng's theorem is a historic breakthrough in the study of conjecture.
The proof of Goldbach's conjecture (Method 1), while correct, does not, however, have the ability to answer: what is the genetic code between the conjecture at 2n and the conjecture at 2 (n+1)?
In order to uncover the secret that the conjecture holds for 2n and also for 2 (n+1), we study Hou Shao-sheng's identity. We have shown that 2n=q+(2n-q), where q≤(2n-q), contains the full possibility of factorising the even 2n into the sum of two odd numbers.
The mathematical representation of Goldbach's conjecture, 2n=pi+pj, is only a part of 2n=q+(2n-q). In order to fully grasp 2n=pi+pj, we must study the basic law of 2n=q+(2n-q). The basic law of 2n=q+(2n-q) is Hou Shaosheng's theorem.
The proof of Hou Shaosheng's theorem is the first difficulty. Before proving Hou Shaosheng's theorem, no one knew what the mathematical formula of Hou Shaosheng's theorem looked like. Therefore, proving Hou Shaosheng's theorem was the first major breakthrough.
Proving the sufficient and necessary condition theorem of the conjecture, Hou Shaosheng only used about 25 minutes, it should be said that the hand can be obtained. However, it took thousands of hours to prove Hou Shaosheng's theorem, and this was after the publication of the Proof of Goldbach's conjecture and the Proof of Fermar's Last Conjecture, and about 10 years of preparation.
The mathematical formula of Hou Shaosheng's theorem contains all the law of change of 2n=q+(2n-q), which lays a theoretical foundation for us to study Goldbach's conjecture comprehensively.
Hou Shaosheng theorem, no answer:
How do all odd prime numbers p in the interval [3,n] combine with odd numbers in the interval [n,2n-3]?
How do all odd composite numbers h in the interval [3,n] combine with odd numbers in the interval [n,2n-3]?
How do all odd prime numbers p in the interval [n,2n-3] combine with odd numbers in the interval [3,n]?
How do all odd composite numbers h in the interval [n,2n-3] combine with odd numbers in the interval [3,n]?
In order to answer the above questions, it is necessary to deduce the inference of Hou Shaosheng's theorem. Proving the inference of Hou Shaosheng's theorem is much easier than proving Hou Shaosheng's theorem. However, it still requires a certain amount of wisdom and a lot of work. Until it is proved, no one knows what the mathematical formula of inference looks like. The Angle from which it should be inferred still needs to be thought over. Therefore, the inference of Hou Shaosheng's theorem is the second major breakthrough.
The essence of the inference of Hou Shaosheng's theorem is to divide the mathematical formula of Hou Shaosheng's theorem, 1 into 4. Each of the four mathematical formulas represents only a part of the mathematical formulas of Hou Shaosheng's theorem.
The four mathematical formulas in the inference describe a certain aspect of Hou Shaosheng's theorem very deeply and carefully, and play an important role in our in-depth understanding of the basic law of 2n=q+(2n-q). Played a key role in proving Goldbach's conjecture.
6.3 Four major theoretical problems are the core theoretical problems in the proof of conjectures
The four major theoretical problems proposed by the author are the core theoretical problems in the proof of Goldbach's conjecture.
Goldbach's conjecture holds, essentially, for 2n it holds, and for 2 (n+1) it still holds.
The proof of Goldbach's conjecture must answer: If the conjecture is true for 2n, why is it still true for 2 (n+1)? What is the close relationship between the establishment of 2n and the establishment of 2k? This is the most critical, the core essence of the conjecture proof, but also the most difficult problem.
The four major theoretical questions theoretically fully answer:the close relationship between the establishment of 2n and the establishment of 2 (n+1).
Theorem 11 in Section 5 proves that: if Goldbach's conjecture 2n=pi+pj is true for 2n, then Goldbach's conjecture 2k=pi++pj+ for 2k has four sources; And as long as one source exists, Goldbach's conjecture will continue to hold at 2k. This is the most important discovery and theory in the proof of Goldbach's conjecture.
2k=pi++pj+ has four sources, which is the fundamental reason and guarantee for the continued establishment of Goldbach conjecture; Is the fundamental mystery of the Goldbach conjecture.
Theorem 12 in Section 5 proves that if Goldbach's conjecture 2n=pi+pj is true for 2n, then 2k=ps++hr+ for 2k has four sources.
Theorem 13 in Section 5 proves that if Goldbach's conjecture 2n=pi+pj is true for 2n, then 2k=ht++hu+ has four sources for 2k.
Theorem 14 in Section 5 proves that if Goldbach's conjecture 2n=pi+pj is true for 2n, then 2k=hk++pd+ for 2k has four sources.
Four major theoretical questions not only theoretically answer the close relationship between 2n establishment and 2k establishment, but also accept the strict test of 8 examples.
The test shows that 2k=pi++pj+ has four sources, which are perfectly consistent with complex mathematical examples.
2k=ps++hr+ has 4 sources; 2k=ht++hu+ has 4 sources; 2k=hk++pd+ has 4 sources; These theories are in perfect agreement with complex mathematical examples.
The test shows that Hou Shaosheng's theorem is correct and the inference of Hou Shaosheng's theorem is correct. Our reasoning process is correct. Readers are welcome to test with other examples.
It has already been pointed out that as long as one of the four sources of 2k=pi++pj+ exists, the 2k time conjecture is guaranteed. Could it be that none of the four sources exist?
This is a central question that must be answered.
5.12 Theorem 17: If the conjecture is true at 2n and k (=n+1) is composite number, then at least one of (pi+2), (hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Theorem 17, proves two sources of 2k=pi++pj+: 2k=(pi+2)+pj; 2k=ps+(hr+2), at least one of them exists.
The clever thing about this theorem proving procedure is that it captures two of the four sources of 2k=pi++pj+ : 2k=(pi+2)+pj, 2k=ps+(hr+2), and at least one of them exists. In a short process, it is proved that conjecture must be true at 2k.
5.13 Theorem 18: If theconjecture is true at 2n and k (=n+1) is compositenumber, then at least one of (hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Theorem 18, proves that2k=pi++pj+1 source :2k=ps+(hr+2), must exist.
5.14 Theorem 19: Ifthe conjecture is true at 2n and k (=n+1) is compositenumber, then at least one of (hk+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Theorem 19, proves that2k=pi++pj+1 source : 2k=(hk+2)+pd, must exist.
In the above proof, the four inferential formulas of Hou Shaosheng's theorem play a decisive role.
We also prove that the formula for calculating the number of odd primes in the interval [n,2n], there must be odd primes in the interval [n,2n].
Now, we have two different theories that can prove Goldbach's conjecture. One theoretical system is based on the sufficient and necessary condition theorem of Goldbach conjecture. The other one is based on Hou Shao-sheng's theorem and centers on the four inferential formulas of Hou Shao-sheng's theorem and the four sources of 2k=pi++pj+. Both proofs satisfy the necessary and sufficient theorems that the conjecture is true!
6.4Our main logical process for proving Goldbach's conjecture is as follows:
6.4.1: Object of study: Goldbach conjecture 2n=pi+pj.
Ask the question: What are the necessary and sufficient conditions for the conjecture to be true?
Answer the question: 2n=pi+pj, the sufficient and necessary condition theorem: (n-△), (n+△), are odd prime numbers.
Ask the question: n+△, in the interval [n,2n]. It must be proved that there are odd primes in the interval [n,2n].
Answer the question: Derive the formula for calculating the number of odd primes in the interval [n,2n].
It is proved that there are odd prime numbers in the interval [n,2n], which satisfies one of the necessary conditions for the conjecture to be established.
The above is a branch of the logical process of proving the conjecture.
6.4.2: The main logical process for proving Goldbach's conjecture is as follows:
Research object: 2n=pi+pj, 2n=q+(2n-q), where q≤(2n-q),q is odd.
The conjecture expression: 2n=pi+pj, is only a part of 2n=q+(2n-q).
Asking questions: Hou Shao-sheng's expansion of identity
Answer the question: Prove Hou Shaosheng's theorem:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+ num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
Where: 2n=pi+pj, pi is an odd prime number in the interval [3,n]; pj is an odd prime number in the interval [n,2n-3].
Ask questions:
How do all odd prime numbers p in the interval [3,n] combine with odd
numbers in the interval [n,2n-3]?
How do all odd composite numbers h in the interval [3,n] combine with odd numbers in the interval [n,2n-3]?
How do all odd prime numbers p in the interval [n,2n-3] combine with odd numbers in the interval [3,n]?
How do all odd composite numbers h in the interval [n,2n-3] combine with odd numbers in the interval [3,n]?
Answer the question: Inference of Hou Shaosheng's theorem:
num(2n=q+(2n-q))=num(2n=pi+pj)+num(2n=ht+hu)
+ num(2n=ps+hr)+num(2n=hk+pd). (3.3.0)
There are always:
num(3≤p≤n)=num(2n=pi+pj)+num(2n=ps+hr); (4.0.1)
num(3≤h≤n)=num(2n=ht+hu)+num(2n=hk+pd); (4.0.2)
num(n≤p≤2n-2)=num(2n=pi+pj)+num(2n=hk+pd); (4.0.3)
num(n≤h≤2n-2)=num(2n=ht+hu)+num(2n=ps+hr). (4.0.4)
Ask questions: From the expression 2n=pi+pj:
2n=pi+pj;2n+2=pi+2+pj;2(n+1)=(pi+2)+pj;
2n=pi+pj;2n+2=pi+2+pj;2(n+1)=pi+(2+pj);
2n=ps+hr;2n+2=ps+2+hr;2(n+1)=ps+(2+hr);
2n=hk+pd;2n+2=hk+2+pd;2(n+1)=(hk+2)+pd;
These questions suggest that 2(n+1)=2k=pi++pj+ has four sources.
Ask the question: It must be proved that 2(n+1)=2k=pi++pj+ has 4 sources.
Answer the question:Section 5 Theorem 11: If the 2n conjecture is
true, then 2k=pi++pj+ has the following four sources, as long as one source exists, it will ensure that the conjecture continues to be true at 2k.
The 4 sources of 2k=pi++pj+ are as follows:
If one of (pi+2) is an odd prime, then 2k=(pi+2)+pj becomes one of 2k=pi++pj+;
If one of (pj+2) is an odd prime, then 2k=pi+(pj+2) becomes one of 2k=pi++pj+;
If one of (hr+2) is an odd prime, then 2k=ps+(hr+2) becomes one of 2k=pi++pj+;
If one of (hk+2) is an odd prime, then 2k=(hk+2)+pd becomes one of 2k=pi++pj+.
Ask the question: As long as one of the four sources exists, Goldbach's conjecture continues to hold true.
Finally, the only question: Is it possible that none of the four sources of 2k=pi++pj+ exist?
Answer the question:
5.12 Theorem 17: If the conjecture is true at 2n and k (=n+1) is
composite number, then at least one of (pi+2), (hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Theorem 17, proves two sources of 2k=pi++pj+: 2k=(pi+2)+pj; 2k=ps+(hr+2), at least one of them exists.
5.13 Theorem 18: If the conjecture is true at 2n and k (=n+1) is composite number, then at least one of (hr+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Theorem 18, proves that 2k=pi++pj+ 1 source :2k=ps+(hr+2), must exist.
5.14 Theorem 19: If the conjecture is true at 2n and k (=n+1) is composite number, then at least one of (hk+2) is an odd prime, which guarantees that the conjecture is true at 2k.
Theorem 19, proves that 2k=pi++pj+ 1 source: 2k=(hk+2)+pd, must exist.
Looking back on the process of proving Goldbach's conjecture, the rule follows:
First, the sufficient and necessary condition theorems of conjectures are proved. The theorem of sufficient and necessary conditions points out the general direction for proving conjectures. In this proof, the proof of Hou Shaosheng's theorem is very important and very difficult. Because that's the theoretical basis for proving the conjecture. On this basis, what other problems can we solve and what progress can we make through our efforts? Every step of the way is to reach the final goal. After we have obtained the four sources of 2k=pi++pj+, our ultimate goal is to prove that at least one of the four sources of 2k=pi++pj+ exists. It is under such logical thinking that the proof of Goldbach's conjecture is finally completed.
So much for the proof of Goldbach's conjecture.
6.5Your help is welcome
Welcome any experts to contact us, welcome any experts to ask questions, welcome any experts to cooperate with us! Welcome anyone who can help us! Please make your valuable contribution to the proof of Goldbach conjecture!
Hou Shao-Sheng Email: ayhss@163.com.