Prerpints.org logo
Preprint
Article

Generalisation Increases the Adaptive Value of Mate-Choice Copying when Immediate Copying is Costly

Altmetrics

Downloads

45

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 September 2024

Posted:

30 September 2024

You are already at the latest version

Alerts
Abstract
When assessing potential mates is costly, there will be selection for copying others. Mate-choice copying, which is the increased chance of mating with another individual after observing them mating with someone else (i.e., individual-based copying), has been documented in several species, including humans. It is touted as an example of the influence of culture on animal and human mating, but alone it is unlikely to lead the cultural evolution of mating. Rather, it requires mate-choice copying with generalisation (i.e., trait-based copying), which is the effect of immediate observations on future mating. This sort of mate-choice copying has been documented in six species, including humans. Here, I extend an existing game-theory model of mate-choice copying to include generalization (Extension 1), a cost to immediate copying (Extension 2), and both previous extensions (Extension 3). The results show that Extensions 1 and 2 decrease the adaptive value of mate-choice copying when compared to the original model. Extension 3 suggests that adding generalisation to mate-choice copying with a cost to immediate copying is a more likely evolutionary trajectory than adding it to mate-choice copying without this cost These results have implications for illuminating the emergence of the cultural evolution of mating preferences.
Keywords: 
Subject: Biology and Life Sciences  -   Ecology, Evolution, Behavior and Systematics

1. Introduction

Mate-choice copying is a type of non-independent mate choice [1] whereby an individual uses public information, more specifically the observed mating behavior of another individual, in making their own mate-choice decisions [2,3]. This phenomenon has been observed in a wide range of taxa, including at least 26 species of invertebrates, fish, birds, and mammals [4]. There is a growing body of literature showing that humans engage in mate-choice copying [reviewed by [5]. The phenomenon has ramifications for sexual selection as it can lead to incredibly high variance in reproductive success [6], and for illuminating the role of social learning—and, by extension, culture—in shaping mating behavior in humans and other animals [7,8,9].
The potential of cultural evolution to shape population-level diversity in mating preferences turns on the distinction between “copying” and “cultural inheritance” of mate choice [7]. Copying involves the immediate use of the socially transmitted information. Cultural inheritance requires generalization—that the socially transmitted information is used to inform future mate choice decisions in addition to current ones. Bowers et al. [10] make a slightly different distinction between “individual-based” copying, where the chances of mating with a particular individual is increased after having observed another mate with that individual, and “trait-based” copying, where the chance of mating with individual that have a particular characteristic is increased after having observed others mating with individuals possessing similar traits. These concepts are illustrated in Figure 1A. With copying or individual-based copying, the socially transmitted information is unlikely to be transmitted beyond the model/copier dyad; with cultural inheritance or trait-based copying, the socially transmitted information becomes are preference that is likely to be transmitted to others, leading to the cultural evolution of mate preferences [11]. Generalization of mate-choice preferences has been demonstrated in the species illustrated in Figure 1B [8,10,12,13,14,15,16,17,18].
Pruett Jones [19] modeled mate-choice copying using evolutionary game theory, namely the logic of evolutionarily stable strategies (ESS). An ESS is a frequency-dependent strategy that affords the greatest net fitness benefit to the individual actors and, when adopted by members of a population, cannot be invaded by alternative strategies via the forces of natural selection [20]. Discrete-strategy ESS models (e.g., Hawk-Dove [21]) assess the proportion of individuals in the population that adopt each strategy. Pure ESSs are the extreme (100%), but intermediate solutions are possible also. In the focal model the strategies are copier and chooser, the ESS proportions of which depend on the costs and benefits of choosing. Copying is supported when the costs are high, or the benefits low, for choosing.
In this paper, I build extensions of the original model [19] to include two important factors: (1) generalization; and (2) the potential for costs to accrue to the copier, the cost to immediate copying, that comes in the form of agonistic relations with the individual being copied and sperm depletion, among other things [4]. The main aim of the paper is to assess whether these factors exert an influence on the adaptive value of mate-choice copying using the same, relatively simple, modeling strategy of the original model. By comparing the results of the original model and its extensions, I hope to illuminate potential evolutionary scenarios for the emergence and maintenance of mate-choice copying in species (such as humans) where there is a cost to immediate copying, such as in monogamous ones, and for explaining the emergence of true cultural inheritance in species with mate-choice copying. This has ramifications, albeit indirectly, for informing debates in the evolutionary behavioural sciences, such as the relative importance of domain specific and domain general mechanisms [22].

2. Models

2.1. Original Model

In Pruett Jones’ [19] original model of mate-choice copying, individuals adopt one of two strategies, chooser and copier, and are paired up at random. Everyone in the dyad makes a mating decision as follows: Choosers select a mate independent of what the other individual in the dyad decides to do. They pay a fitness cost, k, for going to the trouble of sizing up potential mates, but realize a fitness benefit, f, for doing so. This is above and beyond the baseline payoff, W, that is earned for mating. Copiers, on the other hand, mimic the mating decision of the individual with whom they are paired, potentially reaping the benefit, but not paying the cost. The payoff matrix is shown in Table 1.
The ESS proportion of the population adopting the chooser strategy, p, is found by setting the fitness payoff to choosers equal to the fitness payoffs for copiers. This is found when
p (W + f – k) + (1 – p)(W + f – k) = p (W + f) + (1 – p) W
which can be simplified to
W + f – k = p (W + f) + (1 – p) W
and is solved when
p = 1 – (k/f).
Under this model, the ESS proportion of copiers is high except when the benefits of assessing mates oneself far outweigh the costs. Figure 2 shows the ESS proportion of the two strategies by the benefits relative to costs, f/k. When the costs equal or exceed the benefits of assessing mates oneself (i.e., f/k ≤ 1), copying is a pure ESS.

2.2. Extension 1: Generalisation

To extend the original model, I added generalisation. Individuals pair up at random and accrue the immediate fitness costs and benefits in the same manner as the original model. Everyone then mates an additional time in the future and is awarded a fitness payoff for that later event conditioned on the probability, m, that the information gained in the first round is useful in the second. Copiers paired with copiers get the same payoff for the immediate and future mating—the average fitness of potential mates. Copiers paired with choosers get an immediate payoff of the mate choice benefit plus the average fitness of potential mates, and a future payoff that is conditioned on whether the information is useful. In essence, 1-m is a cost of generalizing mate-choice copying. There are several potential sources of such a cost, including that the trait on which generalization has occurred is associated with a mate with lower fitness, and that there are insufficient potential mates with the particular trait on which generalisation has occurred. Choosers, regardless of who they are paired with, get the same payoff for immediate and future mating. The payoff matrix is shown in Table 2.
the fitness payoffs for copiers. This is found when
p [2(W + f – k)] + (1 – p) [2(W + f – k)]
= p [W + f + m (W + f) + (1 – m) W] + (1 – p) 2W
which can be simplified to
2(W + f – k) = p [W + f + m (W + f) + (1 – m) W] + (1 – p) 2W
and is solved when
p = [2( f – k)] / [ f (m+1)].
In this model, as with the original model, copying is a pure ESS when the cost of mate choice is equal to or greater than the benefit (i.e., f/k ≤ 1). As illustrated in Figure 3A, when the benefits outweigh the costs of mate choice, the adaptive value of copying depends on the probability the observed mate choice in the current round of mating is helpful in the future round. When the information acquired is 100% likely to help future mating (i.e., m=1), the ESS proportion of choosers and copiers predicted by the extended model is identical to the proportion predicted by the original. When the information’s usefulness is less than certain (i.e., m < 1) the ESS proportion of copiers is greater without generalization and, at intermediate values of f/k, choosing is a pure ESS. This is a striking contrast to the original model within which choosing is never a pure ESS. The results suggest that adding generalization decreases the adaptive value of mate-choice copying.

2.3. Extension 2: Costs to Immediate Copying

To extend the original model, I added costs to immediate copying, c. While this could encapsulate any of several potential costs, including sperm depletion and an agonistic response from the individual being copied [4], for the purposes of the model it is considered an intrinsic aspect of copiers (e.g., that they spend more time because they have to wait to assess the actions of the individual they copy). When conceptualized in this fashion, the cost is incurred to all copiers regardless of with whom they are paired. The payoffs to choosers are identical to those in the original model. The payoffs to copiers are almost identical to those in the original model, except that the cost of immediate copying is subtracted from them. The payoff matrix is shown in Table 3.
The ESS proportion of the population adopting the chooser strategy, p, is found by setting the fitness payoff to choosers equal to the fitness payoffs for copiers. This is found when
p (W + f – k) + (1 – p)(W + f – k) = p (W + f – c) + (1 – p) W – c
which can be simplified to
W + f – k = p (W + f – c) + (1 – p) W – c
and is solved when
p = (c + f – k) / (f – c).
When there are no costs for immediate copying (i.e., c =0), the extended model is identical to the original model. As can be seen in Figure 3B, there are substantial decreases in the ESS proportion of copiers when the cost of immediate copying is added. When the cost equals or exceeds 50% of the costs of mate choice (i.e., c/k ≥ 0.5) choosing becomes a pure ESS. The results suggest that adding a cost to immediate copying decreases the adaptive value of mate-choice copying.

2.4. Extension 3: Incorporating Both Extensions

To extend the original model, I added both generalisation and the costs of immediate copying. As such, the payoffs were split into current and future components, and cost was added for copiers in the current component. The payoff matrix is shown in Table 4.
The ESS proportion of the population adopting the chooser strategy, p, is found by setting the fitness payoff to choosers equal to the fitness payoffs for copiers. This is found when
p [2(W + f – k)] + (1 – p) [2(W + f – k)]
= p [W + f – c + m (W + f) + (1 – m) W] + (1 – p) [(W– c) + W]
which can be simplified to
2(W + f – k) = p [W + f – c + m (W + f) + (1 – m) W] + (1 – p) [(W– c) + W]
and is solved when
p = (c + 2f – 2k) / [ f (m + 1)].
Although adding either extension by itself leads to decreases or held-constant ESS proportions of copiers, adding the remaining extension to create the current model has contrasting effects on the ESS proportions of copiers depending on which was the starting point. As shown in Figure 4A, adding generalization to a system that already has a cost to immediate copying in some cases can lead to substantial increases in the ESS proportion of copiers. That is, adding generalisation when there is already a cost for immediate copying increases the adaptive value of copying. As shown in Figure 4B, the converse does not appear to be the case. Under no conditions does adding a cost to immediate copying to a system that already includes generalization increase the ESS proportion of copiers. The amount by which the ESS proportion of copiers decreases depends on the value of c/k. This means adding costs to immediate copying when there is already generalisation decreases the adaptive value of mate-choice copying.

3. Discussion

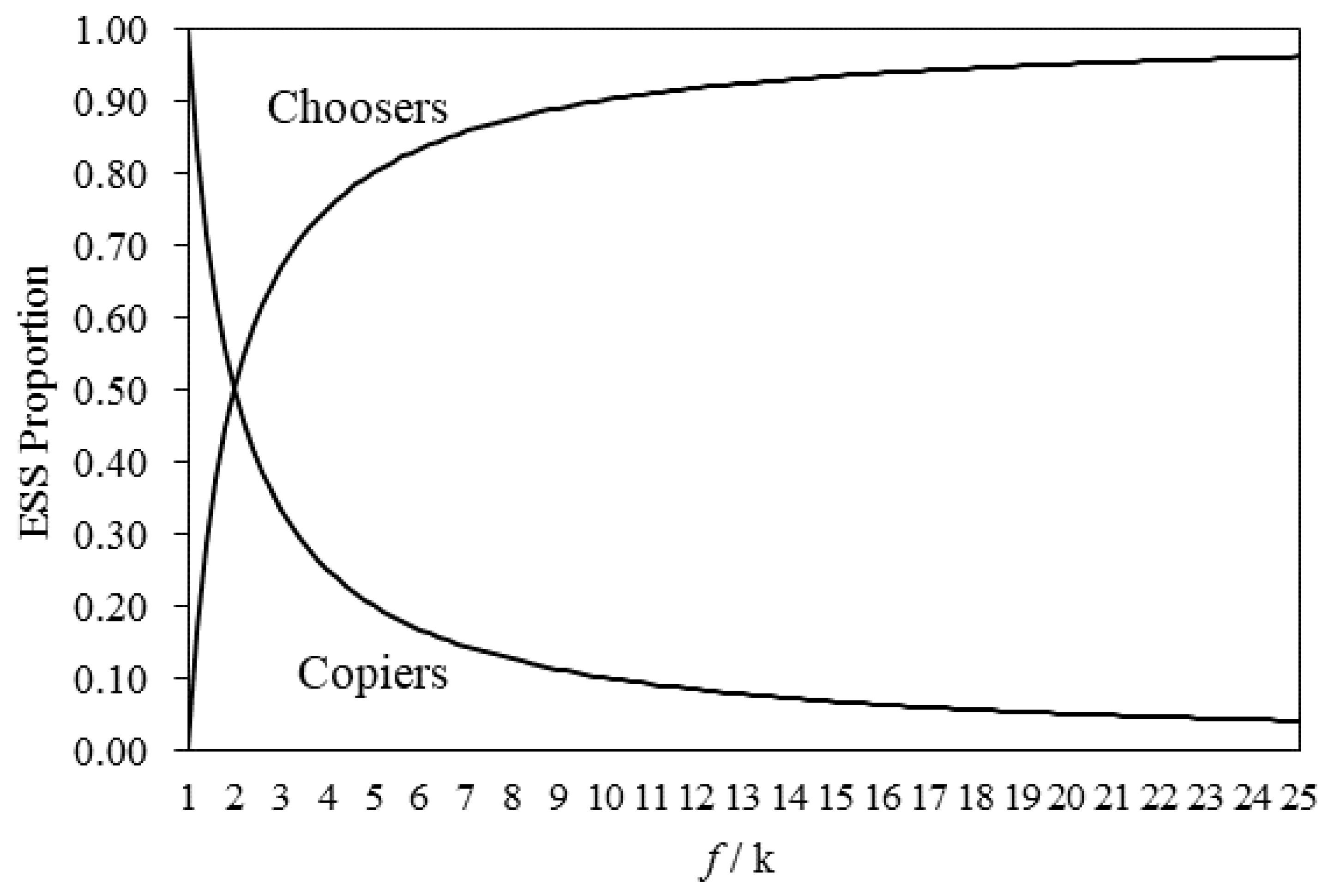
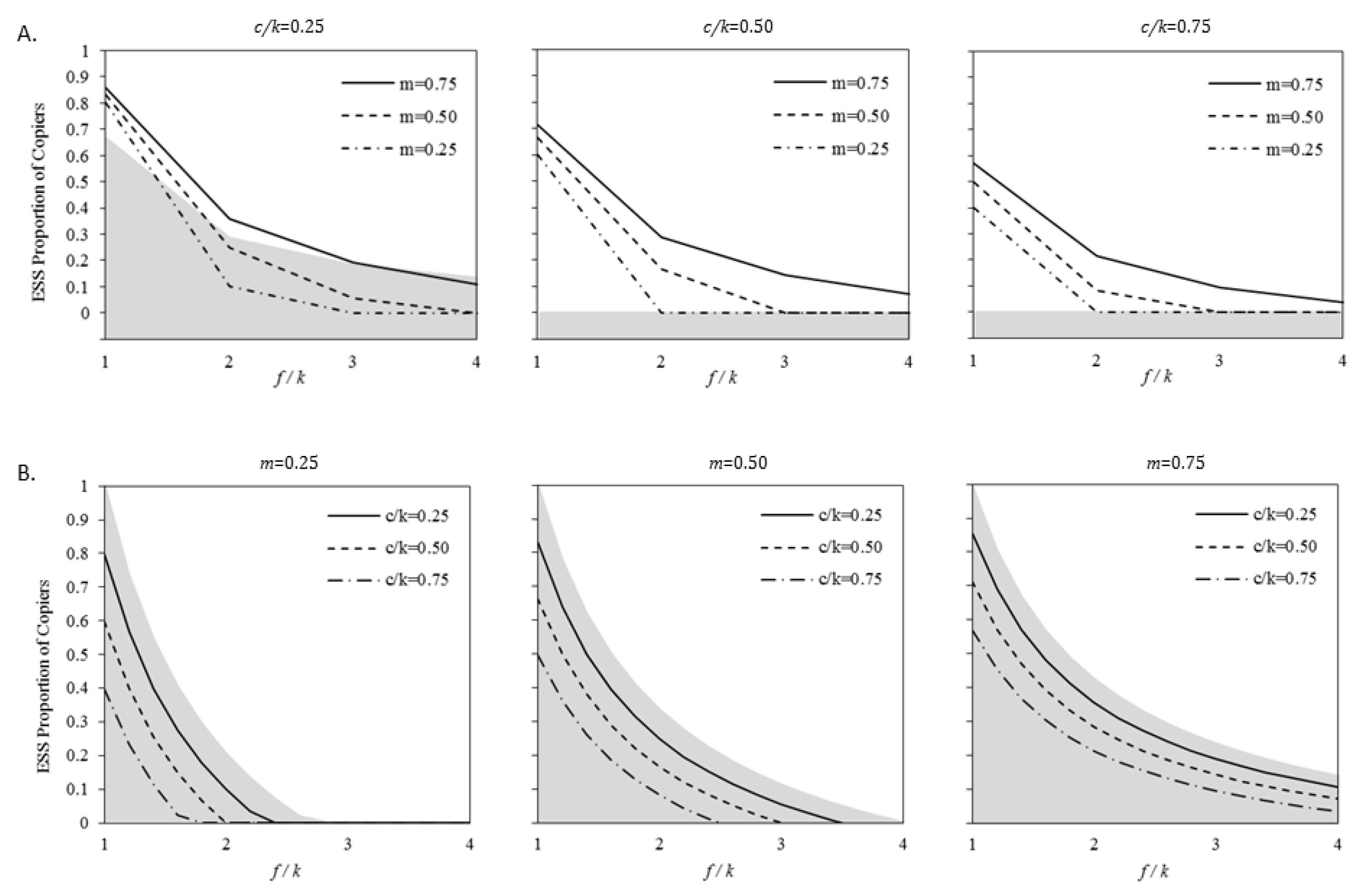
Pruett Jones’s [19] model of mate-choice copying showed that, when there is a cost to choosing a mate by oneself, copying is selected for as a pure or mixed ESS, as shown in Figure 2. Here, I have extended the original model in three ways by adding generalization (Extension 1), a cost to immediate copying (Extension 2), and both generalization and a cost to immediate copying (Extension 3). 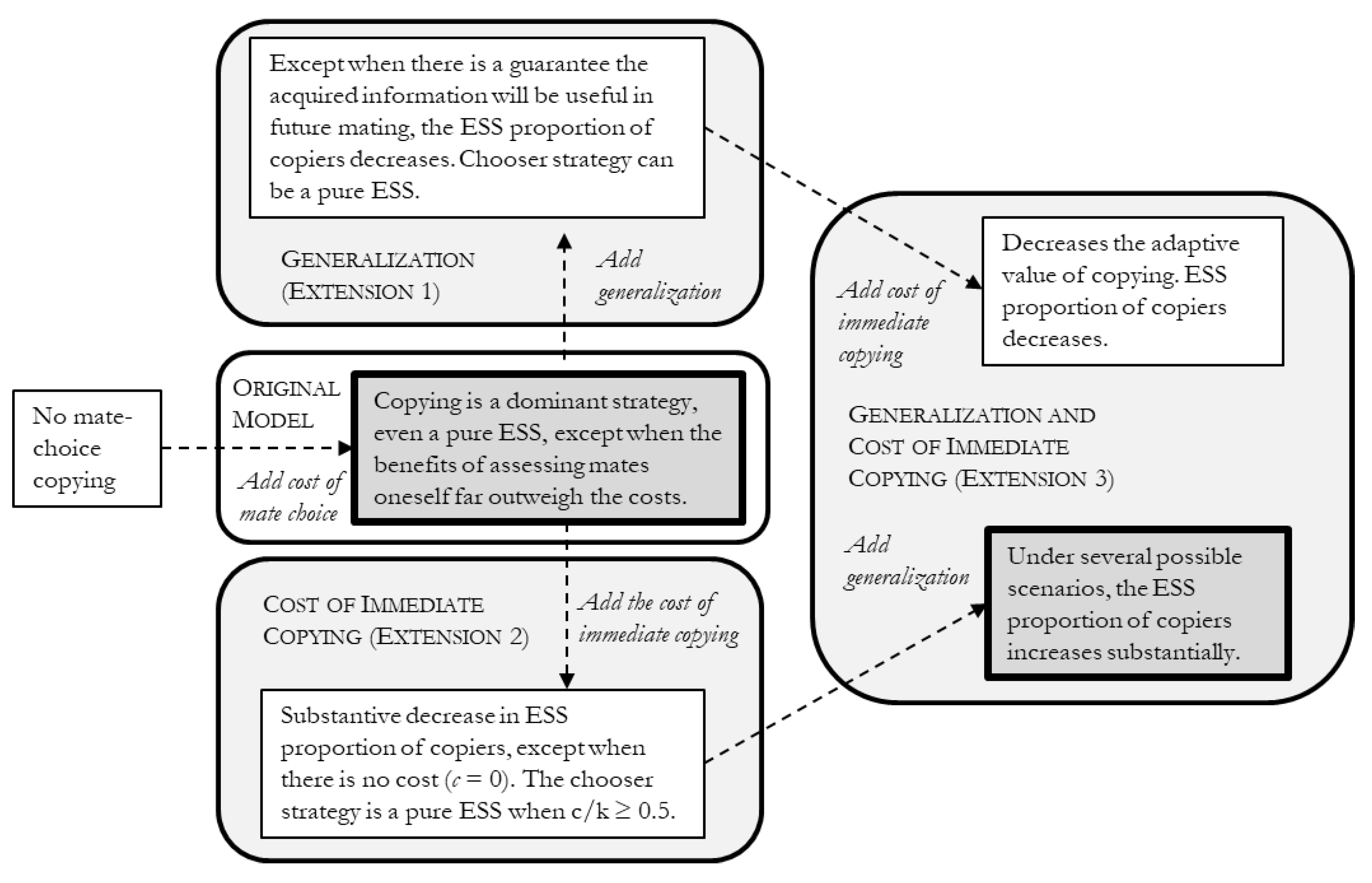The results, outlined in Figure 5, show that when either generalization or a cost to immediate copying is added by itself to the original model, except in a very limited range of circumstances, there is a decrease in the ESS proportion of copiers. Put another way, either factor, by itself, leads to a decrease in the adaptive value of mate-choice copying. When there is already a cost to immediate copying, however, generalization increases the adaptive value of copying. The converse fails to hold. When there is already generalisation, adding a cost to immediate copying decreases the adaptive value of mate-choice copying. These results suggest that a system marked by the “cultural inheritance” of mate choice (i.e., mate-choice copying with generalisation) would be more likely to have evolved from a system that had a cost to immediate copying. That is, a trajectory that went from individual-based copying with a cost to immediate copying → trait-based copying may be more likely than a trajectory that goes from individual-based copying → trait-based copying.
Preprints 119516 g004
Figure 4. Comparing model results: (A) comparing the model with cost to immediate copying (Extension 2) and the model with both extensions (Extension 3), and (B) comparing the model with generalisation (Extension 1) and the model with both extensions (Extension 3). In both, the lines are ESS proportions of copiers in the model with both extensions and the edge of the shaded area are the ESS proportions of copiers in the models with a single extension. As shown in (A), under several conditions, adding generalization to a mate-choice copying system where there is a cost to immediate copying leads to substantive increases in the ESS proportion of copiers (i.e., there is an increase in adaptive value). As shown in (B), under no conditions does adding a cost to immediate copying in a system with generalization increase the ESS proportion of copier. That is, there is a decrease in the adaptive value of copying, however small.
Figure 4. Comparing model results: (A) comparing the model with cost to immediate copying (Extension 2) and the model with both extensions (Extension 3), and (B) comparing the model with generalisation (Extension 1) and the model with both extensions (Extension 3). In both, the lines are ESS proportions of copiers in the model with both extensions and the edge of the shaded area are the ESS proportions of copiers in the models with a single extension. As shown in (A), under several conditions, adding generalization to a mate-choice copying system where there is a cost to immediate copying leads to substantive increases in the ESS proportion of copiers (i.e., there is an increase in adaptive value). As shown in (B), under no conditions does adding a cost to immediate copying in a system with generalization increase the ESS proportion of copier. That is, there is a decrease in the adaptive value of copying, however small.
Preprints 119516 g004
The distribution of mating systems among species that engage in mate-choice copying supports the evolutionary trajectory suggested by the models presented in this paper. Most species that engage in mate-choice copying engage in polygyny or promiscuity to some extent, and many of them are lekking species [4,23,24]. There is only one obligatory-monogamous species with biparental care that engages in mate-choice copying, the zebra finch (Taenipygia guttata)—a species that happens to engage in trait-based mate copying [14,16]. Many of the other species that generalize mate-choice copying have biparental care to some extent. As predicted by my model, generalization might be one way to avoid the costs of mating with an already-mated male, which Vakirtzis [4,25] outlines as follows: (i) increased competition with other females, (ii) diminishing paternal care, (iii) low male mating skew which renders the public information gathered related to mate choice less reliable, (iv) copying unattractive females who are paired with low-quality males, and (v) ambiguous relationship between male qualities and his number of mates. DuBois [26] explores another possibility—that mate choice copying in monogamous species might be adaptive for extrapair copulations. The model results suggest an evolutionary trajectory for the emergence of key features of human mating strategies using a theory-based approach, rather than a purely speculative or induction-based approach.
Preprints 119516 g005
Figure 5. Summary of results, which suggests that generalisation of mate-choice copying (aka trait-based copying) would have been more likely to arise out of a system of mate-choice copying with a cost to immediate copying.
Figure 5. Summary of results, which suggests that generalisation of mate-choice copying (aka trait-based copying) would have been more likely to arise out of a system of mate-choice copying with a cost to immediate copying.
Preprints 119516 g005
The generalization of mate-choice copying has potential ramifications for shaping male displays. Several authors have shown that the intensity and nature of sexual selection on male traits can be influenced by how females use socially acquired information about mate choice [27,28,29]. Wade and Pruett Jones [6] showed that mate-choice copying could lead to increased variance in mating success accompanied by strong directional sexual selection, even traits that reduce male viability [28] and runaway sexual selection in the absence of genetic correlations [31,32]. Others have argued that, while these effects might follow from trait-based copying, they are more likely to lead to stabilizing selection and the fixation of male displays [10,28,33].
One simplification I employed was modelling the future contribution of the socially transmitted information on the copier’s fitness as the consequences of a single future mating event. It is unlikely that many, if any species, reproduce this way so it might be useful to at least consider how the results might change if generalization affected multiple future mating. Because generalization appears to counterbalance the negative effects of a cost to immediate copying, generalizing over multiple future mating would likely increase the fitness consequences of copying when the cost exists.
The approach I have adopted here models equilibrium states and may downplay constraints on the ability of frequency-dependent selection to lead to an ESS [34,35,36]. Evolutionarily stable strategies are those that, when monomorphic in a population, resist the invasion of rare mutants [20]. McNamara and Weissing [35] clarify that although “the reasoning behind an ESS suggests a population that reaches an ESS will not evolve away from this strategy, it does not guarantee that evolution will actually lead to an ESS.” Constraints on their evolution include the specifics of the underlying genetics, the existence of additional equilibria, and the dynamic nature of the adaptive landscape under frequency dependence [35]. Several authors [34,36] have argued for the use of a dynamic approach using the “replicator dynamics” [37] over the sort of static one used here. I offer the following in defense of my choice to adopt a static approach. First, the original model [19] used it. Second, each of the extensions of the original model has a single ESS and a simple strategy set. The dynamic approach would have presented unnecessary complexity. Third, my intention was to derive as-general-as-possible qualitative conclusions from the models. The static approach, it can be argued, is better suited for such a goal.
Of course, any modeling exercise will peel away some of the complexity of the real-world system under study [38]. In the case of human mating (or the mating of most species where mate-choice copying occurs), where strategies are complex rather than binary, the results must always be interpreted with caution. For instance, DuVal et al. [39] have modeled the evolutionary dynamics of preferences for specific traits. At the same time, whether this should be considered a shortcoming or feature of the model depends on one’s aims (as realism and generalizability of a model may trade-off against each other [40]).
The generalization of mate-choice preferences, or trait-based copying, is necessary for the cultural evolution of inter- and intra-population diversity in mating preferences. Much is already known about this diversity in human mating [39,40]; less is known about other species that generalize their preferences (see Figure 1B). One avenue for further research is the investigation of this diversity, including elucidating the cultural evolutionary dynamics for the origin and maintenance of mate-choice preferences. Part of this enterprise will be to systematically unravel the sometimes-intertwined influences of innate and learned factors on mate choice [43,44], which is easier to do in experimentation-amenable species, much more difficult for ethical reasons in humans In addition, future research should address the question of whether mate-choice copying is driven by domain-specific or domain-general mechanisms [22,45], and whether this differs for species with individual- versus trait-based copying.

Funding

While writing this article, GK was supported by the Outside Studies Program, ANU College of Arts and Social Sciences, The Australian National University.

Conflicts of Interest

There were no conflicts of interest.

Author Bio

Geoff Kushnick is a Senior Lecturer in Biological Anthropology (Human Behavioural Ecology) at The Australian National University, Canberra. He holds a PhD in Biocultural Anthropology from the University of Washington, Seattle, and is a Fulbright Scholar. His research interests include theoretical and empirical aspects of the evolution of human reproductive and social behaviour. He has done extensive field-based research in Indonesia and Solomon Islands and is a member of the Cultural Evolution Society.

References

  1. Westneat, D.F.; Walters, A.; McCarthy, T.M.; Hatch, M.I.; Hein, W.K. Alternative mechanisms of nonindependent mate choice. Animal Behaviour 2000, 59, 467-476. [CrossRef]
  2. Hoglund, J.; Alatalo, R.V.; Lundberg, A. Copying the mate choice of others? observations on the female black grouse. Behaviour 1990, 114, 221-231. [CrossRef]
  3. Dugatkin, L.A. Sexual selection and imitation: females copy the mate choice of others. American Naturalist 1992, 139, 1384-1389. [CrossRef]
  4. Vakirtzis, A. Mate choice copying and nonindependent mate choice: a critical review. Annales Zoologici Fennici 2011, 48, 91-107. [CrossRef]
  5. Gouda-Vossos, A.; Nakagawa, S.; Dixson, B.J.W.; Brooks, R.C. Mate Choice Copying in Humans: a Systematic Review and Meta-Analysis. Adaptive Human Behavior and Physiology 2018, 4, 364-386. [CrossRef]
  6. Wade, M.J.; Pruett-Jones, S.G. Female copying increases the variance in male mating success. Proc Nat Acad Sci 1990, 87, 5749-5753. [CrossRef]
  7. Brooks, R. The importance of mate copying and cultural inheritance of mating preferences. Trends in Ecology & Evolution 1998, 13, 45-46. [CrossRef]
  8. Little, A.C.; Jones, B.C.; DeBruine, L.M.; Caldwell, C.A. Social learning and human mate preferences: A potential mechanism for generating and maintaining between-population diversity in attraction. Phil Trans Roy Soc B 2011, 366, 366-375. [CrossRef]
  9. Nöbel, S.; Jacquet, A.; Isabel, G.; Pocheville, A.; Seabright, P.; Danchin, E. Conformity in mate choice, the overlooked social component of animal and human culture. Biological Reviews 2023, 98, 132-149. [CrossRef]
  10. Bowers, R.I.; Place, S.S.; Todd, P.M.; Penke, L.; Asendorpf, J.B. Generalization in mate-choice copying in humans. Behavioral Ecology 2012, 23, 112-124. [CrossRef]
  11. Danchin, E.; Giraldeau, L.-A.; Valone, T.J.; Wagner, R.H. Public information: from nosy neighbors to cultural evolution. Science 2004, 305, 487-491. [CrossRef]
  12. White, D.J.; Galef Jr, B.G. ‘Culture’ in quail: social influences on mate choices of female Coturnix japonica. Animal Behaviour 2000, 59, 975-979. [CrossRef]
  13. Godin, J.-G.J.; Herdman, E.J.E.; Dugatkin, L.A. Social influences on female mate choice in the guppy, Poecilia reticulata: generalized and repeatable trait-copying behaviour. Animal Behaviour 2005, 69, 999-1005. [CrossRef]
  14. Brown, G.R.; Fawcett, T.W. Sexual selection: Copycat mating in birds. Current Biology 2005, 15, R626-R628. [CrossRef]
  15. Witte, K.; Noltemeier, B. The role of information in mate-choice copying in female sailfin mollies (Poecilia latipinna). Behav. Ecol. Sociobiol. 2002, 52, 194-202. [CrossRef]
  16. Swaddle, J.P.; Cathey, M.G.; Correll, M.; Hodkinson, B.P. Socially transmitted mate preferences in a monogamous bird: a non-genetic mechanism of sexual selection. Proceedings of the Royal Society B: Biological Sciences 2005, 272, 1053-1058. [CrossRef]
  17. Mery, F.; Varela, S.A.M.; Danchin, É.; Blanchet, S.; Parejo, D.; Coolen, I.; Wagner, R.H. Public versus personal information for mate copying in an invertebrate. Current Biology 2009, 19, 730-734. [CrossRef]
  18. Danchin, E.; Nöbel, S.; Pocheville, A.; Dagaeff, A.-C.; Demay, L.; Alphand, M.; Ranty-Roby, S.; van Renssen, L.; Monier, M.; Gazagne, E.; et al. Cultural flies: Conformist social learning in fruitflies predicts long-lasting mate-choice traditions. Science 2018, 362, 1025-1030. [CrossRef]
  19. Pruett-Jones, S. Independent versus nonindependent mate choice: do females copy each other? The American Naturalist 1992, 140, 1000-1009. [CrossRef]
  20. Maynard Smith, J. Evolution and the theory of games; Princeton University Press: Princeton, NJ, 1982.
  21. Maynard Smith, J.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15-18. [CrossRef]
  22. Barrett H.C. The shape of thought: how mental adaptations evolve. Oxford University Press: NY, 2015.
  23. Galef, B.G.; White, D.J. Evidence of social effects on mate choice in vertebrates. Behavioural Processes 2000, 51, 167-175. [CrossRef]
  24. White, D.J. Influences of social learning on mate-choice decisions. Learning & Behavior 2004, 32, 105-113. [CrossRef]
  25. Vakirtzis, A.; Roberts, S.C. Nonindependent mate choice in monogamy. Behavioral Ecology 2010, 21, 898-901. [CrossRef]
  26. Dubois, F. Mate choice copying in a monogamous species: should females use public information to choose extrapair males? Animal Behaviour 2007, 74, 1785-1793. [CrossRef]
  27. Agrawal, A.F. The evolutionary consequences of mate choice copying on male traits. Behav. Ecol. Sociobiol. 2001, 51, 33-40. [CrossRef]
  28. Verzijden, M.N.; ten Cate, C.; Servedio, M.R.; Kozak, G.M.; Boughman, J.W.; Svensson, E.I. The impact of learning on sexual selection and speciation. Trends in Ecology & Evolution 2012, 27, 511-519. [CrossRef]
  29. Gibson, R.M.; Höglund, J. Copying and sexual selection. Trends in Ecology & Evolution 1992, 7, 229-232. [CrossRef]
  30. Kirkpatrick, M.; Dugatkin, L.A. Sexual selection and the evolutionary effects of copying mate choice. Behav. Ecol. Sociobiol. 1994, 34, 443-449. [CrossRef]
  31. Bailey, N.W.; Moore, A.J. Runaway sexual selection without genetic correlations: social environments and flexible mate choice initiate and enhance the Fisher process. Evolution 2012, 66, 2674-84. [CrossRef]
  32. Richerson, P.J.; Boyd, R. The role of evolved predispositions in cultural evolution: or, Human Sociobiology meets Pascal's Wager. Ethology and Sociobiology 1989, 10, 195-219. [CrossRef]
  33. Laland, K.N. Sexual selection with a culturally transmitted mating preference. Theoretical Population Biology 1994, 45, 1-15. [CrossRef]
  34. Nowak, M. An evolutionarily stable strategy may be inaccessible. Journal of Theoretical Biology 1990, 142, 237-241. [CrossRef]
  35. McNamara, J.M.; Weissing, F.J. Evolutionary game theory. In Social behaviour: genes, ecology and evolution, Székely, T., Moore, A.J., Komdeur, J., Eds.; Cambridge University Press: Cambridge, 2010; pp. 88-106.
  36. Huttegger, S.M.; Zollman, K.J.S. Methodology in biological game theory. The British Journal for the Philosophy of Science 2013, 64, 637-58. [CrossRef]
  37. Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Mathematical Bioscience 1978, 40, 145-156. [CrossRef]
  38. Kokko, H. Modeling for field biologists and other interesting people; Cambridge University Press: Cambridge, 2007.
  39. DuVal, E.H., Fitzpatrick, C.L., Hobson, E.A., Servedio, M.R. Inferred attractiveness: A generalized mechanism for sexual selection that can maintain variation in traits and preferences over time. PLOS Biology, 2023, 21, e3002269. [CrossRef]
  40. Levins. R. The strategy of model building in population biology. American Scientist, 1966, 54, 421-31.
  41. Darwin, C. The descent of man and sex in relation to sex; John Murray: London, 1871.
  42. Ford, C.S.; Beach, F.A. Patterns of sexual behavior; Harper: NY, 1951.
  43. Dugatkin, L.A. The interface between culturally based preferences and genetic mate preferences: female mate choice in Pocilia reticulata. Proc Nat Acad Sci 1996, 93, 2770-2773. [CrossRef]
  44. Santos, M.; Varela, S.A.M. Genetic and Cultural Evolution of Mate Choice. In Illuminating Human Evolution: 150 Years after Darwin, Bertranpetit, J., Peretó, J., Eds.; Springer Nature Singapore: Singapore, 2022; pp. 187-199.
  45. Street, S.E.; Morgan, T.J.H.; Thornton, A.; Brown, G.R.; Laland, K.N.; Cross, C.P. Human mate-choice copying is domain-general social learning. Scientific Reports 2018, 8, 1715. [CrossRef]
Preprints 119516 g001
Figure 1. Mate-choice copying is normally used to refer to (A) individual-based copying, where an individual preferentially mates with an individual who they observed mating with somebody else. Mate-choice copying can lead to (B) “generalisation” or trait-based copying, where an individual preferentially mates with individuals that have the features of an individual that they observed mating with somebody else. The former can lead to the cultural evolution of mating preferences. Generalisation of mate-choice copying has been observed in several species, including: (C) fruit flies (Drosophila melanogaster), (D) sailfin mollies (Poecilia latipinna), (E) guppies (Poecilia reticulata), (F) zebra finches (Taenipygia guttata), (G) Japanese quail (Coturnix japonica), and (H) humans (Homo sapiens). Credits: fruit fly, CC Attribution 2.0 Generic, Paco Romero-Ferrero; sailfin mollie, CC Attribution-Share Alike 3.0 Unported, Bjoertvedt; guppy, CC Attribution-Share Alike 4.0, Marrabbio2; zebra finches, CC Attribution 4.0 International, Christoph_moning; Japanese quail, public domain; humans, CC Attribution 2.0 Generic, Scarleth White.
Figure 1. Mate-choice copying is normally used to refer to (A) individual-based copying, where an individual preferentially mates with an individual who they observed mating with somebody else. Mate-choice copying can lead to (B) “generalisation” or trait-based copying, where an individual preferentially mates with individuals that have the features of an individual that they observed mating with somebody else. The former can lead to the cultural evolution of mating preferences. Generalisation of mate-choice copying has been observed in several species, including: (C) fruit flies (Drosophila melanogaster), (D) sailfin mollies (Poecilia latipinna), (E) guppies (Poecilia reticulata), (F) zebra finches (Taenipygia guttata), (G) Japanese quail (Coturnix japonica), and (H) humans (Homo sapiens). Credits: fruit fly, CC Attribution 2.0 Generic, Paco Romero-Ferrero; sailfin mollie, CC Attribution-Share Alike 3.0 Unported, Bjoertvedt; guppy, CC Attribution-Share Alike 4.0, Marrabbio2; zebra finches, CC Attribution 4.0 International, Christoph_moning; Japanese quail, public domain; humans, CC Attribution 2.0 Generic, Scarleth White.
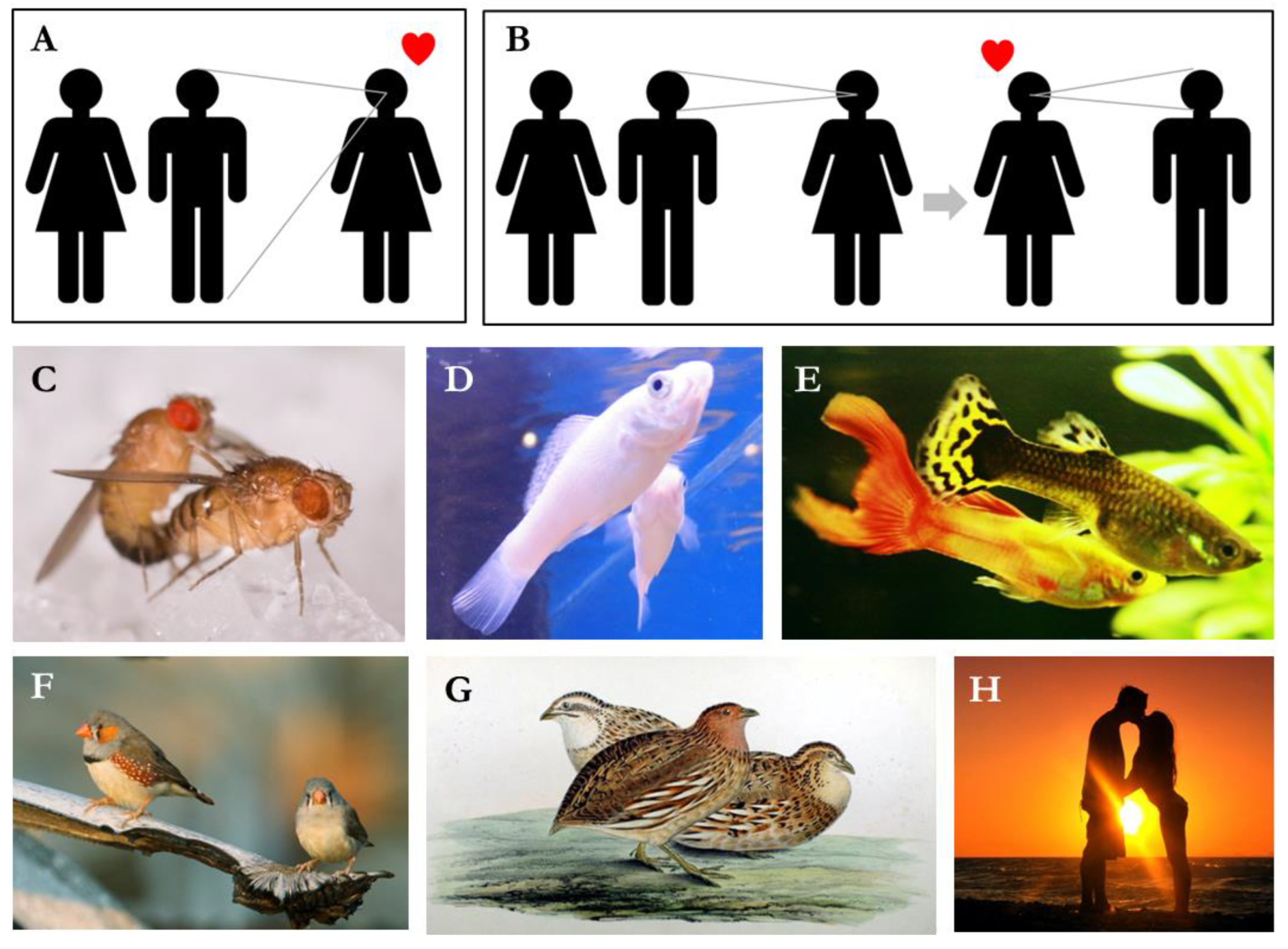
Preprints 119516 g001
Preprints 119516 g002
Figure 2. ESS proportions of choosers and copiers in the original model.
Figure 2. ESS proportions of choosers and copiers in the original model.
Preprints 119516 g002
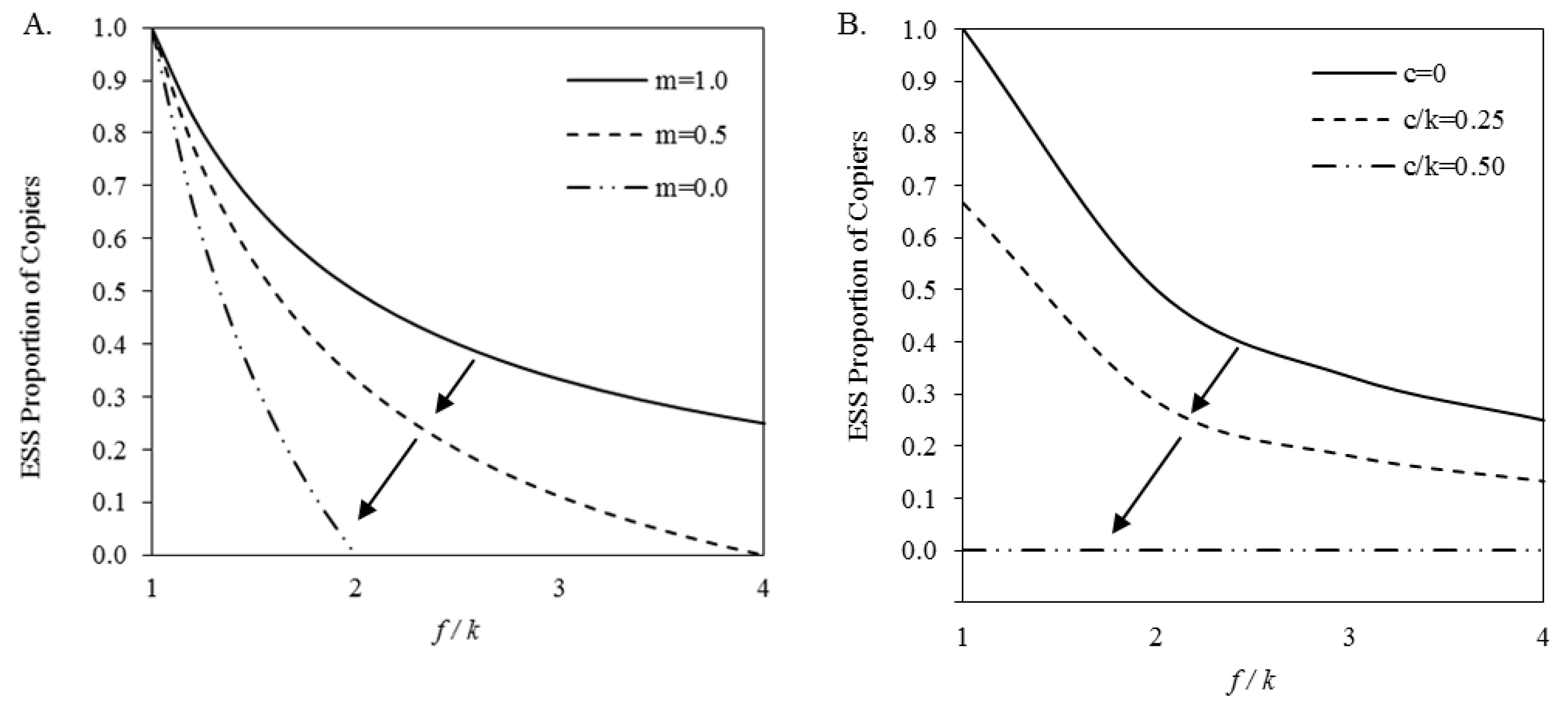
Preprints 119516 g003
Figure 3. Model results for each of the two extensions: (A) In the original model plus generalisation (Extension 1), the ESS proportion of copiers decreases with decreasing values of m, as indicated by the arrows. The extended model’s results are identical to the original model when m=1, but otherwise leads to lower ESS proportion of copiers (i.e.,, adaptive value of copying decreases). At some levels of m, as illustrated, the ESS proportion of copiers is 0. That is, the chooser can be a pure ESS. (B) In the original model plus cost to immediate copying (Extension 2), the ESS proportion of copiers decreases with increasing c, as indicated by the arrows. The extended model’s results reduce to the original model when there is no cost to immediate copying. When the cost of immediate copying is greater than or equal to half the cost of mate choice, the chooser strategy is a pure ESS.
Figure 3. Model results for each of the two extensions: (A) In the original model plus generalisation (Extension 1), the ESS proportion of copiers decreases with decreasing values of m, as indicated by the arrows. The extended model’s results are identical to the original model when m=1, but otherwise leads to lower ESS proportion of copiers (i.e.,, adaptive value of copying decreases). At some levels of m, as illustrated, the ESS proportion of copiers is 0. That is, the chooser can be a pure ESS. (B) In the original model plus cost to immediate copying (Extension 2), the ESS proportion of copiers decreases with increasing c, as indicated by the arrows. The extended model’s results reduce to the original model when there is no cost to immediate copying. When the cost of immediate copying is greater than or equal to half the cost of mate choice, the chooser strategy is a pure ESS.
Preprints 119516 g003
Table 1. Payoff matrix for the original model [1].
Table 1. Payoff matrix for the original model [1].
When paired with:
Chooser Copier
Payoff to: Chooser W + f – k W + f – k
Copier W + f W
Table 2. Payoff matrix for the original model plus generalisation (Extension 1).
Table 2. Payoff matrix for the original model plus generalisation (Extension 1).
When paired with:
Chooser Copier
Immediate Future Immediate Future
Payoff to: Chooser W + f – k W + f – k W + f – k W + f – k
Copier W + f m (W + f) + (1 – m) W W W
Table 3. Payoff matrix for the original model plus costs to immediate copying (Extension 2).
Table 3. Payoff matrix for the original model plus costs to immediate copying (Extension 2).
When paired with:
Chooser Copier
Payoff to: Chooser W + f – k W + f – k
Copier W + f – c W – c
Table 4. Payoff matrix for the original model plus both other extensions (Extension 3).
Table 4. Payoff matrix for the original model plus both other extensions (Extension 3).
When paired with:
Chooser Copier
Immediate Future Immediate Future
Payoff to: Chooser W + f – k W + f – k W + f – k W + f – k
Copier W + f – c m (W + f) + (1 – m) W W – c W
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated