Prerpints.org logo
Preprint
Review

Phase Error Correction in Magnetic Resonance: A Review of Models, Optimization Functions, and Optimizers in Traditional Statistics and Neural Networks

Altmetrics

Downloads

97

Views

73

Comments

0

This version is not peer-reviewed

Submitted:

27 September 2024

Posted:

27 September 2024

Read the latest preprint version here

Alerts
Abstract
Phase errors in magnetic resonance (MR) techniques, including Nuclear Magnetic Resonance (NMR) spectroscopy and Magnetic Resonance Imaging (MRI), pose significant challenges to data accuracy and interpretation. As MR technologies advance, the demand for more sophisticated phase correction methods continues to grow, enhancing diagnostic precision and analytical outcomes. This review explores the evolution of phase correction models, beginning with simple global phase shifts, progressing through traditional linear statistical models, and culminating in modern machine learning techniques—specifically, neural networks. We also examine a range of optimization functions and optimizers, including both MR data-specific and common statistical approaches, applied in phase error correction. Despite notable progress, challenges remain in developing fully automatic phase error correction methods, particularly given the absence of ground truth in real-world MR data. This review highlights key methods, discusses their limitations, and proposes future pathways, including ensemble learning, that could guide further innovation in phase error correction.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Magnetic Resonance (MR) techniques, including Nuclear Magnetic Resonance (NMR) spectroscopy and Magnetic Resonance Imaging (MRI), are fundamental tools in chemical research, medical diagnostics, and various other fields. Despite their significance, the accuracy of these techniques can be compromised by phase errors, which may substantially distort the resulting data.
Phase errors can arise from various factors, including eddy currents, motion artifacts, and timing discrepancies. Several approaches have been developed to address these errors. One effective method involves using multiple acquisitions with different magnetic inductions. By applying positive and negative magnetic fields in a two-step approach, phase errors induced by eddy currents can be canceled out through combination (Bieri, Markl and Scheffler, 2005; Jiru, 2008). Similarly, in phase-contrast MRI, applying gradient pulses in opposite directions helps remove phase errors related to flow and motion, thereby enhancing the accuracy of velocity measurements (Wymer et al., 2020). These techniques leverage multiple data sets or acquisitions to counteract phase distortions and improve overall imaging precision.
However, in many cases, access to multiple acquisitions or data sets may be limited. In such situations, phase error correction techniques become essential to maintain diagnostic precision and analytical capabilities. Despite their importance, phase correction methods can be inherently complex and time-consuming.
To address these challenges, Ernst proposed automatic phase correction methods over fifty years ago (Ernst, 1969). Since then, research has continually focused on refining these automatic techniques to improve their effectiveness and reduce variability. Although automatic methods initially offered a promising alternative to manual corrections, their effectiveness has often fallen short of expectations and, in some cases, may even worsen accuracy (Minderhoud et al., 2020). Consequently, manual phase correction remains widely used, either in conjunction with automatic corrections (Emwas et al., 2018) or as a standalone method (Canlet et al., 2023). Manual correction is still recommended for achieving more accurate results (Ben-Tal et al., 2022).
Recognizing these limitations, current research is actively exploring innovative approaches to enhance the accuracy of automatic phase correction and reduce reliance on manual methods. These advancements underscore the necessity for continued refinement to keep pace with developments in MR technology.
In response to these evolving challenges, this review provides a comprehensive examination of current phase correction methods in MR. By covering a range of MR techniques, including NMR, MRI, and other modalities, this review offers a broader perspective compared to previous studies that often focused on only one or a limited set of technologies (Binczyk, Tarnawski and Polanska, 2015; Haskell, Nielsen and Noll, 2023). It will explore the underlying models used for phase correction, optimization functions designed to enhance these models, and various optimizers employed in both traditional statistical methods and modern neural networks. As MR technologies continue to advance, keeping up with the latest developments in phase correction is essential. This review will summarize the state-of-the-art techniques, highlight current challenges, and suggest future research directions to further advance the field.

2. Phasing Models

Phase correction models are fundamental to addressing phase errors in MR data. Over the years, the evolution of these models has ranged from simple global phase shifts to more complex linear and non-linear approaches, eventually incorporating advanced techniques such as machine learning.
Initially, phase correction relied heavily on manual interaction with software. An experienced expert would zoom in on a specific region of the spectrum—MR frequency domain data—visually detect phase errors, and adjust the phase for a specific signal peak by dragging it upward until the peak exhibited a symmetric Lorentzian shape. This approach essentially applies a global phase correction with a constant adjustment across the entire spectrum but focuses on the selected peak.
However, this method has significant drawbacks. Adjusting the phase for one peak can inadvertently affect all other peaks in the spectrum, leading to suboptimal results. To achieve an overall phase correction for all peaks, the expert must painstakingly adjust each peak individually while monitoring the entire spectrum. This process is time-consuming and mentally exhausting. In some cases, when an expert becomes fatigued, they might mistakenly apply a phase adjustment value from a different spectrum, resulting in incorrect corrections.
Although such errors are rare among experts, the challenges of manual phase correction highlight a critical issue: achieving accurate global phase correction using a constant adjustment value is difficult and labor-intensive.
To address this, we need to optimize global phase correction with a constant value. Manual adjustments of individual peaks are inefficient, necessitating mathematical calculations for improved speed and accuracy. This need led to Ernst's development of the first model for automatic phase correction in 1969 (Ernst, 1969).

2.1. Global Phase Error Correction Using a Constant Phase Adjustment Value

The simplest model for phase correction involves applying a constant phase adjustment across the entire spectrum. This can be expressed by the formula:
θ = c
In this formula, θ represents the phase value to be added to a spectrum. This phase value is equal in magnitude but opposite in sign to the global phase error of the spectrum. The constant c serves as the adjustment value.
The key challenge is determining the appropriate value for c. Ernst (Ernst, 1969) proposed a method for estimating global phase errors based on integrals, which remains widely used today. The global phase correction model can be formulated as follows:
θ = − arctan ⁡ ( ∫ D x d x ∫ A x d x )
In this formula, arctan denotes the inverse tangent function, which is utilized for phase adjustment as phase correction fundamentally involves angle modification. Here, x represents the frequency or location-related variable, D(x) denotes the observed dispersion spectrum, and A(x) stands for the observed absorption spectrum. A(x) and D(x) represent the real and imaginary parts of the complex data in the MR frequency domain, which is commonly referred to as the frequency domain for one-dimensional (1D) MR data and as k-space for multi-dimensional MR data.
While Ernst’s original paper (Ernst, 1969) did not explicitly include a formula involving the dispersion spectrum, it utilized the Hilbert transform of the observed frequency domain data. In theory, when there is no signal decay over time, a pure dispersion spectrum is equivalent to the Hilbert transform of the corresponding pure absorption spectrum, which shifts the phase by 90 degrees. This 90-degree phase difference is a key concept used for phase adjustment in Džakula’s research (Džakula, 2000).
However, real MR signals are subject to decay and various types of errors over time. Therefore, it is more accurate to use the observed dispersion spectrum directly rather than relying on the Hilbert-transformed spectrum. This approach has been adopted in subsequent research. Nonetheless, when the observed dispersion spectrum is unavailable, the Hilbert-transformed spectrum remains a viable alternative.

2.2. Linear Phase Correction Model with Zero and First Order Parameters

The global phase correction model, while useful, does not account for the variability of phase errors across the spectrum. This limitation arises because phase errors can vary with frequency and are not uniformly distributed. To address these variations, a linear phase correction model with zero and first-order parameters was introduced. This model provides a more sophisticated approach by incorporating frequency-dependent terms.
For one-dimensional (1D) frequency domain data, the phase correction model can be expressed as (Sotak, Dumoulin and Newsham, 1984; Craig and Marshall, 1988; Brown, Campbell and Moore, 1989; Montigny et al., 1990; Heuer, 1991; Balacco, 1994; Džakula, 2000; Chen et al., 2002; Jiru, 2008; de Brouwer, 2009; Van, Hernando and Sutton, 2011; Wright, Buydens and Heerschap, 2012; Bao et al., 2013; Worley and Powers, 2014; Worley, Sisco and Powers, 2015; Morris, 2017; Prostko et al., 2022; Rout et al., 2023; Jiang, 2024):
θ = β 0 + β 1 x
In this formula, β0 and β1 represent the zero and first-order parameters, respectively. The variable x can be any function related to position or frequency in the observed absorption spectrum, such as a scaled index (Chen et al., 2002).
For two-dimensional (2D) frequency domain data, the phase correction model can be extended as (Feinauer, Altobelli and Fukushima, 1997; Larry Bretthorst, 2008; Moussavi et al., 2014):
θ = β 0 + β 1 x + β 2 y  
Here, x and y represent the two spatial frequency directions in k-space. This model can be extended further to three-dimensional (3D) and four-dimensional (4D) MR data.

2.3. Linear Phase Correction Model with Higher-Order Terms

In cases where phase errors exhibit non-linear characteristics, the linear model can be further extended to include higher-order terms. This extension allows for a more accurate representation of complex phase error patterns.
For 1D MR data, a linear phase correction model with higher-order terms can be expressed as (Vanvaals and Vangerwen, 1990; Hoffman, Delaglio and Levy, 1992; Hardy et al., 2009; Worley and Powers, 2014; Gan and Hung, 2022; Jaroszewicz et al., 2023):
θ = β 0 + β 1 x + β 2 x 2 + …
For 2D MR data, the model can be written as (Zheng Chang and Qing-San Xiang, 2005):
θ = β 0 + β 1 x + β 2 y + β 3 x 2 + β 4 y 2 + …
This approach can also be extended to three-dimensional (3D) and four-dimensional (4D) MR data, providing enhanced flexibility for correcting non-linear phase errors.

2.4. Neural Networks with Multiple Layers

As discussed in previous sections, traditional phase correction models have evolved from simple global phase shifts to more sophisticated linear models that address frequency-dependent errors and incorporate higher-order terms. While these advancements have significantly improved phase correction, they still face limitations when dealing with complex, non-linear phase error patterns. To overcome these challenges, modern techniques have introduced advanced machine learning approaches, such as neural networks.
Neural networks, particularly those with multiple layers, offer a promising alternative by learning complex, non-linear patterns directly from data. Unlike traditional models that rely on predefined mathematical formulations, neural networks can adaptively learn and correct phase errors based on extensive training data. This adaptability allows them to capture intricate relationships between phase errors and spectral features, making them effective for handling non-linear phase error patterns.
To understand neural networks, consider them as a series of interconnected nodes (neurons), where each node performs a mathematical operation—typically a weighted sum followed by an activation function. In this context, a simple linear regression model can be seen as a basic form of a neural network, consisting of just an input layer and an output layer.
However, a typical neural network includes one or more hidden layers, each applying non-linear activation functions to model complex patterns in the data. The network's final output is generated through a sequence of transformations across all layers, with each layer enhancing the model's ability to correct phase errors effectively. Figure 1 illustrates a neural network architecture consisting of five layers: an input layer, three intermediate hidden layers, and an output layer. This structure demonstrates how the network processes data through multiple stages to improve phase correction.

2.4.1. Unsupervised Neural Network Learning

Neural network learning can be classified into supervised and unsupervised learning, with supervised training being the dominant approach. The key difference between these approaches lies in the use of ground truth data. Supervised learning requires ground truth phase values to be included in the MR dataset during the training process. The trained neural network model can then predict and adjust phase values for new MR datasets. In contrast, unsupervised learning does not rely on ground truth during training. Instead, it identifies patterns and structures within the data without the need for ground truth.
In the context of phase correction, unsupervised learning becomes particularly valuable since phase errors are not directly observable, and these statistical models we have discussed earlier are typically applied within an unsupervised learning framework.
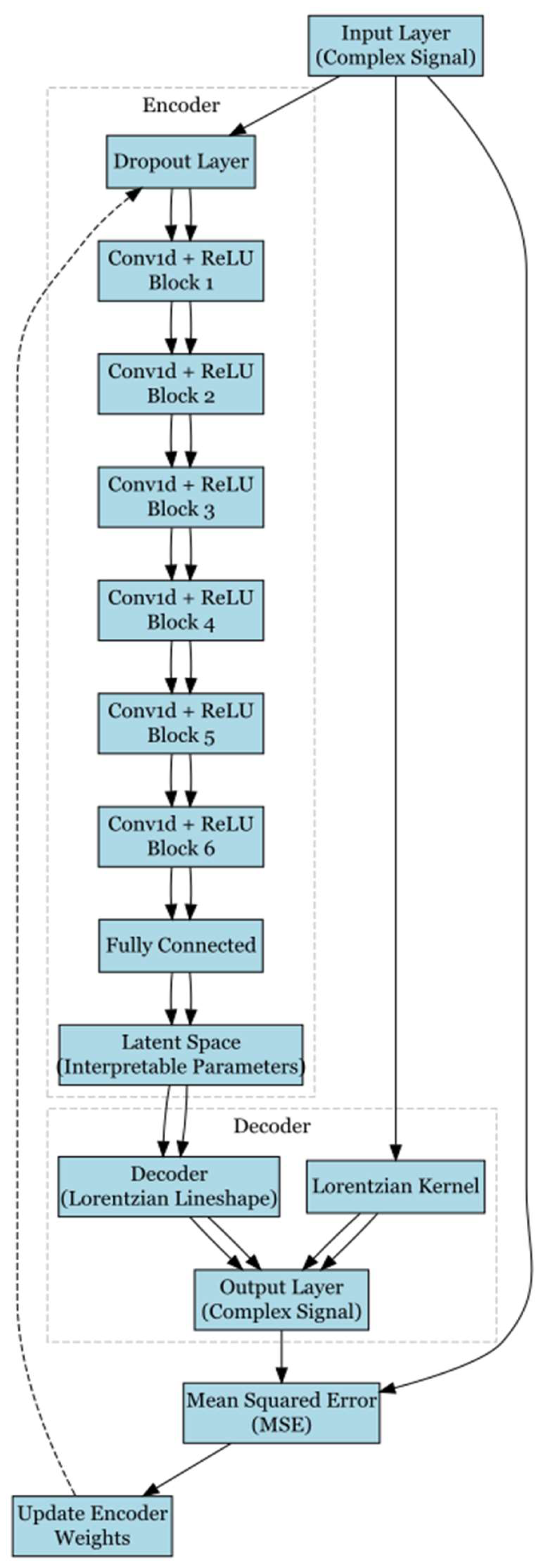
Now, let’s delve deeper into how unsupervised neural network learning can be applied to phase correction. Based on the ideas from (Shamaei et al., 2023), Figure 2 illustrates a neural network architecture designed for unsupervised phase correction using deep autoencoders. This architecture comprises several nonlinear hidden layers and includes two main components: an encoder and a decoder.
The encoder processes MRS (magnetic resonance spectroscopy) signals in complex format, converting them into a simpler form that the network can more easily interpret. It begins with a dropout layer that randomly removes some of data points during each training step. This is followed by six convolutional blocks and a fully connected layer, which combines the features learned by the previous layers to make final predictions.
Each convolutional block includes a one-dimensional convolutional layer (Conv1D) followed by a Rectified Linear Unit (ReLU) activation function.
Convolution is just to merge two functions, illustrating how one function is altered by the other. One-dimensional convolution can be expressed as (https://en.wikipedia.org/wiki/Convolution):
f ∗ g t = f t ∗ g t = ∫ − ∞ + ∞ f τ g t − τ d τ
In digital convolution, a small matrix, known as a filter or kernel, is applied to a larger matrix (input) by sliding it across the input and performing element-wise multiplications. The results of these multiplications are summed to generate a single number for each position of the filter, creating an output matrix or feature map. Unlike simple matrix multiplication, which involves dot products of rows and columns, convolution captures local patterns by repeatedly applying the filter across the entire input, making it essential for tasks like image processing in neural networks.
In 1D convolution (Conv1D), a one-dimensional input data matrix is convolved with a one-dimensional filter of shorter length, producing a one-dimensional output that highlights local patterns in the input sequence. In 2D convolution (Conv2D), a two-dimensional input data matrix is convolved with a two-dimensional filter of fewer elements, generating a two-dimensional output that captures spatial features and patterns within the image.
Each convolutional block in Figure 2 also includes an activation function. The ReLU activation function filters the data by allowing only positive values to pass through and can be expressed as
f x = m a x ⁡ ( 0 ,   x )
These Conv1D and ReLU blocks work together to extract and process relevant features from the input data. The incorporation of these components enables the network to handle the complexities of phase correction more efficiently.
Following the encoder, the decoder utilizes the information provided by the encoder to reconstruct a Lorentzian lineshape of a specific peak in the input signal using the latent space parameters.

2.4.2. Supervised Neural Network Learning

In unsupervised learning, there is no ground truth needed for phase values or absorption spectra without phase errors (Shamaei et al., 2023). The Lorentzian lineshape is used as a reference model for phase adjustments, as shown in Figure 2. When ground truth phase values or absorption spectra without phase errors are available, they can be used for comparison, enabling supervised neural network learning. This approach follows the structure in Figure 1 and the architectural pattern depicted in Figure 2.
Synthetic data are commonly used to establish ground truth for supervised learning. For instance, Jurek (Jurek et al., 2023) utilized the BrainWeb MRI Simulator (https://www.mcgill.ca/bic/neuroinformatics/software-neuroinformatics-tools-and-analysis-brainweb-mri-simulator) with random phase shifts to achieve this goal. The phase correction architecture, based on SRCNN (Super-Resolution Using Deep Convolutional Networks) (C. Dong et al., 2016), includes an input layer, three hidden convolutional layers with non-linear mapping, and an output layer that performs convolutions twice to produce the real and imaginary parts of the phase-corrected image as separate channels. This structure resembles the five layers shown in Figure 1, although the number of nodes differs significantly.
Another example is the FID-A software (Simpson et al., 2017), used in supervised learning by Bugler (Bugler et al., 2024) to obtain ground truth. This approach also involves an input layer, an output layer, and multiple hidden layers. Except for the output layer's convolution, all other convolutional and dense layers use the ReLU activation function, which is independently applied to both the real and imaginary components of the data. A dense layer, or fully connected layer, integrates all information to make decisions or predictions based on identified patterns.

2.4.3. Semi-Supervised Neural Network Learning

Semi-supervised neural network learning combines elements of supervised and unsupervised learning to enhance model performance, particularly when ground truth data is limited. This approach is especially useful in the context of phase correction, where it utilizes both labeled and unlabeled data.
An example of this method can be found in Ma et al. (Ma et al., 2024), where the semi-supervised learning framework consists of two components: supervised learning and unsupervised learning. The supervised learning component, similar to the approach used by Bugler et al. (Bugler et al., 2024), relies on simulated data generated with the FID-A software (Simpson et al., 2017). In contrast, the unsupervised learning component uses an in vivo dataset extracted from the Big GABA repository (Mikkelsen et al., 2017), which serves as template spectra. These templates are modified by introducing additional offsets to simulate real-world variations. The results from these two components are integrated to enhance overall model performance.
However, it is important to note that the unsupervised component is not devoid of supervision, as it utilizes a form of pseudo ground truth. This suggests that the approach is, in fact, supervised learning rather than semi-supervised, as the authors claimed (Ma et al., 2024).
Regarding the architecture in Ma’s study (Ma et al., 2024), the CNN-SR model (convolutional neural network-based spectral registration) is employed for both training processes. Like other neural network models discussed earlier, CNN-SR includes an input layer, an output layer, and several internal hidden layers. Specifically, CNN-SR comprises convolutional layers, batch normalization layers, max-pooling layers, and dense (fully connected) layers. Each hidden layer is followed by a ReLU activation function, while the final output layer uses a linear activation function.

2.5. Supervised Neural Network Combined with High-Order Polynomial Models

In the pursuit of more accurate and robust phase correction, integrating traditional linear models with advanced neural network architectures presents a compelling approach. Neural networks excel at capturing complex, non-linear relationships, while linear models are valued for their simplicity and interpretability. Combining neural network and linear model approaches leverages the strengths of both methods, with higher-order terms in the linear model providing additional enhancement. This hybrid approach captures the broader, non-linear trends identified by the neural network while making finer, detail-oriented adjustments through the linear model, leading to enhanced phase correction performance.
For instance, You et al. (You et al., 2022) demonstrated the effectiveness of combining a 3D multichannel U-Net CNN with a third-order polynomial regression model. The modified 3D U-Net, based on the original U-Net architecture (Ronneberger, Fischer and Brox, 2015), used the tanh activation function instead of ReLU. The network, consisting of more than 30 layers, features a contracting path on the left and an expansive path on the right, forming a U shape. The contracting path follows the standard convolutional network structure, with successive convolution layers, each followed by tanh activation and max pooling, which downsamples the input data.
The tanh activation function introduces non-linearity and ensures that outputs remain within a specific range, facilitating smooth transformations to capture intricate patterns. The tanh function is defined as:
tanh ⁡ x = e x − e − x e x + e − x
This non-linear transformation maps any real-valued input x to the range [-1,1].
As with all supervised neural networks, ground truth data is essential for training the 3D U-Net. In You’s study (You et al., 2022), manually corrected phase values were used as ground truth. These values were then smoothed by fitting them to a third-order polynomial regression model to refine the corrections and reduce local inference errors. After phase correction with the 3D CNN, the adjusted phase values were further refined by fitting them to a third-order polynomial least-squares regression model. This two-step process effectively enhanced phase correction accuracy by combining the deep learning capabilities of the neural network with the precision of polynomial regression, particularly by mitigating spurious local errors that might arise from the neural network’s inferences.
Similarly, Srinivas et al. (Srinivas et al., 2023) employed the same 3D U-Net architecture and tanh activation function as You et al. (You et al., 2022). While the specifics of their ground truth data generation were not fully detailed, it appears to follow a similar strategy. Furthermore, the post-processing step involving third-order polynomial regression of the 3D U-Net inferences was incorporated into the architecture diagram.

3. Optimization Functions for Phase Correction

Phase errors and the corresponding adjustments are not directly observable. Consequently, all phase correction models—whether traditional statistical or neural network-based—require an optimization process to determine appropriate parameters. This is necessary unless phase errors have already been estimated by other methods, such as manual phase estimation, DISPA (Dispersion vs Absorption) approaches (Marshall, 1978; Herring and Phillips, 1984; Sotak, Dumoulin and Newsham, 1984; Craig and Marshall, 1988; WACHTER E. A, SIDKY E. Y and FARRAR$ T. C, 1989; Hoffman, Delaglio and Levy, 1992), or the PAMPAS (Phase Angle Measurement from Peak AreaS) method (Džakula, 2000). When phase errors are already estimated, a simple regression model can be applied without further optimization. However, when phase errors are not pre-estimated, this section discusses several optimization functions that can be used for phase error correction.

3.1. Minimization of Integral of Dispersion Spectrum

Consider a simple linear model given by formula (3):
θ = β 0 + β 1 x
Now, consider formula (2):
θ = − arctan ⁡ ( ∫ D x d x ∫ A x d x )
Using this, we can formulate an optimization function for phase correction. The following optimization function is conceptually similar to, but presented slightly differently from, the so-called Ernst method described in Binczyk’s paper (Binczyk, Tarnawski and Polanska, 2015):
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) ∫ S D x , β 0 , β 1 d x
Binczyk referred to S D x , β 0 ,   β 1 as the magnitude of the dispersion spectrum after phase correction using a linear model with two parameters. Thus, S D x , β 0 ,   β 1 can be considered the absolute value of the dispersion spectrum, as it represents the magnitude component only. However, the integral of the absolute dispersion does not necessarily approach zero; in fact, it might actually reach a maximum when there is no phase error. The integral of the absolute dispersion spectrum does reach a minimum when the dispersion peaks are in a Lorentzian shape, which could occur if the dispersion is actually the absorption spectrum or the negative of the absorption spectrum. Therefore, it might be better to consider D x , β 0 ,   β 1 , representing the intensity rather than the absolute intensity, in the dispersion spectrum. The question remains: even with this consideration, is formula (10), used as one of the objective functions in Jaroszewicz’s study (Jaroszewicz et al., 2023), an effective optimization function?

3.2. Minimization of Absolute Integral of Dispersion Spectrum

We initially believed that formula (10) represented the optimization function based on Ernst’s paper (Ernst, 1969), as claimed in Binczyk’s paper (Binczyk, Tarnawski and Polanska, 2015). However, upon closer examination, this might not be the case. Ernst only stated, “The dispersion mode signal under nonsaturating conditions has a vanishing integral, for slow as well as for arbitrarily fast passage, whereas the integral of the absorption mode signal has a non-zero value” (Ernst, 1969). Clearly, Ernst did not explicitly mention an optimization function; he merely described the characteristics of MR data. Even if we interpret Ernst’s statement as implying optimization, he did not specify whether two individual functions or a combined optimization function should be used.
More importantly, even if we develop an optimization function based on Ernst’s statement—'The dispersion mode signal under nonsaturating conditions has a vanishing integral'—the function should converge to zero rather than merely seeking a minimum. For instance, although −20 is smaller than −2, −2 is closer to zero. On the other hand, if we consider S D x , β 0 ,   β 1 in formula (10) as the absolute dispersion spectrum, it diverges from Ernst’s original concept.
Revisiting formula (2): θ = − arctan ⁡ ( ∫ D x d x ∫ A x d x ) Based on this formula, θ reaches its minimum when the numerator converges to zero, not simply when it reaches a minimum value.
Therefore, the following optimization function, which minimizes the absolute integral of the dispersion spectrum, might make more sense:
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) | ∫ D x , β 0 , β 1 d x |

3.3. Maximization of R Ratio

In his original paper, Ernst (Ernst, 1969) did suggest an optimization function: “It is a rather complicated function of the phase angle α, such that an iterative search procedure must be used to determine the proper phase setting for maximum R.” Here, R is defined as the ratio of the “maximum positive signal excursion to maximum negative signal excursion” (Ernst, 1969), and is mathematically expressed as:
θ ^   = a r g m a x ( θ )   R = a r g m a x ( θ )   m a x ⁡ ( A x , θ ) | m i n ⁡ ( A x , θ ) |
Here, A x ,   θ represents the absorption spectrum after phase correction with the value θ, where x is the variable related to frequency or location. Clearly, this approach aims to find the optimal global phase adjustment for correcting phase errors.

3.4. Minimization of the Integral of Absolute Absorption Spectrum

The integral of the absolute absorption spectrum reaches its minimum when there is no phase error. Therefore, an optimization function—the minimization of the integral of the absolute absorption spectrum—can be formulated as:
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) ∫ | A x , β 0 , β 1 | d x
Here, A x , β 0 ,   β 1 represents the absorption spectrum after phase correction using a linear model with two parameters, where x is the variable related to frequency or location. This optimization function is also referred to as area minimization (de Brouwer, 2009). Although de Brower did not explicitly provide the formula, the concept can be inferred from the MATLAB code in the supplemental file (de Brouwer, 2009).

3.5. Maximization of the Integral of the Absorption Spectrum

Conversely, we can consider another property of the absorption spectrum: the integral of the absorption spectrum reaches its maximum when there is no phase error. This can be mathematically expressed as:
β 0 ^ , β 1 ^ = a r g m a x ( β 0 , β 1 ) ∫ A x , β 0 , β 1 d x
This method was originally suggested by Nelson and Brown (Nelson and Brown, 1989), who also proposed a variation that applies it exclusively to peak regions. It is also the main objective function in Jaroszewicz’s study (Jaroszewicz et al., 2023).
Hardy et al. (Hardy et al., 2009) extended this approach to three-dimensional gradient-echo images by searching for the parameters of a linear model with third-order polynomial terms for phase error correction. In this case, the model involves three position variables and up to 20 parameters: one zero-order term, three first-order terms, six second-order terms, and ten third-order terms. Despite the complexity, the optimization still involves maximizing the integral of the real part of the images, though it is performed in the image domain rather than the frequency domain.

3.6. Minimization of the Sum of Squares of Differences between Heights at Peak-Region Maxima in the Absorption Spectrum and the Magnitude Spectrum

This method was also proposed by Nelson and Brown (Nelson and Brown, 1989). The magnitude spectrum can be calculated using the following equation:
M x = A ( x ) 2 + D ( x ) 2
Here, x represents the frequency or location-related variable, and M(x), A(x), and D(x) are the magnitude, absorption, and dispersion spectra respectively.
The rationale is that peak heights of absorption and magnitude should be the same when there is no phase error. The optimization function can be written as:
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) ∑ p e a k   m a x i m a ( A x , β 0 , β 1 − M ( x ) ) 2
Note that M(x) is independent of the phase.

3.7. Minimization of the Sum of Squares of Negative Values within Peak Regions in the Absorption Spectrum

This function aims to minimize the sum of squares of negative values within the peak regions of the absorption spectrum. The rationale is that after phase correction, the negative values within the peak regions should be minimized. This method was also proposed by Nelson and Brown (Nelson and Brown, 1989).
Formula:
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) ∑ p e a k   r e g i o n s ( min ⁡ 0 , A x , β 0 , β 1 ) 2

3.8. Minimization of Entropy with Negative Peak Penalty

Chen (Chen et al., 2002) proposed an optimization function for phase error correction based on entropy minimization. Entropy minimization is a widely used approach in various machine learning applications.
Entropy measures the average uncertainty associated with a set of states and their corresponding probabilities. The general formula for entropy is given by (https://en.wikipedia.org/wiki/Entropy_(information_theory)):
H X = − ∑ x ∈ X   p x l o g p ( x )
where p(x) represents the probability of a random variable x.
While this formula is conceptually straightforward, there is no direct association between MR data and probabilities. To address this, Chen et al. (Chen et al., 2002) proposed replacing p(x) in formula (18) with normalized derivatives of MR data. Additionally, a penalty term is incorporated. The resulting minimization function, based on Chen’s suggestion, is expressed as:
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) { − ∑ i [ | A i m | ∑ i | A i m | ln ⁡ | A i m | ∑ i | A i m | ] +   γ [ ∑ i I A i < 0 A i 2 ] }
Here, A i a shorthand notation for A ( i ,   β 0 ,   β 1 ) , which represents the i-th data point in the absorption spectrum after applying linear phase correction with two parameters β0​ and β1. The shorthand Ai is used in the formula to simplify the expression, as the full notation would make the formula excessively long. The parameter m denotes the order of the derivative and can range from 1 to 4. The parameter γ is a penalty factor, and I() is an indicator function.
Following Chen’s idea as presented in formula (19), Binczyk proposed a simplified version of this optimization function (Binczyk, Tarnawski and Polanska, 2015):
β 0 ^ ,   β 1 ^ = a r g m i n ( β 0 , β 1 ) { − ∑ i [ | A i | ln ⁡ | A i | ] + P }
In this version, the absolute value of the phased absorption is used instead of the normalized absolute value of the derivative of the phased absorption. Additionally, no detailed information is provided about the penalty term.

3.9. Negative Peak Penalty after Normalization

Instead of treating the negative peak as a penalty term in (19) as proposed by Chen (Chen et al., 2002) , de Brower (de Brouwer, 2009) opted to use the penalty component alone as an optimization function, with a slightly modified formula. This can be expressed by the following formula based on the MATLAB code provided in the supplementary file (de Brouwer, 2009):
β 0 ^ , β 1 ^ = a r g m i n ( β 0 , β 1 ) ∑ i ( A ( i , β 0 , β 1 ) − A ( i , β 0 , β 1 ) ) 2
While de Brower (de Brouwer, 2009) suggested performing normalization before minimization, a constant scaling factor does not impact the minimization process, although it might affect the calculation speed.

3.10. Mean Squared Error

Mean squared error (MSE) is one of the most commonly used loss functions, with a basic formula that is straightforward and can be expressed as:
M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2
Here, n represents the number of data points, y i is the i-th observed value, and ​ y ^ i is the estimated value for ​ y i . Without dividing by n, this formula is known as the sum of squared errors (SSE) or is often referred to as the L2 error. This measure can also be used for phase error correction. For example, it was used as the main component of the loss function to compare the fit and spectra in an extension of the cross-entropy stochastic optimization method (Ravanbakhsh, Poczos and Greiner, 2010). In this case, the other component of the loss function was the absolute error (Ravanbakhsh, Poczos and Greiner, 2010).
While the concept of MSE is straightforward, applying it to data with phase errors can be challenging. Phase errors distort the data, making it difficult to compare with data that is free from such errors. To effectively use MSE for phase correction optimization, it is essential to have ground truth data without phase errors. This can be obtained through synthetic data (Vanvaals and Vangerwen, 1990; Jurek et al., 2023), previously acquired reference spectra of pure solid-state components (Prostko et al., 2022), by manually phasing the data (You et al., 2022; Srinivas et al., 2023), or by using specific mathematical models such as Lorentzian, Gaussian, and Voigt functions (Shamaei et al., 2023).

3.11. Stein's Unbiased Risk Estimate Minimization

Since it is hard to apply MSE without extra ground truth data, Stein's Unbiased Risk Estimate (SURE) was introduced for phase correction optimization process. SURE is an estimate of the mean squared error proposed by Stein (Stein, 1981). It has been applied to MRI data for adaptive phase correction (Pizzolato et al., 2020) and it operates in the image domain. The corresponding loss function is defined as (Pizzolato et al., 2020):
φ I 0 , λ = 1 2 X Y | I 0 − ρ I 0 , λ | 2 − σ ^ 2 + σ ^ 2 X Y ( d i v R ρ I 0 , λ + d i v I ρ I 0 , λ )
Here, the 2D image is composed with X data points in the x direction, and Y data points in the y direction, resulting in X×Y pixels. I 0   is the origin image. ρ I 0 ,   λ represents a regularized or phase-corrected version of the image. σ ^ 2 denotes the noise variance. div is a divergence operator. ℜ[⋅] and ℑ[⋅] represent the real and imaginary parts of the function, respectively. The divergence terms can be estimated with Monte Carlo approach.

3.12. Maximization of Refocusing Ratio

For 2D image domain data with both x and y directions, we assume that the phase error is only related to the x direction. Therefore, the second-order linear model for phase correction is the same as in formula (5), but without additional terms:
θ = β 0 + β 1 x + β 2 x 2
Chang and Xiang (Zheng Chang and Qing-San Xiang, 2005) proposed the following optimization function for phase correction in the image domain, which is slightly reformatted here for clarity:
β 0 ^ , β 1 ^ , β 2 ^ = a r g m a x ( β 0 , β 1 , β 2 ) | ∑ x , y S ( x , y , β 0 , β 1 , β 2 ) | ∑ x , y | S x , y , β 0 , β 1 , β 2 |
While this function may seem complex, it is actually quite straightforward. S ( x , y , β 0 , β 1 ,   β 2 ) refers to the real part of the image data for each pixel after phase correction using a second-order linear model. The ratio of the absolute value of the summation to the summation of absolute values is known as the refocusing ratio (R) (Chang and Xiang, 2005). The R value ranges from 0 to 1, with R=1 indicating no phase error.

3.13. Posterior Probability Maximization

Similar to section 3.12, this approach also works in the 2D image domain but utilizes a different phase correction model, which follows the same form as in formula (4):
θ = β 0 + β 1 x + β 2 y
Bretthorst (Larry Bretthorst, 2008) proposed simplified posterior probability functions for β 1   and β 2 ​, which take the form of Student's t-distribution. Thus, this t-distribution is used to estimate the first-order parameters. Additionally, the zero-order phase parameter that maximizes the posterior probability is estimated using the following formula (Larry Bretthorst, 2008):
( β 0 ) e s t = − 1 2 tan − 1 ⁡ ( X W ) ± 8 σ 2 X 2 + W 2
Where
X = 2 ∑ j ∑ l F R j l F I j l
W = ∑ j ∑ l [ F R j l 2 − F I j l 2 ]
Here, F R j l   and F I j l refer to the real and imaginary components of a pixel at the j-th and l-th intersection in the two directions of the image domain, while, σ 2 represents the noise variance.

3.14. Maximum Likelihood Estimation (MLE) Based Cost Function

To address phase errors induced by motion in 3D imaging, and assuming a linear phase correction model, Van et al. (Van, Hernando and Sutton, 2011) proposed an MLE-based cost function:
( a ^ , a 0 ^ ) = a r g m i n ( a , a 0 ) ( R a , a 0 ) = a r g m i n ( a , a 0 ) ∑ r | e j ∠ I b ~ ( r ) − e j ∠ I 0 r + a · r + a 0 ] | 2
Here, a refers to a vector of the first-order parameters (slopes) of the linear model for the three different dimensions in the image, and a 0 is the intercept (zero order or global parameter) of the linear model. The variable r represents image space across multiple dimensions, j = − 1 (commonly represented as i in mathematics), ∠ is the phase extraction operator, I b ~ r is the image with phase error, and I 0 r is the ideal image without distortion.
Although formula (26) appears complicated, it essentially minimizes the sum of squared errors, but in a nonlinear fashion due to the nature of complex image data.

3.15. Maximization of Pearson Correlation between Magnitude and Real Spectra

Since an ideal real spectrum should have peak heights that match those of the corresponding magnitude spectrum, and they are positively correlated—meaning that when the magnitude spectrum increases, the real spectrum also increases, and when the magnitude spectrum decreases, the real spectrum decreases as well—Wright et al. (Wright, Buydens and Heerschap, 2012) proposed maximizing the Pearson correlation coefficient between the real spectrum and the magnitude spectrum. This is done to optimize zero- and first-order parameters in a linear phase correction model for each of the two specific regions separately: the choline/creatine region (3.36–2.86 ppm) and the citrate region (2.86–2.37 ppm). The formula can be written as:
β 0 ^ , β 1 ^ = a r g m a x ( β 0 , β 1 ) ∑ i ( A ( i , β 0 , β 1 ) − A ( β 0 , β 1 ) ¯ ) ( M ( i , β 0 , β 1 ) − M ( β 0 , β 1 ) ¯ ) ∑ i ( A ( i , β 0 , β 1 ) − A ( β 0 , β 1 ) ¯ ) 2 ( M i , β 0 , β 1 − M β 0 , β 1 ¯ ) 2
Here, A and M represent the real and magnitude spectra, respectively.

3.16. Tail Height Minimization and Penalty for Negative Peaks

Bao et al. (Bao et al., 2013) proposed a two-step process for phase error correction: coarse tuning and fine tuning. In the first step, coarse tuning, the following tail height minimization objective function (OF) is used (Bao et al., 2013):
O F = ∑ i = 1 P N a b s { ∑ k = 0 M R [ p e a k i . S t a r t − k ] − ∑ k = 0 M R [ p e a k i . E n d + k ] }
Here, R refers to the real part of a spectrum, PN is the number of identified peaks, and M denotes the number of chosen points, where 1≤M≤4.
In the second step, fine tuning is based on minimizing the sum of squared errors, with the penalty function (PF) defined as (Bao et al., 2013):
P F = ∑ i = 1 N { T e m p R i − a b s ( T e m p R i ) } 2
Where:
T e m p R i = R i ,                                                                                                                   d e f a u l t   s i t u a l t i o n 0 ,                                                         i f   t h e   i t h   p o i n t   i s   i n   d i s t o r t e d   p e a k s − R i ,                                       i f   t h e   i t h   p o i n t   i s   i n   n e g a t i v e   p e a k s
Here, R(i) indicates the i-th data point in the real part of the spectrum.

3.17. Sum of Squared Error Minimization with Scaling

Worley and Powers (Worley and Powers, 2014) proposed an optimization function to simultaneously search for parameters in a linear phase correction model and a scaling factor. The minimization function is derived from Worley and Powers (2014):
b ^ , ϕ 0 ^ , ϕ 1 ^ = a r g m i n ( b , ϕ 0 , ϕ 1 ) ∑ j = 1 N | b · s ɷ j e i ϕ 0 + ϕ 1 ɷ j − r ( ɷ j ) | 2
In this formula, b is the scaling factor, ϕ0 and ϕ1 are the zero-order and first-order parameters for a linear phase correction model, respectively, and i = − 1 . The index j refers to a point in the spectrum with length N, s(ɷj) is the j-th point of the real part of mean-centered row in data matrix X, r(ɷj) is the corresponding point in a reference spectrum, and ɷj represents the frequency at the j-th point.
If the scaling factor b is ignored, formula (30) reduces to the sum of squared errors (SSE).

3.18. Phase Difference Minimization

This optimization function is specifically designed for MRI data with multiple scans. Due to the long scan time, these images often contain phase errors caused by patient movement relative to the first scan. To correct these phase errors, a simple optimization function can be applied to the region of interest (ROI) (Xia and Chen, 2021):
ϕ ′ ( k x ,   k y )   = a r g m i n ( ϕ k x ,     k y ) ( arg [ G j ′ ( k x   k y ) ] − arg [ G j ( k x   k y ) ] }
Here, ϕ′(kx, ky) is the estimated phase adjustment value at location (kx,ky). The term arg[Gj′(kx, ky)] and arg[Gj(kx, ky) represent the phase values (angles) between two iterations. The initial value of Gj(kx, ky) is set as the first scan’s k-space data, including the phase shift due to movement. Through iterative adjustments, Gj(kx,ky) is updated until the phase difference is minimized, producing a corrected image.

3.19. Mean Absolute Error

The mean absolute error (MAE) is a straightforward metric, and its general formula can be expressed as:
M A E = 1 n ∑ i = 1 n | y i − y ^ i |
Where n represents the number of data points, y i is the i-th observed value, and ​ y ^ i is the estimated value for ​ y i . Without dividing by n, this formula is known as the sum of absolute errors (SAE) or is often referred to as the L1 error.
A significant challenge in directly measuring phase shift MAE is that the phase shift itself is unknown and not directly observable. To address this issue, Bugler et al. (Bugler et al., 2024) trained a convolutional neural network (CNN) model using simulations where the ground truth of the phase shift was known. This approach relies on the availability of ground truth; without it, the method may not be applicable.

3.20. Linear Combination of Mean Absolute Error

The MAE loss function can be extended to a linear combination of multiple MAE loss functions for different variables. Ma et al. (Ma et al., 2024) proposed such a loss function, defined as follows:
L o s s = 100 × R e a l S p e c t r a M A E + I m a g i n a r y S p e c t r a M A E + F r e q u e n c y M A E 10 + P h a e M A E 20
This approach requires ground truth to calculate multiple types of MAEs. Specifically, the real and imaginary MAEs are computed by comparing the pseudo-ground truth template spectra from the BIG GABA database (Mikkelsen et al., 2017), while the frequency and phase MAEs are calculated using comparisons to simulated ground truth.

4. Optimizers in Traditional Statistics and Neural Networks

As discussed earlier, phase errors and the corresponding phase values that require adjustment are not directly observable. Therefore, except in rare cases where phase errors have already been estimated, each phase correction model—whether based on traditional statistical methods or neural networks—requires an optimization process to determine the appropriate parameters.
To execute this optimization, both optimization functions and optimizers are essential. While considerable attention has been paid to developing optimization functions tailored to specific challenges, the optimizers that execute these functions often receive less focus, particularly within traditional statistical methods.
An optimization function represents the goal, while an optimizer is the computational procedure used to achieve that goal. Optimizers are algorithms designed to iteratively adjust model parameters to find the optimal solution. The selection of an optimizer plays a crucial role in the optimization process, affecting aspects like convergence speed and the ability to avoid getting stuck in local minima or maxima, and the overall accuracy of the model. In the following sections, we will examine the optimizers used for phase error correction in both traditional statistical models and neural networks.

4.1. False Position

The False Position method, also known as Regula Falsi, is an ancient technique that combines elements of the bisection method and linear interpolation to iteratively refine a solution. This optimization method starts with an initial “false” position—a guess that serves as an approximation rather than the exact solution. The process involves evaluating the function at the endpoints of the interval and using these values to linearly interpolate a new point within the interval. This new point becomes one of the endpoints for the next iteration, gradually narrowing the interval and honing in on the root. Despite its age, this method has continued to find applications, including zero-order equality (ZOE) method for phase correction (Balacco, 1994).

4.2. Golden Section Bisection

The golden section bisection method is an optimization technique designed to find the minimum or maximum of a unimodal function. It builds on the principles of bisection, similar to the false position method, but with a key difference: it utilizes the golden ratio, approximately 1.618, to divide the search interval into segments that maintain a consistent ratio. By leveraging the golden ratio, this method efficiently narrows down the search space and has been used in various applications. For example, in adaptive phase correction (APC), this method was employed to reduce the number of evaluations in the phase correction optimization process (Pizzolato et al., 2020).

4.3. Simplex

The Simplex algorithm is a well-known method for solving linear programming problems, first proposed by George Dantzig in 1947 (Gass, 2011). The algorithm iteratively explores the vertices of the feasible region to identify the optimal solution. More specifically, the Simplex method moves from one vertex of the feasible region to an adjacent one in order to maximize or minimize the objective function. The algorithm has been widely applied in various optimization processes, including phase error correction (Brown, Campbell and Moore, 1989; Chen et al., 2002; de Brouwer, 2009).

4.4. Nelder-Mead

Unlike the Simplex algorithm, which is used for linear programming, the Nelder-Mead method (Nelder and Mead, 1965) is a direct search optimization technique that utilizes an n-simplex, which is an n-dimensional polytope with n+1 vertices. This method is particularly useful for optimizing non-differentiable functions. It iteratively adjusts the simplex based on function evaluations at its vertices, moving towards the optimum without requiring gradient information. Although the method itself does not require derivatives, the original paper includes a procedure for estimating the Hessian matrix near the minimum, which can be useful for statistical estimation problems. The Hessian matrix is a square matrix of second-order partial derivatives of a scalar-valued function, which describes the local curvature of the function. The Nelder-Mead method has been cited for its effectiveness in various applications, including phase error correction (Binczyk, Tarnawski and Polanska, 2015), and in fact, this is the default method for the famous R function optim().

4.5. Powell’s Method

In Brown’s phase correction paper (Brown, Campbell and Moore, 1989), it was mentioned that one of the optimizers was “Powell’s steepest descent.” However, it appears that “Powell’s steepest descent” is not a recognized algorithm; rather, Powell’s method and steepest descent are distinct methods. In this section, we will focus on Powell’s method and discuss the steepest descent method in the following section.
Powell's method was introduced by Powell in 1964 (Powell, 1964). Unlike many modern optimization techniques, Powell's method is a gradient-free algorithm that minimizes functions without the need for derivative calculations (Vassiliadis and Conejeros, 2001). It achieves minimization by iteratively performing line searches along a set of directions, updating these directions based on the results, all without relying on any gradient or derivative information.

4.6. Steepest Descent

Remarkably, the steepest descent method, developed by Augustin-Louis Cauchy in 1847, remains widely used today (Petrova and Solov’ev, 1997; Andrei, 2022). Cauchy, renowned for his work in mathematics, introduced this gradient-based technique as a practical approach for optimizing functions. It involves selecting a descent direction based on the negative gradient and finding an optimal step size via line search. Despite its simplicity, it remains fundamental in numerical optimization and continues to influence modern methods.

4.7. Quasi-Newton

The Newton-Raphson algorithm, widely used in traditional statistics, refines model parameters iteratively using both first and second derivatives, offering high accuracy with few iterations due to its quadratic convergence rate. However, computing the Hessian matrix can be costly for large-scale problems.
Quasi-Newton methods address this by approximating the inverse Hessian matrix using only first-order derivatives. Notable methods include the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm and its limited-memory variant, L-BFGS. These methods balance computational efficiency and convergence speed, making them suitable for complex problems where exact Hessian calculations are impractical. Quasi-Newton methods have been applied in phase error correction (Brown, Campbell and Moore, 1989; Hardy et al., 2009).

4.8. Hypersphere

Hypersphere optimization techniques constrain the search space within a hypersphere, which is a high-dimensional analogue of a circle or sphere. These methods perform angular searches orthogonal to the direction of steepest descent, reducing the risk of inefficient oscillatory iterations across ridges by stabilizing the search path (Brown, Campbell and Moore, 1989). Recent advancements by Kumar in 2022 (Kumar, Das and Snášel, 2022) have further refined these techniques, introducing improved spherical search strategies with local distribution-induced self-adaptation, making them effective for non-convex optimization problems, both with and without constraints.

4.9. Levenberg-Marquardt Nonlinear Least Squares

The gradient descent method iteratively adjusts parameters to minimize the objective function by moving in the direction of steepest descent. The Gauss-Newton method approximates the Hessian matrix by using the Jacobian (the partial derivatives of the residuals (or errors)) and ignoring the second-order partial derivatives. The Levenberg-Marquardt algorithm combines the directionality of gradient descent with the efficiency of the Gauss-Newton method, making it particularly effective for nonlinear objective functions. It updates parameters by adjusting the step size based on a damping factor, balancing the trade-off between speed and stability during convergence. This approach is especially useful for problems with complex error surfaces, where other methods might struggle with slow convergence or instability. The Levenberg-Marquardt method was employed in the optimization process for phase error correction (Worley and Powers, 2014; Worley, Sisco and Powers, 2015).

4.10. Trust-Region-Reflective

The trust-region-reflective method iteratively approximates the objective function within a “trust region”, an area where the model is expected to closely match the true objective. The region's size adjusts based on the model's performance: it expands if predictions are accurate and contracts if not. This approach prevents overly aggressive updates while allowing steady progress toward the optimal solution. It's particularly effective for complex, nonlinear objective functions with constraints, making it a reliable choice for challenging optimization problems. The Matlab lsqnonlin function, which offers this algorithm, was applied in phase error correction (Van, Hernando and Sutton, 2011).

4.11. Subplex/Sbplx

The Subplex method (Rowan, 1990) was derived from the Nelder-Mead n-simplex method, with Sbplx being a re-implementation of Subplex used in phase error correction (Prostko et al., 2022). Subplex improves upon the standard Nelder-Mead n-simplex approach by breaking the optimization problem into smaller, more manageable subproblems, which can be solved more efficiently. It combines local exploration with global refinement, concentrating on promising regions of the parameter space while remaining adaptable to explore new areas. This blend of local and global search enables Subplex to effectively navigate complex, multimodal objective functions where traditional Nelder-Mead n-simplex methods might become trapped in local optima.

4.12. Stochastic Gradient Descent (SGD)

PyTorch, a Python library based on the original Lua-based Torch, includes the optimization package torch.optim, which has been used in phase error correction (Shamaei et al., 2023), though the specific optimizer was not indicated in that application. While PyTorch offers various optimizers, including LBFGS, which we discussed previously, SGD and Adam are frequently mentioned in the documentation.
Stochastic Gradient Descent (SGD) is a fundamental optimizer for neural networks, particularly effective for large-scale and high-dimensional data. It updates parameters iteratively based on a randomly selected subset of data, making SGD faster and more scalable, but it also introduces noise into the optimization process. Consequently, SGD is commonly combined with the standard backpropagation algorithm (LeCun 1998, Dong 2016) and has been applied in phase error correction (Jurek et al., 2023).
Adam is another method for addressing the noise introduced by SGD and will be discussed in the next section.

4.13. Adaptive Moment Estimation (Adam)

To address the noise introduced by SGD and improve convergence, several enhancements have been developed, including momentum, learning rate schedules, and adaptive learning rates used in methods like AdaGrad, RMSprop, and Adam.
AdaGrad (Adaptive Gradient Algorithm) and RMSProp (Root Mean Square Propagation) are adaptive optimization algorithms that adjust learning rates based on past gradient information. RMSProp reduces the learning rate for frequently occurring features, while AdaGrad adapts the learning rate individually for each parameter. Adam (Adaptive Moment Estimation) combines the benefits of RMSProp and AdaGrad by using both the exponentially decaying average of past gradients and squared gradients, which enhances convergence speed and stability.
Adam has become one of the most widely used optimizers in deep learning, including for phase error correction (You et al., 2022; Shamaei et al., 2023; Srinivas et al., 2023), due to its robustness and efficiency. It performs well in a variety of settings and often requires minimal hyperparameter tuning to achieve good results.

4.14. Bayesian Optimization

Bayesian optimization employs probabilistic models and Bayes’ theorem to strategically determine where to sample next, with the goal of achieving optimal results with as few evaluations as possible. The approach involves building a probabilistic model of the objective function and using this model to guide the search process, effectively balancing the exploration of uncertain areas with the exploitation of known promising regions. Bayesian optimization has been applied in phase error correction (Larry Bretthorst, 2008).

5. Challenges

Despite the wide variety of models, optimization functions, and optimizers developed for MR data phase error correction, not all phase error correction methods in practice rely on fully automated approaches. A recent review by Ben-Tal et al. (Ben-Tal et al., 2022) even suggested that fully manual phase correction should be used, as it provides more accurate results, highlighting the ongoing limitations of automated approaches. So, why does automatic phase error correction still underperform in certain cases? In the following subsections, we explore the key challenges from three perspectives: models, optimization functions, and optimizers.

5.1. Challenges in Phase Error Correction Models

In order to correct phase errors, we need to develop a model if estimated phase errors from other approaches are not already available. This model, whether it is a statistical approach or a machine learning architecture, can estimate the necessary phase adjustment values. These values are then applied to the observed data to adjust the phase and correct the errors.
Among the five modeling approaches discussed in Section "2. Phase Models," global phase error correction with a constant phase adjustment value is the simplest. However, this model is too simplistic to handle phase errors, as phase errors are not constant in real-world MR data.A linear model, which includes both zero-order and first-order parameters, is the most commonly used for phase error correction. It introduces a first-order parameter to adjust for frequency-related phase errors, but it assumes a linear relationship between phase errors and frequency, which cannot adequately address non-linear phase errors.
To manage non-linear phase errors, higher-order terms are introduced into the linear model. While these terms can capture some non-linear phase errors, the non-linear pattern of phase errors cannot be fully addressed by simple quadratic or cubic terms.
Neural networks with multiple layers can handle complex, non-linear patterns, but training often requires ground truth data, typically from simulations, template spectra, or manually phased spectra. Simulation-trained models may struggle with real-world data due to the gap between simulated conditions and actual variability. Template spectra, while standardized, often lack the diversity of real-world signals, leading to poor generalization when models encounter noise, biological variability, or machine-specific differences. Manually phased spectra rely on the expert's skill, and even slight human errors can introduce phase inaccuracies, affecting model quality and consistency. These limitations can weaken the performance and robustness of neural networks trained on such data.
While unsupervised learning does not require ground truth data, it operates under the strong assumption that all peaks follow Lorentzian line shapes (Shamaei et al., 2023), which may not always hold true for real-world data.
Semi-supervised learning, which aims to balance the strengths of both supervised and unsupervised methods, has the potential to overcome these limitations. However, as discussed earlier, Ma’s study (Ma et al., 2024) is not a true example of semi-supervised learning. Instead, it is a supervised approach.
Recent research has added a step involving a linear model with higher-order terms following neural network-based training, making the final model more interpretable and smoothing out potential irregularities from neural network learning. This combination of traditional statistics and modern machine learning has been promising. Although the phased data are not statistically different from manually corrected data, they still fall slightly short, leaving room for improvement, even with sophisticated 3D U-nets (You et al., 2022; Shamaei et al., 2023).

5.2. Challenges in Phase Error Correction Optimization Functions

Since phase errors and phase adjustment values are not directly observable, developing a model—whether it is a statistical model or a machine learning architecture—requires an optimization function. Section 3, “Optimization Functions for Phase Correction,” discusses 20 optimization functions that have been applied to phase error correction. Here, we would like to explore the challenges associated with these optimization functions.

5.2.1. Integral of the Imaginary Component

Minimizing the integral of the imaginary component (dispersion spectrum), as shown in formula (10), follows the approach by Binczyk et al. (Binczyk, Tarnawski and Polanska, 2015). However, this approach does not fully align with the characteristics of an ideal dispersion spectrum. To address this, we propose minimizing the absolute integral of the dispersion spectrum. The ideal dispersion spectrum, without phase errors, has an integral of zero, with one skewed positive peak and one skewed negative peak. When phase errors are present, the integral deviates from zero, becoming either positive or negative. Therefore, while the integral itself is neither a minimum nor a maximum, minimizing the absolute integral could provide an effective solution (formula 11).
However, minimizing an absolute function poses a significant challenge due to its non-differentiability at zero. The derivative of an absolute value function is undefined where the function crosses zero, complicating the use of gradient-based optimization methods. This issue is particularly problematic when trying to minimize the absolute integral to zero, as the function becomes non-smooth, making it difficult to compute gradients and achieve convergence.

5.2.2. Integral of the Real Component

Minimizing the integral of the absolute value of the real component (as described in formula (13)) considers only absolute values. While using absolute values may complicate differentiation, it is essential to note that the integral will never converge to zero; instead, it approaches a minimum positive value when the absorption spectrum is ideal. However, it is important to recognize that a reversed negative peak, which is 180 degrees out of phase with the ideal peak, can also reach this same minimal value.
Conversely, maximizing the integral of the absorption spectrum (as indicated in formula (14)) does not involve absolute values, making it a differentiable function. More significantly, since an ideal absorption spectrum devoid of phase errors contains no negative values, the integral naturally attains its maximum when the absorption is optimal. Therefore, formula (14) serves as an effective optimization function.
Additionally, the formula for maximizing the refocusing ratio in the image domain is presented in formula (24). The refocusing ratio is defined as the ratio of the absolute value of the sum of the real component to the sum of the absolute real component. In this context, the numerator corresponds to the absolute value from formula (14), while the denominator refers to formula (13). The objective is to balance maximizing the absolute sum while managing the sum of the absolute values. While this approach appears logical, it can still yield negative intensity values, as an image with a 180-degree phase error can achieve the maximum refocusing ratio. In such cases, the phase shift inverts the real component without altering its absolute intensity.

5.2.3. Peak Height

The maximization of the R ratio (formula 12) presents some challenges. In essence, the numerator represents the maximum positive peak height, while the denominator represents the smallest absolute height among the negative peaks in the absorption spectrum. Since an ideal absorption spectrum should have no negative peaks, the denominator would ideally be zero. However, as previously discussed, the derivative at zero introduces complications. Furthermore, because the formula is a ratio, a logarithmic transformation is commonly applied to facilitate its maximization, but log(0) is undefined. Thus, the R ratio, as defined in formula (12), is not a suitable maximization function. Additionally, it considers two peaks within the entire spectrum.

5.2.4. Entropy

Minimizing entropy with a negative peak penalty, as outlined in formula (19), offers a balanced approach by accounting for all data points while simultaneously controlling negative values. However, since entropy is typically applied to probability functions, there remains the question of whether scaled absolute derivatives of the absorption spectrum can legitimately be treated as probability functions, especially when high-order derivatives are involved.
Formula (20) is a variation of formula (19), also aiming to minimize entropy with a negative peak penalty, but instead of using derivatives, it applies absolute absorption values directly. While formula (19) raises the issue of whether the scaled absolute derivatives can be considered probability functions, they at least fall within the [0, 1] range required for probabilities. In contrast, absolute absorption values do not adhere to this range.
The good news is that the minimization process remains unaffected by constant factors or additive constants. Therefore, even if the values do not strictly satisfy the probability range, minimizing entropy still holds if we assume the scaled absolute absorption spectrum can be considered a probability function. This assumption may be more reasonable than using derivatives, as an ideal absorption peak resembles a Lorentzian function, which can be interpreted as a probability function.
Following this reasoning, if we ignore the scaling factor in the first term of formula (20) while leaving the second term unchanged, the penalty term in formula (20) —which penalizes the sum of squared negative absorption values—loses some of its impact, thereby reducing the overall effectiveness of the penalty.
Nevertheless, both formulas (19) and (20) still raise the question of whether it is reasonable to apply the concept of entropy to absolute absorption values or to the scaled absolute values of their derivatives.

5.2.5. Squared Errors

Formula (16) is a variation of the sum of squared errors. Its objective is to minimize the difference in peak heights between the absorption peaks and their corresponding peaks in the magnetic spectrum, based on the assumption that ideal absorption should match these heights. While this method is effective for isolated peaks, it may not be as accurate for situations where the ideal absorption peak height does not correspond with the magnetic peak height due to overlapping. Moreover, this approach tends to overlook most data points that are not local maxima.
Formula (17) involves minimizing the sum of squared negative values in the absorption spectrum. This is based on the premise that an ideal absorption spectrum should not contain negative values, making this formula a variation of the sum of squared errors with negative values considered as errors. Although this method is effective for controlling negative values, it does not account for positive values in the spectrum.
Another related idea is to use the negative peak penalty term from formula (19) on its own to develop an optimization function, resulting in formula (21). Instead of using an indicator, formula (21) directly subtracts the absorption value from its absolute value. If the value is positive, the result is 0; if the value is negative, it results in a positive value, which is considered an error, as an ideal absorption spectrum has no negative values. Looking at formula (21), it essentially sums the squared errors if negative values are treated as errors, making it effectively the same as formula (17). As discussed earlier, while this method is effective at controlling negative values, it does not account for the positive values in the spectrum.
When discussing the sum of squared errors, dividing it by the number of terms used to calculate the sum gives the mean squared error, as shown in formula (22), which is a standard statistical measure. The error is measured between the observed value and its fit, estimate, or reference value. Ideally, the reference would be the ground truth; however, in real-world MR data, such a ground truth does not exist. As a result, researchers often rely on synthetic data, template spectra, manually phased data, or specific mathematical models to serve as references. However, as discussed in Section 5.1, these approaches limit the effectiveness of the mean squared error approach.
To address this complicated situation in mean squared errors in MR data without ground truth, Stein's unbiased risk estimate based adaptive phase error correction method was introduced (Pizzolato et al., 2020), and the loss function is shown in formula (23). The main component of the loss function is the sum of squared errors, which measures the difference between the original image and the phase-corrected image. The effectiveness of this approach depends on how closely the original image approximates a phase-error-free image. If the original image deviates significantly from an ideal phase-error-free image, the formula may not perform effectively.
One might wonder why the mean spectrum of real component spectra is not used as a reference for phase error correction, as is common in regular statistical analyses. The reason is that the mean of real component spectra does not produce a phase-error-free spectrum, even with a large sample size. This is because most phase errors are systematic biases and do not follow a normal distribution. These errors are influenced by factors such as machine settings, acquisition conditions, or experimental setups, and they persist across multiple measurements. Consequently, averaging spectra does not eliminate these systematic errors in the same way that averaging can mitigate random noise.
The maximum likelihood estimation-based cost function, also referred to as a minimization function, is shown in formula (26). Despite its seemingly complex form, it essentially represents the sum of squared errors. This method aims to correct phase errors by fitting a model to the distorted image data. However, a significant challenge is obtaining an ideal, distortion-free reference image, which is often unavailable in real-world situations.
The second step of Bao’s method (Bao et al., 2013) also employs the sum of squared errors, as shown in formula (29). This approach is quite similar to the one in formula (21), but with a key modification: it minimizes the sum of squared negative values for non-distorted positive peaks, as well as non-distorted negative peaks after reversing them. However, it disregards the distorted peaks altogether. The drawback of this approach is clear—by ignoring the distorted peaks, which should receive more attention, this method is likely to leave residual phase errors even after the phase correction process.
To address the lack of ground truth, Worley and Powers (Worley and Powers, 2014) used the mean spectrum of the dataset as a reference spectrum, combining phase error correction with a scaling step, as described in formula (30). The goal is to minimize the sum of squared errors between the scaled spectrum and the reference spectrum. However, as previously discussed, most phase errors arise from systematic biases rather than random errors. Minderhoud et al. (Minderhoud et al., 2020) demonstrated that phase errors vary significantly between machines. If all spectra come from the same machine, averaging them will not eliminate phase errors. Therefore, while formula (30) can align each spectrum closer to the mean spectrum, it is unlikely to remove non-random phase errors.

5.2.6. Bayesian

Through a complex Bayesian calculation, Bretthorst (Larry Bretthorst, 2008) derived a posterior probability function in the form of a t-distribution. This function was used to estimate the two first-order phase correction parameters in the image domain, while the formula for estimating the zero-order phase correction parameter is given in formula (25). The challenge lies in whether all the assumptions made during the derivation process can be satisfied with real-world data.

5.2.7. Pearson Correlation

Wright et al. (Wright, Buydens and Heerschap, 2012) proposed maximizing the correlation between the real component spectrum and the magnitude spectrum for two specific peak ranges, as shown in formula (27). While this approach is feasible, it requires that the two specific metabolites be included in all samples. A major limitation of this method is that focusing on just these two ranges may not provide sufficient phase correction for other regions of the spectrum, as much of the data is disregarded. Additionally, an important question arises: does maximizing this correlation truly yield a phase-corrected real component spectrum? It’s important to note that the relationship between the magnitude spectrum ( R e a l 2 + I m a g i n a r y 2 ) and the real component is nonlinear, which raises doubts about whether maximizing the Pearson correlation between them can effectively achieve a phase-free real component spectrum.

5.2.8. Phase Difference

A phase difference-based method is generally challenging because a phase error-free real component is not directly observable, making it difficult to establish a true ground truth for phase values. However, in specific cases, such as correcting phase errors caused by patient movement in MRI data, it is possible to minimize the phase differences between the current scan and the previous scan immediately before it, as outlined in formula (31). This approach uses the initial scan as a reference for iterative corrections. However, if the reference scan itself contains significant phase errors due to movement or other factors, these errors could be propagated rather than corrected, potentially limiting the effectiveness of the method.

5.2.9. Absolute Errors

Similar to squared errors, absolute errors are generally challenging to apply in phase error correction. However, in simulation-based studies where ground truth phase values are available, minimizing the mean absolute error in phase can be used to train a convolutional neural network. (Bugler et al., 2024). As with squared errors, applying simulation-based training to real-world data may lead to a gap between simulated and actual conditions, potentially limiting its effectiveness for phase correction.
Ma et al. (Ma et al., 2024) extended this approach by combining multiple mean absolute errors across the real spectrum, imaginary spectrum, frequency, and phase, as shown in formula (33). However, this method also relies on simulations and template spectra due to the need for ground truth, and thus faces similar limitations as the Bugler et al. approach (Bugler et al., 2024). Additionally, the weighting coefficients in Ma et al. (Ma et al., 2024) appear somewhat arbitrary, with 2000 times more weight given to the real and imaginary spectra based on template spectra from BIG GABA (Mikkelsen et al., 2017) than to phase based on simulations, thereby reducing the contribution of mean absolute errors in phase correction.

5.3. Challenges in Phase Error Correction Optimizers

Optimizers are algorithms that navigate the optimization landscape by adjusting model parameters based on a chosen optimization function. While various optimizers have been applied to phase error correction, each comes with its own set of limitations.
Both the false position and golden section bisection methods can converge under the right conditions and with well-behaved functions. However, they may be less effective for functions with multiple extrema due to their assumptions and fixed search behaviors, which can slow convergence or prevent them from finding the global optimum.
The Simplex algorithm, effective for linear programming problems, struggles with non-linear or non-smooth problems as it is specifically designed for linear objectives and feasible regions. It is not suitable for problems involving non-linear constraints or objective functions and may fail to find optimal solutions in such cases. Similarly, the Nelder-Mead method, a robust optimizer for non-differentiable functions, does not require gradient information. However, it can still suffer from slow convergence and sensitivity to initial conditions.
Powell’s method, another derivative-free optimizer, avoids gradient calculations by performing line searches along iteratively updated directions. It is generally considered robust for smooth, unconstrained optimization but can struggle with non-smooth functions. Conversely, the steepest descent method, which relies on gradients, can be sensitive to the learning rate or step size and often struggles with ill-conditioned problems where the function’s curvature varies significantly.
Quasi-Newton methods face the challenge of memory requirements, as they need to store approximations of the Hessian matrix, which can be demanding for large-scale problems. The computational expense of updating these approximations can also impact efficiency in high-dimensional spaces. While L-BFGS reduces memory usage with a limited-memory approach, it is typically very efficient for large-scale problems, though it may compromise convergence speed compared to full-memory methods.
Hypersphere optimization, involving angular searches, can help avoid inefficient oscillations but can still face issues with local minima and determining how constraints interact with spherical boundaries. Additionally, it may involve computational complexity and scaling challenges, especially in high-dimensional spaces.
The Levenberg-Marquardt algorithm is heavily dependent on the initial guess, which can affect its convergence to local minima. It is also computationally expensive due to iterative updates and Jacobian computations. While it balances speed and stability through a damping factor, careful tuning is required to optimize performance and avoid convergence issues.
The trust-region-reflective method can be computationally demanding due to the need to solve subproblems at each iteration to define and adjust the trust region. The choice of trust region size is critical, as an inappropriate size can lead to slow or inefficient convergence. The method’s computational cost and parameter tuning can impact its performance, especially in complex, nonlinear problems.
Subplex/Sbplx decomposes the problem into smaller, simpler optimization tasks, which can result in increased computational overhead due to multiple local searches. Additionally, managing the trade-off between local refinement and global exploration can impact both the efficiency and convergence of the method, particularly in complex, high-dimensional problems.
Due to the stochastic nature of Stochastic Gradient Descent (SGD), updates can be noisy, potentially causing the optimizer to oscillate around minima, preventing it from settling at the optimum. Choosing the right learning rate is challenging: if the learning rate is too high, it can lead to instability, while if it is too low, convergence may become slow. Recent developments often incorporate adaptive learning rate methods or momentum-based approaches to address these sensitivity issues.
While Adam often converges quickly and efficiently, it may sometimes find solutions that generalize less well than other optimizers like SGD. Its generalization depends on the problem and how it handles sharp vs. flat minima. Adam might not always converge to the global minimum, particularly in complex, non-convex loss landscapes. It is also important to note that Adam's performance can be sensitive to hyperparameter settings, and its computational and memory requirements can be substantial.
Bayesian optimization is effective for costly evaluations but struggles with model selection and tuning complexity. It can be computationally demanding, especially in high-dimensional spaces or with very noisy functions, and requires careful balancing of exploration and exploitation to optimize performance.

6. Conclusions

In this review, we explored five statistical models, several machine learning architectures, 20 optimization functions, and 14 optimizers used for phase error correction. We also examined the challenges each of these methods presents.
Statistical models remain the dominant approach for phase error correction, with the linear model—utilizing zero and first-order parameters—being the most commonly employed. In some cases, higher-order terms are added to enhance accuracy. Recently, machine learning architectures, particularly convolutional neural networks (CNNs), have gained traction in phase error correction due to their capacity for handling complex patterns in data.
Although a wide range of optimization functions are used in phase error correction, they generally fall into two categories:
MR data-specific characteristics, such as phase difference, peak height, the integral of the real component, and the integral of the imaginary component.
Common statistical approaches, including Pearson correlation, absolute errors, squared errors, entropy, and Bayesian methods.
Among these, squared error is the most widely used component in statistical optimization functions. For MR data-specific optimizations, real component integrals are often favored due to their clearer patterns in phase-error-free signals. However, considering multiple MR-specific features simultaneously could potentially improve accuracy in phase correction.
The main challenge in phase error correction, particularly in optimization functions based on statistical measures like squared error, is the absence of ground truth in real-world data. This is a significant hurdle for both statistical models and machine learning methods, including neural networks. Without a clear ground truth, models may struggle to generalize effectively, especially in diverse, noisy environments.
In terms of optimizers, Nelder-Mead is the most commonly applied for statistical model optimization in phase error correction, largely because it is the default method in the optim() function in R. However, many studies do not explicitly mention the optimizer used. On the machine learning side, Adam is the most frequently utilized optimizer. Both methods, however, come with limitations—Nelder-Mead can be sensitive to local minima, and Adam can struggle with generalization, particularly in non-convex loss landscapes.
From our own practice, Quasi-Newton optimizers like BFGS and L-BFGS have shown strong performance across both statistical and machine learning models. While memory requirements can be a challenge—particularly for BFGS—this issue has lessened in importance with modern computing advancements, making these methods more viable for large-scale applications.
Given the extensive array of models, optimization functions, and optimizers currently available, is there still a need for further development? The answer is a resounding yes. Despite the progress made, significant room for improvement remains in fully automatic phase error correction. As Ben-Tal (2022) pointed out, manual correction is still often recommended for achieving the highest accuracy.
Our ongoing research seeks to depart from the conventional optimization-based approaches to phase error correction. Instead, we are exploring a novel method that does not rely on any optimization process, and thus eliminates the need for optimization functions or optimizers altogether. This approach has the potential to serve as a ground truth to guide machine learning models, especially in the context of phase error correction.
For the future of automatic, AI-based phase error correction, which is seamlessly integrated with other MR data pre-processing steps, the collection of MR data from diverse machines, facilities, and environments is crucial. Optimization functions must account for these variances, and ideally, the process would no longer rely on ground truth data. This can be achieved by leveraging MR-specific characteristics more effectively.
The underlying motivation for this review is our belief in the power of ensemble learning—bridging traditional statistical models and machine learning architectures. By dynamically selecting appropriate optimization functions and optimizers tailored to specific datasets, we believe it is possible to achieve fully automated and highly accurate phase error correction. This is the direction we see for the future.

References

  1. Andrei, N. (2022) ‘Steepest Descent Methods’, in N. Andrei (ed.) Modern Numerical Nonlinear Optimization. Cham: Springer International Publishing, pp. 81–107. [CrossRef]
  2. Balacco, G. (1994) ‘A New Criterion for Automatic Phase Correction of High-Resolution NMR-Spectra Which Does Not Require Isolated or Symmetrical Lines’, Journal of Magnetic Resonance, Series A, 110(1), pp. 19–25. [CrossRef]
  3. Bao, Q. et al. (2013) ‘A robust automatic phase correction method for signal dense spectra’, Journal of Magnetic Resonance, 234, pp. 82–89. [CrossRef]
  4. Ben-Tal, Y. et al. (2022) ‘Mechanistic analysis by NMR spectroscopy: A users guide’, Progress in Nuclear Magnetic Resonance Spectroscopy, 129, pp. 28–106. [CrossRef]
  5. Bieri, O., Markl, M. and Scheffler, K. (2005) ‘Analysis and compensation of eddy currents in balanced SSFP’, Magnetic Resonance in Medicine, 54(1), pp. 129–137. [CrossRef]
  6. Binczyk, F., Tarnawski, R. and Polanska, J. (2015) ‘Strategies for optimizing the phase correction algorithms in Nuclear Magnetic Resonance spectroscopy.’, Biomedical engineering online, 14 Suppl 2(Suppl 2), p. S5. [CrossRef]
  7. de Brouwer, H. (2009) ‘Evaluation of algorithms for automated phase correction of NMR spectra’, Journal of Magnetic Resonance, 201(2), pp. 230–238. [CrossRef]
  8. Brown, D.E., Campbell, T.W. and Moore, R.N. (1989) ‘Automated phase correction of FT NMR spectra by baseline optimization’, Journal of Magnetic Resonance (1969), 85(1), pp. 15–23. [CrossRef]
  9. Bugler, H. et al. (2024) ‘Frequency and phase correction of GABA-edited magnetic resonance spectroscopy using complex-valued convolutional neural networks’, Magnetic Resonance Imaging, 111, pp. 186–195. [CrossRef]
  10. C. Dong et al. (2016) ‘Image Super-Resolution Using Deep Convolutional Networks’, IEEE Transactions on Pattern Analysis and Machine Intelligence, 38(2), pp. 295–307. [CrossRef]
  11. Canlet, C. et al. (2023) ‘NMR metabolite quantification of a synthetic urine sample: an inter-laboratory comparison of processing workflows’, Metabolomics, 19(7), p. 65. [CrossRef]
  12. Chen, L. et al. (2002) ‘An efficient algorithm for automatic phase correction of NMR spectra based on entropy minimization’, Journal of Magnetic Resonance, 158(1), pp. 164–168. [CrossRef]
  13. Craig, E.C. and Marshall, A.G. (1988) ‘Automated Phase Correction of Ft Nmr-Spectra by Means of Phase Measurement Based on Dispersion Versus Absorption Relation (Dispa)’, Journal of Magnetic Resonance, 76(3), pp. 458–475. [CrossRef]
  14. Džakula, Ž. (2000) ‘Phase Angle Measurement from Peak Areas (PAMPAS)’, Journal of Magnetic Resonance, 146(1), pp. 20–32. [CrossRef]
  15. Emwas, A.-H. et al. (2018) ‘Recommended strategies for spectral processing and post-processing of 1D (1)H-NMR data of biofluids with a particular focus on urine.’, Metabolomics : Official journal of the Metabolomic Society, 14(3), p. 31. [CrossRef]
  16. Ernst, R.R. (1969) ‘Numerical Hilbert transform and automatic phase correction in magnetic resonance spectroscopy’, Journal of Magnetic Resonance (1969), 1(1), pp. 7–26. [CrossRef]
  17. Feinauer, A., Altobelli, S.A. and Fukushima, E. (1997) ‘NMR measurements of flow profiles in a coarse bed of packed spheres’, Magn Reson Imaging, 15(4), pp. 479–87.
  18. Gan, Z. and Hung, I. (2022) ‘Second-order phase correction of NMR spectra acquired using linear frequency-sweeps’, Magnetic Resonance Letters, 2(1), pp. 1–8. [CrossRef]
  19. Gass, S.I. (2011) ‘George B. Dantzig’, in A.A. Assad and S.I. Gass (eds) Profiles in Operations Research: Pioneers and Innovators. Boston, MA: Springer US, pp. 217–240. [CrossRef]
  20. Hardy, E.H. et al. (2009) ‘Automated phase correction via maximization of the real signal’, Magnetic Resonance Imaging, 27(3), pp. 393–400. [CrossRef]
  21. Haskell, M.W., Nielsen, J.-F. and Noll, D.C. (2023) ‘Off-resonance artifact correction for MRI: A review’, NMR in Biomedicine, 36(5), p. e4867. [CrossRef]
  22. Herring, F.G. and Phillips, P.S. (1984) ‘Automatic phase correction in magnetic resonance using DISPA’, Journal of Magnetic Resonance (1969), 59(3), pp. 489–496. [CrossRef]
  23. Heuer, A. (1991) ‘A new algorithm for automatic phase correction by symmetrizing lines’, Journal of Magnetic Resonance (1969), 91(2), pp. 241–253. [CrossRef]
  24. Hoffman, R.E., Delaglio, F. and Levy, G.C. (1992) ‘Phase correction of two-dimensional NMR spectra using DISPA’, Journal of Magnetic Resonance (1969), 98(2), pp. 231–237. [CrossRef]
  25. Jaroszewicz, M.J. et al. (2023) ‘An automated multi-order phase correction routine for processing ultra-wideline NMR spectra’, Journal of Magnetic Resonance, 354, p. 107528. [CrossRef]
  26. Jiang, A. (2024) ‘Insights into Nuclear Magnetic Resonance Data Pre-processing: A Comprehensive Review’, Journal of Data Science and Intelligent Systems, p. Online First. [CrossRef]
  27. Jiru, F. (2008) ‘Introduction to post-processing techniques.’, European journal of radiology, 67(2), pp. 202–217. [CrossRef]
  28. Jurek, J. et al. (2023) ‘Phase Correction and Noise-to-Noise Denoising of Diffusion Magnetic Resonance Images Using Neural Networks’, in J. Mikyška et al. (eds) Computational Science – ICCS 2023. Cham: Springer Nature Switzerland, pp. 638–652.
  29. Kumar, A., Das, S. and Snášel, V. (2022) ‘Improved spherical search with local distribution induced self-adaptation for hard non-convex optimization with and without constraints’, Information Sciences, 615, pp. 604–637. [CrossRef]
  30. Larry Bretthorst, G. (2008) ‘Automatic phasing of MR images. Part I: Linearly varying phase’, Journal of Magnetic Resonance, 191(2), pp. 184–192. [CrossRef]
  31. Ma, D.J. et al. (2024) ‘Magnetic Resonance Spectroscopy Spectral Registration Using Deep Learning’, Journal of Magnetic Resonance Imaging, 59(3), pp. 964–975. [CrossRef]
  32. Marshall, A.G.; R., D.C. (1978) ‘Dispersion versus Absorption: Spectral Line Shape Analysis for Radiofrequency and Microwave Spectrometry’, Analytical Chemistry, 50(6), p. 756.
  33. Mikkelsen, M. et al. (2017) ‘Big GABA: Edited MR spectroscopy at 24 research sites.’, NeuroImage, 159, pp. 32–45. [CrossRef]
  34. Minderhoud, S.C.S. et al. (2020) ‘The clinical impact of phase offset errors and different correction methods in cardiovascular magnetic resonance phase contrast imaging: a multi-scanner study.’, Journal of cardiovascular magnetic resonance : official journal of the Society for Cardiovascular Magnetic Resonance, 22(1), p. 68. [CrossRef]
  35. Montigny, F. et al. (1990) ‘Automatic phase correction of Fourier-transform NMR data and estimation of peak area by fitting to a Lorentzian shape’, Analytical Chemistry, 62(8), pp. 864–867. [CrossRef]
  36. Morris, G.A. (2017) ‘NMR Data Processing☆’, in J.C. Lindon, G.E. Tranter, and D.W. Koppenaal (eds) Encyclopedia of Spectroscopy and Spectrometry (Third Edition). Oxford: Academic Press, pp. 125–133. [CrossRef]
  37. Moussavi, A. et al. (2014) ‘Correction of gradient-induced phase errors in radial MRI’, Magn Reson Med, 71(1), pp. 308–12. [CrossRef]
  38. Nelder, J.A. and Mead, R. (1965) ‘A Simplex Method for Function Minimization’, The Computer Journal, 7(4), pp. 308–313. [CrossRef]
  39. Nelson, S.J. and Brown, T.R. (1989) ‘The Accuracy of Quantification from 1d Nmr-Spectra Using the Piqable Algorithm’, Journal of Magnetic Resonance, 84(1), pp. 95–109. [CrossRef]
  40. Petrova, S.S. and Solov’ev, A.D. (1997) ‘The Origin of the Method of Steepest Descent’, Historia Mathematica, 24(4), pp. 361–375. [CrossRef]
  41. Pizzolato, M. et al. (2020) ‘Adaptive phase correction of diffusion-weighted images’, NeuroImage, 206, p. 116274. [CrossRef]
  42. Powell, M.J.D. (1964) ‘An efficient method for finding the minimum of a function of several variables without calculating derivatives’, The Computer Journal, 7(2), pp. 155–162. [CrossRef]
  43. Prostko, P. et al. (2022) ‘R Shiny App for the Automated Deconvolution of NMR Spectra to Quantify the Solid-State Forms of Pharmaceutical Mixtures’, Metabolites, 12(12). [CrossRef]
  44. Ravanbakhsh, S. (Moshen), Poczos, B. and Greiner, R. (2010) ‘A Cross-Entropy Method that Optimizes Partially Decomposable Problems: A New Way to Interpret NMR Spectra’, Proceedings of the AAAI Conference on Artificial Intelligence, 24(1), pp. 1280–1286. [CrossRef]
  45. Ronneberger, O., Fischer, P. and Brox, T. (2015) ‘U-Net: Convolutional Networks for Biomedical Image Segmentation’, in N. Navab et al. (eds) Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Cham: Springer International Publishing, pp. 234–241.
  46. Rout, M. et al. (2023) ‘MagMet: A fully automated web server for targeted nuclear magnetic resonance metabolomics of plasma and serum’, Magnetic Resonance in Chemistry, 61(12), pp. 681–704. [CrossRef]
  47. Rowan, T.H. (1990) Functional stability analysis of numerical algorithms. PhD Thesis. University of Texas at Austin.
  48. Shamaei, A. et al. (2023) ‘Model-informed unsupervised deep learning approaches to frequency and phase correction of MRS signals’, Magnetic Resonance in Medicine, 89(3), pp. 1221–1236. [CrossRef]
  49. Simpson, R. et al. (2017) ‘Advanced processing and simulation of MRS data using the FID appliance (FID-A)—An open source, MATLAB-based toolkit’, Magnetic Resonance in Medicine, 77(1), pp. 23–33. [CrossRef]
  50. Sotak, C.H., Dumoulin, C.L. and Newsham, M.D. (1984) ‘Automatic phase correction of fourier transform NMR spectra based on the dispersion versus absorption (DISPA) lineshape analysis’, Journal of Magnetic Resonance (1969), 57(3), pp. 453–462. [CrossRef]
  51. Srinivas, S. et al. (2023) ‘Deep learning phase error correction for cerebrovascular 4D flow MRI.’, Scientific reports, 13(1), p. 9095. [CrossRef]
  52. Stein, C.M. (1981) ‘Estimation of the Mean of a Multivariate Normal Distribution’, The Annals of Statistics, 9(6), pp. 1135–1151.
  53. Van, A.T., Hernando, D. and Sutton, B.P. (2011) ‘Motion-induced phase error estimation and correction in 3D diffusion tensor imaging’, IEEE Trans Med Imaging, 30(11), pp. 1933–40. [CrossRef]
  54. Vanvaals, J.J. and Vangerwen, P.H.J. (1990) ‘Novel Methods for Automatic Phase Correction of Nmr-Spectra’, Journal of Magnetic Resonance, 86(1), pp. 127–147. [CrossRef]
  55. Vassiliadis, V.S. and Conejeros, R. (2001) ‘Powell methodPowell Method’, in C.A. Floudas and P.M. Pardalos (eds) Encyclopedia of Optimization. Boston, MA: Springer US, pp. 2001–2003. [CrossRef]
  56. WACHTER E. A, SIDKY E. Y and FARRAR$ T. C (1989) ‘Calculation of Phase-Correction Constants Using the DISPA Phase-Angle Estimation Techniqu’, JOURNALOF MAGNETIC RESONANCE, 82, pp. 352–359.
  57. Worley, B. and Powers, R. (2014) ‘Simultaneous Phase and Scatter Correction for NMR Datasets’, Chemometr Intell Lab Syst, 131, pp. 1–6. [CrossRef]
  58. Worley, B., Sisco, N.J. and Powers, R. (2015) ‘Statistical removal of background signals from high-throughput 1H NMR line-broadening ligand-affinity screens’, Journal of Biomolecular NMR, 63(1), pp. 53–58. [CrossRef]
  59. Wright, A.J., Buydens, L.M. and Heerschap, A. (2012) ‘A phase and frequency alignment protocol for 1H MRSI data of the prostate’, NMR Biomed, 25(5), pp. 755–65. [CrossRef]
  60. Wymer, D.T. et al. (2020) ‘Phase-Contrast MRI: Physics, Techniques, and Clinical Applications’, RadioGraphics, 40(1), pp. 122–140. [CrossRef]
  61. Xia, Y. and Chen, S. (2021) ‘Magnetic Resonance Imaging Artifact Elimination in the Diagnosis of Female Pelvic Abscess under Phase Correction Algorithm’, Contrast Media & Molecular Imaging, 2021(1), p. 9873775. [CrossRef]
  62. You, S. et al. (2022) ‘Deep Learning Automated Background Phase Error Correction for Abdominopelvic 4D Flow MRI.’, Radiology, 302(3), pp. 584–592. [CrossRef]
  63. Zheng Chang and Qing-San Xiang (2005) ‘Nonlinear phase correction with an extended statistical algorithm’, IEEE Transactions on Medical Imaging, 24(6), pp. 791–798. [CrossRef]
Preprints 119563 g001
Figure 1. An example of a neural network with five layers: two outer layers and three internal layers. (R packages NeuralNetTools and RSNNS were used to generate this plot).
Figure 1. An example of a neural network with five layers: two outer layers and three internal layers. (R packages NeuralNetTools and RSNNS were used to generate this plot).
Preprints 119563 g001
Preprints 119563 g002
Figure 2. Example deep autoencoder architecture diagram for unsupervised phase correction, inspired by Shamaei et al. (Shamaei et al., 2023). Con1d: one-dimensional convolution, ReLU: rectified linear unit. (R packages DiagrammeR and DiagrammeRsvg were used to generate the plot).
Figure 2. Example deep autoencoder architecture diagram for unsupervised phase correction, inspired by Shamaei et al. (Shamaei et al., 2023). Con1d: one-dimensional convolution, ReLU: rectified linear unit. (R packages DiagrammeR and DiagrammeRsvg were used to generate the plot).
Preprints 119563 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated