Prerpints.org logo
Preprint
Article

Cellulose-Based Acoustic Absorber with Macro-Controlled Properties

Altmetrics

Downloads

29

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 September 2024

Posted:

29 September 2024

You are already at the latest version

Alerts
Abstract
Cellulose-based materials are now commonly used, including in the field of acoustic comfort. Often presented as a less environmentally impactful alternative to traditional acoustic absorbents (such as melamine, glass wool, etc.), these cellulose-based materials are more frequently derived from recycling, thus undergoing in most cases the technical process allowing these cellulose fibers to be obtained, thus inheriting the acoustic properties of the latter, with limited or even non-existent control. This paper proposes a manufacturing process that allows for the production of cellulose foam with precise control over its porosity, pore size, and interconnections. In addition to exhibiting remarkable sound absorption properties, this process also enables the fabrication of gradient porous structures and other hybrid materials that can result in remarkable sound absorption properties.
Keywords: 
Subject: Physical Sciences  -   Acoustics

1. Introduction

Soundproofing materials are still extensively developed and studied, as constant improvements in tools and methods allow us to imagine objects that were considered difficult to fabricate just a few years ago [1,2]. Based on the physical laws of acoustics, we have long known how to guarantee, for example, low-frequency absorption or optimal attenuation over a frequency band with a material specifically designed for this function. Recent advancements in material science and engineering have led to the development of innovative porous and fibrous materials with enhanced acoustic performance [3,4]. These advancements are driven by the need to meet specific acoustic requirements in diverse applications, ranging from building acoustics and transportation to industrial noise control and consumer electronics. However, these materials still do not meet the most demanding expectations, particularly in terms of performance-to-size ratio. Indeed, and despite the emergence of acoustic metamaterials with remarkable sound absorption and/or transmission loss, thanks to tunable properties, their adoption for building sound insulation still limited [5].
Recently, the democratization of 3D printing has disrupted the near status quo in acoustic absorbent materials [6]. Indeed, the almost systematic use of products that have become common (melamine, mineral, and/or organic fibers) is now sometimes being replaced by hybrid materials and new concepts [7], guaranteeing better performance for the intended application, often by exploring new paradigms. On the other hand, and beyond the purely technical aspects, the environmental question inevitably arises. Materials with a low carbon footprint [8,9] or bio-sourced materials [10,11] still have to compete with so-called traditional materials. Thus, many have looked into the acoustic performance of recycled materials[12], from all sources, of all materials whatsoever. Among these, we find cellulose, resulting from the recycling of paper and cardboard [13], or derived from residues from industrial plants [14]. As efficient as they are, these green materials often only rarely stand out from their predecessors. Thus, rather than offering comparable performance, why not offer more? Indeed, cellulose foams have shown their interest in sound insulation [15,16,17] following the conclusions of Miranda-Valdez et al. [18] that foam-formed cellulose bio-composites are a promising technology for developing lightweight and sustainable materials, and Taiwo et al. [19], showing that natural fibers present good acoustic properties, specially at high frequencies. But, although efficient, these new cellulose-based materials are obtained "as is", with relatively little control possible depending on the manufacturing parameters.
This article provides an initial look at a porous bio-sourced material composed of homogeneous and isotropic cellulose. Its manufacturing process, described in the following section, allows fine-tuning of structural parameters and, consequently, its acoustic properties. The results also highlight what this process allows in terms of controlled porosity, to the point of offering an absorbent with a continuous porosity gradient [20,21].

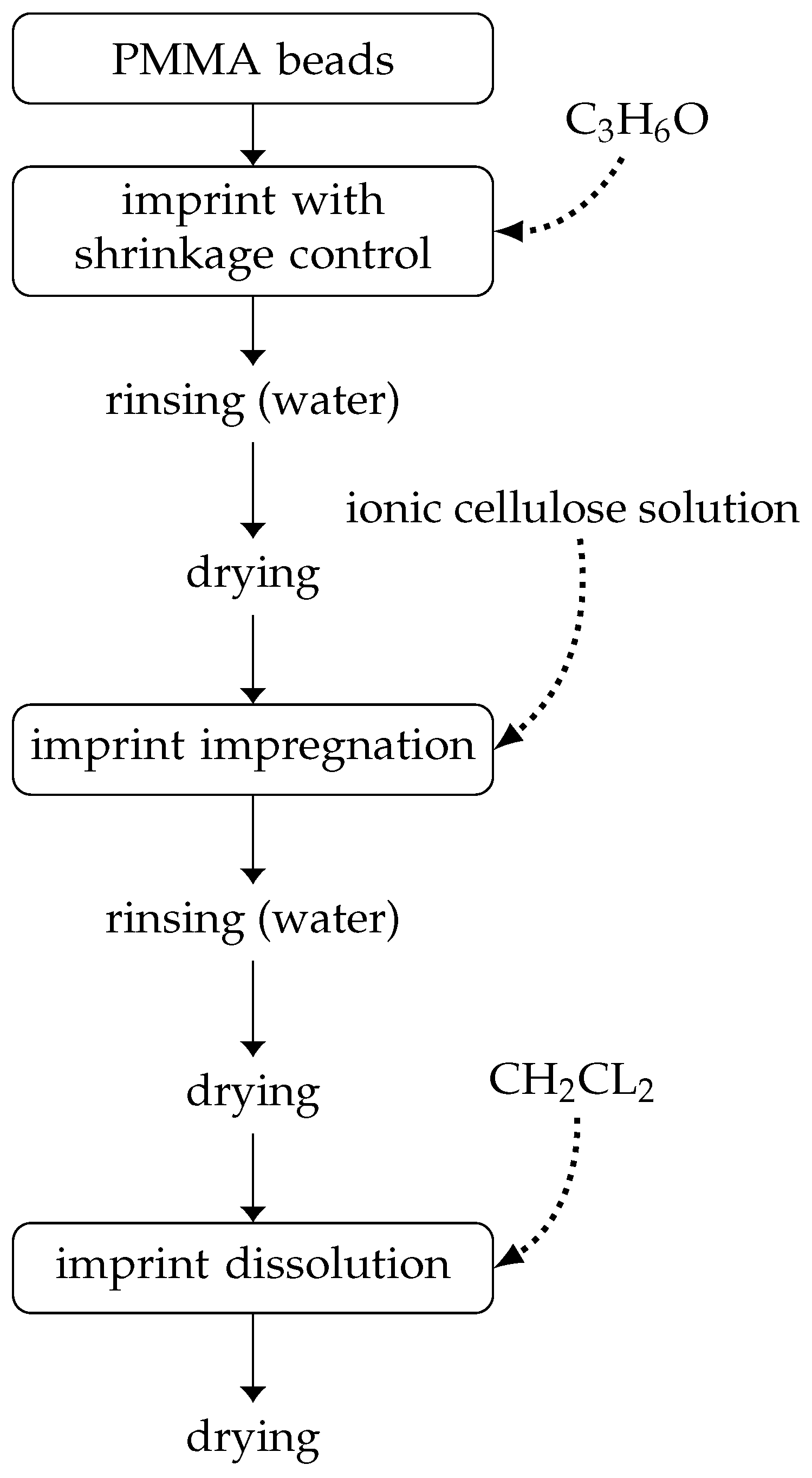
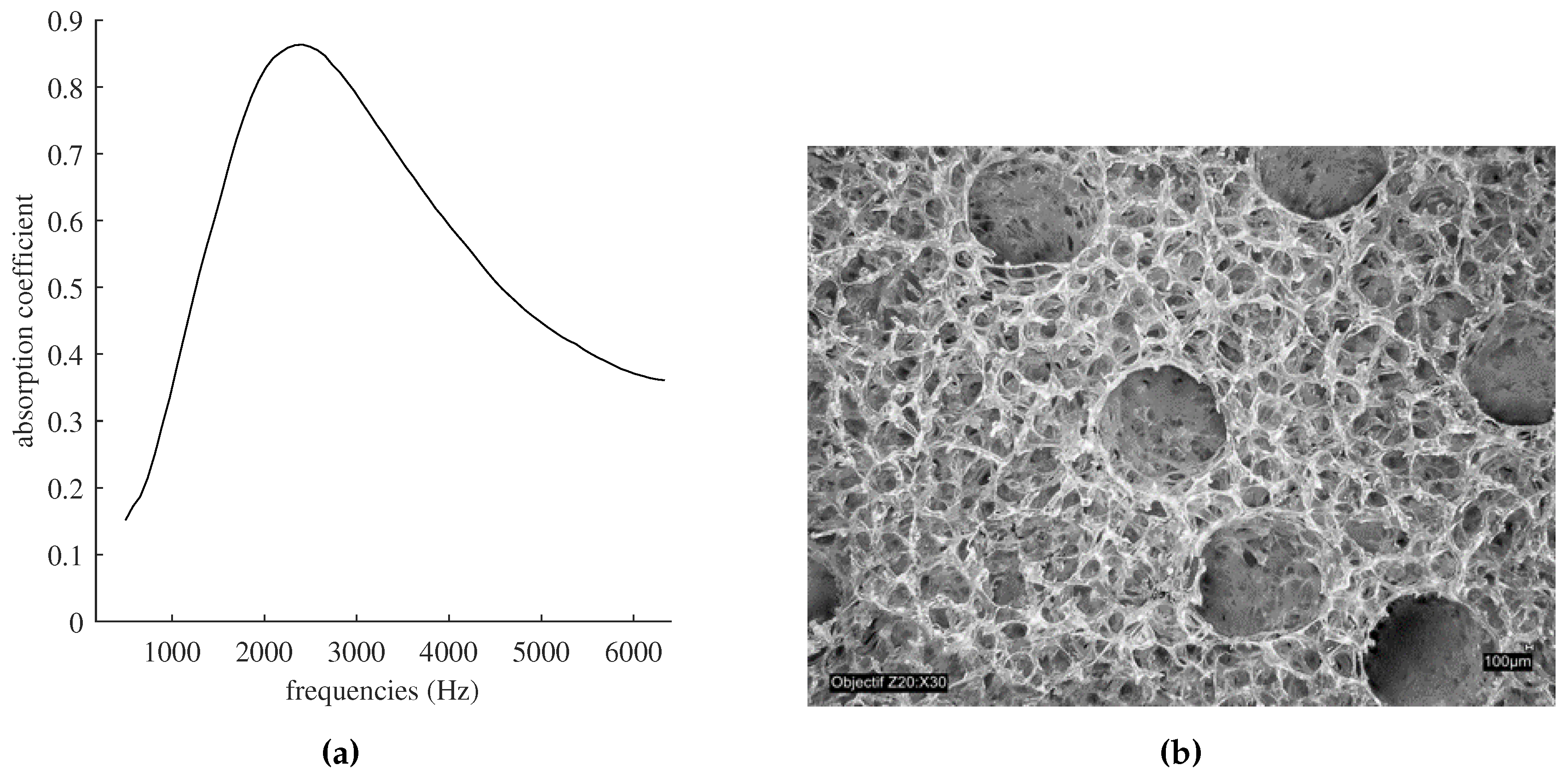
2. Fabrication Process

The fabrication process of the cellulose absorbent is inspired by macro-porous bioceramics, such as tricalcium phosphate ( β TCP [22]). In the context of bone implants, their fabrication is based on the observation that the osseointegration of an implant (its colonization) is ensured by the porous structure of the material. Thus, the manufacturing process of these ceramics allows for the control of their internal structure (pore diameter, interconnection diameter). The originality of the process lies in the molding of an imprint with polymethyl methacrylate (PMMA) beads (cf. Figure 1a). After firing, the PMMA imprint is calcined, leaving only the positive (or skeleton) forming an open-porosity ceramic (cf. Figure 1b).
To obtain our cellulose porous structures, the principle of a mold composed of PMMA beads is kept, in order to allow fine control over the pore size and their interconnections. The acetone ( C 3 H 6 O ) used during this phase has the effect of slowly and uniformly dissolving the PMMA beads and thus causing interpenetration between them. Next, this skeleton is impregnated by ionic solution of cellulose. The cellulose solution is obtained through several steps. The first step involves preparing a solution composed of a mixture of lithium chloride (LiCl) and dimethylacetamide (DMAc) at a concentration of 6% (60 g of LiCl per 1 liter of DMAc). Microcrystalline cellulose naturally contains water, which must be removed through multiple washings: a first washing with methanol (30 minutes, 20°C, stirring), followed by a second washing with DMAc (30 minutes, 20°C, stirring). The cellulose, thus freed of water, is dissolved in the LiCl/DMAc solution for 12 hours at 80°C. The resulting solution is an ionic solution, with cellulose chains interconnected by Li+ and Cl- charges [23]. The final step necessary for obtaining our porous material, as summarized in Figure 2, involves dissolving the PMMA skeleton in dichloromethane ( CH 2 CL 2 ) solution.

3. Macro-Controlled Properties

A first campaign was conducted to verify the repeatability of the manufacturing process. For the construction of the PMMA imprint of the samples, the same particle size is used (between 600 µm and 800 µm). The contraction rate during the construction of the PMMA skeleton is constant and set at 5%. The properties of the samples at the end of the manufacturing process are given in the Table 1 where h and d are the dimensional parameters after complete drying, respectively the height and the diameter of resulting cylinders. Also, the parameters m, V t , and V c are respectively the mass, the total volume, and the cellulose volume of the porous material. The size of the samples used does not allow direct measurement of open porosity. However, and thus the manufacturing method ensures that the pores are interconnected (hypothesis verified by imaging), porosity ϕ is determined by the apparent mass method [24].
Figure 4a shows the coefficients absorption obtained with the 2-microphones method (ISO 10534-2) for the samples of Table 1 recut in height to 25mm. This resizing has a double interest: ensuring an identical height for the 6 samples, but also removing the cellulose film forming on the flat faces, discernible in Figure 3a.
Preprints 119495 g003
Figure 3. The 6 samples characterized in Table 1.
Figure 3. The 6 samples characterized in Table 1.
Preprints 119495 g003
These results show the repeatability of the manufacturing process as well as the homogeneity of pore sizes and interconnections, illustrated by the microscopic view of the cellulose foam in Figure 3b.
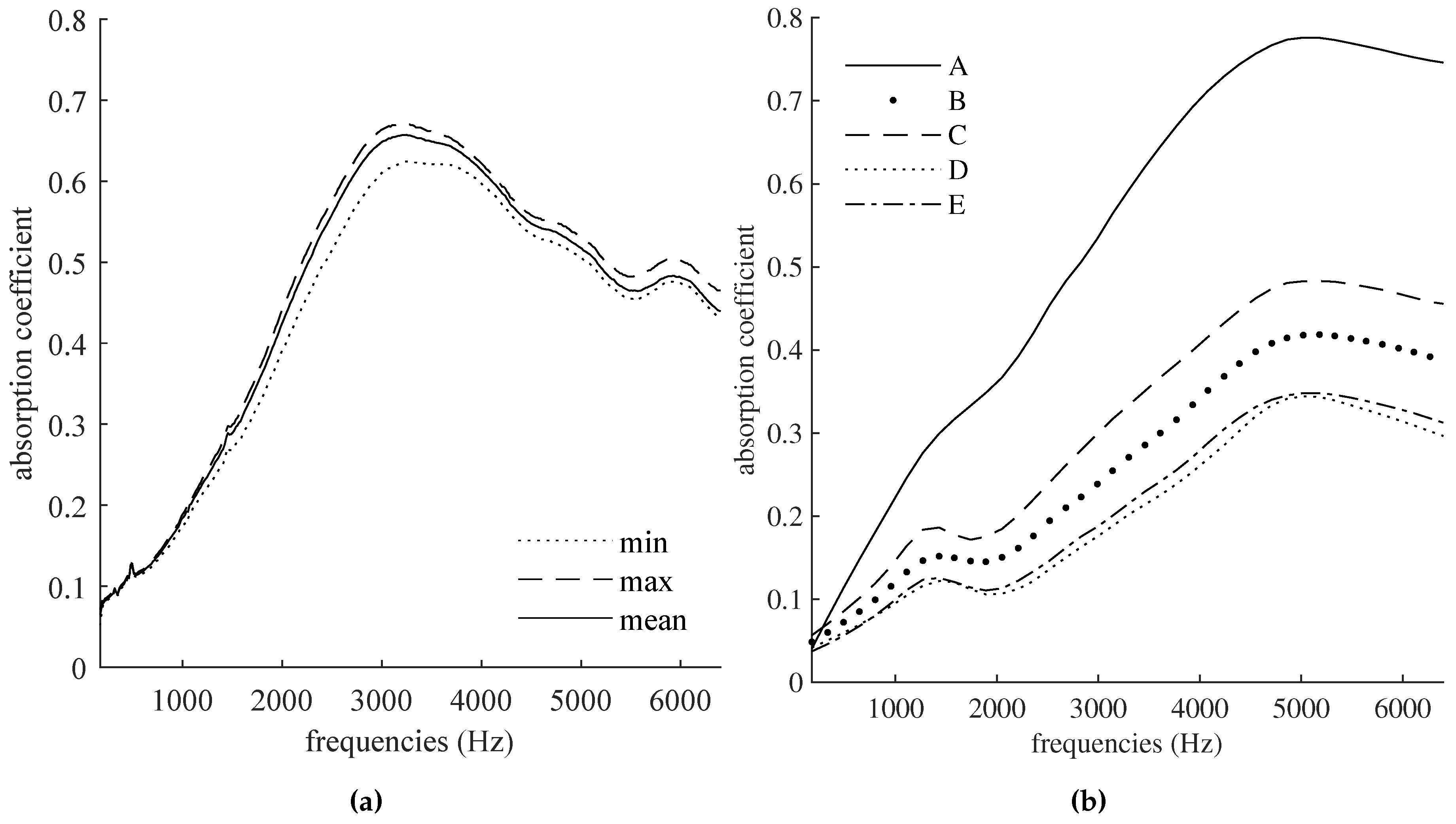
Preprints 119495 g004
Figure 4. Absorptions coefficients of (a) the 6 samples depicted in Table 1 and (b) the 5 samples depicted in Table 2.
Figure 4. Absorptions coefficients of (a) the 6 samples depicted in Table 1 and (b) the 5 samples depicted in Table 2.
Preprints 119495 g004

3.1. Basic Control of Skeletal Structure

The aim is to highlight the possibilities of dimensional modification of the skeleton and to estimate the maximum performance of porous cellulose. The properties of the 5 tested samples are given in Table 2. The parameters which vary during manufacturing are: the diameter D of the PMMA beads (which accounts for the diameter of the pores), the shrinkage rate τ of the skeleton during the forming phase which influences the theoretical diameter ϵ of the interconnections.
Among all the tests carried out, these 5 examples were selected to illustrate the control capabilities that this manufacturing process offered, but also for their structural homogeneity observed under the microscope. They are thus free of artifacts that the process can generate during its different phases (partial crushing of pores, localized tearing, etc.)
The absorption curves (cf. Figure 4b) under normal incidence show that the modification of these parameters influences the acoustic performance of the foams. Thus, reducing the pore size improves absorption with the best performance obtained with the sample whose diameter of the PMMA beads is between 200 µm and 400 µm, with an absorption peak of around 0.8 to 5 kHz. For samples B and C, where the range of ball diameters used is the same, we see a notable difference in performance. This is explained by the fact that the ratio τ will influence directly the diameter of the interconnections. Thus, the larger this diameter, the more reticulated the medium, it is therefore more permeable to the acoustic wave and has a lesser absorption. The performance of porous cellulose is therefore, as expected, dependent on the dimensional characteristics of its skeleton.
The acoustical properties such as the airflow resistivity σ , the tortuosity α ∞ , the viscous characteristic length Λ and the thermal characteristic length Λ ′ are shown for the 5 cellulose sound absorbers in Table 3. The porosity is determined as depicted in previous section while σ is measured directly using an airflow resistivity meter. The other parameters are obtained by an inverse method [25].
As shown in the table and figure, the acoustic effectiveness of porous cellulose is essentially due to its resistivity. For a porous material with oblique cylindrical pores, this value is linked to the radius of the pores by the relation [26]:
σ = 8 η α ∞ ϕ R 2
where R is the radius of the pores. Even if our material does not present this idealized structure, the comparison of the radius R obtained by Eq. 1 and the values of the viscous and thermal characteristic lengths as a function of the resistivity can give an indication of the parameters to vary in order to optimize the acoustic performance of porous cellulose. Thus, the more the size of the pores decreases, the more the resistivity depends on their radius ( ≈ Λ ′ ). Also when the size of the pores increases, it is the radius of the interconnections ( ≈ Λ ) which becomes dominant. According to the tests carried out for the manufacture of porous ceramics, the limit of mechanical resistance of the impression is reached for ϵ < r ¯ / 5 [22], which implies a slight reduction in the radius of the interconnections for the samples with a pore diameter greater than 400 µm. Obtaining a pore diameter of less than 200 µm could improve the acoustic performance of our material. However, impregnation of the cellulose solution with such diameters requires a need for optimization of the current process (risks of partial impregnation and collapse of the skeleton).

3.2. Double Porosity

The process for obtaining a material with double porosity is straightforward. PMMA rods or filaments are added to the beads. Figure 5a shows a test conduct on the basis of sample B of Table 2, with the difference that PMMA rods with a diameter of 1.75 mm were arranged without any concerns about alignment or concern for structuring the desired mesoporous network at the end (cf. Figure 5). We observe a radical change in performance towards low frequencies, a direct consequence of this double porosity. However, with a ratio of only 4 between the pore sizes of the micro and meso networks, we are only halfway towards the admited optimal ratio of 10. Using larger PMMA rods will allow you to get closer to this aim with less concern for the structural integrity of the foam than reducing the size of the beads. Also, this process opens the possibility of directly influencing the tortuosity of the mesoporous network by incorporating a more or less complex interweaving of PMMA filaments, and thus overcome the shape limits of double porosity materials usually obtained by perforation [27].

3.3. Gradient Porous Biomaterials

The manufacturing process showed that it is possible to control the size of the pores and their interconnections. It is also possible to manufacture gradients of porosity and interconnections. The implementation of property gradients is carried out only in the first step of manufacturing the porous cellulose, namely the step of constructing the impression. This is why the manufacturing processes described below only relate to this step; the production of the skeleton and the dissolution of the impression remain identical to those described in the previous sections.

3.3.1. Continuous Interconnection Gradient

First, rather than producing a material presenting a discrete interconnection gradient, which would lead to impedance breaks between each layer of different granularity [28,29], we opted for a continuous gradient. To achieve a continuous gradient of interconnections, PMMA beads are placed in a mold with a perforated bottom. Similar to the basic process, the piston is used to compress the sacrificial material to achieve interpenetration between the beads. The mold is then placed in a crystallizer into which acetone is poured. The negative is impregnated until the acetone level reaches its upper surface by capillarity. As the total immersion time varies between the bottom and the top will differ, different interconnections will be made depending on the height. The interconnection gradient is confirmed by the difference in absorption between the two faces of the sample (cf. Figure 7a), with an imprint similar as the one used to obtain sample D from Table 2 (diameter of the beads ranging from 0.6 to 0.7 mm). The best performance is obtained for the face whose smallest interconnections are against the rigid termination of the impedance tube. The comparison with results of the sample D (same beads diameter, rangong from , similar thickness) reveal an acoustic activity 3 times higher. With the largest interconnections against the rigid termination (so reversed), the gain in acoustic activity remains almost equal although shifted towards high frequencies. Note that these performances are obtained for a sample having a pore size of 600-710 µm which, in the case of constant interconnections, is the one which presents the lowest absorption and the lowest resistivity.
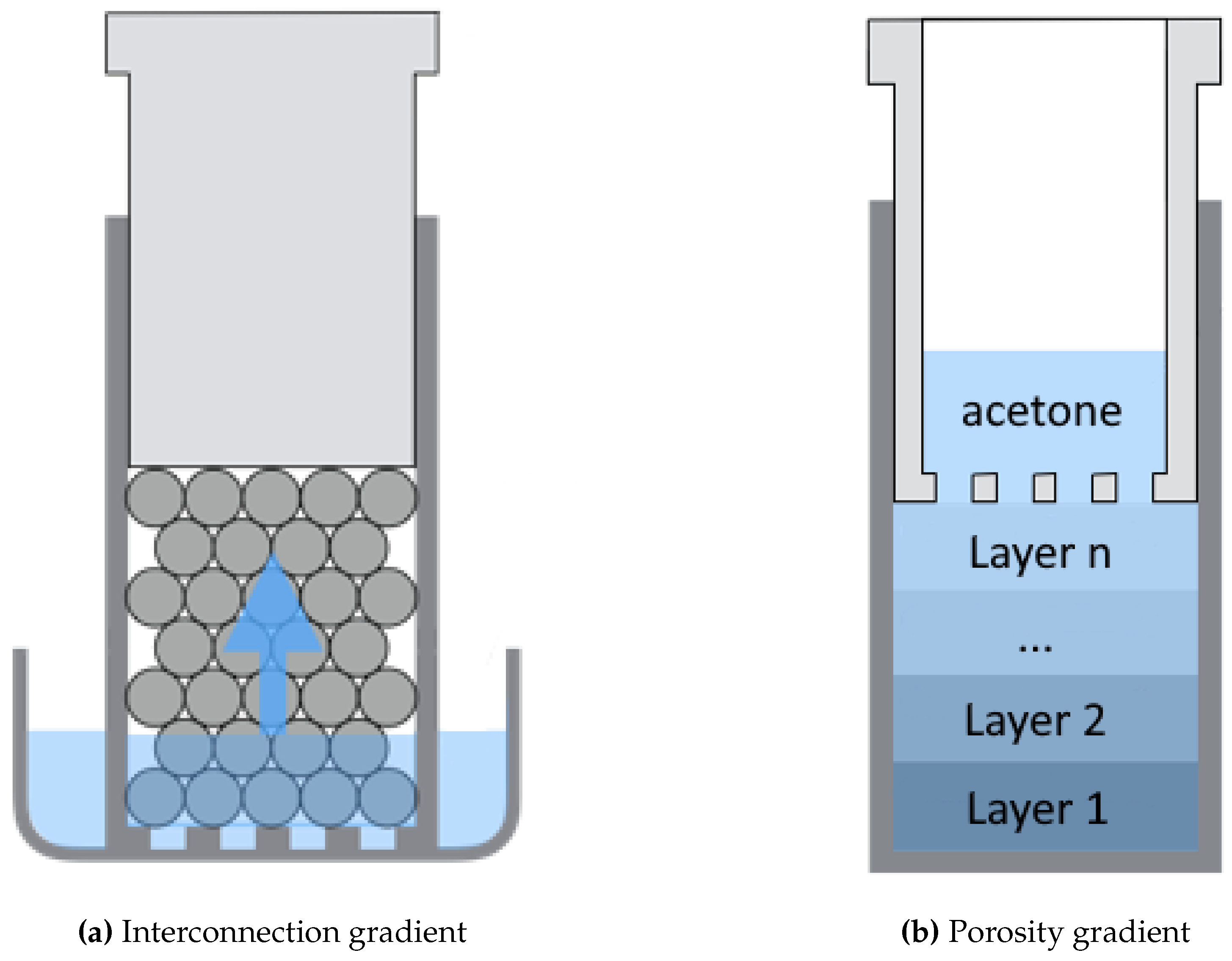
Preprints 119495 g006
Figure 6. First manufacturing step for gradient foams.
Figure 6. First manufacturing step for gradient foams.
Preprints 119495 g006
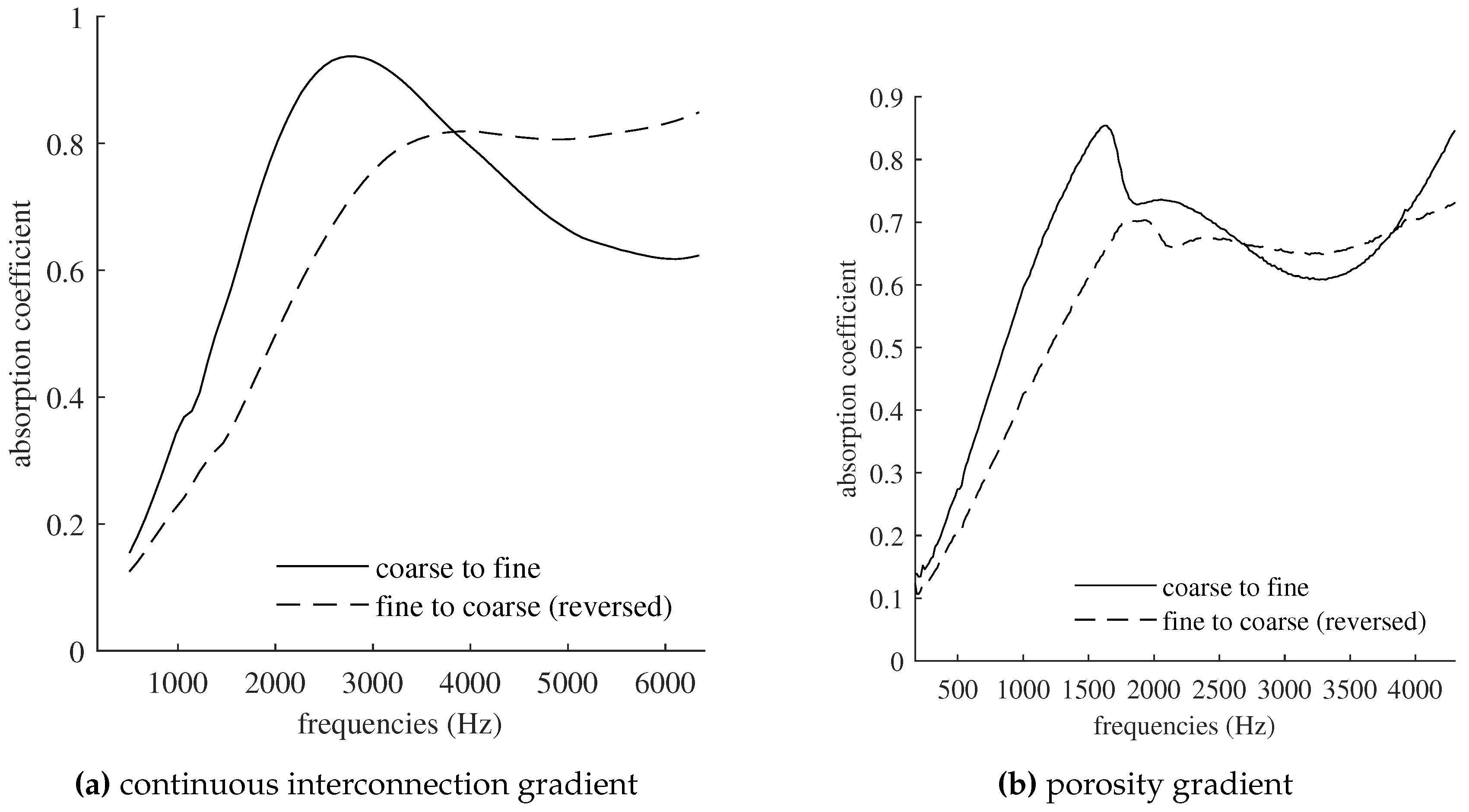
Preprints 119495 g007
Figure 7. Absorption coefficient of gradient porous biomaterials.
Figure 7. Absorption coefficient of gradient porous biomaterials.
Preprints 119495 g007

3.3.2. Porosity Gradient

As in the ceramic manufacturing process, the porosity gradient is obtained by superimposing layers of PMMA beads of different diameters. In order to obtain the impression in a single step, a first layer of balls (smaller diameter) is placed in the mold, then a new layer of balls with a larger diameter is incorporated and so on until the last layer. Between each layer, the surface is flattened by placing a piston (see Figure 6b). A grid is placed on the last layer and the perforated piston is inserted to keep the beads under pressure before immersion with acetone. Results shown in Figure 7b are obtain with a 4 layers of beads (diameters of each layer : above 0.4 to 0.5, above 0.5 to 0.6, above 0.6 to 0.7 and above 0.7 to 0.8 mm), each of identical thickness, resulting on 4.2 cm foam once completely manufactured and dried. Here again, the absorption curves clearly reflect the creation of an orthotropic material: depending on the face in contact with the incident wave, the response of the foam changes significantly.
Figure 8 illustrates the effect of this manufacturing process on the pore size (images and measures performed with the digital microscope KEYENCE VHX-7000N), with an observed ratio that can approach 2 between the two opposite side of the porosity gradient material.
Preprints 119495 g008
Figure 8. Pore size estimation for porosity gradient material acoustically characterized in Figure 7a.
Figure 8. Pore size estimation for porosity gradient material acoustically characterized in Figure 7a.
Preprints 119495 g008
Preprints 119495 g009
Figure 9. Pore size estimation for the continuous interconnection gradient material acoustically characterized in Figure 7b.
Figure 9. Pore size estimation for the continuous interconnection gradient material acoustically characterized in Figure 7b.
Preprints 119495 g009

4. Conclusions

Inspired by a method originally dedicated to obtaining ceramics, the porous materials presented in this article demonstrate the interest of a manufacturing process that is certainly complex but rich in possibilities. Thus, controlling the size of the pores, their interconnections, but above all the possibility of differentiating them spatially (eg. porosity gradient), makes this process particularly relevant for obtaining a material with remarkable properties. Also, this process can make it possible to easily obtain materials that could be described as hybrids. Indeed, incorporating a solid body within the skeleton of PMMA beads, or the addition of fine particles or fibers, is relatively simple and does not require substantial modification of the manufacturing method used here.

References

  1. Al-Qararah, A.M.; Ekman, A.; Hjelt, T.; Ketoja, J.A.; Kiiskinen, H.; Koponen, A.; Timonen, J. A unique microstructure of the fiber networks deposited from foam–fiber suspensions. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2015, 482, 544–553. [CrossRef]
  2. Ferreira, F.V.; Otoni, C.G.; Kevin, J.; Barud, H.S.; Lona, L.M.; Cranston, E.D.; Rojas, O.J. Porous nanocellulose gels and foams: Breakthrough status in the development of scaffolds for tissue engineering. Materials Today 2020, 37, 126–141. [CrossRef]
  3. Zieliński, T.G.; Dauchez, N.; Boutin, T.; Leturia, M.; Wilkinson, A.; Chevillotte, F.; Bécot, F.X.; Venegas, R. Taking advantage of a 3D printing imperfection in the development of sound-absorbing materials. Applied Acoustics 2022, 197, 108941. [CrossRef]
  4. Xue, Y.; Nobles, L.P.; Sharma, B.; Bolton, J.S. Designing hybrid aerogel-3D printed absorbers for simultaneous low frequency and broadband noise control. Materials & Design 2024, 242, 113026. [CrossRef]
  5. Arjunan, A.; Baroutaji, A.; Robinson, J.; Vance, A.; Arafat, A. Acoustic metamaterials for sound absorption and insulation in buildings. Building and Environment 2024, p. 111250. [CrossRef]
  6. Godbold, O.; Soar, R.; Buswell, R. Implications of solid freeform fabrication on acoustic absorbers. Rapid Prototyping Journal 2007, 13, 298–303. [CrossRef]
  7. Setaki, F.; Tian, F.; Turrin, M.; Tenpierik, M.; Nijs, L.; Van Timmeren, A. 3D-printed sound absorbers: Compact and customisable at broadband frequencies. Architecture, Structures and Construction 2023, 3, 205–215. [CrossRef]
  8. Zheng, Z.; Li, Y.; Yang, W. Absorption properties of natural fiber-reinforced sandwich structures based on the fabric structures. Journal of Reinforced Plastics and Composites 2013, 32, 1561–1568. [CrossRef]
  9. Tiuc, A.E.; Vermeşan, H.; Gabor, T.; Vasile, O. Improved sound absorption properties of polyurethane foam mixed with textile waste. Energy Procedia 2016, 85, 559–565. [CrossRef]
  10. Zhu, X.; Kim, B.J.; Wang, Q.; Wu, Q. Recent Advances in the Sound Insulation Properties of Bio-based Materials. BioResources 2014, 9. [CrossRef]
  11. Oldham, D.J.; Egan, C.A.; Cookson, R.D. Sustainable acoustic absorbers from the biomass. Applied Acoustics 2011, 72, 350–363. [CrossRef]
  12. Del Rey, R.; Alba, J.; Arenas, J.P.; Sanchis, V.J. An empirical modelling of porous sound absorbing materials made of recycled foam. Applied Acoustics 2012, 73, 604–609. [CrossRef]
  13. Trematerra, A.; Lombardi, I. Acoustic Properties of Cellulose. IOP Conference Series: Materials Science and Engineering. IOP Publishing, 2017, Vol. 225, p. 012082. [CrossRef]
  14. Arenas, J.P.; Rebolledo, J.; Rey Tormos, R.M.d.; Alba Fernández, J. Sound absorption properties of unbleached cellulose loose-fill insulation material. BioResources 2014, 9, 6227–6240. [CrossRef]
  15. Seciureanu, M.; Nastac, S.M.; Guiman, M.V.; Nechita, P. Cellulose Fibers-Based Porous Lightweight Foams for Noise Insulation. Polymers 2023, 15, 3796. [CrossRef]
  16. Nastac, S.M.; Nechita, P.; Guiman, M.V.; Roman, M.; Rosca, I.C. Applications of Xylan Derivatives to Improve the Functional Properties of Cellulose Foams for Noise Insulation. Polymers 2023, 15, 4648. [CrossRef]
  17. Muchlisinalahuddin, M.; Dahlan, H.; Mahardika, M.; Rusli, M. Cellulose-based Material for Sound Absorption And Its Application–A Short Review. BIO Web of Conferences. EDP Sciences, 2023, Vol. 77, p. 01003. [CrossRef]
  18. Miranda-Valdez, I.Y.; Coffeng, S.; Zhou, Y.; Viitanen, L.; Hu, X.; Jannuzzi, L.; Puisto, A.; Kostiainen, M.A.; Mäkinen, T.; Koivisto, J.; others. Foam-formed biocomposites based on cellulose products and lignin. Cellulose 2023, 30, 2253–2266. [CrossRef]
  19. Taiwo, E.M.; Yahya, K.; Haron, Z. Potential of using natural fiber for building acoustic absorber: A review. Journal of Physics: Conference Series. IOP Publishing, 2019, Vol. 1262, p. 012017. [CrossRef]
  20. Mahasaranon, S.; Horoshenkov, K.V.; Khan, A.; Benkreira, H. The effect of continuous pore stratification on the acoustic absorption in open cell foams. Journal of applied physics 2012, 111. [CrossRef]
  21. Geslain, A.; Groby, J.P.; Dazel, O.; Mahasaranon, S.; Horoshenkov, K.; Khan, A. An application of the Peano series expansion to predict sound propagation in materials with continuous pore stratification. The Journal of the Acoustical Society of America 2012, 132, 208–215. [CrossRef]
  22. Descamps, M.; Duhoo, T.; Monchau, F.; Lu, J.; Hardouin, P.; Hornez, J.; Leriche, A. Manufacture of macroporous β-tricalcium phosphate bioceramics. Journal of the European Ceramic Society 2008, 28, 149–157. [CrossRef]
  23. Joly, N.; Granet, R.; Krausz, P. Crosslinking of cellulose by olefin metathesis. Journal of Carbohydrate Chemistry 2003, 22, 47–55. [CrossRef]
  24. Panneton, R.; Gros, E. A missing mass method to measure the open porosity of porous solids. ACTA Acustica united with Acustica 2005, 91, 342–348.
  25. Atalla, Y.; Panneton, R. Inverse acoustical characterization of open cell porous media using impedance tube measurements. Canadian acoustics 2005, 33, 11–24.
  26. Allard, J.; Allard, J. Sound propagation in cylindrical tubes and porous materials having cylindrical pores. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials 1993, pp. 48–78. [CrossRef]
  27. Liu, X.; Ma, X.; Yu, C.; Xin, F. Sound absorption of porous materials perforated with holes having gradually varying radii. Aerospace Science and Technology 2022, 120, 107229. [CrossRef]
  28. Doutres, O.; Atalla, N. Sound absorption properties of functionally graded polyurethane foam. INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Institute of Noise Control Engineering, 2012, Vol. 2012, pp. 679–688.
  29. Sacristan, C.; Dupont, T.; Sicot, O.; Leclaire, P.; Verdière, K.; Panneton, R.; Gong, X.L. A mixture approach to the acoustic properties of a macroscopically inhomogeneous porous aluminum in the equivalent fluid approximation. The Journal of the Acoustical Society of America 2016, 140, 2847–2855. [CrossRef]
Preprints 119495 g001
Figure 1. PMMA beads and resulting ceramic [22].
Figure 1. PMMA beads and resulting ceramic [22].
Preprints 119495 g001
Preprints 119495 g002
Figure 2. Synoptic of the manufacturing process.
Figure 2. Synoptic of the manufacturing process.
Preprints 119495 g002
Preprints 119495 g005
Figure 5. (a) absorption coefficient and (b) microscopic view of a porous cellulose with double porosity.
Figure 5. (a) absorption coefficient and (b) microscopic view of a porous cellulose with double porosity.
Preprints 119495 g005
Table 1. Properties of the samples at the end of the manufacturing process.
Table 1. Properties of the samples at the end of the manufacturing process.
Sample m (g) h (mm) d (mm) V t ( cm 3 ) V c ( cm 3 ) ϕ (%)
1 0.5492 35.57 28.09 22.04 0.38 0.983
2 0.5720 35.25 28.13 21.91 0.39 0.982
3 0.5894 34.86 27.65 20.93 0.41 0.981
4 0.4612 35.12 25.79 18.35 0.32 0.983
5 0.5479 34.83 27.62 20.87 0.38 0.982
6 0.5792 35.78 27.57 21.36 0.40 0.981
Table 2. Properties of samples depicted in Figure 4b.
Table 2. Properties of samples depicted in Figure 4b.
Sample D (mm) m (g) h (mm) d (mm) τ (%)
A 0.2-0.4 0.17 18.1 22.04 9
B 0.5-0.6 0.22 20.3 21.91 5
C 0.5-0.6 0.21 19.1 20.93 11
D 0.6-0.7 0.23 20.9 18.35 5
E 0.7-0.8 0.21 19.1 20.87 5.9
Table 3. Acoustical properties of samples listed in Table 2 and illustrated in Figure 4b.
Table 3. Acoustical properties of samples listed in Table 2 and illustrated in Figure 4b.
Sample σ ( N . s . m − 4 ) α ∞ Λ (µm) Λ ′ (µm) ϕ
A 5192 1.05 114 192 0.990
B 2045 1.00 273 313 0.989
C 1194 1.07 340 456 0.989
D 685 1.02 468 710 0.989
E 750 1.12 449 590 0.989
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated