Basics of Parametric Decay Instability in Magnetized Plasma

Preprint

Article

Basics of Parametric Decay Instability in Magnetized Plasma

Altmetrics

Downloads

Views

Comments

Ilya Shesterikov^*

This version is not peer-reviewed

Submitted:

26 September 2024

Posted:

29 September 2024

You are already at the latest version

Alerts

Abstract

Parametric decay instabilities frequently occur in wave interactions. These instabilities typically have thresholds for wave amplitudes. They arise when nonlinearity, such as a spatial pressure inhomogenety, couples different waves. For these instabilities to arise, the waves must satisfy frequency and wavenumber matching conditions, which follow from the laws of energy and momentum conservation. However, parametric instabilities are not limited to wave interactions; the simples form of parametric instability is parametrically coupled oscillators. Magnetized plasma represents a unique wave medium in which numerous waves of various polarizations and spatial-temporal scales are easily excited and weakly damped. The greater the number of wave types, the easier it is to satisfy resonance conditions like the frequency and wavenumber matching conditions, and thus parametrically excite, or "drive" new waves from the initial wave. Therefore, in magnetoactive plasma, all known types of parametric instabilities can arise.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

1. Wave Equation

It is natural to start the discussion of the theory of parametric decay instabilities by considering parametric resonance (PR) [1,2,3,4,5,6]. In this case, it is convenient to choose a model that is close to reality and has sufficient simplicity to trace on this model the main qualitative patterns that govern decay parametric instabilities. It is not difficult to choose such a model. In oscillatory systems the discussion of parametric instabilities begins with the analysis of solutions of the Mathieu equation [7,8,9,10,11]. In our case for a wave medium, such as plasma, it is convenient to refer to the following equation:

\partial^{2} u / \partial t^{2} - υ^{2} [1 + ε cos (ω_{0} t - k_{0} x)] \partial^{2} u / \partial x^{2} = 0,

(1)

where we assume the linear dispersion relation

ω = k υ

Obviously, Eq.1 can be considered as one of the simplest generalizations of the Mathieu equation to wave media. In the absence of a term proportional to

ε

, such equations in linear approximation describe many well-known waves: acoustic, magnetosonic, Alfvénic, etc. Thus, for linear acoustic waves in a homogeneous plasma from the equations:

\begin{matrix} \partial ρ / \partial t + ρ_{0} \partial u / \partial x = 0; \\ ρ_{0} \partial u / \partial t = - \partial p / \partial x; p / ρ^{γ} = const, \end{matrix}\}

(2)

where

ρ, u, p

are respectively density, mass velocity and pressure;

γ

is the adiabatic exponent; the index zero denotes unperturbed quantities, follows the equation

\partial^{2} u / \partial t^{2} - υ^{2} \partial^{2} u / \partial x^{2} = 0,

where

υ^{2} \equiv γ p_{0} / ρ_{0}

(sound speed).

Suppose we are interested in low-amplitude Alfvén waves.

The propagation of Alfvén waves can be described by a wave equation:

\frac{\partial^{2} u}{\partial t^{2}} = v_{A}^{2} \frac{\partial^{2} u}{\partial x^{2}}

(3)

where

v_{A} = \frac{B_{0}}{\sqrt{μ_{0} ρ_{0}}}

is the Alfvén speed.

Here the x-axis is directed along

B

, and

(u

denotes any of the components of the mass velocity perpendicular to

B_{0}

Let the density

ρ

be modulated by a sinusoidal pump wave of small amplitude, then

v_{A}^{2} = v_{A_{0}}^{2} [1 + ε cos (ω_{0} t - k_{0} x)] .

(4)

Formal substitution of these values into (2) and (3) leads to equations of type (1). A rigorous derivation of the equations describing the propagation of sound or Alfvén waves in a medium with wave density modulation will give rise to additional harmonic terms associated with other nonlinear terms (such as, for example, the convective term). This circumstance significantly complicates the equations, but does not change the nature of the parametric relationship, so for a qualitative analysis it is sufficient to limit ourselves to the choice of the model equation (1). We can say that Eq.(1) describes a wave medium in which the influence of the pump wave is reduced to the modulation of the wave phase velocities.

2. Parametric Decay Instability (PDI). Regions of Instability

Let’s consider how the parametric coupling arises for a pair of waves

ω_{1}, k 1; ω 2, k 2

described by Eq.(1). It is easy to see that in the absence of a pump wave (

ε = 0

) Eq.(1) describes independent spatiotemporal harmonics with the linear dispersion relation

ω (k) = k v_{A}

To investigate the coupling of waves, it is convenient to switch to Fourier components in (1) for the spatial variables

V_{k} (t) = \int_{- \infty}^{\infty} u (x, t) e^{- i k x} d x

and transfer the term that takes into account the influence of the pump waves to the right-hand side of the equation.

So, we will use the wavenumber representation of

u (x, t)

, which is

V_{k} (t) = \int_{- \infty}^{\infty} u (x, t) e^{- i k x} d x

Given the equation:

\frac{\partial^{2} u}{\partial t^{2}} = v_{A}^{2} [1 + ε \cdot cos (ω_{0} t - k_{0} x)] \frac{\partial^{2} u}{\partial x^{2}}

First, we take the Fourier transform of both sides of the equation with respect to x.

The Fourier transform of

\frac{\partial^{2} u}{\partial t^{2}}

is:

F \{\frac{\partial^{2} u}{\partial t^{2}}\} = \frac{\partial^{2} V_{k} (t)}{\partial t^{2}}

The Fourier transform of

\frac{\partial^{2} u}{\partial x^{2}}

is:

F \{\frac{\partial^{2} u}{\partial x^{2}}\} = - k^{2} V_{k} (t)

Now, consider the term with the cosine function:

F \{v_{A}^{2} [1 + ε cos (ω_{0} t - k_{0} x)] \frac{\partial^{2} u}{\partial x^{2}}\}

The cosine term can be written using Euler’s formula:

cos (ω_{0} t - k_{0} x) = \frac{1}{2} (e^{i (ω_{0} t - k_{0} x)} + e^{- i (ω_{0} t - k_{0} x)})

The Fourier transform of

cos (ω_{0} t - k_{0} x)

will result in two delta functions in the frequency domain:

F \{cos (ω_{0} t - k_{0} x)\} = \frac{1}{2} (e^{i ω_{0} t} δ (k + k_{0}) + e^{- i ω_{0} t} δ (k - k_{0}))

Combining these results, the Fourier transform of the product

[v_{A}^{2} ε cos (ω_{0} t - k_{0} x)] \frac{\partial^{2} u}{\partial x^{2}}

involves the convolution of the individual transforms. Let:

f (x) = cos (ω_{0} t - k_{0} x) a n d g (x) = \frac{\partial^{2} u}{\partial x^{2}}

The convolution in the Fourier domain is:

F {f (x) g (x)} = \frac{1}{2} v_{A}^{2} ε [e^{i ω_{0} t} δ (k + k_{0}) + e^{- i ω_{0} t} δ (k - k_{0})] * (- k^{2} V_{k} (t))

The convolution of a delta function with another function shifts the argument of the function:

- \frac{1}{2} v_{A}^{2} ε [{(k + k_{0})}^{2} V_{k + k_{0}} (t) e^{i ω_{0} t} + {(k - k_{0})}^{2} V_{k - k_{0}} (t) e^{- i ω_{0} t}]

Simplifying, we get:

F \{[v_{A}^{2} ε cos (ω_{0} t - k_{0} x)] \frac{\partial^{2} u}{\partial x^{2}}\} = - \frac{1}{2} v_{A}^{2} ε [{(k_{0} + k)}^{2} V_{k_{0} + k} (t) e^{i ω_{0} t} + {(k_{0} - k)}^{2} V_{k_{0} - k}^{*} (t) e^{- i ω_{0} t}]

Combining everything, the equation in wavenumber space is:

\frac{\partial^{2} V_{k} (t)}{\partial t^{2}} + v_{A}^{2} k^{2} V_{k} (t) + \frac{1}{2} v_{A}^{2} ε [{(k_{0} + k)}^{2} e^{i ω_{0} t} V_{k_{0} + k} (t) + {(k_{0} - k)}^{2} e^{- i ω_{0} t} V_{k_{0} - k}^{*} (t)] = 0

or, taking into account that

ω (k) = v_{A}^{2} k^{2}

, we have:

\frac{\partial^{2} V_{k} (t)}{\partial t^{2}} + ω (k) V_{k} (t) = - \frac{1}{2} ε v_{A}^{2} [{(k_{0} + k)}^{2} e^{i ω_{0} t} V_{k_{0} + k} (t) + {(k_{0} - k)}^{2} e^{- i ω_{0} t} V_{k_{0} - k}^{*} (t)]

(5)

The equation we obtained is actually not a single equation. Considering the continuous spectrum of waves, any waves, it can be said that this is a system of two equations for coupled waves with wave numbers k and $k_{0} \pm k$ . Note that

ε

is a small quantity.

First of all, we note that in the zeroth approximation in $ε$ , all $V_{k}$ oscillate with their own frequencies $ω_{k}$ . The weak coupling does not significantly change the frequency of the oscillator. However, in the case when the forcing force in the right-hand side of Eq.(5) falls into resonance with the natural frequency, the oscillator can be excited.

The resonance condition for the second term in the right-hand side of Eq.(5) has the form:

ω_{0} - ω (k_{0} - k) = ω (k)

, for the first:

ω_{0} + ω (k_{0} + k) = ω (k)

Let the first condition be fulfilled, then the another term is non-resonant and can be ignored.

In turn, the Fourier component

V_{k_{0} - k}

of the resonance part of the equation Eq.(5) is described by the equation

\begin{matrix} d^{2} V_{k_{0} - k}^{*} / d t^{2} + ω^{2} (k_{0} - k) V_{k_{0} - k}^{*} = - (ε / 2) {(2 k_{0} - k)}^{2} v_{A}^{2} exp (i ω_{0} t) V_{2 k_{0} - k} - \\ - (ε / 2) k^{2} v_{A}^{2} exp (- i ω_{0} t) V_{k} \end{matrix}

(6)

In this equation also the second term is resonant. Therefore, considering only the resonant interaction of two coupled oscillators (designated as oscillator 1 and oscillator 2), we obtain the following shortened system:

\begin{matrix} \frac{\partial^{2} V_{k_{1}} (t)}{\partial t^{2}} + ω^{2} (k_{1}) V_{k_{1}} = - \frac{1}{2} v_{A}^{2} ε \cdot {(k_{2})}^{2} e^{- i ω_{0} t} V_{k_{2}}^{*} (t) \\ \frac{\partial^{2} V_{k_{2}} (t)}{\partial t^{2}} + ω^{2} (k_{2}) V_{k_{2}} = - \frac{1}{2} v_{A}^{2} ε \cdot {(k_{1})}^{2} e^{i ω_{0} t} V_{k_{1}} (t) \end{matrix}

(7)

where the notation

k_{2} = k_{0} - k_{1}

is introduced.

Taking into account the resonance conditions for frequencies, it can be said that parametrically related waves are those whose frequencies and wave vectors satisfy the conditions

\begin{matrix} ω_{0} = ω_{1} (k_{1}) + ω_{2} (k_{2}) \\ k_{0} = k_{1} + k_{2} \end{matrix}

(8)

i.e., the conditions of spatiotemporal synchronization. These conditions look like the energy and momentum conservation conditions in quantum mechanics. Thus, they remind us of the deep connection between the quantum mechanical and wave descriptions of wave processes.

In accordance with the above, we will seek the solution (7) in the form

V_{k} = a (t) exp [- i ω (k) t],

where

a (t)

-slowly changing amplitudes of the coupled waves. Then

\{\begin{matrix} - 2 i ω_{1} \frac{\partial a_{1}}{\partial t} = - (\frac{ε}{2}) k_{2}^{2} v_{A}^{2} a_{2}^{*} exp (- i Δ ω t) \\ - 2 i ω_{2} \frac{\partial a_{2}^{*}}{\partial t} = - (\frac{ε}{2}) k_{1}^{2} v_{A}^{2} a_{1} exp (i Δ ω t) \end{matrix}

(9)

where

Δ ω = ω_{0} - ω_{1} - ω_{2} .

It is easy to see that the solution to (9) is:

\begin{matrix} a_{1} \sim exp (- i \frac{Δ ω}{2} t + ν t); \\ a_{2}^{*} \sim exp (i \frac{Δ ω}{2} t + ν t), \end{matrix}

(10)

where

ν = \sqrt{γ_{D}^{2} - {(Δ ω)}^{2} / 4}; γ_{D}^{2} \equiv \frac{ε^{2} k_{1}^{2} k_{2}^{2} v_{A}^{4}}{16 ω_{1} ω_{2}}

(11)

This solution describes a first-order parametric decay instability. It follows from (11) that at zero frequency detuning, i.e., at

Δ ω = 0

[this means strict fulfillment of the resonance conditions (8)], the amplitudes of the waves

a_{1}

and

a_{2}

grow exponentially with an increment

γ = γ_{D}

. In this case, the relationship

ω_{1} ω_{2} > 0

must be fulfilled, which, together with the resonance conditions, gives

ω_{0} > ω_{1}, ω_{2}

In other words, in the case of parametric resonance instability, waves with frequencies less than the pump wave frequency are excited (red satellites). It should be noted that in the absence of dissipation the increment of the decay instability is proportional to the first power of the pump wave amplitude:

γ_{D} \sim ε

Equation (11) determines the width of the first-order instability zone

n = 1

. For detuning

| Δ ω / 2 | > γ_{D}

, the instability disappears. This means that the width of the first PI zone is proportional to the first power of the pump wave amplitude.

Knowing the theory of parametric resonance in oscillatory systems, this conclusion could have been made immediately after reducing the problem to solving the shortened equations (7), which describe a system of two parametrically coupled oscillators.

It should be emphasized that the system of shortened equations is obtained using the conditions of not only temporal $(ω_{0} = ω_{1} + ω_{2})$ , but also spatial $k_{0} = k_{1} + k_{2}$ resonance. The similarity of (1) with Mathieu’s equation, as well as the method of obtaining systems of shortened equations (based on spatiotemporal resonance of modes), allow qualitative conclusions to be drawn about higher-order parametric resonance and the corresponding instability zones.

Obviously, for waves of relatively small amplitude (in our example,

\tilde{ρ} ≪ ρ_{0}

), the increment of the n-th order PI

γ_{n} \approx ε^{n}

Accordingly, the instability zone narrows with increasing n, since

|Δ ω_{n}| / 2 = γ_{n}

, where

Δ ω_{n} = n ω_{0} - ω_{1} - ω_{2}

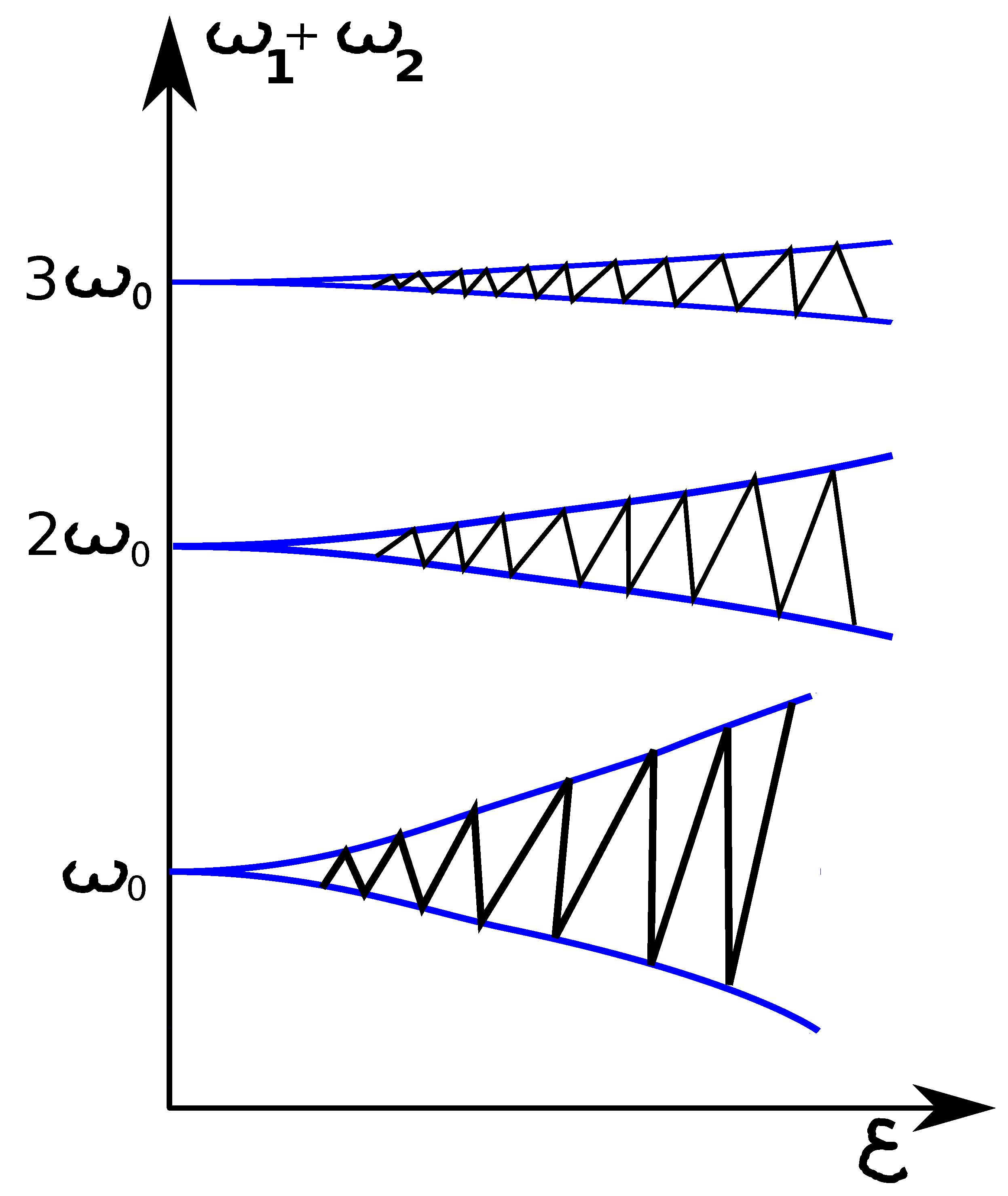
Figure 1 shows the zones of PI of the n-th order.

Instabilities of the first and second orders are of mos practical importance due to decrease in increments and the narrowing of instability zones with increasing n.

PI of the second order manifest themselves in those cases when PI of the first order do not arise due to the impossibility of fulfilling conditions (8).

In systems where PI of the first order are absent, the conditions for the occurrence of PI of the second order are usually met.

3. Thresholds of PDI

Parametric decay instabilities arise when the amplitudes exceed certain values. In the approximation of a homogeneous plasma, these thresholds are determined by the decrements of the excited wave doublet, which can be shown by introducing dissipation terms into equation (7). This is not difficult to do if small imaginary additions to the natural frequencies

ω_{i}

are introduced according to the scheme

ω_{i} \to ω_{i} + i γ_{i}

, where

γ_{i}

are the decrements of the corresponding waves. Assuming

Δ ω = 0

and performing simple calculations and taking dissipation into account, we obtain the following expression for the growth rate of the parametrically excited wave $ν_{D}$ :

ν_{D} = - \frac{γ_{1} + γ_{2}}{2} + \sqrt{γ_{D}^{2} + \frac{{(γ_{1} - γ_{2})}^{2}}{4}},

(12)

The requirement

ν_{D} > 0

gives the expression for the instability threshold in general form:

{\hat{γ^{2}}}_{D} > γ_{1} γ_{2}

(13)

or for the model problem (7):

ε_{thr} = \frac{16 ω_{1} ω_{2} γ_{1} γ_{2}}{k_{1}^{2} k_{2}^{2} v_{A}^{4}}

(14)

From (13), it follows that the threshold disappears when at least one of the decrements of the excited wave pair tends to zero.

4. Conclusions

In this work, we have explored the fundamental dynamics of Parametric Decay Instability (PDI) within a magnetized plasma environment. By analyzing the mathematical frameworks, such as the modified Mathieu equation, and applying it to wave media, we demonstrated how PDI is driven by resonance conditions between waves of different frequencies and wavenumbers. Specifically, we showed that parametric instabilities can arise under the influence of a pump wave, and their occurrence is governed by energy and momentum conservation, similar to quantum mechanical systems.

One of the key findings is that the instability threshold is highly dependent on the amplitudes of the interacting waves, where exceeding a certain amplitude initiates the instability. Furthermore, the resonant conditions dictate the regions of instability, with the first-order instabilities being the most prevalent due to their larger growth rates and broader regions of resonance.

The study also highlights the practical significance of first and second-order parametric instabilities, particularly in scenarios where the conditions for first-order instability are not met. These insights are crucial for understanding wave dynamics in plasma and could have applications in controlled fusion, space physics, and plasma-based devices.

References

Steven H. Strogatz. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Westview Press, 2000.
S. Timoshenko, D.H. Young, and W. Weaver. Vibration Problems in Engineering. Wiley, 1974.
J.P. Den Hartog. Mechanical Vibrations. McGraw-Hill, 1947.
John Guckenheimer and Philip Holmes. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer-Verlag, 1983.
William T. Thomson and Marie Dillon Dahleh. Theory of Vibration with Applications. Prentice Hall, 1998. [CrossRef]
Orazio Svelto. Principles of Lasers. Springer, 1998. [CrossRef]
Steven H. Strogatz. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Westview Press, Boulder, CO, 1st edition, 1994. [CrossRef]
H.C. Luckock. Introduction to Nonlinear Dynamics for Physicists. World Scientific Publishing Company, Singapore, 1990.
George B. Arfken, Hans J. Weber, and Frank E. Harris. Mathematical Methods for Physicists. Elsevier Academic Press, Burlington, MA, 7th edition, 2012.
A.M. Lyapunov. Stability of Motion. Taylor & Francis, London, 1992.
Lawrence Perko. Differential Equations and Dynamical Systems. Springer, New York, NY, 3rd edition, 2013. [CrossRef]

Figure 1. Stability - instability chart of the parametric interaction. (Mathieu equation stability chart).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Basics of Parametric Decay Instability in Magnetized Plasma

Abstract

1. Wave Equation

2. Parametric Decay Instability (PDI). Regions of Instability

3. Thresholds of PDI

4. Conclusions

References

MDPI Initiatives

Important Links

Subscribe