Prerpints.org logo
Preprint
Article

FL-APB: Balancing Privacy Protection and Performance Optimization for Adversarial Training in Federated Learning

Altmetrics

Downloads

111

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 October 2024

Posted:

21 October 2024

You are already at the latest version

Alerts
Abstract
Federated Learning (FL), as a distributed machine learning method, is particularly suitable for training models that require large amounts of data while meeting increasingly strict data privacy and security requirements. Although FL effectively protects the privacy of participants by avoiding the sharing of raw data, balancing the risks of privacy leakage with model performance remains a significant challenge. To address this, this paper proposes a new algorithm—FL-APB (Federated Learning with Adversarial Privacy-Performance Balancing). This algorithm combines adversarial training with privacy protection mechanisms to dynamically adjust privacy and performance budgets, optimizing the balance between the two while enhancing and ensuring performance. Experimental results demonstrate that the FL-APB algorithm significantly improves model performance across various adversarial training scenarios, while effectively protecting the privacy of participants through adversarial training of privacy data.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

Federated Learning (FL) [1,2] is an emerging distributed machine learning approach designed for effective model training in scenarios with high data privacy and security requirements. Unlike traditional centralized learning, FL allows multiple participants to collaboratively train a global model without sharing raw data. Each participant conducts local model training and sends the updated model parameters to a central server for aggregation, while the raw data remains on local devices. This model protects participant privacy while effectively utilizing decentralized data resources, making it widely applicable in fields such as finance, healthcare, and intelligent transportation [3,4,5,6].
The key advantage of FL is its ability to avoid the privacy leakage risks associated with data centralization, aligning with increasingly stringent data privacy regulations (such as GDPR [7]). Furthermore, FL leverages distributed computing resources to enhance training efficiency and reduce the costs and risks of data transmission. Therefore, FL not only aids in building efficient machine learning systems but also provides a viable solution for applying machine learning in scenarios where data privacy and security are critical [8].
Despite its significant privacy protection advantages, FL faces numerous challenges [9,10,11]. First, privacy concerns remain a core issue for FL. Although participants do not need to share raw data, the transmission of model update parameters may reveal sensitive information about the original data, allowing attackers to infer participants’ private data by analyzing patterns in the model updates [12]. Additionally, balancing privacy protection and model performance poses a significant challenge. Excessive privacy protection mechanisms (such as differential privacy) can prevent data leakage but may lead to declines in model performance, affecting accuracy and usability [13].
Second, model performance also encounters various technical challenges. In FL, participants’ data is often heterogeneous (uneven data distribution and significant feature differences), which can hinder model convergence, especially with a large number of participants [14]. Moreover, communication overhead and computational resource constraints can affect training efficiency, making it an important direction of FL research to improve model performance and convergence speed while ensuring privacy [15].
To address the privacy and robustness issues in FL [16], adversarial training (AT) has gradually been introduced into the FL domain [17]. Adversarial training introduces adversarial attack samples during model training, enabling the model to maintain stability and robustness when faced with malicious attacks [18]. This method not only enhances the model’s defense against privacy data leakage attacks but also improves overall model security [19]. However, the application of adversarial training in FL also comes with certain drawbacks.
First, while adversarial training can effectively enhance model robustness, it can slow down convergence speed and increase computational complexity during training. Additionally, the introduction of adversarial samples may result in decreased model performance (such as accuracy). Particularly in FL environments, data heterogeneity and distribution differences exacerbate these issues, making it a pressing challenge to maintain model performance while protecting privacy [20,21,22,23,24].
To balance privacy protection and model performance during FL training, this paper proposes a new algorithm—FL-APB (Federated Learning with Adversarial Privacy-Performance Balancing). Existing methods often focus on improving one aspect of performance, either emphasizing privacy protection at the cost of model accuracy and convergence speed, or prioritizing model performance while neglecting the risks of privacy leakage. Therefore, designing an algorithm that simultaneously considers privacy protection and performance optimization has become the main motivation for this research.
The core idea of FL-APB is to combine adversarial training with privacy protection mechanisms, dynamically adjusting the privacy budget and performance budget during training to achieve a balance between the two. This algorithm maximizes model performance while ensuring privacy protection and mitigates the negative impact of adversarial training through adaptive adjustments.
The goal of this paper is to achieve a balance between privacy protection and performance optimization in FL. To this end, we propose the FL-APB algorithm and validate its effectiveness across different adversarial training methods through theoretical analysis and experimental verification. The main contributions of this paper are as follows:
1. Proposing the FL-APB algorithm, which achieves a balance between privacy protection and performance optimization by dynamically adjusting the privacy budget and performance budget.
2. Introducing adversarial training, which enhances the robustness of FL models while improving overall performance in conjunction with privacy protection.
3. Conducting experimental validation and theoretical analysis to verify the convergence, robustness, privacy protection capabilities, and performance optimization effects of the FL-APB algorithm through multiple sets of experiments, showcasing its application potential in real-world scenarios.
4. Providing a new solution for privacy protection and performance optimization, serving as a reference for further research on balancing privacy protection and performance optimization in FL.
The content of this paper is arranged as follows: Section 2 briefly reviews related work on privacy protection and performance optimization in Federated Learning. Section 3 introduces the FL-APB system model, analyzes issues related to privacy protection and performance optimization, and conducts convergence analysis and privacy-performance trade-off analysis of the FL-APB algorithm. Section 4 provides a brief introduction to the experimental setup. Section 5 analyzes and discusses the experimental results. Section 6 concludes the paper and outlines future research directions.

2. Related Work

In this section, we will systematically review the existing literature on differential privacy within the context of FL, elucidating their applications and inherent limitations, particularly with respect to their impact on model performance. Additionally, we will explore the integration of adversarial training in FL, emphasizing its potential to enhance model robustness while critically examining its detrimental effects on convergence speed and overall performance. Furthermore, we will analyze current research focused on optimizing performance in FL, addressing challenges related to data heterogeneity, accelerating model convergence, and minimizing communication overhead. This analysis will include a discussion of the trade-offs between these optimization techniques concerning privacy protection and performance. Ultimately, we will provide insights into how recent advancements seek to balance privacy protection with performance optimization, setting the stage for the introduction of our proposed FL-APB algorithm.

2.1. Differential Privacy in FL

In FL, data privacy remains a core challenge. To address this, blockchain [25], homomorphic encryption [26], secure multi-party computation (SMPC) [27], and differential privacy (DP) [13] are widely implemented within the FL framework. Among these, DP protects participants’ private data by introducing noise into data or model updates, thus preventing data leakage and safeguarding against potential attacks. Article [28] proposes a user-level differential privacy method (UDP) and derives the theoretical convergence upper bound for the UDP algorithm. Additionally, it introduces a communication round discount (CRD) method that balances computational complexity and convergence performance effectively. Article [29] presents a DP-based FL framework designed for generating personalized models for heterogeneous clients, analyzing its convergence performance and the optimal trade-offs among various metrics. Article [30] introduces a FL method called Dynamic Fisher Personalization and Adaptive Constraint (FedDPA) to address non-IID data distribution and mitigate privacy leakage risks in personalized FL. FedDPA leverages layer-wise Fisher information to assess the informational content of local parameters, allowing it to retain local parameters with high Fisher values during the personalization process and avoid noise interference. It also employs adaptive constraint strategies to enhance the convergence of both personalized and shared parameters. Article [31] proposes a local differential privacy scheme (ACS-FL) aimed at training clustered FL models on heterogeneous IoT data through adaptive clipping, weight compression, and parameter shuffling. ACS-FL achieves a favorable balance between privacy and utility by alleviating the curse of dimensionality, reducing LDP noise, and minimizing communication overhead. Article [32] presents a perturbation algorithm (PDPM) designed to meet personalized local differential privacy (PLDP) requirements. The PDPM algorithm allows clients to adjust privacy parameters based on data sensitivity, providing personalized privacy protection. While these methods effectively enhance privacy and achieve a favorable balance between privacy and utility, they often negatively impact model performance, as excessive noise injection can lead to decreased accuracy.

2.2. Adversarial Training in FL

To further enhance models’ defenses against privacy leaks and malicious attacks, adversarial training has been gradually integrated into FL. In adversarial training, participants generate adversarial samples for model training, enabling models to remain robust against malicious attacks. The paper [33] explores fairness issues in FL, promoting individual fairness through distributed adversarial training without compromising data privacy. The paper [34] proposes a federated adversarial learning paradigm (FAL) tailored for FL, aimed at utilizing decentralized training data. This approach addresses unique vulnerabilities exposed by multi-step local updates prior to aggregation and conducts convergence analysis using appropriate gradient approximation and coupling techniques. The paper [23] introduces a margin-based federated adversarial training method (GEAR), which encourages minority classes to maintain larger margins by introducing a margin-based cross-entropy loss, while regularizing the decision boundary to be smoother, thereby providing an improved decision boundary for the global model. However, while adversarial training enhances model robustness, it inevitably increases training complexity and slows convergence, particularly in heterogeneous FL environments. Furthermore, the introduction of adversarial samples can result in diminished model performance (e.g., accuracy), posing a significant challenge in balancing privacy protection and performance optimization through adversarial training.

2.3. Balancing Privacy and Performance in FL

Despite significant advances in both privacy protection and performance optimization, achieving an effective balance between the two remains a pressing issue. Reference [16] employs a natural adversarial optimization method that trains an encoding function alongside a deep neural network for private attribute classification. This approach proposes a stable and convergent optimization method that successfully learns an encoder meeting privacy requirements while maintaining utility. Article [18] investigates the robustness of machine learning (ML) through adversarial training in both centralized and decentralized environments, exploring the design of ML algorithms to enhance training accuracy across various adversarial training methods. Reference [19] introduces a novel adversarial training framework that explicitly learns a degradation transformation for original video inputs to optimize the trade-off between target task performance and the privacy budget of degraded videos. This framework utilizes different definitions of privacy budgets to maintain high performance in target tasks (such as action recognition) while effectively mitigating privacy breach risks. Article [20] conducts a comprehensive robustness evaluation of existing FL methods to better understand their adversarial vulnerabilities, proposing a new algorithm called Decision Boundary-based Federated Adversarial Training (DBFAT), which incorporates local re-weighting and global regularization components to improve the accuracy and robustness of FL systems. Reference [22] presents a new algorithm, FedDynAT, designed for adversarial training (AT) in federated environments, significantly enhancing both natural and adversarial accuracy while reducing model drift and accelerating convergence. Article [24] examines the FAT problem under label skewness and identifies root causes of training instability and degradation in natural accuracy. To address these issues, a Calibrated FAT (CalFAT) method is proposed, which adaptively calibrates logits to balance classes, thus resolving stability challenges. Existing privacy protection methods often prioritize enhancing privacy defenses while neglecting their impact on model performance; conversely, some performance optimization algorithms focus on accelerating convergence and improving accuracy but do not adequately address privacy protection. Therefore, designing a FL algorithm that concurrently considers both privacy protection and performance optimization has become the primary motivation for this study. To this end, we propose the FL-APB algorithm, which integrates adversarial training with privacy protection mechanisms to dynamically adjust privacy and performance budgets, thereby achieving a balance between privacy protection and performance optimization.

3. System Model

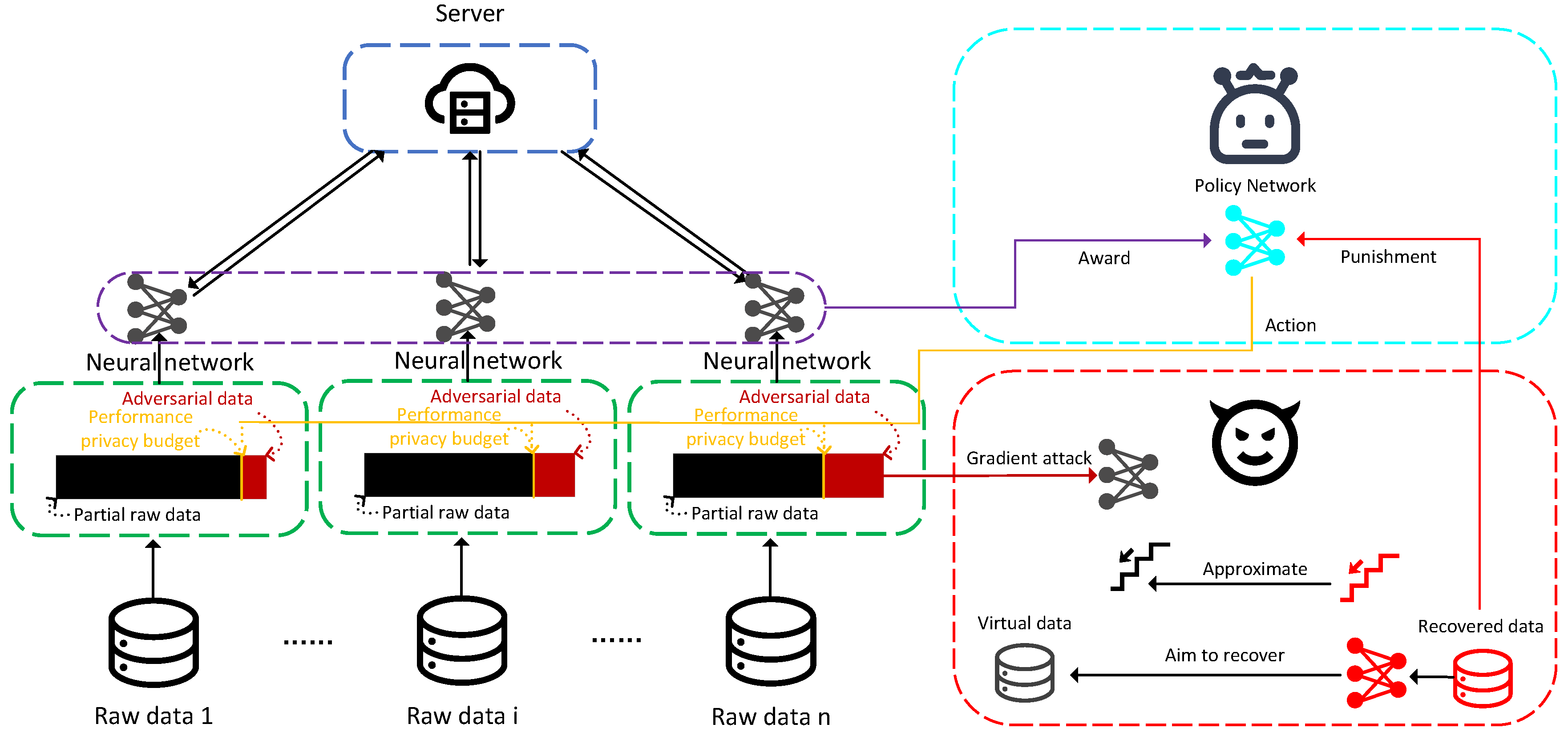
In this section, we introduce the main components and working mechanism of the FL-APB system model. As shown in Figure 1, when FL training is subjected to privacy attacks, the FL-APB algorithm balances privacy and performance budgets by generating adversarial training strategies to prevent attackers from stealing sensitive information.

3.1. Problem Definition

In FL, each participant i has a local dataset D i and a local loss function L i ( w ) , where w represents the global model parameters. The global objective is to minimize the average loss across all participants:
min w 1 N ∑ i = 1 N L i ( w )
To protect user privacy, participant i introduces differential privacy to its local dataset D i , ensuring that model updates satisfy the ϵ -differential privacy ( ϵ - DP ) requirement:
P ( M ( D 1 ) ∈ S ) ≤ e ϵ · P ( M ( D 2 ) ∈ S )
where M represents the mechanism used to compute model updates based on the dataset (such as gradient computation or parameter aggregation), D 1 and D 2 are neighboring datasets that differ by very few data points, S is a subset of possible outcomes (i.e., the space of all potential model updates), and ϵ controls the level of privacy protection, with smaller ϵ providing stronger privacy guarantees.
Specifically, we enhance model robustness and privacy protection through adversarial training by introducing perturbations δ to the input data x. The adversarial training loss is defined as:
L adv ( w ) = E ( x , y ) ∼ D max ∥ δ ∥ ≤ α ℓ ( f w ( x + δ ) , y )
where δ is the adversarial perturbation, α is the perturbation bound, and ℓ ( · ) denotes the model’s loss function.
In adversarial training, the perturbation δ simulates small changes to the input data, which serves a similar purpose as the differences between neighboring datasets in differential privacy.
We can express this relationship as:
P ( M ( x ) ∈ S ) ≤ P ( M ( x + δ ) ∈ S )
where x represents the original input data, and x + δ denotes the input perturbed by the adversarial noise. This equation indicates that adversarial training minimizes the difference in the output distribution of the model before and after introducing the perturbation δ , thereby ensuring the model’s robustness and privacy protection. The perturbation δ thus acts similarly to the mechanism used in differential privacy to control the variation in model outputs, making adversarial training an approximate implementation of differential privacy.
By introducing perturbations to the input data, adversarial training ensures that the model output remains stable even in the presence of minor changes to the dataset (such as the perturbation δ or the alteration of one data point), thereby providing privacy protection. This aligns with the core principle of differential privacy, which seeks to limit the changes in the model’s output to prevent attackers from inferring the original data from model updates.
To simultaneously optimize privacy protection and model performance, we define a total loss function L t , which combines performance loss and privacy protection loss. Privacy and performance budgets control the weights of these components:
L t ( w ) = λ 1 L per ( w ) + λ 2 L pri ( w )
where L per ( w ) represents the model’s performance loss, including either regular training loss or adversarial training loss. L pri ( w ) represents the privacy protection-related loss, such as the impact of noise added to meet differential privacy requirements. λ 1 and λ 2 are dynamic weights, satisfying λ 1 + λ 2 = 1 , used to adjust the balance between privacy protection and performance optimization.

3.1.1. Design of FL-APB

The goal of FL-APB is to minimize the total loss function L t , which integrates model performance loss and privacy protection loss. The objective function is expressed as:
L total ( w , λ 1 , λ 2 ) = λ 1 L per ( w ) + λ 2 L pri ( w )
To dynamically adjust λ 1 and λ 2 , we introduce the Proximal Policy Optimization (PPO) algorithm. PPO is a reinforcement learning algorithm that updates weight parameters through policy gradient methods, ensuring stability and convergence of each update.
FL-APB uses the policy π θ ( λ 1 , λ 2 | s ) to generate weights λ 1 and λ 2 , where s is the current state (such as privacy leakage level and model performance), and θ is the policy parameter. The policy objective is to maximize the reward R t , which is the reward obtained from actions taken in the given state.
The loss function for FL-APB is defined as:
L APB ( θ ) = E t min r t ( θ ) A ^ t , clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t
where r t ( θ ) is the ratio of the current policy to the old policy:
r t ( θ ) = π θ ( λ 1 , λ 2 | s t ) π θ old ( λ 1 , λ 2 | s t )
A ^ t is the advantage function used to evaluate the superiority of the current action relative to other possible actions. ϵ is a parameter controlling the update range, ensuring that the policy update does not exceed the ϵ limit.
In each training iteration, new values of λ 1 and λ 2 are generated to balance privacy loss and performance loss. The weight update formula is:
λ 1 ( t + 1 ) , λ 2 ( t + 1 ) = arg max λ 1 , λ 2 E R t
where R t is the reward for each training round, typically related to the balance between privacy protection and model performance.
The final optimization objective is to minimize the loss function L t , while generating and optimizing weights λ 1 and λ 2 :
min w λ 1 L per ( w ) + λ 2 L pri ( w ) subject to λ 1 , λ 2 ∼ π θ ( λ 1 , λ 2 | s )
Finally, the policy parameters θ are updated to generate better λ 1 and λ 2 :
θ t + 1 = θ t + α ∇ θ L APB ( θ )
where α is the learning rate, and ∇ θ L APB ( θ ) is the policy gradient used to optimize the policy parameters.

3.2. Theoretical Analysis

In this section, we will perform a theoretical analysis of the FL-APB algorithm, focusing on its convergence and the trade-offs between privacy and performance.

3.2.1. Convergence Analysis

Firstly, FL-APB balances privacy leakage and model performance by dynamically adjusting the weights λ 1 and λ 2 for privacy protection and performance optimization. The PPO (Proximal Policy Optimization) reinforcement learning algorithm used in FL-APB has good convergence properties. In each iteration, PPO avoids drastic policy fluctuations by restricting the magnitude of policy updates, ensuring the stability of the training process.
In FL-APB, the core idea of using PPO is to optimize the dynamic weights λ 1 and λ 2 through policy gradients, thereby minimizing the total loss function L t ( w ) in Equation (5). The FL-APB algorithm aims to simultaneously optimize privacy protection and model performance. We have two loss functions: L per ( w ) , which evaluates the model’s standard training error, representing the model’s performance; and L pri ( w ) , which measures the impact of privacy protection, typically including noise introduced by differential privacy. In each local training, the model’s performance loss L per ( w ) and privacy loss L pri ( w ) are independent and can be balanced through dynamic adjustment of weights.
According to the Lagrange multiplier method, we can represent the problem as a constrained optimization problem as shown in Equation (10). To solve this constrained optimization problem, we introduce the Lagrange multiplier μ and define the Lagrangian function L :
L ( w , λ 1 , λ 2 , μ ) = λ 1 L per ( w ) + λ 2 L pri ( w ) + μ ( λ 1 + λ 2 − 1 )
Next, we take the derivatives of L and find the optimal solution by setting the derivatives to zero.
First, we differentiate with respect to λ 1 and λ 2 :
∂ L ∂ λ 1 = L per ( w ) + μ
∂ L ∂ λ 2 = L pri ( w ) + μ
We also handle the constraint λ 1 + λ 2 = 1 :
∂ L ∂ μ = λ 1 + λ 2 − 1
Setting these partial derivatives to zero:
L per ( w ) + μ = 0 ⇒ μ = − L per ( w )
L pri ( w ) + μ = 0 ⇒ μ = − L pri ( w )
Thus:
L per ( w ) = L pri ( w )
This equation suggests that, in theory, the performance loss and privacy loss should be balanced at an optimal point. However, in practical applications, the trade-off between privacy protection and performance often depends on specific requirements. To improve the model’s performance, performance loss should typically decrease over time, while the relative privacy loss may increase as more resources are allocated to privacy protection. This does not mean privacy leakage increases but rather reflects the system’s prioritization of safeguarding privacy. When L per ( w ) = L pri ( w ) , it may not fully meet performance expectations. In such cases, FL-APB automatically adjusts the weight parameters to strike a better balance between performance loss and privacy protection loss.
FL-APB dynamically adjusts the weight parameters λ 1 and λ 2 through the PPO algorithm, iteratively moving toward the optimal balance between privacy protection and performance. The objective of the PPO algorithm is to maximize the reward R t , which is defined as a weighted combination of privacy performance and model performance. In each iteration, the reward R t is assumed to be directly related to this balance, and its formula is given by:
R t = λ 1 ( t ) · per ( w ) − λ 2 ( t ) · pri ( w )
where per ( w ) represents the model performance, pri ( w ) represents the privacy performance, and λ 1 ( t ) and λ 2 ( t ) are dynamic parameters that control the relative importance of these two components.
To integrate this reward function within the PPO framework, we convert R t into a scalar value, enabling it to serve as the feedback signal for policy optimization in each iteration. Specifically, the PPO algorithm adjusts λ 1 and λ 2 by maximizing the expected reward, as expressed in Equation (9). Combined with the PPO policy gradient optimization method, the policy gradient update rule is given by Equation (11).
According to policy gradient theory, the PPO algorithm will converge to the optimal policy after multiple iterations. For FL-APB, this means that the weight parameters λ 1 and λ 2 will gradually converge to an optimal balance point, ensuring that the model meets both performance and privacy protection requirements.
Moreover, the convergence of FL-APB is ensured by the PPO update mechanism, which limits the step size of policy updates through the clipping operation in Equation (8), ensuring that new policies remain within a neighborhood of the old policies, thereby preventing excessive deviations. This mechanism controls the magnitude of policy updates via the parameter ϵ , ensuring small, incremental adjustments. Such controlled updates guarantee that the algorithm converges gradually under various training conditions, resulting in stable weight adjustment strategies.

3.2.2. Privacy and Performance Trade-off Analysis

The core objective of the FL-APB algorithm is to make a reasonable trade-off between model performance and privacy protection. In differential privacy mechanisms, as shown in Equation (2), the privacy leakage level is controlled by the privacy parameter ϵ . A smaller ϵ value implies stronger privacy protection but may negatively impact model performance, such as increased noise during training, leading to slower convergence or decreased performance, i.e.:
L per ( w ) ∝ 1 ϵ and L pri ( w ) ∝ ϵ
This means that when privacy protection (i.e., smaller ϵ ) increases, the performance loss L pri ( w ) becomes larger, and vice versa. Therefore, FL-APB balances the performance loss due to differential privacy and the actual application needs of the model by introducing dynamic weights λ 1 and λ 2 .
Specifically, when the risk of privacy leakage is high, the policy generates a larger λ 2 value to enhance privacy protection and limit the possibility of attackers stealing private data. Conversely, when the model’s performance is poor, the policy generates a larger λ 1 value to prioritize performance optimization. Through this dynamic weight adjustment mechanism, FL-APB can make targeted optimization decisions at different training stages to achieve a balance between privacy and performance.
According to the PPO policy optimization algorithm, the long-term expected reward R t of FL-APB directly reflects the balance between privacy protection and performance optimization. In each training iteration, the policy generates the optimal weight combination λ 1 ( t ) and λ 2 ( t ) based on the current state s t (such as privacy leakage level and model performance) to minimize the loss function and maximize the reward. As training progresses, the policy will converge, allowing the FL system to meet privacy protection requirements while ensuring the model’s performance.

4. Experimental Setup

This section introduces the experimental setup used to evaluate the proposed FL-APB algorithm, including the dataset, baseline methods, evaluation metrics, and implementation details.

4.1. Dataset Description

To thoroughly evaluate the performance of the FL-APB algorithm, we selected the CIFAR-10 dataset, which consists of 60,000 32x32 color images evenly distributed across 10 categories, with each class containing 6,000 images. This dataset is widely used in machine learning research due to its balanced representation of image classes, making it suitable for evaluating FL algorithms.
To simulate a realistic Non-IID scenario in FL, we applied a Dirichlet distribution to partition the dataset. This method enables controlled imbalances in the data distribution by assigning varying proportions of each class to different clients, effectively capturing the diversity of data allocation across clients. The Dirichlet distribution allows for a flexible, client-specific data distribution, where some clients may hold more examples of certain classes than others, mimicking the challenges in real-world data environments. At the same time, we ensured that each client received at least a minimum threshold of data to avoid extreme imbalance, which could undermine the model’s training stability. This approach enhances the experimental design by closely replicating the data heterogeneity often encountered in FL settings.

4.2. Baseline Methods

To validate the effectiveness of the FL-APB algorithm, we compared it with the standard FL algorithm, FedAvg, which lacks privacy protection mechanisms. Specifically, we compared the test accuracy of the model after 100 rounds of training under FL-APB optimization. Additionally, we analyzed the impact of different adversarial training methods (FGSM [35], PGD [36], EOTPGD [37], FFGSM [38], TPGD [39], MIFGSM [40], UPGD, TIFGSM [41], Jitter [42], NIFGSM [43], PGDRS [44], DIFGSM [45], SINIFGSM [43], VMIFGSM [46], VNIFGSM [46], CW [47], PGDL2 [36], PGDRSL2 [44], SPSA [48], PIFGSM [49], PIFGSMPP [50]) on the optimization effectiveness of FL-APB. To further assess the privacy protection capabilities of the FL-APB algorithm, we conducted privacy attack experiments using the DLG and iDLG algorithms on models trained with different methods. In particular, we compared the mean squared error (MSE) between the images recovered by DLG and iDLG and the original private images for both the FL-APB and VANILLA methods. A higher MSE (greater than 1) indicates that the recovered images do not reveal private information, which allows us to evaluate the model’s performance in protecting training data privacy.

4.3. Implementation Details

The experiments were implemented based on the PyTorch framework, using the FedAvg FL algorithm for 100 communication rounds. In each round, 10 participants were randomly selected for training, and the data was distributed in a Non-IID manner. During each round, 50% of the participants were randomly chosen to perform actual model training, using the LeNet convolutional neural network for image classification tasks. The LeNet network consists of three convolutional layers and one fully connected layer, which is suitable for handling image classification problems. For training, the optimizer used for FedAvg was SGD, with a learning rate of 0.15, and a batch size of 16, where each participant conducted 5 local training iterations. In contrast, FL-APB used the Adam optimizer with a learning rate of 3e-4. For the privacy attack experiments, the DLG and iDLG algorithms were employed to test the recovery of the same images under different adversarial perturbations. The optimizer used was LBFGS, with a learning rate of 0.2, and the number of iterations was set to 400.

5. Results and Discussion

This section presents an in-depth performance evaluation of the FL-APB algorithm under different adversarial training scenarios, focusing on the algorithm’s performance in privacy protection and optimization. Through a series of experiments, we verify the effectiveness of the FL-APB algorithm in both model accuracy and privacy protection, and provide a comparative analysis.
The experimental design begins by setting the same privacy and performance budgets to evaluate the FL-APB algorithm under these constraints. To further demonstrate its advantages, we compare it with the standard FL algorithm, FedAvg, with a focus on analyzing the improvements of FL-APB in balancing privacy protection and performance.
Subsequently, we will present detailed experimental results from multiple dimensions, including privacy protection, model performance, and the training process, and explore the differences in FL-APB’s performance under varying experimental conditions and the potential reasons behind these differences.

5.1. Balancing Privacy and Performance

Privacy budgets are typically expressed in the form of differential privacy, used to limit the amount of sensitive information exposed to attacks. A higher privacy budget often implies stronger privacy protection, but it can also lead to a decrease in model performance, as stricter privacy protection requires more noise injection or interference to gradient information.
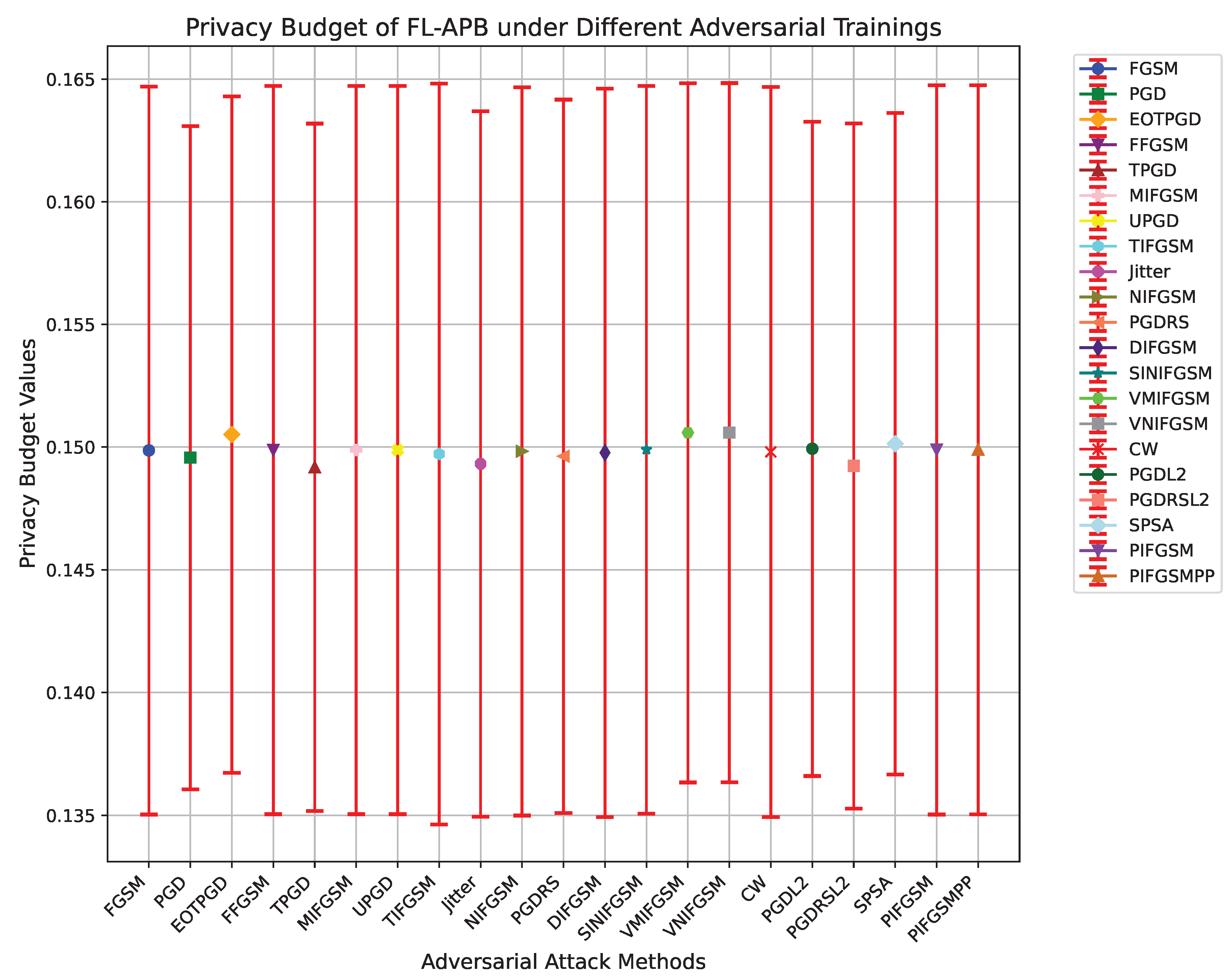
The FL-APB algorithm balances privacy protection and model performance through various adversarial training strategies. Figure 2 shows the privacy budget and standard deviation under multiple adversarial training methods (e.g., FGSM, PGD, MIFGSM, etc.), with detailed values provided in Table 1. From this, we can infer that FL-APB requires different levels of privacy budget investment to maintain system security under different attack strategies.
For instance, under PGDL2 and SPSA adversarial training, FL-APB’s privacy budget is relatively high (close to 0.150), indicating that more resources are required to enhance protection in response to these complex and powerful attacks. In contrast, adversarial trainings like TPGD and Jitter show relatively lower privacy budgets, indicating that these attacks are less severe, requiring less effort to protect system privacy.
Further analysis of the privacy budget and standard deviation of various adversarial attack methods can reveal the fluctuation in privacy protection demands across different communication rounds. A larger standard deviation means that under the given attack, the privacy protection demand of the FL-APB algorithm fluctuates greatly between rounds, leading to lower system stability; a smaller standard deviation indicates less fluctuation in privacy protection demand.
PGDL2 and SPSA have relatively small standard deviations of 0.0133 and 0.0135, respectively, indicating that the privacy protection demand is stable under these attacks, and FL-APB can smoothly adjust the privacy budget to maintain a relatively consistent level of privacy protection.
In contrast, methods like TIFGSM and VNIFGSM show larger standard deviations, 0.0151 and 0.0142, respectively, indicating less stability in FL-APB’s privacy protection demand under these attacks, potentially requiring more complex dynamic adjustment strategies to balance privacy protection.
The size and volatility of the privacy budget are closely related to the complexity and intensity of the attack. More adaptive attacks like PGDL2 and CW (with a privacy budget of 0.1498 and a standard deviation of 0.0148) often require higher privacy budgets to defend against.

5.2. Model Performance

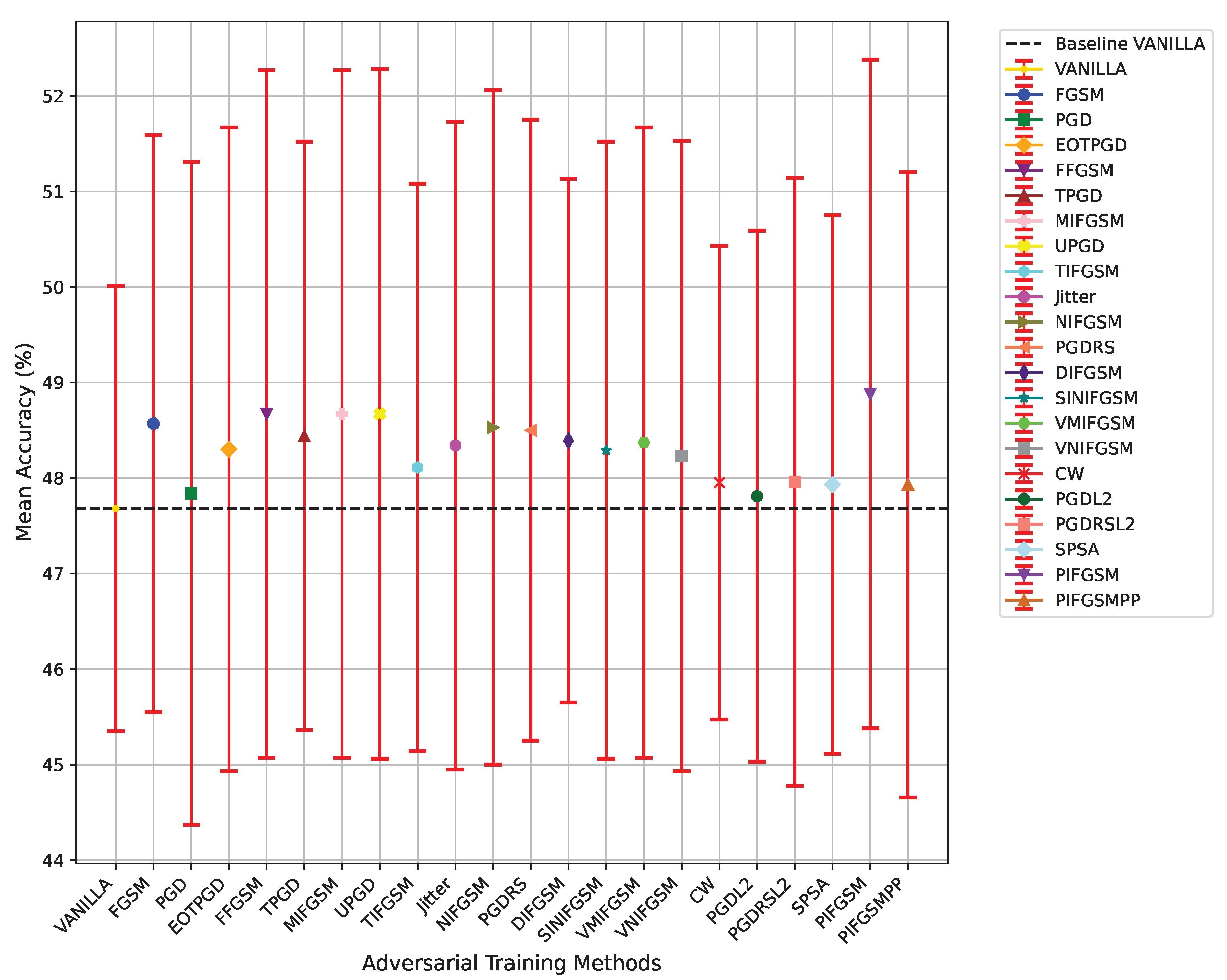
Figure 3 illustrates the average accuracy and standard deviation of the FL-APB algorithm under various adversarial training methods after 100 communication rounds, with specific values provided in Table 1. Adversarial training is a critical approach for enhancing the robustness of FL systems. however, different adversarial training methods can influence model accuracy and performance while protecting against attacks.
As a baseline model, VANILLA achieves an average accuracy of 47.68 % with a standard deviation of 2.33 % , demonstrating relatively stable performance. However, without the incorporation of adversarial training, the baseline model, while stable, exhibits weaker robustness and resistance to privacy attacks.
In comparison to the baseline model, the introduction of adversarial training samples controlled by the FL-APB strategy has resulted in improved average accuracy across most adversarial training methods. For instance, methods such as FGSM ( 48.57 % ) and MIFGSM ( 48.67 % ) demonstrate superior accuracy compared to the baseline, indicating that these adversarial training techniques can maintain or enhance model performance.
Among all adversarial training methods, PIFGSM achieves the highest average accuracy at 48.88 % , with a standard deviation of 3.50 % , reflecting notable robustness and performance advantages. This method enhances model accuracy by integrating multiple attack pathways while maintaining relatively low performance variability. Although most methods exhibit slight improvements in accuracy, others, such as FFGSM ( 48.67 % ) and UPGD ( 48.67 % ), demonstrate larger standard deviations ( 3.60 % and 3.61 % , respectively), indicating significant performance fluctuations across different communication rounds. For these methods with considerable variability, despite their higher average accuracy, their stability may be compromised, potentially leading to performance degradation in certain communication rounds.

5.3. Privacy Protection

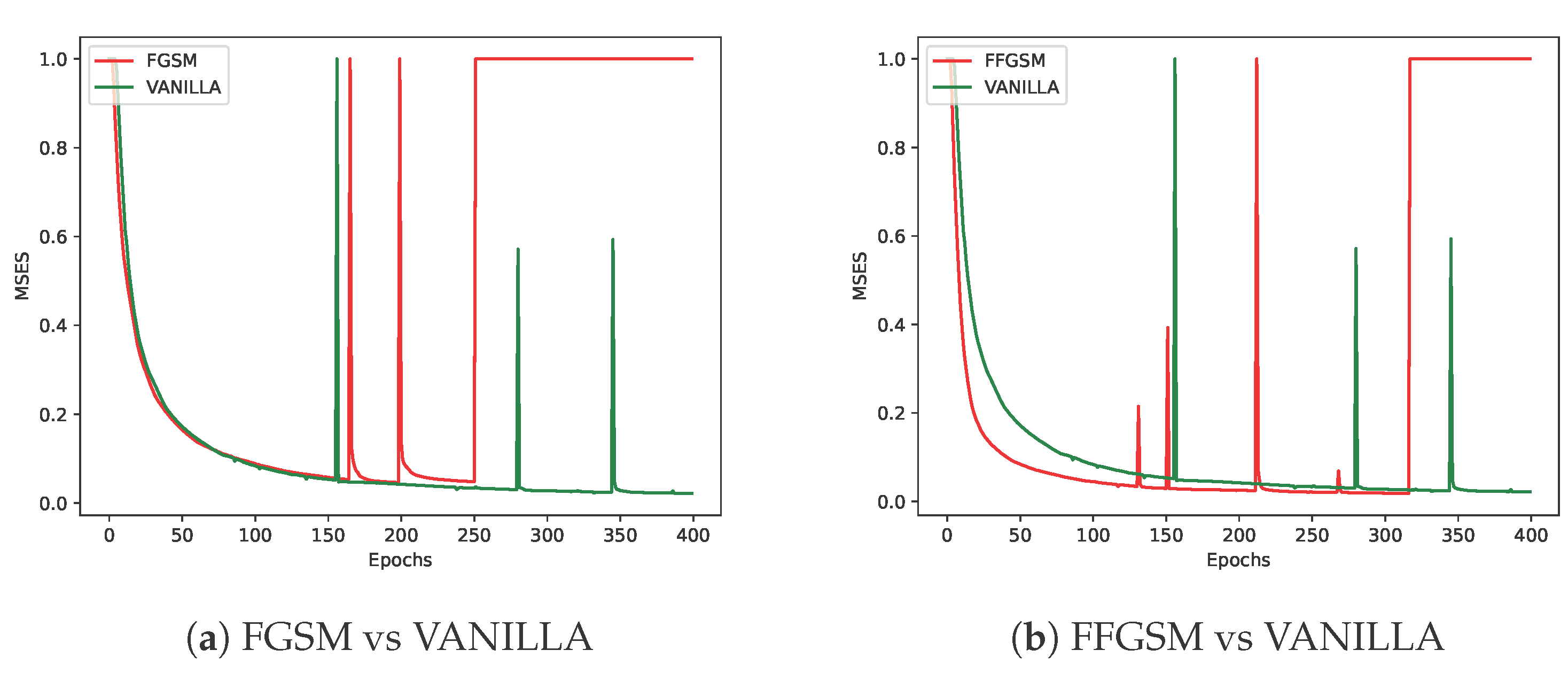
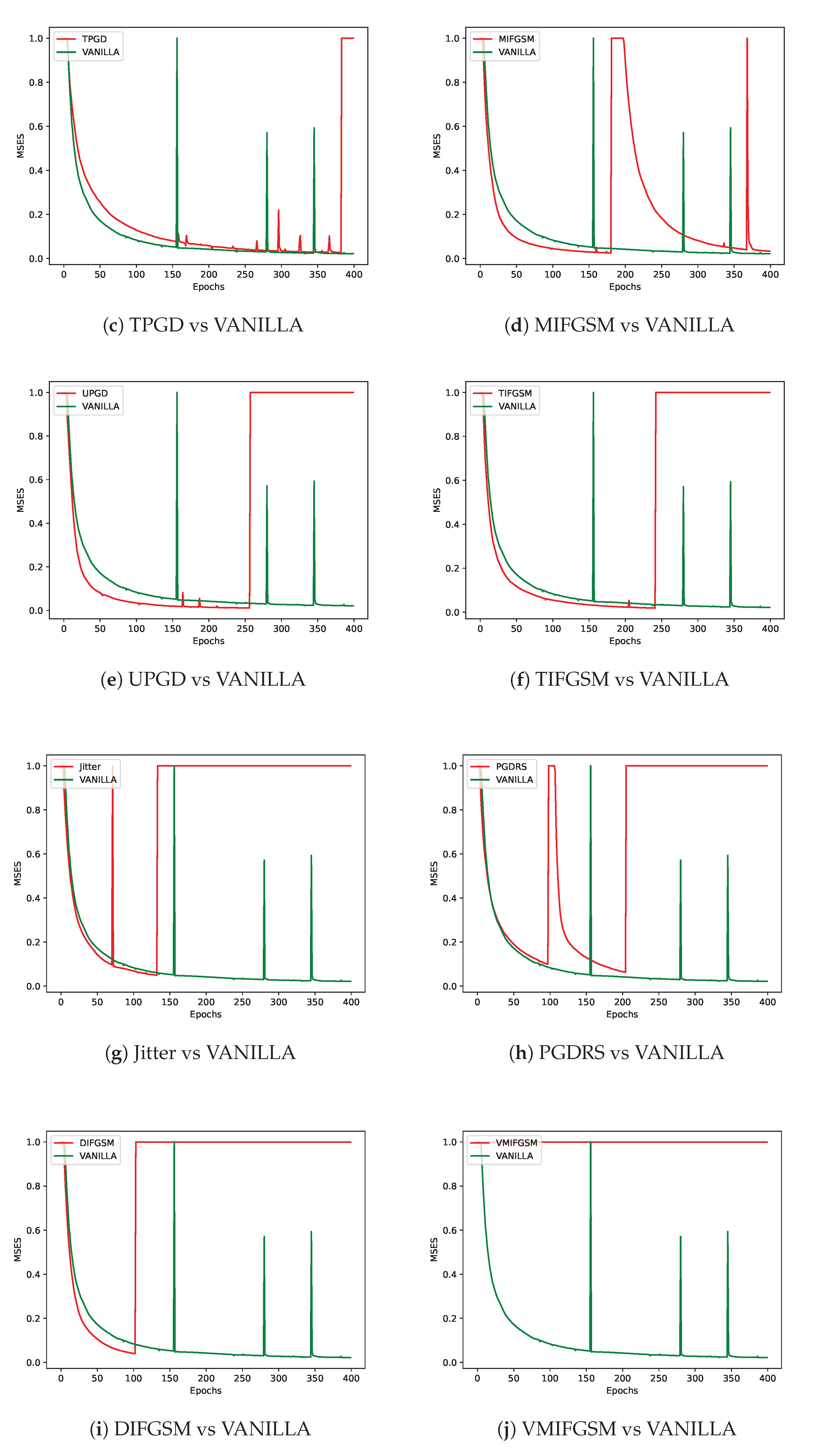
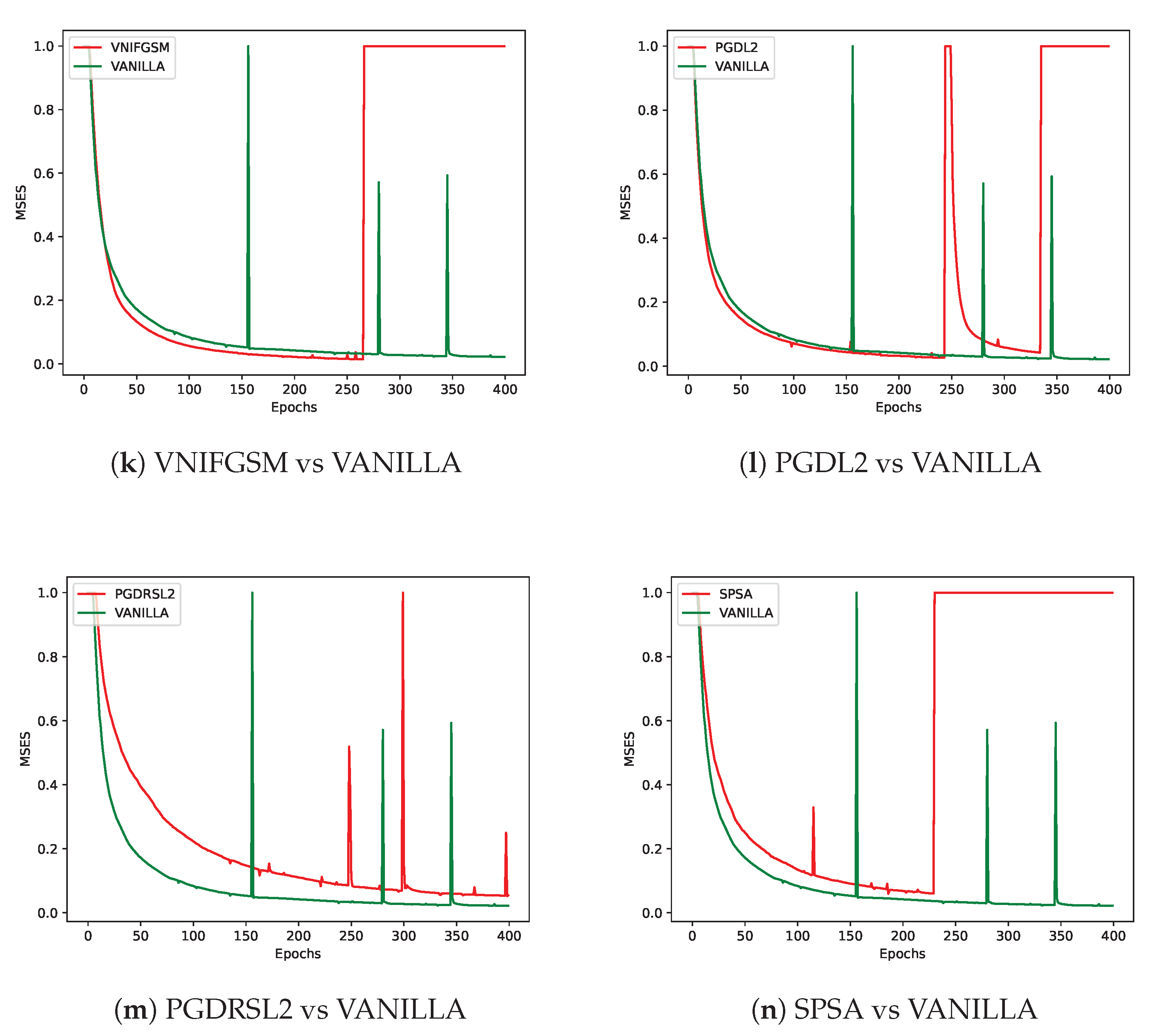
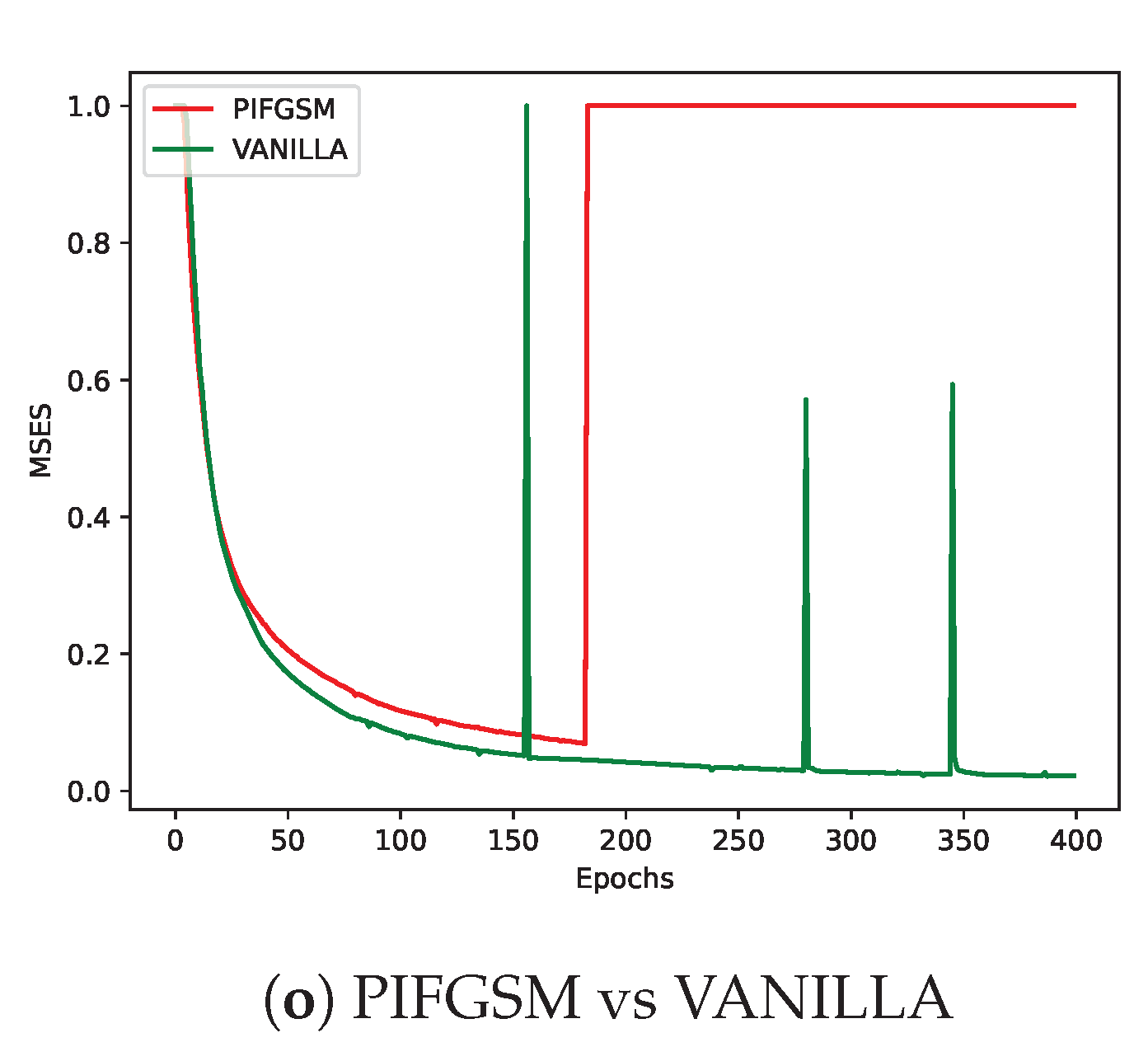
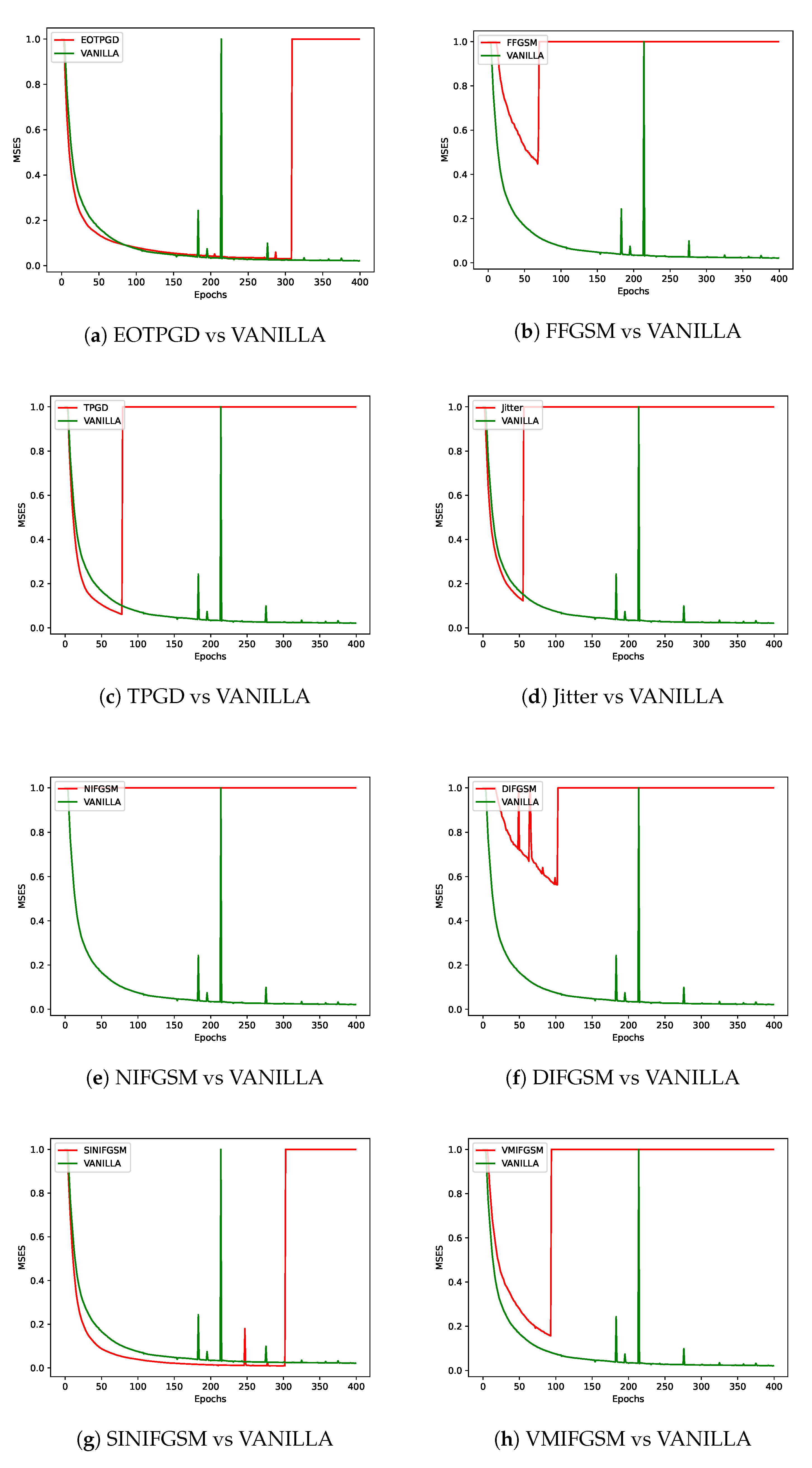
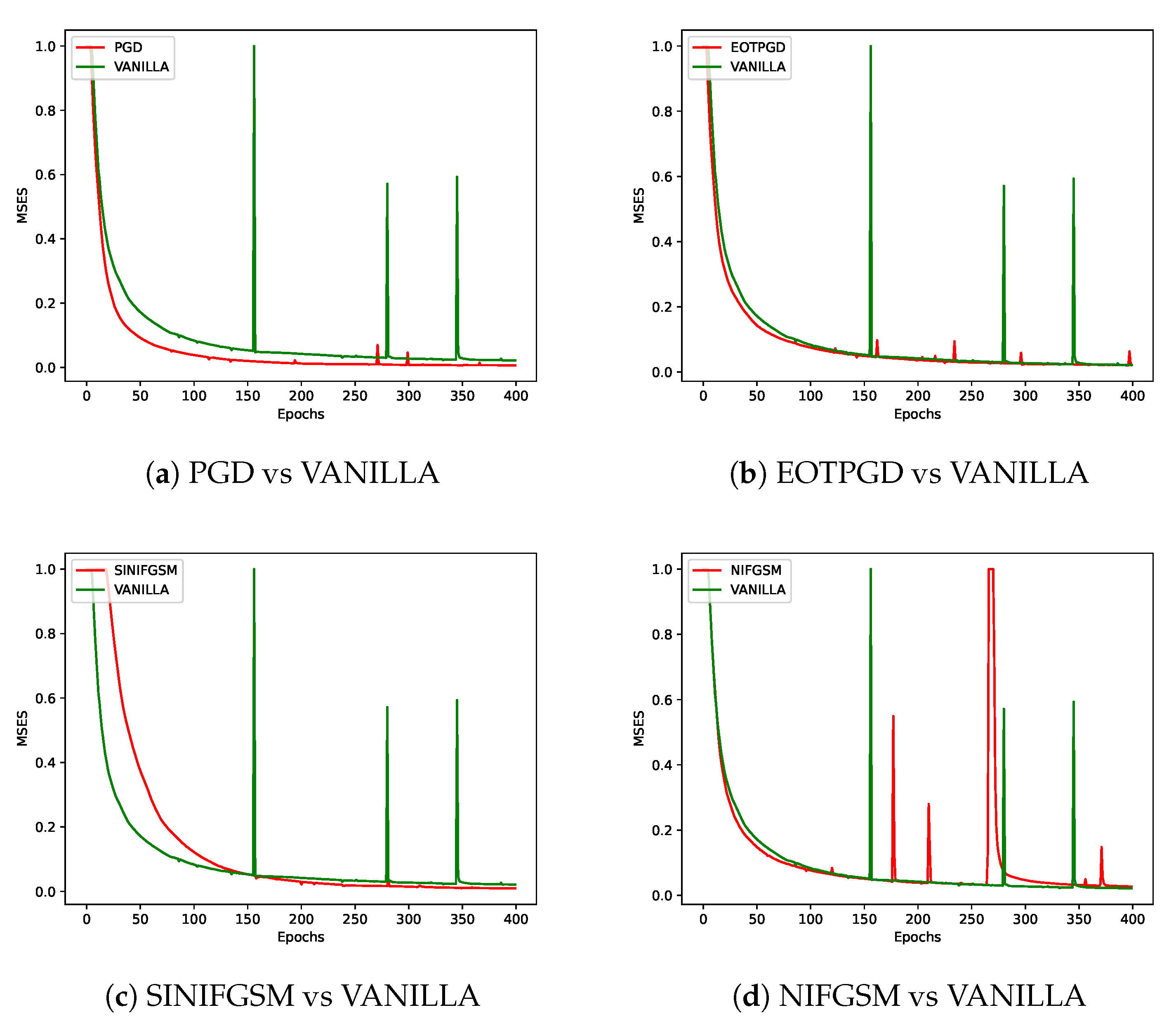
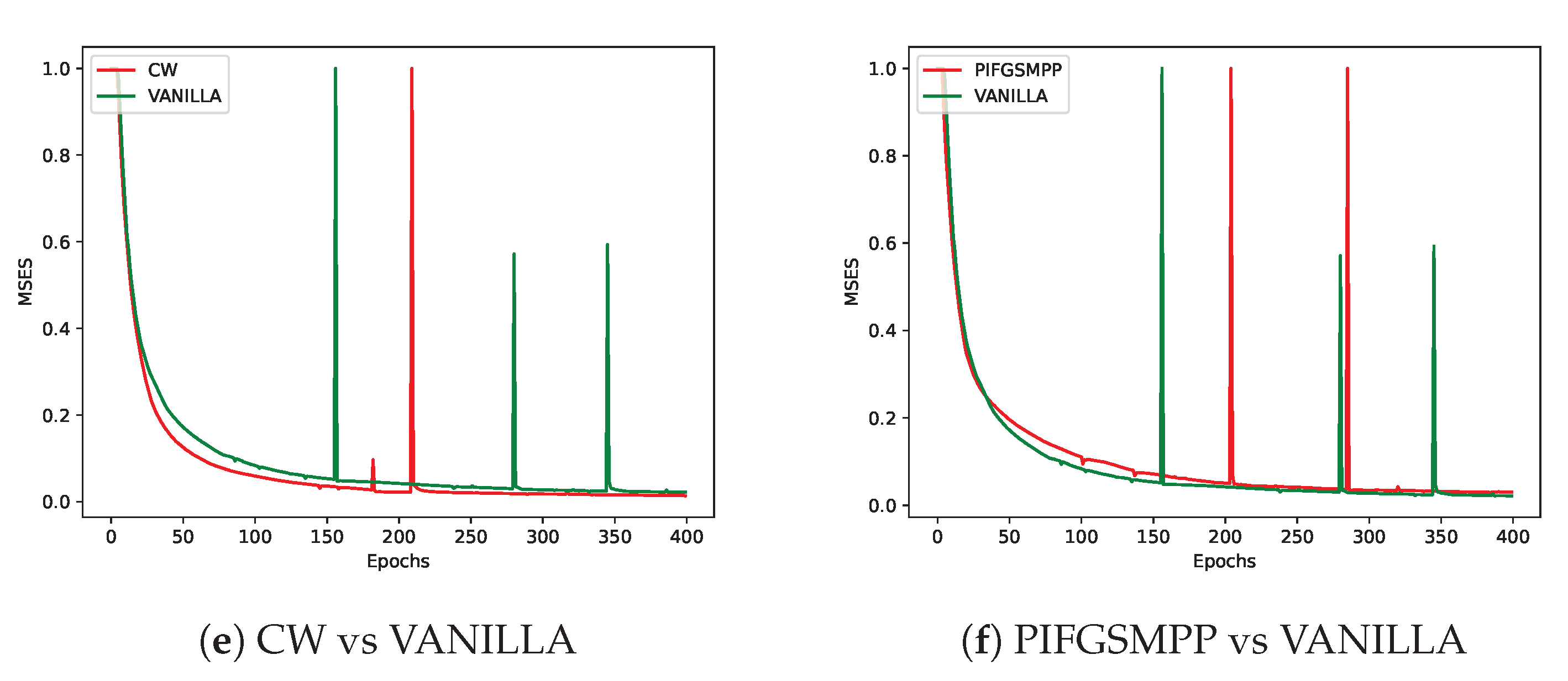
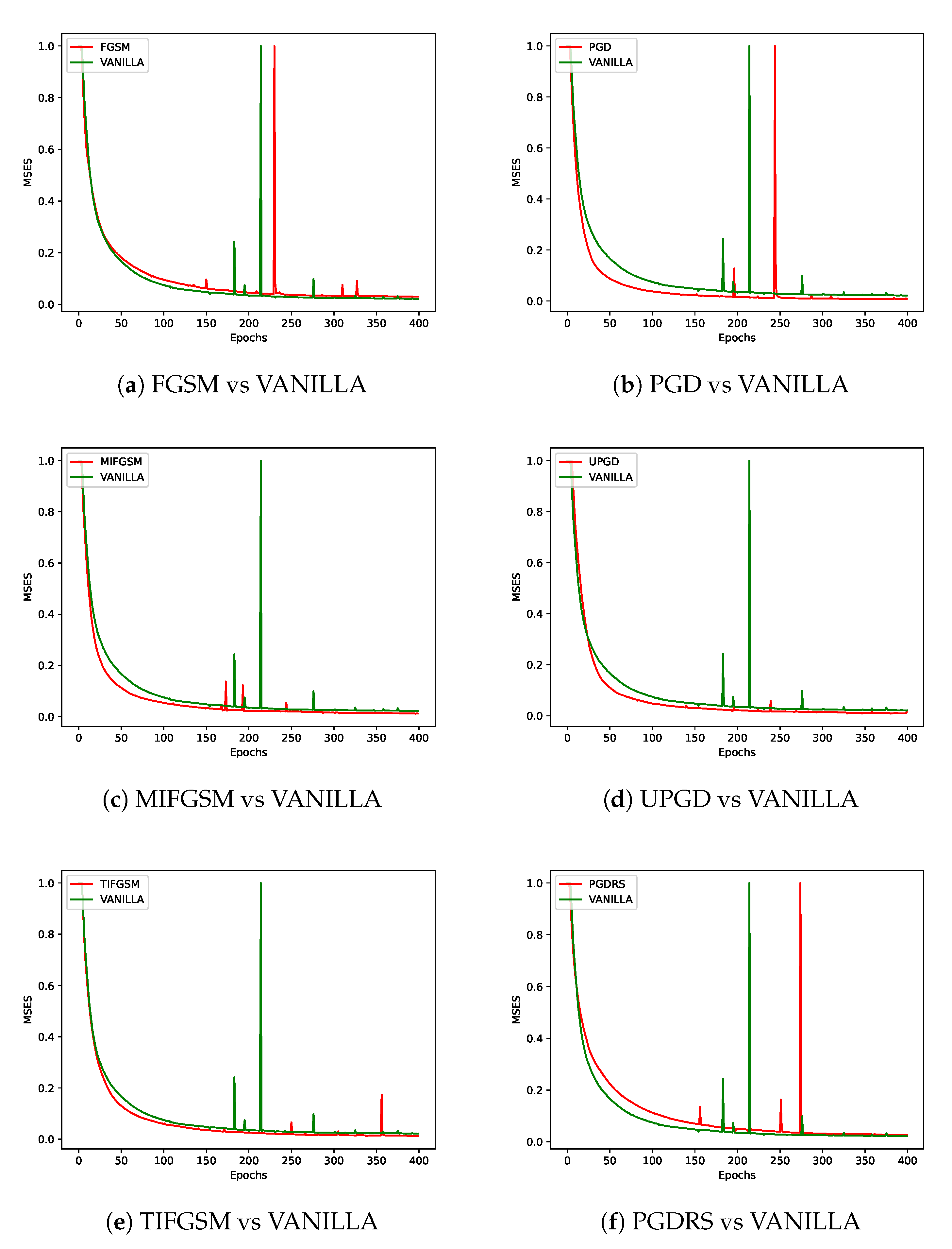
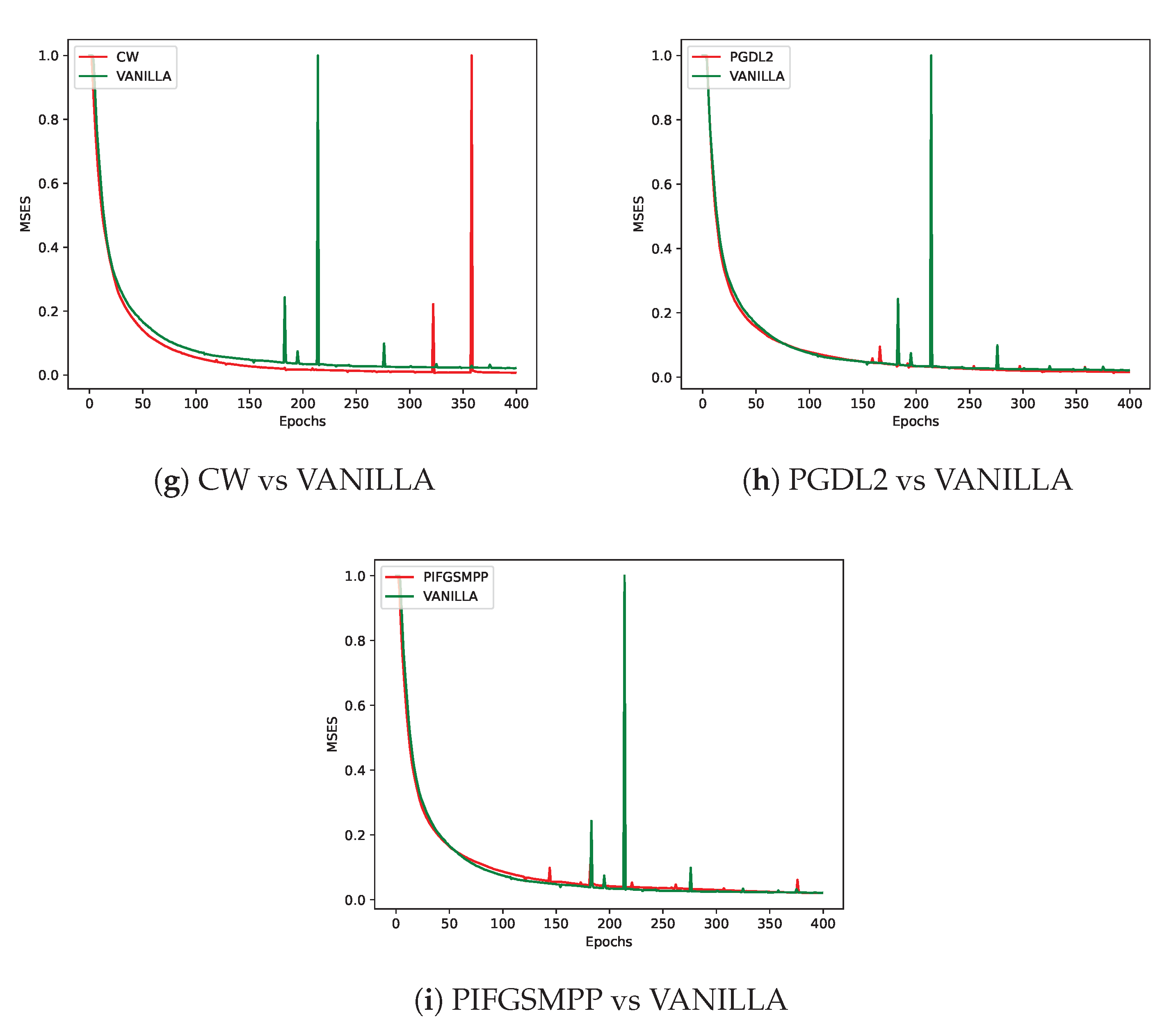
As shown in Figure 4, different adversarial perturbation methods produce visually distinct effects on the same data. FL-APB adjusts the privacy budget and sets varying amounts of data to participate in adversarial training to meet privacy protection requirements. According to Figure 5 and Figure 6, when private data undergoes adversarial perturbation and is subjected to privacy attacks by the DLG and iDLG algorithms, the MSE value typically remains higher than that of VANILLA data as the attack rounds increase. When the MSE exceeds 1, it indicates a failed attack (the lower the MSE, the smaller the difference between the reconstructed data and the original private data, and the better the attack effect). Similarly, as shown in Figure 7 and Figure 8, the performance of adversarial training methods in countering privacy attacks is slightly inferior or superior.

5.4. Discussion

One of the core challenges of the FL-APB algorithm is how to achieve the optimal balance between privacy protection and performance. Although increasing the privacy budget can enhance system security, it may lead to performance losses (e.g., decreased model accuracy, slower convergence, etc.). Therefore, the choice of adversarial training strategy not only affects the strength of privacy protection but also significantly impacts system efficiency and model performance.
For example, the attack methods PIFGSM and FFGSM are able to maintain a relatively low mean privacy budget (about 0.1498) while exhibiting good model prediction accuracy (48.88% and 48.67%, respectively), indicating that they strike a better balance between privacy protection and model performance. On the other hand, EOTPGD has a slightly higher mean privacy budget (0.1505), but its model performance is slightly lower than the two methods mentioned above (48.30%). This result suggests that EOTPGD may expose more privacy but offers a trade-off in maintaining model performance.
Similarly, PGDL2 has a low and stable privacy budget (mean of 0.1499, standard deviation of 0.0133), but its model performance is relatively weak (47.81%), making it suitable for scenarios where high privacy protection is required, but tolerance for model performance degradation is high.
From a defense perspective, Figures 5b and 6b demonstrate the strong defense capabilities of the FFGSM method against the DLG and iDLG algorithms, while Figures 5o and 6l show the excellent performance of PIFGSM in defending against such attacks. However, Figures 7b and 6a indicate that EOTPGD performs poorly in defending against DLG or iDLG attacks, and Figures 5l and 8h also show that PGDL2 has shortcomings in this regard.

6. Conclusion and Prospect

In this study, we investigate the balance between privacy and performance challenges faced by adversarial training in Federated Learning and propose the FL-APB algorithm to effectively regulate the privacy and performance budgets in training models. By comparing the FL-APB algorithm with various adversarial training methods in a Non-IID data environment, we validate the algorithm’s effectiveness in ensuring and enhancing model performance while assessing its capability for privacy protection against adversarial data.
Future research will further explore the adaptability of the FL-APB algorithm across different application scenarios, particularly in more complex Non-IID data environments. Moreover, with the continuous evolution of privacy attack methods and adversarial training techniques, evaluating the privacy protection efficacy against various adversarial attacks and their long-term impact on model performance will be a significant focus of our research. Finally, reducing the computational resource consumption of the algorithm is another essential area that requires attention.

Data Availability Statement

Data are contained within the article.

References

  1. McMahan, H.B.; Moore, E.; Ramage, D.; y Arcas, B.A. Federated learning of deep networks using model averaging. arXiv 2016, arXiv:1602.05629. [Google Scholar]
  2. Konečnỳ, J. Federated Learning: Strategies for Improving Communication Efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
  3. Pinto Neto, E.C.; Sadeghi, S.; Zhang, X.; Dadkhah, S. Federated reinforcement learning in IoT: applications, opportunities and open challenges. Appl. Sci. 2023, 13, 6497. [Google Scholar] [CrossRef]
  4. Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar] [CrossRef] [PubMed]
  5. Rodríguez-Barroso, N.; Jiménez-López, D.; Luzón, M.V.; Herrera, F.; Martínez-Cámara, E. Survey on federated learning threats: Concepts, taxonomy on attacks and defences, experimental study and challenges. Inf. Fusion 2023, 90, 148–173. [Google Scholar] [CrossRef]
  6. Beltrán, E.T.M.; Pérez, M.Q.; Sánchez, P.M.S.; Bernal, S.L.; Bovet, G.; Pérez, M.G.; Pérez, G.M.; Celdrán, A.H. Decentralized federated learning: Fundamentals, state of the art, frameworks, trends, and challenges. IEEE Commun. Surv. Tutor. 2023. [Google Scholar]
  7. Voigt, P.; Von dem Bussche, A. The eu general data protection regulation (gdpr). A Practical Guide, 1st Ed., Cham: Springer International Publishing 2017, 10, 10–5555. [Google Scholar]
  8. Zhang, X.; Kang, Y.; Chen, K.; Fan, L.; Yang, Q. Trading off privacy, utility, and efficiency in federated learning. ACM Trans. Intell. Syst. Technol. 2023, 14, 1–32. [Google Scholar] [CrossRef]
  9. Fang, L.; Susilo, W.; Ge, C.; Wang, J. Public key encryption with keyword search secure against keyword guessing attacks without random oracle. Inf. Sci. 2013, 238, 221–241. [Google Scholar] [CrossRef]
  10. Shaham, S.; Ding, M.; Liu, B.; Dang, S.; Lin, Z.; Li, J. Privacy preserving location data publishing: A machine learning approach. IEEE Trans. Knowl. Data Eng. 2020, 33, 3270–3283. [Google Scholar] [CrossRef]
  11. Ge, C.; Susilo, W.; Liu, Z.; Xia, J.; Szalachowski, P.; Fang, L. Secure keyword search and data sharing mechanism for cloud computing. IEEE Trans. Dependable Secur. Comput. 2020, 18, 2787–2800. [Google Scholar] [CrossRef]
  12. Zhu, L.; Liu, Z.; Han, S. Deep leakage from gradients. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
  13. Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.; Poor, H.V. Federated learning with differential privacy: Algorithms and performance analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef]
  14. Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-iid data. arXiv preprint arXiv:1806.00582, 2018. [Google Scholar]
  15. Sattler, F.; Wiedemann, S.; Müller, K.R.; Samek, W. Robust and communication-efficient federated learning from non-iid data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3400–3413. [Google Scholar] [CrossRef]
  16. Pittaluga, F.; Koppal, S.; Chakrabarti, A. Learning privacy preserving encodings through adversarial training. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV). IEEE; 2019; pp. 791–799. [Google Scholar]
  17. Zizzo, G.; Rawat, A.; Sinn, M.; Buesser, B. Fat: Federated adversarial training. arXiv 2020, arXiv:2012.01791. [Google Scholar]
  18. Dang, L.; Hapuarachchi, T.; Xiong, K.; Lin, J. Improving Machine Learning Robustness via Adversarial Training. In Proceedings of the 2023 32nd International Conference on Computer Communications and Networks (ICCCN). IEEE; 2023; pp. 1–10. [Google Scholar]
  19. Wu, Z.; Wang, Z.; Wang, Z.; Jin, H. Towards privacy-preserving visual recognition via adversarial training: A pilot study. In Proceedings of the Proceedings of the European conference on computer vision (ECCV), 2018, pp. 606–624.
  20. Zhang, J.; Li, B.; Chen, C.; Lyu, L.; Wu, S.; Ding, S.; Wu, C. Delving into the adversarial robustness of federated learning. In Proceedings of the Proceedings of the AAAI conference on artificial intelligence, 2023,; Volume 37, pp. 3711245–11253.
  21. Hong, J.; Wang, H.; Wang, Z.; Zhou, J. Federated robustness propagation: Sharing adversarial robustness in federated learning. arXiv 2021, arXiv:2106.10196. [Google Scholar] [CrossRef]
  22. Shah, D.; Dube, P.; Chakraborty, S.; Verma, A. Adversarial training in communication constrained federated learning. arXiv 2021, arXiv:2103.01319. [Google Scholar]
  23. Chen, C.; Zhang, J.; Lyu, L. Gear: a margin-based federated adversarial training approach. In Proceedings of the International Workshop on Trustable, Verifiable, and Auditable Federated Learning in Conjunction with AAAI, Vol. 2022. 2022. [Google Scholar]
  24. Chen, C.; Liu, Y.; Ma, X.; Lyu, L. Calfat: Calibrated federated adversarial training with label skewness. Adv. Neural Inf. Process. Syst. 2022, 35, 3569–3581. [Google Scholar]
  25. Ressi, D.; Romanello, R.; Piazza, C.; Rossi, S. AI-enhanced blockchain technology: A review of advancements and opportunities. J. Netw. Comput. Appl. 2024, 103858. [Google Scholar] [CrossRef]
  26. Park, J.; Lim, H. Privacy-preserving federated learning using homomorphic encryption. Applied Sciences 2022, 12, 734. [Google Scholar] [CrossRef]
  27. Kanagavelu, R.; Li, Z.; Samsudin, J.; Yang, Y.; Yang, F.; Goh, R.S.M.; Cheah, M.; Wiwatphonthana, P.; Akkarajitsakul, K.; Wang, S. Two-phase multi-party computation enabled privacy-preserving federated learning. In Proceedings of the 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID). IEEE; 2020; pp. 410–419. [Google Scholar]
  28. Wei, K.; Li, J.; Ding, M.; Ma, C.; Su, H.; Zhang, B.; Poor, H.V. User-level privacy-preserving federated learning: Analysis and performance optimization. IEEE Trans. Mob. Comput. 2021, 21, 3388–3401. [Google Scholar] [CrossRef]
  29. Wei, K.; Li, J.; Ma, C.; Ding, M.; Chen, W.; Wu, J.; Tao, M.; Poor, H.V. Personalized federated learning with differential privacy and convergence guarantee. IEEE Trans. Inf. Forensics Secur. 2023. [Google Scholar] [CrossRef]
  30. Yang, X.; Huang, W.; Ye, M. Dynamic personalized federated learning with adaptive differential privacy. Adv. Neural Inf. Process. Syst. 2023, 36, 72181–72192. [Google Scholar]
  31. He, Z.; Wang, L.; Cai, Z. Clustered federated learning with adaptive local differential privacy on heterogeneous iot data. IEEE Internet Things J. 2023. [Google Scholar] [CrossRef]
  32. Shen, X.; Jiang, H.; Chen, Y.; Wang, B.; Gao, L. Pldp-fl: Federated learning with personalized local differential privacy. Entropy 2023, 25, 485. [Google Scholar] [CrossRef] [PubMed]
  33. Li, J.; Zhu, T.; Ren, W.; Raymond, K.K. Improve individual fairness in federated learning via adversarial training. Comput. Secur. 2023, 132, 103336. [Google Scholar] [CrossRef]
  34. Li, X.; Song, Z.; Yang, J. Federated adversarial learning: A framework with convergence analysis. In Proceedings of the International Conference on Machine Learning. PMLR; 2023; pp. 19932–19959. [Google Scholar]
  35. Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
  36. Madry, A. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083 2017. [Google Scholar]
  37. Liu, X.; Li, Y.; Wu, C.; Hsieh, C.J. Adv-bnn: Improved adversarial defense through robust bayesian neural network. arXiv 2018, arXiv:1810.01279. [Google Scholar]
  38. Wong, E.; Rice, L.; Kolter, J.Z. Fast is better than free: Revisiting adversarial training. arXiv 2020, arXiv:2001.03994. [Google Scholar]
  39. Zhang, H.; Yu, Y.; Jiao, J.; Xing, E.; El Ghaoui, L.; Jordan, M. Theoretically principled trade-off between robustness and accuracy. In Proceedings of the International conference on machine learning. PMLR; 2019; pp. 7472–7482. [Google Scholar]
  40. Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018,; pp. 9185–9193.
  41. Dong, Y.; Pang, T.; Su, H.; Zhu, J. Evading defenses to transferable adversarial examples by translation-invariant attacks. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019,; pp. 4312–4321.
  42. Schwinn, L.; Raab, R.; Nguyen, A.; Zanca, D.; Eskofier, B. Exploring misclassifications of robust neural networks to enhance adversarial attacks. Appl. Intell. 2023, 53, 19843–19859. [Google Scholar] [CrossRef]
  43. Lin, J.; Song, C.; He, K.; Wang, L.; Hopcroft, J.E. Nesterov accelerated gradient and scale invariance for adversarial attacks. arXiv 2019, arXiv:1908.06281. [Google Scholar]
  44. Salman, H.; Li, J.; Razenshteyn, I.; Zhang, P.; Zhang, H.; Bubeck, S.; Yang, G. Provably robust deep learning via adversarially trained smoothed classifiers. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
  45. Xie, C.; Zhang, Z.; Zhou, Y.; Bai, S.; Wang, J.; Ren, Z.; Yuille, A.L. Improving transferability of adversarial examples with input diversity. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019; pp. 2730–2739.
  46. Wang, X.; He, K. Enhancing the transferability of adversarial attacks through variance tuning. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021; pp. 1924–1933.
  47. Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 ieee symposium on security and privacy (sp). Ieee; 2017; pp. 39–57. [Google Scholar]
  48. Uesato, J.; O’donoghue, B.; Kohli, P.; Oord, A. Adversarial risk and the dangers of evaluating against weak attacks. In Proceedings of the International conference on machine learning. PMLR; 2018; pp. 5025–5034. [Google Scholar]
  49. Gao, L.; Zhang, Q.; Song, J.; Liu, X.; Shen, H.T. Patch-wise attack for fooling deep neural network. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 2020, Proceedings, Part XXVIII 16. Springer, 2020, August 23–28; pp. 307–322.
  50. Gao, L.; Zhang, Q.; Song, J.; Shen, H.T. Patch-wise++ perturbation for adversarial targeted attacks. arXiv 2020, arXiv:2012.15503. [Google Scholar]
Preprints 121610 g001
Figure 1. FL-APB System Model.
Figure 1. FL-APB System Model.
Preprints 121610 g001
Preprints 121610 g002
Figure 2. Privacy budget of FL-APB algorithm under different adversarial training methods after 100 communication rounds.
Figure 2. Privacy budget of FL-APB algorithm under different adversarial training methods after 100 communication rounds.
Preprints 121610 g002
Preprints 121610 g003
Figure 3. Performance of FL-APB algorithm under different adversarial training methods after 100 communication rounds.
Figure 3. Performance of FL-APB algorithm under different adversarial training methods after 100 communication rounds.
Preprints 121610 g003
Preprints 121610 g004
Figure 4. Perturbations on the same data using different adversarial training methods.
Figure 4. Perturbations on the same data using different adversarial training methods.
Preprints 121610 g004
Preprints 121610 g005aPreprints 121610 g005bPreprints 121610 g005cPreprints 121610 g005d
Figure 5. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing DLG privacy attacks is superior compared to the VANILLA algorithm.
Figure 5. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing DLG privacy attacks is superior compared to the VANILLA algorithm.
Preprints 121610 g005aPreprints 121610 g005bPreprints 121610 g005cPreprints 121610 g005d
Preprints 121610 g006aPreprints 121610 g006b
Figure 6. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing iDLG privacy attacks is superior compared to the VANILLA algorithm.
Figure 6. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing iDLG privacy attacks is superior compared to the VANILLA algorithm.
Preprints 121610 g006aPreprints 121610 g006b
Preprints 121610 g007aPreprints 121610 g007b
Figure 7. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing DLG privacy attacks is somewhat inferior or slightly superior compared to the VANILLA algorithm.
Figure 7. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing DLG privacy attacks is somewhat inferior or slightly superior compared to the VANILLA algorithm.
Preprints 121610 g007aPreprints 121610 g007b
Preprints 121610 g008aPreprints 121610 g008b
Figure 8. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing iDLG privacy attacks is somewhat inferior or slightly superior compared to the VANILLA algorithm.
Figure 8. Under the FL-APB algorithm, the performance of different adversarial training methods in addressing iDLG privacy attacks is somewhat inferior or slightly superior compared to the VANILLA algorithm.
Preprints 121610 g008aPreprints 121610 g008b
Table 1. Comparison of privacy budget and prediction accuracy under different adversarial training methods
Table 1. Comparison of privacy budget and prediction accuracy under different adversarial training methods
Adversarial Training Method Mean Privacy Budget Std Dev of Privacy Budget Mean Prediction Accuracy Std Dev of Prediction Accuracy
VANILLA 0 0 47.68 2.33
FGSM 0.149864 0.014829 48.57 3.02
PGD 0.149572 0.013512 47.84 3.47
EOTPGD 0.150512 0.013789 48.30 3.37
FFGSM 0.149884 0.014836 48.67 3.60
TPGD 0.149184 0.014005 48.44 3.08
MIFGSM 0.149884 0.014836 48.67 3.60
UPGD 0.149884 0.014836 48.67 3.61
TIFGSM 0.149720 0.015097 48.11 2.97
Jitter 0.149320 0.014373 48.34 3.39
NIFGSM 0.149828 0.014835 48.53 3.53
PGDRS 0.149628 0.014538 48.50 3.25
DIFGSM 0.149772 0.014843 48.39 2.74
SINIFGSM 0.149900 0.014828 48.29 3.23
VMIFGSM 0.150588 0.014247 48.37 3.30
VNIFGSM 0.150592 0.014248 48.23 3.30
CW 0.149804 0.014873 47.95 2.48
PGDL2 0.149932 0.013331 47.81 2.78
PGDRSL2 0.149236 0.013958 47.96 3.18
SPSA 0.150136 0.013484 47.93 2.82
PIFGSM 0.149892 0.014858 48.88 3.50
PIFGSMPP 0.149896 0.014856 47.93 3.27
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated