Prerpints.org logo
Preprint
Article

Multi-Criteria Calibration of a Thermo-Mechanical Model of Steel Plate Welding in Vacuum

Altmetrics

Downloads

41

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 September 2024

Posted:

30 September 2024

You are already at the latest version

Alerts
Abstract
This paper proposes a methodology for multi-criteria calibration of a thermo-mechanical model for numerical simulation of welding in vacuum. A finite element model of a steel plate is created. Experimental and computational data are obtained. An inverse problem is formulated for the vector identification of five calibration parameters from the heat flow model. They are evaluated for adequacy with controlled accuracy according to four criteria. An optimization problem is solved using a two-step interactive procedure. The parameter space studying method (PSI) has been applied to the study of multidimensional regions by means of quasi-uniform sounding. A Pareto-optimal set is defined. It is used to determine reduced ranked Pareto subsets by -selection. Salukvadze optimum is also determined.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

There are several welding methods applicable in the space vacuum, laser welding [1] and electric arc welding [2], [3] being the most widely used. An advantage of applying the first method is the possibility for obtaining welds with a deeper penetration, and the second is suitable when lower values of welding current and voltage are needed.
Performing vacuum welding experiments can be done using specialized vacuum chambers [4].
Numerical modeling of welding processes allows for the selection of suitable welding parameters without accomplishing a large number of field experiments. In 1973 Hibbitt presented a model of a welded structure [5]. The task solution consists of two stages. During the first one, the problem concerning heat exchange is solved, taking into account the convection according to Newton’s law, as well as the radiation, according to the Stefan-Boltzmann law. The physical characteristics are assumed to be linear. As a result of this stage, the temperature distribution in the body is obtained. In the second stage, the problem of the stress-strain state is solved, and the loading is the temperature field from the previous stage. The body is freely supported. It assumes that the material is considered to be perfectly elasto-plastic.
In 1975, Friedman presented a two-dimensional model of a butt weld joint, in which the non-linear physical and mechanical properties of the material are taken into account [6]. When solving the heat problem, the heat flow is set as normally distributed function. This issue is studied in more detail by Goldak [7], who experiments with different heat flux (HF) functions: Gaussian distribution, spherical, elliptic, and doubly elliptic.
The most used theoretical heat source model in the thermo-mechanical simulation of various arc welding processes is the model with Gaussian heat intensity distribution and double-ellipsoid shape [8-14]. For this model and its good number of modifications, a significant difficulty represents the determination of the initially unknown thermo-mechanical model parameters, which are usually determined by the so-called “trial and error” method, performing numerical experiments. The aim is to achieve maximum similarity to the experimentally found data related to the width and depth of welding [15]. Methods for calibrating some of these parameters have been proposed as solutions to single-criteria problems of nonlinear optimization, for example in [15-20].
Hartwig et al. [21] propose a physically motivated heat source model using computational fluid dynamics. They take the geometry of the melting pool as an input for a finite element model.
In traditional identification problems, which are characterized as “direct”, the experimentally determined data for the studied object are used to specify the parameters of its mathematical model [22]. In this case, parametric identification means indirect determination of some parameters of the steel plate welding process in a vacuum environment by comparing and evaluating the disagreement between some experimental and model characteristics. The calculated data required for this purpose are obtained by applying a mathematical model that simulates the main thermo-mechanical processes of welding of a test sample. This model contains some heat flow parameters, the theoretical values of which are unavailable for direct measurement when performing a natural experiment. In order to build an adequate mathematical model, it is necessary to indirectly identify these parameters based on available experimental data. According to [23], this procedure is known as “calibration” of the used simulation model applied.
Strychek et al. [24] consider a reverse identification problem for mechanical systems, in which there is no information about some parameters of the investigated sample that are inaccessible for assessment. Using a specific example of a mechanical system, these parameters indicate that in order to increase the model adequacy and the identification effectiveness, it is necessary to use a multi-criteria approach.
In [25], the adequacy of the mathematical welding model is evaluated by statistical processing of the differences between the experimental and simulated data for the widths of the seam on both sides of the plate, as well as the width and height of the “hourglass” neck, using Student’s stochastic criterion.
Walker et al. [19] reduced the initial two-criteria optimization task to a single-criteria one with weighting coefficients, which facilitates the automation of the calibration process, but complicates the optimization task and, in principle, does not solve the problem of compromise uncertainty when selecting a unique solution.
The research presented in [26] demonstrates that the ratio between the front and rear length of the double ellipsoid has a significant effect on the weld dimensions, thermal distortion and residual stresses in the final state of the welded specimen. This ratio is considered a function of the welding speed and referred to an algebraic polynomial of the third degree with three coefficients subjected to calibration. A generalized criterion of closeness between simulated and experimental data has been selected for the differences in width and depth for the weld pool measured at a number of points along the seam. The resulting optimization problem is solved by establishing a global optimization procedure based on applying a genetic algorithm.
In [27], one possible approach for calibrating a double-ellipsoidal heat source model used in the ESI Group’s Sysweld software system is discussed. To compensate for the inevitable limitations of the mathematical description, the three coefficients in the exponential multipliers of the classical model given in [7] have been modified so that they are interpreted as being composed of three constant components determined by measurements of a test specimen, and of three variable ingredients that allow variation in the intensity of the heat flow and, thus, the shape of the pool of liquid metal. These variable ingredients are subject to calibration. For a specific example, the author indicates values of the calibration parameters, which are qualified as optimized, without providing a description of the optimization task or a procedure for solving it. The criteria applied for determining the adequacy between the measured and simulated data are not mentioned, either.
The problem of multi-criteria, as opposed to single-criteria, parametric identification of complex systems is discussed, for example, in [22, 28]. A correct formulation of the multi-criteria parametric identification task is proposed, in which the permissible set of variable parameters is formed in the process of solving the task itself, because it is also limited by criterion constraints. For such tasks, the use of the universal method PSI (Parameter Space Investigation) for studying the space of variable parameters with quasi-uniformly distributed Sobol’s points [29] and the software package MOVI for multicriteria optimization and vector identification [30] is justified.
The numerical simulations required to solve an optimization or inverse identification problem of welding processes remain complex and time-consuming due to their inherent nonlinear, multi-physics and multi-parameter aspects. In order to improve the efficiency of reverse welding identification procedures, a number of publications suggest using a new approach to organize, store and use the required experimental and simulated data [31]. It is related to the availability of an informative computer reference “vademecum” or “virtual metamodel” with quantitative data on the welding properties (residual stresses, deformations, etc.), depending on the input parameters – geometric and material characteristics, boundary conditions, applied loading, etc. This approach enables selecting and real-time obtaining of quasi-optimal spatio-temporal parametric solutions with controlled accuracy of nonlinear thermomechanical problems for a different set of input parameters [32].
The presented research is focused on the usual problem situation of obtaining preliminary reliable information for the realization of non-serial welding in the absence of additive material and convective heat exchange, for which there is insufficient experimental information and modest computational capabilities for computer simulations. The aim is, under these conditions, to propose an efficient computational technology for solving an inverse problem for multi-criteria calibration of a fundamental thermomechanical model of welding of the type proposed in [27], which ensures a better adequacy of the simulated information obtained. To achieve the aim, a procedure for calibrating a finite element model based on experimental data was created. The calibration procedure uses the PSI method combined with a post-optimization analysis by μ-selection.

2. Materials and Methods

2.1. Experiments

The experiments are performed using a vacuum installation with an electric arc discharge and a hollow cathode described in [4]. A diagram of the installation is shown in Figure 1. It consists of a vacuum chamber, a pump unit, devices for micro-flowing and measuring the amount of a plasma-forming gas and welding current sources. A welding torch with a multi-stage arc excitation and a device with progressive movement of the welded part is installed in the chamber. The pump unit providing the necessary underpressure in the chamber consists of three vacuum pumps: a rotary pump with an oil seal, a rotary two-rotor pump and a diffusion pump.
The pressure in the chamber is measured by using a magnetic electric discharge vacuum meter and a resistance vacuum meter. The vacuum depth at which the experiments are conducted is approximately 3 Pa.
The plasma-forming gas is 99.999% pure argon, and its controlled by using a micro-adjuster, and the reading of the corresponding amount is realized by a sensor and a digital device.
Welding current sources are direct current with steep external characteristics. The main current source enables the use of a maximum welding current of up to 300 A.
The hollow cathode is made of tantalum foil. The welding is done without using of filler material.
The welded plate, in accordance with [33], is made of steel S235JR. The size of the plate is 100×60×9 mm. The welding seams is done in longitudinal direction of the plate and the employed configuration is 1G.
The determined geometric characteristics of the welded seam are the width and depth of the weld pool (WP), and the width and depth of the heat affected zone (HAZ). Their determination is made by micro-grinding of the cross section of the samples – Figure 2. Statistically processed mean values are given in Table 1.

2.2. Thermo-Mechanical Model

The numerical modeling of the welding process is related to the formation of a weld seam on a steel plate under vacuum conditions. The physical laws that are related to this process are from the field of the mechanics of the rigid deformable body, heat exchange, fluid mechanics and electromagnetism. In the present work, it is assumed that the equations from the mechanics of the deformable solid body and heat exchange, which are the subject of study in thermo-plasticity, are the most significant ones that are to be taken into account. This understanding is also into the basis of the existing relevant standards [23]. The mathematical model of the selected physical description represents a system of differential equations, including functions of time and spatial coordinates, as well as of preliminary known initial and boundary conditions.
The welding process is accompanied by non-stationary heat exchange, which is described by the condition of temperature equilibrium and Fourier’s law
d i v λ ∙ g r a d T + Q = V ρ U ˙ ,
where: λ is the tensor with the heat-conducting material characteristics, which are a function of the temperature T; Q is the amount of heat in the considered volume; U is the specific enthalpy.
The considered welding process takes place in a vacuum, where convection is absent. Radiant heat transfer is described by the Stefan-Boltzmann law [35].
The electric arc is considered as a moving HF
q = q x , t ,
where the vector x determines the location of the center of the HF at time t.
The HF from the electric arc is considered as volumetrically distributed by a double ellipsoid, as proposed by authors in [7] – Figure 3. In a modified form discussed in [27], for the part in front of the flow center it is modeled by applying the following equation
q x , y ,   ξ = 6 3 f f Q e a b c f π 3 / 2 e − k x 2 / a 2 e − l y 2 / b 2 e − m z 2 / c f 2
, and for the part after the center the following equation is used
q x , y ,   ξ = 6 3 f r Q e a b c r π 3 / 2 e − k x 2 / a 2 e − l y 2 / b 2 e − m z 2 / c r 2 .
Here, Q e denotes the effective heat transmitted by the arc; a , b , c f and c r are the geometric parameters of the double ellipsoid; ξ is the local longitudinal coordinate along the seam direction, f f and f r are HF density coefficients, such that f f + f r = 2; k, l and m are calibration parameters.
The initial body temperature is determined as follows:
T x , t = 0 = 20 ° C .
The temperature strain is described by the applying the following equation:
ε i j T = α T − T 0 δ i j ,
where α is the coefficient of thermal expansion; T and T 0 are the current and initial temperatures, respectively, and δ i j is Kronecker’s delta function.
As can be seen, temperature strain is involved in the total strain equation:
ε ˙ i j = ε ˙ i j E + ε ˙ i j P + ε ˙ i j T ,
where ε ˙ i j E and ε ˙ i j P are the derivatives of the elastic and plastic strains.
The relationship between strains and stresses is determined by applying the generalized Hooke’s law
σ i j = C i j k l ɛ i j .

2.3. Finite Element Desription

The unsteady heat transfer problem is solved by applying finite element method, using the matrix equation below:
C ∙ T ˙ + K T ∙ T = F ,
where C is the capacitance matrix, K T is the heat transfer matrix, and F - the vector describing HF.
The problem of the stress-strain state is solved by using the following matrix equation:
K f ∙ U = P M + P T ,
where K f is the stiffness matrix, U is the nodal displacement vector, P M and P T are the nodal vectors of the mechanical and thermal loads, respectively.
Numerical time integration is accomplished by applying the finite difference method:
T ˙ t + ∆ t T t + ∆ t − T t ∆ t ,
where ∆ t is the time step.

2.4. Computer Model

The computer implementation of the welding process model is performed by specialized software ABAQUS [36]. The geometric model is built according to the shape and dimensions of the plank (100×60×9 mm), taking into account that the problem is symmetrical. The discretization is performed by three-dimensional finite elements DC3D20 with one intermediate node and characteristic size 2.25 mm. The number of the nodes is restricted by the computing capabilities. All calculations are done at cluster of four computers with Intel Xeon processors.
There are some differences regarding the physical properties of the material, proposed by different authors in their papers. Table 2 indicates the accepted values for the thermophysical properties of the material, experimentally determined in [37], after partial linear approximation is performed.
In the considered temperature interval, the S235JR steel has two phase transformations, which leads to the achieving of two peaks in the specific heat capacity. There are two possibilities for describing these jump-like changes. The first one, proposed in [38], is through applying a direct description of this nonlinearity in the specific heat capacity. This leads to obtaining a highly physically nonlinear problem and serious difficulties in the implementation of the applied Newton-Raphson numerical method applied. This difficulty is overcome by exploiting the latent heat due to phase transitions. It is set twice - when certain temperature values are reached in the heating process and in the cooling process. This approach is preferred in the present work. Latent heat values and temperature limits of phase transformations are presented in Table 3.
The boundary conditions of the heat problem are the radiation heat exchange and the heat flow of the electric arc. A constant value of 0.3 is assumed for the emissivity, and the Stefan-Boltzmann constant is 5.57037×10 – 8. The power of the electric arc is 18.5 A, and the electric voltage is 120 V. The welding time 45.5 s is discretized in the numerical model with the number of steps equal to the number of elements in the longitudinal direction. A subroutine DFLUX built into the ABAQUS [36] system has been created to determine the volumetric HF. The accepted arc efficiency is 0.46. The unknown parameters in the heat flow description in equations (3) and (4) are the subject of the calibration considered in this paper.
The boundary conditions for the mechanical problem are the symmetry and the restriction of the displacements at three points, so that free deformation of the plate is possible.
The computer model provides numerical results for the temperature field and the displacement in the transverse direction of the plate. The zones of the WP at a melting temperature of 1593°C and the HAZ at an assumed structural variation temperature of 723°C are obtained. The results are presented in Figure 4. The WP is depicted in gray, the colored zone is the HAZ, and the zone with a temperature below 723°C is dark.

2.5. Optimization Model

The optimization model contains the described thermomechanical model, supplemented with information about the selected variable parameters for model calibration, the intervals of their change and an evaluation system of criteria for closeness with controlled accuracy between experimental and simulated data for the welded specimen.
The optimization model contains five variable parameters united into a vector:
u = [ u 1 , u 2 , … , u 5 ] ,
The physical meaning and nominal values uj°, j ∈ Ij = {1, 2, … , 5} of the variable parameters are presented in Table 4. Interval limits are indicated and set in it
u П = { u E 5 : u − u u + } ,
where u + and u − are the limits of variation of the vector u .
When accomplishing additional probing in the vicinity of a current variable vector assumed as a new nominal u° in order to improve it, it is convenient to expand or contract the new multidimensional parallelepiped area П according to the rule:
u− = u°(1 – n°/200); u+ = u°(1 + n°/200); n°∈{1, 5, 10, 20}.
The selected basic geometric characteristics fv , v ∈ Iv = {1, 2, … , 4}, are presented in Table 1. They are used for establishing a criteria evaluation system for calibrating the mathematical model. The discrepancy fv (u) between the calculated fvc(u) and the measured fvе data from Table 1 is estimated as a percentage using the following vector criterion:
f(u) = [ f1(u), f2(u), … , fv (u), … , f4 (u) ],
where:
fv (u) = ? fvc (u) / fve – 1 ?100, v ∈ Iv ,
f c(u) = [ f1c(u), f2c(u), … , fvc(u), … , f4c(u) ],
f е = [ f1е, f2е, … , fvе, … , f4е ].
The vector criterion (15) for closeness (adequacy) between the calculated and measured data is specified in (16) and being presented as the absolute value of the relative discrepancies fv (u), given in percentage. Since there is no information about the nature and degree of impact of the causal relationships between the variable parametric vector u and the measured geometric characteristics fvе, on the studied process, it is assumed that all criteria are of equal value.
Probing the entire parametric domain П with Sobol’s trial points of the variable vector u may leads to producing unacceptable values of the relative misfit fv (u). To control the closeness between experimental and simulated weld characteristics, it is advisable to introduce a criterion limit on the maximum mismatch
G (f (u)) ≤ 0,
where
G (f (u)) = max v ∈ Iv { fv (u) } – δf +,
and δf +is the maximum allowable relative difference, given in percentage.
The vector identification problem takes the form of a generalized multi-objective optimization problem [29], as it can be presented as follows:
u* = arg Pmin u∈D f (u),
D = {u∈Е5: G (f (u)) ≤ 0, u∈П},
where: Pmin is the operator for determining approximate global Pareto minimum compromise values of the vector criterion f; D – the feasible solution set; G (f (u)) – the imposed criterion constraint. The boundaries of the interval domain Π are determined by numerical experiment so that the Pareto optimal points u* are internal to this domain.
Solving the extremal problem (19) is based on the principle of consistent optimality of V. Pareto [39]. According to this principle, an admissible point u*∈D is globally Pareto optimal if there exists no other admissible point u∈D for which the condition fν (u) ≤ fν (u*) is fulfilled for everyν ∈Iv , as at least for one particular criterion the inequality is strict.
Problem (19) is solved by applying the MATLAB program mviweld, which uses program modules of the psims program for multicriteria parametric optimization, documented in [40]. The optimal solutions (u*p ∈D, f *p = f (u*p )) form two discrete Pareto sets D* = {u*p : u*p = arg Pmin ui ∈D f (ui)} and P* = {f *p: f *p = f (u*p )} with incomparable points u*p∈D*⊆ D и f *p∈P*⊆ F, where: D and F = {f (ui): ui∈D} are respectively the feasible parametric and the attainable criterion sets; i ∈ Ii = {1, 2, … , Ns}; p ∈ Ip = {1, 2, … , NP}, respectively. The selection of a compromise solution (u#∈D*, f # = f*(u#)) can be greatly facilitated if it is made from reasonably reduced subsets of D* and P*.
The optimization is done into two stages. In the first stage, the universal method PSI, used to study multidimensional areas by their quasi-uniform probing with a set number of Ns allowed by the imposed restrictions Sobol’s sample points [29, 30], is implemented.
Using the MATLAB and ABAQUS software systems, for each vector ui ∈ D, i ∈ Ii from the computer model of the simulated object in the SIMULATOR conditional block, achievable values of the criteria f (ui )∈ F (Figure 5) are determined. A conceptual idea of the structure of this block is given in Figure 6. The sets D and F are formed after satisfying the criterion constraint G (f (ui )) ≤ 0, which performs the role of a filter with an adjustable maximum permissible discrepancy δf + between the simulated f c(ui ), and the experimentally determined criterion vector f e. The sample points uji, i ∈ Ii , j ∈ Ij determined by the PSI procedure for Ns = 26 ≡ 128.
The first stage ends with the selection of approximately Pareto optimal sets D* and P*. In cases where any of the sets D or D* turns out to be empty, the “decision maker” (DM) must relax the criterion constraint (17) to obtain a sufficient number of NP solutions (u* p, f (u* p )).
In the second stage, Pareto subsets DR*⊂ D* and PR*⊂ P*, ranked by compromise efficiency, are selected using the minimum values μk* = min p {μkp}, p ∈ Ip , k ∈ Ik = {1, 2, 3} of the components of a vector criterion μ = [μ1, μ2, μ3] with a geometric sense from the set M = {μ(f *p ) ∈ E3: f *p∈P*} [41].
The components μkp of the vector μ p determine the distances between three characteristic points: the positive utopian point fU; the current compromise point f *p and its projection fUN on the hyperline UN with unit vector e = (fN − fU ) / || fN– fU|| which joins the two utopian points – the positive fU = min i∈ Ii {f (ui)} and the negative fN = max i∈ Ii {f (ui)} with components the uncompromising extreme values of the particular criteria.
The position of a Pareto point f *∈P* with respect to the utopian point U and the hyperline UN is estimated using three vectors: r(f *) = f *− fU; p(f *) = (r ⋅ e) e; q(f *) = r − p. Their Euclidean norms determine the scalar geometric components μ1 = || p ||, μ2 = || q ||, μ3 = || r || of the vector μ.
Each p-th Pareto optimal point f *p∈ P*, p ∈ Ip of the set P* using the vector μp = [μ1p, μ2p, μ3p] is transformed into a point of the set M = {μ p∈Е3: p ∈ Ip} of the three- dimensional μ-space. In this space, the Pareto-selection result is easily analyzed visually.
In the set M, all possible combinations of two criteria are examined: {μt p, μh p}, t ≠ h, (t, h) ∈ It h = {(1,2), (2,1), (1,3), (3,1), (2,3), (3,2)}.
Subsets of Pareto optimal points are selected for each pair of criteria Mρ = {μ p∈Е3: μt*p,t ≤ μt p ≤ μt* p,h, t ≠ h, (t, h) ∈ It h, p ∈ Ip } ⊂ M, ρ ∈ Iρ = {6, 5, … , 1}.
The minimizing point μh*p,h = minp ∈ Ip {μh p} of a given criterion μh p, h ∈ Ik is used as the upper limit of the filtering interval in the selection by another criterion μt p, t ≠ h, t ∈ Ik, and the minimum point μt*p,t = minp ∈ Ip {μt p} of the criterion μt p, as a lower limit. Each point selected in this way μR = μ (f R ) ∈ Mρ , ρ ∈ Iρ and its corresponding points f R = f (uR ) ∈ PR* ⊂ P*, uR∈DR*⊂ D* receive as an individual evaluation number Mρ , which determines their trade-off efficiency rank. This number is equal to the number ρ of subsets Mρ in the unified set MR = {∪ρ ∈IρMρ} to which μR belongs. In this way, to analyze the reached compromise efficiency and finalize the solution of the multi-criteria problem, DM has two reduced ranked Pareto subsets DR* and PR*.
The subset of PR* with the highest rank RE = 6 of compromise efficiency usually contains only one point f S = f (uS) which corresponds to the Salukvadze optimal solution (uS = arg min u∈D μ3(f (u)), f S = f (uS)) of problem (19). This solution reveals the potential possibilities of uniformly approaching the private criteria to their uncompromising optimal values under the assumption that they are equivalent [42].
The final compromise solution (u#, f # ) is selected by the DM after analysis of the remaining ranked Pareto subsets in PR*. If the Salukvadze optimal solution (u# = uS, f # = f S ) based on the ideal point concept is evaluated as unacceptable regarding the reached trade-off level by any of the private criteria, the non-empty subsets of PR* are successively analyzed with lower rank RE ∈{5, 4, ... , 1} until a unique selection is made.

2.6. Calculation Procedure

The computer model, simulating the thermomechanical phenomena during welding of the test specimen, was implemented in interaction with the programming environments of the MATLAB and ABAQUS systems. A generalized scheme of the used iterative identification procedure is presented in Figure 7.
It can be executed repeatedly if the DM accepts the determined unique compromise solution (u#, f # ) as a new current nominal (u°, f ° ≡ f (u°)) and set a new interval domain П according to rule (14). The basis of the DM’s decisions is his expert knowledge of the process, which cannot be initially formalized and, for this reason, is not included in the criterion space of the optimization problem. Resuming the procedure is justified if it leads to a significant improvement of the Salukvadze optimal solution.

3. Results

In the performed numerical study, the following basic values of the parameters of the optimization model are selected, when they remain constant within a specific numerical experiment: u− = [3,1,3,1,0.4], u+ = [8,3,8,1.6,0.52], Ns = 26 ≡ 128. For this range of the parameters, the difference between the minimum and maximum values of the results are: 1.92 mm, 0.39 mm 0.94 mm and 0.86 mm. Referred to the experimentally determined data in percentages they are 55%, 76% 89% and 69%. The three variants used with values of allowable mismatch δfv + (given in percentage) are listed in Table 5.
The results obtained after performing the multi-criteria optimization for variant V1 with a maximum permissible discrepancy G = 20% are illustrated in Figure 8. It can be clearly seen, that the point with the highest rank RЕ = 6 is marked with the symbol ( ■ ), and the points of the non-empty ranked Pareto subsets of rank 5, 4, ... , 1 – with ( •, ▲, ►, ◄, ♦ ), respectively.
Figure 9 represents the results obtained after accomplishing variant V2.
The final decision is set for variant V3. The results are visualized in Figure 10.
Three ranked Pareto optimal solutions with criteria values presented in Table 6 are highlighted. Table 7 shows the values of their corresponding ranked Pareto optimal parameters.
The maximum disagreement reached for the unique Salukvadze optimal solution found is 12.47%, and the minimum is 4.75%. The results vector for this model is u = [6.59 1.69 6.59 1,02 0,45].

4. Discussion

The multi-criteria inverse identification task for calibrating the thermomechanical model is implemented with the universal PSI method for quasi-uniform probing of the admissible parametric region with 128 Sobol’s test points.
The second stage is conducted with a three-stage proximity filtering scheme of the simulated data of the μ-selection procedure. Utopian and Nadir points are identified and ranked by trade-off efficiency Pareto subsets. The selection of a unique solution is reached at a limit of 13% Pareto set differences. Thus, a solution with rank RE = 6 of compromise efficiency was singled out and represents Salukvadze optimum. Since it corresponds to the hypothesis of equal- value of the criteria, the compromise levels reached reveal the degree of their simultaneous and uniform reduction. Provided that the determined Salukvadze-optimum is an acceptable solution, the DM may choose it as the final unambiguous solution. It provides equivalence of criteria with a minimum discrepancy of 4.75% and a maximum of 12.47% between measured and calculated data. Ideal calibration parameters would give a maximum discrepancy between the model and the experiments of 0%.
The obtained results demonstrate the good possibility of applying optimization and post-optimization analysis for calibrating a numerical welding model. Variant 1 (V1) has solutions for the six orders of efficiency. Variant 2 (V2) lacks a solution for rank 3, and variant 3 (V3) has solutions only for rank 2, 4 and 6. The third variant gives little opportunity for the DM if replacement of the solution of rank 6 is necessary.
Residual stresses and strains are an important characteristic of the welded structure. In further developments, they should participate in the criterion space.
Improvement of the accuracy of the obtained results can be sought by applying the selective integration-based adaptive mesh refinement approach described in [43].

Author Contributions

Conceptualization I.D. and Y.A.; methodology, V.V.; software, V.V. and I.D.; validation, R.R. and S.M.; investigation, D.G., N.F. and Y.A.; resources, N.F.; data curation, N.F. and D.G.; writing — original draft preparation, V.V. and I.D.; writing — review and editing, I.D. and R.R.; visualization, S.M.; supervision, R.R.; project administration, R.R. All authors have read and agreed to the published version of the manuscript.

Funding

This study is financed by the European Union-NextGenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project № BG-RRP-2.013-0001-C01.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Arata, Y.; Abe, N.; Oda, T.; Tsujii, N. Fundamental Phenomena during Vacuum Laser Welding; ASME: Boston, Massachusetts, USA, 1984; pp 1–7. [CrossRef]
  2. Miller, H. C. A Review of Anode Phenomena in Vacuum Arcs. IEEE Transactions on Plasma Science 1985, Vol. 13, (No. 5), pp 242–252. [CrossRef]
  3. Toya, H.; Hieda, K.; Saitou, T. Preliminary Study on Arc Welding in Vacuum; Matsue, Japan, 2006; pp 762–765. [CrossRef]
  4. Ferdinandov, N.; Gospodinov, D.; Ilieva, M.; Dimitrov, S. Effect of the process parameters on mechanical properties of titanium alloy Ti-6Al-4V welds; Proceedings of University of Ruse; Ruse, Bulgaria, 2017, Vol. 56, book 2, pp 58-65.
  5. Hibbitt, H.; Marcal, P. A Numerical, Thermo-Mechanical Model for the Welding and Subsequent Loading of a Fabricated Structure. Comuters & Structures 1973, Vol. 3, pp 1145–1174.
  6. Friedman, E. Thermomechanical Analysis of the Welding Process Using the Finite Element Method. Trans. ASME 1975, Vol. 97 (No. J3), pp 206–213.
  7. Goldak, J.; Chakravarti A.; Bibby M. A New Finite Element Model for Welding Heat Sources. Metallurgical Transactions B 1984, Vol. 15B, pp 299–305.
  8. Michaleris, P.; Debiccari, A. Prediction of Welding Distortion. AWS Annual Convention 1996, pp 172–181.
  9. Han, Y.; Lee, K.; Han, M.; Chang, H.; Choi, K.; Im, S. Finite Element Analysis of Welding Processes by Way of Hypoelasticity-Based Formulation. Journal of Engineering Materials and Technology 2011, Vol. 133, pp 1–13. [CrossRef]
  10. Fadaei, A.; Mokhtari, H. Finite Element Modeling and Experimental Study of Residual Stress in Repair Butt Weld of St-37 Plates. IJST, Transactions of Mechalical Engineering 2015, Vol. 39, (No. M2), pp 291-307.
  11. Nezamdost, M.; Efahani, M.; Hashemi, S.; Mirbozorgi, S. Investigation of Temperature and Residual Stresses Field of Submerged Arc Welding by Finite Element Method and Experiments. Int. J. Adv. Manuf. Technol. 2016, Vol. 87, pp 615–624. [CrossRef]
  12. Kik, T.; Górka, J. Numerical Simulations of Laser and Hybrid S700MC T-Joint Welding. Materials 2019, Vol. 12, (No. 3), 516. [CrossRef]
  13. Murthy, K.K.R.; Akyel, F.; Reisgen, U.; Olschok, S.; Mahendran, D. Modelling the Evolution of Phases during Laser Beam Welding of Stainless Steel with Low Transformation Temperature Combining Dilatometry Study and FEM. J. Manuf. Mater. Process. 2024, Vol. 8, 50. [CrossRef]
  14. Akrivos, V.; Muransky, O.; Depradeux, L.; Smith, M.C.; Vasileiou, A.; Deaconu, V.; Kapadia, P. On the Accurate Prediction of Residual Stress in a Three-Pass Slot Nickel-Base Repair Weld by Numerical Simulations. J. Manuf. Mater. Process. 2022, Vol. 6, 61. [CrossRef]
  15. Sumanlal, M. S.; Sarin, P.; Varghese, V. J. Three-Dimensional Finite Element Optimization of Bead Shape Developed during Tig Welding of Mild Steel. International Journal of Applied Engineering Research 2018, Vol. 13, (No. 3), pp 104–109.
  16. Bag, S.; Trivedi, A.; De, A. Use of a Multivariate Optimization Algorithm to Develop a Self-Consistent Numerical Heat Transfer Model for Laser Spot Welding. The International Journal of Advanced Manufacturing Technology 2008, Vol. 38, (No. 5), pp 575–585.
  17. Fu, G.; Gu J.; Lourenco, M. I.; Duan, M.; Estefen, S. F. Parameter Determination of Double-Ellipsoidal Heat Source Model and Its Application in the Multi-Pass Welding Process. Ships and offshore structures 2015, Vol. 10, (No. 2), pp 204–217.
  18. Belitzki, A.; Marder, C.; Huissel, A.; Zaeh, M.F. Automated Heat Source Calibration for the Numerical Simulation of Laser Beam Welded Components. Production Engineering 2016, Vol. 10, (No. 2), pp 129-36. [CrossRef]
  19. Walker, T. R.; Bennett, C. J. An Automated Inverse Method to Calibrate Thermal Finite Element Models for Numerical Welding Applications. Journal of Manufacturing Processes 2019, Vol. 47, pp 263–283. [CrossRef]
  20. Escribano-García, R.; Álvarez, P.; Marquez-Monje, D. Calibration of Finite Element Model of Titanium Laser Welding by Fractional Factorial Design. J. Manuf. Mater. Process. 2022, Vol. 6, (No. 6), 15 p. [CrossRef]
  21. Hartwig, P.; Bakir, N.; Scheunemann, L.; Gumenyuk, A.; Schröder, J.; Rethmeier, M. A. Physically Motivated Heat Source Model for Laser Beam Welding. Metals 2024, Vol. 14, (No. 4), 430. [CrossRef]
  22. Statnikov, R. B.; Matusov, I. B. Solved tasks of multi-criteria identification and refinement of experimental samples. Problems of mechanical engineering and machine reliability 2012, No. 5, pp 20–29.
  23. ISO/TS 18166 Numerical Welding Simulation — Execution and Documentation.
  24. Strychek, Y.; Antoniak, P.; Lurie, Z. Y.; Solovyov, V. M. Determination of unknown parameters of a gear pump external gearing by solving the inverse problem of multi-criteria identification. Industrial hydraulics and pneumatics 2017, No. 2, pp 57–69. https://repository.kpi.kharkov.ua/server/api/core/bitstreams/1d1bf4c3-f772-49fb-ab78-fbef39f079e6/content .
  25. Kovalenko, D. V.; Pavlyak, D. A.; Sudnik, V. A.; Kovalenko, I. V. Adequacy of the thermo-hydrodynamic model of through penetration in TIG and A-TIG welding of Nimonic-75 nickel alloy. Automatic Welding 2010, No. 10, pp 5–9.
  26. Yadaiah, N.; Bag, S. Effect of Heat Source Parameters in Thermal and Mechanical Analysis of Linear GTA Welding Process. ISIJ International 2012, Vol. 52, (No. 11), pp 2069–2075. [CrossRef]
  27. Bradáč, J. Calibration of Heat Source Model in Numerical Simulations of Fusion Welding. Machines, Technologies, Materials 2013, No. 11, pp 9–12. https://mech-ing.com/journal/Archive/2013/11/76_Bradac.pdf .
  28. Yakimenko, O. A.; Statnikov, R. B. Multicriteria Parametrical Identification of the Parafoil-Load Delivery System. 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, AIAA 2005 – 1664, 12 р. [CrossRef]
  29. Sobol, I. M.; Statnikov, R. B. Selection of optimal parameters in tasks with many criteria.; Drofa: Moscow, 2006, (in Russ.).
  30. Statnikov, R. B.; Statnikov, A. R. The Parameter Space Investigation Method Toolkit.; Artech House: Boston/ London, 2011.
  31. Lu, Y.; Blal, N.; Gravouil, A. Space-Time POD Based Computational Vademecums for Parametric Studies: Application to Thermo-Mechanical Problems. Advanced Modeling and Simulation in Engineering Sciences 2018, Vol. 5, (No. 3), pp 1–27. [CrossRef]
  32. Chinesta, F.; Leygue, A.; Bordeu, F.; Aguado, J.; Cueto, E.; Gonzalez, D.; Alfaro, I.; Ammar, A.; Huerta, A. PGD-Based Computational Vademecum for Efficient Design. Optimization and Control. Archives of Computational Methods in Engineering 2013, Vol. 20, (No. 1), pp 31–59. [CrossRef]
  33. EN 10025-2:2005 Hot Rolled Products of Structural Steels - Part 2: Technical Delivery Conditions for Non-Alloy Structural Steels.
  34. Draganov, I.; Ferdinandov, N.; Gospodinov, D.; Radev, R.; Mileva, S.; Angelov, Y. Numerical modeling and calibration of steel plate welding in vacuum; Ruse, Bulgaria, 2019; Vol. 58, book 2.1, pp 65-73.
  35. Bergheau, J-M.; Fortunier R. Finite Element Simulation of Heat Transfer. Hoboken: John Wiley & Sons, Inc., NJ, 2008.
  36. ABAQUS. Analysis User’s Manual. Ver. 6.14, Providence, RI, USA.
  37. Milkowska-Piszczek, K.; Korolczuk-Hejnak, M. An Analysis of The Influence of Viscosity on The Numerical Simulations of Temperature Distribution as Demonstrated The CC Process. Archives of Metallurgy and Materials 2011, Vol. 58 (No. 4), pp 1267–1274. [CrossRef]
  38. Muhtarov, I. Residual stresses in thin stainless steel plates subject to TIG welding; Sozopol, Bulgaria, 2011, pp 246–249.
  39. Miettinen, K. Nonlinear Multiobjective Optimization, 2nd ed., Springer: New York, 2012.
  40. Yordanov, Y. T.; Vitliemov, V. G. Optimization with MATLAB. A pragmatic approach.; “Angel Kanchev” University Publishing House: Ruse, Bulgaria, 2013, (in Bulg.).
  41. Cheshankov, B. I.; Ivanov, I. V.; Vitliemov, V. G.; Koev, P. A. PSI-Method Multi-Criteria Optimization Contracting the Set of Trade-Off Solutions. Proceedings of the 15th International Conference on Systems Science, Wrozlaw, Poland, 2004, Vol. 1, pp 281–288,.
  42. Salukvadze, M. E. Vector-Valued Optimization Problems in Optimal Control Theory, 2nd ed., Academic Press: New York, 2012.
  43. Huang, H.; Murakawa, H. A. Selective Integration-Based Adaptive Mesh Refinement Approach for Accurate and Efficient Welding Process Simulation. J. Manuf. Mater. Process. 2023, Vol. 7, (No. 6), 206. [CrossRef]
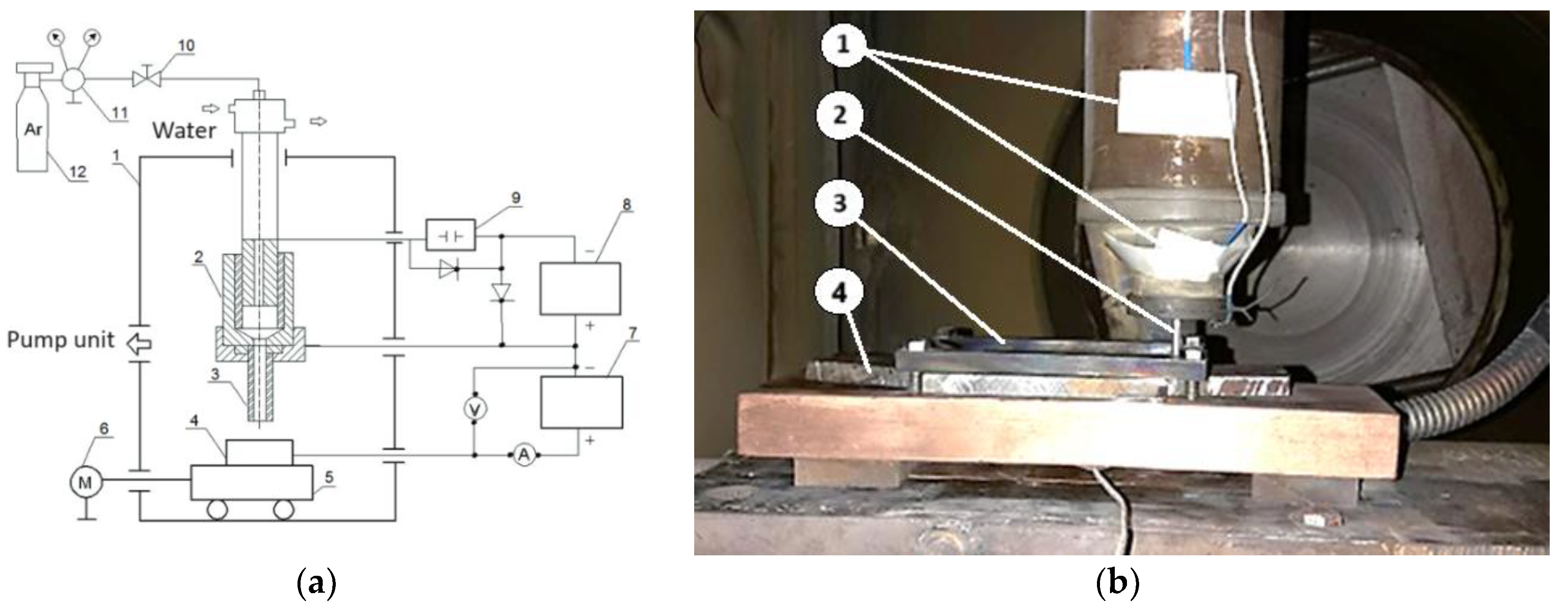
Preprints 119742 g001
Figure 1. Vacuum welding installation: (a) schematic diagram of the laboratory installation: 1 - vacuum chamber; 2 - torch; 3 - cathode; 4 - welded specimen; 5 - manipulator; 6 - electric motor; 7 - main current source; 8 - auxiliary current source; 9 - capacitor battery; 10 - micro-flow; 11 - reducer-valve; 12 - a bottle of plasma-forming gas [4]; (b) position of the test specimen and the welding torch in the vacuum chamber: 1 – thermocouples (shielded); 2 – cathode; 3 – fastening plate; 4 – welded specimen [34].
Figure 1. Vacuum welding installation: (a) schematic diagram of the laboratory installation: 1 - vacuum chamber; 2 - torch; 3 - cathode; 4 - welded specimen; 5 - manipulator; 6 - electric motor; 7 - main current source; 8 - auxiliary current source; 9 - capacitor battery; 10 - micro-flow; 11 - reducer-valve; 12 - a bottle of plasma-forming gas [4]; (b) position of the test specimen and the welding torch in the vacuum chamber: 1 – thermocouples (shielded); 2 – cathode; 3 – fastening plate; 4 – welded specimen [34].
Preprints 119742 g001
Preprints 119742 g002
Figure 2. WP and HAZ.
Figure 2. WP and HAZ.
Preprints 119742 g002
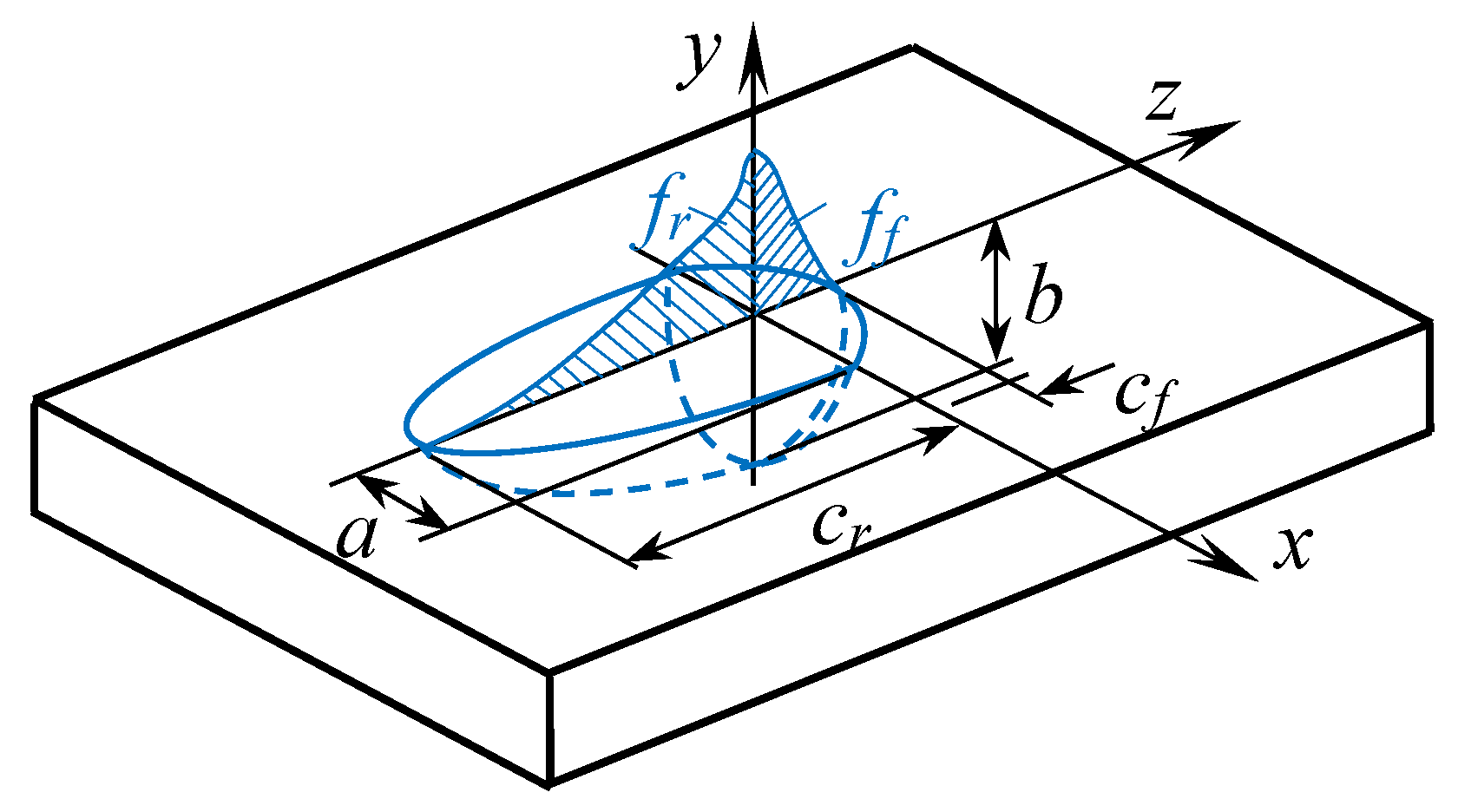
Preprints 119742 g003
Figure 3. Heat flow distribution.
Figure 3. Heat flow distribution.
Preprints 119742 g003
Preprints 119742 g004
Figure 4. Temperature field: (a) b = 4 mm, cf = 0.8 mm, ff = 1.2; (b) b = 16 mm, cf = 0.8 mm,ff = 1.2; (c) b = 28 mm, cf = 0.8 mm, ff = 1.2.
Figure 4. Temperature field: (a) b = 4 mm, cf = 0.8 mm, ff = 1.2; (b) b = 16 mm, cf = 0.8 mm,ff = 1.2; (c) b = 28 mm, cf = 0.8 mm, ff = 1.2.
Preprints 119742 g004
Preprints 119742 g005
Figure 5. Interaction between the PSI procedure and the thermomechanical model simulator.
Figure 5. Interaction between the PSI procedure and the thermomechanical model simulator.
Preprints 119742 g005
Preprints 119742 g006
Figure 6. Schematic of the SIMULATOR block.
Figure 6. Schematic of the SIMULATOR block.
Preprints 119742 g006
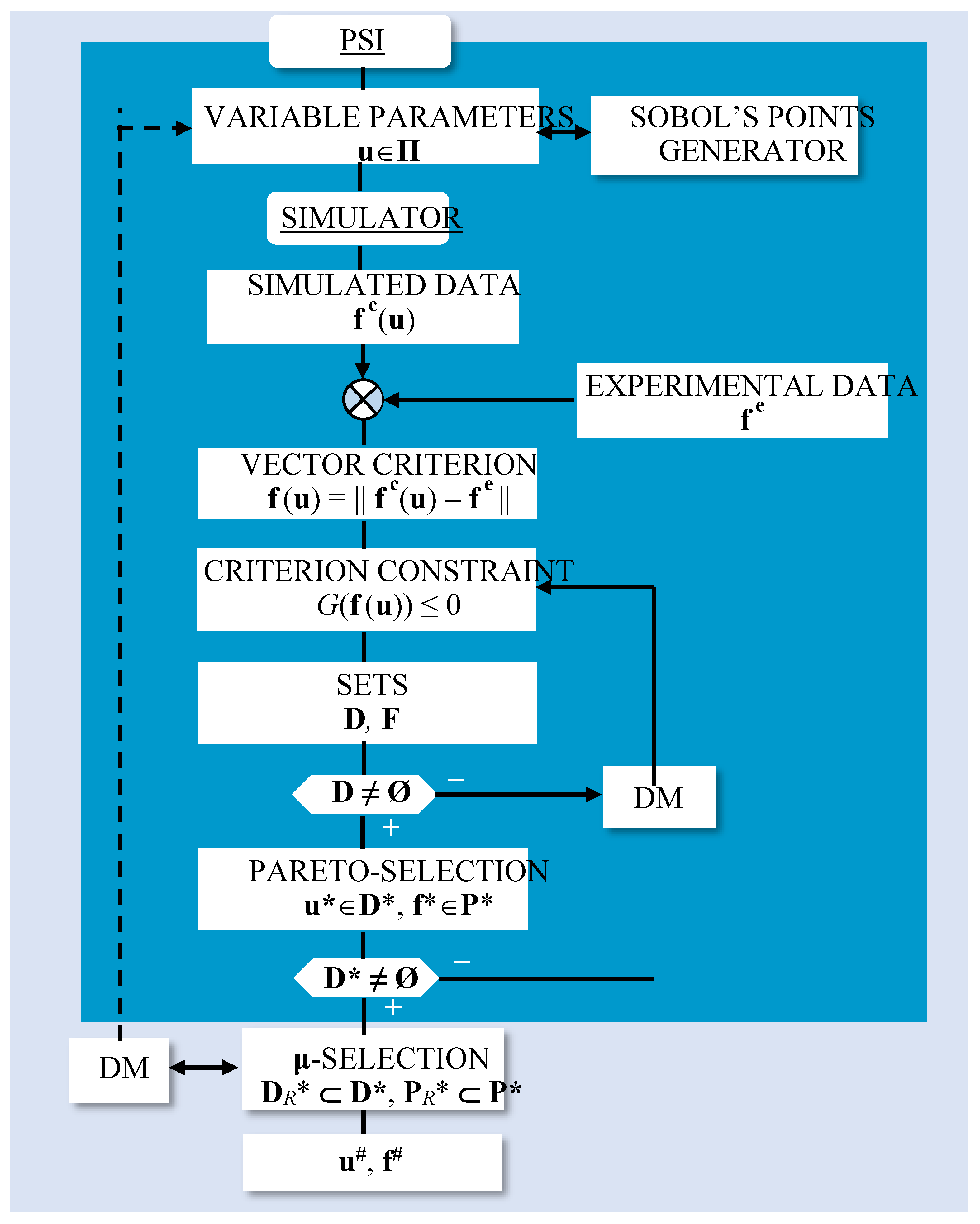
Preprints 119742 g007
Figure 7. Summary of the procedure for multi-criteria identification.
Figure 7. Summary of the procedure for multi-criteria identification.
Preprints 119742 g007
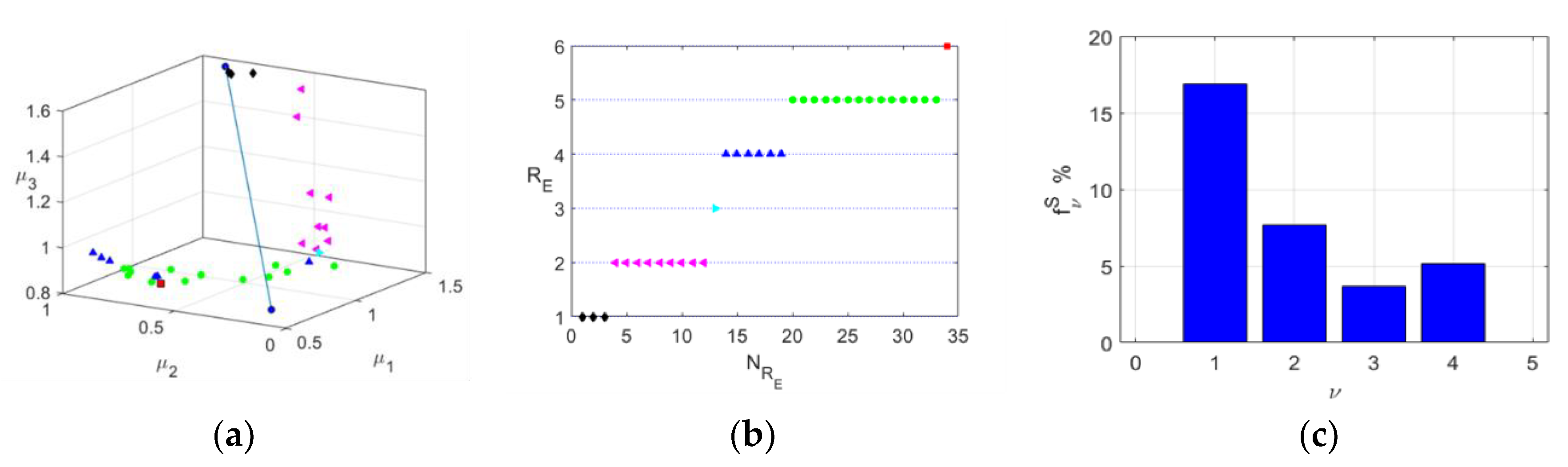
Preprints 119742 g008
Figure 8. Variant V1: (a) Ranked Pareto optimal solutions in μ-space; (b) Number of NRE of ranked Pareto optimal solutions with rank RE ; (c) Salukvadze optimum f (uS).
Figure 8. Variant V1: (a) Ranked Pareto optimal solutions in μ-space; (b) Number of NRE of ranked Pareto optimal solutions with rank RE ; (c) Salukvadze optimum f (uS).
Preprints 119742 g008
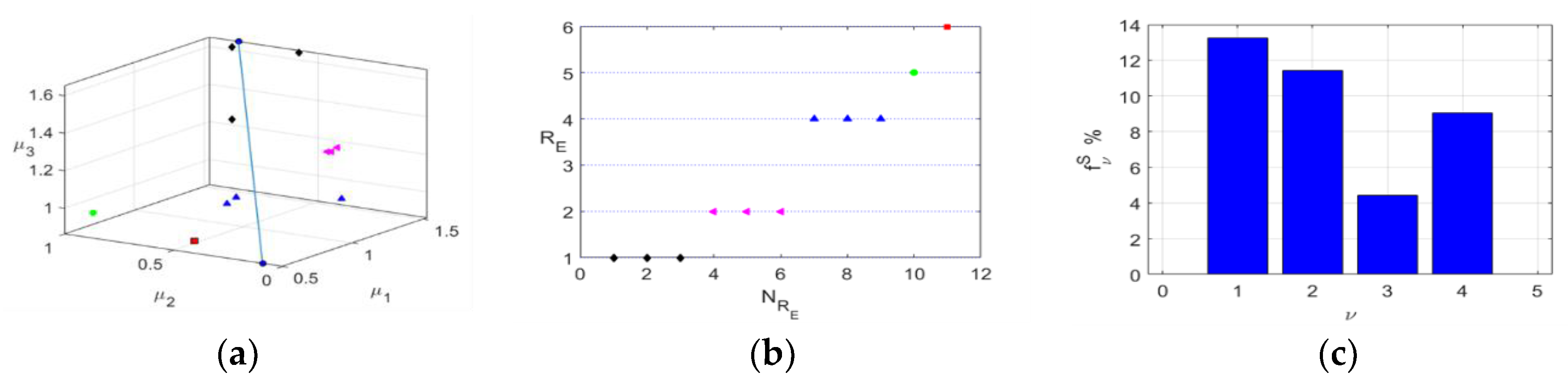
Preprints 119742 g009
Figure 9. Variant V2: (a) Ranked Pareto optimal solutions in μ-space; (b) Number of NRE of ranked Pareto optimal solutions with rank RE ; (c) Salukvadze optimum f (uS).
Figure 9. Variant V2: (a) Ranked Pareto optimal solutions in μ-space; (b) Number of NRE of ranked Pareto optimal solutions with rank RE ; (c) Salukvadze optimum f (uS).
Preprints 119742 g009
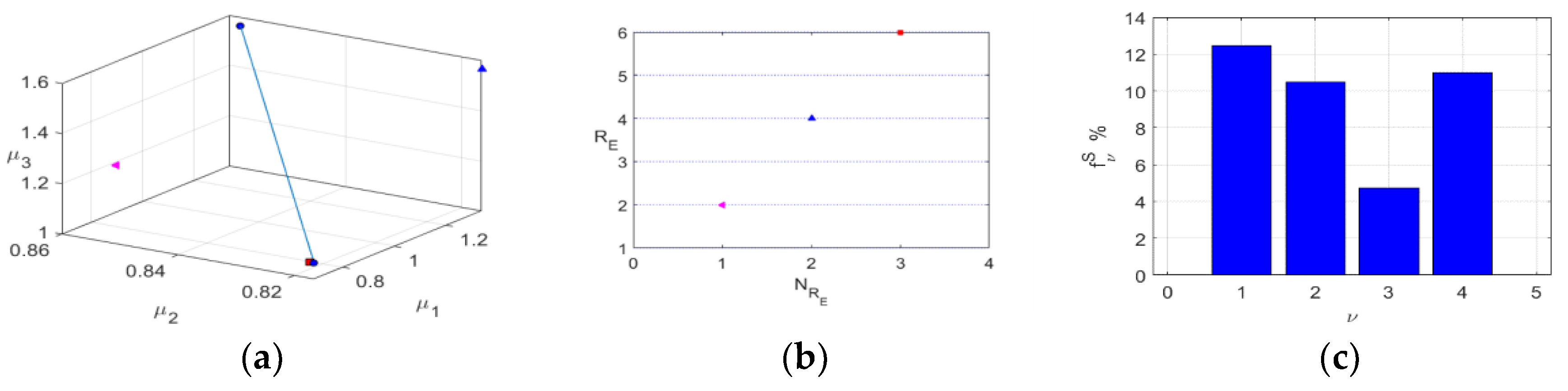
Preprints 119742 g010
Figure 10. Variant V3: (a) Ranked Pareto optimal solutions in μ-space; (b) Number of NRE of ranked Pareto optimal solutions with rank RE ; (c) Salukvadze optimum f (uS).
Figure 10. Variant V3: (a) Ranked Pareto optimal solutions in μ-space; (b) Number of NRE of ranked Pareto optimal solutions with rank RE ; (c) Salukvadze optimum f (uS).
Preprints 119742 g010
Table 1. Geometry of the experimental specimen.
Table 1. Geometry of the experimental specimen.
Dimensions Designation Value, mm
Width of the WP f1е 4.30
Depth of WP f2е 1.65
Width of HAZ f3е 8.40
Depth of HAZ f4е 2.80
Table 2. Physical properties of the material.
Table 2. Physical properties of the material.
Material Properties Temperature, °C Value
Thermal conductivity, W/mK 20 40
1300 30
1600 120
Specific heat capacity, J/kgK 20 400
1540 600
Modulus of elasticity, GPa 20 210
1500 5
Poisson’s ratio, – 20 … 1600 0.27
Coefficient of temperature expansion, K – 1 20 1.25×10–6
1500 1.65×10–6
Yield strength, MPa 20 235
500 100
1000 50
Table 3. Latent heat.
Table 3. Latent heat.
Phase Transformations Latent Heat, kJ Lower Limit, °C Upper Limit, °C
(α – γ) transition 55 700 800
Solid phase – liquid phase 150 1450 1650
Table 4. Variable parameters.
Table 4. Variable parameters.
uj Designation Values
uj– uj° uj+
u1 Depth-related calibration parameter – k 3.00 5.00 8.00
u2 Calibration parameter related to the width – l 1.00 2.00 3.00
u3 Calibration parameter related to length – m 3.00 5.00 8.00
u4 Arc density factor in front of the center of the HF 1.00 1.20 1.60
u5 Arc efficiency 0.40 0.46 0.52
Table 5. Variants of permissible disagreements.
Table 5. Variants of permissible disagreements.
Variant δfv +, %
V1 20
V2 15
V3 13
Table 6. Ranked Pareto optimal values of the criteria fν*(uR ), v ∈ Iv.
Table 6. Ranked Pareto optimal values of the criteria fν*(uR ), v ∈ Iv.
RE f1*R f2*R f3*R f4*R
6 12.471 10.487 4.746 11.017
4 9.738 12.169 5.203 11.827
2 11.601 12.988 4.758 10.537
Table 7. Ranked Pareto optimal values of parameters uj*R, j ∈ Ij .
Table 7. Ranked Pareto optimal values of parameters uj*R, j ∈ Ij .
RE u1*R u2*R u3*R u4*R u5*R
6 3.469 1.938 7.219 1.244 0.434
4 5.734 2.531 3.547 1.047 0.424
2 5.383 2.391 7.961 1.098 0.438
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated