Prerpints.org logo
Preprint
Review

Advancing Additive Manufacturing Through Machine Learning Techniques: A State-of-the-Art Review

Altmetrics

Downloads

140

Views

66

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 September 2024

Posted:

30 September 2024

You are already at the latest version

Alerts
Abstract
In the fourth industrial revolution, artificial intelligence (AI) and machine learning (ML) have increasingly been applied to manufacturing, particularly additive manufacturing (AM), to enhance processes and production. This study provides a comprehensive review of the state-of-the-art achievements in this domain, highlighting not only the widely discussed supervised learning but also the emerging applications of semi-supervised learning and reinforcement learning (RL). These advanced ML techniques have recently garnered significant attention due to their potential to further optimize and automate AM processes. The review aims to offer insights into various ML technologies employed in current research projects and to promote the diverse applications of ML in AM. By exploring the latest advancements and trends, this study seeks to foster a deeper understanding of ML’s transformative role in AM, paving the way for future innovations and improvements in manufacturing practices.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Intelligent manufacturing, also known as smart manufacturing [1,2,3], harnesses cutting-edge technologies, such as artificial intelligence (AI) [4,5,6], machine learning (ML) [7], Internet of Things (IoT) [8,9], robotics [10,11], automation [12,13], and big data analytics [14,15,16], to revolutionize the manufacturing process. By leveraging these advancements, intelligent manufacturing aims to enhance productivity, efficiency, and flexibility in production. Central to intelligent manufacturing is the use of data analytics to gather, analyze, and interpret vast amounts of data generated throughout the production cycle. Artificial intelligence and ML play crucial roles in processing this data, enabling predictive maintenance, quality control, demand forecasting, and process optimization. Furthermore, deploying sensors and IoT devices across the factory floor facilitates seamless connectivity between machines and systems. This connectivity enables real-time monitoring of equipment performance and inventory levels, ensuring smooth transitions during production. Advanced robotics systems within intelligent manufacturing environments can adapt to dynamic conditions, collaborate with human workers, and execute tasks with precision and efficiency. Concurrently, automation streamlines production workflows, reduces labor costs, and improves consistency and quality. Overall, intelligent manufacturing holds the promise of transforming traditional manufacturing practices by forstering greater agility, customization, and efficiency while simultaneously reducing costs and minimizing waste.
Traditional manufacturing processes [17], such as milling or turning, typically involve subtracting materials from a solid bulk. In contrast [18], additive manufacturing (AM) [19], also referred to as 3D printing, constructs objects layer by layer by adding materials precisely where needed based on digital designs. Additive manufacturing offers the flexibility to produce intricate geometries, minimize material wastage, and expedite production timelines. Various techniques have been developed in AM, including fused deposition modeling, stereolithography, selective laser sintering, and others. Fused deposition modeling [20], one of the most widely used and accessible 3D printing technologies, builds objects by depositing successive layers of material, typically thermoplastic filament, to form a 3D structure. This technology is known for its affordability and user-friendliness. Stereolithography [21] utilizes a UV laser to solidify layers of liquid photopolymer resin, resulting in highly detailed and precise parts with smooth surface finishes. Selective laser sintering [22], on the other hand, employs a high-power laser to selectively fuse powdered materials, including metals and ceramics, to create complex and durable objects. Other AM technologies include direct metal laser sintering [23], directed energy deposition [24], electron beam melting [25], binder jetting [26], and material jetting [27]. Additionally, AM has been instrumental in synthesizing bio-inspired materials and structures [28,29]. The versatility and potential of AM extend across industries, from aerospace and automotive to healthcare and consumer goods. Its innovative capabilities are driving profound changes in manufacturing, promising a future shaped by efficiency, customization, and technological advancement.
Artificial intelligence and ML stand at the crossroads of computer science, statistics, mathematics, and cognitive psychology. Artificial intelligence endeavors to engineer systems capable of tasks, typically requiring human intelligence, such as problem-solving, reasoning, and natural language comprehension. Machine learning, a subset of AI, focuses on developing algorithms that enable computers to learn from data without being explicitly programmed. Within ML, supervised and unsupervised learning are prominent paradigms for processing existing data. Supervised ML, encompassing classification and regression, operates on labeled data featuring input features alongside corresponding outputs or targets. Conversely, unsupervised ML tackles unlabelled data, exploring data structure for clustering and dimensionality reduction. Deep learning (DL), a subset of ML, harnesses neural networks with multiple layers to represent transformations and handle complex tasks, such as image recognition [30,31], natural language processing [32], and speech synthesis [33]. This methodology, characterized by its depth, has significantly advanced the field. The ML process entails identifying patterns, correlations, and statistical structures within datasets, empowering the development of intelligent systems for predictive fidelity, decision-making, and task automation. The continuous advancement of AI and ML has catalyzed breakthroughs across diverse domains, including materials science [34,35], hydrology [36], finance [37], and healthcare [38]. Through a combination of rigorous mathematical modeling, algorithm development, and empirical validation, scientists and engineers persistently expand the frontiers of AI and ML, unlocking new capabilities and potentials for intelligent systems.
Reinforcement learning (RL) [39], another vital subset of ML, stands as a fundamental pillar in the realm of AI, mirroring how humans learn to navigate and make decisions in a dynamic environment. Unlike supervised and unsupervised learning, RL doesn’t rely on pre-collected datasets. Instead, the RL agent operates within an environment, iteratively exploring and learning from its experiences to achieve a specific goal through trial and error. Central to RL is the concept of reward, which provides positive or negative feedback from the environment after the agent takes action. The RL agent’s objective is to learn optimal policies or strategies, guiding its decision-making process to maximize cumulative rewards over time. Reinforcement learning has diverse applications across domains like healthcare [40] and recommendation systems [41]. For example, it has excelled in game-playing tasks, often surpassing human performance in games like chess, Go, and video games [42]. In robotics, RL algorithms train robots to efficiently perform complex tasks [43], while in self-driving cars and drones, RL aids in navigation, path-finding [44], and decision-making. Moreover, RL finds utility in algorithmic trading and portfolio optimization, enhancing risk management and investment decisions [45]. In smart grid systems [46], it optimizes energy consumption, facilitates demand response, and integrates renewable energy resources. In summary, RL presents promising solutions for addressing complex real-world challenges where explicit instruction or exhaustive search methods are impractical. Reinforcement learning’s adaptability and learning capabilities make it a versatile tool for tackling diverse problems across multiple domains.
Several reviews [47] have examined the applications of ML in the AM domain. Meng and co-workers [48] provided a thorough overview of supervised and unsupervised ML tasks in AM, focusing on parameter optimization and anomaly detection. They explored regression, classification, and clustering techniques, delving into their roles in enhancing Am processes. In their analysis of regression models, the authors highlighted neural networks and Gaussian process regression as significant tools for parameter optimization [49], property prediction [50], and geometric deviation control [51]. Notably, with its probabilistic characteristics, Gaussian process regression offers the ability to quantify uncertainty [52] – an essential feature in AM applications. The authors discussed popular ML methods like decision trees, support vector machines (SVM), and convolutional neural networks (CNN) [53] for classification tasks related to quality assessment [54], quality prediction, and defect detection [55]. They also addressed challenges such as model overfitting and proposed corresponding solutions to ensure robust performance. Moreover, the authors tackled the issue of dataset size limitations in AM by exploring clustering analysis methods such as the self-organizing map (SOM) model and the least absolute shrinkage and selection operator (LASSO) model. These techniques can effectively handle datasets with constrained sizes, a common challenge in AM research. Overall, this work offered valuable guidance for ideating ML applications, understanding different ML tasks, and selecting appropriate ML models in the AM domain. By synthesizing insights from various ML approaches, their review contributes to advancing the integration of ML techniques in AM processes.
In another comprehensive review, Kuman et al. [56] focused on the applications of ML and data mining techniques in AM design, processes, and production control. They initially summarized the digitization in manufacturing [57] within the framework of Industry 4.0, which encompasses smart factories [58], cyber-physical systems, IoT, and AI. Then, the authors provided an overview of supervised learning, including Bayesian networks, artificial neural networks (ANN), ensemble methods, and CNN. Additionally, they highlighted the role of generative adversarial networks (GAN) alongside CNN [59] in assisting topology design with optimal structures. Modern ML approaches have been employed for synthesizing metamaterials for material design in AM [60]. For AM processes, they reviewed various works utilizing SVM in process parameter optimization [61], long short-term memory (LSTM) in process monitoring [62], CNN in geometric deviation control, and LASSO in cost estimation [63], as well as other works in quality prediction, defects assessment, and closed-loop control. They also outlined the applications of ML in AM planning [64], quality control [65], and printability and dimensional deviation management [66]. Additionally, the authors addressed the unique challenge of data security in AM production. They discussed addressing uncertainty in AM through experiment-based UQ of the AM process [67], melting pool [68], and solidification. In their conclusion, the authors emphasized the integration of AM and ML as a pivotal innovation in the context of the fourth industrial revolution.
The reviews mentioned above primarily concentrated on one subset of ML – supervised learning, and its applications to advance AM process and production. However, they overlooked semi-supervised learning and RL, crucial subsets of ML known for their advantages in data mining, optimizing, and controlling autonomous systems. Furthermore, the rapid accumulation of literature publications in the AM domain warrants an exploration of more recent pioneering studies. Hence, this study endeavors to present a state-of-the-art review of ML in the AM domain, emphasizing recent groundbreaking research and the applications of semi-supervised learning and RL. The structure of this paper is outlined below: Section 2 describes ML techniques. Subsequently, recent pioneering applications of ML and RL in AM are individually reviewed, culminating in the conclusion.

2. Machine Learning

2.1. Supervised Learning

Supervise learning requires a pre-collected dataset to train predictive ML models, with the data labeled with output variables. It can be categorized into two types: regression and classification, depending on the nature of the output targets. Various ML models are available for supervised learning. For regression problems, options include linear and polynomial regression, while logistic regression is commonly used for classification tasks. Other methods, such as SVMs [69], decision trees, and k-nearest neighbors, have variations tailored for handling both regression and classification tasks. These ML algorithms are often referred to as “shallow” because they typically involve only one layer of non-linear transformation to map input features to outputs. For instance, Aoyagi et al. [61] proposed a framework for constructing a process map for AM. They integrated a decision function, representing the porosity density of parts fabricated by AM, into SVM to predict process conditions (good or bad) based on the observations from the parts’ surface. This method was shown to be effective in customizing optimized process conditions with a reduced number of experiments. However, shallow ML algorithms generally have a limited capacity to capture complex patterns in data and are often used for simple tasks.
In contrast, DL models [70] or neural networks with multiple layers of transformations on input features become necessary when dealing with large or complex datasets. One commonly used DL model is the artificial neural network (ANN) or fully connected neural network, which comprises an input layer, one or more hidden layers, and an output layer. The input data is fed into the input layer, where each node represents an input feature. Subsequently, the data passes through the hidden layers successively. Each layer applies weighted connections and activation functions to transform the input data into a more abstract representation. Notably, each neuron in a hidden layer is connected to all neurons in the previous and subsequent layers, rendering the neural network fully connected. Commonly used activation functions include the sigmoid function, rectified linear unit (ReLU) [71], radial basis function (RBF) [72], and the tangent hyperbolic function. The final layer of the network is the output layer, which is responsible for predicting the output targets. The number of nodes in this layer depends on the dimension of the output. No activation functions are typically applied in the output layer for regression tasks, whereas the sigmoid function is used for binary classifications and the softmax function for multiclass classifications. Discrepancies between predictions based on the aforementioned feedforward process and actual outputs result in a so-called loss function. Network training aims to determine proper neuron weights to minimize this loss function. This optimization process involves backpropagation to iteratively update network weights using the gradient descent method or its variations. It’s worth mentioning that physics-informed neural networks [73] have recently garnered attention by incorporating physical laws into neural network training. Consequently, the loss function comprises both data loss and physics loss calculated from differential equations.
Convolutional neural networks (CNNs) [31] constitute a unique class of DL algorithms specifically tailored to process and analyze data with a grid-like topology. Their most prevalent application lies in image processing for computer vision tasks, where images are typically represented as grids of pixels. However, CNNs are versatile and capable of handling various other data types, including videos, two-dimensional grid geological data, three-dimensional volumetric data, and text structured as a one-dimensional grid. A typical CNN architecture comprises convolutional, max-pooling, and fully connected layers, collectively processing input data to make predictions for either regression or classification. Convolutional layers utilize sets of learnable filers or kernels that traverse the input data, performing element-wise multiplication and summation operations, followed by nonlinear activation functions. These operations yield feature maps that capture intricate patterns and feature presentations within the input data. Max-pooling layers are often employed after convolutional layers to downsample the feature maps, effectively reducing the spatial dimensions of the data. Subsequently, the flattened feature maps, as a one-dimensional array, are passed through fully connected layers, whose architecture mirrors that of ANNs, for prediction. During training, the weights and biases of a CNN are iteratively adjusted using optimization algorithms such as gradient descent and backpropagation. This adjustment process minimizes the disparity between predicted outputs and actual targets, enhancing the models’ performance.
Recurrent neural networks (RNNs) [74] constitute another vital class of DL algorithms tailored for handling sequential data, such as text. Unlike standard ANNs, which process a sequence of input independently, RNNs maintain an internal state to retain the memory of past inputs. This dynamic temporal behavior allows them to effectively manage sequences of varying lengths. By sharing network weights across different time steps, RNNs excel at learning patterns within sequential data, making them particularly useful in natural language processing tasks like speech recognition and text generation. Furthermore, when combined with CNNs, RNNs can even process video data consisting of time-series images. However, traditional RNNs encounter a significant hurdle known as the vanishing gradient problem [75], where gradients diminish exponentially over long sequences, making it challenging to learn long-term dependencies. To mitigate this issue, innovative architectures like Long Short-Term Memory (LSTM) [76] and Gated Recurrent Units (GRUs) [77] have been developed. Long short-term memories employ specialized gates – input, forget, and output gates – to regulate the flow of information into and out of the memory cells, facilitating selective retention or discard of information over time. On the other hand, GRUs, while similar to LSTMs, feature a simplified structure with only two gates: an update gate and a reset gate. Recently, the Transformer architecture [78] has emerged as a groundbreaking solution to the limitations of RNNs and CNNs in processing sequential data. Transformers rely exclusively on self-attention mechanisms to weigh the importance of different input elements when generating outputs. This approach enables Transformers to capture long-range dependencies in data more effectively than RNNs and CNNs. Transformers have achieved remarkable success across various natural language processing tasks, including machine translation and question-answering.

2.2. Semi-Supervised Learning

Semi-supervised learning [79] occupies a middle ground between two well-established paradigms: supervised learning, which operates on labeled data samples to establish input-output mappings, and unsupervised learning, which discerns patterns or structures within unlabeled data. In semi-supervised learning, a model is trained using a dataset comprising both labeled and unlabeled samples. The labeled data aids in refining predictions, while the unlabeled data assists in developing more robust representations of the underlying data structure, thereby enhancing the model’s ability to generalize to new, unseen data. Consequently, the overall performance of the model can be significantly improved. Various techniques have been employed in semi-supervised learning, such as self-training, co-training, consistency regularization, and pseudo-labeling. These methods harness the labeled data to initialize the model and then utilize it to make predictions on unlabeled data, iteratively refining the model for enhanced performance.
Self-training [80], a popular semi-supervised learning method, capitalizes on unlabeled data to enhance model performance. Traditionally, this technique involves using an initially trained model on labeled data to generate pseudo-labels for unlabeled samples, which are then incorporated into the training set to update the model. However, this process can be time-consuming and prone to error accumulation due to the use of incorrect pseudo labels. To address these challenges, especially in mitigating error accumulation during self-training, researchers have proposed several alternative solutions. Berthelot et al. [81] introduced a method that averages the results of various augmentation techniques to label unlabeled data samples. Other approaches [82,83,84] have utilized confidence thresholds to control the quality of label assignments, ensuring that only strongly augmented data samples receive labels. Additionally, curriculum labeling [85] has been suggested as another strategy to refine the quality of pseudo-labels during model iterations. Recently, an incremental self-training technique [86] has been developed to discern the positivity of unlabeled data through clustering. This method processes the model in sequential batches to enhance performance. Moreover, a sequential query list has been introduced to streamline the process by reducing the time consumption associated with multiple clustering and queries in iterative learning. These advancements aim to make self-training more efficient and effective in leveraging unlabeled data for model improvement.
Co-training [87,88,89], which originated from self-training, serves as the foundation for the bifurcated method in semi-supervised learning and is readily implementable with most ML algorithms. Initially, co-training algorithms primarily focused on multi-view learning [90,91], which involves training multiple models (referred to as learners) on distinct subsets of features or data samples. Each model learns from labeled data and subsequently collaborates with the other models to label the unlabeled data, leveraging inter-model agreement to reduce uncertainty. Consequently, co-training enhances model generalization by fostering cooperation among multiple learners. The key steps in co-training involve view acquisition, learner differentiation, and label confidence estimation. View acquisition necessitates a delicate balance between the independence and sufficiency of split views. Learner differentiation arises from employing basic models, selecting optimization algorithms, and configuring learner parameters (i.e., model parameters). Estimating label confidence is crucial for avoiding incorrect labeling scenarios. In constrast, single-view learning in co-training does not mandate feature splitting, aiming to previed individual models from converging into similar hypotheses. Single-view learning [92,93,94] capitalizes on view redundancy and conditional independence, thereby providing initial models or learners with richer information form the data.
Notably, pseudo-labeling [95], another popular semi-supervised learning technique, combines the principles of self-training with traditional supervised learning. Pseudo-labeling is effective when the model’s predictions on the unlabeled data are reliable, which typically occurs when the model’s confidence in its predictions is high. However, setting a confidence threshold is essential to avoid including unreliable pseudo-labels, which could degrade performance. Additionally, pseudo-labeling may not be suitable for datasets where the distribution of the labeled and unlabeled data significantly differs. By implementing these advanced techniques, self-training and pseudo-labeling can substantially improve the performance and robustness of ML models, particularly in scenarios where labeled data is scarce or expensive to obtain. Moreover, co-training has been successfully applied across various domains, demonstrating its flexibility and effectiveness in leveraging unlabeled data to improve model performance. By utilizing multiple learners and ensuring high confidence in pseudo-labels, co-training can significantly reduce the reliance on large labeled datasets, making it a valuable technique in semi-supervised learning.

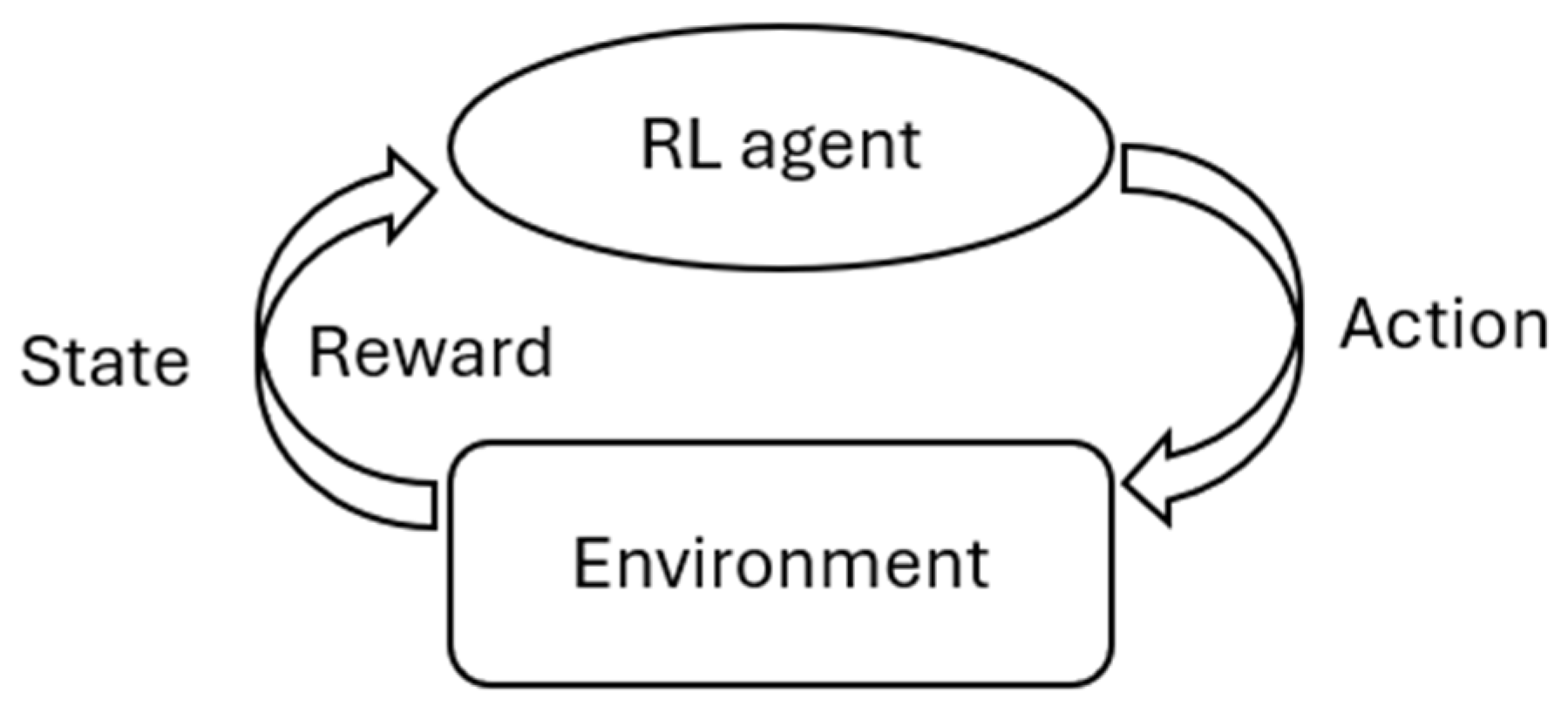
2.3. Reinforcement Learning

Unlike supervised learning, RL [39], another subset of ML, does not rely on pre-existing data sets. Instead, an RL agent (typically a computer program) learns from its experiences by interacting with its surroundings or environment, as depicted in Figure 1. A fundamental assumption in RL is that the environment is fully observable, meaning the agent can determine its environment’s configuration or state through observations. Consequently, the agent can choose an action to take based on the current state. Upon executing the selected action, the environment transitions to another state, and the agent receives a reward as feedback. This learning process is iterative. A mathematical framework known as the Markov decision process [96,97] is commonly used to describe the interaction between the agent and its environment during learning. The key components of this framework include a state space, an action space, a transition function, and a reward function. The transition function denotes the probability of the agent moving from the current state to the next state after taking an action, while the reward function determines the feedback the agent receives during this transition. The objective of RL for an agent is to accumulate rewards, often referred to as the expected return or utility, to the maximum extent possible. The output of RL corresponds to the agent’s optimal behavior function, or the optimal policy, which maps a state to the action the agent should take.
There are two primary classes of methods for solving RL problems: model-based and model-free [39]. Model-based RL methods, such as policy iteration and value interaction, aim to determine optimal value functions using dynamic programming techniques [98]. These value functions quantify the expected return an agent can achieve from specific states or state-action pairs. The state value function represents the total reward an agent can attain starting from a particular state. Conversely, the state-action value function, also known as the action value function, indicates the expected return an agent can obtain by starting from a state and taking a specific action. Once the optimal value functions are derived, determining the optimal policy becomes feasible, as the agent tends to select actions associated with the highest values.
Another type of RL method is model-free, which assumes that agents have no knowledge of transition probabilities and reward functions, reflecting most practical applications. Early model-free RL methods include the Monte Carlo method and Temporal Difference methods, both of which are value-based RL methods. Q-learning [99] is another widely used value-based RL method. During the learning process, the agent selects the best action according to the current knowledge of the action value function at each step, receives a reward as feedback, and updates the action values through the Bellman equation [39]. It should be noted that the epsilon-greedy action selection technique is usually adopted to balance exploration and exploitation. Over many episodes, the action values converge to their optimal values, from which the optimal policy can be derived. Conventional Q-learning is a tabular method where a table stores action values with respect to the finite state and action spaces. If the state space and/or action space are extremely large or continuous, an ANN can be employed to approximate action values. This method is called Deep Q Network (DQN) [100] and is one of the methods in deep reinforcement learning (DRL). In addition to value-based RL methods, another type of model-free RL method is policy-based. These methods directly update and converge to the optimal policy rather than the optimal value function. Policy gradient methods [101] are a typical family of policy-based RL methods, with Proximal Policy Optimization (PPO) [102] being a notable example.

3. Applications of Supervised Learning in Additive Manufacturing

Recent applications of supervised learning in AM include predicting the fatigue life of AM materials such as metal alloys and quality detection of AM-manufactured parts. Various ML methods, particularly DL methods, have been utilized. These include SVMs, ANNs, CNNs, and RNNs.

3.1. Fatigue Life Prediction

Dang et al. [103] addressed the critical aspect of fatigue and service life prediction in AM products by employing support vector regression (SVR). Their study focused on thirty specimens of titanium alloy produced via the laser-induced energy deposition (LDED) method, followed by double-annealing heat treatment. Subsequently, constant-amplitude fatigue tests were conducted across three different stress levels to measure the fatigue lives, which served as labels or outputs. Microstructural analysis, facilitated by an optical microscope and scanning electron microscope (SEM) [104], enabled the examination of the specimens for defects, particularly pores. The input features in their study included the range of stress intensity near pores, pore type, the distance-size ratio (the ratio of the distance from a pore to the free surface to the equivalent diameter of the pore), pore area, and the peak stress applied on the specimen. The range of stress intensity was calculated using Murakami’s approach [105], which was instrumental in evaluating stress distribution around pores. Pore type, a categorical feature, categorized pores into four types based on SEM images, considering pore size and facet visibility. Various SVR models were trained using different combinations of input features. It was found that a model incorporating two features, the range of stress intensity and pore type, demonstrated superior performance in terms of errors and correlation coefficients. Additionally, alternative ML models were evaluated, including ANNs, random forest, and Gaussian process regression. The comparative analysis underscored the effectiveness of the SVR model in accurately predicting fatigue life for the LDED titanium alloy specimens.
Using the ML model to predict the fatigue life of AM products requires fabricating and measuring a sufficient number of samples, which is often impractical. Recent studies have proposed incorporating physics knowledge into “black-box” ML mode to address this issue. Salvati and colleagues presented pioneering work [106] where they developed a physics-informed neural network (PINN) framework to predict the finite fatigue life of defective materials. The dataset was provided by Romano et al. [107], who fabricated aluminum alloy samples using AM techniques like selective laser melting (SLM). These samples underwent CT scans to reconstruct the morphology and location of defects. The morphological features include the defects’ volume, external surface, and the projection of the external surface onto the plane normal to the direction of the applied load. From these features, the sphericity and diameter of the defects can be calculated. Additionally, the distance between the defects and the free surface of the specimen can be evaluated through CT scans. Fatigue testings were conducted by applying a cyclic load of constant stress amplitudes, and the fatigue lives were measured. The samples were then investigated using fractography to detect pores, referred to as killer defects, where fatigue cracks were triggered. In their proposed PINN framework, the neural network is enforced with phenomenological constraints from physics, specifically the linear elastic fracture mechanics (LEFM) model. In addition to the data loss from the direct prediction of the neural network, the physics loss was determined from Basquin’s law for stress-fatigue life diagrams. The sum of these two loss functions was employed in the backpropagation process to optimize the network weights and bias. This research highlighted that incorporating physics laws into the neural network could be highly effective for accurately predicting the finite fatigue life of materials.
In another recent study, Wang et al. [108] introduced physics-guided ML frameworks aimed at enhancing fatigue life prediction in AM materials. Traditionally, the evaluation of fatigue life, particularly fatigue crack growth life, relies on the application of Paris’ law [109], incorporating empirical model parameters. However, this physics-based model often overlooks the influence of defect characteristics such as size and location. To address this limitation, data-driven approaches like ML [110] prove beneficial. The authors employed two ML models, SVR and ANN, with inputs comprising the range of applied stress and defect features. They devised adaptive ML models by employing Bayesian optimization to fine-tune model hyperparameters and k-fold cross-validation for robustness. These models were trained and assessed using three different AM materials, Aluminum alloy [111], Titanium alloy [104], and alloy steel [112], across datasets varying in size from 8 and 30. Their findings suggested employing the ANN model for scenarios with limited data and the SVR model for relatively large datasets. Additionally, they extended this physics-guided ML framework to a probabilistic model using maximum likelihood estimation. The study demonstrated that while the physics-based Paris’ law ensures predicted results consistent with physical observations, data-driven approaches account for the variability in fatigue lives attributed to defect features. Ultimately, the integrated physics-guided ML model maintained high prediction accuracy while mitigating overfitting issues associated with limited fatigue data.
A research study by Fan et al. [113] advanced the development of a generalized ML framework to predict fatigue strength for different AM materials. The dataset was derived from manufacturing and testing six AM materials widely used in aerospace: Ti and Ni-based superalloys. In addition to load conditions like temperature and stress ratio, the model primarily considered material properties such as Young’s modulus, density, and tensile properties, including tensile strength and yield strength. The correlations among input features were investigated. Despite a strong correlation between tensile strength and yield strength, both were included as input features due to their respective importance in plastic deformation ability and resistance to failure. This study employed three advanced supervised learning models: residual neural network (ResNet), gradient boosting decision tree (GBDT), and light gradient boosting machine (LGBM). The findings revealed that the ML model with ResNet outperformed the other two models. Additionally, Gaussian noise was introduced to the input features, demonstrating the robustness of the proposed ML models. However, using GBDT in the ML model resulted in the best robustness compared to the other two ML models.
Gao et al. [114] explored the predictability of various ML models in forecasting the fatigue life of Titanium structures produced via AM methods, such as electron beam melting (EBM). The ML regression models examined in this study comprised multiple linear regression (MLR), ANNs, SVR, and random forests (RF). Initially, the study assessed the influence of density, porosity, yield stress, and fatigue stress on the predicted fatigue life of samples. The resulting correlation matrices and heatmaps emphasized the significant impacts of yield stress and fatigue stress on the target prediction. Consequently, yield stress, which exhibited a positive correlation with fatigue life, and fatigue stress, which demonstrated a negative correlation, were selected as the input features. Following the training and evaluation of the aforementioned four regression models, the authors observed that all models demonstrated excellent predictive capabilities. MLR displayed superior predictive performance at a 95% confidence interval, followed by the SVR model. Furthermore, the study addressed hyperparameter tuning and generalization for each model. Specifically, for the ANN model, three or four neurons were recommended for the first hidden layer. For the SVR model, a coefficient of 0.0001 for the RBF kernel function and a regularization hyperparameter of 30 were suggested. It was also recommended that the RF model utilize three estimators with a maximum tree depth of seven.

3.2. Quality Detection

Convolutional neural networks have become a standard tool for assessing the quality of parts produced through AM, particularly in scenarios where surface polishing post-processing affects wear resistance and residual stresses. Abhilash and Ahmed [115] integrated CNN classification into the process of electrical discharge-assisted postprocessing to enhance the surface quality of AM components. In their study, titanium alloys were prepared using a direct metal laser sintering 3D printer. The researchers selected the lowest discharge energy regime for polishing the samples. Images captured through an optical microscope were fed into a CNN architecture comprising five convolutional layers followed by a fully connected layer for prediction. This task at hand was a multiclass classification problem, with five surface categories reflecting different levels of surface roughness. Each class had 50 data samples (images) that were manufactured and polished under distinct printing and process parameters. To expedite model training, the study leveraged the pre-trained ResNet50 model. Subsequently, the convolutional layer weights were transferred to the proposed CNN model, with only the weights of the fully connected layer and the output layer being fine-tuned. The researchers employed a fivefold cross-validation approach during the model training, achieving an impressive overall accuracy of 96%. Notably, all false negative predictions were confined to borderline classes, indicating the robustness of the CNN model in discerning subtle differences in surface quality.
In a separate study, Ansari et al. [116] investigated defects in surface deformation arising from laser powder-bed fusion (LPBF), which can significantly impact the mechanical and physical properties of manufactured AM parts. However, previous research did not address real-time identification of surface deformation. This study proposed a novel real-time approach to classify surface deformation problems during LPBF processing using a powder-bed image as the input for each data sample. To gather data samples, 13 bar-like geometries were deigned and printed using an EOS printer equipped with cameras and sensors to capture each layer during the printing process. The collected powder-bed images were categorized as either normal or defective. The initial dataset consisted of 1022 images converted to grayscale. Detecting defects early is crucial to halt defect propagation promptly. Hence, the selection of relevant data samples yielded a final dataset comprising 239 normal images and 14 defective images. Given the dataset’s significant imbalance, data augmentation methods were employed. This study utilized CNN to classify the images. Three distinct model architectures were developed and tested, incorporating techniques such as early stopping, learning rate variation, and employing various model evaluation metrics to refine the model. The results showcased exceptional model performance, achieving an accuracy of up to 99%. The study also concluded that employing a balanced dataset through data augmentation could lead to a more generalized and unbiased ML model.
Moreover, Banadaki et al. [117] devised another real-time CNN model integrated into an automated grading system to oversee the fused deposition modeling process, one of the prominent AM processes. They established an image acquisition system equipped with a high-resolution camera to capture the videos during printing. Subsequently, the data was collected by converting the videos to frames representing 21 classes based on the temperature and speed settings of the AM process. The images were manually inspected to retain only those providing proper views of the printing area. Consequently, a total of 5000 images were obtained, from which a randomly selected subset of 100 images formed the testing set. They employed a CNN architecture within a DL framework, incorporating the aggregation layers, such as convolutional and pooling layers between low-level and high-level layers. Low-level layers were utilized for spatial feature extraction, while high-level layers extracted high-order features or patterns before passing them to the fully connected layers for classification. Various metrics, including accuracy, F1-score, sensitivity, and precision, were employed to assess the developed CNN model. Remarkably, exceptional accuracies exceeding 93% were achieved for all classes. Additionally, the F1-scores indicated relatively varied accuracies among classes with different printing settings. Once the quality predictive model was developed, it was utilized to detect the significance of the defects during the 3D printing process and monitor the process’s quality.
Conrad et al. [118] designed a comprehensive end-to-end workflow for efficiently sorting AM-manufactured parts based on specific post-processing requirements. The initial stage of this automated process involved image rendering, wherein synthetic images were generated from CAD models representing the AM parts. Notably, a variety of simulated camera angles were employed during rendering, accompanied by data augmentation techniques to ensure sufficient diversity in the training data. Subsequently, pre-trained image classification neural networks were adopted and fine-tuned using the training image dataset. In the final step, the trained neural network was deployed to recognize the parts, with the resulting classification recommendations presented to the user via a graphic user interface (GUI). The GUI displayed the top three class predictions for the user to assess and compare with the actual part. To evaluate the framework, the authors constructed a test set comprising 30 distinct parts, yielding a total of 1200 images. Three pre-trained CNN architectures, namely MobileNetV2 [119], ResNet-50 [120], and VGG16 [121], were employed, with VGG16 achieving the highest average part classification accuracy. Furthermore, the authors enhanced the industrial applicability of their workflow by integrating physics simulation into the rendering process. In an industrial case study with 215 distinct parts, the part classification accuracies reached 99.04% for the top three predictions and 90.37% for the top one.

3.3. Process Modeling and Control

To mitigate uncertainty in the mechanical properties and quality of parts produced using fused filament fabrication (FFF), Wenzel et al. [122] developed a DL method aimed at enhancing the AM processing system’s reliability by optimizing input parameters and predicting system responses. Latin Hypercube sampling [123] was employed for experimental design to efficiently explore the input feature space and generate data. The DL framework comprised an RNN and an ANN. The RNN was tasked with estimating a behavior vector based on the input parameters and past observations of the system, while the ANN predicted the system responses. This approach facilitated the identification of significant input parameters crucial for establishing a reliable AM processing system. The principle of PIML [124] was integrated into this DL method. Domain knowledge, expressed through physical laws, was utilized to initialize neural networks, facilitating the learning of fundamental correlations between features. This aspect was essential for the method’s applicability across different FFF 3D printing systems. For practical implementation in mass production, the authors addressed the controllability of print bed adhesion. Relevant domain knowledge, including various measurements and datasets, was extracted from scientific literature [125] and incorporated into the proposed neural networks. A case study involved four 3D printers in a temperature- and humidity-controlled environment. Four hundred experiments were designed, resulting in 1273 print bed adhesion measurements, with 20% forming a testing set. Compared to a statistical approach, the proposed method exhibited a significantly lower Root Mean Square Error (RMSE), especially when limited measurements were available.
Modeling over-deposition is critical in controlling laser metal deposition (LMD) processing to prevent additional materials from being melted onto the substrate. Perani et al. [126] developed an LSTM model to simulate over-deposition, focusing on nickel alloys with various shapes deposited via LMD. Data collected during and after deposition included deposition head positions, laser activation signals, melt pool images, and deposited shapes. After data fusion, several new input features were incorporated, such as deposition speed and two variables representing the geometry of deposited shapes. Sequences of input features for 20 deposition steps were fed into the LSTM to predict deposition height for the next time step. The relative errors on the testing sets ranged from 6% to 11%. The results underscored the importance of selecting simple geometries to construct the training set for modeling the LMD deposition process. The authors intended to utilize this model in closed-loop control of deposition parameters during real-time processes, indicating its potential for practical application in enhancing LMD processing control and efficiency.
Inyang-Udoh and colleagues [127] developed a predictive geometry control framework for jet-based AM 3D printing processes. A key component of this learning-and-control framework was a physics-guided data-driven model [128], which utilized a convolutional recurrent neural network (convRNN) to forecast the height evolution of AM manufactured parts across various scenarios. This enabled both feedforward and feedback control. The convRNN model parameters were determined by training the network with data from a limited number of layers during the printing process. Notably, the model could be represented in dual forms, where the layer droplet input pattern became the network parameters, making the network architecture interpretable in physical terms. This model was integrated into a feedforward control scheme, with experimental findings demonstrating its superiority over state-of-the-art open-loop control methods for 3D printing processes. Furthermore, the researchers developed an online learning algorithm for the convRNN model and implemented it into a feedback control system. They also conducted stability analyses of the developed model predictive control framework using Lyapunov theorems. The physics-guided principle allowed minimal computational effort to update the convRNN model while effectively controlling the printing system in practical applications. Additionally, the online learning and feedback control strategy mitigated process uncertainties and enhanced the geometric accuracy of the printed parts.
Huang et al. [129] developed a novel method named Multi-Fidelity Point-Cloud Neural Network (MF PointNN) for surrogate modeling of the melt pool, which is critical for uncertainty quantification and quality control in metallic AM processes, such as electron beam AM. They generated a high-fidelity (HF) dataset comprising 280 data points using finite element modeling and simulation under uncertainty. The input features included controllable and uncontrollable parameters, while the output targets represented the thermal field response. Controllable parameters included preheating temperature, electron beam power, and beam velocity. Uncertainty stemmed from uncontrolled parameters treated as random variables, such as the absorption efficiency of beam power and material and thermal properties of titanium alloy powder, including thermal conductivity, specific heat capacity, and density. Moreover, they derived a low-fidelity (LF) dataset of 280 data points from finite element simulations with coarser meshes compared to those used for HF data. In the proposed MF PointNN framework, an LF PointNN was initially trained based on the LF training samples. Subsequently, by freezing certain network coefficients of the LF PointNN, a new PointNN was fine-tuned using the HF training data. The efficacy of this method was evaluated by comparing predictions with various methods, including finite element analysis, surrogate modeling using Kriging and Singular Value Decomposition (SVD), and a standard MF modeling approach using Kriging and SVD [130]. The results demonstrated that the proposed method enhanced the prediction performance of 3D thermal fields while utilizing a limited number of training data samples, thereby reducing the computation cost associated with finite element analysis.
Yu and co-workers [131] investigated the stability of the cladding layer’s formation during the wire arc additive manufacturing (WAAM) process, which significantly influences the final dimensional precision of WAAM weldments. The experiments utilized the cold metal transfer process, examining four different welding gun offsets in addition to a no-offset setup. Each experiment generates a dataset of 750 samples, comprising temperature distribution images on the weldment sidewall as inputs. The objective was to develop a DL model for cladding layer offset recognition, constituting a multi-class classification problem. The authors employed a CNN, integrating identity maps to facilitate the training of exceptionally deep networks. The overall detection accuracy achieved an impressive 99.84%.

4. Applications of Semi-Supervised Learning in Additive Manufacturing

Manivannan [132] introduced a novel semi-supervised DL approach for automatic quality inspection in AM processes, including selective laster sintering (SLS). Unlike other automated quality inspection systems that rely solely on fully supervised learning and require large amounts of labeled data or images, the proposed approach harnessed both labeled and unlabeled data, thereby reducing the need for manual labeling efforts. In this approach, a CNN was utilized, and the loss function comprised the cross-entropy of the labeled images, the cross-entropy of the pseudo-labeled images (where unlabeled images were assumed to have true labels), and an entropy regularization term [133] representing the probabilities of unlabeled images belonging to the true class. The training procedure involved three steps. Initially, only labeled data was fed into the model, and the CNN weights and biases were iteratively adjusted to minimize the loss function. Next, the output probability of each unlabeled data was predicted, and a margin criterion was applied to assign a weight to the data. Finally, the combination of labeled data and weighted unlabeled data formed a new training set to update the CNN model. This approach was applied to a dataset for SLS powder bed defect detection. The results demonstrated excellent model performance with an accuracy of 98%, comparable to other sate-of-the-art approaches [134], despite using only 25% of the labeled training data samples. Additionally, the author successfully applied the proposed approach to other publicly available defect inspection datasets [135,136,137,138], highlighting its flexible and extensive applicability.
Numerous supervised learning endeavors [139,140,141] have been undertaken to efficiently monitor the quality of products produced through LPBF, a metal AM technique. Nguyen et al. [142,143] proposed a semi-supervised ML approach aimed at minimizing the effort required for labeling training data samples to detect overheating in LPBF. For data collection, they utilized a digital camera to capture layer-by-layer monitoring images of the powder bed following laser scanning or powder recoating. Only the images captured after laser scanning were employed to train the ML model. This model, which featured the DeepLab v3 + network with Xception as its backbone, was designed to classify characteristic appearances at the pixel level. Data augmentation techniques were applied to prevent overfitting and enhance the model’s robustness. Subsequently, the classified apearances were correlated with post-process characteristics such as surface roughness, morphology, and tensile strength to ascertain the quality of LPBF products, which were categorized as anomaly-free, exhibiting lack of fusion, or overheated. The results demonstrated that the trained ML model possessed the capability for defect detection and quality prediction across various geometries of products. The authors suggested that this approach could be extended to other 3D printing processes. Additionally, integrating thermal history data and employing RNNs could further enhance the model’s ability to predict quality and confirm the occurrence overheated defects.
Several studies have focused on anomaly detection during AM processes using ML techniques [144,145,146,147] to anticipate flaws or porosity in products. However, many of these approaches overlooked the dynamic nature of the manufacturing process. In a novel approach, Larsen and Hooper [148] proposed a methodology to construct a data-driven model of the LPBF process dynamics, leveraging high-speed cameras co-axial with the laster to capture real-time process signatures during material fusion. By considering the process dynamics, they framed the problem as utilizing sequences of historical observations (i.e., images), process system states, and control inputs to predict residual error between the predicted and observed states at the current time, termed the dynamic signature. This method involved multiple models. An autoregressive model with additional inputs was employed to approximate the first-order Markov chain governing the evolution of the AM process. Additionally, a variational autoencoder was utilized to extract latent variables associated with the images. Principal component analysis was then appplid to reduce the dimensionality of these latent variables. Suebequently, a variational RNN was developed to process sequence data from previous time steps and predict the current state. Anomally detection was performed by computing Kullback-Leibler divergence at each time step to assess accumulated errors. The effectiveness of this approach was evaluated across various level of porosity in AM products, achieving an impressive receiver operating characteristic area under curve of up to 0.999.
In a separate study, Pandiyan et al. [149] proposed a semi-supervised approach, utilizing ML algorithms exclusively with data from the defect-free regime of LPBF processes to predict anomalies. The experiments involved creating overlapping lines to contract a defect-free cube of nickel-based super-alloy. Various combinations of laster power and scanning velocity were tested to induce different LPBF process regimes, encompassing phenomena such as balling, lack of fusion pores, conduction mode, and keyhole pores. Data acquisition was facilitated using acoustic sensors, with acoustic emission signals being normalized. Two generative CNN architectures were developed in this work. One architecture utilized a variational autoencoder, a commonly employed technique for tasks such as image denoising [150], dimensionality reduction [151], feature extraction, image generation, machine translation, and anomaly detection [152]. Typically, the encoder and decoder networks can efficiently learn the data representation in a dense manner and reconstruct the original input. The other architecture was based on a generative adversarial network [153], consisting of a generative network and a discriminative network, designed to generate new distribution samples from the training set. Both methods yielded impressive accuracies of 96% and 97% for anomaly detection, respectively.

5. Applications of Reinforcement Learning in Additive Manufacturing

Close-loop control systems have been developed to regulate the AM processes, allowing for the adjustment of process parameters during production to ensure quality control. For instance, Wang et al. [154] designed a high-speed thermal sensor and a proportional-integral-derivative (PID) controller, implementing them on an LPBF testbed. They used thermal emission, measured by the thermal sensor, as feedback to the controller because it correlated with the metal pool size. The control output was an analog voltage signal representing laser power. The experiments demonstrated that this system significantly improved printing quality, as assessed through microscopic imaging and 3D scanning. As an important subset of ML, RL offers advantages for handling optimization and control problems, particularly in the context of quality control and scheduling optimization of AM processes.

5.1. Quality Control

In recent years, researchers have increasingly focused on using RL to optimize process parameters in AM processes. Dharmawan et al. [155] proposed a model-based RL and correction framework to control multi-layer and multi-bead (MLMB) deposition in robotic wire arc additive manufacturing (WAAM). The model-based RL approach in this study was utilized to learn an optimal relationship between process inputs and print outputs. To establish the transition from one state to another after taking action (i.e., changing process inputs), the authors collected a dataset along the print path by discretizing it into waypoints with local states and actions. A Gaussian process regression model was then trained as the Kriging dynamics function. Additionally, the quality of the layer’s surface was periodically assessed, and the necessary corrections were made if needed. The authors experimentally demonstrated and evaluated this learning-correction framework on a robotic WAAM system, testing it with bronze and stainless steel materials. Results showed that the standard deviation of the surface height of each printed layer was significantly reduced compared to using single-bead parameters during the WAAM processes.
Knaak et al. [156] proposed a novel analysis approach combining CNN and RL methods to monitor product quality in LPBF AM processes. They employed image-based surface roughness estimation, acquiring high dynamic range optical images of the product’s top surfaces. These images were processed through CNNs to classify surface roughness and defective areas into five categories, ranging from very low roughness to surface distortion. Transfer learning was utilized to enhance the ML model’s performance. Subsequently, a model-based RL method was used to train an agent to learn the optimal policy for selecting the best LPBF process parameters based on a given state during the AM process. This study employed an MDP framework, where the applied laser power, scan velocity, mean surface roughness, and percentage of defective area represented an MDP state. The action space consisted of process parameters, specifically laser power and scan velocity combinations to be applied in the next layer. A random forest algorithm was also used to approximate system dynamics, serving as the transition probability function in this MDP framework for LPBF processes. The agent received rewards based on the percentage of surface defects at each state, with a higher positive reward given for a smaller defective surface area. The optimal policy was learned to maximize accumulated rewards to ensure product quality.
Ogoke and Farimani [157] presented a DRL framework designed to derive a versatile control policy for minimizing the likelihood of melting defects during LPBF processes. In this study, they employed a model-free and policy-based RL method, PPO, in which the policy was directly optimized. The state space was defined by sequential observations of the temperature field, including nine heat maps of the local temperature distribution around the laser’s current position. These heat maps were numerically encoded and fed into a fully connected neural network as the policy network to predict an action. The action space comprised various velocities or powers of the laser, while the reward was defined as the absolute error between the target melt depth and the current depth. The algorithm was trained on a simulator, acting as a virtual environment for the agent to interact with. The simulation involved modeling heat conduction of a moving heat source, approximating the laser, within a rectangular domain. Assumptions included considering only conduction models of heat transfer, assuming thermal properties to be temperature-independent, and treating the powder bed as a solid continuum. The simulation results indicated that the errors could be reduced by up to 91%. Additionally, the authors discussed the potential for extending this method to experimental applications through the NIST AM metrology testbed [158].
Recently, Shi et al. [159] developed another DRL framework to enhance the uniform temperature distribution during the laser directed energy deposition (DED) of nickel-based alloys. They first created a fast and efficient temperature simulation model of the deposition process, reducing computational costs while maintaining AM processing speed. This simulation model assumed a straight-line movement of the laser beam and employed the Rosenthal equation [160] to evaluate temperatures at different sampling points on both sides of the product. In their RL framework, the continuous state space was represented by the substrate’s thermal distribution, the sample’s thermal distribution, and material properties. The available actions included varying laser power, scanning speed, the deposition axis, and the deposition direction. Additionally, the transition probabilities were determined by the temperature simulation model. They employed the PPO algorithm, a policy-based RL method. Specifically, a state, presented by a three-dimensional tensor, was fed into a CNN for feature extraction before applying critic and actor networks to update the policy. Notably, after the optimal policy was learned through simulations, it was evaluated in a DED processing environment. The results demonstrated that the derived policy improved temperature uniformity in the products, thereby enhancing their hardness.
Dharmadhikari et al. [161] introduced an RL methodology transformed into an optimization problem for metal AM processes to ensure repeatability, control material microstructure, and minimize product defects. They proposed an off-policy RL framework based on Q-learning, a value-based RL method, for the agent to learn optimal process parameters, which included combinations of laser power and scan velocity to maintain a steady melt pool depth. Specifically, the state was represented by discrete process parameters, and the actions were the parameter changes. A Q-table was maintained and updated during the learning since both state and action paces were finite. A digital twin, developed based on Eagar-Tsai formulation [162], emulated the laser DED environment with which the agent interacted. The model calibration was conducted experimentally on a laser DED system using various laser powers and scan velocities for single-track and single-layer deposits of SS316L powder on a SS304 substrate. Additionally, the experimentally-derived process map served as a validation tool to evulate the optimal process parameters learned from the RL framework. The authors also investigated the effects of various hyperparameters on the learning process, including domain discretization, the exploration-exploitation tradeoff parameter, discount factor, learning rate, and number of episodes. This study emphasized RL as an alternative approach for process parameter optimization, particularly when system iformationn or large datasets were unavailable.
In another pioneering work, Chung et al. [163] employed a model-free RL method to achieve optimal defect mitigation strategies for quality assurance during fused filament fabrication. The method they used falls into the category of online learning-based methods, designed to update the model incrementally as new data becomes available, rather than training it in a batch mode with a pre-provided and fixed dataset. However, the limited number of samples for shape deviation during the AM process posed a challenge for the practical utilization of online RL. To address this challenge, the authors proposed a transfer-learning-based approach called continual G-learning aimed at detecting and mitigating new defects during printing while reducing the need for extensive training samples. Specifically, continual G-learning integrated both offline and online prior knowledge. Offline prior knowledge was obtained from literature or previously experimental datasets, while online knowledge was acquired during printing. Additionally, both the reward incurred in the AM process and the information cost were considered in the expected return, which was maximized as the objective. The authors designed an experimental platform to evaluate the performance of the proposed RL framework. The results demonstrated that this method significantly improved online defect mitigation in the AM process.

5.2. Scheduling

Reinforcement learning has also been applied to optimize AM scheduling of multiple machines. Alicastro et al. [164] proposed an RL-iterated local search (ILS) meta-heuristics to achieve optimal solutions with low computational costs. The scheduling problem considered in this study was based on the selective Laser Melting (SLM) process to increase the utilization of machines and decrease the average cost of setup and post-processing operations. The problem definition was similar to that of batch processing machine (BPM) problems. However, in an AM scheduling problem, the processing time of a job depends not only on the total volume of the parts but also on the maximum heights of those parts. The proposed ILS algorithm was based on genetic algorithms with the variable neighborhood search, using a Q-learning approach as the local search to improve solution performance. Such a local search could effectively and efficiently choose the best neighborhood to explore for optimal solutions. The computational experiments were conducted to illustrate that the developed method reached optimal solutions faster than other approaches, especially for large productions.
Ying and Lin [165] recently investigated two-stage assembly AM machine scheduling problems (AMMSPs), where multiple parts were produced through job batches in the production stage before being assembled into the final products in the assembly stage. The authors accounted for different specifications of each part and adopted the mixed-integer linear programming (MILP) model [166] to define the AMMSPs as optimization problems. Subsequently, they proposed an RL meta-heuristics, specifically the iterated epsilon-greedy (IEG) algorithm, to balance exploration and exploitation during the scheduling optimization. The goal of the induced optimal scheduling was to reduce the makespan by placing parts in appropriate batches during the production stage and shortening the waiting time for product assembly. To demonstrate the performance of the proposed framework, they utilized the iterated greedy (IG) algorithm as a baseline on a benchmark problem, with numerical experiments and data described in previous works [166,167]. The results underscored that the proposed IEG algorithm was effective, efficient, and robust in solving AM scheduling problems.

6. Conclusions and Outlooks

This state-of-the-art review highlights pioneering works from recent years, focusing on diverse perspectives of ML technologies and their applications in AM processes. In addition to supervised learning, this review emphasized the significance of semi-supervised learning and reinforcement learning, which are gradually gaining traction in the field of AM research due to their distinct advantages. Despite not being widely adopted in AM research, semi-supervised learning offers promising opportunities. Reducing the need for extensive labeling can accelerate ML model training processes. Moreover, semi-supervised learning enables better generalization compared to supervised learning, as the model can learn from a broader data distribution. This aspect is particularly valuable in AM where data collection and labeling can be time-consuming and resource-intensive.
Traditionally, the optimization of process parameters for AM has relied on offline heuristic methods or supervised learning with pre-collected datasets. However, many of these methods may be suboptimal and lack generalization across different manufacturing scenarios. Reinforcement learning, especially online RL methods, presents a promising alternative for AM process control and optimization. Reinforcement learning offers dynamic and adaptable solutions, allowing systems to learn and optimize process parameters in real time based on feedback from the environment. By iteratively interacting with the manufacturing process, RL algorithms can discover optimal strategies for AM, leading to improved efficiency, quality, and flexibility. As the field continues to evolve, integrating RL-based approaches into AM workflows can revolutionize manufacturing practices, enabling more efficient and adaptive production processes.
In conclusion, exploring ML, especially semi-supervised learning and RL, in the context of AM represents a promising avenue for future research and development. Embracing these advanced ML techniques has the potential to address key challenges in AM, leading to enhanced defect detection, quality assurance, process control, optimization, and overall performance.

Author Contributions

Conceptualization, S.X; Writing – Original Draft Preparation, S.X.; Writing – Review & Editing, J.L., Z.W, Y.C, S.T.; Supervision, S.X.; Project Administration, S.X.; Funding Acquisition, S.X.

Funding

This research was funded by the U.S. Department of Education with grant number #P116S210005.

Ethics Statement

Not applicable.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Wang, B.; Tao, F.; Fang, X.; Liu, C.; Liu, Y.; Freiheit, T. Smart Manufacturing and Intelligent Manufacturing: A Comparative Review. Engineering 2020, 7, 738–757. [Google Scholar] [CrossRef]
  2. Yuan, C.; Li, G.; Kamarthi, S.; Jin, X.; Moghaddam, M. Trends in intelligent manufacturing research: a keyword co-occurrence network based review. J. Intell. Manuf. 2022, 33, 425–439. [Google Scholar] [CrossRef]
  3. Phuyal, S.; Bista, D.; Bista, R. Challenges, Opportunities and Future Directions of Smart Manufacturing: A State of Art Review. Sustain. Futur. 2020, 2, 100023. [Google Scholar] [CrossRef]
  4. Arinez, J.F.; Chang, Q.; Gao, R.X.; Xu, C.; Zhang, J. Artificial Intelligence in Advanced Manufacturing: Current Status and Future Outlook. J. Manuf. Sci. Eng. 2020, 142, 1–53. [Google Scholar] [CrossRef]
  5. Kim, S.W.; Kong, J.H.; Lee, S.W.; Lee, S. Recent Advances of Artificial Intelligence in Manufacturing Industrial Sectors: A Review. Int. J. Precis. Eng. Manuf. 2021, 23, 111–129. [Google Scholar] [CrossRef]
  6. Yang, T.; Yi, X.; Lu, S.; Johansson, K.H.; Chai, T. Intelligent Manufacturing for the Process Industry Driven by Industrial Artificial Intelligence. Engineering 2021, 7, 1224–1230. [Google Scholar] [CrossRef]
  7. Wang, J.; Ma, Y.; Zhang, L.; Gao, R.X.; Wu, D. Deep learning for smart manufacturing: Methods and applications. J. Manuf. Syst. 2018, 48, 144–156. [Google Scholar] [CrossRef]
  8. Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent Manufacturing in the Context of Industry 4.0: A Review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
  9. Gupta, P.; Krishna, C.; Rajesh, R.; Ananthakrishnan, A.; Vishnuvardhan, A.; Patel, S.S.; Kapruan, C.; Brahmbhatt, S.; Kataray, T.; Narayanan, D.; et al. Industrial internet of things in intelligent manufacturing: a review, approaches, opportunities, open challenges, and future directions. Int. J. Interact. Des. Manuf. (IJIDeM) 2022, 1–23. [Google Scholar] [CrossRef]
  10. Fan, H.; Liu, X.; Fuh, J.Y.H.; Lu, W.F.; Li, B. Embodied intelligence in manufacturing: leveraging large language models for autonomous industrial robotics. J. Intell. Manuf. 2024, 1–17. [Google Scholar] [CrossRef]
  11. Evjemo, L.D.; Gjerstad, T.; Grøtli, E.I.; Sziebig, G. Trends in Smart Manufacturing: Role of Humans and Industrial Robots in Smart Factories. Curr. Robot. Rep. 2020, 1, 35–41. [Google Scholar] [CrossRef]
  12. Ribeiro, J.; Lima, R.; Eckhardt, T.; Paiva, S. Robotic Process Automation and Artificial Intelligence in Industry 4.0 – A Literature review. Procedia Comput. Sci. 2021, 181, 51–58. [Google Scholar] [CrossRef]
  13. Lievano-Martínez, F.A.; Fernández-Ledesma, J.D.; Burgos, D.; Branch-Bedoya, J.W.; Jimenez-Builes, J.A. Intelligent Process Automation: An Application in Manufacturing Industry. Sustainability 2022, 14, 8804. [Google Scholar] [CrossRef]
  14. Wang, J.; Xu, C.; Zhang, J.; Zhong, R. Big data analytics for intelligent manufacturing systems: A review. J. Manuf. Syst. 2022, 62, 738–752. [Google Scholar] [CrossRef]
  15. Li, C.; Chen, Y.; Shang, Y. A review of industrial big data for decision making in intelligent manufacturing. Eng. Sci. Technol. Int. J. 2022, 29, 101021. [Google Scholar] [CrossRef]
  16. Kozjek, D.; Vrabič, R.; Rihtaršič, B.; Lavrač, N.; Butala, P. Advancing manufacturing systems with big-data analytics: A conceptual framework. Int. J. Comput. Integr. Manuf. 2020, 33, 169–188. [Google Scholar] [CrossRef]
  17. Imad, M.; Hopkins, C.; Hosseini, A.; Yussefian, N.; Kishawy, H. Intelligent machining: a review of trends, achievements and current progress. Int. J. Comput. Integr. Manuf. 2021, 35, 359–387. [Google Scholar] [CrossRef]
  18. Pereira, T.; Kennedy, J.V.; Potgieter, J. A comparison of traditional manufacturing vs additive manufacturing, the best method for the job. Procedia Manuf. 2019, 30, 11–18. [Google Scholar] [CrossRef]
  19. Abdulhameed, O.; Al-Ahmari, A.; Ameen, W.; Mian, S.H. Additive manufacturing: Challenges, trends, and applications. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef]
  20. Kristiawan, R.B.; Imaduddin, F.; Ariawan, D.; Ubaidillah, *!!! REPLACE !!!*; Arifin, Z. A review on the fused deposition modeling (FDM) 3D printing: Filament processing, materials, and printing parameters. Open Eng. 2021, 11, 639–649. [Google Scholar] [CrossRef]
  21. Huang, J.; Qin, Q.; Wang, J. A Review of Stereolithography: Processes and Systems. Processes 2020, 8, 1138. [Google Scholar] [CrossRef]
  22. F. Jabri, A. Ouballouch, L. Lasri. A Review on Selective Laser Sintering 3D Printing Technology for Polymer Materials. Proceedings of CASICAM 2022; Zarbane, K., Beidouri, Z., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 63–71. [Google Scholar]
  23. Venkatesh, K.V.; Nandini, V.V. Direct Metal Laser Sintering: A Digitised Metal Casting Technology. J. Indian Prosthodont. Soc. 2013, 13, 389–392. [Google Scholar] [CrossRef] [PubMed]
  24. Ahn, D.-G. Directed Energy Deposition (DED) Process: State of the Art. Int. J. Precis. Eng. Manuf. Technol. 2021, 8, 703–742. [Google Scholar] [CrossRef]
  25. Galati, M. Chapter 8 - Electron beam melting process: a general overview. In Additive Manufacturing; Pou, J., Riveiro, A., Davim, J.P., Eds.; Elsevier, 2021; pp. 277–301. [Google Scholar] [CrossRef]
  26. Mostafaei, A.; Elliott, A.M.; Barnes, J.E.; Li, F.; Tan, W.; Cramer, C.L.; Nandwana, P.; Chmielus, M. Binder jet 3D printing—Process parameters, materials, properties, modeling, and challenges. Prog. Mater. Sci. 2020, 119, 100707. [Google Scholar] [CrossRef]
  27. Elkaseer, A.; Chen, K.J.; Janhsen, J.C.; Refle, O.; Hagenmeyer, V.; Scholz, S.G. Material jetting for advanced applications: A state-of-the-art review, gaps and future directions. Addit. Manuf. 2022, 60. [Google Scholar] [CrossRef]
  28. Mu, X.; Amouzandeh, R.; Vogts, H.; Luallen, E.; Arzani, M. A brief review on the mechanisms and approaches of silk spinning-inspired biofabrication. Front. Bioeng. Biotechnol. 2023, 11, 1252499. [Google Scholar] [CrossRef]
  29. Mu, X.; Wang, Y.; Guo, C.; Li, Y.; Ling, S.; Huang, W.; Cebe, P.; Hsu, H.; De Ferrari, F.; Jiang, X.; et al. 3D Printing of Silk Protein Structures by Aqueous Solvent-Directed Molecular Assembly. Macromol. Biosci. 2019, 20, 1900191–e1900191. [Google Scholar] [CrossRef]
  30. Foody, G.M.; Mathur, A. Toward intelligent training of supervised image classifications: directing training data acquisition for SVM classification. Remote. Sens. Environ. 2004, 93, 107–117. [Google Scholar] [CrossRef]
  31. Sharma, N.; Jain, V.; Mishra, A. An Analysis Of Convolutional Neural Networks For Image Classification. Procedia Comput. Sci. 2018, 132, 377–384. [Google Scholar] [CrossRef]
  32. Khurana, D.; Koli, A.; Khatter, K.; Singh, S. Natural language processing: state of the art, current trends and challenges. Multimedia Tools Appl. 2022, 82, 3713–3744. [Google Scholar] [CrossRef]
  33. Anumanchipalli, G.K.; Chartier, J.; Chang, E.F. Speech synthesis from neural decoding of spoken sentences. Nature 2019, 568, 493–498. [Google Scholar] [CrossRef] [PubMed]
  34. Xiao, S.; Hu, R.; Li, Z.; Attarian, S.; Björk, K.-M.; Lendasse, A. A machine-learning-enhanced hierarchical multiscale method for bridging from molecular dynamics to continua. Neural Comput. Appl. 2019, 32, 14359–14373. [Google Scholar] [CrossRef]
  35. Xiao, S.; Li, J.; Bordas, S.P.A.; Kim, A.M. Artificial neural networks and their applications in computational materials science: A review and a case study. In Advances in Applied Mechanics; Elsevier, 2023. [Google Scholar] [CrossRef]
  36. Gurbuz, F.; Mudireddy, A.; Mantilla, R.; Xiao, S. Using a physics-based hydrological model and storm transposition to investigate machine-learning algorithms for streamflow prediction. J. Hydrol. 2023, 628. [Google Scholar] [CrossRef]
  37. Hoang, D.; Wiegratz, K. Machine learning methods in finance: Recent applications and prospects. Eur. Financial Manag. 2023, 29, 1657–1701. [Google Scholar] [CrossRef]
  38. Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R.; Rab, S. Significance of machine learning in healthcare: Features, pillars and applications. Int. J. Intell. Networks 2022, 3, 58–73. [Google Scholar] [CrossRef]
  39. Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
  40. Yu, C.; Liu, J.; Nemati, S.; Yin, G. Reinforcement Learning in Healthcare: A Survey. ACM Comput. Surv. 2021, 55, 1–36. [Google Scholar] [CrossRef]
  41. Chen, X.; Yao, L.; McAuley, J.; Zhou, G.; Wang, X. Deep reinforcement learning in recommender systems: A survey and new perspectives. Knowledge-Based Syst. 2023, 264. [Google Scholar] [CrossRef]
  42. Mnih, V. Playing Atari with Deep Reinforcement Learning. 2013. Available online: https://arxiv.org/abs/1312.5602v1 (accessed on 19 September 2021).
  43. Cai, M.; Xiao, S.; Li, J.; Kan, Z. Safe reinforcement learning under temporal logic with reward design and quantum action selection. Sci. Rep. 2023, 13, 1–20. [Google Scholar] [CrossRef]
  44. Li, J.; Cai, M.; Kan, Z.; Xiao, S. Model-free reinforcement learning for motion planning of autonomous agents with complex tasks in partially observable environments. Auton. Agents Multi-Agent Syst. 2024, 38, 1–32. [Google Scholar] [CrossRef]
  45. Hambly, B.; Xu, R.; Yang, H. Recent advances in reinforcement learning in finance. Math. Finance 2023, 33, 437–503. [Google Scholar] [CrossRef]
  46. Li, Y.; Yu, C.; Shahidehpour, M.; Yang, T.; Zeng, Z.; Chai, T. Deep Reinforcement Learning for Smart Grid Operations: Algorithms, Applications, and Prospects. Proc. IEEE 2023, 111, 1055–1096. [Google Scholar] [CrossRef]
  47. Qi, X.; Chen, G.; Li, Y.; Cheng, X.; Li, C. Applying Neural-Network-Based Machine Learning to Additive Manufacturing: Current Applications, Challenges, and Future Perspectives. Engineering 2019, 5, 721–729. [Google Scholar] [CrossRef]
  48. Meng, L.; McWilliams, B.; Jarosinski, W.; Park, H.-Y.; Jung, Y.-G.; Lee, J.; Zhang, J. Machine Learning in Additive Manufacturing: A Review. JOM 2020, 72, 2363–2377. [Google Scholar] [CrossRef]
  49. Tapia, G.; Khairallah, S.; Matthews, M.; King, W.E.; Elwany, A. Gaussian process-based surrogate modeling framework for process planning in laser powder-bed fusion additive manufacturing of 316L stainless steel. Int. J. Adv. Manuf. Technol. 2017, 94, 3591–3603. [Google Scholar] [CrossRef]
  50. Mozaffar, M.; Paul, A.; Al-Bahrani, R.; Wolff, S.; Choudhary, A.; Agrawal, A.; Ehmann, K.; Cao, J. Data-driven prediction of the high-dimensional thermal history in directed energy deposition processes via recurrent neural networks. Manuf. Lett. 2018, 18, 35–39. [Google Scholar] [CrossRef]
  51. Francis, J.; Bian, L. Deep Learning for Distortion Prediction in Laser-Based Additive Manufacturing using Big Data. Manuf. Lett. 2019, 20, 10–14. [Google Scholar] [CrossRef]
  52. Hu, Z.; Mahadevan, S. Uncertainty quantification and management in additive manufacturing: current status, needs, and opportunities. Int. J. Adv. Manuf. Technol. 2017, 93, 2855–2874. [Google Scholar] [CrossRef]
  53. Shen, Z.; Shang, X.; Zhao, M.; Dong, X.; Xiong, G.; Wang, F.-Y. A Learning-Based Framework for Error Compensation in 3D Printing. IEEE Trans. Cybern. 2019, 49, 4042–4050. [Google Scholar] [CrossRef]
  54. Tootooni, M.S.; Dsouza, A.; Donovan, R.; Rao, P.K.; Kong, Z.; Borgesen, P. Classifying the Dimensional Variation in Additive Manufactured Parts From Laser-Scanned Three-Dimensional Point Cloud Data Using Machine Learning Approaches. J. Manuf. Sci. Eng. 2017, 139, 091005. [Google Scholar] [CrossRef]
  55. Gobert, C.; Reutzel, E.W.; Petrich, J.; Nassar, A.R.; Phoha, S. Application of supervised machine learning for defect detection during metallic powder bed fusion additive manufacturing using high resolution imaging. Addit. Manuf. 2018, 21, 517–528. [Google Scholar] [CrossRef]
  56. Kumar, S.; Gopi, T.; Harikeerthana, N.; Gupta, M.K.; Gaur, V.; Krolczyk, G.M.; Wu, C. Machine learning techniques in additive manufacturing: a state of the art review on design, processes and production control. J. Intell. Manuf. 2022, 34, 21–55. [Google Scholar] [CrossRef]
  57. Ghobakhloo, M. Industry 4.0, digitization, and opportunities for sustainability. J. Clean. Prod. 2019, 252, 119869. [Google Scholar] [CrossRef]
  58. Lucke, D.; Constantinescu, C.; Westkämper, E. Smart Factory - A Step towards the Next Generation of Manufacturing. In Manufacturing Systems and Technologies for the New Frontier; Mitsuishi, M., Ueda, K., Kimura, F., Eds.; Springer: London, UK, 2008; pp. 115–118. [Google Scholar]
  59. Behzadi, M.M.; Ilieş, H.T. Real-Time Topology Optimization in 3D via Deep Transfer Learning. Comput. Des. 2021, 135. [Google Scholar] [CrossRef]
  60. Gu, G.X.; Chen, C.-T.; Richmond, D.J.; Buehler, M.J. Bioinspired hierarchical composite design using machine learning: simulation, additive manufacturing, and experiment. Mater. Horizons 2018, 5, 939–945. [Google Scholar] [CrossRef]
  61. Aoyagi, K.; Wang, H.; Sudo, H.; Chiba, A. Simple method to construct process maps for additive manufacturing using a support vector machine. Addit. Manuf. 2019, 27, 353–362. [Google Scholar] [CrossRef]
  62. Zhang, Z.; Liu, Z.; Wu, D. Prediction of melt pool temperature in directed energy deposition using machine learning. Addit. Manuf. 2020, 37, 101692. [Google Scholar] [CrossRef]
  63. Chan, S.L.; Lu, Y.; Wang, Y. Data-driven cost estimation for additive manufacturing in cybermanufacturing. J. Manuf. Syst. 2018, 46, 115–126. [Google Scholar] [CrossRef]
  64. Lu, S.C.-Y. Machine learning approaches to knowledge synthesis and integration tasks for advanced engineering automation. Comput. Ind. 1990, 15, 105–120. [Google Scholar] [CrossRef]
  65. Kumar, S.; Wu, C. Eliminating intermetallic compounds via Ni interlayer during friction stir welding of dissimilar Mg/Al alloys. J. Mater. Res. Technol. 2021, 15, 4353–4369. [Google Scholar] [CrossRef]
  66. Khanzadeh, M.; Chowdhury, S.; Tschopp, M.A.; Doude, H.R.; Marufuzzaman, M.; Bian, L. In-situ monitoring of melt pool images for porosity prediction in directed energy deposition processes. IISE Trans. 2018, 51, 437–455. [Google Scholar] [CrossRef]
  67. Tapia, G.; Elwany, A.; Sang, H. Prediction of porosity in metal-based additive manufacturing using spatial Gaussian process models. Addit. Manuf. 2016, 12, 282–290. [Google Scholar] [CrossRef]
  68. Lopez, F.; Witherell, P.; Lane, B. Identifying Uncertainty in Laser Powder Bed Fusion Additive Manufacturing Models. J. Mech. Des. 2016, 138. [Google Scholar] [CrossRef] [PubMed]
  69. Hsu, C.-W.; Lin, C.-J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Networks 2002, 13, 415–425. [Google Scholar] [CrossRef]
  70. LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
  71. Nair, V.; Hinton, G. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning; 2010; pp. 807–814. [Google Scholar]
  72. Chen, S.; Cowan, C.; Grant, P. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Networks 1991, 2, 302–309. [Google Scholar] [CrossRef]
  73. Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
  74. Heess, N.; Hunt, J.J.; Lillicrap, T.P.; Silver, D. Memory-based control with recurrent neural networks. 2015. Available online: https://arxiv.org/abs/1512.04455v1 (accessed on 27 April 2023).
  75. Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Networks 1994, 5, 157–166. [Google Scholar] [CrossRef]
  76. Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
  77. Gruber, N.; Jockisch, A. Are GRU Cells More Specific and LSTM Cells More Sensitive in Motive Classification of Text? Front. Artif. Intell. 2020, 3. [Google Scholar] [CrossRef]
  78. Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? Proc. AAAI Conf. Artif. Intell. 2023, 37, 11121–11128. [Google Scholar] [CrossRef]
  79. van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2019, 109, 373–440. [Google Scholar] [CrossRef]
  80. Yarowsky, D. Unsupervised word sense disambiguation rivaling supervised methods. The 33rd annual meeting; pp. 189–196.
  81. D. Berthelot, N. Carlini, I. Goodfellow, A. Oliver, N. Papernot, and C. Raffel, “MixMatch: a holistic approach to semi-supervised learning,” in Proceedings of the 33rd International Conference on Neural Information Processing Systems, Red Hook, NY, USA: Curran Associates Inc., 2019.
  82. Q. Xie, Z. Dai, E. Hovy, M.-T. Luong, and Q. V. Le, “Unsupervised data augmentation for consistency training,” in Proceedings of the 34th International Conference on Neural Information Processing Systems, in NIPS ’20. Red Hook, NY, USA: Curran Associates Inc., 2020.
  83. D. Berthelot et al., “ReMixMatch: Semi-Supervised Learning with Distribution Matching and Augmentation Anchoring,” in International Conference on Learning Representations, 2020. [Online]. Available: https://api.semanticscholar.org/CorpusID:213757781.
  84. K. Sohn et al., “FixMatch: simplifying semi-supervised learning with consistency and confidence,” in Proceedings of the 34th International Conference on Neural Information Processing Systems, in NIPS ’20. Red Hook, NY, USA: Curran Associates Inc., 2020.
  85. Cascante-Bonilla, P.; Tan, F.; Qi, Y.; Ordonez, V. Curriculum Labeling: Revisiting Pseudo-Labeling for Semi-Supervised Learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 6912–6920. [Google Scholar] [CrossRef]
  86. M. I. J. Guo, Z. Liu, S. M. I. T. Zhang, and F. I. C. L. P. Chen, “Incremental Self-training for Semi-supervised Learning,” 2024. [Online]. Available: https://api.semanticscholar.org/CorpusID:269283005.
  87. Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the eleventh annual conference on Computational learning theory-COLT’ 98. [CrossRef]
  88. Liu, W.; Li, Y.; Tao, D.; Wang, Y. A general framework for co-training and its applications. Neurocomputing 2015, 167, 112–121. [Google Scholar] [CrossRef]
  89. Ning, X.; Wang, X.; Xu, S.; Cai, W.; Zhang, L.; Yu, L.; Li, W. A review of research on co-training. Concurr. Comput. Pr. Exp. 2021, 35, e6276. [Google Scholar] [CrossRef]
  90. M. Balcan, A. Blum, and K. Yang, “Co-Training and Expansion: Towards Bridging Theory and Practice,” in Advances in Neural Information Processing Systems, L. Saul, Y. Weiss, and L. Bottou, Eds., MIT Press, 2004. [Online]. Available: https://proceedings.neurips.cc/paper_files/paper/2004/file/9457fc28ceb408103e13533e4a5b6bd1-Paper.pdf.
  91. Nigam, K.; Ghani, R. Analyzing the effectiveness and applicability of co-training. CIKM00: Ninth International Conference on Information and Knowledge Management. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 86–93.
  92. S. A. Goldman and Y. Zhou, “Enhancing Supervised Learning with Unlabeled Data,” in International Conference on Machine Learning, 2000. [Online]. Available: https://api.semanticscholar.org/CorpusID:1215747.
  93. Zhou, Z.-H.; Li, M. Tri-training: exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
  94. W. Xi-l, “Semi-supervised regression based on support vector machine co-training,” Comput. Eng. Appl., 2011, [Online]. Available: https://api.semanticscholar.org/CorpusID:201894734.
  95. Ferreira, R.E.P.; Lee, Y.J.; Dórea, J.R.R. Using pseudo-labeling to improve performance of deep neural networks for animal identification. Sci. Rep. 2023, 13, 1–11. [Google Scholar] [CrossRef]
  96. Ding, X.; Smith, S.L.; Belta, C.; Rus, D. Optimal Control of Markov Decision Processes With Linear Temporal Logic Constraints. IEEE Trans. Autom. Control. 2014, 59, 1244–1257. [Google Scholar] [CrossRef]
  97. van Ravenzwaaij, D.; Cassey, P.; Brown, S.D. A simple introduction to Markov Chain Monte–Carlo sampling. Psychon. Bull. Rev. 2016, 25, 143–154. [Google Scholar] [CrossRef]
  98. Beranek, W.; Howard, R.A. Dynamic Programming and Markov Processes. Technometrics 1961, 3, 120. [Google Scholar] [CrossRef]
  99. Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
  100. H. van Hasselt, A. Guez, and D. Silver, “Deep Reinforcement Learning with Double Q-Learning,” in AAAI’16: Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, 2016, pp. 2094–2100.
  101. S. Kakade and J. Langford, “Approximately optimal approximate reinforcement learning,” in In Proc. 19th International Conference on Machine Learning, Citeseer, 2002.
  102. J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov, “Proximal policy optimization algorithms,” arXiv. arXiv, Jul. 19, 2017. Accessed: Nov. 23, 2020. [Online]. Available: https://arxiv.org/abs/1707.06347v2.
  103. Dang, L.; He, X.; Tang, D.; Li, Y.; Wang, T. A fatigue life prediction approach for laser-directed energy deposition titanium alloys by using support vector regression based on pore-induced failures. Int. J. Fatigue 2022, 159. [Google Scholar] [CrossRef]
  104. Wang, X.; He, X.; Wang, T.; Li, Y. Internal pores in DED Ti-6.5Al-2Zr-Mo-V alloy and their influence on crack initiation and fatigue life in the mid-life regime. Addit. Manuf. 2019, 28, 373–393. [Google Scholar] [CrossRef]
  105. Y. Murakami, “18 - Additive manufacturing: effects of defects,” in Metal Fatigue (Second Edition), Y. Murakami, Ed., Academic Press, 2019, pp. 453–483. [CrossRef]
  106. Salvati, E.; Tognan, A.; Laurenti, L.; Pelegatti, M.; De Bona, F. A defect-based physics-informed machine learning framework for fatigue finite life prediction in additive manufacturing. Mater. Des. 2022, 222. [Google Scholar] [CrossRef]
  107. Romano, S.; Brückner-Foit, A.; Brandão, A.; Gumpinger, J.; Ghidini, T.; Beretta, S. Fatigue properties of AlSi10Mg obtained by additive manufacturing: Defect-based modelling and prediction of fatigue strength. Eng. Fract. Mech. 2017, 187, 165–189. [Google Scholar] [CrossRef]
  108. Wang, L.; Zhu, S.-P.; Luo, C.; Liao, D.; Wang, Q. Physics-guided machine learning frameworks for fatigue life prediction of AM materials. Int. J. Fatigue 2023, 172. [Google Scholar] [CrossRef]
  109. Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
  110. He, L.; Wang, Z.; Ogawa, Y.; Akebono, H.; Sugeta, A.; Hayashi, Y. Machine-learning-based investigation into the effect of defect/inclusion on fatigue behavior in steels. Int. J. Fatigue 2021, 155, 106597. [Google Scholar] [CrossRef]
  111. Xie, C.; Wu, S.; Yu, Y.; Zhang, H.; Hu, Y.; Zhang, M.; Wang, G. Defect-correlated fatigue resistance of additively manufactured Al-Mg4.5Mn alloy with in situ micro-rolling. J. Mech. Work. Technol. 2021, 291. [Google Scholar] [CrossRef]
  112. Cui, X.; Zhang, S.; Wang, C.; Zhang, C.; Chen, J.; Zhang, J. Microstructure and fatigue behavior of a laser additive manufactured 12CrNi2 low alloy steel. Mater. Sci. Eng. A 2020, 772, 138685. [Google Scholar] [CrossRef]
  113. Fan, J.; Wang, Z.; Liu, C.; Shi, D.; Yang, X. A tensile properties-related fatigue strength predicted machine learning framework for alloys used in aerospace. Eng. Fract. Mech. 2024, 301. [Google Scholar] [CrossRef]
  114. Gao, S.; Yue, X.; Wang, H. Predictability of Different Machine Learning Approaches on the Fatigue Life of Additive-Manufactured Porous Titanium Structure. Metals 2024, 14, 320. [Google Scholar] [CrossRef]
  115. Abhilash, P.M.; Ahmed, A. Convolutional neural network–based classification for improving the surface quality of metal additive manufactured components. Int. J. Adv. Manuf. Technol. 2023, 126, 3873–3885. [Google Scholar] [CrossRef]
  116. Ansari, M.A.; Crampton, A.; Parkinson, S. A Layer-Wise Surface Deformation Defect Detection by Convolutional Neural Networks in Laser Powder-Bed Fusion Images. Materials 2022, 15, 7166. [Google Scholar] [CrossRef] [PubMed]
  117. Banadaki, Y.; Razaviarab, N.; Fekrmandi, H.; Li, G.; Mensah, P.; Bai, S.; Sharifi, S. Automated Quality and Process Control for Additive Manufacturing using Deep Convolutional Neural Networks. Recent Prog. Mater. 2021, 4, 1–1. [Google Scholar] [CrossRef]
  118. Conrad, J.; Rodriguez, S.; Omidvarkarjan, D.; Ferchow, J.; Meboldt, M. Recognition of Additive Manufacturing Parts Based on Neural Networks and Synthetic Training Data: A Generalized End-to-End Workflow. Appl. Sci. 2023, 13, 12316. [Google Scholar] [CrossRef]
  119. Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. “MobileNetV2: Inverted Residuals and Linear Bottlenecks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA: IEEE, Jun. 2018; pp. 4510–4520. [CrossRef]
  120. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. CoRR 2015, abs/1512.03385.
  121. K. Simonyan and A. Zisserman, “Very Deep Convolutional Networks for Large-Scale Image Recognition,” CoRR, vol. abs/1409.1556, 2014, [Online]. Available: https://api.semanticscholar.org/CorpusID:14124313.
  122. Wenzel, S.; Slomski-Vetter, E.; Melz, T. Optimizing System Reliability in Additive Manufacturing Using Physics-Informed Machine Learning. Machines 2022, 10, 525. [Google Scholar] [CrossRef]
  123. Ye, K.Q. Orthogonal Column Latin Hypercubes and Their Application in Computer Experiments. J. Am. Stat. Assoc. 1998, 93, 1430–1439. [Google Scholar] [CrossRef]
  124. Kapusuzoglu, B.; Mahadevan, S. Physics-Informed and Hybrid Machine Learning in Additive Manufacturing: Application to Fused Filament Fabrication. JOM 2020, 72, 4695–4705. [Google Scholar] [CrossRef]
  125. Spoerk, M.; Gonzalez-Gutierrez, J.; Lichal, C.; Cajner, H.; Berger, G.R.; Schuschnigg, S.; Cardon, L.; Holzer, C. Optimisation of the Adhesion of Polypropylene-Based Materials during Extrusion-Based Additive Manufacturing. Polymers 2018, 10, 490. [Google Scholar] [CrossRef]
  126. Perani, M.; Jandl, R.; Baraldo, S.; Valente, A.; Paoli, B. Long-short term memory networks for modeling track geometry in laser metal deposition. Front. Artif. Intell. 2023, 6, 1156630. [Google Scholar] [CrossRef] [PubMed]
  127. Inyang-Udoh, U.; Chen, A.; Mishra, S. A Learn-and-Control Strategy for Jet-Based Additive Manufacturing. IEEE/ASME Trans. Mechatronics 2022, 27, 1946–1954. [Google Scholar] [CrossRef]
  128. Inyang-Udoh, U.; Mishra, S. A Physics-Guided Neural Network Dynamical Model for Droplet-Based Additive Manufacturing. IEEE Trans. Control. Syst. Technol. 2021, 30, 1863–1875. [Google Scholar] [CrossRef]
  129. Huang, X.; Xie, T.; Wang, Z.; Chen, L.; Zhou, Q.; Hu, Z. A Transfer Learning-Based Multi-Fidelity Point-Cloud Neural Network Approach for Melt Pool Modeling in Additive Manufacturing. ASCE-ASME J Risk Uncert Engrg Sys Part B Mech Engrg 2021, 8. [Google Scholar] [CrossRef]
  130. Shu, L.; Jiang, P.; Zhou, Q.; Shao, X.; Hu, J.; Meng, X. An on-line variable fidelity metamodel assisted Multi-objective Genetic Algorithm for engineering design optimization. Appl. Soft Comput. 2018, 66, 438–448. [Google Scholar] [CrossRef]
  131. Yu, R.; He, S.; Yang, D.; Zhang, X.; Tan, X.; Xing, Y.; Zhang, T.; Huang, Y.; Wang, L.; Peng, Y.; et al. Identification of cladding layer offset using infrared temperature measurement and deep learning for WAAM. Opt. Laser Technol. 2023, 170. [Google Scholar] [CrossRef]
  132. Manivannan, S. Automatic quality inspection in additive manufacturing using semi-supervised deep learning. J. Intell. Manuf. 2022, 34, 3091–3108. [Google Scholar] [CrossRef]
  133. Tanaka, D.; Ikami, D.; Yamasaki, T.; Aizawa, K. Joint Optimization Framework for Learning with Noisy Labels. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; pp. 5552–5560.
  134. Westphal, E.; Seitz, H. A machine learning method for defect detection and visualization in selective laser sintering based on convolutional neural networks. Addit. Manuf. 2021, 41. [Google Scholar] [CrossRef]
  135. M. N. Rizve, K. Duarte, Y. S. Rawat, and M. Shah, “In Defense of Pseudo-Labeling: An Uncertainty-Aware Pseudo-label Selection Framework for Semi-Supervised Learning,” ArXiv, vol. abs/2101.06329, 2021, [Online]. Available: https://api.semanticscholar.org/CorpusID:231632854.
  136. Wang, Y.; Gao, L.; Gao, Y.; Li, X. A new graph-based semi-supervised method for surface defect classification. Robot. Comput. Manuf. 2020, 68, 102083. [Google Scholar] [CrossRef]
  137. Xu, L.; Lv, S.; Deng, Y.; Li, X. A Weakly Supervised Surface Defect Detection Based on Convolutional Neural Network. IEEE Access 2020, 8, 42285–42296. [Google Scholar] [CrossRef]
  138. Huang, Y.; Qiu, C.; Wang, X.; Wang, S.; Yuan, K. A Compact Convolutional Neural Network for Surface Defect Inspection. Sensors 2020, 20, 1974. [Google Scholar] [CrossRef] [PubMed]
  139. Scime, L.; Beuth, J. A multi-scale convolutional neural network for autonomous anomaly detection and classification in a laser powder bed fusion additive manufacturing process. Addit. Manuf. 2018, 24, 273–286. [Google Scholar] [CrossRef]
  140. Chen, Y.; Wang, H.; Wu, Y.; Wang, H. Predicting the Printability in Selective Laser Melting with a Supervised Machine Learning Method. Materials 2020, 13, 5063. [Google Scholar] [CrossRef]
  141. Huang, D.J.; Li, H. A machine learning guided investigation of quality repeatability in metal laser powder bed fusion additive manufacturing. Mater. Des. 2021, 203. [Google Scholar] [CrossRef]
  142. Nguyen, N.V.; Hum, A.J.W.; Tran, T. A semi-supervised machine learning approach for in-process monitoring of laser powder bed fusion. Mater. Today: Proc. 2022, 70, 583–586. [Google Scholar] [CrossRef]
  143. Nguyen, N.V.; Hum, A.J.W.; Do, T.; Tran, T. Semi-supervised machine learning of optical in-situ monitoring data for anomaly detection in laser powder bed fusion. Virtual Phys. Prototyp. 2022, 18. [Google Scholar] [CrossRef]
  144. Okaro, I.A.; Jayasinghe, S.; Sutcliffe, C.; Black, K.; Paoletti, P.; Green, P.L. Automatic fault detection for laser powder-bed fusion using semi-supervised machine learning. Addit. Manuf. 2019, 27, 42–53. [Google Scholar] [CrossRef]
  145. Mitchell, J.A.; Ivanoff, T.A.; Dagel, D.; Madison, J.D.; Jared, B. Linking pyrometry to porosity in additively manufactured metals. Addit. Manuf. 2019, 31, 100946. [Google Scholar] [CrossRef]
  146. Scime, L.; Beuth, J. Using machine learning to identify in-situ melt pool signatures indicative of flaw formation in a laser powder bed fusion additive manufacturing process. Addit. Manuf. 2018, 25, 151–165. [Google Scholar] [CrossRef]
  147. Yuan, B.; Giera, B.; Guss, G.; Matthews, I.; Mcmains, S. Semi-Supervised Convolutional Neural Networks for In-Situ Video Monitoring of Selective Laser Melting. 2019 IEEE Winter Conference on Applications of Computer Vision (WACV). LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 744–753.
  148. Larsen, S.; Hooper, P.A. Deep semi-supervised learning of dynamics for anomaly detection in laser powder bed fusion. J. Intell. Manuf. 2021, 33, 457–471. [Google Scholar] [CrossRef]
  149. Pandiyan, V.; Drissi-Daoudi, R.; Shevchik, S.; Masinelli, G.; Le-Quang, T.; Logé, R.; Wasmer, K. Semi-supervised Monitoring of Laser powder bed fusion process based on acoustic emissions. Virtual Phys. Prototyp. 2021, 16, 481–497. [Google Scholar] [CrossRef]
  150. Gondara, L. Medical Image Denoising Using Convolutional Denoising Autoencoders. 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW). LOCATION OF CONFERENCE, SpainDATE OF CONFERENCE; pp. 241–246.
  151. Mahmud, M.S.; Huang, J.Z.; Fu, X. Variational Autoencoder-Based Dimensionality Reduction for High-Dimensional Small-Sample Data Classification. Int. J. Comput. Intell. Appl. 2020, 19. [Google Scholar] [CrossRef]
  152. Von Hahn, T.; Mechefske, C.K. Self-supervised learning for tool wear monitoring with a disentangled-variational-autoencoder. Int. J. Hydromechatronics 2021, 4, 69. [Google Scholar] [CrossRef]
  153. Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurth, U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef]
  154. Wang, R.; Standfield, B.; Dou, C.; Law, A.C.; Kong, Z.J. Real-time process monitoring and closed-loop control on laser power via a customized laser powder bed fusion platform. Addit. Manuf. 2023, 66. [Google Scholar] [CrossRef]
  155. Dharmawan, A.G.; Xiong, Y.; Foong, S.; Soh, G.S. A Model-Based Reinforcement Learning and Correction Framework for Process Control of Robotic Wire Arc Additive Manufacturing. 2020 IEEE International Conference on Robotics and Automation (ICRA). LOCATION OF CONFERENCE, FranceDATE OF CONFERENCE; pp. 4030–4036.
  156. Knaak, C.; Masseling, L.; Duong, E.; Abels, P.; Gillner, A. Improving Build Quality in Laser Powder Bed Fusion Using High Dynamic Range Imaging and Model-Based Reinforcement Learning. IEEE Access 2021, 9, 55214–55231. [Google Scholar] [CrossRef]
  157. Ogoke, F.; Farimani, A.B. Thermal control of laser powder bed fusion using deep reinforcement learning. Addit. Manuf. 2021, 46, 102033. [Google Scholar] [CrossRef]
  158. Yeung, H.; Lane, B.; Donmez, M.; Fox, J.; Neira, J. Implementation of Advanced Laser Control Strategies for Powder Bed Fusion Systems. Procedia Manuf. 2018, 26, 871–879. [Google Scholar] [CrossRef]
  159. Shi, S.; Liu, X.; Wang, Z.; Chang, H.; Wu, Y.; Yang, R.; Zhai, Z. An intelligent process parameters optimization approach for directed energy deposition of nickel-based alloys using deep reinforcement learning. J. Manuf. Process. 2024, 120, 1130–1140. [Google Scholar] [CrossRef]
  160. D. Rosenthal, “Mathematical Theory of Heat Distribution during Welding and Cutting,” Weld. J., vol. 20, pp. 220–234, 1941.
  161. Dharmadhikari, S.; Menon, N.; Basak, A. A reinforcement learning approach for process parameter optimization in additive manufacturing. Addit. Manuf. 2023, 71. [Google Scholar] [CrossRef]
  162. T. W. Eagar and N.-S. Tsai, “Temperature Fields Produced by Travelling Distributed Heat Sources.,” Weld. J. Miami Fla, vol. 62, no. 12, pp. 346–355, 1983.
  163. Chung, J.; Shen, B.; Law, A.C.C.; Kong, Z. (. Reinforcement learning-based defect mitigation for quality assurance of additive manufacturing. J. Manuf. Syst. 2022, 65, 822–835. [Google Scholar] [CrossRef]
  164. Alicastro, M.; Ferone, D.; Festa, P.; Fugaro, S.; Pastore, T. A reinforcement learning iterated local search for makespan minimization in additive manufacturing machine scheduling problems. Comput. Oper. Res. 2021, 131, 105272. [Google Scholar] [CrossRef]
  165. Ying, K.-C.; Lin, S.-W. Minimizing makespan in two-stage assembly additive manufacturing: A reinforcement learning iterated greedy algorithm. Appl. Soft Comput. 2023, 138. [Google Scholar] [CrossRef]
  166. Kucukkoc, I. MILP models to minimise makespan in additive manufacturing machine scheduling problems. Comput. Oper. Res. 2019, 105, 58–67. [Google Scholar] [CrossRef]
  167. Li, Q.; Kucukkoc, I.; Zhang, D.Z. Production planning in additive manufacturing and 3D printing. Comput. Oper. Res. 2017, 83, 157–172. [Google Scholar] [CrossRef]
Preprints 119738 g001
Figure 1. An RL agent learns by interacting with the environment.
Figure 1. An RL agent learns by interacting with the environment.
Preprints 119738 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated