1. Introduction
Since the dawn of the 21st century, the ocean has emerged as a new frontier for global exploration and development. With advances in marine scientific research, Autonomous Underwater Vehicles (AUVs) have become pivotal in the exploration, development, and study of marine resources, thanks to their remarkable capabilities in autonomous sensing, decision-making, and control [
1,
2]. The degree of autonomy in AUVs is a key metric for assessing their technological progress, while the optimization of motion control systems forms the foundation for achieving high autonomy. However, in the complex and dynamic underwater environment, AUVs face numerous challenges, including strong nonlinear dynamics, internal coupling effects, difficult-to-model dynamic parameters, and unpredictable external disturbances, particularly from random ocean currents. These currents significantly impact heading stability and speed control, increasing the complexity of control strategies. Given the critical importance of energy efficiency for long-distance and prolonged AUV operations, the slender rotating body structure has become the standard in underactuated AUV design due to its efficiency. Nonetheless, this structure's design—having fewer control degrees of freedom than motion degrees of freedom—places higher demands on control strategy formulation. In real marine environments, disturbances from ocean currents and waves are both common and variable [
3,
4]. Failing to address these disturbances effectively can severely undermine control performance or even lead to instability in AUV operations. Therefore, exploring robust control strategies with effective disturbance rejection capabilities is crucial for the safe and efficient operation of underactuated AUVs in complex ocean current environments.
Extensive research has been conducted on adaptive and robust control strategies for underactuated AUVs in challenging marine environments, with the development of accurate disturbance models serving as a prerequisite for efficient robust controller design. For instance, Lu Liu et al. developed an output feedback path-following controller that combines an extended state observer with a projection neural network, effectively addressing internal uncertainties and external disturbances [
5]. Shen et al. proposed a novel model predictive control framework (LMPC) based on Lyapunov stability, which enhances trajectory tracking accuracy through online optimization techniques and introduces a disturbance observer to estimate comprehensive disturbances [
6]. Kim et al. integrated a sliding mode controller with a conventional time-delay controller to improve the position control performance of AUVs in disturbed environments [
7]. Notably, much existing research simplifies ocean current disturbances, often treating them as constant or periodically varying disturbance forces. While this simplification captures some influence of ocean currents, it fails to accurately represent their time-varying and unpredictable nature in real environments. To design motion controllers for AUVs that can adapt flexibly to various ocean current conditions, this paper delves into the multidimensional impacts of ocean currents on underactuated AUVs, providing robust technical support to enhance AUV operational efficiency in complex marine settings.
Furthermore, numerous advanced control algorithms have been widely applied in underwater vehicles, including Fuzzy control [
8], PID control [
9,
10], Linear Quadratic Regulator (LQR) [
11,
12], Backstepping Control (BC) [
13], Sliding Mode Control (SMC), Sliding Mode Control (SMC), Model Predictive Control (MPC) [
6,
14,
15], Adaptive Control [
16], and Robust Control [
17]. Among these, SMC demonstrates significant potential in addressing the challenges discussed in this paper, owing to its strong anti-disturbance capabilities and adaptability to model uncertainties. However, traditional SMC faces issues of control overshoot and output chattering, necessitating ongoing optimization and refinement. Significant breakthroughs have been achieved in the SMC field. Hangil Joe et al. proposed a second-order SMC for AUVs subject to modeling errors and unknown environmental disturbances, effectively suppressing chattering and improving control accuracy [
18]. Konar et al. introduced fractional-order fuzzy SMC, offering a novel solution for depth control in underwater robots, with simulations confirming its excellent transient response and control performance [
19]. Haomiao Yu et al. developed a Proportional-Integral-Derivative Sliding Mode Control (PIDSMC) method, enhancing the anti-disturbance capability of SMC and strengthening motion control robustness [
20]. Nhut Thanh, Xiaoqiang Dai, Jian Xu, and Jianguo Wu combined the advantages of BC and SMC, proposing backstepping sliding mode control strategies that significantly improve error convergence speed and system stability under uncertainties and unknown disturbances [
20,
21,
22,
23,
24]. Although convergence speed has greatly improved, instances remain where tracking errors do not converge to zero within a finite time. To address this issue, Lei Qiao et al. proposed two innovative methods: Adaptive Integral Terminal Sliding Mode Control (AITSMC) and Fast Integral Terminal Sliding Mode Control (AFITSMC), which not only accelerate convergence speed but also achieve zero-error convergence within a finite time frame, enhancing the system's resistance to dynamic uncertainties and time-varying external disturbances [
25]. Van et al. designed a controller that combines adaptive neural networks with integral sliding mode, using switching control terms to optimize error approximation while integral terms eliminate steady-state errors, further enhancing system robustness [
26].
In summary, recognizing the limitations of existing ocean current disturbance models, which often simplify currents to total disturbance forces, this paper innovatively employs a velocity vector synthesis method, transforming absolute velocity into relative velocity that incorporates current effects. This approach establishes a more realistic kinematic and dynamic model for AUVs in marine environments. Regarding control strategy, this paper proposes Backstepping Integral Sliding Mode Control (BISMC), integrating the system decomposition benefits of BC with the rapid response and robustness of SMC. By incorporating Dynamic Surface Control (DSC) technology, the "explosion of derivatives" phenomenon is effectively mitigated, optimizing the controller's transient performance. Additionally, the inclusion of integral terms in the SMC component accelerates convergence and eliminates steady-state errors, enhancing overall robustness. The use of saturation functions in place of traditional switching functions also effectively suppresses control output chattering. To improve depth control accuracy, this paper presents a dual-loop control structure, employing integral sliding mode as the outer loop and BISMC as the inner loop, thereby achieving enhanced control precision.
The remainder of this paper is structured as follows:
Section 2 delves into the motion model, rudder force model, and ocean current disturbance model for underactuated AUVs, laying the essential groundwork for the design of efficient control algorithms.
Section 3 elaborates on the BISMC method and the design of heading and depth controllers based on it. Additionally, a Lyapunov stability analysis will be conducted to theoretically demonstrate the effectiveness of the proposed control strategy for AUV motion control in complex marine environments.
Section 4 will validate the effectiveness and superiority of the proposed method through numerical simulations and comparative experiments. By analyzing experimental results under various operational conditions, the significant advantages of BISMC in enhancing AUV motion control performance will be fully demonstrated. Finally,
Section 5 provides a comprehensive summary of this research.
2. Preliminaries and AUV Modeling
2.1. Model Analysis and Simplification
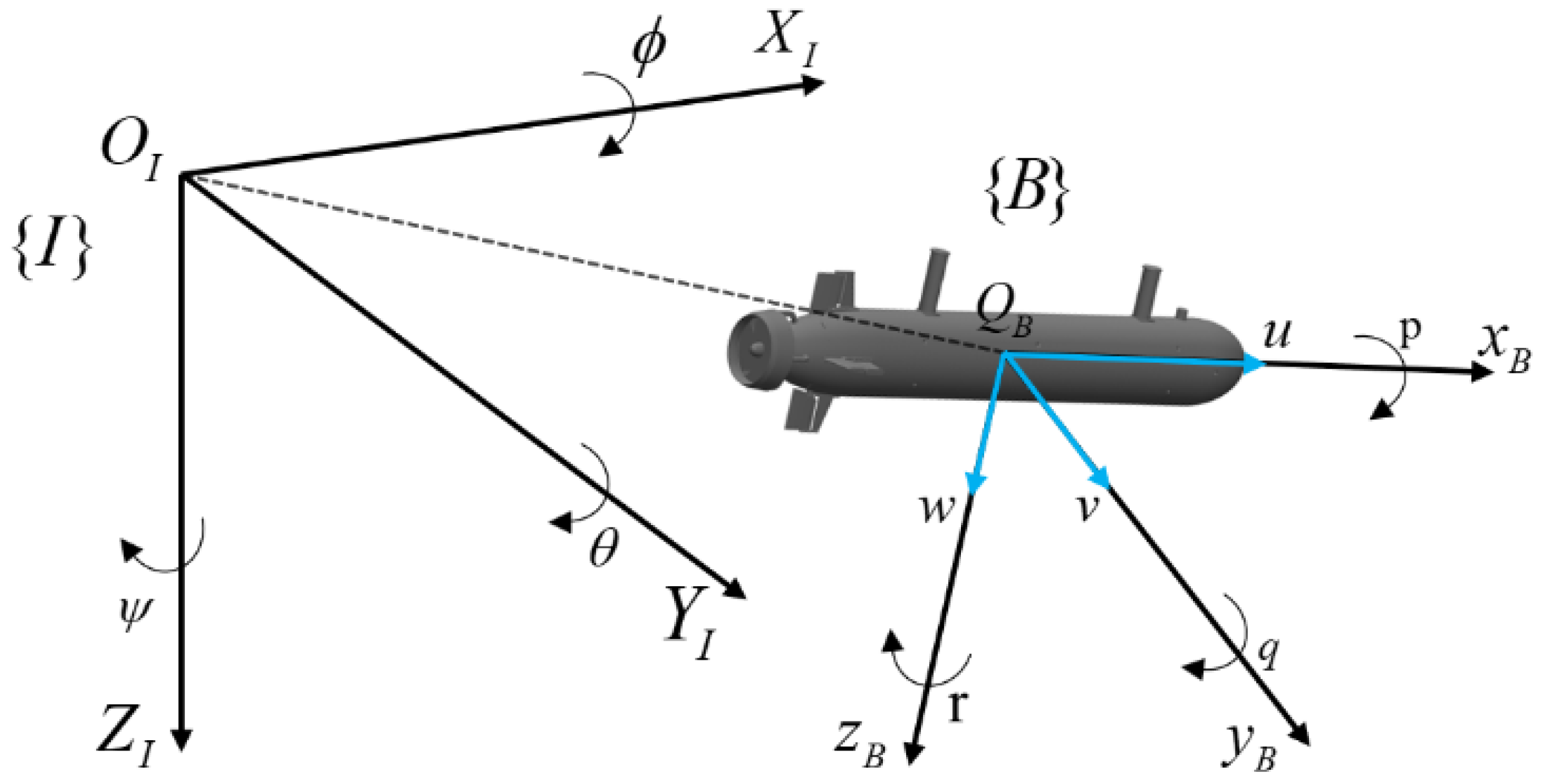
To study the mathematical model of AUVs motion and to determine their velocity and attitude during underwater movement, it is common to establish a body-fixed coordinate system, denoted as {B}, and an inertial coordinate system, denoted as {I} (as shown in
Figure 1). Euler angles can be employed to define the angles between the inertial coordinate system and the body-fixed coordinate system, as well as to describe the position and orientation of the AUV in three-dimensional space. The coordinates
of the AUV's body-fixed coordinate system {B} in the inertial coordinate system are determined by the relative attitude angle
with respect to the inertial coordinate system {I}.
The motion model serves as the foundation for underwater robot motion control, ensuring that the controller maintains robust performance even in the face of various uncertainties present in the underwater environment. If the constructed AUV motion model is overly complex, it can complicate the control system, increase the difficulty of controller design, and potentially lead to control system failure. Conversely, if the motion model is too simplistic, it can significantly diminish the performance of the control system and hinder its ability to accurately represent the true motion patterns of AUVs [
27]. Therefore, it is essential to optimize the spatial motion model of underactuated AUVs effectively. Based on this premise, the following assumptions are made:
Assumption 1. To better analyze and model, the origin of the AUV's body-fixed coordinate system is established at its center of gravity to facilitate improved analysis and modeling.
Assumption 2. The object of study is an underactuated AUV with a rotary body that possesses two planes of symmetry: the left-right symmetric -plane and t the up-down symmetric -plane.
Assumption 3. In typical AUV, the roll recovery torque is relatively substantial, which makes it challenging to induce significant alterations in the marine environment. Consequently, the roll motion is disregarded in this paper [
28].
Based on the above assumptions, referring to relevant papers[
29], and using the Newton-Euler equations for rigid bodies and the Lagrangian formulation, we derive the model for a five-degree-of-freedom underactuated AUV:
In Equation (1), represents the position and attitude vector of the AUVs, denotes the velocity vector of the AUVs in the body-fixed coordinate system, and is the transformation matrix that converts velocities and angular velocities from the body-fixed coordinate system to the inertial coordinate system. is the inertia matrix, which includes the rigid body inertia matrix and added mass. represents the matrix containing the centripetal and Coriolis forces due to the mass matrix and added mass. is the damping force and torque matrix due to hydrodynamic effects, and is the restoring force and torque vector. is the environmental disturbance force matrix, and is the control force matrix, where represents the thrust produced by the propeller, represents the pitch moment produced by the horizontal rudder angle, and represents the yaw moment produced by the vertical rudder angle.
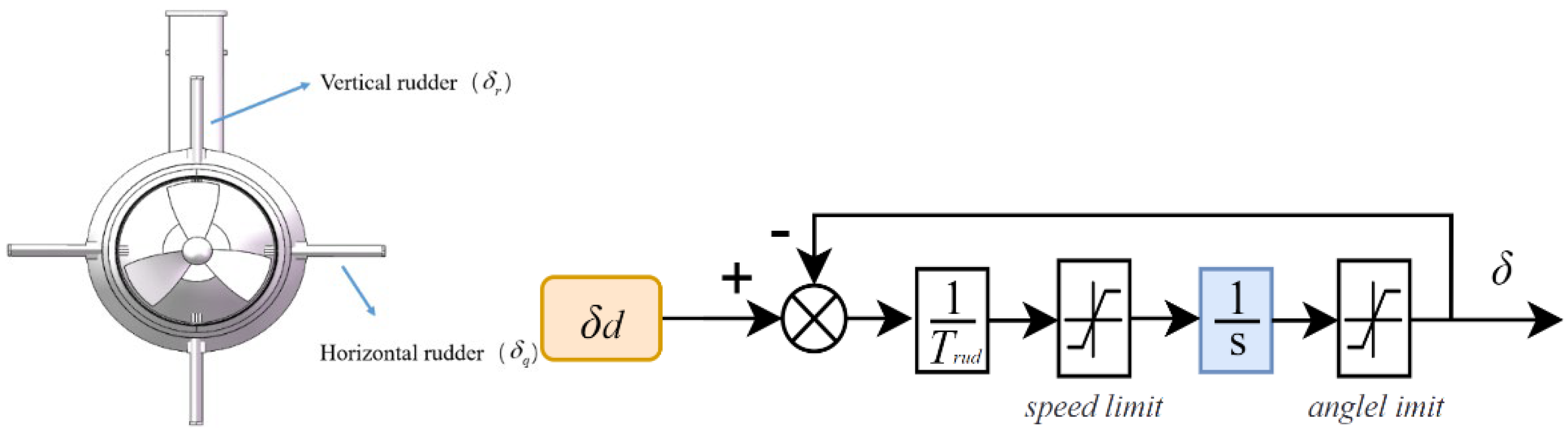
2.3. Rudder Force Model
The mathematical model that describes the vertical and horizontal rudders of the underactuated AUV is as follows:
Where and are the distances from the rudder to the center of buoyancy, and are the lift coefficients of the rudder blades, is the density of seawater, is the area of the rudder blade, is the combined velocity of the AUV, is the rudder servo control gain, is the time constant of the servo, is the commanded rudder angle, and are the rudder angles.
Figure 2.
Cross rudder structure diagram and rudder servo model.
Figure 2.
Cross rudder structure diagram and rudder servo model.
2.4. Ocean current disturbance model
This paper adopts the method of velocity vector synthesis, which, during trajectory calculation, converts absolute velocity into relative velocity considering the current speed. This method applies real-time uncertain disturbances to the AUV to simulate the uncertainties of the real marine environment. Let the velocity of the ocean current in the inertial coordinate system be
, the angle between the projection of the velocity on the
horizontal plane and the
-axis be the horizontal flow direction angle
, and the angle between the projection of the velocity on the
vertical plane and the
-axis be the vertical flow direction angle
. Then, the velocity of the ocean current in the inertial coordinate system
,
, and
is expressed as follows:
Through the transformation matrix that converts from the inertial coordinate system to the body-fixed coordinate system, the velocity of the AUV affected by the ocean currents
,
, and
can be determined.
By substituting the equation into the equation, the motion model of the AUV under ocean current disturbance is obtained as:
Where 、、、、 represents the various hydrodynamic coefficients of the AUV, is the distance between the center of buoyancy and the center of gravity, is the magnitude of the buoyant force, and are the moments of inertia about the Z and Y axes.
In order to meet the convergence conditions for control in the next section, several reasonable assumptions and lemmas are presented as follows:
Assumption 4. The direction angles , of the ocean current change slowly, and sampling is conducted randomly within the range .
Assumption 5. The velocity of the ocean current has an upper bound, satisfying,,where , is a positive constant.
Remark 1. Due to the continuously changing marine environment and limited energy, the disturbances acting on the AUV can be considered as unknown time-varying but bounded signals with finite rates of change. Therefore, assumptions 4 and 5 are reasonable.
Remark 2. As shown in the dynamics model (7), the AUV discussed in this paper has three degrees of freedom. However, since there are no actuators in the sway direction, the number of independent control inputs is two. Therefore, the AUV is a second-order underactuated system.
Remark 3. For marine robots, there is inherent actuator saturation[
4]. Therefore, the propeller thrust, rudder angle of the vertical fin, and rudder angle of the directional fin for the AUV discussed here should be bounded, i.e.,
,
and
,where
,
and
are positive constant.
3. Backstepping Integral Sliding Mode Controller Design
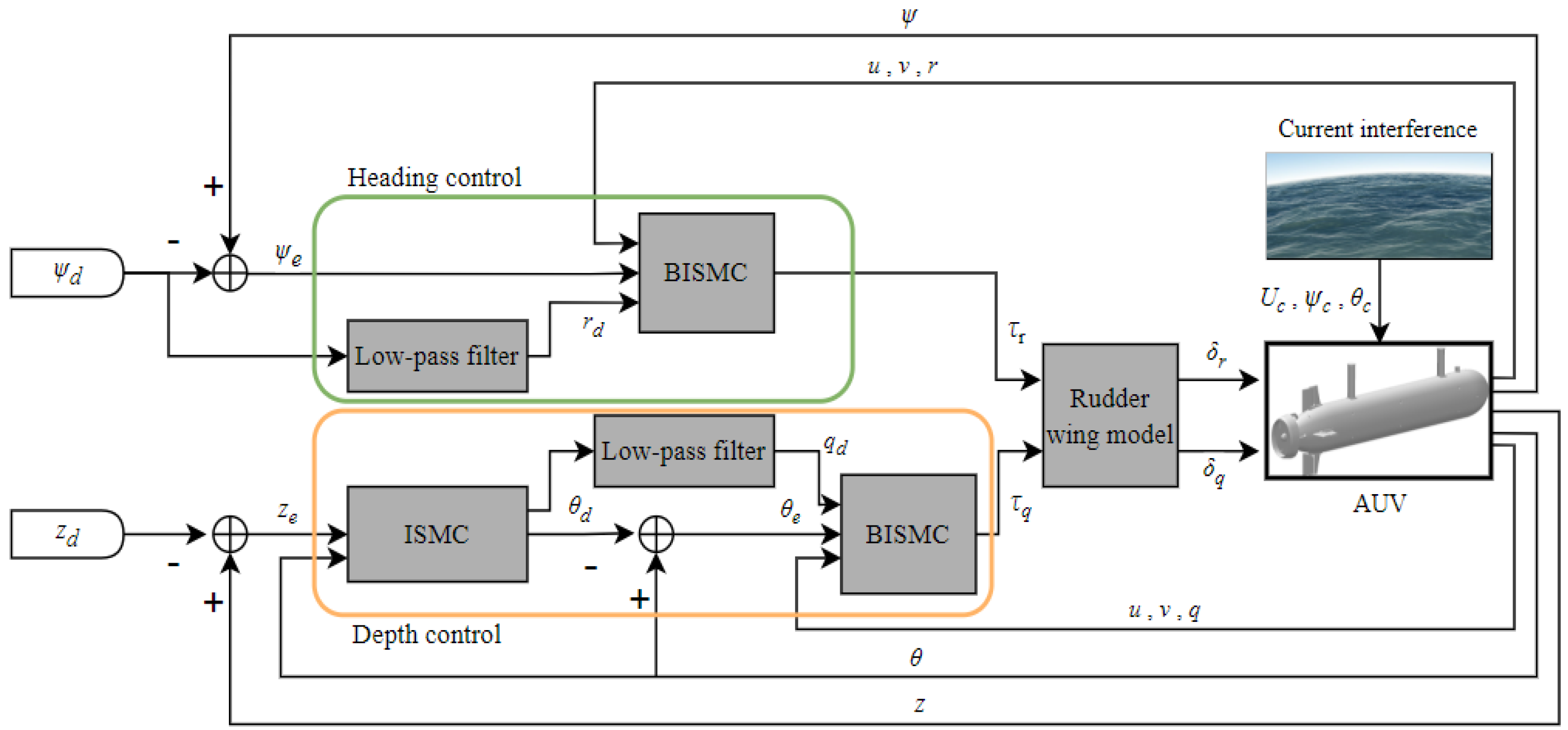
To achieve effective motion control, the proposed BISMC controller demonstrate strong motion control performance in the presence of ocean currents but also provide precise and robust control to address high coupling nonlinearity and model uncertainties. The design of this controller integrates backstepping control and sliding mode control methodologies, with enhancements made to improve performance. The control principle block diagram is depicted in
Figure 3.
3.1. Heading controller design
To simplify the complexity of the controller design, the model for heading control is presented as follows:
Stabilize the heading error
:
Define the Lyapunov function:
Define the heading angular velocity error
:
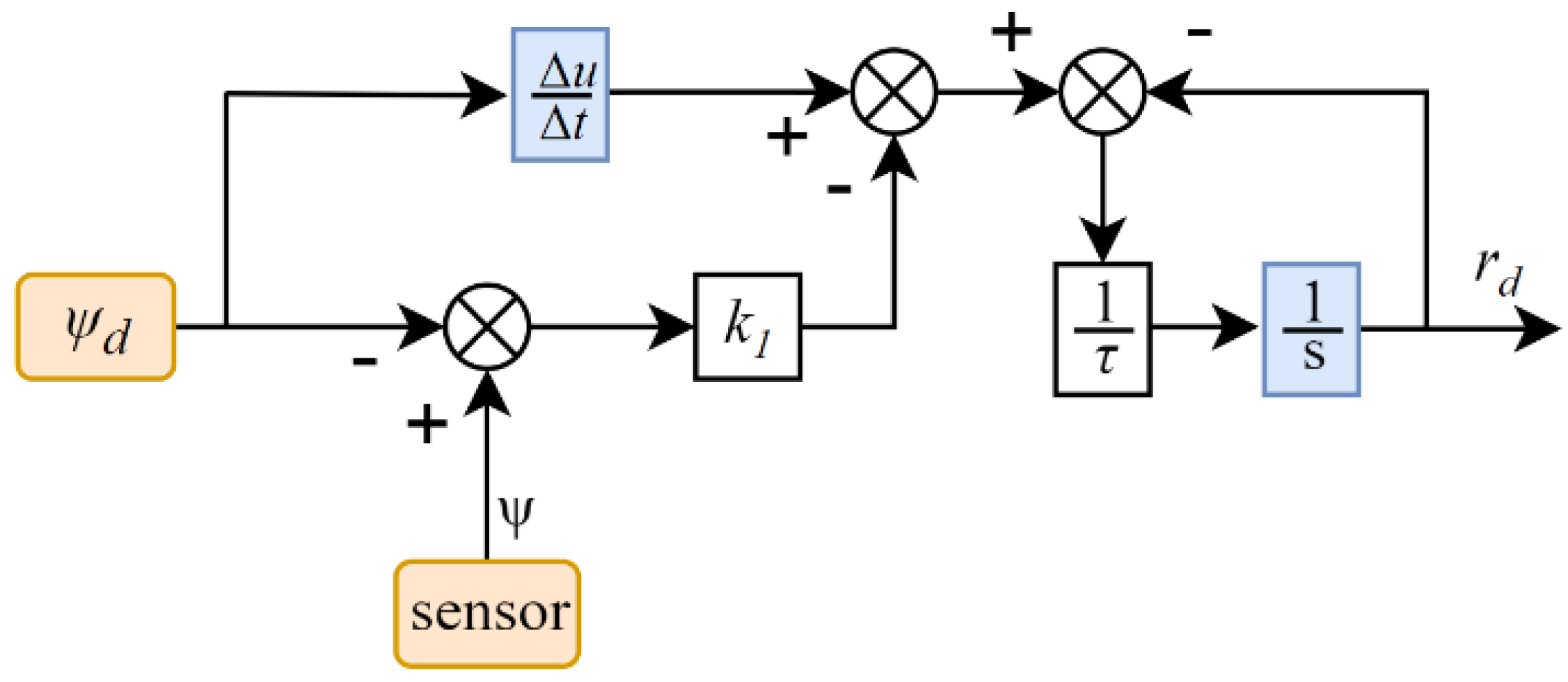
In traditional backstepping design, if
is chosen, it may lead to a "differentiation explosion" when computing
. By adopting the dynamic surface control method and using a first-order integral filter to calculate the derivative of the virtual control, this drawback can be overcome. Let
be the output of the low-pass filter
for
.(as shown in
Figure 4)
Where is a positive constant greater than zero.
Where is a positive constant greater than zero, and the filtering error generated is .
The heading control model is classified as a second-order system. The first layer stabilizes the heading angle using backstepping dynamic surface control, while the second layer stabilizes the heading angular velocity through sliding mode variable structure control. To eliminate the steady-state error associated with sliding mode control, an integral term of the tracking error is incorporated into the traditional sliding mode surface, resulting in the integral sliding mode surface defined as follows:
Where is a positive constant greater than zero.
Define the Lyapunov function:
Where
The control law for the heading control is designed as:
Where 、、 is a positive constant greater than zero.
Remark 4. According to (20), the proposed observer has a saturation function instead of a discontinuous signum function. As a result, unwanted oscillatory effects can be reduced significantly.
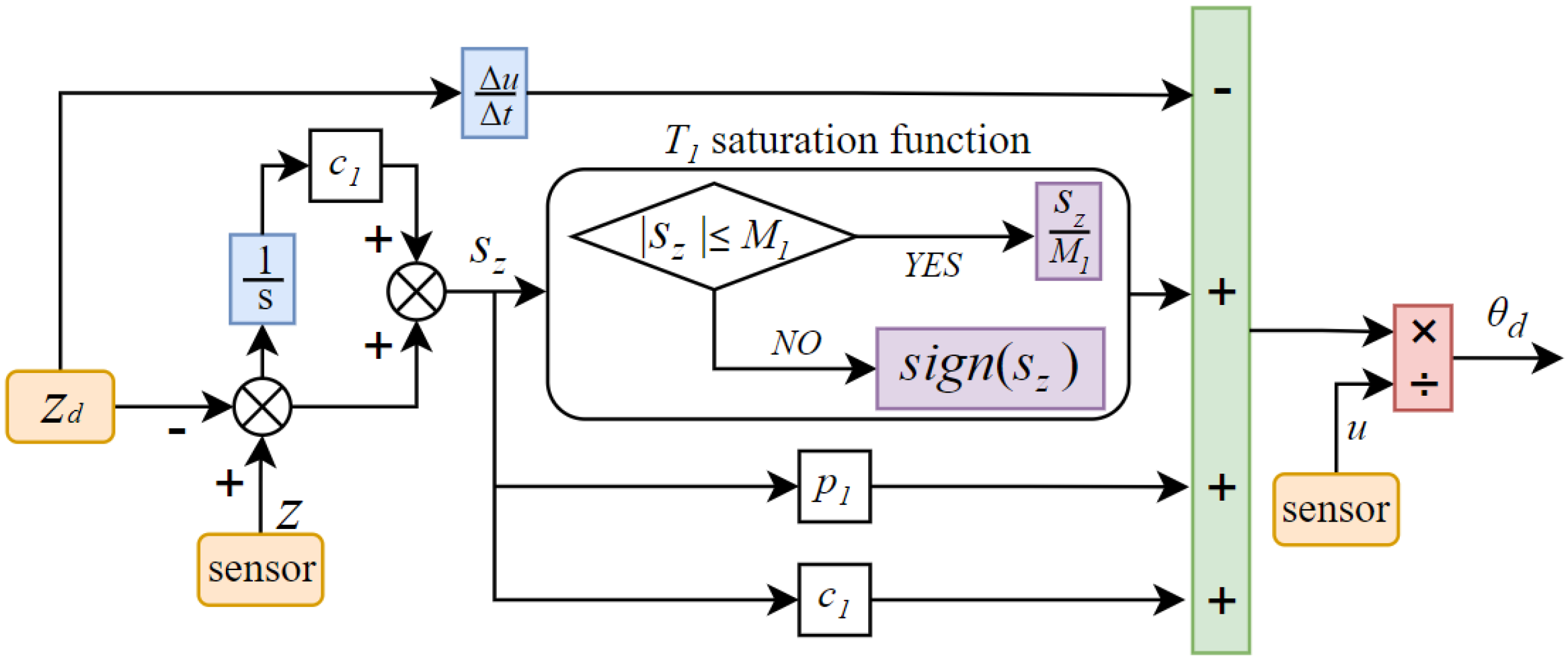
3.2. Depth controller design
The model for depth control is simplified as follows:
Depth control utilizes a dual-loop control strategy, with the integral sliding mode controller functioning as the outer loop.
Figure 5.
Inner loop controller block diagram.
Figure 5.
Inner loop controller block diagram.
The integral sliding mode surface is defined as follows:
Obtain the desired pitch angle
as the virtual control input:
Where 、、 is a positive constant greater than zero.
Backstepping integral sliding mode control serves as the outer loop. Define the pitch error formula:
The subsequent derivation principle is the same as that for heading control (refer to equations (8)-(17)), so the specific steps are omitted.
Then, the control law for depth control is designed as:
Where 、、 is a positive constant greater than zero.
3.3. Lyapunov stability verification
This section analyzes the stability of the proposed heading controller algorithm, and the same method can also be used to prove the stability of the depth control.
For Equation (18), there exists a positive constant such that , which implies that all signals in the closed-loop system are bounded and converge.
Proof: Let at this point, then is bounded, denoted as , thus .
Substituting the control law into Equation
, we obtain:
There exists a positive constant
, take:
Since at this point , then Equation (31) can be rewritten as . To ensure that , take , i.e., .
Equation (31) shows that when , if , then , and consequently .
Furthermore, based on the above reasoning, the following convergence analysis can be performed. According to Theorem [
30], the solution to the inequality equation
is
And converges asymptotically, with the convergence accuracy depending on .
Furthermore, since , if is taken, then can be taken, which is the reason why the low-pass filter can be designed as .
4. Simulation Verification
4.1. Parameters of the underactuated AUV
To verify the effectiveness and robustness of the proposed motion controller, a simulation environment was developed using MATLAB R2022b software. The simulation model of the underactuated AUV is based on the physical data (as shown in
Table 1) of the "Sprite 200"(as shown in
Figure 6) robot in the author's laboratory, with the controller parameters provided in
Table 2 and
Table 3.
This paper presents a comprehensive evaluation of BISMC through four simulation experiments. Case 1 validated fundamental functionality under ideal conditions. Case 2 tested robustness against static disturbances, while Case 3 assessed adaptability in dynamic environments. Case 4 posed the ultimate challenge with random disturbances, mirroring real oceanic conditions.
Additionally, to analyze the AUV motion control performance more clearly and quantitatively, data analysis was conducted on the heading and depth errors. Four key performance indicators: (1) IAE (Integral of Absolute Error), expressed as ; (2) AVE (Average Value of the Absolute Errors), expressed as ; and (3) ITAE (Integrated Time Absolute Error), expressed as ; and (4) ASSE (Average Steady State Error), expressed as , where represents the time after the error converges and stabilizes. For the sake of convenience in statistics, the data tracking the first expected value is taken for calculation.
4.2. Simulation Model Validation
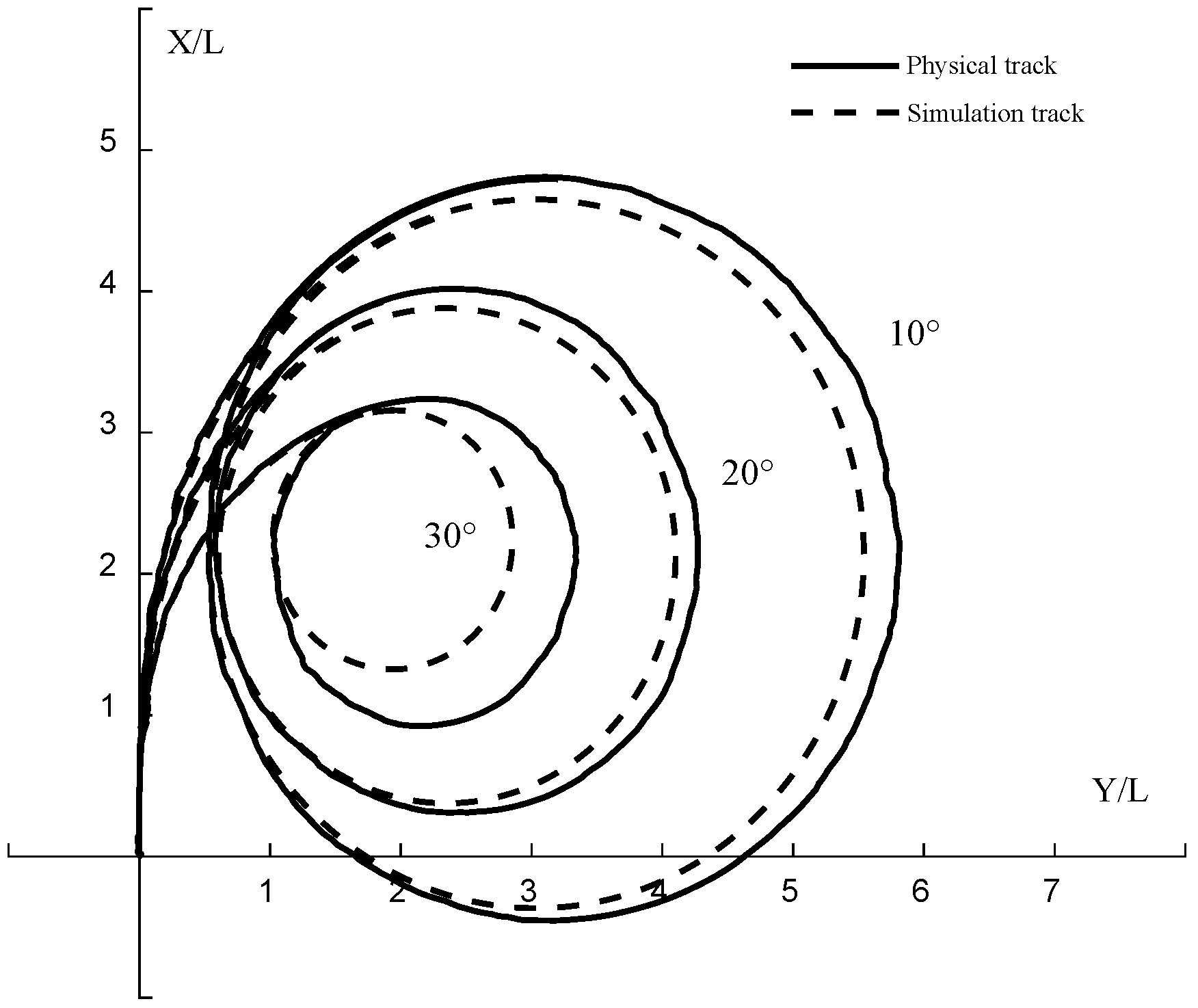
In order to ensure the accuracy, reliability, and practicality of the simulation model, an underactuated AUV entity turning test was conducted on the Shazhou Jinhu Lake in Zhangjiagang(as shown in
Figure 7). The trajectory data of the AUV was exported from the mounted Doppler sensor. During the test, the wind speed was around 1.5 m/s, and the wind direction was westerly.
Figure 8 presents a comparison of the turning rates between the physical model and the simulation under different rudder angles. It is evident that the two are similar and correspond well with each other. Based on this result, we can conclude that the simulation model we have constructed is effective and reliable, and can be utilized for further analysis and research
4.3. Case Results
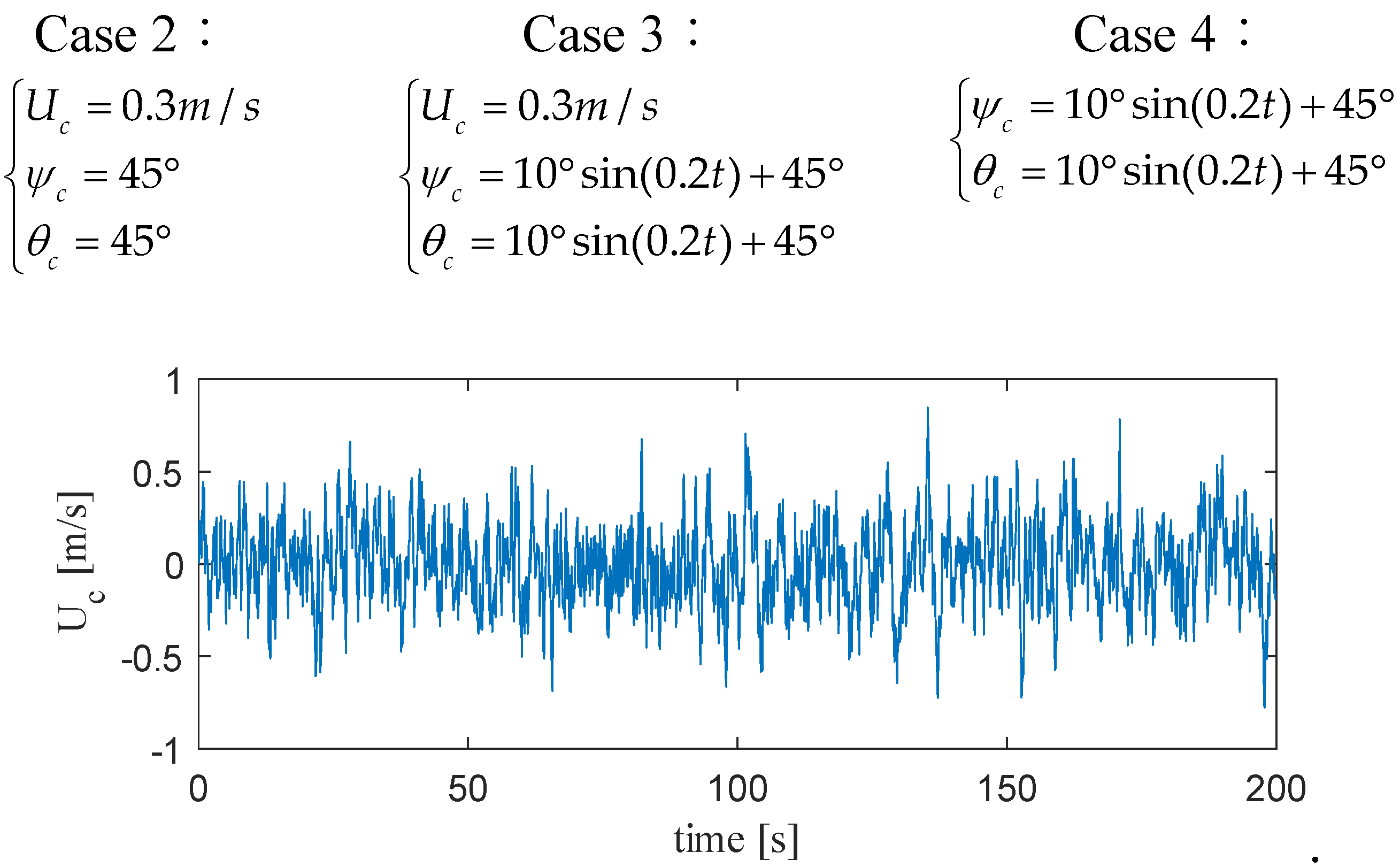
The AUV follows headings of [0°, 20°, 40°, 10°] at 30-second intervals and depths of [0 m, -10 m, -30 m, -20 m] at 50-second intervals. The initial position and velocity of the AUV are both set at , . The propeller speed was set to 1200, and the longitudinal speed stabilized at 2.5m/s after reaching equilibrium. The disturbance of ocean currents in the simulation is introduced into the motion model after the first expected value of AUV tracking. The settings of ocean currents in Cases 2, 3, and 4 are as follows:
Figure 9.
In Case 4, the ocean current velocity is generated by a Gaussian function.
Figure 9.
In Case 4, the ocean current velocity is generated by a Gaussian function.
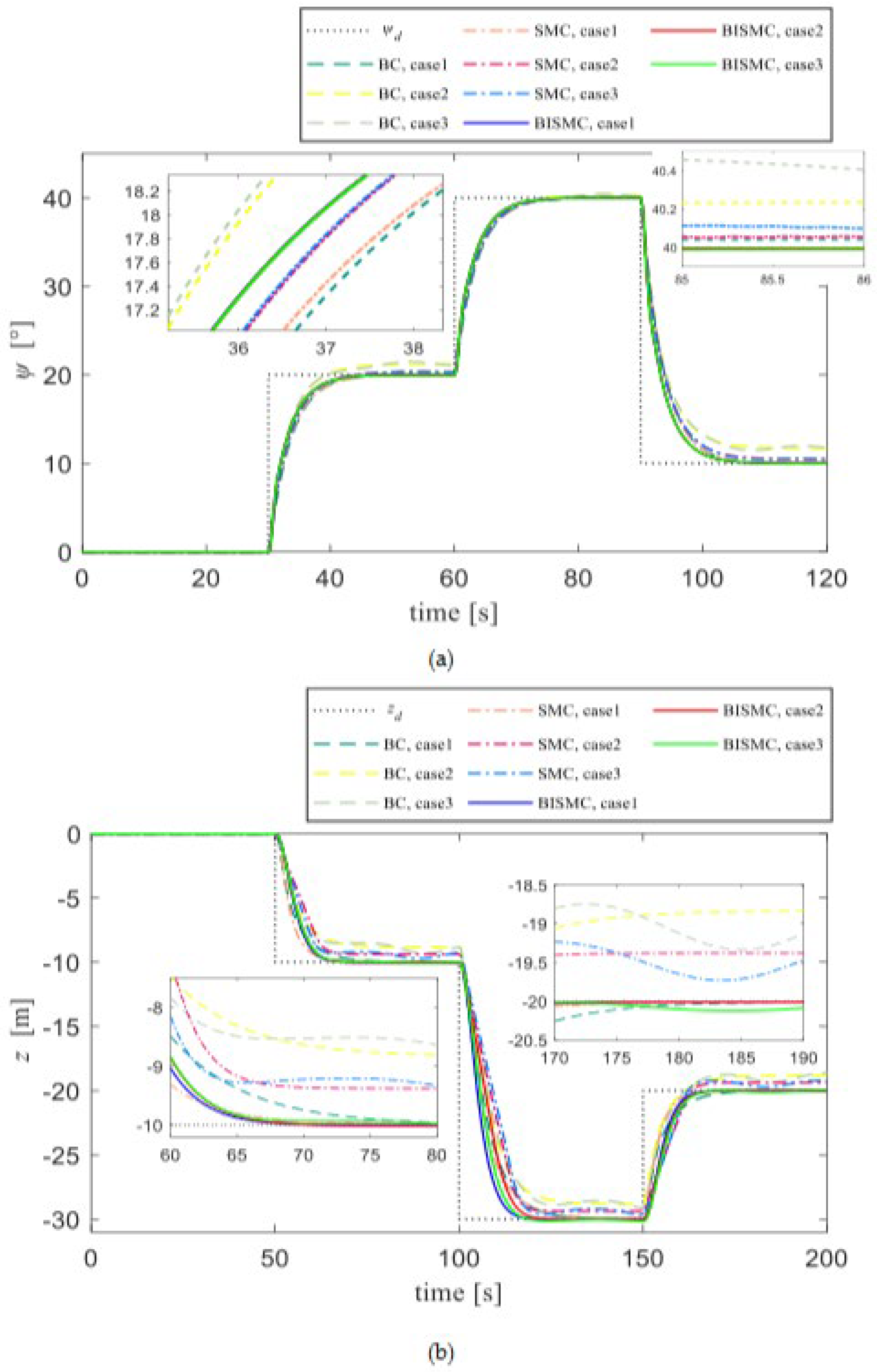
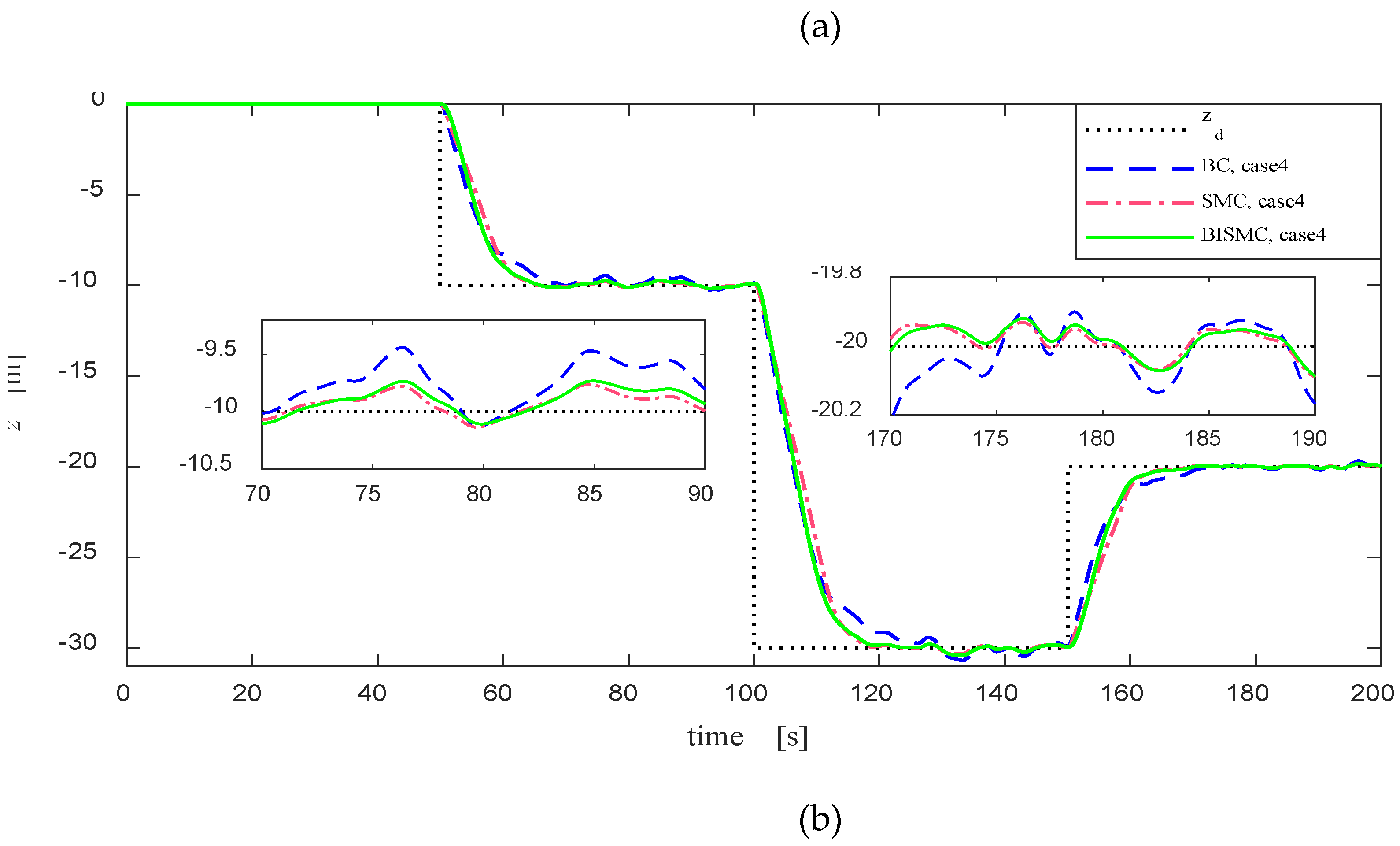
As evident from the comparative analysis in
Figure 10, under the scenario set in case 1, all three controllers exhibit the capability to track the desired heading and depth, with BISMC demonstrating a faster convergence speed. In the scenarios set by case 2 and case 3, both the traditional BC and SMC experience certain static and dynamic errors. Although SMC exhibits smaller steady-state errors due to its lower sensitivity to external disturbances, it still cannot fully counteract deviations caused by environmental factors such as ocean currents. In contrast, BISMC, with its built-in integral term, is able to completely eliminate steady-state errors in motion control, ensuring that tracking errors tend towards zero, thereby achieving a more precise control effect.
Figure 11 and
Figure 12 clearly show that during the 50 to 80 seconds interval when the AUV executes the 10-meter depth command, the horizontal rudder of BISMC does not exhibit any signs of saturation during operation. Furthermore, when the AUV is commanded to dive to a deeper depth of 30 meters (corresponding to the 100 to 130 seconds interval), there are no obvious overshoot phenomena observed during the control process of BISMC. These results effectively demonstrate the remarkable effectiveness of the double closed-loop control design in enhancing depth control accuracy and preventing actuator oversaturation. Additionally, the control output curve of BISMC is smoother compared to SMC, effectively overcoming the issue of chattering.
Table 4 further reinforces the above observations by showcasing that BISMC achieves the lowest values for the three performance indicators: IAE, AVE, and ITAAE. Specifically, in Case 1, for heading control, BISMC reduces the average performance metrics by 15.6% compared to BC and 12.6% compared to SMC, while for depth control, the reductions are 5% and 1.8%, respectively. This result indicates that the integral term in BISMC effectively mitigates internal system disturbances. In Case 2, for heading control, BISMC outperforms BC by an average of 29.3% and SMC by 16.4%, while for depth control, the improvements are 33.5% and 28.7%, respectively. Similarly, in Case 3, BISMC reduces the average performance metrics for heading control by 28.9% compared to BC and 16.5% compared to SMC, and for depth control, the reductions are 37.2% and 32.8%, respectively.
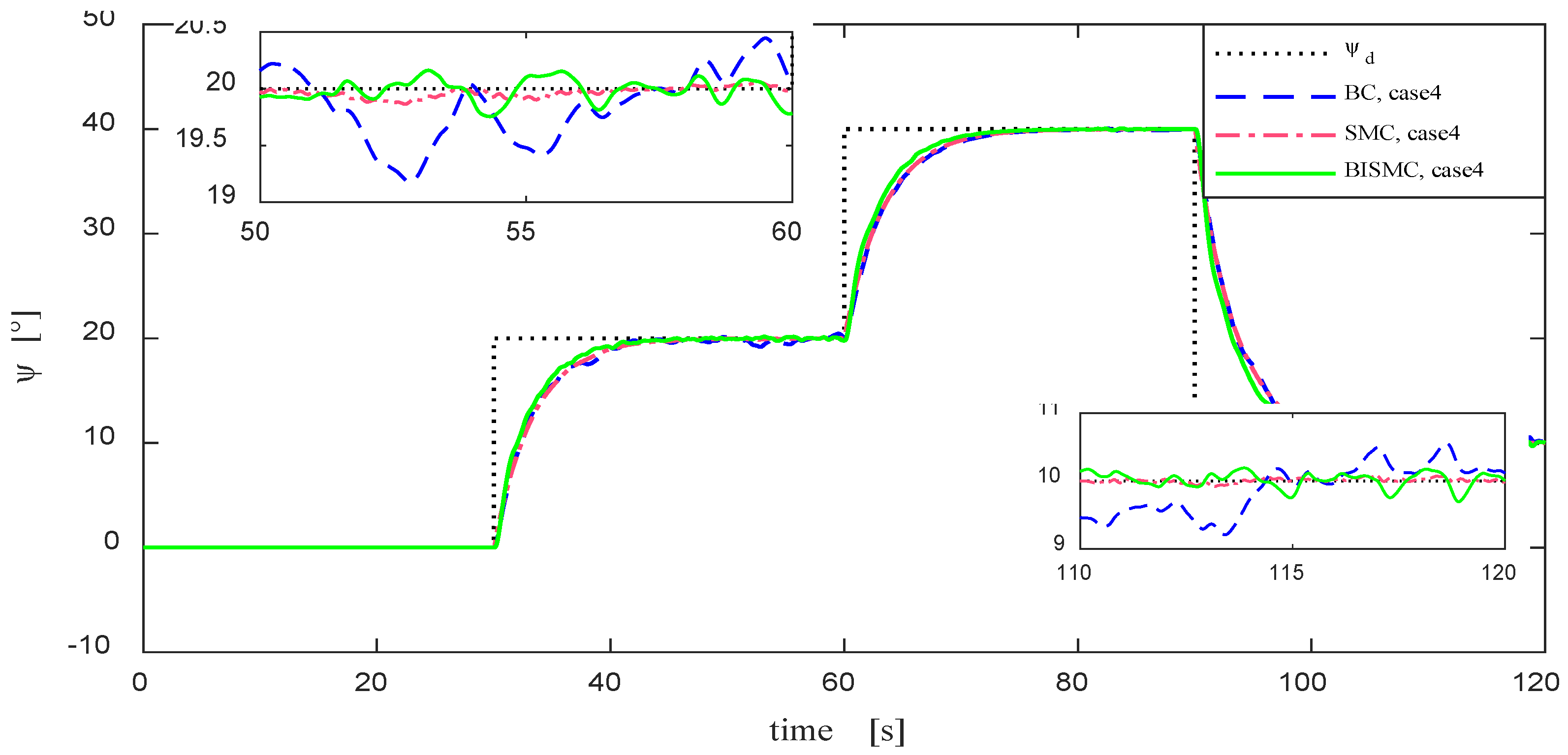
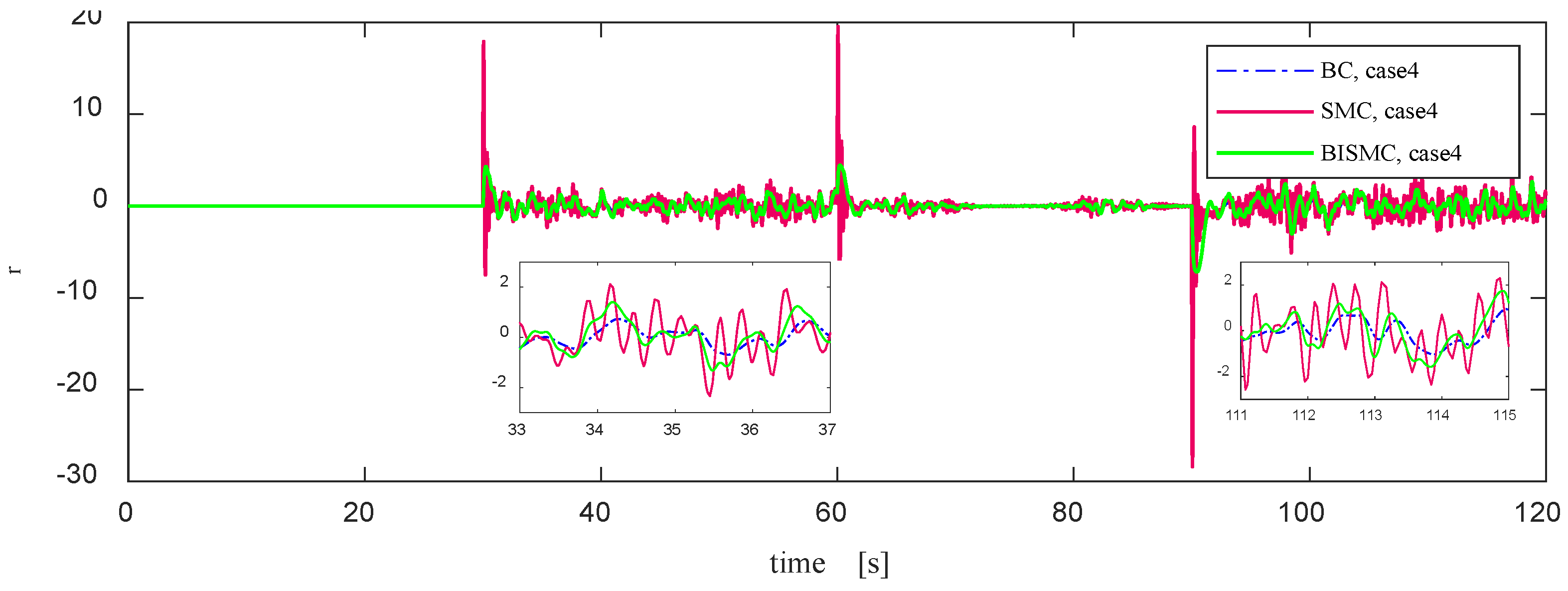
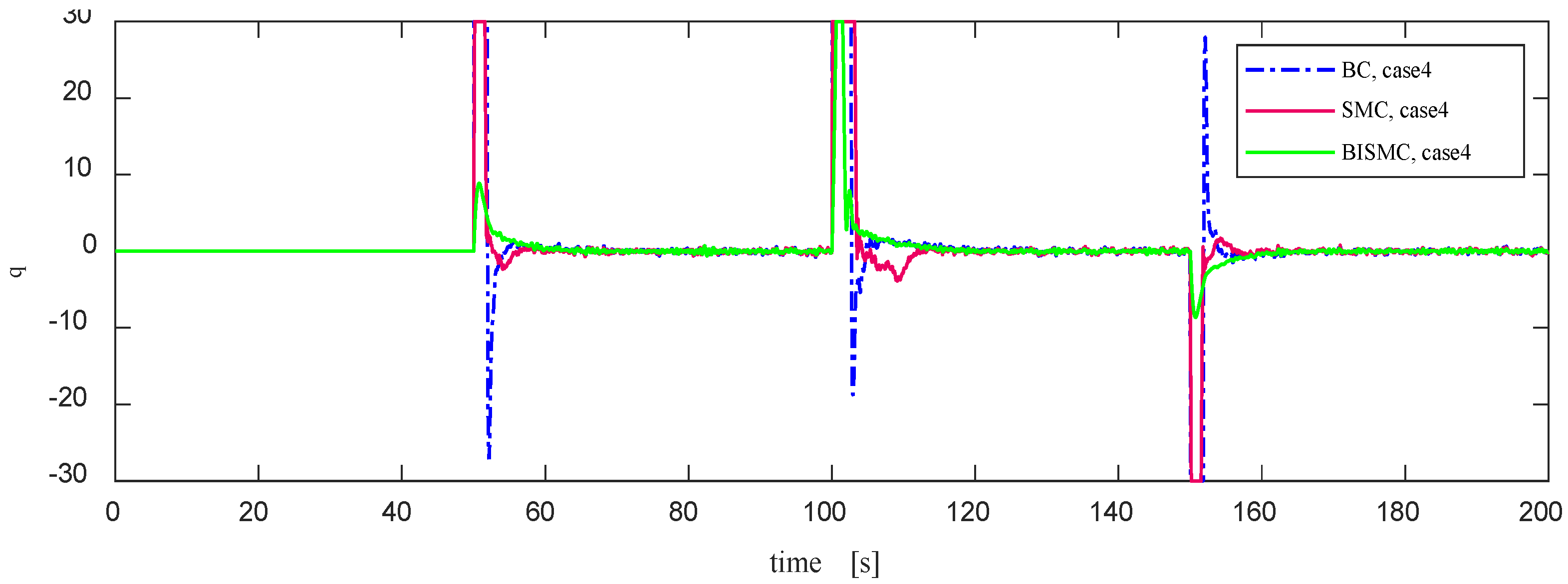
Figure 13 reveals the limitations of BISMC in motion control under the disturbance of random ocean current environments. In contrast, the conventional SMC demonstrates superior performance in heading and depth tracking, with minimal fluctuations after error convergence. The core of this phenomenon lies in the inherent anti-disturbance characteristics of SMC, which makes it particularly adept at handling high-frequency and random ocean current fluctuations, in stark contrast to the low-frequency sea conditions described in previous cases 2 and 3. However, it is noteworthy that SMC's high-precision tracking capability comes at the cost of high-frequency and severe vibrations in the control rudder (as shown in
Figure 14 and
Figure 15), posing a significant challenge to the rudder actuators of Autonomous Underwater Vehicles (AUVs). This can exacerbate wear and shorten their service life, thus limiting its practical application. Since BISMC incorporates a saturation function mechanism in the design of its control law, it effectively eliminates the chattering issue in control output but weakens its ability to counter high-frequency disturbances. As seen in
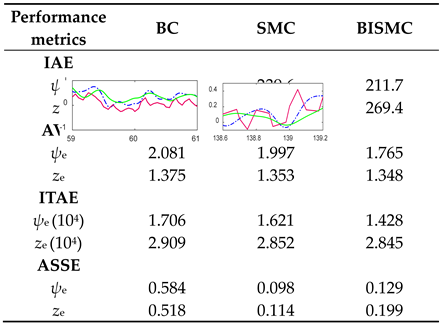
Table 3, while BISMC has a higher steady-state error than SMC, it exhibits advantages in IAT, AVE, and ITAE performance indicators, indicating that BISMC converges faster with less accumulated error during the convergence process.
In summary, although BISMC shows certain deficiencies in dealing with high-frequency ocean current disturbances, it still ensures that AUVs can quickly converge and maintain smooth control output, a feature that holds significant value in practical applications.
Figure 1.
The AUV reference frame.
Figure 1.
The AUV reference frame.
Figure 3.
Control principle diagram.
Figure 3.
Control principle diagram.
Figure 4.
First-order filtering.
Figure 4.
First-order filtering.
Figure 6.
AUV Sprite 200 physical diagram.
Figure 6.
AUV Sprite 200 physical diagram.
Figure 7.
Underactuated AUV Physical Turning Test.
Figure 7.
Underactuated AUV Physical Turning Test.
Figure 8.
Turning curves of the physical model and simulation at rudder angles of 10°, 20°, and 30°.
Figure 8.
Turning curves of the physical model and simulation at rudder angles of 10°, 20°, and 30°.
Figure 10.
Tracking curves for heading and depth in Cases 1, 2, and 3: BC, SMC, and BISMC all successfully track the desired values in Case 1, with BISMC exhibiting the fastest convergence speed.; BC and SMC exhibit static errors in Case 2 and dynamic errors in Case 3; BISMC performs the best among the three cases.
Figure 10.
Tracking curves for heading and depth in Cases 1, 2, and 3: BC, SMC, and BISMC all successfully track the desired values in Case 1, with BISMC exhibiting the fastest convergence speed.; BC and SMC exhibit static errors in Case 2 and dynamic errors in Case 3; BISMC performs the best among the three cases.
Figure 11.
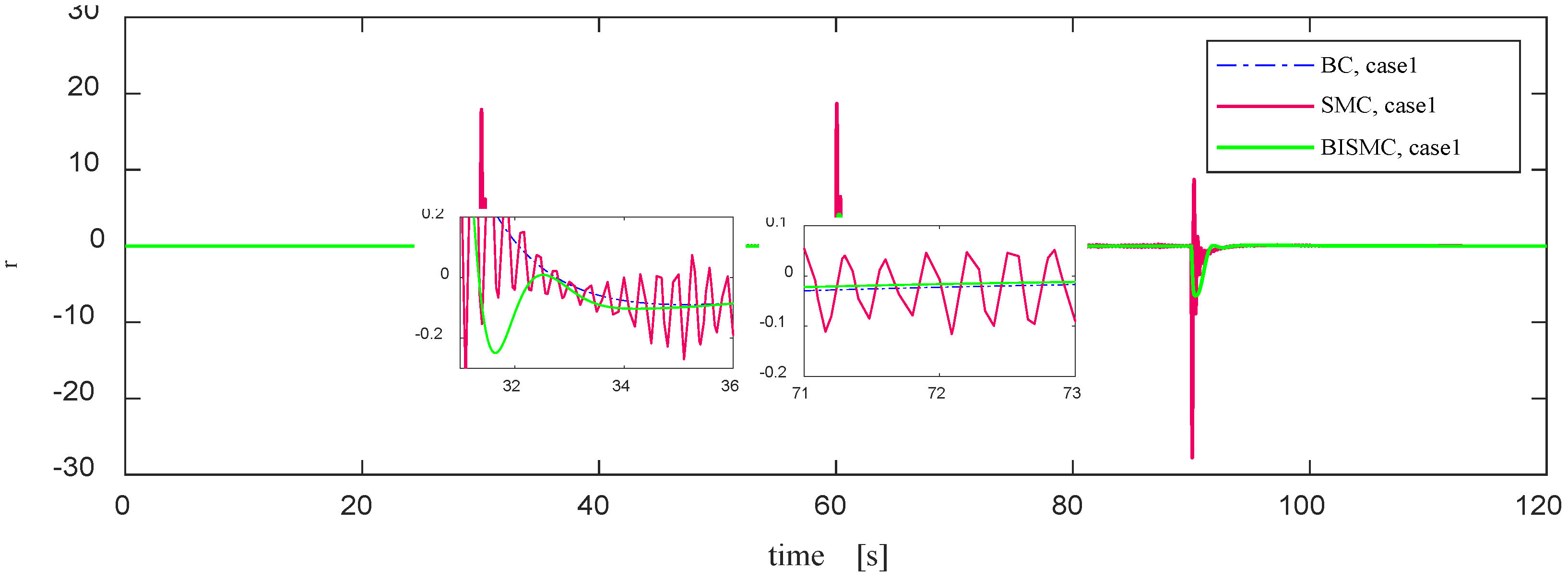
Vertical Rudder Output Curve in Case 1. Between 32-36 seconds, significant chattering is observed in SMC. Due to the coupling between the heading and depth, after the heading reaches equilibrium at 71-73 seconds, rudder force is still required to counteract the influence.
Figure 11.
Vertical Rudder Output Curve in Case 1. Between 32-36 seconds, significant chattering is observed in SMC. Due to the coupling between the heading and depth, after the heading reaches equilibrium at 71-73 seconds, rudder force is still required to counteract the influence.
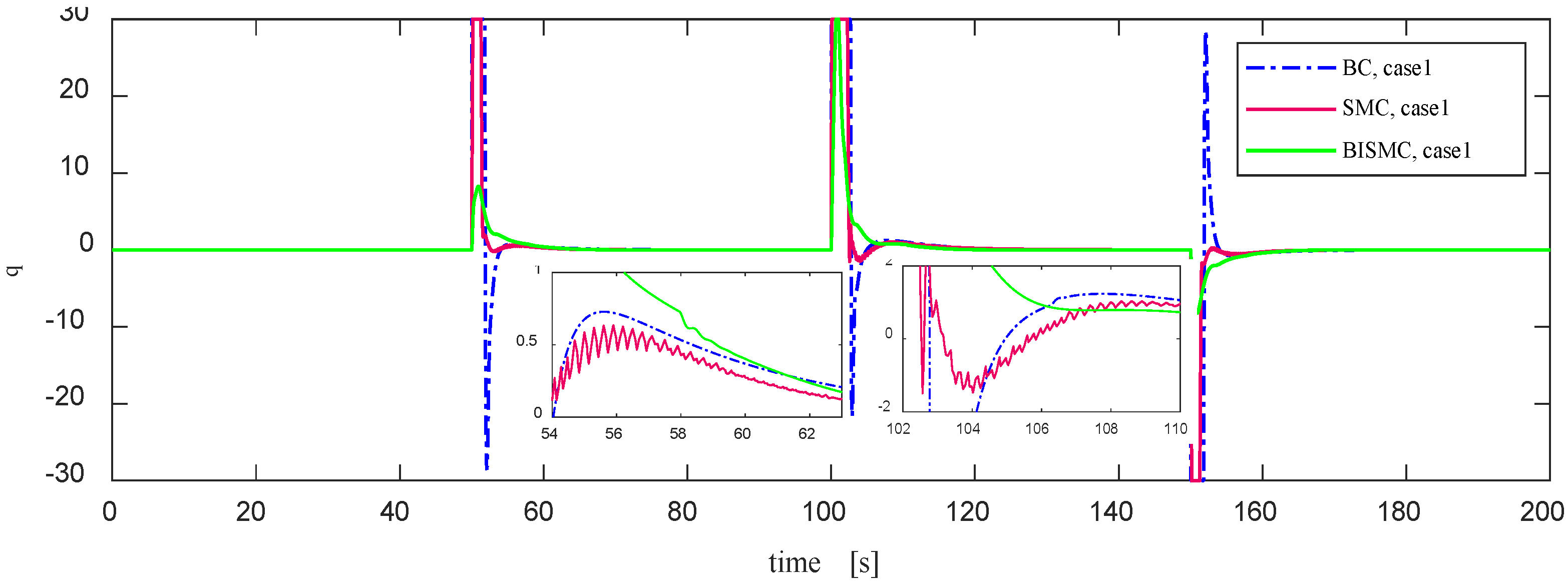
Figure 12.
Horizontal Rudder Output Curve in Case 1. Both BC and SMC exhibit oversaturation and overshoot phenomena while tracking depth. Noticeable chattering is observed in SMC during the intervals of 54-62 seconds and 102-110 seconds.
Figure 12.
Horizontal Rudder Output Curve in Case 1. Both BC and SMC exhibit oversaturation and overshoot phenomena while tracking depth. Noticeable chattering is observed in SMC during the intervals of 54-62 seconds and 102-110 seconds.
Figure 13.
Heading and Depth Tracking in Case 4. SMC exhibits minimal fluctuations after error convergence.
Figure 13.
Heading and Depth Tracking in Case 4. SMC exhibits minimal fluctuations after error convergence.
Figure 14.
Vertical Rudder Output Curve in Case 4. SMC's rudder angle output exhibits the most severe chattering.
Figure 14.
Vertical Rudder Output Curve in Case 4. SMC's rudder angle output exhibits the most severe chattering.
Figure 15.
Horizontal Rudder Output Curve in Case 4. SMC's rudder angle output experiences the most intense chattering.
Figure 15.
Horizontal Rudder Output Curve in Case 4. SMC's rudder angle output experiences the most intense chattering.
Table 1.
AUV parameter list in the simulations.
Table 1.
AUV parameter list in the simulations.
| Parameter |
Value |
Parameter |
Value |
|
1000(kg/m3) |
|
-21.01 |
|
11(kg) |
|
3.834 |
|
1.2(m) |
|
-26.08 |
|
106.0(N) |
|
-96.22 |
|
107.9(N) |
|
-41.9 |
|
0.016(kg·m2) |
|
-21.01 |
|
0.8(kg·m2) |
|
-3.834 |
|
0.8(kg·m2) |
|
-2.918 |
|
0.0296 |
|
-112.4 |
|
-0.683 |
|
2.107 |
|
-1.428 |
|
1.591 |
|
-26.08 |
|
-1.325 |
|
-1.279 |
|
-2.918 |
|
-26.08 |
|
-56.21 |
|
-1.279 |
|
-2.107 |
|
-26.08 |
|
-1.591 |
|
-96.22 |
|
-1.325 |
|
-0.419 |
|
|
Table 2.
Heading controller parameters.
Table 2.
Heading controller parameters.
| BC |
SMC |
BISMC |
| Parameter |
Value |
Parameter |
Value |
Parameter |
Value |
| k1 |
2 |
c1 |
1 |
k1 |
2 |
| k2 |
10 |
E |
6 |
τ |
0.025 |
| |
|
P |
2 |
c1 |
0.5 |
| |
|
|
|
E |
6 |
| |
|
|
|
P |
2 |
| |
|
|
|
M |
5 |
Table 3.
Depth controller parameters.
Table 3.
Depth controller parameters.
| BC |
SMC |
ISMC |
BISMC |
| Parameter |
Value |
Parameter |
Value |
Parameter |
Value |
Parameter |
Value |
| k1 |
1.5 |
c1 |
2 |
c1 |
1 |
k1 |
1.5 |
| k2 |
6 |
c2 |
4 |
E1 |
10 |
τ |
0.025 |
| k3 |
2 |
E |
10 |
P1 |
3 |
c2 |
0.5 |
| |
|
P |
3 |
M1 |
5 |
E2 |
10 |
| |
|
|
|
|
|
P2 |
3 |
| |
|
|
|
|
|
M2 |
5 |
Table 4.
Performance comparison in Cases 1, 2, and 3.
Table 4.
Performance comparison in Cases 1, 2, and 3.
Performance
metrics |
BC |
SMC |
BISMC |
BC |
SMC |
BISMC |
BC |
SMC |
BISMC |
| IAE |
|
|
|
|
|
|
|
|
|
|
ψe
|
248.5 |
239.7 |
210 |
287.5 |
248 |
210 |
286.1 |
248.1 |
210 |
|
ze
|
246.5 |
233.9 |
239.2 |
394.8 |
369.6 |
266.1 |
395.3 |
370.8 |
251.7 |
| AVE |
|
|
|
|
|
|
|
|
|
|
ψe
|
2.07 |
1.998 |
1.75 |
2.395 |
2.067 |
1.75 |
2.384 |
2.068 |
1.75 |
|
ze
|
1.232 |
1.17 |
1.196 |
1.974 |
1.848 |
1.33 |
1.977 |
1.854 |
1.259 |
| ITAE |
|
|
|
|
|
|
|
|
|
|
ψe (104) |
1.682 |
1.623 |
1.412 |
2.136 |
1.736 |
1.412 |
2.128 |
1.736 |
1.412 |
|
ze (104) |
2.593 |
2.464 |
2.493 |
4.325 |
4.002 |
2.795 |
4.353 |
4.040 |
2.661 |
Table 5.
Performance comparison in Cases 4.
Table 5.
Performance comparison in Cases 4.