Preprint
Article
Biomathematics in Cancer Research: Looking into How Mathematical Models Are Used to Understand Tumor Growth and the Effectiveness of Different Treatment Strategies
Altmetrics
Downloads
119
Views
125
Comments
0
This version is not peer-reviewed
Submitted:
29 September 2024
Posted:
30 September 2024
You are already at the latest version
Alerts
Abstract
This paper explores the critical role of biomathematics in cancer research, focusing on how mathematical models enhance our understanding of tumor growth and optimize treatment strategies. It begins with an overview of cancer biology, highlighting the complexities of tumor dynamics and the molecular mechanisms driving growth. The paper then delves into various mathematical modeling approaches, including deterministic, stochastic, and agent-based models, illustrating their applications in predicting tumor behavior and treatment responses. Case studies demonstrate the real-world impact of these models on optimizing chemotherapy, radiation therapy, and immunotherapy. Challenges such as data availability, model complexity, and clinical translation are discussed, alongside future directions in the field, including advances in computational power and personalized medicine. Ultimately, this research emphasizes the transformative potential of biomathematics in improving cancer treatment outcomes and underscores the importance of interdisciplinary collaboration in advancing the field.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
Introduction
Background Information
Cancer, a leading cause of mortality worldwide, presents a significant challenge to global health. According to the World Health Organization, approximately 10 million people died from cancer in 2020, and this number is expected to rise as populations age and risk factors such as smoking, poor diet, and lack of physical activity persist (WHO, 2022). With its complex biology and many subtypes, cancer requires diverse approaches to diagnosis and treatment. Traditional methods like surgery, chemotherapy, and radiation have been pivotal in improving patient outcomes, but cancer remains a formidable adversary. New approaches that integrate biology with advanced technologies are increasingly vital in the fight against this disease.
Historically, cancer research has evolved through significant discoveries, from early understandings of tumors in ancient civilizations to the establishment of oncology as a medical field in the 19th century (McAleer, 2022). The discovery of the cell cycle, DNA structure, and oncogenes have all deepened our understanding of cancer biology, leading to the development of treatments like targeted therapies and immunotherapies. However, despite these advances, the complexity of cancer, particularly its heterogeneity and ability to evolve resistance to therapies, continues to challenge researchers and clinicians. This has led to the incorporation of interdisciplinary approaches, including mathematics, into cancer research.
Biomathematics, the application of mathematical methods to biological problems, has emerged as an essential tool in modern cancer research. By utilizing mathematical models, researchers can simulate the growth of tumors, predict their future behavior, and evaluate how they might respond to various treatment strategies. This integration of mathematical and biological sciences has opened new avenues for understanding the complex dynamics of cancer. Biomathematics allows scientists to move beyond static models and gain insights into the time-dependent processes that govern tumor development, metastasis, and treatment resistance (Vieira et al., 2023). As a result, biomathematics is not only providing a deeper understanding of cancer biology but also improving the design of treatment protocols.
Research Problem and Rationale
The need for a better understanding of tumor dynamics is critical to improving cancer treatment outcomes. Tumor growth is a multifaceted process influenced by genetic mutations, cell proliferation rates, interactions with the immune system, and the surrounding microenvironment. Traditional experimental approaches often fall short of capturing the full scope of these complexities. Mathematical modeling offers a powerful alternative by allowing researchers to analyze how tumors evolve over time, considering factors like angiogenesis, nutrient availability, and immune evasion.
One of the most significant contributions of mathematical models in cancer research is their ability to simulate tumor growth under various treatment scenarios. By incorporating factors such as drug pharmacokinetics, radiation dosage, or immune responses, these models can predict how different treatments will affect tumor size and composition (Vieira et al., 2023). This capability is particularly valuable in personalizing treatment plans for individual patients, as it enables oncologists to predict which therapies might be most effective based on a patient’s unique tumor biology.
Figure 1.
Schematic representation of tumor microenvironment and its dynamic interactions.
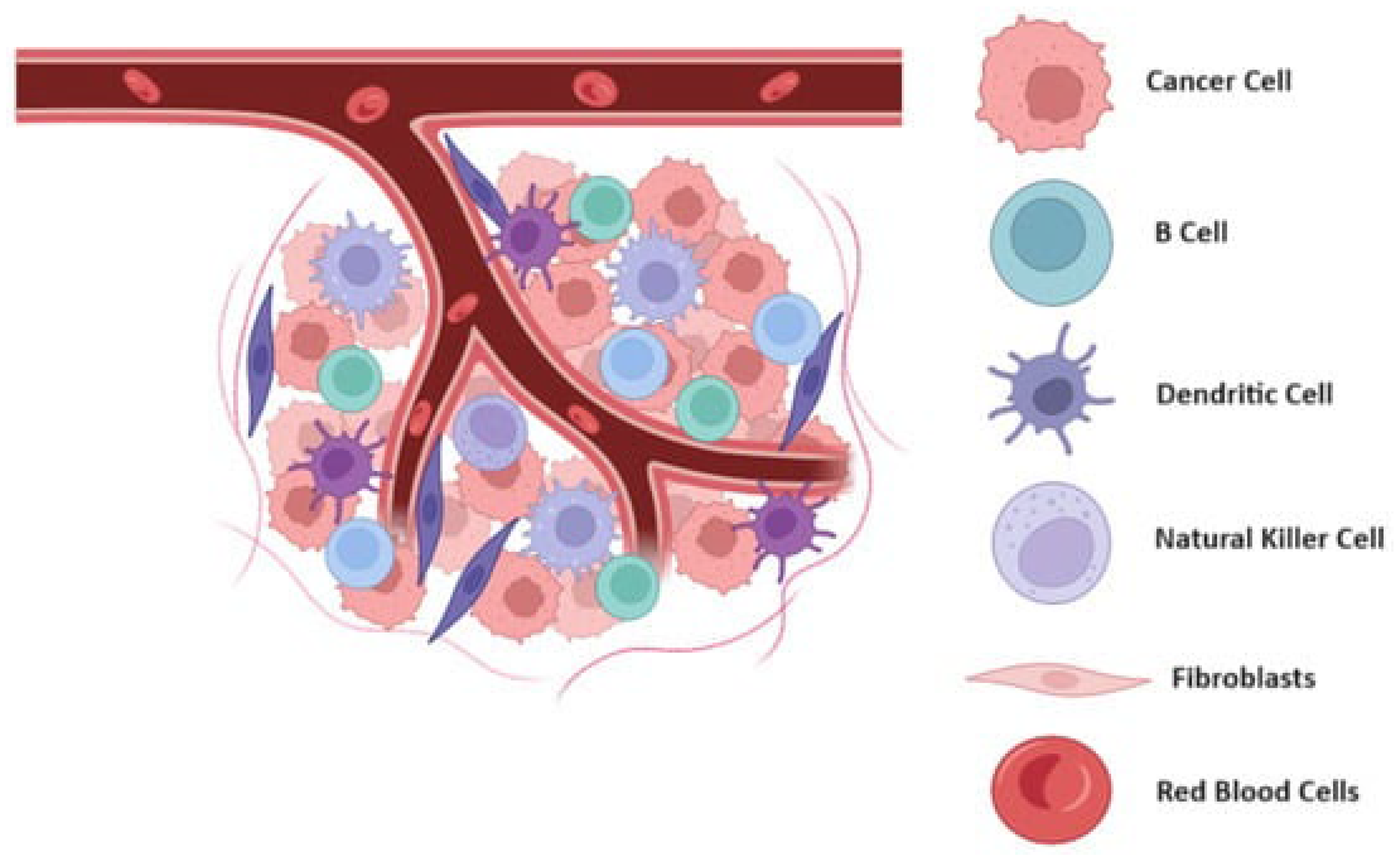
The rationale for using mathematical models is clear: they provide a framework for systematically investigating tumor dynamics, offering predictive power that experimental methods alone cannot achieve (Azizi, 2024). This approach not only enhances our understanding of how tumors grow and spread but also helps in optimizing therapeutic strategies, potentially improving patient survival rates and reducing side effects from overtreatment.
Objectives and Scope
The primary aim of this paper is to explore the role of biomathematics in modeling tumor growth and evaluating the effectiveness of different cancer treatment strategies. By examining how mathematical models simulate tumor behavior and treatment responses, this research will provide insights into the benefits and limitations of current models in cancer research. Furthermore, this paper will address how these models can guide the development of new therapies and enhance existing ones.
The scope of the research includes a discussion of various mathematical models used in cancer research, such as deterministic and stochastic models, as well as the application of these models to specific cancer types. The focus will be on models that predict tumor growth and response to treatments like chemotherapy, radiation, and immunotherapy. While mathematical models offer many advantages, they also come with limitations. These models rely on assumptions that may not always accurately reflect the biological complexities of tumors, and data limitations can restrict their predictive power. By acknowledging these constraints, this paper will also address the challenges and future directions in integrating biomathematics into cancer research.
Thesis Statement
Biomathematics is transforming the landscape of cancer research, offering a new way to understand the intricate dynamics of tumor growth and treatment response. Through mathematical modeling, researchers can simulate tumor behavior under various conditions, predict responses to therapies, and develop more effective, personalized treatment strategies. This paper will demonstrate how the integration of mathematical models into cancer research is enhancing our ability to understand tumor biology, optimize treatment plans, and ultimately improve patient outcomes.
Overview of Cancer Biology and Tumor Growth
Basic Cancer Biology
Cancer is a broad term for a group of diseases characterized by the uncontrolled growth and spread of abnormal cells. Unlike normal cells, which follow a regulated cell cycle, cancer cells divide uncontrollably, forming tumors that can invade nearby tissues and metastasize to distant organs. Tumors can be classified as either benign or malignant (National Cancer Institute, 2021). Benign tumors are non-cancerous and usually do not spread, whereas malignant tumors are cancerous and possess the potential to invade other parts of the body.
Figure 2.
Cancer cell and normal cell.
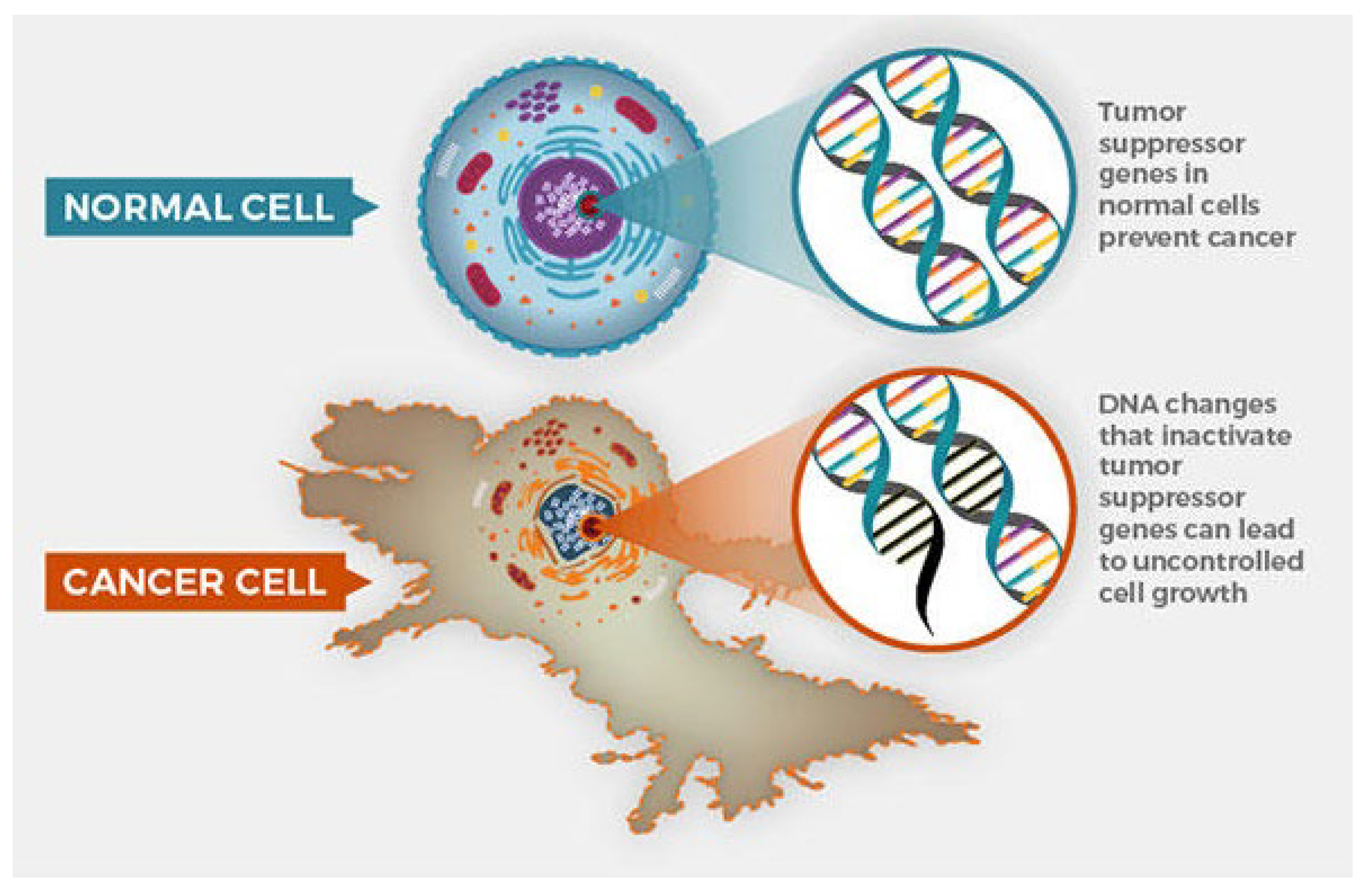
Cancer progresses through several stages, typically defined by the size of the tumor and its spread. In early-stage cancer, the tumor is confined to its original site. As the disease advances, the cancerous cells invade surrounding tissues and, in later stages, may metastasize through the bloodstream or lymphatic system to distant organs. The molecular mechanisms driving tumor growth are rooted in genetic mutations and dysregulation of the cell cycle. Normal cell division is tightly controlled by checkpoints in the cell cycle, where DNA is repaired before the cell divides (National Cancer Institute, 2021). However, in cancer cells, mutations in oncogenes, tumor suppressor genes, and DNA repair genes lead to unchecked proliferation. These genetic alterations can occur due to exposure to carcinogens, such as tobacco smoke or UV radiation, or arise from inherited genetic mutations.
The cell cycle is central to tumor growth, with several key proteins involved in regulating cell division. Mutations in genes like TP53, which encodes a tumor suppressor protein, and genes controlling growth factors like epidermal growth factor receptor (EGFR) contribute to the development and progression of cancer (National Cancer Institute, 2021). As these cells divide uncontrollably, tumors grow and evolve, acquiring further mutations that enhance their survival, proliferation, and ability to evade the immune system.
Tumor Microenvironment
The tumor microenvironment (TME) is composed of the non-cancerous cells, molecules, and blood vessels that surround and interact with the tumor. Far from being passive bystanders, these components play an active role in tumor progression (de Visser & Joyce, 2023). Tumor cells communicate with the surrounding stroma, which includes fibroblasts, immune cells, and the extracellular matrix, to create a supportive niche that promotes growth and invasion.
One critical aspect of the TME is its interaction with the immune system. While the immune system is capable of identifying and eliminating abnormal cells, cancer cells can evade immune detection by expressing proteins that suppress immune responses (de Visser & Joyce, 2023). For example, they can inhibit cytotoxic T-cells, which are responsible for attacking cancer cells, or upregulate immune checkpoint proteins like PD-L1 that act as a shield against immune attack. This immune evasion allows the tumor to grow unchecked.
Figure 3.
The tumor microenvironment (TME) representation.
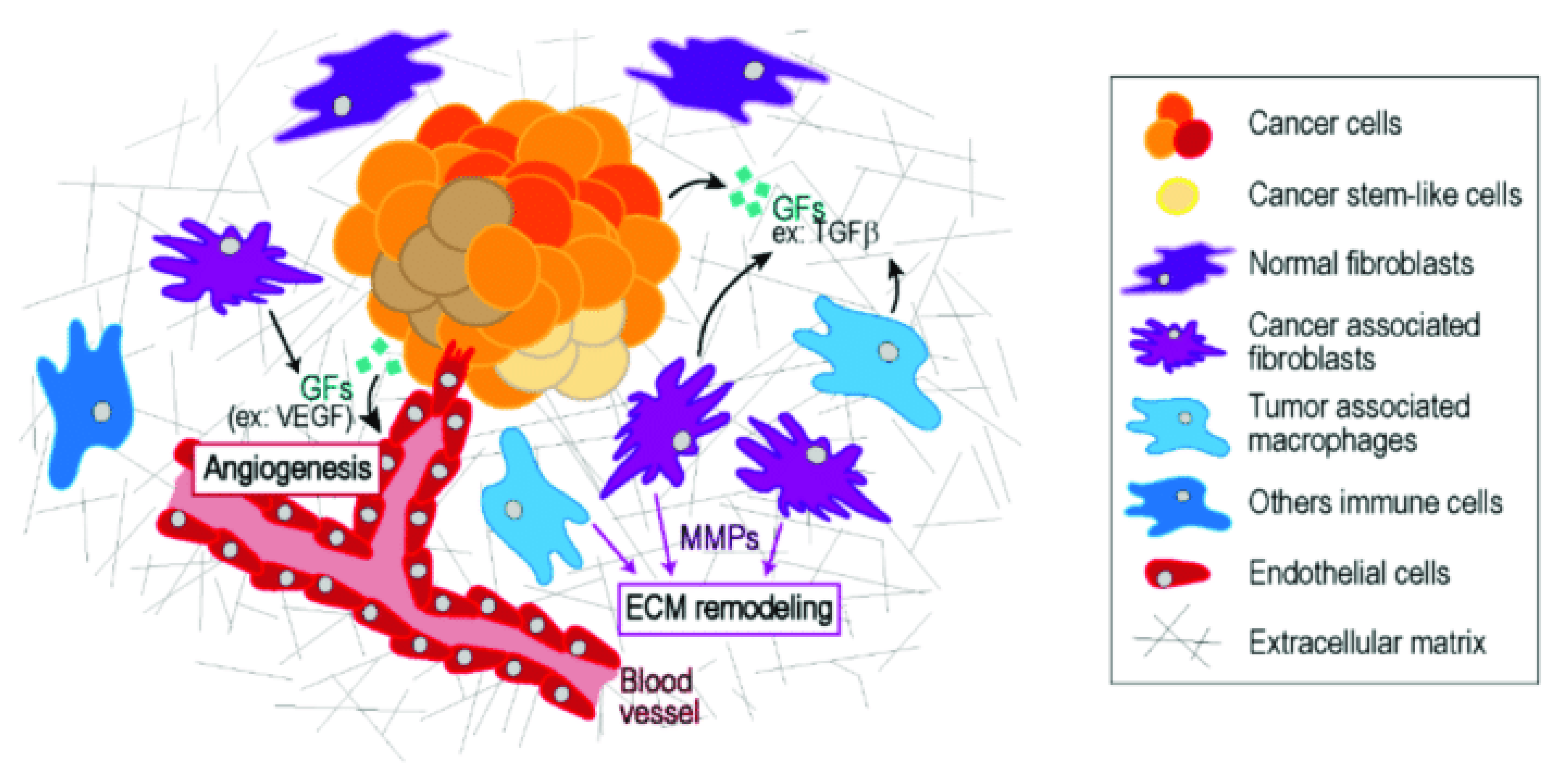
Another key process in the TME is angiogenesis, the formation of new blood vessels that supply the tumor with oxygen and nutrients. As tumors grow, they can outstrip their blood supply, leading to hypoxia (low oxygen levels). In response, cancer cells secrete factors like vascular endothelial growth factor (VEGF), which stimulates the growth of new blood vessels to nourish the expanding tumor (de Visser & Joyce, 2023). This process not only supports tumor growth but also provides a route for cancer cells to enter the bloodstream and metastasize to distant organs.
Tumor Growth Dynamics
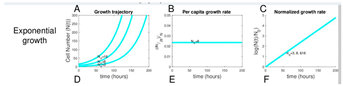
Tumor growth is often described using mathematical models that capture the dynamics of cell proliferation and death. There are several types of growth patterns observed in tumors, with the most common being exponential, logistic, and Gompertzian growth. In the early stages, many tumors grow exponentially, where the number of cells doubles at a constant rate (Nidal Al-Huniti et al., 2020). However, as tumors increase in size and resources like oxygen and nutrients become limited, growth tends to slow down.
The logistic growth model accounts for this deceleration, incorporating the concept of a carrying capacity—the maximum tumor size that the environment can support. In this model, tumor growth follows a sigmoidal curve, where growth is rapid at first but eventually plateaus as the tumor reaches its limits (Nidal Al-Huniti et al., 2020). Gompertzian growth is another commonly used model in cancer biology, characterized by an initial period of exponential growth followed by a progressively slower rate of increase. This model is often more accurate for describing the growth of larger, more established tumors.
Several factors influence tumor growth dynamics, including genetic, environmental, and treatment-related factors. On the genetic level, mutations that enhance cell proliferation or confer resistance to apoptosis (programmed cell death) can accelerate tumor growth. Environmental factors, such as the availability of oxygen, nutrients, and space, also play a critical role. For instance, tumors in nutrient-poor environments may grow more slowly or develop necrotic (dead) areas due to insufficient blood supply (GomezQuiroz & Roman, 2022). Finally, treatments like chemotherapy and radiation can significantly affect tumor growth by killing cancer cells or halting their division. However, cancer cells can adapt to these therapies by acquiring resistance, leading to regrowth and relapse.
Introduction to Biomathematics in Cancer Research
What Is Biomathematics?
Biomathematics, also referred to as mathematical biology, is an interdisciplinary field that applies mathematical techniques to solve biological problems. At its core, biomathematics provides a framework for understanding the complexity of biological systems through models, equations, and algorithms (Vaia, 2019). By translating biological phenomena into mathematical language, biomathematicians can simulate processes, make predictions, and uncover patterns that are not easily discernible through experimental biology alone. In the context of cancer research, biomathematics offers a structured approach to modeling tumor growth, metastasis, and responses to treatment, giving researchers a powerful tool to analyze data and optimize therapeutic strategies.
The scope of biomathematics is vast, covering a wide range of biological applications. It encompasses population dynamics, gene regulation networks, epidemiology, and ecological modeling. In cancer research specifically, biomathematics focuses on tumor dynamics, cellular interactions, drug efficacy, and patient-specific treatment responses (Vaia, 2019). It allows scientists to create detailed models that reflect the complex interplay between cancer cells and their microenvironment, helping them understand the mechanisms driving cancer progression and resistance to therapy.
Historically, the application of mathematics to biological problems has roots in the early 20th century, with pioneers like Alfred J. Lotka and Vito Volterra using differential equations to describe predator-prey dynamics (Israel, 1988). However, it wasn’t until the latter half of the century that biomathematics gained significant traction in cancer research. Early models of tumor growth were primarily empirical, focusing on observed patterns of cell proliferation. As computational power increased, so did the complexity of the models, evolving from simple growth curves to more sophisticated representations that account for genetic mutations, angiogenesis, and immune responses. Today, biomathematics plays a central role in oncology, allowing researchers to study tumor dynamics across various scales, from the molecular to the whole-organism level.
Key Mathematical Concepts in Tumor Modeling
Tumor modeling relies on several key mathematical concepts, each offering unique insights into cancer biology. One of the most fundamental tools in biomathematics is the use of differential equations to describe the changes in tumor size over time (Yin et al., 2019). Differential equations allow researchers to model continuous processes such as cell proliferation, nutrient consumption, and the effect of treatments like chemotherapy or radiation. For example, the Gompertz equation is often used to model tumor growth, providing a realistic description of how tumors grow rapidly at first but slow down as they encounter limitations in resources like oxygen and nutrients.
Figure 4.
mathematical oncology.
Another important concept in tumor modeling is stochastic models, which account for the inherent randomness and variability in biological systems. While differential equations provide a deterministic framework, assuming that given initial conditions always produce the same outcome, stochastic models incorporate the unpredictable nature of processes like gene mutations or the immune system's response to cancer (Yin et al., 2019). These models are particularly useful for understanding rare events, such as the emergence of drug-resistant cancer cells or the probability of metastasis.
Figure 5.
Cellular automation.
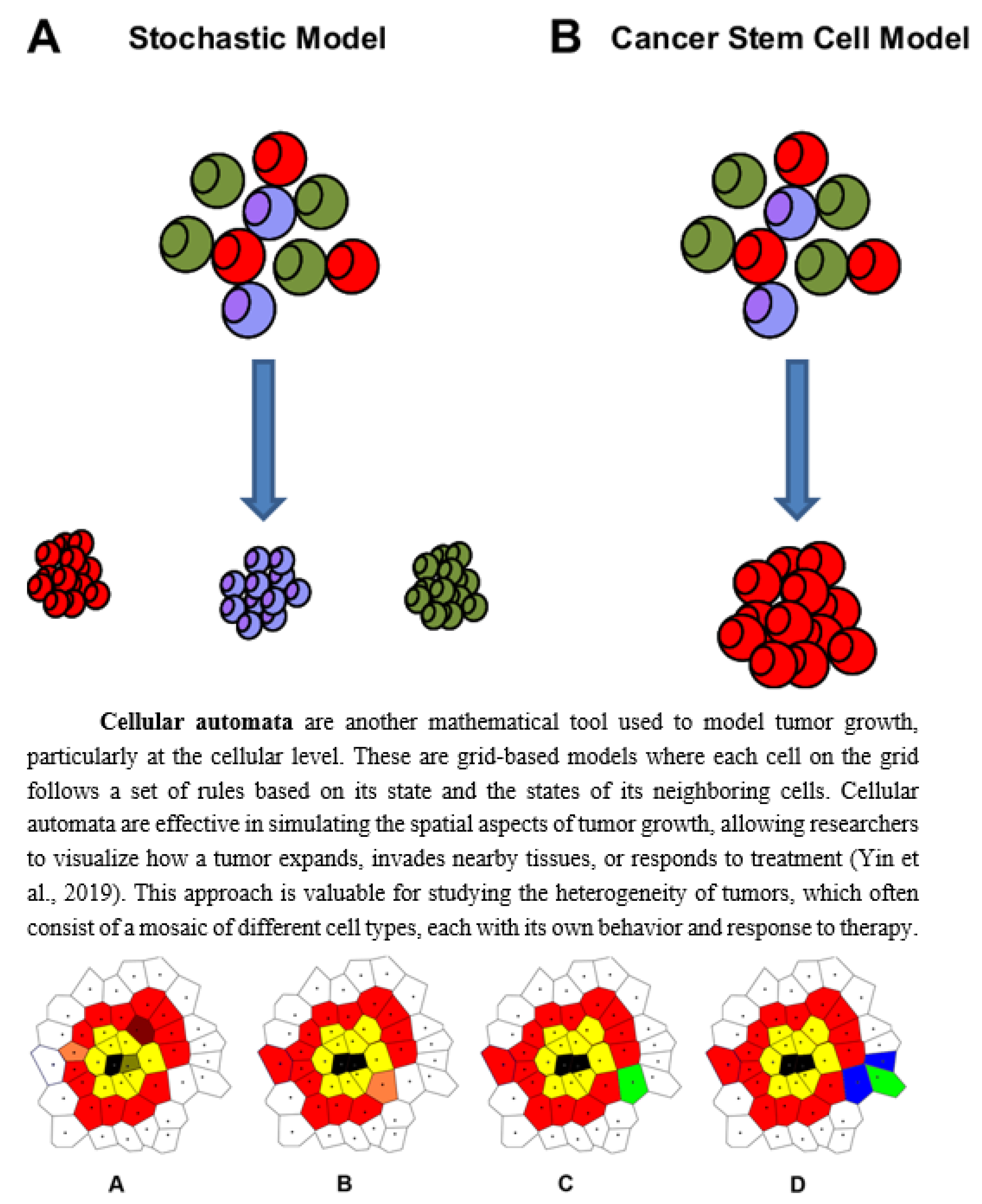
The role of computational tools in mathematical cancer models cannot be overstated. As the complexity of these models has increased, so has the need for sophisticated software and algorithms to solve them. Computational tools allow researchers to run simulations that would be impossible to calculate by hand, often involving millions of variables and interactions (Matin & Setayeshi, 2024). Software platforms like MATLAB, R, and Python’s scientific libraries are commonly used to implement and analyze cancer models. These tools provide the computational power necessary to explore different treatment scenarios, optimize drug dosages, and predict patient outcomes.
Relevance of Biomathematics to Cancer
Mathematical models are indispensable for interpreting biological data in cancer research. One of the main advantages of these models is their ability to integrate vast amounts of data from multiple sources, including genomic, proteomic, and clinical datasets. For instance, by combining genetic mutation data with information on tumor growth rates, researchers can predict how specific mutations will affect tumor behavior and, consequently, how they should be targeted therapeutically (Enderling, 2022). This capability is crucial for the development of precision medicine, where treatments are tailored to the individual characteristics of each patient’s tumor.
Moreover, mathematical models offer a predictive power that is difficult to achieve with experimental methods alone. Through modeling, scientists can simulate how a tumor will evolve over time and how it might respond to different treatments. For example, models that incorporate the dynamics of angiogenesis, the formation of new blood vessels that supply nutrients to the tumor, can predict when a tumor will become hypoxic (oxygen-starved) and how that will influence its growth or resistance to therapies (Enderling, 2022). These predictions can guide treatment decisions, helping oncologists determine the most effective timing and combination of therapies for each patient.
One area where the predictive power of biomathematics has proven particularly valuable is in understanding treatment resistance. Cancer cells often evolve resistance to therapies, rendering treatments less effective over time. Mathematical models can simulate the evolution of resistance by incorporating factors such as genetic mutations, drug pharmacokinetics, and the tumor microenvironment (Enderling, 2022). By identifying the key drivers of resistance, these models can suggest strategies for overcoming it, such as adjusting drug dosages, timing, or combining multiple therapies to prevent the emergence of resistant cell populations.
In the context of clinical trials, mathematical models are also used to optimize trial design and reduce the number of patients needed to test new therapies. By predicting which treatments are most likely to succeed, models can help focus resources on the most promising candidates, accelerating the development of new cancer drugs (Enderling, 2022). Additionally, biomathematical models are used to study the population dynamics of cancer cells, including the interplay between tumor cells, immune cells, and normal tissue. This provides insights into how cancer spreads within the body and why certain cancers metastasize to specific organs.
Mathematical Models for Tumor Growth
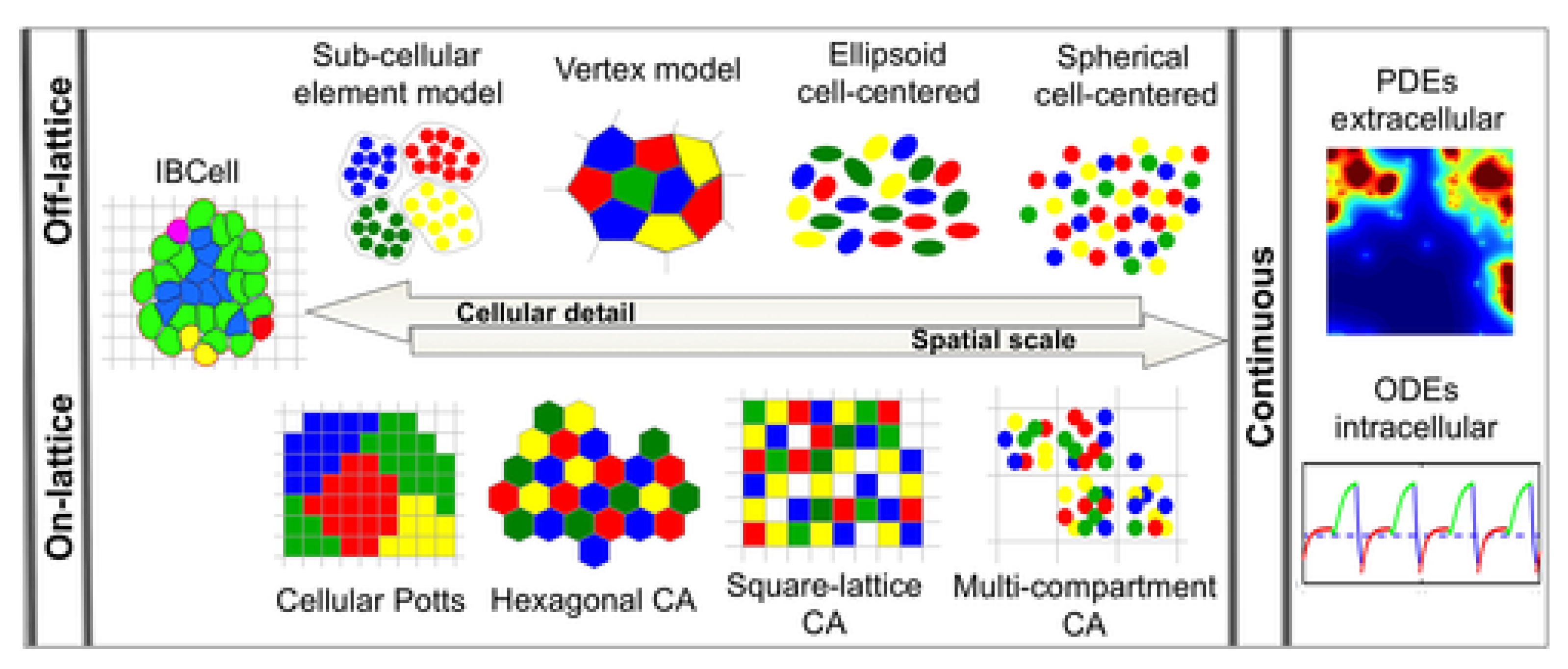
Mathematical models are essential tools in cancer research, offering insights into the complex dynamics of tumor growth. They serve as frameworks for understanding how cancer cells proliferate, interact with their environment, and respond to treatments. Over the years, several classes of mathematical models have been developed to describe different aspects of tumor growth (Wei, 2023). We explored five major types of models: deterministic, stochastic, multiscale, agent-based, and hybrid models, highlighting their roles, applications, and contributions to cancer research.
Deterministic Models
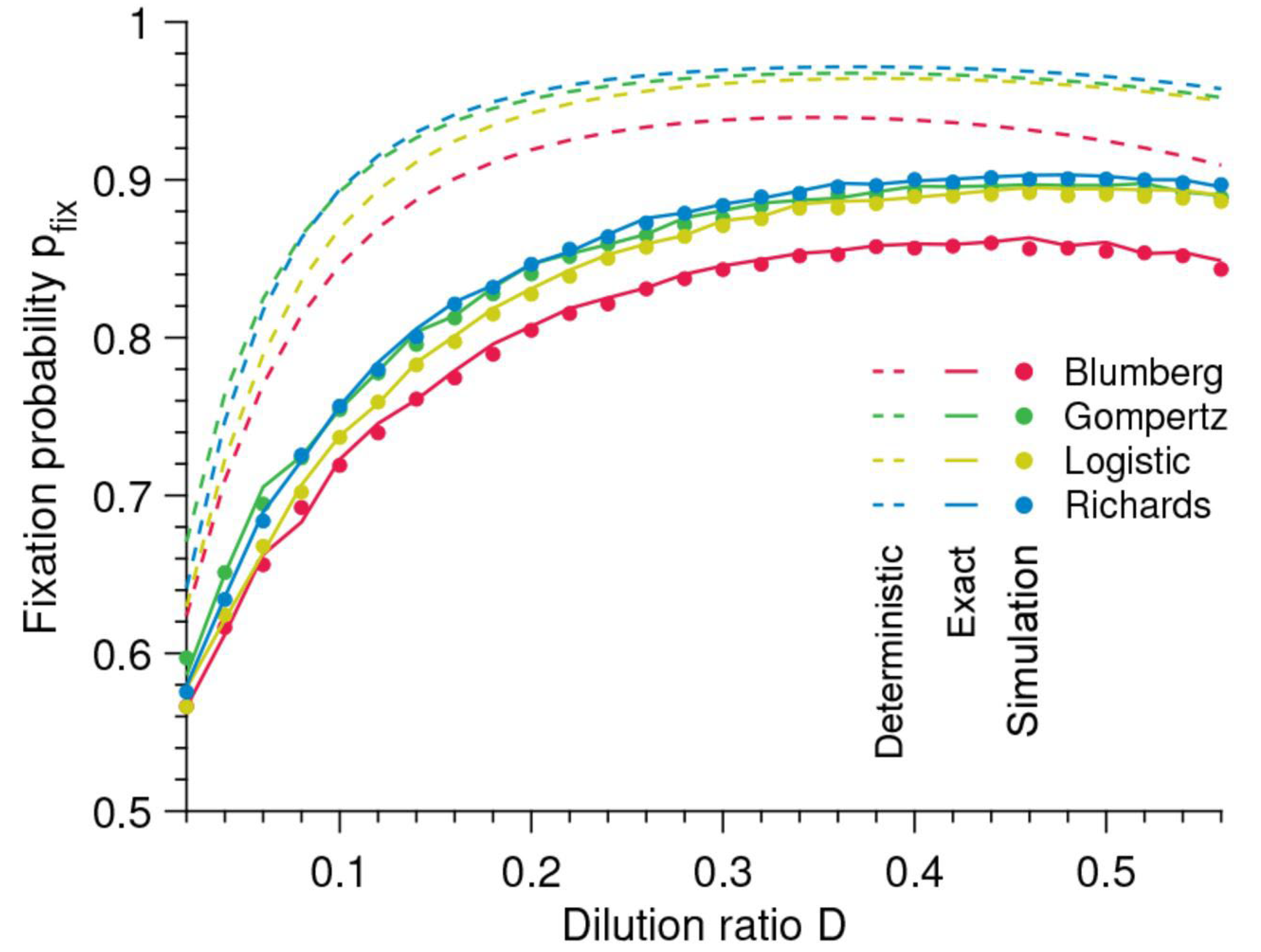
Deterministic models describe tumor growth through mathematical equations that predict the evolution of the tumor size over time. These models are "deterministic" because, given the same initial conditions, they always produce the same outcome without incorporating random variations (Alinei-Poiana et al., 2023). Three of the most commonly used deterministic models are the exponential, logistic, and Gompertz models.
Exponential Growth Model: The simplest model for tumor growth is the exponential model, which assumes that cancer cells divide at a constant rate, leading to a continuous and rapid increase in tumor size (Johnson et al., 2019). Mathematically, the model is expressed as:
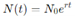
where N(t) is the number of cells at time t1, N0 is the initial number of cells, and r is the growth rate. This model is useful for describing early tumor growth, where resources such as nutrients and space are abundant. However, the exponential model becomes unrealistic as the tumor size increases, as it does not account for the biological limitations that slow growth in larger tumors.
Logistic Growth Model: To account for these limitations, the logistic model introduces a carrying capacity K, which represents the maximum tumor size that the environment can support. The logistic model is expressed as:
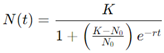
This model shows rapid growth at the beginning, followed by a deceleration as the tumor size approaches K. The logistic model is particularly useful for simulating the behavior of tumors as they face constraints like limited nutrients and immune system pressure (Harshe et al., 2023).
Gompertz Model: The Gompertz model is another refinement that captures the slowing of tumor growth more accurately, especially in later stages. It is expressed as:
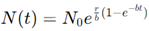
where r and b are constants. The Gompertz model assumes that the growth rate decreases exponentially as the tumor grows, which aligns with empirical data for many solid tumors. It is commonly used in oncology to describe the long-term growth of tumors and to predict treatment responses, especially in the context of chemotherapy.
Applications: Deterministic models are widely used in the early stages of tumor development. For instance, the exponential model is often applied in studies where researchers examine the initial rapid proliferation of cancer cells (Johnson et al., 2019). The logistic and Gompertz models, meanwhile, provide more realistic simulations of tumor growth over extended periods, helping to understand how tumors respond to changes in their environment, such as nutrient depletion or immune responses. These models are foundational in cancer research, forming the basis for more complex approaches.
Stochastic Models
While deterministic models provide clear predictions, biological systems like tumors are inherently random. Stochastic models incorporate elements of randomness to capture this uncertainty, making them more realistic for modeling cancer progression (Odoux et al., 2019).
Figure 6.
Models of tumor development - Stochastic Models.
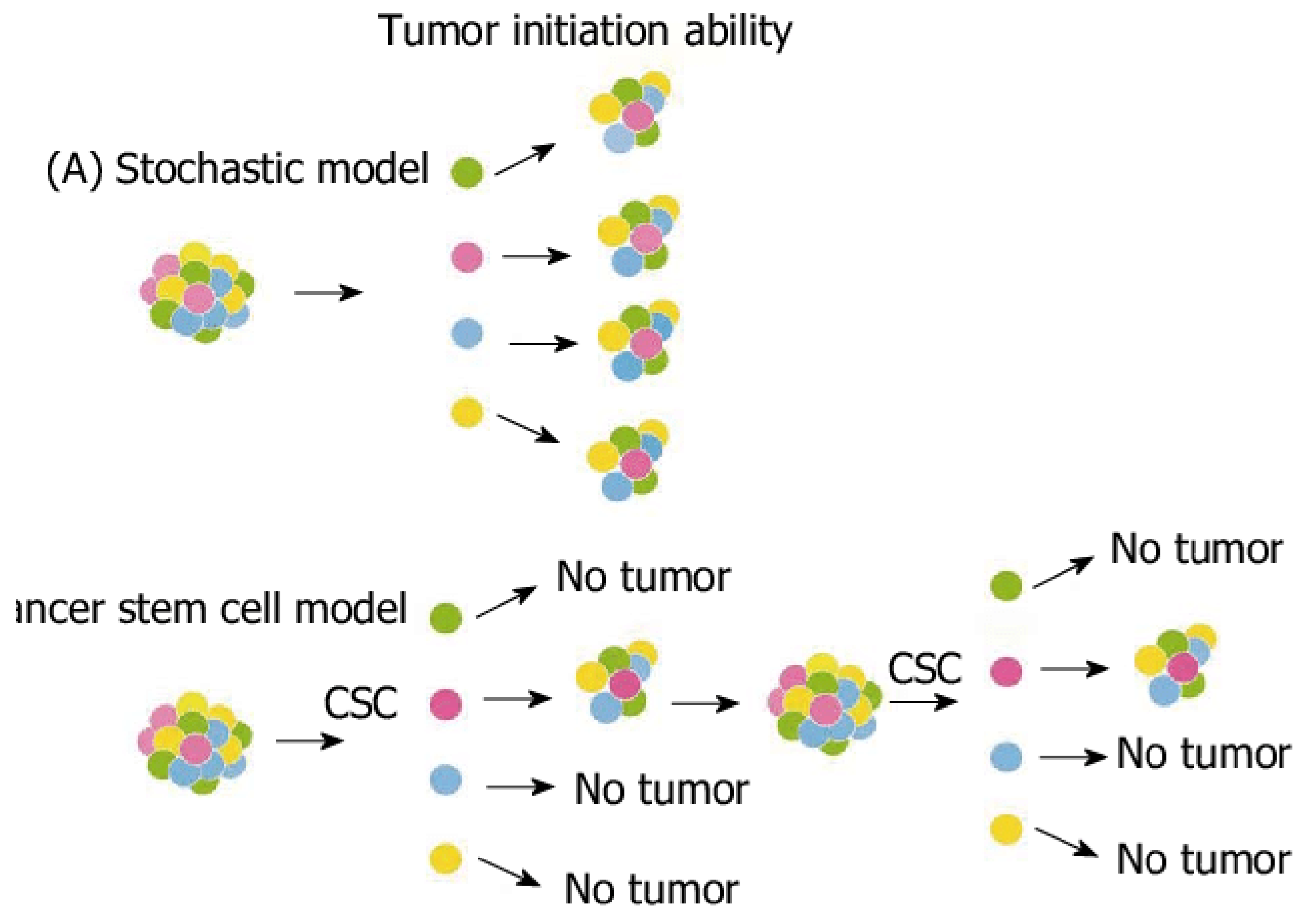
How Randomness is Used: Stochastic models account for random variations in processes like cell division, mutation, and death. For example, in a population of tumor cells, not every cell will divide at the same rate, and some may acquire mutations that affect their growth. The probability of a cell dividing, dying, or mutating is represented by a stochastic process, such as a Poisson or Markov process.
A common stochastic model is the birth-death process, which describes the probability of a cell population growing or shrinking over time. (Lunk, 2019) The transition rates between states (e.g., the probability of a cell dividing or dying) depend on factors like the availability of nutrients or the effects of treatment. Stochastic models are especially useful in capturing rare events, such as the emergence of drug-resistant cancer cells, which may occur infrequently but have a significant impact on treatment outcomes.
Figure 1.
stochastic dynamics of population growth
Incorporation of Random Mutations and Cell Death: Stochastic models are essential for modeling genetic mutations, which occur randomly and can drive cancer progression. By incorporating mutation probabilities, these models can simulate the development of cancer subclones that may be more aggressive or resistant to therapy (Foo et al., 2011). This is crucial for understanding how heterogeneity arises within a tumor and how this heterogeneity influences treatment resistance and metastasis.
Applications: Stochastic models are widely used in cancer research to simulate the random processes that influence tumor evolution. For instance, they can model the impact of random genetic mutations on the development of drug resistance, helping researchers design better treatment strategies. Additionally, stochastic models are often used in the study of cancer metastasis, where the random detachment and spread of cancer cells to distant organs are critical processes (Castaneda et al., 2022).
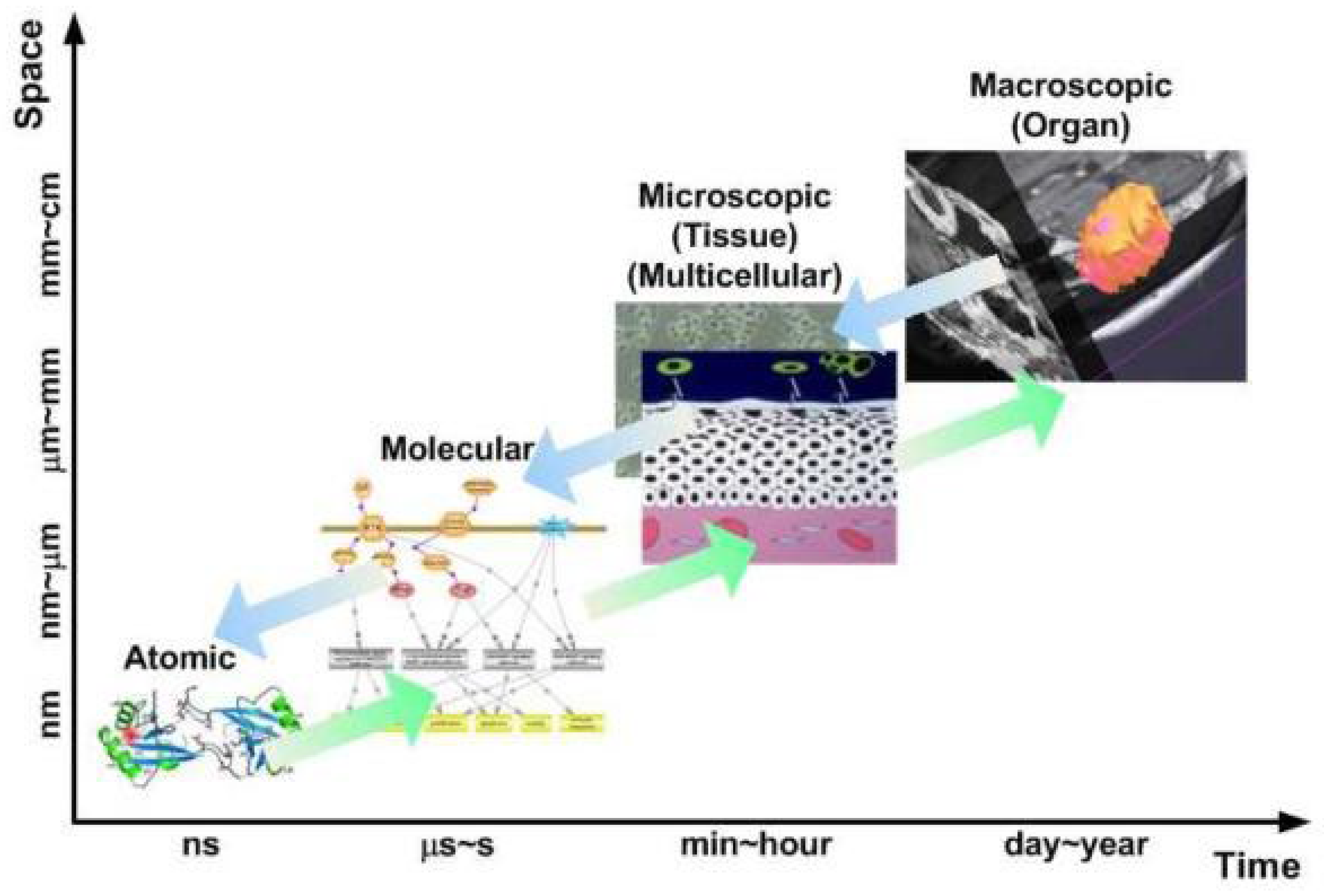
Multiscale Models
Multiscale models bridge different biological scales, from the genetic and molecular level to the tissue and organ level, to provide a more comprehensive picture of tumor growth. Cancer is a multiscale disease, where changes at the genetic or molecular level can have profound effects on cellular behavior, tissue architecture, and organ function (Deisboeck et al., 2011). Multiscale models aim to capture this complexity by integrating information across these different levels.
Figure 8.
Schematic illustration of the biological scales of significant relevance for cancer modeling.
Figure 8.
Schematic illustration of the biological scales of significant relevance for cancer modeling.
Combining Biological Scales: A typical multiscale model might combine a genetic model that describes mutations in cancer cells with a cellular model that simulates how those mutations affect cell behavior (e.g., proliferation or apoptosis) (Nivlouei et al, 2022). This, in turn, is linked to a tissue-scale model that describes how the tumor interacts with its surrounding environment, including blood vessels, immune cells, and extracellular matrix.
Figure 9.
An illustration of the spatiotemporal multiscale modeling framework.
Predicting Metastasis: One of the key applications of multiscale models is in predicting metastasis, the process by which cancer cells spread from the primary tumor to other parts of the body. Metastasis involves multiple steps, including the detachment of cancer cells from the primary tumor, invasion into surrounding tissues, entry into the bloodstream or lymphatic system, and colonization of distant organs (Petinrin et al., 2023). Multiscale models can simulate these processes, providing insights into which factors drive metastasis and how it might be prevented.
Figure 10.
Engineered models to parse apart the metastatic.
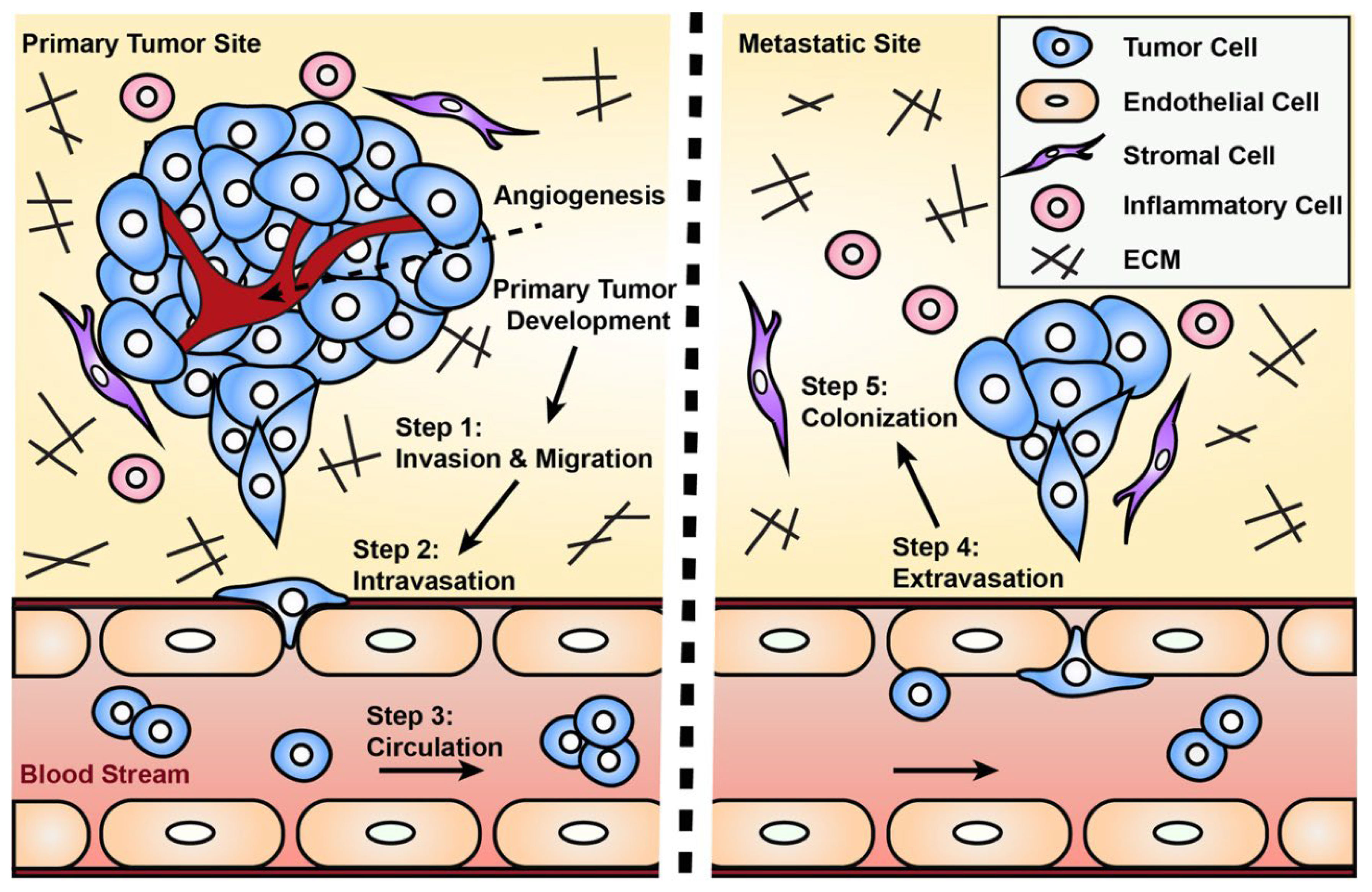
Applications: Multiscale models are highly valuable in understanding the complex interactions that occur within a tumor and between a tumor and its environment. They have been used to study how genetic mutations drive tumor growth, how cancer cells evade the immune system, and how treatments like radiation therapy affect both cancer cells and surrounding normal tissues (Norton et al., 2019). These models are increasingly being used to guide the development of personalized cancer therapies by simulating how a patient’s tumor might respond to different treatment options.
Agent-Based Models
Agent-based models (ABMs) take a different approach to tumor modeling by treating individual cells as "agents" that follow specific rules (Poleszczuk et al., 2016). Each cell is modeled as an independent entity with its own set of behaviors, such as proliferation, migration, or death, which depend on the cell’s internal state and its interactions with other cells and the environment.
Figure 11.
gent-based modeling in cancer biomedicine.
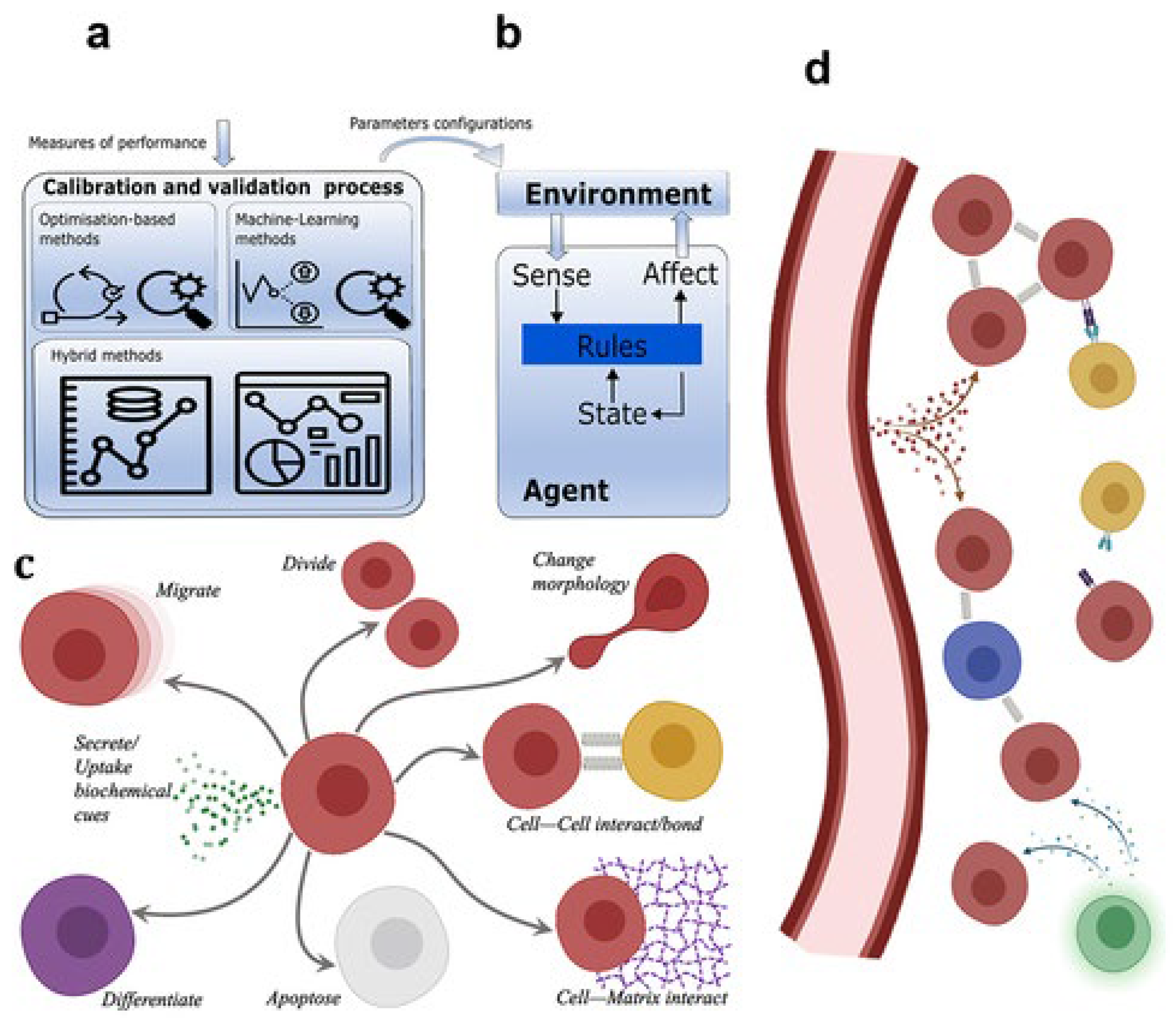
Modeling Individual Cells as Agents: In an ABM, the behavior of each cell is governed by rules that describe how it interacts with its neighbors and the surrounding environment. For example, a cancer cell might proliferate if it has enough nutrients and space, but it might die if it encounters immune cells or is starved of oxygen (West et al., 2023). The overall tumor behavior emerges from the collective actions of thousands or millions of individual cells, each following its own rules.
Benefits of Agent-Based Models: One of the key advantages of ABMs is their ability to capture the heterogeneity of tumor cells. Tumors are not homogeneous masses of identical cells; instead, they consist of a diverse population of cells with different genetic mutations, behaviors, and responses to treatment (Belkhir et al., 2021). ABMs can simulate this heterogeneity, providing insights into how different subpopulations of cancer cells interact with each other and how this affects tumor growth and treatment response.
Applications: ABMs are particularly useful for studying tumor heterogeneity and the spatial organization of tumors. For instance, they have been used to simulate how different cancer cell subpopulations compete for resources within a tumor, how cancer cells invade surrounding tissues, and how treatments like immunotherapy affect individual cancer cells (Belkhir et al., 2021). ABMs are also valuable for studying the interactions between cancer cells and other cell types in the tumor microenvironment, such as immune cells and fibroblasts.
Hybrid Models
Hybrid models combine different mathematical approaches to capture the complexity of tumor growth. For example, a hybrid model might combine a deterministic model that describes the overall growth of the tumor with a stochastic model that captures random mutations and an agent-based model that simulates the behavior of individual cancer cells (Gonçalves & GarcíaAznar, 2023).
Figure 12.
Schematic representation of hybrid models.
Combining Mathematical Approaches: By combining different types of models, hybrid models can provide a more comprehensive view of tumor growth. For instance, a hybrid model might use a deterministic model to describe the overall growth of the tumor while incorporating stochastic elements to account for the randomness of genetic mutations and an agent-based component to simulate the behavior of individual cancer cells (Chamseddine & Rejniak, 2019).
Case Studies: Hybrid models have been used in several case studies to simulate tumor growth and treatment response. One notable example is the use of hybrid models to study the evolution of drug resistance in cancer (Szumilak et al., 2021). By combining deterministic models of tumor growth with stochastic models of mutation and agent-based models of cell behavior, researchers have been able to simulate how cancer cells evolve resistance to chemotherapy and suggest strategies for overcoming this resistance. Hybrid models have also been used to study metastasis, combining multiscale models of tissue invasion with stochastic models of cell migration.
Applications: Hybrid models are becoming increasingly popular in cancer research due to their ability to capture the complexity of tumor growth and treatment response. They are particularly useful for studying the evolution of cancer over time, including the development of drug resistance, the spread of metastasis, and the effects of combination therapies (Chamseddine & Rejniak, 2019). Hybrid models are also being used in personalized medicine, where they can simulate how an individual patient’s tumor might respond to different treatments based on its unique characteristics.
Figure 13.
Mathematical modeling in cancer treatment.
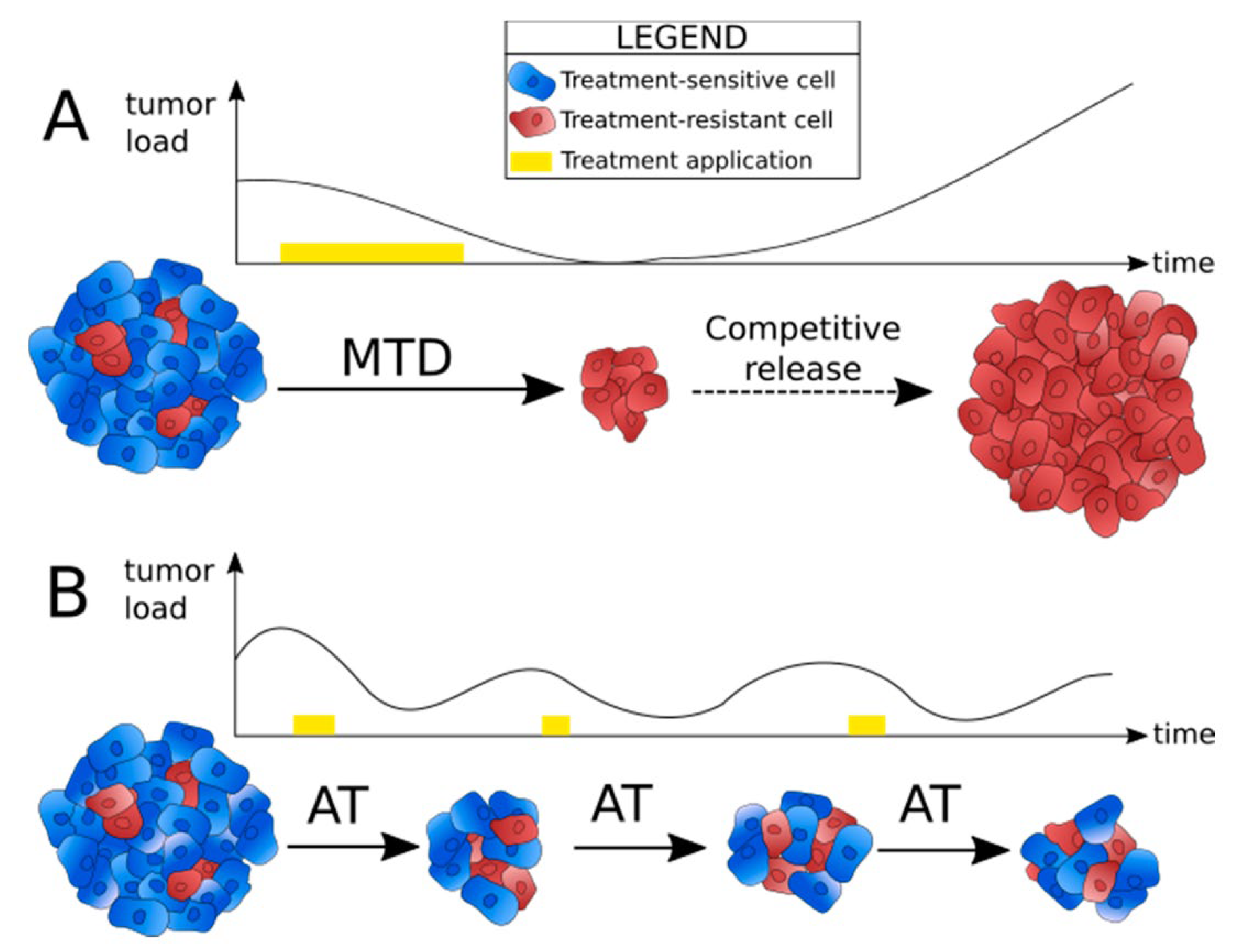
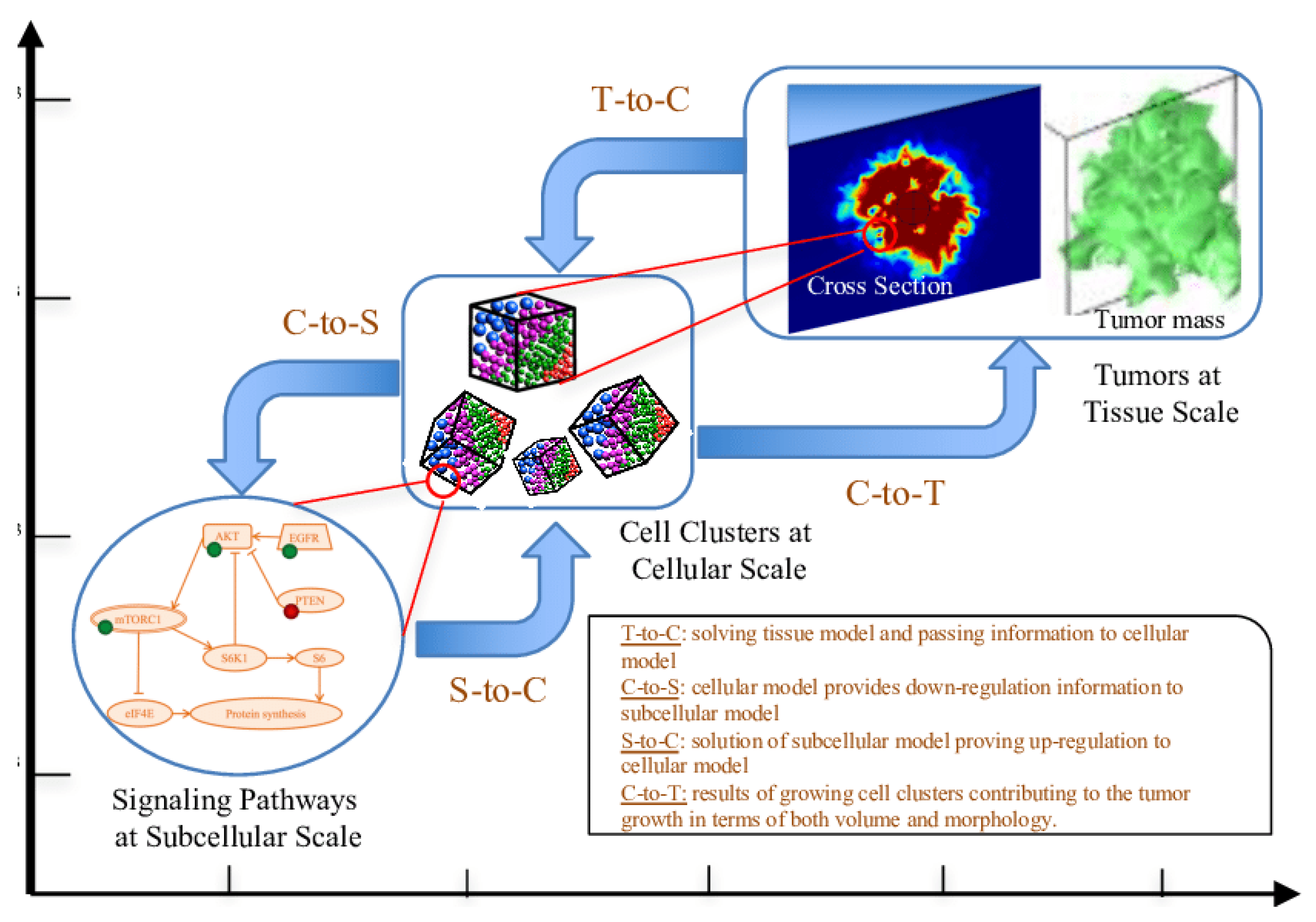
Mathematical Models for Cancer Treatment Optimization
Optimizing cancer treatment is a critical challenge in oncology, and mathematical models have become valuable tools in guiding decisions about therapy selection, drug dosing, and treatment schedules. These models simulate various treatment modalities, chemotherapy, radiation, and immunotherapy, and their interactions with tumor cells, aiming to maximize therapeutic efficacy while minimizing side effects (Michor & Beal, 2015). With advances in machine learning and personalized medicine, mathematical models also play a crucial role in developing patient-specific treatment strategies.
Chemotherapy Modeling
Chemotherapy remains a cornerstone in cancer treatment, but its efficacy is often limited by factors such as drug resistance, toxicity, and tumor regrowth. Mathematical models have been instrumental in addressing these challenges by helping optimize chemotherapy dosage, timing, and combinations.
Optimizing Drug Dosage and Schedules: Mathematical models are used to identify optimal dosing schedules that maximize the killing of cancer cells while minimizing harm to healthy tissue. One common approach is to use pharmacokinetic (PK) and pharmacodynamic (PD) models, which describe how the drug is absorbed, distributed, metabolized, and excreted (PK), and how it affects the tumor and healthy cells (PD) (Sun & Hu, 2018). These models use differential equations to represent the concentration of the drug in the bloodstream over time and its effect on cell populations.
For example, in a standard model, the rate of tumor cell death may depend on the concentration of the drug and the sensitivity of the tumor cells to treatment:
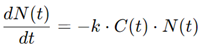
where N(t) is the number of tumor cells at time t1, C(t) is the drug concentration, and k is a constant representing drug efficacy. By simulating various dosing regimens, these models can help determine whether high doses given infrequently or lower doses administered more frequently yield better results.
Modeling Drug Resistance and Tumor Regrowth: One of the major challenges in chemotherapy is the development of drug resistance, which can lead to tumor regrowth after an initial period of remission. Mathematical models of drug resistance typically involve stochastic processes that account for random mutations in cancer cells that make them resistant to chemotherapy (Yin et al., 2019). These models can simulate the emergence of resistant cell populations and help identify treatment strategies that delay or prevent resistance.
For instance, a common approach is to model the growth of both sensitive and resistant cancer cells using a set of differential equations:
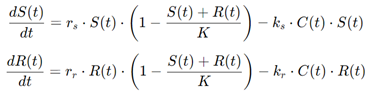
where S(t) and R(t) represent the populations of sensitive and resistant cells, respectively, rs and rr are the growth rates, K is the carrying capacity of the tumor environment, and ks and kr are the effects of the drug on sensitive and resistant cells. These models provide insight into the timing and dosing strategies that might minimize the development of resistance, leading to more effective long-term treatment outcomes.
Radiation Therapy Models
Radiation therapy, another common cancer treatment, relies on high-energy radiation to kill tumor cells by damaging their DNA. The challenge is to deliver a sufficient dose to eradicate the tumor while minimizing damage to surrounding healthy tissue (Bekker et al., 2022). Mathematical models have been developed to optimize radiation therapy protocols by predicting the effects of different doses and schedules on both tumor shrinkage and normal tissue response.
Optimizing Radiation Doses: One of the most widely used models in radiation therapy is the linear-quadratic (LQ) model, which describes the relationship between radiation dose and cell survival (Li, 2023). The model is based on the idea that radiation kills cells through two mechanisms: single-hit lethal events (linear term) and double-hit events (quadratic term). The LQ model is expressed as:

where S(D) is the surviving fraction of cells after a dose D of radiation, and α and β are constants that depend on the sensitivity of the tumor and normal tissues to radiation. By fitting clinical data to the LQ model, researchers can predict how different radiation doses will affect tumor control and normal tissue toxicity, helping to tailor treatment to the individual patient.
Models Predicting Tumor Shrinkage and Normal Tissue Response: In addition to the LQ model, other mathematical frameworks, such as tumor control probability (TCP) models, are used to predict the likelihood of completely eradicating a tumor with a given radiation dose (Spoormans et al., 2022). These models are often combined with normal tissue complication probability (NTCP) models, which predict the risk of damage to healthy tissues. By balancing TCP and NTCP, radiation oncologists can design treatment plans that maximize tumor control while minimizing side effects.
Immunotherapy Modeling
Immunotherapy represents a major breakthrough in cancer treatment, harnessing the power of the immune system to recognize and destroy cancer cells. However, predicting the response to immunotherapy is complex due to the dynamic interactions between cancer cells, immune cells, and the tumor microenvironment (Butner et al., 2022). Mathematical models are playing a critical role in simulating these interactions and guiding the development of more effective immunotherapies.
Simulation of Immune-Tumor Dynamics: Mathematical models of immunotherapy often involve ordinary differential equations (ODEs) that describe the interactions between tumor cells and various components of the immune system, such as T cells, natural killer (NK) cells, and cytokines (Unni & Seshaiyer, 2019). These models simulate how the immune system recognizes and attacks tumor cells, as well as how cancer cells evade immune detection.
For example, a simple model of immune-tumor dynamics might include equations for the growth of tumor cells and the activity of immune cells:
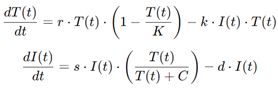
where T(t) is the tumor cell population, I(t) is the immune cell population, r is the tumor growth rate, k is the rate at which immune cells kill tumor cells, s is the immune response rate, and d is the rate of immune cell decay. By adjusting these parameters, the model can simulate different immunotherapy strategies, such as checkpoint inhibitors or CAR-T cell therapy, and predict how the tumor will respond.
Models for Predicting the Efficacy of Immunotherapeutic Agents: Another approach involves agent-based models (ABMs), where individual immune cells and tumor cells are treated as agents with specific behaviors. These models allow for detailed simulations of how immune cells infiltrate the tumor, interact with cancer cells, and respond to immunotherapeutic agents (Norton et al., 2019). ABMs can capture the spatial heterogeneity of tumors and the complex dynamics of immune-tumor interactions, making them valuable tools for designing personalized immunotherapy treatments.
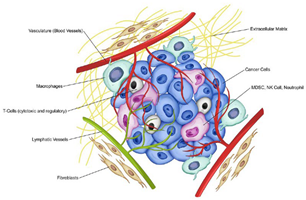
Personalized Medicine
One of the most exciting developments in cancer treatment is the shift toward personalized medicine, where treatment is tailored to the individual patient's tumor characteristics. Mathematical models are central to this approach, as they can integrate data from genomic, proteomic, and clinical sources to predict how a patient will respond to different treatments.
How Models Contribute to Patient-Specific Treatment Plans: In personalized medicine, mathematical models are used to simulate how a patient's unique tumor biology will respond to various treatments (Azizi, 2024). For example, machine learning algorithms can analyze large datasets of patient outcomes and identify patterns that predict treatment success. These models can then be used to develop patient-specific treatment plans that optimize drug selection, dosing, and scheduling.
The Role of Machine Learning and Big Data: Machine learning techniques, such as random forests, support vector machines, and neural networks, are increasingly being integrated into mathematical models of cancer treatment (Panja et al., 2021). These algorithms can process large amounts of data, including genomic and proteomic profiles, to identify biomarkers that predict treatment response. By combining traditional mathematical models with machine learning, researchers can develop more accurate predictions of how individual patients will respond to different therapies.
Combination Therapy Models
Combination therapies, which involve using multiple treatment modalities (e.g., chemotherapy, radiation, and immunotherapy), are often more effective than single therapies in controlling cancer. However, the timing, dosage, and sequencing of these therapies must be carefully optimized to maximize their synergistic effects. Mathematical models are essential for designing combination therapy protocols that achieve the best possible outcomes.
Mathematical Approaches for Combining Different Treatment Modalities: Combination therapy models often involve differential equations that describe the interactions between different treatments and their combined effects on tumor cells (Duarte & Vale, 2022). For example, a model might simulate how chemotherapy and radiation therapy work together to kill tumor cells, with equations representing the effects of each treatment on cell survival and tumor regrowth.
Models Optimizing the Timing and Synergy of Chemotherapy, Radiation, and Immunotherapy: One common challenge in combination therapy is determining the optimal sequence and timing of treatments. Should chemotherapy be given before or after radiation? When should immunotherapy be introduced? Mathematical models can simulate various treatment schedules and predict how the timing of each therapy affects tumor control and side effects. By optimizing the timing and synergy of different treatments, these models can help clinicians design more effective combination therapy protocols.
Case Studies of Mathematical Models in Cancer Research
Mathematical models are invaluable tools in cancer research, providing a means to predict tumor behavior, optimize treatments, and understand patient-specific responses to therapies. These models have been applied in various settings, from simulating tumor growth to personalizing immunotherapy treatments. We explore three case studies that illustrate the real-world impact of mathematical models in cancer research: the Gompertz model for predicting tumor growth, chemotherapy optimization through mathematical approaches, and the use of models in guiding immunotherapy for melanoma patients.
Case Study 1: Predicting Tumor Growth with the Gompertz Model
The Gompertz model is one of the most widely used mathematical models for predicting tumor growth. It is particularly useful for describing the slowing of tumor growth as the tumor approaches a certain size, a characteristic that distinguishes it from simpler exponential growth models (Heesterman et al., 2019). The Gompertz model posits that the growth rate of a tumor decreases exponentially as the tumor size increases, reflecting the biological reality that tumors tend to grow more slowly as they expand and encounter environmental constraints, such as limited nutrients or immune suppression.
The Gompertz equation is given by:
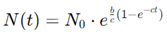
where N(t) is the tumor size at time t1, N0 is the initial tumor size, b is the initial growth rate, and c is a parameter related to the rate of growth deceleration.
Real-world Application: The Gompertz model has been applied in various clinical studies to predict tumor growth dynamics across several cancer types, including breast cancer and gliomas. For example, in a study involving breast cancer patients, the Gompertz model was used to predict the tumor's progression over time, both before and after treatment (Clare et al., 2000). The model’s predictions closely aligned with the observed tumor growth patterns, demonstrating its effectiveness in capturing the sigmoidal nature of tumor growth.
Accuracy and Limitations: While the Gompertz model accurately reflects many observed growth patterns, particularly during the later stages of tumor progression, it has limitations. One significant drawback is its assumption that tumor growth decelerates solely due to size-related constraints, which may oversimplify the complex biological interactions occurring in the tumor microenvironment (Heesterman et al., 2019). For instance, factors such as immune evasion, genetic mutations, and tumor heterogeneity are not explicitly accounted for in this model. Additionally, the Gompertz model may not perform well when tumors are in their early stages of growth, where exponential models might be more appropriate.
Despite these limitations, the Gompertz model remains a valuable tool for predicting tumor growth, particularly when combined with other models that account for early-stage dynamics or tumor-specific factors. Its ability to predict long-term growth trends makes it useful in clinical settings, particularly for monitoring tumor progression or evaluating treatment efficacy over time.
Case Study 2: Optimizing Chemotherapy Through Mathematical Models
Optimizing chemotherapy involves finding the right balance between killing cancer cells and minimizing harm to healthy tissue, a challenge that mathematical models have been instrumental in addressing. Several models have been developed to optimize drug dosing and timing, including those that simulate drug resistance and tumor regrowth.
Application of Models in Chemotherapy Optimization: In a case study involving non-small cell lung cancer (NSCLC) patients, mathematical models were used to simulate different chemotherapy dosing regimens. These models incorporated data on drug pharmacokinetics (how the drug is processed in the body) and pharmacodynamics (the drug's effect on the tumor) to predict the outcomes of various treatment schedules (Smieja, 2023). By adjusting variables such as drug dosage, frequency, and combination therapies, the models identified an optimal regimen that minimized tumor growth while reducing toxicity to healthy tissues.
One of the models employed in this study was based on differential equations that described the interaction between the tumor cells and the chemotherapeutic agents. A simplified version of such a model is:
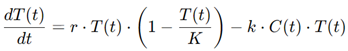
where T(t) is the tumor cell population, r is the tumor growth rate, K is the carrying capacity (reflecting the maximum tumor size), and C(t) is the concentration of the chemotherapeutic agent. By solving this system of equations, the researchers were able to simulate how different chemotherapy schedules affected the tumor's growth trajectory.
Comparison of Model Predictions with Clinical Outcomes: The predictions made by the mathematical model were compared with clinical outcomes from a group of NSCLC patients undergoing chemotherapy. The optimized regimen suggested by the model not only reduced the tumor size more effectively than standard dosing protocols but also led to fewer side effects, as measured by patient-reported symptoms and blood markers of toxicity (Smieja, 2023).. In some cases, the model even predicted the development of drug resistance before it became clinically apparent, allowing for early adjustments to the treatment plan.
Case Study 3: Modeling Immunotherapy in Melanoma
Immunotherapy has revolutionized the treatment of melanoma, particularly with the advent of immune checkpoint inhibitors that boost the body’s natural immune response to cancer cells. However, predicting which patients will respond to immunotherapy remains a challenge due to the complex interplay between tumor cells, immune cells, and the tumor microenvironment (Nomdedeu-Sancho et al., 2023). Mathematical models have been developed to simulate these interactions and provide insights into the effectiveness of immunotherapy.
Mathematical Models of Immune Responses: One of the most widely studied mathematical models for immunotherapy involves ordinary differential equations (ODEs) that describe the interactions between tumor cells and immune cells, such as cytotoxic T cells and natural killer (NK) cells. These models can simulate how the immune system responds to the introduction of immunotherapeutic agents, such as anti-PD-1 or anti-CTLA-4 antibodies (Unni & Seshaiyer, 2019).
A simple model might look like this:
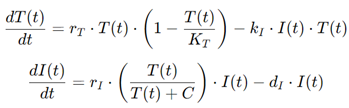
where T(t) represents the tumor population, I(t) represent the immune cell population, rT and rI are the respective growth rates of tumor and immune cells, KT is the tumor carrying capacity, and kI is the rate at which immune cells kill tumor cells. By adjusting parameters such as rI or kI , the model can simulate how the tumor responds to immunotherapy under different conditions.
Impact on Patient Outcomes: A case study involving melanoma patients treated with immune checkpoint inhibitors demonstrated the predictive power of these mathematical models. In this study, the model was used to simulate patient-specific immune responses to anti-PD-1 therapy. The model’s predictions closely matched the observed clinical outcomes, with patients whose immune responses were predicted to be strong showing significant tumor regression, while those with weaker predicted responses had more limited benefits from the treatment (Butner et al., 2021).
This case study highlights the potential of mathematical models to not only predict patient outcomes but also guide treatment strategies. For instance, patients with a predicted weak immune response might benefit from combination therapies that include both checkpoint inhibitors and other treatments, such as chemotherapy or radiation, to enhance the immune system's ability to fight the tumor.
Challenges and Limitations of Mathematical Modeling in Cancer Research
Mathematical modeling has emerged as a powerful tool in cancer research, providing insights into tumor dynamics and aiding in treatment optimization (Vieira, Costa, & Valério, 2023). However, these models are not without their challenges and limitations.
Data Availability and Quality
One of the most significant challenges in mathematical modeling is the availability and quality of biological data. Mathematical models rely heavily on accurate and comprehensive datasets that reflect the biological processes they aim to represent. However, obtaining reliable data can be problematic for several reasons:
Biological Variability: Cancer is a highly heterogeneous disease, with significant variability in tumor biology across different patients. Factors such as genetic mutations, tumor microenvironment, and immune system interactions can influence tumor growth and response to treatment (Vieira, Costa, & Valério, 2023). This variability complicates the development of generalized models that can accurately predict outcomes across a diverse patient population.
Data Scarcity: In many cases, especially for rare cancer types or specific patient subgroups, there is limited biological data available. Clinical studies may not capture all the relevant variables needed for model development, leading to incomplete datasets (Vieira, Costa, & Valério, 2023). This scarcity can significantly impact model accuracy, as models trained on insufficient data may fail to reflect the true dynamics of tumor behavior and treatment response.
Quality of Data: Even when data is available, its quality can vary significantly. Factors such as inconsistent measurement techniques, variations in experimental conditions, and incomplete patient records can introduce noise into the data. Low-quality data can lead to inaccurate model predictions and hinder the validation of model outcomes.
The impact of data availability and quality on model accuracy cannot be overstated. Models developed with insufficient or poor-quality data may yield misleading results, ultimately compromising their utility in clinical settings.
Model Complexity
Another challenge in mathematical modeling is the trade-off between model simplicity and biological realism. While more complex models can capture intricate biological processes, they also present several issues (Vieira, Costa, & Valério, 2023).:
Simplicity vs. Realism: Simplified models often fail to account for the multitude of factors influencing tumor behavior, leading to oversimplified predictions. On the other hand, highly complex models may become difficult to interpret and computationally intensive, making them less practical for real-time applications in clinical settings. Striking the right balance between complexity and usability is a significant challenge in model development.
Validation of Complex Models: Complex models often require extensive validation against experimental or clinical data to ensure their accuracy and reliability. However, the validation process can be resource-intensive and time-consuming. Moreover, if the underlying assumptions of a complex model are incorrect or poorly defined, it may lead to erroneous predictions, further complicating the validation process.
To address these challenges, researchers must carefully consider the trade-offs involved in model complexity and prioritize the inclusion of relevant biological factors while maintaining a manageable level of complexity.
Uncertainty and Variability
Biological variability across patients poses a significant challenge to mathematical modeling in cancer research. Cancer's inherent heterogeneity means that two patients with the same type of cancer can respond very differently to identical treatments. This variability introduces uncertainty in model predictions:
Biological Variability: Individual differences in genetics, tumor microenvironment, and immune response can result in diverse treatment outcomes. Mathematical models that fail to account for this variability may provide inaccurate predictions, leading to suboptimal treatment decisions.
Managing Uncertainty: Quantifying and managing uncertainty in predictions is crucial for the reliability of mathematical models. Techniques such as sensitivity analysis can help identify which parameters have the most significant impact on model outcomes, allowing researchers to focus on the most critical variables (Vieira, Costa, & Valério, 2023).. Additionally, probabilistic models can be employed to incorporate uncertainty into predictions, providing a range of possible outcomes rather than a single deterministic result.
Despite these approaches, managing uncertainty in predictions remains a complex challenge, necessitating ongoing research and refinement of modeling techniques.
Clinical Translation of Models
The ultimate goal of mathematical modeling in cancer research is to translate these models into clinical practice effectively. However, several issues hinder this translation:
Integration into Clinical Practice: Integrating mathematical models into routine clinical decision-making requires collaboration between mathematicians, biologists, and clinicians. There is often a gap in communication between these disciplines, which can impede the effective application of mathematical models in clinical settings (Vieira, Costa, & Valério, 2023).. Clinicians may lack the training to interpret complex mathematical outputs, while mathematicians may not fully understand the clinical context.
Gaps in Personalized Medicine: While mathematical models have the potential to guide personalized treatment strategies, significant gaps remain in their application to personalized medicine. Many existing models are based on average responses rather than patient-specific data, limiting their effectiveness in tailoring treatment plans to individual patients (Vieira, Costa, & Valério, 2023).. Efforts to incorporate genetic, phenotypic, and treatment response data into mathematical models are crucial for advancing the field of personalized cancer therapy.
While mathematical modeling offers tremendous potential in cancer research, it faces several challenges and limitations. Addressing issues related to data availability and quality, model complexity, uncertainty and variability, and clinical translation will be essential for realizing the full potential of these models in improving cancer treatment outcomes. Ongoing research, collaboration, and innovation in modeling approaches are necessary to overcome these hurdles and enhance the impact of mathematical models in cancer research.
Future Directions in Biomathematics and Cancer Research
The field of biomathematics is poised for significant advancements in cancer research, driven by technological innovations, the integration of genetic data, interdisciplinary collaborations, and emerging trends in the understanding of tumor dynamics and treatment strategies.
Advances in Computational Power
The exponential growth in computational power is transforming the capabilities of mathematical modeling in cancer research (Thirumal et al., 2018). Supercomputing and artificial intelligence (AI) play pivotal roles in enhancing the accuracy and efficiency of mathematical models:
Supercomputing: High-performance computing systems enable researchers to run complex simulations that were previously infeasible due to resource constraints. This capability allows for the modeling of intricate biological processes at multiple scales, from molecular interactions to tumor growth dynamics across entire patient populations. With supercomputing, researchers can analyze vast datasets, leading to more robust models that better reflect biological reality.
Artificial Intelligence: AI and machine learning algorithms are increasingly integrated into biomathematics, allowing for the analysis of large datasets and the identification of patterns that may not be apparent through traditional statistical methods. These techniques can enhance predictive modeling, allowing for more accurate forecasts of tumor behavior and treatment outcomes. AI can also facilitate the development of adaptive treatment strategies, where mathematical models are continually updated with new patient data to optimize therapy over time.
The synergy between supercomputing and AI represents a significant leap forward in the ability to develop sophisticated mathematical models that can effectively address the complexities of cancer biology.
Integration with Genomics and Personalized Medicine
The incorporation of genomic data into mathematical models is a critical step toward the realization of personalized cancer treatment:
Genetic Data Integration: As genomic technologies advance, researchers are increasingly able to obtain detailed genetic profiles of tumors. This data can be used to inform mathematical models, allowing for the simulation of how specific genetic alterations influence tumor growth, treatment response, and resistance mechanisms (Hassan et al., 2022). By incorporating individual genetic variations, models can be tailored to reflect the unique biology of each patient's cancer.
Personalized Treatment Strategies: The future of cancer treatment lies in its personalization, and mathematical models will play a key role in this evolution. Models that integrate genomic data can help predict how patients will respond to various therapies, enabling clinicians to design customized treatment plans that optimize effectiveness while minimizing side effects (Hassan et al., 2022). As these models evolve, they may also guide the development of combination therapies that target multiple pathways in cancer cells, further enhancing treatment efficacy.
The integration of genomics and personalized medicine with mathematical modeling promises to revolutionize cancer care by providing more accurate predictions and tailored treatment approaches.
Interdisciplinary Collaborations
The complexities of cancer research necessitate collaboration among diverse fields. Interdisciplinary partnerships will be crucial in advancing biomathematics and its applications in cancer research:
Collaboration between Disciplines: The integration of expertise from mathematicians, biologists, oncologists, and computational scientists is essential for developing models that accurately capture the multifaceted nature of cancer. By working together, these experts can create comprehensive models that reflect biological realities and clinical needs.
Emerging Trends: Increasingly, research institutions and organizations are promoting interdisciplinary cancer research initiatives. These collaborations not only foster innovation but also facilitate the sharing of knowledge and methodologies across disciplines. Such efforts can lead to breakthroughs in understanding tumor behavior, treatment response, and the development of novel therapeutic strategies.
As interdisciplinary collaborations continue to flourish, they will drive forward the field of biomathematics in cancer research, resulting in more effective solutions to the challenges posed by cancer.
Potential Breakthroughs
The advancements in biomathematics and cancer research are likely to yield significant breakthroughs in treatment strategies:
Transforming Treatment Strategies: The development of more sophisticated mathematical models can lead to improved understanding of tumor dynamics, which in turn can guide clinical decision-making. For instance, models that simulate how tumors adapt to therapy can inform treatment adjustments in real time, optimizing patient outcomes.
Predictive Models for New Therapies: Mathematical models will also be instrumental in the testing and development of new therapeutic agents. By simulating the effects of various drugs on tumor growth and patient response, researchers can identify promising candidates for clinical trials, ultimately accelerating the pace of drug development.
Enhancing Cancer Prevention: Beyond treatment, biomathematics has the potential to play a role in cancer prevention strategies. Predictive models that incorporate lifestyle factors, genetic predispositions, and environmental influences can help identify high-risk individuals and guide preventive measures.
The future directions of biomathematics in cancer research hold immense promise for transforming the landscape of cancer treatment and patient care. Advances in computational power, integration with genomics, interdisciplinary collaborations, and potential breakthroughs will pave the way for more effective, personalized, and data-driven approaches to combating cancer. As the field evolves, ongoing investment in research and collaboration will be essential to unlocking the full potential of mathematical modeling in improving cancer outcomes and advancing our understanding of this complex disease.
Conclusions
The exploration of biomathematics in cancer research has revealed significant insights into the dynamics of tumor growth and treatment strategies. As we have seen throughout this paper, mathematical models play a crucial role in enhancing our understanding of cancer biology, optimizing treatment regimens, and ultimately improving patient outcomes. This conclusion aims to summarize the key insights gained from the research, discuss the impact of biomathematics on cancer research, and reflect on the future potential of this evolving field.
Summary of Key Insights
Mathematical models have emerged as powerful tools in the study of cancer, providing a structured framework to simulate the complexities of tumor growth and response to treatment. By leveraging various modeling approaches, such as deterministic, stochastic, multiscale, and agent-based models, researchers have gained deeper insights into the behavior of tumors, the factors influencing their growth, and the dynamics of treatment responses.
Understanding Tumor Growth: Mathematical models have elucidated different growth patterns exhibited by tumors, such as exponential and Gompertzian growth. These models help researchers quantify how tumors expand and respond to internal and external influences, such as genetic mutations, microenvironment interactions, and therapeutic interventions. For instance, the Gompertz model has been particularly useful in predicting tumor dynamics over time, offering valuable insights into how tumors evolve and adapt.
Optimizing Treatment Strategies: The integration of biomathematics into cancer treatment planning has enabled clinicians to personalize therapies for individual patients. Models that incorporate patient-specific data can predict how tumors will respond to chemotherapy, radiation, and immunotherapy, thereby guiding treatment decisions and improving outcomes. The use of mathematical modeling in optimizing drug dosages, schedules, and combinations has the potential to enhance therapeutic efficacy while minimizing adverse effects.
Case Studies of Success: Various case studies have demonstrated the practical application of mathematical models in clinical settings. For example, models predicting the efficacy of immunotherapy in melanoma have significantly influenced treatment strategies, showcasing how mathematical approaches can inform real-world clinical decisions.
Impact on Cancer Research
The integration of biomathematics into cancer research has not only improved our understanding of tumor behavior but has also led to significant advancements in research outcomes and treatment effectiveness. This impact can be seen in several key areas:
Enhanced Predictive Capabilities: Mathematical models allow researchers to analyze large datasets, incorporating genetic, clinical, and environmental factors to make predictions about patient outcomes. This predictive power is invaluable in identifying high-risk patients and tailoring interventions accordingly.
Accelerated Drug Development: The application of mathematical models in preclinical and clinical trial settings has expedited the drug development process. By simulating treatment responses, researchers can identify promising drug candidates more efficiently, leading to faster clinical translations and the introduction of new therapies.
Interdisciplinary Collaboration: The emergence of biomathematics as a critical discipline in cancer research has fostered collaboration among mathematicians, biologists, oncologists, and computational scientists. This interdisciplinary approach has enriched research methodologies and fostered innovation, resulting in more comprehensive and effective cancer research strategies.
Personalized Medicine Revolution: The advancement of personalized medicine, supported by biomathematical models, represents a paradigm shift in cancer treatment. By tailoring therapies based on individual tumor characteristics and responses, researchers and clinicians can achieve better outcomes, ultimately improving survival rates and quality of life for patients.
Final Thoughts
The future of biomathematics in cancer research is bright, with the potential for revolutionary treatments that significantly alter the landscape of oncology. As advancements in computational power and data analysis techniques continue to progress, we can expect even more sophisticated mathematical models to emerge. These models will likely incorporate vast amounts of genomic, proteomic, and clinical data, providing insights that were previously unattainable.
Moreover, the integration of artificial intelligence and machine learning into biomathematical frameworks holds great promise for refining predictive modeling and enhancing treatment personalization. The potential for real-time adaptations in treatment strategies, guided by mathematical models, could further revolutionize how we approach cancer care.
The contributions of biomathematics to cancer research have been profound, impacting our understanding of tumor dynamics, improving treatment effectiveness, and paving the way for personalized medicine. As the field continues to evolve, it stands at the forefront of developing innovative strategies to combat cancer, ultimately striving toward more effective and targeted treatments for patients worldwide. The ongoing commitment to research and collaboration will be essential in unlocking the full potential of biomathematics in transforming cancer care and achieving better outcomes for patients.
References
- Akinbusola, Victoria (2024). Mathematical modeling of neural networks: Bridging the gap between mathematics and neurobiology. World Journal of Advanced Engineering Technology and Sciences, 2024, 13(01), 516–526. [CrossRef]
- Alinei-Poiana, T., Dulf, Eva-H., & Kovacs, L. (2023). Fractional calculus in mathematical oncology. Scientific Reports, 13(1). [CrossRef]
- Azizi, T. (2024). Mathematical Modeling of Cancer Progression. AppliedMath, 4(3), 1065–1079. [CrossRef]
- Bekker, R. A., Kim, S., Pilon-Thomas, S., & Enderling, H. (2022). Mathematical modeling of radiotherapy and its impact on tumor interactions with the immune system. Neoplasia (New York, N.Y.), 28, 100796. [CrossRef]
- Belkhir, S., Thomas, F., & Roche, B. (2021). Darwinian Approaches for Cancer Treatment: Benefits of Mathematical Modeling. Cancers, 13(17), 4448. [CrossRef]
- Butner, J. D., Dogra, P., Chung, C., Pasqualini, R., Arap, W., Lowengrub, J., Cristini, V., & Wang, Z. (2022). Mathematical modeling of cancer immunotherapy for personalized clinical translation. Nature computational science, 2(12), 785–796. [CrossRef]
- Butner, J. D., Wang, Z., Elganainy, D., Al Feghali, K. A., Plodinec, M., Calin, G. A., Dogra, P., Nizzero, S., Ruiz-Ramírez, J., Martin, G. V., Tawbi, H. A., Chung, C., Koay, E. J., Welsh, J. W., Hong, D. S., & Cristini, V. (2021). A mathematical model for the quantification of a patient’s sensitivity to checkpoint inhibitors and long-term tumour burden. Nature Biomedical Engineering, 5(4), 297–308. [CrossRef]
- Castaneda, M., den Hollander, P., Kuburich, N. A., Rosen, J. M., & Mani, S. A. (2022). Mechanisms of cancer metastasis. Seminars in Cancer Biology, 87(1), 17–31. [CrossRef]
- Chamseddine, I. M., & Rejniak, K. A. (2019, July 17). Hybrid modeling frameworks of tumor development and treatment. Wiley Online Library; John Wiley & Sons, Inc. [CrossRef]
- Clare, S. E., Nakhlis, F., & Panetta, J. C. (2000). Molecular biology of breast cancer metastasis. The use of mathematical models to determine relapse and to predict response to chemotherapy in breast cancer. Breast cancer research : BCR, 2(6), 430–435. [CrossRef]
- de Visser, K. E., & Joyce, J. A. (2023, March 13). The evolving tumor microenvironment: From cancer initiation to metastatic outgrowth. Doi.org. [CrossRef]
- Deisboeck, T. S., Wang, Z., Macklin, P., & Cristini, V. (2011). Multiscale cancer modeling. Annual review of biomedical engineering, 13, 127–155. [CrossRef]
- Duarte, D., & Vale, N. (2022). Evaluation of synergism in drug combinations and reference models for future orientations in oncology. Current Research in Pharmacology and Drug Discovery, 3, 100110. [CrossRef]
- Enderling, H. (2022). Mathematical oncology: A new frontier in cancer biology and clinical decision making. Physics of Life Reviews, 40, 60–62. [CrossRef]
- Foo, J., Leder, K., & Michor, F. (2011). Stochastic dynamics of cancer initiation. Physical Biology, 8(1), 015002. [CrossRef]
- GomezQuiroz, L. E., & Roman, S. (2022). Influence of genetic and environmental risk factors in the development of hepatocellular carcinoma in Mexico. Special Issue on Hepatocellular Carcinoma (HCC) and Hepatitis B and c as Its Main Causes Worldwide, 27, 100649. [CrossRef]
- Gonçalves, I. G., & GarcíaAznar, J. M. (2023). Hybrid computational models of multicellular tumour growth considering glucose metabolism. Computational and Structural Biotechnology Journal, 21, 1262–1271. [CrossRef]
- Harshe, I., Enderling, H., & Brady-Nicholls, R. (2023). Predicting Patient-Specific Tumor Dynamics: How Many Measurements Are Necessary?. Cancers, 15(5), 1368. [CrossRef]
- Hassan, M., Awan, F. M., Naz, A., deAndrés-Galiana, E. J., Alvarez, O., Cernea, A., Fernández-Brillet, L., Fernández-Martínez, J. L., & Kloczkowski, A. (2022). Innovations in Genomics and Big Data Analytics for Personalized Medicine and Health Care: A Review. International journal of molecular sciences, 23(9), 4645. [CrossRef]
- Israel, G. (1988). On the contribution of Volterra and Lotka to the development of modern biomathematics. History and Philosophy of the Life Sciences, 10, 37–49.
- Johnson, K. E., Howard, G., Mo, W., Strasser, M. K., Lima, E. A. B. F., Huang, S., & Brock, A. (2019). Cancer cell population growth kinetics at low densities deviate from the exponential growth model and suggest an Allee effect. PLoS Biology, 17(8), e3000399. [CrossRef]
- Li H. (2023). Invalidity of, and alternative to, the linear quadratic model as a predictive model for postirradiation cell survival. Cancer science, 114(7), 2931–2938. [CrossRef]
- Lunk, B. (2019). PICUP Exercise Sets: A Stochastic Model of Birth-Death Population Dynamics. PICUP. https://www.compadre.org/PICUP/exercises/exercise.cfm?A=BirthDeath.
- Matin, H. N., & Setayeshi, S. (2024). A computational tumor growth model experience based on molecular dynamics point of view using deep cellular automata. Artificial Intelligence in Medicine, 148, 102752. [CrossRef]
- McAleer, S. (2022). A history of cancer and its treatment: Presidential Address to the Ulster Medical Society. 7th October 2021. The Ulster Medical Journal, 91(3), 124–129. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9720583/.
- Michor, F., & Beal, K. (2015). Improving Cancer Treatment via Mathematical Modeling: Surmounting the Challenges Is Worth the Effort. Cell, 163(5), 1059–1063. [CrossRef]
- National Cancer Institute. (2021, October 11). What Is Cancer? - National Cancer Institute. Www.cancer.gov. https://www.cancer.gov/about-cancer/understanding/what-is-cancer#.
- Nidal Al-Huniti, Yan, F., Jingyu Jerry Yu, Zheng Rong Lü, Nagase, M., Zhou, D., & Sheng, J. (2020). Tumor Growth Dynamic Modeling in Oncology Drug Development and Regulatory Approval: Past, Present, and Future Opportunities. CPT: Pharmacometrics & Systems Pharmacology, 9(8), 419–427. [CrossRef]
- Nivlouei J., S., Soltani, M., Shirani, E., Salimpour, M. R., Travasso, R., & Carvalho, J. (2022). A multiscale cell-based model of tumor growth for chemotherapy assessment and tumor-targeted therapy through a 3D computational approach. Cell proliferation, 55(3), e13187. [CrossRef]
- Nomdedeu-Sancho, G., Gorkun, A., Mahajan, N., Willson, K., Schaaf, C. R., Votanopoulos, K. I., Atala, A., & Soker, S. (2023). In Vitro Three-Dimensional (3D) Models for Melanoma Immunotherapy. Cancers, 15(24), 5779. [CrossRef]
- Norton, K. A., Gong, C., Jamalian, S., & Popel, A. S. (2019). Multiscale Agent-Based and Hybrid Modeling of the Tumor Immune Microenvironment. Processes (Basel, Switzerland), 7(1), 37. [CrossRef]
- Norton, K.-A., Gong, C., Jamalian, S., & Popel, A. S. (2019). Multiscale Agent-Based and Hybrid Modeling of the Tumor Immune Microenvironment. Processes, 7(1), 37. [CrossRef]
- Odoux, C., Fohrer, H., Hoppo, T., Guzik, L., Stolz, D. B., Lewis, D. W., Gollin, S. M., Gamblin, T. C., Geller, D. A., & Lagasse, E. (2019). A Stochastic Model for Cancer Stem Cell Origin in Metastatic Colon Cancer. Cancer Research, 68(17), 6932–6941. [CrossRef]
- Olushola, A. , Mart, J. , (2022). Fraud Detection Using Machine Learning Techniques. http://dx.doi.org/10.13140/RG.2.2.33044.88961/1.
- Olushola, A. , Mart, J. , Alao, V. , (2023). Implementations Of Artificial Intelligence In Health Care. http://dx.doi.org/10.13140/RG.2.2.36344.62729/1.
- Olushola, A. , Mart, J. , Alao, V. , (2023). Predictive Modelling For Disease Outbreak Prediction. http://dx.doi.org/10.13140/RG.2.2.17470.25929/1.
- Panja, S., Rahem, S., Chu, C. J., & Mitrofanova, A. (2021). Big Data to Knowledge: Application of Machine Learning to Predictive Modeling of Therapeutic Response in Cancer. Current genomics, 22(4), 244–266. [CrossRef]
- Petinrin, O. O., Saeed, F., Toseef, M., Liu, Z., Basurra, S., Muyide, I. O., Li, X., Lin, Q., & Wong, K.-C. (2023). Machine learning in metastatic cancer research: Potentials, possibilities, and prospects. Machine Learning in Metastatic Cancer Research: Potentials, Possibilities, and Prospects, 21, 2454–2470. [CrossRef]
- Poleszczuk, J., Macklin, P., & Enderling, H. (2016). Agent-Based Modeling of Cancer Stem Cell Driven Solid Tumor Growth. Methods in Molecular Biology (Clifton, N.J.), 1516, 335–346. [CrossRef]
- Smieja J. (2023). Mathematical Modeling Support for Lung Cancer Therapy-A Short Review. International journal of molecular sciences, 24(19), 14516. [CrossRef]
- Spoormans, K., Crabbé, M., Struelens, L., De Saint-Hubert, M., & Koole, M. (2022). A Review on Tumor Control Probability (TCP) and Preclinical Dosimetry in Targeted Radionuclide Therapy (TRT). Pharmaceutics, 14(10), 2007. [CrossRef]
- Sun, X., & Hu, B. (2018). Mathematical modeling and computational prediction of cancer drug resistance. Briefings in bioinformatics, 19(6), 1382–1399. [CrossRef]
- Szumilak, M., Wiktorowska-Owczarek, A., & Stanczak, A. (2021). Hybrid Drugs-A Strategy for Overcoming Anticancer Drug Resistance?. Molecules (Basel, Switzerland), 26(9), 2601. [CrossRef]
- Thirumal, R. A., Patil, S., Sarode, S., Sarode, G., Gadbail, A., & Gondivkar, S. (2018). Scope of Mathematical Biology in Cancer Research. The Journal of Contemporary Dental Practice, 19, 1035–1036. [CrossRef]
- Unni, P., & Seshaiyer, P. (2019). Mathematical Modeling, Analysis, and Simulation of Tumor Dynamics with Drug Interventions. Computational and mathematical methods in medicine, 2019, 4079298. [CrossRef]
- Vaia. (2019). Biomathematics: Applications & Implications | Vaia. Vaia. https://www.vaia.com/en-us/explanations/math/applied-mathematics/biomathematics/.
- Vieira, L. C., Costa, R. S., & Valério, D. (2023). An overview of mathematical modelling in cancer research: Fractional calculus as modelling tool. Fractal and Fractional, 7, 8. [CrossRef]
- Vieira, L., Costa, R. S., & Duarte Valério. (2023). An Overview of Mathematical Modelling in Cancer Research: Fractional Calculus as Modelling Tool. Fractal and Fractional, 7(8), 595–595. [CrossRef]
- Wei, H. (2023). Mathematical modeling of tumor growth and treatment: Triple negative breast cancer. Mathematics and Computers in Simulation, 204, 645–659. [CrossRef]
- West, J., Robertson-Tessi, M., & Anderson, A. R. A. (2023). Agent-based methods facilitate integrative science in cancer. Trends in cell biology, 33(4), 300–311. [CrossRef]
- WHO. (2022, February 3). Cancer. World Health Organization. https://www.who.int/news-room/fact-sheets/detail/cancer.
- Yin, A., Moes, D. J. A. R., van Hasselt, J. G. C., Swen, J. J., & Guchelaar, H. (2019). A Review of Mathematical Models for Tumor Dynamics and Treatment Resistance Evolution of Solid Tumors. CPT: Pharmacometrics & Systems Pharmacology, 8(10), 720–737. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





