Preprint
Article
Evaluating the Impact of Windowing Techniques on Fourier Transform Preprocessed Signals for Deep Learning-Based ECG Classification
Altmetrics
Downloads
46
Views
24
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 September 2024
Posted:
01 October 2024
You are already at the latest version
Alerts
Abstract
(1) Background: Arrhythmia, or irregular heart rhythms, are a prevalent cardiovascular condition and can be diagnosed using electrocardiogram (ECG) signals. Advances in deep learning have enabled automated analysis of these signals. However, the effectiveness of deep learning models depends heavily on the quality of signal preprocessing. This study evaluates the impact of different windowing techniques applied to Fourier Transform-preprocessed ECG signals on the classification accuracy of deep learning models. (2) Methods: We applied three windowing techniques—Hamming, Hann, and Blackman—to transform ECG signals into the frequency domain. A 1D Convolutional Neural Network (CNN) was employed to classify the ECG signals into five arrhythmia categories based on features extracted from each windowed signal.(3) Results: The Blackman window yielded the highest classification accuracy, with improved signal-to-noise ratio and reduced spectral leakage compared to the Hamming and Hann windows. (4) Conclusions: The choice of windowing technique significantly influences the effectiveness of deep learning models in ECG classification. Future studies should explore additional preprocessing methods and their clinical applications.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Arrhythmia, characterized by irregular heart rhythms, are among the most prevalent heart conditions. These occur when the heart beats either too fast or too slow due to irregular electrical impulses traveling through the myocardial tissue of the heart. These impulses are responsible for controlling the contraction and relaxation of the myocardium, thus generating the heart’s rhythm. While a healthy heart maintains a consistent rhythm, arrhythmia disrupt this pattern, making it irregular, faster, or slower depending on factors such as the heart’s electrical activity, blood flow, the strength of the myocardial tissue, or heart muscle damage [1].
The ECG signal, demonstrates a unique waveform for every heartbeat cycle, with each part of the signal representing specific events during the cycle. When the atria have filled with blood, the sinoatrial (SA) node fires an electrical impulse that causes atrial depolarization, leading to the formation of the P wave on the ECG. After the P wave, the atria contract for approximately 100 milliseconds. The PQ interval represents the transmission of the signal from the SA node to the atrioventricular (AV) node. Ventricular depolarization follows, marked by the QRS complex, which is initiated by the AV node’s firing. The Q wave reflects electrical impulses traveling through the heart’s lower regions, while the R wave occurs as the signal passes through the ventricles’ lateral sides. The S wave denotes the last phase of ventricular depolarization in the heart’s lower muscles, while atrial repolarization happens concurrently but is obscured by the QRS complex. The ventricles continue contracting during the ST segment, and the T wave signals ventri [2].
By carefully examining these ECG waveforms, segments, and intervals, cardiologists can diagnose various types of arrhythmias. Advances in machine learning and deep learning technologies allow automated analysis of ECG data, extracting key features and enabling the classification of different arrhythmia types. This not only helps detect arrhythmias more efficiently but also assists in making faster, more accurate diagnoses. Through these innovations, arrhythmia detection has become more accessible, improving patient outcomes by allowing for timely intervention.
Deep learning (DL) has demonstrated significant success in medical diagnosis, particularly in the automatic classification of heart abnormalities using ECG signals in recent years [3,4,5,6,7]. DL models learn to map ECG features to their corresponding medical categories, utilizing multiple neural layers. This mapping is optimized through a training process using datasets where neuron weights are adjusted to minimize discrepancies between the predicted and actual categories of the training data. Compared to traditional machine learning methods such as clustering[8] and support vector machines (SVM)[9], DL-based ECG classification offers a more effective way to map ECG signal characteristics to their respective categories[1,10], due to its powerful multi-level abstraction capability for feature extraction.
While existing research has yielded promising outcomes in the analysis of ECG signals, several challenges remain unresolved. One significant issue is the imbalance in data, where normal ECG signals far outnumber abnormal ones, leading to difficulty in effectively addressing the imbalance problem. Additionally, the generalization capabilities of many current models are limited. Due to the significant individual variations in ECG patterns, these methods are often inadequate for clinical application [11]. When applied to real-time hospital data, their performance tends to fall short compared to results from publicly available datasets.
Convolutional Neural Networks (CNNs) have established themselves as potent tools in the morphological analysis of physiological signals, particularly due to their ability to discern invariant patterns and capture pivotal features across the data. This paper presents an innovative approach for ECG signal recognition and classification, which utilizes the strengths of CNNs to analyze signals in both the time and frequency domains. To enhance the model’s performance and address the nuances of complex ECG signal patterns, different Fourier Transform windowing techniques have been explored.
While Fourier Transform has long been a cornerstone in the analysis of ECG signals, its application has predominantly focused on the transformation of signals from the time domain to the frequency domain without a detailed examination of the effects of varying windowing techniques. Previous studies have effectively leveraged the Fourier Transform to identify fundamental frequency components and diagnose arrhythmias, ischemic episodes, and other cardiac abnormalities [5,12,13,14]. However, there exists a notable gap in the literature regarding how different windowing techniques, such as Hann, Hamming, and Blackman, which are known to reduce spectral leakage and improve signal clarity, impact the diagnostic capabilities of Fourier-based ECG analysis. This paper seeks to fill this gap by exploring how these specific windowing techniques enhance the interpretability of Fourier Transformed ECG signals and, in turn, improve the performance of CNNs in classifying cardiac events. This innovative approach promises not only to refine the analysis of ECG data but also to provide more accurate and reliable diagnostic tools that are critical for clinical decision-making.
The primary contributions of this work are summarized as follows: Firstly, Fourier Transform techniques with different window functions—Hamming, Hann, and Blackman—are applied to convert the ECG signals into the frequency domain. This transformation facilitates the extraction of frequency-based features that provide valuable insights into the signal’s characteristics. Secondly, a 1D CNN model is employed to classify the ECG signals into five categories based on the features extracted through each windowing method. This approach not only addresses data imbalances but also enhances the analysis framework by leveraging features derived from various Fourier windowing techniques. The comparative analysis of these window functions aims to identify which method optimally enhances model performance by effectively balancing the resolution and leakage trade-offs inherent in Fourier-based frequency domain feature extraction.
2. Materials and Methods
2.1. Dataset Description
In this study, the Massachusetts Institute of Technology-Beth Israel Hospital (MIT-BIH) Arrhythmia Dataset [15] is utilized. This dataset includes 24-hour ECG recordings collected from 47 individuals, with subjects ranging in age from 23 to 89 years. We utilized excerpts from 30-minute, dual-channel ECG recordings collected from 47 participants between 1975 and 1979. The dataset features two ECG lead signals for each recording, digitized at 360 samples per second with 11-bit resolution over a 10-mV range.
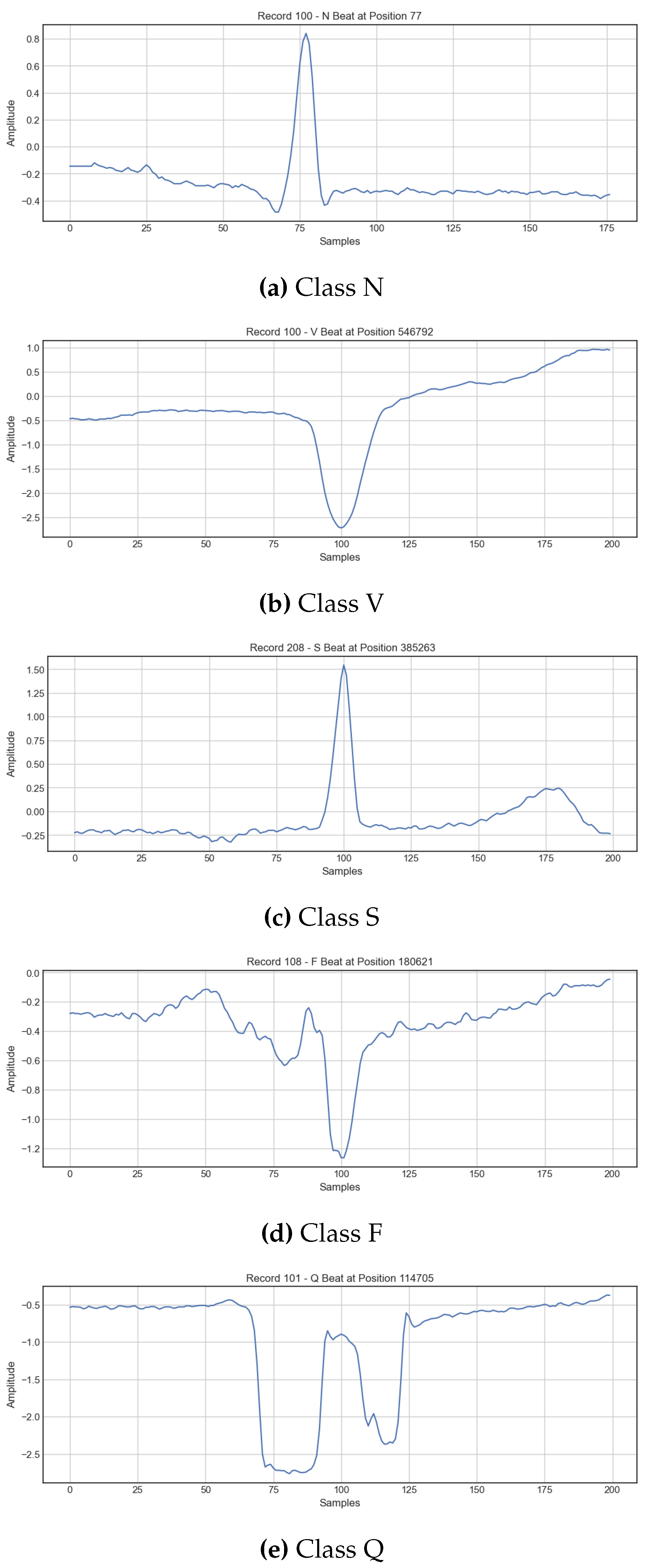
For the purposes of classification, the annotations were grouped into five categories following the AAMI EC57 standard [16]. Class N encompasses "normal beats," as well as "left bundle branch block," "right bundle branch block," "atrial escape," and "nodal junction escape" beats. Class V includes "premature ventricular contractions" and "ventricular escape" beats. Class S contains "atrial premature" (AP) beats, "aberrated premature" beats, "nodal junction premature" beats, and "supraventricular" beats. Class Q, sometimes referred to as "unknown beats," includes "paced beats" (P), "fusion of paced and normal beats" (fPN), and "unclassified beats." Lastly, Class F is comprised of "fusion of ventricular and normal beats" (fVN). These annotations are derived from specific symbols present in the original dataset, which were mapped into the five simplified categories for classification purposes. For example, the "N" label includes symbols such as ’N’, ’L’, ’R’, ’e’, and ’j’, while the "S" label corresponds to symbols like ’A’, ’a’, and ’S’. This mapping was implemented to standardize the labels for the classification task.
For the purposes of classification, the annotations were grouped into five categories following the AAMI EC57 standard [16]. Class N encompasses "normal beats," as well as "left bundle branch block," "right bundle branch block," "atrial escape," and "nodal junction escape" beats. Class V includes "premature ventricular contractions" and "ventricular escape" beats. Class S contains "atrial premature" (AP) beats, "aberrated premature" beats, "nodal junction premature" beats, and "supraventricular" beats. Class Q, sometimes referred to as "unknown beats," includes "paced beats" (P), "fusion of paced and normal beats" (fPN), and "unclassified beats." Lastly, Class F is comprised of "fusion of ventricular and normal beats" (fVN). These annotations are derived from specific symbols present in the original dataset, which were mapped into the five simplified categories for classification purposes. For example, the "N" label includes symbols such as ’N’, ’L’, ’R’, ’e’, and ’j’, while the "S" label corresponds to symbols like ’A’, ’a’, and ’S’. This mapping was implemented to standardize the labels for the classification task. The illustration of each signals were shown in Figure 2.
The classification and understanding of these beats rely heavily on the identification of the PQRST complex, which is fundamental to interpreting ECG signals. The PQRST complex consists of five main components: the P wave, which indicates atrial depolarization; the QRS complex, which represents ventricular depolarization; and the T wave, which denotes ventricular repolarization. Occasionally, a U wave may be present, following the T wave, whose origin is less clearly understood but is thought to be related to the repolarization of the Purkinje fibers. Figure 1 provides a visual representation of these components within a typical ECG waveform. Understanding the morphology and timing of these components is critical for accurate beat classification and diagnosis, as each class of beats exhibits distinct characteristics in terms of the PQRST sequence. For instance, ventricular contractions such as those in Class V may show an abnormal QRS complex, while atrial contractions in Class S alter the P wave’s morphology.
Figure 1.
Illustration of each label in an ECG signal.
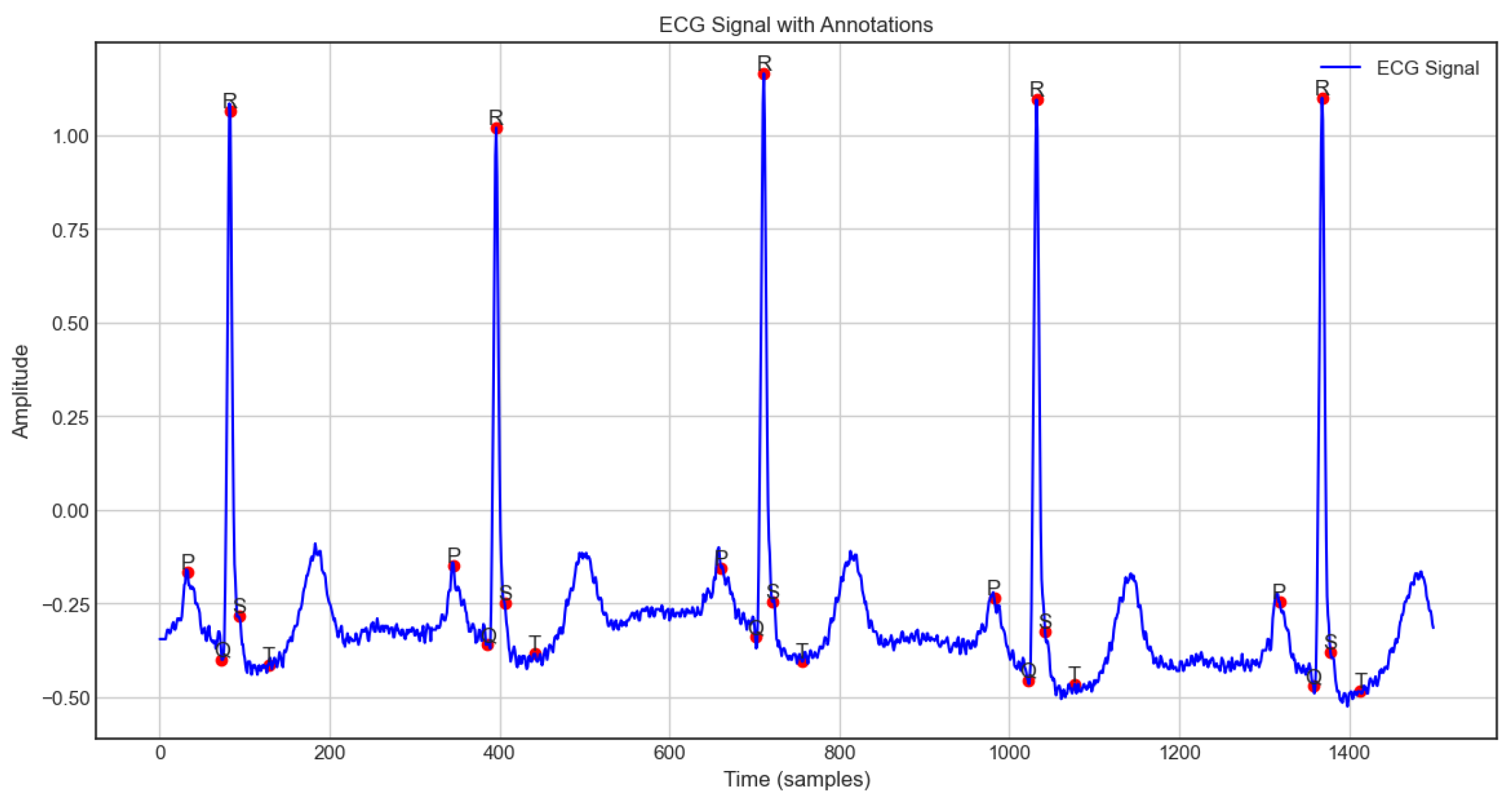
Figure 2.
Illustration of time series signals for each label.
2.2. Signal Preprocessing
2.2.1. Standardization for Signal Normalization
For this study, we chose standardization as the normalization technique, which is particularly suitable for data involving biological signals such as ECGs. Standardization adjusts the data to have zero mean and unit standard deviation. This is achieved by subtracting the mean and dividing by the standard deviation of each data sample. The standardization formula applied to each signal x in the dataset is expressed as:
where represents the mean of the signal, and denotes the standard deviation.
Standardization was selected over other normalization techniques like Min-Max scaling because it effectively addresses features that vary in scale and distribution. The ECG signals, which exhibit significant variations in amplitude and waveform due to factors such as heart size, electrode placement, and physiological conditions, benefit from standardization as it normalizes the range without distorting differences in values or losing information about zero entries.
2.2.2. Noise Reduction Using Moving Average Filters
Noise reduction is a critical preprocessing step in ECG signal analysis to ensure the reliability and accuracy of the data before further processing. Among various techniques available, the moving average filter is widely employed due to its simplicity and effectiveness in smoothing out short-term fluctuations and highlighting longer-term trends in the data.
The moving average filter operates by creating an average of different subsets of the total number of data points available in a signal, effectively smoothing the signal. This is particularly useful in ECG signal processing, where high-frequency noise can obscure the true heart rate signal and other important diagnostic features.
The moving average filter is applied to the ECG signal using the following formula:
where represents the original data points in the signal, represents the output of the moving average filter, and N is the number of data points in the moving average window, which determines how much the data will be smoothed.
In this study, a window size of 5 samples was chosen based on the sampling rate and the expected frequency of the noise components. This window size provides a balance between smoothing the signal to remove high-frequency noise and preserving the essential characteristics of the ECG signal, such as the P wave, QRS complex, and T wave.
2.3. Feature Extraction and Windowing Techniques
Feature extraction is a pivotal aspect of signal processing, especially for tasks that involve the classification of physiological signals like ECGs. The Fourier Transform is a powerful mathematical tool used for decomposing a signal into its constituent frequencies, providing a different perspective that is particularly useful for analyzing the frequency content of signals.
The Fourier Transform [17] transforms a time-domain signal, which is a function of time, into a frequency-domain signal, which is a function of frequency. This transformation reveals the different frequencies present in the signal and their amplitudes, which can be crucial for identifying rhythmic patterns such as those found in heartbeats.
The continuous Fourier Transform of a continuous, time-dependent signal is defined as:
where:
- is the Fourier Transform of ,
- f is the frequency in hertz,
- t is time,
- j is the imaginary unit.
For digital signals, we use the Discrete Fourier Transform (DFT), especially implemented in an efficient manner through the Fast Fourier Transform (FFT) algorithm as show in Equation 4.
where:
- N is the total number of samples,
- is the signal value at sample n,
- represents the frequency component at frequency k.
To enhance the spectral purity of the Fourier analysis, Finite Impulse Response (FIR) filters [18] such as the Hann, Hamming, and Blackman windows are employed to precondition the ECG signal. These filters are specifically designed to address the phenomenon of spectral leakage—where energy from strong frequency components bleeds into neighboring frequencies, potentially obscuring or altering the true spectral content [19].
Applying Finite Impulse Response (FIR) filters in the preprocessing stages of signal analysis enhances the effectiveness of subsequent deep learning models. These filters are crucial for reducing spectral leakage and noise, thereby improving the quality of the signal. Enhanced signal quality ensures that deep learning models train on data that accurately represent the underlying physiological signals, which is particularly vital in ECG analysis. The clear and distinct representation of frequency components achieved through FIR filtering facilitates the extraction of subtle features. This is especially beneficial for convolutional neural networks (CNNs), which rely heavily on high-quality inputs to detect crucial patterns in the data. By improving the signal-to-noise ratio and emphasizing important signal characteristics, FIR filters reduce the complexity of the models required to achieve high performance, thus enhancing training efficiency and predictive accuracy.
Hann Window The Hann window, often referred to as the Hanning window, is designed to reduce spectral leakage effectively [19,20]. It is mathematically defined as:
where n is the sample index ranging from 0 to , and N is the total number of samples in the window. This window function tapers the signal to zero at both ends, thus minimizing the discontinuities at the window boundaries and reducing the resultant spectral leakage.
Hamming Window The Hamming window offers a narrower main lobe compared to the Hann window[19,20], which enhances its ability to resolve close frequency components but at the cost of higher side lobes. It is defined by the expression:
This characteristic provides a better frequency resolution and is beneficial when analyzing complex signals where precision in frequency component separation is crucial.
Blackman Window For applications requiring significant reduction of spectral leakage, the Blackman window is a superior choice[19,20]. It incorporates a second-order cosine term to further attenuate the side lobes, as defined by:
The inclusion of the additional cosine term results in a significantly higher attenuation of the side lobes, making the Blackman window especially effective in situations where leakage needs to be minimized to detect small amplitude frequencies adjacent to large amplitude components.
The selection of specific FIR filters can be strategically aligned with the requirements of the deep learning model, taking into account the characteristics of the ECG signal and the diagnostic objectives. For instance, a Blackman window, known for its superior attenuation of side lobes, can be particularly useful in noisy environments where detailed feature analysis is critical. This strategic alignment ensures that the preprocessing not only augments the capabilities of deep learning models but also optimizes them for more effective learning and improved diagnostic outcomes. Therefore, integrating FIR filters into the preprocessing stage is instrumental in maximizing the potential of advanced machine learning techniques for medical signal analysis, thereby enhancing the overall diagnostic capabilities in clinical settings.
2.4. 1D-CNN Model Architecture
A Convolutional Neural Network (CNN) is a type of deep learning architecture that excels at extracting high-level features from input data. Conceptually similar to a multilayer perceptron (MLP), each neuron in a CNN has an activation function that processes weighted inputs to produce outputs. CNNs are composed primarily of three types of layers: convolutional layers, pooling layers, and fully connected layers [21]. These networks, when adequately trained, find application in various fields such as speech recognition, structural engineering, and image processing.
A 1D-CNN is a variant of the traditional CNN, tailored specifically for handling one-dimensional data, making it particularly effective for sparse datasets that traditional CNNs might struggle with. Unlike 2D-CNNs that use two-dimensional convolutional filters, 1D-CNN utilize one-dimensional filters to extract features from data. This makes 1D-CNN not only more suitable for processing data such as audio or text but also more computationally efficient due to having fewer parameters. Their design allows them to capture local features within the signal, making them robust to slight shifts in time, which is crucial for analyzing time-series data with temporal components.
The first 1D-CNN classification model used in this study is designed to process the ECG signals and classify them into one of the five heartbeat categories. The architecture, as shown in Table, consists of:
- Three convolutional layers with filter sizes of 32, 64, and 64 respectively, and a kernel size of 3. Each convolutional layer is followed by a max pooling layer with a pool size of 2 to reduce the spatial dimensions of the data.
- Flattening layer, which transforms the 1D convoluted data into a flat vector for the fully connected layers.
- Two dense layers: the first dense layer has 64 units, followed by another dense layer with 32 units, both using the ReLU activation function.
- Dropout layer (with a dropout rate of 0.5) is added after the first dense layer to prevent overfitting by randomly deactivating neurons during training.
- The final output layer uses a softmax activation function to predict the probability of each class, with 5 output units corresponding to the five heartbeat categories.
This architecture was chosen for its ability to capture local patterns in the ECG signals while maintaining a manageable number of parameters. The model was trained using the Adam optimizer, with categorical cross-entropy as the loss function since this is a multi-class classification problem. The model was trained for 15 epochs with a batch size of 32, in line with prior research settings. The training dataset was split into 60% training and 40% testing to ensure the model was evaluated on a substantial portion of the data. Validation data was taken from the test set to monitor the model’s performance during training. Additionally, the class distribution in the training and test sets was adjusted to reflect the balanced dataset achieved through SMOTE.
Table 1.
Parameter Tuning of the Proposed 1D CNN Model.
| Parameter | Value |
|---|---|
| Pooling Type | Max Pooling |
| Pooling Size | 2 |
| Units in First Dense Layer | 64 |
| Units in Second Dense Layer | 32 |
| Activation Function | ReLU |
| Dropout Rate | 0.5 |
| Output Layer Activation | Softmax |
| Number of Output Units | 5 |
| Optimizer | Adam |
3. Results
3.1. Effectiveness of FIR Window Functions in Signal Preprocessing
Quantitative Analysis The Signal-to-Noise Ratio (SNR) is a metric in signal processing used to quantify the clarity and quality of a signal relative to the background noise. It is particularly important in the context of ECG signal analysis where distinguishing true signal from noise can influence diagnostic decisions. The SNR is expressed in decibels (dB) and calculated using the following equation [22]:
where represents the power of the desired signal, calculated as the sum of the squares of the signal amplitudes, and denotes the power of the noise, which is determined by the difference between the original and the FIR-filtered signal:
Here, is the amplitude of the original ECG signal at time t, and is the amplitude after applying an FIR filter, such as Hann, Hamming, or Blackman. The application of these filters typically aims to enhance the SNR by reducing the noise components without distorting the essential features of the ECG signal. By improving the SNR, the filtered signal can offer clearer and more discernible cardiac events, facilitating more accurate analysis and interpretation.
In the analysis of FIR filters applied to ECG signals, the Hann and Hamming filters demonstrated superior performance in enhancing the Signal-to-Noise Ratio (SNR), both achieving improvements around 4 dB (Figure 3). The Hamming filter slightly outperformed the Hann filter, suggesting its marginally better efficacy in minimizing spectral leakage and enhancing signal clarity. Conversely, the Blackman filter, while still effective, showed a lower SNR improvement of approximately 3 dB. The observed variations in SNR improvements, denoted by error bars in the results, underscore the consistency of the filters’ effects across multiple datasets. This variability is crucial for understanding the practical implications of filter selection in clinical ECG analysis, where signal integrity can significantly influence diagnostic accuracy.
3.2. Performance of Deep Learning Models on Preprocessed Signals
Confusion Matrix Analysis In classifying ECG signals using different windowing techniques in the preprocessing, the evaluation of classification performance is central, with a specific focus on confusion matrices for the Blackman, Hamming, and Hann windows. Classification matrix is a crucial metric to assess how well the classification algorithms perform under the different spectral conditions induced by the respective window types.
The confusion matrix for the Blackman window exhibits prominent diagonal elements, with a notable 10,467 correct classifications for class F, indicating strong accuracy in classification across the observed categories. Misclassifications are minimal, with the most significant confusion between classes F and V, consisting of 35 instances, which is relatively low in comparison to the total classifications. This suggests that the Blackman window maintains high specificity and sensitivity, particularly in distinguishing between closely related classes.
Similarly, the Hamming window’s confusion matrix shows high values on the diagonal, reflective of effective classification, with class F having 10,458 correct classifications. However, this window displays a broader spread of misclassifications, particularly between classes F and V (38 instances), and between classes S and V (40 instances). These figures suggest a slightly reduced specificity under the Hamming window, which might influence its suitability in applications requiring high precision in class differentiation.
The Hann window’s matrix also demonstrates strong diagonal values, albeit with a slight reduction in sensitivity for class S, which has 2,361 correct classifications—a decrease compared to the other windows. Misclassifications are higher, especially between classes F and S (181 instances), and between classes S and V (44 instances), indicating potential challenges in distinguishing these class pairs more so than with the other window functions.
Overall, the comparison of these three window functions reveals robust classification capabilities across all types, yet highlights subtle differences in their performance. The Blackman window appears to offer the best overall accuracy with the least amount of misclassification, making it potentially more suitable for clinical applications where precise class distinction is crucial. On the other hand, the Hamming and Hann windows, while still effective, exhibit a slightly increased tendency for misclassification between certain classes, which could influence their application in specific diagnostic settings.
Overall Performance The performance analysis of the three window functions— Hamming, Hann, and Blackman—on ECG signal classification provides a detailed insight into their effectiveness across five classes (F, N, S, V, Q), evaluated through metrics such as Precision, Recall, and F1-Score ( Table 2). These metrics are defined as follows:
- Precision: The ratio of correctly predicted positive observations to the total predicted positive observations.where is the number of true positives, and is the number of false positives.
- Recall: The ratio of correctly predicted positive observations to all observations in the actual class.where is the number of false negatives.
- F1-Score: The harmonic mean of Precision and Recall, providing a balance between the two.
All three models demonstrate excellent performance in classifying class F, with notably high precision and recall, suggesting their strong capability in accurately identifying this category with minimal false positives and negatives. Classes N and S also see relatively good performance, although the recall for class N is slightly reduced, indicating fewer true positives detected relative to the actual positives present. This could impact the clinical utility of the model where missing a positive case can have significant consequences.
Figure 4.
Comparison of confusion matrix for ECG signals classification processed using (a) Hann, (b) Hamming, and (c) Blackman windows.
Figure 4.
Comparison of confusion matrix for ECG signals classification processed using (a) Hann, (b) Hamming, and (c) Blackman windows.
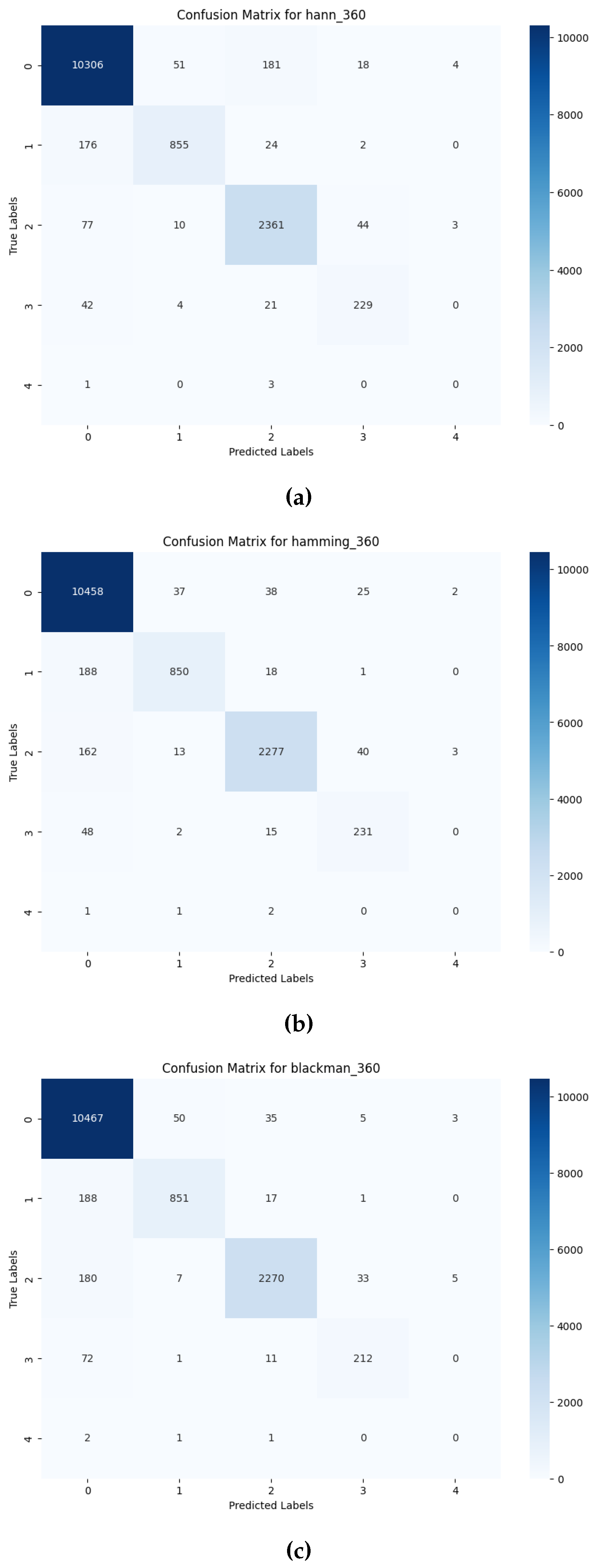
The performance on class V is moderate across all models, with precision slightly lower than other classes, hinting at a higher rate of false positives for this class. This might suggest a common challenge in the classification of this class using window-based spectral analysis, possibly due to the overlap in spectral characteristics between class V and other classes.
A notable observation across all three models is the complete lack of detection of class Q, which exhibits zero values in precision, recall, and F1-Score. This uniform failure to detect class Q likely indicates that class Q represents a type of signal that is undetectable under the current feature extraction and classification methodology employed. This could be due to the absence of distinct or adequate features within the spectral domain that these window functions analyze, or possibly the absence of sufficient representative samples of class Q in the training dataset. Overall, while all three window functions provide robust classification capabilities for most ECG signal classes, the choice among them should consider the specific classification needs and the unique challenges presented by each class. The slight differences in performance metrics between the models can guide the selection of a window function based on whether higher precision or a better-balanced F1-Score is more critical for the intended application.
The results clearly demonstrate the utility of FIR window functions in enhancing the signal-to-noise ratio and reducing artifacts in ECG signals, which in turn significantly improves the performance of deep learning models. The use of Blackman window filtering, in particular, facilitated a more refined feature extraction process, thereby aiding in more accurate heart condition diagnostics. The findings suggest that integrating advanced FIR filtering techniques with deep learning frameworks can significantly advance the field of biomedical signal analysis.
4. Conclusion
This study explored the effectiveness of Finite Impulse Response (FIR) filters— specifically, Hann, Hamming, and Blackman—in enhancing the Signal-to-Noise Ratio (SNR) of ECG signals. The results indicate significant improvements in SNR, which in turn have facilitated more accurate feature extraction by convolutional neural networks (CNNs) used for signal classification.
Our findings demonstrate that the Blackman filter, while providing a slightly lower increase in SNR compared to the Hann and Hamming filters, maintains a balance between noise reduction and signal integrity. The Hann and Hamming filters, on the other hand, showed slightly higher SNR improvements, suggesting their potential for applications requiring maximum noise suppression. Importantly, all tested FIR filters contributed to the enhanced performance of deep learning models by providing cleaner, more distinguishable signal inputs.
4.1. Deep Learning Enhancements
The preprocessing improvements achieved through the application of FIR filters significantly impacted the performance of CNNs. By reducing noise and enhancing signal clarity, these filters allowed the CNNs to better learn and generalize from the training data, resulting in higher accuracy and sensitivity in ECG classification tasks. Specifically, the clarity in the time-domain features post-filter application improved the network’s ability to discern subtle variations in ECG signals, which are often indicative of critical cardiac conditions.
Moreover, the use of these optimized signals in training CNNs led to a reduction in model overfitting. With cleaner data, models were less likely to learn noise as a feature, which is a common problem in medical signal processing. This enhancement was particularly evident in the models’ performance on unseen test data, where generalization is most crucial.
4.2. Implications
The improvement in signal preprocessing, as evidenced by increased SNR, implies that FIR filters play a crucial role in the preprocessing steps for ECG analysis. This enhancement is critical for clinical applications where accurate ECG interpretation can dictate patient diagnosis and treatment plans. Additionally, the integration of these preprocessing techniques with advanced deep learning models presents a promising approach for automated ECG analysis systems, potentially leading to more reliable and scalable solutions in healthcare diagnostics.
4.3. Limitations and Future Work
While the study results are promising, the scope of FIR filters and their configurations could be expanded in future research to include a wider variety of ECG signal conditions and noise types. Further, comparative studies involving other types of digital filters and their impact on different deep learning architectures could provide deeper insights into the optimization of signal preprocessing for medical diagnostics. Future work could also explore the integration of adaptive filtering techniques, which dynamically adjust their parameters in response to changing signal characteristics, offering potential for even more robust ECG analysis systems.
Author Contributions
N.P.M: Conceptualization, Data analysis, Writing – review & editing. H.O: Review & editing.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Antzelevitch, C.; Burashnikov, A. Overview of Basic Mechanisms of Cardiac Arrhythmia, 2011. [CrossRef]
- Varalakshmi, P.; Sankaran, A.P. An improved hybrid AI model for prediction of arrhythmia using ECG signals. Biomedical Signal Processing and Control 2023, 80. [Google Scholar] [CrossRef]
- Xiao, Q.; Lee, K.; Mokhtar, S.A.; Ismail, I.; bin Md Pauzi, A.L.; Zhang, Q.; Lim, P.Y. Deep Learning-Based ECG Arrhythmia Classification: A Systematic Review, 2023. [CrossRef]
- Ahmed, A.A.; Ali, W.; Abdullah, T.A.; Malebary, S.J. Classifying Cardiac Arrhythmia from ECG Signal Using 1D CNN Deep Learning Model. Mathematics 2023, 11. [Google Scholar] [CrossRef]
- Eleyan, A.; Alboghbaish, E. Multi-Classifier Deep Learning based System for ECG Classification Using Fourier Transform. Institute of Electrical and Electronics Engineers Inc., 2023. [CrossRef]
- Ullah, H.; Heyat, M.B.B.; Akhtar, F.; Sumbul.; Muaad, A.Y.; Islam, M.S.; Abbas, Z.; Pan, T.; Gao, M.; Lin, Y.; Lai, D. An End-to-End Cardiac Arrhythmia Recognition Method with an Effective DenseNet Model on Imbalanced Datasets Using ECG Signal. Computational Intelligence and Neuroscience 2022, 2022. [CrossRef]
- Zhang, H.; Liu, C.; Zhang, Z.; Xing, Y.; Liu, X.; Dong, R.; He, Y.; Xia, L.; Liu, F. Recurrence Plot-Based Approach for Cardiac Arrhythmia Classification Using Inception-ResNet-v2. Frontiers in Physiology 2021, 12. [Google Scholar] [CrossRef] [PubMed]
- Yeh, Y.C.; Chiou, C.W.; Lin, H.J. Analyzing ECG for cardiac arrhythmia using cluster analysis. Expert Systems with Applications 2012, 39, 1000–1010. [Google Scholar] [CrossRef]
- Dhyani, S.; Kumar, A.; Choudhury, S. Analysis of ECG-based arrhythmia detection system using machine learning. MethodsX 2023, 10. [Google Scholar] [CrossRef] [PubMed]
- Śmigiel, S.; Pałczyński, K.; Ledziński, D. ECG signal classification using deep learning techniques based on the PTB-XL dataset. Entropy 2021, 23. [Google Scholar] [CrossRef] [PubMed]
- Ansari, Y.; Mourad, O.; Qaraqe, K.; Serpedin, E. Deep learning for ECG Arrhythmia detection and classification: an overview of progress for period 2017–2023, 2023. [CrossRef]
- Aziz, S.; Ahmed, S.; Alouini, M.S. ECG-based machine-learning algorithms for heartbeat classification. Scientific Reports 2021, 11. [Google Scholar] [CrossRef] [PubMed]
- Biran, A.; Jeremic, A. ECG based Human Identification using Short Time Fourier Transform and Histograms of Fiducial QRS Features. SciTePress, 2020, pp. 324–329. [CrossRef]
- Kumar, M.A.; Chakrapani, A. Classification of ECG signal using FFT based improved Alexnet classifier. PLoS ONE 2022, 17. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Mark, R.G. MIT-BIH Arrhythmia Database, 1992. [CrossRef]
- Yang, M.; Liu, W.; Zhang, H. A robust multiple heartbeats classification with weight-based loss based on convolutional neural network and bidirectional long short-term memory. Frontiers in Physiology 2022, 13. [Google Scholar] [CrossRef] [PubMed]
- Bracewell, R.N.; Bracewell, R.N. The Fourier transform and its applications; Vol. 31999, McGraw-Hill New York, 1986.
- Oppenheim, A.V. Discrete-time signal processing; Pearson Education India, 1999.
- Podder, P.; Khan, T.Z.; Khan, M.H.; Rahman, M.M. Comparative Performance Analysis of Hamming, Hanning and Blackman Window, 2014.
- Kaur, M.; Kaur, S.P. High Frequency Noise Removal From Electrocardiogram Using Fir Low Pass Filter Bassed On Window Technique 2018. 8, 27–32.
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mechanical Systems and Signal Processing 2021, 151, 107398. [Google Scholar] [CrossRef]
- Czanner, G.; Sarma, S.V.; Ba, D.; Eden, U.T.; Wu, W.; Eskandar, E.; Lim, H.H.; Temereanca, S.; Suzuki, W.A.; Brown, E.N. Measuring the signal-to-noise ratio of a neuron. Proceedings of the National Academy of Sciences of the United States of America 2015, 112, 7141–7146. [Google Scholar] [CrossRef] [PubMed]
Figure 3.
Comparison of spectral analysis results for ECG signals processed using Hann, Hamming, and Blackman windows.
Figure 3.
Comparison of spectral analysis results for ECG signals processed using Hann, Hamming, and Blackman windows.
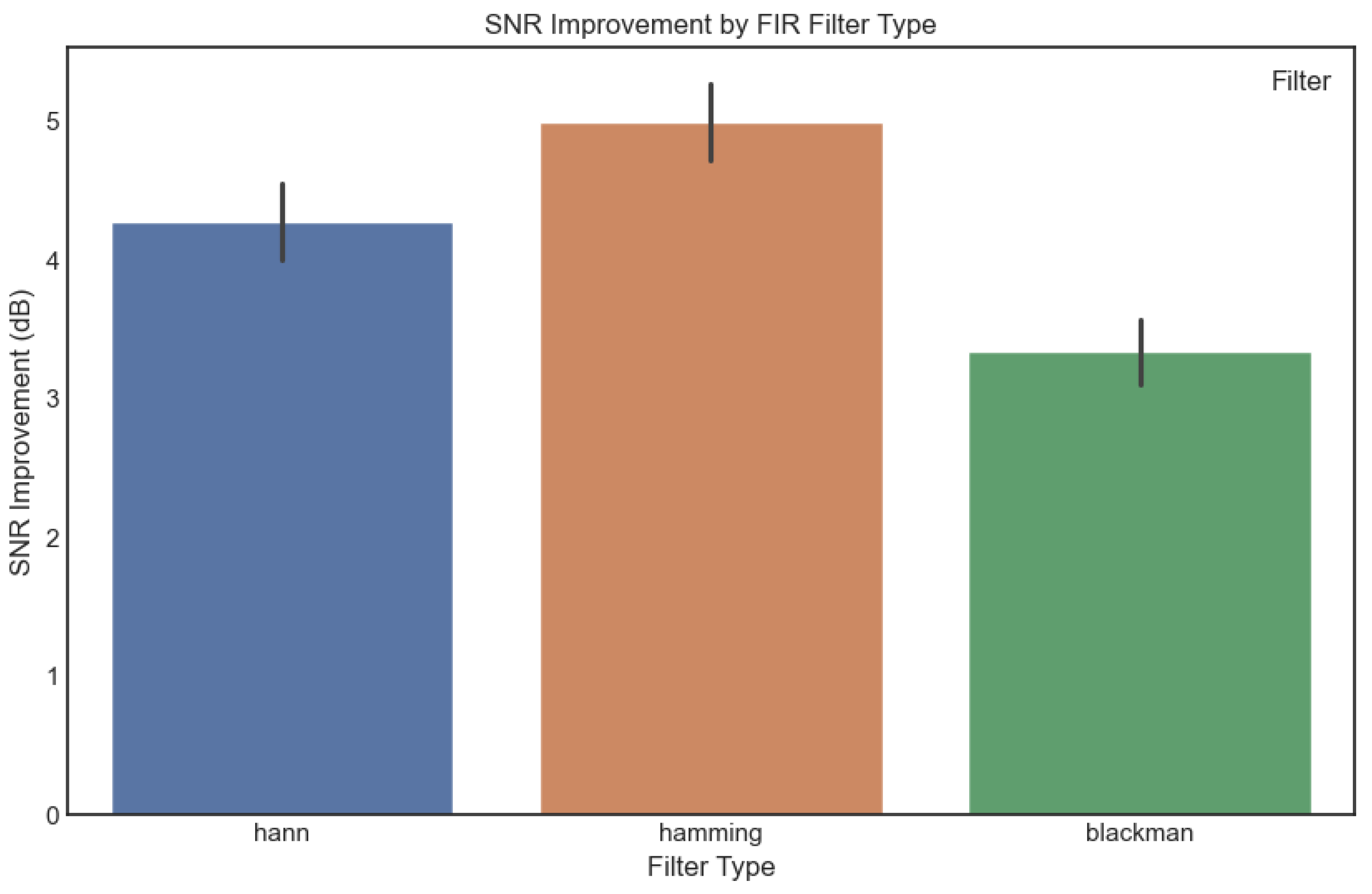
Table 2.
Performance metrics for different window models on ECG signal classification.
| Model | Class | Precision | Recall | F1-Score |
| Hamming | F | 0.963 | 0.990 | 0.977 |
| N | 0.941 | 0.804 | 0.867 | |
| S | 0.969 | 0.913 | 0.940 | |
| V | 0.778 | 0.780 | 0.779 | |
| Q | 0.000 | 0.000 | 0.000 | |
| Hann | F | 0.972 | 0.976 | 0.974 |
| N | 0.929 | 0.809 | 0.865 | |
| S | 0.912 | 0.946 | 0.929 | |
| V | 0.782 | 0.774 | 0.778 | |
| Q | 0.000 | 0.000 | 0.000 | |
| Blackman | F | 0.959 | 0.991 | 0.975 |
| N | 0.935 | 0.805 | 0.865 | |
| S | 0.973 | 0.910 | 0.940 | |
| V | 0.845 | 0.716 | 0.775 | |
| Q | 0.000 | 0.000 | 0.000 | |
| No FIR applied | F | 0.945 | 0.944 | 0.920 |
| N | 0.922 | 0.802 | 0.830 | |
| S | 0.953 | 0.897 | 0.933 | |
| V | 0.785 | 0.710 | 0.725 | |
| Q | 0.000 | 0.000 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






